Формула для расчета индуктивности катушки: Как рассчитать сердечник и витки самодельных катушек индуктивности

Расчёт индуктивности. Часть 2 | HomeElectronics

Всем доброго времени суток. Сегодняшняя статья является продолжением предыдущей. Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников. В прошлой статье я рассказал, как рассчитать индуктивность прямого провода и провода свёрнутого в кольцо (виток), в данной статье будем рассчитывать индуктивность круговых катушек, то есть поперечный профиль, которых представляет собой окружности.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Виды катушек индуктивности

Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности

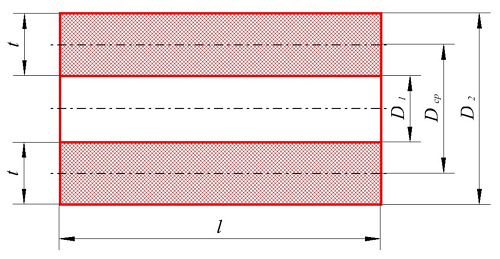
Расчёт индуктивности катушки.

Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:

D₁ – внутренний диаметр, D₂ – внешний диаметр, D_ср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить

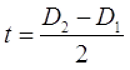
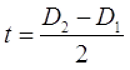
Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:

если l > D_ср – длинная катушка,

если l < D_ср – короткая катушка,

если l << D_ср – очень короткая катушка,

если l = 0 – плоская катушка,

если t ≈ D_ср – толстая катушка,

если t << D_ср – тонкая катушка,

если t = 0 – соленоид.

Особенности расчёта катушек индуктивности

Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода (диаметр, толщина изоляции, шаг намотки), хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением

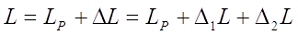
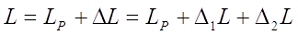
где L_Р – расчётная индуктивность;

∆L – поправка на «изоляцию», ∆L = ∆₁L + ∆₂L;

∆₁L – поправка учитывающая влияние индуктивности витков;

∆₂L – поправка учитывающая влияние взаимной индуктивности витков.

В большинстве случаев, например, при плотной намотке «виток к витку» поправка ∆L составляет несколько процентов от расчётной индуктивности L_Р, поэтому если нет необходимости в точном значении общей индуктивности L, поправку на изоляцию ∆L можно не учитывать.

Особенности расчёта круговых катушек индуктивности состоят в следующем:

1. При определении расчётной индуктивности L_P, средний диаметр принимается равным среднему диаметру реальной катушки;

2. Длина намотки l и толщина намотки t принимается равными шагу обмотки (p – шаг по длине катушки, q – шаг по толщине намотки) умноженному на количество слоёв ω в том или ином направлении

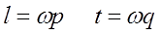
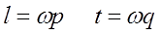
3. Если у катушки в каком-либо направлении (по длине намотки l или по толщине намотки t) имеется только один ряд (или слой), то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.

4. В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d.

5. Так как величина поправки на взаимную индуктивность ∆₂L в несколько раз меньше, чем поправка на индуктивность витков ∆₁L, то при расчётах можно учитывать только ∆₁L.

Приступим к расчётным выражениям, в начале рассчитаем простейшие круговые катушки – соленоид и плоскую катушку.

Расчёт индуктивности соленоида

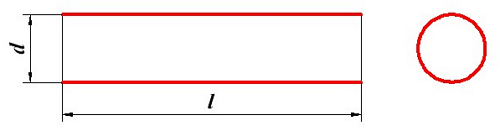
Определение индуктивности соленоида, d – диаметр соленоида, l – длина соленоида.

Соленоид представляет собой катушку, намотанную на каркас в один слой, поэтому толщину слоя можно принять равной нулю t = 0, а расчётная формула индуктивности будет иметь вид

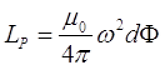
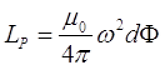
где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

d – диаметр соленоида, м;

Φ – коэффициент, который зависит от отношения α = l/D;

l – длина соленоида, м;

Поправочный коэффициент Φ зависит от отношения длины соленоида l к его диаметру d

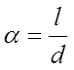
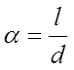
Для длинного соленоида, то есть α > 0,75, поправочный коэффициент составит

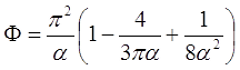
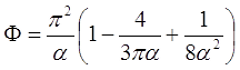
Для короткого соленоида, то есть α < 0,75, поправочный коэффициент составит

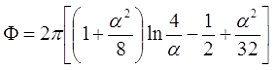
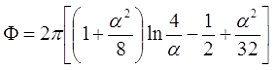
Пример. Необходимо рассчитать соленоид диаметром d = 1 см и длиной l = 5 см, который имеет ω = 75 витков.

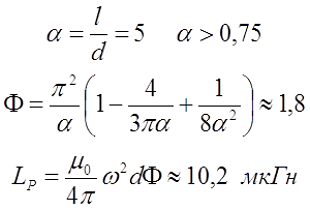
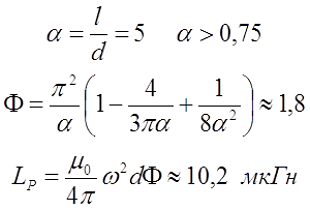
Стоит отметить, что формула расчёта соленоида подходит для большинства однослойных катушек с точностью в несколько процентов.

Индуктивность плоской катушки

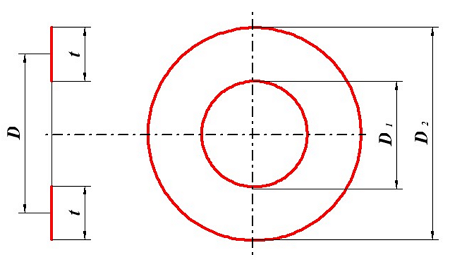
Определение индуктивности плоской катушки, D₁ – внутренний диаметр, D₂ – внешний диаметр, D – средний диаметр, t – толщина намотки.

В данном случае в качестве плоской катушки представлена идеализированная катушка, длина намотки которой приняли равной нулю l = 0, тогда индуктивность такой катушки можно вычислить по следующей формуле

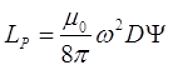
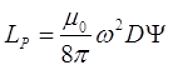
где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

D – средний диаметр катушки, м;

Ψ – коэффициент, который зависит от отношения ρ = t/D­;

t – толщина намотки катушки.

Коэффициент Ψ зависит от соотношения толщины намотки t и среднего диаметра катушки D

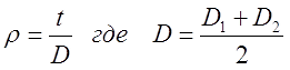
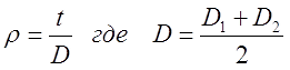
При небольшой толщине намотки, когда ρ < 0,5

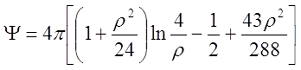
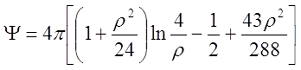
При большой толщине намотки, когда ρ > 0,5

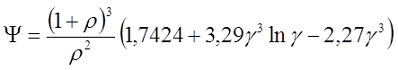
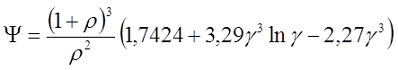
где γ – коэффициент учитывающий соотношение внешнего и внутреннего диаметров обмотки катушки

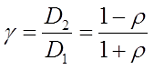
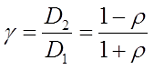
Пример. Рассчитаем плоскую катушку со средним диаметром D = 5 см и толщиной намотки t = 1 см, состоящую из ω = 20 витков.

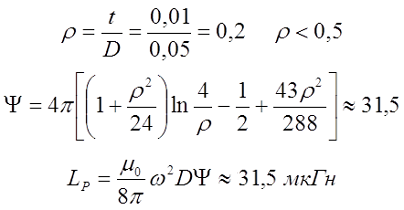
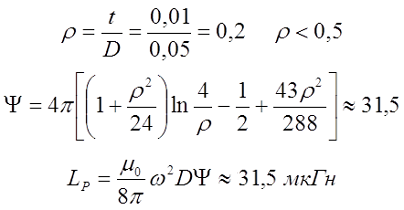
Выражения для индуктивности тонкой катушки позволяют рассчитать индуктивность и большинства катушек с малой длиной и большой толщиной обмоток.

Индуктивность круговой катушки прямоугольного сечения

Теперь перейдём от идеализированных катушек к реальным, которые в своем сечении представляют собой прямоугольник

Индуктивность прямоугольной катушки.

Катушку прямоугольного сечения можно представить в виде соленоида с ненулевой толщиной обмотки t ≠ 0, либо в виде плоской катушки с ненулевой длиной l ≠ 0, поэтому рассчитать необходимую катушку можно либо как соленоид, либо как плоскую катушку, а затем внести поправку.

Таким образом, индуктивность прямоугольной катушки можно вычислить по следующей формуле

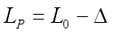
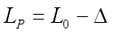
где L₀ – индуктивность идеальной катушки (соленоида или плоской катушки) в зависимости от α = l/D_cp;

l – длина катушки, м;

D_cp – средний диаметр катушки, м;

∆ — поправка на форму катушки.

В принципе реальную катушку индуктивности, в зависимости от отношения длины намотки l к среднему диаметру D_cp, можно разделить на несколько типов:

1. Длинная катушка, у которой α > 0,75.

2. Короткая катушка, имеющая α < 0,75 и γ < 1.

3. Очень короткая катушка, имеет α << 1 и γ > 1.

где

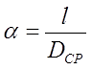
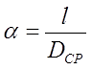
Рассмотрим каждый случай по отдельности.

Индуктивность длинной катушки

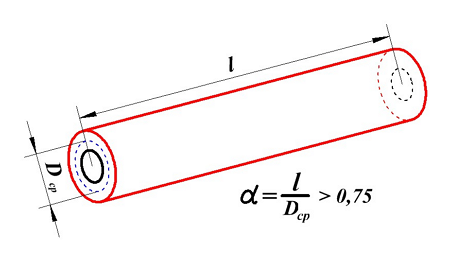
Длинная катушка.

Для длинной катушки (α > 0,75) величина L₀ рассчитывается также как для длинного соленоида, где l – длина соленоида, D_cp – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению

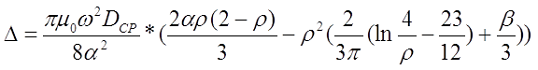
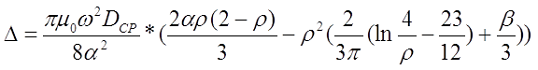
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;

ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру D_CP.

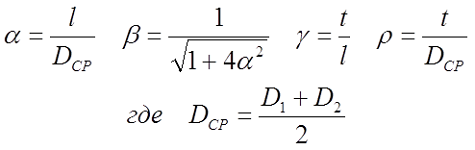
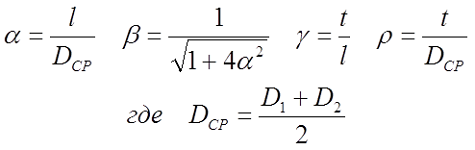
где D₁ – внутренний диаметр, D₂ – внешний диаметр.

Пример. Рассчитаем индуктивность катушки длиной l = 10 см, средним диаметром D_CP = 2 см, количеством витков ω = 100 и толщиной намотки t = 5 мм.

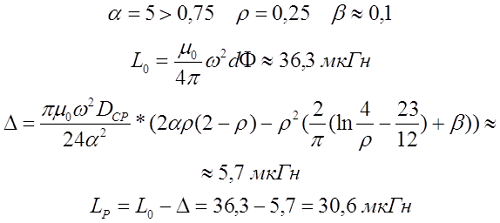
Индуктивность короткой катушки

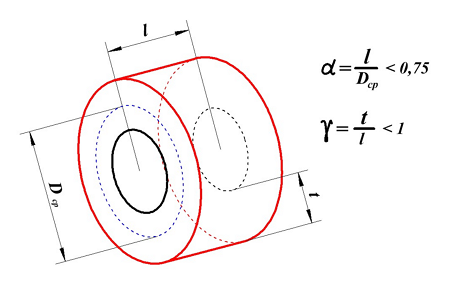
Короткая катушка.

Для короткой катушки (α < 0,75, t < l) величина L₀ рассчитывается также как для короткого соленоида, где l – длина соленоида, D_СР – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению

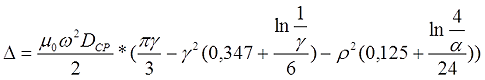
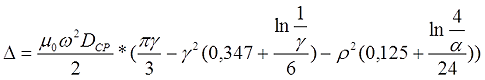
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;

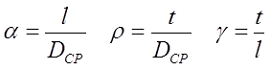
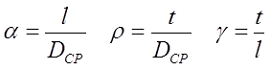
Пример. Рассчитаем индуктивность катушки длиной l = 1 см, средним диаметром D_СР = 2 см, толщиной намотки t = 5 мм, количеством витков ω = 50.

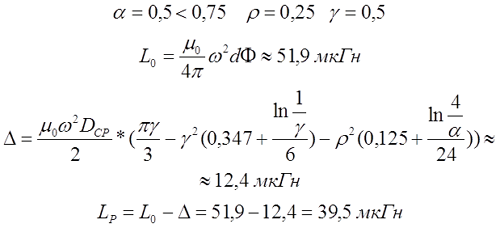
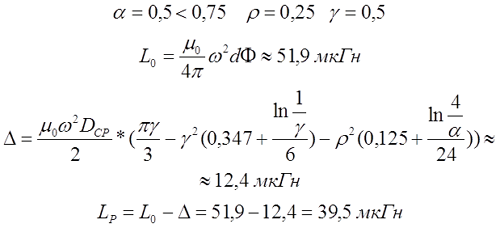
Индуктивность очень короткой катушки

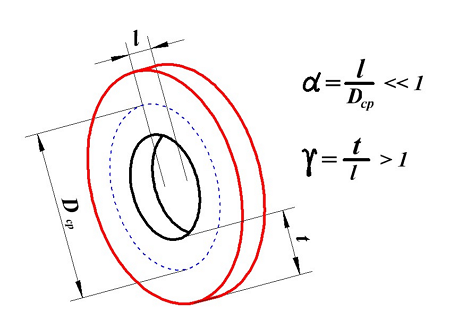
Очень короткая катушка.

Для очень короткой катушки (α << 1, t > l) величина L₀ рассчитывается также как для плоской катушки, где t – толщина намотки, D_cp – средний диаметр катушки, а значение поправки ∆ вычисляется по следующему выражению

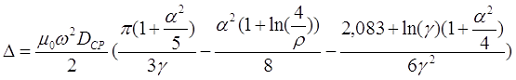
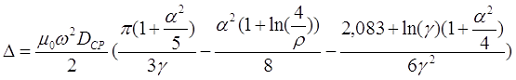
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l, γ < 1;

ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру D_CP.

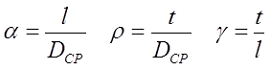
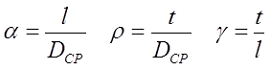
Пример. Рассчитаем индуктивность катушки длиной l = 5 мм, средним диаметром D_CP = 7 см, намотка толщиной t = 1 см, количество витков ω = 150.

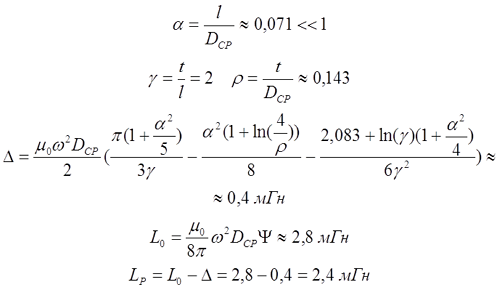
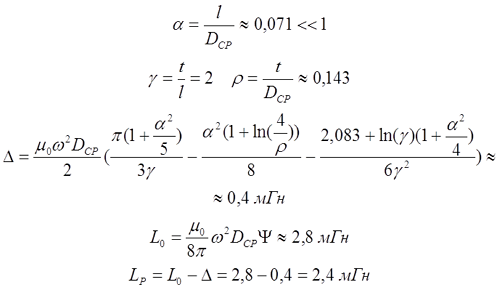
Расчёт поправки на собственную индуктивность витков

Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности L_P и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆₁L и поправки на взаимную индуктивность витков ∆₂L

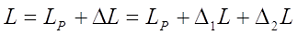
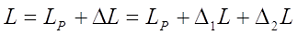
Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки

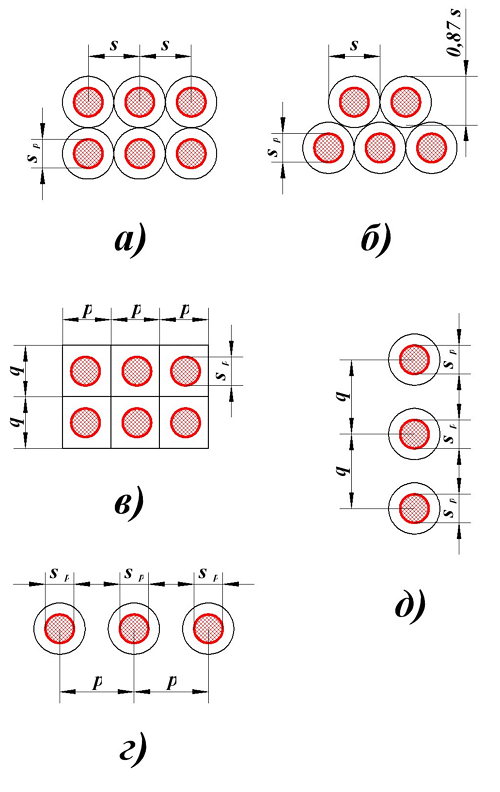
Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.

В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению

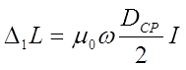
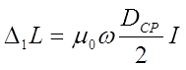
где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

D_СР – средний диаметр катушки, м;

I – коэффициент, зависящий от расположения витков катушки.

Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.

Для варианта а), провод намотан с небольшим коэффициентом заполнения

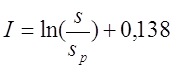
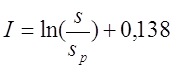
где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта б), провод намотан с большим коэффициентом заполнения

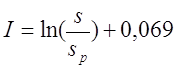
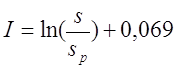
где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки

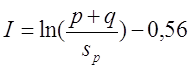
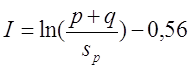
где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности L_P

— если при вычислении расчётной индуктивности L_P толщина намотки t принята равной диаметру голого провода s_P, то коэффициент I будет равен

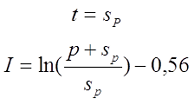
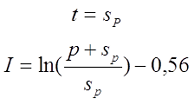
— если при вычислении расчётной индуктивности L_P толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен

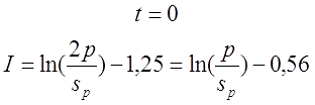
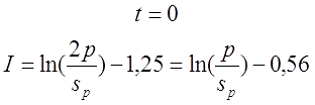
где p – шаг намотки по длине катушки, s_p – диаметр голого провода (без изоляции).

Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая

— если при вычислении расчётной индуктивности L_P длина намотки l принята равной диаметру голого провода s_P, то коэффициент I будет равен

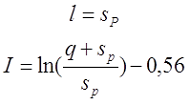
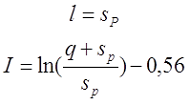
— если при вычислении расчётной индуктивности L_P длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен

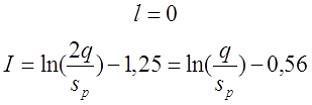
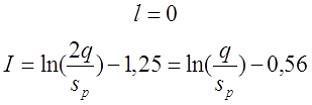
где q – шаг намотки по толщине катушки, s_p – диаметр голого провода (без изоляции).

Расчёт поправки на взаимную индуктивность витков

В общем случае поправка на взаимную индуктивность витков ∆₂L катушки определяется выражением

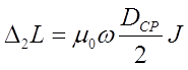
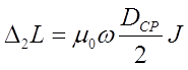
где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

D_СР – средний диаметр катушки, м;

J – коэффициент, зависящий формы катушки и от числа витков катушки.

1. Для катушки выполненной в один слой по длине катушки (соленоид):

а) при определении расчётной индуктивности L_P толщина намотки t принята равной шагу намотки р, то коэффициент J составит

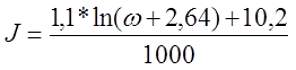
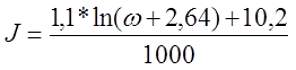
где ω – количество витков катушки.

б) при определении расчётной индуктивности L_P толщина намотки t принята равной нулю (рассчитывается как соленоид), то коэффициент J составит

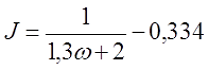
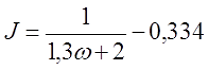
где ω – количество витков катушки.

2. Для катушки, выполненной в один слой по толщине намотки (плоская катушка):

а) при определении расчётной индуктивности L_P длина катушки l принята равной шагу намотки р, то коэффициент J составит

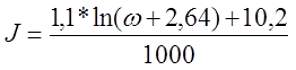
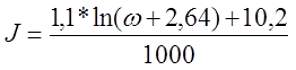
где ω – количество витков катушки.

б) при определении расчётной индуктивности L_P длина катушки l принята равной нулю (рассчитывается как плоская катушка), то коэффициент J составит

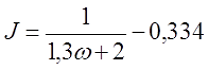
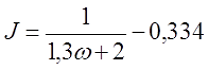
где ω – количество витков катушки.

На сегодня всё. В следующей статье я закончу с индуктивными элементами без сердечников.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Coil32 — Однослойная катушка

Расчет индуктивности однослойной катушки

Однослойная катушка индуктивности представляет собой провод, свернутый в спираль. Для придания жесткости, провод обычно наматывают на цилиндрический каркас. Поэтому в Coil32 в качестве исходных параметров приняты размеры каркаса и диаметр провода, т.к. их легче измерить практически. В расчетных формулах, однако, используются геометрические параметры самой спирали. Во избежании путаницы на этой страничке справки можно подробнее ознакомиться с этими тонкостями.

Однослойные катушки получили широкое распространение, особенно для конструкций коротковолнового и средневолнового любительских и радиовещательных диапазонов. Основные свойства однослойных катушек — высокая добротность, относительно небольшая собственная емкость, удобство изготовления. Рассмотрим методы расчета такой катушки без промежутка между витками — «виток к витку«…

Начнем с того, что в конце XIX века Х.А.Лоренц вывел формулу с применением эллиптических интегралов для расчета соленоида. Отличием модели Лоренца от модели Максвелла являлся тот момент, что витки соленоида представлялись не бесконечно тонким круговым проводом, а бесконечно тонкой спиральной проводящей лентой с шириной равной реальной толщине провода, без промежутка между витками. Формула имеет высокую точность при расчете реальной катушки в случае если последняя имеет большое количества витков и имеет намотку виток к витку. В 1909 г. японский физик Х.Нагаока преобразовал формулу Лоренца и привел ее к виду из которого следовал важный вывод — индуктивность соленоида зависит исключительно от формы и размеров катушки. Формула Нагаока имеет следующий вид:

[2]

, где

• L_s — индуктивность катушки
• N — число витков катушки
• r — радиус намотки
• l — длина намотки
• k_L — коэффициент Нагаока

Важнейшим выводом из анализа этой формулы был тот, что коэффициент Нагаока зависел только от отношения l/D, который был назван форм-фактором катушки. Коэффициент Нагаока вычислялся с применением эллиптических интегралов. Подробнее на этой формуле останавливаться не будем, т.к. Coil32 ее не использует в расчетах. Стоит только отметить, что в случае длинного соленоида формула упрощается до следующего вида:

[3]

где S — площадь поперечного сечения катушки. Эта формула имеет только академический интерес и не пригодна для расчетов реальных катушек, т.к. справедлива только для бесконечно длинных соленоидов, которых в природе не существует.

Однослойную катушку можно рассчитать численным методом, используя формулу Максвелла или формулу Нагаока для соленоида. Однако современные эмпирические формулы дают очень высокую точность расчетов и вполне достаточны для практических целей.

Обзор и выбор эмпирических формул начнем с самой известной формулы Г.Вилера. Обычно именно эта формула чаще всего используется в различных программах, онлайн калькуляторах, справочниках и статьях, посвященных расчетам индуктивностей.

В оригинале эта формула выглядит так:

L = a² N² / ( 9 a + 10 b )

где N — число витков, а a и b — соответственно радиус и длина намотки катушки. Размерности в дюймах. Адаптировав эту формулу для метрической системы (вернее сказать для СГС) и поменяв радиус на диаметр, получаем следующее:

[4]

, где

• L — индуктивность катушки [мкГн];
• N — число витков катушки;
• D — диаметр намотки [см];
• l — длина намотки [см];

Это самый известный у нас вариант этой формулы. Раньше на сайте С.-Петербуржского университета телекоммуникаций — sut.ru был довольно информативный ресурс — dvo.sut.ru, на котором можно было найти много информации о катушках индуктивности, включая и эту формулу. Теперь это ресурс к сожалению удален. Но удалось обнаружить клон этого ресурса на qrz.ru, на который перекочевала даже старая ошибка (0,5ё1.0) в формуле 2.37. Там можно найти и формулу Нагаока (формула 2.28) и выражение коэффициента Нагаока через формулу Вилера (формула 2.29).

Формула была предложена Вилером в далеком 1928 году, когда еще о компьютерах только мечтали и была очень полезна в то время, т.к. позволяла «в столбик» на бумажке рассчитать практическую катушку. Формула «укоренилась» в массовом сознании радиолюбителей. Однако мало кто знает, что она, как любая эмпирическая формула, имеет ограничения. Эта формула дает погрешность до 1% при l/D > 0,4, т.е если катушка не слишком короткая. Для коротких катушек эта формула не пригодна.

Последовало несколько попыток устранить этот недостаток. В 1985 г. Р.Лундин опубликовал две свои эмпирические формулы, одна — для «длинных», другая — для «коротких» катушек, позволяющие рассчитать коэффициент Нагаока с точностью не менее чем 3ppM (±0.0003%), что несомненно выше точности изготовления или измерения индуктивности катушки. Вот калькулятор, основанный на этих формулах.
В 1982 г., спустя 54 года, с наступлением эры компьютеров, Вилер опубликовал свою «длинную» формулу, которая рассчитывала однослойную катушку с погрешностью не более ±0.1%, как длинную, так и короткую. В дальнейшем эта формула была усовершенствована Р.Розенбаумом, а в последствии Р.Вивером (Robert Weaver — анализ и вывод формулы у него на сайте).

[5]

где:

• D_k — диаметр намотки
• N — число витков
• k = l/D_k — форм-фактор катушки, отношение длины намотки к ее диаметру

В результате мы имеем формулу, позволяющую рассчитать однослойную катушку с точностью не менее 18.5 ppM (в сравнении с формулой Нагаока), что хуже чем по формулам Лундина, но во-первых вполне достаточно для практических расчетов, во-вторых мы имеем одну более простую формулу вместо двух, рассчитывающую однослойную катушку независимо от ее форм-фактора.

Формула [5] и используется в онлайн-калькуляторе однослойной катушки, старых версиях Coil32, а также во всех версиях программы для Linux и в J2ME приложении для мобильных телефонов.

В основной версии Coil32 для Windows, а также начиная с версии 3.0 для Android, применена более сложная методика расчета однослойной катушки, учитывающая спиральную форму витков и произвольный шаг намотки.

В 1907 году Э.Роза, сравнивая расчеты по методу Максвелла и по методу Лоренца, вывел таблицу поправок, существенно увеличивающих точность расчета по методу Лоренца, особенно если катушка имеет небольшое число витков. Эти поправки стали именоваться «поправки на круглость провода» — Round Wire Corrections. В дальнейшем эти поправки использовались для увеличения точности расчета коэффициента Нагаока и эмпирических формул Лундина и Вивера. В 2008 г. Р.Вивер создал эмпирический алгоритм, позволяющий численным методом рассчитать «поправки на круглость провода» не прибегая к помощи таблиц. Этот алгоритм применяется в Coil32 начиная с версии 8.0, в онлайн-калькуляторе, а также в версиях Coil32 для Андроид и J2ME, для увеличения точности расчета индуктивности однослойных катушек.

Кроме индуктивности, как основного параметра однослойной катушки, программа Coil32 вычисляет и другие параметры:

Этих данных вполне достаточно для создания реалистичной модели катушки в программах схемотехнического моделирования. Например, в популярных RFSim99 или LTSpice IV. В RFSim99 необходимо поставить галочку в чекбоксе «Вкл. физ. модель» и ввести частоту собственного резонанса и добротность. Тип добротности необходимо выбрать третий — Q(f)=Q(F). В LTSpice необходимо задать R_ser — это наше сопротивление потерь (r) и C_par — это собственная емкость катушки Cs.

Кроме того можно рассчитать дополнительные результаты для параллельного колебательного контура на рабочей частоте. Характеристическое сопротивление такого контура равно реактивному сопротивлению катушки на рабочей частоте.

Назад…      Вперед…

как найти число витков в катушке, формула

Катушка индуктивности является спиральным или винтовым проводником, который преобразовывает энергию электрополя в магнитное поле. Каково более полное определение этого элемента электроцепи, как сделать расчёт катушки индуктивности и что влияет на ее индуктивность? Об этом далее.

Описание устройства

Катушка индуктивности бывает винтовой, спиральной или винтоспиральной, имеющей свернутый изолированный проводник, который обладает значительным показателем индукции при малой емкости с активным сопротивлением. Как следствие, ток протекает через источник тока со значительной инерционностью.

Главный компонент электроцепи

Обратите внимание! Применяется, чтобы подавлять помехи, сглаживать биения, накапливать энергию, ограничивать переменный ток или резонансный/частотно-избирательный контур цепи.

Стоит указать, что ее применение разнообразно. Называется она дросселем, вариометром, соленоидом и токоограничивающим реактором. При этом основные технические характеристики варьируются. Могут отличаться силой тока, сопротивлением потерь, добротностью, емкостью и температурным добротным коэффициентом.

Полное определение из физики

Факторы, влияющие на индукцию

Влияет на индукцию число проводниковых витков, площадь поперечного сечения, длина и материалы. Благодаря увеличению витков повышается индукция и наоборот. Что касается сечения, чем больше источник, тем больше показатель. Также чем больше магнитный вид проницаемости, тем больше индуктивный показатель.

Факторы, влияющие на преобразование энергии в магнитное поле

Расчет

Вычислить число витков, зная конструкцию, можно по формуле нахождения энергии и ее магнитного поля W = LI2/2, где L является индукцией, I — силой тока. Витки находятся из формулы L/d, где d является проводным диаметром. Стоит указать, что есть специальный калькулятор, в который нужно только подставить необходимые параметры. При этом можно определить, однослойный или многослойный проводник.

Схематическое расположение витков в катушке

С сердечником

Стоит отметить, что со стержнем, намоткой, обмоткой индукция вычисляется через замкнутый магнитный поток индуктивных элементов, в то время как без него  учитывается поток, который пронизывает только проводник с токовой энергией. Расчитывая индуктивность подобных элементов, необходимо учесть размеры и материал центральной части. Обобщенно можно представить формулу схематично. При этом требуется взять в расчет источник с сопротивлением магнитной цепи, абсолютной магнитной проницаемостью вещества, площадью поперечного сердечникового сечения и длиной средней силовой линии. Зная это, можно посчитать индукцию. Стоит учитывать погрешность. Она будет равна 25%.

Расчет индуктивности катушки с сердечником

Без сердечника

Стоит указать, что без ферритового, геометрического и цилиндрического сердечника с мощным каркасом источник имеет небольшую индукцию, а с ним она повышается. Это связано с тем, что имеется материальная магнитная проницаемость. Форма бывает разная. Есть броневой, стержневой и тороидальный материал.

Обратите внимание! Рассчитать можно, используя метод эллиптических максвелловских интегралов и специальную онлайн программу.

Расчет индуктивности без сердечника

Катушка — незаменимый компонент любой электросети, который имеет вид скрученного или обвивающего элемента с проводником. Влияет на ее индукцию число проводных витков, площадь сечения, длина и материал сердечника. Отыскать количество витков и посчитать индуктивность с сердечником и без него несложно, главное — руководствоваться приведенными выше рекомендациями.

Coil32 — Методы расчета индуктивности катушки.

Методы расчета индуктивностей

Наиболее полно теоретические основы методов расчета индуктивностей изложены в справочной книге: «Расчет индуктивностей. П.Л.Калантаров Л.А.Цейтлин». Здесь же хотелось бы немного систематизировать подходы к расчету индуктивностей.

Прежде всего отметим, что расчет индуктивности можно вести двумя способами:

∙ Численный метод с различной степенью упрощения задачи

∙ Расчет по упрощенным эмпирическим формулам

Эмпирический подход предполагает подбор (подгонку) относительно несложных аппроксимирующих формул по результатам измерений индуктивности реальных катушек. Расчет по упрощенным эмпирическим формулам имеет ограничения в точности и применим только к катушкам с определенной геометрией намотки. Большинство таких формул можно найти здесь. Несмотря на невысокую точность, такой расчет чаще всего вполне достаточен в радиолюбительской практике.

Численные методы основываются на реальных физических моделях катушек индуктивности и их, в свою очередь, можно разбить на две категории:

1. Расчет в программах основанных на фундаментальных законах классической электродинамики, так называемых электромагнитных симуляторах. К ним можно отнести COMSOL Multiphysics, FEMM, ANSYS, GAL-ANA и т.п. Эти программы используют специальные численные методы, такие как метод моментов и метод конечных элементов. Расчет в таких программах довольно точен, позволяет учесть множество нюансов, рассчитать катушку произвольной формы, однако требует огромных ресурсов компьютера. Применяется при научном анализе или если катушка работает в режиме, когда ее нельзя представлять как сосредоточенный элемент [пример]
2. Численные методы расчета, основанные на фундаментальных формулах физики, применимых к круговым проводникам, выведенных в XIX веке Д.К.Максвеллом. Позволяют провести расчет более точно, чем по эмпирическим формулам, но не требуют запредельных аппаратных ресурсов компьютера. На них следует остановится подробнее, т.к их и использует Coil32…

Расчет индуктивности в программе Coil32 основан на модели Максвелла, в которой катушка представляется как множество соосных бесконечно тонких круговых проводников.
Из Теоремы Гаусса следует, что силовые линии магнитного поля всегда замкнуты. Из этого следует, что магнитный поток порожденный круговым контуром с током весь проходит через поверхность, ограниченную этим контуром. Это обстоятельство отражено в следующей формуле:

Из этой формулы можно вывести определение для собственной индуктивности кругового проводника через двойной контурный интеграл Ф.Е.Неймана для взаимоиндукции [вывод здесь]:

Как показал Д.К.Максвелл, для двух бесконечно тонких круговых соосных проводников этот интеграл имеет однозначное решение, которое выглядит следующим образом:

[1]

, где:

• M — взаимоиндукция;
• r₁, r₂ — радиусы двух бесконечно тонких круговых проводников;
• x — расстояние между центрами кругов, ограниченных этими проводниками;
• K,E — эллиптические интегралы, соответственно первого и второго рода;

Численный метод расчета по формуле Максвелла сводится к численным методам решения эллиптических интегралов.

По формуле Максвелла можно рассчитывать как индуктивность многослойных и однослойных катушек, так и взаимную индуктивность двух отдельных катушек. Погрешности модели, связанные с допущением, что провод бесконечно тонкий и представляет собой набор круговых проводников (хотя на самом деле — это спираль), можно уменьшить с помощью соответствующих поправок.

Рассчитывая взаимоиндукцию проводника «самого на себя», т.е. его самоиндукцию (собственную индуктивность), Максвелл использует понятие — «среднее геометрическое расстояние» — GDM (g), для круглого провода:

g = e^0.25*r_w, где r_w — радиус провода.

Очень важен следующий момент. Вся вышеприведенная логика рассуждений и вывода формул, начиная от формулы Неймана, справедлива в случае равномерного распределения плотности тока вдоль катушки. В подавляющем большинстве практических случаев так и есть. Однако если катушка работает вблизи частот собственного резонанса, начинает проявляться неравномерность распределения плотности тока по проводнику! Другими словами, начинает проявляться зависимость индуктивности от частоты, которая в наших расчетах не учитывается. Поэтому индуктивность катушки можно рассчитать корректно только на частотах не превышающих 60-70% от частоты ее собственного резонанса. Таким образом Coil32 не годится для точных расчетов, например, катушек Тесла или спиральных резонаторов. В этом случае и в случае если катушка работает в режиме выше частоты собственного резонанса — ее нужно представлять только в виде модели длинной линии и рассчитывать в программах-электромагнитных симуляторах, либо пользоваться специальными эмпирическими формулами.

Ссылки:

1. An introduction to the art of Solenoid Inductance Calculation D W Knight 2013
2. Numerical Methods for Inductance Calculation Robert Weaver 2012
3. Inductance Calculation Techniques — Part II: Approximations and Handbook Methods Marc T. Thompson 1999
4. A new method for inductance calculation M.A.Bueno A K T Assis 1995

Как рассчитать индуктивность катушек с замкнутыми сердечниками?

Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Особенности расчёта индуктивных элементов с сердечниками

В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.

Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения

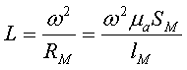
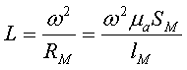
где ω – количество витков катушки,

R_M – сопротивление магнитной цепи,

μ_а – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,

S_M – площадь поперечного сечения сердечника,

l_M – длина средней магнитной силовой линии,

Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.

Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии l_e и эффективная площадь поперечного сечения S_e сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле

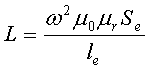
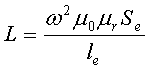
где ω – количество витков катушки,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7,

μ_r – относительная магнитная проницаемость вещества,

S_e – эффективная площадь поперечного сечения сердечника,

l_e – эффективный путь магнитной линии сердечника.

Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм^-1;

С₂ – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм^-3;

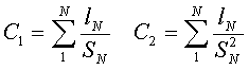
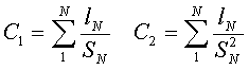
где N – количество разнородных участков сердечника,

l_N – длина N – го участка сердечника,

S_N – площадь N – го участка сердечника.

Тогда величины S_e и l_e определятся из следующих выражений

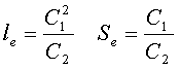
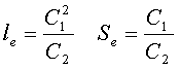
Кроме индуктивности с помощью постоянных С₁ и С­₂ определяют эффективный объём V_e, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С₁ по следующему выражению

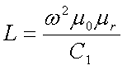
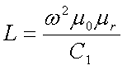
где ω – количество витков катушки,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7,

μ_r – относительная магнитная проницаемость вещества,

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.

Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.

Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.

Расчёт катушки с тороидальным сердечником

Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.

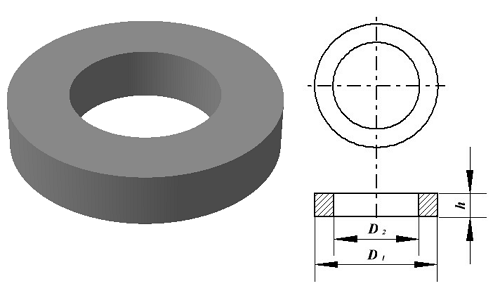
Тороидальный сердечник.

Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D₁ – внешний диаметр, D₂ – внутренний диаметр, h – высота сердечника.

Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С₁ и С₂, которые составляют

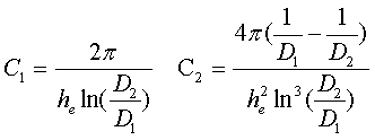
где h_e – эффективная высота сердечника,

D₁ – внешний диаметр сердечника,

D₂ – внутренний диаметр сердечника.

Расчёт эффективной высоты h_e сердечника зависит от конструктивных особенностей.

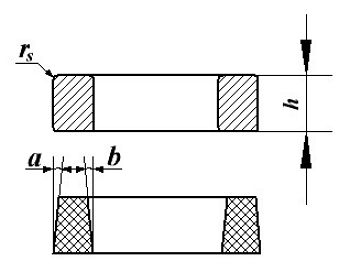
Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).

Рассмотрим несколько случаев:

а) прямоугольное поперечное сечение с острыми кромками

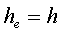
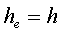
б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления r_s

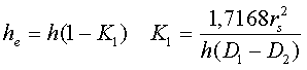
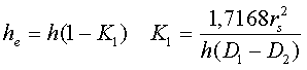
в) трапецеидальное поперечное сечение с острыми кромками

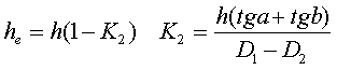
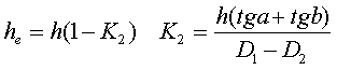
г) трапецеидальное поперечное сечение со скруглёнными кромками

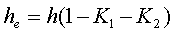
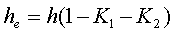
Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D₁ = 20 мм, D₂ = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления r_s = 0,5 мм, относительная магнитная проницаемость материала сердечника μ_r = 1000.

Так как рассчитываем только индуктивность, то в расчёте коэффициента С₂ нет необходимости

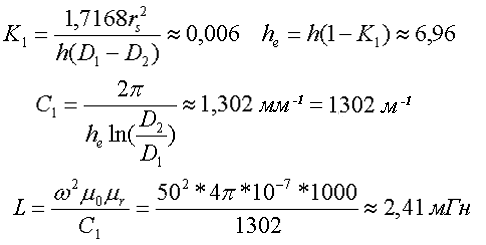
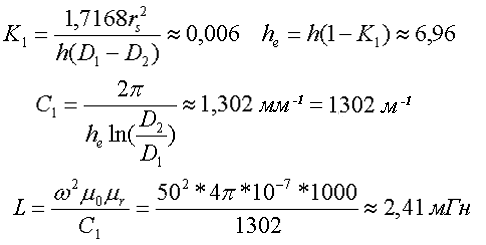
Расчёт катушки с П–образным сердечником прямоугольного сечения

В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.

Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.

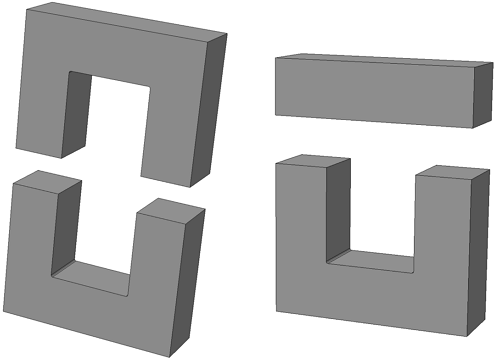
П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).

Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника

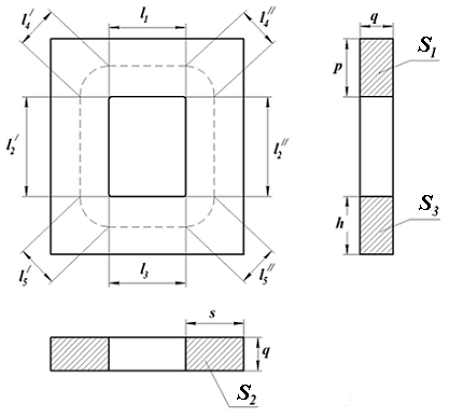
Сечение П-образного прямоугольного сердечника.
Данный сердечник состоит из нескольких участков l₁, l₂, l₃, l₄, l₅ имеющих различное сечение S₁, S₂, S₃, S₄, S₅,. Тогда коэффициенты С₁ и С₂ составят

Неизвестные величины можно найти следующим образом

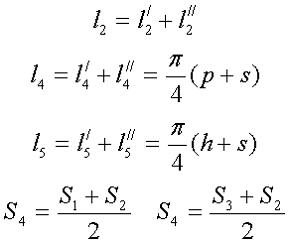
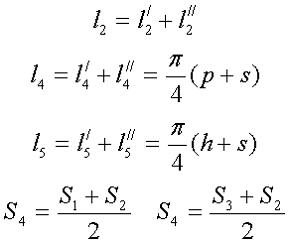
Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μ_r = 1950, количество витков ω = 150.

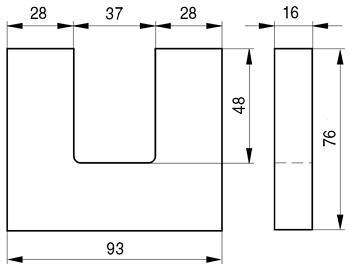
Сердечник Epcos U93/76/16.

Таким образом, расчётные параметры сердечника составят

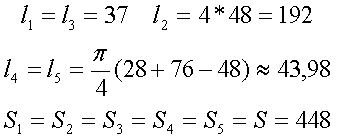
Таким образом коэффициент С1 и индуктивность L составят

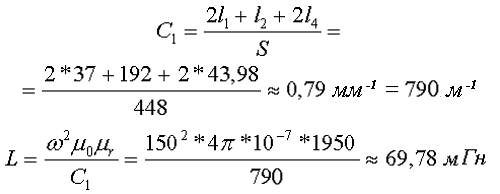
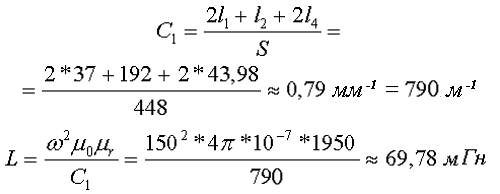
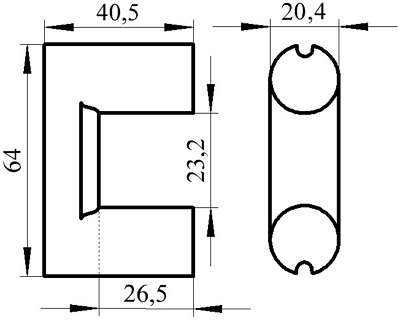
Расчёт катушки с П-образным сердечником круглого сечения

Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей

П-образный сердечник с круговым сечением.

Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.

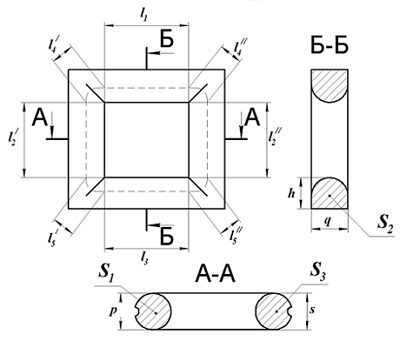
Сечение П-образного сердечника с круговым сечением.

Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь

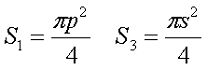
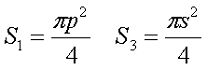
Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μ_r = 2500), количество витков ω = 60.

Сердечник типа SDMR 40 UY20.

Параметры сердечника для расчёта составят

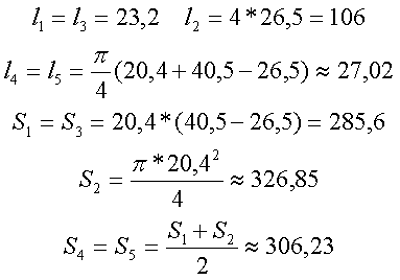
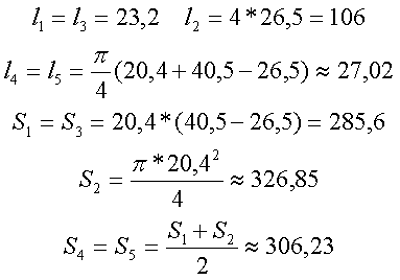
Таким образом коэффициент С1 и индуктивность L составят

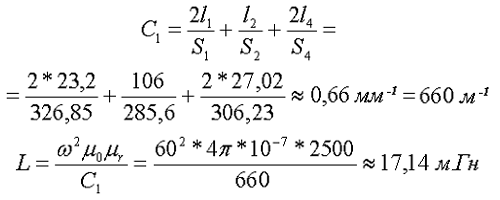
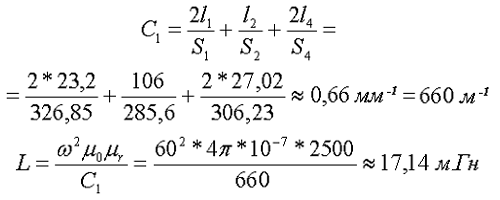
На сегодня всё. Продолжение смотри в следующей статье.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Расчет индуктивности катушек (однослойных)

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность. То что делает катушка индуктивности в колебательных контурах является очень важным и от правильного расчета зависит добротность контура.

Если катушка индуктивности наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке ее более толстым проводом надо несколько увеличить, а тонким —    уменьшить число витков катушки, чтобы получить необходимую индуктивность.

Ресчет катушек индуктивности (однослойных, цилиндрических)

Рис. 1. Пример однослойной катушки индуктивности.

Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников. Расчет однослойных цилиндрических катушек производится по формуле:

где:

• L — индуктивность катушки, мкГн;
• D — диаметр катушки, см;
• I — длина намотки катушки, см;
• n — число витков катушки.

При расчете катушки могут встретиться два случая:

• а) по заданным геометрическим размерам необходимо определить индуктивность катушки;
• б) при известной индуктивности определить число витков и диаметр провода катушки.

В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.

Пример. Определим индуктивность катушки, изображенной на рис. 1; для этого подставим в формулу все необходимые величины:

Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода.

Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и длину намотки, а затем рассчитывают число витков по формуле:

После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле:

где:

• d — диаметр провода, мм,
• l — длина обмотки, мм,
• n — число витков.

Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.

Подставив в последнюю формулу заданные величины, получим:

Диаметр провода:

Если эту катушку наматывать проводом меньшего диаметра, то нужио полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки.

Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки.

Возможно, также придется увеличить и то и другое одновременно, пока не будут получепы необходимые габариты катушки, соответствующие заданной индуктивности.

Следует заметить, что по приведенным пыше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше D половины диаметра то более точные результаты можно получить по формулам:

Как произвести пересчет катушек индуктивности (однослойных, цилиндрических)

Необходимость в пересчете катушек индуктивности возникает при отсутствии нужного диаметра провода, указанного в описании конструкции, и замене его проводом другого диаметра; при изменении диаметра каркаса катушки.

Если отсутствует провод нужного диаметра, что является наиболее частой причиной пересчета катушек, можно воспользоваться проводом другого диаметра.

Изменение диаметра провода в пределах до 25% в ту или другую сторону вполне допустимо и в большинстве конструкций не отражается на качестве их работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как оно уменьшает омическое сопротивление катушки и повышает ее добротность.

Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше определенной допустимой величины.

Пересчет числа витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле:

где:

• n — повое число витков катушки;
• n1 — число витков катушки, указанное в описании;
• d— диаметр имеющеюся провода;
• d1 — диаметр провода, указанный в описании.

В качестве примера произведем пересчет числа витков катушки, изображенной на рис. 1, для провода диаметром 0,8 мм:

(длина намотки l= 18 X 0,8 = 14,4 мм, или 1,44 см).

Таким образом, число витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:

При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков катушки.

Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков ее уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра увеличивается число витков на равное число процентов. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса.

Рис. 2. Катушки индуктивности. Пример.

Так, для примера произведем пересчет числа витков катушки (рис. 2, а), имеющей диаметр 1,5 см, на диаметр, равный 1,8 см (рис. 2, б). Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%.

Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке ее на каркасе большего диаметра нужно уменьшить число витков на 20%, или на 8 витков. Таким образом, новая катушка будет иметь 32 витка.

Проверим пересчет н установим погрешность, допущенную в результате пересчета. Катушка (см. рис. 2, а) имеет индуктивность:

Новая катушка на каркасе с увеличенным ди

Онлайн калькулятор расчета многослойной катушки индуктивности

На практике нередко случаются ситуации, когда при выходе со строя катушки индуктивности, ее необходимо восстановить – намотать новую проволоку взамен старой. При этом вам уже известны геометрические параметры катушки, но требуется узнать, сколько сделать витков, слоев, их толщину и длину необходимого для этого провода. Стоит отметить, что при намотке витки должны ложиться вплотную без зазора.

Для расчета индуктивности многослойной катушки используется такая формула:

Где,

• d – сумма диаметра каркаса и толщины намотки только с одной стороны;
• n – количество витков;
• g – толщина намотанной проволоки;
• h – высота намотанной проволоки;

Из этой формулы, зная величину индуктивности, можно вывести толщину намотки:

Для определения количества витков необходимо воспользоваться формулой:

Где,

• d­_пр – диаметр провода
• h – высота катушки;
• g – толщина намотки.

Расчет количества витков

Длину одного витка можно определить следующим образом:

l_вит = π * d_вит

Где π – это константа, а d_{вит_}— это диаметр витка.

Тогда, зная общее число витков и принимая, что d – это усредненное значение диаметра для всех витков, длина всего провода будет определяться по формуле:

L_w = n * π * d

Через сопротивление провода можно определить его диаметр, для чего понадобится выразить сопротивление через геометрические параметры устройства.

R = ρ * ( L_w / S ),

где ρ – удельное сопротивление металла, из которого изготовлен проводник, а S – площадь проводника, которая определяется по формуле:

Подставив значение площади и длины провода, получим такое выражение для определения сопротивления:

Из значения сопротивления можно вывести формулу для определения диаметра провода, подставив предварительно формулу для вычисления количества витков:

После получения величины диаметра провода, можно определить количество витков, которое подставляется с остальными данными в первую формулу для расчета индуктивности.

Число слоев можно определить, разделив толщину намотки на диаметр провода:

N = g / d_пр

Посредством вышеприведенных вычислений можно определить все параметры многослойной катушки индуктивности, которые помогут вам изготовить устройство с нужными параметрами. Также, чтобы облегчить вычисления вы можете воспользоваться нашим онлайн калькулятором ниже.

Конструкция катушки и вычислитель индуктивности

Эта страница проведет вас через создание собственной катушки DIY / самодельной катушки.
Я сделал это для изготовления катушек для
хрустальные радиоприемники и
Катушки Тесла, но он работает с любой катушкой цилиндрической формы.
Это также полезно, если вы собираетесь использовать свою катушку в
Танк LC резонансный
цепь.

Калькулятор индуктивности предоставляется
ниже, чтобы упростить задачу.

Намотка катушки вручную.

Индуктивность — это часто то, чего вы пытаетесь достичь при разработке катушки.
то есть вы знаете нужную индуктивность, и теперь вам нужно спроектировать катушку
у которого будет такая индуктивность.

Индуктивность

Катушки имеют свойство, называемое индуктивностью.
Что такое индуктивность? Когда электрический ток изменяется при прохождении через
провод катушки, он создает изменяющееся магнитное поле, которое наводит
(производит) напряжение или ЭДС (электродвижущая сила) в проводе, который
противостоит течению.Это называется индукцией и индуктивностью.
— величина, определяющая способность катушки индуцировать это напряжение.
Символ индуктивности — Генри, а единица — H.
на самом деле речь идет о катушке, создающей напряжение в себе,
что является самоиндукцией, но мы просто скажем индукция.

Магнитное поле вокруг катушки.

Параметры для формулы индуктивности

Одна формула для индуктивности выглядит следующим образом:

Где:

• L = индуктивность
• u _r = относительная проницаемость материала сердечника (воздух = 1)
• витков = количество витков на катушке
• area = площадь поперечного сечения жилы в квадратных метрах *,
  включая часть катушки, как показано на схеме
• длина = длина бухты в метрах *

* Калькулятор индуктивности ниже также принимает дюймы, а также
сантиметры и миллиметры, и переводит их в метры за вас.

Как сказано выше, μ _r — это относительный магнитный
проницаемость для всего, что вы используете для сердечника катушки,
цилиндр, на который вы наматываете провод. Это греческая буква мю, μ,
хотя часто для удобства используется буква u, например u _r .
Если это полая картонная или пластиковая трубка, то картонная или пластиковая
считается воздухом, и вы можете использовать 1. Такие материалы, как железо и феррит, имеют
более высокие относительные проницаемости в сотни и тысячи.Для железного сердечника приблизительное число — 100, хотя оно действительно варьируется.
в зависимости от сплава. То же самое и с ферритом, который может иметь ценность
где-то от 20 до 5000, но если вы не знаете, что использовать, тогда
1000 — грубый компромисс.
Поскольку он умножается на остальную часть формулы, это означает, что
материалы дадут более высокое значение индуктивности. Ядра для кристаллического радио
катушки иногда бывают пластиковыми или картонными и поэтому представляют собой катушки с воздушным сердечником,
а иногда это ферритовый сердечник.Сердечники для вторичной обмотки Тесла
катушки обычно пластиковые, а меньшие могут быть картонными, и
поэтому считаются катушками с воздушным сердечником.

И если вы не знакомы с обозначениями 1.26×10 ^-6 , это
просто другой способ записи 0.00000126.

Область включает часть катушки, как показано на схеме выше.
Если площадь рассчитывается с использованием радиуса, включите радиус ядра.
плюс радиус проволоки. При расчете площади по диаметру
затем включите диаметр сердечника плюс диаметр проволоки.Обратите внимание, что
при выполнении расчетов для катушки с очень тонкой проволокой, как в случае
кристалл радио и катушка Тесла, показанная выше (например, 24 калибра / AWG)
тогда размер провода, вероятно, будет незначительным по сравнению с
область жилы, и обычно можно не обращать внимания на провод.

Калькулятор индуктивности

Вот калькулятор индуктивности, который использует приведенную выше формулу. Диаграмма
Вышеуказанное можно использовать в качестве руководства для некоторых параметров.

Видео — Как сконструировать катушку с удельной индуктивностью

В этом видео я подробно объясняю формулу индукции.
а также привести пример и поговорить о других факторах, таких как
емкость катушки, частота и связь.

.

Coil32 — Как рассчитать индуктивность?

Детали

Опубликовано: 02 июня 2015

Просмотров: 7353

Как рассчитать индуктивность? — 5.0 из
5
на основе
2 отзыва

Мы можем использовать различные методы для расчета индуктивности, используя численные методы или справочные формулы.Их условно можно разделить на три уровня — высокий, средний и низкий уровень.

Высокий уровень предполагает использование программ, имеющих общее название — электромагнитные симуляторы. Например, Comsol Multisystems с радиочастотным модулем, Ansys HFSS и др. Их работа основана на дифференциальных уравнениях Максвелла для электромагнитного поля, обеспечивающих граничные условия.
Преимущества: точный расчет индуктивности и других параметров катушки при любой геометрии обмотки в любом частотном диапазоне.
Недостатки: эти программы достаточно сложные и требуют предварительного обучения, требуют больших вычислительных ресурсов, расчет занимает много времени. Может использоваться для профессиональной работы или если индуктор используется на частоте собственного резонанса или выше.

Средний уровень основан на упрощенной модели индуктора, представленной Дж. К. Максвеллом.
Достоинства: приемлемая для практики радиолюбителей точность расчета, возможность использования в простых программах, невысокие требования к вычислительной мощности компьютера.
Недостатки: менее точные расчеты, чем на высоком уровне; расчет невозможен для любой геометрии обмотки и, возможно, только в диапазоне частот, который не превышает 60-70% собственной резонансной частоты (или, скорее, 1-резонанса) катушки.

Нижний уровень основан на простых справочных формулах. Эти формулы основаны на упрощении формул среднего уровня или на основе набора измерений реальных катушек.
Достоинства: простой расчет, нетребовательность к ресурсам компьютера

Недостатки: формулы работают только с ограниченной геометрией обмотки и на частотах намного ниже, чем частота собственного резонанса.

Подробнее о вычислениях среднего уровня, которые использует Col32 … Великий физик Дж.К. Максвелл показал в конце XIX века в своей знаменитой работе «Трактат об электричестве и магнетизме». что взаимную индуктивность между двумя бесконечно тонкими круглыми коаксиальными проводниками можно рассчитать следующим образом:

Где

• M — взаимная индуктивность;
• r1, r2 — радиусы двух круговых нитей;
• x — расстояние между центрами окружностей, ограниченных этими нитями;
• K, E — эллиптические интегралы первого и второго рода;

Численный метод вычисления формулы Максвелла, сведенный к численным методам решения эллиптических интегралов.

С помощью уравнения Максвелла можно рассчитать индуктивность однослойной, многослойной или плоской катушки и взаимную индуктивность двух отдельных катушек. Ошибки, связанные с приближением коаксиальных круговых нитей (фактически речь идет о спирали круглой проволоки), могут быть уменьшены за счет дополнительных поправок.

.

Катушки индуктивности и формулы для расчета индуктивности

Стили корпуса индуктора

Катушки индуктивности — это пассивные устройства, используемые в электронных схемах для хранения энергии в виде
магнитного поля. Они дополняют конденсаторы, накапливающие энергию в виде электрического поля. An
идеальная катушка индуктивности эквивалентна короткому замыканию (0 Ом) для постоянного тока (DC),
и представляет собой противодействующую силу (реактивное сопротивление) переменным токам (AC), которая зависит от
от частоты тока.Реактивное сопротивление (противодействие протеканию тока) индуктора
пропорциональна частоте тока, протекающего через него. Индукторы иногда
называются «катушками», потому что большинство индукторов физически построено из секций, скрученных катушками.
проволоки.

Свойство индуктивности, препятствующее изменению тока, используется для
цель предотвращения прохождения сигналов с более высокочастотной составляющей во время
пропуская сигналы низкочастотных компонентов.Вот почему индукторы иногда
их называют «дросселями», поскольку они эффективно подавляют более высокие частоты. Общий
применение дросселя в цепи смещения радиоусилителя, где коллектор
транзистор должен быть запитан постоянным напряжением, не допуская RF (радиочастоты)
сигнал от проводки обратно в источник постоянного тока.

При использовании в
серия (левый рисунок) или
параллельно (правый рисунок) со своей схемой
комплимент, конденсатор, комбинация индуктора-конденсатора образует цепь, которая резонирует
с определенной частотой, которая зависит от значений каждого компонента.В сериале
В цепи сопротивление току на резонансной частоте равно нулю с идеальными компонентами.
В параллельной цепи (справа) сопротивление току бесконечно с идеальными компонентами.

Реальные индукторы из физических компонентов
демонстрируют больше, чем просто чистую индуктивность, когда присутствуют в цепи переменного тока. Общая схема
Слева показана модель симулятора. Он включает в себя идеальный индуктор с параллельным
резистивный компонент, реагирующий на переменный ток.Резистивная составляющая постоянного тока
соединен последовательно с идеальной катушкой индуктивности, а конденсатор подключен через всю
сборки и представляет собой емкость, присутствующую из-за близости обмоток катушки.
Симуляторы SPICE-типа используют эту или даже более сложную модель для облегчения большего
точные расчеты в широком диапазоне частот.

Связанные страницы по RF Cafe
— Индукторы и
Расчет индуктивности
— Преобразование индуктивности
—
Стандартные значения индуктивности
—
Продавцы индукторов

HamWaves.com
на сайте есть очень сложный калькулятор индуктивности катушки, который позволяет вам вводить
диаметр проводника.

Уравнения (формулы) для объединения катушек индуктивности последовательно и параллельно приведены ниже.
Приведены дополнительные уравнения для катушек индуктивности различной конфигурации.

Индукторы, подключенные к серии

Суммарная индуктивность последовательно соединенных катушек индуктивности равна сумме индивидуальных
индуктивности.Держите единицы измерения постоянными.

Тороид с закрытой намоткой

Прямоугольное сечение

Индуктивность коаксиального кабеля

Индуктивность прямого провода

Эти уравнения применимы, когда
длина проволоки намного больше диаметра проволоки (см.
диаметр проволоки здесь). Справочник ARRL
представляет уравнение для единиц дюймов и мкФ:

Для низких частот — примерно до VHF, используйте эту формулу:

Выше VHF скин-эффект приводит к приближению в верхнем уравнении к единице (1), поэтому
используйте это уравнение:

Прямой провод параллельно плоскости заземления с заземленным одним концом

Справочник ARRL представляет это уравнение для прямого провода, подвешенного над землей.
плоскость, заземленная одним концом на плоскость:

a = радиус проволоки,

l = длина провода параллельно плоскости заземления
h = высота провода над пластиной заземления
к нижней части провода

Индуктивность параллельной линии

Многослойная индуктивность воздушного сердечника

Уиллера
Формула:

Дроссели с параллельным соединением

Полная индуктивность параллельно соединенных катушек индуктивности равна обратной величине индуктивности.
сумма обратных величин индивидуальных индуктивностей.Держите единицы измерения постоянными.

Константы и переменные формулы индуктивности

Следующие физические константы и механические размерные переменные применимы к уравнениям
на этой странице. Единицы для уравнений показаны внутри скобок в конце уравнений;
например, означает, что длина
в дюймах, а индуктивность в Генри. Если единицы не указаны, можно использовать любые
пока они согласованы для всех сущностей; т.е. все счетчики, все мкГн и т. д.

C = Емкость
L = Индуктивность
N = Число витков
W = Энергия
ε _r
= Относительная диэлектрическая проницаемость (безразмерная)
ε ₀
= 8.85 x 10 ^-12 Ф / м (диэлектрическая проницаемость свободного пространства)
µ _r
= Относительная проницаемость (безразмерная)
µ ₀
= 4π
x 10 ^-7 Гн / м (проницаемость свободного пространства)

1 метр = 3,2808 футов <—> 1 фут = 0,3048 метра
1 мм =
0,03937 дюйма <—> 1 дюйм = 25,4 мм

Также точки (не путать с десятичными знаками)
используются для обозначения умножения во избежание двусмысленности.

Индуктивное реактивное сопротивление

Индуктивное реактивное сопротивление (X _L , в Ом) пропорционально частоте (ω,
в радианах / сек или f в Гц) и индуктивности (L в единицах Генри).Чистая индуктивность имеет фазу
угол 90 ° (напряжение отводит ток с фазовым углом 90 °).

Энергия, запасенная в индукторе

Энергия (Вт, в Джоулях), запасенная в катушке индуктивности, равна половине произведения индуктивности.
(L, в Генрие) и ток (I, в амперах) через устройство.

Напряжение на индукторе

Свойство индуктора противодействовать изменению потока тока вызывает противо-ЭДС.
(напряжение) на его выводах, полярность противоположная приложенному напряжению.

Коэффициент качества индуктора

Добротность — это безразмерное отношение реактивного сопротивления к сопротивлению в катушке индуктивности.

Однослойная индуктивность круглой катушки

Уиллера
Формула для d >> a:

Обычно для a = радиус проволоки:

Примечание. Если длина выводов значительна, используйте расчет прямого провода, чтобы добавить это
индуктивность.

Поиск эквивалента «R _Q »

Поскольку
Q индуктора — это отношение реактивной составляющей к резистивной,
эквивалентная схема может быть определена с резистором, подключенным параллельно катушке индуктивности. Эта
уравнение действительно только для одной частоты «f» и должно вычисляться для каждой частоты.
представляет интерес.

.

Калькулятор ВЧ-индуктивности для однослойных спиральных круглых проволочных катушек

Серж Ю. Строобандт, ON4AA

Copyright 2007–2020, под лицензией Creative Commons BY-NC-SA

0. Дом
2. Калькулятор индуктивности

Обеспечение высокого качества

Катушки

, обеспечивающие наивысший коэффициент качества, требуют проволоки, ленты или трубки большого диаметра и обычно имеют кубическую форму ; я.е. длина катушки равна диаметру катушки.

Чем отличается этот калькулятор индуктивности от остальных?

Д-р Джеймс Ф. Корум, K1AON

Вычислитель индуктивности, представленный на этой странице, уникален тем, что использует волноводный режим со спиральной оболочкой n = 0 для определения индуктивности катушки независимо от ее электрической длины. В отличие от калькуляторов квазистатической индуктивности, этот калькулятор индуктивности RF позволяет более точно прогнозировать индуктивность на высоких частотах с помощью , включая эффекты линии передачи , проявляющиеся при более длинных катушках.Кроме того, калькулятор точно следует методологии Национального института стандартов и технологий (NIST) для применения коэффициентов коррекции круглой проволоки и неоднородности, а учитывает как эффект близости, так и скин-эффект.

Разработка этого калькулятора была в основном основана на статье братьев Корум в обзоре микроволн в IEEE 2001 г. ⁷ и формулах коррекции, представленных в книге Дэвида Найта, G3YNH, теоретический обзор, ¹ , дополненной несколькими личными дополнениями.

Какую схему замещения следует использовать?

Обе эквивалентные схемы дают точно такое же полное сопротивление катушки на расчетной частоте.

Для узкополосных приложений около единственной проектной частоты может использоваться эффективная эквивалентная схема. При необходимости могут быть рассчитаны дополнительные эквивалентные схемы для дополнительных расчетных частот.

Схема замещения с сосредоточенными параметрами приведена здесь в основном для сравнения с другими калькуляторами.За счет параллельного добавления сосредоточенной паразитной емкости эта эквивалентная схема пытается имитировать частотную характеристику импеданса катушки. Это будет точно только для ограниченного диапазона частот, сосредоточенного вокруг проектной частоты.

Для чего можно использовать этот калькулятор?

спиральная антенна

Калькулятор возвращает значения для коэффициента осевого распространения β и характеристического импеданса Z _c волновода со спиральной оболочкой n = 0 (T ₀ ) для любых размеров спирали на любой частоте.

Эта информация пригодится при проектировании:

• Нагрузочные катушки High-Q для уменьшения размеров антенны (детали конструкции),
• Одиночная или многоядерная приемная антенна с известной резонансной частотой,
• Спиральные антенны, , эквивалентные стержневой диэлектрической антенне,
• Катушка Тесла источники высокого напряжения (см. Рисунок далее),
• РЧ катушки для магнитно-резонансной томографии (МРТ) ,
• Лампа бегущей волны (ЛБВ) спиралей (рисунок ниже).

В чем проблема других вычислителей индуктивности?

Том Раух, W8JI

Том Раух, W8JI, в своем известном исследовании индукторов с высокой добротностью однажды пожаловался, что многие программы моделирования индукторов не учитывают два важных эффекта:

• Паразитная емкость через катушку индуктивности,
• Эффект близости , вызывает уменьшение Q по мере сближения витков.

Например, JavaScript-калькулятор RF Coil Design от VE3KL игнорирует эти эффекты.

Точно так же некогда очень популярная компьютерная программа, названная «COIL» Брайаном Бизли ex-K6STI, оказалась основана на наборе ошибочных формул, ^1,10,11 , как было тщательно указано Дэвидом Найтом, G3YNH. К счастью, эта программа больше не продается.

Как рассчитывается мода спирального волновода?

Фридрих Вильгельм Бессель

Катушку лучше всего рассматривать как спиральный волновод, по которому распространяется своего рода спиральная поверхностная волна. Фазовая скорость распространения такого спирального волновода составляет с дисперсией, что означает , что означает, что она разная для разных частот. (Это не относится к обычным линиям передачи, таким как коаксиальный или открытый провод.) Более низкие частоты распространяются медленнее по катушке. Фактическая фазовая скорость на конкретной частоте для конкретной волновой моды получается путем решения трансцендентного уравнения на собственные значения, включающего модифицированные функции Бесселя первого (I _n ) и второго рода (K _n ) соответственно для внутреннего и снаружи спирали. ^7,8

Д-р Т. Дж. Деккер

Поскольку такое уравнение не может быть решено обычными аналитическими средствами, настоящий калькулятор определит фазовую скорость β моды спирали оболочки самого низкого порядка (n = 0) на расчетной частоте, используя метод Теодоруса (Дирк) Дж. Деккера ^12–14 комбинированный метод определения корня пополам и секущей . Для этого калькулятора версия SLATEC FORTRAN ¹⁵ алгоритма Деккера была переведена Дэвидом Биннером в код JavaScript, а затем, с уважением, в код Brython.

Аналогичный алгоритм также используется для определения частоты, на которой катушка выглядит как четвертьволновой резонатор. Это первая собственная резонансная частота катушки.

Более подробную информацию об используемых формулах и алгоритмах можно получить непосредственно из исходного кода Brython этого калькулятора.

Почему все еще нужны поправочные коэффициенты?

Несмотря на то, что модель волновода со спиральной оболочкой является наиболее точной из имеющихся на сегодняшний день, она, безусловно, имеет ряд ограничений.Они берут свое начало в самом определении — спирали оболочки, — это: идеализированная анизотропно проводящая цилиндрическая поверхность, проводящая только в спиральном направлении. ⁷

Выбирая спираль оболочки в качестве модели для цилиндрической катушки из круглой проволоки, делаются следующие допущения:

1. Провод отлично проводит.
2. Провод бесконечно тонкий.
3. Витки катушки бесконечно замкнуты.
4. Наконец, поскольку более высокие (n> 0) моды волновода со спиральной оболочкой не учитываются, концевые эффекты в виде неоднородностей поля не рассматриваются. Следовательно, спираль оболочки должна быть очень длинной и относительно тонкой, чтобы концевые эффекты стали незначительными.

К счастью, эти допущения совпадают с допущениями, сделанными при использовании формулы геометрической индуктивности. Это означает, что те же поправочные коэффициенты могут быть применены к результатам модели волновода со спиральной оболочкой, а именно:

• Поправочный коэффициент неоднородности поля k _L согласно Lundin ^1,3 для моделирования конечных эффектов коротких и толстых катушек (высокий \ (\ frac {D} {\ ell} \) соотношение),
• A Поправочный коэффициент самоиндукции круглого провода k _с по Rosa, ^1,4,5
• Коэффициент поправки на взаимную индуктивность круглого провода k _м по Knight, ^1,6
• Уменьшенный эффективный диаметр катушки для моделирования гашения тока в проводе под влиянием близости соседних обмоток,
• Последовательное сопротивление переменному току для моделирования скин-эффекта, включая , дополнительную концевую коррекцию для двух концевых витков, на которые действует только половина эффекта близости.

Есть небольшой разрыв в расчетных индуктивностях?

Да, есть; вокруг ℓ = D. Thomas Bruhns, K7ITM обнаружил этот небольшой недостаток. Это полностью из-за по сути прерывистой формулировки справочной формулы Лундина. Эта приближенная формула используется для получения поправочного коэффициента неоднородности поля k _L без особых вычислительных затрат. Неравномерность расчетных индуктивностей появляется только тогда, когда ℓ = D. Она проявляется только тогда, когда сумма поправочных коэффициентов (k _s + k _m ) относительно мала по сравнению с k _L ; я.е. для очень толстых поворотов с малым шагом. Однако даже в этом случае ошибка не превышает ± 0,0003%. ¹

Делаются ли какие-то другие приближения?

Д-р Дэвид В. Найт, G3YNH

Да, есть еще несколько приближений. Они вводятся только тогда, когда вычислительная выгода существенна и когда влияние на точность меньше любого допустимого производственного допуска. Помимо ранее обсуждавшейся формулы из справочника Лундина, аппроксимационная формула Дэвида Найта ¹ используется для определения поправочного коэффициента k _m для взаимной индуктивности круглого провода. ¹ Эффективный диаметр D _eff также оценивается просто потому, что в настоящее время нет известного способа его расчета (см. Ниже).

Основывается ли этот калькулятор на каких-либо эмпирических данных?

Коэффициент близости Φ, используемый для расчета сопротивления катушки переменному току, интерполируется из таблицы экспериментальных данных Медхерста. ² Фактор близости Φ определяется как отношение общего сопротивления переменного тока, включая вклад эффекта близости к сопротивлению переменного тока без вклада эффекта близости.

\ [\ Phi \ Equiv \ frac {R_ {ac, \ Phi}} {R_ {ac}} \]

Как эффективный диаметр D _eff связан с коэффициентом близости Φ?

Другие вычислители индуктивности обычно используют средний и внутренний физические диаметры (соответственно: D и D — d), чтобы ограничить индуктивность катушки между двумя широко разнесенными теоретическими пределами. ¹ . Однако часто упоминается, что фактический эффективный диаметр D _eff катушки должен быть связан с коэффициентом близости Φ.Чтобы избавиться от неоднозначности результата измерения диапазона индуктивности, была выведена новая наивная формула аппроксимации. В этом приближении эффективный диаметр D _eff является простой функцией фактора близости Φ. В результате этих усилий этот калькулятор индуктивности вернет только одно значение индуктивности.

Эффективный диаметр и его предполагаемая связь с коэффициентом близости Φ (см. Текст)

Хотя расчет индуктивности по этой формуле более конкретен, чем брекетинг эффективного диаметра, он остается приблизительным по двум причинам:

1. Как и в случае с брекетингом диаметра, эта формула в равной степени предполагает, что ток под действием эффекта близости гаснет, сохраняя при этом круговое поперечное распределение.Скорее всего, это не так.
2. Как и в случае брекетинга диаметра, формула не учитывает частотно-зависимые возмущения поперечного распределения тока, такие как скин-эффект.

Эти нарушения в поперечном распределении тока не учитываются и могут перемещать центр распределения тока дальше внутрь. Это уменьшает эффективный диаметр и, как следствие, индуктивность еще больше. Таким образом, индуктивность, полученная с помощью этого калькулятора, будет немного завышена.Тем не менее, указанная индуктивность в большинстве случаев будет более точной и, безусловно, менее неоднозначной, чем теоретические крайние значения (или их среднее значение), указанные другими вычислителями индуктивности.

Индуктивность и, следовательно, добротность вблизи резонанса огромны; Это может быть правильно?

Как объяснялось ранее, правильный способ увидеть индуктор — это спиральный волновод, закороченный на одном конце, поскольку предполагается, что он питается от источника напряжения. На любой частоте можно определить коэффициент осевого распространения β и характеристический импеданс Z _c эквивалентной линии передачи.

Входной импеданс на другом конце будет тангенциальной функцией электрической длины катушки. Следовательно, когда электрическая длина приближается к четверти длины волны или \ (\ frac {\ pi} {2} \) рад, результирующий входной импеданс и, следовательно, индуктивность будут чрезвычайно высокими. Омические потери остаются сравнительно низкими, поэтому добротность Q будет огромной вблизи резонанса.

Катушка Тесла использует это явление для создания чрезвычайно высоких напряжений в диапазоне нескольких сотен кВ. ⁷ Калькуляторы индуктивности, которые не показывают этого реального поведения, основаны на геометрических формулах.

Пробой напряжения воздуха на одном конце катушки Тесла. Источник: oneTesla

Расчетная индуктивность отрицательна; Это может быть правильно?

Вы работаете с катушкой выше ее первой собственной резонансной частоты. Катушка с электрической длиной от 90 ° до 180 ° (и нечетное кратное ей) будет вести себя как конденсатор, а не как катушка индуктивности. Это еще раз указывает на то, что первый собственный резонанс катушки на самом деле является параллельным резонансом. Из-за емкостного поведения в этом диапазоне индуктивность катушки будет отрицательной.

Паразитная емкость C _p намного выше, чем у других калькуляторов; Это может быть правильно?

Понятие паразитной емкости — вот что это такое; корректирующий элемент в схеме с сосредоточенными параметрами катушки, эквивалентный для решения проблемы частотной независимости формулы худшей геометрической индуктивности. ⁷

Используя формулы на основе спирального волновода, настоящий калькулятор работает намного лучше при оценке индуктивностей на высоких частотах. Таким образом, калькулятор компенсирует эквивалент схемы с сосредоточенными параметрами даже больше, чем другие калькуляторы. Это приводит к более высоким значениям для C _p .

В конце концов, от старомодной концепции эквивалента сосредоточенной схемы лучше отказаться. Вместо этого фокусируется на эффективных значениях на проектной частоте для индуктивности, реактивного сопротивления, последовательного сопротивления и ненагруженной Q.

В чем проблема проектирования катушек с использованием EZNEC?

Прагматики из нас, вероятно, хотели бы использовать EZNEC, программу моделирования антенн, которая позволяет вам очень удобно определять спиральные структуры катушек. Однако этот ценный метод не лишен недостатков:

• Катушки в EZNEC определены как полилинии. Спроецированный многоугольник полилинии должен иметь ту же площадь, что и спроецированный круг реальной спиральной катушки. Я предоставлю читателю возможность выполнить это тригонометрическое упражнение.
• Чем больше сегментов в ломаной линии, тем точнее модель будет представлять реальную спиральную катушку. Однако EZNEC имеет нижний предел длины сегмента, который пропорционален длине волны.
• С учетом двух предыдущих пунктов, довольно громоздко оптимизировать конструкцию змеевика с помощью EZNEC.

Катушка EZNEC, модель

На практике часто намного проще, быстрее и точнее прибегнуть к вышеуказанному калькулятору вместо создания геометрической модели катушки EZNEC. После получения результатов с помощью этого калькулятора катушку можно легко смоделировать как нагрузку Лапласа в любой модели антенны EZNEC.

Шаг намотки однослойной катушки определяется как

\ [\ begin {уравнение} p \ эквив \ frac {\ ell} {N} \ end {уравнение} \]

Фактор близости \ (\ Phi \) интерполирован на основе эмпирических данных Медхерста. ^1,2

\ [\ begin {уравнение} \ Phi = f_ \ text {Medhurst} \ left (\ frac {\ ell} {D}, \ frac {p} {d} \ right) \ end {уравнение} \]

Наивная приблизительная формула для эффективного диаметра \ (D_ \ text {eff} \) была выведена автором:

\ [\ begin {уравнение} D_ \ text {eff} = D — d \ cdot \ left (1 — \ frac {1} {\ sqrt {\ Phi}} \ right) \ end {уравнение} \]

Поправочные коэффициенты

\ (k_ \ text {L} \) — коэффициент коррекции неоднородности поля по Лундину.2} — \ frac {4D_ \ text {eff}} {3 \ pi \ ell} \ end {формула} \]

\ (k_ \ text {s} \) — поправочный коэффициент для самоиндукции круглого проводника по Найту и Розе. ^1,4,5

\ [k_ \ text {s} = \ frac {5} {4} — \ ln {\ left (2 \, \ frac {p} {d} \ right)} \]

\ (k _ {\ text {m}} \) — поправочный коэффициент на взаимную индуктивность между обмотками круглого проводника по Найту. ^1,6

\ [k _ {\ text {m}} = \ ln {(2 \ pi)} — \ frac {3} {2} — \ frac {\ ln {(N)}} {6N} — \ frac {0 .2)} \, \ Phi \, \ frac {N — 1} {N} \]

Для одиночного контура поправочный коэффициент близкого конца \ (\ frac {N — 1} {N} \) в приведенной выше формуле заменен коэффициентом 1.

Исправленная геометрическая формула токового листа

Не зависящая от частоты последовательная индуктивность \ (L _ {\ text {s}} \) по геометрической формуле катушки токового слоя с поправкой на неоднородность поля, самоиндукцию круглого проводника и взаимную связь составляет: ^{1,3– 6}

\ [L_ \ text {s} = \ mu_0 \ left [\ pi \ frac {(D_ \ text {eff} N) ^ 2} {4 \ ell} — D_ \ text {eff} N \ frac {k_ \ » текст {s} + k_ \ text {m}} {2} \ right] \]

Характеристический импеданс волноводной моды спиральной оболочки

Эффективный угол наклона рассчитывается по тригонометрии:

\ [\ psi = \ arctan {\ frac {p} {\ pi \, D_ \ text {eff}}} \]

Герц показал, что произвольное электромагнитное поле в однородной линейной изотропной среде без источника может быть определено в терминах единственного векторного потенциала \ (\ Pi \). ¹⁶ Предполагая \ (\ e {\, \ j \ omega t} \) зависимость от времени, волна в поле векторного потенциала Герца может быть записана как:

\ [\ vec {\ Pi} (x) = \ vec {\ Pi} (0) \ e {- \ gamma x} \]

Постоянная распространения \ (\ gamma \) — комплексная величина:

\ [\ gamma = \ alpha + \ j \ beta \]

где:
\ (\ alpha \) — постоянная затухания, а
\ (\ beta \) — фазовая постоянная.

Однако, поскольку затухание в воздушной среде незначительно, принято записывать волновое уравнение исключительно в функции комплексной фазовой постоянной \ (\ beta \):

\ [\ vec {\ Pi} (x) = \ vec {\ Pi} (0) \ e {- \ j \ beta x} \]

где \ (\ beta = \ beta ‘- \ j \ beta’ ‘\),
такие, что \ (\ gamma \ Equiv \ j \ beta = \ j (\ beta ‘- \ j \ beta’ ‘) = \ beta’ ‘+ \ j \ beta’ \ Rightarrow \ beta » \ Equiv \ alpha \) .2} \]

Характеристический импеданс \ (Z_ \ text {c} \) волноводной моды со спиральной оболочкой \ (n = 0 \) на расчетной частоте равен: ⁷

\ [Z_ \ text {c} = \ frac {60 \ beta} {k_0} \, \ text {I} _0 (\ tau a) \; \ text {K} _0 (\ tau a) \]

Формула волновода со спиральной оболочкой и скорректированной оболочкой

\ [L_ \ text {eff, s} = \ frac {Z_ \ text {c}} {\ omega} \, \ tan (\ beta \, \ ell) \; k_ \ text {L} — \ mu_0 D_ \ text {eff} N \ frac {k_ \ text {s} + k_ \ text {m}} {2} \]

Эффективная эквивалентная схема

\ [X_ \ text {eff, s} = \ omega L_ \ text {eff, s} \]

\ [Q_ \ text {eff} \ Equiv \ frac {X_ \ text {eff, s}} {R_ \ text {eff, s}} \]

Схема замещения с сосредоточенными параметрами

Чтобы рассчитать сосредоточенную эквивалентную схему, сначала известная последовательная эффективная эквивалентная схема преобразуется в ее параллельную версию:

\ [R_ \ text {eff, p} = \ left (Q_ \ text {eff} ^ 2 + 1 \ right) R_ \ text {eff, s} \ qquad
X_ \ text {eff, p} = \ frac {Q_ \ text {eff} ^ 2 + 1} {Q_ \ text {eff} ^ 2} X_ \ text {eff, s} \]

Аналогично, эквивалентная схема с сосредоточенными параметрами может быть преобразована в схему только с параллельными компонентами, в которой \ (Q_L \) и \ (R_ \ text {s} \) остаются неизвестными:

\ [R_ \ text {p} = \ left (Q_L ^ 2 + 1 \ right) R_ \ text {s} \ qquad
X_ {L_ \ text {p}} = \ frac {Q_L ^ 2 + 1} {Q_L ^ 2} X_ {L_ \ text {s}} \]

Можно записать еще три тождества; первый гласит, что параллельные резисторы в обеих схемах замещения одинаковые:

\ [R_ \ text {p} = R_ \ text {eff, p} \ qquad
Q_L \ Equiv \ frac {X_ {L_ \ text {s}}} {R_ \ text {s}} \ qquad
X_ {L_ \ text {s}} = \ omega L_ \ text {s} \]

Подстановка позволяет записать сокращенное квадратное уравнение в \ (Q_L \):

\ [R_ \ text {p} = \ left (Q_L ^ 2 + 1 \ right) \ frac {X_ {L \ text {s}}} {Q_L} \ quad
\ Rightarrow \ quad Q_L ^ 2 — \ frac {R_ \ text {p}} {X_ {L \ text {s}}} Q_L +1 = 0 \]

Это дает следующие решения для \ (Q_L \) и \ (R_ \ text {s} \):

\ [Q_L = \ frac {R_ \ text {p}} {2 X_ {L \ text {s}}} + \ sqrt {\ left (\ frac {R_ \ text {p}} {2 X_ {L \ текст {s}}} \ right) ^ 2 — 1} \ qquad
R_ \ text {s} = \ frac {X_ {L_ \ text {s}}} {Q_L} \]

На данный момент известны как \ ({X_ \ text {eff, p}} \), так и его компонент \ (X_ {L_ \ text {p}} \).Следовательно, теперь можно извлечь параллельную паразитную емкость \ (C_ \ text {p} \) на расчетной частоте:

\ [\ frac {1} {X_ {C_ \ text {p}}} = \ frac {1} {X_ \ text {eff, p}} — \ frac {1} {X_ {L_ \ text {p} }} = \ frac {X_ {L_ \ text {p}} — X_ \ text {eff, p}} {X_ \ text {eff, p} \: X_ {L_ \ text {p}}} \ quad
\ Rightarrow \ quad X_ {C_ \ text {p}} = \ frac {X_ \ text {eff, p} \: X_ {L_ \ text {p}}} {X_ {L_ \ text {p}} — X_ \ текст {eff, p}} \]

\ [C_ \ text {p} = — \ frac {1} {\ omega X_ {C_ \ text {p}}} \]

Собственная резонансная частота

Собственная резонансная частота приблизительно равна:

\ [\ beta \ ell \ rightarrow \ frac {\ pi} {2} \]

где:
\ (k_0 = \ sqrt {\ beta ^ 2 — \ tau ^ 2} \),
дисперсионная функция трансцендентной спирали оболочки решается численно для поперечного (радиального) волнового числа,
\ (\ omega = k_0 c_0 \) и \ (f_ \ text {res} = \ frac {\ omega} {2 \ pi} \).

Код Brython этого калькулятора доступен ниже. Код Brython не предназначен для автономной работы, хотя он выглядит почти идентично Python 3. Код Brython выполняется на стороне клиента в браузере, где он транскодируется для защиты Javascript.

8. Роберт Э. Коллин. Основы микроволновой техники. В: 2-е изд. Wiley-IEEE Press; 2001: 580-583.

12. T. J. Dekker, W. Hoffmann. Алгол 60. Процедуры числовой алгебры, часть 2 .Mathematisch Centrum Amsterdam; 1968.

13. T. J. Dekker. Нахождение нуля с помощью последовательной линейной интерполяции. В: Б. Дежон, П. Хенрици, ред. Конструктивные аспекты основной теоремы алгебры . Нью-Йорк; 1969.

16. Дж. А. Страттон. Электромагнитная теория . Макгроу-Хилл; 1941.

.