Эдс самоиндукции расчет. Формула ЭДС индукции определена как
Э. д. с. самоиндукции.
Э. д. с. e L , индуцирования в проводнике или катушке в результате изменения магнитного потока, созданного током, проходящим по этому же проводнику или катушке, носит название э. д. с. самоиндукции (рис. 60). Эта э. д. с. возникает при всяком изменении тока, например при замыкании и размыкании электрических цепей, при изменении нагрузки электродвигателей и пр. Чем быстрее изменяется ток в проводнике или катушке, тем больше скорость изменения пронизывающего их магнитного потока и тем большая э. д. с. самоиндукции в них индуцируется. Например, э. д. с. самоиндукции e L возникает в проводнике АБ (см. рис. 54) при изменении протекающего по нему тока i 1 . Следовательно, изменяющееся магнитное поле индуцирует э. д. с. в том же самом проводнике, в котором изменяется ток, создающий это поле.
Направление э. д. с. самоиндукции определяется по правилу Ленца. Э. д. с. самоиндукции имеет всегда такое направление, при котором она препятствует изменению вызвавшего ее тока.
Следовательно, при возрастании тока в проводнике (катушке) индуцированная в них э. д. с. самоиндукции будет направлена против тока, т. е. будет препятствовать его возрастанию (рис. 61, а), и наоборот, при уменьшении тока в проводнике (катушке) возникает э. д. с. самоиндукции, совпадающая по направлению с током, т. е. препятствующая его убыванию (рис. 61, б). Если же ток в катушке не изменяется, то э. д. с. самоиндукции не возникает.
Из рассмотренного выше правила для определения направления э. д. с. самоиндукции вытекает, что эта э. д. с. оказывает тормозящее действие на изменение тока в электрических цепях. В этом отношении ее действие аналогично действию силы инерции, которая препятствует изменению положения тела. В электрической цепи (рис. 62, а), состоящей из резистора с сопротивлением R и катушки К, ток i создается совместным действием напряжения U источника и э. д. с. самоиндукции e L индуцируемой в катушке. При подключении рассматриваемой цепи к источнику э. д. с. самоиндукции e L (см. сплошную стрелку) сдерживает нарастание силы тока. Поэтому ток i достигает установившегося значения I=U/R (согласно закону Ома) не мгновенно, а в течение определенного промежутка времени (рис. 62, б). За это время в электрической цепи происходит переходный процесс, при котором изменяются e L и i. Точно
сплошную стрелку) сдерживает нарастание силы тока. Поэтому ток i достигает установившегося значения I=U/R (согласно закону Ома) не мгновенно, а в течение определенного промежутка времени (рис. 62, б). За это время в электрической цепи происходит переходный процесс, при котором изменяются e L и i. Точно
так же при выключении электрической цепи ток i не уменьшается мгновенно до нуля, а из-за действия э. д. с. e L (см. штриховую стрелку) постепенно уменьшается.
Индуктивность.
Способность различных проводников (катушек) индуцировать э. д. с. самоиндукции оценивается индуктивностью L. Она показывает, какая э. д. с. самоиндукции возникает в данном проводнике (катушке) при изменении тока на 1 А в течение 1 с. Индуктивность измеряется в генри (Гн), 1 Гн = 1 Ом*с. На практике индуктивность часто измеряют в тысячных долях генри — миллигенри (мГн) и в миллионных долях генри — микрогенри (мкГн).
Индуктивность катушки зависит от числа витков катушки? и магнитного сопротивления R м ее магнитопровода, т.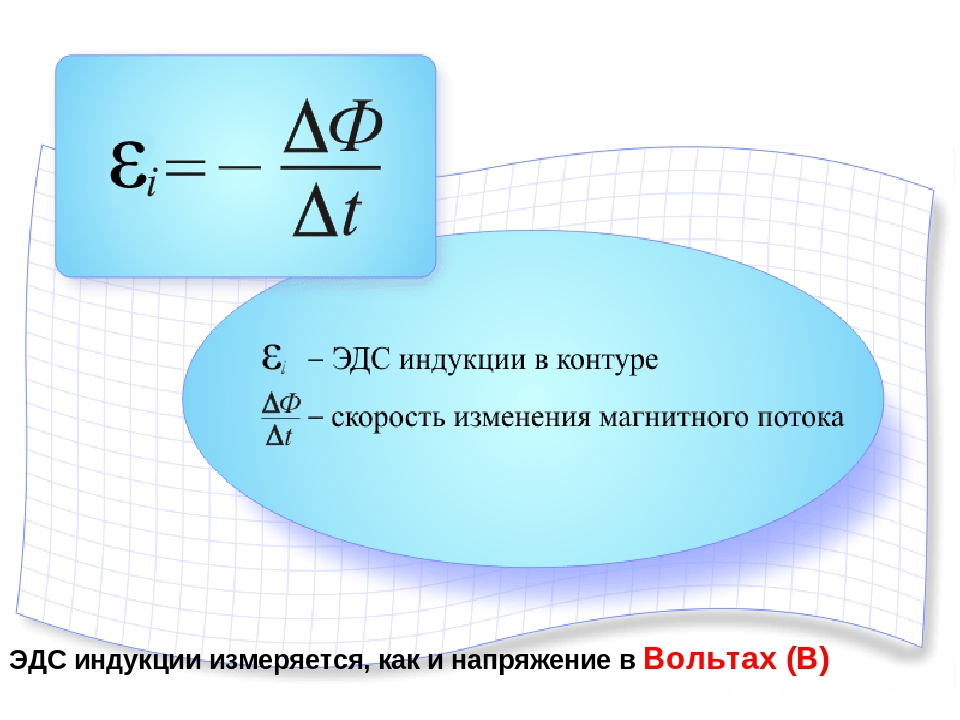 е. от его магнитной проницаемости? а и геометрических размеров l и s. Если в катушку вставить стальной сердечник, ее индуктивность резко возрастает из-за усиления магнитного поля катушки. В этом случае ток 1 А создает значительно больший магнитный поток, чем в катушке без сердечника.
е. от его магнитной проницаемости? а и геометрических размеров l и s. Если в катушку вставить стальной сердечник, ее индуктивность резко возрастает из-за усиления магнитного поля катушки. В этом случае ток 1 А создает значительно больший магнитный поток, чем в катушке без сердечника.
Используя понятие индуктивности L, можно получить для э. д. с. самоиндукции следующую формулу:
e L = – L ?i / ?t
(53)
Где?i – изменение тока в проводнике (катушке) за промежуток времени?t.
Следовательно, э. д. с. самоиндукции пропорциональна скорости изменения тока.
Включение и отключение цепей постоянного тока с катушкой индуктивности.
При подключении к источнику постоянного тока с напряжением U электрической цепи, содержащей R и L, выключателем B1 (рис. 63, а) ток i возрастает до установившегося значения I уст =U/R не мгновенно, так как э. д. с. самоиндукции e L , возникающая в индуктивности, действует против приложенного напряжения V и препятствует нарастанию тока. Для рассматриваемого процесса характерным является постепенное изменение тока i (рис. 63, б) и напряжений u а и u L по кривым — экспонентам.
Для рассматриваемого процесса характерным является постепенное изменение тока i (рис. 63, б) и напряжений u а и u L по кривым — экспонентам.
Изменение i, u а и u L по указанным кривым называется апериодическим.
Скорость нарастания силы тока в цепи и изменения напряжений u а и u L характеризуется постоянной времени цепи
T = L/R
(54)
Она измеряется в секундах, зависит только от параметров R и L данной цепи и позволяет без построения графиков оценить длительность процесса изменения тока. Эта длительность теоретически бесконечно велика. Практически же обычно считают, что она составляет (3-4) Т. За это время ток в цепи достигает 95-98 % установившегося значения. Следовательно, чем больше сопротивление и чем меньше индуктивность L, тем быстрее протекает процесс изменения тока в электрических цепях с индуктивностью. Постоянную времени Т при апериодическом процессе можно определить как отрезок АВ, отсекаемый касательной, проведенной из начала координат к рассматриваемой кривой (например, тока i) на линии, соответствующей установившемуся значению данной величины.
Свойством индуктивности замедлять процесс изменения тока пользуются для создания выдержек времени при срабатывании различных аппаратов (например, при управлении работой песочниц для периодической подачи порций песка под колеса локомотива). На использовании этого явления основана также работа электромагнитного реле времени (см. § 94).
Коммутационные перенапряжения.
Особенно сильно проявляет себя э. д. с. самоиндукции при размыкании цепей, содержащих катушки с большим числом витков и со стальными сердечниками (например, обмотки генераторов, электродвигателей, трансформаторов и пр.), т. е. цепей, обладающих большой индуктивностью. В этом случае возникающая э. д. с. самоиндукции e L может во много раз превысить напряжение U источника и, суммируясь с ним, послужить причиной возникновения перенапряжений в электрических цепях (рис. 64, а), называемых коммутационными
(возникающими при коммутации
— переключениях электрических цепей). Они являются опасными для обмоток электродвигателей, генераторов и трансформаторов, так как могут вызвать пробой их изоляции.
Большая э. д. с. самоиндукции способствует также возникновению электрической искры или дуги в электрических аппаратах, осуществляющих коммутацию электрических цепей. Например, в момент размыкания контактов рубильника (рис. 64, б) образующаяся э. д. с. самоиндукции сильно увеличивает разность потенциалов между разомкнутыми контактами рубильника и пробивает воздушный промежуток. Возникающая при этом электрическая дуга поддерживается в, течение некоторого времени э. д. с. самоиндукции, которая, таким образом, затягивает процесс отключения тока в цепи. Это явление весьма нежелательно, так как дуга оплавляет контакты отключающих аппаратов, что приводит к быстрому выходу их из строя. Поэтому во всех аппаратах, служащих для размыкания электрических цепей, предусматриваются специальные дугогасительные устройства, обеспечивающие ускорение гашения дуги.
Кроме того, в силовых цепях, обладающих значительной индуктивностью (например, обмотки возбуждения генераторов), параллельно цепи R-L (т. е. соответствующей обмотке) включают разрядный резистор R р (рис. 65, а). В этом случае после отключения выключателя В1 цепь R-L не прерывается, а оказывается замкнутой на резистор R р. Ток в цепи i при этом уменьшается не мгновенно, а постепенно — по экспоненте (рис. 65,6), так как э. д. с. самоиндукции e L , возникающая в индуктивности L, препятствует уменьшению тока. Напряжение u p на разрядном резисторе в течение процесса изменения тока также изменяется по экспоненте. Оно равно напряжению, приложенному к цепи R-L, т. е. к зажимам соответ-
е. соответствующей обмотке) включают разрядный резистор R р (рис. 65, а). В этом случае после отключения выключателя В1 цепь R-L не прерывается, а оказывается замкнутой на резистор R р. Ток в цепи i при этом уменьшается не мгновенно, а постепенно — по экспоненте (рис. 65,6), так как э. д. с. самоиндукции e L , возникающая в индуктивности L, препятствует уменьшению тока. Напряжение u p на разрядном резисторе в течение процесса изменения тока также изменяется по экспоненте. Оно равно напряжению, приложенному к цепи R-L, т. е. к зажимам соответ-
ствующей обмотки. В начальный момент U p нач = UR p /R, т. е. зависит от сопротивления разрядного резистора; при больших значениях Rp это напряжение может оказаться чрезмерно большим и опасным для изоляции электрической установки. Практически для ограничения возникающих перенапряжений сопротивление R p разрядного резистора берут не более чем в 4-8 раз больше сопротивления R соответствующей обмотки.
Условия возникновения переходных процессов.
Рассмотренные выше процессы при включении и выключении цепи R-L называют переходными процессами
. Они возникают при включении и выключении источника или отдельных участков цепи, а также при изменении режима работы
, например при скачкообразном изменении нагрузки, обрывах и коротких замыканиях. Такие же переходные процессы имеют место при указанных условиях и в цепях, содержащих конденсаторы, обладающие емкостью С. В ряде случаев переходные процессы являются опасными для источников и приемников, так как возникающие токи и напряжения могут во много раз превышать номинальные значения, на которые рассчитаны эти устройства. Однако в некоторых элементах электрооборудования, в частности в устройствах промышленной электроники, переходные процессы являются рабочими режимами.
Физически возникновение переходных процессов объясняется тем, что катушки индуктивности и конденсаторы являются накопителями энергии, а процесс накопления и отдачи энергии в этих элементах не может происходить мгновенно, следовательно, не может мгновенно измениться ток в катушке индуктивности и напряжение на конденсаторе. Время переходного процесса, в течение которого при включениях, выключениях и изменениях режима работы цепи происходит постепенное изменение тока и напряжения, определяется значениями R, L и С цепи и может составить доли и единицы секунд. После окончания переходного процесса ток и напряжение приобретают новые значения, которые называют установившимися
Время переходного процесса, в течение которого при включениях, выключениях и изменениях режима работы цепи происходит постепенное изменение тока и напряжения, определяется значениями R, L и С цепи и может составить доли и единицы секунд. После окончания переходного процесса ток и напряжение приобретают новые значения, которые называют установившимися
.
Магнитное поле
контура, в котором сила тока изменяется,
индуцирует ток не только в других
контурах, но и в себе самом. Это
явление получило название самоиндукции.
Опытным путём
установлено, что магнитный поток вектора
магнитной индукции поля, создаваемого
текущим в контуре током, пропорционален
силе этого тока:
где L– индуктивность
контура. Постоянная характеристика
контура, которая зависит от его формы
и размеров, а так же от магнитной
проницаемости среды, в которой находится
контур. [L] = Гн (Генри,
1Гн = Вб/А).
Если за время
dtток в контуре изменится
наdI, то магнитный поток,
связанный с этим током, изменится наdФ
=LdIв результате чего в
этом контуре появится ЭДС самоиндукции:
Знак минус показывает, что ЭДС
самоиндукции (а, следовательно, и ток
самоиндукции) всегда препятствует
изменению силы тока, который вызвал
самоиндукцию.
Наглядным
примером явления самоиндукции служат
экстратоки замыкания и размыкания,
возникающие при включении и выключении
электрических цепей, обладающей
значительной индуктивностью.
Энергия магнитного поля
Магнитное поле
обладает потенциальной энергией, которая
в момент его образования (или изменения)
пополняется за счёт энергии тока в цепи,
совершающего при этом работу против
ЭДС самоиндукции, возникающей вследствие
изменения поля.
Работа dAза бесконечно малый промежуток времениdt, в течении которого ЭДС
самоиндукциии токIможно считать
постоянными, равняется:
.
(5)
Знак минус указывает, что
элементарная работа совершается током
против ЭДС самоиндукции. Чтобы определить
работу при изменении тока от 0 до I,
проинтегрируем правую часть, получим:
.
(6)
Эта работа численно равна
приросту потенциальной энергии ΔW п магнитного поля, связанного с этой
цепью, т.е.A= -ΔW п.
Выразим энергию магнитного
поля через его характеристики на примере
соленоида. Будем считать, что магнитное
Будем считать, что магнитное
поле соленоида однородно и в основном
расположено внутри его. Подставим в (5)
значение индуктивности соленоида,
выраженное через его параметры и значение
силы тока I, выраженное
из формулы индукции магнитного поля
соленоида:
, (7)
где N – общее число витков
соленоида; ℓ – его длина; S – площадь
сечения внутреннего канала соленоида.
, (8)
После подстановки имеем:
Разделив обе части на V,
получим объёмную плотность энергии
поля:
(10)
или, с учётом, что
получим,
.
(11)
Переменный ток
2.1 Переменный ток и его основные характеристики
Переменным
называется ток, изменяющийся с течением
времени и по величине и по направлению.
Примером переменного тока может служить
потребляемый промышленный ток. Этот
ток является синусоидальным, т.е.
мгновенное значение его параметров
меняются со временем по закону синуса
(или косинуса):
i
= I 0 sinωt,
u =
U 0 sin(ωt
+ φ 0). (12)
Переменный
синусоидальный ток можно получить, если
вращать рамку (контур) с постоянной
скоростью
в однородном
магнитном поле с индукцией B
(рис. 5). При этом магнитный поток,
5). При этом магнитный поток,
пронизывающий контур, изменяется по
закону
где S– площадь
контура, α = ωt– угол
поворота рамки за время t. Изменение
потока приводит к возникновению ЭДС
индукции
, (17)
направление которой определяется
по правилу Ленца.
Если
контур замкнут (рис.5), то по нему идёт
ток:
.
(18)
График изменения электродвижущей
силыи индукционного токаi
представлен на рис.6.
Переменный
ток характеризуется периодом Т, частотой
ν = 1/Т, циклической частотой
и фазой φ = (ωt
+ φ 0)
Графически значения напряжения и силы
переменного тока на участке цепи будут
представляться двумя синусоидами, в
общем случае сдвинутыми по фазе на φ.
Для
характеристики переменного тока вводятся
понятия действующего (эффективного)
значения тока и напряжения. Эффективным
значением силы переменного тока
называется сила такого постоянного
тока, который выделяет в данном проводнике
столько же тепла за время одного периода,
сколько выделяет тепла и данный переменный
ток.
,
. (13)
Приборы, включенные в цепь
переменного тока (амперметр, вольтметр),
показывают эффективные значения тока
и напряжения.
Электромагнитная индукция – генерирование электротоков магнитными полями, изменяющимися во времени. Открытие Фарадеем и Генри этого феномена ввело определенную симметрию в мир электромагнетизма. Максвеллу в одной теории удалось собрать знания об электричестве и магнетизме. Его исследования предсказывали существование электромагнитных волн перед экспериментальными наблюдениями. Герц доказал их существование и открыл человечеству эпоху телекоммуникаций.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/1-14-210×140..jpg 614w»>
Эксперименты Фарадея
Законы Фарадея и Ленца
Электрические токи создают магнитные эффекты. А возможно ли, чтобы магнитное поле порождало электрическое? Фарадей обнаружил, что искомые эффекты возникают вследствие изменения МП во времени.
Когда проводник пересекается переменным магнитным потоком, в нем индуцируется электродвижущая сила, вызывающая электроток.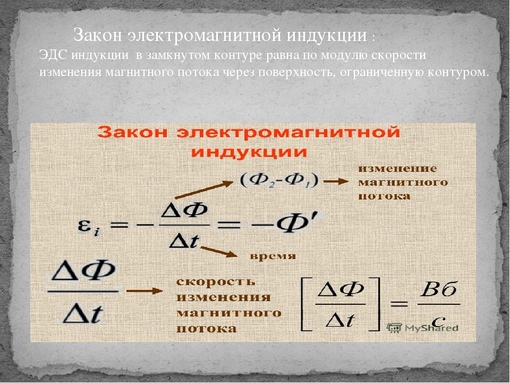 Системой, которая генерирует ток, может быть постоянный магнит или электромагнит.
Системой, которая генерирует ток, может быть постоянный магнит или электромагнит.
Явление электромагнитной индукции регулируется двумя законами: Фарадея и Ленца.
Закон Ленца позволяет охарактеризовать электродвижущую силу относительно ее направленности.
Важно!
Направление индуцированной ЭДС такое, что вызванный ею ток стремится противостоять создающей его причине.
Фарадей заметил, что интенсивность индуцированного тока растет, когда быстрее изменяется число силовых линий, пересекающих контур. Другими словами, ЭДС электромагнитной индукции находится в прямой зависимости от скорости движущегося магнитного потока.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/2-10-768×454..jpg 960w»>
ЭДС индукции
Формула ЭДС индукции определена как:
Е = — dФ/dt.
Знак «-» показывает, как полярность индуцированной ЭДС связана со знаком потока и меняющейся скоростью.
Получена общая формулировка закона электромагнитной индукции, из которой можно вывести выражения для частных случаев.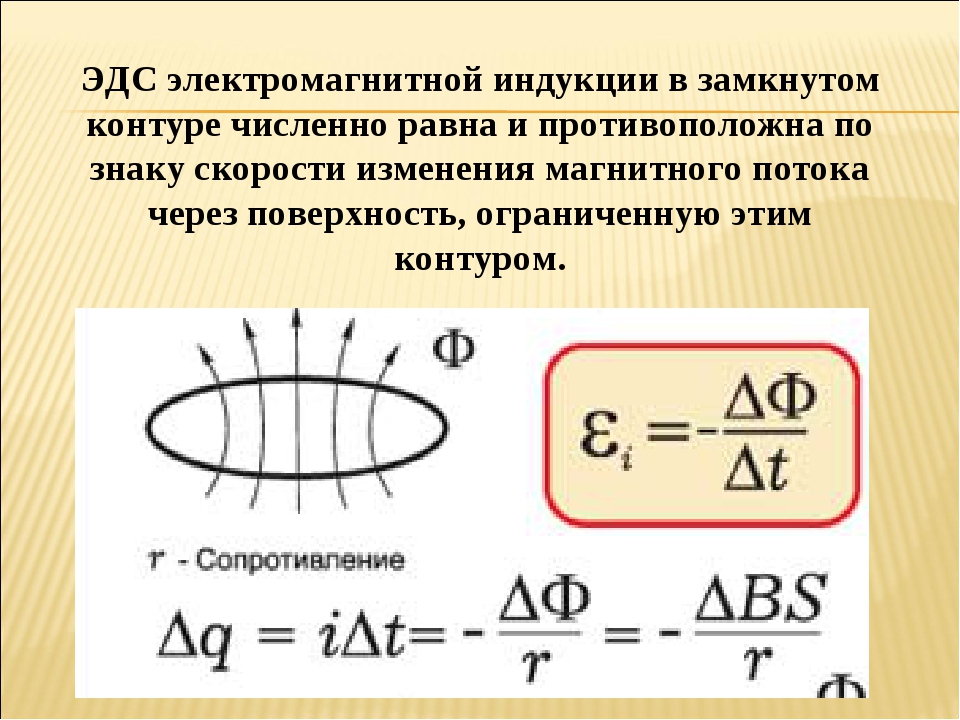
Движение провода в магнитном поле
Когда провод длиной l движется в МП, имеющем индукцию В, внутри него будет наводиться ЭДС, пропорциональная его линейной скорости v. Для расчета ЭДС применяется формула:
- в случае движения проводника перпендикулярно направлению магнитного поля:
Е = — В x l x v;
- в случае движения под другим углом α:
Е = — В x l x v х sin α.
Индуцированная ЭДС и ток будут направлены в сторону, которую находим, пользуясь правилом правой руки: расположив руку перпендикулярно силовым линиям магнитного поля и указывая большим пальцем в сторону перемещения проводника, можно узнать направление ЭДС по оставшимся четырем распрямленным пальцам.
Jpg?x15027″ alt=»Перемещение провода в МП»>
Перемещение провода в МП
Вращающаяся катушка
Работа генератора электроэнергии основана на вращении контура в МП, имеющего N витков.
ЭДС индуцируется в электроцепи всегда, когда магнитный поток ее пересекает, в соответствии с определением магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на поверхностную площадь, через которую проходит МП, и косинус угла, образованного вектором В и перпендикулярной линией к плоскости S).
Из формулы следует, что Ф подвержен изменениям в следующих случаях:
- меняется интенсивность МП – вектор В;
- варьируется площадь, ограниченная контуром;
- изменяется ориентация между ними, заданная углом.
В первых опытах Фарадея индуцированные токи были получены путем изменения магнитного поля В. Однако можно индуцировать ЭДС, не двигая магнит или не меняя ток, а просто вращая катушку вокруг своей оси в МП. В данном случае магнитный поток меняется из-за изменения угла α. Катушка при вращении пересекает линии МП, возникает ЭДС.
Если катушка вращается равномерно, это периодическое изменение приводит к периодическому изменению магнитного потока. Или количество силовых линий МП, пересекаемых каждую секунду, принимает равные значения с равными интервалами времени.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/4-10-768×536..jpg 900w»>
Вращение контура в МП
Важно!
Наведенная ЭДС меняется вместе с ориентацией с течением времени от положительной до отрицательной и наоборот. Графическое представление ЭДС представляет собой синусоидальную линию.
Графическое представление ЭДС представляет собой синусоидальную линию.
Для формулы ЭДС электромагнитной индукции применяется выражение:
Е = В х ω х S x N x sin ωt, где:
- S – площадь, ограниченная одним витком или рамкой;
- N – количество витков;
- ω – угловая скорость, с которой вращается катушка;
- В – индукция МП;
- угол α = ωt.
На практике в генераторах переменного тока часто катушка остается неподвижной (статор), а электромагнит вращается вокруг нее (ротор).
ЭДС самоиндукции
Когда через катушку проходит переменный ток, он генерирует переменное МП, обладающее изменяющимся магнитным потоком, индуцирующим ЭДС. Этот эффект называется самоиндукцией.
Поскольку МП пропорционально интенсивности тока, то:
где L – индуктивность (Гн), определяемая геометрическими величинами: количеством витков на единицу длины и размерами их поперечного сечения.
Для ЭДС индукции формула принимает вид:
Е = — L x dI/dt.
Взаимоиндукция
Если две катушки расположены рядом, то в них наводится ЭДС взаимоиндукции, зависящая от геометрии обеих схем и их ориентации относительно друг друга. Когда разделение цепей возрастает, взаимоиндуктивность снижается, так как уменьшается соединяющий их магнитный поток.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/5-5.jpg 680w»>
Взаимоиндукция
Пусть имеется две катушки. По проводу одной катушки, обладающей N1 витками, протекает ток I1, создающий МП, проходящее через катушку с N2 витками. Тогда:
- Взаимоиндуктивность второй катушки относительно первой:
М21 = (N2 x F21)/I1;
- Магнитный поток:
Ф21 = (М21/N2) x I1;
- Найдем индуцированную ЭДС:
Е2 = — N2 x dФ21/dt = — M21x dI1/dt;
- Идентично в первой катушке индуцируется ЭДС:
Е1 = — M12 x dI2/dt;
Важно!
Электродвижущая сила, вызванная взаимоиндукцией в одной катушке, всегда пропорциональна изменению электротока в другой.
Взаимную индуктивность можно признать равной:
М12 = М21 = М.
Соответственно, E1 = — M x dI2/dt и E2 = M x dI1/dt.
М = К √ (L1 x L2),
где К – коэффициент связи между двумя индуктивностями.
Явление взаимоиндукции используется в трансформаторах – электроаппаратах, позволяющих изменить значение напряжения переменного электротока. Аппарат представляет собой две катушки, намотанные вокруг одного сердечника. Ток, присутствующий в первой, создает меняющееся МП в магнитопроводе и электроток в другой катушке. Если количество витковых оборотов первой обмотки меньше, чем другой, напряжение увеличивается, и наоборот.
При изменении тока в контуре меняется поток магнитной индукции через поверхность , ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи эдс препятствует возрастанию тока, а при уменьшении тока — убыванию.
Направление ЭДС оказывается таким, что при увеличении тока в цепи эдс препятствует возрастанию тока, а при уменьшении тока — убыванию.
Величина ЭДС пропорциональна скорости изменения силы тока I
и индуктивности контура L
:
.
За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи , при этом величина ЭДС самоиндукции может значительно превышать ЭДС источника. Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение самоиндукции при напряжении питающей батареи 12В составляет 7-25кВ.
Wikimedia Foundation
.
2010
.
Смотреть что такое «ЭДС самоиндукции» в других словарях:
эдс самоиндукции
— — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN self induced emfFaraday voltageinductance voltageself induction… …
Это явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока.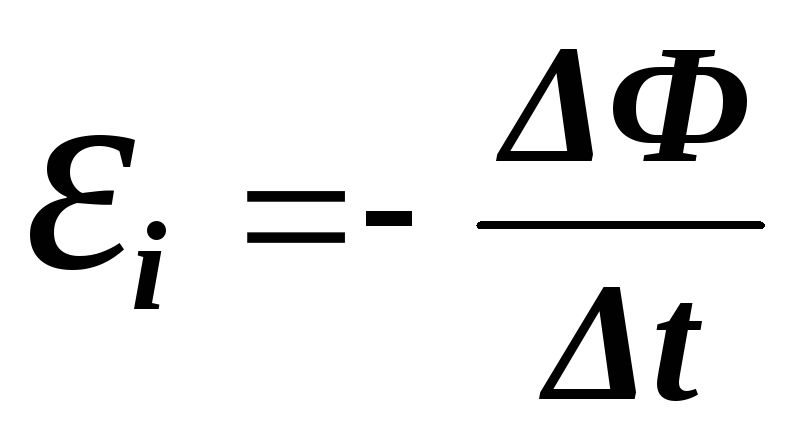 При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение… … Википедия
При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение… … Википедия
— (от лат. inductio наведение, побуждение), величина, характеризующая магн. св ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо… … Физическая энциклопедия
реактивная мощность
— Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… … Справочник технического переводчика
Раздел физики, охватывающий знания о статическом электричестве, электрических токах и магнитных явлениях. ЭЛЕКТРОСТАТИКА В электростатике рассматриваются явления, связанные с покоящимися электрическими зарядами. Наличие сил, действующих между… … Энциклопедия Кольера
Электрический машина, не имеющая подвижных частей и преобразующая переменный ток одного напряжения в переменный ток другого напряжения.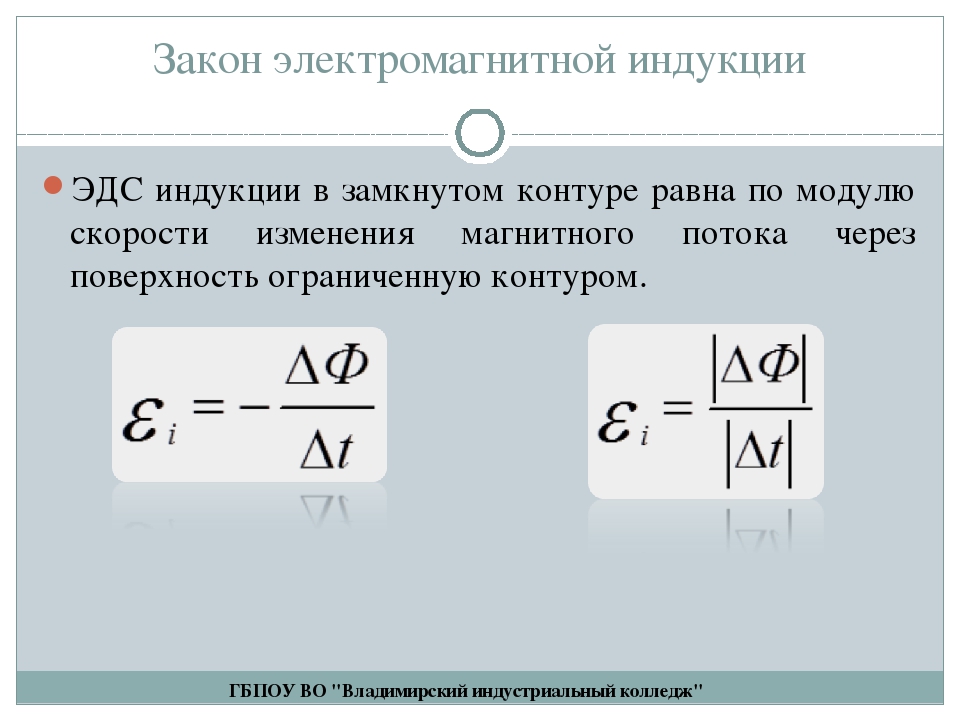 В простейшем случае состоит из магнитопровода (сердечника) и расположенных на нём двух обмоток первичной и… … Энциклопедический словарь
В простейшем случае состоит из магнитопровода (сердечника) и расположенных на нём двух обмоток первичной и… … Энциклопедический словарь
САМОИНДУКЦИЯ Каждый проводник, по которому протекает эл. ток, находится в собственном При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный Это явление называется самоиндукцией. Замыкание цепи При замыкании в эл. цепи нарастает ток, что вызывает в катушке увеличение Размыкание цепи При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, Вывод в электротехнике явление самоиндукции проявляется при замыкании цепи (эл.ток От чего зависит ЭДС самоиндукции? Эл. ток создает собственное магнитное поле. Магнитный поток через контур Индуктивность где Ф — магнитный поток через контур, I — сила тока в контуре. Единицы измерения индуктивности Индуктивность катушки зависит от: ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию Вокруг проводника с током существует магнитное поле, которое обладает энергией. Энергия магнитного поля равнасобственной Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы ВОПРОСЫ К ПРОВЕРОЧНОЙ РАБОТЕ
|
Явление самоиндукции формула. Формула эдс индукции
При изменении тока в контуре меняется поток магнитной индукции через поверхность , ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи эдс препятствует возрастанию тока, а при уменьшении тока — убыванию.
Величина ЭДС пропорциональна скорости изменения силы тока I
и индуктивности контура L
:
.
За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи , при этом величина ЭДС самоиндукции может значительно превышать ЭДС источника. Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение самоиндукции при напряжении питающей батареи 12В составляет 7-25кВ.
Типичное напряжение самоиндукции при напряжении питающей батареи 12В составляет 7-25кВ.
Wikimedia Foundation
.
2010
.
Смотреть что такое «ЭДС самоиндукции» в других словарях:
эдс самоиндукции
— — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN self induced emfFaraday voltageinductance voltageself induction… …
Это явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока. При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение… … Википедия
— (от лат. inductio наведение, побуждение), величина, характеризующая магн. св ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо… … Физическая энциклопедия
реактивная мощность
— Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… … Справочник технического переводчика
[ГОСТ Р 52002 2003]… … Справочник технического переводчика
Раздел физики, охватывающий знания о статическом электричестве, электрических токах и магнитных явлениях. ЭЛЕКТРОСТАТИКА В электростатике рассматриваются явления, связанные с покоящимися электрическими зарядами. Наличие сил, действующих между… … Энциклопедия Кольера
Электрический машина, не имеющая подвижных частей и преобразующая переменный ток одного напряжения в переменный ток другого напряжения. В простейшем случае состоит из магнитопровода (сердечника) и расположенных на нём двух обмоток первичной и… … Энциклопедический словарь
Взаимосвязь электрических и магнитных полей
Электрические и магнитные явления изучались давно, вот только никому не приходило в голову каким-то образом связать эти исследования между собой. И только в 1820 году было обнаружено, что проводник с током действует на стрелку компаса. Это открытие принадлежало датскому физику Хансу Кристиану Эрстеду. Впоследствии его именем была названа единица измерения напряженности магнитного поля в системе СГС: русское обозначение Э (Эрстед), англоязычное — Oe. Такую напряженность магнитное поле имеет в вакууме при индукции в 1 Гаусс.
Такую напряженность магнитное поле имеет в вакууме при индукции в 1 Гаусс.
Это открытие наводило на мысль о том, что из электрического тока можно получить магнитное поле. Но вместе с тем возникали мысли и по поводу обратного преобразования, а именно, как из магнитного поля получить электрический ток. Ведь многие процессы в природе обратимы: из воды получается лед, который можно снова растопить в воду.
На изучение этого очевидного сейчас закона физики после открытия Эрстеда ушло целых двадцать два года. Получением электричества из магнитного поля занимался английский ученый Майкл Фарадей. Делались различной формы и размеров проводники и магниты, искались варианты их взаимного расположения. И только, видимо, случайно ученый обнаружил, что для получения на концах проводника ЭДС необходимо еще одно слагаемое — движение магнита, т.е. магнитное поле должно быть обязательно переменным.
Сейчас это никого уже не удивляет. Именно так работают все электрические генераторы, — пока его чем-то вращают, электроэнергия вырабатывается, лампочка светит. Остановили, перестали вращать, и лампочка погасла.
Остановили, перестали вращать, и лампочка погасла.
Электромагнитная индукция
Таким образом, ЭДС на концах проводника возникает лишь в том случае, если его определенным образом перемещать в магнитном поле. Или, точнее говоря, магнитное поле обязательно должно изменяться, быть переменным. Это явление получило название электромагнитной индукции, по-русски электромагнитное наведение: в этом случае говорят, что в проводнике наводится ЭДС. Если к такому источнику ЭДС подключить нагрузку, то в цепи будет протекать ток.
Величина наведенной ЭДС зависит от нескольких факторов: длины проводника, индукции магнитного поля B, и в немалой степени от скорости перемещения проводника в магнитном поле. Чем быстрее вращать ротор генератора, тем напряжение на его выходе выше.
Замечание: электромагнитную индукцию (явление возникновение ЭДС на концах проводника в переменном магнитном поле) не следует путать с магнитной индукцией — векторной физической величиной характеризующей собственно магнитное поле.
Индукция
Этот способ был рассмотрен . Достаточно перемещать проводник в магнитном поле постоянного магнита, или наоборот перемещать (практически всегда вращением) магнит около проводника. Оба варианта однозначно позволят получить переменное магнитное поле. В этом случае способ получения ЭДС называется индукцией. Именно индукция используется для получения ЭДС в различных генераторах. В опытах Фарадея в 1831 году магнит поступательно перемещался внутри катушки провода.
Взаимоиндукция
Это название говорит о том, что в этом явлении принимают участие два проводника. В одном из них протекает изменяющийся ток, который создает вокруг него переменное магнитное поле. Если рядом находится еще один проводник, то на его концах возникает переменная же ЭДС.
Такой способ получения ЭДС называется взаимоиндукцией. Именно по принципу взаимоиндукции работают все трансформаторы, только проводники у них выполнены в виде катушек, а для усиления магнитной индукции применяются сердечники из ферромагнитных материалов.
Если ток в первом проводнике прекратится (обрыв цепи), или станет пусть даже очень сильным, но постоянным (нет никаких изменений), то на концах второго проводника никакой ЭДС получить не удастся. Вот почему трансформаторы работают только на переменном токе: если к первичной обмотке подключить гальваническую батарейку, то на выходе вторичной обмотки никакого напряжения однозначно не будет.
ЭДС во вторичной обмотке наводится только при изменении магнитного поля. Причем, чем сильнее скорость изменения, именно скорость, а не абсолютная величина, тем больше будет наведенная ЭДС.
Самоиндукция
Если убрать второй проводник, то магнитное поле в первом проводнике будет пронизывать не только окружающее пространство, но и сам проводник. Таким образом, под воздействием своего поля в проводнике наводится ЭДС, которая называется ЭДС самоиндукции.
Явления самоиндукции в 1833 году изучал русский ученый Ленц. На основании этих опытов удалось выяснить интересную закономерность: ЭДС самоиндукции всегда противодействует, компенсирует внешнее переменное магнитное поле, которое вызывает эту ЭДС. Эта зависимость называется правилом Ленца (не путать с законом Джоуля — Ленца).
Эта зависимость называется правилом Ленца (не путать с законом Джоуля — Ленца).
Знак «минус» в формуле как раз и говорит о противодействии ЭДС самоиндукции причинам ее породившим. Если катушку подключить к источнику постоянного тока, ток будет возрастать достаточно медленно. Это очень заметно при «прозвонке» первичной обмотки трансформатора стрелочным омметром: скорость движения стрелки в сторону нулевого деления шкалы заметно меньше, чем при проверке резисторов.
При отключении катушки от источника тока ЭДС самоиндукции вызывает искрение контактов реле. В случае, когда катушка управляется транзистором, например катушка реле, то параллельно ей ставится диод в обратном направлении по отношению к источнику питания. Это делается для того, чтобы защитить полупроводниковые элементы от воздействия ЭДС самоиндукции, которая может в десятки и даже сотни раз превышать напряжение источника питания.
Для проведения опытов Ленц сконструировал интересный прибор. На концах алюминиевого коромысла закреплены два алюминиевых же кольца. Одно кольцо сплошное, а в другом был сделан пропил. Коромысло свободно вращалось на иголке.
Одно кольцо сплошное, а в другом был сделан пропил. Коромысло свободно вращалось на иголке.
При введении постоянного магнита в сплошное кольцо оно «убегало» от магнита, а при выведении магнита стремилось за ним. Те же самые действия с разрезанным кольцом никаких движений не вызывали. Это объясняется тем, что в сплошном кольце под воздействием переменного магнитного поля возникает ток, который создает магнитное поле. А в разомкнутом кольце тока нет, следовательно, нет и магнитного поля.
Немаловажная деталь этого опыта в том, что если магнит будет введен в кольцо и останется неподвижным, то никакой реакции алюминиевого кольца на присутствие магнита не наблюдается. Это лишний раз подтверждает, что ЭДС индукции возникает только в случае изменения магнитного поля, причем величина ЭДС зависит от скорости изменения. В данном случае просто от скорости перемещения магнита.
То же можно сказать и о взаимоиндукции и самоиндукции, только изменение напряженности магнитного поля, точнее скорость его изменения зависит от скорости изменения тока. Для иллюстрации этого явления можно привести такой пример.
Для иллюстрации этого явления можно привести такой пример.
Пусть через две достаточно большие одинаковые катушки проходят большие токи: через первую катушку 10А, а через вторую целых 1000, причем в обеих катушках токи линейно возрастают. Предположим, что за одну секунду ток в первой катушке изменился с 10 до 15А, а во второй с 1000 до 1001А, что вызвало появление ЭДС самоиндукции в обеих катушках.
Но, несмотря на такое огромное значение тока во второй катушке, ЭДС самоиндукции будет больше в первой, поскольку там скорость изменения тока 5А/сек, а во второй всего 1А/сек. Ведь ЭДС самоиндукции зависит от скорости возрастания тока (читай магнитного поля), а не от его абсолютной величины.
Индуктивность
Магнитные свойства катушки с током зависят от количества витков, геометрических размеров. Значительного усиления магнитного поля можно добиться введением в катушку ферромагнитного сердечника. О магнитных свойствах катушки с достаточной точностью можно судить по величине ЭДС индукции, взаимоиндукции или самоиндукции. Все эти явления были рассмотрены выше.
Все эти явления были рассмотрены выше.
Характеристика катушки, которая рассказывает об этом, называется коэффициентом индуктивности (самоиндукции) или просто индуктивностью. В формулах индуктивность обозначается буквой L, а на схемах этой же буквой обозначаются катушки индуктивности.
Единица измерения индуктивности — генри (Гн). Индуктивностью 1Гн обладает катушка, в которой при изменении тока на 1А в секунду вырабатывается ЭДС 1В. Это величина достаточно большая: индуктивностью в один и более Гн обладают сетевые обмотки достаточно мощных трансформаторов.
Поэтому достаточно часто пользуются величинами меньшего порядка, а именно милли и микро генри (мГн и мкГн). Такие катушки применяются в электронных схемах. Одно из применений катушек — колебательные контура в радиоустройствах.
Также катушки используются в качестве дросселей, основное назначение которых пропустить без потерь постоянный ток при этом ослабив переменный (фильтры ). Как правило, чем выше рабочая частота, тем меньшей индуктивности требуются катушки.
Индуктивное сопротивление
Если взять достаточно мощный сетевой трансформатор и сопротивление первичной обмотки, то окажется, что оно всего несколько Ом, и даже близко к нулю. Выходит, что ток через такую обмотку будет очень большим, и даже стремиться к бесконечности. Кажется, короткое замыкание просто неизбежно! Так почему же его нет?
Одним из основных свойств катушек индуктивности является индуктивное сопротивление, которое зависит от индуктивности и от частоты переменного тока, который подведен к катушке.
Нетрудно видеть, что с увеличением частоты и индуктивности индуктивное сопротивление увеличивается, а на постоянном токе вообще становится равным нулю. Поэтому при измерении сопротивления катушек мультиметром измеряется только активное сопротивление провода.
Конструкция катушек индуктивности весьма разнообразна и зависит от частот, на которых работает катушка. Например, для работы в дециметровом диапазоне радиоволн достаточно часто используются катушки, выполненные печатным монтажом. При массовом производстве такой способ очень удобен.
При массовом производстве такой способ очень удобен.
Индуктивность катушки зависит от ее геометрических размеров, сердечника, количества слоев и формы. В настоящее время выпускается достаточное количество стандартных катушек индуктивности похожих на обычные резисторы с выводами. Маркировка таких катушек выполняется цветными кольцами. Также существуют катушки для поверхностного монтажа, применяемые в качестве дросселей. Индуктивность таких катушек составляет несколько миллигенри.
Термин индукция в электротехнике означает возникновение тока в электрической замкнутой цепи, если она находится в изменяющемся Открыта всего-то двести лет назад Майклом Фарадеем. Значительно раньше это мог бы сделать Андре Ампер, проводивший похожие опыты. Он вставлял в катушку металлический стержень, а затем, вот незадача, шел в другую комнату посмотреть на стрелку гальванометра — а вдруг она шевельнется. А стрелка исправно делала свое дело — отклонялась, но пока Ампер странствовал по комнатам — возвращалась на нулевую отметку. Вот так явление самоиндукции дожидалось еще добрый десяток лет, пока катушка, прибор и исследователь окажутся одновременно в нужном месте.
Вот так явление самоиндукции дожидалось еще добрый десяток лет, пока катушка, прибор и исследователь окажутся одновременно в нужном месте.
Главным моментом этого эксперимента было то, что ЭДС индукции возникает только тогда, когда магнитное поле, проходящее через замкнутый контур, изменяется. А вот менять его можно как угодно — или изменять величину самого магнитного поля, или просто перемещать источник поля относительно того же замкнутого контура. ЭДС, которая при этом возникает, назвали “ЭДС взаимоиндукции”. Но это было только начало открытий в области индукции. Еще более удивительным было явление самоиндукции, которое открыл примерно в то же время. В его опытах было обнаружено, что катушки не только индуцировало ток в другой катушке, но и при изменении тока в этой катушке, наводило в ней же дополнительную ЭДС. Вот ее-то и назвали ЭДС самоиндукции. В большое интерес представляет направление тока. Оказалось, что в случае с ЭДС самоиндукции ее ток направлен против своего “родителя” — тока, обусловленного основной ЭДС.
А можно наблюдать явление самоиндукции? Как говорится, нет ничего проще. Соберем две первая — последовательно включенная катушка индуктивности и лампочка, а вторая — только лампочка. Подключим их к аккумулятору через общий выключатель. При включении можно видеть, что лампочка в цепи с катушкой загорается “нехотя”, а вторая лампочка, более быстрая “на подъем”, включается мгновенно. Что происходит? В обеих цепях после включения начинает протекать ток, причем он изменяется от нуля до своего максимума, а как раз изменения тока и дожидается катушка индуктивности, которая порождает ЭДС самоиндукции. Есть ЭДС и замкнутая цепь — значит, есть и ее ток, но направлен он противоположно основному току цепи, который, в конце концов, достигнет максимального значения, определяемого параметрами цепи, и перестанет расти, а раз нет изменения тока — нет и ЭДС самоиндукции. Все просто. Аналогичная картина, но с “точностью до наоборот”, наблюдается при выключении тока. Верная своей “вредной привычке” противодействовать любому изменению тока, ЭДС самоиндукции поддерживает его протекание в цепи после отключения питания.
Сразу же стал вопрос — в чем заключается явление самоиндукции? Было установлено, что на ЭДС самоиндукции влияет скорость изменения тока в проводнике, и можно записать:
Отсюда видно, что ЭДС самоиндукции Е прямопропорциональна скорости изменения тока dI/dt и коэффициенту пропорциональности L, названному индуктивностью. За свой вклад в исследование вопроса, в чем состоит явление самоиндукции, Джордж Генри был вознагражден тем, что его имя носит единица измерения индуктивности — генри (Гн). Именно индуктивность цепи протекания тока определяет явление самоиндукции. Можно представить, что индуктивность — это некое “хранилище” магнитной энергии. В случае увеличения тока в цепи электрическая энергия преобразуется в магнитную, задерживает рост тока, а при уменьшении тока магнитная энергия катушки преобразуется в электрическую и поддерживает ток в цепи.
Наверное, каждому приходилось видеть искру при выключении вилки из розетки — это самый распространенный вариант проявления ЭДС самоиндукции в реальной жизни. Но в быту размыкаются токи максимум 10-20 А, а время размыкания порядка 20 мсек. При индуктивности порядка 1 Гн ЭДС самоиндукции в этом случае будет равна 500 В. Казалось бы, что вопрос, в чем состоит явление самоиндукции, не так и сложен. А на самом деле, ЭДС самоиндукции представляет собой большую техническую проблему. Суть в том, что при разрыве цепи, когда контакты уже разошлись, самоиндукция поддерживает протекание тока, а это приводит к выгоранию контактов, т.к. в технике коммутируются цепи с токами в сотни и даже тысячи ампер. Здесь зачастую речь идет об ЭДС самоиндукции в десятки тысяч вольт, а это требует дополнительного решения технических вопросов, связанных с перенапряжениями в электрических цепях.
Но в быту размыкаются токи максимум 10-20 А, а время размыкания порядка 20 мсек. При индуктивности порядка 1 Гн ЭДС самоиндукции в этом случае будет равна 500 В. Казалось бы, что вопрос, в чем состоит явление самоиндукции, не так и сложен. А на самом деле, ЭДС самоиндукции представляет собой большую техническую проблему. Суть в том, что при разрыве цепи, когда контакты уже разошлись, самоиндукция поддерживает протекание тока, а это приводит к выгоранию контактов, т.к. в технике коммутируются цепи с токами в сотни и даже тысячи ампер. Здесь зачастую речь идет об ЭДС самоиндукции в десятки тысяч вольт, а это требует дополнительного решения технических вопросов, связанных с перенапряжениями в электрических цепях.
Но не все так мрачно. Бывает, что эта вредная ЭДС очень даже полезна, например, в системах зажигания ДВС. Такая система состоит из катушки индуктивности в виде автотрансформатора и прерывателя. Через первичную обмотку пропускается ток, который выключается прерывателем. В результате обрыва цепи возникает ЭДС самоиндукции в сотни вольт (при этом аккумулятор дает всего 12В). Дальше это напряжение дополнительно трансформируется, и на свечи зажигания поступает импульс больше 10 кВ.
Дальше это напряжение дополнительно трансформируется, и на свечи зажигания поступает импульс больше 10 кВ.
Знаете ли Вы,
в чем ложность понятия «физический вакуум»?
Физический вакуум
— понятие релятивистской квантовой физики, под ним там понимают низшее (основное) энергетическое состояние квантованного поля, обладающее нулевыми импульсом, моментом импульса и другими квантовыми числами. Физическим вакуумом релятивистские теоретики называют полностью лишённое вещества пространство, заполненное неизмеряемым, а значит, лишь воображаемым полем. Такое состояние по мнению релятивистов не является абсолютной пустотой, но пространством, заполненным некими фантомными (виртуальными) частицами. Релятивистская квантовая теория поля утверждает, что, в согласии с принципом неопределённости Гейзенберга, в физическом вакууме постоянно рождаются и исчезают виртуальные, то есть кажущиеся (кому кажущиеся?), частицы: происходят так называемые нулевые колебания полей. Виртуальные частицы физического вакуума, а следовательно, он сам, по определению не имеют системы отсчета, так как в противном случае нарушался бы принцип относительности Эйнштейна, на котором основывается теория относительности (то есть стала бы возможной абсолютная система измерения с отсчетом от частиц физического вакуума, что в свою очередь однозначно опровергло бы принцип относительности, на котором постороена СТО). Таким образом, физический вакуум и его частицы не есть элементы физического мира, но лишь элементы теории относительности, которые существуют не в реальном мире, но лишь в релятивистских формулах, нарушая при этом принцип причинности (возникают и исчезают беспричинно), принцип объективности (виртуальные частицы можно считать в зависимсоти от желания теоретика либо существующими, либо не существующими), принцип фактической измеримости (не наблюдаемы, не имеют своей ИСО).
Таким образом, физический вакуум и его частицы не есть элементы физического мира, но лишь элементы теории относительности, которые существуют не в реальном мире, но лишь в релятивистских формулах, нарушая при этом принцип причинности (возникают и исчезают беспричинно), принцип объективности (виртуальные частицы можно считать в зависимсоти от желания теоретика либо существующими, либо не существующими), принцип фактической измеримости (не наблюдаемы, не имеют своей ИСО).
Когда тот или иной физик использует понятие «физический вакуум», он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик , уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование «моря» двух компенсирующих друг друга энергий в вакууме — положительной и отрицательной, а также «моря» компенсирующих друг друга частиц — виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Магнитное поле
контура, в котором сила тока изменяется,
индуцирует ток не только в других
контурах, но и в себе самом. Это
явление получило название самоиндукции.
Опытным путём
установлено, что магнитный поток вектора
магнитной индукции поля, создаваемого
текущим в контуре током, пропорционален
силе этого тока:
где L– индуктивность
контура. Постоянная характеристика
контура, которая зависит от его формы
и размеров, а так же от магнитной
проницаемости среды, в которой находится
контур. [L] = Гн (Генри,
1Гн = Вб/А).
Если за время
dtток в контуре изменится
наdI, то магнитный поток,
связанный с этим током, изменится наdФ
=LdIв результате чего в
этом контуре появится ЭДС самоиндукции:
Знак минус показывает, что ЭДС
самоиндукции (а, следовательно, и ток
самоиндукции) всегда препятствует
изменению силы тока, который вызвал
самоиндукцию.
Наглядным
примером явления самоиндукции служат
экстратоки замыкания и размыкания,
возникающие при включении и выключении
электрических цепей, обладающей
значительной индуктивностью.
Энергия магнитного поля
Магнитное поле
обладает потенциальной энергией, которая
в момент его образования (или изменения)
пополняется за счёт энергии тока в цепи,
совершающего при этом работу против
ЭДС самоиндукции, возникающей вследствие
изменения поля.
Работа dAза бесконечно малый промежуток времениdt, в течении которого ЭДС
самоиндукциии токIможно считать
постоянными, равняется:
.
(5)
Знак минус указывает, что
элементарная работа совершается током
против ЭДС самоиндукции. Чтобы определить
работу при изменении тока от 0 до I,
проинтегрируем правую часть, получим:
.
(6)
Эта работа численно равна
приросту потенциальной энергии ΔW п магнитного поля, связанного с этой
цепью, т.е.A= -ΔW п.
Выразим энергию магнитного
поля через его характеристики на примере
соленоида. Будем считать, что магнитное
поле соленоида однородно и в основном
расположено внутри его. Подставим в (5)
значение индуктивности соленоида,
выраженное через его параметры и значение
силы тока I, выраженное
из формулы индукции магнитного поля
соленоида:
, (7)
где N – общее число витков
соленоида; ℓ – его длина; S – площадь
сечения внутреннего канала соленоида.
, (8)
После подстановки имеем:
Разделив обе части на V,
получим объёмную плотность энергии
поля:
(10)
или, с учётом, что
получим,
.
(11)
Переменный ток
2.1 Переменный ток и его основные характеристики
Переменным
называется ток, изменяющийся с течением
времени и по величине и по направлению.
Примером переменного тока может служить
потребляемый промышленный ток. Этот
ток является синусоидальным, т.е.
мгновенное значение его параметров
меняются со временем по закону синуса
(или косинуса):
i
= I 0 sinωt,
u =
U 0 sin(ωt
+ φ 0). (12)
Переменный
синусоидальный ток можно получить, если
вращать рамку (контур) с постоянной
скоростью
в однородном
магнитном поле с индукцией B
(рис.5). При этом магнитный поток,
пронизывающий контур, изменяется по
закону
где S– площадь
контура, α = ωt– угол
поворота рамки за время t. Изменение
потока приводит к возникновению ЭДС
индукции
, (17)
направление которой определяется
по правилу Ленца.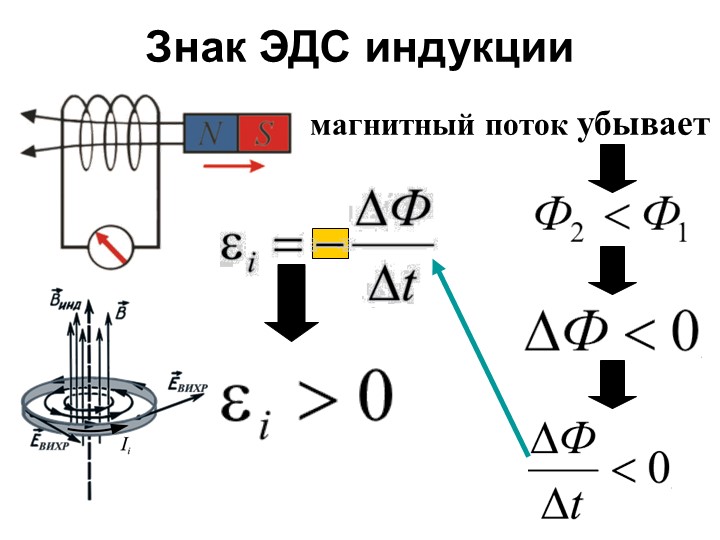
Если
контур замкнут (рис.5), то по нему идёт
ток:
.
(18)
График изменения электродвижущей
силыи индукционного токаi
представлен на рис.6.
Переменный
ток характеризуется периодом Т, частотой
ν = 1/Т, циклической частотой
и фазой φ = (ωt
+ φ 0)
Графически значения напряжения и силы
переменного тока на участке цепи будут
представляться двумя синусоидами, в
общем случае сдвинутыми по фазе на φ.
Для
характеристики переменного тока вводятся
понятия действующего (эффективного)
значения тока и напряжения. Эффективным
значением силы переменного тока
называется сила такого постоянного
тока, который выделяет в данном проводнике
столько же тепла за время одного периода,
сколько выделяет тепла и данный переменный
ток.
,
. (13)
Приборы, включенные в цепь
переменного тока (амперметр, вольтметр),
показывают эффективные значения тока
и напряжения.
Формула определения эдс. Формула эдс индукции. Внутреннее сопротивление источника тока
На концах проводника, а значит, и тока необходимо наличие сторонних сил неэлектрической природы, с помощью которых происходит разделение электрических зарядов .
Сторонними силами
называются любые силы, действующие на электрически заряженные частицы в цепи, за исключением электростатических (т. е. кулоновских).
Сторонние силы приводят в движение заряженные частицы внут-ри всех источников тока: в генераторах, на электростанциях, в гальванических элементах, аккумуляторах и т. д.
При замыкании цепи создается электрическое поле во всех про-водниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны движут-ся от положительно заряженного электрода к отрицательному), а во всей остальной цепи их приводит а движение электрическое поле (см. рис. выше).
В источниках тока в процессе работы по разделению заряженных частиц происходит превращение разных видов энергии в электричес-кую. По типу преобразованной энергии различают следующие виды электродвижущей силы:
— электростатическая
— в электрофорной машине, в которой происходит превращение механической энергии при трении в электрическую;
— термоэлектрическая
— в термоэлементе — внутренняя энергия нагретого спая двух проволок, изготовленных из разных металлов, превращается в электрическую;
— фотоэлектрическая
— в фотоэлементе.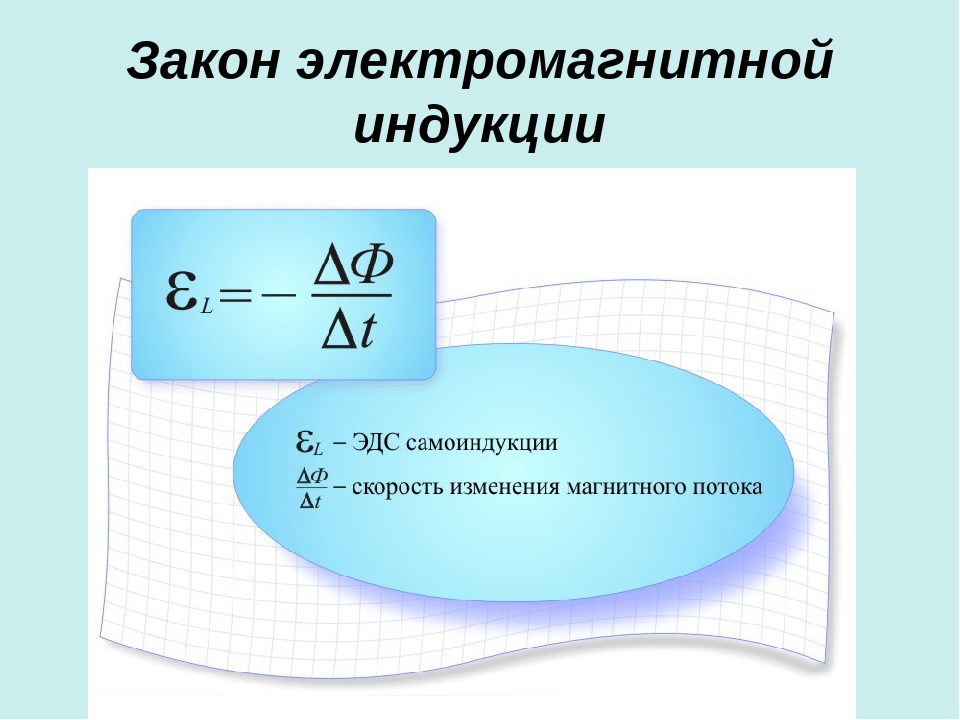 Здесь происходит превращение энергии света в элек-трическую: при освещении некоторых веществ, например, селена, оксида меди (I) , кремния наблюдается потеря отрицательного электрического заряда;
Здесь происходит превращение энергии света в элек-трическую: при освещении некоторых веществ, например, селена, оксида меди (I) , кремния наблюдается потеря отрицательного электрического заряда;
— химическая
— в гальванических элементах, аккумуляторах и др. источниках, в которых происходит превращение химической энергии в электрическую.
Электродвижущая сила (ЭДС)
— характеристика источников тока. Понятие ЭДС было введено Г. Омом в 1827 г. для цепей постоянного тока. В 1857 г. Кирхгофф определил ЭДС как работу сторонних сил при переносе единичного электрического заряда вдоль замкнутого контура:
ɛ = A ст /q
,
где ɛ
— ЭДС источника тока, А ст
— работа сторонних сил , q
— количество перемещенного заряда.
Электродвижущую силу выражают в вольтах.
Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всем контуре, а только на данном участке.
Внутреннее сопротивление источника тока.
Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R
. Ток в замкну-той цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока
и обозначается буквой r
.
В генераторе r
— это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.
Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до со-тни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.
Это позволяет с их помощью получать токи, измеряемые амперами.
«Физика — 10 класс»
Любой источник тока характеризуется электродвижущей силой, или сокращённо ЭДС. Так, на круглой батарейке для карманного фонарика написано: 1,5 В.
Что это значит?
Если соединить проводником два разноимённо заряженных шарика, то заряды быстро нейтрализуют друг друга, потенциалы шариков станут одинаковыми, и электрическое поле исчезнет (рис. 15.9, а).
Сторонние силы.
Для того чтобы ток был постоянным, надо поддерживать постоянное напряжение между шариками. Для этого необходимо устройство (источник тока), которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со стороны электрического поля шариков. В таком устройстве на заряды, кроме электрических сил, должны действовать силы неэлектростатического происхождения (рис. 15.9, б). Одно лишь электрическое поле заряженных частиц (кулоновское поле
) не способно поддерживать постоянный ток в цепи.
Любые силы, действующие на электрически заряженные частицы, за исключением сил электростатического происхождения (т. е. кулоновских), называют сторонними силами
.
Вывод о необходимости сторонних сил для поддержания постоянного тока в цепи станет ещё очевиднее, если обратиться к закону сохранения энергии.
Электростатическое поле потенциально. Работа этого поля при перемещении в нём заряженных частиц по замкнутой электрической цепи равна нулю. Прохождение же тока по проводникам сопровождается выделением энергии — проводник нагревается. Следовательно, в цепи должен быть какой-то источник энергии, поставляющий её в цепь. В нём, помимо кулоновских сил, обязательно должны действовать сторонние, непотенциальные силы. Работа этих сил вдоль замкнутого контура должна быть отлична от нуля.
Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника тока энергию и отдают её затем проводникам электрической цепи.
Сторонние силы приводят в движение заряженные частицы внутри всех источников тока: в генераторах на электростанциях, в гальванических элементах, аккумуляторах и т. д.
д.
При замыкании цепи создаётся электрическое поле во всех проводниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил
(электроны от положительно заряженного электрода к отрицательному), а во внешней цепи их приводит в движение электрическое поле (см. рис. 15.9, б).
Природа сторонних сил.
Природа сторонних сил может быть разнообразной. В генераторах электростанций сторонние силы — это силы, действующие со стороны магнитного поля на электроны в движущемся проводнике.
В гальваническом элементе, например в элементе Вольта, действуют химические силы.
Элемент Вольта состоит из цинкового и медного электродов, помещённых в раствор серной кислоты. Химические силы вызывают растворение цинка в кислоте. В раствор переходят положительно заряженные ионы цинка, а сам цинковый электрод при этом заряжается отрицательно. (Медь очень мало растворяется в серной кислоте.) Между цинковым и медным электродами появляется разность потенциалов, которая и обусловливает ток во внешней электрической цепи.
Действие сторонних сил характеризуется важной физической величиной, называемой электродвижущей силой
(сокращённо ЭДС).
Электродвижущая сила
источника тока равна отношению работы сторонних сил при перемещении заряда по замкнутому контуру к абсолютной величине этого заряда:
Электродвижущую силу как и напряжение, выражают в вольтах.
Разность потенциалов на клеммах батареи при разомкнутой цепи равна электродвижущей силе. ЭДС одного элемента батареи обычно 1-2 В.
Можно говорить также об электродвижущей силе и на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всём контуре, а только на данном участке.
Электродвижущая сила гальванического элемента есть величина, численно равная работе сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому.
Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории перемещения зарядов.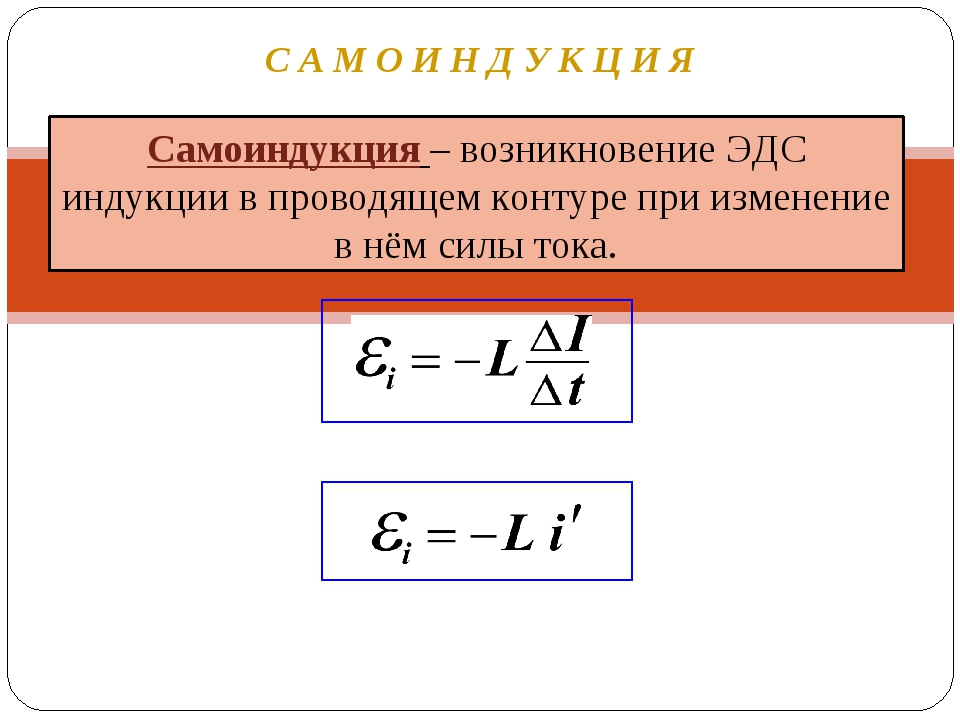
ЭДС (ε
)
— отношение работы сторонних сил по разделению зарядов к величине этого заряда, иначе, способность данного источника давать необходимое количество зарядов необходимой энергии.
— ЭДС.
ЭДС не является силой
в Ньютоновом смысле (неудачное название величины, сохраненное как дань традиции).
ε i
возникает при изменении
магнитного потока Ф
, пронизывающего контур.
Дополнительно
см. презентацию «Электромагнитная индукция» , а также видеофильмы «Электромагнитная индукция «, «Опыт Фарадея «, мультфильмы «Электромагнитная индукция «, «Вращение рамки в магнитном поле (генератор) «
— ЭДС индукции.
— ЭДС индукции при движении одного из проводников контура (так, чтобы менялся Ф). В этом случае проводник длиной l
, движущийся со скоростью v
становится источником тока.
— ЭДС индукции в контуре, вращающемся в магнитном поле со скоростью ω.
Другие формулы, где встречается ЭДС:
— закон Ома для полной цепи. В замкнутой цепи ЭДС рождает электрический ток I.
В замкнутой цепи ЭДС рождает электрический ток I.
Направление индукционного тока определяют по правилам:
— правило Ленца
— возникающий в замкнутом контуре индукционный ток противо
действует тому изменению
магнитного потока, которым вызван данный ток;
— для проводника, движущегося в магнитном поле, иногда проще воспользоваться правилом правой руки
— если расположить раскрытую ладонь правой руки
так, чтобу в нее входили
силовые линии магнитного поля В
, а большой палец
, отставленный в сторону указывал направление скорости v
, то четыре пальца
руки укажут направление индукционного тока I
.
— ЭДС самоиндукции при изменении тока в проводнике.
Электродвижущая сила, в народе ЭДС, также как и напряжение измеряется в вольтах, но носит совсем иной характер.
ЭДС с точки зрения гидравлики
Думаю, вам уже знакома водонапорная башня из прошлой статьи про
Допустим, что башня полностью заполнена водой.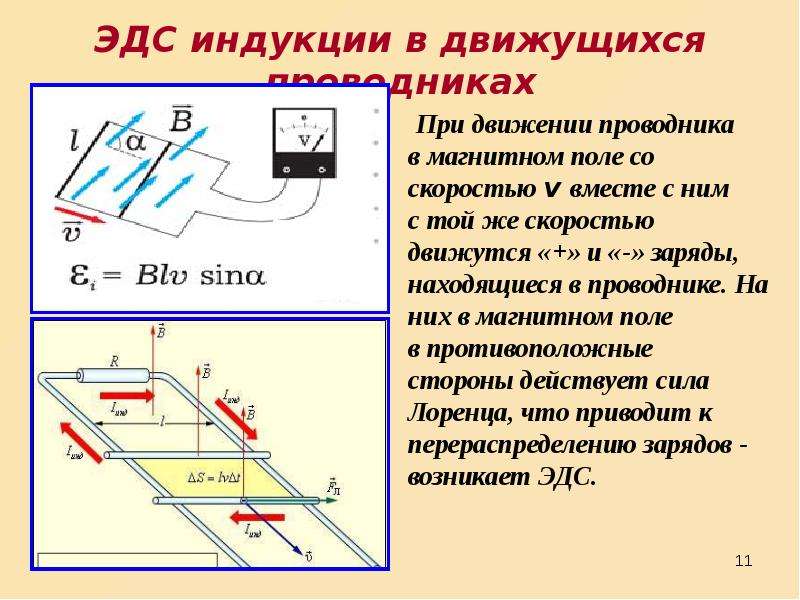 Снизу башни мы просверлили отверстие и врезали туда трубу, по которой вода бежит к вам домой.
Снизу башни мы просверлили отверстие и врезали туда трубу, по которой вода бежит к вам домой.
Сосед захотел полить огурцы, вы решили помыть автомобиль, мать затеяла стирку и вуаля! Поток воды стал меньше и меньше, и вскоре совсем иссяк… Что случилось? Закончилась вода в башне…
Время, которое потребуется, чтобы опустошить башню, зависит от емкости самой башни, а также от того, сколько потребителей будут пользоваться водой.
Все то же самое можно сказать и про радиоэлемент конденсатор :
Допустим мы его зарядили от батарейки 1,5 вольта и он принял заряд. Нарисуем заряженный конденсатор вот так:
Но как только мы цепляем к нему нагрузку (пусть нагрузкой будет светодиод) с помощью замыкания ключа S, в первые доли секунд светодиод будет светиться ярко, а потом тихонько угасать… и пока полностью не потухнет. Время угасания светодиода будет зависеть от емкости конденсатора, а также от того, какую нагрузку мы цепляем к заряженному конденсатору.
Как я уже сказал, это равносильно простой наполненной башне и потребителям, которые пользуются водой.
Но почему тогда в наших башнях вода никогда не заканчивается? Да потому что работает насос подачи воды
! А откуда этот насос берет воду? Из скважины, которая пробурена для добычи подземных вод. Иногда ее еще называют артезианской.
Как только башня полностью наполнится водой, насос выключается. В наших водобашнях насос всегда поддерживает максимальный уровень воды.
Итак, давайте вспомним, что такое напряжение ? По аналогии с гидравликой – это уровень воды в водобашне. Полная башня – это максимальный уровень воды, значит максимальное напряжение. Нет в башне воды – напряжение ноль.
ЭДС электрического тока
Как вы помните из прошлых статей, молекулы воды – это “электроны”. Для возникновения электрического тока, электроны должны двигаться в одном направлении. Но чтобы они двигались в одном направлении, должно быть напряжение и какая-нибудь нагрузка. То есть вода в башне – это напряжение, а люди, которые тратят воду для своих нужд – это нагрузка, так как они создают поток воды из трубы, которая находится у подножия водобашни. А поток – это не что иное, как сила тока.
То есть вода в башне – это напряжение, а люди, которые тратят воду для своих нужд – это нагрузка, так как они создают поток воды из трубы, которая находится у подножия водобашни. А поток – это не что иное, как сила тока.
Также должно соблюдаться условие, что вода должна всегда быть на максимальной отметке, независимо от того, сколько людей тратит ее для своих нужд одновременно, иначе башня опустошится. Для водобашни этим спасительным средством является водонасос. А для электрического тока?
Для электрического тока должна быть какая-то сила, которая бы толкала электроны в одном направлении в течение продолжительного времени. То есть эта сила должна двигать электроны! Электродвижущая сила!
Да, именно так! ЭЛЕКТРОДВИЖУЩАЯ СИЛА! Можно назвать ее сокращенно ЭДС – Э
лектро Д
вижущая С
ила. Измеряется она в вольтах, как и напряжение, и обозначается в основном буквой E
.
Значит, в наших батарейках тоже есть такой “насос”? Есть, и правильней было бы его назвать “насос подачи электронов”). Но, конечно, так никто не говорит. Говорят просто – ЭДС. Интересно, а где спрятан этот насос в батарейке? Это просто-напросто электрохимическая реакция, из-за которой держится “уровень воды” в батарейке, но потом все-таки этот насос изнашивается и напряжение в батарейке начинает проседать, потому как “насос” не успевает качать воду. В конце концов он полностью ломается и напряжение на батарейке стает практически ноль.
Но, конечно, так никто не говорит. Говорят просто – ЭДС. Интересно, а где спрятан этот насос в батарейке? Это просто-напросто электрохимическая реакция, из-за которой держится “уровень воды” в батарейке, но потом все-таки этот насос изнашивается и напряжение в батарейке начинает проседать, потому как “насос” не успевает качать воду. В конце концов он полностью ломается и напряжение на батарейке стает практически ноль.
Реальный источник ЭДС
Источник электрической энергии – это источник ЭДС с внутренним сопротивлением R вн. Это могут быть какие-либо химические элементы питания, наподобие батареек и аккумуляторов
Их внутреннее строение с точки зрения ЭДС выглядит примерно вот так:
Где E
– это ЭДС, а R вн
– это внутреннее сопротивление батарейки
Итак, какие выводы можно сделать из этого?
Если к батарейке не цепляется никакая нагрузка, типа лампы накаливания и тд, то в результате сила тока в такой цепи будет равняться нулю. Упрощенная схема будет такой:
Упрощенная схема будет такой:
Но если мы все-таки присоединим к нашей батарейке лампочку накаливания, то у нас цепь станет замкнутой и в цепи будет течь ток:
Если начертить график зависимости силы в цепи тока от напряжения на батарейке, то он будет выглядеть вот так:
Какой напрашивается вывод? Для того, чтобы замерить ЭДС батарейки, нам достаточно просто взять хороший мультиметр с высоким входным сопротивлением и замерять напряжение на клеммах батарейки.
Идеальный источник ЭДС
Допустим, пусть наша батарейка обладает нулевым внутренним сопротивлением, тогда получается, что R вн =0.
Нетрудно догадаться, что в этом случае падение напряжение на нулевом сопротивлении также будет равняться нулю. В результате, наш график примет вот такой вид:
В результате мы получили просто источник ЭДС. Следовательно, источник ЭДС – это идеальный источник питания, у которого напряжение на клеммах не зависит от силы тока в цепи. То есть, какую нагрузку мы бы не цепляли на такой источник ЭДС, у нас он все равно будет выдавать положенное напряжение без просадки. Сам источник ЭДС обозначается вот так:
То есть, какую нагрузку мы бы не цепляли на такой источник ЭДС, у нас он все равно будет выдавать положенное напряжение без просадки. Сам источник ЭДС обозначается вот так:
На практике идеального источника ЭДС не существует.
Типы ЭДС
– электрохимическая
(ЭДС батареек и аккумуляторов)
– фотоэффекта
(получение электрического тока от солнечной энергии)
– индукции
(генераторы, использующие принцип электромагнитной индукции)
– Эффект Зеебека или термоЭДС
(возникновение электрического тока в замкнутой цепи, состоящей из последовательно соединённых разнородных проводников
, контакты между которыми находятся при различных температурах)
– пьезоЭДС
(получение ЭДС от )
Для поддержания электрического тока в проводнике требуется внешний источник энергии, создающий все время разность потенциалов между концами этого проводника. Такие источники энергии получили название источников электрической энергии (или источников тока).
Источники электрической энергии обладают определенной электродвижущей силой
(сокращенно ЭДС
), которая создает и длительное время поддерживает разность потенциалов между концами проводника. Иногда говорят, что ЭДС создает электрический ток в цепи. Нужно помнить об условности такого определения, так как выше мы уже установили, что причина возникновения и существования электрического тока — электрическое поле.
Источник электрической энергии производит определенную работу, перемещая электрические заряды по всей замкнутой цепи..
Определение:
Работа, совершаемая источником электрической энергии при переносе единицы положительного заряда по всей замкнутой цепи, называется ЭДС источника
За единицу измерения электродвижущей силы принят вольт (сокращенно вольт обозначается буквой В или V — «вэ» латинское).
ЭДС источника электрической энергии равна одному вольту, если при перемещении одного кулона электричества по всей замкнутой, цепи источник электрической энергии совершает работу, равную одному джоулю:
В практике для измерения ЭДС используются как более крупные, так и более мелкие единицы, а именно:
1 киловольт (кВ, kV), равный 1000 В;
1 милливольт (мВ, mV), равный одной тысячной доле вольта (10-3 В),
1 микровольт (мкВ, μV), равный одной миллионной доле вольта (10-6 В).
Очевидно, что 1 кВ = 1000 В; 1 В = 1000 мВ = 1 000 000 мкВ; 1 мВ= 1000 мкВ.
В настоящее, время существует несколько видов источников электрической энергии. Впервые в качестве источника электрической энергии была использована гальваническая батарея, состоящая из нескольких цинковых и медных кружков, между которыми была проложена кожа, смоченная в подкисленной воде. В гальванической батарее химическая энергия превращалась в электрическую (подробнее об этом будет рассказано в главе XVI). Свое название гальваническая батарея получила по имени итальянского физиолога Луиджи Гальвани (1737-1798), одного из основателей учения об электричестве.
Многочисленные опыты по усовершенствованию и практическому использованию гальванических батарей были проведены русским ученым Василием Владимировичем Петровым. Еще в начале прошлого века он создал самую большую в мире гальваническую батарею и использовал ее для ряда блестящих опытов.
Источники электрической энергии, работающие по принципу преобразования химической энергии в электрическую, называются химическими источниками электрической энергии.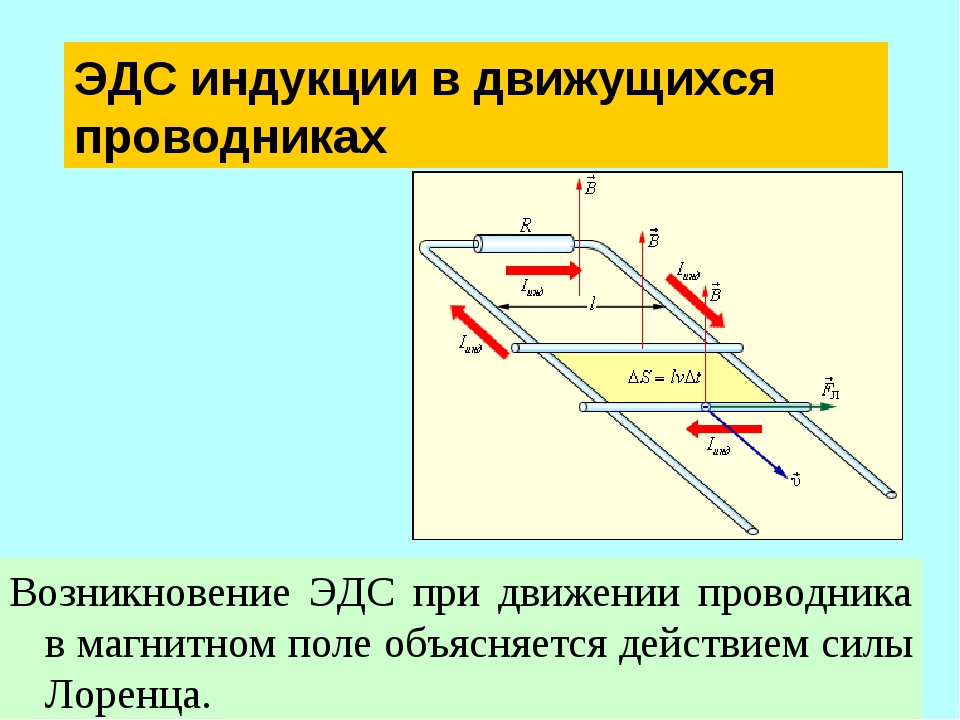
Другим основным источником электрической энергий, получившим широкое применение в электротехнике и радиотехнике, является генератор. В генераторах механическая энергия преобразуется в электрическую.
На электрических схемах источники электрической энергии и генераторы обозначаются так, как это показано на рис. 1.
Рисунок 1. Условные обозначения источников электрической энергии:
а — источник ЭДС, общее обозначение, б — источник тока, общее обозначение; в — химический источник электрической энергии; г — батарея химических источников; д — источник потоянного напряжения; е — источник переменного нарияжения; ж — генератор.
У химических источников электрической энергии и у генераторов электродвижущая сила проявляется одинаково, создавая на зажимах источника разность потенциалов и поддерживая ее длительное время. Эти зажимы называются полюсами источника электрической энергии
. Один полюс источника электрической энергии имеет положительный потенциал (недостаток электронов), обозначается знаком плюс (+) и называется положительным полюсом. Другой полюс имеет отрицательный потенциал (избыток электронов), обозначается знаком минус (-) и называется отрицательным полюсом.
Другой полюс имеет отрицательный потенциал (избыток электронов), обозначается знаком минус (-) и называется отрицательным полюсом.
От источников электрической энергии электрическая энергия передается по проводам к ее потребителям (электрические лампы, электродвигатели, электрические дуги, электронагревательные приборы и т. д.).
Определение
:
Совокупность источника электрической энергии, ее потребителя и соединительных проводов называется электрической цепью.
Простейшая электрическая цепь показана на рис. 2.
Рисунок 2. Б — источник электрической энергии; SA — выключатель; EL — потребитель электрической энергии (лампа).
Для того чтобы по цепи проходил электрический ток, она должна быть замкнутой. По замкнутой электрической цепи непрерывно проходит ток, так как между полюсами источника электрической энергии существует некоторая разность потенциалов. Эта разность потенциалов называется напряжением источника
и обозначается буквой U
. Единицей измерения напряжения служит вольт. Так же как и ЭДС, напряжение может измеряться в киловольтах, милливольтах и микровольтах.
Единицей измерения напряжения служит вольт. Так же как и ЭДС, напряжение может измеряться в киловольтах, милливольтах и микровольтах.
Для измерения величины ЭДС и напряжения применяется прибор, называемый вольтметром
. Если вольтметр подключить непосредственно к полюсам источника электрической энергии, то при разомкнутой электрической цепи он покажет ЭДС источника электрической энергии, а при замкнутой — напряжение на его зажимах: (рис. 3).
Рисунок 3. Измерение ЭДС и напряжения источника электрической энергии:
а- измерение ЭДС источника электрической энергии; б — измерение напряжения на зажимах источника электрической энергии..
Заметим, что напряжение на зажимах источника электрической энергии всегда меньше его ЭДС.
ЭДС индукции. Основные определения и формулы. Электромагнитная индукция. Закон электромагнитной индукции
ЭДС ИНДУКЦИИ
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ
Электромагнитная индукция: в замкнутом
проводящем контуре при изменении магнитного потока (т. е. вектора B! ),
е. вектора B! ),
охватываемого этим контуром, возникает электрический ток индукционный ток.
Правило Ленца: индукционный ток всегда
направлен так, чтобы противодействовать причине его вызывающей.
Закон
электромагнитной индукции: εi =
− ddtΦ
возникающая в контуре
ЭДС индукции.
Если замкнутый
контур, в котором индуцируется ЭДС состоит не из одного витка, а из N витков и, если, магнитный
поток, охватываемый каждым витком одинаков и равен Φ1, то суммарный поток Φ
сквозь поверхность, натянутую на данный контур: Φ = NΦ1 полный магнитный поток
или потокосцепление. εi = −N ddtΦ1 .
Изменение тока в контуре, которое ведет к возникновению
ЭДС индукции в этом же контуре называется самоиндукцией.
Если в пространстве, где находится контур с током
I , нет ферромагнетиков,
то полный магнитный поток через контур пропорционален силе тока I : Φ
= LI , где
L коэффициент пропорциональности
индуктивность контура.
Взаимная
индукция:
Рассмотрим два неподвижных контура 1 и 2, расположенных
достаточно близко друг к другу. Если в контуре 1 течет ток I1, то он создает через контур
2 полный магнитный поток Φ2, пропорциональный (при отсутствии ферромагнетиков)
току I1: Φ
=2 L I21 1.
Аналогично, если в контуре 2 течет ток I2, он создает через контур
1 полный магнитный поток: Φ =1 L I12 2.
Коэффициенты L12
и L21 называют взаимной индуктивностью
контуров.
Теорема взаимности: при отсутствии ферромагнетиков
коэффициенты L12 и L21 одинаковы: L12 =
L21.
Взаимная индукция: при всяком изменении
тока в одном из контуров в другом контуре возникает ЭДС индукции.
Согласно закону электромагнитной индукции, ЭДС,
возникающие в контурах 1 и 2 равны, соответственно: ε1 =
− ddtΦ1 =
−L12 dIdt2 ,
ε2 = − ddtΦ = −L21 dIdt1 .
С учетом явления электромагнитной индукции, закон Ома для контура
1:
R I1 1 =ε1 −
L1 dIdt1 −
L12 dIdt2 , где ε1 сторонняя ЭДС в контуре
1 (помимо индукционных ЭДС), L1 индуктивность контура
1.
Энергия
магнитного поля:
Дополнительная работа, совершаемая сторонними
силами против ЭДС самоиндукции в процессе установления тока: δAдоп =
IdΦ
.
При отсутствии ферромагнетиков контур с индуктивностью
L, по которому течет
ток I обладает энергией:
W =
12 LI2 =
12 IΦ = Φ2L2 магнитная
W dV энергия магнитного поля.
объемная плотность
магнитной энергии. Данное выражение справедливо лишь для случаев, когда
зависимость B H! !(
) линейная, т.е. для пара- и диамагнетиков.
W = L I1 12 2 + L I2 22 2 + L I I12 1 2 магнитная энергия
двух контуров с токами; первые два слагаемых собственная энергия, последнее
слагаемое взаимная энергия.
W dV dV dV полевая трактовка энергии, где B1 магнитное поле тока I1, B2 магнитное поле тока I2.
ЗАДАЧИ ЭДС индукции, ЭДС
самоиндукции:
1.
Провод, имеющий форму параболы y = kx2 , находится в однородном магнитном поле B! ,
перпендикулярном плоскости параболы. Из вершины параболы перемещают поступательно
и без начальной скорости перемычку с постоянным ускорением a. Найти ЭДС индукции в образовавшемся
контуре как функцию времени.
Решение:
За время dt перемычка переместится на dy , и замкнутый контур получит
приращение площади dS =
2xdy .
Если S! ↑↑
B! ,
то dΦ
= BdS .
Поток Φ возрастает и
индукционный ток Iи течет против часовой
стрелки, порождая поле B!и ↑↓
B!
компенсируя изменение Φ .
Тогда εи = − ddtΦ = −B 2xdydt . Но dydt = v = at , x = ky = at2k2 .
Поэтому εи =
−B⋅2at at2k2 =
−Ba 2kat2.
Ответ: Ba t2.
2.
Плоская спираль с большим числом N витков, плотно прилегающих друг к другу, находится
в однородном магнитном поле, перпендикулярном в плоскости спирали. Наружный радиус
спирали равен a. Магнитное
поле изменяется со временем по закону B = B0 sinωt . Найти амплитудное значение ЭДС индукции, наведенной в спирали.
Решение:
Выделим участок спирали толщиной dr . В нем dN = Na dr витков по форме совпадающих
В нем dN = Na dr витков по форме совпадающих
с окружностью радиуса r .
Полный магнитный поток через
этот участок спирали равен dΦ
= B r dNπ
2 =
B Nπa r dr2 .
Полный магнитный
поток через всю спираль равен
Φ = ∫0a dΦ = B Nπa r33 0a=πNa3 2 B0 sinωt.
Тогда B t и амплитуда εи0 =
−πNa3 2ωB0.
Ответ: εи0 =
−πNa3 2ωB0.
3.
По двум металлическим
столбам, поставленным вертикально
Явление э/м индукции.
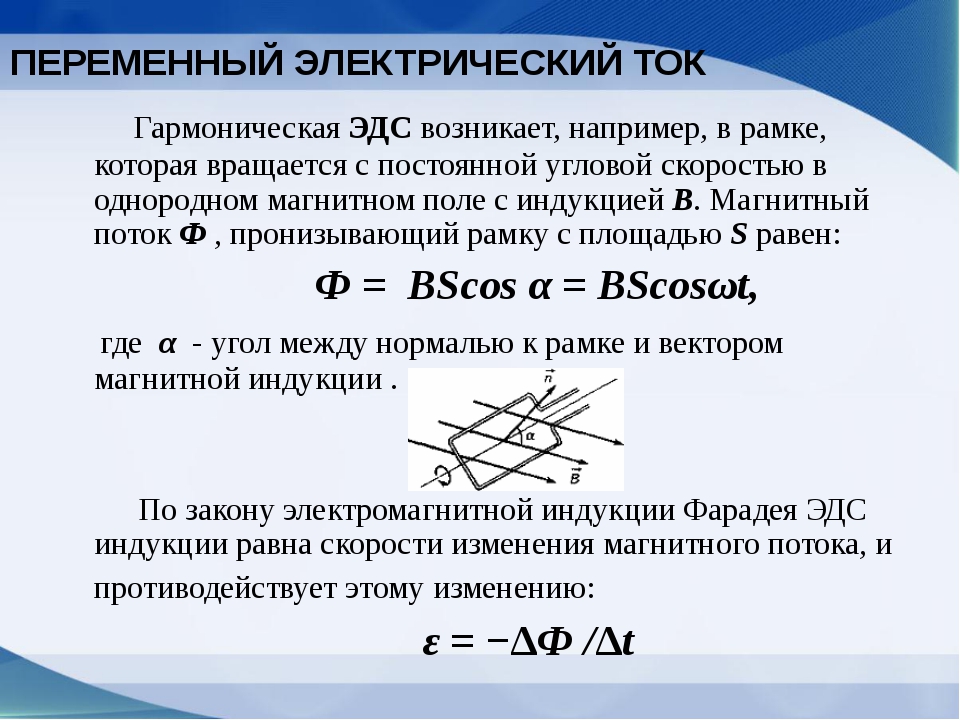 Магн. поток. Закон э/м индукции
Магн. поток. Закон э/м индукции
- Явление электромагнитной индукции
Электрические и магнитные поля порождаются одними и теми же источниками – электрическими зарядами, поэтому можно предположить, что между этими полями существует определенная связь. Это предположение нашло экспериментальное подтверждение в 1831 г. в опытах выдающегося английского физика М.Фарадея. Он открыл явление электромагнитной индукции.
Явление электромагнитной индукции лежит в основе работы индукционных генераторов электрического тока, на которые приходится вся вырабатываемая в мире электроэнергия.
- Магнитный поток
Замкнутый контур, помещенный в однородное магнитное поле
Количественной характеристикой процесса изменения магнитного поля через замкнутый контур является физическая величина называемая магнитным потоком. Магнитным потоком (Ф) через замкнутый контур площадью (S) называют физическую величину, равную произведению модуля вектора магнитной индукции (В) на площадь контура (S) и на косинус угла между вектором В и нормалью к поверхности: Φ = BS cos α.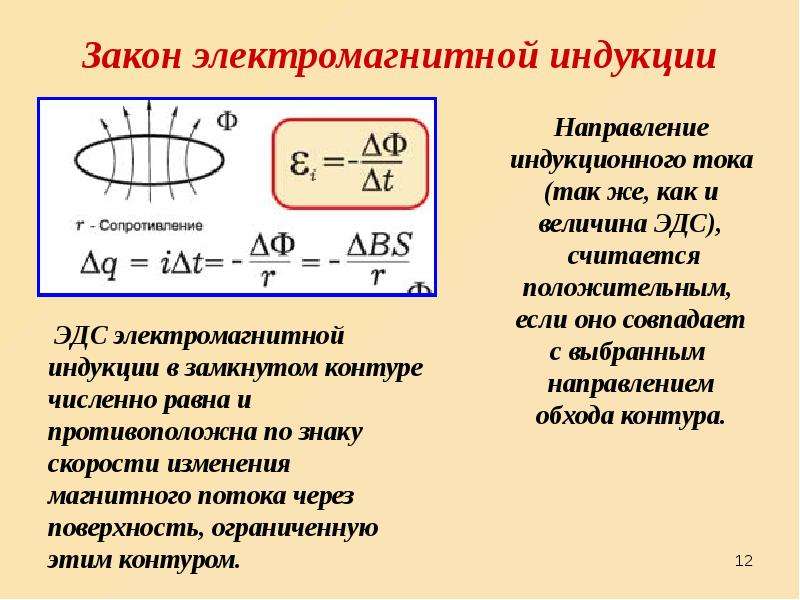 Единица магнитного потока Ф — вебер (Вб): 1 Вб = 1 Тл · 1 м2.
Единица магнитного потока Ф — вебер (Вб): 1 Вб = 1 Тл · 1 м2.
Если вектор магнитной индукции перпендикулярен площади контура, то магнитный поток максимальный.
Если вектор магнитной индукции параллелен площади контура, то магнитный поток равен нулю.
- Закон электромагнитной индукции
Опытным путем был установлен закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром: Эта формула носит название закона Фарадея.
Классической демонстрацией основного закона электромагнитной индукции является первый опыт Фарадея. В нем, чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.
- Правило Ленца
Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский физик Э.Х.Ленц. Согласно правилу Ленца, возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Более кратко это правило можно сформулировать следующим образом: индукционный ток направлен так, чтобы препятствовать причине, его вызывающей. Правило Ленца отражает тот экспериментальный факт, что всегда имеют противоположные знаки (знак «минус» в формуле Фарадея).
опытным путем установил русский физик Э.Х.Ленц. Согласно правилу Ленца, возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Более кратко это правило можно сформулировать следующим образом: индукционный ток направлен так, чтобы препятствовать причине, его вызывающей. Правило Ленца отражает тот экспериментальный факт, что всегда имеют противоположные знаки (знак «минус» в формуле Фарадея).
Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине. Они могли вращаться вокруг оси, как коромысло. При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца оно стремилось «догнать» магнит. При движении же магнита внутри разрезанного кольца никакого движения не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.
Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Закон эдс индукции фарадея для трансформаторов. Закон электромагнитной индукции формула
Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.
Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как
где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м 2 однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.
Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока
Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.
Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.
Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.
При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.
Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи
где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи.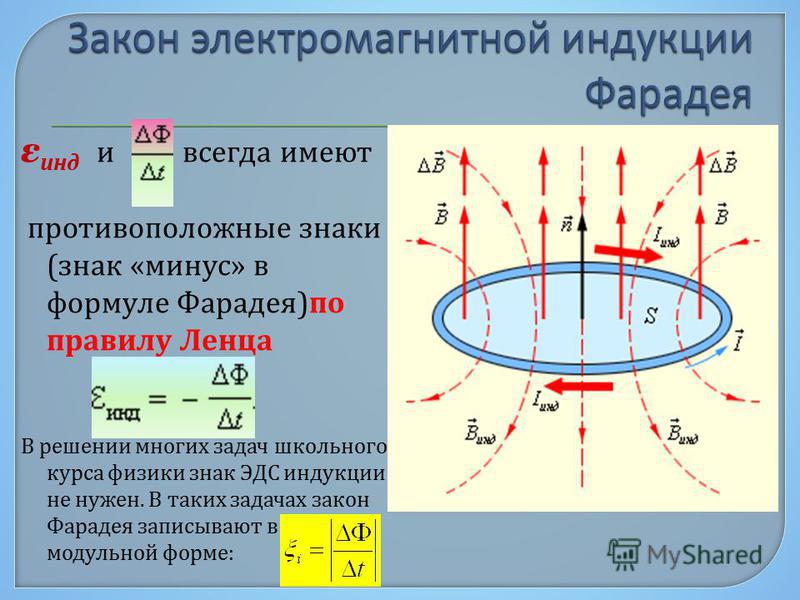 Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции
Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции
Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током
где — индуктивность контура, — сила тока в нем.
Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.
Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.
Рассмотрим теперь задачи.
Из перечисленных в задаче 23.1.1
явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3
). Все остальное — результат магнитного взаимодействия токов.
Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2
), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2
).
Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3
Поэтому при приближении магнита к кольцу (задача 23.1.3
) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4
).
Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4
случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1
).
При вращении рамки 1 (задача 23.1.5
) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2
).
В задаче 23.1.6
индукционный ток возникает только в случае 2 (ответ 2
). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется.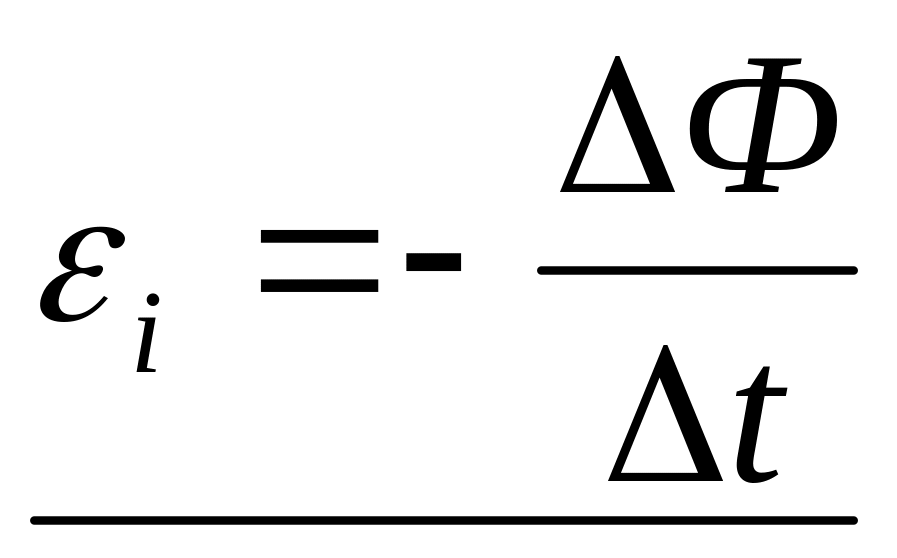 При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток
При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток
В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7
) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2
.
Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8
индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3
).
В задаче 23.1.9
ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4
). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.
Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.
В задаче 23.1.10
во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1
).
При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1
), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1
). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.2.2
— ответ 3
).
Используя формулу (23.3) находим в задаче 32. 2.3
2.3
Гн (ответ 4
).
Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4
) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3
.
Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5
) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2
).
Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6
этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2
).
Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7
), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1
).
При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8
). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2
А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2
). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.
Задача 23.2.9
также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2
). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.
Задача 23.2.10
— единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4
Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4
).
Эмпирически М. Фарадей показал, что сила тока индукции в проводящем контуре прямо пропорциональна скорости изменения количества линий магнитной индукции, которые проходят через поверхность ограниченную рассматриваемым контуром. Современную формулировку закона электромагнитной индукции, используя понятие магнитный поток, дал Максвелл. Магнитный поток (Ф) сквозь поверхность S — это величина, равная:
где модуль вектора магнитной индукции; — угол между вектором магнитной индукции и нормалью к плоскости контура. Магнитный поток трактуют как величину, которая пропорциональна количеству линий магнитной индукции, проходящих сквозь рассматриваемую поверхность площади S.
Появление тока индукции говорит о том, что в проводнике возникает определенная электродвижущая сила (ЭДС). Причиной появления ЭДС индукции является изменение магнитного потока. В системе международных единиц (СИ) закон электромагнитной индукции записывают так:
где — скорость изменения магнитного потока сквозь площадь, которую ограничивает контур.
Знак магнитного потока зависит от выбора положительной нормали к плоскости контура. При этом направление нормали определяют при помощи правила правого винта, связывая его с положительным направлением тока в контуре. Так, произвольно назначают положительное направление нормали, определяют положительное направление тока и ЭДС индукции в контуре. Знак минус в основном законе электромагнитной индукции соответствует правилу Ленца.
На рис.1 изображен замкнутый контур. Допустим, что положительным является направление обхода контура против часовой стрелки, тогда нормаль к контуру () составляет правый винт в направлением обхода контура. Если вектор магнитной индукции внешнего поля сонаправлен с нормалью и его модуль увеличивается со временем, тогда получим:
Если вектор магнитной индукции внешнего поля сонаправлен с нормалью и его модуль увеличивается со временем, тогда получим:
Title=»Rendered by QuickLaTeX.com»>
При этом ток индукции создаст магнитный поток (Ф’), который будет меньше нуля. Линии магнитной индукции магнитного поля индукционного тока () изображены на рис. 1 пунктиром. Ток индукции будет направлен по часовой стрелке. ЭДС индукции будет меньше нуля.
Формула (2) — это запись закона электромагнитной индукции в наиболее общей форме. Ее можно применять к неподвижным контурам и движущимся в магнитном поле проводникам. Производная, которая входит в выражение (2) в общем случае состоит из двух частей: одна зависит от изменения магнитного потока во времени, другая связывается с движением (деформаций) проводника в магнитном поле.
В том случае, если магнитный поток изменяется за равные промежутки времени на одну и ту же величину, то закон электромагнитной индукции записывают как:
Если в переменном магнитном поле рассматривается контур, состоящий из N витков, то закон электромагнитной индукции примет вид:
где величину называют потокосцеплением.
Примеры решения задач
ПРИМЕР 1
| Задание | Какова скорость изменения магнитного потока в соленоиде, который имеет N=1000 витков, если в нем возбуждается ЭДС индукции равная 200 В? |
| Решение | Основой для решения данной задачи служит закон электромагнитной индукции в виде: где — скорость изменения магнитного потока в соленоиде. Следовательно, искомую величину найдем как: Проведем вычисления: |
| Ответ |
ПРИМЕР 2
| Задание | Квадратная проводящая рамка находится в магнитном поле, которое изменяется по закону: (где и постоянные величины). Нормаль к рамке составляет угол с направлением вектора магнитной индукции поля. Стона рамки b. Получите выражение для мгновенного значения ЭДС индукции (). |
| Решение | Сделаем рисунок. За основу решения задачи примем основной закон электромагнитной индукции в виде: |
Явление электромагнитной индукции было открыто Майклом Фарадеем в 1831 г. Он опытным путем установил, что при изменении магнитного поля внутри замкнутого контура в нем возникает электрический ток, который называютиндукционным током.
Он опытным путем установил, что при изменении магнитного поля внутри замкнутого контура в нем возникает электрический ток, который называютиндукционным током.
Опыты Фарадея можно воспроизвести следующим образом: при внесении или вынесении магнита в катушку, замкнутую на гальванометр, в катушке возникает индукционный ток (рис. 24). Если рядом расположить две катушки (например, на общем сердечнике или одну катушку внутри другой) и одну катушку через ключ соединить с источником тока, то при замыкании или размыкании ключа в цепи первой катушки во второй катушке появится индукционный ток (рис. 25). Объяснение этого явления было дано Максвеллом. Любое переменное магнитное поле всегда порождает переменное электрическое поле.
Для количественной характеристики процесса изменения магнитного поля через замкнутый контур вводится физическая величина под названием магнитный поток.Магнитным потоком
через замкнутый контур площадью S называют физическую величину, равную произведению модуля вектора магнитной индукции В
на площадь контура S
и на косинус угла а между направлением вектора магнитной индукции и нормалью к площади контура. Ф = BS cos
Ф = BS cos
α (рис. 26).
Опытным путем был установлен основной закон электромагнитной индукции:ЭДС индукции в замкнутом контуре равна по величине скорости из-менения магнитного потока через контур. ξ = ΔФ/t..
Если рассматривать катушку, содержащую п
витков, то формула основного закона электромагнитной индукции будет выглядеть так: ξ = n ΔФ/t.
Единица измерения магнитного потока Ф — вебер (Вб): 1В6 =1Β c.
Из основного закона ΔФ =ξ t следует смысл размерности: 1 вебер — это величина такого магнитного потока, который, уменьшаясь до нуля за одну секунду, через замкнутый контур наводит в нем ЭДС индукции 1 В.
Классической демонстрацией основного закона электромагнитной индукции является первый опыт Фарадея: чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.
Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский ученый Ленц. Он сформулировал правило, носящее его имя. Индукционный ток имеет такое направление, при котором его магнитное поле стремится скомпенсировать изменение внешнего магнитного потока через контур.
опытным путем установил русский ученый Ленц. Он сформулировал правило, носящее его имя. Индукционный ток имеет такое направление, при котором его магнитное поле стремится скомпенсировать изменение внешнего магнитного потока через контур.
Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине и имеющие возможность вращаться вокруг оси, как коромысло. (рис. 27). При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца кольцо стремилось «догнать» магнит. При движении магнита внутри разрезанного кольца никакого эффекта не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.
В результате многочисленных опытов Фарадей установил основной количественный закон электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток. Возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Фарадей установил, что значение ЭДС электромагнитной индукции E i пропорционально скорости изменения магнитного потока:
Возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Фарадей установил, что значение ЭДС электромагнитной индукции E i пропорционально скорости изменения магнитного потока:
E i = -К , (27.1)
где К – коэффициент пропорциональности, зависящий только от выбора единиц измерения.
В системе единиц СИ коэффициент К = 1, т.е.
E i = — . (27.2)
Эта формула и представляет собой закон электромагнитной индукции Фарадея. Знак минус в этой формуле соответствует правилу (закону) Ленца.
Закон Фарадея можно сформулировать еще таким образом: ЭДС электромагнитной индукции E i в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: ЭДС E i не зависит от способа изменения магнитного потока.
Знак минус в (27.2) показывает, что увеличение потока ( > 0) вызывает ЭДС E i 0 т. е. направления магнитного потока индукционного тока и потока, вызвавшего его, совпадают. Знак минус в формуле (27.2) является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока (а значит и знака и ЭДС индукции), выведенного в 1833 г. Правило Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Иначе говоря, индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.
е. направления магнитного потока индукционного тока и потока, вызвавшего его, совпадают. Знак минус в формуле (27.2) является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока (а значит и знака и ЭДС индукции), выведенного в 1833 г. Правило Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Иначе говоря, индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.
ЭДС индукции выражается в вольтах (В). Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим:
Если замкнутый контур, в котором индуцируется ЭДС индукции, состоит из N витков, то E i будет равна сумме ЭДС, индуцируемых в каждом из витков. И если магнитный поток, охватываемый каждым витком, одинаков и равен Ф, то суммарный поток сквозь поверхность N витков, равен (NФ) – полный магнитный поток (потокосцепление). В этом случае ЭДС индукции равна:
E i = -N× , (27. 3)
3)
Формула (27.2) выражает закон электромагнитной индукции в общей форме. Она применима как к неподвижным контурам, так и к движущимся проводникам в магнитном поле. Входящая в нее производная от магнитного потока по времени в общем случае состоит из двух частей, одна из которых обусловлена изменением магнитной индукции во времени, а другая – движением контура относительно магнитного поля (или его деформацией). Рассмотрим некоторые примеры применения этого закона.
Пример 1. Прямолинейный проводник длиной l движется параллельно самому себе в однородном магнитном поле (рисунок 38). Этот проводник может входить в состав замкнутой цепи, остальные части которой неподвижны. Найдем ЭДС, возникающую в проводнике.
Если мгновенное значение скорости проводника есть v
, то за время dt он опишет площадь dS = l×v
×dt и за это время пересечет все линии магнитной индукции, проходящие через dS. Поэтому изменение магнитного потока через контур, в состав которого входит движущийся проводник, будет dФ = B n ×l×v
×dt. Здесь B n — составляющая магнитной индукции, перпендикулярная к dS. Подставляя это в формулу (27.2) получаем величину ЭДС:
Здесь B n — составляющая магнитной индукции, перпендикулярная к dS. Подставляя это в формулу (27.2) получаем величину ЭДС:
E i = B n ×l×v
. (27.4)
Направление индукционного тока и знак ЭДС определяются правилом Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток. В некоторых случаях возможно определение направления индукционного тока (полярности ЭДС индукции) согласно другой формулировке правила Ленца: индукционный ток в движущемся проводнике направлен таким образом, что возникающая при этом сила Ампера противоположна вектору скорости (тормозит движение).
Разберем численный пример. Вертикальный проводник (автомобильная антенна) длиной l = 2 м движется с востока на запад в магнитном поле Земли со скоростью v
= 72 км/час = 20 м/с. Вычислим напряжение между концами проводника. Так как проводник разомкнут, то тока в нем не будет и напряжение на концах будет равно ЭДС индукции. Учитывая, что горизонтальная составляющая магнитной индукции поля Земли (т.е. составляющая, перпендикулярная к направлению движения) для средних широт равна 2×10 -5 Тл, по формуле (27.4) находим
Учитывая, что горизонтальная составляющая магнитной индукции поля Земли (т.е. составляющая, перпендикулярная к направлению движения) для средних широт равна 2×10 -5 Тл, по формуле (27.4) находим
U = B n ×l×v
= 2×10 -5 ×2×20 = 0,8×10 -3 В,
т.е. около 1 мВ. Магнитное поле Земли направлено с юга на север. Поэтому мы находим, что ЭДС направлена сверху вниз. Это значит, что нижний конец провода будет иметь более высокий потенциал (зарядится положительно), а верхний – более низкий (зарядится отрицательно).
Пример 2. В магнитном поле находится замкнутый проволочный контур, пронизываемый магнитным потоком Ф. Предположим, что этот поток уменьшается до нуля, и вычислим полную величину заряда, прошедшего по цепи. Мгновенное значение ЭДС в процессе исчезновения магнитного потока выражается формулой (27.2). Следовательно, согласно закону Ома мгновенное значение силы тока есть
где R – полное сопротивление цепи.
Величина прошедшего заряда равна
q = = — = . (27.6)
(27.6)
Полученное соотношение выражает закон электромагнитной индукции в форме, найденной Фарадеем, который из своих опытов заключил, что величина заряда, прошедшего по цепи, пропорциональна полному числу линий магнитной индукции, пересеченных проводником (т.е. изменению магнитного потока Ф 1 -Ф 2), и обратно пропорциональна сопротивлению цепи R. Соотношение (27.6) позволяет дать определение единицы магнитного потока в системе СИ: вебер – магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 Ом проходит заряд 1 Кл.
Согласно закону Фарадея, возникновение ЭДС электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае она не может быть причиной возникновения ЭДС индукции. Максвелл для объяснения ЭДС индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора напряженности этого поля по любому неподвижному контуру L проводника представляет собой ЭДС электромагнитной индукции:
Циркуляция вектора напряженности этого поля по любому неподвижному контуру L проводника представляет собой ЭДС электромагнитной индукции:
E i = = — . (27.7)
Линии напряженности вихревого электрического поля представляют собой замкнутые кривые, поэтому при перемещении заряда в вихревом электрическом поле по замкнутому контуру совершается отличная от нуля работа. В этом заключается отличие вихревого электрического поля от электростатического, линии напряженности которого начинаются и заканчиваются на зарядах.
После того, как было установлено, что магнитное поле создаётся электрическими токами, учёные пытались решить обратную задачу — при помощи магнитного поля создать электрический ток. Эту задачу в 1831 г. успешно решил М. Фарадей , который открыл явление электромагнитной индукции. Суть этого явления заключается в том, что в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего этот контур, возникает электрически ток, который называется индукционным
. Схема некоторых опытов Фарадея показана на рис. 3.12.
Схема некоторых опытов Фарадея показана на рис. 3.12.
При изменении положения постоянного магнита относительно катушки, замкнутой на гальванометр, в последней возникал электрический ток, причём направление тока оказывалось различным — в зависимости от направления перемещения постоянного магнита. Аналогичный результат достигался и при перемещении другой катушки, по которой шёл электрический ток. Более того, в большой катушке возникал ток даже при неизменном положении меньшей катушки, но при изменении тока в ней.
На основании подобных опытов М. Фарадей пришёл к выводу, что в катушке всегда возникает электрический ток при изменении магнитного потока, сцепленного с этой катушкой. Величина тока зависит от скорости изменения магнитного потока. Сейчас мы формулируем открытия Фарадея в виде закона электромагнитной индукции
: при любом изменении магнитного потока, сцепленного с проводящим замкнутым контуром, в этом контуре возникает ЭДС индукции, которая определяется как
Знак “-” в выражении (3. 53) означает, что при увеличении магнитного потока магнитное поле, созданное индукционным током, направлено против внешнего магнитного поля. Если же магнитный поток уменьшается по величине, то магнитное поле индукционного тока совпадает по направлению с внешним магнитным полем. Русский учёный Х. Ленц таким образом определил появление знака минус в выражении (3.53) — индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле имеет такое направление, что препятствует изменению магнитного потока, вызвавшего возникновение индукционного тока
53) означает, что при увеличении магнитного потока магнитное поле, созданное индукционным током, направлено против внешнего магнитного поля. Если же магнитный поток уменьшается по величине, то магнитное поле индукционного тока совпадает по направлению с внешним магнитным полем. Русский учёный Х. Ленц таким образом определил появление знака минус в выражении (3.53) — индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле имеет такое направление, что препятствует изменению магнитного потока, вызвавшего возникновение индукционного тока
.
Дадим ещё одну формулировку закона электромагнитной индукции
: ЭДС индукции в замкнутом проводящем контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего этот контур.
Немецкий физик Гельмгольц показал, что закон электромагнитной индукции можно получить из закона сохранения энергии. В самом деле, энергия источника ЭДС по перемещению проводника с током в магнитном поле (см.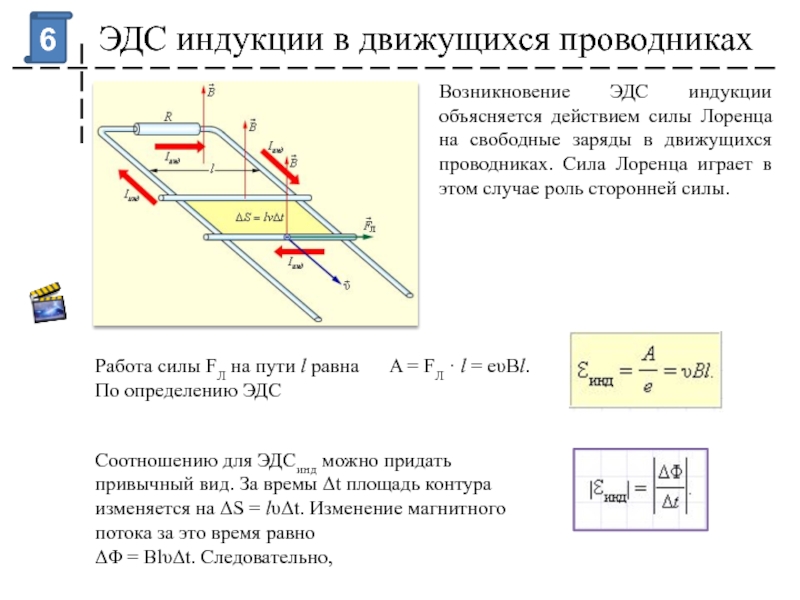 рис.3.37) будет затрачена как на Джоулев разогрев проводника сопротивлением R, так и на работу по перемещению проводника:
рис.3.37) будет затрачена как на Джоулев разогрев проводника сопротивлением R, так и на работу по перемещению проводника:
Тогда из уравнения (3.54) сразу же следует, что
В числителе выражения (3.55) стоит алгебраическая сумма ЭДС, действующих в контуре. Следовательно,
Какова же физическая причина возникновения ЭДС? На заряды в проводнике АВ действует сила Лоренца при движении проводника вдоль оси x. Под действием этой силы положительные заряды будут смещаться вверх, в результате чего электрическое поле в проводнике будет ослаблено. Другими словами, в проводнике появится ЭДС индукции. Следовательно, в рассмотренном нами случае физической причиной возникновения ЭДС является сила Лоренца. Однако, как мы уже отмечали, и в неподвижном замкнутом контуре может появиться ЭДС индукции, если будет изменяться магнитное поле, пронизывающее этот контур.
В этом случае заряды можно считать неподвижными, а на неподвижные заряды сила Лоренца не действует. Чтобы объяснить возникновение ЭДС в этом случае, Максвелл предположил, что всякое изменяющееся магнитное поле порождает в проводнике изменяющееся электрическое поле, которое и является причиной возникновения ЭДС индукции. Циркуляция вектора напряжённости, действующей в этом контуре, таким образом, будет равна ЭДС индукции, действующей в контуре:
Циркуляция вектора напряжённости, действующей в этом контуре, таким образом, будет равна ЭДС индукции, действующей в контуре:
. (3.56)
Явление электромагнитной индукции используется для превращения механической энергии вращения в электрическую — в генераторах электрического тока. Обратный процесс — превращение электрической энергии в механическую, основанный на вращательном моменте, действующем на рамку с током в магнитном поле, используется в электродвигателях.
Рассмотрим принцип действия генератора электрического тока (рис. 3.13). Пусть у нас проводящая рамка вращается между полюсами магнита (это может быть и электромагнит) с частотой w. Тогда угол между нормалью к плоскости рамки и направлением магнитного поля изменяется по закону a = wt
. В этом случае магнитный поток, сцепленный с рамкой, будет изменяться в соответствии с формулой
где S — площадь контура. В соответствии с законом электромагнитной индукции в рамке будет индуцироваться ЭДС
с e max = BSw.
Таким образом, если в магнитном поле вращается с постоянной угловой скоростью проводящая рамка, то в ней будет индуцироваться ЭДС, изменяющаяся по гармоническому закону. В реальных генераторах вращают много витков, соединенных последовательно, а в электромагнитах, для увеличения магнитной индукции, используют сердечники с большой магнитной проницаемостью m
..
Индукционные токи могут возникать и в толще проводящих тел, помещённых в переменное магнитное поле. В этом случае эти токи называются токами Фуко. Эти токи вызывают разогрев массивных проводников. Это явление используется в вакуумных индукционных печах, где сильные токи разогревают металл до плавления. Поскольку разогрев металлов происходит в вакууме, то это позволяет получать особо чистые материалы.
Формула для ЭДС индукции в катушке из-за изменения физики класса 12 JEE_Main
Подсказка: Концепция ЭДС индукции дается законом Фарадея, который гласит:
Любое изменение магнитного поля или магнитного потока катушки вызовет наведенную ЭДС.
$e = — N\dfrac{{d\phi }}{{dt}}$( e — ЭДС индукции, N — число витков катушки и $\phi $ — магнитный поток)
Знак минус приведенное выше уравнение основано на законе Ленца.
Обсудим более подробно два вышеуказанных закона и решим поставленную задачу.
Полное пошаговое решение:
Давайте сначала более подробно объясним закон Ленца и закон Фарадея.
Закон Фарадея гласит, что: ЭДС индукции прямо пропорциональна скорости изменения магнитного потока, создаваемого в катушке из-за протекания тока в проводнике с конечным числом витков.
В математических терминах Закон Фарадея задается как:
$e = — N\dfrac{{d\phi}}{{dt}}$
Знак минус уравнения задается законом Ленца, который утверждает, что;
Направление электрического тока, индуцируемого в проводнике изменяющимся магнитным полем, таково, что магнитное поле таково, что магнитное поле, создаваемое индуцируемым током, противодействует начальному изменяющемуся магнитному полю.
На языке непрофессионала мы можем сформулировать закон Ленца как; Ток или напряжение, которые индуцируются в цепи, противодействуют изменению, которое их вызывает.
Теперь вычислим формулу ЭДС индукции.
Магнитное поле задается как:
$B = \dfrac{\phi }{A}$ (B — магнитное поле, A — площадь и $\phi $ — поток)
Следовательно, поток задается как, $ \phi $ = BA
В соответствии с определением ЭДС индукции скорость изменения потока равна ЭДС индуцирования, поэтому формула принимает следующий вид:
$e = — \dfrac{{дБ.A}}{{dt}}$
Следовательно, вариант C верен.
Примечание. Закон Фарадея применим во многих электрических устройствах, таких как трансформаторы, в которых процесс повышения или понижения тока или напряжения происходит из-за электромагнитной индукции, генераторы переменного тока, которые создают вращающиеся магнитные поля, двигатели постоянного тока, измерительные приборы, такие как счетчики энергии и т. д.
Формула индукционного тока и примеры | Как рассчитать напряжение — видео и расшифровка урока
Формула индукционного тока
После расчета ЭДС индукции в катушке или контуре можно рассчитать индуцированный ток, если известно сопротивление контура или катушки. Это можно сделать с помощью закона Ома, который определяется как
Это можно сделать с помощью закона Ома, который определяется как
{eq}V=IR {/eq}
Где {eq}V {/eq} – напряжение или ЭДС, в данном случае {eq}I {/ eq} — ток, а {eq}R {/eq} — сопротивление. Объединив закон Ома и закон Фарадея, можно записать формулу индуцированного тока. Уравнение индуцированного тока:
$$I = \frac{EMF}{R} $$
Как найти индуктивный ток
Чтобы лучше понять, как найти индуктивный ток, рассмотрим пример. На проволочную петлю радиусом 25 см действует магнитное поле, начинающееся с нуля.2(0,6 — 0,15) = 0,088 $$
Следующим шагом является расчет ЭДС, которая равна
$$ЭДС = -N\frac{\Delta\Phi}{t} $$
Так как пример для петли, а не катушки, {eq}N=1 {/eq}
Подстановка других значений в уравнение дает
$$ЭДС = -(1)\frac{0,088}{0,2} = 0,44 В $ $
Наконец, используя ЭДС индукции и закон Ома, можно рассчитать индукционный ток. Уравнение:
$$I = \frac{EMF}{R} $$
Сопротивление контура равно 3. 5{eq}\Omega {/eq}, поэтому индуцированный ток равен
5{eq}\Omega {/eq}, поэтому индуцированный ток равен
$$I = \frac{0,44}{3,5} = 0,13 A $$
Индуцированное током магнитное поле
Как кратко упоминалось выше, изменяющееся магнитное поле индуцирует ток. И наоборот, также верно, что движущийся ток индуцирует магнитное поле. Это то, что наблюдал Фарадей, когда замыкал цепь, как показано выше. Когда ток начал течь, он индуцировал магнитное поле в одной катушке. Это известно как индуцированное током магнитное поле.Сила магнитного поля определяется величиной движущегося тока, больший ток будет индуцировать более сильное магнитное поле.
Индуктивное напряжение
Согласно закону Фарадея, изменяющееся магнитное поле индуцирует ЭДС. Несмотря на название, единицами измерения электродвижущей силы являются вольты, а не ньютоны. Это означает, что ЭДС представляет собой наведенное напряжение, а не силу. Закон Фарадея гласит, что величина индуцированного напряжения зависит от числа витков в катушке.Это означает, что индуцированное напряжение можно регулировать, соорудив установку с катушкой определенного размера. Это явление используется в трансформаторах, которые используются для увеличения или уменьшения напряжения электричества.
Это явление используется в трансформаторах, которые используются для увеличения или уменьшения напряжения электричества.
Формула наведенного напряжения
Поскольку ЭДС представляет собой наведенное напряжение, закон Фарадея также называют формулой наведенного напряжения.2(4,2 — 0,3) = 1,96 $$
Таким образом, индуцированное напряжение определяется выражением
$$ЭДС = -N\frac{\Delta\Phi}{t} $$
$$ЭДС = -( 25)\frac{1.96}{2} = -24,5 В $$
Итоги урока
Когда изменяющийся магнитный поток проходит через замкнутую цепь, в цепи индуцируется ток. Величина тока зависит от того, насколько быстро и насколько сильно изменяется магнитный поток. Это выражается количественно в законе Фарадея , который гласит
$$ЭДС = -N\frac{\Delta\Phi}{t} $$
цепь известна, индуктивного тока можно рассчитать, используя закон Ома, {eq} V = IR {/eq}. Этот эффект используется в электрических трансформаторах для «повышения» или «понижения» напряжения. Правило правой руки можно использовать для определения направления протекания положительного тока, например, если большой палец указывает в направлении магнитного поля, пальцы согнутся в направлении протекания тока. При рассмотрении электронов поток тока меняется на противоположный.
Этот эффект используется в электрических трансформаторах для «повышения» или «понижения» напряжения. Правило правой руки можно использовать для определения направления протекания положительного тока, например, если большой палец указывает в направлении магнитного поля, пальцы согнутся в направлении протекания тока. При рассмотрении электронов поток тока меняется на противоположный.
Физическая модель низкочастотной электромагнитной индукции в ближнем поле, основанная на прямом взаимодействии электронов передатчика и приемника
Proc Math Phys Eng Sci.2016 июль; 472(2191): 20160338.
Ray T. Smith
1 Факультет электротехники и электроники, Ливерпульский университет, Liverpool L69 3GJ, UK
Fred PM Jjunju
2 Факультет электротехники и электроники 9014 , Ливерпульский университет, Ливерпуль L69 3GJ, Великобритания
Иэн С. Янг
2 Институт интегративной биологии, Ливерпульский университет, Ливерпуль L69 3BX, Великобритания
Стивен Тейлор
1 Факультет электротехники и электроники , University of Liverpool, Liverpool L69 3GJ, UK
Simon Maher
1 Факультет электротехники и электроники, University of Liverpool, Liverpool L69 3GJ, UK
1 Факультет электротехники и электроники, University of Liverpool , Liverpool L69 3GJ, UK
2 Институт интегративной биологии Ливерпульского университета, Liverpool L69 3BX, UK
Получено 13 мая 2016 г . ; Принято 21 июня 2016 г.
; Принято 21 июня 2016 г.
Опубликовано Королевским обществом в соответствии с лицензией Creative Commons Attribution License http://creativecommons.org/licenses/by/4.0/, которая разрешает неограниченное использование при условии указания автора и источника.Эта статья была процитирована другие статьи в PMC.
Abstract
Разработана физическая модель электромагнитной индукции, которая напрямую связывает силы между электронами в передающей и приемной обмотках концентрических коаксиальных конечных катушек в ближней зоне.Применяя принцип суперпозиции, вклады от ускоряющих электронов в последовательных петлях тока суммируются, что позволяет точно предсказать пиковое индуцированное напряжение в приемнике. Результаты показывают хорошее соответствие между теорией и экспериментом для различных приемников с разным радиусом, в пять раз превышающим радиус передатчика. Обсуждаются ограничения линейной теории электромагнитной индукции с точки зрения неравномерного распределения тока, вызванного скин-эффектом. В частности, объяснение с точки зрения электромагнитной энергии и теоремы Пойнтинга противопоставляется более прямому объяснению, основанному на переменной индукции нити накала по поперечному сечению проводника. Поскольку прямая физическая модель, разработанная здесь, имеет дело только с силами между дискретными элементами тока, ее можно легко адаптировать к различным геометриям катушек и широко применять в различных областях исследований, таких как связь ближнего поля, проектирование антенн, беспроводная передача энергии, датчики. приложений и не только.
В частности, объяснение с точки зрения электромагнитной энергии и теоремы Пойнтинга противопоставляется более прямому объяснению, основанному на переменной индукции нити накала по поперечному сечению проводника. Поскольку прямая физическая модель, разработанная здесь, имеет дело только с силами между дискретными элементами тока, ее можно легко адаптировать к различным геометриям катушек и широко применять в различных областях исследований, таких как связь ближнего поля, проектирование антенн, беспроводная передача энергии, датчики. приложений и не только.
Ключевые слова: катушки , электромагнитная индукция, распространение, беспроводная передача энергии, соленоиды, трансформаторы. 1], томография ИМ [2,3] и беспроводная передача энергии [4]. Они все чаще используются в беспроводных подземных сенсорных сетях [5,6] для таких приложений, как мониторинг окружающей среды (в почве [7] и воде [8]), осмотр оползней [9] и наблюдение за подземными трубопроводами [10].Традиционные подходы с использованием беспроводных датчиков сдерживаются сложными средами распространения (например, почвой, камнем, водой).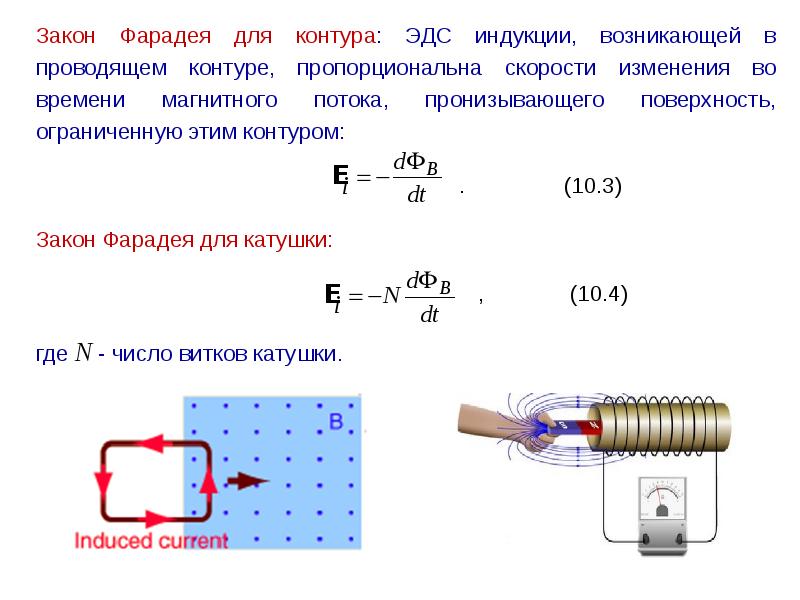 Однако при использовании ближнего поля низкочастотных магнитных полей трудности, связанные с задержкой распространения, замираниями и многолучевым распространением, не столь заметны. Термин ближнее поле относится к безызлучательному распространению на короткие расстояния магнитных или электрических полей вследствие индуктивной или емкостной связи соответственно. Напротив, дальнее поле относится к электромагнитным полям излучения на больших расстояниях от источника, которые получили широкое распространение [11–14].
Однако при использовании ближнего поля низкочастотных магнитных полей трудности, связанные с задержкой распространения, замираниями и многолучевым распространением, не столь заметны. Термин ближнее поле относится к безызлучательному распространению на короткие расстояния магнитных или электрических полей вследствие индуктивной или емкостной связи соответственно. Напротив, дальнее поле относится к электромагнитным полям излучения на больших расстояниях от источника, которые получили широкое распространение [11–14].
Было предпринято несколько ценных исследовательских инициатив по моделированию электромагнитных полей в ближней зоне, которые обычно включают точные представления и/или интенсивные вычисления [15–23], которые, согласно Микки и Антару [24], «не могут привести к значительным результатам». понимание общих вопросов, таких как природа электромагнитного излучения или внутренняя структура антенны ближнего поля». Тем не менее, моделирование ближнего магнитного поля является важной задачей, например, при проектировании сложных схем для определения соответствия стандартам ЭМС [25].
В этой статье мы развиваем метод для случая многовитковой конечной пары катушек передатчика и приемника круговой геометрии, расположенных концентрически. В основе этого метода, адаптированного для расчета ЭДС индукции в приемнике на некотором расстоянии от источника, лежит формула силы Вебера, которую можно рассматривать как модификацию закона Кулона для зарядов, находящихся в относительном движении [26–32] . Эта сила напрямую связана с силой между движущимися зарядами с точки зрения их смещения, относительной радиальной скорости и относительного радиального ускорения в дискретной системе.
Определение границ ближней зоны — неоднозначная задача, поскольку она зависит от геометрии и возбуждения рассматриваемого передатчика. Микки и Антар справедливо подчеркивают в своем подробном и всестороннем обзоре теории антенн в ближнем поле «необходимость продолжительного, всестороннего и строгого рассмотрения темы ближнего поля, рассмотрения, учитывающего специфический характер антенны». электромагнитное поведение в этой зоне [24]». Принято считать, что «ближнее поле» включает, по крайней мере, окружающее пространство до расстояния в одну длину волны и вполне может простираться дальше.Мы также представляем предварительные результаты того, как индуцированное напряжение изменяется как с расстоянием, так и с частотой на основе взаимодействий между частицами в этой зоне.
электромагнитное поведение в этой зоне [24]». Принято считать, что «ближнее поле» включает, по крайней мере, окружающее пространство до расстояния в одну длину волны и вполне может простираться дальше.Мы также представляем предварительные результаты того, как индуцированное напряжение изменяется как с расстоянием, так и с частотой на основе взаимодействий между частицами в этой зоне.
Во-первых, мы исследуем теоретические основы низкочастотной электромагнитной индукции. При этом мы разрабатываем модель прямого действия, которая напрямую связана с распределением тока в конечных катушках передатчика и приемника. Модель подтверждается экспериментальными измерениями путем расчета отклика приемника при увеличении расстояния от источника.Наконец, мы обсуждаем преимущества и ограничения модели и даем предложения для дальнейших исследований.
2. Теория
Рассматриваемый случай электромагнитной индукции иногда называют трансформаторной индукцией. Устройство состоит из коаксиальных катушек, расположенных концентрически, при этом передатчик (T) определяется внутренней катушкой, а приемник (R) — внешней, как показано на рис.
Конфигурация коаксиальных катушек с воздушным сердечником. Передатчик (T) длиной, L T , радиусом, r T с N T тесно навитых витков расположен внутри приемника (R) длиной, L R , радиус, r R и N R плотно намотанные витки.(Онлайн-версия в цвете.)
(a) Закон индукции Фарадея
Закон Фарадея связывает ЭДС индукции e в замкнутой цепи со скоростью изменения магнитного потока в этой цепи. Обычно это дается
, где ∅ – магнитный поток (уравнение (2.1) строго справедливо только для провода бесконечно малого сечения). Для схемы на катушку передатчика подается переменный ток, I = I 0 sin ω t , где I 0 – пиковый ток2 903 и радиальная частота определяется выражением ω = 2 πf .Магнитный поток через приемник следует за током таким образом, что ∅=∅ 0 sin 2 πft , а ЭДС индукции в приемнике определяется выражением
eR=−d∅dt=−∅02πf cos(2πft).
2,2
Для случая бесконечной многовитковой катушки плотность магнитного потока в центральной области определяется как — проницаемость свободного пространства, а n — плотность намотки (= Н / L ).Пиковый магнитный поток на виток, соединяющий передатчик и приемник, определяется как произведение плотности потока на площадь поперечного сечения одного витка ( Bπr 2 T ). Предполагая, что приемник намотан близко к передатчику, так что r R − r T ≅0, тогда пиковая ЭДС, индуцированная в приемнике, определяется выражением
(ER) 0 = -2π2RT2NTNRI0Fε0C2,
2.3
, где ε 0 = диэлектрическая проницаемость свободного пространства, C = скорость света и N T — это плотность поворота передатчика.
(b) Формула взаимной индуктивности Неймана
Более общий метод расчета ЭДС между замкнутыми цепями можно получить из формулы Неймана. Если предположить, что плотность магнитного потока пропорциональна току (закон Био–Савара) и выразить поток через векторный потенциал ( A ), то для замкнутых контуров T и R с элементами d л Т , д л Р на расстоянии р друг от друга
Если предположить, что плотность магнитного потока пропорциональна току (закон Био–Савара) и выразить поток через векторный потенциал ( A ), то для замкнутых контуров T и R с элементами d л Т , д л Р на расстоянии р друг от друга
где
Так что
∅R = μ0it4π∮∮dltr⋅dlr
, потому что ∅ R = м RT I T , где M RT = м TR , который является взаимным индуктивность двух контуров, то формула Неймана имеет вид
MRT=μ04π∮∮1rdlT⋅dlR.
2.4
Взаимная индуктивность между двумя замкнутыми цепями является геометрической величиной, относящейся к размеру, форме и взаимному расположению двух цепей, и не зависит от того, какая цепь действует как передатчик или приемник. Переписывая закон Фарадея с учетом взаимной индуктивности ( M ), переменного тока передатчика I и связанного с ним изменяющегося магнитного потока, ЭДС индукции в приемнике определяется выражением
Предполагая, как и ранее, что приемник намотан близко к передатчику, так что r R − r T ≅0. Тогда, отметив что, м = μ 0 πr 2 T ( N T / L T ) и I = I 0 sin ω t , с числом витков приемника, действующим как множитель, пиковая ЭДС в приемнике определяется как
Тогда, отметив что, м = μ 0 πr 2 T ( N T / L T ) и I = I 0 sin ω t , с числом витков приемника, действующим как множитель, пиковая ЭДС в приемнике определяется как
(eR)0=−2π2rT2nTNRI0fε0c2
, что совпадает с (2.3).
(c) Решение Гровера, когда
r T ≠ r R
Конкретное решение для концентрических коаксиальных катушек различных радиусов приведено в [33] по формуле
М=0.004π2rT2nTNR(B1r1−B2r2),
где r1=rR2+(1/4)(lT+lR)2 и r2=rR2+(1/4)(lT−lR)2
Функции B 1 и B 2 зависят от параметров, p12=rR2/r12, p22=rR2/r22, α = r T / r R 6 и справочные таблицы можно получить из [ ]. Например, используя данные конкретной катушки в настоящем эксперименте, значения для M были рассчитаны как 9,22 мГн ( r T / r R = 1) и 8.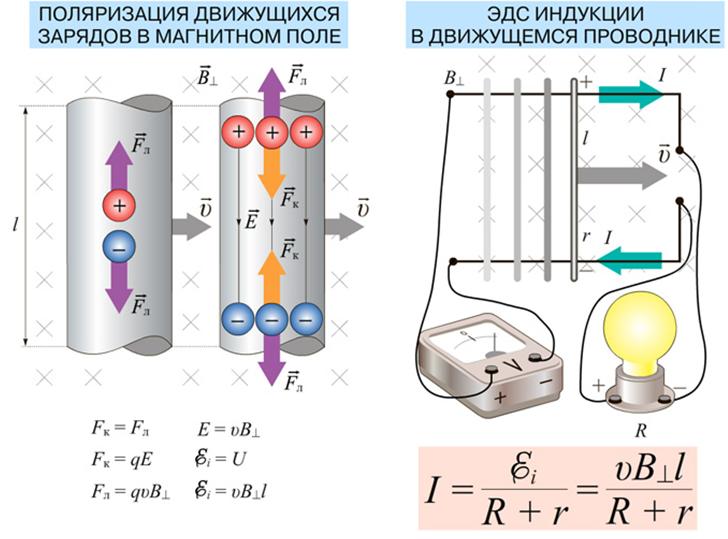 66 мГн ( r T / r R = 0,78), что дает увеличение примерно на 6 %, если предполагается, что приемник плотно намотан.
66 мГн ( r T / r R = 0,78), что дает увеличение примерно на 6 %, если предполагается, что приемник плотно намотан.
(d) Векторный потенциал
Векторный потенциал вне длинного соленоида определяется как A =∅/2 πr , где ∅ — общий магнитный поток внутри катушки передатчика. Тогда электрическое поле снаружи передатчика будет равно E = −∂ A /∂ t = −(1/2 πr )(d∅/ dt ).Приравнивая ∅= LI = μ 0 nIπr 2 T , где L — индуктивность на единицу длины n
2 бесконечной многовитковой катушки единица длины, затем для одной петли радиусом r R , окружающей передатчик
E = -½ ( μ 0 N R T 2 T 2 π F ) I 0 COS Ω T .
Интегрирование по одному контуру и включение множителя для учета N R оборотов приемника
(eR)0=∮E.dl=2πrTE=−2π2rT2nTNRI0fε0c2
, что опять равно (2.3).
3. Подход прямого действия
Рассмотрим два отдельных круговых контура передатчика (T) и приемника (R). Передающая петля имеет радиус 90 203 r 90 204 90 205 T 90 206 и возбуждается переменным током заданной частоты 90 203 f 90 204 , тогда как огибающая приемная петля имеет радиус 90 203 r 90 204 90 205 R 90 206, поперек которой индуцируется ЭДС ( 90 203 r R > r T ), как показано на .
Геометрия одиночных круговых петель, составляющих часть катушек передатчика и приемника. На вставке показана геометрия, спроецированная на двумерную плоскость ( x – y ).
Используя декартову систему координат, мы определяем центр контура приемника как начало координат. При применении закона силы Вебера к этому случаю сила определяется между линейным элементом заряда (= r T δθ ) в передатчике, расположенном в точке M , и единицей заряда, расположенной в приемнике в точке N , где расстояние между этими точками равно MN = r . — единичный вектор вдоль r , u r — относительная скорость вдоль r и u — относительная скорость между M и N . В этом случае, когда в приемнике нет чистого потока тока, относительная скорость между M и N определяется скоростью дрейфа электронов v на M в контуре передатчика. Отсюда в (3.1) u 2 = v 2 .Относительная скорость вдоль R дана как U R = D R / D T = V COS β = V B Sin θ / р . Оба члена u 2 и ur2, которые появляются в (3.1), включают члены v 2 , которыми можно пренебречь для малых токов, оставляя только член ускорения, r (d 2
— единичный вектор вдоль r , u r — относительная скорость вдоль r и u — относительная скорость между M и N . В этом случае, когда в приемнике нет чистого потока тока, относительная скорость между M и N определяется скоростью дрейфа электронов v на M в контуре передатчика. Отсюда в (3.1) u 2 = v 2 .Относительная скорость вдоль R дана как U R = D R / D T = V COS β = V B Sin θ / р . Оба члена u 2 и ur2, которые появляются в (3.1), включают члены v 2 , которыми можно пренебречь для малых токов, оставляя только член ускорения, r (d 2
4 / r 9 t )= r (d u r /d t ) и r определяется тригонометрически, r2θrco. Дифференцируя U R и отмечая, что V = R T (D θ / D T ), игнорирование V 2 Условия, доходность R D u r /d t = r R sin θ (d v /d 4). Поскольку I = n ′ Ave , то v˙=I˙/n′Ae и, следовательно,
Дифференцируя U R и отмечая, что V = R T (D θ / D T ), игнорирование V 2 Условия, доходность R D u r /d t = r R sin θ (d v /d 4). Поскольку I = n ′ Ave , то v˙=I˙/n′Ae и, следовательно,
Fr=rTrR sinθ4πε0c2r2I˙.
3.2
3.2
Разрешение вдоль касательной к петле приемника, дает силу на единицу заряда, как, E T = F R COS γ , где COS γ = — г T sin θ / r и, следовательно,
ET=-rT2rRI˙4πε0c2sin2θr3δθ.
3,3
ЭДС индукции в приемнике определяется путем интегрирования по замкнутому контуру, так что
er=∮E.dl=2πrRET=−2πrT2rR2I˙4πε0c2sin2θr3δθ.
3,4
Дифференцируя ток передатчика, мы получаем пиковую ЭДС в одном контуре приемника как
(eR)0=πrT2rR2I0ε0c2f∫02πsin2θr3dθ.
3,5
Для расчета ЭДС индукции в конечной многовитковой катушке принцип суперпозиции применяется к вкладам тока от каждого отдельного витка катушки. Подынтегральная функция из (3.5) вычисляется для диапазона 90 203 z 90 204 -значений от каждого поворота. Значения z относятся к вертикальному расстоянию между витками, выраженному в диаметре провода, d .Тогда с помощью стандартного численного интегрирования (правило трапеций с интервалами 5 °) получаем
где +z2. Коэффициент 2 учитывает вклад обоих слоев передатчика (т. е. катушка передатчика имеет двойную обмотку). Матрица имеет 20 ( N R ) строк по 650 ( N T /2) столбцов, представляющих все вклады отдельных оборотов, где z -значение равно нулю для случая, когда отдельные витки катушки передатчика и приемника прямо выровнены.Суммирование в (3.6) производится для всех отдельных членов матрицы. Например, суммирование первой строки матрицы дает индуцированное напряжение в первом витке приемника из всех 650 отдельных витков передатчика (см. приложение А).
приложение А).
4. Экспериментальный
Для проверки вышеупомянутого подхода были проведены следующие экспериментальные измерения. Экспериментальная установка состоит из конечной коаксиальной внутренней катушки передатчика и внешней катушки приемника, как показано на рис.Передающая (внутренняя) катушка длиной L T =0,5 м состоит из 1300 витков, дважды намотанных одножильным эмалированным медным проводом диаметром 0,7 мм и плотностью намотки =2600 витков на метр на каркасе из радиус, r T примерно 0,0292 м. Были использованы три приемные катушки с одинаковой плотностью витков и числом витков ( N R = 20), но с разными радиусами r R 0,0375, 0,075 и 0.15 м.
Катушка передатчика была подключена к цифровому генератору сигналов (Lascells, Великобритания), обеспечивающему синусоидальный ток передатчика 3 мА (среднеквадратичное значение), измеренный 5,5-разрядным мультиметром Keithley в диапазоне частот 0–14 кГц. Одновременно измерялось напряжение на приемнике с помощью цифрового осциллографа (Tektronix, США). Принципиальная принципиальная схема показана на . Для улучшения отношения сигнал-шум катушка приемника была экранирована от внешних помех по окружности с помощью экрана из мю-металла (полностью термообработанный, 0.толщиной 35 мм, ASTM A753, сплав 4, магнитные экраны, Великобритания). Все расчеты выполнены с использованием программы Matlab 2014a (MathWorks, США).
Одновременно измерялось напряжение на приемнике с помощью цифрового осциллографа (Tektronix, США). Принципиальная принципиальная схема показана на . Для улучшения отношения сигнал-шум катушка приемника была экранирована от внешних помех по окружности с помощью экрана из мю-металла (полностью термообработанный, 0.толщиной 35 мм, ASTM A753, сплав 4, магнитные экраны, Великобритания). Все расчеты выполнены с использованием программы Matlab 2014a (MathWorks, США).
Принципиальная схема экспериментальной установки для измерения ЭДС индукции в приемной катушке.
5. Результаты
Экспериментальные результаты суммированы в –. показывает ЭДС приемника (от пика до пика) в зависимости от частоты для двух разных радиусов катушки приемника 3,75 и 15 см. Меньшая приемная катушка находится на расстоянии менее примерно 1 см от внешней поверхности передающей катушки, тогда как большая приемная катушка находится на расстоянии примерно 12 см от передающей катушки, а ее диаметр примерно в пять раз больше диаметра передающей катушки. Обе катушки следуют одной и той же тенденции: ЭДС индукции больше для катушки с меньшим радиусом (т.е. ближе к передатчику), чем для большей для каждого измерения. Первоначально тренд ЭДС индукции в зависимости от частоты соответствует линейной характеристике. Это хорошо видно в том числе и смоделированные данные, рассчитанные по (3.6) с эквивалентными параметрами модели. На графике рассчитанный модельный тренд в зависимости от радиусов приемника сравнивается с результатами измерений для трех различных экспериментальных радиусов катушки приемника ( r R =0.0375, 0,075, 0,15 м) на разных частотах.
Обе катушки следуют одной и той же тенденции: ЭДС индукции больше для катушки с меньшим радиусом (т.е. ближе к передатчику), чем для большей для каждого измерения. Первоначально тренд ЭДС индукции в зависимости от частоты соответствует линейной характеристике. Это хорошо видно в том числе и смоделированные данные, рассчитанные по (3.6) с эквивалентными параметрами модели. На графике рассчитанный модельный тренд в зависимости от радиусов приемника сравнивается с результатами измерений для трех различных экспериментальных радиусов катушки приемника ( r R =0.0375, 0,075, 0,15 м) на разных частотах.
ЭДС индукции ( пик – пик пик , мВ) отклик от частоты для радиусов приемника 3,75 и 15 см. (Онлайн-версия в цвете.)
ЭДС индукции ( pk – pk , мВ) в зависимости от частоты в диапазоне 1–8 кГц по сравнению с расчетными данными для радиусов приемника 3,75 и 15 см. (Онлайн-версия в цвете.)
Расчетная ЭДС индукции ( pk – pk , мВ) в зависимости от радиуса приемника для диапазона частот, дополненная измерениями для радиусов приемника 3. 75, 7 и 15 см для f ≤5 кГц. (Онлайн-версия в цвете.)
75, 7 и 15 см для f ≤5 кГц. (Онлайн-версия в цвете.)
6. Обсуждение
Преимущество формулировки, основанной на Вебере, заключается в том, что она может легко работать с различными радиусами приемника и передатчика. Сравнение между экспериментом и теорией показано в и , где смоделированные данные находятся в пределах ошибки эксперимента, в линейном режиме (90 203 f 90 204 < 90 203 приблизительно 90 204, 5 кГц). Согласно модели, ЭДС уменьшается с увеличением радиуса приемника из-за уменьшения межэлектронных сил, так как связь между катушками уменьшается с расстоянием.
Нелинейность, связанная с ЭДС индукции на более высоких частотах, очевидна в . Приблизительно выше 5 кГц характеристика отличается от линейной. Из (3.5) видно, что модель прямого действия линейно зависит от частоты, как и в случае с законом Фарадея, приведенным в (2.3). По закону Фарадея ЭДС индукции зависит от скорости изменения тока, отсюда линейная зависимость от f . Точно так же для подхода прямого действия относительные ускорения электронов также линейно зависят от частоты. Насколько известно авторам, не существует какой-либо удовлетворительной теории, которая могла бы иметь дело со случаем электромагнитной индукции переменной частоты. Фейнман [34] обсуждает попытки модифицировать уравнения Максвелла, все из которых сталкиваются с трудностями, связанными с допущением точечных зарядов, самовоздействием заряда на самого себя (реакцией излучения) и ролью ЭМ массы по сравнению с механической массой.
Насколько известно авторам, не существует какой-либо удовлетворительной теории, которая могла бы иметь дело со случаем электромагнитной индукции переменной частоты. Фейнман [34] обсуждает попытки модифицировать уравнения Максвелла, все из которых сталкиваются с трудностями, связанными с допущением точечных зарядов, самовоздействием заряда на самого себя (реакцией излучения) и ролью ЭМ массы по сравнению с механической массой.
Для модели прямого действия предполагается, что ток равномерно распределяется по поперечному сечению провода и что принцип суперпозиции применяется к последовательным участкам катушки.С увеличением частоты любая модель линейной индукции выйдет из строя, поскольку распределение тока станет неравномерным, что приведет к появлению хорошо известных скин-эффектов и эффектов близости. Явление, получившее название скин-эффекта, было открыто Максвеллом, выдвинувшим гипотезу о неравномерном распределении тока [35]. Высокочастотное сопротивление можно представить как сопротивление постоянному току эквивалентной «кожи» с определенной глубиной проникновения. Эффект близости связан с интерференцией токов между отдельными соседними контурами, поскольку геометрическая форма поля не постоянна, а изменяется с частотой.Это представляет серьезную проблему для любой модели электромагнитной индукции. Однако подход прямого действия имеет внутреннее преимущество, заключающееся в том, что он может учитывать условия ускорения более высокого порядка. На более высоких частотах теория может быть адаптирована для моделирования тонких трубок с током, а не для предположения об однородной плотности тока.
Эффект близости связан с интерференцией токов между отдельными соседними контурами, поскольку геометрическая форма поля не постоянна, а изменяется с частотой.Это представляет серьезную проблему для любой модели электромагнитной индукции. Однако подход прямого действия имеет внутреннее преимущество, заключающееся в том, что он может учитывать условия ускорения более высокого порядка. На более высоких частотах теория может быть адаптирована для моделирования тонких трубок с током, а не для предположения об однородной плотности тока.
Для определения скин-эффекта в различных условиях были разработаны различные концепции и решения [36–42]. Более прямое и физическое объяснение скин-эффекта заключается в большей индуктивности (инерции электронов) нитей вблизи центра проводника по сравнению с нитями на поверхности.То есть инверсии тока на центральных нитях испытывают более высокое сопротивление/реактивное сопротивление по сравнению с инверсиями на поверхности. Следовательно, по мере увеличения частоты ток становится более ограниченным внешними областями проводника. Возможная физическая основа скин-эффекта была предложена с точки зрения электромагнитной массы ( M e ). Калвик [43] предположил, что эффективный заряд электронов проводимости не равен заряду всех имеющихся электронов проводимости и что ток переносится небольшим числом электронов, движущихся с высокой скоростью.Следуя этим рассуждениям, индуктивность можно рассматривать как аналог электромагнитной массы. Гровер [33], напротив, описывает скин-эффект в следующих терминах: «Электромагнитная энергия входит в поверхность провода и все больше и больше ослабляется и отстает по фазе по мере приближения к центру. На очень высоких частотах затухание настолько велико, что амплитуда тока становится незаметной после того, как волна проникнет в провод всего на долю миллиметра». По сути это объяснение, основанное на теореме Пойнтинга, согласно которой энергия, подводимая к проводнику с током, течет не по проводу, а через окружающее ЭМ поле [44].
Возможная физическая основа скин-эффекта была предложена с точки зрения электромагнитной массы ( M e ). Калвик [43] предположил, что эффективный заряд электронов проводимости не равен заряду всех имеющихся электронов проводимости и что ток переносится небольшим числом электронов, движущихся с высокой скоростью.Следуя этим рассуждениям, индуктивность можно рассматривать как аналог электромагнитной массы. Гровер [33], напротив, описывает скин-эффект в следующих терминах: «Электромагнитная энергия входит в поверхность провода и все больше и больше ослабляется и отстает по фазе по мере приближения к центру. На очень высоких частотах затухание настолько велико, что амплитуда тока становится незаметной после того, как волна проникнет в провод всего на долю миллиметра». По сути это объяснение, основанное на теореме Пойнтинга, согласно которой энергия, подводимая к проводнику с током, течет не по проводу, а через окружающее ЭМ поле [44].
Поскольку в настоящее время не существует удовлетворительной общей нелинейной теории электромагнитной индукции, полезно согласовать данные о частоте ЭДС индуцирования с помощью некоторой формы эмпирического закона. Существует линейное изменение примерно до 5 кГц в соответствии с законом Вебера. Приблизительно выше 5 кГц, когда скин-эффект становится все более значительным, задействованы частотные составляющие более высокого порядка. С помощью инструмента подгонки кривой Matlab получаются следующие выражения для значений выше 5 кГц (),
Существует линейное изменение примерно до 5 кГц в соответствии с законом Вебера. Приблизительно выше 5 кГц, когда скин-эффект становится все более значительным, задействованы частотные составляющие более высокого порядка. С помощью инструмента подгонки кривой Matlab получаются следующие выражения для значений выше 5 кГц (),
( e R ) p k − p k ⟨ r R 0375⟩ = 2,3 f 2 − − 22,4 f + 127,5
6,1
и
( E R ) P K — P K ⟨ R R = 0,15⟩ = 2.2 F 2 — 23,1 F + 124 ,
6,2
, где ЭДС индукции представляет собой размах в мВ, а частота – в кГц. Квадратичный ответ получается с коэффициентом детерминации ( R 2 ), рассчитанным как 0.9983 и 0,9986 для уравнений (6. 1) и (6.2) соответственно. Такие эмпирические подгонки для данной геометрии могут оказаться полезными в качестве основы для сравнения взаимной индуктивности в диапазоне частот.
1) и (6.2) соответственно. Такие эмпирические подгонки для данной геометрии могут оказаться полезными в качестве основы для сравнения взаимной индуктивности в диапазоне частот.
Наконец, стоит прокомментировать, почему любая нелинейная теория индукции оказывается трудной. Электрон проводимости, на который действует переменная сила, приходит в вынужденное колебание, при котором на него действуют как восстанавливающая, так и демпфирующая силы. По мере увеличения частоты возбуждения и ограничения потока электронов внешними областями проводника тот же ток через уменьшенную площадь вызовет увеличение скорости дрейфа электронов и, следовательно, увеличение амплитуды колебаний.Затем это приводит к нелинейной восстанавливающей силе (т. е. не слишком отличающейся от пружины, которая может становиться «жестче» или «мягче» в механической системе). Следствием этого является то, что гармоническое движение при малых амплитудах может стать гармоникой при больших амплитудах и, таким образом, привести к возникновению частотных членов более высокого порядка, которые затем необходимы для описания изменения напряжения вторичной обмотки.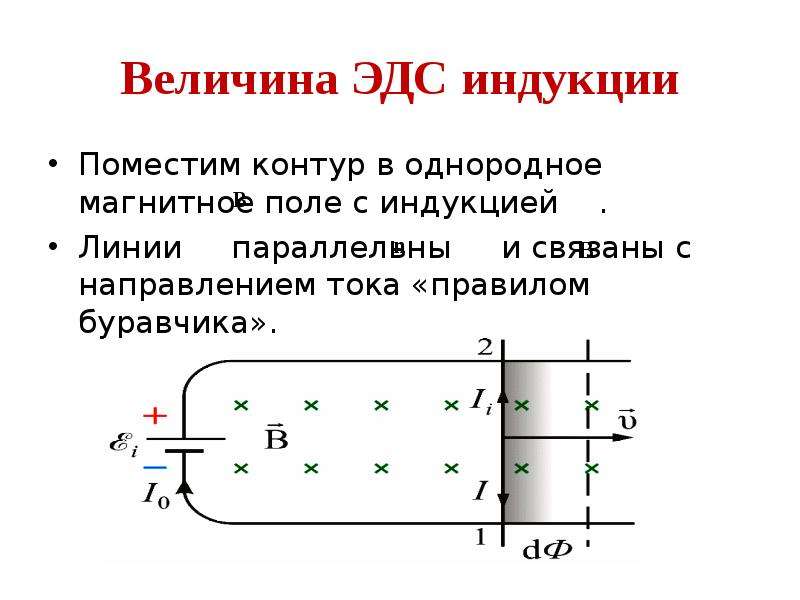
7. Выводы
Для исследованной схемы коаксиальной катушки подход прямого действия показывает хорошее согласие с экспериментальными измерениями для прогнозирования ЭДС индукции в приемной катушке на различных расстояниях от передатчика в ближней зоне (до пятикратного диаметра передающая катушка).Модель представляет интерес за пределами изучаемой здесь конструкции, поскольку ее вполне можно адаптировать для использования с катушками другой геометрии. Модель учитывает радиус каждой катушки, приложенную частоту, амплитуду тока возбуждения и вклад отдельных витков катушки, как указано в (3.6).
Показано, что линейность между ЭДС индукции и частотой сохраняется до частот приблизительно 5 кГц. Кроме того, постепенное ограничение тока внешними областями проводника (скин-эффект) приводит к нелинейной зависимости наведенного напряжения от частоты.Было обнаружено, что данные соответствуют квадратичной зависимости от частоты, как указано в (6.1) и (6.2). Что касается скин-эффекта, стандартное объяснение, основанное на поле, заключается в том, что он включает в себя поток электромагнитной энергии сбоку в проводник в соответствии с теоремой Пойнтинга. Модель, разработанная в этом исследовании, предполагает, что альтернативное объяснение связано с изменением инерции/индуктивности электронов в проводнике. В последнее время возобновился интерес к гидродинамическим аналогам потока электронов в конкретных материалах с некоторыми свидетельствами того, что электронная вязкость играет важную роль в определении электрического сопротивления [45].В связи с этим интересно отметить, что существует также гидродинамическая аналогия с электрической толщиной скин-слоя, связанная с акустическим течением в заполненной воздухом трубе, в которой низкочастотный пульсирующий поток накладывается на существующий установившийся поток [46]. Показано, что скорость частиц достигает максимального значения на расстоянии от стенки трубы, равном dw≈υ/πf, где υ — кинематическая вязкость. Это контрастирует с электрической глубиной скин-слоя, δ=1/πfμ0σ. Поскольку μ 0 является постоянным и ρ = 1/ σ , то δ≈ρ/πf обеспечивает аналогию с электронной вязкостью и электрическим сопротивлением.
Модель, разработанная в этом исследовании, предполагает, что альтернативное объяснение связано с изменением инерции/индуктивности электронов в проводнике. В последнее время возобновился интерес к гидродинамическим аналогам потока электронов в конкретных материалах с некоторыми свидетельствами того, что электронная вязкость играет важную роль в определении электрического сопротивления [45].В связи с этим интересно отметить, что существует также гидродинамическая аналогия с электрической толщиной скин-слоя, связанная с акустическим течением в заполненной воздухом трубе, в которой низкочастотный пульсирующий поток накладывается на существующий установившийся поток [46]. Показано, что скорость частиц достигает максимального значения на расстоянии от стенки трубы, равном dw≈υ/πf, где υ — кинематическая вязкость. Это контрастирует с электрической глубиной скин-слоя, δ=1/πfμ0σ. Поскольку μ 0 является постоянным и ρ = 1/ σ , то δ≈ρ/πf обеспечивает аналогию с электронной вязкостью и электрическим сопротивлением.
Будущая работа будет включать разработку этой модели для других случаев, в том числе конкретных приложений, представляющих интерес, таких как визуализация ИМ, а также изучение возможности расширения модели для включения членов более высокого порядка. Этот подход представляет интерес помимо того, что изучается здесь, поскольку он обеспечивает альтернативные и, возможно, более эффективные средства моделирования электромагнитной индукции в ближнем поле, которые могут быть полезны в смежных областях, таких как связь ближнего поля, радиочастотная идентификация и совместимость с ЭМ.Точность предсказания модели на значительном расстоянии от передатчика означает, что такое расположение может быть адаптировано в качестве эталонного стандарта для калибровки измерителей напряженности поля для приемных рамочных антенн. Кроме того, этот метод может иметь значение для изучения влияния электромагнитных взаимодействий ближнего поля с биологическими телами. Поскольку формулировка силы Вебера описывает движущиеся заряды, и это не обязательно должны быть электроны в медной проволоке, теория вполне может быть распространена на движущиеся заряженные частицы [47–51] или ионные частицы в биомедицинских системах [52–54]. в частности, предоставление информации о влиянии электромагнитной индукции на конкретные биологические процессы.
в частности, предоставление информации о влиянии электромагнитной индукции на конкретные биологические процессы.
Благодарности
Авторы выражают признательность Департаменту электротехники и электроники Ливерпульского университета.
Приложение A
показывает отдельные обороты передатчика-приемника, используемые при суммировании уравнения (3.6).
Рис. 7.
( a ) На схеме показано расположение отдельных витков в схеме приемо-передающей катушки. ( b ) Расширение матрицы из уравнения (3.6) для иллюстрации процедуры суммирования. (Онлайн-версия в цвете.)
Вклад авторов
R.T.S. и С.М. разработал и инициировал проект. Эксперименты проводились RTS при поддержке S.M., F.P.M.J. и И.С.Ю. Рукопись и рисунки были подготовлены R.T.S. и С.М. Все авторы рассмотрели рукопись.
Конкурирующие интересы
У авторов нет конфликта интересов, о котором следует заявить.
Финансирование
Это исследование не получило специального грантового финансирования.
Ссылки
7. Ma J, Zhang X, Huang Q, Cheng L, Lu M. Экспериментальное исследование влияния проводимости грунта на подземный магнитоиндукционный канал. Антенны IEEE и беспроводное распространение. лат. 14, 1782–1785 гг. (doi:10.1109/LAWP.2015.2423687).10. Sun Z, Wang P, Vuran MC, Al-Rodhaan MA, Al-Dhelaan AM, Akyildiz IF.
2011.
MISE-PIPE: беспроводные сенсорные сети на основе магнитной индукции для мониторинга подземных трубопроводов. Специальная сеть.
9, 218–227. (дои: 10.1016/j.adhoc.2010.10.006) [Google Scholar]11. Хуанг И, Бойл К.
2008.
Антенны: от теории к практике . Чичестер, Великобритания: John Wiley & Sons. [Google Академия] 15. Вернер ДХ.
1998.
Метод моментов для эффективного и точного моделирования цилиндрических проволочных антенн средней толщины. IEEE Trans. Антенны Распространение.
46, 373–382. (doi:10.1109/8.662656) [Google Scholar]16. Оверфель П.
1996.
Ближние поля постоянного тока тонкой круглой рамочной антенны произвольного радиуса.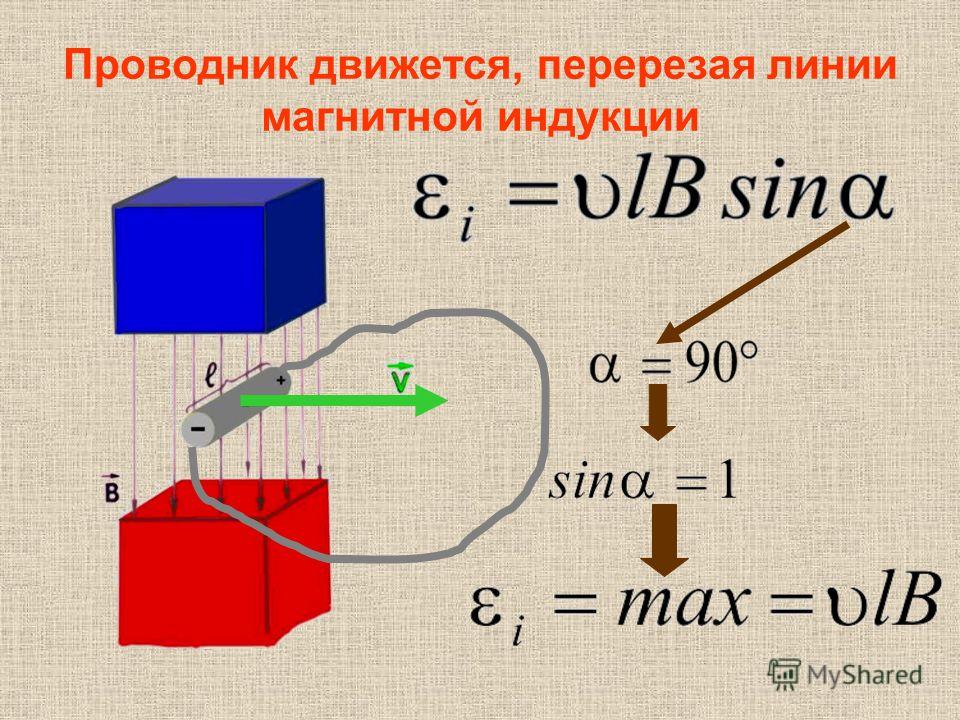 IEEE Trans. Антенны Распространение.
IEEE Trans. Антенны Распространение.
44, 166–171. (doi:10.1109/8.481643) [Google Scholar]18. Вернер Д.Х., Колегроув Т.В.
1999.
О новом цилиндрическом гармоническом представлении для сферических волн. IEEE Trans. Антенны Распространение.
47, 97–100. (doi:10.1109/8.752999) [Google Scholar]19. Фикиорис Г., Папаканеллос П.Дж., Анастассиу Х.Т.
2008.
Об использовании несингулярных ядер в некоторых интегральных уравнениях тонкопроволочных рамочных антенн. IEEE Trans. Антенны Распространение.
56, 151–157.(doi:10.1109/TAP.2007.6) [Google Scholar]
22. Mikki SM, Antar YMM.
2011.
О пространственной структуре антенны электромагнитного ближнего поля . Генеральная ассамблея и научный симпозиум, XXXth URSI 2011, Стамбул, Турция, 13–20 августа . стр. 1–4.
23. Микки С.М., Антар Ю.М.
2015.
Анализ общих взаимодействий ближнего поля с использованием функции Грина тока антенны. Прог. Электромагн. Рез. С
59, 1–9. (doi:10.2528/PIERC15060304) [Google Scholar]
25. Эме Дж., Руде Дж., Клавель Э., Ауин О., Лабарр С., Коста Ф., Экрабе Дж.
Эме Дж., Руде Дж., Клавель Э., Ауин О., Лабарр С., Коста Ф., Экрабе Дж.
2007.
Прогнозирование и измерение ближнего магнитного поля статического преобразователя . In Industrial Electronics, 2007. ISIE 2007. IEEE Int. Symp ., Виго, Испания, 4–7 июня , стр. 2550–2555. Пискатауэй, Нью-Джерси: IEEE.
32. Смит Р.Т., Джунджу Ф.П., Махер С.
2015.
Оценка отклонения электронного пучка поперек соленоида с помощью электродинамики Вебера-Ритца и Максвелла-Лоренца. Прог. Электромагн.Рез.
151, 83–93. (doi:10.2528/PIER15021106) [Google Scholar]33. Гровер Ф.В.
2004.
Расчет индуктивности . Минеола, Нью-Йорк: Dover Publications. [Google Академия] 34. Фейнман Р.П., Лейтон Р.Б., Сэндс М.
1963 год.
Фейнмановские лекции по физике, в основном по электромагнетизму и материи , vol. II
Редвуд-Сити: Эддисон Уэсли. [Google Академия] 35. Максвелл Дж.
1954.
Трактат об электричестве и магнетизме , том. 2
Нью-Йорк, штат Нью-Йорк: Довер. [Google Академия] 38. О КС.
О КС.
2000.
Точное моделирование переходных процессов в линиях электропередачи с использованием скин-эффекта. IEEE Trans. Компьютерный Des. интегр. Цирк. Сист.
19, 389–396. (doi:10.1109/43.833207) [Google Scholar]39. Бир О, Бом П, Прейс К, Вачутка Г.
2000.
Краевой конечно-элементный анализ нестационарных задач скин-эффекта. IEEE Trans. Магн.
36, 835–839. (doi:10.1109/20.877574) [Google Scholar]41. Айелло Г., Альфонцетти С., Борзи Г., Салерно Н.
2001.
Улучшенная схема решения задач скин-эффекта с открытой границей. IEEE Trans. Магн.
37, 3474–3477. (дои: 10.1109/20.952640) [Google Scholar]42. Джафари-Шапурабади Р., Конрад А., Синклер А.
2002.
Сравнение трех формулировок для задач вихревых токов и скин-эффекта. IEEE Trans. Магн.
38, 617–620. (doi:10.1109/20.996161) [Google Scholar]
43. Калвик Э.Г.
1949 год.
Основы электромагнетизма . Кембридж, Великобритания: Издательство Кембриджского университета.
44. Чубыкало А., Эспиноза А.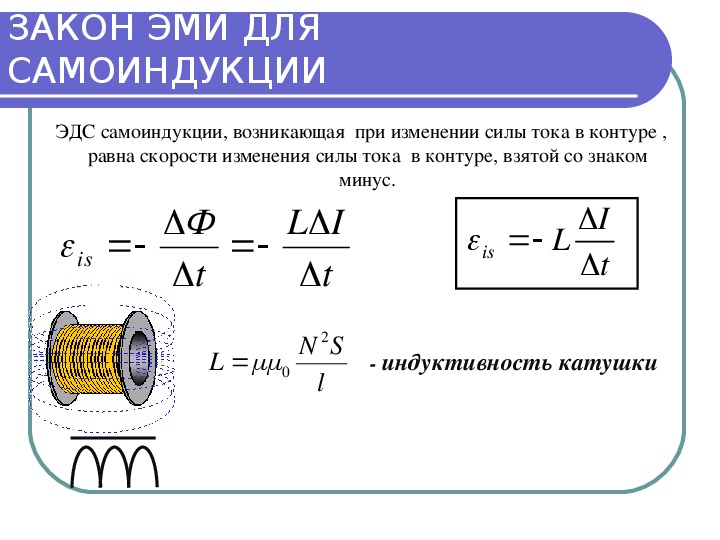 , Цончев Р.
, Цончев Р.
2004.
Экспериментальная проверка совместимости определений плотности электромагнитной энергии и вектора Пойнтинга. евро. физ. Дж. Д
31, 113–120. (doi:10.1140/epjd/e2004-00135-x) [Google Scholar]46. Ричардсон ЭГ.
1961.
Динамика реальных жидкостей . Лондон, Великобритания: Эдвард Арнольд. [Google Академия] 49. Сайед С.У., Махер С., Эйкель Г.Б., Эллис С.Р., Джунджу Ф., Тейлор С., Хирен Р.М.
2015.
Метод прямой визуализации ионов для исследования динамики ионов в мультипольных ионопроводах. Анал. хим.
87, 3714–3720. (doi:10.1021/ac5041764) [PubMed] [Google Scholar]50. Махер С., Сайед С.У., Хьюз Д.М., Гибсон Дж.Р., Тейлор С.2013.
Отображение диаграммы устойчивости квадрупольного масс-спектрометра при приложении статического поперечного магнитного поля. Дж. Ам. соц. Масс-спектр.
24, 1307–1314. (doi:10.1007/s13361-013-0654-5) [PubMed] [Google Scholar]51. Шрикумар Дж., Хоган Т.Дж., Тейлор С.
2012.
Моделирование СМК с учетом влияния давления в ионном источнике электронного удара. IEEE Trans. Инструм. Изм.
IEEE Trans. Инструм. Изм.
61, 3024–3030. (doi:10.1109/TIM.2012.2202166) [Google Scholar]53. Лю С, Дуань В, Сюй С, Чен С, Хе М, Чжан Л, Ю З, Чжоу З.2013.
Воздействие радиочастотного электромагнитного излучения с частотой 1800 МГц вызывает окислительное повреждение оснований ДНК в клеточной линии, полученной из сперматоцитов мыши. Токсикол. лат.
218, 2–9. (doi:10.1016/j.toxlet.2013.01.003) [PubMed] [Google Scholar]
Лекция 15, 11 октября 2000 г.
Лекция 15, 11 октября 2000 г.
индекс курса
Вспомнить с последней лекции:
- Создание магнитных полей:
- Длинный прямой провод: B = m 0 I / 2p r
- Соленоид: B = m 0 n I
- Сила магнитного поля:
- Подвижный заряд: F = q v B sinq
- Провод: F = B I l sinq
- Крутящий момент в токовой петле: t = B I A sinq
- Усилие между двумя проводами: F / l = m 0 I 1 I 2 / 2p d
- привлекательный, когда течения идут в одном направлении
- отталкивающий, когда токи противоположны по направлению
Гл.
 20: Наведенные напряжения и индуктивность
20: Наведенные напряжения и индуктивность
Мы видели, что магнитное поле воздействует на провод, по которому течет ток, и что провод, по которому течет ток, создает магнитное поле.
Токи создаются электрическими полями, так что, похоже, между электричеством и магнетизмом существует какая-то связь.
В этой главе мы установим эту связь, увидев, как магнитное поле может создавать разность потенциалов.
Магнитный поток будет играть важную роль на протяжении всей этой главы.
20.1 ЭДС индукции и магнитный поток
Эксперименты 19 века показали, что изменяющееся магнитное поле может создавать ЭДС.
Мы количественно определяем изменение с точки зрения магнитного потока.
Магнитный поток определяется аналогично электрическому потоку.
Для проволочной петли площадью A в магнитном поле B магнитный поток F определяется выражением:
F = B perp A = B A cosq
где q — угол между перпендикуляром к плоскости петли и магнитным полем B.Единицы магнитного потока в системе СИ — Тм².
Другой способ взглянуть на поток — представить его как количество силовых линий магнитного поля, проходящих через петлю.
Если петля ориентирована перпендикулярно полю (q=0), то поток будет большим.
Если петля ориентирована параллельно полю (q = 90°), силовые линии магнитного поля не проходят через петлю, и поток равен нулю.
Пример: P20.2
Квадратная петля со стороной 2,00 м помещена в магнитное поле с напряженностью 0.300т.
Если поле образует угол 50,0° с нормалью к плоскости петли, как на рис. 20.2, определите магнитный поток через петлю.
Из того, что нам дано, мы используем
F = B A cosq = (0,300T)(2,00m)²cos50,0° = 0,386 Tm²
20.2 Закон индукции Фарадея
Закон индукции Фарадея связывает изменение магнитного потока с ЭДС индукции:
ЭДС = -N (DF / Dt)
где N — число витков в катушке, в которых индуцируется ЭДС, а DF — изменение потока, происходящее за время Dt.Это один из случаев, когда термин ЭДС несколько отличается от напряжения, и поэтому я буду использовать его.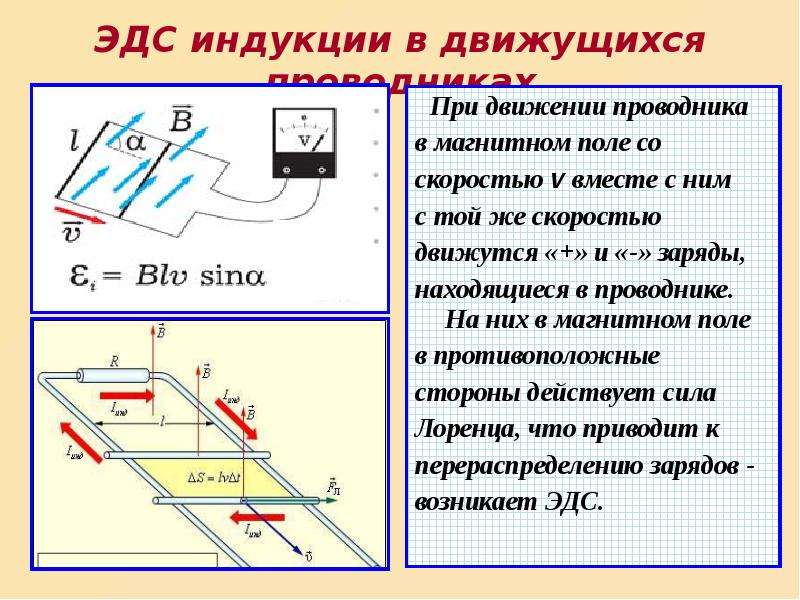
ЭДС индукции пропорциональна изменению магнитного потока, F = BAcosq.
Существует три способа изменения потока:
- изменение величины магнитного поля, В,
- изменение угла между контуром и магнитным полем, q, или
- изменение площади петли, А.
Знак минус напоминает вам, что полярность ЭДС индукции препятствует изменению потока.Это точно указано в законе Ленца:
Полярность ЭДС индукции такова, что она создает ток, магнитное поле которого противодействует изменению магнитного потока через контур.
То есть индуцированный ток имеет тенденцию поддерживать первоначальный поток через цепь.
Пример: P20.13
Проволочная петля радиусом 0,30 м расположена так, что внешнее магнитное поле с напряженностью +0,30 Тл перпендикулярно петле.
Поле меняется на -0,20 Тл за 1,5 с.
(Здесь знаки плюс и минус относятся к противоположным направлениям цикла.)
Найти величину средней ЭДС индукции в контуре за это время.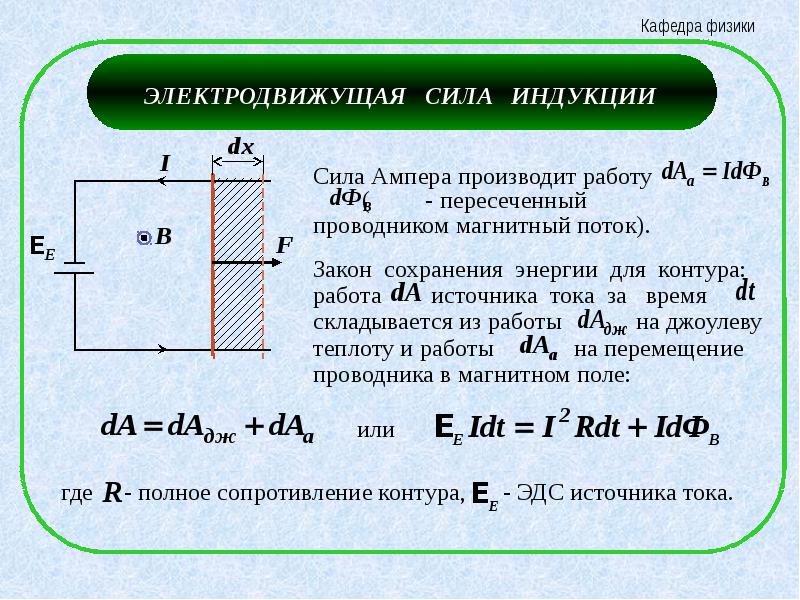
Петля всегда перпендикулярна полю, поэтому нормаль к петле параллельна полю, поэтому q = 0, а cosq = 1.
Таким образом, поток через контур равен F = BA = Bpr².
Первоначально поток равен
F i = (0,30T)p(0,30м) 2 = 0,085Tm²
, а после изменения поля поток равен
F f = (-0,20T)p(0,30м) 2 = -0,057Tm²
Величина средней ЭДС индукции:
ЭДС = DF/Dt = (F i — F f )/Dt = (0.085T — (-0,057T))/1,5 с = 0,095 В = 95 мВ.
Пример: P20.10
Гибкая петля на рис. P20.10 имеет радиус 12 см и находится в магнитном поле напряженностью 0,15 Тл.
Петлю захватывают в точках А и В и растягивают до закрытия.
Если для замыкания контура требуется 0,20 с, найти величину средней ЭДС индукции в нем за это время.
Это тот случай, когда изменение потока вызвано изменением площади контура.
И магнитное поле, и угол q остаются постоянными.Когда петля растянута так, что ее площадь равна нулю, поток через петлю равен нулю.
Таким образом, изменение потока равно его первоначальному значению:
F i = BA cosq = (0,15T)p(0,12m)² = 6,8×10 -3 Tm²
Средняя ЭДС индукции равна:
ЭДС = N (DF / Dt) = (6,8×10 -3 Тм²)/(0,20 с) = 3,4×10 -2 В = 34 мВ.
20.3 ЭДС движения
Интересным применением закона Фарадея является создание ЭДС посредством движения проводника.В качестве простого примера рассмотрим проводящий стержень, движущийся перпендикулярно однородному магнитному полю с постоянной скоростью v.
На первый взгляд у нас есть просто стержень, а не полная проводящая петля, и мы рассмотрим, что происходит, используя только силу, действующую на движущийся заряд, F = qvBsinq.
Эта сила будет действовать на свободные заряды в проводнике.
Он будет иметь тенденцию перемещать отрицательный заряд к одному концу и оставлять другой конец стержня с чистым положительным зарядом.
Разделенные заряды создадут электрическое поле, которое будет стремиться сблизить заряды.Когда существует равновесие, магнитная сила F=qvB будет уравновешивать электрическую силу F=qE, так что свободный заряд в стержне не будет ощущать результирующей силы.
Таким образом, в равновесии E = vB.
Разность потенциалов на концах стержня определяется как DV = E l, или
DV = E л = B л v
Эта разность потенциалов существует из-за избытка заряда на концах проводника, создаваемого движением через магнитное поле.
Если направление движения меняется на противоположное, меняется и полярность разности потенциалов.
Теперь давайте посмотрим, что произойдет, если мы добавим токопроводящие шины для верхней и нижней части стержня, чтобы они соприкасались, и резистор между ними, чтобы замкнуть контур.
Мы можем применить закон Фарадея к полной петле.
Изменение потока через петлю пропорционально изменению площади от движения стержня:
DF = B DA = B 1 Dx.
Используя закон Фарадея, мы находим величину ЭДС равной (N = 1):
ЭДС = DF/Dt = B l Dx/Dt = B l v
где я использовал соотношение v = Dx/Dt.Это тот же результат, который мы получили, рассматривая проводящий стержень сам по себе.
Если проводящая цепь имеет полное сопротивление, R, то ток равен
I = ЭДС / R = B l v / R
Пример: P20.18
Над областью, где вертикальная составляющая магнитного поля Земли 40,0 мкТл направлена вниз, провод длиной 5,00 м удерживается в направлении восток-запад и перемещается горизонтально на север со скоростью 10,0 м/с.
Рассчитайте разность потенциалов между концами провода и определите, какой конец положительный.
Вертикальная составляющая магнитного поля перпендикулярна проводу и его движению, так что это то, что нам нужно.
Использование выражения, полученного для DV, дает:
DV = B l v = (40,0 мкТл)(5,00 м)(10,0 м/с) = 2,00 мВ
Чтобы определить, какой конец положительный, рассмотрим положительный заряд, движущийся на север через нисходящее магнитное поле.
Правило правой руки дает силу, направленную на запад.
Таким образом, западный конец провода будет иметь чистый положительный заряд и более положительный потенциал.
Взаимный | Определение собственной индуктивности | Формула
При изменении потокосцепления с катушкой (или проводником) в катушке индуцируется ЭДС. Эта ЭДС может быть вызвана следующими двумя способами:
- Вращением катушки в стационарном магнитном поле или вращением магнитного поля в стационарной катушке (как в генераторах переменного и постоянного тока). Индуцированная ЭДС таким образом известна как динамически индуцированная ЭДС. Он так называется потому, что в этом случае движется либо магнитное поле, либо катушка.
- Магнитное поле и катушка неподвижны. Но поток, связанный с катушкой, изменяется за счет изменения тока, создающего этот поток (как в трансформаторах). Индуцированная ЭДС таким образом называется статически индуцированной ЭДС. Он так называется, потому что магнитное поле и катушка в этом случае стационарны. ЭДС статического электричества можно разделить на следующие две категории: 91 100
- ЭДС самоиндукции
- ЭДС взаимной индукции
ЭДС самоиндукции
ЭДС, индуцируемая в катушке из-за изменения потока, создаваемого ею при соединении с ее собственными витками, называется ЭДС самоиндукции.
Рассмотрим катушку с N витками на железном сердечнике, подключенную к батарее, как показано на рисунке. По катушке протекает ток I , он создает поток φ. Этот поток также связан со своими витками. Если ток, протекающий через катушку, изменяется за счет изменения переменного сопротивления R, это изменяет поток, связанный с катушкой, и, следовательно, в катушке индуцируется ЭДС.
Наведенная таким образом ЭДС называется ЭДС самоиндукции. Направление ЭДС индукции таково, что оно препятствует изменению тока i.е. причина, которая его производит (закон Ленца).
Величина ЭДС самоиндукции прямо пропорциональна скорости изменения потока, связанного с катушкой (закон Фарадея). Но скорость изменения потока, связанного с катушкой, прямо пропорциональна скорости изменения тока в катушке.
Следовательно, ЭДС самоиндукции, e α – d I /dt
Или e = – L(d I /dt) ……….(i)
постоянная пропорциональности и известна как коэффициент собственной индуктивности или собственной индуктивности или индуктивности катушки.
Свойство катушки сопротивляться любому изменению тока, протекающего через нее, известно как собственная индуктивность или индуктивность катушки.
Собственная индуктивность, L = (N 2 µ o µ r a) ÷ l
где N = число витков катушки,
a = площадь поперечного сечения магнитопровода,
l = длина магнитной цепи.
Катушка приобретает это свойство за счет ЭДС самоиндукции в катушке при изменении тока, протекающего через нее.
Как показано на рисунке, если ток в катушке увеличивается (за счет изменения сопротивления реостата), ЭДС самоиндукции устанавливается в таком направлении, чтобы противодействовать нарастанию тока, т.е. ЭДС индуцирования противоположна ЭДС приложенного напряжения.
Аналогично, если ток в катушке уменьшается, ЭДС самоиндукции устанавливается в таком направлении, чтобы противодействовать падению тока, т.е. направление ЭДС самоиндукции совпадает с направлением направления приложенное напряжение.
Можно отметить, что собственная индуктивность не препятствует изменению тока, поскольку для преодоления этого противодействия батарея поставляет дополнительную энергию. Однако задерживает изменение тока через катушку .
Можно отметить, что наличие индуктивности в цепи проявляется только при изменении тока в цепи.
Например, при установившихся (прямых) потоках через катушку, имеющую индуктивность (в силу своих геометрических и магнитных свойств), не будет проявляться ее наличие.
Однако, когда через ту же катушку протекает переменный (непрерывно изменяющийся) ток, он будет эффективно демонстрировать свое присутствие.
Единицей индуктивности является Генри (Гн).
Если в приведенном выше уравнении (i) e = 1 вольт и d I /dt = 1 А/сек, то L = 1 Гн.
Следовательно, говорят, что катушка (или цепь) имеет индуктивность один Генри, если в нем индуцируется ЭДС в 1 вольт при изменении тока через него со скоростью один ампер в секунду.
Из приведенного выше выражения видно, что индуктивность обратно пропорциональна сопротивлению магнитной цепи.Следовательно, катушка, намотанная на магнитный сердечник (низкое сопротивление), имеет большую индуктивность, чем эквивалентная катушка с воздушным сердечником.
ЭДС взаимной индукции
ЭДС, индуцированная в катушке из-за изменения потока, создаваемого другой катушкой, называется ЭДС взаимной индукции.
Рассмотрим катушку X, имеющую N 1 витков, и катушку Y, имеющую N 2 витков, намотанную на железный стержень. Когда эти катушки соединены по схеме, как показано на рисунке, ток протекает через катушку X и создает поток φ 1 .
Часть этого потока также связана с катушкой Y. Если ток, протекающий через катушку X, изменить путем изменения переменного сопротивления R, он изменяет поток, связанный с другой катушкой Y, и, следовательно, в катушке Y индуцируется ЭДС .
Индуцированная таким образом ЭДС известна как взаимно индуцированная ЭДС. Направление взаимно индуцированной ЭДС таково, что она противодействует изменению тока в катушке X, т. е. причине, которая его производит (закон Ленца).
математически, взаимно индуцированные EMF, E M α — D I 1 / DT
или E M = — M (D I 1 / DT)
Где М — постоянная пропорциональности, известная как коэффициент взаимной индуктивности или взаимной индуктивности катушки.
Взаимная индуктивность между двумя катушками может быть определена как свойство второй катушки, благодаря которому она препятствует изменению тока в первой катушке. Выражения для взаимной индуктивности:
м = (N 1 N 2 μ O μ R1 A 1 ) ÷ L 1 ) ÷ L 1
M = (N 1 N 2 μ O μ R2 A R2 A 2 ) ÷ L 2
, где, N 1 , N 2 = количество оборотов катушек,
A 1 , 2 = площади поперечного сечения магнитопроводов,
l 1 , l 2 = длины магнитопроводов.
Коэффициент сцепления
Доля магнитного потока, создаваемого током в первой катушке, которая связана со второй катушкой, называется коэффициентом связи (k) между двумя катушками.
Коэффициент связи, k = M ÷ √(L 1 L 2 )
где M = взаимная индуктивность между двумя катушками,
L 1 = собственная индуктивность первой катушки,
L 2 = Самоиндукция второй катушки.
Значение k равно единице, если поток, создаваемый одной катушкой, полностью связан с другой. Из-за эффекта утечки потока значение k всегда меньше единицы. Значение взаимной индуктивности зависит от значения коэффициента связи (k). Его значение максимально при k = 1,
Электромагнетизм | Все сообщения
© http://www.yourelectricalguide.com/ определение и формула собственной индуктивности.
Как рассчитать ЭДС катушки? – М.В.Организинг
Как рассчитать ЭДС катушки?
Расчет ЭДС индукции Закон Фарадея гласит: ЭДС индукции равна скорости изменения магнитного потока.Магнитный поток = напряженность магнитного поля x площадь = BA. Следовательно… Индуцированная ЭДС = (изменение плотности магнитного потока x площадь)/изменение во времени.
Что такое ЭДС индукции в физике?
Его можно определить как создание разности потенциалов в катушке из-за изменения магнитного потока через нее. Проще говоря, говорят, что электродвижущая сила или ЭДС индуцируется, когда изменяется поток, связанный с проводником или катушкой.
Как найти ЭДС индукции в контуре?
Рассчитайте производную по времени потока, dΦB/dt.Величина ЭДС индукции, |εind| равно |dΦB/dt|. Если вам нужно найти ток, вы часто можете найти его, используя закон Ома, I = ε/R, где R — сопротивление провода.
Как рассчитать максимальную ЭДС индукции?
ЭДС=2Bℓw2ωsinωt=(ℓw)Bωsinωt ЭДС знак равно 2 B ℓ ш 2 ω грех ω т знак равно ( ℓ ш ) B ω грех . — максимальная (пиковая) ЭДС. Обратите внимание, что частота колебаний f = ω/2π, а период T = 1/f = 2π/ω.
Какой пример динамической ЭДС?
ДИНАМИЧЕСКАЯ ЭДС Таким образом, следуя одному из двух процессов, проводник пересекает магнитное поле, и в катушке индуцируется ЭДС.Это явление имеет место в электрических генераторах и противо-ЭДС двигателей, а также в трансформаторах.
Чему равна ЭДС индукции в цепи?
Чтобы быть абсолютно точным, если изменить магнитный поток через катушку, возникнет напряжение. Это напряжение известно как ЭДС индукции. Магнитный поток является мерой количества силовых линий магнитного поля, проходящих через площадь.
Что является основной причиной ЭДС индукции?
Самая основная причина индуцированной ЭДС — изменение магнитного потока.Размещение катушки с током, которая постоянно движется в стабильном и статическом магнитном поле. Это вызовет изменение вектора площади и, следовательно, будет генерироваться ЭДС.
Что такое ЭДС самоиндукции?
Определение: ЭДС самоиндукции — это ЭДС, индуцированная в катушке из-за изменения потока, вызванного ее связью с ее собственными витками. Это явление ЭДС самоиндукции можно дополнительно понять на следующем примере, приведенном ниже: Рассмотрим катушку, имеющую N витков, как показано на рисунке выше.
Может ли быть отрицательное ЭДС?
Напряжение всегда не отрицательное. Знак минус в законе Фарадея (законе Ленца) не означает, что ЭДС (или ток) всегда указывает в каком-то «отрицательном» направлении. Это означает, что ток всегда течет таким образом, чтобы противостоять изменению потока, что хорошо показано в этом видеоклипе.
Что такое ЭДС движения?
ЭДС, индуцированная движением относительно магнитного поля B, называется ЭДС движения и определяется как. ЭДС = Bℓv (B, ℓ и v перпендикулярны), где ℓ — длина объекта, движущегося со скоростью v относительно поля.
Как сделать ЭДС?
ЭДС индуцируется в катушке или проводнике всякий раз, когда происходит изменение потокосцепления. В зависимости от того, каким образом происходят изменения, различают два типа: Когда проводник перемещается в стационарном магнитном поле, чтобы вызвать изменение потокосцепления, ЭДС индуцируется статически.
Как определить полярность ЭДС индукции?
Когда ЭДС генерируется изменением магнитного потока в соответствии с законом Фарадея, полярность ЭДС индукции определяется законом Ленца.
Можно ли вызвать ЭДС в разомкнутой цепи?
Да, ЭДС может существовать без протекания тока. Рассмотрим закон Ома: V= IR ; V = ЭДС индукции. Для разомкнутой цепи R -> бесконечность Следовательно, I = V / бесконечность = 0 даже для некоторого ненулевого значения V. Это то же самое, что и изолированная ячейка. ЭДС будет индуцироваться в проводе только в том случае, если он проходит через переменное магнитное поле.
Какова полярность ЭДС индукции?
Иногда трудно определить полярность ЭДС индукции. Закон Ленца гласит, что индуцированная ЭДС, возникающая в результате изменения магнитного потока, имеет полярность, которая приводит к индуцированному току, направление которого таково, что индуцированное магнитное поле противодействует первоначальному изменению потока.
Что понимается под полярностью ЭДС индукции?
Когда ЭДС генерируется изменением магнитного потока в соответствии с законом Фарадея, полярность ЭДС индукции такова, что она создает ток, магнитное поле которого противодействует изменению, которое его вызывает. Если оно уменьшается, индуцированное поле действует в направлении приложенного поля, пытаясь сохранить его постоянным.
Что такое собственная индуктивность L?
В электрической цепи, когда ЭДС индуцируется в той же цепи, в которой изменяется ток, этот эффект называется самоиндукцией ( L ), но иногда его обычно называют обратной ЭДС, поскольку его полярность противоположна направлению приложенное напряжение.
Какой закон определяет направление ЭДС индукции?
Закон Ленца используется для определения направления индукционного тока. Закон электромагнитной индукции Ленца гласит, что направление индуцированного тока в данном магнитном поле таково, что он противостоит индуцированному изменению за счет изменения магнитного поля.
Что подразумевается под полярностью?
1 : качество или состояние, присущее телу, которое проявляет противоположные свойства или силы в противоположных частях или направлениях или которое проявляет противоположные свойства или силы в противоположных частях или направлениях: состояние наличия полюсов.
Что такое полярный и неполярный?
Полярные молекулы возникают, когда существует разница в электроотрицательности между связанными атомами. Неполярные молекулы возникают, когда электроны поровну распределяются между атомами двухатомной молекулы или когда полярные связи в более крупной молекуле компенсируют друг друга.
Какие бывают два типа полярности?
1.7 Полярность. Полярность относится к электрическим условиям, определяющим направление тока относительно электрода. Состояние полярности электродов бывает двух типов: (1) прямая полярность и (2) обратная полярность.
Что такое полярное и неполярное соединение?
Полярная ковалентная связь представляет собой тип ковалентной связи, образованной между двумя неидентичными атомами. Неполярная ковалентная связь – это ковалентная связь, в которой разница в электроотрицательности между связанными атомами меньше 0,5.
Как узнать, является молекула полярной или неполярной?
- Если расположение симметрично и стрелки одинаковой длины, молекула неполярна.
- Если стрелки разной длины и если они не уравновешивают друг друга, молекула полярна.
- Если расположение асимметрично, молекула полярна.
Как определить, является соединение полярным или неполярным?
Взгляните еще раз на воду. Вода связана с двумя атомами водорода, а также имеет две неподеленные пары электронов. Имеет четырехгранную изогнутую форму. Чтобы определить, является ли молекула полярной, вы должны посмотреть на векторы частичного заряда на двух связях в молекуле.
Что такое неполярное соединение?
соединение, состоящее из молекул, обладающих симметричным распределением заряда, так что не существует ни положительных, ни отрицательных полюсов, и которые не ионизируются в растворе, например, углеводороды.
В чем разница между полярной и неполярной ковалентной связью?
Связи, которые являются частично ионными, называются полярными ковалентными связями. Неполярные ковалентные связи с равным распределением электронов связи возникают, когда электроотрицательности двух атомов равны.
Является ли CO2 полярным или неполярным?
И CO2, и h3O имеют две полярные связи. Однако диполи в линейной молекуле СО2 компенсируют друг друга, а это означает, что молекула СО2 неполярна.
Почему CO полярен, а CO2 неполярен?
Он содержит две полярные связи, расположенные симметрично.Углерод образует двойную связь с каждым атомом кислорода. Но геометрия CO2 является линейной, так что дипольные моменты двух связей сокращаются, и нет результирующего молекулярного дипольного момента. Таким образом, молекула неполярна.
Какой тип молекулы представляет собой CO2?
ковалентный
Является ли CCl4 полярной или неполярной молекулой?
CCl4, представляющий собой четыреххлористый углерод, неполярен, поскольку все четыре связи симметричны и вытянуты во всех направлениях.
Почему CCl4 неполярная молекула?
Молекула CCl4 неполярна по своей природе из-за своей симметричной тетраэдрической структуры.Однако связь C-Cl является полярной ковалентной связью, но четыре связи компенсируют полярность друг друга и образуют неполярную молекулу CCl4.
Что такое формула ЭДС индукции? – Easyrwithpractice.com
Что такое формула ЭДС индукции?
Закон Фарадея гласит: ЭДС индукции равна скорости изменения магнитного потока. Магнитный поток = напряженность магнитного поля x площадь = BA. Следовательно… Индуцированная ЭДС = (изменение плотности магнитного потока x площадь)/изменение во времени. Следовательно, ЭДС индукции = (Bπr2n)/t.
Как рассчитать ЭДС индукции в контуре?
ЭДС, индуцированная в цепи, прямо пропорциональна скорости изменения магнитного потока через цепь во времени. Предположим, что петля, охватывающая площадь А, находится в однородном магнитном поле. = ВА cos θ. ЭДС индукции равна ε = – d/dt (BA cos θ).
Как рассчитать среднюю индуцированную ЭДС?
Мы используем закон индукции Фарадея, чтобы найти среднюю ЭДС, индуцированную за время Δt: ЭДС=−NΔΦΔt ЭДС = − N Δ Φ Δ t .
Какова средняя ЭДС индукции?
Средняя ЭДС индукции равна изменению магнитного потока во времени. Таким образом, ЭДС индукции будет равна 0,
.
Какова средняя ЭДС?
В исследовании, в ходе которого измерялось ЭМП почти в 1000 домах в США, средний уровень ЭМП в 50% домов был 0,6 мГс или меньше, а в 95% средний уровень ЭМП был ниже 3 мГс. Имейте в виду, что это средние уровни ЭМП в доме.
Как рассчитать ЭДС?
Если мы знаем результирующую энергию и количество заряда, прошедшего через ячейку.Это самый простой способ расчета ЭДС. Электродвижущая сила клетки… Формула для расчета ЭДС.
| \varepsilon | электродвижущая сила |
|---|---|
| Е | энергия в цепи |
| В | Заряд цепи. |
Можно ли генерировать ЭДС без вращающейся катушки?
(c) Да, можно генерировать ЭДС без вращения катушки. Вместо вращения, если позволить катушке двигаться со скоростью ⊥r к полю, то также индуцируется ЭДС движения.Также при изменении А и В индуцируется ЭДС.
Что такое принцип работы генератора переменного тока?
Генераторы переменного тока
работают по принципу закона электромагнитной индукции Фарадея, который гласит, что электродвижущая сила — ЭДС или напряжение — генерируется в проводнике с током, пересекающем однородное магнитное поле.
Как магнитный поток связан с изменениями катушки в генераторе?
Ответ: Перемещение магнита рядом с катушкой изменяет магнитное поле в катушке, что, в свою очередь, изменяет магнитный поток, связанный с катушкой.Следовательно, в цепи индуцируется ЭДС, следовательно, возникает ток. Ответ: ЭДС увеличивается на 12,
.
Почему ЭДС максимальна, когда плоскость якоря параллельна магнитному полю?
Когда плоскость якоря параллельна силовым линиям магнитного поля, скорость изменения связанного с ней магнитного потока максимальна. Следовательно, э.д.с. наведенная в якоре в этой ориентации максимальна.
От каких факторов зависит ЭДС индукции?
Индуцированный э.м.ф. прямо пропорциональна B, напряженности магнитного поля, в котором вращается катушка. ЭДС индукции прямо пропорциональна w, угловой скорости катушки. ЭДС индукции также меняется со временем и зависит от момента времени t.
Почему ЭДС максимальна, когда поток равен нулю?
Величина ЭДС индукции пропорциональна скорости изменения магнитного потока. Чем быстрее вращается катушка, тем больше максимальное значение ЭДС индукции, так как увеличение угловой скорости вызывает более быстрое изменение магнитного потока.ЭДС индукции проходит через нуль, когда кривая потока имеет нулевой наклон.
При каком угле поворота ЭДС индукции максимальна объясните обоснованно?
Когда плоскость якоря параллельна силовым линиям магнитного поля, скорость изменения связанного с ней магнитного потока максимальна. Следовательно, ЭДС, индуцируемая в якоре в этой ориентации, максимальна.
Зависит ли ЭДС индукции от сопротивления?
Из формулы видно, что ЭДС индукции не зависит от сопротивления катушки или провода.Однако, если индуцированная ЭДС создает ток, то этот производимый ток будет зависеть от сопротивления катушки или провода.
ЭДС прямо пропорциональна сопротивлению?
Ответ: Сила тока прямо пропорциональна разности электрических потенциалов и обратно пропорциональна сопротивлению.
Всегда ли ЭДС индукции действует на уменьшение?
5 Всегда ли ЭДС индукции уменьшает магнитный поток в цепи? Ответ Нет. Согласно закону Ленца, ЭДС индукции противодействует причине, вызвавшей ее.
Какие факторы влияют на ЭМП?
Минимум, что требуется для индукции ЭДС, это проводник, поток и движение проводника в магнитном поле. Из этого уравнения видно, что ЭДС индукции зависит от плотности потока, эффективной длины проводника, скорости проводника и угла между направлением скорости и направлением потока.
Какой закон определяет направление ЭДС индукции?
Закон Ленца
Всегда ли ЭДС индукции уменьшает магнитный поток через катушку?
Полярность ЭДС индукции такова, что она создает ток, магнитное поле которого противостоит вызывающему его изменению.Наведенное магнитное поле внутри любого контура провода всегда поддерживает постоянный магнитный поток в контуре. Это неотъемлемое поведение генерируемых магнитных полей резюмируется в законе Ленца.
Что дает закон Ленца?
Закон Ленца гласит, что ток, индуцируемый в цепи из-за изменения магнитного поля, направлен на противодействие изменению потока и создает механическую силу, противодействующую движению. Это означает, что направление обратной ЭДС индуцированного поля противоположно изменяющемуся току, который является ее причиной.
Где используется закон Ленца?
Закон Ленца используется в электромагнитных тормозах и индукционных варочных панелях. Он также применяется к электрическим генераторам, генераторам переменного тока.
Является ли ЭДС движения силой?
ЭДС, вызванная движением проводника поперек магнитного поля, является движущей электродвижущей силой. Уравнение задается как E = -vLB. Стержень проводника движется с постоянной скоростью и помещается в магнитное поле.



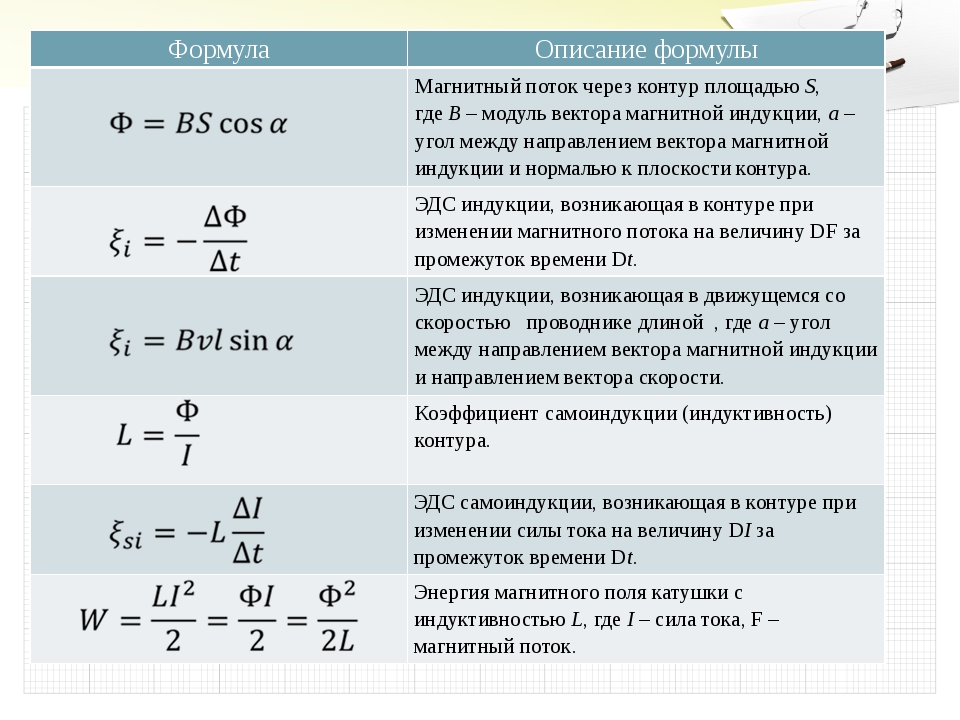
 Перечислить 6 способов
Перечислить 6 способов