Плоский конденсатор, теория и примеры задач
Большое число конденсаторов, которые применяют в технике, приближены по типу к плоскому конденсатору. Это конденсатор, который представляет собой две параллельные проводящие плоскости (обкладки), которые разделяет небольшой промежуток, заполненный диэлектриком. На обкладках сосредоточены равные по модулю и противоположные по знаку заряды.
Электрическая емкость плоского конденсатора
Электрическая емкость плоского конденсатора очень просто выражается через параметры его частей. Изменяя площадь пластин конденсатора и расстояние между ними легко убедиться, что электрическая емкость плоского конденсатора прямо пропорциональна площади его пластин (S) и обратно пропорциональна расстоянию между ними (d):
Формулу для расчета емкости плоского конденсатора просто получить при помощи теоретических расчетов.
Положим, что расстояние между пластинами конденсатора много меньше, чем их линейные размеры.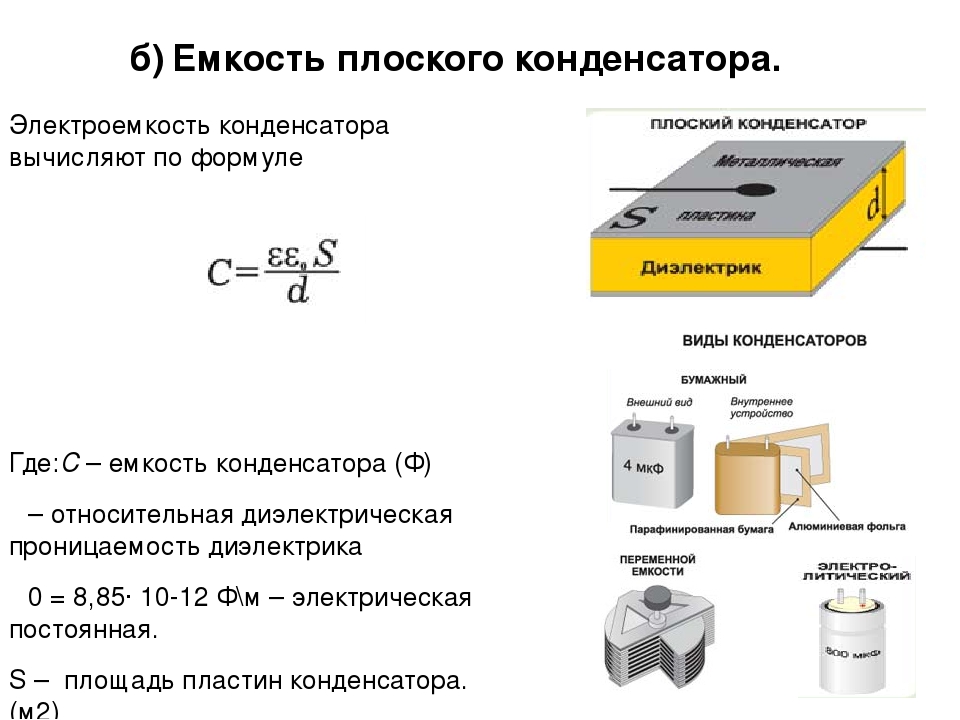 Тогда краевыми эффектами можно пренебречь, и электрическое поле между обкладками считать однородным. Поле (E), которое создают две бесконечные плоскости, несущие одинаковый по модулю и противоположный по знаку заряд, разделенные диэлектриком с диэлектрической проницаемостью , можно определить при помощи формулы:
Тогда краевыми эффектами можно пренебречь, и электрическое поле между обкладками считать однородным. Поле (E), которое создают две бесконечные плоскости, несущие одинаковый по модулю и противоположный по знаку заряд, разделенные диэлектриком с диэлектрической проницаемостью , можно определить при помощи формулы:
где — плотность распределения заряда по поверхности пластины. Разность потенциалов между рассматриваемыми обкладками конденсатора, находящимися на расстоянии d будет равна:
Подставим правую часть выражения (3) вместо разности потенциалов в (1) учитывая, что , имеем:
Энергия поля плоского конденсатора и сила взаимодействия его пластин
Формула энергии поля плоского конденсатора записывается как:
где – объем конденсатора; E – напряженность поля конденсатора. Формула (5) связывает энергию конденсатора с зарядом на его обкладках и напряженностью поля.
Механическую (пондемоторную) силу, с которой пластины плоского конденсатора взаимодействуют между собой можно найти, если использовать формулу:
В выражении (6) минус показывает, что пластины конденсатора притягиваются друг к другу.
Примеры решения задач
Емкость плоского конденсатора — Студопедия
Напряженность поля внутри конденсатора (рис. 5.11):
Рис. 5.11
Напряжение между обкладками:
где – расстояние между пластинами.
Так как заряд , то
| . | (5.4.7) |
Как видно из формулы, диэлектрическая проницаемость вещества очень сильно влияет на емкость конденсатора. Это можно увидеть и экспериментально: заряжаем электроскоп, подносим к нему металлическую пластину – получили конденсатор (за счет электростатической индукции, потенциал увеличился). Если внести между пластинами диэлектрик с ε, больше, чем у воздуха, то емкость конденсатора увеличится.
Из (5.4.6) можно получить единицы измерения ε0:
| (5.4.8) |
.
Емкость цилиндрического конденсатора
Разность потенциалов между обкладками цилиндрического конденсатора, изображенного на рисунке 5. 12, может быть рассчитана по формуле:
12, может быть рассчитана по формуле:
где λ – линейная плотность заряда,R1 иR2 – радиусы цилиндрических обкладок,l– длина конденсатора, .
Рис. 5.12
Тогда, так как , получим
| (5.4.9) |
Понятно, что зазор между обкладками мал: то есть
Тогда
Емкость шарового конденсатора (рис. 5.13)
Рис. 5.13
Из п. 3.6 мы знаем, что разность потенциала между обкладками равна:
Тогда, так как , получим
.
Это емкость шарового конденсатора, где R1 и R2 – радиусы шаров.
В шаровом конденсаторе – расстояние между обкладками. Тогда
| (5.4.11) |
27. Диэлектрики в электрическом поле. Поляризация диэлектрика. Диэлектрическая проницаемость. Электрическое смещение.
Диэлектрики в электрическом поле. Поляризация диэлектрика. Диэлектрическая проницаемость. Электрическое смещение.
Диэлектрик (изолятор) — вещество, практически не проводящее электрический ток. Концентрация свободных носителей заряда в диэлектрике не превышает 108 см−3. Основное свойство диэлектрика состоит в способности поляризоваться во внешнем электрическом поле. С точки зрения зонной теории твёрдого тела диэлектрик — вещество с шириной запрещённой зоны больше 3 эВ.
Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.
Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией.
· Вектор поляризации применим для описания макроскопического состояния поляризации не только обычных диэлектриков, но и сегнетоэлектриков, и, в принципе, любых сред, обладающих сходными свойствами. Он применим не только для описания индуцированной поляризации, но и спонтанной поляризации (у сегнетоэлектриков).
Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема.
Диэлектри́ческая проница́емость среды — физическая величина, характеризующая свойства изолирующей (диэлектрической) среды и показывающая зависимость электрической индукции от напряжённости электрического поля.
Определяется эффектом поляризации диэлектриков под действием электрического поля (и с характеризующей этот эффект величиной диэлектрической восприимчивости среды).
Различают относительную и абсолютную диэлектрические проницаемости.
ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ
индукция электрическая, — векторная величина D, характеризующая электрич. поле. В нек-рой точке поля Э. с. равно геом. сумме напряжённости электрического поля Е, умноженной на электрическую постоянную ЕС, и поляризованности Р: D = е0Е + Р. Если среда изотропна, то D = ее0Е, где е — относит. диэлектрическая проницаемость среды. Во многих случаях, например, если однородный и изотропный диэлектрик заполняет всё пространство, где имеется электрич. поле, или часть его, ограниченную эквипотенциальными поверхностями, Э. с. не зависит от диэлектрич. проницаемости е и совпадает с Э. с. в этой же точке для электрич. поля, создаваемого в вакууме той же системой свободных зарядов. Единица Э. с. (в СИ) — кулон на квадратный метр(Кл/м2).
поле. В нек-рой точке поля Э. с. равно геом. сумме напряжённости электрического поля Е, умноженной на электрическую постоянную ЕС, и поляризованности Р: D = е0Е + Р. Если среда изотропна, то D = ее0Е, где е — относит. диэлектрическая проницаемость среды. Во многих случаях, например, если однородный и изотропный диэлектрик заполняет всё пространство, где имеется электрич. поле, или часть его, ограниченную эквипотенциальными поверхностями, Э. с. не зависит от диэлектрич. проницаемости е и совпадает с Э. с. в этой же точке для электрич. поля, создаваемого в вакууме той же системой свободных зарядов. Единица Э. с. (в СИ) — кулон на квадратный метр(Кл/м2).
28. Постоянный ток. Стационарное электрическое поле. Закон Ома для однородного участка цепи.
Постоя́нный ток, (англ. direct current) — электрический ток, который с течением времени не изменяется по величине и направлению.
Постоянный ток Переменный синусоидальный ток Пульсирующий ток, форма импульсов близка к пилообразной Произвольно изменяющийся ток
Стационарное электрическое поле — электрическое поле неизменяющихся электрических токов при условии неподвижности проводников с токами.
Стационарное электрическое поле связано с наличием электрического тока, и это упрощает измерения разности потенциалов между любыми двумя точками поля — для этого достаточно прикоснуться к этим точкам щупами, которые подключены к гальванометру. Стационарное электрическое поле, создаваемое системой неподвижных зарядов, называется электростатическим полем. Стационарное электрическое поле в проводнике, как и электрическое поле неподвижных зарядов, характеризуется напряженностью электрического поля, которая неизменна по времени в любой из точек проводника.
Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.
В своей оригинальной форме он был записан его автором в виде :
Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r.
В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает
29. Электродвижущая сила. Закон Ома для полной (замкнутой) цепи.
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура.
В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура.
По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил , под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд, к величине этого заряда. Тогда в замкнутом контуре ЭДС будет равна:
где — элемент контура.
Закон Ома для полной цепи:
где:
· — ЭДС источника напряжения,
· — сила тока в цепи,
· — сопротивление всех внешних элементов цепи,
· — внутреннее сопротивление источника напряжения.
Из закона Ома для полной цепи вытекают следствия:
· При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
· При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
И источник может быть назван источником тока.
Часто[2] выражение
где есть напряжение или падение напряжения, (или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
30. Закон Ома для неоднородного участка. Законы Кирхгофа.
Закон Ома для неоднородного участка цепи имеет вид:
где R — общее сопротивление неоднородного участка.
ЭДС может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.е. ЭДС способствует движению положительных зарядов в данном направлении, то > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то < 0.
Это связано с полярностью включения ЭДС в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.е. ЭДС способствует движению положительных зарядов в данном направлении, то > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то < 0.
Законы Кирхгофа.
Расстояние между пластинами в плоском конденсаторе. Калькулятор онлайн.
Онлайн калькулятор вычисления расстояния между пластинами в плоском конденсаторе, позволит найти расстояние между пластинами через электроемкость и площадь пластины, а
также через площадь пластины, напряжение и заряд на пластине. Калькулятор произведет вычисление и даст подробное решение. Единицы измерения, могут включать любые приставки Си.
Калькулятор автоматически переведет одни единицы в другие. -9 Фарад.
-9 Фарад.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
|
Калькулятор вычисления энергии W заряженного конденсатора.  Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
|
Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвекторы величин |
| Конвертер единиц длины |
| Калькуляторы (Теория чисел) |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
Электроёмкость плоского конденсатора | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Плоским конденсатором обычно называют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Простота конструкции такого конденсатора позволяет сравнительно просто рассчитывать его электроемкость и получать значения, совпадающие с результатами эксперимента.
| Рис. 4.71. Плоский конденсатор на электрометре |
Укрепим две металлические пластины на изоляционных подставках и соединим с электрометром так, что одна из пластин будет присоединена к стержню электрометра, а вторая — к его металлическому корпусу (рис. 4.71). При таком соединении электрометр будет измерять разность потенциалов между пластинами, которые образуют плоский конденсатор из двух пластин. Проводя исследования, необходимо помнить, что
при постоянном значении заряда пластин уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
Сообщим пластинам разноименные заряды и отметим отклонение стрелки электрометра. Приближая пластины друг к другу (уменьшая расстояние между ними), заметим уменьшение разности потенциалов. Таким образом, при уменьшении расстояния между пластинами конденсатора его электроемкость увеличивается. При увеличении расстояния показания стрелки электрометра увеличиваются, что является свидетельством уменьшения электроемкости.
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
C ~ 1 / d,
где d — расстояние между обкладками.
| Рис. 4.72. График зависимости емкости плоского конденсатора от расстояния между пластинами |
Рис. 4.73. При расчетах емкости плоских конденсаторов учитывают площадь перекрытия пластин 4.73. При расчетах емкости плоских конденсаторов учитывают площадь перекрытия пластин |
Эту зависимость можно изобразить графиком обратной пропорциональной зависимости (рис. 4.72).
Будем смещать пластины одну относительно другой в параллельных плоскостях, не изменяя расстояния между ними.
При этом площадь перекрытия пластин будет уменьшаться (рис. 4.73). Увеличение разности потенциалов, отмеченное электрометром, будет свидетельствовать об уменьшении электроемкости.
Увеличение площади перекрытия пластан приведет к увеличению емкости.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
C ~ S,
где S — площадь пластин.
Рис. 4.74. График зависимости емкости плоского конденсатора от площади его пластин График зависимости емкости плоского конденсатора от площади его пластин |
Эту зависимость можно представить графиком прямой пропорциональной зависимости (рис. 4.74).
Возвратив пластины в начальное положение, внесем в пространство между ними плоский диэлектрик. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увеличении электроемкости конденсатора. Если между пластинами поместить другой диэлектрик, то изменение электроемкости будет иным.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика.
C ~ ε,
где ε — диэлектрическая проницаемость диэлектрика. Материал с сайта http://worldofschool.ru
| Рис. 4.75. График зависимости емкости плоского конденсатора от диэлектрической проницаемости диэлектрика |
Такая зависимость показана на графике рис. 4.75.
4.75.
Результаты опытов можно обобщить в виде формулы ёмкости плоского конденсатора:
C = εε0S / d,
где S — площадь пластины; d — расстояние между ними; ε — диэлектрическая проницаемость диэлектрика; ε0 — электрическая постоянная.
Конденсаторы, которые состоят из двух пластин, в практике применяются очень редко. Как правило, конденсаторы имеют много пластин, соединенных между собой по определенной схеме.
На этой странице материал по темам:
При збільшенні площі перекриття пластин конденсатора , що буде з електроємністю
Сообщение на тему электроемкость
График электроемкости плоского конденсатора от площади его пластин
График зависимости емкости c плоского конденсатора
График зависимости электроемкости от расстояния
Вопросы по этому материалу:
Какое строение плоского конденсатора?
По изменению какой величины в опыте можно делать заключение об изменении электроемкости?
В какой последовательности проводится опыт, в котором устанавливалась зависимость электроемкости конденсатора от его параметров?
Как зависит электроемкость плоского конденсатора от активной площади пластин?
Как зависит электроемкость плоского конденсатора от расстояния между пластинами?
Как влияет диэлектрик на электроемкость конденсатора?
Билет №29 — Администратор — Каталог статей
Конденсатор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.
Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью каждая, расположенных на расстоянии друг от друга, в системе СИ выражается формулой: , где — относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (в вакууме равна единице), — электрическая постоянная, численно равная Ф/м (эта формула справедлива, лишь когда много меньше линейных размеров пластин).
Если на обкладках конденсатора электроемкостью С находятся электрические заряды +q и —q, то согласно формуле напряжение между обкладками конденсатора равно
В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения Uдо 0.
Среднее значение напряжения в процессе разрядки равно
Для работы А, совершаемой электрическим полем при разрядке конденсатора, будем иметь:
Следовательно, потенциальная энергия Wp конденсатора электроемкостью С, заряженного до напряжения U, равна
Энергия конденсатора обусловлена тем, что электрическое поле между его обкладками обладает энергией. Напряженность Е поля пропорциональна напряжению U, поэтому энергия электрического поля пропорциональна квадрату его напряженности.
3.1.9 Конденсатор. Электроёмкость конденсатора. Электроёмкость плоского конденсатора
Видеоурок 1: Емкость конденсатора — Физика в опытах и экспериментах
Видеоурок 2: Емкость плоского конденсатора. Классификация конденсаторов
Классификация конденсаторов
Лекция: Конденсатор. Электроёмкость конденсатора. Электроёмкость плоского конденсатора
Для определения понятия конденсатора, необходимо воспользоваться всеми знаниями по поводу проводников и диэлектриков, поскольку и те, и другие одновременно используются для изготовления конденсаторов.
Ёмкость конденсатора
Во время изучения понятия конденсаторов будем использовать термин «уединенный конденсатор». Он значит, что данное проводящее тело находится вне поля действия других тел. Рассмотрим проводник, у которого имеется какой-то определенный потенциал «фи». Данный потенциал является пропорциональным к величине заряда проводника. Данный коэффициент принято обозначать 1/С. В данном случае величина, что находится в знаменателе, является электрической ёмкостью имеющегося проводника.
Если рассматривать некоторый объемный шар в виде проводника, то его ёмкость можно определить по следующей формуле:
Эпсилон нулевое — это электрическая постоянная.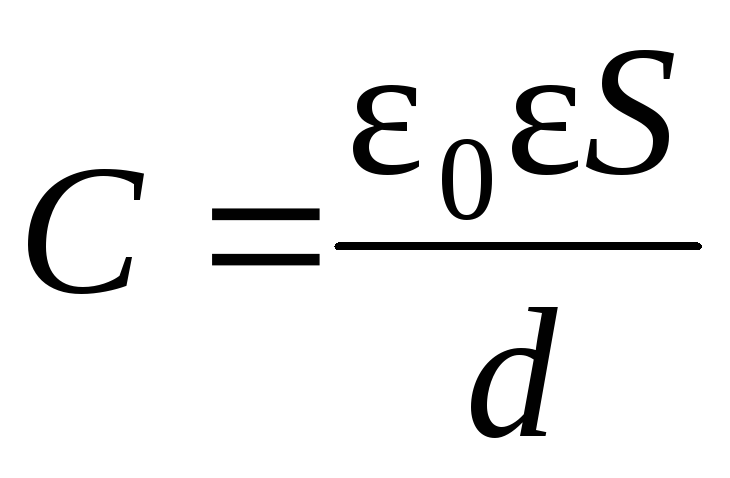
Судя из данной формулы, можно сделать вывод, что емкость сферического проводника зависит исключительно от внешнего диэлектрика, а также от радиуса сферы, то есть её размера. То есть, чем больше сфера, тем больше её емкость. Иными словами можно сказать, что ёмкость — это некая тара, которая вмещает в себя величину заряда.
Итак,
Ёмкость — это некая ФВ, позволяющая определить величину заряда, необходимую для изменения потенциала проводника на 1 В.
Ёмкость измеряется в фарадах (Ф).
Самым главным для нас сферическим проводником является Земля. Посчитать её емкость достаточно просто. Если принять радиус за 6400 км, а окружающую диэлектрическую среду мы знаем — это воздух, то получим:
Плоский конденсатор
Самым простым примером для исследования конденсаторов являются плоские конденсаторы. Структура плоского конденсатора достаточно проста. Он состоит из двух металлических плоскостей (обкладок), которые параллельно расположены друг к другу, и располагаются на некотором расстоянии. Между данными пластинами имеется диэлектрик.
Между данными пластинами имеется диэлектрик.
Самым простым примером плоского конденсатора является тот, у которого в виде диэлектрика воздух, то есть Ɛ = 1.
Обе обкладки имеют противоположный заряд -q, +q. Схематически конденсатор изображают следующим образом:
Следует отметить, что поле в конденсаторе показывается линиями, выходящими из положительно заряженной пластины, и входящими в отрицательно заряженную пластину.
Для определения его ёмкости следует воспользоваться следующей формулой:
Как уже говорилось раньше, ёмкость зависит исключительно от геометрических размеров конденсатора, а также от диэлектрика между пластинами.
Емкость — модуль AQA 4
Щелкните здесь, чтобы получить ответы на вопросы и домашнее задание по конденсаторам.
Щелчок — конденсатор отвечает.
Конденсатор — это накопитель заряда. Заряды (Q) измеряются в кулонах (C).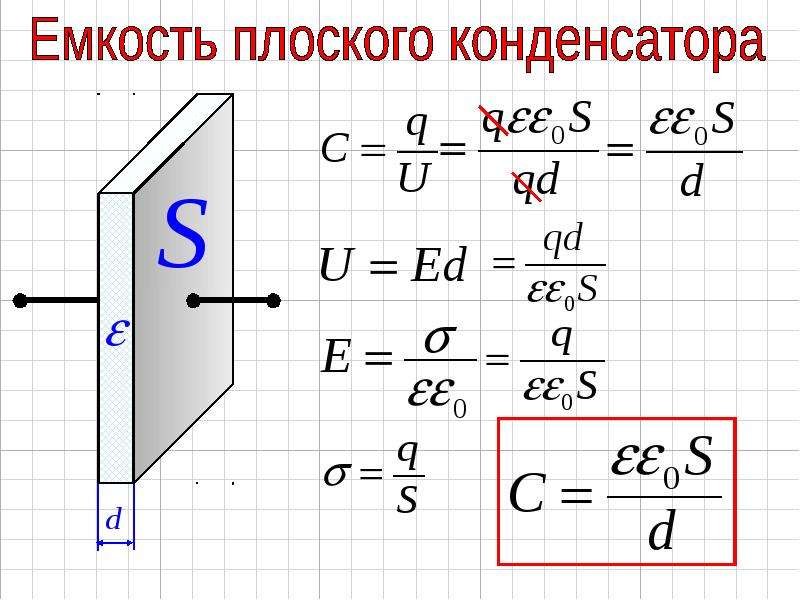 Один электрон несет заряд 1,6 x 10 -19 Кл.
Один электрон несет заряд 1,6 x 10 -19 Кл.
Конденсатор — это две металлические пластины, разделенные изолятором (или диэлектриком).
Обозначение цепи конденсатора:
Емкость
Емкость конденсатора измеряется в фарадах (Ф).Один фарад — это один кулон заряда на вольт (1 Ф = 1 CV -1 ).
C = емкость, измеренная в фарадах (F)
Q = заряд, измеренный в кулонах (C)
V = разность потенциалов, измеренная в вольтах (V)
1 фарад — это очень большая емкость. Обычно конденсаторы имеют емкость порядка микрофарад (10 -6 Ф), нанофарада (10 -9 Ф), пикофарада (10 -12 Ф).
Энергия, запасаемая конденсатором
Заряд (Q), накопленный на конденсаторе, прямо пропорционален разности потенциалов (V) на пластинах конденсатора.
Площадь под линией на графике равна энергии (E), запасенной в конденсаторе, и измеряется в джоулях (Дж).
E = энергия, запасенная на конденсаторе, измеренная в джоулях (Дж)
Q = заряд конденсатора, измеренный в кулонах (C)
V = разность потенциалов, измеренная в вольтах (В)
C = емкость конденсатора, измеренная в фарадах ( F)
Разряд конденсатора
Когда конденсатор разряжается, электроны с отрицательной (-) пластины текут на положительную (+) пластину конденсатора, и в цепи течет ток. На приведенном ниже графике показана экспоненциальная кривая спада при отложении заряда разряженного конденсатора от времени.
На приведенном ниже графике показана экспоненциальная кривая спада при отложении заряда разряженного конденсатора от времени.
Q = заряд конденсатора в момент t, измеренный в кулонах (Кл)
Q 0 = заряд конденсатора при t = 0 секунд, измеренный в кулонах (Кл)
t = время, в течение которого конденсатор был наработан разряд, измеренный в секундах (с)
C = емкость конденсатора, измеренная в кулонах (C)
R = сопротивление в цепи разряда, измеренное в омах (Вт)
Постоянная времени CR
Постоянная времени CR показывает, насколько быстро конденсатор разряжается.Если постоянная времени CR большая, конденсатору потребуется больше времени для разряда, чем если бы постоянная времени CR мала.
Постоянная времени CR = емкость x сопротивление
(секунды / с) (фарады / Ф) (Ом / Вт)
Постоянная времени равна времени, за которое заряд конденсатора достигает 1 / e (37%) от своего начального значения. Мы можем найти значение постоянной времени CR из графика.
Разность потенциалов и емкость
Разность потенциалов и емкость
Следующий текст используется только для обучения, исследований, стипендий, образовательных целей и информационных целей в соответствии с принципами добросовестного использования.
Мы благодарим авторов текстов и исходный веб-сайт, который дает нам возможность поделиться своими знаниями
Физика
Разница потенциалов (p.d.) между двумя точками — это работа, проделанная для переноса заряда в 1 кулон от одной точки к другой *.
Единица измерения разности потенциалов — Вольт (обозначение В)
Вольт
Разница потенциалов между двумя точками составляет один вольт, если один Джоуль работы выполняется при переносе заряда в один кулон из одной точки в другую.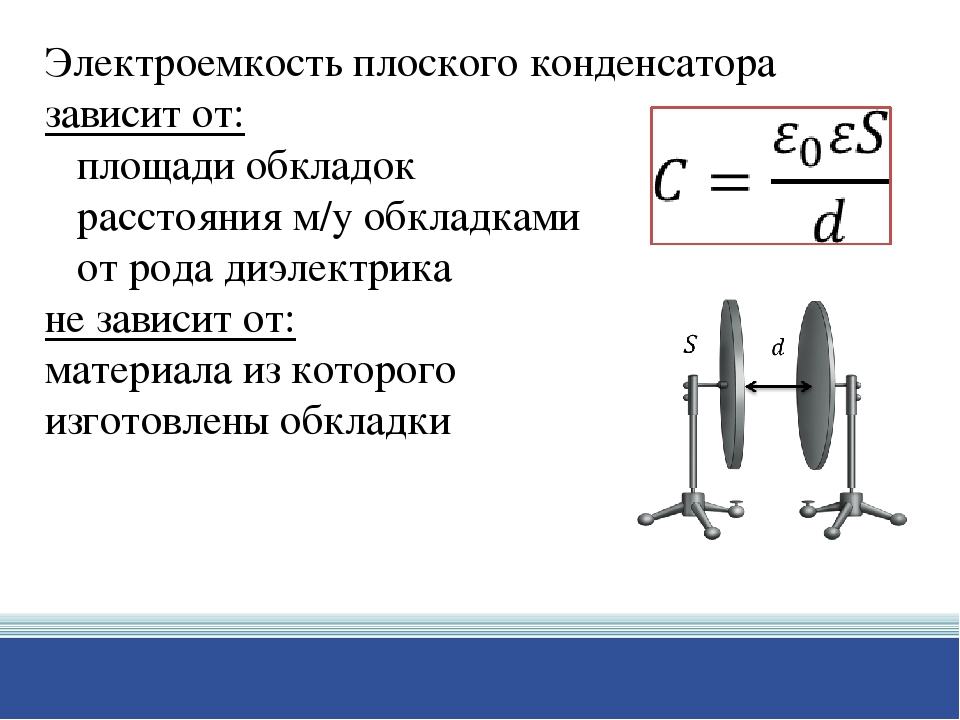
Более распространенным (но менее правильным) словом для термина «разность потенциалов» является «напряжение».
Обратите внимание, что разность потенциалов всегда находится между двумя точками.
Взаимосвязь между работой, зарядкой и напряжением
Работа = Напряжение × Заряд:
См. Решенные задачи 1–6, стр. 236.
В частности, следует попробовать задачи 5 и 6, но, возможно, решение № 5 следует оставить до 6-го года обучения. Затем попробуйте 1 — 8, стр. 237.
Потенциал в точке *
Потенциал в точке относится к работе, проделанной по переносу положительного заряда из этой точки на землю.
Завершение программы Cert Physics Syllabus: потенциальная разница
Содержание | Глубина обработки | Деятельность | СТС |
| Определение разности потенциалов: | Соответствующие расчеты. |
Емкость *
Обозначение емкости — C
Не путайте «Емкость» (символ C) с «Зарядом» (символ Q).
Конденсатор — это электрическое устройство, используемое для хранения заряда
Емкость проводника — это отношение заряда проводника к его потенциалу *.
Единица измерения емкости — Фарада; символ F.
(Это похоже на определение сопротивления, которое мы встретим в следующей главе.)
Параллельный пластинчатый конденсатор *
Рассмотрим две противоположно заряженные параллельные пластины, как показано *
Из диаграммы мы видим, что емкость будет увеличиваться, если общая площадь между пластинами (A) увеличивается, или если расстояние между пластинами (d) уменьшается.
Следовательно, C µ A и C µ Þ C µ Þ C = k
Пропорциональная константа оказывается e (помните, что мы сталкивались с этим в предыдущей главе как часть закона Кулона) и представляет собой диэлектрическую проницаемость среды между двумя пластинами.
Þ
См. Рабочие примеры 11 и 12, стр. 241. Затем попробуйте вопросы 1–5, стр. 243
Для демонстрации факторов, влияющих на емкость параллельного пластинчатого конденсатора *
- Подключите две параллельные пластины к цифровому мультиметру (DMM), установленному для измерения емкости.Обратите внимание на емкость.
- Увеличьте расстояние между ними — обратите внимание, что емкость уменьшается.
- Немного сдвиньте одну пластину в сторону (уменьшая площадь перекрытия) — обратите внимание, что емкость уменьшается.

- Поместите разные плиты изоляционного материала между пластинами — обратите внимание, что емкость самая низкая, когда между пластинами нет ничего (воздуха) *.
Две формулы для энергии, запасенной в конденсаторе *
Вт =
Чтобы показать, что заряженный конденсатор накапливает энергию
- Установите, как показано.
- Включите переключатель, чтобы зарядить конденсатор.
- Снимите аккумулятор и соедините клеммы вместе, чтобы «замкнуть» цепь.
- Лампа будет мигать по мере разряда конденсатора, показывая, что в нем накапливается энергия.
Общие области применения конденсаторов
- «Вспышка» на фотоаппарате
- Сглаживание колебаний постоянного тока
- Допускает переменный ток (a.
 c.), чтобы пройти через него, но блокирует постоянный ток (d.c.) *.
c.), чтобы пройти через него, но блокирует постоянный ток (d.c.) *. - Используется в цепях, чтобы пропускать только переменный ток определенной частоты *
Завершение программы Cert Physics Syllabus: Capacitance
Содержание | Глубина обработки | Деятельность | СТС |
| |||
Конденсаторы и | Определение: C = Q / V | ||
Конденсатор с параллельными пластинами. | Демонстрация того, что емкость зависит от общей площади, расстояния между пластинами, и природы диэлектрика. | Общее использование конденсаторов: | |
Энергия, накопленная в конденсаторе. Использование W = ½ CV 2 Конденсаторы — проведите а. | Конденсатор зарядный — разряд через лампу или низковольтный постоянный ток. мотор. Соответствующие расчеты. |
Дополнительный кредит
* Определение потенциальной разницы
Примечание:
Если заряд +1 переходит в положительную точку, то нужно работать, чтобы получить его, но если он переходит в отрицательную точку, то это (заряд +1).
Это похоже на утверждение, что камень на вершине утеса имеет потенциальную энергию, скажем, 100 Джоулей.
Чтобы поднять камень наверх, вы должны потратить 100 Джоулей работы на скале или, альтернативно, если бы камень упал на землю , сделал бы 100 Джоулей работы.
* W = V Q
Теперь, если вы знаете, сколько гравитационной энергии имеет камень (из формулы для гравитационной потенциальной энергии E = mgh), вы можете рассчитать скорость, с которой он ударится о землю (из формулы для кинетической энергии E = ½ mv2).
От сохранения энергии; Потенциальная энергия = кинетическая энергия: mgh = ½ мв2
Как камень будет ускоряться к земле, так и положительный заряд будет ускоряться в сторону отрицательной точки.
Фактически, если вы знаете, сколько потенциальной энергии должно было иметь заряд вначале, то есть потенциал между двумя точками (из формулы W = QV), вы можете рассчитать его скорость, когда он достигнет второй точки (если вы знаете его массу) снова используя
Потенциальная энергия = кинетическая энергия или QV = ½ мв2
* Потенциал в точке
Помните выше, что мы отметили, что разность потенциалов всегда находится между двумя точками?
Очень часто нам нужно знать, насколько сложно передать положительный заряд от земли положительному объекту.
Поскольку это происходит так часто, мы отказываемся от термина «разность потенциалов» и просто называем разность потенциалов между землей и объектом «потенциалом объекта» — это также известно как «потенциал в точке».
Из этого должно быть очевидно, что чем больше положительного заряда у объекта, тем больше работы потребуется для того, чтобы подвести к нему еще один положительный заряд, и поэтому потенциал в этой точке будет больше.
Теперь вы можете бросить вызов себе и объяснить, как можно использовать электроскоп с золотым листом для сравнения разности потенциалов между одним объектом и землей по сравнению с другим объектом и землей (большой совет см. На стр. 235).
* Емкость
Представьте емкость с водой.
Количество воды, которое может вместить контейнер (его вместимость), будет зависеть, помимо прочего, от того, насколько быстро поднимется уровень воды при наливании воды; если уровень воды быстро поднимается, это означает, что емкость должна быть довольно узкой и, следовательно, не может содержать много воды.
Мы бы пришли к выводу, что контейнер имел небольшую «емкость».
Электрический конденсатор можно сравнить с этим резервуаром для воды, и скорость увеличения потенциала конденсатора дает нам представление о том, сколько заряда конденсатор может удерживать; если небольшой заряд на нем значительно увеличивает его потенциал, то его емкость должна быть небольшой.
Помните, что «значительно повышает свой потенциал» означает, что необходимо проделать гораздо больше работы, чтобы повысить его эффективность.
Так, например, если конденсатор имеет емкость 2 фарада, то установка на него заряда в 6 кулонов увеличит его потенциал на 3 вольта (от C = Q / V, поэтому V = Q / C).
Однако, если бы емкость конденсатора составляла 200 фарад, установка на него заряда в 6 кулонов повысила бы его потенциал только на 0,03 вольт.
* Определение Емкость
Если, когда вас попросят определить емкость, вы ответите, что « используется для хранения заряда» , вы получите нулевые оценки, потому что это не определение.
* C = Q / V
Формулу C = Q / V легче запомнить, если переставить ее как Q = CV
.
* Конденсатор с параллельными пластинами
Потенциал положительно заряженного объекта является показателем того, сколько работы потребуется сделать, чтобы подвести к нему другой положительно заряженный объект.
Следовательно, чем больше положительного заряда на объекте, тем больше будет его потенциал.
Однако, если мы поднесем отрицательно заряженный объект близко к положительно заряженному объекту, их электрические поля будут стремиться нейтрализовать друг друга, и тогда станет легче подвести больше положительного заряда к исходному — положительно заряженному — объекту.
Это означает, что потенциал исходного объекта уменьшается, просто поднося к нему противоположно заряженный проводник.
Это принцип, на котором основан конденсатор с параллельными пластинами.
* Рассмотрим две противоположно заряженные параллельные пластины, как показано на рисунке
Ключ к этому — помнить, что чем больше их электрические поля нейтрализуют друг друга, тем больше будет емкость системы.
* Две формулы для энергии, запасенной в конденсаторе
W = ½ CV2, W = Q2 / 2C
Вам не нужно знать, как вывести эти формулы, но на самом деле это очень просто, и, по крайней мере, для меня легче вывести их с нуля, чем запомнить.
Их вывод включает формулы W = QV и C = Q / V.
Я могу показать вам доску через 5 минут, если вы спросите меня.
Обратите внимание: если вы начнете с Q = CV и замените это на W = QV, вы получите W = CV без коэффициента 1/2!
Чтобы объяснить, откуда берется множитель ½, требуется пройтись по выводам, так что продолжайте — спросите меня!
Кстати, в учебниках эту явную аномалию не объясняют.
* Допускает переменный ток (a.c.), чтобы пройти через него, но блокирует постоянный ток (d.c.) *.
На первой диаграмме (постоянный ток), когда цепь замкнута, происходит внезапное движение электронов, но поскольку цепь не замкнута, дальнейшего потока нет.
На второй диаграмме пластины непрерывно заряжаются и разряжаются; время (и, следовательно, частота) зависит от размера пластин (см. следующий пункт).
Строго говоря, ток не «проходит» через конденсатор, а просто действует так, как будто он есть.
* Используется в цепях, чтобы пропускать только переменный ток определенной частоты
Это, в свою очередь, используется в радиоприемниках для приема только определенных частот , соответствующих радиоволнам, исходящим от определенной радиостанции.
Часть электронной схемы, отвечающая за это, называется «RC-цепью» (сопротивление, емкость).
При смене станций в радио вы действительно меняете емкость этой части цепи.
Как это работает?
Чем больше размер конденсатора, тем больше времени требуется для разряда (и зарядки). Теперь, если время, необходимое для зарядки и разрядки, соответствует частоте переменного тока, который, в свою очередь, несет звуковую информацию от радиостанции, тогда этот сигнал будет пропущен и в конечном итоге достигнет динамиков.
* Для демонстрации факторов, влияющих на емкость параллельного пластинчатого конденсатора
Примечание. Альтернативная демонстрация приведена на странице 242, но понять, что происходит, до смешного сложно — учебник не объясняет это полностью.
Описанная демонстрация вполне адекватна и очень проста.
* Поместите разные плиты изоляционного материала между пластинами — обратите внимание, что емкость самая низкая, когда между пластинами нет ничего (или воздуха).
Это может показаться запутанным, поэтому, если вас это беспокоит, попросите меня объяснить, почему.
Экзаменационные вопросы
- [2005] [2004] [2009] [2002 OL]
Определите разность потенциалов.
Назовите прибор, используемый для измерения разности потенциалов.
- [2009] [2008] [2004] [2002 OL]
Определите емкость.
Назовите электрический компонент, представленный на схеме.
- [2006 год] [2006 год] [2007 год] [2010]
Дайте одно использование конденсатора.
Какие из следующих устройств настраиваются при настройке на радиостанцию?
Трансформатор, диод, конденсатор, реостат
Перечислите факторы, влияющие на емкость конденсатора с параллельными пластинами.
Как бы вы продемонстрировали, что емкость конденсатора с параллельными пластинами зависит от расстояния между его пластинами?
Какой положительный заряд сохраняется на конденсаторе 5 мкФ при подключении к напряжению 120 В постоянного тока? поставка?
- [2006]
- Пластины заполненного воздухом конденсатора с параллельными пластинами имеют общую площадь 40 см2 и расположены на расстоянии 1 см друг от друга. Конденсатор подключен к источнику постоянного тока 12 В. поставка. Рассчитайте емкость конденсатора.
(Проницаемость свободного пространства = 8.85 × 10-12 Фм-1)
- Рассчитайте величину заряда на каждой пластине.
- Каков чистый заряд конденсатора?
Опишите эксперимент, демонстрирующий, что конденсатор может накапливать энергию.
- Конденсатор подключен к переключателю, батарее и лампочке, как показано на схеме. Когда переключатель переводится из положения A в положение B, лампочка загорается на короткое время.
- Что происходит с конденсатором, когда переключатель находится в положении A?
- Почему лампочка загорается, когда переключатель находится в положении B?
- Когда переключатель находится в положении A, конденсатор имеет заряд 0.6 C, рассчитайте его емкость.
Рассчитайте энергию, запасенную в конденсаторе 5 мкФ, когда к нему приложена разность потенциалов 20 В.
Конденсатор емкостью 100 мкФ заряжается до разности потенциалов 20 В. Какая энергия хранится в конденсаторе?
Сколько энергии хранится в конденсаторе емкостью 100 мкФ, когда он заряжается до разности потенциалов 12 В?
Способность конденсатора накапливать энергию — основа дефибриллятора.Во время сердечного приступа камеры сердца не могут перекачивать кровь, потому что их мышечные волокна сокращаются и расслабляются беспорядочно. Чтобы спасти жертву, необходимо потрясти сердечную мышцу, чтобы восстановить нормальный ритм.
Дефибриллятор используется для разряда сердечной мышцы.
Конденсатор на 64 мкФ в дефибрилляторе заряжен до разности потенциалов 2500 В.
Конденсатор разряжается за 10 миллисекунд через электроды, прикрепленные к груди пострадавшего от сердечного приступа.
- Рассчитайте заряд, накопленный на каждой пластине конденсатора.
- Рассчитайте энергию, запасенную в конденсаторе.
- Рассчитайте среднюю мощность, генерируемую при разряде конденсатора.
- [2004]
- На принципиальной схеме показан конденсатор емкостью 50 мкФ, соединенный последовательно с резистором, батареей на 6 В и переключателем.
Разность потенциалов на конденсаторе равна 2.Первоначально 24 В при токе 80 мкА.
Рассчитайте заряд конденсатора в этот момент.
- Вычислите количество энергии, накопленной в конденсаторе, когда он полностью заряжен.
- Опишите, что происходит в цепи, когда напряжение 6 В постоянного тока питание заменяется на 6 В переменного тока. поставка.
На схеме A показан конденсатор, подключенный к лампочке, и напряжение 12 В переменного тока. поставка.
На схеме B показан тот же конденсатор, подключенный к лампочке, но подключенный к напряжению 12 В.c. поставка.
Что происходит в каждом случае, когда переключатель замкнут? Поясните свой ответ.
Решения для экзаменов
- Разность потенциалов между двумя точками — это работа, совершаемая при переносе заряда в 1 кулон из одной точки в другую.
- Вольтметр
- Емкость проводника — это отношение заряда проводника к его потенциалу.
- А конденсатор
- Магазин заряда / (радио) настройки / сглаживания / накопления энергии / вспышки для фотоаппаратов, зарядного устройства для телефона, блоков d.c.
- Конденсатор
- Общая площадь пластин, расстояние друг от друга, диэлектрическая проницаемость диэлектрика между пластинами.
- Подключите две параллельные пластины к цифровому мультиметру (DMM), установленному для измерения емкости.
Обратите внимание на емкость.
Увеличьте расстояние между ними — обратите внимание, что емкость уменьшается.
- Q = CV = (5 × 10–6) (120)
Q = 6.0 × 10–4 C
C = [(8.85 × 10-12) (40 × 10-4)] / (0,01)
C = 3,54 × 10-12 F
Q = (3,54 x 10-12) (12) = 4,2 (5) x 10-11 C
- Ноль
- Установите, как показано.
- Включите переключатель, чтобы зарядить конденсатор.
- Снимите аккумулятор и соедините клеммы вместе, чтобы «замкнуть» цепь.
- Лампа будет мигать по мере разряда конденсатора, показывая, что в нем накапливается энергия.
- Заряжается (на пластинах накапливается заряд).
- Конденсатор разряжается, и через лампочку на короткое время проходит ток.
- C = Q / V = 0,6 / 6 = 0,1 Фарад
- E = ½ CV2 = ½ (5 x 10-6) (20) 2 = 1,0 x 10-3 Дж
- E = ½CV2 Þ E = ½ (100 × 10-6) (20) 2 = 0,02 Дж
- E = ½ CV2 = ½ (100 × 10-6) (12) 2 = 7,2 × 10-3 Дж
- C = Q / v Þ q = CV Þ q = (64 × 10-6) (2500) Þ q = 0.16 C
- E = ½ CV2 = ½ (64 × 10-6) (2500) 2 = 200 Дж
- P = Вт / t = (200) / (10 × 10-3) = 20000 Вт
- C = Q / V Þ Q = CV = (50 × 10−6) (2,24) = 1,12 × 10-4 C
- E = ½ CV2 = ½ (50 × 10−6) (6) 2 = 9 × 10−4 Дж
Обратите внимание, что здесь мы используем 6 В в качестве разности потенциалов на конденсаторе, потому что, хотя разность потенциалов вначале составляет 2,24 В, когда конденсатор полностью заряжен, требуется максимальное количество энергии для увеличения заряда.
- Ток будет течь непрерывно.
- На схеме A лампа горит, потому что конденсатор «проводит» переменный ток. (он постоянно заряжается и разряжается).
На схеме B лампа не горит, потому что конденсатор не проводит постоянный ток.
Источник: http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/20.%20Potential%20Difference%20and%20Capacitance.doc
Ссылка на веб-сайт: http://www.thephysicsteacher.ie
Автор: не указан в исходном документе текста выше
Разность потенциалов и емкость
Разность потенциалов и емкость
На главную
Разность потенциалов и емкость
Это правильное место, где можно найти ответы на свои вопросы, например:
Кто? Какие ? Когда ? Куда ? Зачем ? Который ? Как ? Что означают разность потенциалов и емкость? Что означают разность потенциалов и емкость?
Примечания по физике разности потенциалов и емкостей
Аланпедия.com с 1998 года год от года новые сайты и инновации
На главную — Заявление об ограничении ответственности — Свяжитесь с нами
Конденсаторы
и емкость
Различные типы конденсаторов
Конденсатор — электронное устройство для накопления заряда. Конденсаторы можно найти почти во всех электронных схемах, кроме самых простых. Существует много разных типов конденсаторов, но все они работают одинаково.Упрощенный вид конденсатора представляет собой пару металлических пластин, разделенных зазором, в котором находится изолирующий материал, известный как диэлектрик. Этот упрощенный конденсатор также выбран, поскольку символ электронной схемы для конденсатора представляет собой пару параллельных пластин, как показано на рисунке 1.
Рис. 1. Символ неполяризованного конденсатора.
Обычно электроны не могут войти в проводник, если не существует пути для выхода такого же количества электронов. Однако лишние электроны могут быть «втиснуты» в проводник без пути для выхода, если электрическое поле может развиваться в пространстве относительно другого проводника.Количество дополнительных свободных электронов, добавленных к проводнику (или отнятых свободных электронов), прямо пропорционально величине потока поля между двумя проводниками.
В этом упрощенном конденсаторе диэлектрик — воздух. Когда на клеммы конденсатора подается напряжение В , электроны перетекают на одну из пластин и уносятся с другой пластины. Общее количество электронов в конденсаторе остается прежним. На одной отрицательной пластине их больше, а на положительной — меньше.
Рисунок 2. Зарядка конденсатора от аккумулятора
Если бы напряжение было увеличено, увеличившаяся разность потенциалов между пластинами подтолкнула бы больше электронов к отрицательно заряженной пластине. Мы могли измерить заряд, накопленный на пластине, в зависимости от различных приложенных напряжений.
При нулевом напряжении пластины конденсатора нейтральны, поэтому заряд не сохраняется. (мы предполагаем, что мы начали с полностью разряженного конденсатора), при напряжении V заряд на пластинах равен Q, а при удвоенном напряжении заряд удваивается.Мы обнаружили, что с увеличением напряжения заряд увеличивается линейно. Мы можем построить это как прямую линию.
Предположим, что мы уходим, проводим некоторые исследования и возвращаемся с лучшим конденсатором, который хранит больше заряда для данного напряжения, мы можем построить график зависимости сохраненного заряда от приложенного напряжения.
Это будет представлено как другая линия с более крутым уклоном. Если бы мы построили много графиков для разных конденсаторов, мы получили бы много прямых линий. Мы можем сказать, что мера емкости — это то, сколько заряда сохраняется при заданном напряжении.Иногда это выражается как Q = CV .
Конечно, при зарядке конденсатора должна выполняться работа по перемещению заряда. Следовательно, энергия должна подаваться, и эта энергия доступна, когда конденсатор разряжен.
Проделанная работа определяется как W = qV . Первоначально заряд легко перемещается на пластины конденсатора, однако по мере того, как больше заряда перемещается на пластины конденсатора, сила отталкивания между зарядами затрудняет добавление заряда, когда сила отталкивания зарядов равна мощности батареи, больше нельзя перемещать заряд на пластины.Следовательно, средняя работа составляет 1/2 qV . Если мы посмотрим на наш график зависимости заряда от напряжения, мы увидим, что это то же самое, что и площадь под кривой. В общем, проделанная работа равна переданной энергии. Математически,
Факторы, влияющие на емкость
Как можно увеличить емкость конденсатора с параллельными пластинами? Есть три фактора, которые влияют на емкость конденсатора с параллельными пластинами.
Площадь
Конденсатор переменной емкости
Увеличивая площадь пластин, мы можем направить на пластины больше заряда до того, как силы отталкивания станут проблемой.Следовательно, емкость пропорциональна площади перекрытия пластин. В переменном конденсаторе площадь перекрытия может быть увеличена или уменьшена путем вращения взаимопроникающих пластин, таким образом увеличивая или уменьшая емкость. Пластины электролитических конденсаторов протравлены для получения шероховатой поверхности, которая еще больше увеличивает площадь поверхности.
Разделение
Уменьшение расстояния между пластинами снижает напряжение на конденсаторе, поскольку электрическое поле не зависит от расстояния между пластинами.Напряжение на конденсаторе В = Ед . Следовательно, напряжение увеличивается. Для постоянного заряда Q , C = Q / V = Q / Ed.
Диэлектрическая проницаемость
Емкость конденсатора с параллельными пластинами определяется выражением C = ε r A / d , где A — площадь пластин, d — расстояние между пластинами, а ε r — площадь пластин. относительная проницаемость диэлектрика между пластинами. Относительная проницаемость — это некоторый коэффициент, K , умножающий допустимость свободного пространства ε 0 .ε 0 имеет значение 8,85×10 -12 F.m -1 .
Полный список относительных допусков можно найти практически для любого диэлектрического материала. Чем больше относительная проницаемость, тем больше емкость конденсатора. Хорошие материалы — слюда, полистирол, масло.
ε r = K ε 0
Конденсаторные сети
Рисунок 3. Последовательные и параллельные конденсаторные сети
серии
Рассмотрим последовательную сеть конденсаторов, показанную на рисунке 3a.где положительная пластина соединена с отрицательной пластиной следующего. Какова эквивалентная емкость сети? Посмотрите на пластины посередине, эти пластины физически отключены от цепи, поэтому общий заряд на них должен оставаться постоянным. Отсюда следует, что когда на оба конденсатора подается напряжение, заряд + Q на положительной пластине конденсатора C 1 должен уравновешиваться зарядом — Q на отрицательной пластине конденсатора C. 2 .В результате оба конденсатора обладают одинаковым зарядом Q. Падения потенциала В 1 и В 2 на двух конденсаторах в целом разные. Однако сумма этих падений равна общему падению потенциала В , приложенному к входным и выходным проводам. В = В 1 + В 2 . Эквивалентная емкость пары снова равна C T = Q / V .Таким образом, 1/ C T = V / Q = ( V 1 + V 2 ) / Q = V 1 / Q + V 2 / Q дающий
Обычно для конденсаторов N , соединенных последовательно, это
Подключая конденсаторы в сериях, вы сохраняете меньше заряда, так есть ли смысл подключать конденсаторы последовательно? Иногда это делается потому, что конденсаторы имеют максимальное рабочее напряжение, и, если последовательно соединить два конденсатора с максимальным напряжением 900 вольт, вы можете увеличить рабочее напряжение до 1800 вольт.
Параллельный
Для параллельной схемы, такой как на рисунке 3b. напряжения одинаковы для всех компонентов. Однако общий заряд делится между двумя конденсаторами, так как он должен распределяться таким образом, чтобы напряжение на них было одинаковым. Кроме того, поскольку конденсаторы могут иметь разные емкости C 1 и C 2 , заряды Q 1 и Q 2 также должны быть разными.Эквивалентная емкость C T пары конденсаторов — это просто отношение Q / V , где Q = Q 1 + Q 2 — это общий накопленный заряд. Отсюда следует, что C T = Q / V = (Q 1 + Q 2 ) / V = Q 1 / V + Q 2 / В подача
Из предыдущего обсуждения довольно очевидно, что для конденсаторов N , подключенных параллельно, общая емкость составляет
Общая емкость увеличивается за счет параллельного добавления конденсаторов, поэтому мы создаем большую емкость, чем это возможно при использовании одного конденсатора.В лабораториях физики высоких энергий часто есть большие батареи конденсаторов, которые могут накапливать большое количество энергии, высвобождаемой за очень короткое время. Самая большая батарея конденсаторов в 2006 году может хранить 50 МДж энергии.
Конденсаторы зарядные и разрядные
Цепь, состоящая из батареи, переключателя, резистора и конденсатора в последовательном контуре, называется RC-цепью. Закон Кирхгофа для этой схемы имеет вид
V = IR + Q / C .Если выразить чисто в терминах заряда, это становится
V = dQ / dt R + Q / C .
Это дифференциальное уравнение, решение которого является экспоненциальной функцией. Когда переключатель замкнут, конденсатор со временем заряжается:
Q = Q f (1 — e -t / RC ),
, где Q — это заряд в момент времени t , а Q f — окончательный заряд конденсатора.Обратите внимание, что Q никогда не равно Q f , но поскольку t становится чрезвычайно большим, Q становится произвольно близким к Q f . Произведение RC называется постоянной времени RC и является характеристической величиной RC цепи. Когда t = RC , конденсатор заряжен до доли (1–1 / e , около 63%) от своего окончательного значения. Необходимо использовать постоянную времени, а не какое-то конечное время, поскольку процесс асимптотический.Его значение — произвольный выбор; мы, естественно, выбираем значение в терминах экспоненциального основания (когда показатель отрицательный).
.

 -9 Фарад.
-9 Фарад. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

 c.), чтобы пройти через него, но блокирует постоянный ток (d.c.) *.
c.), чтобы пройти через него, но блокирует постоянный ток (d.c.) *.
 c. но не
c. но не