Измерение сопротивлений и мощности методом вольтметра, аьперметра и ваттметра. Измерение сопротивления методом вольтметра и амперметра

4.3. Измерение сопротивления методом амперметра и вольтметра

16

Подключить к мультиметру по очереди резисторы с сопротивлениями R2, R3, R4 и записать полученные показания прибора RИ2, RИ3, RИ4.

Рассчитать относительные погрешности δR1, δR2, δR3 и δR4 измерения сопротивлений резисторов (см. пример расчета).

Перевести полученные относительные погрешности в абсолютные - по грешности R1, R2, R3 и R4.

Записать результаты измерений в виде RX=RИ±ΔR.

4.3.1.Описание метода амперметра и вольтметра.

Расчет погрешности

Измерения сопротивлений с помощью метода амперметра и вольтметра являются косвенными измерениями непосредственной оценки. Косвенное измерение – это определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.

Вотличие от прямых измерений, где результат получают сразу по измерительному прибору, предназначенному для искомой величины, в косвенных измерениях результат получают путем расчета, используя результаты прямых измерений связанных величин и констант.

При выполнении расчета возможны допущения и упрощения, приводящие к методической погрешности измерения в целом.

Вкачестве принципа измерения в методе амперметра и вольтметраис пользуется закон Ома. Для получения значения сопротивления необходимо одновременно измерить напряжение на исследуемом элементе и ток через него. С этой целью собирается электрическая цепь, содержащая источник питания постоянного (или переменного) тока, амперметр, вольтметр и исследуемый элемент. Параметры источника питания в большинстве случаев подбираются в соответствии с номинальным или рабочим режимом исследуемого элемента, что особенно актуально для элементов с нелинейной вольтамперной характеристикой, когда сопротивление элемента не постоянно и сильно зависит от тока и напряжения в реализуемом режиме работы (полупроводниковые элементы, лампа накаливания и др.).

Пределы измерения выбираемых приборов должны соответствовать -напряжению и току в цепи(ближайшие большие значения из стандартного ряда

17

пределов относительно измеряемого тока и напряжения), что позволяет минимизировать инструментальную погрешность измерения.

Для примера рассмотрим в качестве объекта измерений полупроводниковый диод. Так как вольтамперная характеристика(ВАХ) диода (рис. 11) нелинейна, его сопротивление для любых двух несовпадающих режимов работы (разное напряжение и ток) будет также различным.

I, A

Обратное смещение

Прямое смещение

К	IПР	А	А
А		В	К
UОБР	D	UПР	U, B

RА<RВ<RС

Рис. 11. Вольтамперная характеристика диода Особенно сильно отличаются сопротивления при прямом смещении дио-

да (потенциал анода больше потенциала катода) и обратном смещении (обратная полярность напряжения). Различия в значениях сопротивления диода визуально можно оценить по ВАХ. Если провести прямую через рабочую точку элемента на ВАХ и начало координат, угол наклона будет иметь однозначную связь с сопротивлением. Прямые, проведенные через разные рабочие точки (рис. 11), проходят под разными углами к оси напряжения ВАХ.

В большинстве случаев при нахождении сопротивления по показаниям приборов для упрощения расчетов делаются допущения, что внутреннее сопротивление вольтметра равно бесконечности(RV=¥), а амперметра – нулю (RA=0), и их включение не влияет на результат измерения. Фактически же, в зависимости от чувствительности и предела измерения приборов, сопротивление милливольтметров и вольтметров может находиться в диапазоне примерно 102…108 Ом, а амперметров, миллиамперметров и микроамперметров – в диапазоне10-4…105Ом. В этом случае оправданность допущений необходимо проверять, сопоставляя сопротивления выбранных приборов с предварительно оцененным значением измеряемого сопротивления. Если сопротивления при-

18

боров оказываются соизмеримы с сопротивлением объекта измерения, может возникать существенная методическая составляющая погрешности измерения.

Влияние сопротивления приборов на процесс измерения может быть определено при анализе схем включения измерительных приборов в цепь. Так как показания с приборов необходимо снимать одновременно, возможны две схемы включения (рис. 12).

Рис. 12. Схемы цепей для измерения сопротивлений методом амперметра и вольтметра

Измеренное значение сопротивления чаще всего определяется по показаниям приборов UV и IA независимо от схемы их включения:

ИЗМ		UV
RX	=
			I A .		(4)

Действительное значение сопротивления, не содержащее методической погрешности, может быть определено через напряжение и ток непосредственно на исследуемом элементе UX и IX:

Д		U Х
RX	=
			I Х .		(5)

Неучтенное при измерении влияние потребления измерительными приборами энергии из цепи приводит к расхождению измеренного и действительного значений и возникновению методической погрешности:

	RИЗМ- R Д
dМ=	X	X	×100%
		RXД
			.	(6)

В схеме рис. 12а напряжения на вольтметре и на измеряемом сопротивлении совпадают (UV = UX), но ток через амперметр IА отличается от тока IХ че-

			19
рез измеряемое сопротивление			на значение тока через вольтметр(IA	¹ IX;
IA = IX + IV; IX = IA - IV). Действительное значение сопротивления				в этом
случае выражается через показания приборов следующим образом
RXД=	UV
	I А- IV.		(7)

Ток через вольтметр зависит от его напряжения и сопротивленияRV (определяется по справочным данным непосредственно или расчетом с использованием предела измерения вольтметра и тока полного отклонения):

Примечание: сопротивление вольтметра RV определяется по справочным данным непосредственно или расчетом по закону Ома с использованием предела измерения вольтметра UН и тока полного отклонения измерительного механизма I0 (приводятся в справочнике).

При измерении сопротивления RX по схеме (рис. 12а) параллельно ему оказывается включенным вольтметр. Вследствие этого фактически измеряется эквивалентное сопротивление участка цепи, содержащего измеряемое сопротивление и вольтметр, и измеренное значение будет всегда меньше действительного. Методическая погрешность всегда отрицательна. Влияние вольтметра на результат будет минимальным при выполнении условияRV>>RX. При этом ток вольтметра будет существенно меньше, чем ток через исследуемый элемент, и им можно пренебречь. Параметры амперметра на результат и методическую погрешность в этом случае не влияют.

В схеме рис. 12б амперметр и измеряемое сопротивление находятся в одной ветви (IA = IX), но напряжение на вольтметре не совпадает с напряжением на исследуемом элементе (UV ¹ UX). Разница в напряжениях равна напряжению на амперметре (UV = UX + UA ; UX = UV- UA ). Действительное значение сопротивления, не содержащее методической погрешности:

Д		UV -UA
RX	=
			I А .		(9)

Напряжение на амперметре находится с использованием тока через -амперметр (показание амперметра) и сопротивления RА:

20

Сопротивление амперметра RА приводится в справочниках непосредственно или вычисляется по отношению напряжения на амперметреU0 при номинальном токе (справочные данные), к собственно номинальному току IН.

При измерении сопротивления по рассматриваемой схеме включения фактически измеряется суммарное сопротивление исследуемого элемента и амперметра, в результате чего измеренное значение всегда будет больше действительного, а методическая погрешность всегда положительна. Влияние амперметра на результат будет минимальным при выполнении условияRA<<RX, так

как соотношение сопротивлений при последовательном соединении определяет распределение напряжений, и напряжение на амперметре будет гораздо меньше, чем на исследуемом элементе. В рассмотренной цепи на результат и методическую погрешность не влияет сопротивление вольтметра.

Поэтому можно сделать вывод, что схема рис 12а используется для измерения малых сопротивлений – когда RX << RV., а схема рис 12б используется для измерения больших сопротивлений – когда RX >> RA.

При практическом применении метода амперметра-вольтметрацелесообразно перед выбором схемы включения приборов:

а) предварительно оценить значение сопротивления исследуемого элемента;

б) осуществить выбор приборов, исходя из требуемых пределов измерения тока и напряжения;

в) определить сопротивления приборов и рассчитать соотношения RV/RX

и RX/RA.

Если соотношение RV/RX будет больше, чем второе RX/RA, то меньшую методическую погрешность будет давать схема рис. 12а, в противном случае схема рис. 12б.

Если выбрана схема включения, в которой в указанных соотношениях сопротивления будут отличаться в 100 и более раз, то в большинстве измерительных задач можно пренебречь методической погрешностью, и результат получать по приближенной формуле (4).

Предложенный подход позволяет минимизировать методическуюпо грешность при расчете по приближенной формуле.

Если при расчете сопротивления производить учет сопротивления приборов, не делая допущений (расчет по точным формулам (7) и (9)), то методическая погрешность при включении приборов по любой из рассмотренных схем будет исключена.

Расчеты по точным формулам с учетом сопротивлений приборов дают результат без методической погрешности независимо от выбранной схемы включения.

Инструментальная погрешность косвенных измерений в данном случае определяется погрешностями примененных средств измерений– амперметра и вольтметра.

21

При косвенных измерениях результат является функцией от результатов

прямых измерений величин X1 ,

X 2 , … ,

X m , т.е.Y = f ( X1 ,X 2 , …,X m ).

Для двух наиболее часто встречающихся функций Y1=X1.X2 и Y1=X1/X2

относительная погрешность обычно вычисляется по формуле

æ DC

ö2

æ DC

ö2

1

2

2

2

dY = ±

ç

÷

ç

÷

ç

C1

÷

+ ç

C2

÷ = ±dх1 +dх2 ,

è

ø

è

ø

(11)

где DX1 иDX2 – абсолютные, аdx1 иdx2 – относительные погрешности прямых измерений величин X1 и X2.

Применительно к методу амперметра-вольтметравыражение(11) примет

вид:

					æ	IН	ö2	æ	UН	ö2
	2		2
				= ±	ç		÷	ç		÷	,
	dR = ±d A +dV				ç K А ×		÷	+ ç KV ×		÷
					è	IИЗМø		è	U ИЗМø		(12)

где dА иdV – относительные погрешности прямых измерений тока амперметром и напряжения вольтметром, определяемые исходя из класса точности амперметра KA или вольтметра KV, предела измерения амперметра IН и вольтметра UН и показаний амперметра IИЗМ и вольтметра UИЗМ.

Абсолютная погрешность DR может быть вычислена как:

±DR=dR.RИЗМ/100 (Ом).

Достоинства метода амперметра-вольтметра:

Метод позволяет при выполнении измерения моделировать рабочий -режим элемента в реальной электрической цепи, что особенно важно при измерении сопротивлений нелинейных элементов.

При возможности выбора параметров источника питания и пределов измерения приборов в широком диапазоне, метод позволяет измерять как малые сопротивления (порядка 10-6Ом) так и большие (до 109 Ом).

Измерение может быть выполнено без применения прибора для измерения сопротивления (омметра).

При использовании источника переменного тока и приборов на переменный ток метод позволяет определить полное сопротивление элемента Z.

Может использоваться для измерения мощности участка цепи. В цепи с источником постоянного тока активная мощность P=U.I (Вт), с источником переменного тока – полная мощность S=U.I (ВА).

Недостатки метода амперметра-вольтметра:

Требует дополнительного источника питания с регулируемыми парамет-

рами.

studfiles.net

50.Измерение мощности методом вольтметра-амперметра.

Метод амперметра – вольтметра основан на использовании известного из курса электротехники соотношения R=U/I, являющегося математическим выражением закона Ома. В формуле R – сопротивление участка электрической цепи, на котором при протекании тока I происходит падение напряжения U. Чтобы определить сопротивление заземлителя, надо пропустить через него определенный ток и измерить падение напряжения на участке растекания. После этого произвести простое вычисление по формуле. Данный способ измерения сопротивления заземления имеет следующие недостатки: а) Необходимо пользоваться одновременно двумя измерительными приборами, а потом производить расчет. б) Для того чтобы получить достаточно точные результаты измерений, нужен источник довольно значительного по величине тока (десятки ампер) с хорошей стабилизацией, чтобы обеспечить возможность снятия показаний двух приборов: амперметра и вольтметра. в) Большой ток может явиться источником дополнительной погрешности, так как при большой плотности переменного тока происходит возрастание полного сопротивления стальных проводников по сравнению с сопротивлением этих же проводников постоянному току. г) Вольтметр должен иметь достаточно большое внутреннее сопротивление. д) Блуждающие переменные и постоянные токи в земле могут внести дополнительную и иногда существенную погрешность при измерениях.

Две возможные схемы измерения мощности при помощи амперметра и вольтметра приведены на рис. 1.а и б.

Рис.1Для схемы, изображенной на рис. 1,а. расчетное значение мощности

отличается от мощности, потребляемой нагрузкой, на величину мощности Рv = UаIv , потребляемой вольтметром.Для схемы, изображенной на pиc. 1,б, расчетное значение мощности, потребляемой нагрузкой,

отличается от мощности потребляемой нагрузкой, на величину мощности РА=UаIн, потребляемой амперметром.При измерении мощности в цепях переменного тока формулы можно использовать только при резистивной нагрузке, т.е. при cos=1. При реактивной нагрузке в результате расчета получают полную мощность. Для исключения погрешностей, вызванных: подключением измерительных приборов, в результаты расчетов вводят поправки:

для схемы рис. 1,а или

для схемы рис. 1.б, где Rv - сопротивление вольтметра, а Rа - сопротивление амперметра.

studfiles.net

Измерение сопротивлений методом вольтметра-амперметра - PDF

Расширение пределов измерения амперметра

Федеральное агентство по образованию РФ Ухтинский государственный технический университет 21 Расширение пределов измерения амперметра Методические указания к лабораторной работе для студентов всех специальностей

Подробнее

R x R R2 R 1 R 2. R x = R. (2.4) l 2. l 1 B D

Методические указания к выполнению лабораторной работы.. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРОВОДНИКОВ МЕТОДОМ МОСТИКА УИТСТОНА Филимоненкова Л.В. Электростатика и постоянный ток: Методические указания к выполнению

Подробнее

ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики

Ю. В. Тихомиров ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики С ЭЛЕМЕНТАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. ОПТИКА для студентов всех специальностей всех форм обучения МОСКВА - 2012 ЦЕЛЬ РАБОТЫ

Подробнее

РЕОСТАТ И ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ

Лабораторная работа 306 РЕОСТАТ И ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ Приборы и принадлежности: источник тока, два вольтметра, два миллиамперметра, реостат, нагрузочные резисторы. Введение. Реостат устройство для регулирования

Подробнее

ε, r R 1 R 2 С1 «ПОСТОЯННЫЙ ТОК»

С1 «ПОСТОЯННЫЙ ТОК» На рисунке показана электрическая цепь, содержащая источник тока (с отличным от нуля внутренним сопротивлением), два резистора, конденсатор, ключ К, а также амперметр и идеальный вольтметр.

Подробнее

Измерение сопротивления на постоянном токе

Федеральное агентство по образованию РФ Ухтинский государственный технический университет 4 Измерение сопротивления на постоянном токе Методические указания к лабораторной работе для студентов всех специальностей

Подробнее

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ФОРМУЛЫ

На рисунке показана цепь постоянного тока. Внутренним сопротивлением источника тока можно пренебречь. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (

Подробнее

ЛАБОРАТОРНЫЕ РАБОТЫ ПО ФИЗИКЕ

ПРАВИТЕЛЬСТВО САНКТ-ПЕТЕРБУРГА КОМИТЕТ ПО НАУКЕ И ВЫСШЕЙ ШКОЛЕ САНКТ-ПЕТЕРБУРГСКОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «АВТОТРАНСПОРТНЫЙ И ЭЛЕКТРОМЕХАНИЧЕСКИЙ

Подробнее

ИЗМЕРЕНИЯ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ

Федеральное агентство по образованию «Уральский государственный технический университет УПИ имени первого Президента России Б.Н. Ельцина» В.С. Проскуряков, С.В. Соболев ИЗМЕРЕНИЯ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ВИРТУАЛЬНЫЙ

Подробнее

Лабораторная работа 22

Лабораторная работа Определение электроемкости конденсатора по осциллограмме его разряда через резистор Методическое руководство Москва 04 г. Определение электроемкости конденсатора по осциллограмме его

Подробнее

Расширение пределов измерения амперметра

МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Ухтинский государственный технический университет» (УГТУ) 1 Расширение пределов

Подробнее

(3.1) (3.2) (3.3) (3.4) η=f(i) P 1, η. 0,5 P 1 =f(i)

Методические указания к выполнению лабораторной работы.1.3 ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПОЛЕЗНОЙ МОЩНОСТИ И КОЭФФИЦИЕНТА ПОЛЕЗНОГО ДЕЙСТВИЯ БАТАРЕИ ЭЛЕМЕНТОВ ОТ СИЛЫ ТОКА В ЦЕПИ Филимоненкова Л.В. Электростатика

Подробнее

Индуктивность в цепи переменного тока

Лабораторная работа 7 Индуктивность в цепи переменного тока Цель работы: исследование зависимости сопротивления соленоида от частоты синусоидального тока, определение индуктивности соленоида, а также взаимной

Подробнее

ИЗМЕРЕНИЕ АКТИВНЫХ СОПРОТИВЛЕНИЙ

Федеральное агентство по образованию Уральский государственный технический университет УПИ Э.Г. Миронов ИЗМЕРЕНИЕ АКТИВНЫХ СОПРОТИВЛЕНИЙ Методические указания к лабораторной работе 6 Учебное электронное

Подробнее

E - нормальный элемент Вестона.

ЛАБОРАТОРНАЯ РАБОТА 3-7: ИЗМЕРЕНИЕ ЭЛЕКТРОДВИЖУЩИХ СИЛ ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ МЕТОДОМ КОМПЕНСАЦИИ Студент группа Допуск Выполнение Защита Цель работы: ознакомление с методами компенсации и применение

Подробнее

ИССЛЕДОВАНИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Министерство образования и науки Российской федерации Федеральное агентство по образованию Саратовский государственный технический университет ИССЛЕДОВАНИЕ ЦЕПИ ПОСТОЯННОГО ТОКА Методические указания к

Подробнее

docplayer.ru

Измерение сопротивлений и мощности методом вольтметра, аьперметра и ваттметра

Работа № 11

ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ И МОЩНОСТИ МЕТОДОМ

ВОЛЬТМЕТРА, АЬПЕРМЕТРА И ВАТТМЕТРА

11.1. Цель работы

11.1.1. Ознакомиться со схемами измерения сопротивления на постоянном и переменном токах методом вольтметра, амперметра и ваттметра.

11.1.2. Ознакомиться со схемами измерения активной мощности на постоянном токе методом вольтметра и амперметра.

11.1.3. Усвоить методику расчета методической погрешности и погрешности измерений.

11.2. Задание

11.2.1. Изучить особенности измерений сопротивления и мощности методом вольтметра, амперметра и ваттметра.

11.2.2. Измерить:

а) активную Rxи реактивную Xx составляющие, а также модуль Zx полного сопротивления образца;

б) мощность потребляемую резистором Rx на постоянном токе методом вольтметра и амперметра.

11.2.3. Вычислить:

а) приближенные значения активной и реактивной составляющие, а также модуля полного сопротивления образца;

б) действительные значения тех же сопротивлений;

в) приближенное и действительное значения мощности и Px ;

г) максимальные абсолютные погрешности определения сопротивлений Rx, Xx, модуля Zx - ∆Rmax,∆Xmax,∆Zmax и мощности Px - ∆Pmax ;

д) методические погрешности определения сопротивлений Rx, Xx,модуля Zx и мощности Px . 11.3. Теоретическая часть

Измерение сопротивлений на постоянном токе может производиться вольтметром и амперметром косвенным методом по двум схемам, показанным на рис.11.1.

а) б)

U= Rx U= Rx

Рис.11.1 Схемы для измерения сопротивлений и мощности на постоянном токе.

Измеряя амперметром величину тока IA , а вольтметром – напряжение UV , по известному соотношению получают лишь приближенное значение искомой величины

(11.1)

Отличие найденного значения от действительного обусловлено тем, что при расчете не учтены внутренние сопротивления измерительных приборов.

В связи с этим действительное значение сопротивления Rx определяется следующими выражениями:

Для схемы рис11.1а

(11.2)

где RA – внутреннее сопротивление амперметра;

для схемы рис.11.1б

(11.3)

где RV –внутреннее сопротивление вольтметра.

Как видно из выражений (11.2+11.3), при подсчете искомого значения сопротивления по формуле (11.1) возникает методическая погрешность.

При измерении по схеме рис.11.1а погрешность вызвана тем, что вольтметр измеряет напряжения на резисторе и амперметре.

В схеме рис.11.1б погрешность появляется вследствие измерения амперметром общего тока проходящего через резистор и вольтметр.

Поскольку на практике расчет сопротивления часто производится по формуле (11.1), то необходимо знать, какая из этих схем дает меньшую погрешность.

В связи с этим целесообразно найти выражения для относительных погрешностей обеих схем.

Для схем рис.11.1а относительная погрешность измерения сопротивления равна:

(11.4)

Для схемы рис.11.1б

(11.5)

Таким образом, схема рис.11.1а обеспечивает малую погрешность в тех случаях, когда измеряемое сопротивление велико по сравнению с сопротивлением амперметра ,т.е. при выполнении условия

>> (11.6)

Схема рис.11.1б пригодна для измерений при соблюдении условия

(11.7)

На практике данные условия считаются выполнимыми, если

>>50 и (11.8)

Способ амперметра и вольтметра может найти применение для измерения сопротивлений также и на переменном токе. Однако в этом случае возможно измерить только модуль полного сопротивления . Для определения активной и реактивной составляющих сопротивления необходимо кроме амперметра и вольтметра включить ваттметр по одной из схем рис.11.2.

а) б)

Рис.11.2. Схемы для измерения сопротивлений на переменном токе.

Приближенные значения модуля сопротивления и его составляющих и для обеих схем находятся из соотношений:

,

(11.9)

, .

Методическая погрешность в данном случае определяется теми же факторами, что и в случае измерений на постоянном токе.

При измерении по схеме рис.11.1а действительные значения искомых величин ,, находятся из выражений:

,

(11.10)

где,-активная и реактивная составляющие полного сопротивления амперметра,

, -активная и реактивная составляющие полного сопротивления токовой обмотки ваттметра.

Методические погрешности ,, определения соответственно , и равны:

, (11.11)

. (11.12)

Как видно из выражений (11.11 + 11.12 ) данную схему целесообразно применять для измерения сопротивлений, у которых активная и реактивная составляющие значительно больше суммы активных и реактивных составляющих внутренних сопротивлений амперметра и последовательной цепи ваттметра, т.е. при выполнении условий

>>+, >>+ . (11.13)

На практике условия считаются выполненными аналогично (11.8). Т.к. питание рассматриваемой схемы осуществляется от сети переменного тока частотой 50 Гц, то из-за малости величин и погрешностью можно пренебречь.

При измерении по схеме рис.11.2б действительные значения величин , и находятся из выражений:

, , (11.14)

.

Методические погрешности определяются соответственно:

, (11.15)

. (11.16)

Согласно соотношениям (11.14 ÷11.15) схему рис.11.2б следует принять для измерения сопротивлений, у которых активная составляющая значительно меньше сопротивлений, представляющих собой параллельное соединение активных и реактивных сопротивлений вольтметра и цепи напряжения ваттметра, т.е. при выполнении условий

, , (11.17)

т.к. величины и невелики, то данную схему можно применять для измерения сопротивлений, реактивная составляющая которых очень мала.

Для измерения сопротивлений с большими реактивными составляющими применяются так называемые низкокосинусный ваттметры, т.к при использовании обычных ваттметров отсчет значений мощности ведется начальных отметках шкалы, что приводит к значительной погрешности измерения.

Одним из методов измерения мощности на постоянном токе является метод амперметра и вольтметра, В этом случае измерения мощности проводятся по двум схемам, показанным на рис.11.1.

Приближенное значение мощности для обеих схем равно

, (11.18)

где , -показания амперметра и вольтметра соответственно.

Найденное значение отличается от действительного , так как при расчете не учитывается собственное потребление мощности измерительными приборами.

Действительное значение мощности определяется выражениями:

для схемы рис.11.1а

(11.19)

для схемы рис.11.1б

(11.20)

где , -собственное потребление мощности амперметром и вольтметром.

Методические погрешности находятся:

Для схемы рис.11.1а

(11.21)

для схемы рис.11.1б

, (11.22)

где , - падения напряжения на амперметре и ,

, -токи, протекающие через вольтметр и .

Схемы рис.11.1а и рис.11.1б обеспечивают малую погрешность измерений при выполнении тех же условий, что и измерения сопротивлений.

Погрешность измерений не зависит от измеряемой величины и схемы включения измерительных приборов и определяется классом точности приборов

, (11.23)

где ,, -классы точности амперметра, вольтметра и ваттметра,

,,-номинальные значения тока, напряжения и мощности измерительных приборов.

11.4. Описание лабораторной установки.

Лабораторная установка состоит из двух схем, показанных на рис.11.3.

Схема, изображенная на рис.11.3а, предназначена для измерения сопротивлений и мощности на постоянном токе, схема рис.11.3б – для измерения сопротивлений на переменном токе.

В схеме рис.11.3а вольтметр V при помощи переключателя П можно включать или перед амперметром А (положение а) или после него (положение б). Реостат Р служит для регулировки напряжения питания схемы.

П2 В схеме рис.11.3а при помощи переключателя П1 и П2 можно включать вольтметр и катушку напряжения ваттметра как перед амперметром и токовой катушкой ваттметра (положение а), так и после них (положение б). Регулировка напряжения в данной схеме осуществляется автотрасформатором типа ЛАТР.

а) б)

а

b

а

а

b

b П1

Zx

П

P

~U

220в

ATp

Rx

U=

5+17в

Рис.11.3. Схема лабораторной установки.

11.5. Порядок выполнения работы

11.5.1. Измерить сопротивление и мощности на постоянном токе:

а) собрать схему рис.11.3а, используя образцы неизвестных

сопротивлений, указанных преподавателем;

б) перевести ползунок реостата Р в нижнее по схеме положение и включить напряжение питания схемы;

в) установить напряжение питания схемы, при котором стрелка амперметра отклонится приблизительно на середину шкалы. Записать показания амперметра и вольтметра в таблицу 11.1;

г) перевести переключатель П в положение ”b” и записать новые показания вольтметра и амперметра в таблицу 11.1;

д) пункты в,г повторить при 2x других значениях тока, превышающих предыдущие;

е) в графу ”Примечания” таблицы 11.1 записать значения внутренних сопротивлений приборов и пределы используемого диапазона (в делениях и в измеряемых единицах).

Таблица 11.1

Измерение сопротивлений и мощности на постоянном токе

Положение переключателя П	№ п.п	IA			UV			Примечания
		дел	CA	A	дел	CV	V
а	1 2 3
b	1 2 3

11.5.2. измерить сопротивление на переменном токе:

а) собрать схему рис.11.3б;

б) повторить пункт 11.5.1б, осуществляя регулировку в схеме ползунком автотрансформатора АТр.;

в) повторить пункты 11.5.1 в-е, коммутируя цепи переключателями П1 и П2, регулируя напряжение питания схемы ползунком автотрансформатора и записывая показания приборов в таблицу 11.2.

Таблица 11.2

Измерение сопротивлений на переменном токе

Поло-жение пере-ключа- теля П	№ п.п	IA			UV			PW			Приме- чания
		дел	CA	A	дел	CV	V	дел	CW	W
а	1 2 3
b	1 2 3

11.5.3. Результаты расчетов записать в таблицы 11.3-11.5.

Таблица 11.3

Результаты измерения сопротивления на постоянном токе

Поло-жение пере-ключа- теля П	№ п.п	R1		Погрешн.		R2 или R3		Погрешн.		Приме- чания
		Ω		%		Ω		%
		без корр.	с корр.			без корр.	с корр.
а	1 2 3 ср.
b	1 2 3 ср.

Таблица 11.3

Результаты измерения сопротивления на постоянном токе

Поло-жение клю-чей П1 и П2

№ п.п

погрешн. мет.

∆R max

∆X max

∆Z max

Ω

Ω

Ω

Ω

Ω

Ω

%

%

%

%

Ω

Ω

Ω

а

1 2 3 ср.

b

1 2 3 ср.

Таблица 11.5

Результаты измерения мощности на постоянном токе

Положение ключей П1 и П2	№ п.п					∆P max
		W	W	%	%	W
а	1 2 3 ср.
b	1 2 3 ср.

11.6. Контрольные вопросы

1. Из чего исходят при выборе варианта схемы для измерения сопротивления на постоянном токе, используя вольтметр и амперметр?

2. В каких случаях при измерении мощности на постоянном токе используют схему рис.11.1а, когда пользуются схемой рис.11.1б.

3. Почему методом вольтметра и амперметра невозможно измерять мощность на переменном токе?

4. Что вызывает погрешности при измерениях сопротивлений, используя вольтметр, амперметр и ваттметр?

5. Что вызывает погрешности при измерениях мощности, используя вольтметр и амперметр?

6. Можно ли рассчитать величину и , пользуясь показаниями приборов, полученными в разных схемах – амперметра по схеме рис.11.1а и вольтметра по схеме рис.11.1б.

7. Как рассчитать методические погрешность при измерениях сопротивлений и мощности методом вольтметра, амперметра и ваттметра?

8. Как рассчитать погрешности измерений, обусловленные погрешностями измерительных приборов при измерении сопротивлений и мощности методом вольтметра, амперметра и ваттметра?

9. Почему методическая погрешность по схеме рис.11.1а имеет положительный знак, а по схеме 11.1б.- отрицательный знак?

10. Можно ли замерить одновременно индуктивность катушки и емкость конденсатора, используя вольтметр, амперметр и ваттметр?

dereksiz.org

Измерение индуктивностей методом вольтметра - амперметра

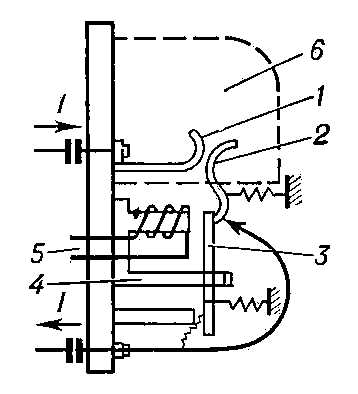
⇐ ПредыдущаяСтр 24 из 54Следующая ⇒

Метод вольтметра - амперметра применяется для измерения сравнительно больших индуктивностей при питании измерительной схемы от источника низкой частоты F = 50...1000 Гц.

Схема измерений представлена на рис. 3, а. Полное сопротивление Z катушки индуктивности рассчитывается по формуле

Z = (R2+X2)0,5 = U/I

на основе показаний приборов переменного тока V~ и mA~. Верхний (по схеме) вывод вольтметра присоединяют к точке а при Z << Zв и к точке б при Z >> Za, где Zв и Za - полные входные сопротивления соответственно вольтметра V~ и миллиамперметра mA~. Если потери малы, т. е. R << X = 2*π*F*Lx, то измеряемая индуктивность определяется формулой

Lx ≈ U/(2*π*F*I).

Катушки большой индуктивности с целью уменьшения их габаритов обычно изготовляются со стальными сердечниками. Наличие последних приводит к нелинейной зависимости магнитного потока от тока, протекающего через катушку. Эта зависимость становится особенно сложной для катушек, работающих с подмагничиванием, через обмотки которых протекают одновременно переменный и постоянный токи. Поэтому индуктивность катушек со стальными сердечниками зависит от значения и характера протекающего через них тока. Например, при большой постоянной составляющей тока происходит магнитное насыщение сердечника и индуктивность катушки резко уменьшается. Кроме того, проницаемость сердечника и индуктивность катушки зависят от частоты переменного тока. Отсюда следует, что измерение индуктивности катушек со стальными сердечниками необходимо проводить в условиях, близких к их рабочему режиму. В схеме на рис. 3, а это обеспечивается при дополнении её цепью постоянного тока, показанной штриховой линией. Необходимый ток подмагничивания устанавливается реостатом R2 по показаниям миллиамперметра постоянного тока mA. Разделительный конденсатор С и дроссель Др разделяют цепи питания постоянного и переменного тока, устраняя взаимное влияние между ними. Приборы переменного тока, применяемые в данной схеме, не должны реагировать на постоянные составляющие измеряемого ими тока или напряжения; для вольтметра V~ это легко обеспечивается посредством включения последовательно с ним конденсатора ёмкостью в несколько микрофарад.

Рис. 3. Схемы измерения индуктивности методом вольтметра - амперметра.

Другой вариант измерительной схемы, позволяющий обойтись без миллиамперметра переменного тока, приведён на рис. 3, б. В этой схеме реостатами R1 и R2 (их можно заменить потенциометрами, включёнными параллельно источникам питания) устанавливают требуемый режим испытания по переменному и постоянному току. В положении 1 переключателя В вольтметр V~ измеряет переменное напряжение U1 на катушке Lx. При переводе переключателя в положение 2 фактически контролируется значение переменного тока в цепи по падению напряжения U2 на опорном резисторе Rо. Если потери в катушке малы, т. е. R << 2*π*F*Lx, то измеряемую индуктивность можно рассчитать по формуле

Lx ≈ U1*Rо/(2*π*F*U2).

Мостовой метод измерения параметров катушек индуктивности. Универсальные измерительные мосты

Мосты, предназначенные для измерения параметров катушек индуктивности, формируются из двух плеч активного сопротивления, плеча с объектом измерений, сопротивление которого в общем случае является комплексным, и плеча с реактивным элементом - конденсатором или катушкой индуктивности.

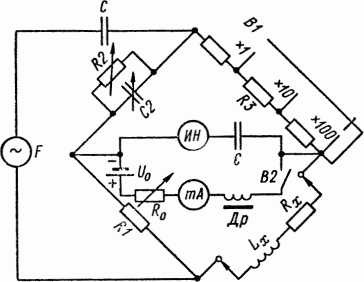
Рис. 4. Схема магазинного моста для измерения индуктивностей и сопротивлений потерь.

В измерительных мостах магазинного типа в качестве реактивных элементов предпочитают использовать конденсаторы,

поскольку в последних потери энергии могут быть сделаны пренебрежимо малыми, а это способствует более точному определению параметров исследуемых катушек. Схема такого моста представлена на рис. 4. Регулируемым элементом здесь является конденсатор С2 переменной ёмкости (или магазин ёмкостей), зашунтированный переменным резистором R2; последний служит для уравновешивания фазового сдвига, создаваемого сопротивлением потерь Rx в катушке с индуктивностью Lx. Применяя условие равновесия амплитуд (Z4Z2 = Z1Z3), находим:

(Rx2 + (2*&pi*F*Lx)2)0,5 : ((1/R2)2 + (2*&pi*F*C2)2)0,5 = R1R3.

Так как фазовые углы φ1 = φ3 = 0, то условие равновесия фаз (φ4 +φ2 =φ1 + φ3) можно записать в виде равенства φ4 + φ2 = 0, или φ4 = -φ2, или tg φ4 = -tg φ2. Учитывая, что для плеча с Lx справедлива формула (tg φ =X/R), а для плеча с ёмкостью С2 - формула (tg φ =R/X) при отрицательном значении угла φ2, имеем

2*&pi*F*Lx / Rx = 2*&pi*F*C2R2

Решая совместно приведённые выше уравнения, получим:

Lx = C2R1R3; (1)Rx = R1R3 / R2. (2)

Из последних формул следует, что конденсатор С2 и резистор R2 могут иметь шкалы для непосредственной оценки значений Lx и Rx, причём регулировки амплитуд и фаз, производимые ими, взаимонезависимы, что позволяет быстро уравновешивать мост.

Для расширения диапазона измеряемых величин один из резисторов R1 или R3 обычно выполняется в виде магазина сопротивлений.

При необходимости измерения параметров катушек со стальными сердечниками схема моста на рис. 4 дополняется источником постоянного напряжения Uо, реостатом Rо и миллиамперметром постоянного тока mA, служащими для регулировки и контроля тока подмагничивания, а также дросселем Др и конденсатором С, разделяющими цепи переменной и постоянной составляющих тока.

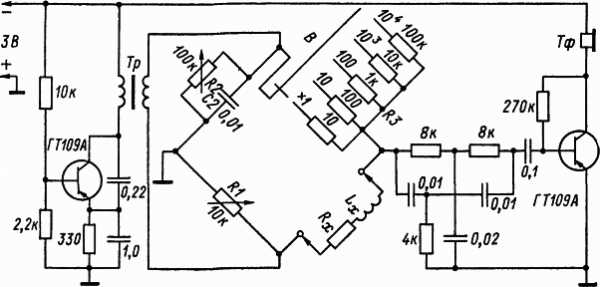
Рис. 5. Схема магазинного моста для измерения индуктивностей и добротностей

На рис. 5 приведена схема другого варианта магазинного моста, в которой конденсатор С2 имеет постоянную ёмкость, а резисторы R1 и R2 взяты переменными. Расширение диапазона измерений осуществляется посредством включения в мост резисторов R3 различных номиналов. Из формул (1) и (2) следует, что регулировки амплитуд и фаз в этой схеме оказываются взаимозависимыми, поэтому уравновешивание моста достигается путём попеременного изменения сопротивлений резисторов R1 и R2. Оценка индуктивностей Lx производится по шкале резистора R1 с учётом множителя, определяемого установкой переключателя В. Отсчёт по шкале резистора R2 обычно производится в значениях добротности катушек

QL = 2*π*F*Lx/Rx = 2*π*F*C2R2.

при частоте F источника питания. В справедливости последней формулы можно убедиться, если левую и правую части равенства (1) разделить на соответствующие части равенства (2).

При указанных на схеме данных измерительный мост позволяет измерять индуктивности примерно от 20 мкГн до 1, 10, 100 мГн; 1 и 10 Гн (без стальных сердечников) и добротности до значения QL ≈ 60. Источником питания служит транзисторный генератор с частотой колебаний F ≈ 1 кГц. Напряжение разбаланса усиливается транзисторным усилителем, нагруженным на телефоны Тф. Двойной Т-образный RC-фильтр, настроенный на частоту 2F ≈ 2 кГц, подавляет вторую гармонику колебаний источника, что облегчает уравновешивание моста и снижает погрешность измерений.

Мостовые измерители индуктивностей, ёмкостей и активных сопротивлений имеют ряд идентичных элементов. Поэтому они часто совмещаются в одном приборе - универсальном измерительном мосте. Универсальные мосты высокой точности базируются на магазинных схемах типа приведённых на рис. 5. Они содержат источник постоянного напряжения или выпрямитель (питающий схему измерения Rx), генератор низкой частоты с выходной мощностью в несколько ватт, многокаскадный усилитель напряжения разбаланса, нагруженный на магнитоэлектрический гальванометр; последний при измерении активных сопротивлений включается непосредственно в измерительную диагональ моста. Требуемая схема измерений формируется с помощью довольно сложной системы коммутации. В таких мостах иногда применяют индикаторы логарифмического типа, чувствительность которых резко падает, если мост не уравновешен.

Рис. 6. Схема универсального реохордного моста для измерения сопротивлений, ёмкостей и индуктивностей

Значительно проще универсальные мосты реохордного типа, измеряющие параметры радиодеталей с погрешностью порядка 5-15%. Возможная схема такого моста представлена на рис. 6. Мост питается при всех видах измерений напряжением с частотой примерно 1 кГц, которое возбуждается транзисторным генератором, выполненным по схеме индуктивной трёхточки. Индикатором баланса служит высокоомный телефон Тф. Резисторы R2 и R3 заменены проволочным реохордом (или, чаще, обычным потенциометром), позволяющим уравновешивать мост плавным изменением отношения сопротивлений R2/R3. Это отношение отсчитывается по шкале реохорда, диапазон показаний которой обычно ограничивается крайними значениями 0,1 и 10. Измеряемая величина определяется при уравновешенном мосте как произведение отсчёта по шкале реохорда на множитель, определяемый установкой переключателя В. Каждому виду и пределу измерений отвечает включение в схему моста соответствующего опорного элемента требуемого номинала - конденсатора Со (С1), резистора Rо (R4) или катушки индуктивности Lо (L4).

Особенностью рассматриваемой схемы является то, что измеряемые элементы Rx и Lx включаются в первое плечо моста (при опорных элементах Rо и Lо, находящихся в четвёртом плече), а Сх, наоборот, - в четвёртое плечо (при Со - в первом плече). Благодаря этому оценка всех измеряемых величин производится по аналогичным формулам типа

AX = Aо(R2/R3),

где Ах и Ао - значения величин соответствующих измеряемого и опорного элементов.

Переменный резистор R5 служит для компенсации фазовых сдвигов и улучшения балансировки моста при измерении индуктивностей. С той же целью иногда включают переменный резистор небольшого сопротивления в цепь опорного конденсатора Со предела измерений больших ёмкостей, которые часто имеют заметные потери.

С целью исключения влияния руки оператора движок реохорда обычно соединяют с корпусом прибора.

Читайте также:

lektsia.com

Работа фпэ-01. Измерение активного сопротивления методом амперметра и вольтметра

Цель работы: ознакомиться с измерительными приборами непосредственного отсчета (амперметрами и вольтметрами), методом измерения сопротивлений в электрических цепях постоянного тока, основными видами погрешностей измерений и способами их уменьшения.

Краткое теоретическое введение

1. Основным законом постоянного электрического тока является закон Ома, согласно которому на однородном участке цепи, в котором не действуют сторонние ЭДС, сила тока, текущего по проводнику, пропорциональна разности потенциалов на его концах и обратно пропорциональна его сопротивлению:

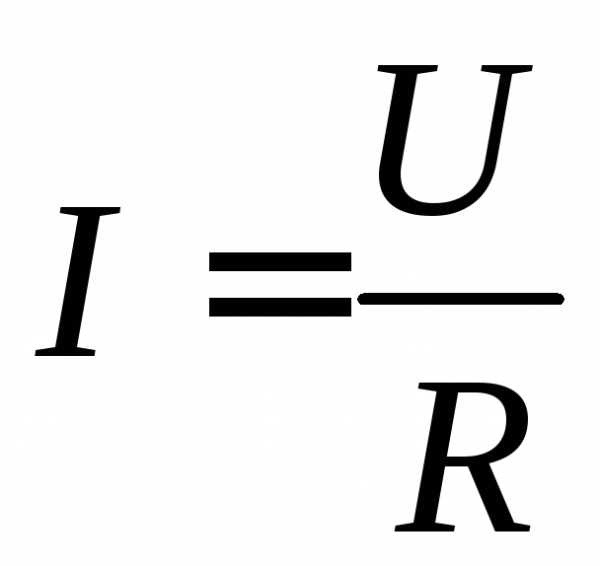(1)

Для поддержания в электрической цепи постоянного тока необходимо непрерывное действие электродвижущей силы, так как носители зарядов при своем движении испытывают некоторое сопротивление. Сопротивление металлических проводников можно качественно объяснить взаимодействием (рассеянием) свободных электронов проводимости, движущихся упорядоченно под действием поля, с атомами и ионами, расположенными в узлах кристаллической решетки. Атомы (ионы), находясь в состоянии теплового колебательного движения, препятствуют перемещению электронов, уменьшая силу тока.

Сопротивлением проводника называют физическую величину, характеризующую свойство проводника затруднять прохождение электрического тока.

Сопротивление зависит от материала проводника, его геометрической формы и размеров, от температуры, а также от конфигурации (распределения) тока по проводнику.

В простейшем случае однородного цилиндрического проводника длиной 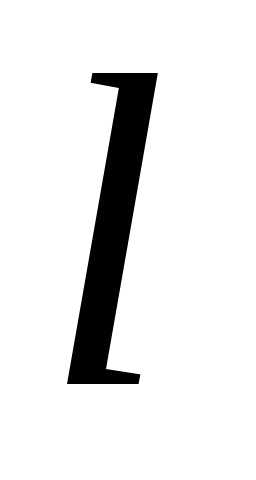и площадью поперечного сечения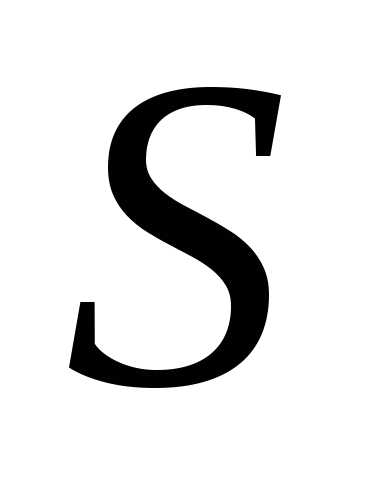сопротивление

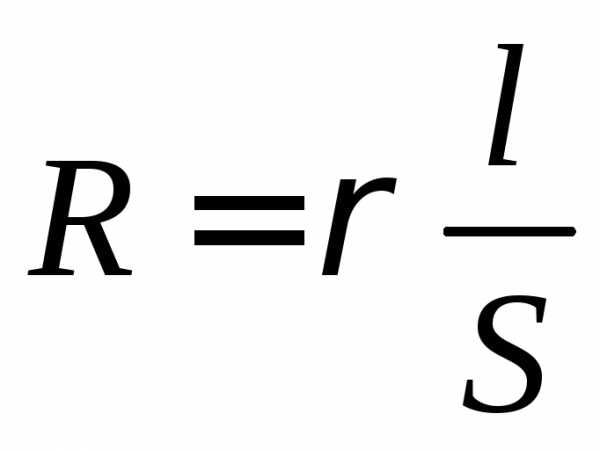(2)

где 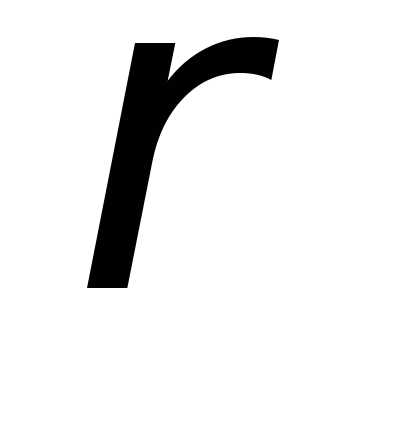– удельное электрическое сопротивление.

В системе СИ сопротивление измеряется в Омах. 1 Ом равен сопротивлению участка электрической цепи, в которой протекает постоянный ток силой 1А при напряжении на его концах 1 В. Для измерения больших сопротивлений используют следующие единицы измерения: 1кОм=103 Ом, 1 МОм=106 Ом.

2. Измерение тока производится амперметрами, включаемыми последовательно в цепь, в которой измеряется ток.

Обмотку амперметра выполняют из небольшого числа витков толстого провода, поэтому при включении прибора в электрическую цепь сопротивление этой ее части практически не изменяется. При этом мощность, потребляемая прибором, оказывается ничтожной.

Включенные таким образом амперметры используются как приборы непосредственной оценки, они показывают численное значение измеряемого тока.

В цепях постоянного тока, в основном, используются амперметры магнитоэлектрической, реже электромагнитной системы. Амперметр рассчитан на определенное предельное значение силы тока. Для расширения его предела измерения в электрических цепях постоянного тока используются шунты. Это специально тарированные (калибровочные) резисторы, включаемые параллельно с амперметром.

3. Измерение напряжения, действующего в электрической цепи постоянного тока, осуществляется с помощью вольтметров, включаемых параллельно к участку цепи, напряжение на котором необходимо измерить. При этом они используются как приборы непосредственной оценки и указывают численное значение измеряемого напряжения. В цепях постоянного тока обычно используются вольтметры магнитоэлектрической и электромагнитной систем. Для расширения предела измерения вольтметров последовательно с их обмоткой включают тарированные (калибровочные) добавочные резисторы, помещенные внутри прибора или отдельно от него.

Для снижения мощности, потребляемой вольтметрами, обмотки последних выполняют из большего числа витков тонкого провода с достаточно большим сопротивлением.

4. В тех случаях, когда искомое сопротивление значительно больше сопротивления амперметра, последовательно с которым оно включено, измерение методом амперметра и вольтметра осуществляется по схеме, представленной на рис. 1. Определяемое сопротивление

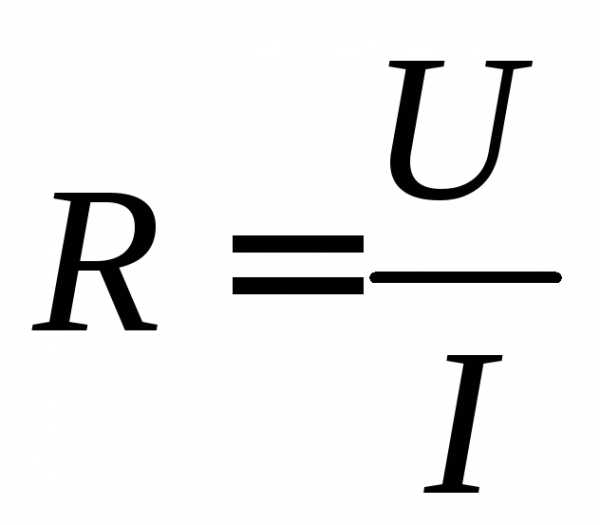(3)

где 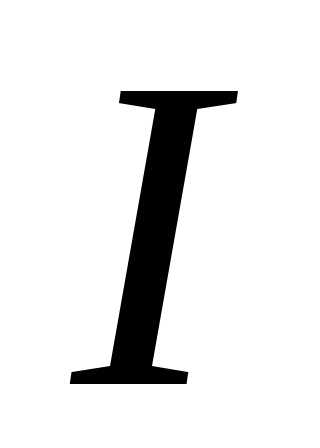– сила тока, показываемая амперметром, а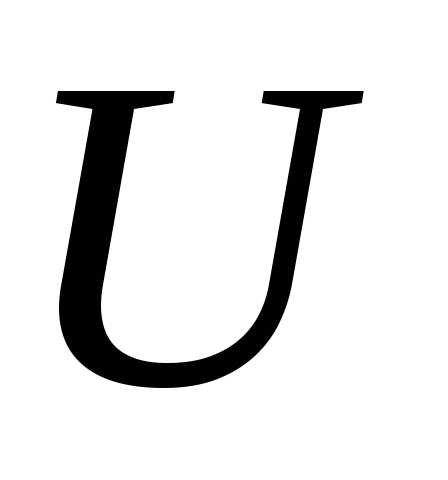– напряжение, показываемое вольтметром.

При этом пренебрегают падением напряжения на амперметре, считая, что подводимое напряжение полностью приложено к измеряемому сопротивлению, хотя вольтметр учитывает падение напряжения и на амперметре:

(4)

где 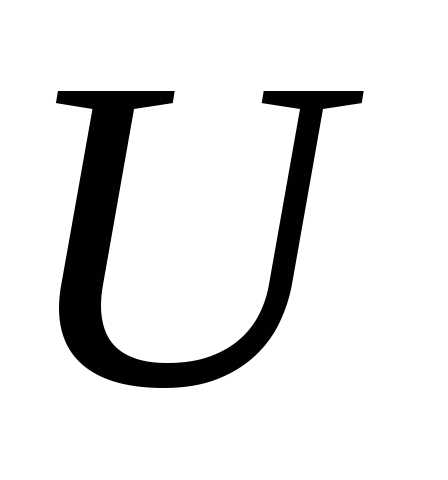– показание вольтметра,

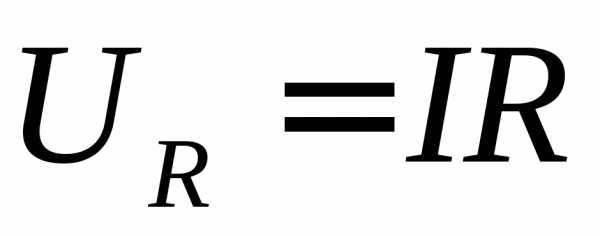–падение напряжения на сопротивлении R.

–падение напряжения на амперметре сопротивлением .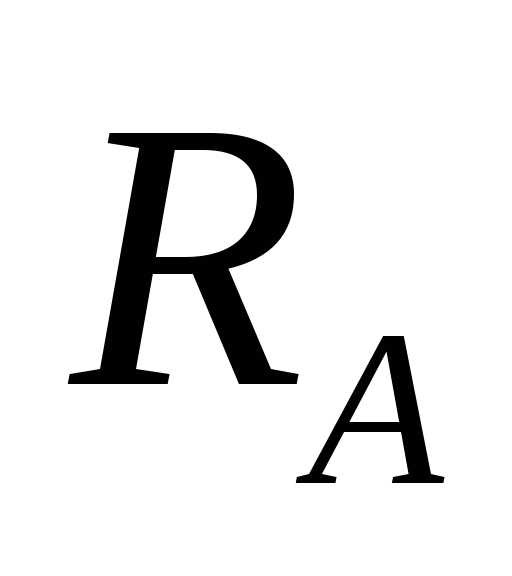

Истинное значение напряжения на сопротивлении R будет

т.е. оно меньше показания вольтметра 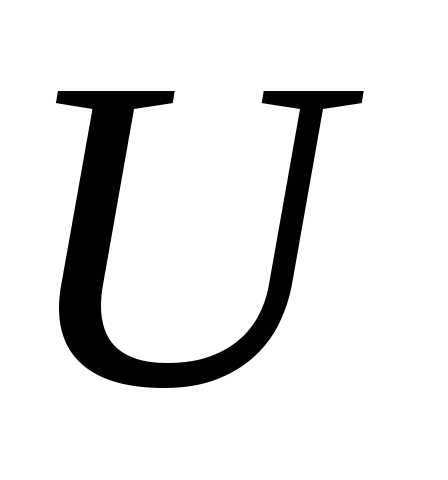на значение.

При точном определении измеряемого сопротивления с учетом погрешности, вносимой амперметром, его значение рассчитывается по формуле:

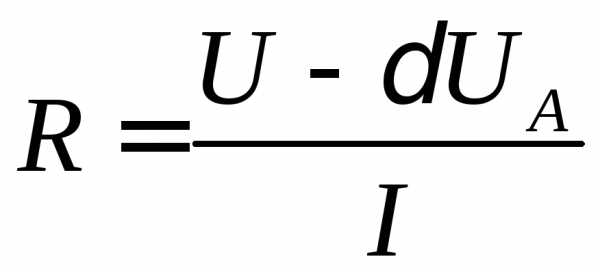(5)

Если поправка выходит за пределы погрешности, определяемой классом точности используемого прибора, то ее следует учитывать при измерениях.

Относительная погрешность при измерениях по данной схеме равняется:

(6)

5. Для определения малых сопротивлений, соизмеримых с сопротивлением амперметра, следует использовать схему на рис. 2, позволяющую исключить влияние сопротивления амперметра.

Искомое сопротивление вновь находится по формуле (3). Однако при этом пренебрегают током, протекающим через вольтметр. Для точного определения сопротивления с учетом погрешности, вносимой вольтметром, его значение рассчитывается по формуле:

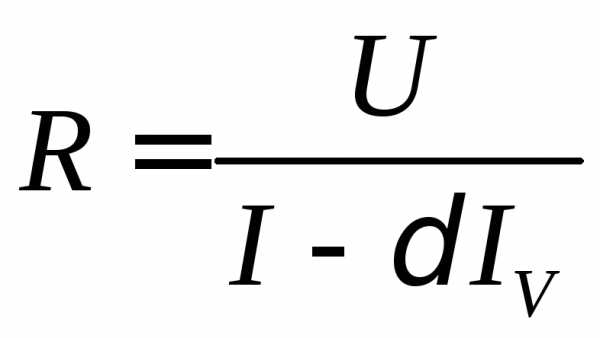(7)

где – ток, текущий через вольтметр.

Если погрешность 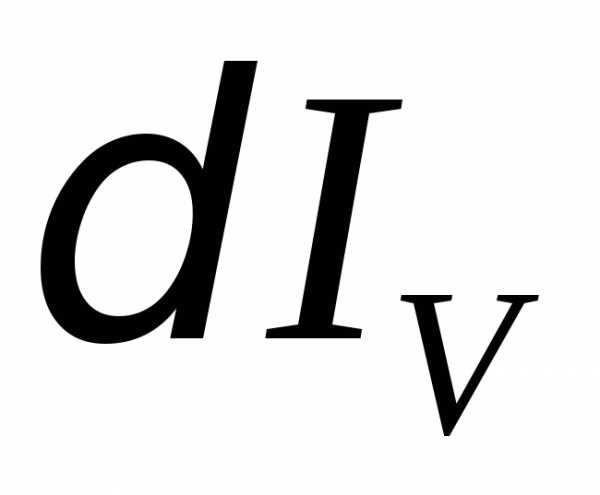превышает предел погрешности, определяемый классом точности используемого прибора, ее следует учитывать при измерениях.

Относительная поправка измерения по этой схеме равняется:

(8)

Таким образом, выбор выгодной (точной) схемы зависит от соотношения сопротивлений нагрузки и используемых приборов.

studfiles.net

4.6. Измерение сопротивлений

Метод вольтметра - амперметра

Метод вольтметра - амперметра наиболее простой, но и наименее точный, т.к. этому методу присуща методическая систематическая погрешность. Если включить приборы по схеме (рис. 4.12, а), то напряжение измеряется  правильно,  но амперметр показывает сумму токов вольтметра и измеряемого сопротивления.  При схеме включения, показанной на (рис. 4.12, а), результаты получаются точнее   при   измерении малых сопротивлений Rв»Rх, а при измерении больших лучше использовать схему (рис. 4.12, б), с неправильно   измеряемым   напряжением,   учитывающим   напряжение на амперметре. При этом сопротивлении Rx » Ra, где Rв и Rа - соответственно, сопротивления вольтметра и амперметра.

Метод вольтметра - амперметра применяют и для измерения реактивных сопротивлений (емкостных или индуктивных) при питании схем напряжением переменного тока. Однако в этих случаях результат измерения будет показывать значение полного сопротивления. Для определения всех параметров в схему дополнительно включают либо ваттметр, и тогда Z=U/I; R=Р/I2; Х= ; либо сопротивление подключается в цепь постоянного тока, считая, что омическое сопротивление равно активному. В некоторых случаях активным сопротивлением пренебрегают, считая, что полное сопротивление равно реактивному и производя соответствующие расчеты.

Мостовой метод измерения.

Мостовой метод измерения наиболее точный. Измерять сопротивления можно мостами постоянного тока (см. гл. 3). Измерение сопротивлений, емкостей, индуктивностей и других параметров определяется мостами переменного тока.

Непосредственный метод измерения.

При непосредственном методе измерений сопротивлений используют омметры и мегомметры с магнитоэлектрическими логометрами в качестве измерительных механизмов. Измеряемое сопротивление включается либо последовательно, либо параллельно измерительному механизму. В первом случае измеряются большие сопротивления, во втором, малые; обе схемы обычно компонуются в одном приборе. Основным достоинством приборов логометрического типа является независимость показаний прибора от напряжения источника питания. Для непосредственных измерений сопротивлений также широко используются электронные омметры. Несмотря на недостатки (невысокая чувствительность и точность) они относительно просты, дешевы и надежны.

Измерение сопротивления с помощью потенциометра.

При измерении сопротивления с помощью потенциометра последовательно с измеряемым сопротивлением включа­ется образцовое сопротивление R0, близкое по значению к измеряемому. Через оба сопротивления пропускают посто­янный ток и с помощью потенциометра определяют падение напряжения сначала на образцовом, затем на измеряемом и, наконец, опять на образцовом сопротивлениях. Последнюю операцию проводят для того, чтобы убедиться, что ток в процессе измерений не изменился. Измеряемое сопротивле­ние RХ=RОUХ/UО [Ом], где UХ и U0 - падение напряжения, соответственно, на измеряемом и образцовом В или мВ сопротивлениях.

4.5. Измерение частоты< Предыдущая Следующая >5. Измерение магнитных велечин

xn----8sbnaarbiedfksmiphlmncm1d9b0i.xn--p1ai

---

• 
  Допустимая температура воздуха на рабочем месте в холодное время года
• 
  Как не платить за не воду
• 
  Ремонт коллектора электродвигателя
• 
  Что такое электрический контактор
• 
  Гост размеры резистор
• 
  Низкие высокие средние частоты
• 
  Ленинградская область аэс
• 
  Магнитная проницаемость вакуума равна
• 
  Показания счетчиков электроэнергии до какого числа передавать
• 
  Заземляющий реактор
• 
  Источник питания для антенны