Формула тока. Как найти ток. Вычисляем и определяем ток по формуле закона Ома.
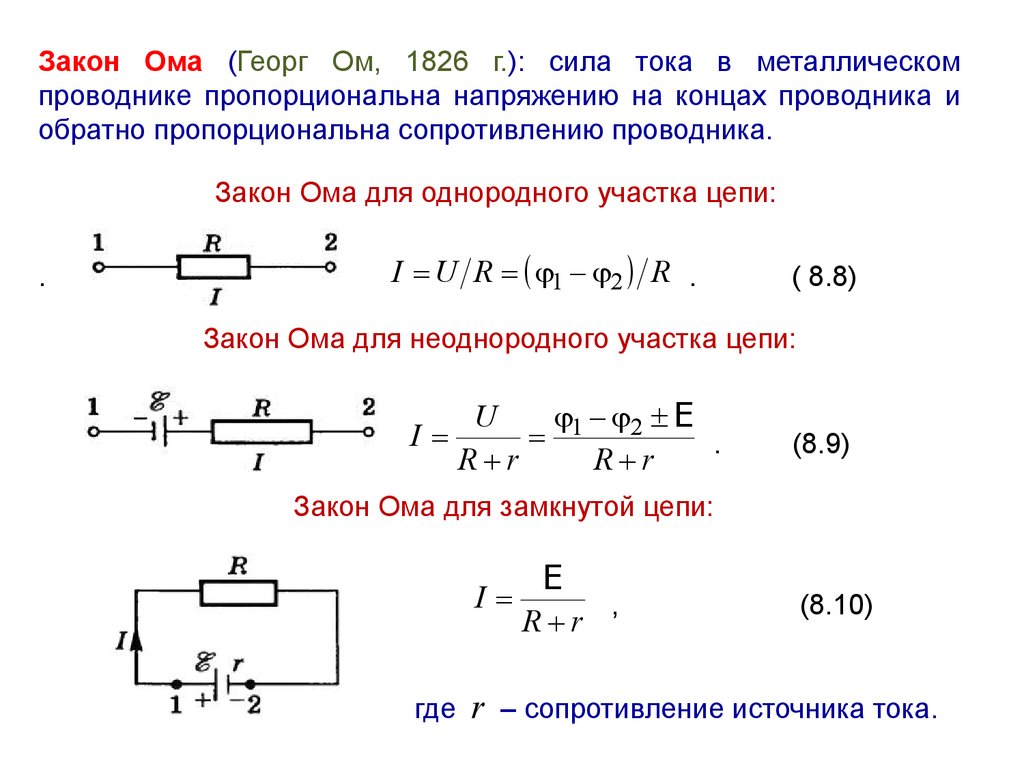
Основополагающей формулой для нахождения силы тока является классический закон Ома, который гласит, что сила тока равна напряжение деленное на сопротивление. И эта основополагающая формула любого электрика и электроника, которая постоянно используется для быстрого вычисления силы тока той или иной цепи. Из любых двух известных величин закона Ома (это ток, напряжение и сопротивление) всегда можно найти третью. В случае нахождения напряжения мы перемножаем ток на сопротивление, ну а при вычислении тока или сопротивления всегда напряжение делим на ту величину, которая известная (сила тока или сопротивление).
Стоит сказать, что данная формула тока подходит как для переменного, так и для постоянного тока. Хотя для переменного имеются некоторые нюансы. А именно: это случаи, когда мы используем активную нагрузку (нагреватели, лампочки). Формула тока показывает зависимость напряжения, сопротивления, и собственно силы тока.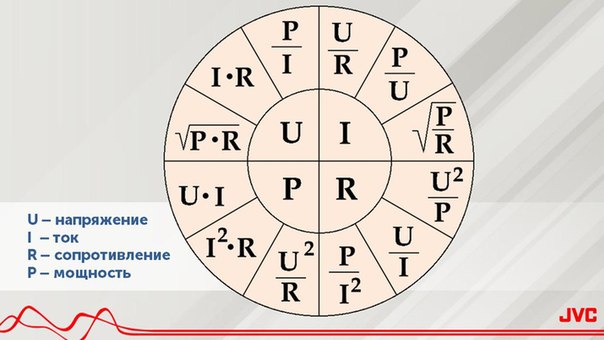
Поскольку немаловажной характеристикой, используемой в области электричества, является также электрическая мощность, то для нахождения силы тока применять можно и её. Электрическая мощность, это произведение силы тока на напряжение. И чтобы найти силу тока необходимо мощность поделить на известное напряжение. Например, нам известна мощность нагревательного элемента, которая равна 880 Вт. Мы также знаем напряжение, что будет подаваться на него, равное 220 В. Нам нужно найти силу тока, которая будет протекать по цепи питания данного нагревателя. Для этого мы просто 880 ватт делим на 220 вольт, что даст на силу тока в 4 ампера.
Теперь как можно вычислить по формуле тока (по закону Ома) этот самый ток зная напряжение и сопротивление. Итак, у нас всё то же напряжение 220 вольт, и есть тот же нагревательный элемент. Мы мультиметром, тестером измеряем сопротивление элемента (у нагревателя с мощностью 880 ватт и рассчитанного на напряжение 220 вольт оно будет 55 ом). И что бы найти силу тока мы напряжение 220 вольт делим на сопротивление нагревателя 55 ом, в итоге получаем всю ту же силу тока в 4 ампера.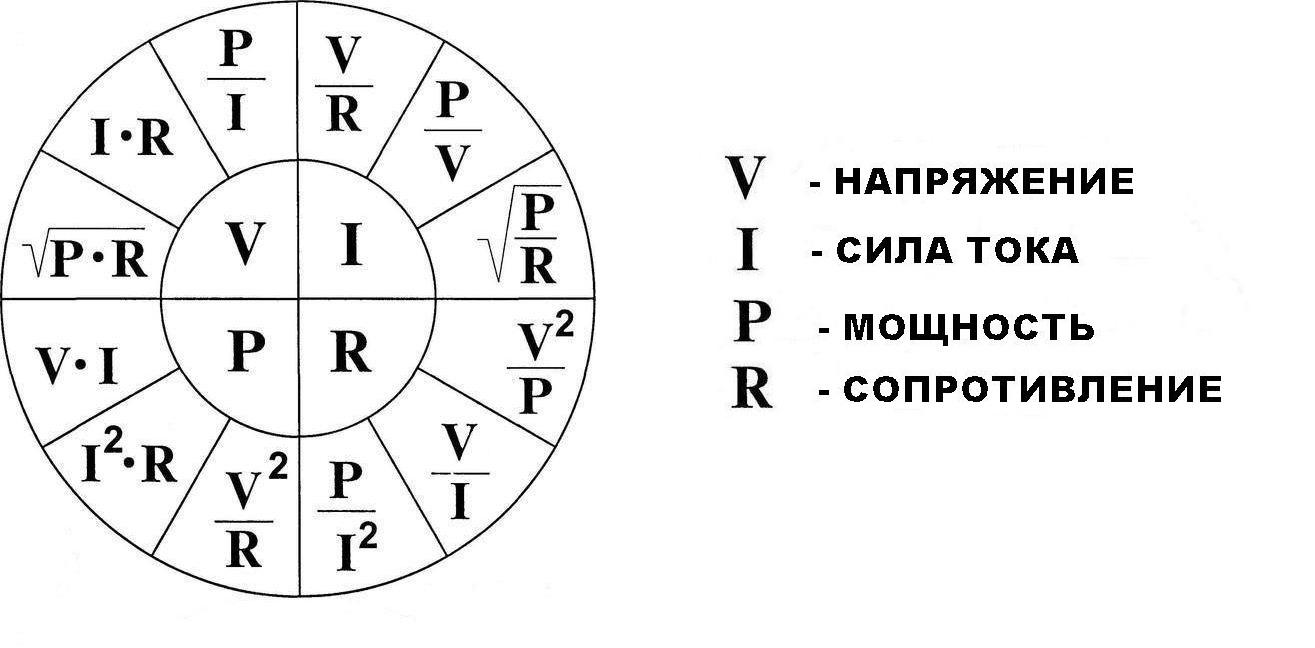
Просто нужно хорошо запомнить эти две формулы тока (его нахождение через мощность и через сопротивление с известным напряжением). Тогда вы быстро и без труда в голове сможете вычислять как силу тока электрической цепи, так и любые другие электрические величины (напряжение, сопротивление, мощность).
Ну, а если вы больше практик, тогда просто берите в руки измерители и меряйте. Напомню, напряжение мы измеряем параллельным прикладыванием щупов тестера, мультиметра к контактам, на которых будет измерять величину разности потенциалов. Силу тока же мы меряем уже путем разрыва цепи, где нужно измерить силу тока, то есть разрываем электрическую цепь в начале (поближе к источнику питания) и между этим разрывом подсоединяем щупы нашего измерителя тока (амперметра). Не забывайте, что переменный ток должен соответствовать своему положению на переключателе тестера, а постоянный своему месту (иначе вы получите неверные значения измеряемого тока).
P.S. Для лучшего запоминания закона Ома вы просто держите в голове, что при делении напряжение всегда в верху, то есть если по закону Ома мы находим напряжение, то перемножаем ток на сопротивление, ну в двух других случаях (при нахождении сопротивления или тока) мы всегда напряжение делим на известную величину, получая вторую, которая ранее была неизвестна.
Как найти сопротивление тока формула. Электрическое сопротивление. Определение, единицы измерения, удельное, полное, активное, реактивное
Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени. Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций. В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление.
Если известна мощность и напряжение
Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:
После несложных мы получаем формулу для вычислений
Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:
Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:
Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:
Р1 = Р2/η
Здесь P2 – активная полезная мощность на валу, η – КПД,
оба этих параметра обычно указывают на шильдике.
Находим полную мощность с учетом cosФ (он также указывается на шильдике):
S = P1/cosφ
Определяем потребляемый ток по формуле:
Iном = S/(1,73·U)
Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.
Если известно напряжение или мощность и сопротивление
Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь , с его помощью проводим расчёт силы тока через сопротивление и напряжение.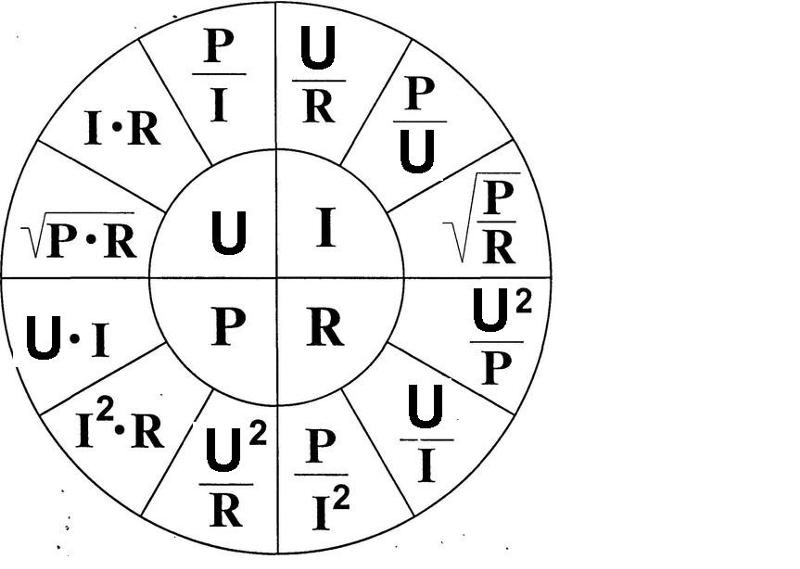
Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:
При этом согласно тому же закону Ома:
P=I 2 *R
Значит расчёт проводим по формуле:
I 2 =P/R
Или возьмем выражение в правой части выражения под корень:
I=(P/R) 1/2
Если известно ЭДС, внутреннее сопротивление и нагрузка
Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:
I=E/(R+r)
Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.
Закон Джоуля-Ленца
Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником. Для этого вспомним .
Для этого вспомним .
Его формула выглядит так:
Q=I 2 Rt
Тогда расчет проводите так:
I 2 =QRt
Или внесите правую часть уравнения под корень:
I=(Q/Rt) 1/2
Несколько примеров
В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.
Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.
I=U/R=12/3=4 Ампера
При параллельном соединении двух элементов Rобщее можно рассчитать так:
Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67
Тогда дальнейшие вычисления можно проводить так:
В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.
Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.
Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению
Так записывается основная формула:
Путем преобразования основной формулы можно найти и другие две величины:
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Формула мгновенной электрической мощности:
Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.
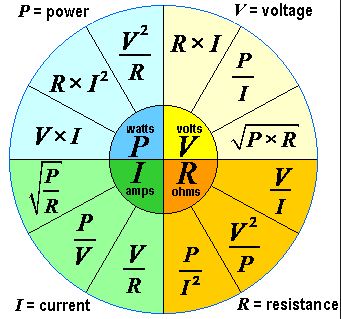
Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.
Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.
Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.
Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.
Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.
Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.
Этот круг также, как и треугольник можно назвать магическим.
Среди прочих показателей, характеризующих электрическую цепь, проводник, стоит выделить электрическое сопротивление. Оно определяет способность атомов материала препятствовать направленному прохождению электронов. Помощь в определении данной величины может оказать как специализированный прибор – омметр, так и математические расчеты на основании знаний о взаимосвязях между величинами и физическими свойствами материала. Измерение показателя производится в Омах (Ом), обозначением служит символ R.
Закон Ома – математический подход при определении сопротивления
Соотношение, установленное Георгом Омом, определяет взаимосвязь между напряжением, силой тока, сопротивлением, основанную на математическом взаимоотношении понятий. Справедливость линейной взаимосвязи – R = U/I (отношение напряжения к силе тока) – отмечается не во всех случаях.
Единица измерения [R] = B/A = Ом. 1 Ом – сопротивление материала, по которому идет ток в 1 ампер при напряжении в 1 вольт.
Эмпирическая формула расчета сопротивления
Объективные данные о проводимости материала следуют из его физических характеристик, определяющих как его собственно свойства, так и реакции на внешние влияния. Исходя из этого проводимость зависит от:
- Размера.
- Геометрии.
- Температуры.
Атомы проводящего материала сталкиваются с направленными электронами, препятствуя их дальнейшему продвижению. При высокой концентрации последних атомы не способны им противостоять и проводимость оказывается высокой. Большие значения сопротивления характерны для диэлектриков, которые отличаются практически нулевой проводимостью.
Большие значения сопротивления характерны для диэлектриков, которые отличаются практически нулевой проводимостью.
Одной из определяющих характеристик каждого проводника является его удельное сопротивление – ρ. Оно определяет зависимость сопротивления от материала проводника и воздействий извне. Это фиксированная (в пределах одного материала) величина, которая представляет данные проводника следующих размеров – длина 1 м (ℓ), площадь сечения 1 кв.м. Поэтому взаимосвязь между данными величинами выражается соотношением: R = ρ* ℓ/S:
- Проводимость материала падает по мере увеличения его длины.
- Увеличение площади сечения проводника влечет за собой снижение его сопротивления. Такая закономерность обусловлена уменьшением плотности электронов, а, следовательно, и контакт частиц материала с ними становится более редким.
- Рост температуры материала стимулирует рост сопротивления, в то время как падение температуры влечет за собой его снижение.
Расчет площади сечения целесообразно производить согласно формуле S = πd 2 / 4.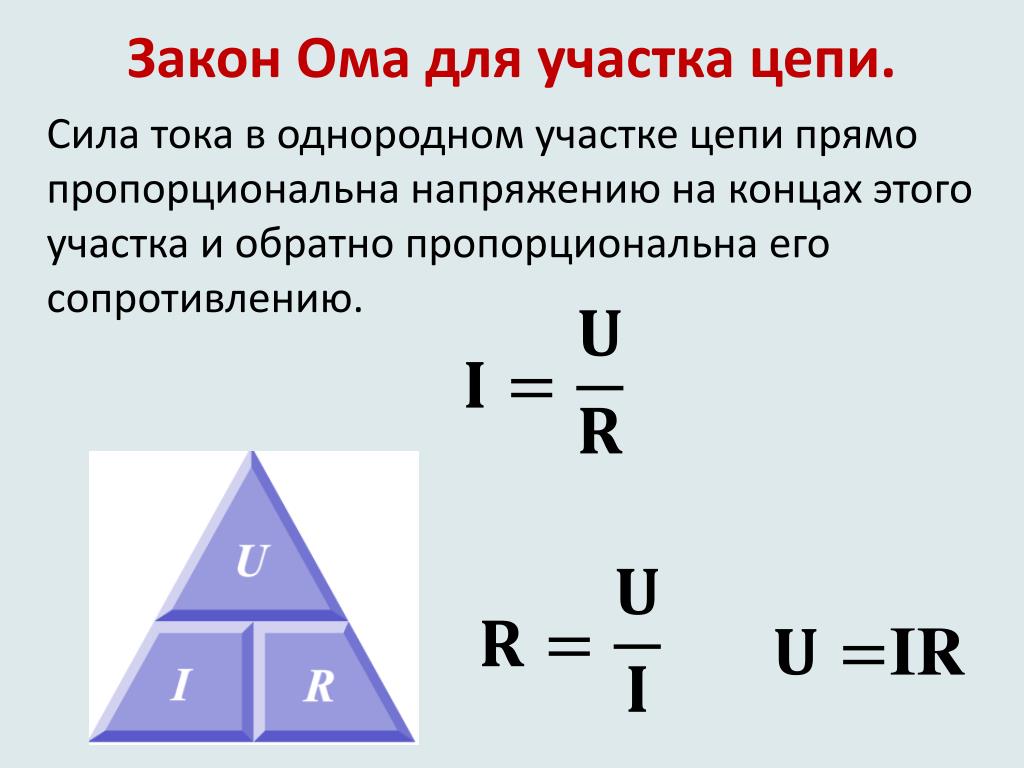 В определении длины поможет рулетка.
В определении длины поможет рулетка.
Взаимосвязь c мощностью (P)
Исходя из формулы закона Ома, U = I*R и P = I*U. Следовательно, P = I 2 *R и P = U 2 /R.
Зная величину силы тока и мощность, сопротивление можно определить как: R = P/I 2 .
Зная величину напряжения и мощности, сопротивление легко вычислить по формуле: R = U 2 /P.
Сопротивление материала и величины других сопутствующих характеристик могут быть получены с применением специальных измерительных приборов или на основании установленных математических закономерностей.
Одним из физических свойств вещества является способность проводить электрический ток. Электропроводимость (сопротивление проводника) зависит от некоторых факторов: длины электрической цепи, особенностей строения, наличия свободных электронов, температуры, тока, напряжения, материала и площади поперечного сечения.
Протекание электрического тока через проводник приводит к направленному движению свободных электронов. Наличие свободных электронов зависит от самого вещества и берется из таблицы Д. И. Менделеева, а именно из электронной конфигурации элемента. Электроны начинают ударяться о кристаллическую решетку
Наличие свободных электронов зависит от самого вещества и берется из таблицы Д. И. Менделеева, а именно из электронной конфигурации элемента. Электроны начинают ударяться о кристаллическую решетку
элемента и передают энергию последней. В этом случае возникает тепловой эффект при действии тока на проводник.
При этом взаимодействии они замедляются, но затем под действием электрического поля, которое их ускоряет, начинают двигаться с той же скоростью. Электроны сталкиваются огромное количество раз. Этот процесс и называется сопротивлением проводника.
Следовательно, электрическим сопротивлением проводника считается физическая величина, характеризующая отношение напряжения к силе тока.
Что такое электрическое сопротивление: величина, указывающая на свойство физического тела преобразовывать энергию электрическую в тепловую, благодаря взаимодействию энергии электронов с кристаллической решеткой вещества. По характеру проводимости различаются:
- Проводники (способны проводить электрический ток, так как присутствуют свободные электроны).

- Полупроводники (могут проводить электрический ток, но при определенных условиях).
- Диэлектрики или изоляторы (обладают огромным сопротивлением, отсутствуют свободные электроны, что делает их неспособными проводить ток).
Обозначается эта характеристика буквой R и измеряется в Омах (Ом)
. Применение этих групп веществ является очень значимым для разработки электрических принципиальных схем приборов.
Для полного понимания зависимости R от чего-либо нужно обратить особое внимание на расчет этой величины.
Расчет электрической проводимости
Для расчета R проводника применяется закон Ома, который гласит: сила тока (I) прямо пропорциональна напряжению (U) и обратно пропорциональна сопротивлению.
Формула нахождения характеристики проводимости материала R (следствие из закона Ома для участка цепи): R = U / I.
Для полного участка цепи эта формула принимает следующий вид: R = (U / I) — Rвн, где Rвн — внутреннее R источника питания.
Способность проводника к пропусканию электрического тока зависит от многих факторов: напряжения, тока, длины, площади поперечного сечения и материала проводника, а также от температуры окружающей среды.
В электротехнике для произведения расчетов и изготовления резисторов учитывается и геометрическая составляющая проводника.
От чего зависит сопротивление: от длины проводника — l, удельного сопротивления — p и от площади сечения (с радиусом r) — S = Пи * r * r.
Формула R проводника: R = p * l / S.
Из формулы видно, от чего зависит удельное сопротивление проводника:
R, l, S. Нет необходимости его таким способом рассчитывать, потому что есть способ намного лучше. Удельное сопротивление можно найти в соответствующих справочниках для каждого типа проводника (p — это физическая величина равная R материала длиною в 1 метр и площадью сечения равной 1 м².
Однако этой формулы мало для точного расчета резистора, поэтому используют зависимость от температуры.
Влияние температуры окружающей среды
Доказано, что каждое вещество обладает удельным сопротивлением, зависящим от температуры.
Для демонстрации это можно произвести следующий опыт. Возьмите спираль из нихрома или любого проводника (обозначена на схеме в виде резистора), источник питания и обычный амперметр (его можно заменить на лампу накаливания). Соберите цепь согласно схеме 1.
Схема 1 — Электрическая цепь для проведения опыта
Необходимо запитать потребитель и внимательно следить за показаниями амперметра. Далее следует нагревать R, не отключая, и показания амперметра начнут падать при росте температуры. Прослеживается зависимость по закону Ома для участка цепи: I = U / R. В данном случае внутренним сопротивлением источника питания можно пренебречь: это не отразится на демонстрации зависимости R от температуры. Отсюда следует, что зависимость R от температуры присутствует.
Физический смысл роста значения R обусловлен влиянием температуры на амплитуду колебаний (увеличение) ионов в кристаллической решетке.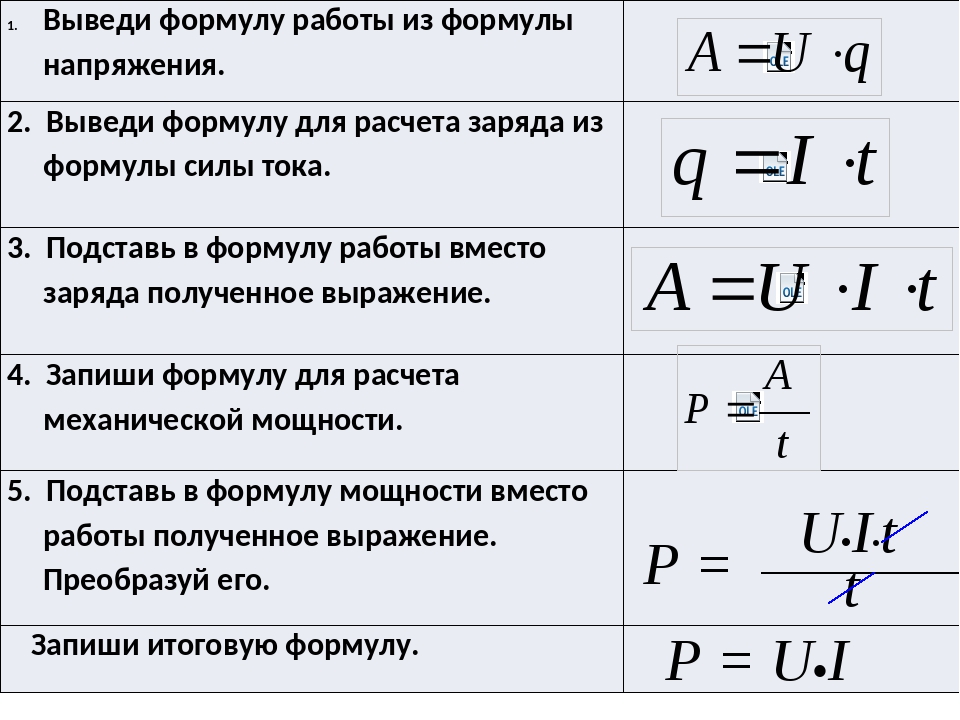 В результате этого электроны чаще сталкиваются и это вызывает рост R.
В результате этого электроны чаще сталкиваются и это вызывает рост R.
Согласно формуле: R = p * l / S, находим показатель, который зависит от температуры
(S и l — не зависят от температуры). Остается p проводника. Исходя из это получается формула зависимости от температуры: (R — Ro) / R = a * t, где Ro при температуре 0 градусов по Цельсию, t — температура окружающей среды и a — коэффициент пропорциональности (температурный коэффициент).
Для металлов «a» всегда больше нуля, а для растворов электролитов температурный коэффициент меньше 0.
Формула нахождения p, применяемая при расчетах: p = (1 + a * t) * po, где ро — удельное значение сопротивления, взятое из справочника для конкретного проводника. В этом случае температурный коэффициент можно считать постоянным. Зависимость мощности (P) от R вытекает из формулы мощности: P = U * I = U * U / R = I * I * R. Удельное значение сопротивления еще зависит и от деформаций материала, при котором нарушается кристаллическая решетка.
При обработке металла в холодной среде при некотором давлении происходит пластическая деформация. При этом кристаллическая решетка искажается и растет R течения электронов. В этом случае удельное сопротивление также увеличивается. Этот процесс является обратимым и называется рекристаллическим отжигом, благодаря которому часть дефектов уменьшается.
При действии на металл сил растяжения и сжатия последний подвергается деформациям, которые называются упругими. Удельное сопротивление уменьшается при сжатии, так как происходит уменьшение амплитуды тепловых колебаний. Направленным заряженным частицам становится легче двигаться
. При растяжении удельное сопротивление увеличивается из-за роста амплитуды тепловых колебаний.
Еще одним фактором, влияющим на проводимость, является вид тока, проходящего по проводнику.
Сопротивление в сетях с переменным током ведет себя несколько иначе, ведь закон Ома применим только для схем с постоянным напряжением. Следовательно, расчеты следует производить иначе.
Полное сопротивление обозначается буквой Z и состоит из алгебраической суммы активного, емкостного и индуктивного сопротивлений.
При подключении активного R в цепь переменного тока под воздействием разницы потенциалов начинает течь ток синусоидального вида. В этом случае формула выглядит: Iм = Uм / R, где Iм и Uм — амплитудные значения силы тока и напряжения. Формула сопротивления принимает следующий вид: Iм = Uм / ((1 + a * t) * po * l / 2 * Пи * r * r).
Емкостное сопротивление (Xc) обусловлено наличием в схемах конденсаторов. Необходимо отметить, что через конденсаторы проходит переменный ток и, следовательно, он выступает в роли проводника с емкостью.
Вычисляется Xc следующим образом: Xc = 1 / (w * C), где w — угловая частота и C — емкость конденсатора или группы конденсаторов. Угловая частота определяется следующим образом:
- Измеряется частота переменного тока (как правило, 50 Гц).
- Умножается на 6,283.
Индуктивное сопротивление (Xl) — подразумевает наличие индуктивности в схеме (дроссель, реле, контур, трансформатор и так далее). Рассчитывается следующим образом: Xl = wL, где L — индуктивность и w — угловая частота. Для расчета индуктивности
Рассчитывается следующим образом: Xl = wL, где L — индуктивность и w — угловая частота. Для расчета индуктивности
необходимо воспользоваться специализированными онлайн-калькуляторами или справочником по физике. Итак, все величины рассчитаны по формулам и остается всего лишь записать Z: Z * Z = R * R + (Xc — Xl) * (Xc — Xl).
Для определения окончательного значения необходимо извлечь квадратный корень из выражения: R * R + (Xc — Xl) * (Xc — Xl). Из формул следует, что частота переменного тока играет большую роль, например, в схеме одного и того же исполнения при повышении частоты увеличивается и ее Z. Необходимо добавить, что в цепях с переменным напряжением Z зависит от таких показателей:
- Длины проводника.
- Площади сечения — S.
- Температуры.
- Типа материала.
- Емкости.
- Индуктивности.
- Частоты.
Следовательно и закон Ома для участка цепи имеет совершенно другой вид: I = U / Z
. Меняется и закон для полной цепи.
Расчеты сопротивлений требуют определенного количества времени, поэтому для измерений их величин применяются специальные электроизмерительные приборы, которые называются омметрами. Измерительный прибор состоит из стрелочного индикатора, к которому последовательно включен источник питания.
Измеряют R все комбинированные приборы
, такие как тестеры и мультиметры. Обособленные приборы для измерения только этой характеристики применяются крайне редко (мегаомметр для проверки изоляции силового кабеля).
Прибор применяется для прозвонки электрических цепей на предмет повреждения и исправности радиодеталей, а также для прозвонки изоляции кабелей.
При измерении R необходимо полностью обесточить участок цепи во избежание выхода прибора из строя. Для это необходимо предпринять следующие меры предосторожности:
В дорогих мультиметрах есть функция прозвонки цепи, дублируемая звуковым сигналом, благодаря чему нет необходимости смотреть на табло прибора.
Таким образом, электрическое сопротивление играет важную роль в электротехнике.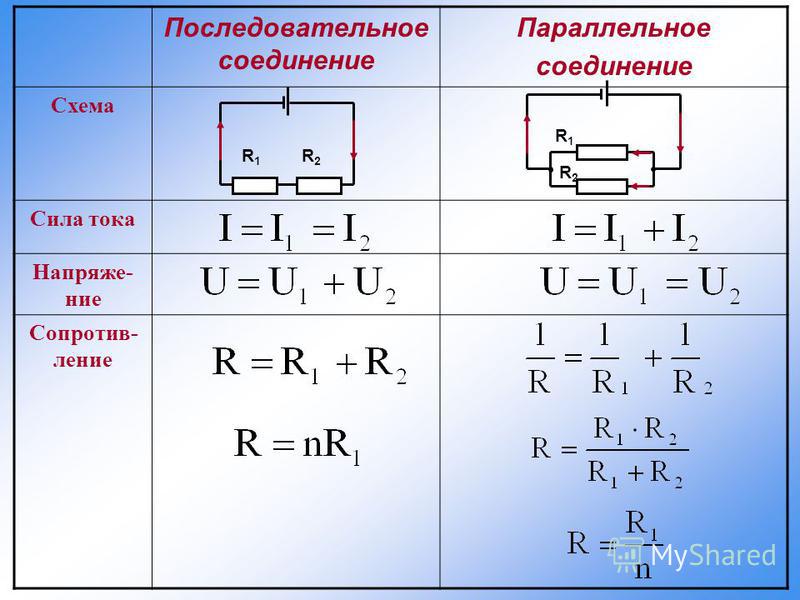 Оно зависит в постоянных цепях от температуры, силы тока, длины, типа материала и площади
Оно зависит в постоянных цепях от температуры, силы тока, длины, типа материала и площади
поперечного сечения проводника
. В цепях переменного тока эта зависимость дополняется такими величинами, как частота, емкость и индуктивность. Благодаря этой зависимости существует возможность изменять характеристики электричества: напряжение и силу тока. Для измерений величины сопротивления применяются омметры, которые используются также и при выявлении неполадок проводки, прозвонки различных цепей и радиодеталей.
Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “ “
Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.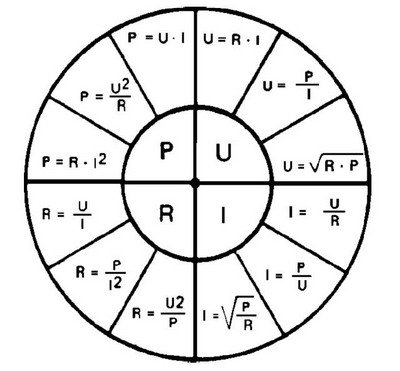
Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.
В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.
Соотношения закона Ома
Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:
В этой таблице используются следующие общепринятые обозначения физических величин:
U
— напряжение (В),
I
— ток (А),
Р
— мощность (Вт),
R
— сопротивление (Ом),
Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток- 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.
Известно, что напряжение на ее выводах составляет 100 В, а ток- 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.
А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:
I = U / R
Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.
Что же в этой формуле есть что? Рассмотрим переменные подробнее.
> U пит
(иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.
К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.
> I
: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.
> R
: искомое сопротивление токоограничивающего резистора, в омах.
В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:
R = U/I = 8,5 В / 0,050 А= 170 Ом
Расчёты сопротивления
Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.
Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.
> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.
> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.
Расчет сопротивления последовательных резисторов
Формула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:
Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)
В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.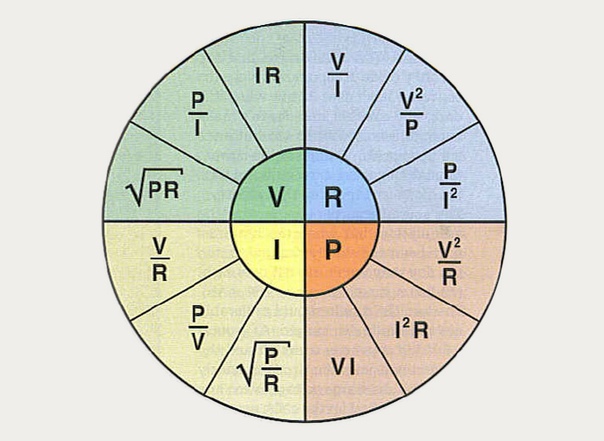
Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.
Расчет сопротивления параллельных резисторов
Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид:
R общ = R1 * R2 / (R1 + R2)
где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим
776,47 = 2640000 / 3400
Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:
Расчёты ёмкости
Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.
Расчет емкости параллельных конденсаторов
Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:
Собщ = CI + С2 + СЗ + …
В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.
Расчет емкости последовательных конденсаторов
Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:
Собщ = С1 * С2 /(С1+С2)
где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи
Расчет емкости трех и более последовательно соединенных конденсаторов
В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:
Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует.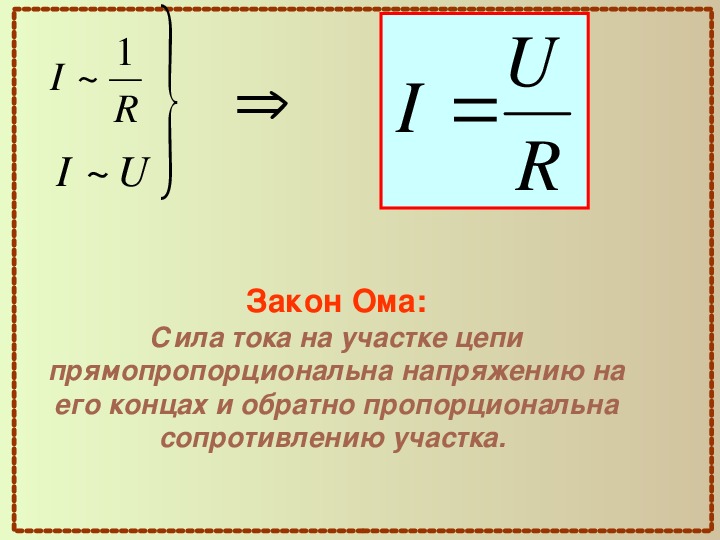 Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.
Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.
Расчёт энергетических уравнений
Наиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:
ватт-часы = Р х Т
В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.
Расчёт постоянной ёмкости RC-цепочки
В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).
Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.
Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.
T = RC
В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.
Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.
Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:
Расчёты частоты и длины волны
Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Расчет частоты сигнала
Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны:
Частота = 300000 / длина волны
Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.
Частота же дана в мегагерцах.
Расчет длины волны сигнала
Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:
Длина волны = 300000 / Частота
Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.
Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:
6000 миллиметров = 300000
/ 50 МГц
Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!
чему равно напряжение, как найти сопротивление нагрузки
В наши дни электричество играет в жизни человека очень большую роль, в следствие чего базовые знания в области физики и электротехники нужны практически каждому.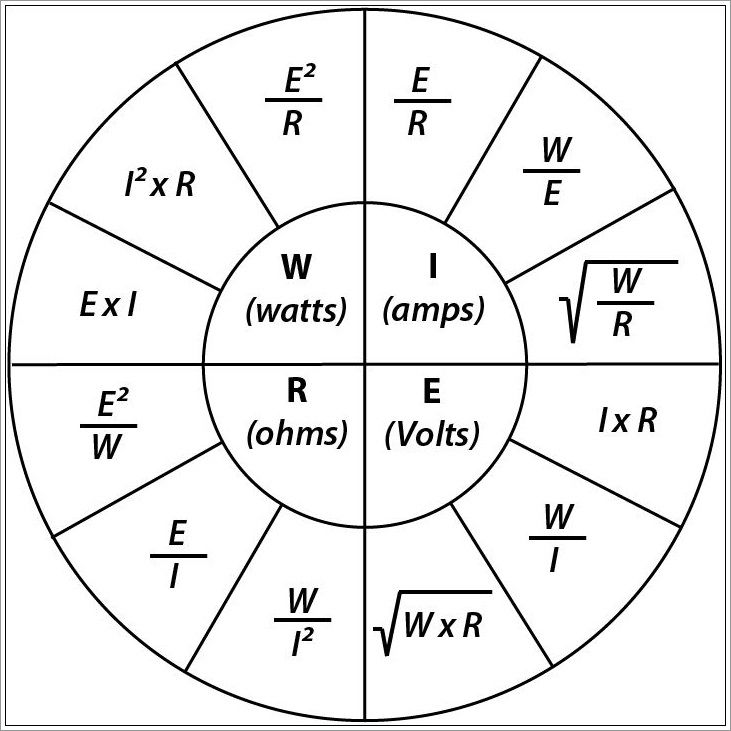 Напряжение является одной из главных физических величин, которая позволяет объяснить теорию возникновения электрического поля и методы подбора оптимального сечения кабеля для применения его в повседневной жизни.
Напряжение является одной из главных физических величин, которая позволяет объяснить теорию возникновения электрического поля и методы подбора оптимального сечения кабеля для применения его в повседневной жизни.
Что такое напряжение в сети электричества.
Напряжение – это физическая величина, которая характеризует электрическое поле. Иными словами, оно показывает, какую работу оно совершает при перемещении одного положительного заряда на определённое расстояние.
Показатель напряжения на вольтметре
За единицу напряжения в международной системе принимается такой показатель на концах проводника, при котором заряд в 1 Кл совершает работу в 1 Дж для перемещения его по этому проводнику. Общепринятой единицей измерения напряжения считается 1 В – Вольт.
Важно! Работа измеряется в Джоулях, заряды в Кулонах, а напряжение в Вольтах, следовательно, 1 Вольт равняется 1 Джоулю, деленному на 1 Кулон.
Чему равно напряжение.
Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.
Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.
Изображение вольтметра и электрической цепи
Напряжение обозначается латинской [U], а измеряется в [В]. Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.
Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении.
Электрическое поле
Формула закона Ома
Свои опыты Ом направлял на изучение такой физической величины, как сопротивление, в результате чего в 1826 году он стал автором закона, который не потерял совей актуальность вплоть до сегодняшнего дня. Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.
Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.
Также, Ом сделал вывод, что каждый проводник обладает индивидуальными свойствами проводимости.
Сопротивление обозначается заглавной латинской [R] и измеряется в Омах. Сопротивление – физическая величина, характеризующая свойства проводника оказывать влияние на идущий по нему ток. Оно прямо пропорционально напряжению в сети и обратно пропорционально силе тока. В виде формулы данный закон можно записать как R = U/I, где U – напряжение, а I – сила тока. 1 Ом равняется 1 Вольту, деленному на 1 Ампер.
Запомните! Реостат – прибор, обеспечивающий возможность изменять сопротивление. Прежде всего, он влияет на показатель R в цепи, а, следовательно, на 2 другие величины, описанные в законе Ома. Силу тока может помочь определить амперметр.
Ползунковый реостат
Из формулы закона Ома можно вывести практически любую зависимость, связанную с электричеством.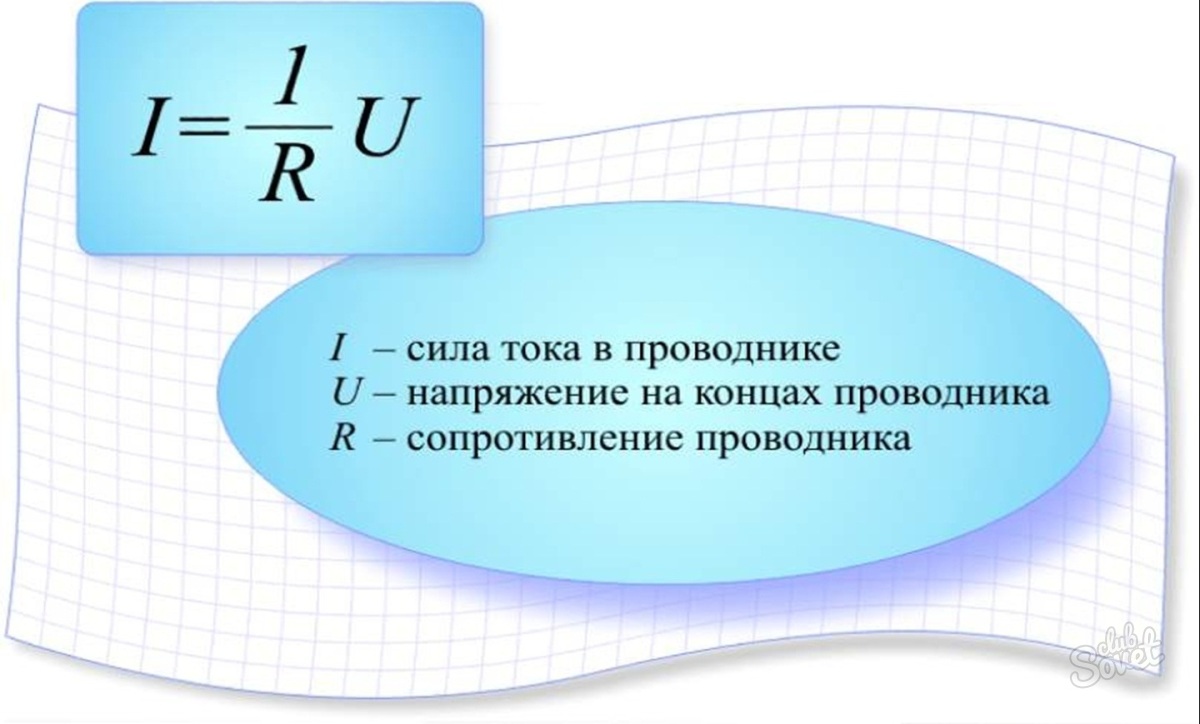 Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.
Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.
Важно! В виде формулы нахождение сопротивления через удельное сопротивление выглядит так: R = ρ*(l/S), где l – длина проводника, а S – площадь поперечного сечения.
Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества. Измеряется в Омах, умноженных на метр: [ρ] = [Ом*м].
Ом и формула
Как найти сопротивление нагрузки
Сопротивление нагрузки обозначается латинскими буквами Rn или Rн. По сути, это является тем же сопротивлением участка цепи и вычисляется также по формулам закона Ома.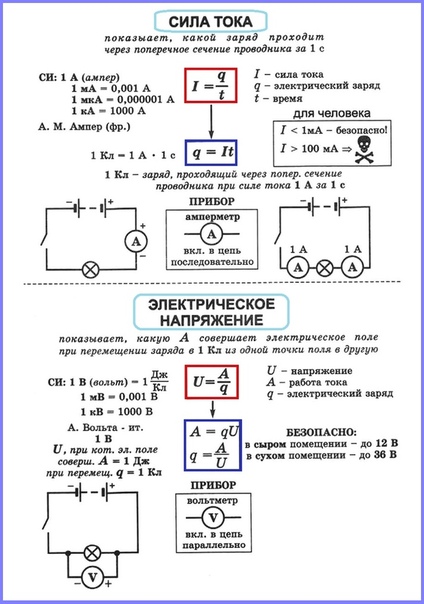 Нагрузка обозначается символами, которые на электрической схеме изображаются в виде крестиков в кружке – лампочкой; то есть двигатель, лампа, конкретный прибор и т. д.
Нагрузка обозначается символами, которые на электрической схеме изображаются в виде крестиков в кружке – лампочкой; то есть двигатель, лампа, конкретный прибор и т. д.
Каждая нагрузка имеет своё собственное сопротивление. Например, если к сети подключена одна лампочка, то сопротивление нагрузки – показатель этого единственного прибора в цепи. Если к цепи подключено несколько нагрузок, то сопротивление считается суммарно для каждой из них.
Сопротивление нагрузки вычисляется в соответствии с законом Ома, то есть Rn = U/I. Если к сети подключено несколько нагрузок, то оно будет рассчитываться следующим образом: сначала находится сопротивление каждой отдельной «лампочки». Далее Rn вычисляется в зависимости от того, какой тип подключения в цепи: последовательное или параллельное. При параллельном 1/R = 1/R1 + 1/R2 + 1/Rn, где n –количество подключенных приборов. Если же соединение последовательное, общее R равно сумме всех R цепи.
Последовательное/параллельное соединения
Как найти с помощью формулы напряжение
Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно.
Измерение напряжения
По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.
Важно! Определить напряжение можно и через мощность электрического тока. Мощность [P] равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t. Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Мощность [P] равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t. Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Как найти силу тока через сопротивление и напряжение
Сила тока обозначается латинскими [I] или [Y], и она зависит от количества заряда, перенесенного от одного полюса к другому за определенный промежуток времени, т.е. I = q/t. Измеряется сила тока в амперах, а узнать её значение в цепи можно при помощи амперметра.
Мужчина считает силу тока
Существуют формулы определения силы тока через напряжение и сопротивление. В первом случае произведение силы тока на время равняется работе, деленной на напряжение: I*t = A/U, во втором – по закону Ома, I = U/R. Через мощность сила будет равняться P/U.
При последовательном соединении, сила тока одинакова на всех участках цепи, следовательно, равна общему значению в цепи. В противоположном случае сила электрического тока равняется сумме силы тока всех нагрузок.
Таким образом, существует огромное множество формул для нахождения силы тока, напряжения и сопротивления. Они всегда могут пригодиться для теории, а на практике всегда помогут специальные приборы – амперметр и вольтметр.
Как рассчитать индукционные токи, напряжения и контуры — видео и стенограмма урока
Приложения
Трансформаторы — это устройства, используемые для повышения или понижения напряжения. Они состоят из железного металлического сердечника в форме рамы для картины. По обеим сторонам железного сердечника находятся петли из проволоки. Напряжение первичной обмотки влияет на напряжение вторичной обмотки. Если вторичная катушка имеет больше петель, чем первичная, напряжение повышается до более высокого напряжения. Если вторичная катушка имеет меньше петель, чем первичная, напряжение снижается до более низкого напряжения.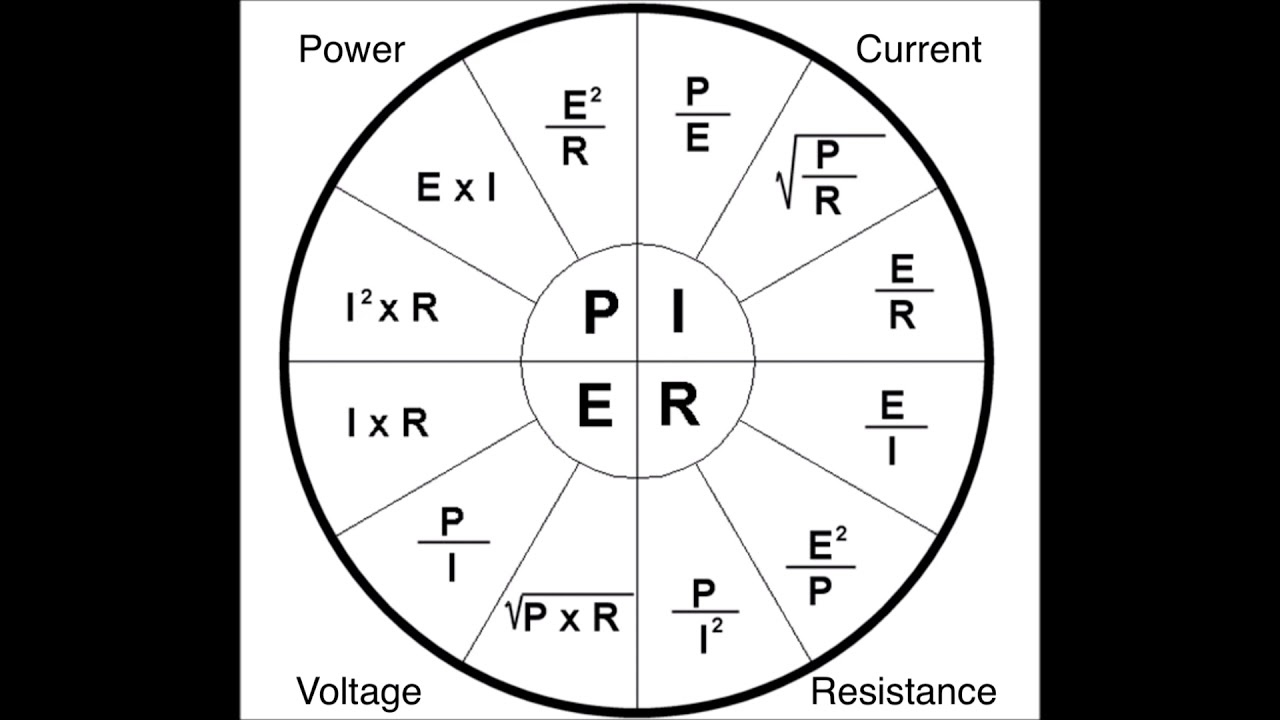 Это используется при передаче электроэнергии от электростанций к жилым домам и предприятиям.
Это используется при передаче электроэнергии от электростанций к жилым домам и предприятиям.
Электрические зубные щетки заряжаются благодаря наведенному напряжению. Внутри зарядного устройства находится катушка провода. Зарядное устройство имеет катушку, которая испытывает изменяющееся магнитное поле из-за переменного тока в электрической системе дома. Поскольку магнитное поле меняется из-за переменного тока, в катушке индуцируется ток, который заряжает электрическую зубную щетку.
Теперь давайте проведем расчет индуцированных напряжений и токов из-за изменяющихся магнитных полей.
Пример
Подсказка: круглый проводник радиусом 10 см подвергается воздействию магнитного поля 0,1 Тл, направленного вверх. Круглый проводник перпендикулярен магнитному полю и имеет сопротивление 0,2 Ом. Магнитное поле увеличивается до 0,5 Тл за 0,5 секунды. Какова величина индуцированного напряжения, индуцированного тока и направления тока?
Решение: Всегда полезно нарисовать сценарий.
Нам нужно определить ΔΦ , то есть изменение магнитного потока. Поскольку петля круглая, площадь будет рассчитана с использованием уравнения площади окружности πr2 .
Теперь мы можем подставить ΔΦ в наше уравнение:
Как видим, индуцированное напряжение ≈ 0.025 В. Силу тока в петле можно определить по закону Ома.
V = IR
I = V / R
I = 0,025 В / 0,2 Ω
I ≈ 0.13 Ampere
Мы можем определить направление тока, указывая на правую руку большой палец вверх, потому что проволочная петля не хочет, чтобы магнитное поле менялось, и оно уменьшается в направлении вниз. Правый большой палец направлен вверх, правые пальцы сгибаются влево.Глядя вниз на петлю, это будет поток против часовой стрелки.
Правый большой палец направлен вверх, правые пальцы сгибаются влево.Глядя вниз на петлю, это будет поток против часовой стрелки.
Итоги урока
Давайте повторим. Закон Фарадея определяет индуцированное напряжение в замкнутом контуре проводника при изменении магнитного потока. Магнитный поток — это величина магнитного поля, проникающего перпендикулярно через площадь. Катушка провода, которая подвергается изменению магнитного поля и/или изменению площади катушки, вызывает изменение магнитного потока.
Это индуцирует напряжение, создающее электрический ток через провод. Направление тока будет создавать магнитное поле в направлении, которое будет пытаться поддерживать постоянное чистое магнитное поле.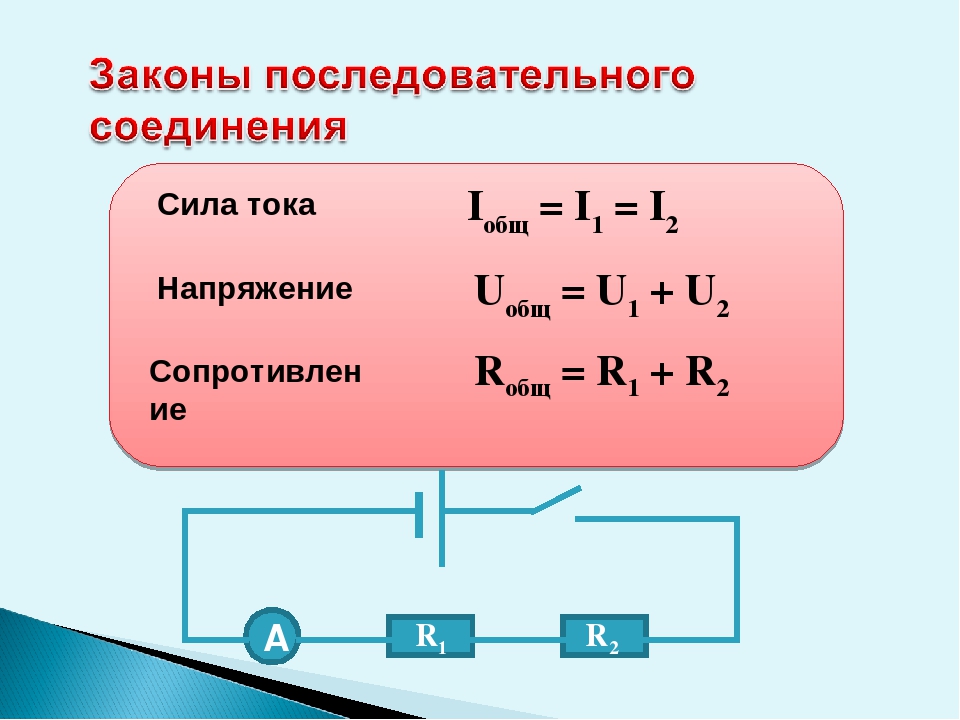
Закон Ома ( В = IR ) можно использовать для определения наведенного тока в контуре.
Трансформаторы — это устройства, повышающие или понижающие напряжение в зависимости от количества витков провода вокруг первичной и вторичной катушек на противоположных сторонах железного сердечника. Они используются при передаче электроэнергии от электростанций к жилым домам и предприятиям, а также в системах зарядки электрических зубных щеток.
Что такое амперы, ватты, вольты и омы?
В электрической системе увеличение тока или напряжения приводит к увеличению мощности.Допустим, у вас есть система с 6-вольтовой лампочкой, подключенной к 6-вольтовой батарее. Выходная мощность лампочки составляет 100 Вт. Используя уравнение I = P/V , мы можем рассчитать, какой ток в амперах потребуется, чтобы получить 100 Вт от этой 6-вольтовой лампочки.
Вы знаете, что P = 100 Вт, а V = 6 В. Итак, вы можете изменить уравнение, чтобы найти I и подставить числа.
I = 100 Вт/6 В = 16,67 ампер
Что произойдет, если вы используете 12-вольтовую батарею и 12-вольтовую лампочку, чтобы получить мощность 100 Вт?
I = 100 Вт/12 В = 8.33 ампера
Итак, эта последняя система производит ту же мощность, но с вдвое меньшим током. Преимущество заключается в использовании меньшего тока для получения того же количества энергии. Сопротивление в электрических проводах потребляет мощность, и потребляемая мощность увеличивается по мере увеличения тока, проходящего через провода. Вы можете увидеть, как это происходит, немного переставив два уравнения. Что вам нужно, так это уравнение для мощности с точки зрения сопротивления и тока. Давайте переформулируем первое уравнение:
I = V/R можно переформулировать как V = I*R
Теперь вы можете подставить уравнение для V в другое уравнение:
P = V*I подставив V, мы получим P = I*R*I, или P = I 2 *R
Это уравнение говорит вам о том, что мощность, потребляемая проводами, увеличивается, если сопротивление проводов увеличивается (например, если провода становятся меньше или из менее проводящего материала).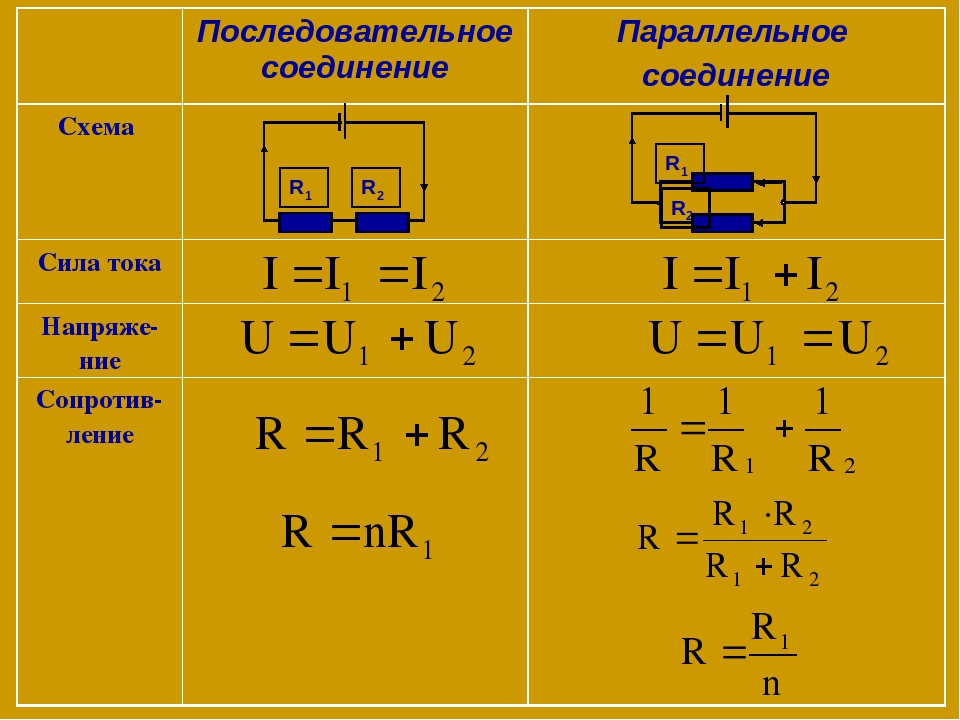 Но она резко возрастает, если ток, проходящий по проводам, увеличивается. Таким образом, использование более высокого напряжения для снижения тока может сделать электрические системы более эффективными. КПД электродвигателей также улучшается при более высоких напряжениях.
Но она резко возрастает, если ток, проходящий по проводам, увеличивается. Таким образом, использование более высокого напряжения для снижения тока может сделать электрические системы более эффективными. КПД электродвигателей также улучшается при более высоких напряжениях.
Это повышение эффективности заставило автомобильную промышленность задуматься о переходе с 12-вольтовых электрических систем на 42-вольтовые системы в 1990-х годах. По мере того, как все больше автомобилей поставлялось с электрическими удобствами — видеодисплеями, подогревом сидений, «умным» климат-контролем — им требовались толстые пучки проводов для подачи достаточного тока.Переход на систему с более высоким напряжением обеспечит большую мощность при использовании более тонкой проводки.
Переключение так и не произошло, потому что автопроизводители смогли повысить эффективность с помощью цифровых технологий и более эффективных электрических насосов на 12 вольт. Но в некоторых новых моделях используются гибридные системы с отдельным 48-вольтовым генератором для питания расширенных функций, таких как отключение на холостом ходу, при одновременном повышении общей эффективности системы.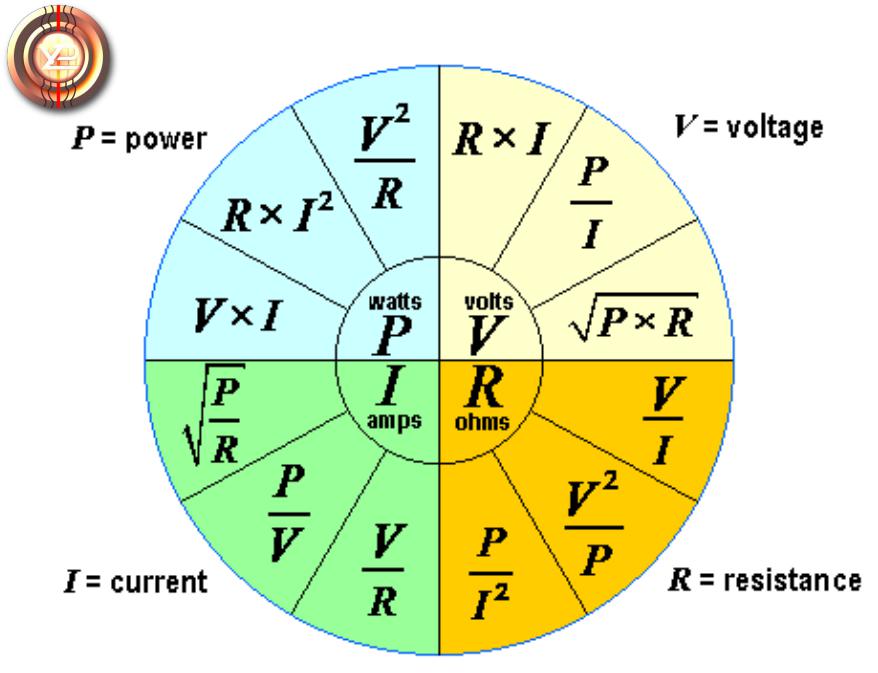
Чтобы узнать больше об электричестве и смежных темах, перейдите по ссылкам на следующей странице.
Первоначально опубликовано: 31 октября 2000 г.
Закон Ома — StatPearls — NCBI Bookshelf
Введение
Закон Ома представляет собой взаимосвязь между тремя физическими явлениями: током, напряжением и сопротивлением. Ток определяется как поток положительного заряда от источника к источнику отрицательного заряда. Единицами тока являются Кл/с для количества заряда (Кл), который проходит в единицу времени (с). Ампер (А) — общепринятая единица измерения тока, равная 1 Кл/с, а символ тока — I.Ток — это внутреннее свойство, поскольку оно зависит от других аспектов, таких как размер системы. Чтобы точно сравнить величину тока для разных систем, ток нормализуется по площади или массе системы. Это описывается следующим образом:
Где J – плотность тока в л/(м·м) или л/г в зависимости от того, как сравниваются системы, I – сила тока (А), A – площадь поперечного сечения. (м·м), а m – масса (г). Обратите внимание, что часто j используется для тока вместо I, чтобы избежать путаницы с мнимыми числами.Поэтому следует обратить внимание на определения символов, так как они могут различаться в каждом конкретном случае.
(м·м), а m – масса (г). Обратите внимание, что часто j используется для тока вместо I, чтобы избежать путаницы с мнимыми числами.Поэтому следует обратить внимание на определения символов, так как они могут различаться в каждом конкретном случае.
Напряжение — это еще одна часть закона Ома, определяющая объем работы, необходимой для перемещения заряда. Единицей измерения напряжения является Дж/Кл, что соответствует вездесущей единице Вольт (В). Напряжение измеряет электрический потенциал, которым обладает объект по отношению к заряду. При подаче напряжения над зарядом совершается работа, которая обеспечивает движение заряда. Величина заряда по сравнению с отдельным зарядом, известная как точечный заряд, может быть определена следующим образом:
Где V — электрический потенциал (В), k — постоянная 8.99 E 9 Н·м·м/(C·C), q – заряд точки (C), r – расстояние от точечного заряда (м).
Сопротивление — это противодействие движению заряда. Сопротивление аналогично эффектам трения в текущей воде или скользящем объекте. Единицами сопротивления являются Омы, которые обозначаются заглавной греческой буквой Омега. Для расчета величины сопротивления объекта можно использовать следующее уравнение:
Единицами сопротивления являются Омы, которые обозначаются заглавной греческой буквой Омега. Для расчета величины сопротивления объекта можно использовать следующее уравнение:
Где R — сопротивление (Омега), Rho — удельное сопротивление объекта (Омега·м), l — длина объекта (м ), а A – площадь поперечного сечения объекта (м·м).Удельное сопротивление для каждого объекта разное и зависит от структуры материала. Расчет удельного сопротивления выходит за рамки этой статьи.
Сопротивление также может быть нормализовано для обеспечения подходящего сравнения в каждом конкретном случае. Нормализованное сопротивление определяется по формуле:
Где R — нормализованное сопротивление (Омега·м·м). Сопротивление, препятствующее прохождению заряда, обратно пропорционально току. Поскольку текущая нормировка относится к единицам площади, нормализация сопротивления умножается на единицы площади поперечного сечения из-за обратной зависимости.
Обратная величина сопротивления (1/R) известна как проводимость, которая измеряет способность объекта проводить заряд, выраженный в единицах Сименс (S).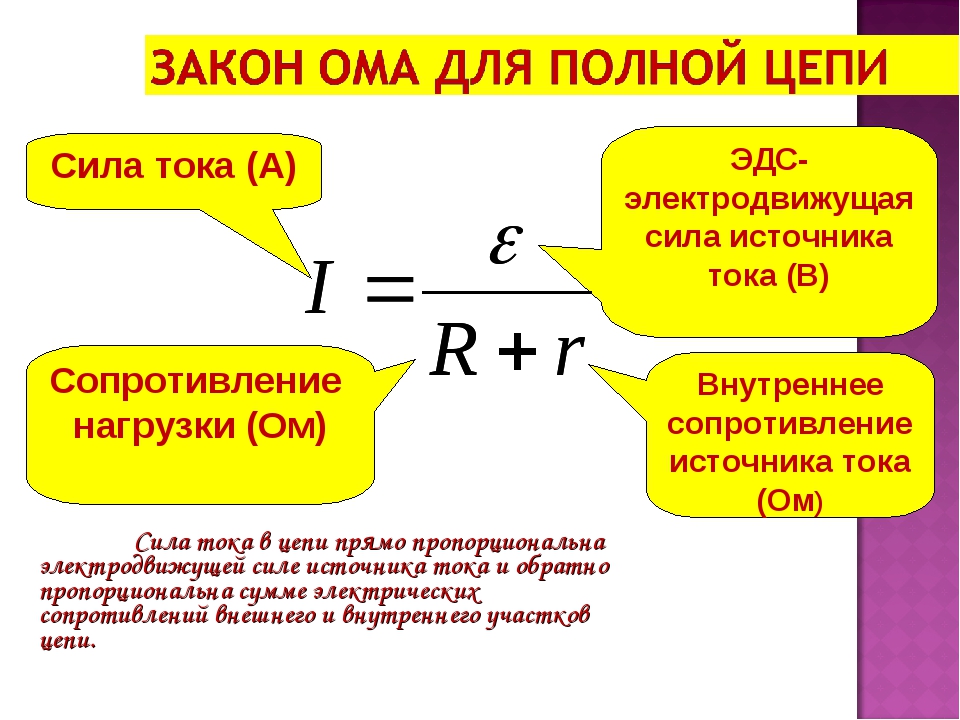 Дальнейшее обсуждение проводимости выходит за рамки этой статьи; однако стоит отметить обратную зависимость проводимости от сопротивления.
Дальнейшее обсуждение проводимости выходит за рамки этой статьи; однако стоит отметить обратную зависимость проводимости от сопротивления.
Учитывая ток, напряжение и сопротивление, закон Ома определяется как:
Для обеспечения согласованности единиц измерения необходим анализ размеров.[1][2][3][4]
Функция
Закон Ома изначально был эмпирическим выводом, основанным на соотношении между током и напряжением; однако он оставался неизменным в микроскопических и макроскопических наблюдениях.Закон Ома широко используется в электронике и при создании схем, а также при разработке аккумуляторов и других электрохимических приложениях. Область действия закона Ома не ограничивается схемотехникой, поскольку его также можно использовать для создания молекул и полимеров. Каждый атом содержит протоны и электроны, которые можно использовать для создания химических связей с другими атомами. При подаче напряжения на материал происходит окислительно-восстановительная реакция, при которой один электрон отрывается от одной молекулы и присоединяется к другой. Это имеет множество исследовательских приложений, таких как хранение энергии, химия материалов, органическая химия и многое другое. Эти приложения используют закон Ома и позволяют ученым создавать материалы новыми способами.
Это имеет множество исследовательских приложений, таких как хранение энергии, химия материалов, органическая химия и многое другое. Эти приложения используют закон Ома и позволяют ученым создавать материалы новыми способами.
Чтобы выбрать правильное напряжение, необходимо учитывать сопротивление, а также необходимое количество заряда. Если есть большое сопротивление и малое напряжение, тока не будет достаточно для подачи заряда повсюду. И наоборот, если напряжение слишком велико, ток может повредить схему устройства или разрушить молекулы.Использование электричества по закону Ома требует внимания к потребностям приложения, чтобы получить желаемую мощность.
Проблемы, вызывающие озабоченность
Основная проблема, связанная с законом Ома, заключается в том, что расчеты могут стать сложными из-за сложных схем и электрохимических явлений. Например, общее сопротивление состоит из различных типов сопротивления, таких как омическое сопротивление, сопротивление переносу массы и сопротивление переносу заряда.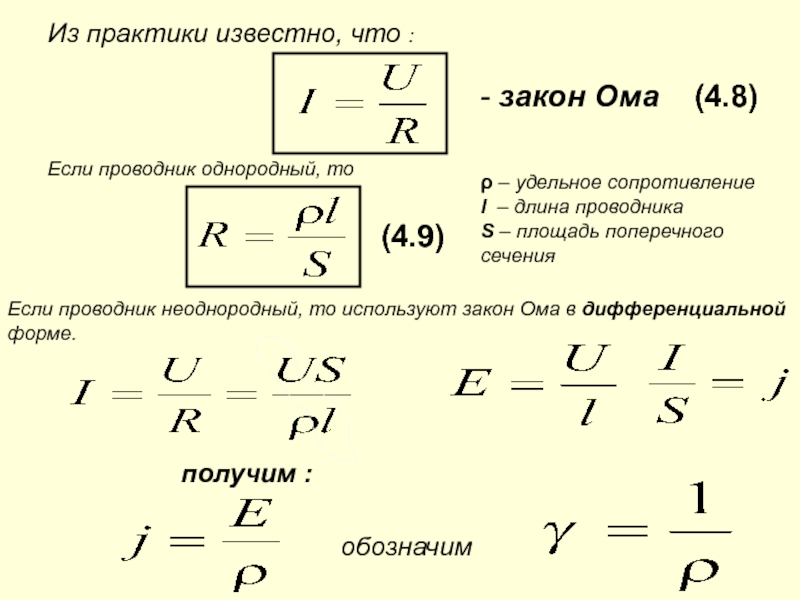 При оптимизации электрических характеристик устройств существует компромисс: уменьшение одного сопротивления может увеличить другое.Это основное соображение при проектировании и исследованиях оптимизации, чтобы определить, какие значения лучше всего подходят для данного приложения. Часто эти различные типы сопротивления трудно измерить, и для получения точных значений требуются сложные машины. Кроме того, сопротивление также меняется со временем по мере ухудшения структурной целостности устройства. Это также может изменить ожидаемые результаты закона Ома, если это не учитывать.
При оптимизации электрических характеристик устройств существует компромисс: уменьшение одного сопротивления может увеличить другое.Это основное соображение при проектировании и исследованиях оптимизации, чтобы определить, какие значения лучше всего подходят для данного приложения. Часто эти различные типы сопротивления трудно измерить, и для получения точных значений требуются сложные машины. Кроме того, сопротивление также меняется со временем по мере ухудшения структурной целостности устройства. Это также может изменить ожидаемые результаты закона Ома, если это не учитывать.
Клиническое значение
Закон Ома используется в каждом электрическом устройстве для подачи правильного количества заряда с учетом сопротивления.Хотя клиницистам не нужно будет легко рассчитывать напряжение, ток и сопротивление для этих устройств, понимание взаимосвязи может дать представление о том, как работают электрические устройства. Закон Ома также присутствует в человеческом теле и имеет множество применений. Например, нервы в нервной системе используют электрические свойства для передачи сообщений друг другу. Эти электрические сигналы могут быть отображены с помощью датчиков и лучше поняты клиницистами. Гао и др. и Су и др. изучили электрические свойства костей и продвинулись в лечении заболеваний костей.Человеческое тело содержит множество электрических путей и процессов. Поняв основное управляющее уравнение, клиницисты могут работать над решением проблем по-новому.
Например, нервы в нервной системе используют электрические свойства для передачи сообщений друг другу. Эти электрические сигналы могут быть отображены с помощью датчиков и лучше поняты клиницистами. Гао и др. и Су и др. изучили электрические свойства костей и продвинулись в лечении заболеваний костей.Человеческое тело содержит множество электрических путей и процессов. Поняв основное управляющее уравнение, клиницисты могут работать над решением проблем по-новому.
Улучшение результатов работы команды здравоохранения
Закон Ома представляет собой взаимосвязь между тремя физическими явлениями: током, напряжением и сопротивлением. Ток определяется как поток положительного заряда от источника к источнику отрицательного заряда. Закон Ома изначально был эмпирическим выводом, основанным на соотношении между током и напряжением; однако он оставался неизменным в микроскопических и макроскопических наблюдениях.Закон Ома широко используется в электронике и при создании схем, а также при разработке аккумуляторов и других электрохимических приложениях.
Основы закона
Ом – напряжение, ток и сопротивление
В предыдущем уроке мы обсуждали применение тока, напряжения и важность закона Кулона в электричестве. Но без закона Ома работа электрической цепи становится неполной.
Для выполнения этого также задействован Закон Ома . Немецкий физик Георг Симон Ом открыл закон Ома и нашел зависимость между током, напряжением и сопротивлением.
Из этого руководства вы узнаете, как применять закон Ома к различным приложениям в электротехнике и электронике.
Как известно, электрический ток течет в виде заряженных электронов. Другими словами, меньший поток электронов означает, что в цепи присутствует высокое сопротивление. А высокий поток электронов означает наличие низкого сопротивления.
Электронный ток — это количество электронов, перемещающихся в секунду. Однако для практических приложений нам нужно меньше заряда электрона.Для упрощения использовались две единицы измерения, известные как Ампер и Кулон .
Кулон, обозначенный как « Q» , выражает достаточное количество электрического заряда.
Электрический заряд равен 6 миллионам электронов, умноженным на 1 миллион электронов. Этот результирующий заряд снова умножается на один миллион электронов.
Ампер, представленный «А» , представляет собой силу единичного тока или количество электронов, перемещающихся в секунду, в данном случае один кулон в секунду.
Ампер слишком велик для некоторых приложений. Таким образом, он снова делится на части, известные как миллиампер ( мА) и микроампер ( мкА ).
1 А = 1000 мА = 1 000 000 мкА 1 мА = 1/1000 А = 1000 мкА
Теперь поговорим о сопротивлении. Поскольку состав различных материалов различен, некоторые материалы оказывают большее сопротивление потоку электронов, чем другие металлы. Это электрическое явление известно как сопротивление .
Теперь, если мы приложим движущую силу или Электромагнитную силу (ЭДС) к проводнику, большое количество электронов будет течь быстро. Это доказывает, что сопротивление проводника низкое.
С другой стороны, приложение того же ЭДС к изолятору будет производить меньше электронов. Следовательно, сопротивление изолятора велико.
Сопротивление выражается в Ом и обозначается заглавной греческой буквой «Ом ». Единицей измерения ЭДС является вольт.Один Вольт — это движущая сила, необходимая для создания силы тока 1 А в цепи с сопротивлением 1 Ом.
Электрический ток представляет собой измерительный прибор, называемый амперметром, а электрическое сопротивление измеряется с помощью омметра.
Как работает закон Ома?
Закон Ома связывает электрические величины, такие как ток, напряжение, мощность и сопротивление. Чтобы узнать практическое использование закона Ома, вот пример.
Подключите провод определенного сопротивления последовательно с 1. Источник батареи 5 В и предположим, что амперметр показывает ток 0,2 А. Теперь, если мы увеличим напряжение до 3 В, амперметр покажет большее значение тока, скажем, 0,4 А.
Источник батареи 5 В и предположим, что амперметр показывает ток 0,2 А. Теперь, если мы увеличим напряжение до 3 В, амперметр покажет большее значение тока, скажем, 0,4 А.
Указывает, что при поддержании постоянного сопротивления и увеличении напряжения ток удваивается. Повторяя этот процесс увеличения и уменьшения напряжения при неизменном сопротивлении, напряжение будет пропорционально току.
То же самое произойдет, если мы изменим длину проводника, сохранив приложенное напряжение постоянным.
Если мы изменим длину провода на более короткий или более длинный, это будет иметь некоторый эффект из-за сопротивления провода.
Например, если приложить постоянную ЭДС 1,5 В и длину провода 2 м, потребляемый ток составит 0,3 А.
Теперь, если мы изменим длину провода на 1 м, ток будет меньше 0,1 (но не 0,3) из-за меньшего расстояния и меньшего сопротивления, которое нужно преодолеть.
Теория закона Ома
Когда вы берете металлический проводник и пропускаете через него некоторый ток, разность потенциалов между двумя концами проводника остается постоянной.
Определение закона Ома
Закон Ома гласит, что «ток, протекающий через электрическую цепь, изменяется при приложении напряжения, но сопротивление обратно пропорционально сопротивлению материала проводника».
Формула закона Ома представлена уравнением
V=IR
«В» — падение потенциала (напряжение) на резисторе.
«I» — ток, протекающий в цепи через резистор
.
«R» — значение сопротивления резистора, выраженное в омах.
Приведенное выше уравнение I=V/R отображает следующие факты.
- Изменение тока в зависимости от приложенного входного напряжения
Если сопротивление проводника поддерживается постоянным, напряжение будет увеличиваться с увеличением тока, а напряжение будет уменьшаться с уменьшением тока.
- Ток и сопротивление обратны друг другу
Теперь оставьте напряжение в цепи постоянным параметром. Если изменить сопротивление, ток тоже будет меняться.
Если изменить сопротивление, ток тоже будет меняться.
Предположим, если сопротивление увеличить, ток в цепи уменьшится, а если сопротивление уменьшить, то ток возрастет.
- Связь между напряжением и током
Зависимость между напряжением и током является линейной. то есть при большем напряжении ток будет выше, а ток ниже при меньшем напряжении.
Аналогия закона Ома
Связь между напряжением, током и сопротивлением можно узнать, найдя третью величину из двух известных величин.
Двумя известными значениями могут быть напряжение, ток или сопротивление.
Расчет закона Ома
Закон Ома можно представить в трех формах. Чтобы понять просто, закон Ом окружность или закон Ом треугольник используется в электрических цепях, чтобы узнать третью величину двух других величин.
Метод круга или треугольника используется для запоминания закона Ома.
Здесь я использую круг по закону Ом, чтобы узнать напряжение, ток и сопротивление.
- Для расчета напряжения (В) округлите значение напряжения (В), как показано ниже. Ток и сопротивление связаны.
В= I x R
- Чтобы рассчитать ток (Ампер) , округлите ток (I), как показано ниже. Это будет ток, протекающий в цепи.
И = В/Р
- Аналогично узнать сопротивление (Ом) , округлив сопротивление(R), получится сопротивление проводника.
Р = В/И
Объединяя напряжение, ток и сопротивление, мы можем получить общую зависимость, чтобы нарисовать график закона Ом .
Из графика видно, что при увеличении тока в электрической цепи напряжение увеличивается линейно, и наоборот.
Для упрощения связи Закон Ома Таблица дана для быстрого ознакомления.
| Закон Ома | Известные значения | Связь 1 | Связь 2 |
|---|---|---|---|
| V=IR | Ток и сопротивление | Напряжение прямо пропорционально току | Напряжение прямо пропорционально сопротивлению |
| I=V/R | Напряжение и сопротивление | Ток обратно пропорционален сопротивлению | Ток прямо пропорционален напряжению |
| R=V/I | Напряжение и ток | Сопротивление прямо пропорционально напряжению | Сопротивление обратно пропорционально току |
Теперь дайте нам знать как использовать формулы закона Ома на практике.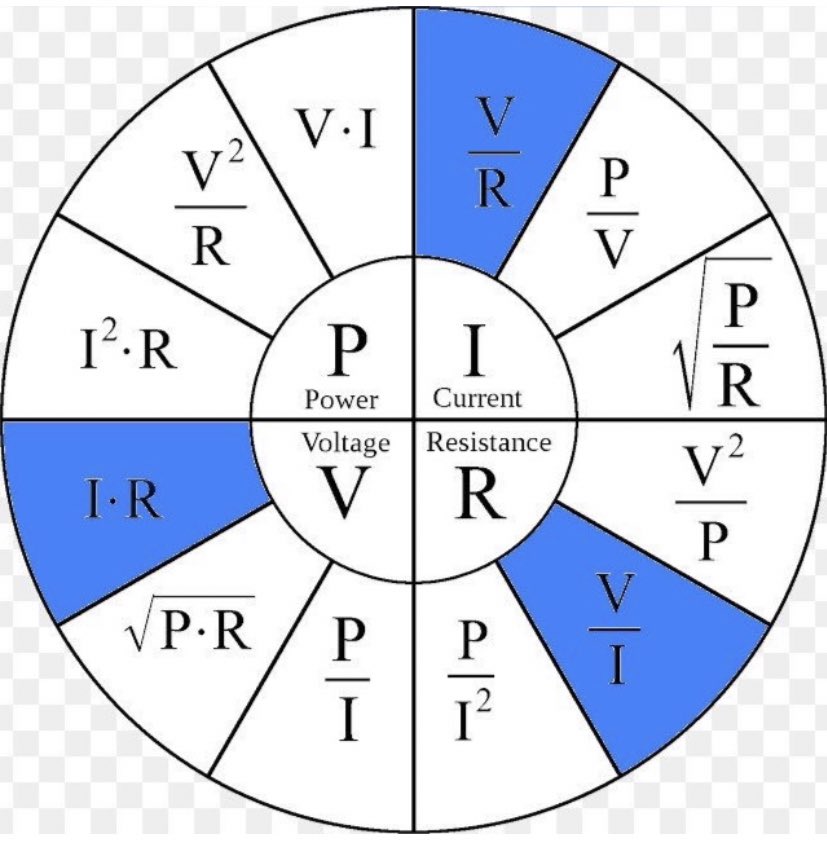
Примеры закона Ома
1 . Определение силы тока в цепи
Дано: Напряжение=5В, Сопротивление=500Ом, I=?
Формула:
I=V/R = 5/500= 0,01 А.
Итак, при подаче потенциала 5 В через резистор 500 Ом протекает ток 0,01 А.
2. Определение напряжения в цепи
Дано: Сопротивление = 100 Ом, I = 2 А, Напряжение =?
Формула:
В=ИК = 2*100=200 В
Итак, напряжение батареи по схеме 200В.
3. Определение сопротивления в цепи
Дано: ток = 2 А, напряжение = 5 В, сопротивление =?
Формула:
R=V/I = 5/2=2,5 Ом
Итак, сопротивление 2,5 Ом должно быть подключено последовательно к источнику батареи.
Практическое применение закона Ома
1. Конструкция источника питания (в виде делителя напряжения)
Закон
Ома полезен при разработке источников питания для электронных схем. Делители напряжения определяют регулируемый выход для правильного функционирования схемы. Это достигается выбором правильного сопротивления по закону Ома.
Делители напряжения определяют регулируемый выход для правильного функционирования схемы. Это достигается выбором правильного сопротивления по закону Ома.
2. Аналоговые датчики
Некоторые типы датчиков выдают текущее значение на выходе. Например, радарный датчик дает ток на выходе 4-20 мА.
Этот выходной ток следует преобразовать в напряжение с помощью уравнения сопротивления. Полученное аналоговое напряжение затем обрабатывается через АЦП (аналого-цифровой преобразователь).
3. Регулятор скорости
Закон
Ом широко используется в приложениях для управления скоростью. Он используется в потенциометре , также известном как « POT ». Сопротивление ручки изменяется медленно, что увеличивает напряжение и вращает двигатель или вентилятор.
4. Упрощение схем
Он также используется для сокращения сложных электрических цепей с использованием уравнения Закона Кирхгофа о напряжении и Закона тока Кирхгофа . Последовательные и параллельные цепи могут быть реализованы просто с использованием закона Ома.
Последовательные и параллельные цепи могут быть реализованы просто с использованием закона Ома.
Заключение
В реальной жизни важно узнать ток и напряжение для любого применения. Небольшое отклонение выходной нагрузки может сжечь или повредить цепь. Чтобы избежать этого, требуется применить принципы закона Ома и построить действующую электронную систему.
электрический ток
Направленное движение носителей электрического заряда, т. е. электронов, движущихся в определенном направлении, называется электрическим током.Сами по себе электроны представляют собой очень маленькие элементарные частицы, имеющие одинаковый отрицательный заряд.
Электрический ток течет только в замкнутой цепи. Замкнутая цепь состоит как минимум из источника электроэнергии и электрического устройства или компонента, которые соединены электрическими проводниками (например, электрическими проводами). Эти проводники могут быть металлами, а также жидкостями или газами. Примечание: Важно проверить, где может протекать электрический ток! Иногда предмет или тело включаются случайно, если они соприкасаются (соприкасаются) с электрическими проводниками.
Чем выше напряжение на источнике питания, тем больше сила тока (необходимое условие: все компоненты остаются неизменными, а температура остается неизменной). Кроме того: чем выше сопротивление электрического проводника, тем меньше сила тока, если напряжение остается прежним.
Если вы знаете напряжение и электрическое сопротивление электрической цепи, то можете рассчитать силу тока по этой формуле:
Сила тока — это физическая величина, обозначающая количество электронов, которые проходят через определенную площадь поперечного сечения электрического проводника в течение одной секунды.(Вы можете представить это как ворота, которые подсчитывают электроны, проходящие определенное место в проводнике). Сила тока сокращается символом формулы I . Символ формулы I происходит от слова интенсивность . Цель состоит в том, чтобы описать, насколько сильным является электрический ток. Интенсивность помогает понять, что сила тока велика, если через площадь поперечного сечения за определенный промежуток времени проходит особенно большое количество электронов.
Сила тока указывается в амперах.Своим названием он обязан французскому физику Андре-Мари Амперу, который жил с 1775 по 1836 год во Франции. Сила тока в один Ампер будет достигнута, если за одну секунду через поперечное сечение проводника пройдет 6,24 квинтиллиона (6 240 000 000 000 000 000) электронов.
Сила электрического тока является мерой количества заряда ( Q ), прошедшего площадь сечения за определенный период времени ( t ). Он описывается следующей формулой:
(Небольшое напоминание: Q — это символ заряда, а t — символ времени.)
Эти модели проводника помогут вам понять, что означает высокая или низкая сила тока. Чем выше сила тока, тем больше электронов проходит через
дирижер в течение определенного периода времени:
Высокая сила тока; много электронов за период времени:
Малая сила тока; несколько электронов за период времени:
Примечание. В реальном проводнике электроны движутся не так прямолинейно; они скорее движутся зигзагообразным курсом.
Вот несколько примеров сильных сторон тока из вашей повседневной жизни:
| лампочка | о | 0,4 Ампера |
| фонарик | до | 0,6 Ампер |
| тостер | о | 5,2 Ампера |
| печь для выпечки | до | 12 ампер |
| электровоз | около | 150 ампер |
| молния | до | 1.000.000 Ампер |
Закон Ома
Закон Ома
Далее: Сопротивление и удельное сопротивление
Вверх: Электрический ток
Предыдущий: Электрические цепи
Рассмотрим снова простую цепь, в которой постоянный ток течет через
один проводящий провод, соединяющий положительные и отрицательные клеммы
батареи напряжением. Какая связь между нынешним
течет по проводу, а разность потенциалов приложена к
два конца провода возле аккумулятора? Если бы мы исследовали эту взаимосвязь экспериментально, то быстро пришли бы к выводу, что ток
прямо пропорционально разности потенциалов. Другими словами,
Другими словами,
| (126) |
где константа пропорциональности называется (электрическим) сопротивлением
провода. Вышеприведенная формула называется законом Ома после ее
Первооткрыватель, немецкий физик начала девятнадцатого века Георг Симон Ом.
Единицей электрического сопротивления является ом (), т.е.
эквивалентно вольту на ампер:
| (127) |
Есть небольшое расхождение между тем, что мы говорим
сейчас, и то, что мы сказали ранее.В разд. 5, мы утверждали, что
электрическое поле внутри проводника равно нулю. Однако при наличии разности потенциалов
между началом и концом проводника, как описано выше,
тогда должно быть
электрическое поле, распространяющееся по длине провода. В самом деле, если
В самом деле, если
провод прямой, и электрический потенциал уменьшается равномерно с
расстояние, пройденное по проводу, то продольное электрическое
напряженность поля определяется выражением (см. раздел 5.3), где — длина провода.Ранее полученный результат о том, что электрическое поле внутри
проводника эквивалентно утверждению, что проводники обладают нулевой электрической
сопротивление. Это следует из того, что если равно нулю, то электрическое поле, а значит, и потенциал
разность , должна быть равна нулю, иначе протекал бы бесконечный ток
по закону Ома. Получается, что хорошие проводники ( т.е. ,
медь, серебро, алюминий и большинство других металлов) обладают
ненулевой электрический
сопротивления. Однако обычно эти сопротивления настолько малы, что
если бы мы соединили клеммы батареи вместе с помощью
провод, сделанный из хорошего проводника, то ток, который будет течь
в проводе, по закону Ома, была бы настолько велика, что
повредить провод и аккумулятор.Мы обычно называем такую схему
короткое замыкание . Для предотвращения слишком больших токов от
Для предотвращения слишком больших токов от
проточные, обычные электрические цепи содержат компоненты, называемые резисторами ,
электрическое сопротивление которых на много порядков больше, чем
проводников в цепи. Когда мы применяем Ома
закону, к цепи мы обычно подсчитываем только чистое сопротивление
все
резисторы в цепи, а сопротивлениями межсоединений пренебречь
провода.Это означает, что все основные падения электрического потенциала, как мы
проехать по цепи от одного вывода батареи к другому,
происходят внутри резисторов. Падение потенциала в проводнике
самих проводов обычно ничтожно мало.
Таким образом, во всех смыслах и целях хорошие проводники и провода
сделанные из хороших проводников, ведут себя так, как будто они
имеют нулевое сопротивление и содержат нулевое электрическое поле.
Далее: Сопротивление и удельное сопротивление
Вверх: Электрический ток
Предыдущий: Электрические цепи
2007-07-14
Electric Power — Summary – The Physics Hypertext
- … .

- Механика
- Кинематика
- Движение
- Расстояние и перемещение
- Скорость и Скорость
- Ускорение
- Уравнения движения
- Свободное падение
- Графики движения
- Кинематика и исчисление
- Кинематика в двух измерениях
- Снаряды
- Параметрические уравнения
- Динамика I: Сила
- Силы
- Сила и масса
- Действие-реакция
- Вес
- Динамика
- Статика
- Трение
- Силы в двух измерениях
- Центростремительная сила
- Системы отсчета
- Энергия
- Работа
- Энергия
- Кинетическая энергия
- Потенциальная энергия
- Сохранение энергии
- Мощность
- Простые машины
- Динамика II: Импульс
- Импульс и импульс
- Сохранение импульса
- Импульс и энергия
- Импульс в двух измерениях
- Вращательное движение
- Вращательная кинематика
- Инерция вращения
- Вращательная динамика
- Вращательная статика
- Угловой момент
- Энергия вращения
- Прокатка
- Вращение в двух измерениях
- Сила Кориолиса
- Планетарное движение
- Геоцентризм
- Гелиоцентризм
- Всемирная гравитация
- Орбитальная механика I
- Гравитационная потенциальная энергия
- Орбитальная механика II
- Сила тяжести вытянутых тел
- Периодическое движение
- Пружины
- Простой гармонический осциллятор
- Маятники
- Резонанс
- Эластичность
- Жидкости
- Плотность
- Давление
- Плавучесть
- Поток жидкости
- Вязкость
- Аэродинамическое сопротивление
- Режимы течения
- Кинематика
- Теплофизика
- Тепло и температура
- Температура
- Тепловое расширение
- Атомная природа материи
- Газовые законы
- Кинетико-молекулярная теория
- Фазы
- Калориметрия
- Явное тепло
- Скрытая теплота
- Химическая потенциальная энергия
- Теплопередача
- Проводка
- Конвекция
- Радиация
- Термодинамика
- Тепло и работа
- Диаграммы давление-объем
- Двигатели
- Холодильники
- Энергия и энтропия
- Абсолютный ноль
- Тепло и температура
- Волны и оптика
- Волновые явления
- Природа волн
- Периодические волны
- Интерференция и суперпозиция
- Интерфейсы и барьеры
- Звук
- Природа звука
- Интенсивность
- Эффект Доплера (звук)
- Ударные волны
- Дифракция и интерференция (звук)
- Стоячие волны
- бьет
- Музыка и шум
- Физическая оптика
- Природа света
- Поляризация
- Эффект Доплера (свет)
- Черенковское излучение
- Дифракция и интерференция (свет)
- Тонкопленочная интерференция
- Цвет
- Геометрическая оптика
- Отражение
- Преломление
- Сферические зеркала
- Сферические линзы
- Аберрация
- Волновые явления
- Электричество и магнетизм
- Электростатика
- Электрический заряд
- Закон Кулона
- Электрическое поле
- Электрический потенциал
- Закон Гаусса
- Проводники
- Электростатические приложения
- Конденсаторы
- Диэлектрики
- Батареи
- Электрический ток
- Электрический ток
- Электрическое сопротивление
- Электроэнергия
- Цепи постоянного тока
- Резисторы в цепях
- Батареи в цепях
- Конденсаторы в цепях
- Правила Кирхгофа
- Магнитостатика
- Магнетизм
- Электромагнетизм
- Закон Ампера
- Электромагнитная сила
- Магнитодинамика
- Электромагнитная индукция
- Закон Фарадея
- Закон Ленца
- Индуктивность
- Цепи переменного тока
- Переменный ток
- RC-цепи
- Цепи РЛ
- LC-цепи
- Электромагнитные волны
- Уравнения Максвелла
- Электромагнитные волны
- Электромагнитный спектр
- Электростатика
- Современная физика
- Относительность
- Пространство-время
- Масса-энергия
- Общая теория относительности
- кванта
- Излучение черного тела
- Фотоэлектрический эффект
- Рентген
- Антиматерия
- Волновая механика
- Волны материи
- Атомные модели
- Полупроводники
- Конденсированные вещества
- Ядерная физика
- Изотопы
- Радиоактивный распад
- Период полураспада
- Энергия связи
- Деление
- Фьюжн
- Нуклеосинтез
- Ядерное оружие
- Радиобиология
- Физика элементарных частиц
- Квантовая электродинамика
- Квантовая хромодинамика
- Квантовая динамика вкуса
- Стандартная модель
- Помимо стандартной модели
- Относительность
- Фундаменты
- Единицы
- Международная система единиц
- Гауссова система единиц
- Британско-американская система единиц
- Разные единицы
- Время
- Преобразование единиц измерения
- Измерение
- Значащие цифры
- Порядок величины
- Графики
- Графическое представление данных
- Линейная регрессия
- Изогнутый фитинг
- Исчисление
- Векторов
- Тригонометрия
- Сложение и вычитание векторов
- Векторное разрешение и компоненты
- Умножение на вектор
- Ссылка
- Специальные символы
- Часто используемые уравнения
- Физические константы
- Астрономические данные
- Периодическая таблица элементов
- Люди в физике
- Единицы
- Задняя часть
- Предисловие
- Об этой книге
- Связаться с автором
- Гленнелерт.

- Гленнелерт.
- Предисловие
- Механика