Каким образом можно измерять малые сопротивления мостиком уитстона: Как измерять неэлектрические величины с помощью моста Уитстона

Как измерять неэлектрические величины с помощью моста Уитстона

Как измерять неэлектрические величины с помощью моста Уитстона

Измерительный мост (мост Уитстона, мостик Витстона) — электрическая схема или устройство для измерения электрического сопротивления.

Мост Уитстона представляет собой электрическую схему, предназначенную для измерения величины электрического сопротивления. Впервые данная схема была предложена британским физиком Самуэлем Кристи в 1833 году, а в 1843 году она была усовершенствована изобретателем Чарльзом Уитстоном. Принцип работы данной схемы схож с действием механических аптекарских часов, только уравниваются здесь не силы, а электрические потенциалы.

Схема моста Уитстона содержит две ветви, потенциалы средних выводов (D и B) которых уравниваются в процессе проведения измерений. Одна из ветвей моста включает в себя резистор Rx, значение сопротивления которого необходимо определить.

Противоположная ветвь содержит реостат R2 — сопротивление регулируемой величины. Между средними выводами ветвей включен индикатор G, в качестве которого может выступать гальванометр, вольтметр, нуль-индикатор или амперметр.

В ходе измерительного процесса сопротивление реостата постепенно изменяют до тех пор, пока индикатор не покажет ноль. Это значит, что потенциалы средних точек моста, между которыми он включен, равны друг другу, и разность потенциалов между ними равна нулю.

Когда стрелка индикатора (гальванометра) отклонена в ту или иную сторону от нуля, это значит что через него протекает ток, и следовательно мост еще не находится в балансе. Если же на индикаторе ровно ноль — мост сбалансирован.

Очевидно, если отношение верхнего и нижнего сопротивлений в левом плече моста равно отношению сопротивлений правого плеча моста — наступает баланс (или равновесие) моста просто в силу нулевой разности потенциалов между выводами гальванометра.

И если значения трех сопротивлений моста (включая текущее сопротивление реостата) сначала измерены с достаточно небольшой погрешностью, то искомое сопротивление Rx будет найдено с достаточно высокой точностью. Считается что сопротивлением гальванометра можно пренебречь.

Мост Уитстона по сути универсален, и применим отнюдь не только для измерений сопротивлений резисторов, но и для нахождения самых разных неэлектрических параметров, достаточно лишь чтобы сам датчик неэлектрической величины был резистивным.

Тогда сопротивление чувствительного элемента-датчика, изменяясь под неэлектрическим воздействием на него, может быть измерено при помощи мостовой схемы Уитстона, и соответствующая неэлектрическая величина может быть таким образом найдена с малой погрешностью.

Таким образом можно найти значение величины: механической деформации (тензометрические датчики), температуры, освещенности, теплопроводности, теплоемкости, влажности, и даже состав вещества.

Современные измерительные приборы на базе моста Уитстона обычно снимают показания с моста через аналого-цифровой преобразователь, подключенный к цифровому вычислительному устройству, такому как микроконтроллер с вшитой программой, которая осуществляет линеаризацию (замена нелинейных данных приближенными линейными), масштабирование и преобразование полученных данных в численное значение измеряемой неэлектрической величины в соответствующих единицах измерения, а также коррекцию погрешностей и вывод в читаемом цифровом виде.

Например напольные весы примерно по такому принципу и работают. Кроме того программными методами тут же может быть проведен гармонический анализ и т. д.

Так называемые тензорезисторы (резистивные датчики механического напряжения) находят применение в электронных весах, в динамометрах, манометрах, торсиометрах и тензометрах.

Тензорезистор просто наклеивается на деформируемую деталь, включается в плечо моста, при этом напряжение в диагонали моста будет пропорционально механическому напряжению, на которое реагирует датчик — его сопротивление изменяется.

При разбалансе моста измеряют величину этого разбаланса, и таким образом находят например вес какого-нибудь тела. Датчик, кстати, может быть и пьезоэлектрическим, если измеряется быстрая или динамическая деформация.

Когда необходимо измерить температуру, применяются резистивные датчики, сопротивление которых изменяется вместе с изменением температуры исследуемого тела или среды. Датчик может даже не контактировать с телом, а воспринимать тепловое излучение, как это происходит в болометрических пирометрах.

Принцип действия болометрического пирометра основан на изменении электрического сопротивления термочувствительного элемента вследствие его нагревания под воздействием поглощаемого потока электромагнитной энергии. Тонкая пластинка из платины, зачерненная для лучшего поглощения излучения, из-за своей малой толщины под действием излучения быстро нагревается и ее сопротивление повышается.

Похожим образом действуют термометры сопротивления с положительным температурным коэффициентом и терморезисторы с отрицательным температурным коэффициентом на базе полупроводников.

При изменении температуры косвенным путем можно измерить теплопроводность, теплоемкость, скорость потока жидкости или газа, концентрацию компонентов газовой смеси и т. д. Именно косвенные измерения такого рода применяются в газовой хроматографии и в термокаталитических датчиках.

Фоторезисторы изменяют свое сопротивление под действием освещенности, а для измерения потоков ионизирующего излучения — используются специализированные резистивные датчики.

Ранее ЭлектроВести писали, что Украина готовится к присоединению к энергетической системы Европы. На фоне этого между двумя энергетическими компаниями Украины «НЭК«Укрэнерго» и «НАЭК«Энергоатом» возник конфликт, потому что компании видят решение вопроса интеграции с энергосистемой ЕС по-разному. В Укренерго предлагают сделать вставку постоянного тока на границе энергосистемы Украины и Бурштынской ТЭС, а Энергоатом представил проект «Энергомост «Украина – ЕС».

По материалам: electrik.info.

Уитстона мостик для переменного тока

    Принципиальная схема для проведения кондуктометрических измерений представлена на рис. 8.3. Это обычный мостик Уитстона, питаемый переменным током от генератора 2. Постоянный ток нежелателен, так как вызывает электролиз раствора. В то же время применение моста переменного тока приводит к появлению так называемого реактивного сопротивления вследствие конечной величины емкости измерительной ячейки Rx в цепи, что особенно заметно при работе с растворами, имеющими большое сопротивление. По этой причине, кстати, нельзя свести к нулю силу тока в диагонали моста гв. Сопротивление 7 м известно (магазин сопротивлений). Положение передвижного контакта в подбирается таким образом, чтобы нуль-инструмент 1 не показывал ток (или ток был минимальным). Тогда сопротивление ячейки R можно рассчитать по формуле [c.172]








    Для проведения кондуктометрического титрования необходимо измерять сопротивление раствора или его электропроводность. Определение электропроводности раствора проводят при помощи мостика Кольрауша, аналогичного известному мостику Уитстона, с той только разницей, что для предотвращения электролиза исследуемого раствора применяют переменный ток. На рис. 199 приведена схема мостика Кольрауша. В качестве источника тока применяют обычно зуммер или высокочастотный ламповый генератор, конструкция которого описана ниже. Для обнаружения переменного тока применяют телефон или специальный гальванометр переменного тока.  [c.355]

    Схема прибора Кольрауша показана на рис. 134. Сосудик для измерения электропроводности образует одно плечо мостика Уитстона—аЬ, магазин сопротивлений Я образует другое—ас, калиброванная проволока сдвижном образует третье—М и четвертое—С(1 плечи мостика. Переменный ток подводится к мостику при помощи какого-либо источника переменного тока О через Ьс. Телефон О, применяемый для установления наличия или отсутствия тока в мостике, соединен через 0(1. Так как при употреблении переменного тока для получения баланса в мостике одинаково важны как сопротивления пле-чей, так и их реактансы, т. е. емкости и индуктивности, то применяется переменный конденсатор С. Когда положение контакта гГ соответствует отсутствию или минимуму звука в телефоне Х), потенциалы точек а и с одинаковы или очень близки. При этом соблюдается следующее соотношение  [c.322]

    Уитстона 322, 564 Мостики переменного тока 323 Мутность 682 [c.734]

    Для измерения электропроводности применяют установку, содержащую мостик Уитстона — Кирхгофа. На одном плече мостика включен последовательно сосуд с электродами для определения электропроводности (рис. 80). На другом плече включен ящик сопротивления (магазин сопротивления). Концы плеч мостика в точке С соединены между собой, а другими концами А и В) подсоединены к противоположным концам проволоки реохорда АОВ, укрепленной на метровой линейке с делениями по 1 мм. В конечных точках (Л и В) проволоки реохорда ответвляется проволока, соединенная с параллельно включенным телефоном 4. С помощью другой проволоки в точке С подключается источник переменного тока, который соединен другой проволокой со специальным движком (Д), который можно устанавливать в [c.491]

    Сопротивление можно измерять с помощью мостика Уитстона, в котором неизвестное сопротивление уравновешивается известным. Для измерения сопротивления ячеек, содержащих растворы электролитов, используется переменный ток. При пропускании переменного тока через сосуд с платинированными электродами направление электролиза меняется на обратное в соответствии с изменением направления тока. Покрытие из платиновой черни, образующееся при электролитическом осаждении, адсорбирует газы и катализирует реакции с их участием. Это препятствует образованию непроводящей газовой пленки. [c.344]

    Прибор Кольрауша. Обычной аппаратурой для измерения сопротивления, а следовательно, и электропроводности является мостик Уитстона. Этот метод для измерения электропроводности впервые был применен Кольраушем, использовавшим переменный ток, и до сих пор является универсальным и доступным методом. Схема прибора Кольрауша приведена на рис. 72. Сосудик для измерения электропроводности образует одно плечо мостика Уитстона с сопротивлением Рх, постоянное сопротивление образует другое калиброванная проволока аЬ с движком С образует третье (Яг) и четвертое (i з) плечи мостика. В диагонали мостика включены источник переменного тока / и гальванометр переменного тока 2. При замыкании выключателя 6 напряжение источника тока 1 будет подводиться к точкам а и Ь . В точке й потенциал имеет промежуточное значение по сравнению с потенциалами в точках а и Ь . Кроме того, на ветви мостика —Яз должна быть точка с таким же потенциалом, как и в точке . Эту точку легко найти перемещением скользящего контакта с до тех пор, пока в гальванометре не будет наблюдаться отклонений ни влево, ни вправо. Когда положению контакта с соответствует отсутствие тока в гальванометре 2, потенциалы точек а и с будут одинаковыми. При этом отношение  [c.171]

    Прибор Кольрауша. Обычной аппаратурой для измерения сопротивления, а следовательно, и электропроводности, является мостик Уитстона. Этот метод для измерения электропроводности впервые был применен Кольраушем, использовавшим переменный ток, и до сих пор является универсальным и доступным методом. [c.167]

    Поскольку для большинства целей не требуется очень точных результатов, то во многих типах приборов для кон-дуктометрического титрования за счет меньшей степени точности достигается большее удобство в обращении [28]. В некоторых случаях сохраняют схему мостика Уитстона, однако телефон заменяют каким-либо визуальным прибором (см. стр. 55). При других упрощенных методах кондуктометрического титрования переменный ток пропускают через сосуд и его силу измеряют подходящим прибором, включенным последовательно если величина приложенного напряжения постоянна, то, по закону Ома, сила тока прямо пропорциональна электропро- [c.120]

    Электролитическое разложение уменьшается до ничтожных размеров при применении мостика Уитстона с питанием прибора от сети переменного тока. В таком приборе используют гальванометр для переменного тока. Можно снизить затраты на аппаратуру, заменив гальванометр парой наушников. В идеальном случае в точке компенсации звук не должен ощущаться. Практически же побочные явления индукции обычно вызывают слабый звук, который в точке компенсации соответствует минимальной слышимости. Употребляемая на практике частота переменного тока составляет 60 или 1000 герц. Единственным преимуществом 60-периодного тока является его широкая доступность. Предпочтительнее применять 1000-пер йодный ток, особенно при использовании наушников в качестве детектора. Этот ток можно получить при помощи лампового генератора или камертона, приводимого в действие электрическим током микрофонный зуммер). Применять телефонную технику неудобно, так как в рабочей комнате должна соблюдаться полная тишина, вследствие чего этот метод вытесняется другими. Применение радиочастот (порядка 10 герц) будет обсуждаться позднее. [c.15]

    При этом пользуются мостиком Уитстона (рис. 15) где 5 — гальванический элемент, 6 — катушка Румкорфа для переменного тока, 7 — телефон. (Гальванометр, конечно, неприменим.) а, Ь, с, (1 суть четыре ветви мостика. При действии элемента 5 телефон звучит, и лишь в том случае, [c.87]

    Для измерения сопротивления пользуются мостиком Уитстона, действующим на переменном токе. Принцип [c.30]

    Измерение электрической проводимости растворов по способу Кольрауша основано на использовании известной из физики схемы мостика Уитстона (рис. 35). Реохорд представляет собой линейку длиной 1 м (с миллиметровыми делениями), на которую натянута проволока из сплава манганина (85% Си, 12% Мп, 3% N1) или константана. Сечение проволоки выбирают такое, чтобы сопротивление ее было не менее 7 Ом. Установка питается переменным током звуковой частоты. При измерении сопротивления электролита оптимальная частота тока 800—1000 Гц. В качестве источника переменного тока используют индукционную [c.121]

    Для определения электропроводности растворов пользуются мостиком Уитстона, питаемого для устранения явления поляризации и электролиза переменным током. [c.75]

    В основе прибора лежит оптический мост, аналогичный мостику Уитстона, применяемому для измерений электрических сопротивлений. Разность между интенсивностью света флуоресценции пробы и интенсивностью света калиброванного опорного источника света измеряется оптическим мостом. При помощи механического прерывателя на фотоумножитель по очереди подается свет от пробы и от этого источника. Возникающее переменное напряжение на выходе фотоумножителя подается на вход первого каскада усилителя переменного тока, у которого отсутствует дрейф нуля. Во втором каскаде усилителя включен фазовый детектор. В зависимости от знака разности интенсивностей света пробы и опорного источника на выходе детектора появляется полол ительный или отрицательный сигнал. Выход фазового детектора подключен к нулевому регистрирующему прибору. Положение равновесия (интенсивность света лампы равна интенсивности света пробы) соответствует нулевому положению этого прибора. Поляризационные фильтры для выравнивания интенсивностей не применяют. Количество света, необходимое для выравнивания интенсивностей света, указывается на шкале интенсивности флуоресценции. Каждому из 100 делений шкалы соответствует определенная порция световой энергии лампы, управляемой эксцентриком. [c.131]

    Электропроводность растворов почти всегда определяют путем измерения сопротивления в ячейке, включаемой в одно из плеч мостика Уитстона, как это показано на рис. 1. На этом рисунке А обозначает источник переменного тока Е — неизвестное сопротивление ячейки Е , Е и Е — известные сопротивления и / — детектор. Сопротивление Д3 регулируют до тех пор, пока [c.222]

    Электрическую проводимость определяют, используя мостик Уитстона, питаемый генератором (рис. VI.36). Для питания моста используется ток частотой порядка 1000 Гц. В качестве эталонного сопротивления включают магазины сопротивлений типа Р-58. Можно использовать комплектные приборы для определения электрической проводимости растворов — мосты переменного тока и кондуктометры. В прямой кондуктометрии используют ячейки с жестко закрепленными электродами (рис. VI.36, б). В методах кондуктометрического титрования используются вышеназванные ячейки или ячейки с погружными электродами (рис. VI.36, в). [c.170]

    Отличие мостика Кольрауша от обычного мостика Уитстона заключается в том, что он питается переменным током высокой частоты (2000—3000 герц), от звукового генератора ЗГ—10 (позиция 1), схема состоит из барабанного реохорда 2 магазина сопротивления 3 сосудика для измерения электропроводимости 5. В качестве нуль-инструмента применяется чувствительный прибор, заменяющий осциллограф (оптический глаз) — 4. [c.347]

    Именно, составим цепь мостика Уитстона — Кольрауша, изображенную на рис. 345. В круглую кювету с плоским стеклянным дном С и металлической стенкой М поместим второй металлический электрод, очерченный по форме береговой линии Южно-Американского материка, как по производящей . Наполним кювету водопроводной водой и будем питать цепь переменным током от малой индукционной катушки I и слушать звук ее в телефонной трубке Г, включенной между ползунком Р реохорда К и тонким электродом-зондом iS. Звук будет стихать до минимума, когда этот зонд станет попадать в точки, обладающие тем я е потенциалом, как и нож ползунка Р, касающийся реохорда. [c.578]

    Определение электропроводности. Для определения электропроводности растворов применяют схему мостика Уитстона в специальном видоизменении Кольрауша, изображенную на рис. 10. На этом рисунке А — аккумулятор с напряжением в 4 в / — индукционная катушка для преобразования постоянного тока в переменный (постоянный ток неприменим вследствие поляризации электродов, погруженных в раствор электролита) г — сосуд с электродами (платиновыми пластинками) и с раствором, сопротивление которого г надо определить Я — известное сопротивление О — контакт, скользящий по никелиновой струне АВ, [c. 68]

    Измерение электропроводности барита в змеевике производится по обычнон схеме мостика Уитстона, в которой два плеча составляют измеряемое сопротивление и магазин сопротивлений (10—1000 ом), а другие два плеча — мостик Кольра-уша (реохорд на барабане). Питание мостика переменным током частотой 800— 10000 щ осуществляется от звукового генератора типа ЗГ-2. В диагональ схемы в качестве нуль-инструмента включают электронный осциллограф типа ЭО-4 или ЭО-5. [c.380]

    Измерение электропроводности раствора Ва(ОН)а производится по обычной схеме мостика Уитстона. Удобным прибором является кондуктометр, -конструкции Гусева и Сентюрина [76], позволяющий измерять сопротивление раствора с точностью 0,1%. Более громоздкой является установка, включающая звуковой генератор типа ЗГ-2 и электронный осциллограф типа ЭО-4 или ЭО-5 в качестве нуль-инструмента. Питание мостика осуществляется переменным током частотой 1000 гц. Определение проводят следующим образом.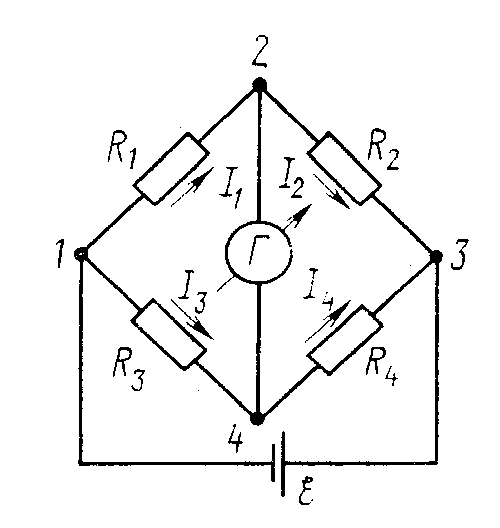 Лодочку с навеской помещают в левую часть трубки для сожжения, но не близко к шлифу включают печь 10 с трубкой 9, заполненной окисью меди. Печь 6 отодвигают вправо до конца и включают. Соединяют все части прибора и пускают кислород со скоростью 10—15 мл мин. Проверяют герметичность прибора. Вся регулировка скорости газа производится краиом 2. Через 20 мин. продувания всего прибора при температуре в печи с окисью меди 600—700° С отключают змеевик-поглотитель (не прерывая тока газа) и запол- [c.384]

    Прибор Кольрауша. Для измерения электрической проводимости применяется мостик Уитстона. Метод впервые был применен Кольраушем, использовавшим переменный ток. Схема прибора Кольрауша показана на рис. 6.4. Сосуд для измерения проводимости образует одно плечо мостика Уитстона с сопротивлением Рх, постоянное сопротивление Яг образует другое плечо калиброванная проволока аЬ с движком с образует третье (Яг) и четвертое (/ з) плечи мостика. В диагонали мостика включены источник переменного тока I и гальванометр пер 1енного тока 2. При замыкании выключателя 6 напряжение источника тока 1 подводится к точкам а и Ь- В точке с потенциал имеет промежуточное значение по сравнению с потенциалами в точках а и 6. Кроме того, на ветви мостика Рц—должна быть точка с таким потенциалом, как и в точке й. Эту точку легко найти перемещением скользящего контакта с до тех пор, пока стрелка гальванометра не перестанет отклоняться ни влево, ни вправо. Когда найдено положение контакта, при котором отсутствует ток в. гальванометре 2, потенциалы точек с1 и с одинаковы. При этом отношение равно отношению Я2[Яг и [c.94]

    Отличие мостика Кольрауша от обычного мостика Уитстона заключается в том, что он питается переменным током высокой частоты, а в качестве нуль-инструмента применяется телефон. Применение переменного тока необходимо потому, что при питании постоянным током здесь происходил бы электролиз, вследствие чего менялась бы концентрация электролита у электродов и возрастало бы сопротивление. При этом у электродов могут накапливаться продукты электролиза, вызывая полярйза-цию, в результате чего может появляться э. д. с. обратного направления, вызывающая кажущееся изменение сопротивлен йя.  [c.98]

    Быстродействие и высокая точность—главные преимущества этого метода. Может быть использован переменный ток с выпрямительным мостиком. Сопротивление может замеряться с помощью моста -Уитстона. Может быть предусмотрена температурная ав.токомпенса-ция. [c.418]

    Точные измерения электропроводности расплавленных силикатных минералов, рассмотренных выше, представляют весьма большие экспериментальные трудности. Качественные исследования предпринимал Дёльтер , но очень скоро он убедился в том, что газы, содержащиеся в природных силикатах, чрезвычайно мешают измерениям. Дёльтер применял в качестве электролитической ванны сосуд в форме параллелепипеда из каолиновых и кварцевых огнеупоров, в который помещал платиновые электроды. Он исследовал расплавы так же, как изучают водные растворы электролитов, т. е. пользуясь мостиком Уитстона, малым индуктором переменного тока и определением минимума звука с помощью телефона. Точность таких измерений весьма невелика. Позже Дёльтер пользовался платиновым тиглем, причем одним из электродов служил образец, другим—тщательно центрированный платиновый цилиндр. Усовершенст- [c.149]

    Метод Фулда для плавленных промышленных стекол значительно усовершенствовали Хенлейн и То-мас в частности, они изменили расположение электродов, улучшили регулировку плотности тока, la также ввели тщательный контроль над изменениями сопротивления в зависимости от температуры. Измерения производились на переменном токе мостиком Уитстона с ламповым усилителем принципиальная схема измерительной цепи представлена яа фиг. 167 и 168. Особое вни- [c.152]

    В камере датчика газоанализатора расположены два чувствительных термоэлемента из слюдяных пластин, обмотанных платиновой проволокой. Один из них находится рядом с постоянным магнитом. Термоэлементы образуют мостик Уитстона и нагреваются пропускаемым через них переменным электрическим током 120 в от стандартного феррорезонансного стабилизатора напряжения. При пропускании продуктов сгорания, содержащих кислород, через камеру датчика поток их будет отклоняться в сторону термоэлемента, расположенного рядом с магнитом, и тем больше, чем выше содержание кислорода в анализируемой пробе. Следовательно, этот термоэлемент будет охлансдаться потоком газов интенсивнее, чем не имеющий магнитного поля. В результате температура и электрическое сопротивление термоэлементов станут различными, что и вызовет нарушение электрического равновесия моста и отклонение стрелки указывающего прибора газоанализатора. В качестве указывающего (вторичного) прибора газоанализатора МГК-348 применяется электронный потенциометр переменного тока ВПГ-359. Кислородные газоанализаторы МГК-348 выпускаются на различные пределы измерений. Для анализа топочных газов применяется газоанализатор с пределом измерения кислорода от О до 10%. [c.422]

    Однако подавляющее большинство исследований электропроводности растворов было выполнено с помощью методики с использованием слабого переменного тока большой частоты, предложенной Кольраушем в 1868 г.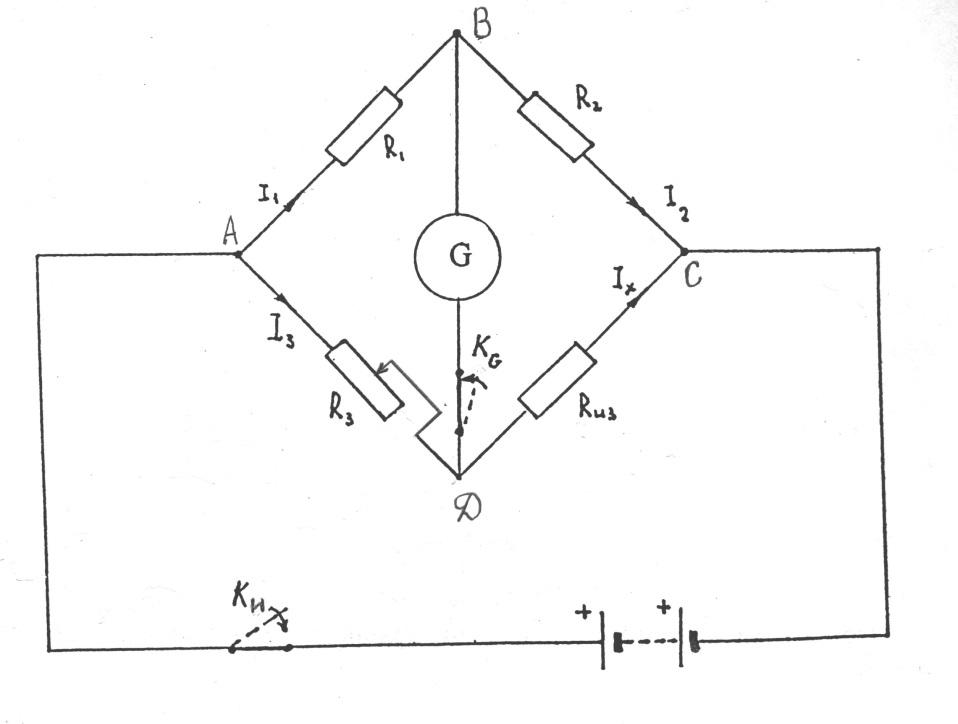 Основная идея применения переменного тока состоит в том, что поскольку направление тока меняется около 1000 раз в 1 сек., то поляризация, вызываемая каждым толчком тока, полностью нейтрализуется следующим толчком при условии, что переменный ток симметричен. При этом полностью компенсируются все изменения концентрации, которые могут иметь место. В качестве источника переменного тока Кольрауш пользовался индукционной катушкой, а в качестве нульинструмента применял в своих первых работах бифилярный гальванометр позже, в 1880 г., он использовал для этой цели телефон, который в усовершенствованном виде до сих пор является наиболее часто применяемым прибором для обнаружения переменного тока при измерениях электропроводности электролитов. Электролит помещался в специальный сосуд, и его сопротивление измерялось с помощью мостика Уитстона, схематически изображенного на рис. 9. Сосуд С включен в ветвь ab, а магазин сопротивлений представляет собой ветвь ас источник переменного тока обозначен через S, а телефон — через Н. В мостике самого простого образца, которым часто пользуются для обычных лабораторных целей, ветви bd и de представляют собой однородную (предпочтительно платино-иридиевую) проволоку, натянутую на прямую шкалу длиной 1 м (так называемый метровый мостик, или реохорд) или намотанную на цилиндрический барабан из шифера .  [c.64]

    Конструкция мостика для переменного тока. Условия равновесия мостика Уитстона, которые определяются уравне—нием (7), применимы к переменному току лишь в том случае, если Яг, Я2, Яз и являются чистыми сопротивлениями. Представляется маловероятным, чтобы магазины сопротивлений были совершенно безиндукционными и не обладали никакой емкостью кроме того, сосуд для определения электропроводности и его соединительные трубки всегда эквивалентны сопротивлению, шунтированному емкостью. Одно из следствий этого обстоятельства состоит в том, что токи, проходящие через две ветви мостика Яг и Я2), оказываются не в фазе и невозможно найти такое положение, при котором звук в телефоне исчезал бы полностью. В большинстве случаев можно устранить это затруднение путем включения конденсатора К параллельно с магазином сопротивления Я , как было указано на стр. 53. [c.74]

    Определение электропроводности при высоком напряжении и высокой частоте. Измерение электропроводности электролитов с помощью переменного тока очень высокой частоты или высокого напряжения приобрело особый интерес в связи с современными теориями растворов электролитов. В этих особых условиях обычный метод мостика Уитстона неприменим в связи с этим были использованы некоторые другие экспериментальные методы. Основная трудность заключается в определении положения равновесия было показано, что наиболее подходящим для этой цели является бареттерный мостик. Одна из разновидностей такого мостика изображена на рис. 19, II по существу это мостик Уитстона. Одна из ветвей его содержит самоиндукции и и небольшую бареттерную лампу с тонкой нитью параллельно с бареттером включена самоиндукция М , предназначенная для связи с главным контуром, и конденсатор Сг. Другая ветвь мостика содержит самоиндукции и 4 и бареттер 1 , который по своим свойствам должен быть идентичен 1 , этот бареттер также шунтирован самоиндукцией Жа и конденсатором С . Две другие ветви мостика составляют переменные сопротивления и Постоянное напряжение накладывается на мостик с помощью батареи постоянного тока, нульинструментом служит гальванометр Г. Включенная последовательно с гальванометром самоиндукция препятствует прохождению через него индуцированных токов. В начале опыта мостик уравновешивается с помощью сопротивлений и [c.83]

    В первую очередь можно упомянз ть о гальванометрах переменного тока — Лидса и Нортрупа или любого другого типа. Для кондуктометрического титрования особенно рекомендуется прибор, снабженный гальванометром и приспособлениями для использования переменного тока из сети с напряжением ПОУ и с 60 периодами. Он не подходит для очень точных измерений, и, кроме того, во время титрования могут возникнуть некоторые затруднения вследствие поля ризации электродов н нагревания раствора в сосудике.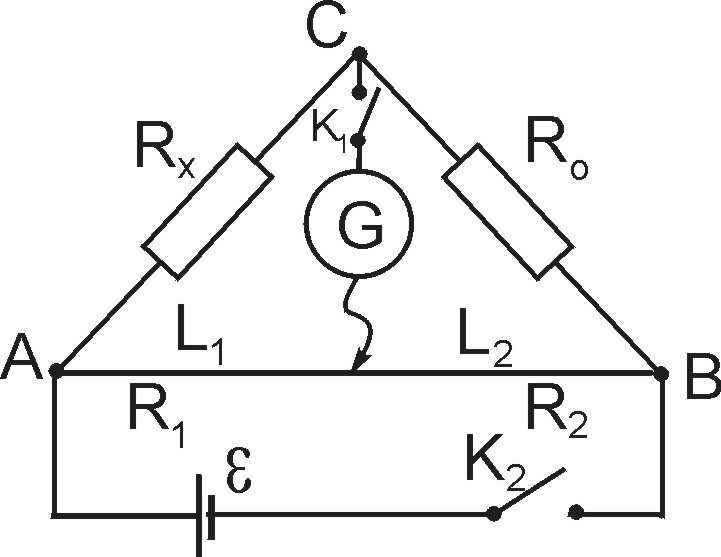 Если удастся преодолеть эти затруднения, то гальванометр переменного тока окажется самым простым прибором для нахождения точки компенсации иа мостике Уитстона. [c.166]

    Продажный аппарат, акваметр Бекмана (рис. 313), специально предназначен для титрования воды по методу Фишера. В этом приборе используется пара платиновых электродов, на которые подается переменное напряжение 50 ле и с которыми титрование проводится до внезапного прекращения тока. Сопротивление раствора между этими электродами включается в цепь мостика Уитстона, нескомпенсированное напряжение которого усиливается и, усиленное, служит для питания фазо-чувствительного детектора, который в свою очередь управляет клапаном бюретки, регулируемым магнитом. Таким образом, если привести в действие аппарат от руки, то титрование, раз начавшееся, будет продолжаться до тех пор, пока в точке эквивалентности резко не из- [c.390]

Мост для измерения больших сопротивлений

Мосты для измерения больших сопротивлений  [c. 231]

Резистор с тремя выводами Рис. 14.22. Мост для измерения больших сопротивлений  [c.232]

Для измерения электросопротивления существуют различные методы, из которых наиболее распространены способ моста Уитстона для измерения больших сопротивлений (от 10 до 10000 ом) и способ двойного моста Томсона для измерения малых сопротивлений (от 1 мком до 1 ом).  [c.195]

И. м. переменного тока применяются для измерения активного сопротивления, индуктивности, взаимоиндуктивности, емкости, частоты переменного тока, диэлектрич. потерь (угла потерь) и т. п. И. м. переменного тока также применяются для измерения неэлектрических величин. В большинстве случае И. м. переменного тока применяются в качестве уравновешенных мостов. В качестве нулевых приборов применяют вибрационные гальванометры, гальванометры постоянного тока с различными выпрямителями, электродинамометры, телефоны и т. д. Для повышения чувствительности нулевого прибора применяют электронные усилители. В качестве источников тока применяют машины переменного тока технической и звуковой частоты, ламповые генераторы, переключатели и прерыватели (зуммеры) и т. п. Плечи И. м. переменного тока составляются из сопротивлений, к-рые в общем случае обладают активным сопротивлением, индуктивностью и емкостью и полное сопротивление к-рых выражается комплексом Z = = К -j- /ж. В частном случае та или иная величина выбирается настолько малой, что ею можно пренебречь, что ве.дет к упрощению расчетных ф-л. Особенно большие упрощения достигаются при применении активных сопротивлений, распределенные индуктивность и емкость к-рых пренебрежительно малы (б е з-реактивные сопротивления) и для к-рых можно принять Z = Д. Значение  [c.552]

Поскольку гальванометр магнитоэлектрической системы реагирует на внешние, возможно имеющиеся в грунте напряжения постоянного тока, перед ним включается конденсатор. Посторонние напряжения переменного тока с частотой 16% или 50 Гц тоже не могут повлиять на результат измерения, поскольку рабочая частота измерительных мостов переменного тока при схеме с вибропреобразователями составляет 108 Гц, а по схеме с транзисторами — около 135 Гц. Первая высшая гармоника в мостовой схеме выпрямителя станции катодной зашиты (100 Гц) обычно вызывает заметные биения. Однако при не слишком больших амплитудах и в этом случае еще возможно выявление нуля путем настройки одинаковых отклонений по обе стороны от нулевой точки. Некоторые характеристики приборов для измерения сопротивления представлены в табл. 3.2. В принципе все четырехполюсные приборы для измерения сопротивления могут быть использованы при закорачивании обеих клемм Ei и также и для измерения сопротивлений растеканию тока в грунт.  [c.114]

Для измерения величины сигнал поступает на сетку левой половины Л4 и далее с ее анода передается на измерительный мостик ПП — ППц, в диагональ которого включен микроамперметр (150 мт). С целью лучшего сглаживания низкочастотных пульсаций стрелки прибора введена шунтирующая емкость jg и балластное сопротивление У 24. Последнее не только улучшает сглаживание за счет повышения сопротивления шунтируемой емкости цепи, но и служит для согласования с анодной нагрузкой сопротивления моста. Делитель R2,R2s на входе этого каскада введен для предотвращения нелинейности шкалы микроамперметра при чрезмерно больших сигналах на сетке лампы. Плечи делителя выбирают так, чтобы полное отклонение стрелки микроамперметра от входного сигнала имело место в пределах линейного участка характеристики лампы. Включенный таким образом микроамперметр работает линейно (в пределах 3 %) в диапазоне от 10 до 100 % шкалы. Следует отметить, что введение регулировки цены деления измерителя величины неуравновешенности до входа левой половины лампы регламентирует постоянство режимов работы всех последующих каскадов, предельным сигналом которых является сигнал, соответствующий полному отклонению стрелки микроамперметра. Это обеспечивает сохранение линейности работы 38  [c.38]

Непрерывность цепи заземляющих проводников проверяют измерением их сопротивления различными приборами измерителем сопротивления заземления, мостами, омметрами и др. Пользование мегаомметром для этих целей недопустимо, так как он измеряет очень большие сопротивления, напряжение мегаомметра велико, в результате чего плохой контакт может быть ошибочно принят за хороший.  [c.287]

Лабораторные работы по изучению фазового состава сплавов методом измерения удельного электросопротивления и температурного коэффициента удельного электросопротивления можно выполнять любым из методов, указанных на с. 119—122. Метод выбирают в зависимости от приборов, имеющихся в лаборатории. Более желательно применение двойного моста. При использовании метода амперметра — вольтметра или простого моста лучше применять образцы из проволоки малого диаметра (0,5—1 мм), но большой длины (1—2 м) с тем, чтобы сопротивление было возможно большим. Проволоку лучше навить в виде спирали, более удобной для измерений и проведения термической обработки.  [c.131]

Для измерения очень малых сопротивлений применяются двойные Т-образные мосты, потенциометры, микроомметры, выполненные по схеме логометра, и т. п. Все эти приборы выполняются таким образом, чтобы по возможности уменьшить влияние сопротивления в местах перехода (измерительные контакты— контролируемая поверхность). По их измерительной цепи течет ток до 20 а и более. При измерениях сопротивлений больше ома применяют мостовые, электронные схемы, в которых измеряемое сопротивление включается в цепи контура генератора, катод —сетка лампы и т. д. В этих схемах нет необходимости заботиться об уменьшении влияния мест перехода.  [c.379]

Точка затвердевания бензойной кислоты. Обычно процедура наблюдения температуры затвердевания кислоты в ампуле сводилась к следующему. Ампула нагревалась в электрической печи, температура в которой на несколько градусов превышала точку затвердевания кислоты и обычно была равна примерно 130° С. Когда кислота совершенно расплавлялась и нагревалась до температуры печи, ампулу вынимали из печи и быстро и энергично встряхивали, для того чтобы кислота равномерно остывала. Для более быстрого охлаждения небольшого объема кислоты на конец боковой трубки (Л на фиг. 1) одевали колпачок из влажной бумаги. Это вызывало кристаллизацию небольшого количества кислоты и таким образом предупреждало чрезмерное переохлаждение массы жидкости. В случае отсутствия кристаллов кислота иногда сильно переохлаждалась (до 15° С), и затем внезапно образовывалось слишком большое количество твердой фазы. Внезапное появление (при охлаждении ампулы) в массе жидкости каши из тонких игольчатых кристаллов представляет совершенно нормальное явление. Хотя затвердевает при этом лишь небольшая часть кислоты, но кристаллы так хорошо переплетаются друг с другом, что не падают на дно ампулы. После этого ампула заворачивается в кусок мягкой ткани и помещается в сосуд Дьюара Для обеспечения изоляции отверстие сосуда Дьюара закрывается ватой. Перед помещением ампулы в сосуд Дьюара последний нагревали приблизительно до температуры затвердевания кислоты, погружая в него на 15—20 мин. аналогичную ампулу, также наполненную затвердевающей бензойной кислотой. Это делалось для предотвращения быстрого затвердевания кислоты, предназначенной для измерений, которое может произойти из-за потери значительного количества тепла в холодном сосуде. Поместив исследуемую ампулу в сосуд Дьюара, в гнездо для термометра вводят термометр сопротивления.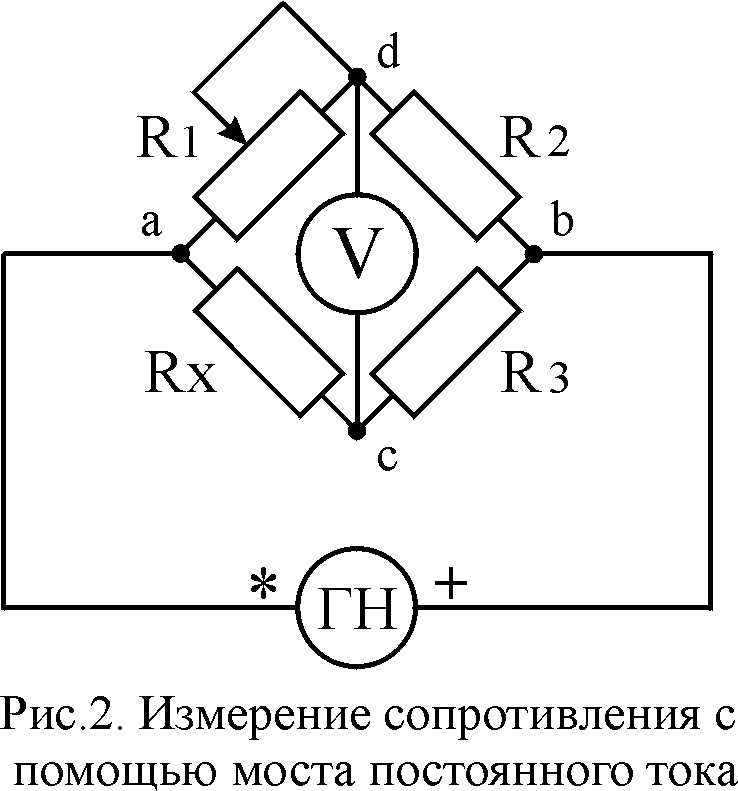 Спустя примерно 10 мин. приступают к измерениям сопротивления, которые продолжают до тех пор, пока сопротивление не достигнет максимума (обычно через 30 мин. или несколько дольше). Производились две отдельные серии измерений сопротивления одна при токе через термометр, равном 1,00 ла, другая—при токе, равном 1,41 ма. Во втором случае отдаваемая мощность была вдвое больше, чем в первом. Для определения сопротивления, соответствующего нулевому току через термометр, надо из сопротивления, соответствующего току через термометр, равному 1 ма, вычесть разность значений сопротивлений для обеих серий измерений. Обычно наблюдения проводили с несколькими ампулами, причем к мосту с помощью переключателя последовательно подключалось несколько термометров.  [c.356]

Для изготовления термометров сопротивления широко применяется платина, которая имеет высокую температуру плавления и химически инертна. Результаты измерений, полученных при помощи платиновых термометров сопротивления, характеризуются высокой воспроизводимостью. Использование современной техники позволяет создавать компактные термометры сопротивления (диаметром до 1 мм), которые обладают малой тепловой инерционностью благодаря их незначительной теплоемкости. Химически инертная платиновая проволока легко отжигается и калибруется. Платиновые термометры сопротивления обычно имеют стандартное сопротивление 100 Ом при 273 К. Зависимость сопротивления этих термометров от температуры приведена в справочных таблицах. Результаты измерений с погрешностью 0,5 К при измерениях температур до 250 °С получают без предварительной калибровки для обеспечения более точных измерений необходимо либо проводить дополнительную калибровку, либо использовать другие, более точные термометры. Так как сопротивление платины в области комнатных температур изменяется всего на 0,4% на 1 К, сопротивление и, следовательно, сила тока и разность потенциалов в используемом термометре должны быть измерены с очень большой точностью. При измерении с такой точностью следует обращать внимание на внешнее сопротивление проводников (например, контуров моста), на влияние паразитных термоэдс, возникающих в местах спайки и соединительных клеммах, и дополнительного нагревания платинового сопротивления измеряющим током. Дополнительное нагревание термометра сопротивления приводит к тому, что измеренная температура оказывается выше истинной. Это один из самых существенных источников погрешностей в результатах калориметрических экспериментов при использовании платиновых термометров сопротивления.  [c.21]

Напряжение подается через повышающий трансформатор I к эталонному конденсатору 2 и конденсатору с испытуемым образцом 3. При помощи переменного сопротивления 4 и переменного конденсатора 5 мост уравновешивается. Для достижения необходимой чувствительности моста при измерении малых углов потерь применяют ламповый усилитель 7, усиливающий ток в 80— 100 раз. При высокой чувствительности моста большое значение приобретает тщательная экранировка моста для защиты от посторонних влияний. Для этой цели служит экранная система 8, причем охранные кольца заземляются наглухо.  [c.410]

И результат измерения не зависит от сопро-тивления соединительного провода Л,. В практич. выполнении в большинстве случаев делают Лз = Л5 и Ri=R . Применимость моста Томсона длн измерения малых сопротивлений достигнута тем, что благодаря дополнительному разветвлению и особому способу включения малых сопротивлений переходные сопротивления контактов оказываются включенными последовательно с относительно большими сопротивлениями. Особый способ включения заключается в применении двух пар зажимов у малых сопротивлений одна пара служит для подвода тока, а другая, расположенная обычно ближе к сопротивлению, сл5 жит для измерительных целей. Вторая пара зажимов (т. н. потенциальные зажи-м ы) хотя и имеет переходное сопротивление контактов, но это сопротивление не входит в цепь проводника, подводящего ток к сопротивлению. На схеме через г обозначены переходные сопротивления контактов и соединительных проводников. Эти сопротивления ( i. 2. 7. 7) либо совершенно не входят в состав тех частей схемы, к-рые имеют значение для определения искомого сопротивления, или (Гз, 7-4, Г5 и г,) оказываются включенными последовательно с такими сопротивлениями, порядок к-рых м.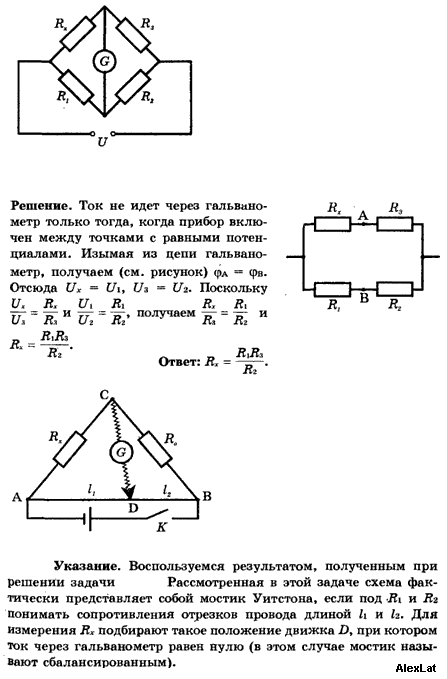 б. выбран (Л3, Л , Л5, Ле). Обычно значение последних выбирается не ниже 10 Q.  [c.557]

Далее приводятся примеры мостовых схем, которые используются для измерения величины индуктивности и сопротивления катушки индуктивности. Для более подробной информации см. главу 9. Мост Максвелла (Рис. 9.86) используется для измерения индуктивности катушек, обладающих высокой добротностью. Мост Максвелла—Вина применяется только для измерения индуктивности катушек с малой добротностью. Мост Оуэна (Рис. 9.8а) используется для катушек с большой индуктивностью. Мост Хея (Рис. 9.8в) разработан для измерения параметров катушек индуктивности с очень высокими значениями добротности.  [c.233]

Термисторы дают значительно большие изменения сопротивления на градус по сравнению с металлическими проволочными элементами (см. пункт 1 главы 8). Их малые размеры обеспечивают небольшую теплоемкость и, следовательно, малое время реакции на температурные изменения. Температурный диапазон, в котором они могут применяться, зависит от типа термистора и составляет -100. ..300°С. В малых диапазонах изменения температуры может быть достигнута точность 0.1 °С или лучше. Однако их характеристики имеют тенденцию изменяться со временем. Для измерения сопротивления термистора может применяться мост Уитстона. Здесь нет необходимости компенсации сопротивления подводящих проводов, так как их сопротивление пренебрежимо мало по сравнению с сопротивлением термистора.  [c.326]

Мостовые методы широко применяют для измерения как малых, так и больших сопротивлений, различающихся на несколько порядков. Различают простой или одинарный и двойной электрические мосты. Первый проще, позволяет с достаточной точностью измерять высокоомные сопротивления, по при измерении малых сопротивлений погрешность возрастает. Двойной мост дает возможность с приемлемой погрешностью измерять даже весьма малые сопротивления.  [c.59]

Серийные электронные автоматические уравновешенные мосты могут быть использованы для измерения температуры с полупроводниковыми термометрами сопротивления. В этом случае вследствие большой разницы в характеристиках металлических и полупроводниковых термосопротивлений измерительная схема моста должна быть пересчитана.  [c.118]

Коммутационный блок деформаций помимо переключателя имеет дополнительные сопротивления для компенсации влияния переходных сопротивлений в подвижных контактах и стальную пластину, установленную на резиновых прокладках, с закрепленными на ней тремя парами тензодатчиков, являющихся тремя ветвями двух измерительных мостов двух каналов деформаций. Четвертые ветви измерительных мостов образуются рабочими тензодатчиками. В каждом канале их может быть от одного до 30 (и больше), так как переключатель при круговом обходе имеет 50 контактов. В положениях переключателя от / до 50 в два измерительных канала подключаются последовательно все 30 тензодатчиков каждого канала. В положении 31 в измерительные каналы для контроля повторно подключаются тензодатчики, подключаемые ранее в положении 1. В положении 32 к измерительным каналам подключаются тензодатчики, установленные на стальной пластине внутри коммутационного блока. Это дает возможность на цикловых записях иметь контроль поведения каналов при измерениях, проверить работу токосъемника и контролировать баланс мостовой схемы во времени. При переходе к положению 33 измерительные мосты каналов деформаций получают активный разбаланс от подключения в соответствующие плечи дополнительных сопротивлений по 0,90 ом, что на цикловой записи дает масштабную ступеньку определенной величины. Один из контактов переключателя коммутационного блока используется для отметки синфазности. Питание привода переключателя осуществляется через пульт управления подачей кратковременных импульсов тока.  [c.122]

Большим преимуществом схемы моста перед компенсационной схемой является также возможность быстрого измерения температуры. Если в компенсационной схеме для определения Гх требуется измерить две величины — воп е , то при измерении по мостовой схеме для получения точного значения сопротивления термометра достаточно одного измерения. Это особенно важно три быстром изменении температуры.  [c.97]

Мосты для измерения больщих сопротивлений Измеряют большие сопротивления  [c.208]

На Рис. 14.22 показан модифицированный вариант моста Уитстона, который может быть использован для измерения больших значений сопротивлений. При измерении больших сопротивлений появляются проблемы, связанные с наличием утечек по параллельным цепям, поэтому в этом случае используются резисто-  [c.231]

Специфический для германиевых термометров сопротивления эффект возникает вследствие довольно высокого значения коэффициента Пельтье для легированного германия. Он проявляется в том, что сопротивление элемента по постоянному и по переменному току различно [53, 54]. Прохождение постоянного тока через германиевый термометр сопротивления приводит к возникновению градиента температуры вдоль элемента вследствие выделения и поглощения тепла Пельтье на спаях элемента с выводами. Наличие градиента температуры вызывает появление небольшой термо-э.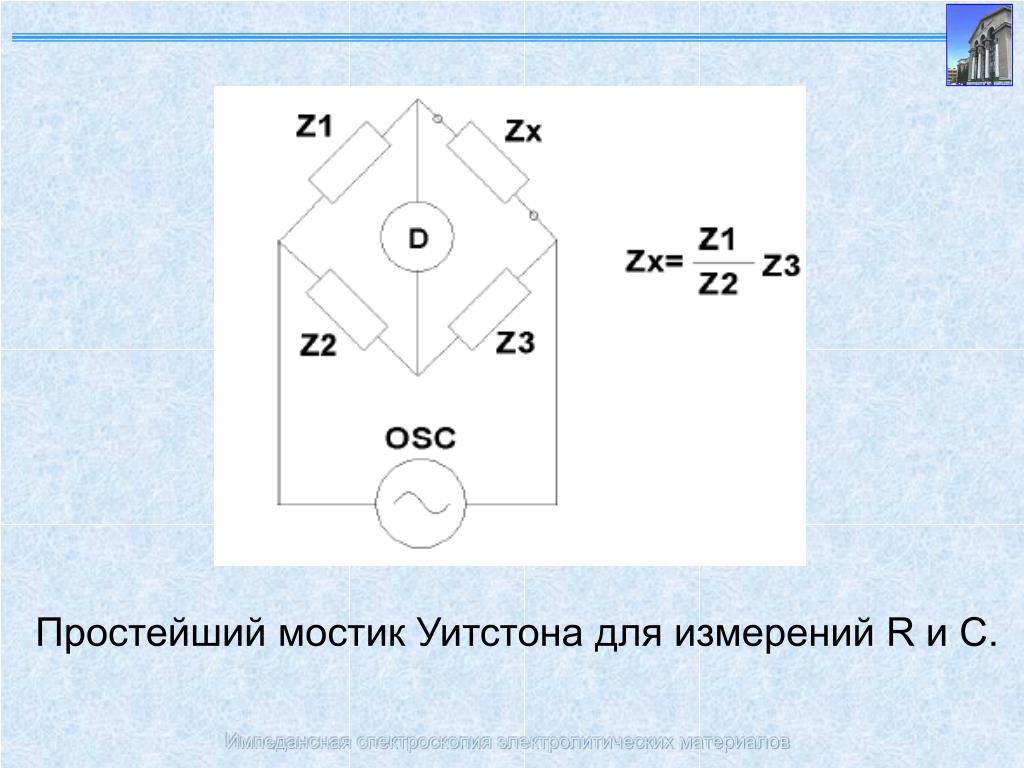 д. с. на потенциальных выводах, что приводит к некоторой погрешности в измерении сопротивления. Если же используется не постоянный, а переменный ток частоты f, то от каждого конца элемента распространяются затухающие тепловые волны. Затухание носит экспоненциальный характер, причем показатель экспоненты пропорционален Уf, так что по мере возрастания частоты тепловые волны все больше сосредоточиваются у концов элемента. Для четырехпроводных элементов в форме моста этот эффект исчезает, когда частота измерительного тока поднимается до такого значения, что тепловые волны перестают достигать потенциальных выводов. В этом случае на потенциальных выводах измеряется истинное сопротивление. Частота, на которой это происходит, зависит от температуропроводности и  [c.237]

Электрические термометры сопротивления в комплекте с логометрами или автоматическими уравновешенными мостами применяются для измерений температур воды, воздуха и газов до 500°С. Для измерения температуры перегретого пара электрические термометры не рекомендуются вследствие их невибростойкости и большой инерционности.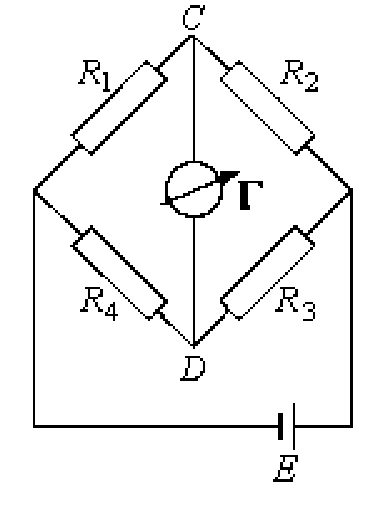  [c.162]

Для измерения М. применяют установки, работающие по принципу механооптич. рычага, позволяющие наблюдать относит, изменения длины образца Ещё большую чувствительность дают радиотехн. и ин-терференц. методы. Распространён также метод проволочных датчиков, в к-ром на образец наклеивают проволочку (с большим уд. сопротивлением), включённую в одно из плеч измерит, моста. Применяются также разл. методики измерения д и н а м и ч. М. (в переменных магн. полях).  [c.12]

Для определения сопротивления есть два точных метода — измерение двойным мостом Кельвина и методом падения потенциала. В методе двойного моста образец составляет одно плечо специальной цепи Витстона и сопротивление измеряется в условиях баланса. Это, повидимому, самый точный метод измерения малых сопротивлений при комнатных температурах, но при более высоких температурах он не так удобен, так как для получения достаточной точности необходим большой ток  [c.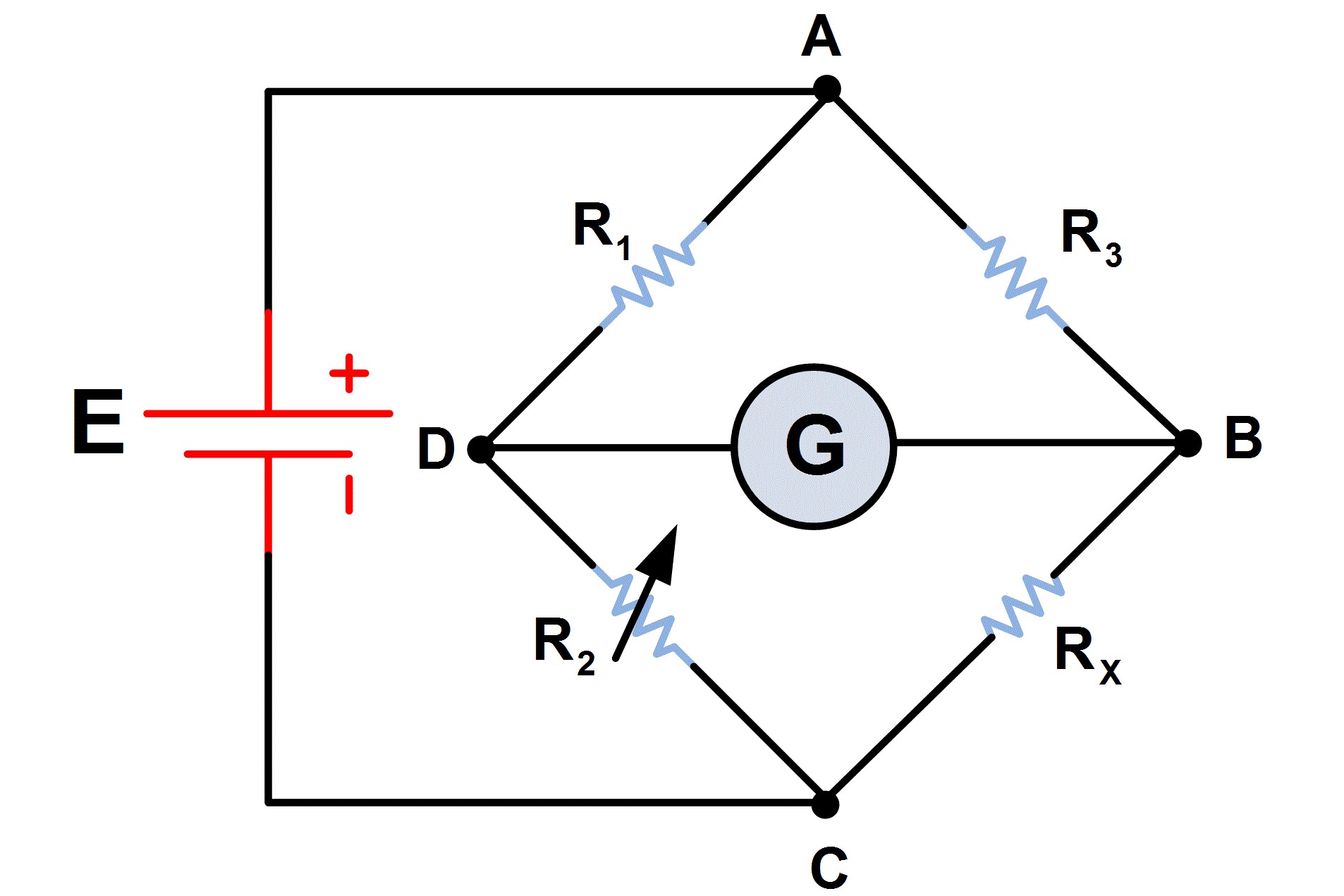 299]

Методы и средства измерения сопротивлений. Сопротивление образца может быть измерено прямо или косвенно. В первом случае применяют электронные омметры (мегаоммет- ры, тераомметры), реже мосты постоянного тока, позволяющие отсчитать значение измеряемого сопротивления непосредственно по шкале прибора. При косвенных измерениях значение сопротивления определяют расчетным путем по результатам измерения тока, протекающего в образце, при известном значении напряжения, приложенного к образцу, или измеряя падение напряжения па образце при известном токе в нем. Для измерения тока и напряжения применяют чувствительные магнитоэлектрические или электростатические приборы с электронными или фотогальванометри-ческими усилителями. Косвенные измерения, в отличие от прямых, позволяют найти сопротивление образца при определенном приложенном напряжении, однако сам процесс измерения усложняется, требует больше времени и дополнительных расчетов.  [c.360]

Наиболее часто значения С и tg б на частоте 50 Гц определяют при помощи мостов переменного тока. Предел измерения моста по емкости должен быть не менее емкости образца, а по tg б превышать примерно в 2 раза tg 6 образца. Принципиальная схема такого моста показана на рис. 29.23, а. Мост питается через повышающий трансформатор, позволяющий получать напряжение на мосте до 10 кВ. В два плеча, примыкающие к высоковольтной>. вершине, включают испытуемый образец Сх и. высоковольтный конденсатор Со, охранный электрод образца соединяют с заземленным экраном моста. В такой схеме все напряжение питания практически приходится на емкостные плечи, так как их сопротивление переменному току много больше сопротивлений других плеч. Это позвояет безопасно уравновешивать мост изменением j и Да. Для защиты цепи в случае пробоя образца предусмотрены разрядники.  [c.370]

Большое сопротивление термистора также во многих случаях является положительным фактором при измерении температуры, так как благодаря этому измерение сопротивления термистора может проводиться со значительно меньшей абсолютной точностью, чем, например, измерение сопротивления платинового термометра.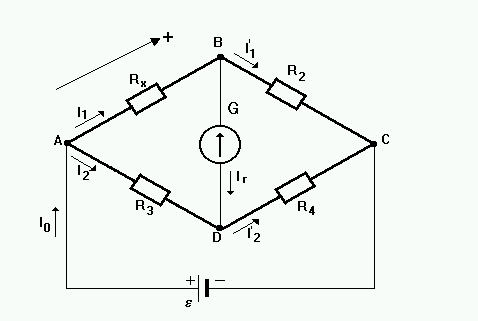 Так, для того чтобы измерять температуру с точностью 0,001°, сопротивление стоомного платинового термометра при 25° необходимо измерять с точностью 0,0004 ом, а сопротивление десятиомного платинового термометра — с точностью 0,00004 ом. Сопротивление же термистора при тех же условиях обычно бывает достаточно измерять с точностью 1— 5 ом. Например для термистора, параметры которого приведены в табл. 9, измерение сопротивления при 25° с точностью 2 ом соответствует точности измерения температуры 0,001°. При таких сравнительно невысоких требованиях к абсолютной точности для измерения сопротивления термисторов вполне могут быть использованы обычные мосты промышленного изготовления, например МТБ, так как непостоянство переходных сопротивлений контактов в декадах моста в этом случае не может заметно сказаться на измерениях. В применении сложных и дорогих термометрических мостов при работе с термисторами нет никакой необходимости.  [c.128]

Из кривых, приведенных на фиг. 1, можно видеть, что сопротивления термисторов обычно велики. Температурный коэффициент сопротивления термисторов имеет отрицательный знак, а абсолютная величина его часто на несколько порядков больше температурного коэффициента сопротивления платиновых термометров при тех же температурах. Большая чувствительность термисторов позволяет применять для измерения температур простые мосты и потенциометрические схемы, тогда как при использовании платиновых термометров сопротивления аналогичные измерения потребовали бы специального измерительного оборудования. Большая величина сопротивления термисторов упрощает проблему подводящих проводов. Это обстоятельство позволяет удалять термисторы от измерительных схем или использовать, где это необходимо, подводящие провода с плохой теплопроводностью и электропроводностью. В результате небольших габаритов и небольшой теплоемкости термисторы имеют меньшее время релаксации, чем другие термометры сопротивления, что удобно при измерении быстро меняющихся температур. Кроме того, термисторный термометр легче привести в тепловой контакт с объектом, температура которого измеряется.  [c.166]

Применение схем замещения или двойного уравновешивания возможно лишь в сравнительно узком диапазоне частот, так как трудно иметь в одном приборе набор безреактивных сопротивлений, необходимых для измерения е и б образцов разнообразных изоляционных материалов в большом интервале частот 10 . . . 10 гц. Поэтому рассмотренные выше схемы с переменным 7 используют при фиксированной частоте, обычно 1000 гц. Если необходимо снимать частотные зависимости е и б, то для этой цели часто применяют неуравновешенный ди еренциальный мост (рис. 3-8, а, б). Два плеча моста образованы двумя вторичными полуобмотками дифференциального трансформатора, третье плечо представляет собой образцовый переменный конденсатор, четвертое — испытуемый образец. В измерительной диагонали включено высокоомное образцовое сопротивление напряжение в диагонали моста измеряется вольтметром Уц с высокоомным входом й с малой входной емкостью Сд. К достоинствам этого метода относятся возможность изменения частоты в широких пределах, наличие только одного регулируемого элемента — образцового конденсатора — и возможность отсчета б по шкале стрелочного прибора, измеряющего напряжение Уд в диагонали моста. то напряжение пропорционально разности токов, протекающих через конденсаторы С и С . При условии равенства емкостей  [c.64]

На рис. 6.26, а показана схема цклю-чения в электрическую цепь двух ТС Лт1 и Рг2, с помощью которых может быть измерена разность температур. Для этой цели может быть использована и схема с прибором типа КБ (рис. 6.26,6), основанные на компенсационном методе измерения разности напряжений, возникающего при изменении сопротивления ТС в зависимости от температуры и напряжения, возникающего в диагонали неуравновешенного моста. Достоинством прибора являются наличие в нем бесконтактного линейного преобразователя, включающего обмотку возбуждения и измерительную обмотку, напряжение которой пропорционально перемещению подвижного магнитопровода. Для согласования фаз измеряемого напряжения и напряжения компенсации питание прибора производится от специального трансформатора Тр, первичная обмотка которого включается в цепь питания последовательно с обмоткой компенсирующего преобразователя. Такое включение исключает влияние изменения частоты тока и питающего напряжения, а также температуры окружающей среды на точность измерения. Для уменьшения влияния соединительных линий на точность измерения ТС подключается к одноточечному прибору по четырехпроводной, а в многоточечных по трехпроводной схеме. Благодаря большим сопротивлениям Р, включенным в токовые цепи, токи практически не зависят от изменения сопротивления тс.  [c.186]

Неуравновеше н н ый мост Уитстона применяется гл. обр. для измерения неэлектрич. величин. Сопротивления одного, двух или всех четырех плеч изменяются под действием какого-либо явления (напр, температуры), при этом первоначально существовавшее равновесие нарушается, напряжение между точками С VI В становится неравным нулю и по гальванометру (или другому прибору, включенному между этими точками) протекает ток тем больший, чем больше нарушение равновесия. При помощи неуравновешенного И. м. может производиться сопоставление двух величин. Для этой цели заставляют одну из величин действовать на одно или два плеча, а другую величину на другое или два других плеча. В основе расчета неуравновешенных Значения токов г, и г .  [c.555]

Следующие примеры показывают применение мостовых схем для измерения величины емкости. В главе 9 содержится более подробная информация по этой теме. Мост Де Сьюти (Рис. 9.9а) определяет значение емкости, сравнивая его со значением другой известной емкости, однако здесь на точность измерений оказывает большое влияние коэффициент мощности конденсатора, из-за этого во многих случаях применение этой мостовой схемы сильно ограничено. Мост Шеринга (Рис. 9.9в) используется для измерения емкости и сопротивления конденсатора, и следовательно, для определения диэлектрических потерь. Мост Вина (Рис. 9.96) имеет целый ряд применений. Он может быть использован для измерения величины емкости, если известна частота применяемого источника питания, и, наоборот, такая мостовая схема может применяться для определения частоты, если значение емкости известно. Мост Вина также может употребляться в качестве средства подавления какой-то определенной частоты.  [c.233]

Предполагается также, что сопротивления проводов и g не изменяются за время между двумя измерениями и что равенство илеч и та1 же ие нарушается. При многих измерениях эти требования выполнить нетрудно, поскольку сопротивление проводов j и б д обычно может быть выбрано малым но сравнению сХ и поэтому малыми изменениями и j во время измерения можно пренебречь. Для многих случаев не пмеет также большого значения дополнительная затрата времени для вторичного уравновешивания моста.  [c.171]

В камере датчика газоанализатора расположены два чувствительных термоэлемента из слюдяных пластин, обмотанных платиновой проволокой, один из которых находится рядом с постоянным магнитом. Термоэлементы включены в электрическую схему моста Уитстона и нагреваются пропускаемым через них переменным электрическим током 120 в через стандартный феррорезонансный стабилизатор напряжения.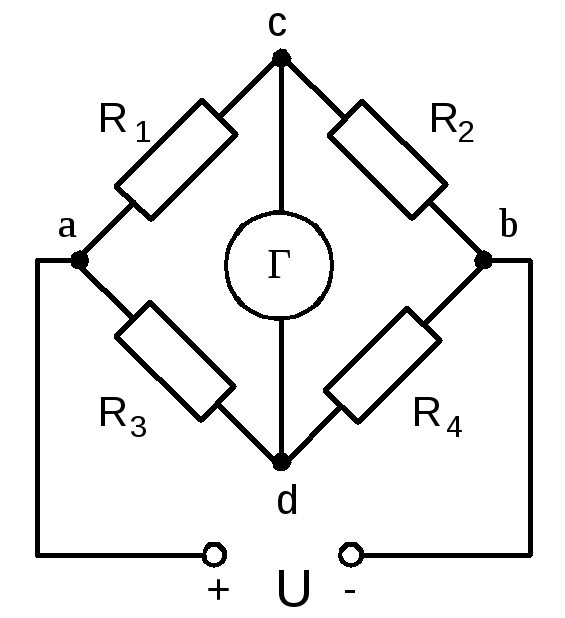 При пропускании через камеру датчика продуктов сгорания, содержащих в себе кислород, поток их будет отклоняться в сторону термоэлемента, лежащего рядом с магнитом, и тем больше, чем больше будет содержание кислорода в анализируемой пробе. Вследствие этого термоэлемент будет охлаждаться потоком газов иптенсивнее, чем другой термоэлемент, пе имеющий магнитного поля, в результате чего температура термоэлементов и их электрическое сопротивление станут различными, что и вызовет нарушение электрического равновесия моста и отклонение стрелки указывающего прибора газоанализатора. В качестве указывающего (вторичного) прибора газоанализатора МГК-348 применяется электронный потенциометр переменного тока ВПГ-359. Кислородные газоанализаторы МГК-348 выпускаются на различные пределы измерений и для анализа топочных газов применяется газоанализатор с пределом измерений от О до 10% О2.  [c.308]

Основные затруднения при работе с термометрами сопротивления связаны с необходимостью иметь электроизмерительные приборы высокого класса точности (потенциометр или мост, гальванометры с высокой чувствительностью к напряжению и т.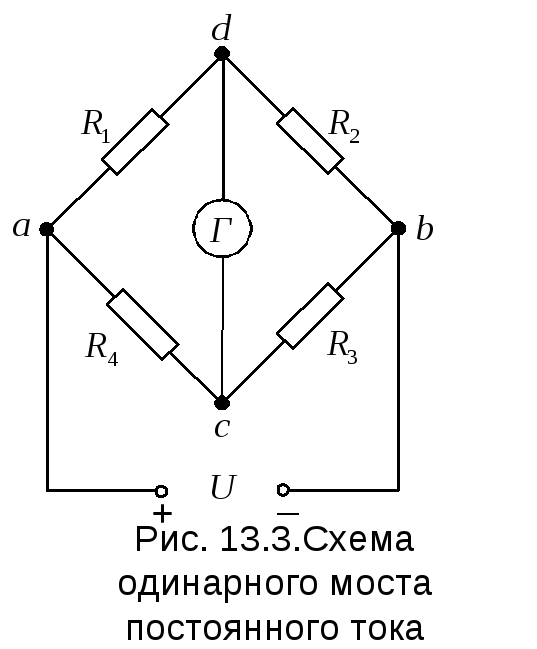 д.) и с необходимостью проведения довольно сложной градуировки термометра. Измерение температуры термометром сопротивления усложняется еще тем, что температура в этом случае (в отличие, например, от измерения ее ртутным термометром) не измеряется непосредственно, а должна быть вычислена по значению сопротивления. Однако, несмотря на это, термометры сопротивления, особенно в наиболее точных калориметрических работах, в последнее время используются все чаще. Этому немало способствует быстрое развитие промышленности электроизмерительных приборов, в связи с чем потенциометры высокого класса точнтости и высокочувствительные гальванометры получили весьма широкое распространение и стали не менее доступными приборами, чем высокочувствительные ртутные термометры и необходимые для их использования оптические трубы большого увеличения.  [c.133]

Поправка на неравенство постоянных сопротивлений моста и сопротивлений Л и В мосте Мюллера сопротивления плечей X и не равны точно нулю, когда все курбели стоят на нуле. Разность в сопротивлениях этих плечей (включая и подводы к коммутатору) вводит ошибку в вычисляемое по уравнению Каллендара значение температуры. Эта ошибка исключается, если применять описанную Мюллером [7] проверку нуля . Кроме того, имеется ошибка, связанная с неравенством постоянных сопротивлений моста. Если отношение сопротивлений не превышает 1,000003, то ошибка в измеренной температуре кипения серы не будет больше 0,0001° С при этом следует ежедневно измерять сопротивление термометра в точке льда и применять полученное значение для расчета произведенных в тот же день измерений температур.  [c.297]

Среднее отклонение от соответствующего каждой серии наблюдений среднего значения было равно 0,000032 ом в точке плавления льда И 0,000043д ом в точке затвердевания бензойной кислоты. Отношение ЭТИХ значений примерно равно отношению соответствующих значений полного сопротивления, равных 25 и 37 ом. Это наводит на мысль, что главной причиной разброса экспериментальных данных для обеих точек может оказаться мост. Если это верно, то обе постоянные точки воспроизводятся примерно с одинаковой точностью и возможно с большей действительной точностью, чем это следует из результатов измерений.  [c.376]

З ичения t/i и /i определяют по показаниям приборов на стороне переменного тока. Конденсатор С является блокировочным и его емкость должна быть много больше емкости испытываемого образца (примерно в 100 раз). Сопротивление R служит для запирания переменной составляющей тока в цепи постоянного тока значение R — порядка 1 ЬЛом. Вместо сопротивления R может быть использован дроссель. Более то1Чно з начен ие ре-верси вной емкости находят, пользуясь приборами д я измерения емкости при низких напряжениях ((Например, НИЕ 1) или описанным выше мостом МСК к конденсатору, помимо переменного, подводят и регулируемое постоянное напряжение от вспомогательного источника (фиг. 21-52 к зажимам моста образец присоединен через конденсатор С).  [c.56]

Лабораторная работа № 12 измерение удельного электрического сопротивления металлических проводников

Лабораторная работа № 12

ИЗМЕРЕНИЕ УДЕЛЬНОГО ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ

МЕТАЛЛИЧЕСКИХ ПРОВОДНИКОВ

В работе рассмотрены вопросы, связанные с протеканием электрического тока в металлических материалах, описан метод измерения электросопротивления проводников на основе использования моста Уитстона. Приведены расчетные формулы, схема электрической цепи и описан порядок выполнения работы и оформления отчета.

1. Электрический ток в металлах

Электрический ток представляет собой упорядоченное, направленное движение электрических зарядов. В металлах носителями заряда являются свободные электроны, или электроны проводимости, отрицательно заряженные частицы, несущие элементарный заряд Кл. Направленное движение электронов возникает в пределах всего металлического проводника при наличии в нем электрического поля.

Способность вещества проводить ток характеризуется удельной электрическойпроводимостью (электропроводностью) , которая обратно пропорциональна его удельному электрическому сопротивлению. Значения  и  зависят от природы проводника и условий, при которых он находится, в частности, от температуры. Все металлы, находящиеся в твердой фазе, обладают кристаллической решеткой, которая никогда не бывает совершенной. Рассеяние электронов проводимости при их движении в металле, которое и приводит к возникновению электрического сопротивленияR проводника, обусловлено тепловыми колебаниями решетки и ее дефектностью. Строгое объяснение механизма электропроводности металлов дает квантовая теория твердого тела.

В соответствии с законом Ома в интегральной форме сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике

(1)

причем, в данном случае совпадает с разностью потенциалов на его концах. Для проволочного образца

(2)

где — длина проводника,

— площадь его поперечного сечения.

Электрический ток характеризуется также с помощью вектора плотности тока, , который численно равен силе тока через расположенную в данной точке площадку, перпендикулярную к направлению движения носителей заряда, отнесенной к величине этой площадки,

. (3)

Направление совпадает с направлением вектора напряженности электрического поля в металлическом проводнике. Поскольку за направление тока условились принимать направление движения положительных зарядов, то вектор противоположен по направлению упорядоченному движению электронов в металле.

Согласно закону Ома в дифференциальной форме

, (4)

Рис.1. Зависимость плотности тока от напряженности электрического поля в металлическом проводнике

проводнике

Классическая теория электропроводности предполагает, что электроны проводимости в металле ведут себя подобно молекулам идеального газа, сталкивающимися преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. Оценка средней скорости хаотического теплового движения электронов при комнатной температуре дает значение м/с.

При включении электрического поля на хаотическое движение электронов накладывается их упорядоченное направленное движение со средней скоростью, которую можно оценить по формуле

(5)

где — концентрация свободных электронов.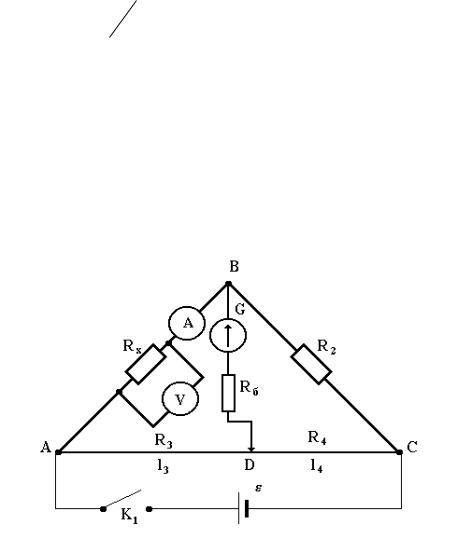 Для разных металлов значения 1/м³.

2. Расчет моста Уитстона на основе правил Кирхгофа

Рис.2. Схема моста Уитстона

В настоящей работе определение сопротивления осуществляется при помощи моста постоянного тока, называемого мостом Уитстона.

Мост Уитстона (рис. 2) включает в себя четыре сопротивления, образующих своего рода четырехугольник, в одну диагональ которого включается источник тока , а в другую — гальванометр G, прибор, фиксирующий протекание тока. Само название «;мостовая схема»; связано с тем, что указатель тока G, как мост, переброшен между двумя параллельными ветвями ABС и ADC. В ветвь AВС входят два сопротивления: неизвестное R_x и эталонное (задаваемое самим экспериментатором), а в ветвь ADC — сопротивления и R₄, причем для дальнейших расчетов нужны не их численные значения, а их соотношение.

Для облегчения расчетов разветвленных цепей разработан ряд вспомогательных приемов, один из которых основан на применении двух правил Кирхгофа.

Первое правило Кирхгофа относится к узлам цепи: алгебраическая сумма сходящихся в узле токов равна нулю

. (6)

Правило знаков: втекающие в узел токи считаются положительными, вытекающие из него — отрицательными.

Второе правило Кирхгофа относится к отдельным замкнутым контурам разветвленной цепи: в любом замкнутом контуре алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС, встречающихся в этом контуре,

. (7)

Для определения знаков в суммах выбирают положительное направление обхода контура. Правило знаков: ток, совпадающий по направлению с направлением обхода, считается положительным; ЭДС , потенциал которой возрастает в направлении обхода, также входит в уравнение (9) со знаком «;+»;. Уравнение (9) можно составить для любых независимых замкнутых контуров в данной разветвленной цепи.

Рассчитаем схему моста Уитстона на основе правил Кирхгофа. Выбираем направление токов так, как показано на рис. 2. Обходить контуры будем по часовой стрелке. Для определения искомого сопротивления R _{xдостаточно написать следующие уравнения Кирхгофа:}

= 0 — для узла В;

= 0 — для узла D;

= 0 — для контура ABDA;

= 0 — для контура BCDB,

где R — сопротивление гальванометра.

Для измерения сопротивления с помощью моста Уитстона сопротивления и подбираются таким образом, чтобы ток через гальванометр был равен нулю (I_r = 0), т.е. потенциалы точек B и Dдолжны быть одинаковыми. При этом . Такое состояние моста называется сбалансированным, или равновесным, и система уравнений (10) значительно упрощается.

Решая эту систему уравнений, получаем формулу для определения

. (8)

3. Применение реохорда в схеме моста Уитстона

В соответствии с рис. 2 и формулой (11) для определения необходимо знать и отношение . Это отношение может быть заменено отношением величин, пропорциональных сопротивлениям, что и осуществляется в данной работе.

В рабочей схеме (рис. 3) ветвью ADC является калиброванная проволока реохорда. Вдоль реохорда перемещается скользящий по проволоке контакт D, благодаря которому можно изменять соотношение сопротивлений и и добиваться отсутствия тока в гальванометре G. Обозначим длину плеча , а плеча . Каждое из проволочных сопротивлений и выразим формулой (2), где , и — величины, относящиеся к проволоке реохорда. Тогда выражение (11) примет вид

. (9)

Рис. 3. Рабочая схема установки

Таким образом, измерение сопротивления мостовым методом связано с определением длин плеч реохорда и сбалансированного моста при известном сопротивлении .

В данной работе используется реохорд барабанного типа, в котором однородная проволока намотана по цилиндрической спирали. В этом случае длина проволоки на участке AD равна , где — длина одного витка проволоки, — число витков на участке AD. Длина проволоки на участке DC равна , где — число витков на участке DC. Подставляя и в выражение (12), получим расчетную формулу для определения :

. (10)

Величину сопротивления лучше подбирать такой, чтобы при окончательной балансировке моста скользящий контакт D был ближе к середине реохорда, что соответствует минимальному значению погрешности.

B заключение отметим, что с помощью описанного метода нельзя определять с достаточной точностью слишком малые сопротивления. Это связано с тем, что начинает сказываться сопротивление контактов и подводящих проводов, а также нагревание плеч моста при прохождении по ним тока.

4. Описание рабочей схемы

На кафедре физики УГТУ-УПИ используется установка, смонтированная на стенде, фотография которого приведена на титульном файле данной компьютерной работы. Схема электрической цепи моста представлена на рис.3. -сопротивление проволоки, которое следует определить. В качестве плеча используется магазин сопротивления. Ветвью ADC является реохорд барабанного типа, в котором однородная калиброванная проволока намотана по цилиндрической спирали на барабан. Подвижным контактом является ролик, осью которого служит прямолинейный стержень. При вращении барабана ролик скользит (катится) по витками проволоки, перемещаясь вдоль стержня. Положение ролика определяется с помощью двух шкал — линейной и круговой. Круговая шкала, разделенная на 100 частей, нанесена на торце барабана; цена деления этой шкалы соответствует 0,01 части длины витка проволоки (или 0,01 оборота). Таким образом, положение ролика и, следовательно, точность отсчетов левого и правого плеча определяется с точностью до 0,01 оборота. Ток в нуль-гальванометре G, включенном в диагональ моста, в момент его компенсации должен быть равен нулю. Экспериментатор по стрелке гальванометра определяет момент компенсации.

В компьютерном варианте данной работы достаточно точно моделируются условия проведения опытов: на экране дисплея воспроизводятся реохорд с подвижным контактом и нуль-гальванометр, измеряющий ток в диагонали моста, что позволяет перемещением с помощью мышки скользящего контакта добиться компенсации моста, снять показания левого плеча реохорда с точностью до 0,01 оборота, рассчитать значение правого плеча и найти сопротивление исследуемого образца. Предусмотрено проведение пяти опытов с различными сопротивлениями , при этом величина получается с некоторым разбросом числовых значений, требующих вычисления его среднего значения и статистической обработки опытных данных. Экспериментатор сам выбирает значение эталонного сопротивления (20, 30, 40, 50, 60 Ом) и, наблюдая за стрелков гальванометра и перемещая с помощью мышки подвижный контакт (ролик) реохорда, добивается компенсации моста. При этом от экспериментатора требуется аккуратность в проведении опыта и правильность записи результатов измерений, обработки опытных данных, расчета искомой величины и погрешности результата измерений. Работать следует только с клавиатурой и мышкой.

Однако прежде чем выполнять экспериментальную часть работы, следует внимательно прочитать теоретическую часть данного руководства и ответить на контрольные вопросы.

5. Порядок выполнения работы

1. Навести курсор на «Измерения», нажать левую клавишу мышки. При этом на дисплее Вашего компьютера появится модель реохорда с подвижным контактом.

2. Ознакомиться с приборами и заполнить таблицу «Средства измерений и их характеристики» отчета (смотри ниже Приложение 2).

3.Записать в отчет данные.

4.Навести курсор на . Результаты измерений внести в таблицу 2 отчета..

6. Рассчитать по основной расчетной формуле. Сравнить полученный результат с табличным значением удельного заряда электрона.

7. Рассчитать границу относительной и абсолютной погрешности результата измерения по формуле, приведенной в отчете. В случае значительного расхождения опытных и табличных значений повторить измерения.

8. Оформить отчет (см. Приложение 2) и сдать его преподавателю на проверку.

1. Составить перечень приборов и указать их характеристики, заполнив соответствующую таблицу отчета.

4. .

2..

3. Установить на магазине значение сопротивления R₂ = 20 Ом.

4. и отсчитать значения и .

Измерения повторить еще четыре раза, увеличивая каждый раз значения на 10 Ом. Результаты всех измерений занести в табл.П.2.

5. По формуле (13) произвести расчеты и результаты занести в табл.П.2.

6. По выражению (14) рассчитать , занести в табл.П.2 и найти среднее значение IMG SRC=»/images/881/1760991/e6add3c.gif» NAME=»Object78″ ALIGN=ABSMIDDLE WIDTH=28 HEIGHT=22>>. Полученный результат сравнить с контрольными данными.

7.

8. По формуле

, (11)

определить значение удельного сопротивления проволоки и сравнить его с контрольными данными.

13. Произвести расчеты погрешностей в определении и .

14. Оформить отчет согласно «;Приложению»;.

Контрольные вопросы

1. Что представляет собой электрический ток? Какие частицы являются cвободными носителями заряда в металлах?

2. Какова причина электрического сопротивления при протекании тока в металлах?

3. Сформулировать закон Ома для однородного участка цепи в интегральной и дифференциальной формах.

4. Существует ли движение носителей заряда в металлическом проводнике при отсутствии в нем электрического поля?

5. Сформулировать правила Кирхгофа.

6.Какова принципиальная схема работы моста постоянного тока? В чем заключается принцип ее работы?

ФОРМА ОТЧЕТА

Титульный лист

У Г Т У — У П И

Кафедра физики

ОТЧЕТ

по лабораторной работе N 12

“Измерение удельного электрического сопротивления металлических проводников”

Студент____________________

Группа ________________________

Дата __________________________

Преподаватель…………………………

1. Расчетные формулы:

1.1. Формула для расчета величины

, где — известное сопротивление;

— числа витков (оборотов) реохорда, соответствующие левому и правому плечам реохорда (общее число оборотов реохорда равно 50) .

1.2. Формула для определения удельного электросопротивления

где d — диаметр исследуемого проволочного образца; l — длина проволоки.

2.Схема рабочей цепи

3. Средства измерений и их характеристики

Таблица П.1

Исследуемое сопротивление (проволочка)

l = 4,84 м, l = 0,01м,

d = 0,35 мм, d = 0,01 мм.

4. Результаты измерений и расчетные значения

Таблица П. 2

5. Расчеты искомых величин.

5.1 Расчет среднего значения сопротивления по пяти результатам:

= ……………….Ом.

5.2. Расчет удельного сопротивления материала исследуемого образца:

…………….Омм

6.Оценка границ погрешностей измерения .

Cреднее значение =…………………Ом.

Расчет среднеквадратичного отклонения:

= …………………Ом;

коэффицент Стьюдента, значение которого берется из таблицы (для числа измерений n=5 он равен 2,77).

Расчет абсолютной погрешности R_x:

……………..Ом;

………………Ом при Р=0,95

6.3. Расчет относительной и абсолютной погрешности удельного сопротивления:

……………………;

……………Омм при Р=0,95.

7.Окончательные результаты

R _x =………..+/-……..Ом при P = 0,95;

 = …………+/-….Омм при P = 0,95;

8. Выводы: сравнить полученные результаты измерений с табличным значением удельного сопротивления нихрома (при комнатной температуре оно равно 1,1 мкОмм), проанализировать погрешности измерений и т. д.

схема, принцип действия и т.д.

Мост Уитстона — это одна из наиболее часто используемых мостовых схем в контрольно-измерительных приборах.

Схема моста Уитстона часто используется в системах измерения температуры. В этих системах устройство, называемое термометр сопротивления или терморезистор, обычно помещается в одной из ветвей схемы мостика.

Принципиальная схема мостика Уитстона

Обратите внимание на основы электричества и на приборы электроники.

Величина тока в мосте Уитстона определяется величиной разности сопротивлений: чем больше разность, тем больше будет течь ток; а если разность сопротивлений меняется, количество протекающего тока будет тоже меняться. Именно это свойство делает схему мосте Уитстона очень полезной в контрольно-измерительных устройствах и системах управления. Точные измерения переменных величин процессов достигаются тем, что переменные параметры процессов изменяют сопротивление в схеме мостика. Даже очень малые изменения величины сопротивления могут быть обнаружены при измерении тока, протекающего через мостик.

Принцип работы моста Уитстона

Схема моста Уитстона имеет два плеча сопротивления, каждое из которых содержит два резистора. Третья ветвь схемы — это соединение между двумя параллельными ветвями. Эта третья ветвь называется мостиком. Ток течет от отрицательной клеммы батарейки к верхней точке мостовой схемы. Затем, ток делится между двумя параллельными ветвями, причем количество тока, протекающее по каждой из ветвей, зависит от величины сопротивления в ветви. Наконец, ток возвращается к положительной клемме батарейки.

При равных величинах сопротивлений равное количество тока течет в каждой из ветвей. По мостику ток не течет, на что указывает нулевое положение измерителя. При этом условии о мостике говорят, что он уравновешен.

Уравновешенная схема мостика Уитстона

При неравных величинах сопротивления в ветвях, ток течет в схеме от ветви с большим сопротивлением к ветви с меньшим сопротивлением. Это будет верно, пока два верхних резистора фиксированы и равны по величине, как это имеет место в схемах мостика Уитстона, используемых в контрольно-измерительных системах. Измеритель на рисунке показывает, что ток в мостике течет слева направо.

Неуравновешенная схема мостика Уитстона

Практикум введение в технику эксперимента лабораторная работа 1

КАФЕДРА ОБЩЕЙ
ФИЗИКИ

Практикум

ВВЕДЕНИЕ В ТЕХНИКУ ЭКСПЕРИМЕНТА

Лабораторная
работа 1

ИЗМЕРЕНИЕ
АКТИВНЫХ СОПРОТИВЛЕНИЙ

Задача посвящена знакомству с
распространенными приборами измерения
активного сопротивления: аналоговыми
– стрелочным омметром и мостом постоянного
тока, а также электронно-цифровым
омметром.

Общие сведения

В
проводнике обычно сила тока I
пропорциональна напряжению U,
приложенному к нему. Коэффициент
пропорциональности между ними R
называется электрическим сопротивлением
R=U/I (закон Ома). Таким образом,
экспериментально можно найти сопротивление
участка цепи, подключив эту цепь к
источнику ЭДС и измерив амперметром
протекающий через данный элемент ток
I, а вольтметром – напряжение на нем
U.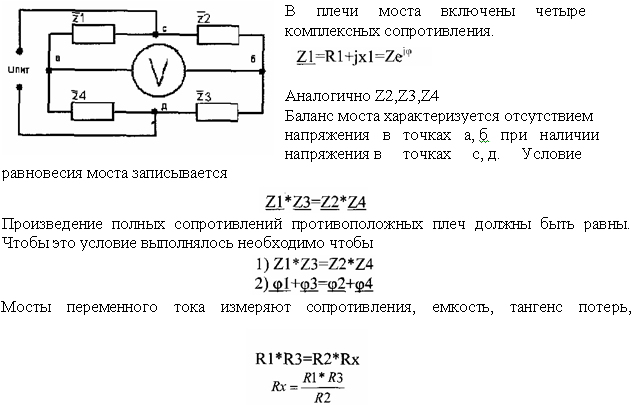 Относительная погрешность измерения
при этом будет складываться из
относительных погрешностей измерения
тока и напряжения _R
=
.
Этот метод универсален, но требует двух
одновременных измерений разными
приборами и математической операции
деления. О его применении в практике
можно отметить следующее:

1. Он
является единственно возможным для
измерения сопротивления элементов
непосредственно в работающих электрических
цепях с протекающими в них токами.

2. Этот
метод является основным в лабораторных
физических экспериментах, требующих
измерения сопротивления, поскольку
позволяет установить при измерении
любую величину напряжения или тока,
которые потребуются по условиям
эксперимента и не повредят измеряемый
элемент.

3. Данный
метод позволяет измерить сопротивления
нелинейных элементов, у которых величина
сопротивления зависит от поданного
напряжения или тока (например, зависимость
сопротивления полупроводникового p/n
перехода от приложенного напряжения).

Тем не
менее, часто приходится сталкиваться
с более простой ситуацией, когда нужно
измерить сопротивление отдельных,
никуда не подключенных линейных элементов
цепи, сопротивления которых постоянно.
Для таких случаев нашли применение
более удобные специальные приборы –
омметры, индикаторы которых позволяют
сразу прочитать сопротивление измеряемого
элемента при его подключении к прибору
без каких-либо дополнительных расчетов.
Данные приборы содержат внутреннюю
электрическую цепь с источником ЭДС и
измеритель с индикатором. Омметры могут
быть цифровыми и аналоговыми.

Аналоговые омметры.

Это
самые простые и дешевые приборы, до сих
пор имеющие широкое распространение.
Обычно они входят в состав многофункциональных
электроизмерительных приборов –
стрелочных мультиметров или «тестеров»,
способных, помимо сопротивления, измерять
также напряжение и силу тока. Данные
приборы содержат внутренний источник
постоянной ЭДС. В режиме измерения
сопротивления измеряемый элемент
подключается в измерительную цепь
прибора вместе со стрелочным гальванометром
таким образом, чтобы ток через гальванометр
зависел от сопротивления подключенного
элемента. Это позволяет проградуировать
шкалу гальванометра непосредственно
в единицах сопротивления.

В
зависимости от величины измеряемого
сопротивления применяются два варианта
включения измеряемого сопротивления
R_X и гальванометра-амперметра
А – последовательный (рис.1) и
параллельный (рис.2). Эти варианты легко
отличить по виду шкалы сопротивлений,
нанесенной на амперметр. В последовательном
варианте (рис.1, шкала k)
нуль шкалы, т.е. точка R_X = 0,
находится справа, поскольку при R_X
= 0 внешняя часть последовательной цепи
замкнута накоротко и ток через амперметр
будет максимальным. Крайняя левая точка
шкалы при этом соответствует R_X
=
,
т.к. в разомкнутой цепи ток через амперметр
отсутствует. Реальные схемы омметров
содержат переменный резистор, который
служит для калибровки положения стрелки
на правом конце шкалы перед
началом измерений, но его учет не
существенен для понимания принципа
работы.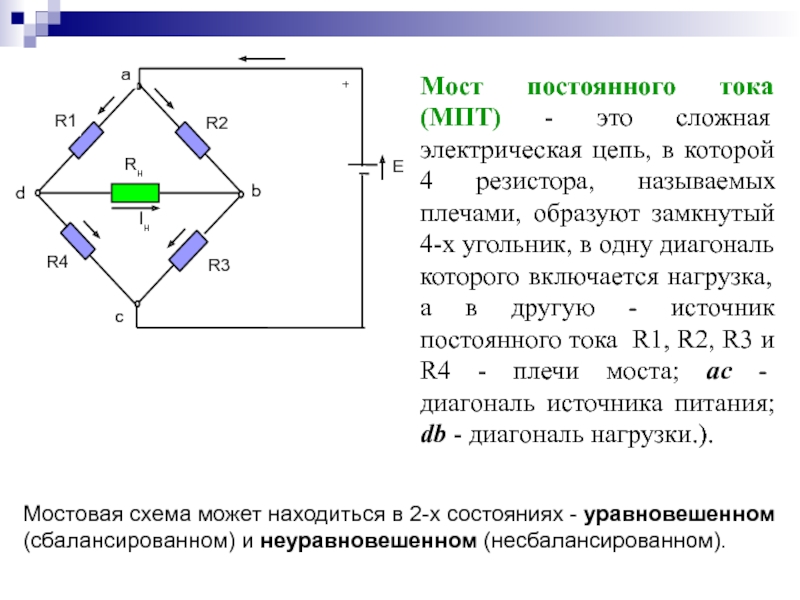

В
параллельном случае (рис.2, шкала )
ситуация обратная: R_X = 0
соответствует крайнему левому положению
стрелки (ток гальванометра равен нулю),
т.к. при этом гальванометр замкнут
накоротко и ток течет мимо него. При R_X
= ∞ ток максимален, так как весь ток
течет только через гальванометр, не
ответвляясь на участок R_X.

Как видно из рисунка, шкалы
сопротивлений неравномерны. Части шкал,
где можно проводить измерения с
гарантируемой точностью, отмечены
сплошной линией.

Рассмотрим
возможности обоих схем с точки зрения
точности измерений и диапазона измеряемых
сопротивлений.

Пусть
I_max – максимальный ток,
измеряемый амперметром, а R_A
– его собственное сопротивление.

В
последовательной схеме ток через
амперметр равен

, (1)

где R_A
– внутреннее сопротивление амперметра.
Если пренебречь погрешностью градуировки
шкалы и ошибками считывания, то погрешность
измерения сопротивления R_X
определяется только точностью самого
амперметра. Обычно используются
амперметры магнитоэлектрической
системы, у которых отклонение стрелки
прямо пропорционально силе тока. Тогда
максимальная погрешность считается
постоянной на всей шкале и составляет

I =
k_А·I_max, (2)

где k_А
·100% – класс точности амперметра. Найдем,
к какой погрешности измеряемого
сопротивления приводит данная ошибка
в измерении силы тока. Считая, что ошибки
малы, приращение тока I
заменим первым дифференциалом (1),
откуда получаем связь между приращениями
тока и сопротивления:

.

Рис.3 Относительная погрешность
в зависимости от величины измеряемого
сопротивления.
R_A
– сопротивление гальванометра

Учитывая, что для данной схемы I_max
= U/R_A, и используя (2), для
относительной максимальной погрешности
измерения сопротивления _R
получаем:

.
(3)

График
данной функции показан на рис.3. Он имеет
минимум при R_Х = R_А,
то есть при измерении сопротивлений,
близких к собственному сопротивлению
гальванометра, относительная погрешность
измерений минимальна и составляет _min
= 4k_A. При удалении от этой точки
погрешности быстро растут, поэтому
реально можно проводить измерения в
интервале, приблизительно составляющем
0. 1R_AR_X R_A,в
котором относительная погрешность не
превосходит 10k_A.

Таким
образом, в данном методе относительная
погрешность измерения R_X
превосходит собственный класс точности
применяемого гальванометра.

Минимальное
сопротивление, измеряемое данной схемой,
определяется сопротивлением гальванометра
согласно вышеуказанному неравенству
R_X  0.1·R_A.
Обычно оно составляет десятки Ом и
уменьшить его, не меняя гальванометр,
нельзя.

Предел
измерения со стороны больших сопротивлений
определяется условием R_X R_A.
Его можно легко расширить увеличением
R_А, для чего в многодиапазонных
омметрах последовательно с гальванометром
подключают добавочные сопротивления
R_доб. Поскольку
на всех диапазонах максимальный ток
через амперметр должен быть один и тот
же, соответствующий правой границе
шкалы, то вместе с R_доб
нужно менять чувствительность прибора,
подключая параллельно ему шунтирующее
сопротивление R.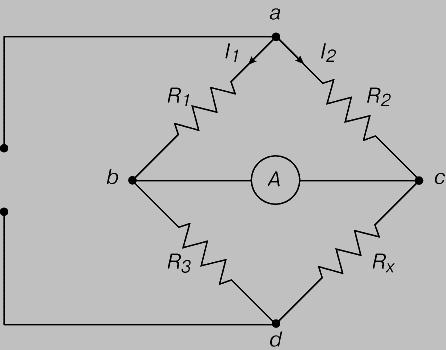
Величины R_доб
и R выбираются таким
образом, чтобы показания последовательных
диапазонов отличались в 10 раз, т.е. на
диапазоне n (n
= 0, 1, 2…) показания шкалы надо было
умножать на 10ⁿ, а
сама шкала k
оставалась бы одной и той же для всех
диапазонов. Диапазоны обычно обозначаются
как 1 (n
= 0), 10 (n
= 1), 100 (n
= 2) и т.д.

Верхний
предел измерений данной схемы теоретически
не ограничен, но при больших R_доб
требуется источник с большой ЭДС.
Подключение такого дополнительного
внешнего источника предусматривается
в некоторых омметрах (например, мультиметр
Ц4324) на диапазонах больших сопротивлений,
порядка 1 МОм и выше (диапазон 1000),
для которых ЭДС внутреннего источника
недостаточно.

Согласно
(1), ток через измеряемый элемент растет
с уменьшением его сопротивления. Поэтому
данный метод нужно с осторожностью
применять к измерению маломощных
элементов с малым сопротивлением,
поскольку это может привести к их
перегреву и повреждению. При измерении
малых сопротивлений из-за большого тока
происходит также быстрый разряд
автономного гальванического элемента
питания омметра.

Параллельная
схема работает следующим образом.
При отсутствии R_X (т.е. R_X = )
весь ток течет через гальванометр и
стрелка устанавливается на правом конце
шкалы. Подключение R_X уменьшает
сопротивление параллельного участка
цепи, состоящего из гальванометра и R_X,
при этом увеличивается ток через резистор
R и, следовательно, увеличивается
падение напряжения на нем U_R.
Напряжение на гальванометре, равное U
– U_R, при этом уменьшается, что
вызывает уменьшение тока через
гальванометр. Легко показать, что ток
через него следующим образом зависит
от R_X:

. (4)

Повторяя
для зависимости (4) те же расчеты, что и
для (1), получаем для относительной ошибки
измерений следующую формулу, которая
полностью идентична (3) если заменить
сопротивление амперметра R_А
на R’,

Поскольку
R’, согласно (4), равно сопротивлению
параллельно соединенных сопротивлений
R_А и R, то всегда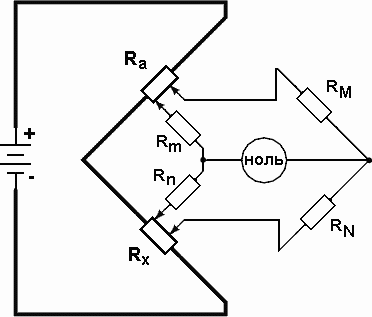_. R’ R_А. Поэтому нижний
предел измерений данной схемы, равный
в данном случае  0.1R’,
получается меньше, чем у последовательной
схемы, и обычно составляет единицы или
даже десятые доли Ома. Верхний предел
измерения, который ограничен приблизительным
условием R_x
10R’, обычно
составляет 100-300 Ом. Такая параллельная
схема используется в некоторых омметрах
(например, в мультиметре Ц4324 и др.)
только для одного диапазона малых
сопротивлений (диапазон «Омы» или
).

Отметим,
что рассмотренные погрешности измерений
являются максимально возможными. Если
считать, что результат может с равной
вероятностью лежать внутри этого
максимального интервала ошибки, то
вероятную ошибку можно оценить, как
_R =
R/.

Выводы:
Обе рассмотренные схемы имеют сравнительно
небольшую точность, что связано как с
самим методом, так и с субъективными
ошибками считывания показаний на
неравномерных шкалах. К их недостаткам
относится также рост силы тока через
измеряемый элемент и рост потребляемой
от источника ЭДС мощности при измерении
малых сопротивлений. Относительная
точность измерений максимальна в центре
шкалы и уменьшается к ее краям. При
измерениях требуется частая калибровка
прибора ввиду уменьшения с течением
времени величины ЭДС гальванического
источника и возрастания его внутреннего
сопротивления.

Преимуществом
метода является простота конструкции,
низкая цена и простота получения
результата. Примером такого прибора
может служить мультиметр Ц4324,
позволяющий измерять сопротивления в
диапазоне 1 Ом 
500 кОм (диапазоны 1
– 100), а с добавочным
внешним источником ЭДС – до 5 МОм
(диапазон 1000).

Измерение сопротивления
мостом постоянного тока

Рис.4 Измерительный
мост Уитстона

Измерительный мост Уитстона содержит
4 плеча. Источник ЭДС включается в одну
из диагоналей моста, а гальванометр G,
служащий нуль-индикатором тока, – в
другую (рис.4). Измеряемый резистор R_X
подключается в одно из плеч моста. В
процессе измерения резисторы R_1-3
подбираются так, чтобы ток через
гальванометр обратился в нуль (баланс
моста). В этом случае потенциалы точек
1 и 2 будут одинаковы, что возможно, только
если отношения сопротивлений резисторов
в верхней и нижней ветви равны:

R₂/R₁ = R_Х/R₃, (5)

откуда
R_Х = R₃(R₂/R₁).
Обычно в мостах, для удобства подсчета
результата, дискретно устанавливаются
фиксированные величины n = R₂/R₁,
выбираемые, как степень 10ⁿ,
в пределах 10^­-3 … 10⁺⁴, а
сопротивление плеча R₃ можно
подбирать с большой точностью, обычно
с помощью нескольких последовательно
соединенных декадных наборов резисторов,
последовательно устанавливающих сотни,
десятки, единицы и десятичные доли Ома.
Процесс измерения сводится к подбору
– сначала n, а затем
R₃ – до получения нуля на
гальванометре и, далее, к перемножению
полученных величин R_X
= n
R₃. Условие баланса (5) не зависит
от ЭДС источника U,
поэтому постоянство ЭДС здесь не
существенно и калибровка не нужна. В
принципе, можно использовать и источник
переменного тока, если при этом применить
гальванометр переменного тока.

Точность
измерения мостом определяется точностью
номиналов эталонных сопротивлений R_1-3
и точностью определения момента баланса
моста. Точность определения баланса, в
свою очередь, зависит от чувствительности
гальванометра и величины ЭДС источника
питания U, поскольку
все напряжения в схеме, в том числе и
сигнал рассогласования U₁₂,
прямо пропорциональны U.
Однако величину ЭДС нельзя брать слишком
большой, чтобы не вызвать избыточного
тепловыделения на плечах моста и
связанного с этим изменения их
сопротивления. Оптимальная величина
напряжения U зависит
от сопротивления измеряемого резистора,
и обычно в мостах его можно выбирать из
нескольких значений, начиная измерения
обязательно с наименьшего. Поскольку
гальванометр в данной схеме используется
только для регистрации нулевого значения,
чувствительность его должна быть
предельно высокой, при этом точность
градуировки остальной части его шкалы,
кроме окрестности нуля, роли не играет.
Чтобы не повредить чувствительный
гальванометр сильным током при большой
разбалансировке моста, последовательно
с гальванометром включают ограничительное
сопротивление (режим «грубо»),
которое затем, с приближением к точке
точного баланса, можно отключить (режим
«точно»).

Оценим
точность измерения мостовой схемой.
Для упрощения пренебрежем током через
гальванометр. Это оправдано, поскольку
при балансе моста этот ток близок к
нулю, т.е. значительно меньше всех
остальных токов в плечах моста. Тогда
разветвлением токов в точках 1 и 2 можно
пренебречь, и разность потенциалов U₁₂
между точками 1 и 2 определяется простым
соотношением

U₁₂
=
(6)

Найдем,
к какой погрешности измеряемого
сопротивления приводит погрешность U
гальванометра при измерении U₁₂.
Считая, что ошибки малы, приращение U₁₂
заменяем первым дифференциалом (6)

U₁₂


откуда
получаем связь между погрешностью
гальванометра U_{и соответствующей ей ошибкой измерения
сопротивления:}

Учитывая,
что R_X = n R₃,
для относительной погрешности получаем

Поскольку
погрешность гальванометра U
и ЭДС источника U
постоянны, поведение _R
определяется множителем K(n)
=
,
график которого показан на рис.5.
Относительная погрешность минимальна
при отношении плеч моста n = 1,
где она равна
,
и быстро возрастает при удалении от
этой точки.

Падение
точности с увеличением n,
то есть при измерении больших сопротивлений,
можно частично компенсировать увеличением
напряжения питания моста U.
Верхний предел измеряемых мостом
Уитстона сопротивлений обычно составляет
сотни МОм. Его можно увеличить (вплоть
до 10¹² Ом), но при этом требуется
высокое напряжения питания и применение
высокочувствительного гальванометра.

Н

Рис.5 Относительная погрешность
измерений мостом в зависимости от
отношения плеч моста n

ижний предел измеряемых сопротивлений
обычно составляет 0.1–1 Ом, что
определяется как уменьшением точности
регистрации баланса моста при n

Выводы:
Измерения с мостовой схемой относятся
к одним из наиболее точных методов
измерения сопротивления с относительной
погрешностью, достигающей 10^–5.
Это объясняется тем, что в мостовой
схеме происходит непосредственное
высокоточное сравнение измеряемого
сопротивления с эталонными резисторами
высокой точности и стабильно­сти. К
недостаткам метода можно отнести
трудоемкость и медленность измерений,
что, однако, преодолено в современных
автоматических мостах, где подбор
баланса происходит автоматически под
управлением микропроцессора.

Цифровые омметры

В
цифровых приборах результат измерений
представляется на цифровом индикаторе.
Обычно цифровые приборы являются
многофункциональными мультиметрами,
которые могут измерять напряжение, силу
тока и сопротивление. Основу таких
приборов составляет вольтметр на базе
аналого-цифрового преобразователя
(АЦП) – устройстве, преобразующем
аналоговую величину – напряжение – в
цифровой код. Принцип работы омметра
обычно основан на измерении данным
цифровым вольтметром падения напряжения
на измеряемом резисторе при протекании
через него заранее известного
фиксированного тока, создаваемого
специальной схемой ­– стабилизатором
тока. Поскольку величина этого напряжения
прямо пропорциональна сопротивлению,
показания цифрового индикатора вольтметра
можно легко перевести в единицы
сопротивления.

Цифровые
омметры, как и все цифровые приборы,
имеют большие преимущества перед
аналоговыми, благодаря которым они во
многих научных и технических измерениях
вытеснили последние. Это:

1) Высокая точность измерений. Типичные
значения погрешности составляют
0.001–0.5% от предела измерений.

2) Широкий
диапазон измеряемых сопротивлений
10^–3­­ –10⁹ Ом.

3) Высокая
скорость измерения.

4) Отсутствие характерных для стрелочных
приборов субъективных зрительных ошибок
считывания со шкал.

5) Сила тока через измеряемый элемент
не зависит от его сопротивления и обычно
очень мала, что исключает его перегрев
или повреждение.

6) Возможность вывода результатов в
цифровой виде на компьютер через шину
интерфейса.

В то же
время, цифровая индикация результатов
субъективно менее наглядна, чем у
стрелочных приборов. Особенно это
проявляется, если измеряемая величина
меняется во времени, т.к. это сопровождается
непрерывным мельканием цифр. Поэтому
в некоторых случаев и высокоточные
цифровые приборы содержат, наряду с
цифровым, и стрелочный индикатор для
наглядного визуального представления
результата.

Как и
любые приборы, имеющие аналоговые
электронные схемы, цифровые омметры не
обладают полной стабильностью параметров.
Поэтому, в отличие от мостов, электронные
омметры для поддержания точности
измерений должны периодически проходить
калибровку (поверку) на эталонных
резисторах. Кроме этого, для них важен
тепловой режим, разогрев прибора перед
началом измерений, что указывается в
инструкциях по эксплуатации.

Многие
цифровые мультиметры могут автоматически
выбирать оптимальный диапазон измерений,
более дешевые приборы имеют индикатор
перегрузки, напоминающий оператору о
необходимости смены диапазона. В режиме
вольтметра и амперметра данные приборы
имеют, как правило, защиту от перегрузки
на входе, то есть при ошибке в выборе
диапазона они не выходят из строя, как
многие стрелочные аналоговые приборы.

В
последнее время в практике физических
измерений широко используются
многофункциональные цифровые измерительные
приборы, выполненные в формате стандартных
плат расширения персональных ЭВМ и
способные, в числе прочих функций,
измерять и сопротивление. Большим
удобством таких устройств является их
полная интеграция с ЭВМ, что облегчает
создание автоматизированных измерительных
и управляющих систем, для чего используются
специально разработанные для них языки
программирования высокого уровня
(например, широко распространенная
система Labview).

Экспериментальная
часть

Рис.6  Экспериментальные
платы

При выполнении задачи
производится измерение разными методами
сопротивлений резисторов, установленных
на учебной плате. Плата содержит 9
резисторов с клеммами подключения: 3
столбца, по 3 резистора в каждом столбце.
Некоторые платы содержат по 4 резистора
в столбце, всего 12 (номера резисторов в
таких платах далее обозначены в скобках).

Номер
платы необходимо записать.

Выдержки
из заводских описаний используемых в
задаче приборов, содержащие все
необходимые сведения для работы с ними,
выдаются в начале занятия. Их нужно
обязательно прочитать перед началом
работы.

Упражнение 1. Измерения
стрелочным омметром

Измеряются
сопротивления резисторов в столбцах 1
и 2: R₁ — R₆
(R₁ – R₈).

Рекомендации
по работе: Сначала при отключенном
приборе нужно проверить установку
стрелки на начало шкалы (левый
предел) и, в случае необходимости,
отрегулировать ее механическим
винтом-корректором. В дальнейшем этот
винт трогать нельзя. Перед началом
измерений и, желательно, при каждом
переключении диапазона, необходимо в
соответствии с описанием прибора
проверять калибровку конца шкалы
(правый предел).

Ко всем
измеренным значениям нужно найти
погрешность, рассчитанную по классу
точности прибора и с учетом субъективной
точности считывания по шкале. При
измерениях нужно самостоятельно выбрать
и указать оптимальный диапазон, на
котором точность измерений максимальна.
Если точность на двух соседних диапазонах
имеет один порядок, нужно привести
данные измерений на обоих диапазонах.

Вероятный
источник ошибок: неправильная калибровка
прибора перед измерением, плохие контакты
при подключении.

Упражнение 2.
Измерения мостом Уитстона

Измеряются
сопротивления резисторов в столбце 2:
R₄ – R₆
(R₅ – R₈).

Рекомендации
по работе.

Используемые
в задаче универсальные мосты, помимо
простого моста Уитстона (режим 
2 з), имеют также режим двойного
моста Томсона (режим  4 з). Нужно
проверить, чтобы переключателем был
включен первый из них.

Измерение
малых сопротивлений (R 2 з, но
при этом для получения правильного
ответа нужно вычесть из полученного
результата сопротивление самих
соединительных проводов, которое надо
предварительно измерить.

Подключать
гальванометр при подборе баланса моста
нужно начиная всегда с кнопки «Грубо«,
и переходя на «Точно«, когда
стрелка будет близка к нулю.

Мост
MO-62 имеет возможность
внешнего питания от сети переменного
тока. Постоянный ток, необходимый для
работы моста, получается выпрямлением
переменного напряжения после понижающего
трансформатора, дающего два напряжения,
36 В или 1,5 В. При измерениях нужно
начинать с меньшего напряжения 1,5 В,
и если измеренное сопротивление больше
указанного на приборе значения (10 Ом),
можно переключиться на напряжение 36 В
для увеличения точности измерений.

Мост,
входящий в состав прибора УПИП-60М, не
имеет сетевого питания и на него надо
подавать постоянное напряжение от
внешнего блока питания.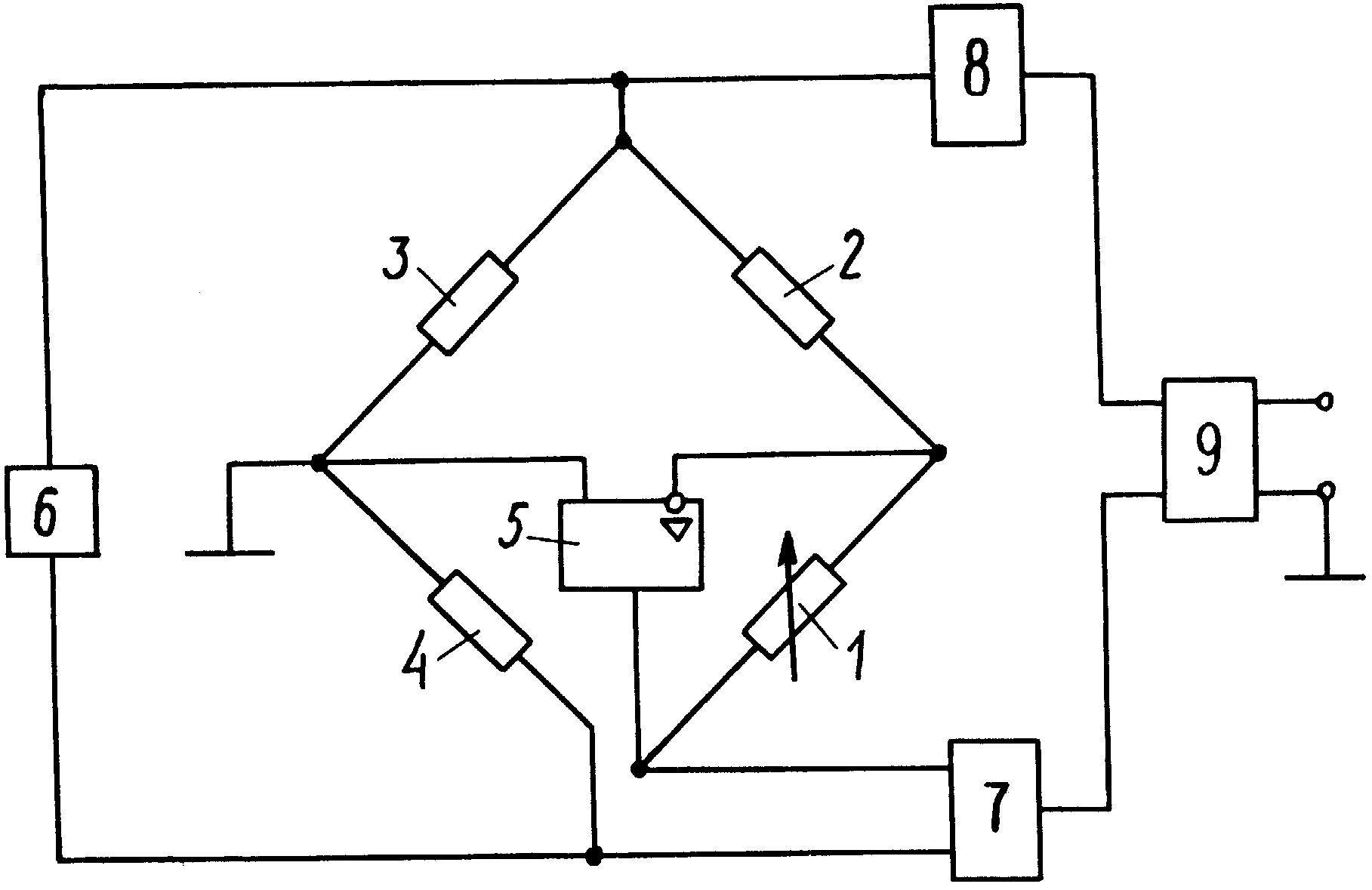 Величина
напряжения указана на мосте и не должна
превышать 10 В. Начинать измерения
лучше при меньшем напряжении 3 В.

Точность
измерений указана на крышке мостов, где
она приведена отдельно для случая
питания от переменного или постоянного
тока, в виде процента от измеренной
величины.

Перед
включением питания моста нужно проверить
установку на нуль стрелки гальванометра,
и в случае необходимости подправить ее
механическим винтом-корректором.

Если стрелка на нуль шкалы не выставляется,
но близка к нулю, следует запомнить по
шкале это положение и при нахождении
баланса моста устанавливать стрелку
на этот «реальный» нуль.

Вероятный
источник ошибок: неправильное включение
режима моста, неправильно выбранное
напряжение питания, плохие контакты,
игнорирование сопротивления проводов
(для малых сопротивлений)

Упражнение 3. Измерения
цифровым омметром

Измеряется
сопротивление всех резисторов платы
R₁ — R₉
(R₁ – R₁₂).
Расчет погрешности измерений проводится
по формулам, которые нужно найти в
описании прибора и записать в отчете.
При ручном выборе диапазона нужно
стремиться к получению максимального
числа цифр в результате.

Индикатор
цифровых приборов всегда показывает
окончательный результат, который не
надо больше пересчитывать.

В некоторых приборах перегрузка, то
есть выход измеряемой величины за
пределы диапазона, индицируется
появлением на индикаторе определенного
числа, например, 120, которое, естественно,
нельзя рассматривать как результат
измерения. Способ индикации перегрузки
обязательно указывается в описании
прибора.

Часть
измерений нужно провести в автоматическом
режиме.

Вероятный
источник ошибок: неправильный выбор
диапазона при ручном режиме, неправильное
считывание результата с индикатора.

В
заключение нужно сравнить результаты
измерений для резисторов, выполненные
всеми тремя приборами. В случае большого
несоответствия надо сделать повторные
измерения и выяснить причину ошибки.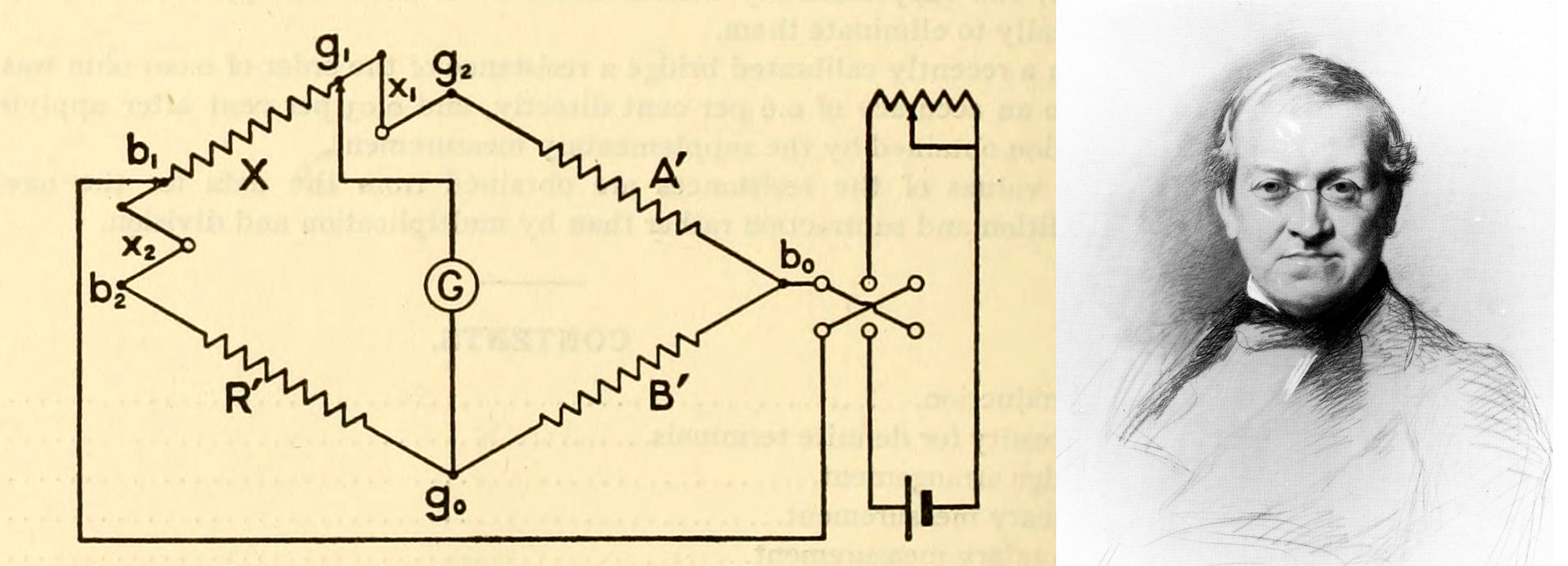

Оформление отчета

Отчет
должен содержать конспект с изложением
основных особенностей методов измерений.
Результаты измерений сопротивлений
резисторов нужно представить в виде
таблицы с нумерацией резисторов,
соответствующей указанной на платах
(по столбцам) следующего вида
(указаны произвольные цифры):

Плата № …

Вопросы к допуску и сдаче задачи

Преимущества и недостатки, область
применения, погрешности измерения для
следующих методов измерения сопротивления:

– Омметр с последовательным включением
гальванометра

– Омметр с параллельным включением
гальванометра

– Мостовая схема измерения сопротивлений

– Цифровые омметры

– Сравнительная характеристика всех
изученных способов измерения сопротивления:
область применения, погрешности
измерения.

– Нахождение погрешностей измерения
на неравномерных шкалах стрелочных
приборов.

Литература:

1. Соболев
Д.А.. Введение в технику физического
эксперимента. с.8-35

Дополнительная литература:

2. Мейзда Ф. Электронные
измерительные приборы и методы
измерений.
Москва. Мир. 1990
г.

Сопротивление куба. Решение задач на расчет электрического сопротивления с помощью моделей Как рассчитать сопротивление в кубе

Транскрипт

1
Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. Часть I.Расчёт сопротивлений Закон Ома. Сопротивление. Последовательное и параллельное соединение.симметричные схемы. Мостики. Преобразование звезда-треугольник. Цепи с перемычками. Бесконечные цепочки и сетки.. Определите эквивалентное сопротивление проволочных структур, представленных на рисунке. Сопротивление каждого звена структуры, т.е. проволочки между узлами вне зависимости от длины равно. а) б) в) г) д) е) ё) 2. Nточек соединены друг с другом одинаковыми проводниками с сопротивлением каждый. Определить эквивалентное сопротивление схемы между двумя соседними точками. 3. В мосте Уитстона сопротивления подбирают таким образом, что чувствительный гальванометр показывает нуль.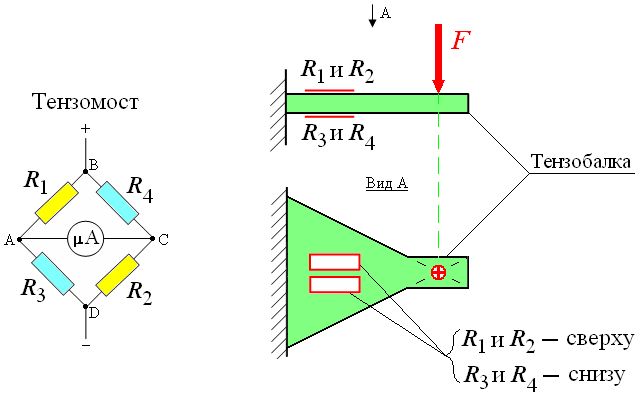 а) Считая сопротивления, 2 и r известными, определите величину сопротивления rx. б)если поменять местами батарею и гальванометр, то снова получится мостовая схема. Сохранится ли баланс в новой схеме? 4. Найдите эквивалентное сопротивление участка цепи. а) 2 б) 2 в) Определите эквивалентное сопротивление участка цепи,содержащего перемычки с пренебрежимо малым сопротивлением. а) б) Электрическая цепь составлена из семи последовательно соединенных резисторов = ком, 2 = 2 ком, 3 = 3 ком, 4 = 4 ком, 5 = 5 ком, 6 = 6 ком, 7 = 7 ком и четырех перемычек. На вход подается напряжение U = 53,2 В. Укажите резисторы, через которые протекают минимальный и максимальный токи, и определите значения этих токов.

2
Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 7. Цепь, состоящая из трех резисторов и четырех одинаковых перемычек (две нижние соединены параллельно), подключена к источнику с напряжением U = 0 В. Считая известными = 3 Ом,определите силу тока в перемычке В.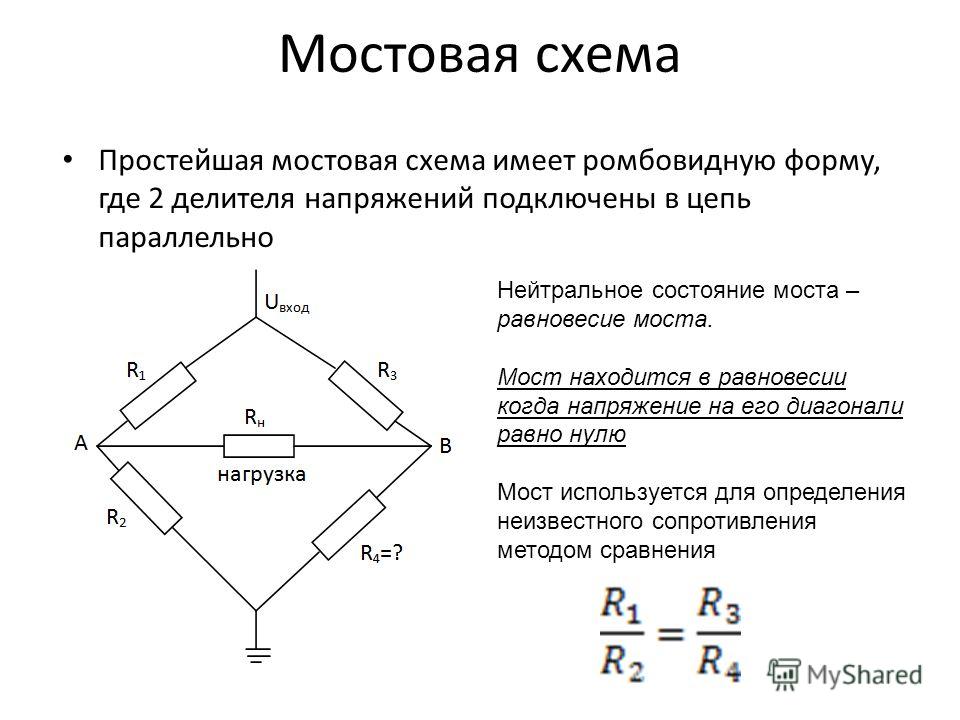 Сопротивление перемычек гораздо меньше сопротивления резисторов. U 2 В 8. Куб собран из одинаковых резисторов, имеющих сопротивления. Два резистора заменены на идеальные перемычки, как указано на рисунке. Найдите общее сопротивление получившейся системы между контактами и B. Какие резисторы из оставшихся можно убрать, и это не изменит общее сопротивление системы? Если известно, что через большинство резисторов в схеме течет ток I = 2, какой общий ток входит в систему в узле? Какой ток течет через идеальную перемычку `? ` K M C L В В` 9. Определите сопротивление проволочной сетки между указанными выводами. Рамка, выделенная толстой линией, имеет пренебрежимо малое сопротивление. Сопротивлениекаждого из остальных звеньев сетки равно. 0. Определите эквивалентное сопротивление полубесконечных цепочек резисторов, представленных на рисунке. 2 2 а) б) в) Определите эквивалентное сопротивление бесконечноразветвляющейся цепочки, состоящей из резисторов с сопротивлением. 2. Бесконечная сетка с квадратными ячейками изготовлена из проволоки. Сопротивление каждого ребра сетки равно. На рисунке C середина ребра B. Известно, что при подключении омметра между точками и B он показывает сопротивление /2. Какое сопротивление покажет омметр, подключенный между точками и C? 3. Определите сопротивление бесконечных плоских сеток с сопротивлением одной стороны ячейки, измеренное между узлами и В. а) б) в) В В В 4. Определите сопротивление бесконечной объемной кубической сетки с сопротивлением одной стороны ячейки, измеренное между соседними узлами и В.

3
Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 5. Пустотелый металлический шар имеет радиус r = 0 см и толщину стенок d = мм. Он изготовлен из меди, за исключением полоски на «экваторе» шириной a = 2 мм, которая выполнена из алюминия. Когда на «полюса» шара было подано напряжение U = 0, мв, через него пошел ток I = 5,2. Опыт повторили с другим шаром, у которого вместо алюминиевой полоски была железная. Какой ток пойдет через этот шар? Удельное сопротивление алюминия 0,03 Ом мм 2 /м, железа 0,0 Ом мм 2 /м. 6. Кольцо радиуса r = 0 см изготовлено из проволоки сечением S = 5 мм 2. Материал проволоки неоднороден и его удельное сопротивление зависит от угла φ так, как показано на графике. Сопротивление между всевозможными парами точек кольца измеряют омметром. Какое максимальное сопротивление может быть получено при таких измерениях?

4
Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. Измерения силы тока и напряжения. мперметр, вольтметр и омметр. Часть II.Измерительные приборы. Определите неизвестные параметры электрической цепи. (Приборы считать идеальными). U 0 2 а) U 0 = 24 B = 2 I -? U v-? б) 2 U I 4 = = 2 2 = 3 3 = 2 4 = 20 5 = 0 U-? I 6 =? 2. Определите показание амперметра в изображенной на рисунке цепи. Напряжение источника U =,5 В, сопротивление каждого резистора = ком. 3. На участке цепи, схема которого приведена на рисунке, включены резисторы с сопротивлениями = 6 Ом, 2 = 3 Ом, 3 = 5 Ом, 4 = 8 Ом. Показания первого амперметра I = 0,. Найдите показания второго амперметра. 4. По известным показаниям приборов определите неизвестные. Сопротивления амперметров считать гораздо меньшим, чем сопротивление резисторов. Приборы одинаковые. 6 а) б) в) В 5 B 5 2 3В г) д) B Как будут изменяться показания идеальных приборов при перемещении ползунка реостата/потенциометра в направлении, указанном стрелкой или при размыкании ключа? 3 а) б) в) г) Ɛ,r Ɛ,r 6. Схема собрана из некоторого количества различающихся между собой резисторов, реостата, идеальных батарейки, вольтметра и амперметра. Ползунок реостата сдвигают, немного увеличивая его сопротивление. В какую сторону изменятся показания вольтметра и амперметра?

5
Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 7. Определите показания вольтметра, подключенного между двумя узлами фрагмента электрической цепи, если показания амперметров и 3 равны I = 2, I3 = 9 соответственно, а сопротивление резисторов = 0 Ом. I2 I3 I 8.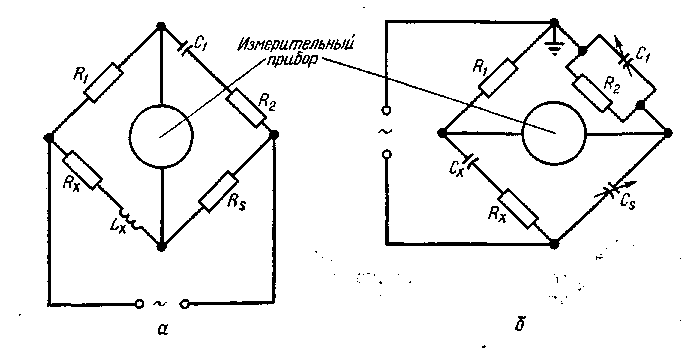 Электрическая цепь в форме тетраэдра содержит четыре одинаковых резистора, идеальный источник постоянного напряжения и идеальный амперметр, который показывает силу тока I = 2. Если заменить амперметр идеальным вольтметром, он покажет напряжение U = 2 В. Определите напряжение U0 источника и сопротивление одного резистора. 9. Электрическая цепь представляет собой сетку, состоящую из одинаковых звеньев, имеющих одинаковые сопротивления. Одно из звеньев заменено на идеальный вольтметр. На схему подано напряжение U0 = 9,7 В. Найдите показание вольтметра. U0 0. Электрическая цепь представляет собой сетку, состоящую из одинаковых звеньев, имеющих одинаковые сопротивления. Одно из звеньев заменено на идеальный вольтметр. На схему подано напряжение U0 = 73 В. Найдите показание вольтметра. U0. Экспериментатор из нескольких одинаковых резисторов и одинаковых вольтметров собрал схему, изображенную на рисунке. Чему будет равна сумма показаний всех вольтметров, если на контакты В подать напряжение U = 6 В. Сопротивление вольтметров гораздо больше сопротивления резисторов. 2. Участок схемы состоит из неизвестных сопротивлений. Как, имея источник, идеальные амперметр и вольтметр, соединительные провода с нулевым сопротивлением, измерить сопротивление, подключенного к точкам и B, не разрывая ни одного контакта в схеме? W C K В N D C L E D F G 3. Знаток физики собрал схему из трех одинаковых резисторов, подключил ее к источнику постоянного напряжения (который можно считать идеальным) и измерил вольтметром напряжение сначала между точками и D, а потом между точками и B. У него получилось U = 3 В и U2 = 0,9 В соответственно. Тогда знаток физики соединил точки и C проводом (сопротивлением которого можно пренебречь) и измерил напряжение между точками B и D. Что он получил? 4. Схема, приведенная на рисунке, содержит 50 разных амперметров и 50 одинаковых вольтметров. Показания первого вольтметра U = 9,6 В, первого амперметра I = 9,5 м, второго амперметра I2 = 9,2 м. Определите по этим данным сумму показаний всех вольтметров. 5. Если к батарее подключен только первый вольтметр, то он показывает 4 В. Если подключен только второй — то он показывает 4,5 В. Если к батарее подключены последовательно оба этих вольтметра, то вместе они показывают 5 В. Какими будут показания этих двух вольтметров, если их подключить к этой же батарее параллельно? 2 B

6
Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 6. Электрическая цепь состоит из двух одинаковых вольтметров, и двух амперметров. Их показания U = 0 В, U2 = 20 В, I = 50 м, I2 = 70 м соответственно. Определите сопротивление резистора, получив ответ в общем виде. 7. Электрическая цепь состоит из батарейки, шести резисторов, значения сопротивлений которых = Ом, 2 = 2 Ом, 3 = 3 Ом, 4 = 4 Ом, и трех одинаковых амперметров, внутреннее сопротивление r которых мало. Вычислите показания амперметров, если напряжение батарейки U = 99 В. 8. Найдите показания одинаковых вольтметров. Сопротивления вольтметров гораздо больше сопротивлений резисторов = 0 Ом. Напряжение на входе U = 4,5 В. 9. К батарее с ЭДС Ɛ = 9 В и неизвестным внутренним сопротивлением подключены последовательно амперметр и вольтметр. Сопротивления приборов неизвестны. Если параллельно вольтметру включено сопротивление (его величина тоже неизвестна), то показание амперметра вдвое увеличивается, а показание вольтметра вдвое уменьшается. Каким стало показание вольтметра после подключения сопротивления? 20. Определите показания одинаковых омметров в схемах, представленных на рисунке.сопротивление каждого из резисторов в схемах равно. а) б) в) 2. Электрическая цепь представляет собой сетку, состоящую из одинаковых звеньев, имеющих одинаковые сопротивления. Два из звеньев заменены на одинаковые омметры. Найдите показания омметров. 22. Определите сумму показаний омметров в схеме, представленной на рисунке. Ɛ,r Ɛ 2,r Из одинаковых омметров собрали цепь, изображённую на рисунке. Один из приборов показывает сопротивление = 2000 Ом. Определите сумму показаний двух оставшихся омметров. 24. Построить график зависимости показаний правого омметра в зависимости от сопротивления реостата, которое может изменяться в пределах от 0 до 2. Собственное сопротивление омметра. Омметры считать одинаковыми. 0-2

7
Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. Часть III.Источники напряжения. Нелинейные элементы Закон Джоуля-Ленца. Источники напряжения. Электродвижущая сила источника тока. Закон Ома для полной цепи. Соединения источников тока. Нелинейные элементы.. Схема, изображенная на рисунке, собрана из одинаковых лампочек и подключена к источнику напряжения. Расположите лампочки в порядке возрастания яркости. 2. К регулируемому источнику напряжения подключена схема из четырех резисторов, как показано на рисунке. мперметр показывает ток 2,5. На двух резисторах выделяется мощность 50 Вт, на других двух 200 Вт. Ключ K замыкают, а напряжение источника изменяют так, чтобы амперметр опять показывал 2,5. Какие мощности будут выделяться на резисторах после этого? 3. Цепочка из двух последовательно соединённых резисторов подключена к источнику постоянного напряжения U = 2 В. Сопротивление одного из них = 4 Ом. При каком значении сопротивления 2 второго резистора тепловая мощность, выделяющаяся на нём, будет максимальна? Найти эту максимальную мощность. 4. Имеются одинаковые резисторы, имеющие форму правильного цилиндра. Боковая поверхность каждого резистора хорошо теплоизолирована, и при его нагревании теплоотдача происходит только через торцы. Один из резисторов подсоединили к идеальной батарее. При этом он нагрелся до температуры t = 38 C. Потом к этой батарее последовательно подключили три таких резистора, плотно совместив их торцы и обеспечив хороший электрический контакт. До какой температуры нагреются резисторы? Комнатная температура t0 = 20 C. Мощность теплоотдачи пропорциональна разности температур резистора и окружающей среды. Сопротивление резисторов при нагревании не изменяется. 5. Цилиндрический проводник радиуса r состоит из двух однородных участков с удельными сопротивлениями ρ и ρ2 и соединяющего их неоднородного участка длины L. Какая тепловая мощность выделяется в неоднородном участке, если напряжение на ρ ρ 2 2r единицу длины проводника с удельным сопротивлением ρ равно u и L удельное сопротивление неоднородного участка линейно меняется от ρ до ρ2? 6. К идеальному источнику тока подключен резистор сопротивлением. Напряжение источника равно U. Оказалось, что температура резистора T зависит от времени t как T = T0 + αt (T0 и α известные константы). Резистор имеет массу m и изготовлен из вещества с удельной теплоемкостью c. Чему равна тепловая мощность, отдаваемая резистором в окружающую среду? 7. Сопротивление резистора линейно растет с температурой, а мощность теплоотдачи с его поверхности прямо пропорциональна разности температур резистора и окружающей среды. Если пропускать через резистор очень малый ток, его сопротивление равно 0. Когда величина тока, протекающего через резистор, приближается к I0, резистор быстро разогревается и плавится. Какое напряжение будет на резисторе, если через него пропустить ток I0/2? 8. К резистору, сопротивление которого зависит от температуры по закону (t) = 0 (+ αt), где t температура в С, αи 0 — неизвестные коэффициенты, подключают источник тока. Через некоторое время источник отключают от резистора. График зависимости температуры резистора от времени показан на рисунке. Мощность теплоотдачи резистора в окружающую среду пропорциональна разности температур резистора и окружающей среды: P = βt,гдеβ неизвестный коэффициент. Считая, что температура резистора одинакова во всех его точках, найдитеα.

8
Сейчас не удается отобразить рисунок. Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 9. Найдите ЭДС и внутреннее сопротивление эквивалентного источника (Ɛэ = φ φb) Ɛ Ɛ 2 а) б) в) 2r r B 2 r B Ɛ Ɛ r г) д) r е) 2Ɛ B B Ɛ Ɛ r Ɛ 2 Ɛ r B Ɛ r 2Ɛ Ɛ B r 0. Имеется цепь, содержащая N = 000 одинаковых источников тока с ЭДС Ɛ и внутренним сопротивлением r каждый. Между точками иb(на дуге СВ) находится m источников тока. Найдите разность потенциалов между точками и B. Какой будет эта разность потенциалов, если элементы будут обращены друг к другу одноименными полюсами?. Экспериментатор собрал электрическую цепь, состоящую из разных батареек с пренебрежимо малыми внутренними сопротивлениями и одинаковых плавких предохранителей, сопротивление которых тоже очень мало, и нарисовал ее схему (предохранители на схеме обозначены черными прямоугольниками). Экспериментатор помнит, что в тот день при проведении опыта все предохранители остались целыми. Напряжения некоторых батареек известны. Восстановите неизвестные значения напряжений. 2. На рисунке приведены идеализированные вольтамперные характеристики диода и резистора. Постройте вольтамперную характеристику участка цепи, содержащего диод и резистор, соединенные: а) параллельно; б) последовательно. I0 0 I U0 2U0 D U 3. На рисунке приведены идеализированные вольтамперные характеристики диода и резистора. Постройте вольтамперную характеристику участка цепи, содержащего диод и два резистора. -0,4-0,2 3,0 2,0,0 0 -,0 I, D 0,2 0,4 0,6 U, В а) б) 4. На рисунке приведены вольтамперные характеристики резистора и участка цепи, состоящего из резистора и нелинейного элемента, соединенных: а) последовательно; б) параллельно. -0,4-0,2 3,0 2,0,0 0 I, Σ 0,2 0,4 0,6 U, В Постройте вольтамперную характеристику нелинейного элемента. -,0 0,5 5. Определите, через какой нелинейный элемент пойдёт больший ток, 2 0,4 если его подключить к источнику с U0 = 0,5 В и r = Ом. 3 0,3 0,2 I, 0, 0 0, 0,2 0,3 0,4 0,5 0,6 U,В

9
Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 6. Найдите величину тока, идущего через диод, в цепи, представленной на рисунке.напряжение идеального источника U и сопротивление известны. 4 U 2 7. В одно из плеч моста включён нелинейныйэлементx,для которого зависимость силы тока Ix от приложенного напряжения Ux дается формулой:ix = Ux 3, где = 0,25 /В 3. Найти мощность Nx,выделяющуюсяна нелинейном элементе в условиях, когда ток через гальванометр Г отсутствует. Сопротивления остальных плеч моста = 2 Ом, 2 = 4 Ом и 3 = Ом. 8. Когда в настольную лампу вставили лампочку, на которой рассеивается мощность W = 60 Вт, то оказалось, что на соединительных проводах лампы рассеивается мощность W2 = 0 мвт. Какая мощность будет рассеиваться на соединительных проводах, если поставить лампочку мощностью W3 = 00 Вт? Напряжение в сети в обоих случаях считать равным U = 220 В. 9. Сопротивление элемента X меняется в зависимости от напряжения на нем. Если напряжение U Uкр сопротивление равно 2. Из трех элементов X собирают схему, показанную на рисунке. Найдите зависимость тока через схему от напряжения на ней. 20. Напряжение источника, подключенного к цепи, состоящей из одинаковых резисторов сопротивлением = Ом и нелинейного элемента, можно изменять. Зависимость показаний амперметра от напряжения источника задана на графике. Положительное направление тока задано на схеме электрической цепи. Восстановите по этим данным вольтамперную характеристику нелинейного элемента. 2. Электрическая цепь, схема которой представлена на рисунке, содержит три одинаковых резистора = 2 = 3 = и три одинаковых диода D, D2, D3. Вольтамперная характеристика диода представлена на графике. Определите силу тока через амперметр I в зависимости от напряжения UВ между точками и В. мперметр идеальный. Постройте график зависимости I от UB, указав значения тока и напряжения в характерных точках. 22. В вашем распоряжении имеется неограниченное количество резисторов произвольного сопротивления и диодов. Диоды пропускают ток только в одном направлении, при этом падение напряжения на них равно В (см. рис. а). Какую схему нужно собрать, чтобы она имела такую зависимость тока от напряжения, как показано на рис. б? Постарайтесь использовать как можно меньше элементов. Контрольная работа. Постоянный ток. на 0 Ом (на одном из параллельно соединённых резисторов) 2. 3/30

10
3. 0/ м 5. 4 м Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год.

Электричество. Постоянный ток. Кирхгоф Задача 1. Электрическая цепь (см. рисунок) состоит из двух одинаковых вольтметров и двух амперметров. Их показания: U 1 = 10.0 В, U 2 = 10.5 В, I 1 = 50 ма, I 2 =

И. В. Яковлев Материалы по физике MathUs.ru Содержание Электрические цепи 1 Всероссийская олимпиада школьников по физике………………. 1 2 Московская физическая олимпиада………………………

Мастер-класс «Электродинамика. Постоянный ток. Работа и мощность тока». 1. По проводнику течёт постоянный электрический ток. Величина заряда, проходящего через проводник, возрастает с течением времени

1 Постоянный электрический ток Справочные сведения. ОПРЕДЕЛЕНИЕ СИЛЫ ТОКА Пусть через некоторую поверхность, площадь которой S, перпендикулярно ей, за время проходит заряд q. Тогда силой тока называется

Вариант 1 Начальный уровень 1. На рисунке изображен график зависимости силы тока в проводнике от напряжения на его концах. Чему равно сопротивление проводника? А. 8 Ом. Б. 0,125 Ом. В. 16 Ом. Г. 2 Ом.

С1.1. На фотографии изображена электрическая цепь, состоящая из резистора, реостата, ключа, цифровых вольтметра, подключенного к батарее, и амперметра. Используя законы постоянного тока, объясните, как

На рисунке показана цепь постоянного тока. Внутренним сопротивлением источника тока можно пренебречь. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (

Задание 12. 1. На рисунке изображена схема электрической цепи, состоящей из трёх резисторов и двух ключей К1 и К2. К точкам А и В приложено постоянное напряжение. Максимальное количество теплоты, выделяемое

И. В. Яковлев Материалы по физике MathUs.ru Нелинейные элементы Вольт-амперная характеристика нелинейного элемента электрической цепи является нелинейной функцией. Задача 1. (Всеросс., 1993, финал, 9)

И. В. Яковлев Материалы по физике MathUs.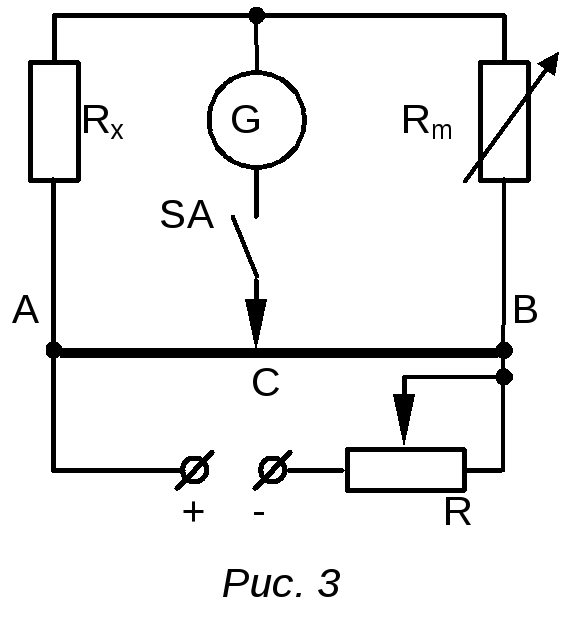 ru Вычисление сопротивлений Задача 1. («Курчатов»016, 8) В лаборатории есть два куска медной проволоки одинакового поперечного сечения. Сопротивление этих кусков,

189 1) В каждом узле цепи сумма втекающих токов равна сумме вытекающих токов, иными словами, алгебраическая сумма всех токов в каждом узле равна нулю. 2) В любом замкнутом контуре, произвольно выбранном

Вариант 1 1. Сила тока в проводнике равномерно нарастает от 0 до 3 А в течение 10 с. Определить заряд, прошедший в проводнике за это время. Ответ: 15Кл. 2. Три батареи аккумуляторов с ЭДС 12 В, 5 В и 10

1. Сила тока в проводнике равномерно нарастает от 0 до 3 А в течение 10 с. Определить заряд, прошедший в проводнике за это время. Ответ: 15Кл. 2. Три батареи аккумуляторов с ЭДС 12 В, 5 В и 10 В и одинаковыми

Уральский федеральный университет имени первого Президента России Б.Н. Ельцина Специализированный учебно-научный центр Летняя школа 2019 Физика Разбор задач и критерии проверки Задача 1.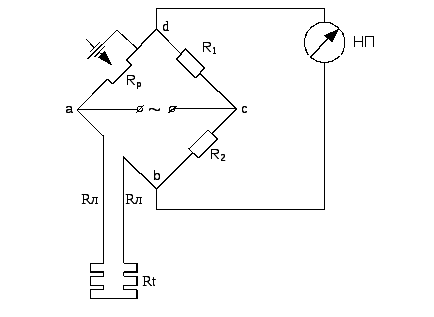 Найти сопротивление

Занятие 19 Постоянный ток. Соединения проводников Задача 1 Перенос вещества происходит в случае прохождения электрического тока через: 1) Металлы и полупроводники 2) Полупроводники и электролиты 3) Газы

В схеме на рисунке сопротивление резистора и полное сопротивление реостата равны R, ЭДС батарейки равна E, её внутреннее сопротивление ничтожно (r = 0). Как ведут себя (увеличиваются, уменьшаются, остаются

Отложенные задания (69) Общее сопротивление участка цепи, изображенного на рисунке, равно 9 Ом. Сопротивления резисторов R 1 и R 2 равны. Чему равно сопротивление каждого резистора? 1) 81 Ом 2) 18 Ом 3)

И. В. Яковлев Материалы по физике MthUs.ru Правила Кирхгофа В статье «ЭДС. Закон Ома для полной цепи» мы вывели закон Ома для неоднородного участка цепи (то есть участка, содержащего источник тока): ϕ

С1.1. На рисунке приведена электрическая цепь, состоящая из гальванического элемента, реостата, трансформатора, амперметра и вольтметра. В начальный момент времени ползунок реостата установлен посередине

Физика 8.1-8.2. Примерный банк заданий Часть 1. Постоянный ток 1. На рисунке приведён участок электрической цепи, по которому течёт ток. В каком из проводников сила тока наименьшая? 1) 1 2) 2 3) 3 4) 4

«ЗАКОНЫ ПОСТОЯННОГО ТОКА». Электрическим током называют упорядоченное направленное движение заряженных частиц. Для существования тока необходимы два условия: Наличие свободных зарядов; Наличие внешнего

Средний уровень Решите устно Задания по теме «Расчет электрических цепей» 8 класс 5.. Резисторы с сопротивлением 5 Ом и 0 Ом соединены один раз последовательно, другой — параллельно. В каком случае их

ЛАБОРАТОРНАЯ РАБОТА 5 ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРОВОДНИКОВ Цель работы: изучение методов измерения сопротивлений, изучение законов электрического тока в цепях с последовательным и параллельным соединением

И. В. Яковлев Материалы по физике MathUs.ru Самоиндукция Пусть через катушку протекает электрический ток I, изменяющийся со временем. Переменное магнитное поле тока I порождает вихревое электрическое поле,

Задания 15 по физике 1. Электрическая цепь состоит из источника постоянного напряжения с ЭДС = 40 В и внутренним сопротивлением r=2 Ом, резистора с переменным сопротивлением и амперметра. На каком из приведенных

Иркутский государственный технический университет Кафедра общеобразовательных дисциплин ФИЗИКА Лабораторная работа 3.3. «Определение неизвестных сопротивлений при помощи мостовой схемы» доц. Щепин В.И.

Измерение мощности и работы тока в электрической лампе. Цель работы: Научиться определять мощность и работу тока в лампе. Оборудование: Источник тока, ключ, амперметр, вольтметр, лампа, секундомер. Ход

ФИЗИК, 11 класс, УМК 2 Вариант 1, Октябрь 2012 Краевая диагностическая работа по ФИЗИКЕ Вариант 1 Часть 1 При выполнении заданий 1 7 в бланке ответов 1 под номером выполняемого задания поставьте знак «х»

Постоянный электрический ток. Сила тока Постоянный электрический ток.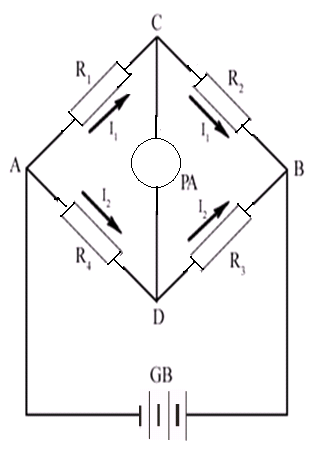 Напряжение Закон Ома для участка цепи Электрическое сопротивление. Удельное сопротивление вещества Электродвижущая сила. Внутреннее

И. В. Яковлев Материалы по физике MathUs.ru Мощность тока Задача 1. («Курчатов», 2017, 8) С помощью электромотора груз массой 50 кг поднимают вверх. При этом груз движется с постоянной скоростью 3,5 см/с.

Юльметов А. Р. Постоянный электрический ток. Электрические измерения Методические указания к выполнению лабораторных работ Оглавление P3.2.4.1. Амперметр как омическое сопротивление в цепи………….

Pdf — файл pitf.ftf.nstu.ru => Преподаватели => Суханов И.И. Лабораторная работа 11 Изучение работы источника постоянного тока Цель работы для цепи «источник тока с нагрузкой» экспериментально получить

Тест по физике 1 вариант A1. Если при неизменном напряжении на концах проводника увеличить сопротивление проводника в 2 раза, то сила тока в проводнике 1) не изменится 3) уменьшится в 2 раза 2) увеличится

И. В. Яковлев Материалы по физике MathUs.ru Содержание Электрические цепи 1 Всероссийская олимпиада школьников по физике………………. 1 2 Московская олимпиада школьников по физике………………..

Московский физико-технический институт Эквивалентные преобразования электрических цепей. Методическое пособие по подготовке к олимпиадам. Составитель: Паркевич Егор Вадимович Москва 2014 Введение. В электротехнике

И. В. Яковлев Материалы по физике MathUs.ru Мощность тока Задача 1. Резисторы с сопротивлениями 2R и 3R соединены последовательно и подключены к источнику постоянного напряжения U. Найдите мощность, выделяющуюся

ПОСТОЯННЫЙ ТОК 2008 Цепь состоит из источника тока с ЭДС 4,5В и внутренним сопротивлением r=,5oм и проводников сопротивлением =4,5 Oм и 2= Oм Работа, совершенная током в проводнике за 20 мин, равна r ε

И. В. Яковлев Материалы по физике MathUs.ru Вычисление сопротивлений Задача 1. (МОШ, 2014, 9 10) Имеются 10 резисторов сопротивлением 1 ком. Нарисуйте схему электрической цепи, сопротивление которой как

Государственное высшее учебное заведение «ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра физики ОТЧЁТ по лабораторной работе 49 ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПОЛЕЗНОЙ МОЩНОСТИ И КОЭФФИЦИЕНТА ПОЛЕЗНОГО

Незаряженные стеклянные кубики 1 и 2 сблизили вплотную и поместили в электрическое поле положительно заряженного шара, как показано в верхней части рисунка. Затем кубики раздвинули и уже потом убрали заряженный

I вариант Тест по теме «Постоянный электрический ток». 1. Для возникновения тока в проводнике необходимо, чтобы… А — на его свободные заряды в определенном направлении действовала сила. Б — на его свободные

Задача 1 Демонстрационный вариант отборочного этапа Электроника 9 класс Как изменится сила взаимодействия между двумя точечными зарядами, если увеличить расстояние между ними в 2 раза? 1 уменьшится в 2

Нурушева Марина Борисовна старший преподаватель кафедры физики 023 НИЯУ МИФИ Электрический ток Электрический ток это направленное (упорядоченное) движение заряженных частиц. Условия существования электрического

Министерство образования Республики Беларусь Учреждение образования «МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОДОВОЛЬСТВИЯ» Кафедра физики ИЗУЧЕНИЕ ЗАКОНОВ ПОСТОЯННОГО ТОКА. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ МОСТИКОМ

Федеральное агентство по образованию РФ Ухтинский государственный технический университет 4 Измерение сопротивления на постоянном токе Методические указания к лабораторной работе для студентов всех специальностей

Министерство образования Российской Федерации ГОУ ВПО УГТУ-УПИ Кафедра физики ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ ПО ФИЗИКЕ ТЕМА: ЗАКОНЫ ПОСТОЯННОГО ТОКА МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

ЛАБОРАТОРНАЯ РАБОТА 3 Изучение электропроводности металлов Теоретическое введение Электропроводность металлов Если на концах проводника поддерживается постоянная разность потенциалов, то внутри проводника

1 вариант 1. Определите силу тока и падение напряжения на проводнике R1 электрической цепи, изображенной на рисунке 121, если R1 = 2 Ом, R2 = 4 Ом, R3 = 6 Ом, ЭДС аккумулятора Ε = 4 В, его внутреннее сопротивление

Работа электрического тока, мощность, закон Джоуля Ленца 1. Чему равно время прохождения тока силой 5 А по проводнику, если при напряжении на его концах 120 В в проводнике выделяется количество теплоты,

Объяснение явлений 1. На рис. 1 приведена схема установки, с помощью которой исследовалась зависимость напряжения на реостате от величины протекающего тока при движении ползунка реостата справа налево.

Сила тока и заряд.. Сила тока в лампочке от карманного фонаря I = 0,3 А. Сколько электронов N проходит через поперечное сечение нити накала за время t = 0, c?.3. Какой заряд q пройдет по проводнику сопротивлением

Лабораторная работа Измерение сопротивления проводников мостиком Уитстона Оборудование: реохорд, набор неизвестных сопротивлений, гальванометр, источник постоянного тока, два ключа, магазин сопротивлений.

Лабораторная работа 3.3 ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ МОЩНОСТИ И КПД ИСТОЧНИКА ПОСТОЯННОГО ТОКА ОТ ВНЕШНЕЙ НАГРУЗКИ 3.3.. Цель работы Целью работы является знакомство с компьютерным моделированием цепей постоянного

Физика. 8 класс. Демонстрационный вариант 2 (90 минут) 1 Диагностическая тематическая работа 2 по подготовке к ОГЭ по ФИЗИКЕ по теме «Постоянный ток» Инструкция по выполнению работы На выполнение диагностической

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ

Электродинамика 1. При подключении резистора с неизвестным сопротивлением к источнику тока с ЭДС 10 В и внутренним сопротивлением 1 Ом напряжение на выходе источника тока равно 8 В. Чему равна сила тока

Решение задач по теме «Электродинамика» Захарова В.Т., учитель физики МАОУ СОШ 37 Задание 14. Пять одинаковых резисторов с сопротивлением 1 Ом соединены в электрическую цепь, через которую течёт ток I

Цель работы: познакомиться с одним из методов измерения электрического сопротивления резисторов. Проверить правила сложения сопротивлений при различных способах соединения резисторов. Задача: собрать схему

ПОДГОТОВКА к ОГЭ ЧАСТЬ 1 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ 1.Два точечных заряда будут притягиваются друг к другу, если заряды 1.одинаковы по знаку и любые по модулю 2.одинаковы по знаку и обязательно одинаковы по

Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа 4» г. Сергиев Посад Лабораторная работа «Измерение ЭДС и внутреннего сопротивления источника тока» 10 «А» класс

Тест по физике Законы электрического тока 8 класс 1 вариант 1. В каких единицах измеряют силу тока? 1) В кулонах (Кл) 2) В амперах (А) 3) В омах (Ом) 4) В вольтах (В) 2. Известно, что через поперечное

Тема 12. Постоянный электрический ток 1. Электрический ток и сила тока Имеющиеся в веществе свободные носители заряда (электроны и/или ионы) в обычном состоянии движутся хаотично. Если создать внешнее

При выполнении заданий 1 7 в поле ответа запишите одну цифру, которая соответствует номеру правильного ответа. 1 На рисунке изображены два одинаковых электрометра, шары которых имеют заряды противоположных

65 7. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 7. Электрический ток, сила и плотность тока Электрическим током называется упорядоченное (направленное) движение электрических зарядов. Сила тока скалярная физическая

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «Общая физика и физика нефтегазового производства»

Отложенные задания (25) В области пространства, где находится частица с массой 1 мг и зарядом 2 10 11 Кл, создано однородное горизонтальное электрическое поле. Какова напряжённость этого поля, если из

Лабораторная работа 1 Измерение выталкивающей силы научиться измерять выталкивающую силу, действующую на тела разной формы, погруженные в воду. Приборы и материалы: тела цилиндрической, кубической и неправильной

Рассмотрим классическую задачу. Дан куб, рёбра которого представляют собой проводники с каким-то одинаковым сопротивлением. Этот куб включается в электрическую цепь между всевозможными его точками. Вопрос: чему равно сопротивление куба
в каждом из этих случаев? В данной статье репетитор по физике и математике рассказывает о том, как решается эта классическая задача. Присутствует также видеоурок, в котором вы найдёте не только подробное объяснение решения задачи, но и реальную физическую демонстрацию, подтверждающую все вычисления.

Итак, куб может быть включен в цепь тремя различными способами.

Сопротивление куба между противоположными вершинами

В этом случае ток, дойдя до точки A
, распределяется между тремя рёбрами куба. При этом, поскольку все три ребра эквивалентны с точки зрения симметрии, ни одному из рёбер нельзя придать большую или меньшую «значимость». Поэтому ток между этими рёбрами должен распределиться обязательно поровну. То есть сила тока в каждом ребре равна :

В результате получается, что падение напряжения на каждом из этих трёх рёбер одинаково и равно , где — сопротивление каждого ребра. Но падение напряжение между двумя точками равно разности потенциалов между этими точками. То есть потенциалы точек C
, D
и E
одинаковы и равены . Из соображений симметрии потенциалы точек F
, G
и K
также одинаковы.

Точки с одинаковым потенциалом можно соединять проводниками. Это ничего не изменит, потому что по этим проводникам всё равно не потечёт никакой ток:

В результате получим, что рёбра AC
, AD
и AE
T
. Точно также рёбра FB
, GB
и KB
соединятся в одной точке. Назовём её точкой M
. Что касается оставшихся 6 рёбер, то все их «начала» окажутся соединены в точке T
, а все концы — в точке M
. В результате мы получим следующую эквивалентную схему:

Сопротивление куба между противолежащими углами одной грани

В данном случае эквивалентными являются рёбра AD
и AC
. По ним потечёт одинаковый ток . Кроме того, эквивалентными также являются KE
и KF
. По ним потечёт одинаковый ток . Ещё раз повторим, что ток между эквивалентными рёбрами должен распределиться поровну, в противном случае нарушится симметрия:

Таким образом, в данном случае одинаковым потенциалом обладают точки C
и D
, а также точки E
и F
. Значит эти точки можно объединить. Пусть точки C
и D
объединятся в точке M
, а точки E
и F
— в точке T
. Тогда получится следующая эквивалентная схема:

На вертикальном участке (непосредственно между точками T
и M
) ток не течёт. Действительно, ситуация аналогична уравновешенному измерительному мосту . Это означает, что данной звено можно исключить из цепи. После этого посчитать общее сопротивление не составит труда:

Сопротивление верхнего звена равно , нижнего — . Тогда общее сопротивление равно:

Сопротивление куба между прилежащими вершинами одной грани

Это последний возможный вариант подключения куба в электрическую цепь. В этом случае эквивалентными рёбрами, через которые будет течь одинаковый ток, являются рёбра AC
и AD
. И, соответственно, одинаковые потенциалы будут иметь точки C
и D
, а также симметричные им точки E
и F
:

Вновь соединяем попарно точки с одинаковыми потенциалами. Мы можем это сделать, потому что ток между этими точками не потечёт, даже если соединить их проводником. Пусть точки C
и D
объединятся в точку T
, а точки E
и F
— в точку M
. Тогда можно нарисовать следующую эквивалентную схему:

Общее сопротивление полученной схемы рассчитывается стандартными способами. Каждый сегмент из двух параллельно соединённых резисторов заменяем на резистор сопротивлением . Тогда сопротивление «верхнего» сегмента, состоящего из последовательно соединённых резисторов , и , равно .

Этот сегмент соединён со «средним» сегментом, состоящим из одного резистора сопротивлением , параллельно. Сопротивление цепи, состоящей из двух параллельно соединённых резисторов сопротивлением и , равно:

То есть схема упрощается до ещё более простого вида:

Как видно, сопротивление «верхнего» П-образного сегмента равно:

Ну а общее сопротивление двух параллельно соединённых резисторов сопротивлением и равно:

Эксперимент на измерению сопротивления куба

Чтобы показать, что всё это не математический трюк и что за всеми этими вычислениями стоит реальная физика, я решил провести прямой физической эксперимент по измерению сопротивления куба. Вы можете посмотреть этот эксперимент в видео, которые находится в начале статьи. Здесь я размещу фотографии экспериментальной установки.

Специально для этого эксперимента я спаял куб, рёбрами которого являются одинаковые резисторы. Также у меня есть мультиметр, который я включил в режиме измерения сопротивления. Сопротивление одиночного резистора равно 38.3 кОм:

Цели: обучающая
: систематизировать
знания и умения учащихся решать задачи ан расчет
эквивалентных сопротивлений с помощью моделей,
каркасов и т.д.

Развивающая: развитие навыков логического
мышления абстрактного мышления, умений заменять
схемы эквивалентности, упрощать расчет схем.

Воспитательная: воспитание чувства
ответственности, самостоятельности,
необходимости навыков приобретенных на уроке в
будущем

Оборудование: проволочный каркас куба,
тетраэдера, сетки бесконечной цепочки
сопротивлений.

ХОД УРОКА

Актуализация:

1. Учитель: “Вспомним последовательное
соединение сопротивлений”.

Учащиеся на доске зарисовывают схему.

и записывают

U об =U 1 +U 2

Y об =Y 1 =Y 2

Учитель: вспомним параллельное соединение
сопротивлений.

Учащийся на доске зарисовывает элементарную
схему:

Y об =Y 1 =Y 2

; для для n равных

Учитель: А теперь будем решать задачи на расчет
эквивалентного сопротивления участок цепи
представлен в виде геометрической фигуры, либо
металлической сетки.

Задача № 1

Проволочный каркас в виде куба, рёбра которого
представляют равные сопротивления R. Рассчитать
эквивалентное сопротивление между точками А и В.
Чтобы рассчитать эквивалентное сопротивление
данного каркаса необходимо заменить
эквивалентной схемой. Точки 1, 2, 3 имеют
одинаковый потенциал, их можно соединить в один
узел. А точки (вершины) куба 4, 5, 6 можно соединить в
другой узел по той же причине. Учащиеся имеют на
каждой парте такую модель. После выполнения
описанных действий зарисовывают эквивалентную
схему.

На участке АС эквивалентное сопротивление ; на СD ; на DB ; и окончательно
для последовательного соединения сопротивлений
имеем:

По тому же принципу потенциалы точек А и 6 равны,
В и 3 равны. Учащиеся совмещают эти точки на своей
модели и получают эквивалентную схему:

Расчёт эквивалентного сопротивления такой
цепи прост

Задача № 3

Эта же модель куба, с включением в цепь между
точками 2 и В. Учащиеся соединяют точки с равными
потенциалами 1 и 3; 6 и 4. Тогда схема будет
выглядеть так:

Точки 1,3 и 6,4 имеют равные потенциалы, и ток по
сопротивлениям между этими точками не потечёт и
схема упрощается до вида; эквивалентное
сопротивление которой рассчитывается так:

Задача № 4

Равносторонняя треугольная пирамида, ребро
которой имеет сопротивление R. Рассчитать
эквивалентное сопротивление при включении в
цепь.

Точки 3 и 4 имеют равный потенциал, поэтому по
ребру 3,4 ток не потечёт. Учащиеся убирают его.

Тогда схема будет выглядеть так:

Эквивалентное сопротивление рассчитывается
так:

Задача № 5

Металлическая сетка с сопротивлением звена
равном R. Рассчитать эквивалентное сопротивление
между точками 1 и 2.

В точке 0 можно звенья отделить, тогда схема
будет иметь вид:

—
сопротивление одной половины симметричной по 1-2
точкам. Параллельно ей такая же ветвь, поэтому

Задача № 6

Звезда состоит из 5-и равносторонних
треугольников, сопротивление каждого.

Между точками 1 и 2 один треугольник параллелен
четырём, последовательно соединенным между
собой

Имея опыт расчёта эквивалентного
сопротивления проволочных каркасов можно
приступить к расчету сопротивлений цепи,
содержащий бесконечное число сопротивлений.
Например:

Если отделить звено

от общей схемы, то схема не изменится, тогда
можно представить ввиде

или ,

решаем данное уравнение относительно R экв.

Итог урока: мы научились абстрактно
представлять схемы участков цепи, заменять их
эквивалентными схемами, которые позволяют легко
рассчитать эквивалентное сопротивление.

Указание: Эту модель представить в виде:

Цели: обучающая
: систематизировать
знания и умения учащихся решать задачи ан расчет
эквивалентных сопротивлений с помощью моделей,
каркасов и т.д.

Развивающая: развитие навыков логического
мышления абстрактного мышления, умений заменять
схемы эквивалентности, упрощать расчет схем.

Воспитательная: воспитание чувства
ответственности, самостоятельности,
необходимости навыков приобретенных на уроке в
будущем

Оборудование: проволочный каркас куба,
тетраэдера, сетки бесконечной цепочки
сопротивлений.

ХОД УРОКА

Актуализация:

1. Учитель: “Вспомним последовательное
соединение сопротивлений”.

Учащиеся на доске зарисовывают схему.

и записывают

U об =U 1 +U 2

Y об =Y 1 =Y 2

Учитель: вспомним параллельное соединение
сопротивлений.

Учащийся на доске зарисовывает элементарную
схему:

Y об =Y 1 =Y 2

; для для n равных

Учитель: А теперь будем решать задачи на расчет
эквивалентного сопротивления участок цепи
представлен в виде геометрической фигуры, либо
металлической сетки.

Задача № 1

Проволочный каркас в виде куба, рёбра которого
представляют равные сопротивления R. Рассчитать
эквивалентное сопротивление между точками А и В.
Чтобы рассчитать эквивалентное сопротивление
данного каркаса необходимо заменить
эквивалентной схемой. Точки 1, 2, 3 имеют
одинаковый потенциал, их можно соединить в один
узел. А точки (вершины) куба 4, 5, 6 можно соединить в
другой узел по той же причине. Учащиеся имеют на
каждой парте такую модель. После выполнения
описанных действий зарисовывают эквивалентную
схему.

На участке АС эквивалентное сопротивление ; на СD ; на DB ; и окончательно
для последовательного соединения сопротивлений
имеем:

По тому же принципу потенциалы точек А и 6 равны,
В и 3 равны. Учащиеся совмещают эти точки на своей
модели и получают эквивалентную схему:

Расчёт эквивалентного сопротивления такой
цепи прост

Задача № 3

Эта же модель куба, с включением в цепь между
точками 2 и В. Учащиеся соединяют точки с равными
потенциалами 1 и 3; 6 и 4. Тогда схема будет
выглядеть так:

Точки 1,3 и 6,4 имеют равные потенциалы, и ток по
сопротивлениям между этими точками не потечёт и
схема упрощается до вида; эквивалентное
сопротивление которой рассчитывается так:

Задача № 4

Равносторонняя треугольная пирамида, ребро
которой имеет сопротивление R. Рассчитать
эквивалентное сопротивление при включении в
цепь.

Точки 3 и 4 имеют равный потенциал, поэтому по
ребру 3,4 ток не потечёт. Учащиеся убирают его.

Тогда схема будет выглядеть так:

Эквивалентное сопротивление рассчитывается
так:

Задача № 5

Металлическая сетка с сопротивлением звена
равном R. Рассчитать эквивалентное сопротивление
между точками 1 и 2.

В точке 0 можно звенья отделить, тогда схема
будет иметь вид:

—
сопротивление одной половины симметричной по 1-2
точкам. Параллельно ей такая же ветвь, поэтому

Задача № 6

Звезда состоит из 5-и равносторонних
треугольников, сопротивление каждого.

Для развития творческих способностей учащихся представляют интерес задачи на решение резисторных схем постоянного тока методом равнопотенциальных узлов. Решение этих задач сопровождается последовательным преобразованием исходной схемы. Причём наибольшее изменение она претерпевает после первого шага, когда используется данный метод. Дальнейшие преобразования связаны с эквивалентной заменой последовательных или параллельных резисторов.

Для преобразования цепи пользуются тем свойством, что во всякой цепи точки с одинаковыми потенциалами можно соединять в узлы. И наоборот: узлы цепи можно разделить, если после этого потенциалы точек, входящих в узел, не изменятся.

В методической литературе часто пишут так: если схема содержит проводники с одинаковыми сопротивлениями, расположенными симметрично
относительно какой-либо оси или плоскости симметрии, то точки этих проводников, симметричные относительно этой оси или плоскости, имеют одинаковый потенциал. Но вся сложность в том, что такую ось или плоскость никто на схеме не обозначает и отыскать её непросто.

Предлагаю другой, упрощённый способ решения подобных задач.

Задача 1
. Проволочный кубик (рис. 1) включён в цепь между точками
А к В.

Найдите его общее сопротивление, если сопротивление каждого ребра равно
R.

Поставим кубик на ребро АВ
(рис. 2) и «распилим» его на две
параллельные половинки
плоскостью
АА 1
B
1 В

, проходящей через нижнее и верхнее ребро.

Рассмотрим правую половинку куба. Учтём, что нижнее и верхнее ребро расщепились пополам и стали в 2 раза тоньше, а их сопротивления увеличились в 2 раза и стали по 2R
(рис. 3).

1) Находим сопротивление
R 1

трёх верхних проводников, соединённых последовательно:

4) Находим общее сопротивление этой половинки куба (рис. 6):

Находим общее сопротивление куба:

Получилось сравнительно просто, понятно и доступно для всех.

Задача 2
. Проволочный кубик подключён в цепь не ребром, а диагональю
АС
любой грани. Найдите его общее сопротивление, если сопротивление каждого ребра равно
R
(рис. 7).

Снова ставим кубик на ребро АВ. «Распиливаем» кубик на две
параллельные половинки
той же вертикальной плоскостью (см. рис. 2).

Опять рассматриваем правую половинку проволочного куба. Учитываем, что верхнее и нижнее ребро расщепились пополам и их сопротивления стали по 2R
.

С учётом условия задачи имеем следующее соединение (рис. 8).

Схема моста Уитстона

| Теория, примеры и приложения

В этом руководстве мы узнаем о мосте Уитстона. Мы увидим принцип работы моста Уитстона, несколько примеров схем и некоторые важные приложения.

Введение в мост Уитстона

В реальном мире мы сталкиваемся с различными сигналами, некоторые из них измеряются по изменению сопротивления, а некоторые — по индуктивности и емкости.

Если рассматривать сопротивление, большинство промышленных датчиков, таких как температура, деформация, влажность, смещение, уровень жидкости и т. Д.производит изменение значения сопротивления для переменного изменения. Следовательно, существует потребность в формировании сигнала для каждого датчика сопротивления.

Обычно измерение сопротивления делится на три типа: измерение низкого сопротивления, измерение среднего сопротивления и измерение высокого сопротивления. Если измерение сопротивления составляет от нескольких миллиом до микроом, то это считается измерением низкого сопротивления.

Это измерение фактически используется в исследовательских целях.Если измерение составляет от 1 Ом до 100 кОм, это обычно считается измерением сопротивления среды. Измерения потенциометров, термисторов и т. Д. Подпадают под эту категорию.

При этом считается измерением очень высокое сопротивление от 100 кОм до более 100 мегаом. Для определения среднего значения сопротивления используются разные методы, но в основном используется мост Уитстона.

Что такое мост Уитстона?

Самая распространенная и простая мостовая сеть для определения сопротивления — это мост Уитстона постоянного тока.Этот мост используется там, где необходимо измерять небольшие изменения сопротивления, например, в сенсорных приложениях. Это используется для преобразования изменения сопротивления в изменение напряжения преобразователя.

Комбинация этого моста с операционным усилителем широко используется в промышленности для различных преобразователей и датчиков. Мост Уитстона состоит из четырех резисторов, которые в форме ромба соединены с источником питания и индикаторными приборами, как показано на рисунке.

Этот мост используется для очень точного определения неизвестного сопротивления путем его сравнения с известным значением сопротивлений.В этом мосту для определения сопротивления используется нулевое или сбалансированное состояние.

Для этого моста в сбалансированном состоянии напряжение в точках C и D должно быть одинаковым. Следовательно, ток через гальванометр не течет. Для сбалансированного состояния один из резисторов должен быть переменным.

На рисунке

Напряжение в точке D = V × R _X / (R ₃ + R _X )

Напряжение в точке C = V × R ₂ / (R ₁ + R ₂ )

Напряжение (В) на гальванометре или между C и D составляет,

V _CD = V × R _X / (R ₃ + R _X ) — V R ₂ / (R ₁ + R ₂ )

Когда мост сбалансирован V _CD = 0,

Итак,

V × R _X / (R ₃ + R _X ) = V R ₂ / (R ₁ + R ₂ )

R _X R ₁ + R _X R ₂ = R ₂ R ₃ + R ₂ R _X

R ₁ R _X = R ₂ R ₃

R ₂ / R ₁ = R _X / R ₃

Это условие балансировки моста.И для нахождения неизвестного значения сопротивления

R _X = R ₃ × (R ₂ / R ₁ )

Из приведенного выше уравнения R4 или Rx можно вычислить из известного значения сопротивления R3 и отношения R2 / R1. Следовательно, в большинстве случаев значения R2 и R1 являются фиксированными, а значение R3 является переменным, так что достигается нулевое значение и мост балансируется.

Принцип работы

Без гальванометра мостовая схема выглядит как схема делителя напряжения, как показано на рисунке ниже.Рассмотрим R ₁ = 20 Ом, R ₂ = 40 Ом для одного плеча, а для другого рассмотрим те же значения R ₃ и R ₄ соответственно.

Текущий поток в первом плече

I ₁ = V / (R ₁ + R ₂ )

I ₁ = 12 В / (20 + 40)

I ₁ = 0,2 А

А напряжение в точке C равно падению напряжения на резисторе R ₂ ,

В _R2 = I ₁ × R ₂ = 0.2 × 40 = 8 В

Аналогично, напряжение на R ₁ составляет 4 В (0,2 × 20). Из-за тех же значений сопротивления, напряжения для R ₄ и R ₃ будут такими же, как и для R ₁ и R ₂ соответственно. Следовательно, в точках A и B напряжения одинаковы, поэтому гальванометр показывает нулевое значение, поскольку разность потенциалов равна нулю. В этом случае считается, что мост находится в сбалансированном состоянии.

Предположим, что если мы поменяем местами резисторы во втором плече, ток останется таким же из-за последовательной цепи.Но напряжение на резисторе R ₄ меняется, т.е. 0,2 * 20 = 4В. Таким образом, в этом состоянии напряжения в точках A и B различны и существует разность потенциалов 8 — 4 = 4 В. Это неуравновешенное состояние моста.

Пример моста Уитстона

Сверху мост Уитстона неуравновешен, когда показание вольтметра не равно нулю. Это показание может быть положительным или отрицательным, в зависимости от значений напряжений на клеммах счетчика.Давайте рассмотрим приведенную ниже схему моста Уитстона, которая подключена, чтобы найти неизвестное значение сопротивления с использованием декадной коробки резисторов, чтобы получить переменное сопротивление R ₃ .

Мы знаем, что условие баланса моста —

R ₄ = R ₃ × R ₂ / R ₁

R _x = R _{КОРОБКА} × (10 x 10 ³ ) / (10 x 10 ³ )

R _x = R _{КОРОБКА}

В данном случае мост Уитстона балансируется путем регулировки декадного сопротивления до тех пор, пока вольтметр не покажет нулевое значение.И соответствующее значение сопротивления в коробке равно неизвестному сопротивлению. Предположим, что если условие нулевого напряжения возникает на 250 Ом декадной ячейки сопротивления, то неизвестное сопротивление также равно 250 Ом.

Мост Уитстона для измерения деформации

Чаще всего для измерения деформации используются тензодатчики, электрическое сопротивление которых изменяется пропорционально деформации в устройстве. На практике диапазон сопротивления тензодатчика составляет от 30 Ом до 3000 Ом.Для данной деформации изменение сопротивления может составлять лишь часть полного диапазона. Поэтому для измерения очень небольшой части изменений сопротивления с высокой точностью используется конфигурация моста Уитстона. На рисунке ниже показан мост Уитстона, в котором неизвестный резистор заменен тензодатчиком.

В приведенной выше схеме два резистора R ₁ и R ₂ равны друг другу, а R ₃ — переменный резистор. Без приложения силы к тензодатчику реостат изменяют и, наконец, устанавливают так, чтобы вольтметр показывал нулевое отклонение.Это называется условием балансировки моста. Это состояние означает, что датчик не подвергается деформации.

Если тензодатчик либо растянут, либо сжимается, сопротивление может увеличиваться или уменьшаться. Следовательно, это вызывает разбалансировку моста. Это дает показание напряжения на вольтметре, соответствующее изменению деформации. Если напряжение, приложенное к тензодатчику, больше, то разница напряжений на выводах измерителя больше. Если деформация равна нулю, мост уравновешивается, и счетчик показывает нулевое значение.

Речь идет об измерении сопротивления с помощью моста Уитстона для точного измерения. Из-за дробного измерения сопротивления мосты Уитстона в основном используются при измерениях тензодатчиков и термометров.

Приложения

1. Мост Уитстона используется для точного измерения очень низких значений сопротивления.
2. Мост Уитстона вместе с операционным усилителем используется для измерения физических параметров, таких как температура, деформация, свет и т. Д.
3. Мы также можем измерить емкость, индуктивность и импеданс, используя вариации моста Уитстона.

Знать о схеме моста Уитстона Работа с приложением

Термин «мост Уитстона» также называют мостом сопротивления, который был изобретен «Чарльзом Уитстоном». Эта мостовая схема используется для расчета неизвестных значений сопротивления и как средство регулирования измерительного прибора, амперметров, вольтметров и т. Д.Но нынешние цифровые миллиметры предлагают самый простой способ рассчитать сопротивление. В последние дни мост Уитстона используется во многих приложениях, таких как; его можно использовать с современными операционными усилителями для подключения различных датчиков и преобразователей к схемам усилителя. Эта мостовая схема состоит из двух простых последовательных и параллельных сопротивлений между клеммой источника напряжения и клеммами заземления. Когда мост сбалансирован, клемма заземления создает нулевую разность напряжений между двумя параллельными ветвями.Мост Уитстона состоит из двух клемм i / p и двух клемм o / p, включающих четыре резистора, расположенных в форме ромба.

Мост Уитстона

Мост Уитстона и его работа

Мост Уитстона широко используется для измерения электрического сопротивления. Эта схема состоит из двух известных резисторов, одного неизвестного резистора и одного переменного резистора, соединенных в виде моста. При настройке переменного резистора ток в гальванометре становится равным нулю, соотношение двух неизвестных резисторов равно отношению значения неизвестного сопротивления и настроенного значения переменного сопротивления.Используя мост Уитстона, можно легко измерить неизвестное значение электрического сопротивления.

Схема моста Уитстона

Схема моста Уитстона показана ниже. Эта схема спроектирована с четырьмя плечами, а именно AB, BC, CD и AD, и состоит из электрического сопротивления P, Q, R и S. Среди этих четырех сопротивлений P и Q известны фиксированные электрические сопротивления. Гальванометр подключается между клеммами B и D через переключатель S1.Источник напряжения подключается к клеммам A и C через переключатель S2. Переменный резистор «S» подключен между выводами C и D. Потенциал на выводе D изменяется при изменении значения переменного резистора. Например, токи I1 и I2 протекают через точки ADC и ABC. Когда значение сопротивления плеча CD изменяется, ток I2 также будет изменяться.

Схема моста Уитстона

Если мы склонны регулировать переменное сопротивление, одно положение вещей может вернуться один раз, когда на резисторе S падает напряжение, равное I2.S становится особенно способным к падению напряжения на резисторе Q, т.е. I1.Q. Таким образом, потенциал точки B становится равным потенциалу точки D, следовательно, разность потенциалов b / n этих двух точек равна нулю, следовательно, ток через гальванометр равен нулю. Тогда отклонение гальванометра равно нулю при замкнутом переключателе S2.

Вывод моста Уитстона

Из приведенной выше схемы токи I1 и I2 равны

I1 = V / P + Q и I2 = V / R + S

Теперь потенциал точки B относительно точки C — падение напряжения на транзисторе Q, тогда уравнение:

I1Q = VQ / P + Q …………………………….. (1)

Потенциал точки D по отношению к C — это падение напряжения на резисторе S, тогда уравнение:

I2S = VS / R + S ………………………… .. (2)

Из приведенных выше уравнений 1 и 2 мы получаем

VQ / P + Q = VS / R + S

` Q / P + Q = S / R + S

P + Q / Q = R + S / S

P / Q + 1 = R / S + 1

P / Q = R / S

R = SxP / Q

Здесь В приведенном выше уравнении значения P / Q и S известны, поэтому значение R можно легко определить.

Электрические сопротивления моста Уитстона, такие как P и Q, имеют определенное соотношение, они равны 1: 1; 10: 1 (или) 100: 1, известное как плечо передаточного числа, а плечо реостата S всегда изменяется от 1 до 1000 Ом или от 1 до 10 000 Ом

Пример моста Уитстона

Следующая схема представляет собой несбалансированный мост Уитстона, рассчитайте напряжение o / p на точках C и D, и значение резистора R4 необходимо для балансировки мостовой схемы.

Пример моста Уитстона

Первое последовательное плечо в приведенной выше схеме — ACB
Vc = (R2 / (R1 + R2)) X Vs
R2 = 120 Ом, R1 = 80 Ом, Vs = 100
Подставьте эти значения в приведенные выше уравнение
Vc = (120 / (80 + 120)) X 100
= 60 вольт
Второе последовательное плечо в приведенной выше схеме — ADB

VD = R4 / (R3 + R4) X Vs

VD = 160 / ( 480 + 160) X 100
= 25 Вольт
Напряжение на точках C и D задается как
Vout = VC-VD
Vout = 60-25 = 35 вольт.
Значение резистора R4, необходимого для балансировки моста Уитстона, определяется как:
R4 = R2 R3 / R1
120X480 / 80
720 Ом.

Итак, наконец, мы можем сделать вывод, что мост Уитстона имеет два вывода i / p и два вывода o / p, а именно A и B, C и D. Когда приведенная выше схема сбалансирована, напряжение на выводах o / p равно нулю вольт. . Когда мост Уитстона неуравновешен, напряжение o / p может быть либо + ve, либо -ve в зависимости от направления дисбаланса.

Применение моста Уитстона

Применение моста Уитстона — детектор света, использующий схему моста Уитстона

Схема светового детектора моста Уитстона

Сбалансированные мостовые схемы используются во многих электронных приложениях для измерения изменений интенсивности света, деформации или давления.Различные типы резистивных датчиков, которые могут использоваться в схеме моста Уитстона, включают: потенциометры, LDR, тензодатчики, термисторы и т. Д.

Мосты Уитстона применяются для измерения электрических и механических величин. Но простое применение моста Уитстона — это измерение освещенности с помощью фоторезистивного устройства. В схеме моста Уитстона светозависимый резистор размещен на месте одного из резисторов.

LDR — это пассивный резистивный датчик, который используется для преобразования уровней видимого света в изменение сопротивления, а затем в напряжение.LDR можно использовать для измерения и контроля уровня освещенности. LDR имеет сопротивление в несколько мегаумов в тусклом или темном свете около 900 Ом при интенсивности света 100 люкс и до 30 Ом при ярком свете. Подключив резистор, зависящий от света, в схему моста Уитстона, мы можем измерять и контролировать изменения уровней освещенности.

Это все о мосте Уитстона и принципе моста Уитстона, его работе с приложением. Мы надеемся, что вы лучше понимаете эту концепцию.Кроме того, любые вопросы или сомнения относительно этой статьи или проектов электроники, пожалуйста, дайте свой отзыв, комментируя в разделе комментариев ниже.

Фото:

Как работает мост Уитстона для тензодатчиков?

Чтобы измерить деформацию с помощью тензодатчика сопротивления, он должен быть подключен к электрической цепи, способной измерять мельчайшие изменения сопротивления, соответствующие деформации. В тензодатчиках обычно используются четыре элемента тензодатчика, электрически соединенные для образования мостовой схемы Уитстона (рис. 2-6).

Мост Уитстона — это схема с разделенным мостом, используемая для измерения статического или динамического электрического сопротивления. Выходное напряжение схемы моста Уитстона выражается в выходных милливольтах на входной вольт. Схема Уитстона также хорошо подходит для температурной компенсации.

Уравнение моста Уитстона: если R1, R2, R3 и R4 равны, а напряжение VIN приложено между точками A и C, то выходной сигнал между точками B и D не будет показывать разность потенциалов.Однако, если R4 изменить на какое-то значение, которое не равно R1, R2 и R3, мост станет несимметричным, и на выходных клеммах появится напряжение. В так называемой конфигурации G-моста датчик переменной деформации имеет сопротивление Rg, а другие плечи являются резисторами фиксированного значения.

Однако датчик может занимать одно, два или четыре плеча моста Уитстона, в зависимости от области применения. Общая деформация или выходное напряжение цепи (VOUT) эквивалентно разнице между падением напряжения на R1 и R4, или Rg.Это также можно записать как:

Подробнее см. Рисунок 2-6. Мост считается сбалансированным, когда R1 / R2 = Rg / R3 и, следовательно, VOUT равен нулю.
Любое небольшое изменение сопротивления тензодатчика приведет к нарушению баланса моста, что сделает его пригодным для определения деформации. Когда мост настроен так, что Rg является единственным активным тензодатчиком, небольшое изменение Rg приведет к выходному напряжению с моста. Если калибровочный коэффициент равен GF, измерение деформации связано с изменением Rg следующим образом:

Количество активных тензодатчиков, которые следует подключить к мосту, зависит от области применения.Например, может быть полезно соединить датчики, которые находятся на противоположных сторонах балки, один при сжатии, а другой при растяжении. В такой конфигурации можно эффективно удвоить выходную мощность моста при той же деформации. В установках, где все рычаги подсоединены к тензодатчикам, температурная компенсация тензодатчиков является автоматической, поскольку изменение сопротивления из-за колебаний температуры будет одинаковым для всех плеч моста Уитстона.
В четырехэлементном мосту Уитстона обычно два датчика соединены при сжатии и два при растяжении.Например, если R1 и R3 находятся в состоянии растяжения (положительное), а R2 и R4 — в состоянии сжатия (отрицательное), то выходной сигнал будет пропорционален сумме всех деформаций, измеренных отдельно. Для датчиков, расположенных на соседних опорах, мост становится неуравновешенным пропорционально разнице в деформации. Для датчиков на противоположных опорах мост балансирует пропорционально сумме деформаций. Независимо от того, измеряется ли деформация изгиба, осевая деформация, деформация сдвига или деформация кручения, устройство тензодатчика будет определять соотношение между выходной мощностью и типом измеряемой деформации.Как показано на рис. 2-6, если положительная деформация растяжения возникает на датчиках R2 и R3, а отрицательная деформация испытывается на датчиках R1 и R4, общий выходной сигнал, VOUT, будет в четыре раза превышать сопротивление одного датчика. В этой конфигурации компенсируются температурные изменения измерителя пятна.

Схема моста Шеврон

Шевронный мост показан на Рисунке 2-7. Это многоканальная схема, которая служит для компенсации изменений сопротивлений перемычек путем их периодического переключения.Здесь четыре позиции каналов используются для переключения цифрового вольтметра (DVM) между конфигурациями G-моста (один активный датчик) и H-моста (два активных датчика). Измерительное устройство DVM всегда использует источник питания и внутренний H-мост. Эта конструкция наиболее популярна для измерения деформации вращающихся машин, где она позволяет уменьшить количество требуемых контактных колец.

Четырехпроводная омическая цепь

Хотя схема моста Уитстона является одним из самых популярных методов измерения электрического сопротивления, можно использовать и другие методы.Основное преимущество четырехпроводной омической схемы состоит в том, что подводящие провода не влияют на измерение, поскольку напряжение регистрируется непосредственно на элементе тензодатчика.

Установка четырехпроводной омической схемы может состоять из вольтметра, источника тока и четырех выводных резисторов R1, соединенных последовательно с измерительным резистором Rg (рисунок 2-8). Вольтметр подключается к клеммам измерения сопротивления DVM, а источник тока подключается к клеммам источника сопротивления DVM.Для измерения величины деформации в цепь подается слабый ток (обычно один миллиампер). В то время как вольтметр измеряет падение напряжения на Rg, абсолютное значение сопротивления вычисляется мультиметром на основе значений тока и напряжения.
Измерение обычно выполняется, сначала измеряя значение сопротивления датчика в ненапряженном состоянии, а затем выполняя второе измерение с приложенной деформацией. Разница в измеренных сопротивлениях датчика, деленная на сопротивление без деформации, дает дробное значение деформации.Это значение используется с калибровочным коэффициентом (GF) для расчета деформации.
Четырехпроводная схема также подходит для автоматической компенсации смещения напряжения. Напряжение сначала измеряется при отсутствии тока. Это измеренное значение затем вычитается из показания напряжения при протекании тока. Полученная разность напряжений затем используется для вычисления сопротивления датчика. Из-за своей чувствительности четырехпроводные тензодатчики обычно используются для измерения низкочастотных динамических деформаций. При измерении деформаций более высоких частот необходимо усилить выходной сигнал моста.Та же схема также может использоваться с полупроводниковым тензометрическим датчиком и высокоскоростным цифровым вольтметром. Если чувствительность ДВМ составляет 100 микровольт, источник тока — 0,44 миллиампера, сопротивление тензометрического элемента — 350 Ом и его коэффициент измерения — 100, то разрешающая способность измерения составит 6 микродеформаций.

Цепь постоянного тока

Сопротивление можно измерить, возбуждая мост постоянным напряжением или источником постоянного тока.Поскольку R = V / I, если либо V, либо I остается постоянным, другой будет изменяться в зависимости от сопротивления. Можно использовать оба метода.
Хотя теоретического преимущества использования источника постоянного тока (рисунок 2-9) по сравнению с постоянным напряжением нет, в некоторых случаях выход моста будет более линейным в системе постоянного тока. Кроме того, если используется источник постоянного тока, отпадает необходимость в измерении напряжения на мосту; следовательно, к тензодатчику необходимо подключить только два провода.
Цепь постоянного тока наиболее эффективна при измерении динамической деформации. Это связано с тем, что если динамическая сила вызывает изменение сопротивления тензодатчика (Rg), можно измерить изменяющуюся во времени составляющую выходного сигнала (VOUT), в то время как медленно меняющиеся эффекты, такие как изменения сопротивления выводов из-за температуры варианты будут отклонены. При использовании этой конфигурации температурные дрейфы становятся практически незначительными.

Применение и установка

Выходной сигнал цепи тензодатчика представляет собой сигнал напряжения очень низкого уровня, требующий чувствительности 100 микровольт или выше.Низкий уровень сигнала делает его особенно восприимчивым к нежелательным шумам от других электрических устройств. Емкостная связь, вызванная проложением выводных проводов слишком близко к силовым кабелям переменного тока или токами заземления, является потенциальным источником ошибок при измерении деформации. Другие источники ошибок могут включать в себя магнитно-индуцированные напряжения, когда выводные провода проходят через переменные магнитные поля, паразитные (нежелательные) контактные сопротивления выводных проводов, нарушение изоляции и эффекты термопары на стыке разнородных металлов.Сумма таких помех может привести к значительному ухудшению качества сигнала.

Экранирование

Большинство проблем с электрическими помехами и шумом можно решить с помощью экранирования и защиты. Экран вокруг проводов измерительных выводов улавливает помехи, а также может уменьшить любые ошибки, вызванные ухудшением изоляции. Экранирование также защитит измерение от емкостной связи. Если измерительные провода проложены рядом с источниками электромагнитных помех, такими как трансформаторы, скручивание проводов минимизирует ухудшение сигнала из-за магнитной индукции.Скручиванием провода, индуцированный магнитным потоком ток инвертируется, и области, которые пересекает магнитный поток, компенсируются. В промышленных процессах практически без исключения используются скрученные и экранированные подводящие провода.

Ограждение

Защита самой аппаратуры так же важна, как и защита проводов. Ограждение представляет собой коробку из листового металла, окружающую аналоговую схему и соединенную с экраном. Если токи заземления протекают через тензометрический элемент или его подводящие провода, схема моста Уитстона не может отличить их от потока, создаваемого источником тока.Защита гарантирует, что клеммы электрических компонентов имеют одинаковый потенциал, что предотвращает протекание постороннего тока.
Подключение защитного провода между испытуемым образцом и отрицательной клеммой источника питания обеспечивает дополнительный путь тока вокруг измерительной цепи. При размещении защитного провода на пути тока, вызывающего ошибку, все задействованные элементы (т.е. плавающий источник питания, тензодатчик, все другое измерительное оборудование) будут иметь тот же потенциал, что и испытательный образец.Используя скрученные и экранированные подводящие провода и интегрируя цифровые видеомагнитофоны с защитой, можно практически устранить ошибку синфазного шума.

Эффекты отведений

Тензодатчики иногда устанавливают на расстоянии от измерительного оборудования. Это увеличивает вероятность ошибок из-за колебаний температуры, снижения чувствительности выводов и изменений сопротивления выводов. В двухпроводной установке (рисунок 2-10A) два провода соединены последовательно с тензодатчиком, и любое изменение сопротивления подводящего провода (R1) будет неотличимо от изменений сопротивления тензодатчика. (Rg).
Чтобы скорректировать эффект отведения проволоки, к верхнему плечу моста можно ввести дополнительный третий вывод, как показано на Рисунке 2-10B. В этой конфигурации провод C действует как измерительный провод, по которому не течет ток, а провода A и B находятся на противоположных сторонах моста. Это минимально приемлемый метод подключения тензодатчиков к мосту, чтобы по крайней мере частично устранить влияние ошибок удлинительного провода. Теоретически, если подводящие провода к датчику имеют одинаковое номинальное сопротивление, одинаковый температурный коэффициент и поддерживаются при одинаковой температуре, достигается полная компенсация.В действительности провода изготавливаются с допуском около 10%, а трехпроводная установка не исключает полностью двухпроводных ошибок, но снижает их на порядок. Если желательно дальнейшее улучшение, следует рассмотреть вариант установки с четырехпроводным подключением и компенсацией смещения (рисунки 2-10C и 2-10D).
В двухпроводных установках погрешность, вызванная сопротивлением выводного провода, зависит от отношения сопротивлений R1 / Rg. Ошибка вывода обычно не имеет значения, если сопротивление выводного провода (R1) мало по сравнению с сопротивлением датчика (Rg), но если сопротивление выводного провода превышает 0.1% от номинального сопротивления датчика, этот источник погрешности становится значительным. Следовательно, в промышленных приложениях длину подводящих проводов следует минимизировать или исключить путем размещения преобразователя непосредственно у сенсора.

Температура и манометрический коэффициент

Материалы, чувствительные к деформации, такие как медь, изменяют свою внутреннюю структуру при высоких температурах. Температура может изменить не только свойства элемента тензодатчика, но также может изменить свойства основного материала, к которому прикреплен тензодатчик.Различия в коэффициентах расширения материала датчика и основного материала могут вызвать изменение размеров чувствительного элемента. Следовательно, потребуется схема температурной компенсации.
Расширение или сжатие тензометрического элемента и / или основного материала приводит к ошибкам, которые трудно исправить. Например, изменение удельного сопротивления или температурного коэффициента сопротивления тензометрического элемента изменяет нулевую точку отсчета, используемую для калибровки устройства.
Измерительный коэффициент — это чувствительность датчика к деформации.Производитель всегда должен предоставлять данные о температурной чувствительности манометрического коэффициента. На рис. 2-11 показано изменение коэффициентов измерения для различных материалов тензодатчиков в зависимости от рабочей температуры. Медно-никелевые сплавы, такие как Advance, имеют калибровочные коэффициенты, которые относительно чувствительны к колебаниям рабочей температуры, что делает их наиболее популярным выбором для материалов для тензодатчиков.

Техническое обучение

Техническое обучение

Учебник по теории моста Уитстона формула математическая

Мост Уитстона

В реальном мире мы сталкиваемся с различными сигналами, некоторые из них измеряются изменениями сопротивления, а некоторые — индуктивностью и емкостью.Если мы рассмотрим сопротивление, большинство промышленных датчиков, таких как температура, деформация, влажность, смещение, уровень жидкости и т. Д., Производят изменение значения сопротивления для переменного изменения. Следовательно, существует потребность в формировании сигнала для каждого датчика сопротивления.

Обычно измерение сопротивления делится на три типа: измерение низкого сопротивления, измерение среднего сопротивления и измерение высокого сопротивления. Если измерение сопротивления составляет от нескольких миллиом до микроом, то это считается измерением низкого сопротивления.

Это измерение фактически используется в исследовательских целях. Если измерение составляет от 1 Ом до 100 кОм, это обычно считается измерением сопротивления среды. Измерения потенциометров, термисторов и т. Д. Подпадают под эту категорию. Считается, что измерение очень высокого сопротивления составляет от 100 кОм до более 100 МОм. Для определения среднего значения сопротивления используются разные методы, но в основном используется мост Уитстона.

ЧАСТЬ 1 — Конфигурация

Самая распространенная и простая мостовая сеть для определения сопротивления — это мост Уитстона постоянного тока.Этот мост используется там, где необходимо измерять небольшие изменения сопротивления, например, в сенсорных приложениях. Это используется для преобразования изменения сопротивления в изменение напряжения преобразователя.

Комбинация этого моста с операционным усилителем широко используется в промышленности для различных преобразователей и датчиков. Мост Уитстона состоит из четырех резисторов, которые в форме ромба соединены с источником питания и индикаторными приборами, как показано на рисунке.

Этот мост используется для очень точного поиска неизвестного сопротивления путем его сравнения с известным значением сопротивлений.В этом мосту для определения сопротивления используется нулевое или сбалансированное состояние. Для этого моста в сбалансированном состоянии напряжение в точках C и D должно быть одинаковым. Следовательно, ток через гальванометр не течет. Для сбалансированного состояния один из резисторов должен быть переменным.

Напряжение в точке D = Vin × RX / (R3 + RX)

Напряжение в точке C = Vin × R2 / (R1 + R2)

Итак, теперь напряжение между C и D — это напряжение на D минус напряжение en C.У нас есть формулы для каждого из вышеперечисленных, поэтому все, что нам нужно сделать, это сделать ВД — ВД. Так:

ВК — VD = V × RX / (R3 + RX) — V R2 / (R1 + R2)

Но, очень важно. Мы ищем сбалансированный мост. Это когда VCD = 0V. Итак, теперь мы подразумеваем, что к нашему уравнению, VC — VD = 0; И тогда мы можем узнать, какое значение должно иметь Rx, чтобы получить сбалансированный мост.

0 = V × RX / (R3 + RX) — V R2 / (R1 + R2)

V × RX / (R3 + RX) = V R2 / (R1 + R2)
RXR1 + RXR2 = R2R3 + R2RX
R1RX = R2R3
R2 / R1 = RX / R3

Это условие балансировки моста.И для нахождения неизвестного значения сопротивления:

RX = R3 × (R2 / R1)

Из приведенного выше уравнения R4 или Rx могут быть вычислены из известного значения сопротивления R3 и отношения R2 / R1. Следовательно, в большинстве случаев значения R2 и R1 являются фиксированными, а значение R3 является переменным, так что достигается нулевое значение и мост балансируется.

ЧАСТЬ 2 — Пример

Итак, в качестве примера мы подключаем к нашему мосту тензодатчик вместо Rx. Приведем значения.С одной стороны у нас, скажем, два резистора по 20 Ом, а питание — 10 вольт . Используя формулу делителя, получаем, что напряжение на C равно 5V . Мы меняем сопротивление R3 , пока не получим 5 В в точке D, и давайте посмотрим, что датчик тоже 20 Ом.

Этот датчик увеличивает сопротивление под воздействием сил. На практике диапазон сопротивления тензодатчика составляет от 30 Ом до 3 тысяч Ом. Для данной деформации изменение сопротивления может составлять лишь часть полного диапазона.Поэтому для измерения части изменений сопротивления с высокой точностью используется конфигурация моста Уитстона.

На первом этапе мост балансируется, поэтому мы имеем CD, равный 0 вольт. Мы прикладываем силу к датчику, и сопротивление становится больше, поэтому падение напряжения на датчике теперь больше. Допустим, теперь сопротивление составляет 35 Ом. Напряжение на D теперь будет 6,36 В, поэтому напряжение на CD будет отрицательным 1,36 В. Итак, мы передаем измерения силы на очень небольшие изменения сопротивления, а затем на значения напряжения, чтобы мы могли использовать это в наших проектах, возможно, подключить его к микроконтроллеру.

Почему мы его используем?

Но теперь вы можете задаться вопросом, почему бы не использовать датчик напрямую с делителем напряжения? Что ж, такого рода датчики могут изменять свое сопротивление из-за других факторов, например, температуры.
Допустим, мы прикладываем силу к датчику и измеряем 20 Ом в комнате с температурой 30 градусов. Затем мы прикладываем ту же силу, но в комнате под углом 50 градусов, и получаем 18 Ом. Это означает, что показания датчика ненадежны, потому что они также будут меняться с температурой, а мы этого не хотим.

Но если мы поместим это в мост Уетстона вместе с другими резисторами, которые также будут изменяться в зависимости от температуры, выход не будет затронут, потому что вся система зависит от температуры, но только датчик подвергается воздействию силы, поэтому мы отделили погрешность температуры от датчик манометра.
Мы могли бы использовать эту установку с датчиками манометра, светозависимыми резисторами или термисторами, чтобы мы могли измерять силы, свет или температуру. Это простая схема, которую легко понять.

ЧАСТЬ 3 — Приложения

1. Мост Уитстона используется для точного измерения очень низких значений сопротивления.
2. Мост Уитстона вместе с операционным усилителем используется для измерения физических параметров, таких как температура, напряжение, свет и т. Д.
3. Мы также можем измерять величины емкости, индуктивности и импеданса, используя вариации моста Уитстона.

Помогите мне, поделившись этим постом

нулевых измерений | Физика

Цели обучения

К концу этого раздела вы сможете

• Объясните, почему прибор для измерения нуля более точен, чем стандартный вольтметр или амперметр.
• Продемонстрируйте, как можно использовать мост Уитстона для точного расчета сопротивления в цепи.

Стандартные измерения напряжения и тока изменяют измеряемую цепь, внося погрешности в измерения. Вольтметры потребляют дополнительный ток, тогда как амперметры уменьшают ток. Нулевые измерения уравновешивают напряжения так, чтобы через измерительный прибор не протекал ток и, следовательно, не изменялась измеряемая цепь.Нулевые измерения, как правило, более точны, но также более сложны, чем использование стандартных вольтметров и амперметров, и по-прежнему имеют пределы точности. В этом модуле мы рассмотрим несколько конкретных типов нулевых измерений, потому что они распространены и интересны, и они дополнительно освещают принципы электрических цепей.

Предположим, вы хотите измерить ЭДС батареи. Представьте, что произойдет, если вы подключите аккумулятор напрямую к стандартному вольтметру, как показано на рисунке 1.(Как только мы отметим проблемы с этим измерением, мы рассмотрим нулевое измерение, которое повысит точность.) Как обсуждалось ранее, фактическая измеряемая величина — это напряжение на клеммах В, , которое связано с ЭДС батареи на В = emf — Ir , где I — протекающий ток, а r — внутреннее сопротивление батареи. ЭДС могла быть точно рассчитана, если бы r были очень точно известны, но обычно это не так.Если бы ток I можно было сделать нулевым, тогда V = ЭДС, и поэтому ЭДС можно было бы непосредственно измерить. Однако стандартным вольтметрам для работы необходим ток; таким образом, необходим другой метод.

Рис. 1. Аналоговый вольтметр, прикрепленный к батарее, потребляет небольшой, но ненулевой ток и измеряет напряжение на клеммах, которое отличается от ЭДС батареи. (Обратите внимание, что заглавная буква E символизирует электродвижущую силу или ЭДС.) Поскольку внутреннее сопротивление батареи точно не известно, невозможно точно рассчитать ЭДС.

Потенциометр — это прибор для измерения нуля для измерения потенциалов (напряжений). (См. Рис. 2.) Источник напряжения подключен к резистору R, например, длинным проводом, и пропускает через него постоянный ток. Существует устойчивое падение потенциала (падение IR ) вдоль провода, так что переменный потенциал может быть получен путем создания контакта в различных местах вдоль провода. На рис. 2 (b) показана неизвестная ЭДС _x (обозначена шрифтом E _x на рисунке), подключенная последовательно с гальванометром.Обратите внимание, что ЭДС _x противостоит другому источнику напряжения. Расположение точки контакта (см. Стрелку на чертеже) регулируют до тех пор, пока гальванометр не покажет ноль. Когда гальванометр показывает ноль, ЭДС _x = IR _x , где R _x — это сопротивление участка провода до точки контакта. Поскольку через гальванометр не протекает ток, он не проходит через неизвестную ЭДС, и поэтому ЭДС _x определяется непосредственно. Теперь очень точно известный стандарт ЭДС _s заменяется на ЭДС _x , и точка контакта регулируется до тех пор, пока гальванометр снова не покажет ноль, так что ЭДС _s = IR _s .В обоих случаях через гальванометр не проходит ток, поэтому ток I через длинный провод одинаков. Принимая соотношение [латекс] \ frac {{\ text {emf}} _ {x}} {{\ text {emf}} _ {s}} \\ [/ latex], I отменяет, давая

[латекс] \ frac {{\ text {emf}} _ {x}} {{\ text {emf}} _ {s}} = \ frac {{IR} _ {x}} {{IR} _ { s}} = \ frac {{R} _ {x}} {{R} _ {s}} \\ [/ latex].

Решение для ЭДС _x дает

[латекс] {\ text {emf}} _ {x} = {\ text {emf}} _ {s} \ frac {{R} _ {x}} {{R} _ {s}} \\ [ /латекс].

Рисунок 2. Потенциометр, устройство измерения нуля. (a) Источник напряжения, подключенный к резистору с длинным проводом, пропускает через него постоянный ток I . (b) Неизвестная ЭДС (обозначена шрифтом E _x на рисунке) подключается, как показано, и точка контакта по R регулируется до тех пор, пока гальванометр не покажет ноль. Отрезок провода имеет сопротивление R _x и скрипт E _x , где соединение I не влияет на соединение, поскольку через гальванометр не протекает ток.Таким образом, неизвестная ЭДС пропорциональна сопротивлению отрезка провода.

Поскольку для R используется длинный однородный провод, соотношение сопротивлений R _x / R _s такое же, как отношение длин провода, который обнуляет гальванометр для каждой ЭДС. Три величины в правой части уравнения теперь известны или измерены, и ЭДС _x может быть вычислена. Погрешность этого расчета может быть значительно меньше, чем при прямом использовании вольтметра, но она не равна нулю.Всегда есть некоторая неопределенность в соотношении сопротивлений R _x / R _s и стандартной ЭДС _s . Кроме того, невозможно определить, когда гальванометр показывает ровно ноль, что вносит ошибку как в R _x , так и в R _s , а также может повлиять на ток I .

Измерения сопротивления и мост Уитстона

Существует множество так называемых омметров , предназначенных для измерения сопротивления.На самом деле наиболее распространенные омметры прикладывают напряжение к сопротивлению, измеряют ток и вычисляют сопротивление по закону Ома. Их показания — это рассчитанное сопротивление. Две конфигурации омметров с использованием стандартных вольтметров и амперметров показаны на рисунке 3. Точность таких конфигураций ограничена, поскольку измерители изменяют как напряжение, подаваемое на резистор, так и ток, протекающий через него.

Рисунок 3. Два метода измерения сопротивления стандартными измерителями.(a) Предполагая, что напряжение источника известно, амперметр измеряет ток, и сопротивление рассчитывается как [латекс] R = \ frac {V} {I} \\ [/ latex]. (b) Поскольку напряжение на клеммах В зависит от тока, лучше его измерить. V наиболее точно известен, когда I мал, но сам I наиболее точно известен, когда он большой.

Мост Уитстона — это устройство измерения нуля для расчета сопротивления путем уравновешивания падения потенциала в цепи.(См. Рисунок 4.) Устройство называется мостом, потому что гальванометр образует мост между двумя ветвями. Для выполнения нулевых измерений в схемах используются различные мостовые устройства . Резисторы R ₁ и R ₂ точно известны, а стрелка через R ₃ указывает, что это переменное сопротивление. Можно точно прочитать значение R ₃ . При неизвестном сопротивлении R _x в цепи, R ₃ регулируется до тех пор, пока гальванометр не покажет ноль.Тогда разность потенциалов между точками b и d равна нулю, что означает, что b и d имеют одинаковый потенциал. При отсутствии тока, протекающего через гальванометр, он не влияет на остальную цепь. Таким образом, ветви abc и adc параллельны, и каждая ветвь имеет полное напряжение источника. То есть у IR капли по abc и adc одинаковы. Поскольку b и d имеют одинаковый потенциал, падение IR вдоль ad должно равняться падению IR вдоль ab.

Таким образом,

I ₁ R ₁ = I ₂ R ₃ .

Опять же, поскольку b и d имеют одинаковый потенциал, падение IR вдоль постоянного тока должно равняться падению IR вдоль bc. Таким образом,

I ₁ R ₂ = I ₂ R _x .

Соотношение этих двух последних выражений дает

[латекс] \ frac {{I} _ {1} {R} _ {1}} {{I} _ {1} {R} _ {2}} = \ frac {{I} _ {2} { R} _ {3}} {{I} _ {2} {R} _ {x}} \\ [/ latex].

Подавление токов и решение для R _x дает

[латекс] {R} _ {\ text {x}} = {R} _ {3} \ frac {{R} _ {2}} {{R} _ {1}} \\ [/ latex].

Рис. 4. Мост Уитстона используется для расчета неизвестных сопротивлений. Переменное сопротивление R ₃ регулируется до тех пор, пока гальванометр не покажет ноль при замкнутом переключателе. Это упрощает схему, позволяя рассчитать R _x на основе падений IR , как описано в тексте.

Это уравнение используется для вычисления неизвестного сопротивления, когда ток через гальванометр равен нулю. Этот метод может быть очень точным (часто до четырех значащих цифр), но он ограничен двумя факторами.Во-первых, невозможно получить ток через гальванометр точно равным нулю. Во-вторых, всегда есть неопределенности в R ₁ , R ₂ и R ₃ , которые способствуют неопределенности в R _x .

Проверьте свое понимание

Определите другие факторы, которые могут ограничить точность нулевых измерений. Может ли использование более чувствительного цифрового устройства, чем гальванометр, повысить точность нулевых измерений?

Решение

Одним из факторов может быть сопротивление проводов и соединений при нулевом измерении.Их невозможно обнулить, и они могут со временем меняться. Другим фактором могут быть температурные колебания сопротивления, которые можно уменьшить, но полностью исключить нельзя путем выбора материала. Цифровые устройства, чувствительные к меньшим токам, чем аналоговые, действительно улучшают точность нулевых измерений, поскольку они позволяют приблизить ток к нулю.

Сводка раздела

• Нулевые методы измерения позволяют достичь большей точности за счет балансировки цепи, чтобы ток не протекал через измерительное устройство.
• Одним из таких устройств для определения напряжения является потенциометр.
• Еще одно устройство измерения нуля для определения сопротивления — мост Уитстона.
• Другие физические величины также могут быть измерены с помощью методов нулевого измерения.

Концептуальные вопросы

1. Почему нулевое измерение может быть более точным, чем измерение с использованием стандартных вольтметров и амперметров? Какие факторы ограничивают точность нулевых измерений?

2.Если потенциометр используется для измерения ЭДС ячейки порядка нескольких вольт, почему наиболее точным является, чтобы стандартная ЭДС _s была того же порядка величины, а сопротивления — в диапазоне нескольких Ом?

Задачи и упражнения

1. Какова ЭДС _x ячейки, измеряемая в потенциометре, если ЭДС стандартной ячейки составляет 12,0 В и потенциометр уравновешивает R _x = 5.000 Ом и R _с = 2 .500 Ом?

2. Рассчитайте ЭДС _x сухого элемента, для которого потенциометр сбалансирован, когда R _x = 1.200 Ом, в то время как для щелочного стандартного элемента с ЭДС 1,600 В требуется R _с = 1,247 Ω для балансировки потенциометра.

3. Когда неизвестное сопротивление R _x помещено в мост Уитстона, можно уравновесить мост, отрегулировав R ₃ на 2500 Ом. Что будет R _x , если [латекс] \ frac {{R} _ {2}} {{R} _ {1}} = 0.625 \ [/ латекс]?

4. На какое значение необходимо отрегулировать R ₃ , чтобы сбалансировать мост Уитстона, если неизвестное сопротивление R _x равно 100 Ом, R ₁ равно 50,0 Ом, а R ₂ — это 175 Ом?

5. (a) Что такое неизвестная ЭДС _x в потенциометре, который уравновешивается, когда R _x составляет 10,0 Ом, и уравновешивается, когда R _s составляет 15,0 Ом для стандартного 3.000-В ЭДС? (b) Та же ЭДС _x помещается в тот же потенциометр, который теперь уравновешивается, когда R _s составляет 15,0 Ом для стандартной ЭДС 3,100 В. При каком сопротивлении R _x будет балансироваться потенциометр. ?

6. Предположим, вы хотите измерить сопротивление в диапазоне от 10,0 Ом до 10,0 кОм, используя мост Уитстона с [латексом] \ frac {{R} _ {2}} {{R} _ {1}} = 2.000 \ \[/латекс]. В каком диапазоне можно регулировать R ₃ ?

Глоссарий

нулевых измерений:

методы более точного измерения тока и напряжения за счет балансировки цепи так, чтобы ток не протекал через измерительное устройство

потенциометр:

прибор измерения нуля для измерения потенциалов (напряжений)

Омметр:

прибор, который прикладывает напряжение к сопротивлению, измеряет ток, вычисляет сопротивление по закону Ома и обеспечивает считывание этого рассчитанного сопротивления

мостовое устройство:

устройство, образующее мост между двумя ветвями цепи; некоторые мостовые устройства используются для измерения нуля в схемах

Мост Уитстона:

прибор для измерения нуля для расчета сопротивления путем уравновешивания падения потенциала в цепи

Избранные решения проблем и упражнения

1.24,0 В

3. 1,56 кОм

5. (а) 2,00 В (б) 9,68 Ом

6. Диапазон = от 5,00 Ом до 5,00 кОм

Мост Уитстона — Производство тензодатчиков

Конфигурации тензометрических датчиков

с четвертьмостом, полумостом и полным мостом Уитстона.

Все конфигурации тензодатчиков основаны на концепции моста Уитстона.
Мост Уитстона представляет собой сеть из четырех резистивных ветвей. Одна или несколько из этих ног могут быть активными чувствительными элементами.На рисунке 1-1 показана принципиальная схема моста Уитстона.

Рисунок 1-1 . Принципиальная электрическая схема моста Уитстона

Мост Уитстона — это электрический эквивалент двух параллельных цепей делителя напряжения. R1 и R2 составляют одну схему делителя напряжения, а R4 и R3 составляют вторую схему делителя напряжения. Выходной сигнал моста Уитстона измеряется между средними узлами двух делителей напряжения.
Физические явления, такие как изменение деформации, приложенной к образцу, или температурный сдвиг, изменяют сопротивление чувствительных элементов в мосте Уитстона.Конфигурация моста Уитстона используется для измерения небольших изменений сопротивления, создаваемых чувствительными элементами, соответствующих физическим изменениям в образце.
Конфигурации тензодатчиков устроены как мосты Уитстона. Датчик — это совокупность всех активных элементов моста Уитстона. Существует три типа конфигураций тензодатчиков: четвертьмостовой, полумостовой и полный мост. Количество плеч активного элемента в мосту Уитстона определяет тип конфигурации моста.Обратитесь к Таблице 1-1, чтобы узнать, сколько активных элементов находится в каждой конфигурации.

Каждая из этих трех конфигураций подразделяется на несколько типов конфигураций. Ориентация активных элементов и вид измеряемой деформации определяют тип конфигурации

.

Акронимы, формулы и определения переменных

На рисунках и уравнениях в этом документе акронимы, формулы и переменные определены как:

e — измеренная деформация (+ e — деформация растяжения, -e — деформация сжатия).
e _S — смоделированная деформация.
GF — манометрический коэффициент, который должен указывать производитель манометра.
R _г — номинальное сопротивление датчика, которое должно быть указано производителем датчика.
R _L — сопротивление свинца. Если длина проводов велика, RL может значительно повлиять на точность измерения.
Rs — значение резистора калибровки шунта.
U — отношение ожидаемого напряжения сигнала к напряжению возбуждения при включенной схеме калибровки шунта.Параметр U появляется в уравнениях для моделируемой деформации и определяется следующим уравнением:

n — коэффициент Пуассона, определяемый как отрицательное отношение поперечной деформации к осевой деформации (продольной) деформации.
В _CH — напряжение измеренного сигнала.
В _EX — напряжение возбуждения.
В _r — это отношение напряжений, которое используется в уравнениях преобразования напряжения в деформацию и определяется следующим уравнением:

Четвертьмост типа I

В этом разделе представлена ​​информация о конфигурации четвертьмостового тензодатчика типа I.Четвертьмост типа I измеряет осевую деформацию или деформацию изгиба.

Рисунок 1-2 . Четверть-мостовой тип I для измерения осевой деформации и деформации изгиба

Четвертьмост типа I имеет следующие характеристики:

• Один активный тензометрический элемент устанавливается в основном направлении осевой деформации или деформации изгиба.
• Пассивный резистор завершения четвертьмоста (фиктивный резистор) требуется в дополнение к завершению полумоста.
• Изменение температуры в образце снижает точность измерений.
• Чувствительность при 1000 мкс составляет ~ 0,5 мВ _{на выходе} / В _EX на входе.

Рисунок 1-3. Четвертьмостовая схема типа I

Следующие символы относятся к принципиальной схеме и уравнениям:

• R1 и R2 — полумостовые резисторы завершения.
• R3 — четвертьмостовой завершающий резистор (фиктивный резистор).
• R4 — активный тензометрический элемент, измеряющий деформацию растяжения (+ e).

Для преобразования показаний напряжения в единицы деформации используйте следующее уравнение:

Чтобы смоделировать влияние на деформацию применения шунтирующего резистора через R ₃ , используйте следующее уравнение:

Четвертьмост типа II

В этом разделе представлена ​​информация о конфигурации четвертьмостового тензодатчика типа II.
Четвертьмост типа II измеряет осевую деформацию или деформацию изгиба.

Рисунок 1-4. Четверть-мостовой тип II для измерения осевой деформации и деформации изгиба

Четвертьмост типа II имеет следующие характеристики:

• Один активный тензометрический элемент и один пассивный термочувствительный четвертьмостовой элемент (фиктивный датчик). Активный элемент устанавливается в направлении осевой деформации или деформации изгиба. Манекен устанавливается в тесном тепловом контакте с образцом деформации, но не прикрепляется к образцу, и обычно устанавливается поперек (перпендикулярно) основной оси деформации.
• Эту конфигурацию часто путают с конфигурацией полумоста I типа, с той разницей, что в конфигурации полумоста I типа элемент R3 активен и связан с образцом деформации для измерения влияния коэффициента Пуассона.
• Завершающие резисторы обеспечивают завершение полумоста.
• Компенсирует температуру.
• Чувствительность при 1000 мкс составляет ~ 0,5 мВ _{на выходе} / В _EX на входе.

Рисунок 1-5.Принципиальная схема четвертьмостового типа II

Следующие символы относятся к принципиальной схеме и уравнениям:

• R ₁ и R ₂ — полумостовые резисторы завершения.
• R ₃ — четвертьмостовой термочувствительный элемент (манекен).
• R ₄ — активный тензометрический элемент, измеряющий деформацию растяжения (+ e).

Для преобразования показаний напряжения в единицы деформации используйте следующее уравнение:

Чтобы смоделировать влияние на деформацию применения шунтирующего резистора через R ₃ , используйте следующее уравнение:

Полумост типа I

В этом разделе представлена ​​информация о конфигурации полумостового тензодатчика типа I.Полумост типа I измеряет осевую деформацию или деформацию изгиба.

Рисунок 1-6. Полумост для измерения осевой деформации и деформации изгиба, тип I

Полумост типа I имеет следующие характеристики:

• Два активных тензометрических элемента. Один установлен в направлении осевой деформации, другой действует как датчик Пуассона и устанавливается поперек (перпендикулярно) главной оси деформации.
• Завершающие резисторы обеспечивают завершение полумоста.
• Чувствителен как к осевой деформации, так и к деформации изгиба.
• Компенсирует температуру
• Компенсирует совокупное влияние на измерение основной деформации из-за коэффициента Пуассона материала образца.
• Чувствительность на 1000 мкс составляет ~ 0,65 мВ _{на выходе} / В _EX на входе.

Рисунок 1-7. Схема полумостового типа I

Следующие символы относятся к принципиальной схеме и уравнениям:

• R ₁ и R ₂ — полумостовые резисторы завершения.
• R ₃ — активный тензометрический элемент, измеряющий сжатие от эффекта Пуассона (–ne).
• R ₄ — активный тензометрический элемент, измеряющий деформацию растяжения (+ e).

Для преобразования показаний напряжения в единицы деформации используйте следующее уравнение:

Чтобы смоделировать влияние на деформацию применения шунтирующего резистора через R ₃ , используйте следующее уравнение:

Полумост типа II

В этом разделе представлена ​​информация о конфигурации полумостового тензодатчика типа II.
Полумост типа II измеряет только деформацию изгиба.

Рисунок 1-8. Полумост типа II, отклоняющий осевую и измерительную деформацию изгиба

Конфигурация полумоста типа II имеет следующие характеристики:

• Два активных тензометрических элемента. Один установлен в направлении деформации изгиба на одной стороне деформированного образца (вверху), другой — в направлении деформации изгиба на противоположной стороне (внизу).
• Завершающие резисторы обеспечивают завершение полумоста.
• Чувствителен к деформации изгиба.
• Отклоняет осевую деформацию.
• Компенсирует температуру.
• Чувствительность на 1000 мкс составляет ~ 1 мВ _{на выходе} / В _EX на входе.

Рисунок 1-9. Принципиальная схема полумоста типа II

Следующие символы относятся к принципиальной схеме и уравнениям:

• R ₁ и R ₂ — полумостовые резисторы завершения.
• R ₃ — активный тензометрический элемент, измеряющий деформацию сжатия (–e).
• R ₄ — активный тензометрический элемент, измеряющий деформацию растяжения (+ e).

Для преобразования показаний напряжения в единицы деформации используйте следующее уравнение:

Чтобы смоделировать влияние на деформацию применения шунтирующего резистора через R ₃ , используйте следующее уравнение:

Полный мост I

В этом разделе представлена ​​информация для полномостового тензодатчика типа I.
Мостовой мост типа I измеряет только деформацию изгиба.

Рисунок 1-10. Полномостовой мост типа I для подавления осевой и измерения деформации изгиба

Конфигурация полного моста типа I имеет следующие характеристики:

• Четыре активных тензометрических элемента. Два устанавливаются в направлении деформации изгиба на одной стороне деформированного образца (вверху), два других — в направлении деформации изгиба на противоположной стороне (внизу).
• Очень чувствителен к деформации изгиба.
• Отклоняет осевую деформацию.
• Компенсирует температуру.
• Компенсирует сопротивление проводов.
• Чувствительность на 1000 мкс составляет ~ 2,0 мВ _{на выходе} / В _EX на входе.

Рисунок 1-11. Принципиальная схема полного моста типа I

Следующие символы относятся к принципиальной схеме и уравнениям:

Для преобразования показаний напряжения в единицы деформации используйте следующее уравнение:

Чтобы смоделировать влияние на деформацию применения шунтирующего резистора через R ₃ , используйте следующее уравнение:

Полный мост типа II

В этом разделе представлена ​​информация о конфигурации тензодатчика типа II с полным мостом.
Полный мост типа II измеряет только деформацию изгиба.

Рисунок 1-12. Полномостовой мост, тип II, отклоняющий осевую и измерительную деформацию изгиба

Конфигурация полного моста типа II имеет следующие характеристики:

• Четыре активных тензометрических элемента. Два из них устанавливаются в направлении деформации изгиба: один с одной стороны деформированного образца (вверху), другой — с противоположной стороны (внизу). Два других действуют вместе как пуассоновский манометр и устанавливаются поперек (перпендикулярно) главной оси деформации, причем один на одной стороне образца деформации (вверху), а другой — на противоположной стороне (внизу).
• Отклоняет осевую деформацию.
• Компенсирует температуру.
• Компенсирует совокупное влияние на измерение основной деформации из-за коэффициента Пуассона материала образца.
• Компенсирует сопротивление проводов.
• Чувствительность на 1000 мкс составляет ~ 1,3 мВ _{на выходе} / В _EX на входе.

Рисунок 1-13. Принципиальная схема полного моста типа II

Следующие символы относятся к принципиальной схеме и уравнениям:

• R ₁ — активный тензодатчик, измеряющий эффект Пуассона сжатия (–ne).
• R ₂ — активный тензодатчик, измеряющий эффект Пуассона при растяжении (+ ne).
• R ₃ — активный тензометрический элемент, измеряющий деформацию сжатия (–e).
• R 4 — активный тензометрический элемент, измеряющий деформацию растяжения (+ e).

Для преобразования показаний напряжения в единицы деформации используйте следующее уравнение:

Чтобы смоделировать влияние на деформацию применения шунтирующего резистора через R ₃ , используйте следующее уравнение:

Полный мост, тип III

В этом разделе представлена ​​информация для полномостового тензодатчика типа III.
Мостовой мост типа III измеряет только осевую деформацию.

Рисунок 1-14. Полномостовой тип III для измерения осевой и отклоняющей деформации изгиба

Конфигурация полного моста типа III имеет следующие характеристики:

• Четыре активных тензометрических элемента. Два устанавливаются в направлении осевой деформации, причем один на одной стороне деформируемого образца (вверху), а другой — на противоположной стороне (внизу). Два других действуют вместе как пуассоновский манометр и устанавливаются поперек (перпендикулярно) главной оси деформации, причем один на одной стороне образца деформации (вверху), а другой — на противоположной стороне (внизу).
• Компенсирует температуру.
• Не допускает деформации изгиба.
• Компенсирует совокупное влияние на измерение основной деформации из-за коэффициента Пуассона материала образца.
• Компенсирует сопротивление проводов.
• Чувствительность на 1000 мкс составляет ~ 1,3 мВ _{на выходе} / В _EX на входе.

Рисунок 1-15. Принципиальная схема полного моста типа III

Следующие символы относятся к принципиальной схеме и уравнениям:

• R ₁ — активный тензодатчик, измеряющий эффект Пуассона сжатия (–ne).
• R ₂ — активный тензометрический элемент, измеряющий деформацию растяжения (+ e).
• R ₃ — активный тензометрический элемент, измеряющий эффект Пуассона сжатия (–ne).
• R ₄ — активный тензометрический элемент, измеряющий деформацию растяжения (+ e).

Для преобразования показаний напряжения в единицы деформации используйте следующее уравнение:

Чтобы смоделировать влияние на деформацию применения шунтирующего резистора через R ₃ , используйте следующее уравнение:

Общие сведения о схеме тензометрического датчика с мостом Уитстона

Тензодатчик в основном работает по принципу простого металлического проводника, который имеет тенденцию влиять на его длину, площадь поперечного сечения и сопротивление из-за приложенного напряжения.Это связано с тем, что длина провода прямо пропорциональна сопротивлению провода и обратно пропорциональна его площади поперечного сечения согласно следующему уравнению.

R = ρ \ frac {L} {A}
Здесь R = сопротивление провода,
ρ = удельное сопротивление
L = длина провода
и A = площадь поперечного сечения провода

Величина деформации, вызванной напряжением, определяется путем измерения изменения сопротивления датчика в результате изменения размеров объекта из-за приложенной силы.Это изменение сопротивления меньше по сравнению с сопротивлением тензодатчика, и, следовательно, его необходимо точно измерить для определения деформации. Чтобы измерить это небольшое изменение сопротивления, используется схема моста Уитстона. Он позволяет с большой точностью измерять относительные изменения тензодатчика в диапазоне от 10 ^-4 до 10 ^-2 Ом / Ом.

Типичная мостовая схема Уитстона состоит из простой сети из четырех резисторов с одинаковым сопротивлением, соединенных встык, образуя квадрат, как показано на рисунке ниже.К одной паре диагональных углов схемы прикладывается напряжение возбуждения, а на другой паре измеряется выходной сигнал моста. Выходная мощность моста, то есть значение V ₀ , зависит от соотношения сопротивлений резисторов, то есть R ₁ : R ₄ и R ₂ : R ₃ .

Когда мост уравновешен и на тензодатчик не возникает деформаций, соотношение между четырьмя сопротивлениями может быть выражено как:

\ frac {R1} {R4} = \ frac {R2} {R3}

Теперь, поскольку V ₀ = V ₊ — V _—, это подразумевает V ₀ = 0

Формы цепей моста Уитстона

В некоторых приложениях, в зависимости от задачи измерения, как правило, только некоторые из плеч моста содержат активные тензодатчики, а остальная часть состоит из резисторов завершения моста.Сюда входят устройства моста, такие как четвертьмост, полумост или диагональный мост. Для приложений с очень строгими требованиями к точности предпочтительна полная перемычка.

Мост Квартал Уитстона

В случае увеличения сопротивления одного из резисторов в мосте из-за приложенной силы мост больше не остается сбалансированным. Эта конфигурация известна как тензодатчик четвертьмостового моста.

Здесь \ frac {R1} {(R4 + ΔR)} ≠ \ frac {R2} {R3} и V0 ≠ 0

Теперь, используя формулу делителя напряжения, получаем
VC = \ frac {R1} {(R1 + R2)} VEX
VD = \ frac {(R4 + ΔR)} {(R4 + ΔR) + R3}) VEX
Кроме того, падение напряжения V ₀ можно выразить как:
V0 = \ frac {(R + ΔR)} {(R + (R + ΔR))} VEX — \ frac {R} {(R + R)} VEX [Так как R1 = R2 = R3 = R4 = R]
При дальнейшем упрощении мы получаем
V0 = \ frac {(Vex ΔR)} {(4R + 2ΔR)}
Теперь, поскольку R >> ΔR и 4R >> 2ΔR , получаем следующее окончательное уравнение:
V0 = \ frac {Vex} {4} \ times \ frac {ΔR} {R}

В приведенном выше уравнении ΔR / R — электрическая деформация, а калибровочный коэффициент называется отношением электрической деформации и механической деформации.Следовательно, приведенное выше уравнение можно переписать как:
V0 = \ frac {Vex} {4} \ times k \ times ϵ
, где k = калибровочный коэффициент
и ϵ = механическая деформация
В четвертьмостовой схеме, как расстояние между тензодатчиком и тремя другими сопротивлениями неизвестно, может существовать значительное сопротивление провода, которое может повлиять на измерение. В этом случае сопротивление тензодатчика будет не единственным измеряемым сопротивлением, но сопротивление провода также будет влиять на измерение выходного напряжения.Этот нежелательный эффект можно свести к минимуму, добавив третий провод, подключенный непосредственно к верхнему проводу тензодатчика.

Половина моста Уитстона
Когда мы устанавливаем два активных тензодатчика на изгибающуюся балку, размещая один спереди и один сзади, мы получаем схему полумоста. Это связано с тем, что половина из четырех резисторов в цепи теперь являются тензодатчиками. При таком расположении оба тензодатчика будут реагировать на индуцированную деформацию, тем самым делая мост более чувствительным к приложенной силе.По сравнению с четвертьмостовой конфигурацией, полумостовая схема дает удвоенное выходное напряжение для заданной деформации, тем самым улучшая чувствительность схемы в два раза.

Рассмотрим пример консольной балки, которая прикреплена к лабораторному столу, и к концу балки прилагается груз. В установке есть тензодатчик, прикрепленный к верхней поверхности балки, а другой прикреплен к нижней поверхности (см. Случай 1). Поскольку балка деформируется из-за приложенной силы, верхний датчик деформации растягивается, а нижний датчик деформации сжимается.Следовательно, выходное напряжение в этом случае можно выразить как:

V0 = \ frac {Vex} {4} \ times \ frac {(ΔR3 — ΔR4)} {R}
V0 = \ frac {Vex} {4} \ times k \ times (ϵ3-ϵ4) (с ϵ3 = -ϵ4 = ϵ)
V0 = \ frac {Vex} {2} \ times k \ times ϵ

Если тензодатчики подключены по диагонали напротив друг друга, как показано на рисунке выше (случай 2), выходное напряжение будет выражено как:
V0 = \ frac {Vex} {4} \ times \ frac {(ΔR2 — ΔR4)} {R}
V0 = \ frac {Vex} {4} \ times k \ times (ϵ2 + ϵ4) (с ϵ2 = ϵ4 = ϵ)
V0 = \ frac {Vex} {2} \ times k \ раз ϵ

Полный мост Уитстона
При замене всех резисторов схемы моста Уитстона четырьмя активными тензодатчиками мы получаем полную мостовую схему.Такая конфигурация обеспечивает большие выходные сигналы тензодатчиков, улучшает температурную компенсацию и предлагает еще большую чувствительность. Полномостовой тензодатчик Мост Уитстона дает линейный выходной сигнал, чем другие конфигурации, поскольку выходное напряжение прямо пропорционально приложенной силе, без какого-либо другого приближения, в отличие от четверть- и полумостовых конфигураций.

В этой схеме два диагонально прикрепленных тензодатчика, которые установлены на нижней части консольной балки, сжимаются, а два других растягиваются во время процесса.Это вызывает как положительные, так и отрицательные изменения сопротивлений в цепи. При приложении силы сопротивления всех тензодатчиков изменяются на величину ΔR, что дает следующее уравнение:
V0 = \ frac {VEX} {4} \ times (\ frac {ΔR1} {R1} — \ frac {ΔR2 } {R2} + \ frac {ΔR3} {R3} — \ frac {ΔR4} {R4})
V0 = \ frac {VEX} {4} \ times \ frac {k} {4} (ϵ1-ϵ2 + ϵ3 -ϵ4)

Как известно, полумостовая и полная мостовая конфигурации обеспечивают большую чувствительность и точность.