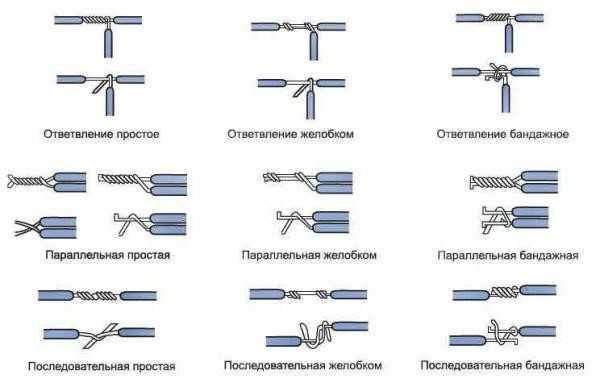
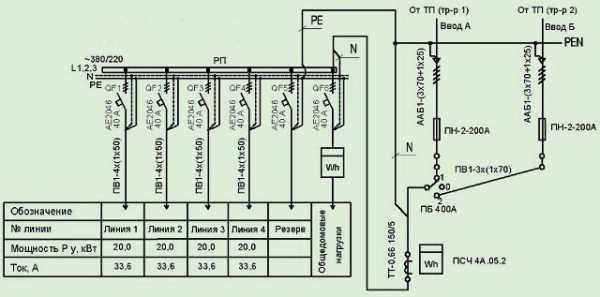
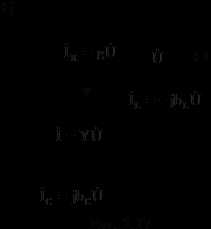Невоспроизводимые косвенные измерения. Косвенное измерение примеры

7. Виды и методы измерений. Прямые измерения. Косвенные измерения. Совместные измерения?

Цель измерения – получение значения этой величины в форме, наиболее удобной для использования.

Классификация измерений

П о х а р а к т е р и с т и к е т о ч н о с т и:

• Равноточные измерения – ряд измерений какой-либо величины, выполненных в одинаковых условиях.

• Неравноточные измерения – ряд измерений, выполненных СИ различной точности и в разных условиях.

П о к о л и ч е с т в у и з м е р и т е л ь н о й и н ф о р м а ц и и:

Однократные измерения – число измерений равно числу измеряемых величин.

Многократные измерения – минимальное число измерений величины больше трех.

П о в ы р а ж е н и ю р е з у л ь т а т а и з м е р е н и й:

Абсолютные измерения -- это такие, при которых используются прямое измерение одной (иногда нескольких) основной величины и физическая константа. Так, в известной формуле Эйнштейна E =mc2 масса (m) – основная физическая величина, которая может быть измерена прямым путем (взвешиванием), а скорость света (с) – физическая константа.

Относительные измерения - установление отношения измеряемой величины к однородной, применяемой в качестве единицы.

Прямые измерения – непосредственное сравнение физической величины с ее мерой. Например, при определении длины предмета линейкой происходит сравнение искомой величины (количественного выражения значения длины) с мерой, т.е. линейкой.

Косвенные измерения - искомое значение величины устанавливают по результатам прямых измерений таких величин, которые связаны с искомой определенной зависимостью.

П о м е т р о л о г и ч е с к о м у н а з н а ч е н и ю:

Технические измерения – с помощью рабочих средств. Применяются в науке и технике, с целью контроля параметров изделий, процессов и т.д.

Метрологические измерения – при помощи эталонов и образцовых средств измерения, с целью воспроизведения единиц физических величин для передачи их размера рабочим средствам измерений.

П о с п о с о б у п о л у ч е н и я р е з у л ь т а т о в и з м е р е н и й :

Совместные измерения - измерения одновременно двух или нескольких разноименных величин для нахождения зависимости между ними.

Совокупные измерения – это проводимые одновременно измерения одноименных величин, при которых значения искомых величин находят решением системы уравнений, получаемых при измерениях этих величин в различных состояниях.

Методы измерения (МИ) – способ получения результата измерений путем использования принципов и средств измерений.

МИ подразделяются на:

Преимущество – быстрота измерений, обусловливающая незаменимость для практического применения. Недостаток – ограниченная точность.

• Метод сравнения с мерой – измеряемая величина сравнивается с величиной, воспроизводимой мерой. Пример: измерение длины линейкой.

Преимущество – большая точность измерения, чем при методе непосредственной оценки. Недостаток – большие затраты времени на подбор мер.

• Метод противоставления – измеряемая величина и величина, воспроизводимая мерой, единовременно действует на прибор сравнения, с помощью которого устанавливают соотношение между этими величинами.

Например, взвешивание на равноплечных весах, при котором измеряется масса, определяется как сумма массы гирь, ее уравновешивающих, и показаний по шкале весов.

Преимущество – уменьшение воздействия на результаты измерения факторов, влияющих на искажение сигналов измерительной информации. Недостаток – увеличение времени взвешивания.

• Косвенный метод измерения – измерение физической величины одного наименования, связанной с другой искомой величиной, определенной функциональной зависимостью, с последующим расчетом путем решения управления. Косвенные методы широко применяются при химических методах испытания.

Преимущества – возможность измерения величин, для которых отсутствуют методы непосредственной оценки или они не дают достоверных результатов или связаны со значительными затратами. Недостатки – повышенные затраты времени и средств на измерение.

studfiles.net

Косвенные измерения

Пусть А, В, С, … - величины, измеряемые непосредственно,

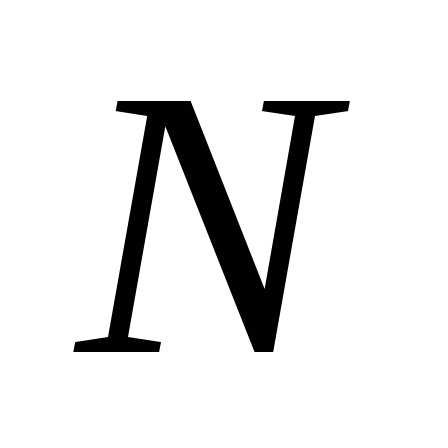- результат косвенного измерения, причем

Задача ставится так: найти погрешность косвенного измерения , которую оно приобретает вследствие наличия погрешностей у прямых измерений А,В,С,…. Будем искать для выражение в виде , если Здесьявляются средними арифметическими значениями, найденными по результатам прямых измерений. Разложение функции в ряд Тейлора около точки со значениями аргументов 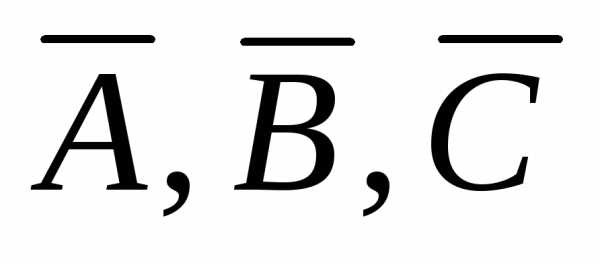, … имеет вид

(10)

где символ обозначает частную производную функциипо переменной х. Отметим, что частная производная функции нескольких переменных по некоторой из них вычисляется по правилам дифференцирования функции одной переменной, при фиксированных значениях всех остальных, т.е. при вычислении производной их следует считать константами.

По определению, точка, в окрестности которой лежит истинное значение физической величины задается равенством

. (11)

тогда из (10) следует, что

(12)

Разделив обе части этого выражения на (11), получим

(13)

Отношение есть относительная погрешность величиныN. Из (12) следует

Введем величину

(14)

которая соответствует худшему для нас варианту оценки искомой величины N и представляет собой предельную абсолютную погрешность косвенного измерения. Тогда

Аналогично можно получить формулу предельной относительной погрешности косвенного измерения

(15)

На практике, рассчитывая погрешность косвенного измерения, значок “max” часто не пишут, однако всегда имеют в виду предельные погрешности, определяемые выражениями (14) и (15). Предельная абсолютная погрешность косвенного измерения вычисляется как дифференциал от по переменным А, В,…, причем производные вычисляются в точке, где частные дифференциалы берутся по абсолютной величине и роль дифференциалов dА, dВ, … играют погрешности прямых измерений Аналогичное правило можно сформулировать для вычисления предельной относительной погрешности косвенного измерения с той лишь разницей, что дифференциал следует брать не от , а от

Полученные нами формулы предельных абсолютной и относительной погрешностей косвенного измерения гарантируют при надежности, для которой мы вычисляем А, В, … прямых измерений доверительный интервал для косвенного измерения. Но этот интервал является “предельным”, завышенным. В теории ошибок существует метод сужения доверительного интервала косвенного измерения. Однако для целей учебной лаборатории достаточно ограничиться вычислением его предельного значения.

Остается лишь дать рекомендации, какой из формул – (14) или (15) – выгоднее пользоваться в конкретных случаях. Если косвенное измерение является алгебраической суммой прямых измерений, то удобнее вычислять абсолютную погрешность . Однако в большинстве случаев приходится иметь дело с более сложными функциональными зависимостями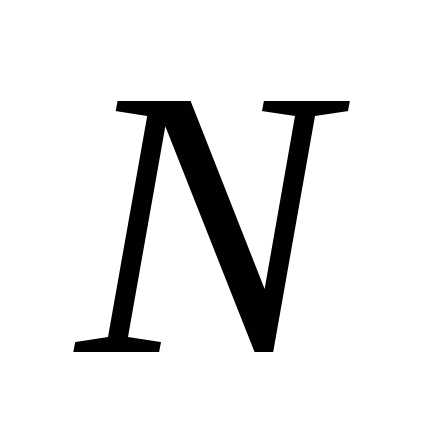от А, В, … Тогда удобнее вычислять сначала относительную погрешность величины, а затем абсолютную, - умножив среднее значение величинына ее относительную погрешность (для записи окончательного результата нужна именно абсолютная погрешность).

Пример.

В качестве иллюстрации применения приведенных общих формул для расчета абсолютной и относительной погрешности косвенного измерения рассмотрим задачу экспериментального определения плотности вещества, из которого изготовлен параллелепипед.

Впредположении однородности вещества параллелепипеда его плотность определяется формулой

(I)

где m масса параллелепипеда, а, b, с – соответственно его длина, ширина и высота. Величины m, а, b, с определяются в прямых измерениях, тогда как вычисляется по формуле (I), т.е. является результатом косвенного измерения. Аналитическая структура формулы (I) такова, что удобнее сначала вычислить относительную погрешность измерения, а затем относительную. Действительно, логарифмируя (I), получим

Тогда

(II)

Подставляя выражение (II) в (15), находим

(III)

где m, a, b, c – абсолютные погрешности соответствующих величин. Тогда абсолютная погрешность косвенного измерения вещества вычисляется по формуле

(IV)

где

ПРАВИЛА ЗАПИСИ И ВЫЧИСЛЕНИЙ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Все верные цифры приближенного числа, начиная с первой, отличной от нуля, называются значащими. Верными является цифры числа, стоящие в разрядах белее высоких, чем разряд первой отличной от нуля цифры его погрешности. Абсолютная погрешность не слишком ответственных измерений округляется до первой, отличной от нуля цифры. Если эта цифра единица, то ее часто уточняют, указывая следующую за ней цифру. Относительная погрешность округляется до первых двух цифр. В конечных результатах указываются все значащие цифры и первая сомнительная. Окончательные результаты записываются в нормальном виде, т.е. в виде произведения двух сомножителей, первым из которых является рассматриваемый результат, причем первая значащая цифра его написана в разряде единиц, остальные - в разрядах десятых, сотых и т.д. долей; вторым сомножителем является 10 в соответствующей степени. Примеры правильно записанных приближенных чисел:

Значащие цифры в приведенных приближенных числах подчеркнуты.

Точность приближенных чисел находится в прямом соответствия с количеством значащих цифр в этих числах. Нетрудно проверить, что относительная погрешность приближенных чисел, имеющих одну значащую цифру, изменяется в пределах от нескольких процентов до нескольких десятков процентов, имеющих 2-значащие цифры - от нескольких десятков долей процента до нескольких процентов, имеющих 3-значащие цифры - от нескольких сотых долей процента до нескольких десятых долей процента и т.д. В учебной лаборатории мы имеем дело с результатами измерений, а которых только одна, две, редко три цифры является значащими.

Рассматривая формулы предельных погрешностей, мы установили, что почти во всех случаях (за редкими исключениями) относительная погрешность косвенного измерения оказывается больше, чем относительная погрешность наименее точного из прямых измерений. Следовательно, количество значащих цифр в косвен­ном измерении не может быть большим, чем количество значащих цифр в наименее точном прямом измерении. Поэтому результаты прямых измерений и промежуточных вычислений рекомендуется округлять так, чтобы в них было на одну цифру больше, чем в наименее точном прямом измерении. Конечный ответ округляется в соответствии с его погрешностью. Однако еще до его вычисления из грубого предварительного анализа результатов прямых измерений может быть ясно, сколько в нем будет цифр.

ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

При построения графиков следует учитывать погрешности изображаемых величин, а также заботиться о том, чтобы их графическое представление не сообщило им дополнительных ошибок. Масштаб должен выбираться по возможности таким образом, чтобы 1) самое малое деление шкалы было одного порядка с погрешностью наносимой величины, 2) линия графика в своей средней части должна быть расположена под углом к координатным осям, близким к 45°. Вследствие имеющихся погрешностей каждый результат на графике представляет собой не точку, а целую область, прямоугольник. Поэтому линия графика должна быть плавной линией, преходящей в каком-либо месте через каждый такой прямоугольник. Примерный вид графика изображен на рисунке.

В некоторых случаях изобразить погрешность на графике нет возможности. Тогда она должна быть указана на соответствующей шкале.

studfiles.net

Невоспроизводимые косвенные измерения

Иногда при выполнении косвенных измерений невозможно повторить наблюдения в тождественных условиях относительно одного или нескольких аргументов измеряемой функции. Например, при измерении коэффициента вязкости жидкости в нее бросают металлические шарики (дробинки). Каждый из брошенных в жидкость шариков сразу же достать нельзя. Условия опытов, повторенных с разными шариками, не будут одинаковыми из-за различия размеров и формы шариков, различного состояния их поверхностей и т.д. В этом случае говорят, что косвенные измерения невоспроизводимы. Тем не менее коэффициент вязкости характеризует одну и ту же исследуемую жидкость, и расчет должен давать близкие значения этого коэффициента для всех шариков.

Для невоспроизводимых косвенных измерений рекомендуется следующий порядок обработки их результатов.

1) Определить значение искомой функции для каждогоого невоспроизводимого наблюдения, исходя из найденных экспериментальных значений аргументов,

2) Каждое из определенных таким образом значений рассматривается затем как случайная величина с нормальным законом распределения погрешностей. Иначе говоря, значениярассматриваются как результаты прямых многократных измерений физической величины. В соответствии с этим в качестве наиболее вероятного значения берется среднее арифметическое

,

а погрешность вычисляется по формуле (как случайная погрешность)

,

т.е. по правилам обработки результатов прямых многократных измерений.

Примеры обработки результатов косвенных измерений

Пример 1. В работе № 103 коэффициент поверхностного натяжения жидкости определяется по расчетной формуле

(16)

где – сила поверхностного натяжения,и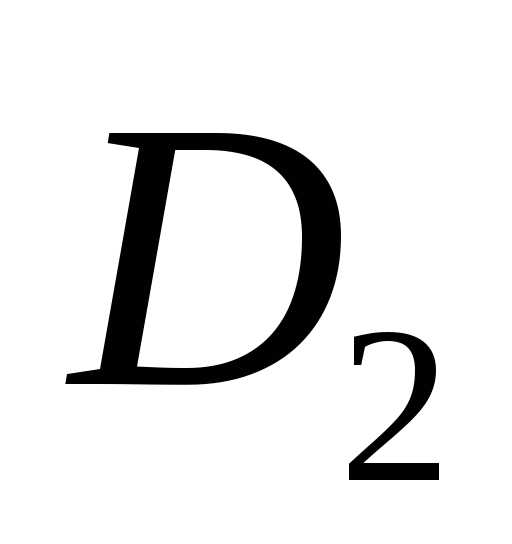– внутренний и внешний диаметры кольца соответственно.

Для получения расчетной формулы погрешности учтем, что выражение (16) относительно удобно для логарифмирования (содержит три множителя:) и, следовательно, целесообразно искать погрешность по формуле (15) с учетом замены соответствующих значений функции и аргументов:

Прологарифмировав выражение (16), получим

Находим частные производные

Выражение для расчета относительной погрешности будет

Отсутствие в данной формуле значения относительной погрешности числа обусловлено тем, что в настоящее время значение этого числа известно с высокой точностью.

Пример 2. В работе № 108 требуется определить отношение теплоемкостей (коэффициент Пуассона) воздуха 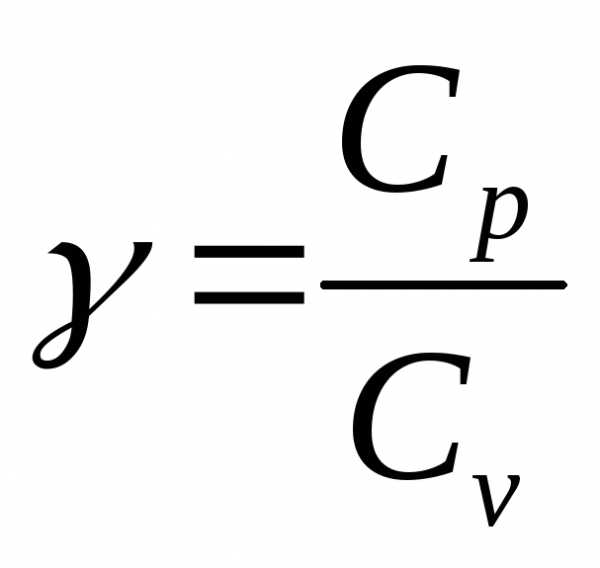. Расчетная формула имеет вид

(17)

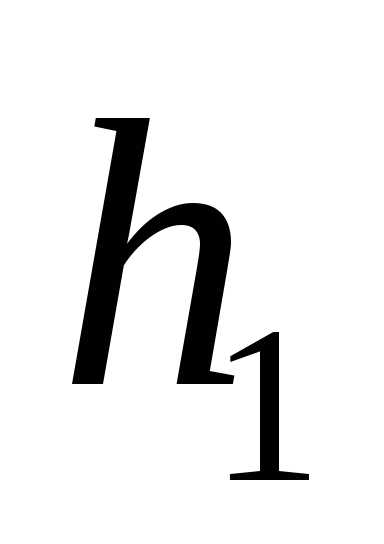где и– разности уровней жидкости (воды) в манометре для некоторых двух состояний воздуха в сосуде.

Косвенные измерения в данном эксперименте являются невоспроизводимыми, поскольку, повторяя опыт, накачать и выпустить каждый раз одинаковое количество воздуха невозможно. Значения вычисляются в каждом наблюдении по результатам прямых измерений величини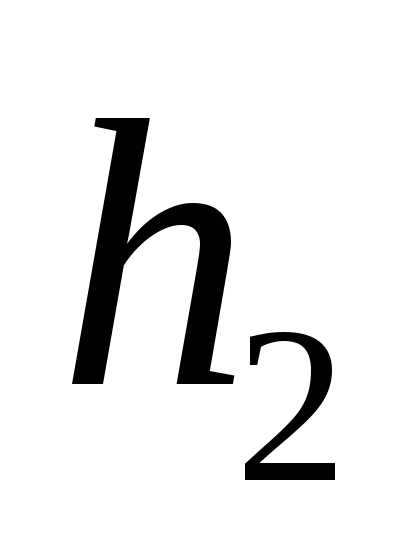, а затем обрабатываются как результаты прямых многократных измерений. Следовательно, доверительная погрешностьопределяется как случайная по формуле

.

Пример 3. В лабораторной работе № 117 коэффициент жесткости пружины определяется по формуле

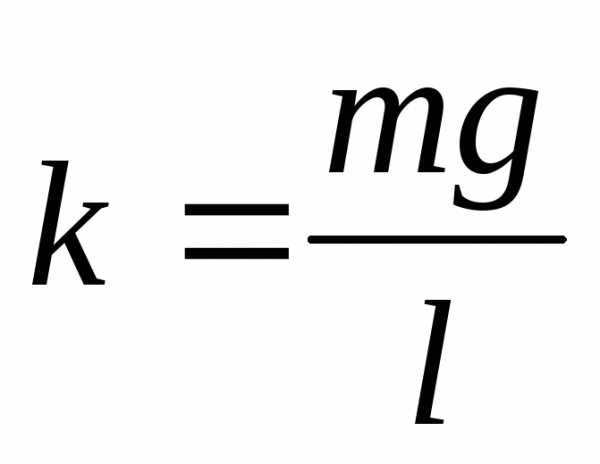, (18)

где – коэффициент жесткости,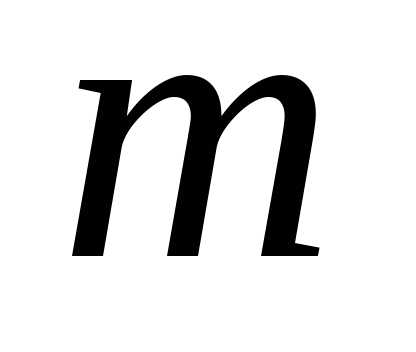– масса груза,– среднее удлинение пружины при увеличении массы груза на 50 г,– ускорение свободного падения (на широте Санкт–Петербурга).

Воспользовавшись алгоритмом обработки результатов косвенных измерений в случае удобной для логарифмирования расчетной формулы, получим (см. пример 1) выражение

в котором погрешностью ускорения свободного падения можно пренебречь в силу ее малости.

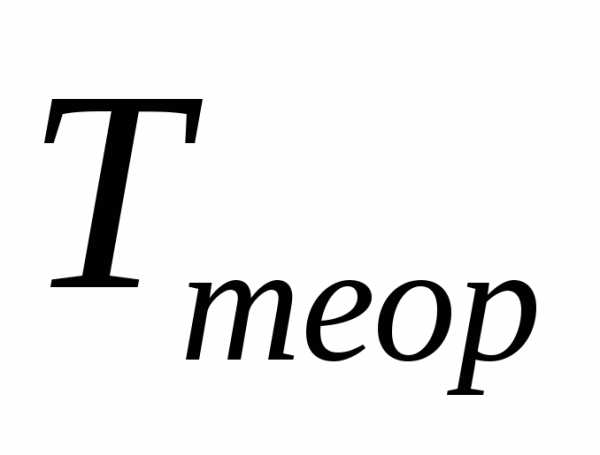В этой работе требуется также найти экспериментальное и расчетное значения периодов колебания груза и(масса груза задается преподавателем). Соответствующие формулы погрешностей имеют следующий вид:

а) для расчетного значения периода колебания груза

б) для периода колебаний, измеренного с помощью секундомера,

.

Пример 4. В работе № 131 термический коэффициент линейного расширения твердых тел определяется соотношением

(19)

где – приращение длины образца при изменении температуры на,– длина исследуемого образца при комнатной температуре.

Выражение (19) удобно для логарифмирования, поэтому относительную погрешность измеряемой величины находим как в примере 1, выполняя математические операции логарифмирования и дифференцирования. В результате получаем формулу

где –доверительные погрешности соответствующих аргументов.

В данной работе может быть использован и алгоритм обработки результатов косвенных невоспроизводимых измерений, если полученные на разных участках исследуемого температурного диапазона значения термического коэффициента линейного расширения не будут соответствовать четко выраженной монотонной зависимости.

studfiles.net

Косвенные измерения

Пусть А, В, С, … - величины, измеряемые непосредственно,

- результат косвенного измерения, причем

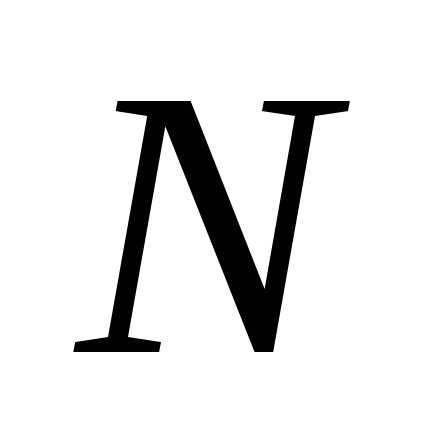Задача ставится так: найти погрешность косвенного измерения , которую оно приобретает вследствие наличия погрешностей у прямых измерений А,В,С,…. Будем искать для выражение в виде , если Здесьявляются средними арифметическими значениями, найденными по результатам прямых измерений. Разложение функции в ряд Тейлора около точки со значениями аргументов , … имеет вид

(10)

где символ обозначает частную производную функциипо переменной х. Отметим, что частная производная функции нескольких переменных по некоторой из них вычисляется по правилам дифференцирования функции одной переменной, при фиксированных значениях всех остальных, т.е. при вычислении производной их следует считать константами.

По определению, точка, в окрестности которой лежит истинное значение физической величины задается равенством

. (11)

тогда из (10) следует, что

(12)

Разделив обе части этого выражения на (11), получим

(13)

Отношение есть относительная погрешность величиныN. Из (12) следует

Введем величину

(14)

которая соответствует худшему для нас варианту оценки искомой величины N и представляет собой предельную абсолютную погрешность косвенного измерения. Тогда

Аналогично можно получить формулу предельной относительной погрешности косвенного измерения

(15)

На практике, рассчитывая погрешность косвенного измерения, значок “max” часто не пишут, однако всегда имеют в виду предельные погрешности, определяемые выражениями (14) и (15). Предельная абсолютная погрешность косвенного измерения вычисляется как дифференциал от по переменным А, В,…, причем производные вычисляются в точке, где частные дифференциалы берутся по абсолютной величине и роль дифференциалов dА, dВ, … играют погрешности прямых измерений Аналогичное правило можно сформулировать для вычисления предельной относительной погрешности косвенного измерения с той лишь разницей, что дифференциал следует брать не от , а от

Полученные нами формулы предельных абсолютной и относительной погрешностей косвенного измерения гарантируют при надежности, для которой мы вычисляем А, В, … прямых измерений доверительный интервал для косвенного измерения. Но этот интервал является “предельным”, завышенным. В теории ошибок существует метод сужения доверительного интервала косвенного измерения. Однако для целей учебной лаборатории достаточно ограничиться вычислением его предельного значения.

Остается лишь дать рекомендации, какой из формул – (14) или (15) – выгоднее пользоваться в конкретных случаях. Если косвенное измерение является алгебраической суммой прямых измерений, то удобнее вычислять абсолютную погрешность . Однако в большинстве случаев приходится иметь дело с более сложными функциональными зависимостями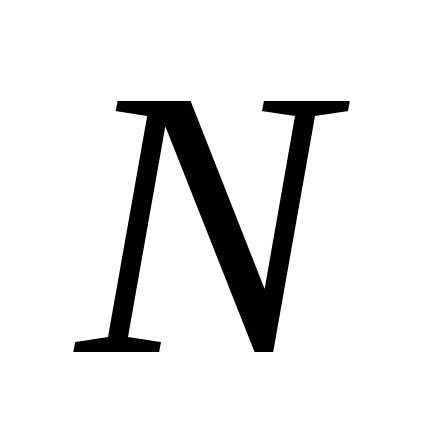от А, В, … Тогда удобнее вычислять сначала относительную погрешность величины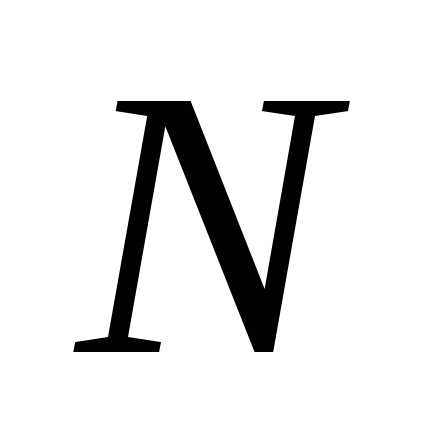, а затем абсолютную, - умножив среднее значение величинына ее относительную погрешность (для записи окончательного результата нужна именно абсолютная погрешность).

Пример.

В качестве иллюстрации применения приведенных общих формул для расчета абсолютной и относительной погрешности косвенного измерения рассмотрим задачу экспериментального определения плотности вещества, из которого изготовлен параллелепипед.

Впредположении однородности вещества параллелепипеда его плотность определяется формулой

(I)

где m масса параллелепипеда, а, b, с – соответственно его длина, ширина и высота. Величины m, а, b, с определяются в прямых измерениях, тогда как вычисляется по формуле (I), т.е. является результатом косвенного измерения. Аналитическая структура формулы (I) такова, что удобнее сначала вычислить относительную погрешность измерения, а затем относительную. Действительно, логарифмируя (I), получим

Тогда

(II)

Подставляя выражение (II) в (15), находим

(III)

где m, a, b, c – абсолютные погрешности соответствующих величин. Тогда абсолютная погрешность косвенного измерения вещества вычисляется по формуле

(IV)

где

ПРАВИЛА ЗАПИСИ И ВЫЧИСЛЕНИЙ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Все верные цифры приближенного числа, начиная с первой, отличной от нуля, называются значащими. Верными является цифры числа, стоящие в разрядах белее высоких, чем разряд первой отличной от нуля цифры его погрешности. Абсолютная погрешность не слишком ответственных измерений округляется до первой, отличной от нуля цифры. Если эта цифра единица, то ее часто уточняют, указывая следующую за ней цифру. Относительная погрешность округляется до первых двух цифр. В конечных результатах указываются все значащие цифры и первая сомнительная. Окончательные результаты записываются в нормальном виде, т.е. в виде произведения двух сомножителей, первым из которых является рассматриваемый результат, причем первая значащая цифра его написана в разряде единиц, остальные - в разрядах десятых, сотых и т.д. долей; вторым сомножителем является 10 в соответствующей степени. Примеры правильно записанных приближенных чисел:

Значащие цифры в приведенных приближенных числах подчеркнуты.

Точность приближенных чисел находится в прямом соответствия с количеством значащих цифр в этих числах. Нетрудно проверить, что относительная погрешность приближенных чисел, имеющих одну значащую цифру, изменяется в пределах от нескольких процентов до нескольких десятков процентов, имеющих 2-значащие цифры - от нескольких десятков долей процента до нескольких процентов, имеющих 3-значащие цифры - от нескольких сотых долей процента до нескольких десятых долей процента и т.д. В учебной лаборатории мы имеем дело с результатами измерений, а которых только одна, две, редко три цифры является значащими.

Рассматривая формулы предельных погрешностей, мы установили, что почти во всех случаях (за редкими исключениями) относительная погрешность косвенного измерения оказывается больше, чем относительная погрешность наименее точного из прямых измерений. Следовательно, количество значащих цифр в косвен­ном измерении не может быть большим, чем количество значащих цифр в наименее точном прямом измерении. Поэтому результаты прямых измерений и промежуточных вычислений рекомендуется округлять так, чтобы в них было на одну цифру больше, чем в наименее точном прямом измерении. Конечный ответ округляется в соответствии с его погрешностью. Однако еще до его вычисления из грубого предварительного анализа результатов прямых измерений может быть ясно, сколько в нем будет цифр.

ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

При построения графиков следует учитывать погрешности изображаемых величин, а также заботиться о том, чтобы их графическое представление не сообщило им дополнительных ошибок. Масштаб должен выбираться по возможности таким образом, чтобы 1) самое малое деление шкалы было одного порядка с погрешностью наносимой величины, 2) линия графика в своей средней части должна быть расположена под углом к координатным осям, близким к 45°. Вследствие имеющихся погрешностей каждый результат на графике представляет собой не точку, а целую область, прямоугольник. Поэтому линия графика должна быть плавной линией, преходящей в каком-либо месте через каждый такой прямоугольник. Примерный вид графика изображен на рисунке.

В некоторых случаях изобразить погрешность на графике нет возможности. Тогда она должна быть указана на соответствующей шкале.

studfiles.net

Измерения косвенные - Справочник химика 21

    Аппараты периодического действия с мешалками и теплообменниками широко применяются в лакокрасочной промышленности [1] и, в частности, при производстве лаковых (алкидных) смол. Контроль за ходом химического процесса в таких аппаратах обычно осуществляется путем измерения косвенного параметра — температуры реакционной смеси 7 (/). Технологический режим производства смол предусматривает три основные стадии 1) нагрев смеси исходных веществ (растительных масел, глицерина, пента-эритрита и др.) до температуры 230—250° С 2) выдержка реакционной смеси при постоянной температуре 3) слив продуктов реакции. [c.279]     По способу получения результата измерения подразделяют на прямые и косвенные. Прямые (абсолютные) измерения — при которых искомое значение измеряемой величины определяют путем непосредственного сравнения ее с мерами или с помощью прибора, проградуированного в принятых единицах измерений. Косвенные измерения состоят в определении измеряемой величины по результатам прямых измерений одной или нескольких других величин, связанных с искомой величиной определенной функциональной зависимостью. [c.182]

    С целью установления правильности геометрической формы деталей и узлов, отклонения их размеров от заданных чертежом и определения износа проводят измерения, которые подразделяют на прямые (абсолютные) и косвенные. При прямых измерениях искомое значение измеряемой величины определяют либо путем непосредственного сравнения ее с мерами, либо с помощью прибора, проградуированного в принятых единицах измерений. Косвенные измерения состоят в определении измеряемой величины по результатам прямых измерений одной или нескольких других величин, связанных с искомой величиной определенной функциональной зависимостью. Методы измерения и контроля подразделяют на контактные и бесконтактные. Контактные измерения выполняют путем контакта измерительного наконечника с поверхностью измеряемой детали, причем характер контакта может быть точечным, линейным или поверхностным. Бесконтактные измерения (оптические, пневматические и др.) выполняют без механического контакта между измерительным наконечником и измеряемой деталью. [c.470]

    Погрешности косвенных измерений. Косвенным называют такое измерение, при котором вначале проводят прямые измерения некоторых величин ( 1, Х2,. ..), а затем по формулам, связывающим эти величины с измеряемой величиной у, вычисляют ее значение. Наиболее часто вычисление результатов косвенных измерений и их ошибок производят по уравнениям  [c.7]

    Общая теория ошибок —специальная область прикладной математики, использующая математический аппарат дифференциального исчисления и посвященная различным аспектам оценки погрешностей косвенных измерений. Косвенными принято называть такие измерения, результат которых находится не в ходе прямого эксперимента, а путем расчета с помощью конкретных функциональных зависимостей, у которых в качестве аргументов выступают результаты тех или иных прямых измерений. [c.116]

    Достоинством прямых методов является возможность охарактеризовать структуру порового пространства без введения дополнительных допущений, необходимых при измерении косвенными методами. Однако прямые методы дают характеристику плоскостной структуры порового пространства, в то время как косвенные методы отражают в интегральной форме пространственное строение, которое определяет основные свойства пористой среды. [c.68]

    Средние размеры, получаемые при измерении косвенными методами, зависят от используемых для этого свойств капель оптических, электрических, механических, термодинамических и т. д. (см. гл. VI. ). Например, при фотометрическом методе средний размер капель равен [c.115]

    Непосредственное измерение А/-вых внутри аппарата сопряжено со значительными трудностями. Поэтому целесообразнее воспользоваться измерением косвенных параметров уровня раздела фаз или перепада давления в колонне, которые однозначно связаны с и Д2-вых- [c.317]

    Радикал Прямое измерение Косвенное измерение Рассчитанные значения  [c.430]

    Наконец, укажем еще, что различные полиморфные формы органических веществ могут сильно отличаться по растворимости. Это обстоятельство заслуживает внимания, когда, как в случае жиров [100], низко плавящиеся и поэтому легко растворимые формы стабилизируются примесями. Таким образом, найденная растворимость, отличающаяся от других измерений, косвенно указывает на загрязнение. [c.127]

    Количественной мерой смачиваемости поверхности веществ служит величина косинуса краевого угла смачивания 0. Определение краевых углов смачивания порошков прямыми методами затруднительно, так как мениски, образующиеся на частица-х порошка, практически недоступны для наблюдения и измерения. Косвенные пути, [c.115]

    Эти методы измерения косвенно характеризуют степень фиксации молекулярной структуры химических волокон. [c.124]

    Кроме того, в указанной монографии приводятся интегральные интенсивности линий, полученные фотоэлектрическим методом и выраженные в единой шкале, а также ширины линий, измеренные косвенным методом по величине 1о и ив ряде случаев степени деполяризации -ЛИНИЙ. При сравнении интегральных интенсивностей линий индивидуальных веществ интенсивность линии 802 см циклогексана принята равной 500. Эти данные могут быть широко использованы для решения аналитических и структурных задач. [c.330]

    Критические плотности тока прямыми методами получены из потенциоста-тнческих поляризационных кривых или подобных измерений. Косвенный метод исходит из соотношения / — = Л / , где I—время, необходимое для до- [c.88]

    Зачастую непрерывное автоматическое измерение показателей качества невозможно или в значительной степени затруднено. Управление качеством продукции при этом производится на основании измерения косвенных параметров, статистически или функционально связанных с показателями качества. При наличии жесткой функциональной зависимости качества продукции от параметров и возможности измерения этих параметров задача определения показателей качества сводится к типичному случаю косвенных измерений. Значение искомой величины при косвенных измерениях получают на основании известной зав исимости, связывающей ее с другими величинами, подвергаемыми прямым измерениям. Как правило, в этом случае процедура контроля и управления качеством сводится к оптимальному управлению в рамках АСУТП. Однако осуществление контроля качества на основании косвенных измерений не всегда возможно и оправдано из-за трудности практической реализации автоматического измерения большого количества параметров сложности получения достаточно точных математических зависимостей показателей качества от измеряемых параметров длительности и большой периодичности анализов при лабораторном контроле параметров. [c.85]

    Внедрение хроматографов в систему промышленного контроля и авао-матического регулирования в настоящее время чрезвыча11но акутально. Существующие схемы автоматического регулирования производственных процессов на химико-технологических, нефтеперерабатывающих и других аналогичных предприятиях в большинстве случаев базируются на измерении косвенных параметров температуры, давления, расхода, уровня и т. д. Схемы управления, построенные на этих датчиках, как правило, не обеспечивают оптимального ведения процесса. [c.439]

    Замкнутые системы. Повышение точности стабилизации МЭЗ может быть достигнуто путем регулирования по отклонению МЭЗ от заданного значения. Ввиду того, что контролировать непосред-етвенно величину МЭЗ при непрерывном режиме работы практически невозможно, информация о фактической величине зазора может быть получена измерением косвенных параметров, функционально связанных с величиной МЭЗ, а именно 1) напряжения на электродах ячейки 7 2) общего технологического тока /  [c.133]

    К+-селективные электроды на основе валиномицина применяли для прямого определения калия в растворах [62], морской воде (методом стандартных добавок) [71 ], природных и сточных водах при использовании их в автоматизированных проточных системах, снабженных мини-компьютером и печатным устройством [72], и в сыворотке крови [73, 74]. Этими же электродами измеряли коэффициенты активности КС в смешанных растворах (КС1 - -+ Г аС ) [75] и активность К в равновесии с аденозинтрифосфа-том. В результате этих измерений Речниц и Мохан [76] определили константу образования комплекса калия с аденозинтрифосфатом (КАТФ ") Кобр = 219. Полученное значение почти в 20 раз превышало измеренное косвенным путем (10—14). Активность калия определяли при pH = 9,2, добавляя растворы К2Н2АТФ (примерно 0 М) и КОН (0,05 М) в 50 мл дистиллированной воды [77]. Концентрацию свободных ионов К" определяли измерением [c.229]

    Дейнтон и др. [62] и Кэмп и др. [148[ исследовали быстро исчезающие спектры поглощения, возникающие в разбавленных растворах нафталина в бензоле при действии коротких импульсов электронов (2 мксек). Этим путем наблюдалось сенсибилизированное растворителем образование триплетного состояния нафталина. ]Тосворти [183] наблюдала перенос энергии возбуждения от бензола к диметилфума-рату и антрацену. Перенос энергии вызывает изомеризацию диметил-фумарата, измеряемую аналитически, и возбуждение антрацена до триплетного состояния, обнаруживаемое путем кинетических измерений ультрафиолетовых спектров в растворах, облученных импульсами излучения. Антрацен, по-видимому, конкурирует с реакцией фумарата, и величины для антрацена и фумарата равны 746 и 320 л моль соответственно. Принимая коэффициент экстинкции равным 7-10 (при 430 нм), можно вычислить величину С образования триплетного состояния антрацена, составляющую 1,1, и О(диметилмалеат) 2. Хотя в этих экспериментах наблюдаются реакции фумарата и антрацена, возбужденных в триплетное состояние, не было доказано, что это то же самое состояние возбуждения, которое переносится донором. Позже Кандэлл и Гриффитс [60] показали, что выход триплетного состояния антрацена в бензоле при добавлении высоких концентраций циклогексена, являющегося тушителем триплетного состояния бензола, может уменьшиться только на 40%, поэтому только часть триплетов антрацена могла образоваться путем реакции переноса энергии триплетов. (Это очень важный результат, делающий ненадежными многие опубликованные величины выхода радиолитического образования триплетного состояния бензола, измеренные косвенными путями. Однако можно возразить, что использованная высокая концентрация циклогексена фундаментально изменяет характеристики ароматической системы, поэтому необходимы очень тщательные исследования, прежде чем отбросить прежние предположения, основанные на ряде хороших корреляций.) [c.126]

    Из этого следует, что температура плавления целлюлозы должна быть очень высокой. Действител .-но, целлюлоза не может быть переведена в расплав, так как при температуре около 300° С начинается процесс быстрого термического распада, первой стадией которого является дегидратация. Температура стеклования целлюлозы, измеренная косвенным путем лежит в области 320—350° С. Если принять во внимание эмпирическое отношб -ние Гс пл = 0,5—0,67, то можно считать, что целлюлозы лежит в области 600—800° С. [c.54]

chem21.info

5.11 Косвенное измерение

Определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.

Пример - Определение плотности тела цилиндрической формы по результатам прямых измерений массы, высотыи диаметра цилиндра, связанных с плотностью уравнением

.

Примечание - Во многих случаях вместо термина косвенное измерение применяют термин косвенный метод измерений

5.12 Совокупные измерения

Проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.

Примечание - Для определения значений искомых величин число уравнений должно быть не меньше числа величин.

Пример - Значение массы отдельных гирь набора определяют по известному значению массы одной из гирь и по результатам измерений (сравнений) масс различных сочетаний гирь

5.13 Совместные измерения

Проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними

5.14 наблюдение при измерении;

наблюдение 

de Messbeobachtung

en observation

fr observation

Операции, проводимые при измерении и имеющие целью своевременно и правильно произвести отсчет.

Примечание - Не следует заменять термин измерение термином наблюдение

5.15 отсчет показаний средства измерений;

отсчет показаний;

отсчет 

Фиксация значения величины или числа по показывающему устройству средства измерений в заданный момент времени.

Пример - Зафиксированное в данный момент времени по табло бытового электрического счетчика значение, равное 505,9 кВт·ч, является отсчетом его показаний на этот момент

5.16 измерительный сигнал

de 

en measurement signal

fr signal de mesure

Сигнал, содержащий количественную информацию об измеряемой физической величине

5.17 измерительная информация

de Messinformation

en measurement information

fr information de mesure

Информация о значениях физических величин

5.18 измерительная задача

Задача, заключающаяся в определении значения физической величины путем ее измерения с требуемой точностью в данных условиях измерений

5.19 объект измерения

Тело (физическая система, процесс, явление и т.д.), которое характеризуется одной или несколькими измеряемыми физическими величинами.

Пример - Коленчатый вал, у которого измеряют диаметр; технологический процесс, во время которого измеряют температуру; спутник Земли, координаты которого измеряются. Это все объекты измерения

5.20 область измерений

Совокупность измерений физических величин, свойственных какой-либо области науки или техники и выделяющихся своей спецификой.

Примечание - Выделяют ряд областей измерений: механические, магнитные, акустические, измерения ионизирующих излучений и др.

5.21 вид измерений

Часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин.

Пример - В области электрических и магнитных измерений могут быть выделены как виды измерений: измерения электрического сопротивления, электродвижущей силы, электрического напряжения, магнитной индукции и др.

5.22 подвид измерений

Часть вида измерений, выделяющаяся особенностями измерений однородной величины (по диапазону, по размеру величины и др.).

Пример - При измерении длины выделяют измерения больших длин (в десятках, сотнях, тысячах километров) или измерения сверхмалых длин - толщин пленок

6 Средства измерительной техники

           

6.1 средства измерительной техники;

измерительная техника

Обобщающее понятие, охватывающее технические средства, специально предназначенные для измерений.

Примечание - К средствам измерительной техники относят средства измерений и их совокупности (измерительные системы, измерительные установки), измерительные принадлежности, измерительные устройства

6.2 средство измерений

de Messmittel

en measuring instrument

fr instrument de mesure;

appareil mesure

Техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени.

Примечания 

1 Приведенное определение вскрывает суть средства измерений, заключающуюся, во-первых, в "умении" хранить (или воспроизводить) единицу физической величины; во-вторых, в неизменности размера хранимой единицы. Эти важнейшие факторы и обусловливают возможность выполнения измерения (сопоставление с единицей), т.е. "делают" техническое средство средством измерений. Если размер единицы в процессе измерений изменяется более чем установлено нормами, таким средством нельзя получить результат с требуемой точностью. Это означает, что измерять можно лишь тогда, когда техническое средство, предназначенное для этой цели, может хранить единицу, достаточно неизменную по размеру (во времени).

2 При оценивании величин по условным шкалам шкалы выступают как бы "средством измерений" этих величин

studfiles.net

косвенное измерение - это... Что такое косвенное измерение?

 косвенное измерение indirect measurement

Большой англо-русский и русско-английский словарь. 2001.

• косвенное зондирование
• косвенное наблюдение

Смотреть что такое "косвенное измерение" в других словарях:

• косвенное измерение — Определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Пример. Определение плотности D тела цилиндрической формы по результатам прямых… …   Справочник технического переводчика

• косвенное измерение — 3.6 косвенное измерение (indirect measurement): Измерение, посредством которого отдельные компоненты и/или группы компонентов, которые не присутствуют в рабочей эталонной газовой смеси, определяются, используя относительные коэффициенты… …   Словарь-справочник терминов нормативно-технической документации

• Косвенное измерение — Основная статья: Измерение Измерения как экспериментальные процессы весьма разнообразны. Это объясняется множеством экспериментальных величин, различным характером измерения величин, различными требованиями точности измерения и другие. Наиболее… …   Википедия

• косвенное измерение — netiesioginis matavimas statusas T sritis automatika atitikmenys: angl. indirect measurement vok. indirekte Messung, f; mittelbare Messung, f rus. косвенное измерение, n pranc. mesurage indirect, m; mesure indirecte, f …   Automatikos terminų žodynas

• косвенное измерение — netiesioginis matavimas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydžio vertės radimas netiesioginiu būdu, kai ieškomoji vertė randama naudojant kitų dydžių tiesioginių matavimų rezultatus. pavyzdys( iai) Vienalytės medžiagos… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• косвенное измерение — netiesioginis matavimas statusas T sritis fizika atitikmenys: angl. indirect measurement vok. indirekte Messung, f rus. косвенное измерение, n pranc. mesure indirecte, f …   Fizikos terminų žodynas

• Косвенное измерение — 1. Измерение, при котором искомое значение величины определяют, исходя из результатов прямых измерений других величин, связанных с искомой величиной известной функциональной зависимостью Употребляется в документе: ОСТ 45.159 2000 Отраслевая… …   Телекоммуникационный словарь

• Косвенное измерение (вычисление) отдельных комплексных показателей функционирования ТОУ — Косвенное автоматическое измерение (вычисление) выполняется путем преобразования совокупности частных измеряемых величин в результирующую (комплексную) измеряемую величину с помощью функциональных преобразований и последующего прямого измерения… …   Словарь-справочник терминов нормативно-технической документации

• Косвенное измерение (вычисление) отдельных комплексных показателей Функционирования ТОУ — Кос во см ос автоматическое измерение (вычисление) выполняется путем преобразования совокупности частных измеряемых величии в результирукчцук» (комплексную) измеряем)» величину с помощью функциональных преобразований и последующего прямого… …   Словарь-справочник терминов нормативно-технической документации

• Измерение (физика) — Измерение  совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом средстве (средстве измерений). Получившееся значение называется числовым значением… …   Википедия

• Измерение — У этого термина существуют и другие значения, см. Измерение (значения). Измерение  совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом… …   Википедия

dic.academic.ru

---

• 
  Схема генератор
• 
  Подпороговый ток оказывает на клетку
• 
  Соединение проводов пуэ
• 
  Однолинейная схема электроснабжения многоквартирного дома
• 
  Частота тока на что влияет
• 
  Чертежи николы тесла
• 
  Установка люминесцентных светильников
• 
  При параллельном соединении элементов
• 
  Светильник для уличного освещения
• 
  Защита узип предохранителями
• 
  Звезда треугольник схема