Магнитная индукция соленоида: Электричество и магнетизм

Электричество и магнетизм

Если длина соленоида много больше его диаметра (l >> 2R), мы возвращаемся к формуле для поля в бесконечно длинном соленоиде (6.20). Относительная разница этих двух значений равна

По условию эта разница мала: , то есть мало отношение диаметра соленоида к его длине: 2R/l << 1. Поэтому можно воспользоваться формулой разложения квадратного корня

Отсюда

или

Подставляя численное значение d, находим, что разница будет менее половины процента при выполнении соотношения

Иными словами, соленоид может рассматриваться как бесконечно длинный, если его длина в двадцать или более раз превышает радиус.

Пример 2. Найти магнитное поле В_е в крайней торцевой точке оси соленоида конечной длины l. Сравнить с результатом предыдущего примера.

Решение. Магнитное поле в торцевой точке оси соленоида конечной длины l дается тем же интегралом (6.19), но теперь пределы интегрирования будут выглядеть иначе

Отношение полей в средней и крайней точках оси соленоида равно

Это отношение всегда меньше единицы (то есть поле на торце меньше поля в середине соленоида). При l >> R имеем 

Этот результат легко понять. Представим себе бесконечный соленоид, который мысленно рассекаем пополам в точке наблюдения. Можно считать, что поле в этой точке создается двумя одинаковыми «полубесконечными» соленоидами, расположенными по разные стороны от нее. Ясно, что при удалении одного из них точка наблюдения становится торцом оставшегося «полубесконечного» соленоида, а магнитная индукция в ней уменьшиться именно в два раза.

Это — так называемый краевой эффект. Пример демонстрирует, что недостаточно выполнения соотношения l >> R, чтобы пользоваться формулами для бесконечно длинного соленоида; надо еще, чтобы точка наблюдения находилась далеко от его концов.

На рис. 6.25 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг соленоида. Поле соленоида, ось которого лежит в плоскости пластинки, сосредоточено в основном внутри соленоида. Силовые линии внутри имеют вид параллельных прямых вдоль оси катушки, а поле снаружи практически отсутствует.

Рис. 6.25. Визуализация силовых линий магнитного поля

Видео 6.1.  Силовые линии магнитного поля проводников с током различной формы: прямой ток, соленоид, один виток.

ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА — Студопедия

Приборы и принадлежности: лабораторная установка с соленоидом, источник питания, милливольтметр, амперметр.

Краткая теория

Соленоидом называется цилиндрическая катушка, содержащая большое, число витков провода, по которому идет ток. Если шаг вин­товой линии проводника, образующего катушку, мал, то каждый ви­ток с током можно рассматривать как отдельный круговой ток, а соленоид — как систему последовательно соединенных круговых токов одинакового радиуса, имеющих общую ось.

Магнитное поле внутри соленоида можно представить как сумму магнитных полей, создаваемых каждым витком. Вектор индукции маг­нитного поля внутри соленоида перпендикулярен плоскости витков, т.е. направлен по оси соленоида и образует с направлением кольце­вых токов витков правовинтовую систему. Примерная картина силовых линий магнитного поля соленоида показана на рис. 1. Силовые линии магнитного поля замкнуты.

На рис, 2 показано сечение соленоида длиной L и с числом витков N и радиусом поперечного сечения R. Кружки с точками обозначают сечения витков катушки, по которым идет ток I , на­правленный от чертежа на нас, а кружки с крестиками — сечения вит­ков, в которых ток направлен за чертеж.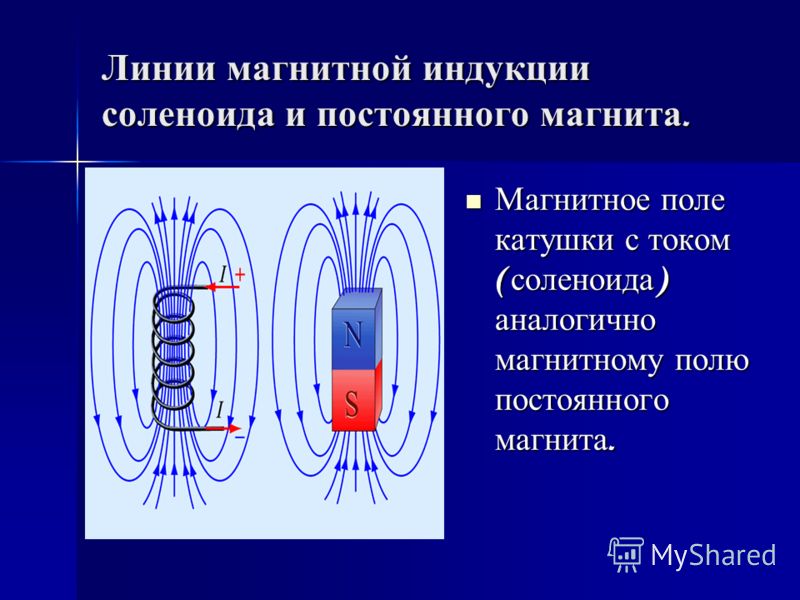 Число витков на единицу длины соленоида обозначим .

Индукция магнитного поля в точке А , расположенной на оси соленоида, определяется путем интегрирования магнитных полей, со­здаваемых каждым витком, и равна

, (1)

где и — углы, образуемые с осью соленоида радиус-векто­рами и , проведенными из точки А к крайним виткам солено­ида, -магнитная проницаемость среды, магнитная постоянная.

Таким образом, магнитная индукция В прямо пропорциональна си­ле тока, магнитной проницаемости среды, заполняющей соленоид, и числу витков на единицу длины. Магнитная индукция также зависит от положения точки А относительно концов соленоида. Рассмотрим нес­колько частных случаев:

1. Пусть точка А находится в центре соленоида, тогда , и . Если соленоид достаточно длинный, то и (2)

2. Пусть точка A находится в центре крайнего витка, тогда , и . Если солено­ид достаточно длинный, то , и (3)

Из формул (2) и (3) видно, что магнитная индукция соленоида на его краю вдвое меньше по сравнению с ее величиной в центре.

3. Если длина соленоида во много раз больше радиуса его витков
(«бесконечно» длинный соленоид), то для всех точек, лежащих внутри
соленоида на его оси, можно положить . Тогда
поле можно считать в центральной части соленоида однородным и рассчитывать его по формуле

(4)

Однородность магнитного поля нарушается вблизи краев соленоида. В этом случае индукцию можно определять по формуле

, (5)

где k — коэффициент, учитывающий неоднородность поля.

Экспериментальное изучение магнитного поля соленоида в данной работе осуществляется с помощью специального зонда — маленькой катушки, укрепленной внутри штока с масштабной линейкой. Ось катуш­ки совпадает с осью соленоида, катушка подключается к милливольт­метру переменного тока, входное сопротивление которого много боль­ше сопротивления катушки-зонда. Если через соленоид идет перемен­ный ток стандартной частоты ( =50 Гц), то внутри соленоида и на его краях индукция переменного магнитного поля изменяется по закону (см. (5)):

Амплитуда магнитной индукции в этой формуле зависит от положения точки внутри соленоида. Если поместить в соленоид катуш­ку-зонд, то в соответствии с законом электромагнитной индукции, в ней возникает ЭДС индукции:

, (6)

где N₁ — число витков в катушке, S — площадь поперечного сече­ния катушки, Ф — магнитный поток ( , т.к. ось катушки совпадает с осью соленоида и, следовательно, вектор магнитной ин­дукции перпендикулярен плоскости поперечного сечения катушки.).

Так как величина индукции B изменяется по закону , , то из (6) получается формула для расчета ЭДС:

(7)

Из выражения (7) видно, что амплитуда ЭДС зависит от . Таким образом, измеряя амплитуду ЭДС, можно определить :

(8)

Коэффициент k учитывающий неоднородность магнитного поля соленоида на краях, можно о определить., по формуле. (5), зная и :

(9)

где — амплитуда переменного тока, идущего через соленоид.

Из формул (7) и (9) следует, что амплитуда ЭДС индукции прямо пропорциональна амплитуде переменного тока :

(10)

Включенные в цепь переменного тока амперметр и милливольт­метр измеряют действующие значения тока и ЭДС , которые связаны с амплитудами и соотношениями:

;

Для действующих значений тока и ЭДС формула (10) имеет вид

(11)

Из формулы (11) следует, что отношение пропорциональ­но коэффициенту K неоднородности индукции магнитного поля в точке соленоида, где проводятся измерения

(12)

где А — коэффициент пропорциональности.

В данной работе требуется выполнить два задания: 1) опреде­лить распределение индукции вдоль оси соленоида при некотором постоянном значении тока; 2) определить значение коэффициента к.

Техника безопасности:

1. Не подключают/ самостоятельно источник питания и милливольтметр к сети 220 В.

2. Не производить переключения цепей, находящихся под напряжением.

Не прикасаться к неизолированным частям цепей.

3. Не оставлять без присмотра включенную схему.

Порядок выполнения работы

Задание № 1. Исследование распределения индукции магнитного поля вдоль оси соленоида.

1. Собрать измерительную цепь по схеме, приведенной на рис. 3. Для этого в цепь соленоида включить источник питания и амперметр, а к выводам катушки — зонда — милливольтметр (для измерения ) В данной установке катушка-зонд имеет следующие параметры: =200 витков, S=2*10^-4м², частота переменного тока = 50 Гц, Число витков на единицу длины соленоида n = 2400 1/м

1- лабораторный стенд Z — шток «

2- катушка-зонд

3- соленоид
5- амперметр

6- источник питания с регулятором выход­ного напряжения (тока), 7- милливольтметр.

2. Установить шток с масштабной линейкой так, чтобы катушка-зонд оказалась примерно в середине соленоида.

3.Включить источник питания соленоида и установить ток соленоида (по амперметру), равный =25мА. Включить милливольтметр и после прогрева (5 мин) снять показания .

4.Перемещая шток с масштабной линейной, измерить при помощи
милливольтметра действующее значение ЭДС индукции через каждый
сантиметр положения линейки. По формуле (8) вычислить .
Результаты измерений и расчетов занести в таблицу 1 (учтите, что ).

Таблица I

Погрешность в каждой точке, соленоида определяется как систематическая погрешность косвенных измерений:

где м², виток; =1 Гц; — погреш­ность измерения ; по милливольтметру.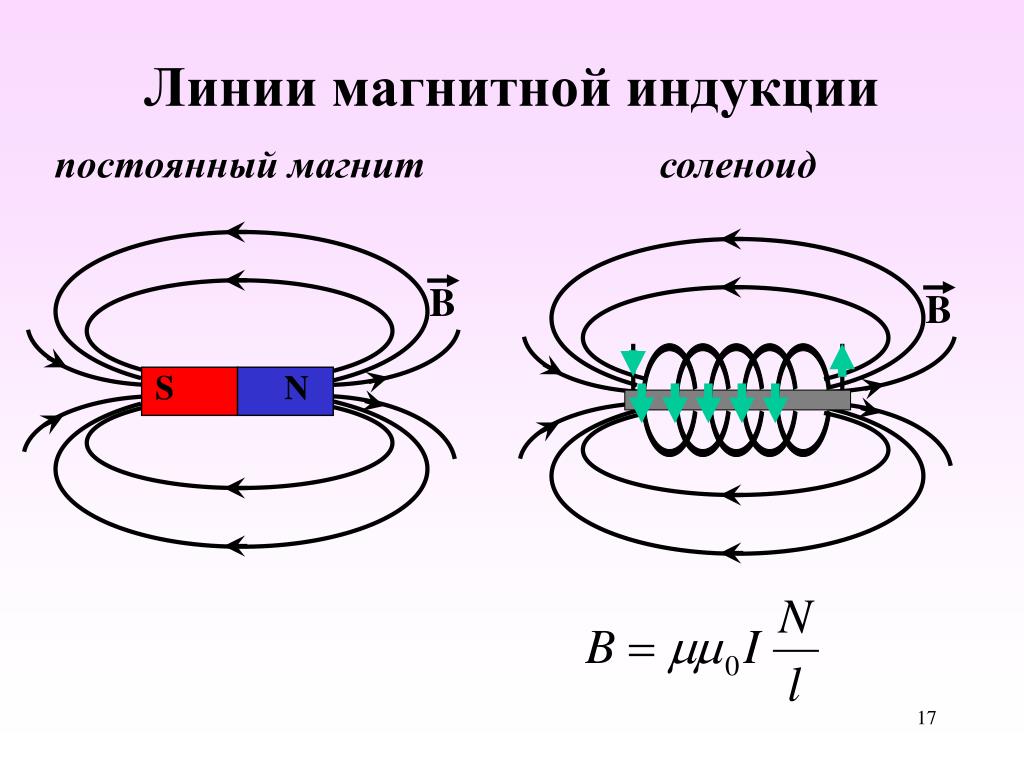

5.Построить график

6.Зная амплитуду тока и число витков на единицу
длины соленоида n, определить в центре соленоида по
формуле (4) и сравнить с измеренным в той же точке значением

Задание 2. Измерение коэффициента неоднородности’ магнитного
поля соленоида.

1. Снять зависимость для данного соленоида. Дня этого установить шток в положение, когда катушка-зонд находится у края соленоидами, изменяя действующее значение тока соленоида с помощью источника питания, снять значения и и занести в таблицу 2.

Таблица 2.

По формуле (12) рассчитать , где

Контрольные вопросы

1. Сформулируйте закон электромагнитной индукции.

2. Нарисуйте картину силовых линий соленоида.

3. Перечислите основные способы исследования магнитного поля.

4. В каких случаях для исследования магнитного поля можно исполь­зовать катушку-зонд?

5. Выведите формулу для вектора магнитной индукции бесконечно длинного соленоида.

Литература

3. Скорохватов Н.А. Курс лекций по электромагнетизму. М: МИИГАиК, 2006.

4. Савельев И.В., Курс общей физики, т. 2 (любое издание).

5. Трофимова Т.И., Курс физики (любое издание).

Магнитное поле бесконечно длинного соленоида

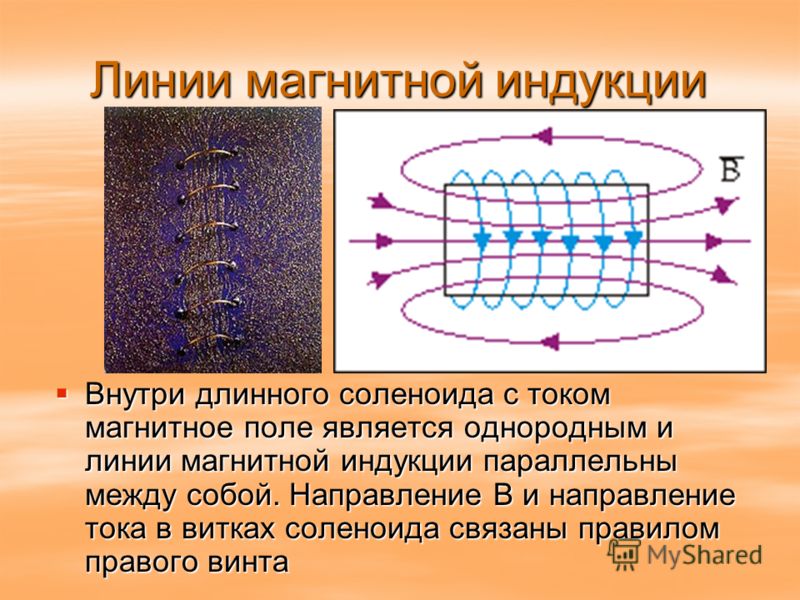
Соленоид — это проволочная катушка цилиндрической формы. Его можно представить себе как множество сложенных в стопку круговых витков с током. Силовые линии магнитного поля, создаваемого электри­ческим током в соленоиде, показаны на рис. 6.6. Как видно из этого рисунка, внутри соленоида силовые линии почти прямые. Чем длин­нее соленоид, т.е. чем больше его длина по сравнению с его радиусом, тем меньше кривизна силовых линий внутри соленоида. В таком случае вектор Вмагнитной индукции поля внутри соленоида будет направлен параллельно его оси. Причем так, что его направление будет связано с направлением тока в соленоиде правилом правого винта. Направим ось х вдоль оси соленоида. При этом проекция вектора магнитной индукции на ось х будет равна его модулю, а все другие его проекции будут равны нулю:

B_x =B, B_y =B_z =0.

Подставим эти проекции вектора Вв уравнение (6.12). Получим

¶B/¶x = 0

Из этого равенства вытекает, что внутри соленоида вектор магнитной индукции не только сохраняет свое направление, но его модуль здесь всюду одинаков. Таким образом, приходим к выводу, что внутри длин­ного соленоида магнитное поле является однородным.

.

Рис. 6.6. Магнитное поле соленоида

Найдем модуль вектора магнитной индукции поля внутри соленоида при помощи теоремы (6.8) о циркуляции этого вектора. В качестве кон­тура С, по которому будем вычислять циркуляцию вектора магнитной индукции, выберем ломанную линию, изображенную пунктиром на рис.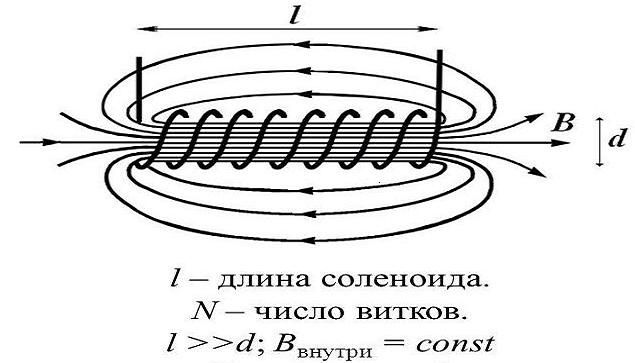 6.6. Отрезок этой линии длиной l находится внутри соленоида и совпа­дает с одной из силовых линий магнитного поля. Две перпендикулярные этому отрезку прямые начинаются на его концах и уходят в бесконеч­ность. Во всех точках этих прямых вектор магнитной индукции или перпендикулярен им (внутри соленоида), или равен нулю (вне соленои­да). Поэтому скалярное произведение Вdlв этих точках равно нулю. Таким образом, циркуляция магнитной индукции по рассматриваемому контуру С будет равна интегралу по отрезку силовой линии длиной l. С учетом того, что модуль вектора магнитной индукции есть постоянная величина будем иметь

= =B =B l

Пусть число витков соленоида, охватываемых контуром С, равно N. При этом сумма токов, охватываемых контуром, будет равна NI, где I — сила тока в одном витке соленоида. Теорема (6.8) приводит к равенству

Вl = μ_o NI,

из которого найдем магнитную индукцию поля в соленоиде:

В = μ_o nI

(6. 14)

где n=N/l

n-число витков, приходящихся на единицу длины соленоида.

Магнитное поле прямого тока

Рассмотрим магнитное поле, создаваемое электрическим током, теку­щим по тонкому бесконечно длинному проводу. Такая система обладает цилиндрической симметрией. Вследствие этого магнитное поле должно обладать следующими свойствами:

1) на любой прямой, параллельной проводу с током, вектор магнитной индукции должен быть всюду оди­наков;

2) при повороте всего магнитного поля целиком вокруг провода оно не изменяется. В таком случае силовыми линиями магнитного поля должны быть окружности, центры которых лежат на оси провода с то­ком (рис, 6.7), а вектор В на любой из этих окружностей всюду имеет один и тот же модуль.

При помощи теоремы (6.8) о циркуляции вектора магнитной индук­ции найдем модуль этого вектора. С этой целью вычислим циркуляцию магнитной индукции по одной из силовых линий С, радиус которой ра­вен а. Так как вектор В является касательным к силовой линии, он коллинеарен векторному элементу dl этой линии. Поэтому

=

где В — модуль вектора магнитной индукции, который, как было сказано, всюду на окружности С один и тот же. Вынесем В за знак интеграла. После интегрирования будем иметь

= В 2p a

Рис. 6.7. Силовые линии магнитного поля прямого токи

Так как контур С охватывает всего один провод с током I, теорема (6.8) приводит к равенству

2p a В = μ_oI

Отсюда найдем, что на расстоянии а от бесконечного прямого провода с током I индукция создаваемого им магнитного поля будет

В = μ_oI/(2p a) (6.15)

Как видно из рис. 6.7, направление вектора В и направление тока I связаны правилом правого винта. В том, что это действительно так, нетрудно убедиться при помощи закона Био — Савара — Лапласа.

Взаимодействие токов

Рассмотрим два тонких параллельных друг другу прямых провода с токами I₁и I₂ (рис. 6.8.). Если расстояние R между проводами много меньше их длины, то магнитную индукцию поля, создаваемого первым проводом на этом расстоянии, можно найти по формуле (6.15):

В = μ_oI₁/(2p R)

Направление вектора В₁связано с направлением тока I₁правилом пра­вого винта. Этот вектор изображен на рис. 6.8.

Рис. 6.8. Взаимодействие токов

Магнитное поле, создаваемое первым током, будет действовать на вто­рой провод с силой Ампера F₂₁, которая определяется формулой (5. 8):

F₂₁= I₂[l₂B₁]

где l₂ — вектор, длина которого равна длина l рассматриваемого участка второго провода. Этот вектор направлен вдоль провода по направлению тока. Модуль силы (6.17) будет

F₂₁ =I₂l B₁. (6.18)

Подставив выражение (6.16) в формулу (6.18), получим следующее выра­жение для силы, с которой первый провод действует на участок второго провода длины l:

F₂₁ =μ_oI₁ I₂ l /(2p R)

Направление силы F₂₁найдем по формуле (6.17). Когда токи I₁, I₂ текут в одном направлении эта сила будет направлена в сторону первого провода. Сила F₁₂, с которой второй провод действует на участок первого провода длины l, равна по модулю и противоположна по направлению силе F₂₁ .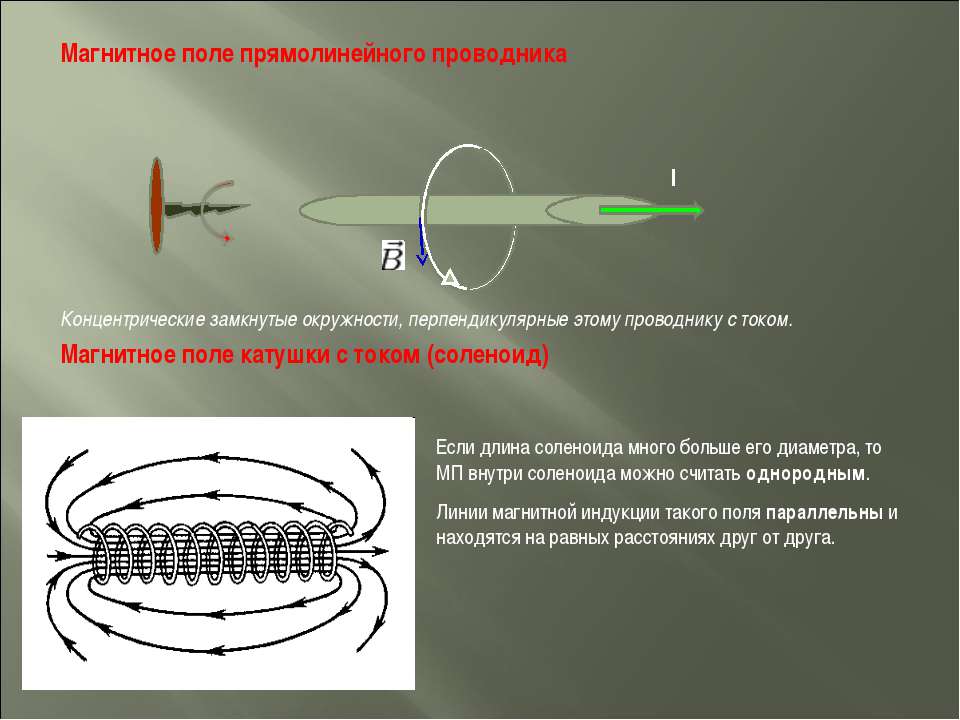

Итак, установлено, что параллельные провода с токами, текущими в одном направлении, притягиваются. Нетрудно доказать, что провода с токами, текущими в противоположных направлениях, отталкиваются друг от друга.

При помощи формулы (6.19) определена единица силы тока в СИ. Как известно, эта единица называется ампер. По определению два длинных тонких провода с токами силой в один ампер, расположенные парал­лельно на расстоянии 1 м один от другого, взаимодействуют с силой 2 • 10^-7 Н на 1 м длины. Подставив эти значения в формулу (6.19), найдем, что магнитная постоянная

m₀ = 4p 10^-7 Н/м.

Единица заряда в СИ — кулон — выражается через единицу силы тока: Кл = А*с. Измерения силы взаимодействия двух точечных зарядов в 1 Кл привели к значению F = 9 • 10⁹ Н при расстоянии между зарядами R = 1 м. Используя эти значения, найдем электрическую постоянную e₀из закона Кулона

F =|Q₁Q₂|/(4pe₀R²)

Интересно отметить, что величина

1/Öe₀m₀ =3 10⁸ м/с

численно равна скорости света в пустоте.

Читайте также:





Магнитное поле бесконечного соленоида

Соленоидом называется проводник, намотанный на цилиндрическую поверхность.

Если витки соленоида намотаны вплотную друг к другу, то соленоид удобно представлять в виде совокупности витков одинакового радиуса, расположенных параллельно друг другу вдоль оси соленоида. Центры витков расположены на оси, плоскости витков перпендикулярны оси. Токи во всех витках одинаковы.

Как показано в разд. 3.4, вектор магнитной индукции на оси витка параллелен ей. Следовательно, и суммарное поле всех витков на оси соленоида параллельно этой оси.

Поскольку соленоид симметричен относительно оси, проходящей через центры витков, постольку и созданное им магнитное поле должно быть симметричным относительно этой оси.

Следовательно, магнитное поле параллельно оси соленоида и в остальных точках, расположенных внутри соленоида.

Магнитное поле вне бесконечного соленоида равно нулю. Это можно доказать следующим образом.

_______________________

* Иногда этот закон называют теоремой о циркуляции вектора магнитной индукции.

Вначале допустим, что магнитное поле вне соленоида всё же существует.

Тогда оно должно быть симметричным относительно оси соленоида. Это значит, что силовые линии магнитного поля вне соленоида должны быть параллельны его оси.

Для определения индукции магнитного поля вне соленоида воспользуемся законом полного тока.

Найдём циркуляцию вектора магнитной индукции по прямоугольному контуру, у которого сторона ab проходит вдоль витков соленоида вблизи от них, а сторона cd находится бесконечно далеко от витков.

Скалярное произведение Bdl во всех точках сторон bc и da равно нулю, так как угол между В и dl на этих сторонах прямой.

Магнитное поле бесконечно далеко от соленоида равно нулю, поэтому вклад участка cd в циркуляцию также равен нулю.

Прежде чем определять вклад участка ab , найдём алгебраическую сумму токов, охваченных контуром abcd.

Поскольку контур не охватывает ни один виток соленоида, сумма токов равна нулю.

Следовательно, и циркуляция вектора В по контуру abcd должна быть равна нулю.

Но это означает, что и на участке ab скалярное произведение равно нулю. Это возможно лишь в том случае, если индукция магнитного поля и вблизи от поверхности соленоида равна нулю.

Таким образом, магнитное поле вне бесконечно длинного соленоида действительно равно нулю.

Теперь найдём индукцию магнитного поля внутри соленоида.

В качестве контура интегрирования выберем прямоугольник 1234, две стороны которого параллельны оси соленоида, охватывающий несколько витков соленоида.

Циркуляция В по этому контуру равна

На участках 2—3 и 4—1 индукция поля в соленоиде В_с перпендикулярна элементу контура dl, поэтому скалярное произведение В_с и dl равно нулю.

Интеграл на участке 3—4 также равен нулю, так как поле вне бесконечного соленоида равно нулю.

Следовательно, , где l₁₂ – длина стороны 1—2 контура интегрирования.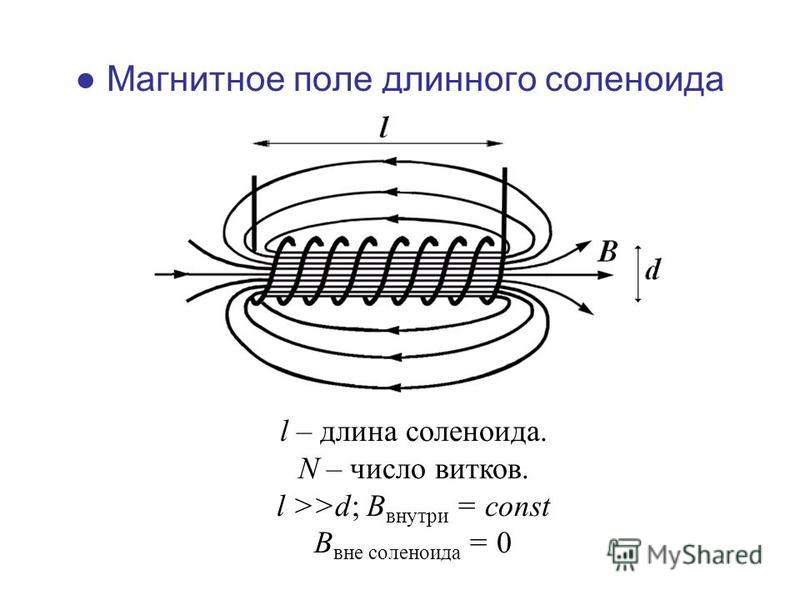

При вычислении интеграла были учтены следующие соображения:

– внутри соленоида направление магнитной индукции и направление обхода контура совпадают, поэтому скалярное произведение Bdl равно произведению модулей этих векторов;

– модуль вектора магнитной индукции во всех точках участка контура 1—2 одинаков, поэтому В можно вынести за знак интеграла;

– интеграл , поэтому циркуляция равняется произведению модуля магнитной индукции на длину участка 1—2.

Ток, охваченный этим контуром, равен nl₁₂I, где n – количество витков на единице длины соленоида, I – ток в одном витке.

На основе закона полного тока циркуляция вектора магнитной индукции равна произведению m_о на алгебраическую сумму токов, охваченных контуром,

Bl₁₂ = m_onl₁₂I;

сокращая длину участка 1—2, получаем выражение для расчёта индукции магнитного поля внутри бесконечного соленоида:

B = m_onI.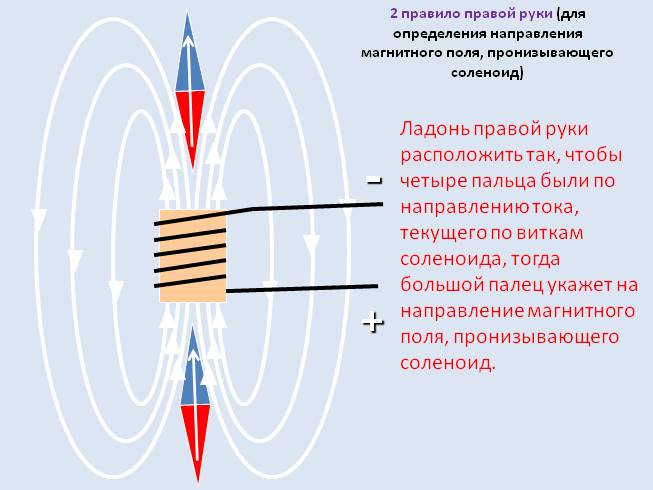

Обратите внимание на то, что величина В внутри соленоида не зависит от расстояния между точкой и осью соленоида. Это значит, что магнитное поле внутри бесконечного соленоида однородно.

Магнитное поле тороида

Тороидом называется соленоид, свёрнутый в кольцо.

Поскольку тороид симметричен относительно оси, проходящей через его центр перпендикулярно плоскости, в которой лежит тороид, то и магнитное поле должно быть симметрично относительно этой оси. Следовательно, силовые линии магнитного поля в тороиде также должны быть симметричны относительно той же самой оси.

В качестве контура интегрирования удобно выбрать окружность, совпадающую с какой-либо силовой линией магнитного поля.

В этом случае циркуляция вектора магнитной индукции (направления В и dl во всех точках контура совпадают, поэтому скалярное произведение Bdl равно произведению их модулей; магнитная индукция во всех точках контура одинакова, следовательно, её можно вынести за знак интеграла).

Ток, охваченный контуром, , где N – число витков тороида.

Тогда в соответствии с законом полного тока

и

.

Обратите внимание: магнитная индукция поля внутри тороида зависит от расстояния между центром тороида и точкой внутри него. Величина В обратно пропорциональна расстоянию r.

Можно показать, что поле вне тороида равно нулю (примерно так же, как это было сделано в предыдущем разделе для поля вне соленоида).

Индуктивность соленоида

Рассмотрим произвольный замкнутый контур с током I. В соответствии с законом Био–Савара–Лапласа индукция магнитного поля, созданного контуром, прямо пропорциональна силе тока в проводнике.

Магнитный поток, охваченный контуром, прямо пропорционален индукции магнитного поля внутри контура и его площади .

Если охваченная контуром площадь неизменна, то величина магнитного потока прямо пропорциональна В и, следовательно, силе тока в контуре I

Ф = LI.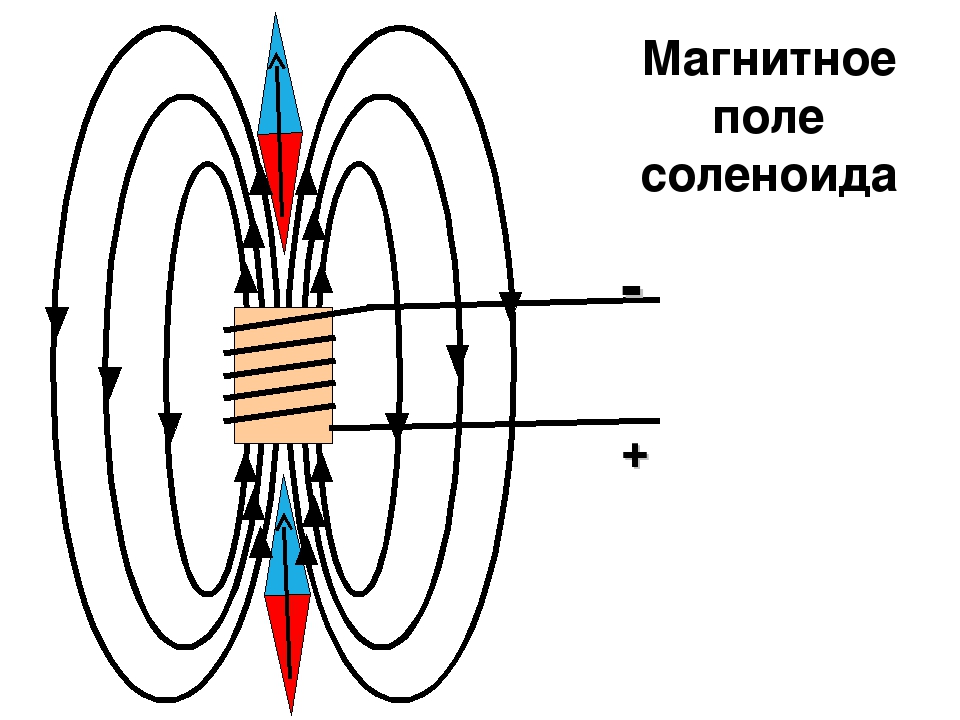

Коэффициент пропорциональности L называется коэффициентом индуктивности, или индуктивностью контура.

Индуктивность является размерным коэффициентом пропорциональности. В системе СИ размерность индуктивности [L] = Гн (генри).

Найдём выражение для расчёта индуктивности соленоида.

Как показано в разд. 3.11.1, магнитная индукция поля внутри соленоида В = m_оnI.

Магнитный поток через один виток соленоида Ф = m_оnIS =
= , где l длина соленоида, N – количество витков соленоида на длине l, S – площадь витка соленоида.

Магнитный поток через N витков соленоида равен .

Это означает, что для соленоида

и отсюда индуктивность соленоида

,

где V – объём соленоида.

Таким образом, индуктивность соленоида без сердечника определяется плотностью витков и объёмом соленоида.

Магнитное поле в веществе

Магнитное поле создаётся электрическим током.

Если один ток создаёт магнитное поле в вакууме, а второй, такой же – в веществе, то созданные ими магнитные поля будут разными. Причём в некоторых веществах магнитное поле будет слабее поля в вакууме, в других – сильнее.

По соотношению поля в веществе и в вакууме вещества делят на три класса: диамагнетики, парамагнетики и ферромагнетики.

В данном разделе будут рассмотрены причины, по которым разные вещества намагничиваются по-разному.

Намагничивание магнетика

Всякое вещество является магнетиком. Это значит, что всякое вещество способно намагничиваться, т. е. под действием внешнего магнитного поля в нём возникает дополнительное, собственное магнитное поле. Другими словами – индукция магнитного поля внутри магнетика В складывается из индукции внешнего поля В_о и индукции собственного поля В¢:

В = В_о+В¢.

Механизм намагничивания вещества был раскрыт французским учёным Андре Мари Ампером, который предположил, что во всех молекулах вещества циркулируют круговые токи. Каждый такой ток создаёт магнитное поле. Но, поскольку в отсутствие магнитного поля молекулярные токи ориентируются хаотически, суммарное магнитное поле всех этих токов равно нулю.

Появление внешнего магнитного поля вызывает упорядочение ориентации молекулярных круговых токов, в результате чего суммарное магнитное поле молекулярных токов становится отличным от нуля, а магнетик – намагниченным.

Намагничивание магнетика количественно характеризуют намагниченностью J, которая определяется выражением

,

где – суммарный магнитный момент всех молекул, находящихся в элементарном объёме DV в окрестности интересующей нас точки.

Размерность вектора намагниченности [J] = [p_m]/[V] =
А^.м²/м³ = А/м.

Итак, намагничивание вещества есть результат упорядочивания ориентации молекулярных токов внешним магнитным полем. Условно это можно представить так, как показано на рисунке.

Как видно из рисунка, токи внутри объёма магнетика компенсируют друг друга.

Токи же, выходящие на боковую поверхность, компенсироваться не будут.

Поэтому намагничение вещества можно трактовать как результат появления на боковой поверхности магнетика макроскопического тока намагничивания I¢.

Читайте также:





Магнитное поле однослойного соленоида

Соленоид – это цилиндрическая обмотка из провода по которой протекает постоянный или
переменный электрический ток. Обмотка может наноситься в один или несколько слоёв виток к витку.{N} I_i.\]

(1)

Если пренебречь краевыми эффектами, то первое и третье слагаемые в (1) будут равны нулю, так как магнитное поле
перпендикулярно контуру и $B_l=0$. Если контур выбрать так, что $AD$ будет лежать на большом расстоянии от
соленоида, где поле стремиться к нулю, то и четвёртое слагаемое в (1) также превратиться в нуль. Тогда, учитывая
приближение однородности поля получим:

где $L$ – длина соленоида, $N$ – количество витков. Если ввести понятие плотности витков (число
витков на единицу длины) $n=N/L$, то индукцию магнитного поля внутри соленоида (2) можно записать в виде:

Рис. 2: Соленоид с произвольными размерами $L$ и $R$.

Чтобы получить точное выражение для индукции магнитного поля в любой точке на оси конечного соленоида необходимо
воспользоваться законом Био-Савара-Лапласа (Рис. 2), который приводит к следующему выражению:

\[B=\frac12\mu_0 nI (\cos\alpha_2-\cos\alpha_1).2}},\]

(5)

где $R$ – радиус соленоида. А на краю полубесконечного соленоида:

\[B=\frac12 \mu_0 nI.\]

(6)

Калькулятор

Индукция магнитного поля бесконечного соленоида (3)

Индукция магнитного поля конечного соленоида (5)

Распределение индукция магнитного внутри конечного соленоида (4)

Магнитное поле соленоида

Соленоидом
называется совокупность N
одинаковых витков изолированного
проводящего провода, равномерно
намотанных на общий каркас или сердечник.
По виткам проходит одинаковый ток.
Магнитные поля, созданные каждым витком
в отдельности, складываются по принципу
суперпозиции. Индукция магнитного поля
внутри соленоида велика, а вне его —
мала. Для бесконечно длинного соленоида
индукция магнитного поля вне соленоида
стремится к нулю. Если длина соленоида
во много раз больше диаметра его витков,
то соленоид можно практически считать
бесконечно
длинным.
Магнитное
поле такого соленоида целиком сосредоточено
внутри него и является однородным
(рис.6).

Величину
индукции магнитного поля внутри
бесконечно длинного соленоида можно
определить, используя теорему
о циркуляции вектора
:циркуляция
вектора
по произвольному замкнутому контуру
равна алгебраической сумме токов,
охватываемых контуром, умноженной на
магнитную постоянную μ_о:

,
(20)

где
μ₀ =
4π 10^-7
Гн/м.

Рис.6.
Магнитное поле соленоида

Для
определения величины магнитной индукции
В внутри соленоида выберем замкнутый
контур ABCD
прямоугольной формы, где
— элемент длины контура, задающий
направление обхода (рис.6). При этом длиныAB
и CD
будем считать бесконечно малыми.

Тогда
циркуляция вектора
по замкнутому контуруABCD,
охватывающему N
витков, равна:

(21)

На
участках AB
и CD
произведение
,
так как вектораивзаимно перпендикулярны. Поэтому

.
(22)

На
участке DA
вне соленоида интеграл,
так как магнитное поле вне контура
равно нулю.

Тогда формула (21)
примет вид:

,
(23)

где
l
– длина участка BC.
Сумма токов, охватываемых контуром,
равна

,
(24)

где
I_c – сила
тока соленоида; N – число
витков, охватываемых контуром ABCD.

Подставив (23) и
(24) в (20), получим:

. (25)

Из
(25) получим выражение для индукции
магнитного поля бесконечно длинного
соленоида:

.
(26)

Так
как число витков на единицу длину
соленоида n
равно:

(27)

то
окончательно получим:

.
(28)

Если внутрь
соленоида помещен сердечник, то формула
(28) для В примет вид:

.
(29),

где

— магнитная проницаемость материала
сердечника.

Таким
образом, индукция
В магнитного поля соленоида определяется
током соленоида I_c,
числом витком n
на единицу длины соленоида и магнитной
проницаемостью материала сердечника.

Цилиндрический магнетрон

Магнетроном
называется двухэлектродная электронная
лампа (диод), содержащая накаливаемый
катод и холодный анод и помещенная во
внешнее магнитное поле.

Анод
диода имеет форму цилиндра радиусом
.
Катод представляет собой полый цилиндр
радиусом,
вдоль оси которого расположена нить
накала, как правило, изготавливаемая
из вольфрама (рис.7).

Раскалённый
катод в результате явления термоэлектронной
эмиссии испускает термоэлектроны,
которые образуют вокруг катода электронное
облако. При подаче анодного напряжения
(рис.8),
электроны начинают перемещаться от
катода к аноду вдоль радиусов, что
приводит к возникновению анодного тока.
Анодный ток регистрируется миллиамперметром.

Рис.7.
Схема диода

Рис.8.
Электрическая схема цепи

Величина
анодного напряжения регулируется
потенциометром R_A.
Чем больше анодное напряжение, тем
большее количество электронов за единицу
времени достигает анода, следовательно,
тем больше анодный ток.

Напряжённость
электрического поля Е между катодом и
анодом такая же, как и в цилиндрическом
конденсаторе:

,
(30)

где
r
– расстояние от оси катода до данной
точки пространства между катодом и
анодом.

Из
формулы (30) следует, что напряжённость
поля Е обратно пропорциональна расстоянию
r
до оси катода. Следовательно, напряженность
поля максимальна у катода.

Так как

r_к <<r_a,

(31)

то
значение логарифма ln
стремится к большой величине. Тогда с
увеличением расстояния r
напряженность электрического поля
между катодом и анодом снижается до
нуля. Поэтому, можно считать, что электроны
приобретают скорость под действием
поля только вблизи катода, и дальнейшее
их движение к аноду происходит с
постоянной по величине скоростью.

Внешнее
магнитное поле, в которое помещён диод,
создаётся соленоидом (рис.8). Длина
соленоида l
много больше диаметра его витков, поэтому
поле внутри соленоида можно считать
однородным. Ток в цепи соленоида
изменяется с помощью потенциометра R_C
(рис.8) и регистрируется амперметром.

Характер
движения электронов в зависимости от
величины поля соленоида показан на
рис.9. Если ток в цепи соленоида отсутствует,
то индукция магнитного поля В = 0.
Тогда электроны движутся от катода к
аноду практически по радиусам.

Увеличение
тока в цепи соленоида приводит к
возрастанию величины В. При этом,
траектории движения электронов начинают
искривляться, однако все электроны
достигают анода. В анодной цепи будет
течь ток такой же, как и в отсутствии
магнитного поля.

Рис.9.
Зависимость анодного тока I_A
от величины тока соленоида I_c
в идеальном (1) и реальном (2) случаях, а
также характер движения электронов в
зависимости от величины поля соленоида.

При
некотором значении тока в соленоиде
радиус окружности, по которой движется
электрон, становится равным половине
расстояния между катодом и анодом:

..
(32)

Электроны
в этом случае касаются анода и уходят
к катоду (рис.9). Такой режим работы диода
называется критическим.
При этом по соленоиду течёт критический
ток I_кр,
которому соответствует критическое
значение индукции магнитного поля В =
В_кр.

При
В = В_кр
анодный ток в идеальном случае должен
скачком уменьшиться до нуля. При В > В_кр
электроны не попадают на анод (рис.9), и
анодный ток также будет равен нулю
(рис.9, кривая 1).

Однако
на практике, вследствие некоторого
разброса скоростей электронов и нарушения
соосности катода и соленоида, анодный
ток уменьшается не скачком, а плавно
(рис.9, кривая 2). При этом значение силы
тока соленоида, соответствующее точке
перегиба на кривой 2, считается критическим
I_кр.
Критическому значению тока соленоида
соответствует анодный ток, равный:

,
(33)

где
– максимальное значение анодного тока
при В = 0.

Зависимость
анодного тока I_A
от величины индукции магнитного поля
В (или от тока в соленоиде) при постоянном
анодном напряжении и постоянном накале
называется сбросовой
характеристикой магнетрона.

МАГНИТНОЕ ИНДУКЦИОННОЕ ПОЛЕ СОЛЕНОИД — СОЛЕНОИД

	СОЛЕНОИД А соленоид представляет собой длинную плотно намотанную цилиндрическую катушку из проволоки. ПОЛЕ ИЗ-ЗА СОЛЕНОИДА Когда через соленоид пропускается ток, создается магнитное поле, которое прочный и однородный внутри, при этом незначительно слабый снаружи. Для последняя информация, бесплатные компьютерные курсы и важные заметки посетите: www.citycollegiate.com ВЫРАЖЕНИЕ ДЛЯ ПЛОТНОСТИ ПОТОКА (B) Кому вычислить B рассмотрим прямоугольный путь a, b, c и d. Путь состоит для элементов длины l 1 , l 2 , л 3 и л 4 . Рассчитаем произведение (B.Dl) для каждого элемента. Для элемент l 1 (B.Dl) 1 = Bl 1 Cosq С B находится по оси l 1 . т.е. q = 0 (B.Dl 1 ) = Bl 1 Cos0 (B.Dl 1 ) = Bl 1 (1) (Б.Dl 1 ) = Bl 1 Для элемент l 2 : (B.Dl) 2 = Bl 2 Cosq С l 2 перпендикулярно B, т.е. q = 90 o (B.Dl) 2 = Bl 2 Cos90 o = Bl 2 (0) = 0 Для элемент l 3 : (Б.Dl) 3 = Bl 3 Cosq С B незначительно, т.е. B = 0 вне катушки. (B.Dl) 3 = 0. л 3 Cosq (B.Dl) 3 = 0 Для элемент l 4 : (B.Dl) 4 = Bl 4 Cosq С l 4 перпендикулярно B i.е. q = 90 o . (B.Dl) 4 = Bl 4 Cos90 o = Bl 4 (0) = 0. Сейчас, применяя закон цепи ампер: S (B.Dl) n = m o (текущий прилагается) B.l 1 + 0 + 0 + 0 = m o (текущий прилагается) Б.l 1 = m o (текущий прилагается) Сейчас, если количество витков на единицу длины = n А если ток в каждом витке = I Тогда ток в петле abcda = nIl 1 . B.l 1 = m o (НИЛ 1 ) B = m o nI Это — выражение для магнитной индукции соленоида.Он показывает, B единообразно с длинным соленоидом. направление B — вдоль оси соленоида. Для последняя информация, бесплатные компьютерные курсы и важные заметки посетите: www.citycollegiate.com Самоиндукция с помощью электромагнитной индукции — Учебные материалы для IIT JEE Полный курс физики — 11 класс ПРЕДЛАГАЕМАЯ ЦЕНА: рупий.2 968 Просмотр подробностей Мы уже обсуждали тему конденсаторов, которые представляют собой устройства для хранения энергии с использованием электрических полей.Как и конденсатор, индуктор также является довольно часто используемым элементом в электрических цепях. Он хранит магнитную энергию. Как мы знаем, когда ток течет по проводнику, вокруг него создается магнитное поле, и, следовательно, оно связано с магнитным потоком. Если магнитный поток, связанный с катушкой, равен Φ, а ток, протекающий через нее, равен I, то ее индуктивность определяется выражением L = Φ ⁄ l . Величина ‘L’ называется самоиндукцией катушки . Он не зависит от тока, но зависит от проницаемости сердечника и размеров катушки. В 1824 году Эрстед обнаружил, что ток, проходящий через катушку, создает магнитное поле, способное сдвигать стрелку компаса. Спустя семь лет Фарадей и Генри обнаружили прямо противоположное. Они заметили, что движущееся магнитное поле индуцирует ток в электрическом проводнике. Процесс генерации электрического тока в проводнике путем помещения проводника в изменяющееся магнитное поле называется электромагнитной индукцией или просто индукцией. Это называется индукцией, потому что ток индуцируется в проводнике магнитным полем. Индуктивность возникает при возникновении индукции в электрической цепи, которая влияет на поток электричества. Он обозначается буквой L. Самоиндукция или просто индуктивность, следовательно, может быть определена как свойство цепи, в которой изменение тока приводит к изменению напряжения в той же цепи. Когда ток индуцируется в одной цепи второй соседней цепью, это называется взаимной индуктивностью . Когда переменный ток протекает через кусок провода в цепи, создается электромагнитное поле, которое постоянно растет, сжимается и меняет направление из-за постоянно меняющегося тока в проводе.Это магнитное поле, которое продолжает меняться, будет индуцировать электрический ток в любом другом проводе, который приближается к проводу в цепи. Ток, протекающий по второму проводу, также будет полностью идентичен току, протекающему по первому. На приведенном ниже рисунке показана индуктивность, которая объясняет поведение провода при противодействии любому изменению электрического тока через катушку. Индуктивность L, выведенная из закона Фарадея , может быть определена как эдс, генерируемая для противодействия изменению тока. Единица для L = вольт в секунду / ампер = Генри Единицей измерения индуктивности является Генри (Гн), которая показывает зависимость скорости изменения магнитного поля. Один генри — это величина индуктивности, которая требуется для генерирования одного вольт индуцированного напряжения, когда ток изменяется со скоростью один ампер в секунду. Мы использовали здесь термин ток, а не магнитное поле, потому что ток может создавать магнитное поле и им легче управлять, чем магнитный поток. Рассмотрим схему, в которой соленоид подключен к ячейке через резистор. Когда переключатель разомкнут, ток в цепи равен нулю. Когда переключатель замкнут, в нем течет ток. Поскольку ток в цепи увеличивается от нуля до определенного значения, связанное с ним магнитное поле изменяется, что вызывает индукцию ЭДС на соленоиде. Поскольку Φ B = LI, а ∈ = -dφ B / dt Следовательно, ∈ = — L dI / dt Индуктивность идеального соленоида Пропустите ток I через соленоид.Магнитное поле из-за тока, протекающего внутри соленоида, составляет B = μ 0 nI, где n — количество витков на единицу длины. Если площадь поперечного сечения соленоида A, то поток, связанный с длиной l, равен . Φ = nlBA. (При условии, что соленоид идеальный и длинный) где l — длина соленоида Теперь B = μ 0 nI Итак, Φ B = nBA = (n) (μ 0 нИ) A Φ B = μ 0 n 2 IA Самоиндуктивность катушки Рассмотрим катушку из N витков и площади поперечного сечения A, по которой проходит ток I.Длина катушки l (l ≥√A) Сравнивая с Φ = LI, получаем, L = μ 0 n 2 A Моделирование алюминиевой рампы (Для просмотра нажмите кнопку воспроизведения и продолжите) Алюминиевая рампа; На этой анимации показано, как на магнит, скользящий по рампе, действует закон Ленца. Мы используем его, чтобы проиллюстрировать лабораторную станцию, которую делают студенты. Проблема (JEE Advanced): Катушка с индуктивностью 1 Гн и незначительным сопротивлением подключена к источнику питания, напряжение которого равно V = 4 В.Если напряжение приложено, когда t = 0, то найти энергию, запасенную в катушке за 4 с. Решение: Мы знаем, что V = L dI / dt Итак, 4t = L dI / dt Или, Таким образом, запасенная энергия, U = ½ LI 2 = ½ (1) (32) 2 = 512 Дж Из приведенного выше наблюдения мы заключаем, что энергия, запасенная в катушке за 4 с, будет 512 Дж. Индуктивное реактивное сопротивление Уменьшение протекания тока в цепи в результате индукции называется индуктивным реактивным сопротивлением.При внимательном рассмотрении катушки с проволокой и использовании закона Ленца становится ясно, что индуктивность уменьшает протекание тока в цепи. Как показано на рисунке ниже, первичный ток показан красным, а магнитное поле, создаваемое током, показано синим. Чтобы определить направление магнитного поля, направьте большой палец правой руки в направлении тока. Магнитное поле от одной петли провода будет пересекать другие петли в катушке, и это вызовет ток, который выделен зеленым цветом.Согласно закону Ленца , индуцированный ток должен течь в направлении, противоположном первичному току . Индуцированный ток, работающий против первичного тока, приводит к уменьшению протекания тока в цепи. Индуктивное реактивное сопротивление будет увеличиваться с увеличением количества витков в катушке. Индуктивное реактивное сопротивление также снижает протекание тока в цепи. Но можно отличить индуктивное реактивное сопротивление от сопротивления в цепи, отметив синхронизацию между синусоидальными волнами напряжения и тока переменного тока.В цепи переменного тока, содержащей только резистивные компоненты, напряжение и ток будут синфазными, что означает, что пики и спады их синусоидальных волн будут происходить одновременно. Но при наличии индуктивного реактивного сопротивления фаза тока сдвигается так, что ее пики и спады не возникают одновременно с пиками напряжения. Обратитесь к этому видео, чтобы узнать больше об индуктивности: — Причина образования индуцированной эл.м.ф. это изменение магнитного потока, связанного с контуром. Величина наведенной э.д.с. не зависит от величины изменения магнитного потока. Это зависит только от того, насколько быстро (скорость изменения во времени) изменяется поток. Индуцированная ЭДС всегда имеет тенденцию противодействовать причине ее возникновения. Величина самоиндуцированного e.m.f не является константой схемы и зависит от характера источника тока в ней. Коэффициент самоиндукции L является константой цепи и не зависит от характера источника тока в ней. Вопрос 1 Свойство катушки, у которой счетчик э.д.с. индуцируется в нем, когда ток через катушку изменяется, известный как (а) самоиндукция (б) взаимная индуктивность Серия (c), повышающая индуктивность (г) емкость Вопрос 2 Какой из следующих элементов схемы накапливает энергию в электромагнитном поле? (а) индуктивность (б) конденсатор (в) переменный резистор (г) сопротивление Вопрос 3 Выше самоиндукции катушки, (а) меньше его витков (b) опустите e.м.ф индуцированный (в) больше производимый им поток (г) больше задержка установления через него установившегося тока Вопрос 4 Количество витков и длина сердечника индуктивной катушки увеличены вдвое. Его собственная индуктивность составит (а) без изменений (б) удвоено (в) делить пополам (г) четырехкратный Самоиндуктивность Самоиндукция Далее: Взаимная индуктивность Up: Магнитная индукция Предыдущий: Индуктивность Рассмотрим длинный соленоид длины и радиуса, который имеет количество витков на единицу длины, и несет ток.Продольный ( т.е. , направленный по ось соленоида) магнитное поле внутри соленоида примерно однородное, и дается (907) Этот результат легко получить, интегрировав закон Ампера по прямоугольной петля, длинные стороны которой проходят параллельно оси соленоида, одна внутри соленоид и другой снаружи, короткие стороны которого перпендикулярны ось. Магнитный поток через каждый виток контура .Общий поток через провод соленоида с витками (908) Таким образом, самоиндукция соленоида равна (909) Обратите внимание, что самоиндуктивность зависит только от геометрических величин, таких как число витков на единицу длины соленоида и площадь поперечного сечения витков. Предположим, что ток, протекающий через соленоид, изменился.Мы должны Предположим, что изменение достаточно медленное, чтобы мы могли пренебречь смещением в наших расчетах эффекты тока и запаздывания. Это означает, что типичный масштаб времени изменения должен быть намного больше, чем время прохождения светового луча цепь. Если это так, то приведенные выше формулы остаются в силе. Изменение тока подразумевает изменение магнитного потока, связывающего соленоид провод, так как . Согласно Фарадею закон, это изменение генерирует e.м.ф. в проводе. По закону Ленца э.д.с. это так что касается противодействия смене нынешнего — т.е. , то это обратный ЭДС. Мы можем написать (910) где — сгенерированная ЭДС. Рисунок 51: Предположим, что у нашего соленоида есть электрическое сопротивление. Разрешите нам подключите концы соленоида к клеммам батареи е.м.ф. . Что сейчас произойдет? Эквивалентная схема представлена ​​на рис.51. Индуктивность и сопротивление соленоида представлены идеальным индуктор« и идеальный резистор«, соединенные последовательно. Падение напряжения на катушке индуктивности и резисторе равна ЭДС. батареи, . Падение напряжения на резисторе просто, тогда как падение напряжения на катушке индуктивности (, т.е. , обратная ЭДС) составляет . Здесь — ток, протекающий через соленоид. Следует, что (911) Это дифференциальное уравнение для тока.Мы можем изменить это на дать (912) Общее решение (913) Константа фиксируется граничными условиями. Предположим, что аккумулятор подключается в то время, когда. Отсюда следует, что так что (914) Эта кривая изображена на рис.52. Видно, что после подключения АКБ ток возрастает и достигает своего установившегося значения (которое исходит от закон), на характерном масштабе времени (915) Эту шкалу времени иногда называют постоянной времени цепи , или несколько невообразимо, L по времени R схемы. Рисунок 52: Теперь мы можем оценить значение самоиндукции.Задний Э.д.с. генерируется в катушке индуктивности, когда ток пытается измениться, эффективно предотвращает ток от нарастания (или падения) намного быстрее времени. Этот эффект иногда выгодно, но часто это очень неприятно. Все элементы схемы обладают некоторой самоиндукцией, а также некоторым сопротивлением и, следовательно, имеют конечное время. Это означает, что когда мы включаем цепь, ток не подскакивает мгновенно до своего установившегося значения. Вместо этого нарастание распределяется по времени L / R цепи.Это хорошая вещь. Если бы ток увеличивался мгновенно, тогда чрезвычайно большое электрическое поля будут генерироваться внезапным скачком индуцированного магнитного поля, ведущего, неизбежно к пробою и возникновению электрической дуги. Итак, если бы такого не было как самоиндукция, то каждый раз, когда вы включаете или выключаете электрическую цепь будет синяя вспышка из-за дуги между проводниками. Самоиндуктивность тоже может быть плохо. Предположим, у нас есть необычный блок питания, и мы хотим использовать его для передачи электрического сигнала по проводу (или линии передачи).Конечно, провод или линия передачи будут обладать как сопротивлением, так и индуктивностью, и, следовательно, будет иметь некоторое характерное время. Предположим, что мы попробуйте послать прямоугольный сигнал по проводу. Поскольку ток в проводе не может подниматься или опускаться быстрее времени, передний и задний края сигнал со временем сглаживается. Типичная разница между сигнал, поступающий в провод (верхний график), и тот, который выходит из другой конец (нижняя кривая) показан на рис.53. Ясно, что мало Дело в том, что у вас есть необычный источник питания, если вы также не обладаете низкой индуктивностью провод или линия передачи, так что сигнал от источника питания может быть передается на какое-то нагрузочное устройство без серьезных искажений. Рисунок 53: Далее: Взаимная индуктивность Up: Магнитная индукция Предыдущий: Индуктивность Ричард Фицпатрик 2006-02-02 Магнитная индукция Ресурс исследования Исследовать Искусство и гуманитарные науки Бизнес Инженерная технология Иностранный язык История Математика Наука Социальная наука Лучшие подкатегории Продвинутая математика Алгебра Основы математики Исчисление Геометрия Линейная алгебра Предалгебра Предварительный камень Статистика и вероятность Тригонометрия другое → Лучшие подкатегории Астрономия Астрофизика Биология Химия Науки о Земле Наука об окружающей среде Наука о здоровье Физика другое → Лучшие подкатегории Антропология Закон Политология Психология Социология другое → Лучшие подкатегории Бухгалтерский учет Экономика Финансы Менеджмент другое → Лучшие подкатегории Аэрокосмическая техника Биоинженерия Химическая инженерия Гражданское строительство Компьютерные науки Электротехника Промышленное проектирование Машиностроение Веб-дизайн другое → Лучшие подкатегории Архитектура . alexxlab Посмотреть все записи автора alexxlab → Вам также может понравиться Ротор якорь статор: Роторы, якоря и статоры 03.04.202101.10.2020 Центр сбк передача показаний электроэнергии: Передать показания | Центр-СБК 15.05.201928.09.2020 Монтажный чертеж: ГОСТ 2.109-73 Единая система конструкторской документации. Основные требования к чертежам 14.08.202118.11.2020 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт