Метод контурных токов онлайн | FaultAn.ru
Программа онлайн-расчёта позволяет по нарисованной вручную схеме производить расчёт электрических цепей различными методами, в том числе по методу контурных токов.
Схема составляется путём перетаскивания элементов из панели элементов и последующим их соединением между собой. Подробная инструкция представлена на видео.
Доступны все основные элементы для линейных электрических цепей: источник ЭДС, источник тока, резистор, конденсатор, катушка индуктивности. Для каждого элемента задаются свои параметры. Программа позволяет производить расчёт как цепей постоянного тока, так и цепей переменного тока. Для цепей переменного тока расчёт производится комплексным методом.
Рассмотрим пример нахождения токов в ветвях методом контурных токов для схемы, приведённой ниже.
Рассматриваемая схема
Рассматриваемая схема
Исходные данные:
- E1: Номер элемента: 1, Амплитудное значение: 5, Начальная фаза: 45
- R1: Номер элемента: 1, Сопротивление, Ом: 1
- R2: Номер элемента: 2, Сопротивление, Ом: 2
- L1: Номер элемента: 1, Сопротивление, Ом: 2
- C1: Номер элемента: 1, Сопротивление, Ом: 1
- C2: Номер элемента: 2, Сопротивление, Ом: 1
- J1: Номер элемента: 1, Амплитудное значение: 1, Начальная фаза: 0
После задания параметров всех элементов необходимо нажать кнопку «Расчёт», после чего программа формирует полное решение задачи, а на исходной схеме отображает принятые положительные направления токов и обозначения узлов. Ниже приведён текст решения.
Принятые положительные направления токов и обозначения узлов
Принятые положительные направления токов и обозначения узлов
Рассчитаем схему по методу контурных токов.
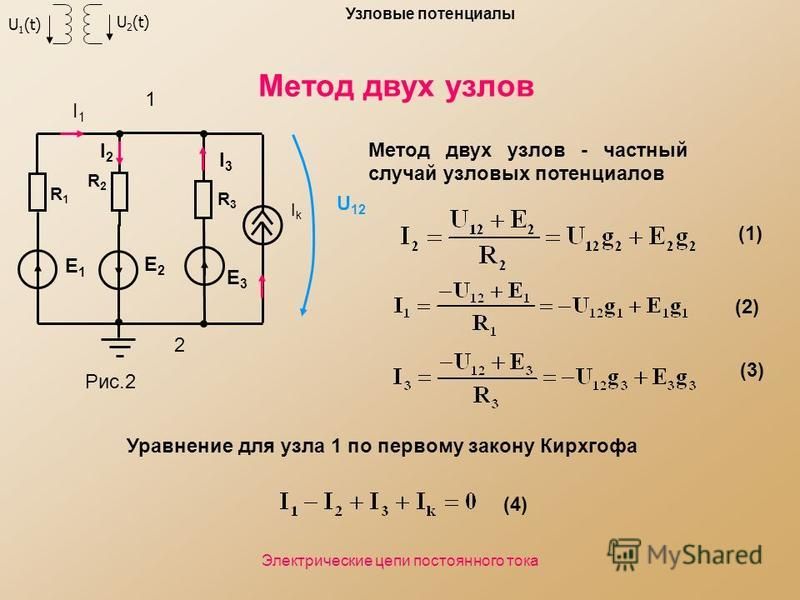
В данной схеме: узлов — 3, ветвей без источников тока — 4, независимых контуров — 2.
Количество уравнений, составляемых по методу контурных токов, равно Nв — Nу + 1, где Nв — число ветвей без источников тока, Nу — число узлов.
Для данной схемы количество уравнений, составляемых по методу контурных токов, равно 4 — 3 + 1 = 2.
Произвольно зададим направления обхода контуров и соответствующие контурные токи.
Принятые направления обхода контуров:
Контур №1 обходится через элементы E1, R1, C1 в указанном порядке. Через эти элементы протекает контурный ток I11.
Контур №2 обходится через элементы R2, L1, C1, C2 в указанном порядке. Через эти элементы протекает контурный ток I22.
Дополнительно зададим контурные токи, создаваемые источниками тока.
Контурный ток J11 протекает через элементы J1, R2, L1 в указанном порядке.
Составим уравнения по методу контурных токов.
Составим уравнение для контура №1:
Составим уравнение для контура №2:
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми контурными токами. Система уравнений по методу контурных токов для исходной цепи выглядит следующим образом:
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
Решим систему уравнений и получим искомые контурные токи:
Произвольно зададим направления токов в ветвях.
Принятые направления токов:
Ток I1 направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы E1, R1.
Ток I2 направлен от узла ‘3 у.’ к узлу ‘1 у.’ через элементы R2, L1.
Ток I3 направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы C1.
Ток I4 направлен от узла ‘2 у.’ к узлу ‘3 у.’ через элементы C2.
Рассчитаем токи в ветвях исходя из полученных контурных токов.
Проверим баланс мощностей.
Определим мощность, потребляемую приёмниками:
Подставим числовые значения и получим:
Определим мощность, отдаваемую источниками:
где SE — мощность, отдаваемая источниками ЭДС, SJ — мощность, отдаваемая источниками тока.
Определим мощность SE, отдаваемую источниками ЭДС:
где I’ означает сопряжённый комплексный ток.
Подставим числовые значения и получим:
Определим мощность SJ, отдаваемую источниками тока. Далее J’ означает сопряжённый комплексный ток источника тока.
Определим мощность SJ1, отдаваемую источником тока J1:
Определим напряжение на источнике тока J1, обозначенное как UJ1. Для этого рассмотрим контур, проходящий через элементы J1, R2, L1 в указанном порядке, и составим для этого контура уравнение по второму закону Кирхгофа. Получим:
Получим:
Выразим из полученного уравнения напряжение UJ1 и подставим числовые значения. Получим:
Мощность, отдаваемая источником тока J1, равна:
Суммарная мощность, отдаваемая источниками тока, равна:
Мощность, отдаваемая источниками, равна:
Итак, Sпр = 12 — 6j, Sист = 12 — 6j. Баланс мощностей сходится.
После завершения расчёта строятся векторные диаграммы токов и напряжений.
Векторные диаграммы токов
Векторные диаграммы токов
Векторные диаграммы напряжений
Векторные диаграммы напряжений
Решение задач ТОЭ – методы, алгоритмы и примеры решения
Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
Решение задач занимают важное место в курсе ТОЭ, так как в процессе их решения проверяется степень усвоения теоретического материала, и приобретаются навыки, необходимые для приложения теории к практике.
На примерах решения задач по ТОЭ представлены основные разделы современной теории электрических цепей, составляющие предмет теоретических основ электротехники (ТОЭ).
Объем теоретического материала курса ТОЭ, представленный в виде кратких физических схем и подробно изложенных алгоритмов, позволяет непосредственно перейти к решению как типовых, так и задач, выходящих за рамки курса ТОЭ.
Реализуется естественный принцип выборочного прочтения и быстрого нахождения нужной информации.
Решение задач по ТОЭ делится на разделы, каждый из которых содержит краткое описание методов и алгоритмов решения задач ТОЭ.
Общие рекомендации при решении задач ТОЭ:
• заданные условия задачи должны быть тщательно проанализированы. Для этого их необходимо прочесть, как минимум, дважды: сначала бегло, схватывая смысл задания в целом, а затем медленно, стараясь подметить мелкие и, на первый взгляд, незначительные детали;
• не стоит решать задачу по схеме, изображенной в расчетной работе, билете. Схему следует перерисовать в привычном для себя виде;
Схему следует перерисовать в привычном для себя виде;
• краткие условия задачи желательно приводить справа от расчетной схемы. На схеме должны быть обозначены все необходимые токи и напряжения, причем, желательно, все величины, относящиеся к одной ветви, обозначать одинаковым индексом: E1, U1, I1, R1. В расчетах не должно быть величин, которые не были бы обозначены на схеме;
• полученный результат (результаты) расчета должен быть проверен, будь это баланс мощностей, векторная диаграмма, отдельное уравнение по одному из законов Кирхгофа или просто логическое рассуждение.
Решение экзаменационных задач ТОЭ онлайн ВКонтаке Василий Новицкий
Содержание
1 Методы расчета электрических цепей при постоянных токах и напряжениях
1.1 Методы решения, основанные на законах Ома и Кирхгофа
1.2 Метод наложения
1. 3 Метод контурных токов
3 Метод контурных токов
1.4 Метод узловых потенциалов. Метод узлового напряжения (двух узлов)
1.5 Метод эквивалентного генератора (источника ЭДС)
1.6 Методы расчета нелинейных электрических цепей постоянного тока
2 Магнитное поле и магнитные цепи при постоянных токах
2.1 Методы расчета магнитных цепей постоянного тока
2.2 Катушки и трансформаторы со стальными сердечниками
2.3 Магнитное поле, индуктивность
3 Методы расчета линейных цепей синусоидального тока
3.1 Расчет цепей переменного тока методом векторных диаграмм
3.2 Символический метод расчета цепей синусоидального тока
3.3 Резонанс в электрической цепи
3.4 Цепи со взаимными индуктивностями
4 Анализ схем при несинусоидальных (негармонических) периодических воздействиях
4.1 Алгоритм расчета схем при несинусоидальных периодических воздействиях
4.2 Примеры расчета схем при несинусоидальных периодических воздействиях
5 Трехфазные цепи
5. 1 Основные определения и отношения
1 Основные определения и отношения
5.2 Расчет симметричных режимов работы трехфазных цепей
5.3 Расчет несимметричных режимов работы трехфазных цепей (метод симметричных составляющих)
6 Анализ общих свойств пассивных четырехполюсников
7 Методы анализа переходных процессов в линейных цепях с сосредоточенными параметрами
7.1 Физические основы переходных процессов
7.2 Математический аппарат и алгоритмы расчетов
7.2.1 Классический метод анализа переходного процесса
7.2.2 Операторный метод расчета (метод преобразования Лапласа)
7.2.3 Расчет методом интеграла Дюамеля
8 Нелинейные цепи переменного тока
8.1 Графические и графоаналитические методы расчета
8.2 Аналитические методы расчета
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
RSS
Электротехника ТОЭ: 3.2.2. Метод контурных токов
Теория / 3. 2. Методы расчета сложных электрических цепей / 3.2.2. Метод контурных токов
2. Методы расчета сложных электрических цепей / 3.2.2. Метод контурных токов
Метод контурных токов позволяет уменьшить число
уравнений, составляемых по законам Кирхгофа до числа независимых контуров.
Метод контурных токов основан на том свойстве, что ток
в каждой ветви может быть представлен в виде алгебраической суммы независимых
контурных токов, протекающих в этой ветви.
Рассмотрим электрическую цепь (рис. 3.4), аналогичную
той, что рассматривали в предыдущем случае.
Определим число независимых контуров:
Считаем, что в каждом контуре протекает свой,
независимый от других контуров, ток. Направление контурных токов обозначаем круговой
стрелкой. Выберем направление контурных токов по часовой стрелке и запишем для
каждого контура уравнение по второму закону Кирхгофа с использованием контурных
токов, считая положительным направлением для каждого контура направление
контурного тока:
Эту систему уравнений можно привести к следующему виду:
При расчете цепей методом контурных токов удобнее
пользоваться готовой математической моделью, которая представляет собой систему
линейных алгебраических уравнений:
Здесь R11, R22, R33 –
собственные сопротивления контуров, равные сумме всех сопротивлений, входящих в
контур:
Все остальные сопротивления являются взаимными:
R12 = R21 = R2 – взаимное сопротивление
между первым и
вторым контурами;
R23 = R32 = R4 – взаимное
сопротивление между
вторым и третьим контурами;
R13 = R31 =
0; – взаимное сопротивление между первым
и третьим контурами.
Из схемы можно видеть, что первый и третий контуры не
имеют общей ветви, а граничат только через узел, поэтому их взаимное сопротивление
равно нулю
Е11 = Е1; Е22
= –Е2; Е33
= Е3 +Е2 – контурные ЭДС.
Если действие э.д.с. совпадает с направлением
контурного тока, то ЭДС имеет знак
«плюс», если не совпадает – «минус».
При использовании математической модели следует
направления всех контурных токов выбирать одинаковыми. В этом случае члены,
расположенные по главной диагонали и
содержащие собственные сопротивления контуров, будут положительны, а
члены, содержащие взаимные сопротивления, – отрицательны.
Если число уравнений больше двух, то систему удобнее
решать матричным методом.
Составим главный определитель системы
Частные определители получим, заменяя соответствующие
столбцы матриц столбцами свободных членов
Контурные токи находим из выражений:
Для того чтобы определить истинные токи в ветвях,
следут пользоваться следующими правилами. Если в ветви протекает только один
Если в ветви протекает только один
контурный ток, то истинный ток равен этому контурному току, причем, если
условно положительное направление истинного тока совпадает с направлением
контурного тока, то ставим знак контурного тока, если не совпадает – противоположный. Если в ветви протекает два
контурных тока, то за положительный принимаем тот, направление которого
совпадает с направлением истинного тока. Для заданной схемы истинные токи
определятся выражениями:
Достоинством этого метода по отношению к предыдущему
является то, что количество уравнений, составляемых по законам Кирхгофа,
уменьшается.
К недостаткам можно отнести введение в расчеты фиктивных величин –
контурных токов, через посредство которых находят истинные токи.
Электротехника. Метод контурных токов — Botva-Project
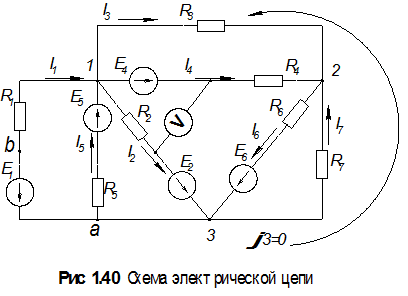
Сегодня мы разберем еще один важный (и по секрету, наш любимый) метод определения токов в цепи постоянного тока. Это метод контурных токов. На наш взгляд он проще, чем уравнения Кирхгофа, хотя бы потому, что уравнений в системе, которую придется решать, ровно в два раза меньше. Итак, рассмотрим ту же электрическую цепь постоянного тока, которую мы рассчитывали по методу Кирхгофа. Напомним, как выглядит схема
Итак, рассмотрим ту же электрическую цепь постоянного тока, которую мы рассчитывали по методу Кирхгофа. Напомним, как выглядит схема
В данной схеме нас интересует количество независимых контуров, выбираем их так же, как мы делали это в прошлый раз. Здесь три независимых контура.
В каждой ветви цепи наносим стрелками направления неизвестных токов, так же, как мы делали ранее (если вы уже рассчитали цепь любым другим способом, то направления и нумерацию токов имеет смысл сохранить, чтобы была возможность сравнить результаты расчета двумя методами). В методе Кирхгофа мы это делали так, повторим.
И последний штрих — в каждом контуре выбираем направление обхода и рисуем контурный ток. Мы любим брать те же направления, что и в методе Кирхгофа, как минимум для того, чтобы не рисовать два раза одно и тоже. Контурные токи обозначают большой буквой I, с нижним индексом 11, 22, 33.
Подготовительная часть работы завершена, переходим непосредственно к определению токов. Записывается три уравнения (по числу контурных токов). По сути каждое уравнение представляет собой что-то, похожее на второй закон Кирхгофа, только для контурного тока.
Записывается три уравнения (по числу контурных токов). По сути каждое уравнение представляет собой что-то, похожее на второй закон Кирхгофа, только для контурного тока.
В общем виде система уравнений для трех контуров имеет вид
Контурные токи, само собой, неизвестны, их надо определить. Сопротивления R11, R22, R33 — это полные сопротивления каждого контура, взятые со знаком «плюс». То есть обходим по кругу каждый контур и суммируем все сопротивления, которые в него входят.
Для контура 1 — это резисторы 1 и 2, для контура 2 — резистор 4, для контура 3 — резистор 5.
Сопротивления типа Rij — это сопротивления ветвей, общих для i и j контуров. То есть, если мы хотим определить R12, мы находим ветвь, общую для контуров 1 и 2, и записываем ее сопротивление. Знак при этом определяется направлением контурных токов: если токи в двух контурах направлены одинаково, то сопротивление ветви берется в «плюсом»; если токи направлены в разные стороны, то берется с «минусом». На примере сопротивления R12: общая для контуров 1 и 2 ветвь — это ветвь между узлами 2 и 4 (ветвь №2 согласно нумерации токов). Резисторов на ней нет, так что сопротивление R12=0. Знак, конечно, в таком случае значения не имеет, но токи I11 и I22 в данной ветви направлены противоположно, так что если бы сопротивление было, то мы бы записали его в систему со знаком «минус». Сопротивления с индексами ij и ji, разумеется, равны.
На примере сопротивления R12: общая для контуров 1 и 2 ветвь — это ветвь между узлами 2 и 4 (ветвь №2 согласно нумерации токов). Резисторов на ней нет, так что сопротивление R12=0. Знак, конечно, в таком случае значения не имеет, но токи I11 и I22 в данной ветви направлены противоположно, так что если бы сопротивление было, то мы бы записали его в систему со знаком «минус». Сопротивления с индексами ij и ji, разумеется, равны.
Для всех ветвей системы получается более чем просто:
В правых частях уравнения идут суммы ЭДС источников напряжения. Принцип тот же, что и во втором законе Кирхгофа: суммируем ЭДС, учитывая знаки. Если направление ЭДС совпадает с направлением контурного тока, то берем его с плюсом, если не совпадает — то с минусом.
На примере контура 1: в контуре 1 только один источник напряжения E1, направление которого противоположно направлению контурного тока. Значит,
Для всех контуров получаем
Теперь мы готовы записать и решить полную систему уравнений для трех контурных токов. Получается так:
Получается так:
Упрощая и сокращая то, что упрощается и сокращается, получим несложную систему уравнений с тремя неизвестными, из которой однозначно определяются контурные токи.
Определив контурные токи, мы должны еще определить токи в ветвях. Это делается совсем несложно. Идем по порядку по ветвям нашей цепи и смотрим, как из контурных токов суммируются токи в ветвях. В образовании тока ветви 1 принимает участие только один контурный ток I11, причем он направлен в другую сторону. Значит
В ветви 2 ток I2 складывается из контурных токов I11 и I22, причем I22 берется с «плюсом» (направление тока I2 и I22 совпадают), а I11 — с «минусом» (направления I2 и I11 противоположны)
Для всех ветвей
Вот и все, задача решена. Остается только сравнить результаты с ответами, полученными другим методом, и убедиться, что все сделано правильно.
Всегда ваша, Botva-Project
Метод контурных токов | Онлайн журнал электрика
Методика расчета цепи способом контурных токов
В способе контурных токов за неведомые величины принимаются расчетные (контурные) токи, которые типо протекают в каждом из независящих контуров. Таким макаром, количество неведомых токов и уравнений в системе равно числу независящих контуров цепи.
Таким макаром, количество неведомых токов и уравнений в системе равно числу независящих контуров цепи.
Расчет токов веток по способу контурных токов делают в последующем порядке:
1 Вычерчиваем принципную схему цепи и обозначаем все элементы.
2 Определяем все независящие контуры.
3 Произвольно задаемся направлением протекания контурных токов в каждом из независящих контуров (по часовой стрелке либо против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные числа (I11, I22, I33 и т. д.) либо римские числа.
4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независящих контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учесть и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях нужно брать от каждого тока в отдельности.
Падение напряжения на потребителях в таких ветвях нужно брать от каждого тока в отдельности.
5 Решаем хоть каким способом полученную систему относительно контурных токов и определяем их.
6 Произвольно задаемся направлением реальных токов всех веток и обозначаем их. Маркировать реальные токи нужно таким макаром, чтоб не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские числа (I1, I2, I3 и т. д.).
7 Перебегаем от контурных токов к реальным, считая, что реальный ток ветки равен алгебраической сумме контурных токов, протекающих по данной ветки.
При алгебраическом суммировании без конфигурации знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветки. В неприятном случае контурный ток множится на минус единицу.
Пример расчёта сложной цепи способом контурных токов
В цепи, изображённой на рисунке 1, высчитать все токи способом контурных токов. Характеристики цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.
Характеристики цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.
Рис. 1. Схема электронной цепи для примера расчета по способу контурных токов
Решение. Для расчета сложной цепи этим способом довольно составить два уравнения, по числу независящих контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. набросок 1).
По второму закону Кирхгофа относительно контурных токов составляем уравнения:
Решаем систему и получаем контурные токи I11 = I22 = 3 А.
Произвольно задаемся направлением реальных токов всех веток и обозначаем их. На рисунке 1 такими токами являются I1, I2, I3. Направление у этих токов однообразное – вертикально ввысь.
Перебегаем от контурных токов к реальным. В первой ветки протекает только один контурный ток I11. Направление его совпадает с направлением реального тока ветки. В таком случае реальный ток I1 + I11 = 3 А.
Реальный ток 2-ой ветки формируется 2-мя контурными I11 и I22. Ток I22 совпадает по направлению с реальным, а I11 ориентирован навстречу реальному. В итоге I2 = I22 — I11 = 3 — 3 = 0А.
В третьей ветки протекает только контурный ток I22. Направление этого тока обратно направлению реального, потому для I3 можно записать I3 = -I22 = -3А.
Необходимо подчеркнуть, как положительный факт, что в способе контурных токов по сопоставлению с решением по законам Кихгофа приходится решать систему уравнений наименьшего порядка. Но этот способ не позволяет сходу определять реальные токи веток.
Пацкевич В. А.
Школа для электрика
Методическая разработка урока «Метод контурных токов» (10 класс). Профильный уровень
Методическая разработка урока физики для профильного класса
(политехнический, физико-математический)
Урок 12/114 10 класс
Тема: Метод контурных токов.
Цели урока:
образовательная: научить учащихся производить расчеты сложных электрических цепей;
развивающая: сформировать умения анализировать, развитие логики мышления, поиска способов рационального решения физических задач;
воспитательная: воспитание мотивации учения.
Содержание урока:
Организационный момент
Проверка знаний.
Фронтальный опрос.
Вопросы:
Дайте определение узла электрической цепи. Начертите на доске электрический узел, укажите направление электрических токов в подводящих к узлу ветвях.
Сформулируйте первое правило Кирхгофа.

Запишите первое правило Кирхгофа для начерченного на доске (рис. 1) узла.
Рис. 1. Рис.2.
Какое соединение элементов электрической цепи можно считать ветвью?
Сформулируйте второе правило Кирхгофа, запишите второе правило Кирхгофа для предложенной схемы (рис. 2).
Объясните, как записать второе правило Кирхгофа, если в ветви находятся несколько источников тока?
Как влияет полярность включения источника тока в электрическую цепь на знак ЭДС в уравнении?
Индивидуальный опрос у доски с одновременным решением задачи № 1 в тетрадях учащихся.
ЗАДАЧА № 1.
В предложенной электрической цепи определите силу тока во всех резисторах, используя законы Кирхгофа.
Рис. 3
Решение задачи:
Напишем 1 закон Кирхгофа для узлов А, В, С:
А: I1 — I2 + I4 = 0;
В: I5 – I1 + I3 = 0;
С: I6 – I4 – I5 = 0.
Выберем направление обхода контуров ADBA, BDCB и ABCA и напишем 2 закон Кирхгофа для этих контуров:
ADBA: ε1 = I2 . R2 + I1 . R1 + I3 . R3 ;
R3 ;
BDCB: ε2 = I5 . R5 — I3 . R3 + I6 . R6 ;
ABCA : 0 = I4 . R4 — I1 . R1 – I5 . R5 .
Подставим численные значения сопротивлений резисторов и источников тока в полученные уравнения и объединим их систему из шести уравнений с шестью неизвестными:
Выразим из наиболее простого уравнения системы один из неизвестных токов и, подставив это неизвестное в остальные уравнения, преобразуем уравнения системы с учетом полученного выражения, и, понижая с каждым преобразованием ранг системы уравнений, найдем численные значения неизвестных, входящих в эту систему уравнений:
Подставим полученные значения силы тока в резисторах в уравнения Кирхгофа, убедимся в правильности расчетов:
Изучение нового материала.

Вопросы: Расчет электрических цепей с помощью метода контурных токов.
Расчет электрической цепи методом контурных токов.
Для сравнения уровня сложности расчетов произведем расчет электрической цепи Рис. 3., предложенной в предыдущей задаче, методом контурных токов:
Основным достоинством, рассматриваемого метода расчета электрической цепи, метода контурных токов является то, что для вычисления силы токов в каждом элементе цепи количество уравнений в системе соответствует количеству контуров рассчитываемой электрической цепи. В нашем случае необходимо составить всего три уравнения, что в два раза меньше чем в системе уравнений рассчитываемой при использовании законов Кирхгофа.
Выберем в контурах ADBA, BDCB и ABCA произвольно направления контурных токов J1, J2 и J3. Составим систему из трех уравнений:
Составим систему из трех уравнений:
Подставив в полученную систему уравнений численные значения резисторов и ЭДС, рассчитаем контурные токи:
Сила тока в отдельных резисторах определяется как векторная сумма контурных токов, протекающих через эти резисторы:
I1 = J1 – J3 = 0,2 А; I2 = J1 = 0,6 А;
I3 = J2 – J1 = 0,4 А; I4 = J3 = 0,4 А;
I5 = J2 – J3 = 0,6 А; I6 = J2 = 1А.
Результаты расчета проверяются с помощью законов Кирхгофа.
Закрепление изученного материала.
Учащимся предлагается самостоятельно записать уравнения, необходимые для расчета следующей электрической цепи (рис. 4) методом контурных токов:
Рис. 4.
Для предложенной электрической цепи выберем 3 контура:
1 – контур: С, R2 ,ε1,R1, А, R3, С
2 – контур: С, R3, А, R4, В, R6, D, R5, С
3 – контур: D, R6, В, R7, ε2, R8, D
Составим уравнения согласно второму правилу Кирхгофа для выбранных контуров:
ε1= J1 . (R1 + R2 + R3 + r1) – J2 . R3 (1).
(R1 + R2 + R3 + r1) – J2 . R3 (1).
0 = J2 . (R3 + R4 + R5 + R6) – J1 . R3 – J3 . R6 (2).
ε 2= J3 . (R6 + R7 + R8 + r2) – J2 . R6 (3).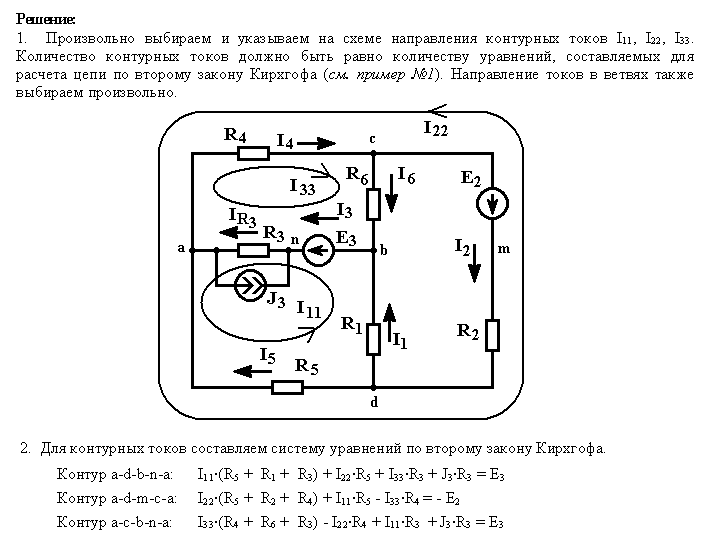
После решения системы трех уравнений с тремя неизвестными найдем токи в элементах цепи:
I1 = I2 =J1, I3 =J1 – J2,
I4 = I5 =J2, I3 =J1 – J2,
I6 = J2 – J3, I7 = I8 =J3.
Самостоятельная работа учащихся по решению задач.
Используя метод контурных токов, вычислите численные значения силы тока в каждом элементе, найдите падение напряжения на всех резисторах, предложенной электрической цепи:
ЗАДАЧА № 2.
Рассчитайте электрическую цепь методом контурных токов:
Дано:
ε1 = 50 В
ε2 = 40 В
R1 = 7 Ом
R2 = 10 Ом
R3 = 6 Ом
r1 = 3 Ом
r2 = 4 Ом.
Определить:
I1 , I2 , I3,
U1, U2, U3.
РЕШЕНИЕ:
В цепи два простых контура. Выберем направление контурных токов J1 и J2 с учетом полярности ЭДС источников тока.
Для контура C,ε1, r1, R1, A, R2,C: ε1= J1 . (R1 + R2 + r1) + J2 . R2 (1).
Для контура C, R2, A, R3 , ε1, r1, ,C: ε2= J2 . (R3 + R2 + r2) + J1 . R2 (2).
R2 (2).
Подставляя в выражения (1) и (2) численные значения сопротивления резисторов и ЭДС источников тока, получаем систему из двух уравнений:
50 = J1 . (7 + 10 + 3) + J2 . 10, 5 = 2J1 + J2 , J1 = 2 А;
40 = J2 . (6 + 10 + 4) + J1 . 10. 4 = 2J2 + J1. J2 = 1 А.
Рассчитаем токи в отдельных резисторах: I1 = J1 = 2А; I2 = J1 + J2 = 3А; I3 = J2 = 1А.
Рассчитаем падение напряжения на резисторах: U1 = I1 . R1 = 2 . 7 = 14 B, U2 = I2 . R2 = 3 . 10 = 30 B, U3 = I3 . R3 = 1 . 6 = 6 B.
Ответ: I1 = 2А; I2 = 3А; I3 = 1А. U1 = 14 B, U2 = 30 B, U3 = 6 B.
Подведение итогов урока.
Задание на дом.

Рассчитайте методом контурных токов электрические цепи:
ЗАДАЧА № 1.
Дано:
ε1 = 20 В
ε2 = 30 В
R1 = 16 Ом
R2 = 10 Ом
R3 = 20 Ом
R4 = 7 Ом
R5 = 10 Ом
r1 = 3 Ом
r2 = 4 Ом.
Определить:
I1 , I2 , I3, I4 , I5 ,
U1, U2, U3, U4, U5.
ЗАДАЧА № 2.
Дано:
ε1 = 20 В
ε2 = 30 В
R1 = 16 Ом
R2 = 10 Ом
R3 = 20 Ом
R4 = 8 Ом
R5 = 20 Ом
r1 = 2 Ом
r2 = 4 Ом.
Определить:
I1 , I2 , I3, I4 , I5 ,
U1, U2, U3, U4, U5.
ЗАДАЧА № 3.
Дано:
ε1 = 100 В
ε2 = 50 В
R1 = 20 Ом
R2 = 30 Ом
R3 = 20 Ом
R4 = 20 Ом
R5 = 75 Ом
R6 = 78 Ом
r1 = 5 Ом
r2 = 2 Ом.
Определить:
I1 , I2 , I3, I4 , I5 , I6,
U1, U2, U3, U4, U5, U6.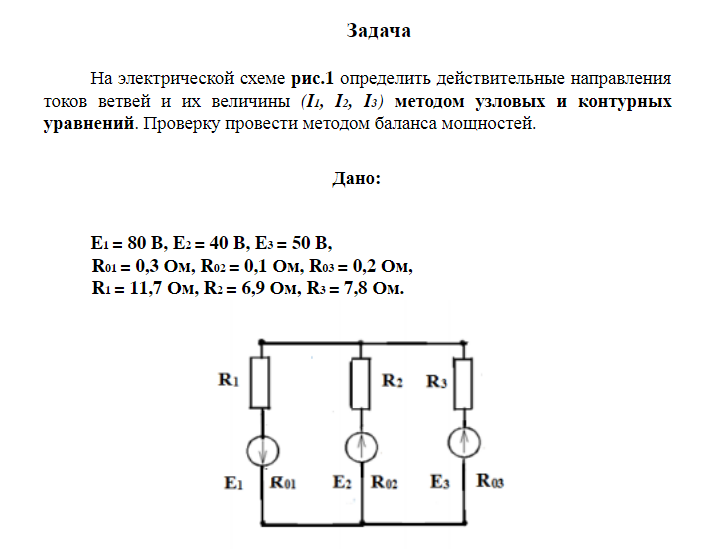
Задача 1.1. Для представленной электрической схемы определить токи во всех ветвях схемы методом контурных токов. Решение: Определяем количество независимых контуров и обозначаем их контурные токи. Далее составляем систему уравнений для первого, второго и третьего контуров по второму закону Кирхгофа.
А мы решаем дальше. Пояснения к первому уравнению: в своем замкнутом контуре №1 контурный ток I11 без учета воздействия других контурных токов как бы «соберет» все сопротивления в этом контуре под знак «плюс». Однако, ток I33 в третьем контуре пройдет в обратном направлении через сопротивление R4 по сравнению с током первого контура через это же сопротивление, поэтому из произведение запишется со знаком «минус». А вот контурный ток I22 второго контура пройдет через сопротивление R1 в том же направлении, что и контурный ток первого контура через это же сопротивление. А значит присоединится к нам их произведение со знаком «плюс». Все слагаемые представляют из себя произведение тока на сопротивление, т.е. — это напряжение. И сумма этих слагаемых, т.е. напряжений данного контура должна равняться ЭДС, входящей в данный контур. А это по условию 110В. Далее придется, как это ни грустно, заняться математикой. Домножим второе уравнение (при умножении обоих частей равенства на одно и тоже число или при делении — равенство не нарушается) на три и сложим его с третьим уравнением. Это позволит нам избавиться от одного неизвестного, а именно контурного тока контура №1. Третье же уравнение перепишем без изменений.
Задача 2.1. Решить предыдущую задачу методом узловых потенциалов. Исходные данные: сопротивление нагрузочных резисторов — R1 = 2Ом, R2 = 3Ом, R3 = 4Ом, R4 = 6Ом, R5 = 10Ом, R6 = 10Ом. Внутренние сопротивления источников ( в схеме не нарисованы, но учитывать надо) — r2 = 1Ом, r3 = 2Ом. ЭДС источников питания — Е2 = 110В, Е3 = 220В. Составить баланс мощностей. Решение: Для начала необходимо составить уравнения по закону Кирхгофа.
;;; ; ; Составим уравнения по закону Кирхгофа для трех узлов. Теперь подставим в эту систему вышенайденные значения для вычисления токов. Получим следующую систему для решения нашей задачи: Далее мы приводим все выражения к общему знаменателю 12, приводим в каждом выражении подобные слагаемые и в получившейся системе уравнений первое из них домножаем на 5,5 и складываем со вторым. Получаем: Сложив первое уравнение со вторым и переписав два последних, получим следующую систему уравнений: Из первого уравнения находим, что Подставив найденное значение во второе и третье уравнения системы, приведем подобные слагаемые и таким образом перейдем к системе уже из двух уравнений с двумя неизвестными: Теперь домножим первое уравнение ситемы на три, а второе на одиннадцать и сложим их. , откуда находим, что Подставив данное значение в любое из двух уравнений последней системы, получим, что Оставшееся неизвестным значение потенциала φ2 находится подстановкой вышенайденных потенциалов φ3 и φ4 в любую систему из трех уравнений. Посчитав, получится, что φ2 = 97,672. Далее по ранее определенным нами формулам для нахождения токов в ветвях находим, что: Как видите, значение тока первой ветви I1 получилось отрицательным. Т.е. на самом деле он будет протекать в противоположном напрвлении по сравнению с тем, которое мы выбрали в начале задачи. Точно также по остальным формулам ;; ; ; находятся и остальные токи. Получим, что I2 = 4,6307A; I3 = 14,1403A; I4 = 8,9986A; I5 = 4,368A; I6 = 9,7672A. Задача 3.1. Решить задачу с применением законов Ома и методом узловых потенциалов. Начертить потенциальную диаграмму контура, не содержащего ЭДС. Исходная схема представлена ниже. Исходные данные: Напряжение источника питания Е = 20В, сопротивления R1 = 3 Ома, R2 = 6 Ом, R3 = 4 Ома, R4 = 8 Ом, R5 = 10 Ом. Решение: Самое простое решение — это упростить схему и решить задачу применением законов Ома. Поскольку каждые из 2-х сопротивлений R1 и R4, а также R2 и R5 включены последовательно, то их значения можно сложить и получить преобразованную схему более простого вида для лучшего понимания и удобства вычисления. Ее вид на рисунке справа. Из схемы видно, что сопротивления R1,4 и R2,5 соединены параллельно. Решим эту же задачу методом узловых потенциалов. В данном случае примем за нулевой потенциал второго узла, т.е. φ2 = 0 (можно и первый — значения не имеет) и воспользуемся формулой межузлового напряжения:Применительно к нашей задаче, получим: Токи ветвей составят:Как видно, из двух методов решения мы пришли к одинаковым результатам. Для построения потенциальной диаграммы нам необходимо найти потенцалы всех точек №№1,2,3,4. |
Метод и анализ тока
Mesh | Анализ сети постоянного тока
Метод Mesh-Current , также известный как метод Loop Current Method , очень похож на метод ответвленных токов в том, что он использует одновременные уравнения, закон напряжения Кирхгофа и закон Ома для определения неизвестных токов в сети.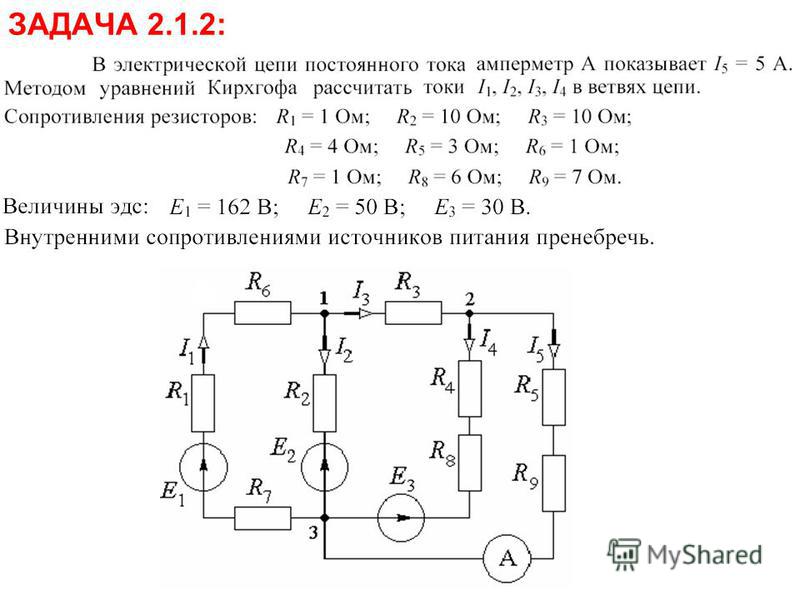 Он отличается от метода ответвленного тока тем, что , а не , использует закон тока Кирхгофа, и он обычно позволяет решить схему с меньшим количеством неизвестных переменных и меньшим количеством одновременных уравнений, что особенно удобно, если вам приходится решать без калькулятор.
Он отличается от метода ответвленного тока тем, что , а не , использует закон тока Кирхгофа, и он обычно позволяет решить схему с меньшим количеством неизвестных переменных и меньшим количеством одновременных уравнений, что особенно удобно, если вам приходится решать без калькулятор.
Mesh Current, традиционный метод
Давайте посмотрим, как этот метод работает на том же примере проблемы:
Определение циклов
Первым шагом в методе Mesh Current является определение «контуров» в цепи, охватывающей все компоненты. В нашем примере схемы петля, образованная B 1 , R 1 и R 2 , будет первой, а петля, образованная B 2 , R 2 и R 3 , будет первой. секунда.Самая странная часть метода Mesh Current — это представление циркулирующих токов в каждой из петель. На самом деле, этот метод получил свое название от идеи, что эти токи соединяются вместе между петлями, как наборы вращающихся шестерен:
Выбор направления каждого тока совершенно произволен, как и в методе ветвления тока, но результирующие уравнения легче решить, если токи проходят в одном направлении через пересекающиеся компоненты (обратите внимание, как токи I 1 и I 2 оба идут «вверх» через резистор R 2 , где они «зацепляются» или пересекаются).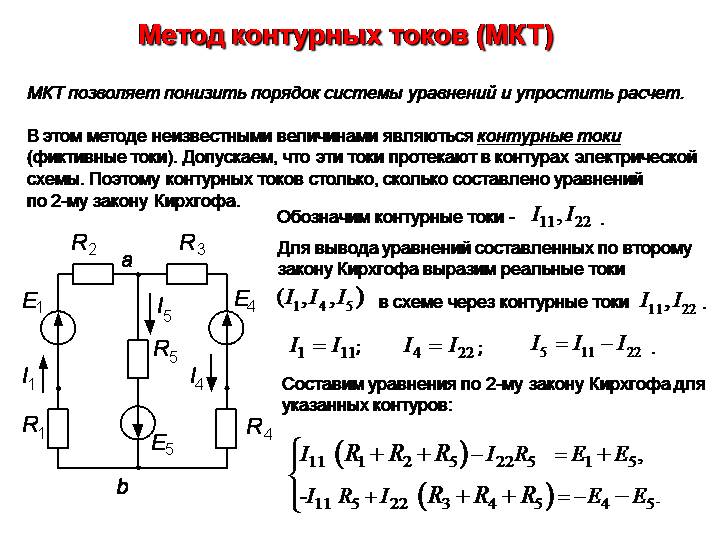 Если предполагаемое направление тока сетки неверно, ответ для этого тока будет иметь отрицательное значение.
Если предполагаемое направление тока сетки неверно, ответ для этого тока будет иметь отрицательное значение.
Маркируйте полярность падения напряжения
Следующим шагом является маркировка всех полярностей падения напряжения на резисторах в соответствии с предполагаемыми направлениями токов сетки. Помните, что конец резистора «вверх по потоку» всегда будет отрицательным, а конец «вниз по потоку» резистора — положительным по отношению друг к другу, поскольку электроны заряжены отрицательно. Полярность батареи, конечно же, определяется ориентацией их символов на схеме и может «согласовываться» или «не совпадать» с полярностью резистора (предполагаемое направление тока):
Используя закон Кирхгофа о напряжении, мы теперь можем обойти каждый из этих контуров, сгенерировав уравнения, представляющие падение напряжения и полярность компонентов.Как и в случае с методом ответвленного тока, мы будем обозначать падение напряжения на резисторе как произведение сопротивления (в омах) и соответствующего тока сетки (на данный момент эта величина неизвестна).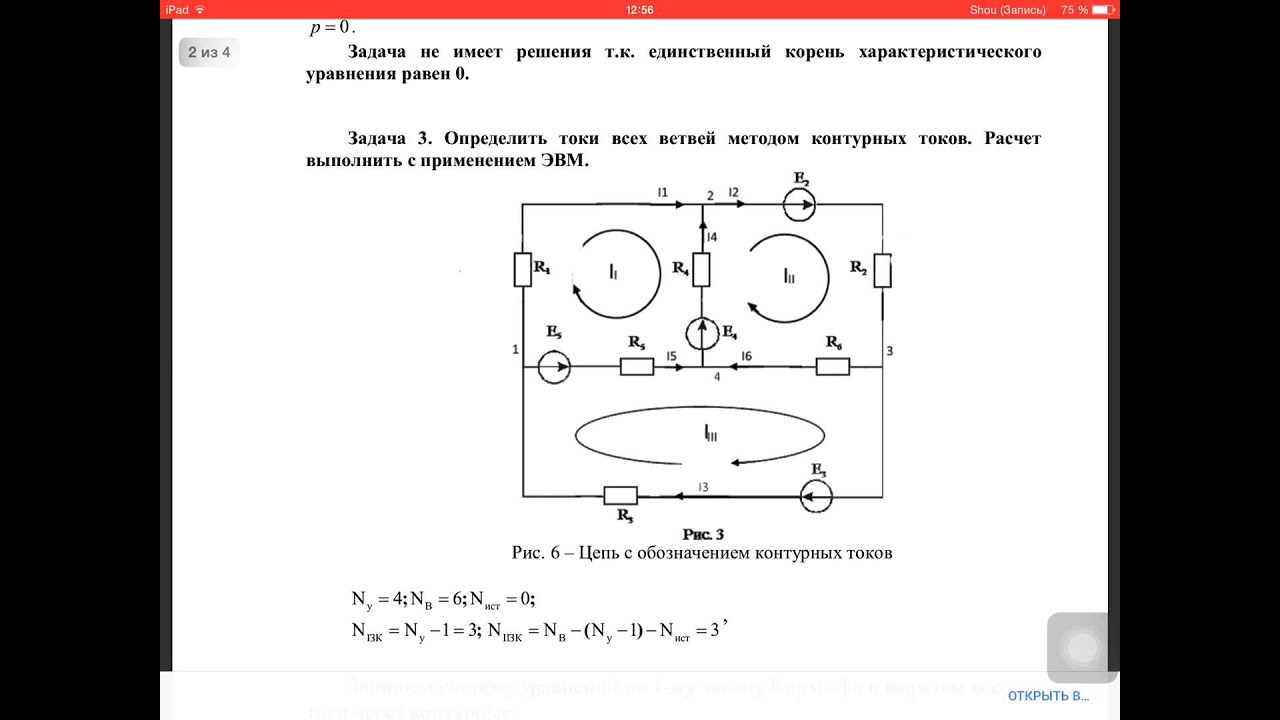 Там, где два тока объединяются, мы запишем этот член в уравнении с током резистора, равным сумме двух объединенных токов.
Там, где два тока объединяются, мы запишем этот член в уравнении с током резистора, равным сумме двух объединенных токов.
Отслеживание левого контура цепи с помощью уравнений
Отслеживание левого контура цепи, начиная с левого верхнего угла и двигаясь против часовой стрелки (выбор начальных точек и направлений в конечном счете не имеет значения), считая полярность, как будто у нас в руках вольтметр, красный щуп на точке впереди и черные идут сзади, получаем уравнение:
Обратите внимание, что средний член уравнения использует сумму токов сетки I 1 и I 2 в качестве тока через резистор R 2 .Это связано с тем, что токи сетки I 1 и I 2 проходят в одном направлении через R 2 и, таким образом, дополняют друг друга. Распределив коэффициент 2 на члены I 1 и I 2 , а затем объединив члены I 1 в уравнении, мы можем упростить как таковое:
На данный момент у нас есть одно уравнение с двумя неизвестными. Чтобы иметь возможность решить для двух неизвестных токов сетки, мы должны иметь два уравнения. Если мы проследим другой контур цепи, мы можем получить другое уравнение КВЛ и иметь достаточно данных для решения двух токов.Существо привычки, которым я являюсь, я начну с верхнего левого угла правой петли и проведу против часовой стрелки:
Чтобы иметь возможность решить для двух неизвестных токов сетки, мы должны иметь два уравнения. Если мы проследим другой контур цепи, мы можем получить другое уравнение КВЛ и иметь достаточно данных для решения двух токов.Существо привычки, которым я являюсь, я начну с верхнего левого угла правой петли и проведу против часовой стрелки:
Упрощая уравнение, как и прежде, мы получаем:
Поиск неизвестного
Теперь, имея два уравнения, мы можем использовать один из нескольких методов для математического решения неизвестных токов I 1 и I 2 :
Перерисовать схему
Зная, что эти решения представляют собой значения для токов ячеек , а не токов ветвей , мы должны вернуться к нашей диаграмме, чтобы увидеть, как они сочетаются друг с другом, чтобы дать токи через все компоненты:
Решение -1 ампер для I 2 означает, что мы изначально предположили, что направление тока неверно.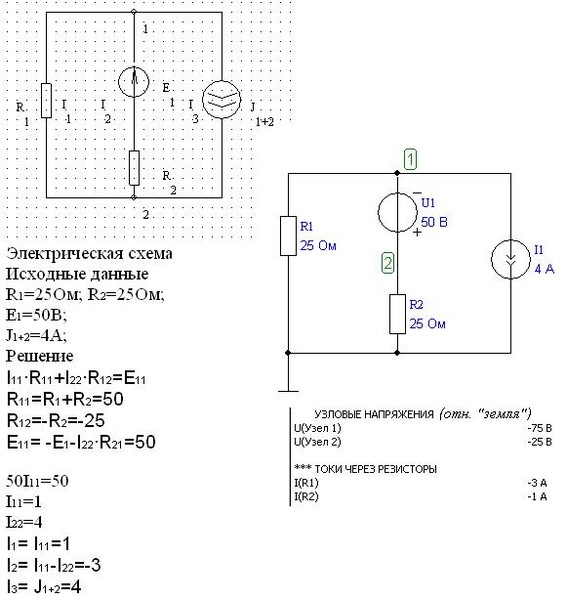 На самом деле I 2 течет против часовой стрелки со значением (положительным) 1 ампер:
На самом деле I 2 течет против часовой стрелки со значением (положительным) 1 ампер:
Это изменение направления тока по сравнению с первоначально предполагаемым изменит полярность падения напряжения на R 2 и R 3 из-за тока I 2 . Отсюда мы можем сказать, что ток через R 1 составляет 5 ампер, а падение напряжения на R 1 является произведением тока и сопротивления (E=IR), 20 вольт (положительное слева и отрицательное на право).
Также можно с уверенностью сказать, что ток через R 3 составляет 1 ампер, с падением напряжения 1 вольт (E=IR), положительный слева и отрицательный справа. Но что происходит на R 2 ?
Ток сетки I 1 идет «вниз» через R 2 , а ток сетки I 2 идет «вверх» через R 2 . Чтобы определить фактический ток через R 2 , мы должны увидеть, как взаимодействуют токи сетки I 1 и I 2 (в данном случае они противоположны), и алгебраически сложить их, чтобы получить окончательное значение. Так как I 1 идет «вниз» при 5 амперах, а I 2 идет «вверх» при 1 ампер, реальный ток через R 2 должен иметь значение 4 ампера, идущий «вниз». :
Так как I 1 идет «вниз» при 5 амперах, а I 2 идет «вверх» при 1 ампер, реальный ток через R 2 должен иметь значение 4 ампера, идущий «вниз». :
Ток силой 4 ампера через резистор R 2 с сопротивлением 2 Ом дает нам падение напряжения 8 вольт (E=IR), положительное вверху и отрицательное внизу.
Преимущество анализа тока сетки
Основным преимуществом анализа Mesh Current является то, что он обычно позволяет решать большие сети с меньшим количеством неизвестных значений и меньшим количеством одновременных уравнений.В нашей примерной задаче потребовалось три уравнения для решения метода Branch Current и только два уравнения с использованием метода Mesh Current. Это преимущество тем больше, чем сложнее сети:
Чтобы решить эту сеть с помощью Branch Currents, нам нужно установить пять переменных для учета каждого уникального тока в цепи (от I 1 до I 5 ). Для этого потребуется пять уравнений для решения в виде двух уравнений KCL и трех уравнений KVL (два уравнения для KCL в узлах и три уравнения для KVL в каждом контуре):
Для этого потребуется пять уравнений для решения в виде двух уравнений KCL и трех уравнений KVL (два уравнения для KCL в узлах и три уравнения для KVL в каждом контуре):
Я полагаю, что если у вас нет ничего лучше, чем потратить свое время, кроме как решить пять неизвестных переменных с пятью уравнениями, вы можете не возражать против использования метода анализа тока ветвления для этой цепи.Для тех из нас, у кого есть более важных дела, которые нужно сделать в наше время, метод Mesh Current намного проще, требуя для решения только трех неизвестных и трех уравнений:
Меньшее количество уравнений для работы является неоспоримым преимуществом, особенно при одновременном решении уравнений вручную (без калькулятора).
Несбалансированный мост Уитстона
Другим типом схемы, которая хорошо подходит для Mesh Current, является несбалансированный мост Уитстона.Возьмем, к примеру, эту схему:
.
Поскольку отношения R 1 /R 4 и R 2 /R 5 не равны, мы знаем, что на резисторе R 3 будет напряжение и некоторая величина тока через него. Как обсуждалось в начале этой главы, этот тип схемы не поддается обычному последовательно-параллельному анализу и может быть проанализирован только каким-либо другим методом.
Как обсуждалось в начале этой главы, этот тип схемы не поддается обычному последовательно-параллельному анализу и может быть проанализирован только каким-либо другим методом.
Мы могли бы применить метод ветвления тока к этой цепи, но для этого потребовалось бы шесть токов (от I 1 до I 6 ), что привело бы к решению очень большого набора одновременных уравнений.Однако, используя метод Mesh Current, мы можем решить для всех токов и напряжений с гораздо меньшим количеством переменных.
Нарисовать сетку
Первым шагом в методе Mesh Current является получение достаточного количества токов сетки для учета всех компонентов в цепи. Глядя на нашу мостовую схему, должно быть очевидно, куда поместить два из этих токов:
Направление этих сетчатых токов, конечно, произвольно. Однако двух токов сетки в этой схеме недостаточно, потому что ни I 1 , ни I 2 не проходят через батарею.Итак, мы должны добавить третий ток сетки, I 3 :
Здесь я выбрал I 3 для петли от нижней стороны батареи, через R 4 , через R 1 и обратно к верхней стороне батареи. Это не единственный путь, который я мог бы выбрать для I 3 , но он кажется самым простым.
Это не единственный путь, который я мог бы выбрать для I 3 , но он кажется самым простым.
Этикетка Полярность падения напряжения на резисторе
Теперь мы должны пометить полярность падения напряжения на резисторе, следуя каждому из предполагаемых направлений тока:
Обратите внимание на одну очень важную вещь: на резисторе R 4 полярность соответствующих токов сетки не совпадает.Это связано с тем, что эти токи сетки (I 2 и I 3 ) проходят через R 4 в разных направлениях. Это не исключает использования метода анализа Mesh Current, но немного усложняет его. Однако позже мы покажем, как избежать конфликта токов R 4 . (см. пример ниже)
Использование KVL
Создание уравнения KVL для верхнего контура моста, начиная с верхнего узла и трассируя по часовой стрелке:
В этом уравнении мы представляем общие направления токов их суммами через общие резисторы. Например, на резисторе R 3 со значением 100 Ом падение напряжения представлено в приведенном выше уравнении КВЛ выражением 100 (I 1 + I 2 ), поскольку оба тока I 1 и I 2 пройти через R 3 справа налево. То же самое можно сказать и о резисторе R 1 , где выражение падения напряжения показано как 150 (I 1 + I 3 ), так как оба резистора I 1 и I 3 проходят через него снизу вверх. резистор, и, таким образом, работайте вместе с , чтобы создать его падение напряжения.
Например, на резисторе R 3 со значением 100 Ом падение напряжения представлено в приведенном выше уравнении КВЛ выражением 100 (I 1 + I 2 ), поскольку оба тока I 1 и I 2 пройти через R 3 справа налево. То же самое можно сказать и о резисторе R 1 , где выражение падения напряжения показано как 150 (I 1 + I 3 ), так как оба резистора I 1 и I 3 проходят через него снизу вверх. резистор, и, таким образом, работайте вместе с , чтобы создать его падение напряжения.
Сгенерировать уравнение КВЛ для нижнего контура моста будет не так просто, так как у нас есть два тока, идущих друг против друга через резистор R 4 . Вот как я это делаю (начиная с правого узла и двигаясь против часовой стрелки):
Обратите внимание, что второй член в исходной форме уравнения имеет значение резистора R 4 , равное 300 Ом, умноженное на разность между I 2 и I 3 (I 2 — I 3 ) . Вот как мы представляем комбинированный эффект двух токов сетки, проходящих в противоположных направлениях через один и тот же компонент. Здесь очень важен выбор соответствующих математических знаков: 300(I 2 — I 3 ) не означает то же самое, что 300 (I 3 — I 2 ). Я решил написать 300 (I 2 — I 3 ), потому что в первую очередь я думал об эффекте I 2 (создание положительного падения напряжения, измерение с помощью воображаемого вольтметра на R 4 , красный свинец на снизу и черный стержень сверху), и, во вторую очередь, от эффекта I 3 (создание отрицательного падения напряжения, красный стержень снизу и черный стержень сверху).Если бы я сначала думал о влиянии I 3 , а затем о влиянии I 2 , удерживая воображаемые выводы вольтметра в одних и тех же положениях (красный внизу и черный вверху), выражение было бы таким: -300(I 3 — I 2 ).
Вот как мы представляем комбинированный эффект двух токов сетки, проходящих в противоположных направлениях через один и тот же компонент. Здесь очень важен выбор соответствующих математических знаков: 300(I 2 — I 3 ) не означает то же самое, что 300 (I 3 — I 2 ). Я решил написать 300 (I 2 — I 3 ), потому что в первую очередь я думал об эффекте I 2 (создание положительного падения напряжения, измерение с помощью воображаемого вольтметра на R 4 , красный свинец на снизу и черный стержень сверху), и, во вторую очередь, от эффекта I 3 (создание отрицательного падения напряжения, красный стержень снизу и черный стержень сверху).Если бы я сначала думал о влиянии I 3 , а затем о влиянии I 2 , удерживая воображаемые выводы вольтметра в одних и тех же положениях (красный внизу и черный вверху), выражение было бы таким: -300(I 3 — I 2 ). Обратите внимание, что это выражение математически эквивалентно первому: +300(I 2 — I 3 ).
Обратите внимание, что это выражение математически эквивалентно первому: +300(I 2 — I 3 ).
Хорошо, это касается двух уравнений, но мне все еще нужно третье уравнение, чтобы завершить мой набор одновременных уравнений из трех переменных, трех уравнений.Это третье уравнение должно также включать напряжение батареи, которое до этого момента не фигурирует ни в двух предыдущих уравнениях KVL. Чтобы сгенерировать это уравнение, я снова начерчу петлю с моим воображаемым вольтметром, начиная с нижней (отрицательной) клеммы батареи, двигаясь по часовой стрелке (опять же, направление, в котором я делаю шаг, является произвольным и не обязательно должно совпадать с направлением). тока сетки в этом контуре):
Решение для токов
Решение для I 1 , I 2 и I 3 с использованием любого метода совместного уравнения, который мы предпочитаем:
Пример: Используйте Octave, чтобы найти решение для I 1 , I 2 и I 3 из приведенной выше упрощенной формы уравнений.
Решение: В Octave, клоне Matlab® с открытым исходным кодом, введите коэффициенты в матрицу A между квадратными скобками с элементами столбца, разделенными запятыми, и строками, разделенными точкой с запятой. Введите напряжения в вектор-столбец: b. Неизвестные токи: I 1 , 2 и I 3 вычисляются командой: x=A\b. Они содержатся в векторе-столбце x.
октава: 1>A = [300,100,150;100,650,-300;-150,300,-450]
А =
300 100 150
100 650 -300
-150 300 -450
октава:2> b = [0;0;-24]
б =
0
0
-24
октава: 3> х = A\b
х =
-0.093793
0,077241
0,136092
Отрицательное значение, полученное для I 1 , говорит нам о том, что предполагаемое направление тока сетки было неверным. Таким образом, фактические значения тока через каждый резистор таковы:
Расчет падения напряжения на каждом резисторе:
Моделирование SPICE подтверждает точность наших расчетов напряжения:
несбалансированный мост из Уитстона v1 1 0 р1 1 2 150 р2 1 3 50 р3 2 3 100 р4 2 0 300 р5 3 0 250 .постоянный ток v1 24 24 1 .print dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0) .конец v1 v(1,2) v(1,3) v(3,2) v(2) v(3) 2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E+01 1.931E+01
Пример:
(a) Найдите новый путь для тока I 3 , который не создает конфликтной полярности на любом резисторе по сравнению с I 1 или I 2 . R 4 был компонентом-нарушителем. (b) Найдите значения для I 1 , I 2 и I 3 .(c) Найдите токи пяти резисторов и сравните их с предыдущими значениями.
Решение:
(a) Маршрут I 3 через R 5 , R 3, и R 1 , как показано:
Обратите внимание, что конфликт полярности на R 4 удален. Более того, ни один из других резисторов не имеет конфликтующей полярности.
(b) Octave, клон Matlab с открытым исходным кодом (бесплатный), дает вектор тока сетки в «x»:
октава: 1> Ля = [300,100,250;100,650,350;-250,-350,-500]
А =
300 100 250
100 650 350
-250 -350 -500
октава:2> b = [0;0;-24]
б =
0
0
-24
октава: 3> х = A\b
х =
-0. 093793
-0,058851
0,136092
093793
-0,058851
0,136092
Не все токи I 1 , I 2 и I 3 такие же (I 2 ), что и у предыдущего моста, из-за разных путей контура. Однако токи резисторов сравниваются с предыдущими значениями:
IR1 = I1 + I3 = -93,793 млн лет + 136,092 млн лет = 42,299 млн лет назад
IR2 = I1 = -93,793 мА
IR3 = I1 + I2 + I3 = -93,793 млн лет -58,851 млн лет + 136,092 млн лет = -16,552 млн лет
IR4 = I2 = -58,851 мА
IR5 = I2 + I3 = -58.851 млн лет + 136,092 млн лет = 77,241 млн лет назад
Поскольку токи резисторов такие же, как и предыдущие значения, напряжения резисторов будут идентичными, и их не нужно будет вычислять повторно.
ОБЗОР:
- Шаги для метода анализа Mesh Current:
- (1) Изобразите токи сетки в петлях цепи, достаточные для учета всех компонентов.
- (2) Отметьте полярность падения напряжения на резисторе на основе предполагаемых направлений токов сетки.

- (3) Напишите уравнения KVL для каждого контура цепи, заменяя E произведением IR в каждом члене уравнения резистора. Когда два тока сетки пересекаются через компонент, выражайте ток как алгебраическую сумму этих двух токов сетки (т. е. I 1 + I 2 ), если токи проходят в одном направлении через этот компонент. Если нет, выразите ток как разницу (т. е. I 1 — I 2 ).
- (4) Решение для неизвестных токов сетки (одновременные уравнения).
- (5) Если какое-либо решение отрицательное, то предполагаемое направление тока неверно!
- (6) Алгебраически сложите токи сетки, чтобы найти текущие компоненты, совместно использующие несколько токов сетки.
- (7) Определите падение напряжения на всех резисторах (E=IR).
Текущая сетка при осмотре
Мы еще раз взглянем на «метод сеточного тока», когда все токи движутся по часовой стрелке (по часовой стрелке). Мотивация состоит в том, чтобы упростить написание уравнений сетки, игнорируя полярность падения напряжения на резисторе. Однако мы должны обратить внимание на полярность источников напряжения относительно предполагаемого направления тока. Знак падения напряжения на резисторе будет следовать фиксированной схеме.
Однако мы должны обратить внимание на полярность источников напряжения относительно предполагаемого направления тока. Знак падения напряжения на резисторе будет следовать фиксированной схеме.
Если мы напишем набор обычных уравнений тока сетки для приведенной ниже схемы, где мы обращаем внимание на знаки падения напряжения на резисторах, мы можем преобразовать коэффициенты в фиксированный шаблон:
После перестановки мы можем писать уравнения путем проверки. Знаки коэффициентов следуют фиксированному шаблону в паре выше или наборе из трех в правилах ниже.
Текущие правила сетки:
- Этот метод предполагает использование обычных источников напряжения тока. Замените любой источник тока, подключенный параллельно резистору, эквивалентным источником напряжения, включенным последовательно с эквивалентным сопротивлением.
- Игнорируя направление тока или полярность напряжения на резисторах, нарисуйте токовые петли против часовой стрелки, пересекающие все компоненты.
 Избегайте вложенных циклов.
Избегайте вложенных циклов. - Напишите уравнения закона напряжения через неизвестные токи: I 1 , I 2 и I 3 .Коэффициент 1 уравнения 1, коэффициент 2 уравнения 2 и коэффициент 3 уравнения 3 являются положительными суммами сопротивлений вокруг соответствующих контуров.
- Все остальные коэффициенты отрицательны и представляют сопротивление, общее для пары контуров. Коэффициент 2 в уравнении 1 — это резистор, общий для контуров 1 и 2, коэффициент 3 — резистор, общий для контуров 1 и 3. Повторите для других уравнений и коэффициентов.
- +(сумма петли 1 R)I1 — (общая петля R 1-2)I2 — (общая петля R 1-3)I3 = E1
-(общая петля R 1-2)I1 + (сумма петли 2 R )I2 — (общая R петля 2-3)I3 = E2
-(общая R петля 1-3)I1 — (общая R петля 2-3)I2 + (сумма R петли 3)I3 = E3 - Правая часть уравнений равна источнику напряжения потока электронов.Повышение напряжения по отношению к предполагаемому току против часовой стрелки является положительным и равно 0 при отсутствии источника напряжения.

- Решите уравнения для токов сетки: I 1 , I 2 и I3. Решите для токов через отдельные резисторы с KCL. Решите для напряжений с Законом Ома и KVL.
Несмотря на то, что приведенные выше правила относятся к схеме с тремя ячейками, правила могут быть распространены на ячейки меньшего или большего размера. На рисунке ниже показано применение правил. Все три тока текут в одном направлении по часовой стрелке.Для каждой из трех петель записывается одно уравнение КВЛ. Обратите внимание, что на резисторах не указана полярность. Нам это не нужно для определения знаков коэффициентов. Хотя нам нужно обратить внимание на полярность источника напряжения по отношению к направлению тока. I 3 ток по часовой стрелке вытекает из положительной клеммы (+) источника l24V, а затем возвращается к клемме (-). Это повышение напряжения для обычного протекания тока. Следовательно, правая часть третьего уравнения равна -24 В.
В Octave введите коэффициенты в матрицу A с элементами столбцов, разделенными запятыми, и строками, разделенными точкой с запятой. Введите напряжения в вектор-столбец b. Решите для неизвестных токов: I 1 , I 2 и I 3 с помощью команды: x=A\b. Эти токи содержатся в векторе-столбце x. Положительные значения указывают на то, что все три тока сетки текут в предполагаемом направлении по часовой стрелке.
Введите напряжения в вектор-столбец b. Решите для неизвестных токов: I 1 , I 2 и I 3 с помощью команды: x=A\b. Эти токи содержатся в векторе-столбце x. Положительные значения указывают на то, что все три тока сетки текут в предполагаемом направлении по часовой стрелке.
октава: 2> Ля=[300,-100,-150;-100,650,-300;-150,-300,450]
А =
300 -100 -150
-100 650 -300
-150 -300 450
октава:3> b=[0;0;24]
б =
0
0
24
октава: 4> х=А\б
х =
0.093793
0,077241
0,136092
Токи сетки соответствуют предыдущему решению с использованием другого метода измерения тока сетки. Расчет напряжений и токов резисторов будет идентичен предыдущему решению. Здесь не нужно повторяться.
Обратите внимание, что тексты по электротехнике основаны на обычном токе. Метод loop-current, mesh-current в этих текстах будет запускать предполагаемые токи сетки по часовой стрелке . Условный ток течет через клемму (+) батареи по цепи, возвращаясь к клемме (-).Обычный рост тока-напряжения соответствует отслеживанию предполагаемого тока от (-) до (+) через любые источники напряжения.
Условный ток течет через клемму (+) батареи по цепи, возвращаясь к клемме (-).Обычный рост тока-напряжения соответствует отслеживанию предполагаемого тока от (-) до (+) через любые источники напряжения.
Далее следует еще один пример предыдущей схемы. Сопротивление вокруг контура 1 составляет 6 Ом, вокруг контура 2: 3 Ом. Общее сопротивление обоих контуров равно 2 Ом. Обратите внимание на коэффициенты I 1 и I 2 в паре уравнений. Отслеживание предполагаемого тока контура 1 по часовой стрелке через B 1 от (+) до (-) соответствует увеличению напряжения потока электронов.
Таким образом, знак 28 В положительный. Петля 2 против часовой стрелки предполагала токовые дорожки (-) к (+) через B 2 , падение напряжения. Таким образом, знак B 2 отрицательный, -7 во втором уравнении сетки. Опять же, на резисторах нет маркировки полярности. Они также не фигурируют в уравнениях.
Токи I 1 = 5 А и I 2 = 1 А являются положительными. Оба они текут в направлении петель по часовой стрелке.Это сопоставимо с предыдущими результатами.
Оба они текут в направлении петель по часовой стрелке.Это сопоставимо с предыдущими результатами.
Сводка:
- Метод модифицированного тока сетки позволяет избежать необходимости определять знаки коэффициентов уравнения, рисуя все токи сетки по часовой стрелке для обычного потока тока.
- Однако нам необходимо определить знак любых источников напряжения в контуре. Источник напряжения положителен, если предполагаемый ток против часовой стрелки течет с батареей (источником). Знак отрицательный, если предполагаемый ток против часовой стрелки течет против батареи.
- Подробнее см. в правилах выше.
СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:
Анализ сетки
Анализ сетки получен из замкнутых контуров в сети с использованием законов напряжения Кирхгофа
Шаги:
- Выберите направление тока замкнутого контура.

- Применение закона Кирхгофа к каждому замкнутому контуру
- Решите полученные одновременные уравнения Лайнера для токов в замкнутом контуре, используя определители.
- Выберите направление тока замкнутого контура.
Пример 1: Найдите ток через каждую ветвь.
Шаг 1: Выберите направление тока замкнутого контура I1 и I2. Шаг 2: Примените закон напряжения Кирхгофа к каждому замкнутому контуру Для первого контура Для второй петли Шаг 3: Одновременное уравнение |
Пример 2: Найти V 0
Самый левый Следующий слева Следующий слева Самый правый Решение i 1 = 20 А, i 2 = 12 А, i 3 = 7 А и i 4 = 3 А Следовательно: В 0 =(12-7)4=20В |
Пример 3: Для следующей цепи:
- Найти общее значение сопротивления R T
- Найти текущий i
- Найти напряжение на отдельных резисторах
- Проверка закона напряжения Кирхгофа
Пример 4: Для следующей цепи:
- Найти V 1
- Найти V 2
- Проверка закона напряжения Кирхгофа для замкнутого контура
Практические задачи :
(Щелкните изображение, чтобы посмотреть решение)
Задача 1: Найдите i 1 и i 2 .
Посмотреть решение
Решение: Левый справа Решение i 1 =2A и i 2 =4A |
Задача 2 : Найдите i 0 .
Посмотреть решение
Решение: Слева справа Средний Решение i 1 =16А; i 2 = 11 А и i 3 = 6 А i 0 = (i 1 -i 2 )=5А
|
Задача 3: Найдите напряжение на резисторе 10 Ом
Посмотреть решение
Решение: Слева справа Топ Решение i 1 = -5A, i 2 = 6A и i 3 = -2A Следовательно: В 10 Ом =i 2 (10)В=60 В |
Задача 4 : Найдите мощность на резисторе 32 Ом.
Посмотреть решение
Решение: Слева справа Топ Решение i 1 = -5A, i 2 = -15A и i 3 = -20A Следовательно: P 32 Ом =i 1 2 R=25(32)=800 Вт |
Проблема 5 : в следующей схеме:
а.Найдите ток и через лампочку.
б. Найдите номинал резистора лампочки в следующей цепи
Посмотреть решение
Решение: Уравнение мощности равно Тогда ток можно рассчитать как Номинал резистора лампочки |
Упражнения:
Опрос:
Метод контурного тока
Метод контурного тока
Далее: Эквивалентные схемы
Up: Законы Кирхгофа
Предыдущий: Текущий метод ветвления
Этот метод также называют методом петли сетки. За независимые текущие переменные принимают циркулирующую
За независимые текущие переменные принимают циркулирующую
ток в каждом из внутренних контуров.
- Отметьте на схеме токи внутреннего контура.
- Получить выражения для изменения напряжения вокруг каждого внутреннего помещения
петля. - Решить систему алгебраических уравнений.
В зависимости от проблемы в конечном итоге может потребоваться
алгебраически суммировать два контурных тока, чтобы получить необходимое
внутренняя ветвь тока для окончательного ответа.
Рассмотрим пример схемы моста Уитстона, показанной на рис.
рисунок 1.6.
Мы хотим рассчитать токи вокруг петель.
Три тока идентифицируются как: ток по часовой стрелке
вокруг большого внутреннего контура, включающего ЭДС,
ток по часовой стрелке вокруг верхнего равностороннего треугольника, а
ток по часовой стрелке вокруг нижнего равностороннего треугольника.
Выражения петли напряжения для трех токовых петель:
Рисунок 1.6:
Петлевой метод для схемы моста Уитстона.
Сбор терминов, содержащих один и тот же ток, дает
Если используются значения параметров, показанные на диаграмме,
текущие значения могут быть найдены путем решения множества одновременных
уравнения, чтобы дать
Более того, если мы пронумеруем отдельные токи через каждый резистор
используя ту же схему, что и для каждого компонента (ток через
есть, имеет и т.) и определить как
ток из батареи, затем
Это те же самые токи, которые можно было бы обнаружить, используя только метод Кирхгофа.
уравнения; однако здесь нам пришлось обрабатывать только три одновременных
уравнений вместо шести.
Пример:
Используйте метод контурного тока, чтобы определить напряжение, развивающееся на
клеммы AB в схеме, показанной на рисунке 1.7.
Рисунок 1.7: Пример схемы для анализа с использованием
метод петлевого тока.Рассмотрим токовую петлю по часовой стрелке через два
резисторы и два потенциала.
Точно так же рассмотрим ток по часовой стрелке вокруг другого
внутренний контур, состоящий из трех резисторов и .
Закон Кирхгофа даетРешение двух приведенных выше уравнений для неизвестных контурных токов
и даетНапряжение на AB определяется просто
Далее: Эквивалентные схемы
Up: Законы Кирхгофа
Предыдущий: Текущий метод ветвления
Вт, 13 июля, 16:55:15 по восточному поясному времени 1999
Mesh Analysis (Loop Current Method)
Mesh Analysis или Loop Current Method — это теория или метод анализа электрической сети, который можно использовать для решения цепей с несколькими источниками и несколькими примыкающими контурами или сетками, как показано на следующем рисунке:
Решение любого схема с использованием метода или теоремы анализа сетки включает следующие шаги:
1. Для каждого замкнутого контура предполагается, что по контуру циркулирует ток. Ток в каждом контуре помечен изогнутой стрелкой и соответствующей меткой тока, например: I1, I2, I3…. . Направление тока во всех петлях делается согласованным (по часовой стрелке или против часовой стрелки), как показано на рисунке ниже:
Для каждого замкнутого контура предполагается, что по контуру циркулирует ток. Ток в каждом контуре помечен изогнутой стрелкой и соответствующей меткой тока, например: I1, I2, I3…. . Направление тока во всех петлях делается согласованным (по часовой стрелке или против часовой стрелки), как показано на рисунке ниже:
Анализ сетки
2. Затем рассчитывается ток, протекающий через каждую ветвь. Если ветвь лежит только на одной сетке, то ток, протекающий через ветвь, является током, протекающим через сетку, а если ветвь является общей для двух сеток, то ток, протекающий через ветвь, представляет собой алгебраическую сумму токов, протекающих через ячейки на в которой лежит ветвь, как показано на рисунке ниже:
Анализ сетки
3.Затем в каждой сетке или цикле формируется уравнение с использованием KVL, как указано ниже:
вкл. , цикл 1:
, цикл 1:
вкл., цикл 2:
вкл., цикл 3:
4. Затем уравнения решаются, чтобы найти сетку. токи I1. I2, I3 и, в конечном счете, ток и падение напряжения в каждой ветви.
Суперсетка и зависимые источники:
Суперсетка — это сетка, в которой источник тока содержится между двумя сетками. Зависимые источники — это источник, который зависит от другого источника.Когда цепь или сетка содержит эти два особых случая, применение метода анализа сетки требует особого рассмотрения.
Чтобы применить метод анализа сетки в Super Mesh:
Мы должны создать одно уравнение для обеих соседних сеток, включающее источник тока, а источник тока должен быть связан с током сетки двух сеток. Например: В следующей суперсетке:
Суперсетка
Уравнения для анализа сетки:
и ,
Чтобы применить метод анализа сетки в сетке, которая содержит зависимые источники:
источник, как будто это независимый источник, и тогда мы должны связать зависимый источник с другими токами сетки.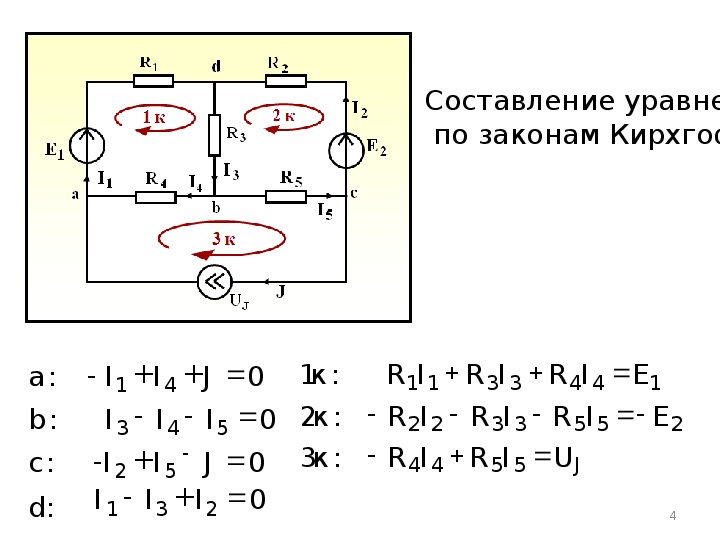 Например: В следующей сетке:
Например: В следующей сетке:
Зависимый источник
Уравнения для анализа сетки:
И,
Метод анализа сетки в действии:
Давайте решим следующую схему, используя анализ сетки или метод контурного тока. :
Анализ сетки
Здесь,
Уравнение для сетки с текущей сеткой I2:
Или,
Уравнение для объединенной сетки I1, I3 (поскольку это суперсетка):
Или, 0 900 ,
Таким образом, решая эти уравнения, мы получаем:
Анализ сетки — обзор
Анализ сетки использует KVL (Уравнение 10.1) составить уравнения, которые приводят к токам и напряжениям в цепи. При анализе сетки вы пишете уравнения, основанные на напряжениях в контуре, но решаете токов контура . Когда у вас есть контурные токи, вы можете вернуться назад и найти любое напряжение в контуре, применяя базовые определения напряжения/тока, данные в главе 9. (Как вы могли догадаться, в узловом анализе все наоборот: вы пишете уравнение или уравнения, основанные на токах, но в конечном итоге решаются для узловых напряжений. ) Анализ сетки может быть выполнен с использованием алгоритма, который обеспечивает пошаговую процедуру, которую можно применить к любой неэлектронной схеме.(Для электронных схем может потребоваться использование как KVL, так и KCL, и они рассматриваются в главе 12.) Пример этого алгоритма анализа сетки приведен в примере 10.1.
) Анализ сетки может быть выполнен с использованием алгоритма, который обеспечивает пошаговую процедуру, которую можно применить к любой неэлектронной схеме.(Для электронных схем может потребоваться использование как KVL, так и KCL, и они рассматриваются в главе 12.) Пример этого алгоритма анализа сетки приведен в примере 10.1.
Пример 10.1
Найдите напряжение на конденсаторе в сети на рис. 10.3. Обратите внимание, что источник синусоидальный, поэтому в этом примере можно использовать векторный анализ.
Решение: Возможно, вы уже решили сеть, подобную этой, в задаче 12 главы 9, используя расширенную версию закона Ома. Однако представленный здесь алгоритмический подход может быть применен к гораздо более сложным сетям.
Схема имеет одну сетку (т. е. петлю) и три узла. Узловой анализ требует одновременного решения двух уравнений, тогда как сеточный анализ требует решения только одного уравнения, что делает его очевидным выбором. Единственная хитрость в анализе сетки состоит в том, чтобы точно следить за направлением или полярностью изменений напряжения: вверх или вниз, в соответствии с увеличением или уменьшением напряжения. На самом деле это не так уж сложно при использовании алгоритмического подхода, описанного здесь.Для этого примера шаги представлены достаточно подробно, но они непосредственно применимы к широкому кругу сетевых проблем.
На самом деле это не так уж сложно при использовании алгоритмического подхода, описанного здесь.Для этого примера шаги представлены достаточно подробно, но они непосредственно применимы к широкому кругу сетевых проблем.
Шаг 1 . Примените сетевое преобразование, чтобы все элементы были представлены их вектором или нотацией домена Лапласа. Эти преобразования суммированы в главе 9 (таблица 9.5) и могут использоваться для получения векторных или лапласовых представлений различных элементов. Поскольку в этом примере мы имеем дело с синусоидальным стимулом, мы используем первое.В преобразованной схеме источники представлены векторными переменными, такими как В S ∠ θ , а пассивным элементам заданы соответствующие импедансы векторов: R Ом, jωL или Ом. / ДжωС Ом. Помещение символа Ω на рисунке указывает нам, что элементы были преобразованы в фазор или обозначение Лапласа. Иногда в источниках напряжения используются среднеквадратичные значения в векторной области, но в этом тексте будут использоваться пиковые значения, поскольку они более распространены. Это действительно не имеет значения, если вы последовательны и знаете, какие единицы измерения используются.
Это действительно не имеет значения, если вы последовательны и знаете, какие единицы измерения используются.
Шаг 2 . В анализе сетки этот шаг состоит из определения тока сетки (или токов, если задействовано более одного контура). Этот ток полностью проходит по контуру либо по часовой стрелке, либо против часовой стрелки, теоретически на ваш выбор. Контур в этом примере замыкается двумя заземлениями, которые находятся под одним и тем же напряжением и, следовательно, по существу связаны. Чтобы быть последовательным, мы всегда предполагаем в этом тексте, что ток проходит по часовой стрелке вокруг сетки.Конечно, ток действительно может течь в противоположном направлении, но это просто означает, что значение, которое мы находим для этого тока, будет отрицательным. Определение направления тока определяет полярность напряжения для пассивных элементов, поскольку ток должен течь на положительную сторону пассивного элемента. Помните, источнику напряжения не важен ток, и он поставляется с уже заданной полярностью. После выполнения этих двух шагов схема выглядит так, как показано на рисунке 10.4.
После выполнения этих двух шагов схема выглядит так, как показано на рисунке 10.4.
Шаг 3 . Применить КВЛ. Мы просто обходим сетку, суммируя напряжения, но это алгебраическая сумма . Присвойте положительные значения, если есть увеличение напряжения и отрицательные значения, если есть уменьшение напряжения. Начните с нижнего левого угла (ниже источника) и мысленно продолжайте движение по петле по часовой стрелке. Пересечение источника приводит к повышению напряжения, поэтому этот вход положительный; следующие два компонента имеют падение напряжения (от + до -), поэтому их записи отрицательны:
VS-VR-VC=0
Обычно мы подставляем фактические числа для этих напряжений, но сейчас мы будем писать уравнение с точки зрения R и C .Подставляя V R = RI(ω) , и:
Vc=1jωCI(ω)
Уравнение KVL принимает вид:
VS−RI(ω)−1jωCI(ω)=0 (ω)(R+1jωC)=0
На самом деле, чтобы разработать это уравнение сетки, мы могли бы начать с любого места в цикле и двигаться либо по часовой стрелке, либо против часовой стрелки, но опять же для согласованности, и поскольку это действительно не имеет значения , мы всегда идем по часовой стрелке и начинаем с нижнего левого угла схемы.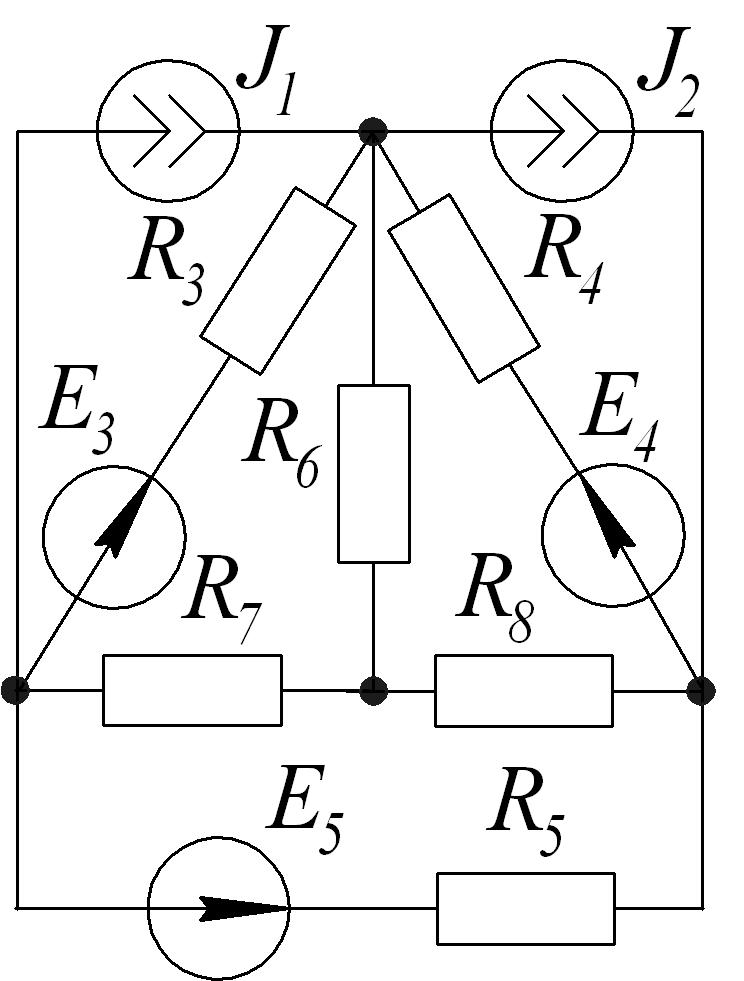
Шаг 4 .Решите для текущих . Поместите источник(и) с одной стороны, а термины для пассивных элементов – с другой. Затем найдите I ( ω ).
VS(ω)=(R+ZC)I(ω)I(ω)=VSR+ZC
Шаг 5 . Решите для любых интересующих нас напряжений. В этой задаче нам нужно напряжение на конденсаторе. Из уравнения, определяющего конденсатор: В С (ω ) = Z С ( ω)I(ω ).Подставив наше решение для I(ω) выше в это уравнение:
VC=ZC(ω)I(ω)=ZC(ω)VSR+ZC(ω)
Иногда вам нужно оставить решение в этой форме , с переменными значениями ваших элементов, например, когда вы не знаете конкретных значений, или когда в схеме может использоваться несколько разных значений, или когда задача будет решаться на компьютере. В этом случае у нас есть определенные значения для наших элементов, поэтому мы можем подставить значения для R , Z C и V S и решить:
VC=(−j25) 4∠3010−j25=(25∠−90)4∠3027∠−68=100∠−6027∠−68=3. 7∠8 вольт
7∠8 вольт
03 Анализ контуров цепей постоянного тока [PDF]
12 страниц • 2083 слова • PDF • 225,6 КБ
Загружено 21.09.2021 07:28
Модуль 2 Цепь постоянного тока Версия 2 EE IIT, Kharagpur
Урок 4 Анализ контуров резистивной цепи в контексте постоянного напряжения и тока Версия 2 EE IIT, Kharagpur
Цели • •
Значение анализа цепи; различать термины «сетка» и «петля». Предоставить более общий и мощный инструмент анализа цепей, основанный только на законе напряжения Кирхгофа (KVL).
L.4.1 Введение Метод последовательно-параллельного преобразования, который мы изучили в уроке 3 для анализа цепей постоянного тока, логически упрощает каждый шаг от предыдущего шага и логически ведет к следующему шагу. К сожалению, если схема сложная, этот метод (упрощение и реконструкция) становится математически трудоемким, трудоемким и может привести к ошибкам в расчетах. На самом деле, чтобы преодолеть эти трудности, доступны некоторые методы, которые вообще не требуют особых размышлений, и нам нужно только следовать четко определенной и верной процедуре. Один из самых популярных методов, который будет обсуждаться на этом уроке, известен как метод анализа «сетка или петля», который основан на фундаментальных принципах законов цепей, а именно законе Ома и законе напряжения Кирхгофа. Некоторые простые проблемы с цепями будут проанализированы с помощью ручного расчета, чтобы понять процедуру, связанную с анализом тока сетки или контура.
Один из самых популярных методов, который будет обсуждаться на этом уроке, известен как метод анализа «сетка или петля», который основан на фундаментальных принципах законов цепей, а именно законе Ома и законе напряжения Кирхгофа. Некоторые простые проблемы с цепями будут проанализированы с помощью ручного расчета, чтобы понять процедуру, связанную с анализом тока сетки или контура.
L.4.1.1 Значение анализа цепи Метод, с помощью которого можно определить переменную (напряжение или ток) цепи, называется анализом.Основное различие между «сеткой» и «петлей» обсуждается в уроке 3 на примере. «Сетка» — это любой замкнутый путь в данной схеме, внутри которого нет ни одного элемента (или ответвления). Сетка обладает следующими свойствами: (i) каждый узел замкнутого пути точно сформирован двумя ветвями (ii) никакие другие ветви не окружены замкнутым путем. Сетки можно рассматривать как напоминающие оконные перегородки. С другой стороны, «петля» также является замкнутым путем, но внутри замкнутого пути может быть одна или несколько ветвей или элементов.
L.4.2 Решение электрической цепи на основе метода ячеистого (контурного) тока Рассмотрим простую сеть постоянного тока, как показано на рисунке 4.1, чтобы найти токи в различных ветвях, используя метод ячеистого (контурного) тока.
Версия 2 EE IIT, Kharagpur
Применение КВЛ вокруг сетки (петли)-1: (примечание в сетке-1, I1 известен как локальный ток, а другие токи сетки I 2 и I 3 известны как внешние токи.)
Va — Vc — ( I1 — I 3 ) R2 — ( I1 — I 2 ) R4 = 0
Va — Vc = ( R2 + R4 ) I1 — R4 I 2 — R2 I 3 = R11 I 1 — R12 I 2 − R13 I 3
(4.1)
Применение КВЛ вокруг сетки (петли)-2: (аналогично в сетке-2, I 2 — местный ток, а I1 и I 3 известны как посторонние токи)
−Vb − (I 2 − I 3 ) R3 − ( I 2 − I1 ) R4 = 0 − Vb = − R4 I1 + ( R3 + R4 ) I 2 − R3 I 3 = − R21 I1 + R22 I 2 − R23 I 3 Применение КВЛ вокруг сетки (петли)-3: Vc — I 3 R1 — ( I 3 — I 2 ) R3 — ( I 3 — I1 ) R2 = 0
(
(4.2)
)
Vc = — R2 I1 — R3 I 2 + R1 + R2 + R3 I 3 = — R31 I1 — R32 I 2 + R33 I 3
(4. 3)
3)
. …….. + Rii I i − Ri ,i +1I i +1 − …. RiN IN
ii
→ просто означает взять алгебраическую сумму всех источников напряжения вокруг i-го
меш. th Rii → означает полное собственное сопротивление вокруг i-й сетки.
th Rij → означает взаимное сопротивление между ячейками i и j.
Версия 2 EE IIT, Харагпур
Примечание. Обычно Rij = R ji (верно только для линейных двусторонних цепей) I i → неизвестные токи сетки для сети.Подведем итоги: Шаг 1. Нарисуйте схему на плоской поверхности без пересечения проводников. Шаг 2: Тщательно обозначьте токи сетки ( I i ) по часовой стрелке. Шаг 3: Напишите уравнения сетки, проверив схему (количество уравнений независимой сетки (контура) = количество ветвей (b) — количество основных узлов (n) + 1). Примечание. Для анализа резистивной сети, содержащей источники напряжения и тока с использованием метода «сетчатых» уравнений, важно отметить следующие шаги: •
Если возможно, преобразовать источник тока в источник напряжения.
•
В противном случае определите напряжение на источнике тока и напишите уравнения сетки, как если бы эти напряжения источника были известны. Дополните набор уравнений одним уравнением для каждого источника тока, выражающим известный ток сетки или разницу между двумя токами сетки.
•
Анализ сетки действителен только для цепей, которые можно изобразить в двумерной плоскости таким образом, чтобы ни один элемент не пересекался с другим.
Пример-L-4.1: Найдите ток через «ветвь ab» ( I ab ) и напряжение ( Vcg ) на источнике тока, используя метод Mesh-current.
Версия 2 EE IIT, Kharagpur
Решение: Предположим, что напряжение на источнике тока равно v1 («c» имеет более высокий потенциал, чем «g» (потенциал земли и принимается за нулевой потенциал) и обратите внимание, что I2 = -2A (поскольку заданный ток направление ( I 2 ) противоположно току источника) Контур — 1: (Прикладывание КВЛ) Va — ( I1 — I 3 ) R2 — ( I1 — I 2 ) R4 = 0 ⇒ 3 = 3I1 — 2 I 2 — I 3 3I1 − I 3 = − 1
(4. 4)
4)
Контур — 2: (Приложение КВЛ) Предположим, что напряжение на источнике тока равно v1 и его верхний конец поставлен в соответствие со знаком плюс.−v1 − ( I 2 − I1 ) R4 − ( I 2 − I 3 ) R3 = 0 ⇒ − v1 = − 2 I1 + 6 I 2 − 4 I 3 (примечание: I 2 = −2 A )
2 I1 + 12 + 4 I 3 = v1
(4.5)
Петля — 3: (Приложение КВЛ) — I 3 R1 — ( I 3 — I 2 ) R3 — ( I 3 — I1 ) R2 = 0 ⇒ — I1 — 4 I 2 + 8 I 3 = 0 I1 − 8I 3 = 8
(Примечание: I 2 = −2 A )
(4.6)
Версия 2 EE IIT, Kharagpur
Решение уравнений (4.4) и (4.6) ), получаем I 1 = − I3 = −
48 = −0,6956 A и 69
25 = −1,0869 A , I ab = I 1 − I 3 = 0.39 А , I bc = I 2 − I 3 = −0,913 A 23
и
I bg = I 1 − I 2 = 1,304 A
— знак тока означает, что ток течет в обратном направлении (в нашем В этом случае ток течет через резистор 4 Ом из точки «с» в точку «b»). Из уравнения (4.5) можно получить v1 == 6,27 вольт. Другой способ: −v1 + vbg + vbc = 0 ⇒ v1 = vcg = 6,27 вольт.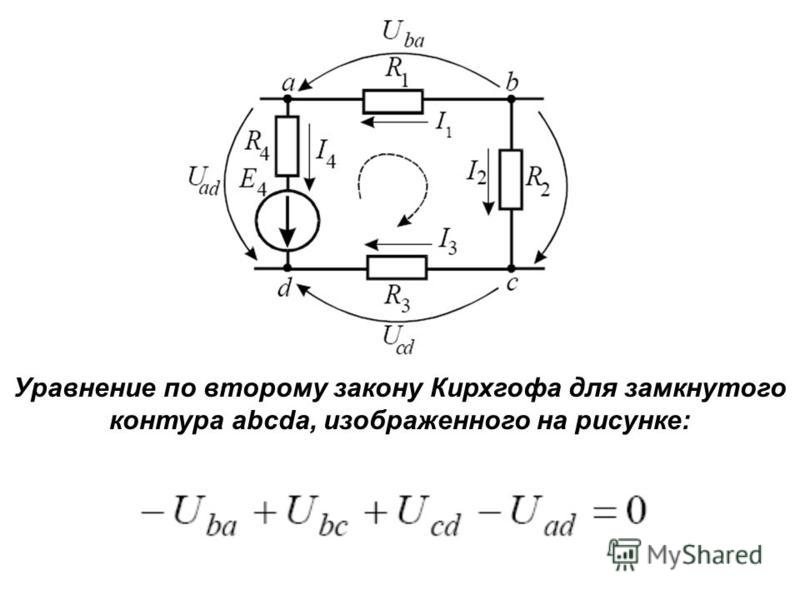 Пример-L-4.2 Для схемы, показанной на рис. 4.3 (а), найдите Vx, используя метод тока сетки.
Пример-L-4.2 Для схемы, показанной на рис. 4.3 (а), найдите Vx, используя метод тока сетки.
Решение: Крайний правый источник тока (6 А) можно легко преобразовать в источник напряжения.Обратите внимание, что величина тока источника составляет 6 А, а его внутреннее сопротивление равно 6 Ом. Данная схема перечерчена и показана на рис. 4.3 (в) Версия 2 EE IIT, Kharagpur
Контур-1: (Записать KVL, отметить I1 =12 A ) Vx − (I1 − I 2 ) × 3 − 18 = 0 ⇒ Vx + 3 I 2 = 54
(4.7)
Петля-2: (записать КВЛ) 18 − ( I 2 − I1 ) × 3 − I 2 × 6 − 36 = 0 ⇒ 9 I 2 =18 ⇒ I 2 = 2 А Используя значение I 2 = 2 А в уравнении (4.7), получаем Vx = 48 вольт. Пример-L-4.3 Найдите vR для схемы, показанной на рисунке 4.4, используя метод «текущей сетки». Рассчитайте мощность, поглощаемую или отдаваемую источниками и всеми элементами.
Версия 2 EE IIT, Kharagpur
Решение: Предположим, что напряжение на источнике тока равно ‘v’, а нижний конец источника тока помечен знаком плюс. Для контура № 1: (уравнение КВЛ)
Для контура № 1: (уравнение КВЛ)
v − (I1 − I 2 )×100 − I1×100 = 0 ⇒ v − 200 I1 + 100 I 2 = 0
(4.8)
Можно отметить что из рисунка, что ток, протекающий через резистор 100 Ом (в средней ветви), равен 10 мА.Более конкретно, можно записать следующее выражение: I 2 ×100 = 0 ⇒ v + 200 I 2 − 100 I1 = − 20
(4.10)
Решая уравнения (4.8)–(4.10), можно получить контурные токи как I1 = − 0,095 = − 95 мА (Знак -ve указывает на то, что назначенное направление тока контура неверно или, другими словами, направление тока контура ( I1 ) против часовой стрелки.) и I 2 = -0,105 = -105 мА (обратите внимание, направление тока контура ( I 2 ) против часовой стрелки.) ).Теперь напряжение на резисторе 100 Ом (крайняя правая ветвь) определяется как vR = I 2 × 100 = — 0,105 × 100 = -10,5 вольт. .Это указывает на то, что клемма резистора (b), расположенная рядом с источником напряжения, более положительна, чем другой конец клеммы резистора
Версия 2 EE IIT, Kharagpur
(a). Из уравнения (4.8) v = -8,5 вольт, а это означает, что «верхний» конец источника тока более положительный, чем нижний «конец». Мощность, отдаваемая источником напряжения = 20 × 0,105 = 2.1 Вт (обратите внимание, что ток уходит с положительной клеммы источника напряжения). С другой стороны, мощность, полученная или поглощенная источником тока = 8,5 × 0,01 = 0,085 Вт (поскольку ток поступает на положительный вывод (верхний вывод) источника тока). Мощность, поглощаемая всеми сопротивлениями, равна = (0,105) 2 × 100 + (0,095) 2 × 100 + (10 × 10–3) 2 × 100 = 2,015 Вт. Далее можно заметить, что отдаваемая мощность (Pd = 2,1 Вт) = потребляемая мощность (Pab = 0,085 + 2,015 = 2,1 Вт) = 2,1 Вт
Из уравнения (4.8) v = -8,5 вольт, а это означает, что «верхний» конец источника тока более положительный, чем нижний «конец». Мощность, отдаваемая источником напряжения = 20 × 0,105 = 2.1 Вт (обратите внимание, что ток уходит с положительной клеммы источника напряжения). С другой стороны, мощность, полученная или поглощенная источником тока = 8,5 × 0,01 = 0,085 Вт (поскольку ток поступает на положительный вывод (верхний вывод) источника тока). Мощность, поглощаемая всеми сопротивлениями, равна = (0,105) 2 × 100 + (0,095) 2 × 100 + (10 × 10–3) 2 × 100 = 2,015 Вт. Далее можно заметить, что отдаваемая мощность (Pd = 2,1 Вт) = потребляемая мощность (Pab = 0,085 + 2,015 = 2,1 Вт) = 2,1 Вт
л.4.3 Проверьте свое понимание
[Оценки: 50]
T.4.1 Чтобы написать уравнение Кирхгофа по закону напряжения для контура, мы движемся вокруг контура по часовой стрелке, рассматривая рост напряжения в уравнении контура как ——- члены и напряжение падает как ——— условия. [2] T. 4.2 При написании уравнения закона Кирхгофа для контура напряжения, как мы поступаем в ситуации, когда вокруг контура присутствует идеальный источник тока? [2] Т.4.3 Что это означает, когда контурный ток выходит с положительным значением из математического решения системы уравнений? Что означает появление отрицательного значения контурного тока? [2] Т.4.4 В методе тока сетки ток, протекающий через резистор, можно вычислить, зная —— ток контура и ———- ток контура. [2] T.4.5 Найдите ток через резистор 6 Ом для схемы, рис. 4.5, используя метод «сетевого тока», и, следовательно, рассчитайте напряжение на источнике тока. [10]
4.2 При написании уравнения закона Кирхгофа для контура напряжения, как мы поступаем в ситуации, когда вокруг контура присутствует идеальный источник тока? [2] Т.4.3 Что это означает, когда контурный ток выходит с положительным значением из математического решения системы уравнений? Что означает появление отрицательного значения контурного тока? [2] Т.4.4 В методе тока сетки ток, протекающий через резистор, можно вычислить, зная —— ток контура и ———- ток контура. [2] T.4.5 Найдите ток через резистор 6 Ом для схемы, рис. 4.5, используя метод «сетевого тока», и, следовательно, рассчитайте напряжение на источнике тока. [10]
Версия 2 EE IIT, Kharagpur
(Ответ: 3,18 А; 13,22 В) .
найти
ток
через [12]
(Ответ: I AB = — 3 A; I AC = — 3 A; I CD = — 2 A и I EF = 0 A. ) T. 4.7. Найдите ток, протекающий через резистор RL = 1 кОм для цепи, показанной на рис. 4.7, методом «сетевого тока». Какова мощность, отдаваемая или потребляемая независимым источником тока? [10]
(Ответ: 1 мА; 10 мВт) Т. 4.8 Используя метод «сетевого тока», найдите ток, протекающий через резистор 2 Ом для цепи, показанной на рисунке 4.8 и, следовательно, вычислить мощность, потребляемую одним и тем же резистором 2 Ом. [10]
4.8 Используя метод «сетевого тока», найдите ток, протекающий через резистор 2 Ом для цепи, показанной на рисунке 4.8 и, следовательно, вычислить мощность, потребляемую одним и тем же резистором 2 Ом. [10]
Версия 2 EE IIT, Харагпур
(Ответ: 6 A ; 72 Вт )
______________________________________________________________
Версия 2 EE IIT, Харагпур
Mesh Current Method | Уравнения сетки по методу контроля
Текущий метод сетки:
В сеточном методе к сети применяется закон Кирхгофа о напряжении (KVL). Из этой сети мы должны написать уравнения сетки в терминах токов сетки.Здесь мы используем токи сетки вместо токов ветвей. Здесь каждой сетке назначается отдельный ток сетки. Предположим, что направление Mesh Current Method — по часовой стрелке. Затем к сети применяется КВЛ для записи уравнений в терминах неизвестных токов сетки.
Ток ответвления можно определить, взяв алгебраическую сумму токов сетки, которые являются общими для этого ответвления.
Для определения токов сетки и токов ветвей необходимо выполнить следующие шаги.
Рассмотрим простую сеть, как показано на рисунке 1.20.
Шаг 1: Сначала каждой сетке назначается отдельный ток сетки. Предположим, что все направления токов сетки направлены по часовой стрелке. Он состоит из двух сеток (PQSP и QRSQ) и двух течений сетки (I 1 и I 2 ).
Шаг 2: Если два тока сетки (I 1 и I 2 ) протекают через элементы сети, фактический ток в элементе цепи представляет собой алгебраическую сумму двух (I 1 и I 2 ).В этой сети токи сетки I 1 и I 2 протекают в R 2 . Сначала мы рассматриваем одно направление, то есть от Q к S, ток равен I 1 – I 2 , а если пойти в другом направлении. то есть от S до Q, ток I 2 – I 1.
Шаг 3: Напишите уравнение для каждой сетки в терминах токов сетки, применяя KVL. При написании уравнений сетки мы назначаем рост потенциала как положительный (+) знак, а падение потенциала — как отрицательный (-) знак.
При написании уравнений сетки мы назначаем рост потенциала как положительный (+) знак, а падение потенциала — как отрицательный (-) знак.
Шаг 4: Предположим, что любое значение тока сетки становится отрицательным в решении, фактическое или истинное направление тока сетки против часовой стрелки, т. е. противоположно направлению по часовой стрелке.
Когда мы применяем КВЛ к фигуре 1.20, мы получаем два уравнения.
Сетка PQSP
Сетка QRSQ
Метод Mesh Current Method I 1 и I 2 можно найти, решив уравнения (27) и (28).
Шаг 5: Ток ответвления можно легко определить, используя токи сетки I 1 и I 2 .
Уравнения сетки по методу проверки:
Процедуру записи уравнения сетки в матричной форме можно упростить следующим образом.
- Преобразование источника тока в источник эквивалентного напряжения путем преобразования источника.

- Все сопротивления, через которые протекает контурный ток I 1 , суммируются и обозначаются R 11 . Это называется собственным сопротивлением контура 1.
- Суммируются все сопротивления, через которые протекают контурные токи I 1 в первом контуре и I 2 во втором контуре.Обозначается R 12 . Знак члена R 12 отрицательный, если два тока I 1 и I 2 через R 12 направлены в противоположные стороны; в противном случае знак положительный.
- Пусть V 1 будет действующим напряжением на первом контуре, через который протекает ток контура I 1 . Знак V 1 положителен, если направление V 1 совпадает с направлением I 1 (т. е. помогает току I 1 , в противном случае знак V 1 отрицательный).V 1 записывается в правой части уравнения.
Теперь справа записывается ноль, если в первом контуре, через который протекает I 1 , нет источника.



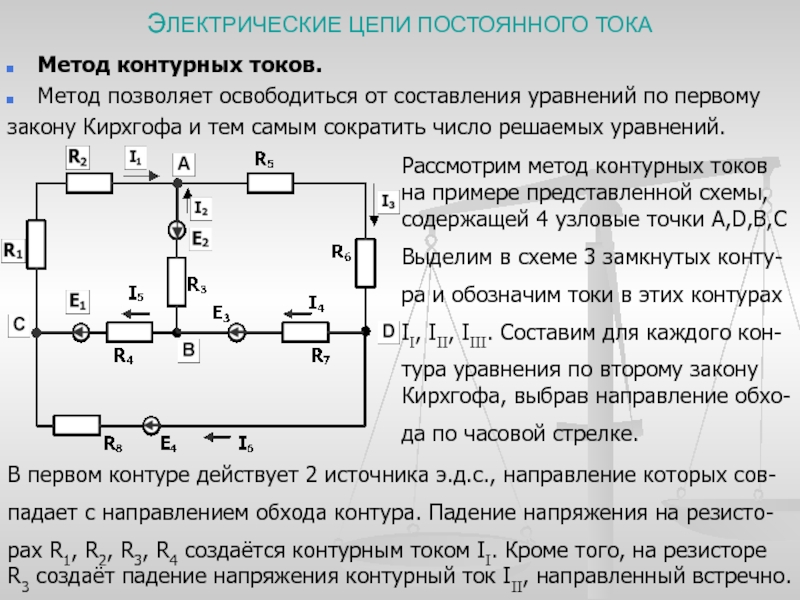
 Для определения этих токов составляют уравнения по второму закону Кирхгофа. Число независимых контуров определяется как К = В — Y + 1, где В — число ветвей, Y — число узлов. В нашем случае на представленной схеме мы имеем шесть ветвей (первая через через резистор R1, вторая — через R2 и r2, треться — через R3 и r3, четвертая через R4, пятая через R5 и шестая ветвь проходит через R6). Узлов (параметр Y) в схеме — четыре (по количеству пересечений соединяемых проводов — на схеме показаны точками). Таким образом, посчитав, получим количество независимых контуров — три: К = 6 — 4 + 1 = 3. Количество независимых контуров соответствует требуемому количеству уравнений в составляемой системе. Впрочем, количество независимых контуров можно определить визуально по схеме. Каждый контур должен быть в своих границах и не «залезать» в соседний. Независимые контуры можно обозначить римскими цифрами, а замыкающиеся в них контурные токи отметить индексами, соответствующими своему контуру (I11, I22, I33).
Для определения этих токов составляют уравнения по второму закону Кирхгофа. Число независимых контуров определяется как К = В — Y + 1, где В — число ветвей, Y — число узлов. В нашем случае на представленной схеме мы имеем шесть ветвей (первая через через резистор R1, вторая — через R2 и r2, треться — через R3 и r3, четвертая через R4, пятая через R5 и шестая ветвь проходит через R6). Узлов (параметр Y) в схеме — четыре (по количеству пересечений соединяемых проводов — на схеме показаны точками). Таким образом, посчитав, получим количество независимых контуров — три: К = 6 — 4 + 1 = 3. Количество независимых контуров соответствует требуемому количеству уравнений в составляемой системе. Впрочем, количество независимых контуров можно определить визуально по схеме. Каждый контур должен быть в своих границах и не «залезать» в соседний. Независимые контуры можно обозначить римскими цифрами, а замыкающиеся в них контурные токи отметить индексами, соответствующими своему контуру (I11, I22, I33). Для единообразия все контурные токи можно направить в одну сторону, например, по направлению часовой стрелки, но принципиального значения это не имеет. Иногда визуально удобнее их направлять по направлению полярности источника ЭДС, там, где этот источник в контур входит. А если он в контуре не один, то в любом направлении. На правильности вычисления это никак не скажется. При составлении уравнений по методу контурных токов, следует учитывать, что в контурах, где имеются источники ЭДС, численные значения этих ЭДС необходимо принимать положительными, если их направление совпадает с выбранным направлением контурного тока, и отрицательными, если их направление не совпадает с выбранным направлением контурного тока. Решая совместно уравнения, составленные по второму закону Кирхгофа, находят величины контурных токов. Токи в ветвях цепи находятся через контурные токи по методу наложения.
Для единообразия все контурные токи можно направить в одну сторону, например, по направлению часовой стрелки, но принципиального значения это не имеет. Иногда визуально удобнее их направлять по направлению полярности источника ЭДС, там, где этот источник в контур входит. А если он в контуре не один, то в любом направлении. На правильности вычисления это никак не скажется. При составлении уравнений по методу контурных токов, следует учитывать, что в контурах, где имеются источники ЭДС, численные значения этих ЭДС необходимо принимать положительными, если их направление совпадает с выбранным направлением контурного тока, и отрицательными, если их направление не совпадает с выбранным направлением контурного тока. Решая совместно уравнения, составленные по второму закону Кирхгофа, находят величины контурных токов. Токи в ветвях цепи находятся через контурные токи по методу наложения.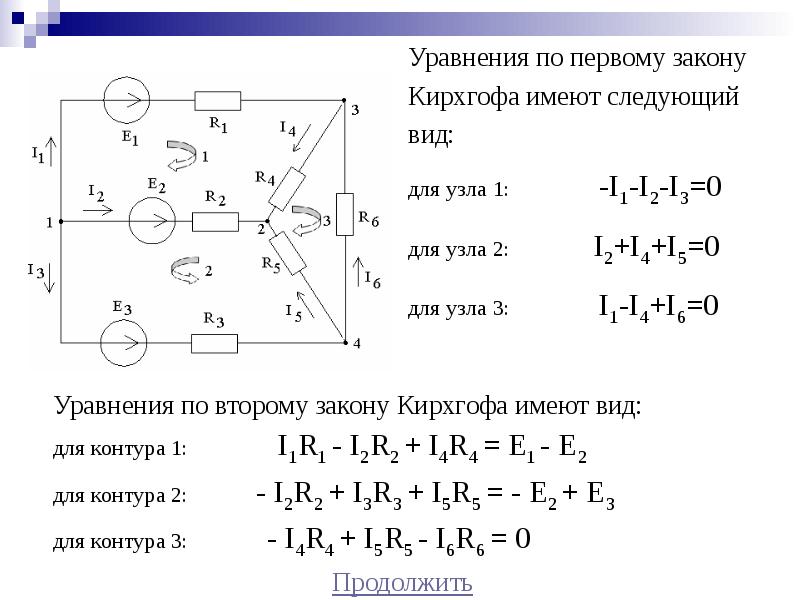 ..
..
 Тогда получим:
Тогда получим: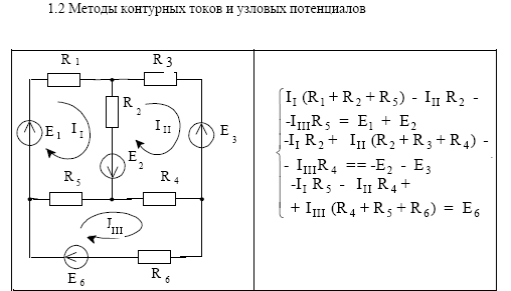 После подстановки получим, что — контурный ток второго контура.
После подстановки получим, что — контурный ток второго контура. Получаем: I1 = I11 + I22 = 4,625 + 14,14 = 18,765 A. Получили I1 = 18,765 A. Через резистор R2 пройдет только контурный ток I11, поэтому I2 = I11 = 4,625 А. Через R3 пройдет только второй контурный ток, поэтому I3 = I22 = 14,14 A. Через R4 контурный ток I33 пройдет против направления контурного тока I11, поэтому I4 = I11 — I33 = 4,625 — (- 4,37) = 8,995 А. Через R5 пройдет только третий контурный ток, поэтому I5 = I33 = — 4,37 A, т.е. на схеме его фактическое направление будет противоположно направлению контурного тока. Через R6 второй и третий контурные токи пройдут в одном направлении, поэтому I6 =I22 + I33 = 14,14 + (- 4,37) = 9,77 A. Собственно, вот все токи и нашли.
Получаем: I1 = I11 + I22 = 4,625 + 14,14 = 18,765 A. Получили I1 = 18,765 A. Через резистор R2 пройдет только контурный ток I11, поэтому I2 = I11 = 4,625 А. Через R3 пройдет только второй контурный ток, поэтому I3 = I22 = 14,14 A. Через R4 контурный ток I33 пройдет против направления контурного тока I11, поэтому I4 = I11 — I33 = 4,625 — (- 4,37) = 8,995 А. Через R5 пройдет только третий контурный ток, поэтому I5 = I33 = — 4,37 A, т.е. на схеме его фактическое направление будет противоположно направлению контурного тока. Через R6 второй и третий контурные токи пройдут в одном направлении, поэтому I6 =I22 + I33 = 14,14 + (- 4,37) = 9,77 A. Собственно, вот все токи и нашли. Если же ток I направлен навстречу ЭДС, то источник ЭДС работает как потребитель энергии, и его мощность записывается в левую часть уравнения с отрицательным знаком. Получаем:
Если же ток I направлен навстречу ЭДС, то источник ЭДС работает как потребитель энергии, и его мощность записывается в левую часть уравнения с отрицательным знаком. Получаем: При расчете сложной цепи с составлением уравнений по закону Кирхгофа выбирают произвольно (обратите внимание — произвольно) направление токов в ветвях. Решая предыдущую задачу, мы выяснили истинное направление всех токов в данной схеме, поэтому для интереса просто изменили направление тока I1, чтобы показать, что результат отт выбора направлений не изменится. Как и в предыдущей задаче, если значение тока получится положительным — значит истинное направление совпадает с произвольно выбранным. Если получится отрицательным — значит истинное направление противоположно выбранному. Только и всего.
При расчете сложной цепи с составлением уравнений по закону Кирхгофа выбирают произвольно (обратите внимание — произвольно) направление токов в ветвях. Решая предыдущую задачу, мы выяснили истинное направление всех токов в данной схеме, поэтому для интереса просто изменили направление тока I1, чтобы показать, что результат отт выбора направлений не изменится. Как и в предыдущей задаче, если значение тока получится положительным — значит истинное направление совпадает с произвольно выбранным. Если получится отрицательным — значит истинное направление противоположно выбранному. Только и всего. Известно, что одна любая точка схемы может быть заземлена без изменения токораспределения в схеме. Поэтому один из узлов схемы нужно мысленно заземлить, т.е. принять его потенциал равным нулю. При этом число неизвестных в методе узловых потенциалов равно числу уравнений, которые могут быть составлены для схемы по первому закону Кирхгофа. После определения потенциалов узлов токи в ветвях рассчитываются по закону Ома. Для ветвей с источниками ЭДС ток вычисляется по формуле:
Известно, что одна любая точка схемы может быть заземлена без изменения токораспределения в схеме. Поэтому один из узлов схемы нужно мысленно заземлить, т.е. принять его потенциал равным нулю. При этом число неизвестных в методе узловых потенциалов равно числу уравнений, которые могут быть составлены для схемы по первому закону Кирхгофа. После определения потенциалов узлов токи в ветвях рассчитываются по закону Ома. Для ветвей с источниками ЭДС ток вычисляется по формуле: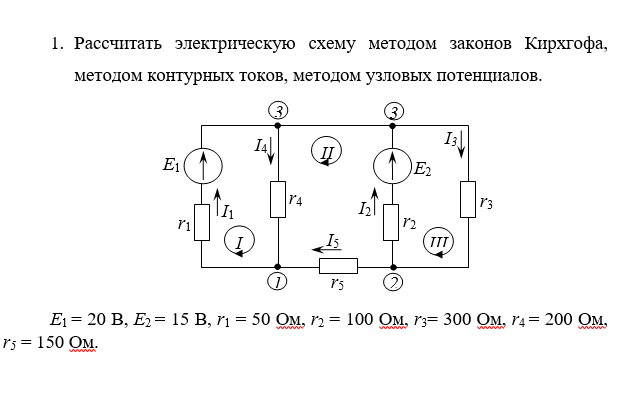 При этом ток, входящий в узел будем записывать со знаком «плюс», а выходящий со знаком «минус». Можно и наоборот — значения не имеет. Получим:
При этом ток, входящий в узел будем записывать со знаком «плюс», а выходящий со знаком «минус». Можно и наоборот — значения не имеет. Получим: Таким образом получим уравнение с одним неизвестным:
Таким образом получим уравнение с одним неизвестным: Вывод: значения почти одинаковые и нет разницы, каким именно способом решать задачу.
Вывод: значения почти одинаковые и нет разницы, каким именно способом решать задачу. Поэтому, посчитав их общее сопротивление по формуле результирующего сопротивления 2-х параллельно включенных резисторов и учитывая тот факт, что это сопротивление будет последовательно включено с резистором R3, получим общее сопротивление всей электрической цепи (пренебрегая внутренним сопротивлением источника питания):Получаем, что Rобщ = 10,5185 Ом. Соответственно, общий ток I1 всей цепи по закону Ома составит: I1 = E/Rобщ = 1,9014А. Далее находим токи отдельных ветвей:. Соответственно,.
Поэтому, посчитав их общее сопротивление по формуле результирующего сопротивления 2-х параллельно включенных резисторов и учитывая тот факт, что это сопротивление будет последовательно включено с резистором R3, получим общее сопротивление всей электрической цепи (пренебрегая внутренним сопротивлением источника питания):Получаем, что Rобщ = 10,5185 Ом. Соответственно, общий ток I1 всей цепи по закону Ома составит: I1 = E/Rобщ = 1,9014А. Далее находим токи отдельных ветвей:. Соответственно,. Начнем обходить левый контур по часовой стрелке от точки №2 до точки №2 — по замкнутому кругу. Потенциал точки №2 в начале решения мы приняли равным нулю, т.е. φ2 = 0. Находим далее: →→→В идеале потенциал φ2 должен был получиться нулю, но из-за округлений в промежуточных вычислениях образовалась небольшая погрешность, но это не страшно. Округлив полученные значения потенциалов до сотых долей можно прийти к идеальному нулю. Потенциальная диаграмма строится просто — по оси Х откладываются сопротивления, концам которых соответствуют точки №№1,2,3,4, а по оси Y — соответствующие этим точкам значения вычисленных потенциалов в этих точках.
Начнем обходить левый контур по часовой стрелке от точки №2 до точки №2 — по замкнутому кругу. Потенциал точки №2 в начале решения мы приняли равным нулю, т.е. φ2 = 0. Находим далее: →→→В идеале потенциал φ2 должен был получиться нулю, но из-за округлений в промежуточных вычислениях образовалась небольшая погрешность, но это не страшно. Округлив полученные значения потенциалов до сотых долей можно прийти к идеальному нулю. Потенциальная диаграмма строится просто — по оси Х откладываются сопротивления, концам которых соответствуют точки №№1,2,3,4, а по оси Y — соответствующие этим точкам значения вычисленных потенциалов в этих точках. постоянный ток v1 24 24 1
.print dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0)
.конец
v1 v(1,2) v(1,3) v(3,2) v(2) v(3)
2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E+01 1.931E+01
постоянный ток v1 24 24 1
.print dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0)
.конец
v1 v(1,2) v(1,3) v(3,2) v(2) v(3)
2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E+01 1.931E+01
 093793
-0,058851
0,136092
093793
-0,058851
0,136092
 Избегайте вложенных циклов.
Избегайте вложенных циклов.