Большая Энциклопедия Нефти и Газа. Мощность трехфазная

Мощность - трехфазная система - Большая Энциклопедия Нефти и Газа, статья, страница 2

Мощность - трехфазная система

Cтраница 2

Сумма показаний этих ваттметров дает мощность трехфазной системы.  [17]

При несимметричной нагрузке одного ваттметра для определения мощности трехфазной системы недостаточно.  [18]

Таким образом, мощность трехфазной системы а2, &2, с2 при частоте / 2 создается за счет преобразования мощности трехфазной системы alf bit ct при частоте / 1; а также за счет мощности приводного электродвигателя Д, который может питаться и от иной системы.  [19]

Для измерения мощности трехфазной системы применяют различные схемы включения ваттметров.  [20]

Каждый однофазный ваттметр измеряет мощность одной фазы. Для получения мощности трехфазной системы необходимо взять сумму показаний трех ваттметров.  [21]

Для измерения мощности трехфазной системы применяют различные схемы включения ваттметров.  [22]

Своеобразная особенность этого метода измерения заключается в том, что даже при симметричном приемнике показания двух ваттметров в большинстве случаев не одинаковые, причем показание одного из них может быть и отрицательным. В этом случае мощность трехфазной системы равна алгебраической сумме показаний двух ваттметров.  [23]

Своеобразная особенность этого метода измерения заключается в том, что даже при симметричном приемнике показания двух ваттметров в большинстве случаев не одинаковые, причем показание одного из них может быть и отрицательным. В этом случае мощность трехфазной системы равна алгебраической сумме показаний двух ваттметров.  [24]

При переключении с треугольника на звезду сила линейного тока в цепи уменьшается в 3 раза, а сила фазного тока - в V 3 раз. Соответственно в 3 раза уменьшается и мощность трехфазной системы.  [26]

Если стрелка одного из ваттметров стремится переместиться влево от нуля, то необходимо изменить направления тока в какой-либо из катушек прибора и определить мощность установки как разность показаний обоих ваттметров. Так как пользование двумя ваттметрами неудобно, то для измерения мощности трехфазной системы применяют один двухэлементный ваттметр.  [28]

Если стрелка одного из ваттметров стремится переместиться влево от нуля, то необходимо изменить направление тока в катушке напряжения этого прибора и определить мощность установки как разность показаний обоих ваттметров. Так как пользование двумя ваттметрами неудобно, то для измерения мощности трехфазной системы часто применяют один двухэлементный ваттметр. Как показывает само название, этот ваттметр состоит из двух однофазных ваттметров ( элементов), включаемых по схеме ( см. рис. 106) и воздействующих на общую подвижную часть. Этот прибор производит автоматическое сложение или вычитание мощностей, измеряемых его отдельными элементами.  [29]

При этом обмотки напряжения ваттметров включаются на фазное напряжение, а в обмотках тока протекают токи соответствующих фаз. Таким образом, каждый ваттметр измеряет мощность одной фазы, а сумма показаний ваттметров дает мощность трехфазной системы. Схема измерения мощности методом трех ваттметров может быть использована и при соединении нагрузки треугольником.  [30]

Страницы:      1    2    3

www.ngpedia.ru

Мощность трехфазной цепи

АрхеологияАрхитектураАстрономияАудитБиологияБотаникаБухгалтерский учётВойное делоГенетикаГеографияГеологияДизайнИскусствоИсторияКиноКулинарияКультураЛитератураМатематикаМедицинаМеталлургияМифологияМузыкаПсихологияРелигияСпортСтроительствоТехникаТранспортТуризмУсадьбаФизикаФотографияХимияЭкологияЭлектричествоЭлектроникаЭнергетика

Метод непосредственной оценки Метод непосредственной оценки предполагает измерение сопротивления постоянному току с помощью омметра. Омметром называют измерительный прибор непосредственного отсчёта для определения электрических активных (активные сопротивлений также называют омическими сопротивлениями) сопротивлений. Обычно измерение производится по постоянному току, однако, в некоторых электронных омметрах возможно использование переменного тока. Разновидности омметров: мегаомметры, тераомметры, гигаомметры, миллиомметры, микроомметры, различающиеся диапазонами измеряемых сопротивлений. По принципу действия омметры можно разделить на магнитоэлектрические - с магнитоэлектрическим измерителем или магнитоэлектрическим логометром (мегаомметры) и электронные, которые бывают аналоговые или цифровые. «Действие магнитоэлектрического омметра основано на измерении силы тока, протекающего через измеряемое сопротивление при постоянном напряжении источника питания. Для измерения сопротивлений от сотен Ом до нескольких мегаом измеритель и измеряемое сопротивление rx включают последовательно. В этом случае сила тока I в измерителе и отклонение подвижной части прибора a пропорциональны: I = U/(r0 + rx), где U — напряжение источника питания; r0 — сопротивление измерителя. При малых значениях rx (до нескольких ом) измеритель и rx включают параллельно».[5] За основу логометрических мегаомметров берется логометр, к плечам которого подключаются в разных комбинациях (в зависимости от предела измерения) образцовые внутренние резисторы и измеряемое сопротивление, показание логометра зависит от соотношения этих сопротивлений. В качестве источника высокого напряжения, необходимого для проведения таких измерений, в подобных приборах обычно используют механический индуктор — электрогенератор с ручным приводом, в некоторых мегаомметрах вместо индуктора применяется полупроводниковый преобразователь напряжения. Принцип действия электронных омметров основан на преобразовании измеряемого сопротивления в пропорциональное ему напряжение с помощью операционного усилителя. Измеряемый резистор включается в цепь обратной связи (линейная шкала) или на вход усилителя. Цифровой омметр представляет собой измерительный мост с автоматическим уравновешиванием. Уравновешивание производится цифровым управляющим устройством методом подбора прецизионных резисторов в плечах моста, после чего измерительная информация с управляющего устройства подаётся на блок индикации. «При измерении малых сопротивлений может возникать дополнительная погрешность из-за влияния переходного сопротивления в точках подключения. Чтобы избежать этого применяют так называемый метод четырехпроводного подключения. Сущность метода состоит в том, что используются две пары проводов — по одной паре на измеряемый объект подается ток определенной силы, с помощью другой пары с объекта на прибор подаётся падение напряжения пропорциональное силе тока и сопротивлению объекта. Провода подсоединяются к выводам измеряемого двухполюсника таким образом, чтобы каждый из токовых проводов не касался непосредственно соответствующего ему провода напряжения, при этом получается, что переходные сопротивления в местах контактов не включаются в измерительную цепь» Дата введения 1971-01-01 Настоящий стандарт устанавливает условные графические обозначения электроизмерительных приборов на схемах, выполняемых вручную или автоматизированным способом, изделий всех отраслей промышленности и строительства. (Введен дополнительно, Изм. № 1, 3). Обозначения электроизмерительных приборов приведены в таблице. Наименование Обозначение 1а. Датчик измеряемой неэлектрической величины 1. Прибор электроизмерительный   а) показывающий б) регистрирующий в) интегрирующий (например, счетчик электрической энергии) Примечания: 1. При необходимости изображения нестандартизованных электроизмерительных приборов следует попользовать сочетания соответствующих основных обозначении, например, комбинированный прибор, показывающий и регистрирующий. 2. Для указания назначения электроизмерительного прибора в его обозначение вписывают условные графические обозначения, установленные в стандартах ЕСКД. а также буквенные обозначения единиц измерения или измеряемых величин, которые помещают внутри графического обозначения электроизмерительного прибора a) амперметр б) вольтметр в) вольтметр двойной г) вольтметр дифференциальный д) вольтамперметр е) ваттметр W ж) ваттметр суммирующий ∑W з) варметр (измеритель активной мощности) var и) микроамперметр μA к) миллиамперметр тА л) милливольтметр mV м) омметр Ω н) мегаомметр MΩ о) частотомер Hz п) волномер λ р) фазометр: измеряющий сдвиг фаз φ измеряющий коэффициент мощности cosφ с) счетчик ампер-часов Ah т) счетчик ватт-часов Wh у) счетчик вольт-ампер-часов реактивный varh ф) термометр, пирометр t° (допускаетсяΘо) х) индикатор полярности + - и) тахометр n ч) измеритель давления Paили Р т) измеритель уровня жидкости ш) измеритель уровня сигнала dB 3. В обозначения электроизмерительных приборов допускается вписывать необходимые данные согласно действующим стандартам на электроизмерительные приборы. 4. Если необходимо указать характеристику отсчетного устройства прибора, то в его обозначение вписывают следующие квалифицирующие символы: а) прибор, подвижная часть которого может отклоняться в одну сторону от нулевой отметки:   вправо влево б) прибор, подвижная часть которого может отклоняться в обе стороны от нулевой отметки допускается применять обозначение в) прибор вибрационной системы г) прибор с цифровым отсчетом д) прибор с непрерывной регистрацией (записывающий) е) прибор с точечной регистрацией (записывающий) ж) прибор печатающий с цифровой регистрацией з) прибор с регистрацией перфорированием Например:   вольтметр с цифровым отсчетом вольтметр с непрерывной регистрацией амперметр, подвижная часть которого отклоняется в обе стороны от нулевой отметки 2. Гальванометр 3. Синхроноскоп 4. Осциллоскоп 5. Осциллограф 6. Гальванометр осциллографический: а) тока или напряжения б) мгновенной мощности 7. Счетчик импульсов 8. Электрометр 9. Болометр полупроводниковый 10. Датчик температуры 10а. Датчик давления Примечание: При необходимости указания конкретной величины, в которую преобразуется неэлектрическая величина, допускается применять следующие обозначения, например, датчик давления 11. Термоэлектрический преобразователь: а) с бесконтактным нагревом б) с контактным нагревом По ГОСТ 2.768-90 По ГОСТ 2.768-90 П. 12 по ГОСТ 2.728-74 13. Часы вторичные Примечание. Для указания часов, минут и секунд используют следующее обозначение 14. Часы первичные 15. Часы с контактным устройством 16. Часы синхронные, например, на 50 Гц 17. Индикатор максимальной активной мощности, имеющий обратную связь с ваттметром 18. Дифференциальный вольтметр 19. Соленомер 20. Самопишущий комбинированный ваттметр и варметр 21. Счетчик времени 22. Счетчик ватт-часов, измеряющий энергию, передаваемую в одном направлении 23. Счетчик ватт-часов с регистрацией максимальной активной мощности 24. Отличительный символ функции счета числа событий 25. Счетчик электрических импульсов с ручной установкой на n(установка на нуль при n =0) 26. Счетчик электрических импульсов с установкой на нуль электрическим путем 27. Счетчик электрических импульсов с несколькими контактами; контакты замыкаются соответственно на каждой единице (10°), десятке (101), сотне (102), тысяче (103) событий, зарегистрированных счетным устройством 28. Счетное устройство, управляемое кулачком и управляющее замыканием контакта через каждые п событий Примечания к п.1-28 1. При изображении обмоток измерительных приборов разнесенным способом используют следующие обозначения:   а) обмотка токовая б) обмотка напряжения в) обмотка секционирования с отводами:   токовая напряжения г) обмотка секционирования переключаемая: токовая напряжения 2. Обмотка в схемах измерительных приборов, отражающих их взаимное расположение в измерительном механизме, изображают следующим образом:   а) обмотка токовая б) обмотка напряжения в) обмотки токовые для сложения или вычитания г) обмотки напряжения для сложения или вычитания Например, механизм измерительный:   амперметра однообмоточного вольтметра однообмоточного ваттметра однофазного ваттметра трехфазного одноэлементного с двумя токовыми обмотками ваттметра трехфазного двухэлементного ваттметра трехфазного трехэлементного логометра магнитоэлектрического (например, омметра-логометра) логометра ферродинамического (например, частотомера) логометра электродинамического (например, фазометра однофазного) логометра трехобмоточного (например, фазометра трехфазного с двумя токовыми обмотками) логометра четырехобмоточного (например, синхроноскопа трехфазного) логометра четырехобмоточного (например, фазометра трехфазного с одной токовой обмоткой) 3. Выводные контакты обмоток допускается не изображать, если это не приведет к недоразумению   4. Выводные контакты обмоток допускается не зачернять, например, вольтметр однообмоточный СОЕДИНЕНИЯ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ способы соединений элементов электрич. цепей, при к-рых ветви цепи образуют соответственно трёхлучевую звезду и треугольник. Наибольшее распространение С. з. и т. получили в трёхфазных электрич. цепях. При соединении звездой концы обмоток трёх фаз генератора (трансформатора, электродвигателя) объединяются в общую нейтральную точку, а начала обмоток присоединяются к трём отходящим проводам ("линейные провода"). При соединении треугольником конец каждой фазы соединяется с началом следующей и к полученным трём узлам присоединяются линейные провода. Если и генератор и приёмник электроэнергии соединены звездой, то нейтр. точки могут быть связаны четвёртым (нейтр.) проводом. У симметричных приёмников, соединённых звездой или треугольником, сопротивления всех трёх фаз одинаковы. В симметричной трёхфазной цепи, соединённой треугольником, напряжения Uл между линейными проводами равны напряжениям Uф на фазах приёмника, а силы тока в линейных проводах в корень из 3 раз больше, чем в фазах приёмника. При соединении звездой линейные напряжения больше фазных в корень из 3 раз, а силы тока в линейных проводах и в фазах одинаковы. См. рис. Схемы соединений звездой и треугольником трёхфазной (симметричной) цепи: а - звездой; б - треугольником; Uл - линейное напряжение; Uф - фазное напряжение; Iл - сила линейного тока; Iф - сила фазного тока Трехфазная система ЭДС   Трехфазные электрические цепи представляют собой частный случай многофазных цепей. Многофазная система электрических цепей есть совокупность нескольких однофазных электрических цепей, в каждой из которых действуют синусоидальные ЭДС одной и той же частоты, создаваемые общим источником энергии и сдвинутые друг относительно друга по фазе на один и тот же угол. Термин «фаза» применяется для обозначения угла, характеризующего стадию периодического процесса, а также для названия однофазной цепи, входящей в многофазную цепь. Обычно применяют симметричные многофазные системы, у которых амплитудные значения ЭДС одинаковы, а фазы сдвинуты друг относительно друга на один и тот же угол /m, где m — число фаз. Наиболее часто в электротехнике используют двухфазные, трехфазные, шестифазные цепи. В электроэнергетике наибольшее практическое значение имеют трехфазные системы. Трехфазные цепи — это совокупность трех однофазных цепей, в которых действуют синусоидальные ЭДС одной и той же частоты, сдвинутые по фазе друг относительно друга на угол /3. Источником электрической энергии в трехфазной цепи является синхронный генератор, в трех обмотках которого, конструктивно сдвинутых друг относительно друга на угол /3 и называемых фазами, индуцируются три ЭДС в свою очередь, также сдвинуты относительно друг друга на угол /3. Устройство трехфазного синхронного генератора схематически показано на рис. 1. В пазах сердечника статора расположены три одинаковые обмотки. На переднем торце статора витки обмоток оканчиваются зажимами А, В, С (начало обмоток) и соответственно зажимами X, Y, Z (концы обмоток). Начала обмоток смещены относительно друг друга на угол /3, и соответственно их концы также cдвинуты относительно друг друга на угол /3. ЭДС в обмотках статора индуцируются в результате пересечения их витков магнитным полем, которое возбуждается постоянным током, проходящим по обмотке вращающегося ротора, которая называется обмоткой возбуждения. При равномерной частоте вращения ротора в обмотках статора индуцируются синусоидальные ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на угол /3. Трехфазная система ЭДС, индуцируемых в статоре синхронного генератора, обычно представляет собой симметричную систему.На электрических схемах обмотки статора трехфазного генератора условно изображают так, как показано на рис. 2 (а). За условное положительное направление ЭДС в каждой фазе генератора принимают направление от конца к началу обмотки. На рис. 2 (б) показано изменение мгновенных значений ЭДС трехфазного генератора, а на рис. 3 (а, б) даны его векторные диаграммы для прямой и обратной последовательности чередования фаз. Последовательность, с которой ЭДС в фазных обмотках генератора принимает одинаковые значения, называют порядком чередования фаз или последовательностью фаз. Если ротор генератора вращать в направлении, указанном на рис. 1, то получается последовательность чередования фаз ABC, т. е. ЭДС фазы В отстает по фазе от ЭДС фазы А, и ЭДС фазы С отстает по фазе от ЭДС фазы В. Такую систему ЭДС называют системой прямой последовательности. Если изменить направление вращения ротора генератора на противоположное, то последовательность чередования фаз будет обратной. У генераторов роторы всегда вращаются в одном направлении, вследствие чего последовательность чередования фаз никогда не изменяется. На практике у генераторов обычно применяется прямая последовательность чередования фаз. От последовательности чередования фаз зависит направление вращения трехфазных синхронных и асинхронных двигателей. Достаточно поменять местами две любые фазы двигателя, как возникает обратная последовательность чередования фаз и, следовательно, противоположное направление вращения двигателя.Последовательность фаз необходимо также учитывать при параллельном включении трехфазных генераторов. Прибор SONEL типа TKF-11 показывает наличие напряжения всех фаз, контролирует симметрию всех напряжений и отсутствие симметрии, а также определяет правильность чередования фаз. Мощность трехфазной цепи Каждую фазу нагрузки в трехфазной цепи можно рассматривать как цепь однофазного переменного тока. Соотношения для мгновенной, активной, реактивной, полной и комплексной мощностей ранее были получены. Мгновенные мощности фаз можно определить согласно выражению: . Суммарная мгновенная мощность будет равна Тогда получим   где - активная мощность одной фазы, а - суммарная активная мощность нагрузки. Получаем вывод: суммарная мгновенная мощность симметричной трехфазной цепи не изменяется во времени и равна суммарной активной мощности всей цепи. Реактивная и полная мощности определяются так: Через линейные токи и напряжения мощности могут быть определены: ; При несимметричной нагрузке суммарные мощности определяются как алгебраические суммы мощностей отдельных фаз. Активная мощность трехфазного приемника равна сумме активных мощностей фаз и аналогично для реактивной. Полная мощность трехфазной цепи будет равна: ;

studopedya.ru

Измерение мощности трехфазной системы | Онлайн журнал электрика

При симметричной трехфазной нагрузке довольно найти мощность Рф, потребляемую в одной фа­зе, потому что измеряемая мощность трехфазной нагрузки Р = ЗРФ. Простые условия для такового измерения имеются, когда нагрузка соединена звездой с доступной нулевой точкой. В этих случаях цепь тока ваттметра врубается после­довательно с одной из фаз нагрузки (рис. 1), а цепь напряже­ния ваттметра врубается на напряжение той фазы, ток которой проходит через ваттметр. Если нулевая точка недоступна либо нагрузка соединена по схеме треугольника, применяется искусственная нулевая точка. Так именуется нулевая точка звезды, образованной из сопротивления цепи напряжения ваттметра rn.вт  и 2-ух других равных ему дополнительных сопротивлений: rв и rc (рис. 2). При правиль­ном соединении с искусственной нулевой точкой цепь напряжения

Рис. 1

ваттметра находится под фазным напряжением и через ватт­метр проходит фазный ток. В таких критериях ваттметр определяет фазную мощность Рфи мощность трехфазной нагрузки снова определяется средством умножения показания ваттметра на 3. Обычно завод-изготовитель снабжает ваттметр искусственной нулевой точкой для измерения в трехфазных системах.Измерения мощности в трехфазных трехпроводных системах при несимметричной нагрузке почти всегда выполня­ются по методу 2-ух ваттметров (рис. 3). Специфичной осо­бенностью этого метода будет то событие, что не только лишь при несимметричной, но даже пр,и симметричной нагруз­ке показания 2-ух ваттметров почти всегда не равны, а показания 1-го из ваттметров могут стать отрицательными. Мощность трехфазной системы в данном случае приходится опре­делять как алгебраическую сумму показаний 2-ух ватт­метров.

Рис. 2

Справедливость такового метода доказывается на основании уравнений моментальной мощности, выраженной через секундные значения напряжений и токов. Моментальная мощность хоть какой фа­зы равна произведению моментальных значений фазных напряже­ний и тока, а моментальная мощность трехфазной системы равна сумме моментальных фазных мощностей. К примеру, при соедине­нии звездой

Р = uAiA + uВiВ + uCiC

Но согласно первому закону Кирхгофа при соединении звездой без нулевого провода

iA + iВ + iC и,  как следует,

iC  = – ( iA  + iВ)=0

Подставив это значение в уравнение мощности, получим:

p = (uA — uC ) iА + (uВ— ис) iВ

Разность фазных напряжений равна  соответственному линей­ному   напряжению:

uA— uC  =  uAC,  uВ — ис = uВC  на  основании  чего

p = uAC iА + uВC iВ

Как следует,  мощность трехфазной системы  может быть

выражена суммой 2-ух произведений , а эти

два  произведения  могут  быть   измерены   двумя   ваттметрами,

включенными в согласовании со схемой метода  (рис. 3).

Рис. 3 Схема метода 2-ух ваттметров

Нет нужды особо обосновывать справедливость метода 2-ух ваттметров для соединения треугольником, потому что при опреде­ленных значениях линейных напряжений и токов мощность не находится в зависимости от метода соединения нагрузки.

Отметим своеобразную особенность методов 2-ух ваттмет­ров: система линейных напряжений в обычной последова­тельности обозначается иАВ, ивс, иСА, а в уравнение этого спо­соба заходит напряжение иАС. Такая перестановка индексов обо­значает, что по отношению к первому ваттметру необходимо поменять фазу напряжения на 180°. Для этого довольно соединить «на­чало» (зажим со знаком звездочки) цепи напряжения первого ваттметра с проводом А, а «конец» этой цепи (зажим, у кото­рого обозначено номинальное напряжение) с проводом С.

Рассредотачивание мощности трехфазной системы меж показа­ниями 2-ух ваттметров зависит приемущественно от величины и знака сдвига фаз ср. Проследим эту зависимость в простом случае при симметричной нагрузке. Если заместо моментальной мощ­ности в уравнение (101) подставить активную (среднюю) мощ­ность трехфазной системы, то нужно поменять секундные значения напряжения и токов действующими и ввести в уравне­ние косинусы сдвигов фаз меж надлежащими напряже­ниями и токами. Таким макаром, уравнение мощности воспримет последующий вид:

р = р1 + р2 = uAC iА cosф1 + ивс iВ cosф2

При симметричной нагрузке по величине линейные токи

iА = iВ  = Iл

равны меж собой так же, как и линейные напряжения

uAC = ивс = ил

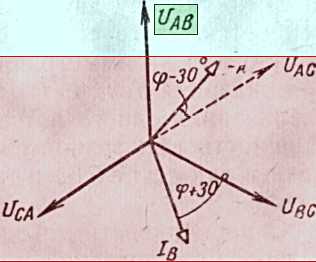
Рис, 4 Векторная диаграмма к методу 2-ух ваттметров

На рис. 4 построена векторная диаграмма трехфазной си­стемы, на которой вектор uAC построен равным по величине и обратным по направлению иСА

На основании этой диаграммы угол сдвига фаз меж век­торами uAC и iА и угол сдвига фаз ф2меж векторами ивс и iВ будут соответственно ф1 = ф – 30о и ф2 = ф + 30о. Как следует, показания 2-ух ваттметров, составляющие мощность трехфазной системы, выразятся последующим образом:

р = р1 + р2 = илIл cos( ф – 30о) + илIл cos( ф + 30о)

Это выражение указывает, что при симметричной нагрузке показания ваттметров равны только при ф = 0. Если же ф >60о то стрелка второго ваттметра отклоняется за нуль шкалы, а что­бы отсчитать в таких критериях показание второго ваттметра, необходимо переключить (т. е. поменять местами в схеме) зажимы цепи напряжения прибора. Нередко для из­менения фазы тока на 180° в цепи напря­жения в корпус ваттметра встраивается особый тумблер. Показания второго ваттметра после переключения следует считать отрицательными и, что­бы найти мощность трехфазной ус­тановки, необходимо эти показания вычитать из показаний первого ваттметра.

Для измерения мощности в трехфазных четырехпроводных системах простым является метод 3-х ваттметров. В любой из линейных проводов врубается цепь тока 1-го из ваттметров, а цепь напряжения каждого из ваттметров вклю­чается меж подходящим линейным проводом и нулевым проводом системы (рис. 5).

Рис, 5 Схема 3-х ваттметров

При таком соединении любой из ваттметров определяет мощ­ность одной фазы системы. Как следует, активная мощность всей трехфазной системы будет равна обычный сумме показаний 3-х ваттметров:

р = р1 + р2 + р3

В промышленных установках на распределительных щитах обширно используются ваттметры трехфазного тока. Они представляют собой два (для трехпроводной системы) либо три (для четырехпроводной системы) измерительных механизма, связанных общей осью и таким методом воздействующих на общую стрелку. Эти измерительные механизмы врубаются в трехфаз­ную цепь соответственно методу 2-ух ваттметров либо методу 3-х ваттметров.

elektrica.info

Трёхфазная система электроснабжения — Википедия РУ

Звезда

 

Звездой называется такое соединение, когда концы фаз обмоток генератора (G) соединяют в одну общую точку, называемую нейтральной точкой или нейтралью. Концы фаз обмоток потребителя (M) также соединяют в общую точку.

Провода, соединяющие начала фаз генератора и потребителя, называются линейными. Провод, соединяющий две нейтрали, называется нейтральным.

Трёхфазная цепь, имеющая нейтральный провод, называется четырёхпроводной. Если нейтрального провода нет — трёхпроводной.

Если сопротивления Za, Zb, Zc потребителя равны между собой, то такую нагрузку называют симметричной.

Линейные и фазные величины

Напряжение между фазным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя фазными проводами (UAB, UBC, UCA) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:

IL=IF;UL=3×UF{\displaystyle I_{L}=I_{F};\qquad U_{L}={\sqrt {3}}\times {U_{F}}} 

Несложно показать, что линейное напряжение сдвинуто по фазе на π/6{\displaystyle \pi /6}  относительно фазных:

uLab=uFa−uFb=UF[cos⁡(ωt)−cos⁡(ωt−2π/3)]=2UFsin⁡(−π/3)sin⁡(ωt−π/3)=3UFcos⁡(ωt+π−π/3−π/2){\displaystyle u_{L}^{ab}=u_{F}^{a}-u_{F}^{b}=U_{F}[\cos(\omega t)-\cos(\omega t-2\pi /3)]=2U_{F}\sin(-\pi /3)\sin(\omega t-\pi /3)={\sqrt {3}}U_{F}\cos(\omega t+\pi -\pi /3-\pi /2)} 

uL=3UFcos⁡(ωt+π/6){\displaystyle u_{L}={\sqrt {3}}U_{F}\cos(\omega t+\pi /6)} 

Мощность трёхфазного тока

Для соединения обмоток звездой, при симметричной нагрузке, мощность трёхфазной сети равна:

P=3UFIFcosφ=3UL3ILcosφ=3ULILcosφ{\displaystyle P=3U_{F}I_{F}cos\varphi =3{\frac {U_{L}}{\sqrt {3}}}I_{L}cos\varphi ={\sqrt {3}}U_{L}I_{L}cos\varphi } 

Последствия отгорания (обрыва) нулевого провода в трехфазных сетях

  Существующие виды защиты от линейного напряжения, которые можно найти в продаже в электротехнических магазинах   Шины для раздачи нулевых проводов (синяя) и проводов заземления(зеленая)

При симметричной нагрузке в трёхфазной системе питание потребителя линейным напряжением возможно даже при отсутствии нейтрального провода. Однако, при питании нагрузки фазным напряжением, когда нагрузка на фазы не является строго симметричной, наличие нейтрального провода обязательно. При его обрыве или значительном увеличении сопротивления (плохом контакте) происходит так называемый «перекос фаз», в результате которого подключенная нагрузка, рассчитанная на фазное напряжение, может оказаться под произвольным напряжением в диапазоне от нуля до линейного (конкретное значение зависит от распределения нагрузки по фазам в момент обрыва нулевого провода). Это зачастую является причиной выхода из строя бытовой электроники в квартирных домах, который может приводить к пожарам. Пониженное напряжение также может послужить причиной выхода из строя техники.

Проблема гармоник, кратных третьей

Современная техника всё чаще оснащается импульсными сетевыми источниками питания. Импульсный источник без корректора коэффициента мощности потребляет ток узкими импульсами вблизи пиков синусоиды питающего напряжения на интервалах зарядки конденсатора входного выпрямителя. Большое количество таких источников питания в сети создаёт повышенный ток третьей гармоники питающего напряжения. Токи гармоник, кратных третьей, вместо взаимной компенсации, математически суммируются в нейтральном проводнике (даже при симметричном распределении нагрузки) и могут привести к его перегрузке даже без превышения допустимой мощности потребления по фазам. Такая проблема существует, в частности, в офисных зданиях с большим количеством одновременно работающей оргтехники. Решением проблемы третьей гармоники является применение корректора коэффициента мощности (пассивного или активного) в составе схемы производимых импульсных источников питания. Требования стандарта IEC 1000-3-2 накладывают ограничения на гармонические составляющие тока нагрузки устройств мощностью от 50 Вт. В России количество гармонических составляющих тока нагрузки нормируется стандартами ГОСТ Р 54149-2010, ГОСТ 32144-2013 (с 1.07.2014), ОСТ 45.188-2001.

Треугольник

 Треугольник — такое соединение, когда конец первой фазы соединяется с началом второй фазы, конец второй фазы с началом третьей, а конец третьей фазы соединяется с началом первой.

Соотношение между линейными и фазными токами и напряжениями

Для соединения обмоток треугольником, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:

IL=3×IF;UL=UF{\displaystyle I_{L}={\sqrt {3}}\times {I_{F}};\qquad U_{L}=U_{F}} 

Мощность трёхфазного тока при соединении треугольником

Для соединения обмоток треугольником, при симметричной нагрузке, мощность трёхфазного тока равна:

P=3UFIFcosφ=3ULIL3cosφ=3ULILcosφ{\displaystyle P=3U_{F}I_{F}cos\varphi =3U_{L}{\frac {I_{L}}{\sqrt {3}}}cos\varphi ={\sqrt {3}}U_{L}I_{L}cos\varphi } 

Распространённые стандарты напряжений

Страна Частота, Гц Напряжение (фазное/линейное), Вольт

Россия	50	230/400[2]
Страны ЕС	50	230/400, 400/690 (промышленные сети)
Япония	50 (60)	120/208
США	60	120/208, 277/480 240 (только треугольник)

http-wikipediya.ru

Мощность трехфазного тока

 

Активная мощность, отдаваемая трехфазным генератором и по­требляемая трехфазным потребителем, определяется суммой ак­тивных мощностей каждой фазы потребителя:

(16.25)

Аналогичное определение можно отнести и к реактивной мощ­ности трехфазного тока, т. е.

(16.26)

Полная, мощность трехфазного потребителя равна

(16.27)

Очевидно, что при равномерной нагрузке фаз ( и ) активная мощность трехфазного тока равна утроенному значению активной мощности каждой фазы

(16.28)

Однако на практике удобней оперировать линейными величи­нами, так как доступными являются линейные провода, а не об­мотки генератора или двигателя.

При соединении потребителя звездой при равномерной нагруз­ке фаз

, а

Тогда

При соединении потребителей треугольником при равномерной нагрузке фаз

, а

Тогда

Таким образом, при равномерной нагрузке фаз при соединении потребителей звездой и треугольником мощности трехфазного тока определяются выражениями:

активная мощность (16.29)

реактивная мощность (16.30)

полная, мощность (16.31)

или при неравномерной нагрузке по (16.27)

При неравномерной нагрузке фаз полная, или кажущаяся, мощность трехфазного тока может быть определена суммой полных мощностей каждой фазы, выраженной в комплексной фор­ме, а именно

(16.32)

Равномерную нагрузку в трехфазных цепях обеспечивают элек­трические двигатели трехфазного тока, обмотки которых могут быть соединены или звездой, или треугольником.

 

 

Похожие статьи:

poznayka.org

Мощность в трёхфазных цепях

Мгновенная мощность трёхфазного генератора равна сумме мгновенных мощностей всех трёх фаз:

(8.18)

или

(8.19)

При отсутствии нейтрального (нулевого) провода уравнение (8.18) приобретает вид:

,

так как в этом случае , а по определению

Активная мощность Р трёхфазного генератора согласно (8.18), равна сумме активных мощностей всех трёх фаз

,

которая в соответствии с ( ) приводится к виду

В симметричной системе

(8.20)

и, следовательно, независимо от схемы соединения фаз

(8.21)

Применяя (8.18) к расчёту мгновенного значения мощности в трёхфазной симметричной системе, можно убедиться, что р = Р, т.е. сумма мгновенных значений мощностей всех трёх фаз – величина постоянная.

где

р = Р à Постоянство мощности в симметричном решении – одно из крупных достоинств трёхфазной (и вообще – многофазной) цепи. При этом трёхфазные электродвигатели и генераторы имеют благоприятные условия для работы, так как в таком решении отсутствуют пульсации момента, что наблюдается у однофазных электрических машинах.

Реактивная мощность Q трёхфазного генератора определяется как алгебраическая сумма реактивных мощностей всех фаз:

(8.22)

и, в частности, для симметричной системы независимо от схемы соединения фаз

(8.23)

Полная мощность S симметричной трёхфазной системы определяется согласно ( )

(8.24)

Коэффициент мощности λ для трёхфазной цепи вычисляется как

(8.25)

Запишем комплексную форму полной мощности , где - комплексная полная мощность, - комплексное действующее значение напряжения, - сопряжённое комплексное действующее значение тока.

(8.26)

Р – активная мощность, Q – реактивная мощность

Для трёхфазной цепи:

(8.27)

Действительная часть этого выражения представляет собой активную мощность:

(8.28)

Суммарная активная мощность, потребляемая несимметричной трёхфазной цепью, может быть в соответствии с этим выражением измерена при помощи трёх ваттметров, активная мощность равна сумме показаний трёх ваттметров. Такой метод измерения применяется при наличии нейтрального провода, или искусственно создаётся нейтральный ток.

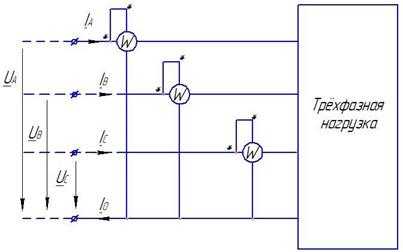
Рис.8.13.

В случае отсутствия нейтрального (нулевого) провода измерение может быть произведено с помощью двух ваттметров (рис.8.14).

Рис.8.14.

В этом случае выражение (8.27) преобразуется следующим образом: искомый ток из условия:

, получаем:

или

(8.29)

В соответствии с (8.29) при изменении активной мощности двумя ваттметрами к одному из них подводится напряжение и ток , к другому – напряжение и ток (рис.8.14.). Показания ваттметров складываются алгебраически.

Информационно-методическое обеспечение дисциплины:

1. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Т1, Т2. - М.: Высшая школа, 1981.
2. Бессонов Л.А. Теоретические основы электротехники. Т1, Т2. - М.: Высшая школа, 1984.
3. Ионкин П.А. и др. Теоретические основы электротехники. Т1. - М.: Высшая школа 1981.
4. Основы теории цепей /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов/ М.: Высшая школа, 1989.
5. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи. – М.: Высшая школа, 1990.
6. Матханов П.Н. Основы анализа электрических цепей. Нелинейные цепи. – М.: Высшая школа, 1990.
7. Сборник задач и упражнений по ТОЭ под ред. П.А. Ионкина. – М.: Энергоиздат, 1982.
8. Шебес М.Р. Задачник по теории линейных электрических цепей. – М.: Высшая школа, 1989.
9. Задачник по ТОЭ под ред. К.М. Поливанова– М.: Энергия, 1975.
10. Дмитриев Б.Ф. Общая электротехника. Линейные электрические цепи.

 

Похожие статьи:

poznayka.org

---

• 
  Как работает генератор в автомобиле
• 
  Источник питания для гальваники
• 
  Управление шаговыми двигателями с помощью компьютера
• 
  Систему счисления
• 
  Фильтр схема
• 
  Как обозначается на схеме фаза и ноль
• 
  Коронки для подрозетников диаметр
• 
  Www vladimir esplus ru
• 
  Международная система си
• 
  Утилизация старых аккумуляторов
• 
  Www ecard dit mos ru