Вектор индукции магнитного поля — формулы и определение с примерами
Полем физической величины называют множество ее значений, заданных не-прерывным образом в пространстве. Если физическая величина — скаляр, то поле называется скалярным, например поле температур нагретого металлического шара. Если физическая величина — вектор, то поле называется векторным. Примером может служить электростатическое поле, задаваемое в пространстве вектором его напряженности.
Вокруг магнитов существует особое состояние пространства — магнитное поле. Земля является гигантским магнитом.
Уже в VI в. до н. э. в Китае было известно, что некоторые руды (например, магнитный железняк) обладают способностью притягиваться друг к другу и притягивать на расстоянии железные предметы. Поскольку впервые куски таких руд были обнаружены возле города Магнезии в Малой Азии, то в Древней Греции они получили название магнитов (естественных магнитов).
После того как в Древнем Китае обратили внимание на способность естественных магнитов ориентироваться в магнитном поле Земли, магниты стали применяться как компасы и получили название «указатель юга» (рис. 131).
131).
Позже, в XI в., китайцы изобрели компас со стрелкой, позволяющий быстро ориентироваться на местности при любой погоде (рис. 132).
Наибольшим притягивающим действием обладают определенные зоны магнита, называемые полюсами.
Термин «полюсы магнита» от греческого слова — ось, конец оси был введен Петром Перегрином в 1269 г. в книге «Письма о магнитах».
Северным магнитным полюсом магнита называют обращенный на север конец свободно ориентирующегося в пространстве магнита. Обозначают северный полюс буквой N.
Противоположный конец магнита, направленный на юг, называется южным магнитным полюсом. Его обозначают буквой S.
Простейшие опыты с магнитной стрелкой показывают, что магниты могут притягиваться или отталкиваться. Разноименные магнитные полюса (как и в случае электрических зарядов) притягиваются, а одноименные — отталкиваются.
Таким образом, в пространстве вокруг магнита существует магнитное поле, которое можно обнаружить по действию сил на другие магниты, внесенные в область существования поля.
Так как сила — величина векторная, то и магнитное поле является векторным полем.
Для количественной характеристики магнитного поля в каждой точке пространства вводится физическая векторная величина — вектор индукции магнитного поля.
Термин «индукция» происходит от латинского слова induction — наведение.
Для определения вектора индукции магнитного поля в данной точке пространства необходимо знать его модуль и направление. За направление вектора индукции магнитного поля в данной точке пространства принимается направление, которое указывает северный полюс свободной магнитной стрелки, помещенной в исследуемую область пространства.
Силу, с которой один магнит действует на другой, можно рассматривать как результат действия магнитного поля, созданного первым магнитом, на второй (или наоборот).
Заметим, что структуру магнитного поля можно сделать «видимой» с помощью железных опилок, помещенных вблизи магнита на плоской подставке: при легком потряхивании опилки располагаются вдоль характерных кривых (рис.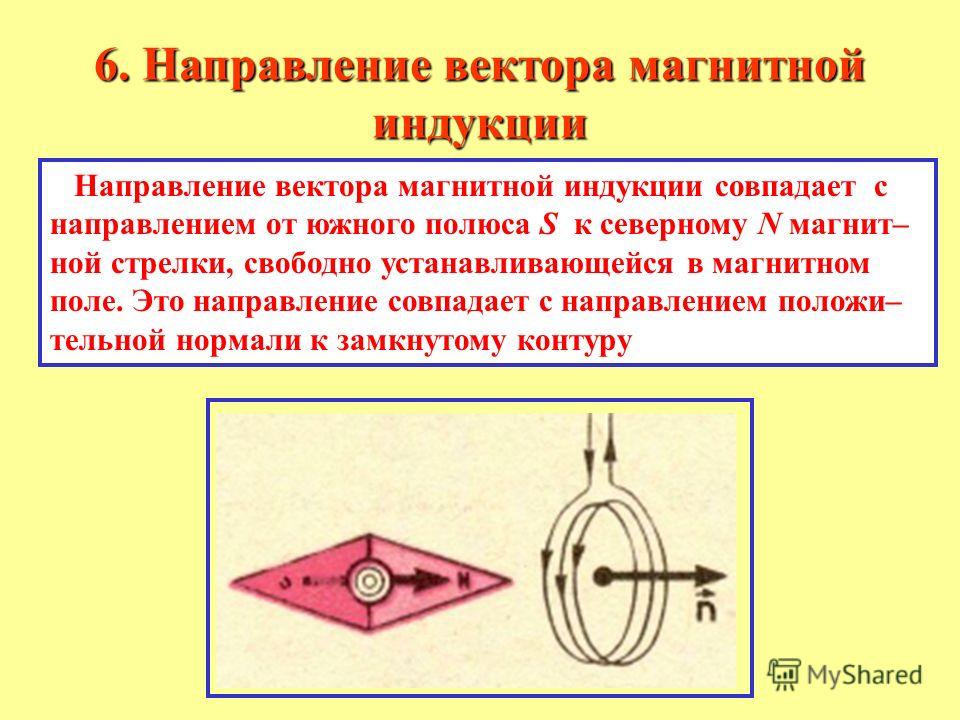 133,134), называемых «магнитными» линиями.
133,134), называемых «магнитными» линиями.
В 1831 г. Фарадей пояснил: «Под магнитными кривыми понимают линии магнитных сил. Эти линии вырисовываются железными опилками; к ним касательно располагались бы весьма небольшие магнитные стрелочки».
При несомненном сходстве электростатического и магнитного полей между ними имеется существенное отличие. Электростатическое поле потенциально, и его силовые линии разомкнуты — они начинаются на положительных зарядах и заканчиваются на отрицательных.
Магнитное поле является вихревым, поскольку его магнитные линии замкнуты: они не имеют ни начала, ни конца (рис. 135).
Эти линии не начинаются на северном полюсе и не заканчиваются на южном — они замыкаются внутри магнита, нигде не прерываясь. Это значит, что магнитное поле не имеет источников — магнитных зарядов.
Вследствие того что магнитные линии поля непрерывны, в любом магнитном образце всегда существуют два разноименных полюса. Иными словами, полюса магнита — места «выхода» наибольшего количества линий из магнита или их «входа» в него. Место, из которого выходят магнитные линии, соответствует северному магнитному полюсу, а место, где они входят в магнит, — южному.
Место, из которого выходят магнитные линии, соответствует северному магнитному полюсу, а место, где они входят в магнит, — южному.
Сильные магнитные свойства, кроме железа и стали, обнаруживают такие металлы, как никель, кобальт, гадолиний.
Вектор индукции магнитного поля. Графическое изображение магнитных полей
Векторное поле, модуль и направление которого во всех точках пространства одинаковы, называется однородным. Так как модуль напряженности поля характеризуется густотой расположения изображающих его линий, то из определения однородного поля следует, что силовые линии такого поля — параллельные прямые, равноотстоящие друг от друга. Примером может служить электростатическое поле плоского конденсатора.
В 1820 г. Ханс Кристиан Эрстед обнаружил действие проводника с током на магнитную стрелку. Расположив прямой провод параллельно стрелке компаса до включения тока (рис. 136, а), он заметил, что после включения тока стрелка поворачивается на некоторый угол, стремясь установиться в плоскости, перпендикулярной проводнику (рис.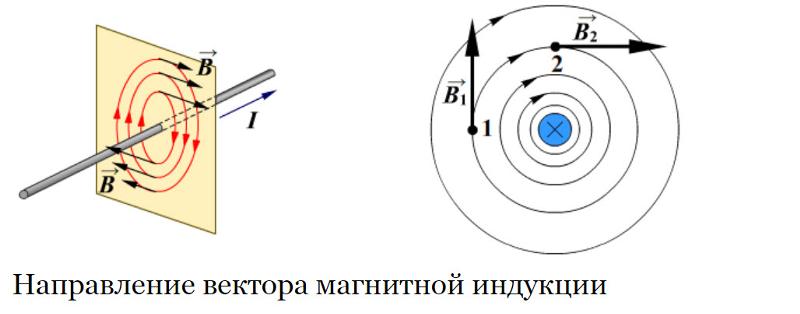 136, б, в).
136, б, в).
Эрстед также заметил, что направление вращения стрелки менялось на противоположное при изменении направления тока в цепи (полярности батареи) (см. рис. 136, б, в).
Угол поворота стрелки зависел от силы тока в проводнике и расстояния от него до стрелки, но не зависел от материала, из которого был изготовлен проводник.
Эксперименты Эрстеда впервые показали связь между электрическими и магнитными явлениями. Изучение этой связи привело к целому ряду открытий, позволивших создать современную электро- и радиотехнику.
Значительный вклад в развитие новой области физики внес французский физик Андре Мари Ампер, в честь которого и названа единица силы тока.
Действие проводника с током на магнитную стрелку показывает, что в пространстве, окружающем такой проводник, существует магнитное поле, связанное с током в проводнике. Таким образом, причина появления этого поля — движение электрических зарядов, так как проводник, по которому проходит ток, остается электрически нейтральным и сила Кулона между ним и стрелкой не действует.
Ампер в 1820 г. обнаружил, что два гибких проводника с током (рис. 137, а), расположенных параллельно друг другу, притягиваются (рис. 137, б), если по ним проходят токи одинакового направления, и отталкиваются (рис. 137, в), если по ним проходят токи противоположных направлений.
С увеличением силы тока проводники будут притягиваться или отталкиваться сильнее. При уменьшении или увеличении расстояния между проводниками их взаимодействие соответственно возрастает или убывает.
Притяжение или отталкивание электрически нейтральных проводников при прохождении через них электрического тока называют магнитным взаимодействием токов. Так как ток — это упорядоченное движение электрических зарядов, то магнитное взаимодействие токов — это взаимодействие упорядоченно движущихся электрических зарядов. Магнитное взаимодействие движущихся зарядов объясняется тем, что всякий движущийся заряд создает в окружающем пространстве магнитное поле, способное действовать на другие движущиеся заряды.
Основные свойства магнитного поля:
- оно материально, т. е. является одной из форм существования материи;
- порождается только движущимися электрическими зарядами;
- действует только на движущиеся электрические заряды;
- обнаруживается по действию на проводники с током, на движущиеся заряженные частицы иди на магнитные материалы.
Для силовой характеристики магнитного поля был введен вектор индукции магнитного поля (или просто индукции поля). Модуль вектора можно определить по аналогии с силовой характеристикой электрического поля — напряженностью, которая вводилась как отношение электрической силы, действующей на пробный электрический заряд со стороны поля, к величине этого заряда. В экспериментах по взаимодействию магнитного поля и проводников с током было обнаружено, что модуль силы взаимодействия пропорционален силе тока I в проводнике и длине части проводника l, находящейся в области магнитного поля индукции .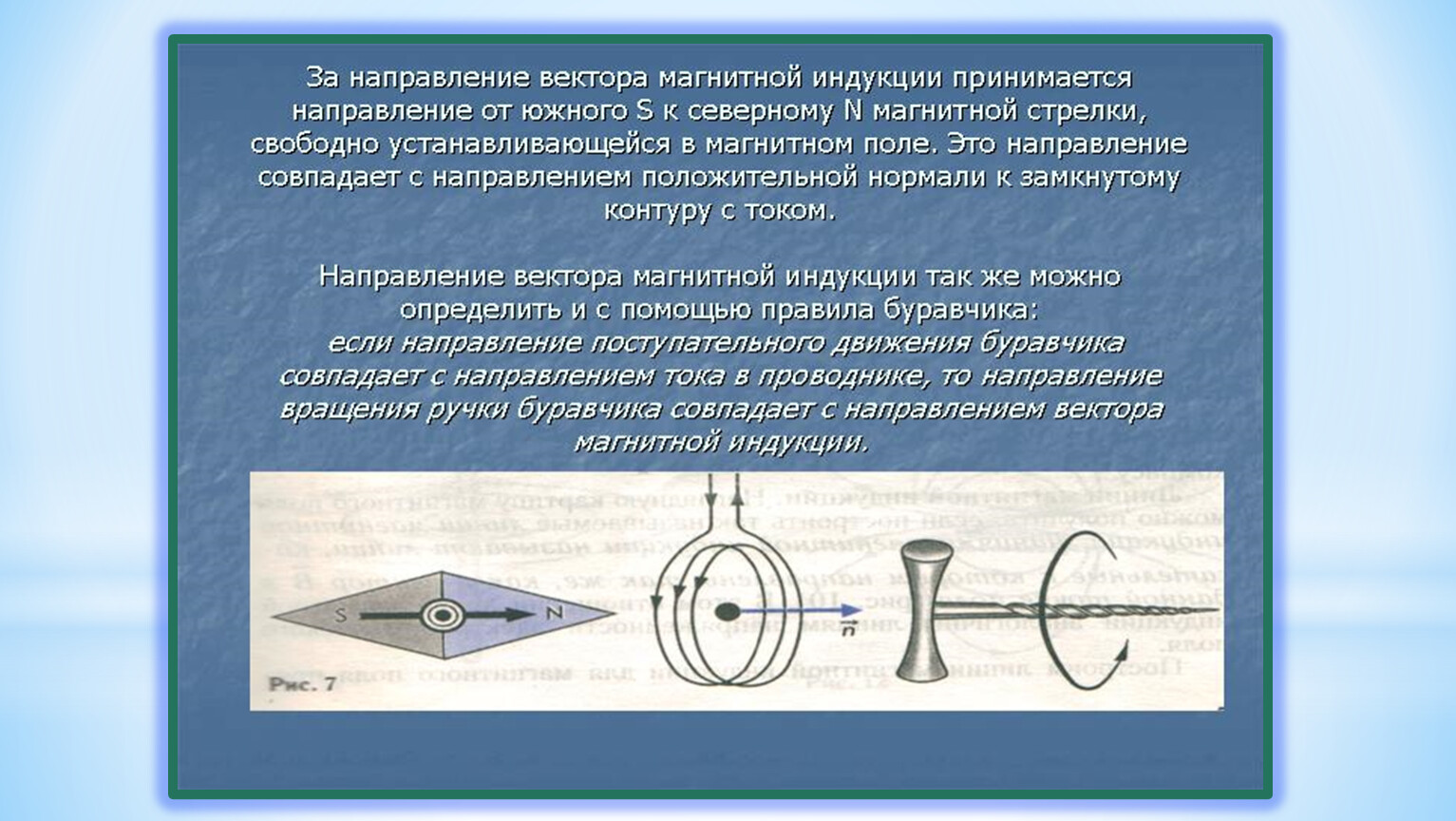
Подчеркнем, что рассматриваемая сила взаимодействия зависит также от угла а между прямолинейным проводником и направлением вектора индукции магнитного поля . Эта сила равна нулю, если направление вектора параллельно проводнику, и максимальна, если направление вектора перпендикулярно ему.
Таким образом, модуль вектора индукции магнитного поля можно определить как отношение максимальной магнитной силы, действующей на проводник с током единичной длины, к силе тока:
За направление вектора индукции магнитного поля в данной точке пространства принимается направление, указываемое северным полюсом свободной магнитной стрелки, которая является аналогом пробного заряда в электростатике (рис. 138).
В СИ единицей индукции магнитного поля является тесла:
Один тесла — индукция такого однородного магнитного поля, в котором на один метр длины прямого проводника, перпендикулярного вектору магнитной индукции с током силой один ампер действует сила один ньютон.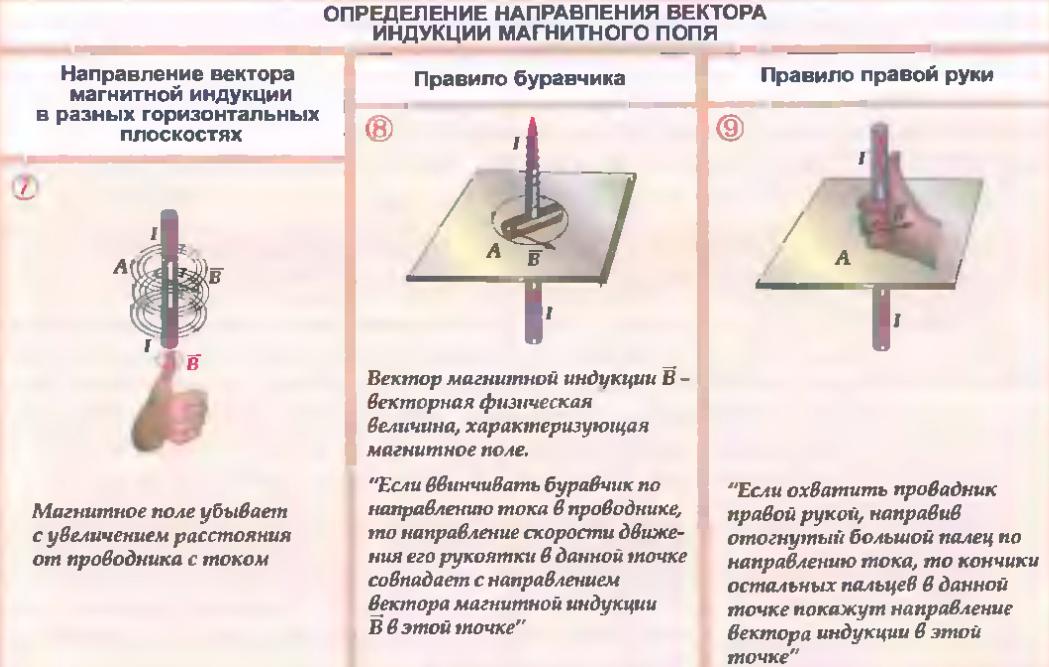
Наименование «тесла» присвоено единице индукции магнитного поля в честь сербского ученого, инженера и видного изобретателя электро- и радиотехники Николы Тесла.
Поле с индукцией 1 Тл — это очень сильное магнитное поле. Так, индукция магнитного поля Земли у ее поверхности составляет примерно для обычных магнитов — не превышает 0,01 Тл, для мощных электромагнитов достигает величин от 1 Тл до 2 Тл, для сверхпроводящих электромагнитов — свыше 10 Тл.
На рисунках принято обозначать направление индукции магнитного поля, перпендикулярного плоскости рисунка, специальными символами. Символ означает, что линии входят в плоскость рисунка (как оперение улетающей от Вас стрелы), символ — выходят из нее (как наконечник стрелы, летящей к Вам).
Для магнитного поля, так же как и для электрического, справедлив принцип суперпозиции:
- если магнитное поле в данной точке пространства создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником с током в отдельности:
Графически магнитные поля изображаются с помощью специальных линий, называемых линиями индукции магнитного поля. Касательная к любой линии в каждой точке направлена вдоль индукции магнитного поля Свойства линий индукции, с одной стороны, сходны со свойствами силовых линий электростатического поля — они не могут пересекаться; густота линий больше там, где модуль вектора больше. С другой стороны, отличаются — линии индукции магнитного поля всегда замкнуты, так как магнитное поле является вихревым (непотенциальным).
Касательная к любой линии в каждой точке направлена вдоль индукции магнитного поля Свойства линий индукции, с одной стороны, сходны со свойствами силовых линий электростатического поля — они не могут пересекаться; густота линий больше там, где модуль вектора больше. С другой стороны, отличаются — линии индукции магнитного поля всегда замкнуты, так как магнитное поле является вихревым (непотенциальным).
Для определения направления вектора индукции магнитного поля прямого тока Джеймс Клерк Максвелл предложил правило буравчика (рис. 139): направление вектора индукции магнитного поля соответствует направлению вращения буравчика (правого винта), если движение острия буравчика совпадает с направлением тока в проводнике.
Правило буравчика можно также использовать для определения направления вектора индукции магнитного поля в центре кругового проводника с током (рис. 140): направление вектора индукции магнитного поля соответствует направлению движения острия буравчика, если вращение рукоятки буравчика совпадает с направлением тока в проводнике.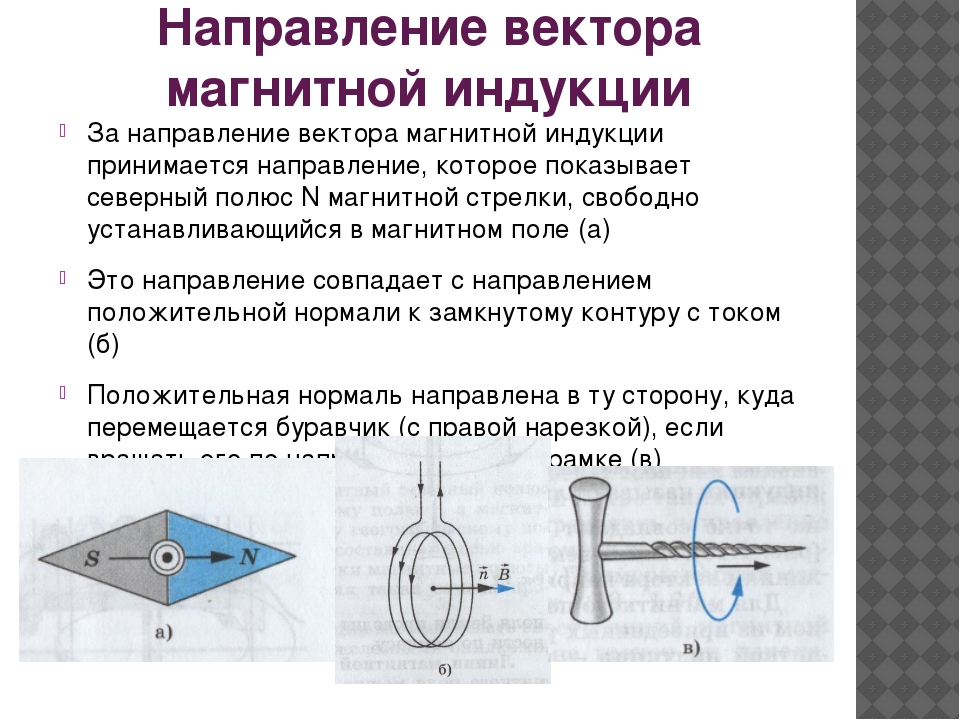
Для определения направления линий индукции магнитного поля прямолинейного проводника с током можно также использовать правило обхвата правой руки (рис. 141): проводник мысленно обхватывается правой рукой так, чтобы большой палец указывал направление тока, тогда остальные пальцы окажутся согнуты в направлении линий индукции магнитного поля.
Для определения направления силы взаимодействия магнита и витка с током необходимо знать положение магнитных полюсов витка. Это можно сделать с помощью правила буравчика, анализируя места «выхода» линий индукции магнитного поля из плоскости витка и их «входа» в плоскости витка.
Для определения «полюсов» кругового тока удобно пользоваться правилом часовой стрелки (рис. 142):
- северный полюс кругового тока находится с той стороны плоскости витка с током, глядя на которую, мы видим прохождение тока через виток в направлении против хода часовой стрелки; южный полюс — с той стороны витка, глядя на которую, видим прохождение тока через виток по ходу часовой стрелки.

Примеры магнитных полей
Для решения задач важно знать формулы, которые описывают магнитные поля, создаваемые проводниками с токами для их различных простейших конфигураций.
Модуль индукции магнитного поля бесконечного прямолинейного проводника с током силой I на расстоянии r от проводника в вакууме (рис. 143, 144) определяется по формуле
где — магнитная постоянная.
Модуль индукции магнитного поля тока силой I в центре тонкого кругового витка радиусом r в вакууме (рис. 145, 146) определяется по формуле
Катушка, витки которой последовательно обходятся током в определенном направлении, называется соленоидом. Если длина соленоида гораздо больше радиуса его витков, магнитное поле внутри него при плотной намотке витков можно считать однородным (по аналогии с электрическим полем внутри плоского конденсатора). Магнитное поле соленоида аналогично магнитному полю прямого магнита. Для определения полюсов соленоида удобно пользоваться правилом буравчика или правилом часовой стрелки.
Для определения полюсов соленоида удобно пользоваться правилом буравчика или правилом часовой стрелки.
Термин «соленоид» (от греческого слова — трубкообразный) введен Ампером в 1826 г.
Модуль индукции магнитного поля, создаваемого током силой I, проходящим по соленоиду внутри него, в точках, достаточно удаленных от его концов, в вакууме (рис. 147, 148) определяется по формуле
где N — число витков обмотки соленоида, l — длина соленоида.
Интересно, что замкнутый в кольцо соленоид (тороид) не имеет полюсов, так как все его линии магнитной индукции замыкаются внутри него (рис. 149).
§ 2 учебника К.Ю. Богданова для 11 класса
§ 2. магнитная индукция. правило буравчика. вихревой характер
магнитного поля
Магнитное поле характеризуется
вектором магнитной индукции. Правило буравчика позволяет определить направление
вектора магнитной индукции проводника с током. Все магнитные поля вихревые.
Характеристикой магнитного поля является вектор магнитной
индукции или индукции магнитного поля, обозначаемый В.
За направление вектора магнитной индукции в данной точке поля принимают
направление, в котором указывает N-полюс свободно вращающейся магнитной стрелки (рис. 2а).
Ориентацию рамки с током в магнитном поле тоже можно использовать для определения
направления вектора магнитной индукции, так как её плоскость устанавливается в
поле перпендикулярно вектору магнитной индукции (см. §1). При этом направление
вектора магнитной индукции определяют с помощью правила правого буравчика,
согласно которому, если вращать ручку буравчика по направлению тока в рамке, то
сам буравчик будет перемещаться в направлении вектора магнитной индукции (рис.
2б). Направление, в котором
перемещается правый буравчик, ещё называют положительной нормалью к
плоскости рамки с током.
Линиями магнитной индукции называют линии, касательные к
которым имеют то же направление, что и вектор магнитной индукции в этой точке поля.
Линии магнитной индукции служат силовыми характеристиками поля, как и силовые
линии электрического поля. Очевидно, что, как и силовые линии электрического
поля, линии магнитной индукции не могут пересекаться между собой. Картину линий
магнитной индукции поля можно построить с помощью магнитной стрелки или рамки с
током, помещая их в различные точки поля.
Как следует из опытов Эрстеда (см. §1), прямолинейный проводник
с током создаёт вокруг себя магнитное поле. На рис.2в показаны линии
магнитной индукции поля прямолинейного проводника, которые представляют собой
концентрические окружности, лежащие в плоскости, перпендикулярной этому
проводнику. Направление вектора магнитной индукции в этом случае можно
определить опять же с помощью правого буравчика: если направление поступательного
движения буравчика совпадает с направлением тока, то направление движения ручки
буравчика указывает на направление вектора магнитной индукции.
Видно (см. рис.2в), что линии магнитной индукции
прямолинейного проводника с током оказались замкнутыми, т.е. линиями без начала
и конца. Поля, характеризуемые замкнутыми силовыми линиями, называют вихревыми.
Из курса физики за 10 класс известно, что силовые линии электростатического
поля всегда имеют начало и конец, начинаясь на положительных и оканчиваясь на отрицательных
электрических зарядах. В отличие от электростатических
все магнитные поля являются вихревыми.
Замкнутость линий магнитной индукции – фундаментальное свойство
магнитного поля, вызванное тем, что изолированных магнитных зарядов, подобных
электрическим, не существует. Любое магнитное поле, возникающее при движении
электрических зарядов, всегда содержит N и S-полюса, и сколько бы мы ни дробили
постоянный магнит, каждая его песчинка всегда будет содержать разноимённые
магнитные полюса.
Вопросы для повторения:
·
Как магнитная стрелка и рамка с током помогают определить
направление вектора магнитной индукции?
·
Дайте определение линий магнитной индукции.
·
Опишите магнитное поле прямолинейного проводника с током.
·
Как правило буравчика помогает
определить направление вектора магнитной индукции прямолинейного проводника с
током?
·
Какие поля называют вихревыми?
Рис. 2. (а) – определение направления вектора магнитной
индукции с помощью магнитной стрелки; (б) — применение правила буравчика
для определения направления вектора магнитной индукции и положительной нормали
рамки с током; (в) — применение правила буравчика для определения
направления вектора магнитной индукции прямолинейного проводника с током.
Физика — 9
2.3
Известно, что действие электрического поля на электрический заряд, помещенный в это поле, определяется напряженностью электрического поля. Напряженность электрического поля — векторная величина, являющаяся силовой характеристикой электрического поля, равна силе, действующей на единичный положительный заряд. Магнитное поле также действует на магнит, помещенный в это поле, значит, у него тоже имеется силовая характеристика.
Напряженность электрического поля — векторная величина, являющаяся силовой характеристикой электрического поля, равна силе, действующей на единичный положительный заряд. Магнитное поле также действует на магнит, помещенный в это поле, значит, у него тоже имеется силовая характеристика.
Исследованние
1
Определим направление силы действия
магнитного поля
Оборудование: полосовой магнит, маленькие
магнитные стрелки (6-8 штук), деревянные опоры.
Ход исследования:
- Поместите полосовой магнит на деревянные опоры (обратите внимание, чтобы рядом не было железных изделий). Поместите магнитные стрелки в разных точках магнитного поля полосового магнита.

- Изобразите на рабочем листке прерывистой линией положения магнитных стрелок, полученных под действием магнитного поля (a).
Обсудите результат:
- Какая закономерность наблюдается в положении магнитных стрелок, полученных в магнитном поле полосового магнита?
- Какие имеются предположения о направлении силы действия магнитного поля?
Силовая характеристика магнитного поля. Условно за силовую характеристику магнитного поля была принята индукция магнитного поля (или магнитная индукция). Она обозначается буквой и характеризует воздействие на магнит (или тело с магнитными свойствами), помещенный в данное магнитное поле. Магнитная индукция является векторной физической величиной.
• Направление вектора индукции магнитного поля — направление северного полюса магнитной стрелки, помещенной в данной точке магнитного поля.
Линии магнитной индукции. Как вы знаете, магнитное поле невидимо, однако его картину можно смоделировать при помощи линий магнитной индукции (или силовыми линиями магнитного поля):
• Линии магнитной индукции — это такие линии магнитного поля, касательные к каждой точке которых совпадают с направлением вектора магнитной индукции в данной точке (b).
Цепочки из магнитных стрелок вокруг магнита отображают форму линий магнитной индукции.
Линии магнитной индукции выходят из северного полюса магнита и входят в южный полюс.
Формула индукции магнитного поля, B
Направлением вектора магнитной индукции считают направление на север магнитной стрелки, которая может свободно вращаться в магнитном поле.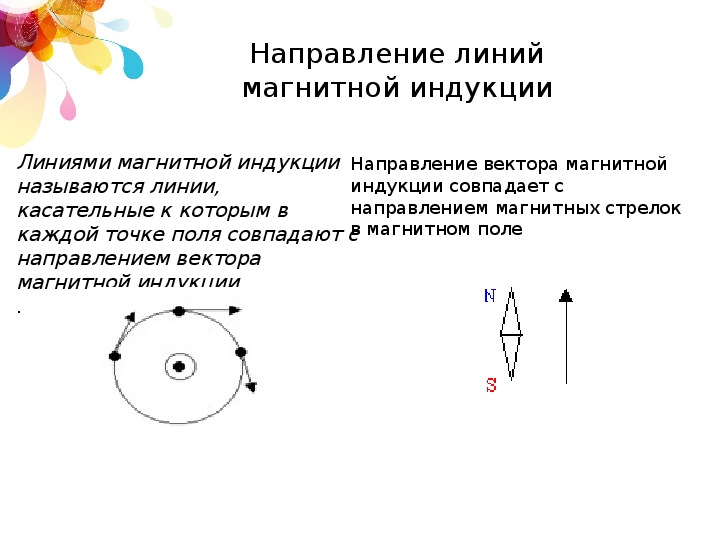 Такое же направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре.
Такое же направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре.
Модуль вектора магнитной индукции можно установить, используя силу, которая действует на проводники с током, помещенные в магнитное поле (силу Ампера). Тогда модуль вектора равен частному от деления максимальной силы (), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ():
Рассматривая силу Лоренца, которая действует на заряженную частицу, движущуюся в магнитном поле, получают формулу для магнитной индукции в виде:
где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.
Формулой, которая определяет величину вектора магнитной индукции в данной точке магнитного поля, считают так же следующее выражение:
где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля. Вращающий момент (M), действующий на контур с током I в однородном магнитном поле можно вычислить как:
Вращающий момент (M), действующий на контур с током I в однородном магнитном поле можно вычислить как:
где S – площадь, которую обтекает ток I. Следует помнить, что максимальный вращающий момент получается тогда, когда плоскость контура параллельна линиям магнитной индукции поля ().
Принцип суперпозиции магнитных полей
Если магнитное поле получается в результат наложения нескольких магнитных полей то, магнитная индукция поля (), может быть найдена как векторная сумма магнитных индукций отдельных полей ():
Закон Био-Савара-Лапласа, как формула для вычисления величины индукции магнитного поля
Закон Био-Савара – Лапласа является одним из распространенных законов, который позволяет вычислить вектор магнитной индукции () в любой точке магнитного поля, создаваемого в вакууме элементарным проводником с током:
где I – сила тока; – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; – магнитная постоянная. Вектор является перпендикулярным к плоскости, в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
Вектор является перпендикулярным к плоскости, в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связывает формула:
где – относительная магнитная проницаемость вещества.
Частные случаи формул для вычисления модуля вектора магнитной индукции
Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):
где R – радиус витка.
Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:
где r – расстояние от оси проводника до точки, в которой рассматривается поле.
В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:
где n – количество витков соленоида на единицу длины; I – сила тока в витке. {-7}$ Гн/м(Н/А2)- магнитная постоянная,
{-7}$ Гн/м(Н/А2)- магнитная постоянная,
$\bar{j}$ – вектор намагниченности среды в исследуемой точке поля.
Для магнитного поля в вакууме напряженность магнитного поля определяется выражением:
$$\bar{H}=\frac{\bar{B}}{\mu_{0}}$$
В изотропной среде формула (1) преобразуется к виду:
$$\bar{H}=\frac{\bar{B}}{\mu_{0} \mu}$$
где $\mu$ – скалярная величина, называемая
относительной магнитной проницаемостью среды (или просто магнитной проницаемостью). В изотропной среде векторы напряженности
магнитного поля и магнитной индукции совпадают по направлению.
Иногда напряженность магнитного поля $d \bar{H}$ определяют как
векторную величину, направленную по касательной к силовой линии поля, по модулю равной отношению силы (dF), с которой поле
воздействует на единичный элемент тока (dl), который расположен перпендикулярно полю в вакууме, к магнитной постоянной:
$$d H=\frac{d F}{\mu_{0} I d l}$$
Закон Био-Савара-Лапласа
Это важнейший в электромагнетизме закон.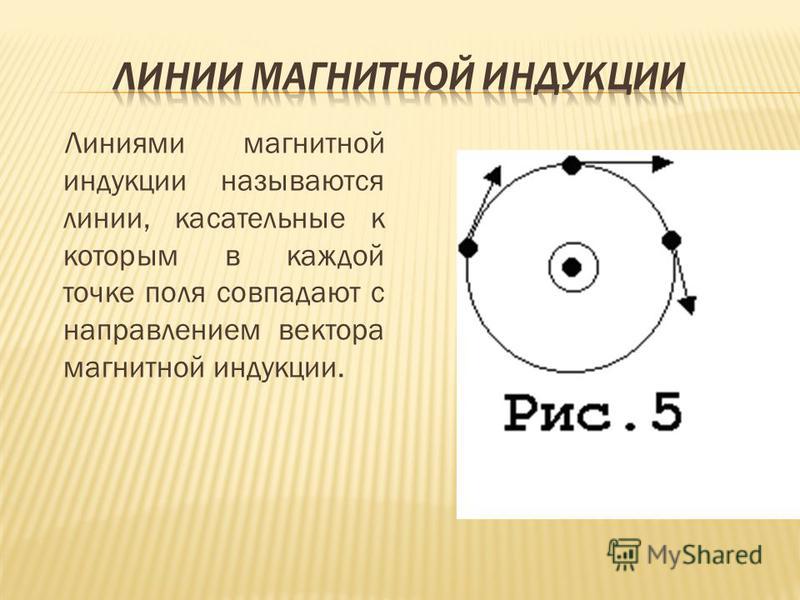 {3}} d \bar{l} \times \bar{r}(5)$$
{3}} d \bar{l} \times \bar{r}(5)$$
где $d \bar{l}$ – вектор элемента проводника, который по модулю равен длине
проводника, направление совпадает с направлением тока; $\bar{r}$ – радиус–вектор,
который проводят от рассматриваемого элементарного проводника к точке рассмотрения поля;
$r=|\bar{r}|$ .
Вектор $d \bar{H}$ – перпендикулярен плоскости, в которой находятся
векторы $d \bar{l}$ и
$\bar{r}$, и направлен так, что из его конца вращение вектора
$d \bar{l}$ по кратчайшему пути до совмещения с вектором
$\bar{r}$ происходило по часовой стрелке. Для нахождения направления вектора
$d \bar{H}$ можно использовать правило буравчика (Буравчик (винт) вращаем так,
чтобы его поступательное движение совпадало с направлением тока, тогда направление, по которому вращается ручка винта, совпадает с направлением
вектора напряженности поля, которое создает рассматриваемый ток).
Закон Био-Савара-Лапласа дает возможность вычислять величину полной напряженности магнитного поля, которое создает ток, текущий по проводнику любой формы.
Для нахождения полной напряженности магнитного поля, которое создает в исследуемой точке ток I, который течет по проводнику l, следует
векторно суммировать все элементарные напряженности $d \bar{H}$, порождаемые
элементами проводника и найденные по формуле (4).
Единицы измерения
Основной единицей измерения момента силы в системе СИ является: [H]=А/м
Примеры решения задач
Пример
Задание. Чему равна напряженность (H) в центре кругового витка (R — радиус витка) с током I.
Решение. Каждый элементарный ток витка магнитное поле в центре окружности, напряженность которого направлена по
положительной нормали к плоскости контура витка (рис.1). Поэтому, если элементарную напряженность поля найти по закону Био-Савара –
Лапласа, то векторное сложение элементарных полей можно будет заменить на алгебраическое.
В соответствии с законом Био-Савара – Лапласа dH равно:
$$d \bar{H}=\frac{1}{4 \pi} \frac{I}{r^{3}} d \bar{l} \times \bar{r}(1. {2}}$
{2}}$
Читать дальше: Формула напряженности электрического поля.
Направление вектора магнитной индукции. Электромагнитная индукция Куда направлено магнитное поле
Раскройте ладонь левой руки и выпрямите все пальцы. Большой палец отогните под углом в 90 градусов по отношению ко всем остальным пальцам, в одной плоскости с ладонью.
Представьте, что четыре пальца ладони, которые вы держите вместе, указывают направление скорости движения заряда, если он положительный, или противоположное скорости направление, если заряд отрицательный.
Вектор магнитной индукции, который всегда направлен перпендикулярно скорости, будет, таким образом, входить в ладонь. Теперь посмотрите, куда указывает большой палец – это и есть направление силы Лоренца.
Сила Лоренца может быть равна нулю и не иметь векторной составляющей. Это происходит в том случае, когда траектория заряженной частицы расположена параллельно силовым линиям магнитного поля. В таком случае частица имеет прямолинейную траекторию движения и постоянную скорость. Сила Лоренца никак не влияет на движение частицы, потому что в этом случае она вообще отсутствует.
В таком случае частица имеет прямолинейную траекторию движения и постоянную скорость. Сила Лоренца никак не влияет на движение частицы, потому что в этом случае она вообще отсутствует.
В самом простом случае заряженная частица имеет траекторию движения, перпендикулярную силовым линиям магнитного поля. Тогда сила Лоренца создает центростремительное ускорение, вынуждая заряженную частицу двигаться по окружности.
Обратите внимание
Сила Лоренца была открыта в 1892 году Хендриком Лоренцом, физиком из Голландии. Сегодня она достаточно часто применяется в различных электроприборах, действие которых зависит от траектории движущихся электронов. Например, это электронно-лучевые трубки в телевизорах и мониторах. Всевозможные ускорители, разгоняющие заряженные частицы до огромных скоростей, посредством силы Лоренца задают орбиты их движения.
Полезный совет
Частным случаем силы Лоренца является сила Ампера. Ее направление вычисляют по правилу левой руки.
Источники:
- Сила Лоренца
- сила лоренца правило левой руки
Действие магнитного поля на проводник с током означает, что магнитное поле влияет на движущиеся электрические заряды. Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь голландского физика Х. Лоренца
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь голландского физика Х. Лоренца
Инструкция
Сила — , значит можно определить ее числовое значение (модуль) и направление (вектор).
Модуль силы Лоренца (Fл)равен отношению модуля силы F, действующей на участок проводника с током длиной ∆l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника: Fл = F/N ( 1). Вследствие, несложных физических преобразований, силу F можно представить в виде: F= q*n*v*S*l*B*sina (формула 2), где q – заряд движущейся , n – на участке проводника, v – скорость частицы, S –площадь поперечного сечения участка проводника, l –длина участка проводника, B – магнитная индукция, sina – синус угла между векторами скорости и индукции. А количество движущихся частиц преобразовать до вида: N=n*S*l (формула 3). Подставьте формулы 2 и 3 в формулу 1, сократите величины n, S, l, получается для силы Лоренца: Fл = q*v*B*sin a.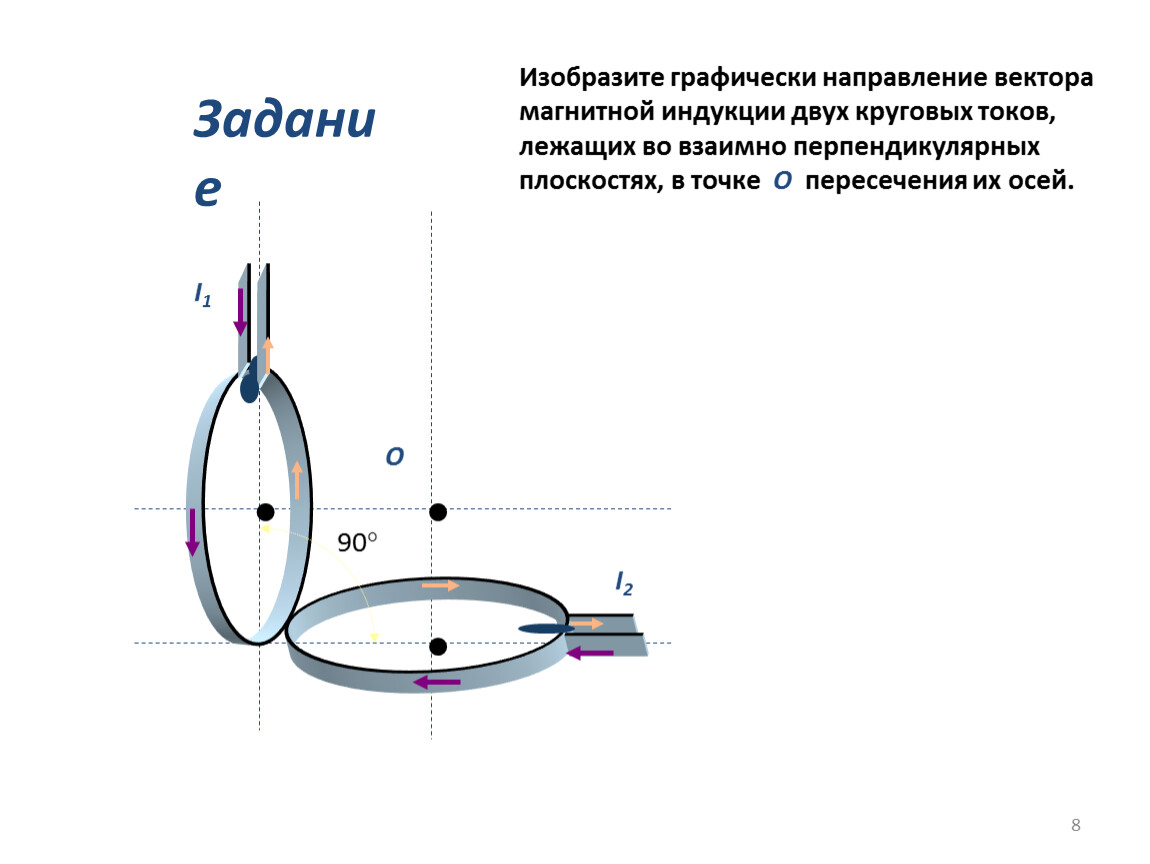 (12).
(12).
Направление силы Лоренца определяется правилом левой руки. Для его применения представьте следующее взаиморасположение трех перпендикулярных друг другу векторов. Расположите левую руку так, чтобы вектор магнитной индукции входил в ладонь, четыре пальца были направлены в сторону движения положительной (против движения отрицательной) частицы, тогда отогнутый на 90 градусов большой палец укажет направление силы Лоренца см рисунок).
Применяется сила Лоренца в телевизионных трубках мониторов, телевизоров.
Источники:
- Г. Я Мякишев, Б.Б. Буховцев. Учебник по физике. 11 класс. Москва. «Просвещение». 2003г
- решение задач на силу лоренца
Истинным направлением тока является то, в котором движутся заряженные частицы. Оно, в свою очередь, зависит от знака их заряда. Помимо этого, техники пользуются условным направлением перемещения заряда, не зависящим от свойств проводника.
Инструкция
Для определения истинного направления перемещения заряженных частиц руководствуйтесь следующим правилом. Внутри источника они вылетают из электрода, который от этого заряжается с противоположным знаком, и движутся к электроду, который по этой причине приобретает заряд, по знаку аналогичный частиц. Во внешней же цепи они вырываются электрическим полем из электрода, заряд которого совпадает с зарядом частиц, и притягиваются к противоположно заряженному.
Внутри источника они вылетают из электрода, который от этого заряжается с противоположным знаком, и движутся к электроду, который по этой причине приобретает заряд, по знаку аналогичный частиц. Во внешней же цепи они вырываются электрическим полем из электрода, заряд которого совпадает с зарядом частиц, и притягиваются к противоположно заряженному.
В металле носителями тока являются свободные электроны, перемещающиеся между узлами кристаллической . Поскольку эти частицы заряжены отрицательно, внутри источника считайте их движущимися от положительного электрода к отрицательному, а во внешней цепи — от отрицательного к положительному.
В неметаллических проводниках заряд переносят также электроны, но механизм их перемещения иной. Электрон, покидая атом и тем самым превращая его в положительный ион, заставляет его захватить электрон с предыдущего атома. Тот же электрон, который покинул атом, ионизирует отрицательно следующий. Процесс повторяется непрерывно, пока в цепи ток. Направление движения заряженных частиц в этом случае считайте тем же, что и в предыдущем случае.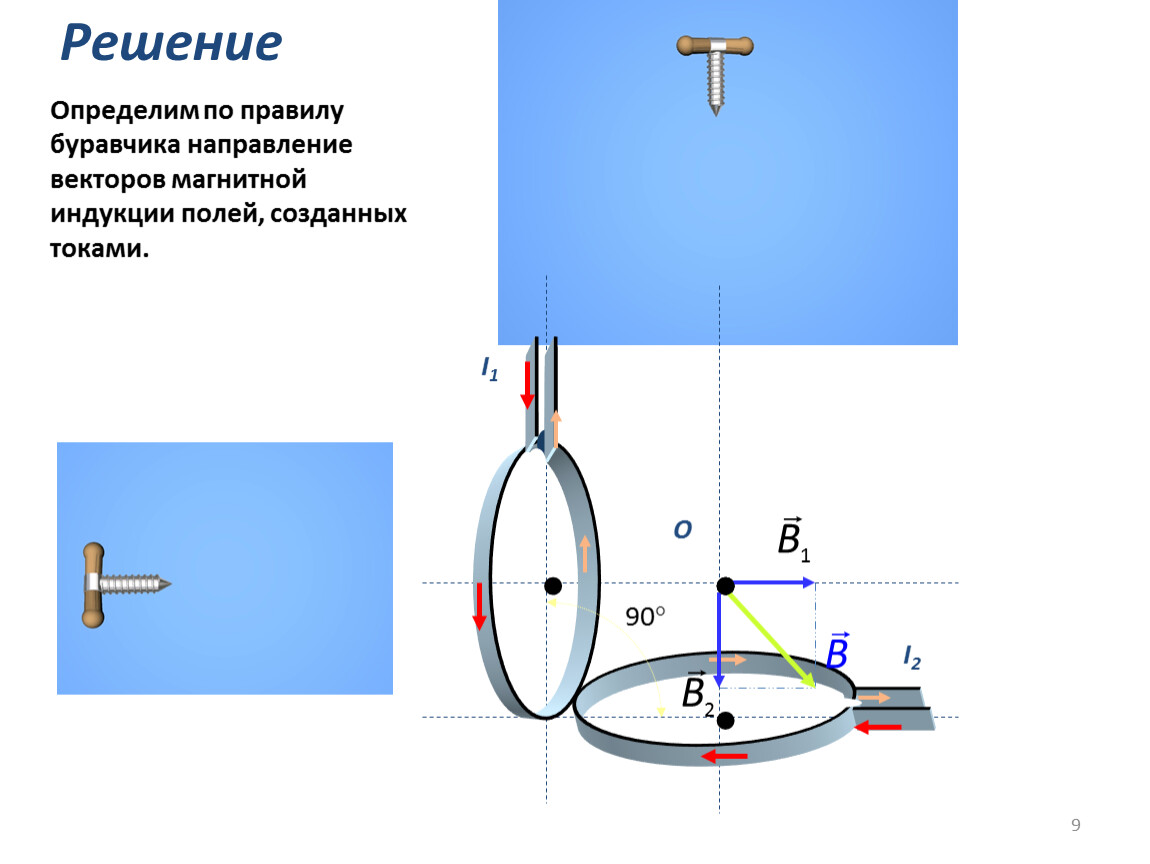
Полупроводники двух видов: с электронной и дырочной проводимостью. В первом носителями являются электроны, и потому направление движения частиц в них можно считать таким же, как в металлах и неметаллических проводниках. Во втором же заряд переносят виртуальные частицы — дырки. Упрощенно можно сказать, что это своего рода пустые места, электроны в которых отсутствуют. За счет поочередного сдвига электронов дырки движутся в противоположном направлении. Если совместить два полупроводника, один из которых обладает электронной, а другой — дырочной проводимостью, такой прибор, называемый диодом, будет обладать выпрямительными свойствами.
В вакууме заряд переносят электроны, движущиеся от нагретого электрода (катода) к холодному (аноду). Учтите, что когда диод выпрямляет, катод является отрицательным относительно анода, но относительно общего провода, к которому присоединен противоположный аноду вывод вторичной обмотки трансформатора, катод заряжен положительно. Противоречия здесь нет, если учесть наличие падения напряжения на любом диоде (как вакуумном, так и полупроводниковом).
В газах заряд переносят положительные ионы. Направление перемещения зарядов в них считайте противоположным направлению их перемещения в металлах, неметаллических твердых проводниках, вакууме, а также полупроводниках с электронной проводимостью, и аналогичным направлению их перемещения в полупроводниках с дырочной проводимостью. Ионы значительно тяжелее электронов, отчего газоразрядные приборы обладают высокой инерционностью. Ионные приборы с симметричными электродами не обладают односторонней проводимостью, а с несимметричными — обладают ей в определенном диапазоне разностей потенциалов.
В жидкостях заряд всегда переносят тяжелые ионы. В зависимости от состава электролита, они могут быть как отрицательными, так и положительными. В первом случае считайте их ведущими себя аналогично электронам, а во втором — аналогично положительным ионам в газах или дыркам в полупроводниках.
При указании направления тока в электрической схеме, независимо от того, куда перемещаются заряженные частицы на самом деле, считайте их движущимися в источнике от отрицательного полюса к положительному, а во внешней цепи — от положительного к отрицательному. Указанное направление считается условным, а принято оно до открытия строения атома.
Указанное направление считается условным, а принято оно до открытия строения атома.
Источники:
- направление тока
Сидите, разлагаете молекулы на атомы,
Забыв, что разлагается картофель на полях.
В. Высоцкий
Как описать гравитационное взаимодействие при помощи гравитационного поля? Как описать электрическое взаимодействие при помощи электрического поля? Почему электрическое и магнитное взаимодействия можно рассматривать как две составляющие единого электромагнитного взаимодействия?
Урок-лекция
Гравитационное поле
. В курсе физики вы изучали закон всемирного тяготения, в соответствии с которым все тела притягиваются друг к другу с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Рассмотрим какое-либо из тел Солнечной системы и обозначим его массу через m. В соответствии с законом всемирного тяготения на это тело действуют все другие тела Солнечной системы, и суммарная гравитационная сила, которую мы обозначим через F, равна векторной сумме всех этих сил. Поскольку каждая из сил пропорциональна массе m, то суммарную силу можно представить в виде Векторная величина зависит от расстояния до других тел Солнечной системы, т. е. от координат выбранного нами тела. Из определения, которое было дано в предыдущем параграфе, следует, что величина G является полем. Данное поле имеет название гравитационное поле
Поскольку каждая из сил пропорциональна массе m, то суммарную силу можно представить в виде Векторная величина зависит от расстояния до других тел Солнечной системы, т. е. от координат выбранного нами тела. Из определения, которое было дано в предыдущем параграфе, следует, что величина G является полем. Данное поле имеет название гравитационное поле
.
Казимир Малевич. Черный квадрат
Выскажите свое предположение, почему именно эта репродукция картины Малевича сопровождает текст параграфа.
Вблизи поверхности Земли сила, действующая на какое-либо тело, например на вас, со стороны Земли, намного превосходит все остальные гравитационные силы. Это знакомая вам сила тяжести. Так как сила тяжести связана с массой тела соотношением F g = mg, то G вблизи поверхности Земли есть просто ускорение свободного падения.
Поскольку величина G не зависит от массы или какого-либо другого параметра выбранного нами тела, то очевидно, что если в ту же самую точку пространства поместить другое тело, то сила, действующая на него, будет определяться той же самой величиной и, умноженной на массу нового тела. Таким образом, действие гравитационных сил всех тел Солнечной системы на некоторое пробное тело можно описать как действие гравитационного поля на это пробное тело. Слово «пробное» означает, что этого тела может и не быть, поле в данной точке пространства все равно существует и не зависит от наличия этого тела. Пробное тело служит просто для того, чтобы можно было измерить это поле измерением суммарной гравитационной силы, действующей на него.
Таким образом, действие гравитационных сил всех тел Солнечной системы на некоторое пробное тело можно описать как действие гравитационного поля на это пробное тело. Слово «пробное» означает, что этого тела может и не быть, поле в данной точке пространства все равно существует и не зависит от наличия этого тела. Пробное тело служит просто для того, чтобы можно было измерить это поле измерением суммарной гравитационной силы, действующей на него.
Совершенно очевидно, что в наших рассуждениях можно и не ограничиваться Солнечной системой и рассматривать любую, сколь угодно большую систему тел.
Гравитационную силу, создаваемую некоторой системой тел и действующую на пробное тело, можно представить как действие гравитационного поля, создаваемого всеми телами (за исключением пробного) на пробное тело.
Электромагнитное поле
. Электрические силы очень похожи на гравитационные, только действуют они между заряженными частицами, причем для одноименно заряженных частиц это силы отталкивания, а для разноименно заряженных — силы притяжения.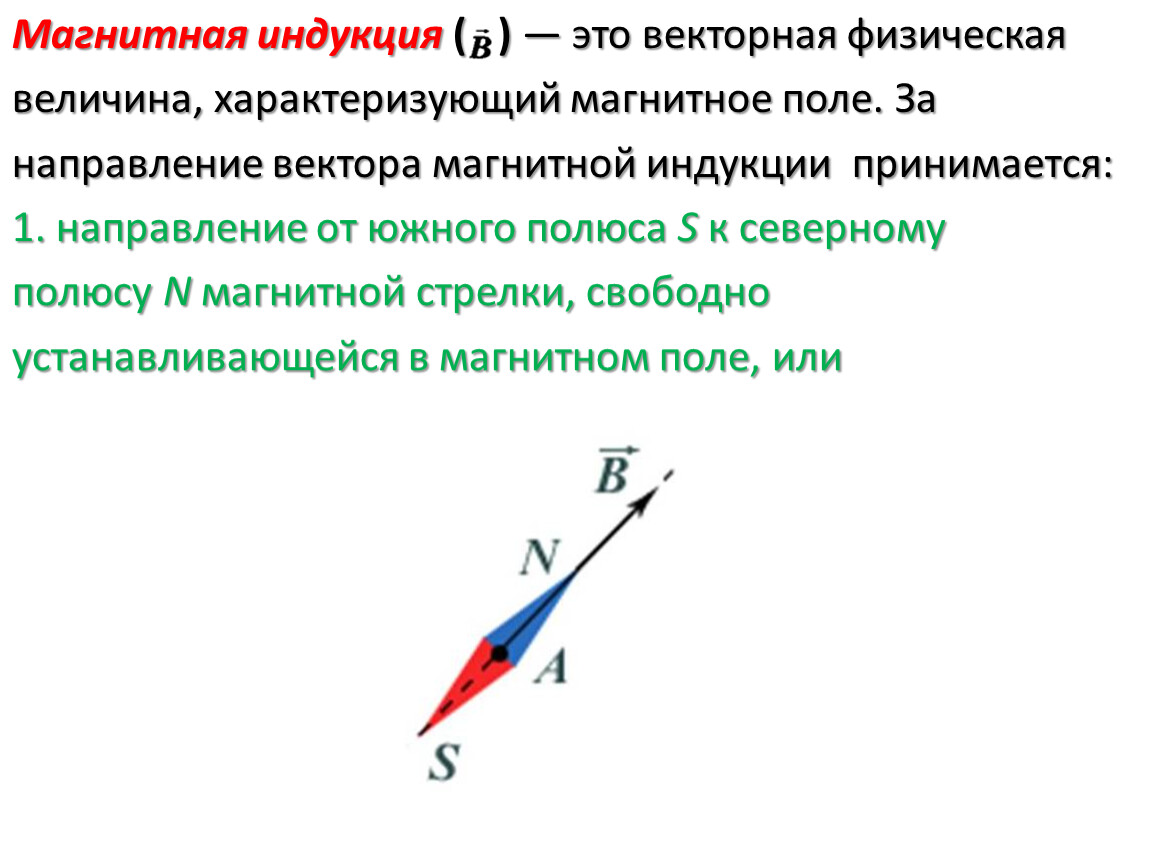 Закон, подобный закону всемирного тяготения, — это закон Кулона. В соответствии с ним сила, действующая между двумя заряженными телами, пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между телами.
Закон, подобный закону всемирного тяготения, — это закон Кулона. В соответствии с ним сила, действующая между двумя заряженными телами, пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между телами.
В силу аналогии между законом Кулона и законом всемирного тяготения то, что говорилось о гравитационных силах, можно повторить для электрических сил и представить силу, действующую со стороны некоторой системы заряженных тел на пробный заряд q, в виде F е = qE Величина Е характеризует знакомое вам электрическое поле и называется напряженностью электрического поля. Вывод, касающийся гравитационного поля, можно почти дословно повторить для электрического поля.
Взаимодействие между заряженными телами (или просто зарядами), как уже говорилось, очень похоже на гравитационное взаимодействие между любыми телами. Однако есть одно очень существенное отличие. Гравитационные силы не зависят от того, движутся тела или неподвижны. А вот сила взаимодействия между зарядами изменяется, если заряды движутся. Например, между двумя одинаковыми неподвижными зарядами действуют силы отталкивания (рис. 12, а). Если же эти заряды движутся, то силы взаимодействия изменяются. В дополнение к электрическим силам отталкивания появляются силы притяжения (рис. 12, б).
Например, между двумя одинаковыми неподвижными зарядами действуют силы отталкивания (рис. 12, а). Если же эти заряды движутся, то силы взаимодействия изменяются. В дополнение к электрическим силам отталкивания появляются силы притяжения (рис. 12, б).
Рис. 12. Взаимодействие двух неподвижных зарядов (а), взаимодействие двух движущихся зарядов (б)
Вы уже знакомы с этой силой из курса физики. Именно эта сила вызывает притяжение двух параллельных проводников с током. Эту силу называют магнитной силой. Действительно, в параллельных проводниках с одинаково направленными токами заряды движутся, как показано на рисунке, а значит, притягиваются магнитной силой. Сила, действующая между двумя проводниками с током, есть просто сумма всех сил, действующих между зарядами.
Электрическую силу, создаваемую некоторой системой заряженных тел и действующую на пробный заряд, можно представить как действие электрического поля, создаваемого всеми заряженными телами (за исключением пробного) на пробный заряд.
Почему же в этом случае исчезает электрическая сила? Все очень просто. Проводники содержат как положительные, так и отрицательные заряды, причем количество положительных зарядов в точности равно количеству отрицательных зарядов. Поэтому в целом электрические силы компенсируются. Токи же возникают вследствие движения только отрицательных зарядов, положительные заряды в проводнике неподвижны. Поэтому магнитные силы не компенсируются.
Механическое движение всегда относительно, т. е. скорость всегда задается относительно некоторой системы отсчета и изменяется при переходе от одной системы отсчета к другой.
А теперь посмотрите внимательно на рисунок 12. Чем различаются рисунки а и б? На рисунке 6 заряды движутся. Но это движение только в определенной, выбранной нами системе отсчета. Мы можем выбрать другую систему отсчета, в которой оба заряда неподвижны. И тогда магнитная сила исчезает. Это наводит на мысль, что электрическая и магнитная силы — это силы одной природы.
И это действительно так. Опыт показывает, что существует единая электромагнитная сила
Опыт показывает, что существует единая электромагнитная сила
, действующая между зарядами, которая по-разному проявляется в различных системах отсчета. Соответственно можно говорить о едином электромагнитном поле
, которое представляет собой совокупность двух полей — электрического и магнитного. В различных системах отсчета электрическая и магнитная составляющие электромагнитного поля могут проявляться по-разному. В частности, может оказаться, что в какой-то системе отсчета исчезает электрическая или магнитная составляющая электромагнитного поля.
Из относительности движения следует, что электрическое взаимодействие и магнитное взаимодействие есть две составляющие единого электромагнитного взаимодействия.
Но если это так, то можно повторить вывод, касающийся электрического поля.
Электромагнитную силу, создаваемую некоторой системой зарядов и действующую на пробный заряд, можно представить как действие электромагнитного поля, создаваемого всеми зарядами (за исключением пробного) на пробный заряд.
Многие силы, действующие на тело, находящееся в вакууме или в непрерывной среде, можно представить как результат действия на тело соответствующих полей. К подобным силам относятся, в частности, гравитационная и электромагнитная силы.
- Во сколько раз гравитационная сила, действующая на вас со стороны Земли, больше гравитационной силы, действующей со стороны Солнца? (Масса Солнца в 330 ООО раз больше массы Земли, а расстояние от Земли до Солнца 150 млн км.)
- Магнитная сила, действующая между двумя зарядами, как и электрическая сила, пропорциональна произведению зарядов. Куда будут направлены магнитные силы, если на рисунке 12, б один из зарядов заменить противоположным по знаку зарядом?
- Куда будут направлены магнитные силы на рисунке 12, б, если скорости обоих зарядов изменить на противоположные?
Инструкция
Чтобы узнать направление магнитных для прямого проводника с , расположите его так, чтобы электрический ток шел в направлении от вас (например, в лист бумаги).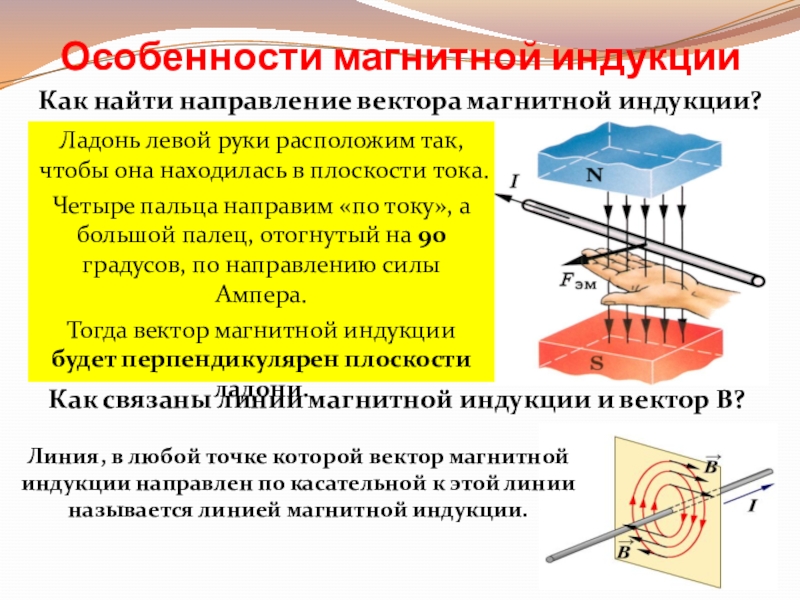 Попробуйте вспомнить, как двигается бур или закручиваемый отверткой винт: по часовой и . Изобразите это движение рукой, чтобы понять направление линий. Таким образом, линии магнитного поля направлены по часовой стрелке. Отметьте их схематично на чертеже. Этот метод правилом буравчика.
Попробуйте вспомнить, как двигается бур или закручиваемый отверткой винт: по часовой и . Изобразите это движение рукой, чтобы понять направление линий. Таким образом, линии магнитного поля направлены по часовой стрелке. Отметьте их схематично на чертеже. Этот метод правилом буравчика.
Если проводник расположен не в том направлении, мысленно встаньте таким образом или поверните конструкцию так, чтобы ток от вас удалялся. Затем вспомните движение бура или винта и поставьте направление магнитных линий по часовой стрелке.
Если правило буравчика кажется вам сложным, попробуйте использовать правило правой руки. Чтобы с его помощью определить направление магнитных линий, расположите руку используйте правую руку с оттопыренным большим пальцем. Большой палец направьте по движению проводника, а 4 остальных пальца – в направлении индукционного тока. Теперь обратите внимание, силовые линии магнитного поля входят в вашу ладонь.
Для того, чтобы использовать правило правой руки для катушки с током, обхватите его мысленно ладонью правой руки так, чтобы пальцы были направлены вдоль тока в витках. Посмотрите, куда смотрит отставленный большой палец – это и есть направление магнитных линий внутри соленоида. Этот способ поможет определить ориентацию металлической болванки, если вам нужно зарядить магнит при помощи катушки с током.
Посмотрите, куда смотрит отставленный большой палец – это и есть направление магнитных линий внутри соленоида. Этот способ поможет определить ориентацию металлической болванки, если вам нужно зарядить магнит при помощи катушки с током.
Чтобы определить направление магнитных линий при помощи магнитной стрелки, расположите несколько таких стрелок вокруг провода или катушки. Вы увидите, что оси стрелок направлены по касательным к окружности. С помощью этого метода можно найти направление линий в каждой точке пространства и доказать их непрерывность.
Сила Ампера действует на проводник с током в магнитном поле. Ее можно измерить непосредственно при помощи динамометра. Для этого к движущемуся под действием силы Ампера проводнику прикрепите динамометр и уравновесьте им силу Ампера. Для того чтобы рассчитать эту силу, измерьте ток в проводнике, индукцию магнитного поля и длину проводника.
Вам понадобится
- — динамометр;
- — амперметр;
- — тесламетр;
- — линейка;
- — подковообразный постоянный магнит
Инструкция
Непосредственное измерение силы Ампера. Соберите цепь таким образом, чтобы она замыкалась цилиндрическим проводником, который может свободно катиться по двум параллельным проводникам, замыкая их, практически без механического сопротивления (силы трения). Между этими проводниками установите подковообразный магнит. Подключите к цепи источник тока, и цилиндрический проводник начнет катиться по параллельным проводникам. Прикрепите к этому проводнику чувствительный динамометр, и вы измерите значение силы Ампера, действующей на проводник с током в магнитном поле в Ньютонах.
Соберите цепь таким образом, чтобы она замыкалась цилиндрическим проводником, который может свободно катиться по двум параллельным проводникам, замыкая их, практически без механического сопротивления (силы трения). Между этими проводниками установите подковообразный магнит. Подключите к цепи источник тока, и цилиндрический проводник начнет катиться по параллельным проводникам. Прикрепите к этому проводнику чувствительный динамометр, и вы измерите значение силы Ампера, действующей на проводник с током в магнитном поле в Ньютонах.
Расчет силы Ампера. Соберите такую же цепь, была описана в предыдущем пункте. Узнайте индукцию магнитного поля, в котором проводник. Для этого внесите датчик тесламетра между параллельными полосами постоянного магнита и снимите с него показания в теслах. Включите в собранную цепь амперметр последовательно. С помощью измерьте длину цилиндрического проводника в .
Подключите собранную цепь к источнику тока, узнайте силу тока в ней, используя амперметр. Измерения производите в амперах. Для того чтобы рассчитать значение силы Ампера, найдите произведение значений магнитного поля на силу тока и длину проводника (F=B I l). В том случае, если между направлениями тока и магнитной индукции угол не равен 90º, измерьте его и умножьте результат на синус этого угла.
Для того чтобы рассчитать значение силы Ампера, найдите произведение значений магнитного поля на силу тока и длину проводника (F=B I l). В том случае, если между направлениями тока и магнитной индукции угол не равен 90º, измерьте его и умножьте результат на синус этого угла.
Определение направления силы Ампера. Найдите направление силы Ампера по правилу левой руки. Для этого поместите левую руку таким образом, чтобы линии магнитной индукции входили в ладонь, а четыре пальца показывали направление движения электрического тока (от положительного к отрицательному полюсу источника). Тогда отставленный на 90º большой палец руки покажет направление действия силы Ампера.
Чтобы правильно определить вектор магнитной индукции нужно узнать не только его абсолютную величину, но и направление. Абсолютная величина определяется при измерении взаимодействия тел через магнитное поле, а направление — по характеру движения тел и специальным правилам.
Вам понадобится
- — проводник;
- — источник тока;
- — соленоид;
- — правый буравчик.
 (-6). Результат поделите на длину соленоида L, B=N I μ/L. Направление вектора магнитной индукции внутри соленоида определите так же, как и в случае с одним витком проводника.
(-6). Результат поделите на длину соленоида L, B=N I μ/L. Направление вектора магнитной индукции внутри соленоида определите так же, как и в случае с одним витком проводника.Вектор магнитной индукции является силовой характеристикой магнитного поля. В лабораторных заданиях по физике направление вектора индукции, который обозначается на схемах стрелкой и буквой В, определяется в зависимости от имеющегося в наличии проводника.
Вам понадобится
- — магнит;
- — магнитная стрелка.
Инструкция
Если вам дан постоянный магнит, найдите его полюса: полюс красят в синий цвет и отмечают латинской буквой N, южный обычно цвета с буквой S. Графически изобразите линии магнитного поля, которые выходят из северного полюса и входят в южный. Постройте по касательной вектор. Если никаких пометок или краски на полюсах магнита нет, узнайте направление вектора индукции с помощью магнитной стрелки, полюса которой вам известны.
Установите стрелку рядом с .
 Один из концов стрелки притянется . Если к магниту притянулся северный полюс стрелки, значит на магните это южный полюс, и наоборот. Используйте правило, что силовые линии магнитного поля выходят из северного полюса магнита (не стрелки!) и входят в южный.
Один из концов стрелки притянется . Если к магниту притянулся северный полюс стрелки, значит на магните это южный полюс, и наоборот. Используйте правило, что силовые линии магнитного поля выходят из северного полюса магнита (не стрелки!) и входят в южный.Найдите направление вектора индукции магнитного поля в витке с током с помощью правила буравчика. Возьмите буравчик или штопор и поставьте его перпендикулярно плоскости заряженного витка. Начните вращать буравчик по направлению движения тока в витке. Поступательное движение буравчика укажет направление линий магнитного поля в центре витка.
При наличии прямого проводника соберите полную замкнутую цепь, включив в нее проводник. Учтите, что за направление тока в цепи принимается движение тока от положительного полюса источника тока к отрицательному. Возьмите штопор или представьте, что вы держите его в правой руке.
Закручивайте буравчик в направлении движения тока в проводнике. Движение рукояти штопора покажет направление силовых линий поля.
 Зарисуйте линии на схеме. Постройте к ним по касательной вектор, который покажет направление индукции магнитного поля.
Зарисуйте линии на схеме. Постройте к ним по касательной вектор, который покажет направление индукции магнитного поля.Узнайте, в какую сторону направлен вектор индукции в катушке или соленоиде. Соберите цепь, подключив катушку или соленоид к источнику тока. Примените правило правой руки. Представьте, что вы обхватили катушку так, что четыре вытянутых пальца показывают направление тока в катушке. Тогда отставленный на 90 градусов большой палец укажет направление вектора индукции магнитного поля внутри соленоида или катушки.
Используйте магнитную стрелку. Приблизьте магнитную стрелку к соленоиду. Синий ее конец (обозначенный буквой N или синей краской) покажет направление вектора. Не забудьте о том, что силовые линии в соленоиде — прямые.
Видео по теме
Источники:
- Магнитное поле и его характеристики
Индукция возникает в проводнике при пересечении силовых линий поля, если его перемещать в магнитном поле. Индукция характеризуется направлением, которое можно определить по установленным правилам.

Вам понадобится
- — проводник с током в магнитном поле;
- — буравчик или винт;
- — соленоид с током в магнитном поле;
Инструкция
Чтобы узнать направление индукции, следует воспользоваться одним из двух : правилом буравчика или правилом правой руки. Первое в основном для прямого провода, в котором ток. Правило правой руки применяют для катушки или соленоида, питаемого током.
Чтобы узнать направление индукции по правилу буравчика, определите полярность провода. Ток всегда течет от положительного полюса к отрицательному. Расположите буравчик или винт вдоль провода с током: носик буравчика должен смотреть на отрицательный полюс, а рукоятка в сторону положительного. Начните вращать буравчик или винт как бы закручивая его, то есть по часовой стрелке. Возникающая индукция имеет вид замкнутых окружностей вокруг питаемого током провода. Направление индукции будет совпадать с направлением вращения рукоятки буравчика или шляпки винта.

Правило правой руки говорит:
Если взять катушку или соленоид в ладонь правой руки, чтобы четыре пальца лежали по направлению течения тока в витках, то большой палец, отставленный в бок, укажет направление индукции.Давно известно, что кусочки магнитного железняка способны притягивать к себе металлические предметы: гвозди, гайки, металлические опилки, иголки и др. Такой способностью их наделила природа. Это естественные магниты
.Подвергнем воздействию естественного магнита брусок из железа. Через некоторое время он сам намагнитится и начнёт притягивать другие металлические предметы. Брусок стал искусственным магнитом
. Уберём магнит. Если намагничивание при этом исчезнет, то говорят о временном намагничивании
.
Если же оно останется, то перед нами постоянный магнит.
Концы магнита, притягивающие металлические предметы наиболее сильно, называют полюсами магнита.
Слабее всего притяжение в его средней зоне. Её называют нейтральной зоной
Её называют нейтральной зоной
.Если к средней части магнита прикрепить нить и позволить ему свободно вращаться, подвесив его к штативу, то он развернётся таким образом, что один из его полюсов будет ориентирован строго на север, а другой строго на юг. Конец магнита, обращённый на север, называют северным полюсом
(N
), а противоположный – южным
(S
).Взаимодействие магнитов
Магнит притягивает другие магниты, не соприкасаясь с ними. Одноимённые полюсы разных магнитов отталкиваются, а разноимённые притягиваются. Не правда ли, это напоминает взаимодействие электрических зарядов?
Электрические заряды оказывают действие друг на друга с помощью электрического поля
, образующегося вокруг них. Постоянные магниты взаимодействуют на расстоянии, потому что вокруг них существует магнитное поле
.Физики XIX века пытались представить магнитное поле как аналог электростатического. Они рассматривали полюсы магнита как положительный и отрицательный магнитные заряды (северный и южный полюсы соответственно).
 Но вскоре поняли, что изолированных магнитных зарядов не существует.
Но вскоре поняли, что изолированных магнитных зарядов не существует.Два одинаковых по величине, но разных по знаку электрических заряда называют электрическим диполем
. Магнит имеет два полюса и является магнитным диполем
.Заряды в электрическом диполе можно легко отделить друг от друга, разрезав на две части проводник, в разных частях которого они находятся. Но с магнитом так не получится. Разделив таким же способом постоянный магнит, мы получим два новых магнита, каждый из которых тоже будет иметь два магнитных полюса.
Тела, имеющие собственное магнитное поле, называются магнитами
. Различные материалы по-разному притягиваются к ним. Это зависит от структуры материала. Свойство материалов создавать магнитное поле под воздействием внешнего магнитного поля, называется магнетизмом
.Наиболее сильно притягиваются к магнитам ферромагнетики
.
Причём их собственное магнитное поле, создаваемое молекулами, атомами или ионами, в сотни раз превосходит вызвавшее его внешнее магнитное поле. Ферромагнетиками являются такие химические элементы, как железо, кобальт, никель, а также некоторые сплавы.
Ферромагнетиками являются такие химические элементы, как железо, кобальт, никель, а также некоторые сплавы.Парамагнетики
– вещества, намагничивающиеся во внешнем поле в его направлении. Притягиваются к магнитам слабо. Химические элементы алюминий, натрий, магний, соли железа, кобальта, никеля и др. – примеры парамагнетиков.Но есть материалы, которые не притягиваются, а отталкиваются от магнитов. Их называют диамагнетиками
.
Они намагничиваются против направления внешнего магнитного поля, но отталкиваются от магнитов довольно слабо. Это медь, серебро, цинк, золото, ртуть и др.Опыт Эрстеда
Однако магнитное поле создают не только постоянные магниты.
В 1820 г. датский физик Ханс Кристиан Э́рстед на одной из своих лекций в университете демонстрировал студентам опыт по нагреванию проволоки от «вольтова столба». Один из проводов электрической цепи оказался на стеклянной крышке морского компаса, лежащего на столе. Когда учёный замкнул электрическую цепь и по проводу пошёл ток, магнитная стрелка компаса вдруг отклонилась в сторону.
 Конечно, Эрстед поначалу подумал, что это просто случайность. Но, повторив опыт в тех же условиях, он получил тот же результат. Тогда он начал менять расстояние от провода до стрелки. Чем бόльшим оно было, тем слабее отклонялась стрелка. Но и это ещё не всё. Пропуская ток через провода, сделанные из разных металлов, он обнаружил, что даже те из них, которые не обладали магнитными свойствами, вдруг становились магнитами, когда через них проходил электрический ток. Стрелка отклонялась, даже когда её отделяли от провода с током экранами из материалов, не проводящих ток: дерева, стекла, камней. Даже когда её поместили в резервуар с водой, она всё равно продолжала отклоняться. При разрыве электрической цепи магнитная стрелка компаса возвращалась в исходное состояние. Это означало, что проводник, по которому идёт электрический ток, создаёт магнитное поле
Конечно, Эрстед поначалу подумал, что это просто случайность. Но, повторив опыт в тех же условиях, он получил тот же результат. Тогда он начал менять расстояние от провода до стрелки. Чем бόльшим оно было, тем слабее отклонялась стрелка. Но и это ещё не всё. Пропуская ток через провода, сделанные из разных металлов, он обнаружил, что даже те из них, которые не обладали магнитными свойствами, вдруг становились магнитами, когда через них проходил электрический ток. Стрелка отклонялась, даже когда её отделяли от провода с током экранами из материалов, не проводящих ток: дерева, стекла, камней. Даже когда её поместили в резервуар с водой, она всё равно продолжала отклоняться. При разрыве электрической цепи магнитная стрелка компаса возвращалась в исходное состояние. Это означало, что проводник, по которому идёт электрический ток, создаёт магнитное поле
, заставляющее стрелку устанавливаться в определённом направлении.Ханс Кристиан Эрстед
Магнитная индукция
Силовой характеристикой магнитного поля является магнитная индукция
. Это векторная величина, определяющая его действие на движущиеся заряды в данной точке поля.
Это векторная величина, определяющая его действие на движущиеся заряды в данной точке поля.Направление вектора магнитной индукции совпадает с направлением северного полюса магнитной стрелки, находящейся в магнитном поле.
Единица измерения магнитной индукции в системе СИ – тесла (Тл)
. Измеряют магнитную индукции приборами, которые называются тесламетрами
.Если векторы магнитной индукции поля одинаковы по величине и направлению во всех точках поля, то такое поле называется однородным.
Нельзя путать понятие индукции магнитного поля
и явление электромагнитной индукции
.Графически магнитное поле изображают с помощью силовых линий.
Силовыми линиями
, или линиями магнитной индукции
, называют линии, касательные к которым в данной точке совпадают с направлением вектора магнитной индукции. Густота этих линий отображает величину вектора магнитной индукции.Картину расположения этих линий можно получить с помощью простого опыта.
 Рассыпав на куске гладкого картона или стекла железные опилки и положив его на магнит, можно увидеть, как опилки располагаются по определённым линиям. Эти линии имеют форму силовых линий магнитного поля.
Рассыпав на куске гладкого картона или стекла железные опилки и положив его на магнит, можно увидеть, как опилки располагаются по определённым линиям. Эти линии имеют форму силовых линий магнитного поля.Линии магнитной индукции всегда замкнуты
. Они не имеют ни начала, ни конца. Выходя из северного полюса, они входят в южный и замыкаются внутри магнита.Поля с замкнутыми векторными линиями называются вихревыми
. Следовательно, магнитное поле является вихревым. В каждой его точке вектор магнитной индукции имеет своё направление. Его определяют по направлению магнитной стрелки в этой точке или по правилу буравчика
(для магнитного поля вокруг проводника с током).Правило буравчика (винта) и правило правой руки
Эти правила дают возможность просто и довольно точно определить направление линий магнитной индукции, не используя никаких физических приборов.
Чтобы понять, как работает правило буравчика
, представим себе, что правой рукой мы вкручиваем бур или штопор.
Если направление поступательного движения буравчика совпадает с направлением движения тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитной индукции.
Разновидностью данного правила является правило правой руки
.Если мысленно обхватить правой рукой проводник с током таким образом, чтобы отогнутый на 90° большой палец показывал направление тока, то остальные пальцы покажут направление линий магнитной индукции поля, создаваемого этим током, и направление вектора магнитной индукции, направленного по касательной к этим линиям.
Магнитный поток
Поместим в однородное магнитное поле плоский замкнутый контур. Величина, равная количеству силовых линий, проходящих через поверхность контура, называется магнитным потоком
.Ф = В·
S·
cosα
,где Ф
– величина магнитного потока;В
– модуль вектора индукции;S
– площадь контура;α
– угол между направлением вектора магнитной индукции и нормалью (перпендикуляром) к плоскости контура.
С изменением угла наклона меняется величина магнитного потока.
Если плоскость контура перпендикулярна магнитному полю (α
= 0), то магнитный поток, проходящий через неё будет максимальным.Ф max = В·S
Если же контур расположен параллельно магнитному полю (α
=90 0), то поток в этом случае будет равен нулю.Сила Лоренца
Мы знаем, что электрическое поле действует на любые заряды, независимо от того находятся ли они в состоянии покоя или движутся. Магнитное поле способно оказывать воздействие только на движущиеся заряды.
Выражение для силы, действующей со стороны магнитного поля на движущийся в нём единичный электрический заряд, установил нидерландский физик-теоретик Хендрик Антон Ло́ренц
.Силу эту назвали силой Лоренца
.Хендрик Антон Лоренц
Модуль силы Лоренца определяют по формуле:
F =
q·
v·
B·
sinα
,где q
– величина заряда;v
– скорость движения заряда в магнитном поле;B
— модуль вектора индукции магнитного поля;α
— угол между вектором индукции и вектором скорости.
Куда же направлена сила Лоренца? Это легко определить с помощью правила левой руки
: «Если расположить ладонь левой руки таким образом, чтобы четыре вытянутых пальца показывали направление движения положительного электрического заряда, а силовые линии магнитного поля входили в ладонь, то отогнутый на 90 0 большой палец покажет направление силы Лоренца
».Закон Ампера
В 1820 г. после того как Эрстед установил, что электрический ток создаёт магнитное поле, известный французский физик Андре Мари Ампер
продолжил исследования по взаимодействию между электрическим током и магнитом.Андре Мари Ампер
В результате проведенных опытов учёный выяснил, что на прямой проводник с током, находящийся в магнитном поле с индукцией В
, со стороны поля действует сила
F
, пропорциональная силе тока и индукции магнитного поля
. Этот закон получил название закона Ампера
, а силу назвали силой Ампера
.
F =
I·
L·
B·
sinα
,
где I
– сила тока в проводнике;L
— длина проводника в магнитном поле;B
— модуль вектора индукции магнитного поля;α
— угол между вектором магнитного поля и направлением тока в проводнике.Сила Ампера имеет максимальное значение, если угол α
равен 90 0 .Направление силы Ампера, как и силы Лоренца, также удобно определять по правилу левой руки.
Располагаем левую руку таким образом, чтобы четыре пальца указывали направление тока, а линии поля входили в ладонь. Тогда отогнутый на 90 0 большой палец укажет направление силы Ампера.
Наблюдая взаимодействие двух тонких проводников с током, учёный выяснил, что параллельные проводники с током, притягиваются, если токи в них текут в одном направлении, и отталкиваются, если направления токов противоположны
.
Магнитное поле Земли
Наша планета представляет собой гигантский постоянный магнит, вокруг которого существует магнитное поле. Этот магнит имеет северный и южный полюсы. Вблизи них магнитное поле Земли проявляется наиболее сильно. Стрелка компаса устанавливается вдоль магнитных линий. Один конец её направлен к северному полюсу, другой к южному.
Магнитные полюсы Земли время от времени меняются местами. Правда, случается это не часто. За последний миллион лет это происходило 7 раз.
Магнитное поле защищает Землю от космического излучения, которое разрушительно действует на всё живое.
На магнитное поле Земли влияет солнечный ветер
, представляющий собой поток ионизированных частиц, вырывающихся из солнечной короны с огромной скоростью. Особенно он усиливается во время вспышек на Солнце. Пролетающие мимо нашей планеты частицы создают дополнительные магнитные поля, в результате чего изменяются характеристики магнитного поля Земли. Возникают магнитные бури
. Правда, длятся они недолго. И спустя некоторое время магнитное поле восстанавливается. Но проблем они могут создать немало, так как влияют на работу линий электропередач, радиосвязи, вызывают сбои в работе различных приборов, ухудшают работу сердечно-сосудистой, дыхательной и нервной систем человека. Особенно чувствительны к ним метеозависимые люди.
Правда, длятся они недолго. И спустя некоторое время магнитное поле восстанавливается. Но проблем они могут создать немало, так как влияют на работу линий электропередач, радиосвязи, вызывают сбои в работе различных приборов, ухудшают работу сердечно-сосудистой, дыхательной и нервной систем человека. Особенно чувствительны к ним метеозависимые люди.Темы кодификатора ЕГЭ
: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.
Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?
Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.

1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».
Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.
При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.
Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.
При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.
Вывод
.Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует
) электрический ток во второй катушке. Этот ток называется индукционным током
Этот ток называется индукционным током
.Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.
Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.
Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.
Обнаруженное явление Фарадей назвал электромагнитной индукцией
(т. е. «наведение электричества магнетизмом»).2. Для подтверждения догадки о том, что индукционный ток порождается переменным
магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.Гальванометр снова фиксировал ток во второй катушке.
 Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки
Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки
.3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.
Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.
Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.

Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».
Магнитный поток
Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.
Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией .
Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1
).Рис. 1.
В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:
(1)
Теперь рассмотрим общий случай, когда вектор образует угол с нормалью к плоскости контура (рис. 2
).Рис. 2.
Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции (а та составляющая, которая параллельна контуру, не «течёт» сквозь него).
 Поэтому, согласно формуле (1), имеем . Но , поэтому
Поэтому, согласно формуле (1), имеем . Но , поэтому(2)
Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть ), то магнитный поток становится равным нулю.
А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2)
, а затем все эти магнитные потоки суммируем.Единицей измерения магнитного потока является вебер
(Вб). Как видим,Вб = Тл · м = В · с. (3)
Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как ).
 Но множители и как раз и образуют магнитный поток!
Но множители и как раз и образуют магнитный поток!Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.
Электромагнитная индукция
— это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур
.ЭДС индукции
Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы
, вызывающие движение зарядов.Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции
и обозначается .Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура
.
Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.
Закон электромагнитной индукции Фарадея
Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.
Если за малое время изменение магнитного потока равно , то скорость
изменения магнитного потока — это дробь (или, что тоже самое, производная магнитного потока по времени).Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:
Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.
Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:
(4)
ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3)
мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4)
Стало быть, единицы измерения обеих частей пропорциональности (4)
совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:(5)
Это и есть закон электромагнитной индукции
или закон Фарадея
. Дадим его словесную формулировку.Закон электромагнитной индукции Фарадея
. При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока
.Правило Ленца
Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком
. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем
.Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное
магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.
Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный
магнитный поток, создаваемый магнитным полем индукционного тока.Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.
Правило Ленца
. Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока
.Правило Ленца позволяет находить направление индукционного тока в любой ситуации.
Рассмотрим некоторые примеры применения правила Ленца.
Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)
). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока.
 Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против
Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против
внешнего магнитного поля.Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)
).Рис. 3. Магнитный поток возрастает
Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4
). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.Рис. 4. Магнитный поток убывает
Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону
, что и внешнее магнитное поле.В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.

Взаимодействие магнита с контуром
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера.
 Результат получается следующий.
Результат получается следующий.Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет
.Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна
. Это значит, что мы, приближая магнит, должны преодолевать
силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания
.
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.
Закон Фарадея + Правило Ленца = Снятие модуля
Выше мы обещали снять модуль в законе Фарадея (5)
. Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5)
, величина ЭДС может получаться как положительной, так и отрицательной.Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным
. Противоположное направление обхода контура называется, соответственно, отрицательным
. Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.Магнитный поток через контур считается положительным alt=»(\Phi > 0)»>
, если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным .
Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным .ЭДС индукции считается положительной alt=»(\mathcal E_i > 0)»>
, если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.
Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен: alt=»\Phi > 0″>
.Рис. 5. Магнитный поток возрастает
Стало быть, в данном случае имеем .
 Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.
Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть, alt=»\mathcal E_i > 0″>
(рис. 6
).Рис. 6. Магнитный поток возрастает alt=»\Rightarrow \mathcal E_i > 0″>
Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока
:(6)
Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.
Вихревое электрическое поле
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое
. Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем
. Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.
Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7
).Рис. 7. Вихревое электрическое поле при увеличении магнитного поля
Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис.
 8
8
).Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля
Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.
Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.
1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура
.Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость вихревого электрического поля одинакова во всех точках кольца. Работа силы , с которой вихревое поле действует на заряд , равна:
Следовательно, для ЭДС индукции получаем:
ЭДС индукции в движущемся проводнике
Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.
Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно . Рельсы находятся в вертикальном однородном магнитном поле .
 По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9
По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9
).Рис. 9. Движение проводника в магнитном поле
Возьмём внутри стержня положительный свободный заряд . Вследствие движения этого заряда вместе со стержнем со скоростью на заряд будет действовать сила Лоренца:
Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!).
Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда от точки к точке наша сторонняя сила совершит работу:
(Длину стержня мы также считаем равной .) Стало быть, ЭДС индукции в стержне окажется равной:
(7)
Таким образом, стержень аналогичен источнику тока с положительной клеммой и отрицательной клеммой . Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке , отрицательные — к точке .

Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце будет возрастать кулоновская сила, с которой положительный свободный заряд отталкивается от и притягивается к — и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7)
.Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении (от «плюса источника» к «минусу» N
). Предположим, что сопротивление стержня равно (это аналог внутреннего сопротивления источника тока), а сопротивление участка равно (сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:Замечательно, что выражение (7)
для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это.
За время наш стержень проходит путь и занимает положение (рис. 9
9
). Площадь контура возрастает на величину площади прямоугольника :Магнитный поток через контур увеличивается. Приращение магнитного потока равно:
Скорость изменения магнитного потока положительна и равна ЭДС индукции:
Мы получили тот же самый результат, что и в (7)
. Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю и, стало быть, препятствует возрастанию магнитного потока через контур.На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.
На рамку с электрическим током одинаковое ориентирующее действие оказывает магнитное поле
На рамку с электрическим током одинаковое ориентирующее действие оказывает магнитное поле
(*ответ*) постоянного тока
(*ответ*) постоянного магнита
переменного тока
алюминиевого бруска
Намагничивание тела – изменение индукции магнитного поля вещества при наложении _ магнитного поля
(*ответ*) внешнего
Направление вектора индукции магнитного поля в данной точке пространства совпадает с направлением
(*ответ*) северного полюса магнитной стрелки, помещенной в эту точку
силы, действующей на неподвижный заряд в этой точке
силы, действующей на движущийся заряд в этой точке
южного полюса магнитной стрелки, помещенной в эту точку
Направление вектора магнитной индукции устанавливают при помощи правила _ (ответ с большой буквы)
(*ответ*) Буравчика
Объемная _ энергии магнитного поля – энергия, заключенная в единице объема пространства, где распределяется магнитное поле
(*ответ*) плотность
По катушке индуктивностью L1 = 0,6 Гн течет ток I1 = 15 А, а по катушке с индуктивностью L2 = 15 Гн течет ток I2 = 0,6 А. Сравните энергии магнитного поля этих катушек
Сравните энергии магнитного поля этих катушек
(*ответ*) W1 > W2
W1 = W2
W1
W1= W2 = 0
Под действием силы Лоренца меняется _ скорости частицы
(*ответ*) направление
Поле с замкнутыми силовыми линиями называется _ полем
(*ответ*) вихревым
Полная сила, действующая на электрический заряд, равна: _ сумме сил электрического и магнитного полей
(*ответ*) геометрической
Постоянный магнит выдвигают из алюминиевого кольца, подвешенного на нити: первый раз северным полюсом, второй — южным полюсом. При этом алюминиевое кольцо
(*ответ*) оба раза отталкивается от магнита
оба раза притягивается магнитом
первый раз притягивается, второй раз — отталкивается
первый раз отталкивается, второй — притягивается
При взаимодействии двух параллельных друг другу проводников, если в первом случае электрический ток в них идет в одном направлении, а во втором случае — в противоположных направлениях, то в
(*ответ*) первом случае притягиваются, а во втором случае отталкиваются друг от друга
обоих случаях притягиваются друг к другу
обоих случаях отталкиваются друг от друга
первом случае отталкиваются, а во втором случае притягиваются друг к другу
При возрастании напряженности электрического поля направление вектора индукции возникающего магнитного поля образует _ винт с направлением вектора
(*ответ*) правый
При замыкании цепи, содержащей источник постоянной ЭДС, определенное значение силы тока устанавливается
(*ответ*) постепенно с течением времени
мгновенно
с большой задержкой
равномерно
При изменении магнитного потока через поверхность, ограниченную контуром, в контуре появляется _ индукции (ответ дать аббревиатурой)
(*ответ*) ЭДС
При отключении источника в замкнутых контурах электрический ток прекращается
(*ответ*) не мгновенно
мгновенно
с большой задержкой
равномерно
При убывании напряженности электрического поля направление вектора магнитной индукции образует _ винт с направлением вектора
(*ответ*) левый
Происхождение магнитного поля постоянного магнита из ферромагнетика определяется
(*ответ*) суммой магнитных полей круговых токов электронов, движущихся вокруг атомных ядер
суммой собственных магнитных полей электронов
суммой собственных магнитных полей атомных ядер
магнитным полем, созданным источником тока при намагничивании и «законсервировано» в магните
Процесс превращения звуковых колебаний воздуха в колебания электрического тока осуществляется при помощи
(*ответ*) микрофонаОтветов: 1 | Категория вопроса: Подготовка к ЕГЭ
Поле магнитной индукции – обзор
4.
 14 Парамагнитные и ферромагнитные материалы
14 Парамагнитные и ферромагнитные материалыВ парамагнитном материале атомы содержат постоянные магнитные дипольные моменты, возникающие из-за спина и орбитального углового момента электронов. К кристаллу приложено внешнее магнитное поле индукции B, где магнитная восприимчивость χm есть константа пропорциональности между вектором намагниченности M (объемная плотность магнитных диполей) и напряженностью магнитного поля H, так что
(4.182)M=χmH
Это линейное соотношение с χm применимо только к линейным магнитным материалам. В вакууме χm=0, а в немагнитных материалах оно обычно очень мало, в пределах от 10–4 до 10–5; например, χm=-0,94×10-5 для меди.
Магнитное поле индукции B представляет собой сумму вектора намагниченности M материала и напряженности внешнего магнитного поля H, где сумма умножается на константу проницаемости вакуума µ0, где
(4,183)B=µ0( H+M)
Индукционное магнитное поле B возникает из-за микроскопических (атомных) и макроскопических (проводов) токов; тогда как напряженность магнитного поля H возникает только из-за макроскопических токов.
 Индукционное магнитное поле B будет стремиться выровнять дипольные моменты, потому что энергия меньше при параллельном выравнивании диполей. Индуцированное магнитное поле выровненных магнитных диполей M добавляется к приложенному извне магнитному полю H. Таким образом, магнитное поле равно
Индукционное магнитное поле B будет стремиться выровнять дипольные моменты, потому что энергия меньше при параллельном выравнивании диполей. Индуцированное магнитное поле выровненных магнитных диполей M добавляется к приложенному извне магнитному полю H. Таким образом, магнитное поле равно(4,185)µr=1+χm
Материалы с относительной магнитной проницаемостью µr<1 являются диамагнитными. Материалы с µr>1, но с µr≅1 являются парамагнитными.Материалы с µr≫1 являются ферромагнитными, а ферромагнитные материалы являются нелинейными, поэтому χm и µr зависят от напряженности приложенного магнитного поля H.
Магнитная проницаемость µ определяется как
(4,186)µ=µ0µr
В линейных магнитных материалах константа пропорциональности между индукционным магнитным полем B и напряженностью приложенного магнитного поля H представляет собой магнитную проницаемость µ, где
(4,187)B=µH
изменяется в зависимости от напряженности приложенного магнитного поля H, где μ может быть большим и иметь репрезентативные значения в диапазоне от 250 для кобальта, 600 для никеля и 5000 для мягкого железа.

Тепловое движение атомов, которое приводит к хаотизации ориентации диполей, должно преодолеваться приложенным магнитным полем или более низкими температурами. Восприимчивость при низких температурах и магнитных полях подчиняется закону Кюри, где для постоянной С характеристика материала равна
(4,188)χ=CT
Ферромагнетизм – это намагниченность, возникающая на небольших участках материала без приложения внешнего магнитного поля. поле. Естественная намагниченность в ферромагнитных материалах, возникающая из-за спинов неспаренных электронов, достигает максимума при Т=0К и падает до нуля при ферромагнитной температуре Кюри TC.При температурах выше TC ферромагнитный материал становится парамагнитным, и его магнитная восприимчивость подчиняется модифицированному соотношению Кюри, в котором
(4,189)χ=CT−TC
тогда материал становится ферромагнитным с постоянной намагниченностью. Ферромагнитный материал не намагничен в одном направлении по всему объему, а имеет множество меньших областей или доменов.
 Каждый домен полностью намагничен в одном направлении, но ориентация доменов случайна, так что направление намагниченности меняется от одного домена к другому.Случайная ориентация доменов возникает из-за того, что случайные домены создают более низкое энергетическое состояние, чем полностью выровненные домены. Приложенное магнитное поле несколько выравнивает эти домены, так что их магнитные поля более выровнены, тем самым увеличивая магнитное поле материала в целом. Увеличение приложенного магнитного поля выше магнитного поля насыщения не приводит к дальнейшему увеличению намагниченности материала, поскольку домены достигают максимально возможного взаимного выравнивания. При снятии внешнего магнитного поля домены и их границы не возвращаются полностью к исходной ориентации, поэтому домены проявляют гистерезис.Единственными ферромагнитными элементами являются железо, кобальт, никель, гадолиний и диспрозий.
Каждый домен полностью намагничен в одном направлении, но ориентация доменов случайна, так что направление намагниченности меняется от одного домена к другому.Случайная ориентация доменов возникает из-за того, что случайные домены создают более низкое энергетическое состояние, чем полностью выровненные домены. Приложенное магнитное поле несколько выравнивает эти домены, так что их магнитные поля более выровнены, тем самым увеличивая магнитное поле материала в целом. Увеличение приложенного магнитного поля выше магнитного поля насыщения не приводит к дальнейшему увеличению намагниченности материала, поскольку домены достигают максимально возможного взаимного выравнивания. При снятии внешнего магнитного поля домены и их границы не возвращаются полностью к исходной ориентации, поэтому домены проявляют гистерезис.Единственными ферромагнитными элементами являются железо, кобальт, никель, гадолиний и диспрозий.Напомним, что одинаковые атомные электроны должны быть неразличимы (следовательно, полная волновая функция должна быть симметричной), но пространственная и спиновая волновые функции компонентов могут быть симметричными или асимметричными, если произведение волновых функций спина и пространственных компонентов равно асимметричный.
 В трехмерных кристаллических полосах, где имеет место ферромагнитное действие, и в других неферромагнитных, парамагнитных элементах кулоновское отталкивание между парой электронов имеет тенденцию перемещать электроны дальше друг от друга в антисимметричное пространственное состояние минимальной энергии.Эта асимметрия полной волновой функции требует симметричного спинового состояния, в котором спины неспаренных электронов выровнены в одном направлении. Таким образом, кулоновская сила, которая раздвигает электроны для минимизации энергии, затем приводит к их выравниванию с параллельными спинами в парамагнитных и ферромагнитных материалах.
В трехмерных кристаллических полосах, где имеет место ферромагнитное действие, и в других неферромагнитных, парамагнитных элементах кулоновское отталкивание между парой электронов имеет тенденцию перемещать электроны дальше друг от друга в антисимметричное пространственное состояние минимальной энергии.Эта асимметрия полной волновой функции требует симметричного спинового состояния, в котором спины неспаренных электронов выровнены в одном направлении. Таким образом, кулоновская сила, которая раздвигает электроны для минимизации энергии, затем приводит к их выравниванию с параллельными спинами в парамагнитных и ферромагнитных материалах.Обменная сила или взаимодействие между пространственной и спиновой компонентами волновой функции для двух или более электронов отвечает за эту связь электронных спинов с параллельным выравниванием в парамагнитных и ферромагнитных материалах.В случае ферромагнетиков трехмерная зона заполнена не полностью, близкое расположение атомов железа позволяет неразличить электроны соседних атомов, и обменное взаимодействие теперь распространяется на электроны соседних атомов.
 Для сохранения полной асимметричной волновой функции для набора электронов, принадлежащих близко расположенным соседним атомам, которые имеют перекрывающиеся d-оболочки неспаренных электронов, есть две возможности. В ферромагнитном случае (скажем, для атомов железа) пространственная волновая функция может быть асимметричной, а спиновая — симметричной.В этом случае кулоновская энергия минимизируется за счет разделения электронов, но разделение позволяет неспаренным электронам выровнять свои спины параллельно. Другая возможность заключается в том, что пространственная волновая функция будет симметричной, а электроны локализованы вместе, и, следовательно, их спиновая волновая функция должна быть антисимметричной, что требует антипараллельности спинов электронов. Антиферромагнитная возможность не минимизирует кулоновскую энергию в железе и не реализуется.Однако такие материалы, как MnO 2 , являются антиферромагнитными.
Для сохранения полной асимметричной волновой функции для набора электронов, принадлежащих близко расположенным соседним атомам, которые имеют перекрывающиеся d-оболочки неспаренных электронов, есть две возможности. В ферромагнитном случае (скажем, для атомов железа) пространственная волновая функция может быть асимметричной, а спиновая — симметричной.В этом случае кулоновская энергия минимизируется за счет разделения электронов, но разделение позволяет неспаренным электронам выровнять свои спины параллельно. Другая возможность заключается в том, что пространственная волновая функция будет симметричной, а электроны локализованы вместе, и, следовательно, их спиновая волновая функция должна быть антисимметричной, что требует антипараллельности спинов электронов. Антиферромагнитная возможность не минимизирует кулоновскую энергию в железе и не реализуется.Однако такие материалы, как MnO 2 , являются антиферромагнитными.Формула магнитного поля
Когда по проводу проходит электрический ток, вокруг него образуется магнитное поле.
 Линии магнитного поля образуют концентрические окружности вокруг проволоки. Направление магнитного поля зависит от направления тока. Его можно определить с помощью «правила правой руки», указав большим пальцем правой руки в направлении течения. Направление линий магнитного поля совпадает с направлением ваших согнутых пальцев.Величина магнитного поля зависит от величины тока и расстояния от несущего заряд провода. В формулу входит константа . Это называется проницаемостью свободного пространства и имеет значение . Единицей магнитного поля является Тесла, т.
Линии магнитного поля образуют концентрические окружности вокруг проволоки. Направление магнитного поля зависит от направления тока. Его можно определить с помощью «правила правой руки», указав большим пальцем правой руки в направлении течения. Направление линий магнитного поля совпадает с направлением ваших согнутых пальцев.Величина магнитного поля зависит от величины тока и расстояния от несущего заряд провода. В формулу входит константа . Это называется проницаемостью свободного пространства и имеет значение . Единицей магнитного поля является Тесла, т..
B = величина магнитного поля (Тесла, Тл)
= проницаемость свободного пространства ()
I = величина электрического тока (Ампер, А)
r = расстояние (м)
Формула магнитного поля Вопросы:
1) Какова величина магнитного поля 0.10 м от провода с током 3,00 А? Если ток имеет направление вектора вне страницы (или экрана), то каково направление магнитного поля?
Ответ: Величину магнитного поля можно рассчитать по формуле:
Величина магнитного поля составляет 6,00 x 10 -6 Тл, что также может быть записано как (микро-Тесла).

Направление магнитного поля можно определить с помощью «правила правой руки», указав большим пальцем правой руки в направлении тока. Направление линий магнитного поля совпадает с направлением ваших согнутых пальцев. Течение имеет векторное направление вне страницы, поэтому ваши пальцы будут сгибаться в направлении против часовой стрелки. Следовательно, линии магнитного поля направлены против часовой стрелки, образуя круги вокруг провода.
2) Если величина магнитного поля 2.00 м от провода составляет 10,0 нТл (нано-Тесла), какова величина электрического тока, переносимого по проводу? Если силовые линии магнитного поля образуют круги по часовой стрелке в плоскости страницы (или экрана), каково направление вектора электрического тока?
Ответ: Величину электрического тока можно рассчитать, переставив формулу магнитного поля:
Величина магнитного поля указана в нано-Тесла. Приставка «нано» означает 10 -9 и так далее.
 Таким образом, величина магнитного поля на указанном расстоянии составляет:
Таким образом, величина магнитного поля на указанном расстоянии составляет:В = 10,0 нТл
Величина тока в проводе:
Величина электрического тока в проводе 0,100А.
Направление электрического тока можно определить с помощью «правила правой руки».Линии магнитного поля образуют круги по часовой стрелке в плоскости страницы, поэтому представьте, что вы сгибаете правую руку так, чтобы ваши пальцы были направлены по часовой стрелке. Для этого большой палец должен указывать на страницу (или экран). Следовательно, направление электрического тока в страницу (или экран).
Магнитный поток и электромагнитная индукция
Магнитный поток и электромагнитная индукция
Магнитный поток
Как и в случае с электрическими полями, мы вводим силовых линий , чтобы помочь визуализировать
магнитное поле. Магнитные силовые линии в регионе дают ощущение
Магнитные силовые линии в регионе дают ощущение
величина и направление магнитного поля в этой области. Если в данный
точка число силовых линий велико, то поле в этой точке равно
большой. Направление силовых линий дает
направление поля.Рассмотрим этот лист бумаги и предположим, что существует константа
магнитное поле. Рассмотрим три случая:Случай 1. B проходит сквозь лист и перпендикулярен листу. Там
будет много силовых линий, проходящих через бумагу.Случай 2. B параллельна этому листу бумаги, поэтому силовые линии не
проникать сквозь бумагу.Магнитный поток
прохождение через площадь определяется как пропорциональная количеству магнитных
силовые линии, проходящие через площадь.Так, в первом случае с полем
перпендикулярно этому листу, поток максимален, и
во втором случае, когда поле параллельно этому листу, поток равен нулю.
Корпус 3. B находится под углом к листу. Определим A как вектор, перпендикулярный странице и имеющий величину, равную
площадь листа. Тогда в этом общем случае магнитный поток определяется какF B BA cosq , где q — угол между B и A .
Для случая 1: q = 0 и F B
= БА cos0 = БА ,
а для случая 2: q =
90 град. и F B = 0,Если вы понимаете магнитный поток, то Закон электромагнитной индукции Фарадея понять легче.
Предположим, что магнитное поле, проходящее через эту страницу, увеличивается в размерах. Сказать,
через интервал времени Dt магнитное
поток через страницу увеличивается на величину DF B .Скорость изменения магнитного потока дает
повышение до индуцированного напряжения, соотношение, называемое законом Фарадея ,V индуцированный = — DF B /Dt.

Если по всей границе этой страницы был проложен провод, то
это индуцированное напряжение имело бы такой же эффект, как если бы мы подключили провод к
батарея напряжением, В индуцируется . Это,
в проводе возникнет индукционный ток.Примеры [в классе]
Магнитное поле, создаваемое тонким прямым проводом — Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как закон Био-Савара используется для определения магнитного поля, создаваемого тонким прямым проводом.
- Определить зависимость магнитного поля от тонкого прямого провода в зависимости от расстояния до него и тока, протекающего в проводе.
- Нарисуйте магнитное поле, создаваемое тонким прямым проводом, используя второе правило правой руки.
Какой ток необходим для создания значительного магнитного поля, возможно, такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса.
 Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? В главе 28 мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода? Мы можем использовать закон Био-Савара, чтобы ответить на все эти вопросы, включая определение магнитного поля длинного прямого провода.
Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? В главе 28 мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода? Мы можем использовать закон Био-Савара, чтобы ответить на все эти вопросы, включая определение магнитного поля длинного прямого провода.(рис.) показан участок бесконечно длинного прямого провода, по которому течет ток I .Чему равно магнитное поле в точке P , расположенной на расстоянии R от провода?
Участок тонкого прямого провода с током. Независимая переменная имеет пределы и
Начнем с рассмотрения магнитного поля, создаваемого токоведущим элементом, расположенным в позиции x .
 Используя правило правой руки 1 из предыдущей главы, указывает за пределы страницы для любого элемента вдоль проводника. Таким образом, в точке P магнитные поля, обусловленные всеми элементами тока, имеют одинаковое направление.Это означает, что мы можем вычислить там чистое поле, оценивая скалярную сумму вкладов элементов. С имеем из закона Био-Савара
Используя правило правой руки 1 из предыдущей главы, указывает за пределы страницы для любого элемента вдоль проводника. Таким образом, в точке P магнитные поля, обусловленные всеми элементами тока, имеют одинаковое направление.Это означает, что мы можем вычислить там чистое поле, оценивая скалярную сумму вкладов элементов. С имеем из закона Био-СавараПроволока симметрична относительно точки O , поэтому мы можем установить пределы интегрирования от нуля до бесконечности и удвоить ответ, а не интегрировать от отрицательной бесконечности до положительной бесконечности. Исходя из рисунка и геометрии, мы можем написать выражения для r и через х и R , а именно:
Подставляя эти выражения в (рисунок), интегрирование магнитного поля становится равным
Оценка интегральных выходов
Подстановка пределов дает нам решение
Силовые линии магнитного поля бесконечного провода имеют круглую форму с центром в проводе ((Рисунок)), и они идентичны во всех плоскостях, перпендикулярных проводу.
 Поскольку поле уменьшается с расстоянием от провода, расстояние между линиями поля должно соответственно увеличиваться с расстоянием. Направление этого магнитного поля можно найти с помощью второй формы правила правой руки (показано на (рис.)). Если вы держите провод правой рукой так, чтобы большой палец был направлен вдоль тока, то ваши пальцы обхватывают провод в том же смысле, что и
Поскольку поле уменьшается с расстоянием от провода, расстояние между линиями поля должно соответственно увеличиваться с расстоянием. Направление этого магнитного поля можно найти с помощью второй формы правила правой руки (показано на (рис.)). Если вы держите провод правой рукой так, чтобы большой палец был направлен вдоль тока, то ваши пальцы обхватывают провод в том же смысле, что и.
Некоторые линии магнитного поля бесконечной проволоки. Направление можно найти с помощью правила правой руки.
Направление силовых линий можно наблюдать экспериментально, поместив несколько маленьких стрелок компаса на окружность рядом с проводом, как показано на (рис.). Когда в проводе нет тока, иглы выравниваются с магнитным полем Земли. Однако, когда по проводу проходит большой ток, все стрелки компаса касаются окружности. Железные опилки, разбросанные по горизонтальной поверхности, также очерчивают линии поля, как показано на (рис.).
Форму линий магнитного поля длинного провода можно увидеть с помощью (а) маленькой стрелки компаса и (б) железных опилок.

Расчет магнитного поля, вызванного тремя проводами Три провода расположены по углам квадрата, и все они передают на страницу ток силой 2 ампера, как показано на (рис.). Вычислите величину магнитного поля в другом углу квадрата, точке P , если длина каждой стороны квадрата равна 1 см.
На страницу подается ток по трем проводам. Магнитное поле определяется в четвертом углу квадрата.
Стратегия Рассчитывается магнитное поле каждого провода в нужной точке.Диагональное расстояние рассчитывается по теореме Пифагора. Затем направление вклада каждого магнитного поля определяется путем рисования круга с центром в точке провода и в направлении желаемой точки. Направление вклада магнитного поля от этого провода тангенциально к кривой. Наконец, работая с этими векторами, вычисляется результирующая.
Решение Провода 1 и 3 имеют одинаковую величину вклада магнитного поля в точке P :
Провод 2 имеет большее расстояние и вклад магнитного поля в точке P из:
Показаны векторы для каждого из вкладов магнитного поля.

Магнитное поле в направлении x имеет вклад от провода 3 и x -компонента провода 2:
y -составляющая аналогично вкладу от провода 1 и y -компонента провода 2:
Таким образом, чистое магнитное поле является результатом этих двух компонентов:
Значение Геометрия в этой задаче приводит к тому, что вклады магнитного поля в направлениях x и y имеют одинаковую величину.Это не обязательно так, если бы токи были разных значений или если бы провода располагались в разных положениях. Независимо от численных результатов, работа с компонентами векторов даст результирующее магнитное поле в нужной точке.
Проверьте свое понимание Используя (рисунок), сохраняя одинаковые токи в проводах 1 и 3, какой должен быть ток в проводе 2, чтобы противодействовать магнитным полям от проводов 1 и 3, чтобы в точке не было результирующего магнитного поля П?
4 ампера вытекает из страницы
Резюме
- Напряженность магнитного поля, создаваемого током в длинном прямом проводе, определяется как (длинный прямой провод), где I — ток, R — кратчайшее расстояние до провода, а константа — магнитная проницаемость свободное место.

- Направление магнитного поля, создаваемого длинным прямым проводом, определяется правилом правой руки 2 (RHR-2): Направьте большой палец правой руки в направлении тока, а остальные пальцы согните в направлении магнитного поля. петли поля, созданные им.
Концептуальные вопросы
Как бы вы расположили два длинных прямых провода с током так, чтобы между ними не было результирующей магнитной силы? ( Подсказка : Какая ориентация приведет к тому, что один провод не будет подвергаться воздействию магнитного поля от другого?)
Вы должны убедиться, что токи текут перпендикулярно друг другу.
Проблемы
Типичный ток в молнии равен А. Оцените магнитное поле на расстоянии 1 м от молнии.
Величина магнитного поля на расстоянии 50 см от длинного тонкого прямого провода равна Какова сила тока через длинный провод?
По линии электропередачи, натянутой на высоте 7,0 м над землей, протекает ток силой 500 А.
 Каково магнитное поле на земле непосредственно под проводом? Сравните свой ответ с магнитным полем Земли.
Каково магнитное поле на земле непосредственно под проводом? Сравните свой ответ с магнитным полем Земли.По длинному прямому горизонтальному проводу течет слева направо ток силой 20 А.Если провод поместить в однородное магнитное поле, величина которого направлена вертикально вниз, какова результирующая величина магнитного поля на высоте 20 см над проводом? 20 см ниже провода?
Оба ответа имеют величину магнитного поля
По двум длинным параллельным проводам, показанным на прилагаемом рисунке, текут токи в одном направлении. Чему равно магнитное поле в точке P?
На прилагаемом рисунке показаны два длинных прямых горизонтальных провода, расположенных параллельно и на расстоянии 2 a друг от друга.Если по обоим проводам течет ток I в одном и том же направлении, (а) каково магнитное поле в точке (б)
В точке P1 чистое магнитное поле равно нулю. На P2, на страницу.

Повторите расчеты предыдущей задачи с обратным направлением тока в нижнем проводе.
Рассмотрим область между проводами предыдущей задачи. На каком расстоянии от верхнего провода суммарное магнитное поле минимально? Предположим, что токи равны и текут в противоположных направлениях.
Магнитное поле минимально на расстоянии a от верхнего провода или на полпути между проводами.
Соленоид
Соленоид
Соленоид [nb 1] представляет собой катушку, свернутую в плотно упакованную спираль. В физике термин соленоид относится к длинной тонкой петле из проволоки, часто обернутой вокруг металлического сердечника, которая создает магнитное поле, когда через нее проходит электрический ток.Соленоиды важны, потому что они могут создавать управляемые магнитные поля и могут использоваться в качестве электромагнитов. Термин соленоид относится конкретно к магниту, предназначенному для создания однородного магнитного поля в объеме пространства (где может проводиться какой-либо эксперимент).

В технике термин соленоид может также относиться к различным преобразователям, которые преобразуют энергию в линейное движение. Этот термин также часто используется для обозначения соленоидного клапана, который представляет собой интегрированное устройство, содержащее электромеханический соленоид, который приводит в действие пневматический или гидравлический клапан, или соленоидный переключатель, представляющий собой особый тип реле, внутри которого используется электромеханический соленоид для управлять электрическим выключателем; например, соленоид автомобильного стартера или линейный соленоид, который является электромеханическим соленоидом.
Магнитное поле соленоида
Внутри
Это вывод магнитного поля вокруг соленоида, достаточно длинного, чтобы можно было игнорировать краевые эффекты. На диаграмме справа мы сразу знаем, что поле направлено в положительном направлении z внутри соленоида и в отрицательном направлении z снаружи соленоида.

Мы видим это, применяя правило захвата правой рукой для поля вокруг провода.Если мы обхватим провод правой рукой так, чтобы большой палец был направлен в направлении тока, изгиб пальцев покажет, как ведет себя поле. Поскольку мы имеем дело с длинным соленоидом, все компоненты магнитного поля, не направленные вверх, компенсируются симметрией. Снаружи происходит аналогичная отмена, и поле направлено только вниз.
Теперь рассмотрим воображаемый контур c , расположенный внутри соленоида. По закону Ампера мы знаем, что линейный интеграл B (вектор магнитного поля) вокруг этого контура равен нулю, так как он не содержит электрических токов (можно также предположить, что электрическое поле контура, проходящее через контур, постоянно при такие условия: постоянный или постоянно изменяющийся ток через соленоид).Выше мы показали, что поле внутри соленоида направлено вверх, поэтому горизонтальные части контура c ничего не дают в интеграл. Таким образом, интеграл верхней стороны 1 равен интегралу нижней стороны 2.
 Поскольку мы можем произвольно изменять размеры петли и получать тот же результат, единственное физическое объяснение состоит в том, что подынтегральные функции на самом деле равны, то есть магнитное поле внутри соленоида радиально однородно. Заметьте, однако, что ничто не запрещает ему изменяться в продольном направлении, что на самом деле и происходит.
Поскольку мы можем произвольно изменять размеры петли и получать тот же результат, единственное физическое объяснение состоит в том, что подынтегральные функции на самом деле равны, то есть магнитное поле внутри соленоида радиально однородно. Заметьте, однако, что ничто не запрещает ему изменяться в продольном направлении, что на самом деле и происходит.Снаружи
Аналогичный аргумент можно применить к петле и , чтобы сделать вывод, что поле снаружи соленоида является радиально однородным или постоянным. Этот последний результат, строго верный только вблизи центра соленоида, где силовые линии параллельны его длине, важен, поскольку он показывает, что поле снаружи практически равно нулю, поскольку радиусы поля вне соленоида будут стремиться к бесконечность.
Можно также использовать интуитивный аргумент, чтобы показать, что поле вне соленоида на самом деле равно нулю.Линии магнитного поля существуют только в виде петель, они не могут расходиться или сходиться в точке, как линии электрического поля (см.
 Закон Гаусса для магнетизма). Линии магнитного поля следуют вдоль продольного пути соленоида внутри, поэтому они должны идти в противоположном направлении снаружи соленоида, чтобы линии могли образовать петлю. Однако объем снаружи соленоида намного больше, чем объем внутри, поэтому плотность силовых линий магнитного поля снаружи сильно снижается. Теперь вспомним, что поле снаружи постоянно.Чтобы общее количество линий поля сохранялось, внешнее поле должно стремиться к нулю по мере того, как соленоид становится длиннее.
Закон Гаусса для магнетизма). Линии магнитного поля следуют вдоль продольного пути соленоида внутри, поэтому они должны идти в противоположном направлении снаружи соленоида, чтобы линии могли образовать петлю. Однако объем снаружи соленоида намного больше, чем объем внутри, поэтому плотность силовых линий магнитного поля снаружи сильно снижается. Теперь вспомним, что поле снаружи постоянно.Чтобы общее количество линий поля сохранялось, внешнее поле должно стремиться к нулю по мере того, как соленоид становится длиннее.Количественное описание
Теперь мы можем рассмотреть воображаемый контур b . Возьмите линейный интеграл B вокруг петли с длиной петли l . Горизонтальные компоненты равны нулю, а внешнее поле практически равно нулю, поэтому закон Ампера дает нам:
где μ 0 — магнитная постоянная, N 9016 6 число витков, электрический ток.Это уравнение для соленоида без сердечника.
 Этимология Соленоид : 1827, французский solenoide , греческий solen «труба, канал» + сочетание формы греческого eidos «форма, форма» [1]
Этимология Соленоид : 1827, французский solenoide , греческий solen «труба, канал» + сочетание формы греческого eidos «форма, форма» [1] - Объясните, как закон Био-Савара используется для определения магнитного поля, создаваемого током в проволочной петле в точке вдоль линии, перпендикулярной плоскости петли.
- Определить магнитное поле дуги тока.
- Напряженность магнитного поля в центре круглой петли определяется выражением [латекс]B=\frac{{\mu }_{0}I}{2R}\phantom{\rule{0.2em}{0ex}} \text{(в центре петли)},[/latex] где R — радиус петли. РХР-2 дает направление поля вокруг петли.
- Это изменение потока магнитного поля, которое приводит к возникновению электродвижущей силы (или напряжения).

- Магнитный поток (часто обозначаемый Φ или Φ B ) через поверхность представляет собой компонент магнитного поля, проходящего через эту поверхность.
- В наиболее общем виде магнитный поток определяется как [латекс]\Phi_{\text{B}} = \iint_{\text{A}} \mathbf{\text{B}} \cdot \text{d} \mathbf {\text{A}}[/латекс].Это интеграл (сумма) всего магнитного поля, проходящего через бесконечно малые элементы площади dA.
- площадь вектора : Вектор, величина которого представляет собой рассматриваемую площадь, а направление перпендикулярно площади поверхности.
- гальванометр : Аналоговый измерительный прибор, обозначаемый буквой G, который измеряет ток, используя отклонение стрелки, вызванное силой магнитного поля, действующей на проводник с током.
- Минус в законе Фарадея означает, что ЭДС создает ток I и магнитное поле B, которые противодействуют изменению потока Δэто известно как закон Ленца.
- Закон индукции Фарадея является фундаментальным принципом работы трансформаторов, катушек индуктивности и многих типов электродвигателей, генераторов и соленоидов.

- Закон Фарадея гласит, что ЭДС, индуцированная изменением магнитного потока, зависит от изменения потока Δ, времени Δt и числа витков катушки.
- электродвижущая сила : (ЭДС) — напряжение, создаваемое батареей или магнитной силой в соответствии с законом Фарадея.Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.
- соленоид : Катушка проволоки, которая действует как магнит, когда через нее проходит электрический ток.
- поток : Скорость передачи энергии (или другой физической величины) через данную поверхность, в частности, электрический поток или магнитный поток.
- Закон индукции Фарадея можно использовать для расчета ЭДС движения, когда изменение магнитного потока вызывается движущимся элементом в системе.
- То, что движущееся магнитное поле создает электрическое поле (и наоборот, что движущееся электрическое поле создает магнитное поле), частично является причиной того, что электрические и магнитные силы теперь рассматриваются как разные проявления одной и той же силы.
- Любое изменение магнитного потока индуцирует электродвижущую силу (ЭДС), противодействующую этому изменению — процесс, известный как индукция.
 Движение является одной из основных причин индукции.
Движение является одной из основных причин индукции. - электродвижущая сила : (ЭДС) — напряжение, создаваемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.
- магнитный поток : Мера силы магнитного поля в данной области.
- индукция : Генерация электрического тока переменным магнитным полем.
- Входная ЭДС, питающая двигатель, может противопоставляться собственной ЭДС двигателя, называемой обратной ЭДС двигателя.
- Если ЭДС движения может вызвать петлю с током в проводнике, то ток называется вихревым током.
- Вихревые токи могут создавать значительное сопротивление, называемое магнитным демпфированием, при соответствующем движении.
- электродвижущая сила : (ЭДС) — напряжение, создаваемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.
- Закон индукции Фарадея : Основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).

- Закон индукции Фарадея — это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу.

- Альтернативная дифференциальная форма закона индукции Фарадея выражается в уравнении [латекс]\nabla \times \vec {\text{E}} = — \frac{\partial \vec {\text{B}}}{ \partial \text{t}}[/latex].
- Закон индукции Фарадея — одно из четырех уравнений Максвелла, управляющих всеми электромагнитными явлениями.
- векторная площадь : Вектор, величина которого представляет собой рассматриваемую площадь и направление которого перпендикулярно плоскости.
- Уравнения Максвелла : Набор уравнений, описывающих, как электрические и магнитные поля генерируются и изменяются друг другом, а также зарядами и токами.
- Теорема Стокса : утверждение об интегрировании дифференциальных форм на многообразиях, которое упрощает и обобщает несколько теорем векторного исчисления.
- Электрический генератор вращает катушку в магнитном поле, индуцируя ЭДС, определяемую как функция времени ε=NABw sinωt.
- обеспечивают почти всю мощность для электросетей, которые обеспечивают большую часть мировой электроэнергии.

- Двигатель становится генератором, когда его вал вращается.
- электродвижущая сила : (ЭДС) — напряжение, создаваемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и, следовательно, на самом деле не является силой.
- турбина : любая из различных вращающихся машин, которые используют кинетическую энергию непрерывного потока жидкости (жидкости или газа) для вращения вала.
- В большинстве электродвигателей для создания силы используется взаимодействие магнитных полей и проводников с током.
- Ток в проводнике состоит из движущихся зарядов. Следовательно, катушка с током в магнитном поле также будет ощущать силу Лоренца.
- В двигателе катушка с током в магнитном поле испытывает силу с обеих сторон катушки, которая создает крутящую силу (называемую крутящим моментом), которая заставляет ее вращаться.
- Сила Лоренца : Сила, действующая на заряженную частицу в электромагнитном поле.

- крутящий момент : Вращательное или скручивающее действие силы; (единица СИ ньютон-метр или Нм; британская единица фут-фунт или фут-фунт)
- Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге.Изменение тока ΔI 1 /Δt в одном индуцирует ЭДС ЭДС2 во втором: ЭДС 2 = −M ΔI 1 /Δt, где М определяется как взаимная индуктивность между двумя устройствами.
- Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
- Устройство, обладающее значительной собственной индуктивностью, называется индуктором, а ЭДС, индуцируемая в нем изменением тока через него, равна ЭДС = −L ∆I/∆t.
- Закон индукции Фарадея : Основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).
- трансформатор : Статическое устройство, которое передает электрическую энергию от одной цепи к другой посредством магнитной связи.
 Их основное применение заключается в передаче энергии между различными уровнями напряжения, что позволяет выбрать наиболее подходящее напряжение для производства, передачи и распределения электроэнергии по отдельности.
Их основное применение заключается в передаче энергии между различными уровнями напряжения, что позволяет выбрать наиболее подходящее напряжение для производства, передачи и распределения электроэнергии по отдельности. - ЭДС движения и ЭДС индукции — это одно и то же явление, просто наблюдаемое в разных системах отсчета. Эквивалентность этих двух явлений побудила Эйнштейна заняться специальной теорией относительности.
- ЭДС, возникающая из-за относительного движения петли и магнита, определяется как [латекс]\varepsilon_{\text{движение}} = \text{vB} \times \text{L}[/latex] (уравнение.1), где L — длина объекта, движущегося со скоростью v относительно магнита.
- ЭДС можно рассчитать с двух разных точек зрения: 1) через магнитную силу, действующую на движущиеся электроны в магнитном поле, и 2) через скорость изменения магнитного потока. Оба дают одинаковый результат.

- специальная теория относительности : Теория, которая (пренебрегая эффектами гравитации) примиряет принцип относительности с наблюдением, что скорость света постоянна во всех системах отсчета.
- магнитное поле : Состояние в пространстве вокруг магнита или электрического тока, в котором присутствует определяемая магнитная сила и где присутствуют два магнитных полюса.
- система отсчета : Система координат или набор осей, в которых измеряется положение, ориентация и другие свойства объектов в ней.
- ЭДС движения, создаваемая движущимся проводником в однородном поле, определяется следующим образом: [latex]\varepsilon = \text{Blv}[/latex].
- Чтобы стержень двигался с постоянной скоростью v, мы должны постоянно прикладывать внешнюю силу F ext к стержню во время его движения.

- Закон Ленца гарантирует, что движение стержня противоположно, и поэтому закон сохранения энергии не нарушается.
- ЭДС движения : ЭДС (электродвижущая сила), индуцированная движением относительно магнитного поля.
- Закон индукции Фарадея : Основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).
- Энергия необходима для создания магнитного поля как для работы против электрического поля, создаваемого изменяющимся магнитным полем, так и для изменения намагниченности любого материала в пределах магнитного поля.2[/латекс].
- проницаемость : Количественная мера степени намагниченности материала в присутствии приложенного магнитного поля (измеряется в ньютонах на ампер в квадрате в единицах СИ).

- индуктор : пассивное устройство, вводящее индуктивность в электрическую цепь.
- ферромагнетик : Материалы, обладающие постоянным магнитным свойством.
- Трансформаторы часто используются в нескольких точках в системах распределения электроэнергии, а также во многих бытовых адаптерах питания.
- Уравнение трансформатора гласит, что отношение вторичных и первичных напряжений в трансформаторе равно отношению количества витков в их катушках: [латекс]\frac{\text{V}_\text{s}}{\text{ V}_\text{p}} = \frac{\text{N}_\text{s}}{\text{N}_\text{p}}[/latex].
- Предполагая, как и мы, что сопротивление пренебрежимо мало, выходная электрическая мощность трансформатора равна его входной мощности.
 Это приводит нас к другому полезному уравнению: [латекс]\frac{\text{I}_\text{s}}{\text{I}_\text{p}} = \frac{\text{N}_\ text{p}}{\text{N}_\text{s}}[/latex]. Если напряжение увеличивается, ток уменьшается. И наоборот, если напряжение уменьшается, ток увеличивается.
Это приводит нас к другому полезному уравнению: [латекс]\frac{\text{I}_\text{s}}{\text{I}_\text{p}} = \frac{\text{N}_\ text{p}}{\text{N}_\text{s}}[/latex]. Если напряжение увеличивается, ток уменьшается. И наоборот, если напряжение уменьшается, ток увеличивается. - магнитный поток : Мера силы магнитного поля в данной области.
- Закон индукции Фарадея : Основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).
Ссылки
Внешние ссылки
9004 Магнитное поле токовой петли — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
Круговой контур на рис. 12.11 имеет радиус R , по нему течет ток I , и он лежит в плоскости xz .Чему равно магнитное поле, обусловленное током в произвольной точке P по оси петли?
Рисунок 12.11 Определение магнитного поля в точке P вдоль оси проволочного контура с током.
Мы можем использовать закон Био-Савара, чтобы найти магнитное поле, создаваемое током.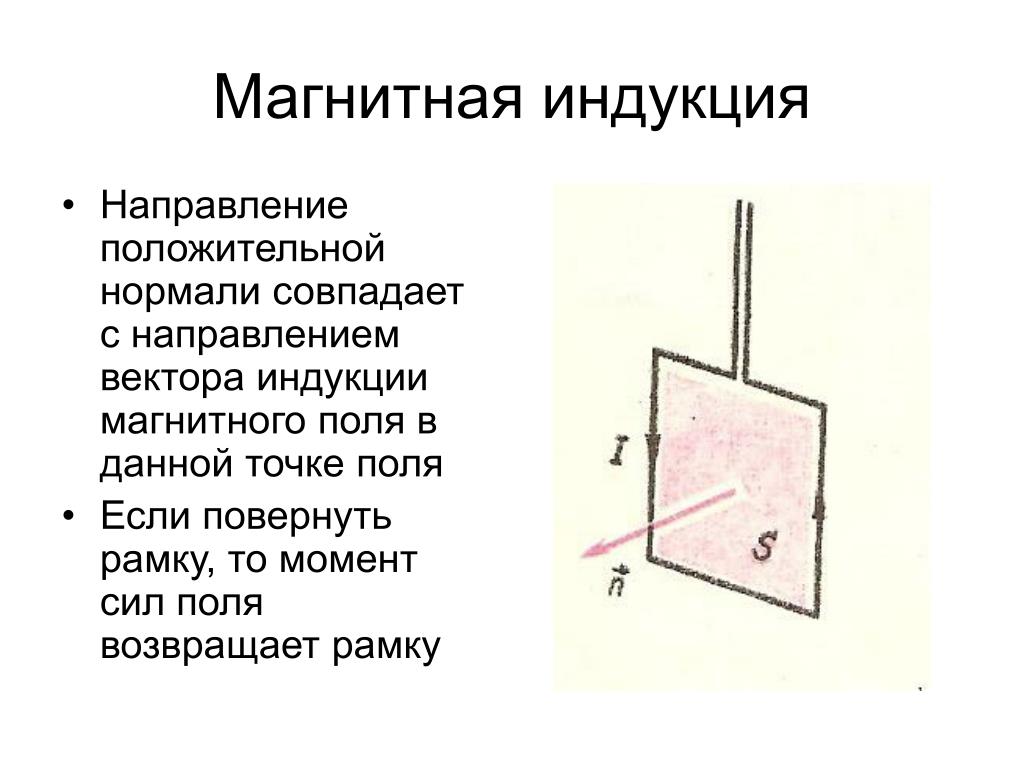 Сначала мы рассмотрим произвольные сегменты на противоположных сторонах петли, чтобы качественно показать векторными результатами, что чистое направление магнитного поля находится вдоль центральной оси петли.Отсюда мы можем использовать закон Био-Савара, чтобы получить выражение для магнитного поля.
Сначала мы рассмотрим произвольные сегменты на противоположных сторонах петли, чтобы качественно показать векторными результатами, что чистое направление магнитного поля находится вдоль центральной оси петли.Отсюда мы можем использовать закон Био-Савара, чтобы получить выражение для магнитного поля.
Пусть P будет расстоянием y от центра петли. Согласно правилу правой руки, магнитное поле [латекс]d\stackrel{\to }{\textbf{B}}[/latex] на уровне P , создаваемое элементом тока [латекс]I\phantom{\rule {0.2em}{0ex}}d\stackrel{\to }{\textbf{l}},[/latex] направлен под углом [latex]\theta[/latex] над осью y , как показано . Поскольку [latex]d\stackrel{\to }{\textbf{l}}[/latex] параллелен вдоль оси x , а [latex]\hat{\textbf{r}}[/latex] находится в yz -плоскость, два вектора перпендикулярны, поэтому мы имеем
[латекс] дБ = \ frac {{\ mu } _ {0}} {4 \ pi} \ phantom {\ rule {0.{\prime}[/latex], перпендикулярные оси y , поэтому сокращаются, и при расчете чистого магнитного поля необходимо учитывать только компоненты вдоль оси y . {3}}.{3}}.[/латекс]
{3}}.{3}}.[/латекс]
Расчет магнитного поля из-за круговой токовой петли в точках вне оси требует довольно сложной математики, поэтому мы просто посмотрим на результаты. Линии магнитного поля имеют форму, показанную на рис. 12.12. Обратите внимание, что одна линия поля следует за осью петли. Это линия поля, которую мы только что нашли. Кроме того, в непосредственной близости от провода линии поля почти круглые, как линии длинного прямого провода.
Рисунок 12.12 Эскиз силовых линий магнитного поля круглой петли с током.
Пример
Магнитное поле между двумя контурами
Два витка провода пропускают одинаковый ток 10 мА, но текут в противоположных направлениях, как показано на Рисунке 12.13. Одна петля имеет радиус [латекс]R=50\phantom{\rule{0.2em}{0ex}}\text{см}[/латекс], а другая петля имеет радиус [латекс]2R= 100\phantom{\rule{0.2em}{0ex}}\text{см}.[/latex] Расстояние от первого контура до точки, где измеряется магнитное поле, равно 0,25 м, а расстояние от этой точки до вторая петля 0. 75 м. Какова величина суммарного магнитного поля в точке P ?
75 м. Какова величина суммарного магнитного поля в точке P ?
Рисунок 12.13 Две петли разных радиусов имеют одинаковый ток, но текут в противоположных направлениях. Магнитное поле в точке P равно нулю.
Стратегия
Магнитное поле в точке P было определено по уравнению 12.15. Поскольку токи текут в противоположных направлениях, чистое магнитное поле представляет собой разницу между двумя полями, создаваемыми катушками.{\text{−9}}\text{T}\phantom{\rule{0.2em}{0ex}}\text{вправо}.\hfill \end{массив}[/latex]
Значение
Катушки Гельмгольца
обычно имеют петли одинакового радиуса с током, текущим в одном направлении, чтобы иметь сильное однородное поле в средней точке между петлями. Аналогичное применение распределения магнитного поля, создаваемого катушками Гельмгольца, можно найти в магнитной бутылке, которая может временно улавливать заряженные частицы. См. Магнитные силы и поля для обсуждения этого.
Проверьте свое понимание
Используя пример 12.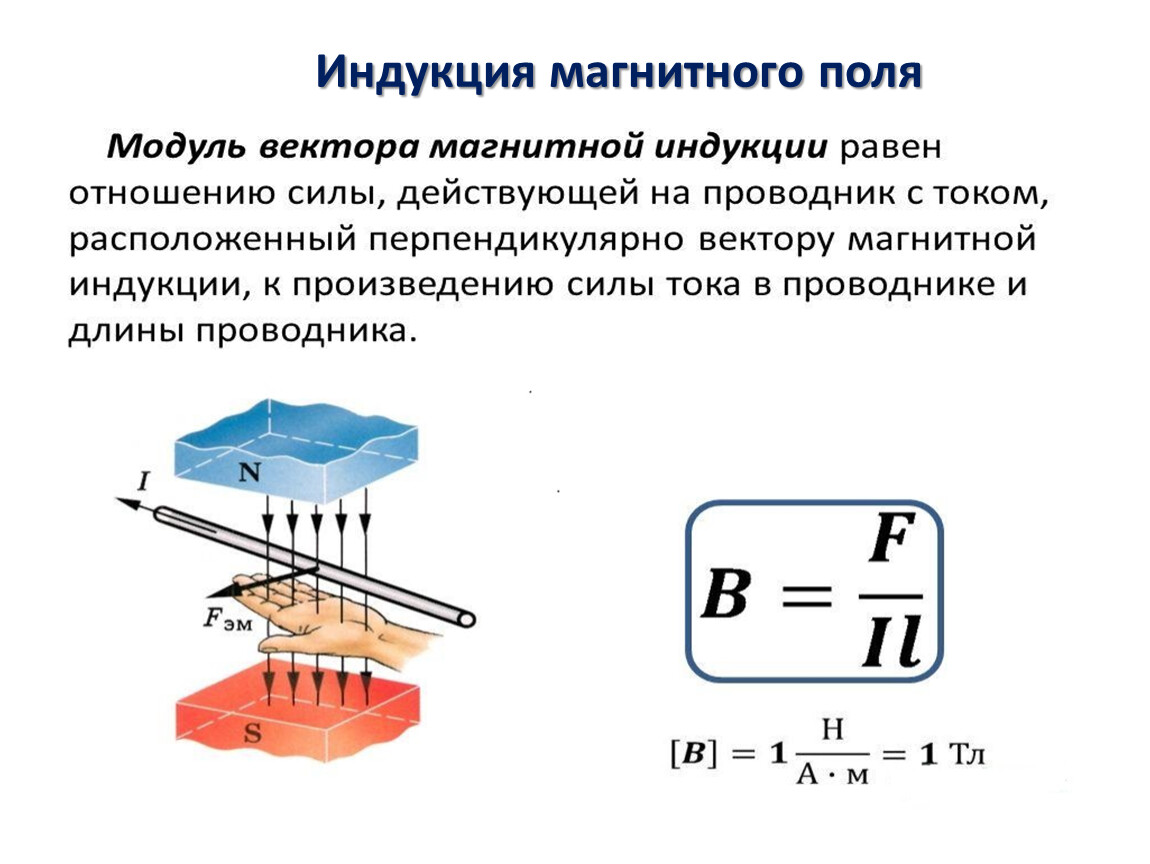 5, на какое расстояние вам пришлось бы переместить первую катушку, чтобы иметь нулевое измеряемое магнитное поле в точке P ?
5, на какое расстояние вам пришлось бы переместить первую катушку, чтобы иметь нулевое измеряемое магнитное поле в точке P ?
Показать решение
Резюме
Концептуальные вопросы
Является ли магнитное поле токовой петли однородным?
Что происходит с длиной подвешенной пружины, когда через нее проходит ток?
Показать решение
Длина пружины уменьшается, поскольку каждая катушка имеет магнитное поле, создаваемое северным полюсом, рядом с южным полюсом следующей катушки.
По двум концентрическим круглым проводам разного диаметра текут токи в одном направлении. Опишите силу, действующую на внутреннюю проволоку.{\text{−5}}\text{T}[/латекс]
По круговой петле радиусом R течет ток I . {3\text{/}2}}[/latex]
{3\text{/}2}}[/latex]
Для катушек в предыдущей задаче, каково магнитное поле в центре каждой катушки?
Лицензии и атрибуты
Магнитное поле токовой петли. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/12-4-magnet-field-of-current-loop. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction
Применение магнитной индукции — физика
Индуцированная ЭДС и магнитный поток
Закон индукции Фарадея гласит, что электродвижущая сила индуцируется изменением магнитного потока.
Цели обучения
Объясните взаимосвязь между магнитным полем и электродвижущей силой
Ключевые выводы
Ключевые моменты
Основные термины
Индуцированная ЭДС
Устройство, которое Фарадей использовал для демонстрации того, что магнитные поля могут создавать токи, показано на следующем рисунке.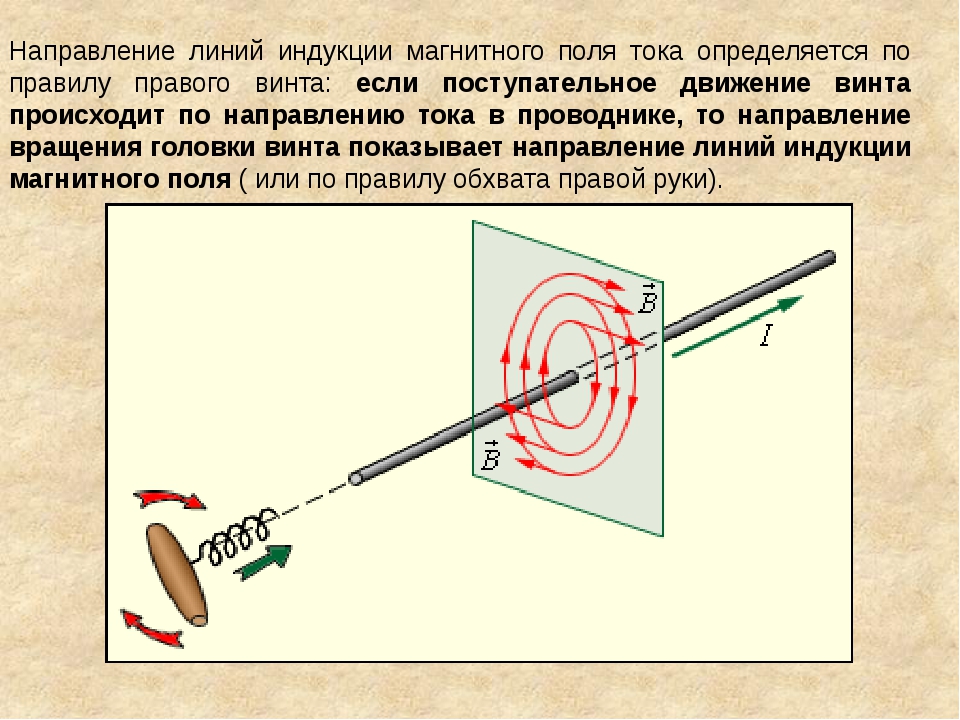 Когда переключатель замкнут, магнитное поле создается в катушке в верхней части железного кольца и передается (или направляется) на катушку в нижней части кольца. Гальванометр используется для обнаружения любого тока, наведенного в отдельной катушке на дне.
Когда переключатель замкнут, магнитное поле создается в катушке в верхней части железного кольца и передается (или направляется) на катушку в нижней части кольца. Гальванометр используется для обнаружения любого тока, наведенного в отдельной катушке на дне.
Аппарат Фарадея : Это аппарат Фарадея для демонстрации того, что магнитное поле может производить ток.Изменение поля, создаваемого верхней катушкой, индуцирует ЭДС и, следовательно, ток в нижней катушке. Когда переключатель размыкается и замыкается, гальванометр регистрирует токи в противоположных направлениях. Через гальванометр не протекает ток, когда переключатель остается замкнутым или разомкнутым.
Было обнаружено, что каждый раз, когда переключатель замыкается, гальванометр регистрирует ток в одном направлении в катушке на дне. Каждый раз, когда переключатель размыкается, гальванометр регистрирует ток в противоположном направлении.Интересно, что если переключатель остается замкнутым или разомкнутым какое-то время, ток через гальванометр отсутствует. Замыкание и размыкание переключателя индуцирует ток. Именно изменение магнитного поля создает ток. Более важным, чем текущий ток, является электродвижущая сила (ЭДС), которая его вызывает. Ток является результатом ЭДС, индуцированной изменяющимся магнитным полем, независимо от того, есть ли путь для протекания тока.
Замыкание и размыкание переключателя индуцирует ток. Именно изменение магнитного поля создает ток. Более важным, чем текущий ток, является электродвижущая сила (ЭДС), которая его вызывает. Ток является результатом ЭДС, индуцированной изменяющимся магнитным полем, независимо от того, есть ли путь для протекания тока.
Магнитный поток
Магнитный поток (часто обозначаемый Φ или Φ B ) через поверхность представляет собой компонент магнитного поля, проходящего через эту поверхность.Магнитный поток через некоторую поверхность пропорционален числу силовых линий, проходящих через эту поверхность. Магнитный поток, проходящий через поверхность векторной площади А, равен
[латекс]\Phi_\text{B} = \mathbf{\text{B}} \cdot \mathbf{\text{A}} = \text{BA} \cos\theta[/latex],
, где B — величина магнитного поля (в единицах Тесла, Тл), A — площадь поверхности, а θ — угол между силовыми линиями магнитного поля и нормалью (перпендикуляром) к A.
Для переменного магнитного поля сначала рассмотрим магнитный поток [латекс]\текст{d}\Phi _\text{B}[/латекс] через элемент бесконечно малой площади dA, где мы можем считать поле постоянным:
Переменное магнитное поле : Каждая точка на поверхности связана с направлением, называемым нормалью к поверхности; тогда магнитный поток через точку является составляющей магнитного поля вдоль этого нормального направления.
[латекс]\текст{d}\Phi_\текст{B} = \mathbf{\text{B}} \cdot \text{d}\mathbf{\text{A}}[/latex]
Общая поверхность A может быть затем разбита на бесконечно малые элементы, и тогда общий магнитный поток через поверхность будет поверхностным интегралом
[латекс]\Phi_\text{B} = \iint_\text{A} \mathbf{\text{B}} \cdot \text{d}\mathbf {\text{A}}[/latex].
Закон индукции Фарадея и закон Ленца
Закон индукции Фарадея гласит, что ЭДС, индуцированная изменением магнитного потока, равна [латекс]\текст{ЭДС} = -\текст{N}\frac{\Delta \Phi}{\Delta \text{t}}[ /латекс], когда поток изменяется на Δ за время Δt.
Цели обучения
Выразите закон индукции Фарадея в виде уравнения
Ключевые выводы
Ключевые моменты
Основные термины
Закон индукции Фарадея
Закон индукции Фарадея — это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).Это основной принцип работы трансформаторов, катушек индуктивности и многих типов электродвигателей, генераторов и соленоидов.
Эксперименты Фарадея показали, что ЭДС, вызванная изменением магнитного потока, зависит лишь от нескольких факторов. Во-первых, ЭДС прямо пропорциональна изменению потока Δ. Во-вторых, ЭДС максимальна, когда изменение времени Δt наименьшее, то есть ЭДС обратно пропорциональна Δt. Наконец, если катушка имеет N витков, будет создаваться ЭДС в N раз больше, чем для одиночной катушки, так что ЭДС прямо пропорциональна N.Уравнение для ЭДС, индуцированной изменением магнитного потока, имеет вид
.
[латекс]\текст{ЭДС} = -\текст{N}\frac{\Delta \Phi}{\Delta \text{t}}[/latex].
Это соотношение известно как закон индукции Фарадея. Единицами ЭДС, как обычно, являются вольты.
Закон Ленца
Знак минус в законе индукции Фарадея очень важен. Минус означает, что ЭДС создает ток I и магнитное поле B, противодействующие изменению потока Δ, это известно как закон Ленца. Направление (заданное знаком минус) ЭДС настолько важно, что его называют законом Ленца в честь русского Генриха Ленца (1804–1865), который, подобно Фарадею и Генри, независимо исследовал аспекты индукции. Фарадей знал об этом направлении, но Ленц указал его, поэтому ему приписывают его открытие.
Фарадей знал об этом направлении, но Ленц указал его, поэтому ему приписывают его открытие.
Закон Ленца : (a) Когда этот стержневой магнит вталкивается в катушку, напряженность магнитного поля в катушке увеличивается. Ток, наведенный в катушке, создает другое поле в направлении, противоположном направлению стержневого магнита, чтобы противостоять увеличению. Это один из аспектов закона Ленца: индукция препятствует любому изменению потока. (b) и (c) — две другие ситуации. Убедитесь сами, что показанное направление индуцированной катушки B действительно противостоит изменению потока и что показанное направление тока согласуется с правилом правой руки.
Энергосбережение
Закон Ленца является проявлением закона сохранения энергии. Индуцированная ЭДС создает ток, противодействующий изменению потока, потому что изменение потока означает изменение энергии. Энергия может войти или уйти, но не мгновенно. Закон Ленца является следствием. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. На самом деле, если бы индуцированная ЭДС была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
На самом деле, если бы индуцированная ЭДС была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
ЭДС движения
Движение в стационарном относительно Земли магнитном поле индуцирует ЭДС движения (электродвижущая сила).
Цели обучения
Определите процесс, вызывающий движущую электродвижущую силу
Ключевые выводы
Ключевые моменты
Основные термины
Как видно из предыдущих Атомов, любое изменение магнитного потока индуцирует электродвижущую силу (ЭДС), противодействующую этому изменению — процесс, известный как индукция. Движение является одной из основных причин индукции. Например, магнит, перемещаемый к катушке, индуцирует ЭДС, а катушка, перемещаемая к магниту, создает аналогичную ЭДС. В этом Атоме мы концентрируемся на движении в магнитном поле, стационарном относительно Земли, производя то, что можно условно назвать ЭДС движения.
ЭДС движения
Рассмотрим ситуацию, показанную на рис. Стержень движется со скоростью v по паре проводящих рельсов, разделенных расстоянием ℓ, в однородном магнитном поле B. Рельсы неподвижны относительно B и подключены к постоянному резистору R ( резистор может быть любым, от лампочки до вольтметра). Рассмотрим область, окруженную движущимся стержнем, рельсами и резистором. B перпендикулярна этой площади, и площадь увеличивается по мере движения стержня. Таким образом, магнитный поток, заключенный между рельсами, стержнем и резистором, увеличивается.При изменении потока индуцируется ЭДС в соответствии с законом индукции Фарадея.
ЭДС движения : (a) ЭДС движения=Bℓv индуцируется между рельсами, когда этот стержень движется вправо в однородном магнитном поле. Магнитное поле B направлено внутрь страницы, перпендикулярно движущимся стержню и рельсам и, следовательно, ограниченной ими области. (b) Закон Ленца дает направления индуцированного поля и тока, а также полярность индуцированной ЭДС. Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или выходит за пределы страницы.Правило правой руки дает показанное направление тока, и полярность стержня будет управлять таким током.
Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или выходит за пределы страницы.Правило правой руки дает показанное направление тока, и полярность стержня будет управлять таким током.
Чтобы найти величину ЭДС, индуцированной вдоль движущегося стержня, воспользуемся законом индукции Фарадея без знака:
[латекс]\текст{ЭДС} = \текст{N}\frac{\Delta \Phi}{\Delta \text{t}}[/latex].
В этом уравнении N=1 и поток Φ=BAcosθ. Имеем θ=0º и cosθ=1, так как B перпендикулярно A. Теперь Δ=Δ(BA)=BΔA, так как B однородно. Обратите внимание, что площадь, заметаемая стержнем, равна ΔA=ℓx.Ввод этих величин в выражение для ЭДС дает:
[латекс]\текст{ЭДС} = \frac{\text{B}\Delta \text{A}}{\Delta \text{t}} = \text{B} \frac{\text{l} \ Дельта \text{x}}{\Delta \text{t}} = \text{Blv}[/latex].
Чтобы найти направление индуцированного поля, направление тока и полярность индуцированной ЭДС, мы применяем закон Ленца, как описано в Законе Фарадея об индукции: закон Ленца. Как видно на рис. 1 (b), поток увеличивается, так как увеличивается площадь охвата.Таким образом, индуцированное поле должно противостоять существующему и быть за пределами страницы. (Правило правой руки требует, чтобы я вращался против часовой стрелки, что, в свою очередь, означает, что вершина стержня положительна, как показано.)
Как видно на рис. 1 (b), поток увеличивается, так как увеличивается площадь охвата.Таким образом, индуцированное поле должно противостоять существующему и быть за пределами страницы. (Правило правой руки требует, чтобы я вращался против часовой стрелки, что, в свою очередь, означает, что вершина стержня положительна, как показано.)
Электрическое поле против магнитного поля
Существует много связей между электрической силой и магнитной силой. То, что движущееся магнитное поле создает электрическое поле (и наоборот, движущееся электрическое поле создает магнитное поле), является одной из причин, по которой электрические и магнитные силы теперь рассматриваются как различных проявлений одной и той же силы (впервые замеченной Альбертом Эйнштейном). .Это классическое объединение электрических и магнитных сил в то, что называется электромагнитной силой , является источником вдохновения для современных усилий по объединению других базовых сил.
Обратная ЭДС, вихревые токи и магнитное демпфирование
Обратная ЭДС, вихревые токи и магнитное демпфирование возникают из-за наведенной ЭДС и могут быть объяснены законом индукции Фарадея.
Цели обучения
Объясните взаимосвязь между движущей электродвижущей силой, вихревыми токами и магнитным демпфированием
Ключевые выводы
Ключевые моменты
Основные термины
Обратная ЭДС
Двигатели и генераторы очень похожи. (Читайте наши атомы в разделе «Электрические генераторы» и «Электродвигатели».) Генераторы преобразуют механическую энергию в электрическую, тогда как двигатели преобразуют электрическую энергию в механическую. Кроме того, двигатели и генераторы имеют одинаковую конструкцию. Когда катушка двигателя поворачивается, магнитный поток изменяется, и индуцируется электродвижущая сила (ЭДС), соответствующая закону индукции Фарадея. Таким образом, двигатель действует как генератор всякий раз, когда его катушка вращается.Это произойдет независимо от того, вращается ли вал с помощью внешнего источника, такого как ременная передача, или под действием самого двигателя. То есть, когда двигатель совершает работу и его вал вращается, возникает ЭДС. Закон Ленца говорит нам, что ЭДС индукции противостоит любым изменениям, поэтому входной ЭДС, питающей двигатель, будет противодействовать ЭДС, создаваемая самим двигателем, называемая обратной ЭДС двигателя.
Вихревой поток
Как обсуждалось в разделе «ЭДС движения», ЭДС движения индуцируется, когда проводник движется в магнитном поле или когда магнитное поле движется относительно проводника.Если ЭДС движения может вызвать петлю с током в проводнике, мы называем этот ток вихревым током. Вихревые токи могут создавать значительное сопротивление, называемое магнитным демпфированием, при соответствующем движении.
Рассмотрим устройство, показанное на рис., которое раскачивает маятник между полюсами сильного магнита. Если поплавок металлический, при входе в поле и выходе из него возникает значительное сопротивление, что быстро гасит движение. Если, однако, груз представляет собой металлическую пластину с прорезями, как показано на (b), эффект магнита будет намного меньше.Никакого заметного влияния на боб, сделанный из изолятора, не наблюдается.
Устройство для изучения вихревых токов и магнитного демпфирования : Обычное физическое демонстрационное устройство для изучения вихревых токов и магнитного демпфирования. а) Движение металлического маятника, качающегося между полюсами магнита, быстро затухает под действием вихревых токов. (b) На движение металлического поплавка с прорезями мало влияет, что означает, что вихревые токи становятся менее эффективными. (c) На непроводящем грузе также нет магнитного демпфирования, поскольку вихревые токи чрезвычайно малы.
а) Движение металлического маятника, качающегося между полюсами магнита, быстро затухает под действием вихревых токов. (b) На движение металлического поплавка с прорезями мало влияет, что означает, что вихревые токи становятся менее эффективными. (c) На непроводящем грузе также нет магнитного демпфирования, поскольку вихревые токи чрезвычайно малы.
показывает, что происходит с металлической пластиной, когда она входит в магнитное поле и выходит из него. В обоих случаях на него действует сила, противодействующая его движению. Когда он входит слева, поток увеличивается, поэтому возникает вихревой ток (закон Фарадея) в направлении против часовой стрелки (закон Ленца), как показано. В поле находится только правая сторона контура тока, так что слева на него действует непротиворечивая сила (правило правой руки). Когда металлическая пластина находится полностью внутри поля, вихревой ток отсутствует, если поле однородно, так как поток в этой области остается постоянным.Но когда пластина покидает поле справа, поток уменьшается, вызывая вихревой ток в направлении по часовой стрелке, который, опять же, испытывает силу влево, еще больше замедляя движение. Аналогичный анализ того, что происходит, когда пластина качается справа налево, показывает, что ее движение также затухает при входе в поле и выходе из него.
Аналогичный анализ того, что происходит, когда пластина качается справа налево, показывает, что ее движение также затухает при входе в поле и выходе из него.
Проводящая пластина, проходящая между полюсами магнита : Более подробный вид на проводящую пластину, проходящую между полюсами магнита.Когда он входит в поле и выходит из него, изменение потока вызывает вихревой ток. Магнитная сила на токовой петле противодействует движению. Когда пластина полностью находится внутри однородного поля, ток и магнитное сопротивление отсутствуют.
Когда металлическая пластина с прорезями входит в поле, как показано на , ЭДС индуцируется изменением потока, но она менее эффективна, поскольку прорези ограничивают размер токовых петель. Более того, в соседних петлях есть токи в противоположных направлениях, и их эффекты компенсируются.При использовании изоляционного материала вихревые токи чрезвычайно малы, поэтому магнитным демпфированием на изоляторах можно пренебречь. Если необходимо избежать вихревых токов в проводниках, то они могут быть щелевыми или изготовлены из тонких слоев проводящего материала, разделенных изоляционными листами.
Если необходимо избежать вихревых токов в проводниках, то они могут быть щелевыми или изготовлены из тонких слоев проводящего материала, разделенных изоляционными листами.
Вихревые токи, индуцированные в металлической пластине с прорезями : Вихревые токи, индуцированные в металлической пластине с прорезями, попадая в магнитное поле, образуют небольшие петли, и силы, действующие на них, имеют тенденцию компенсироваться, тем самым делая магнитное сопротивление почти нулевым.
Изменение магнитного потока создает электрическое поле
Закон индукции Фарадея гласит, что изменение магнитного поля создает электрическое поле: [латекс]\varepsilon = -\frac{\partial \Phi_\text{B}}{\partial \text{t}}[/latex].
Цели обучения
Описать взаимосвязь между изменяющимся магнитным полем и электрическим полем
Ключевые выводы
Ключевые моменты
Основные термины
Мы изучили закон индукции Фарадея в предыдущих атомах. Мы узнали взаимосвязь между индуцированной электродвижущей силой (ЭДС) и магнитным потоком. В двух словах, закон гласит, что изменение магнитного поля [латекс](\frac{\text{d} \Phi_\text{B}}{\text{dt}})[/latex] создает электрическое поле [латекс] (\varepsilon)[/latex], закон индукции Фарадея выражается как [latex]\varepsilon = -\frac{\partial \Phi_\text{B}}{\partial \text{t}}[/latex], где [latex]\varepsilon[/latex] — ЭДС индукции, а [latex]\Phi_\text{B}[/latex] — магнитный поток. («N» опущено из нашего предыдущего выражения. Количество включенных витков катушки может быть включено в магнитный поток, поэтому коэффициент необязателен.) Закон индукции Фарадея — это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС). В этом Атоме мы узнаем об альтернативном математическом выражении закона.
В двух словах, закон гласит, что изменение магнитного поля [латекс](\frac{\text{d} \Phi_\text{B}}{\text{dt}})[/latex] создает электрическое поле [латекс] (\varepsilon)[/latex], закон индукции Фарадея выражается как [latex]\varepsilon = -\frac{\partial \Phi_\text{B}}{\partial \text{t}}[/latex], где [latex]\varepsilon[/latex] — ЭДС индукции, а [latex]\Phi_\text{B}[/latex] — магнитный поток. («N» опущено из нашего предыдущего выражения. Количество включенных витков катушки может быть включено в магнитный поток, поэтому коэффициент необязателен.) Закон индукции Фарадея — это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС). В этом Атоме мы узнаем об альтернативном математическом выражении закона.
Эксперимент Фарадея : Эксперимент Фарадея, показывающий индукцию между витками провода: Жидкостная батарея (справа) обеспечивает ток, который течет через маленькую катушку (А), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется.Но когда маленькую катушку перемещают внутрь или наружу из большой катушки (В), магнитный поток через большую катушку изменяется, вызывая ток, который регистрируется гальванометром (G).
Когда катушки неподвижны, ток не индуцируется.Но когда маленькую катушку перемещают внутрь или наружу из большой катушки (В), магнитный поток через большую катушку изменяется, вызывая ток, который регистрируется гальванометром (G).
Дифференциальная форма закона Фарадея
Магнитный поток равен [латекс]\Phi_\text{B} = \int_\text{S} \vec {\text{B}} \cdot \text{d} \vec {\text{A}}[/ латекс], где [латекс]\vec {\text{А}}[/латекс] — площадь вектора над замкнутой поверхностью S. Устройство, способное поддерживать разность потенциалов, несмотря на протекание тока, является источником электродвижущей силы .(ЭМП) Определение математически [латекс]\varepsilon = \oint_\text{C} \vec {\text{E}} \cdot \text{d}\vec {\text{s}}[/latex], где интеграл оценивается по замкнутому циклу C.
Закон Фарадея теперь можно переписать {\ partial \ text {t}} (\ int \ vec {\ text {B}} \ cdot \ text {d} \ vec {\ text {A}}) [/latex]. Используя теорему Стокса в векторном исчислении, левая часть равна [латекс]\oint_\text{C} \vec {\text{E}} \cdot \text{d}\vec {\text{s}} = \int_\text{S} (\nabla \times \vec {\text{E}}) \cdot \text{d}\vec {\text{A}}[/latex]. Также обратите внимание, что в правой части [латекс]\frac{\partial}{\partial \text{t}} (\int \vec {\text{B}} \cdot \text{d}\vec {\ текст {A}}) = \ int \ frac {\ partial \ vec {\ text {B}}} {\ partial \ text {t}} \ cdot \ text {d} \ vec {\ text {A}} [ /латекс]. Таким образом, мы получаем альтернативную форму закона индукции Фарадея: \text{t}}[/latex].Это также называется дифференциальной формой закона Фарадея. Это одно из четырех уравнений Максвелла, управляющих всеми электромагнитными явлениями.
Также обратите внимание, что в правой части [латекс]\frac{\partial}{\partial \text{t}} (\int \vec {\text{B}} \cdot \text{d}\vec {\ текст {A}}) = \ int \ frac {\ partial \ vec {\ text {B}}} {\ partial \ text {t}} \ cdot \ text {d} \ vec {\ text {A}} [ /латекс]. Таким образом, мы получаем альтернативную форму закона индукции Фарадея: \text{t}}[/latex].Это также называется дифференциальной формой закона Фарадея. Это одно из четырех уравнений Максвелла, управляющих всеми электромагнитными явлениями.
Электрогенераторы
Электрические генераторы преобразуют механическую энергию в электрическую; они индуцируют ЭДС, вращая катушку в магнитном поле.
Цели обучения
Объясните, как в электрических генераторах индуцируется электродвижущая сила
Ключевые выводы
Ключевые моменты
Генераторы
Основные термины
Электрические генераторы — это устройства, преобразующие механическую энергию в электрическую.Они индуцируют электродвижущую силу (ЭДС), вращая катушку в магнитном поле. Это устройство, которое преобразует механическую энергию в электрическую. Генератор заставляет электрический заряд (обычно переносимый электронами) течь через внешнюю электрическую цепь. К возможным источникам механической энергии относятся: поршневой или турбинный паровой двигатель, вода, падающая через турбину или водяное колесо, двигатель внутреннего сгорания, ветряная турбина, рукоятка, сжатый воздух или любой другой источник механической энергии. Генераторы обеспечивают почти всю мощность для электросетей, которые обеспечивают большую часть мировой электроэнергии.
Генераторы обеспечивают почти всю мощность для электросетей, которые обеспечивают большую часть мировой электроэнергии.
Генератор паровой турбины : Современный генератор паровой турбины.
Базовая настройка
Рассмотрим установку, показанную на рис. Заряды в проводах петли испытывают магнитную силу, потому что они движутся в магнитном поле. На заряды в вертикальных проводах действуют силы, параллельные проводу, вызывающие токи. Однако те, кто находится в верхнем и нижнем сегментах, чувствуют силу, перпендикулярную проводу; эта сила не вызывает тока.Таким образом, мы можем найти ЭДС индукции, рассматривая только боковые провода. ЭДС движения определяется как ЭДС=Bℓv, где скорость v перпендикулярна магнитному полю B (см. наш атом на «ЭДС движения»). Здесь скорость составляет угол θ с B, так что ее составляющая, перпендикулярная B, равна vsinθ.
Схема электрического генератора : Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, которая изменяется синусоидально во времени. Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для создания тока, а не наоборот.
Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для создания тока, а не наоборот.
Таким образом, в этом случае ЭДС, индуцируемая с каждой стороны, равна ЭДС=Bℓvsinθ, и они имеют одинаковое направление. Полная ЭДС [латекс]\varepsilon[/латекс] вокруг контура тогда:
[латекс]\varepsilon = 2 \text{Blv} \sin{\theta}[/латекс].
Это выражение верно, но оно не дает ЭДС как функцию времени. Для нахождения зависимости ЭДС от времени предположим, что катушка вращается с постоянной угловой скоростью ω.Угол θ связан с угловой скоростью соотношением θ=ωt, так что:
[латекс]\varepsilon = 2 \text{Blv} \sin{\omega \text{t}}[/latex].
Теперь линейная скорость v связана с угловой скоростью соотношением v=rω. Здесь r=w/2, так что v=(w/2)ω, и:
[латекс]\varepsilon = 2 \text{Bl} \frac{\text{w}}{2} \omega \sin{\omega \text{t}} = (\text{lw})\text{B }\omega \sin{\omega \text{t}}[/latex].
Заметив, что площадь петли равна A=ℓw, и учитывая N петель, мы находим, что:
[latex]\varepsilon = \text{NABw}~\sin{\omega \text{t}}[/latex] — ЭДС, индуцируемая в генераторной катушке из N витков и площади A, вращающейся с постоянной угловой скоростью в однородное магнитное поле Б.
Генераторы, показанные в этом Атоме, очень похожи на двигатели, показанные ранее. Это не случайно. Фактически двигатель становится генератором, когда его вал вращается.
Электродвигатели
Электродвигатель — это устройство, преобразующее электрическую энергию в механическую.
Цели обучения
Объясните, как создается сила в электродвигателях
Ключевые выводы
Ключевые моменты
Основные термины
Основные принципы работы двигателя такие же, как у генератора, за исключением того, что двигатель преобразует электрическую энергию в механическую (движение).(Сначала прочитайте наш атом об электрических генераторах.) Большинство электродвигателей используют взаимодействие магнитных полей и проводников с током для создания силы. Электродвигатели используются в таких разнообразных областях, как промышленные вентиляторы, воздуходувки и насосы, станки, бытовая техника, электроинструменты и дисковые накопители.
Сила Лоренца
Если бы вы поместили движущуюся заряженную частицу в магнитное поле, она испытала бы силу, называемую силой Лоренца:
[латекс]\текст{F}=\текст{q}\times \text{v}\times \text{B}[/latex]
Правило правой руки : Правило правой руки, показывающее направление силы Лоренца
, где v — скорость движущегося заряда, q — заряд, а B — магнитное поле. Ток в проводнике состоит из движущихся зарядов. Следовательно, катушка с током в магнитном поле также будет ощущать силу Лоренца. Для прямолинейного провода с током, который не движется, сила Лоренца равна:
Ток в проводнике состоит из движущихся зарядов. Следовательно, катушка с током в магнитном поле также будет ощущать силу Лоренца. Для прямолинейного провода с током, который не движется, сила Лоренца равна:
[латекс]\текст{F}=\текст{I}\times \text{L}\times \text{B}[/latex]
где F — сила (в ньютонах, Н), I — сила тока в проводе (в амперах, А), L — длина провода, находящегося в магнитном поле (в м) , а B — напряженность магнитного поля (в теслах, Тл).Направление силы Лоренца перпендикулярно как направлению тока, так и магнитного поля, и его можно найти с помощью правила правой руки, показанного на рис. Правой рукой направьте большой палец в направлении тока, и укажите пальцем в направлении магнитного поля. Теперь ваш безымянный палец будет указывать в направлении силы.
Крутящий момент : Сила на противоположных сторонах катушки будет направлена в противоположные стороны, поскольку заряды движутся в противоположных направлениях. Это означает, что катушка будет вращаться.
Это означает, что катушка будет вращаться.
Механика двигателя
И двигатели, и генераторы можно объяснить с точки зрения катушки, которая вращается в магнитном поле. В генераторе катушка подключается к внешней цепи, которая затем включается. Это приводит к изменению потока, который индуцирует электромагнитное поле. В двигателе катушка с током в магнитном поле испытывает силу с обеих сторон катушки, которая создает крутящую силу (называемую крутящим моментом), которая заставляет ее вращаться.Любая катушка с током может чувствовать силу в магнитном поле. Эта сила представляет собой силу Лоренца, действующую на движущиеся заряды в проводнике. Сила на противоположных сторонах катушки будет противоположной, потому что заряды движутся в противоположных направлениях. Это означает, что катушка будет вращаться.
Индуктивность
Индуктивность — это свойство устройства, которое говорит о том, насколько эффективно оно индуцирует ЭДС в другом устройстве или на самом себе.
Цели обучения
Описать свойства индуктора, различая взаимную индуктивность и самоиндукцию
Ключевые выводы
Ключевые моменты
Основные термины
Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы (см.«) Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется индуктивностью.
Взаимная индуктивность
Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. Посмотрите, где простые катушки наводят друг в друге ЭДС.
Взаимная индуктивность в катушках : Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор.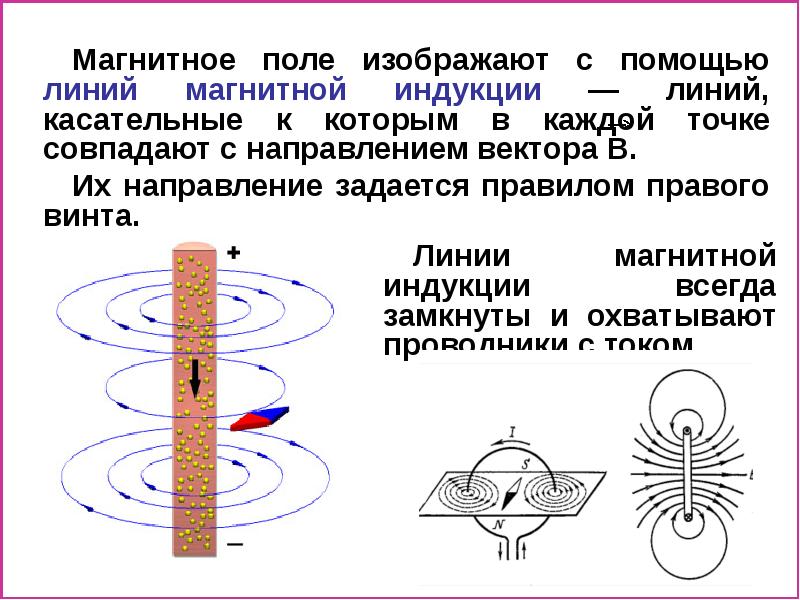 Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что «E2 индуцируется» представляет ЭДС индукции в катушке 2.)
Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что «E2 индуцируется» представляет ЭДС индукции в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, поток изменяется за счет изменения тока. Поэтому мы сосредоточимся на скорости изменения тока ΔI/Δt как на причине индукции. Изменение тока I 1 в одном устройстве, катушке 1, индуцирует ЭДС 2 в другом.Мы выражаем это в форме уравнения как
[латекс]\текст{ЭДС}_2 = -\текст{M} \frac{\Delta \text{I}_1}{\Delta \text{t}}[/latex],
, где М определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность М, тем эффективнее связь.
Природа здесь симметрична. Если мы изменим ток I2 в катушке 2, мы индуцируем ЭДС1 в катушке 1, которая равна
[латекс]\текст{ЭДС}_1 = -\текст{M} \frac{\Delta \text{I}_2}{\Delta \text{t}}[/latex],
, где М такое же, как и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью
Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью
М.
Самоиндукция
Самоиндукция, действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока ΔI через устройство.ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается
[латекс]\текст{ЭДС} = -\текст{L} \frac{\Delta \text{I}}{\Delta \text{t}}[/latex],
, где L — собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется индуктором. Опять же, знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока.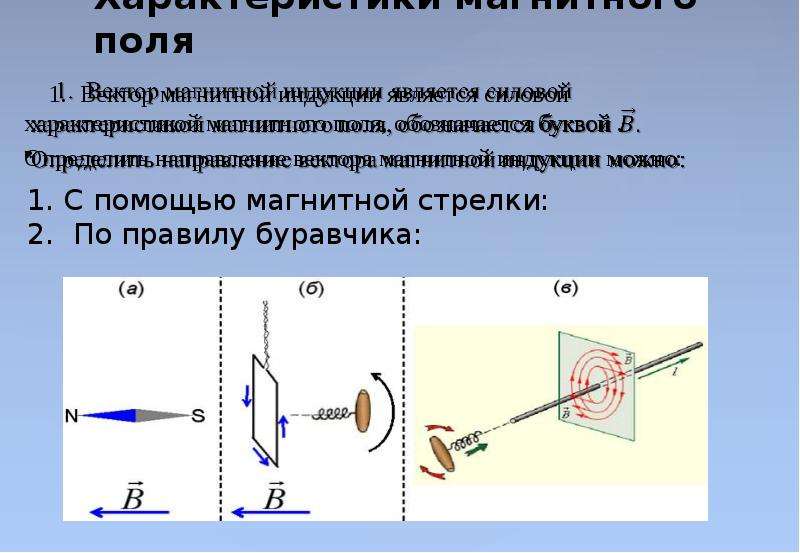
Количественная интерпретация ЭДС движения
A ЭДС движения – это электродвижущая сила (ЭДС), вызванная движением относительно магнитного поля B.
Цели обучения
Сформулируйте два представления, применяемые для расчета электродвижущей силы
Ключевые выводы
Ключевые моменты
Основные термины
Электродвижущая сила (ЭДС), вызванная движением относительно магнитного поля B, называется ЭДС движения. Вы могли заметить, что ЭДС движения очень похожа на индуцированную ЭДС, вызванную изменяющимся магнитным полем.В этом Атоме мы видим, что это действительно одно и то же явление, показанное в разных системах отсчета.
ЭДС движения
В случае, когда петля проводника движется в магнит, показанный на (а), магнитная сила, действующая на движущийся заряд в петле, определяется выражением [latex]evB[/latex] (сила Лоренца, e: заряд электрона).
Петля проводника, движущаяся в магните : (a) ЭДС движения. Петля с током движется в неподвижный магнит. Направление магнитного поля на экран.(б) Наведенная ЭДС. Токовая петля неподвижна, а магнит движется.
Под действием силы электроны будут накапливаться на одной стороне (нижний конец рисунка) до тех пор, пока поперек стержня не установится достаточное электрическое поле, противодействующее движению электронов, то есть [латекс]\текст{eE}[/ латекс]. Приравнивая две силы, получаем [латекс]\текст{Е} = \текст{vB}[/латекс].
Следовательно, ЭДС движения по длине L стороны петли определяется выражением [латекс]\varepsilon_{\text{движение}} = \text{vB} \times \text{L}[/latex] (уравнение .1), где L — длина объекта, движущегося со скоростью v относительно магнита.
Индуцированная ЭДС
Поскольку скорость изменения магнитного потока, проходящего через петлю, равна [латекс]\текст{В}\frac{\text{dA}}{\text{dt}}[/латекс](A: площадь петли через которое проходит магнитное поле), индуцированная ЭДС [латекс]\varepsilon_{\text{индуцируемая}} = \text{BLv}[/латекс] (уравнение 2).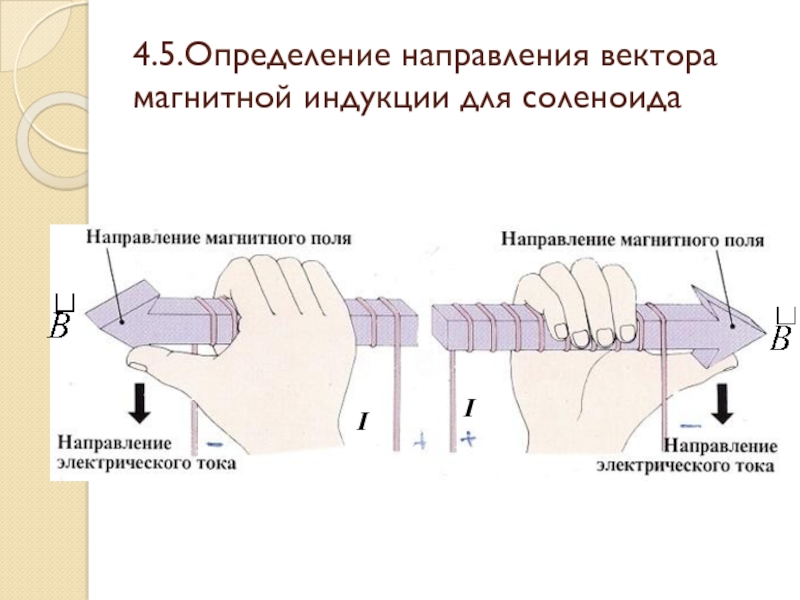
Эквивалентность ЭДС движения и индукции
Из уравнения. 1 и уравнение 2 мы можем подтвердить, что ЭДС движения и наведения дают одинаковый результат.На самом деле эквивалентность этих двух явлений и побудила Альберта Эйнштейна заняться специальной теорией относительности. В своей основополагающей статье по специальной теории относительности, опубликованной в 1905 году, Эйнштейн начинает с упоминания об эквивалентности двух явлений:
«……например, взаимное электродинамическое действие магнита и проводника. Наблюдаемое здесь явление зависит только от относительного движения проводника и магнита, тогда как обычная точка зрения проводит резкое различие между двумя случаями, в которых движется то одно, то другое из этих тел.В самом деле, если магнит движется, а проводник покоится, то вблизи магнита возникает электрическое поле с определенной энергией , производящее ток в местах, где части проводника расположенный. Но если магнит неподвижен, а проводник движется, то вблизи магнита не возникает никакого электрического поля. В проводнике, однако, мы находим электродвижущую силу, которой самой по себе нет соответствующей энергии, но которая порождает — при условии равенства относительного движения в двух обсуждаемых случаях — электрические токи того же пути и силы, что и производимые электрическими силами в первом случае.“
В проводнике, однако, мы находим электродвижущую силу, которой самой по себе нет соответствующей энергии, но которая порождает — при условии равенства относительного движения в двух обсуждаемых случаях — электрические токи того же пути и силы, что и производимые электрическими силами в первом случае.“
Механическая работа и электрическая энергия
Механическая работа, совершаемая внешней силой для создания ЭДС движения, преобразуется в тепловую энергию; в процессе сохраняется энергия.
Цели обучения
Применение закона сохранения энергии для описания производства движущей электродвижущей силы с механической работой
Ключевые выводы
Ключевые моменты
Основные термины
Мы узнали об ЭДС движения ранее (см. наш Атом в разделе «ЭДС движения»). Для простой установки, показанной ниже, ЭДС движения [латекс](\varepsilon)[/латекс], создаваемая движущимся проводником (в однородном поле), определяется следующим образом:
[латекс]\varepsilon = \text{Blv}[/латекс]
, где B — магнитное поле, l — длина проводящего стержня, v — (постоянная) скорость его движения. ( B , l и v перпендикулярны друг другу, как показано на изображении ниже. )
)
ЭДС движения : (a) ЭДС движения=Bℓv индуцируется между рельсами, когда этот стержень движется вправо в однородном магнитном поле. Магнитное поле B направлено внутрь страницы, перпендикулярно движущимся стержню и рельсам и, следовательно, ограниченной ими области. (b) Закон Ленца дает направления индуцированного поля и тока, а также полярность индуцированной ЭДС. Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или выходит за пределы страницы. Правило правой руки дает показанное направление тока, и полярность стержня будет управлять таким током.
Сохранение энергии
В этом атоме мы будем рассматривать систему с энергетической точки зрения . При движении стержня с током i на него будет действовать сила Лоренца
.
[латекс]\текст{F}_\текст{L} = \текст{iBL}[/латекс].
Чтобы стержень двигался с постоянной скоростью v , мы должны постоянно прикладывать внешнюю силу F ext (равную по модулю F L и противоположную по направлению) к стержню вдоль его движения . Поскольку стержень движется со скоростью 90 557 v 90 282 , мощность 90 557 P 90 282, передаваемая внешней силой, будет: 90 005
Поскольку стержень движется со скоростью 90 557 v 90 282 , мощность 90 557 P 90 282, передаваемая внешней силой, будет: 90 005
[латекс]\текст{P} = \text{F}_{\text{ext}} \text{v} = (\text{iBL})\times \text{v} = \text{i} \ варепсилон[/латекс].
На последнем шаге мы использовали первое уравнение, о котором говорили. Обратите внимание, что это именно мощность, рассеиваемая в петле (= ток [латекс]\умножить [/латекс] напряжение). Таким образом, мы заключаем, что механическая работа, совершаемая внешней силой для поддержания движения стержня с постоянной скоростью, преобразуется в тепловую энергию в петле.В более общем смысле механическая работа, совершаемая внешней силой для создания ЭДС движения, преобразуется в тепловую энергию. Энергия сохраняется в процессе.
Закон Ленца
В «Атоме» «Закон индукции Фарадея и закон Ленца» мы узнали, что закон Ленца является проявлением сохранения энергии. Как мы видим на примере с этим атомом, закон Ленца гарантирует, что движение стержня противоположно из-за тенденции природы сопротивляться изменению магнитного поля. Если бы индуцированная ЭДС была направлена в ту же сторону, что и изменение потока, то существовала бы положительная обратная связь, заставляющая стержень улетать от малейшего возмущения.
Если бы индуцированная ЭДС была направлена в ту же сторону, что и изменение потока, то существовала бы положительная обратная связь, заставляющая стержень улетать от малейшего возмущения.
Энергия в магнитном поле
Магнитное поле накапливает энергию. Плотность энергии определяется как [латекс]\текст{u} = \frac{\mathbf{\text{B}}\cdot\mathbf{\text{B}}}{2\mu}[/latex].
Цели обучения
Выразите плотность энергии магнитного поля в виде уравнения
Ключевые выводы
Ключевые моменты
Основные термины
Энергия необходима для создания магнитного поля как для работы против электрического поля, создаваемого изменяющимся магнитным полем, так и для изменения намагниченности любого материала в пределах магнитного поля.Для недисперсионных материалов эта же энергия высвобождается при разрушении магнитного поля. Следовательно, эту энергию можно смоделировать как «запасенную» в магнитном поле.
Магнитное поле, создаваемое соленоидом : Магнитное поле, создаваемое соленоидом (вид в разрезе), описываемое линиями поля. Энергия «запасается» в магнитном поле.
Энергия, запасенная в магнитном поле
Для линейных недисперсионных материалов (таких, что B = µ H, где µ, называемая проницаемостью, не зависит от частоты), плотность энергии равна:
[латекс]\текст{u} = \frac{\mathbf{\text{B}}\cdot\mathbf{\text{B}}}{2\mu} = \frac{\mu\mathbf{\text {H}}\cdot\mathbf{\text{H}}}{2}[/латекс].
Плотность энергии — это количество энергии, хранящейся в данной системе или области пространства на единицу объема. Если поблизости нет магнитных материалов, μ можно заменить на μ 0 . Однако приведенное выше уравнение нельзя использовать для нелинейных материалов; необходимо использовать более общее выражение (приведенное ниже).
В общем, дополнительная работа на единицу объема δВт , необходимая для того, чтобы вызвать небольшое изменение магнитного поля δ Б, составляет:
[латекс]\дельта\текст{W} = \mathbf{\text{H}}\cdot\delta\mathbf{\text{B}}[/латекс].
Когда отношение между H и B известно, это уравнение используется для определения работы, необходимой для достижения заданного магнитного состояния. Для гистерезисных материалов, таких как ферромагнетики и сверхпроводники, необходимая работа также зависит от того, как создается магнитное поле. Однако для линейных недисперсионных материалов общее уравнение приводит непосредственно к более простому уравнению плотности энергии, приведенному выше.
Энергия, накопленная в поле соленоида
Энергия, накопленная индуктором, равна количеству работы, необходимой для установления тока через индуктор и, следовательно, магнитного поля.2[/латекс].
Трансформаторы
Трансформаторы преобразуют напряжение из одного значения в другое; его функция определяется уравнением трансформатора.
Цели обучения
Применение уравнения трансформатора для сравнения вторичного и первичного напряжения
Ключевые выводы
Ключевые моменты
Основные термины
Трансформаторы изменяют напряжение с одного значения на другое. Например, такие устройства, как сотовые телефоны, ноутбуки, видеоигры, электроинструменты и небольшие бытовые приборы, имеют трансформатор (встроенный в их съемный блок), который преобразует 120 В в напряжение, подходящее для устройства.Трансформаторы также используются в нескольких точках в системах распределения электроэнергии, как показано на рис. . Энергия передается на большие расстояния при высоком напряжении, поскольку для заданной мощности требуется меньший ток (это означает меньшие потери в линии). Поскольку высокое напряжение представляет большую опасность, для получения более низкого напряжения в месте расположения пользователя используются трансформаторы.
. Энергия передается на большие расстояния при высоком напряжении, поскольку для заданной мощности требуется меньший ток (это означает меньшие потери в линии). Поскольку высокое напряжение представляет большую опасность, для получения более низкого напряжения в месте расположения пользователя используются трансформаторы.
Настройка трансформатора : Трансформаторы изменяют напряжение в нескольких точках системы распределения электроэнергии. Электроэнергия обычно вырабатывается при напряжении более 10 кВ и передается на большие расстояния при напряжении более 200 кВ, иногда до 700 кВ, для ограничения потерь энергии.Местное распределение электроэнергии в районы или предприятия проходит через подстанцию и передается на короткие расстояния при напряжении от 5 до 13 кВ. Оно снижено до 120, 240 или 480 В для обеспечения безопасности на объекте отдельного пользователя.
Рассматриваемый здесь тип трансформатора основан на законе индукции Фарадея и очень похож по конструкции на аппарат Фарадея, который использовался для демонстрации того, что магнитные поля могут создавать токи (показано на рис. ). Две катушки называются первичной и вторичной катушками.При нормальном использовании входное напряжение подается на первичную обмотку, а вторичная создает преобразованное выходное напряжение. Железный сердечник не только улавливает магнитное поле, создаваемое первичной катушкой, но и увеличивает его намагниченность. Поскольку входное напряжение переменного тока, изменяющийся во времени магнитный поток направляется на вторичную обмотку, индуцируя ее выходное напряжение переменного тока.
). Две катушки называются первичной и вторичной катушками.При нормальном использовании входное напряжение подается на первичную обмотку, а вторичная создает преобразованное выходное напряжение. Железный сердечник не только улавливает магнитное поле, создаваемое первичной катушкой, но и увеличивает его намагниченность. Поскольку входное напряжение переменного тока, изменяющийся во времени магнитный поток направляется на вторичную обмотку, индуцируя ее выходное напряжение переменного тока.
Простой трансформатор : Типичная конструкция простого трансформатора состоит из двух катушек, намотанных на ферромагнитный сердечник, ламинированный для минимизации вихревых токов.Магнитное поле, создаваемое первичной обмоткой, в основном ограничивается и усиливается сердечником, который передает его вторичной обмотке. Любое изменение тока в первичной обмотке индуцирует ток во вторичной обмотке. На рисунке показан простой трансформатор с двумя катушками, намотанными по обеим сторонам многослойного ферромагнитного сердечника. Набор катушек на левой стороне сердечника помечен как первичный, а его номер указан как N p. Напряжение на первичной обмотке определяется как V p. Набор катушек на правой стороне сердечника помечен как вторичный, а их количество представлено как Ns.Напряжение на вторичной обмотке определяется как V s. Символ трансформатора также показан под диаграммой. Он состоит из двух катушек индуктивности, разделенных двумя равными параллельными линиями, представляющими сердечник.
Набор катушек на левой стороне сердечника помечен как первичный, а его номер указан как N p. Напряжение на первичной обмотке определяется как V p. Набор катушек на правой стороне сердечника помечен как вторичный, а их количество представлено как Ns.Напряжение на вторичной обмотке определяется как V s. Символ трансформатора также показан под диаграммой. Он состоит из двух катушек индуктивности, разделенных двумя равными параллельными линиями, представляющими сердечник.
Уравнение трансформатора
Для простого трансформатора, показанного на рис., выходное напряжение V s почти полностью зависит от входного напряжения V p и соотношения числа витков в первичной и вторичной обмотках. Закон индукции Фарадея для вторичной катушки дает индуцированное выходное напряжение V s как:
[латекс]\текст{V}_\текст{s} = -\текст{N}_\текст{s} \frac{\Delta \Phi}{\Delta \text{t}}[/latex],
, где N s — количество витков во вторичной обмотке, а Δ/Δt — скорость изменения магнитного потока. Обратите внимание, что выходное напряжение равно ЭДС индукции (V s = ЭДС s ), при условии, что сопротивление катушки мало. Площадь поперечного сечения катушек одинакова с обеих сторон, как и напряженность магнитного поля, поэтому /Δt одинаково с обеих сторон. Входное первичное напряжение V p также связано с изменением потока:
Обратите внимание, что выходное напряжение равно ЭДС индукции (V s = ЭДС s ), при условии, что сопротивление катушки мало. Площадь поперечного сечения катушек одинакова с обеих сторон, как и напряженность магнитного поля, поэтому /Δt одинаково с обеих сторон. Входное первичное напряжение V p также связано с изменением потока:
[латекс]\текст{V}_\текст{p} = -\текст{N}_\текст{p} \frac{\Delta \Phi}{\Delta \text{t}}[/latex].
Соотношение этих двух последних уравнений дает полезное соотношение:
[латекс]\frac{\text{V}_\text{s}}{\text{V}_\text{p}} = \frac{\text{N}_\text{s}}{\ текст{N}_\текст{p}}[/латекс].
Это известно как уравнение трансформатора , которое просто утверждает, что отношение вторичного напряжения к первичному в трансформаторе равно отношению числа витков в его катушках. Выходное напряжение трансформатора может быть меньше, больше или равно входному напряжению, в зависимости от соотношения числа витков в их катушках. Некоторые трансформаторы даже обеспечивают переменную мощность, позволяя выполнять подключение в разных точках вторичной обмотки.Повышающий трансформатор — это тот, который увеличивает напряжение, тогда как понижающий трансформатор уменьшает напряжение.
Некоторые трансформаторы даже обеспечивают переменную мощность, позволяя выполнять подключение в разных точках вторичной обмотки.Повышающий трансформатор — это тот, который увеличивает напряжение, тогда как понижающий трансформатор уменьшает напряжение.
Предполагая, как и мы, что сопротивление пренебрежимо мало, выходная электрическая мощность трансформатора равна его входной мощности. Приравнивание входной и выходной мощности,
[латекс]\текст{P}_\текст{p} = \text{I}_\text{p} \text{V}_\text{p} = \text{I}_\text{s} \text{V}_\text{s} = \text{P}_\text{s}[/latex].
Объединяя этот результат с уравнением трансформатора, мы находим:
[латекс]\frac{\text{I}_\text{s}}{\text{I}_\text{p}} = \frac{\text{N}_\text{p}}{\ текст{N}_\текст{s}}[/латекс].
Таким образом, если напряжение увеличивается, ток уменьшается. И наоборот, если напряжение уменьшается, ток увеличивается.
.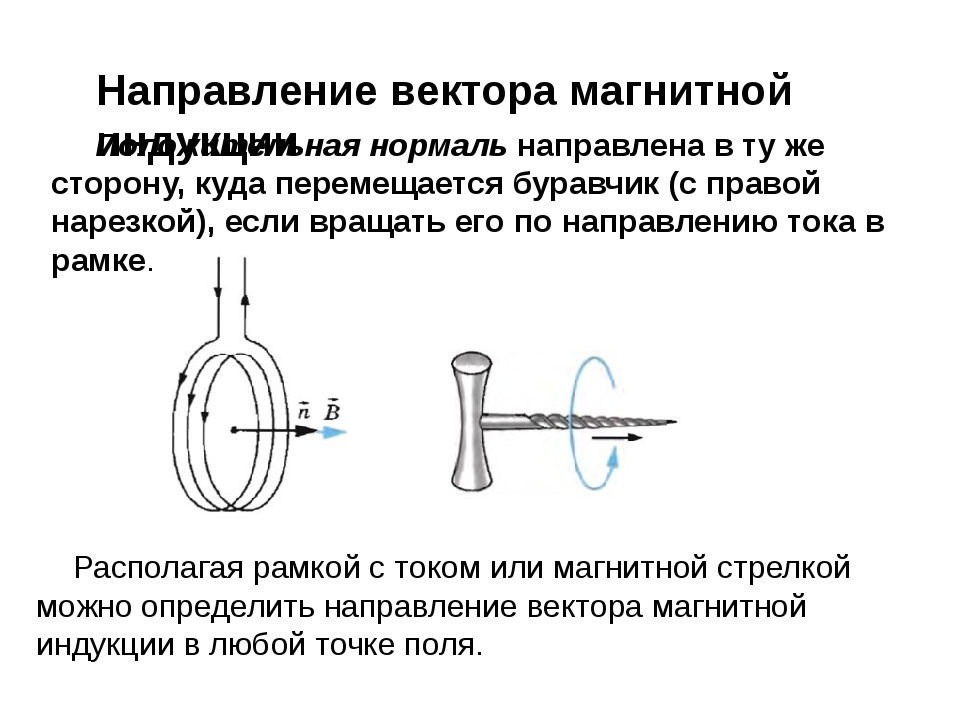



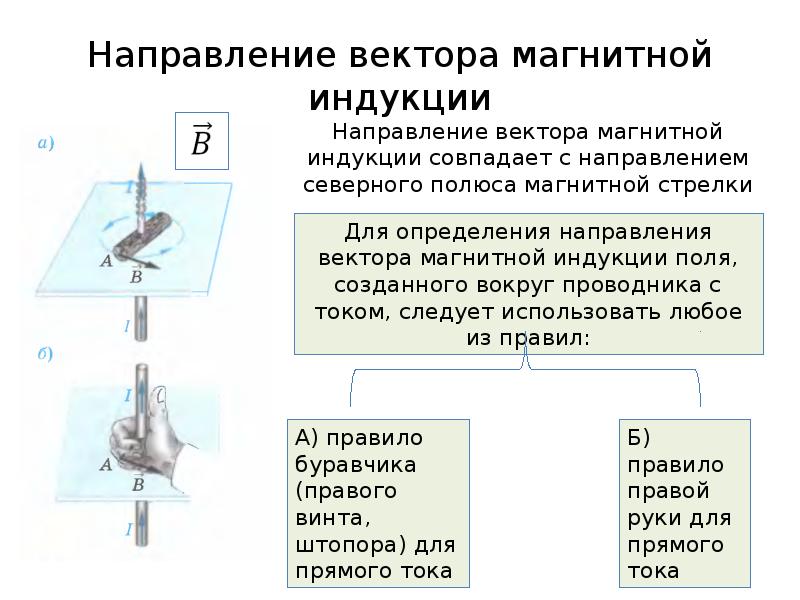 (-6). Результат поделите на длину соленоида L, B=N I μ/L. Направление вектора магнитной индукции внутри соленоида определите так же, как и в случае с одним витком проводника.
(-6). Результат поделите на длину соленоида L, B=N I μ/L. Направление вектора магнитной индукции внутри соленоида определите так же, как и в случае с одним витком проводника. Один из концов стрелки притянется . Если к магниту притянулся северный полюс стрелки, значит на магните это южный полюс, и наоборот. Используйте правило, что силовые линии магнитного поля выходят из северного полюса магнита (не стрелки!) и входят в южный.
Один из концов стрелки притянется . Если к магниту притянулся северный полюс стрелки, значит на магните это южный полюс, и наоборот. Используйте правило, что силовые линии магнитного поля выходят из северного полюса магнита (не стрелки!) и входят в южный. Зарисуйте линии на схеме. Постройте к ним по касательной вектор, который покажет направление индукции магнитного поля.
Зарисуйте линии на схеме. Постройте к ним по касательной вектор, который покажет направление индукции магнитного поля.

 Её называют нейтральной зоной
Её называют нейтральной зоной Но вскоре поняли, что изолированных магнитных зарядов не существует.
Но вскоре поняли, что изолированных магнитных зарядов не существует. Ферромагнетиками являются такие химические элементы, как железо, кобальт, никель, а также некоторые сплавы.
Ферромагнетиками являются такие химические элементы, как железо, кобальт, никель, а также некоторые сплавы. Конечно, Эрстед поначалу подумал, что это просто случайность. Но, повторив опыт в тех же условиях, он получил тот же результат. Тогда он начал менять расстояние от провода до стрелки. Чем бόльшим оно было, тем слабее отклонялась стрелка. Но и это ещё не всё. Пропуская ток через провода, сделанные из разных металлов, он обнаружил, что даже те из них, которые не обладали магнитными свойствами, вдруг становились магнитами, когда через них проходил электрический ток. Стрелка отклонялась, даже когда её отделяли от провода с током экранами из материалов, не проводящих ток: дерева, стекла, камней. Даже когда её поместили в резервуар с водой, она всё равно продолжала отклоняться. При разрыве электрической цепи магнитная стрелка компаса возвращалась в исходное состояние. Это означало, что проводник, по которому идёт электрический ток, создаёт магнитное поле
Конечно, Эрстед поначалу подумал, что это просто случайность. Но, повторив опыт в тех же условиях, он получил тот же результат. Тогда он начал менять расстояние от провода до стрелки. Чем бόльшим оно было, тем слабее отклонялась стрелка. Но и это ещё не всё. Пропуская ток через провода, сделанные из разных металлов, он обнаружил, что даже те из них, которые не обладали магнитными свойствами, вдруг становились магнитами, когда через них проходил электрический ток. Стрелка отклонялась, даже когда её отделяли от провода с током экранами из материалов, не проводящих ток: дерева, стекла, камней. Даже когда её поместили в резервуар с водой, она всё равно продолжала отклоняться. При разрыве электрической цепи магнитная стрелка компаса возвращалась в исходное состояние. Это означало, что проводник, по которому идёт электрический ток, создаёт магнитное поле Это векторная величина, определяющая его действие на движущиеся заряды в данной точке поля.
Это векторная величина, определяющая его действие на движущиеся заряды в данной точке поля. Рассыпав на куске гладкого картона или стекла железные опилки и положив его на магнит, можно увидеть, как опилки располагаются по определённым линиям. Эти линии имеют форму силовых линий магнитного поля.
Рассыпав на куске гладкого картона или стекла железные опилки и положив его на магнит, можно увидеть, как опилки располагаются по определённым линиям. Эти линии имеют форму силовых линий магнитного поля.




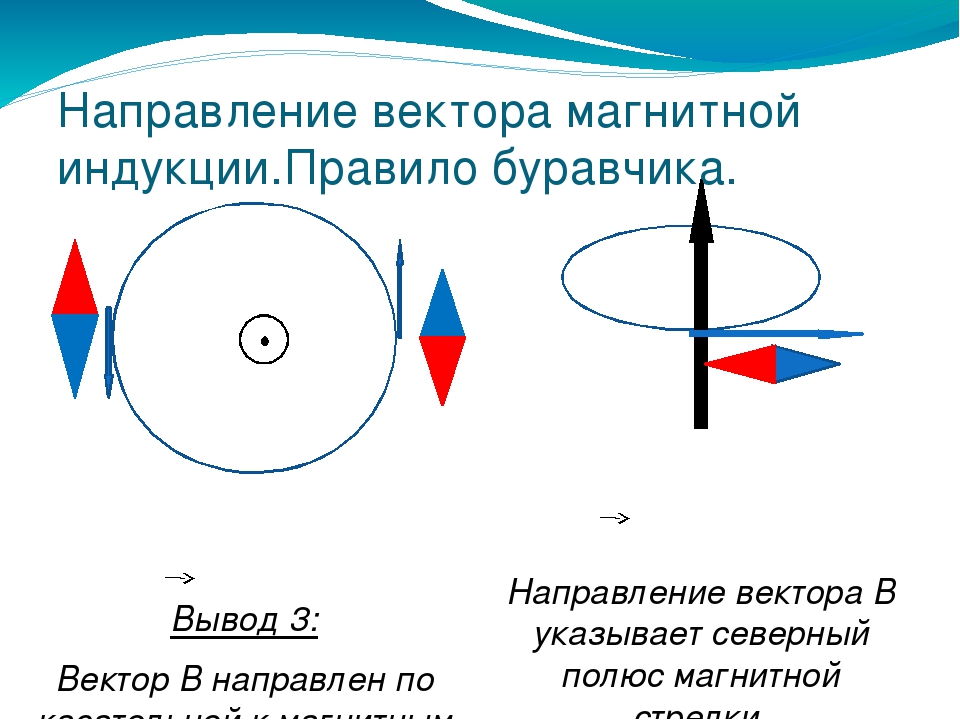 Правда, длятся они недолго. И спустя некоторое время магнитное поле восстанавливается. Но проблем они могут создать немало, так как влияют на работу линий электропередач, радиосвязи, вызывают сбои в работе различных приборов, ухудшают работу сердечно-сосудистой, дыхательной и нервной систем человека. Особенно чувствительны к ним метеозависимые люди.
Правда, длятся они недолго. И спустя некоторое время магнитное поле восстанавливается. Но проблем они могут создать немало, так как влияют на работу линий электропередач, радиосвязи, вызывают сбои в работе различных приборов, ухудшают работу сердечно-сосудистой, дыхательной и нервной систем человека. Особенно чувствительны к ним метеозависимые люди.
 Этот ток называется индукционным током
Этот ток называется индукционным током Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки
Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки
 Поэтому, согласно формуле (1), имеем . Но , поэтому
Поэтому, согласно формуле (1), имеем . Но , поэтому Но множители и как раз и образуют магнитный поток!
Но множители и как раз и образуют магнитный поток!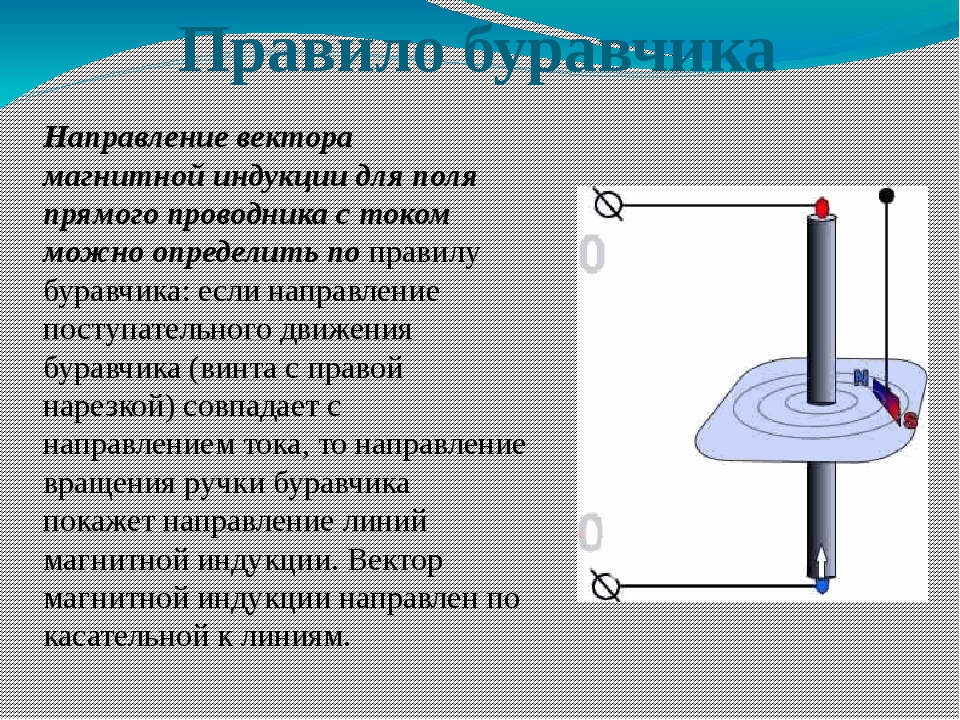
 Стало быть, единицы измерения обеих частей пропорциональности (4)
Стало быть, единицы измерения обеих частей пропорциональности (4)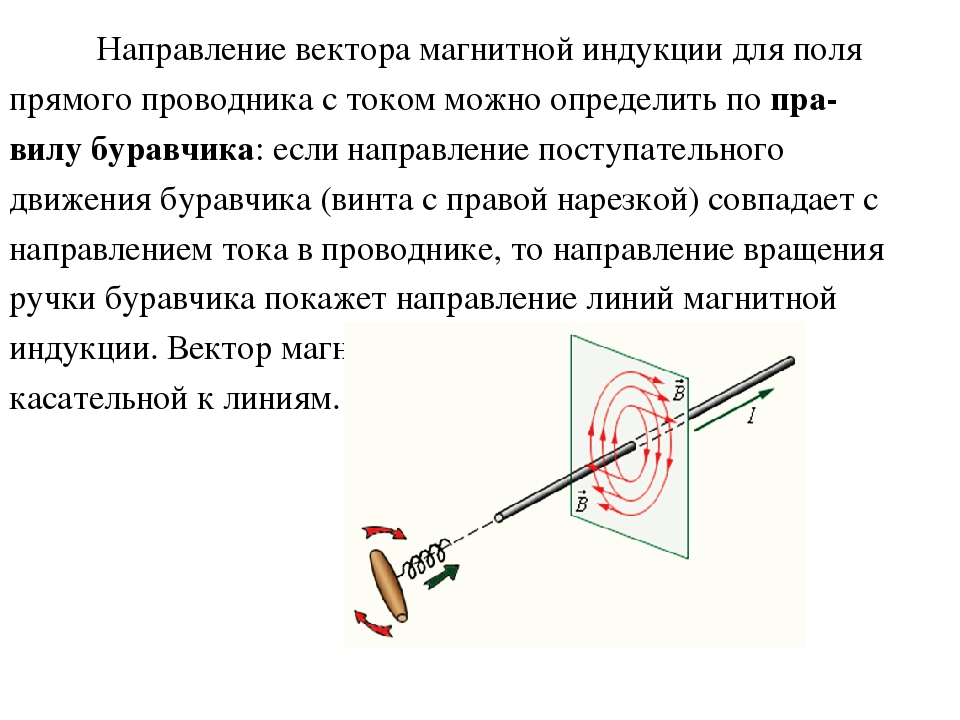
 Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против
Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против
 Результат получается следующий.
Результат получается следующий.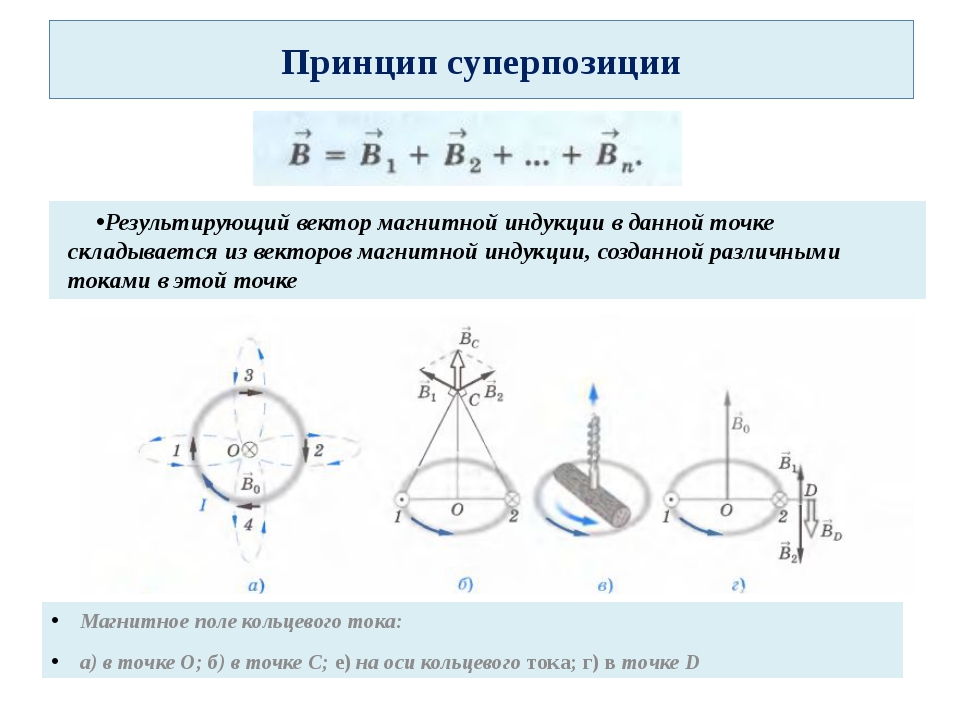
 Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным .
Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.
Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации. Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток. 8
8
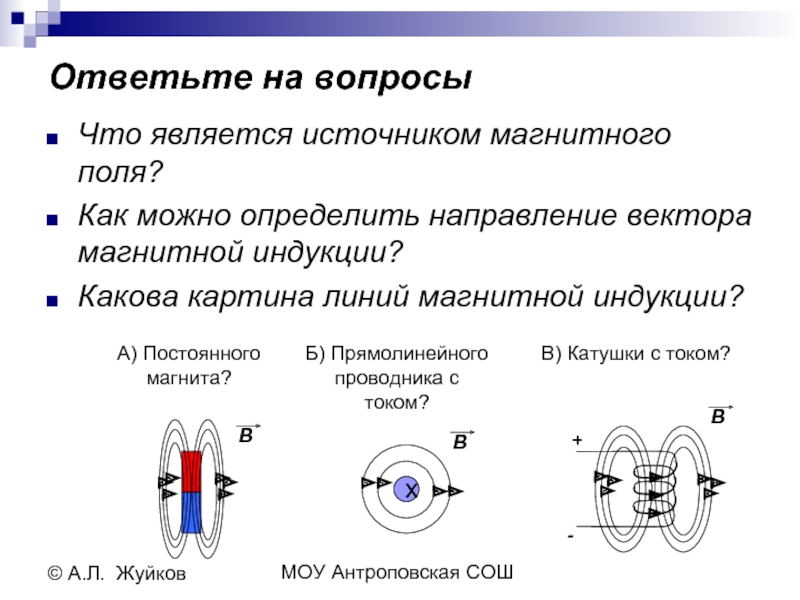 По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9
По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9
 9
9 Сравните энергии магнитного поля этих катушек
Сравните энергии магнитного поля этих катушек 14 Парамагнитные и ферромагнитные материалы
14 Парамагнитные и ферромагнитные материалы Индукционное магнитное поле B будет стремиться выровнять дипольные моменты, потому что энергия меньше при параллельном выравнивании диполей. Индуцированное магнитное поле выровненных магнитных диполей M добавляется к приложенному извне магнитному полю H. Таким образом, магнитное поле равно
Индукционное магнитное поле B будет стремиться выровнять дипольные моменты, потому что энергия меньше при параллельном выравнивании диполей. Индуцированное магнитное поле выровненных магнитных диполей M добавляется к приложенному извне магнитному полю H. Таким образом, магнитное поле равно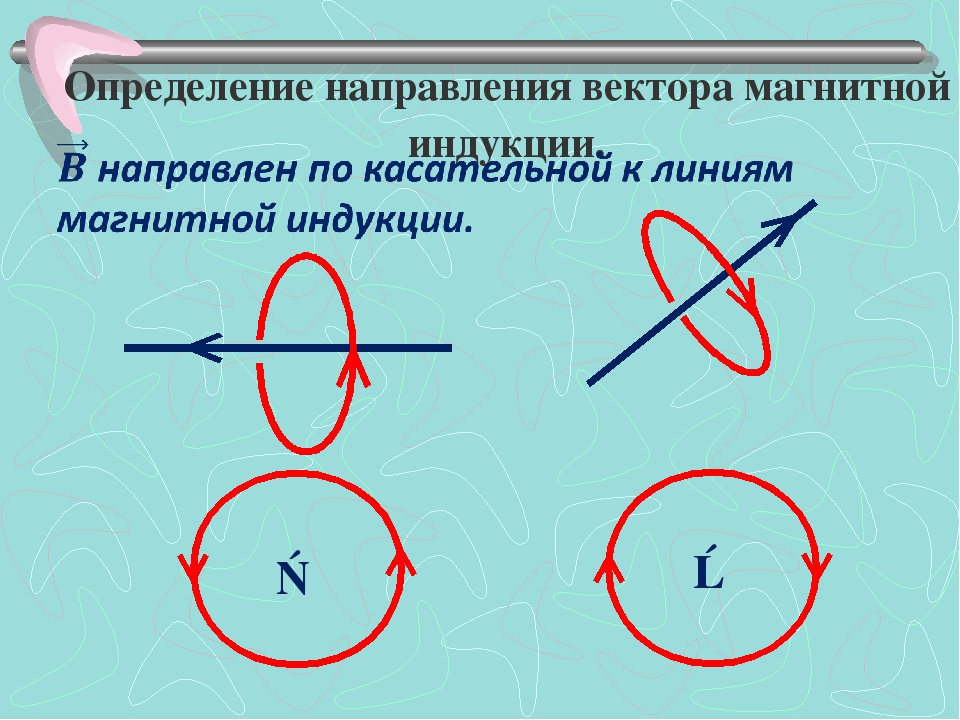
 Каждый домен полностью намагничен в одном направлении, но ориентация доменов случайна, так что направление намагниченности меняется от одного домена к другому.Случайная ориентация доменов возникает из-за того, что случайные домены создают более низкое энергетическое состояние, чем полностью выровненные домены. Приложенное магнитное поле несколько выравнивает эти домены, так что их магнитные поля более выровнены, тем самым увеличивая магнитное поле материала в целом. Увеличение приложенного магнитного поля выше магнитного поля насыщения не приводит к дальнейшему увеличению намагниченности материала, поскольку домены достигают максимально возможного взаимного выравнивания. При снятии внешнего магнитного поля домены и их границы не возвращаются полностью к исходной ориентации, поэтому домены проявляют гистерезис.Единственными ферромагнитными элементами являются железо, кобальт, никель, гадолиний и диспрозий.
Каждый домен полностью намагничен в одном направлении, но ориентация доменов случайна, так что направление намагниченности меняется от одного домена к другому.Случайная ориентация доменов возникает из-за того, что случайные домены создают более низкое энергетическое состояние, чем полностью выровненные домены. Приложенное магнитное поле несколько выравнивает эти домены, так что их магнитные поля более выровнены, тем самым увеличивая магнитное поле материала в целом. Увеличение приложенного магнитного поля выше магнитного поля насыщения не приводит к дальнейшему увеличению намагниченности материала, поскольку домены достигают максимально возможного взаимного выравнивания. При снятии внешнего магнитного поля домены и их границы не возвращаются полностью к исходной ориентации, поэтому домены проявляют гистерезис.Единственными ферромагнитными элементами являются железо, кобальт, никель, гадолиний и диспрозий. В трехмерных кристаллических полосах, где имеет место ферромагнитное действие, и в других неферромагнитных, парамагнитных элементах кулоновское отталкивание между парой электронов имеет тенденцию перемещать электроны дальше друг от друга в антисимметричное пространственное состояние минимальной энергии.Эта асимметрия полной волновой функции требует симметричного спинового состояния, в котором спины неспаренных электронов выровнены в одном направлении. Таким образом, кулоновская сила, которая раздвигает электроны для минимизации энергии, затем приводит к их выравниванию с параллельными спинами в парамагнитных и ферромагнитных материалах.
В трехмерных кристаллических полосах, где имеет место ферромагнитное действие, и в других неферромагнитных, парамагнитных элементах кулоновское отталкивание между парой электронов имеет тенденцию перемещать электроны дальше друг от друга в антисимметричное пространственное состояние минимальной энергии.Эта асимметрия полной волновой функции требует симметричного спинового состояния, в котором спины неспаренных электронов выровнены в одном направлении. Таким образом, кулоновская сила, которая раздвигает электроны для минимизации энергии, затем приводит к их выравниванию с параллельными спинами в парамагнитных и ферромагнитных материалах.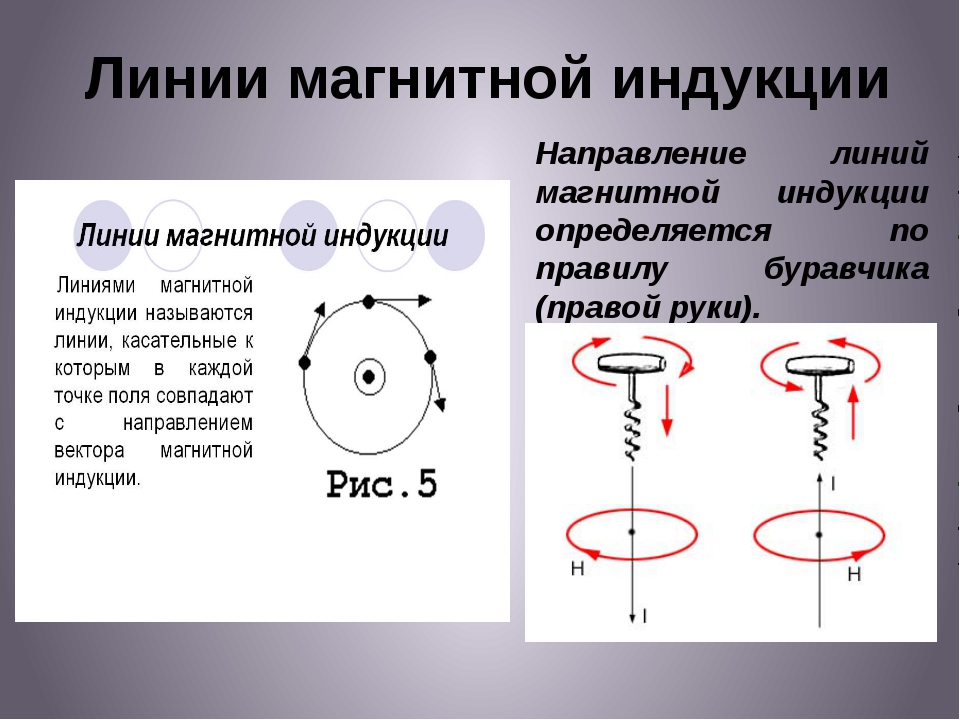 Для сохранения полной асимметричной волновой функции для набора электронов, принадлежащих близко расположенным соседним атомам, которые имеют перекрывающиеся d-оболочки неспаренных электронов, есть две возможности. В ферромагнитном случае (скажем, для атомов железа) пространственная волновая функция может быть асимметричной, а спиновая — симметричной.В этом случае кулоновская энергия минимизируется за счет разделения электронов, но разделение позволяет неспаренным электронам выровнять свои спины параллельно. Другая возможность заключается в том, что пространственная волновая функция будет симметричной, а электроны локализованы вместе, и, следовательно, их спиновая волновая функция должна быть антисимметричной, что требует антипараллельности спинов электронов. Антиферромагнитная возможность не минимизирует кулоновскую энергию в железе и не реализуется.Однако такие материалы, как MnO 2 , являются антиферромагнитными.
Для сохранения полной асимметричной волновой функции для набора электронов, принадлежащих близко расположенным соседним атомам, которые имеют перекрывающиеся d-оболочки неспаренных электронов, есть две возможности. В ферромагнитном случае (скажем, для атомов железа) пространственная волновая функция может быть асимметричной, а спиновая — симметричной.В этом случае кулоновская энергия минимизируется за счет разделения электронов, но разделение позволяет неспаренным электронам выровнять свои спины параллельно. Другая возможность заключается в том, что пространственная волновая функция будет симметричной, а электроны локализованы вместе, и, следовательно, их спиновая волновая функция должна быть антисимметричной, что требует антипараллельности спинов электронов. Антиферромагнитная возможность не минимизирует кулоновскую энергию в железе и не реализуется.Однако такие материалы, как MnO 2 , являются антиферромагнитными. Линии магнитного поля образуют концентрические окружности вокруг проволоки. Направление магнитного поля зависит от направления тока. Его можно определить с помощью «правила правой руки», указав большим пальцем правой руки в направлении течения. Направление линий магнитного поля совпадает с направлением ваших согнутых пальцев.Величина магнитного поля зависит от величины тока и расстояния от несущего заряд провода. В формулу входит константа . Это называется проницаемостью свободного пространства и имеет значение . Единицей магнитного поля является Тесла, т.
Линии магнитного поля образуют концентрические окружности вокруг проволоки. Направление магнитного поля зависит от направления тока. Его можно определить с помощью «правила правой руки», указав большим пальцем правой руки в направлении течения. Направление линий магнитного поля совпадает с направлением ваших согнутых пальцев.Величина магнитного поля зависит от величины тока и расстояния от несущего заряд провода. В формулу входит константа . Это называется проницаемостью свободного пространства и имеет значение . Единицей магнитного поля является Тесла, т.
 Таким образом, величина магнитного поля на указанном расстоянии составляет:
Таким образом, величина магнитного поля на указанном расстоянии составляет: Магнитные силовые линии в регионе дают ощущение
Магнитные силовые линии в регионе дают ощущение
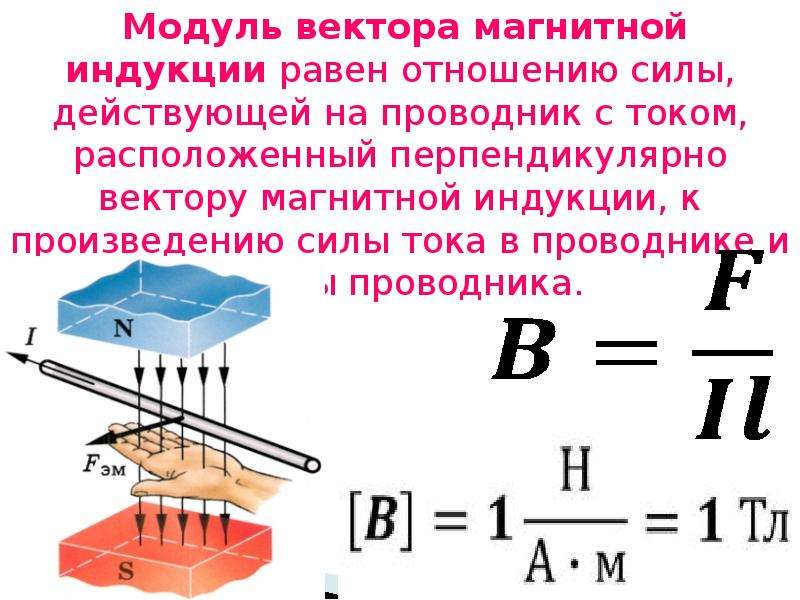
 Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? В главе 28 мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода? Мы можем использовать закон Био-Савара, чтобы ответить на все эти вопросы, включая определение магнитного поля длинного прямого провода.
Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? В главе 28 мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода? Мы можем использовать закон Био-Савара, чтобы ответить на все эти вопросы, включая определение магнитного поля длинного прямого провода. Используя правило правой руки 1 из предыдущей главы, указывает за пределы страницы для любого элемента вдоль проводника. Таким образом, в точке P магнитные поля, обусловленные всеми элементами тока, имеют одинаковое направление.Это означает, что мы можем вычислить там чистое поле, оценивая скалярную сумму вкладов элементов. С имеем из закона Био-Савара
Используя правило правой руки 1 из предыдущей главы, указывает за пределы страницы для любого элемента вдоль проводника. Таким образом, в точке P магнитные поля, обусловленные всеми элементами тока, имеют одинаковое направление.Это означает, что мы можем вычислить там чистое поле, оценивая скалярную сумму вкладов элементов. С имеем из закона Био-Савара Поскольку поле уменьшается с расстоянием от провода, расстояние между линиями поля должно соответственно увеличиваться с расстоянием. Направление этого магнитного поля можно найти с помощью второй формы правила правой руки (показано на (рис.)). Если вы держите провод правой рукой так, чтобы большой палец был направлен вдоль тока, то ваши пальцы обхватывают провод в том же смысле, что и
Поскольку поле уменьшается с расстоянием от провода, расстояние между линиями поля должно соответственно увеличиваться с расстоянием. Направление этого магнитного поля можно найти с помощью второй формы правила правой руки (показано на (рис.)). Если вы держите провод правой рукой так, чтобы большой палец был направлен вдоль тока, то ваши пальцы обхватывают провод в том же смысле, что и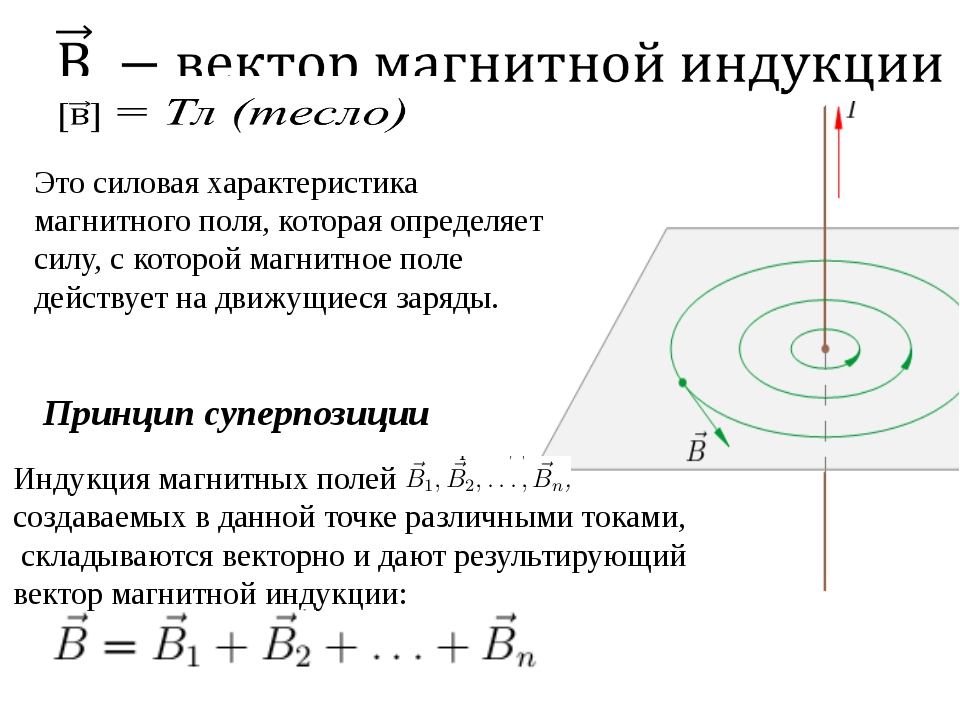


 Каково магнитное поле на земле непосредственно под проводом? Сравните свой ответ с магнитным полем Земли.
Каково магнитное поле на земле непосредственно под проводом? Сравните свой ответ с магнитным полем Земли.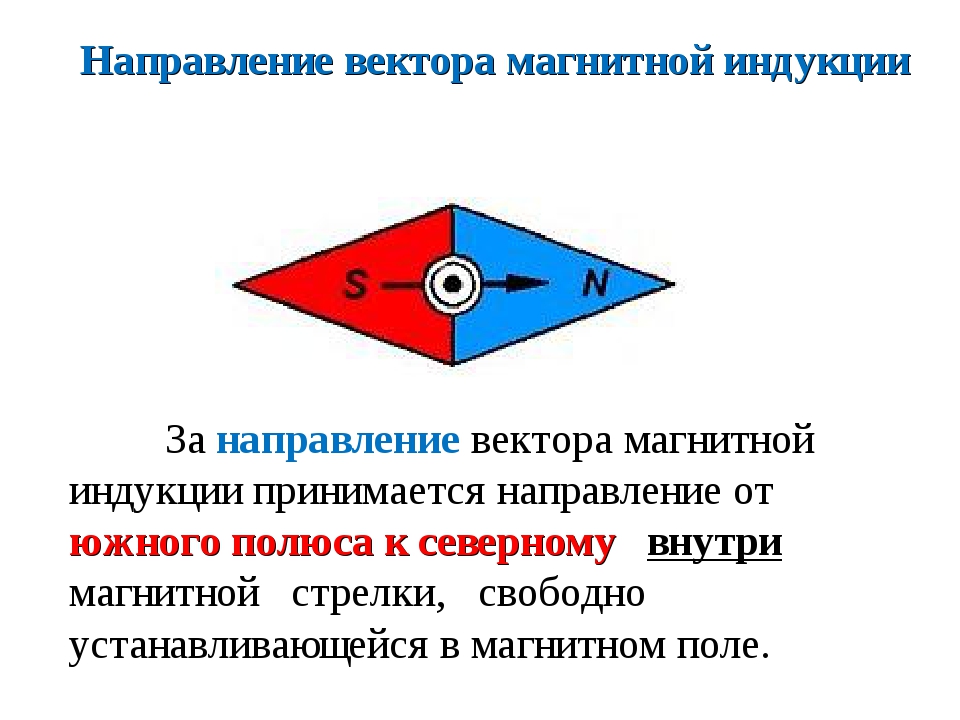


 Поскольку мы можем произвольно изменять размеры петли и получать тот же результат, единственное физическое объяснение состоит в том, что подынтегральные функции на самом деле равны, то есть магнитное поле внутри соленоида радиально однородно. Заметьте, однако, что ничто не запрещает ему изменяться в продольном направлении, что на самом деле и происходит.
Поскольку мы можем произвольно изменять размеры петли и получать тот же результат, единственное физическое объяснение состоит в том, что подынтегральные функции на самом деле равны, то есть магнитное поле внутри соленоида радиально однородно. Заметьте, однако, что ничто не запрещает ему изменяться в продольном направлении, что на самом деле и происходит. Закон Гаусса для магнетизма). Линии магнитного поля следуют вдоль продольного пути соленоида внутри, поэтому они должны идти в противоположном направлении снаружи соленоида, чтобы линии могли образовать петлю. Однако объем снаружи соленоида намного больше, чем объем внутри, поэтому плотность силовых линий магнитного поля снаружи сильно снижается. Теперь вспомним, что поле снаружи постоянно.Чтобы общее количество линий поля сохранялось, внешнее поле должно стремиться к нулю по мере того, как соленоид становится длиннее.
Закон Гаусса для магнетизма). Линии магнитного поля следуют вдоль продольного пути соленоида внутри, поэтому они должны идти в противоположном направлении снаружи соленоида, чтобы линии могли образовать петлю. Однако объем снаружи соленоида намного больше, чем объем внутри, поэтому плотность силовых линий магнитного поля снаружи сильно снижается. Теперь вспомним, что поле снаружи постоянно.Чтобы общее количество линий поля сохранялось, внешнее поле должно стремиться к нулю по мере того, как соленоид становится длиннее. Этимология Соленоид : 1827, французский solenoide , греческий solen «труба, канал» + сочетание формы греческого eidos «форма, форма» [1]
Этимология Соленоид : 1827, французский solenoide , греческий solen «труба, канал» + сочетание формы греческого eidos «форма, форма» [1] 

 Движение является одной из основных причин индукции.
Движение является одной из основных причин индукции.



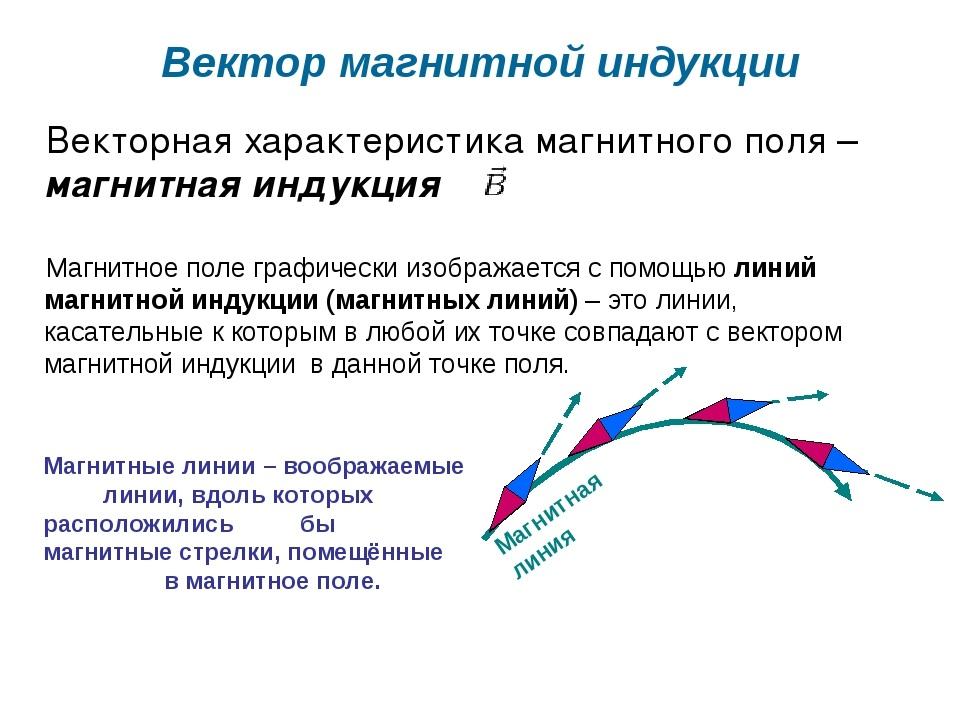 Их основное применение заключается в передаче энергии между различными уровнями напряжения, что позволяет выбрать наиболее подходящее напряжение для производства, передачи и распределения электроэнергии по отдельности.
Их основное применение заключается в передаче энергии между различными уровнями напряжения, что позволяет выбрать наиболее подходящее напряжение для производства, передачи и распределения электроэнергии по отдельности.
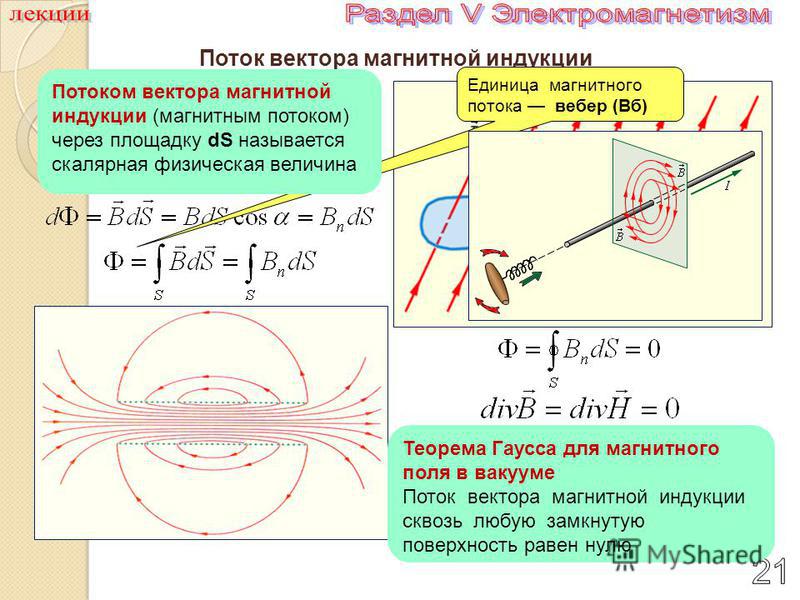

 Это приводит нас к другому полезному уравнению: [латекс]\frac{\text{I}_\text{s}}{\text{I}_\text{p}} = \frac{\text{N}_\ text{p}}{\text{N}_\text{s}}[/latex]. Если напряжение увеличивается, ток уменьшается. И наоборот, если напряжение уменьшается, ток увеличивается.
Это приводит нас к другому полезному уравнению: [латекс]\frac{\text{I}_\text{s}}{\text{I}_\text{p}} = \frac{\text{N}_\ text{p}}{\text{N}_\text{s}}[/latex]. Если напряжение увеличивается, ток уменьшается. И наоборот, если напряжение уменьшается, ток увеличивается.