Урок 9. конденсатор и катушка индуктивности в цепи переменного электрического тока — Физика — 11 класс
Физика, 11 класс
Урок 9. Конденсатор и катушка индуктивности в цепи переменного электрического тока
Перечень вопросов, рассматриваемых на уроке:
Процессы, происходящие в цепи переменного электрического тока при наличии конденсатора и катушки индуктивности;
Устройство и принцип действия генератора переменного тока и трансформатора;
Автоколебания;
Проблемы передачи электроэнергии и способы повышения эффективности её использования.
Глоссарий по теме
Автоколебания – незатухающие колебания в системе, поддерживаемые за счет постоянного источника энергии.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами.
Трансформатор – устройство, применяемое для повышения или понижения переменного напряжения.
Коэффициент трансформации – величина равная отношению напряжений в первичной и вторичной обмотках трансформатора.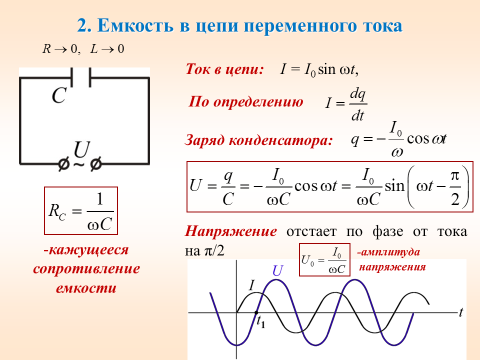
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.
Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.
Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004
Основное содержание урока
Переменный ток, которым мы пользуемся, вырабатывается с помощью генераторов переменного тока на электростанциях. Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.
В июле 1832 года Фарадей получил анонимное письмо, в котором автор описывал устройство созданного им генератора постоянного тока. Ознакомившись с содержанием письма Фарадей тут же отослал его в редакцию научного журнала.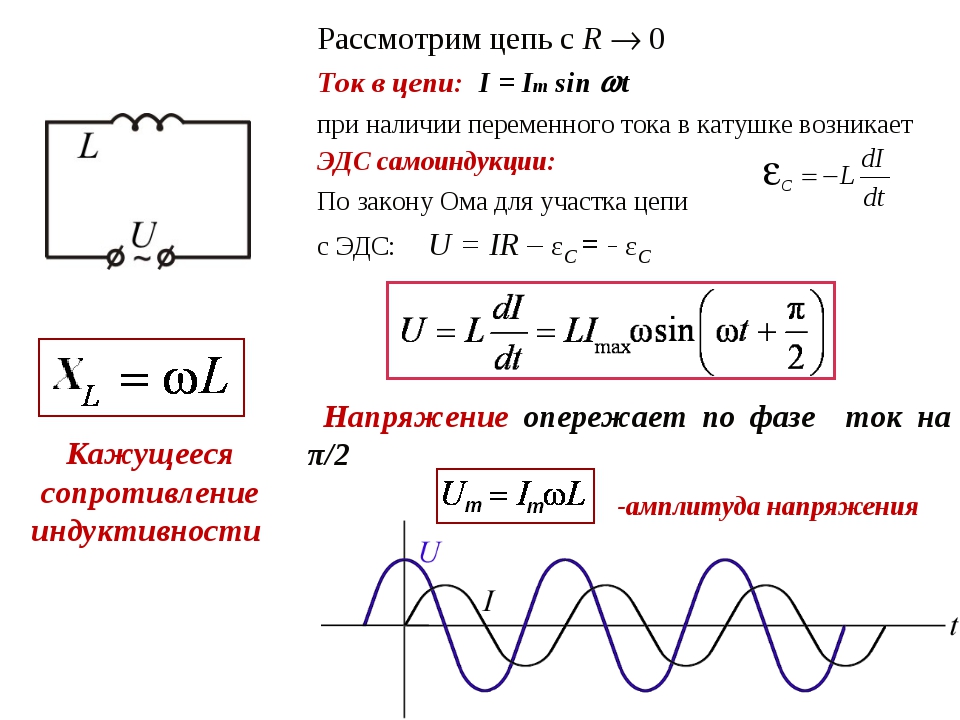
Автор этого письма не назвал себя, его фамилия осталась неизвестной.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами. Впоследствии генераторы постоянного тока непрерывно совершенствовались. Потом, когда начали использовать переменный ток они уступили место генераторам переменного тока. Переменный ток в основном вырабатывается генераторами переменного тока. Простой моделью генератора может служить прямоугольная рамка, вращающаяся в магнитном поле. При вращении рамки, магнитный поток пронизывающий площадь поверхности, ограниченную рамкой, меняется по гармоническому закону:
N- число витков.
Возникает ЭДС индукции который меняется по гармоническому закону.
ЭДС индукции в рамке равна:
Если с помощью контактных колец и скользящих по ним щёток соединить концы рамки с электрической цепью, то в цепи возникнет переменный ток.
В современной энергетике для производства электроэнергии используются электромеханические индукционные генераторы.
Принцип действия таких генераторов основан на явлении электромагнитной индукции. Основными частями генератора являются статор и ротор. Неподвижная часть генератора называется статором, а вращающаяся – ротором.
Постоянный ток не может идти по цепи содержащей конденсатор, т. к. цепь оказывается разомкнутой. При включении конденсатора в цепь переменного тока конденсатор будет периодически заряжаться и разряжаться с частотой равной частоте приложенного напряжения. В результате периодически меняющихся процессов зарядки и разрядки конденсатора в цепи течет переменный ток. Лампа накаливания, включенная в цепь переменного тока последовательно с конденсатором кажется горящей непрерывно, т.к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.
Величину ХC, обратную произведению циклической частоты на электрическую ёмкость конденсатора называют ёмкостным сопротивлением.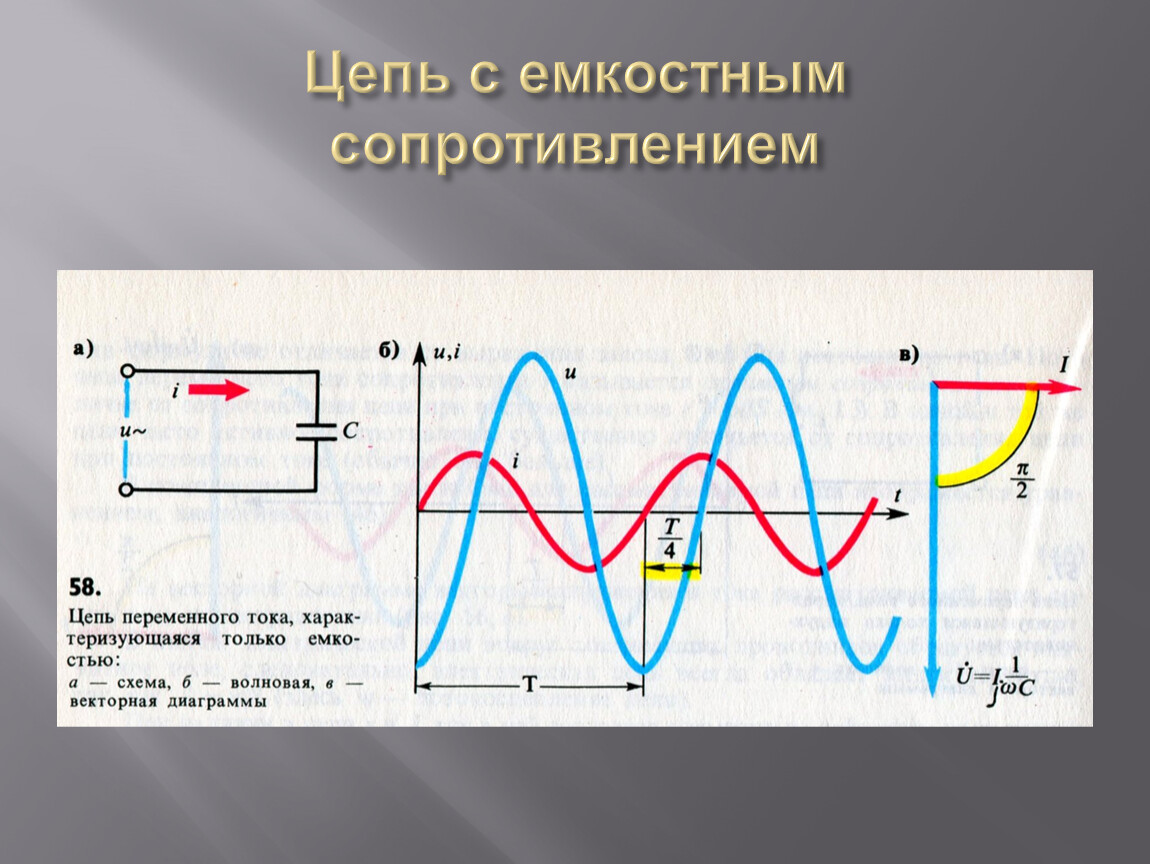
Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току. Чем больше ёмкость конденсатора и частота колебаний, тем больше ток перезарядки. При наличии в цепи переменного тока конденсатора колебания силы тока опережают по фазе колебания напряжения конденсаторе на 90º. Сдвиг фазы колебаний силы тока на 90º относительно фазы колебания напряжения на конденсаторе приводит к тому, что мощность переменного тока в течение одной четверти периода имеет положительный знак, а в течение второй четверти – отрицательный. Поэтому среднее значение мощности за период равно нулю.
Индуктивность в цепи, так же, как и ёмкость, влияет на силу переменного тока. Объясняется это явлением самоиндукции. В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов.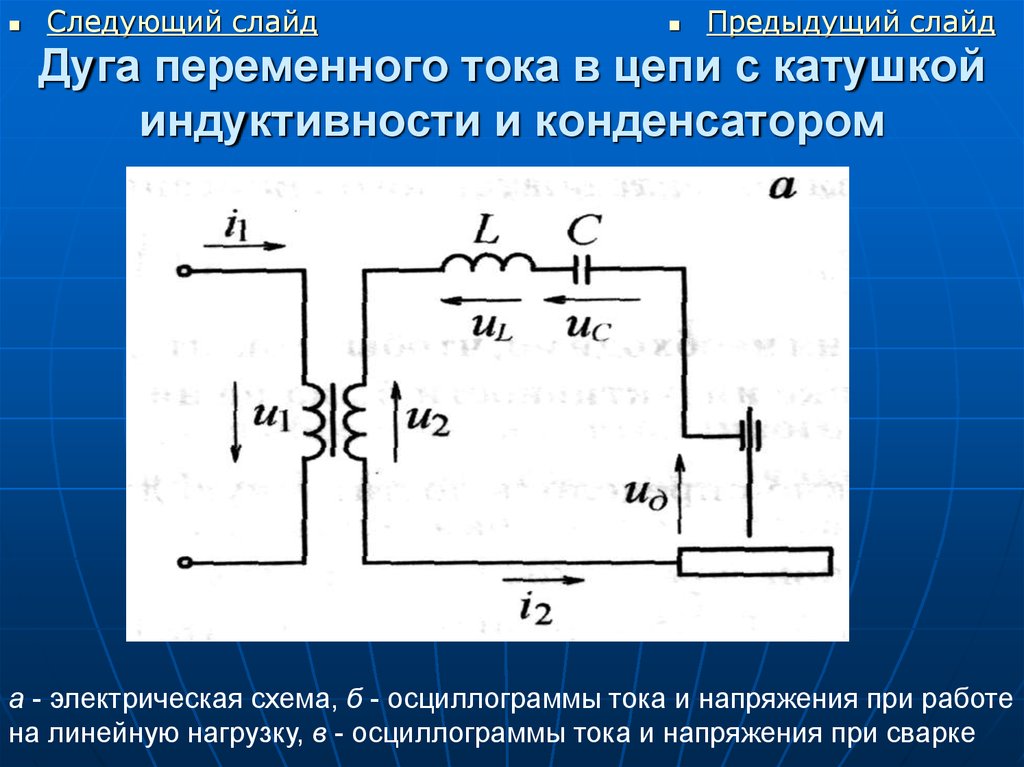
Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.
Величину ХL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
Если частота равна нулю, то индуктивное сопротивление тоже равно нулю. Поэтому постоянный ток как бы не «замечает» катушку индуктивности в цепи.
Колебания напряжения на катушке опережают по фазе колебания силы тока на 90º.
Сдвиг фазы колебаний приводит к тому, что средняя мощность за период колебаний равна нулю.
Генератор на транзисторе используется для создания высокочастотных электромагнитных колебаний.
Для потребления электрической энергии нужно доставить его от источника к потребителю.
Для этого строят линии электропередачи. При передаче электроэнергии на расстояние возникают потери энергии вследствие нагревания проводов. Тепловые потери можно определить используя закон Джоуля – Ленца:
Из этой формулы следует, что для уменьшения потерь энергиинужно уменьшить сопротивление или повысить напряжение. Уменьшения сопротивления проводов ЛЭП требует увеличения их площади поперечного сечения, что приведет к увеличению массы проводов. Увеличение массы проводов связано с большими расходами на укрепление столбов линии электропередачи, для их удержания и на производство металла для них. Наиболее эффективным является увеличение напряжения.
Для изменения напряжения в сети используют трансформаторы. Трансформатор был изобретен в 1876 году Яблочковым и в 1882 году усовершенствован Усагиным. Простейший трансформатор состоит из двух катушек, надетых на общий замкнутый стальной сердечник. Эти катушки называются обмотками трансформатора. Обмотка трансформатора, подключаемая к источнику переменного напряжения, называют первичной, а другая к которой присоединяют нагрузку – вторичной.
Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.
Величина равная отношению напряжений в первичной и вторичной обмотках трансформатора называют коэффициентом трансформации. Его обозначают буквой «k».
k– коэффициент трансформации.
U1 иU2 – напряжения на первичной и на вторичной обмотке.
N1 и N2— число витков на первичной и на вторичной обмотке.
Если k < 1 — трансформатор повышающий,
k > 1 — трансформатор понижающий.
КПД трансформатора равен отношению мощности в нагрузке к мощности, подаваемой из сети на первичную обмотку:
Для передачи электроэнергии на расстояние напряжение повышают с помощью трансформатора, а для потребления — понижают.
В массивных проводниках при изменении магнитного поля возникают индукционные токи (токи Фуко), которые нагревают проводник. Чтобы эти индукционные токи не нагревали сердечник трансформатора его делают не сплошным, а из отдельных пластин, скрепленных вместе.
Закон Ома гласит: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
Из формулы закона Ома для переменного тока мы видим, что при постоянной амплитуде напряжения, амплитуда силы тока зависит от частоты. Амплитуда силы тока будет максимальной, если полное сопротивление минимально. Полное сопротивление цепи минимально при равенстве индуктивного и ёмкостного сопротивления. В этом заключается условие возникновения резонанса в электрической цепи.
Резонанс в электрической цепи – это явление резкого возрастания амплитуды колебаний силы тока в контуре при совпадении частоты вынужденных колебаний с частотой собственных колебаний контура.
Явление резонанса широко используется в радиотехнике, в схемах настройки радиоприемников. Меняя электроемкость конденсатора в колебательном контуре можно настроить его на нужную волну, т.е. выделить частоту на которой работает передающая станция
Разбор тренировочных заданий
1. Каково амплитудное значение ЭДС, возникающей в рамке из 50 витков, если она вращается с циклической частотой 180 рад/с в магнитном поле индукцией 0,4 Тл? Площадь рамки 0,02 м2.
Дано:
N=50
ω=180 рад/с
B=0,4 Тл
S=0,02 м2
_________
Ԑm=?
Решение:
Ответ: 72 В.
2. Катушка с индуктивностью 0,08 Гн присоединена к источнику переменного тока частотой 1000 Гц. При этом вольтметр показывает 100 В. Определить амплитуду тока в цепи. Ответ округлить до десятых.
Дано:
L=0,08 Гн
ν= 1000 Гц
U=100 В
__________
Im=?
Решение:
Напишем закон Ома для переменного тока
Т.
к. ХC и R равны нулю, то
Учитывая, что , получаем:
Найдем амплитудное значение напряжения:
Подставим числовые данные в формулу для расчета амплитуды силы тока:
Ответ: Im = 0,3 А.
Однофазные цепи переменного тока (страница 2)
Решение:
Полное сопротивление схемы
Полная мощность на входе схемы
Потери мощности в обмотке катушки
Активная мощность схемы
Коэффициент мощности схемы
Из таблиц тригонометрических величин .
Активное сопротивление схемы
сопротивление дуги
Индуктивное сопротивление цепи представлено индуктивным сопротивлением катушки:
Эту же величину можно определить из треугольника сопротивлении (рис. 25, масштаб )
Искомая индуктивность катушки
Если бы вместо катушки был включен реостат, то сопротивление схемы имело бы ту же величину 6 Ом, но было бы чисто активным:
откуда
Потери мощности в катушке
Потери мощности в реостате
Отсюда ясно, что к.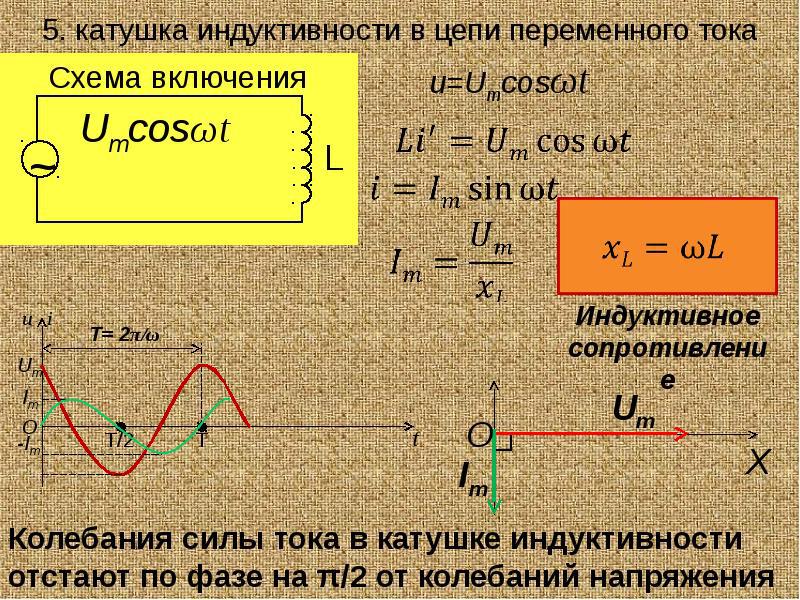
п. д. схемы выше при «погашении» избытка напряжения индуктивной катушкой. Действительно, к. п. д. при наличии катушки
к. п. д. при наличии реостата
Не следует забывать, что «погашение» избытка напряжения катушкой (или конденсатором) ухудшает коэффициент мощности (в данном примере при наличии катушки и при наличии реостата).
22. Последовательно с катушкой, параметры которой и L=15,92 мГн, включен реостат сопротивлением, . Цепь включена на напряжение U=130 В при частоте f=50 Гц.
Определить ток в цепи; напряжение на катушке и реостате; коэффициент мощности цепи и катушки.
Решение:
Индуктивное сопротивление катушки
Полное сопротивление катушки
Активное сопротивление цепи, состоящей из последовательно соединенных катушки и реостата,
Полное сопротивление цепи
На основании закона Ома ток в цепи
Напряжение на катушке
Напряжение на реостате
Арифметическая сумма много больше приложенного напряжения U=130 В.
Коэффициент мощности цепи
Коэффициент мощности катушки
Следовательно, реостат увеличивает коэффициент мощности и сопротивление цепи, но уменьшает ток, увеличивает потребление энергии схемой.
Действительно, активная мощность катушки
активная мощность реостата
Так как цепь неразветвленная и ток один, то с него целесообразно начать построение векторной диаграммы (рис. 26).
Напряжение на реостате, представляющем собой чисто активное сопротивление, совпадает по фазе с током; на диаграмме вектор этого напряжения совпадает по направлению с вектором тока. Из конца вектора в сторону опережения вектора тока I, под углом в сторону, противоположную вращению стрелки часов, откладываем вектор напряжения на катушке . Векторы построены так с целью сложения по правилу многоугольника.
23. Неразветвленная цепь составлена из двух катушек: у первой катушки индуктивность и сопротивление , у второй катушки индуктивность и сопротивление .
Определить ток в цепи и напряжения на каждой катушке, а также построить в масштабе векторную диаграмму, если частота f=50 Гц и приложенное напряжение U=12,6 В.
Решение:
Индуктивное сопротивление первой катушки
т. е. оно численно равно активному сопротивлению , что обусловливает отставание тока по фазе от напряжения на 1/8 периода (на 45°).
Действительно, тангенс угла сдвига фаз
Индуктивное сопротивление второй катушки
Так как ее активное сопротивление то тангенс угла сдвига фаз
Построим в масштабе треугольник сопротивлений для рассматриваемой цепи. Для этого зададимся масштабом сопротивлений . Тогда на диаграмме сопротивление 1,57 Ом будет изображено отрезком 15,7 мм, сопротивление 2,7 Ом — отрезком 27 мм и т. д. На рис. 27 отрезок, изображающий активное сопротивление , отложен в горизонтальном направлении, а отрезок, изображающий индуктивное сопротивление , — в вертикальном направлении под прямым углом к .
Полное сопротивление первой катушки является гипотенузой прямоугольного треугольника. Из вершины с этого треугольника в горизонтальном направлении отложен отрезок, изображающий сопротивление , и под прямым углом к нему вверх — отрезок, изображающий сопротивление . Гипотенуза се прямоугольного треугольника означает полное сопротивление второй катушки.
Из рис. 27 видно, что отрезок ае, изображающий полное сопротивление z неразветвленной цепи из двух катушек, не равен сумме отрезков ас и се, т. е. . Чтобы определить полное сопротивление z рассматриваемой цепи, следует сложить отдельно активные (, отрезок аf) и индуктивные (, отрезок ef) сопротивления катушек.
Гипотенуза ае, означающая полное сопротивление z цепи, определяется по теореме Пифагора:
Ток в цепи определяется по закону Ома:
Напряжение на первой катушке
Напряжение на второй катушке
Строим векторную диаграмму (рис. 28), приняв масштабы:
а) для тока ; тогда вектор тока изобразится отрезком длиной 25 мм;
б) для напряжения ; при этом вектор напряжения будет иметь длину 55,2 мм, вектор напряжения — длину 71 мм, а вектор приложенного напряжения — длину 126 мм.
Начало вектора совмещено с концом вектора для возможности сложения векторов напряжений но правилу многоугольника (напряжение, приложенное к неразветвленной цепи катушек, равно геометрической сумме напряжений отдельных катушек).
Конденсатор в цепи переменного тока
Если конденсатор включить в цепь постоянного тока, то такая цепь будет разомкнутой, так как обкладки конденсатора разделяет диэлектрик, и ток в цепи идти не будет. Иначе происходит в цепи переменного тока. Переменный ток способен течь в цепи, если она содержит конденсатор. Это происходит не из-за того, что заряды вдруг получили возможность перемещаться между пластинами конденсатора. В цепи переменного тока происходит периодическая зарядка и разрядка конденсатора, который в нее включен благодаря действию переменного напряжения.
Рассмотрим цепь на рис.1, которая включает конденсатор. Будем считать, что сопротивление проводов и обкладок конденсатора не существенно, напряжение переменного тока изменяется по гармоническому закону:
По определению емкость на конденсаторе равна:
Следовательно, напряжение на конденсаторе:
Из выражения (3), очевидно, что заряд на конденсаторе будет изменяться по гармоническому закону:
Сила тока равна:
Сравнивая законы колебаний напряжения на конденсаторе и силы тока, видим, что колебания тока опережают напряжение на .
Этот факт отражает то, что в момент начала зарядки конденсатора сила тока в цепи является максимальной при равенстве нулю напряжения. В момент времени, когда напряжение достигает максимума, сила тока падает до нуля.
В течение периода, при зарядке конденсатора до максимального напряжения, энергия, поступающая в цепь, запасается на конденсаторе, в виде энергии электрического поля. За следующую четверть периода данная энергия возвращается обратно в цепь, когда конденсатор разряжается.
Амплитуда силы тока (), исходя из выражения (5), равна:
Емкостное сопротивление конденсатора
Физическую величину, равную обратному произведению циклической частоты на емкость конденсатора называют его емкостным сопротивлением ():
Роль емкостного сопротивления уподобляют роли активного сопротивления (R) в законе Ома:
где – амплитудное значение силы тока; – амплитуда напряжения. Для емкостного сопротивления действующая величина силы тока имеет связь с действующим значением напряжения аналогичную выражению (8) (как сила тока и напряжение для постоянного тока):
На основании (9) говорят, что сопротивление конденсатора переменному току.
При увеличении емкости конденсатора растет ток перезарядки. Тогда как сопротивление конденсатора постоянному току является бесконечно большим (в идеальном случае), ёмкостное сопротивление конечно. С увеличением емкости и (или) частоты уменьшается.
Примеры решения задач
Конденсатор, катушка и резонанс в цепи переменного тока 🐲 СПАДИЛО.РУ
Опишем колебания, которые происходят в цепи переменного тока при включении в нее конденсатора и катушки индуктивности. А также рассмотрим условия, при выполнении которых в цепи переменного тока наступает резонанс. Получим формулы для вычисления амплитуд напряжений, введем понятия емкостного и индуктивного сопротивления и выясним, какую роль играют эти величины.
Конденсатор в цепи переменного тока
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см.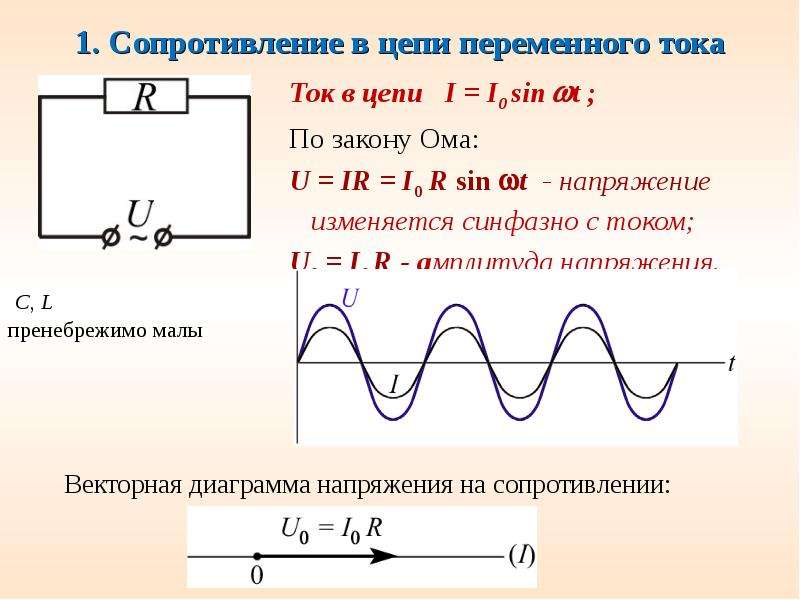
рисунок ниже).
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
u=φ1−φ2=qC..
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
qC..=Umaxcos.ωt
Следовательно, заряд конденсатора меняется по гармоническому закону:
q=CUmaxcos.ωt
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i=q´=−CUmaxsin.ωt=CUmaxcos.(ωt+π2..)
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π2.. (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
Амплитуда силы тока равна:
Imax=UmaxCω
Примем, что:
1Cω..=XC
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Определение
I=UXC..
Величина XC, равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура qmax=10−6 Кл. Амплитудное значение силы тока в контуре Imax=10−3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q2max2C..=LI2max2..
Отсюда:
LC=q2maxI2max..
√LC=qmaxImax..
T=2π√LC=2πqmaxImax..=2·3,1410−610−3..≈6,3·10−3 (с)
Катушка индуктивности в цепи переменного тока
Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).
Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока.
Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля →Ei, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля →Eк, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства →Ei=−→Eк следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции ei) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать:
ei=−u
Напомним, что сила переменного тока изменяется по гармоническому закону:
i=Imaxsin.ωt
Тогда ЭДС самоиндукции равна:
ei=−Li´=−LωImaxcos.ωt
Так как u=−ei, то напряжение на концах катушки оказывается равным:
u= LωImaxcos.ωt=LωImaxsin.(ωt+π2..)=Umax(ωt+π2..)
Амплитуда напряжения равна:
Umax=LωImax
Следовательно, колебания напряжения на катушке опережают колебания силы тока на π2.., или колебания силы тока отстают от колебаний напряжения на π2.., что одно и то же.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).
Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна:
Imax=UmaxLω..
Введем обозначение:
Lω=XL
Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим:
Определение
I=UXL..
Величина XL, равная произведению циклической частоты на индуктивность, называется индуктивным сопротивлением. Индуктивное сопротивление зависит от частоты. Поэтому в цепи постоянного тока, в котором отсутствует частота, индуктивное сопротивление катушки равно нулю.
Пример №2. Катушка с индуктивным сопротивлениемXL=500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока Imax в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.
Индуктивное сопротивление катушки выражается формулой:
XL=Lω=2πνL
Отсюда:
Так как амплитуда напряжения связана с его действующим значением соотношением Umax=U√2, то для амплитуды силы тока получаем:
Резонанс в электрической цепи
Механические и электромагнитные колебания имеют разную природу, но процессы, происходящие при этом, идентичны. Поэтому можно предположить, что резонанс в электрической цепи так же реален, как резонанс в колебательной системе, на которую действует периодическая сила.
Напомним, что в механической системе резонанс тем более заметен, чем меньше в колебательной системе трение между ее элементами. Роль трения в электрической цепи играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника, который при этом нагревается. Следовательно, резонанс в электрической цепи будет отчетливо наблюдаться при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная частота колебаний в колебательном контуре определяется формулой:
ω0=1√LC..
Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру равна собственной частоте колебательного контура:
ω=ω0=1√LC..
Определение
Резонанс в электрическом колебательном контуре — явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
После включения внешнего переменного напряжения резонансное значение силы тока в цепи устанавливается не моментально, а постепенно. Амплитуда колебаний силы тока возрастает до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
I2maxR2..=UmaxImax2..
Упростив это уравнение, получим:
ImaxR=Umax
Следовательно, амплитуда установившихся колебаний силы тока при резонансе определяется уравнением:
Imax=UmaxR..
При сопротивлении, стремящемся к нулю, сила тока возрастает до бесконечно больших значений. При большом сопротивлении сила тока возрастает незначительно. Это хорошо видно на графике ниже.
Пример №3. В цепь переменного тока с частотой ν = 500 Гц включена катушка индуктивностью L = 10 мГн. Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?
Электрическая цепь, описываемая в условии, представляет собой колебательный контур. Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (ν = ν0).
Но:
ν0=12π√LC..
Тогда:
ν=12π√LC..
Отсюда:
Задание EF22579
К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой ν.
Индуктивность L катушки колебательного контура можно плавно менять от максимального значения Lmax до минимального Lmin, а ёмкость его конденсатора постоянна.
Ученик постепенно уменьшал индуктивность катушки от максимального значения до минимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.
Алгоритм решения
1.Установить, что вызывает увеличение амплитуды силы тока.
2.Объяснить, какие изменения вызвало уменьшение индуктивности.
3.Объяснить, при каком условии в течение всего эксперимента амплитуда силы тока может только расти.
Решение
В колебательном контуре источником тока возбуждаются вынужденные колебания. Частота этих колебаний равна частоте источника — ν. Амплитуда колебаний зависит от того, как соотносятся между собой внешняя частота и частота собственных электромагнитных колебаний, которая определяется формулой:
ν0=12π√LC..
По мере увеличения внешней частоты от нуля до ν0 амплитуда растет. Она достигает максимума тогда, когда происходит резонанс. При этом внешняя частота равна частоте собственных электромагнитных колебаний: ν = ν0. Затем амплитуда начинает убывать.
В данном случае, ученик меняет не внешнюю частоту, а частоту собственных электромагнитных колебаний. При плавном уменьшении индуктивности контура от максимального значения Lmax до минимального Lmin частота возрастает от ν0min до ν0max. Причем:
ν0min=12π√LminC..
ν0max=12π√LmaxC..
Из того факта, что амплитуда всё время увеличивалась, можем сделать вывод, что частота ν0 всё время приближалась к частоте источника тока, при этом ν > ν0max. В противном случае наблюдалось бы уменьшений амплитуды силы тока.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22785
В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.
Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях.
Ответ:
а) период колебаний силы тока в контуре
б) фаза колебаний напряжения на конденсаторе
в) заряд конденсатора
г) энергия магнитного поля катушки
д) амплитуда колебаний напряжения на катушке
Алгоритм решения
- Определить, от чего зависит каждая из перечисленных величин.
- Установить, какие величины меняются, а какие нет.
Решение
В колебательном контуре происходят гармонические колебания. Поэтому период колебаний силы тока в контуре — величина постоянная.
Фаза — это величина, которая определяет положение колебательной системы в любой момент времени. Поскольку в системе происходят колебания, фаза меняется.
Заряд конденсатора — колебания происходят за счет постоянной перезарядки конденсатора. Следовательно, эта величина тоже меняется.
Энергия магнитного поля катушки — в колебательном контуре происходят взаимные превращения энергии магнитного поля катушки в энергию электрического поля конденсатора, и обратно. Поэтому энергия магнитного поля катушки постоянно меняется.
В условии задачи сказано, что колебания незатухающие. Это значит, что полная механическая энергия колебательной системы сохраняется. Поскольку именно от нее зависит амплитуда колебаний напряжения на катушке, то эта величина также остается постоянной.
Ответ: ад
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18656 На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.
Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2..=4π√LC2π√LC..=2
Отсюда:
T2=T12..=4·10−62..=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор | оценить
| U, B | UR, B | UC, B | I, мА | φ, град. | R, Ом | ХΔ, Ом | Z, Ом | Примечание |
· Вычислите:
Фазовый угол
Полное сопротивление цепи
Активное сопротивление цепи
Емкостное реактивное сопротивление цепи
·Выберите масштабы и постройте векторную диаграмму напряжений (рис. 5) и треугольник сопротивлений (рис. 6).
Рис. 3.5 Рис. 3.6
Контрольные вопросы:
- Что называется периодом?
- Что называется частотой?
- Для переменного напряжения и тока записать выражения мгновенных напряжений и токов, дать определение амплитуды и начальной фазы.
- Дать определение действующего напряжения (тока), указать его связь с амплитудой напряжения (тока).
- Дать определения мгновенной и активной мощности.
- Объяснить назначение приборов в измерительной цепи.
- Какие элементы обладают активным сопротивлением.
- Какой вид имеет временная диаграмма напряжений и тока при последовательном соединении R и C-цепей?
- Изобразите треугольники напряжений, сопротивлений и мощностей для цепи с активно-ёмкостной нагрузкой. Чем они отличаются от треугольников для активно-индуктивной нагрузки?
Лабораторная работа 4
Дата добавления: 2016-12-04; просмотров: 1927 | Нарушение авторских прав
Рекомендуемый контект:
Похожая информация:
Поиск на сайте:
Начальная фаза. Сдвиг фаз
Но т.к. витки сдвинуты в пространстве, то наводимая в них ЭДС будет достигать амплитудных и нулевых значений не одновременно.
В начальный момент времени ЭДС витка будет:
В этих выражениях углы и называются фазными, или фазой. Углы и называются начальной фазой. Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
Разность начальных фаз двух синусоидальных величин одинаковой частоты и амплитуды называется углом сдвига фаз
Разделив угол сдвига фаз на угловую частоту, получим время, прошедшее с начала периода:
Графическое изображение синусоидальных величин
Синусоидальные величины можно изображать графически при помощи синусоид или вращающихся векторов.
Любая синусоидальная величина характеризуется:
1. Амплитудой;
2. Угловой частотой;
3. Начальной фазой.
При изображении величины с помощью синусоиды ординаты синусоиды в масштабе представляют собой мгновенное значение, абсциссы – промежутки времени.
При этом длина вектора равна амплитудному значению величины, угол между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью . Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.
Совокупность нескольких синусоид называется синусоидальной (волновой) диаграммой.
Совокупность нескольких векторов называется векторной диаграммой.
Сложение и вычитание синусоидальных величин
Для сложения двух синусоидальных величин с помощью синусоид необходимо сложить их ординаты в каждый момент времени.
Для того, чтобы сложить две величины с помощью векторов, необходимо к концу первого вектора добавить второй, не изменяя его величины и направления. Соединив начало первого вектора с концом второго, получим суммарный вектор.
Цепи переменного тока с активным сопротивлением
На величину тока и его характер в цепях переменного тока оказывает влияние не только сопротивление, определяемое материалом и геометрическими размерами, но и наличием в цепи емкости и индуктивности. Любая электрическая цепь обладает сопротивлением, индуктивностью и емкостью. Однако, часто тот или иной элемент преобладает над другим, поэтому их влиянием можно пренебречь.
Один и тот же проводник имеет различное сопротивление в цепях постоянного и переменного тока, причем, в цепях переменного тока это сопротивление больше.
Это объясняется тем, что переменный ток в отличие от постоянного, который протекает по сечению проводника с равномерной плотностью, частично вытесняется из внутренних слоев проводника к наружным. В результате чего плотность тока в различных слоях неодинакова. Это явление называется поверхностным эффектом. Это объясняется тем, что внутренние слои проводника сцеплены с большим числом магнитных силовых линий, чем наружные, и поэтому в них наводится большая ЭДС самоиндукции, которая препятствует протеканию тока и вытесняет его к наружным слоям, где ЭДС самоиндукции меньше.
Разделив обе части равенства на , получим действующие значения .
Ток и напряжение в цепи с активным сопротивлением совпадают по фазе.
Таким образом, мощность состоит из постоянной составляющей и переменной составляющей , среднее значение которых за период равно нулю. Таким образом, постоянная составляющая мощности выражает среднее за период значение мощности и называется активной мощностью:
Мощность в оба полупериода положительна. Это означает, что цепь с сопротивлением r только потребляет энергию из сети и назад ее не возвращает, т.к. она преобразуется в другие виды энергии.
Цепи переменного тока с индуктивностью
ЭДС самоиндукции в любой момент времени уравновешивается напряжением:
Т.о. в цепи с индуктивностью напряжение опережает ток на угол 900.
— индуктивное (реактивное) сопротивление.
— закон Ома для цепи с индуктивностью.
Физически индуктивное сопротивление характеризует препятствие, оказываемое переменному току в результате наличия ЭДС самоиндукции.
Мощность цепи:
Т.о. мощность изменяется с двойной частотой и может быть положительной и отрицательной. Когда она «+» индуктивность потребляет электрическую энергию от источника и запасает ее от магнитного поля. Когда мощность «-» индуктивность возвращает запасенную энергию обратно к источнику.
Т.о. между источником и индуктивностью происходит непрерывный обмен энергией, при котором:
— цепь работает потребителем
— цепь работает генератором.
Максимальное значение мощности цепи индуктивности называется реактивной мощностью:
Энергия, запасенная в магнитном поле катушки, равна
Цепь переменного тока с емкостью
— закон Ома для цепи с емкостью.
— реактивное емкостное сопротивление
Т.о. ток в цепи с емкостью опережает напряжение на угол 900.
Физически емкостное сопротивление характеризует препятствие, оказываемое переменному току цепью с емкостью. В результате поляризации диэлектрика конденсатора в нем образуется свое внутренне электрическое поле, которое направлено противоположно внешнему полю, приложенному к диэлектрику.
Мощность цепи:
Мощность изменяется с двойной частотой относительно тока и напряжения. В течении первой четверти периода, когда напряжение, приложенное к конденсатору, возрастает, мгновенная мощность положительна. Это означает, что конденсатор получает и запасает энергию источника в виде электрического поля.
В течении второй четверти, когда напряжение, приложенное к конденсатору, уменьшается, запасенная энергия возвращается к источнику, т.е.
— цепь работает потребителем;
— цепь работает источником.
Максимальное значение мощности цепи с емкостью называют реактивной емкостной мощностью:
Она характеризует скорость обмена энергией между источником и цепью с емкостью.
Максимальное значение энергии, запасенной в цепи:
Неразветвленная цепь переменного тока с активным сопротивлением и индуктивностью
Таким сопротивлением (активным и индуктивным) обладают катушки индуктивности, обмотки трансформаторов и электрических машин.
Т.о. напряжение опережает ток в этой цепи на угол , причем .
Мощность цепи:
Т.о. мгновенная мощность состоит из двух составляющих: постоянной и переменной , среднее значение за период которой равно нулю.
Мощность принимает как положительные так и отрицательный значения. Когда мощность положительна, то цепь потребляет энергию, а когда мощность отрицательна, то цепь возвращает запасенную энергию в цепь. Но т.к. потребляет энергию и активное сопротивление и индуктивное, а возвращает в цепь только индуктивность, то положительная будет значительно больше.
Треугольники напряжений, сопротивлений, мощностей
Если стороны треугольника напряжений уменьшить на ток, то получим треугольник мощностей.
— реактивная мощность
— активная мощность
Коэффициент мощности показывает, какая часть полной мощности потребляется безвозвратно.
Цепь переменного тока с активным сопротивлением, емкостью и индуктивностью
Допустим:
Общий случай неразветвленной цепи
Резонанс напряжений
Результирующий ток резко увеличивается, т.к. индуктивное и емкостное сопротивления компенсируют друг друга.
Если параметры цепи подобрать так, что , то напряжения на емкости и индуктивности будут превышать напряжение на зажимах цепи в раз. Отношение называется добротностью цепи (контура).
Т.о. напряжение на емкости и индуктивности будут превышать напряжение сети в раз, что может привести к пробою диэлектрика в конденсаторе или сопротивлений изоляции индуктивности, поэтому явление резонанса напряжений в электрических цепях нежелательно, но в то же время в радиотехнике его используют (колебательные контуры приемника и передатчика).
Возникновение напряжений на L и С, превышающих напряжение на зажимах цепи объясняется способностью емкости и индуктивности накапливать электрическую энергию.
Между емкостью и индуктивностью происходит непрерывный обмен энергией, который называется собственными колебаниями.
Частоту собственных колебаний можно определить при условии, что .
Резонансные кривые
Зависимость параметров цепи от частоты характеризуется резонансными кривыми.
Разветвленные цепи переменного тока
Рассмотрим цепь с двумя параллельно соединенными катушками.
Для определения тока неразветвленной части цепи необходимо разложить токи и на активные и реактивные составляющие.
Характеристики синусоидальных величин: мгновенное, амплитудное, действующее, среднее значение, период, частота (угловая и циклическая), фаза − мгновенные значения синусоидальных функций обозначают маленькими буквами: i, e, u. Они являются функциями времени.
Зависимость их от времени выражается соотношениями:
− фаза — аргумент синусоидальной функции (wt + j) — показывает, какое значение имеет синусоидальная функция в данный момент времени;
− начальная фаза j — показывает, какое значение имеет синусоидальная функция в момент на чала отсчета, т.е. при t = 0;
− угловая (циклическая) частота изменения тока:
, рад/c.
Для нашей сети w = 314 рад/c.
− Действующее значение переменного тока.
Действующим значением I переменного тока называют такое значение постоянного I, который, протекая по сопротивлению R, за время, равное одному периоду Т изменения тока, выделяет в нем такое же количество теплоты Q, что и переменный ток i. Поясним определение на примере:
После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:
Аналогичные соотношения могут быть получены также для напряжения и ЭДС:
Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.
Учитывая, например, что действующее значение напряжения в нашей сети составляет 220 В, можно определить амплитудное значение фазного напряжения Um = UÖ2 = 307 В. Связь между действующим и амплитудным значениями напряжений важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.
Цепи переменного тока с резистором: напряжение, ток, мощность, векторная диаграмма
Мгновенное значение мощности. В цепи, содержащей активное, индуктивное и емкостное сопротивления, в которой ток I и напряжение u в общем случае сдвинуты по фазе на некоторый угол ?, мгновенное значение мощности р равно произведению мгновенных значений силы тока i и напряжения u. Кривую мгновенной мощности р можно получить перемножением мгновенных значений тока i и напряжения u при различных углах t (рис. 199, а. Из этого рисунка видно, что в некоторые моменты времени, когда ток и напряжение направлены навстречу друг другу, мощность имеет отрицательное значение.
Возникновение в электрической цепи отрицательных значений мощности является вредным. Это означает, что в такие периоды времени приемник возвращает часть полученной электроэнергии обратно источнику; в результате уменьшается мощность, передаваемая от источника к приемнику. Очевидно, что чем больше угол сдвига фаз, тем больше время, в течение которого часть электроэнергии возвращается обратно к источнику, и тем больше возвращаемая обратно энергия и мощность.
Активная и реактивная мощности. Мгновенная мощность может быть представлена в виде суммы двух составляющих 1 и 2 (рис. 199,б). Составляющая 1 соответствует изменению мощности в цепи с активным сопротивлением (см. рис. 175,б).
Среднее ее значение, которое называют активной мощностью,
P = UI cos
Она представляет собой среднюю мощность, которая поступает от источника к электрическим установкам при переменном токе.
Составляющая 2 изменяется подобно изменению мощности в цепи с реактивным сопротивлением (индуктивным или емкостным, см. рис. 179, а и б). Среднее ее значение равно нулю, поэтому для оценки этой составляющей пользуются ее амплитудным значением, которое называют реактивной мощностью:
Q = UI sin
Рассматривая кривые мощности (см. рис. 199,б), можно установить, что только активная мощность может обеспечить преобразование в приемнике электрической энергии в другие виды энергии. Эта мощность в течение всего периода имеет положительный знак, т. е. соответствующая ей электрическая энергия 2, называемая активной, непрерывно переходит от источника 1 к приемнику 4 (рис. 200, а). Реактивная мощность никакой полезной работы создать не может, так как среднее значение ее в течение одного периода равно нулю. Как видно из рис. 199,б, эта мощность становится то положительной, то отрицательной, т. е. соответствующая ей электрическая энергия ,3, называемая реактивной,
Рис. 199. Зависимость мгновенной мощности р (а) и ее составляющих (б) от угла t
Рис. 200. Диаграмма, иллюстрирующая передачу электрической энергии между источником и приемником, содержащим активное и реактивное сопротивления, при отсутствии компенсатора (а) и при наличии его (б): 1 — источник; 2,3 — условные изображения активной и реактивной энергии; 4 — приемник; 5 — компенсатор непрерывно циркулирует по электрической цепи от источника электрической энергии 1 к приемнику 4 и обратно (см. рис. 200, а).
Возникновение реактивной мощности в цепи переменного тока возможно только при включении в эту цепь накопителей энергии, таких как катушка индуктивности или конденсатор. В первом случае электрическая энергия, поступающая от источника, накапливается в электромагнитном поле катушки индуктивности, а затем отдается обратно; во втором случае она накапливается в электрическом поле конденсатора, а затем возвращается обратно к источнику. Постоянная циркуляция реактивной мощности от источника к приемникам загружает генераторы переменного тока и электрические сети реактивными токами, не создающими полезной работы, и тем самым не дает возможности использовать их по прямому назначению для выработки и передачи потребителям активной мощности. Поэтому в производственных условиях стараются по возможности уменьшить реактивную мощность, потребляемую электрическими установками.
Полная мощность. Источники электрической энергии переменного тока (генераторы и трансформаторы) рассчитаны на определенный номинальный ток Iном и определенное номинальное напряжение Uном, которые зависят от конструкции машины, размеров ее основных частей и пр. Увеличить значительно номинальный ток или номинальное напряжение нельзя, так как это может привести к недопустимому нагреву обмоток машины или пробою их изоляции. Поэтому каждый генератор или трансформатор может длительно отдавать без опасности аварии только вполне определенную мощность, равную произведению его номинального тока на номинальное напряжение. Произведение действующих значений тока и напряжения называется полной мощностью,
S = UI
Следовательно, полная мощность представляет собой наибольшее значение активной мощности при заданных значениях тока и напряжения. Она характеризует ту наибольшую мощность, которую можно получить от источника переменного тока при условии, что между проходящим по нему током и напряжением отсутствует сдвиг фаз. Полную мощность измеряют в вольт-амперах (В*А) или киловольт-амперах (кВ*А).
Связь между мощностями Р, Q и S можно определить из векторной диаграммы напряжений (рис. 201, а). Если умножить на ток I все стороны треугольника ABC, то получим треугольник мощностей А’В’С’ (рис. 201,б), стороны которого равны Р, Q и S. Из треугольника мощностей имеем:
S = (P2 + Q2)
Из этого выражения следует, что при заданной полной мощности S (т. е. напряжении U и токе I) чем больше реактивная мощность Q, которая проходит через генератор переменного тока или трансформатор, тем меньше активная мощность Р, которую он может отдать приемнику. Иными словами, реактивная мощность не позволяет полностью использовать всю расчетную мощность источников переменного тока для выработки полезно используемой электрической энергии.
То же самое относится и к электрическим сетям. Ток I = (Ia2 + Ip2), который можно безопасно пропускать по данной электрической сети, определяется, главным образом, поперечным сечением ее проводов. Поэтому если часть Iр проходящего по сети тока (см. рис. 194,б) идет на создание реактивной мощности, то должен быть уменьшен активный ток Iа, обеспечивающий создание активной мощности, которую можно пропустить по данной сети.
Рис. 201. Векторная диаграмма напряжений (а) и треугольник мощностей (б) для цепи переменного тока
Если задана активная мощность Р, то при увеличении реактивной мощности Q возрастут реактивный ток Iр и общий ток I, проходящий по проводам генераторов переменного тока, трансформаторов, электрических сетей и приемников электрической энергии. При этом увеличиваются и потери мощности Р = I2Rпp в активном сопротивлении Rпp этих проводов.
Таким образом, бесполезная циркуляция электрической энергии между источником переменного тока и приемником, обусловленная наличием в нем реактивных сопротивлений, требует также затраты определенного количества энергии, которая теряется в проводах всей электрической цепи.
Коэффициент мощности. Из формулы (75) следует, что активная мощность Р зависит не только от тока I и напряжения U, но и от величины cos, называемой коэффициентом мощности:
cos = P/(UI) = P/S = P/(P2 + Q2)
По значению cos можно судить, как использует мощность источника данный приемник или электрическая цепь. Чем больше cos ?, тем меньше sin, следовательно, согласно формулам (75) и (76) при заданных U и I, т. е. S, тем больше активная и меньше реактивная мощности, отдаваемые источником. При повышении cos и постоянной активной мощности Р, поступающей в приемник, уменьшается ток в цепи I = P/(U cos). При этом уменьшаются потери мощности P = I2Rпp в проводах и обеспечивается возможность дополнительной загрузки источника и электрической сети, т. е. лучшего их использования.
Если приемник питается от источника при неизменном токе нагрузки, то повышение cos ведет к возрастанию активной мощности Р, используемой приемником. При cos = 1 реактивная мощность равна нулю, и вся мощность, отдаваемая источником, является активной. Поэтому на всех предприятиях и во всех отраслях народного хозяйства стремятся всемерно повышать коэффициент мощности и доводить его по возможности до единицы.
Значения коэффициента мощности электрических установок переменного тока различны. Электрические лампы обладают, главным образом, активным сопротивлением, поэтому при их включении сдвиг фаз между током и напряжением практически отсутствует. Следовательно, для осветительной нагрузки коэффициент мощности можно считать равным единице. Коэффициент мощности для двигателей переменного тока зависит от нагрузки. При номинальной расчетной нагрузке двигателя cos = 0,8-0,9, а у крупных двигателей даже выше. При недогрузке двигателей коэффициент мощности их резко снижается (при холостом ходе cos = 0,25-0,3).
Повышение коэффициента мощности. Cos повышают различными способами. Основной из них — включение параллельно приемникам электрической энергии специальных устройств, называемых компенсаторами. В качестве последних чаще всего используют батареи конденсаторов (статические компенсаторы), но могут быть применены также и синхронные электрические машины (вращающиеся компенсаторы).
Способ повышения cos с помощью статического компенсатора (рис. 202, а) называют компенсацией сдвига фаз, или компенсацией реактивной мощности. При отсутствии компенсатора от источника к приемнику, содержащему активное и индуктивное сопротивления, поступает ток i1 который отстает от напряжения и на некоторый угол сдвига фаз. При включении компенсатора Хс по нему проходит ток ic, опережающий напряжение и на 90°. Как видно из векторной диаграммы (рис. 202,б), при этом в цепи источника будет проходить ток i < i1 и угол сдвига фаз его относительно напряжения также будет меньше.
Для полной компенсации угла сдвига фаз, т. е. для получения cos = 1 и минимального значения тока Imin, необходимо, чтобы ток компенсатора Iс был равен реактивной составляющей I1p = I1 sin1 тока I1.
При включении компенсатора 5 (см. рис. 200,б) источник 1 и электрическая сеть разгружаются от реактивной энергии 3, так как она циркулирует уже по цепи «приемник — компенсатор». Благодаря этому достигаются существенное повышение использования генераторов переменного тока и электрических сетей и уменьшение потерь энергии, возникающих при бесполезной циркуляции реактивной энергии между источником 1 и приемником 4.
Рис. 202. Схема, иллюстрирующая способ повышения cos с помощью компенсатора (а), и векторная диаграмма (б)
Компенсатор в этом случае выполняет роль генератора реактивной энергии, так как токи Iсв конденсаторе и I1р в катушке индуктивности (см, рис. 202,б) направлены навстречу один другому (первый опережает по фазе напряжение на 90°, второй отстает от него на 90°), вследствие чего включение компенсатора уменьшает общий реактивный ток Iр и сдвиг фаз между током I и напряжением U. При надлежащем подборе реактивной мощности компенсатора можно добиться, что вся реактивная энергия 3 (см. рис. 200,б), поступающая в приемник 4, будет циркулировать внутри контура «приемник — компенсатор», а генератор и сеть не будут участвовать в ее передаче. При этих условиях от источника 1 к приемнику 4 будет передаваться только активная мощность 2, т. е. cos будет равен единице.
В большинстве случаев по экономическим соображениям в электрических установках осуществляют неполную компенсацию угла сдвига фаз и ограничиваются значением cos = 0,95.
Последовательное соединение активного и реактивного элементов
В общем случае в цепях переменного тока обычно имеются все виды сопротивлений: активное, индуктивное и емкостное. Например, электрические двигатели переменного тока могут быть представлены эквивалентной схемой, состоящей из индуктивного сопротивления имеющихся в нем катушек и активного сопротивления образующих эти катушки проводов.
Рис. 192. Схема цепи переменного тока, содержащей последовательно включенные активное, индуктивное и емкостное сопротивления (а), векторные диаграммы (б и а), кривые тока и напряжения и (г)
Воздушные линии электропередачи или кабельные линии обычно представляют в виде совокупности активного, индуктивного и емкостного сопротивлений. Активное сопротивление обусловлено сопротивлением электрических проводов, индуктивное — индуктивностью линии, а емкостное — емкостью, возникающей между отдельными проводами, между проводами и землей или же между отдельными жилами кабеля и между жилами кабеля и его оболочкой.
Расчет электрических цепей переменного тока существенно отличается от расчета цепей постоянного тока, так как при переменном токе в активном, индуктивном и емкостном сопротивлениях имеют место различные сдвиги фаз между токами и напряжениями.
Ток, напряжение и полное сопротивление. При последовательном включении в цепь переменного тока активного R, индуктивного XL и емкостного Хс сопротивлений (рис. 192, а) к ним приложены напряжения: активное ua = iR, индуктивное uL = iXL и емкостное uc = iXc. Мгновенное значение напряжения и, приложенного к данной цепи, согласно второму закону Кирхгофа равно алгебраической сумме напряжений:
u = ua + uL + uc
Но для действующих значений эта формула неприменима, так как между всеми указанными напряжениями имеется сдвиг по фазе (амплитудные значения этих напряжений не совпадают по времени).
Рис. 193. Треугольник со противлении
Для этого строят векторную диаграмму, на которой откладывают в определенном масштабе векторы тока и напряжений. Из этих напряжений первое совпадает по фазе с током, второе опережает его на 90°. Векторная диаграмма (рис. 192,б) построена для цепи, в которой индуктивное сопротивление XL больше емкостного Xc, а рис. 192, в — для цепи, в которой XL меньше Хс. Напряжение U (действующее значение) может быть определено из треугольника ЛВС по теореме Пифагора:
U = (U2a + (UL – Uc)2)
Таким образом, из-за наличия угла сдвига фаз напряжение U всегда меньше алгебраической суммы Ua + UL + UC. Разность UL – UC = Up называется реактивной составляющей напряжения.
Рассмотрим, как изменяются ток и напряжение в последовательной цепи переменного тока.
В цепи, содержащей все три вида сопротивления, ток i и напряжение и оказываются сдвинутыми по фазе на некоторый угол ср (рис. 192, г).
Полное сопротивление и угол сдвига фаз. Если подставить в формулу (71) значения Ua = IR; UL = lL и UC=I/(C), то будем иметь: U = ((IR)2+ 2), откуда получаем формулу закона Ома для последовательной цепи переменного тока:
I = U / ( (R2+ 2) ) = U / Z (72)
где Z = (R2+ 2) = (R2+ (XL – Xc)2)
Величину Z называют полным сопротивлением цепи, оно измеряется в омах. Разность L — l/(C) называют реактивным сопротивлением цепи и обозначают буквой X. Следовательно, полное сопротивление цепи
Z = (R2+ X2)
Соотношение между активным, реактивным и полным сопротивлениями цепи переменного тока можно также получить по теореме Пифагора из треугольника сопротивлений (рис. 193). Треугольник сопротивлений А’В’С’ можно получить из треугольника напряжений ABC (см. рис. 192,б), если разделить все его стороны на ток I.
Угол сдвига фаз определяется соотношением между отдельными сопротивлениями, включенными в данную цепь. Из треугольника А’В’С (см. рис. 193) имеем:
sin ? = X / Z; cos? = R / Z; tg? = X / R
Например, если активное сопротивление R значительно больше реактивного сопротивления X, угол сравнительно небольшой. Если в цепи имеется большое индуктивное или большое емкостное сопротивление, то угол сдвига фаз возрастает и приближается к 90°. При этом, если индуктивное сопротивление больше емкостного, напряжение и опережает ток i на угол; если же емкостное сопротивление больше индуктивного, то напряжение и отстает от тока i на угол.
Идеальная катушка индуктивности, реальная катушка и конденсатор в цепи переменного тока.
Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.
>Емкостное сопротивление конденсатора определяется по формуле. Сопротивление конденсатора
Сопротивление конденсатора.
Замкнем цепь. Конденсатор начал заряжаться и сразу стал источником тока, напряжения, Э. Д. С.. На рисунке видно что Э. Д. С. конденсатора направлена против заряжающего его источника тока.
Противодействие электродвижущей силы заряжаемого конденсатора заряду этого конденсатора называется емкостным сопротивлением.
Вся энергия затрачиваемая источником тока на преодоление емкостного сопротивления превращается в энергию электрического поля конденсатора. Когда конденсатор будет разряжаться вся энергия электрического поля вернется обратно в цепь в виде энергии электрического тока. Таким образом емкостное сопротивление является реактивным, т.е. не вызывающим безвозвратных потерь энергии.
Почему постоянный ток не проходит через конденсатор, а переменный ток проходит?
Включим цепь постоянного тока. Лампа вспыхнет и погаснет, почему? Потому что в цепи прошел ток заряда конденсатора. Как только конденсатор зарядится до напряжения батареи ток в цепи прекратится.
А теперь замкнем цепь переменного тока. В I четверти периода напряжение на генераторе возрастает от 0 до максимума. В цепи идет ток заряда конденсатора. Во II четверти периода напряжение на генераторе убывает до нуля. Конденсатор разряжается через генератор. После этого конденсатор вновь заряжается и разряжается. Таким образом в цепи идут токи заряда и разряда конденсатора. Лампочка будет гореть постоянно.
В цепи с конденсатором ток проходит во всей замкнутой цепи, в том числе и в диэлектрике конденсатора. В заряжающемся конденсаторе образуется электрическое поле которое поляризует диэлектрик. Поляризация это вращение электронов в атомах на вытянутых орбитах.
Одновременная поляризация огромного количества атомов образует ток, называемый током смещения. Таким образом в проводах идет ток и в диэлектрике причем одинаковой величины.
Емкостное сопротивление конденсатора определяется по формуле
Рассматривая график делаем вывод: ток в цепи с чисто емкостным сопротивлением опережает напряжение на 90 0 .
Возникает вопрос каким образом ток в цепи может опережать напряжение на генераторе? В цепи идет ток от двух источников тока поочередно, от генератора и от конденсатора. Когда напряжение на генераторе равно нулю ток в цепи максимален. Это ток разряда конденсатора.
Активное сопротивление, индуктивность и емкость в цепи переменного тока.
Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальная фаза напряжения будет иметь некоторое значение φ. При таком условии мгновенные значения силы тока и напряжения и будут выражаться следующими формулами:
i = I m sinωt
u = U m sin(ωt + φ)
a) Активное сопротивление в цепи переменного тока. Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным . Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току.
В цепи переменного тока, имеющей только активное сопротивление, например, в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. φ = 0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.
Будем считать, что напряжение на зажимах цепи меняется по гармоническому закону: и = U т cos ωt.
Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома:
по фазе с колебаниями напряжения.
b) Катушка индуктивности в цепи переменного тока. Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление X L , которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω: X L = ωL.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь. Для этого предварительно найдем связь между напряжением на катушке и ЭДС самоиндукции в ней. Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой.
Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля E i , порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля Е к, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства E i = -Е к следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции e i) равна по модулю и противоположна по знаку удельной работе кулоновского поля . Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать: e i = -и.
При изменении силы тока по гармоническому закону i = I m sin соsωt, ЭДС самоиндукции равна: е i = -Li» = -LωI m cos ωt. Так как e i = -и, то напряжение на концах катушки оказывается равным
и = LωI m cos ωt = LωI m sin (ωt + π/2) = U m sin (ωt + π/2)
гдеU m = LωI m — амплитуда напряжения.
Следовательно, колебания напряжения на катушке опережают по фазе колебания силы тока на π/2, или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на π/2.
Если ввести обозначение X L = ωL, то получим . Величину X L , равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением. Согласно формуле , значение силы тока связано с значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.
Индуктивное сопротивление зависит от частоты ω. Постоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю. Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток .
c) Конденсатор в цепи переменного тока. Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.
Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока.
Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Х с . Оно обратно пропорционально емкости С и круговой частоте ω: Х с =1/ωС.
Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь.
Напряжение на конденсаторе u = q/C равно напряжению на концах цепи u = U m cosωt.
Следовательно, q/C = U m cosωt. Заряд конденсатора меняется по гармоническому закону:
q = CU m cosωt.
Сила тока, представляющая собой производную заряда по времени, равна:
i = q» = -U m Cω sin ωt =U m ωC cos(ωt + π/2).
Следовательно, колебания силы тока опережают по фазе колебания напряжения на конденсаторе на π/2.
Величину Х с , обратную произведению ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома. Значение силы тока связано с значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока. Это и позволяет рассматривать величину Х с как сопротивление конденсатора переменному току (емкостное сопротивление).
Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Х с. С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты ω.
В заключение отметим, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.
Из сравнения формул X L = ωL и Х с =1/ωС видно, что катушки индуктивности. представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Индуктивное Х L и емкостное Х C сопротивления называют реактивными.
d) Закон ома для электрической цепи переменного тока.
Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С
Мы видели, что при включении по отдельности в цепь активного сопротивления R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами:
; ; I m = U m ωC .
Амплитуды же напряжений на активном сопротивлении, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так: U m = I m R; U m = I m ωL;
В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах. Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.
Действительно, ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлениями. Однако только на активном сопротивлении колебания напряжения и тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний тока на π/2, а на катушке индуктивности колебания напряжения опережают колебания тока на π/2. Если учесть сдвиг фаз между складываемыми напряжениями, то окажется, что
Для получения этого равенства нужно уметь складывать колебания напряжений, сдвинутые по фазе друг относительно друга. Проще всего выполнить сложение нескольких гармонических колебаний с помощью векторных диаграмм. Идея метода основана на двух довольно простых положениях.
Во-первых, проекция вектора с модулем х m вращающегося с постоянной угловой скоростью совершает гармонические колебания: х = х m cosωt
Во-вторых, при сложении двух векторов проекция суммарного вектора равна сумме проекций складываемых векторов.
Векторная диаграмма электрических колебаний в цепи, изображенной на рисунке, позволит нам получить соотношение между амплитудой силы тока в этой цепи и амплитудой напряжения. Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока I m . Этот вектор изобразим в виде горизонтальной стрелки. Напряжение на активном сопротивлении совпадает по фазе с силой тока. Поэтому вектор U mR , должен совпадать по направлению с вектором I m . Его модуль равен U mR = I m R
Колебания напряжения на индуктивном сопротивлении опережают колебания силы тока на π/2, и соответствующий вектор U m L должен быть повернут относительно вектора I m на π/2. Его модуль равен U m L = I m ωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор U m L следует повернуть налево. (Можно было бы, конечно, поступить и наоборот.)
Его модуль равен U mC =I m /ωC . Для нахождения вектора суммарного напряжения U m нужно сложить три вектора: 1) U mR 2) U m L 3) U mC
Вначале удобнее сложить два вектора: U m L и U mC
Модуль этой суммы равен , если ωL > 1/ωС. Именно такой случай изображен на рисунке. После этого, сложив вектор (U m L + U mC) с вектором U mR получим вектор U m , изображающий колебания напряжения в сети. По теореме Пифагора:
Из последнего равенства можно легко найти амплитуду силы тока в цепи:
Таким образом, благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи, изображенной на рисунке, выражается так:
От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин:
Это и есть закон Ома для переменного тока в цепи, изображенной на рисунке 43. Мгновенное значение силы тока меняется со временем гармонически:
i = I m cos (ωt+ φ), где φ — разность фаз между силой тока и напряжением в сети. Она зависит от частоты ω и параметров цепи R, L, С.
e) Резонанс в электрической цепи. При изучении вынужденных механических колебаний мы познакомились с важным явлением — резонансом. Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой внешней силы. При малом трении происходит резкое увеличение амплитуды установившихся вынужденных колебаний. Совпадение законов механических и электромагнитных колебаний сразу же позволяет сделать заключение о возможности резонанса в электрической цепи, если эта цепь представляет, собой колебательный контур, обладающий определенной собственной частотой колебаний.
Амплитуда тока при вынужденных колебаниях в контуре, совершающихся под действием внешнего гармонически изменяющегося напряжения, определяется формулой:
При фиксированном напряжении и заданных значениях R, L и С, сила тока достигает максимума при частоте ω, удовлетворяющей соотношению
Эта амплитуда особенно велика при малом R. Из этого уравнения можно определить значение циклической частоты переменного тока, при которой сила тока максимальна:
Эта частота совпадает с частотой свободных колебаний в контуре с малым активным сопротивлением.
Резкое возрастание амплитуды вынужденных колебаний тока в колебательном контуре с малым активным сопротивлением происходит при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура. В этом состоит явление резонанса в электрическом колебательном контуре.
Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности. Эти напряжения становятся одинаковыми и во много раз превосходят внешнее напряжение.
Действительно,
U м, С,рез =
U м, L ,рез =
Внешнее напряжение связано с резонансным током так:
U м = . Если тоU m , C ,рез = U m , L ,рез >> U m
При резонансе сдвиг фаз между током и напряжением становится равным нулю.
Действительно, колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. Резонансные амплитуды этих напряжений одинаковы. В результате напряжения на катушке и конденсаторе полностью компенсируют друг друга, и падение напряжения происходит только на активном сопротивлении.
Равенство нулю сдвига фаз между напряжением и током при резонансе обеспечивает оптимальные условия для поступления энергии от источника переменного напряжения в цепь. Здесь полная аналогия с механическими колебаниями: при резонансе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).
Конденсаторы, как и резисторы, относятся к наиболее многочисленным элементам радиотехнических устройств. Основное свойство конденсаторов, это способность накапливать электрический заряд . Основной параметр конденсатора это его емкость .
Емкость конденсатора будет тем значительнее, чем больше площадь его обкладок и чем тоньше слой диэлектрика между ними. Основной единицей электрической емкости является фарада (сокращенно Ф), названная так в честь английского физика М. Фарадея. Однако 1 Ф — это очень большая емкость. Земной шар, например, обладает емкостью меньше 1 Ф. В электро- и радиотехнике пользуются единицей емкости, равной миллионной доле фарады, которую называют микрофарадой (сокращенно мкФ) .
Емкостное сопротивление конденсатора переменному току зависит от его емкости и частоты тока: чем больше емкость конденсатора и частота тока, тем меньше его емкостное сопротивление.
Керамические конденсаторы обладают сравнительно небольшими емкостями — до нескольких тысяч пикофарад. Их ставят в те цепи, в которых течет ток высокой частоты (цепь антенны, колебательный контур), для связи между ними.
Простейший конденсатор представляет собой два проводника электрического тока, например: — две металлические пластины, называемые обкладками конденсатора, разделенные диэлектриком, например: — воздухом или бумагой. Чем больше площадь обкладок конденсатора и чем ближе они расположены друг к другу, тем больше электрическая емкость этого прибора. Если к обкладкам конденсатора подключить источник постоянного тока, то в образовавшейся цепи возникнет кратковременный ток и конденсатор зарядится до напряжения, равного напряжению источника тока. Вы можете спросить: почему в цепи, где есть диэлектрик, возникает ток? Когда мы присоединяем к конденсатору источник тока, электроны в проводниках образовавшейся цепи начинают двигаться в сторону положительного полюса источника тока, образуя кратковременный поток электронов во всей цепи. В результате обкладка конденсатора, которая соединена с положительным полюсом источника тока, обедняется свободными электронами и заряжается положительно, а другая обкладка обогащается свободными электронами и, следовательно, заряжается отрицательно. Как только конденсатор зарядится, кратковременный ток в цепи, называемый током зарядки конденсатора, прекратится.
Если источник тока отключить от конденсатора, то конденсатор окажется заряженным. Переходу избыточных электронов с одной обкладки на другую препятствует диэлектрик. Между обкладками конденсатора тока не будет, а накопленная им электрическая энергия будет сосредоточена в электрическом поле диэлектрика. Но стоит обкладки заряженного конденсатора соединить каким-либо проводником «лишние» электроны отрицательно заряженной обкладки перейдут по этому проводнику на другую обкладку, где их недостает, и конденсатор разрядится. В этом случае в образовавшейся цепи также возникает кратковременный ток, называемый током разрядки конденсатора. Если емкость конденсатора большая, и он заряжен до значительного напряжения, момент его разрядки сопровождается появлением значительной искры и треска. Свойство конденсатора накапливать электрические заряды и разряжаться через подключенные к нему проводники используется в колебательном контуре радиоприемника.
Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемых обкладками ), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок (см. рис.). Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки). Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.
С точки зрения метода комплексных амплитуд конденсатор обладает комплексным импедансом
,
Где j — мнимая единица, ω — циклическая частота (рад/с ) протекающего синусоидального тока, f — частота в Гц , C — ёмкость конденсатора (фарад ). Отсюда также следует, что реактивное сопротивление конденсатора равно: . Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).
Резонансная частота конденсатора равна
При f > f p конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f p , на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2-3 раза ниже резонансной.
Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:
где U — напряжение (разность потенциалов), до которого заряжен конденсатор.
Ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС.
Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.
Общее описание
Физически электронное устройство — конденсатор — представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь. Конструктивно прибор может быть различного размера и формы, но его структура остаётся неизменной, то есть всегда происходит чередование проводящего и диэлектрического слоев.
Слово «конденсатор» произошло от латинского «condensatio» — «накопление». Научное определение гласит, что накопительный электрический прибор — это двухполюсник, характеризующийся постоянным и переменным значениями ёмкости и большим сопротивлением. Предназначен он для накопления энергии и заряда. За единицу измерения ёмкости принят фарад (F).
На схемах конденсатор изображается в виде двух прямых, соответствующих проводящим пластинам прибора, и перпендикулярно к их серединам нарисованными отрезками — выводами устройства.
Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным. Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом — отрицательного.
Длительность этого процесса зависит от ёмкости прибора и активного сопротивления. Расположенный между выводами диэлектрик мешает перемещению частиц между обкладками. Но это будет происходить лишь до того момента, пока разность потенциалов источника питания и напряжение на выводах конденсатора не сравняются. В этот момент ёмкость станет максимально возможной, а электроток — минимальным.
Если на элемент перестают подавать напряжение, то при подключении нагрузки конденсатор начинает отдавать свой накопленный заряд ей. Его ёмкость уменьшается, а в цепи снижаются уровни напряжения и тока. Иными словами, накопительный прибор сам превращается в источник питания. Поэтому если конденсатор подключить к переменному току, то он начнёт периодически перезаряжаться, то есть создавать определённое сопротивление в цепи.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними.
Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе. Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние.
Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X < 0, в элементе проявляется ёмкостное сопротивление.
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное — с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
Ёмкостное сопротивление
Для понимания процесса следует представить конденсатор в электрической цепи, по которой течёт переменный ток. Причём в этой цепи нет других элементов. Значение тока, проходящего через конденсатор, и напряжения, приложенного к его обкладкам, изменяется по времени. Зная любое из этих значений, можно найти другое.
Пускай ток изменяется по синусоидальной зависимости I (t) = Im * sin (w*t+ f 0). Тогда напряжение можно описать как U (t) = (Im/C*w) *sin (w*t+ f 0 -p/2). При учёте в формуле сдвига фаз на 90 градусов, возникающего между сигналами, вводится комплексная величина j, называемая мнимой единицей. Поэтому формула для нахождения тока будет выглядеть как I = U /(1/j*w*C). Но учитывая, что комплексное число только обозначает смещение напряжения относительно тока, а на их амплитудные значения не влияет, его можно убрать из формулы, тем самым значительно её упростив.
Так как по закону Ома сопротивление прямо пропорционально напряжению на участке цепи и обратно пропорционально току, то преобразуя формулы, можно будет получить следующее выражение:
- Xc = 1/w*C = ½*p*f*C. Единица измерения — ом.
Становится понятно, что ёмкостное сопротивление зависит не только от ёмкости, но и от частоты. При этом чем больше эта частота, тем меньшее сопротивление конденсатор будет оказывать проходимому через него току. По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.
На практике всё немного по-другому. Чем ближе частота сигнала приближается к нулевому значению, тем больше становится сопротивление конденсатора, но при этом разрыв цепи наступить всё равно не может. Связанно это с током утечки. В случае когда частота стремится к бесконечности, сопротивление конденсатора должно становиться нулевым, но этого тоже не происходит — из-за присутствия паразитной индуктивности и всё того же тока утечки.
Индуктивная составляющая
При прохождении переменного сигнала через накопитель, его можно представить в виде последовательно включённой с источником питания катушки индуктивности. Эта катушка характеризуется большим сопротивлением в цепи переменного сигнала, чем постоянного. Значение силы тока в определённой точке времени находится как I = I 0 * sinw .
Приняв во внимание, что мгновенная величина напряжения U 0 обратна по знаку мгновенному значению ЭДС самоиндукции E 0, а также используя правило Ленца, можно получить выражение E = L * I, где L — индуктивность.
Следовательно: U = L*w * I 0 *cosw*t = U 0 *sin (wt + p /2) , причём ток отстаёт от напряжения на p /2. Используя закон Ома и приняв, что сопротивление катушки равно w * L, получится формула для участка электрической цепи, имеющая только индуктивную составляющую: U 0 = I 0 / w * L.
Таким образом, индуктивное сопротивление будет равно Xl = w * L, измеряется оно также в омах. Из полученного выражения видно, что чем больше частота сигнала, тем сильнее будет сопротивление прохождению тока.
Пример расчёта
Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R 2 +Xc 2 ) ½.
Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.
В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет
Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 −6 ) = 3,2 кОм.
По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.
Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 −3 + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (50002+32002)½ = 5 936 Ом =5,9 кОм.
Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.
Емкость в цепи переменного тока
Положим теперь, что участок цепи содержит конденсатор емкости , причем сопротивлением и индуктивностью можно пренебречь. Выясним, по какому закону будет изменяться напряжение на концах участка цепи в этом случае. Полагаем, что сила тока изменяется по закону .
Напряжение на конденсаторе равно
. (6.4)
Ток можно записать через величину заряда протекающего через сечение проводника и увеличивающего заряд конденсатора за промежуток времени
. (6.5)
Тогда заряд конденсатора можно найти интегрированием
. (6.6)
Поскольку сила тока в цепи изменяется по закону
, (6.7)
то заряд равен
. (6.8)
Постоянная интегрирования здесь обозначает произвольный постоянный заряд конденсатора, не связанный с колебаниями тока, и поэтому мы положим . Следовательно, с учетом формулы (6.4) можно записать для напряжения
(6.9)
Рисунок 6.4 Рисунок 6.5
Сравнение выражений (6.7) и (6.9) показывает, что при гармонических колебаниях тока в цепи напряжение на конденсаторе изменяется также по гармоническому закону, однако колебания напряжения на конденсаторе отстают по фазе от колебаний тока на
Изменение тока и напряжения во времени изображено графически на рисунке 6.5.
Полученный результат имеет простой физический смысл. Напряжение на конденсаторе в какой – либо момент времени определяется существующим зарядом конденсатора. Но этот заряд был образован током, протекавшим предварительно в более ранней стадии колебаний. Поэтому колебания напряжения, как и колебания заряда, запаздывают относительно колебаний тока. Так, например, когда в момент времени сила тока равна нулю (рисунок 6.5), то на пластинах конденсатора еще имеется заряд, перенесенный током в предыдущий промежуток времени, и напряжение не равно нулю. Для обращения в нуль этого заряда нужно, чтобы в течение промежутка времени, равного , проходил ток положительного направления. Однако, когда заряд конденсатора (а значит, и напряжение) станет равным нулю, сила тока уже не будет равна нулю (рисунок 6.5)–она принимает максимальное значение.
Формула (6.9) показывает, что амплитуда напряжения на конденсаторе равна
. (6.10)
Сравнивая это выражение с законом Ома для участка цепи постоянного тока , мы видим, что величина
, (6.11)
зависящая от емкости конденсатора , играет роль сопротивления участка цепи. Поэтому она получила название кажушегося сопротивления емкости или емкостным сопротивлением. Емкостное сопротивление равно отношению амплитуды напряжения на емкости к амплитуде силы тока в цепи. В Международной системе единиц СИ емкостное сопротивление выражается в омах. . Емкостное сопротивление равно величине, обратной произведению электрической емкости ( в ) и циклической частоты переменного тока (в ).
Полученные результаты можно представить в виде векторной диаграммы (рисунок 6.6). Здесь вектор, изображающий колебания напряжения, уже не совпадает с осью токов. Он повернут в отрицательном направлении (по часовой стрелке) на угол . Модуль этого вектора равен амплитуде напряжения .
Рисунок 6.6
Из формулы (6.11) видно, что сопротивление емкости зависит также от частоты . Поэтому при очень высоких частотах даже малые емкости могут представлять совсем небольшое сопротивление для переменного тока.
Закон Ома для участка цепи переменного тока. Разность фаз между колебаниями силы тока и напряжения
«Любое
препятствие
преодолевается
настойчивостью».
Леонардо
да Винчи
Задача
1.
В цепь переменного тока включена катушка с индуктивностью 75 мГн. Найдите
действующее значение напряжения на данном участке цепи, если действующее
значение силы тока равно 2 А, а частота колебаний равна 50 Гц.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ
Из закона Ома для участка цепи
Тогда действующее напряжение будет равно
Индуктивное сопротивление определяется по формуле
Т.к. циклическая частота равна
индуктивное сопротивление будет равно
С учётом последней формулы действующее значение напряжения
|
|
|
Ответ:
47 В.
Задача
2.
В цепь переменного тока включены резистор с сопротивлением 20 Ом и
конденсатор с ёмкостью 10 мкФ. Известно, что напряжение на конденсаторе
изменяется по закону ,
а амплитудный ток, протекающий по данному участку равен 5 А.
Какое напряжение покажет вольтметр, указанный на схеме?
|
ДАНО:
|
СИ
|
РЕШЕНИЕ
Запишем закон Ома для цепей переменного тока
Полное сопротивление определяется по формуле (с учётом
Действующее значение напряжения определяется по формуле
С другой стороны действующие значения напряжения и силы
Тогда получим
Запишем уравнение гармонических колебаний в общем виде
По условию задачи задано следующее уравнение
Сопоставляя эти два уравнения можно определить, что
Тогда действующее значение напряжения
|
|
|
Ответ:
79 В.
Задача
3.
Дана цепь переменного тока со следующими параметрами: активное сопротивление
равно 20 Ом, индуктивность равна 15 мГн, электроёмкость конденсатора равна
55 мкФ, частота равна 50 Гц, амплитудное напряжение равно 220 В.
Найдите амплитудные токи, протекающие в каждом элементе цепи, а также суммарный
ток.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ
При параллельном соединении
Закон Ома для участка цепи
Исходя из него, запишем
Индуктивное сопротивление определяется по формуле
Ёмкостное сопротивление определяется по формуле
Тогда получим
Циклическую частоту можно определить по формуле
Тогда сила тока в резисторе,
Запишем закон Ома для цепей переменного тока
В котором полное сопротивление определяется как
Тогда сила тока
|
|
|
Задача
4.
Конденсатор и катушка индуктивности последовательно подключены к источнику
переменного напряжения. Частоту колебаний увеличивают от 50 Гц до 80 Гц. Как
изменится значение амплитудного тока? Резонансная частота колебаний равна 70
Гц.
|
ДАНО:
|
РЕШЕНИЕ
Запишем закон Ома для цепей переменного тока
В соответствии с ним,
Полное сопротивление определяется по формуле
Исходя из того, что в цепи
В соответствии с полученным
Тогда отношение полных сопротивлений
Собственная частота колебательного контура определяется по
Тогда получаем, что отношение полных сопротивлений равно
Т.к. циклическая частота определяется по формуле
то получаем
Тогда отношение полных сопротивлений равно
Можно получить косвенное
|
|
|
Ответ:
амплитудный ток увеличится в 6,67 раза.
Задача
5.
В цепь переменного тока последовательно включен резистор с сопротивлением 10
Ом, катушка и конденсатор с ёмкостью 200 нФ. Известно что при частотах 1 кГц и
1,5 кГц в цепи наблюдаются одинаковые амплитудные токи. Найдите индуктивность
катушки и разность фаз между током и напряжением при указанных частотах.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ
Запишем закон Ома для цепей переменного тока
В соответствии с этим,
Запишем теперь формулу, по
На основании данной формулы
Преобразуем полученное
Преобразуем получившуюся формулу
Циклическая частота определяется по формуле
Тогда индуктивность катушки равна
Разность фаз определяется по формуле
В соответствии с полученной
|
|
|
Колебаний в LC-цепи — Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, почему заряд или ток колеблются между конденсатором и катушкой индуктивности, соответственно, при последовательном соединении
- Опишите взаимосвязь между зарядом и током, колеблющимся между конденсатором и катушкой индуктивности, соединенными последовательно
Следует отметить, что и конденсаторы, и катушки индуктивности накапливают энергию в своих электрических и магнитных полях соответственно.Цепь, содержащая как катушку индуктивности ( L ), так и конденсатор ( C ), может колебаться без источника ЭДС путем сдвига энергии, накопленной в цепи, между электрическим и магнитным полями. Таким образом, концепции, которые мы развиваем в этом разделе, непосредственно применимы к обмену энергией между электрическим и магнитным полями в электромагнитных волнах или свете. Начнем с идеализированной схемы с нулевым сопротивлением, содержащей индуктивность и конденсатор, — это схема LC .
Схема LC показана на (Рисунок). Если конденсатор содержит заряд до того, как переключатель замкнут, тогда вся энергия цепи изначально хранится в электрическом поле конденсатора ((Рисунок) (a)). Эта энергия
Когда переключатель замкнут, конденсатор начинает разряжаться, создавая ток в цепи. Ток, в свою очередь, создает в индукторе магнитное поле. Конечным результатом этого процесса является передача энергии от конденсатора с его уменьшающимся электрическим полем к индуктору с его увеличивающимся магнитным полем.
(a – d) Колебания накопителя заряда при изменении направления тока в цепи LC . (e) Графики показывают распределение заряда и тока между конденсатором и катушкой индуктивности.
В (Рисунок) (b) конденсатор полностью разряжен, и вся энергия хранится в магнитном поле индуктора. В этот момент ток достигает максимального значения, а энергия в катушке индуктивности равна
.
Поскольку в цепи нет сопротивления, энергия не теряется из-за джоулева нагрева; таким образом, максимальная энергия, запасенная в конденсаторе, равна максимальной энергии, сохраненной позже в катушке индуктивности:
В произвольный момент времени, когда заряд конденсатора равен q (t) , а ток равен i (t) , полная энергия U в цепи равна
Поскольку нет рассеивания энергии,
После достижения максимума ток i (t) продолжает переносить заряд между пластинами конденсатора, тем самым перезаряжая конденсатор.Поскольку катушка индуктивности сопротивляется изменению тока, ток продолжает течь, даже если конденсатор разряжен. Этот непрерывный ток заставляет конденсатор заряжаться с противоположной полярностью. Электрическое поле конденсатора увеличивается, в то время как магнитное поле индуктора уменьшается, и общий эффект заключается в передаче энергии от индуктора обратно к конденсатору. Согласно закону сохранения энергии, максимальный заряд, который повторно приобретает конденсатор, составляет. Однако, как показано (Рисунок) (c), пластины конденсатора заряжены на напротив от того, что было изначально.
После полной зарядки конденсатор снова передает свою энергию катушке индуктивности до тех пор, пока он снова полностью не разрядится, как показано на (Рисунок) (d). Затем, в последней части этого циклического процесса, энергия возвращается к конденсатору, и исходное состояние схемы восстанавливается.
Мы проследили цепь через один полный цикл. Его электромагнитные колебания аналогичны механическим колебаниям массы на конце пружины. В последнем случае энергия передается назад и вперед между массой, имеющей кинетическую энергию, и пружиной, имеющей потенциальную энергию.При отсутствии трения в системе масса-пружина колебания будут продолжаться бесконечно. Точно так же колебания цепи LC без сопротивления продолжались бы вечно, если бы их не беспокоили; однако эта идеальная схема LC с нулевым сопротивлением неприменима, и любая схема LC будет иметь, по крайней мере, небольшое сопротивление, которое со временем будет излучать и терять энергию.
Частоту колебаний в цепи без сопротивления LC можно найти по аналогии с системой масса-пружина.Для схемы, полная электромагнитная энергия U составляет
Для системы масса-пружина, полная механическая энергия E составляет
Эквивалентность двух систем очевидна. Чтобы перейти от механической системы к электромагнитной, мы просто заменяем m на L , v на i , k на 1/ C и x на q . Теперь x (t) даёт
, где Следовательно, заряд конденсатора в цепи LC равен
, где угловая частота колебаний в контуре
Наконец, ток в цепи LC находится путем взятия производной по времени от q (t) :
Временные изменения q и I показаны на (Рисунок) (e) для.
Цепь LC В цепи LC собственная индуктивность равна H, а емкость равна F. Вся энергия хранится в конденсаторе, который имеет заряд C. (a) Какова угловая частота колебания в цепи? б) Каков максимальный ток, протекающий через цепь? (c) Сколько времени нужно, чтобы конденсатор полностью разрядился? (d) Найдите уравнение, представляющее q (t) .
Стратегия
Угловая частота цепи LC приведена на (Рисунок).Чтобы найти максимальный ток, максимальная энергия в конденсаторе устанавливается равной максимальной энергии в катушке индуктивности. Время разряда конденсатора, если он изначально заряжен, составляет четверть периода цикла, поэтому, если мы вычислим период колебаний, мы сможем выяснить, какая четверть от этого времени составляет это время. Наконец, зная начальный заряд и угловую частоту, мы можем составить уравнение косинуса, чтобы найти q ( t ).
Решение
- Из (рисунок) угловая частота колебаний
- Ток максимален, когда вся энергия накапливается в катушке индуктивности.Из закона сохранения энергии,
т.
Этот результат также можно найти по аналогии с простым гармоническим движением, где ток и заряд — это скорость и положение осциллятора.
- Конденсатор полностью разряжается за одну четверть цикла или за время T /4, где T — период колебаний. С
время, необходимое для полной разрядки конденсатора, составляет
- Конденсатор полностью заряжен, поэтому Используя (рисунок), получаем
Таким образом, и
Значение Энергетическая взаимосвязь, установленная в части (b), — не единственный способ приравнять энергии.В большинстве случаев часть энергии накапливается в конденсаторе, а часть энергии — в катушке индуктивности. Мы можем поместить оба члена в каждую сторону уравнения. Исследуя схему только при отсутствии заряда конденсатора или тока в катушке индуктивности, мы упрощаем уравнение энергии.
Проверьте свое понимание Угловая частота колебаний в цепи LC составляет рад / с. (а) Если, что такое C ? (б) Предположим, что вся энергия хранится в катушке индуктивности.Каково значение (c) Второй идентичный конденсатор подключен параллельно исходному конденсатору. Какая угловая частота этой схемы?
Сводка
- Энергия, передаваемая колебательным образом между конденсатором и катушкой индуктивности в цепи LC , происходит с угловой частотой.
- Заряд и ток в цепи даны по формуле
.
Концептуальные вопросы
Применяются ли правила Кирхгофа к цепям, содержащим катушки индуктивности и конденсаторы?
Может ли элемент схемы иметь как емкость, так и индуктивность?
Что в цепи LC определяет частоту и амплитуду колебаний энергии в катушке индуктивности или конденсаторе?
Амплитуда колебаний энергии зависит от начальной энергии системы.Частота в цепи LC зависит от значений индуктивности и емкости.
Проблемы
Конденсатор емкостью 5000 пФ заряжается до 100 В и затем быстро подключается к катушке индуктивности 80 мГн. Определите (а) максимальную энергию, запасенную в магнитном поле индуктора, (б) пиковое значение тока и (в) частоту колебаний цепи.
Собственная индуктивность и емкость цепи LC составляют 0,20 мГн и 5,0 пФ.Какая угловая частота колеблется в цепи?
Какова собственная индуктивность цепи LC , которая колеблется с частотой 60 Гц при емкости?
В колеблющейся цепи LC максимальный заряд конденсатора составляет, а максимальный ток через катушку индуктивности составляет 8,0 мА. а) Каков период колебаний? (б) Сколько времени проходит между моментом, когда конденсатор не заряжен, и следующим моментом, когда он полностью заряжен?
а.; б.
Собственная индуктивность и емкость колеблющегося контура LC соответственно. а) Какова частота колебаний? (b) Если максимальная разность потенциалов между пластинами конденсатора составляет 50 В, каков максимальный ток в цепи?
В колеблющейся цепи LC максимальный заряд конденсатора составляет. Определите заряд конденсатора и ток через катушку индуктивности, когда энергия распределяется поровну между электрическим и магнитным полями.Выразите свой ответ в виде L и C .
В схеме, показанной ниже, одновременно размыкается и замыкается. Определите (а) частоту возникающих колебаний, (б) максимальный заряд конденсатора, (в) максимальный ток через катушку индуктивности и (г) электромагнитную энергию колебательного контура.
Схема LC в AM-тюнере (в автомобильной стереосистеме) использует катушку с индуктивностью 2.5 мГн и конденсатор переменной емкости. Если собственная частота схемы должна регулироваться в диапазоне от 540 до 1600 кГц (диапазон AM), какой диапазон емкости требуется?
Глоссарий
- LC контур
- , состоящая из источника переменного тока, катушки индуктивности и конденсатора
Цепь
23.12 Схемы переменного тока серии RLC — Физика колледжа: OpenStax
Сводка
- Рассчитайте полное сопротивление, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и / или ток в последовательной цепи RLC.
- Нарисуйте принципиальную схему последовательной цепи RLC.
- Объясните значение резонансной частоты.
Когда один в цепи переменного тока, все катушки индуктивности, конденсаторы и резисторы препятствуют току. Как они себя ведут, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в Ом не складываются просто так. Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично полностью нейтрализуют влияние друг друга. На рисунке 1 показана последовательная цепь RLC с источником переменного напряжения, поведение которой является предметом этого раздела.Суть анализа схемы RLC — это частотная зависимость [latex] \ boldsymbol {X_L} [/ latex] и [latex] \ boldsymbol {X_C} [/ latex] и их влияние на фазу. зависимости напряжения от тока (установлено в предыдущем разделе). Это приводит к частотной зависимости схемы с важными «резонансными» характеристиками, которые лежат в основе многих приложений, таких как радиотюнеры.
Рисунок 1. Последовательная цепь RLC с источником переменного напряжения.
Комбинированный эффект сопротивления [латекс] \ boldsymbol {R} [/ latex], индуктивного реактивного сопротивления [латекс] \ boldsymbol {X_L} [/ latex] и емкостного реактивного сопротивления [латекс] \ boldsymbol {X_C} [/ latex] равен определяется как импеданс , аналог сопротивления в цепи постоянного тока по переменному току. Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:
[латекс] \ boldsymbol {I_0 =} [/ latex] [латекс] \ boldsymbol {\ frac {V_0} {Z}} [/ latex] [латекс] \ boldsymbol {\ textbf {или} \; I _ {\ textbf {rms}} =} [/ latex] [latex] \ boldsymbol {\ frac {V _ {\ textbf {rms}}} {Z}}.[/ латекс]
Здесь [latex] \ boldsymbol {I_0} [/ latex] — пиковый ток, [latex] \ boldsymbol {V_0} [/ latex] — пиковое напряжение источника, а [latex] \ boldsymbol {Z} [/ latex] — сопротивление цепи. Единицы измерения импеданса — омы, и его влияние на схему такое, как и следовало ожидать: чем больше импеданс, тем меньше ток. Чтобы получить выражение для [latex] \ boldsymbol {Z} [/ latex] в терминах [latex] \ boldsymbol {R} [/ latex], [latex] \ boldsymbol {X_L} [/ latex] и [latex] \ boldsymbol {X_C} [/ latex], теперь мы рассмотрим, как напряжения на различных компонентах связаны с напряжением источника.Эти напряжения обозначены [латекс] \ boldsymbol {V_R} [/ latex], [latex] \ boldsymbol {V_L} [/ latex] и [latex] \ boldsymbol {V_C} [/ latex] на Рисунке 1.
Сохранение заряда требует, чтобы ток был одинаковым в каждой части цепи все время, так что мы можем назвать токи в [латексе] \ boldsymbol {R} [/ latex], [латексе] \ boldsymbol {L} [ / latex] и [latex] \ boldsymbol {C} [/ latex] равны и находятся в фазе. Но из предыдущего раздела мы знаем, что напряжение на катушке индуктивности [латекс] \ boldsymbol {V_L} [/ latex] опережает ток на одну четверть цикла, напряжение на конденсаторе [латекс] \ boldsymbol {V_C} [ / latex] следует за током на четверть цикла, а напряжение на резисторе [латекс] \ boldsymbol {V_R} [/ latex] точно совпадает по фазе с током.2}}, [/ latex]
где [латекс] \ boldsymbol {V_ {0R}} [/ latex], [latex] \ boldsymbol {V_ {0L}} [/ latex] и [latex] \ boldsymbol {V_ {0C}} [/ latex] — пиковое напряжение на [латексе] \ boldsymbol {R} [/ latex], [latex] \ boldsymbol {L} [/ latex] и [latex] \ boldsymbol {C} [/ latex] соответственно. Теперь, используя закон Ома и определения из главы 23.11. Реактивность, индуктивная и емкостная, мы заменяем [latex] \ boldsymbol {V_0 = I_0Z} [/ latex] в приведенное выше, а также [latex] \ boldsymbol {V_ {0R} = I_0R} [/ latex], [latex] \ boldsymbol {V_ {0L} = I_0X_L} [/ latex] и [latex] \ boldsymbol {V_ {0C} = I_0X_C} [/ latex], получается
[латекс] \ boldsymbol {I_0Z = \ sqrt {{I_0} ^ 2R ^ 2 + (I_0X_L — I_0X_C) ^ 2} = I_0 \ sqrt {R ^ 2 + (X_L — X_C) ^ 2}}.2}}, [/ latex]
, который является сопротивлением цепи переменного тока серии RLC . Для схем без резистора возьмите [латекс] \ boldsymbol {R = 0} [/ latex]; для тех, у кого нет индуктора, возьмите [латекс] \ boldsymbol {X_L = 0} [/ latex]; а для тех, у кого нет конденсатора, возьмите [латекс] \ boldsymbol {X_C = 0} [/ latex].
Рис. 2. На этом графике показаны отношения напряжений в цепи RLC к току. Напряжения на элементах схемы складываются, чтобы равняться напряжению источника, которое, как видно, не совпадает по фазе с током.
Пример 1: Расчет импеданса и тока
Цепь серии RLC имеет резистор [latex] \ boldsymbol {40.0 \; \ Omega} [/ latex], индуктивность 3,00 мГн и [латексный] \ boldsymbol {5.00 \; \ mu F} [/ латекс ] конденсатор. (a) Найдите полное сопротивление цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для [latex] \ boldsymbol {L} [/ latex] и [latex] \ boldsymbol {C} [/ latex] одинаковы. 2}} \\ [1em ] & \ boldsymbol {\ sqrt {(40.2}} \\ [1em] & \ boldsymbol {190 \; \ Omega \; \ textbf {at} \; 10.0 \; \ textbf {кГц}}. \ end {array} [/ latex]
Обсуждение для (а)
В обоих случаях результат почти такой же, как и наибольшее значение, и импеданс определенно не является суммой отдельных значений. Понятно, что [latex] \ boldsymbol {X_L} [/ latex] доминирует на высоких частотах, а [latex] \ boldsymbol {X_C} [/ latex] — на низких частотах.
Решение для (b)
Текущий [латекс] \ boldsymbol {I _ {\ textbf {rms}}} [/ latex] можно найти, используя версию закона Ома для переменного тока в уравнении [латекс] \ boldsymbol {I_ {rms} = V_ {rms} / Z} [/ latex]:
[латекс] \ boldsymbol {I _ {\ textbf {rms}} =} [/ latex] [latex] \ boldsymbol {\ frac {V _ {\ textbf {rms}}} {Z}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {120 \; \ textbf {V}} {531 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {= 0.226 \; \ textbf {A}} [/ latex] при 60,0 Гц
Наконец, на частоте 10,0 кГц мы находим
[латекс] \ boldsymbol {I _ {\ textbf {rms}} =} [/ latex] [latex] \ boldsymbol {\ frac {V _ {\ textbf {rms}}} {Z}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {120 \; \ textbf {V}} {190 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {= 0,633 \; \ textbf {A}} [/ latex] на 10,0 кГц
Обсуждение для (а)
Ток при 60,0 Гц такой же (до трех цифр), что и для одного конденсатора в Примере 1.Конденсатор преобладает на низкой частоте. Ток на частоте 10,0 кГц лишь немного отличается от того, который был обнаружен для одной катушки индуктивности в главе 23.11. Пример 1. Катушка индуктивности преобладает на высокой частоте.
Как цепь RLC ведет себя в зависимости от частоты источника управляющего напряжения? Объединяя закон Ома, [латекс] \ boldsymbol {I _ {\ textbf {rms}} = V _ {\ textbf {rms}} / Z} [/ latex], и выражение для импеданса [латекс] \ boldsymbol {Z} [/ латекс] из [латекса] \ boldsymbol {Z = \ sqrt {R ^ 2 + (X_L-X_C) ^ 2}} [/ latex] дает
[латекс] \ boldsymbol {I _ {\ textbf {rms}} =} [/ latex] [латекс] \ boldsymbol {\ frac {V _ {\ textbf {rms}}} {\ sqrt {R_2 + (X_L-X_C) ^ 2}}}.[/ латекс]
Реактивные сопротивления изменяются в зависимости от частоты: [latex] \ boldsymbol {X_L} [/ latex] большое на высоких частотах и [latex] \ boldsymbol {X_C} [/ latex] большое на низких частотах, как мы видели в трех предыдущих примерах. . На некоторой промежуточной частоте [latex] \ boldsymbol {f_0} [/ latex] реактивные сопротивления будут равны и отменены, давая [latex] \ boldsymbol {Z = R} [/ latex] — это минимальное значение для импеданса, и максимальное значение для результатов [latex] \ boldsymbol {I _ {\ textbf {rms}}} [/ latex]. Мы можем получить выражение для [latex] \ boldsymbol {f_0} [/ latex], взяв
[латекс] \ boldsymbol {X_L = X_C}.[/ латекс]
Замена определений [latex] \ boldsymbol {X_L} [/ latex] и [latex] \ boldsymbol {X_C} [/ latex],
[латекс] \ boldsymbol {2 \ pi f_0 L =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {2 \ pi f_0 C}}. [/ Latex]
Решение этого выражения для [latex] \ boldsymbol {f_0} [/ latex] дает
[латекс] \ boldsymbol {f_0 =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {2 \ pi \ sqrt {LC}}}, [/ латекс]
, где [latex] \ boldsymbol {f_0} [/ latex] — это резонансная частота цепи серии RLC .Это также собственная частота , на которой цепь будет колебаться, если не будет управляться источником напряжения. В [латексе] \ boldsymbol {f_0} [/ latex] эффекты катушки индуктивности и конденсатора нейтрализуются, так что [латекс] \ boldsymbol {Z = R} [/ latex] и [латекс] \ boldsymbol {I _ {\ textbf {rms}}} [/ latex] — это максимум.
Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденное колебание — в данном случае вызываемое источником напряжения — на собственной частоте системы.Приемник в радиоприемнике представляет собой схему RLC , которая лучше всего колеблется в своем [латексе] \ boldsymbol {f_0} [/ latex]. Переменный конденсатор часто используется для настройки [latex] \ boldsymbol {f_0} [/ latex], чтобы получить желаемую частоту и отклонить другие. На рисунке 3 представлен график зависимости тока от частоты, иллюстрирующий резонансный пик в [латексе] \ boldsymbol {I _ {\ textbf {rms}}} [/ latex] в [латексе] \ boldsymbol {f_0} [/ latex] . Две кривые относятся к двум разным цепям, которые различаются только величиной сопротивления в них.Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не так сильно резонирует и, например, не будет такой избирательной в радиоприемнике.
Рисунок 3. График зависимости тока от частоты для двух последовательных цепей RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f 0 , но для более высокого сопротивления он ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду В 0 .
Пример 2: Расчет резонансной частоты и тока
Для той же цепи серии RLC , имеющей резистор [latex] \ boldsymbol {40.0 \; \ Omega} [/ latex], индуктивность 3,00 мГн и [латексный] \ boldsymbol {5.00 \; \ mu F} [ / латекс] конденсатор: (а) Найдите резонансную частоту. (b) Рассчитайте [латекс] \ boldsymbol {I _ {\ textbf {rms}}} [/ latex] при резонансе, если [latex] \ boldsymbol {V _ {\ textbf {rms}}} [/ latex] составляет 120 В.
Стратегия
Резонансная частота находится с помощью выражения в [latex] \ boldsymbol {f_0 = \ frac {1} {2 \ pi \ sqrt {LC}}} [/ latex].Ток на этой частоте такой же, как если бы в цепи был только резистор.
Решение для (a)
Ввод данных значений для [latex] \ boldsymbol {L} [/ latex] и [latex] \ boldsymbol {C} [/ latex] в выражение, данное для [latex] \ boldsymbol {f_0} [/ latex] в [ latex] \ boldsymbol {f_0 = \ frac {1} {2 \ pi \ sqrt {LC}}} [/ latex] дает
[латекс] \ begin {array} {r @ {{} = {}} l} \ boldsymbol {f_0} & \ boldsymbol {\ frac {1} {2 \ pi \ sqrt {LC}}} \\ [1em ] & \ boldsymbol {\ frac {1} {2 \ pi \ sqrt {(3.{-6} \; \ textbf {F})}} = 1,30 \; \ textbf {кГц}.} \ End {array} [/ latex]
Обсуждение для (а)
Мы видим, что резонансная частота находится между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого и следовало ожидать, поскольку конденсатор преобладает на низкой частоте, а катушка индуктивности — на высокой. Их эффекты такие же на этой промежуточной частоте.
Решение для (b)
Ток определяется законом Ома.В резонансе два реактивных сопротивления равны и компенсируются, так что полное сопротивление равно только сопротивлению. Таким образом,
[латекс] \ boldsymbol {I _ {\ textbf {rms}} =} [/ latex] [latex] \ boldsymbol {\ frac {V _ {\ textbf {rms}}} {Z}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {120 \; \ textbf {V}} {40.0 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {= 3.00 \; \ textbf {A}}. [/ latex]
Обсуждение для (б)
В резонансе ток больше, чем на более высоких и более низких частотах, рассмотренных для той же цепи в предыдущем примере.
Если ток изменяется с частотой в цепи RLC , то мощность, подаваемая на нее, также зависит от частоты. Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток в цепи RLC не совпадают по фазе. Существует фазовый угол [латекс] \ boldsymbol {\ phi} [/ latex] между источником напряжения [латекс] \ boldsymbol {V} [/ latex] и текущим [латексом] \ boldsymbol {I} [/ латексом ], который можно найти по номеру
[латекс] \ boldsymbol {\ textbf {cos} \; \ phi =} [/ latex] [латекс] \ boldsymbol {\ frac {R} {Z}}.{\ circ}} [/ latex] и что напряжение и ток совпадают по фазе, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Причина в том, что напряжение и ток не совпадают по фазе, а также потому, что [latex] \ boldsymbol {I _ {\ textbf {rms}}} [/ latex] ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность составляет
[латекс] \ boldsymbol {P _ {\ textbf {ave}} = I _ {\ textbf {rms}} V _ {\ textbf {rms}} \ textbf {cos} \; \ phi}, [/ latex]
Таким образом, [latex] \ boldsymbol {\ textbf {cos} \; \ phi} [/ latex] называется коэффициентом мощности , который может находиться в диапазоне от 0 до 1.Например, при разработке эффективного двигателя желательны коэффициенты мощности, близкие к 1. На резонансной частоте [латекс] \ boldsymbol {\ textbf {cos} \; \ phi = 1} [/ latex].
Пример 3: Расчет коэффициента мощности и мощности
Для той же цепи серии RLC , имеющей резистор [latex] \ boldsymbol {40.0 \; \ Omega} [/ latex], индуктор 3,00 мГн, [латексный] \ boldsymbol {5.00 \; \ mu F} [/ латексный] конденсатор и источник напряжения с [латексом] \ boldsymbol {V _ {\ textbf {rms}}} [/ latex] на 120 В: (a) Рассчитайте коэффициент мощности и фазовый угол для [латекса] \ boldsymbol { f = 60.0 \ textbf {Hz}} [/ latex]. (б) Какова средняя мощность при 50,0 Гц? (c) Найдите среднюю мощность на резонансной частоте цепи.
Стратегия и решение для (а)
Коэффициент мощности при 60,0 Гц находится из
.
[латекс] \ boldsymbol {\ textbf {cos} \; \ phi =} [/ latex] [латекс] \ boldsymbol {\ frac {R} {Z}}. [/ Latex]
Мы знаем [латекс] \ boldsymbol {Z = 531 \; \ Omega} [/ latex] из Примера 1, так что
[латекс] \ boldsymbol {cos \; \ phi =} [/ latex] [латекс] \ boldsymbol {\ frac {40.{\ circ}} [/ latex] не в фазе).
Стратегия и решение для (b)
Средняя мощность при 60,0 Гц —
[латекс] \ boldsymbol {P_ {ave} = I _ {\ textbf {rms}} V _ {\ textbf {rms}} \ textbf {cos} \; \ phi} [/ латекс]
[latex] \ boldsymbol {I _ {\ textbf {rms}}} [/ latex] оказалось равным 0,226 A в Примере 1. Ввод известных значений дает
[латекс] \ boldsymbol {P _ {\ textbf {ave}} = (0,226 \; \ textbf {A}) (120 \; \ textbf {V}) (0,0753) = 2,04 \; \ textbf {W at} \ ; 60,0 \; \ textbf {Гц}}.[/ латекс]
Стратегия и решение для (c)
На резонансной частоте мы знаем [latex] \ boldsymbol {\ textbf {cos} \; \ phi = 1} [/ latex] и [latex] \ boldsymbol {I _ {\ textbf {rms}}} [/ latex ] в Примере 2 оказалось равным 6,00 А. Таким образом,
[латекс] \ boldsymbol {P _ {\ textbf {ave}} = (3.00 \; \ textbf {A}) (120 \; \ textbf {V}) (1) = 360 \; \ textbf {W}} [ / латекс] при резонансе (1,30 кГц)
Обсуждение
Как ток, так и коэффициент мощности больше в резонансе, производя значительно большую мощность, чем на более высоких и низких частотах.
Мощность, подаваемая в цепь переменного тока серии RLC , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, а резистор рассеивает именно то, что источник напряжения вводит в цепь. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, например радиоволн. Такое излучение может происходить и даже быть желательным, как мы увидим в следующей главе об электромагнитном излучении, но оно также может быть подавлено, как в случае в этой главе.Схема аналогична колесу автомобиля, движущегося по рифленой дороге, как показано на рисунке 4. Ровные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз. Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний. Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, хранящейся в индукторе) и потенциальной энергией, хранящейся в автомобильной пружине (аналогично отсутствию тока и энергии, хранящейся в электрическом поле конденсатора).Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.
Рисунок 4. Принудительное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC . Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту.
Чистая цепь LC с незначительным сопротивлением колеблется на [latex] \ boldsymbol {f_0} [/ latex], той же резонансной частоте, что и цепь RLC .Он может служить эталоном частоты или схемой часов — например, в цифровых наручных часах. При очень маленьком сопротивлении требуется лишь очень небольшая подводимая энергия для поддержания колебаний. Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рисунке 5 показана аналогия между цепью LC и грузом на пружине.
Рис. 5. Цепь LC аналогична массе, колеблющейся на пружине без трения и без движущей силы.Энергия движется вперед и назад между катушкой индуктивности и конденсатором, точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.
Исследование PhET: комплект для конструирования цепей (AC + DC), Virtual Lab
Создавайте цепи с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных инструментов, таких как вольтметры и амперметры.
Рисунок 6. Комплект для конструирования цепей (AC + DC), виртуальная лаборатория
- Аналогом сопротивления для переменного тока является импеданс [латекс] \ boldsymbol {Z} [/ latex], комбинированный эффект резисторов, катушек индуктивности и конденсаторов, определяемый версией закона Ома для переменного тока:
[латекс] \ boldsymbol {I_0 =} [/ latex] [латекс] \ boldsymbol {\ frac {V_0} {Z}} [/ latex] [латекс] \ boldsymbol {\ textbf {или} \; I _ {\ textbf {rms}} =} [/ latex] [latex] \ boldsymbol {\ frac {V _ {\ textbf {rms}}} {Z}}, [/ latex]
, где [latex] \ boldsymbol {I_0} [/ latex] — это пиковый ток, а [latex] \ boldsymbol {V_0} [/ latex] — это пиковое напряжение источника. {\ circ}} [/ latex] для чисто резистивной цепи или цепи RLC в резонансе.
- Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением
[латекс] \ boldsymbol {P _ {\ textbf {ave}} = I _ {\ textbf {rms}} V _ {\ textbf {rms}} \; \ textbf {cos} \; \ phi}, [/ latex]
[латекс] \ boldsymbol {\ textbf {cos} \; \ phi} [/ latex] называется коэффициентом мощности, который находится в диапазоне от 0 до 1.
Концептуальные вопросы
1: Зависит ли резонансная частота цепи переменного тока от пикового напряжения источника переменного тока? Объясните, почему да или почему нет.
2: Предположим, у вас есть двигатель с коэффициентом мощности значительно меньше 1. Объясните, почему было бы лучше улучшить коэффициент мощности как метод улучшения выходной мощности двигателя, чем увеличивать входное напряжение.
Задачи и упражнения
1: Схема RL состоит из [латексного] \ boldsymbol {40.0 \; \ Omega} [/ latex] резистора и индуктора 3,00 мГн. (a) Найдите его импеданс [латекс] \ boldsymbol {Z} [/ latex] при 60,0 Гц и 10.0 кГц. (b) Сравните эти значения [latex] \ boldsymbol {Z} [/ latex] со значениями, найденными в Примере 1, в котором также был конденсатор.
2: Схема RC состоит из [латексного] \ boldsymbol {40.0 \; \ Omega} [/ latex] резистора и [латексного] \ boldsymbol {5.00 \; \ mu F} [/ латексного] конденсатора. . (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения [latex] \ boldsymbol {Z} [/ latex] со значениями, найденными в Примере 1, в котором также был индуктор.
3: Схема LC состоит из [латексного] \ bold символа {3.00 \; \ textbf {mH}} [/ latex] индуктор и [латексный] \ boldsymbol {5.00 \; \ mu F} [/ latex] конденсатор. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения [latex] \ boldsymbol {Z} [/ latex] со значениями, найденными в Примере 1, в котором также был резистор.
4: Какова резонансная частота индуктора 0,500 мГн, подключенного к [латексному] \ boldsymbol {40.0 \; \ mu F} [/ латексный] конденсатор?
5: Для приема AM-радио вам нужна цепь RLC , которая может резонировать на любой частоте от 500 до 1650 кГц.Это достигается с помощью фиксированной [латексной] \ boldsymbol {1.00 \; \ mu \ textbf {H}} [/ latex] катушки индуктивности, подключенной к переменному конденсатору. Какой диапазон емкости нужен?
6: Предположим, у вас есть запас катушек индуктивности от 1,00 нГн до 10,0 Гн и конденсаторов от 1,00 пФ до 0,100 F. Каков диапазон резонансных частот, который может быть достигнут при сочетании одного индуктора и одного конденсатор?
7: Какая емкость вам нужна для получения резонансной частоты 1.00 ГГц, при использовании катушки индуктивности 8,00 нГн?
8: Какая индуктивность необходима для создания резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ и 2,00 мкФ?
9: Самая низкая частота в диапазоне FM-радио составляет 88,0 МГц. (а) Какая индуктивность необходима для создания этой резонансной частоты, если она подключена к конденсатору 2,50 пФ? (b) Конденсатор регулируемый, что позволяет регулировать резонансную частоту до 108 МГц. Какой должна быть емкость на этой частоте?
10: Схема серии RLC имеет символ [латекс] \ bold {2.50 \; \ Omega} [/ latex] резистор, [латексный] \ boldsymbol {100 \; \ mu \ textbf {H}} [/ latex] индуктор и [латексный] \ boldsymbol {80.0 \; \ mu \ textbf {F}} [/ latex] конденсатор. (a) Найдите полное сопротивление цепи при 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет [латекс] \ boldsymbol {V _ {\ textbf {rms}} = 5.60 \; \ textbf {V}} [/ latex], то что такое [латекс] \ boldsymbol {I _ {\ textbf { rms}}} [/ latex] на каждой частоте? (d) Какова резонансная частота контура? (e) Что такое [латекс] \ boldsymbol {I _ {\ textbf {rms}}} [/ latex] при резонансе?
11: Схема серии RLC имеет символ [латекс] \ bold {1.00 \; \ textbf {k} \ Omega} [/ latex] резистор, катушка индуктивности [latex] \ boldsymbol {150 \; \ mu \ textbf {H}} [/ latex] и конденсатор 25,0 нФ. (а) Найдите полное сопротивление цепи при 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет [латекс] \ boldsymbol {V _ {\ textbf {rms}} = 408 \; \ textbf {V}} [/ latex], то что такое [латекс] \ boldsymbol {I _ {\ textbf { rms}}} [/ latex] на каждой частоте? (d) Какова резонансная частота контура? (e) Что такое [латекс] \ boldsymbol {I _ {\ textbf {rms}}} [/ latex] при резонансе?
12: Схема серии RLC имеет символ [латекс] \ bold {2.50 \; \ Omega} [/ latex] резистор, [латексный] \ boldsymbol {100 \; \ mu H} [/ latex] индуктор и [латексный] \ boldsymbol {80.0 \; \ mu \ textbf {F} } [/ латексный] конденсатор. (a) Найдите коэффициент мощности [латекс] \ boldsymbol {f = 120 \; \ textbf {Hz}} [/ latex]. (б) Каков фазовый угол при 120 Гц? (c) Какая средняя мощность при 120 Гц? (d) Найдите среднюю мощность на резонансной частоте цепи. 2}} [/ latex]
- резонансная частота
- — частота, при которой полное сопротивление в цепи минимально, а также частота, с которой цепь будет колебаться, если не будет управляться источником напряжения; рассчитывается по [latex] \ boldsymbol {f_0 = \ frac {1} {2 \ pi \ sqrt {LC}}} [/ latex]
- фазовый угол
- обозначается [latex] \ boldsymbol {\ phi} [/ latex], величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи
- Коэффициент мощности
- — величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе; рассчитывается по [latex] \ boldsymbol {\ textbf {cos} \; \ phi} [/ latex]
Решения
Задачи и упражнения
1: (a) [латекс] \ boldsymbol {40.02 \; \ Omega} [/ latex] при 60,0 Гц, [латекс] \ boldsymbol {193 \; \ Omega} [/ latex] при 10,0 кГц
(b) При 60 Гц, с конденсатором [латекс] \ boldsymbol {\ textbf {Z} = 531 \; \ Omega} [/ latex], что более чем в 13 раз выше, чем без конденсатора. Конденсатор имеет большое значение на низких частотах. На 10 кГц, с конденсатором [латекс] \ boldsymbol {\ textbf {Z} = 190 \; \ Omega} [/ latex], примерно так же, как без конденсатора. Конденсатор оказывает меньшее влияние на высоких частотах.
3: (a) [латекс] \ boldsymbol {529 \; \ Omega} [/ latex] на 60.0 Гц, [латекс] \ boldsymbol {185 \; \ Omega} [/ latex] при 10,0 кГц
(b) Эти значения близки к значениям, полученным в Примере 1, потому что на низкой частоте преобладает конденсатор, а на высокой частоте преобладает индуктор. Таким образом, в обоих случаях резистор вносит небольшой вклад в общий импеданс.
5: от 9,30 нФ до 101 нФ
7: 3,17 пФ
9: (a) [латекс] \ boldsymbol {1.31 \; \ mu \ textbf {H}} [/ latex]
(б) 1,66 пФ
11: (a) [латекс] \ boldsymbol {12.{\ circ}} [/ латекс]
(в) 26,4 Вт
(г) 166 Вт
15: 16,0 Вт
Колебания напряжения — обзор
41.9.1 Компенсация мерцания лампы
Спектральная плотность колебаний напряжения, создаваемых дуговой печью, приблизительно обратно пропорциональна квадратному корню из частоты. Люди испытывают субъективную реакцию на мерцание лампы; как правило, пики человеческой чувствительности для ламп накаливания на 230 В чуть ниже 10 Гц.Как видно из рис. 41.44 , взвешенная комбинация этих характеристик показывает, что частоты, наиболее часто вызывающие визуальное раздражение, лежат в диапазоне от 2 до 25 Гц. Если колебания напряжения на частоте 10 Гц превышают примерно 0,2%, они могут вызвать заметное мерцание светового выхода лампы накаливания 230 В. Лампа на 110 В той же мощности имеет более тяжелую нить накала с большей теплоемкостью, что приводит к меньшему отклику на колебания напряжения, а частота наиболее возмущающих воздействий снижается примерно до 5–6 Гц.
Рисунок 41.44. Чувствительность глаз к мерцанию, вызванному дуговой печью
Цепь, питающую дуговую печь, можно упростить до схемы, показанной на рис. 41.45 , где точка общего соединения (pcc) — это точка в сети, к которой подключены другие потребители. . Сопротивление источника питания обычно мало по сравнению с реактивным сопротивлением, X с , и падение напряжения в этой точке, В p , в основном связано с изменением спроса на переменную ток в дуговой печи.Если SVC не установлен, реактивный ток, I s , в источнике питания такой же, как реактивный ток печи, I q , и мы получаем:
Рисунок 41.45. Упрощенная схема питания дуговой печи. PCC является точкой общего соединения (с другими потребителями)
Таким образом, относительно легко оценить величину провалов напряжения, вызванных колебаниями var, но трудно оценить раздражение, вызванное последовательностью быстрых провалов напряжения.Чтобы оценить и количественно оценить влияние колеблющихся провалов напряжения на человеческий глаз и мозг, Международный союз электрообогрева (UIE) разработал измеритель мерцания, который был одобрен IEC. Фликерметр измеряет последовательные колебания напряжения и с помощью алгоритмов, разработанных на основе первых принципов, преобразует их в числовые значения, которые сравниваются с тем, что 50% населения считают порогом восприятия мерцания лампы. Для этого порогового уровня мерцания лампы мерцание UIE даст числовое значение 1.0 для «интенсивности кратковременного мерцания» (Pst).
Фликерметр может применяться только при вводе печи в эксплуатацию и не может использоваться напрямую для прогнозирования уровней мерцания. Однако простая процедура оценки для целей планирования была получена эмпирическим путем из записей жалоб на мерцание на многих установках. Эта процедура оценивает «депрессию напряжения короткого замыкания» (SCVD) для предлагаемой дуговой печи; это изменение напряжения на pcc, которое могло бы быть вызвано изменением потребления варки печи с холостого хода на устойчивое трехфазное короткое замыкание на электродах.Если SCVD превышает примерно 2%, потребители, скорее всего, испытают достаточное раздражение, чтобы пожаловаться на мерцание лампы. Для электродуговой печи с SCVD около 1,3% фликерметр UIE обычно показывает максимальное значение Pst около 1.
Критерий SCVD может использоваться для оценки максимальной мощности печи, которая должна быть подключена к данной системе. но его можно использовать только для определения номинала компенсатора для уменьшения мерцания при условии, что компенсатор способен уменьшать все частоты мерцания в диапазоне визуального раздражения в разумной степени одинаково.Если компенсатор имеет приемлемую линейную частоту колебаний в зависимости от характеристики скорости отклика примерно до 25 Гц, тогда, если он подключен, как показано на рис. 41.45 , расчет SCVD в установившемся режиме можно использовать для оценки его номинального значения, т. Е. Тока компенсатора. jI c составляет разницу между допустимым — jI s и значением — jI q . Для уменьшения мерцания необходима высокая скорость реакции.Было показано, что если компенсатор имеет задержку времени регулирования 10 мс, независимо от его номинала, он может дать очень небольшое снижение мерцания; при временной задержке 20 мс или более диапазон частот в пределах диапазона визуального раздражения будет сильно выделен. Компенсатор конденсатора с тиристорным переключением, например, не может достичь необходимой скорости отклика для уменьшения мерцания дуговых печей в частотном диапазоне выше 5 Гц, где человеческий глаз наиболее чувствителен.
Насыщенный реактор с компенсацией гармоник без схемы коррекции крутизны спада был использован для снижения фликера до 3: 1.Он успешно использовался во многих установках в качестве компенсатора сборных шин ( Рисунок 41.46 (a) ), будучи спроектированным на основе критерия SCVD. Схема реактор с отводом / насыщенный реактор ( Рисунок 41.46 (b) ) была использована для получения снижения фликера до 7: 1 для одной дуговой печи. В этой схеме насыщенные реакторы являются однофазными устройствами, и коррекция наклона достигается за счет измененных соотношений обмоток реактора; этот компенсатор по своей сути компенсирует несбалансированные нагрузки дуговой печи и дает мгновенный отклик.Он вызывает значительные гармонические искажения и требует серьезной фильтрации.
TCR, используемый в качестве компенсатора шин, можно сделать пригодным для компенсации дуговых печей с уменьшением мерцания около 2: 1. Преобразователи с питанием от источника напряжения из-за их более низкого реактивного сопротивления и способности к гораздо более быстрому отклику могут превзойти обычные TCR; имеющиеся данные указывают на возможность уменьшения мерцания примерно на 4: 1.
Глава 7. Переменный ток — Анкит Патшала
Глава 7.Переменный ток — Анкит Патшала
Глава 7. Переменный ток
Напряжение переменного тока, приложенное к резистору
* Изменяющееся во времени напряжение, которое изменяется подобно синусоидальной функции, называется напряжением переменного тока.
* Ток, вызываемый переменным напряжением, называется переменным током.
* Переменный ток предпочтительнее постоянного тока главным образом потому, что переменное напряжение можно легко и эффективно преобразовать с более низкого напряжения на более высокое и наоборот с помощью трансформаторов.
* В чистом резисторе ток, протекающий через резистор, находится в фазе с разностью потенциалов на нем.
* Соотношение мгновенного напряжения и мгновенного тока в резисторе постоянно.
Мощность переменного тока, среднеквадратичный ток, напряжение и векторы
* Среднеквадратичный ток определяется как корень среднего квадрата тока.
* При аренде переменного тока: I среднеквадратичное значение = I м / √2 = 0,707 x I м
* Действующее значение напряжения или действующее значение напряжения: В = V м / √2
* Средняя мощность, рассеиваемая любым переменным током в резисторе, P = I 2 действующее значение R
* Вектор — это синусоидальная волна, амплитуда, фаза и частоты не зависят от времени.
Напряжение переменного тока, приложенное к катушке индуктивности
* Индуктор — это электрический компонент, который может накапливать энергию в магнитном поле, создаваемом переменным током, протекающим через него.
* Любое изменение тока через катушку индуктивности вызывает на ней ЭДС, пропорциональную скорости изменения тока.
* Мощность, подаваемая на катушку индуктивности в среднем в цепи переменного тока за один полный цикл, равна нулю.
(P) = — \ frac {i_ {m} v_ {m}} {2} (sin 2 ωt) = 0
Напряжение переменного тока, приложенное к конденсатору
* Конденсатор является электронным компонент, который может накапливать электростатический заряд.Он может быть похож на крошечный аккумулятор.
* Простой конденсатор состоит из двух проводящих пластин, разделенных изоляционным материалом, называемым диэлектриком.
* Когда конденсатор полностью заряжен, заряд конденсатора препятствует протеканию через него тока, и ток в цепи падает до нуля в установившемся состоянии.
* Емкостное реактивное сопротивление, X c , является обратным произведению угловой частоты ω и емкости C,
X c = 1 / ωC
* Мощность, подаваемая на конденсатор в среднем в цепи, равна нулю .{2 + (x_ {C} — x_ {L}) ²)}}}
Контур LCR — резонанс
* Резонанс — это явление, наблюдаемое в системах, которые имеют тенденцию колебаться с некоторой фиксированной частотой под влиянием внешней периодической силы, необходимой для поддержания его колебаний.
* Условие резонанса в цепи LCR: X c = X L
* Резонансная частота: ω 0 = 1 / \ sqrt {LC}
* Резонанс возможен только в цепи, имеющей как емкостную, так и индуктивную компоненты как условие, X c = X L должно быть выполнено.
* Полоса пропускания контура: 2∆ω = ω 0 / Q
* Резкость резонанса: ω 0 / 2∆ω = ω 0 L / R
* Добротность: Q = ω 0 L / R = 1 / ω 0 CR
* Более высокое значение добротности приводит к более резкому резонансу при уменьшении полосы пропускания.
Мощность в цепи переменного тока
* Мощность в цепи переменного тока: P av = V rms I rms (cos φ) P av = I 2 rms Z cos φ
* Коэффициент мощности: cosφ
* Ток в чисто индуктивной или чисто емкостной цепи, где коэффициент мощности равен нулю, известен как ток Ватта.
LC-колебания
* Явление LC-колебаний можно наблюдать, когда заряженный конденсатор включен в цепь последовательно с катушкой индуктивности.
* В генераторе LC зарядка и разрядка конденсатора имеют колебательный характер.
* Для колебания LC: q = qm cos (\ omega _ {0} t) i = im sin (\ omega _ {0} t)
Где:
i m = ω 0 q m
q = мгновенный заряд конденсатора
i = мгновенный ток в цепи
q м = максимальный заряд конденсатора в установившемся режиме
ω 0 = угловая частота
t = время
* Полная энергия в LC-цепь всегда постоянна.
U всего = q 2 m / 2C
Трансформаторы
* Трансформатор — это устройство, используемое для увеличения или уменьшения напряжения переменного тока.
* Трансформаторы работают по принципу взаимной индукции. Согласно принципу взаимной индукции, когда две катушки расположены близко друг к другу и если одна из катушек пропускает изменяющийся во времени ток, ток индуцируется в другой катушке.
* Для идеального трансформатора отношение выходного напряжения к входному напряжению равно отношению входного тока к выходному току, которое равно отношению количества витков вторичной катушки к числу витков в первичной катушке.
V s / V p = i p / i s = N s / N p
* Если вторичная катушка имеет большее количество витков, чем первичная, трансформатор называется понижающий трансформатор.
* Если вторичная обмотка имеет меньшее количество витков, чем первичная, трансформатор называется понижающим трансформатором.
Ошибка
: Контент защищен !!
Видеоурок: Цепи переменного тока
Стенограмма видеозаписи
В этом уроке мы научимся вычислять некоторые важные величины, связанные с током, напряжением и мощностью в цепях переменного тока.Мы также узнаем о различных возможных отношениях между переменным током и переменным напряжением в зависимости от того, является ли цепь резистивной, емкостной или индуктивной.
Начнем с определения переменного тока. Ток — это скорость, с которой заряд течет по пути. В электрической цепи, такой как эти резисторы, соединенные последовательно, путь формируется проводами и компонентами цепи. Как видно из этого примера, существует два возможных направления тока в этой цепи.Заряд может течь по цепи либо по часовой стрелке, либо в обратном направлении, против часовой стрелки. Если мы введем в цепь источник электродвижущей силы или ЭДС, например, ячейку с напряжением, то создаваемая ячейкой ЭДС будет управлять током в цепи. В этом случае обычный ток будет иметь направление по часовой стрелке, потому что обычный ток определяется как идущий от положительного вывода к отрицательному выводу ячейки.
Если мы физически перемещаем и возвращаемся вокруг ячейки, мы меняем местами положительные и отрицательные выводы относительно остальной цепи, и теперь направление тока будет против часовой стрелки.В обоих этих примерах с током, управляющим ячейкой в цепи, ток является постоянным током, потому что он имеет только одно направление, определяемое ориентацией ячейки. Существует другой тип источника, называемый источником переменного напряжения, который может плавно переключаться между положительным выводом вверху и отрицательным выводом внизу, отрицательным выводом вверху и положительным выводом внизу, как и наши две ориентации ячейки.
Следовательно, ЭДС от источника переменного напряжения будет переключаться взад и вперед между движением тока по часовой стрелке и против часовой стрелки по цепи.Поэтому мы называем такой ток переменным током, потому что он переключается между двумя возможными направлениями в цепи. Точно так же мы называем ЭДС, создаваемую нашим источником, переменной ЭДС, потому что она управляет током, меняющим направление. Прежде чем мы узнаем о простом источнике переменной ЭДС, стоит понять, как мы представим постоянный ток и переменный ток на графике.
Чтобы построить график зависимости тока от времени, нам нужно представить ток в конкретное время с помощью числа.Допустим, что величина нашего числа будет величиной силы тока. И затем, поскольку ток имеет одно из двух возможных направлений, мы позволим положительным числам представлять ток в одном направлении, а отрицательные числа — току в противоположном направлении. Неважно, какое направление мы выберем в качестве положительного, а какое — в качестве отрицательного, если мы придерживаемся определенного контура. Итак, нарисуем постоянный ток. Это течение имеет только одно направление. Эта синяя линия представляет постоянный ток.
Обратите внимание, что этот ток непостоянен во времени; он меняет размеры. Но значение всегда больше нуля, что означает, что всегда имеет направление, связанное с положительным током. Итак, это постоянный ток, потому что он имеет только одно направление. Эта зеленая линия также представляет постоянный ток. Величина этого тока постоянна во времени, но его значение всегда меньше нуля. Таким образом, он имеет направление, противоположное току, представленному синей линией. С другой стороны, ток, представленный этой оранжевой кривой, не постоянный, а переменный ток.Значение этого тока переключается с больше нуля в некоторые моменты на меньше нуля в другое время. Другими словами, этот ток меняет направление.
Хорошо, теперь перейдем к переменной ЭДС, создаваемой простым генератором переменного тока. Самый простой генератор переменного тока состоит из проволочной петли в однородном магнитном поле. Когда петля вращается в поле, магнитный поток, проходящий через петлю, изменяется, что вызывает индукцию переменного ЭДС на выводах петли. Давайте выведем количественную формулу для этой ЭДС как функции времени.Затем мы можем использовать эту формулу, чтобы понять некоторые количественные и качественные свойства ЭДС, а также переменные величины в целом. Мы начнем с закона индукции Фарадея, который гласит, что индуцированная ЭДС равна отрицательной величине измененного магнитного потока через петлю по времени.
Хорошо, давайте посчитаем поток через наш цикл. Мы можем думать о магнитном потоке как о величине магнитного поля, проходящего через петлю. Таким образом, если площадь петли равна, а сила магнитного поля равна, то полное магнитное поле, проходящее через петлю, будет просто раз.Это верно, когда петля полностью перпендикулярна полю. Но помните, наша петля вращается. Вот два снимка петли в магнитном поле, если смотреть сбоку. На первом изображении петля перпендикулярна магнитному полю, и мы ясно видим, что она пересекает пять силовых линий магнитного поля.
Однако на втором рисунке, поскольку петля повернулась на угол, петля теперь пересекает только три силовые линии магнитного поля, несмотря на то, что она имеет одинаковую длину.Таким образом, даже несмотря на то, что площадь петли не изменилась, общее магнитное поле, проходящее через петлю, безусловно, изменилось, и поэтому поток также изменился. Чтобы вычислить этот новый поток, отметим, что исходная петля, представленная сплошной линией, пересекает то же количество силовых линий магнитного поля, что и другая меньшая вертикальная петля, представленная этой вертикальной пунктирной линией. И мы знаем, каков поток через этот другой контур, потому что он перпендикулярен магнитному полю. Это просто площадь этой петли, умноженная на силу магнитного поля.
Теперь поток через оба контура одинаков. Таким образом, мы можем сказать, что петля, представленная сплошной линией, имеет эффективную площадь, равную площади петли, представленной пунктирной линией. Чтобы вычислить эту эффективную площадь, сначала назовем длину сплошной линии. Во-вторых, поскольку петля вращается с некоторой фиксированной скоростью, мы можем заменить угол величиной 𝜔, умноженной на 𝑡. — угловая скорость вращения, поэтому 𝜔 умноженное на — это общий угол поворота петли. Затем мы замечаем, что, поскольку две пунктирные линии на этой диаграмме параллельны, угол между двумя оранжевыми линиями также равен.Это позволяет нам рассчитать длину оранжевой пунктирной линии как 𝑙, умноженное на cos.
Нам не нужно корректировать ширину петли, потому что она всегда перпендикулярна магнитному полю на протяжении всего вращения. Таким образом, это позволяет нам записать эффективную площадь петли как ширину петли, умноженную на длину петли, умноженную на cos. Но ширина, умноженная на длину, — это всего лишь исходная площадь петли. Таким образом, эффективная площадь для расчета магнитного потока при вращении контура в поле — это площадь контура, умноженная на cos, где 𝜔 — угловая скорость вращения, а — прошедшее время.Корректируя наше предыдущее выражение для потока, чтобы получить поток в любой конкретный момент времени, нам нужно только включить коэффициент cos.
Это превращает наш исходный коэффициент площади в эффективную площадь. Рассчитанный нами поток — это поток для одной петли. Но многие генераторы на самом деле содержат несколько контуров для увеличения выходной мощности ЭДС. Если имеется 𝑛 идентичных контуров, и каждый контур имеет поток cos 𝜔𝑡, то общий поток через все контуры будет 𝑛 раз cos 𝜔𝑡.Давайте теперь найдем отрицательное значение изменения этого выражения относительно времени, чтобы получить ЭДС.
Единственная часть нашего выражения для потока, которая зависит от времени, — это cos 𝜔𝑡. Это означает, что мы можем записать ЭДС как, все они постоянны во времени, умноженные на отрицательное изменение cos 𝜔𝑡 во времени. Оказывается, это изменение отрицательное 𝜔 sin 𝜔𝑡. И когда мы принимаем отрицательное значение этого, мы получаем отрицательный отрицательный 𝜔 sin 𝜔𝑡. И у нас остался только положительный грех. Это дает нам окончательное выражение для переменной электродвижущей силы, создаваемой генератором переменного тока.У нас есть, что ЭДС равна 𝑛, количество витков провода, умноженное на 𝐴, площадь каждой петли, умноженное на, напряженность магнитного поля, умноженную на, скорость вращения петель, умноженную на sin, время с момента, когда петля была вертикальной.
Теперь, когда мы закончили наш количественный вывод, давайте воспользуемся этой формулой, чтобы понять некоторые качественные свойства этой переменной ЭДС. Чтобы получить качественное представление об этой ЭДС, первое, что мы сделаем, это построим график. График зависимости ЭДС от времени имеет синусоидальную форму из-за части sin выражения для ЭДС.Поскольку синусоидальная функция изменяется от положительной до отрицательной, крайние значения ЭДС просто задаются константой перед синусом 𝑛𝐴𝐵𝜔. Аналогичным образом мы можем ясно видеть из этого графика, что ЭДС принимает как положительные, так и отрицательные значения. В физическом смысле это соответствует способности ЭДС управлять током как в положительном, так и в отрицательном направлении конкретной цепи.
Кроме того, как мы видим, значение ЭДС изменяется со временем.Поэтому полезно попытаться найти какое-то значение, которое будет отражать среднее поведение ЭДС. Одно из естественных значений, которое мы могли бы рассмотреть, — это среднее арифметическое значение ЭДС за один цикл. Мы назовем это 𝐸 sub avg для средней ЭДС. И мы найдем его, найдя полную ЭДС за один цикл, деленную на длину цикла. Однако, если мы внимательно посмотрим на наш график, мы увидим, что каждый раз, когда ЭДС достигает некоторого положительного значения, есть соответствующий момент, когда ЭДС достигает отрицательного значения с той же величиной.Но это означает, что общая ЭДС этих двух времен равна нулю, поскольку значения отменяются.
Применяя это ко всему циклу, мы видим, что полная ЭДС за весь цикл равна нулю, потому что все положительные ЭДС компенсируются соответствующими отрицательными ЭДС. Если полная ЭДС равна нулю, то и средняя ЭДС равна нулю. Это истинный факт, но он не несет никакой информации о пиковых значениях ЭДС. И на самом деле, независимо от того, сколько существует проволочных петель, какова их площадь, какова сила магнитного поля или какова скорость вращения, средняя ЭДС от генератора переменного тока всегда будет равна нулю.Поэтому нам нужен другой вид среднего, который будет включать информацию о пиковых значениях ЭДС. Одно значение, которое окажется особенно полезным для приложений электроники, — это среднеквадратичное значение, или среднеквадратичное значение.
Каждое слово, корень, среднее значение и квадрат относится к одному из этапов вычисления среднеквадратичного значения. Первый шаг — возвести каждое число в квадрат. Поскольку квадрат отрицательного числа является положительным числом, это гарантирует, что все числа, с которыми мы имеем дело, теперь положительны.Следующий шаг — найти среднее этих чисел в квадрате. Оно всегда будет положительным или нулевым, поскольку квадратное число либо положительно, либо равно нулю. Последний шаг — извлечь квадратный корень из среднего, найденного на втором шаге. Мы делаем этот шаг, чтобы сбалансировать возведение в квадрат, которое мы сделали на первом шаге. Оказывается, среднеквадратичное значение синусоиды имеет очень красивую и простую форму.
Среднеквадратичное значение синусоиды ровно на единицу больше квадратного корня из двух максимального значения. Это означает, что среднеквадратичная ЭДС, создаваемая нашим генератором, равна единице над квадратным корнем из двух.Обратите внимание, что это действительно значение, которое содержит информацию о максимальном размере ЭДС. Кроме того, как очень полезное приближение, один квадратный корень из двух был приблизительно равен 0,7. Таким образом, среднеквадратичное значение ЭДС составляет примерно 0,7. Теперь, когда мы понимаем некоторые средние свойства переменной ЭДС, мы можем применить аналогичные принципы к току и мощности в цепях переменного тока.
В цепи переменного тока, если ЭДС следует синусоиде во времени, то же самое происходит и с током.График зависимости тока от времени будет иметь форму, очень похожую на график зависимости ЭДС от времени. Он будет синусоидальной формы с максимальным размером пика, который может быть как положительным, так и отрицательным. Следовательно, как и в случае с ЭДС, мы будем иметь, что среднее арифметическое значение тока за один цикл равно нулю, а среднеквадратичное значение тока равно единице над квадратным корнем из двукратного максимального значения тока, или примерно в 0,7 раза. максимальный ток. В нормальной резистивной цепи постоянного тока рассеиваемая мощность равна квадрату силы тока, умноженного на сопротивление.Для цепей переменного тока, которые являются чисто резистивными, где ток изменяется со временем, это соотношение все еще сохраняется, пока мы также указываем, что мощность теперь изменяется со временем.
Максимальная мощность будет рассеиваться, когда ток достигнет своего положительного или отрицательного максимального значения. Однако, в отличие от тока и ЭДС, рассеиваемая мощность всегда больше или равна нулю, потому что — положительное число или ноль. И хотя 𝐼 может быть отрицательным, в квадрате всегда положительно или равно нулю.Следовательно, если мы попытаемся взять среднее арифметическое мощности за один цикл тока, мы не получим просто ноль. На самом деле мы получаем половину максимальной мощности или половину пика, умноженного на квадрат 𝑅. Но половина равна единице над квадратным корнем из двух в квадрате, поэтому мы можем переписать 𝑃 среднее как единицу из квадратного корня, умноженного на двукратный максимальный ток, как величину, возведенную в квадрат, умноженную на.
Но это полезно, потому что у нас есть определение единицы на квадратный корень из двукратного максимального тока.Это просто среднеквадратичный ток. Тогда мы можем видеть, что средняя мощность, рассеиваемая в цепи переменного тока, такая же, как мощность, которая рассеивалась бы в цепи постоянного тока, если бы ток в цепи постоянного тока имел то же значение, что и действующее значение для цепи постоянного тока. ток в цепи переменного тока. Таким образом, использование среднеквадратичного значения тока не только дает нам информацию о пиковом значении тока, но также дает нам связь между средней мощностью, рассеиваемой в цепи переменного тока, и мощностью, рассеиваемой в цепи постоянного тока.
Хорошо, давайте теперь посмотрим, как переменное напряжение и переменный ток соотносятся друг с другом в резистивных, емкостных и индуктивных цепях. Чтобы проиллюстрировать эти отношения, мы нарисовали три схемы. Каждая схема имеет источник переменного напряжения, подключенный к одному компоненту. В первой цепи компонент представляет собой резистор сопротивления. Во второй цепи это конденсатор емкости. А в третьей цепи это индуктор индуктивности. Буква 𝐿 используется в честь физика Генриха Ленца, потому что закон Ленца играет важную роль в индукторах.Чтобы облегчить сравнение, мы будем рассматривать каждый источник переменного напряжения как идентичный, чтобы каждая цепь имела одинаковый управляющий ток переменной ЭДС.
Для каждой цепи мы нарисовали синусоидальную ЭДС на графике в виде синей пунктирной кривой. Давайте теперь посмотрим, что мы ожидаем от тока для каждой цепи. Для резистивной цепи или цепи 𝑅 действует закон Ома, который гласит, что напряжение и ток прямо пропорциональны. Об этом четко говорит закон Ома: 𝑉 равно и справедливо даже при переменном токе.В этом случае ток, представленный сплошной зеленой линией, будет иметь точно такую же форму, что и ЭДС, но с другой величиной. В емкостной или 𝐶-цепи ЭДС и ток не прямо пропорциональны. Скорее, ток следует по этой сплошной зеленой кривой, которая равна нулю в моменты, когда ЭДС максимальна, и максимальна в моменты, когда ЭДС равна нулю.
Если мы внимательно посмотрим, то увидим, что ток следует синусоиде той же формы, что и ЭДС, но достигает своего максимального значения на четверть периода раньше, чем ЭДС.На языке фаз мы видим, что ток опережает ЭДС на 90 градусов. Чтобы интуитивно понять эту взаимосвязь, вспомните, что напряжение на конденсаторе определяется количеством заряда на пластинах. А ток — это поток заряда во времени. Таким образом, ЭДС заставляет ток в цепи заряжать конденсатор.
Если мы вспомним, что обычный ток определяется как поток положительного заряда от положительного вывода источника напряжения к отрицательному выводу источника напряжения, мы можем видеть, что результирующий заряд на конденсаторе будет положительным с той же стороны. как положительный вывод источника напряжения и отрицательный на той же стороне, что и отрицательная сторона источника напряжения, поскольку положительный заряд течет в верхнюю пластину и уходит от нижней пластины.Если ЭДС от источника переменного напряжения больше, чем напряжение на конденсаторе, ток будет проходить через конденсатор, накапливающий заряд, как показано на рисунке.
Таким образом, пока ЭДС становится больше, мы ожидаем, что ток будет течь, как показано. С другой стороны, если ЭДС становится более отрицательной по сравнению с напряжением на конденсаторе, мы ожидаем, что ток будет течь в противоположном направлении. Глядя на наш график, мы видим, что, действительно, когда ЭДС переходит от своего наиболее положительного к самому отрицательному значению — другими словами, ЭДС уменьшается — ток отрицательный.И когда ЭДС изменяется от самого отрицательного до самого положительного значения — другими словами, увеличивается — ток становится положительным. В индуктивной цепи или 𝐿 цепи ток будет иметь такой же сдвиг, что и емкостная цепь, но в другом направлении.
Таким образом, в этом случае максимальная электродвижущая сила возникает за четверть периода до максимального тока. Другими словами, ЭДС опережает ток на 90 градусов. Чтобы понять это интуитивно, вспомните, что, когда ЭДС пропускает ток через катушку индуктивности, она создает магнитное поле, указывающее в определенном направлении, которое колеблется вместе с током.При изменении ЭДС изменяется ток в индукторе, что изменяет величину магнитного поля. По закону Ленца это изменяющееся магнитное поле индуцирует ток, препятствующий этому изменению. Это вызывает задержку тока, и в результате ЭДС изменяется раньше, чем ток, что приводит к опережению фазы на 90 градусов.
Прежде чем мы рассмотрим то, что мы узнали, стоит отметить, что ЭДС в каждой из этих цепей является синусоидальной. Таким образом, ток также является синусоидальным, хотя иногда он отстает или опережает ЭДС.
Хорошо, давайте рассмотрим ключевые моменты, которые мы усвоили в этом уроке. В центре нашего внимания были цепи переменного тока. Мы определили переменный ток как ток, который периодически меняет направление со временем. Мы видели, что если график переменного тока представляет собой синусоиду, и действительно для любой синусоиды, определенное среднее значение — это среднее арифметическое, равное нулю. Однако мы можем определить другое среднее значение, называемое среднеквадратическим, которое не равно нулю. Для особого случая синусоиды среднеквадратичное значение равно единице над квадратным корнем из двукратного максимального значения, что приблизительно равно 0.В 7 раз больше максимального значения.
Мы также видели, что синусоидальный переменный ток часто вызывается синусоидальной электродвижущей силой, создаваемой генератором переменного тока. Мы вывели формулу: количество витков, умноженное на площадь каждого контура, умноженное на напряженность магнитного поля, умноженное на угловую частоту вращения, умноженное на грех, умноженное на, умноженное на время, прошедшее с момента, когда петля была перпендикулярна магнитному полю, чтобы дать ЭДС в любой заданной точке. время. Мы видели, что в резистивной цепи ЭДС и ток синфазны.В емкостной цепи ток опережает ЭДС на 90 градусов. А в индуктивной цепи ЭДС опережает ток на 90 градусов. Наконец, мы увидели, что средняя мощность, рассеиваемая в резистивной цепи переменного тока, равна среднеквадратичному значению тока, умноженному на сопротивление.
Как работают индукторы? — Utmel
Катушки индуктивности — это элементы накопления энергии, которые преобразуют электрическую энергию в магнитную энергию для хранения. Он похож на трансформатор, но индуктор имеет только одну обмотку.Конструкция индуктора обычно состоит из каркаса, обмотки, экрана, упаковочного материала, железного сердечника и магнитопровода.
Каталог
Ⅰ Введение
Индукторы — это элементы накопления энергии, которые преобразуют электрическую энергию в магнитную для хранения. Он похож на трансформатор, но индуктор имеет только одну обмотку. Конструкция индуктора обычно состоит из каркаса, обмотки, экрана, упаковочного материала, железного сердечника и магнитопровода.Индуктор — это пассивный электронный компонент, который может накапливать электрическую энергию в виде магнитного потока. Когда ток течет, справа от направления тока создается магнитное поле. В своей основной форме индуктор может быть такой же простой, как проволочная катушка. Сделав провода вокруг сердечника, можно увеличить индуктивность вдвое. Характеристики материала магнитопровода имеют большое влияние на значение индуктивности, и характеристики индуктивности также могут быть оптимизированы за счет формы.
Катушки индуктивности обладают важными характеристиками, которые инженеры могут использовать для управления энергией и управляющими сигналами. Основные характеристики индуктора: 1. В отличие от резистора, электрическая энергия, связанная с индуцированным током, не будет рассеиваться в виде тепла, а будет накапливаться в соответствующем магнитном поле. 2. Когда ток индуктора прерывается, он возвращается в цепь; 3. Поведение катушки индуктивности зависит от частоты; 4. Когда магнитное поле накапливает энергию, которую оно может принять, индуктор «насыщается».После этого, если произойдет увеличение тока, сила магнитного поля не будет увеличиваться, а избыточная электрическая энергия будет рассеиваться в виде тепла.
Используя эти характеристики, катушки индуктивности обычно используются для моделирования цепей фильтров и управления потоком энергии в импульсных преобразователях мощности.
Ⅱ Единица индуктивности
Поскольку индуктивность была обнаружена американским ученым Джозефом Генри, единицей индуктивности является «Генри». Единица индуктивности — Генри (Гн).6 мкГн.
Когда на катушку индуктивности подается напряжение, скорость нарастания тока зависит от напряжения и значения индуктивности. Потенциал 1 В на катушке индуктивности 1H увеличивает ток со скоростью 1 А в секунду. Применимая здесь формула: V = L * di / dt. Ток в 1 А через катушку может создавать магнитный поток 1 Вт, поэтому эта катушка имеет индуктивность 1 Гн.
Кроме того, существуют индукторы общего назначения и прецизионные индукторы, как показано ниже:
| Прецизионный индуктор | Общий индуктор | ||||||
| Symbol | F | G | J | K | K | K | M |
| Допуск | 1% | 2% | 5% | 10% | 15% | 20% | |
Ⅲ Что делает индуктор?
1.Роль индукторов в переменном токе
Когда переменный ток течет в индуктор, и индуктор будет препятствовать его изменению. Он не сразу становится большим, а увеличивается медленно. Когда питание переменного тока отключено, индуктор переменного тока не потеряет сразу, а постепенно станет меньше.
Этот процесс хорошо видно по изменению яркости лампы накаливания. В цепи переменного тока последовательно в цепь включены индукторы, лампы накаливания, переключатели и т. Д.При замкнутом выключателе лампа накаливания включается не мгновенно, а из темного в яркое. Когда выключатель выключен, лампа накаливания не выключается внезапно. Он меняется от светлого к темному. Весь процесс ясно показывает, что рабочая функция индуктора заключается в стабилизации тока. Электрическая энергия преобразуется в магнитную энергию, а затем магнитная энергия преобразуется в электрическую. В обоих процессах первый представляет собой лампу накаливания от темного к яркому, а второй — от яркого к темному.
2. Роль индукторов в фильтрации индуктивности
В цепи постоянного тока, когда через индуктор протекает ток, в катушке мгновенно создается индуцированное магнитное поле, и магнитное поле индуцирует ток. . Направление индуцированного тока и тока, протекающего через катушку индуктивности, противоположны, что будет препятствовать прохождению внешнего тока. Текущий ток стабилизируется, и индуцированное магнитное поле больше не будет изменяться, так что постоянный ток может течь плавно.Из этого процесса мы видим, что индуктивность фактически препятствует изменению тока. При прохождении через переменный ток, поскольку переменный ток изменяется в любое время, индуктивность всегда сопротивляется этому изменению и препятствует прохождению переменного тока.
Рисунок 1. Схема фильтра & pi; -типа
Препятствующее влияние катушки индуктивности на переменный ток называется индуктивным реактивным сопротивлением, и оно связано с частотой переменного тока и индуктивностью.Чем выше частота переменного тока, тем больше индуктивность и индуктивное реактивное сопротивление. Воспользовавшись этой функцией, мы часто используем ее при фильтрации источников питания. На рисунке выше показана схема фильтра типа & pi;, состоящая из конденсатора и катушки индуктивности. После фильтрации конденсатора в сигнале постоянного тока будут небольшие колебания. Однако катушка индуктивности может препятствовать изменению тока, так что она может подавлять эти небольшие колебания, тем самым выводя более чистую мощность постоянного тока.
За исключением описанных выше эффектов блокировки и фильтрации, индуктор также выполняет функции подавления помех электромагнитных волн, фильтрации сигналов, стабилизации тока и фильтрации шума.
Ⅳ Как работают индукторы?
Рисунок 2. Простая конструкция индуктора
На принципиальной схеме индуктор выглядит следующим образом:
Рисунок 3. Обозначение индуктора
Когда через провод течет ток, вокруг него создается концентрическое магнитное поле. В это время, если провод сгибается в «форму пружины», как показано на рисунке, магнитный поток внутри индуктора будет указывать в том же направлении, тем самым усиливая магнитное поле.Регулируя количество витков, можно создать магнитное поле, пропорциональное количеству витков. Это принцип работы индуктора.
Рисунок 4. Принцип индуктора
Магнитное поле создается, когда ток проходит через индуктор, и наоборот, изменения магнитного поля создают ток. (Закон электромагнитной индукции)
E = L ・ (di / dt)
L: Самоиндукция катушки индуктивности E: обратная ЭДС
Противоэлектродвижущая сила E, генерируемая в катушке индуктивности, пропорциональна скорости изменения тока на единицу времени (di / dt), поэтому этого не происходит, когда определенный ток продолжает течь в том же направлении, что и постоянный ток.Другими словами, катушка индуктивности не влияет на постоянный ток, а только на переменный ток, чтобы блокировать ток. Используя это свойство индуктора, его можно использовать в качестве сопротивления (импеданса) в цепи переменного тока. Полное сопротивление Z (единица Ом) индуктора составляет:
Z = ωL = 2πfL
f — частота переменного тока, а L — самоиндуктивность индуктора.
Катушка индуктивности — это пассивный электронный компонент, который может накапливать электрическую энергию в виде магнитного потока. Обычно провод наматывают, при прохождении тока магнитное поле создается с правой стороны от направления тока.
Рисунок 5. Магнитное поле индуктора
Формула расчета значения индуктивности приведена ниже. Чем больше количество валков, тем сильнее магнитное поле. В то же время увеличение площади поперечного сечения или изменение магнитопровода может усилить магнитное поле.
Рисунок 6. Формула расчета значения индуктивности
Итак, давайте посмотрим, что происходит с индуктором, когда через него протекает переменный ток.Переменный ток относится к току, величина и направление которого периодически меняются со временем. Когда через катушку индуктивности проходит переменный ток, создаваемое током магнитное поле отключает другие обмотки, создавая обратное напряжение, которое препятствует изменению тока. В частности, когда ток внезапно увеличивается, электродвижущая сила в направлении, противоположном току, то есть в направлении уменьшения тока, будет генерироваться, чтобы препятствовать увеличению тока.И наоборот, когда ток уменьшается, он генерируется в направлении увеличения тока.
Рисунок 7. Переменный ток течет через катушку индуктивности
Если направление тока меняется на противоположное, также будет генерироваться обратное напряжение. Прежде чем ток будет заблокирован обратным напряжением, ток будет обратным, так что ток не сможет течь. С другой стороны, постоянный ток не изменяется из-за тока, поэтому нет обратного напряжения и нет опасности короткого замыкания.Другими словами, индуктор — это компонент, который пропускает постоянный ток, но не переменный.
Рисунок 8. Обратный ток течет через катушку индуктивности
Следующий рисунок поможет вам понять, как индуктор работает в цепи:
Рисунок 9. индуктор работает в цепи
Здесь вы видите батарею, лампочку, катушку вокруг (желтого) железного блока и выключатель. Катушка — это индуктор.Если вы прочитали принцип работы электромагнита, вы будете знать, что индуктор — это электромагнит.
Если убрать дроссель из схемы, то получится обычная вспышка. Закройте выключатель, и лампочка загорится. Если индуктор установлен в схеме, как показано, его роль будет совершенно иной.
Лампочка представляет собой резистор (сопротивление выделяет тепло и заставляет нить накаливания в лампочке светить). Сопротивление провода в катушке намного ниже (это просто провод), поэтому, когда вы включите переключатель, вы увидите, что лампочка тускло светится.Большая часть тока будет проходить через контур через цепь с низким сопротивлением. На самом деле происходит следующее: когда вы замыкаете выключатель, лампочка сначала горит ярко, а затем гаснет. Когда вы включаете выключатель, лампочка становится очень яркой, а затем быстро гаснет.
Это дроссель вызывает это странное явление. Когда ток начинает течь в катушке впервые, катушка образует магнитное поле. Во время формирования магнитного поля катушка препятствует протеканию тока.Как только магнитное поле сформировано, ток обычно может проходить через провод. Когда переключатель разомкнут, магнитное поле вокруг катушки заставляет ток течь в катушке до тех пор, пока магнитное поле не исчезнет. Этот ток может поддерживать свечение лампы в течение некоторого времени, даже когда выключатель разомкнут. Другими словами, индуктор может накапливать энергию в своем магнитном поле и обычно предотвращает любое изменение количества тока, протекающего через него.
Представьте себе поток воды …
Интуитивный способ понять принцип работы индуктора — представить узкую водопроводную трубу с протекающей по ней водой и тяжелое водяное колесо с лопастью, погруженной в водопроводную трубу.Представьте, что вода в водопроводе изначально не течет. Теперь вы пытаетесь заставить воду течь. Водяное колесо будет останавливать поток воды, пока оно не начнет вращаться со скоростью воды. Если вы попытаетесь остановить поток воды в водопроводной трубе, вращающееся водяное колесо будет продолжать перемещать воду до тех пор, пока скорость водяного колеса не уменьшится до скорости потока воды. Принцип работы индуктора такой же, то есть поток электронов в проводе — индуктор препятствует изменению потока электронов.
Рекомендуемый артикул:
Основы индуктивности: структура, параметры и измерения
Срок
| Определение | ||
Условие
| Определение | ||
Срок
| Определение
| ||
Условие
| Определение | ||
Термин
| Определение | ||
Срок
| Определение | ||
Клемма
| Определение
| ||
Срок
| Определение | ||
Термин
| Определение | ||
Клемма
| Определение | ||
| Срок | Определение
| ||
Срок
| Определение | ||
| Срок | Определение | ||
Срок
| Определение
| ||
Термин
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение | ||
Термин
| Определение | ||
Срок
| Определение | ||
Срок
| Определение | ||
Срок
| Определение | ||
Срок действия
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Срок
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Клемма
| Определение | ||
Условие
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение | ||
Срок
| Определение | ||
Термин
| Определение
| ||
Термин
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение
| ||
Клемма
| Определение | ||
Термин
| Определение
| ||
Термин
| Определение | ||
Термин
| Определение | ||
Термин
| Определение
| ||
Условие
| Определение | ||
Термин
| Определение | ||
Term
| Определение | ||
Клемма
| Определение | ||
Условие
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Условие
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение | ||
Термин
| Определение
| ||
Клемма
| Определение | ||
Термин
| Определение | ||
Срок
| Определение | ||
Срок
| Определение | ||
Условие
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Клемма
| Определение | ||
Термин
| Определение | ||
Срок
| Определение | ||
Термин
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение
| ||
Термин
| Определение
| ||
Термин
| Определение | ||
Срок
| Определение | ||
Член
| Определение | ||
Срок
| Определение | ||
Условие
| Определение | ||
Термин
| Определение | ||
Срок
| Определение | ||
Срок
| Определение | ||
Клемма
| Определение | ||
Срок
| Определение | ||
Термин
| Определение | ||
Условие
| Определение | ||
Термин
| Определение | ||
Условие
| Определение
| ||
Условие
| Определение | ||
Клемма
| Определение | ||
Условие
| Определение | ||
Срок
| Определение | ||
| Срок | Определение
| ||
Термин
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение | ||
Клемма
| Определение | ||
Член
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Условие
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Срок
| Определение
| ||
Термин
| Определение | ||
 | |||