Закон сохранения энергии в механике. Общефизический закон сохранения энергии. Диссипация энергии. Общефизический закон сохранения энергии

2. Понятие энергии. Общефизический закон сохранения энергии

Важнейшими понятиями механики являются: сила, импульс, момент импульса, энергия. Эти физические величины определяются в качестве мер.

Сила- это векторная мера взаимодействия.

Импульс- это векторная мера движения при линейных перемещениях (переносах) тел в пространстве.

Момент импульса - это векторная мера движения при изменении ориентации (поворотах) тел в пространстве.

Энергия- это всеобщая скалярная мера движения и взаимодействия всех видов материи.

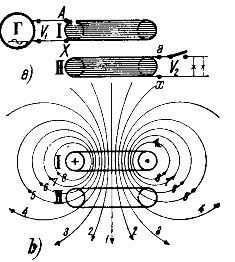
блок

S1*

S2* S2*

шкив S1

Р В S2 r

r S2

груз

G G

а) б)

Рис.2.

Пояснение. Дополнительный блок применяется для увеличения высоты подъёма груза и улучшения переброски нити на шкиве. На первой схеме - а) груз опускается, и нить на шкиве разматывается. На второй схеме - б) груз поднимается, т.к. нить после опускания груза перебрасывается на другую сторону шкива и теперь наматывается на его обод. Момент силы натяжения нити Мр= r∙ х∙ S1. В первом случае момент силы S1 "помогает" шкиву вращаться и угловая скорость  увеличивается. Во втором случае шкив продолжает вращаться по инерции, но момент силы S1"тормозит" шкив и угловая скорость  уменьшается, так что шкив (вместе с грузом) через некоторое время остановится.

На схемах показаны направления скорости груза, движущегося под действием силы тяжести G и натяжения нити S2. При движении груза сила G>S2.

Силы S были бы равны между собой (S1=S*1=S2=S*2) при условии, что блок невесом и на его оси нет трения. В реальной схеме эти силы равны попарно (S1=S*1; S2=S*2). Объясните, почему в первом случае S*2>S*1, а во втором- S*1>S*2. Как это влияет на высоту подъёма груза после переброски нити?

Общефизическое понятие энергии сформировалось в XIX в., когда было установлено, что все виды взаимодействия и движения возможны только при наличии особой физической величины, получившей название «энергия». При этом энергия переходит из одной формы в другую: механическую, внутреннюю, электромагнитную, химическую, ядерную и др. Такое разделение форм энергии условно. Например, внутренней энергией называется сумма кинетической энергии хаотического движения атомов и молекул и энергии взаимодействия таких частиц, которая складывается из энергии электромагнитного и гравитационного взаимодействий.

Установлено, что при переходе из одной формы в другую суммарное значение энергии не изменяется, и на этом основании сформулирован общефизический закон сохранения энергии: в изолированной системе энергия может переходить из одной формы в другую, но её количество остается постоянным.

В космологической механике предполагается, что в Большой Вселенной (включающей в себя всю совокупность Галактик) количество энергии сохраняется неизменным. Отметим, что в Большой Вселенной суммарное значение сил, импульсов и моментов импульсов оказывается равным нулю вследствие полной балансировки этих векторных величин.

Примечание. Система тел называется изолированной, если составляющие систему тела не взаимодействуют с внешними объектами. В этом смысле Большая Вселенная по определению является изолированной системой.

studfiles.net

5.4. Общефизический закон сохранения энергии

Классическая механика учитывает только кинетическую энергию макроскопического движения тел и их макроскопических частей, а также их потенциальную энергию. Но она полностью отвлекается от внутреннего атомистического строения вещества. При ударе, трении и аналогичных процессах кинетическая энергия видимого движения тел не пропадает. Она только переходит в кинетическую энергию невидимого беспорядочного движения атомов и молекул вещества, а также в потенциальную энергию их взаимодействия. Эта часть энергии получила название внутренней энергии.

Беспорядочное движение атомов и молекул воспринимается нашими органами чувств в виде тепла.

Таково физическое объяснение кажущейся потери механической энергии при ударе, трении и пр.

В физике закон сохранения энергии распространяют не только на явления, рассматриваемые в механике, но на все без исключения процессы, происходящие в природе.

Полное количество энергии в изолированной системе тел и полей всегда остается постоянным; энергия лишь может переходить из одной формы в другую.

В основе закона сохранения энергии лежит такое свойство времени как однородность, т.е. равнозначность всех моментов времени, заключающаяся в том, что замена момента времени t1 моментом времени t2, без изменения значений координат и скоростей тел не изменяет механических свойств системы. Поведение системы, начиная с момента времени t2 будет таким же, каким оно было бы, начиная с момента t1.

Общефизический закон сохранения энергии не может быть выведен из уравнений механики, и должен рассматриваться как одно из наиболее широких обобщений опытных фактов.

Лекция №6. Закон сохранения момента импульса

6.1. Момент силы и момент импульса относительно неподвижного начала

Пусть О – какая-либо неподвижная точка в инерциальной системе отсчета. Ее называют началом или полюсом. Обозначим через 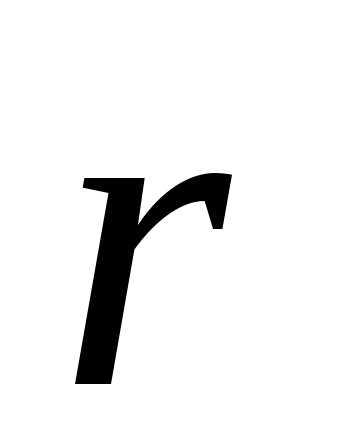радиус-вектор, проведенный из этой точки к точке A приложения силы (рис. 1) .

Моментом силы относительно точки О называется векторное произведение радиуса-вектора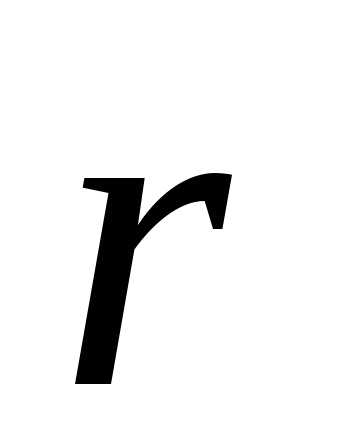 на силу : , , (1)

–угол между векторами 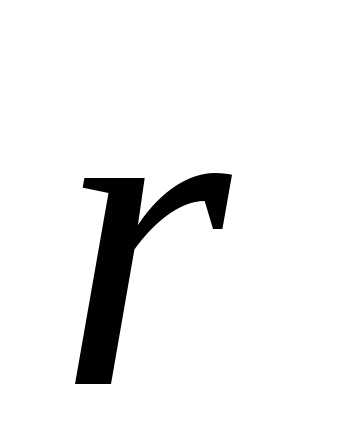и ; направление выбирается так, чтобы последовательность векторов 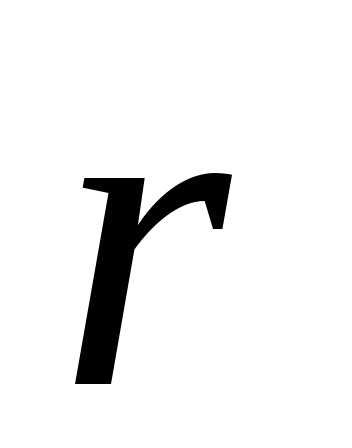,,образовывала правовинтовую систему, т. е. если смотреть вдоль вектора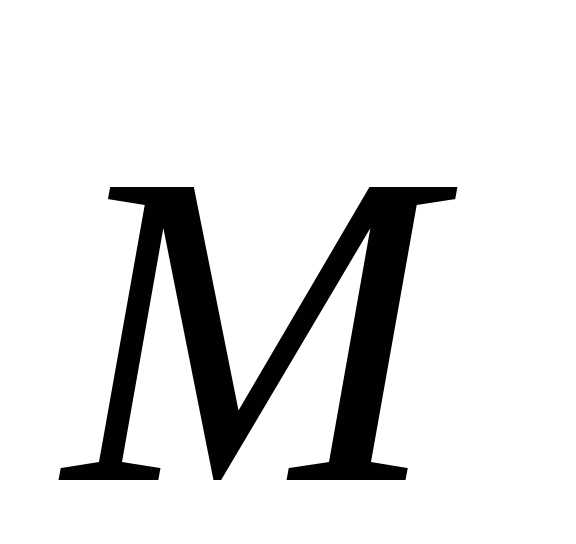, то поворот по кратчайшему пути от первого сомножителя в (1) ко второму осуществлялся по часовой стрелке, таким образом совпадает с направлением поступательного движения правого буравчика, рукоятка которого вращается от к по наикратчайшему пути.

Моментом 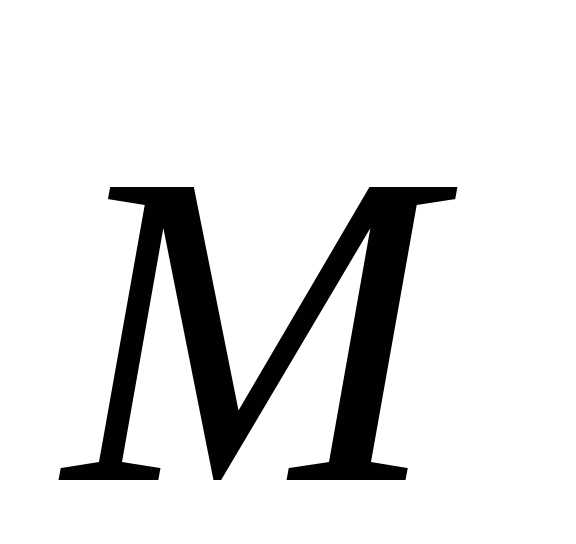нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки

. (2)

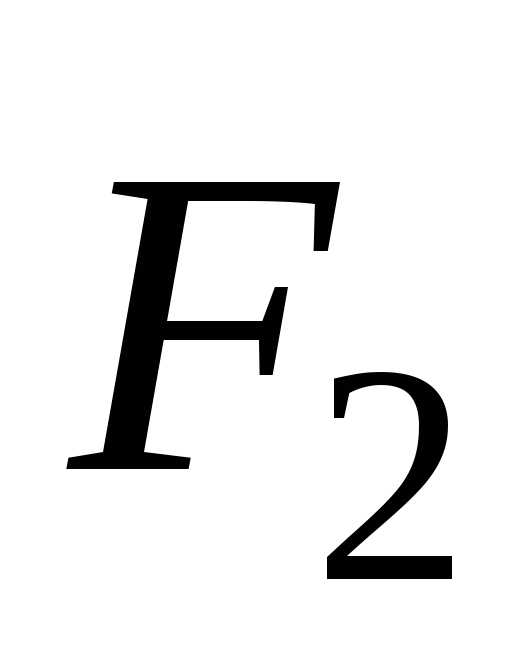Отметим частный случай двух равных параллельных сил и , направленных в противоположные стороны.

Такие силы образуют так называемую пару сил. В этом случае

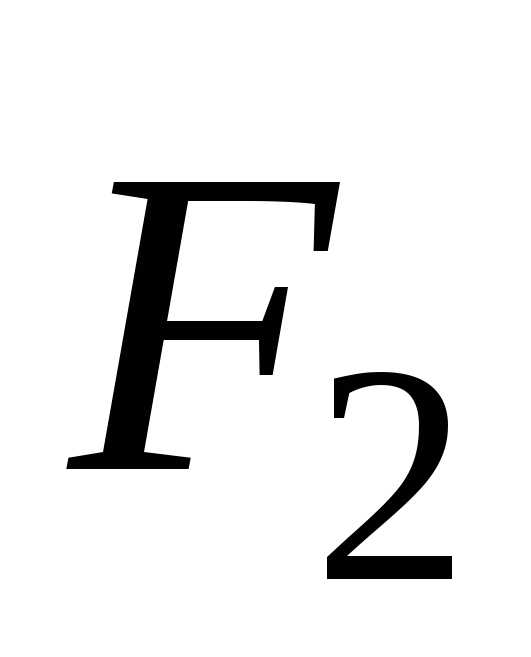т. е. момент пары сил равен моменту одной из этих сил относительно точки приложения другой. Очевидно, что момент пары сил не зависит от выбора точки О. В частности, если равные и противоположно направленные силы и действуют вдоль одной и той же прямой, то они коллинеарны с вектором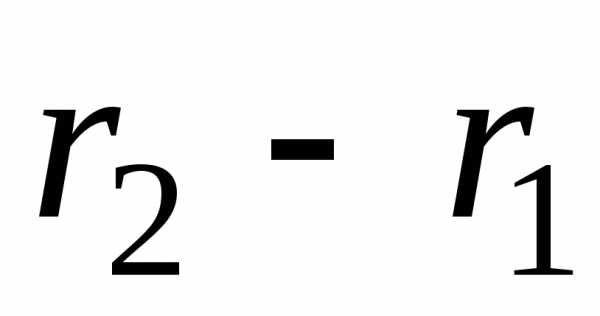, и поэтому момент пары таких сил равен нулю.

Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора 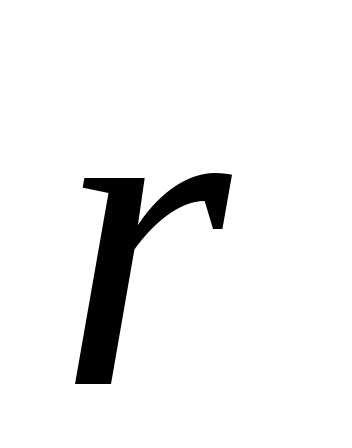на импульс :

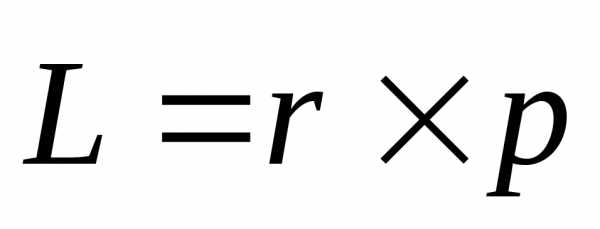. (3)

Для системы n материальных точек моментом импульса относительно некоторой точки О называется векторная сумма моментов импульсов этих точек относительно того же начала:

. (4)

studfiles.net

Закон сохранения энергии в механике. Общефизический закон сохранения энергии. Диссипация энергии

Пусть:

- дана система материальных точек массами mi, i=1,2…n;

- - равнодействующая внутренних консервативных сил, действующих на i – тую точку системы;

- - равнодействующая внешних консервативных сил, действующих на i – тую точку системы;

- неконсервативные силы отсутствуют;

- vi<<c.

Запишем для всех точек системы второй закон Ньютона в виде:

, где i=1,2…n.

Пусть за dt каждая из точек под действием сил переместится на . Умножая каждое из предыдущих уравнений на соответствующее ему последующее, имеем:

, где i=1,2…n ,

или: , где i=1,2…n .

Сложим эти уравнения и получим:

. (3.5.1)

Первый член этого равенства – приращение кинетической энергии системы, так как: .

Второй член равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т.е. равен элементарному приращению потенциальной энергии системы:

Тогда уравнение (3.5.1)можно записать в виде:

Откуда: . Т.е. полная механическая энергия такой системы сохраняется. Итак:

Закон сохранения полной механической энергии:В системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется.

Этот закон связан с однородностью времени, т.е. инвариантностью физических законов относительно выбора начала отсчета времени.

Существует еще один вид систем – диссипативные системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс называется диссипацией (рассеянием) энергии. Строго говоря, все системы в природе – диссипативные.

Общефизический закон сохранения энергии: В изолированной системе энергия может переходить из одной формы в другую, но ее количество остается постоянным.

Соударение тел.

Примером применения законов сохранения импульса и энергии при решении реальной физической задачи является удар абсолютно упругих и неупругих тел.

Удар(или соударение) - это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Исходя из данного определения, кроме явлений, которые можно отнести к ударам в прямом смысле этого слова (столкновения атомов или биллиардных шаров), сюда можно отнести и такие, как удар человека о землю при прыжке с трамвая и т.д. При ударе в телах возникают столь значительные внутренние силы, что внешними силами, действующими на них, можно пренебречь. Это позволяет рассматривать соударяющиеся тела как замкнутую систему и применять к ней законы сохранения.

Тела во время удара претерпевают деформацию. Сущность удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Наблюдения показывают, что относительная скорость тел после удара не достигает своего прежнего значения. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей. Отношение нормальных составляющих относительной скорости тел после и до удара называется коэффициентом восстановления : .

Если для сталкивающихся тел =0, то такие тела называются абсолютно неупругими,если =1 - абсолютно упругими.На практике для всех тел 0< <1 (например, для стальных шаров 0,56, для шаров из слоновой кости 0,89, для свинца 0). Однако в некоторых случаях тела можно с большой точностью рассматривать либо как абсолютно упругие, либо как абсолютно неупругие.

Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называется линией удара. Удар называется центральным,если тела до удара движутся вдоль прямой, проходящей через их центры масс. Мы будем рассматривать только центральные абсолютно упругие и абсолютно неупругие удары.

Абсолютно упругий удар- столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.

Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии.

Обозначим скорости шаров массами и до удара через и (рис. 3.4). При прямом центральном ударе векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей. Их направления учтем знаками: положительное значение припишем движению вправо, отрицательное - движению влево.

При указанных допущениях законы сохранения имеют вид:

, (3.6.1)

. (3.6.2)

Произведя соответствующие преобразования в выражениях (3.6.1) и (3.6.2), получим

, (3.6.3)

, (3.6.4)

откуда: . (3.6.5)

Решая уравнения (3.6.3) и (3.6.5), находим

, (3.6.6)

. (3.6.7)

Рассмотрим несколько частных случаев.

1) При =0

, (3.6.8)

. (3.6.9)

Проанализируем выражения (3.6.8) и (3.6.9) для двух шаров различных масс:

а) > . Первый шаг продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью ( ). Скорость второго шара после удара больше, чем скорость первого после удара ( ) (рис. 3.5).

б) < . Направление движения первого шара при ударе изменяется - шар отскакивает обратно. Второй шар движется в ту же сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т.е. (рис. 3.6).

в) >> (например, столкновение шара со стеной). Из уравнений (3.6.8) и (3.6.9) следует, что , .

2) При = выражения (3.6.6) и (3.6.7) будут иметь вид

, ,

т.е. шары равной массы "обмениваются" скоростями.

Абсолютно неупругий удар- столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстречу друг другу (рис. 3.7).

Если массы шаров и , их скорости до удара и , то, используя закон сохранения импульса, можно записать

откуда

. (3.6.10)

Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом.

Выясним, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие не от самих деформаций, а от их скоростей, то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения механической энергии не должен соблюдаться. Вследствие деформации происходит "потеря" кинетической энергии, перешедшей в тепловую или другие формы энергии. Эту "потерю" можно определить по разности кинетической энергии тел до и после удара:

Используя (3.6.10), получим

Если ударяемое тело было первоначально неподвижно ( ), то

, .

Когда >> (масса неподвижного тела очень большая), то v<< и почти вся кинетическая энергия тела при ударе переходит в другие формы энергии. Поэтому, например, для получения значительной деформации наковальня должна быть массивнее молотка. Наоборот, при забивании гвоздей в стену масса молотка должна быть гораздо большей ( >> ), тогда и практически вся энергия затрачивается на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.

Абсолютно неупругий удар - пример того, как происходит "потеря" механической энергии под действием диссипативных сил.

megaobuchalka.ru

§ 3.7. Внутренняя энергия. Общефизический закон сохранения энергии

Макроскопическая механика учитывает только кинетическую энергию макроскопического движения тел и их макроскопических частей, а также их потенциальную энергию. Но она полностью отвлекается от внутреннего атомистического строения вещества. При ударе, трении и аналогичных процессах кинетическая энергия видимого движения тел не пропадает. Она только переходит в кинетическую энергию невидимого беспорядочного движения атомов и молекул вещества, а также в потенциальную энергию их взаимодействия. Эта часть энергии тела получила название внутренней энергии. Беспорядочное движение атомов и молекул воспринимается нашими органами чувств в виде тепла. Таково физическое объяснение кажущейся потери механической энергии при ударе, трении и пр.

Представление о теплоте как о беспорядочном движении атомов и молекул окончательно утвердилось во второй половине ХIХ века. Примерно тогда же в физике утвердился и взгляд на закон сохранения энергии как на общефизический закон, не знающий никаких исключений. Согласно этому закону энергия никогда не создается и не уничтожается, она может только переходить из одной формы в другую. Однако необходимо расширить понятие энергии, введя новые формы ее: энергию электромагнитного поля, ядерную энергию и пр. При этом необходимо заметить, что дать окончательную классификацию различных видов энергии не представляется возможным. Это можно было бы сделать, если бы окончательно были установлены все законы природы, и развитие науки, во всяком случае в ее основах, было бы окончательно завершено.

Деление энергии на кинетическую и потенциальную имеет смысл только в механике и не охватывает всех форм энергии. Кроме того, отнесение энергии к тому или иному виду часто зависит от точки зрения. Например, в макроскопической механике упругая энергия сжатого идеального газа считается потенциальной. Но с молекулярной точки зрения упругость газа объясняется тепловым движением его молекул. Поэтому с этой точки зрения ту же энергию следует считать кинетической.

Общефизический принцип сохранения энергии охватывает, таким образом, не только явления, рассматриваемые в макроскопической механике, но и такие физические явления, к которым законы такой механики не применимы. Поэтому он не может быть выведен из уравнений макроскопической механики, а должен рассматриваться как одно из наиболее широких обобщений опытных фактов.

§ 3.8. Силы и потенциальная энергия

Взаимодействие тел можно описывать либо с помощью сил, либо с помощью потенциальной энергии как функции координат взаимодействующих частиц. В макроскопической механике применимы оба способа. Первый способ обладает несколько большей общностью, так как он применим и к таким силам (например, силам трения), для которых нельзя ввести потенциальную энергию. Второй же способ применим только в случае консервативных сил.

Зная действующие силы как функции координат материальных точек системы, можно вычислить ее потенциальную энергию. Эта задача решается интегрированием. Можно поставить и обратную задачу: вычислить действующие силы по заданной потенциальной энергии как функции координат взаимодействующих материальных точек. Эта задача решается с помощью более простой математической операции – дифференцирования.

Рассмотрим сначала отдельную материальную точку, находящуюся в силовом поле каких-то неподвижных тел. Если силы консервативные, то можно ввести потенциальную энергию U, которой обладает материальная точка в рассматриваемом силовом поле. Величина U будет функцией радиуса – вектора r этой точки или ее координат х, у, z. Пусть точка претерпела произвольное бесконечно малое перемещение dr. Если F – сила, действующая на нее, то работа этой силы при таком перемещении будет равна убыли потенциальной энергии:

Fdr = - dU (3.26)

или это уравнение перепишем:

. (3.27)

Допустим, что перемещение происходит вдоль какой-либо одной координатной оси, например оси Х. Тогда

и, следовательно,

. (3.28)

Индексы у, z означают, что при смещении, а следовательно, и при дифференцировании координаты у и z должны оставаться постоянными. Иными словами, U (x, у, z) при дифференцировании должна рассматриваться как функция одного аргумента х ; остальные два аргумента, у и z, являются параметрами, которые при дифференцировании по х должны оставаться постоянными. Величины, получающиеся в результате такого дифференцирования, называются частными производными функции U. Они обозначаются символом ¶, в отличие от символа d, применяемого при дифференцировании функций одного независимого переменного. Аналогичные соображения справедливы и для проекций силы вдоль остальных двух осей Y и Z. Таким образом,

. (3.29)

Если функция U(x, у, z) известна, то нахождение составляющих Fх, Fу, Fzcводится к вычислению ее частных производных по координатам. Разумеется, формулы (3.29) относятся только к случаю консервативных сил.

Пример.

Измеряя потенциальную энергию растянутой спиральной пружины, нашли, что она определяется выражением U = Ѕ kx2 , где х – удлинение пружины, а k – постоянная. Направим ось Х вдоль оси пружины, закрепив один конец ее, а другой будем удерживать рукой. Тогда U будет функцией только одной координаты х. Растянутая пружина действует на руку с силой

Знак минус указывает, что сила F направлена в сторону, противоположную смещению, т.е. является силой притяжения.

Три формулы (3.29) можно объединить в одну векторную формулу. С этой целью умножим эти формулы на единичные векторы координатных осей i, j, k и сложим. В результате получим

F = - gradU, (3.30)

где символом grad U обозначена сумма

. (3.31)

Она, согласно соотношению (3.31), является вектором. Вектор, определяемый соотношением (3.31), называется градиентом скаляра U. Для него, наряду с обозначением grad U, применяется также ÑU. Здесь Ñ («набла») означает символический вектор или оператор

называемый оператором Гамильтона или набла-оператором.

studfiles.net

14. Полная механическая энергия и закон ее изменения. Закон сохранения механической энергии. Общефизический закон сохранения и превращения энергии.

Полной механической энергией системы тел называется сумма кинетической и потенциальной энергий:

E = Eк + Eп.

Существует 2 причины изменения энергии системы: действие внешних и действие внутренних непотенциальных сил.

Очевидно, что полная механическая энергия замкнутой системы, в которой действуют только потенциальные(силы, работа которых зависит только от начального и конечного положения точек их приложения и не зависит ни от вида траекторий, ни от закона движения этих точек.) силы, не изменяется при любых перемещениях тел. Это утверждение называется законом сохранения механической энергии.

Общефизический закон сохранения энергии: В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии — сущность неуничтожимости материи и ее движения.

15. Механический принцип относительности и преобразования Галилея. Классический закон сложения скоростей.

В классической механике справедлив механический принцип относительности (принцип относительности Галилея): законы динамики одинаковы во всех инерциальных системах отсчета.

Рассмотрим две системы отсчета: неподвижную (К) и движущуюся относительно первой вдоль оси Х с постоянной Х с постоянной скоростью (K’). Координаты тела М в системе К x:y:z , а в системе К’ - x’:y’:z’. Эти координаты связаны между собой соотношениями, которые называются преообразованием Галилея Отсчет времени начат с момента, когда начало координат обеих систем совпадают. Продифференцировав по времени t, получим выражение правила сложения скоростей в классической механике: υ=υ'+υ0Классический закон сложения скоростей формулируется следующим образом: скорость движения материальной точки по отношению к системе отсчета, принимаемой за неподвижную, равна векторной сумме скоростей движения точки в подвижной системе и скорости движения подвижной системы относительно неподвижной.

16. Постулаты специальной теории относительности (сто). Относительность понятия одновременности. Преобразования Лоренца.

В основе специальной теории относительности лежат два принципа или постулата, сформулированные Эйнштейном в 1905 г.

1) Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна.

2) Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую.

Постулаты Эйнштейна находятся в противоречии не друг с другом, а с формулами преобразования Галилея. Поэтому на смену галилеевых преобразований СТО предложила другие формулы преобразования при переходе из одной инерциальной системы в другую – так называемые преобразования Лоренца, которые при скоростях движения, близких к скорости света, позволяют объяснить все релятивисткие эффекты, а при малых скоростях (υ << c) переходят в формулы преобразования Галилея. Таким образом, новая теория (СТО) не отвергла старую классическую механику Ньютона, а только уточнила пределы ее применимости. Такая взаимосвязь между старой и новой, более общей теорией, включающей старую теорию как предельный случай, носит название принципа соответствия.

Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики.

Одним из важнейших следствий из преобразований Лоренца является вывод об относительности одновременности. Пусть, например, в двух разных точках системы отсчета K' (x'1 ≠ x'2) одновременно с точки зрения наблюдателя в K' (t'1 = t'2 = t') происходят два события. Согласно преобразованиям Лоренца, наблюдатель в системе K будет иметь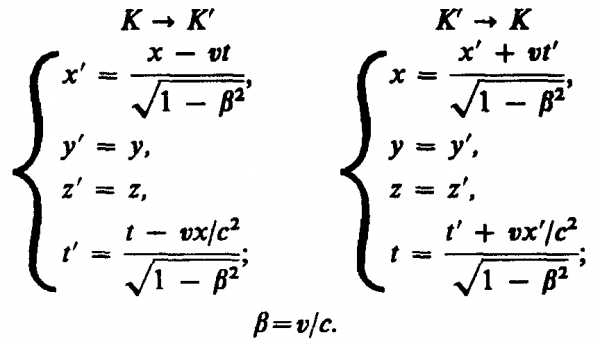

studfiles.net

2. Понятие энергии. Общефизический закон сохранения энергии

Сила- это векторная мера взаимодействия.

Импульс- это векторная мера движения при линейных перемещениях (переносах) тел в пространстве.

Момент импульса - это векторная мера движения при изменении ориентации (поворотах) тел в пространстве.

Энергия- это всеобщая скалярная мера движения и взаимодействия всех видов материи.

блок

S1*

S2* S2*

шкив S1

Р В S2 r

r S2

груз

G G

а) б)

Рис.2.

studfiles.net

§ 3.7. Внутренняя энергия. Общефизический закон сохранения энергии

§ 3.8. Силы и потенциальная энергия

Fdr =  dU (3.26)

или это уравнение перепишем:

. (3.27)

Допустим, что перемещение происходит вдоль какой-либо одной координатной оси, например оси Х. Тогда

и, следовательно,

. (3.28)

Индексы у, z означают, что при смещении, а следовательно, и при дифференцировании координаты у и z должны оставаться постоянными. Иными словами, U (x, у, z) при дифференцировании должна рассматриваться как функция одного аргумента х ; остальные два аргумента, у и z, являются параметрами, которые при дифференцировании по х должны оставаться постоянными. Величины, получающиеся в результате такого дифференцирования, называются частными производными функции U. Они обозначаются символом , в отличие от символа d, применяемого при дифференцировании функций одного независимого переменного. Аналогичные соображения справедливы и для проекций силы вдоль остальных двух осей Y и Z. Таким образом,

. (3.29)

Пример.

Измеряя потенциальную энергию растянутой спиральной пружины, нашли, что она определяется выражением U = ½ kx2 , где х – удлинение пружины, а k – постоянная. Направим ось Х вдоль оси пружины, закрепив один конец ее, а другой будем удерживать рукой. Тогда U будет функцией только одной координаты х. Растянутая пружина действует на руку с силой

F =  gradU, (3.30)

где символом grad U обозначена сумма

. (3.31)

Она, согласно соотношению (3.31), является вектором. Вектор, определяемый соотношением (3.31), называется градиентом скаляра U. Для него, наряду с обозначением grad U, применяется также U. Здесь  («набла») означает символический вектор или оператор

называемый оператором Гамильтона или набла-оператором.

studfiles.net

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

Закон сохранения энергии в механике. Общефизический закон сохранения энергии. Диссипация энергии. Общефизический закон сохранения энергии

2. Понятие энергии. Общефизический закон сохранения энергии

5.4. Общефизический закон сохранения энергии

Лекция №6. Закон сохранения момента импульса

6.1. Момент силы и момент импульса относительно неподвижного начала

Закон сохранения энергии в механике. Общефизический закон сохранения энергии. Диссипация энергии

§ 3.7. Внутренняя энергия. Общефизический закон сохранения энергии

§ 3.8. Силы и потенциальная энергия

14. Полная механическая энергия и закон ее изменения. Закон сохранения механической энергии. Общефизический закон сохранения и превращения энергии.

15. Механический принцип относительности и преобразования Галилея. Классический закон сложения скоростей.

16. Постулаты специальной теории относительности (сто). Относительность понятия одновременности. Преобразования Лоренца.

2. Понятие энергии. Общефизический закон сохранения энергии

§ 3.7. Внутренняя энергия. Общефизический закон сохранения энергии

§ 3.8. Силы и потенциальная энергия

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация