Что такое Сименс. Определение Сименса. Формула Сименса
Сименс (обозначение: См, S) — единица измерения электрической проводимости в системе СИ, величина обратная ому.
Сименс (англ. siemens ) — единица электрической проводимости, адмитанса (полной проводимости) и реактивной проводимости в системе СИ и в системе метр-килограмм-секунда. Наиболее важной характеристикой проводника является величина тока, протекающего через него, когда приложено электрическое напряжение. Проводник имеет проводимость один сименс, если разность потенциалов один вольт создаёт в проводнике ток в один ампер. Проводимость проводника в сименсах является обратной величиной к его сопротивлению в омах; сименс раньше назывался «мо» (mho) или обратный ом.
Сименс — единица измерения электропроводности (проводимости) в системе СИ. Она эквивалентна ранее использовавшейся единице mho . Обычно проводимость обозначают символом G, но для ионной проводимости принято использовать символ L.
Иными словами, проводимость в сименсах – это просто единица, делённая на сопротивление в омах. В уравнениях проводимость обозначается буквой G.
“Siemens” является формой единственного и множественного числа; “1 siemen” – неправильное написание.
До Второй мировой войны (в СССР до 1960-х годов) сименсом называлась единица электрического сопротивления, соответствующая сопротивлению столба ртути длиной 1 м и диаметром 1 мм при 0 °C. Она соответствует примерно 0,9534 Ом. Эта единица была введена Сименсом в 1860 году и конкурировала с Омом, который победил на Всемирном конгрессе Электротехников в 1881 году. Тем не менее, единица широко использовалась связистами во всём мире до середины XX века.
Через другие единицы измерения СИ сименс выражается следующим образом:
См = 1 / Ом = А / В = кг-1·м-2·с³А²
Единица названа в честь немецкого учёного и предпринимателя Вернера фон Сименса.
Раньше применялось название мо, обозначалось перевёрнутой буквой Ω: \mho (в Юникоде U+2127, ℧).
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 См | декасименс | даСм | daS | 10−1 См | децисименс | дСм | dS |
| 102 См | гектосименс | гСм | hS | 10−2 См | сантисименс | сСм | cS |
| 103 См | килосименс | кСм | kS | 10−3 См | миллисименс | мСм | mS |
| 106 См | мегасименс | МСм | MS | 10−6 См | микросименс | мкСм | µS |
| 109 См | гигасименс | ГСм | GS | 10−9 См | наносименс | нСм | nS |
| 1012 См | терасименс | ТСм | TS | 10−12 См | пикосименс | пСм | pS |
| 1015 См | петасименс | ПСм | PS | 10−15 См | фемтосименс | фСм | fS |
| 1018 См | эксасименс | ЭСм | ES | 10−18 См | аттосименс | аСм | aS |
| 1021 См | зеттасименс | ЗСм | ZS | 10−21 См | зептосименс | зСм | zS |
| 1024 См | йоттасименс | ИСм | YS | 10−24 См | йоктосименс | иСм | yS |
| применять не рекомендуется | |||||||
Электрическая проводимость тел оценивается количественно в специальных единицах, называемых сименс (сокращенно См), и обозначается символом G.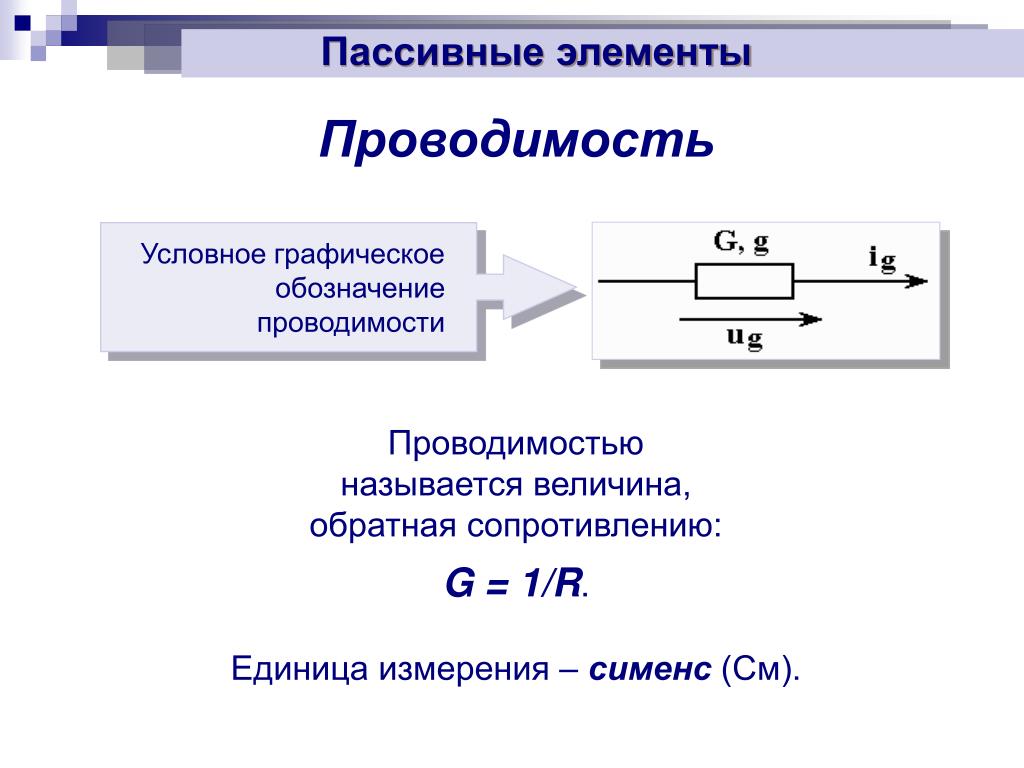 1 См — это электрическая проводимость проводника, между концами которого создается напряжение 1 В при силе тока 1 А. Электрическая проводимость тела пропорциональна площади его поперечного сечения S и обратно пропорциональна его длине I
1 См — это электрическая проводимость проводника, между концами которого создается напряжение 1 В при силе тока 1 А. Электрическая проводимость тела пропорциональна площади его поперечного сечения S и обратно пропорциональна его длине I
Препятствие, которое преодолевает ток при прохождении по проводнику, называется электрическим сопротивлением. За единицу электрического сопротивления принят 1 ом. Ом определяется как сопротивление, оказываемое неизменяющемуся электрическому току при температуре тающего льда ртутным столбом, имеющим повсюду одинаковое поперечное сечение, равное 1 мм , длину 106,300 см и массу 14,4521 г. Величина, обратная величине электрического сопротивления, называется электропроводностью, или проводимостью. Единицей электропроводности считается сименс, равный одному обратному ому. Электрическое сопротивление будет тем больше, чем больше длина
Электрическая проводимость – это способность вещества или материала пропускать через себя электрический ток. Измеряется электрическая проводимость в Сименсах, в честь немецкого физика Эрнста Сименса. Эта характеристика материала находится в обратной зависимости от его электрического сопротивления. То есть чем больше проводимость, тем меньше сопротивление и наоборот.
Измеряется электрическая проводимость в Сименсах, в честь немецкого физика Эрнста Сименса. Эта характеристика материала находится в обратной зависимости от его электрического сопротивления. То есть чем больше проводимость, тем меньше сопротивление и наоборот.
Как правило, электрической проводимостью обладают проводники и полупроводники. Диэлектрики не проводят ток, а следовательно и не имеют проводимости.
Помимо электрической проводимости измеряют еще и удельную проводимость материала. Она показывает отношение между проходящим через материал током и электрическим полем, которое его вызвало.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Проводимость
Добавлено 4 января 2021 в 17:10
Сохранить или поделиться
Когда учащиеся впервые видят формулу общего параллельного сопротивления, возникает естественный вопрос: «Откуда эта штука?». Это действительно странная арифметика, и ее происхождение заслуживает хорошего объяснения.
Это действительно странная арифметика, и ее происхождение заслуживает хорошего объяснения.
В чем разница между сопротивлением и проводимостью?
Сопротивление, по определению, является мерой «трения», которое компонент представляет для прохождения через него тока. Сопротивление обозначается заглавной буквой «R» и измеряется в единицах «Ом». Однако мы также можем думать об этом электрическом свойстве с обратной ему точки зрения: насколько легко току течь через компонент, а не насколько трудно.
Если сопротивление – это термин, которое мы используем для обозначения меры того, насколько трудно току течь, то хорошим термином, чтобы выразить, насколько легко ток течет, будет проводимость. Математически проводимость – это величина, обратная сопротивлению:
\[проводимость = \frac{1}{сопротивление}\]
Чем больше сопротивление, тем меньше проводимость; и наоборот.
Это должно быть интуитивно понятно, потому что сопротивление и проводимость – противоположные способы обозначения одного и того же важного электрического свойства.
Если сравнивать сопротивления двух компонентов и обнаружится, что компонент «A» имеет сопротивление вдвое меньше сопротивления компонента «B», то в качестве альтернативы мы могли бы выразить это соотношение, сказав, что компонент «A» в два раза более проводящий, чем компонент «B». Если компонент «A» имеет сопротивление, равное только одной трети от сопротивления компонента «B», то мы можем сказать, что он в три раза более проводящий, чем компонент «B», и так далее.
Единица измерения проводимости
В продолжение этой идеи были придуманы символ и единица измерения проводимости. Символ представляет собой заглавную букву «G», а единицей измерения был mho, что означает «ohm» (ом), написанное в обратном порядке (вы думали, что у электронщиков нет чувства юмора?).
Несмотря на свою уместность, единицы измерения mho в последующие годы были заменены единицей Сименс (сокращенно «См», или, в англоязычной литературе, «S»). Это решение об изменении названий единиц измерения напоминает изменение единицы измерения температуры в градусах стоградусной шкалы (degrees centigrade – от латинских слов «centum», т. е. «сто», и «gradus») на градусы Цельсия (degrees Celsius) или изменение единицы измерения частоты c.p.s. (циклов в секунду) в герцы. Если вы ищете здесь какой-то шаблон переименования, то Сименс, Цельсий и Герц – это фамилии известных ученых, имена которых, к сожалению, о природе единиц говорят нам меньше, чем их первоначальные обозначения.
е. «сто», и «gradus») на градусы Цельсия (degrees Celsius) или изменение единицы измерения частоты c.p.s. (циклов в секунду) в герцы. Если вы ищете здесь какой-то шаблон переименования, то Сименс, Цельсий и Герц – это фамилии известных ученых, имена которых, к сожалению, о природе единиц говорят нам меньше, чем их первоначальные обозначения.
Возвращаясь к нашему примеру с параллельной схемой, мы должны быть в состоянии увидеть, что несколько путей (ветвей) для тока уменьшают общее сопротивление всей цепи, поскольку ток может легче проходить через всю цепь из нескольких ветвей, чем через любую из них отдельно. Что касается сопротивления, дополнительные ветви приводят к меньшему общему значению (ток встречает меньшее сопротивление). Однако с точки зрения проводимости дополнительные ветви приводят к большему общему значению (ток протекает с большей проводимостью).
Общее сопротивление параллельной цепи
Общее сопротивление параллельной цепи меньше, чем любое из сопротивлений отдельных ветвей, потому что параллельные резисторы вместе «сопротивляются» меньше, чем по отдельности:
Рисунок 1 – Полное сопротивление параллельной цепи
Общая проводимость параллельной цепи
Общая проводимость параллельной цепи больше, чем проводимость любой из отдельных ветвей, потому что параллельные резисторы «проводят» вместе лучше, чем по отдельности:
Рисунок 2 – Полная проводимость параллельной цепи
Чтобы быть более точным, полная проводимость в параллельной цепи равна сумме отдельных проводимостей:
\[G_{общ} = G_1 + G_2 + G_3 + G_4\]
Если мы знаем, что проводимость – это не что иное, как математическая величина, обратная (1/x) сопротивлению, мы можем перевести каждый член приведенной выше формулы в сопротивление, подставив величину, обратную каждой соответствующей проводимости:
\[\frac{1}{R_{общ}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \frac{1}{R_{4}}\]
Решая приведенное выше уравнение для полного сопротивления (вместо значения, обратного общему сопротивлению), мы получим следующую формулу:
\[R_{общ} = \frac{1}{\frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \frac{1}{R_{4}}}\]
Итак, мы, наконец, пришли к нашей загадочной формуле сопротивления! Проводимость (G) редко используется в качестве практического параметра, поэтому при анализе параллельных цепей часто используется приведенная выше формула.
Резюме
- Проводимость – параметр, противоположный сопротивлению: это мера того, насколько легко электрический ток проходит через что-то.
- Проводимость обозначается буквой «G» и измеряется в сименсах (сокр. См).
- Математически проводимость равна величине, обратной сопротивлению: G = 1/R.
Оригинал статьи:
Теги
ОбучениеПараллельная цепьПроводимостьСопротивление
Сохранить или поделиться
Проводимости | Цепи переменного тока
Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению
где y=1/z — величина обратная полному сопротивлению, называется полной проводимостью.
Комплексная проводимость и комплексное сопротивление взаимно обратны. Комплексную проводимость можно представить в виде
где — действительная часть комплексной проводимости, называется активной проводимостью; — значение мнимой части комп-лексной проводимости, называется реактивной проводимостью;
Из ( 3. 30) и ( 3.29) следует, что для схемы, представленной на рис. 3.12, комплексная проводимость
30) и ( 3.29) следует, что для схемы, представленной на рис. 3.12, комплексная проводимость
где
и называются соответственно активной, индуктивной и емкостной проводимостями.
Реактивная проводимость
Индуктивная и емкостная проводимости — арифметические величины, а реактивная проводимость b — алгебраическая величина и может быть как больше, так и меньше нуля. Реактивная проводимость b ветви, содержащей только индуктивность, равна индуктивной проводимости , а реактивная проводимость b ветви, содержащей только емкость, равна емкостной проводимости с обратным знаком, т. е. .
Сдвиг по фазе между напряжением и током зависит от соотношения индуктивной и емкостной проводимостей. Для схемы по рис. 3.12 на рис. 3.14 представлены векторные диаграммы для трех случаев, а именно При построении этих диаграмм начальная фаза напряжения принята равной нулю, поэтому , как это следует из ( 3.28), равны и противоположны по знаку ().
Рассматривая схему на рис. 3.12 в целом как пассивный двухполюсник, можно заметить, что при заданной частоте она эквивалентна в первом случае параллельному соединению сопротивления и индуктивности, во втором — сопротивлению и в третьем — параллельному соединению сопротивления и емкости. Второй случай называется резонансом. При заданных L и С соотношение между зависит от частоты, а поэтому от частоты зависит и вид эквивалентной схемы.
3.12 в целом как пассивный двухполюсник, можно заметить, что при заданной частоте она эквивалентна в первом случае параллельному соединению сопротивления и индуктивности, во втором — сопротивлению и в третьем — параллельному соединению сопротивления и емкости. Второй случай называется резонансом. При заданных L и С соотношение между зависит от частоты, а поэтому от частоты зависит и вид эквивалентной схемы.
Обратим внимание на то, что в схеме рис. 3.12 каждая из параллельных ветвей содержит по одному элементу. Поэтому получилось такое простое выражение для У, в которое проводимости элементов входят как отдельные слагаемые.
Заметим, что обозначения применяются не только для сопротивлений и проводимостей, но и для элементов схемы, характеризуемых этими величинами. В таких случаях элементам схемы дают те же самые наименования, какие присвоены величинам, которые обозначаются этими буквами. Комплексные сопротивления или проводимости как элементы схемы имеют условное обозначение в виде прямоугольника (см. рис. 3.1). Точно так же обозначают реактивные сопротивления или проводимости, если хотят отметить, что они могут быть как индуктивными, так и емкостными сопротивлениями или проводимостями.
рис. 3.1). Точно так же обозначают реактивные сопротивления или проводимости, если хотят отметить, что они могут быть как индуктивными, так и емкостными сопротивлениями или проводимостями.
Проводимость — 2012 — Справка по SOLIDWORKS
Проводимость представляет собой механизм переноса тепла, в котором термическая энергия переносится от одной точки к другой через взаимодействие между атомами или молекулами материи. Проводимость имеет место в твердых телах, жидкостях и газах.
Проводимость не включает какое-либо объемное движение материи. Газы переносят тепло прямым соударением между энергетическими молекулами и их теплопроводность ниже по сравнению с твердыми телами, так как они представляют собой разреженную среду. Проведение энергии в жидкостях такое же, как и в газах, за исключением того, что ситуация здесь значительно сложнее, так как молекулы располагаются намного ближе друг к другу и поля сил молекулярного взаимодействия оказывают значительное влияние на энергетический обмен в процессе соударений. Неметаллические твердые тела переносят тепло колебаниями кристаллической решетки, поэтому здесь нет места движению среды по мере распространения по ней тепла. Металлы являются лучшими проводниками по сравнению с неметаллами при нормальных температурах, так как они обладают свободными электронами, несущими термическую энергию.
Неметаллические твердые тела переносят тепло колебаниями кристаллической решетки, поэтому здесь нет места движению среды по мере распространения по ней тепла. Металлы являются лучшими проводниками по сравнению с неметаллами при нормальных температурах, так как они обладают свободными электронами, несущими термическую энергию.
Перенос тепла проводимостью подчиняется закону Фурье, который устанавливает, что скорость проведения тепла Qпроводимости пропорциональна площади переноса тепла (A) и температурному градиенту (dT/dx) или:
Qпроводимости = — K A (dT/dx)
где K или теплопроводность измеряет способность материала к проведению тепла. Единицами величины K являются Вт/м.oC или (БТЕ/с)/дюйм.oF. Для планарного слоя, показанного ниже, скорость теплопроводности задается отношением
Q
проводимости = — K A ( T
H — T
C )/L
На этом рисунке показывается диапазон значений для теплопроводности жидкостей, неметаллических твердых тел и чистых металлов при нормальных температуре и давлении.
Температурная зависимость теплопроводности (K)
Для большинства материалов K меняется вместе с температурой. Коэффициент возрастает с ростом температуры в газах при низких давлениях, но может либо возрастать, либо падать в металлах и жидкостях.
В следующей таблице приводятся значения теплопроводности (в Вт/м.oK) в отношении температур (в oK) для выбранных материалов:
|
Металл
|
Температура (oK)
| |||||||
|
103
|
173
|
273
|
373
|
473
|
573
|
673
|
873
| |
|
Нержавеющая сталь
|
|
|
|
15
|
17
|
19
|
21
|
25
|
|
Свинец
|
40
|
37
|
36
|
34
|
33
|
32
|
17 (жидк.
|
20 (жидк.)
|
|
Платина
|
78
|
73
|
72
|
72
|
72
|
73
|
74
|
77
|
|
Цинк
|
124
|
122
|
122
|
117
|
110
|
106
|
100
|
60 (жидк.
|
|
Кремний
|
856
|
342
|
168
|
112
|
82
|
66
|
54
|
38
|
Метод индукционного каротажного зондирования (ИКЗ)
Индукционным каротажным зондированием (ИКЗ) называют изучение удельного сопротивления (удельной электропроводности) пересеченных скважиной горных пород, основанное на измерении вторичного поля вихревых токов, индуцированных в породе. В основе метода лежит закон электромагнитной индукции (закон Фарадея), устанавливающий взаимосвязь между магнитными и электрическими явлениями. Вертикальная разрешающая способность метода – 35 см, горизонтальная разрешающая способность метода – 250 см.
|
|
Прибор 4ИК-Т-76
|
Прибор 4ИК-1Т
|
Прибор 5ИК-Т-76
|
|---|---|---|---|
|
Длина, м
|
3,95
|
5,35
|
3,95
|
|
Диаметр, мм
|
76
|
76
|
76
|
|
Масса, кг
|
40
|
80
|
40
|
|
Максимальная рабочая температура, °С
|
120
|
175
|
120
|
|
Максимальное рабочее давление, МПа
|
80
|
140
|
80
|
|
Максимальная скорость записи, м/ч в интервале М 1:200 (детальных исследований)
|
1800
|
2000
|
1800
|
|
Диаметр исследуемых скважин, мм
|
от 110
|
от 90
|
от 110
|
|
Положение в скважине
|
свободное/
|
свободное/
|
свободное/
|
|
Комбинируемость
|
транзитный
|
транзитный
|
транзитный
|
|
Радиус исследования
|
|
|
|
|
зонд 3И2.
|
2,97
|
2,97
|
2,97
|
|
зонд 3И1.26
|
1,82
|
1,82
|
1,82
|
|
зонд 3И0.85
|
1,23
|
1,23
|
1,23
|
|
зонд 3И0.5
|
0,72
|
0,72
|
0,72
|
|
зонд 3И0.
|
—
|
—
|
0,4
|
ПРИНЦИПИАЛЬНАЯ КОНСТРУКЦИЯ МОДУЛЯ
Прибор 5ИК-Т-76 содержит 5 (4, в случае с прибором 4ИК-Т-76) трехкатушечных индукционных зондов, каждый из которых имеет 2 генераторные (основную и компенсационную) и одну (общую для всех зондов) измерительную катушку L1. Генераторные катушки совместно с измерительной образуют следующие зонды:
L2, L3, L1 – зонд 3И0.3, питается генератором U1;
L4, L5, L1 – зонд 3И0.5, питается генератором U2;
L6, L7, L1 – зонд 3И0.85, питается генератором U3;
L8, L9, L1 – зонд 3И1.26, питается генератором U4;
L10, L11, L1 – зонд 3И2.05, питается генератором U5.
Подвижность электронов и дырок.
 Электронная проводимость
Электронная проводимость
из «Физическая химия твердого тела»
Здесь вместо Хе мы используем специальное обозначение для удельной электронной проводимости т, чтобы подчеркнуть ее отличие от ионной проводимости х. Как и в предыдущих главах, п означает число электронов проводимости и дырок в единице объема верхние индексы (—) и ( + ) указывают знак носителя и относятся соответственно к электронам проводимости и дыркам. [c.189]
Концентрации электронных носителей в зависимости от температуры и состава кристаллов были вычислены в гл. 4 для полупроводников и в гл. 5 для нестехиометрических ионных кристаллов. Поэтому в данном разделе задача описания электронной проводимости твердых тел сводится к определению подвижности электронных носителей. [c.189]
В отличие от ионных проводников, для которых, как отмечалось в предыдущем разделе, выбор носителей бывает двояким, для электронных проводников носители принято выбирать вполне однозначно это электроны в зоне проводимости для проводников п-типа и электронные дырки для проводников р-типа. Поэтому для них подвижность всегда относится к указанным частицам. [c.189]
Поэтому для них подвижность всегда относится к указанным частицам. [c.189]
Рассмотрим теперь кристаллы с различными типами химической связи. [c.192]
Температурная зависимость удельного электросопротивления натрия [72]. [c.193]
Типичный пример зависимости удельного электросопротивления от температуры изображен на рис. 6.8 для металлического натрия. При температурах, достаточно удаленных от абсолютного нуля и от точки плавления, удельное сопротивление р=1/а линейно растет с температурой в соответствии с теоретической зависимостью (6.72). Однако эта зависимость нарушается при очень низких температурах, при которых энергия колебаний атомов уже не равна ЪкТ, а убывает при уменьшении температуры по законам квантовой статистики. Линейная зависимость р от Г также нарушается в области предельно высоких температур, близких к точке плавления. Это явление связано с быстрым возрастанием при высоких температурах концентраций вакансий, которые приводят к дополнительному рассеянию электронов и к появлению избыточного сопротивления металла. Измерения избыточного сопротивления иногда используют для оценки концентраций вакансий в металлах. [c.193]
Измерения избыточного сопротивления иногда используют для оценки концентраций вакансий в металлах. [c.193]
Здесь любопытна следующая особенность. В примесных полупроводниках концентрация примесных ионов равна концентрации электронных носителей [0+] = [е ] [А ] = [е+]. Поэтому формула (6.57) с учетом (6.76) дает для электропроводности полупроводника при рассеянии на примесных ионах значение, не зависящее от концентрации последних. [c.194]
Температурная зависимость подвижности электронов проводимости и дырок в валентных полупроводниках при рассеянии на акустических фононах и ионизованной примеси кривая 2 соответствует большей концентрации примеси. [c.195]
В зависимости от природы полупроводника, содержания примеси и температуры подвижность носителей в полупроводниках может изменяться в широком диапазоне — от л 1 до 10 см2/(В-с). [c.195]
На рис. 6.10, а изображена в логарифмических координатах температурная зависимость подвижности квазисвободных электронов в германии, легированном мышьяком, для той же серии образцов, для которой в гл. 4 обсуждалась температурная зависимость концентрации электронов (см. рис. 4.3). На рис. 6.10, а обращает на себя внимание, во-первых, довольно широкий диапазон изменения подвижности (3 порядка величины), во-вторых, различный характер кривых при малых и больших содержаниях примеси. [c.195]
4 обсуждалась температурная зависимость концентрации электронов (см. рис. 4.3). На рис. 6.10, а обращает на себя внимание, во-первых, довольно широкий диапазон изменения подвижности (3 порядка величины), во-вторых, различный характер кривых при малых и больших содержаниях примеси. [c.195]
Температурная зависимость подвижности носителей (а) и электропроводности (б) германия, легированного мышьяком 154]. Концентрация Аз возрастает от 1-го к 6-му образцу. [c.196]
На рис. 6.10,6 изображен график Аррениуса для электропроводности тех же образцов. Как и на рис. 4,3 для концентрации носителей, пунктирная прямая относится к области собственной электропроводности. [c.197]
За исключением кривой 6, отвечающей вырожденному состоянию, кривые для примесной электропроводности имеют четкие максимумы. Нисходящие участки кривых в области промежуточных температур (от 20—80 К ДО комнатной) соответствуют горизонтальным участкам на рис.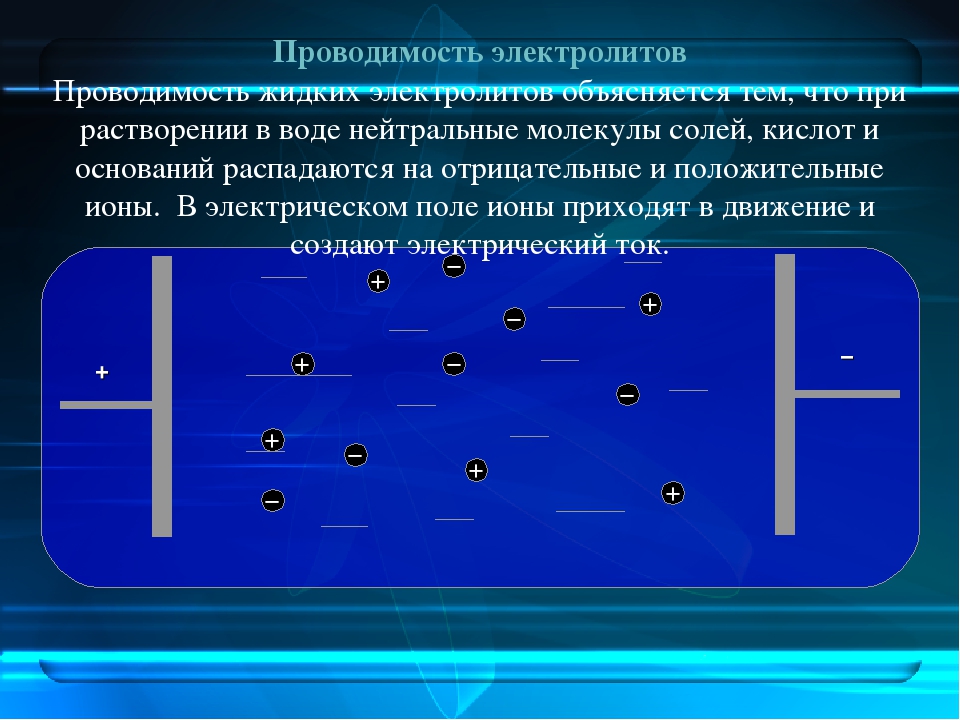 4.3 для концентрации носителей в области истощения доноров здесь уменьшение электропроводности с ростом температуры обусловлено уменьшением подвижности носителей при их постоянной концентрации. [c.197]
4.3 для концентрации носителей в области истощения доноров здесь уменьшение электропроводности с ростом температуры обусловлено уменьшением подвижности носителей при их постоянной концентрации. [c.197]
Ионные кристаллы. Как уже указывалось в разделе 1.6, механизм движения электронов в ионных кристаллах зачастую отличается от такового в валентных полупроводниках и осуществляется перескоками их из устойчивого состояния на одном ионе в аналогичное состояние на другом. В отличие от туннельного механизма движения квазисвободных электронов в валентных полупроводниках такой механизм движения локализованных электронов называют прыжковым. [c.197]
Различное поведение электронов и дырок в кристаллах с ковалентной и ионной химической связью обусловлено различным характером взаимодействия избыточного электрона с окружающей средой кристалла. В любом веществе избыточный электрон, находящийся в зоне проводимости, или дырка в валентной зоне поляризуют окружающую среду. В телах, состоящих из нейтральных атомов, таких, как валентные полупроводники, поляризация сводится к образованию электрических диполей на каждом из окружающих атомов благодаря смещению их внешних электронных оболочек относительно положительного ионного остатка. Такой вид поляризации соответствует высокочастотной (оптической) диэлектрической постоянной и характеризуется очень малым временем релаксации, при котором поляризационное искажение среды успевает следовать за вызвавшим его избыточным электроном при движении последнего по кристаллу. Поэтому энергетическое состояние кристалла не изменяется при переходе электрона от одного узла к соседнему, и движение электронных носителей по кристаллу не требует затрат энергии, т. е. электроны проводимости и дырки являются квазисвободными частицами. [c.197]
В телах, состоящих из нейтральных атомов, таких, как валентные полупроводники, поляризация сводится к образованию электрических диполей на каждом из окружающих атомов благодаря смещению их внешних электронных оболочек относительно положительного ионного остатка. Такой вид поляризации соответствует высокочастотной (оптической) диэлектрической постоянной и характеризуется очень малым временем релаксации, при котором поляризационное искажение среды успевает следовать за вызвавшим его избыточным электроном при движении последнего по кристаллу. Поэтому энергетическое состояние кристалла не изменяется при переходе электрона от одного узла к соседнему, и движение электронных носителей по кристаллу не требует затрат энергии, т. е. электроны проводимости и дырки являются квазисвободными частицами. [c.197]
Принято различать иоляроны большого радиуса и поляропы малого радиуса. К первому типу относят поляроны, у которых эффективный радиус поляризованной области гораздо больше постоянной решетки ко второму типу — поляроны, у которых эффективный радиус сравним с постоянной решетки или меньше ее. [c.198]
[c.198]
Таким образом, полярон малого радиуса основное время жизни проводит в автолокализованном состоянии, когда избыточный электрон или дырка вращаются вокруг определенных ионов и только изредка перескакивают к соседним, в конечном итоге хаотически блуждая по кристаллу. В этом отношении картина прыжкового механизма миграции электронных носителей в ионных кристаллах аналогична механизму ионной проводимости, рассмотренному в предыдущем разделе, причем движение электронов проводимости аналогично движению междуузельных ионов, а дырок — движению вакансий. [c.200]
Температурная зависимость подвижности поляронов малого радиуса в ионных кристаллах при рассеянии на оптических фононах. [c.202]
График температурной зависимости подвижности поляронов, соответствующий формуле (6.88) при рассеянии на оптических фононах, схематически изображен на рис. 6.11 в координатах Аррениуса. Здесь обращает на себя внимание ход кривой, противоположный представленному на рис. 6.8 в отличие от квазисвободных электронов в атомных полупроводниках подвижность поляронов малого радиуса имеет минимум в области промежуточных температур. Пунктирный участок кривой изображает переход к рассеянию туннелирующих поляронов на заряженных точечных дефектах решетки, играющих в ионных кристаллах ту же роль, что и примесные ионы в валентных полупроводниках. [c.202]
6.8 в отличие от квазисвободных электронов в атомных полупроводниках подвижность поляронов малого радиуса имеет минимум в области промежуточных температур. Пунктирный участок кривой изображает переход к рассеянию туннелирующих поляронов на заряженных точечных дефектах решетки, играющих в ионных кристаллах ту же роль, что и примесные ионы в валентных полупроводниках. [c.202]
Вернуться к основной статье
4. Проводимость | 4. Последовательные и параллельные цепи | Часть1
4. Проводимость
Проводимость
Когда начинающие радиолюбители видят уравнение для расчета общего сопротивления параллельной цепи, у них возникает естественный вопрос, «Откуда оно взялось?». В этой статье мы попытаемся дать ответ на данный вопрос.
Ввиду того что электроны, сталкиваясь с частицами проводника,
преодолевают некоторое сопротивление движению, принято говорить, что
проводники обладают электрическим сопротивлением. Сопротивление обозначается буквой «R» и измеряется в Омах. Однако, всякий проводник можно характеризовать не только его сопротивлением, но и
Сопротивление обозначается буквой «R» и измеряется в Омах. Однако, всякий проводник можно характеризовать не только его сопротивлением, но и
так называемой проводимостью — способностью проводить электрический
ток. Проводимость есть величина, обратная сопротивлению:
Чем больше сопротивление, тем меньше проводимость и наоборот. Сопротивление и проводимость являются противоположными способами обозначения одного и того же электрического свойства материалов. Если при сравнении сопротивлений двух компонентов выясняется, что сопротивление компонента «А» составляет половину от сопротивления компонента «Б», то мы можем альтернативно выразить эту связь, сказав, что проводимость компонента «А» в два раза выше проводимости компонента «Б». Если сопротивление компонента «А» составляет одну треть от сопротивления компонента «Б», то можно сказать, что компонент «А» в три раза проводимее компонента «Б», и так далее.
Обозначается проводимость буквой «G», а ее единицей измерения первоначально было «Мо», то есть «Ом» записанный задом наперед. Но, несмотря на уместность этой единицы, позже она была заменена на «Сименс» (сокращенно — См или S).
Теперь давайте вернемся к нашему примеру параллельной цепи. Если рассматривать ее с точки зрения сопротивления, то наличие нескольких путей (ветвей) для потока электронов снижает общее сопротивление этой цепи, так как электронам легче течь по нескольким путям, чем по одному, обладающему некоторым сопротивлением. Если рассматривать цепь с точки зрения проводимости, то несколько путей для потока электронов наоборот, увеличивают проводимость схемы.
Общее сопротивление параллельной цепи меньше любого из ее отдельных сопротивлений, поскольку несколько параллельных ветвей создают меньше препятствий потоку электронов, чем каждый резистор по отдельности:
Общая проводимость параллельной цепи больше проводимости любой ее отдельной ветви, поскольку параллельно соединенные резисторы лучше проводят электрический ток, чем каждый резистор по отдельности:
Точнее будет сказать, что общая проводимость параллельной цепи равна сумме ее отдельных проводимостей:
Зная, что проводимость равна 1/R, мы можем преобразовать эту формулу в следующий вид:
Из данной формулы видно, что общее сопротивление параллельной цепи будет равно:
Ну вот мы и нашли ответ на поставленный в начале статьи вопрос! Вам следует знать, что проводимость очень редко используется на практике, в связи с чем данная статья носит чисто образовательный характер.
Краткий обзор:
- Проводимость — это величина противоположная сопротивлению.
- Проводимость обозначается буквой «G» и измеряется в Мо или Сименсах.
- Математически проводимость обратна сопротивлению: G=1/R
Электропроводность электрическая | IOPSpark
Проводимость
Электричество и магнетизм
Электропроводность, электрическая
Глоссарий Определение
за
16-19
Описание
Электропроводность материала — это внутреннее объемное свойство, которое вместе с пространственными размерами и формой образца материала определяет электрическую проводимость (и, следовательно, электрическое сопротивление) этого образца.
Электропроводность обычно обозначается символом σ .
Электропроводность определяется уравнением
σ = L R A
, где R — электрическое сопротивление образца материала длиной L и однородной площадью поперечного сечения A .
Электропроводность обратна удельному сопротивлению:
σ = 1 ρ
, где ρ — удельное электрическое сопротивление материала.
Обсуждение
Модель электропроводности в твердых телах, известная как зонная теория, может объяснить огромный диапазон проводимостей, наблюдаемых в различных материалах. В этой модели электроны в твердом теле могут иметь только определенные диапазоны энергии, называемые энергетическими зонами.
Электрический ток в твердом теле включает электроны, которые могут свободно перемещаться через твердое тело и не связаны с каким-либо конкретным атомным ядром. Эти электроны известны как электроны проводимости, и их энергия находится в так называемой зоне проводимости.
Эти электроны известны как электроны проводимости, и их энергия находится в так называемой зоне проводимости.
В присутствии электрического поля электроны проводимости приобретают дрейфовую скорость вдоль направления поля, и это движение представляет собой электрический ток. Чем больше плотность электронов проводимости, тем больше ток для данного электрического поля и, следовательно, больше проводимость.
Электроны, которые остаются связанными с определенными атомами и не могут свободно перемещаться через материал, известны как валентные электроны. Валентные электроны имеют более низкую энергию, чем электроны проводимости; их энергии лежат в валентной зоне.Между зоной проводимости и валентной зоной находится диапазон энергий, которые «запрещены» — электроны в твердом теле не могут иметь энергии в этом диапазоне. Разность энергий между валентной зоной и зоной проводимости называется шириной запрещенной зоны. Валентный электрон может перейти в зону проводимости, если он приобретет дополнительную энергию, которая по крайней мере равна ширине запрещенной зоны.
В металлах зоны проводимости и валентные зоны перекрываются, каждый атом вносит один или несколько электронов в зону проводимости, и проводимость высокая.Передача энергии металлу (например, путем нагревания) не приводит к значительному увеличению числа электронов проводимости.
В полупроводнике плотность электронов проводимости меньше, чем в металле – в среднем значительно меньше одного на атом. Поэтому проводимость ниже. Однако для полупроводников характерна малая ширина запрещенной зоны. Относительно легко продвигать валентные электроны в зону проводимости (например, нагревая или освещая материал), что увеличивает проводимость.Также возможно изменить структуру энергетических зон, комбинируя два или более полупроводниковых элемента (например, GaAs) и/или «легируя» полупроводник небольшим количеством примесей — и, таким образом, создавать «дизайнерские» полупроводниковые материалы с особыми свойствами.
У изоляторов очень мало электронов проводимости, так как их ширина запрещенной зоны очень велика. У них очень низкая проводимость.
У них очень низкая проводимость.
Единица СИ
См -1
Выражено в основных единицах СИ
кг -1 м -3 с 3 А 2
Другие широко используемые единицы
Ом -1 м -1
Математические выражения
- σ = L R A
- σ = 1 ρ
где R — электрическое сопротивление образца материала длиной L и площадью поперечного сечения A
где ρ — удельное электрическое сопротивление материала
В контексте
Твердые материалы с электропроводностью более ~ 10 5 См м -1 классифицируются как проводники, материалы с проводимостью от ~ 10 5 См м -1 и ~ 10 –6 См 9 –1 являются полупроводниками, а вещества с более низкой проводимостью классифицируются как изоляторы. Серебро имеет самую высокую проводимость среди всех металлических элементов. В таблице 1 ниже приведены значения электропроводности различных материалов при 20°C, иллюстрирующие огромный диапазон значений.
Серебро имеет самую высокую проводимость среди всех металлических элементов. В таблице 1 ниже приведены значения электропроводности различных материалов при 20°C, иллюстрирующие огромный диапазон значений.
| Материал | Проводимость σ / См м -1 |
|---|---|
| Серебро | 6,30 × 10 7 |
| Медь | 5,96 × 10 7 |
| Титан | 2.38 × 10 6 |
| Константан | 2,04 × 10 6 |
| Нихром | 9,09 × 10 6 |
| GaAs | 5 × 10 от -8 до 10 3 |
| Аморфный углерод | от 1,25 до 2 × 10 3 |
| Морская вода | 4,8 |
| Силикон | 1.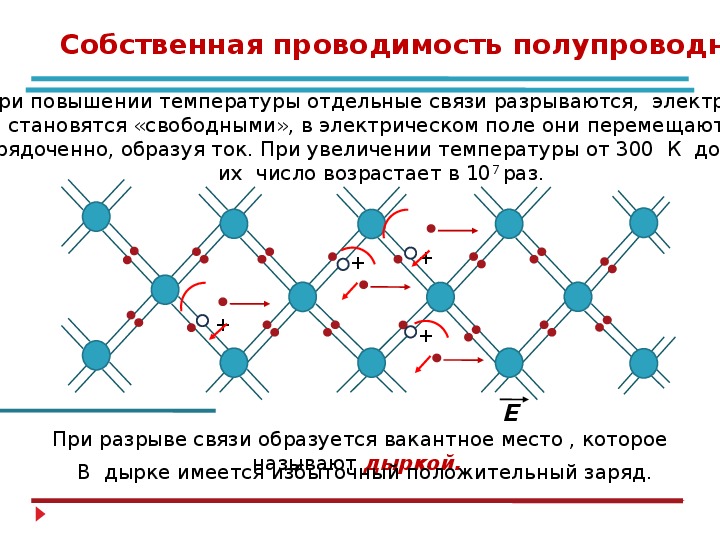 56 × 10 -3 56 × 10 -3 |
| Стекло | 10 -11 до 10 -16 |
| Сера | 10 -16 |
| Парафиновый воск | 10 -18 |
| Тефлон | 10 -23 до 10 -26 |
| Коэффициенты скорости передачи (модель Ходжкина-Хаксли) | |||||
| β H , β м , β N N | — «- | ||||
| δ S , δ V , Δ V | Двумерный [M -2 ] и трехмерный [M -3 ] Dirac Delta Функции | ||||
| ε | ε | диэлектрическая проницаемость [f / m] | |||
| E | Электромологическая сила (EMF) [V] | ||||
| θ | скорость проводимости (волна) [м / с] | ||||
| λ | мембранная длина постоянной [см] (~ √ ( R M / R I ) = √ ( R м A / 2ρ 5 I )) | ||||
| магнитная проницаемость среды [Гн/м = Vs/Am] | , 0 | электрохимический потенциал иона в целом и в эталонном состоянии [Дж/моль] | |||
| ν | узловая ширина [м] | ||||
| Плотность [C / M 3 ] | |||||
| ρ I B , ρ O B O B 6 B 6 B | Внутриклеточные и интерстициальные стойкие резистивы (KωCM] | ||||
| ρ M B | Мембранное удельное сопротивление биджина [KΩCM] | ||||
| ρ T B | Hultomain THE | ||||
| ρ I , ρ o | Внутриклеточные и интерстициальные сопротивления [KΩCM] | ||||
| σ | проводимость [См/м] | ||||
| σ i b , σ i b 6 Uctivities [MS / CM] | |||||
| Σ I , σ o , Σ o | Внутриклеточные и интерстициальные проводимости [MS / CM] | ||||
| τ | Мембрана времени постоянной [мс] (= R м C C M в одномерной проблеме, = R M C M в двумерной проблеме) | ||||
| Φ, θ | Долгота (азимут), значимость, в сферической Полярные координаты | ||||
| Φ | Φ | потенциал [V] | |||
| Φ I , φ O | Потенциал внутри и снаружи мембраны [MV] | ||||
| Φ le | Взаимный электрический скалярный потенциальное поле электрического провода вследствие единичного обратного тока [В/А] | ||||
| Φ LM | обратное магнитное скалярное потенциальное поле магнитного провода вследствие обратного тока в единицу времени Производное [vs / a] | ||||
| φ, ψ | 2 скалярных функция (в теореме Грина) | ||||
| χ | поверхность до объема соотношение клетки [1 / см] | ||||
| ω | радиальный Частота [RAD] (= 2πF) | Ω | твердый угол [SR (стенадиан) = M 2 / м 2 ] | ||
| A | RADIUS [M], радиус волокна [ M] | ||||
| единицы единицы | |||||
| A | Азимут Угол в сферических координатах [°] | ||||
| A | A | Район поперечного сечения [M] | |||
| Магнитный Векторный потенциал [WB / M = VS / M] | Магнитная индукция (плотность магнитного поля) [WB / M 2 = VS / M 2 ] | ||||
| LM | индукция магнитного поля Ведущий из-за взаимного тока единичного времени производной [WBS / AM 2 = VS 2 / am 2 ] | C | концентрация частиц [MOL / M 3 ] | ||
| Ведущий вектор | |||||
| C I , C O , C O , C O | Внутриклеточные и внеклеточные ионные концентрации (моновалентное ион) [моль / м 3 ] | ||||
| C K | Концентрация ионов K TH проницаемый ион [моль / м 3 ] | ||||
| C м | Мембранная емкость на единицу длины [F / см Длина волокна] | ||||
| C | электрический заряд [C (Кулон) = As] | ||||
| C m | емкость мембраны на единицу площади (удельная емкость) [Ф/см] | Толщина двойного слоя, диаметр [M] | |||
| D I , D O | Волокно внутренние и внешние миелиновые диаметры [M] | ||||
| D | Нормальная поверхность внешней поверхности | ||||
| D D | ФИКС (диффузионная констанция) [см 2 / S = CM 3 / (CMS)] | ||||
| D | D | Электрическое перемещение [C / M 2 ] 2 ] | |||
| E | Угол высоты в сферических координатах [°] | ||||
| Электрическое поле [V / M] | |||||
| le | Отправочное электрическое поле электрического ведущего к единице обратного тока [В/Ам] | ||||
| LM | обратное электрическое поле магнитопровода, вызванное обратным током единичной производной по времени [Вс/Ам] 9014 6 | ||||
| F | Постоянная Фарадея [9. 64910 4 C / Mol] 64910 4 C / Mol] | ||||
| F | Магнитный поток [WB = VS] | ||||
| г K , г Na , г L | Мембранные проводи на единицу длины блока для калия, натрия и хлорида (утечка) [MS / CM Viber длина] | ||||
| г K , г Na , г L 6 | мембранные проводки на единицу площади для калия, натрия и хлорида (утечка) [мСм/см 2 ] | ||||
| G K max , G Na max | |||||
| г м | H | Расстояние (высота) [M ] 90 146 | |||
| H H | Мембранная толщина [M] | ||||
| H, M, N 6 | Gating Primations (Ходжкин-Хаксли) | ||||
| HCT | HCT | ||||
| Магнитное поле [A / M] | |||||
| LM LM | Отправочное магнитное поле магнитного свинца из-за обратного тока единичного времени производной [S / M] | ||||
| I м | Мембранный ток на единицу длины I | электрический ток [А] | |||
| I a | приложенный установившийся (или стимулирующий) ток [А] | 22 I , I 5 I O O | осевые токи [A] и осевые токи на единицу площади [A / CM 2 ] Внутри и снаружи соты | I K , I Na , i L | мембранный ток, переносимый ионами калия, натрия и хлорида (утечка) на единицу длины [А/см длины волокна] | 906 I 906 I 9025 9022 902 5 Na 6, I 6, I L 6 L L | Мембранный ток, пересеченный калием, натрием, и хлорид (утечки) ионы на единицу площади [A / CM] | I L | ведущий ток General [A] | I | I м | Мембранный ток на единицу площади [A / CM 2 ] (= I 5 MC + I MR ), Мембранная мембрана объем блока [А/см] | i mC , i mI , i mR | емкостная, ионная и резистивная составляющие тока aπ2 на единицу длины мембраны MC , = 2π AI MI MI , = 2π AI MR ) | 8 MC , I , I MI , I MR | емкостный , Ионные и резистивные компоненты мембранного тока на единицу площади [A / CM] |
| I R | Общий обратный ток [A] | ||||
| I RH 6 | Реобазический ток На единицу площади [A / CM 2 ] | ||||
| I S | Стимул Ток на единицу площади [A / CM 2 ] | J , J K | Ионный поток, ионный поток из-за k Th ION [ML / (см 2 S)] | ||
| J D , J E | ионный поток из-за диффузии , Из-за электрического поля [моль / (см 2 ы)] | ||||
| электрический ток плотности [A / M 2 ] | |||||
| DV | Source Element | ||||
| I [ | плотность приложенного тока [А/см 2 ], приложенный дипольный момент на единицу объема [Асм/см 3 ] | ||||
| i , o 9014 CM 2 ] 9 ] | |||||
| I F , I V V | Поток (поток) и вихревые компоненты исходного вихря впечатленной плотности тока [A / CM 2 ] | Радиальные и тангенциальные компоненты впечатленной плотности тока [A / CM 2 ] | |||
| L | Поле свинца в целом [A / M 2 ] | ||||
| Le Le | Электрическое свинцовое поле из-за блока взаимного тока [1 / м 2 ] | ||||
| LI | Поле свинцовой подачи электродов подачи тока для единицы тока [1 / м 2 ] (в измерении импеданса) | ||||
LM LM | Магнитное свинцовое поле из-за обратного тока единичного времени производной [S / M 2 ] | | ||||
| K | Константы | ||||
| K (K) , E (k) | полные эллиптические интегралы | ||||
| J J | источник вторичного тока для электрических полей [A / CM 2 ] | ||||
| L | |||||
| LIC 6 | |||||
| L | L | Индуктивность [H = WB / A = VS / A] | |||
| Магнитный дипольный момент Объемный источник [am 2 ] | |||||
| м | Векторные величины в сферических координатах |
| м 1 , м 2 , м 3 | пиковый амплитуды в начальной, средней и терминальной фазах комплекса QRS на ЭКГ [мВ] и МКГ [пТл] | |
| n | число родинок | ||||
| длина в норме (единица измерения) 9 | |||||
| j | нормаль к поверхности S j направлена от заштрихованной области к дважды заштрихованной | ||||
| электрическая диполь e момент на единицу площади [Ам/м 2 = А/м] | |||||
| электрический дипольный момент объемного источника [Ам] | |||||
| P | |||||
| P CL 5 CL , P 5 K , P 5 Na Na Na Na | Мембранная проницаемость ионов хлорида, калия и натрия [м / с] | ||||
| R | Radius, расстояние [M], Вектор величины в сферических полярных координатах | ||||
| R | R | R | Radius Vector | R 5 I , R O | осевые и междоузельные сопротивления на единицу длины [кОм/см длины волокна] (r i = 1/σ i ρa 2 ) |
| r m 6 мэмб Сопротивление Ране, умноженное на единицу длины [кОм·см длины волокна] (= R м /2ρa) | |||||
| R | газовая постоянная [8.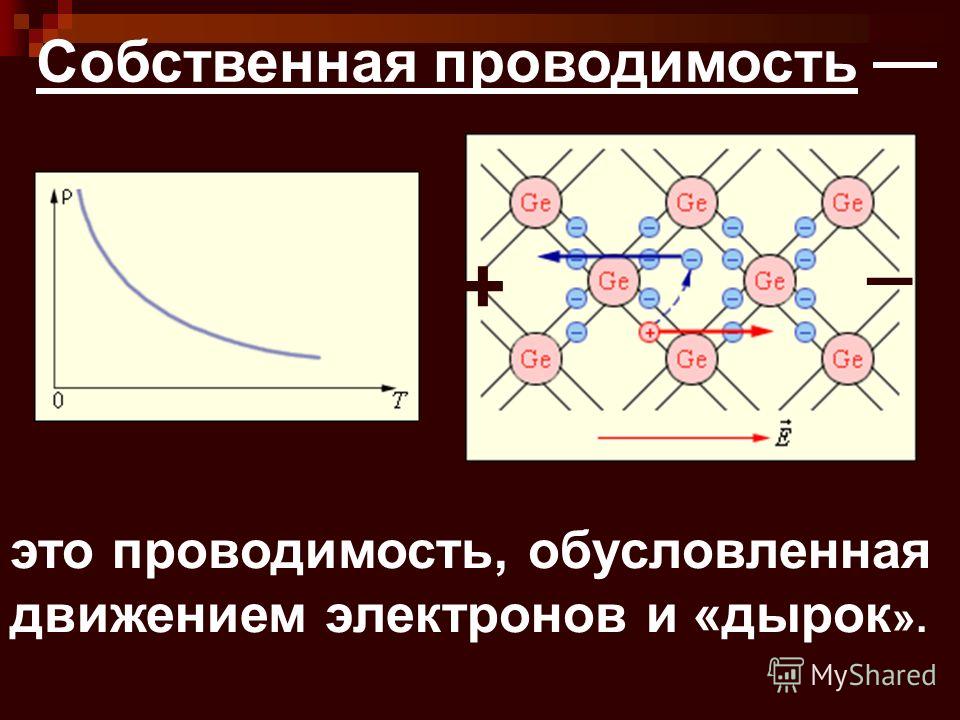 314 J / (Молк)] 314 J / (Молк)] | ||||
| R 5 I , R O , R O O | осевые сопротивления внутриклеточных и интерстициальных СМИ [kω] | ||||
| R M | Мембрана Сопротивление времен устойчивости (утешение сопротивления) [KΩCM 2 ] | ||||
| R | R S S S | Устойчивость к серии [Mω] | |||
S CL , S 5 K , S NA Na | Электрические плотности тока Из-за хлорида, калия и ионов натрия ионов [A / CM 2 ] | | T | Время [S] | ||
| T | Температура [°C], абсолютная температура [K] | ||||
| u | ионная подвижность [см 2 /(Вс)] | ||||
| v 9014] скорость [c 46 | |||||
| V V V | объем [M 3 ] | ||||
| V | V | Напряжение [V] | Напряжение [V] | ||
| V ‘ | V ‘ | Отклонение мембранного напряжения от состояния отдыха [MV ] (= V M — 5 м — V R ) R ) | |||
| V C C | Зажимая напряжение [MV] | ||||
| V L | Ведущее напряжение в целом [V] | ||||
| V LE | Напряжение свинца электрического свинца из-за единицы взаимного тока [V] | ||||
| V LM LM | Световольное напряжение магнитного свинца из-за взаимного тока единичная производная по времени [В] | ||||
| В K , В Na , В L | Нернст oride (утечка) ионы [MV] | ||||
| V | V м | мембранное напряжение [MV] (= φ I — φ O ) | |||
| V R , V TH TH 9 | Отдых и пороговые напряжения мембраны [MV] | ||||
| V R R R R R R R | Напряжение разворота [MV] | ||||
| V Z | Измеренное напряжение (в измерении импендиатации ) [V] | ||||
| W W | работа [J / MOL] | ||||
| X, Y, Z | Прямоугольные координаты | ||||
| Z | Валентность ионов | ||||
| Z | импеданс [Ом] |
Проводимость воды — Lenntech
Определение и описание
Проводимость вещества определяется как « способность или способность проводить или передавать тепло, электричество или звук ».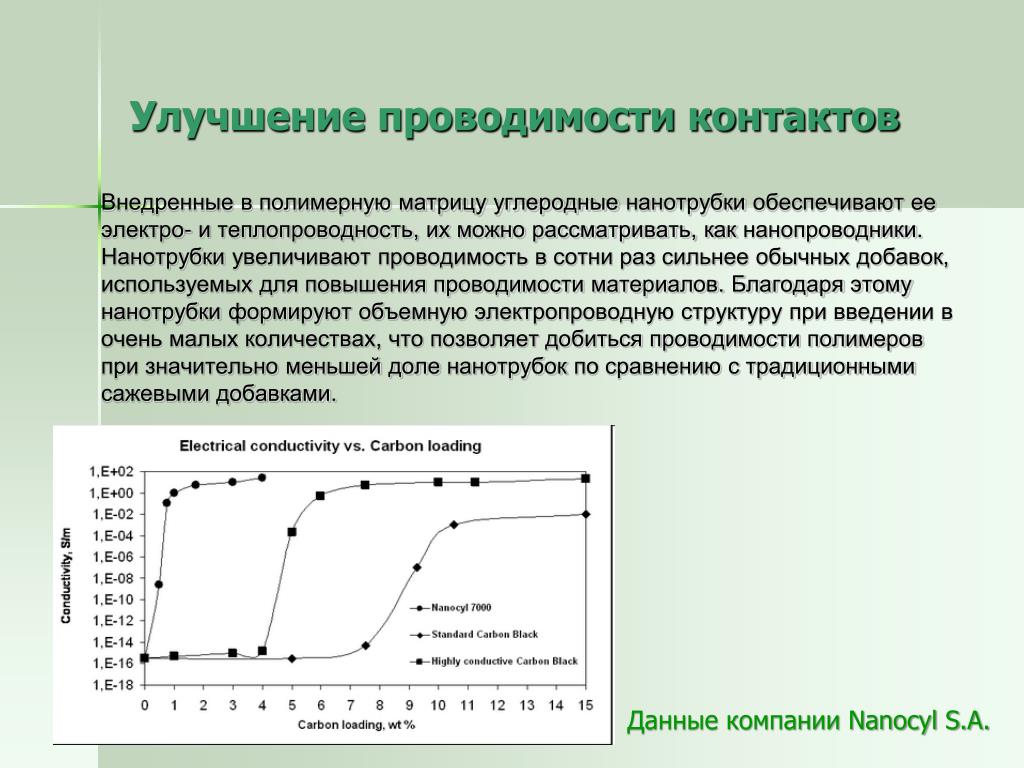 Его единицами являются сименсы на метр [См/м] в СИ и миллимгоны на сантиметр [ммхо/см] в обычных единицах измерения США. Его символ k или s.
Его единицами являются сименсы на метр [См/м] в СИ и миллимгоны на сантиметр [ммхо/см] в обычных единицах измерения США. Его символ k или s.
Электропроводность (EC)
Электрический ток возникает в результате движения электрически заряженных частиц в ответ на силы, действующие на них со стороны приложенного электрического поля. В большинстве твердых материалов ток возникает из-за потока электронов, который называется электронной проводимостью. Во всех проводниках, полупроводниках и многих изолированных материалах существует только электронная проводимость, а электрическая проводимость сильно зависит от количества электронов, доступных для участия в процессе проводимости.Большинство металлов являются чрезвычайно хорошими проводниками электричества из-за большого количества свободных электронов, которые могут быть возбуждены в пустом и доступном энергетическом состоянии.
В воде и ионных материалах или жидкостях может происходить результирующее движение заряженных ионов. Это явление создает электрический ток и называется ионной проводимостью.
Это явление создает электрический ток и называется ионной проводимостью.
Электропроводность определяется как отношение между плотностью тока (Дж) и напряженностью электрического поля (е) и противоположно удельному сопротивлению (r, [Вт*м]):
с = Дж/е = 1 /r
Серебро имеет самую высокую электропроводность среди всех металлов: 63 x 10 6 См/м.
Проводимость воды
Чистая вода не является хорошим проводником электричества. Обыкновенная дистиллированная вода в равновесии с углекислым газом воздуха имеет электропроводность около 10 х 10 -6 Вт -1 *м -1 (20 дСм/м). Поскольку электрический ток переносится ионами в растворе, проводимость увеличивается по мере увеличения концентрации ионов.
Таким образом, проводимость увеличивается по мере растворения в воде ионных частиц.
Типичная электропроводность воды:
Сверхчистая вода 5.5 · 10 -6 См/м
Питьевая вода 0,005 – 0,05 См/м
Морская вода 5 См/м
Электропроводность и TDS
TDS или Total Dissolved Solids – это мера общего содержания ионов в растворе .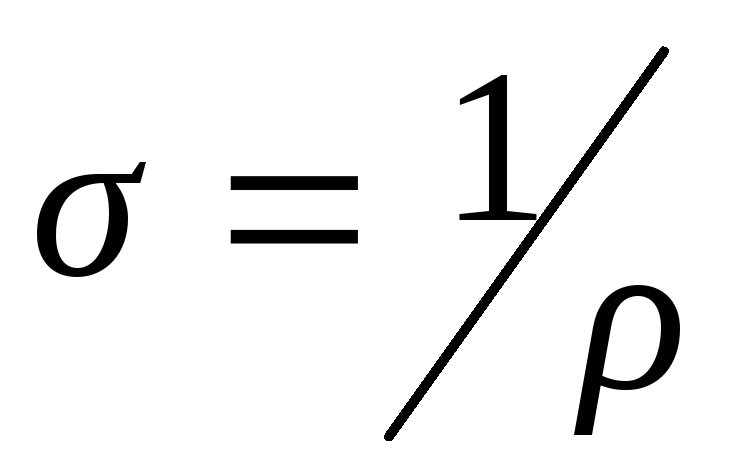 EC на самом деле является мерой ионной активности раствора с точки зрения его способности пропускать ток. В разбавленном растворе TDS и EC достаточно сопоставимы. TDS пробы воды на основе измеренного значения EC можно рассчитать с помощью следующего уравнения:
EC на самом деле является мерой ионной активности раствора с точки зрения его способности пропускать ток. В разбавленном растворе TDS и EC достаточно сопоставимы. TDS пробы воды на основе измеренного значения EC можно рассчитать с помощью следующего уравнения:
TDS (мг/л) = 0.5 x EC (дСм/м или ммо/см) или = 0,5 * 1000 x EC (мСм/см)
Приведенное выше соотношение можно также использовать для проверки приемлемости химических анализов воды. Не относится к сточным водам.
По мере того, как раствор становится более концентрированным (TDS > 1000 мг/л, EC > 2000 мс/см), близость ионов раствора друг к другу снижает их активность и, следовательно, их способность проводить ток, хотя физическое количество растворенных твердых веществ не влияет. При высоких значениях TDS отношение TDS/EC увеличивается, и соотношение стремится к TDS = 0.9 х ЕС.
В этих случаях указанное выше соотношение не следует использовать и каждый образец должен быть охарактеризован отдельно.
Для воды для сельскохозяйственных и ирригационных целей значения EC и TDS связаны друг с другом и могут быть преобразованы с точностью около 10% с помощью следующего уравнения:
TDS (мг/л) = 640 x EC (ds/ м или ммо/см).
В процессе обратного осмоса вода нагнетается через полунепроницаемую мембрану, оставляя за собой примеси.Этот процесс способен удалить 95-99% TDS, обеспечивая чистую или сверхчистую воду.
Используйте калькуляторы Lenntech для расчета содержания TDS на основе анализа воды и преобразования TDS в EC или наоборот.
6.8A: Электрическая проводимость и удельное сопротивление
Удельное электрическое сопротивление и проводимость являются важными свойствами материалов. Различные материалы имеют разную проводимость и удельное сопротивление. Электропроводность основана на свойствах электротранспорта.Их можно измерить несколькими методами с использованием различных инструментов. Если электричество легко проходит через материал, этот материал имеет высокую проводимость. Некоторые материалы с высокой проводимостью включают медь и алюминий. Электропроводность — это мера того, насколько легко электричество проходит через материал.
Электропроводность против удельного сопротивления
Проводимость и удельное сопротивление обратно пропорциональны друг другу. Когда проводимость низкая, удельное сопротивление высокое.Когда сопротивление низкое, проводимость высокая. Уравнение выглядит следующим образом:
Когда проводимость низкая, удельное сопротивление высокое.Когда сопротивление низкое, проводимость высокая. Уравнение выглядит следующим образом:
\[ \rho = \dfrac{1}{\sigma}\]
где
- Удельное сопротивление обозначается \(\rho\) и измеряется в Ом-метрах (\(Ом·м\)),
- Электропроводность обозначается \(\сигма\) и измеряется в Siemens (\(1/Ом·м\)).
Поскольку проводимость является мерой того, насколько легко протекает электричество, удельное электрическое сопротивление измеряет, насколько материал сопротивляется потоку электричества.
Свойства электрического транспорта
Проще говоря, электричество — это движение электронов через материал. Когда электроны движутся через материал, они вступают в контакт с атомами материала. Столкновения замедляют электроны. Каждое столкновение увеличивает удельное сопротивление материала. Чем легче электроны проходят через материал, тем меньше происходит столкновений и тем выше проводимость.
При повышении температуры проводимость металлов обычно уменьшается, а проводимость полупроводников увеличивается.Это, конечно, предполагает, что материал однороден, что не всегда так. Вы можете рассчитать удельное сопротивление, используя следующее уравнение
\[\dfrac{E}{J} = ρ\]
Как вы уже читали, ρ — это символ удельного сопротивления. \(E\) представляет собой электрическое поле и измеряется в вольтах на метр (В/м). J — плотность тока, выраженная в амперах на квадратный метр (А/м2). Электрическое поле рассчитывается путем деления напряжения на длину l, на которую подается напряжение.
\[E=\dfrac{V}{l}\]
Плотность тока рассчитывается по уравнению ниже
\[J=\dfrac{I}{A}\]
I — ток, который делится на площадь поперечного сечения, А, по которому протекает ток.
Удельное сопротивление против сопротивления
Удельное сопротивление и сопротивление — разные вещи. Удельное сопротивление не зависит от размера или формы. Сопротивление, однако, есть. Вы можете рассчитать сопротивление с помощью приведенного ниже уравнения.
Сопротивление, однако, есть. Вы можете рассчитать сопротивление с помощью приведенного ниже уравнения.
\[ R=\dfrac{V}{I} \]
R относится к сопротивлению и измеряется в Ом. \(V\) — напряжение и измеряется в вольтах. I измеряет ток, и его единицей измерения являются ампер (А).
Каталожные номера
Электропроводность и удельное сопротивление, Хини, Майкл, электрические измерения, обработка сигналов и дисплеи.июль 2003 г.
- Леви, Питер М. и Шуфэн Чжан. «Электропроводность магнитных многослойных структур». Physical Review Letters 65.13 (1990): 1643-646. Распечатать.
Проблемы
- Какова плотность тока материала с удельным сопротивлением 12 Ом·м и напряженностью электрического поля 64 В/м?
- Если напряжение 6 В проходит через вещество радиусом 2 м и длиной 3 м, каково электрическое поле?
- Каково электрическое поле материала, если сила тока равна 25 А, измеренное сопротивление равно 78 Ом, плотность тока равна 24 А/м2, а длина тока составляет 100 м?
- Материал имеет напряжение 150В и ширину 24м.
 Материал также имеет силу тока 62 А и проходит расстояние 5 м. Какая проводимость?
Материал также имеет силу тока 62 А и проходит расстояние 5 м. Какая проводимость? - Металл изначально имеет электрон, сталкивающийся с каждым пятым атомом, и его температура увеличивается от 6К до 100К. Полупроводник изначально имеет электрон, сталкивающийся с каждым пятым атомом, и его температура увеличивается от 6 К до 100 К. Какой материал будет иметь большее удельное сопротивление? Почему?
Ответы на задачи:
1. E/J = ρ —> J=E/ρ = 64 В/м/12 Ом·м = 5.33 А/м 2
2. E=В/л = 6В/3м = 2В/м
3. Е=V/1
V=IR —> E=IR/l = 25 A x 78 Ом/100 м = 19,5 В/м
4. E/J = ρ
Э=В/л
J=I/A —> ρ=(В/л)/(I/А) = (150 В/5 м)/(62 А/(24 м x 5 м) = 58 Ом·м
ρ = 1/σ —> 1/ρ = σ = 1/58 Ом·м
5. Материалом с наибольшим удельным сопротивлением является металл, поскольку при повышении температуры удельное сопротивление металлов с большей вероятностью увеличивается, а у полупроводников обычно уменьшается удельное сопротивление при повышении температуры.
Авторы и авторство
- Майкл Форд (UCD) и Александра Кристман (UCD)
Что такое теплопроводность? Обзор
Изменение теплопроводности
Теплопроводность конкретного материала сильно зависит от ряда факторов. К ним относятся градиент температуры, свойства материала и длина пути, по которому следует тепло.
Теплопроводность окружающих нас материалов существенно отличается от материалов с низкой теплопроводностью, таких как воздух со значением 0.024 Вт/м·K при 0°C для металлов с высокой проводимостью, таких как медь (385 Вт/м·K).
Теплопроводность материалов определяет, как мы их используем, например, материалы с низкой теплопроводностью отлично подходят для изоляции наших домов и предприятий, в то время как материалы с высокой теплопроводностью идеально подходят для приложений, где необходимо быстро и эффективно перемещать тепло из одной области. к другому, как в кухонной утвари и системах охлаждения в электронных устройствах. Выбирая материалы с теплопроводностью, соответствующей применению, мы можем добиться наилучших возможных характеристик.
Выбирая материалы с теплопроводностью, соответствующей применению, мы можем добиться наилучших возможных характеристик.
Теплопроводность и температура
В связи с тем, что молекулярное движение является основой теплопроводности, температура материала оказывает большое влияние на теплопроводность. Молекулы будут двигаться быстрее при более высоких температурах, и поэтому тепло будет передаваться через материал с большей скоростью. Это означает, что теплопроводность одного и того же образца может резко измениться при повышении или понижении температуры.
Способность понять влияние температуры на теплопроводность имеет решающее значение для обеспечения того, чтобы продукты вели себя должным образом при воздействии термического стресса. Это особенно важно при работе с продуктами, выделяющими тепло, такими как электроника, и при разработке огнезащитных и теплозащитных материалов.
Теплопроводность и структура
Значения теплопроводности существенно различаются между материалами и сильно зависят от структуры каждого конкретного материала. Некоторые материалы будут иметь разные значения теплопроводности в зависимости от направления распространения тепла; это анизотропные материалы. В этих случаях тепло легче перемещается в определенном направлении из-за того, как устроена структура.
Некоторые материалы будут иметь разные значения теплопроводности в зависимости от направления распространения тепла; это анизотропные материалы. В этих случаях тепло легче перемещается в определенном направлении из-за того, как устроена структура.
При обсуждении тенденций теплопроводности материалы можно разделить на три категории; газы, неметаллические твердые вещества и металлические твердые вещества. Различные способности этих трех категорий с точки зрения передачи тепла можно объяснить различиями в их структурах и движениях молекул.
Газы имеют более низкую относительную теплопроводность, так как их молекулы не так плотно упакованы, как в твердых телах, и поэтому теплопередача сильно зависит от свободного движения молекул и молекулярной скорости.
Газы плохо передают тепло. Напротив, молекулы неметаллических твердых тел связаны в сеть решеток, и поэтому теплопроводность в основном возникает за счет колебаний в этих решетках. Непосредственная близость этих молекул по сравнению с молекулами газов означает, что неметаллические твердые вещества имеют более высокую теплопроводность из двух, однако внутри этой группы существуют большие различия.
Это изменение частично связано с количеством воздуха, присутствующего в твердом теле. Материалы с большим количеством воздушных карманов являются отличными изоляторами, а материалы с более плотной упаковкой будут иметь более высокое значение теплопроводности.
Теплопроводность металлических твердых тел еще раз отличается от предыдущих примеров. Металлы обладают самой высокой теплопроводностью среди всех материалов, за исключением графена, и обладают уникальным сочетанием тепло- и электропроводности.Оба этих атрибута передаются одними и теми же молекулами, и связь между ними объясняется законом Видемана-Франца. Этот закон свидетельствует о том, что при определенной температуре электропроводность будет пропорциональна теплопроводности, однако с повышением температуры теплопроводность материала будет расти, а электропроводность уменьшаться.
Испытание и измерение теплопроводности
Теплопроводность является важнейшим компонентом взаимосвязи между материалами, и способность понять ее позволяет нам добиться наилучших результатов от материалов, которые мы используем во всех аспектах нашей жизни. Эффективное тестирование и измерение теплопроводности имеют решающее значение для этой цели. Методы измерения теплопроводности можно разделить на стационарные и переходные. Это разграничение является определяющей характеристикой того, как работает каждый метод. Методы стационарного состояния требуют, чтобы образец и эталонные образцы находились в тепловом равновесии до начала измерений. Переходные методы не требуют выполнения этого правила и поэтому дают результаты быстрее.
Эффективное тестирование и измерение теплопроводности имеют решающее значение для этой цели. Методы измерения теплопроводности можно разделить на стационарные и переходные. Это разграничение является определяющей характеристикой того, как работает каждый метод. Методы стационарного состояния требуют, чтобы образец и эталонные образцы находились в тепловом равновесии до начала измерений. Переходные методы не требуют выполнения этого правила и поэтому дают результаты быстрее.
Исследовательские работы
Получение пористой муллитовой керамики с низкой теплопроводностью
В этом исследовании анализируется муллитовая керамика, образованная в результате вспенивания и отверждения крахмалом порошка муллита, а также то, как изменяется ее теплопроводность в зависимости от пористости керамики.Теплопроводность измерялась с помощью метода плоскостного источника (TPS) Hot Disc с помощью TPS 2500 S. По мере увеличения пористости муллитовой керамики увеличивается и теплопроводность.
Нанографит/парафиновый материал с фазовым переходом и высокой теплопроводностью
Композиты нанографита (НГ)/парафина были приготовлены в качестве композиционных материалов с фазовым переходом. Добавление ПГ повысило теплопроводность композиционного материала. Материал, содержащий 10% NG, имел теплопроводность 0.9362 Вт/м•К
Каталожные номера:
Неф, Р. Гиперфизика. «Теплопроводность». Государственный университет Джорджии.
Доступно по адресу: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/thercond.html#c1
Учебный материал по неразрушающему контролю. «Теплопроводность». Ресурсный центр по неразрушающему контролю.
Доступно по адресу: https://www.ndeed.org/EducationResources/CommunityCollege/Materials/Physical_Chemical/ThermalConductivity.htm
Уильямс, М. «Что такое теплопроводность?». Физ.орг. 9 декабря 2014 г.
Доступно по ссылке: http://phys.org/news/2014-12-what-is-heat-conduction. html
html
Что вы подразумеваете под теплопроводностью? Получено из определения теплопроводности
.
Thermtest База данных тепловых свойств материалов. Список теплопроводностей
Проводимость | Последовательные и параллельные цепи
Когда учащиеся впервые видят уравнение параллельного сопротивления, возникает естественный вопрос: «Откуда взялось это ?» Это действительно странная часть арифметики, и ее происхождение заслуживает хорошего объяснения.
В чем разница между сопротивлением и проводимостью?
Сопротивление, по определению, является мерой трения компонента, представляющего протекающий через него ток. Сопротивление обозначается заглавной буквой «R» и измеряется в единицах измерения «Ом». Однако мы можем также думать об этом электрическом свойстве в терминах его обратного: насколько легко для тока течь через компонент, а не как сложно .
Если сопротивление — это слово, которое мы используем, чтобы символизировать меру того, насколько трудно течь току, то хорошим словом для выражения того, насколько легко течь току, будет проводимость . Математически проводимость обратно пропорциональна сопротивлению:
Математически проводимость обратно пропорциональна сопротивлению:
Чем больше сопротивление, тем меньше проводимость — и наоборот.
Это должно иметь интуитивно понятный смысл, поскольку сопротивление и проводимость являются противоположными способами обозначения одного и того же существенного электрического свойства.
Если сравнить сопротивления двух компонентов и обнаружить, что компонент «А» имеет половину сопротивления компонента «В», то мы могли бы в качестве альтернативы выразить это отношение, сказав, что компонент «А» имеет удвоенную проводимость , чем компонент «В.Если компонент «А» имеет только одну треть сопротивления компонента «В», то мы могли бы сказать, что его проводимость в раз больше, чем в три раза по , чем у компонента «В», и так далее.
Единица проводимости
Развивая эту идею, были созданы символ и единица измерения проводимости. Символ — заглавная буква «G», а единица измерения — mho , что означает «Ом», написанный наоборот (и вы не думали, что у инженеров-электронщиков есть чувство юмора!).
Несмотря на свою уместность, единица mho была заменена в последующие годы единицей Siemens (сокращенно заглавной буквой «S»).Это решение об изменении названий единиц напоминает изменение единицы измерения температуры с градусов по Цельсию на градусов по Цельсию или изменение единицы частоты с c.p.s. (циклов в секунду) до Герц . Если вы ищете здесь закономерность, Сименс, Цельсий и Герц — это все фамилии известных ученых, имена которых, к сожалению, говорят нам о природе единиц меньше, чем их первоначальные обозначения.
Как примечание, единица Сименс никогда не выражается без последней буквы «с».Другими словами, не существует такой вещи, как единица «симен», как в случае с «омом» или «мхо». Причиной этого является правильное написание фамилий соответствующих ученых.
Единица измерения электрического сопротивления была названа в честь кого-то по имени «Ом», тогда как единица измерения электрической проводимости была названа в честь кого-то по имени «Сименс», поэтому было бы неправильным «обозначать в единственном числе» последнюю единицу, поскольку ее конечная буква «s» не соответствует обозначают множественность.
Вернемся к нашему примеру с параллельной цепью. Мы должны увидеть, что несколько путей (ветвей) для тока уменьшают общее сопротивление всей цепи, поскольку ток может легче течь через всю сеть из нескольких ветвей, чем через какую-либо одну. одних только сопротивлений этих ветвей.С точки зрения сопротивления дополнительные ответвления приводят к меньшему общему количеству (текущее встречается с меньшим сопротивлением). Однако с точки зрения проводимости дополнительные ответвления приводят к большей сумме (ток течет с большей проводимостью).
Общее параллельное сопротивление
Суммарное параллельное сопротивление на меньше, чем на , чем любое из сопротивлений отдельных ответвлений, потому что сопротивление параллельных резисторов вместе меньше, чем по отдельности:
Суммарная параллельная проводимость
Суммарная параллельная проводимость на больше , чем проводимость любой из отдельных ветвей, потому что параллельные резисторы лучше проводят вместе, чем по отдельности:
Точнее, общая проводимость в параллельной цепи равна сумме отдельных проводимостей:
Если мы знаем, что проводимость есть не что иное, как математическая обратная величина (1/x) сопротивления, мы можем перевести каждый член приведенной выше формулы в сопротивление, подставив обратную величину каждой соответствующей проводимости:
Решая приведенное выше уравнение для полного сопротивления (вместо обратной величины полного сопротивления), мы можем инвертировать (обратить) обе части уравнения:
Итак, мы наконец пришли к нашей загадочной формуле сопротивления! Проводимость (G) редко используется в качестве практического измерения, поэтому приведенная выше формула часто используется при анализе параллельных цепей.
ОБЗОР:
- Проводимость противоположна сопротивлению: мера того, насколько легко электрический ток проходит через что-то.
- Проводимость обозначается буквой «G» и измеряется в единицах мОм или Сименс .
- Математически проводимость равна обратной величине сопротивления: G = 1/R
РОДСТВЕННЫЕ РАБОЧИЕ ЛИСТЫ:
Руководство инструктора — Проводимость — Роберт Б.Институт водных ресурсов Анниса (AWRI) — образование и информационно-пропагандистская деятельность
Что такое проводимость?
Проводимость или удельная проводимость — это мера способности воды проводить электрический ток. Проводимость зависит от количества ионов или заряженных частиц в воде. Легкость или сложность протекания электрического тока через жидкости позволяет разделить их на две большие категории: электролиты и неэлектролиты. Электричество легко проходит через воду с высоким содержанием электролитов или ионов и плохо проходит через материалы с низким содержанием электролитов, такие как чистая вода или многие органические растворители, такие как спирт или масло. Противодействие потоку электричества называется сопротивлением и измеряется в единицах, называемых омами. Вещества с низким сопротивлением и высокой проводимостью легко проводят электричество.
Противодействие потоку электричества называется сопротивлением и измеряется в единицах, называемых омами. Вещества с низким сопротивлением и высокой проводимостью легко проводят электричество.
Как измеряется электропроводность?
Кондуктометр используется для измерения способности пробы воды проводить электричество. Удельная проводимость измеряется путем пропускания тока между двумя электродами (на расстоянии один сантиметр друг от друга), которые помещаются в образец воды. Единица измерения проводимости выражается либо в микросименсах (мкСм/см), либо в микромосах (мкм/см), что является обратной величиной единицы сопротивления, ома.Приставка «микро» означает, что оно измеряется в миллионных долях мхо. MicroSiemens и micromhos являются эквивалентными единицами. Дистиллированная вода имеет диапазон электропроводности от 0,5 до 2 мкСм/см. Электропроводность питьевой воды обычно составляет от 50 до 1500 мкСм/см, а бытовые сточные воды могут иметь проводимость выше 10 000 мкСм/см. Чем теплее вода, тем выше проводимость с увеличением примерно на 1,9% на градус Цельсия. Электропроводность указана при стандартной температуре 25,0°C.
Чем теплее вода, тем выше проводимость с увеличением примерно на 1,9% на градус Цельсия. Электропроводность указана при стандартной температуре 25,0°C.
Какое значение имеет проводимость?
Определение электропроводности полезно в исследованиях на воде, поскольку оно дает оценку растворенного в воде ионного вещества.Низкие значения удельной электропроводности характерны для качественных, олиготрофных (низкопитательных) озерных вод. Высокие значения удельной электропроводности наблюдаются в эвтрофных озерах, где больше питательных веществ для растений (удобрений). Очень высокие значения являются хорошими индикаторами возможных мест загрязнения. Например, промышленные выбросы, дорожная соль и неисправные септиктенки могут повышать проводимость. Внезапное изменение проводимости может указывать на прямой сброс или другой источник загрязнения в воду.
Показания электропроводности не предоставляют информацию о конкретном ионном составе и концентрациях.

 )
) )
) 05
05 3
3 Символы, которые появляются только в одном соединении или являются очевидными расширениями тех, что указаны в списке, не обязательно включаются. Они определяются в тексте по мере их введения.
Символы, которые появляются только в одном соединении или являются очевидными расширениями тех, что указаны в списке, не обязательно включаются. Они определяются в тексте по мере их введения. Материал также имеет силу тока 62 А и проходит расстояние 5 м. Какая проводимость?
Материал также имеет силу тока 62 А и проходит расстояние 5 м. Какая проводимость?