Соединение резисторов — как считать общее сопротивление | PoweredHouse
Применяются следующие соединения резисторов: параллельное, последовательное и смешанное.
Последовательное соединение резисторов
Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.
Принципиальная схема последовательного соединения:
Как видно в цепи последовательно соединено три резистора (их может быть и больше). Сопротивление первого резистора R1 = 20 Ом. Второго R2 = 70 Ом. Третьего R3 = 10 Ом.
Как видно в цепи последовательно соединено три резистора (их может быть и больше). Сопротивление первого резистора R1 = 20 Ом. Второго R2 = 70 Ом. Третьего R3 = 10 Ом.
Для подсчета общего (эквивалентного) сопротивление при последовательном соединении нужно сложить все номинальные сопротивления резисторов входящих в цепь:
R = R1 + R2 + R3 + . .. + Rn.
.. + Rn.
R = 20 + 70 + 10 = 100 Ом.
В представленной схеме для наглядности приведены напряжения на каждом из трех участков. И падение напряжения происходит в зависимости от сопротивления конкретного резистора. Сила тока в цепи общая для всех резисторов (I = I1 = I2 = I3). Поэтому согласно закону Ома сила тока при известном напряжении источника питания (в данном случае U = 220 В) определяется по формуле:
I = U / R = U / (R1 + R2 + R3 + … + Rn).
I = 220 / (20 + 70 + 10) = 220 / 100 = 2,2 A.
Формулы нахождения напряжения на участке цепи при известной силе тока (в данном случае I = I1 = I2 = I3 = 2,2 A):
- U1 = I × R1.
- U2 = I × R2.
- U3 = I × R3.
- Un = I × Rn.
Соответственно U1 = 2,2 × 20 = 44 В; U2 = 2,2 × 70 = 154 В; U3 = 2,2 × 10 = 22 В.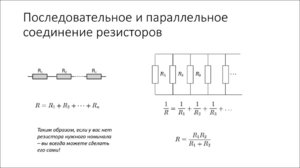 В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).
В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).
Рассмотренные три резистора в последовательной цепи можно заменить одним с сопротивлением 100 Ом:
Если можно несколько резисторов заменить одним, то возникает логичный вопрос, зачем применяется такое комбинирование. Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.
В цепи из последовательно соединенных резисторов главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление. К примеру, если соединить три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате получиться составной с сопротивлением 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом. А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.
А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.
Параллельное соединение резисторов
Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.
При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un. По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + … + In. Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + . .. + 1 / Rn. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
.. + 1 / Rn. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:
1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.
R ≈ 1 / 0,164 ≈ 6,097 Ом.
Для наглядности смоделируем в программе Electronics Workbench замену трех параллельно соединенных резисторов одним (R = 6,097 Ом):
Как видно, расчет был произведен правильно, так как сила тока в цепи с резистором 6,097 Ом равна силе тока в цепи с параллельным соединением (36,08 A ≈ 36,14 A).
Для наглядности смоделируем в программе Electronics Workbench замену трех параллельно соединенных резисторов одним (R = 6,097 Ом):
Как видно, расчет был произведен правильно, так как сила тока в цепи с резистором 6,097 Ом равна силе тока в цепи с параллельным соединением (36,08 A ≈ 36,14 A).
Выделим основные особенности параллельного соединения резисторов:
- Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.

- Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
- Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
- Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).
Смешанное соединение резисторов
Смешанное соединение резисторов — это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.
Пример цепи со смешанным соединением резисторов:
Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:
Определяется общее сопротивление участков с параллельным соединением резисторов.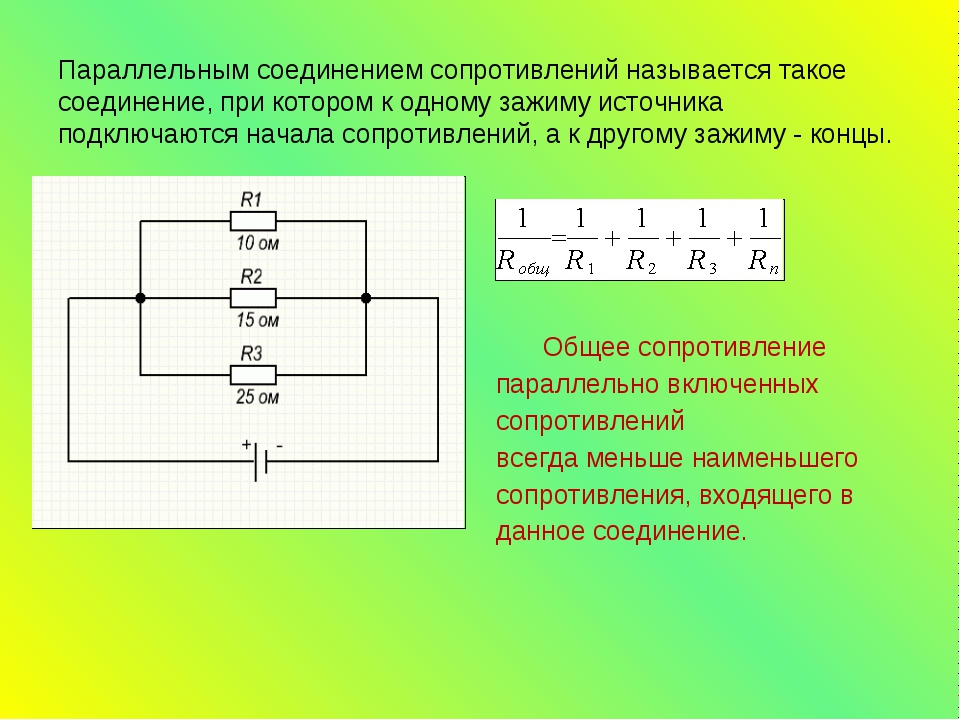 Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление.После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений.Далее рассчитывается сопротивление полученной простой схемы.
Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление.После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений.Далее рассчитывается сопротивление полученной простой схемы.
Определяется общее сопротивление участков с параллельным соединением резисторов.Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление.После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений.Далее рассчитывается сопротивление полученной простой схемы.
PS:
Параллельное соединение резисторов используется для получения меньшего сопротивления из имеющихся простейших радиоэлектронных элементов. При таком способе соединения складываются проводимости. Поэтому чем больше параллельно включенных резисторов, тем ниже получается общее сопротивление или выше проводимость соответственного участка электрической цепи – носителям электрических зарядов легче его преодолеть.
Последовательное соединение резисторов используется с целью большего ограничения протеканию электрическому току, то есть приводит к повышению сопротивления соответственного участка электрической цепи или для снижения ее проводимости.
Важнейшим параметром резистора является мощность рассеивания. При любом способе соединения, не важно, при последовательном, при параллельном или при смешанном, происходит сложение мощностей рассеивания отдельных резисторов. Поэтому все вместе они способны рассеять больше тепла, а соответственно и пропустить большие токи не перегреваясь, что широко применяется в радиолюбительской практике.
Читайте также:
Моделирование пробоя фазы на корпус в системе TT. Потенциал на нуле
Соединение резисторов — пример расчета
Суммарное сопротивление при последовательном соединении. Последовательное и параллельное соединение сопротивлений
Содержание:
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для — последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав , нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +
20, +
10, +
5, +
2, +
1% и так далее до величины +
0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, сила тока будет составлять I = U/R = 100/390 = 0,256 A.На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
- P 1 = I 2 x R 1 = 0,256 2 x 200 = 13,11 Вт;
- P 2 = I 2 x R 2 = 0,256 2 x 100 = 6,55 Вт;
- P 3 = I 2 x R 3 = 0,256 2 x 51 = 3,34 Вт;
- P 4 = I 2 x R 4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы — с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R 1 +1/R 2 +1/R 3 +1/R 4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I 1 = U/R 1 = 100/200 = 0,5A; I 2 = U/R 2 = 100/100 = 1A; I 3 = U/R 3 = 100/51 = 1,96A; I 4 = U/R 4 = 100/39 = 2,56A.
 На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P 1 = U 2 /R 1 = 100 2 /200 = 50 Вт; P 2 = U 2 /R 2 = 100 2 /100 = 100 Вт; P 3 = U 2 /R 3 = 100 2 /51 = 195,9 Вт; P 4 = U 2 /R 4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р 1 +Р 2 +Р 3 +Р 4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Содержание:
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле.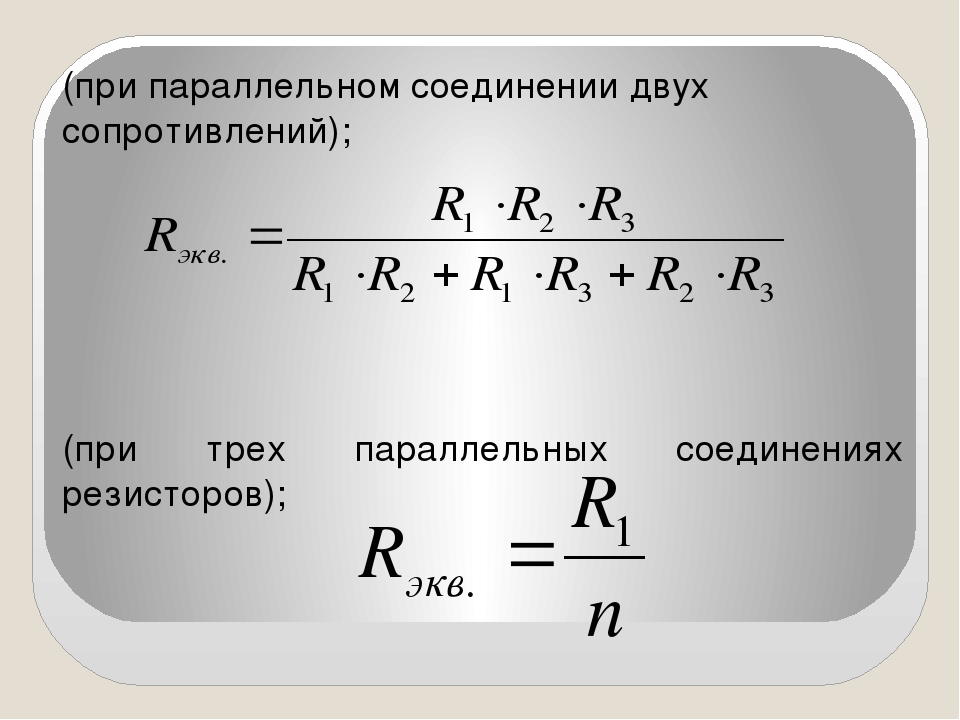 Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему.
 Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR. - Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Параллельное соединение
резисторов.
При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви
(рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис.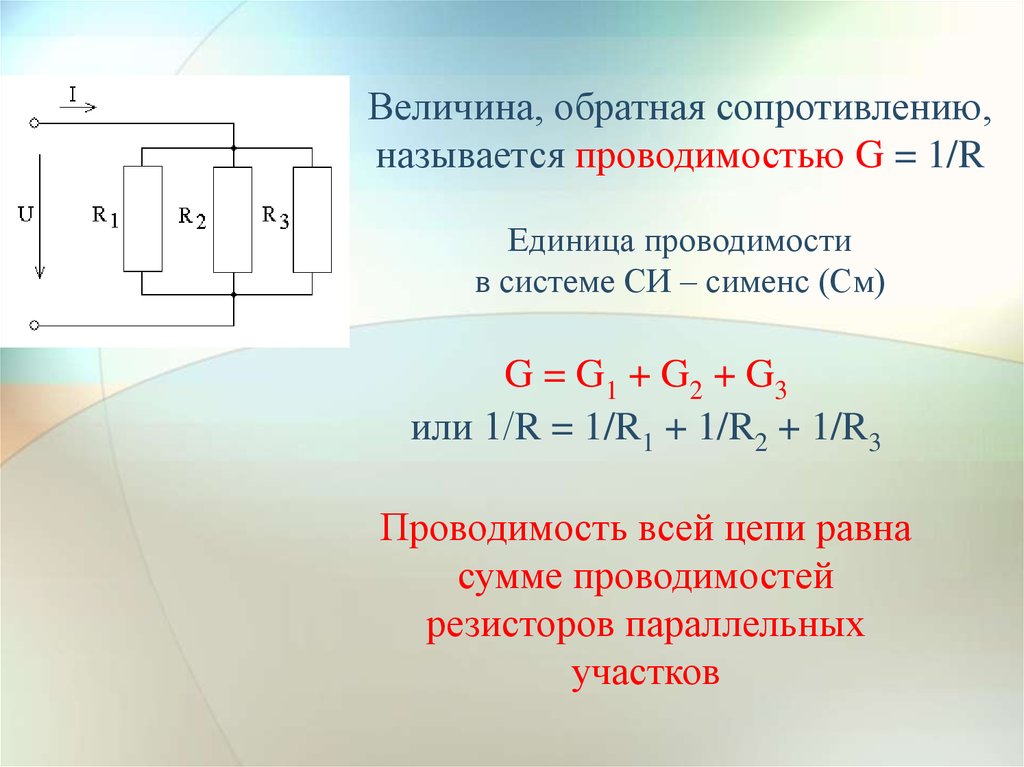 26, б.
26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк
(23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк
=
1/R 1 + 1/R 2 + 1/R 3
(24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов
:
G эк = G 1 + G 2 +G 3
(25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3
(26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n
(27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n
(28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных.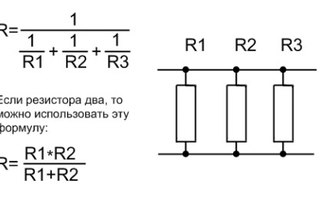 Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.
С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Виды соединений
Резистор — пассивный элемент
, присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:
- Постоянные.
- Переменные.
Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:
- Последовательное.

- Параллельное.
- Смешанное.
Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.
Последовательное соединение проводников
В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно
. Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.
Но если резисторов очень много, то проще воспользоваться специальным калькулятором.
Примером последовательного соединения проводников в быту является ёлочная гирлянда.
Параллельное соединение резисторов
При параллельном соединении проводников
эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.
Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.
В таких схемах значение напряжения постоянно
. То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.
Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник.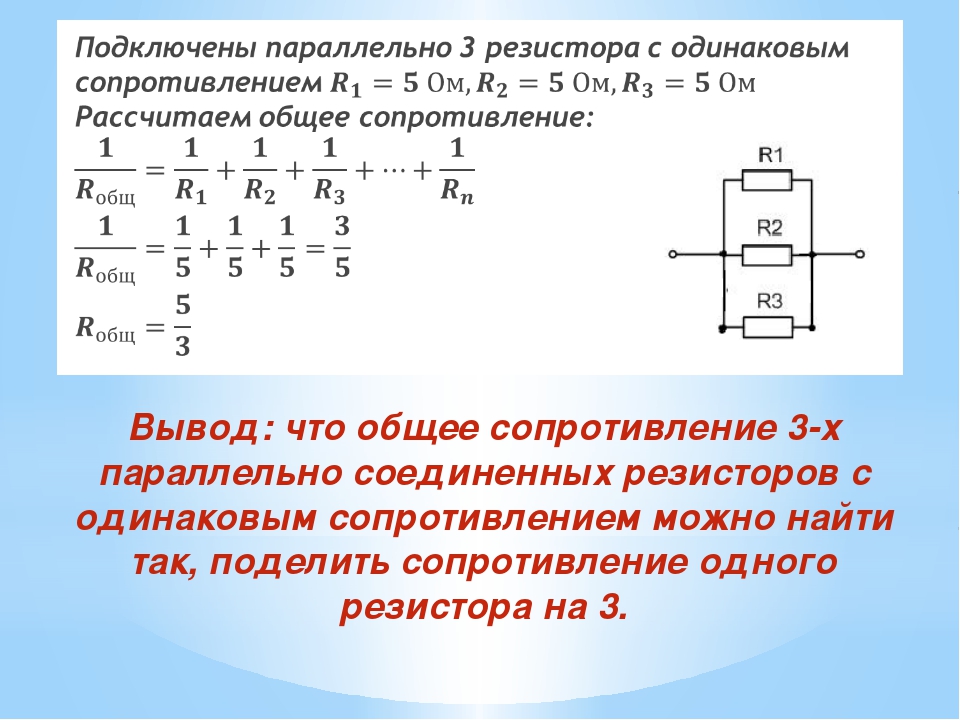 равно отношению напряжения источника к сопротивлению этого проводника.
равно отношению напряжения источника к сопротивлению этого проводника.
Примеры параллельного соединения проводников:
- Освещение.
- Розетки в квартире.
- Производственное оборудование.
Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.
Смешанное соединение проводников
Этот вид соединения состоит из каскадов резисторов
. Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор
для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.
В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.
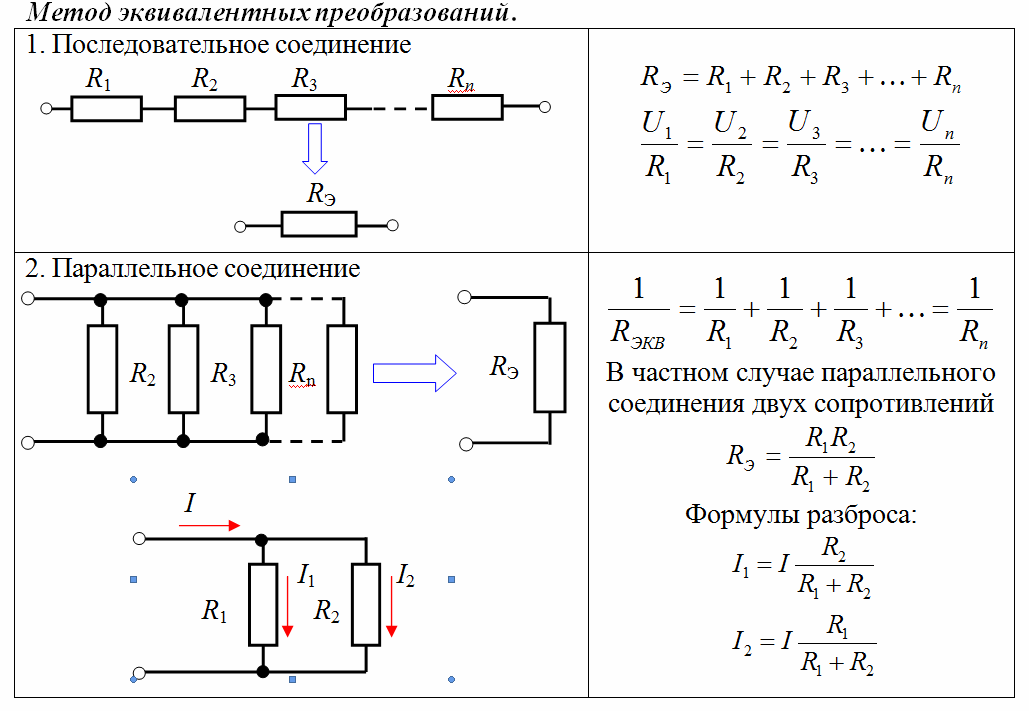
Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.
Шаги
Последовательное соединение
Определите, является ли цепь последовательной.
Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.
Сложите сопротивления отдельных элементов.
Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь. Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.
- Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.
Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.
Подставьте известные значения в формулу, описывающую закон Ома.
Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.
- Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: R O = 12 В / 8 А = 1,5 Ом.
Параллельное соединение
Определите, является ли цепь параллельной.
Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
Вычислите общее сопротивление на основе сопротивления каждой ветви.
Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления: , где R 1 – сопротивление первой ветви, R 2 – сопротивление второй ветви и так далее до последней ветви R n .Вычислите сопротивление по известной силе тока и напряжению.
Сделайте это, если сопротивление каждого элемента цепи не известно.
Подставьте известные значения в формулу закона Ома.

Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: R O = 9 В / 3 А = 3 Ом.
Поищите ветви с нулевым сопротивлением.
Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.
Комбинированное соединение
Разбейте комбинированную цепь на последовательную и параллельную.
Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.
- Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом.
 За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
Найдите сопротивление параллельной цепи.
Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи: 1 R O = 1 R 1 + 1 R 2 + 1 R 3 + . . . 1 R n {\displaystyle {\frac {1}{R_{O}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+{\frac {1}{R_{3}}}+…{\frac {1}{R_{n}}}}
.
Упростите цепь.
После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.
- В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.
Сложите сопротивления резисторов, соединенных последовательно.
Заменив параллельную цепь одним элементом, вы получили последовательную цепь.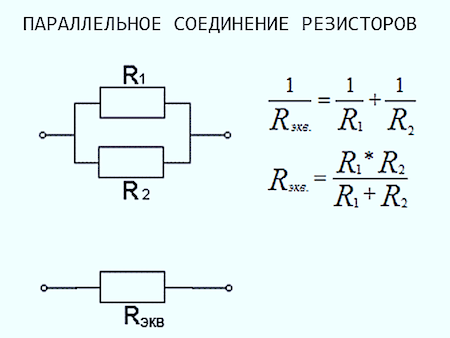 Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
Калькулятор параллельных сопротивлений • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов.
Пример. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно.
Входные данные
Добавить резистор
Выходные данные
Эквивалентное сопротивление
R ом (Ом)
Введите величины сопротивлений в поля R1, R2 и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы сопротивления в миллиомах (мОм), омах (Ом), килоомах (кОм) или мегаомах (МОм) и нажмите кнопку Рассчитать.
1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.
Эквивалентное сопротивление Req группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.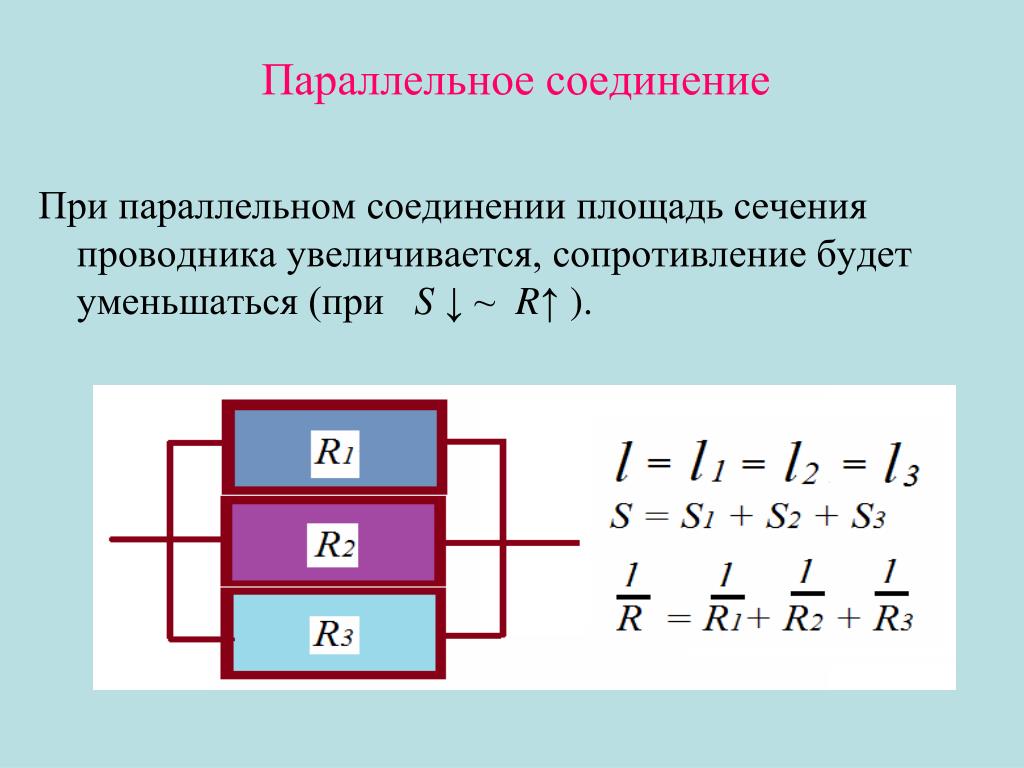
или
Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:
Эта формула для Req и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:
Если параллельно соединены только два резистора, формула упрощается:
или
Если имеется n соединенных параллельно одинаковых резисторов R, то их эквивалентное сопротивление будет равно
Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.
Общий ток через группу резисторов равен сумме токов в отдельных резисторах.
При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.
Различные постоянные и переменные резисторы
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).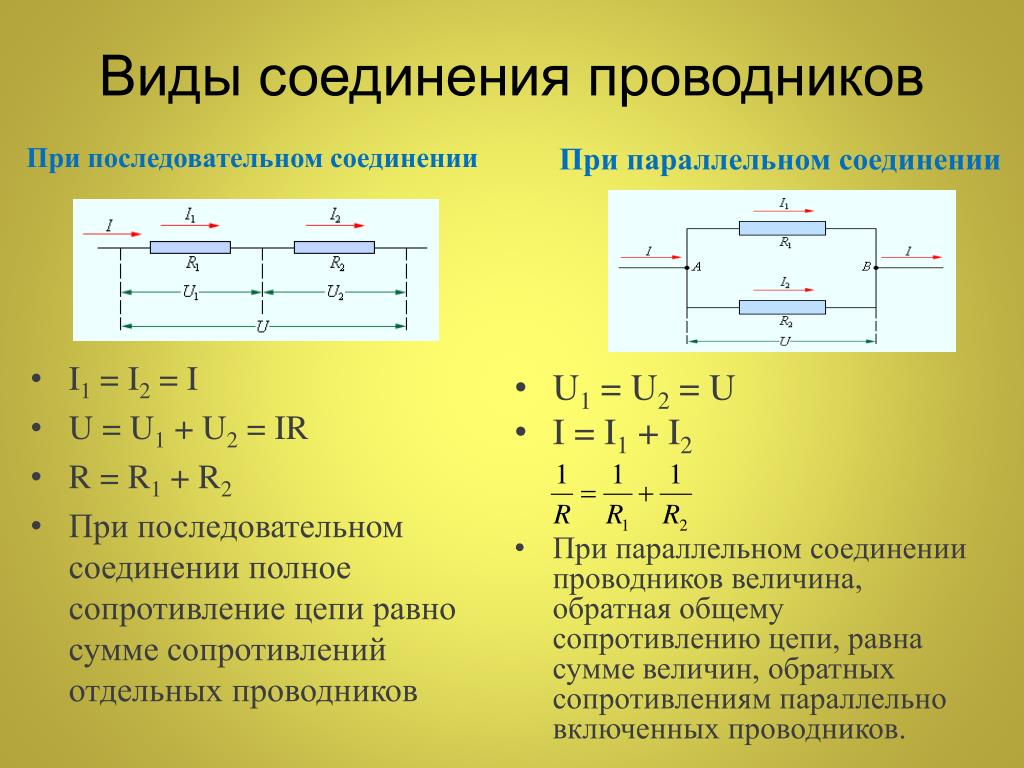
Установленный в мультиметре шунт для измерения ток до 20 ампер. Отметим, что если этим мультиметром измеряется большой ток непрерывно более 10 секунд, шунт перегреется и его сопротивление изменится, что приведет к ошибке измерения
Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Резисторы поверхностного монтажа на печатной плате
Автор статьи: Анатолий Золотков
Калькулятор соединения резисторов онлайн. Параллельное соединение резисторов
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Несмотря на то что для резисторов предусмотрены различные номиналы
, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Параллельное соединение: общая информация
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление
Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление
, используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
R(общ)=R1*R2/R1+R2.
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Видео: Пример расчёта сопротивления
Универсальная схема расчета
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель
, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше
по сравнению с номиналом любого элемента, подключаемого в цепь.
Пример расчёта
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом.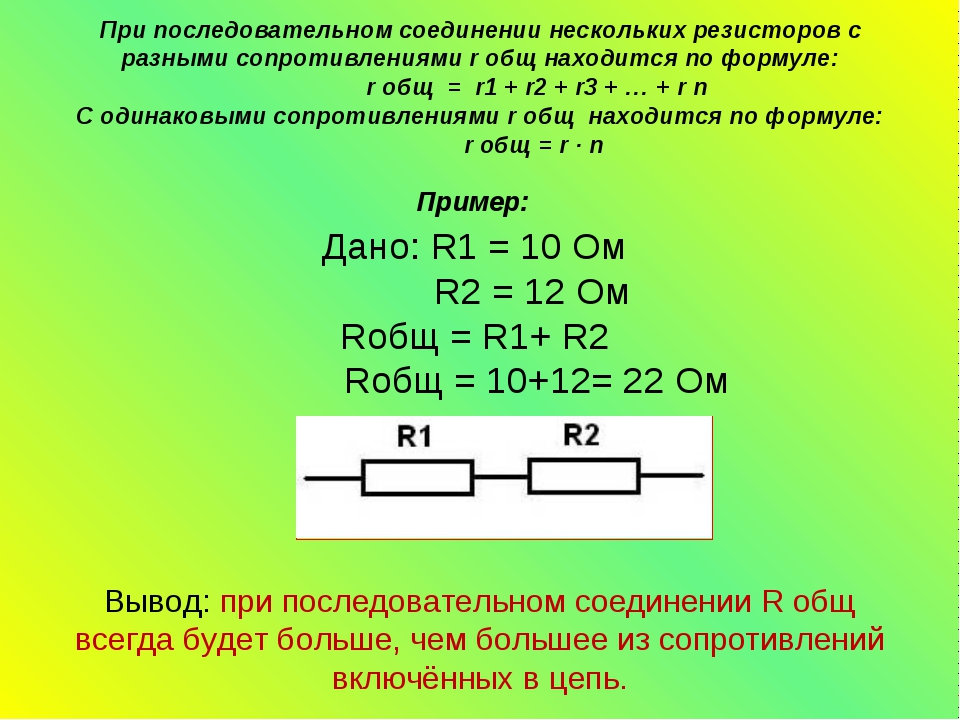 Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=
1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом
: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Видео: Правильное подключение светодиодов
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью
, где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Параллельное соединение резисторов
— одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.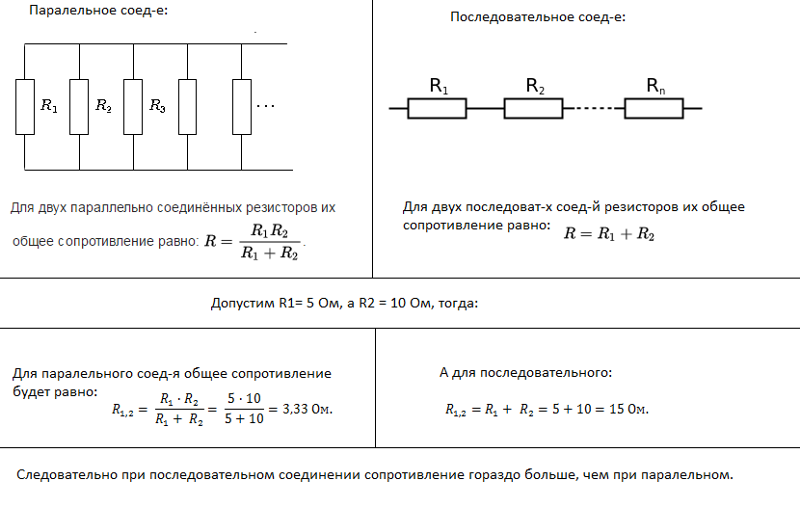 Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .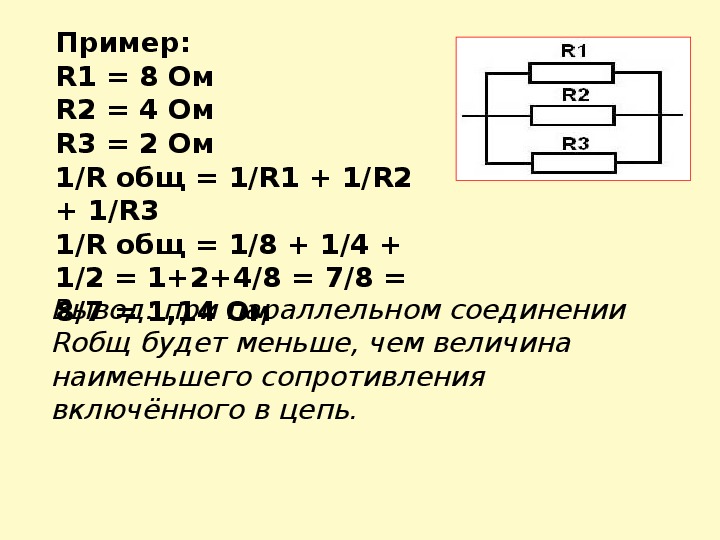
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.
Эквивалентное сопротивление R eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.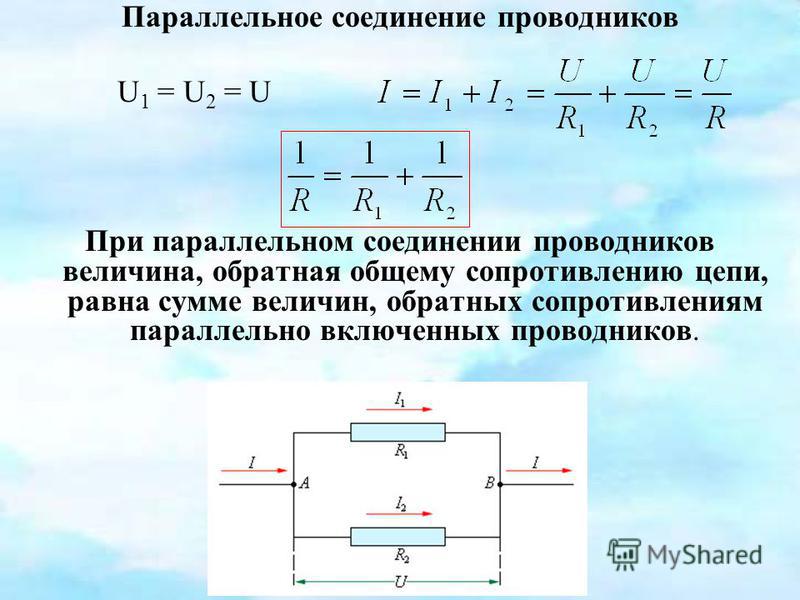
Иными словами, проводимость G
параллельно соединенных резисторов равна сумме проводимостей этих резисторов:
Эта формула для R eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:
Если параллельно соединены только два резистора, формула упрощается:
Если имеется n
соединенных параллельно одинаковых резисторов R
, то их эквивалентное сопротивление будет равно
Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.
При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства
. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2
на 3
и 47 Ом
и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром.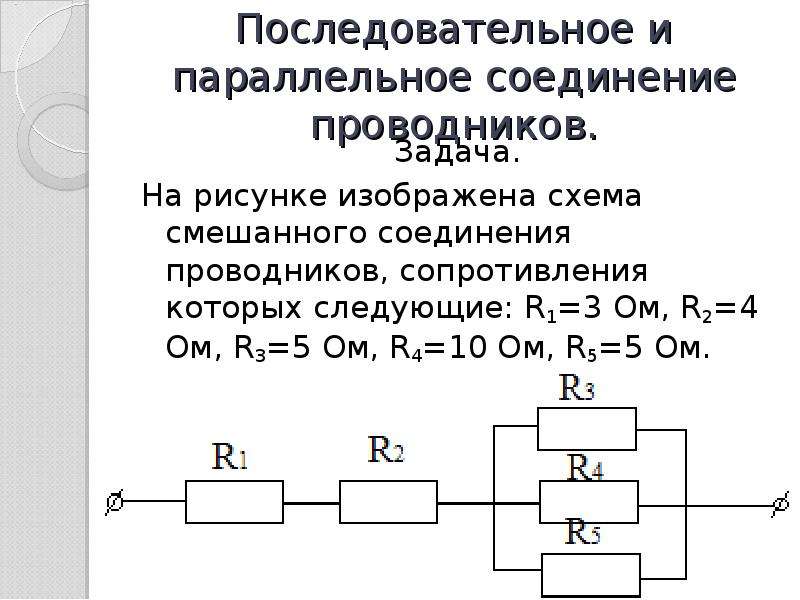 Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно
учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом
и мощностью 1 Вт
. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А
), а сопротивление каждого из них равно 50 Ом
, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт
. В результате на каждом из них выделится по 0,5 Вт
В результате на каждом из них выделится по 0,5 Вт
мощности. В сумме это и будет тот самый 1 Вт
.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи. Во втором варианте все элементы установлены последовательно: конец одного элемента соединен с началом следующего. В такой схеме сила тока на всех элементах одинаковая, а падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подсоединены начала всех элементов, а ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль.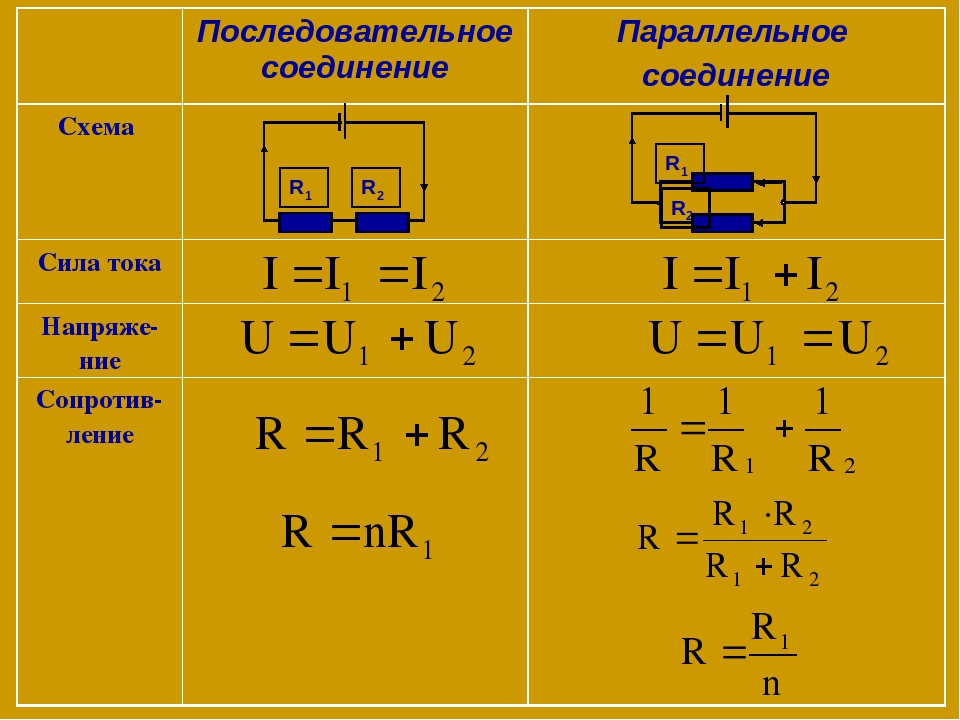 Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.
Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.
Расчет общего сопротивления при параллельном соединении резисторов
В отличие от последовательного соединения, где для нахождения общего сопротивления достаточно сложить значение каждого элемента, для параллельного то же самое будет справедливо для проводимости. А так как она обратно пропорциональна сопротивлению, получим формулу, представленную вместе со схемой на следующем рисунке:
Необходимо отметить одну важную особенность расчета параллельного соединения резисторов: общее значение будет всегда меньше, чем самое маленькое из них. Для резисторов справедливо как для постоянного, так и для переменного тока. Катушки и конденсаторы имеют свои особенности.
Сила тока и напряжение
При расчете параллельного сопротивления резисторов необходимо знать, как рассчитать напряжение и силу тока.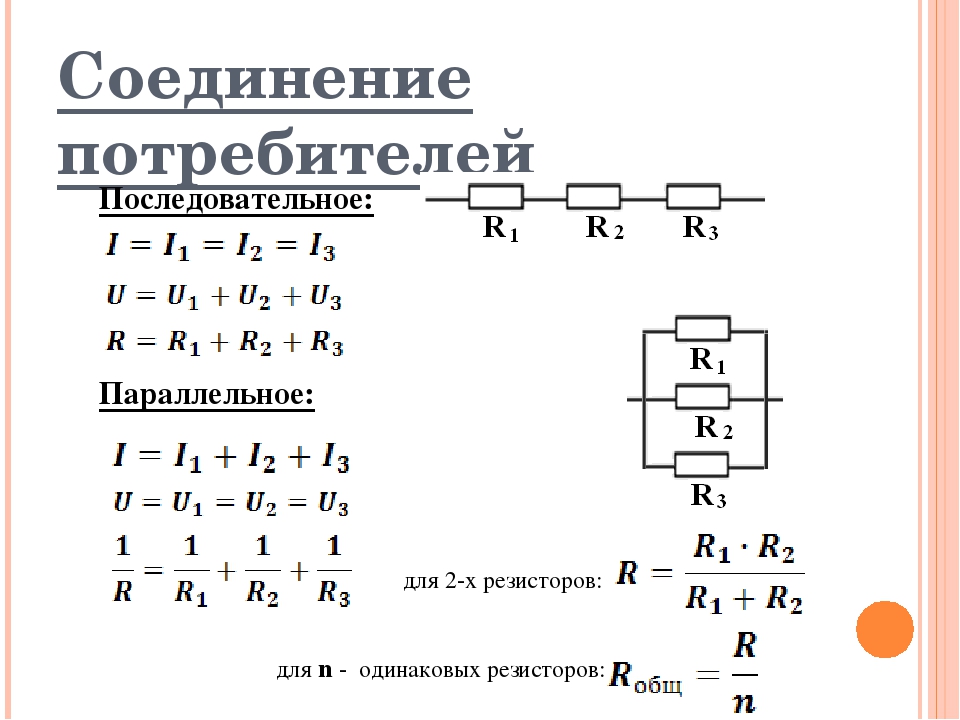 В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.
В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.
Исходя из первой формулировки закона Кирхгофа, получим, что сумма сходящихся в одном узле токов равна нулю. Направление выбираем по направлению протекания тока. Таким образом, положительным направлением для первого узла можно считать входящий ток от источника питания. А отрицательными будут отходящие из каждого резистора. Для второго узла картина противоположна. Исходя из формулировки закона, получим, что суммарный ток равен сумме токов, проходящих через каждый параллельно соединенный резистор.
Итоговое напряжение же определяется по второму закону Кирхгофа. Оно одинаково для каждого резистора и равно общему. Эта особенность используется для подключения розеток и освещения в квартирах.
Пример расчета
В качестве первого примера приведем расчет сопротивления при параллельном соединении одинаковых резисторов. Сила тока, протекающая через них, будет одинаковой. Пример расчета сопротивления выглядит так:
Пример расчета сопротивления выглядит так:
По этому примеру прекрасно видно, что общее сопротивление ниже в два раза, чем каждое из них. Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного. А также прекрасно соотносится с увеличением проводимости в два раза.
Второй пример
Рассмотрим пример параллельного соединения трех резисторов. Для расчета используем стандартную формулу:
Похожим образом рассчитываются схемы с большим количеством параллельно соединенных резисторов.
Пример смешанного соединения
Для смешанного соединения, например, представленного ниже, расчет будет производиться в несколько этапов.
Для начала последовательные элементы можно условно заменить одним резистором, обладающим сопротивлением, равным сумме двух заменяемых. Далее общее сопротивление считаем тем же способом, что и для предыдущего примера. Данный метод подойдет и для других более сложных схем. Последовательно упрощая схему, можно получить необходимое значение.
Например, если вместо резистора R3 будут подключены два параллельных, потребуется сначала рассчитать их сопротивление, заменив их эквивалентным. А далее то же самое, что и в примере выше.
Применение параллельной схемы
Параллельное соединение резисторов находит свое применение во многих случаях. Последовательное подключение увеличивает сопротивление, а для нашего случая оно уменьшится. Например, для электрической цепи требуется сопротивление в 5 Ом, но есть только резисторы на 10 Ом и выше. Из первого примера мы знаем, что можно получить в два раза меньшее значение сопротивления, если установить два одинаковых резистора параллельно друг другу.
Уменьшить сопротивление можно еще больше, например, если две пары параллельно соединенных резисторов соединить параллельно относительно друг друга. Можно уменьшить сопротивление еще в два раза, если резисторы имеют одинаковое сопротивление. Комбинируя с последовательным соединением, можно получить любое значение.
Второй пример — это использование параллельного подключения для освещения и розеток в квартирах.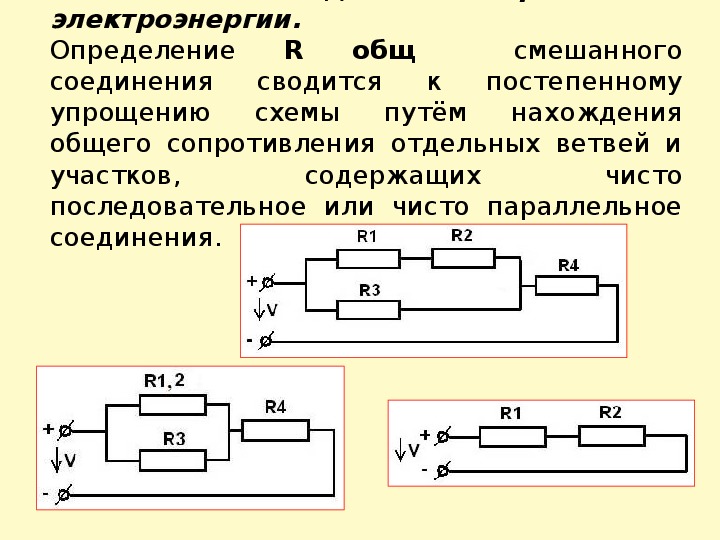 Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.
Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.
Еще один пример использования параллельного подключения — это защитное заземление электрооборудования. Например, если человек касается металлического корпуса прибора, на который произойдет пробой, получится параллельное соединения его и защитного проводника. Первым узлом будет место прикосновения, а вторым нулевая точка трансформатора. По проводнику и человеку будет течь разный ток. Величину сопротивления последнего принимают за 1000 Ом, хотя реальное значение зачастую гораздо больше. Если бы не было заземления, весь ток, протекающий в схеме, пошел бы через человека, так как он был бы единственным проводником.
Параллельное соединение может использоваться и для батарей. Напряжение при этом остается прежним, однако в два раза возрастает их емкость.
Итог
При подключении резисторов параллельно, напряжение на них будет одинаковым, а ток равен сумме протекающих через каждый резистор. Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.
Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.
Необходимо учитывать при расчете параллельного соединения резисторов то, что итоговое сопротивление будет всегда меньше самого маленького. Это также можно объяснить суммированием проводимости резисторов. Последняя будет возрастать при добавлении новых элементов, соответственно и проводимость будет уменьшаться.
формула расчета расчета общего сопротивления
Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи. Во втором варианте все элементы установлены последовательно: конец одного элемента соединен с началом следующего. В такой схеме сила тока на всех элементах одинаковая, а падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подсоединены начала всех элементов, а ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль. Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.
Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.
Расчет общего сопротивления при параллельном соединении резисторов
В отличие от последовательного соединения, где для нахождения общего сопротивления достаточно сложить значение каждого элемента, для параллельного то же самое будет справедливо для проводимости. А так как она обратно пропорциональна сопротивлению, получим формулу, представленную вместе со схемой на следующем рисунке:
Необходимо отметить одну важную особенность расчета параллельного соединения резисторов: общее значение будет всегда меньше, чем самое маленькое из них. Для резисторов справедливо как для постоянного, так и для переменного тока. Катушки и конденсаторы имеют свои особенности.
Сила тока и напряжение
При расчете параллельного сопротивления резисторов необходимо знать, как рассчитать напряжение и силу тока.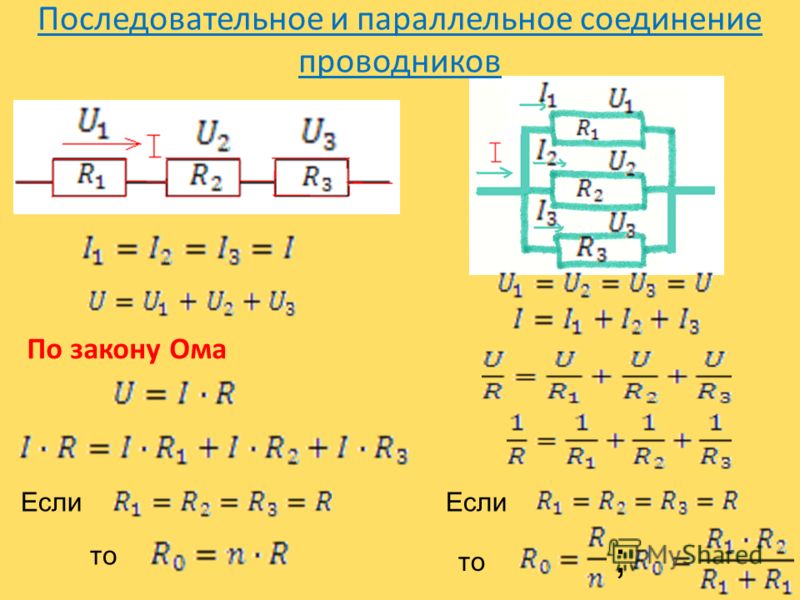 В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.
В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.
Исходя из первой формулировки закона Кирхгофа, получим, что сумма сходящихся в одном узле токов равна нулю. Направление выбираем по направлению протекания тока. Таким образом, положительным направлением для первого узла можно считать входящий ток от источника питания. А отрицательными будут отходящие из каждого резистора. Для второго узла картина противоположна. Исходя из формулировки закона, получим, что суммарный ток равен сумме токов, проходящих через каждый параллельно соединенный резистор.
Итоговое напряжение же определяется по второму закону Кирхгофа. Оно одинаково для каждого резистора и равно общему. Эта особенность используется для подключения розеток и освещения в квартирах.
Пример расчета
В качестве первого примера приведем расчет сопротивления при параллельном соединении одинаковых резисторов. Сила тока, протекающая через них, будет одинаковой. Пример расчета сопротивления выглядит так:
Пример расчета сопротивления выглядит так:
По этому примеру прекрасно видно, что общее сопротивление ниже в два раза, чем каждое из них. Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного. А также прекрасно соотносится с увеличением проводимости в два раза.
Второй пример
Рассмотрим пример параллельного соединения трех резисторов. Для расчета используем стандартную формулу:
Похожим образом рассчитываются схемы с большим количеством параллельно соединенных резисторов.
Пример смешанного соединения
Для смешанного соединения, например, представленного ниже, расчет будет производиться в несколько этапов.
Для начала последовательные элементы можно условно заменить одним резистором, обладающим сопротивлением, равным сумме двух заменяемых. Далее общее сопротивление считаем тем же способом, что и для предыдущего примера. Данный метод подойдет и для других более сложных схем. Последовательно упрощая схему, можно получить необходимое значение.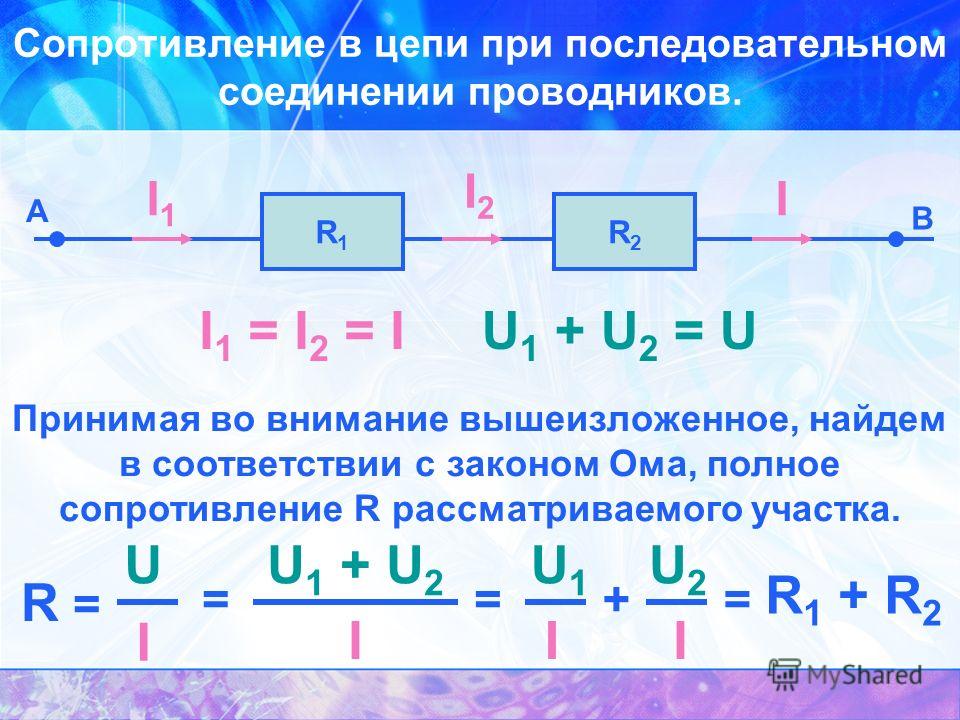
Например, если вместо резистора R3 будут подключены два параллельных, потребуется сначала рассчитать их сопротивление, заменив их эквивалентным. А далее то же самое, что и в примере выше.
Применение параллельной схемы
Параллельное соединение резисторов находит свое применение во многих случаях. Последовательное подключение увеличивает сопротивление, а для нашего случая оно уменьшится. Например, для электрической цепи требуется сопротивление в 5 Ом, но есть только резисторы на 10 Ом и выше. Из первого примера мы знаем, что можно получить в два раза меньшее значение сопротивления, если установить два одинаковых резистора параллельно друг другу.
Уменьшить сопротивление можно еще больше, например, если две пары параллельно соединенных резисторов соединить параллельно относительно друг друга. Можно уменьшить сопротивление еще в два раза, если резисторы имеют одинаковое сопротивление. Комбинируя с последовательным соединением, можно получить любое значение.
Второй пример — это использование параллельного подключения для освещения и розеток в квартирах. Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.
Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.
Еще один пример использования параллельного подключения — это защитное заземление электрооборудования. Например, если человек касается металлического корпуса прибора, на который произойдет пробой, получится параллельное соединения его и защитного проводника. Первым узлом будет место прикосновения, а вторым нулевая точка трансформатора. По проводнику и человеку будет течь разный ток. Величину сопротивления последнего принимают за 1000 Ом, хотя реальное значение зачастую гораздо больше. Если бы не было заземления, весь ток, протекающий в схеме, пошел бы через человека, так как он был бы единственным проводником.
Параллельное соединение может использоваться и для батарей. Напряжение при этом остается прежним, однако в два раза возрастает их емкость.
Итог
При подключении резисторов параллельно, напряжение на них будет одинаковым, а ток равен сумме протекающих через каждый резистор. Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.
Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.
Необходимо учитывать при расчете параллельного соединения резисторов то, что итоговое сопротивление будет всегда меньше самого маленького. Это также можно объяснить суммированием проводимости резисторов. Последняя будет возрастать при добавлении новых элементов, соответственно и проводимость будет уменьшаться.
Метод ключевых ситуаций на уроке физики «Параллельное и последовательное соединение проводников» в 8-м классе
Рассмотрены примеры использования метода ключевых ситуаций при изучении темы «Параллельное и последовательное соединение проводников» в 8 классе.
Ключевые моменты.
- Расчет сопротивления цепи при параллельном и последовательном соединении проводников.
- Распределение сил токов и напряжений при последовательном и параллельном соединении проводников.
Расчет сопротивления цепи при параллельном и последовательном соединении проводников
Первый уровень.
Имеется три проводника сопротивлением по 3 Ом каждый. Как надо соединить эти проводники, чтобы сопротивление цепи было максимальным? минимальным? Рассчитайте сопротивление для каждого случая.
Второй уровень.
Три одинаковых проводника соединены последовательно. Как изменится сила тока в цепи, если последовательно с ними подключить еще один проводник?
Как изменится сила тока, если к параллельно включенным проводникам добавить еще один?
Третий уровень.
Как получить сопротивления 16 Ом и 36 Ом, используя три одинаковых сопротивления по 24 Ом?
Или
Из одинаковых резисторов по 10 Ом требуется составить цепь сопротивлением 6 Ом. Какое наименьшее количество резисторов для этого потребуется?
Начертите схему цепи.
Методика решения задач
После рассмотрения закономерностей последовательного и параллельного соединения предлагается для устного решения ряд задач первого уровня.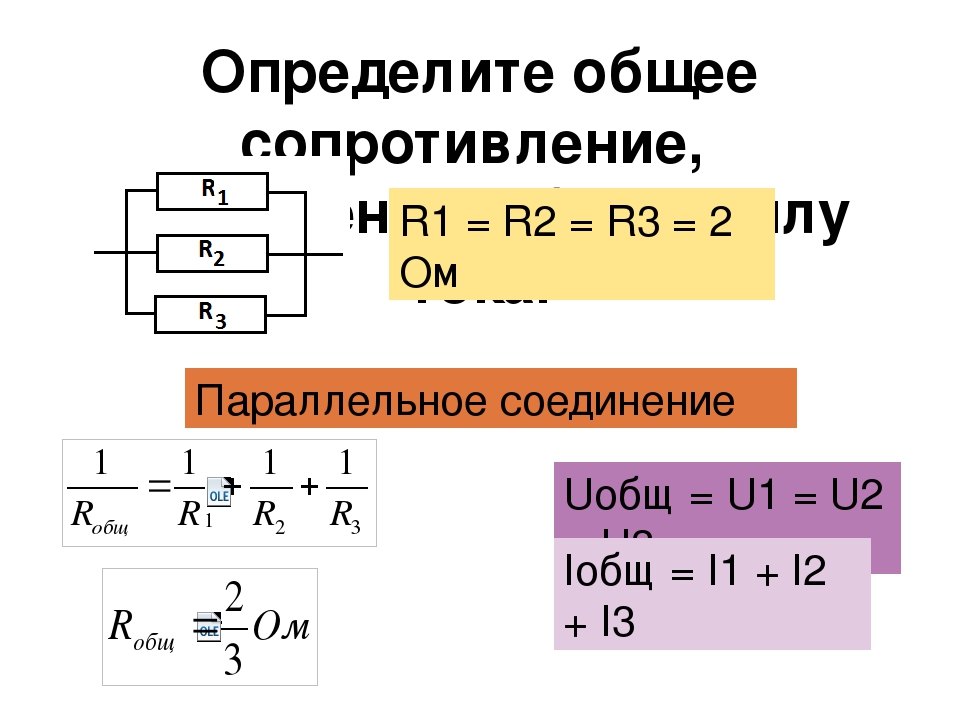
Учитель: Рассчитайте сопротивление цепи, состоящей из двух проводников по 2 Ом, соединенных последовательно.
Ученики: При последовательном соединении проводников сопротивления складываются. Следовательно, ответ – 4 Ом.
Учитель: Каким станет сопротивление, если добавить еще один проводник 2 Ом? 10 Ом?
Ученики: 6 Ом, 14 Ом.
Если будем последовательно подключать еще проводники, как будет меняться общее сопротивление цепи?
Ученики: Увеличиваться.
Учитель: Попробуем обобщить результаты и сделать выводы. Если включаем последовательно n проводников сопротивлением R каждый, чему равно общее сопротивление цепи?
Ученики: Rобщ = nR.
Учитель: Как изменяется общее сопротивление последовательно включенных проводников при подключении каждого последующего проводника?
Ученики. Увеличивается.
Увеличивается.
Учитель: Заметим также, что общее сопротивление цепи при последовательном включении проводников будет больше каждого, даже самого большого.
Рассмотрим аналогичную задачу, но проводники соединены параллельно. Итак, два проводника по 2 Ом соединены параллельно. Каково общее сопротивление цепи?
Ученики: при параллельном соединении складываются величины обратные сопротивлениям. Следовательно, воспользовавшись формулой 1/R = 1/R1 + 1/R2, получаем 1 Ом.
Учитель: А если величина сопротивлений по 4 Ом?
Ученики: Воспользуемся этой же формулой. Общее сопротивление цепи – 2 Ом.
Учитель: Посмотрите на результаты и скажите, как рассчитать без данной формулы общее сопротивление параллельно включенных резисторов, если их величины одинаковы?
Ученики: Rобщ = R/n.
Учитель: А значит, если мы будем подключать параллельно еще резисторы, общее сопротивление будет…?
Ученики: Уменьшаться.
Учитель: Верно. А теперь добавим к нашим резисторам по 2 Ом параллельно в первом случае сопротивление 1/2 Ом, во втором — 1000 Ом. Что получим?
Ученики: Получаем в первом случае — 1/3 Ом, во втором — 1000/1001 Ом.
Учитель: Проанализируем результаты. При параллельном подключении маленького сопротивления общее сопротивление уменьшилось и стало меньше самого маленького. При подсоединении большого сопротивления общее все равно уменьшилось и его величина все равно меньше самого маленького.
Запомним наши выводы. Во-первых, при последовательном соединении одинаковых резисторов сопротивлением R общее сопротивление цепи nR, при параллельном включении — R/n. Во-вторых, при последовательном соединении общее сопротивление — больше самого большого, при параллельном – меньше самого маленького.
(В дальнейшем эти выводы пригодятся при рассмотрении причин короткого замыкания)
После этого можно предложить для устного или полу-устного решения задачи первого, второго и третьего уровней, помогая использовать при рассуждениях полученные знания.
Ученики: (Задача второго уровня) Если к последовательно подключить еще один проводник, то общее сопротивление увеличится: 4R → 5R. I = U/R, следовательно, при неизменном напряжении сила тока уменьшится: I1 = U/4R → I2 = U/5R → сила тока уменьшится в 5/4 раз = 1,25 раз. При параллельном соединении общее сопротивление уменьшиться: R/4 → R/5 → сила тока увеличится в 1,25 раз.
Задача третьего уровня.
Ученики: Максимальное и минимальное сопротивления, которые можно получить, используя данные резисторы – 72 Ом и 8 Ом соответственно. Значит, надо использовать оба вида соединений. Два параллельно включенных резистора дают 12 Ом + последовательно еще 24 Ом. (Рисуют схему). Два последовательно включенных дают сопротивление 48 Ом + параллельно с ними 24 Ом. Получаем 16 Ом (схема).
Учитель: В качестве домашнего задания подумайте, какие еще сопротивления можно получить. Используя данные резисторы.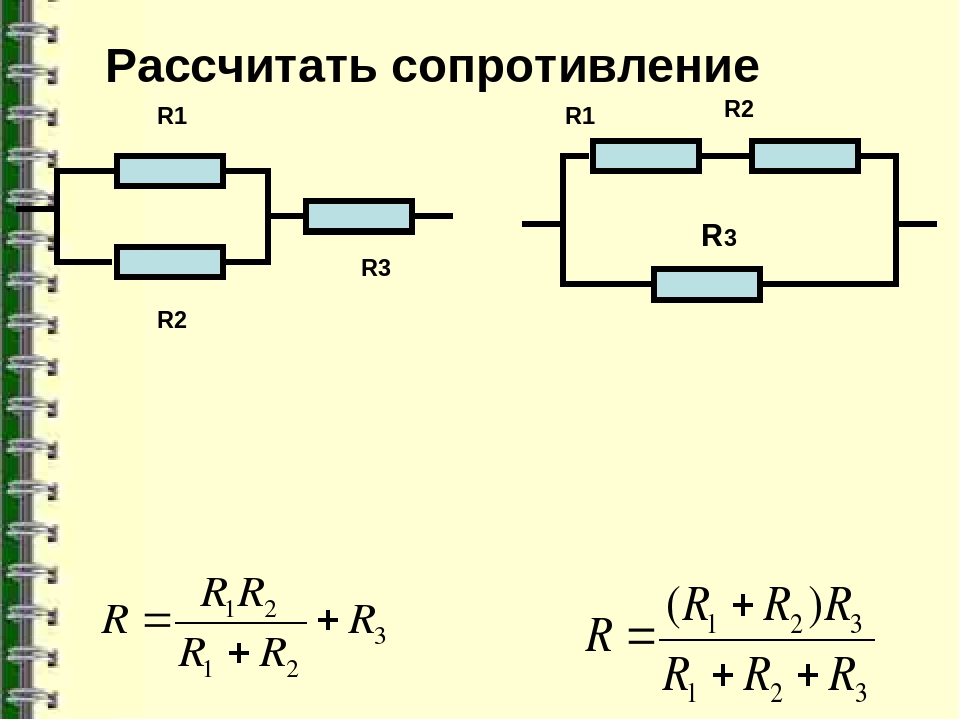
Можно в качестве домашнего задания предложить вторую задачу.
Распределение сил токов и напряжений при последовательном и параллельном соединении проводников
Первый уровень.
Два резистора сопротивлением 3 Ом и 6 Ом соединены последовательно (параллельно). К концам цепи приложено напряжение 36 В. Найдите силу тока и напряжение на каждом резисторе.
Второй уровень.
Три резистора сопротивлением 3 Ом, 6 Ом и 18 Ом соединены последовательно (параллельно). К концам цепи приложено напряжение 36 В. Найдите силу тока и напряжение на каждом резисторе.
Третий уровень.
К участку цепи приложено напряжение 6 В. Сопротивление каждого резистора 1 Ом. Сравните напряжения и силу тока в резисторах.
Методика разбора задач на уроке
- Учитель, познакомив с закономерностями последовательного и параллельного соединения, предлагает решить задачу первого уровня.
 Сначала задача решается с помощью формул: Rобщ = R1+ R2, I = U/ Rобщ, I = I1 = I2, U1 = IR1, U2 = IR2 (или U2 = U – U1).
Сначала задача решается с помощью формул: Rобщ = R1+ R2, I = U/ Rобщ, I = I1 = I2, U1 = IR1, U2 = IR2 (или U2 = U – U1). - Затем учитель просит учеников предложить другой способ решения и подводит их к следующим рассуждениям: так как второе сопротивление в 2 раза больше, то напряжение на нем в два раза меньше, а их сумма известна и равна 36 В. Следовательно, если на первое сопротивление приходится одна часть напряжения, то на второе – две части, всего – три части. 36 В делим на три части. Получаем, что на каждую часть приходится 12 В. Следовательно, напряжение на первом резисторе равно 12 В, на втором – 24 В. То есть задача сводится к известной из курса математики «задаче на части».
- Задачу второго уровня можно решить двумя способами для закрепления. Ученикам предложить высказаться в пользу одного или другого метода.
- После предыдущих упражнений третью задачу можно решить устно: напряжение на резисторах 1 и 4 одинаково и равно 6 В.
 Следовательно, сила тока тоже одинакова и равна 6 А. Напряжение на среднем участке 6 В. Сопротивление среднего участка в два раза больше. Следовательно, сила тока в два раза меньше и равна 3 А. напряжения на резисторах 2 и 3 одинаковы и равны 3 В.
Следовательно, сила тока тоже одинакова и равна 6 А. Напряжение на среднем участке 6 В. Сопротивление среднего участка в два раза больше. Следовательно, сила тока в два раза меньше и равна 3 А. напряжения на резисторах 2 и 3 одинаковы и равны 3 В.
Проверим: общее сопротивление резисторов 1 и 4 равно ½ Ом. Общее сопротивление резисторов 2 и 3 равно 2 Ом. Сопротивление всего участка 2/5 Ом. Сила тока на всем участке 15 А. Совпадает с полученным результатом 6А+6А+3А = 15 А.
Лабораторная работа №4
Лабораторная работа №4
ЛАБОРАТОРНАЯ
РАБОТА №4
Исследование
сопротивлений резисторов при параллельном соединении.
Цель
работы: опытом
проверить
закономерности электрической цепи при параллельном соединении резисторов.
1.Пояснение
к работе
Краткие
теоретические сведения
Параллельным соединением сопротивлений называется такое соединение, при
котором к одному зажиму источника подключаются начала сопротивлений, а
к другому зажиму — концы.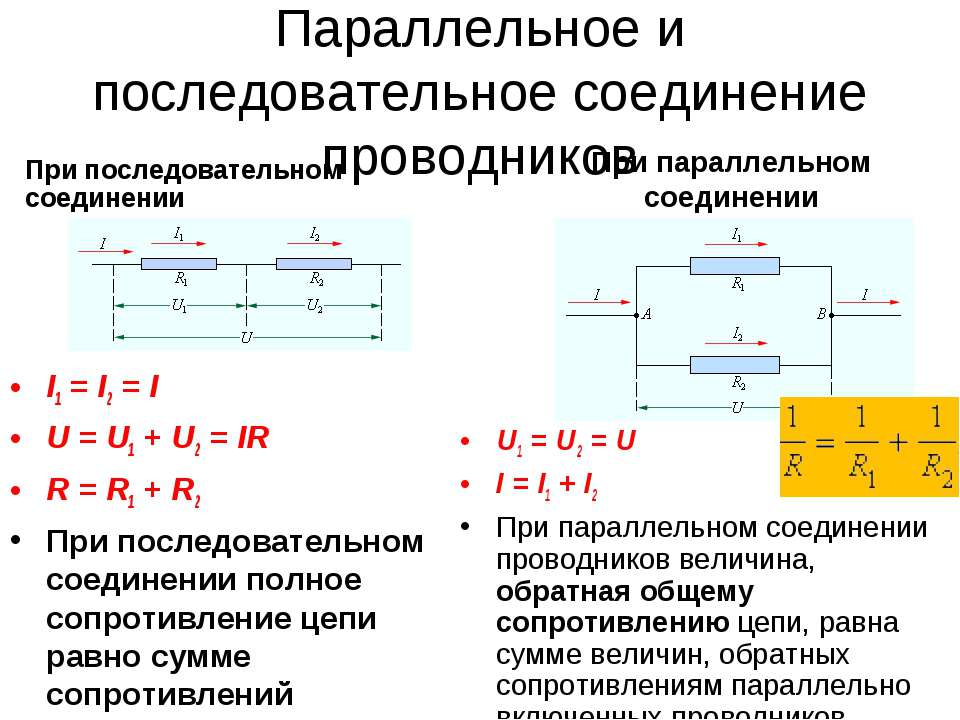
Общее
сопротивление
параллельно включенных сопротивлений определяется по формуле:
Общее
сопротивление параллельно включенных сопротивлений всегда меньше наименьшего
сопротивления, входящего в данное соединение. На
вышеуказанном рисунке мы можем сразу сказать что общее сопротивление
будет меньше 10 ом.Первый
частный случай
Если параллельно включено только два резистора то
их общее сопротивление можно определить по формуле:
Второй частный случай
Если параллельно включено любое
количество резисторов одинаковых сопротивлений то их общее
сопротивление можно определить если сопротивление одного
резистора разделить на количество резисторов.
Распределение токов и напряжения
в параллельных ветвях
Так как начала всех сопротивлений сведены в одну общую точку, а концы -
в другую, то очевидно, что разность потенциалов на концах любого из
параллельно включенных сопротивлений равна разности потенциалов между
общими точками.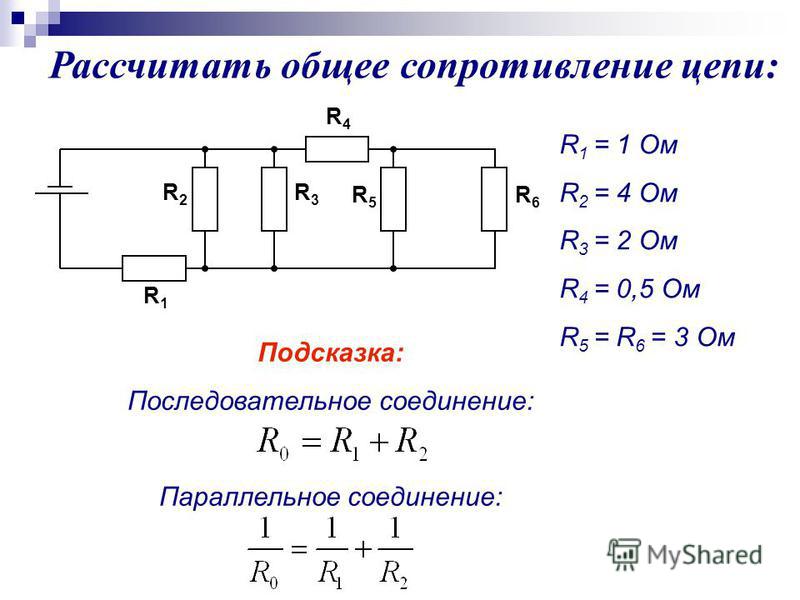
Итак,
при
параллельном соединении сопротивлений напряжения на них равны между
собой.
Если разветвление подключено
непосредственно к зажимам источника тока, то напряжение на каждом из
сопротивлений равно напряжению на зажимах источника.
Второе
свойство цепи с параллельным соединением
заключается в том, что
электрический ток распределяется по параллельным ветвям обратно
пропорционально их сопротивлениям.
Это значит что, чем больше
сопротивление, тем меньше
по нему пойдет ток.
Рассматривая точку разветвления А,
замечаем, что к ней притекает ток I, а токи I1, I2, I3 утекают из нее.
Так как движущиеся электрические заряды не скапливаются в точке, то
очевидно, что суммарный заряд, притекающий к точке разветвления, равен
суммарному заряду утекающему от нее:
Следовательно, третье
свойство параллельного соединения может сформулирована
так:
Величина
тока в не разветвленной части цепи равна сумме токов в параллельных
ветвях.
2.Техническое
задание
2.1.Собрать
электрическую цепь (рисунок 1)
Рисунок
1. Схема электрическая
принципиальная.
2.2.Снять
показания приборов и записать их в таблицу
2.3.Произвести
расчеты
2.4.Ответить
на контрольные вопросы
2.5.
Сделать
вывод
| Расчетные формулы
(расчет установкой): | |
| Расчетные формулы
(расчетом): |
3.Работа
в лаборатории
3. 1.
1.
Собрать схему (Рисунок 2).
Рисунок 2. Схема исследования.
3.2.
Установить на схеме величины R1=70
Ом + N, R2=100
Ом + N
и R3=150
Ом + N,
где N — номер студента по журналу
(мощность резисторов более
1 Вт).
3.3. Включить
источник и установить напряжение U=15 В, 24 В.
3.4.
Измерить величину тока, протекающего во всей цепи и занести значение в
таблицу 1.
3.5.
Измерить величину тока, протекающего в каждом резисторе и записать в
таблицу 1.
3.6. Расчитать проводимость каждого резистора и записать в таблицу 1
(установкой).
3.7. Рассчитать проводимость каждого резистора через ток и напряжение и
записать в таблицу 1 (расчетом).
3.8.
Отключить схему.
Таблица 1 — Измеренные
параметры
|
№ измер.
|
Измерением
|
Установкой
|
Расчетом
| ||||||||||||
|
U
|
I
|
I1
|
I2
|
I3
|
g1
|
g2
|
g3
|
gэ
|
Rэ
|
g1
|
g2
|
g3
|
gэ
|
Rэ
| |
|
А
|
А
|
А
|
А
|
А
|
См
|
См
|
См
|
См
|
Ом
|
См
|
См
|
См
|
См
|
Ом
| |
|
1
|
15
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
|
24
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Содержание отчета
Содержание отчета
4.1.
Название и цель работы
4.2.
Схемы
4.3.
Таблицы
4.4.
Расчеты по формулам
4.5.
Ответы на контрольные вопросы
4.6.
Вывод
5.Контрольные вопросы
5.1.
Какое соединение резисторов называют паралельным?
5.2. Как определить общее сопротивление резисторов при паралельным
соединении?
5.3. Чему равен общий ток цепи и напряжение на участках при паралельным
соединении?
5.4. Как определяется мощность на участках цепи и всей цепи
при паралельным соединении?
Назад в оглавление
Сайт создан в системе uCoz
простых параллельных цепей | Последовательные и параллельные цепи
На этой странице мы опишем три принципа, которые вы должны понимать в отношении параллельных цепей:
- Напряжение: Напряжение одинаково для всех компонентов в параллельной цепи.

- Ток: Общий ток цепи равен сумме токов отдельных ответвлений.
- Сопротивление: Индивидуальные сопротивления уменьшают , чтобы получить меньшее общее сопротивление, а не добавляют к сумме .
Давайте рассмотрим несколько примеров параллельных схем, демонстрирующих эти принципы.
Начнем с параллельной цепи, состоящей из трех резисторов и одной батареи:
Напряжение в параллельных цепях
Первый принцип параллельных цепей заключается в том, что напряжение одинаково для всех компонентов в цепи . Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени.
Следовательно, в приведенной выше схеме напряжение на R 1 равно напряжению на R 2 , которое равно напряжению на R 3 , которое равно напряжению на батарее.
Это равенство напряжений может быть представлено в другой таблице для наших начальных значений:
Применение закона Ома для простых параллельных цепей
Как и в случае с последовательными цепями, применяется то же предостережение для закона Ома: значения напряжения, тока и сопротивления должны быть в одном контексте, чтобы расчеты работали правильно.
Однако в приведенном выше примере схемы мы можем немедленно применить закон Ома к каждому резистору, чтобы найти его ток, потому что мы знаем напряжение на каждом резисторе (9 вольт) и сопротивление каждого резистора:
На данный момент мы все еще не знаем, каков общий ток или общее сопротивление для этой параллельной цепи, поэтому мы не можем применить закон Ома к крайнему правому столбцу («Всего»). Однако, если хорошенько подумать о том, что происходит, должно стать очевидным, что общий ток должен равняться сумме токов всех отдельных резисторов («ветвей»):
Когда общий ток выходит из положительной (+) клеммы аккумулятора в точке 1 и проходит по цепи, часть потока разделяется в точке 2, чтобы пройти через R 1 , еще часть разделяется в точке 3, чтобы пройти через R 2 , а остаток проходит через R 3 .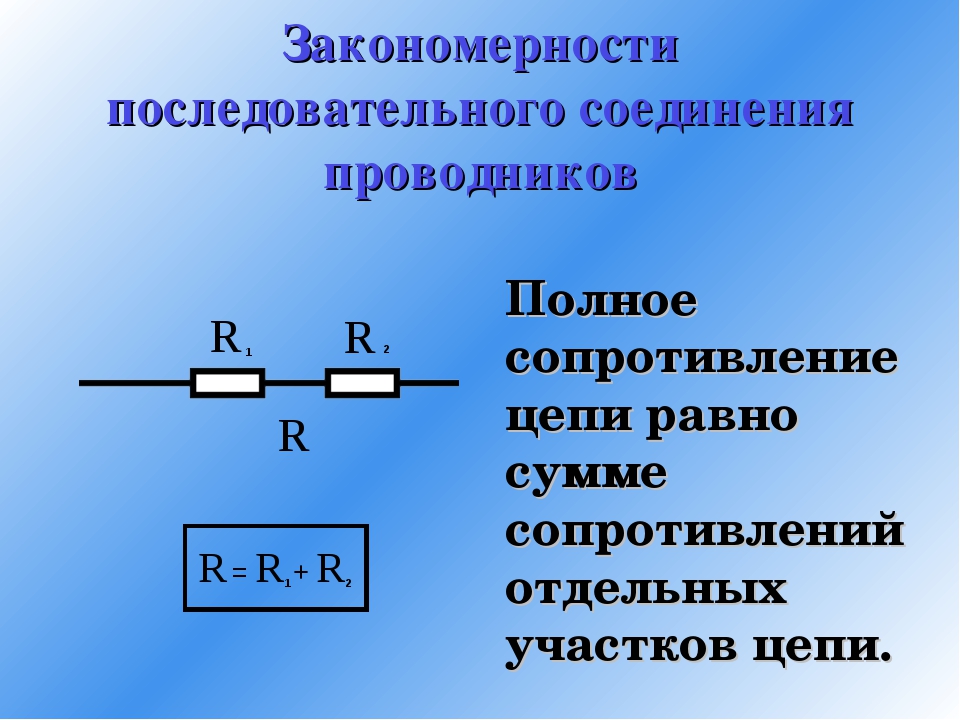 Подобно реке, разветвляющейся на несколько более мелких ручьев, суммарный расход всех ручьев должен равняться расходу всей реки.
Подобно реке, разветвляющейся на несколько более мелких ручьев, суммарный расход всех ручьев должен равняться расходу всей реки.
То же самое происходит, когда токи через R 1 , R 2 и R 3 объединяются, чтобы течь обратно к отрицательной клемме батареи (-) в направлении точки 8: протекание тока из точки 7 к точке 8 должна быть равна сумме токов (ветвей) через R 1 , R 2 и R 3 .
Это второй принцип параллельных цепей: общий ток цепи равен сумме токов отдельных ветвей .
Используя этот принцип, мы можем заполнить место IT в нашей таблице суммой I R1 , I R2 и I R3 :
Как рассчитать общее сопротивление в параллельных цепях
Наконец, применив закон Ома к крайнему правому столбцу («Всего»), мы можем вычислить общее сопротивление цепи:
Уравнение сопротивления в параллельных цепях
Обратите внимание на очень важную вещь.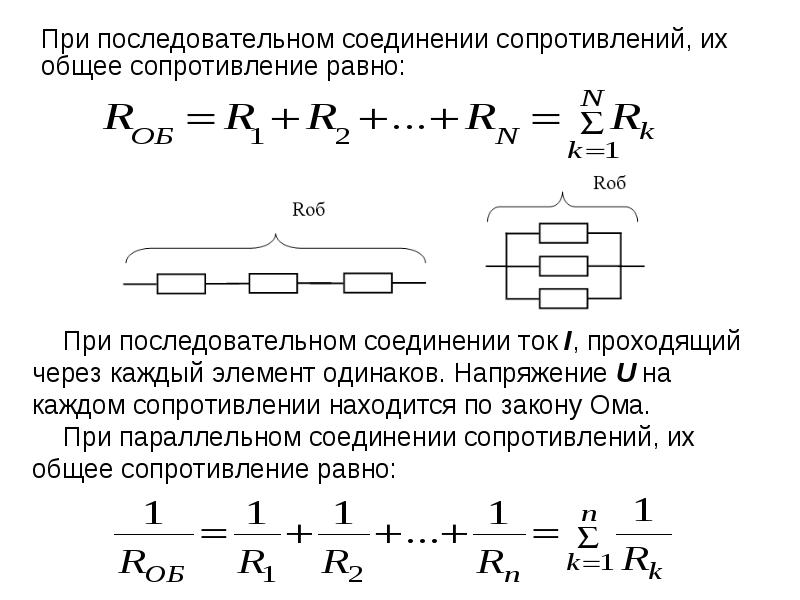 Общее сопротивление цепи составляет всего 625 Ом: меньше, чем , чем любой из отдельных резисторов.В последовательной цепи, где общее сопротивление было суммой отдельных сопротивлений, общее сопротивление должно было быть на больше, чем на , чем у любого из резисторов по отдельности.
Общее сопротивление цепи составляет всего 625 Ом: меньше, чем , чем любой из отдельных резисторов.В последовательной цепи, где общее сопротивление было суммой отдельных сопротивлений, общее сопротивление должно было быть на больше, чем на , чем у любого из резисторов по отдельности.
Однако здесь, в параллельной цепи, верно обратное: мы говорим, что отдельных сопротивлений уменьшают , а не добавляют , чтобы получить общее количество .
Этот принцип завершает нашу триаду «правил» для параллельных цепей, точно так же, как было обнаружено, что для последовательных цепей действуют три правила для напряжения, тока и сопротивления.
Математически соотношение между общим сопротивлением и отдельными сопротивлениями в параллельной цепи выглядит так:
Как изменить схемы нумерации параллельных цепей для SPICE
Та же базовая форма уравнения работает для любого количества резисторов, соединенных вместе параллельно, просто добавьте столько членов 1/R в знаменатель дроби, сколько необходимо для размещения всех параллельных резисторов в цепи.
Как и в случае с последовательной схемой, мы можем использовать компьютерный анализ для перепроверки наших расчетов.Во-первых, конечно, мы должны описать наш пример схемы компьютеру в терминах, которые он может понять. Начну с перерисовки схемы:
И снова мы обнаруживаем, что первоначальная схема нумерации, используемая для обозначения точек в цепи, должна быть изменена в пользу SPICE.
В SPICE все электрически общие точки должны иметь одинаковые номера узлов. Вот как SPICE знает, что с чем и как связано.
В простой параллельной цепи все точки являются электрически общими в одном из двух наборов точек.Для схемы нашего примера провод, соединяющий верхние части всех компонентов, будет иметь один номер узла, а провод, соединяющий нижние части компонентов, будет иметь другой.
Оставаясь верным соглашению о включении нуля в качестве номера узла, я выбираю числа 0 и 1:
Подобный пример делает назначение номеров узлов в SPICE достаточно понятным для понимания.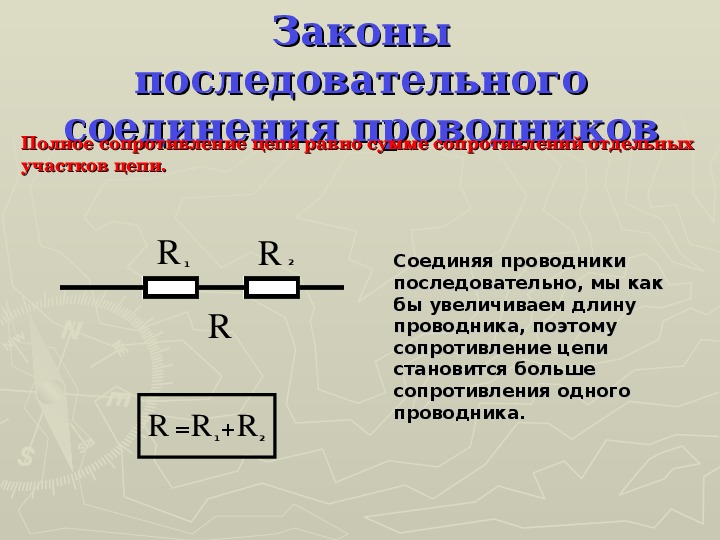 Поскольку все компоненты имеют общие наборы чисел, компьютер «знает», что все они соединены параллельно друг с другом.
Поскольку все компоненты имеют общие наборы чисел, компьютер «знает», что все они соединены параллельно друг с другом.
Чтобы отобразить токи ветвей в SPICE, нам нужно вставить источники нулевого напряжения в линию (последовательно) с каждым резистором, а затем сопоставить наши измерения тока с этими источниками.
По какой-то причине создатели программы SPICE сделали так, чтобы ток мог рассчитываться только от до источника напряжения. Это несколько раздражающее требование программы моделирования SPICE. При добавлении каждого из этих «фиктивных» источников напряжения необходимо создать несколько новых номеров узлов, чтобы соединить их с соответствующими ветвевыми резисторами:
.
Как проверить результаты компьютерного анализа
Все фиктивные источники напряжения установлены на 0 вольт, чтобы не влиять на работу схемы.
Файл описания схемы или netlist выглядит так:
Параллельная схема v1 1 0 р1 2 0 10к г2 3 0 2к р3 4 0 1к vr1 1 2 постоянный ток 0 vr2 1 3 dc 0 vr3 1 4 постоянный ток 0 .dc v1 9 9 1 .print DC v (2,0) v (3,0) v (4,0) .print DC я (vr1) я (vr2) я (vr3) .конец
Запустив компьютерный анализ, мы получили следующие результаты (я снабдил распечатку описательными метками):
| v1 | v(2) | v(3) | v(4) |
|---|---|---|---|
| 9.000E+00 | 9.000E+00 | 9.000E+00 | 9.000E+00 |
| аккумулятор | Напряжение R1 | Напряжение R2 | Напряжение R3 |
Напряжение
| v1 | я (vr1) | я (vr2) | я (vr3) |
|---|---|---|---|
| 9.000E+00 | 9.000E-04 | 4.500E-03 | 9.000E-03 |
| аккумулятор | R1 ток | R2 ток | R3 ток |
Напряжение
Эти значения действительно соответствуют рассчитанным ранее по закону Ома: 0.9 мА для I R1 , 4,5 мА для I R2 и 9 мА для I R3 . Разумеется, при параллельном соединении все резисторы имеют одинаковое падение напряжения (9 вольт, как и батарея).
Разумеется, при параллельном соединении все резисторы имеют одинаковое падение напряжения (9 вольт, как и батарея).
Три правила параллельных цепей
Таким образом, параллельная цепь определяется как цепь, в которой все компоненты соединены между одним и тем же набором электрически общих точек. Другими словами, все компоненты подключены через терминалы друг друга.Из этого определения следуют три правила параллельных цепей:
- Все компоненты имеют одинаковое напряжение.
- Сопротивление уменьшается до меньшего общего сопротивления.
- Суммарные токи ветвей равны большему общему току.
Как и в случае с последовательными цепями, все эти правила уходят корнями в определение параллельной цепи. Если вы полностью понимаете это определение, то правила — не что иное, как сноски к определению.
ОБЗОР:
- Компоненты в параллельной цепи имеют одинаковое напряжение: E Всего = E 1 = E 2 = .
 . . Е п
. . Е п - Общее сопротивление в параллельной цепи на меньше , чем любое из отдельных сопротивлений: R Всего = 1 / (1/R 1 + 1/R 2 + . . . 1/R n )
- Общий ток в параллельной цепи равен сумме токов отдельных ответвлений: I Всего = I 1 + I 2 + .. . я n .
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
21.1 Резисторы, включенные последовательно и параллельно – College Physics: OpenStax
На рис. 3 показаны резисторы , соединенные параллельно , подключенные к источнику напряжения. Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).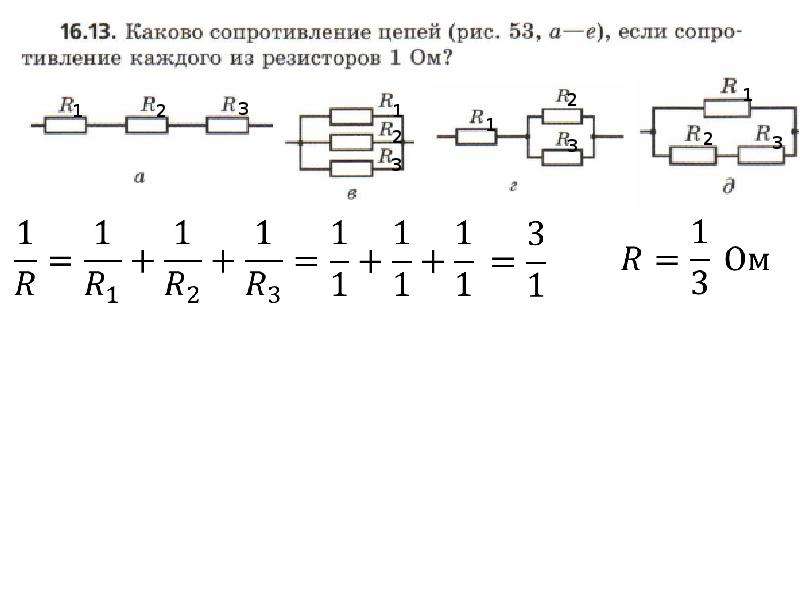 Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое верно и в вашем доме, или в любом здании. (См. рис. 3(b).)
Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое верно и в вашем доме, или в любом здании. (См. рис. 3(b).)
Чтобы найти выражение для эквивалентного параллельного сопротивления [латекс]\boldsymbol{R_{\textbf{p}}}[/латекс], рассмотрим протекающие токи и то, как они связаны с сопротивлением. Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, составляют [латекс]\boldsymbol{I_1 = \frac{V}{R_1}}[/латекс], [латекс]\boldsymbol{I_2 = \ frac{V}{R_2}}[/latex] и [латекс]\boldsymbol{I_3 = \frac{V}{R_3}}[/latex].Сохранение заряда подразумевает, что полный ток [латекс]\boldsymbol{I}[/латекс], создаваемый источником, представляет собой сумму этих токов:
[латекс]\boldsymbol{I =}[/латекс] [латекс]\ boldsymbol{\frac{V}{R_1}}[/латекс] [латекс]\boldsymbol{+}[/латекс] [латекс]\boldsymbol{\frac{V}{R_2}}[/латекс] [латекс]\ boldsymbol{+}[/латекс] [латекс]\boldsymbol{\frac{V}{R_3}}[/latex] [латекс]\boldsymbol{= V}[/latex] [латекс]\boldsymbol{(\frac{ 1}{R_1}}[/latex] [латекс]\boldsymbol{+}[/latex] [латекс]\boldsymbol{\frac{1}{R_2}}[/latex] [латекс]\boldsymbol{+}[ / латекс] [латекс] \ жирный символ {\ гидроразрыва {1} {R_3})}. [/латекс]
[/латекс]
[латекс]\boldsymbol{I =}[/латекс] [латекс]\boldsymbol{\frac{V}{R_p}}[/латекс] [латекс]\boldsymbol{= V}[/латекс ] [latex]\boldsymbol{(\frac{1}{R_p})}.[/latex]
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая любое количество резисторов, общее сопротивление [латекс]\boldsymbol{R_p}[/латекс] параллельного соединения связано с отдельными сопротивлениями как
[латекс]\boldsymbol{\frac{1}{R_p}} [/латекс] [латекс]\жирныйсимвол{=}[/латекс] [латекс]\жирныйсимвол{\гидроразрыва{1}{R_1}}[/латекс] [латекс]\жирныйсимвол{+}[/латекс] [латекс] \boldsymbol{\frac{1}{R_2}}[/латекс] [латекс]\boldsymbol{+}[/латекс] [латекс]\boldsymbol{\frac{1}{R_3}}[/латекс] [латекс] \boldsymbol{+ \cdots}[/latex]
В результате этого соотношения общее сопротивление [latex]\boldsymbol{R_p}[/latex] меньше наименьшего из индивидуальных сопротивлений.(Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.
Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рисунке 3 такие же, как и при последовательном соединении, рассмотренном ранее: [латекс]\boldsymbol{V = 12.0 \;\textbf{V}}[/latex], [латекс]\boldsymbol{R_1 = 1,00 \;\Omega}[/latex], [латекс]\boldsymbol{R_2 = 6,00 \;\Omega}[/latex ] и [латекс]\boldsymbol{R_3 = 13,0 \;\Omega}[/латекс]. а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов определяется по приведенной ниже формуле. Ввод известных значений дает
[латекс]\boldsymbol{\frac{1}{R_p}}[/latex] [латекс]\boldsymbol{=}[/latex] [латекс]\boldsymbol{\frac{1}{R_1}}[/latex ] [латекс]\boldsymbol{+}[/латекс] [латекс]\boldsymbol{\frac{1}{R_2}}[/латекс] [латекс]\boldsymbol{+}[/латекс] [латекс]\boldsymbol{ \frac{1}{R_3}}[/latex] [латекс]\boldsymbol{=}[/latex] [латекс]\boldsymbol{\frac{1}{1. 00 \;\Omega}}[/латекс] [латекс]\boldsymbol{+}[/латекс] [латекс]\boldsymbol{\frac{1}{6.00 \;\Omega}}[/латекс] [латекс]\ жирный символ {+} [/ латекс] [латекс] \ жирный символ {\ гидроразрыва {1} {13,0 \; \ Омега}}. [/ латекс]
00 \;\Omega}}[/латекс] [латекс]\boldsymbol{+}[/латекс] [латекс]\boldsymbol{\frac{1}{6.00 \;\Omega}}[/латекс] [латекс]\ жирный символ {+} [/ латекс] [латекс] \ жирный символ {\ гидроразрыва {1} {13,0 \; \ Омега}}. [/ латекс]
Таким образом,
[латекс]\boldsymbol{\frac{1}{R_p}}[/latex] [латекс]\boldsymbol{=}[/latex] [латекс]\boldsymbol{\frac{1.00}{\Omega}}[/ латекс] [латекс]\boldsymbol{+}[/латекс] [латекс]\boldsymbol{\frac{0.1667}{\Omega}}[/латекс] [латекс]\boldsymbol{+}[/латекс] [латекс]\ boldsymbol{\frac{0,07692}{\Omega}}[/latex] [латекс]\boldsymbol{=}[/latex] [латекс]\boldsymbol{\frac{1.2436}{\Омега}}[/латекс]
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны инвертировать это, чтобы найти общее сопротивление [латекс]\boldsymbol{R_p}[/латекс]. Это дает
[латекс]\boldsymbol{R_p =}[/латекс] [латекс]\boldsymbol{\frac{1}{1.2436}}[/латекс] [латекс]\boldsymbol{\Omega = 0,8041 \;\Omega}. [ /латекс]
[ /латекс]
Общее сопротивление с правильным количеством значащих цифр равно [латекс]\boldsymbol{R_p = 0,804 \;\Омега}[/латекс]
Обсуждение для (а)
[латекс]\boldsymbol{R_p}[/латекс], как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, подставив [латекс]\жирныйсимвол{R_p}[/латекс] вместо полного сопротивления. Это дает
[латекс]\boldsymbol{I =}[/латекс] [латекс]\boldsymbol{\frac{V}{R_p}}[/латекс] [латекс]\boldsymbol{=}[/латекс] [латекс]\boldsymbol {\ frac {12,0 \; \ textbf {V}} {0,8041 \; \ Omega}} [/ латекс] [латекс] \ жирный символ {= 14,92 \; \ textbf {A}} [/ латекс]
Обсуждение для (б)
Ток [latex]\boldsymbol{I}[/latex] для каждого устройства намного больше, чем для таких же устройств, соединенных последовательно (см. предыдущий пример).Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.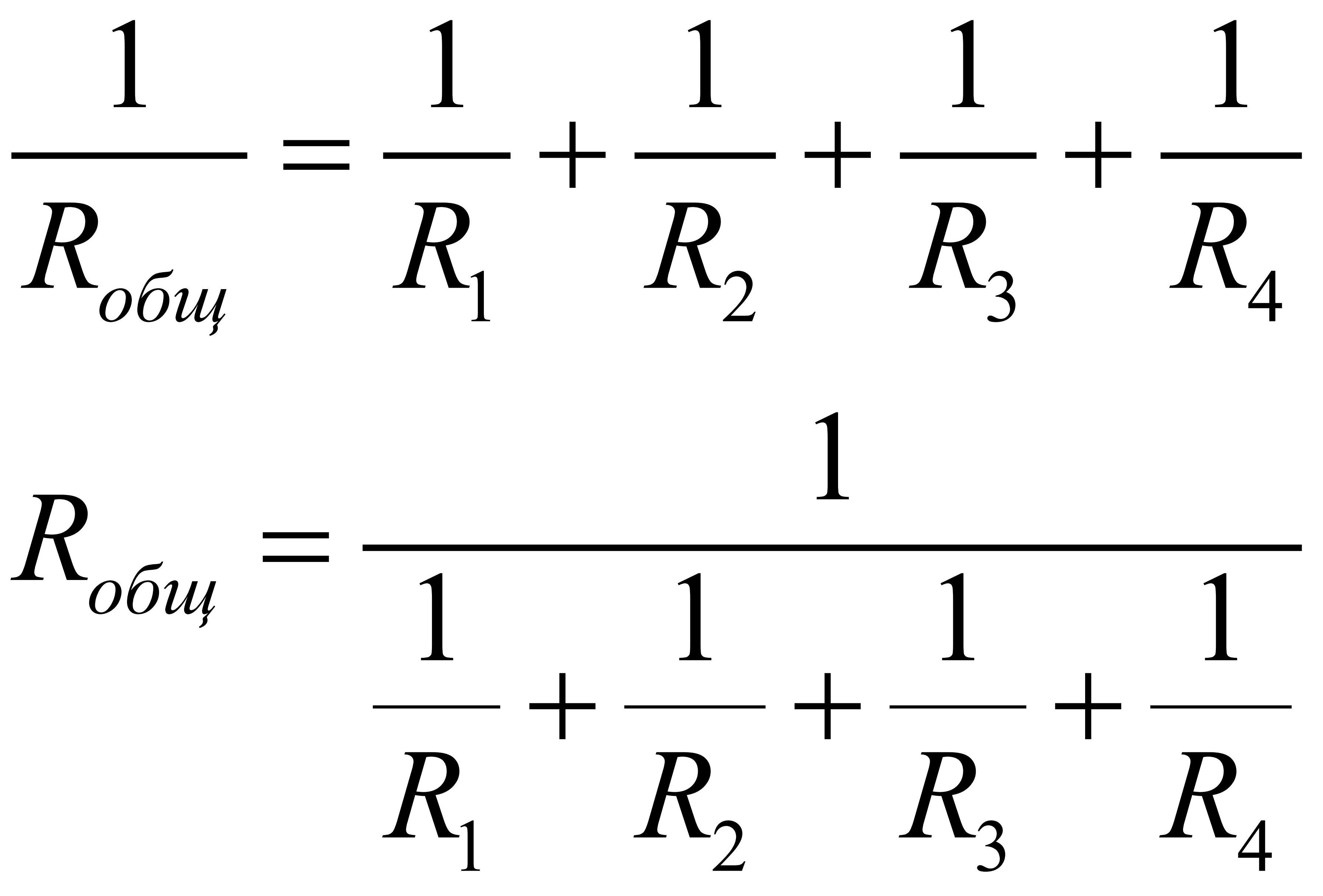
Стратегия и решение для (с)
Индивидуальные токи легко рассчитать по закону Ома, так как на каждый резистор подается полное напряжение. Таким образом,
[латекс]\boldsymbol{I_1 =}[/латекс] [латекс]\boldsymbol{\frac{V}{R_1}}[/латекс] [латекс]\boldsymbol{=}[/латекс] [латекс]\boldsymbol {\frac{12,0 \;\textbf{V}}{1,00 \;\Omega}}[/latex] [латекс]\boldsymbol{= 12.0 \;\textbf{A}}.[/латекс]
Аналогично
[латекс]\boldsymbol{I_2 =}[/латекс] [латекс]\boldsymbol{\frac{V}{R_2}}[/латекс] [латекс]\boldsymbol{=}[/латекс] [латекс]\boldsymbol {\ frac {12,0 \;\ textbf{V}}{6,00 \;\Omega}}[/latex] [латекс]\boldsymbol{= 2,00 \;\textbf{A}}[/latex]
и
[латекс]\boldsymbol{I_3 =}[/латекс] [латекс]\boldsymbol{\frac{V}{R_3}}[/латекс] [латекс]\boldsymbol{=}[/латекс] [латекс]\boldsymbol {\frac{12,0 \;\textbf{V}}{13,0 \;\Omega}}[/latex] [латекс]\boldsymbol{= 0.92 \;\textbf{A}}.[/latex]
Обсуждение для (с)
Общий ток представляет собой сумму отдельных токов:
[латекс]\boldsymbol{I_1 + I_2 + I_3 = 14,92 \;\textbf{A}}. [/latex]
[/latex]
Это соответствует закону сохранения заряда.
Стратегия и решение для (d)
Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.2}{13.0 \;\Omega}}[/latex] [латекс]\boldsymbol{= 11.1 \;\textbf{W}} .[/latex]
Обсуждение для (д)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к одному и тому же источнику напряжения.
Стратегия и решение для (e)
Общая мощность также может быть рассчитана несколькими способами. Выбор [латекс]\жирный символ{P = IV}[/латекс] и ввод общего тока дает
[латекс]\boldsymbol{P = IV = (14.92 \;\textbf{A})(12,0 \;\textbf{V}) = 179 \;\textbf{W}}.[/latex]
Обсуждение для (e)
Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт:
[латекс]\boldsymbol{P_1 + P_2 + P_3 = 144 \;\textbf{W} + 24,0 \;\textbf{W} + 11,1 \;\textbf{W} = 179 \;\textbf{W}}. [/латекс]
[/латекс]
Это согласуется с законом сохранения энергии.
Общее обсуждение
Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.
Резисторы в параллельном соединении
Обзор
Резисторы в цепи могут быть соединены последовательно или параллельно. Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.
Резисторы, соединенные параллельно
Резисторы соединены параллельно, если каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с пренебрежимо малым сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Резисторы параллельно
Параллельное соединение резисторов.
Каждый резистор потребляет такой же ток, как если бы он был единственным резистором, подключенным к источнику напряжения.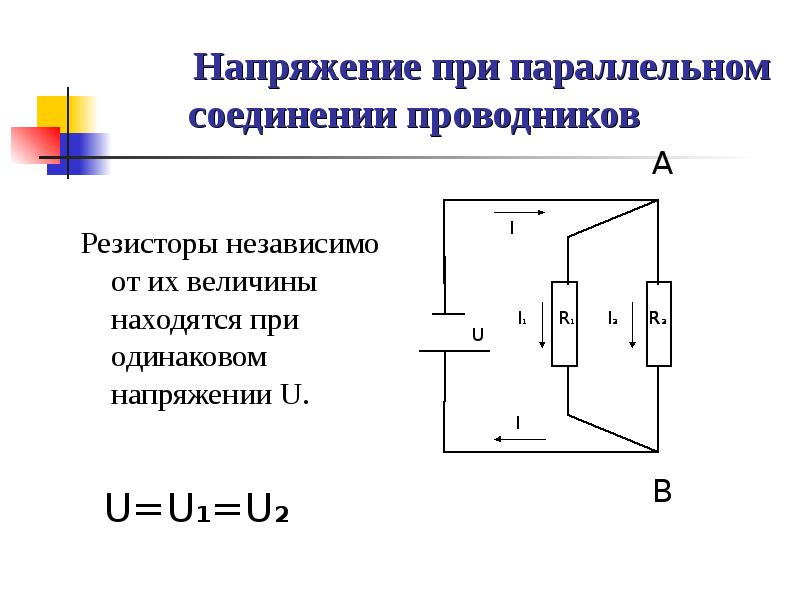 Это касается электросхем в доме или квартире. Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.
Это касается электросхем в доме или квартире. Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.
Закон Ома и параллельные резисторы
Каждый резистор в цепи имеет полное напряжение.Согласно закону Ома, токи, протекающие через отдельные резисторы, равны $I_1 = \frac{V}{R_1}$, $I_2 = \frac{V}{R_2}$ и $I_3 = \frac{V}{R_3. }$. Сохранение заряда подразумевает, что полный ток равен сумме этих токов:
Параллельные резисторы
Три резистора, подключенные параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление.
$I = I_1 + I_2 + I_3.$
Подстановка выражений для отдельных токов дает:
$I = \frac{V}{R_1} + \frac{V}{R_2} + \frac{V}{R_3}$
или
$I = V( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3})$
Отсюда следует, что полное сопротивление в параллельной цепи равно сумме обратной величины каждого отдельного сопротивления.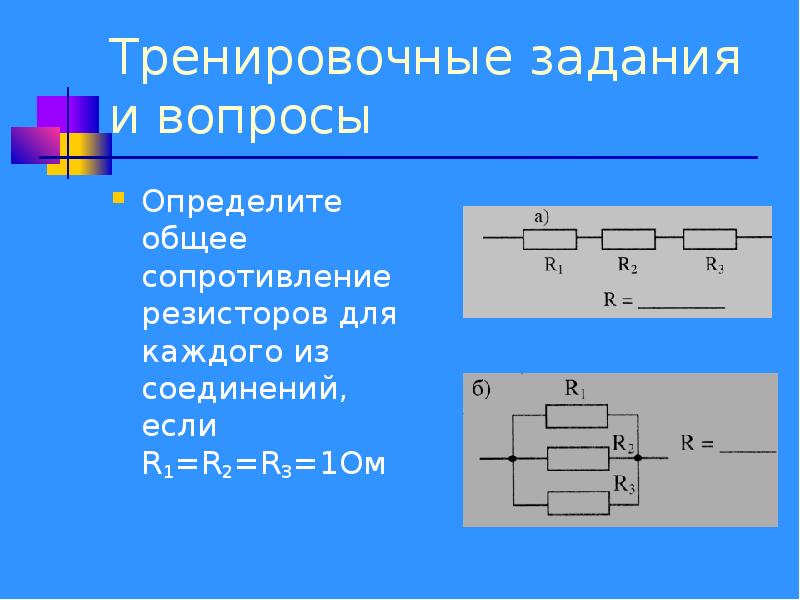 Следовательно, для каждой цепи с числом $n$ или резисторами, соединенными параллельно,
Следовательно, для каждой цепи с числом $n$ или резисторами, соединенными параллельно,
$R_{n \;(параллельно)} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} … + \frac{1}{R_n}. $
Это соотношение приводит к тому, что общее сопротивление меньше, чем наименьшее из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника протекает больший ток, чем по каждому из них по отдельности, поэтому общее сопротивление меньше.
На каждый параллельно подключенный резистор подается одинаковое полное напряжение источника, но общий ток делится между ними.Примером этого является подключение двух лампочек в параллельную цепь с батареей 1,5 В. В последовательной цепи две лампочки будут в два раза тусклее при подключении к одному аккумуляторному источнику. Однако, если бы две лампочки были соединены параллельно, они были бы такими же яркими, как если бы они были подключены к батарее по отдельности. Поскольку к обеим лампочкам приложено одинаковое полное напряжение, батарея также разрядится быстрее, поскольку она, по сути, подает полную энергию обеим лампочкам.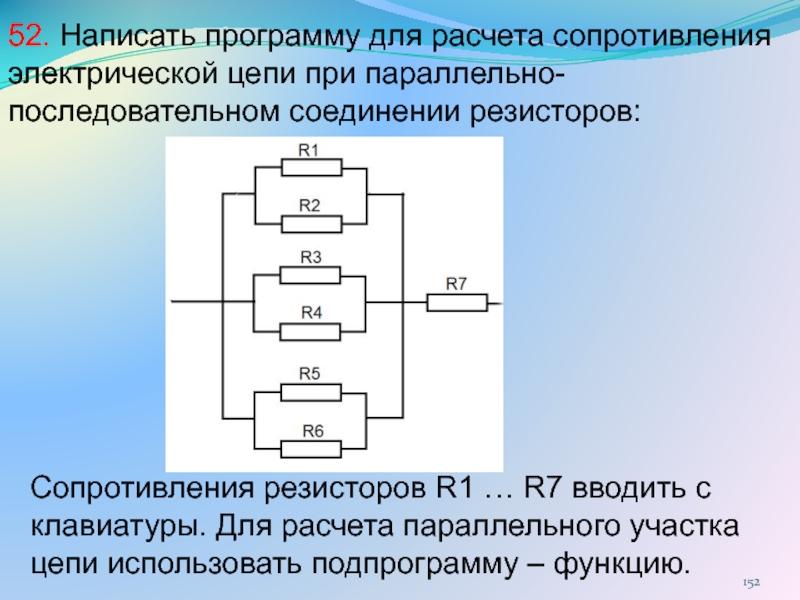 В последовательной цепи батарея будет работать так же долго, как и с одной лампочкой, только яркость затем будет делиться между лампочками.
В последовательной цепи батарея будет работать так же долго, как и с одной лампочкой, только яркость затем будет делиться между лампочками.
Резисторы — Learn.sparkfun.com
Добавлено в избранное
Любимый
51
Серия
и параллельные резисторы
Резисторы в электронике всегда соединены вместе, обычно либо в последовательной, либо в параллельной цепи. Когда резисторы соединены последовательно или параллельно, они создают общее сопротивление Ом, которое можно рассчитать с помощью одного из двух уравнений.Знание того, как комбинируются значения резисторов, пригодится, если вам нужно создать конкретное значение резистора.
Резисторы серии
При последовательном соединении значения резисторов просто складываются.
N резисторы последовательно. Общее сопротивление равно сумме всех последовательных резисторов.
Так, например, если вы просто должны иметь 12,33 кОм; резистор, найдите некоторые из наиболее распространенных номиналов резисторов 12 кОм; и 330 Ом, и соединить их последовательно.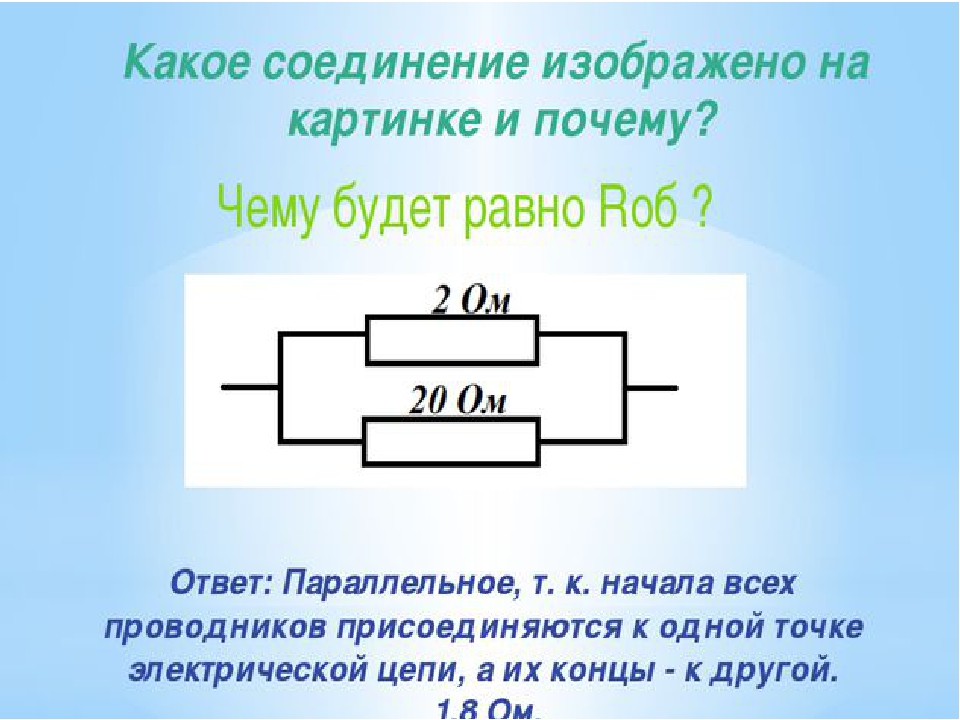
Параллельные резисторы
Найти сопротивление параллельных резисторов не так-то просто. Общее сопротивление N резисторов, включенных параллельно, обратно величине суммы всех обратных сопротивлений. Это уравнение может иметь больше смысла, чем последнее предложение:
.
Резисторы N параллельно. Чтобы найти общее сопротивление, инвертируйте каждое значение сопротивления, сложите их, а затем инвертируйте.
(Инверсия сопротивления на самом деле называется проводимостью , так что говоря более кратко: проводимость параллельных резисторов представляет собой сумму каждой из их проводимостей).
Как частный случай этого уравнения: если у вас есть только два резистора , подключенных параллельно, их общее сопротивление можно рассчитать с помощью этого немного менее инвертированного уравнения:
В качестве даже более специального случая этого уравнения, если у вас есть два параллельных резистора равного значения , общее сопротивление составляет половину их значения. Например, если два 10кОм; резисторы включены параллельно, их общее сопротивление 5кОм.
Например, если два 10кОм; резисторы включены параллельно, их общее сопротивление 5кОм.
Сокращенный способ сказать, что два резистора подключены параллельно, — это использовать параллельный оператор: || .Например, если R 1 параллельно с R 2 , концептуальное уравнение может быть записано как R 1 ||R 2 . Гораздо чище и скрывает все эти неприятные частицы!
Сети резисторов
В качестве специального введения в расчет полных сопротивлений учителя электроники просто любят подвергать своих учеников поиску сумасшедших, запутанных резисторных цепей.
Нормальный вопрос сети резисторов может звучать примерно так: «Каково сопротивление от клемм A до B в этой цепи?»
Чтобы решить такую проблему, начните с задней части схемы и упростите ее по направлению к двум терминалам.В этом случае R 7 , R 8 и R 9 расположены последовательно и могут быть сложены вместе.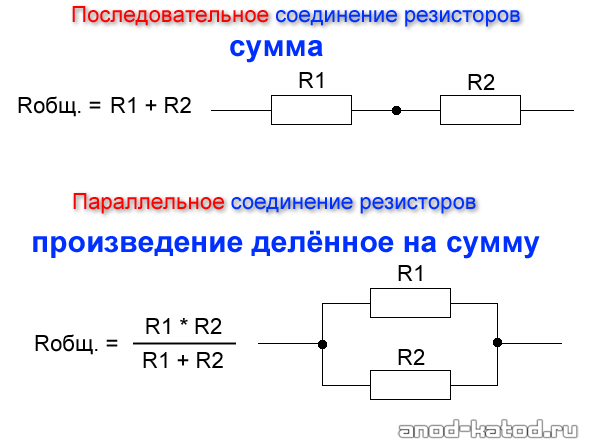 Эти три резистора подключены параллельно R 6 , поэтому эти четыре резистора можно объединить в один с сопротивлением R 6 ||(R 7 +R 8 +R 9 ). Делаем нашу схему:
Эти три резистора подключены параллельно R 6 , поэтому эти четыре резистора можно объединить в один с сопротивлением R 6 ||(R 7 +R 8 +R 9 ). Делаем нашу схему:
Теперь четыре крайних правых резистора можно еще больше упростить. R 4 , R 5 и наш набор R 6 — R 9 идут последовательно и могут быть добавлены.Тогда все эти последовательные резисторы подключены параллельно R 3 .
И это всего три последовательных резистора между выводами A и B . Добавьте их вверх! Таким образом, общее сопротивление этой цепи равно: R 1 +R 2 +R 3 ||(R 4 +R 5 +R 6 ||(R 7 +R 8 +R 9 )).
← Предыдущая страница
Номинальная мощность
Сопротивление в параллельной цепи
Сопротивление в параллельной цепи
На приведенной в качестве примера схеме, рис. 3-44, есть два резистора, подключенных параллельно к 5-вольтовой батарее.Каждый имеет значение сопротивления 10 Ом. Образуется полная цепь, состоящая из двух параллельных путей, и ток течет, как показано на рисунке.
3-44, есть два резистора, подключенных параллельно к 5-вольтовой батарее.Каждый имеет значение сопротивления 10 Ом. Образуется полная цепь, состоящая из двух параллельных путей, и ток течет, как показано на рисунке.
Рис. 3-44. — Два одинаковых резистора, соединенных параллельно.
Вычисление отдельных токов показывает, что через каждое сопротивление проходит половина ампера. Суммарный ток, протекающий от батареи к соединению резисторов и возвращающийся от резисторов к батарее, равен 1 ампер.
Общее сопротивление цепи можно рассчитать, используя
значения полного напряжения (E T ) и полного тока (I T ).
ПРИМЕЧАНИЕ. С этого момента в примерах задач будут использоваться сокращения и символы для электрических величин.
Дано:
Решение:
Это вычисление показывает, что общее сопротивление равно 5 Ом; половину значения любого из двух резисторов.
Поскольку общее сопротивление параллельной цепи меньше любого из отдельных резисторов, общее сопротивление параллельной цепи не является суммой значений отдельных резисторов, как это было в случае последовательной цепи. Общее сопротивление резисторов, включенных параллельно, также называют ЭКВИВАЛЕНТНЫМ СОПРОТИВЛЕНИЕМ.
Общее сопротивление резисторов, включенных параллельно, также называют ЭКВИВАЛЕНТНЫМ СОПРОТИВЛЕНИЕМ.
(R экв. ). Термины «полное сопротивление» и «эквивалентное сопротивление» взаимозаменяемы.
Существует несколько методов определения эквивалентного сопротивления параллельных цепей. Лучший метод для данной схемы зависит от количества и номинала резисторов. Для схемы, описанной выше, где все резисторы имеют одинаковое значение, используется следующее простое уравнение:
Это уравнение действительно для любого количества параллельно соединенных резисторов РАВНОГО ЗНАЧЕНИЯ.
Пример. Четыре резистора по 40 Ом соединены параллельно. Каково их эквивалентное сопротивление?
Дано:
Решение:
На рис. 3-45 показаны два резистора разного номинала, соединенные параллельно. Поскольку показан общий ток, можно рассчитать эквивалентное сопротивление.
Рис. 3-45. — Пример схемы с неодинаковыми параллельными резисторами.
Дано:
Решение:
Эквивалентное сопротивление цепи, показанной на рис. 3-45, меньше любого из двух резисторов (R 1 , R 2 ).Важно помнить, что эквивалентное сопротивление параллельной цепи всегда меньше сопротивления любой ветви.
3-45, меньше любого из двух резисторов (R 1 , R 2 ).Важно помнить, что эквивалентное сопротивление параллельной цепи всегда меньше сопротивления любой ветви.
Эквивалентное сопротивление можно найти, если известны значения отдельных сопротивлений и напряжение источника. Вычислив ток каждой ветви, добавив токи ветви для расчета общего тока и разделив напряжение источника на общий ток, можно найти общее значение. Этот метод хоть и эффективен, но несколько длителен. Более быстрый метод нахождения эквивалентного сопротивления заключается в использовании общей формулы для параллельных резисторов:
. Если вы примените общую формулу к цепи, показанной на рис. 3-45, вы получите то же значение эквивалентного сопротивления (2 Ом), что и было. полученный в предыдущем расчете, в котором использовались напряжение источника и общий ток.
Дано:
Решение:
Приведите дроби к общему знаменателю.
Поскольку обе стороны обратны (разделены на одну), обратной функцией пренебрегаем.
Формула, которую вы дали для равных резисторов, включенных параллельно
, является упрощением общей формулы для параллельных резисторов
Существуют другие упрощения общей формулы для параллельных резисторов, которые можно использовать для расчета общего или эквивалентное сопротивление в параллельной цепи.
ВЗАИМНЫЙ МЕТОД. — Этот метод основан на взятии обратной величины каждой части уравнения. Это представляет общую формулу для параллельных резисторов как:
Эта формула используется для расчета эквивалентного сопротивления ряда неравных параллельных резисторов. Вы должны найти наименьший общий знаменатель в решении этих задач. Если вы немного затрудняетесь найти наименьший общий знаменатель, освежите его в Mathematics Volume 1, NAVEDTRA 10069 (Series).
Пример: Три резистора соединены параллельно, как показано на рис. 3-46. Номиналы резисторов: R 1 = 20 Ом, R 2 = 30 Ом, R 3 = 40 Ом. Чему равно сопротивление? (Используйте метод обратной связи.)
Чему равно сопротивление? (Используйте метод обратной связи.)
Рисунок 3-46. — Пример параллельной схемы с неодинаковыми ветвевыми резисторами.
Дано:
Решение:
МЕТОД ПРОИЗВЕДЕНИЯ НА СУММУ. — Удобный метод нахождения эквивалентного или общего сопротивления двух параллельных резисторов заключается в использовании следующей формулы.
Это уравнение, называемое формулой произведения на сумму, используется так часто, что его следует запомнить.
Пример. Каково эквивалентное сопротивление резисторов сопротивлением 20 Ом и 30 Ом, соединенных параллельно, как показано на рис. 3-47?
Рис. 3-47. — Параллельная схема с двумя неодинаковыми резисторами.
Дано:
Решение:
Четыре одинаковых резистора соединены параллельно, каждый резистор имеет омическое сопротивление 100 Ом, каково эквивалентное сопротивление?
Три параллельно соединенных резистора имеют номиналы 12 кОм, 20 кОм и 30 кОм. Чему равно сопротивление?
Чему равно сопротивление?
Два параллельно соединенных резистора имеют номиналы 10 кОм и 30 кОм. Чему равно сопротивление?
Серия
и параллельно — AP Physics 1
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как
в виде
ChillingEffects. org.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится
на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
4.1 Резисторы последовательно и параллельно
Резисторы последовательно
Когда резисторы включены последовательно? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током, должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то R1.R1.на рис. 4.2(а) может быть сопротивлением стержня отвертки, R2R2 — сопротивлением ее рукоятки, R3R3 — сопротивлением тела человека, и R4R4 сопротивление ее обуви.
Например, если ток течет через человека, держащего отвертку, в землю, то R1.R1.на рис. 4.2(а) может быть сопротивлением стержня отвертки, R2R2 — сопротивлением ее рукоятки, R3R3 — сопротивлением тела человека, и R4R4 сопротивление ее обуви.
На рис. 4.3 показаны резисторы, последовательно подключенные к источнику напряжения. Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор.Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить силу тока, надев обувь на резиновой подошве с высоким сопротивлением. Это могло бы быть недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением для устройства, которое уменьшило бы рабочий ток.
Рисунок 4.3. Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа).
Чтобы убедиться, что последовательное сопротивление действительно добавляется, давайте рассмотрим потери электроэнергии, называемые падением напряжения, в каждом резисторе на рисунке 4.3.
В соответствии с законом Ома падение напряжения V,V на резисторе при протекании через него тока рассчитывается по уравнению V=IR,V=IR, где II равно току в амперах (А), а RR равно сопротивление в омах Ω.Ω. Другой способ представить это так: VV — это напряжение, необходимое для того, чтобы ток II протекал через сопротивление R. R.
.
Таким образом, падение напряжения на R1R1 равно V1=IR1,V1=IR1, на R2R2 — V2=IR2, V2=IR2, а на R3R3 — V3=IR3.V3=IR3. Сумма этих напряжений равна выходному напряжению источника; то есть
4.1 В=В1+В2+В3.В=В1+В2+В3.
Это уравнение основано на законах сохранения энергии и сохранения заряда. Электрическая потенциальная энергия может быть описана уравнением PE=qV, PE=qV, где qq — электрический заряд, а VV — напряжение. Таким образом, энергия, подаваемая источником, составляет qV,qV, а рассеиваемая резисторами —
4.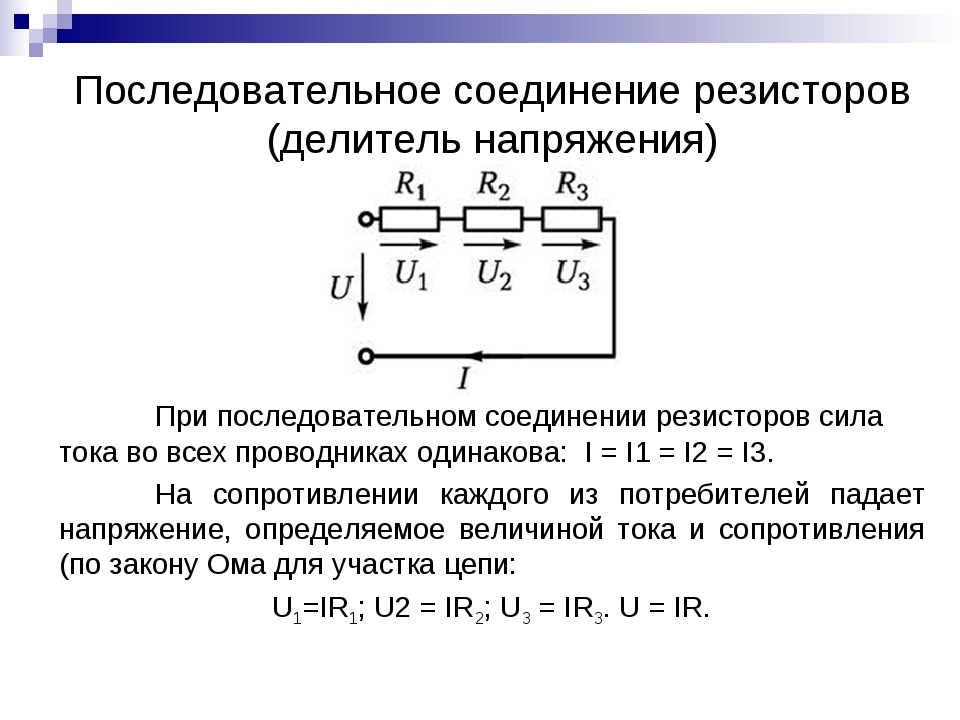 2 qV1+qV2+qV3.qV1+qV2+qV3.
2 qV1+qV2+qV3.qV1+qV2+qV3.
Связи: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что полный заряд и полная энергия постоянны в любом процессе.Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого места назначения энергии. Таким образом, qV=qV1+qV2+qV3.qV=qV1+qV2+qV3. Заряд qq компенсируется, что дает V=V1+V2+V3, V=V1+V2+V3, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда, и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
4.3 V=IR1+IR2+IR3=I(R1+R2+R3). V=IR1+IR2+IR3=I(R1+R2+R3).
V=IR1+IR2+IR3=I(R1+R2+R3).
Обратите внимание, что для эквивалентного последовательного сопротивления Rs,Rs мы имеем
Это означает, что общее или эквивалентное последовательное сопротивление RsRs трех резисторов равно Rs=R1+R2+R3.Rs=R1+R2+R3.
Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, общее сопротивление RsRs последовательного соединения равно
.
4.5 Rs=R1+R2+R3+…,Rs=R1+R2+R3+…,
, как было предложено. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.
Пример 4.1 Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рис. 4.3 составляет 12,0–12,0 В, а сопротивления равны R1=1,00 Ом, R1=1,00 Ом, R2=6,00 Ом, R2=6,00 Ом и R3=13,0 Ом. R3=13,0 Ом. . а) Чему равно полное сопротивление? б) Найдите силу тока.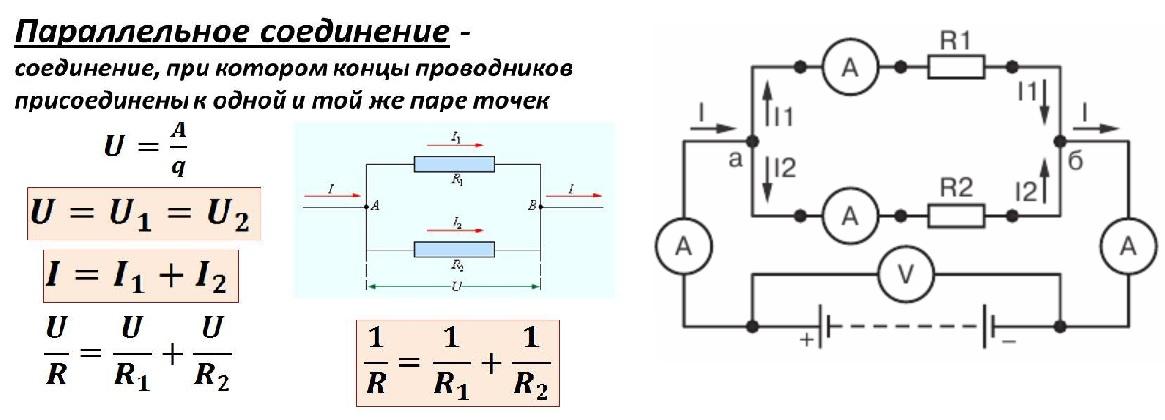 (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
(c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление представляет собой просто сумму отдельных сопротивлений, определяемую уравнением
.
4.6 Rs=R1+R2+R3=1,00 Ом+6,00 Ом+13,0 Ом=20,0 Ом. Rs=R1+R2+R3=1.00 Ом+6,00 Ом+13,0 Ом=20,0 Ом.
Стратегия и решение для (b)
Ток находится по закону Ома, V=IR.V=IR. Ввод значений приложенного напряжения и общего сопротивления дает ток в цепи.
4.7 I=VRs=12,0 В20,0 Ом=0,600 AI=VRs=12,0 В20,0 Ом=0,600 А
Стратегия и решение для (с)
Напряжение — или падение IRIR — на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает
4.8 V1=IR1=(0,600 А)(1,0 Ом)=0,600 В.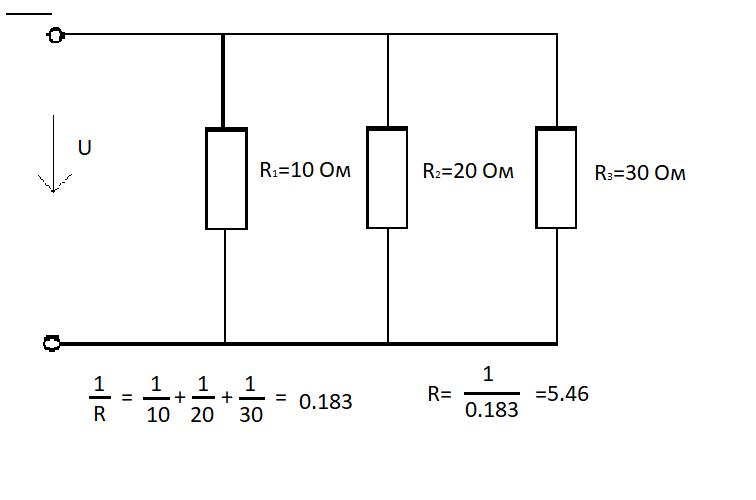 V1=IR1=(0,600 А)(1,0 Ом)=0,600 В.
V1=IR1=(0,600 А)(1,0 Ом)=0,600 В.
Аналогично
4,9 V2=IR2=(0,600 А)(6,0 Ом)=3,60 VV2=IR2=(0,600 А)(6,0 Ом)=3,60 В
и
4.10 V3=IR3=(0,600 А)(13,0 Ом)=7,80 В. V3=IR3=(0,600 А)(13,0 Ом)=7,80 В.
Обсуждение для (с)
Три падения IRIR добавляют к 12,0 В, 12,0 В, как и предполагалось.
4.11 V1+V2+V3=(0,600+3,60+7,80)V=12,0 VV1+V2+V3=(0,600+3,60+7,80)V=12,0 В
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля, P=IV,P=IV, где PP — электрическая мощность.В этом случае через каждый резистор протекает одинаковый полный ток. Подставив закон Ома V=IRV=IR в закон Джоуля, мы получим мощность, рассеиваемую первым резистором, как
.
4.12 P1=I2R1=(0,600 А)2(1,00 Ом)=0,360 Вт. P1=I2R1=(0,600 А)2(1,00 Ом)=0,360 Вт.
Аналогично
4.13 P2=I2R2=(0,600 А)2(6,00 Ом)=2,16 WP2=I2R2=(0,600 А)2(6,00 Ом)=2,16 Вт
и
4.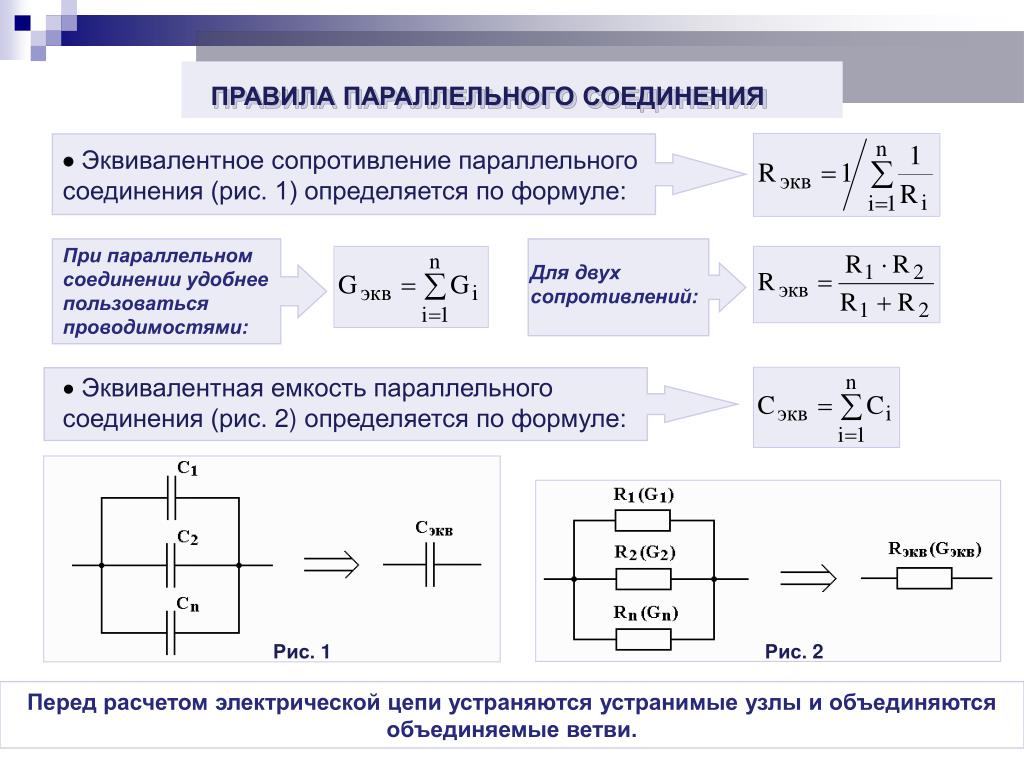 14 P3=I2R3=(0,600 А)2(13,0 Ом)=4,68 Вт. P3=I2R3=(0,600 А)2(13,0 Ом)=4,68 Вт.
14 P3=I2R3=(0,600 А)2(13,0 Ом)=4,68 Вт. P3=I2R3=(0,600 А)2(13,0 Ом)=4,68 Вт.
Обсуждение для (д)
Мощность также можно рассчитать, используя либо P=IVP=IV, либо P=V2R,P=V2R, где VV — падение напряжения на резисторе (не полное напряжение источника).Будут получены одинаковые значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать P=IV,P=IV, где VV — напряжение источника. Это дает
4,15 P=(0,600 А)(12,0 В)=7,20 Вт.P=(0,600 А)(12,0 В)=7,20 Вт.
Обсуждение для (e)
Обратите внимание, кстати, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, как и мощность, выдаваемая источником. То есть
4.16 P1+P2+P3=(0,360+2,16+4,68)W=7,20 Вт. P1+P2+P3=(0,360+2,16+4,68)W=7,20 Вт.
Мощность — это энергия в единицу времени (ватты), поэтому для сохранения энергии необходимо, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.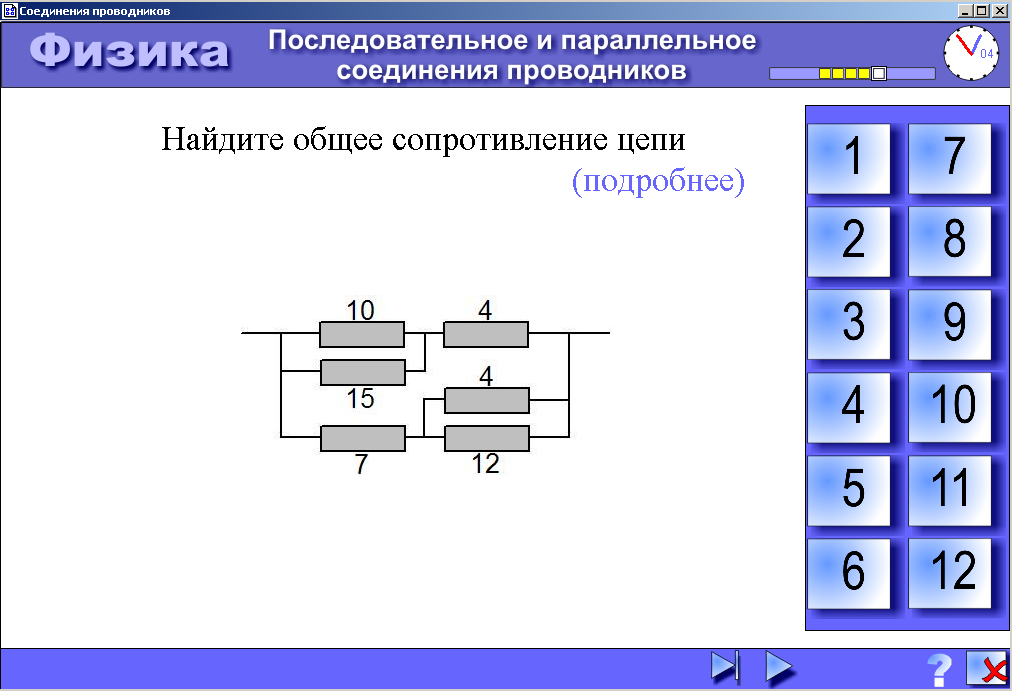


 На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.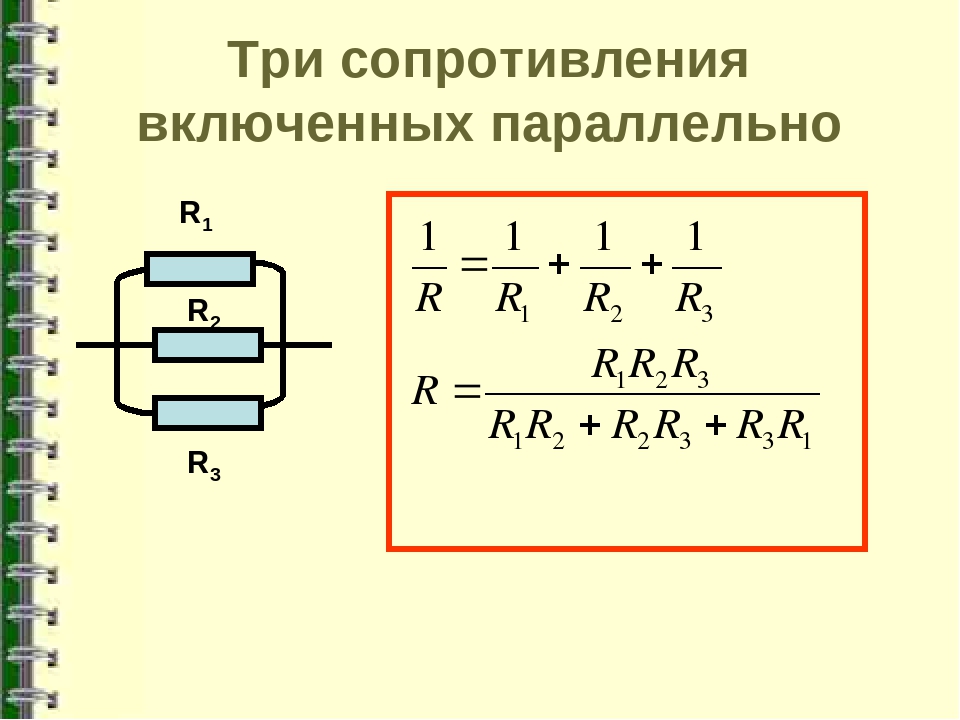 Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.

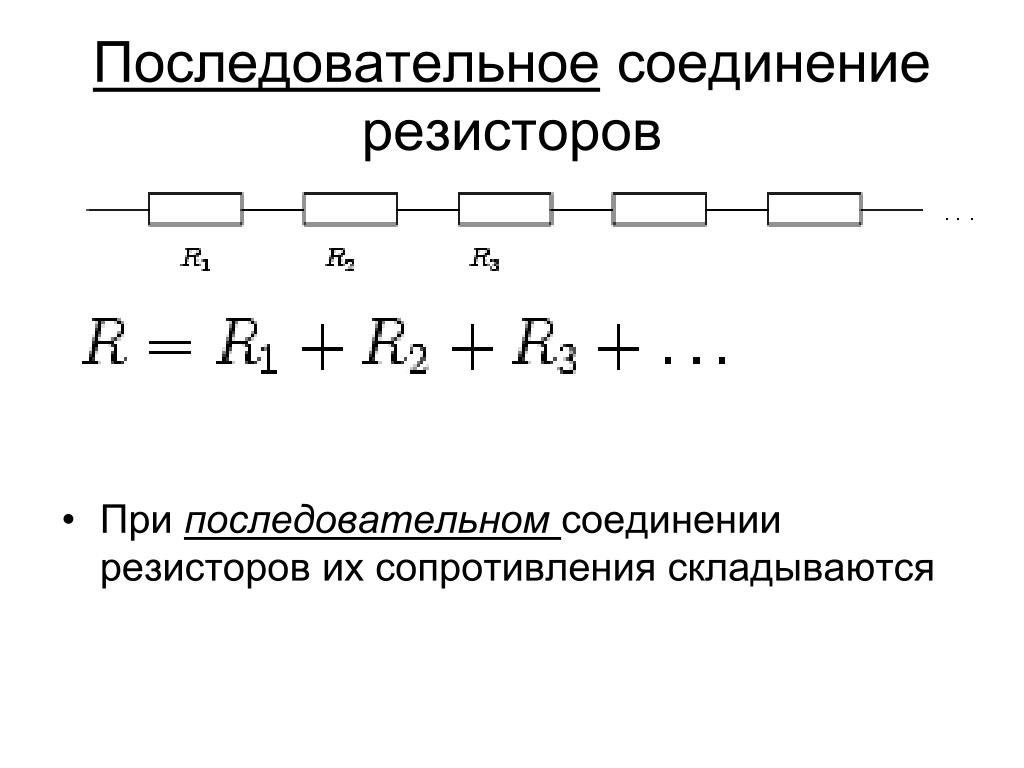 За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи. Сначала задача решается с помощью формул: Rобщ = R1+ R2, I = U/ Rобщ, I = I1 = I2, U1 = IR1, U2 = IR2 (или U2 = U – U1).
Сначала задача решается с помощью формул: Rобщ = R1+ R2, I = U/ Rобщ, I = I1 = I2, U1 = IR1, U2 = IR2 (или U2 = U – U1).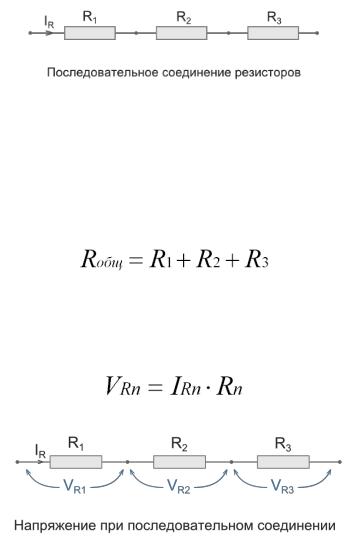 Следовательно, сила тока тоже одинакова и равна 6 А. Напряжение на среднем участке 6 В. Сопротивление среднего участка в два раза больше. Следовательно, сила тока в два раза меньше и равна 3 А. напряжения на резисторах 2 и 3 одинаковы и равны 3 В.
Следовательно, сила тока тоже одинакова и равна 6 А. Напряжение на среднем участке 6 В. Сопротивление среднего участка в два раза больше. Следовательно, сила тока в два раза меньше и равна 3 А. напряжения на резисторах 2 и 3 одинаковы и равны 3 В.
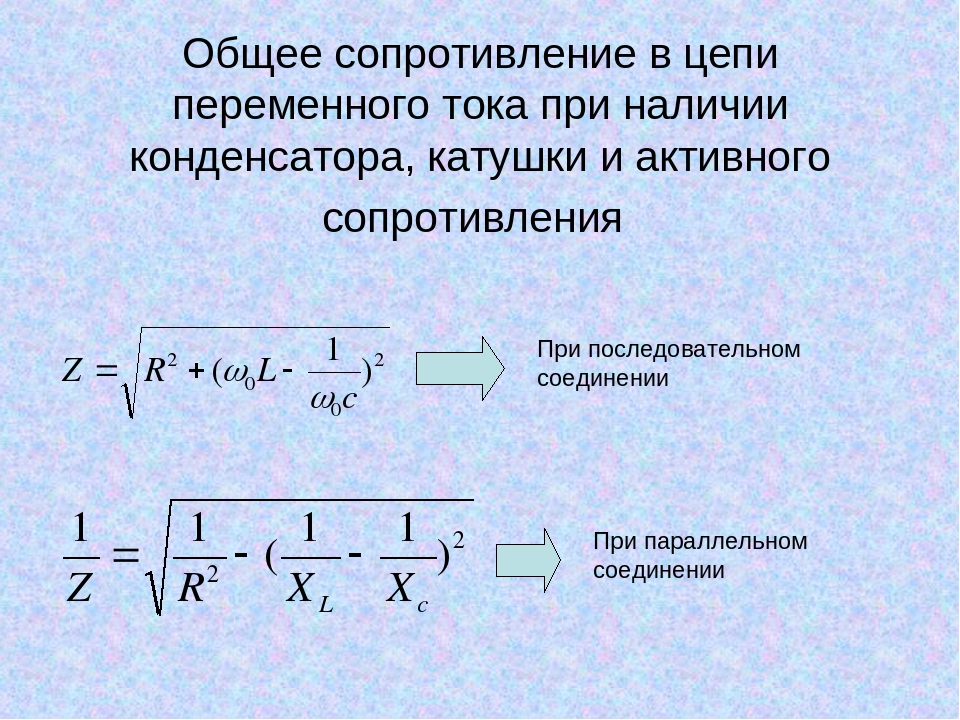
 dc v1 9 9 1
.print DC v (2,0) v (3,0) v (4,0)
.print DC я (vr1) я (vr2) я (vr3)
.конец
dc v1 9 9 1
.print DC v (2,0) v (3,0) v (4,0)
.print DC я (vr1) я (vr2) я (vr3)
.конец
 . . Е п
. . Е п