Определение параллельное соединение: ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ — это… Что такое ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ?

Параллельное соединение — урок. Физика, 8 класс.

При параллельном соединении все потребители подключены к источнику тока независимо друг от друга и образуют разветвлённую цепь.

При параллельном соединении все потребители подключены к одному источнику тока, между клеммами которого имеется определённое напряжение.

Каждый потребитель получает полное напряжение цепи.
 

U=U1=U2=U3=…

При параллельном соединении общий ток является суммой токов, протекающих через отдельные потребители.

I=I1+I2+I3+…

Общее сопротивление потребителей, находящихся в параллельном соединении, будет наименьшим (меньше, чем наименьшее из сопротивлений параллельно подключённых потребителей).
Если параллельно соединены \(n\) потребителей, а сопротивление каждого из них одинаково и равно \(R\), тогда общее сопротивление цепи будет равно \(R : n\).

Можно сделать вывод о том, что при увеличении числа потребителей общая сила тока неограниченно возрастает, что может привести к пожару.

Обрати внимание!

В одну розетку нельзя включать несколько мощных потребителей, так как перенагруженные провода нагреваются и могут загореться.

В квартире потребители включены в параллельное соединение. Подводка электричества, входящего в квартиру, состоит из нескольких проводов, которые проходят через счётчик, измеряющий потребление электроэнергии. Электрический ток течёт через предохранители, которые подключены последовательно и предусмотрены для определённой силы тока в цепи. Они размыкают цепь в случае опасной перегрузки.

Электрический кабель, который используется в электрической цепи квартиры, имеет три провода. Третий провод является заземлением.

Преимуществом параллельного соединения является то, что при отключении одного из потребителей, остальные продолжают работать.

Источники:

Fizika 9. klasei/Ilgonis Vilks. — Rīga: Zvaigzne ABC, 2008. — 159 lpp.: izmantotā literatūra: 117, lpp.
(Физика для 9 класса// Илгонис Вилкс. — Рига: Zvaigzne ABC, 2008. — 159 стр.: использованная литература: 117. стр.)
Fizika pamatskolai 2. daļa// V. Rasmane, A. Vītols, Ā. Cacāne. — Rīga: RAKA, 2006. — 136 lpp.: il.-izmantotā literatūra: 84, lpp.
(Физика для начальной школы, 2 часть// Расмане В., Витолс А., Цацане А. — Рига: RAKA, 2006. — 136 стр.: ил.-использованная литература: 84. стр.)
http://www.ndg.lv/latvian/Macibas/FizInter/b2.2.4.htm
http://www.goerudio.com/demo/paralelais_slegums
http://www.ndg.lv/latvian/Macibas/FizInter/b2.2.4.htm

Параллельное соединение проводников | Физика

При параллельном соединении все проводники (резисторы, лампы и т.д.) подключаются к одной и той же паре точек A и B (рис. 43). Связь между общими значениями силы тока, напряжения и сопротивления с их значениями на отдельных участках цепи при этом отличается от той, что была при последовательном соединении.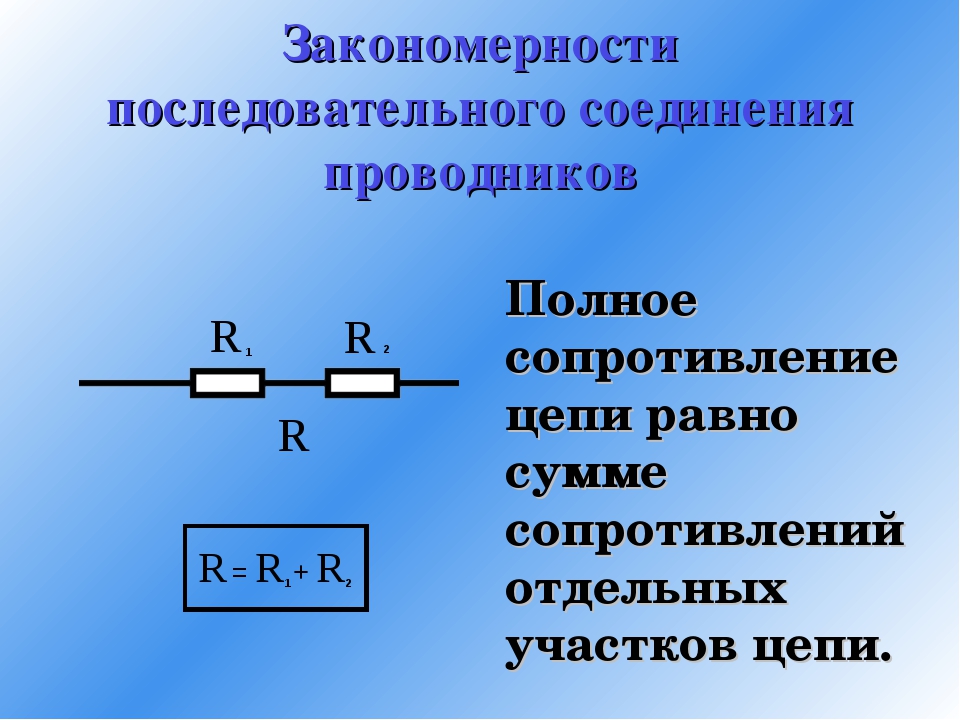 Теперь соответствующие формулы имеют вид

I = I₁ + I₂, (17.1)     U = U₁ = U₂, (17.2)      R = (R₁R₂) / (R₁ + R₂). (17.3)

Чтобы убедиться в справедливости этих соотношений, следует собрать цепь и с помощью амперметра и вольтметра произвести необходимые измерения.

Итак, при параллельном соединении проводников напряжение на всех участках цепи одно и то же, общая сила тока равна сумме сил токов на отдельных проводниках, а общее сопротивление двух проводников находится как отношение произведения их сопротивлений к их сумме.

Первые две из этих закономерностей справедливы для любого числа параллельно соединенных проводников, последняя — только для двух.

Если R₁ = R₂, то

R = (R₁R₂) / (R₁ + R₂) = R₁²/2R₁ = R₁/2      (17.4)

Мы видим, что общее сопротивление двух одинаковых проводников в 2 раза меньше сопротивления одного проводника. Эта закономерность допускает обобщение: если параллельно соединено n одинаковых потребителей электроэнергии (резисторов, ламп и т.д.), то их общее сопротивление в n раз меньше сопротивления каждого из них:

R = R₁/n      (17.5)

Отсюда следует, что с увеличением числа проводников общее сопротивление будет становиться все меньше и меньше. Это может показаться странным. На самом деле ничего удивительного в этом нет: ведь при параллельном соединении проводников происходит как бы увеличение общей площади их поперечного сечения, а с увеличением площади сечения проводника, как известно, его сопротивление уменьшается.

Отличительной особенностью параллельного соединения нескольких потребителей является то, что при выключении одного из них остальные продолжают работать. Так, например, вывернув одну лампу в цепи, изображенной на рисунке 44, мы увидим, что другая будет по-прежнему гореть.

Большинство потребителей электроэнергии — электронагревательные приборы, холодильники, швейные машины, магнитофоны, телевизоры и т. д. — рассчитаны на напряжение сети 220 В. Поэтому все они должны включаться в сеть параллельно, ибо только в этом случае они окажутся под одним и тем же напряжением (220 В) и будут продолжать работать при выключении одного из них.

На рисунке 45 приведена упрощенная схема квартирной электропроводки. Провода сети, между которыми существует напряжение 220 В, обозначены буквами Ф и О. Первый из них называют фазным, второй — нулевым. Нулевой провод соединен с землей. Именно с ним соединяют все потребители. И наоборот, все выключатели соединяют с фазным проводом. Такой порядок подключения потребителей и выключателей обеспечивает наибольшую безопасность человека.

??? 1. Какое соединение называют параллельным? 2. Начертите схему цепи, изображенной на рисунке 44. 3. Какие три закономерности справедливы для параллельного соединения проводников? 4. Как находится общее сопротивление параллельно соединенных проводников, когда они одинаковые? 5. Перечислите все элементы электрической цепи, изображенной на рисунке 45. 6. Предположим, что при замене лампы человек случайно коснулся металлического контакта в патроне лампы и одновременно с этим какой-либо заземленной части здания (например, батареи отопления). Под каким напряжением он окажется? Рассмотрите ситуацию, когда лампа и выключатель подсоединены к проводам сети так, как это показано на рисунке 45. Что произойдет, если лампу и выключатель поменять местами? 7. Почему у вольтметров делают большое внутреннее сопротивление, а у амперметров — малое?

Параллельное соединение резисторов определение — Морской флот

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.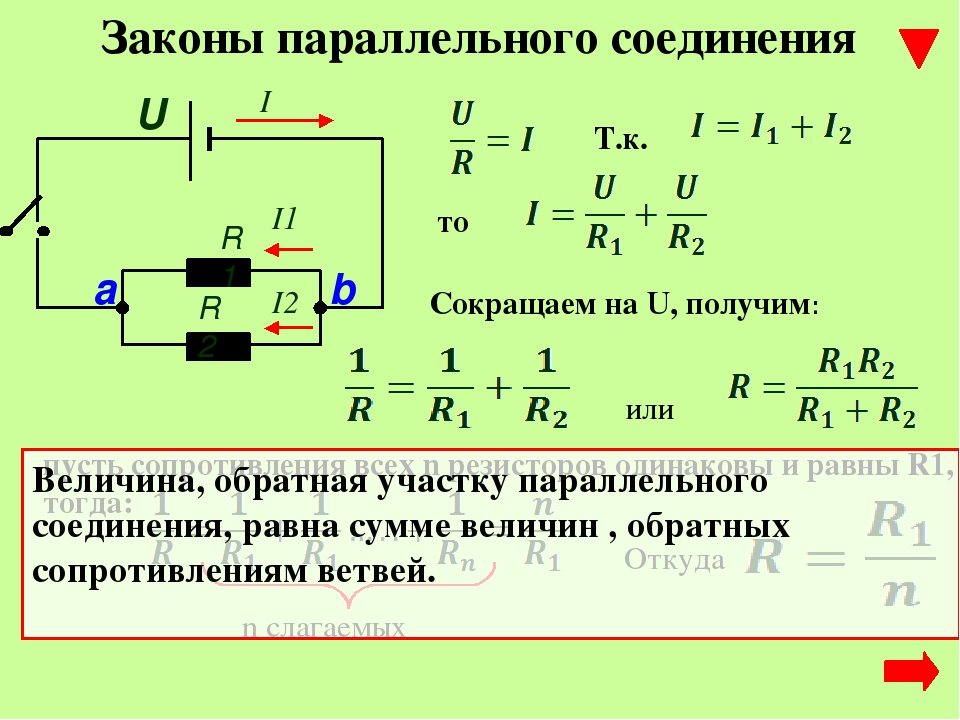

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн).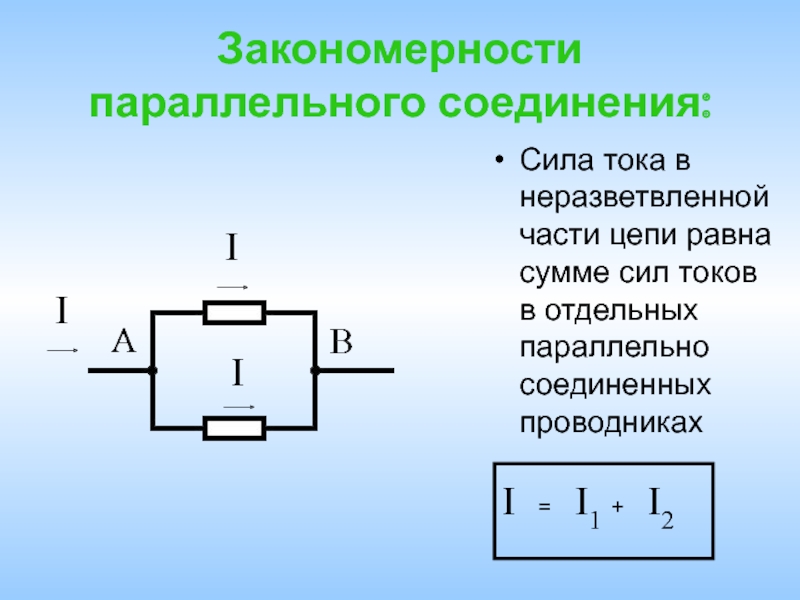 В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте.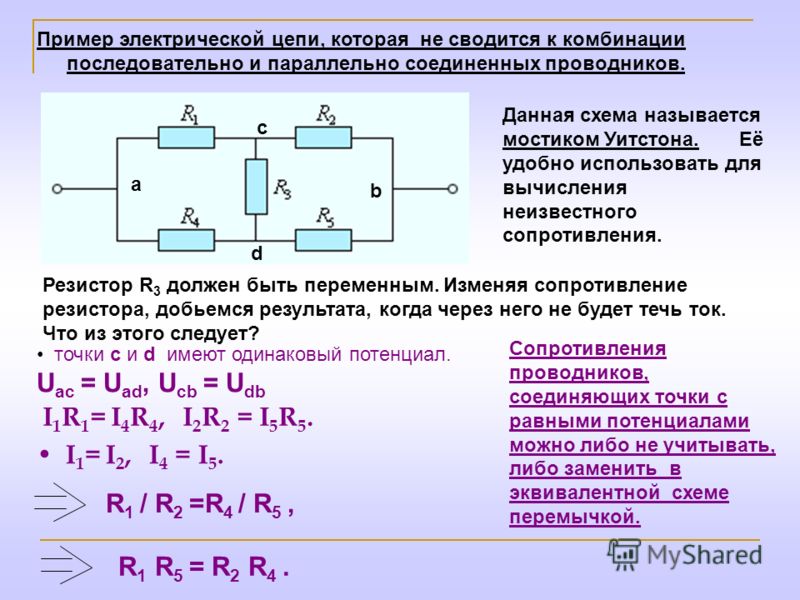 Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

1. Номинал резистора в 16 Ом подойдет.
2. Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

1. Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
2. Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом.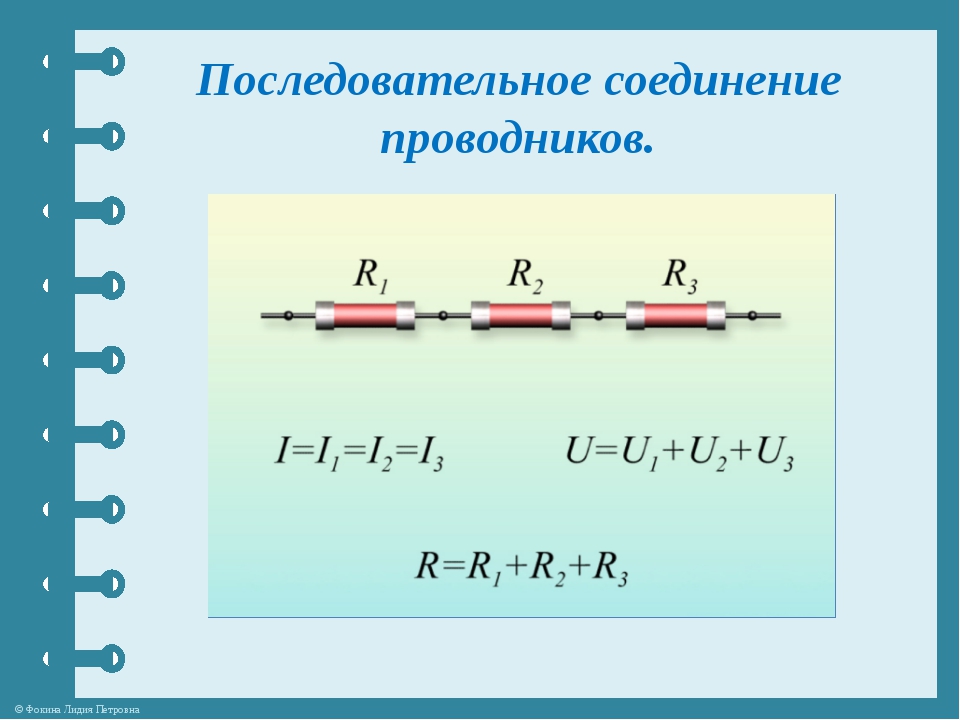 Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

1. Ток не изменяется на участке цепи.
2. Общее напряжение равно сумме падений напряжений на каждом резисторе.
3. Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

1. I = I1 = I2 = 0,5 (А).
2. Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
3. Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Электрическое сопротивление характеризует свойство проводника препятствовать прохождению через него электрического тока. У каждого материала есть свое удельное сопротивление. Это табличная величина, и условно она считается постоянной.

Условно, потому что во многом эта характеристика зависит от внешних условий, например температуры. Сопротивление же какого-либо конкретного элемента (мы будем говорить о резисторах) складывается из многих факторов, например, из геометрических параметров, а когда речь идет о цепи переменного тока, то в расчеты включают также индуктивное и емкостное сопротивление, но об этом мы расскажем позже. Пока же — немного теории.

Закон Ома

В 1826 году немецкий физик Георг Ом на основе своих опытов вывел закон, согласно которому сила тока на участке цепи прямо пропорциональна напряжению, которое к нему приложено, и обратно пропорциональна сопротивлению участка. Из школьного курса мы знаем этот закон:

I=U/R

Позже он был сформулирован и для полной цепи:

I=ε/(R+r)

Где ε — ЭДС источника, R — сопротивление цепи, а r — сопротивление источника.

Мощность прибора

Электрический заряд при своем перемещении совершает работу.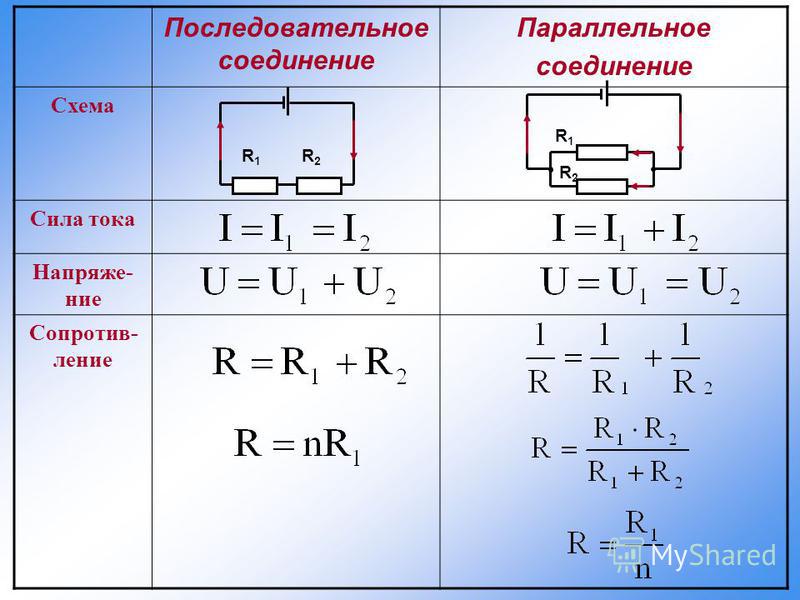 2/R

Последовательное и параллельное соединение

В реальной жизни мы редко имеем дело с одним проводником и одним источником. Достаточно взглянуть в любую принципиальную электрическую схему, например, такую простенькую:

(это схема микроволновки «Электроника»)

можно увидеть, что элементы в схеме соединены по-разному, но мы покажем вам базовые закономерности, которые работают в цепях.

Правила Кирхгофа

Если взять замкнутую электрическую цепь, по которой течет заряд, то можно определенно сказать: он никуда не денется. Сумма всех зарядов, которые текут в одной цепи, всегда одинакова. Это называется законом сохранения заряда, частным случаем общего закона сохранения (как говорится, если в одном месте что-то убудет, в другом непременно прибудет).

Отсюда мы и выводим тот факт, что в каждом узле цепи сумма токов равна нулю. То есть, если ток «приходит» в точку по ветке и «уходит» по двум — значит, первый равен сумме второго и третьего.

На этой картинке мы видим, что I1+I4=I2+I3

Это называется первым правилом Кирхгофа.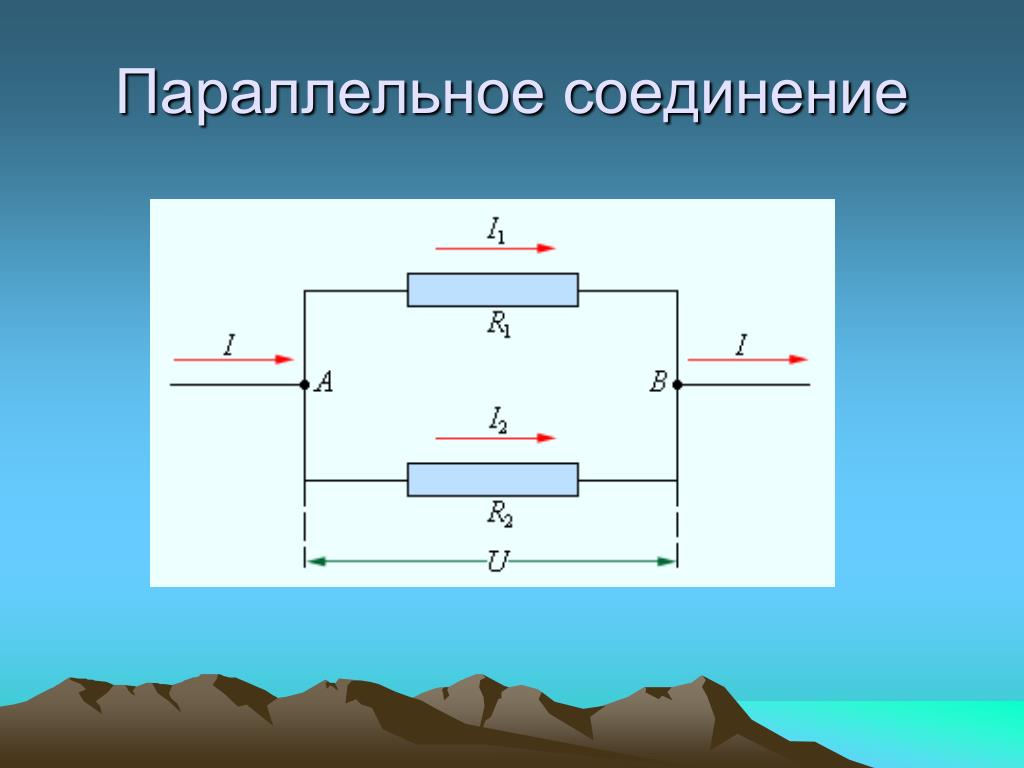

Если наша цепь не будет содержать узлов, значит, ток в ней будет величиной постоянной, а элементы, один за другим поставленные в цепь, будут давать падение напряжения. При этом общее напряжение в цепи останется тем же. Отсюда вытекает второе правило Кирхгофа: сумма напряжений на участках цепи будет равна ЭДС источников тока, входящий в эту цепь. Если у нас источник один, то будет верно равенство:

ε=U1+U2+U3+…+Un

Сумма падений напряжения будет, таким образом, нулевой.

В ситуациях, когда мы имеем дело с переменным током, падение будет наблюдаться на участках с конденсаторами и катушками — в цепях переменного тока у них появляется сопротивление (об этом позже).

Теперь, когда мы познакомились с теоретической частью, можем перейти к более приближенному к суровой реальности вопросу, а именно — расчету последовательного и параллельного соединения резисторов.

Примеры расчетов

Рассчитаем параметры цепей с разным типом соединения.

Как мы видим из рисунка, резисторы соединены один за другим, последовательным способом.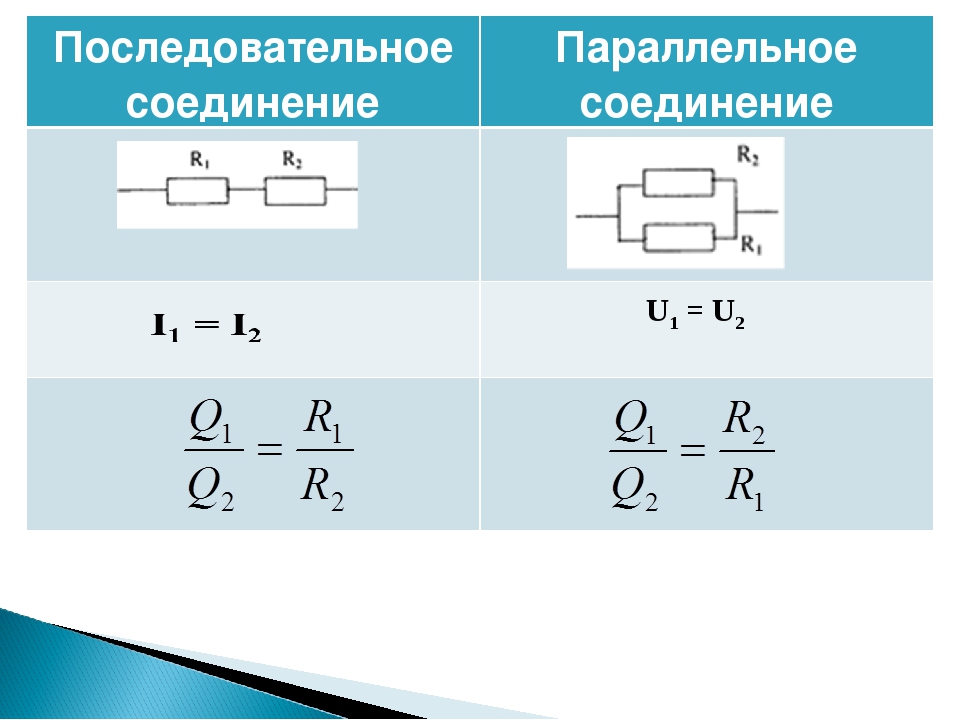 2/R

Исходя из вышеперечисленных закономерностей, вы сможете рассчитывать самые причудливые соединения резисторов, можете попрактиковаться, взяв в библиотеке задачник.

Типы резисторов

Как уже было сказано ранее, элемент, который ставится в цепь для нагрузки, называется резистором. Ставят его для разных целей, главным образом для того, чтобы изменить тот или иной параметр на участке цепи. Например, понизить напряжение или силу тока, чтобы деталь, стоящая за резистором, не сгорела.

Предприятиями выпускается большой ассортимент таких изделий, и их можно по-разному классифицировать. Номинально резистор имеет то сопротивление, которое указано на нем, а по факту оно может зависеть от напряжения в сети (нелинейность), иметь разброс параметра (иногда до 20% доходит). По применяемой технологии резисторы можно разделить на:

1. проволочные;
2. композитные;
3. металлофольговые;
4. угольные;
5. интегральные.

Фактическое сопротивление такого элемента может зависеть от температуры окружающей среды и даже от частоты, если мы имеем дело с переменным током. Дело в том, что часть ассортимента резисторов выполнены по проволочной технологии, то есть фактически они представляют собой мини-катушку. При малых частотах (50 Гц) это в расчет не берется, а вот на высоких (мегагерцы) паразитная индуктивность и индуктивное сопротивление может сказаться на работе схемы. Поэтому при выборе резистора для работы с высокочастотными схемами внимательно смотрите. по какой технологии он сделан. Отдайте предпочтение тонкослойным и композиционным изделиям.

Помимо этого, большое распространение получили переменные резисторы, значение сопротивления которых можно регулировать. Делается это чаще всего отверткой. Необходимость в таких изделиях продиктована разбросом параметров у обычных резисторов, а подстроечный вариант позволяет регулировать сопротивление.

Все вышесказанное актуально для цепей постоянного тока и переменного при невысоких частотах, и все это — при нормальных условиях внешней среды. Расчеты цепей при нарушении этих условий нуждаются в дополнительной корректировке: это связано с ограниченностью действия закона Ома. С чем связаны ограничения? Вот несколько примеров:

1. при сверхнизких температурах многие проводники проявляют такое интересное явление, как сверхпроводимость;
2. также сопротивление может разниться при нагревании;
3. неприменим закон Ома для описания электрического тока в газах;
4. наконец, обычный резистор можно просто пробить высоким напряжением.

Все это прекрасно работает. Не верите — можете поэкспериментировать у себя дома или провести замеры тестером. Например, изучить елочную гирлянду или показания счетчиков при включенных электроприборах (напомню, что в гирлянде лампочки соединены последовательно, а розетки в доме — параллельно). Удачи!

Последовательное и параллельное соединение проводников

Последовательное соединение проводников

Проводники в электрических цепях могут соединяться как последовательным, так и параллельным способами.

Определение 1

В условиях последовательного соединения проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

I1 =I2=I.

Рисунок 1.9.1. Последовательное соединение проводников.

Опираясь на закон Ома, можно заявить, что напряжения U1 и U2 на проводниках равняются следующим выражениям:

U1=IR1, U2=IR2.

Общее напряжение U на обоих проводниках эквивалентно сумме напряжений U1 и U2:

U=U1+U2=I(R1+R2)=IR,

где R является электрическим сопротивлением всей цепи.

Из этого следует, что общее сопротивление R равняется сумме сопротивлений на входящих в данную цепь отдельных проводников:

R=R1+R2.

Данный результат применим для любого количества последовательно соединенных проводников.

Параллельное соединение проводников

Определение 2

В условиях параллельного соединения (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках эквивалентны друг другу, из чего следует:

U1=U2=U.

Совокупность существующих в обоих проводниках токов I1+I2 равняется значению тока в неразветвленной цепи, то есть:

I=I1 + I2.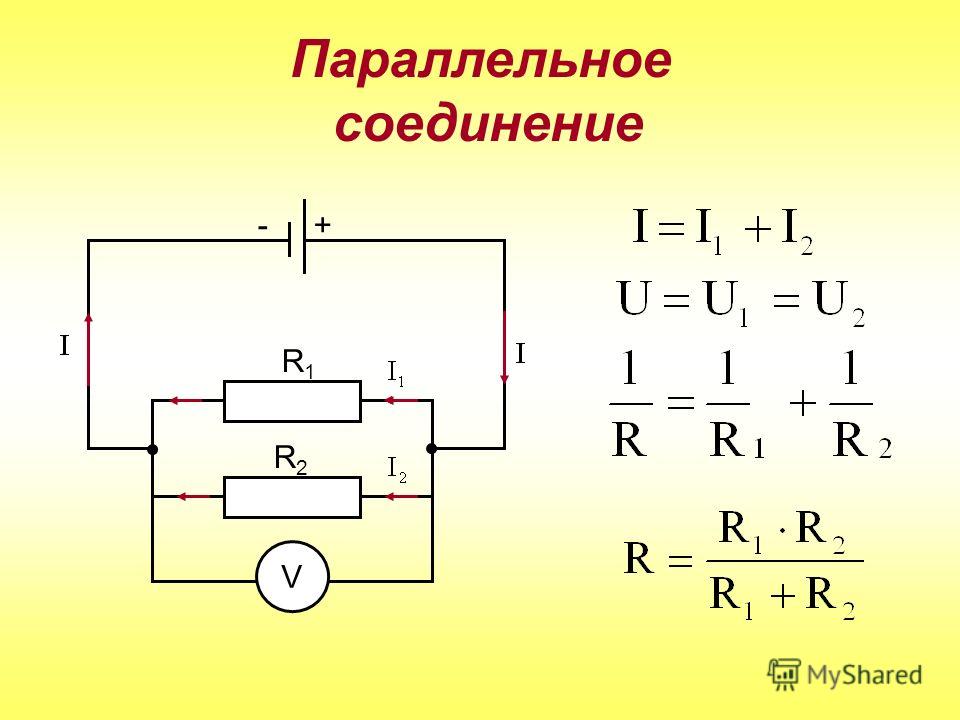

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Данный результат исходит из того, что заряды не могут копиться в точках разветвления, то есть в узлах A и B, цепи постоянного тока.

Пример 1

Так, например, узлу A за время Δt сообщается заряд IΔt, а уходит из узла за то же время зарядI1Δt+I2Δt. Таким образом, подтверждается выражение I=I1 + I2.

Рисунок 1.9.2.Параллельное соединение проводников.

Опираясь на закон Ома, запишем для каждой ветви:

I1=UR1, I2=UR2, I=UR,

где R является электрическим сопротивлением всей цепи, получим

1R=1R1+1R2

Определение 3

В условиях параллельного соединения проводников обратная общему сопротивлению цепи величина, равняется сумме величин, обратных сопротивлениям параллельно включенных проводников.

Полученный вывод может быть применим для любого количества включенных параллельно проводников.

Применение формул для расчета сопротивления сложной цепи

Формулы для последовательного и параллельного соединений проводников дают возможность во многих случаях рассчитывать сопротивление сложной цепи, которая состоит из многих резисторов. На рис. 1.9.3 проиллюстрирована подобная сложная цепь и указана последовательность необходимых для расчета вычислений.

Рисунок 1.9.3. Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах (Ом).

Стоит акцентировать внимание на том факте, что далеко не каждая сложная цепь, состоящая из проводников с разными сопротивлениями, может быть рассчитана с использованием формул для последовательного и параллельного соединений. На рис. 1.9.4 изображена электрическая цепь, которую рассчитать данным методом не получится.

Рисунок 1.9.4. Пример электрической цепи, не сводящейся к комбинации последовательно и параллельно соединенных проводников.

Аналогичные иллюстрированной на рисунке 1. 9.4 цепи, так же, как и цепи с разветвлениями, содержащие более одного источника, можно рассчитать, используя правила Кирхгофа.

Параллельное соединение проводников

Параллельное соединение проводников

Автор: edu1

Методическая копилка —

Физика

Конспект

открытого урока

 физики в 8 классе

по теме:

«Параллельное соединение

проводников»

  Учитель физики  МБОУ  «СОШ№6»

Пчелина Ирина Валентиновна

Тип урока: изучение нового материала.

Цель урока:

-организовать деятельность по изучению, запоминанию и осмыслению темы:

«Параллельное соединение  проводников».

Задачи урока:

Обучающие:

-обеспечить экспериментальное  ознакомление обучаемых с параллельным соединением проводников и закономерностями этого соединения;

-планируется, что к окончанию  урока  обучающиеся будут знать  соотношение при параллельном соединении величин силы тока, напряжения и сопротивления на отдельных участках и во всей цепи;                                                                                                    

-продолжить формирование умений и навыков работы с лабораторным оборудованием.    

Развивающие:

-способствовать развитию у обучаемых исследовательских умений и навыков;

-продолжить работу по формированию умений делать выводы и обобщения на основе результатов проведенного исследования;

Личностные:

-содействовать формированию умения работать в коллективе;

-создать условия для воспитания творческого отношения к учебной деятельности.

Оборудование:

1.Демонстрационный набор для исследования электрических цепей постоянного тока (лаборатория L-микро).

2.Набор для лабораторных работ «Электричество»(L-микро).

3.Компьютер, проектор.

План    урока

1.Актуализация знаний.

2.Изучение  нового.

                          3.Решение устно тестов на закрепление.

                          4.Самостоятельная работа.

5.Домашнее задание.

6.Рефлексия.

Изучая электрические явления, мы встретились с целым рядом физических величин и терминов, некоторые из которых нам были совершенно не знакомы.

А какие же вы теперь уже знаете электрические  величины, характеристики  электрических цепей?

-ответыобучаемых

(электрический ток, сила тока, напряжение, сопротивление).

Какой закон связывает эти величины?  (закон Ома)

Мы уже знаем, что существует множество различных и сложных электрических цепей. Мы начали изучать пока  самые простые  соединения.

Какое соединение проводников вы  знаете?  Что представляет собой последовательное соединение потребителей?

Назовите закономерности последовательного соединения проводников.

Какой же основной недостаток этого соединения?

У вас на столах  лабораторное  оборудование.  Какие измерительные приборы  находятся на столах?

Что измеряют амперметром и как он включается в цепь?

Что измеряют вольтметром?  Как его включают в цепь?

На доске  собрана электрическая цепь последовательного соединения с одним резистором.    А теперь подключим вольтметр для измерения напряжения на резисторе.  Учитель  замыкает цепь.

Объясните,  как вы это делали? Сколько проводников вы подключали к одной клемме резистора или лампочки?

А если бы  вы подключили вместо вольтметра еще один резистор,  как бы он был подключен к первому?

А как  вы думаете, что же мы сегодня на уроке будем изучать?

            Учитель объявляет тему урока:

«Параллельное соединение проводников»

Как же нужно соединить два проводника  параллельно?

Вспомните, как мы давали определение последовательного соединения проводников. И попробуйте сформулировать определение параллельного соединения проводников.

Сегодня на уроке вы проведете исследование  параллельного соединения проводников и выясните законы этого соединения.

У вас на столах необходимые  приборы и алгоритм выполнения  исследования.

Обучающиеся выполняют исследования и делают  выводы о закономерностях параллельного соединения проводников.

I=I₁+I₂            U=U₁=U₂

Любой прибор имеет погрешности измерения.  (Можно повторить абсолютную и относительную погрешность измерения).

Давайте сделаем измерения более точными  цифровыми приборами на доске.

Наши измерения подтверждают сделанные  ранее выводы.

Продолжим наши исследования.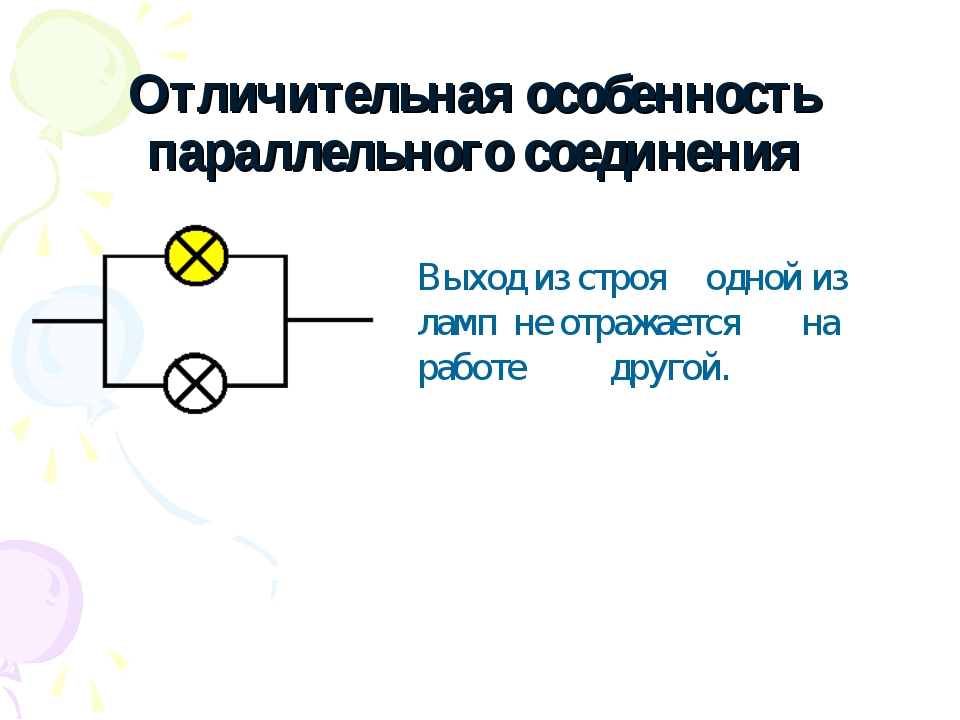

Уберите из цепи один резистор. Существует ли после этого ток в цепи?

Особенностью параллельного соединения является то, что при выключении одного из потребителей все остальные  продолжают  работать.

А теперь выясним, как определяется  сопротивление проводников, соединенных параллельно.

При последовательном соединении проводников как бы увеличивается длина     проводника,  следовательно, увеличивается и сопротивление.

Можно сказать, что при параллельном соединении увеличивается площадь поперечного сечения (показать  пучок проводников). Как  изменится общее сопротивление проводников?

Выведем математическую формулу  для сопротивления.

1/R=1/R₁+1/R₂

Вывод: при параллельном сопротивлении общее сопротивление в цепи уменьшается.

Наши теоретики приготовили  мини-пректы  о параллельном соединении.

А сейчас  на экране  для вас  задания, которые  выполним  устно.На экране 4 теста.

Решение и  разбор  задач из задачника «Самостоятельные и контрольные работы» 8класс Л.А.Кирик.

1.Два резистора сопротивления,  которых 20 Ом и 40 Ом, подключены к батарейке. Сила тока в первом резисторе  0,2А. Какой ток протекает во втором резисторе?

2.Моток проволоки сопротивлением 20 Ом разрезали на две равные части и соединили параллельно. Каково сопротивление соединенной таким образом проволоки?

3.Проводники сопротивлением 15 Ом и 20 Ом соединены  параллельно. Вычислите общее сопротивление соединения.

Самостоятельное выполнение тестов. Взаимопроверка при обмене вариантов с соседом по парте.             

Домашнее задание: § 49. Упражнение 33(1,2,3).

Рефлексия:

Как вам  помогли  опыты разобраться с параллельным соединением проводников?        Как мы подведем итог урока? Что  вы делали сегодня на уроке, что узнали нового, чему научились? (ответы детей).

Возьмите свои карточки и положите их в соответствующий контейнер.

Если вы узнали новое, научились, и вам было интересно, то положите зеленую карточку в  зеленый контейнер.

Если вы что-то не совсем усвоили, но считаете,что дома с учебником вы разберетесь во всем, то опустите желтую  карточку в желтый контейнер.

А если вы ничего не поняли на уроке и вам потребуется дополнительная консультация учителя, то опустите красную карточку в красный контейнер.

Конспект урока физики в 8 классе по теме «Параллельное соединение проводников»

Напряжение при параллельном соединении двух резисторов. Формула для расчета параллельного соединения сопротивлений. Мощность при паралл ельном соединение

Последовательное и параллельное соединение резисторов

Последовательное соединение резисторов

Последовательное соединение
–
это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление Rобщ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение
–
это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление Rобщ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление Rобщ

o
Цепь разбивают на участки с только пареллельным или только последовательным соединением. o
Вычисляют общее сопротивление для каждого отдельного участка.

o
Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

o
Если резисторы соединяются последоватеьно — складывать.

o
Если резисторы соединяются параллельно — использовать условное обозначение «||». o
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1.

Параллельное соединение
резисторов.
При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви
(рис. 26, а). Заменяя

лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или

I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк
(23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R эк

=
1/R 1 + 1/R 2 + 1/R 3
(24)

Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов
:

G эк = G 1 + G 2 +G 3

(25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3
(26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R эк =R 1 R 2 /(R 1 +R 2)

при трех параллельно включенных резисторах

R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R эк = R1 / n
(27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n
(28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Эквивалентные преобразования электрических схем.

Определение последовательного соединения элементов

Последовательное соединение элементов электрической цепи — это такое соединение, когда вывод одного элемента подключен к выводу другого элемента. В этом месте подключения нет узлов. Следующий элемент так же подключен к выводу другого элемента и т.д…

На рисунке ниже показано последовательное подключение четырех сопротивлений.

Формулы для расчета эквивалентного сопротивления при последовательном подключении элементов

При последовательном подключении сопротивлений их эквивалентное сопротивление равно сумме сопротивлений.

R экв =ΣR i =R1 + R2 + R3 +…+Rn

При последовательном соединении индуктивностей их эквивалентное сопротивление равно сумме индуктивностей (без учета взаимной индуктивности).

L экв =ΣL i =L1 + L2 + L3 +…+Ln

При последовательном подключении емкостей обратная величина от эквивалентной емкости равна сумме обратных величин емкостей.

1/С экв =Σ(1/C i)=1/С1+1/С2+1/С3+…+1/Cn

Свойства последовательного соединения элементов

При последовательном подключении элементов через них протекает одинаковый ток.

Согласно закону Ома и второму закону Кирхгофа экивалентное (суммарное) напряжение на участке последовательно соединенных сопротивлений равно сумме напряжений на каждом элементе. U общ = U1+U2+U3+U4 = I·(R1+R2+R3+R4). На данном принципе построены простейшие делители напряжения.

Определение параллельного соединения

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

Смешанное соединение
. Это сочетание последовательного и параллельного соединения элементов.

Эквивалентное сопротивление для последовательно-параллельного соединения элементов:

R экв = R 1 +R 2 R 3 / (R 2 +R 3)

Сложное соединение
. Это соединение, имеющее три и более узлов. В сложных цепях встречаются соединения сопротивлений в виде звезды и треугольника.

Формулы преобразования треугольника сопротивлений в эквивалентную трехлучевую звезду имеют вид:

Формулы обратного преобразования ветвей трехлучевой звезды в эквивалентный треугольник:

,

РЕЖИМЫ РАБОТЫ ИСТОЧНИКОВ ПИТАНИЯ

Различают четыре режима работы источников питания. Е

Режим холостого хода
. В режиме холостого хода концы источника разомкнуты: (R х = ∞).

Этот режим используют для измерения ЭДС источника. Параметры режима холостого хода: I х = 0; R х = ∞; U х = E; (U х =E-Ir; r= 0; U х = E)

Режим короткого замыкания
. В режиме короткого замыкания концы источника соединены накоротко: (R к = 0).

Номинальный режим
. Это режим работы источника питания при номинальных значениях тока и напряжения. Номинальные значения тока и напряжения приводятся в паспорте источника питания.

Согласованный режим
. Это режим работы источника питания с максимальной мощностью Р=Р mах. Такое возможно при условии, когда R вн =R вш. Формула мощности для согласованного режима:

P max = I 2 R = E 2 / 4R.

Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.

Определения

Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:

• Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
• Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.

На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.

Использование параллельного и последовательного соединения проводников

Термины, применяемые к электрическим цепям

Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.

Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.

Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:

• Внешняя часть цепи, где заряды движутся, увлекаемые полем.
• Внутренняя часть цепи, где заряды движутся против напряженности.

Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:

Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.

Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.

При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.

Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников

Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:

Посчитать сопротивления элементов при последовательном и параллельном соединении

Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:

1. При последовательном включении суммируются сопротивления, при параллельном — проводимости:
   1. Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
   2. Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
   3. Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.

Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.

У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.

Пример решения уравнений Кирхгофа

Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:

1. Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
2. Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.

Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.

Возьмем три постоянных сопротивления R1, R2 и R3
и включим их в цепь так, чтобы конец первого сопротивления R1
был соединен с началом второго сопротивления R
2, конец второго — с началом третьего R
3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1
).

Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.

Рис 1

Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:

U = U1 + U2 + U3

где

U1 = IR1 U2 = IR2
и U3 = IR3

или

IR = IR1 + IR2 + IR3

Вынеся в правой части равенства I
за скобки, получим IR = I(R1 + R2 + R3)
.

Поделив теперь обе части равенства на I
, будем окончательно иметь R = R1 + R2 + R3

Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.

Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1
== 10 Ом, R
2 = 20 Ом и R
3 = 50 Ом). Соединим их последовательно (рис. 2
) и подключим к источнику тока, ЭДС которого равна 60 В ( пренебрегаем).

Рис. 2. Пример последовательного соединения трех сопротивлений

Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R
= 10 + 20 + 50 = 80 Ом.

Найдем ток в цепи : 60 / 80
= 0
,75 А

Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U
1 = 0,75х 10 = 7,5 В, U
2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.

Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U
= 7,5+15 + 37,5 = 60 В.

Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.

Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.

Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.

Рис 3. Параллельное соединение сопротивлений

Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1
и I
2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.

Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.

Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.

Значит, до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).

Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1
, а во второй — I
2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I

до разветвления (до точки а).

Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки.
I = I1 + I2

Выражая это формулой, получим

Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи
.

Рассмотрим теперь, каково будет соотношение между токами в ветвях.

Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3
, непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1
и U2 на сопротивлениях R1
и R2, так как он соединен с началом и концом каждого сопротивления.

Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.

Это дает нам право написать, что U = U1 = U2
,

где U — напряжение на зажимах источника тока; U1
— падение напряжения на сопротивлении R1
, U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR
.

Поэтому для каждой ветви можно написать: U1 = I1R1
и U2 = I2R2
, но так как U1
= U2, то и I1R1 = I2R2
.

Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1
т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.

Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей.
Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.

Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1
и R
2, подключенных к источнику тока. Пусть R1
= 10 Ом, R2 = 20 Ом и U = 3 В.

Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:

I1 =
U / R1 = 3 / 10 = 0
,3 А = 300 мА

I
2 =
U / R
2 = 3 / 20 = 0,15 А = 150 мА

Общий ток в цепи I = I1
+I2
= 300 + 150 = 450 мА

Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.

Действительно, R1
== 10 Ом вдвое меньше R
2 = 20 Ом, при этом I1
= 300 мА вдвое больше I2
= 150 мА. Общий ток в цепи I
= 450 мА разветвился на две части так, что большая его часть (I1
= 300 мА) пошла через меньшее сопротивление (R1
= 10 Ом), а меньшая часть (R2
= 150 мА) -через большее сопротивление (R
2 = 20 Ом).

Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.

Рис. 4

Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.

Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления.
Такое сопротивление называется эквивалентным сопротивлением.

Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R
, где I
— ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.

Точно так же для каждой ветви I1 = U1 / R1
, I2 = U2 / R2
, где I1
и I
2 — токи в ветвях; U1
и U2 — напряжение на ветвях; R1
и R2
— сопротивления ветвей.

По закону разветвленной цепи: I = I1 + I2

Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2

Так как при параллельном соединении U = U1 = U2
, то можем написать U / R = U / R1 + U / R2

Вынеся U в правой части равенства за скобки, получим U / R = U
(1 / R1 +
1 / R2
)

Разделив теперь обе части равенства на U
, будем окончательно иметь 1 / R
=
1 / R1 +
1 / R2

Помня, что проводимостью называется величина, обратная сопротивлению
, мы можем сказать, что в полученной формуле 1 / R —
проводимость внешней цепи; 1 / R1
проводимость первой ветви; 1 / R2-
проводимость второй ветви.

На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.

Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.

Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.

Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?

Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.

Чтобы убедиться в этом, рассмотрим следующий пример.

Возьмем три сопротивления R1 = 10 Ом, R2
= 20 Ом и R3
= 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5
).

Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями

Применяя для этой цепи формулу 1 / R
=
1 / R1 +
1 / R2
, можем написать 1 / R
=
1 / R1 +
1 / R2 +
1 / R3
и, подставляя известные величины, получим 1 / R
=
1 /
10 +
1 /
20 +
1 /
60

Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6
Следовательно, эквивалентное сопротивление
R = 6 Ом.

Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений
, т. е. меньше сопротивления R1.

Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.

Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3
равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1
,2 А I
2 = U/R
2 = 12 /
20 = 1
,6 А I
3 = U/R1 = 12 /
60 =
0,2
А

Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3
=1,2 + 0,6 + 0,2 =
2 А.

Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.

I = U
/
R
= 12 / 6 = 2
А

Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.

В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.

На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.

Например, если соединены параллельно два сопротивления R1
и R2
, то формулу 1 / R
=
1 / R1 +
1 / R2
можно преобразовать так: 1/R = (R2 + R1) / R1 R2
и, решая равенство относительно R, получить R = R1
х R2 /
(R1 + R2
), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.

Рабочий лист параллельных цепей постоянного тока серии

— Электрические цепи постоянного тока

Позвольте электронам сами дать вам ответы на ваши собственные «практические проблемы»!

Примечания:

По моему опыту, студентам требуется много практики с анализом цепей, чтобы стать профессионалом. С этой целью инструкторы обычно предоставляют своим ученикам множество практических задач, над которыми нужно работать, и дают ученикам ответы, с которыми они могут проверить свою работу. Хотя такой подход позволяет студентам овладеть теорией схем, он не дает им полноценного образования.

Студентам нужна не только математическая практика. Им также нужны настоящие практические схемы построения схем и использование испытательного оборудования. Итак, я предлагаю следующий альтернативный подход: ученики должны построить свои собственные «практические задачи» с реальными компонентами и попытаться математически предсказать различные значения напряжения и тока. Таким образом, математическая теория «оживает», и учащиеся получают практические навыки, которых они не приобрели бы, просто решая уравнения.

Еще одна причина для следования этому методу практики — научить студентов научному методу : процессу проверки гипотезы (в данном случае математических предсказаний) путем проведения реального эксперимента.Студенты также разовьют реальные навыки поиска и устранения неисправностей, поскольку они время от времени делают ошибки при построении схем.

Выделите несколько минут времени со своим классом, чтобы ознакомиться с некоторыми «правилами» построения схем, прежде чем они начнутся. Обсудите эти проблемы со своими учениками в той же сократической манере, в которой вы обычно обсуждаете вопросы рабочего листа, вместо того, чтобы просто говорить им, что они должны и не должны делать. Я никогда не перестаю удивляться тому, насколько плохо студенты понимают инструкции, представленные в типичном формате лекции (монолог инструктора)!

Примечание для тех инструкторов, которые могут жаловаться на «потраченное впустую» время, необходимое ученикам для построения реальных схем вместо того, чтобы просто математически анализировать теоретические схемы:

Какова цель студентов, посещающих ваш курс?

Если ваши ученики будут работать с реальными схемами, им следует по возможности учиться на реальных схемах.Если ваша цель — обучить физиков-теоретиков, то во что бы то ни стало придерживайтесь абстрактного анализа! Но большинство из нас планирует, чтобы наши ученики что-то делали в реальном мире с образованием, которое мы им даем. «Потраченное впустую» время, потраченное на создание реальных схем, принесет огромные дивиденды, когда им придет время применить свои знания для решения практических задач.

Кроме того, когда студенты создают свои собственные практические задачи, они учатся выполнять первичных исследований , тем самым давая им возможность продолжить свое образование в области электротехники / электроники в автономном режиме.

В большинстве наук реалистичные эксперименты намного сложнее и дороже, чем электрические схемы. Профессора ядерной физики, биологии, геологии и химии хотели бы, чтобы их студенты применяли передовую математику в реальных экспериментах, не представляющих опасности для безопасности и стоивших меньше, чем учебник. Они не могут, но вы можете. Воспользуйтесь удобством, присущим вашей науке, и заставит ваших учеников практиковать математику на множестве реальных схем!

Схемы серии

(часть 1) — Видеолекция по схемам

В начале четвертой главы мы упомянули, что собираемся рассмотреть четыре основных способа построения схем, и первый метод, который мы собираемся рассмотреть, и самый простой — это последовательные схемы.

Техническому специалисту важно разбираться в последовательных схемах. Последовательная схема характеризуется как имеющая только один путь для прохождения тока, поэтому здесь у нас есть источник ЭДС и подключенный компонент, так как здесь внизу у нас есть источник напряжения и компонент, подключенный, в данном случае лампочка, но в обоих В этих случаях существует только один путь для прохождения тока. Есть только один способ протекания тока, нет альтернативных путей, есть только один путь, и это делает его последовательной схемой.

Компоненты серии

соединены таким образом, что существует только один путь для прохождения тока без каких-либо ответвлений в цепи.

Цепи серии

Если каждый электрон, который покидает отрицательный вывод источника питания, имеет только один путь для прохождения тока, тогда схема представляет собой последовательную цепь, и в этом случае вы видите здесь отрицательную сторону этого… и положительную… каждый проходящий электрон имеет только один путь для тока, поэтому мы будем называть его последовательной схемой.В последовательной цепи, поскольку существует только один путь для прохождения тока, через каждый компонент протекает тот же ток, что и через всю цепь. Это важный аспект последовательной цепи. Поскольку существует только один путь для прохождения тока, то это тот же ток, который проходит через R2, R3 и R1, то есть такая же величина. Это похоже на то, как мы говорили об этой гидравлической системе и о том, что в гидравлической системе есть насос, и если это контур, то такое же количество жидкости, которое проходит через него, проходит через это, и это была аналогия с гидравлическим насосом, который мы говорилось в предыдущих уроках.

Теперь, вот эта конкретная схема, у меня есть вопрос по вышеуказанным последовательным схемам … ну, это, очевидно, последовательная схема … в этом случае мы начинаем с нашего источника напряжения, ток входит и проходит через все … ток от источник идет от R2, но теперь у нас есть то, что мы называем разветвлением, и это будет параллельная схема, поэтому схема будет проходить через эту ветвь резисторов здесь, а затем вернуться через эту схему. Это уже не действительно последовательная схема.Это последовательная схема, но здесь есть параллельная ветвь, и позже в этой главе мы рассмотрим параллельные схемы.

Интуитивные отношения

Цепи серии

, этот раздел называется интуитивными отношениями, а интуитивные отношения — это вещи, которые просто имеют смысл, а в последовательных цепях есть некоторые вещи, которые просто интуитивно понятны для последовательной цепи, и в вашем тексте будет немного обсуждения. каждый из них, если неясно, как я это преодолел.Во-первых, все токи в последовательной цепи равны, весь ток через эту конкретную цепь будет одинаковым. Общее сопротивление больше любого сопротивления. Возможно, это очевидно, но общее сопротивление всех компонентов будет больше, чем какое-либо одно сопротивление. Аналогичным образом, общая мощность больше, чем рассеиваемая мощность любого одного компонента, поэтому общая рассеиваемая мощность этой схемы будет больше, чем рассеиваемая мощность любого отдельного компонента. Падение большего сопротивления приводит к большему падению напряжения.Это может быть не так очевидно, но если мы вспомним, что напряжения … помните, мы говорили о том, что такое напряжение с точки зрения закона Ома? Мы сказали, что напряжение равно I, умноженному на R, теперь помните, что у нас есть один и тот же ток, протекающий по всей цепи, поэтому мы говорим, что ток будет таким, мы просто покажем плоскую стрелку, показывающую горизонтальную, плоское соотношение не изменится. Если сопротивление увеличивается, то падение напряжения на этом компоненте будет увеличиваться, и поэтому у нас здесь три компонента, это самые большие 30 кОм, поэтому это будет самое большое падение напряжения, основанное на формуле, согласно которой ток, умноженный на сопротивление, равен напряжению и самое большое сопротивление и все токи равны, падение здесь будет самым большим.

Наконец, последнее интуитивное соотношение, полное напряжение больше, чем напряжение любого компонента, поэтому общее напряжение в этом случае составляет 120 вольт, и оно будет больше, чем падение любого отдельного напряжения, и эти отношения называются интуитивными отношениями для последовательных цепей. схемы.

Математические отношения

Математические соотношения, в последовательной цепи существуют следующие соотношения в отношении текущего напряжения и сопротивления. Первый, у нас есть что-то здесь, называемое IA, в этом случае A имеет отношение к приложенному току, ток, который выходит из нашего источника питания, равен тому, который проходит через R1, R2 и R3, и математически это то, что состояния.Сопротивление, в данном случае RT — это полное сопротивление. В этом случае общее сопротивление всех компонентов будет равно R1 + R2 + R3. Затем у нас есть VT для напряжения, и снова это общее напряжение, в данном случае 120 вольт, но оно будет равно падению напряжения на R1, R2 и R3. Приложенное напряжение в замкнутом контуре равно сумме падений составляющих напряжения. Это важное соотношение известно как закон напряжения Кирхгофа.

Полярность падений напряжения

Когда через резистор протекает ток, на этом резисторе возникает соответствующее падение напряжения.Точка, где ток входит в резистор, является отрицательной, а точка выхода тока будет положительной. Итак, здесь у нас есть источник питания, он подает ток, ток течет в этом направлении, и обратите внимание, что мы находимся здесь на отрицательной клемме, но первая точка здесь, где мы вводим компонент, полярность будет отрицательной, а затем другая сторона будет положительной. Когда мы будем моделировать наши схемы, вы сможете использовать вольтметр, чтобы измерить это и подтвердить, что это действительно так.Полярность здесь будет минус к положительному, минус к положительному, минус к положительному. Это имеет смысл, если вы думаете, что у вас есть батарея, и у вас есть только один компонент, вот этот компонент, и батарея имеет положительный или отрицательный полюс, что полярность в компоненте будет такой же; положительное будет на положительной стороне, отрицательное — на отрицательной. В любом случае, точка, где ток входит в компонент, будет отрицательной стороной компонента.

Уравнения с обратной связью

Следующая процедура может использоваться для создания уравнения с обратной связью для описания последовательной цепи.В этом есть два шага. Сначала пометьте полярность падений напряжения и источников, так что здесь у нас есть полярность, мы делали это ранее нормально, положительный к минусу, а затем минус к положительному минусу к положительному минусу к положительному. Начните с любой точки схемы и запишите напряжения, указывающие полярность, по мере продвижения по петле в любом направлении. Помните, что полярность падения напряжения определяется направлением тока. Наконец, переместитесь по контуру и запишите напряжения на выходных концах компонентов.

Закон Кирхгофа о напряжении

Мы можем это сделать… перейдем к следующему слайду; на следующем слайде немного больше места. На самом деле мы применяем закон напряжения Кирхгофа, и другой способ сформулировать этот закон состоит в том, что алгебраическая сумма всех падений напряжения и всех источников напряжения в любом замкнутом контуре равна нулю. Вы можете сделать это, суммируя полярность каждого компонента в зависимости от того, где этот ток входит в компоненты. Мы смотрим на это и думаем, что ток течет в этом направлении, и мы собираемся оценить полярность на основе того, где ток входит в этот конкретный компонент.Давайте начнем с этого момента. Полярность, при которой ток поступает в источник питания, положительная, поэтому мы начинаем со 120, а затем собираемся суммировать на основе того, где ток входит в компонент. Мы начинаем здесь с положительного значения, затем мы входим в этот компонент, и у нас есть знак «минус», поэтому мы идем -60 и продолжаем около -40, продолжаем примерно до -20. Если мы сложим эти значения, сумма будет равна нулю. Это то, о чем мы упоминали на предыдущем слайде, что сумма всех напряжений по кругу будет равна нулю, и это еще один способ сформулировать закон Кирхгофа.Если бы вы были обычным человеком и хотели бы пойти в другом направлении, вы могли бы сделать это с тем же успехом, но вы должны быть последовательны, если собираетесь это делать. Если мы скажем, что положительные силы движутся в этом направлении, тогда мы начнем с этого момента, и мы начнем с -120, идущим в этом направлении, + 20, +40, а затем +60, но снова сумма будет нулем.

Теперь я собираюсь посоветовать вам прочитать текст по этой конкретной теме, и есть несколько симуляций схем, которые вы можете сделать в мультисимметричной симуляции, чтобы подтвердить это, и вам нужно иметь возможность войти в симуляцию, подключить мультиметр и фактически измерить их. падает и убедитесь сами, что это так и закон Кирхгофа имеет смысл.Если вы алгебраически просуммируете все значения в последовательной схеме, сумма будет равна нулю.

Здесь мы рассмотрели закон напряжения Кирхгофа при решении уравнения замкнутого контура, мы рассмотрели полярность и падение напряжения, мы рассмотрели математические зависимости, мы рассмотрели некоторые интуитивно понятные взаимосвязи между последовательными цепями и мы посмотрели, что такое последовательная цепь. и что не является последовательной схемой. На этом мы завершаем наш раздел, посвященный последовательным схемам.

Видеолекции, созданные Тимом Фигенбаумом в Общественном колледже Северного Сиэтла.

Параллельные схемы

: определение и примеры — научный класс (видео)

Что такое параллельная цепь?

Прежде чем мы перейдем к определению параллельной цепи, давайте сделаем быстрый обзор некоторых основ электрических цепей, в основном напряжения, тока, сопротивления и некоторых законов. Вот те, которые нам понадобятся:

• Напряжение (В, в вольтах — В) — это электрическая сила, ответственная за движение электрического заряда.
• Ток (I, в амперах — А) — это мера движения электрического заряда во времени.
• Сопротивление (R, в Ом) — это мера того, насколько компонент препятствует прохождению тока через него.
• Текущий закон Кирхгофа ( KCL ) — это просто утверждение, что заряд должен сохраняться, и поэтому сумма токов, идущих в цепь узла (точка в цепи, где соединены два или более компонента) должна равняется сумме токов, выходящих из того же узла:

• Закон Кирхгофа о напряжении ( KVL ) гласит, что если вы просуммируете напряжения вокруг любого контура в цепи, вы получите ноль:

Применение определения: пример

Давайте начнем с рассмотрения технического определения параллельной цепи.Говорят, что два или более электрических компонента подключены параллельно, если общий электрический ток, протекающий в параллельной сети, делится между компонентами, а затем повторно объединяется с тем же полным током. Это определение может показаться не самым интуитивным, поэтому посмотрите на последствия. Параллельная цепь будет иметь следующие определяющие характеристики:

• Она начинается с двух или более компонентов, соединенных вместе в схему
• Каждый из компонентов должен иметь только два электрических контакта (провода, токопроводящие дорожки и т. Д.)
• Компоненты соединены таким образом, что все они используют один и тот же узел на каждой стороне компонента
• Напряжение на всех компонентах, подключенных параллельно, одинаковое
• Ток, протекающий в параллельном соединении, такой же, как ток, текущий, и равен сумме отдельных токов, протекающих через каждый компонент

Давайте изобразим это практическое определение следующим образом:

Напряжение на всех трех компонентах (В) одинаково, и уравнение KCL для любого узла (верхнего или нижнего) одинаково, поэтому все три компонента работают параллельно:

Применение определения — другой пример

Когда вы пытаетесь решить, параллельны ли несколько элементов схемы, вы не можете просто посмотреть, как она нарисована; необходимо использовать электрические характеристики параллельной цепи.Вот пример:

Какие компоненты образуют параллельную цепь? Только компоненты №1 и №2, потому что оба они удовлетворяют следующим трем условиям:

• Они используют одни и те же узлы в каждой из своих точек подключения
• У каждого из них одинаковое напряжение (В)
• Ток, протекающий по двум компонентам, разделяется на I1 и I2, а затем снова объединяется.

Мы не можем сказать, что компонент № 3 или компонент № 4 работает параллельно с № 1 и № 2, потому что они не используют одни и те же узлы на каждой стороне, и отдельные напряжения на этих компонентах должны иметь значения меньше V .Мы можем показать это, используя уравнение КВЛ для цикла, который содержит компоненты №2, №3 и №4. Пусть V3 и V4 — напряжения на компонентах №3 и №4 соответственно. Тогда:

Если V3 и V4 не равны нулю (исключения приведены в следующем разделе), то они должны быть меньше V.

Важное исключение

А как насчет использования выключателей, предохранителей и автоматических выключателей в цепях? Они параллельны? Если нет, то нарушаем ли мы принцип параллельной схемы для остальных компонентов? Взгляните на следующую схему, которая представляет собой простую модель некоторых электрических компонентов в автомобиле:

Компоненты (например, фары, радио, дворники и т. Д.)) обозначены как R1, R2 и R3. Слева вы можете увидеть автомобильный аккумулятор на 12 В. Эта конкретная схема также содержит три предохранителя и два переключателя. Фактически, мы можем сказать, что когда переключатели замкнуты, их внутреннее сопротивление приблизительно равно нулю, и поэтому они выглядят как провода. Точно так же предохранители и автоматические выключатели при правильной работе имеют практически нулевое сопротивление, поэтому они тоже выглядят как короткое замыкание. Таким образом, при исправной работе предохранителей и замкнутых переключателях схема теперь выглядит так:

Теперь мы видим, что это действительно параллельная схема.

Другой пример — батареи, подключенные параллельно

В большинстве случаев, когда вы вставляете батареи в устройство, вы подключаете их последовательно. Причина, по которой вы это делаете, заключается в том, что напряжения складываются при последовательном подключении батарей. Например, вы можете вставить четыре батарейки типа АА 1,5 В в устройство, которое работает от 6 В. Что будет, если подключить батареи параллельно? Что ж, сначала вы должны убедиться, что они одинакового напряжения. Почему? Потому что, как мы видели, напряжение на параллельно соединенных компонентах должно быть одинаковым.При параллельном подключении двух батарей разного напряжения могут произойти повреждения. Параллельное подключение нескольких батарей с одинаковым напряжением просто увеличивает общий ток, который вы можете подать в цепь до того, как батареи разрядятся.

Вот конкретное приложение. Предположим, у вас есть прицеп, и электрические системы работают от автомобильного аккумулятора на 12 В. Вы замечаете, что можете отправиться в поход без зарядки аккумулятора в течение 3 дней. Что, если вы захотите продержаться 6 дней? Если вы подключите вторую батарею 12 В параллельно с первой, то каждая батарея будет обеспечивать только половину тока, необходимого для одиночной батареи.Поскольку ток — это движение заряда, вы удвоили количество заряда, доступное для кемпинга! Вот упрощенное изображение:

Резюме урока

Параллельная схема — это схема, которая имеет следующие характеристики: 1) она включает два или более компонентов, каждый из которых имеет ровно два контакта; 2) компоненты используют одни и те же узлов с обеих сторон; 3) все компоненты, включенные параллельно, имеют одинаковое напряжение на них; и 4) ток делит, проходя через компоненты, и затем рекомбинирует на другой стороне до того же полного тока.Цепи показаны как электрически параллельные с использованием закона по току Кирхгофа ( KCL ) и закона по напряжению Кирхгофа ( KVL ), а не по тому, как нарисована цепь. Батареи, соединенные параллельно, должны иметь одинаковое напряжение источника; Срок службы батареи умножается на количество параллельно подключенных батарей.

Самый быстрый словарь в мире: Vocabulary.com

Что такое параллельная цепь — как сделать, характеристики, применение

Поведение схемы полностью зависит от конфигурации ее компонентов схемы.В зависимости от конфигурации подключения эти схемы делятся на параллельные и последовательные схемы. В этом посте раскрывается смысл параллельной схемы, как создать параллельную схему, ее различные характеристики, приложения, преимущества и недостатки.

Что такое параллельная схема

Цепь называется параллельной цепью, когда два или более компонента подключены к одному узлу, и обе стороны компонентов подключены непосредственно к батарее или любому другому источнику.Ток в параллельной цепи имеет два или более путей для прохождения через него.

Наиболее распространенным примером параллельной схемы является подключение автомобильных фар. Если фары автомобиля были включены последовательно, то при выходе из строя одного из огней другой также выключится, что означает потерю запаса прочности.

Рис. 1 — Пример включения фар автомобиля по параллельной цепи

Как сделать параллельную цепь

Два или более компонента схемы подключены к общему источнику напряжения, образуя параллельную схему.На рисунке ниже показана типичная параллельная схема, в которой резисторы (R1, R2, R3, R4) подключены параллельно. Обе стороны резисторов подключены непосредственно к источнику напряжения. Параллельный путь называется ветвью, и напряжение на всех ветвях одинаковое, но ток может быть разным.

Рис. 2 — Принципиальная схема параллельной цепи

Характеристики параллельной цепи

Основные характеристики параллельной схемы перечислены ниже:

Токи ответвления в параллельной цепи

По закону Ома I = E / R. Это означает, что каждый резистор в этой цепи будет потреблять ток от источника. Следовательно, полный ток, потребляемый от источника, равен сумме токов ответвления, и ток, протекающий по каждому пути, зависит от сопротивления ответвления. Однако напряжение остается прежним и создает разность потенциалов на его выводах.

Общий ток (I _t ) можно рассчитать по формуле

I _t = I ₁ + I ₂ + I ₃ +….Я _№

Где (I ₁ + I ₂ + I ₃ +… .I _n ) — токи ответвления

Предположим, что параллельная цепь построена с двумя резисторами (R1 и R2) с разными номиналами (10 Ом и 5 Ом) соответственно. Напряжение 10 В подается на резисторы, в результате чего ток 1 А, потребляемый от батареи через R1, и 2 А, протекающий через R2, выводится из уравнения I = E / R .

Следовательно, два тока ответвления в цепи равны 1А и 2А, что в сумме составляет 3А.

I _t = 1 + 2 = 3A

Сопротивления в параллельной цепи

Суммарное сопротивление любого количества резисторов рассчитывается по формуле

Взаимно R1 = 1 / R1 = 1/10 = 0,1

Взаимно с R2 = 1 / R2 = 1/5 = 0,2

Сумма указанных выше обратных величин = 0,3

R _t = 1 / 0,3 = 3,33 Ом

Питание в параллельной цепи

Когда известны значения полного тока и приложенного напряжения, мощность можно рассчитать по формуле P = EI .В приведенном выше примере приложенное напряжение (E) = 10 В и I = 3 А

.

∴P = 10 x 3 = 30 Вт

Приложения параллельной цепи

Применения параллельных цепей включают:

• Электропроводка к розеткам электропитания в каждом доме выполнена в виде параллельных цепей.
• В источниках питания постоянного тока в автомобильной промышленности используются параллельные схемы.
• Компьютерное оборудование разработано с использованием параллельных схем.

Преимущества параллельной схемы

К преимуществам параллельных цепей относятся:

• На каждый компонент в цепи распределяется одинаковое напряжение.
• На ток не влияет даже при добавлении или удалении дополнительных компонентов (резисторов) из цепи.

Недостатки параллельной цепи

Недостатки параллельных цепей перечислены ниже:

• Конструкция более сложна по сравнению с последовательными схемами.
• Дорого построить.
• Короткое замыкание может произойти случайно при параллельном подключении и быть опасным.
• Даже если один из компонентов неисправен, ток все равно может проходить через цепь.

  Также читают: 
 Цепь серии  - принцип работы, характеристики, применение, преимущество 
  Что такое цифровой вольтметр - как он работает, типы, применение, преимущества 
  Что такое технология Li-Fi - как она работает, применение и преимущества  

Лакшми имеет степень бакалавра в области электроники и связи и имеет опыт работы в RelQ Software в качестве инженера-испытателя и HP в качестве руководителя службы технической поддержки. Она является автором, редактором и партнером Electricalfundablog.

параллельная цепь в предложении — как использовать «параллельную цепь» в предложении

SentencesMobile

• Аналогичный эффект наблюдается с токами в параллельной цепи.
• Измеритель искажений — это фактически измеритель уровня с двумя переключаемыми параллельными цепями на входе.
• Эти группы аккумуляторов соединены параллельно.
• Иногда, особенно в цепях 110 кВ, по параллельной цепи проходят тяговые линии для электрификации железных дорог.
• : Вы спрашиваете о последовательных и параллельных цепях?
• Замыкание клемм в этом случае будет означать, что у вас параллельная цепь.
• Затем можно рассчитать сопротивление между клеммами, используя формулы для последовательных и параллельных цепей.
• Упражнения становятся все более сложными и охватывают основные электрические концепции, такие как ток, напряжение, сопротивление и параллельные цепи.
• Выемки 14, 21 и 28 — это выемки на выводах последовательностей выемок последовательной, последовательно-параллельной и параллельной схемы.
• : Технический ответ состоит в том, что отрезок провода между ногами птицы и птицей образует параллельную цепь.
• В предложении сложно увидеть параллельную схему.
• Параллельная цепь последовательного резистора и конденсатора правильных номиналов образует мост Зобеля.
• :: См. Также Последовательные и параллельные цепи. Предшествующий доклад) 07: 54, 6 мая 2009 г. (UTC)
• Я бы подключил фары параллельно и надежно и безопасно подключил один конец этой параллельной цепи к батарее.
• В этих условиях линейный ток очень мал из-за высокого электрического импеданса параллельной цепи при антирезонансе.
• Правильно ли я заключил, что при сочетании последовательных и параллельных цепей, таких как эта, все три лампы светят одинаково ярко?
• Для номера 5 вам нужно будет знать формулу для параллельных резисторов, которую можно найти в резисторе № Последовательная и параллельная цепи.
• Независимое увеличение в последовательной или параллельной цепи.правда или ложь ? Предыдущие вклады) 17: 51, 17 ноября 2013 г. (UTC)
• В параллельной цепи все компоненты подключены к одинаковому напряжению, и ток делится между различными компонентами в соответствии с их сопротивлением.
• FMMC описывают параллельные схемы: движение обрабатывается параллельно с другими прогнозами движения; если движение соответствует предсказанию — возникает чувство свободы воли.
• В параллельных цепях каждая лампа имеет свою собственную цепь, поэтому все лампы, кроме одной, могут перегореть, а последняя будет продолжать работать.

• Другие предложения ： 1 2 3

Определение параллели по физике.

Примеры параллелей в следующих темах:

• Комбинации конденсаторов: последовательные и параллельные

  • Как и любой другой вид электрического схемного устройства, конденсаторы могут использоваться последовательно и / или параллельно внутри схем.
  • Схема может содержать конденсаторы, которые включены как последовательно, так и параллельно .
  • Однако они оба находятся в параллельно с C3.
  • На этом изображении показаны конденсаторы C1, C2 и так далее до Cn в параллельно .
  • Рассчитайте общую емкость конденсаторов, соединенных последовательно и параллельно

• Параллельные резисторы

  • Резисторы в цепи можно подключать последовательно или параллельно .
  • Следовательно, для каждой цепи с числом $ n $ или резисторами, подключенными параллельно ,
  • $ R_ {n \; ( параллельно )} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} … + \ frac {1} { R_n}. $
  • Три резистора, подключенных по параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление .
  • Рассчитайте общее сопротивление в цепи с резисторами, подключенными параллельно

• Структурный параллелизм в предложении

  • А что такое параллелизм ?
  • Параллельный : Мы можем заплатить маркой, иеной, долларом или фунтом.
  • Параллель : Это время не для слов, а для действий.
  • В некоторых случаях вы должны выяснить, какие части предложения являются параллельными по смыслу, прежде чем делать их параллельными по структуре.
  • Заглавное предложение не является параллельным утверждением .

• Комбинированные схемы

  • Комбинированная цепь может быть разбита на аналогичные части, которые являются последовательными или параллельными .
  • В этом случае сопротивление провода последовательно с другими сопротивлениями, которые находятся в параллельно .
  • На исходном изображении две обведенные кружком части показывают резисторы, которые соединены параллельно .
  • Следующий шаг показывает, что два обведенных резистора соединены параллельно .
  • Эта комбинация из семи резисторов состоит из и параллельных частей.

• Как называются скелетные мышцы

  • Анатомическое расположение пучков скелетных мышц может быть описано как параллель , конвергентная, перистая или сфинктерная.
  • Параллельные мышцы характеризуются пучками, которые проходят на параллелей друг к другу, и сокращение этих групп мышц действует как продолжение сокращения одиночного мышечного волокна.
  • Параллельные мышцы можно разделить на веретенообразные и негибридные типы в зависимости от их формы.
  • Двуглавая мышца плеча является примером веретенообразной параллельной мышцы и отвечает за сгибание предплечья.
  • Fascicles тянут за сухожилие под углом, таким образом, не перемещаясь так далеко на параллельных мышцах во время сокращения.

• Повторение и параллельность

  • Повторение и параллелизм может добавить ясности и выразительности вашей речи.
  • Параллелизм — это особенно эффективный метод, позволяющий структурировать, упорядочивать и сбалансировать вашу речь, помимо прояснения аргументов.
  • Параллелизм работает таким же образом, но без механического повторения слов или идей и вместо этого строит их из аналогичных примеров.
  • Параллелизм — очень эффективный способ избавиться от повторения, предложив множество различных способов выражения одной и той же мысли или идеи.
  • См. Ниже, как в этих двух динамиках использовалось параллелизм :

• Параллельные и перпендикулярные линии

  • Две прямые на плоскости, которые не пересекаются и не касаются в одной точке, называются параллельными линиями .
  • Символ параллель — это $ \ параллель $.
  • $ f (x) $ \ parallel $ $ g (x) $ утверждает, что две прямые на параллельны друг другу.
  • Для двух параллельных прямых $ f (x) $ и $ g (x) $, верно следующее:
  • В 2D две прямые параллельны , если у них есть наклон.

• Конденсатор с параллельными пластинами

  • Конденсатор с параллельными пластинами — это электрический компонент, используемый для хранения энергии в электрическом поле между двумя заряженными плоскими поверхностями.
  • Для этого атома мы сосредоточимся на параллельных конденсаторах с пластинами.
  • Для конденсатора с параллельными пластинами емкость (C) связана с диэлектрической проницаемостью (ε), площадью поверхности (A) и расстоянием между пластинами (d):
  • Краткий обзор параллельных пластин и эквипотенциальных линий с точки зрения электростатики.

• Конденсатор с параллельными пластинами

  • Конденсатор с параллельными пластинами — это конденсатор, который включает в себя две проводящие пластины, каждая из которых соединена с проводами, отделенными друг от друга тонким пространством.
  • Одним из наиболее часто используемых конденсаторов в промышленности и в академической среде является конденсатор с параллельными пластинами .
  • Назначение конденсатора — накапливать заряд, а в конденсаторе с параллельными пластинами и одна пластина принимает на себя избыток положительного заряда, а другая становится более отрицательной.

• Зарядка аккумулятора: последовательные и параллельные ЭДС

  • При последовательном включении источников напряжения их ЭДС и внутренние сопротивления складываются; в параллелях они остаются прежними.
  • Когда используется более одного источника напряжения, они могут быть подключены последовательно или параллельно , аналогично резисторам в цепи.
  • Но общее внутреннее сопротивление уменьшено, так как внутренние сопротивления находятся в параллелях .
  • Таким образом, параллельное соединение может производить больший ток.
  • Параллельные комбинации часто используются для подачи большего тока.

.