Последовательное соединение конденсаторов распределение напряжений. Последовательное соединение конденсаторов
Содержание:
В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.
Последовательное соединение
При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = i c1 = i c2 = i c3 = i c4 .
В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Q общ = Q 1 = Q 2 = Q 3 .
Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Q общ = Q 1 = Q 2 = Q 3 .
Если рассмотреть три конденсатора С 1 , С 2 и С 3 , соединенные в последовательную цепь, то выясняется, что средний конденсатор С 2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.
Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью.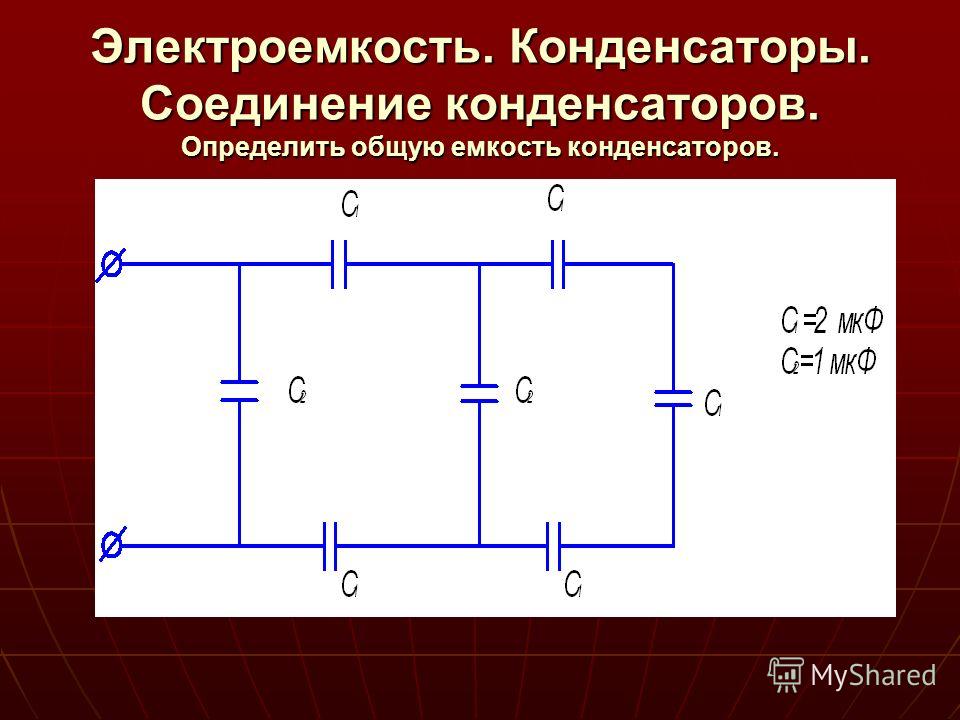 Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.
Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.
Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/C общ = 1/C 1 + 1/C 2 + 1/C 3 .
Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.
Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.
Смешанное соединение
Параллельное соединение конденсаторов
Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами.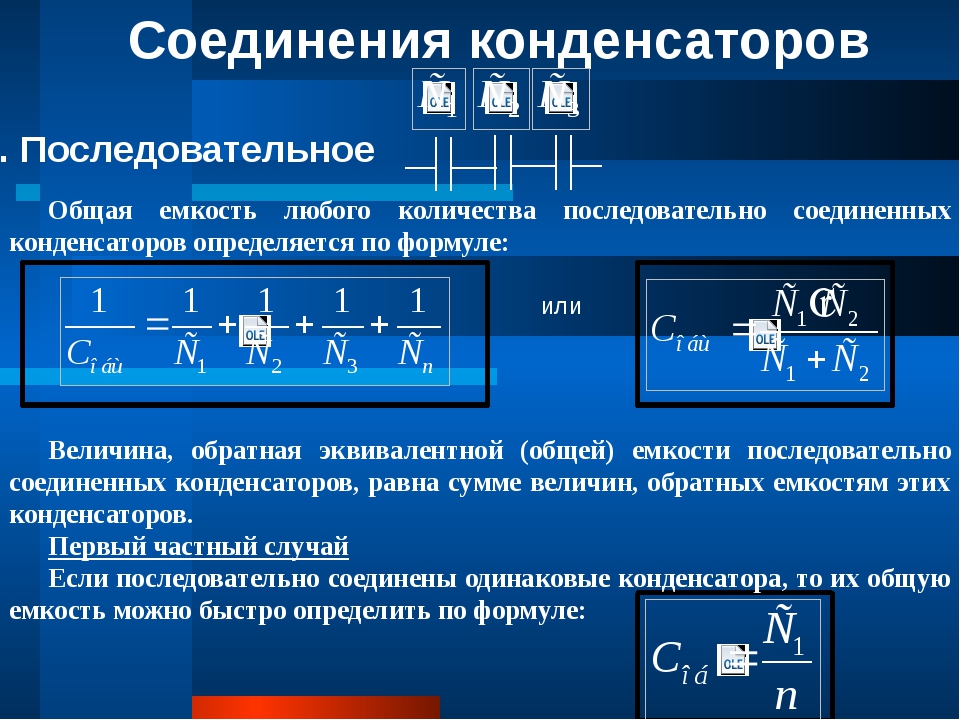 Таким образом в одной точке может соединяться сразу несколько элементов.
Таким образом в одной точке может соединяться сразу несколько элементов.
Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, С общ = С 1 + С 2 + С 3 .
Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.
Практически все электрические цепи включают в себя емкостные элементы.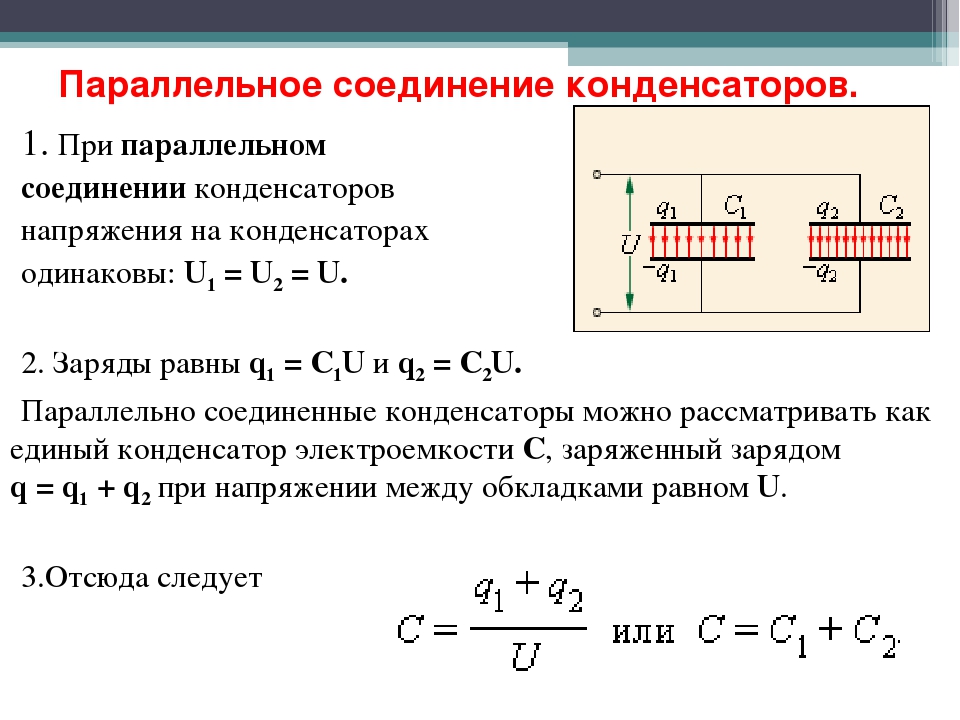 Соединение конденсаторов между собой выполняют по схемам. Их необходимо знать как при расчетах, так и при выполнении монтажа.
Соединение конденсаторов между собой выполняют по схемам. Их необходимо знать как при расчетах, так и при выполнении монтажа.
Последовательное соединение
Конденсатор, а в просторечии – «ёмкость», та деталь, без которой не обходится ни одна электрическая или электронная плата. Даже в современных гаджетах он присутствует, правда, уже в измененном виде.
Вспомним, что представляет собой этот радиотехнический элемент. Это накопитель электрических зарядов и энергии, 2 проводящие пластины, между которыми расположен диэлектрик. При прикладывании к пластинам источника постоянного тока через устройство кратковременно потечет ток, и оно зарядится до напряжения источника. Его емкость используют для решения технических задач.
Само это слово произошло задолго до того, как придумали устройство. Термин появился ещё тогда, когда люди считали, что электричество – это что-то типа жидкости, и ею можно наполнить какой-нибудь сосуд. Применительно к конденсатору – он неудачен, т.к. подразумевает, что прибор может вместить только конечное количество электричества. Хотя это и не так, но термин остался неизменным.
подразумевает, что прибор может вместить только конечное количество электричества. Хотя это и не так, но термин остался неизменным.
Чем больше пластины, и меньше расстояние между ними, тем больше . Если его обкладки соединить с каким-либо проводником, то через этот проводник произойдет быстрый разряд.
В координатных телефонных станциях с помощью этой особенности происходит обмен сигналами между приборами. Длина импульсов, необходимых для команд, таких как: «соединение линии», «ответ абонента», «отбой», регулируется величиной ёмкости установленных в цепь конденсаторов.
Единица измерения ёмкости – 1 Фарад. Т.к. это большая величина, то пользуются микрофарадами, пикофарадами и нанофарадами, (мкФ, пФ, нФ).
На практике, выполнив последовательное соединение, можно добиться увеличения прикладываемого напряжения. В этом случае поданное напряжение получают 2 внешние обкладки собранной системы, а обкладки, находящиеся внутри, заряжаются с помощью распределения зарядов. К таким приемам прибегают, когда под рукой не оказывается нужных элементов, зато есть детали других номиналов по напряжению.
К таким приемам прибегают, когда под рукой не оказывается нужных элементов, зато есть детали других номиналов по напряжению.
К участку, имеющему 2 последовательно соединенных конденсатора, рассчитанных на напряжение 125 В, можно подключить питание 250 В.
Если для постоянного тока, конденсатор является препятствием за счет своего диэлектрического промежутка, то с переменным – все иначе. Для токов разных частот, подобно катушкам и резисторам, сопротивление конденсатора будет меняться. Токи высокой частоты он пропускает хорошо, а для их собратьев низкой частоты создает барьер.
У радиолюбителей есть способ – через емкость 220-500 пФ к радиоприемнику подключают вместо антенны сеть освещения напряжением 220 В. Ток с частотой 50 Гц он отфильтрует, а токи высокой частоты пропустит. Это сопротивление конденсаторов легко рассчитать по формуле для емкостного сопротивления:RC =1/6*f*C.
- Rc – емкостное сопротивление, Ом;
- f – частота тока, Гц;
- C – емкость данного конденсатора, Ф;
- 6 – округленное до целой части число 2π.

Но не только прикладываемое напряжение к цепи можно изменить, пользуясь подобной схемой включения. Так добиваются изменений емкостей при последовательных соединениях. Для легкости запоминания придумали подсказку, что общее значение емкости, полученное при выборе подобной схемы, получается всегда меньше меньшей из двух, включенных в цепочку.
Если так соединить 2 детали одинаковой ёмкости, то их общее значение будет вдвое меньше каждой из них. Расчеты последовательных соединений конденсатора можно выполнить по приведенной ниже формуле:
Собщ = С1*С2/С1+С2,
Пусть С1=110 пФ, а С2=220 пФ, тогда Собщ = 110×220/110+220 = 73 пФ.
Не стоит забывать про простоту и удобство монтажа, а также обеспечение качественной работы собранного устройства или оборудования. В последовательных соединениях у емкостей должен быть 1 производитель. А если детали всей цепочки будут одной партии выпуска, то проблем с эксплуатацией созданной цепи не будет.
Параллельное соединение
Накопители электрического заряда постоянной емкости, различают:
- керамические;
- бумажные;
- слюдяные;
- металлобумажные;
- электролитические конденсаторы.

Их делят на 2 группы: низковольтные и высоковольтные. Применяют их в фильтрах выпрямителей, для связи между низкочастотными участками цепей, в блоках питания различных устройств и т.д.
Конденсаторы переменной ёмкости тоже существуют. Они нашли свое предназначение в настраиваемых колебательных контурах теле- и радиоприемников. Емкость регулируется за счет изменения положения пластин относительно друг друга.
Рассмотрим соединение конденсаторов, когда их выводы соединятся попарно. Подобное включение подходит для 2 или более элементов, рассчитанных на одно и то же напряжение. Номинальное напряжение, которое указано на корпусе детали, превышать нельзя. В противном случае произойдет пробой диэлектрика, и элемент выйдет из строя. Но в цепь, где присутствует напряжение меньше номинального, конденсатор включать можно.
Параллельным включением конденсаторов можно добиться увеличения общей ёмкости. В некоторых устройствах необходимо обеспечить большое накопление электрического заряда. Существующих номиналов не хватает, приходится выполнять параллели и использовать то, что есть под рукой. Определить общую величину полученного соединения просто. Для этого нужно просто сложить величины всех используемых элементов.
Существующих номиналов не хватает, приходится выполнять параллели и использовать то, что есть под рукой. Определить общую величину полученного соединения просто. Для этого нужно просто сложить величины всех используемых элементов.
Для вычисления емкостей конденсаторов формула имеет вид:
Собщ = С1+С2, где С1 и С2 – емкость соответствующих элементов.
Если С1=20 пФ, а С2=30 пФ, то Собщ = 50 пФ. Деталей в в параллели может быть n-ое количество.
На практике такое соединение находит применение в специальных устройствах, используемых в энергетических системах, и на подстанциях. Их монтируют, зная, как соединить конденсаторы для увеличения емкости, в целые блоки из батарей.
Для того чтобы поддерживать равновесие реактивной мощности как в энергоснабжающих установках, так и в установках энергопотребителей, существует необходимость включать в работу компенсирующие устройства реактивной мощности (УКРМ). Для снижения потерь и регулировки напряжения в сетях при расчетах устройства необходимо знать величины реактивных сопротивлений конденсаторов, используемых в установке.
Случается, что возникает необходимость вычислить по формуле напряжение на конденсаторах. В этом случае будем исходить из того, что С=q/U, т.е. отношение заряда к напряжению. И если величина заряда – q, а ёмкость – C, можем получим искомое число, подставляя значения. Она имеет вид:
Смешанное соединение
При расчете цепи, представляющей собой совокупность рассмотренных выше комбинаций, поступают так. Сначала ищем в сложной цепи конденсаторы, которые соединены между собой либо параллельно, либо последовательно. Заменив их эквивалентным элементом, получим более простую схему. Потом в новой схеме с участками цепи проводим те же манипуляции. Упрощаем до тех пор, пока не останется только параллельное или последовательное соединение. Их рассчитывать мы уже научились в этой статье.
Параллельно-последовательное соединение применимо для увеличения емкости, батареи или для того, чтобы приложенное напряжение не превышало рабочего напряжения конденсатора.
Практически на любой электронной плате применяются конденсаторы, устанавливаются они и в силовых схемах. Для того чтобы компонент мог выполнять свои функции, он должен обладать определёнными характеристиками. Иногда возникает ситуация, когда необходимого элемента нет в продаже или его цена неоправданно завышена.
Для того чтобы компонент мог выполнять свои функции, он должен обладать определёнными характеристиками. Иногда возникает ситуация, когда необходимого элемента нет в продаже или его цена неоправданно завышена.
Выйти из сложившегося положения можно, используя несколько элементов, а необходимые характеристики получают, применяя параллельное и последовательное соединения конденсаторов между собой.
Немного теории
Конденсатор — пассивный электронный компонент, с переменной или постоянной величиной ёмкости, которое предназначено для накопления заряда и энергии электрического поля.
При выборе этих электронных компонентов руководствуются двумя основными характеристиками:
Условное обозначение неполярного постоянного конденсатора на схеме, показано на рис. 1, а. Для полярного электронного компонента дополнительно отмечают положительный вывод — рис. 1, б.
Способы соединения конденсаторов
Составление батарей конденсаторов позволяет изменить суммарную ёмкость или рабочее напряжение. Для этого могут применяться такие способы соединения:
Для этого могут применяться такие способы соединения:
- последовательное;
- параллельное;
- смешанное.
Последовательное соединение
Последовательное подключение конденсаторов показано на рис. 1, в. Применяют такое соединение в основном для увеличения рабочего напряжения. Дело в том, что диэлектрики каждого из элементов расположены друг за другом, поэтому при таком соединении напряжения складываются.
Суммарная ёмкость
последовательно соединённых элементов можно рассчитать по формуле, которая для трёх компонентов будет иметь вид, показанный на рис. 1, е.
После преобразования в более привычную для нас форму, формула примет вид рис. 1, ж.
Если, соединённые последовательно, компоненты имеют одинаковые ёмкости, то расчёт значительно упрощается. В этом случае суммарную величину можно определить, разделив номинал одного элемента на их количество. Например, если требуется определить, какова ёмкость при последовательном соединении двух конденсаторов по 100 мкФ, то эту величину можно рассчитать, разделив 100 мкФ на два, то есть суммарная ёмкость равна 50 мкФ.
Максимально упростить расчёты последовательно соединённых компонентов
, позволяет использование онлайн-калькуляторов, которые без проблем можно найти в сети.
Параллельное подключение
Параллельное подключение конденсаторов показано на рис. 1, г. При таком соединении рабочее напряжение не изменяется, а ёмкости складываются. Поэтому для получения батарей большой ёмкости, используют параллельное соединение конденсаторов. Калькулятор для расчёта суммарной ёмкости не понадобится, так как формула имеет простейший вид:
С сум = С 1 + С 2 + С 3.
Собирая батарею для запуска трёхфазных асинхронных электродвигателей, часто применяют параллельное соединение электролитических конденсаторов. Обусловлено это большой ёмкостью этого типа элементов и небольшим временем запуска электродвигателя. Такой режим работы электролитических компонентов допустим, но следует выбирать те элементы, у которых номинальное напряжение минимум в два раза превышает напряжение сети.
Смешанное включение
Смешанное подключение конденсаторов — это сочетание параллельного и последовательного соединений
.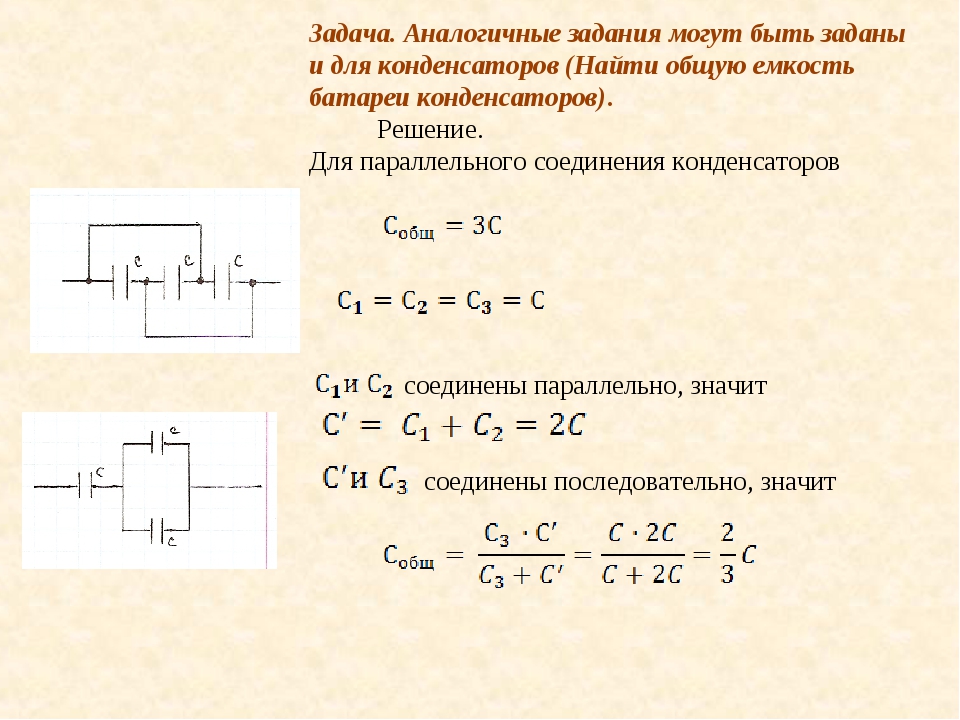
Схематически такая цепочка может выглядеть по-разному. В качестве примера рассмотрим схему, изображённую на рис. 1, д. Батарея состоит из шести элементов, из которых С1, С2, С3, соединены параллельно, а С4, С5, С6 — последовательно.
Рабочее напряжение можно определить сложением номинальных напряжений С4, С5, С6 и напряжения одного из параллельно подключённых конденсаторов. Если параллельно соединённые элементы имеют разные номинальные напряжения, то для расчёта берут меньшее из трёх.
Для определения суммарной ёмкости, схему разбивают на участки с одинаковым соединением элементов, производят расчёт для этих участков, после чего определяют общую величину.
Для нашей схемы последовательность вычислений следующая:
- Определяем ёмкость параллельно соединённых элементов и обозначаем её С 1-3.
- Рассчитываем ёмкость последовательно соединённых элементов С 4-6.
- На этом этапе можно начертить упрощённую эквивалентную схему, в которой вместо шести элементов изображаются два — С 1-3 и С 4-6.
 Эти элементы схемы соединены последовательно. Остаётся произвести расчёт такого соединения и мы получим искомую.
Эти элементы схемы соединены последовательно. Остаётся произвести расчёт такого соединения и мы получим искомую.
В жизни подробные знания о смешанном соединении могут только пригодится радиолюбителям.
Электрические конденсаторы широко используются в радиоэлектронной аппаратуре. Они лидируют по количеству применения в блоках аппаратуры и по некоторым критериям уступают лишь резисторам. Конденсаторы присутствуют в любом электронном устройстве и их потребность в современной электронике постоянно растет. Наряду с имеющейся широкой номенклатурой, продолжаются разработки новых типов, которые имеют улучшенные электрические и эксплуатационные характеристики.
Что такое конденсатор?
Конденсатором называется элемент электрической цепи, который состоит из проводящих электродов, изолированных друг от друга диэлектриком.
Конденсаторы отличают по емкости, а именно по отношению заряда к разности потенциалов, который передается этим зарядом.
В международной системе СИ за единицу емкости принимают емкость конденсатора
с возрастанием потенциала на один вольт при сообщении заряда в один кулон. Эта единица называется фарадой. Она слишком велика для применения в практических целях. Поэтому принято использовать более мелкие единицы измерения, такие как пикофарад (пФ), нанофарад (нФ) и микрофарад (мкФ).
Эта единица называется фарадой. Она слишком велика для применения в практических целях. Поэтому принято использовать более мелкие единицы измерения, такие как пикофарад (пФ), нанофарад (нФ) и микрофарад (мкФ).
Группы по виду диэлектрика
Диэлектрики применяют для изоляции пластин друг от друга. Они изготавливаются из органических и неорганических материалов. Нередко, в качестве диэлектрика, применяют оксидные пленки металлов.
По виду диэлектрика элементы делят на группы:
- органические;
- неорганические;
- газообразные;
- оксидные.
Элементы с органическим диэлектриком изготавливают путем намотки тонких лент специальной бумаги или пленки. Также применяют комбинированный диэлектрик
с фольговыми или металлизированными электродами. Такие элементы могут быть как высоковольтные (свыше 1600 В), так и низковольтные (до 1600 В).
В изделиях с неорганическим диэлектриком используют керамику, слюду, стекло и стеклокерамику, стеклоэмаль. Их обкладки состоят из тонкого слоя металла, который нанесен на диэлектрик путем металлизации. Бывают высоковольтные, низковольтные и помехоподавляющие.
Их обкладки состоят из тонкого слоя металла, который нанесен на диэлектрик путем металлизации. Бывают высоковольтные, низковольтные и помехоподавляющие.
В качестве газообразного диэлектрика используют сжатый газ (фреон, азот, элегаз), воздух или вакуум. По характеру изменения емкости и выполняемой функции такие элементы бывают постоянными и переменными.
Наибольшее распространение получили элементы с вакуумным диэлектриком. Они имеют большие удельные емкости (по сравнению с газообразным диэлектриком) и более высокую электрическую прочность. Элементы с вакуумным диэлектриком обладают стабильностью параметров
при температурных изменениях окружающей среды.
Область применения – передающие устройства, работающие на коротких, средних и длинных волнах диапазонов с частотой до 30-80 МГц.
Элементы с оксидным диэлектриком бывают:
- общего назначения;
- пусковые;
- импульсные;
- неполярные;
- высокочастотные;
- помехоподавляющие.

Диэлектриком является оксидный слой, который наносится на анод электрохимическим путем.
Условные обозначения
Элементы обозначаются по сокращенной и полной системе.
При сокращенной системе наносятся буквы и цифры
, где буквой обозначается подкласс, цифрой — группа в зависимости от применяемого диэлектрика. Третий элемент указывает регистрационный номер типа изделия.
При полном условном обозначении указываются параметры и характеристики в следующей последовательности:
- условное обозначение конструктивного исполнения изделия;
- номинальное напряжение изделия;
- номинальная емкость изделия;
- допустимое отклонение емкости;
- температурная стабильность емкости изделия;
- номинальная реактивная мощность изделия.
Подбор номинала
Конденсаторы могут соединяться друг с другом различными способами.
На практике нередко возникают ситуации, когда при монтаже схемы или замене неисправного элемента, приходится использовать ограниченное количество радиодеталей. Не всегда удается подобрать элементы нужного номинала.
Не всегда удается подобрать элементы нужного номинала.
В этом случае приходится применять последовательное и параллельное соединение конденсаторов.
При параллельной схеме соединения, их суммарная величина составит сумму емкостей
отдельных элементов. При этой схеме подключения все обкладки элементов соединяются по группам. Один из выводов каждого элемента соединяется в одну группу, а другой вывод в другую группу.
При этом напряжение на всех обкладках будет одинаково
, потому что все группы подключены к одному источнику питания. Фактически получается одна емкость, суммарной величины всех емкостей в данной цепи.
Чтобы получить большую емкость, применяют параллельное соединение конденсатора.
Например, необходимо подключить двигатель с тремя фазами к однофазной сети 220 В. Для рабочего режима двигателя необходима емкость величиной в 135 мкФ. Ее найти очень трудно, но можно получить, применив параллельное соединение элементов на 5, 30 и 100 мкФ. В результате сложения получаем необходимую единицу в 135 мкФ.
Последовательно соединение конденсаторов
Последовательное соединение конденсаторов используют, если необходимо получить емкость меньшую емкости элемента. Такие элементы выдерживают более высокие напряжения. При последовательном соединении конденсаторов, обратная величина общей емкости равняется сумме обратных величин отдельных элементов. Для получения требуемой величины нужны определенные конденсаторы, последовательное соединение которых даст необходимую величину.
При последовательном соединении конденсаторов каждый его вывод соединяется с одним выводом другого элемента. Получается некая цепочка из последовательно соединенных конденсаторов, где крайние выводы подключаются к источнику питания.
Емкость общей батареи всегда меньше минимальной емкости элементов, входящих в нее. То есть, половина от емкости каждой из этих емкостей.
При последовательном соединении конденсаторов увеличивается расстояние между обкладками элементов.
Например, при последовательном соединении двух элементов напряжением 200 В можно смело включать в схему напряжением до 1000 В.
Данный метод соединения используется гораздо реже
, потому что емкости такой величины и рабочего напряжения можно приобрести в магазинах.
Таким образом, зная принцип общего расчета параллельного и последовательного соединения конденсаторов, всегда можно выйти из затруднительного положения, имея под рукой ограниченное количество номиналов.
Под последовательным соединением подразумевают случаи, когда два или больше элемента имеют вид цепи, при этом каждый из них соединяется с другим только в одной точке. Зачем конденсаторы так размещаются? Как это правильно сделать? Что необходимо знать? Какие особенности последовательное соединение конденсаторов имеет на практике? Какая формула результата?
Что необходимо знать для правильного соединения?
Увы, но здесь не всё так легко сделать, как может показаться. Многие новички думают, что если на схематическом рисунке написано, что необходим элемент на 49 микрофарад, то достаточно его просто взять и установить (или заменить равнозначным). Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно. Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим. Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет.
Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно. Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим. Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет.
Зачем так делают?
Когда с ними проводятся такие манипуляции, то электрические заряды на обкладках отдельных элементов будут равны: КЕ=К 1 =К 2 =К 3 . КЕ — конечная емкость, К — пропускаемое значение конденсатора. Почему так? Когда заряды поступают от источника питания на внешние обкладки, то на внутренних может быть осуществлен перенос величины, которая является значением элемента с наименьшими параметрами. То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ — то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ. Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула:
То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ — то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ. Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула:
- ОЕ — общая емкость;
- Н — напряжение;
- КЕ — конечная емкость.
Что ещё необходимо знать, чтобы правильно соединить конденсаторы?
Для начала не забывайте, что кроме ёмкости они ещё обладают номинальным напряжением. Почему? Когда осуществляется последовательное соединение, то напряжение распределяется обратно пропорционально их ёмкостям между ними самими. Поэтому использовать такой подход имеет смысл только в тех случаях, когда любой конденсатор сможет предоставить минимально необходимые параметры работы. Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну. Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов. Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы.
Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну. Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов. Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы.
Ток при последовательном соединении
Из-за того, что у него существует только один возможный путь протекания, он будет иметь одно значение для всех конденсаторов. При этом количество накопленного заряда везде обладает одинаковым значением. От емкости это не зависит. Посмотрите на любую схему последовательного соединения конденсаторов. Правая обкладка первого соединена с левой второго и так далее. Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи. Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток. И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться.
Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи. Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток. И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться.
Падение напряженности и общая емкость
Каждый элемент понемногу рассеивает напряжение. Учитывая, что емкость ему обратно пропорциональна, то чем она меньше, тем большим будет падение. Как уже упоминалось ранее, последовательно соединённые конденсаторы обладают одинаковым электрическим зарядом. Поэтому при делении всех выражений на общее значение можно получить уравнение, которое покажет всю емкость. В этом последовательное и параллельное соединение конденсаторов сильно разнятся.
Пример № 1
Давайте воспользуемся представленными в статье формулами и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300. Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ.
Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300. Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ.
Пример № 2
Давайте, чтобы закрепить наработки, решим ещё одну задачу. Имеется 100 конденсаторов. Емкость каждого элемента составляет 2 мкФ. Необходимо определить их общую емкость. Нужно их количество умножить на характеристику: 100*2=200 мкФ. Итак, общая емкость конденсатора при последовательном соединении составляет 200 микрофарад. Как видите, ничего сложного.
Заключение
Итак, мы проработали теоретические аспекты, разобрали формулы и особенности правильного соединения конденсаторов (последовательно) и даже решили несколько задачек. Хочется напомнить, чтобы читатели не упускали из внимания влияние номинального напряжения. Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект.
Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект.
Электрическая емкость (страница 1)
Решение:
При перемещении пластины емкость конденсатора в данный момент времени определяется той частью площади пластин, по которой они перекрывают друг друга. В моменты времени t1 и t2 площади
где l=10 см-длина стороны пластины. В эти моменты времени конденсатор имеет емкости
а заряды на его пластинах
11 Найти заряд, который нужно сообщить двум параллельно соединенным конденсаторам с емкостями C1 = 2 мкФ и С2=1 мкФ, чтобы зарядить их до разности потенциалов V=20кВ.
Решение:
Общий заряд параллельно соединенных конденсаторов
12 Два одинаковых плоских конденсатора соединены параллельно и заряжены до разности потенциалов V0 = 6 В. Найти разность потенциалов V между пластинами конденсаторов, если после отключения конденсаторов от источника тока у одного конденсатора уменьшили расстояние между пластинами вдвое.
Найти разность потенциалов V между пластинами конденсаторов, если после отключения конденсаторов от источника тока у одного конденсатора уменьшили расстояние между пластинами вдвое.
Решение:
13 Два конденсатора с емкостями С1 = 1 мкФ и С2 = 2мкФ зарядили до разностей потенциалов V1=20B и V2 = 50 В. Найти разность потенциалов V после соединения — конденсаторов одноименными полосами.
Решение:
14 Конденсатор емкости C1 = 20 мкФ, заряженный до разности потенциалов V1 = 100B, соединили параллельно с заряженным до разности потенциалов V1=40 В конденсатором, емкость которого С2 неизвестна (соединили одноименно заряженные обкладки конденсаторов). Найти емкость С2 второго конденсатора, если разность потенциалов между обкладками конденсаторов после соединения оказалась равной V=80 В.
Решение:
15 Конденсатор емкости С1=4мкФ, заряженный до разности потенциалов V1 = 10B, соединен параллельно с заряженным до разности потенциалов V2 = 20 В конденсатором емкости С2 = 6 мкФ (соединили разноименно заряженные обкладки конденсаторов). Какой заряд окажется на пластинах первого конденсатора после соединения?
Какой заряд окажется на пластинах первого конденсатора после соединения?
Решение:
Заряды конденсаторов до их соединения q1 = C1V1 и q2 = C2V2. После соединения разноименно заряженных обкладок конденсаторов общий заряд q = |q2-q1| = (C1 + C2)V и заряд первого конденсатора где V-разность потенциалов между обкладками конденсаторов после соединения; отсюда
16 Конденсатор, заряженный до разности потенциалов V1 = 20 В, соединили параллельно с заряженным до разности потенциалов V2 = 4 В конденсатором емкости С2 = 33 мкФ (соединили разноименно заряженные обкладки конденсаторов). Найти емкость С1 первого конденсатора, если разность потенциалов между обкладками конденсаторов после их соединения V=2 В.
Решение:
После соединения разноименных обкладок общий заряд q = CV равен разности зарядов q1 = C1V1 и q2 = C2V2 отдельных конденсаторов, где С=С1 + С2 — общая емкость после соединения. Таким образом,
Таким образом,
17 Конденсатор емкости С1 = 1 мкФ, заряженный до разности потенциалов V1 = 100B, соединили с конденсатором емкости С2 = 2 мкФ, разность потенциалов V2 на обкладках которого неизвестна (соединили разноименно заряженные обкладки конденсаторов). Найти разность потенциалов V2, если разность потенциалов между обкладками конденсаторов после соединения оказалась равной V=200 В.
Решение:
До соединения заряды первого и второго конденсаторов
После соединения разноименных обкладок общий заряд
Двойной знак мы здесь поставили потому, что заранее не известно, какой из зарядов, q2 или q1 больше; отсюда
Решение со знаком минус соответствует случаю, когда знаки зарядов на пластинах первого конденсатора после соединения пластин не меняются, а со знаком плюс-случаю, когда эти знаки становятся обратными. Так как в нашем случае , а величина |V2| должна быть всегда положительной, то существует лишь одно решение-со знаком плюс. В результате |V2| = 350 В.
В результате |V2| = 350 В.
18 Два проводящих шара с радиусами R1 и R2 расположены так, что расстояние между ними во много раз больше радиуса большего шара. На шар радиуса R1 помещен заряд q. Каковы будут заряды на шарах после соединения их проводником, если второй шар не был заряжен? Емкостью проводника, соединяющего шары, пренебречь.
Решение:
19 Два проводящих шара с радиусами R1 = 8см и R2 = 20 см, находящихся на большом расстоянии друг от друга, имели электрические заряды q1=40 нКл и q2=— 20 нКл. Как перераспределятся заряды, если шары соединить проводником? Емкостью проводника, соединяющего шары, пренебречь.
Решение:
Соединение шаров проводником эквивалентно параллельному соединению конденсаторов. После соединения
20 Два проводящих шара с радиусами R1 = 10см и R2 = 5см, заряженных до потенциалов φ1=20B и φ2=10В, соединяются проводником. Найти поверхностные плотности зарядов на шарах σ1 и σ2 после их соединения. Расстояние между шарами велико по сравнению с их радиусами. Емкостью проводника, соединяющего шары, пренебречь.
Найти поверхностные плотности зарядов на шарах σ1 и σ2 после их соединения. Расстояние между шарами велико по сравнению с их радиусами. Емкостью проводника, соединяющего шары, пренебречь.
Решение:
Заряды на шарах до и после соединения Общий потенциал шаров после соединения определим из условия сохранения заряда
Заряды на первом и втором шарах после соединения
Поверхностные плотности зарядов на шарах
21 Плоский воздушный конденсатор, заряженный до разности потенциалов V0 = 800 В, соединили параллельно с таким же по размерам незаряженным конденсатором, заполненным диэлектриком. Какова диэлектрическая проницаемость e диэлектрика, если после соединения разность потенциалов между пластинами конденсаторов оказалась равной V=100В?
Решение:
22 Найти емкость С трех плоских воздушных конденсаторов, соединенных параллельно. Размеры конденсаторов одинаковы: площадь пластины S=314 см2, расстояние между пластинами d=1 мм. Как изменится емкость трех конденсаторов, если пространство между пластинами одного конденсатора заполнить слюдой (диэлектрическая проницаемость ε1 = 7), а другого — парафином (диэлектрическая проницаемость ε2 = 2)?
Как изменится емкость трех конденсаторов, если пространство между пластинами одного конденсатора заполнить слюдой (диэлектрическая проницаемость ε1 = 7), а другого — парафином (диэлектрическая проницаемость ε2 = 2)?
Решение:
Емкость трех конденсаторов без диэлектрика При заполнении двух конденсаторов диэлектриками емкость трех конденсаторов
23 В заряженном плоском конденсаторе, отсоединенном от источника тока, напряженность электрического поля равна Е0. Половину пространства между пластинами конденсатора заполнили диэлектриком с диэлектрической проницаемостью ε (толщина диэлектрика равна расстоянию между пластинами). Найти напряженность электрического поля Е в пространстве между пластинами, свободном от диэлектрика.
Решение:
Если d-расстояние между пластинами и С0 — емкость конденсатора без диэлектрика, то разность потенциалов между пластинами конденсатора (без диэлектрика) и заряд на пластинах Конденсатор, половина которого заполнена диэлектриком, можно рассматривать как два соединенных параллельно конденсатора (рис. 341), причем один не содержит диэлектрика и имеет емкость а в другом все пространство между пластинами заполнено диэлектриком, и поэтому его емкость Полная емкость конденсатора, половина которого заполнена диэлектриком, При отключенном источнике тока заряд на пластинах сохраняется, поэтому разность потенциалов между пластинами V=q/C, и напряженность электрического поля в пространстве между пластинами, свободном от диэлектрика,
341), причем один не содержит диэлектрика и имеет емкость а в другом все пространство между пластинами заполнено диэлектриком, и поэтому его емкость Полная емкость конденсатора, половина которого заполнена диэлектриком, При отключенном источнике тока заряд на пластинах сохраняется, поэтому разность потенциалов между пластинами V=q/C, и напряженность электрического поля в пространстве между пластинами, свободном от диэлектрика,
24 Два последовательно соединенных конденсатора с емкостями C1 = 1 мкФ и С2 = 3 мкФ подключены к источнику тока с напряжением V =220 В. Найти напряжение на каждом конденсаторе.
Решение:
Если V1 и V2 — напряжения на первом и втором конденсаторах, то V= V1 + V2, а заряды на них одинаковы и равны
q=C1V1=C2V2; отсюда
При последовательном соединении конденсаторов на конденсаторе меньшей емкости напряжение больше, чем на конденсаторе большей емкости.
25 Два последовательно соединенных конденсатора с емкостями C1 = 1 мкФ и С2 = 2 мкФ подключены к источнику тока с напряжением V =900 В. Возможна ли работа такой схемы, если напряжение пробоя конденсаторов Vпр = 500 В?
Решение:
Напряжения на первом и втором конденсаторах (см. задачу 24). Работать при указанном в условии задачи напряжении пробоя конденсаторов нельзя, ибо произойдет пробой первого, а затем и второго конденсаторов.
26 Два последовательно соединенных конденсатора подключены к источнику тока с напряжением V= 200 В (рис. 79). Один конденсатор имеет постоянную емкость C1 = 0,5 мкФ, а другой — переменную емкость С2 (от Cmin = 0,05 мкФ до Сmах = 0,5 мкФ). В каких пределах изменяется напряжение на переменном конденсаторе при изменении его емкости от минимальной до максимальной?
Решение:
При изменении емкости переменного конденсатора С2 от Cmin до Сmax, напряжение на нем V изменяется в пределах (см. задачу 24)
задачу 24)
27 При последовательном соединении трех различных конденсаторов емкость цепи С0 = 1 мкФ, а при параллельном соединении емкость цепи С=11мкФ. Найти емкости конденсаторов С2 и С3, если емкость конденсатора С1 = 2 мкФ.
Решение:
28 При последовательном соединении трех различных конденсаторов емкость цепи С0 = 0,75 мкФ, а при параллельном соединении емкость цепи С = 7 мкФ. Найти емкости конденсаторов С2 и С3 и напряжения на них V2 и V3 (при последовательном соединении), если емкость конденсатора C1 = 3 мкФ, а напряжение на нем V1 = 20B.
Решение:
При последовательном соединении конденсаторов имеем
при параллельном
Из этих уравнений находим
Согласно теореме Виета С2 и С3 должны быть корнями квадратного уравнения
Решая его, найдем
Заряды на всех конденсаторах при последовательном соединении равны между собой:
29 Три последовательно соединенных конденсатора с емкостями С1 = 100пФ, С2 = 200 пФ, С3 = 500 пФ подключены к источнику тока, который сообщил им заряд q=10нКл.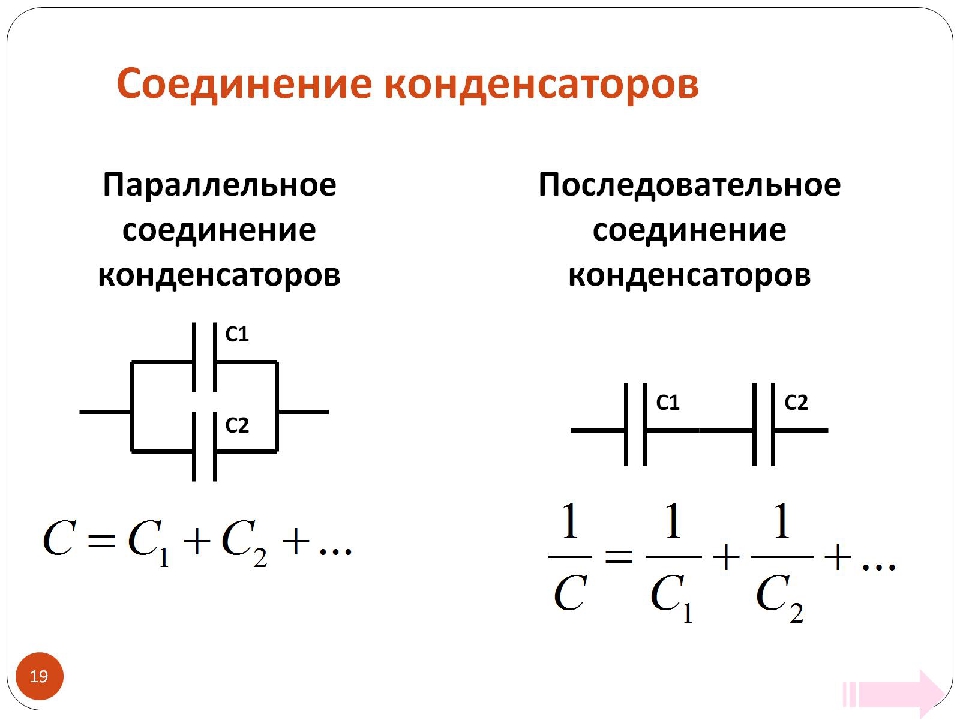 Найти напряжения на конденсаторах V1, V2 и V3, напряжение источника тока V и емкость всех конденсаторов С0.
Найти напряжения на конденсаторах V1, V2 и V3, напряжение источника тока V и емкость всех конденсаторов С0.
Решение:
При последовательном соединении конденсаторов заряд каждого конденсатора равен q, поэтому
Напряжение источника тока равно полному напряжению на всех конденсаторах:
Так как при последовательном соединении
то
30 Три последовательно соединенных конденсатора с емкостями С1=0,1мкФ, С2 = 0,25 мкФ и С3 = 0,5 мкФ подключены к источнику тока с напряжением V =32 В. Найти напряжения V1, V2 и V3 на конденсаторах.
Решение:
31 Два одинаковых воздушных конденсатора емкости С=100пФ соединены последовательно и подключены к источнику тока с напряжением V= 10 В. Как изменится заряд на конденсаторах, если один из них погрузить в диэлектрик с диэлектрической проницаемостью ε = 2?
Решение:
При последовательном соединении конденсаторов заряды на конденсаторах равны. До погружения одного из них в диэлектрик заряд на каждом конденсаторе
До погружения одного из них в диэлектрик заряд на каждом конденсаторе
после погружения одного из них в диэлектрик заряды конденсаторов будут
Учитывая, что
Изменение заряда на конденсаторах
32 Два плоских воздушных конденсатора с одинаковыми емкостями соединены последовательно и подключены к источнику тока. Пространство между пластинами одного из конденсаторов заполняют диэлектриком с диэлектрической проницаемостью ε = 9. Во сколько раз изменится напряженность электрического поля Е в этом конденсаторе?
Решение:
Первоначальная напряженность электрического поля в каждом конденсаторе
где d-расстояние между пластинами конденсатора. После заполнения одного конденсатора диэлектриком напряженность электрического поля в нем
Отношение напряженностей
33 Решить предыдущую задачу для случая, когда конденсаторы после зарядки отключаются от источника тока.
Решение:
После отключения конденсатора от источника тока и заполнения его диэлектриком заряд на нем не изменяется:
Напряженность электрического поля в конденсаторе, заполненном диэлектриком,
Отношение напряженностей
34 Два плоских воздушных конденсатора с одинаковыми емкостями С=10пФ соединены последовательно. Насколько изменится емкость конденсаторов, если пространство между пластинами одного из них заполнить диэлектриком с диэлектрической проницаемостью ε = 2?
Насколько изменится емкость конденсаторов, если пространство между пластинами одного из них заполнить диэлектриком с диэлектрической проницаемостью ε = 2?
Решение:
Изменение емкости соединенных конденсаторов
35 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d введена параллельно обкладкам проводящая пластинка, размеры которой равны размерам обкладок, а ее толщина намного меньше d. Найти емкость конденсатора с проводящей пластинкой, если пластинка расположена на расстоянии l от одной из обкладок конденсатора.
Решение:
После введения пластинки образовалось два последовательно включенных конденсатора с емкостями
(рис. 342). Их общую емкость определим из соотношения
где С-первоначальная емкость конденсатора. Таким образом, после введения пластинки при любом ее положении С0 = С.
36 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d введена параллельно обкладкам проводящая пластинка, размеры которой равны размерам обкладок, а толщина dп = d/3
Решение:
Введение проводящей пластинки между обкладками конденсатора приводит к образованию двух последовательно включенных конденсаторов с расстояниями между обкладками d1 и d2 и емкостями
(рис.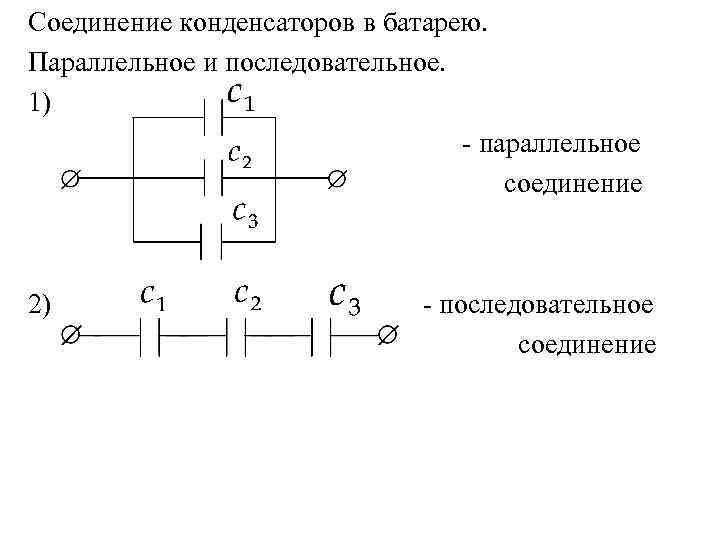 343). Их общую емкость находим из соотношения
343). Их общую емкость находим из соотношения
При -первоначальная емкость конденсатора.
37 Плоский воздушный конденсатор заряжен до разности потенциалов V0 = 50 В и отключен от источника тока. После этого в конденсатор параллельно обкладкам вносится проводящая пластинка толщины dп= 1 мм. Расстояние между обкладками d=5 мм, площади обкладок и пластинки одинаковы. Найти разность потенциалов V между обкладками конденсатора с проводящей пластинкой.
Решение:
Емкости конденсатора до и после внесения проводящей пластинки толщины dп (см. задачу 36)
Заряд конденсатора, отключенного от источника тока, не изменяется:
отсюда разность потенциалов между обкладками конденсатора после внесения проводящей пластинки
38 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d вводится параллельно обкладкам диэлектрическая пластинка толщины d1<d/ Диэлектрическая проницаемость пластинки равна ε, площади обкладок и пластинки одинаковы и равны S.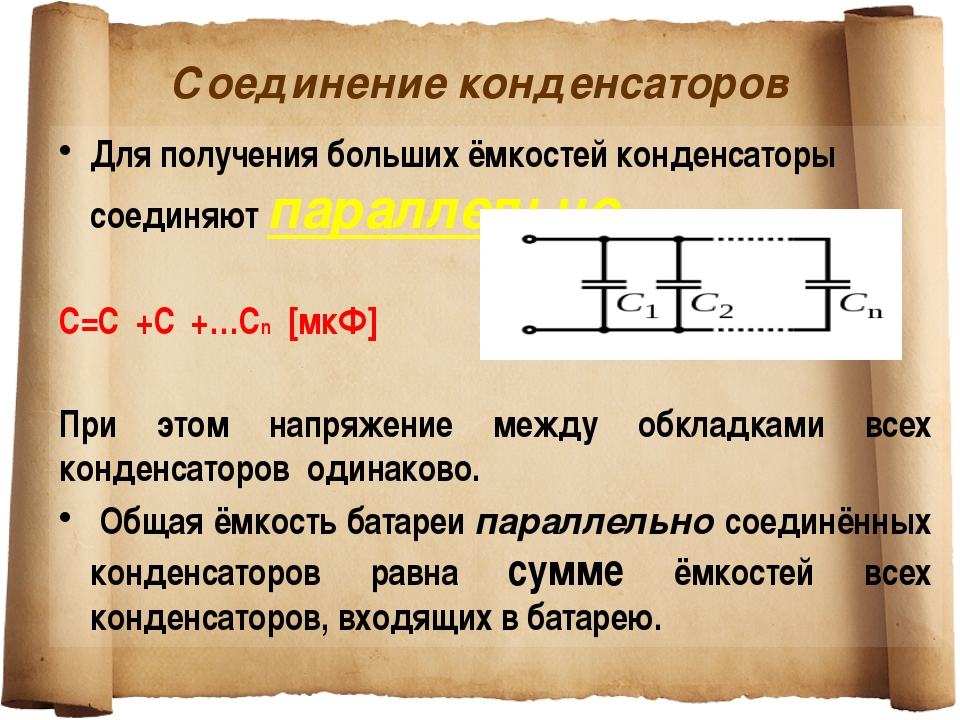 Найти емкость конденсатора с диэлектрической пластинкой.
Найти емкость конденсатора с диэлектрической пластинкой.
Решение:
Задачи по теме «Соединение конденсаторов» | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Тема:
Задачи по электродинамике
- Четыре конденсатора имеют емкости 2пФ, 5пФ, 10пФ и 20пФ. Определить их общую емкость при параллельном и последовательном соединении.
- Конденсатор переменной емкости состоит из 12 пластин, площадь каждой из которых составляет 10 см2. Воздушный зазор между соседними пластинами составляет 1 мм. Какую максимальную емкость имеет конденсатор?
- Два конденсатора электроемкостью 2 мкФ и 4 мкФ соединены последовательно и заряжены так, что разность потенциалов между крайними точками соединения составляет 60 В. Найти заряд и разность потенциалов каждого конденсатора.
- Два конденсатора, электроемкости которых 4 мкФ и 1 мкФ, соединены последовательно и заряжены от источника тока.
 Разность потенциалов на соединении составляет 220 В. Определить заряд и разность потенциалов на каждом конденсаторе.
Разность потенциалов на соединении составляет 220 В. Определить заряд и разность потенциалов на каждом конденсаторе. - Разность потенциалов на обкладках конденсатора электроемкостью 6 мкФ составляет 127 В. Его соединили параллельно с конденсатором, имеющим электроемкость 4 мкФ и разность потенциалов 220 В. Определить электроемкость батареи и разность потенциалов между ее выводами.
Ответы:
1. 37 пФ; 1,18 пФ. Материал с сайта http://worldofschool.ru
2. ≈ 102 пФ.
3. 8 • 10-5Кл; 40 В; 20 В.
4. 176 • 10-6 Кл; 44 В; 176 В.
5. 10 мкФ; 164 В.
На этой странице материал по темам:
Решение задач по конденсаторам
Смешанное соединение конденсаторов решение задач
Чотири конденсатори мають ємность 2пф 5пф 10пф 20пф
Работа по теме смешанное соединение конденсаторов
Краткий конспект на тему соединения конденсаторов
Глава 11.
 Емкость . Введение в электронику
Емкость . Введение в электронику
ЦЕЛИ
После изучения этой главы студент должен быть в состоянии:
• Объяснить, что такое емкость.
• Знать, в каких единицах измеряется емкость.
• Знать различные типы конденсаторов.
• Уметь определить общую емкость последовательной и параллельной цепей.
• Дать объяснение постоянной времени RC и ее связи с емкостью.
Емкость позволяет сохранять энергию в электростатическом поле. Емкость существует всегда, когда два проводника разделены изолятором.
В этой главе рассматривается емкость и ее применения в цепях постоянного тока. Более подробно емкость рассмотрена в главе 15.
11-1. ЕМКОСТЬ
Емкость — это способность устройства хранить электрическую энергию в электростатическом поле. Конденсатор — это устройство, которое обладает определенной емкостью. Конденсатор состоит из двух проводников, разделенных изолятором (рис. 11-1).
Конденсатор состоит из двух проводников, разделенных изолятором (рис. 11-1).
Рис. 11-1. Конденсатор состоит из двух обкладок (проводников), разделенных диэлектриком (изолятором).
Проводники называются обкладками, а изолятор — диэлектриком. На рис. 11-2 даны схематические изображения конденсаторов.
Рис. 11-2. Схематическое обозначение конденсаторов.
Когда источник тока подсоединен к конденсатору, ток течет до тех пор пока конденсатор не зарядится. Конденсатор заряжается избытком электронов на одной обкладке (отрицательный заряд) и дефицитом электронов на другой обкладке (положительный заряд).
Диэлектрик предотвращает перемещение электронов между обкладками. Как только конденсатор зарядится, ток прекращается. Напряжение на конденсаторе равно напряжению источника тока.
Заряженный конденсатор может быть отключен от источника тока и использован как источник энергии.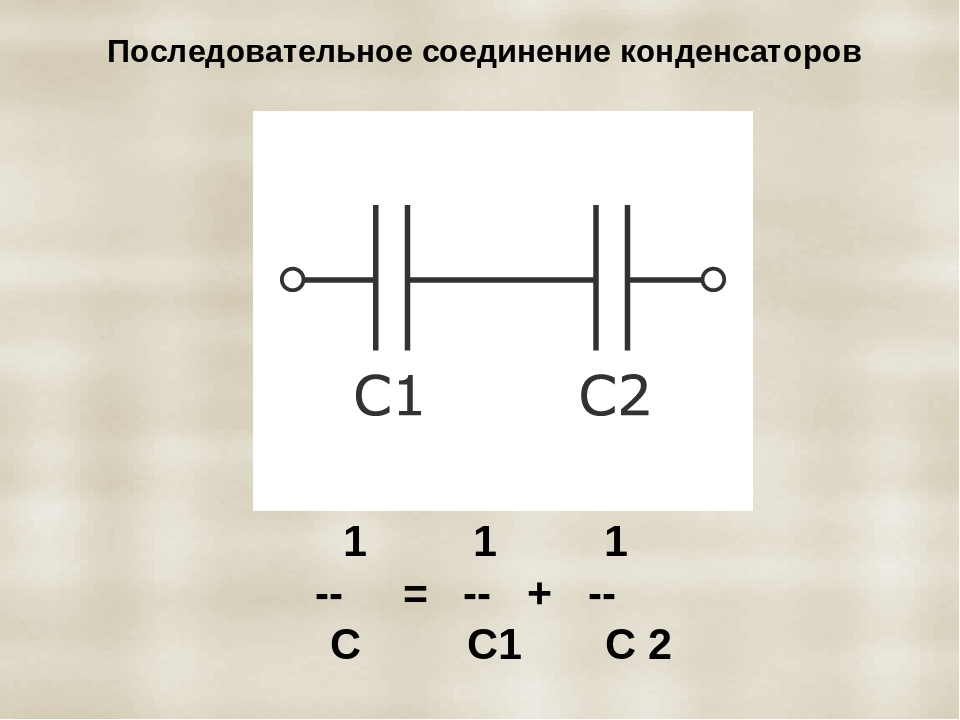 Однако как только конденсатор теряет энергию, напряжение на нем резко падает. В цепи постоянного тока конденсатор после начальной зарядки работает как разомкнутая цепь.
Однако как только конденсатор теряет энергию, напряжение на нем резко падает. В цепи постоянного тока конденсатор после начальной зарядки работает как разомкнутая цепь.
Разомкнутая цепь — это цепь с бесконечным сопротивлением.
Предупреждение: так как конденсатор при отключении от источника тока может удерживать потенциал источника тока достаточно долго, обращайтесь со всеми конденсаторами, как с заряженными. Никогда не касайтесь обоих выводов конденсатора рукой до тех пор, пока не разрядите его путем закорачивания выводов. Конденсатор в цепи может удерживать потенциал неопределенно долго, если у него нет пути для разряда.
Количество энергии, сохраняемой в конденсаторе, пропорционально размеру конденсатора. Конденсаторы, используемые в учебных лабораториях, обычно малы и наносят небольшой удар током при разряде через тело. Однако если конденсатор большой и заряжен высоким напряжением, его удар может быть смертельным. С заряженными конденсаторами следует обращаться так же, как и с любыми другими источниками тока.
С заряженными конденсаторами следует обращаться так же, как и с любыми другими источниками тока.
Основной единицей измерения емкости является фарада (Ф). Фарада — это такая емкость, которая может сохранить 1 кулон заряда при напряжении на конденсаторе 1 вольт.
Фарада слишком большая единица для обычных целей, и поэтому обычно используются микрофарады (мкФ) и пикофарады (пФ). Для обозначения емкости используется буква С.
1 микрофарада = 0,000001 или 1/1000 000 фарады,
1 пикофарада = 0,000000000001 или 1/1000000000000 фарады
11-1. Вопросы
1. Что такое емкость?
2. Нарисуйте схематическое изображение емкости.
3. Какие предосторожности необходимо соблюдать при работе с конденсаторами?
4. В каких единицах измеряется емкость?
5. Какие единицы обычно используются для обозначения емкости конденсаторов?
11-2. КОНДЕНСАТОРЫ
КОНДЕНСАТОРЫ
На емкость конденсатора влияют четыре фактора:
1. Площадь обкладок
2. Расстояние между обкладками.
3. Тип диэлектрического материала.
4. Температура.
Конденсаторы бывают постоянные и переменные. Постоянный конденсатор имеет определенное значение емкости, которое не может быть изменено. Емкость переменного конденсатора можно изменять, изменяя либо расстояние между обкладками (подстроечный конденсатор), либо перекрытие между двумя наборами пластин (переменный конденсатор).
Емкость прямо пропорциональна площади обкладок.
Например, увеличение площади обкладок в два раза в те же два раза увеличивает емкость, если, конечно, все другие факторы остаются неизменными.
Емкость обратно пропорциональна расстоянию между обкладками. Другими словами, если обкладки раздвинуть, величина электрического поля между ними уменьшится.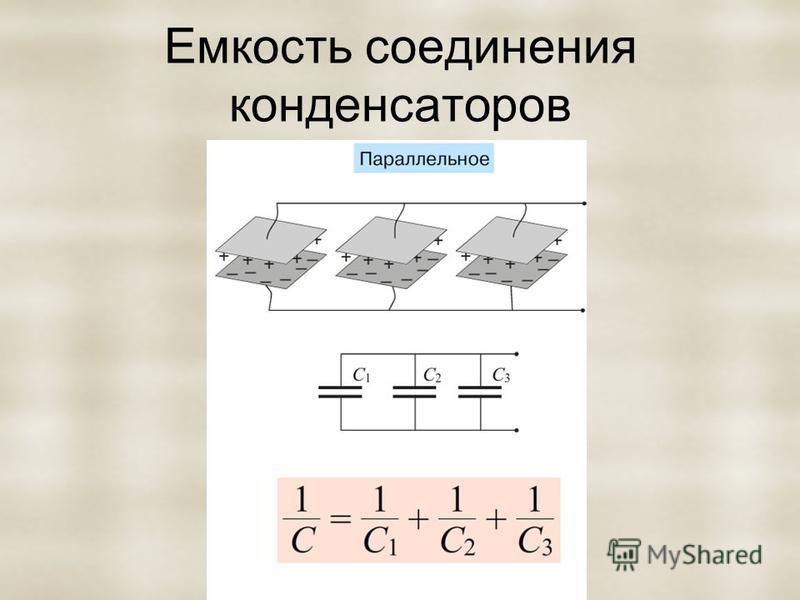
Способность конденсаторов сохранять электрическую энергию зависит от электростатического поля между обкладками и искажения электронных орбит в диэлектрическом материале. Степень этого искажения зависит от природы диэлектрического материала и определяется его диэлектрической постоянной. Диэлектрическая постоянная — это мера эффективности материала как диэлектрика. Эта постоянная сравнивает способность материала к искажению электронных орбит и сохранению энергии в электрическом поле со способностью воздуха, диэлектрическая постоянная которого равна 1. Бумага имеет диэлектрическую постоянную от 2 до 3; слюда — от 5 до 6; а титан — от 90 до 170.
Температура конденсатора из всех четырех факторов имеет наименьшее значение. Для большинства приложений общего назначения рассматривать ее нет необходимости.
Конденсаторы бывают различных типов и конструкций в соответствии с требованиями электронной промышленности. Электролитические конденсаторы обладают большой емкостью при малых размерах и весе (рис.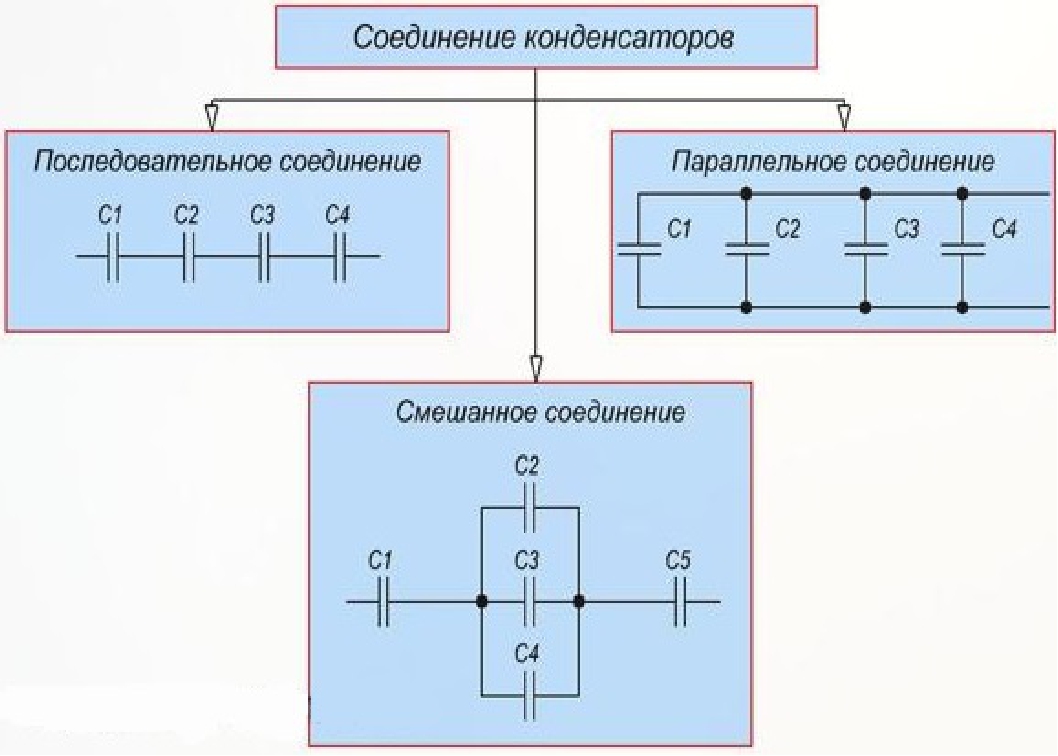 11-3).
11-3).
Рис. 11-3. Электролитические конденсаторы.
Электролитические конденсаторы состоят из двух металлических обкладок из фольги, разделенных тонкой материей или другим гигроскопическим материалом, насыщенным химической пастой, называемой электролитом.
Электролит является хорошим проводником и служит частью отрицательной обкладки. Диэлектрик образуется окислением положительной обкладки. Слой окисла является тонким и хорошим изолятором. Электролитический конденсатор является поляризованным, имеет положительный и отрицательный выводы. При включении электролитического конденсатора в цепь должна соблюдаться полярность.
Бумажные и пластиковые конденсаторы сконструированы как рулоны фольги, разделенной диэлектриком (рис. 11-4).
Рис. 11-4. Бумажные и пластиковые конденсаторы
Бумажный диэлектрик имеет меньшее сопротивление, чем пластиковая диэлектрическая пленка, но пластиковая пленка в настоящее время используется чаще.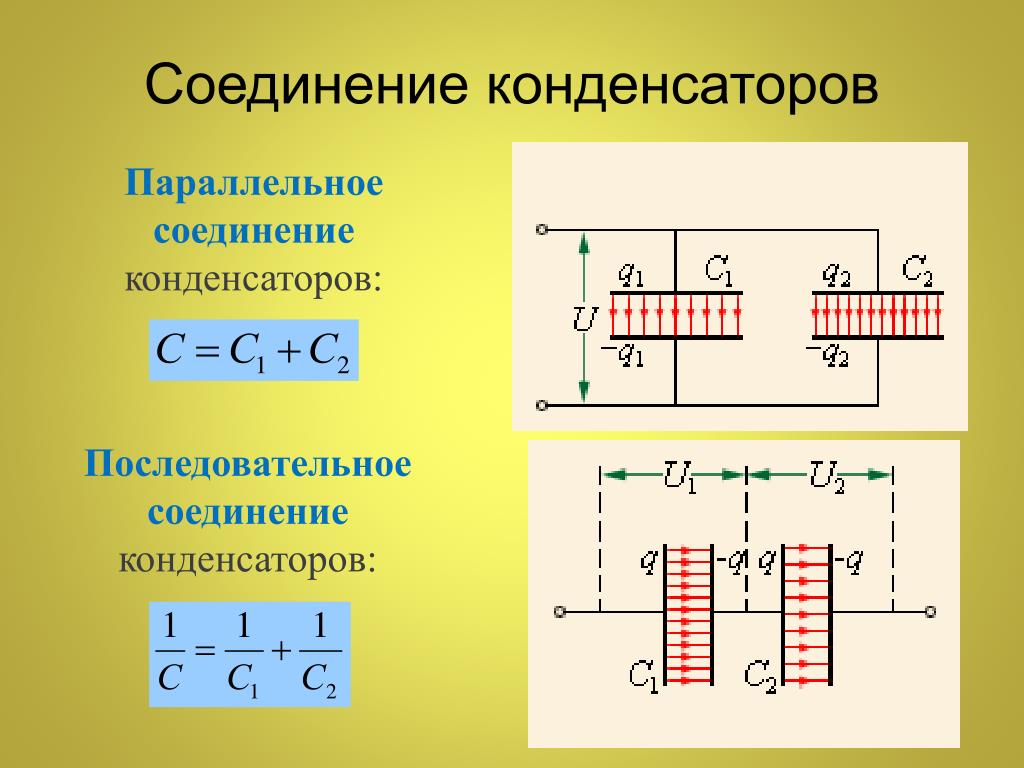 Пластиковая пленка позволяет нанести металлическую пленку прямо на нее. Это уменьшает расстояние между обкладками, и в результате конденсатор получается компактнее.
Пластиковая пленка позволяет нанести металлическую пленку прямо на нее. Это уменьшает расстояние между обкладками, и в результате конденсатор получается компактнее.
Керамические дисковые конденсаторы популярны вследствие того, что их производство обходится очень дешево (рис. 11-5). Они используются в качестве емкостей от 0,1 микрофарады и меньше. Керамический материал является диэлектриком. Это выносливые, надежные конденсаторы для широкого применения.
Рис. 11-5. Керамические дисковые конденсаторы.
Переменные конденсаторы также имеют различные размеры и формы (рис. 11-6). Переменные конденсаторы бывают выравнивающие, подстроечные и настроечные. Выравнивающие и подстроечные конденсаторы должны настраиваться специалистом. Настроечные конденсаторы могут настраиваться пользователем.
Рис. 11-6. Переменные конденсаторы.
Подобно резисторам и катушкам индуктивности, конденсаторы могут соединяться последовательно, параллельно и последовательно-параллельно. Последовательное соединение конденсаторов эффективно увеличивает толщину диэлектрика. Это уменьшает общую емкость, так как емкость обратно пропорциональна расстоянию между обкладками. Общая емкость последовательно соединенных конденсаторов вычисляется подобно общему сопротивлению параллельно соединенных резисторов:
Последовательное соединение конденсаторов эффективно увеличивает толщину диэлектрика. Это уменьшает общую емкость, так как емкость обратно пропорциональна расстоянию между обкладками. Общая емкость последовательно соединенных конденсаторов вычисляется подобно общему сопротивлению параллельно соединенных резисторов:
1/СT = 1/С1 + 1/С2 + 1/С3 +… + 1/Сn
Когда конденсаторы различной емкости соединяются последовательно, наименьший конденсатор заряжается до наивысшего напряжения.
Параллельное соединение конденсаторов эффективно увеличивает площадь обкладок. Это приводит к тому, что общая емкость равна сумме отдельных емкостей:
СT = С1 + С2 + С3 +… + Сn
11-2. Вопросы
Вопросы
1. Какие четыре фактора влияют на емкость конденсатора?
2. Каковы преимущества электролитических конденсаторов?
3. Как иначе называются переменные конденсаторы?
4. По какой формуле определяется общая емкость последовательной цепи?
5. По какой формуле определяется общая емкость параллельной цепи?
11-3. ПОСТОЯННАЯ ВРЕМЕНИ ЦЕПИ RC
Постоянная времени цепи RC отражает соотношение между временем, сопротивлением и емкостью. На рис. 11-7 изображена RC цепь.
Рис. 11-7. Цепь, используемая для определения постоянной времени RC.
Время, необходимое для заряда и разряда конденсатора прямо пропорционально величине сопротивления и емкости. Постоянная времени цепи определяет время, требуемое для того, чтобы конденсатор зарядился до 63,2 % от величины приложенного напряжения или разрядился на 63,2 % от этой величины. Постоянная времени определяется следующей формулой:
Постоянная времени определяется следующей формулой:
t = RC,
где
t — время в секундах, R — сопротивление в омах, С — емкость в фарадах.
ПРИМЕР: Чему равна постоянная времени цепи, состоящей из конденсатора емкостью в 1 микрофараду и резистора величиной 1 МОм?
Дано:
С = 1 мкФ; R = 1 МОм
t =?
Решение:
t = RC
t = (1000000)(0,000001)
t = 1 сек.
Постоянная времени цепи не равна времени, требуемого для полного заряда или разряда конденсатора. Рис. 11-8 показывает, сколько постоянных времени требуется для полного заряда и разряда конденсатора. Заметим, что для полного заряда или разряда конденсатора требуется время, примерно в пять раз большее постоянной времени цепи.
Заметим, что для полного заряда или разряда конденсатора требуется время, примерно в пять раз большее постоянной времени цепи.
Рис. 11-8. График зависимости заряда и разряда конденсатора от времени.
11-3. Вопросы
1. Что такое постоянная времени цепи RC?
2. Как определяется постоянная времени цепи RC?
3. Сколько постоянных времени цепи требуется для полного заряда или разряда конденсатора?
4. Конденсаторы емкостью 1 мкФ и 0,1 мкФ соединены последовательно. Чему равна полная емкость цепи?
5. Конденсатор емкостью 0,015 мкФ заряжен до 25 вольт. Чему будет равно напряжение на нем через 25 миллисекунд после подсоединения к его выводам резистора 2 МОм?
РЕЗЮМЕ
• Емкость — это способность сохранять электрическую энергию в электростатическом поле.
• Конденсатор состоит из двух проводников, разделенных изолятором.
• Схематическое обозначение постоянного конденсатора следующее:
• Схематическое обозначение переменного конденсатора следующее:
• Единицей измерения емкости является фарада (Ф).
• Поскольку фарада — это большая единица, обычно используются микрофарады (мкФ) и пикофарады (пФ).
• Емкость обозначается буквой С.
• На емкость влияют следующие факторы:
а. Площадь обкладок конденсатора.
б. Расстояние между обкладками.
в. Тип диэлектрического материала
г. Температура.
• Конденсаторы бывают следующих типов: электролитические, бумажные, пластиковые и керамические.
• Емкость последовательно соединенных конденсаторов вычисляется по следующей формуле:
1/СT = 1/С1 + 1/С2 + 1/С3 +… + 1/Сn
• Емкость параллельно соединенных конденсаторов вычисляется по следующей формуле:
СT = С1 + С2 + С3 +… + Сn
• Постоянная времени цепи RC определяется формулой:
t = RC.
Для полного заряда или разряда конденсатора требуется время, примерно в пять раз больше постоянной времени цепи.
Глава 11. САМОПРОВЕРКА
1. Где в конденсаторе сохраняется заряд?
2. Четыре конденсатора с емкостями 1,5 мкФ, 0,05 мкФ, 2000 пФ и 25 пФ соединены последовательно. Чему равна полная емкость цепи?
3. Четыре конденсатора с емкостями 1,5 мкФ, 0,05 мкФ, 2000 пФ и 25 пФ соединены параллельно. Чему равна полная емкость цепи?
Соединение конденсаторов Почему переменный ток проходит через конденсатор
Соединение конденсаторов Почему переменный ток проходит через конденсатор, а постоянный — нет? (Постоянному току обкладки мешают, а переменный их обходит) ШУТКА ДНЯ
Воздушные конденсаторы: диэлектрик – воздух.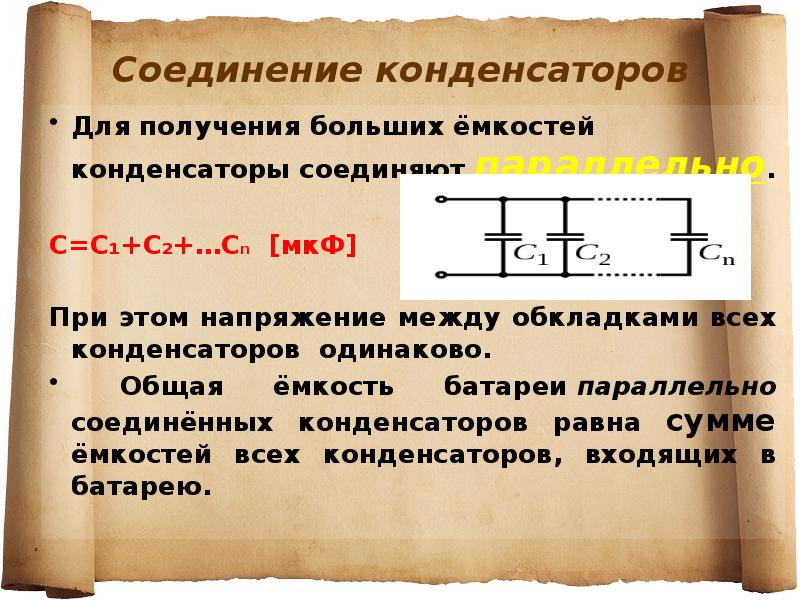 Применяются редко из-за громоздкости. Бумажные конденсаторы (КБ, КБГ, БМ, БГМ, где Г — герметизированный, М – малогабаритный): диэлектриком служит пропитанная изоляционным составом бумага. Обкладки – ленты из металлической фольги. Металло-бумажные (МБГ, МБМ) обкладки напыляют на бумажную ленту, пропитанную изоляционным составом и покрытую лаком. Слюдяные: изолятор – слюда с серебряным напылением.
Применяются редко из-за громоздкости. Бумажные конденсаторы (КБ, КБГ, БМ, БГМ, где Г — герметизированный, М – малогабаритный): диэлектриком служит пропитанная изоляционным составом бумага. Обкладки – ленты из металлической фольги. Металло-бумажные (МБГ, МБМ) обкладки напыляют на бумажную ленту, пропитанную изоляционным составом и покрытую лаком. Слюдяные: изолятор – слюда с серебряным напылением.
Керамические: диэлектрик – высококачественная керамика с напылением серебра. Электролитический (КЭ, ЭМ): диэлектрик – тонкий слой окиси на фольге. Другая обкладка – из пропитанной электролитом бумажной ленты. При включении обязательно соблюдать полярность. В переменный ток включать на короткое время.
Последовательное соединение конденсаторов.
При последовательном соединении общая емкость меньше самой малой из соединенных емкостей. Последовательное соединение применяется если напряжение в цепи больше напряжения одного конденсатора (Общее напряжение участка распределяется между отдельными конденсаторами пропорционально их емкости: чем больше емкость, тем меньше напряжение между его пластинами).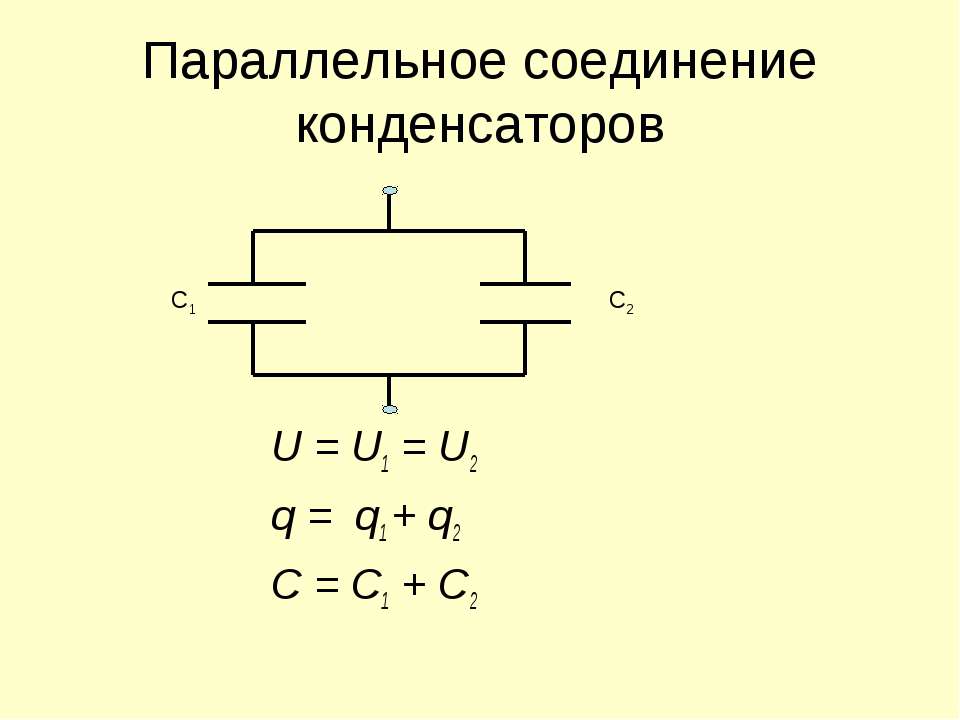
Параллельное соединение конденсаторов
Параллельное соединение применяется, когда нужно увеличить общую емкость конденсаторов. Напряжение на каждом конденсаторе равно общему, поэтому можно подводить напряжение, не превышающее рабочее напряжение каждого из них.
Задача № 1 В цепь напряжением 600 В необходимо включить емкость 2 мк. Ф. В нашем распоряжении имеются четыре конденсатора емкостью 2 мк. Ф, но рабочее напряжение которых 300 В. Как нужно соединить конденсаторы для включения их в цепь?
Задача № 2 Определить общую емкость пяти конденсаторов, если они соединены так, как показано на рисунке:
Практическая работа № 1 Задание № 1 10 мк. Ф 2 п. Ф 40 п. Ф 500 п. Ф Ф мк. Ф Ф
Самостоятельно: 2. Два конденсатора емкостью С 1=500 п. Ф, С 2=1000 п. Ф соединены последовательно. Определить их общую емкость. 3. Два конденсатора емкостью С 1 = 2 н. Ф и С 2=6 мк. Ф соединены параллельно. Определить общую емкость цепи. 4. Сколько конденсаторов по 150 п. Ф нужно соединить параллельно, чтобы получить емкость 600 п. Ф?
3. Два конденсатора емкостью С 1 = 2 н. Ф и С 2=6 мк. Ф соединены параллельно. Определить общую емкость цепи. 4. Сколько конденсаторов по 150 п. Ф нужно соединить параллельно, чтобы получить емкость 600 п. Ф?
в чём измеряется и от чего зависит величина, как её определить, формулы расчёта
Один из наиболее важных эффектов, используемых в электронике, — ёмкость конденсаторов. Способность накапливать и хранить электрический заряд нашла применение практически во всех аналоговых цепях и логических схемах. Пассивные устройства, запасающие энергию в виде электрического поля, называли конденсаторами уже в те времена, когда учёные ещё очень мало знали о природе электричества.
История накопителей заряда
Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.
Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.
Первое устройство для хранения полученных зарядов было создано в 1745 г. двумя электриками (так тогда называли людей, изучающих природу статического электричества), работающими независимо друг от друга: Эвальдом фон Клейстом, деканом собора в Пруссии, и Питером ван Мюссенбруком, профессором математики и физики в университете Лейдена.
Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:
Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:
- 1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
- 1750 г. — опыты Бенджамина Франклина с батареями конденсаторов;
- 1837 г. — публикация Майклом Фарадеем теории диэлектрической поляризации — научной основы работы накопителей;
- конец XIX в. — начало практического применения лейденских банок вместе с первыми устройствами постоянного тока;
- начало XX в. — изобретение слюдяных и керамических конденсаторов.
Физика ёмкостных характеристик
Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.
Если подключить к пластинам источник напряжения, то одна из них получит избыток электронов, а на другой сформируется их дефицит. Ионы и электроны на каждой из этих пластин притягиваются друг к другу, но благодаря диэлектрическому барьеру они не соединяются, а накапливаются на плоскостях проводников. В результате первая пластина (электрод) окажется заряженной отрицательно, а вторая — положительно. Неподвижные заряды создают постоянное электрическое поле, теоретически сохраняемое неограниченное количество времени в незамкнутой электрической цепи.
Поток электронов на пластины называется зарядным током, продолжающим присутствовать до тех пор, пока напряжение на пластинах не сравняется с приложенным. В этот момент конденсатор считается полностью заряженным, то есть зарядов на пластинах становится так много, что они отталкивают вновь поступающие. При подключении к заряженному устройству нагрузки электроны и ионы находят новый путь друг к другу. В этом случае конденсатор работает как источник тока до момента потери разности потенциалов на электродах.
Способность конденсатора хранить заряд Q (измеряется в кулонах) называют ёмкостью. Чем больше площадь пластин и меньше расстояние между ними (благодаря усилению эффекта притяжения зарядов между обкладками), тем большая ёмкость устройства. Степень приближения пластин ограничивается способностью диэлектрика сопротивляться разрядке пробоем между ними. Таким образом, три характеристики определяют производительность конденсатора:
- геометрия пластин;
- расстояние между ними;
- диэлектрический материал между пластинами.
Единица и формулы расчёта
Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.
Математическое выражение фарада
Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.
Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:
- пикофарад — 10—12 Ф;
- нанофарад — 10—9 Ф;
- микрофарад — 10—6 Ф.
Диэлектрическая проницаемость
Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:
Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:
- А — площадь меньшей пластины;
- d — расстояние между ними;
- ε — абсолютная проницаемость используемого диэлектрического материала.
Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.
На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:
- 1,0006 — воздух;
- 2,5—3,5 — бумага;
- 3—10 — стекло;
- 5—7 — слюда.

Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.
Практические измерения
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме.
Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.
Идея суперконденсатора
Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.
Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному.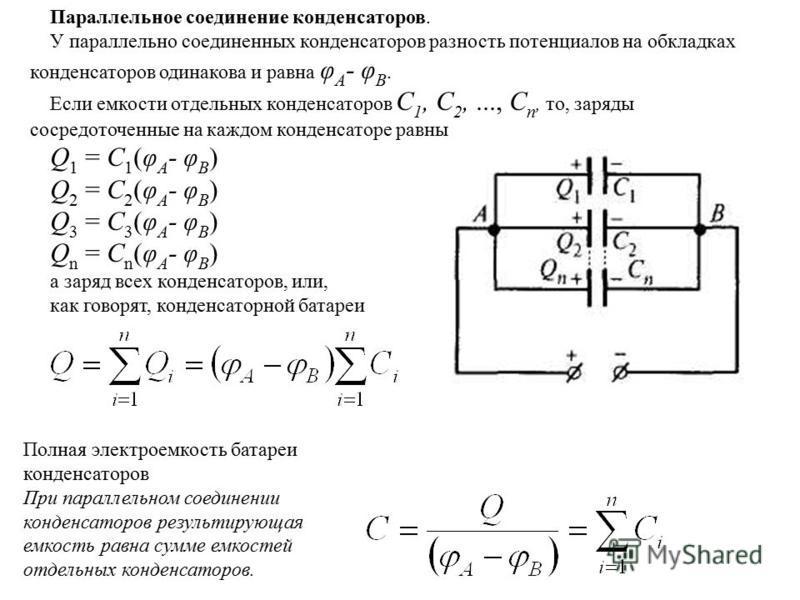 Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ. Основные недостатки аккумуляторов по сравнении и конденсаторами:
Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ. Основные недостатки аккумуляторов по сравнении и конденсаторами:
- непродолжительный жизненный цикл;
- невысокая удельная мощность;
- узкий диапазон температур зарядки и разрядки;
- неспособность быстро отдать весь запас энергии.
Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.
Крупнейшие коммерческие устройства обладают ёмкостью до нескольких тысяч фарад, но их возможности всё равно несопоставимы с аккумуляторами, поэтому подобные устройства используются для хранения зарядов в течение относительно короткого периода времени. Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.
Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.
Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками. Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.
Расчет общей емкости — Физика средней школы
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как рассчитать общую емкость параллельно? — Кухня
конденсаторов, подключенных параллельно Это показано ниже. Чтобы рассчитать общую общую емкость ряда конденсаторов, подключенных таким образом, вы складываете отдельные емкости по следующей формуле: CTotal = C1 + C2 + C3 и т.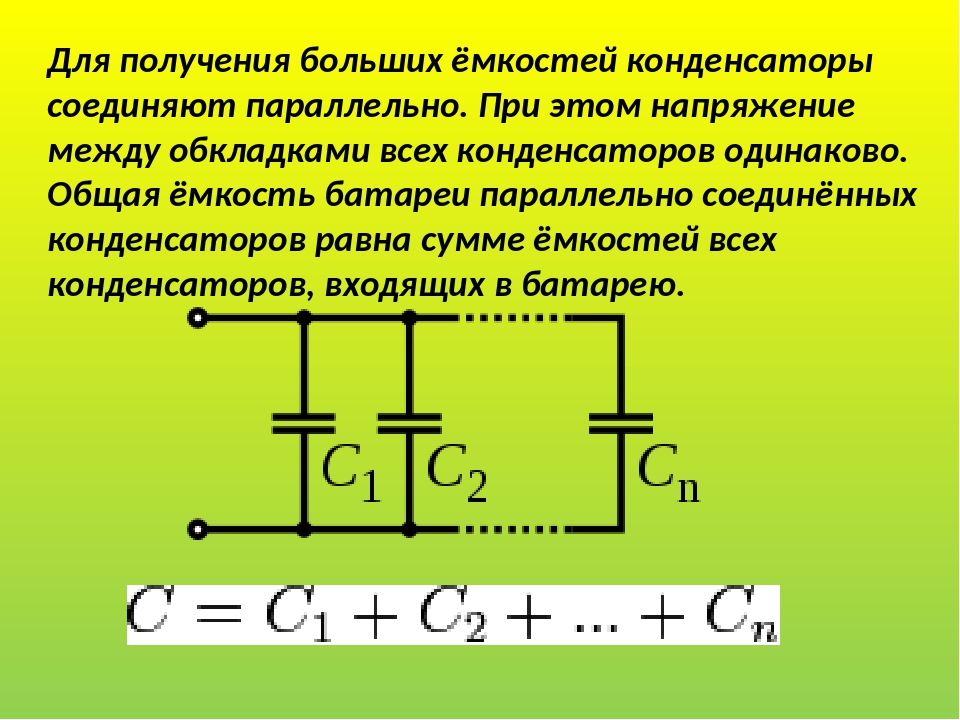 Д. Пример: Чтобы рассчитать общую емкость для этих трех конденсаторов в параллельно.
Д. Пример: Чтобы рассчитать общую емкость для этих трех конденсаторов в параллельно.
Какова общая емкость параллельно?
При параллельном подключении конденсаторов общая емкость складывается из емкостей отдельных конденсаторов. Если два или более конденсатора соединены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.
Какова общая емкость для двух конденсаторов, соединенных параллельно?
Когда конденсаторы размещаются параллельно друг другу, общая емкость — это просто сумма всех емкостей.Это аналогично тому, как резисторы добавляются последовательно. Так, например, если у вас есть три конденсатора номиналом 10 мкФ, 1 мкФ и 0,1 мкФ, подключенные параллельно, общая емкость будет 11,1 мкФ (10 + 1 + 0,1).
Как определить емкость конденсатора с параллельными пластинами?
Обобщенное уравнение емкости конденсатора с параллельными пластинами имеет вид: C = ε (A / d), где ε представляет собой абсолютную диэлектрическую проницаемость используемого диэлектрического материала. Диэлектрическая проницаемость, ε o , также известная как «диэлектрическая проницаемость свободного пространства», имеет значение постоянной 8.84 x 10 — 12 Фарад на метр.
Диэлектрическая проницаемость, ε o , также известная как «диэлектрическая проницаемость свободного пространства», имеет значение постоянной 8.84 x 10 — 12 Фарад на метр.
Как рассчитать общую емкость серии?
Для конденсаторов, соединенных последовательно, общую емкость можно найти, сложив значения, обратные величине отдельных емкостей, и взяв обратную величину от суммы.
Как определить общую емкость комбинации конденсаторов?
Как и в случае любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением C = QV C = Q V.Обратите внимание на рис. 1, что противоположные заряды величины Q текут к обеим сторонам изначально незаряженной комбинации конденсаторов при приложении напряжения V.
Как найти эквивалентную емкость параллельной цепи?
Для конденсаторов, соединенных параллельно, эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети, Cp = C1 + C2 + C3 +
Как рассчитать емкость?
Емкость определяется делением электрического заряда на напряжение по формуле C = Q / V. Его единица — Фарад.
Его единица — Фарад.
При параллельном подключении конденсаторов общая емкость всегда составляет?
Пояснение: При параллельном подключении конденсаторов общая емкость равна сумме емкостей каждого из конденсаторов. Следовательно, Ctotal = C1 + C2 + C3. 2.
Как рассчитать емкость параллельных пластин с диэлектриками?
Емкость конденсатора с параллельными пластинами определяется как: c = ϵAd c = ϵ A d, где ε — диэлектрическая проницаемость, A — площадь пластин конденсатора (при условии, что они имеют одинаковый размер и форму), а d — толщина диэлектрика.
Что такое конденсатор с параллельными пластинами получить формулу?
Формула конденсатора с параллельными пластинами имеет вид: C = kϵ0Ad. Где o — диэлектрическая проницаемость пространства (8,854 × 10-12 Ф / м), k — относительная диэлектрическая проницаемость диэлектрического материала. d — расстояние между пластинами.
Что вы подразумеваете под конденсатором с параллельными пластинами, чтобы получить выражение для емкости конденсатора с параллельными пластинами?
Разность потенциалов пластин V = Ред. ⟹ V = Aϵo Qd Емкость C = VQ Таким образом, мы получаем емкость конденсатора с параллельными пластинами C = dAϵo
⟹ V = Aϵo Qd Емкость C = VQ Таким образом, мы получаем емкость конденсатора с параллельными пластинами C = dAϵo
Как рассчитать конденсаторы последовательно привести примеры?
Вот правила расчета емкостей при последовательном включении. Если конденсаторы одинаковой стоимости, вам повезло.Все, что вам нужно сделать, это разделить значение одного из отдельных конденсаторов на количество конденсаторов. Например, общая емкость двух конденсаторов по 100 мкФ составляет 50 мкФ.
3.6 Последовательные и параллельные конденсаторы — Douglas College Physics 1207
Сводка
- Выведите выражения для полной емкости последовательно и параллельно.
- Обозначение последовательной и параллельной частей в комбинации конденсаторов.
- Рассчитайте эффективную емкость последовательно и параллельно с учетом индивидуальных емкостей.
Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько подключений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Существует два простых и распространенных типа подключения: серия и параллельный , для которых мы можем легко вычислить общую емкость. Некоторые более сложные соединения также могут быть связаны с последовательными и параллельными соединениями.
Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Существует два простых и распространенных типа подключения: серия и параллельный , для которых мы можем легко вычислить общую емкость. Некоторые более сложные соединения также могут быть связаны с последовательными и параллельными соединениями.
На рис. 1 (а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и в случае любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением C = Q / V.
Обратите внимание на рис. 1, что противоположные заряды величиной Q протекают по обе стороны от первоначально незаряженной комбинации конденсаторов при приложении напряжения В, . Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов создавались заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах. Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов. (См. Рисунок 1 (b).) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов. (См. Рисунок 1 (b).) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
Рис. 1. (a) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине Q .(b) Эквивалентный конденсатор имеет большее расстояние между пластинами d . При последовательном соединении общая емкость меньше, чем у любого из отдельных конденсаторов.
Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение C = Q / V для V дает V = C / Q . Напряжения на отдельных конденсаторах равны. Общее напряжение складывается из отдельных напряжений:
V = V 1 + V 2 + V 3
Теперь, называя общую емкость C серии = C s для последовательной емкости, считайте, что
Вводя выражения для V 1 , V 2 и V 3 , получаем
Отменяя Q s, получаем уравнение для полной емкости в серии C , равное
, где «…» означает, что выражение действительно для любого количества конденсаторов, соединенных последовательно.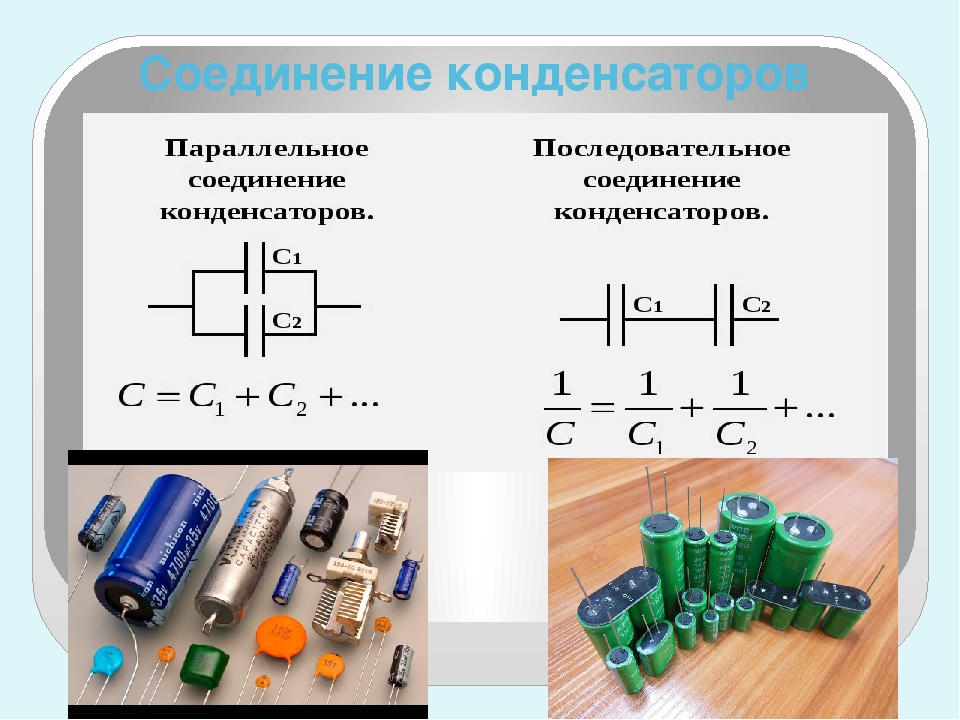 Выражение этой формы всегда приводит к общей емкости C , которая меньше любой из отдельных емкостей C 1 , C 2 , C 3 , …, как показано в следующем примере.
Выражение этой формы всегда приводит к общей емкости C , которая меньше любой из отдельных емкостей C 1 , C 2 , C 3 , …, как показано в следующем примере.
Общая емкость в серии,
C с
Общая емкость в серии:
Пример 1: Что такое последовательная емкость?
Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны 1.000, 5.000 и 8.000 мкФ.
Стратегия
Имея данную информацию, общую емкость можно найти, используя уравнение для емкости в серии.
Решение
Ввод заданных емкостей в выражение для дает.
Обращение для нахождения C серии или C s урожайности.
Обсуждение
Общая последовательная емкость C с меньше наименьшей индивидуальной емкости, как было обещано. При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только целочисленные вычисления) равен 40. Таким образом,
При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только целочисленные вычисления) равен 40. Таким образом,
, так что
На рис. 2 (а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь полную емкость найти легче, чем в последовательном случае.Чтобы найти эквивалентную общую емкость C параллельно или C p , сначала отметим, что напряжение на каждом конденсаторе составляет В, , то же самое, что и у источника, поскольку они подключены напрямую к нему через дирижер. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют такой же заряд, как и при индивидуальном подключении к источнику напряжения. Общая сумма начислений Q — это сумма отдельных сборов:
Общая сумма начислений Q — это сумма отдельных сборов:
Q = Q 1 + Q 2 + Q 3
Рис. 2. (a) Конденсаторы, включенные параллельно. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, поэтому общая параллельная емкость — это просто сумма отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.
Используя соотношение Q = CV , мы видим, что общий заряд составляет Q всего = C p V , а отдельные заряды составляют Q 1 = C 1 V , Q 2 = C 2 V , и Q 3 = C 3 V . Ввод их в предыдущее уравнение дает
Q итого = Q 1 + Q 2 + Q 3
C p V = C 1 V + C 2 V + C 3 V
C p = C 1 + C 2 + C 3
Исключая V из уравнения, мы получаем уравнение для полной емкости параллельно C p :
C p = C 1 + C 2 + C 3 +….
Общая емкость при параллельном подключении — это просто сумма отдельных емкостей. (И снова «… » указывает на то, что выражение действительно для любого количества конденсаторов, подключенных параллельно.) Так, например, если конденсаторы в приведенном выше примере были подключены параллельно, их емкость была бы
C p = C 1 + C 2 + C 3 = 1.000 мкФ + 5.000 мкФ + 8.000 мкФ = 14.000 мкФ
Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на Рисунке 2 (b).
Общая емкость параллельно,
C p
Общая емкость параллельно C p = C 1 + C 2 + C 3 +….
Более сложные соединения конденсаторов иногда могут быть последовательными и параллельными. (См. Рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую.
Рисунок 3. (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C 1 и C 2 идут последовательно; их эквивалентная емкость C S меньше, чем у любого из них. (c) Обратите внимание, что C S параллельно с C 3 .Таким образом, общая емкость равна сумме C S и C 3 .
Смесь последовательной и параллельной емкости
Найдите общую емкость комбинации конденсаторов, показанной на рисунке выше. Предположим, что емкости известны с точностью до трех десятичных знаков.
C p = C 1 + C 2 + C 3 = 1.000 мкФ + 5.000 мкФ + 8. 000 мкФ = 14.000 мкФ
000 мкФ = 14.000 мкФ
C p = C 1 + C 2 + C 3 = 1.000 мкФ + 5.000 мкФ + 8.000 мкФ = 14.000 мкФ
C 1 = 1.000 мкФ, C 2 = 5.000 мкФ и C 3 = 8.000 мкФ. Округлите ответ до трех десятичных знаков.
Стратегия
Чтобы определить общую емкость, мы сначала определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы С 1 и С 2 включены последовательно.Их комбинация, Cs на рисунке, параллельна C 3 .
Решение
Поскольку C 1 и C 2 включены последовательно, их общая емкость определяется выражением. Ввод их значений в уравнение дает
Инвертирование дает
Cs = 0,833 мкФ
Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; Таким образом, общая сумма составляет
Обсуждение
Этот метод анализа комбинаций конденсаторов по частям, пока не будет получена общая сумма, может быть применен к более крупным комбинациям конденсаторов.
- Суммарная емкость в серии
- Общая емкость параллельно C p = C 1 + C 2 + C 3 +…
- Если схема содержит комбинацию конденсаторов, включенных последовательно и параллельно, определите последовательную и параллельную части, вычислите их емкости, а затем найдите общую сумму.
Концептуальные вопросы
1: Если вы хотите хранить большое количество энергии в конденсаторной батарее, подключите ли вы конденсаторы последовательно или параллельно? Объяснять.
Задачи и упражнения
1: Найдите общую емкость комбинации конденсаторов на рисунке 4.
Рисунок 4. Комбинация последовательного и параллельного подключения конденсаторов.
2: Предположим, вам нужна конденсаторная батарея с общей емкостью 0,750 Ф и у вас есть множество конденсаторов 1,50 мФ. Какое наименьшее число вы могли бы связать вместе, чтобы достичь своей цели, и как бы вы их связали?
3: Какую общую емкость можно получить, подключив 5. 00 мкФ и конденсатор 8,00 мкФ вместе?
00 мкФ и конденсатор 8,00 мкФ вместе?
4: Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.
Рисунок 5. Комбинация последовательного и параллельного подключения конденсаторов.
5: Найдите общую емкость комбинации конденсаторов, показанной на рисунке ниже
Рисунок 6. Комбинация последовательного и параллельного подключения конденсаторов.
6: Необоснованные результаты
(а) Ан 8.Конденсатор 00 мкФ подключен параллельно другому конденсатору, что дает общую емкость 5,00 мкФ . Какая емкость у второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Решения
Задачи и упражнения
1: 0,293 мкФ
3: 3,08 мкФ в последовательной комбинации, 13,0 мкФ в параллельной комбинации
4: 2. 79 мкФ
79 мкФ
6: (a) -3,00 мкФ (b) У вас не может быть отрицательного значения емкости. (c) Предположение, что конденсаторы были подключены параллельно, а не последовательно, было неверным. Параллельное соединение всегда дает большую емкость, в то время как здесь предполагалась меньшая емкость. Это могло произойти, только если конденсаторы подключены последовательно.
Видео с вопросом: Определение общей емкости конденсаторов серии
Стенограмма видео
Цепь на схеме содержит два последовательно включенных конденсатора.Какая общая емкость цепи? Ответить с ближайшим микрофарадом.
Хорошо, в этом вопросе нам дали схему, которая показывает простую схему, в которой у нас есть ячейка, соединенная последовательно с двумя конденсаторами. Емкости каждого из этих двух конденсаторов обозначены на диаграмме в единицах микрофарад. Емкость того, что слева, составляет 150 мкФ, а этого — 250 мкФ. Нас просят определить общую емкость.Для этого нам нужно вспомнить, что, когда у нас есть несколько конденсаторов, соединенных последовательно, то один по общей емкости, который мы обозначили как 𝐶 нижний индекс 𝑇, определяется как сумма обратных величин отдельных емкостей. Итак, если мы обозначим эти емкости индексами один, два, три и т. Д., То это будет один больше один плюс один больше 𝐶 два плюс один больше три и так далее для любых дополнительных конденсаторов, соединенных последовательно.
Нас просят определить общую емкость.Для этого нам нужно вспомнить, что, когда у нас есть несколько конденсаторов, соединенных последовательно, то один по общей емкости, который мы обозначили как 𝐶 нижний индекс 𝑇, определяется как сумма обратных величин отдельных емкостей. Итак, если мы обозначим эти емкости индексами один, два, три и т. Д., То это будет один больше один плюс один больше 𝐶 два плюс один больше три и так далее для любых дополнительных конденсаторов, соединенных последовательно.
В этом вопросе у нас есть только два последовательно включенных конденсатора в нашей цепи, поэтому нам нужны только первые два члена в правой части этого уравнения.Обозначим этот конденсатор емкостью 150 мкФ как один, а этот конденсатор емкостью 250 мкФ как два. Тогда в этом уравнении вместо величин один и 𝐶 два мы можем использовать наши значения 150 и 250 мкФ. Это дает нам выражение, которое говорит, что единица общей емкости 𝐶 нижний индекс равна единице более 150 мкФ плюс одна более 250 мкФ.
Чтобы сложить две дроби, мы хотим, чтобы у этих дробей был общий знаменатель. Один простой способ сделать это — умножить крестиком.Итак, мы берем 250 из знаменателя правой дроби и умножаем числитель и знаменатель левой дроби на эти 250. Затем мы берем 150 из знаменателя левой дроби и умножаем числитель и знаменатель правой дроби на эти 150. Теперь у нас есть две дроби с одинаковым знаменателем, равным 250, умноженным на 150 в микрофарадах. Получается 37500 микрофарад. Теперь мы можем сложить эти две дроби, чтобы получить результат 400, разделенный на 37500 микрофарад.Затем оценка этой дроби дает результат 0,0106, повторяющийся с единицами обратных микрофарад.
Обратите внимание, что мы получили эти единицы обратных микрофарад, потому что у нас была величина с единицами микрофарад в знаменателе дроби. Теперь наличие единиц обратных микрофарад, или единицы, деленной на микрофарады, имеет здесь полный смысл, потому что то, что мы вычислили, было делением единицы на общую емкость 𝐶 нижний индекс 𝑇. В вопросе мы пытаемся найти значение самой общей емкости, так что это значение 𝐶 нижнего индекса 𝑇.Это означает, что для получения ответа нам нужно взять обратное значение этого результата для одного более 𝐶 нижнего индекса 𝑇. Таким образом, у нас есть это выражение для полной емкости 𝐶 нижний индекс. Разделение единицы на количество в единицах единицы сверх микрофарад даст результат в единицах микрофарад.
В вопросе мы пытаемся найти значение самой общей емкости, так что это значение 𝐶 нижнего индекса 𝑇.Это означает, что для получения ответа нам нужно взять обратное значение этого результата для одного более 𝐶 нижнего индекса 𝑇. Таким образом, у нас есть это выражение для полной емкости 𝐶 нижний индекс. Разделение единицы на количество в единицах единицы сверх микрофарад даст результат в единицах микрофарад.
Когда мы вычисляем выражение, мы обнаруживаем, что этот результат равен точно 93,75 мкФ. Это значение равно общей емкости цепи, которую нас попросили найти.Но последнее, что осталось сделать, это заметить, что нас попросили дать этот ответ до ближайшего микрофарада. Округление этого результата до ближайшей микрофарады дает нам ответ для полной емкости 94 мкФ.
Видео с вопросом: Определение общей емкости конденсаторов последовательно и параллельно
Стенограмма видео
Цепь на схеме содержит конденсаторы, включенные последовательно и параллельно. Какая общая емкость цепи? Дайте ответ с точностью до микрофарада.
Какая общая емкость цепи? Дайте ответ с точностью до микрофарада.
На схеме, представленной нам, показана схема, в которой ячейка подключена к комбинации конденсаторов. Мы видим, что эта схема имеет две параллельные ветви с включенными конденсаторами. Через середину проходит эта ветвь, которую мы обозначим как ветвь A. И мы видим, что на ней есть конденсаторы. Один с емкостью 75 мкФ, а другой — с емкостью 55 мкФ.Затем здесь есть ветвь, которую мы обозначим как ветвь B. И она содержит только один конденсатор емкостью 35 мкФ.
Нас просят определить общую емкость цепи. А для этого нам нужно вспомнить, как мы объединяем конденсаторы последовательно и параллельно. Когда несколько конденсаторов соединяются последовательно, величина, обратная величине общей емкости, равна сумме обратных величин отдельных емкостей. То есть, если мы соединим группу конденсаторов последовательно с емкостями один, 𝐶 два, 𝐶 три и т. Д., То один над общей емкостью 𝐶 индекс T будет равен единице больше, один плюс один больше, два плюс один больше 𝐶 три и так далее.
Между тем, если у нас есть несколько конденсаторов, подключенных параллельно, мы просто складываем отдельные емкости, чтобы получить общую емкость. На нашей схеме мы видим, что ветвь, обозначенная буквой A, состоит из двух последовательно соединенных конденсаторов. Обозначим общую емкость этой ветви, так что это общая емкость этих двух конденсаторов, соединенных последовательно, как нижний индекс 𝐶 A. Мы также обозначим эту емкость 75 микрофарад как один, а эту емкость в 55 микрофарад как два.Тогда из нашего общего выражения для конденсаторов, соединенных последовательно, мы знаем, что один над нижний индекс A равен единице над одним плюс один над двумя.
Поскольку нам известны значения 𝐶 one и 𝐶 two, то мы можем использовать это уравнение, чтобы найти значение нижнего индекса A. Для этого мы хотим сделать нижний индекс A объектом уравнения. . Мы начнем с умножения обеих частей уравнения на нижний индекс A, 𝐶 один и 𝐶 два. Расширяя скобки с правой стороны, мы можем переписать уравнение следующим образом. В этой дроби слева нижний индекс в числителе заменяется нижним индексом в знаменателе. В этой первой дроби справа единица в числителе и знаменателе сокращается. Во второй дроби справа двойка в числителе и знаменателе сокращается.
В этой дроби слева нижний индекс в числителе заменяется нижним индексом в знаменателе. В этой первой дроби справа единица в числителе и знаменателе сокращается. Во второй дроби справа двойка в числителе и знаменателе сокращается.
Как только мы избавимся от отмененных терминов, мы получим вот это выражение. Затем мы можем вынести за скобки индекс 𝐶, который появляется в обоих членах справа. Последний шаг, который нам нужно сделать, чтобы получить нижний индекс A в качестве предмета этого уравнения, — разделить обе части на один плюс два так, чтобы справа один плюс два в числителе компенсировался единицей в знаменатель.Если мы затем запишем уравнение наоборот, мы получим, что Индекс A равен 𝐶 один раз 𝐶 два, разделенных на 𝐶 один плюс два.
Итак, это уравнение говорит нам, как рассчитать общую емкость 𝐶 нижний индекс A двух конденсаторов 𝐶 один и два, соединенных вместе последовательно.
Давайте теперь освободим немного места, чтобы мы могли подставить наши значения 𝐶 один и два из этой схемы. Подставив туда один равен 75 микрофарад, а 𝐶 два равен 55 микрофарадам, мы получим это выражение для нижнего индекса A.В числителе 75 микрофарад умноженные на 55 микрофарад. И это получается как 4125 с единицей микрофарад в квадрате. Затем в знаменателе 75 микрофарад плюс 55 микрофарад, что получается как 130 микрофарад.
Подставив туда один равен 75 микрофарад, а 𝐶 два равен 55 микрофарадам, мы получим это выражение для нижнего индекса A.В числителе 75 микрофарад умноженные на 55 микрофарад. И это получается как 4125 с единицей микрофарад в квадрате. Затем в знаменателе 75 микрофарад плюс 55 микрофарад, что получается как 130 микрофарад.
В единицах измерения мы можем исключить один из двух множителей микрофарад в числителе и микрофарад в знаменателе. Это оставляет нам единицы для 𝐶 нижнего индекса A микрофарад. Затем вычисление выражения дает результат с двумя десятичными знаками 31.73 мкФ. Итак, мы нашли значение нижнего индекса 𝐶 A, которое представляет собой емкость ветви, обозначенной на нашей принципиальной схеме буквой A. Поскольку ветвь B содержит только один конденсатор, мы знаем, что его емкость как раз равна этому значению в 35 микрофарад. Обозначим это как 𝐶, индекс B.
Теперь мы находимся в положении, когда у нас есть две параллельные ветви. Это ветвь A и ветвь B. И мы знаем емкость каждой ветви. Это наши значения для 𝐶 нижнего индекса A и 𝐶 нижнего индекса B.Если мы освободим немного места на плате, то сможем использовать наше общее выражение для конденсаторов, соединенных параллельно, чтобы найти общую емкость этих двух ветвей.
Это наши значения для 𝐶 нижнего индекса A и 𝐶 нижнего индекса B.Если мы освободим немного места на плате, то сможем использовать наше общее выражение для конденсаторов, соединенных параллельно, чтобы найти общую емкость этих двух ветвей.
Это общее выражение говорит нам, что для конденсаторов, соединенных параллельно, мы просто складываем отдельные емкости. В нашем случае это значения для нижнего индекса A и 𝐶 нижнего индекса B. Таким образом, общая емкость 𝐶 нижнего индекса T равна нижнему индексу A плюс 𝐶 нижнему индексу B. Затем мы можем подставить в наши значения 𝐶 нижний индекс A и 𝐶 нижний индекс B и вычислите сумму, чтобы получить значение общей емкости 𝐶 индекс T.
Нас в вопросе просят дать ответ с точностью до микрофарад. Округляя до ближайшей микрофарад, получаем ответ для полной емкости схемы, равной 67 микрофарад.
19.6 Последовательные и параллельные конденсаторы — College Physics chapters 1-17
Сводка
- Выведите выражения для полной емкости последовательно и параллельно.

- Обозначение последовательной и параллельной частей в комбинации конденсаторов.
- Рассчитайте эффективную емкость последовательно и параллельно с учетом индивидуальных емкостей.
Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько подключений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Существует два простых и распространенных типа подключения: серия и параллельный , для которых мы можем легко вычислить общую емкость.Некоторые более сложные соединения также могут быть связаны с последовательными и параллельными соединениями.
На рис. 1 (а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением [латекс] \ boldsymbol {C = \ frac {Q} {V}} [/ latex].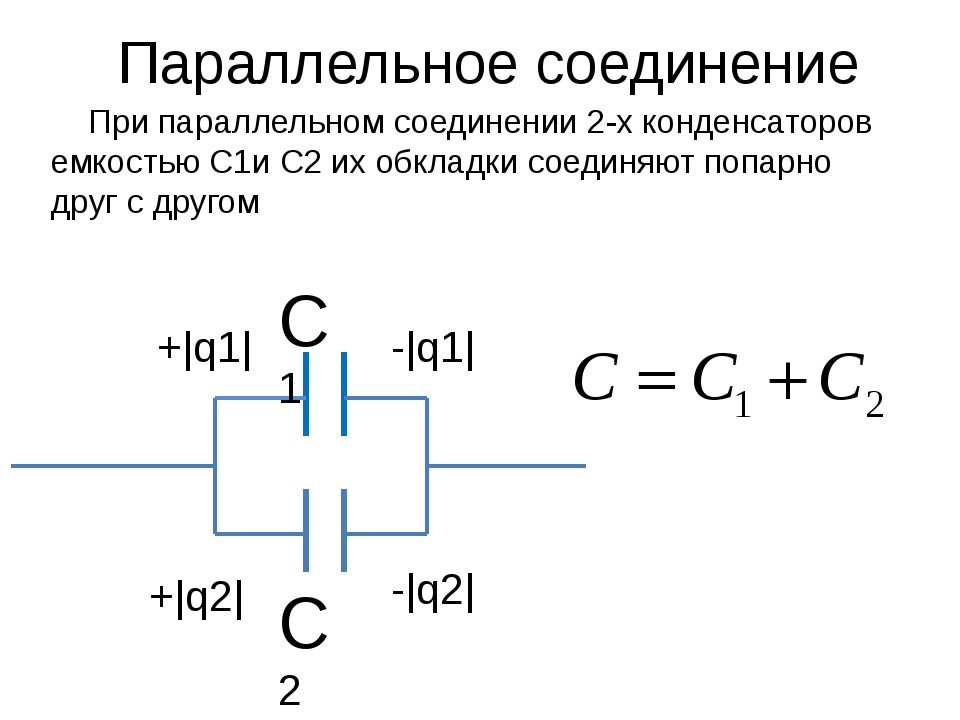
Обратите внимание на рис. 1, что противоположные заряды величиной [латекс] \ boldsymbol {Q} [/ latex] текут по обе стороны от первоначально незаряженной комбинации конденсаторов при приложении напряжения [латекс] \ boldsymbol {V} [/ латекс] .Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов создавались заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах. Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов. (См. Рисунок 1 (b).) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
Рис. 1. (a) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине Q . (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d .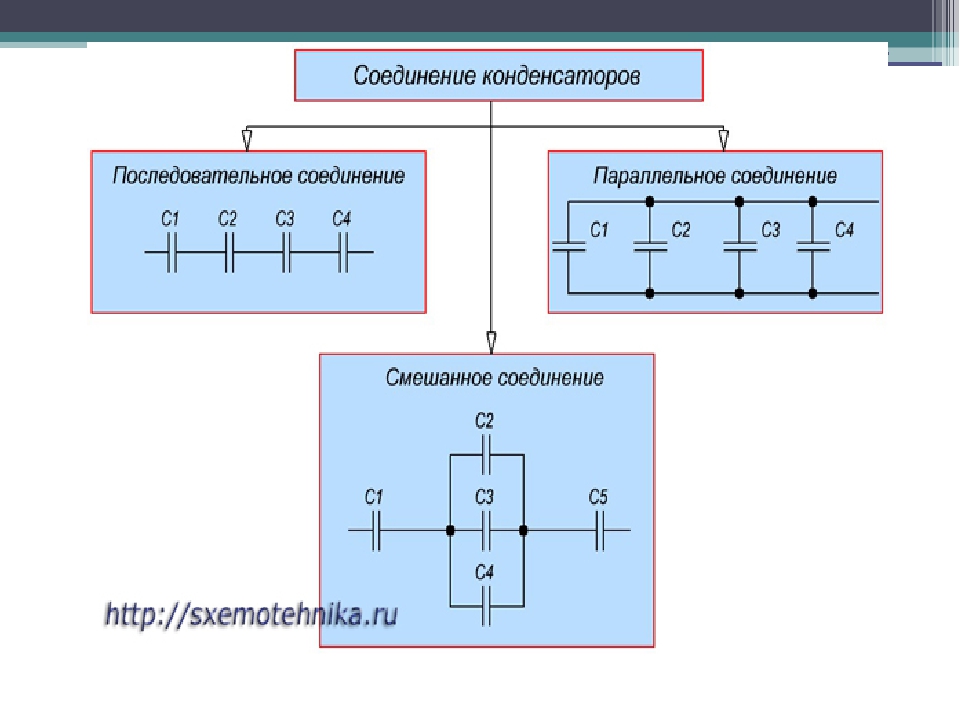 При последовательном соединении общая емкость меньше, чем у любого из отдельных конденсаторов.
При последовательном соединении общая емкость меньше, чем у любого из отдельных конденсаторов.
Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение [latex] \ boldsymbol {C = \ frac {Q} {V}} [/ latex] для [latex] \ boldsymbol {V} [/ latex] дает [латекс] \ boldsymbol {V = \ frac {Q} {C}} [/ latex].Таким образом, напряжения на отдельных конденсаторах составляют [латекс] \ boldsymbol {V_1 = \ frac {Q} {C_1}} [/ latex], [латекс] \ boldsymbol {V_2 = \ frac {Q} {C_2}} [/ латекс ] и [латекс] \ boldsymbol {V_3 = \ frac {Q} {C_3}} [/ latex]. Общее напряжение складывается из отдельных напряжений:
[латекс] \ boldsymbol {V = V_1 + V_2 + V_3}. [/ Latex]
Теперь, назвав общую емкость [латекс] \ boldsymbol {C_S} [/ latex] для последовательной емкости, примите во внимание, что
[латекс] \ boldsymbol {V =} [/ latex] [латекс] \ boldsymbol {\ frac {Q} {C_S}} [/ latex] [латекс] \ boldsymbol {= V_1 + V_2 + V_3}. [/ латекс]
[/ латекс]
Вводя выражения для [latex] \ boldsymbol {V_1} [/ latex], [latex] \ boldsymbol {V_2} [/ latex] и [latex] \ boldsymbol {V_3} [/ latex], получаем
[латекс] \ boldsymbol {\ frac {Q} {C_S} = \ frac {Q} {C_1} + \ frac {Q} {C_2} + \ frac {Q} {C_3}}. [/ Latex]
Убирая [латекс] \ boldsymbol {Q} [/ latex] s, мы получаем уравнение для полной емкости в серии [латекс] \ boldsymbol {C_S} [/ latex] равным
[латекс] \ boldsymbol {\ frac {1} {C_S}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {C_1}} [/ латекс ] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {C_2}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol { \ frac {1} {C_3}} [/ latex] [latex] \ boldsymbol {+ \ cdots}, [/ latex]
, где «…» означает, что выражение действительно для любого количества конденсаторов, соединенных последовательно.Выражение этой формы всегда приводит к общей емкости [латекс] \ boldsymbol {C_S} [/ latex], которая меньше любой из отдельных емкостей [латекс] \ boldsymbol {C_1} [/ latex], [латекс] \ boldsymbol {C_2} [/ latex],…, как показано в следующем примере.
Общая емкость в серии,
C с
Общая емкость в серии: [латекс] \ boldsymbol {\ frac {1} {C_S} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} + \ cdots } [/ латекс]
Пример 1: Что такое последовательная емкость?
Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны 1.000, 5.000 и 8.000 [латекс] \ mu \ textbf {F} [/ latex].
Стратегия
Имея данную информацию, общую емкость можно найти, используя уравнение для емкости в серии.
Решение
Ввод заданных емкостей в выражение для [latex] \ boldsymbol {\ frac {1} {C_S}} [/ latex] дает [latex] \ boldsymbol {\ frac {1} {C_S} = \ frac {1} { C_1} + \ frac {1} {C_2} + \ frac {1} {C_3}} [/ латекс].
[латекс] \ boldsymbol {\ frac {1} {C_S}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {1.000 \; \ mu \ textbf {F}}} [/ latex] [latex] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {5. 000 \; \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {8.000 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol { =} [/ latex] [латекс] \ boldsymbol {\ frac {1.325} {\ mu \ textbf {F}}} [/ latex]
000 \; \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {8.000 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol { =} [/ latex] [латекс] \ boldsymbol {\ frac {1.325} {\ mu \ textbf {F}}} [/ latex]
Инвертирование для поиска [latex] \ boldsymbol {C_S} [/ latex] дает [latex] \ boldsymbol {C_S = \ frac {\ mu \ textbf {F}} {1.325} = 0.755 \; \ mu \ textbf {F} }[/латекс].
Обсуждение
Общая последовательная емкость [латекс] \ boldsymbol {C_s} [/ latex] меньше наименьшей индивидуальной емкости, как было обещано.При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только целочисленные вычисления) равен 40. Таким образом,
[латекс] \ boldsymbol {\ frac {1} {C_S}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {40} {40 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {8} {40 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {5} {40 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {=} [/ латекс] [латекс] \ boldsymbol {\ frac {53} {40 \; \ mu \ textbf {F}}}, [/ латекс]
, так что
[латекс] \ boldsymbol {C_S =} [/ latex] [латекс] \ boldsymbol {\ frac {40 \; \ mu \ textbf {F}} {53}} [/ latex] [латекс] \ boldsymbol {= 0 . 755 \; \ mu \ textbf {F}}. [/ latex]
755 \; \ mu \ textbf {F}}. [/ latex]
На рис. 2 (а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь полную емкость найти легче, чем в последовательном случае. Чтобы найти эквивалентную общую емкость [латекс] \ boldsymbol {\ textbf {C} _ {\ textbf {p}}} [/ latex], сначала отметим, что напряжение на каждом конденсаторе составляет [латекс] \ boldsymbol {V} [ / latex], то же самое, что и у источника, так как они подключаются к нему напрямую через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.Таким образом, конденсаторы имеют такой же заряд, как и при индивидуальном подключении к источнику напряжения. Общий заряд [латекс] \ boldsymbol {Q} [/ latex] — это сумма отдельных зарядов:
[латекс] \ boldsymbol {Q = Q_1 + Q_2 + Q_3}. [/ Latex]
Рис. 2. (a) Конденсаторы, включенные параллельно. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, поэтому общая параллельная емкость — это просто сумма отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.
(b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.
Используя соотношение [латекс] \ boldsymbol {Q = CV} [/ latex], мы видим, что общий заряд составляет [латекс] \ boldsymbol {Q = C _ {\ textbf {p}} V} [/ latex], и индивидуальные расходы: [латекс] \ boldsymbol {Q_1 = C_1 V} [/ latex] , [латекс] \ boldsymbol {Q_2 = C_2 V} [/ latex] , и [латекс] \ boldsymbol {Q_3 = C_3 V} [/ латекс]. Ввод их в предыдущее уравнение дает
[латекс] \ boldsymbol {C _ {\ textbf {p}} V = C_1 V + C_2 V + C_3 V}. [/ Latex]
Исключая [латекс] \ boldsymbol {V} [/ latex] из уравнения, мы получаем уравнение для полной емкости параллельно [латекс] \ boldsymbol {C _ {\ textbf {p}}} [/ latex]:
[латекс] \ boldsymbol {C _ {\ textbf {p}} = C_1 + C_2 + C_3 \ cdots} [/ latex].
Общая емкость при параллельном подключении — это просто сумма отдельных емкостей. (И снова «… » указывает на то, что выражение действительно для любого количества конденсаторов, подключенных параллельно. ) Так, например, если конденсаторы в приведенном выше примере были подключены параллельно, их емкость была бы
) Так, например, если конденсаторы в приведенном выше примере были подключены параллельно, их емкость была бы
[латекс] \ boldsymbol {C _ {\ textbf {p}} = 1.000 \; \ mu \ textbf {F} + 5.000 \; \ mu \ textbf {F} + 8.000 \; \ mu \ textbf {F} = 14.000 \; \ mu \ textbf {F}}. [/ latex]
Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на Рисунке 2 (b).
Общая емкость параллельно,
C p [латекс] \ boldsymbol {C _ {\ textbf {p}}} [/ latex]
Общая емкость параллельно [латекс] \ boldsymbol {C _ {\ textbf {p}} = C_1 + C_2 + C_3 + \ cdots} [/ latex]
Более сложные соединения конденсаторов иногда могут быть последовательными и параллельными. (См. Рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую.
Рисунок 3. (a) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C 1 и C 2 идут последовательно; их эквивалентная емкость C S меньше, чем у любого из них. (c) Обратите внимание, что C S параллельно с C 3 .Таким образом, общая емкость равна сумме C S и C 3 .
См. Пример 2 для расчета общей емкости цепи. (b) C 1 и C 2 идут последовательно; их эквивалентная емкость C S меньше, чем у любого из них. (c) Обратите внимание, что C S параллельно с C 3 .Таким образом, общая емкость равна сумме C S и C 3 .
Смесь последовательной и параллельной емкости
Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех десятичных знаков ([латекс] \ boldsymbol {C_1 = 1.000 \; \ mu \ textbf {F}} [/ latex ], [латекс] \ boldsymbol {C_2 = 5.000 \; \ mu \ textbf {F}} [/ latex] и [латекс] \ boldsymbol {C_3 = 8.000 \; \ mu \ textbf {F}} [/ latex]) и округлите ответ до трех десятичных знаков.
Стратегия
Чтобы определить общую емкость, мы сначала определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы [латекс] \ boldsymbol {C_1} [/ latex] и [латекс] \ boldsymbol {C_2} [/ latex] включены последовательно. Их комбинация, обозначенная на рисунке [латекс] \ boldsymbol {C_S} [/ latex], параллельна [латексу] \ boldsymbol {C_3} [/ latex].
Решение
Поскольку [латекс] \ boldsymbol {C_1} [/ latex] и [latex] \ boldsymbol {C_2} [/ latex] включены последовательно, их общая емкость определяется выражением [латекс] \ boldsymbol {\ frac {1} {C_S } = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3}} [/ latex].Ввод их значений в уравнение дает
[латекс] \ boldsymbol {\ frac {1} {C_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {C_2}} [/ латекс ] [латекс] \ boldsymbol {=} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {1.000 \; \ mu \ textbf {F}}} [/ латекс] [латекс] \ boldsymbol {+} [ / latex] [латекс] \ boldsymbol {\ frac {1} {5. 000 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ гидроразрыв {1.200} {\ mu \ textbf {F}}}. [/ latex]
000 \; \ mu \ textbf {F}}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ гидроразрыв {1.200} {\ mu \ textbf {F}}}. [/ latex]
Инвертирование дает
[латекс] \ boldsymbol {C _ {\ textbf {S}} = 0.833 \; \ mu \ textbf {F}}. [/ Latex]
Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; Таким образом, общая сумма составляет
[латекс] \ begin {array} {r @ {{} = {}} l} \ boldsymbol {C _ {\ textbf {tot}}} & \ boldsymbol {C_S + C_S} \\ [1em] & \ boldsymbol { 0.833 \; \ mu \ textbf {F} + 8.000 \; \ mu \ textbf {F}} \\ [1em] & \ boldsymbol {8.833 \; \ mu \ textbf {F}}. \ end {array} [/ latex]
Обсуждение
Этот метод анализа комбинаций конденсаторов по частям, пока не будет получена общая сумма, может быть применен к более крупным комбинациям конденсаторов.
- Общая емкость последовательно [латекс] \ boldsymbol {\ frac {1} {C _ {\ textbf {S}}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1 } {C_3} + \ cdots} [/ латекс]
- Общая емкость параллельно [латекс] \ boldsymbol {C _ {\ textbf {p}} = C_1 + C_2 + C_3 + \ cdots} [/ latex]
- Если схема содержит комбинацию конденсаторов, включенных последовательно и параллельно, определите последовательную и параллельную части, вычислите их емкости, а затем найдите общую сумму.

Концептуальные вопросы
1: Если вы хотите хранить большое количество энергии в конденсаторной батарее, подключите ли вы конденсаторы последовательно или параллельно? Объяснять.
Задачи и упражнения
1: Найдите общую емкость комбинации конденсаторов на рисунке 4.
Рисунок 4. Комбинация последовательного и параллельного подключения конденсаторов.
2: Предположим, вам нужна конденсаторная батарея с общей емкостью 0,750 Ф и у вас есть множество конденсаторов 1,50 мФ. Какое наименьшее число вы могли бы связать вместе, чтобы достичь своей цели, и как бы вы их связали?
3: Какую общую емкость можно получить, подключив символ [латекс] \ bold {5.00 \; \ mu \ textbf {F}} [/ latex] и конденсатор [latex] \ boldsymbol {8.00 \; \ mu \ textbf {F}} [/ latex] вместе?
4: Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.
Рисунок 5. Комбинация последовательного и параллельного подключения конденсаторов.
5: Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.
Рисунок 6. Комбинация последовательного и параллельного подключения конденсаторов.
6: Необоснованные результаты
(a) Конденсатор [латекс] \ boldsymbol {8.00 \; \ mu \ textbf {F}} [/ latex] подключен параллельно другому конденсатору, что дает общую емкость [латекс] \ boldsymbol {5.00 \; \ mu \ textbf {F}} [/ латекс]. Какая емкость у второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Решения
Задачи и упражнения
1: [латекс] \ boldsymbol {0.293 \; \ mu \ textbf {F}} [/ латекс]
3: [латекс] \ boldsymbol {3.08 \; \ mu \ textbf {F}} [/ latex] в последовательной комбинации, [латекс] \ boldsymbol {13. 0 \; \ mu \ textbf {F}} [/ латекс ] в параллельной комбинации
0 \; \ mu \ textbf {F}} [/ латекс ] в параллельной комбинации
4: [латекс] \ boldsymbol {2.79 \; \ mu \ textbf {F}} [/ латекс]
6: (a) [латекс] \ boldsymbol {-3.00 \; \ mu \ textbf {F}} [/ latex]
(b) У вас не может быть отрицательного значения емкости.
(c) Предположение, что конденсаторы были подключены параллельно, а не последовательно, было неверным.Параллельное соединение всегда дает большую емкость, в то время как здесь предполагалась меньшая емкость. Это могло произойти, только если конденсаторы подключены последовательно.
Общая емкость
Емкость C — один из основных параметров электрических цепей после сопротивления R и индуктивности L. Емкость C определяется как отношение заряда Q к напряжению V → C = Q / V. Единица измерения емкости — Фарад → [C] = 1F, Фарад — производная единица системы СИ.Иногда необходимо рассчитать емкость электрической цепи, которая содержит несколько конденсаторов в своей топологии, поэтому часто говорят, что вычисляется общая емкость электрической цепи . Иногда во время анализа цепей необходимо рассчитать общую емкость, которая видна на клеммах конкретной цепи.
Иногда во время анализа цепей необходимо рассчитать общую емкость, которая видна на клеммах конкретной цепи.
Конденсаторы, соединенные последовательно
Электрическая схема содержит три последовательно включенных конденсатора, имеющих разные номиналы.Предметом является обозначение общей емкости , из конденсаторов, соединенных последовательно . Каждый конденсатор будет иметь одинаковый электрический заряд Q, собранный на его электродах, потому что конденсаторы соединены последовательно. На первом электроде это будет электрический заряд + Q, а на втором электроде — электрический заряд -Q. Общая емкость цепи обозначена как C X .
Конденсаторы, соединенные последовательно
Конденсаторы, включенные параллельно
Электрическая цепь содержит три конденсатора, которые включены параллельно и имеют разные номиналы.Предметом является обозначение общей емкости из конденсаторов, соединенных параллельно . Каждый конденсатор будет иметь одинаковое напряжение между электродами, потому что конденсаторы подключены параллельно. Конденсаторы будут иметь разные электрические заряды, собранные между электродами, но все они будут иметь одинаковое напряжение между электродами, поскольку они подключены параллельно. Общая емкость цепи обозначена как C X .
Каждый конденсатор будет иметь одинаковое напряжение между электродами, потому что конденсаторы подключены параллельно. Конденсаторы будут иметь разные электрические заряды, собранные между электродами, но все они будут иметь одинаковое напряжение между электродами, поскольку они подключены параллельно. Общая емкость цепи обозначена как C X .
Конденсаторы, включенные параллельно
Емкость плоского конденсатора
Предмет этого краткого пояснения состоит в том, чтобы обозначить формулу для емкости плоского конденсатора .Основная причина получения математической формулы для емкости плоского конденсатора заключается в том, что она зависит только от геометрических размеров и постоянных материала. Емкость плоского конденсатора будет обозначаться с применением следующих вещей:
• определение электрической емкости
• закон Гаусса
• уравнение для электрического потока
• размеры плоского конденсатора
• знание констант материала → относительная электрическая проницаемость и электрическая проницаемость вакуума
• знание плотности электрического заряда на площади
Емкость плоского конденсатора
Общая емкость — пример 1
Электрическая схема построена из четырех конденсаторов разного номинала. Предметом является обозначение общей емкости электрической цепи, видимой со стороны клемм источника питания. Конденсаторы включены в схему смешанным образом, так как два из них включены последовательно, а еще два — параллельно. Общая емкость цепи обозначена как C X .
Предметом является обозначение общей емкости электрической цепи, видимой со стороны клемм источника питания. Конденсаторы включены в схему смешанным образом, так как два из них включены последовательно, а еще два — параллельно. Общая емкость цепи обозначена как C X .
Общая емкость — пример 1
Общая емкость — пример 2
Электрическая схема построена из пяти конденсаторов разного номинала.Предметом является обозначение общей емкости электрической цепи, видимой со стороны клемм источника питания. Конденсаторы соединены в цепи смешанным способом, поскольку два из них соединены последовательно, а еще два соединены параллельно, поэтому для некоторых конкретных ветвей в цепи необходимо рассчитать емкость последовательного соединения конденсаторов, а иногда и емкость параллельного соединения. конденсаторы тоже должны быть рассчитаны. Общая емкость цепи обозначена как C X .
Общая емкость — пример 2
Общая емкость — пример 3
Электрическая схема содержит в своей топологии семь конденсаторов.


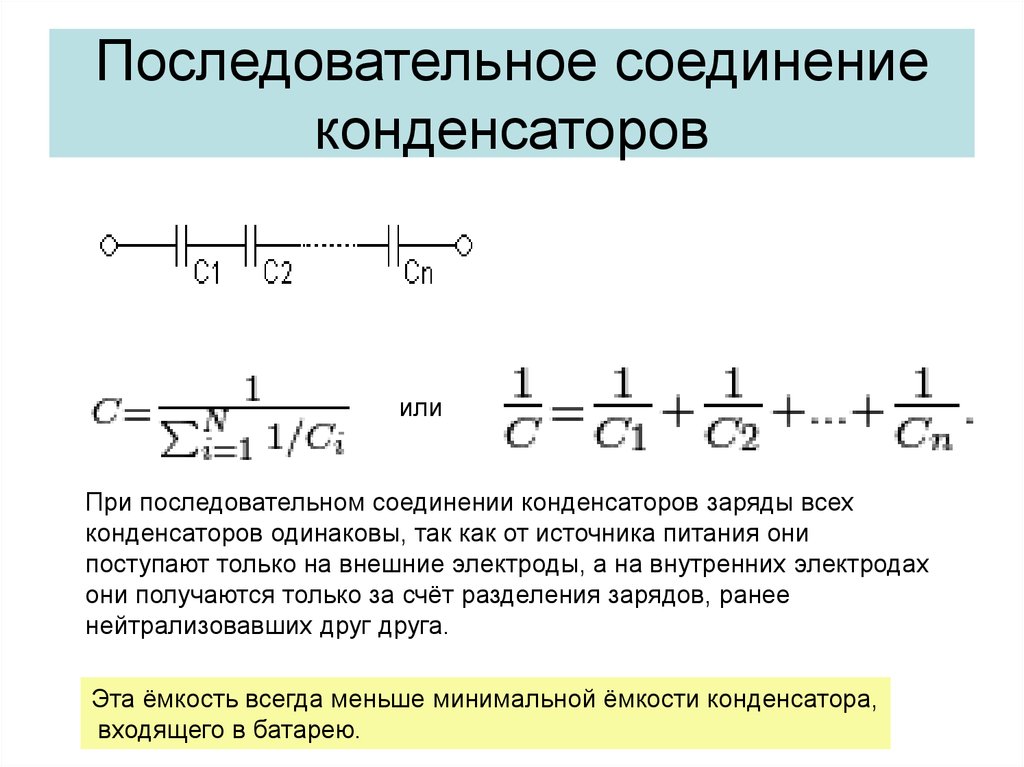
 Эти элементы схемы соединены последовательно. Остаётся произвести расчёт такого соединения и мы получим искомую.
Эти элементы схемы соединены последовательно. Остаётся произвести расчёт такого соединения и мы получим искомую.
 Разность потенциалов на соединении составляет 220 В. Определить заряд и разность потенциалов на каждом конденсаторе.
Разность потенциалов на соединении составляет 220 В. Определить заряд и разность потенциалов на каждом конденсаторе.
 Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.
Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.
