Определить токи в ветвях методом контурных токов: Метод контурных токов, метод узловых потенциалов

Содержание

Метод контурных токов, метод узловых потенциалов

Ранее рассматривались простейшие одноконтурные (двухконтурные) электрические цепи и схемы с двумя узлами. Были описаны способы преобразования схем, с помощью которых в ряде случаев удаётся упростить расчёт разветвлённой электрической цепи.

В случае, когда электрическая схема достаточно сложна и не приводится к схеме одноконтурной цепи, пользуются более общими методами расчёта. Описанные ниже методы применимы для цепей постоянного и переменного тока.

Метод контурных токов позволяет уменьшить количество уравнений системы до числа

— число уравнений (сост. по II закону Кирхгофа).

Если в цепи некоторые узлы соединяются ветвями, не меняющими проводимость (они могут содержать источники тока), то число уравнений К, составляемых по методу контурных токов уменьшается на NT.

Метод основывается на том свойстве, что ток в любой ветви цепи может быть представлен в виде алгебраической суммы независимых контурных токов, протекающих в этой ветви.

При пользовании методом сначала выбирают и обозначают независимые контурные токи (по любой ветви должен протекать хотя бы один выбранный ток).

— число независимых контурных токов, их необходимо выбирать проходящими по ветви, не содержащими источников тока.

Пусть электрическая цепь содержит n контуров (независимых). Согласно II закону Кирхгофа получаем следующую систему из n линейных уравнений:

При этом следует считать

, если условные положительные направления контурных токов в одной ветви контуров K и m совпадают, и , если они противоположны.

где D1 D2 Dn — дополнение

D — определитель системы.

Расчёт установившегося режима в цепи переменного тока комплексным методом выполняется в следующей последовательности:

Составляется электрическая схема, на которой все источники и пассивные элементы представляются комплексными величинами соответственно напряжений, токов, сопротивлений (проводимостей).

Выбирается условно положительное направление для комплексных значений напряжений, ЭДС и токов.

Согласно уравнениям электрических цепей (Ома, Кирхгофа) в комплексной форме составляются алгебраические уравнения для рассчитываемой цепи.

Уравнения цепи разрешаются относительно искомых переменных (токов, напряжений) в их комплексной форме.

Метод узловых потенциалов

Метод позволяет уменьшить количество уравнений системы до числа

, где Ny – число узлов электрической схемы.

Сущность метода заключается в том, что сначала определяются потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, определяются с помощью законов Ома.

При составлении уравнений по МУП сначала полагают равным нулю потенциал какого-либо узла, для оставшихся

составляют уравнения по I-му закону Кирхгофа.

Если в цепи некоторые узлы соединяются ветвями, не имеющими сопротивлений (они могут содержать источники напряжений), то число KI уравнений, составленных по МУП, уменьшается на Nн (число ветвей с нулевыми сопротивлениями).

— число уравнений по МУП.

Прежде, чем перейти к изложению самого метода, напомним, что в случае, когда между двумя узлами имеются несколько параллельных ветвей с источниками ЭДС (или без них), их можно привести к одной эквивалентной схеме.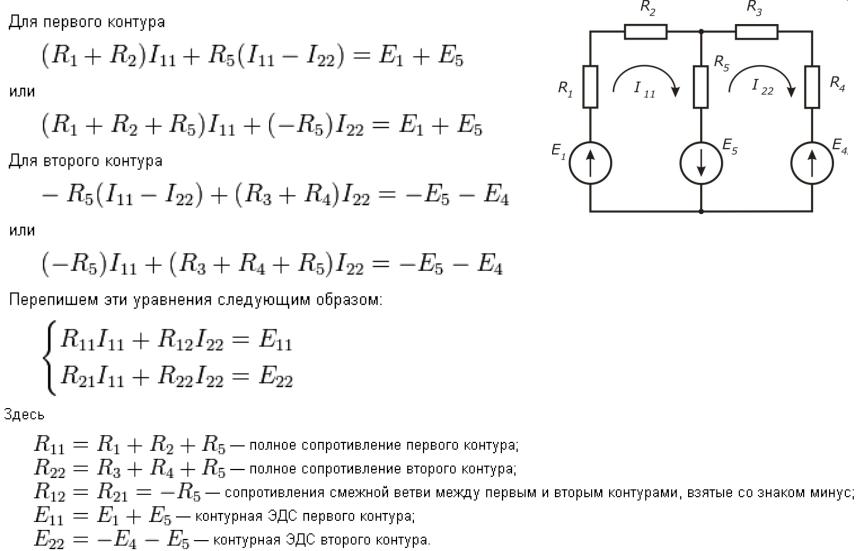

Это представление эквивалентной схемой параллельных ветвей с источниками ЭДС даёт нам право без ограничения общности считать, что между любой парой узлов включена только одна ветвь.

Дальше будем предполагать, что

, т.е. между узлами цепи не включены идеальные источники ЭДС.

В качестве примера составим уравнение по методу узловых напряжений для цепи, изображённой на рис. 3.

Задано:

и параметры всех элементов.

Расчёт цепи производим комплексным методом:

Для узлов 1, 2, 3 имеем уравнения:

(1)

Y11=Y12+Y10+Y13; Y22=Y20+Y12+Y23; Y33=Y30+Y13+Y23

Решив систему из 3-х уравнений относительно узловых напряжений, находим напряжения на ветвях и токи в них. Метод узловых напряжений применим к независимым контурам.

Положительное направление всех узловых напряжений принято считать к опорному узлу.

Первое уравнение Кирхгофа для некоторого узла К можно записать:

(1)

Для 1-ого узла:

Значения Z1; Z2; Z3; E1 и E2 у нас были определены ранее (см. 1-ый способ решения).

Ответ:

Между узлами К и m имеется ветвь с источниками ЭДС (EKm), сопротивлением ZKm, то ток в этой цепи (ветви), направленный от К к m связан соотношениями:

Первый закон Кирхгофа для рис. 1 имеет вид (1).

Напряжение можно выразить через узловые напряжения в виде:

Получаем:

или

Обозначив

, где YKK – сумма проводимостей всех ветвей, присоединённых к К-ому узлу, имеем: — что и является основным уравнением для К-ого узла по МУП.

В развёрнутой форме совокупность уравнений по МУП имеет вид:

Решая эту систему, найдём узловые напряжения, причём для К-ого узла величина

будет: ,

где D — главный определитель системы, DmK – его алгебраическое дополнение.

После того, как узловые напряжения найдены, определения токов в ветвях цепи имеют вид:

Если в ветви содержатся ЭДС, то ток равен

Метод узловых напряжений применяется к независимым узлам.

Если к К-ому узлу подтекает ток от источника тока, то он должен быть включен в ток IKK со знаком «+», если утекает, то со знаком «-».

Если между какими-либо двумя узлами нет ветви, то соответствующая проводимость равна 0.

Yii – собственная проводимость всех ветвей, подходящих к узлу i (всегда со знаком «+»).

Yiк – взаимная проводимость между узлами i и к (входит в уравнение всегда со знаком «-» при выбранном направлении всех узловых напряжений к базисному узлу).

Ток I1 называется узловым током 1-ого узла. Это расчётная величина, равная алгебраической сумме токов, полученных от деления ЭДС ветвей, подходящих к 1-ому узлу, на сопротивления данных ветвей. В эту сумму со знаком «+» входят токи тех ветвей, ЭДС которых направлена к 1-ому узлу.

Y11 – проводимость всех ветвей, сходящихся в 1-ом узле.

Y12 – проводимость взаимная – равняется сумме проводимостей всех ветвей, соединяющих узел 1 с узлом 2 (берётся со знаком «-»).

Пример:

Е2=Е3 = 1 В

IK3 = 1 A

IK2 = 1 A

R1 = 13 Ом

R2 = 5 Ом

R3 = 9 Ом

R4 = 7 Ом

R5 = 1 Ом

R6 = 4 Ом

Определить токи в ветвях.

Для определения напряжения между двумя произвольными точками схемы необходимо ввести в левую часть уравнений искомое напряжение вдоль пути, как бы дополняющего незамкнутый контур до замкнутого.

Алгоритм расчета цепи методом контурных токов.

1.4. Метод узловых потенциалов.

14 Метод узловых потенциалов Теоретические сведения Метод расчета, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов Этот метод наиболее рационально применять

Подробнее

УНИВЕРСИТЕТ ИТМО. Денисова А.В.

УНИВЕРСИТЕТ ИТМО Кафедра электротехники и прецизионных электромеханических систем Денисова А. В. Методическое пособие в помощь к выполнению домашних заданий по курсу «Электротехника» и «Общая электротехника»

Подробнее

Расчетно-графическая работа 1

Расчетно-графическая работа 1 Расчет цепей с источниками постоянных воздействий Пример решения: Дано: N M 3 4 5 6 7 Решение: 1 1) По заданному номеру варианта изобразим цепь, подлежащую расчету, выпишем

Подробнее

2.8. Метод контурных токов.

При использовании законов Кирхгофа число уравнений равно числу ветвей Для уменьшения числа уравнений (и неизвестных величин) используют методы контурных токов узловых потенциалов и эквивалентных генераторов

Подробнее

МЕТОДЫ РАСЧЕТА СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С. П. КОРОЛЕВА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)»

Подробнее

Практическая работа 5

Практическая работа 5 Тема: Расчёт электрических цепей с использованием законов Ома и Кирхгофа. Цель: научиться рассчитывать электрические цепи постоянного тока, используя законы Ома и Кирхгофа. Ход работы

Подробнее

Работа по теме : «Сложные цепи»

Работа по теме «Сложные цепи» Определить токи в ветвях и режимы работы источников в схеме, где E, E — ЭДС источника энергии; 0, 0 — их внутреннее сопротивление;,,, 4, 5 — сопротивление резисторов. Данные

Подробнее

Методы анализа сложных линейных цепей.

ЛЕКЦИЯ. Методы анализа сложных линейных цепей. Существуют универсальные методы, позволяющие автоматически описывать связь между током и напряжением на различных участках цепи. Эти методы позволяют сократить

Подробнее

Постоянный ток «на ладони»

Постоянный ток «на ладони» Теоретические сведения. Топология цепи ее строение. Разобраться со строением цепи можно, зная определения ее элементов. Ветвь — участок цепи, содержащий один или несколько последовательно

Подробнее

Методы анализа сложных линейных цепей.

ЛЕКЦИЯ 6. Методы анализа сложных линейных цепей. Существуют универсальные методы, позволяющие автоматически описывать связь между током и напряжением на различных участках цепи. Эти методы позволяют сократить

Подробнее

РАСЧЕТ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Ивановский государственный политехнический университет ( И В Г П У) Т е к с т и л ь н ы й и н с т и т у т К а федра автоматики и радиоэлектроники Методические указания к расчетно-графическим заданиям по

Подробнее

I 3 b I 11 E 1 I 5 I 6 I 33

Задача 1 Для заданной схемы необходимо: 1) составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы; 2) определить токи во всех ветвях методом контурных токов; 3)

Подробнее

E — нормальный элемент Вестона.

ЛАБОРАТОРНАЯ РАБОТА 3-7: ИЗМЕРЕНИЕ ЭЛЕКТРОДВИЖУЩИХ СИЛ ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ МЕТОДОМ КОМПЕНСАЦИИ Студент группа Допуск Выполнение Защита Цель работы: ознакомление с методами компенсации и применение

Подробнее

РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ

Федеральное агентство по образованию Уральский государственный технический университет УПИ имени первого Президента России Б.Н. Ельцина В.В. Муханов, А.Г. Бабенко РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ Учебное электронное

Подробнее

Глава 1. Основные законы электрической цепи

Глава 1. Основные законы электрической цепи 1.1 Параметры электрической цепи Электрической цепью называют совокупность тел и сред, образующих замкнутые пути для протекания электрического тока. Обычно физические

Подробнее

Электротехника и электроника

Федеральное агентство связи Государственное образовательное учреждение высшего профессионального образования Поволжский государственный университет телекоммуникаций и информатики Кафедра электродинамики

Подробнее

от частоты — Фазо-частотная

7 Комплексный коэффициент передачи I I -реакция ток или напряжение цепи на внешнее воздействие F ток или напряжение F F K — комплексный коэффициент передачи, передаточная F функция или передаточная характеристика

Подробнее

4.

МЕТОДЫ РАСЧЁТА РЕЗИСТИВНЫХ СХЕМ

28 4. МЕТОДЫ РАСЧЁТА РЕЗИСТИВНЫХ СХЕМ В данной главе рассматриваются методы расчёта, применяемые при анализе линейных схем в статическом режиме, т. е. при постоянных сигналах. В соответствии с компонентными

Подробнее

Лекция 2. АНАЛИЗ РЕЗИСТИВНЫХ ЦЕПЕЙ

4 Лекция. АНАЛИЗ РЕЗИСТИВНЫХ ЦЕПЕЙ План. Задача анализа электрических цепей. Законы Кирхгофа.. Примеры анализа резистивных цепей. 3. Эквивалентные преобразования участка цепи. 4. Заключение. Задача анализа

Подробнее

Основныезаконы электротехники

Основныезаконы электротехники Схема это графическое изображение электрической цепи. Ветвь это участок схемы, вдоль котороготечетодинитотжеток. Узел это место соединения трех или большего числа ветвей Контур

Подробнее

ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики

Ю. В. Тихомиров ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики С ЭЛЕМЕНТАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. ОПТИКА для студентов всех специальностей всех форм обучения МОСКВА — 2012 ЦЕЛЬ РАБОТЫ

Подробнее

Лабораторная работа 12*

Лабораторная работа 2 ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ Цель работы найти и построить эквипотенциальные поверхности и силовые линии электрического поля между двумя электродами произвольной формы; определить

Подробнее

Лекция 2. АНАЛИЗ РЕЗИСТИВНЫХ ЦЕПЕЙ

4 Лекция АНАЛИЗ РЕЗИСТИВНЫХ ЦЕПЕЙ План Задача анализа электрических цепей Законы Кирхгофа Примеры анализа резистивных цепей 3 Эквивалентные преобразования участка цепи 4 Выводы Задача анализа электрических

Подробнее

Расчетно-графическая работа 1

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ КАФЕДРА ТЕОРЕТИЧЕСКИ Х

Подробнее

РАСЧЕТ ЦЕПИ ПОСТОЯННОГО ТОКА

Расчетно-графическое задание 1 для студентов института дистанционного обучения. РАСЧЕТ ЦЕПИ ПОСТОЯННОГО ТОКА методом контурных токов и эквивалентного генератора Вариант *** ( вариант определяется тремя

Подробнее

3. Постоянный электрический ток.

3 Постоянный электрический ток Закон Ома для однородного участка цепи: где разность потенциалов на концах участка Сопротивление однородного участка проводника: l l S σs где удельное сопротивления σ удельная

Подробнее

2007, Ravenbird ВВ-2-06

ТИПОВОЙ РАСЧЁТ ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ Вариант Красняков А.М. МИРЭА, 2007 Рис.. Исходная схема.. Упростить схему (рис. ), заменив последовательно и параллельно соединённые резисторы четвёртой

Подробнее

ЦЕЛЬ ДОМАШНЕГО ЗАДАНИЯ

ЦЕЛЬ ДОМАШНЕГО ЗАДАНИЯ 3 1. Освоить анализ линейных цепей с использованием метода комплексных амплитуд. 2. Закрепить методы расчета линейных цепей. 3. Овладеть построением векторных диаграмм. 4. Уяснить

Подробнее

Теоретические сведения.

2.2. Операторный метод расчета переходных процессов. Теоретические сведения. Расчет переходных процессов в сложных цепях классическим методом очень часто затруднен нахождением постоянных интегрирования.

Подробнее

Лекция 3. МЕТОД УЗЛОВЫХ НАПРЯЖЕНИЙ

6 Лекция. МЕТОД УЗЛОВЫХ НАПРЯЖЕНИЙ План. Метод узловых напряжений.. Алгоритм формирования узловых уравнений.. Формирование узловых уравнений для схем с ИТУН.. Модифицированный метод узловых напряжений.

Подробнее

АНАЛИЗ СЛОЖНЫХ ЛИНЕЙНЫХ ЦЕПЕЙ

Министерство образования и науки Российской Федерации Федеральное агентство по образованию ГОУ ВПО «УГТУ — УПИ имени первого Президента России Б. Н. Ельцина» АНАЛИЗ СЛОЖНЫХ ЛИНЕЙНЫХ ЦЕПЕЙ Методические указания

Подробнее

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ К РАСЧЕТУ СЛОЖНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА ПО КУРСУ «ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ» для студентов электротехнических и электроэнергетических специальностей

Подробнее

РАСЧЕТ ЛИНЕЙНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Московский государственный технический университет имени Н.Э. Баумана В.И. Волченсков, Г.Ф. Дробышев РАСЧЕТ ЛИНЕЙНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА Издательство МГТУ им. Н.Э. Баумана Московский государственный

Подробнее

Рис.1 — исходная схема

Рис.1 — исходная схема Параметры элементов цепи для приведенной схемы: R 1 := Ом R 2 :=62 Ом R 3 := Ом R 4 :=44 Ом R 5 :=76 Ом R 6 := Ом R 7 :=71 Ом R 8 := Ом Xl 1 :=27 Ом Xl 2 := Ом Xl 3 :=47 Ом Xl 4

Подробнее

Контрольная работа.

Задачи:

ЭЛЕКТРОТЕХНИКА (Учебно-методическое пособие) Контрольная работа. Задачи: 1.Расчет цепи, состоящей из линейных и нелинейных элементов. 2.Расчет сложной электрической цепи постоянного тока. 3.Расчет электрической

Подробнее

ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА

Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта ГОУ ВПО «Дальневосточный государственный университет путей сообщения» Кафедра «Телекоммуникации» АВСтафеев

Подробнее

Теоретические сведения.

Глава 2. Методы расчета переходных процессов. 2.1. Классический метод расчета. Теоретические сведения. В первой главе были рассмотрены методы расчета цепи, находящейся в установившемся режиме, то есть

Подробнее

Линейные электрические цепи

Федеральное агентство по образованию Рубцовский индустриальный институт ГОУ ВПО «Алтайский государственный технический университет им ИИ Ползунова» ВТ Гетманов Линейные электрические цепи Курс лекций по

Подробнее

★ Метод контурных токов — электротехника .

{t}={\begin{pmatrix}-1&amp,0&amp,1\\-1&amp 0\\0&amp 1&amp,1\\1&amp,0&amp,0\\0&amp,1&amp,0\\0&amp 1\\\end{pmatrix}},\квад \mathbf {Z} ={\begin{pmatrix}Z_{1}&amp,0&amp 0&amp 0\\0&amp,Z_{2}&amp,0&amp 0&amp,0\\0&amp Z_{3}&amp,0&amp 0\\0&amp 0&amp,Z_{4}&amp,0&amp,0\\0&amp 0&amp Z_{5}&amp,0\\0&amp 0&amp 0&amp,Z_{6}\\\end{pmatrix}},\квад \mathbf {J} ={всегда\begin{pmatrix по}0\\0\\0\\0\\J_{5}\\0\конец{pmatrix по}},\Quad с \mathbf {E} ={всегда\begin{pmatrix по}0\\0\\0\\у, {4}\\0\\у, {6}\конец{pmatrix все}}}

В умножаемой матрицы в соответствии с матричным уравнением:

C Z = (С Z =) − Z 1 (З 1) − Z 2 0 Z 4 0 Z 2 (З 2 0 З 4 0 З 2) − Z 3 0 Z 5 0 Z 1 0 Z 3 0 Z 6 (З 3 0 З 5 0 З 1 0 З 3 0 З 6), {\свойства стиль отображения значение \mathbf {CZ} ={\begin{pmatrix}-Z_{1}&amp Z_{2}&amp,0&amp,Z_{4}&amp,0&amp,0\\0&amp,Z_{2}&amp Z_{3}&amp,0&amp,Z_{5}&amp,0\\Z_{1}&amp,0&amp,Z_{3}&amp,0&amp Z_{6}\end{pmatrix}},}

C Z C t = Z 1 (С З С т = з 1) Z 2 (З 2) Z 4 (З 4) − Z 2 (З 2) − Z 1 (З 1) − Z 2 Z 2 (З 2 З 2) Z 3 (З 3) Z 5 (З 5) − Z 3 (З 3) − Z 1 (З 1) − Z 3 Z 1 (З 3 З 1) Z 3 (З 3) Z 6 (З 6), {\свойства стиль отображения значение \mathbf {CZC^{Т}} ={всегда\begin{pmatrix по}Z_{1} Z_{2} Z_{4}&амп-Z_{2}&амп-Z_{1}\\-Z_{2}&амп Z_{2} Z_{3} Z_{5}&амп-Z_{3}\\-Z_{1}&амп-Z_{3}&амп Z_{1} Z_{3} Z_{6}\конец{pmatrix все}},}

C Z C t I 2 = Z 1 (С З С Т и 2 = З 1) Z 2 (З 2) Z 4 (З 4) ⋅ I 4 − Z 2 (З 2) ⋅ I 5 − Z 1 (З 1) ⋅ I 6 − Z 2 (З 2) ⋅ I 4 Z 2 (З 2) Z 3 (З 3) Z 5 (З 5) ⋅ I 5 − Z 3 (З 3) ⋅ I 6 − Z 1 (З 1) ⋅ I 4 − Z 3 (З 3) ⋅ I 5 Z 1 (З 1) Z 3 (З 3) Z 6 (З 6) ⋅ I 6), {\свойства стиль отображения значение \mathbf {CZC^{Т}призраки{2}} ={всегда\begin{pmatrix по}Z_{1} Z_{2} Z_{4}\cDOT на Призраки{4}-Z_{2}\cDOT на призраки{5}-Z_{1}\cDOT на Призраки{6}\\-Z_{2}\cDOT на Призраки{4} Z_{2} Z_{3} Z_{5}\cDOT на призраки{5}-Z_{3}\cDOT на Призраки{6}\\-Z_{1}\cDOT на Призраки{4}-Z_{3}\cDOT на призраки{5} Z_{1} Z_{3} Z_{6}\cDOT на Призраки{6}\конец{pmatrix все}},}

E Z J = 0 E 4 Z 5 J 5 E 6 (З J = 0 И 0 Е 4 З 5 ДЖ 5-Е 6), C E Z J = E 4 Z 5 J 5 E 6 (З Ф = Е 4 З 5 ДЖ 5-Е 6) {\свойства стиль отображения значение \mathbf {Е от ZJ} ={всегда\begin{pmatrix по}0\\0\\0\\у, {4}\\Z_{5}J_{5}\\У, {6}\конец{pmatrix все}},\Quad с \mathbf {СЕ от ZJ} ={всегда\begin{pmatrix все}, что{4}\\Z_{5}J_{5}\\У, {6}\конец{pmatrix по}}}

Раскрывая матричное представление, мы получим следующую систему уравнений:

{ Z 1 ({ З 1) Z 2 (З 2) Z 4 (З 4) ⋅ I 4 − Z 2 (З 2) ⋅ I 5 − Z 1 (З 1) ⋅ I 6 = E 4 (Я 6 = Е 4) − Z 2 (З 2) ⋅ I 4 Z 2 (З 2) Z 3 (З 3) Z 5 (З 5) ⋅ I 5 − Z 3 (З 3) ⋅ I 6 = Z 5 J 5 (Я 6 = З 5 ДЖ 5) − Z 1 (З 1) ⋅ I 4 − Z 3 (З 3) ⋅ I 5 Z 1 (З 1) Z 3 (З 3) Z 6 (З 6) ⋅ I 6 = E 6 (Я 6 = Е 6). {\свойства стиль отображения значение {\начать{случаи}Z_{1} Z_{2} Z_{4}\cDOT на Призраки{4}-Z_{2}\cDOT на призраки{5}-Z_{1}\cDOT на Призраки{6}=у, {4}\\-Z_{2}\cDOT на Призраки{4} Z_{2} Z_{3} Z_{5}\cDOT на призраки{5}-Z_{3}\cDOT на Призраки{6}=Z_{5}J_{5}\\-Z_{1}\cDOT на Призраки{4}-Z_{3}\cDOT на призраки{5} Z_{1} Z_{3} Z_{6}\cDOT на Призраки{6}=У, {6}\конец{случаи}}. }

Метод контурных токов и PSpice. OrCAD PSpice. Анализ электрических цепей

Метод контурных токов, метод узловых потенциалов (Реферат)

Метод контурных
токов, метод узловых потенциалов

Ранее рассматривались простейшие
одноконтурные (двухконтурные) электрические
цепи и схемы с двумя узлами. Были описаны
способы преобразования схем, с помощью
которых в ряде случаев удаётся упростить
расчёт разветвлённой электрической
цепи.

В случае, когда электрическая схема
достаточно сложна и не приводится к
схеме одноконтурной цепи, пользуются
более общими методами расчёта. Описанные
ниже методы применимы для цепей
постоянного и переменного тока.

Метод контурных токов позволяет уменьшить
количество уравнений системы до числа

— число уравнений (сост. по II закону
Кирхгофа).

Если в цепи некоторые узлы соединяются
ветвями, не меняющими проводимость (они
могут содержать источники тока), то
число уравнений К, составляемых по
методу контурных токов уменьшается на
NT.

Метод основывается на том свойстве, что
ток в любой ветви цепи может быть
представлен в виде алгебраической суммы
независимых контурных токов, протекающих
в этой ветви.

При пользовании методом сначала выбирают
и обозначают независимые контурные
токи (по любой ветви должен протекать
хотя бы один выбранный ток).

—
число независимых контурных токов, их
необходимо выбирать проходящими по
ветви, не содержащими источников тока.

Пусть электрическая цепь содержит n
контуров (независимых). Согласно II закону
Кирхгофа получаем следующую систему
из n линейных уравнений:

При этом следует считать
,
если условные положительные направления
контурных токов в одной ветви контуров
K и m совпадают, и
,
если они противоположны.

где D1 D2
Dn — дополнение

D —
определитель системы.

Расчёт установившегося режима в цепи
переменного тока комплексным методом
выполняется в следующей последовательности:

Составляется электрическая схема, на
которой все источники и пассивные
элементы представляются комплексными
величинами соответственно напряжений,
токов, сопротивлений (проводимостей).

Выбирается условно положительное
направление для комплексных значений
напряжений, ЭДС и токов.

Согласно уравнениям электрических
цепей (Ома, Кирхгофа) в комплексной форме
составляются алгебраические уравнения
для рассчитываемой цепи.

Уравнения цепи разрешаются относительно
искомых переменных (токов, напряжений)
в их комплексной форме.

Метод узловых потенциалов

Метод позволяет уменьшить количество
уравнений системы до числа
,
где Ny – число узлов электрической схемы.

Сущность метода заключается в том, что
сначала определяются потенциалы всех
узлов схемы, а токи ветвей, соединяющих
узлы, определяются с помощью законов
Ома.

При составлении уравнений по МУП сначала
полагают равным нулю потенциал какого-либо
узла, для оставшихся

составляют уравнения по I-му закону
Кирхгофа.

Если в цепи некоторые узлы соединяются
ветвями, не имеющими сопротивлений (они
могут содержать источники напряжений),
то число KI уравнений, составленных по
МУП, уменьшается на Nн (число ветвей с
нулевыми сопротивлениями).

— число уравнений по МУП.

Прежде, чем перейти к изложению самого
метода, напомним, что в случае, когда
между двумя узлами имеются несколько
параллельных ветвей с источниками ЭДС
(или без них), их можно привести к одной
эквивалентной схеме.

Это представление эквивалентной схемой
параллельных ветвей с источниками ЭДС
даёт нам право без ограничения общности
считать, что между любой парой узлов
включена только одна ветвь.

Дальше будем предполагать, что
,
т.е. между узлами цепи не включены
идеальные источники ЭДС.

В качестве
примера составим уравнение по методу
узловых напряжений для цепи, изображённой
на рис. 3.

Задано:

и параметры
всех элементов.

Расчёт цепи
производим комплексным методом:

Для узлов 1, 2,
3 имеем уравнения:

(1)

Y11=Y12+Y10+Y13;
Y22=Y20+Y12+Y23; Y33=Y30+Y13+Y23

Решив систему
из 3-х уравнений относительно узловых
напряжений, находим напряжения на ветвях
и токи в них. Метод узловых напряжений
применим к независимым контурам.

Положительное
направление всех узловых напряжений
принято считать к опорному узлу.

Первое уравнение
Кирхгофа для некоторого узла К можно
записать:

(1)

Для 1-ого узла:

Значения Z1;
Z2; Z3; E1 и E2 у нас были определены ранее
(см. 1-ый способ решения).

Ответ:

Между
узлами К и m имеется ветвь с источниками
ЭДС (EKm), сопротивлением ZKm, то ток в этой
цепи (ветви), направленный от К к m связан
соотношениями:

Первый закон
Кирхгофа для рис. 1 имеет вид (1).

Напряжение
можно выразить через узловые напряжения
в виде:

Получаем:

или

Обозначив
,
где YKK – сумма проводимостей всех ветвей,
присоединённых к К-ому узлу, имеем:

—
что и является основным уравнением для
К-ого узла по МУП.

В развёрнутой
форме совокупность уравнений по МУП
имеет вид:

Решая эту систему, найдём узловые
напряжения, причём для К-ого узла величина

будет:

где D
— главный определитель системы, DmK
– его алгебраическое дополнение.

После того, как узловые напряжения
найдены, определения токов в ветвях
цепи имеют вид:

Если в ветви содержатся ЭДС, то ток равен

Метод узловых
напряжений применяется к независимым
узлам.

Если к К-ому
узлу подтекает ток от источника тока,
то он должен быть включен в ток IKK со
знаком «+», если утекает, то со знаком
«-».

Если между
какими-либо двумя узлами нет ветви, то
соответствующая проводимость равна 0.

Yii – собственная
проводимость всех ветвей, подходящих
к узлу i (всегда со знаком «+»).

Yiк – взаимная
проводимость между узлами i и к (входит
в уравнение всегда со знаком «-» при
выбранном направлении всех узловых
напряжений к базисному узлу).

Ток I1 называется
узловым током 1-ого узла. Это расчётная
величина, равная алгебраической сумме
токов, полученных от деления ЭДС ветвей,
подходящих к 1-ому узлу, на сопротивления
данных ветвей. В эту сумму со знаком «+»
входят токи тех ветвей, ЭДС которых
направлена к 1-ому узлу.

Y11 – проводимость
всех ветвей, сходящихся в 1-ом узле.

Y12 – проводимость
взаимная – равняется сумме проводимостей
всех ветвей, соединяющих узел 1 с узлом
2 (берётся со знаком «-»).

Пример:

Е2=Е3
= 1 В

IK3 = 1 A

IK2 = 1 A

R1 =
13 Ом

R2 =
5 Ом

R3 =
9 Ом

R4 = 7 Ом

R5 = 1 Ом

R6 = 4 Ом

Определить
токи в ветвях.

Для определения
напряжения между двумя произвольными
точками схемы необходимо ввести в левую
часть уравнений искомое напряжение
вдоль пути, как бы дополняющего незамкнутый
контур до замкнутого.

Список литературы

Для подготовки данной работы были
использованы материалы с сайта
http://revolution. allbest.ru

Электротехника ТОЭ: 3.2.2. Метод контурных токов

Теория / 3.2. Методы расчета сложных электрических цепей / 3.2.2. Метод контурных токов

Метод контурных токов позволяет уменьшить число
уравнений, составляемых по законам Кирхгофа до числа независимых контуров.

Метод контурных токов основан на том свойстве, что ток
в каждой ветви может быть представлен в виде алгебраической суммы независимых
контурных токов, протекающих в этой ветви.

Рассмотрим электрическую цепь (рис. 3.4), аналогичную
той, что рассматривали в предыдущем случае.

Определим число независимых контуров:

Считаем, что в каждом контуре протекает свой,
независимый от других контуров, ток. Направление контурных токов обозначаем круговой
стрелкой. Выберем направление контурных токов по часовой стрелке и запишем для
каждого контура уравнение по второму закону Кирхгофа с использованием контурных
токов, считая положительным направлением для каждого контура направление
контурного тока:

Эту систему уравнений можно привести к следующему виду:

При расчете цепей методом контурных токов удобнее
пользоваться готовой математической моделью, которая представляет собой систему
линейных алгебраических уравнений:

Здесь R₁₁, R₂₂, R₃₃ –
собственные сопротивления контуров, равные сумме всех сопротивлений, входящих в
контур:

Все остальные сопротивления являются взаимными:

R₁₂ = R₂₁ = R₂ – взаимное сопротивление
между первым и
вторым контурами;

R₂₃ = R₃₂ = R₄ – взаимное
сопротивление между
вторым и третьим контурами;

R₁₃ = R₃₁ =
0; – взаимное сопротивление между первым
и третьим контурами.

Из схемы можно видеть, что первый и третий контуры не
имеют общей ветви, а граничат только через узел, поэтому их взаимное сопротивление
равно нулю

Е₁₁ = Е₁; Е₂₂
= –Е₂; Е₃₃
= Е₃ +Е₂ – контурные ЭДС.

Если действие э.д.с. совпадает с направлением
контурного тока, то ЭДС имеет знак
«плюс», если не совпадает – «минус».

При использовании математической модели следует
направления всех контурных токов выбирать одинаковыми. В этом случае члены,
расположенные по главной диагонали и
содержащие собственные сопротивления контуров, будут положительны, а
члены, содержащие взаимные сопротивления, – отрицательны.

Если число уравнений больше двух, то систему удобнее
решать матричным методом.

Составим главный определитель системы

Частные определители получим, заменяя соответствующие
столбцы матриц столбцами свободных членов

Контурные токи находим из выражений:

Для того чтобы определить истинные токи в ветвях,
следут пользоваться следующими правилами. Если в ветви протекает только один
контурный ток, то истинный ток равен этому контурному току, причем, если
условно положительное направление истинного тока совпадает с направлением
контурного тока, то ставим знак контурного тока, если не совпадает – противоположный. Если в ветви протекает два
контурных тока, то за положительный принимаем тот, направление которого
совпадает с направлением истинного тока. Для заданной схемы истинные токи
определятся выражениями:

Достоинством этого метода по отношению к предыдущему
является то, что количество уравнений, составляемых по законам Кирхгофа,
уменьшается.

К недостаткам можно отнести введение в расчеты фиктивных величин –
контурных токов, через посредство которых находят истинные токи.

Метод контурных токов

Дата публикации: 13 января 2015.
Категория: Статьи.

Метод контурных токов применяется для расчета сложных электрических цепей, имеющих больше двух узловых точек. На рисунке 1, а изображена такая электрическая цепь. В ней три контура, причем средний контур имеет участки, входящие в состав двух соседних контуров, которые входят в состав одного контура.

Рисунок 1. Метод контурных токов пример

Сущность метода контурных токов заключается в предположении, что в каждом контуре проходит свой ток (контурный ток). Тогда на общих участках, расположенных на границе соседних контуров, будет протекать ток, равный алгебраической сумме токов этих контуров.

Выберем положительные направления трех контурных токов так, как указано на чертеже стрелками. Затем составим уравнения по второму закону Кирхгофа, обходя все три контура в одном направлении, например в направлении движения часовой стрелки.

Для контура I:

E₁ = I₁ × r₁ + (I₁ – I₂) × r₂ .

(а)

Для контура II:

0 = I₂ × r₃ + (I₂ – I₁) × r₂ + (I₂ – I₃) × r₄ .

(б)

Для контура III:

E₂ = I₃ × r₅ + (I₃ – I₂) × r₄ .

(в)

Как мы видим, число уравнений равно числу контуров, то есть число уравнений меньше, чем при решении задачи по законам Кирхгофа. Решая систему уравнений, находим контурные токи, по которым определяются токи в ветвях. Пример решения задач методом контурных токов показан ниже.

Пример 1. Определить, как распределяются токи в цепи, представленной на рисунке 1, а, если E₁ = 14 В, E₂ = 20 В, r₁ = 2 Ом, r₂ = 3 Ом, r₃ = 4 Ом, r₄ = 2 Ом, r₅ = 6 Ом. Произведем расчет методом контурных токов.

Решение.

Уравнение для контура I по формуле (а):

14 = I₁ × 2 + (I₁ – I₂) × 3 ,

14 = 2I₁ + 3I₁ – 3I₂ ,

14 = 5I₁ – 3I₂ .

(а’)

Уравнение для контура II по формуле (б):

0 = I₂ × 4 + (I₂ – I₁) × 3 + (I₂ – I₃) × 2 ,

0 = 4I₂ + 3I₂ – 3I₁ + 2I₂ – 2I₃ ,

0 = 9I₂ – 3I₁ – 2I₃ .

(б’)

Уравнение для контура III, по формуле (в):

20 = I₃ × 6 + (I₃ – I₂) × 2 ,

20 = 6I₃ + 2I₃ – 2I₂ ,

20 = 8I₃ – 2I₂ ,

10 = 4I₃ – I₂ .

(в’)

Складывая выражения (а’) и (б’), получим:

или

Складывая выражения (в’) и (г), получим:

или

Подставляя значение тока I₂ в уравнение (в’), получим:

10 = 4I₃ – 2 ,

10 + 2 = 4I₃ ,

откуда

Подставляя значение тока I₂ в уравнение (а’), получим:

14 – 5I₁ – 6 ,

20 = 5I₁ ,

откуда

Таким образом, все контурные токи найдены.

Определяем на отдельных участках цепи алгебраически, складывая протекающие по ним токи. Токораспределение на отдельных участках цепи показано на рисунке 1, б.

Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.

Метод петлевых (или ячеистых) токов Максвелла

Метод петлевых или ячеистых токов обычно используется при решении сетей, имеющих определенную степень сложности. Такая степень сложности уже начинается для сети из трех ячеек. Иногда может быть даже удобно использовать метод петлевых или ячеистых токов для решения схемы с двумя ячейками.

Метод ячеистого тока предпочтительнее обычного метода или метода ветвления, потому что неизвестные на начальном этапе решения сети равны количеству ячеек, т.е.е. сеточные токи. Отсутствует необходимость в написании уравнений узлового тока, как это делается в общем методе или методе тока ответвления, где используются токи ответвления. Существует столько же уравнений напряжения сетки, сколько и независимых петлевых или петлевых токов. Следовательно, токи M-сетки получаются путем решения напряжений M-сетки или петлевых уравнений для M неизвестных. После решения для токов сетки требуется только разделение сливных токов сетки на соответствующие токи ответвления с помощью очень простых алгебраических манипуляций.

Этот метод устраняет большую часть утомительной работы, связанной с методом тока ответвления, и лучше всего подходит, когда источники энергии являются источниками напряжения, а не источников тока. Этот метод можно использовать только для планарных схем.

Процедура написания уравнений следующая:

1. Предположим наименьшее количество токов сетки, чтобы по крайней мере один ток сетки связывался с каждым элементом. Для удобства предполагается, что все токи в сетке имеют направление по часовой стрелке.

Количество токов в сетке равно количеству ячеек в цепи.

2. Для каждой сетки запишите уравнение закона напряжения Кирхгофа. Если через элемент протекает более одного тока сетки, следует использовать алгебраическую сумму токов. Алгебраическая сумма токов сетки может быть суммой или разностью токов, протекающих через элемент, в зависимости от направления токов сетки.

3. Решите приведенные выше уравнения и по токам сетки найдите токи ответвления.

На рис. 36 показаны две батареи E ₁ и E ₂, соединенные в сеть, состоящую из трех резисторов.

Пусть токи контура для двух ячеек равны I ₁ и I ₂ (оба предполагаются по часовой стрелке). Очевидно, что ток через R3 (если рассматривать его как часть первого контура) равен (I ₁ — 1 ₂). Однако, когда R3 считается частью второго контура, ток через него равен (I ₂ — I ₁).

Применяя закон напряжения Кирхгофа к двум петлям, мы получаем

E ₁ — R ₁ R ₁ — R ₃ (I ₁ — I ₂) = 0

E ₁ — I ₁ (R ₁ + R ₃) + I ₂ R ₃ = 0

— I ₂ R ₂ — E ₂ — R ₃ (I ₂ — I ₁) = 0

— I ₂ R ₂ — E ₂ –I ₂ R ₃ + I ₂ R ₃ = 0

I ₁ R ₃ — I ₂ (R ₂ — R ₃) — E ₃ = 0

Два приведенных выше уравнения могут быть решены не только для определения токов контура, но и токи ответвления как

Пример 7 . Определите токи через различные резисторы схемы, показанной на рис. 37, используя концепцию сетки

Solution. См. Рис. 37.

Поскольку есть две сетки, пусть токи контура будут такими, как показано.

Применяя закон Кирхгофа к петле 1, получаем

24-4 I ₁-2 (I ₁ — I ₂) = 0

-6 I ₁ + 2 I ₁ + 24 = 0

3 I ₁ — I ₂ = 12

Для цикла 2 имеем

-2 (I ₂ — I ₁) — 6 I ₂ — 12 = 0

2 I ₁ — 8 I ₂ — 1 ₂ = 0

I ₁ — 4 I ₁ = 6

Решение (i) и (ii) , получаем I ₂ = 42/11 A

и I ₂ = — 6/11

Следовательно, ток через резистор 4 Q = 42/11 A (от L к M).(Отв.)

Ток через резистор 6 Ом = 6/11 А (от N до M). (Отв.)

Ток через резистор 2 Ом = 42/11 — (- 6/11) = 48/11 А (от M к P)

Пример 8 . Определите ток, подаваемый каждой батареей в цепи, показанной на рис. 38.

Решение. См. Рис. 38.

Поскольку есть три сетки, пусть токи трех контуров будут такими, как показано.

Применяя закон Кирхгофа к петле 1, получаем

20-5 I1 — 3 (I ₁ — I ₂) — 5 = 0

8 I ₁-3 I ₂ = 15

Для цикла 2 имеем

-4 I ₂ + 5-2 (I ₂ — I ₃) + 5 + 5-3 (I ₂ — I ₁) = 0

3 I ₁ — 9 I ₂ + 2 I ₃ = — 15

Для цикла 3 имеем

— 8 I ₃ — 30 — 5 — 2 (I ₃ — I ₂) = 0

2 I ₂ — 10 I ₃ = 35

Исключая I ₁ из (i) и (ii), мы получаем

63 I ₂ — 16 I ₃ = 165

Решая (iii) и (iv), получаем

I ₂ = 1.82 A и I ₃ = — 3,15 A

(знак — ve означает, что ток направлен против часовой стрелки)

Подставляя значение 12 в (i), мы получаем

I ₁ = 2,56 A

Ток через батарею B 1 (ток разряда) = I ₁ = 2,56 A. (Ответ)

Ток через батарею B2 (ток зарядки) = I ₁ — I ₂ = 2,56-1,82 = 0,74 A (Ответ)

Ток через батарею B s (ток разряда) = I ₂ + I ₃ = 1.82 + 3,15 = 4,97 А. (Ответ)

Ток через батарею B4 (ток разряда) = I ₂ = 1,82 А. (Ответ)

Ток через батарею B5 (ток разряда) = I ₃ = 3,15 А. (Отв.)

Пример 9. Определите токи через различные ветви мостовой схемы, показанной на рис. 39.

Решение. См. Рис. 39.

Предполагаются три тока сетки, как показано

Уравнения для трех сеток:

Для контура 1: 240 — 20 (I ₁ — I ₂) — 500 (I ₁ — I ₂) = 0

— 70 I ₁ + 20 I ₂ + 50 I ₃ = — 240

70 I ₁ — 20 I ₂-50 I ₃ = 240

Для цикла 2: — 30 i2 — 40 (I ₂ — I ₂) — 200 (I ₂ — I ₁) = 0

20 I ₁-90 I ₂ + 40 I ₃ = 0

2 I1 — 9 I ₂ + 40 I ₃ = 0

Для цикла 3: 60 i ₃ — 500 (I ₃ — I ₁) — 40 (I ₃ — I ₂) = 0

50 I ₁ + 40 I ₂ — 150 I ₃ = 0

5 I ₁ + 4 I ₂-15 I ₃ = 0

Решая эти уравнения, получаем

I ₁ = 6. 10 A, I ₂ = 2,56 A, I ₃ = 2,72 A

Ток через резистор 30 Ом = I3 = 2,73 A (от A до B)

Ток через резистор 60 Ом = I ₃ = 2,72 A (От B до C). (Отв.)

Ток через резистор 20 Ом = I ₁ — I ₂ = 6,10–2,56 = 3,54 A (от A до D).

Ток через резистор 50 Ом = I ₁ — I ₃ = 6,10–2,72 = 3,38 А (от D до C).

Ток через резистор 40 Ом = I ₃ — I ₂ = 2.72-2,56 = 0,16 А (от D к B).

Физика для науки и техники II

из отдела академических технологий на Vimeo.

Пример — Правила Кирхгофа

Лектор: Хорошо. Приведем пример, связанный с Правилами Кирхгофа.

Предположим, что у нас есть простая схема с тремя электродвижущими силами: Epsilon1, подключенный к сопротивлению r1, Epsilon2, подключенный к резистору r2, и, наконец, Epsilon 3, подключенный к резистору, скажем, r3. И вы легко можете в этой схеме, что мы не можем пойти дальше и напрямую применить закон Ома из-за существования этих трех электродвижущих сил, или трех батарей.

Предположим, что нас интересует энергия, рассеиваемая в единицу времени через каждое из этих сопротивлений. Итак, вопрос в том, чтобы найти мощность, рассеиваемую через каждый резистор. Теперь, если вы вспомните, что мощность, рассеиваемая через резистор, была равна i в квадрате, умноженном на r, другими словами, ток, протекающий через этот резистор, в квадрате, умноженный на сопротивление этого резистора.

Таким образом, чтобы иметь возможность определить эту величину, если предположить, что нам даны числовые значения Epsilon1, Epsilon2, Epsilon3, а также r1, r2 и r3, и нам необходимо определить ток, протекающий через каждое из этих сопротивлений.

Допустим, пусть Epsilon1 равен 2 вольтам, Epsilon2 равен 4 вольтам, а Epsilon3 равен, скажем, 10 вольт, и r1 равно 1 Ом, r2 равно 2 Ом, и, наконец, r3 равно 4 ом например.

Итак, зная значения этих электродвижущих сил, а также сопротивления, чтобы иметь возможность определить мощность, рассеиваемую через каждый резистор, нам нужно выяснить, какой ток протекает через каждый резистор, и для этого мы будем применять правила Кирхгофа.

Что ж, при этом мы можем использовать два разных метода. Скажем, первый метод, который мы называем методом текущей ветви. Хорошо, во-первых, мы собираемся отметить направление стрелки ЭДС, и поскольку они указывают от отрицательного к положительному, для Эпсилон1 он будет указывать вверх, для Эпсилон2 снова будет указывать вверх, а также для Эпсилон3, потому что это отрицательный конец, и это положительный конец для этих электродвижущих сил.

В качестве второго шага мы собираемся назначить ток для каждой ветви этой цепи.Под ответвлением мы понимаем пути между точками соединения. Как видите, это одна точка соединения, а это еще одна точка соединения. Это единственные точки, в которых у нас есть провода, которые соединяются друг с другом или разделяют два разных пути.

Следовательно, это одна ветвь, эта — другая ветвь, а эта — другая ветвь. Итак, в качестве первого шага мы назначим ток для каждой ветви, и при этом направление потока не имеет значения.Другими словами, мы можем выбрать любое направление, в котором захотим.

Для этого, например, давайте выберем ток i1, протекающий через первую ветвь, i1. Следовательно, i1 движется по этой ветке. Опять же, я выбрал i1 по часовой стрелке для этой ветви. Я мог бы легко выбрать прямо противоположное направление, и это будет нормально.

Итак, если мы посмотрим на среднюю ветвь, в этом случае я собираюсь выбрать, что это за путь, ток, текущий в нисходящем направлении, и я назову его i2.И, наконец, я собираюсь выбрать третью ветвь, по которой ток снова течет по часовой стрелке, поэтому я назову ее i3.

Опять же, направление протекания этих токов совершенно произвольно. Мы можем выбрать любое направление, в котором захотим. Другими словами, мы могли бы легко выбрать только противоположные направления этих потоков, но мы выбираем их произвольно, а затем отмечаем их для каждой ветви как i1, i2, i3 и т. Д. И т. Д.

После назначения ветвей следующим шагом будет выбор направления для обхода возможных петель.На первый взгляд, мы можем легко увидеть, что у нас есть один цикл здесь, а другой — здесь. Обозначим эти петли как первую и вторую петли.

Для первого цикла мы просто выберем направление прохождения этого цикла. Что ж, я собираюсь выбрать направление по часовой стрелке и покажу это направление пунктирными линиями со стрелкой на моей принципиальной схеме. И для другого цикла я снова выберу направление по часовой стрелке и покажу его на диаграмме.

Поскольку мы выбираем эти направления для прохождения схемы или этих петель, это направление снова полностью произвольно, мы можем выбрать их против часовой стрелки, мы можем выбрать одно из них по часовой стрелке, а другое — против часовой стрелки.

Итак, все зависит от нашего выбора, и у нас есть полная свобода выбора этих направлений. Как только мы выберем направление, в котором будем проходить каждый из этих циклов, мы продолжим и запишем уравнения цикла.

Допустим, петля первая. Мы начнем с произвольной точки. Мы можем начать, например, прямо перед ЭДС Epsilon1, и, начиная с этой точки, мы будем отслеживать этот цикл по часовой стрелке.

Теперь, поскольку мы движемся по часовой стрелке, когда мы пересекаем Эпсилон1, мы пересечем его в том же направлении, что и стрелка ЭДС, и из правил мы знаем, что если мы это сделаем, потенциал увеличится на + Эпсилон1 вольт.А дальше продолжим. Теперь мы собираемся пересечь Эпсилон2. В этом случае мы пересечем его в направлении, противоположном стрелке ЭДС. Следовательно, потенциал уменьшится на -Эпсилон2 вольт.

Теперь мы пересечем r2 в направлении протекания тока, и, как вы помните, если вы пересечете резистор, сопротивление в направлении протекания тока, то потенциал уменьшится. Итак, у нас будет знак минус рядом с током, который равен i2, умноженному на сопротивление, r2.

Продолжаем движение по часовой стрелке.Теперь мы пересечем r1 в направлении тока. Опять же, потенциал уменьшится в текущее время, в этом случае он будет в i1, умноженном на сопротивление, которое равно r1.

Цикл завершен. Алгебраическая сумма изменений потенциала в сумме будет равна нулю, и это наше уравнение номер один, связанное с первым циклом. Мы сделаем то же самое для второго цикла.

Мы собираемся начать снова в определенный момент. Начнем раньше, чем Эпсилон2. Опять же, мы будем отслеживать цикл по часовой стрелке.При этом мы пересечем Эпсилон2 в том же направлении, что и стрелка ЭДС. Следовательно, потенциал увеличится на Эпсилон2 вольта. Затем, двигаясь по часовой стрелке, мы пересечем Эпсилон3 в направлении, противоположном стрелке ЭДС, поэтому потенциал уменьшится на -Эпсилон3 вольт.

Теперь мы будем пересекать r3 в том же направлении, что и ток, поэтому снова мы испытаем уменьшение потенциала, и это будет равное количество раз, то есть i3, умноженное на сопротивление, и это будет r3.

Теперь, двигаясь по часовой стрелке, мы пересечем r2 в направлении, противоположном течению тока. Следовательно, потенциал увеличится на ток, умноженный на сопротивление, и это будет i2, умноженное на r2.

Цикл завершен. Алгебраическая сумма этих изменений потенциала даст в сумме ноль, и это уравнение номер два. Итак, когда мы смотрим на это уравнение, мы получаем значения Epsilon1, Epsilon2, r2, r1, Epsilon3, r3 и r2. Итак, неизвестными нам являются токи, а именно i1, i2 и i3.И здесь у нас есть три неизвестных, но два уравнения. Чтобы иметь возможность найти неизвестные, нам нужно еще одно уравнение, и оно будет исходить из правила перехода, а затем правило перехода просто говорит, что сумма токов в переходе должна быть равна сумме токов, поступающих из этого перекрестка.

И когда мы смотрим на точки соединения, которыми являются эти две точки, мы можем выбрать любую из них. Если мы посмотрим на это здесь, мы увидим, что i1 входит в это соединение, в то время как i2 выходит, а также i3 выходит.Итак, правило соединения гласит, что входящий i1 должен быть равен i2 плюс i3, и именно они выходят из этого соединения.

Если мы воспользуемся другой точкой соединения здесь, это даст нам то же самое уравнение. В этом случае i2 и i3 входят, а i1 выходит, поэтому i2 плюс i3 будет равно i1, что является тем же уравнением, что и здесь.

Теперь, как вы можете видеть, у нас есть одно уравнение здесь, другое уравнение там и третье уравнение здесь.У нас есть три уравнения и три неизвестных, поэтому мы можем легко решить эти уравнения одновременно, чтобы получить i1, i2 и i3.

После получения этих токов мощность, рассеиваемая на первом резисторе, будет равна i1 в квадрате, умноженном на r1, через второй резистор будет равна i2 в квадрате, умноженном на r2, а через третий будет равна i3 в квадрате, умноженном на r3. Точно так же мощность, генерируемая ЭДС, Epsilon1, будет равна, назовем ее p-sub-Epsilon1.Это будет равно i1, умноженному на Epsilon1.

Epsilon2, мощность, генерируемая Epsilon2, будет в i2 раз больше Epsilon2, и аналогично для Epsilon3 у нас будет i3, умноженная на Epsilon3, потому что это токи, которые накачиваются или генерируются этими электродвижущими силами.

Так вот, я упомянул, что, выбирая направление этих токов через каждую из этих ветвей, мы сказали, что мы полностью свободны в том направлении, которое хотели бы выбрать. В конце нашего алгебраического расчета оказывается — если оказывается, что i1 отрицательное, это просто означает, что фактическое направление потока тока прямо противоположно выбранному нами.

Итак, важная вещь — это информация о величине величины, значение, которое мы найдем, когда решим эти три уравнения одновременно.

Опять же, когда мы смотрим на мощность, вырабатываемую этими источниками питания, в зависимости от знака этих токов, которые мы получим, если мы получим положительный ток, это означает, что эта батарея подает энергию в цепь, и если мы имеют значение -current, поэтому мощность, связанная с этим источником питания, будет отрицательной, что указывает на то, что этот источник питания заряжается, эта батарея заряжается в этой цепи.

И, конечно же, подаваемая мощность всегда должна быть равна рассеиваемой мощности. Другими словами, сумма мощностей, энергии за единицу времени, должна быть равна сумме энергии за единицу времени, рассеиваемой через каждый резистор, а также, если есть батареи, которые заряжаются в цепи, тогда мощность потребляется этими батареями.

Я не буду вдаваться в подробности одновременного решения этих трех уравнений. Я оставлю это вам в качестве домашнего задания, и, конечно же, вы просто замените эти символы их числовыми значениями здесь, и чтобы иметь возможность решать их одновременно, вы можете просто решить одно из неизвестных с точки зрения двух других и подставьте это в следующее уравнение.Следовательно —

Например, здесь я хочу, чтобы он был равен i2 плюс i3, и если вы просто возьмете это i1 и замените его или подставите в первое уравнение, тогда вы получите два уравнения в терминах i2 и i3. , первое уравнение и второе. Вы можете решить одно из них для одного из неизвестных, скажем, i2 через i3, а затем подставить его в первое уравнение. Тогда вы получите одно уравнение и одно неизвестное, которые вы легко решите. Как только вы получите один из токов, вы можете проследить его в обратном направлении, чтобы получить два других уравнения.

Теперь я покажу вам другой метод решения той же схемы, и для этого я перерисую схему здесь. Здесь Epsilon1 с сопротивлением r1, здесь Epsilon2 с сопротивлением r2, а ЭДС Epsilon3 с сопротивлением r3. Итак, это оригинальная схема. Давайте назовем его здесь методом два, и этот метод также называется методом тока цикла.

В этом случае снова давайте сначала нарисуем стрелки ЭДС для каждого из этих источников питания, указывающие от отрицательного к положительному концу.И поэтому в этом случае вместо того, чтобы назначать ток для каждой ветви, мы назначим ток контура для каждого контура в цепи, и мы увидим, что чистый ток i1 протекает через первый контур по часовой стрелке, а для второго контура давайте выберем ток i2 течет против часовой стрелки. Итак, это направление по часовой стрелке, а это — против часовой стрелки.

Следовательно, вместо того, чтобы назначать токи ответвления, мы назначаем токи контура. Опять же, мы выбираем направление течения этих токов совершенно произвольно.Я просто выбрал один из них как направление по часовой стрелке, другой как направление против часовой стрелки.

Опять же, я собираюсь проследить, я собираюсь выбрать направление для отслеживания каждой из этих петель, поэтому я выберу эту по часовой стрелке, а я выберу другую — я могу выбрать ее по часовой стрелке. направлении или против часовой стрелки. Выберем его в данном случае против часовой стрелки.

Опять же, все эти направления произвольны. Вы можете выбрать любое направление, которое захотите.Это наш второй цикл, и мы запишем уравнения цикла, начиная с первого цикла. Давайте снова начнем прямо перед электродвижущей силой, Epsilon1. Мы собираемся пересечь его по часовой стрелке, следовательно, от отрицательной клеммы к положительной, другими словами в направлении стрелки ЭДС, поэтому потенциал увеличится на эпсилон1 вольт.

Теперь, двигаясь по часовой стрелке, мы собираемся пересечь Эпсилон2 в направлении, противоположном стрелке ЭДС, поэтому потенциал уменьшится на Эпсилон2 вольт. Теперь мы собираемся пересечь r2 в направлении тока. Почему? Когда мы смотрим на эту среднюю ветвь, i1 движется или течет в нисходящем направлении, а также i2 течет в нисходящем направлении.

Итак, чистый ток, протекающий через эту среднюю ветвь, является суммой этих двух токов. Когда мы пересекаем его по часовой стрелке, мы собираемся пересечь r2 в том же направлении, что и ток, поэтому потенциал будет уменьшаться на чистый ток, который в i1 плюс i2 умножается на сопротивление r2.

Теперь вернемся к сопротивлению r1. Мы будем пересекать это снова в том же направлении, в котором течет ток, поэтому потенциал будет уменьшаться в текущее время, а это i1 умноженное на r1. Петля завершена. Алгебраическая сумма изменений потенциала будет равна нулю.

Теперь посмотрим на вторую петлю. Во втором цикле, начиная прямо перед Epsilon2 и идя против часовой стрелки, поэтому мы начнем здесь, потому что в этом случае мы выбрали направление — я выбрал направление движения против часовой стрелки, поэтому я собираюсь пересечение Эпсилон2 в направлении, противоположном стрелке ЭДС. Следовательно, потенциал уменьшится на -Эпсилон2 вольт.

Двигаясь против часовой стрелки, я пересечу r2 в том же направлении, что и чистый ток. Следовательно, мы снова увидим снижение потенциала, минус. Чистый ток проходит по средней ветви i1 плюс i2 и умножается на сопротивление r2. Двигаясь против часовой стрелки, мы пересечем r3. Ток также течет в том же направлении, следовательно, в направлении потока тока. Мы испытаем уменьшение потенциала, и это будет в i3 раза больше r3.

Теперь мы пересечем Эпсилон3, двигаясь против часовой стрелки, в том же направлении, что и стрелка ЭДС, поэтому потенциал увеличится на Эпсилон3 вольт.

Мы вернулись к тому моменту, с которого начали. Петля завершена. Опять же, алгебраическая сумма этих изменений потенциала будет равна нулю.

Как вы теперь видите, в этом случае у нас есть только два неизвестных, ток контура i1 и i2, и у нас есть два уравнения. Итак, когда мы применяем метод тока контура, правило соединения не имеет значения, и у нас будет количество уравнений, равное нашим неизвестным, как только мы выразим уравнения контура, и мы можем легко решить это алгебраически.

Если вы предпочитаете использовать этот метод, вы должны быть осторожны при назначении токов. Здесь я выбрал ток первой петли по часовой стрелке, второй — против часовой стрелки. При этом я закончил, что чистый ток, протекающий через среднюю ветвь, как сумма этих двух токов, потому что они текут в одном направлении вдоль этой ветви.

Что ж, если бы я выбрал i2, я могу это сделать. Для этого нет никаких ограничений. I2 также по часовой стрелке.Если я это сделаю, то i2 будет течь вверх через среднюю ветвь, а i1 будет течь вниз через среднюю ветвь. Тогда чистый ток будет разницей между этими двумя токами.

И поскольку до того, как мы решим проблему, мы не будем знать, какая из них больше, чем другая, то единственный способ определить чистый поток — чистое направление потока тока — это предположить, что один из них больше другого. один. Итак, в этом случае мы сделаем предположение и скажем, что, например, net i1 больше, чем i2.

В этом случае, поскольку i1 идет вниз, тогда как i2 идет вверх, а i1 больше, чем i2, чистый поток будет идти вниз. И затем мы сохраняем это предположение во всех наших уравнениях цикла, когда мы записываем эти уравнения цикла.

Опять же, в конце вычислений, если окажется, что i2 больше, чем i1, что в этом случае мы собираемся получить с отрицательным значением для чистого тока через эту среднюю ветвь, то это означает что фактическое направление потока прямо противоположно выбранному нами.Но сила тока будет одинаковой в любом направлении, которое мы выберем.

Опять же, как только значения тока получены, можно определить мощность, рассеиваемую через r1, которая будет равна i1 в квадрате, умноженном на r2, но для сопротивления r2, p2 рассеиваемая мощность будет равна чистому току, протекающему через r2 в квадрате, что i1 плюс i2 в квадрате, умноженное на r2 и r3, опять же, позвольте мне просто записать. p3 будет равно току через r3, и это будет i2 в квадрате, умноженном на r3, а p1 будет i1 в квадрате, умноженном на r1.

Итак, используя эти выражения, мы можем легко определить, сколько энергии рассеивается или преобразуется в тепло за каждую секунду.

Отвод по текущему способу

Применение метода тока ответвления для расчета токов и напряжений в электрических цепях. Рассмотрены электрические цепи постоянного тока и электрические цепи переменного тока. Метод тока ответвления основан на текущем законе Кирхгофа ( KCL ) и законе напряжения Кирхгофа ( KVL ).

Текущий закон Кирхгофа (KCL) говорит нам, что алгебраическая сумма токов, которые текут в узел и вытекают из него, равна нулю. Текущий закон Кирхгофа произошел от принцип сохранения электрического заряда . Когда мы применяем текущий закон Кирхгофа, мы используем соглашение, согласно которому токи, которые текут в направлении к узлу, имеют знак «+», а токи, которые текут в направлении от узла, имеют знак «-».

Закон напряжения Кирхгофа (KVL) говорит нам, что алгебраическая сумма напряжений в заданной сетке равна нулю. Закон напряжения Кирхгофа произошел от принципа сохранения энергии . Применение закона летучести Кирхгофа выглядит следующим образом. В указанной сетке отмечаем направление циркуляции напряжений. Когда напряжения в сетке имеют одинаковое направление, мы даем им знак «+», иначе мы даем им знак «-».

Порядок действий по методу по току ветви следующий. В этом методе мы должны написать уравнения для закона тока Кирхгофа и закона напряжения Кирхгофа.Количество уравнений для каждого закона указано и дается следующими формулами:
Количество уравнений для текущего закона Кирхгофа равно количеству узлов минус один. Мы записываем это символически:
KCL → (n-1)
где:
n — количество узлов
Количество уравнений для закона напряжения Кирхгофа равно количеству ветвей в цепи минус количество уравнений для текущего закона Кирхгофа. Помните, что текущий источник — это не ветвь. Условно запишем это:
KVL → m- (n-1)
, где
m — количество ветвей,
n — количество узлов.

Пример метода тока ответвления 1

Применение метода тока ответвления для электрической цепи, построенной из четырех источников напряжения и пяти резисторов.

Метод тока ответвления — пример 1

Пример 2 метода тока ответвления

Применение метода тока ответвления для электрической цепи, построенной из двух источников тока, трех источников напряжения и четырех резисторов.

Метод тока ответвления — пример 2

Пример 3 метода ветвления тока

Применение метода тока ответвления для электрической цепи, построенной из двух источников тока, трех источников напряжения и пяти резисторов.

Метод тока ответвления — пример 3

Пример 4 метода тока ответвления

Электрическая схема представляет собой модель однофазного от трехфазного электродвигателя переменного тока. Модель фазы асинхронного двигателя часто используется для теоретического расчета токов. В этом упражнении метод тока ответвления будет использоваться, чтобы найти выражения для токов в модели двигателя переменного тока.

Метод тока ответвления — пример 4

Пример 5 текущего метода ветвления

Метод тока ответвления будет применяться для расчета токов ответвления в электрической цепи переменного тока.Электросхема построена с источником переменного напряжения E , источником переменного тока I . Электрическая схема также имеет в своей топологии пассивные элементы. Схема содержит три импеданса, которые складываются из следующих элементов: индуктивности L1, конденсатора C1 и резистора R1. Токи ответвлений рассчитываются в примере с применением комплексных чисел.

Метод тока ответвления — пример 5

Пример метода 6 тока ветви

Токи ответвлений будут рассчитаны в электрической цепи переменного тока.Электрическая схема содержит в своей топологии один источник переменного напряжения В _с и один источник переменного тока I _с. Поскольку это цепь переменного тока, все вычисления производятся с использованием комплексных чисел. Схема построена с пятью импедансами, которые связаны с пассивными элементами, такими как индуктивности L1 и L2, резисторы R1 и R2 и один конденсатор C1.

Метод тока ответвления — пример 6

Пример 7 метода текущего ветвления

Токи ответвления будут рассчитаны для электрической цепи постоянного тока.Электрическая схема содержит в своей топологии источник напряжения, два резистора, один индуктивный и один конденсатор. Мы применяем метод тока ответвления для электрических цепей в стабильном (непереходном) состоянии. Для электрического постоянного тока мы относимся к идеальной индуктивности и идеальным конденсаторам особым образом. Идеальная индуктивность — это короткое замыкание на постоянный ток . Идеальный конденсатор — прерыватель на постоянный ток .

Метод тока ответвления — пример 7

Пример метода тока ветвления 8

Токи ответвления будут рассчитаны для электрической цепи постоянного тока. Электрическая схема построена из двух источников напряжения и пяти резисторов. Схема имеет в своей топологии две сетки. Источники напряжения подключаются в цепь по-разному, поэтому вы должны учитывать этот факт при написании уравнений Кирхгофа. Общее сопротивление цепи будет вычислено с целью найти значение основного тока цепи .

Метод тока ответвления — пример 8

Простой анализ тока в сетке для электрических цепей

Анализ тока в сетке используется для анализа электрической цепи с использованием текущих токов в замкнутом контуре цепи.Даже у нас уже есть закон Ома и законы Кирхгофа, эти два дают нам больше математических уравнений, которые нужно решить. Анализ тока сетки или Циркуляционные токи Максвелла или Метод токов петли может значительно уменьшить количество уравнений.

Этот метод отличается от метода Branch Current, который не использует законы Кирхгофа и предполагается использовать для менее неизвестных переменных. Этот анализ сетки также отличается от преобразования звезда-дельта, если у нас нет конфигурации звезды или дельты.

Анализ сетки предоставляет нам другой метод анализа электрических цепей с использованием тока сетки или тока петли в качестве основных переменных.

Более удобно использовать ток сетки, а не ток, протекающий через элементы в цепи, потому что нам придется решать меньше уравнений.

Обратите внимание, что цикл — это замкнутый путь, в котором ни один узел не прошел более одного раза. Сетка — это петля, не содержащая никаких других петель.

Теперь приступим к использованию этих двух методов для разработки двух мощных методов анализа схем:

Узловой анализ
Анализ сетки

Когда узловой анализ использует KCL для определения узловых напряжений в цепи в качестве основных переменных, анализ сетки использует KVL для определения тока сетки в цепи.

Имейте в виду: анализ тока сетки может использоваться только в планарной схеме . Что такое планарная схема? Это схема, которую можно перерисовать так, чтобы ветви не пересекали друг друга, в противном случае непланарную схему можно увидеть на рисунке.(1).

Рисунок 1. Непланарная схема

Схема может иметь пересекающиеся ветви и оставаться плоской, если ее можно перерисовать так, чтобы в ней не было пересекающихся ветвей, как показано на рисунке. (2).

Рис. 2. Планарная схема

Что такое петля и сетка

Нам нужно полностью понимать термин «сетка», поскольку мы будем упоминать его каждый раз, когда будем использовать этот метод тока сетки. Сетка — это, по сути, «исключительный» цикл. Я уверен, что вы хорошо знаете, что такое петля в электрической цепи.

Для сравнения обратите внимание на рисунок (3) ниже:

Рисунок 3. Ячеистая схема

Давайте обновим это теперь, что такое петля в электрической цепи?

Цикл состоит из набора узлов. Если ток течет от начального узла и проходит через набор узлов, не проходя один и тот же узел дважды, это означает, что ток течет в одном цикле.

На рисунке выше видно, что схема имеет 3 контура, обозначенных стрелками 1, 2 и 3 по часовой стрелке.Но есть ли у нас еще 3 сетки? Вот в чем вопрос.

Не дайте себя обмануть представлением стрелок в схеме, поскольку и петля, и сетка представлены стрелками по часовой стрелке или против часовой стрелки.

Сетка обычно имеет то же значение, что и петля, но сетка — это петля без петли внутри нее.

Разница вас не поразила? Обратите внимание:

Сетка — это петля, не содержащая никаких других петель внутри нее.

Мы не нуждаемся в дополнительных объяснениях. Из рисунка (3) выше только петли 1 и 2 считаются сетками, потому что петля 3 содержит другие петли (петли 1 и 2). Следовательно, на рисунке (3) у нас есть 3 петли (1, 2 и 3) и 2 ячейки (1 и 2).

На рисунке (3) пути abefa и bcdeb являются сетками, но путь abcdefa не является сеткой.

Как мы читали ранее, ток, протекающий через сетку или замкнутый контур, известен как , ток сетки . Мы выполним KVL в любых условиях при использовании анализа сетки.

Для лучшего и легкого понимания, мы запретим использование токовой цепи в анализе сетки на этот раз для плоской схемы. Это не означает, что анализ сетки ограничен только источником напряжения. Вы поймете, почему здесь, внизу.

При анализе сетки схемы с n сетками мы используем следующие три шага.

Шаги для определения токов сетки:

Назначьте токи сетки i ₁ , i ₂ ,…., i _n к сеткам n .
Примените KVL к каждой из n сеток. Используйте закон Ома, чтобы выразить напряжения через сеточные токи.
Решите полученные одновременные уравнения n , чтобы получить токи сетки.

Анализ тока сетки

Перейдем к методу тока сетки. Мы будем использовать приведенный выше рисунок (3). Мы присвоим источникам напряжения и резисторам метки, как показано ниже:

Затем мы наложим сетки с направлением по часовой стрелке, а затем назначим метки токам и полярности для резисторов. Помните, что мы назначаем положительную полярность клемме резистора, на которую впервые подается ток. Поскольку R ₃ находится в пересечении между сетками 1 и 2, мы присвоим ему i ₃.

Мы получим следующие уравнения:

Для сетки 1 ( i ₁):

Для сетки 2 ( i ₂):

И это уравнения для двух сеток, которые у нас есть.Но как решить 3 неизвестные переменные всего с 2 уравнениями?

Ответ: ЭТО БУДЕТ ТРУДНО

Но чтобы упростить задачу, мы можем написать i ₃ с другим уравнением.

Как? Проверьте процедуру анализа тока сетки ниже:

Процедура анализа тока сетки

Для вас, кто еще не изучал анализ тока сетки или хочет освежить свою память, мы внимательно изучим его шаг за шагом. Чтобы не усложнять ситуацию после прочтения объяснения выше, мы все равно будем использовать рисунок.(3) в качестве примера с известными значениями переменных.

Текущие направления анализа сетки

Сначала мы определяем текущие направления для каждой сетки. Вам решать, идут ли они по часовой стрелке или против часовой стрелки, или их сочетание. Теперь пойдем по часовой стрелке.

Маркировка элементов схемы

Теперь мы помечаем все элементы схемы с положительной и отрицательной полярностью в зависимости от направления тока, используя пассивное знаковое соглашение.Для токов, проходящих через R ₃, это зависит от того, какую сетку мы анализируем в данный момент. Ниже вы найдете объяснение.

Найдите уравнения сетки KVL

Мы запишем все уравнения KVL для решения схемы. Но перед этим давайте дадим номера для каждой переменной, которая у нас есть. Окончательная схема будет:

Мы будем использовать направление по часовой стрелке для каждой сетки.

Для сетки 1,

Получаем:

Значение В ₁ = -3, потому что сетка 1 входит в клемму источника напряжения со своей отрицательной полярностью.

Для сетки 2,

Мы получаем:

Если вы все еще не уверены в токах, входящих в R ₃, предположим, что мы анализируем сетку 1. Если мы проанализируем сетку 1, мы будем отдать приоритет i ₁. Посмотрите на рисунок ниже.

Для сетки 1 сумма токов, входящих в R ₃, будет

Если мы проанализируем сетку 2,

Теперь у нас есть ‘2’ уравнения для ‘2’ сеток .

Для сетки 1,

Для сетки 2,

Решите уравнения сетки KVL

Как указывалось ранее, для каждой сетки « n » будут уравнения KVL « n ». У нас есть:

Мы меняем уравнение сетки 1 на:

Подставляя это в уравнение сетки 2,

Подставляя i ₁ в уравнение сетки 1,

Это означает, что направление i ₂ против часовой стрелки 0.73075 A. С текущими значениями были обнаружены, вы можете найти другие переменные, какие захотите.

Анализ тока сетки с источником тока

Приведенный выше пример представляет собой анализ сетки с источником напряжения. Теперь разберем схему с источниками тока. Он не будет сильно отличаться от источника напряжения, но нам действительно нужно знать разницу в шагах. Например, мы будем использовать схему ниже:

Нам нужно найти значение i .

Сначала мы назначаем ток сетки,

Теперь запишем все уравнения KVL.Мы получим 3 уравнения, поскольку в схеме 3 сетки.

Для сетки I ₁,

Почему мы получаем ценность без каких-либо усилий? Потому что в сетке 1 есть текущий источник без пересечения с другим током сетки.

Для сетки I ₂ и I ₃,

Когда есть источник тока в пересекающейся ветви, мы называем эту схему супер сеткой. Глубина supermesh будет объяснена в следующем посте, посвященном Supermesh Analysis.

Из supermesh:

Подстановка I ₃ в это уравнение приводит к

Следовательно,

Анализ сетки 3 петли

Если схема имеет 3 сетки, решение будет достаточно просто пока нет источника тока в ветви пересечения с другим током сетки. Ниже приведен пример анализа трех петель сетки с единственным источником напряжения и тока в одной сетке, чтобы упростить задачу.

Мы назначаем ток сетки,

Для сетки 1,

Для сетки 2,

Для сетки 3,

Подставляем уравнение сетки 3 в сетку 2,

Теперь нам нужно найти V . Через резистор проходит ток сетки i ₁ и i ₂. Поскольку положительная полярность находится на верхней стороне,

Несбалансированный мост Уитстона

Использование анализа тока сетки оказалось более простым в использовании для анализа несбалансированного моста Уитстона. Например, мы будем использовать схему ниже:

Мы будем рисовать ток сетки внутри петель по часовой стрелке, как показано ниже:

Как вы видели, у нас есть три сетки, и это означает, что мы получим три уравнения. Решить 2 уравнения сетки внутри моста проще, потому что у нас есть источник тока в сетке 1.

Для начала давайте проанализируем источник тока. Из сетки 1,

Из сетки 2,

Из сетки 3,

Следовательно,

Пример анализа тока сетки

Для лучшего понимания целесообразно проанализировать больше схем .Давайте изучим приведенные ниже примеры:

1. Найдите значение токов ответвления I ₁, I ₂ и I ₃ схемы на рисунке. (4) ниже, используя анализ сетки. . Предположим, что направление тока сетки для обоих контуров — по часовой стрелке.

Рисунок 4

Решение:

Сначала мы запишем все уравнения KVL. Для двух сеток мы получим два уравнения:

Для сетки 1

(1.1)

Для сетки 2,

(1.2)

Используя подстановку,

Подставляем (1.2) в (1.1) и получаем

Из (1.2) получаем

Таким образом,

2. Найдите значение i на рисунке (5) ниже, используя анализ сетки!

Рисунок 5

Изобразим токи сетки на рисунке. (6):

Рисунок 6

Для сетки I ₁,

Для сетки I ₂,

Часто задаваемые вопросы

Как найти ток при анализе сетки?

1. Обозначьте сетки , , (открытые окна схемы).
2. Назначьте текущую переменную каждой сетке , , используя в согласованном направлении (по часовой стрелке или против часовой стрелки).
3. Напишите уравнения закона напряжения Кирхгофа вокруг каждой ячейки .
4. Решите полученную систему уравнений для всех токов сетки .

Каковы преимущества использования анализа тока сетки при решении электронных схем?

Основное преимущество анализа Mesh Current состоит в том, что он обычно позволяет получить решение большой сети с меньшим количеством неизвестных значений и меньшим количеством одновременных уравнений.В нашем примере задачи потребовалось три уравнения для решения метода ветвления Current и только два уравнения с использованием метода Mesh Current .

В чем разница между сеточным и узловым анализом?

Этот метод отличается от узлового метода тем, что в качестве переменных цепи используются токи ячеек вместо узловых напряжений . … Метод узловых использует закон токов Кирхгофа для учета узловых напряжений , а метод ячеек использует закон напряжений Кирхгофа для учета токов ячеек . Сетка — это петля, не содержащая других петель.

Законы Кирхгофа (ток и напряжение): что это такое и почему это важно?

Обновлено 28 декабря 2020 г.

Автор: GAYLE TOWELL

По мере того, как электрические цепи становятся все более сложными, с множеством ветвей и элементов, становится все сложнее определить, какой ток может протекать через ту или иную ветвь, и как это исправить. Полезно иметь систематический способ анализа цепей.

Важные определения

Чтобы понять законы Кирхгофа, необходимо несколько определений:

Напряжение В — это разность потенциалов на элементе схемы. Он измеряется в вольтах (В).
Ток I — это мера скорости потока заряда через точку в цепи. Он измеряется в амперах (А).
Сопротивление R — это мера сопротивления элемента схемы протеканию тока.Он измеряется в омах (Ом).
Закон Ома связывает эти три величины следующим уравнением: V = IR.

Что такое законы Кирхгофа?

В 1845 году немецкий физик Густав Кирхгоф формализовал следующие два правила о схемах:

1. Правило соединения (также известное как закон Кирхгофа или KCL): Сумма всех токов, протекающих в переходе в цепь должна равняться общему току, вытекающему из перехода.

Другой способ выражения этого закона состоит в том, что алгебраическая сумма токов, текущих в переход, равна 0. Это означало бы рассматривать любые токи, текущие в переход, как положительные, а любые, вытекающие из них, как отрицательные. Поскольку общий приток должен равняться общему оттоку, это эквивалентно утверждению, что суммы будут равны 0, поскольку это равносильно перемещению оттекающих к другой стороне уравнения с отрицательным знаком.

Этот закон выполняется при простом применении сохранения заряда.Все, что входит, должно равняться тому, что вытекает. Представьте, что водопроводные трубы соединяются и разветвляются подобным образом. Точно так же, как вы ожидаете, что общая вода, текущая в переход, будет равна общему количеству воды, вытекающей из перехода, так и с текущими электронами.

2. Правило цикла (также известное как закон напряжения Кирхгофа или KVL): Сумма разностей потенциалов (напряжений) вокруг замкнутого контура в цепи должна равняться 0.

Чтобы понять второй закон Кирхгофа, представьте себе что бы случилось, если бы это было неправдой.Рассмотрим одноконтурный контур, в котором есть несколько батарей и резисторов. Представьте, что вы начинаете с точки A и двигаетесь по петле по часовой стрелке. Вы набираете напряжение, когда идете через батарею, а затем падаете, когда вы проходите через резистор, и так далее.

Обойдя весь круг, вы снова окажетесь в точке A . Сумма всех разностей потенциалов при обходе контура должна тогда равняться разнице потенциалов между точкой A и самой собой.Ну, одна точка не может иметь два разных значения потенциала, поэтому эта сумма должна быть 0.

В качестве аналогии рассмотрим, что произойдет, если вы пойдете по круговой пешеходной тропе. Предположим, вы начинаете с точки A и начинаете поход. Часть похода ведет в гору, часть — под гору и так далее. После завершения цикла вы снова вернетесь в точку A . Это обязательно тот случай, когда сумма ваших приростов и перепадов высоты в этом замкнутом контуре должна быть равна 0 именно потому, что высота в точке A должна равняться самой себе.

Почему важны законы Кирхгофа?

При работе с простой последовательной цепью определение тока в контуре требует только знания приложенного напряжения и суммы сопротивлений в контуре (с последующим применением закона Ома).

В параллельных цепях и электрических цепях с комбинациями Однако для последовательных и параллельных элементов задача определения тока, протекающего через каждую ветвь, быстро усложняется. Ток, входящий в соединение, будет разделяться по мере того, как он входит в разные части цепи, и без тщательного анализа неочевидно, сколько будет проходить в каждую сторону.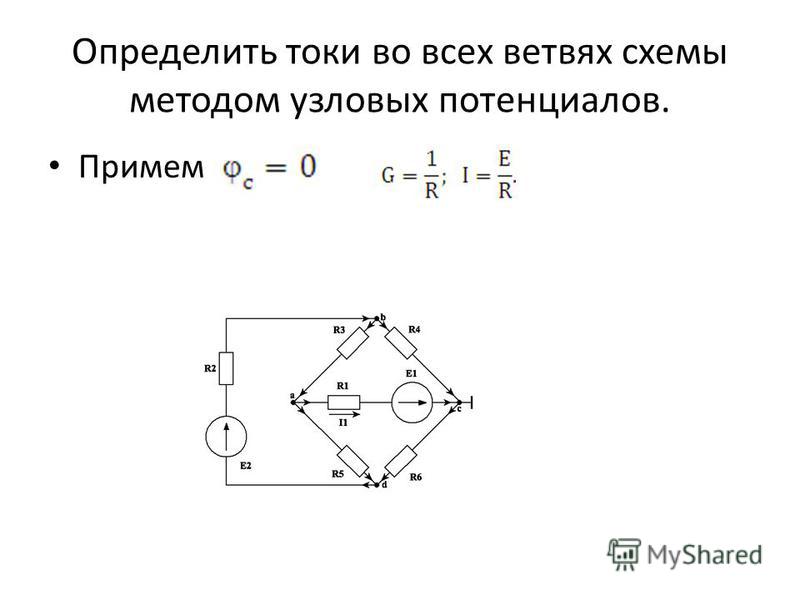

Два правила Кирхгофа позволяют анализировать все более сложные схемы. Хотя требуемые алгебраические шаги по-прежнему довольно сложны, сам процесс прост. Эти законы широко используются в области электротехники.

Возможность анализировать схемы важна для предотвращения перегрузки элементов схемы. Если вы не знаете, какой ток будет протекать через устройство или какое напряжение упадет на нем, вы не будете знать, какой будет выходная мощность, и все это имеет значение для функционирования устройства.

Как применять законы Кирхгофа

Правила Кирхгофа можно применить для анализа принципиальной схемы, выполнив следующие шаги:

Для каждой ветви i схемы пометьте неизвестный ток, протекающий через нее, как I _i и выберите направление для этого тока. (Направление не обязательно должно быть правильным. Если окажется, что этот ток на самом деле течет в противоположном направлении, то вы просто получите отрицательное значение при решении для этого тока позже. )

Для каждой петли в цепи выберите направление. (Это произвольно. Вы можете выбрать против часовой стрелки или по часовой стрелке. Это не имеет значения.)

Для каждого цикла начните с одной точки и двигайтесь в выбранном направлении, складывая разности потенциалов по каждому элементу. Эти разности потенциалов можно определить следующим образом:

Если ток проходит в положительном направлении через источник напряжения, это положительное значение напряжения. Если ток проходит через источник напряжения в отрицательном направлении, напряжение должно иметь отрицательный знак.
Если ток проходит в положительном направлении через резистивный элемент, то вы используете закон Ома и добавляете -I _i × R (падение напряжения на этом резисторе) для этого элемента. Если ток проходит в отрицательном направлении через резистивный элемент, вы добавляете + I _i × R для этого элемента.
После того, как вы обошли контур, установите эту сумму всех напряжений равной 0. Повторите действия для всех контуров в цепи.

Для каждого перехода сумма токов, текущих в этот переход, должна равняться сумме токов, вытекающих из этого перехода.Запишите это в виде уравнения.

Теперь у вас должен быть набор одновременных уравнений, который позволит вам определять ток (или другие неизвестные величины) во всех ветвях цепи. Последний шаг — решить эту систему алгебраически.

Примеры

Пример 1: Рассмотрим следующую схему:

Применяя шаг 1, для каждой ветви мы маркируем неизвестные токи.

••• na

Применяя Шаг 2, мы выбираем направление для каждой петли в схеме следующим образом:

••• na

Теперь мы применяем Шаг 3: Для каждой петли, начиная с одной точки и обходя в выбранном направлении складываем разности потенциалов по каждому элементу и устанавливаем сумму равной 0.

Для цикла 1 на диаграмме мы получаем:

-I_1 \ times 40 — I_3 \ times 100 + 3 = 0

Для цикла 2 на диаграмме получаем:

-I_2 \ times 75-2 + I_3 \ times 100 = 0

Для шага 4 мы применяем правило соединения. На нашей диаграмме есть два соединения, но оба они дают эквивалентные уравнения. А именно:

I_1 = I_2 + I_3

Наконец, на шаге 5 мы используем алгебру для решения системы уравнений для неизвестных токов:

Используйте уравнение соединения, чтобы подставить в уравнение первого контура:

— (I_2 + I_3) \ times 40 — I_3 \ times 100 + 3 = -40I_2 — 140I_3 + 3 = 0

Решите это уравнение для I ₂ :

I_2 = \ frac {3-140I_3} {40}

Подставьте это в уравнение второго цикла:

— [(3-140I_3) / 40] \ times 75-2 + 100I_3 = 0

-3 \ times 75/40 + (140 \ times 75/40) I_3 — 2 + 100I_3 = 0 \\ \ подразумевает I_3 = (2 + 3 \ times 75/40) / (140 \ times 75/40 + 100) = 0.021 \ text {A}

Используйте значение I ₃ , чтобы найти I ₂ :

I_2 = (3-140 \ times (0,021)) / 40 = 0,0015 \ text {A}

I_1 = I_2 + I_3 = 0,021 + 0,0015 = 0,0225 \ text {A}

Итак, окончательный результат таков: I ₁ = 0,0225 A, I ₂ = 0,0015 A и I ₃ = 0,021 A.

Подстановка этих текущих значений в исходные уравнения проверяет правильность, поэтому мы можем быть достаточно уверены в результате!

Попробуйте повторить эту же задачу еще раз, но сделайте другой выбор для ваших текущих меток и направлений петли.Если все сделать аккуратно, вы должны получить тот же результат, показывая, что первоначальный выбор действительно произвольный.

(Обратите внимание, что если вы выберете разные направления для обозначенных токов, тогда ваши ответы для них будут отличаться знаком минус; однако результаты все равно будут соответствовать тому же направлению и величине тока в цепи.)

Пример 2: Какова электродвижущая сила (ЭДС) ε батареи в следующей цепи? Какой ток в каждой ветке?

••• na

Сначала мы маркируем все неизвестные токи.Пусть I ₂ = ток вниз через среднюю ветвь и I ₁ = ток вниз через крайнюю правую ветвь. Изображение уже показывает текущий I в крайнем левом ответвлении с пометкой.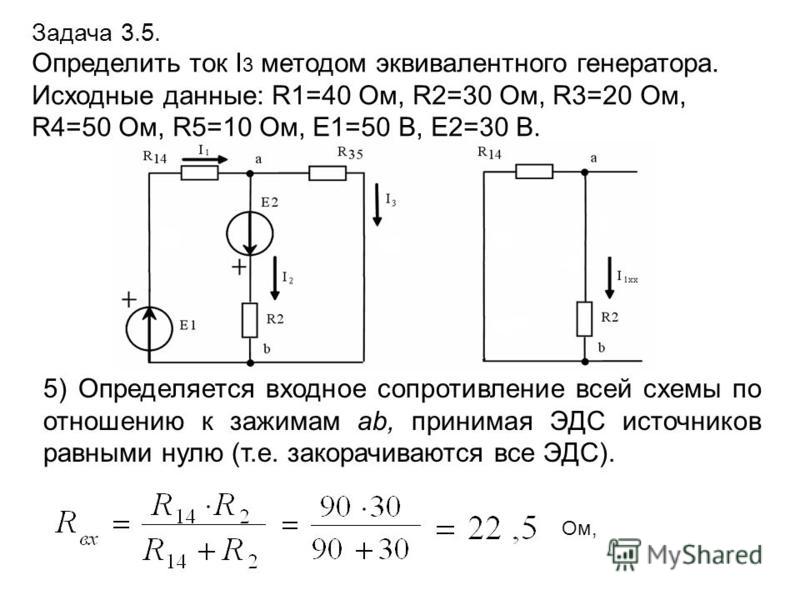

Выбор направления по часовой стрелке для каждого контура и применение законов Кирхгофа дает следующую систему уравнений:

\ begin {align} & I_1 = I-I_2 \\ & \ varepsilon — 4I — 6I_2 + 8 = 0 \\ & — 12I_1 — 8 + 6I_2 = 0 \ end {align}

Для решения замените I — I ₂ на I ₁ в третьем уравнении, а затем подставьте данное значение для I и решите это уравнение относительно I ₂ .Как только вы узнаете I ₂ , вы можете подставить I и I ₂ в первое уравнение, чтобы получить I ₁ . Затем вы можете решить второе уравнение относительно ε . Следуя этим шагам, вы получите окончательное решение:

\ begin {align} & I_2 = 16/9 = 1,78 \ text {A} \\ & I_1 = 2/9 = 0,22 \ text {A} \\ & \ varepsilon = 32/3 = 10.67 \ text {V} \ end {align}

Опять же, вы всегда должны проверять свои окончательные результаты, вставляя их в исходные уравнения. Совершать простые алгебраические ошибки очень легко!

(PDF) Фундаментальный метод токовой петли с использованием техники «виртуальных источников напряжения» для особых случаев

International Journal of Electrical Engineering Education 40/3

Фундаментальный метод токовой петли с использованием техники «виртуальных источников напряжения»

для

особые случаи

Джордж Э. Хатзаракис, 1 Марина Д. Торторели1 и Анастасиос Д. Циолас2

1 Кафедры электротехники и электроники, Педагогический факультет и

Технологическое образование (ASPETE), Афины, Греция

2 Вычислительный факультет, Аристотелианский университет Греция

Эл. Почта: geaxatz @ otenet.gr, [email protected]

Аннотация Новый метод, основанный на использовании виртуальных источников напряжения, делает любую электрическую цепь

решаемой с помощью фундаментального метода токовой петли простым и понятным способом для студентов. Таким образом, систематизируется метод

основного токового контура (особенно для неплоских цепей), и трудности

, представленные до сих пор для специальных категорий цепей, перестают существовать.

Ключевые слова основной цикл; связь; неконвертируемый источник тока; Особые случаи; дерево; виртуальное напряжение

источник

Систематическое решение электрической цепи требует топологических концепций, подобных

, которые упоминаются во многих учебниках по электрическим цепям.1,2,3 Наиболее важные con-

cepts — это граф, дерево и основная петля.

Каждой электрической цепи соответствует график, который представляет собой результат геометрической фигуры —

из схемы, когда каждая ветвь неактивного элемента схемы заменяется

линейной частью или изогнутой частью; источники напряжения цепи замкнуты накоротко, а источники тока

разомкнуты.

Если граф можно нарисовать на плоскости таким образом, что любые две его ветви имеют размер

, которые нельзя пересекать ни в одной точке, кроме узла схемы, то этот граф называется планарным графом

и схема, планарная схема (рис.1 (а, б)). В противном случае они называются

неплоским графом и неплоской схемой соответственно (рис. 1 (c)).

Граф, для которого переход от одного узла к другому осуществляется посредством следующих

непрерывных ветвей, называется связным графом (рис. 2 (а)). В противоположном случае

он называется несвязным графом (рис. 2 (б)).

Для связного графа схемы дерево (T) — это связная часть графа

, которая содержит все узлы и одновременно не содержит никаких петель.

ветвей дерева называются ветвями дерева, а остальные ветви (составляющие

в графе) называются связями (LT) или хордами.

Основное свойство, проистекающее непосредственно из определения дерева, состоит в том, что если граф

имеет n узлов, то дерево также имеет n узлов, но имеет n-1 ветвей.

На рисунке 3 показаны два дерева T1 и T2 связного графа и их связи LT1 и

LT2, соответственно.

Очевидно, возможные деревья связного графа являются результатом всех комбинаций

ветвей графа, удовлетворяющих свойствам дерева.

Для данного дерева в связном графе основной цикл (FL) — это каждый цикл, который

Метод токовой сетки | Прядильные числа

Метод Mesh Current — один из двух хорошо организованных методов решения схемы. (Другой — метод напряжения узла.)

Метод сеточного тока — прекрасное применение закона напряжения Кирхгофа (KVL).

Содержание

Куда мы направляемся

Метод токовой сетки

Определите сетки (открытые окна схемы).Нарисуйте и назовите текущие стрелки сетки с одинаковым направлением (все по часовой стрелке или все против часовой стрелки).
Решите простые сеточные токи, которые проходят через источник постоянного тока.
Напишите закон Кирхгофа по напряжению вокруг каждой ячейки.
Решите получившуюся систему уравнений, чтобы получить токи сетки.
Найдите токи и напряжения элементов с помощью закона Ома.

Исключение: если схема неплоская , или у вас есть источник тока, совместно используемый двумя сетками, используйте метод тока контура.Метод токовой петли — это небольшая вариация метода токовой петли.

Петли и сетки

Нам нужно понять два специальных терминальных термина: петля и петля .

Контур — это любой замкнутый контур вокруг контура. Чтобы отследить цикл, начните с любого терминала компонента и проследите путь через соединенные элементы, пока не вернетесь туда, где вы начали. Есть только одно правило: циклу разрешено проходить через элемент только один раз (поэтому вы не получите циклы, которые выглядят как восьмерка).В приведенной выше схеме есть три цикла, два сплошных цикла, $ \ text I $ и $ \ text {II} $, и один пунктирный цикл, $ \ text {III} $, по всей внешней стороне.

Если мы проследим петли по часовой стрелке, три петли в нашей схеме пройдут через

$ \ begin {align}
& \ text {Цикл I:} && \ text {V1 — R1 — R3} \\
& \ text {Цикл II:} && \ text {R3 — R2 — V2} \\
& \ text {Цикл III: (пунктир)} && \ text {V1 — R1 — R2 — V2}
\ end {выровнены} $

Сетка — петля с ограничениями; сетка — это петля, не содержащая других петель.В приведенной выше схеме петли $ \ text I $ и $ \ text {II} $ представляют собой ячейки и , потому что внутри нет петель меньшего размера.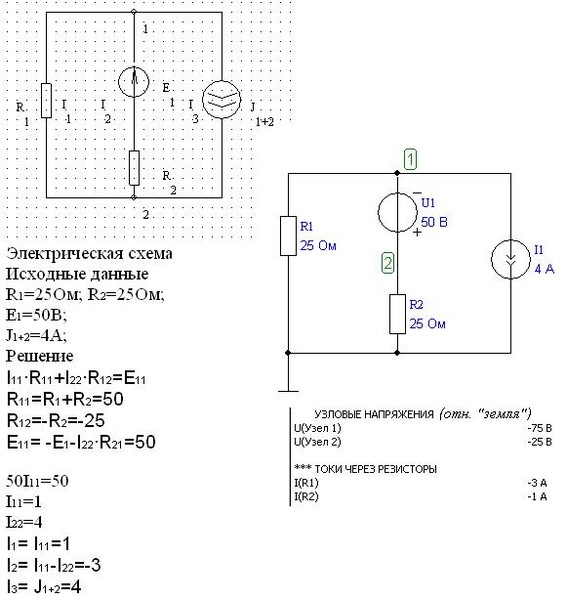 Пунктирная петля снаружи не является сеткой, потому что она содержит две другие петли.

В методе тока сетки мы используем сетки для генерации уравнений KVL. Это всегда дает нам нужное количество независимых уравнений.

Что означает слово сетка ?

Обыденное слово сетка имеет два значения:

Сетка описывает материал , составляющий сеть из проволоки или нити, например: «Наши рыболовные сети сделаны из сетки из прочного корда.”

Сетка

— это также пространство между отдельными нитями сети из проволоки или нити: «Если сетка слишком большая, маленькая рыба может проплыть через отверстия и ускользнуть».

При анализе цепей ток сетки течет через провода, образующие границу каждой сетки. Это первое значение. Чтобы быстро идентифицировать сетки, вы ищите «открытые окна» схемы. Это второе значение.

Сетка тока

Теперь мы даем определение другому новому термину, mesh current . До сих пор ток обычно относился к элементу , току (ток, протекающий через элемент). Когда мы используем термин mesh current , мы говорим о воображаемом токе, текущем вокруг сетки.

Сетка тока — немного странная идея, но придерживайтесь меня. В следующей схеме давайте определим токи сетки $ i _ {\ text I} $ и $ i _ {\ text {II}} $, текущие по сеткам $ \ text I $ и $ \ text {II} $, с положительное направление токов указано стрелками.

Понятно, что $ i _ {\ text I} $ — это ток, протекающий в источнике $ \ text V1 $ и резисторе $ \ text R1 $. Аналогично, $ i _ {\ text {II}} $ — это ток, протекающий в резисторе $ \ text R2 $ и источнике $ \ text V2 $. Но что происходит с током в $ \ text R3 $?

Давайте внимательно посмотрим на $ \ text R3 $ в средней ветви схемы. Какой ток элемента протекает через $ \ text R3 $?

Как нарисованы токи сетки, похоже, что они оба проходят через $ \ text R3 $ в противоположных направлениях.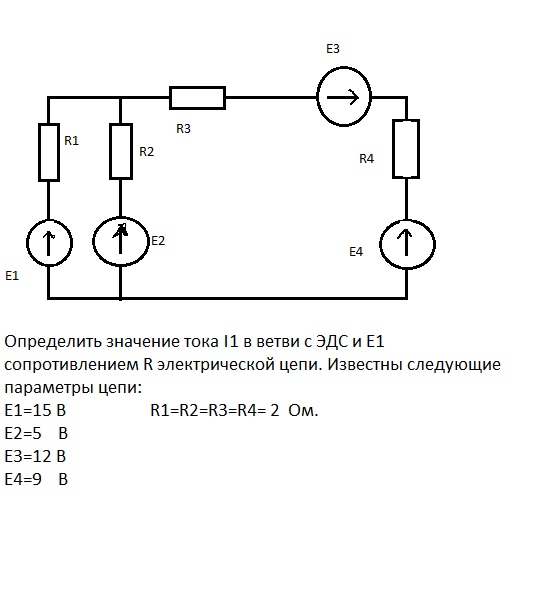 Может ли это быть правдой? Да, может, потому что мы можем использовать очень важную концепцию, называемую принципом суперпозиции .

Суперпозиция

Суперпозиция — красивое слово для прибавления . В случае $ \ text R3 $, когда мы говорим, что два тока сетки, $ i _ {\ text I} $ и $ i _ {\ text {II}} $ складываются в фактический ток в резисторе, $ i_ { \ text R3} $ используем принцип суперпозиции .

$ i _ {\ text R3} = + i _ {\ text I} — i _ {\ text {II}}

Два тока сетки накладываются друг на друга (добавить), чтобы сформировать ток элемента в $ \ text R3 $.Стрелка для текущей сетки $ i _ {\ text I} $ указывает в том же направлении, что и текущая ветвь $ i _ {\ text R3} $, давая ей знак $ + $ в уравнении суперпозиции. Стрелка для текущей сетки $ i _ {\ text {II}} $ указывает в противоположном направлении, поэтому в уравнении появляется знак $ — $.

Линейность

Мы можем использовать суперпозицию с идеальными резисторами потому, что идеальный резистор имеет свойство Линейность . Резисторы линейны, потому что если мы умножаем напряжение на константу $ a $, то ток умножается на ту же константу $ a $.

$ v = i \, \ text

R $

$ a \, v = a \, i \, \ text

R $

Линейность — это то, что позволяет нам использовать принцип суперпозиции. Мы используем суперпозицию, когда определяем два тока сетки, протекающие в одном элементе схемы. А это означает, что мы можем использовать метод Mesh Current для решения схем!

Чтобы узнать больше о линейности и суперпозиции, ознакомьтесь с разделом «Линейность и суперпозиция».

Сетка действующая практика

задача 1 Найти текущий элемент $ i _ {\ text {Rx}} $,

$ \ large i _ {\ text {Rx}} = $ ______ $ \ text {mA}

показать ответ

$ 4 \, \ text {mA} $ течет вниз через $ \ text {Rx} $ в том же направлении, что и текущая стрелка элемента, $ i _ {\ text {Rx}} $.

$ 3 \, \ text {mA} $ течет вверх через $ \ text {Rx} $, противоположно направлению текущей стрелки элемента $ i _ {\ text {Rx}} $.

Путем наложения, $ i _ {\ text {Rx}} = +4 \, \ text {mA} — 3 \, \ text {mA} = +1 \, \ text {mA} $

задача 2 Найти текущий элемент $ i _ {\ text {Ry}} $,

$ \ large i _ {\ text {Ry}} = $ ______ $ \ text {mA}

показать ответ

Сетка $ \ text I $ имеет $ 2 \, \ text {mA} $, противоположные направлению текущей стрелки элемента, $ i _ {\ text {Ry}} $.Так что он идет со знаком минус.

Сетка $ \ text {II} $ имеет $ -2 \, \ text {mA} $, текущие в том же направлении, что и текущая стрелка элемента, $ i _ {\ text {Rx}} $. Так что это тоже идет со знаком минус.

Путем наложения, $ i _ {\ text {Ry}} = -2 \, \ text {mA} — 2 \, \ text {mA} = -4 \, \ text {mA} $

Сеточные токи немного странные. Вот почему я люблю использовать этот метод всякий раз, когда могу.

Метод течения сетки

Метод Mesh Current Method следует этой последовательности шагов:

Определите сетки (открытые окна схемы). Нарисуйте и назовите текущие стрелки сетки с одинаковым направлением (все по часовой стрелке или все против часовой стрелки).
Решите простые сеточные токи, которые проходят через источник постоянного тока.
Напишите закон Кирхгофа по напряжению вокруг каждой ячейки.
Решите полученную систему уравнений, чтобы найти сеточные токи.
Найдите токи и напряжения элементов с помощью суперпозиции и закона Ома.

Давайте продемонстрируем метод сеточного тока с этой схемой,

Определите сетки

Наша схема состоит из двух сеток.Мы идентифицируем два тока сетки и называем их $ i _ {\ text I} $ и $ i _ {\ text {II}} $. Это будут наши независимые переменные. Важно: текущие направления совпадают. Оба текут по часовой стрелке.

Определив ток в каждой ячейке, вы гарантированно получите достаточно независимых уравнений для решения схемы.

Решите токи easy mesh

В нашей схеме нет источников тока, поэтому нет токов с простой сеткой. Однако, если вы посмотрите на пример схемы в статье о методе узлового напряжения, вы увидите, что источник тока есть.Если вы атакуете эту схему методом Mesh Current Method, через источник тока слева проходит один ток сетки, что делает его «простым». Этот ток сетки имеет то же значение, что и текущий источник.

пример схемы из статьи о напряжении узла

Запишите закон напряжения Кирхгофа вокруг каждой ячейки

Чтобы подготовиться, мы помечаем схему токами элементов (зеленые стрелки) и напряжениями элементов (оранжевые $ + $ и $ — $), используя условные обозначения для пассивных компонентов.

Необходимый навык: Набросайте чертёж на схеме!

Сначала нарисуйте токи элементов (перед назначением напряжений). Рекомендуется направлять токи в том же направлении, что и ток ближайшей сетки. Вы не всегда можете это сделать. (Обратите внимание, где $ i _ {\ text {II}} $ течет напротив стрелки тока $ 1 \, \ text k \ Omega $. Это нормально, в конце концов все будет хорошо.)
Затем добавьте напряжения элементов со знаком $ + $ рядом со стрелкой входящего тока (соглашение о пассивных знаках).

Теперь напишите уравнение для каждой сетки, используя закон напряжения Кирхгофа. Каждый член в уравнении представляет собой напряжение, а сумма равна нулю. Вот как включить каждый термин напряжения:

Если через резистор протекает ток одной ячейки, введите напряжение как сопротивление $ \ times $ ток ячейки.
Если через компонент протекают два тока сетки, включите их разницу в выражение закона Ома, как мы это делали выше в практике тока сетки.
Когда вы подходите к источнику напряжения, он просто входит в качестве значения напряжения.

Уравнение для сетки $ \ text I $, пошаговое описание

Мы начинаем с левого нижнего угла схемы и движемся по часовой стрелке по сетке $ \ text I $.

Первым элементом, к которому мы подходим, является источник напряжения $ 5 \, \ text V $. Сначала мы видим оранжевый знак $ — $ источника напряжения. Это означает, что мы испытаем повышение напряжения , проходящее через источник. Поскольку это рост, он входит в уравнение со знаком $ + $, как $ + 5 \, \ text V $.

$ \ text {mesh I:} \ quad + 5 \, \ text V \,… $

Второй элемент — это резистор $ 2 \, \ text k \ Omega $. Напряжение на этом резисторе равно $ 2 \, \ text k \ Omega \ cdot i _ {\ text {I}} $. (Вот что значит «выполнять закон Ома в своей голове».) Зеленая стрелка тока этого резистора направлена в том же направлении, что и ток сетки $ i_ \ text {I} $. Оранжевый знак напряжения $ + $ говорит нам, что мы будем испытывать падение напряжения , проходящее через этот компонент, поэтому этот член входит в уравнение со знаком $ — $, как $ -2000 \, i _ {\ text I} $ .

$ \ text {mesh I:} \ quad + 5 \, \ text V — 2000 \, i _ {\ text I} \,… $

Далее мы подошли к резистору $ 1 \, \ text k \ Omega $. Это сложный вопрос. Он имеет два тока сетки, текущие в противоположных направлениях: $ i _ {\ text I} $ и $ i _ {\ text {II}} $. Ток элемента в резисторе равен $ (i _ {\ text I} — i _ {\ text {II}}) $. Мы помещаем $ i _ {\ text I} $ первым, потому что он течет в том же направлении, что и ток зеленого элемента. Таким образом, термин напряжения равен $ 1 \, \ text k \ Omega \ cdot (i _ {\ text I} — i _ {\ text {II}}) $.Сначала мы подходим к оранжевому значку напряжения $ + $, который говорит нам о падении напряжения через резистор. Следовательно, этот член входит в уравнение со знаком $ — $, как $ -1 \, \ text k \ Omega \ cdot (i _ {\ text I} — i _ {\ text {II}}) $.

$ \ text {mesh I:} \ quad + 5 \, \ text V — 2000 \, i _ {\ text I} — 1000 \, (i _ {\ text {I}} — i _ {\ text {II} }) \,…

Обход сетки $ \ text I $ завершен, и мы устанавливаем сумму напряжений равной нулю,

$ \ text {mesh I:} \ quad + 5 \, \ text V — 2000 \, i _ {\ text I} — 1000 \, (i _ {\ text {I}} — i _ {\ text {II} }) = 0 $

Сводка сетки $ \ text I $

Уравнение для сетки $ \ text {II} $, пошаговое описание

Мы начинаем с нижней части резистора $ 1 \, \ text k \ Omega $ и перемещаемся по сетке по часовой стрелке.

Первым элементом является резистор $ 1 \, \ text k \ Omega $, через который протекают два тока сетки. Общий ток резистора равен $ (i _ {\ text I} — i _ {\ text {II}}) $. Первый член — $ i _ {\ text I} $, потому что он соответствует направлению текущей стрелки зеленого элемента. Поскольку мы вводим этот резистор снизу, под его оранжевым знаком $ — $, мы будем испытывать повышение напряжения , проходящее через него, поэтому член, который мы включаем в уравнение, равен $ + 1000 \, (i _ {\ text I } — i _ {\ text {II}}) $.

$ \ text {mesh II:} \ quad +1000 \, (i _ {\ text I} — i _ {\ text {II}}) \,… $

Следующий компонент — резистор $ 2 \, \ text k \ Omega $ в правом верхнем углу схемы, через который проходит только $ i _ {\ text {II}} $. Это падение напряжения, поэтому оно входит в уравнение как $ -2000 \ cdot i _ {\ text {II}} $.

$ \ text {mesh II:} \ quad +1000 \, (i _ {\ text I} — i _ {\ text {II}}) — 2000 \, i _ {\ text {II}} \,… $

Последнее, к чему мы подошли, это источник $ 2 \, \ text V $. Для источников просто введите значение их напряжения. Мы видим, как через этот источник проходит падение напряжения , поэтому оно входит в уравнение как $ -2 \, \ text V $.

$ \ text {mesh II:} \ quad +1000 \, (i _ {\ text I} — i _ {\ text {II}}) — 2000 \, i _ {\ text {II}} -2 \, \ текст V \,… $

И завершаем установкой суммы на ноль,

$ \ text {mesh II:} \ quad +1000 \, (i _ {\ text I} — i _ {\ text {II}}) — 2000 \, i _ {\ text {II}} -2 \, \ текст V = 0 $

Сводка сетки $ \ text {II} $

Решите систему уравнений сетки

Уравнения сетки скопированы сверху,

$ \ begin {align}
& \ text {сетка I:} && + 5 \, \ text V — 2000 \, i _ {\ text I} — 1000 \, (i _ {\ text {I}} — i _ {\ text {II}}) = 0 \\
& \ text {сетка II:} && + 1000 \, (i _ {\ text I} — i _ {\ text {II}}) — 2000 \, i _ {\ text {II}} -2 \, \ text V = 0
\ end {align}

долл. США

Для начала перемножим члены и переместим константы вправо,

$ \ begin {align}
& \ text {сетка I:} && — 2000 \, i _ {\ text I} — 1000 \, i _ {\ text {I}} + 1000 \, i _ {\ text {II}} = -5 \\
& \ text {сетка II:} && +1000 \, i _ {\ text I} — 1000 \, i _ {\ text {II}} — 2000 \, i _ {\ text {II}} = +2
\ end {align}

долл. США

Объедините похожие термины, чтобы получить аккуратную систему уравнений,

$ \ begin {align}
& \ text {сетка I:} && — 3000 \, i _ {\ text I} + 1000 \, i _ {\ text {II}} = -5 \\

& \ text {сетка II:} && +1000 \, i _ {\ text I} — 3000 \, i _ {\ text {II}} = +2
\ end {align}

долл. США

Наша стратегия будет заключаться в том, чтобы исключить $ i _ {\ text I} $, умножив уравнение $ \ text {mesh II} $ на $ 3 $ и добавив его к первому уравнению.Вот умножение уравнения сетки $ \ text {II} $,

$ \ begin {align}
& \ text {сетка II:} & 3 \ times [+1000 \, i _ {\ text I} — 3000 \, i _ {\ text {II}} = +2 \,] \\
& & = [+3000 \, i _ {\ text I} — 9000 \, i _ {\ text {II}} = +6 \,]
\ end {align}

долл. США

Теперь сложите два уравнения. Условия $ i _ {\ text I} $ отменяются, остается только термин $ i _ {\ text {II}} $,

$ \ begin {align}
& \ text {сетка I:} & [\ cancel {-3000 \, i _ {\ text I}} + 1000 \, i _ {\ text {II}} & = -5 \,] \\
& \ text {сетка II:} & \ underline {+ \ quad [\ cancel {+3000 \, i _ {\ text I}} — 9000 \, i _ {\ text {II}}} & \ underline {\: = +6 \,]} \\
&& — 8000 \, i _ {\ text {II}} & = +1 \\
&& i _ {\ text {II}} & = +1 \, / — 8000 \\
&& i _ {\ text {II}} & = -0. 125 \, \ text {mA}
\ end {align}

долл. США

Текущая сетка $ i _ {\ text {II}} $ вышла со знаком минус. Это означает, что этот ток течет против часовой стрелки, противоположно направлению стрелки тока сетки $ i _ {\ text {II}} $.

У нас одна сетка тока. Пойдем за другой.
Вставьте $ i _ {\ text {II}} $ в уравнение сетки, чтобы получить другой ток. Давайте воспользуемся уравнением для сетки $ \ text {I} $,

$ \ begin {align}
\ text {mesh I:} \ quad -3000 \, i _ {\ text I} + 1000 \, i _ {\ text {II}} & = -5 \\
— 3000 \, i _ {\ text I} + 1000 \, (-0.125) & = -5 \\
— 3000 \, i _ {\ text I} & = -5 + 0,125 \\
i _ {\ text I} & = -4,875 \, / — 3000 \\
i _ {\ text I} & = +1,625 \, \ text {mA}
\ end {align}

долл. США

Два тока сетки теперь решены.

Переходим к нахождению токов и напряжений для отдельных элементов.

Решите для токов и напряжений элементов

Для любого элемента, несущего только один ток сетки, мы сразу узнаем его ток элемента. Это то же самое, что и ток сетки,

$ i_ {2 \, \ text k \ Omega \ text {left}} = + i _ {\ text I} = \ blueD {+1.625 \, \ text {mA}}

долл. США

$ i_ {2 \, \ text k \ Omega \ text {right}} = + i _ {\ text {II}} = \ blueD {-0,125 \, \ text {mA}} $

Резистор $ 1 \, \ text k \ Omega $ в середине несет два тока сетки, поэтому мы используем суперпозицию, чтобы найти ток элемента,

$ i_ {1 \ text k \ Omega} = i _ {\ text I} — i _ {\ text {II}} = +1,625 \, \ text {mA} — (-0,125 \, \ text {mA}) = \ blueD {+1.75 \, \ text {mA}}

долл. США

И, наконец, мы находим напряжение в узле между тремя резисторами, используя закон Ома для резистора $ 1 \, \ text k \ Omega $,

$ v_ {1 \ text k \ Omega} = 1 \, \ text k \ Omega \ cdot 1.75 \, \ text {mA} = \ goldD {1.75 \, \ text V}

долл. США

Поздравляем! Мы проанализировали схему, используя метод Mesh Current.

Выбор метода

У нас есть два эффективных метода анализа цепей: узловое напряжение и сеточный ток. Который лучший? Это зависит от схемы. Подсчитайте количество сеток и сравните это с количеством узлов. Какое число меньше: сетки или узлы? Лучше всего выбрать метод с меньшим количеством одновременных уравнений. Если сетки и узлы одинаковы или почти одинаковы, выберите метод, который вам лучше всего понятен.

Исключение: неплоские схемы

Описанный выше метод сеточного тока работает с планарными схемами (схемами, которые можно рисовать плоскими, без пересечения проводов). Цепи в этой статье плоские, и большинство цепей, с которыми вы столкнетесь, тоже будут. Схема неплоская , если нет возможности провести ее без пересечения проводов. Мы должны сделать небольшую модификацию метода сетки, и он получит имя Loop Current Method .Большинство шагов одинаковы, но мы можем включать петли в дополнение к сеткам. Мы поговорим больше о неплоских и петлях в статье о методе тока петли.

Резюме

Шаги метода Mesh Current Method:

Определите сетки (открытые окна схемы). Назначьте текущую переменную каждой сетке, используя согласованное направление (по или против часовой стрелки).
Решите простые сетки, которые проходят через источник постоянного тока.
Напишите закон Кирхгофа по напряжению вокруг каждой ячейки.
Если через резистор протекает ток одной ячейки, то значение напряжения записывается как $ \ text R \, i_ {mesh} $.
Если два тока сетки протекают в противоположных направлениях , член напряжения входит как $ \ text R \, (i_ {mesh 1} — i_ {mesh 2}) $.
Если два тока сетки протекают в одном и том же направлении в резисторе , напряжение входит как $ \ text R \, (i_ {mesh 1} + i_ {mesh 2}) $.
Источники напряжения соответствуют их значениям напряжения.
Решите систему уравнений.
Найдите токи и напряжения элементов, используя закон Ома.

Если схема неплоская или имеется общий источник тока между двумя сетками, лучше всего использовать метод тока контура.

Метод контурных токов, метод узловых потенциалов

Алгоритм расчета цепи методом контурных токов.

1.4. Метод узловых потенциалов.

УНИВЕРСИТЕТ ИТМО. Денисова А.В.

Расчетно-графическая работа 1

2.8. Метод контурных токов.

МЕТОДЫ РАСЧЕТА СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Практическая работа 5

Работа по теме : «Сложные цепи»

Методы анализа сложных линейных цепей.

Постоянный ток «на ладони»

Методы анализа сложных линейных цепей.

РАСЧЕТ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

I 3 b I 11 E 1 I 5 I 6 I 33

E — нормальный элемент Вестона.

РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ

Глава 1. Основные законы электрической цепи

Электротехника и электроника

от частоты — Фазо-частотная

4.

Лекция 2. АНАЛИЗ РЕЗИСТИВНЫХ ЦЕПЕЙ

Основныезаконы электротехники

ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики

Лабораторная работа 12*

Лекция 2. АНАЛИЗ РЕЗИСТИВНЫХ ЦЕПЕЙ

Расчетно-графическая работа 1

РАСЧЕТ ЦЕПИ ПОСТОЯННОГО ТОКА

3. Постоянный электрический ток.

2007, Ravenbird ВВ-2-06

ЦЕЛЬ ДОМАШНЕГО ЗАДАНИЯ

Теоретические сведения.

Лекция 3. МЕТОД УЗЛОВЫХ НАПРЯЖЕНИЙ

АНАЛИЗ СЛОЖНЫХ ЛИНЕЙНЫХ ЦЕПЕЙ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

РАСЧЕТ ЛИНЕЙНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Рис.1 — исходная схема

Контрольная работа.

ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА

Теоретические сведения.

Линейные электрические цепи

★ Метод контурных токов — электротехника .

Метод контурных токов и PSpice. OrCAD PSpice. Анализ электрических цепей

Читайте также

Форматы контурных шрифтов

Обзор PSpice

Направления токов

Метод узловых потенциалов и PSpice

Библиотека элементов PSpice

9. Приборы в PSpice

Анализ на PSpice

Обозначения токов и напряжений в Probe

Временные диаграммы гармонических токов

Приложение A. Краткое описание директив PSpice

Приложение B. Компоненты и директивы PSpice

Приложение D.

2.2. Выходной файл программы PSPICE

10.1. PSPICE как статический логический анализатор

Глава 13 Возможности применения программы PSPICE

Метод контурных токов, метод узловых потенциалов (Реферат)

Электротехника ТОЭ: 3.2.2. Метод контурных токов

Метод контурных токов

Метод петлевых (или ячеистых) токов Максвелла

Физика для науки и техники II

Отвод по текущему способу

Пример метода тока ответвления 1

Пример 2 метода тока ответвления

Пример 3 метода ветвления тока

Пример 4 метода тока ответвления

Пример 5 текущего метода ветвления

Пример метода 6 тока ветви

Пример 7 метода текущего ветвления

Пример метода тока ветвления 8

Простой анализ тока в сетке для электрических цепей

Что такое петля и сетка

Анализ тока сетки

Процедура анализа тока сетки

Текущие направления анализа сетки

Маркировка элементов схемы

Найдите уравнения сетки KVL

Решите уравнения сетки KVL