ФИЗИКА: ЗАДАЧИ на Последовательное соединение
Задачи на Последовательное соединение
проводников с решениями
Формулы, используемые на уроках «Задачи на Последовательное соединение проводников»
Название величины | Обозначение | Единица измерения | Формула |
Сила тока | I | А | I = U / R |
Напряжение | U | В | U = IR |
Сопротивление | R | Ом | R = U/I |
Сила тока на участке цепи | I | A | I = I1 = I2 |
Напряжение на концах участка | U | B | U = U1 + U2 |
Сопротивление участка цепи | R | Ом | R = R1 + R2 |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.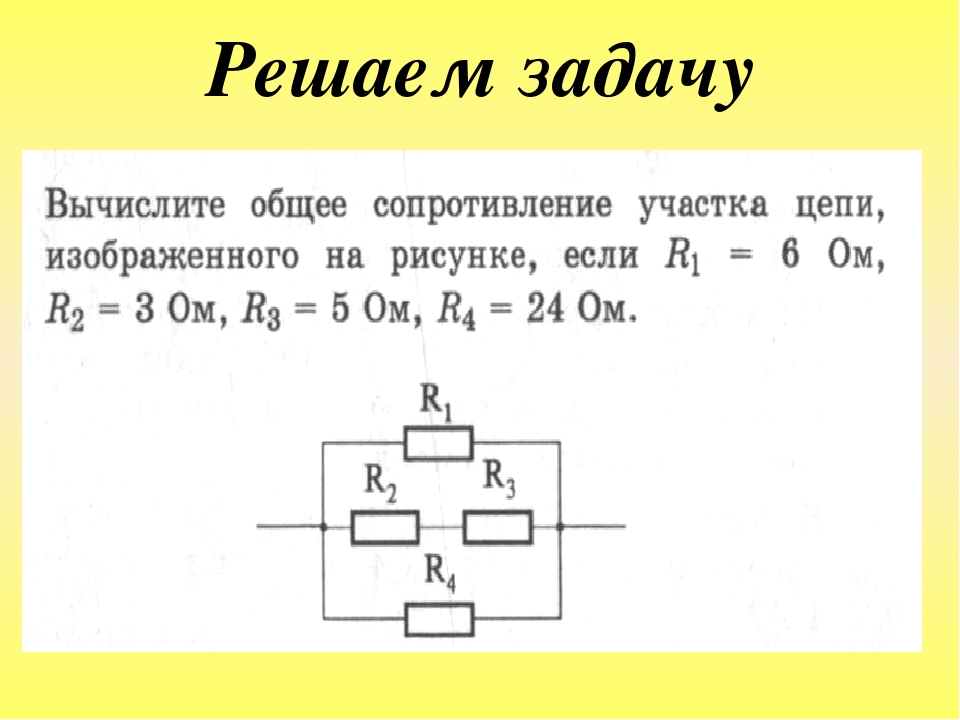
Два проводника сопротивлением 2 Ом и 3 Ом соединены последовательно. Сила тока в цепи 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение.
Задача № 2.
Два проводника сопротивлением 20 Ом и 30 Ом соединены последовательно. Напряжение на концах первого проводника 12 В. Определить сопротивление цепи, силу тока в цепи, напряжение на втором проводнике и полное напряжение.
Задача № 3.
Два резистора соединены последовательно. Сопротивление первого 12 Ом, полное сопротивление 30 Ом. Сила тока в цепи 2 А. Определить сопротивление первого резистора, напряжение на каждом проводнике и полное напряжение.
Задача № 4.
В каких пределах можно менять сопротивление в цепи, если сопротивление реостата R имеет пределы 0…10 Ом? Сопротивление резистора R1 равно 20 Ом.
Ответ: Сопротивления R и R1 соединены параллельны. Сопротивление цепи будет изменяться в пределах от 20 до 30 Ом.
Сопротивление цепи будет изменяться в пределах от 20 до 30 Ом.
Задача № 5.
Последовательно с нитью накала радиолампы сопротивлением 3,9 Ом включен резистор, сопротивление которого 2,41 Ом. Определите их общее сопротивление.
Задача № 6.
Общее сопротивление последовательно включенных двух ламп сопротивлением 15 Ом каждая и реостата равно 54 Ом. Определите сопротивление реостата.
Задача № 7.
Два резистора сопротивлением 8 и 1 кОм соединены последовательно. Определите показание вольтметра, подключенного между точками А и С, если сила тока в цепи равна 3 мА. Что будет показывать вольтметр, подключенный между точками А и В, В и С?
Задача № 8.
В цепь включены последовательно три проводника сопротивлениями: R1=5 Ом, R2=6 Ом, R3= 12 Ом. Какую силу тока показывает амперметр и каково напряжение между точками А и В, если показание вольтметра 1,2 В?
Задача № 9.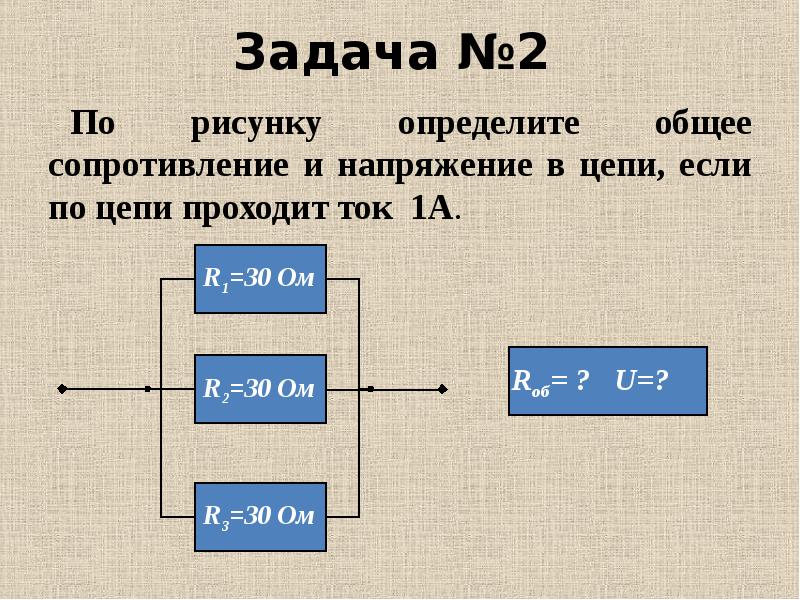
Последовательно с электрической лампой включен реостат. Начертите схему цепи и определите сопротивление реостата и лампы, если напряжение на зажимах цепи 12 В. Вольтметр, подключенный к реостату, показывает 8 В. Сила тока в цепи 80 мА.
Краткая теория для решения Задачи на Последовательное соединение проводников.
Это конспект по теме «ЗАДАЧИ на Последовательное соединение проводников». Выберите дальнейшие действия:
План-конспект урока по физике по теме: ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ-Урок решения задач.Викторина -сказка «Физическая страна».
УРОК 1.
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ: «Последовательное и параллельное соединение проводников».
ЦЕЛИ УРОКА:
Сформировать умение находить неизвестные величины при последовательном и параллельном соединении.
ЗАДАЧИ УРОКА:
образовательные:
- экспериментально определить сопротивление резистора при последовательном соединении проводников;
- продолжить формирование умений и навыков собирать простейшие электрические цепи, а также пользоваться измерительными приборами (амперметром и вольтметром).

воспитательные:
- продолжить воспитание отношение к физике как к экспериментальной науке;
- продолжить работу по формированию умений работать в коллективе (умение высказать свою точку зрения и выслушать точку зрения товарища, умение уважительного отношения к мнению товарища и др.).
развивающие:
- продолжить работу по формированию умений делать выводы и обобщения на основе результатов проведённого исследования;
- продолжить развитие мышления, творческих и исследовательских способностей учащихся.
ОБОРУДОВАНИЕ:
Для всех: Презентация, универсальный стенд.
На каждую парту:
- амперметр,
- вольтметр,
- резистор,
- ключ,
- источник питания,
- соединительные провода.
ХОД УРОКА:
- Организационная часть.
Оцените свое эмоциональное состояние в начале урока..
- Проверка пройденного материала.
Ребята решают задачу, данные берут из практической работы, которую проводят на уроке.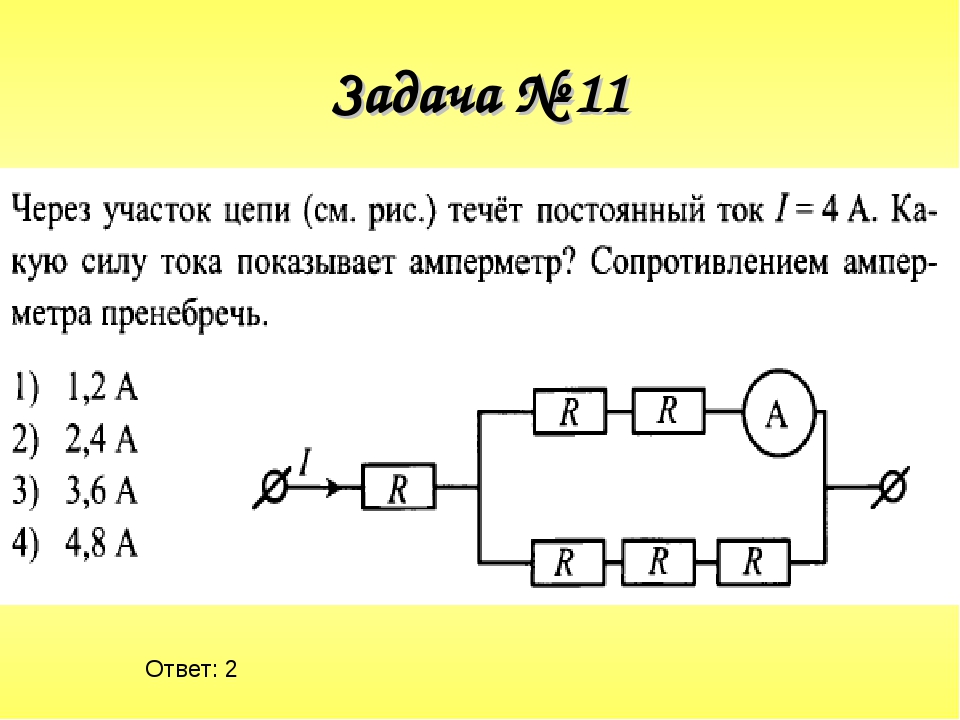
- Соберите электрическую цепь по схеме:
- Снимите показания амперметра и вольтметра.
- По полученным данным определите сопротивление резистора.
- 1. Проверка знаний учащихся по теме.
Демонстрация. Последовательное соединение проводников.
На столе три ученика выбирают формулы, с помощью которых можно вычислить напряжение, силу тока и сопротивление при последовательном соединении проводников.
- Как включаются в цепь потребители при последовательном соединении?
При последовательном соединении потребителей они включаются в цепь поочередно друг за другом без разветвлений проводов между ними.
рис.
а)
- Чему равна сила тока в цепи при последовательном соединении?
Сила тока в цепи при последовательном соединении везде одинакова.
I = I1 = I2. ( Проверка правильности написания формулы)
- Чему равно напряжение в цепи при последовательном соединении?
Напряжение в цепи равно сумме напряжений на отдельных участках.
U = U1 + U2. . ( Проверка правильности написания формулы)
- Чему равно общее сопротивление в цепи при последовательном соединении?
Общее сопротивление в цепи складывается из сопротивлений отдельных проводников.
R = R1 + R2. . ( Проверка правильности написания формулы)
- 1. Закрепление материала по теме. Решение задач.
- Каковы показания вольтметров, если амперметр показывает 1,5 А. (Рис. 1).
Дано: Решение:
R1= 4 Ом. Т. к. проводники соединены последовательно, то
R2= 2 Ом. Iобщ.=I1=I2.
I= 1,5 А. U1=I1 R1; U2=I2R2.
U1= ? U1=1,5 А 4 Ом = 6В.
U2= ? U2= 1,5А 2 Ом = 3В
Ответ: U1=6В, U2=3В.
Рис. 1.
- Проверка знаний учащихся по теме.
Демонстрация.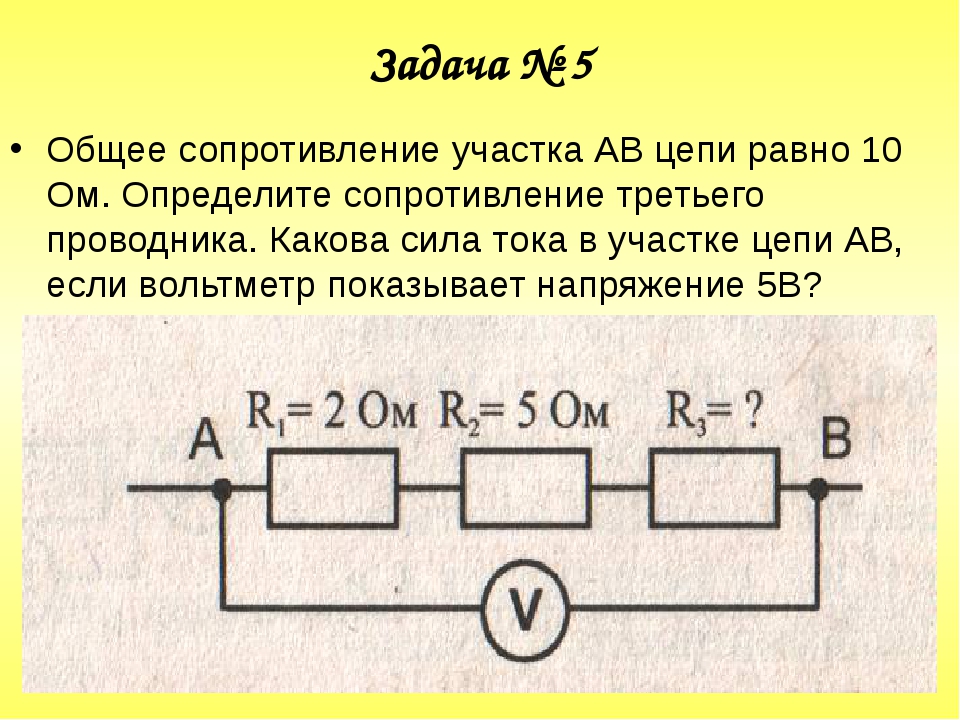 Параллельное соединение проводников.
Параллельное соединение проводников.
На столе три ученика выбирают формулы, с помощью которых можно вычислить напряжение, силу тока и сопротивление при параллельном соединении проводников.
- Как включаются в цепь потребители при параллельном соединении?
При параллельном соединении все проводники подключаются к одной и той же паре точек А и В.
рис.
а)
- Чему равна сила тока в цепи при параллельном соединении?
Сила тока в цепи при параллельном соединении равна сумме сил токов на \отдельных участках.
I = I1 + I2. ( Проверка правильности написания формулы)
- Чему равно напряжение в цепи при параллельном соединении?
Напряжение при параллельном соединении на всех участках цепи одно и то же.
U = U1 = U2. . ( Проверка правильности написания формулы)
- Чему равно общее сопротивление в цепи при параллельном соединении?
Сопротивление в цепи при параллельном соединении находится как отношение произведения их сопротивлений к их сумме.
R = R1 R2. . ( Проверка правильности написания формулы)
R1 + R2.
4.2. Закрепление материала по теме. Решение задач.
2.Определить общее сопротивление (Рис. 2)
Дано: Решение:
R1= 40 Ом. Т. к. проводники соединены параллельно, то:
R2= 20 Ом. 1 = 1 + 1
Rобщ.= ? Rобщ R1 R2
R = R1 R2. . = 40 60 = 24 Ом.
R1 + R2. 40+60
Ответ: Rобщ.= 24 Ом.
Рис. 2.
4.3. Решение задач.
3.Каковы показания амперметров, если стрелка вольтметра показывает 6В.
(Рис. 3)
Дано: Решение:
R1= 4 Ом. Т. к. проводники соединены параллельно, то:
R2=3 Ом. U = U1 = U2 = 6В
U = 6В I1= U/ R1
I1= ? I2= U/ R2
I2= ? I1= 6В/ 4Ом = 1,5 А
I2= 6В / 3 Ом = 2 А.
Ответ: I1= 1,5 А; I2= 2А.
Рис. 3.
- Общее сопротивление участка АВ цепи равно 10 Ом. Определите сопротивление третьего проводника. Какова сила тока в участке цепи АВ, если вольтметр показывает напряжение 5В.
(Рис. 4)
Дано: Решение:
R1=2 Ом. Т. к. проводники соединены последовательно, то:
R2=5 Ом. R = R1 + R2 + R 3
U = 5В R 3= R — R1 — R2
R = 10 Ом R 3= 10 Ом – 2 Ом – 5 Ом = 3 Ом.
I общ = U/ R
I общ.= ? I общ = 5В / 10 Ом = 0,5 А.
R 3= ? Ответ: R 3= 3 Ом., I общ = 0,5 А.
Рис. 4.
Последовательное и параллельное соединение — Википедия. Что такое Последовательное и параллельное соединение
Последовательное соединение проводников.
Параллельное соединение проводников.
Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включённых проводников.
Последовательное соединение
При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I=I1=I2=⋯=In{\displaystyle I\mathrm {=} I_{1}=I_{2}=\cdots =I_{n}} (так как сила тока определяется количеством электронов, проходящим через поперечное сечение проводника, и если в цепи нет узлов, то все электроны в ней будут течь по одному проводнику).
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника питания, равно сумме напряжений на отдельных участках цепи: U=U1+U2+⋯+Un{\displaystyle U\mathrm {=} U_{1}+U_{2}+\cdots +U_{n}}.
Резисторы
- R=R1+R2+⋯+Rn{\displaystyle R=R_{1}+R_{2}+\cdots +R_{n}}
Катушка индуктивности
- L=L1+L2+⋯+Ln{\displaystyle L=L_{1}+L_{2}+\cdots +L_{n}}
Электрический конденсатор
- 1C=1C1+1C2+⋯+1Cn{\displaystyle {\frac {1}{C}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\cdots +{\frac {1}{C_{n}}}}.
Мемристоры
- M=M1+M2+⋯+Mn{\displaystyle M=M_{1}+M_{2}+\cdots +M_{n}}
Выключатели
Цепь замкнута, когда замкнуты все выключатели. Цепь разомкнута, когда разомкнут хотя бы один выключатель. (См.также Логическая операция И).
Параллельное соединение
Сила тока в неразветвлённой части цепи равна сумме сил тока в отдельных параллельно соединённых проводниках: I=I1+I2+⋯+In{\displaystyle I\mathrm {=} I_{1}+I_{2}+\cdots +I_{n}}
Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же: U=U1=U2=⋯=Un{\displaystyle U\mathrm {=} U_{1}=U_{2}=\cdots =U_{n}}
Резисторы
При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость 1R{\displaystyle {\frac {1}{R}}} складывается из проводимостей каждого резистора 1Ri{\displaystyle {\frac {1}{R_{i}}}})
Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее (искомое) сопротивление.
Доказательство
Для двух параллельно соединённых резисторов их общее сопротивление равно: R=
Frontiers | Эффективная многозадачность: параллельная или последовательная обработка нескольких задач
Введение
Основная цель исследований в области многозадачности в когнитивной психологии и когнитивной нейробиологии — понять и оптимизировать лежащие в основе процессы, чтобы повысить эффективность при одновременном решении нескольких задач. Растущие требования к обработке информации из-за увеличения количества мультимедийных взаимодействий требуют повышения эффективности. Есть ли у человеческого разума структурные и функциональные средства для эффективной многозадачности? Архитектурные свойства нервной системы допускают широко распределенную одновременную нейронную обработку в миллиардах нейронов.Однако при многозадачности возникают серьезные потери производительности при объединении даже простейших когнитивных задач для одновременного выполнения. Основываясь на современной литературе, мы отвечаем на два ключевых вопроса о многозадачности: (1) Что представляет собой эффективная и адаптивная многозадачность? (2) Какие процессы определяют эффективность многозадачности?
Большинство исследователей объясняют типичное снижение производительности при многозадачности структурным ограничением мощности, так называемым узким местом обработки (например,g. , Pashler, 1998), при котором определенные когнитивные процессы протекают последовательно (т. е. только по одному). Такая концептуализация многозадачности исключает возможность параллельной (то есть одновременной) когнитивной обработки нескольких компонентов задачи. Другие утверждают, что в целом возможна параллельная обработка (например, посредством разделения мощности, Tombu and Jolicoeur, 2003), но эта последовательная обработка отражает более эффективную и, следовательно, в первую очередь преследуемую стратегию многозадачности (например,г., Логан и Гордон, 2001; Миллер и др., 2009). В этом обзоре мы изложим эту дискуссию, в частности, сосредоточив внимание на характеристиках вариантов последовательной и параллельной обработки и на том, как они теоретически концептуализируются, а также эмпирически оцениваются в многозадачности. Для этого мы ограничиваем данный обзор ситуациями многозадачности, в которых две задачи с ускоренным выбором и реакцией должны выполняться одновременно, т.
, Pashler, 1998), при котором определенные когнитивные процессы протекают последовательно (т. е. только по одному). Такая концептуализация многозадачности исключает возможность параллельной (то есть одновременной) когнитивной обработки нескольких компонентов задачи. Другие утверждают, что в целом возможна параллельная обработка (например, посредством разделения мощности, Tombu and Jolicoeur, 2003), но эта последовательная обработка отражает более эффективную и, следовательно, в первую очередь преследуемую стратегию многозадачности (например,г., Логан и Гордон, 2001; Миллер и др., 2009). В этом обзоре мы изложим эту дискуссию, в частности, сосредоточив внимание на характеристиках вариантов последовательной и параллельной обработки и на том, как они теоретически концептуализируются, а также эмпирически оцениваются в многозадачности. Для этого мы ограничиваем данный обзор ситуациями многозадачности, в которых две задачи с ускоренным выбором и реакцией должны выполняться одновременно, т. Е. Двойные задачи (обзоры последовательной многозадачности, то есть переключения задач, см. В Monsell, 2003; Kiesel. и другие., 2010; Koch et al., 2010). Мы более подробно остановимся на вопросе, почему люди преследуют общее стремление выполнять более одной задачи одновременно (участвуя в параллельной обработке) с намерением повысить эффективность своей производительности, в то время как последовательная обработка на самом деле более эффективна. Чтобы представить более полную картину дискуссии о параллельной и последовательной обработке, мы также обсудим, при каких обстоятельствах принятие стратегии параллельной обработки представляет собой благоприятное решение для многозадачности.
Е. Двойные задачи (обзоры последовательной многозадачности, то есть переключения задач, см. В Monsell, 2003; Kiesel. и другие., 2010; Koch et al., 2010). Мы более подробно остановимся на вопросе, почему люди преследуют общее стремление выполнять более одной задачи одновременно (участвуя в параллельной обработке) с намерением повысить эффективность своей производительности, в то время как последовательная обработка на самом деле более эффективна. Чтобы представить более полную картину дискуссии о параллельной и последовательной обработке, мы также обсудим, при каких обстоятельствах принятие стратегии параллельной обработки представляет собой благоприятное решение для многозадачности.
Возможности и ограничения когнитивной системы для многозадачности
Последовательная обработка в связи с ограниченными ресурсами
Одновременное выполнение двух или более задач обычно приводит к серьезным потерям производительности с точки зрения увеличения задержек ответа и / или количества ошибок (Welford, 1952; Kahneman, 1973; Pashler, 1994). На теоретическом уровне эти двойные затраты часто объясняются ограничением структурных возможностей когнитивной обработки. Ранние работы по многозадачности, основанные на теории обработки информации, предполагали, что доступ к этому единственному каналу обработки планируется последовательно, по одной задаче за раз.Например, когда первая задача (T1) переходит в стадию обработки с ограниченной производительностью, обработка дополнительной задачи (T2) останавливается до тех пор, пока обработка критической стадии T1 не будет завершена (см. Рисунок 1). Следуя этой логике, планирование последовательных задач является следствием узкого места обработки с ограниченной производительностью, которое носит структурный характер (Welford, 1952; Broadbent, 1958). Этот взгляд на структурные ограничения и процесс пассивного составления расписания узких мест является основным предположением влиятельной и до сих пор широко принятой модели узких мест с отбором ответов (RSB) (Pashler and Johnston, 1989; Pashler, 1994).
На теоретическом уровне эти двойные затраты часто объясняются ограничением структурных возможностей когнитивной обработки. Ранние работы по многозадачности, основанные на теории обработки информации, предполагали, что доступ к этому единственному каналу обработки планируется последовательно, по одной задаче за раз.Например, когда первая задача (T1) переходит в стадию обработки с ограниченной производительностью, обработка дополнительной задачи (T2) останавливается до тех пор, пока обработка критической стадии T1 не будет завершена (см. Рисунок 1). Следуя этой логике, планирование последовательных задач является следствием узкого места обработки с ограниченной производительностью, которое носит структурный характер (Welford, 1952; Broadbent, 1958). Этот взгляд на структурные ограничения и процесс пассивного составления расписания узких мест является основным предположением влиятельной и до сих пор широко принятой модели узких мест с отбором ответов (RSB) (Pashler and Johnston, 1989; Pashler, 1994). Следуя логике этапов когнитивной обработки (Sternberg, 1969), этапы периферийной обработки двух задач (например, восприятие, двигательная реакция) выполняются параллельно. Ограничение мощности возникает на этапах центральной обработки (например, выбор ответа), которые не выполняются одновременно (см. Рис. 1A, Pashler, 1984; Pashler and Johnston, 1989). Этот взгляд на ограничение структурных возможностей для стадий центральной обработки по-прежнему преобладает в когнитивной нейробиологии человека и психологии из учебников, скорее всего, из-за наблюдения, что даже самые простые и / или хорошо обученные когнитивные операции подвержены существенным ограничениям обработки в сочетании с другой задачей. (е.г., Леви и др., 2006). Однако существует меньше единого мнения о том, отражает ли это узкое место обработки структурное (Pashler, 1998) или стратегическое (Meyer and Kieras, 1997) ограничение.
Следуя логике этапов когнитивной обработки (Sternberg, 1969), этапы периферийной обработки двух задач (например, восприятие, двигательная реакция) выполняются параллельно. Ограничение мощности возникает на этапах центральной обработки (например, выбор ответа), которые не выполняются одновременно (см. Рис. 1A, Pashler, 1984; Pashler and Johnston, 1989). Этот взгляд на ограничение структурных возможностей для стадий центральной обработки по-прежнему преобладает в когнитивной нейробиологии человека и психологии из учебников, скорее всего, из-за наблюдения, что даже самые простые и / или хорошо обученные когнитивные операции подвержены существенным ограничениям обработки в сочетании с другой задачей. (е.г., Леви и др., 2006). Однако существует меньше единого мнения о том, отражает ли это узкое место обработки структурное (Pashler, 1998) или стратегическое (Meyer and Kieras, 1997) ограничение.
Рис. 1. Схематическое изображение последовательной обработки задач (A) и различных форм параллельной обработки (B, C) двух задач в рамках предполагаемого этапа центральной обработки с ограниченной производительностью. Пунктирными линиями показаны изменения в шаблонах результатов при использовании различных форм параллельной обработки.Обратите внимание, что хотя теоретические модели объясняются в терминах модели времени отклика (RT), та же логика применима и к частоте ошибок. (A) Иллюстрация модели узкого места выбора ответа (RSB) как объяснение серьезных ограничений двойной обработки задач (Pashler, 1994). Каждая задача состоит из различных этапов обработки (например, P — восприятие; RS — выбор ответа; MR — двигательный ответ). Обработка в несколько этапов может происходить параллельно (белым цветом). Обработка других критических этапов не может происходить одновременно (затенено), потому что они полагаются на один и тот же канал обработки с ограниченной пропускной способностью.Когда обе задачи существенно перекрываются (например, асинхронность начала короткого стимула, SOA), обработка задачи 2 (T2) прерывается, потому что обработка RS2 должна ждать, пока обработка RS1 не будет завершена (психологический рефрактерный период, PRP).
Пунктирными линиями показаны изменения в шаблонах результатов при использовании различных форм параллельной обработки.Обратите внимание, что хотя теоретические модели объясняются в терминах модели времени отклика (RT), та же логика применима и к частоте ошибок. (A) Иллюстрация модели узкого места выбора ответа (RSB) как объяснение серьезных ограничений двойной обработки задач (Pashler, 1994). Каждая задача состоит из различных этапов обработки (например, P — восприятие; RS — выбор ответа; MR — двигательный ответ). Обработка в несколько этапов может происходить параллельно (белым цветом). Обработка других критических этапов не может происходить одновременно (затенено), потому что они полагаются на один и тот же канал обработки с ограниченной пропускной способностью.Когда обе задачи существенно перекрываются (например, асинхронность начала короткого стимула, SOA), обработка задачи 2 (T2) прерывается, потому что обработка RS2 должна ждать, пока обработка RS1 не будет завершена (психологический рефрактерный период, PRP). При длинном SOA прерывание не происходит, поскольку критические этапы не перекрываются. Это приводит к типичной схеме снижения производительности в T2 при короткой SOA (высокая двойная нагрузка) по сравнению с длинной SOA (низкая двойная нагрузка). На обработку задачи 1 (T1) очень мало влияет временное перекрытие задач. (B) Перекрестные помехи относятся к наблюдению, что обработка T2 влияет на обработку T1, что было принято как свидетельство параллельной обработки, несмотря на предполагаемый RSB. Эффекты перекрестных помех обычно измеряются в задержке ответа в T1 (RT1). Влияние обработки T2 на обработку на центральном этапе в T1 может быть как выгодным, так и дорогостоящим при уменьшении или увеличении RT1 соответственно (например, Koch and Prinz, 2002). Важно отметить, что любое влияние обработки T2 на T1, сокращение или удлинение RT1, будет распространяться обратно на T2 (Ferreira and Pashler, 2002; Miller and Reynolds, 2003; Schubert et al., 2008). Таким образом, изменения RT1 из-за перекрестных помех также должны быть доступны в задержке ответа в T2 (RT2).
При длинном SOA прерывание не происходит, поскольку критические этапы не перекрываются. Это приводит к типичной схеме снижения производительности в T2 при короткой SOA (высокая двойная нагрузка) по сравнению с длинной SOA (низкая двойная нагрузка). На обработку задачи 1 (T1) очень мало влияет временное перекрытие задач. (B) Перекрестные помехи относятся к наблюдению, что обработка T2 влияет на обработку T1, что было принято как свидетельство параллельной обработки, несмотря на предполагаемый RSB. Эффекты перекрестных помех обычно измеряются в задержке ответа в T1 (RT1). Влияние обработки T2 на обработку на центральном этапе в T1 может быть как выгодным, так и дорогостоящим при уменьшении или увеличении RT1 соответственно (например, Koch and Prinz, 2002). Важно отметить, что любое влияние обработки T2 на T1, сокращение или удлинение RT1, будет распространяться обратно на T2 (Ferreira and Pashler, 2002; Miller and Reynolds, 2003; Schubert et al., 2008). Таким образом, изменения RT1 из-за перекрестных помех также должны быть доступны в задержке ответа в T2 (RT2).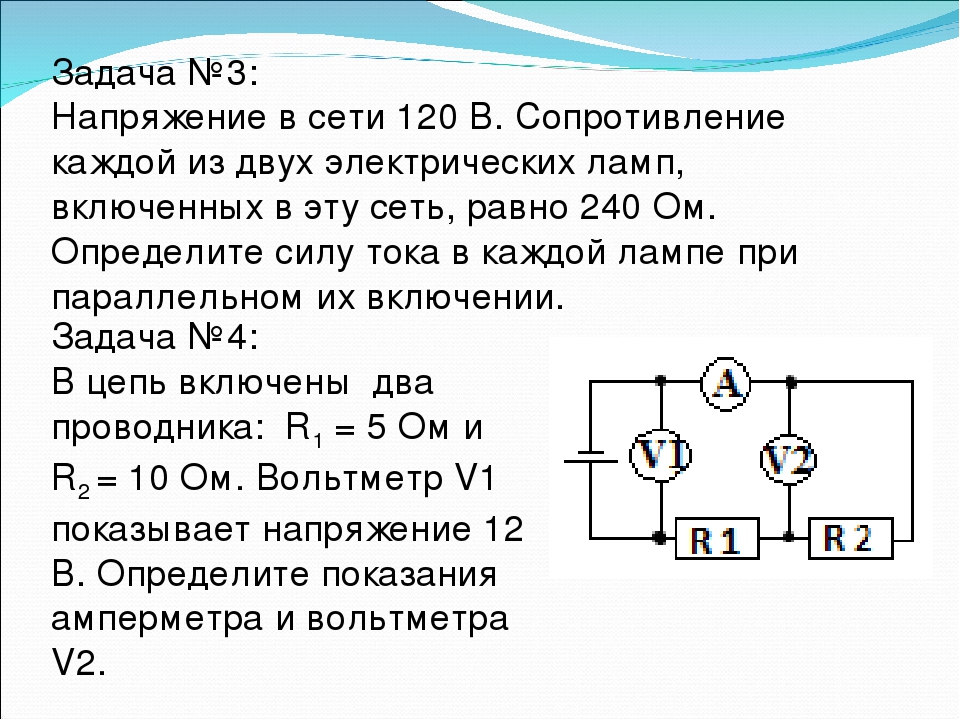 Теоретически эффекты перекрестных помех несовместимы с классическими моделями одноканальной теории (например, моделью RSB) и требуют объяснений с точки зрения разделения пропускной способности (см. C ). Однако предположения о последовательной обработке в соответствии с моделью RSB можно сохранить, если предположить, что различные подкомпоненты RS2 могут работать параллельно. Таким образом, некоторые авторы отличают процессы активации ответа (RA) от более классических процессов выбора ответа как основу для взаимодействия центральных компонентов между двумя задачами (Hommel, 1998; Lien and Proctor, 2002; Schubert et al., 2008). (C) Модели емкости предполагают, что центральное узкое место не является неизменным, а гибким. Ограничение обработки возникает, потому что два центральных процесса требуют доступа к одним и тем же когнитивным ресурсам. Доступные ресурсы распределяются между двумя задачами на период, в течение которого оба центральных этапа перекрываются.
Теоретически эффекты перекрестных помех несовместимы с классическими моделями одноканальной теории (например, моделью RSB) и требуют объяснений с точки зрения разделения пропускной способности (см. C ). Однако предположения о последовательной обработке в соответствии с моделью RSB можно сохранить, если предположить, что различные подкомпоненты RS2 могут работать параллельно. Таким образом, некоторые авторы отличают процессы активации ответа (RA) от более классических процессов выбора ответа как основу для взаимодействия центральных компонентов между двумя задачами (Hommel, 1998; Lien and Proctor, 2002; Schubert et al., 2008). (C) Модели емкости предполагают, что центральное узкое место не является неизменным, а гибким. Ограничение обработки возникает, потому что два центральных процесса требуют доступа к одним и тем же когнитивным ресурсам. Доступные ресурсы распределяются между двумя задачами на период, в течение которого оба центральных этапа перекрываются. Распределение ресурсов по текущим задачам зависит от факторов задачи (например, инструкции, стимулы). Экстремальные формы могут имитировать центральное узкое место, при этом 100% ресурсов выделяются для T1 и 0% для T2.Чем больше ресурсов распределяется между двумя задачами (например, 70/30 или 50/50), тем выше увеличение RT1 и уменьшение RT2 при коротком SOA. Предполагается, что это распределение ресурсов реализуется с помощью механизмов когнитивного контроля (подробности см. В тексте).
Распределение ресурсов по текущим задачам зависит от факторов задачи (например, инструкции, стимулы). Экстремальные формы могут имитировать центральное узкое место, при этом 100% ресурсов выделяются для T1 и 0% для T2.Чем больше ресурсов распределяется между двумя задачами (например, 70/30 или 50/50), тем выше увеличение RT1 и уменьшение RT2 при коротком SOA. Предполагается, что это распределение ресурсов реализуется с помощью механизмов когнитивного контроля (подробности см. В тексте).
Это теоретическое предположение о том, что ограничения центральной обработки вызывают затраты на двойную задачу, в значительной степени было получено из экспериментальных парадигм, в которых представлены две задачи реакции выбора с различными временными интервалами (т. Е. Асинхронность начала стимула, SOA) между стимулом T1 (S1) и стимул T2 (S2; e.г., Пашлер, 1984; Пашлер и Джонстон, 1989; Шуберт, 1999). Временным перекрытием задач (и, следовательно, двойной нагрузкой) можно экспериментально манипулировать, чтобы исследовать затраты на двойную задачу и, таким образом, оценить микроструктуру взаимодействия двойной задачи (Pashler and Johnston, 1989; McCann and Johnston, 1992; Fischer et al. , 2007; обзоры см. В Pashler, 1994, 1998; Meyer and Kieras, 1997).
, 2007; обзоры см. В Pashler, 1994, 1998; Meyer and Kieras, 1997).
В то время как производительность в Задаче 1, как предполагалось, не зависит от манипулирования временным перекрытием задач, производительность в Задаче 2 была предположена, что критически зависит от временной близости обеих задач (рис. 1A).Чем больше временное перекрытие между обеими задачами (чем короче SOA между S1 и S2), тем медленнее ответы и выше частота ошибок в Задаче 2. Разница во времени ответа в Задаче 2 (RT2) между короткой и длинной SOA была назвали психологический рефрактерный период эффектом (PRP) (Pashler, 1994; Meyer and Kieras, 1997). Эффект PRP отражает широко используемую меру затрат на двойную задачу, возникающую на этапе выбора ответа с ограниченными возможностями при выполнении двойной задачи (рис. 1A).Важно отметить, что эти затраты на двойную задачу (т. Е. Приращение производительности при большом временном перекрытии задач по сравнению с низким временным перекрытием задач) служат маркером эффективности многозадачности.
Демонстрация параллельной обработки при предположении ограниченных ресурсов
В парадигме PRP допущение параллельной обработки означает, что центральная когнитивная обработка в T2 может выполняться параллельно с центральной обработкой стадии с ограниченной пропускной способностью в T1 (Рисунки 1B, C). Структурные модели узких мест отрицают возможность центральной обработки T2 во время узких мест (т.е.е., ПРП). Тем не менее, параллельная обработка T2 на этапе узкого места T1 была продемонстрирована с помощью двух разных подходов, что привело к двум различным шаблонам результатов, то есть локусу логики резервирования и логике обратных перекрестных помех .
В локусе резервной логики (Пашлер и Джонстон, 1989; Макканн и Джонстон, 1992) возможность параллельной обработки оценивается с помощью показателей производительности Т2. Для этого манипулируют длительностью (например, сложностью) центрального когнитивного процесса в T2.В этих случаях особенно важна взаимосвязь между легкими и сложными условиями и SOA.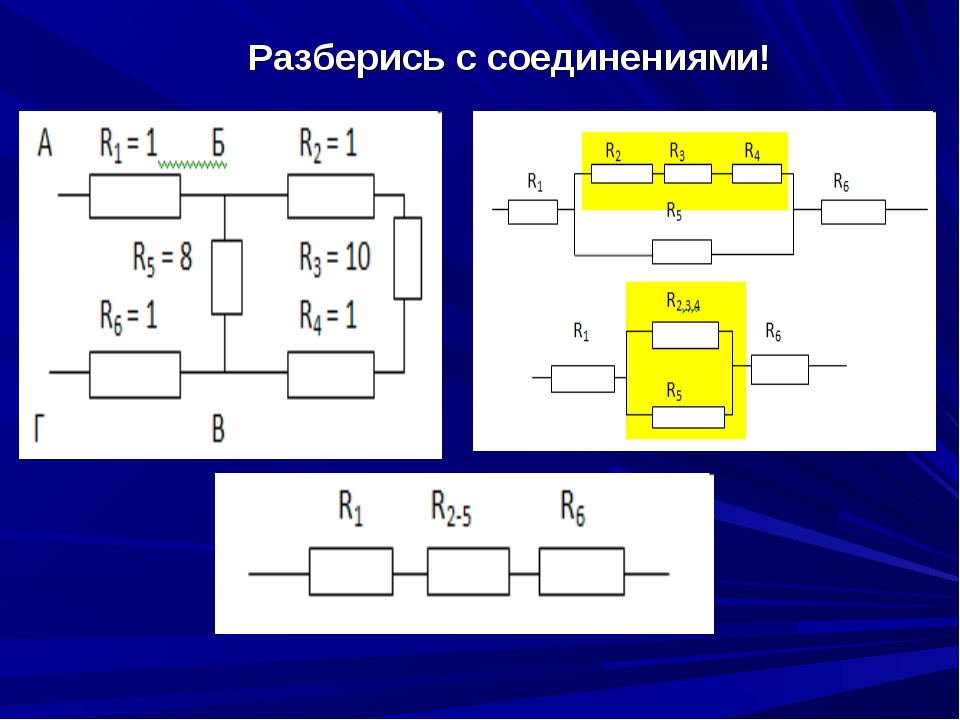 Если при коротком SOA разница в сложности не достигается, предполагается поглощение узкого места (и, следовательно, параллельная обработка во время узкого места). Если управляемый центральный процесс не может продолжаться во время узкого места, манипуляции продолжительностью / сложностью должны выявить аддитивность с манипуляциями SOA. Манипуляция должна быть видна в одинаковой степени как в короткой, так и в длинной SOA (для успешной демонстрации параллельной центральной обработки с использованием локуса резерва см. Oriet et al., 2005; Фишер и др., 2007; Фишер и Шуберт, 2008; Янчик, 2013).
Если при коротком SOA разница в сложности не достигается, предполагается поглощение узкого места (и, следовательно, параллельная обработка во время узкого места). Если управляемый центральный процесс не может продолжаться во время узкого места, манипуляции продолжительностью / сложностью должны выявить аддитивность с манипуляциями SOA. Манипуляция должна быть видна в одинаковой степени как в короткой, так и в длинной SOA (для успешной демонстрации параллельной центральной обработки с использованием локуса резерва см. Oriet et al., 2005; Фишер и др., 2007; Фишер и Шуберт, 2008; Янчик, 2013).
Логика обратных перекрестных помех основана на эмпирическом открытии, что обработка двух задач редко происходит независимо (Navon and Miller, 1987). Вероятность взаимодействия между задачами увеличивается, особенно в условиях высокой временной близости (т. Е. Короткого SOA) и высокой схожести задач (т. Е. Обе задачи разделяют пространственное перекрытие). Рисунок 1B иллюстрирует возможность перекрестных помех .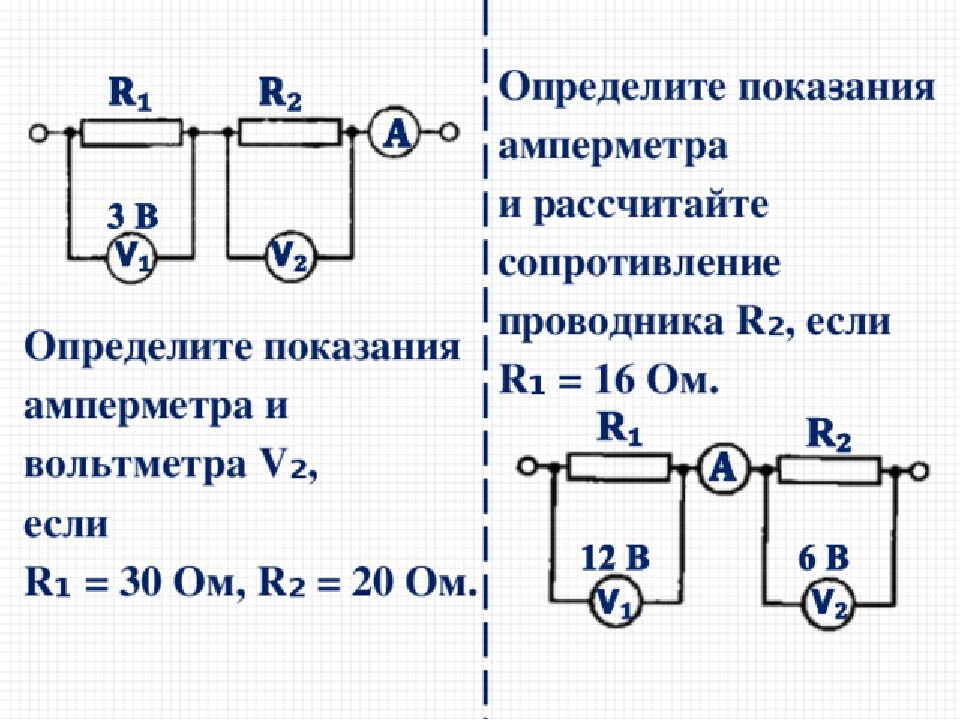 Центральная обработка задач T2 влияет на центральную обработку T1 до завершения обработки узких мест Задачи 1 (Duncan, 1979; Navon and Miller, 1987, 2002; Hommel, 1998; Logan and Schulkind, 2000; Koch and Prinz, 2002; Miller, 2006). ; Фишер и др., 2007). Как следствие, любые процессы T1, подверженные центральному узкому месту, либо облегчаются, либо продлеваются. Таким образом, в отличие от локуса логики резервов, свидетельство параллельной обработки, основанной на логике перекрестных помех, происходит из модуляции показателей производительности в T1, вызванной центральной обработкой T2.
Центральная обработка задач T2 влияет на центральную обработку T1 до завершения обработки узких мест Задачи 1 (Duncan, 1979; Navon and Miller, 1987, 2002; Hommel, 1998; Logan and Schulkind, 2000; Koch and Prinz, 2002; Miller, 2006). ; Фишер и др., 2007). Как следствие, любые процессы T1, подверженные центральному узкому месту, либо облегчаются, либо продлеваются. Таким образом, в отличие от локуса логики резервов, свидетельство параллельной обработки, основанной на логике перекрестных помех, происходит из модуляции показателей производительности в T1, вызванной центральной обработкой T2.
Основополагающее исследование с использованием этой логики было проведено Хоммелем (1998). В его эксперименте участники реагировали на цвет (красный / зеленый) букв в T1 и на свою идентичность (H / S) в T2.Эффекты перекрестных помех на RT1 были продемонстрированы, когда коды ответов для обеих задач перекрывались. Более конкретно, ручные ответы T1 на цвета букв (например, красный — слева и зеленый — справа ответ) и словесные ответы T2 на буквенное обозначение (например, произнесение слева на H и справа на S) вызывали существенные перекрестные помехи (продолжение RT1), когда словесный ответ справа совпадал с ручным ответом слева (несоответствие категории ответа). Обработка T2 способствовала активации ответа T1 (уменьшение RT1), когда словесный ответ справа сопровождался ручным ответом справа (соответствие категории ответа). Процессы трансляции SR T1 и T2 не были последовательными и дискретными, но происходили параллельно, когда между задачами было обеспечено пространственное перекрытие (см. Также Logan and Schulkind, 2000; Koch and Prinz, 2002; Miller and Alderton, 2006; Fischer et al. 2007; Schubert et al., 2008; Janczyk et al., 2014). Это открытие значительной центральной обработки T2 во время PRP бросает вызов одноканальной теории последовательной обработки (Pashler, 1984).Вместо этого наблюдаемая картина результатов соответствует предположению о совместном использовании мощности. Однако обнаружение перекрестных помех можно согласовать с понятием модели RSB, если добавить различие между активацией ответа (RA) и идентификацией ответа (RI). В то время как первый не имеет ограничений пропускной способности, что допускает перекрестные помехи, последний требует всех центральных ресурсов, вызывая узкое место (Hommel, 1998; Lien and Proctor, 2002; Schubert et al.
Обработка T2 способствовала активации ответа T1 (уменьшение RT1), когда словесный ответ справа сопровождался ручным ответом справа (соответствие категории ответа). Процессы трансляции SR T1 и T2 не были последовательными и дискретными, но происходили параллельно, когда между задачами было обеспечено пространственное перекрытие (см. Также Logan and Schulkind, 2000; Koch and Prinz, 2002; Miller and Alderton, 2006; Fischer et al. 2007; Schubert et al., 2008; Janczyk et al., 2014). Это открытие значительной центральной обработки T2 во время PRP бросает вызов одноканальной теории последовательной обработки (Pashler, 1984).Вместо этого наблюдаемая картина результатов соответствует предположению о совместном использовании мощности. Однако обнаружение перекрестных помех можно согласовать с понятием модели RSB, если добавить различие между активацией ответа (RA) и идентификацией ответа (RI). В то время как первый не имеет ограничений пропускной способности, что допускает перекрестные помехи, последний требует всех центральных ресурсов, вызывая узкое место (Hommel, 1998; Lien and Proctor, 2002; Schubert et al. , 2008).
, 2008).
Еще одно свидетельство параллельной центральной обработки в двойных задачах было получено из электрофизиологических исследований.Поведенческие перекрестные помехи, как сообщалось в Hommel (1998), сопровождаются отклонениями в потенциале латерализованной готовности (LRP) в T2, отражая процессы RA T2, которые начинаются до завершения обработки центрального узкого места в T1 (Lien et al., 2007) . Точно так же, измеряя LRP во время обработки T1, Ko и Miller (2014) показали, что время между началом S1 и началом LRP с блокировкой стимула модулировалось центральной обработкой T2, таким образом обеспечивая дополнительные доказательства параллельной центральной обработки T2.
Параллельная обработка без использования ограниченных ресурсов
Строгое понятие ограниченных ресурсов и последующей последовательной обработки подвергалось сомнению как на экспериментальной, так и на теоретической основе. Его можно проследить до ранних концепций фильтра внимания Дойча и Дойча (1963) и допущения о множественных специализированных ресурсах (Норман и Боброу, 1975; Викенс, 1984; но см. Оллпорт, 1980).
Оллпорт, 1980).
В ранних работах 1970-х годов были выявлены такие факторы, как схожесть задач и практика выполнения задач, которые решающим образом определяют возможность параллельной обработки задач.Например, Allport et al. (1972) утверждал, что затраты на выполнение двух задач возникают не из-за превышения мощности одноканального процессора, а из-за сложности разделения двух одинаковых задач. Комбинируя две совершенно разные задачи (например, повторение непрерывной речи и чтение сложной фортепианной музыки с листа), пианисты смогли продемонстрировать параллельную обработку обеих задач с качеством, сопоставимым с обработкой одной задачи (Allport et al., 1972; см. также Shaffer, 1975; Wickens, 1984). Точно так же Шаффер (1975) показал, что участники, умеющие печатать на машинке, могут легко выполнять копирование текста (набор текста с листа) с задачей словесного дублирования, но не могут объединить задачу набора текста со звуком с чтением с листа (для более недавнего исследование роли сочетаний модальностей при определении затрат на двойную задачу, см. Stelzel et al., 2005; Хазельтин и Рутрафф, 2006; Hazeltine et al., 2006; Уэстегге и Кох, 2013; Halvorson and Hazeltine, 2015). Хотя вышеупомянутые ранние исследования выявили впечатляющие возможности многозадачности, многие из этих исследований подверглись критике, поскольку их время выполнения задач позволяло быстро переключаться между обработкой компонентов задачи (например, мультиплексированием). Таким образом, можно предположить, что результаты только имитируют параллельную обработку, а не представляют ее.
Stelzel et al., 2005; Хазельтин и Рутрафф, 2006; Hazeltine et al., 2006; Уэстегге и Кох, 2013; Halvorson and Hazeltine, 2015). Хотя вышеупомянутые ранние исследования выявили впечатляющие возможности многозадачности, многие из этих исследований подверглись критике, поскольку их время выполнения задач позволяло быстро переключаться между обработкой компонентов задачи (например, мультиплексированием). Таким образом, можно предположить, что результаты только имитируют параллельную обработку, а не представляют ее.
Еще одна демонстрация параллельной обработки была достигнута путем администрирования большого количества двухзадачных практик.Spelke et al. (1976) обучили двух участников читать короткие рассказы, записывая списки слов под диктовку. Обучение длилось 17 недель (пять занятий по 1 часу в неделю). После тренинга выполнение двойных задач приблизилось к качеству выполнения индивидуальных одиночных задач. Поскольку люди легко развивают навыки на практике, авторы постулировали, что возможность приобретения навыков в любой области может поставить под сомнение общую концепцию ограниченных когнитивных способностей. В 2001 году предположение о параллельной обработке в обширной практике возродилось, в основном из-за реализации парадигм двойной задачи, контролируемой синхронизацией и интерференцией.В влиятельном исследовании Schumacher et al. (2001) представили две задачи реакции на выбор (например, визуально-руководство и слухово-голосовую задачу) одновременно (SOA = 0 мс) и с равным приоритетом задачи. Эффективность многозадачности была зафиксирована в степени, в которой выполнение каждой задачи в контексте двойной задачи приравнивается к производительности одной задачи. Критерий идеального разделения времени (выполнение двух заданий равно выполнению одного задания) был достигнут всего после пяти практических занятий (см. Также Ruthruff et al., 2001; Hazeltine et al., 2002; Оберауэр и Клигл, 2004 г .; Липельт и др., 2011а, б; Strobach et al., 2012). Сторонники модели RSB, однако, утверждали, что практика приводит к сокращению этапов обработки, что, в свою очередь, уменьшает влияние узкого места вместо его обхода (например, предположения о скрытых узких местах, см.
В 2001 году предположение о параллельной обработке в обширной практике возродилось, в основном из-за реализации парадигм двойной задачи, контролируемой синхронизацией и интерференцией.В влиятельном исследовании Schumacher et al. (2001) представили две задачи реакции на выбор (например, визуально-руководство и слухово-голосовую задачу) одновременно (SOA = 0 мс) и с равным приоритетом задачи. Эффективность многозадачности была зафиксирована в степени, в которой выполнение каждой задачи в контексте двойной задачи приравнивается к производительности одной задачи. Критерий идеального разделения времени (выполнение двух заданий равно выполнению одного задания) был достигнут всего после пяти практических занятий (см. Также Ruthruff et al., 2001; Hazeltine et al., 2002; Оберауэр и Клигл, 2004 г .; Липельт и др., 2011а, б; Strobach et al., 2012). Сторонники модели RSB, однако, утверждали, что практика приводит к сокращению этапов обработки, что, в свою очередь, уменьшает влияние узкого места вместо его обхода (например, предположения о скрытых узких местах, см.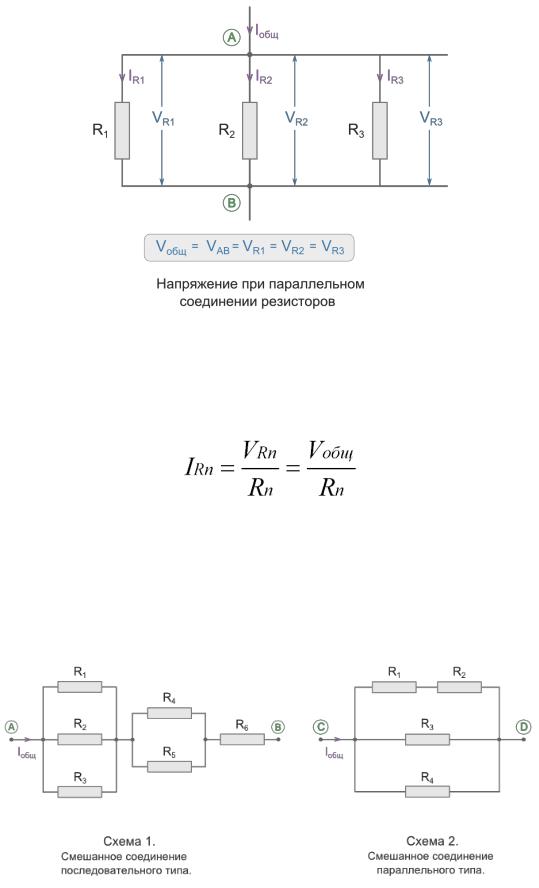 , Например, Ruthruff et al., 2003; Dux et al. др., 2009).
, Например, Ruthruff et al., 2003; Dux et al. др., 2009).
Теоретические модели, допускающие параллельную обработку
Ресурсные модели представляют собой основную группу теоретических моделей, которые допускают возможность параллельной обработки задач.В соответствии с теориями одноканального доступа они также предполагают строгое ограничение возможностей центральной когнитивной обработки. Однако, в отличие от модели RSB, они включают идею о том, что доступные несколько ограниченные ресурсы могут быть запланированы и выделены для обработки конкретных задач (Канеман, 1973; Норман и Боброу, 1975). Расширением предположения о неспецифических центральных ресурсах (Канеман, 1973) является идея о множественных конкретных ресурсах (Wickens, 1984, 2002).При условии наличия нескольких ресурсов параллельная обработка может происходить, например, если компоненты задачи запланированы в разных потоках обработки, которые координируются и планируются разными ресурсами (например, Salvucci and Taatgen, 2008).
Согласно ресурсным моделям, возникают двойные затраты, поскольку обработка различных компонентов задачи требует одних и тех же ограниченных ресурсов (Канеман, 1973; Навон и Миллер, 2002; Томбу и Джоликер, 2003). В этих случаях ресурсы распределяются по принципу «все или ничего».Классический эффект PRP будет отражать крайнюю форму разделения ресурсов 100% ресурсов для T1 и 0% для T2, имитируя узкое место центральной обработки с ограниченной пропускной способностью из-за инструкции приоритета T1. Однако, в отличие от моделей RSB, ограниченные ресурсы обработки могут совместно использоваться двумя задачами в разных пропорциях (например, 80% T1 и 20% T2). Чем больше ресурсов используется совместно, тем больше выполняется параллельная обработка. В соответствии с этой логикой модели распределения мощности включают центральное допущение узкого места (Navon and Miller, 2002; Tombu and Jolicoeur, 2002, 2003; Lehle and Hübner, 2009) и учитывают часто наблюдаемые результаты перекрестных помех между задачами в парадигмах, подобных PRP. (Hommel, 1998; Logan, Schulkind, 2000; Koch, Prinz, 2002; Miller, 2006; Fischer et al., 2007; Schubert et al., 2008; Кох, 2009).
(Hommel, 1998; Logan, Schulkind, 2000; Koch, Prinz, 2002; Miller, 2006; Fischer et al., 2007; Schubert et al., 2008; Кох, 2009).
Предложение гибкого распределения ресурсов требует определения того, как распределяются ресурсы внимания. Высказывались аргументы в пользу того, что распределение ресурсов внимания не является случайным, а зависит от инструкций (Lehle, Hübner, 2009; Lehle et al., 2009), приоритета задачи и ценности результата (Wickens et al., 2003). Он отражает стратегическое планирование ресурсов, обычно реализуемое процессами когнитивного контроля (Meyer and Kieras, 1997; Logan and Gordon, 2001; Sigman and Dehaene, 2006).Предположение о стратегическом и гибком распределении вычислительной мощности подтверждается недавними открытиями функциональной магнитно-резонансной томографии (фМРТ), показывающими, что области мозга, связанные с когнитивным контролем, активируются во время двойной задачи (например, Szameitat et al., 2002; Marois and Ivanoff, 2005; Dux et al., 2006; Stelzel et al.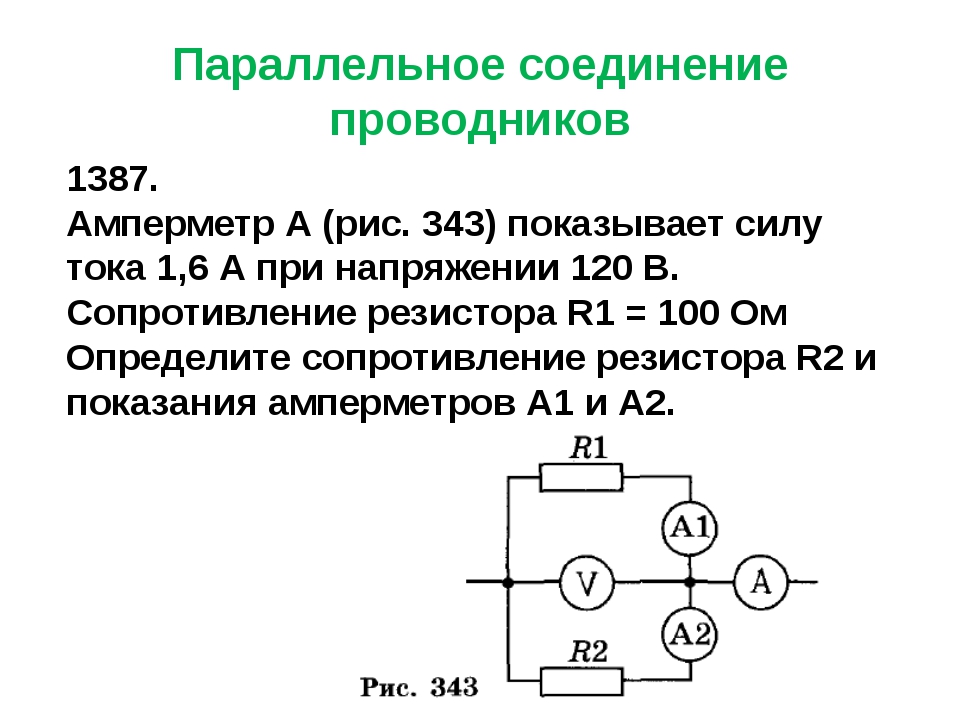 , 2009; Tombu et al., 2011). Кроме того, недавнее исследование фМРТ, в котором принята парадигма двойной задачи, представленная Miller et al. (2009) для создания условий более последовательной по сравнению с более параллельной обработкой задач (подробности см. Ниже) предоставили доказательства различных нейроанатомических коррелятов выбора ответа в зависимости от ограничений обработки задачи.Более подробно, в условиях повышенной обработки параллельных задач механизмы выбора ответа работали на уровне полосатого тела, тогда как в условиях повышенной обработки последовательной обработки выбор ответа сопровождался преимущественно латеральной активацией префронтальной коры (Yildiz and Beste, 2014).
, 2009; Tombu et al., 2011). Кроме того, недавнее исследование фМРТ, в котором принята парадигма двойной задачи, представленная Miller et al. (2009) для создания условий более последовательной по сравнению с более параллельной обработкой задач (подробности см. Ниже) предоставили доказательства различных нейроанатомических коррелятов выбора ответа в зависимости от ограничений обработки задачи.Более подробно, в условиях повышенной обработки параллельных задач механизмы выбора ответа работали на уровне полосатого тела, тогда как в условиях повышенной обработки последовательной обработки выбор ответа сопровождался преимущественно латеральной активацией префронтальной коры (Yildiz and Beste, 2014).
Теории, которые постулируют участие функций когнитивного контроля для объяснения ограничений многозадачности, не обязательно предполагают общие ограниченные ресурсы. Ограничения многозадачности возникают из-за конкурирующих процессов, которым требуется доступ к одним и тем же локальным ресурсам и ресурсам для конкретных задач (Navon and Gopher, 1979).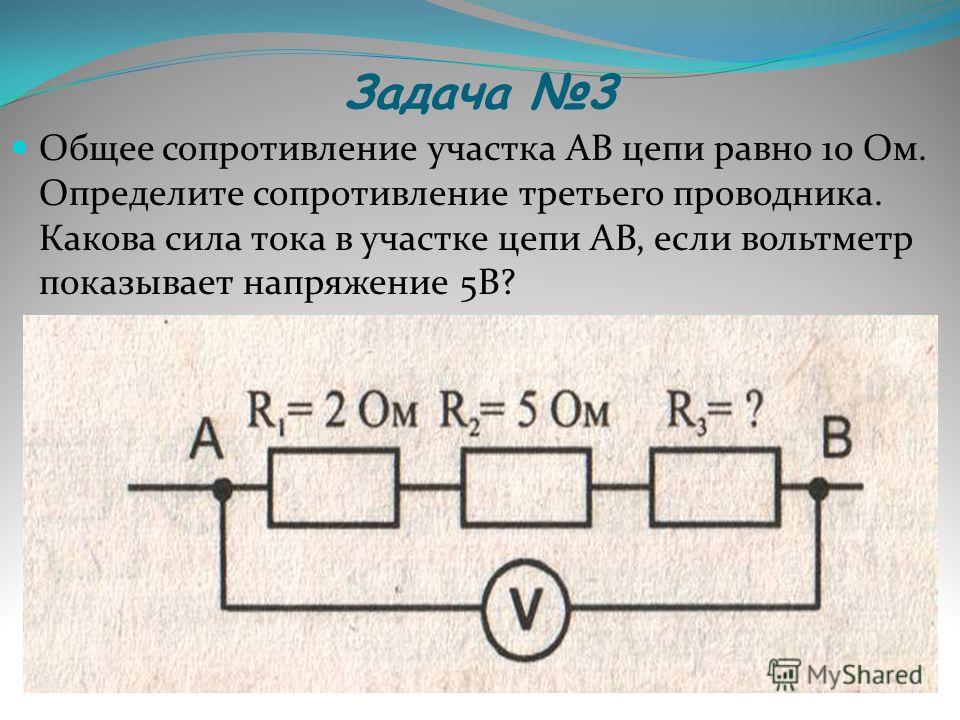 Это понятие важно, потому что вместо указания структурных ограничений ограниченной емкости наблюдаемые ограничения отражают функциональные ограничения (например, вычислительные ограничения). Функциональные ограничения возникают, когда одно и то же представление используется «для разных целей несколькими процессами» (Feng et al., 2014, стр. 130). Например, в теориях когнитивного контроля двойной задачи, таких как теория исполнительного контроля визуального внимания (ECTVA) (Logan and Gordon, 2001), наблюдение за последовательной обработкой задач является результатом попытки избежать взаимодействия между обработкой нескольких компонентов задачи ( е.g., между привязками «стимул-ответ»). Это было сформулировано в терминах двойной задачи привязки , которая описывает задачу правильно сопоставить стимулы каждой задачи (S1 и S2) с правильными ответами в каждой задаче (R1 и R2 для Задачи 1 и Задачи 2, соответственно. ). Чтобы решить проблему привязки и, следовательно, минимизировать риск обратной реакции и / или путаницы, принята стратегия последовательной обработки (Logan and Gordon, 2001).
Это понятие важно, потому что вместо указания структурных ограничений ограниченной емкости наблюдаемые ограничения отражают функциональные ограничения (например, вычислительные ограничения). Функциональные ограничения возникают, когда одно и то же представление используется «для разных целей несколькими процессами» (Feng et al., 2014, стр. 130). Например, в теориях когнитивного контроля двойной задачи, таких как теория исполнительного контроля визуального внимания (ECTVA) (Logan and Gordon, 2001), наблюдение за последовательной обработкой задач является результатом попытки избежать взаимодействия между обработкой нескольких компонентов задачи ( е.g., между привязками «стимул-ответ»). Это было сформулировано в терминах двойной задачи привязки , которая описывает задачу правильно сопоставить стимулы каждой задачи (S1 и S2) с правильными ответами в каждой задаче (R1 и R2 для Задачи 1 и Задачи 2, соответственно. ). Чтобы решить проблему привязки и, следовательно, минимизировать риск обратной реакции и / или путаницы, принята стратегия последовательной обработки (Logan and Gordon, 2001). Когнитивная система может гибко реагировать на требования ситуации с двойным заданием (Meyer and Kieras, 1997), принимая стратегию последовательной обработки, если риск реверсирования задач высок.Как следствие, последовательная обработка двух задач представляется более эффективной стратегией обработки в целом (Logan and Gordon, 2001; Miller et al., 2009) с функцией уменьшения интерференции между задачами (Navon and Miller, 1987; Logan и Gordon, 2001; Tombu and Jolicoeur, 2003; Lehle, Hübner, 2009; Oberauer, Bialkova, 2011). Таким образом, выбор режима последовательной обработки отражает функциональный и стратегический вариант (см. Также Hazeltine et al., 2008).
Когнитивная система может гибко реагировать на требования ситуации с двойным заданием (Meyer and Kieras, 1997), принимая стратегию последовательной обработки, если риск реверсирования задач высок.Как следствие, последовательная обработка двух задач представляется более эффективной стратегией обработки в целом (Logan and Gordon, 2001; Miller et al., 2009) с функцией уменьшения интерференции между задачами (Navon and Miller, 1987; Logan и Gordon, 2001; Tombu and Jolicoeur, 2003; Lehle, Hübner, 2009; Oberauer, Bialkova, 2011). Таким образом, выбор режима последовательной обработки отражает функциональный и стратегический вариант (см. Также Hazeltine et al., 2008).
Почему люди используют режим параллельной обработки задач перед лицом повышенного интерференции между задачами?
Мы установили, что люди могут применять стратегию параллельной обработки компонентов задачи при одновременном выполнении более одной задачи.Учитывая, что параллельная обработка связана с повышенными рисками межзадачного взаимодействия и менее эффективна, почему участники должны выбирать эту стратегию обработки в первую очередь? Miller et al. (2009) дали первый ответ на этот вопрос, показав, что параллельная обработка может превзойти последовательную обработку с точки зрения эффективности двойной задачи. Они определили эффективность двойной задачи как общее время, необходимое для выполнения двух задач (RT1 + RT2 = общее время реакции, TRT).В двух экспериментах применялась логика PRP с двумя независимыми задачами, и соотношение коротких и длинных SOA варьировалось при манипулировании пропорциями SOA для всего списка, то есть участники выполняли списки в основном с короткими SOA и списки с в основном длинными SOA. Авторы не только показали, что списки с в основном короткими SOA дают типичные шаблоны результатов параллельной обработки (т. Е. Увеличенное RT1 и уменьшенное RT2, рис. 1C), но также показали, что манипуляции с SOA на уровне списка определяют эффективность режимов параллельной и последовательной обработки.Важно отметить, что в списках с в основном короткими SOA параллельная обработка оказалась более эффективной, чем последовательная.
(2009) дали первый ответ на этот вопрос, показав, что параллельная обработка может превзойти последовательную обработку с точки зрения эффективности двойной задачи. Они определили эффективность двойной задачи как общее время, необходимое для выполнения двух задач (RT1 + RT2 = общее время реакции, TRT).В двух экспериментах применялась логика PRP с двумя независимыми задачами, и соотношение коротких и длинных SOA варьировалось при манипулировании пропорциями SOA для всего списка, то есть участники выполняли списки в основном с короткими SOA и списки с в основном длинными SOA. Авторы не только показали, что списки с в основном короткими SOA дают типичные шаблоны результатов параллельной обработки (т. Е. Увеличенное RT1 и уменьшенное RT2, рис. 1C), но также показали, что манипуляции с SOA на уровне списка определяют эффективность режимов параллельной и последовательной обработки.Важно отметить, что в списках с в основном короткими SOA параллельная обработка оказалась более эффективной, чем последовательная. В типичных парадигмах PRP временная близость между задачами (SOA) довольно сбалансирована. Таким образом, здесь может показаться благоприятной стратегия последовательной обработки.
В типичных парадигмах PRP временная близость между задачами (SOA) довольно сбалансирована. Таким образом, здесь может показаться благоприятной стратегия последовательной обработки.
Еще одна причина того факта, что мы в основном наблюдаем последовательную обработку при тестировании участников с типичными PRP-подобными парадигмами двойной задачи в наших лабораториях, — это сильная инструкция приоритета T1. Сильный акцент на производительности T1 способствует распределению ресурсов, которое в первую очередь или даже полностью приносит пользу обработке T1 (например,g., 100% доступных ресурсов распределяются на T1). Соответственно, шаблоны результатов, говорящие о последовательной обработке, неудивительны. Тем не менее, когда отменяются конкретные инструкции по приоритету, участники свободно выбирают умеренную стратегию параллельной обработки (Lehle and Hübner, 2009), что приводит к увеличению перекрестных помех между задачами (рисунок 1B). Объяснение того, почему участники могут выбрать менее эффективный режим обработки, было предложено Lehle et al. (2009), показав, что параллельная обработка связана с меньшими умственными усилиями, что подтверждается снижением уровней периферических физиологических показателей и субъективных оценок усилий параллельно по сравнению с более последовательной обработкой.Следовательно, хотя параллельная обработка не является самым эффективным способом обработки с двумя задачами (в большинстве случаев), похоже, что она отражает менее трудоемкую стратегию обработки по сравнению со строгой последовательной обработкой. Имея возможность выбора, участники, кажется, принимают метод обработки с наименьшими умственными усилиями (Hull, 1943; Kool et al., 2010).
(2009), показав, что параллельная обработка связана с меньшими умственными усилиями, что подтверждается снижением уровней периферических физиологических показателей и субъективных оценок усилий параллельно по сравнению с более последовательной обработкой.Следовательно, хотя параллельная обработка не является самым эффективным способом обработки с двумя задачами (в большинстве случаев), похоже, что она отражает менее трудоемкую стратегию обработки по сравнению со строгой последовательной обработкой. Имея возможность выбора, участники, кажется, принимают метод обработки с наименьшими умственными усилиями (Hull, 1943; Kool et al., 2010).
Переход между режимами параллельной и последовательной обработки как маркер адаптивного поведения
Несмотря на то, что вопрос о том, возможна ли и в какой степени параллельная обработка задач при выполнении двойной задачи, часто обсуждается в литературе (Han and Marois, 2013), нам, когнитивным психологам, возможно, не стоит задавать себя в этом контексте. .Вместо этого, по нашему мнению, в результате работы, кратко изложенной выше, возникают два ключевых вопроса, которыми будут руководствоваться текущие дискуссии и будущие исследования: (1) Как осуществляется переход между этими дополнительными режимами обработки двух задач? (2) При каких условиях параллельная и последовательная обработка являются более адаптивным и, следовательно, предпочтительным выбором? В ответ на первый вопрос мы предполагаем, что оптимизированная и эффективная многозадачность отражает способность гибко применять параллельный или последовательный режим обработки задач, в зависимости от ситуационных требований.Многозадачность требует, чтобы человек поддерживал баланс между двумя антагонистическими типами оптимизации производительности, то есть минимизацией межзадачного взаимодействия (за счет увеличения последовательной обработки задач ) и минимизации умственных усилий (за счет разрешения более параллельной обработки ). Гибкая регулировка степени более последовательной или параллельной обработки двух задач в соответствии с изменяющимися требованиями задачи и контекста отражает высокий уровень адаптируемости в динамических средах, включая онлайн-анализ контекстных функций, их преобразование в требования к производительности, реализацию оптимального режима обработки и непрерывный мониторинг требований к окружающей среде и производительности в качестве основы для дальнейшей настройки, где это необходимо (Goschke, 2013; Fischer et al.
.Вместо этого, по нашему мнению, в результате работы, кратко изложенной выше, возникают два ключевых вопроса, которыми будут руководствоваться текущие дискуссии и будущие исследования: (1) Как осуществляется переход между этими дополнительными режимами обработки двух задач? (2) При каких условиях параллельная и последовательная обработка являются более адаптивным и, следовательно, предпочтительным выбором? В ответ на первый вопрос мы предполагаем, что оптимизированная и эффективная многозадачность отражает способность гибко применять параллельный или последовательный режим обработки задач, в зависимости от ситуационных требований.Многозадачность требует, чтобы человек поддерживал баланс между двумя антагонистическими типами оптимизации производительности, то есть минимизацией межзадачного взаимодействия (за счет увеличения последовательной обработки задач ) и минимизации умственных усилий (за счет разрешения более параллельной обработки ). Гибкая регулировка степени более последовательной или параллельной обработки двух задач в соответствии с изменяющимися требованиями задачи и контекста отражает высокий уровень адаптируемости в динамических средах, включая онлайн-анализ контекстных функций, их преобразование в требования к производительности, реализацию оптимального режима обработки и непрерывный мониторинг требований к окружающей среде и производительности в качестве основы для дальнейшей настройки, где это необходимо (Goschke, 2013; Fischer et al. , 2014).
, 2014).
Поднимая вопрос о том, могут ли участники сверху вниз управлять своим режимом многозадачной обработки, недавние исследования свидетельствуют о том, что люди могут реализовать существенные поблочные переключения между более параллельными и более последовательными режимами обработки задач, продолжая выполнять та же задача, когда ей поручено это сделать (Lehle and Hübner, 2009). В рамках ECTVA (Logan and Gordon, 2001) предполагается, что инструкции определяют набор параметров когнитивного контроля (например,g., приоритет задачи, дыхание внимания и т. д.), что в применении к контексту двойной задачи означает, что они определяют степень последовательной и параллельной обработки. На уровне когнитивного процесса степень обработки последовательной задачи может быть затем переведена в два аспекта, а именно: (а) приоритизация обработки задачи 1 (Stelzel et al., 2009) и (б) временное запрещение дополнительной задачи 2. обработки (Koch et al., 2010).
В дополнение к нисходящему регулированию, есть свидетельства контекстно-зависимых сдвигов между более параллельной и более последовательной двойной обработкой задач. Например, вышеупомянутое ожидание временного перекрытия между двумя задачами (Miller et al., 2009) и сложность задачи определяют степень параллельной обработки задачи по сравнению с последовательной (например, сложность задачи вызывает тенденцию к увеличению последовательной двойной обработки задач, которая является отражается в более резком снижении RT2 с увеличением SOA; Luria and Meiran, 2005; Fischer et al., 2007). Недавно мы также предоставили доказательства полной корректировки снизу вверх параллельной обработки по сравнению с последовательной (Fischer et al., 2014). Используя подход перекрестных помех (рис. 1B), мы проверили, могут ли участники извлечь статистические непредвиденные обстоятельства (то есть вероятность межзадачного взаимодействия) из контекста задачи и использовать эту информацию для корректировки объема параллельной обработки задач по сравнению с последовательной. В частности, условия двойной задачи с высоким риском перекрестных помех (80% испытаний перекрестных помех) и условия двойной задачи с низким риском перекрестных помех (20% испытания перекрестных помех) были представлены в определенных местах на экране.
Например, вышеупомянутое ожидание временного перекрытия между двумя задачами (Miller et al., 2009) и сложность задачи определяют степень параллельной обработки задачи по сравнению с последовательной (например, сложность задачи вызывает тенденцию к увеличению последовательной двойной обработки задач, которая является отражается в более резком снижении RT2 с увеличением SOA; Luria and Meiran, 2005; Fischer et al., 2007). Недавно мы также предоставили доказательства полной корректировки снизу вверх параллельной обработки по сравнению с последовательной (Fischer et al., 2014). Используя подход перекрестных помех (рис. 1B), мы проверили, могут ли участники извлечь статистические непредвиденные обстоятельства (то есть вероятность межзадачного взаимодействия) из контекста задачи и использовать эту информацию для корректировки объема параллельной обработки задач по сравнению с последовательной. В частности, условия двойной задачи с высоким риском перекрестных помех (80% испытаний перекрестных помех) и условия двойной задачи с низким риском перекрестных помех (20% испытания перекрестных помех) были представлены в определенных местах на экране.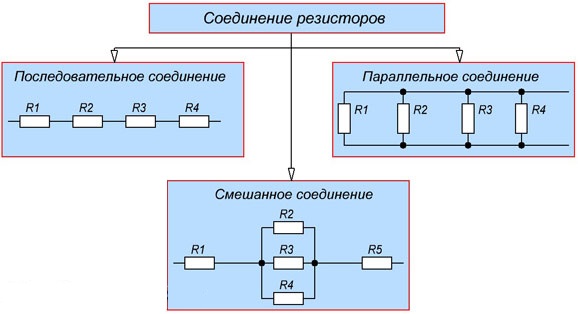 Хотя общая вероятность перекрестных помех составляла 50/50, участники смогли отрегулировать силу экранирования задачи (посредством усиленной последовательной обработки) в зависимости от местоположения. Объем последовательной обработки был значительно увеличен для местоположения с высокой вероятностью перекрестных помех, что привело к снижению перекрестных помех для испытаний в этом месте. В испытаниях, представленных в месте с низкой вероятностью помех, экранирование было уменьшено и наблюдались более высокие уровни параллельной обработки.Следовательно, если контекст требует большей защиты обработки T1 от влияний T2, экранирование задач увеличивается, что приводит к меньшему количеству параллельной обработки.
Хотя общая вероятность перекрестных помех составляла 50/50, участники смогли отрегулировать силу экранирования задачи (посредством усиленной последовательной обработки) в зависимости от местоположения. Объем последовательной обработки был значительно увеличен для местоположения с высокой вероятностью перекрестных помех, что привело к снижению перекрестных помех для испытаний в этом месте. В испытаниях, представленных в месте с низкой вероятностью помех, экранирование было уменьшено и наблюдались более высокие уровни параллельной обработки.Следовательно, если контекст требует большей защиты обработки T1 от влияний T2, экранирование задач увеличивается, что приводит к меньшему количеству параллельной обработки.
Изучая факторы, влияющие на выполнение дополнительных задач на приоритетные двигательные движения, мы продемонстрировали, что предыдущая история испытаний (то есть конфликт между задачами в предыдущем испытании) влияет на баланс между параллельной и последовательной обработкой задач (Scherbaum et al. , 2015). Используя задачи непрерывного моторного выполнения (то есть движения мыши в обеих задачах), мы показали, что большое количество перекрестных помех во время предыдущего испытания (N-1) привело к принятию более последовательного режима обработки задач, о чем свидетельствует сокращение перекрестные помехи в испытании N.Такие последовательные модуляции обычно объясняются конфликтами ответов, запускающими набор когнитивного контроля (Gratton et al., 1992; Botvinick et al., 2001). В контексте двойной задачи это отражает тенденцию к увеличению обработки последовательных задач для уменьшения перекрестных помех.
, 2015). Используя задачи непрерывного моторного выполнения (то есть движения мыши в обеих задачах), мы показали, что большое количество перекрестных помех во время предыдущего испытания (N-1) привело к принятию более последовательного режима обработки задач, о чем свидетельствует сокращение перекрестные помехи в испытании N.Такие последовательные модуляции обычно объясняются конфликтами ответов, запускающими набор когнитивного контроля (Gratton et al., 1992; Botvinick et al., 2001). В контексте двойной задачи это отражает тенденцию к увеличению обработки последовательных задач для уменьшения перекрестных помех.
Далее мы продемонстрировали, что баланс между дополнительными режимами обработки двойной задачи определяется внутренними ситуационными особенностями, такими как изменения в настроении человека, состояние когнитивного контроля перед выполнением задачи или уровни острого стресса.Сначала мы провели процедуру индукции настроения (с контролируемыми эффектами возбуждения) перед двойной задачей с перекрестными помехами. Участники, которые прошли протокол индукции отрицательного настроения, продемонстрировали более высокий уровень обработки серийных задач (например, меньшее вмешательство между задачами), чем участники, которые подверглись индукции положительного настроения (Zwosta et al., 2013). Во-вторых, мы изменили уровень параллельной обработки по сравнению с последовательной.
Участники, которые прошли протокол индукции отрицательного настроения, продемонстрировали более высокий уровень обработки серийных задач (например, меньшее вмешательство между задачами), чем участники, которые подверглись индукции положительного настроения (Zwosta et al., 2013). Во-вторых, мы изменили уровень параллельной обработки по сравнению с последовательной.
22 Параллельные вычисления | Программирование на R для науки о данных
- R Программирование для науки о данных
- Добро пожаловать
- Оставайтесь на связи!
- 1 Предисловие
- 2 История и обзор R
- 2.1 Что такое R? html»> 2,2 Что такое S?
- 2,3 Философия S
- 2,4 Вернуться к
- 2,5 Основные характеристики R
- 2,6 Бесплатное программное обеспечение
- 2,7 Конструкция системы R
- 2,8 Ограничения R
- 2,9 Ресурсы R
- 2.9.1 Официальные руководства
- 2.
 9.2 Полезные стандартные тексты на S и R
9.2 Полезные стандартные тексты на S и R - 2.9.3 Прочие ресурсы
рэнд
- 3,1 Установка
- 3,2 Начало работы с интерфейсом R
- 4,1 Ввод ввода
- 4,2 Оценка
- 4.3 R Объекты
- 4,4 Номера html»> 4,5 Атрибуты
- 5,1 Чтение и запись данных
- 5.2 Чтение файлов данных с таблицей чтения
() - 5,3 Чтение больших наборов данных с таблицей чтения
- 5,4 Расчет требований к памяти для объектов R
Пакет- html»> 7.1 Использование
dput () и dump () - 8.1 Файловые соединения
- 8,2 Строки чтения текстового файла
- 8,3 Чтение из URL-соединения
- 9,1 Подмножество вектора
- 9.
 2 Подмножество матрицы
2 Подмножество матрицы- 9.2.1 Размеры капельной матрицы
- 9,3 Списки подмножеств
- 9,4 Подмножество вложенных элементов списка
- 9,5 Извлечение нескольких элементов списка
- 9,6 Частичное соответствие
- 9,7 Удаление значений NA
- 10.1 Векторизованные матричные операции
- 11,1 Даты в R
- 11,2 Раз в
- 11,3 Операции с датой и временем
- 11,4 Резюме
рэндов
dplyr - 12,1 Фреймы данных
- 12.2
dplyrПакет - 12,3
dplyrГрамматика- 3.1″ data-path=»managing-data-frames-with-the-dplyr-package.html»> 12.3.1 Общий
dplyrСвойства функции
dplyr выберите () фильтр () упорядочить () переименовать () мутировать () group_by () %>% - 13,1
если—иначе - 13,2
дляпетель - 13.3 Вложенный
дляпетель - 13,4
в то время какПетли - 13,5
повторПетли - 13,6
следующий,перерыв - 13,7 Резюме
- 14,1 Функции в R
- 14,2 Ваша первая функция
- 14.3 Сопоставление аргументов
- 14,4 Ленивая оценка
- 14,5 Аргумент
... - 14,6 Аргументы, следующие после
...Аргумент - 14,7 Резюме
- 15,1 Отклонение значений привязки к символу
- 15,2 Правила определения объема
- 15.3 Лексическая область видимости: почему это важно?
- 15,4 Лексическая и динамическая область видимости
- 15,5 Приложение: оптимизация
- 15,6 График вероятности
- 15,7 Резюме
- 16,1 Цикл в командной строке
- 16,2
внахлест () - 16.3
сапр () - 16,4
раздельный () - 16,5 Разделение фрейма данных
- 16,6 штуцер
- 16,7
применить () - 16,8 Суммы столбцов и строк и средние значения
- 16,9 Другие способы подачи заявления
- 16.10
отображение () - 16.11 Векторизация функции
- 16.12 Сводка
- 17,1 Перед тем, как начать
- 17,2 Основные функции R
- 17,3
grep () - 17,4
grepl () - 17,5
regexpr () - 17,6
sub ()иgsub () - 17.7
regexec () - 17,8 Стрингер
- 17,9 Резюме
- 18,1 Что-то не так!
- 18,2 Выяснение того, что не так
- 18,3 Инструменты отладки в R
- 18,4 Использование
traceback () - 18.5 Использование
debug () - 18,6 Использование
recovery () - 18,7 Резюме
- 19,1 Использование
system.time () - 19,2 Определение времени для более длинных выражений
- 19,3 Профиль R
- 19,4 Использование
summaryRprof () - 19.5 Резюме
- 20,1 Генерация случайных чисел
- 20,2 Установка начального числа случайных чисел
- 20,3 Моделирование линейной модели
- 20,4 Случайная выборка
- 20,5 Резюме
- 21,1 Сводка
- 21,2 Загрузка и обработка необработанных данных
- 21.2.1 Чтение данных за 1999 год
Electronics Club — Сопротивление — последовательно, параллельно, Ом, проводники, изоляторы
Electronics Club — Сопротивление — последовательно, параллельно, Ом, проводники, изоляторы
Сопротивление | В серии |
Параллельно | Проводники и изоляторы
Следующая страница: Закон Ома
См. Также: Резисторы | Импеданс
Сопротивление — это свойство компонента, которое ограничивает поток заряда .Энергия используется, поскольку напряжение на компоненте пропускает через него ток и
эта энергия проявляется в компоненте как тепло.
Сопротивление измеряется в омах, символ ом — омега.
.
1
довольно мала для электроники, поэтому сопротивления часто указываются в
k
и м.
1 к
= 1000
1 млн
= 1000000.
Резисторы, используемые в электронике, могут иметь сопротивление всего 0,1.
или до 10 млн.
Rapid Electronics: резисторы
Резисторы, подключенные последовательно
При последовательном соединении резисторов их суммарное сопротивление равно
отдельные сопротивления суммируются.Например, если резисторы R1 и R2
соединенные последовательно, их общее сопротивление R определяется выражением:
| Два резистора в серии : | R = R1 + R2 |
Это можно расширить для большего количества резисторов:
| Резисторы в серии : | R = R1 + R2 + R3 + R4 + … |
Комбинированное сопротивление в серии всегда будет на больше , чем любое из
индивидуальные сопротивления.
Параллельно подключенные резисторы
При параллельном подключении резисторов их суммарное сопротивление меньше любого из отдельных сопротивлений.
Существует специальное уравнение для суммарного сопротивления двух резисторов R1 и R2, включенных параллельно:
| Два резистора в параллели : | R = | R1 × R2 |
| R1 + R2 |
Для более чем двух резисторов , подключенных параллельно необходимо использовать более сложное уравнение.Это суммирует , равное («на один больше») каждого сопротивления, чтобы получить
обратная комбинированного сопротивления, R:
| Резисторы параллельно : | 1 | = | 1 | + | 1 | + | 1 | +… |
| R | R1 | R2 | R3 |
Более простое уравнение для двух резисторов , включенных параллельно, намного проще в использовании!
Комбинированное сопротивление , включенного параллельно , всегда будет на меньше , чем любое из
индивидуальные сопротивления.
Проводники, полупроводники и изоляторы
Сопротивление объекта зависит от его формы и материала
из которого он сделан.Для данного материала объекты с меньшим поперечным сечением
или большая длина будет иметь большее сопротивление.
Материалы можно разделить на три группы:
Проводники — низкое сопротивление
Примеры включают металлы (алюминий, медь, серебро и т. Д.) И углерод.
Металлы используются для изготовления соединительных проводов, контактов переключателей и нитей ламп.
Резисторы изготавливают из углерода или длинных катушек из тонкой проволоки.
Полупроводники — умеренное сопротивление
Примеры включают германий и кремний.Полупроводники используются для изготовления диодов, светодиодов, транзисторов и интегральных схем (микросхем).
Изоляторы — высокое сопротивление
Примеры включают большинство пластмасс, таких как полиэтилен и ПВХ (поливинилхлорид), бумагу, дерево, резину и стекло.
ПВХ используется как внешнее покрытие для проводов, чтобы предотвратить их соприкосновение.
Рекомендуемая книга
Я рекомендую Электронику для детей
как хорошее введение в электричество и электронику.
Напечатанный в цвете с множеством иллюстраций, он знакомит с общими компонентами простых, но интересных проектов.
строить на каждом этапе.Книга начинается с предположения об отсутствии предшествующих знаний, а затем тщательно строятся простые объяснения.
о том, как работают компоненты, а также о практических методах, включая снятие изоляции с проводов, пайку и использование мультиметра.
Основные моменты включают освещение светодиода лимонами, использование реле для включения светодиода, создание музыкального инструмента, включение сигнала восхода солнца,
игра по угадыванию цвета, проверка секретного кода и финальный проект используют три микросхемы для создания отличной игры.
Автор, Эйвинд Нидал Даль, проделал огромную работу, предоставив четкие пошаговые инструкции с макетом (или полосой).
макеты, а также электрические схемы для проектов.Как технический рецензент книги, я сам создавал все проекты, и я очень
с радостью рекомендую его всем, кто хочет весело и познавательно познакомиться с электроникой.
Следующая страница: Закон Ома | Исследование
Политика конфиденциальности и файлы cookie
Этот сайт не собирает личную информацию.
Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет
используется только для ответа на ваше сообщение, оно не будет передано никому.На этом веб-сайте отображается реклама, если вы нажмете на
рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден.
Рекламодателям не передается никакая личная информация.
Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации.


 9.2 Полезные стандартные тексты на S и R
9.2 Полезные стандартные тексты на S и R 2 Подмножество матрицы
2 Подмножество матрицы