Переходные процессы в линейных электрических цепях. (Лекция 6)
1. Лекция 6
ЛЕКЦИЯ 6
2. Переходные процессы в линейных электрических цепях
2
Переходные процессы в линейных
электрических цепях
В электрических цепях возможны включения и отключения отдельных
ветвей, короткие замыкания участков цепи, различного рода
переключения. Любые изменения в электрических цепях можно
представить в виде переключений или коммутаций. Характер
коммутации указывается в схеме с помощью рубильника со стрелкой.
По направлению стрелки можно судить, замыкается или размыкается
рубильник.
При коммутации в цепи возникают переходные
процессы, т.е. процессы перехода токов и
напряжений от одного установившегося значения к
другому.
Изменения токов и
напряжений вызывают одновременное изменение энергии
электрического и магнитного полей, связанных с элементами цепи емкостями и индуктивностями.
Однако энергия электрического поля и энергия магнитного поля могут
изменяться только непрерывно, так как скачкообразное изменение
потребовало бы от источника бесконечно большой мощности.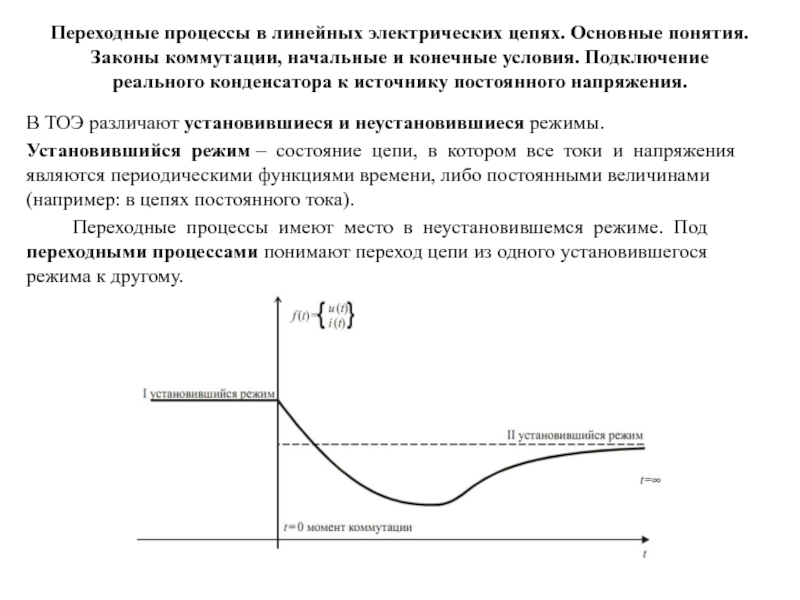 На этом
На этом
рассуждении основаны законы коммутации.
3
Первый закон. В любой ветви с индуктивностью ток не
может изменяться скачком и в момент коммутации
сохраняет то значение, которое он имел
непосредственно перед моментом коммутации
,
где
— ток в ветви с индуктивностью в момент
коммутации, сразу после коммутации. Знак «+» в
формуле обычно не записывается. Время переходного
процесса отсчитывается от момента коммутации;
— ток в индуктивности непосредственно перед
коммутацией.
4
Второй закон. Напряжение на емкости сразу после
коммутации сохраняет то значение, которое оно имело
непосредственно перед моментом коммутации.
,
где
— напряжение на емкости в момент
коммутации;
— напряжение на емкости непосредственно
перед моментом коммутации.
5
Допущения, применяемые при анализе переходных
процессов:
1. Полагают, что переходный процесс длится
бесконечно большое время.
2. Считают, что замыкание и размыкание рубильника
происходит мгновенно, без образования электрической
дуги.
3. Принимают, что к моменту коммутации предыдущие
переходные процессы в цепи закончились.
6
Свободный ток определяют по формуле:
Количество слагаемых в формуле равно числу реактивных
элементов (индуктивностей и емкостей) в схеме.
— корни характеристического уравнения.
— постоянные интегрирования, определяются с
помощью начальных условий.
Начальные условия — это переходные токи и напряжения в
момент коммутации, в момент времени
Переходные процессы в линейных электрических цепях
1. Сущность переходного процесса заключается в том, что электриская цепь переходит из одного установившегося состояния (режима) в другое. Переходные режимы играют важную роль в различных областях инженерной практики. Например, в электрических нагревательных печах качество выпускаемого материала и производительность зависят от характера протекания переходного процесса. Чрезмерно быстрое нагревание может стать причиной брака, а чрезмерно медленное — отрицательно сказывается на качестве материала и, кроме того, ведет к снижению производительности.
Чрезмерно быстрое нагревание может стать причиной брака, а чрезмерно медленное — отрицательно сказывается на качестве материала и, кроме того, ведет к снижению производительности.
2. Одним из широко применяемых электрических аппаратов является электромагнитное реле. Катушка реле обладает индуктивностью L и сопротивлением R. Контакты реле могут быть замыкающими и размыкающими. При включении реле на постоянное напряжение U ток в цепи катушки нарастает. Переходный процесс выражается уравнением
, или , где ; .
Варьированием параметров L и R можно воздействовать на скорость протекания переходного процесса.
Если контактное устройство срабатывает через заданный промежуток времени после замыкания цепи катушки, то к этому моменту ток достигнет величины .
Если Же Контактное устройство выполнено так, что оно срабатывает, когда ток достигает заданной величины , то промежуток времени, в течение которого произойдет срабатывание, определится по формуле
3. Процесс заряда и разряда конденсатора является основой для простейшего релаксационного генератора — генератора несинусоидального напряжения. Такой генератор создает пилообразное напряжение, которое при заряде сравнительно медленно возрастает и быстро убывает при разряде конденсатора. Схема такого генератора, состоящего из резистора R, Конденсатора С и неоновой лампы, показана на рис. 8. Заряд конденсатора С производится через резистор R в течение времени и напряжение возрастает по экспоненциальному закону , где . Когда напряжение достигает напряжения зажигания неоновая лампа зажигается, начинается ее тлеющий разряд, сопротивление ее резко падает (R » ) и начинается разряд через лампу. Значение падает по экспоненте , где . Когда упадет до значения напряжения гашения лампы, снова повторяется заряд через R, Затем разряд через и Далее процесс периодически повторяется по пилообразной кривой, показанной на рис.
Процесс заряда и разряда конденсатора является основой для простейшего релаксационного генератора — генератора несинусоидального напряжения. Такой генератор создает пилообразное напряжение, которое при заряде сравнительно медленно возрастает и быстро убывает при разряде конденсатора. Схема такого генератора, состоящего из резистора R, Конденсатора С и неоновой лампы, показана на рис. 8. Заряд конденсатора С производится через резистор R в течение времени и напряжение возрастает по экспоненциальному закону , где . Когда напряжение достигает напряжения зажигания неоновая лампа зажигается, начинается ее тлеющий разряд, сопротивление ее резко падает (R » ) и начинается разряд через лампу. Значение падает по экспоненте , где . Когда упадет до значения напряжения гашения лампы, снова повторяется заряд через R, Затем разряд через и Далее процесс периодически повторяется по пилообразной кривой, показанной на рис. 9. На выходе генератора это пилообразное напряжение обозначено через .
9. На выходе генератора это пилообразное напряжение обозначено через .
Переходные процессы в линейных электрических цепях — 4.0 out of
5
based on
1 vote
Переходные процессы в линейных электрических цепях
(государственный технический университет)
ФИЛИАЛ «ВЗЛЕТ»
Кафедра РЭВС
РАЛДЫГИН И.К.
КОНСПЕКТ ЛЕКЦИЙ ПО КУРСУ
«Основы теории цепей». Часть 3.
Переходные процессы в линейных электрических цепях
Учебное пособие для студентов радиотехнической специальности.
|
Ахтубинск – 2004
Предисловие к 3-ей части
В третьей части конспекта по Основам теории цепей (ОТЦ) кратко изложены два метода расчета переходных процессов в линейных электрических цепях: Классический метод и Операторный метод. И классический и операторный методы расчета теоретически можно применять для решения задач любой сложности. Каким из них пользоваться определяется автором.
И классический и операторный методы расчета теоретически можно применять для решения задач любой сложности. Каким из них пользоваться определяется автором.
Однако классический метод физически более прозрачен, чем операторный, в котором решение уравнений во многом формализовано. Операторный метод имеет перед классическим явное преимущество если для расчета переходных процессов использовать прикладную программу Mathcad
2000
, особенно в тех случаях, когда воздействующее напряжение является линейно возрастающее или в виде всплеска одной или несколько экспонент.
Глава 1. Основные сведения о переходных процессах в линейных электрических цепях
1.1 Возникновение и общая характеристика переходных процессов
Выше рассматривались цепи, в которых выполнялись два условия: 1) Источники энергии были подключены к цепи теоретически бесконечно давно; 2) Никаких изменений в состоянии цепи не производилось. Такой режим работы цепи называется установившимся или принужденным.
Переходным называют электромагнитный процесс, возникающий в электрической цепи, при переходе от одного установившегося режима к другому. Этот переход может происходить вследствие преднамеренного или случайного отключения цепи, а также подключения ее под напряжение, вследствие обрыва или короткого замыкания в цепи.
Любые изменения в цепи можно представить в виде переключений, которые называются коммутацией. Коммутация на схемах обозначается в виде ключа со стрелкой, обозначающей замыкание или размыкание:
Теоретически считается, что коммутация производится мгновенно.
Установившийся режим работы цепи при заданных и неизменных ее параметрах полностью определяется источником энергии: постоянный ток, переменный ток.
После коммутации, т.е. во время переходного процесса, токи и напряжения в цепи определяются не только внешними, но и внутренними источниками энергии, в качестве которых выступают индуктивности и емкости.
Дело в том, что в режиме, который существовал до коммутации, в катушках и конденсаторах было накоплено определенное количество энергии:
В момент коммутации (t=0) начинается перераспределение энергии между внутренними накопителями и внешними источниками; при этом часть энергии необратимо преобразуется в тепло.
По истечении какого-то времени после коммутации в цепи установится новый режим, который будет обусловлен только внешними источниками энергии. При отключении цепи от внешних источников переходной процесс будет существовать только за счет энергии накопленной в индуктивностях и емкостях, т.е. только за счет внутренней энергии. Новый установившийся режим, в этом случае, будет характеризоваться отсутствием тока в цепи.
Задача анализа переходного процесса заключается в том, чтобы установить по какому закону и как долго будет происходить переход от одного режима к другому.
В соответствии с законом непрерывности энергии напряжение на емкости и ток через индуктивность не могут изменяться скачком, т.к. в этом случае мощность, равная скорости изменения энергии обращалась бы в бесконечность, что физически невозможно.
На основании изложенного сформулированы два закона коммутации:
· Заряд и напряжение на емкости в момент коммутации остаются такими же, какими они были непосредственно перед коммутацией, а затем плавно изменяются;
· Ток через индуктивность в момент коммутации остается таким же, каким он был непосредственно перед коммуникацией, а затем плавно изменяется.
Математически законы коммутации записываются в следующем виде:
Ток через емкость и напряжение на индуктивности могут изменяться скачком.
1.2 Начальные условия
Значения токов, напряжений и их производных в момент коммутации называют начальными условиями.
Начальные условия подразделяются на зависимые и независимые.
Напряжение на емкости и ток через индуктивность, непосредственно перед коммутацией, называются независимыми начальными условиями, т.к. их значения не зависят от вида и места коммутации и определяются только энергетическим состоянием цепи непосредственно перед коммутацией.
Зависимыми начальными условиями являются токи через емкость и напряжение на индуктивности в момент коммутации. Они зависит от вида и места коммутации и в общем случае, в момент коммутации, могут изменяться скачком.
Независимые начальные условия определяются в цепи до коммутации, а зависимые начальные условия определяются в цепи образовавшейся в момент коммутации.
1.3 Математические основы анализа переходных процессов
Электромагнитные процессы в линейных электрических цепях в установившемся режиме описываются законами Кирхгофа для мгновенных или комплексных значений токов и напряжений.
Для определения законов изменения токов и напряжений в переходном режиме необходимо линейные уравнения, составленные по законам Кирхгофа для мгновенных значений, записать в виде дифференциальных уравнений, а затем решить эти уравнения относительно искомых токов и напряжений.
Таким образом, анализ переходных процессов сводится к решению обыкновенных дифференциальных уравнений с правой частью.
На практике для решения дифференциальных уравнений применяют классический и операторный методы расчета.
Суть классического метода расчета рассмотрим на конкретном примере.
Пусть задана электрическая цепь из последовательно соединенных RC элементов Рис.1.1.
Рис. 1.1. Цепь RC в момент t=0 при нулевых начальных условиях, Uc
(0)=0, подключается к источнику постоянного напряжения
Определим, в общем виде, законы изменения напряжения на емкости и ток в цепи после коммутации.
Решение.
При анализе переходных процессов классическим методом необходимо составить уравнения по законам Кирхгофа для мгновенных значений токов и напряжений. В данном случае можно составить только одно уравнение по второму закону Кирхгофа:
(1.1)
Поскольку исходное алгебраическое уравнение (1.1) можно записать в дифференциальной форме:
(1.2)
При анализе переходных процессов в качестве искомых функций могут выступать токи и напряжения на пассивных элементах цепи, образовавшейся после коммутации. Для общности обозначений, принятых в математике, условимся в дальнейшем искомую функцию обозначать Y
(
t
)
.
Тогда дифференциальное уравнение (1.2) можно записать в виде:
(1.3)
где — постоянная времени.
Из курса математики известно, что полное решение дифференциального уравнения (1.3) представляется в виде суммы двух составляющих:
(1.4)
где Y
пр
(
t
)
— принужденная составляющая;
Y
св
(
t
)
— свободная составляющая.
Принужденная составляющая искомого тока или напряжения определяется из анализа установившегося режима в цепи, образовавшейся после коммутации, для чего применяются любые известные методы расчета: по законам Кирхгофа, методом контурных токов и др.
Таким образом, принужденная составляющая зависит от вида источника напряжения и параметров цепи, образовавшейся после коммутации.
Свободная составляющая искомого тока или напряжения представляет собой решение уравнения (1.3) без правой части:
(1.5)
а именно:
(1.6)
где — постоянная интегрирования, которая зависит от начальных условий;
— корень характеристического уравнения
(1.7)
Свободная составляющая является результатом действия внутренних источников энергии, когда они не уравновешены внешними источниками. Свободная составляющая с течением времени затухает и в пределе стремится к нулю.
Свободная составляющая не зависит от вида воздействующих внешних источников энергии, и ее характер определяется только свойствами цепи, образовавшейся после коммутации.
Таким образом, закон изменения искомого тока или напряжения в переходном режиме определяется двумя факторами: свойствами цепи образовавшейся после коммутации и приложенным напряжением.
Глава 2. Переходные процессы в цепях первого порядка
2.1 Общий алгоритм расчета переходных процессов в цепях первого порядка классическим методом
Электрической цепью первого порядка называется цепь, которая включает в себя только один накопитель энергии (индуктивности или емкость) или сколько угодно накопителей одного характера, но которые могут быть заменены одним эквивалентным.
На основании вышеизложенного составлен алгоритм расчета переходных процессов в цепях первого порядка, который сводится к выполнению следующих операций.
1. Расчет независимых начальных условий производится в цепи непосредственно перед коммутацией, в результате чего определяются значения напряжений на емкости и ток через индуктивность в момент коммутации:
Независимые начальные условия бывают нулевые, когда UC
(0) = 0,
iL
(0) = 0
и ненулевые, когда UC
(0)
¹ 0,
iL
(0)
¹ 0
.
2. Расчет зависимых начальных условий производится в цепи, которая образовалась после коммутации. Для этого необходимо составить уравнения по законам Кирхгофа и рассмотреть их на момент коммутации t
=0
. После этого определяются зависимые начальные условия, например, для цепи Рис.1.1:
3. Расчет принужденных составляющих производится в цепи, которая образовалась после коммутации, используя известные методы расчета установившихся процессов. В результате определяются принужденные составляющие искомых токов и напряжений Y
пр
(
t
)
.
Например, для цепи Рис.1.1:
4. Составление характеристического уравнения и определение его корня. Для решения дифференциального уравнения первого порядка, например (1.5), необходимо составить характеристическое уравнение первого порядка и найти его корень.
Характеристическое уравнение можно составить двумя способами, например, для цепи Рис.1.1:
· либо путем формальной замены оператора дифференцирования оператором
· либо для цепи, образовавшейся после коммутации, составить комплексное входное сопротивление, а затем путем формальной замены j
*
w
=
P
получить операторное сопротивление, которое приравнять к нулю и найти корень этого уравнения.
Например, для цепи Рис.1.1:
5. Определение свободных составляющих искомых токов и напряжений.
Свободные составляющие всех токов и напряжение в цепях первого порядка представляют собой решение дифференциального уравнения без правой части (1.5) и записываются в виде:
(2.1)
Например, для цепи Рис.1.1 свободные составляющие для тока в цепи и напряжения на емкости имеют вид:
Они отличаются друг от друга только постоянными интегрирования.
6. Расчет постоянных интегрирования. Для расчета постоянных интегрирования, входящих в (2.1), необходимо составить полное решение дифференциального уравнения и рассмотреть его на момент коммутации :
(2.2)
При t
=0
имеем:
(2.3)
Например, для цепи Рис.1.1:
7. Запись полного решения дифференциального уравнения (2.3):
Для цепи Рис.1.1 получим:
(2.4)
2.2 Переходные процессы в цепи
RC
при подключении ее к источнику постоянного напряжения и коротком замыкании
Рассмотрим электрическую цепи, изображенную на Рис.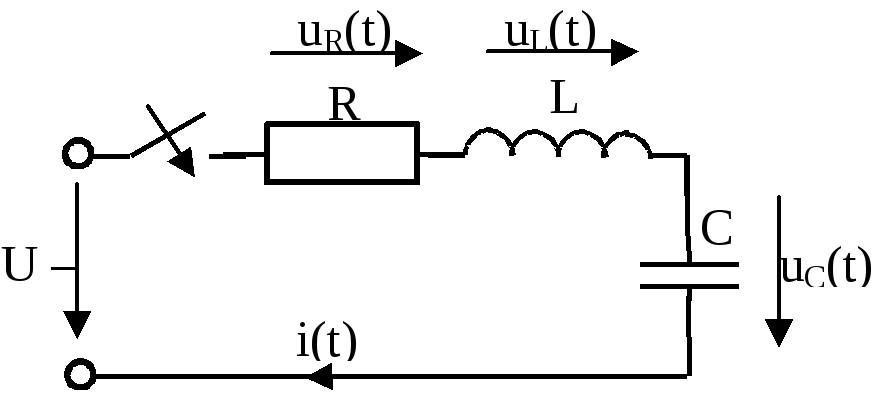 2.1, которая в момент , при нулевых начальных условиях UC
2.1, которая в момент , при нулевых начальных условиях UC
(0)=0
, подключается к источнику постоянного напряжения E
, а затем в момент t
1
>
0
в цепи происходит короткое замыкание, (ключ K
2
замыкается, а ключ K
1
размыкается).
Рис. 2.1. Цепь RC при подключении к источнику постоянного напряжения (ключ замыкается, ключ — разомкнут) и коротком замыкании (ключ — размыкается, а ключ — замыкается).
Определим законы изменения напряжений на емкости и на резисторе после первой и второй коммутаций.
Законы изменения напряжений на емкости и резисторе после первой коммутации получены при изложении алгоритма расчета переходных процессов в цепях первого порядка (2.4).
Определим теперь эти законы после второй коммутации, полагая, что вторая коммутация произошла в момент t
>
0
.
Фактически требуется рассчитать переходные процессы в цепи RC при ненулевых начальных условиях.
Следуя принятому алгоритму, получим следующее:
1. Независимые начальные условия. Напряжение на емкости в момент t
1
будет:
2. Зависимые начальные условия определим из уравнения, составленного по второму закону Кирхгофа, для цепи образовавшейся после второй коммутации:
3. Принужденные составляющие после второй коммутации будут равны нулю, т.к. в цепи нет источника напряжения:
4. Характеристическое уравнение остается таким же как после первой коммутации:
5. Свободные составляющие не зависят от входного напряжения, поэтому определяются по формуле (2.1).
6. Постоянные интегрирования определяются по формуле (2.3).
7. Законы изменения напряжений на емкости и на резисторе после второй коммутации принимают вид:
Из формулы (2.4) видно, что нарастание напряжения на емкости происходит тем быстрее, чем меньше постоянная времени. Для различных моментов времени напряжение на емкости, отнесенное к входному напряжению, характеризуется следующими данными (Таблица 2. 1).
1).
Таблица 2.1.
| 0 | ||||||
| 0 | 0,63 | 0,86 | 0,95 | 0985 | 0,993 |
Переходной процесс теоретически продолжается бесконечно долго. Однако, как видно из приведенной таблицы, в цепях первого порядка он заканчивается через время, равное (4…
5)*
t
после коммутации. В связи с этим принято считать, что длительность переходного процесса в цепях первого порядка составляет
В заключение отметим, что описанные выше переходные процессы возникают при подключении цепи RC к одиночному прямоугольному импульсу напряжением E
и длительностью t
1.
В связи с этим характер изменения напряжений на емкости и резисторе будет определяться соотношением между постоянной времени цепи и длительностью импульса.
Ниже приведен пример расчета переходных процессов в цепи RC по программе Mathcad (Рис.2.2), а также пример электронного моделирования работы этой цепи по программе Electronics Workbench (Рис.2.3 и Рис.2.4). Из этих рисунков видно, что результаты расчетов и результаты моделирования практически совпадают.
2.3 Переходные процессы в цепи
RC
при подключении ее к источнику синусоидального напряжения
Рассмотрим цепи RC Рис.1.1, которая при нулевых начальных условиях UC
(0)=0
подключается к источнику синусоидального напряжения
Определим для этой цепи закон изменения напряжения на емкости UC
(
t
)
после коммутации, применив вышеприведенный алгоритм.
1. Независимые начальные условия UC
(0)=0
.
2. Зависимые начальные условия
На момент коммутации , получим
3. Амплитуда принужденной составляющей напряжения на емкости определяется по общему правилу расчета одноконтурных цепей.
Определим модуль входного сопротивления
и его аргумент
Определяем комплексную амплитуду тока в цепи в установившемся режиме
Определим комплексную амплитуду напряжения на емкости
Теперь можно записать принужденную составляющую напряжения на емкости
4.5. Характеристическое уравнение и его корень, а также свободная составляющая не зависят от вида входного напряжения и определяются по ранее приведенным формулам
5. Постоянная интегрирования:
6. Закон изменения напряжения на емкости принимает следующий вид:
Ниже приведен пример 2.2 расчета переходных процессов в цепи RC при подключении ее к источнику синусоидального напряжения при нулевых начальных условиях Рис.2.5. На Рис.2.6 приведены результаты электронного моделирования этой цепи при синусоидальном воздействии.
Из этих рисунков видно, что результаты расчетов по программе Mathcad (Рис.2.5) и результаты электронного моделирования по программе Elecrronics Workbench (Рис. 2.6) практически совпадают.
2.6) практически совпадают.
В первый полупериод после коммутации напряжение на емкости в 1,7 раза больше принужденной составляющей, что необходимо учитывать при выборе пробивного напряжения на конденсаторе.
2.4 Переходные процессы в цепи
RL
при подключении ее к источнику постоянного напряжения и коротком замыкании
Рассмотрим электрическую цепь, состоящую из последовательно соединенных RL элементов Рис.2.7.
Рис. 2.7. Цепь RL в момент t
=0
при нулевых начальных условиях i
(0)=0
подключается к источнику постоянного напряжения; в момент ключ размыкается, а ключ замыкается.
Определим законы изменения напряжений на резисторе и индуктивности после первой коммутации и после второй.
Вначале определим U
2
(
t
) ,
UL
(
t
)
после первой коммутации: K
1
— замкнут, K
2
— разомкнут.
1. Независимые начальные условия
2. Зависимые начальные условия
На момент первой коммутации имеем
Отсюда следует, что индуктивность в момент коммутации представляет собой разрыв цепи. До коммутации напряжение на индуктивности было равно нулю, а в момент коммутации оно скачком принимает значение, равное входному напряжению.
3. Принужденные составляющие.
В установившемся режиме в цепи будет протекать постоянный ток, при котором индуктивное сопротивление равно нулю и поэтому
4. Характеристическое уравнение и его корень
где — постоянная времени цепи RL.
5. Свободные составляющие
6. Постоянные интегрирования
7. Законы изменения напряжений на индуктивности и резисторе после первой коммутации:
Переходные процессы в цепи RL при коротком замыкании (после второй коммутации).
Переходные процессы в цепи RL Рис.2.7 происходят при ненулевых начальных условиях.
1. Независимые начальные условия на момент t
1
>0
:
2. Зависимые начальные условия
Зависимые начальные условия
3. Принужденные составляющие.
В цепи после второй коммутации нет источников напряжения, поэтому
4. Характеристическое уравнение и его корень после второй коммутации такие же, как после первой:
5. Свободные составляющие
6. Постоянные интегрирования
7. Законы изменения напряжений на индуктивности и резисторе после второй коммутации:
Ниже приведен пример расчета переходных процессов в цепи RL, выполненный по программе Mathcad (Рис.2.8), а также результат электронного моделирования переходных процессов (Рис.2.9), который получен по программе ElectronicsWorkbench (EWB). Из анализа Рис.2.8 и Рис.2.9 видно, что кривые U
2
(
t
)
и UL
(
t
)
первого рисунка практически совпадают с одноименными кривыми второго рисунка.
2.5 Подключение цепи RL к источнику синусоидального напряжения
Пусть цепь RL Рис.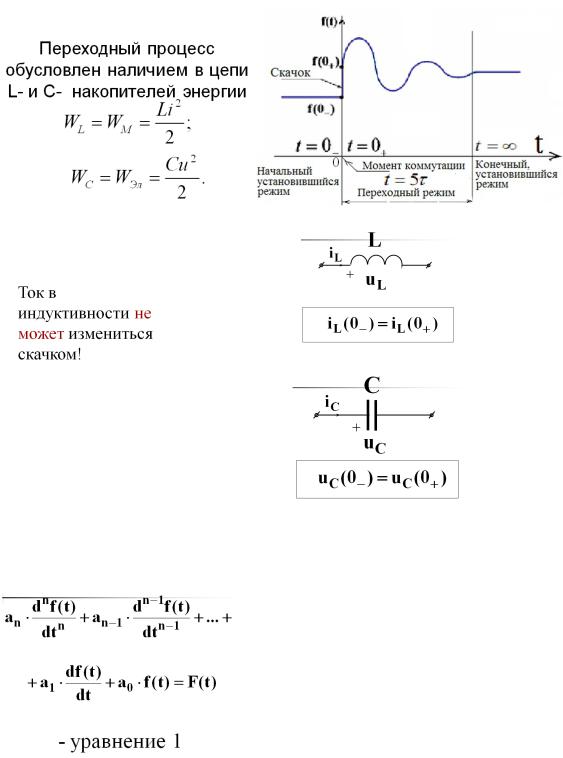 2.7. при нулевых начальных условиях подключается к источнику синусоидального напряжения с начальной фазой не равной нулю:
2.7. при нулевых начальных условиях подключается к источнику синусоидального напряжения с начальной фазой не равной нулю:
Определим закон изменения тока в цепи после коммутации.
1. Независимые начальные условия i
(0)=0
.
2. Зависимые начальные условия
На момент коммутации t
=0
имеем
Отсюда получаем:
3. Принужденная составляющая тока в цепи:
где
Отсюда амплитуда принужденной составляющей тока
Мгновенное значение принужденной составляющей тока
4.5. Характеристическое уравнение и его корень, а также свободная составляющая тока не зависят от вида входного напряжения и определяются по ранее приведенным формулам:
6. Постоянная интегрирования
7. Закон изменения тока в цепи RL при подключении ее к источнику синусоидального напряжения
Ниже приведен пример 2.4 расчета переходных процессов в цепи RL при подключении ее к источнику синусоидального напряжения.
Из приведенных формул видно, что при подключении цепи RL к источнику синусоидального напряжения ток в переходном режиме содержит две составляющие: синусоиду и экспоненту и его значение, в первый момент после коммутации, зависит от фазы включения.
Если включение произошло в момент, когда y
=
f
, то свободная составляющая будет отсутствовать и в цепи сразу будет установившийся режим (удачное включение). Наоборот, неудачное включение имеет место, когда начальная фаза входного напряжения будет y
=
f
±
90
°
.
Если при этом постоянная времени велика, то в начальный момент после коммутации ток переходного режима может достигнуть почти удвоенной амплитуды принужденной составляющей, что наглядно показано на Рис.2.10, где ток переходного режима в 1,66 раза больше амплитуды принужденной составляющей.
2.6 Синтез цепи
RC
с заданными параметрами переходного процесса
Выше рассматривались переходные процессы при заданных параметрах RC-элементов.
На практике возникает необходимость в решении обратной задачи: рассчитать потребные значения RC-элементов, при которых обеспечивалась бы заданная длительность переходного процесса и заданное значение выходного напряжения, снимаемого с резистора.
Рассмотрим электрическую цепь, изображенную на Рис.2.11.
Рис. 2.11. Исходная схема для расчета неизвестных R1
и C
На вход этой цепи подается последовательность однополярных прямоугольных импульсов напряжением E
B
, длительностью ti
, с частотой f
и скважностью 2.
Для синхронного управления ключевыми схемами с помощью цепи Рис.2.11 необходимо сформировать остроконечные импульсы, длительность которых была бы во много раз меньше длительности прямоугольных импульсов на входе цепи. Другими словами, заряд и разряд конденсатора должен происходить за время много меньше, чем длительность прямоугольного импульса
где K
<<1
— коэффициент длительности переходного процесса в цепи Рис.2.11.
При этом заданными величинами должны быть: сопротивление нагрузки R
2
, с которого снимается напряжение и максимальное значение U
2
этого напряжение (U
2
<
E
).
Решение.
Из условия задачи следует, что необходимо определить два параметра:
R
1
— балластное (регулировочное) сопротивление;
C
— емкость конденсатора цепи Рис.2.11.
В соответствии с принятым алгоритмом расчета переходных процессов в цепях первого порядка получаем следующее.
1. Независимые начальные условия:
где U
2
— потребное значение напряжения на нагрузке в момент коммутации.
2. Зависимые начальные условия.
К зависимым начальным условиям, в данном случае, относится напряжение на балластном сопротивление . Для определения этого напряжения составим уравнение по второму закону Кирхгофа и рассмотрим его на момент коммутации (на момент воздействия первого импульса):
На момент воздействия первого импульса t
=0
имеем
Поскольку UC
(0)=0,
U
2
(0)=
U
2
, следовательно, U
1
(0)
должно быть равным:
С другой стороны на момент t
=0
можно записать
Разделив левые и правые части этих соотношений, получим:
Для определения потребного значения емкости примем во внимание, что длительность переходного процесса в спроектированной цепи должно составлять не более
Это означает, что должно выполняться равенство:
5*
t
=K*ti
или 5*(R1
+R2
)*C=K*ti
.
Отсюда получаем потребное значение емкости
Расчет законов изменения напряжений на емкости и резисторах R
1
,
R
2
в цепи Рис.2.11 можно производить по формулам, приведенным в примере 2.1. Однако, ограничимся расчетом потребных значений R
1
,
C
, но выполним электронное моделирование спроектированной цепи.
Результаты расчетов и электронного моделирования приведены в примере 2.5.
Из Рис.2.12, где приведены результаты электронного моделирования, видно, что для спроектированной цепи RC переходной режим является «штатным». Данную цепь можно рассматривать как генератор остроконечных импульсов или преобразователь напряжения: прямоугольные импульсы преобразуются в остроконечные.
Глава 3. Переходные процессы в цепях второго порядка
3.1 Общая характеристика переходных процессов в цепях второго порядка
Цепями второго порядка называются цепи, в которых содержится два накопителя энергии: индуктивность и емкость.
Электрические цепи второго порядка бывают разветвленными и неразветвленными. К неразветвленным цепям второго порядка относится последовательный колебательный контур. К разветвленным цепям второго порядка относятся Г-образные фильтры нижних и верхних частот.
Электромагнитные процессы в цепях второго порядка описываются дифференциальными уравнениями второго порядка.
Например, дифференциальное уравнение относительно тока в последовательном колебательном контуре можно получить из уравнения, составленного по второму закону Кирхгофа, для мгновенных значений тока и напряжений:
После дифференцирования (3.2) получим дифференциальное уравнение второго порядка относительно тока
Обозначим, как и ранее, искомый ток i
(
t
)
через Y
и разделим левую и правую части (3.3) на L
, получим дифференциальное уравнение второго порядка:
где — коэффициент затухания;
— резонансная частота контура;
— правая часть дифференциального уравнения (3. 3).
3).
Из курса математики известно, что решение дифференциального уравнения второго порядка, также как и первого, представляется в виде двух слагаемых:
где Y
пр
(
t
)
— принужденная составляющая искомого тока или напряжения, которая зависит от вида источника напряжения, оставшегося в цепи после коммутации;
Y
св
(
t
)
— свободная составляющая, характер которой определяется только структурой цепи образовавшейся после коммутации.
Для решения дифференциального уравнения второго порядка, также как и первого, и по тем же правилам, составляется характеристическое уравнение, которое, в общем, имеет вид:
Корни этого уравнения:
где .
Свободная составляющая искомого тока или напряжения записывается в виде:
(3.8)
где A
1
,
A
2
— неизвестные постоянные интегрирования, которые зависят от начальных условий.
Допустим, что для цепи второго порядка составлено характеристическое уравнение (3.6) и определены его корни (3.7), а также найдены принужденные составляющие искомых токов и напряжений. Тогда общее решение дифференциального уравнения можно записать в виде:
. (3.9)
Для определения двух неизвестных и необходимо составить два уравнения.
В качестве первого уравнения используется уравнение (3.9), а в качестве второго – используется первая производная от (3.9).
Рассматривая (3.9) и (3.10) на момент t
=0
, получим два уравнения с двумя неизвестными A
1
и A
2
:
Совместное решение системы (3.11) дает:
После подстановки корней характеристического уравнения (3.6) и найденных постоянных интегрирования (3.12) в формулу общего решения (3.9) и преобразования, получим закон изменения искомого тока или напряжения:
(3.13)
где a
=
Y
(0)-
Y
пр
(0)
; b
=
Y
’(0)-
Y
’пр
(0)
— постоянные коэффициенты, зависящие от начальных условий.
Отметим, что формула (3.13) является общей для всех токов и напряжений в данной цепи второго порядка. При этом меняются только коэффициенты a
и b
и их размерность.
При решении конкретных задач могут представиться три случая.
Случай 1
.
Корни характеристического уравнения (3.7) действительные и разные, что возможно при d>wk
.
В этом случае после коммутации в цепи возникает апериодический режим, при котором все токи и напряжения изменяются плавно, без колебаний, а их законы описываются уравнением (3.13).
Случай 2
.
Корни характеристического уравнения (3.7) действительные и одинаковые, что возможно при d=wk
.
В этом случае в цепи после коммутации возникает критический режим.
При d
=
w
k
,
b
=
Ö
d
2
—
w
k
2
=0,
P
1
=
P
2
=-
d
,
формула (3.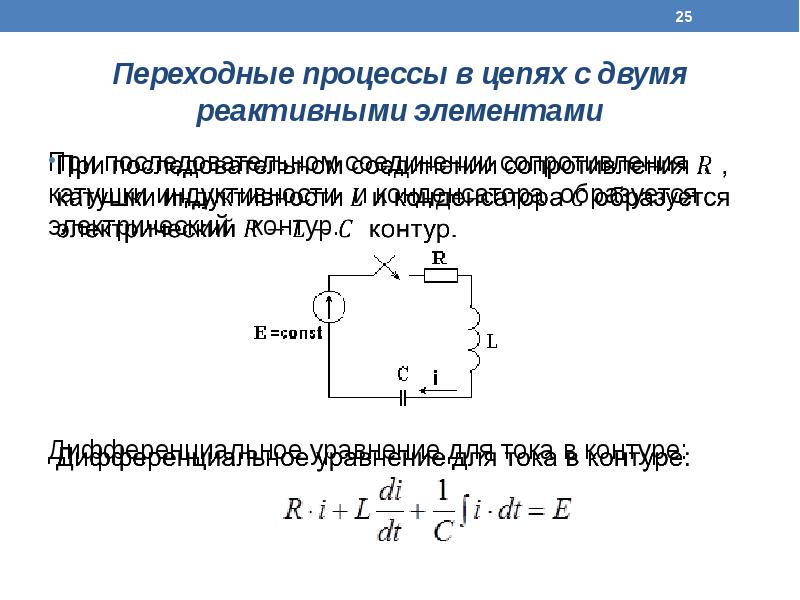 13) приобретает другой вид, поскольку
13) приобретает другой вид, поскольку
Подстановка полученных результатов в (3.13) дает формулу для расчета законов изменения токов и напряжений в критическом режиме:
В критическом режиме токи и напряжения, как видно из (3.14), изменяются также плавно, как в апериодическом режиме.
Критический режим лежит на границе между апериодическим и колебательным, к рассмотрению которого приступаем.
Случай 3
.
Корни характеристического уравнения (3.7) комплексные сопряженные, что возможно при d
<
w
k
.
В этом случае в цепи после коммутации возникает колебательный режим.
При d
<
w
k
имеем:
где — частота свободных колебаний.
Корни характеристического уравнения в этом случае принимают вид:
P
1
= —
d
+
j
*
w
св
; P
2
= —
d
—
j
*
w
св
.
Если в формуле (3.13) заменить b = j
*
w
св
, то получим:
.
Поскольку, законы изменения токов и напряжений в колебательном режиме принимают вид:
(3.15)
Подчеркнем еще раз, что формулы (3.13), (3.14) и (3.15) являются общими для всех токов и напряжений в цепях второго порядка.
3.2 Алгоритм расчета переходных процессов в цепях второго порядка
На основании вышеизложенного можно предложить следующий алгоритм расчета переходных процессов в цепях второго порядка.
1. Расчет независимых начальных условий производится в цепи до коммутации, в результате чего определяются ток через индуктивность и напряжение на емкости:
2. Расчет зависимых начальных условий производиться для цепи, образовавшейся после коммутации. Для этого составляются уравнения по первому и второму законам Кирхгофа для мгновенных значений токов и напряжений. Затем эти уравнения необходимо рассмотреть на момент t
=0
.
В уравнениях, составленных на момент t
=0
, известными будут: e
(0),
iL
(0)
и UC
(0)
, а неизвестными UL
(0)
и iC
(0)
, которые и определяются.
3. Расчет первых производится на момент t
=0
.
Для определения постоянных коэффициентов a
и b
, входящих в формулы (3.13), (3.14) и (3.15), необходимо знать значения не только искомых функций, но и их первых производных на момент t
=0
.
Первые производные искомых функций определяются путем дифференцирования уравнений, составленных по законам Кирхгофа, и рассмотрения их на момент t
=0
.
При этом в первую очередь определяются первые производные тока через индуктивность и напряжение на емкости, для чего используются уравнения связи между током и напряжением этих элементов.
. (3.16)
После этого определяются первые производные Y
’(0)
.
4. Расчет принужденных составляющих и их первых производных на момент t
=0
.
Принужденные составляющие искомых токов и напряжений определяются любым известным методом расчета установившихся режимов в цепи образовавшейся после коммутации (по законам Кирхгофа, методом контурных токов и др).
Затем полученные выражения для мгновенных значений принужденных токов и напряжений необходимо продифференцировать по времени, после чего определить: Y
пр
(0)
и Y
пр
’(0)
.
5. Расчет постоянных коэффициентов a
и b
.
Постоянные коэффициенты a
и b
определяются по формулам:
6. Составление характеристического уравнения, определение и анализ его корней, выбор расчетной формулы для свободной составляющей.
Одним из описанных выше методов составляется характеристическое уравнение, например, Z
(
P
)=0
и определяются его корни P
1
и P
2
.
На основании анализа корней характеристического уравнения выбирается одна из трех формул (3.13), (3.14), (3.15) для расчета законов изменения тока или напряжения после коммутации.
3.3 Переходные процессы в последовательном колебательном контуре при подключении его к источнику постоянного напряжения
Рассмотрим последовательный колебательный контур (Рис.3.1), который относится к неразветвленным цепям второго порядка.
Пусть данный контур при нулевых начальных условиях подключается к источнику постоянного напряжения .
Рис. 3.1. Последовательный колебательный контур
Определим для этих условий законы изменения тока в цепи и напряжений на пассивных элементах после коммутации.
Расчет законов будем вести по принятому выше алгоритму.
1. Независимые начальные условия.
Цепь до коммутации была обесточена, поэтому
2. Зависимые начальные условия.
Зависимым начальным условием, в данном случае, является напряжение на индуктивности. Для его определения составим единственно возможное уравнение по второму закону Кирхгофа для мгновенных значений напряжений и рассмотрим его на момент t
Для его определения составим единственно возможное уравнение по второму закону Кирхгофа для мгновенных значений напряжений и рассмотрим его на момент t
=0
.
.
На момент t
=0
получим:
Поскольку i
(0)=0
и UC
(0)=0
, постольку
Напряжение на индуктивности в момент коммутации скачком принимает значение, равное приложенному напряжению.
3. Первые производные и их значения на момент t
=0
.
В соответствии с (3.16), имеем:
(3.18)
.
Производную напряжения на индуктивности найдем после дифференцирования уравнения (3.17) и рассмотрения его на момент t
=0
.
На момент t
=0
, имеем
Таким образом, первые производные для рассматриваемого случая:
4. Принужденные составляющие и их первые производные на момент t
=0
.
В цепи образовавшейся после коммутации (Рис.3.1), через какое-то время конденсатор зарядится до уровня приложенного напряжения , ток в цепи прекратится, т. к. постоянный ток через емкость не проходит. Принужденные составляющие и их первые производные соответственно будут равны:
к. постоянный ток через емкость не проходит. Принужденные составляющие и их первые производные соответственно будут равны:
5. Постоянные коэффициенты a
и b
определяются по общей формуле:
.
6. Характеристическое уравнение и его корни.
Характеристическое уравнение, соответствующее дифференциальному уравнению второго порядка (3.4), получим из комплексного входного сопротивления цепи Рис.3.1 путем формальной замены j
*
w
®
P
.
Приравняв к нулю Z
(
P
)
и выполнив очевидные преобразования, получим характеристическое уравнение (3.6), корни которого зависят от конкретных значений RLC-элементов рассматриваемого контура Рис.3.1.
(3.20)
В данном случае корни (3.20) определяются по формулам:
где — коэффициент затухания свободной составляющей;
— резонансная частота последовательного контура Рис.3.1;
— постоянная величина.
Как было сказано выше, в цепях второго порядка, в зависимости от вида корней характеристического уравнения (3. 19), после коммутации может возникнуть один из трех возможных режимов: апериодический, критический или колебательный.
19), после коммутации может возникнуть один из трех возможных режимов: апериодический, критический или колебательный.
Найдем закон изменения напряжений на пассивных элементах цепи Рис.3.1 при подключении ее к источнику постоянного напряжения при нулевых начальных условиях для упомянутых случаев.
3.3.1 Апериодический режим
Апериодический режим наступает, если корни характеристического уравнения (3.20) действительные и разные, а это возможно если
где — волновое сопротивление контура;
— добротность контура.
Таким образом, в последовательном колебательном контуре (Рис.3.1) апериодический режим наступает при Q
<0.5
.
В связи с этим при анализе переходных процессов в последовательном колебательном контуре отпадает надобность в составлении характеристического уравнения и определении его корней.
В апериодическом режиме законы изменения тока и напряжений на пассивных элементах описываются формулой (3.13).
Если подставить в (3.13) найденные значения коэффициентов a
и b
(см. п.5) и выполнить простейшие преобразования, то получим законы изменения напряжений на пассивных элементах последовательного колебательного контура (3.1) в апериодическом режиме:
Для иллюстрации законов изменения напряжений на пассивных элементах последовательного колебательного контура в апериодическом режиме зададимся произвольными значениями E
,
L
,
C
,
, а сопротивление нагрузки R
выберем таким, чтобы Q
<0.5
и по формулам (3.20) рассчитаем и построим соответствующие графики.
Пример таких расчетов приведен на Рис.3.2.
3.3.2 Критический режим
Критический режим в последовательном колебательном контуре наступает, если корни характеристического уравнения действительные и одинаковые, а это возможно, если:
Таким образом, критический режим в последовательном колебательном контуре наступает при Q<0. 5.
5.
Законы изменения напряжений на пассивных элементах цепи Рис.3.1 в критическом режиме описываются формулой (3.14).
Если подставить в (3.14) значения a
и b
(см. п.5) и выполнить простейшие преобразования, то получим:
Для иллюстрации законов изменения напряжений на пассивных элементах последовательного колебательного контура в критическом режиме выберем значения E
,
L
и C
такими как в примере 3.1, а сопротивление нагрузки выберем из условия Q
=0.5
.
Пример расчетов по формулам (3.21) приведен на Рис.3.3.
Из сравнения рисунков 3.2 и 3.3 следует, что изменения напряжений на резисторе (ток в цепи) в критическом режиме происходят более плавно, чем в апериодическом.
Кроме того, в критическом режиме конденсатор заряжается, примерно, в 2,6 раза быстрее, чем в апериодическом.
Если ограничить длительность переходного процесса в критическом режиме временем t
пер
=5/
d
, при котором UC
(
t
пер
)=0. 96*
96*
E
, то возникает возможность синтеза последовательного колебательного контура в заданной длительностью переходного процесса в критическом режиме.
Пусть задано сопротивление нагрузки R
в цепи рис.3.1, которая подключается к источнику постоянного напряжения при нулевых начальных условиях. Необходимо найти такие значения L
и C
, при которых в цепи возникает критический режим, длительность которого должна составлять t
пер
.
Решение.
В критическом режиме t
пер
=5/
d
;
Совместное решение этих уравнений дает формулы для расчета потребных значений индуктивности и емкости
3.3.3 Колебательный режим
Колебательный режим в последовательном колебательном контуре возникает, если корни характеристического уравнения комплексные и сопряженные, а это возможно если
В этом случае
где — частота свободных колебаний.
В колебательном режиме законы изменения напряжений на пассивных элементах контура определяются по формуле (3. 15).
15).
Подстановка коэффициентов a
и b
(3.19) в формулу (3.15) дает законы изменения напряжений на пассивных элементах контура Рис.3.1:
.
Для иллюстрации законов изменения напряжений на пассивных элементах последовательного колебательного контура в колебательном режиме (3.22) выберем значения E
,
L
и C
такими же, как в примерах 3.1 и 3.2, а сопротивление нагрузки выберем из условия Q
=5
.
Пример расчетов по формулам (3.22) приведен на Рис.3.4.
Из анализа изложенного следует, что при Q
>0.5
в последовательном контуре Рис.3.1 возникают затухающие колебания, при которых происходит непрерывный обмен энергией между индуктивностью и емкостью.
Затухание свободных колебаний происходит вследствие необратимых потерь энергии в активном сопротивлении R
.
Длительность переходного процесса в колебательном режиме определятся коэффициентом затухания
Чем больше Q
, т. е. чем меньше R
е. чем меньше R
, тем дольше продолжается переходной процесс.
Частота свободных колебаний всегда меньше резонансной частоты контура
и при
Из Рис.3.4 видно, что напряжение на емкости в начале переходного процесса почти в два раза превышает приложенное напряжение, что необходимо учитывать при выборе пробивного напряжения конденсатора.
Таким образом, режим переходного процесса в колебательном контуре, при подключении его к источнику постоянного напряжения, целиком определяется комбинацией значений RLC-элементов:
При Q
<0.5
— в цепи после коммутации наступает апериодический режим;
при Q
=0.5
— критический режим;
при Q
>0.5
— колебательный режим.
Глава 4. Операторный метод расчета переходных процессов в линейных электрических цепях
4.1 Общие сведения
В предыдущих главах был изложен классический метод расчета переходных процессов в линейных электрических цепях.
Такие процессы описываются линейными дифференциальными уравнениями с постоянными коэффициентами. Для их решения классическим методом необходимо определить постоянные интегрирования, зависящие от начальных условий. По мере усложнения электрических схем и возрастания порядка дифференциальных уравнений трудности, связанные с нахождением постоянных интегрирования, увеличиваются.
Решение упомянутых уравнений может быть выполнено операторным методом, где не требуется дополнительно определить постоянные интегрирования.
При использовании операторного метода действительные функции времени, называемые оригиналами, заменяются их операторными изображениями. В результате чего исходные дифференциальные уравнения заменяются алгебраическими; затем после решения алгебраических уравнений производится обратный переход в область функций действительного переменного.
Связь между оригиналом f
(
t
)
и его изображением устанавливается прямым преобразованием Лапласа:
гдеP
=
s
+
j
*
w
— комплексное число.
Из определения изображения (4.1) следует, что каждый оригинал имеет единственное изображение. В свою очередь, оригинал вполне определяется своим изображением.
Фразу «оригинал f
(
t
)
имеет своим изображением F
(
P
)
» принято записывать в виде знака соответствия :
или
Существует обратное функциональное преобразование, дающее возможность определить оригинал по его изображению (4.1):
Формула (4.2) называется обратным преобразование Лапласа.
4.2 Изображения простейших функций
При исследовании переходных процессов в электрических цепях чаще всего возникает необходимость в определении изображений единичной функции l
(
t
)
, линейной функции a
*
t
, экспоненциальной функции , синусоидальной и косинусоидальной функции, их производных и интегралов.
Единичная функция задается условием:
Изображение единичной функции:
Изображение постоянной величины E
:
Изображение линейной функции:
Изображение экспоненты:
Изображения тригонометрических функций:
Изображение производной от функции f
(
t
)
:
Изображение интеграла от функции f
(
t
)
:
Операция дифференцирования оригинала заменяется операцией умножения на P
изображения, а операция интегрирования оригинала заменяется операцией деления изображения на P
.
4.3 Операторное сопротивление. Закон Ома в операторной форме
Рассмотрим вначале пассивные RLC-элементы и определим их операторные сопротивления.
Пусть через индуктивность при нулевых начальных условиях i
(0)=0
протекает ток i
(
t
)
, изображение которого I
(
P
)
.
По закону электромагнитной индукции напряжение на индуктивности:
Умножим обе части этого равенства на множитель и выполним прямое преобразование Лапласа:
По теореме дифференцирования оригинала, при i
(0)=0
, получим:
Отсюда получаем выражение для операторного сопротивления индуктивности:
(4.3)
Рассмотрим теперь емкость C
, которая при нулевых начальных условиях подключается к источнику напряжения UC
(
t
)
, изображение которого UC
(
P
)
.
Ток и напряжение на емкости связаны уравнением:
Применим к левой и правой частям этого выражения прямое преобразование Лапласа, в результате получим:
Отсюда находим операторное сопротивление емкости:
.
Рассмотрим теперь последовательный колебательный контур Рис.3.1, который при нулевых начальных условиях подключается к источнику , изображение которогоE
(
P
)
.
По второму закону Кирхгофа можем записать (3.17):
(4.5)
Применим к этому уравнению прямое преобразование Лапласа, в результате, с учетом (4.3) и (4.4), получим:
(4.6)
или
где — операторное сопротивление последовательного колебательного контура.
Формула (4.6) представляет собой закон Ома в операторной форме. Нетрудно заметить, что структура операторного и комплексного сопротивлений подобны по форме:
Для перехода от комплексного сопротивления к операторному достаточно заменить j
*
w
на P
.
Сопротивление цепи в операторной форме есть новая более общая форма сопротивления, которая может применяться для решения задач, относящихся к любому режиму цепи при любой форме внешнего воздействия. Тогда как комплексное сопротивление применимо лишь при синусоидальном воздействии на цепь.
Наряду с операторным сопротивлением применяется операторная проводимость, которая, по определению, является величиной обратной сопротивлению.
4.4 Законы Кирхгофа в операторной форме
Первый закон Кирхгофа для мгновенных значений токов в узле электрической цепи:
Полагая, что каждый ток, входящий в узел или выходящий из него, имеет свое изображение Ik
(
P
)
, получим первый закон Кирхгофа в операторной форме:
который формулируется так: алгебраическая сумма изображений токов в узле электрической цепи равна нулю.
Соответственно второй закон Кирхгофа для любого замкнутого контура
где ek
(
t
),
Uk
(
t
)
— мгновенные значения э.д.с. и напряжений на пассивных элементах данного замкнутого контура, записывается в операторной форме:
Естественно, что при составлении уравнений по законам Кирхгофа в операторной форме необходимо задаться положительными направлениями всех токов и э. д.с., а также соблюдать все правила при составлении уравнений по законам Кирхгофа для действительных функций времени.
д.с., а также соблюдать все правила при составлении уравнений по законам Кирхгофа для действительных функций времени.
4.5 Эквивалентные операторные схемы
Вышеприведенные формулы (4.7) и (4.8), выражающие законы Кирхгофа в операторной форме справедливы при нулевых начальных условиях:
iL
(0)=0 и
UC
(0)=0.
Если до возникновения переходного процесса цепь обладала запасом энергии в виде электрического и магнитного полей, то, естественно, этот запас энергии необходимо учесть при составлении операторных уравнений. Надо ожидать, что законы Ома и Кирхгофа в этом случае изменяются в своей записи и примут более общую форму, из которой, как частный случай, должны вытекать формулы для нулевых начальных условий.
При ненулевых начальных условиях формула (4.3) принимает следующий вид:
гдеi
(0)
— ток через индуктивность в момент коммутации (t=0
).
Этому операторному уравнению соответствует следующая эквивалентная операторная схема замещения (Рис. 4.1)
4.1)
а) в)
Рис. 4.1. Исходная а) и в) операторная схема замещения индуктивности: EL
=
L
*
i
(0)
– внутренний источник напряжения, направление которого совпадает с направлением тока.
При ненулевых начальных условиях уравнение (4.4) принимает вид:
где UC
(0)
— напряжение на емкости в момент коммутации.
Операторному уравнению (4.10) соответствует следующая эквивалентная операторная схема замещения (Рис.4.2):
Рис. 4.2. Исходная а) и в) эквивалентная операторная схема замещения емкости
— внутренний источник напряжения, направление которого противоположно направлению тока.
Расчет переходных процессов операторным методом сводится к выполнению следующих операций:
· вместо источников напряжений, оставшихся в цепи после коммутации, вводятся их операторные изображения e
(
t
)
®
E
(
P
)
;
· вместо всех искомых токов и напряжений на пассивных элементах вводятся пока неизвестные их изображения:
· вместо индуктивности и емкости рисуются их операторные схемы замещения, как показано на Рис. 4.1 и Рис.4.2; при этом комплексные сопротивления заменяются операторными, а при ненулевых начальных условиях в операторную схему замещения вводятся внутренние источники напряжений
4.1 и Рис.4.2; при этом комплексные сопротивления заменяются операторными, а при ненулевых начальных условиях в операторную схему замещения вводятся внутренние источники напряжений
Активное сопротивление остается без изменений.
Искомые изображения токов и напряжений могут быть определены любым известным методом расчета установившихся режимов (по законам Кирхгофа, методом контурных токов и др.).
Рассмотрим, для примера, электрическую схему Рис.4.3а, в которой до коммутации был установившийся режим. В момент коммутации t
=0
происходит короткое замыкание резистора R
1
и в цепи возникает переходной процесс.
Определим изображения токов в ветвях с индуктивностью и емкостью.
а) в)
Рис. 4.3. Исходная а) и ее операторная схема замещения в)
Операторный метод, как и классический, предусматривает, в первую очередь, определить независимые начальные условия.
В исходной схеме до коммутации был установившийся режим, при котором:
Для определения неизвестных изображений токов через индуктивность и емкость составим операторную схему замещения (рис. 4.3 в), а затем составим два уравнения по второму закону Кирхгофа:
4.3 в), а затем составим два уравнения по второму закону Кирхгофа:
где
Отсюда определяем неизвестные изображения токов
(4.11)
4.6 Определение оригинала по известному изображению
Из вышеизложенного следует, что по законам Ома и Кирхгофа в операторной форме всегда можно найти изображения искомых токов и напряжений. После этого возникает обратная задача: по известному изображению тока или напряжения, например (4.11), найти соответствующий ему оригинал i
(
t
)
, т.е. найти закон изменения тока или напряжения в функции времени.
Для нахождения оригинала пользуются готовыми таблицами, которые приводятся в учебниках и справочниках, где приводятся изображения и соответствующие им оригиналы.
Однако, в настоящее время расчет переходных процессов операторным методом можно выполнять с помощью программы Mathcad, которая позволяет производить прямое и обратное преобразование не прибегая в таблицам: laplace, invlaplace.
На нескольких примерах покажем, как производится расчет переходных процессов операторным методом в среде Mathcad.
4.6.1 Расчет переходных процессов в цепях первого порядка операторным методом
Пример 4.1.
Рассчитать реакцию цепи RC (Рис.4.4) при воздействии на нее одиночного прямоугольного импульса.
Рис. 4.4. Одиночный прямоугольный импульс с напряжением E
и длительностью T
воздействует на цепь RC в момент t
=0
Для описания единичной функции в среде Mathcad имеется встроенная функция Хевисайда, Ф(
t
)
которая представляет собой источник постоянного напряжения в 1 В
.
Одиночный прямоугольный импульс, изображенный на Рис.4.4, описывается так:
U1
(t)=E*(
Ф
(t)-
Ф
(t-T)).
где Ф(
t
—
T
)
— функция Хевисайда, смещенная по оси времени вправо на T
.
Результаты расчетов переходных процессов в цепи RC, выполненные операторным методом в среде Mathcad, представлены на Рис. 4.5.
4.5.
Сравнение законов изменения напряжений на резисторе и емкости, полученные классическим методом Рис.2.2 и операторным методом Рис.4.5, показывает, что они совпадают.
Пример 4.2.
Рассчитать реакцию цепи RC (Рис.4.4) при подключении ее к источнику синусоидального напряжения.
Результаты расчетов представлены на Рис.4.6.
Сравнение Рис.4.6 с рис.2.6 показывает, что они совпадают.
Пример 4.3.
Рассчитать реакцию цепи RC (Рис.4.4), если входное напряжение представляет затухающую экспоненту.
Результаты расчетов представлены на Рис.4.7.
4.6.2 Расчет переходных процессов в цепях второго порядка операторным методом
Пример 4.4.
Рассчитать переходные процессы в последовательном колебательном контуре (Рис.4.8) операторным методом при подключении его к источнику постоянного напряжения U
1
(
t
)
.
Рис. 4.8. Последовательный колебательный контур при нулевых начальных условиях подключается к источнику напряжения U
1
(
t
)
.
Реакция цепи (Рис.4.8) при подключении ее к источнику постоянного напряжения U
1
(
t
)=E
представлена на Рис.4.9 и Рис.4.10 для критического и колебательного режимов соответственно.
Сравнение этих рисунков с результатами расчетов, выполненными классическим методом (Рис.3.3 и рис.3.4), показывает, что они совпадают.
Пример 4.5.
Реакция цепи RLC (Рис.4.8) при воздействии одиночного прямоугольного импульса (опер ХЕВИСАЙД LRC) показана на Рис.4.11.
ЛИТЕРАТУРА
1. Атабеков Г.И. Основы теории цепей. Учебник для вузов. М., «Энергия», 1969 г. 424с. с ил.
2. Г.В. Зевеке Г.В., П.А. Ионкин, А.В. Нетушил, С.В. Страхов. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия» 1975 г. 752с. с ил.
3. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи: Учебник для электротехн., энерг., приборостроит. спец. вузов.-8-е изд., перераб. и доп.-М.: Высш. шк., 1984.-559с., ил.
и доп.-М.: Высш. шк., 1984.-559с., ил.
4. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники: В 2-х т. Учебник для вузов. Том 1.-3-е изд., перераб. и доп.-Л.: Энергоиздат. Ленингр. отд-ние, 1981.-536с., ил.
5. Дьяконов В. Д. Mathcad 2000: Учебный курс-СПб: Питер, 2000.-592с.: ил.
6. М. Херхагер, Х. Партоль Mathcad 2000 полное руководство: перевод с нем.-К.: Издательская группа BHV. 2000.-416с.
7.Карлащук В.И. Электронная лаборатория на IBMPC. Программа ElectronicsWorkbench и ее применение. «Салон-Р», 2000.-506с.
СОДЕРЖАНИЕ
Предисловие к 3-ей части
Глава 1. Основные сведения о переходных процессах в линейных электрических цепях
1.1 Возникновение и общая характеристика переходных процессов
1.2 Начальные условия
1.3 Математические основы анализа переходных процессов
Глава 2. Переходные процессы в цепях первого порядка
2.1 Общий алгоритм расчета переходных процессов в цепях первого порядка классическим методом
2. 2 Переходные процессы в цепях RC при подключении ее к источнику постоянного напряжения и коротком замыкании
2 Переходные процессы в цепях RC при подключении ее к источнику постоянного напряжения и коротком замыкании
2.3 Переходные процессы в цепях RC при подключении ее к источнику синусоидального напряжения
2.4 Переходные процессы в цепях RL при подключении ее к источнику постоянного напряжения и коротком замыкании
2.5 Подключение цепи RL к источнику синусоидального напряжения
2.6 Синтез цепи RC с заданными параметрами переходного процесса
Глава 3 Переходные процессы в цепях второго порядка
3.1 Общая характеристика переходных процессов в цепях второго порядка
3.2 Алгоритм расчета переходных процессов в цепях второго порядка
3.3 Переходные процессы в последовательном колебательном контуре при подключении его к источнику постоянного напряжения
3.3.1 Апериодический режим
3.3.2 Критический режим
3.3.3 Колебательный режим
Глава 4. Операторный метод расчета переходных процессов в линейных электрических цепях
4. 1 Общие сведения
1 Общие сведения
4.2 Изображения простейших функций
4.3 Операторное сопротивление. Закон Ома в операторной форме
4.4 Законы Кирхгофа в операторной форме
4.5 Эквивалентные операторные схемы
4.6 Определение оригинала по известному изображению
4.6.1 Расчет переходных процессов в цепях первого порядка операторным методом
4.6.2 Расчет переходных процессов в цепях второго порядка операторным методом
Литература
Переходные процессы в линейных электрических цепях (ЛЭЦ) с сосредоточенными параметрами
8. Переходные процессы в ЛЭЦ с сосредоточенными параметрами.
В предыдущих разделах рассматривались установившиеся
процессы в линейных электрических цепях (ЛЭЦ), т.е. такие процессы, при которых
и либо не
изменены во (цепи = ) либо
представляют периодические функции (цепи ).
8.1 Возникновение переходных процессов (п/пр) и порядок составления
уравнения, характеризующих п/пр.
Наступлению установившегося процесса, отлично от
первоначального режима работы цепи, предшествует переходный процесс, при
котором и изменяются
не периодически.
Переход от одного режима работы цепи к другому режиму
может быть вызван изменением параметров или схемы цепи, называемым в общем
случае в электротехнике коммутацией.
включение, выключение.
Можно считать, что коммутация цепи производится
мгновенно, т.е. на включение или переключение цепи время не расходуется. Тем не менее переход
режима работы цепи к последующему установившемуся процессу происходит не
мгновенно, а в течение некоторого времени. Объясняется это тем, что каждому
состоянию цепи соответствует определенный запас энергии электрических и магнитных полей.
Переход к новому режиму связан с нарастанием или
убыванием энергии этих полей, которые не могут изменятся мгновенно, без
скачков, т.к. в противном случае мощность достигла
бы бесконечных значений, что физически, невозможно. Поэтому в случае размыкание
ветви с индуктивной катушкой, в месте размыкания неизбежно возникает искра, в
сопротивлении которой расходуется энергия, накопленная в магнитном поле индуктивной
катушки.
Аналогично, если замкнуть накоротко зажимы
конденсатора, который был заряжен, то запасенная энергия рассеется между
контактами и в сопротивлении соединяющего проводом.
Практически время п/пр определяется малым интервалом,
по истечению которого и настолько
приближаются к установившимся значениям, что разница оказывается практически
неощутимой. Чем интенсивнее происходит рассеивание энергии в сопротивлениях,
тем быстрее протекает п/пр.
В одних случаях п/пр в ЭЦ нежелательны и опасны
(например, пир к.з. в энергитических системах). В других случаях п/пр
представляет нормальный, естественный режим работы цепи (напр., в
радиопередающих и радиоприемных устройствах, САР и др.).
Существуют различные методы расчета п/пр в АЭЦ:
классический, операторный, спектральный метод интеграл Дюамеля, метод
переменных состояния. Настоящий раздел посвящен классическому методу решения дифференциальных
уравнений, описывающих п/пр.
8.2Порядок составления уравнений, характеризующих переходный процесс.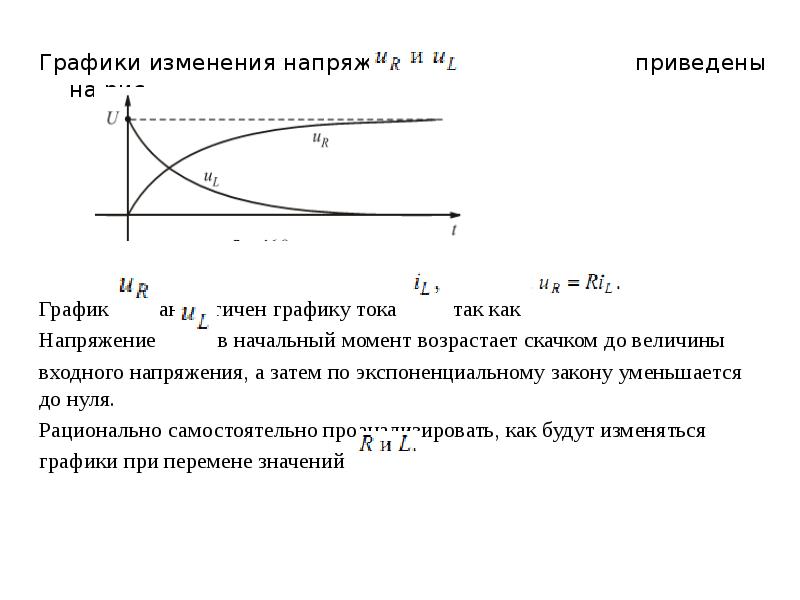
Сущность классического метода анализа
п/пр заключается в следующем:
1) составляется система интегро-дифференциальных
уравнений для мгновенных значений токов, напряжений и зарядов рассматриваемой
цепи после коммутации, т.е. после замыкания или размыкания ключа,
2) путем повторного дифференцирования система
интегро-дифференциальных преобразуется в систему дифференциальных уравнений;
3) система дифференциальных уравнений решается
относительно одной переменной величины (путем исключения переменных,
подстановок
Переходные процессы в линейных электрических цепях
}Переходные процессы в линейных электрических цепях.
Определения
1. Коммутация это какое-либо включение, выключение, переключение пассивных и активных ветвей и элементов схемы, приводящее к изменению конфигурации схемы или ее параметров. Предполагается, что коммутация совершается мгновенно (время коммутации равно нулю). Момент времени непосредственно до коммутации называется: 0- (“минус ноль”, момент непосредственно после: 0+ (“плюс ноль”).
Момент времени непосредственно до коммутации называется: 0- (“минус ноль”, момент непосредственно после: 0+ (“плюс ноль”).
Для схемы до коммутации и после коммутации характерны некоторые установившиеся режимы. В результате коммутации в схеме возникает некий режим перехода от установившегося процесса до коммутации к установившемуся процессу после коммутации. Это и есть переходный процесс. Теоретически длительность переходного процесса равна бесконечности, т.е. режим в цепи асимптотически приближается к установившемуся. Практически малым отличием режима от установившегося пренебрегают, и считают, что длительность переходного процесса конечна.
Законы коммутации
- В индуктивном элементе ток и магнитный поток в момент коммутации не изменяются, т.е.
(1)
Ток индуктивности сразу после коммутации равен току индуктивности непосредственно перед коммутацией (то же для магнитных потоков). В переходном процессе ток индуктивности и ее магнитный поток изменяются, начиная с этого значения.
В переходном процессе ток индуктивности и ее магнитный поток изменяются, начиная с этого значения.
- Напряжение емкостного элемента и его заряд в момент коммутации не изменяются.
(2)
Напряжение на емкости и ее электрический заряд сразу после коммутации равны напряжению на емкости и электрическому заряду непосредственно перед коммутацией. В переходном процессе напряжение на емкости и ее электрический заряд изменяются, начиная с этого значения.
Обоснование законов коммутации
Если в момент коммутации меняется скачком, то и, следовательно, из-за чего нарушается второй закон Кирхгофа, чего не может быть.
Аналогично.
Если в момент коммутации меняется скачком, то и, следовательно, из-за чего нарушается первый закон Кирхгофа, чего не может быть.
Обоснование законов коммутации из закона сохранения энергии.

Энергия магнитного поля индуктивности:
Энергия электрического поля емкости:
,
— мощность.
, , если или меняются скачком, то соответствующая мощность и стремятся к , следовательно, для скачкообразного изменения или схему надо подключить к источнику питания бесконечной мощности, чего быть не может.
Сформулированные законы коммутации не являются универсальными: существуют схемы, для которых они не выполняются. Эти схемы называются некорректными, для их расчета существуют специальные методы.
Значения в начальный момент времени токов индуктивностей и напряжений на ёмкостях называются независимыми начальными условиями. Значения других величин в начальный момент времени , , , называются зависимыми начальными условиями, они могут изменяться скачком в момент коммутации и определяются по независимым начальным условиям с помощью первого и второго закона Кирхгофа.
Зависимость токов и напряжений в схеме от времени представляем в виде суммы двух составляющих: принужденной и свободной:
, . (3)
Принужденная составляющая описывает установившийся режим цепи после коммутации, она определяется свойствами цепи и источника питания. Если источник постоянный, то установившийся режим постоянный и принужденная составляющая постоянная. Если источник периодический, то установившийся режим и принужденная составляющая — периодические.
Свободная составляющая отражает зависимость переходного процесса от свойств цепи конфигурации и параметров.
Математически переходный процесс в линейной схеме описывается линейным обыкновенным дифференциальным уравнением с постоянными коэффициентами n-ого порядка, где n число индуктивностей и емкостей в схеме, т.е. элементов, накапливающих энергию, источники напряжения и тока входят в правую часть этого ОДУ. Принужденная составляющая является частным решением неоднородного ОДУ, свободная составляющая общим решением однородного ОДУ.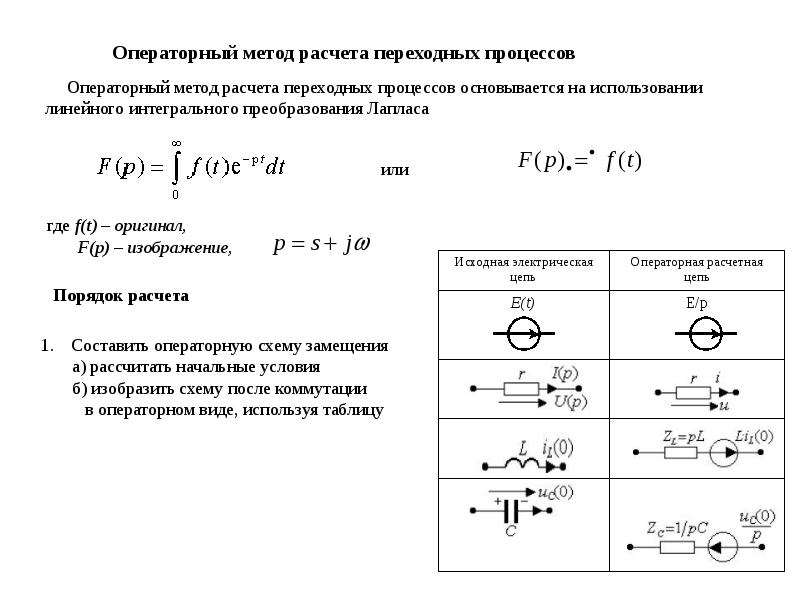 Для ОДУ n-ого порядка требуется n начальных условий. Они могут быть получены из n независимых условий: токов индуктивностей и напряжений емкостей в момент коммутации.
Для ОДУ n-ого порядка требуется n начальных условий. Они могут быть получены из n независимых условий: токов индуктивностей и напряжений емкостей в момент коммутации.
Метод расчета переходных процессов в линейных цепях состоящий в поиске решения ОДУ n-ого порядка называется классическим методом расчета переходных процессов. При этом само ОДУ в явном виде не записывается.
Пример 1
Включение RC-цепи на постоянное напряжение.
Найти , ключ замыкается
В замкнутом состоянии цепь является контуром, запишем для него второй закон Кирхгофа:
, т.к.
т.е.
Это ОДУ — линейное с постоянными коэффициентами.
Принужденное напряжение частное решение неоднородного ДУ — ищем в виде константы:
:
Общее решение однородного уравнения будет иметь вид:
— постоянная времени.
Постоянная B ищется из нескольких условий: по закону коммутации , до коммутации ключ был разомкнут и все напряжения в схеме были равны нулю (она была отключена от источника)
Это и есть начальное условие для нашей задачи.
Решение ищем в виде:
отсюда
, (4)
Пример 2
Ключ замыкается
По законам Кирхгофа составим систему ОДУ:
;
(5)
,
откуда
подставим в систему уравнений и продифференцируем по t:
(6)
Независимые начальные условия
;
определим из схемы до коммутации
ввиду того, что , , , постоянный ток через ёмкость не течет.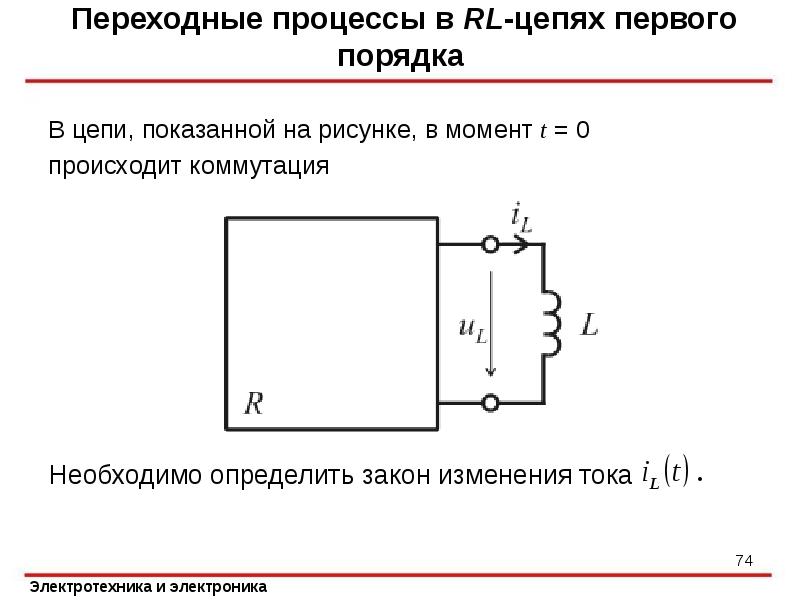
Запишем искомую величину в виде суммы свободной и принужденной составляющей:
Принужденная составляющая есть установившаяся составляющая после коммутации, когда переходный процесс закончился.
,
Постоянный ток через емкость не течет.
Чтобы найти свободную составляющую переходного процесса, которая является общим решением однородного уравнения, необходимо записать характеристическое уравнение системы ОДУ (или ОДУ ей эквивалентного) и найти его корни. Из системы (6) можно исключить и , и для полученного ОДУ записать характеристическое уравнение. Но можно составить главный определитель системы (5) и приравнять его нулю:
отсюда
Корни характеристического уравнения:
— соответствует установившемуся режиму. Два других найдем из уравнения
или
Дискриминант этого квадратного уравнения имеет вид:
1) — корни действительные, разные
) — корни действительные, одинаковые
) — корни комплексные сопряженные
В первом случае свободная составляющая имеет вид
Во втором случае:
В третьем случае:
— есть действительная часть корней, св модуль мнимых частей корней.
Пусть в нашем случае корни действительные, различные, тогда, с учетом:
,
решение примет вид:
Для определения постоянных интегрирования и , запишем значение и его производную в начальный момент времени:
значения и определим из системы (5), записанной для начального момента времени :
.
Из законов коммутации:
,
тогда:
,
Для определения начального значения производной продифференцируем систему (5) и подставим
отсюда
из второго уравнения исходной системы при
Алгебраические уравнения для постоянных интегрирования:
Классический и операторный методы анализа переходных процессов в линейных электрических цепях
Репозиторий БГУИР: Теория электрических цепей. Справочник : учебно-метод. пособие : в 3 ч. Ч. 2 : Классический и операторный методы анализа переходных процессов в линейных электрических цепях
Справочник : учебно-метод. пособие : в 3 ч. Ч. 2 : Классический и операторный методы анализа переходных процессов в линейных электрических цепях
Skip navigation
Please use this identifier to cite or link to this item:
https://libeldoc.bsuir.by/handle/123456789/1301
| Title: | Теория электрических цепей. Справочник : учебно-метод. пособие : в 3 ч. Ч. 2 : Классический и операторный методы анализа переходных процессов в линейных электрических цепях |
| Authors: | Курулев, А. П. |
| Keywords: | учебно-методические пособия справочники электрические цепи методы анализа переходные процессы линейные электрические цепи |
| Issue Date: | 2012 |
| Publisher: | БГУИР |
| Citation: | Курулёв, А.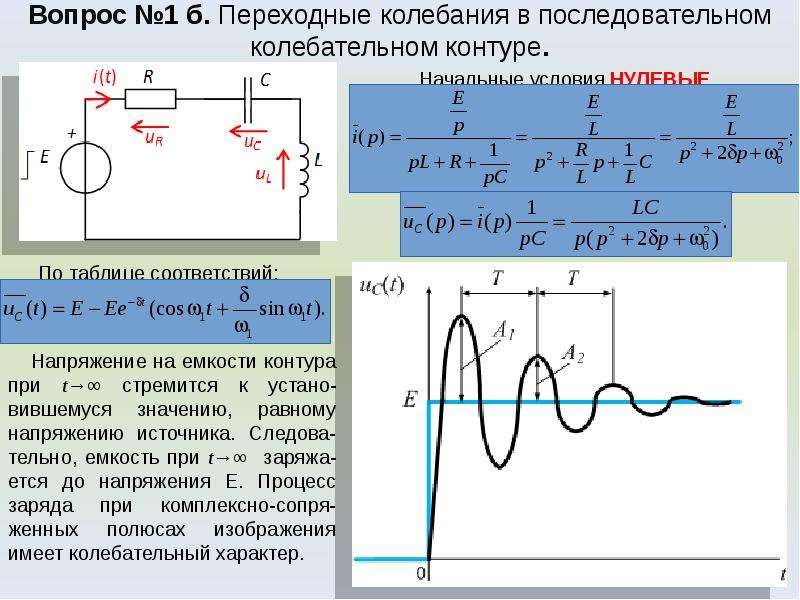 П. Теория электрических цепей. Справочник : учебно-метод. пособие : в 3 ч. Ч. 2 : Классический и операторный методы анализа переходных процессов в линейных электрических цепях / А. П. Курулёв. — Минск : БГУИР, 2012. — 52 с. П. Теория электрических цепей. Справочник : учебно-метод. пособие : в 3 ч. Ч. 2 : Классический и операторный методы анализа переходных процессов в линейных электрических цепях / А. П. Курулёв. — Минск : БГУИР, 2012. — 52 с. |
| Abstract: | В учебно-методическом пособии представлен справочный материал по
двум темам теории электрических цепей: классический (временной) метод анализа переходных процессов в линейных электрических цепях первого и второго порядка при подключении к источникам постоянного и синусоидального напряжения и операторный метод, в основе которого лежат преобразования Лапласа. Предназначено для студентов специальностей вузов, закреплённых за УМО по образованию в области информатики и радиоэлектроники, и преподавателей вузов читающих лекции и ведущих практические и лабораторные занятия по теории электрических цепей. |
| URI: | https://libeldoc.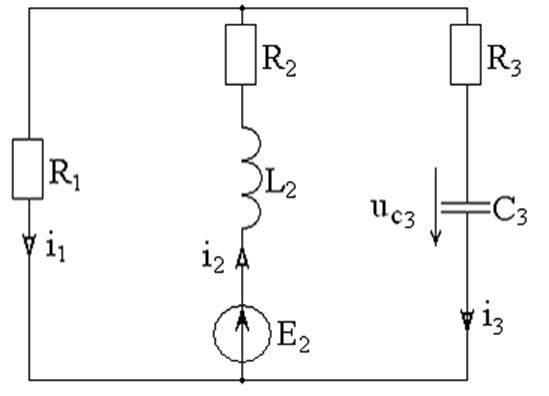 bsuir.by/handle/123456789/1301 bsuir.by/handle/123456789/1301 |
| ISBN: | 978-985-488-906-1 (ч. 2) |
| Appears in Collections: | Кафедра теоретических основ электротехники |
Items in DSpace are protected by copyright, with all rights reserved, unless otherwise indicated.
Переходные процессы в линейных электрических цепях с сосредоточенными параметрами
«ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ»
I. Расчет цепи второго порядка.
[pic 1]
Параметры цепи:
[pic 2],
[pic 3],
[pic 4],
[pic 5],
[pic 6].
Определить закон изменения напряжения [pic 7] после коммутации.
1. Классический метод.
1. Расчет докоммутационного установившегося режима.
[pic 8]
По методу двух узлов
[pic 9],
[pic 10],
[pic 11]
Законы коммутации:
[pic 12]
[pic 13].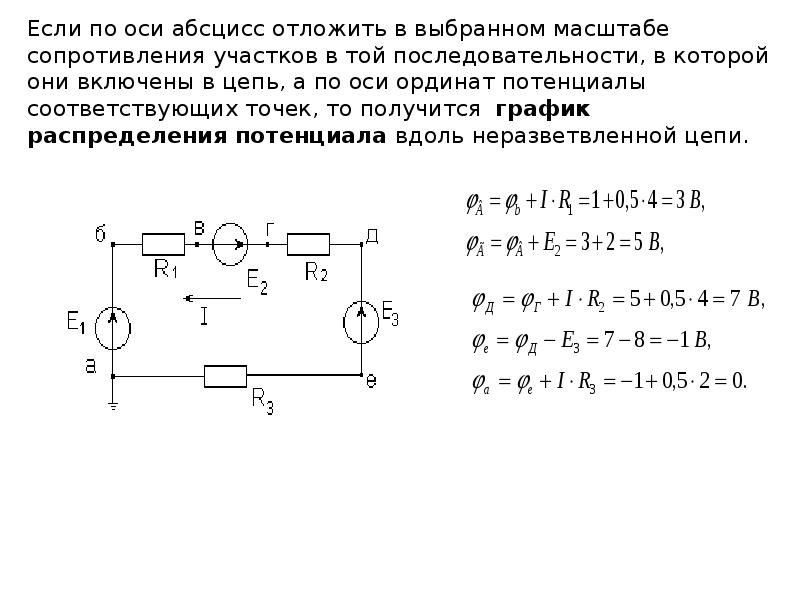
2. Расчет принужденной составляющей напряжения [pic 14].
Рассматриваемая цепь в принужденном режиме имеет вид:
[pic 15]
[pic 16].
3. Расчет свободной составляющей напряжения [pic 17].
Составим характеристическое уравнение методом входного сопротивления.
[pic 18]
В произвольной ветви разорвем цепь и запишем входное сопротивление:
[pic 19],
заменив [pic 20] на [pic 21], получим
[pic 22]
Приравняем [pic 23], получим характеристическое уравнение
[pic 24]
Подставим численные значения параметров цепи:
[pic 25],
корни характеристического уравнения
[pic 26].
Свободная составляющая напряжения
[pic 27].
4. Полное решение для напряжения [pic 28] после коммутации имеет вид
[pic 29]
5. Определение постоянных интегрирования [pic 30], используя законы коммутации и уравнения Кирхгофа при [pic 31].
[pic 32],
дифференцируя уравнение [pic 33] и подставляя [pic 34], получим уравнение
[pic 35].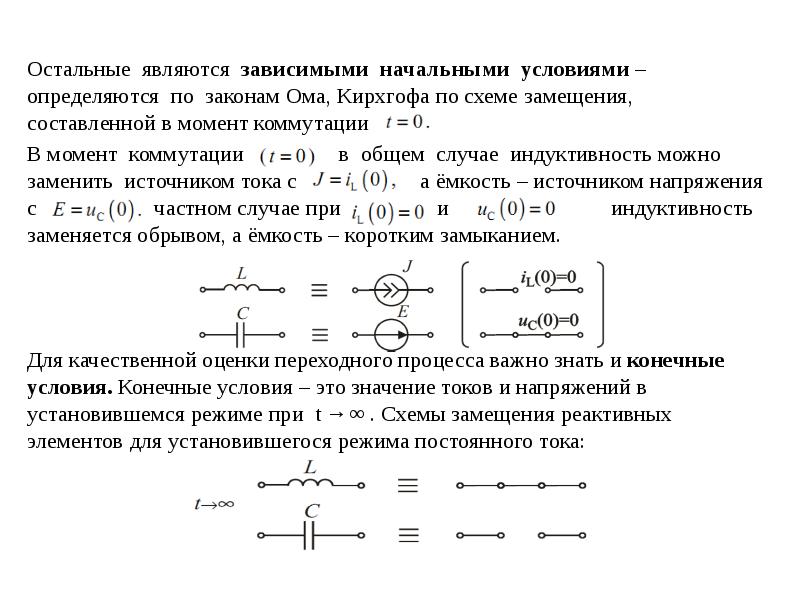
[pic 36]
Составляем уравнения по законам Кирхгофа при [pic 37]
[pic 38]
Из уравнения (4) выразим
[pic 39]
подставим в уравнение (5)
[pic 40]
откуда
[pic 41],
из уравнения (3) найдем
[pic 42]
[pic 43]
Дифференцируя уравнение (7), получим
[pic 44]
[pic 45].
Далее находим
[pic 46]
[pic 47],
[pic 48],
[pic 49].
Анализ переходных процессов — обзор
В этой главе мы систематически разработали различные методы анализа переходных процессов в электрических цепях первого и второго порядка. Наиболее важные факты и результаты, обсуждаемые в этой главе, можно резюмировать следующим образом:
Переходные процессы в электрических цепях возникают из-за наличия элементов накопления энергии (т. е. катушек индуктивности и конденсаторов).
Переходные процессы в электрических цепях могут быть вызваны начальными условиями, источниками или обоими.
Анализ переходных процессов можно разбить на два основных этапа:
- 1.
Определение начальных условий для элементов накопления энергии с использованием непрерывности напряжения на конденсаторе и непрерывности тока через индуктор.
- 2.
Анализ электрических цепей после коммутации. Этот шаг обычно включает решение начальных задач для обыкновенных дифференциальных уравнений.
Анализ переходных процессов, возбуждаемых начальными условиями, требует решения однородных дифференциальных уравнений при ненулевых начальных условиях.
Анализ переходных процессов, возбуждаемых источниками, требует решения неоднородных дифференциальных уравнений при нулевых начальных условиях.
Анализ переходных процессов, возбуждаемых источниками, требует решения неоднородных дифференциальных уравнений при нулевых начальных условиях.
Анализ переходных процессов, возбуждаемых начальными условиями и источниками, требует решения неоднородных уравнений при ненулевых начальных условиях.
Полное решение линейного неоднородного дифференциального уравнения можно представить в виде суммы частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения.
В случае возбуждения от источников переменного тока частное решение неоднородного уравнения может быть найдено с помощью метода фазора для расчета установившегося отклика.Частное решение имеет физический смысл принудительного ответа .
Общее решение соответствующего однородного уравнения имеет физический смысл свободной (переходной) реакции . Его расчет требует решения характеристических уравнений и определения неизвестных констант из начальных условий.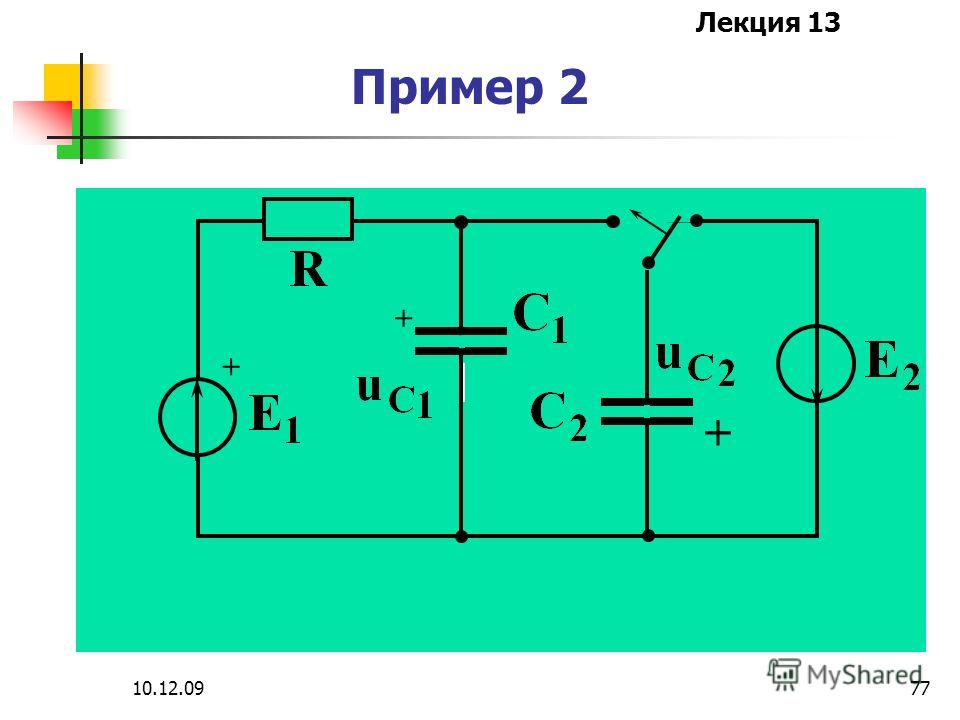
Характер переходного (свободного) отклика цепей второго порядка определяется корнями характеристического уравнения.Существует четыре различных случая:
- а)
передемпфированная реакция, когда два корня действительны, отрицательны и различны;
- b)
критически затухающий отклик, когда два корня действительны, отрицательны и идентичны;
- c)
отклик с недостаточным демпфированием, когда два корня комплексные и сопряженные;
- d)
незатухающий отклик, когда два корня являются мнимыми и сопряженными.
Механизм передаточных функций является очень мощным инструментом для анализа переходных процессов в электрических цепях.(с) находится как функция комплексной частоты с . Значение этой функции на частоте возбуждения ( с = jω ) полностью определяет переменный установившийся (вынужденный) отклик, а полюса передаточной функции определяют показатели степени и, следовательно, форму свободного отклика. Описанный подход носит алгебраический характер; он полностью избегает вывода и решения дифференциальных уравнений и полностью использует технику векторной техники.
Описанный подход носит алгебраический характер; он полностью избегает вывода и решения дифференциальных уравнений и полностью использует технику векторной техники.
Для расчета отклика электрической цепи на произвольный источник можно использовать интеграл свертки .Интеграл свертки имеет следующий вид: возбуждения источником напряжения v s ( t ), а i δ ( t ) – единичная импульсная характеристика, вызванная единичным импульсным возбуждением источника. Единичная импульсная характеристика может быть найдена как производная по времени единичной ступенчатой характеристики, которая, в свою очередь, может быть найдена из анализа переходных процессов электрической цепи, возбуждаемой единичным источником постоянного тока.Таким образом, анализ электрической цепи с помощью интеграла свертки состоит из двух основных этапов: а) расчет единичной импульсной характеристики; б) вычисление интеграла свертки для произвольного (но заданного) источника напряжения v s ( t ).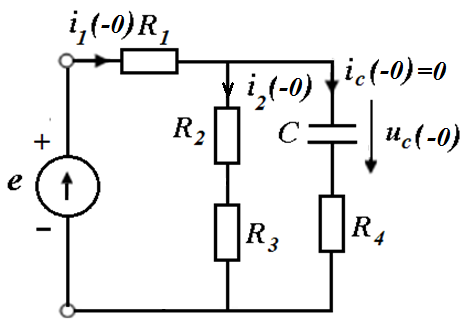 Выражения, подобные (7.464), справедливы для интегралов свертки, когда требуемой характеристикой схемы является напряжение и/или возбуждение схемы является источником тока.
Выражения, подобные (7.464), справедливы для интегралов свертки, когда требуемой характеристикой схемы является напряжение и/или возбуждение схемы является источником тока.
Диод представляет собой элемент с двумя выводами, сопротивление которого зависит от полярности приложенного напряжения.Идеальные диоды действуют как короткое замыкание, если приложенное напряжение положительное, и они действуют как разомкнутая цепь, если приложенное напряжение отрицательное. Диоды используются в схемах выпрямителей для преобразования источников переменного напряжения в источники постоянного напряжения. Один диод можно использовать для создания полуволнового выпрямителя . Схема диодного моста может быть использована для построения двухполупериодного выпрямителя . Элементы накопления энергии используются в схемах выпрямителей для снижения уровня пульсаций. Методы анализа переходных процессов электрических цепей могут быть использованы для анализа стационарного состояния выпрямителей .
Курсы PDH онлайн. PDH для профессиональных инженеров. ПДХ Инжиниринг.
«Мне нравится широта ваших курсов HVAC; не только экологичность или энергосбережение
курсы.»
Рассел Бейли, ЧП
Нью-Йорк
«Это укрепило мои текущие знания и научило меня дополнительно нескольким новым вещам
для раскрытия мне новых источников
информации.»
Стивен Дедак, ЧП
Нью-Джерси
«Материал был очень информативным и организованным. Я многому научился, и они были
очень быстро отвечают на вопросы.
Это было на высшем уровне. Будет использоваться
снова. Спасибо.»
Блэр Хейворд, ЧП
Альберта, Канада
«Легкий в использовании веб-сайт.Хорошо организовано. Я действительно воспользуюсь вашими услугами снова.
Я действительно воспользуюсь вашими услугами снова.
Я передам вашу компанию
имя для других на работе.»
Рой Пфлейдерер, ЧП
Нью-Йорк
«Справочный материал был превосходным, и курс был очень информативным, тем более что я думал, что уже знаком
с реквизитами Канзас
Авария в городе Хаятт.»
Майкл Морган, ЧП
Техас
«Мне очень нравится ваша бизнес-модель. Мне нравится возможность просмотреть текст перед покупкой. Я нашел класс
информативный и полезный
на моей работе.»
Уильям Сенкевич, Ч.Е.
Флорида
«У вас отличный выбор курсов и очень информативные статьи.Вы
— лучшее, что я нашел.»
Рассел Смит, ЧП
Пенсильвания
«Я считаю, что такой подход позволяет работающему инженеру легко зарабатывать PDH, предоставляя время для проверки
материал.»
Хесус Сьерра, ЧП
Калифорния
«Спасибо, что разрешили мне просмотреть неправильные ответы.На самом деле
человек узнает больше
от сбоев.»
Джон Скондрас, ЧП
Пенсильвания
«Курс был хорошо составлен, и использование тематических исследований является эффективным
способ обучения.»
Джек Лундберг, ЧП
Висконсин
«Я очень впечатлен тем, как вы представляете курсы; т.э., что позволяет
студент для ознакомления с курсом
материал перед оплатой и
получение викторины.»
Арвин Свангер, ЧП
Вирджиния
«Спасибо, что предлагаете все эти замечательные курсы. Я, конечно, выучил и
очень понравилось.»
Мехди Рахими, ЧП
Нью-Йорк
«Я очень доволен предлагаемыми курсами, качеством материала и простотой поиска и
подключение к Интернету
курсы.»
Уильям Валериоти, ЧП
Техас
«Этот материал в значительной степени оправдал мои ожидания. Курс был легким для понимания. Фотографии в основном давали хорошее представление о
обсуждаемые темы.»
Майкл Райан, ЧП
Пенсильвания
«Именно то, что я искал. Нужен 1 балл по этике, и я нашел его здесь.»
Джеральд Нотт, ЧП
Нью-Джерси
«Это был мой первый онлайн-опыт получения необходимых кредитов PDH. Это был
информативно, выгодно и экономично.
Очень рекомендую
всем инженерам.»
Джеймс Шурелл, ЧП
Огайо
«Я ценю, что вопросы «реального мира» и имеют отношение к моей практике, и
не основано на каком-то непонятном разделе
законов, которые не применяются
до «обычная» практика.»
Марк Каноник, ЧП
Нью-Йорк
«Отличный опыт! Я многому научился, чтобы использовать его в своем медицинском устройстве
организация.»
Иван Харлан, ЧП
Теннесси
«Материал курса имеет хорошее содержание, не слишком математический, с хорошим акцентом на практическое применение технологий.»
Юджин Бойл, П.Е.
Калифорния
«Это был очень приятный опыт. Тема была интересной и хорошо представлена,
а онлайн формат был очень
доступный и простой
использование. Большое спасибо.»
Патрисия Адамс, ЧП
Канзас
«Отличный способ добиться соответствия непрерывному обучению PE в рамках временных ограничений лицензиата.»
Джозеф Фриссора, ЧП
Нью-Джерси
«Должен признаться, я действительно многому научился. Распечатанная викторина помогает во время
просмотр текстового материала. я
также оценил просмотр
предоставлены фактические случаи.»
Жаклин Брукс, ЧП
Флорида
«Документ Общие ошибки ADA в проектировании помещений очень полезен.
тест требовал исследований в
документ но ответы были
всегда в наличии.»
Гарольд Катлер, ЧП
Массачусетс
«Это было эффективное использование моего времени. Спасибо за разнообразие выбора
в дорожной технике, что мне нужно
для выполнения требований
Сертификация PTOE.»
Джозеф Гилрой, ЧП
Иллинойс
«Очень удобный и доступный способ заработать CEU для выполнения моих требований в штате Делавэр.»
Ричард Роудс, ЧП
Мэриленд
«Узнал много нового о защитном заземлении. До сих пор все курсы, которые я проходил, были отличными.
Надеюсь увидеть больше 40%
Курсы со скидкой.»
Кристина Николас, ЧП
Нью-Йорк
«Только что сдал экзамен по радиологическим стандартам и с нетерпением жду дополнительных
курсы. Процесс прост, и
намного эффективнее, чем
необходимость путешествовать.»
Деннис Мейер, ЧП
Айдахо
«Услуги, предоставляемые CEDengineering, очень полезны для профессионалов
Инженеры для приобретения блоков PDH
в любое время.Очень удобно.»
Пол Абелла, ЧП
Аризона
«Пока все было отлично! Поскольку я постоянно работаю матерью двоих детей, у меня не так много
пора искать куда
получить мои кредиты от.»
Кристен Фаррелл, ЧП
Висконсин
«Это было очень информативно и поучительно.Легко понять с иллюстрациями
и графики; определенно делает его
легче впитывать все
теорий.»
Виктор Окампо, инженер.
Альберта, Канада
«Хороший обзор принципов полупроводников. Мне понравилось проходить курс по телефону
.
мой собственный темп во время моего утра
на метро
на работу.»
Клиффорд Гринблатт, ЧП
Мэриленд
«Просто найти интересные курсы, скачать документы и получить
викторина. Я бы очень рекомендую
вам в любой PE нуждающийся
Единицы CE.»
Марк Хардкасл, ЧП
Миссури
«Очень хороший выбор тем во многих областях техники.»
Рэндалл Дрейлинг, ЧП
Миссури
«Я заново узнал то, что забыл. Я также рад помочь финансово
от ваш рекламный адрес электронной почты который
сниженная цена
на 40%.»
Конрадо Касем, П.Е.
Теннесси
«Отличный курс по разумной цене. Буду пользоваться вашими услугами в будущем.»
Чарльз Флейшер, ЧП
Нью-Йорк
«Это был хороший тест, и я фактически проверил, что я прочитал профессиональную этику
Коды
и Нью-Мексико
правила.»
Брун Гильберт, П.Е.
Калифорния
«Мне очень понравились занятия. Они стоили времени и усилий.»
Дэвид Рейнольдс, ЧП
Канзас
«Очень доволен качеством тестовых документов. Буду использовать CEDengineerng
при необходимости дополнительного
Сертификация
.»
Томас Каппеллин, П.Е.
Иллинойс
«У меня истек срок действия курса, но вы все равно выполнили обязательство и дали
мне то, за что я заплатил — много
с благодарностью!»
Джефф Ханслик, ЧП
Оклахома
«CEDengineering предлагает удобные, экономичные и актуальные курсы
для инженера.»
Майк Зайдл, П.Е.
Небраска
«Курс был по разумной цене, а материал был кратким и
в хорошем состоянии.»
Глен Шварц, ЧП
Нью-Джерси
«Вопросы соответствовали урокам, а материал урока
хороший справочный материал
для дизайна под дерево.»
Брайан Адамс, П.Е.
Миннесота
«Отлично, удалось получить полезную информацию с помощью простого телефонного звонка.»
Роберт Велнер, ЧП
Нью-Йорк
«У меня был большой опыт прохождения курса «Строительство прибрежных районов — Проектирование»
Корпус Курс и
очень рекомендую.»
Денис Солано, ЧП
Флорида
«Очень понятный, хорошо организованный веб-сайт. Материалы курса этики штата Нью-Джерси были очень
прекрасно приготовлено.»
Юджин Брекбилл, ЧП
Коннектикут
«Очень хороший опыт. Мне нравится возможность загружать учебные материалы на
обзор везде и
когда угодно.»
Тим Чиддикс, ЧП
Колорадо
«Отлично! Поддерживайте широкий выбор тем на выбор.»
Уильям Бараттино, ЧП
Вирджиния
«Процесс прямой, никакой чепухи. Хороший опыт.»
Тайрон Бааш, П.Е.
Иллинойс
«Вопросы на экзамене были пробными и демонстрировали понимание
материала. Тщательный
и полный.»
Майкл Тобин, ЧП
Аризона
«Это мой второй курс, и мне понравилось то, что курс предложил мне, что
поможет в моей линии
работы.»
Рики Хефлин, ЧП
Оклахома
«Очень быстрая и простая навигация. Я определенно воспользуюсь этим сайтом снова.»
Анджела Уотсон, ЧП
Монтана
«Прост в исполнении. Нет путаницы при подходе к сдаче теста или записи сертификата.»
Кеннет Пейдж, П.Е.
Мэриленд
«Это был отличный источник информации о нагревании воды с помощью солнечной энергии. Информативный
и отличное освежение.»
Луан Мане, ЧП
Коннетикут
«Мне нравится подход к подписке и возможности читать материалы в автономном режиме, а затем
вернись, чтобы пройти тест.»
Алекс Млсна, П.Е.
Индиана
«Я оценил количество информации, предоставленной для класса. Я знаю
это вся информация, которую я могу
использование в реальных жизненных ситуациях.»
Натали Дерингер, ЧП
Южная Дакота
«Материалы обзора и образец теста были достаточно подробными, чтобы я мог
успешно завершено
курс.»
Ира Бродская, ЧП
Нью-Джерси
«Веб-сайт прост в использовании, вы можете скачать материал для изучения, а затем вернуться
и пройти тест. Очень
удобный а на моем
собственное расписание.»
Майкл Гладд, ЧП
Грузия
«Спасибо за хорошие курсы на протяжении многих лет.»
Деннис Фундзак, ЧП
Огайо
«Очень легко зарегистрироваться, получить доступ к курсу, пройти тест и распечатать PDH
сертификат
. Спасибо за создание
процесс простой.»
Фред Шайбе, ЧП
Висконсин
«Положительный опыт.Быстро нашел подходящий мне курс и закончил
PDH за один час в
один час.»
Стив Торкилдсон, ЧП
Южная Каролина
«Мне понравилась возможность загрузки документов для ознакомления с содержанием
и пригодность до
наличие для оплаты
материал .»
Ричард Ваймеленберг, ЧП
Мэриленд
«Это хорошее пособие по ЭЭ для инженеров, не являющихся электриками.»
Дуглас Стаффорд, ЧП
Техас
«Всегда есть место для улучшения, но я ничего не могу придумать в вашем
процесс, которому требуется
улучшение.»
Томас Сталкап, ЧП
Арканзас
«Мне очень нравится удобство прохождения викторины онлайн и получения немедленного
Сертификат
.»
Марлен Делани, ЧП
Иллинойс
«Обучающие модули CEDengineering — очень удобный способ доступа к информации по
многие различные технические области снаружи
по собственной специализации без
необходимость путешествовать.»
Гектор Герреро, ЧП
Грузия
Анализ переходных процессов линейной цепи
— MATLAB & Simulink
В этом примере показано стационарное и переходное моделирование линейной цепи.
H. Le-Huy (Университет Лаваля, Квебек) и G. Sybille (Hydro-Quebec)
Описание
Эта схема представляет собой упрощенную модель трехфазной энергосистемы на 230 кВ. Представлена только одна фаза системы передачи.2/2000e6 = 26,45 Ом или L = 0,0702 Гн, R = X/10 = 2,645 Ом). Источник питает нагрузку RL через линию передачи длиной 150 км. Распределенные параметры линии (R = 0,035 Ом/км, L = 0,92 мГн/км, C = 12,9 нФ/км) моделируются одним пи-участком (ветвь RL1 5,2 Ом; 138 мГн и двумя шунтирующими емкостями С1 и С2 по 0,967). мкФ). Нагрузка (75 МВт — 20 МВар на фазу) моделируется параллельным блоком нагрузки RLC.
Автоматический выключатель используется для переключения нагрузки на приемном конце линии передачи.Первоначально замкнутый выключатель размыкается при t = 2 цикла, затем снова включается при t = 7 циклов. Блоки измерения тока и напряжения предоставляют сигналы для целей визуализации.
Моделирование
1. Моделирование с использованием непрерывного решателя (ode23tb)
Запустите моделирование и наблюдайте переходные процессы линейного напряжения и тока нагрузки во время переключения нагрузки и обратите внимание, что моделирование начинается в установившемся режиме. Используйте кнопки масштабирования осциллографа, чтобы наблюдать переходное напряжение при повторном включении выключателя.
2. Использование Powergui для получения векторов установившегося состояния и установки начальных состояний
Откройте блок Powergui и выберите «Стационарное напряжение и ток» для измерения установившегося напряжения и тока. Используя Powergui, выберите «Настройка начальных состояний», чтобы получить значения начального состояния (напряжение на конденсаторах и ток в индуктивностях). Теперь сбросьте все начальные состояния до нуля, нажав кнопку «Обнулить», а затем «Применить», чтобы подтвердить изменения.Перезапустите симуляцию и наблюдайте переходные процессы при запуске симуляции. Используя то же окно Powergui, вы также можете установить для выбранных состояний определенные значения.
3. Дискретизация схемы и моделирование с фиксированными шагами
Блок Powergui также можно использовать для дискретизации схемы и ее моделирования с фиксированными шагами. Откройте PowerGuy. Выберите «Дискретизировать электрическую модель» и задайте шаг расчета 50e-6 с. Модель в пространстве состояний теперь будет дискретизирована с использованием трапецеидального интегрирования с фиксированным шагом.Точность результатов теперь зависит от времени расчета. Перезапустите симуляцию и сравните результаты симуляции с методом непрерывной интеграции. Измените шаг расчета дискретной системы и обратите внимание на влияние на точность быстрых переходных процессов.
4. Использование векторного метода моделирования
Теперь вы будете использовать третий метод моделирования. Метод «фазорного моделирования» состоит в замене модели в пространстве состояний схемы набором алгебраических уравнений, оцениваемых на фиксированной частоте, и замене синусоидальных источников напряжения и тока векторами (комплексными числами).Этот метод позволяет быстро вычислить векторы напряжения и тока на выбранной частоте, игнорируя быстрые переходные процессы. Особенно эффективно исследование электромеханических переходных процессов генераторов и двигателей с низкочастотными модами колебаний. Откройте блок Powergui и выберите «Фазорное моделирование». Перезапустите симуляцию. Обратите внимание, что величина напряжения и тока 60 Гц теперь отображается на осциллографе. Если дважды щелкнуть блок измерения напряжения или тока, можно выбрать вывод векторных сигналов в четырех различных форматах: Комплексный, Действительный/Изображение, Величина/Угол (в градусах) или просто Величина (значение по умолчанию).Обратите внимание, что вы не можете отправить сложный сигнал на осциллограф.
Электрические переходные процессы в энергосистемах
Дата публикации: 21 октября 2020 г. Последнее обновление: 21 октября 2020 г. Абдур Рехман
Электрические переходные процессы могут возникать в энергосистемах из различных источников и оказывать неблагоприятное воздействие на оборудование и надежность энергосистемы. Лучше всего знать о возможных источниках на вашем предприятии и защищаться от них. Читайте дальше, чтобы узнать больше о переходных процессах в энергосистеме.
Возможно, вы уже слышали слово «переходный процесс», означающее что-то, что длится в течение очень короткого периода времени, но когда дело доходит до систем электроснабжения, переходные процессы — это и многое другое.
Мы только что запустили нашу серию Power Systems Engineering Vlog , и в этой серии мы собираемся рассказать о всевозможных исследованиях и комментариях по инженерным системам питания. Мы рассмотрим различные блоги, написанные AllumiaX. Это весело, живо, по сути это видеоблог, и мы надеемся, что вы присоединитесь к нам и получите от этого пользу.
Что такое электрические переходные процессы?
Внезапные и кратковременные всплески энергии, вызванные линиями питания или передачи данных и связи в коммунальном предприятии или любом другом объекте, известны как электрические переходные процессы.
Имеют характеристику чрезвычайно высокого напряжения, которое вызывает большой ток в электрической цепи, длящийся от менее чем микросекунды до нескольких миллисекунд. Следовательно, система переходит из устойчивого состояния в кратковременное возмущенное состояние и обратно.Стабильное состояние после затухания переходного процесса также называется установившимся состоянием.
Большинство электрических переходных процессов не имеют большой величины, но все же являются критическими из-за их влияния на работу цепей и прерывающих или защитных устройств.
Переходные процессы в энергосистемах следуют по пути наименьшего сопротивления к земле и могут нагревать компоненты схемы и полупроводниковые устройства, вызывая неисправности и отказы. Кроме того, значительное количество этих электрических переходных процессов имеет достаточную величину, чтобы вызвать пробой изоляции оборудования в энергосистеме.
Неблагоприятные условия во время переходного процесса могут нанести серьезный ущерб оборудованию защиты энергосистемы и распределительному устройству. Их влияние на устройства зависит от самого устройства и его расположения в системе электропитания.
Поэтому инженеры по энергосистемам всегда изобретают способы и средства для ограничения величины создаваемых переходных процессов и контроля их воздействия на работающее оборудование.
Причины переходных процессов в энергосистемах
Существуют различные причины переходных процессов в энергосистеме, однако все пути и источники, из которых могут возникать переходные процессы, можно классифицировать как внутренние или внешние источники.
Внутренние источники
Электрическая система или объект состоит из множества различных компонентов и устройств, как внутри объекта, так и за пределами коммунальной сети. Внутри объекта индуктивные компоненты, такие как трансформаторы и двигатели, могут генерировать переходные напряжения в электрических системах. Когда ток в этих устройствах нарушается, магнитное поле разрушается, что приводит к импульсам напряжения или переходным процессам. Несколько факторов, таких как расположение переходного процесса в системе, размер источника, временной интервал и время нарастания, влияние на соседнее оборудование и конфигурация электрической системы, определяют общий эффект этих электрических переходных процессов.Несколько источников переходных напряжений на объекте представлены в следующем списке:
- Переключение конденсаторов
- Прерывание тока (двигатели и т. д.)
- Работа с силовой электроникой (тиристоры и т. д.)
- Электростатический разряд
- (Дуговая) сварка
- Копировальные машины
- Неисправность проводки или работа автоматического выключателя
- Замыкание контактов и реле
- Загрузка загрузки или отключение
Внутренние источники не производят скачков напряжения большой величины.Опыт показывает, что переходные процессы, вызванные внутренними источниками, едва ли увеличат напряжение системы вдвое по сравнению с нормальным значением.
Внешние источники
Несколько источников переходных напряжений, находящихся вне установки:
- Молния
- Переключение конденсаторов
- Линейно-кабельное переключение
- Переключение трансформатора
- Срабатывание токоограничивающего предохранителя
Хотя переходные процессы напряжения, возникающие вне электрической системы, могут влиять на работу объекта, более распространены внутренние переходные процессы и источники напряжения.Повседневная работа устройств на объекте, таких как двигатели, сварочные станции, электропечи, печи, индукционные нагреватели и т. д., может вызывать переходные процессы напряжения, влияющие на соседнее оборудование.
Типы переходных процессов
Согласно определению стандарта IEEE 1159-2019, существует два типа переходных процессов: импульсные и колебательные.
Внезапное и не связанное с сетью изменение частоты напряжения или тока или того и другого, которое является однонаправленным по полярности, классифицируется как импульсный переходный процесс и называется Импульсным.Примером импульсивного переходного процесса может быть переходный процесс молнии или электростатический разряд.
И наоборот, внезапное и не относящееся к силовой частоте изменение напряжения или тока или того и другого, которое является двунаправленным по полярности, классифицируется как колебательный переходный процесс. Примером причины может быть включение батареи конденсаторов или коммутация кабеля.
Природа переходных процессов в энергосистемах
Переходные напряжения обычно длятся от менее микросекунд до нескольких миллисекунд.
В зависимости от того, где они возникают в энергосистеме, переходные процессы можно разделить на два типа.
Если переходный процесс возникает между любыми двумя силовыми или сигнальными проводниками, он называется нормальным переходным процессом.
Если это происходит одинаково между и в фазе от каждого силового или сигнального проводника к земле, это называется синфазным переходным процессом.
Повреждение оборудования может быть вызвано переходными процессами несколькими способами, включая пробой диэлектрика, электрическое перекрытие, разрушение, тепловые и мгновенные перегрузки пиковой мощности, а также превышение пределов dV/dt и dI/dt .
Переходные процессы также могут привести к тому, что диэлектрический материал станет электропроводным, если он имеет достаточно большую величину. В случае, когда воздух является диэлектриком, например, при физическом разделении двух проводящих сред с двумя разными потенциалами напряжения, пробой диэлектрика обычно называют электрическим перекрытием (или вспышкой дуги). Электрические напряжения, связанные с переходными процессами напряжения, преобразуются в механическую энергию, что приводит к разрушению материалов компонентов как на микроскопическом, так и на макроуровне.
Переходные процессы также производят тепловую энергию, неблагоприятно изменяя изоляционный материал на молекулярном уровне. Скорость изменений напряжения и тока, связанных с переходными процессами, также играет важную роль в воздействии этих нагрузок на открытые материалы и компоненты.
Эффекты электрических переходных процессов
Влияние скачков напряжения на электронное оборудование обычно подпадает под одну из четырех категорий:
- Периодическое прерывание
- Хроническая деградация
- Скрытый сбой
- Катастрофический сбой
Прерывистое прерывание — это когда в сеть передачи данных или управления вводится кратковременное событие, что приводит к потере или повреждению данных.Это может привести к блокировке, отключению или неправильной работе нагрузки или устройства.
Хроническая деградация может происходить, когда повторяющиеся переходные процессы снижают целостность и надежность незащищенного компонента. В течение нескольких дней, недель или даже месяцев кумулятивный эффект переходных напряжений приводит к возможной неработоспособности уязвимого компонента. Поскольку переходные напряжения в этом случае часты и относительно постоянны, возможно определить местонахождение их источника.
Скрытые отказы аналогичны хронической деградации, за исключением того, что они вызваны значительным переходным событием, которое повреждает компоненты, но не до такой степени, что компонент не может выполнять свою предназначенную функцию. С течением времени — опять же дней, недель или даже месяцев — обычные нагрузки, вызванные нормальной работой, приводят к неработоспособности компонента. Этот тип режима труднее устранять, поскольку основная причина сбоя могла возникнуть в неопределенное время в прошлом.
Катастрофические отказы из-за переходных напряжений легко идентифицируются и обнаруживаются, поскольку поврежденный компонент или устройство почти сразу перестает функционировать должным образом, и даже повреждение может быть видимым. В этом случае пиковая величина или скорость нарастания напряжения переходного процесса превышают номинальный порог компонента таким образом, что создается постоянный разомкнутая цепь или короткое замыкание внутри компонента. Вероятность корреляции отказа компонента с нарушением энергосистемы при таком типе события обычно выше.
Устройства, такие как микропроцессорные устройства и программируемые логические контроллеры (ПЛК), особенно подвержены повреждениям из-за скачков напряжения. Соответственно, воздействие скачков напряжения может снизить надежность и сократить срок службы этих типов оборудования. По мере развития технологий и сокращения масштабов этих устройств компоненты устройств становятся меньше, а их восприимчивость к повреждениям от переходных процессов напряжения увеличивается.
Было показано, что переходные напряжения могут мешать нормальной работе оборудования, что приводит к неустойчивому поведению и снижению качества конечного продукта.Кроме того, перерывы в непрерывных производственных процессах могут привести к потере доходов из-за простоя производства.
Устройства для смягчения переходных процессов
Переходные процессы или скачки напряжения в энергосистеме могут быть вызваны переключением или другими причинами, но наиболее важными и опасными являются скачки напряжения, вызванные молнией. Обычно используемые устройства для защиты от грозовых перенапряжений:
- Экран заземления
- Воздушные грозозащитные тросы
- Грозозащитные разрядники или устройства защиты от перенапряжений
1.Экран заземления
Электростанции и подстанции состоят из дорогостоящего оборудования, которое нуждается в защите от прямых ударов молнии. Это достигается за счет использования заземляющего экрана, представляющего собой сеть медных проводников, размещенных вокруг и над оборудованием наподобие экрана или клетки. Этот экран подключается к заземлению не менее чем в двух точках. В случае прямого удара молнии экран отводит молнию от оборудования на землю, тем самым защищая оборудование.Для подробного объяснения видео, нажмите здесь.
2. Воздушные заземляющие провода
Другим эффективным способом защиты линий электропередачи от ударов молнии является использование грозозащитного троса. Заземляющие провода располагаются выше линейных проводников и заземляются вблизи башни или столба таким образом, чтобы в случае удара молнии молния перехватывалась заземляющим проводом и направлялась на землю, защищая, таким образом, линейные проводники. Для подробного объяснения видео, нажмите здесь.
3. Грозовые разрядники
Экран заземления и заземляющие провода не могут обеспечить защиту оборудования от скачков напряжения, которые могут достигать клемм оборудования. Здесь используется молниеотвод. Молниезащитный разрядник работает, отводя скачок высокого напряжения на землю. Он состоит из искрового разрядника, последовательно соединенного с нелинейным резистором. Он подключается параллельно устройству, которое он должен защищать, т. е. между линией и землей. Длина зазора установлена таким образом, что нормального линейного напряжения недостаточно, чтобы вызвать дугу через зазор, но опасно высокое напряжение разрушит воздушную изоляцию и сформирует дугу.Свойство нелинейного сопротивления заключается в том, что его сопротивление уменьшается с увеличением напряжения (или тока) и наоборот. Для подробного объяснения видео, нажмите здесь
Чтобы узнать больше об устройствах, которые защищают от переходных процессов и скачков напряжения, следите за нашим блогом, написанным на
Устройства защиты от перенапряжения
Анализ переходных процессов и исследование стабильности с использованием программного обеспечения
Чтобы обеспечить надежную работу энергосистемы и правильно спланировать ее расширение, инженеры по энергосистемам проводят различные исследования сети.Наиболее распространенные виды сетевых исследований:
- Анализ короткого замыкания (или неисправности),
- Анализ потока мощности (или нагрузки),
- Анализ стабильности и
- Анализ электромагнитных переходных процессов.
Среди них исследования, связанные с электромагнитными переходными процессами, вероятно, являются наиболее сложными.
Крайне важно понимать переходные процессы в электроэнергетических системах и влияние возникающих в результате помех для надежной работы и устойчивости энергосистемы.С этой целью инженеры по энергосистемам используют инструмент численного анализа Альтернативная программа переходных процессов — Программа электромагнитных переходных процессов (ATP-EMTP). Этот инструмент широко используется для распознавания и решения переходных процессов в силовых сетях и компонентах.
АТП-ЭМТП — универсальный программный комплекс для цифрового моделирования переходных процессов как электромагнитной, так и электромеханической природы. При этом можно моделировать сложные сети и системы управления произвольной структуры. Он имеет широкие возможности моделирования и дополнительные важные функции, помимо расчета переходных процессов.За последние 20 лет он постоянно улучшался благодаря вкладу международных групп и органов.
Благодаря своей точности, быстроте и удобному интерфейсу EMTP используется во всем мире в качестве справочного инструмента основными субъектами отрасли энергосистем (энергетическими компаниями, компаниями и консультантами) для проектов, проектирования и проектирования или для решения проблем. и необъяснимые сбои. Он стал стандартом де-факто в отрасли из-за его способности эффективно и быстро выполнять моделирование очень больших энергосистем, его численной надежности и стабильности механизма моделирования.
Выполнение исследования переходной устойчивости
Исследование переходной стабильности представляет собой двухэтапный процесс, включающий:
Идентификация и квантование переходных процессов
Рассматриваемая энергосистема подвергается критическому анализу и моделируется с использованием программы электромагнитных переходных процессов (EMTP) для обнаружения основной причины переходных помех, и после ее выявления в программе моделируется «наихудший сценарий». Ключевые параметры переходного возмущения, такие как его величина, скорость нарастания, продолжительность, частота и энергия, извлекаются из моделирования.
Разработка подходящей схемы смягчения последствий
Выбирается и разрабатывается подходящая схема смягчения в соответствии с параметрами, извлеченными из моделирования, и характеристической частотной характеристикой рассматриваемой системы, чтобы обеспечить наилучшее всестороннее решение для снижения переходных процессов до безопасного уровня.
AllumiaX, LLC проводит исследования переходной стабильности. Некоторые из схем смягчения последствий, в которых AllumiaX, LLC имеет опыт, включают в себя демпферы и разрядники в качестве подавителей переходных процессов. Нажмите, чтобы узнать больше и получить предложение для вашего объекта
Принципы работы ATP-EMTP
Программное обеспечение использует трапецеидальное правило интегрирования для решения дифференциальных уравнений компонентов системы во временной области.
Для обеспечения ненулевых начальных условий либо автоматически выполняется стационарное векторное решение, либо они могут быть введены пользователем для более простых компонентов.
Программа также предлагает возможность взаимодействия с такими модулями, как Transient Analysis of Control Systems и MODELS (язык моделирования), позволяющими моделировать системы управления и компоненты с нелинейными характеристиками, такими как дуги и корона.
Допускаются помехи, симметричные или асимметричные, такие как грозовые перенапряжения, неисправности или любые операции переключения.
Переходные процессы могут происходить естественным образом или быть вызваны работой устройства в помещении, но в любом случае они неизбежны. Поэтому важно смоделировать объект, имея в виду такие случаи, и установить устройства защиты от переходных процессов после проведения детального изучения объекта с использованием программного обеспечения для анализа переходных процессов для надежной и безопасной энергосистемы.
Об авторе
Абдур Рехман (Abdur Rehman) — профессиональный инженер-электрик с более чем восьмилетним опытом работы с оборудованием от 208 В до 115 кВ как в коммунальных, так и в промышленных и коммерческих помещениях. Особое внимание он уделяет исследованиям в области защиты энергосистем и инженерии.
Введение в защиту от переходных процессов
Переходные процессы (кратковременные скачки напряжения или тока) могут нарушить работу или повредить устройства, подключенные к сигнальным линиям или линиям электропередач.Обычные источники энергии переходных процессов, связанные с молнией, электростатическим разрядом и цепями, испытывающими внезапное изменение тока из-за размыкания выключателя или короткого замыкания.
Устройства защиты от переходных процессов пытаются перенаправить энергию в этих переходных процессах, используя различия между формой волны переходного процесса и предполагаемой формой волны сигнала или мощности. Наиболее распространенные схемы защиты от переходных процессов ограничивают амплитуду напряжения, амплитуду тока или время перехода в цепи, которую они защищают.
Устройства ограничения напряжения
На рис. 1 показано, как можно использовать устройство защиты от переходных процессов с ограничением напряжения для защиты входа компонента СБИС, установленного на печатной плате. При нормальных напряжениях сигнала или питания устройство имеет высокое сопротивление и не оказывает существенного влияния на работу схемы. Однако, если напряжение на устройстве превышает пороговое значение, импеданс на его клеммах внезапно уменьшается, отводя ток от защищаемого компонента.
Рис. 1. Ограничивающая напряжение защита от переходных процессов на печатной плате.
Диоды
Диоды
, пожалуй, самые распространенные защитные устройства для низковольтных приложений. Несмещенный диод обычно имеет высокий импеданс, когда потенциал на его клеммах ниже примерно 0,5 вольт. Импеданс быстро падает при более высоких напряжениях. Диоды могут быть объединены последовательно для достижения более высоких пороговых напряжений или могут использоваться диоды Зенера с обратным смещением.Как правило, диоды используются в приложениях, требующих порогового напряжения от 0,5 до нескольких вольт.
Диоды
являются ограничивающими напряжение устройствами , что означает, что они проводят ток, достаточный для удержания напряжения на пороговом уровне. Они относительно быстродействующие с достаточно коротким временем отклика для защиты чувствительных полупроводниковых входов. Однако диоды, как правило, не способны рассеивать много энергии до выхода из строя. Неисправный диод может выглядеть как обрыв цепи или короткое замыкание, но, скорее всего, он выйдет из строя из-за короткого замыкания.
Варисторы
Варисторы — это еще один тип устройства ограничения напряжения, часто изготавливаемого из порошка оксида металла. Варисторы могут иметь пороговое напряжение от 0,5 до 10 вольт. Как правило, они способны рассеивать больше энергии, чем диоды, но они также, вероятно, имеют большую паразитную емкость, что может сделать их непригодными для приложений с высокоскоростными сигналами. Как и у диодов, у них больше шансов выйти из строя накоротко, чем разомкнуться.
Тиристоры
Тиристоры представляют собой полупроводниковые устройства, подобные диодам.Однако они, как правило, способны рассеивать гораздо больше энергии, чем диоды, и их можно найти с различными пороговыми напряжениями. В отличие от диодов и варисторов, тиристоры являются ломовыми приборами, а это значит, что они эффективно «закорачивают» при превышении их порогового напряжения и падении напряжения на них почти до нуля.
Газоразрядные устройства
Молниезащита для раннего телефонного оборудования в домах состояла из двух заостренных кусков металла, расположенных в непосредственной близости.Когда напряжение на этих металлических деталях превышало пороговое значение, воздух между металлическими частями разрушался, образуя дугу. Это по-прежнему эффективная схема защиты от переходных процессов для больших напряжений, но сегодняшние устройства заключены в стеклянную или пластиковую трубку, заполненную газом, который разрушается более предсказуемо, чем воздух.
Газоразрядные трубки способны рассеивать относительно большое количество энергии без повреждений. Они также имеют относительно низкую емкость, поэтому они с меньшей вероятностью будут искажать быстрые или высокочастотные сигналы.Как правило, они разрабатываются с пороговыми напряжениями от 10 до 100 вольт и представляют собой ломовые устройства, такие как тиристоры.
Газоразрядные трубки, скорее всего, не открываются, из-за чего трудно определить, правильно ли они работают. Однако неисправная газоразрядная трубка не помешает нормальной работе устройства, к которому она подключена. Неоновые лампы ведут себя как газоразрядные лампы и могут быть недорогим способом обеспечения первичной защиты от переходных процессов (порог ~ 70 вольт) для многих приложений.
Токоограничивающие устройства
Такие устройства, как предохранители, автоматические выключатели и устройства тепловой защиты, срабатывают от тока, а не от напряжения. Эти устройства размещаются последовательно с силовыми или сигнальными линиями, ведущими к защищаемому оборудованию. Обычно они имеют очень низкий импеданс, но размыкаются (становятся высокоимпедансными), когда через них протекает слишком большой ток. После срабатывания устройства ограничения тока блокируют передачу энергии на защищаемое оборудование, не рассеивая эту мощность в виде тепла.Поэтому практически нет ограничений на количество энергии (или мощности), с которой они могут справиться. Однако токоограничивающие устройства обычно не реагируют достаточно быстро, чтобы защитить оборудование от быстрых переходных процессов, вызванных молнией или электростатическим разрядом.
Устройства ограничения времени перехода
Устройствам ограничения напряжения и тока требуется определенное время для срабатывания. Если переходный процесс быстрый, повреждение может произойти до того, как защитное устройство успеет сработать.Часто лучшей защитой от переходных процессов является простой конденсатор или ферритовая шайба, предназначенная для замедления любого изменения напряжения или тока из-за наведенного переходного процесса.
На рис. 2 показано, как конденсатор на чувствительном входе компонента СБИС может замедлить время нарастания, связанное с любыми индуцируемыми переходными процессами. Часто входы интегральных схем реагируют на очень быстрые переходные процессы, даже если это не требуется для правильной работы устройства. Например, вход сброса на микропроцессоре обычно не переключается на частой основе.Когда он переключается, обычно не имеет значения, происходит ли переключение в микросекундах или миллисекундах. Тем не менее, эти входы часто реагируют на переходные процессы порядка наносекунд. Замедление этих входов путем добавления шунтирующего конденсатора может устранить проблемы, связанные с очень быстрыми переходными процессами (например, вызванными электростатическим разрядом), без какого-либо неблагоприятного воздействия на работу устройства.
Рис. 2. Использование фильтрующего конденсатора для замедления реакции на быстрый вход.
Конденсаторы
имеют ряд преимуществ перед другими устройствами защиты от переходных процессов.Они относительно малы, недороги, а их линейное поведение относительно легко предсказать и смоделировать. Они имеют относительно большую емкость хранения энергии по сравнению с устройствами, которые они защищают, поэтому они вряд ли выйдут из строя при правильном размере. Хотя конденсаторы обычно ведут себя как короткозамкнутые при воздействии напряжения выше их номинального значения, их поведение в этих условиях ненадежно; поэтому конденсаторы не следует использовать в качестве устройств защиты от переходных процессов, ограничивающих напряжение.
Ферритовые шарики или резисторы могут использоваться для обеспечения защиты от переходных процессов с ограничением времени перехода для устройств с низким импедансом (например,г. высокоемкие) входы. Ферритовые шарики имеют то преимущество, что на них не падает постоянное напряжение. Однако при использовании ферритового шарика важно следить за тем, чтобы сигнальный или силовой токи не насыщали ферритовый материал.
Анализ цепей
Анализ цепей
Майк Брукс
18 лекций в осеннем семестре
Цели
Чтобы дать учащимся понимание законов, управляющих состоянием покоя,
частотная область и слабосигнальное поведение электрических цепей, а также
способность применять это понимание к анализу и проектированию схем
поведение. Дать учащимся понимание анализа и разработки общих
схемы, например, с операционными усилителями.
Результаты обучения
К концу курса студент должен понимать и уметь применять
как для анализа, так и для проектирования: — общий процесс проектирования, включая
моделирование — описание компонентов (резисторы и управляемые источники) —
Законы Кирхгофа — эквивалентность: модели Тевенина и Нортона — суперпозиция —
узловой анализ — обработка контролируемых источников — описание компонентов
— конденсаторы и катушки индуктивности — значение соотношения фаз — понятие
комплексные напряжения и токи — распространение законов Кирхгофа на комплексные напряжения
и токи — актуальность теорем о линейных цепях в частотной области
поведение — асимптотическое поведение Операционный усилитель (операционный усилитель) —
характеристики операционного усилителя — математические операции, которые можно выполнить
с операционниками — обратная связь и стабильность; ограничения полосы пропускания.Первый заказ
переходные процессы: — пассивные цепи CR и LR — переходные процессы в активных цепях.
Линии передачи: — прямые и обратные волны, отражения, стоячие волны.
Учебный план
Переменные цепи; напряжение, ток, заряд и мощность Элементы цепи
Законы Кирхгофа для тока и напряжения Узловой анализ резисторных цепей
Анализ переходных процессов RC- и RL-цепей 1-го порядка Суперпозиция Thevenin и
Теоремы Нортона Управляемые источники Векторы и векторный анализ Трансфер
функции и фильтры Схемы операционных усилителей, систематический узловой анализ, мощность
в цепях переменного тока, линиях электропередач.
Учебник
Есть два рекомендуемых учебника, оба из которых охватывают в целом схожий материал:
(1) «Анализ инженерных цепей», Ирвин, Нелмс и Патнаик, Вили, 11-е изд.
2015. ISBN 9781118960639, 39 [Уили,
Амазонка].
(2) «Анализ инженерных цепей», авторы Hayt, Kemmerly & Durbin, McGraw Hill,
8-е изд. 2011. ISBN 9780073529578, 48 [Макгроу
Холм,
Амазонка]. Распродано, но все еще доступно.
Список лекций
- Введение и основные понятия [слайды,
раздаточный материал] - Цепи резисторов [слайды,
раздаточный материал] - Узловой анализ [слайды,
раздаточный материал] - Линейность и суперпозиция [слайды,
раздаточный материал] - Эквивалент Norton/Thevenin [слайды,
раздаточный материал] - Идеальные операционные усилители [слайды,
раздаточный материал] - Отрицательный отзыв [слайды,
раздаточный материал] - Нелинейные компоненты [слайды,
раздаточный материал] - Реактивные компоненты [слайды,
раздаточный материал] - Фазоры [слайды,
раздаточный материал] - Частотные характеристики [слайды,
раздаточный материал] - Резонанс [слайды,
раздаточный материал] - Цепи фильтров [слайды,
раздаточный материал] - Мощность в цепях переменного тока [слайды,
раздаточный материал] - Переходные процессы 1-го порядка (Часть 1) [слайды,
раздаточный материал] - Переходные процессы 1-го порядка (Часть 2) [слайды,
раздаточный материал] - Линии электропередачи [слайды,
раздаточный материал] - Фазоры и линии передачи [слайды,
раздаточный материал]
Полный комплект раздаточных материалов (4.6 МБ)
Учебные вопросы
Есть четыре обучающие задачи для обсуждения в обучающих программах, которые происходят
в недели 4/5, 6/7, 8/9 и 10/11 соответственно.
Таблицы задач
- Цепи резисторов [пробы,
решения] - Узловой анализ, линейность, суперпозиция [probs,
решения] - Norton/Thevenin, операционные усилители, диоды [пробы,
решения] - Реактивные компоненты и фазовращатели [пробы,
решения] - Фильтры и резонанс [проблемы,
решения] - Трансформаторы и переходные процессы [пробы,
решения] - Линии передачи [проблемы,
решения]
Полный набор задач + решения
Лекции по пересмотру
- Узловой анализ и частотные характеристики [слайды,
раздаточный материал] - Переходные процессы и линии передачи [слайды,
раздаточный материал]
Полный комплект раздаточных материалов для повторных лекций
Прошлые экзаменационные работы
Формат экзамена: Экзамен состоит из трех обязательных вопросов.Вопрос 1 стоит 40%
и содержит восемь частей, охватывающих весь курс. Вопросы 2 и 3 находятся на
одна тема и стоит 30% каждая.
Обратите внимание, что экзамены до 2009 г. проводились по несколько иной программе. В
в частности, следующие разделы больше не включены: Параметры двух портов
(2008:1j), исключение Гаусса (2007:2c), области применения (2008:3d),
Nullators and Norators (2008:4c), Модели компонентов слабого сигнала (2008:4e),
Произведение усиления на полосу пропускания (2006: 4c), Зенеровские диоды (программа 2008/9).
«Обратная связь» и «Линии передачи» были добавлены в учебный план в
2011 г.; последняя тема ранее была включена в учебную программу по коммуникациям.
2007, 2008, 2009, 2010, 2011,
2012, 2013, 2014,
2015, 2016,
2017
Анализ переходных процессов электрических цепей
1. Генерация переходного процесса и правило переключения маршрутов
Что такое переходный процесс
Стабильное состояние: стабильное рабочее состояние, не обязательно напряжение и ток поддерживать постоянным , Вы также можете нажать Периодическое изменение 。
Переходное состояние: из устойчивого состояния Преобразование или переход В другое стабильное состояние.
Пример перехода:
Пример перехода:
Причины переходных процессов
- Внутренняя причина: Содержит компоненты накопления энергии
- Внешняя причина: произошло изменение маршрутов
Значение изучения переходных процессов
- Использование: генерация требуемого сигнала
- Предупреждение: возможно чрезмерное напряжение или чрезмерный ток
Задачи по изучению переходных процессов
- Общая задача: решить дифференциальное уравнение связи между возбуждением и откликом
- Конкретные задачи:
- Начальное значение f (0+) f(0+)f(0+)
- Установившееся значение f (∞) f(\infty)f(∞)
- Постоянная времени τ
- Решение дифференциального уравнения или кривая
Правило изменения
Существенная причина отсутствия мутации:
Энергия электрического поля W c и энергия магнитного поля W L , хранящиеся в накопителе энергии, не изменяются в момент переключения.
Контурное правило: в момент переключения напряжение конденсатора u c и ток дросселя i L не могут изменяться.
C: U C (0 +) = U C (0-)
L: I L (0+) = I L (0-)
Когда C и L являются константами , величина заряда и цепь магнитного потока сохраняются
Определение начального значения и установившегося значения
- Определение начальной стоимости
- Найдите 0- из u c и i L
- Получить 0+ из u c и i L
- Найти начальные значения других токов и напряжений
[Примечание]
1. Ток в C и напряжение в L, а также напряжение и ток в сопротивлении могут резко изменяться
2. Начальный запас энергии равен 0: C короткое замыкание, L разомкнутая цепь
Начальный запас энергии: C эквивалентен к источнику постоянного напряжения, L эквивалентен источнику постоянного тока
- Определение установившегося значения
- C эквивалентно разомкнутой цепи, а L эквивалентно короткому замыканию, т. е. ic (∞) = 0 i~c~(\infty)=0i c (∞)=0 ,u L (∞) = 0 u ~ L ~ (\ infty) = 0 и L ( ∞ ) =0
- Найти установившиеся значения других токов и напряжений
- Напряжение, отображаемое вольтметром, на самом деле является напряжением, протекающим через него самого
- В момент переключения на обоих концах вольтметра появится высокое обратное напряжение, которое повредит вольтметр.
- Решение: 1. Перед отключением выключателя возьмите вольтметр; 2. Подключить отводящий диод
.
2. Отклик RC-цепи
Нулевой ответ ввода
Определение: после переключения цепи силовое возбуждение отсутствует, реакция цепи формируется начальным значением емкостного элемента
u c (0+)=u c (0-)=U 0
для получения линейного однородного дифференциального уравнения первого порядка: RC ducdt + uc = 0 RC\frac{\mathrm{ d} u_{c}}{\mathrm{d } t} +u_{c}=0RCdtd uc+uc=0
общее решение:
uc ( t ) = U 0 e − t τ = uc ( 0 + ) e — t τ u_ {c} \ left ( t \ right ) = U_ {0} e ^ {\ frac {-t} {\ tau}} = u_ {c} \ left ( 0+ \ right ) e^{\frac{-t}{\tau} } uc(t)=U0eτ−t=uc(0+)eτ−t(t≥0)
Скорость разряда:
- Постоянная времени τ \tauτ =RC (единицы с) определяет, насколько быстро затухает c (обычно 3~5τ \tauτ , что переходный процесс в основном завершен)
- U 0 определенно, чем больше C, тем больше Q, тем больше запас энергии, тем медленнее разряд
- Чем больше R, тем меньше i, тем медленнее разряд
Энергия, полученная на сопротивлении, равна энергии, потребляемой при разряде
Ответ нулевого состояния
Определение: после переключения происходит силовое возбуждение, и отклик цепи генерируется внешним силовым возбуждением
u c (0+)=u c (0-)=0 (эквивалентно короткому замыканию)
для получения линейного неоднородного дифференциального уравнения первого порядка:
RC ducdt + uc = U RC\ frac{\mathrm{d} u_{c}} {\mathrm{d} t} +u_{c}=URCdtd uc+uc=U
общее решение:
uc ( t ) = U ( 1 − е — т τ ) знак равно uc ( ∞ ) ( 1 — е — т τ ) u_ {c} \ влево ( т \ вправо ) = U \ влево (1-e ^ {\ frac {-t} {\ тау}} \right)=u_{c} \left ( \infty\right )\left(1-e^{\frac{-t}{\tau}} \right) uc(t)=U(1−eτ− t)=uc(∞)(1−eτ−t)(t≥0)
(Установившаяся составляющая + переходная составляющая)
Полный ответ
Определение: при возбуждении от источника питания начальное значение емкости конденсатора не равно неоднородное дифференциальное уравнение :
RC ducdt + uc = U RC\frac {\ mathrm{d} u_{c}}{\mathrm{d} t} +u_{c}=URCdtd uc+uc=U
