Формула расчета последовательного соединения конденсатора
Конденсаторы, наряду с резисторами и диодами, входят в тройку наиболее распространённых электронных компонентов. Различные их соединения встречаются в подавляющем большинстве электробытовых приборов. Их можно встретить в персональных компьютерах, пылесосах, лампочках и даже смартфонах.
Конденсаторы
Как правильно соединять конденсаторы
Чтобы узнать, как подключить конденсатор правильно, нужно разобраться, к какому именно типу он относится. Данных электронных приборов существует огромное множество. Все конденсаторы подразделяются на две группы:
- полярные (электролитические) – подключая их, необходимо учитывать, где у детали плюсовой, а где минусовой контакт;
- неполярные (все остальные) – эти конденсаторы способны работать от переменного тока, у них не бывает положительных и отрицательных клемм.
Затем нужно учесть конструкцию электронного компонента. С этой точки зрения конденсаторы могут быть:
С этой точки зрения конденсаторы могут быть:
- Выводными. Подключаются к плате с помощью тонких медных ножек, покрытых (лужёных) для защиты слоем припоя.
- Для поверхностного монтажа (SMD). В основном применяются в компактной электронике. Очень миниатюрны, часто в поперечнике не превышают 1 мм.
Также важно принять во внимание рабочее напряжение конденсатора. Это особенно принципиально для электролитических приборов данного типа, ведь при превышении их номинального вольтажа они, вероятнее всего, взорвутся, разбрызгивая во все стороны кипящий электролит.
Важно! На крышке электролитического конденсатора имеются две насечки. Эти слабые места служат для мгновенной разгерметизации изделия в случае избыточного внутреннего давления. При ремонте и наладке оборудования следует избегать направленности насечек на лицо или одежду. При внештатной ситуации с их стороны может брызнуть горячий электролит.
Не менее критичен порог максимального напряжения и для прочих видов конденсаторов, особенно имеющих мелкие габариты и не способных длительно выдерживать перегрузки.
Последний, но не наименее важный фактор, который следует учесть при соединении конденсаторов, – это их ёмкость. Она измеряется в микрофарадах (в честь Майкла Фарадея). Это их главная характеристика, поэтому конденсаторы часто называют электрическими ёмкостями. В некоторых электронных устройствах этот параметр может существенно отклоняться как в меньшую, так и в большую сторону. В других – недопустимо погрешность и на 1 %.
Схема последовательного соединения
Последовательное соединение конденсаторов подразумевает, что правая ножка каждой предстоящей ёмкости будет подключена к левому выводу последующей. Иными словами, детали объединяются в цепь, в которой они идут друг за другом, как люди в длинной очереди в магазине.
Если подключаются электролитические конденсаторы, то плюс одной детали соединяется с минусом другой, по тому же принципу, как и батарейки в различных портативных гаджетах.
Последовательное включение ёмкостей
В случае с распаянными на плате SMD деталями у каждой детали есть своё место, подключаются они тонкими медными проводниками – дорожками при помощи паяльника (редко) или термофена.
SMD детали
При последовательном соединении двух и более ёмкостей их рабочее напряжение суммируется. Нередко такой подход используется радиолюбителями, когда у них нет детали на нужный вольтаж. Формула для вычисления рабочего напряжения линейки из n конденсаторов выглядит следующим образом:
Uобщ.посл = U1 + U2 + … + Un.
Здесь U1, U2… – максимальный вольтаж каждого отдельно взятого конденсатора.
С ёмкостью линейки последовательно включенных деталей всё обстоит иначе. Она наоборот снижается. Объясняется это конструктивными особенностями этих приборов, а именно виртуальным увеличением расстояния между их обкладками. При последовательном соединении общая ёмкость определяется следующим выражением:
1/Cобщ.посл = (1/С1) + (1/С2) + … + (1/Сn).
Здесь C1, C2… – ёмкости отдельных конденсаторов.
Имеется более простой расчет этого параметра, но он пригоден только в том случае, если подключены два конденсатора, не более:
Cобщ. посл = С1*С2/(С1 + С2).
посл = С1*С2/(С1 + С2).
Параллельное и комбинированное соединение
Выделяются другие способы соединения, а именно комбинированное и параллельное подключение конденсаторов. Для них справедливы иные физические законы.
Параллельные конденсаторы
Напряжение всей группы при параллельном соединёнии конденсаторов равно вольтажу самого наименьшего из них. Т.е., если имеется цепь из трёх конденсаторов на 16, 25 и 50 В, то максимум, который на них можно подать, это 16 В. В такой схеме к каждой отдельной ёмкости будет приложено полное напряжение источника питания.
Ёмкость такой батареи складывается. Вызвано это виртуальным сложением площадей обкладок всех отдельных конденсаторов. На языке физики это выглядит так:
Cобщ.пар = С1 + С2 + … + Сn.
Зачем нужно такое соединение? Оно используется для увеличения ёмкости конденсаторов, например, в высоковольтной части сварочных инверторов и многих мощных блоках питания.
Дополнительная информация. Параллельное соединение позволяет снизить общее внутреннее сопротивление сборки, следовательно, и её нагрев. Тем самым можно увеличить срок службы ёмкости.
Параллельное соединение позволяет снизить общее внутреннее сопротивление сборки, следовательно, и её нагрев. Тем самым можно увеличить срок службы ёмкости.
Комбинированное (смешанное) соединение наиболее сложное. В нём встречаются как последовательные, так и параллельные элементы. Расчёт параметров таких схем даётся с опытом. Для простоты его принято изучать по треугольнику, разбивая на более простые части.
Смешанное соединение
Из схемы очевидно, что конденсаторы C1 и C2 включены последовательно. Их общую ёмкость можно рассчитать по вышеописанной формуле – Cобщ.посл. Далее схема упрощается. Здесь уже имеются два параллельных конденсатора Cобщ.посл и C3. Вычисляется по вышестоящей формуле Cобщ.пар. В итоге сложный для восприятия элемент цепи превращается в один эквивалентный конденсатор. Данная методика описывает алгоритм упрощения, с помощью которого можно рассчитывать гораздо более сложные конденсаторные фигуры (квадрат, куб и т.п.).
Ток при последовательном соединении конденсаторов
Электрический ток бывает двух видов: постоянным и переменным. Для работы ёмкостей это имеет большое значение.
Для работы ёмкостей это имеет большое значение.
Конденсатор и постоянный ток
Постоянный ток через конденсатор не проходит вообще. Справедливо это и для линейки из последовательно соединённых ёмкостей. Объясняется такой эффект опять же конструкцией самого электронного прибора. Конденсатор имеет две металлические обкладки. В простых электролитических приборах они сделаны из алюминиевой фольги. Между ними расположен тонкий слой диэлектрика (оксид алюминия). Если приложить к обкладкам разность потенциалов (напряжение), то ток потечёт, но только очень короткое время, пока конденсатор полностью ни зарядится. Далее движение носителей заряда прекратится, т.к. они не смогут пройти через диэлектрик. В этот момент можно сказать, что электрический ток равен нулю, и конденсатор его не пропускает.
Конденсатор и переменный ток
При переменном токе носители заряда периодически меняют своё направление. В случае с бытовой сетью изменение происходит 50 раз в секунду. Поэтому говорят, что частота тока в розетке равна 50 Гц.
Важно! Конденсаторы способны накапливать и длительно удерживать заряд. При работе с ёмкостями, заряженными от сети 220 В, их всегда следует разряжать сопротивлением в 100-1000 ом. Несоблюдение правила однажды приведёт к неприятному удару током.
Конденсатор определённо пропустит переменный ток, но не факт, что весь. Количество носителей заряда, которые смогут пройти через этот электронный прибор, зависит от ёмкости конденсатора, приложенного к нему напряжения и частоты смены направления зарядов. Математически это выражается так:
I = 2pfCU.
Здесь I – это электрический ток с частотой f, проходящий через конденсатор ёмкостью C, если к его обкладкам приложить напряжение U. 2 – просто число, а p = 3.14.
Такая способность конденсаторов ограничивать переменный ток широко применяется в аудиотехнике для построения различных звуковых фильтров. Изменяя ёмкость, можно влиять на частоту сигнала, которую она пропускает.
Фильтр на основе ёмкости
Падение напряженности и общая емкость
Ёмкость конденсатора – это величина, определяющая количество заряда, который он способен в себе сохранить. Выражение имеет следующий вид:
Выражение имеет следующий вид:
C = q/U.
Здесь q – заряд, накопленный между обкладками конденсатора, U – напряжение к ним приложенное.
Вышеописанная формула представляет общий случай. На практике при расчете ёмкости конденсатора следует учитывать ряд других переменных:
C = E0ES/d,
где:
- E0 – электрическая постоянная, равная 8,85*10-12 Ф/м,
- E – диэлектрическая проницаемость среды, в которой располагаются обкладки конденсатора,
- S – их площадь пересечения,
- d – расстояние между обкладками.
Стандартная модель конденсатора имеет следующий вид.
Модель конденсатора
Обкладки чаще всего изготовлены из тонкого листового алюминия и скручены в рулон. Делается это для увеличения их площади, ведь так ёмкость конденсатора становится существенно больше.
От выбора диэлектрика, устанавливаемого производителем между обкладками конденсатора, зависит номинальное и максимальное напряжение прибора. Это, в свою очередь, определяет его сферу применения. Если к обкладкам приложить чрезмерную разность потенциалов, то напряжённость поля между ними превысит допустимый уровень, и произойдёт пробой диэлектрика. Подобная ситуация особенно пагубно влияет на электролитические конденсаторы и ионисторы. В случае их пробоя прибор частично или полностью теряет способность накапливать заряд и в дальнейшем становится непригодным для работы.
Это, в свою очередь, определяет его сферу применения. Если к обкладкам приложить чрезмерную разность потенциалов, то напряжённость поля между ними превысит допустимый уровень, и произойдёт пробой диэлектрика. Подобная ситуация особенно пагубно влияет на электролитические конденсаторы и ионисторы. В случае их пробоя прибор частично или полностью теряет способность накапливать заряд и в дальнейшем становится непригодным для работы.
При последовательном и параллельном включении разных конденсаторов существенно изменяются их характеристики. Данное свойство этих деталей активно используется инженерами-электронщиками и радиолюбителями. Знание принципов подключения позволяет им более продуктивно разрабатывать новые устройства.
Видео
Параллельное и последовательное соединение конденсаторов: способы, правила, формулы
Любая электроника в доме может выйти из строя.
Однако сразу бежать в сервис не стоит – простейшие приборы может продиагностировать и починить даже начинающий радиолюбитель. К примеру, сгоревший конденсатор виден невооружённым глазом. Но как быть, если под рукой нет детали подходящего номинала? Конечно, соединить 2 и более в цепь. Сегодня поговорим о таких понятиях, как параллельное и последовательное соединение конденсаторов, разберемся, как его выполнить, узнаем о способах соединения, правилах его выполнения.
Не всегда удаётся подобрать конденсатор нужного номинала
Читайте в статье:
Нет конденсатора нужного номинала: что делать
Очень часто начинающие домашние мастера, обнаружив поломку прибора, стараются самостоятельно обнаружить причину. Увидев сгоревшую деталь, они стараются найти подобную, а если это не удаётся, несут прибор в ремонт. На самом деле, не обязательно, чтобы показатели совпадали. Можно использовать конденсаторы меньшего номинала, соединив их в цепь. Главное – сделать это правильно. При этом достигается сразу 3 цели – поломка устранена, приобретён опыт, сэкономлены средства семейного бюджета.
Попробуем разобраться, какие способы соединения существуют и на какие задачи рассчитаны последовательное и параллельное соединение конденсаторов.
Часто без соединения конденсаторов в батарею не обойтись. Главное – сделать это правильно
Соединение конденсаторов в батарею: способы выполнения
Существует 3 способа соединения, каждый из которых преследует свою определённую цель:
- Параллельное – выполняется в случае необходимости увеличить ёмкость, оставив напряжение на прежнем уровне.
- Последовательное – обратный эффект. Напряжение увеличивается, ёмкость уменьшается.
- Смешанное – увеличивается как ёмкость, так и напряжение.
Теперь рассмотрим каждый из способов более подробно.
Параллельное соединение: схемы, правила
На самом деле всё довольно просто. При параллельном соединении расчёт общей ёмкости можно вычислить путём простейшего сложения всех конденсаторов. Итоговая формула будет выглядеть следующим образом: Собщ= С₁ + С₂ + С₃ + … + Сn. При этом напряжение на каждом их элементов будет оставаться неизменным: Vобщ= V₁ = V₂ = V₃ = … = Vn.
При этом напряжение на каждом их элементов будет оставаться неизменным: Vобщ= V₁ = V₂ = V₃ = … = Vn.
Соединение при таком подключении будет иметь следующий вид:
Получается, что подобный монтаж подразумевает подключение всех пластин конденсаторов к точкам питания. Такой способ встречается наиболее часто. Но может произойти ситуация, когда важно увеличить напряжение. Разберёмся, каким образом это сделать.
Последовательное соединение: способ, используемый реже
При использовании способа последовательного подключения конденсаторов напряжение в цепи возрастает. Оно складывается из напряжения всех элементов и выглядит так: Vобщ= V₁ + V₂ + V₃ +…+ Vn. При этом ёмкость изменяется в обратной пропорции: 1/Собщ= 1/С₁ + 1/С₂ + 1/С₃ + … + 1/Сn. Рассмотрим изменения ёмкости и напряжения при последовательном включении на примере.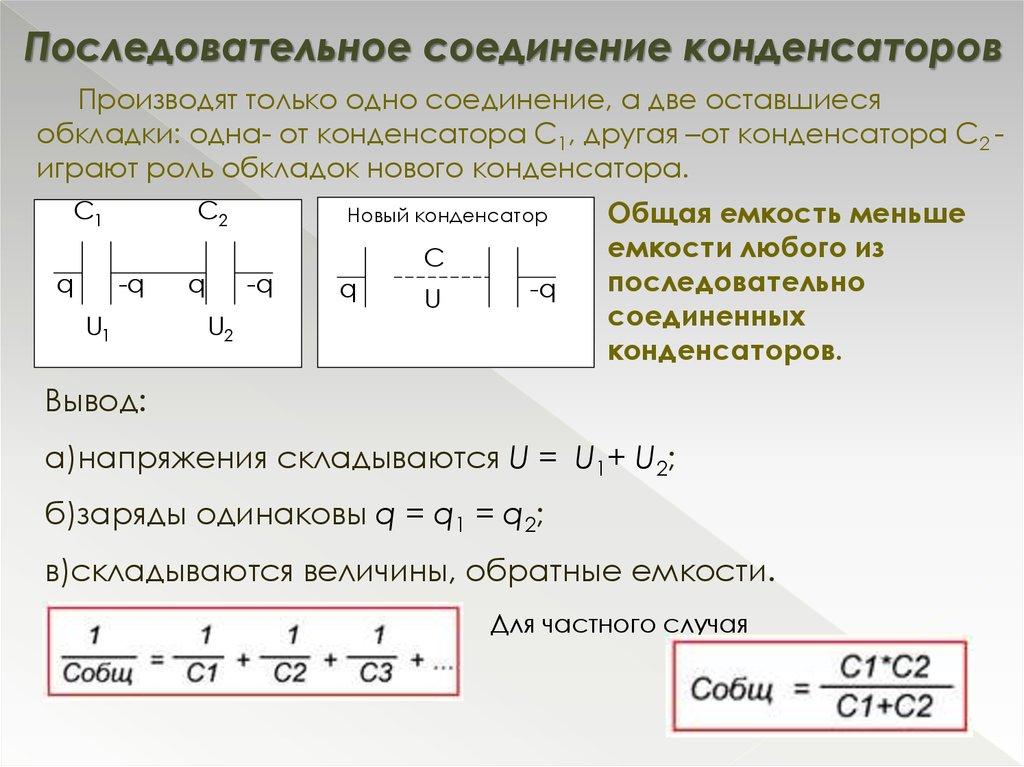
Дано: 3 конденсатора с напряжением 150 В и ёмкостью 300 мкф. Подключив их последовательно, получим:
- напряжение: 150 + 150 + 150 = 450 В;
- ёмкость: 1/300 + 1/300 + 1/300 = 1/С = 299 мкф.
Внешне подобное подключение обкладок (пластин) будет выглядеть так:
Выполняют такое соединение в том случае, если есть опасность пробоя диэлектрика конденсатора при подаче напряжения в цепь. Но ведь существует и ещё один способ монтажа.
Полезно знать! Применяют также последовательное и параллельное соединение резисторов и конденсаторов. Это делается с целью снижения подаваемого на конденсатор напряжения и исключения его пробоя. Однако следует учитывать, что напряжения должно быть достаточно для работы самого прибора.
Смешанное соединение конденсаторов: схема, причины необходимости применения
Такое подключение (его ещё называют последовательно-параллельным) применяют в случае необходимости увеличения, как ёмкости, так и напряжения. Здесь вычисление общих параметров немного сложнее, но не настолько, чтобы нельзя было разобраться начинающему радиолюбителю. Для начала посмотрим, как выглядит такая схема.
Здесь вычисление общих параметров немного сложнее, но не настолько, чтобы нельзя было разобраться начинающему радиолюбителю. Для начала посмотрим, как выглядит такая схема.
Составим алгоритм вычислений.
- всю схему нужно разбить на отдельные части, высчитать параметры которых просто;
- высчитываем номиналы;
- вычисляем общие показатели, как при последовательном включении.
Выглядит подобный алгоритм следующим образом:
Преимущество смешанного включения конденсаторов в цепь по сравнению с последовательным или параллельным
Смешанное соединение конденсаторов решает задачи, которые не под силу параллельным и последовательным схемам. Его можно использовать при подключении электродвигателей либо иного оборудования, его монтаж возможен отдельными участками. Монтаж его намного проще за счёт возможности выполнения отдельными частями.
Интересно знать! Многие радиолюбители считают этот способ более простым и приемлемым, чем два предыдущих. На самом деле, так и есть, если полностью понять алгоритм действий и научиться пользоваться им правильно.
На самом деле, так и есть, если полностью понять алгоритм действий и научиться пользоваться им правильно.
Смешанное, параллельное и последовательное соединение конденсаторов: на что обратить внимание при его выполнении
Соединяя конденсаторы, в особенности электролитические, обратите внимание на строгое соблюдение полярности. Параллельное присоединение подразумевает подключение «минус/минус», а последовательное – «плюс/минус». Все элементы должны быть однотипны –плёночные, керамические, слюдяные либо металлобумажные.
А вот что умеют делать всем известные китайские «изобретатели» – такой конденсатор явно долго не протянет
Полезно знать! Выход из строя конденсаторов часто происходит по вине производителя, экономящего на деталях (чаще это приборы китайского производства). Поэтому правильно рассчитанные и собранные в схему элементы будут работать намного дольше. Конечно, при условии отсутствия замыкания в цепи, при котором работа конденсаторов невозможна в принципе.
Калькулятор расчёта ёмкости при последовательном соединении конденсаторов
А что делать, если необходимая ёмкость неизвестна? Не каждому хочется самостоятельно рассчитывать необходимую ёмкость конденсаторов вручную, а у кого-то на это просто нет времени. Для удобства производства подобных действий редакция Seti.guru предлагает нашему уважаемому читателю воспользоваться онлайн-калькулятором расчёта конденсаторов при последовательном соединении или вычисления ёмкости. В работе он необычайно прост. Пользователю необходимо лишь ввести в поля необходимые данные, после чего нажать кнопку «Рассчитать». Программы, в которые заложены все алгоритмы и формулы последовательного соединения конденсаторов, а также вычислений необходимой ёмкости, моментально выдаст необходимый результат.
Как рассчитать энергию заряженного конденсатора: выводим окончательную формулу
Первое, что для этого необходимо сделать – рассчитать, с какой силой притягиваются обкладки друг к другу. Это можно сделать по формуле F = q₀ × E, где q₀ является показателем величины заряда, а E – напряжённостью обкладок. Далее нам необходим показатель напряжённости обкладок, который можно вычислить по формуле E = q / (2ε₀S), где q – заряд, ε₀ – постоянная величина, S – площадь обкладок. В этом случае получим общую формулу для расчёта силы притяжения двух обкладок: F = q₂ / (2ε₀S).
Далее нам необходим показатель напряжённости обкладок, который можно вычислить по формуле E = q / (2ε₀S), где q – заряд, ε₀ – постоянная величина, S – площадь обкладок. В этом случае получим общую формулу для расчёта силы притяжения двух обкладок: F = q₂ / (2ε₀S).
Итогом наших умозаключений станет вывод выражения энергии заряженного конденсатора, как W = A = Fd. Однако это не окончательная формула, которая нам необходима. Следуем далее: учитывая предыдущую информацию, мы имеем: W = dq₂ / (2ε₀S). При ёмкости конденсатора, выражаемой как C = d / (ε₀S) получаем результат W = q₂ / (2С). Применив формулу q = СU, получим итог: W = CU² /2.
Редакция Seti.guru советует сохранить эту памятку
Конечно, для начинающего радиолюбителя все эти расчёты могут показаться сложными и непонятными, но при желании и некоторой усидчивости с ними можно разобраться. Вникнув в смысл, он поразится, насколько просто производятся все эти расчёты.
Вникнув в смысл, он поразится, насколько просто производятся все эти расчёты.
Для чего нужно знать показатель энергии конденсатора
По сути, расчёт энергии применяется редко, однако есть области, в которых это знать необходимо. К примеру, фотовспышка камеры – здесь вычисление показателя энергии очень важно. Она накапливается за определённое время (несколько секунд), а вот выдаётся мгновенно. Получается, что конденсатор сравним с аккумулятором – разница лишь в ёмкости.
Ни одна фотовспышка не сможет работать без накопителя энергии, такого, как конденсатор
Подводя итог
Порой без соединения конденсаторов не обойтись, ведь не всегда можно подобрать подходящие по номиналам. Поэтому знание того как это сделать может выручить при поломке бытовой техники или электроники, что позволит значительно сэкономить на оплате труда специалиста по ремонту. Как наверняка уже понял Уважаемый читатель, сделать это несложно и под силу даже начинающим домашним мастерам. А значит стоит потратить немного своего драгоценного времени и разобраться в алгоритме действий и правилах их выполнения.
Правильность соединения конденсаторов гарантирует их долгую бесперебойную работу
Надеемся, что информация, изложенная в сегодняшней статье, была полезна нашим читателям. Возможно, у Вас остались какие-либо вопросы? В этом случае их можно изложить в обсуждении ниже. Редакция Seti.guru с удовольствием на них ответит в максимально короткие сроки. Если же Вы имеете опыт самостоятельного соединения конденсаторов (неважно, положительный он или отрицательный), убедительная просьба поделиться им с другими читателями. Это поможет начинающим мастерам более полно понять алгоритм действий и избежать ошибок. Пишите, делитесь, спрашивайте. А напоследок мы предлагаем посмотреть короткий, но довольно информативный видеоролик по сегодняшней теме.
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
Сократив выражение на Q, получим знакомую формулу:
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
Так как заряд конденсатора
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С1 = 10 мкФ, C2 = 2 мкФ, C3 = 5 мкФ, а C4 = 1 мкФ?
При последовательном соединении общая емкость равна:
При параллельном соединении общая емкость равна:
Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С1 = 7 мкФ, С2 = 2 мкФ, С3 = 1 мкФ.
Сначала найдем общую емкость параллельного участка цепи:
Затем найдем общую емкость для всей цепи:
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Советуем прочесть — Заряд и разряд конденсатора
Последовательное подключение конденсаторов — Всё о электрике
Соединение конденсаторов
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.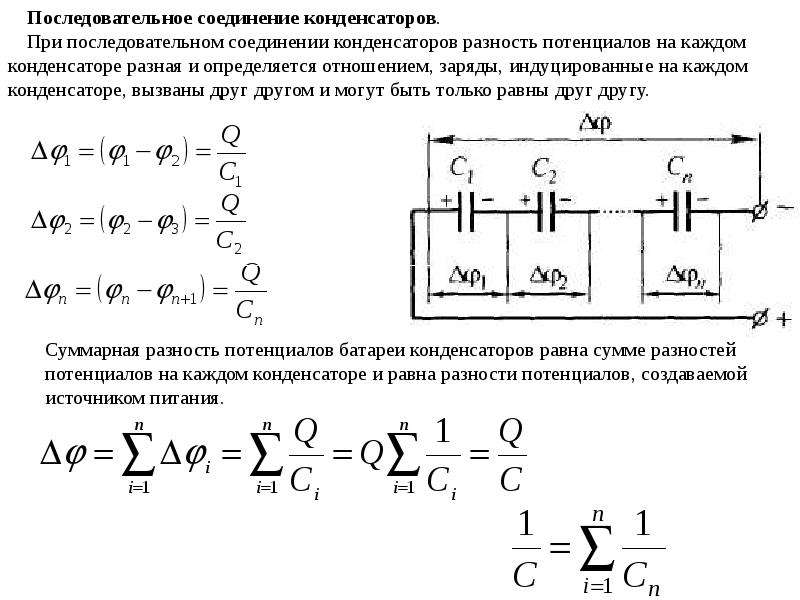
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние.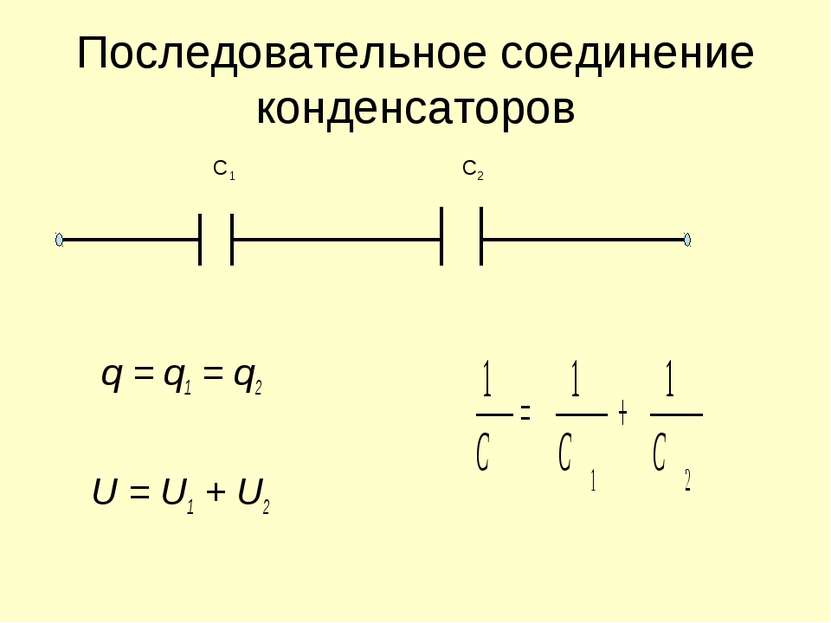 При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.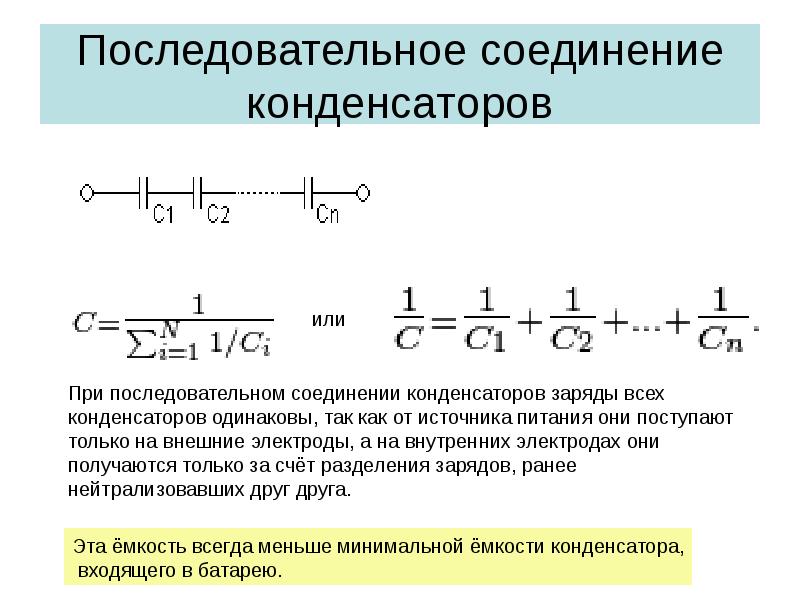
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5.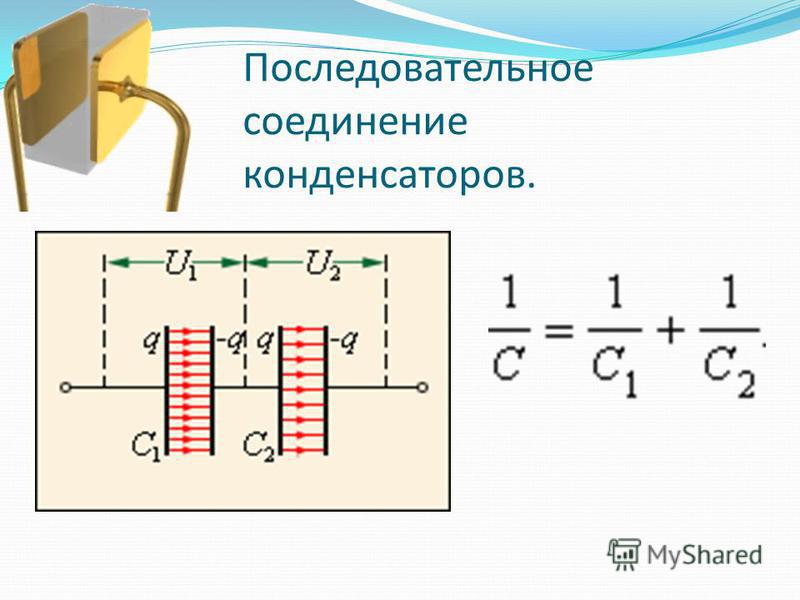 Пример расчета последовательно-параллельного соединения конденсаторов.
Пример расчета последовательно-параллельного соединения конденсаторов.
Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
Сократив выражение на Q, получим знакомую формулу:
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
Так как заряд конденсатора
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С1 = 10 мкФ, C2 = 2 мкФ, C3 = 5 мкФ, а C4 = 1 мкФ?
При последовательном соединении общая емкость равна:
При параллельном соединении общая емкость равна:
Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С1 = 7 мкФ, С2 = 2 мкФ, С3 = 1 мкФ.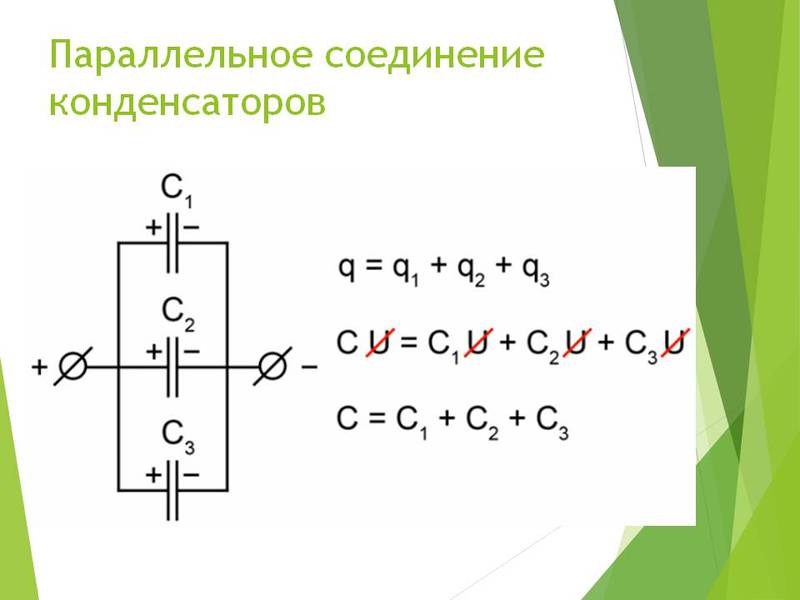
Сначала найдем общую емкость параллельного участка цепи:
Затем найдем общую емкость для всей цепи:
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Способы подключения конденсаторов в электрическую цепь
Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей. Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.
Параллельное включение конденсаторов в цепь
Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.
Параллельное соединение конденсаторов:
Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.
Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.
При параллельном соединении конденсаторов емкость равняется:
Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.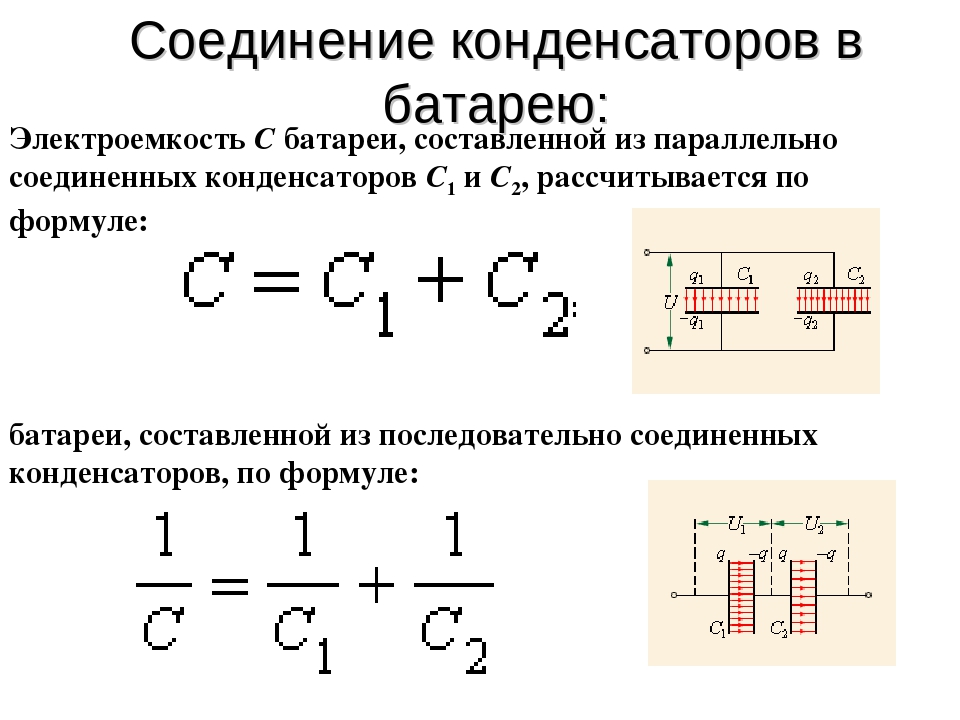
Конденсаторы, соединенные параллельно, имеют напряжение:
Последовательное включение конденсаторов в цепь
Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.
Последовательное соединение конденсатора:
При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния. По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.
Формула нахождения заряда на конденсаторе, схема подключения конденсатора:
Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости. Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.
Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.
Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.
Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:
Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:
Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:
Смешанное включение емкостных накопителей в схему
Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.
Участок цепи подсоединенных смешанным включением накопителей емкости:
Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:
- разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
- вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
- проводим нахождение эквивалентной емкости на параллельном участке;
- когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
- рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.
Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:
- Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.

- Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
- Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.
Вывод
Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников. В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.
Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.
{SOURCE}
При последовательном соединении конденсаторов — Всё о электрике
Соединение конденсаторов: руководство для начинающих
В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.
Параллельное соединение
Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии
Схема параллельного крепления
Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор.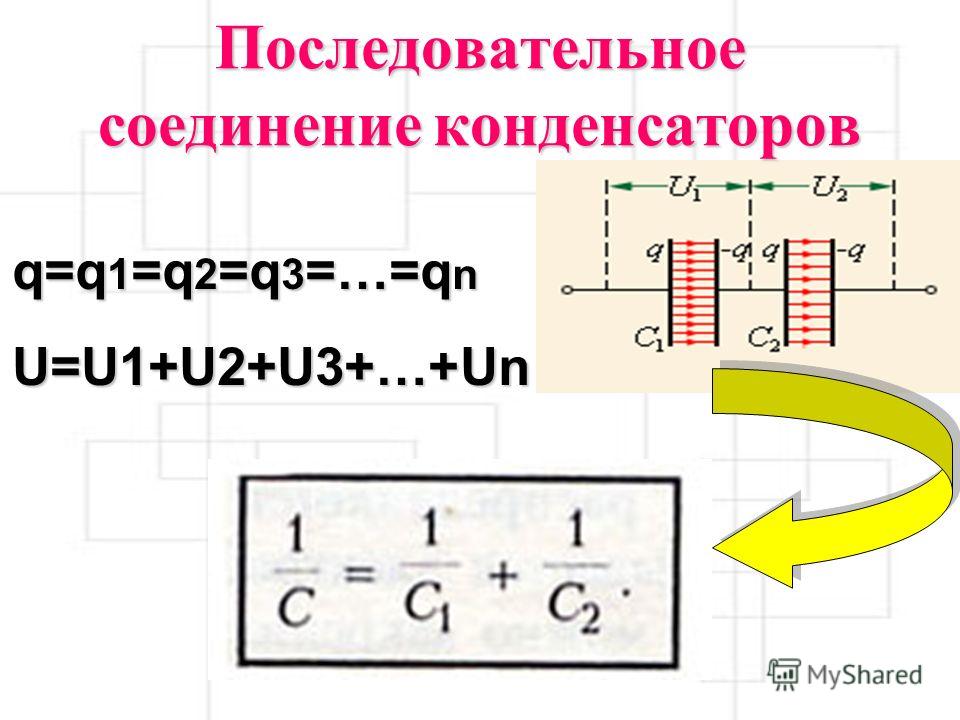 Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.
Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.
Схема — напряжение на накопителях
В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:
Последовательное соединение
Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.
Схема — схема последовательного соединения
Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.
Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:
i = ic1 = ic2 = ic3 = ic4, то есть токи проходящие через каждый конденсатор равны между собой.
Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:
А так определяется общая суммарная емкость конденсаторов при последовательном соединении:
Видео: как соединять конденсаторы параллельным и последовательным методом
Смешанное подключение
Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.
Схема: смешанное соединение конденсаторов
Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:
- Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
- Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
- Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока. Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
- Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
Сократив выражение на Q, получим знакомую формулу:
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
Так как заряд конденсатора
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С1 = 10 мкФ, C2 = 2 мкФ, C3 = 5 мкФ, а C4 = 1 мкФ?
При последовательном соединении общая емкость равна:
При параллельном соединении общая емкость равна:
Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С1 = 7 мкФ, С2 = 2 мкФ, С3 = 1 мкФ.
Сначала найдем общую емкость параллельного участка цепи:
Затем найдем общую емкость для всей цепи:
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Соединение конденсаторов
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Емкость при последовательном соединении — Всё о электрике
Соединение конденсаторов
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.
Параллельное соединение электролитов
Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
Сократив выражение на Q, получим знакомую формулу:
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
Так как заряд конденсатора
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С1 = 10 мкФ, C2 = 2 мкФ, C3 = 5 мкФ, а C4 = 1 мкФ?
При последовательном соединении общая емкость равна:
При параллельном соединении общая емкость равна:
Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С1 = 7 мкФ, С2 = 2 мкФ, С3 = 1 мкФ.
Сначала найдем общую емкость параллельного участка цепи:
Затем найдем общую емкость для всей цепи:
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Соединение конденсаторов: руководство для начинающих
В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.
Параллельное соединение
Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии
Схема параллельного крепления
Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.
Схема — напряжение на накопителях
В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:
Последовательное соединение
Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.
Схема — схема последовательного соединения
Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.
Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:
i = ic1 = ic2 = ic3 = ic4, то есть токи проходящие через каждый конденсатор равны между собой.
Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:
А так определяется общая суммарная емкость конденсаторов при последовательном соединении:
Видео: как соединять конденсаторы параллельным и последовательным методом
Смешанное подключение
Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.
Схема: смешанное соединение конденсаторов
Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:
- Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
- Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
- Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока. Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
- Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.
{SOURCE}
Физика для науки и техники II
Подключение конденсаторов серии 5.8 от Office of Academic Technologies на Vimeo.
- Демонстрация: энергия, запасенная в конденсаторе
- Пример: подключение конденсаторов
5.08 Последовательное подключение конденсаторов
Хорошо. Теперь займемся последовательным соединением конденсаторов. В этом случае снова давайте рассмотрим три конденсатора с емкостью C1, C2 и C3.А для того, чтобы соединить их последовательно, соединяем их друг за другом. Чтобы конденсаторы устанавливались последовательно, сумма разностей потенциалов на каждом конденсаторе должна быть равна разности потенциалов, приложенной ко всей комбинации. Поэтому мы говорим, что конденсаторы соединены последовательно, если сумма разностей потенциалов на каждом конденсаторе равна разности потенциалов, приложенной к комбинации.
Итак, как я упоминал ранее, в этом случае мы подключаем конденсаторы C1, C2 и C3 один за другим, вот так.Подобно сцепкам вагонов поезда на одном рельсе или пути. Затем мы применяем разность потенциалов к комбинации, подключая эти два конца к клеммам источника питания, скажем, батареи, которая вырабатывает разность потенциалов V вольт, и вводим здесь переключатель. Здесь у нас есть конденсатор с емкостью C1, конденсатор 2 с емкостью C2 и C3 для третьего конденсатора.
Как только мы замкнем здесь переключатель, опять же, как и в предыдущем случае, так как эти заряды постоянно отталкивают друг друга, скажем, на выводах источника питания батареи, и положительные заряды пройдут через этот доступный путь чтобы как можно дальше уйти друг от друга.И они будут собраны на левой пластине конденсатора C1 как q1 плюс q1. Точно так же отрицательные будут продолжаться по этому пути и собираются на выводах правой пластины конденсатора C3 как минус, скажем, q.
Но поскольку они подключены, эти пластины подключены к клеммам источника питания, поэтому эти заряды, величина заряда q1, и если вы назовете его как q3, все они будут равны друг другу, и все они будут быть равным заряду q, скажем так.Поэтому, давайте обозначим этот вот здесь как плюс q, а другой как минус q. Опять же, они напрямую подключены к клеммам этого источника питания.
Итак, как мы помним из конструкции конденсатора, мы сказали, что это устройство, которое состоит из двух проводящих пластин, разделенных изолирующей средой. Итак, эти среды между пластинами каждого из этих конденсаторов являются изолирующими средами. Другими словами, они не создают среду для легкого перемещения зарядов.Они изоляторы. Итак, когда мы смотрим на эту схему в целом, на самом деле это разомкнутая цепь. Другими словами, у нас нет полностью замкнутого пути для движения зарядов.
Тогда мы можем легко задать вопрос, хорошо, мы можем понять, почему пластина конденсатора C1 заряжается положительно, и почему пластина конденсатора C3 получает отрицательный заряд, потому что они напрямую подключены к клеммам источника питания. тогда как эта пластина, другая пластина C3 и затем другая пластина C1, а также конденсатор C2 будут заряжаться во время этого процесса, потому что у них нет прямой проводящей связи с клеммами источника питания.
Что ж, когда мы посмотрим — давайте рассмотрим вот этот блок. Как мы видим, эта единица здесь является пластиной конденсатора C2 и этой пластиной конденсатора C3, и почему вся эта область здесь является проводящей средой. Он разделен этими изолирующими точками. Эта проводящая среда, кусок проволоки и, скажем, металлические пластины этих конденсаторов, имеют большое количество свободных электронов. Итак, как только эта другая пластина заряжена до значения минус q, эти отрицательные заряды будут отталкивать эти свободные электроны в этой среде от самих себя.Таким образом, эти свободные электроны будут двигаться как можно дальше для них, и это другая граница этой области, и они будут собираться и собираться, следовательно, на правой боковой пластине конденсатора C2.
Таким образом, поскольку мы собираемся иметь это избыточное количество отрицательного заряда, свободных электронов, отталкиваемых этим минусом q, мы получим минус q заряда, который будет собираться на этой пластине, на правой боковой пластине. этот конденсатор С2. Поскольку эти заряды будут перемещаться от этого конца к этой области, то на другом конце здесь не будет такого большого количества отрицательного заряда.Следовательно, эта пластина будет заряжена положительным q.
И, конечно же, аналогичный тип зарядки будет иметь место и для другого устройства. Этот отрицательный заряд будет отталкивать такое же количество свободных электронов как можно дальше от этой области. Таким образом, эта пластина будет заряжаться минус q, и поскольку, следовательно, они покинут другую область, не имеющую такого большого отрицательного заряда, эта пластина будет заряжаться положительно q. Следовательно, другие пластины и конденсаторы, которые не подключены напрямую к источнику питания, будут заряжаться в результате индукции.
Итак, первое свойство этого соединения или комбинации, мы можем сказать, что заряды, накопленные на каждом конденсаторе в последовательной комбинации, будут равны друг другу. Другими словами, q1 будет равно q2, что будет равно q3, и все они будут равны количеству заряда, полученному от источника питания, то есть q. Опять же, это напрямую связано с принципом сохранения заряда.
И если вы посмотрите на второе свойство, и оно напрямую проистекает из общей особенности последовательной комбинации, как мы заявили здесь выше, разность потенциалов по всей комбинации будет равна сумме разностей потенциалов на каждом конденсаторе.Другими словами, если вы просто возьмете наш вольтметр и измеряете разность потенциалов во всей комбинации, подключив наш вольтметр к этим двум точкам, через комбинацию, мы собираемся считывать вольт вольт независимо от напряжения, подаваемого источником питания. Так что это будет считывать нас вольт.
А затем, если мы измеряем разность потенциалов на первом конденсаторе, мы получим V1 вольт. На C2 мы будем читать V2 вольт, а на C3 мы будем читать V3 вольт. И мы увидим, что разность потенциалов во всей комбинации, которая составляет V вольт, будет равна V1 плюс V2 плюс V3.И это общее свойство последовательного соединения. Разность потенциалов по всей комбинации равна сумме разностей потенциалов по каждому компоненту в последовательном соединении.
Теперь, как мы сделали в случае параллельного соединения, мы собираемся упростить эту схему, заменив все эти 3 конденсатора при последовательном соединении одним конденсатором. И давайте назовем это эквивалентом C, так что этот единственный конденсатор будет выполнять ту же работу в цепи, которую эти три выполняли в последовательной комбинации.Опять же, давайте представим здесь наш переключатель. Та же батарея обеспечивает такую же разность потенциалов в вольт, что и в предыдущем случае, и как только мы включим переключатель, как только мы его закроем, эти положительные заряды снова будут двигаться по этому пути и собираться вдоль левой боковой пластины. эквивалентного конденсатора. А положительные будут перемещаться по другому пути и собираются на правой боковой пластине эквивалента C. И, конечно же, зарядка будет продолжаться до тех пор, пока мы не достигнем высокой плотности заряда, чтобы они создавали достаточно сильную силу отталкивания для входящих зарядов.И в это время конденсатор будет полностью заряжен.
Если мы запишем эквивалент конденсатора C, емкость этого конденсатора, эквивалентного C, по его определению, она будет равна общему заряду, хранящемуся на месте конденсатора, который равен q, деленному на разность потенциалов между пластинами. этого конденсатора. И это будет равно любой разности потенциалов, генерируемой этой батареей. А это V.
Отсюда, если вы решите для разности потенциалов, мы можем записать это выражение как q в эквиваленте C, количество заряда, накопленного в конденсаторе, деленное на емкость конденсатора.Конечно, мы можем записать аналогичные выражения для конденсаторов C1, C2 и C3. Разность потенциалов относительно C1, которая была V1, будет равна q1 над C1. Но поскольку в последовательной комбинации количество заряда, хранящегося в каждом конденсаторе, одинаково, q1 равно q. Следовательно, для V1 у нас будет q над C1. И аналогично, V2 будет равно q2 над C2, и это тоже будет равно q над C2, так как снова q2 равно q. В дальнейшем V3 будет равняться q3 над C3. И снова, поскольку q3 равно q из свойства 1, у нас будет q больше C3 для этого конденсатора.
Используя свойство 2 из свойства 2, поскольку V равно V1 плюс V2 плюс V3, а в терминах заряда и емкости, мы можем записать V как q в эквиваленте C. Это будет равно для V1. У нас будет q над V1, плюс для V2 у нас будет q над C2, плюс для V3 у нас будет q над C3. Поскольку заряд является общим для каждого из этих членов, делящих обе части уравнения на q, мы можем исключить qs и получить окончательное выражение, в котором 1 по сравнению с эквивалентом C равняется 1 по C1 плюс 1 по C2 плюс 1 по C3 .
Теперь мы можем легко увидеть тенденцию. Если мы соединим конденсаторы последовательно, то мы увидим, что обратная величина эквивалентных конденсаторов становится суммой обратных величин конденсаторов или емкостей в последовательной комбинации. Мы можем обобщить это для числа N конденсаторов, подключенных последовательно, один по сравнению с эквивалентом C, эквивалентная емкость всей комбинации становится равной сумме инверсий каждой емкости в комбинации или последовательной комбинации. Здесь также легко заметить, что после последовательного подключения конденсаторов результирующая емкость становится меньше наименьшей емкости в комбинации.Другими словами, общая емкость цепи уменьшается, когда мы соединяем конденсаторы последовательно.
Одна вещь, которую вы всегда должны быть очень осторожны, используя это уравнение для вычисления эквивалентной емкости цепи, это выражение дает вам обратную величину эквивалентной емкости. Таким образом, чтобы получить эквивалент C или эквивалентную емкость, после того, как мы вычислим правую часть этого уравнения, вы должны сделать обратную величину, чтобы получить эквивалентную емкость этих конденсаторов.
конденсаторов последовательно и параллельно
конденсаторов последовательно и параллельно
Далее: Энергия в конденсаторах
Up: Емкость
Предыдущая: Диэлектрики
Конденсаторы — один из стандартных компонентов электронных схем.
Кроме того, часто встречаются сложные комбинации конденсаторов.
в практических схемах. Это,
поэтому полезно иметь набор правил для определения эквивалентной емкости
некоторого общего расположения конденсаторов.Оказывается, всегда можно найти
эквивалентная емкость при повторном
применение два простых правила . Эти правила относятся к подключенным конденсаторам.
последовательно и параллельно.
Рассмотрим два конденсатора, подключенных параллельно : , то есть , с
положительно заряженные пластины подключены к общему «входному» проводу, а отрицательно
заряженные пластины, прикрепленные к общему «выходному» проводу — см. рис.15. Какая эквивалентная емкость
между входным и выходным проводами? В этом случае потенциал
разница между двумя конденсаторами одинакова и равна
разность потенциалов между входным и выходным проводами. Общий заряд
однако, хранящиеся в двух конденсаторах делятся между
конденсаторы, поскольку он должен распределяться так, чтобы напряжение на
два то же самое. Поскольку конденсаторы могут иметь разную емкость, и,
сборы также могут быть разными.Эквивалентная емкость
пары конденсаторов — это просто соотношение, где
общий накопленный заряд. Следует, что
| (113) |
давая
| (114) |
Здесь мы воспользовались тем фактом, что напряжение является общим для всех трех
конденсаторы. Таким образом, правило:
Эквивалентная емкость двух конденсаторов, соединенных параллельно
представляет собой сумму отдельных емкостей.
Для конденсаторов, подключенных параллельно, уравнение. (114) обобщает на
.
Рассмотрим два конденсатора, подключенных в серию : , т. Е. , в линию так, что
положительная пластина одного прикреплена к отрицательной пластине другого — см.
Рис.16.
Фактически, предположим, что положительная обкладка конденсатора 1 подключена
к проводу «вход» отрицательная обкладка конденсатора 1 подключается к
положительная пластина конденсатора 2 и отрицательная пластина конденсатора
2 подключается к проводу «выход».Какая эквивалентная емкость между входными и выходными проводами?
В этом случае важно понимать, что заряд, хранящийся в
два конденсатора одинаковые. Это легче всего увидеть, если рассмотреть
«внутренние» пластины: , то есть , отрицательная пластина конденсатора 1, и
положительная пластина конденсатора 2. Эти пластины физически отключены.
от остальной части схемы, поэтому общий заряд на них должен
быть постоянным. Если предположить, что кажется разумным, что эти пластины несут нулевой заряд
когда к двум конденсаторам приложена нулевая разность потенциалов, следует
что при наличии ненулевой разности потенциалов заряд на положительном
пластина конденсатора 2 должна быть уравновешена равным и противоположным зарядом
на отрицательной пластине конденсатора 1.Поскольку отрицательная пластина
Конденсатор 1 несет заряд, положительная пластина должна нести заряд.
Аналогичным образом, поскольку положительная пластина конденсатора 2 несет заряд,
отрицательная пластина должна нести заряд. В итоге оба конденсатора
обладают таким же накопленным зарядом. Потенциал падает, и
два конденсатора, как правило, разные. Однако сумма этих
капель равняется общему падению потенциала на входе и выходе
провода: , т.е. ,. Эквивалентная емкость пары
конденсаторы снова
.Таким образом,
| (115) |
давая
| (116) |
Здесь мы использовали тот факт, что заряд является общим для всех трех
конденсаторы.
Следовательно, правило таково:
Величина, обратная эквивалентной емкости двух конденсаторов, подключенных в
серия — это сумма обратных величин отдельных емкостей.
Для конденсаторов, соединенных последовательно, уравнение.(116) обобщает на
Далее: Энергия в конденсаторах
Up: Емкость
Предыдущая: Диэлектрики
2007-07-14
Серия
и параллельное соединение конденсаторов
Параллельное соединение конденсаторов:
На схеме ниже показан пример параллельно подключенных конденсаторов. В этом случае одинаковое напряжение U присутствует на всех конденсаторах.
Конденсаторы несут следующие заряды:
Общий заряд Q , генерируемый источником постоянного тока, равен сумме отдельных зарядов:
Суммирование значений в скобках дает общую емкость C для параллельной цепи:
Другими словами:
| Общая емкость конденсаторов, подключенных параллельно, равна сумме отдельных емкостей. |
Параллельное подключение конденсаторов эквивалентно увеличению площади пластины.
Серия Подключение конденсаторов:
Последовательное подключение нескольких конденсаторов к источнику напряжения, как показано на схеме ниже, вызывает перенос заряда Q по всей цепи.
В результате на каждом из конденсаторов должен быть индуцирован одинаковый заряд Q. Тогда напряжение U i на каждом из компонентов зависит от соответствующих емкостей:
Общий потенциал равен сумме индивидуальных потенциалов:
Следовательно, общая емкость последовательного соединения определяется следующим образом:
Другими словами:
| Для конденсаторов, соединенных последовательно, обратная величина полной емкости равна сумме обратных величин отдельных емкостей. |
В этом случае общая емкость меньше наименьшей индивидуальной емкости. Последовательное подключение конденсаторов эквивалентно увеличению расстояния между пластинами.
Какова общая емкость C следующей цепи, состоящей из четырех конденсаторов?
НАЖМИТЕ ЗДЕСЬ ДЛЯ УКАЗАТЕЛЬНОЙ СТРАНИЦЫ | |||||||
| |||||||
ФАЙЛ PDF — | |||||||
Конденсаторы — это компоненты, которые используются для хранения | |||||||
Конденсатор состоит из двух проводов, разделенных | |||||||
КАК РАБОТАЕТ КОНДЕНСАТОР | |||||||
Когда цепь включена, светодиод излучает свет, и конденсатор заряжается.Когда переключатель повернут | |||||||
Конденсаторы электролитические поляризованные Неэлектролитические конденсаторы обычно имеют меньшую емкость. ЕМКОСТЬ — означает емкость конденсатора. | |||||||
Обратите внимание на электролитический | |||||||
Внимательно посмотрите фотографии двух типов | |||||||
Простая схема (см. Ссылку ниже) в основном представляет собой переключатель, который | |||||||
ПОМНИТЕ — есть | |||||||
НАЖМИТЕ ЗДЕСЬ ДЛЯ ПРИМЕРЫ — КАК | |||||||
Специальные технические предметы — WIMA — Компетентность в конденсаторах
Максимально допустимое напряжение переменного тока, которое может быть приложено к конденсаторам в приложениях с синусоидальной формой волны , можно определить по графикам в соответствующих диапазонах конденсаторов.
Тем не менее, при наличии условий импульса необходимо соблюдать следующую процедуру, чтобы гарантировать, что правильный номинал конденсатора выбран для конкретного режима работы:
Номинальное напряжение U r : Номинальное напряжение конденсатора относительно нулевого потенциала Контрольная точка должна учитывать, что диэлектрическая прочность пленки конденсатора уменьшается с увеличением частоты. Следовательно, при расчете требуемого номинального напряжения конденсатора необходимо учитывать поправочный коэффициент k; где k = электрическая прочность пленки на частоте f в% показана на графике 1.
График 1: Диэлектрическая прочность полипропиленовой пленки как коэффициент частоты (общие рекомендации).
Расчет необходимой диэлектрической прочности показан в следующем примере (U мин , U макс имеют одинаковую полярность).
Кроме того, среднеквадратичное значение напряжения, полученное из размаха напряжения, не должно быть больше номинального номинального напряжения переменного тока конденсатора, чтобы избежать начального уровня ионизации:
U среднеквадратичное значение AC номинальное значение
Максимальный ток: Градиент напряжения или время нарастания импульса принимается за точку отсчета при расчете максимального номинального тока концевых контактов.Максимально возможная токовая нагрузка на концевые контакты рассчитывается по нарастанию напряжения импульса (время нарастания импульса F).
I макс = F x C x 1,6
Данные о номинальном времени нарастания импульса Fr для импульсов, равных номинальному номинальному напряжению, приведены в технических характеристиках различных типов. При малом повышении напряжения во время работы (U PP ) допустимая токовая нагрузка рассчитывается следующим образом:
например, U r = 63 В, U PP = 12 В, F r = 50 В / мкс.
следовательно, F макс
63/12
x 50 = 262,5 В / мкс.
При использовании максимального номинального тока необходимо учитывать самонагрев на более высоких частотах, и он не должен превышать 8 К.
Рассеивание (тепловые потери): Тепло, рассеиваемое конденсатором при воздействии несинусоидальных напряжений или в импульсном режиме можно приблизительно определить по следующей формуле:
| P V | = U среднеквадратичное значение 2 x ωC x tanδ |
| P V | = рассеиваемая мощность в ваттах (макс.Вт на К). |
| U СКЗ | = среднеквадратичное значение доли переменного напряжения |
| ω | = 2π x f, где f — частота повторения импульсного сигнала. |
| С | = емкость в Фарадах |
| tanδ | = коэффициент рассеяния, соответствующий частоте самой крутой части импульса. |
частота импульсов =
1 / ширина импульса
Повышение температуры в K =
расчетное рассеивание / удельное рассеивание
(см. таблицу 1)
| Модуль печатной схемы PCM (в мм) | Удельное рассеивание в ваттах на K выше температуры окружающей среды |
| 2.5 5 7,5 10 15 22,5 27,5 37,5 | 0,0025 0,004 0,006 0,0075 0,012 0,015 0,025 0,03 |
Таблица 1: Данные относятся к обычным условиям сборки и вентиляции, избегая теплового излучения внутри корпуса оборудования.
В приложениях, где надежность имеет решающее значение, рекомендуется измерять температуру поверхности конденсатора и учитывать, что температура внутри этого конденсатора будет примерно на 5 К выше температуры корпуса.
Определение допустимого переменного напряжения и переменного тока на заданных частотах.
Чтобы определить допустимое напряжение переменного тока (синусоидальное) для приложений в более высокочастотном спектре, для соответствующей серии WIMA доступны графики, показывающие снижение номинального напряжения переменного тока с частотой. Диаграммы относятся к допустимому самонагреву:
Δϑ <10 К.
Например, для WIMA MKP 10 / 0,01 мкФ / 630 В постоянного тока / 400 В переменного тока это показывает — при f = 50 кГц — допустимое напряжение переменного тока
U действующее значение = 280 В (график 2).
График 2: Допустимое напряжение переменного тока в зависимости от частоты при повышении внутренней температуры на 10 ° C (общие рекомендации).
Напряжение переменного тока, указанное на диаграммах, также можно использовать для определения максимального эффективного тока
| X C = 1 / ω x C = 1 / 2π x 50 кГц x 0,01 мкФ | X C = 318 Ом |
| I C = U C / X C = 280 В ~ / 318 МОм | Я С = 0.88 А |
Расчетное максимальное значение действующего тока
| I P = I C x √2 = 0,88 A x √2 | I P = 1,24 А |
не должен превышать максимальный номинальный ток, указанный при расчете максимального времени нарастания импульса (см. F max выше). В этом случае необходимо соответственно снизить рабочее напряжение переменного тока.
| | | Характеристики Приложения | | | | |
|
| UMR | Радиальный | Ультраминиатюрный | от -40 до + 85º с | 4-50 | 0.1-470 | 1000 часов |
|
| MR | Радиальный | Миниатюрный тип | от -40 до + 105 ° C | 6.3-63 | 0,1-470 | 1000 часов |
|
| MHR | Радиальный | 105ºC | от -40 до + 105 ° C | 6.3-63 | 0,1-470 | 1000 часов |
|
| GPR | Радиальный | 85ºC @ | от -40 до + 85 ° C | 6.3–100 | 0,1-22000 | 2000 часов |
от -25 до + 85 ° C | 160-450 | 0,47-820 | |||||
|
| RH | Радиальный | 105ºC @ | от -40 до + 105 ° C | 6.3–100 | 0,1-15000 | 2000 часов |
от -25 до + 105 ° C | 160-450 | 0,47-330 | |||||
|
| LL | Радиальный | Ток малой утечки @ | от -40 до + 105 ° C | 6.3-63 | 0,1-2200 | 2000 часов |
|
| НП | Осевое радиальное | Неполяризованный @ | от -40 до + 105 ° C | 10–250 | 0.47-2200 | 2000 часов |
|
| БП | Радиальный | Биполяризованный @ | от -40 до + 105 ° C | 6.3–100 | 0,47-6800 | 2000 часов |
|
| GLR | Радиальный | Низкое сопротивление / | от -55 до + 105 ° C | 6.3-100 | 0,47-4700 | 5000 часов |
|
| AX | Осевой
| 105ºC | от -40 до + 105 ° C | 6.3–100 | 0,47-15000 | 2000 часов |
от -25 до + 105 ° C | 160-400 | 0,47-220 | |||||
|
| LPR | Вставка
| Печатная плата Snap-in @ | от -40 до + 85 ° C | 10-100 | 470-68000 | 2000 часов |
от -25 до + 85 ° C | 160-450 | 47-2700 | |||||
|
| л.с. | Вставка
| 105ºC @ | от -40 до + 105 ° C | 10-100 | 330-68000 | 2000 часов |
от -25 до + 105 ° C | 160-400 | 33-2200 | |||||
|
| СТ | Винт | Винтовые клеммы Тип | от -40 до + 85º с | 10-100 | 220–330 000 | 2000 часов |
от -25 до + 85º с | 160-450 | ||||||
|
| ERC | Радиальный | E. |

 Однако сразу бежать в сервис не стоит – простейшие приборы может продиагностировать и починить даже начинающий радиолюбитель. К примеру, сгоревший конденсатор виден невооружённым глазом. Но как быть, если под рукой нет детали подходящего номинала? Конечно, соединить 2 и более в цепь. Сегодня поговорим о таких понятиях, как параллельное и последовательное соединение конденсаторов, разберемся, как его выполнить, узнаем о способах соединения, правилах его выполнения.
Однако сразу бежать в сервис не стоит – простейшие приборы может продиагностировать и починить даже начинающий радиолюбитель. К примеру, сгоревший конденсатор виден невооружённым глазом. Но как быть, если под рукой нет детали подходящего номинала? Конечно, соединить 2 и более в цепь. Сегодня поговорим о таких понятиях, как параллельное и последовательное соединение конденсаторов, разберемся, как его выполнить, узнаем о способах соединения, правилах его выполнения.