Калькулятор последовательного и параллельного соединения конденсаторов
Перевод единиц Ёмкости электрической, электрической емкости, маркировка конденсаторов — таблица + Таблица перевода величин емкостей и обозначений конденсаторов
| Перевести из: | Перевести в: | ||||
| Ф | абФ | Ф до 1948 г. | μФ | статФ | |
| 1 Ф = фарада = F = farad (единица СИ) это: | 1,0 | 1.0×10-9 | 1.000495 | 1.0×106 | 8.987584×1011 |
| 1 абФ = Абфарад = Abfarad = единица СГСМ = EM unit это: | 1.0×109 | 1,0 | 1.000495×109 | 1.0×1015 | 8.987584×1020 |
1Ф до 1948 г. = «farad international»: | 0.999505 | 9.995052×10-10 | 1,0 | 9.995052×105 | 8.9831369×1011 |
| 1 микрофарад = μФ = μF: | 1.0×10-6 | 1.0×10-15 | 1.000495×10-6 | 1,0 | 8.987584×105 |
| 1 Статфарад = статФ = Statfarad = единица СГСЭ = ES unit это: | 1.112646×10-12 | 1.112646×10-21 | 1.131968×10-12 | 1.112646×10-6 | 1,0 |
- Приставки: мили-, микро-, нано-, пико- — таблица тут
- Формулы емкости конденсатора.
Последовательное и параллельное соединение конденсаторов
На практике часто используются тела, обладающие малыми (и очень малыми) размерами, которые могут накопить большой заряд, при этом имея небольшой потенциал. Такие объекты называют конденсаторами. Одна из основных характеристик конденсатора – это его емкость.
Имея в резерве набор конденсаторов, обладающих разными параметрами, можно расширить спектр величин емкостей и диапазон рабочих напряжений, если применять их соединения.
Различают три типа соединений конденсаторов: последовательное, параллельное и смешанное (параллельное и последовательное).
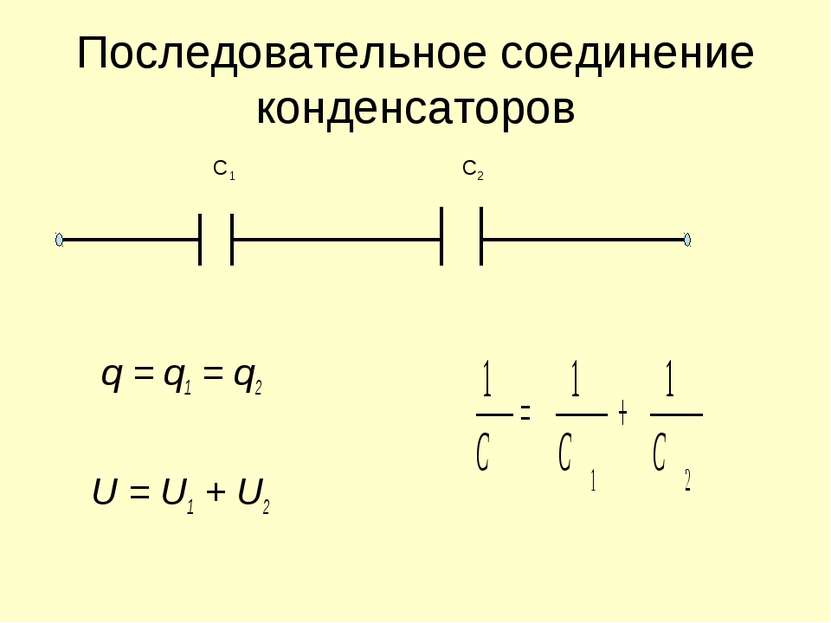
Последовательное соединение конденсаторов
Последовательное соединение изконденсаторов изображено на рис. 1
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды. Электрическая емкость последовательного соединения конденсаторов вычисляется по формуле:
где– электрическая емкость i-го конденсатора.
Если емкости конденсаторов при последовательном соединении равны, то емкость последовательного их соединения составляет:
где– предельное напряжение каждого конденсатора соединения. При последовательном соединении конденсаторов следует следить за тем, чтобы ни на один из конденсаторов батареи не падало напряжение, превышающее его максимальное рабочее напряжение.
Параллельное соединение конденсаторов
Параллельное соединение N конденсаторов изображено на рис. 2.
При параллельном соединении конденсаторов соединяют обкладки, обладающие зарядами одного знака (плюс с плюсом; минус с минусом). В результате такого соединения одна обкладка каждого конденсатора имеет одинаковый потенциал, например,, а другая. Разности потенциалов на обкладках всех конденсаторов при их параллельном соединении равны.
При параллельном соединении конденсаторов суммарная емкость соединения рассчитывается как сумма емкостей отдельных конденсаторов:
При параллельном соединении конденсаторов напряжение равно самой наименьшей величине рабочего напряжения конденсатора из состава рассматриваемого соединения.
Зарядка и разрядка
Рассмотрим такую схему:
Пока переключатель находится в положении 1, на конденсаторе создаётся напряжение — он заряжается.
Заряд Q на пластине в определённый момент времени расчитывается по формуле:
C — ёмкость, e — экспонента (константа ≈ 2.71828), t — время с момента начала зарядки.
Заряд на второй пластине по значению всегда точно такой же, но с противоположным знаком. Если резистор
R убрать, останется лишь небольшое сопротивление проводов (оно и станет значением R)
и зарядка будет происходить очень быстро.
Изобразив функцию на графике, получим такую картину:
Как видно, заряд растёт не равномерно, а обратно-экспоненциально. Это связанно с тем, что по
мере того, как заряд копится, он создаёт всё большее и большее обратное напряжение Vc,
которое «сопротивляется» Vin.
Заканчивается всё тем, что Vc становится равным по значению Vin и
ток перестаёт течь вовсе. В этот момент говорят, что конденсатор достиг точки насыщения (equilibrium).
Заряд при этом достигает максимума.
Вспомнив , мы можем изобразить зависимость силы тока в нашей
цепи при зарядке конденсатора.
Теперь, когда система находится в равновесии, поставим переключатель в положение 2.
На пластинах конденсатора заряды противоположных знаков, они создают напряжение — появляется ток
через нагрузку (Load). Ток пойдёт в противоположном направлении, если сравнивать с направлением
источника питания. Разрядка тоже будет происходить наоборот: сначала заряд будет теряться быстро,
затем, с падением напряжения создаваемого им же, всё медленее и медленее. Если за Q
обозначить заряд, который был на конденсаторе изначально, то:
Эти величины на графике выглядят следующим образом:
Опять же, через некоторое время система придёт в состояние покоя: весь заряд потеряется, напряжение
исчезнет, течение тока прекратится.
Если снова воспользоваться переключателем, всё начнётся по кругу. Таким образом конденсатор
ничего не делает кроме как размыкает цепь когда напряжение постоянно; и «работает», когда напряжение
резко меняется. Это его свойство и определяет когда и как он применяется на практике.
Это его свойство и определяет когда и как он применяется на практике.
Принцип работы схем на балластном конденсаторе
В этой схеме конде-р является фильтром тока. Напряжение на нагрузку поступает только до момента полного заряда конде-ра, время которого зависит от его ёмкости. При этом никакого тепловыделения не происходит, что снимает ограничения с мощности нагрузки.
Чтобы понять, как работает эта схема и принцип подбора балластного элемента для LED, напомню, что напряжение – скорость движения электронов по проводнику, сила тока – плотность электронов.
Для диода абсолютно безразлично, с какой скоростью через него будут «пролетать» электроны. Расчет конде-ра основан на ограничении тока в цепи. Мы можем подать хоть десять киловольт, но если сила тока составит несколько микр оампер, количества электронов, проходящих через светоизлучающий кристалл, хватит для возбуждения лишь крохотной части светоизлучателя и свечения мы не увидим.
В то же время при напряжении несколько вольт и силе тока десятки ампер плотность потока электронов значительно превысит пропускную способность матрицы диода, преобразовав излишки в тепловую энергию, и наш LED элемент попросту испарится в облачке дыма.
Кодовая маркировка, дополнение
В соответствии со стандартами IEC на практике применяется четыре способа кодировки номинальной емкости.
А. Маркировка 3 цифрами
Первые две цифры указывают на значение емкости в пигофарадах (пф), последняя — количество нулей. Когда конденсатор имеет емкость менее 10 пФ, то последняя цифра может быть «9». При емкостях меньше 1.0 пФ первая цифра «0». Буква R используется в качестве десятичной запятой. Например, код 010 равен 1.0 пФ, код 0R5 — 0.5 пф.
| Код | Емкость | Емкость | Емкость |
| 109 | 1,0 | 0,001 | 0,000001 |
| 159 | 1,5 | 0,0015 | 0,000001 |
| 229 | 2,2 | 0,0022 | 0,000001 |
| 339 | 3,3 | 0,0033 | 0,000001 |
| 479 | 4,7 | 0,0047 | 0,000001 |
| 689 | 6,8 | 0,0068 | 0,000001 |
| 100* | 10 | 0,01 | 0,00001 |
| 150 | 15 | 0,015 | 0,000015 |
| 220 | 22 | 0,022 | 0,000022 |
| 330 | 33 | 0,033 | 0,000033 |
| 470 | 47 | 0,047 | 0,000047 |
| 680 | 68 | 0,068 | 0,000068 |
| 101 | 100 | 0,1 | 0,0001 |
| 151 | 150 | 0,15 | 0,00015 |
| 221 | 220 | 0,22 | 0,00022 |
| 331 | 330 | 0,33 | 0,00033 |
| 471 | 470 | 0,47 | 0,00047 |
| 681 | 680 | 0,68 | 0,00068 |
| 102 | 1000 | 1,0 | 0,001 |
| 152 | 1500 | 1,5 | 0,0015 |
| 222 | 2200 | 2,2 | 0,0022 |
| 332 | 3300 | 3,3 | 0,0033 |
| 472 | 4700 | 4,7 | 0,0047 |
| 682 | 6800 | 6,8 | 0,0068 |
| 103 | 10000 | 10 | 0,01 |
| 153 | 15000 | 15 | 0,015 |
| 223 | 22000 | 22 | 0,022 |
| 333 | 33000 | 33 | 0,033 |
| 473 | 47000 | 47 | 0,047 |
| 683 | 68000 | 68 | 0,068 |
| 104 | 100000 | 100 | 0,1 |
| 154 | 150000 | 150 | 0,15 |
| 224 | 220000 | 220 | 0,22 |
| 334 | 330000 | 330 | 0,33 |
| 474 | 470000 | 470 | 0,47 |
| 684 | 680000 | 680 | 0,68 |
| 105 | 1000000 | 1000 | 1,0 |
* Иногда последний ноль не указывают.
В. Маркировка 4 цифрами
Возможны варианты кодирования 4-значным числом. Но и в этом случае последняя цифра указывает количество нулей, а первые три — емкость в пикофарадах.
| Код | Емкость | Емкость | Емкость |
| 1622 | 16200 | 16,2 | 0,0162 |
| 4753 | 475000 | 475 | 0,475 |
Рис. 6
С. Маркировка емкости в микрофарадах
Вместо десятичной точки может ставиться буква R.
| Код | Емкость |
| R1 | 0,1 |
| R47 | 0,47 |
| 1 | 1,0 |
| 4R7 | 4,7 |
| 10 | 10 |
| 100 | 100 |
D. Смешанная буквенно-цифровая маркировка емкости, допуска, ТКЕ, рабочего напряжения
В отличие от первых трех параметров, которые маркируются в соответствии со стандартами, рабочее напряжение у разных фирм имеет различную буквенно-цифровую маркировку.
| Код | Емкость |
| p10 | 0,1 пФ |
| Ip5 | 1,5 пФ |
| 332p | 332 пФ |
| 1НО или 1nО | 1,0 нФ |
| 15Н или 15n | 15 нФ |
| 33h3 или 33n2 | 33,2 нФ |
| 590H или 590n | 590 нФ |
| m15 | 0,15мкФ |
| 1m5 | 1,5 мкФ |
| 33m2 | 33,2 мкФ |
| 330m | 330 мкФ |
| 1mO | 1 мФ или 1000 мкФ |
| 10m | 10 мФ |
Кодовая маркировка электролетических конденсаторов для поверхностного монтажа
Приведенные ниже принципы кодовой маркировки применяются такими известными фирмами, как «Panasonic», «Hitachi» и др. Различают три основных способа кодирования
А. Маркировка 2 или 3 символами
Код содержит два или три знака (буквы или цифры), обозначающие рабочее напряжение и номинальную емкость. Причем буквы обозначают напряжение и емкость, а цифра указывает множитель. В случае двухзначного обозначения не указывается код рабочего напряжения.
Причем буквы обозначают напряжение и емкость, а цифра указывает множитель. В случае двухзначного обозначения не указывается код рабочего напряжения.
| Код | Емкость | Напряжение |
| А6 | 1,0 | 16/35 |
| А7 | 10 | 4 |
| АА7 | 10 | 10 |
| АЕ7 | 15 | 10 |
| AJ6 | 2,2 | 10 |
| AJ7 | 22 | 10 |
| AN6 | 3,3 | 10 |
| AN7 | 33 | 10 |
| AS6 | 4,7 | 10 |
| AW6 | 6,8 | 10 |
| СА7 | 10 | 16 |
| СЕ6 | 1,5 | 16 |
| СЕ7 | 15 | 16 |
| CJ6 | 2,2 | 16 |
| CN6 | 3,3 | 16 |
| CS6 | 4,7 | 16 |
| CW6 | 6,8 | 16 |
| DA6 | 1,0 | 20 |
| DA7 | 10 | 20 |
| DE6 | 1,5 | 20 |
| DJ6 | 2,2 | 20 |
| DN6 | 3,3 | 20 |
| DS6 | 4,7 | 20 |
| DW6 | 6,8 | 20 |
| Е6 | 1,5 | 10/25 |
| ЕА6 | 1,0 | 25 |
| ЕЕ6 | 1,5 | 25 |
| EJ6 | 2,2 | 25 |
| EN6 | 3,3 | 25 |
| ES6 | 4,7 | 25 |
| EW5 | 0,68 | 25 |
| GA7 | 10 | 4 |
| GE7 | 15 | 4 |
| GJ7 | 22 | 4 |
| GN7 | 33 | 4 |
| GS6 | 4,7 | 4 |
| GS7 | 47 | 4 |
| GW6 | 6,8 | 4 |
| GW7 | 68 | 4 |
| J6 | 2,2 | 6,3/7/20 |
| JA7 | 10 | 6,3/7 |
| JE7 | 15 | 6,3/7 |
| JJ7 | 22 | 6,3/7 |
| JN6 | 3,3 | 6,3/7 |
| JN7 | 33 | 6,3/7 |
| JS6 | 4,7 | 6,3/7 |
| JS7 | 47 | 6,3/7 |
| JW6 | 6,8 | 6,3/7 |
| N5 | 0,33 | 35 |
| N6 | 3,3 | 4/16 |
| S5 | 0,47 | 25/35 |
| VA6 | 1,0 | 35 |
| VE6 | 1,5 | 35 |
| VJ6 | 2,2 | 35 |
| VN6 | 3,3 | 35 |
| VS5 | 0,47 | 35 |
| VW5 | 0,68 | 35 |
| W5 | 0,68 | 20/35 |
В. Маркировка 4 символами
Маркировка 4 символами
Код содержит четыре знака (буквы и цифры), обозначающие емкость и рабочее напряжение. Буква, стоящая вначале, обозначает рабочее напряжение, последующие знаки — номинальную емкость в пикофарадах (пФ), а последняя цифра — количество нулей. Возможны 2 варианта кодировки емкости: а) первые две цифры указывают номинал в пикофарадах, третья — количество нулей; б) емкость указывают в микрофарадах, знак m выполняет функцию десятичной запятой. Ниже приведены примеры маркировки конденсаторов емкостью 4.7 мкФ и рабочим напряжением 10 В.
С. Маркировка в две строки
Если величина корпуса позволяет, то код располагается в две строки: на верхней строке указывается номинал емкости, на второй строке — рабочее напряжение. Емкость может указываться непосредственно в микрофарадах (мкФ) или в пикофарадах (пф) с указанием количества нулей (см. способ В). Например, первая строка — 15, вторая строка — 35V — означает, что конденсатор имеет емкость 15 мкФ и рабочее напряжение 35 В.
Последовательное и параллельное соединение конденсаторов
Опубликовано Июль 30, 2015
Все наверняка уже знают, что собой представляют последовательное и параллельное соединения. Соединение, при котором конец одного устройства соединен с началом следующего, называется последовательным.
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов. получаемая цепь выглядит следующим образом:
Эта схема состоит из следующих элементов: трех конденсаторов C1. C2. С3 и источника электрической энергии E .
Мы видим, что конденсаторы подключены по всем правилам последовательного соединения, то есть вывод конденсатора C1 соединён с началом конденсатора C2. ну а конец конденсатора C2 соединен с началом третьего конденсатора C3
Стоит обратить внимание на то, как распределяются ёмкости каждого
При таком соединении, все ёмкостя следующим образом.
Дело в том, что общая емкость всех включенных конденсаторов не будит превышать емкости любого из конденсаторов. Проще говоря, если в данной группе конденсаторов, будит конденсатор с наименьшей емкостью, например, в 100 миро фарад, то общая емкость трех конденсаторов не будит превышать этих ста микрофарад. Общую емкость можно рассчитать по следующей формуле: Если в цепи имеются всего лишь два последовательно соединенных конденсатора, то общая емкость определяется по формуле:
Проще говоря, если в данной группе конденсаторов, будит конденсатор с наименьшей емкостью, например, в 100 миро фарад, то общая емкость трех конденсаторов не будит превышать этих ста микрофарад. Общую емкость можно рассчитать по следующей формуле: Если в цепи имеются всего лишь два последовательно соединенных конденсатора, то общая емкость определяется по формуле:
Параллельное соединение конденсаторов
При параллельном соединении, начала всех конденсаторов соединяются в одну точку, а концы в другую, как показано на рисунке ниже:
Так при параллельном соединении, емкости всех конденсаторов складываются: То есть, емкость каждого конденсатора, включенного параллельно суммируется и получается одна большая емкость, которую можно на схеме представить одним конденсатором.
Это как два пишем один в уме, только в данном случаи один рисуем, а три в уме.
Смешанное соединение конденсаторов
Смешанное соединение конденсаторов выглядит следующим образом:
И представляет с собой различные сочетания параллельного и последовательного соединений. Для вычисления общей емкости таких соединений, применяют метод замещения: все конденсаторы делят на последовательно и параллельно соединенные группы, рассчитывают ёмкость каждой группы в отдельности, так что в конце выйдет две параллельных или последовательных емкостей, которые можно без труда посчитать. Например, дана следующая схема и следующие данные:
C1=0.4Ф C2=0.8Ф C3=0,73Ф Необходимо найти общую емкость всех трех конденсаторов. Как мы видим конденсаторы C1 и C2 соединены последовательно, а конденсатор C3 по отношению к первым двум параллельно. Посчитав общую емкость последовательно соединенных конденсаторов C1 и C2, их можно представить, как один конденсатор C1,2. Теперь нам не составит труда посчитать емкость двух параллельно соединенных конденсаторов, просто сложив их ёмкости.
Применения параллельного и последовательного соединений конденсаторов нашло свое применение в тех случаях, когда необходимо получить ту или иную величину емкости. Допустим у вас нет подходящего конденсатора, но есть куча других. Выполнив несколько не хитрых расчетов можно подобрать необходимую емкость.
Допустим у вас нет подходящего конденсатора, но есть куча других. Выполнив несколько не хитрых расчетов можно подобрать необходимую емкость.
Последовательное соединение
При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = ic1 = ic2 = ic3 = ic4.
В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Qобщ= Q1 = Q2 = Q3.
Если рассмотреть три конденсатора С1, С2 и С3, соединенные в последовательную цепь, то выясняется, что средний конденсатор С2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.
Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.
Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.
Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.
Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.
Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.
Таблица перевода емкостей и обозначений конденсаторов
| μF микрофарады | nF нанофарады | pF пикофарады | Code / Код трех-цифровой |
|---|---|---|---|
| 1μF | 1000nF | 1000000pF | 105 |
| 0.82μF | 820nF | 820000pF | 824 |
| 0.8μF | 800nF | 800000pF | 804 |
| 0.7μF | 700nF | 700000pF | 704 |
| 0.68μF | 680nF | 680000pF | 624 |
| 0.6μF | 600nF | 600000pF | 604 |
| 0.56μF | 560nF | 560000pF | 564 |
| 0.5μF | 500nF | 500000pF | 504 |
0. 47μF 47μF | 470nF | 470000pF | 474 |
| 0.4μF | 400nF | 400000pF | 404 |
| 0.39μF | 390nF | 390000pF | 394 |
| 0.33μF | 330nF | 330000pF | 334 |
| 0.3μF | 300nF | 300000pF | 304 |
| 0.27μF | 270nF | 270000pF | 274 |
| 0.25μF | 250nF | 250000pF | 254 |
| 0.22μF | 220nF | 220000pF | 224 |
| 0.2μF | 200nF | 200000pF | 204 |
| 0.18μF | 180nF | 180000pF | 184 |
| 0.15μF | 150nF | 150000pF | 154 |
| 0.12μF | 120nF | 120000pF | 124 |
| 0.1μF | 100nF | 100000pF | 104 |
| 0.082μF | 82nF | 82000pF | 823 |
| 0.08μF | 80nF | 80000pF | 803 |
| 0.07μF | 70nF | 70000pF | 703 |
| 0.068μF | 68nF | 68000pF | 683 |
| 0.06μF | 60nF | 60000pF | 603 |
| 0.056μF | 56nF | 56000pF | 563 |
| 0.05μF | 50nF | 50000pF | 503 |
| 0.047μF | 47nF | 47000pF | 473 |
| μF микрофарады | nF нанофарады | pF пикофарады | Code / Код трех-цифровой |
| 0.04μF | 40nF | 40000pF | 403 |
0. 039μF 039μF | 39nF | 39000pF | 393 |
| 0.033μF | 33nF | 33000pF | 333 |
| 0.03μF | 30nF | 30000pF | 303 |
| 0.027μF | 27nF | 27000pF | 273 |
| 0.025μF | 25nF | 25000pF | 253 |
| 0.022μF | 22nF | 22000pF | 223 |
| 0.02μF | 20nF | 20000pF | 203 |
| 0.018μF | 18nF | 18000pF | 183 |
| 0.015μF | 15nF | 15000pF | 153 |
| 0.012μF | 12nF | 12000pF | 123 |
| 0.01μF | 10nF | 10000pF | 103 |
| 0.0082μF | 8.2nF | 8200pF | 822 |
| 0.008μF | 8nF | 8000pF | 802 |
| 0.007μF | 7nF | 7000pF | 702 |
| 0.0068μF | 6.8nF | 6800pF | 682 |
| 0.006μF | 6nF | 6000pF | 602 |
| 0.0056μF | 5.6nF | 5600pF | 562 |
| 0.005μF | 5nF | 5000pF | 502 |
| 0.0047μF | 4.7nF | 4700pF | 472 |
| 0.004μF | 4nF | 4000pF | 402 |
| 0.0039μF | 3.9nF | 3900pF | 392 |
| 0.0033μF | 3.3nF | 3300pF | 332 |
| 0.003μF | 3nF | 3000pF | 302 |
| 0.0027μF | 2.7nF | 2700pF | 272 |
0. 0025μF 0025μF | 2.5nF | 2500pF | 252 |
| 0.0022μF | 2.2nF | 2200pF | 222 |
| 0.002μF | 2nF | 2000pF | 202 |
| 0.0018μF | 1.8nF | 1800pF | 182 |
| μF микрофарады | nF нанофарады | pF пикофарады | Code / Код трех-цифровой |
| 0.0015μF | 1.5nF | 1500pF | 152 |
| 0.0012μF | 1.2nF | 1200pF | 122 |
| 0.001μF | 1nF | 1000pF | 102 |
| 0.00082μF | 0.82nF | 820pF | 821 |
| 0.0008μF | 0.8nF | 800pF | 801 |
| 0.0007μF | 0.7nF | 700pF | 701 |
| 0.00068μF | 0.68nF | 680pF | 681 |
| 0.0006μF | 0.6nF | 600pF | 621 |
| 0.00056μF | 0.56nF | 560pF | 561 |
| 0.0005μF | 0.5nF | 500pF | 52 |
| 0.00047μF | 0.47nF | 470pF | 471 |
| 0.0004μF | 0.4nF | 400pF | 401 |
| 0.00039μF | 0.39nF | 390pF | 391 |
| 0.00033μF | 0.33nF | 330pF | 331 |
| 0.0003μF | 0.3nF | 300pF | 301 |
| 0.00027μF | 0.27nF | 270pF | 271 |
| 0.00025μF | 0.25nF | 250pF | 251 |
| 0.00022μF | 0. 22nF 22nF | 220pF | 221 |
| 0.0002μF | 0.2nF | 200pF | 201 |
| 0.00018μF | 0.18nF | 180pF | 181 |
| 0.00015μF | 0.15nF | 150pF | 151 |
| 0.00012μF | 0.12nF | 120pF | 121 |
| 0.0001μF | 0.1nF | 100pF | 101 |
| 0.000082μF | 0.082nF | 82pF | 820 |
| 0.00008μF | 0.08nF | 80pF | 800 |
| 0.00007μF | 0.07nF | 70pF | 700 |
| μF микрофарады | nF нанофарады | pF пикофарады | Code / Код трех-цифровой |
| 0.000068μF | 0.068nF | 68pF | 680 |
| 0.00006μF | 0.06nF | 60pF | 600 |
| 0.000056μF | 0.056nF | 56pF | 560 |
| 0.00005μF | 0.05nF | 50pF | 500 |
| 0.000047μF | 0.047nF | 47pF | 470 |
| 0.00004μF | 0.04nF | 40pF | 400 |
| 0.000039μF | 0.039nF | 39pF | 390 |
| 0.000033μF | 0.033nF | 33pF | 330 |
| 0.00003μF | 0.03nF | 30pF | 300 |
| 0.000027μF | 0.027nF | 27pF | 270 |
| 0.000025μF | 0.025nF | 25pF | 250 |
| 0.000022μF | 0.022nF | 22pF | 220 |
| 0.00002μF | 0.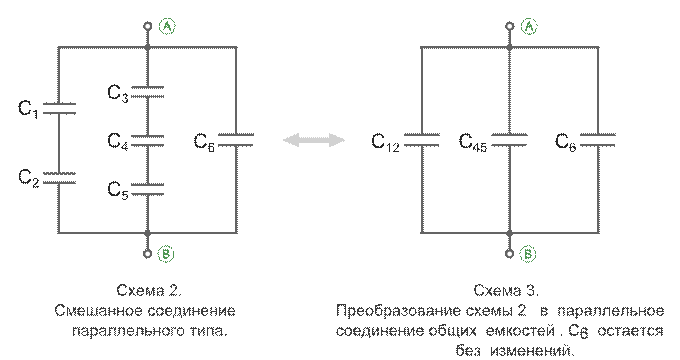 02nF 02nF | 20pF | 200 |
| 0.000018μF | 0.018nF | 18pF | 180 |
| 0.000015μF | 0.015nF | 15pF | 150 |
| 0.000012μF | 0.012nF | 12pF | 120 |
| 0.00001μF | 0.01nF | 10pF | 100 |
| 0.000008μF | 0.008nF | 8pF | 080 |
| 0.000007μF | 0.007nF | 7pF | 070 |
| 0.000006μF | 0.006nF | 6pF | 060 |
| 0.000005μF | 0.005nF | 5pF | 050 |
| 0.000004μF | 0.004nF | 4pF | 040 |
| 0.000003μF | 0.003nF | 3pF | 030 |
| 0.000002μF | 0.002nF | 2pF | 020 |
| 0.000001μF | 0.001nF | 1pF | 010 |
| μF микрофарады | nF нанофарады | pF пикофарады | Code / Код трех-цифровой |
Цветовая кодировка керамических конденсаторов.
На корпусе конденсатора, слева — направо, или сверху — вниз наносятся цветные
полоски.
Как правило, номинал емкости оказывается закодирован первыми тремя полосками.
Каждому цвету, в первых двух полосках,соответствует своя цифра:
черный — цифра 0;
коричневый — 1;
красный — 2;
оранжевый — 3;
желтый — 4;
зеленый — 5;
голубой — 6;
фиолетовый — 7;
серый — 8;
белый — 9.
Таким образом, если например, первая полоска коричневая а вторая желтая,
то это соответствует числу -14. Но это число не будет величиной номинальной
емкости конденсатора, его еще необходимо умножить на множитель, закодированный
третьей полоской.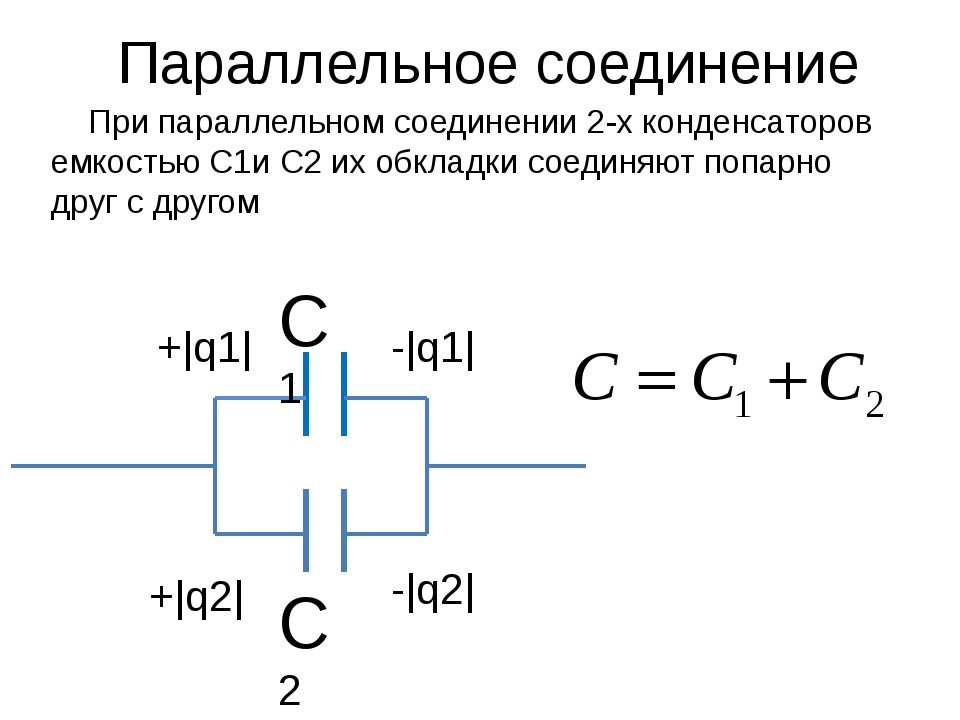
В третьей полоске цвета имеют следующие значение:
оранжевый — 1000;
желтый — 10000;
зеленый — 100000.
Допустим, что цвет третьей полоски нашего конденсатора — желтый.
Умножаем 14 на 10000, получаем емкость в пикофарадах -140000, иначе, 140 нанофарад или 0,14 микрофарад.
Четвертая полоска обозначает допустимые отклонения от номинала емкости(точность), в
процентах:
белый — ± 10 %;
черный — ± 20%.
Пятая полоска — номинальное рабочее напряжение.
Красный цвет — 250 Вольт, желтый — 400.
Соединение конденсаторов Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим необходимый конденсатор. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь 2 – 3 конденсатора на 470 микрофарад. Ставить конденсатор на 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров за одним конденсатором?
Важно
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение конденсаторов. На практике вам вряд ли это пригодиться.
На практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого конденсатора;
С2 – ёмкость второго конденсатора;
С3 – ёмкость третьего конденсатора;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости конденсаторов нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если рассчитываем ёмкости в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах
Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады или нанофарады можно воспользоваться специальной таблицей. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно пересчитать значения величин.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Для большего количества последовательно включенных конденсаторов потребуется другая формула. Она более запутанная, да и не всегда пригождается
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении конденсаторов их результирующая ёмкость будет всегда меньше наименьшей ёмкости, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсатор ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость составного конденсатора будет меньше 5.
Совет
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – ёмкость конденсатора.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из конденсаторов.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате ёмкость составного конденсатора составит 5 нанофарад.
Маркировка СМД (SMD) конденсаторов.
Размеры СМД конденсаторов невелики, поэтому маркировка их производится весьма лаконично.
Рабочее напряжение нередко кодируется буквой(2-й и 3-й варианты на рисунке ниже) в соответствии с.
Номинальная емкость может кодироваться либо с помощью (вариант 2 на рисунке), либо с использованием двухзначного
буквенно-цифровой кода(вариант 1 на рисунке). При использовании последнего, на корпусе можно обнаружить таки две(а не одну букву) с одной цифрой(вариант 3 на рисунке).
Первая буква может является как кодом изготовителя(что не всегда интересно), так и указываеть на номинальное рабочее напряжение(более полезная информация), вторая — закодированным значением
в пикоФарадах(мантиссой). Цифра — показатель степени(указывает сколько нулей необходимо добавить к мантиссе).
Например EA3 может означать, что номинальное напряжение конденсатора 16в(E) а емкость — 1,0 *1000 = 1 нанофарада,
BF5 соответсвенно, напряжение 6,3в(В), емкость — 1,6* 100000 = 0,1 микрофарад и.т.д.
| Буква | Мантисса. |
Подведем итоги о блокировочных конденсаторах
Теперь у нас достаточно информации, чтобы сформулировать краткий набор рекомендаций для успешной блокировки:
- В случае сомнений обеспечьте каждый питающий вывод керамическим конденсатором 0,1 мкФ, предпочтительно размером 0805 или меньше, параллельно танталовому или керамическому конденсатору 10 мкФ.

- Если речь идет только о высокочастотном шуме, возможно, вы можете опустить конденсатор на 10 мкФ или заменить его чем-то меньшим.
- Если вам необходимо компенсировать продолжительные колебания питания, которые потребуют большого количества сохраненного заряда, вам может потребоваться обеспечить каждую микросхему дополнительным более крупным конденсатором, скажем, 47 мкФ.
- Если ваш проект включает в себя очень высокие частоты или особенно чувствительную схему, используйте симулятор для анализа переходных процессов (AC анализ) вашей цепи блокировки. (Возможно, будет сложно найти точные спецификации на ESR и ESL, особенно учитывая, что ESR конденсатора может значительно варьироваться в зависимости от частоты – просто сделайте всё возможное.) При необходимости добавьте керамические конденсаторы с малой ESL для улучшения высокочастотных характеристик импеданса.
- Устанавливайте высокочастотные керамические конденсаторы как можно ближе к питающему выводу и используйте короткие дорожки и сквозные отверстия для минимизации паразитных емкости и сопротивления. Размещение более крупных конденсаторов, предназначенных для низкочастотной блокировки, не столь критично, но они также должны быть близки к микросхеме (в пределах полдюйма (12,7 мм) или около того).
Список источников
- dpva.ru
- elektrikaetoprosto.ru
- radioprog.ru
- electric-220.ru
- wiki.amperka.ru
- orenburgelectro.ru
- electricremont.ru
- www.gamesdraw.ru
- sibay-rb.ru
Поделитесь с друзьями!
При последовательном соединении конденсаторов их суммарная емкость
Соединение конденсаторов
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается
.
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф. )
)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.
Параллельное соединение электролитов
Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел
). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Соединение конденсаторов: руководство для начинающих
В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.
Параллельное соединение
Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии
Схема параллельного крепления
Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.
Схема — напряжение на накопителях
В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:
Последовательное соединение
Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.
Схема — схема последовательного соединения
Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.
Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:
i = ic1 = ic2 = ic3 = ic4, то есть токи проходящие через каждый конденсатор равны между собой.
Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:
А так определяется общая суммарная емкость конденсаторов при последовательном соединении:
Видео: как соединять конденсаторы параллельным и последовательным методом
Смешанное подключение
Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.
Схема: смешанное соединение конденсаторов
Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:
- Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
- Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
- Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока. Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
- Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.
Соединение конденсаторов
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Последовательное соединение конденсаторов
Конденсаторы, наряду с резисторами и диодами, входят в тройку наиболее распространённых электронных компонентов. Различные их соединения встречаются в подавляющем большинстве электробытовых приборов. Их можно встретить в персональных компьютерах, пылесосах, лампочках и даже смартфонах.
Как правильно соединять конденсаторы
Чтобы узнать, как подключить конденсатор правильно, нужно разобраться, к какому именно типу он относится. Данных электронных приборов существует огромное множество. Все конденсаторы подразделяются на две группы:
- полярные (электролитические) – подключая их, необходимо учитывать, где у детали плюсовой, а где минусовой контакт;
- неполярные (все остальные) – эти конденсаторы способны работать от переменного тока, у них не бывает положительных и отрицательных клемм.
Затем нужно учесть конструкцию электронного компонента. С этой точки зрения конденсаторы могут быть:
- Выводными. Подключаются к плате с помощью тонких медных ножек, покрытых (лужёных) для защиты слоем припоя.
- Для поверхностного монтажа (SMD). В основном применяются в компактной электронике. Очень миниатюрны, часто в поперечнике не превышают 1 мм.
Также важно принять во внимание рабочее напряжение конденсатора. Это особенно принципиально для электролитических приборов данного типа, ведь при превышении их номинального вольтажа они, вероятнее всего, взорвутся, разбрызгивая во все стороны кипящий электролит.
Важно! На крышке электролитического конденсатора имеются две насечки. Эти слабые места служат для мгновенной разгерметизации изделия в случае избыточного внутреннего давления. При ремонте и наладке оборудования следует избегать направленности насечек на лицо или одежду. При внештатной ситуации с их стороны может брызнуть горячий электролит.
Не менее критичен порог максимального напряжения и для прочих видов конденсаторов, особенно имеющих мелкие габариты и не способных длительно выдерживать перегрузки.
Последний, но не наименее важный фактор, который следует учесть при соединении конденсаторов, – это их ёмкость. Она измеряется в микрофарадах (в честь Майкла Фарадея). Это их главная характеристика, поэтому конденсаторы часто называют электрическими ёмкостями. В некоторых электронных устройствах этот параметр может существенно отклоняться как в меньшую, так и в большую сторону. В других – недопустимо погрешность и на 1 %.
Схема последовательного соединения
Последовательное соединение конденсаторов подразумевает, что правая ножка каждой предстоящей ёмкости будет подключена к левому выводу последующей. Иными словами, детали объединяются в цепь, в которой они идут друг за другом, как люди в длинной очереди в магазине.
Если подключаются электролитические конденсаторы, то плюс одной детали соединяется с минусом другой, по тому же принципу, как и батарейки в различных портативных гаджетах.
В случае с распаянными на плате SMD деталями у каждой детали есть своё место, подключаются они тонкими медными проводниками – дорожками при помощи паяльника (редко) или термофена.
При последовательном соединении двух и более ёмкостей их рабочее напряжение суммируется. Нередко такой подход используется радиолюбителями, когда у них нет детали на нужный вольтаж. Формула для вычисления рабочего напряжения линейки из n конденсаторов выглядит следующим образом:
Uобщ.посл = U1 + U2 + … + Un.
Здесь U1, U2… – максимальный вольтаж каждого отдельно взятого конденсатора.
С ёмкостью линейки последовательно включенных деталей всё обстоит иначе. Она наоборот снижается. Объясняется это конструктивными особенностями этих приборов, а именно виртуальным увеличением расстояния между их обкладками. При последовательном соединении общая ёмкость определяется следующим выражением:
1/Cобщ.посл = (1/С1) + (1/С2) + … + (1/Сn).
Здесь C1, C2… – ёмкости отдельных конденсаторов.
Имеется более простой расчет этого параметра, но он пригоден только в том случае, если подключены два конденсатора, не более:
Cобщ.посл = С1*С2/(С1 + С2).
Параллельное и комбинированное соединение
Выделяются другие способы соединения, а именно комбинированное и параллельное подключение конденсаторов. Для них справедливы иные физические законы.
Напряжение всей группы при параллельном соединёнии конденсаторов равно вольтажу самого наименьшего из них. Т.е., если имеется цепь из трёх конденсаторов на 16, 25 и 50 В, то максимум, который на них можно подать, это 16 В. В такой схеме к каждой отдельной ёмкости будет приложено полное напряжение источника питания.
Ёмкость такой батареи складывается. Вызвано это виртуальным сложением площадей обкладок всех отдельных конденсаторов. На языке физики это выглядит так:
Cобщ.пар = С1 + С2 + … + Сn.
Зачем нужно такое соединение? Оно используется для увеличения ёмкости конденсаторов, например, в высоковольтной части сварочных инверторов и многих мощных блоках питания.
Дополнительная информация. Параллельное соединение позволяет снизить общее внутреннее сопротивление сборки, следовательно, и её нагрев. Тем самым можно увеличить срок службы ёмкости.
Комбинированное (смешанное) соединение наиболее сложное. В нём встречаются как последовательные, так и параллельные элементы. Расчёт параметров таких схем даётся с опытом. Для простоты его принято изучать по треугольнику, разбивая на более простые части.
Из схемы очевидно, что конденсаторы C1 и C2 включены последовательно. Их общую ёмкость можно рассчитать по вышеописанной формуле – Cобщ.посл. Далее схема упрощается. Здесь уже имеются два параллельных конденсатора Cобщ.посл и C3. Вычисляется по вышестоящей формуле Cобщ.пар. В итоге сложный для восприятия элемент цепи превращается в один эквивалентный конденсатор. Данная методика описывает алгоритм упрощения, с помощью которого можно рассчитывать гораздо более сложные конденсаторные фигуры (квадрат, куб и т.п.).
Ток при последовательном соединении конденсаторов
Электрический ток бывает двух видов: постоянным и переменным. Для работы ёмкостей это имеет большое значение.
Конденсатор и постоянный ток
Постоянный ток через конденсатор не проходит вообще. Справедливо это и для линейки из последовательно соединённых ёмкостей. Объясняется такой эффект опять же конструкцией самого электронного прибора. Конденсатор имеет две металлические обкладки. В простых электролитических приборах они сделаны из алюминиевой фольги. Между ними расположен тонкий слой диэлектрика (оксид алюминия). Если приложить к обкладкам разность потенциалов (напряжение), то ток потечёт, но только очень короткое время, пока конденсатор полностью ни зарядится. Далее движение носителей заряда прекратится, т.к. они не смогут пройти через диэлектрик. В этот момент можно сказать, что электрический ток равен нулю, и конденсатор его не пропускает.
Конденсатор и переменный ток
При переменном токе носители заряда периодически меняют своё направление. В случае с бытовой сетью изменение происходит 50 раз в секунду. Поэтому говорят, что частота тока в розетке равна 50 Гц.
Важно! Конденсаторы способны накапливать и длительно удерживать заряд. При работе с ёмкостями, заряженными от сети 220 В, их всегда следует разряжать сопротивлением в 100-1000 ом. Несоблюдение правила однажды приведёт к неприятному удару током.
Конденсатор определённо пропустит переменный ток, но не факт, что весь. Количество носителей заряда, которые смогут пройти через этот электронный прибор, зависит от ёмкости конденсатора, приложенного к нему напряжения и частоты смены направления зарядов. Математически это выражается так:
Здесь I – это электрический ток с частотой f, проходящий через конденсатор ёмкостью C, если к его обкладкам приложить напряжение U. 2 – просто число, а p = 3.14.
Такая способность конденсаторов ограничивать переменный ток широко применяется в аудиотехнике для построения различных звуковых фильтров. Изменяя ёмкость, можно влиять на частоту сигнала, которую она пропускает.
Падение напряженности и общая емкость
Ёмкость конденсатора – это величина, определяющая количество заряда, который он способен в себе сохранить. Выражение имеет следующий вид:
Здесь q – заряд, накопленный между обкладками конденсатора, U – напряжение к ним приложенное.
Вышеописанная формула представляет общий случай. На практике при расчете ёмкости конденсатора следует учитывать ряд других переменных:
где:
- E0 – электрическая постоянная, равная 8,85*10-12 Ф/м,
- E – диэлектрическая проницаемость среды, в которой располагаются обкладки конденсатора,
- S – их площадь пересечения,
- d – расстояние между обкладками.
Стандартная модель конденсатора имеет следующий вид.
Обкладки чаще всего изготовлены из тонкого листового алюминия и скручены в рулон. Делается это для увеличения их площади, ведь так ёмкость конденсатора становится существенно больше.
От выбора диэлектрика, устанавливаемого производителем между обкладками конденсатора, зависит номинальное и максимальное напряжение прибора. Это, в свою очередь, определяет его сферу применения. Если к обкладкам приложить чрезмерную разность потенциалов, то напряжённость поля между ними превысит допустимый уровень, и произойдёт пробой диэлектрика. Подобная ситуация особенно пагубно влияет на электролитические конденсаторы и ионисторы. В случае их пробоя прибор частично или полностью теряет способность накапливать заряд и в дальнейшем становится непригодным для работы.
При последовательном и параллельном включении разных конденсаторов существенно изменяются их характеристики. Данное свойство этих деталей активно используется инженерами-электронщиками и радиолюбителями. Знание принципов подключения позволяет им более продуктивно разрабатывать новые устройства.
Видео
Последовательное и параллельное соединение конденсаторов
Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-пареллельным (смешанным).
Если провести аналогию между соединением конденсаторов и соединением резисторов , то стоит отметить, что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений:
Формула Cобщ при параллельном соединении конденсаторов = формула Rобщ при последовательном соединении резисторов.
Формула Cобщ при последовательном соединении конденсаторов = формула Rобщ при параллельном соединении резисторов.
Параллельное соединение конденсаторов
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов.
При параллельном соединении формируется один большой конденсатор с площадью обкладок, равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме емкостей всех конденсаторов в цепи.
Параллельное соединение конденсаторов
Напряжение при параллельном соединении
На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит, потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение). Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения.
Падение напряжения при параллельном соединении
Ток при параллельном соединении
Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:
- ic — ток конденсатора
- C — Емкость конденсатора
- ΔVC/Δt – Скорость изменения напряжения
При параллельном соединении через каждый конденсатор потечет одельный ток, в зависимости от емкости конденсатора:
Ток при параллельном соединении
Последовательное соединение конденсаторов
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов в форме цепи, в которой каждый отдельный конденсатор соединяется с другим отдельным конденсатором только в одной точке.
Последовательное соединение конденсаторов
Ток при последовательном соединении
Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения:
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора.
Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд:
Посмотрим на последовательную цепь из трех конденсаторов на рисунке выше. Правая обкладка первого конденсатора С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3. Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи.
В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится.
При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи.
Площадь и расстояние между обкладками при последовательном соединении
Падение напряжения и общая емкость при последовательном соединении
На каждый отдельный конденсатор в последовательной цепи падает разное напряжение. Поскольку емкость обратно пропрциональна напряжению (С = Q/V), то чем меньше емкость конденсатора, тем большее напряжение на него упадет.
Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов:
Падение напряжения при последовательном соединении
Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3.
Разделив все выражение на Qобщ мы получим уравнение для общей емкости при последовательном соединении:
Из данного уравнения можно легко вывести формулу общей емкости для любого частного случая последовательного соединения.
Например, общая емкость для трех конденсаторов:
Общая емкость для двух конденсаторов:
Смешанное соединение конденсаторов
Если в цепи есть и последовательное и параллельное соединение, то такую цепь называют смешанной или последовательно-параллельной. Тем не менее, смешанное соединение может иметь как последовательный, так и параллельный характер.
Смешанное соединение конденсаторов
Общая емкость смешанного соединения конденсаторов
Чтобы посчитать общую емкость смешанного соединения конденсаторов, следуют такому же алгоритму, как и при расчете общего сопротивления смешанного соединения резисторов.
- Цепь разбивают на участки с только пареллельным или только последовательным соединением
- Вычисляют общую емкость для каждого отдельного участка.
- Вычисляют общую емкость для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 2:
Преобразование смешанного соединения в параллельное
Зачем все это нужно?
Вполне справедливым может оказаться вопрос, для чего надо соединять конденсаторы последовательно, если общая емкость будет меньше? Скорее всего, первым что приходит в голову — это чтобы получить новый эквивалентный конденсатор с меньшей емкостью. Но в производстве микросхем вряд ли будут делать подобное, поскольку, во -первых, обычно нужно экономить место на печатной плате, а во-вторых, нет смысла тратить деньги на два компонента или больше, если можно купить один с требуемой емкостью.
Но если в параллельном или последовательном соединении конденсаторов еще есть хоть какая-то логика, то кому вообще нужно смешанное?
Дело в том, что емкостью, то есть способностью накапливать электрический заряд, обладает любое тело в природе, даже человеческое. Если мы говорим о электрической цепи, то все ее элементы на практике обладают емкостью, и их можно представить как конденсаторы. Часто такую емкость еще называют паразитической, потому как она создает разного рода помехи.
Например, у нас есть какая-то электронная цепь с множеством различных компонентов, которая принимает сигнал, обрабатывает его определенным образом и выдает на выход результат. Известно, что время задержки сигнала, в основном, зависит от паразитической емкости электронных компонентов схемы. Поскольку должно пройти время зарядки паразитической емкости, прежде чем она начнет пропускать сигнал. Если мы хотим узнать время задержки, нужно посчитать общую емкость всех компонентов, конвертировав их в цепь из конденсаторов.
Последовательное соединение конденсаторов
Последовательное соединение конденсаторов – батарея, образованная цепочкой конденсаторов. Отсутствует ветвление, выход одного элемента подключается к входу следующего.
Физические процессы при последовательном соединении
При последовательном соединении конденсаторов заряд каждого равноценен. Обусловлено природным принципом равновесия. С источником соединены только крайние обкладки, другие заряжаются путем перераспределения меж ними зарядов. Используя равенство, находим:
q = q1 = q2 = U1 C1 = U2 C2, откуда запишем:
Напряжения меж конденсаторами распределяются обратно пропорционально номинальным емкостям. В сумме оба составляют вольтаж питающей сети. При разряде конструкция способна отдать заряд q вне зависимости от того, сколько конденсаторов включено последовательно. Емкость батареи найдем из формулы:
C = q/u = q/(U1 + U2), подставляя выражения, приведенные выше, приводя к общему знаменателю:
Вычисление общей емкости батареи
При последовательном соединении конденсаторов в батарею складываются величины, обратные номинальным емкостям. Приводя последнее выражение к общему знаменателю, переворачивая дроби, получаем:
Выражение используется для нахождения емкости батареи. Если конденсаторов более двух, формула усложняется. Для нахождения ответа номиналы перемножаются меж собой, выходит числитель дроби. В знаменатель ставят попарные произведения двух номиналов, перебирая комбинации. Практически иногда удобнее вести вычисление через обратные величины. Полученным результатом разделить единицу.
Соединение последовательное конденсаторов
Формула сильно упрощается, если номиналы батареи одинаковы. Требуется просто цифру поделить общим числом элементов, получая результирующее значение. Напряжение распределится равномерно, следовательно, достаточно номинал питающей сети разбить поровну на общее число. При питании аккумулятором 12 вольт, 4-х емкостях, на каждой упадет 3 вольта.
Одно упрощение сделаем для случая, когда номиналы равны, одна емкость включена переменная, чтобы подстраивать результат. Тогда максимальное напряжение каждого элемента удастся приближенно найти, разделив вольтаж источника уменьшенным на единицу количеством. Получится результат с заведомым запасом. Что касается переменной емкости, требования намного жёстче. В идеале рабочее значение перекрывает вольтаж источника.
Необходимость в последовательном соединении
На первый взгляд идея соединения конденсаторов батареей последовательным образом покажется лишенной смысла. Первое преимущество очевидно: падают требования к максимальному напряжению обкладок. Больше рабочий вольтаж, дороже изделие. Подобным образом мир видит радиолюбитель, владеющий рядом низковольтных конденсаторов, желающий применить железо составной частью высоковольтной цепи.
Рассчитывая по приведенным выше формулам действующие напряжения элементом, можно легко решить поставленную задачу. Рассмотрим для пущей наглядности пример:
Пусть установлены аккумулятор напряжением 12 вольт, три емкости номиналами 1, 2 и 4 нФ. Найдем напряжение при последовательном соединении элементов батареей.
Для нахождения трех неизвестных потрудитесь составить равное количество уравнения. Известно из курса высшей математики. Результат будет выглядеть следующим образом:
- U1 + U2 + U3 = 12;
- U1/U2 = 2/1 = 2, откуда запишем: U1 = 2U2;
- U2/U3 = 4/2 = 2, откуда видно: U2 = 2U
Не сложно заметить, последние два выражения подставим первому, выразив 12 вольт через вольтаж третьего конденсатора. Получится следующее:
4U3 + 2U3 + U3 = 12, откуда находим, напряжение третьего конденсатора составляет 12/7 = 1,714 вольта, U2 – 3,43 вольта, U1 – 6,86 вольта. Сумма чисел дает 12, каждое меньше напряжения питающего аккумулятора. Причем тем больше разница, чем меньший номинал у соседей. Из этого правила следует: в последовательном соединении конденсаторы низкой емкости показывают большее рабочее напряжение. Найдем для определенности номинал составленной батареи, заодно проиллюстрируем формулу, поскольку выше описана чисто словесно:
С = С1С2С3/(С1С2 + С2С3 + С1С3) = 8/(2 + 8 + 4) = 8/14 = 571 пФ.
Результирующий номинал меньше каждого конденсатора, составляющего последовательное соединение. Из правила видно: максимальное влияние на суммарную емкость оказывает меньший. Следовательно, при необходимости подстройки полного номинала батареи должен быть переменный конденсатор. В противном случае поворот винта не окажет большого влияния на конечный результат.
Видим очередной подводный камень: после подстройки распределение напряжений по конденсаторам изменится. Просчитайте крайние случаи, дабы вольтаж не превысил рабочее значение для составляющих батарею элементов.
Программные пакеты исследования электрических цепей
Помимо онлайн- калькуляторов расчета последовательного соединения конденсаторов присутствуют и инструменты помощнее. Большой минус общедоступных средств объясняется нежеланием сайтов проверять программный код, значит, содержат ошибки. Плохо, если одна емкость выйдет из строя, сломленная процессом испытаний неправильно собранной схемы. Не единственный недостаток. Иногда схемы гораздо сложнее, разобраться комплексно невозможно.
В отдельных приборах встречаются фильтры высокой частоты, использующие конденсатор, включенные каскадами. Тогда на схеме помимо замыкания через резистор на землю образуется последовательное соединение емкостей. Обычно не применяют формулу, показанную выше. Принято считать, каждый каскад фильтра существует отдельно, результат прохождения сигнала описывается амплитудно-частотной характеристикой. Графиком, показывающим, как сильно обрежет на выходе спектральную составляющую сигнала.
Желающим провести ориентировочные расчеты рекомендуется ознакомиться с программным пакетом персонального компьютера Electronics Workbench. Конструктив выполнен по английским стандартам, потрудитесь учитывать нюанс: обозначение резисторов на электрической схеме изломанным зигзагом. Номиналы, названия элементов будут изложены на иностранный манер. Не мешает пользоваться оболочкой, предоставляющей оператору гору источников питания различного толка.
И главное – Electronics Workbench позволит задать контрольные точки на каждой, в режиме реального времени посмотреть напряжение, ток, спектр, форму сигнала. Полагается дополнить проект амперметром, вольтметром, прочими аналогичного толка приборами.
При помощи такого программного пакета смоделируете ситуацию, посмотрите, сколько падает напряжения на элементе батареи. Уберегает от громоздких расчетов, намного ускоряя процесс проектирования схемы. Одновременно исключаются ошибки. Легко и просто становится добавлять, удалять конденсаторы с немедленной оценкой результата.
Рабочий пример
Скрин показывает рабочий стол Electronics Workbench 5.12 с собранной электрической схемой последовательного соединения конденсаторов. Каждый емкостью 1 мкФ, одинаковые элементы взяты для целей демонстрации. Чтобы каждый мог без труда проверить правильность.
Последовательная батарея конденсаторов
Обратим вначале внимание на источник. Переменное напряжение частотой 60 Гц. В стране разработчика действует иной стандарт, нежели российские. Рекомендуется правой кнопкой мыши щелкнуть источник, посетить свойства, выставить:
- Частоту (frequency) 50 Гц вместо 60 Гц.
- Действующее значение напряжения (voltage) 220 вольт вместо 120.
- Фазу (phase – имитация реактивности) взять согласно своим нуждам.
Для буквоедов будет полезно полистать свойства элементов цепи. У источника вольны задать допустимое отклонение напряжения (voltage tolerance) в процентах. Достаточно добавить один резистор размером 1 кОм, цепь становится фильтром верхних частот. Рекомендуется не упрощать действия. Поставить правильно знак заземления, убедиться: схема полностью тривиальна. В противном случае результаты заставят надолго поломать голову.
Проиллюстрированный скрином фильтр верхних частот обнаруживает подъем амплитудно-частотной характеристики в районе 1 кГц. При нахождении полосы пропускания необходимо учесть: вертикальная шкала логарифмическая. Посему срез на уровне 70% максимума не соответствует семи десятым высоты пологой части пика. Заядлым любителям будет интересна фазочастотная характеристика, в окне расположенная снизу.
Тот и другой график строятся из меню Analysis раздел AC Frequency. А еще тут… Fourier. Доступно посмотреть спектр выходного сигнала. В нашем случае не будет ничего интересного, поскольку собрали унылый пассивный фильтр, колебание на входе гармоническое. Гораздо интереснее наблюдать спектр импульсного сигнала.
Раздел Transient показывает отклик на подачу фронта питающего напряжения. На графике фактически представлен процесс заряда батареи, откуда найдем постоянную времени по уровню 0,7 максимума. Тонкости понятны желающим собрать сглаживающий фильтр амплитудного детектора. Как видно из графика, значение составляет 250 мкс. Параметр определяется из окна следующим образом:
- Считается, за три постоянные времени цепи заряд конденсаторов, разряд производится приблизительно на 95%.
- Легко заметить, точка находится в районе 800 мкс.
- Следует разделить значение на три, получится постоянная времени батареи последовательно соединенных конденсаторов.
По-другому постоянная времени вычисляется произведением сопротивления на общую емкость батареи. Пользуясь приведенными выше формулами, вычислим: С = 1 мкФ / 4 = 250 нФ. Осталось умножить значение на 1000 Ом, получится 250 мкс. Программный пакет Electronics Workbench 5.12 при умелом использовании высвобождает уйму свободного времени.
Раздобыть программный пакет расчета электрики
В интернете бытует мнение: автором Electronics Workbench выступает дочерняя компания корпорации National Instruments, разрабатывающая программное обеспечение. Неправда. Из окна авторских прав упомянутого приложения видно: разработка выполнена отделом Interactive Image Technologies.
Вышеозначенное подразделение обрело самостоятельность в 1995 году. Отдел направленно занимался рекламными и обучающими материалами. Electronics Workbench разработан для целей обучения студентов Канады. Потом программный продукт распространился всемирно, с некоторых пор именуется Multisim.
Обновленный программный продукт продают официальные дилеры, перечень представлен официальным сайтом компании National Instruments: russia.ni.com/contact. На момент исследования счастливчиками, получившими право купить ПО не выезжая за город, назовем жителей Москвы, Санкт-Петербурга. Удачи решившимся связаться с официальными представителями, в Multisim добавлены новые фишки:
- Более 36000 схемных элементов.
- Возможность разработки печатных плат на основе собранной электрической схемы.
- Продвинутые опции анализа вместо убогости, демонстрируемой скринам, версии 20-летней давности.
Параллельное и последовательное соединение конденсаторов: способы, правила, формулы
Любая электроника в доме может выйти из строя. Однако сразу бежать в сервис не стоит – простейшие приборы может продиагностировать и починить даже начинающий радиолюбитель. К примеру, сгоревший конденсатор виден невооружённым глазом. Но как быть, если под рукой нет детали подходящего номинала? Конечно, соединить 2 и более в цепь. Сегодня поговорим о таких понятиях, как параллельное и последовательное соединение конденсаторов, разберемся, как его выполнить, узнаем о способах соединения, правилах его выполнения.
Нет конденсатора нужного номинала: что делать
Очень часто начинающие домашние мастера, обнаружив поломку прибора, стараются самостоятельно обнаружить причину. Увидев сгоревшую деталь, они стараются найти подобную, а если это не удаётся, несут прибор в ремонт. На самом деле, не обязательно, чтобы показатели совпадали. Можно использовать конденсаторы меньшего номинала, соединив их в цепь. Главное – сделать это правильно. При этом достигается сразу 3 цели – поломка устранена, приобретён опыт, сэкономлены средства семейного бюджета.
Попробуем разобраться, какие способы соединения существуют и на какие задачи рассчитаны последовательное и параллельное соединение конденсаторов.
Соединение конденсаторов в батарею: способы выполнения
Существует 3 способа соединения, каждый из которых преследует свою определённую цель:
- Параллельное – выполняется в случае необходимости увеличить ёмкость, оставив напряжение на прежнем уровне.
- Последовательное – обратный эффект. Напряжение увеличивается, ёмкость уменьшается.
- Смешанное – увеличивается как ёмкость, так и напряжение.
Теперь рассмотрим каждый из способов более подробно.
Параллельное соединение: схемы, правила
На самом деле всё довольно просто. При параллельном соединении расчёт общей ёмкости можно вычислить путём простейшего сложения всех конденсаторов. Итоговая формула будет выглядеть следующим образом: Собщ= С₁ + С₂ + С₃ + … + Сn. При этом напряжение на каждом их элементов будет оставаться неизменным: Vобщ= V₁ = V₂ = V₃ = … = Vn.
Соединение при таком подключении будет иметь следующий вид:
Получается, что подобный монтаж подразумевает подключение всех пластин конденсаторов к точкам питания. Такой способ встречается наиболее часто. Но может произойти ситуация, когда важно увеличить напряжение. Разберёмся, каким образом это сделать.
Последовательное соединение: способ, используемый реже
При использовании способа последовательного подключения конденсаторов напряжение в цепи возрастает. Оно складывается из напряжения всех элементов и выглядит так: Vобщ= V₁ + V₂ + V₃ +…+ Vn. При этом ёмкость изменяется в обратной пропорции: 1/Собщ= 1/С₁ + 1/С₂ + 1/С₃ + … + 1/Сn. Рассмотрим изменения ёмкости и напряжения при последовательном включении на примере.
Дано: 3 конденсатора с напряжением 150 В и ёмкостью 300 мкф. Подключив их последовательно, получим:
- напряжение: 150 + 150 + 150 = 450 В,
- ёмкость: 1/300 + 1/300 + 1/300 = 1/С = 299 мкф.
Внешне подобное подключение обкладок (пластин) будет выглядеть так:
Выполняют такое соединение в том случае, если есть опасность пробоя диэлектрика конденсатора при подаче напряжения в цепь. Но ведь существует и ещё один способ монтажа.
Полезно знать! Применяют также последовательное и параллельное соединение резисторов и конденсаторов. Это делается с целью снижения подаваемого на конденсатор напряжения и исключения его пробоя. Однако следует учитывать, что напряжения должно быть достаточно для работы самого прибора.
Смешанное соединение конденсаторов: схема, причины необходимости применения
Такое подключение (его ещё называют последовательно-параллельным) применяют в случае необходимости увеличения, как ёмкости, так и напряжения. Здесь вычисление общих параметров немного сложнее, но не настолько, чтобы нельзя было разобраться начинающему радиолюбителю. Для начала посмотрим, как выглядит такая схема.
Составим алгоритм вычислений.
- всю схему нужно разбить на отдельные части, высчитать параметры которых просто,
- высчитываем номиналы,
- вычисляем общие показатели, как при последовательном включении.
Выглядит подобный алгоритм следующим образом:
Преимущество смешанного включения конденсаторов в цепь по сравнению с последовательным или параллельным
Смешанное соединение конденсаторов решает задачи, которые не под силу параллельным и последовательным схемам. Его можно использовать при подключении электродвигателей либо иного оборудования, его монтаж возможен отдельными участками. Монтаж его намного проще за счёт возможности выполнения отдельными частями.
Интересно знать! Многие радиолюбители считают этот способ более простым и приемлемым, чем два предыдущих. На самом деле, так и есть, если полностью понять алгоритм действий и научиться пользоваться им правильно.
Смешанное, параллельное и последовательное соединение конденсаторов: на что обратить внимание при его выполнении
Соединяя конденсаторы, в особенности электролитические, обратите внимание на строгое соблюдение полярности. Параллельное присоединение подразумевает подключение «минус/минус», а последовательное – «плюс/минус». Все элементы должны быть однотипны –плёночные, керамические, слюдяные либо металлобумажные.
Полезно знать! Выход из строя конденсаторов часто происходит по вине производителя, экономящего на деталях (чаще это приборы китайского производства). Поэтому правильно рассчитанные и собранные в схему элементы будут работать намного дольше. Конечно, при условии отсутствия замыкания в цепи, при котором работа конденсаторов невозможна в принципе.
Калькулятор расчёта ёмкости при последовательном соединении конденсаторов
А что делать, если необходимая ёмкость неизвестна? Не каждому хочется самостоятельно рассчитывать необходимую ёмкость конденсаторов вручную, а у кого-то на это просто нет времени. Для удобства производства подобных действий редакция Seti.guru предлагает нашему уважаемому читателю воспользоваться онлайн-калькулятором расчёта конденсаторов при последовательном соединении или вычисления ёмкости. В работе он необычайно прост. Пользователю необходимо лишь ввести в поля необходимые данные, после чего нажать кнопку «Рассчитать». Программы, в которые заложены все алгоритмы и формулы последовательного соединения конденсаторов, а также вычислений необходимой ёмкости, моментально выдаст необходимый результат.
Как рассчитать энергию заряженного конденсатора: выводим окончательную формулу
Первое, что для этого необходимо сделать – рассчитать, с какой силой притягиваются обкладки друг к другу. Это можно сделать по формуле F = q₀ × E, где q₀ является показателем величины заряда, а E – напряжённостью обкладок. Далее нам необходим показатель напряжённости обкладок, который можно вычислить по формуле E = q / (2ε₀S), где q – заряд, ε₀ – постоянная величина, S – площадь обкладок. В этом случае получим общую формулу для расчёта силы притяжения двух обкладок: F = q₂ / (2ε₀S).
Итогом наших умозаключений станет вывод выражения энергии заряженного конденсатора, как W = A = Fd. Однако это не окончательная формула, которая нам необходима. Следуем далее: учитывая предыдущую информацию, мы имеем: W = dq₂ / (2ε₀S). При ёмкости конденсатора, выражаемой как C = d / (ε₀S) получаем результат W = q₂ / (2С). Применив формулу q = СU, получим итог: W = CU² /2.
Конечно, для начинающего радиолюбителя все эти расчёты могут показаться сложными и непонятными, но при желании и некоторой усидчивости с ними можно разобраться. Вникнув в смысл, он поразится, насколько просто производятся все эти расчёты.
Для чего нужно знать показатель энергии конденсатора
По сути, расчёт энергии применяется редко, однако есть области, в которых это знать необходимо. К примеру, фотовспышка камеры – здесь вычисление показателя энергии очень важно. Она накапливается за определённое время (несколько секунд), а вот выдаётся мгновенно. Получается, что конденсатор сравним с аккумулятором – разница лишь в ёмкости.
Подводя итог
Порой без соединения конденсаторов не обойтись, ведь не всегда можно подобрать подходящие по номиналам. Поэтому знание того как это сделать может выручить при поломке бытовой техники или электроники, что позволит значительно сэкономить на оплате труда специалиста по ремонту. Как наверняка уже понял Уважаемый читатель, сделать это несложно и под силу даже начинающим домашним мастерам. А значит стоит потратить немного своего драгоценного времени и разобраться в алгоритме действий и правилах их выполнения.
Надеемся, что информация, изложенная в сегодняшней статье, была полезна нашим читателям. Возможно, у Вас остались какие-либо вопросы? В этом случае их можно изложить в обсуждении ниже. Редакция Seti.guru с удовольствием на них ответит в максимально короткие сроки. Если же Вы имеете опыт самостоятельного соединения конденсаторов (неважно, положительный он или отрицательный), убедительная просьба поделиться им с другими читателями. Это поможет начинающим мастерам более полно понять алгоритм действий и избежать ошибок. Пишите, делитесь, спрашивайте. А напоследок мы предлагаем посмотреть короткий, но довольно информативный видеоролик по сегодняшней теме.
Загрузка…
Формула расчета последовательного соединения конденсатора
Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом.
Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей.
Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.
Параллельное включение конденсаторов в цепь
Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.
Параллельное соединение конденсаторов:
Параллельное соединение конденсаторов
Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.
Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.
При параллельном соединении конденсаторов емкость равняется:
Формула и расшифровка
Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.
Конденсаторы, соединенные параллельно, имеют напряжение:
Формула
Последовательное включение конденсаторов в цепь
Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.
Последовательное соединение конденсатора:
Формула
При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния.
По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак.
Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.
Формула нахождения заряда на конденсаторе, схема подключения конденсатора:
Последовательное соединение конденсаторов
Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости.
Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки.
Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.
Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.
Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:
Основные моменты
Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:
Формула
Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:
Формула
Смешанное включение емкостных накопителей в схему
Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.
Участок цепи подсоединенных смешанным включением накопителей емкости:
Схема подключения конденсаторов
Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:
- разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
- вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
- проводим нахождение эквивалентной емкости на параллельном участке;
- когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
- рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.
Последовательное, параллельное и смешанное соединение конденсаторов
Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:
- Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.
- Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
- Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.
Вывод
Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников.
В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом.
Происходит увеличение емкости накопителя, и меняется работа двухполюсника.
Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.
Источник: https://domelectrik.ru/baza/komponenty/soedinenie-kondensatorov
Соединения конденсаторов. Энергия электрического поля конденсатора
| Соединения конденсаторов . | |
| Параллельное соединение конденсаторов | |
| Обкладки конденсаторов соединяют попарно, т.е. в системе остается два изолированных проводника, которые и представляют собой обкладки нового конденсатора | |
Вывод: При параллельном соединении конденсаторов
Т.о., общая емкость больше емкости любого из параллельно соединенных конденсаторов | |
| Последовательное соединение конденсаторов | |
| Производят только одно соединение, а две оставшиеся обкладки — одна от конденсатора С1 другая от конденсатора С2 — играют роль обкладок нового конденсатора. | |
Вывод: При последовательном соединении конденсаторов
Т.о., общая емкость меньше емкости любого из последовательно соединенных конденсаторов. | |
| Энергия электрического поля конденсатора. Формулы справедливы для любого конденсатора. | Пример: С=2мкФ; U=1000В. t=10-6c.W=1 Дж — опасно для жизни! |
| Плотность энергии. Формула справедлива для полей любых конденсаторов и, кроме того, для полей, меняющихся со временем (неэлектростатических). |
Источник: https://www.eduspb.com/node/1763
Соединение конденсаторов — Основы электроники
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока.
Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы.
Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов.
Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость.
А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
- Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник: http://www.sxemotehnika.ru/soedinenie-kondensatorov.html
Параллельное и последовательное соединение конденсаторов, схемы, расчет
Радиоэлементы можно соединить между собой тремя способами. Существует параллельное и последовательное соединение конденсаторов, а также смешанный тип. Всегда можно точно определить емкость равноценного конденсатора по этому показателю.
Его можно поменять на ряд соединенных в цепь других, более мелких по емкости конденсаторов.
Для равнозначного конденсаторы должно быть выполнено некоторое условие, а именно подключенное напряжение к конденсатору равно напряжению на зажимах этой группы этих.
Таким же образом подключается все радиоэлементы, существующие на данный момент. Главным образом используются параллельное и последовательное соединение конденсаторов. В данной статьи рассмотрены все типы соединений конденсаторов. В качестве бонуса. в статье есть видеоролик и статья, посвященные этой теме.
Виды соединения конденсаторов в обмотке.
Последовательное и параллельное соединение конденсаторов
Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-пареллельным (смешанным).
Если провести аналогию между соединением конденсаторов и соединением резисторов, то стоит отметить, что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений: Формула Cобщ при параллельном соединении конденсаторов = формула Rобщ при последовательном соединении резисторов.
- Cобщ — общая емкость.
- Rобщ — общее сопротивление.
При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q.
Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.
Соединения конденсаторов.
Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3.
Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.
Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.
Материал в тему: все о переменном конденсаторе.
Параллельное соединение конденсаторов
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов.
При параллельном соединении формируется один большой конденсатор с площадью обкладок, равной сумме площадей обкладок всех отдельных компонентов.
Поскольку емкость конденсаторов прямо пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме емкостей всех конденсаторов в цепи.
Напряжение при параллельном соединении
На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит, потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение). Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения. Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:
- ic — ток конденсатора
- C — Емкость конденсатора
- ΔVC/Δt – Скорость изменения напряжения
Будет интересно➡ Несколько фактов об электролитических конденсаторах
При параллельном соединении через каждый конденсатор потечет одельный ток, в зависимости от емкости конденсатора:
Последовательное соединение конденсаторов
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины, а остальные пластины заряжаются через влияние.
При этом заряд пластины будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения.
Типы соединений конденсаторов.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы. Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов в форме цепи, в которой каждый отдельный конденсатор соединяется с другим отдельным конденсатором только в одной точке. Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения.
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости.
Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора.
Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд.
Стоит почитать: все об электолитических конденсаторах.
Правая обкладка первого конденсатора С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3. Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи. В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится. При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.
Будет интересно➡ Формула расчёта сопротивления конденсатора
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи.
На каждый отдельный конденсатор в последовательной цепи падает разное напряжение. Поскольку емкость обратно пропрциональна напряжению (С = Q/V), то чем меньше емкость конденсатора, тем большее напряжение на него упадет.
Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов.
Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3. Из данного уравнения можно легко вывести формулу общей емкости для любого частного случая последовательного соединения.
Источник: https://ElectroInfo.net/kondensatory/chem-otlichajutsja-parallelnoe-i-posledovatelnoe-soedinenie-kondensatorov.html
Последовательное соединение конденсаторов
Последовательное соединение конденсаторов – батарея, образованная цепочкой конденсаторов. Отсутствует ветвление, выход одного элемента подключается к входу следующего.
Физические процессы при последовательном соединении
При последовательном соединении конденсаторов заряд каждого равноценен. Обусловлено природным принципом равновесия. С источником соединены только крайние обкладки, другие заряжаются путем перераспределения меж ними зарядов. Используя равенство, находим:
q = q1 = q2 = U1 C1 = U2 C2, откуда запишем:
U1/U2 = C2/C1.
Напряжения меж конденсаторами распределяются обратно пропорционально номинальным емкостям. В сумме оба составляют вольтаж питающей сети. При разряде конструкция способна отдать заряд q вне зависимости от того, сколько конденсаторов включено последовательно. Емкость батареи найдем из формулы:
C = q/u = q/(U1 + U2), подставляя выражения, приведенные выше, приводя к общему знаменателю:
1/С = 1/С1 + 1/С2.
Вычисление общей емкости батареи
При последовательном соединении конденсаторов в батарею складываются величины, обратные номинальным емкостям. Приводя последнее выражение к общему знаменателю, переворачивая дроби, получаем:
С = C1C2/(C1 + C2).
Выражение используется для нахождения емкости батареи. Если конденсаторов более двух, формула усложняется. Для нахождения ответа номиналы перемножаются меж собой, выходит числитель дроби. В знаменатель ставят попарные произведения двух номиналов, перебирая комбинации. Практически иногда удобнее вести вычисление через обратные величины. Полученным результатом разделить единицу.
Соединение последовательное конденсаторов
Формула сильно упрощается, если номиналы батареи одинаковы. Требуется просто цифру поделить общим числом элементов, получая результирующее значение. Напряжение распределится равномерно, следовательно, достаточно номинал питающей сети разбить поровну на общее число. При питании аккумулятором 12 вольт, 4-х емкостях, на каждой упадет 3 вольта.
Одно упрощение сделаем для случая, когда номиналы равны, одна емкость включена переменная, чтобы подстраивать результат.
Тогда максимальное напряжение каждого элемента удастся приближенно найти, разделив вольтаж источника уменьшенным на единицу количеством. Получится результат с заведомым запасом.
Что касается переменной емкости, требования намного жёстче. В идеале рабочее значение перекрывает вольтаж источника.
Необходимость в последовательном соединении
На первый взгляд идея соединения конденсаторов батареей последовательным образом покажется лишенной смысла. Первое преимущество очевидно: падают требования к максимальному напряжению обкладок. Больше рабочий вольтаж, дороже изделие. Подобным образом мир видит радиолюбитель, владеющий рядом низковольтных конденсаторов, желающий применить железо составной частью высоковольтной цепи.
Рассчитывая по приведенным выше формулам действующие напряжения элементом, можно легко решить поставленную задачу. Рассмотрим для пущей наглядности пример:
Пусть установлены аккумулятор напряжением 12 вольт, три емкости номиналами 1, 2 и 4 нФ. Найдем напряжение при последовательном соединении элементов батареей.
Решение:
Для нахождения трех неизвестных потрудитесь составить равное количество уравнения. Известно из курса высшей математики. Результат будет выглядеть следующим образом:
- U1 + U2 + U3 = 12;
- U1/U2 = 2/1 = 2, откуда запишем: U1 = 2U2;
- U2/U3 = 4/2 = 2, откуда видно: U2 = 2U
Не сложно заметить, последние два выражения подставим первому, выразив 12 вольт через вольтаж третьего конденсатора. Получится следующее:
4U3 + 2U3 + U3 = 12, откуда находим, напряжение третьего конденсатора составляет 12/7 = 1,714 вольта, U2 – 3,43 вольта, U1 – 6,86 вольта. Сумма чисел дает 12, каждое меньше напряжения питающего аккумулятора.
Причем тем больше разница, чем меньший номинал у соседей. Из этого правила следует: в последовательном соединении конденсаторы низкой емкости показывают большее рабочее напряжение.
Найдем для определенности номинал составленной батареи, заодно проиллюстрируем формулу, поскольку выше описана чисто словесно:
С = С1С2С3/(С1С2 + С2С3 + С1С3) = 8/(2 + 8 + 4) = 8/14 = 571 пФ.
Результирующий номинал меньше каждого конденсатора, составляющего последовательное соединение. Из правила видно: максимальное влияние на суммарную емкость оказывает меньший. Следовательно, при необходимости подстройки полного номинала батареи должен быть переменный конденсатор. В противном случае поворот винта не окажет большого влияния на конечный результат.
Видим очередной подводный камень: после подстройки распределение напряжений по конденсаторам изменится. Просчитайте крайние случаи, дабы вольтаж не превысил рабочее значение для составляющих батарею элементов.
Программные пакеты исследования электрических цепей
Помимо онлайн- калькуляторов расчета последовательного соединения конденсаторов присутствуют и инструменты помощнее.
Большой минус общедоступных средств объясняется нежеланием сайтов проверять программный код, значит, содержат ошибки. Плохо, если одна емкость выйдет из строя, сломленная процессом испытаний неправильно собранной схемы.
Не единственный недостаток. Иногда схемы гораздо сложнее, разобраться комплексно невозможно.
В отдельных приборах встречаются фильтры высокой частоты, использующие конденсатор, включенные каскадами. Тогда на схеме помимо замыкания через резистор на землю образуется последовательное соединение емкостей.
Обычно не применяют формулу, показанную выше. Принято считать, каждый каскад фильтра существует отдельно, результат прохождения сигнала описывается амплитудно-частотной характеристикой.
Графиком, показывающим, как сильно обрежет на выходе спектральную составляющую сигнала.
Желающим провести ориентировочные расчеты рекомендуется ознакомиться с программным пакетом персонального компьютера Electronics Workbench.
Конструктив выполнен по английским стандартам, потрудитесь учитывать нюанс: обозначение резисторов на электрической схеме изломанным зигзагом. Номиналы, названия элементов будут изложены на иностранный манер.
Не мешает пользоваться оболочкой, предоставляющей оператору гору источников питания различного толка.
И главное – Electronics Workbench позволит задать контрольные точки на каждой, в режиме реального времени посмотреть напряжение, ток, спектр, форму сигнала. Полагается дополнить проект амперметром, вольтметром, прочими аналогичного толка приборами.
При помощи такого программного пакета смоделируете ситуацию, посмотрите, сколько падает напряжения на элементе батареи. Уберегает от громоздких расчетов, намного ускоряя процесс проектирования схемы. Одновременно исключаются ошибки. Легко и просто становится добавлять, удалять конденсаторы с немедленной оценкой результата.
Рабочий пример
Скрин показывает рабочий стол Electronics Workbench 5.12 с собранной электрической схемой последовательного соединения конденсаторов. Каждый емкостью 1 мкФ, одинаковые элементы взяты для целей демонстрации. Чтобы каждый мог без труда проверить правильность.
Последовательная батарея конденсаторов
Обратим вначале внимание на источник. Переменное напряжение частотой 60 Гц. В стране разработчика действует иной стандарт, нежели российские. Рекомендуется правой кнопкой мыши щелкнуть источник, посетить свойства, выставить:
- Частоту (frequency) 50 Гц вместо 60 Гц.
- Действующее значение напряжения (voltage) 220 вольт вместо 120.
- Фазу (phase – имитация реактивности) взять согласно своим нуждам.
Для буквоедов будет полезно полистать свойства элементов цепи. У источника вольны задать допустимое отклонение напряжения (voltage tolerance) в процентах.
Достаточно добавить один резистор размером 1 кОм, цепь становится фильтром верхних частот. Рекомендуется не упрощать действия. Поставить правильно знак заземления, убедиться: схема полностью тривиальна.
В противном случае результаты заставят надолго поломать голову.
Построение графиков
Проиллюстрированный скрином фильтр верхних частот обнаруживает подъем амплитудно-частотной характеристики в районе 1 кГц.
При нахождении полосы пропускания необходимо учесть: вертикальная шкала логарифмическая. Посему срез на уровне 70% максимума не соответствует семи десятым высоты пологой части пика.
Заядлым любителям будет интересна фазочастотная характеристика, в окне расположенная снизу.
Тот и другой график строятся из меню Analysis раздел AC Frequency. А еще тут… Fourier. Доступно посмотреть спектр выходного сигнала. В нашем случае не будет ничего интересного, поскольку собрали унылый пассивный фильтр, колебание на входе гармоническое. Гораздо интереснее наблюдать спектр импульсного сигнала.
График отклика
Раздел Transient показывает отклик на подачу фронта питающего напряжения. На графике фактически представлен процесс заряда батареи, откуда найдем постоянную времени по уровню 0,7 максимума. Тонкости понятны желающим собрать сглаживающий фильтр амплитудного детектора. Как видно из графика, значение составляет 250 мкс. Параметр определяется из окна следующим образом:
- Считается, за три постоянные времени цепи заряд конденсаторов, разряд производится приблизительно на 95%.
- Легко заметить, точка находится в районе 800 мкс.
- Следует разделить значение на три, получится постоянная времени батареи последовательно соединенных конденсаторов.
По-другому постоянная времени вычисляется произведением сопротивления на общую емкость батареи. Пользуясь приведенными выше формулами, вычислим: С = 1 мкФ / 4 = 250 нФ. Осталось умножить значение на 1000 Ом, получится 250 мкс. Программный пакет Electronics Workbench 5.12 при умелом использовании высвобождает уйму свободного времени.
Версия ПО
Раздобыть программный пакет расчета электрики
В интернете бытует мнение: автором Electronics Workbench выступает дочерняя компания корпорации National Instruments, разрабатывающая программное обеспечение. Неправда. Из окна авторских прав упомянутого приложения видно: разработка выполнена отделом Interactive Image Technologies.
Вышеозначенное подразделение обрело самостоятельность в 1995 году. Отдел направленно занимался рекламными и обучающими материалами. Electronics Workbench разработан для целей обучения студентов Канады. Потом программный продукт распространился всемирно, с некоторых пор именуется Multisim.
Обновленный программный продукт продают официальные дилеры, перечень представлен официальным сайтом компании National Instruments: russia.ni.com/contact. На момент исследования счастливчиками, получившими право купить ПО не выезжая за город, назовем жителей Москвы, Санкт-Петербурга. Удачи решившимся связаться с официальными представителями, в Multisim добавлены новые фишки:
- Более 36000 схемных элементов.
- Возможность разработки печатных плат на основе собранной электрической схемы.
- Продвинутые опции анализа вместо убогости, демонстрируемой скринам, версии 20-летней давности.
Источник: https://VashTehnik.ru/enciklopediya/posledovatelnoe-soedinenie-kondensatorov.html
Как правильно соединять конденсаторы? Параллельное и последовательное соединение конденсаторов
КатегорииСправочная Статьи для новичков
Всем привет. Этот маленький пост посвящу теме соединения конденсаторов.
На практике, часто бывает так, что в наличии нет конденсатора нужного номинала для установки, а технику нужно срочно отремонтировать. Как раз для таких случаев нам необходимы знания о правилах соединения конденсаторов.
Способов соединения конденсаторов существуют всего два. Это последовательное и параллельное соединение. Сейчас более детально рассмотрим оба способа.
Параллельное соединение конденсаторов.
Это наиболее частый вид соединения конденсаторов. При подключении параллельно, емкость конденсатора увеличивается, а напряжение остается прежним.
Формула параллельного соединения конденсаторов: С= С1+С2+С3…
Рассмотрим на примере. Предположим, что необходим конденсатор 100 мкф 50в, а у Вас в наличии только 47мкф на 50в.
Если соединить эти конденсаторы параллельно (плюс к плюсу а минус к минусу) то общая емкость получившегося конденсатора будет ровняться около 94 мкф на 50в.
Это допустимое отклонение, так что можно свободно устанавливать в технику.
Параллельное соединение конденсаторов
Последовательное соединение конденсаторов.
При подключении, таким образом, общая емкость уменьшается, а напряжение работы конденсатора растёт.
Рассчитывается последовательное подключение конденсаторов по такой формуле:
Формула расчета последовательного соединения конденсаторов
Для примера подключим 3 конденсатора номиналом 100мкф на 100в последовательно. Согласно формуле, делим единицу, на емкость конденсаторов. Потом суммируем . Далее единицу делим на результат.
(1:100)+(1:100)+(1:100) = 0,01 + 0,01 + 0,01 = 0,03 далее 1 : 0,03 = 33 мкф на 300вольт (напряжение суммируем 100+100+100 = 300в). Итого 33мкф на 300в.
- В работе, последовательное соединение использую редко, но иногда бывает.
- Рекомендую ознакомиться со статей о ESR конденсаторов.
- Всем спасибо за просмотр.
Весь инструмент и расходники, которые я использую в ремонтах находится здесь.
Если у Вас возникли вопросы по ремонту телевизионной техники, вы можете задать их на нашем новом форуме . (9
Источник: https://my-chip.info/kak-pravilno-soedinyat-kondensatory-parallelnoe-i-posledovatelnoe-soedinenie-kondensatorov/
Последовательное и параллельное соединение проводников, резисторов, конденсаторов и катушек индуктивности. Онлайн расчёты
В«- РЇ тебе как электрику РѕР±СЉСЏСЃРЅСЏСЋ: Надя СЃРїРёС‚ СЃ мужиками последовательно, Р° Света параллельно. Кто РёР· РЅРёС… шмара вавилонская? — РќСѓ, Света наверное.
— Р’РѕС‚! Рђ РјРЅРµ, как кладовщику, видится немного РґСЂСѓРіРѕРµ: «РїРѕР±Р»СЏРґСѓС€РєР° обыкновенная» — 2 штуки! В» В«- Рђ теперь скажи РјРЅРµ отрок, как течёт электричество РїРѕ проводам электрическим, Рё цепям рукотворным, последовательным РґР° параллельным, РѕС‚ плюса Рє РјРёРЅСѓСЃСѓ СЃРѕ скоростью света РІ вакууме? — РЎ Божьей помощью, батюшка! РЎ Божьей помощью…В» РќСѓ РґР° ладно, достаточно! Шутки — штуками, Р° РїРѕСЂР° Р±С‹ уже дело делать. Так что «Копайте РїРѕРєР° здесь! Рђ СЏ тем временем схожу узнаю — РіРґРµ надо…В», Р° заодно набросаю пару-тройку калькуляторов РЅР° заданную тему. Р�так.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
РџСЂРё параллельном соединении падение напряжения между РґРІСѓРјСЏ узлами, объединяющими элементы цепи, одинаково для всех элементов, Р° сила тока РІ цепи равна СЃСѓРјРјРµ СЃРёР» токов РІ отдельных параллельно соединённых проводниках. РџРѕСЏСЃРЅРёРј СЂРёСЃСѓРЅРєРѕРј СЃ распределением напряжений, токов Рё формулами. Р РёСЃ.1 Расчёт проведём для 4 резисторов (РїСЂРѕРІРѕРґРЅРёРєРѕРІ), соединённых последовательно или параллельно. Если элементов РІ цепи меньше, то оставляем лишние поля РІ таблице РЅРµ заполненными. Заодно, РїСЂРё желании узнать распределение значений токов Рё напряжений РЅР° каждом РёР· элементов РїСЂРё последовательном Рё параллельном соединениях, есть возможность ввести величину общего напряжения РІ цепи U. Рђ есть возможность РЅРµ вводить… Короче, РІСЃРµ вводные, помеченные * — Рє заполнению РЅРµ обязательны.
РАСЧЁТ СОПРОТ�ВЛЕН�Й ПР� ПАРАЛЛЕЛЬНОМ � ПОСЛЕДОВАТЕЛЬНОМ СОЕД�НЕН�� проводников
Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая РЅР° Р РёСЃ.1 для РїСЂРѕРІРѕРґРЅРёРєРѕРІ Рё резисторов, остаётся РІ полной силе Рё для катушек СЃ конденсаторами, распределение напряжений Рё токов тоже РЅРёРєСѓРґР° РЅРµ девается, трансформируется лишь осмысление того, что токи эти Рё напряжения обязаны быть переменными. Почему переменными? Рђ потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет РІ первом приближении бесконечность, Р° катушек — ноль, соответственно Рё токи Р±СѓРґСѓС‚ равны либо нулю, либо бесконечности, Р° для переменных значений иметь СЏСЂРєРѕ выраженную зависимость РѕС‚ частоты.
Поэтому, для желающих рассчитать величины напряжений Рё токов РІ последовательных или параллельных цепях, состоящих РёР· конденсаторов Рё катушек индуктивности, имеет полный смысл выяснить РЅР° странице ссылка РЅР° страницу значения реактивных сопротивлений данных элементов РїСЂРё интересующей Вас частоте Рё подставить эти значения РІ таблицу для расчёта РїСЂРѕРІРѕРґРЅРёРєРѕРІ Рё резисторов. Рђ РІ качестве общего напряжения РІ цепи — подставлять действующее значение амплитуды переменного тока.
Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:
РЎ = РЎ1+ РЎ2+….+ РЎn Рё 1/L = 1/L1+ 1/L2 +…+ 1/Ln для параллельных цепей Рё
L = L1 + L2 +….+ Ln Рё 1/РЎ = 1/РЎ1+ 1/РЎ2+…+ 1/РЎn для последовательных. Как Рё РІ предыдущей таблице вводные, помеченные * — Рє заполнению РЅРµ обязательны.
- РАСЧЁТ ЁМКОСТ� ПР� ПАРАЛЛЕЛЬНОМ � ПОСЛЕДОВАТЕЛЬНОМ СОЕД�НЕН�� конденсаторов
- РАСЧЁТ �НДУКТ�ВНОСТ� ПР� ПАРАЛЛЕЛЬНОМ � ПОСЛЕДОВАТЕЛЬНОМ СОЕД�НЕН�� катушек
Ну и в завершении ещё одна таблица. Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.
Источник: https://vpayaem.ru/information12.html
Калькулятор | ColorAndCode
| LCD1602/2004 — HD44780 | |
Параллельное соединение резисторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
Последовательное соединение резисторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
Параллельное соединение конденсаторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
Последовательное соединение конденсаторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
| Реактивное сопротивление конденсатора | |
| Реактивное сопротивление конденсатора (+) | |
| Реактивное сопротивление катушки индуктивности | |
| Реактивное сопротивление катушки индуктивности (+) | |
| Обратное определение при параллельном соединении резисторов и последовательном конденсаторов | |
| Определение индуктивности из частоты и реактивного сопротивления | |
| Определение емкости из частоты и реактивного сопротивления | |
| Проводники | |
| Цилиндрические однослойные катушки | |
| Цилиндрические однослойные катушки (+) | |
Тороидальные катушки на ферритовых кольцах
Дополнительно: — Возможность использовать данные из справочника. | |
| Программирование ДПКД (делитель с переменным коэффициентом деления) | |
Сопротивление резистора для светодиода
Дополнительно: — Возможность использовать данные из справочника; — Вывод номинала в 4-х цветной маркировке для ряда E24 +/- 5 %. | |
| Расчёт схемы на основе NE555 | |
| Расчёт схем на основе LM317, LM338, LM350 | |
| Расчёт схем на основе LM2596 | |
| Расчет катушек на ферритовых кольцах фирмы Amidon |
|
| Расчёт индуктивности квадратной плоской катушки |
|
| Индуктивность прямого провода над проводящей подложкой |
Дополнительный материал в статье:
— Полупроводниковая светотехника № 4 за 2019 год
— Радиолюбитель № 3 за 2010 год
— Компоненты и технологии № 6 за 2010 год
Формирование исследовательских умений и навыков студентов как составной части профессиональной компетенции
Библиографическое описание:
Янченко, И. В. Формирование исследовательских умений и навыков студентов как составной части профессиональной компетенции / И. В. Янченко, В. С. Окунева. — Текст : непосредственный // Проблемы и перспективы развития образования : материалы I Междунар. науч. конф. (г. Пермь, апрель 2011 г.). — Т. 2. — Пермь : Меркурий, 2011. — С. 161-163. — URL: https://moluch.ru/conf/ped/archive/17/156/ (дата обращения: 22.03.2021).
Лабораторный
практикум по дисциплинам естественнонаучного профиля занимает
важнейшее место в формировании профессиональной компетенции инженера,
так как формирует навыки и умения, необходимые для организации и
проведения экспериментальных исследований. Анализ литературы,
посвященной организации практикумов показывает, что ученые и педагоги
стремятся создать образовательную технологию, которая в отличие от
традиционных способов проведения лабораторных практикумов, позволит
исключить формализм в выполнении работ практикума, который неизбежен
при его выполнении строго по методическим указаниям.
Исследовательская
ориентация учебного процесса при выполнении,
обработке, анализе результатов, вычислении погрешностей и оценки
достоверности результатов эксперимента учит студента сомневаться и
проверять информацию, доказывать собственное мнение и отстаивать
результаты. При этом активизируются познавательные способности
студентов, развиваются умения и навыки исследовательской
деятельности. Виртуальные лабораторные работы и модели не дают
практических навыков работы с реальным оборудованием, при их
выполнении нет неизбежно возникающей особой атмосферы сотрудничества
преподавателя и студента.
В качестве
одной из исследовательских работ, мы предлагаем студентам с помощью
конденсатора с известной электроемкостью определить электроемкость
неизвестного конденсатора и проверить законы параллельного и
последовательного соединения конденсаторов с помощью «мостика
Уинстона».
Студенту
предлагается самостоятельно собрать мостик Уинстона из приборов:
конденсаторы, реохорд, реостат, источник тока, гальванометр, набор
проводников и провести эксперимент, подтверждающий закон
параллельного и последовательного соединения конденсаторов (см.
рисунок). На
стадии теоретической части исследования с помощью правил Кирхгофа
студент выводит формулу для экспериментального определения
неизвестной электроемкости конденсатора
по известной электроемкости конденсатора
.
Идея, лежащая в основе
экспериментальной части исследования: собираем мостик Уинстона с
одним конденсатором неизвестно электроемкости и добиваемся нулевой
разности потенциалов между точкой М и движком реохорда. Определив
длины плеч реохорда, вычислим электроемкость неизвестного
конденсатора
,
по известной электроемкости конденсатора
.
С каждым
конденсатором, включая их последовательно в цепь, проводим
эксперимент и по формуле
определения электроемкости неизвестных конденсаторов:
где
-
емкость неизвестного конденсатора,
-
емкость известного конденсатора,
-
правое плечо реохорда,
-
левое плечо реохорда.
Результаты первой части
эксперимента по определению электроемкости двух конденсаторов
представлены в таблице 1.
Таблица результатов №1
|
№ опыта |
,мкФ |
Конденсатор
|
Конденсатор
| ||||
|
,см |
,см |
,мкФ |
,см |
,см |
,мкФ | ||
|
1 |
1 |
10 |
40 |
4,00 |
7 |
43 |
6,14 |
|
2 |
2 |
18 |
32 |
3,56 |
13 |
37 |
5,69 |
|
3 |
3 |
22 |
28 |
3,82 |
16 |
34 |
6,38 |
|
Среднее
|
3,79 |
Среднее
|
6,07 | ||||
После
измерений и вычисления электроемкостей конденсаторов
и
проверим соблюдение законов
параллельного и последовательного соединения конденсаторов для этого
соединяем их
параллельно и подключаем в цепь в точках АМ, как подключали один
конденсатор. Выше описанным способом добиваясь нулевой разности
потенциалов между точками М и движком реохорда экспериментально
определяем их электроемкость, как электроемкость одного конденсатора.
Результаты эксперимента представлены в таблице 2.
Таблица результатов №2
|
Параллельное
| ||||
|
№
опыта |
,мкФ |
результаты
| ||
|
,см |
,см |
,
| ||
|
1 |
1 |
5 |
45 |
9,00 |
|
2 |
2 |
8 |
42 |
10,50 |
|
3 |
3 |
12 |
38 |
9,50 |
|
Среднее
|
9,67 | |||
Далее
разбираем параллельное соединение конденсаторов
и
и соединяем их последовательно, подключив в цепь в точках АМ.
Добиваясь нулевой разности потенциалов между точками М и движком
реохора экспериментально определяем их общую электроемкость при
последовательном соединении. Результаты эксперимента представлены в
таблице 3.
Таблица результатов №3
|
Последовательное
| ||||
|
№
опыта |
,мкФ |
результаты
| ||
|
,см |
,см |
,
| ||
|
1 |
1 |
13 |
37 |
2,85 |
|
2 |
2 |
15 |
35 |
2,33 |
|
3 |
3 |
18 |
32 |
1,78 |
|
Среднее
|
2,32 | |||
Для
проверки полученных результатов эксперимента используем формулы для
вычисления электроемкости параллельно и последовательно соединенных
конденсаторов. Для параллельного соединения:
,
где
— теоретическое значение емкости батареи при параллельном соединении,
— экспериментальное
значение емкости первого конденсатора,
— экспериментальное значение емкости второго конденсатора.
Для последовательного
соединения:
где
— теоретическое значение емкости батареи при последовательном
соединении,
— экспериментальное
значение емкости первого конденсатора,
— экспериментальное значение емкости второго конденсатора.
Полученные результаты
эксперимента студент сводит в одну таблицу 4.
Таблица результатов №4
|
3,79 |
6,07 |
9,67 |
9,86 |
2,32 |
2,33 |
Сравнивая
экспериментальное и теоретическое значения емкости
конденсаторов при параллельном соединении,
видим, что отклонение составляет:
Сравнивая экспериментальное
и теоретическое значения емкости
конденсаторов при последовательном соединении,
видим, что отклонение составляет:
Анализ полученных
результатов студентом приводит к выводу о допустимости и довольно
высокой точности использования «мостика Уинстона» для
определения неизвестной электроемкости конденсатора по известной
электроемкости.
Наблюдение
на протяжении нескольких семестров за поведением и реакциями
студентов первого курса на свой первый, конечно не без участия
преподавателя, научно-исследовательский опыт показало, что
исследовательский метод проведения лабораторных практикумов
активизирует познавательную деятельность и способствует созданию
положительной мотивации, что, безусловно, сказывается на изучении
дисциплины в целом. Студент на своем опыте осознает, что полученные
знания являются средством для решения учебно-исследовательских, а
затем реальных экспериментальных и практических задач.
В этом состоит ценность
лабораторного практикума в техническом ВУЗ, он способствует
формированию профессиональных компетенций инженера, деятельность
которого заключается в решении технических задач, совершенствовании и
внедрении новых технологий.
Необходимо
отметить, что исследовательский метод проведения лабораторного
практикума требует от преподавателя изучения индивидуальных
особенностей и учебных возможностей студента, индивидуального
руководства процессом деятельности студента на практикуме,
перспективного планирования их деятельности. Невозможно и нет
необходимости превращать весь процесс обучения в исследование,
необходимо разумное сочетание исследовательского подхода и
традиционного проведения лабораторного практикума. Особенность работы
в лабораториях физики связана с постоянным индивидуальным общением
преподавателя и студента, именно поэтому на лабораторном практикуме
возможно, создать оптимальные условия для формирования
исследовательских компетенций.
Литература:
Т.И. Трофимова. Курс
физики в 2-х томах.- М.:Высшая школа, 1997.- Т.1.- 188с.
Основные термины (генерируются автоматически): лабораторный практикум, последовательное соединение, параллельное соединение, результат эксперимента, таблица результатов, конденсатор, неизвестный конденсатор, нулевая разность потенциалов, последовательное соединение конденсаторов, студент.
Последовательное соединение конденсаторов распределение напряжений. Последовательное соединение конденсаторов
Содержание:
В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.
Последовательное соединение
При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = i c1 = i c2 = i c3 = i c4 .
В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Q общ = Q 1 = Q 2 = Q 3 .
Если рассмотреть три конденсатора С 1 , С 2 и С 3 , соединенные в последовательную цепь, то выясняется, что средний конденсатор С 2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.
Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.
Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/C общ = 1/C 1 + 1/C 2 + 1/C 3 .
Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.
Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.
Смешанное соединение
Параллельное соединение конденсаторов
Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.
Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, С общ = С 1 + С 2 + С 3 .
Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.
Практически все электрические цепи включают в себя емкостные элементы. Соединение конденсаторов между собой выполняют по схемам. Их необходимо знать как при расчетах, так и при выполнении монтажа.
Последовательное соединение
Конденсатор, а в просторечии – «ёмкость», та деталь, без которой не обходится ни одна электрическая или электронная плата. Даже в современных гаджетах он присутствует, правда, уже в измененном виде.
Вспомним, что представляет собой этот радиотехнический элемент. Это накопитель электрических зарядов и энергии, 2 проводящие пластины, между которыми расположен диэлектрик. При прикладывании к пластинам источника постоянного тока через устройство кратковременно потечет ток, и оно зарядится до напряжения источника. Его емкость используют для решения технических задач.
Само это слово произошло задолго до того, как придумали устройство. Термин появился ещё тогда, когда люди считали, что электричество – это что-то типа жидкости, и ею можно наполнить какой-нибудь сосуд. Применительно к конденсатору – он неудачен, т.к. подразумевает, что прибор может вместить только конечное количество электричества. Хотя это и не так, но термин остался неизменным.
Чем больше пластины, и меньше расстояние между ними, тем больше . Если его обкладки соединить с каким-либо проводником, то через этот проводник произойдет быстрый разряд.
В координатных телефонных станциях с помощью этой особенности происходит обмен сигналами между приборами. Длина импульсов, необходимых для команд, таких как: «соединение линии», «ответ абонента», «отбой», регулируется величиной ёмкости установленных в цепь конденсаторов.
Единица измерения ёмкости – 1 Фарад. Т.к. это большая величина, то пользуются микрофарадами, пикофарадами и нанофарадами, (мкФ, пФ, нФ).
На практике, выполнив последовательное соединение, можно добиться увеличения прикладываемого напряжения. В этом случае поданное напряжение получают 2 внешние обкладки собранной системы, а обкладки, находящиеся внутри, заряжаются с помощью распределения зарядов. К таким приемам прибегают, когда под рукой не оказывается нужных элементов, зато есть детали других номиналов по напряжению.
К участку, имеющему 2 последовательно соединенных конденсатора, рассчитанных на напряжение 125 В, можно подключить питание 250 В.
Если для постоянного тока, конденсатор является препятствием за счет своего диэлектрического промежутка, то с переменным – все иначе. Для токов разных частот, подобно катушкам и резисторам, сопротивление конденсатора будет меняться. Токи высокой частоты он пропускает хорошо, а для их собратьев низкой частоты создает барьер.
У радиолюбителей есть способ – через емкость 220-500 пФ к радиоприемнику подключают вместо антенны сеть освещения напряжением 220 В. Ток с частотой 50 Гц он отфильтрует, а токи высокой частоты пропустит. Это сопротивление конденсаторов легко рассчитать по формуле для емкостного сопротивления:RC =1/6*f*C.
- Rc – емкостное сопротивление, Ом;
- f – частота тока, Гц;
- C – емкость данного конденсатора, Ф;
- 6 – округленное до целой части число 2π.
Но не только прикладываемое напряжение к цепи можно изменить, пользуясь подобной схемой включения. Так добиваются изменений емкостей при последовательных соединениях. Для легкости запоминания придумали подсказку, что общее значение емкости, полученное при выборе подобной схемы, получается всегда меньше меньшей из двух, включенных в цепочку.
Если так соединить 2 детали одинаковой ёмкости, то их общее значение будет вдвое меньше каждой из них. Расчеты последовательных соединений конденсатора можно выполнить по приведенной ниже формуле:
Собщ = С1*С2/С1+С2,
Пусть С1=110 пФ, а С2=220 пФ, тогда Собщ = 110×220/110+220 = 73 пФ.
Не стоит забывать про простоту и удобство монтажа, а также обеспечение качественной работы собранного устройства или оборудования. В последовательных соединениях у емкостей должен быть 1 производитель. А если детали всей цепочки будут одной партии выпуска, то проблем с эксплуатацией созданной цепи не будет.
Параллельное соединение
Накопители электрического заряда постоянной емкости, различают:
- керамические;
- бумажные;
- слюдяные;
- металлобумажные;
- электролитические конденсаторы.
Их делят на 2 группы: низковольтные и высоковольтные. Применяют их в фильтрах выпрямителей, для связи между низкочастотными участками цепей, в блоках питания различных устройств и т.д.
Конденсаторы переменной ёмкости тоже существуют. Они нашли свое предназначение в настраиваемых колебательных контурах теле- и радиоприемников. Емкость регулируется за счет изменения положения пластин относительно друг друга.
Рассмотрим соединение конденсаторов, когда их выводы соединятся попарно. Подобное включение подходит для 2 или более элементов, рассчитанных на одно и то же напряжение. Номинальное напряжение, которое указано на корпусе детали, превышать нельзя. В противном случае произойдет пробой диэлектрика, и элемент выйдет из строя. Но в цепь, где присутствует напряжение меньше номинального, конденсатор включать можно.
Параллельным включением конденсаторов можно добиться увеличения общей ёмкости. В некоторых устройствах необходимо обеспечить большое накопление электрического заряда. Существующих номиналов не хватает, приходится выполнять параллели и использовать то, что есть под рукой. Определить общую величину полученного соединения просто. Для этого нужно просто сложить величины всех используемых элементов.
Для вычисления емкостей конденсаторов формула имеет вид:
Собщ = С1+С2, где С1 и С2 – емкость соответствующих элементов.
Если С1=20 пФ, а С2=30 пФ, то Собщ = 50 пФ. Деталей в в параллели может быть n-ое количество.
На практике такое соединение находит применение в специальных устройствах, используемых в энергетических системах, и на подстанциях. Их монтируют, зная, как соединить конденсаторы для увеличения емкости, в целые блоки из батарей.
Для того чтобы поддерживать равновесие реактивной мощности как в энергоснабжающих установках, так и в установках энергопотребителей, существует необходимость включать в работу компенсирующие устройства реактивной мощности (УКРМ). Для снижения потерь и регулировки напряжения в сетях при расчетах устройства необходимо знать величины реактивных сопротивлений конденсаторов, используемых в установке.
Случается, что возникает необходимость вычислить по формуле напряжение на конденсаторах. В этом случае будем исходить из того, что С=q/U, т.е. отношение заряда к напряжению. И если величина заряда – q, а ёмкость – C, можем получим искомое число, подставляя значения. Она имеет вид:
Смешанное соединение
При расчете цепи, представляющей собой совокупность рассмотренных выше комбинаций, поступают так. Сначала ищем в сложной цепи конденсаторы, которые соединены между собой либо параллельно, либо последовательно. Заменив их эквивалентным элементом, получим более простую схему. Потом в новой схеме с участками цепи проводим те же манипуляции. Упрощаем до тех пор, пока не останется только параллельное или последовательное соединение. Их рассчитывать мы уже научились в этой статье.
Параллельно-последовательное соединение применимо для увеличения емкости, батареи или для того, чтобы приложенное напряжение не превышало рабочего напряжения конденсатора.
Практически на любой электронной плате применяются конденсаторы, устанавливаются они и в силовых схемах. Для того чтобы компонент мог выполнять свои функции, он должен обладать определёнными характеристиками. Иногда возникает ситуация, когда необходимого элемента нет в продаже или его цена неоправданно завышена.
Выйти из сложившегося положения можно, используя несколько элементов, а необходимые характеристики получают, применяя параллельное и последовательное соединения конденсаторов между собой.
Немного теории
Конденсатор — пассивный электронный компонент, с переменной или постоянной величиной ёмкости, которое предназначено для накопления заряда и энергии электрического поля.
При выборе этих электронных компонентов руководствуются двумя основными характеристиками:
Условное обозначение неполярного постоянного конденсатора на схеме, показано на рис. 1, а. Для полярного электронного компонента дополнительно отмечают положительный вывод — рис. 1, б.
Способы соединения конденсаторов
Составление батарей конденсаторов позволяет изменить суммарную ёмкость или рабочее напряжение. Для этого могут применяться такие способы соединения:
- последовательное;
- параллельное;
- смешанное.
Последовательное соединение
Последовательное подключение конденсаторов показано на рис. 1, в. Применяют такое соединение в основном для увеличения рабочего напряжения. Дело в том, что диэлектрики каждого из элементов расположены друг за другом, поэтому при таком соединении напряжения складываются.
Суммарная ёмкость
последовательно соединённых элементов можно рассчитать по формуле, которая для трёх компонентов будет иметь вид, показанный на рис. 1, е.
После преобразования в более привычную для нас форму, формула примет вид рис. 1, ж.
Если, соединённые последовательно, компоненты имеют одинаковые ёмкости, то расчёт значительно упрощается. В этом случае суммарную величину можно определить, разделив номинал одного элемента на их количество. Например, если требуется определить, какова ёмкость при последовательном соединении двух конденсаторов по 100 мкФ, то эту величину можно рассчитать, разделив 100 мкФ на два, то есть суммарная ёмкость равна 50 мкФ.
Максимально упростить расчёты последовательно соединённых компонентов
, позволяет использование онлайн-калькуляторов, которые без проблем можно найти в сети.
Параллельное подключение
Параллельное подключение конденсаторов показано на рис. 1, г. При таком соединении рабочее напряжение не изменяется, а ёмкости складываются. Поэтому для получения батарей большой ёмкости, используют параллельное соединение конденсаторов. Калькулятор для расчёта суммарной ёмкости не понадобится, так как формула имеет простейший вид:
С сум = С 1 + С 2 + С 3.
Собирая батарею для запуска трёхфазных асинхронных электродвигателей, часто применяют параллельное соединение электролитических конденсаторов. Обусловлено это большой ёмкостью этого типа элементов и небольшим временем запуска электродвигателя. Такой режим работы электролитических компонентов допустим, но следует выбирать те элементы, у которых номинальное напряжение минимум в два раза превышает напряжение сети.
Смешанное включение
Смешанное подключение конденсаторов — это сочетание параллельного и последовательного соединений
.
Схематически такая цепочка может выглядеть по-разному. В качестве примера рассмотрим схему, изображённую на рис. 1, д. Батарея состоит из шести элементов, из которых С1, С2, С3, соединены параллельно, а С4, С5, С6 — последовательно.
Рабочее напряжение можно определить сложением номинальных напряжений С4, С5, С6 и напряжения одного из параллельно подключённых конденсаторов. Если параллельно соединённые элементы имеют разные номинальные напряжения, то для расчёта берут меньшее из трёх.
Для определения суммарной ёмкости, схему разбивают на участки с одинаковым соединением элементов, производят расчёт для этих участков, после чего определяют общую величину.
Для нашей схемы последовательность вычислений следующая:
- Определяем ёмкость параллельно соединённых элементов и обозначаем её С 1-3.
- Рассчитываем ёмкость последовательно соединённых элементов С 4-6.
- На этом этапе можно начертить упрощённую эквивалентную схему, в которой вместо шести элементов изображаются два — С 1-3 и С 4-6. Эти элементы схемы соединены последовательно. Остаётся произвести расчёт такого соединения и мы получим искомую.
В жизни подробные знания о смешанном соединении могут только пригодится радиолюбителям.
Электрические конденсаторы широко используются в радиоэлектронной аппаратуре. Они лидируют по количеству применения в блоках аппаратуры и по некоторым критериям уступают лишь резисторам. Конденсаторы присутствуют в любом электронном устройстве и их потребность в современной электронике постоянно растет. Наряду с имеющейся широкой номенклатурой, продолжаются разработки новых типов, которые имеют улучшенные электрические и эксплуатационные характеристики.
Что такое конденсатор?
Конденсатором называется элемент электрической цепи, который состоит из проводящих электродов, изолированных друг от друга диэлектриком.
Конденсаторы отличают по емкости, а именно по отношению заряда к разности потенциалов, который передается этим зарядом.
В международной системе СИ за единицу емкости принимают емкость конденсатора
с возрастанием потенциала на один вольт при сообщении заряда в один кулон. Эта единица называется фарадой. Она слишком велика для применения в практических целях. Поэтому принято использовать более мелкие единицы измерения, такие как пикофарад (пФ), нанофарад (нФ) и микрофарад (мкФ).
Группы по виду диэлектрика
Диэлектрики применяют для изоляции пластин друг от друга. Они изготавливаются из органических и неорганических материалов. Нередко, в качестве диэлектрика, применяют оксидные пленки металлов.
По виду диэлектрика элементы делят на группы:
- органические;
- неорганические;
- газообразные;
- оксидные.
Элементы с органическим диэлектриком изготавливают путем намотки тонких лент специальной бумаги или пленки. Также применяют комбинированный диэлектрик
с фольговыми или металлизированными электродами. Такие элементы могут быть как высоковольтные (свыше 1600 В), так и низковольтные (до 1600 В).
В изделиях с неорганическим диэлектриком используют керамику, слюду, стекло и стеклокерамику, стеклоэмаль. Их обкладки состоят из тонкого слоя металла, который нанесен на диэлектрик путем металлизации. Бывают высоковольтные, низковольтные и помехоподавляющие.
В качестве газообразного диэлектрика используют сжатый газ (фреон, азот, элегаз), воздух или вакуум. По характеру изменения емкости и выполняемой функции такие элементы бывают постоянными и переменными.
Наибольшее распространение получили элементы с вакуумным диэлектриком. Они имеют большие удельные емкости (по сравнению с газообразным диэлектриком) и более высокую электрическую прочность. Элементы с вакуумным диэлектриком обладают стабильностью параметров
при температурных изменениях окружающей среды.
Область применения – передающие устройства, работающие на коротких, средних и длинных волнах диапазонов с частотой до 30-80 МГц.
Элементы с оксидным диэлектриком бывают:
- общего назначения;
- пусковые;
- импульсные;
- неполярные;
- высокочастотные;
- помехоподавляющие.
Диэлектриком является оксидный слой, который наносится на анод электрохимическим путем.
Условные обозначения
Элементы обозначаются по сокращенной и полной системе.
При сокращенной системе наносятся буквы и цифры
, где буквой обозначается подкласс, цифрой — группа в зависимости от применяемого диэлектрика. Третий элемент указывает регистрационный номер типа изделия.
При полном условном обозначении указываются параметры и характеристики в следующей последовательности:
- условное обозначение конструктивного исполнения изделия;
- номинальное напряжение изделия;
- номинальная емкость изделия;
- допустимое отклонение емкости;
- температурная стабильность емкости изделия;
- номинальная реактивная мощность изделия.
Подбор номинала
Конденсаторы могут соединяться друг с другом различными способами.
На практике нередко возникают ситуации, когда при монтаже схемы или замене неисправного элемента, приходится использовать ограниченное количество радиодеталей. Не всегда удается подобрать элементы нужного номинала.
В этом случае приходится применять последовательное и параллельное соединение конденсаторов.
При параллельной схеме соединения, их суммарная величина составит сумму емкостей
отдельных элементов. При этой схеме подключения все обкладки элементов соединяются по группам. Один из выводов каждого элемента соединяется в одну группу, а другой вывод в другую группу.
При этом напряжение на всех обкладках будет одинаково
, потому что все группы подключены к одному источнику питания. Фактически получается одна емкость, суммарной величины всех емкостей в данной цепи.
Чтобы получить большую емкость, применяют параллельное соединение конденсатора.
Например, необходимо подключить двигатель с тремя фазами к однофазной сети 220 В. Для рабочего режима двигателя необходима емкость величиной в 135 мкФ. Ее найти очень трудно, но можно получить, применив параллельное соединение элементов на 5, 30 и 100 мкФ. В результате сложения получаем необходимую единицу в 135 мкФ.
Последовательно соединение конденсаторов
Последовательное соединение конденсаторов используют, если необходимо получить емкость меньшую емкости элемента. Такие элементы выдерживают более высокие напряжения. При последовательном соединении конденсаторов, обратная величина общей емкости равняется сумме обратных величин отдельных элементов. Для получения требуемой величины нужны определенные конденсаторы, последовательное соединение которых даст необходимую величину.
При последовательном соединении конденсаторов каждый его вывод соединяется с одним выводом другого элемента. Получается некая цепочка из последовательно соединенных конденсаторов, где крайние выводы подключаются к источнику питания.
Емкость общей батареи всегда меньше минимальной емкости элементов, входящих в нее. То есть, половина от емкости каждой из этих емкостей.
При последовательном соединении конденсаторов увеличивается расстояние между обкладками элементов.
Например, при последовательном соединении двух элементов напряжением 200 В можно смело включать в схему напряжением до 1000 В.
Данный метод соединения используется гораздо реже
, потому что емкости такой величины и рабочего напряжения можно приобрести в магазинах.
Таким образом, зная принцип общего расчета параллельного и последовательного соединения конденсаторов, всегда можно выйти из затруднительного положения, имея под рукой ограниченное количество номиналов.
Под последовательным соединением подразумевают случаи, когда два или больше элемента имеют вид цепи, при этом каждый из них соединяется с другим только в одной точке. Зачем конденсаторы так размещаются? Как это правильно сделать? Что необходимо знать? Какие особенности последовательное соединение конденсаторов имеет на практике? Какая формула результата?
Что необходимо знать для правильного соединения?
Увы, но здесь не всё так легко сделать, как может показаться. Многие новички думают, что если на схематическом рисунке написано, что необходим элемент на 49 микрофарад, то достаточно его просто взять и установить (или заменить равнозначным). Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно. Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим. Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет.
Зачем так делают?
Когда с ними проводятся такие манипуляции, то электрические заряды на обкладках отдельных элементов будут равны: КЕ=К 1 =К 2 =К 3 . КЕ — конечная емкость, К — пропускаемое значение конденсатора. Почему так? Когда заряды поступают от источника питания на внешние обкладки, то на внутренних может быть осуществлен перенос величины, которая является значением элемента с наименьшими параметрами. То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ — то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ. Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула:
- ОЕ — общая емкость;
- Н — напряжение;
- КЕ — конечная емкость.
Что ещё необходимо знать, чтобы правильно соединить конденсаторы?
Для начала не забывайте, что кроме ёмкости они ещё обладают номинальным напряжением. Почему? Когда осуществляется последовательное соединение, то напряжение распределяется обратно пропорционально их ёмкостям между ними самими. Поэтому использовать такой подход имеет смысл только в тех случаях, когда любой конденсатор сможет предоставить минимально необходимые параметры работы. Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну. Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов. Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы.
Ток при последовательном соединении
Из-за того, что у него существует только один возможный путь протекания, он будет иметь одно значение для всех конденсаторов. При этом количество накопленного заряда везде обладает одинаковым значением. От емкости это не зависит. Посмотрите на любую схему последовательного соединения конденсаторов. Правая обкладка первого соединена с левой второго и так далее. Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи. Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток. И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться.
Падение напряженности и общая емкость
Каждый элемент понемногу рассеивает напряжение. Учитывая, что емкость ему обратно пропорциональна, то чем она меньше, тем большим будет падение. Как уже упоминалось ранее, последовательно соединённые конденсаторы обладают одинаковым электрическим зарядом. Поэтому при делении всех выражений на общее значение можно получить уравнение, которое покажет всю емкость. В этом последовательное и параллельное соединение конденсаторов сильно разнятся.
Пример № 1
Давайте воспользуемся представленными в статье формулами и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300. Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ.
Пример № 2
Давайте, чтобы закрепить наработки, решим ещё одну задачу. Имеется 100 конденсаторов. Емкость каждого элемента составляет 2 мкФ. Необходимо определить их общую емкость. Нужно их количество умножить на характеристику: 100*2=200 мкФ. Итак, общая емкость конденсатора при последовательном соединении составляет 200 микрофарад. Как видите, ничего сложного.
Заключение
Итак, мы проработали теоретические аспекты, разобрали формулы и особенности правильного соединения конденсаторов (последовательно) и даже решили несколько задачек. Хочется напомнить, чтобы читатели не упускали из внимания влияние номинального напряжения. Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект.
конденсаторов последовательно и параллельно
Цели обучения
К концу этого раздела вы сможете:
- Выведите выражения для полной емкости последовательно и параллельно.
- Обозначает последовательные и параллельные части при соединении конденсаторов.
- Рассчитайте эффективную емкость последовательно и параллельно с учетом индивидуальных емкостей.
Несколько конденсаторов могут быть соединены вместе в различных приложениях.Несколько подключений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Существует два простых и распространенных типа соединений: серия и параллельно , для которых мы можем легко вычислить общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного.
Емкость серии
На рисунке 1а показано последовательное соединение трех конденсаторов с приложенным напряжением.Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением [латекс] C = \ frac {Q} {V} \\ [/ latex].
Обратите внимание на рис. 1, что противоположные заряды величиной Q протекают по обе стороны от первоначально незаряженной комбинации конденсаторов при приложении напряжения В, . Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов создавались заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах.Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов. (См. Рисунок 1b.) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
Рис. 1. (a) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине равна Q. (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d.Последовательные соединения производят общую емкость, которая меньше, чем у любого из отдельных конденсаторов.
Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение [латекс] C = \ frac {Q} {V} \\ [/ latex] для В дает [латекс ] V = \ frac {Q} {C} \\ [/ latex]. Таким образом, напряжения на отдельных конденсаторах равны [латексному] V_1 = \ frac {Q} {C_1}, V_2 = \ frac {Q} {C_2}, \ text {и} V_3 = \ frac {Q} {C_3} \\ [/латекс].
Общее напряжение складывается из отдельных напряжений:
В = В 1 + В 2 + В 3 .
Теперь, называя общую емкость C S последовательной емкостью, считайте, что
[латекс] V = \ frac {Q} {C _ {\ text {S}}} = V_1 + V_2 + V_3 \\ [/ latex].
Вводя выражения для V 1 , V 2 и V 3 , получаем
[латекс] \ frac {Q} {C _ {\ text {S}}} = \ frac {Q} {C_ {1}} + \ frac {Q} {C_ {2}} + \ frac {Q} { C_ {3}} \\ [/ латекс].
Отменяя Q s, получаем уравнение для полной емкости в серии C S , равное
[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} { C_ {3}} + \ точки, \\ [/ latex]
, где «…» означает, что выражение действительно для любого количества конденсаторов, соединенных последовательно.Выражение этой формы всегда приводит к общей емкости C S , которая меньше любой из отдельных емкостей C 1 , C 2 ,…, как показано в примере 1.
Общая емкость в серии,
C с
Общая емкость в серии:
[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} { C_ {3}} + \ dots \\ [/ latex]
Пример 1. Что такое серийная емкость?
Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны 1.000, 5.000 и 8.000 мкФ.
Стратегия
Имея данную информацию, общую емкость можно найти, используя уравнение для емкости в серии.
Решение
Ввод заданных емкостей в выражение для [latex] \ frac {1} {C _ {\ text {S}}} \\ [/ latex] дает [latex] \ frac {1} {C _ {\ text {S} }} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} \\ [/ latex].
[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {1.000 \ mu \ text {F}} + \ frac {1} {5.000 \ mu \ text {F} } + \ frac {1} {8.000 \ mu \ text {F}} = \ frac {1.325} {\ mu \ text {F}} \\ [/ latex]
Преобразование для нахождения C S дает [латекс] C _ {\ text {S}} = \ frac {1.325} {\ mu \ text {F}} = 0,755 \ mu \ text {F} \\ [/ латекс].
Обсуждение
Общая последовательная емкость C с меньше наименьшей индивидуальной емкости, как было обещано. При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только целочисленные вычисления) равен 40.Таким образом,
[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {40} {40 \ mu \ text {F}} + \ frac {8} {40 \ mu \ text {F} } + \ frac {5} {40 \ mu \ text {F}} = \ frac {53} {40 \ mu \ text {F}} \\ [/ latex]
, так что
[латекс] C _ {\ text {S}} = \ frac {40 \ mu \ text {F}} {53} = 0,755 \ mu \ text {F} \\ [/ latex]
Конденсаторы параллельно
На рис. 2а показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти легче, чем в последовательном случае. Чтобы найти эквивалентную общую емкость C, , p , сначала отметим, что напряжение на каждом конденсаторе составляет В, , то же самое, что и у источника, поскольку они подключены непосредственно к нему через проводник.(Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют такой же заряд, как и при индивидуальном подключении к источнику напряжения. Общая сумма начислений Q представляет собой сумму отдельных начислений: Q = Q 1 + Q 2 + Q 3 .
Рис. 2. (a) Конденсаторы, включенные параллельно. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, поэтому общая параллельная емкость — это просто сумма отдельных емкостей.(b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.
Используя соотношение Q = CV , мы видим, что общий заряд составляет Q = C p V , а отдельные расходы составляют Q 1 = C 1 V , Q 2 = C 2 V , и Q 3 = C 3 V .Ввод их в предыдущее уравнение дает
C p V = C 1 V + C 2 V + C 3 V .
Исключая из уравнения В , получаем уравнение для полной емкости параллельно
C p : C p = C 1 + C 2 + C 3 +….
Общая емкость при параллельном подключении — это просто сумма отдельных емкостей. (И снова «… » означает, что выражение действительно для любого количества конденсаторов, подключенных параллельно.) Так, например, если конденсаторы в Примере 1 были подключены параллельно, их емкость составила бы
C p = 1.000 мкФ + 5.000 мкФ + 8.000 мкФ = 14000 мкФ.
Эквивалентный конденсатор для параллельного подключения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на рисунке 2b.
Общая емкость параллельно,
C p
Общая емкость параллельно C p = C 1 + C 2 + C 3 +…
Более сложные соединения конденсаторов иногда могут быть последовательными и параллельными. (См. Рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую.
Рис. 3. (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C 1 и C 2 находятся последовательно; их эквивалентная емкость C S меньше, чем у любого из них. (c) Обратите внимание, что C S параллельно с C 3 . Таким образом, общая емкость составляет сумму C S и C 3 .
Пример 2. Смесь последовательной и параллельной емкостей
Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех десятичных знаков ( C 1 = 1.000 мкФ, C 2 = 3.000 мкФ и C 3 = 8.000 мкФ) и округлите ответ до трех десятичных знаков.
Стратегия
Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы включены последовательно, а какие — параллельно.Конденсаторы C 1 и C 2 включены последовательно. Их комбинация, обозначенная на рисунке C S , параллельна C 3 .
Решение
Поскольку C 1 и C 2 включены последовательно, их общая емкость определяется как [латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} { C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} \\ [/ latex]. Ввод их значений в уравнение дает
[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} = \ frac {1} { 1.000 \ mu \ text {F}} + \ frac {1} {5.000 \ mu \ text {F}} = \ frac {1.200} {\ mu \ text {F}} \\ [/ latex].
Инвертирование дает C S = 0,833 мкФ.
Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; Таким образом, общая сумма составляет
[латекс] \ begin {array} {lll} C _ {\ text {tot}} & = & C _ {\ text {S}} + C _ {\ text {S}} \\\ text {} & = & 0.833 \ mu \ text {F} +8.000 \ mu \ text {F} \\\ text {} & = & 8.833 \ mu \ text {F} \ end {array} \\ [/ latex]
Обсуждение
Этот метод анализа комбинаций конденсаторов по частям, пока не будет получена общая сумма, может быть применен к большим комбинациям конденсаторов.
Сводка раздела
- Общая емкость последовательно [латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ гидроразрыв {1} {C_ {3}} + \ dots \\ [/ latex]
- Общая емкость параллельно C p = C 1 + C 2 + C 3 +…
- Если схема содержит комбинацию конденсаторов, включенных последовательно и параллельно, определите последовательную и параллельную части, вычислите их емкости, а затем найдите общую сумму.
Концептуальные вопросы
- Если вы хотите хранить большое количество энергии в конденсаторной батарее, подключите ли вы конденсаторы последовательно или параллельно? Объяснять.
Задачи и упражнения
- Найдите общую емкость комбинации конденсаторов на рисунке 4.
Рисунок 4. Комбинация последовательного и параллельного подключения конденсаторов.
- Предположим, вам нужна конденсаторная батарея с общей емкостью 0.750 Ф, и у вас есть множество конденсаторов емкостью 1,50 мФ. Какое наименьшее число вы могли бы связать вместе, чтобы достичь своей цели, и как бы вы их связали?
- Какую общую емкость можно получить, соединив вместе конденсатор 5,00 мкФ и конденсатор 8,00 мкФ?
- Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.
Рисунок 5. Комбинация последовательного и параллельного подключения конденсаторов.
- Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.
Рисунок 6. Комбинация последовательного и параллельного подключения конденсаторов.
- Необоснованные результаты. (a) Конденсатор на 8,00 мкФ подключен параллельно другому конденсатору, что дает общую емкость 5,00 мкФ. Какая емкость у второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Избранные решения проблем и упражнения
1. 0,293 мкФ
3.3,08 мкФ в последовательном соединении, 13,0 мкФ в параллельном соединении
4. 2,79 мкФ
6. (a) –3,00 мкФ; (б) У вас не может быть отрицательного значения емкости; (c) Предположение, что конденсаторы были подключены параллельно, а не последовательно, было неверным. Параллельное соединение всегда дает большую емкость, в то время как здесь предполагалась меньшая емкость. Это могло произойти, только если конденсаторы подключены последовательно.
8.3: Последовательные и параллельные конденсаторы
Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях.Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серии и параллельно , для которых мы можем легко вычислить общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Серия конденсаторов
На рисунке \ (\ PageIndex {1} \) показано последовательное сочетание трех конденсаторов, расположенных в ряд внутри схемы.Как и в случае любого конденсатора, емкость комбинации связана как с зарядом, так и с напряжением:
\ [C = \ dfrac {Q} {V}. \]
Когда эта последовательная комбинация подключена к батарее с напряжением В , каждый из конденсаторов получает одинаковый заряд Q . Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен \ (+ Q \), а заряд на пластине, подключенной к отрицательной клемме, равен \ (- Q \). Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю.Однако падение потенциала \ (V_1 = Q / C_1 \) на одном конденсаторе может отличаться от падения потенциала \ (V_2 = Q / C_2 \) на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть , все конденсаторы последовательной комбинации имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи удаляется с пластины первого конденсатора (который мы обозначаем как \ (- Q \)), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как \ ( + Q \)) и т. Д.
Рисунок \ (\ PageIndex {1} \): (a) Три конденсатора соединены последовательно.Величина заряда на каждой пластине равна Q. (b) Сеть конденсаторов на (a) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей на (a), а заряд на его пластинах равен Q.
Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны, соответственно, \ (V_1 = Q / C_1 \), \ (V_2 = Q / C_2 \) и \ (V_3 = Q / C_3 \). Эти потенциалы должны суммироваться с напряжением батареи, давая следующий баланс потенциалов:
\ [V = V_1 + V_2 + V_3.\]
Потенциал \ (V \) измеряется на эквивалентном конденсаторе, который держит заряд \ (Q \) и имеет эквивалентную емкость \ (C_S \). Вводя выражения для \ (V_1 \), \ (V_2 \) и \ (V_3 \), получаем
\ [\ dfrac {Q} {C_S} = \ dfrac {Q} {C_1} + \ dfrac {Q} {C_2} + \ dfrac {Q} {C_3}. \]
Отменяя заряд Q , мы получаем выражение, содержащее эквивалентную емкость \ (C_S \) трех последовательно соединенных конденсаторов:
\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3}.\]
Это выражение можно обобщить на любое количество конденсаторов в последовательной сети.
Комбинация серии
Для конденсаторов, соединенных последовательно, эквивалентная емкость, обратная величине, равна сумме обратных величин индивидуальных емкостей:
\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} + \ dots \ label {capseries} \]
Пример \ (\ PageIndex {1} \): эквивалентная емкость последовательной сети
Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны \ (1.000 мкФ \), \ (5.000 мкФ \) и \ (8.000 мкФ \).
Стратегия
Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capseries} с тремя членами.
Раствор
Вводим данные емкости в уравнение \ ref {capseries}:
\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} + \ dfrac {1} {8.000 \ mu F} \\ [4pt] & = \ dfrac {1.325} {\ mu F}. \ End {align *} \]
Теперь инвертируем этот результат и получаем
\ [\ begin {align *} C_S & = \ dfrac {\ mu F} {1.325} \\ [4pt] & = 0.755 \ mu F. \ end {align *} \ nonumber \]
Значение
Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.
Параллельная комбинация конденсаторов
Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке \ (\ PageIndex {2a} \).Поскольку конденсаторы соединены параллельно, , все они имеют одинаковое напряжение V на своих пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость \ (C_p \) параллельной сети, отметим, что общий заряд Q , хранящийся в сети, является суммой всех отдельных зарядов:
\ [Q = Q_1 + Q_2 + Q_3. \]
В левой части этого уравнения используется соотношение \ (Q = C_pV \), которое выполняется для всей сети.В правой части уравнения мы используем соотношения \ (Q_1 = C_1 V \), \ (Q_2 = C_2V \) и \ (Q_3 = C_3V \) для трех конденсаторов в сети. Таким образом получаем
\ [C_pV = C_1V + C_2V + C_3V. \]
Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:
\ [C_p = C_1 + C_2 + C_3. \]
Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.
Параллельная комбинация
Для конденсаторов, соединенных параллельно, эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,
\ [C_p = C_1 + C_2 + C_3 + … \ label {capparallel} \]
Рисунок \ (\ PageIndex {2} \): (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен непосредственно к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.
Пример \ (\ PageIndex {2} \): эквивалентная емкость параллельной сети
Найдите полезную емкость для трех конденсаторов, соединенных параллельно, учитывая, что их индивидуальные емкости равны \ (1.0 \ mu F \), \ (5.0 \ mu F \) и \ (8.0 \ mu F \).
Стратегия
Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capparallel} с тремя членами.
Раствор
Ввод заданных емкостей в уравнение \ ref {capparallel} дает
\ [\ begin {align *} C_p & = C_1 + C_2 + C_3 \\ [4pt] & = 1.0 \ mu F + 5.0 \ mu F + 8.0 \ mu F \\ [4pt] & = 14.0 \ mu F.\ end {align *} \]
Значение
Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.
Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на Рисунке \ (\ PageIndex {3} \). Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости.Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.
Рисунок \ (\ PageIndex {3} \): (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. (b) \ (C_1 \) и \ (C_2 \) идут последовательно; их эквивалентная емкость \ (C_S \) c) Эквивалентная емкость \ (C_S \) подключена параллельно с \ (C_3 \). Таким образом, эквивалентная емкость всей сети является суммой \ (C_S \) и \ (C_3 \).
Пример \ (\ PageIndex {3} \): эквивалентная емкость сети
Найдите общую емкость комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {3} \). Предположим, что емкости известны с точностью до трех десятичных знаков (\ (C_1 = 1.000 мкФ, C_2 = 5.000 мкФ, C_3 = 8.000 мкФ \)). Округлите ответ до трех десятичных знаков.
Стратегия
Сначала мы определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы \ (C_1 \) и \ (C_2 \) включены последовательно.Их комбинация, помеченная \ (C_S \), параллельна \ (C_3 \).
Раствор
Поскольку \ (C_1 \) и \ (C_2 \) включены последовательно, их эквивалентная емкость \ (C_S \) получается с помощью уравнения \ ref {capseries}:
\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} \\ [4pt] & = \ dfrac {1.200} {\ mu F} \ end {align *} \]
Для этого
\ [C_S = 0,833 \ mu F. \ nonumber \]
Емкость \ (C_S \) соединена параллельно с третьей емкостью \ (C_3 \), поэтому мы используем уравнение \ ref {capparallel}, чтобы найти эквивалентную емкость C всей сети:
\ [\ begin {align *} C & = C_S + C_3 \\ [4pt] & = 0.833 \ mu F + 8.000 \ mu F \\ [4pt] & = 8.833 \ mu F. \ end {align *} \]
Сеть конденсаторов
Определите чистую емкость C комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {4} \), когда емкости равны \ (C_1 = 12,0 мкФ, C_2 = 2,0 мкФ \) и \ (C_3 = 4,0 мкФ \). Когда на комбинации поддерживается разность потенциалов 12,0 В, найдите заряд и напряжение на каждом конденсаторе.
Рисунок \ (\ PageIndex {4} \): (a) Комбинация конденсаторов.(b) Эквивалентная комбинация из двух конденсаторов. Стратегия
Сначала мы вычисляем чистую емкость \ (C_ {23} \) параллельного соединения \ (C_2 \) и \ (C_3 \). Тогда C — это чистая емкость последовательного соединения \ (C_1 \) и \ (C_ {23} \). Мы используем соотношение \ (C = Q / V \), чтобы найти заряды \ (Q_1, Q_2 \) и \ (Q_3 \), а также напряжения \ (V_1, V_2 \) и \ (V_3 \) на конденсаторы 1, 2 и 3 соответственно.
Решение Эквивалентная емкость для \ (C_2 \) и \ (C_3 \) составляет
\ [C_ {23} = C_2 + C_3 = 2.0 мк F + 4,0 мк F = 6,0 мк F. \]
Вся комбинация из трех конденсаторов эквивалентна двум последовательно включенным конденсаторам,
\ [\ dfrac {1} {C} = \ dfrac {1} {12.0 \ mu F} + \ dfrac {1} {6.0 \ mu F} = \ dfrac {1} {4.0 \ mu F} \ Rightarrow C = 4,0 мкм F. \]
Рассмотрим эквивалентную комбинацию из двух конденсаторов на рисунке \ (\ PageIndex {2b} \). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд, \ (Q_1 = Q_ {23} \). Кроме того, конденсаторы разделяют разность потенциалов 12,0 В, поэтому
\ [12.0 V = V_1 + V_ {23} = \ dfrac {Q_1} {C_1} + \ dfrac {Q_ {23}} {C_ {23}} = \ dfrac {Q_1} {12.0 \ mu F} + \ dfrac {Q_1 } {6.0 \ mu F} \ Rightarrow Q_1 = 48.0 \ mu C. \]
Теперь разность потенциалов на конденсаторе 1 равна
.
\ [V_1 = \ dfrac {Q_1} {C_1} = \ dfrac {48,0 \ mu C} {12,0 \ mu F} = 4,0 В. \]
Поскольку конденсаторы 2 и 3 подключены параллельно, они имеют одинаковую разность потенциалов:
\ [V_2 = V_3 = 12,0 В — 4,0 В = 8,0 В. \]
Следовательно, заряды на этих двух конденсаторах равны, соответственно,
\ [Q_2 = C_2V_2 = (2.0 мкФ) (8,0 В) = 16,0 мкФ, \]
\ [Q_3 = C_3V_3 = (4,0 мкФ) (8,0 В) = 32,0 мкФ \]
Значение Как и ожидалось, чистая плата за параллельную комбинацию \ (C_2 \) и \ (C_3 \) составляет \ (Q_ {23} = Q_2 + Q_3 = 48,0 \ mu C. \)
Упражнение \ (\ PageIndex {1} \)
Определите полезную емкость C каждой сети конденсаторов, показанной ниже. Предположим, что \ (C_1 = 1,0 пФ, C_2 = 2,0 пФ, C_3 = 4,0 пФ \) и \ (C_4 = 5,0 пФ \). Найдите заряд на каждом конденсаторе, предполагая, что разность потенциалов равна 12.0 В в каждой сети.
- Ответьте на
\ (C = 0,86 пФ, Q_1 = 10 пКл, Q_2 = 3,4 пКл, Q_3 = 6,8 пКл \)
- Ответ б
\ (C = 2,3 пФ, Q_1 = 12 пКл, Q_2 = Q_3 = 16 пКл \)
- Ответ c
\ (C = 2,3 пФ, Q_1 = 9,0 пКл, Q_2 = 18 пКл, Q_3 = 12 пКл, Q_4 = 15 пКл \)
Работа конденсаторов в последовательной и параллельной цепях
Последовательные и параллельные конденсаторы
Конденсаторы серии
Последовательные конденсаторы означают, что два или более конденсатора соединены в одну линию i.Положительная пластина одного конденсатора соединена с отрицательной пластиной следующего конденсатора. Все конденсаторы, включенные последовательно, имеют одинаковый заряд (Q) и одинаковый зарядный ток (i C ).
Рассмотрим N- количество конденсаторов, подключенных последовательно, тогда
Q T = Q 1 = Q 2 = Q 3 = ———- = Q N
I C = I 1 = I 2 = I 3 = ——— = I N
Вернуться к списку
Конденсаторы в последовательном соединении:
Следующие схемы показывают последовательное соединение группы конденсаторов.
Последовательное соединение N-количество конденсаторов:
Последовательное соединение 2-х конденсаторов:
В этой схеме заряд (Q), хранящийся во всех конденсаторах, одинаков, потому что каждый конденсатор имеет заряд, который течет от соседнего конденсатора. Падение напряжения на всех конденсаторах отличается друг от друга. Но полное падение напряжения, приложенное между входными и выходными линиями схемы, равно сумме всех индивидуальных падений напряжения каждого конденсатора.Эквивалентная емкость цепи составляет C eq = Q / V.
Таким образом,
V T = V 1 + V 2
C экв = Q / V 1 + Q / V 2
1 / C экв = (V 1 + V 2 ) / Q
V T = Q / C экв = Q / C 1 + Q / C 2
Вернуться к списку
Конденсаторы серии Equation
1 / Ceq = 1 / C1 + 1 / C2 +……… + 1 / CN
Когда конденсаторы включены последовательно, величина, обратная эквивалентной емкости, равна сумме обратных величин отдельных емкостей конденсаторов в цепи.
На рисунке 2 величина, обратная эквивалентной емкости цепи, равна сумме значений обратных емкостей двух конденсаторов C 1 и C 2 , выражение приведено ниже.
1 / C экв = 1 / C 1 + 1 / C 2
Вернуться к списку
Конденсаторы в серии Пример № 1:
Мы предполагаем, что номиналы двух конденсаторов на рисунке 2 выше равны 0.4 мкФ и 0,5 мкФ соответственно. Теперь мы можем рассчитать эквивалентную емкость для двух последовательно соединенных конденсаторов как
1 / C экв = 1 / C 1 + 1 / C 2
1 / C экв = (C 1 + C 2 ) / C 1 C 2
C экв = (C 1 C 2 ) / (C 1 + C 2 )
C экв = (0,4 мкФ * 0,5 мкФ) / (0.4 мкФ + 0,5 мкФ)
C экв = 0,22 мкФ
Мы знаем, что эквивалентная емкость конденсаторов при последовательном включении меньше, чем значение наименьшего конденсатора в цепи. Таким образом, здесь мы также получаем эквивалентное значение 0,22 мкФ, что меньше наименьшей емкости 0,4 мкФ в последовательном соединении данной цепи с двумя конденсаторами.
Вернуться к списку
Последовательные конденсаторы Пример № 2
Вычислите эквивалентную емкость, и отдельные падения напряжения на наборе из двух последовательно соединенных конденсаторов равны нулю.1 мкФ и 0,2 мкФ соответственно при подключении к 12 В переменного тока. поставлять.
1 / C экв = 1 / C 1 + 1 / C 2
C экв = (C 1 C 2 ) / (C 1 + C 2 )
C экв = (0,1 мкФ * 0,2 мкФ) / (0,1 мкФ + 0,2 мкФ)
C экв = 0,066 мкФ = 66 нФ
Падение напряжения на двух последовательно соединенных конденсаторах составляет:
V 1 = (C 2 * V T ) / (C 1 + C 2 ) = (0.2 мкФ * 12 В) / (0,1 мкФ + 0,2 мкФ) = 8 В
V 2 = (C 1 * V T ) / (C 1 + C 2 ) = (0,1 мкФ * 12 В) / (0,1 мкФ + 0,2 мкФ) = 4 В
Из этих результатов мы заметили, что эквивалентная емкость 66 нФ меньше наименьшей емкости 0,1 мкФ из данных двух конденсаторов. Отдельные падения напряжения на данных двух конденсаторах различны. Но сумма отдельных падений напряжения обоих конденсаторов равна общему напряжению.т.е. 8 В + 4 В = 12 В.
Теперь посчитаем заряд, накопленный в отдельном конденсаторе,
Q 1 = V 1 * C 1 = 8 В * 0,1 мкФ = 0,8 мкКл
Q 2 = В 2 * C 2 = 4 В * 0,2 мкФ = 0,8 мкКл
Здесь мы заметили, что одинаковый заряд 0,8 мкКл сохраняется в обоих конденсаторах C 1 и C 2 , которые соединены последовательно.
Вернуться к списку
Конденсаторы в серии Сводка:
Эквивалентная емкость конденсаторов, соединенных последовательно, обратная эквивалентной емкости равна сумме обратных величин всех индивидуальных емкостей последовательно соединенных конденсаторов.Все конденсаторы, соединенные последовательно, имеют одинаковый заряд (Q). Зарядный ток (i C ) также одинаков для всех отдельных конденсаторов, которые соединены последовательно, например, i C = i 1 = i 2 и т. Д.
Падение напряжения для отдельных конденсаторов в Последовательное соединение разные. Но сумма всех отдельных падений напряжения равна общему напряжению в цепи. т.е. V T = V 1 + V 2 и т. д.Большое значение емкости приведет к меньшему падению напряжения, а небольшое значение емкости приведет к большему падению напряжения.
Вернуться к списку
Конденсаторы в параллельных цепях
Конденсаторы, включенные параллельно, означает, что два или более конденсатора подключены параллельно, то есть оба их вывода подключены к каждому выводу другого конденсатора или конденсаторы соответственно. Все конденсаторы, которые соединены параллельно, имеют одинаковое напряжение, равное V T , приложенному между входными и выходными клеммами схемы.Тогда на параллельные конденсаторы подается «общее напряжение». т.е. V T = V 1 = V 2 и т. д.
Эквивалентная емкость C eq цепи, в которой конденсаторы соединены параллельно, равна сумме всех отдельных емкостей конденсаторов, сложенных вместе. Это связано с тем, что верхняя пластина каждого конденсатора в цепи соединена с верхней пластиной соседних конденсаторов. Таким же образом нижняя пластина каждого конденсатора в цепи соединяется с нижней пластиной соседних конденсаторов.
Следующие схемы показывают параллельное соединение между группами конденсаторов.
Параллельное соединение n конденсаторов:
Параллельное соединение 2-х конденсаторов:
На рисунке 4 общий заряд (Q) в цепи разделен между двумя конденсаторами, это означает, что заряд Q распределяется между конденсаторами, подключенными параллельно. Потому что падение напряжения на отдельных конденсаторах равно общему напряжению, приложенному к цепи.Но общий заряд Q равен сумме всех зарядов отдельных конденсаторов, соединенных параллельно. т.е. из приведенного выше рисунка 4 два разных конденсатора C1 и C2 имеют два разных заряда Q 1 и Q 2 соответственно. Здесь Q = Q 1 + Q 2
Теперь мы видим эквивалентную емкость конденсаторов C1 и C2, соединенных параллельно, что показано на рисунке 4 выше.
Мы знаем формулу:
Q = C экв V T
Здесь Q = Q 1 + Q 2
И V T = V 1 = V 2
C экв = Q / V T = (Q 1 + Q 2 ) / V T = (Q 1 / V T ) + (Q 2 / V T )
Вернуться к списку
Параллельные конденсаторы Уравнение:
C eq = C 1 + C 2 + C 3 + ———— + C N
Эквивалентная емкость конденсаторов, подключенных в параллельность равна сумме отдельных емкостей конденсаторов в цепи.
На рисунке 4 значение эквивалентной емкости (C eq ) равно сумме значений емкости C 1 и C 2 , выражение показано ниже.
Ceq = C1 + C2
Вернуться к списку
Конденсаторы параллельно Пример № 1:
Рассмотрим значения емкости двух конденсаторов C 1 = 0,2 мкФ и C 2 = 0,3 мкФ, которые показаны на рисунке 4 выше.Теперь рассчитайте эквивалентную емкость цепи.
Мы знаем, что эквивалентная емкость
C экв = C 1 + C 2
C экв = 0,2 мкФ + 0,3 мкФ
C экв = 0,5 мкФ
Один важный момент, который следует помнить о параллельно соединенных цепях конденсаторов, эквивалентная емкость (C eq ) любых двух или более конденсаторов, соединенных вместе параллельно, всегда будет больше, чем значение самого большого конденсатора в цепи, поскольку мы складываем значения. .Таким образом, в нашем примере выше C eq = 0,5 мкФ, тогда как конденсатор наибольшей емкости в цепи составляет всего 0,3 мкФ.
Вернуться к списку
Конденсаторы в параллельном соединении Пример № 2:
Вычислите эквивалентную емкость на наборе из двух параллельно включенных конденсаторов, показанном на рисунке 4.
(а) Один конденсатор емкостью 0,1 мкФ, подключенный параллельно с емкостью 0,2 мкФ.
(b) Один конденсатор емкостью 750 нФ, подключенный параллельно с 0.5 мкФ.
(а) Эквивалентная емкость,
C экв. = C 1 + C 2
C экв. = 0,1 мкФ + 0,2 мкФ
C экв = 0,3 мкФ
(б) Эквивалентная емкость,
C экв = C 1 + C 2
C экв = 750 нФ + 0,5 мкФ
C экв = 750 нФ + 500 нФ
C экв = 1250 нФ = 1.25 мкФ
В двух вышеупомянутых случаях мы наблюдали, что значение эквивалентной емкости (C eq ) двух конденсаторов, соединенных параллельно, больше, чем значение самого большого конденсатора в цепи, поскольку мы складываем значения. В разделе (а) значение C eq = 0,3 мкФ, тогда как конденсатор с наибольшей емкостью составляет всего 0,2 мкФ. В разделе (b) значение C eq = 1,25 мкФ, тогда как самый большой конденсатор в цепи составляет всего 0,5 мкФ.
Вернуться к списку
Конденсаторы в параллельном соединении
Эквивалентная емкость группы конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов.то есть C экв = C 1 + C 2 . Потому что падение напряжения на отдельном конденсаторе равно общему напряжению, приложенному между входными и выходными клеммами схемы. т.е. V T = V 1 = V 2 . Заряды, хранящиеся в отдельных конденсаторах, различны, но сумма всех зарядов отдельных конденсаторов равна общему количеству зарядов, протекающих в цепи. то есть Q = Q 1 + Q 2 .
Зарядный ток, протекающий в цепи, распределяется по всем конденсаторам в цепи.Но общий зарядный ток равен сумме всех отдельных зарядных токов конденсаторов в цепи. т.е. i C = i 1 + i 2 и т. д. Эквивалентное значение емкости группы конденсаторов, соединенных параллельно, всегда больше, чем значение самого большого конденсатора в цепи.
Вернуться к списку
конденсаторов последовательно и параллельно
конденсаторов последовательно и параллельно
Далее: Энергия в конденсаторах
Up: Емкость
Предыдущая: Диэлектрики
Конденсаторы — один из стандартных компонентов электронных схем.Кроме того, часто встречаются сложные комбинации конденсаторов.
в практических схемах. Это,
поэтому полезно иметь набор правил для определения эквивалентной емкости
некоторого общего расположения конденсаторов. Оказывается, всегда можно найти
эквивалентная емкость при повторном
применение два простых правила . Эти правила относятся к подключенным конденсаторам.
последовательно и параллельно.
Рассмотрим два конденсатора, подключенных параллельно : , т. Е. , с
положительно заряженные пластины подключены к общему « входному » проводу, а отрицательно
заряженные пластины присоединены к общему « выходному » проводу — см. рис. 15. Какая эквивалентная емкость
между входным и выходным проводами? В этом случае потенциал
разница между двумя конденсаторами одинакова и равна
разность потенциалов между входным и выходным проводами.Общий заряд
, однако, хранящиеся в двух конденсаторах делятся между
конденсаторы, так как он должен распределяться так, чтобы напряжение на
два то же самое. Поскольку конденсаторы могут иметь разную емкость, и,
и сборы тоже могут быть разными. Эквивалентная емкость
пары конденсаторов — это просто соотношение, где
— общий накопленный заряд. Следует, что
| (113) |
давая
| (114) |
Здесь мы воспользовались тем фактом, что напряжение является общим для всех трех
конденсаторы.Таким образом, правило таково:
Эквивалентная емкость двух конденсаторов, соединенных параллельно
представляет собой сумму отдельных емкостей.
Для конденсаторов, подключенных параллельно, уравнение. (114) обобщает на
.
Рассмотрим два конденсатора, подключенных в серию : , т. Е. , в линию так, что
положительная пластина одного прикреплена к отрицательной пластине другого — см.
Инжир.16.
Фактически, предположим, что положительная обкладка конденсатора 1 подключена
к проводу « вход » отрицательная обкладка конденсатора 1 подключается к
положительная пластина конденсатора 2 и отрицательная пластина конденсатора
2 подключается к проводу « выход ».
Какая эквивалентная емкость между входными и выходными проводами?
В этом случае важно понимать, что заряд, хранящийся в
два конденсатора одинаковые. Это легче всего увидеть, если рассмотреть
« внутренние » пластины: i.е. , отрицательная пластина конденсатора 1, и
положительная пластина конденсатора 2. Эти пластины физически отключены.
от остальной части схемы, поэтому общий заряд на них должен
Остаются неизменными. Если предположить, что кажется разумным, что эти пластины несут нулевой заряд
когда к двум конденсаторам приложена нулевая разность потенциалов, следует
что при наличии ненулевой разности потенциалов заряд на положительном
пластина конденсатора 2 должна быть уравновешена равным и противоположным зарядом
на отрицательной пластине конденсатора 1.Поскольку отрицательная пластина
Конденсатор 1 несет заряд, положительная пластина должна нести заряд.
Аналогичным образом, поскольку положительная пластина конденсатора 2 несет заряд,
отрицательная пластина должна нести заряд. В итоге оба конденсатора
обладают таким же накопленным зарядом. Потенциал падает, и
два конденсатора, как правило, разные. Однако сумма этих
падение равняется общему падению потенциала на входе и выходе
провода: т.е. ,. Эквивалентная емкость пары
конденсаторы снова
.Таким образом,
| (115) |
давая
| (116) |
Здесь мы воспользовались тем фактом, что заряд является общим для всех трех
конденсаторы.
Следовательно, правило таково:
Величина, обратная эквивалентной емкости двух конденсаторов, подключенных в
серия — это сумма обратных величин отдельных емкостей.
Для конденсаторов, соединенных последовательно, уравнение.(116) обобщает на
Далее: Энергия в конденсаторах
Up: Емкость
Предыдущая: Диэлектрики
2007-07-14
Калькулятор конденсаторов серии
• Калькуляторы электрических, ВЧ и электроники • Онлайн-преобразователи единиц
1 мФ = 0,001 F. 1 мкФ = 0,000001 = 10 F. 1 нФ = 0,000000001 = 10 F. 1 пФ = 0,000000000001 = 10 ¹² F.
Согласно второму правилу Кирхгофа, падение потенциала В , В и В ₃ на каждом конденсаторе в группе из трех последовательно соединенных конденсаторов обычно различно, и общее падение потенциала В равно к их сумме:
По определению емкости и с учетом того факта, что заряд Q группы конденсаторов, соединенных последовательно, является общим для всех конденсаторов, эквивалентная емкость C eq трех конденсаторов, подключенных в серия определяется как
или
Для группы из n конденсаторов, соединенных последовательно, эквивалентная емкость C eq 9 0044 является обратной величиной суммы обратных емкостей отдельных конденсаторов:
или
Эта формула для C eq используется для вычислений в этом калькуляторе.Например, три конденсатора, 10, 15 и 20 мкФ, соединенные последовательно, будут давать 4,62 мкФ:
Только для двух последовательных конденсаторов:
или
При наличии n одинаковых конденсаторов C подключенных последовательно, тогда эквивалентная емкость будет
Обратите внимание, что формула для расчета общей емкости нескольких последовательно соединенных конденсаторов такая же, как и для расчета сопротивления группы резисторов, соединенных параллельно.
Также обратите внимание, что для группы, содержащей любое количество конденсаторов, соединенных последовательно, эквивалентная емкость всегда меньше, чем наименьший конденсатор в группе конденсаторов, и добавление любого нового конденсатора всегда будет уменьшать эквивалентную емкость группы.
Конденсаторы на печатной плате
Что касается падения напряжения на каждом конденсаторе, то это отдельная история. Даже если все конденсаторы, подключенные последовательно, равны, падение напряжения может быть различным, поскольку нельзя ожидать, что конденсаторы будут иметь одинаковую емкость и ток утечки.Конденсатор с наименьшей емкостью будет принимать наибольшее напряжение и, следовательно, будет самым слабым звеном в цепи.
Балансировочные резисторы уменьшают влияние изменения емкости
Чтобы помочь в равном распределении напряжения при последовательном подключении конденсаторов, к каждому конденсатору часто добавляются сбалансированные резисторы высокой стоимости, чтобы гарантировать, что напряжение распределяется поровну. Резисторы действуют как делители напряжения и уменьшают влияние изменения емкости.Даже с этими резисторами лучше оставить значительный запас рабочего напряжения конденсаторов.
Если несколько конденсаторов соединены параллельно , разность потенциалов В на конденсаторах одинакова и равна разности потенциалов между соединительными проводами. Общий заряд Q делится между конденсаторами, и если их емкости различаются, отдельные заряды Q₁ , Q и Q также будут разными.Общий заряд определяется как
Конденсаторы, подключенные параллельно
Учитывая, что по определению емкости, эквивалентная емкость
мы получим
или
Для n конденсаторов параллельно,
То есть, если несколько конденсаторов подключены параллельно, их эквивалентная емкость определяется простым сложением емкостей всех конденсаторов в группе.
Как вы, наверное, заметили, конденсаторы ведут себя прямо противоположно резисторам: если резисторы подключены последовательно, их эквивалентные значения всегда будут выше, чем значения любых резисторов, подключенных последовательно, а их параллельное соединение приведет к уменьшению значений.
Конденсаторы на печатной плате
Серия
и параллельный калькулятор емкости Apogeeweb
Часто задаваемые вопросы
1.Как рассчитать параллельную емкость?
Общее значение емкости конденсаторов, соединенных параллельно, фактически вычисляется путем сложения площадей пластин. Другими словами, общая емкость равна сумме всех отдельных емкостей, включенных параллельно.
2. Как отличить последовательный конденсатор от параллельного?
Когда разность потенциалов на пластинах одинакова, они параллельны. Когда ток через них равен, они включены последовательно.
3. Зачем нужно последовательно включать конденсаторы?
Причина, по которой вы можете соединять конденсаторы последовательно, заключается в том, чтобы увеличить эффективное управление напряжением цепи. Конденсаторы имеют номинальное напряжение пробоя, превышение которого значительно увеличивает вероятность отказа. Два одинаковых конденсатора будут иметь половину напряжения на каждом.
4. Последовательные или параллельные конденсаторы накапливают больше энергии?
Энергия, запасенная в конденсаторе, является функцией напряжения на конденсаторе.Напряжение будет выше, когда они подключены параллельно, поэтому при параллельном подключении сохраняется больше энергии.
5. Какова основная функция конденсатора?
Конденсатор — это электронный компонент, который накапливает и выделяет электричество в цепи. Он также пропускает переменный ток, не пропуская постоянный ток. Конденсатор является неотъемлемой частью электронного оборудования и поэтому почти всегда используется в электронных схемах.
6. В чем разница между последовательным и параллельным подключением?
В последовательной цепи сумма напряжений, потребляемых каждым отдельным сопротивлением, равна напряжению источника.Компоненты, соединенные параллельно, соединяются несколькими путями, так что ток может разделяться; одинаковое напряжение приложено к каждому компоненту.
7. Почему последовательно подключенные конденсаторы уменьшают емкость?
Полное сопротивление двух последовательно соединенных конденсаторов равно сумме индивидуальных сопротивлений двух конденсаторов. Поскольку импеданс пропорционален обратной величине емкости, больший импеданс последовательной цепи означает меньшую емкость.
8.Что произойдет, если резистор и конденсатор соединить параллельно?
Когда резисторы и конденсаторы смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °. Ток в цепи будет иметь фазовый угол от 0 ° до + 90 °.
9. Как узнать, включен ли последовательный конденсатор параллельно?
Если у каждого конденсатора ОБЕ клеммы подключены к ОБЕИМ клеммам других, то они параллельны.Если у каждого конденсатора только одна клемма подключена к одной клемме другого конденсатора, они соединены последовательно.
10. Почему последовательно подключенные конденсаторы уменьшают емкость?
Полное сопротивление двух последовательно соединенных конденсаторов равно сумме индивидуальных сопротивлений двух конденсаторов. Поскольку импеданс пропорционален обратной величине емкости, больший импеданс последовательной цепи означает меньшую емкость.
11. Как соединить параллельно конденсаторы и резисторы?
Детальная операция начинается с 1:42.
12. Почему мы используем конденсаторы в цепях постоянного тока?
При использовании в цепи постоянного или постоянного тока конденсатор заряжается до напряжения питания, но блокирует прохождение тока через него, потому что диэлектрик конденсатора непроводящий и в основном является изолятором.
13. Преобразует ли конденсатор переменный ток в постоянный?
Конденсатор не может самостоятельно преобразовывать переменный ток в постоянный, но хороший синхронизированный переключатель, который пропускает выбранные пики и отклоняет части формы волны переменного тока, сделает это.
14. Что произойдет, если конденсатор подключен к постоянному току?
Когда конденсаторы подключены к источнику постоянного напряжения постоянного тока, они становятся заряженными до значения приложенного напряжения, действуя как устройства временного хранения и сохраняя или удерживая этот заряд неопределенно долго, пока присутствует напряжение питания.
15. Есть ли у конденсаторов положительная и отрицательная сторона?
Большинство электролитических конденсаторов поляризованного типа, то есть напряжение, подключенное к клеммам конденсатора, должно иметь правильную полярность, т.е.е. положительное на положительное и отрицательное на отрицательное.
16. Как решить проблемы, связанные с подключением конденсаторов последовательно и параллельно?
Видео ниже показывает, как рассчитать емкость в последовательной и параллельной цепи, а также дает лабораторный пример, демонстрирующий работу математики.
Серия Подключение конденсаторов
На рис. 1 (а) показано, что два конденсатора подключены последовательно. Для каждого конденсатора он имеет одинаковый ток, а соотношение тока и напряжения соответствует
.
«
(а) (б)
Рисунок 1.Последовательное соединение
Итак, два конденсатора соединены последовательно, эквивалентная емкость
Эквивалентная схема показана на рисунке 1 (б). Когда конденсаторы соединены последовательно, напряжение на каждом конденсаторе соответствует
.
Параллельное соединение конденсаторов
На рис. 2 (а) показано, что два конденсатора подключены параллельно. Для каждого конденсатора оно имеет одинаковое напряжение, а соотношение тока и напряжения соответствует
.
Рисунок 2.Cicuit параллельных конденсаторов
Два конденсатора подключены параллельно, эквивалентная емкость
Эквивалентная схема показана на рисунке 2 (б). При параллельном подключении конденсаторов ток на каждом конденсаторе соответствует
.
Разница между последовательными конденсаторами и параллельными конденсаторами
При последовательном соединении конденсаторов емкость уменьшается (для расчета общей емкости после последовательного соединения см. Метод параллельного подключения резисторов), а выдерживаемое напряжение увеличивается.
Конденсаторы подключаются параллельно, емкость увеличивается (добавление каждой емкости), а выдерживаемое напряжение наименьшее. Последовательный конденсатор: чем больше число последовательно, тем меньше емкость, но выше выдерживаемое напряжение. Отношение емкости: 1 / C = 1 / C1 + 1 / C2 + 1 / C3 Параллельная емкость: чем больше параллельное соединение, тем больше емкость, но выдерживаемое напряжение не изменяется, его отношение емкости: C = C1 + C2 + C3
См. Более подробную информацию о конденсаторах, включенных последовательно и параллельно.Кликните сюда!
Онлайн-расчет емкости конденсатора последовательного включения
Калькуляторы и формулы для расчета последовательного включения конденсатора
Последовательное соединение конденсатора
Когда конденсаторы соединены последовательно, полный ток протекает через все конденсаторы.
Расчет последовательного включения конденсаторов
Чтобы рассчитать емкость, введите значения отдельных конденсаторов, разделенных точкой с колонкой.
Пример: 3.3; 12; 22
Экспоненты не допускаются. Вместо этого введите значения в подходящей единице измерения.
Если вы введете все значения в нано-фарадах, результат также отобразится в нано-фарадах.
|
Формулы для расчета общей мощности
Общая емкость последовательного соединения рассчитывается с использованием обратной величины отдельных конденсаторов.Отдельные обратные значения добавляются для расчета общей емкости.
Итак, формула для трех последовательно соединенных конденсаторов:
\ (\ displaystyle \ frac {1} {C_ {ges}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} \)
Следующая формула может использоваться для расчета общей емкости двух последовательно соединенных конденсаторов.
\ (\ Displaystyle C_ {ges} = \ гидроразрыва {C_1 · C_2} {C_1 + C_2} \)
|
Индекс электрики:
База
URI,
проволочное сопротивление,
падение напряжения на кабеле,
внутреннее сопротивление,
сопротивление-температура-дрейф,
таблица температурных коэффициентов,
децибел-фактор,
децибел-напряжение-мощность,
переменное напряжение,
переменное напряжение и время,
частота-длина волны,
переменное напряжение и угол,
частота-периодичность-время,
Цепь конденсатора / R / L
конденсаторная серия,
конденсатор-импеданс,
постоянная времени,
c-заряд-состояние,
c-разрядное состояние,
RC-последовательная цепь,
Резисторы
резисторы, включенные параллельно,
вольтметр-последовательный резистор,
шунтирующий резистор,
делитель напряжения,
нагруженный делитель напряжения,
пи-аттенюатор,
/ t-аттенюатор,
LED-резистор,
.

