Расчет конденсаторов: Расчёт ёмкости конденсатора онлайн / Калькулятор / Элек.ру

Как подобрать конденсатор для однофазного электродвигателя или трехфазного

Что делать, если требуется подключить двигатель к источнику, рассчитанному на другой тип напряжения (например, трехфазный двигатель к однофазной сети)? Такая необходимость может возникнуть, в частности, если нужно подключить двигатель к какому-либо оборудованию (сверлильному или наждачному станку и пр.). В этом случае используются конденсаторы, которые, однако, могут быть разного типа. Соответственно, надо иметь представление о том, какой емкости нужен конденсатор для электродвигателя, и как ее правильно рассчитать.

Что такое конденсатор

Конденсатор состоит из двух пластин, расположенных друг напротив друга. Между ними помещается диэлектрик. Его задача – снимать поляризацию, т.е. заряд близкорасположенных проводников.

Существует три вида конденсаторов:

• Полярные. Не рекомендуется использовать их в системах, подключенных к сети переменного тока, т. к. вследствие разрушения слоя диэлектрика происходит нагрев аппарата, вызывающий короткое замыкание.
• Неполярные. Работают в любом включении, т.к. их обкладки одинаково взаимодействуют с диэлектриком и с источником.
• Электролитические (оксидные). В роли электродов выступает тонкая оксидная пленка. Считаются идеальным вариантом для электродвигателей с низкой частотой, т.к. имеют максимально возможную емкость (до 100000 мкФ).

Как подобрать конденсатор для трехфазного электродвигателя

Задаваясь вопросом: как подобрать конденсатор для трехфазного электродвигателя, нужно принять во внимание ряд параметров.

Чтобы подобрать емкость для рабочего конденсатора, необходимо применить следующую расчетную формулу: Сраб.=k*Iф / U сети, где:

• k – специальный коэффициент, равный 4800 для подключения «треугольник» и 2800 для «звезды»;
• Iф – номинальное значение тока статора, это значение обычно указывается на самом электродвигателе, если же оно затерто или неразборчиво, то его измеряют специальными клещами;
• U сети – напряжение питания сети, т. е. 220 вольт.

Таким образом вы рассчитаете емкость рабочего конденсатора в мкФ.

Еще один вариант расчета – принять во внимание значение мощности двигателя. 100 Ватт мощности соответствуют примерно 7 мкФ емкости конденсатора. Осуществляя расчеты, не забывайте следить за значением тока, поступающего на фазную обмотку статора. Он не должен иметь большего значения, чем номинальный показатель.

В случае, когда пуск двигателя производится под нагрузкой, т.е. его пусковые характеристики достигают максимальных величин, к рабочему конденсатору добавляется пусковой. Его особенность заключается в том, что он работает примерно в течение трех секунд в период пуска агрегата и отключается, когда ротор выходит на уровень номинальной частоты вращения. Рабочее напряжение пускового конденсатора должно быть в полтора раза выше сетевого, а его емкость – в 2,5-3 раза больше рабочего конденсатора. Чтобы создать необходимую емкость, вы можете подключить конденсаторы как последовательно, так и параллельно.

Как подобрать конденсатор для однофазного электродвигателя

Асинхронные двигатели, рассчитанные на работу в однофазной сети, обычно подключаются на 220 вольт. Однако если в трехфазном двигателе момент подключения задается конструктивно (расположение обмоток, смещение фаз трехфазной сети), то в однофазном необходимо создать вращательный момент смещения ротора, для чего при запуске применяется дополнительная пусковая обмотка. Смещение ее фазы тока осуществляется при помощи конденсатора.

Итак, как подобрать конденсатор для однофазного электродвигателя?

Чаще всего значение общей емкости Сраб+Спуск (не отдельного конденсатора) таково: 1 мкФ на каждые 100 ватт.

Есть несколько режимов работы двигателей подобного типа:

• Пусковой конденсатор + дополнительная обмотка (подключаются на время запуска). Емкость конденсатора: 70 мкФ на 1 кВт мощности двигателя.
• Рабочий конденсатор (емкость 23-35 мкФ) + дополнительная обмотка, которая находится в подключенном состоянии в течение всего времени работы.
• Рабочий конденсатор + пусковой конденсатор (подключены параллельно).

Если вы размышляете: как подобрать конденсатор к электродвигателю 220в, стоит исходить из пропорций, приведенных выше. Тем не менее, нужно обязательно проследить за работой и нагревом двигателя после его подключения. Например, при заметном нагревании агрегата в режиме с рабочим конденсатором, следует уменьшить емкость последнего. В целом, рекомендуется выбирать конденсаторы с рабочим напряжением от 450 В.

Как выбрать конденсатор для электродвигателя – вопрос непростой. Для обеспечения эффективной работы агрегата нужно чрезвычайно внимательно рассчитать все параметры и исходить из конкретных условий его работы и нагрузки.

Расчет емкости конденсатора для трехфазного двигателя

При подключении асинхронного трехфазного электродвигателя на 380 В в однофазную сеть на 220 В необходимо рассчитать емкость фазосдвигающего конденсатора, точнее двух конденсаторов — рабочего и пускового конденсатора. Онлайн калькулятор для расчета емкости конденсатора для трехфазного двигателя в конце статьи.

Как подключить асинхронный двигатель?

Подключение асинхронного двигателя осуществляется по двум схемам: треугольник (эффективнее для 220 В) и звезда (эффективнее для 380 В).

На картинке внизу статьи вы увидите обе эти схемы подключения. Здесь, я думаю, описывать подключение не стоит, т.к. это описано уже тысячу раз в Интернете.

Во основном, у многих возникает вопрос, какие нужны емкости рабочего и пускового конденсаторов.

Пусковой конденсатор

Ознакомьтесь также с этими статьями

Стоит отметить, что на небольших электродвигателях, используемых для бытовых нужд, например, для электроточила на 200-400 Вт, можно не использовать пусковой конденсатор, а обойтись одним рабочим конденсатором, я так делал уже не раз — рабочего конденсатора вполне хватает. Другое дело, если электродвигатель стартует со значительной нагрузкой, то тогда лучше использовать и пусковой конденсатор, который подключается параллельно рабочему конденсатору нажатием и удержанием кнопки на время разгона электродвигателя, либо с помощью специального реле. Расчет емкости пускового конденсатора осуществляется путем умножения емкостей рабочего конденсатора на 2-2.5, в данном калькуляторе используется 2.5.

При этом стоит помнить, что по мере разгона асинхронному двигателю требуется меньшая емкость конденсатора, т.е. не стоит оставлять подключенным пусковой конденсатор на все время работы, т.к. большая емкость на высоких оборотах вызовет перегрев и выход из строя электродвигателя.

Как подобрать конденсатор для трехфазного двигателя?

Конденсатор используется неполярный, на напряжение не менее 400 В. Либо современный, специально на это рассчитанный (3-й рисунок), либо советский типа МБГЧ, МБГО и т.п. (рис.4).

Итак, для расчета емкостей пускового и рабочего конденсаторов для асинхронного электродвигателя введите данные в форму ниже, эти данные вы найдете на шильдике электродвигателя, если данные неизвестны, то для расчета конденсатора можно использовать средние данные, которые подставлены в форму по умолчанию, но мощность электродвигателя нужно указать обязательно.

Онлайн калькулятор расчета емкости конденсатора

Советуем к прочтению другие наши статьи

Расчет емкости конденсатора22:

как рассчитать с помощью онлайн калькулятора

Конденсаторы – это компоненты, способные хранить электрозаряд или электрическую энергию. Простейшая форма элемента – это две пластины из металла с диэлектриком между ними, не допускающим электрического соединения обкладок. При подаче напряжения в межобкладочном пространстве образуется электрическое поле, с положительным зарядным знаком на одной пластине и с отрицательным – на другой. Распределение заряда одинаково с обеих сторон.

Различные типы конденсаторов

Емкость конденсатора

Для конденсаторного элемента емкость – это потенциальная мера хранения энергии. Она имеет символ С и рассчитывается в фарадах (Ф). Наиболее часто можно встретить единицы, масштабированные в меньшую сторону: микро-, нано-, пикофарады.

Емкость конденсатора можно выразить через заряд (q) и напряжение (V):

C = q/V = (I x t)/V, где:

• t – время,
• I – сила тока.

Емкость определяется также структурными размерами конденсатора:

C = (ε x ε0 x S)/d.

Из этой формулы получается, что емкость тем больше, чем:

• больше поверхность пластины S;
• меньше расстояние между ними d;
• лучше дипольное образование в изоляторе (больше диэлектрическая проницаемость ε):

ε0 = 8,85 х 10 ( в -12 степени), Ф/м – диэлектрическая проницаемость в вакууме.

Для увеличения емкости плоского конденсатора надо увеличить плоскость его пластин, уменьшить межобкладочное расстояние или применить для изолятора материал с большим значением ε.

Формулы емкости для различных конденсаторов

Элементы обладают фиксированной емкостью, определенной производителем, значение которой нельзя изменить.

Конденсаторы с переменной емкостью

Для этих элементов характерна способность менять емкость. Простейший из них состоит из нескольких половин дисков (одной), фиксированных и электрически связанных друг с другом.

Другая группа аналогичных половин диска установлена на общей оси. При вращении вала фиксированная на нем половина диска устанавливается между неподвижными половинами, и происходит изменение емкости.

Конденсатор с переменной емкостью

Характеристики конденсатора

1. Диэлектрическая постоянная ε является мерой того, как изолирующий материал влияет на емкость конденсатора;
2. Диэлектрическая прочность определяет самое высокое напряжение, которое может быть приложено к конденсаторному элементу. В случае его превышения происходит пробой;
3. Температурная зависимость. В фильтрах и резонансных схемах важную роль играет температурный коэффициент ТК. В зависимости от температуры, меняется отдаваемая мощность. Изменение может быть со знаком «плюс» и «минус». Некоторые схемы требуют точности расчета конденсатора.

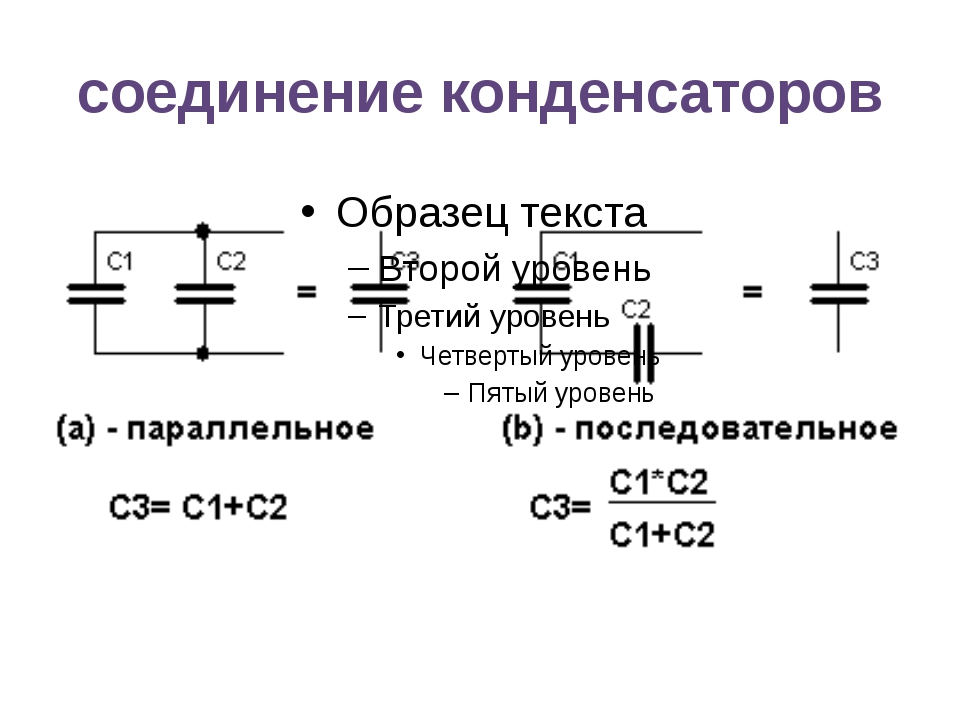
Соединение конденсаторов

В электрических цепях нередко производят подключения, состоящие из нескольких конденсаторов, имеющих разные типы соединений.

Последовательное соединение

Если левая пластина первого конденсатора несет заряд со знаком «плюс», правая из-за электростатической индукции получит его со знаком «минус». При этом он будет смещен от левой обкладки второго конденсатора, что, в свою очередь, положительно зарядит ее и т. д.

Последовательное соединение конденсаторных элементов

Напряжение, приложенное к общей емкости конденсаторов, будет складываться из напряжений на каждом из них:

V = V1 + V2 + V3 + …

Так как:

• V1 = q/С1;
• V2 = q/С2;
• V3 = q/С3,

а для всей батареи последовательных элементов:

V = q/С,

то q/С = q/С1 + q/С2 + q/С3.

Количество электричества в последовательной цепи одинаково, значит допустимо разделить обе части уравнения на q.

Рассчитать емкость элементов, собранных в последовательную цепь, можно по формуле:

1/С = 1/С1 + 1/С2 + 1/С3 + …

Важно! Величина, обратная суммарной емкости конденсаторных элементов, соединенных в последовательную цепь, составляет сумму обратных величин емкостей отдельных компонентов.

Параллельное соединение

Когда емкость конденсаторов мала, они включаются параллельно. Как рассчитать общую емкость такой цепи, определяется теми же зависимостями, но с учетом того, что напряжение на конденсаторных пластинах будет одинаковым:

V = V1 = V2 = V3 = …

Параллельное соединение конденсаторных элементов

Количество электричества на каждом конденсаторе составит:

q1 = V x C1, q2 = V x C2, q3 = V x C3.

Общий заряд конденсаторной батареи:

q = q1 + q2 + q3 = V/C1 + V/C2 + V/C3 = V x (C1 + C2 + C3), а С = С1 + С2 + С3.

Важно! При параллельном соединении конденсаторных элементов каждый из них подключен на полное напряжение электроцепи, а общая емкость суммируется.

В сети есть сайты, имеющие калькулятор для расчета конденсатора при разных конфигурациях электросхемы, а также позволяющих определить емкость, задавая свои структурные параметры, как для плоских, так и для цилиндрических элементов.

Расчет конденсатора для электродвигателя

Трехфазный электромотор можно подключить к однофазной линии, которая позволит управлять им с помощью конденсатора. При этом надо произвести расчет емкости конденсатора.

Чтобы узнать значение в микрофарадах, которое нужно получить от конденсаторного элемента, и найти оптимальный пусковой момент в однофазной линии, надо знать технические характеристики мотора.

Схемы включения электромотора с конденсатором

1. Активная мощность определяется:

Р = √3 x V x I x соsφ.

Она может быть указана на таблице, прикрепленной к мотору. Напряжение – 220 В в однофазном режиме. Величина соsφ также указывается производителем (обычно для электродвигателей соsφ = 0,8-0,85).

2. Отсюда можно найти силу тока:

I = P/(√3 x V x  соsφ).

3. Емкость конденсатора для соединенных звездой двигательных обмоток Сраб = 4800 x I /V, для соединенных в Δ – Сраб = 2800 x I/V;
4. Для пускового конденсаторного элемента Спуск = 2,5 С.

Сетевой калькулятор онлайн производит и такой тип расчетов. Для этого вводятся параметры электромотора и питающей сети, в результате получается емкостное значение.

Видео

Оцените статью:

Расчёт растягивающих конденсаторов LC контура настройки

Как загнать пределы перестройки конденсатора переменной ёмкости (КПЕ) в колеба-
тельном LC контуре в нужный диапазон изменения
частоты.
Онлайн калькулятор ёмкостей конденсаторов растяжки.

«В процессе конструирования генераторов сигналов и задающих генераторов передатчиков радиолюбители часто сталкиваются с трудностями
приобретения конденсатора переменной ёмкости с нужными пределами изменения ёмкости. Я предлагаю читателям простой способ расчёта ёмкостей
дополнительных конденсаторов С1 и С2 (см. рисунок), включение которых в колебательный контур генератора позволяет получить нужный
диапазон перестройки».

Рис.1 Общая схема колебательного контура с растягивающими конденсаторами

Так начинается очень полезная статья, опубликованная в журнале Радио, 1992, №11, с.23, под авторством С. Бирюкова. Далее там приведены
уравнения и довольно громоздкие итоговые формулы для расчёта величин растягивающих конденсаторов С1 и С2, а также практический пример
расчёта контура с КПЕ.

Для желающих освоить теоретическую часть процесса порекомендую обратиться к статье в журнале, а для практиков приведу простую таблицу,
позволяющую без излишнего напряга, калькулятора и деревянных счёт в режиме онлайн рассчитать значения искомых конденсаторов.

К тому же формулы уважаемого автора не учитывают ёмкости, обозначенной на Рис.1 — С_конт.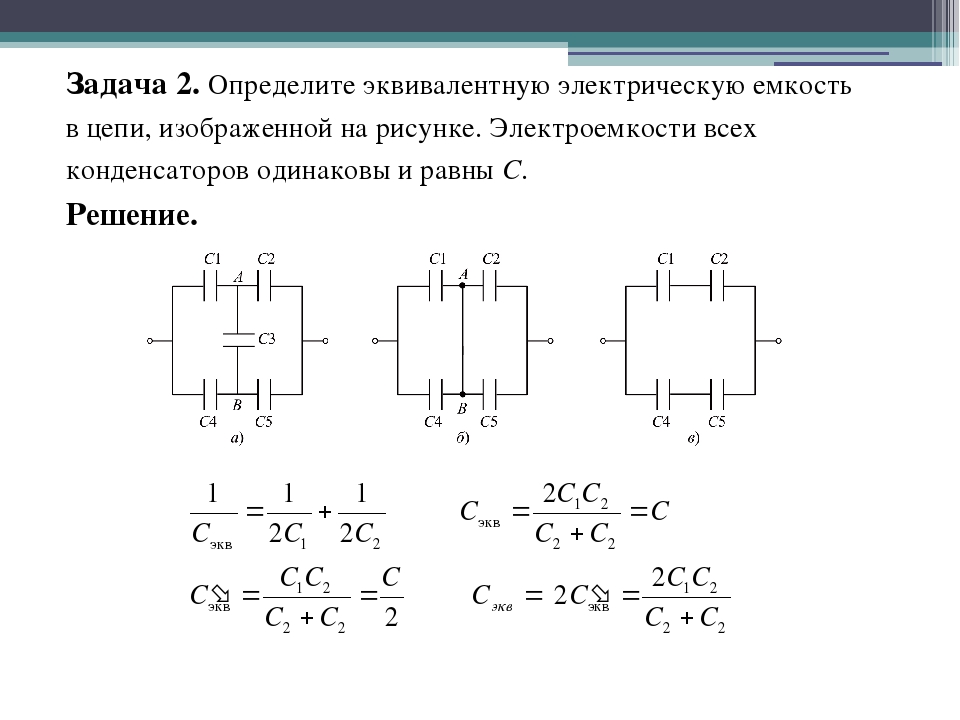

Тем не менее, эта ёмкость в реальном устройстве всегда присутствует и численно равна сумме: собственной ёмкости катушки индуктивности,
общей ёмкости подключённых к ней радиоэлементов, а также ёмкости проводников печатного или какого-либо иного монтажа. И надо сильно
постараться, чтобы величина этой суммарной ёмкости уложилась в десяток пикофарад. Даже при довольно продуманном монтаже значение
С_конт, как правило, составляет 15…20 пФ.

Короче, для максимальной достоверности итогового результата — величину этой ёмкости учитывать необходимо!

КАЛЬКУЛЯТОР РАСЧЁТА РАСТЯГИВАЮЩИХ КОНДЕНСАТОРОВ LC-КОНТУРА.

Необходимо иметь в виду, что выбираемые значения исходных величин должны быть корректными. Например, это относится к частотам диапазона,
который не должен быть чрезмерно широк для выбранного КПЕ. Важно следить за тем, чтобы посчитанный номинал ёмкости С1 был больше
величины «максимальная ёмкость КПЕ с учётом С1, С2». Если это не так, то надо либо уменьшить индуктивность катушки, либо снизить
ширину диапазона перестройки. Возможны иные варианты ограничений, в которых пользователь может разобраться самостоятельно, действуя
методом проб и ошибок.

Ну а воспользовавшись простыми, как ситцевые трусы формулами для расчёта последовательно — параллельного соединения конденсаторов, можно
решить обратную задачу и посмотреть, какой будет полоса перестройки контура при впаивании в схему конденсаторов из имеющегося у радиолюбителя
ряда.

КАЛЬКУЛЯТОР ЧАСТОТ ПЕРЕСТРОЙКИ LC-КОНТУРА С РАСТЯГИВАЮЩИМИ КОНДЕНСАТОРАМИ.

Данный калькулятор не подвержен влиянию вводимых данных и покажет корректный результат при любых значениях исходных величин.

Расчет конденсатора для трехфазного двигателя в однофазной сети

Для включения трехфазного электродвигателя (что такое электродвигатель ➠) в однофазную сеть обмотки статора могут быть соединены в звезду или треугольник.

Напряжение сети подводят к началам двух фаз. К началу третьей фазы и одному из зажимов сети присоединяют рабочий конденсатор 1 и отключаемый (пусковой) конденсатор 2, который необходим для увеличения пускового момента.

Пусковая емкость конденсаторов

Сп = Ср + Со,

где Ср — рабочая емкость,
Со — отключаемая емкость.

После пуска двигателя конденсатор 2 отключают.

Рабочую емкость конденсаторного двигателя для частоты 50 Гц определяют по формулам:

для схемы на рис. а: Ср = 2800 Iном / U;
для схемы на рис. б: Ср = 4800 Iном / U;
для схемы на рис. в: Ср = 1600 Iном / U;
для схемы на рис. г: Ср = 2740 Iном / U,

где Ср — рабочая емкость при номинальной нагрузке, мкФ;
Iном — номинальный ток фазы двигателя, А;
U — напряжение сети, В.

Нагрузка двигателя с конденсатором не должна превышать 65—85% номинальной мощности, указанной на щитке трехфазного двигателя.

Если пуск двигателя происходит без нагрузки, то пусковая емкость не требуется — рабочая емкость будет в то же время пусковой. В этом случае схема включения упрощается.

При пуске двигателя под нагрузкой, близкой к номинальному моменту необходимо иметь пусковую емкость Сп = (2,5 ÷ 3) Ср.

Выбор конденсаторов по номинальному напряжению производят по соотношениям:

для схемы на рис. а, б: Uк = 1,15 U;
для схемы на рис. в: Uк = 2,2 U;
для схемы на рис. г: Uк = 1,3 U,

где Uк и U — напряжения на конденсаторе и в сети.

Купить конденсаторы для запуска двигателя:
CBB60 3/4/5/6/10/12/14/16 мкФ 500 В;
CBB60 20 мкФ 450 В;
CBB60 25 мкФ 450 В;
CBB60 35 мкФ 450 В;
CBB60 50 мкФ 450 В;
CBB60 60 мкФ 450 В;
CBB60 80 мкФ 450 В;
CD60 100 мкФ 450 В;
CBB60 120 мкФ 450 В.

Основные технические данные некоторых конденсаторов приведены в таблице.

Если трехфазный электродвигатель, включенный в однофазную сеть, не достигает номинальной частоты вращения, а застревает на малой скорости, следует увеличить сопротивление клетки ротора проточкой короткозамыкающих колец или увеличить воздушный зазор шлифовкой ротора на 15—20%.

В том случае, если конденсаторы отсутствуют, можно использовать резисторы, которые включаются по тем же схемам, что и при конденсаторном пуске. Резисторы включаются вместо пусковых конденсаторов (рабочие конденсаторы отсутствуют).

Сопротивление (Ом) резистора может быть определено по формуле

,

где R — сопротивление резистора;
κ и I— кратность пускового тока и линейный ток в трехфазном режиме.

Пример расчета рабочей емкости конденсатора для двигателя

Определить рабочую емкость для двигателя АО 31/2, 0.6 кВт, 127/220 В, 4.2/2.4 А, если двигатель включен по схеме, изображенной на рис. а, а напряжение сети равно 220 В. Пуск двигателя без нагрузки.

Решение

1. Рабочая емкость Ср = 2800 x 2.4 / 220 ≈ 30 мкФ.

2. Напряжение на конденсаторе при выбранной схеме Uк = 1,15 x U = 1,15 x 220 = 253 В.

По таблице выбираем три конденсатора МБГО-2 по 10 мкФ каждый с рабочим напряжением 300 В. Конденсаторы включать параллельно.

Источник: В.И. Дьяков. Типовые расчеты по электрооборудованию.

Видео о том, как подключить электродвигатель на 220 вольт:

Помощь студентам

Расчет конденсаторов шины питания мощных преобразовательных устройств — Компоненты и технологии

Одними из значимых элементов схемы и конструкции импульсного преобразователя являются конденсаторы шины питания. Неграмотный выбор ЭК и неправильный расчет режимов его работы может заметно снизить надежность аппаратуры и стать причиной неожиданных отказов. Компания RIFA предлагает методику расчета конденсаторов, позволяющую не только оценить мощность потерь в конкретных условиях эксплуатации, но и достаточно точно спрогнозировать срок их службы.

Особенностям топологии и конструкции преобразователей высокой мощности посвящено достаточно много литературы (см., например, [3, 4]). Технология выполнения соединений имеет решающее значение в устройствах, коммутирующих с высокими скоростями токи в десятки, сотни и даже тысячи ампер. Именно такие режимы работы характерны для современных мощных импульсных устройств, использующих в качестве силовых ключей транзисторы MOSFET или IGBT. Неправильно выполненная топология шин, высокое значение распределенных паразитных индуктивностей проводников приводит к появлению импульсных перенапряжений, что подчас является причиной отказа силовых полупроводников. Распределенные параметры шин достаточно сложно поддаются расчету или измерению, серьезной проблемой является анализ уровня переходных перенапряжений, особенно в предельных режимах, таких, как режим аварийного отключения транзисторов при коротком замыкании нагрузки.

Не менее значимыми элементами схемы и конструкции импульсного преобразователя являются конденсаторы шины питания. Как правило, мы не особо задумываемся о расчете режимов при выборе электролитических конденсаторов (ЭК) для маломощных схем. Такая «невнимательность» совершенно недопустима при расчете конденсаторов силовой шины питания. Неграмотный выбор ЭК и неправильный расчет режимов его работы может заметно снизить надежность аппаратуры и стать причиной неожиданных отказов.

Рис. 1. Инвертор для ветрогенератора фирмы SEMIKRON. На рисунке видны силовые модули SKiiP IGBT и многослойные шины питания с установленными на них конденсаторами

Как правило, производители ЭК в технической документации приводят минимальный набор параметров: предельное напряжение, допустимый ток пульсаций при заданной частоте, тангенс угла потерь, эквивалентное последовательное сопротивление (ESR), эквивалентная последовательная индуктивность (ESL). В спецификациях более «продвинутых» изготовителей ЭК можно найти таблицу поправочных коэффициентов для тока пульсаций и показатели надежности. Например, конденсаторы HU3/HU4 фирмы Hitachi имеют ресурс свыше 600 тыс. часов при номинальном токе пульсаций и температуре 50 °С. Этот же параметр не превышает 4 тыс. часов при предельной температуре. Однако при расчете схемы разработчику хотелось бы знать, сколько конкретно прослужат емкости при заданных рабочих режимах. Это необходимо и для определения минимального номинала ЭК, поскольку современные высоковольтные конденсаторы вносят значительный вклад в стоимость изделия и имеют существенные габариты.

Одним из мировых лидеров в производстве конденсаторов различного назначения, фирмой RIFA, разработана методика расчета, позволяющая не только оценить мощность потерь конденсаторов в конкретных условиях эксплуатации, по и достаточно точно спрогнозировать срок их службы. Подобный расчет может оказать неоценимую помощь разработчику силовой электронной техники.

Потери в ЭК

Суммарные потери проще всего оценить, зная ток утечки Il, среднеквадратичное (RMS) значение переменного тока I, текущего через конденсатор, и значения эквивалентных сопротивлений ЭК.

Общее омическое сопротивление R состоит из сопротивления металла и электролита.

Диэлектрические потери пропорциональны энергии, запасенной в конденсаторе: W_С = CU²/2. Мощность P₁, рассеиваемая в ЭК, может быть записана следующим образом:

где f — частота перезаряда конденсатора.

Условимся, что ток через ЭК имеет синусоидальную форму. В этом случае потери будут составлять:

Поскольку I = ω × C × U, a ω = 2π × f, то

Сомножитель (A + B 9 f) представляет собой известный всем cosφ. Однако пользоваться углом φ неудобно, так как обычно он близок к 90°, поэтому при расчетах ЭК применяют угол δ = 90 — φ, называемый углом потерь. Таким образом, tan δ = sin (90 — φ)/cos(90 — φ) ≅ sin (90 — φ) так как cos (90 — φ) ≅ 1 Формула приобретает нормальный вид:

Ошибка, возникающая из-за принятой аппроксимации, несущественна для расчетов потерь ЭК, а измерение tan δ намного проще, чем cos φ. Этот параметр называется тангенсом угла потерь и приводится в данных на ЭК.

Подставляя в (2) U = I/(ω × C), получаем:

Таким образом можно определить R_S или ESR — эквивалентное последовательное сопротивление, значение которого также приводится в технических характеристиках (по крайней мере у серьезных производителей).

Как видно из уравнения (6), параметр R_S является частотно зависимым. Примерный вид графика зависимости R_S от частоты приведен на рис. 2. Это несколько затрудняет расчет потерь. Кроме того, если ток имеет сложный спектральный состав, необходимо знать величину каждой гармоники. Однако, если низшие гармоники достаточно велики и частотно зависимый компонент мал по сравнению с омическим сопротивлением, расчет становится простым. Обычно на частотах свыше 500 Гц R_S практически не зависит от частоты.

Рис. 2. Зависимость ESR от частоты

Температура перегрева ЭК зависит от R_S и среднеквадратичного значения переменного тока I. Назовем температуру в наиболее нагретой точке конденсатора (точке перегрева) T_hs, а температуру окружающей среды — T_a. В рабочем диапазоне перегрев является линейной функцией мощности потерь Р. Тогда справедливо следующее соотношение:

где R_th — тепловое сопротивление «точка перегрева — окружающая среда». Некоторые дополнительные потери P_L создает и ток утечки I_L:

Однако данными потерями, как правило, можно пренебречь, особенно в соотношении с мощностью, рассеиваемой как самими конденсаторами, так и балластными резисторами при последовательном соединении конденсаторов.

Срок службы и надежность

Два основных параметра, влияющих на ресурс и надежность ЭК, — это рабочее напряжение и температура. Для срока службы L_op можно записать соотношение:

где U_op — рабочее напряжение, U_R — предельно допустимое напряжение, L_opR — срок службы ЭК при напряжении U_R.

Показатель степени n = 5 при 0,8U_R < U < U_R; n = 3 при 0,5U_R < U < 0,8U_R. Это означает, что снижение рабочего напряжения на 21% увеличивает срок службы вдвое. Если U < 0,5U_R срок службы практически не зависит от напряжения.

Срок службы имеет экспоненциальную температурную зависимость. График зависимости может быть описан выражением:

Надежность ЭК оказывается тем выше, чем выше его диаметр. Формула, учитывающая диаметр, имеет следующий вид:

(Для конденсаторов, рассчитанных на 105° вместо 85° в показателе степени должно быть 105).

Значение f(D) для некоторых значений диаметра ЭК стандартной конструкции приведено ниже:

L_op определяется, как время, в течение которого параметры ЭК находятся в пределах определенных допусков. У каждой фирмыпроизводителя значения допусков свои. RIFA так определяет предельное состояние ЭК:

• Изменение емкости более 15%.
• Увеличение tanδ более чем в 1,3 раза.
• Увеличение ESR более чем в 2 раза.

Когда большое количество ЭК (назовем его N₀) испытывается при заданных условиях, то через определенное время некоторые параметры ЭК подойдут к своему предельному значению. Количество ЭК, сохраняющих свои параметры в пределах допусков, — R(t) будет со временем становиться все меньше в соответствии с выражением:

где — частота отказов.

Вероятность отказа F(t) можно определить как:

где S(t) — вероятность, что 1 конденсатор прослужит время t.

Можно также определить зависимость срока службы L_op от вероятности отказа следующим образом:

где m — среднее время между отказами.

L_op и λ экспоненциально зависят от температуры: λ возрастает, а L_op — снижается.

Упрощенное выражение для выглядит следующим образом:

Для 105° конденсаторов в показателе степени надо заменить 85 на 105.

Тепловая модель электролитического конденсатора

Токи перезаряда конденсатора вызывают потери на его омическом сопротивлении. Потери также создаются за счет тока утечки и изменения напряжения на диэлектрике. Эти потери проявляются в повышении температуры ЭК — ΔT, пропорциональном мощности потерь Р.

где R_th — тепловое сопротивление конденсатора.

Наиболее нагретая точка ЭК имеет температуру T_hs. Обычно эта точка расположена в геометрическом центре ЭК. Тепло распространяется во все стороны через электролит, фольгу, выводы, корпус и т. д. Обозначим R_thhc — тепловое сопротивление «точка перегрева — корпус», а R_thca — тепловое сопротивление «корпус — окружающая среда». Если ЭК установлен на теплосток, появляется тепловое сопротивление «корпус — теплоотвод» R_thcс, зависящее от размера, формы теплостока и способа охлаждения.

На тепловые режимы при импульсном характере работы влияние оказывает также тепловая емкость конденсатора C_th, которая зависит от массы и материала ЭК. В модели ЭК такую емкость можно было бы установить параллельно каждому сопротивлению. Однако емкостью, параллельной R_thca, можно пренебречь из-за низкой теплоемкости воздуха.

На рис. 3 приведены эквивалентные тепловые схемы для случая естественного охлаждения (слева) и установки ЭК на радиатор (справа). Tt — температура выводов конденсатора. Температура корпуса Tc измеряется в точке, противоположной выводам.

Рис. 3. Эквивалентные тепловые схемы ЭК

В таблице 1, приведенной ниже, приведены тепловые характеристики (при естественном охлаждении) некоторых типоразмеров ЭК фирмы RIFA.

Таблица 1. Тепловые сопротивления и тепловые емкости ЭК RIFA

Приведенные цифры являются основными данными для расчета нагрева ЭК, в какой бы схеме он не работал. К сожалению, в каталогах большинства фирм-производителей (и в отечественных ТУ тоже) тепловые характеристики конденсаторов не приводятся.

Параллельное и последовательное соединение ЭК

Соединение ЭК используется для повышения емкости, увеличения допустимого напряжения или тока пульсаций и не вызывает, на первый взгляд, никаких проблем. Однако проблемы существуют и связаны они в первую очередь с возникновением переходных помех при включении из-за паразитной индуктивности соединительных проводов.

На рис. 4 показано параллельное соединение 4 конденсаторов C1…C4 емкостью по 3300 мкФ.

Рис. 4. Эквивалентная схема при параллельном соединении конденсаторов

В схему включены сопротивления и индуктивности подводящих проводов, паразитные индуктивности ЭК и сопротивления R_s (ESR). Эпюры напряжений в точке 5 схемы (см. рис. 5) даны для двух значений температуры — 20 и 85 °С. Разница в переходном напряжении (135 В для 20 °С и 165 В для 85 °С) объясняется тем, что Rs изменяет свое значение от 22 мОм при 20 °С до 7 мОм при 85 °С. Величина перенапряжения зависит и от номинала конденсатора. Интересно, что пик напряжения практически не зависит от величины нагрузки. Это объясняется тем, что импеданс схемы очень низок по сравнению с нагрузкой. Следует отметить, что в реальных схемах, как правило, используется режим «плавного» заряда, что необходимо для ограничения зарядного тока конденсаторов. В этом случае перенапряжения при включении не наблюдается.

Рис. 5. Эпюры напряжений при включении схемы

Последовательное соединение ЭК используется для высоковольтных схем. При этом часто приходится включать конденсаторы последовательно — параллельно для получения необходимой величины емкости.

Анализ переходных искажений в комбинированной схеме производится аналогично описанному выше. Следует учесть паразитные параметры проводов между последовательно соединенными конденсаторами. Стоит помнить и про разброс номиналов конденсаторов, который может привести к значительным перенапряжениям на некоторых из них.

Особенностью последовательного соединения ЭК является то, что параллельно каждому ЭК необходимо установить балластный резистор для устранения перекоса напряжения из-за разности токов утечки конденсаторов. Номиналы уравнивающих резисторов можно рассчитать по формуле:

где С — емкость в мкФ, R — сопротивление в кОм.

Формула 17 выведена на основании известного соотношения для тока утечки I_L = k × C × U_R, где константа k = 3 × 10^-3. Ток резистора I_R должен быть значительно больше тока утечки ЭК, который имеет разброс и зависит от условий эксплуатации. Обычно ток балластного резистора превышает номинальное значение тока утечки ЭК в 10…20 раз. Часто оказывается, что правильно рассчитанный уравнивающий резистор рассевает довольно большую мощность и с этим приходится мириться.

На ЭК присутствует также переменное напряжение пульсаций. Резисторы обеспечивают уравнивание для постоянного тока и низких частот. На частотах порядка сотен герц и выше коэффициент деления напряжения определяется только соотношением емкостей.

Причины отказов ЭК

Основная причина деградации и выхода из строя ЭК — диффузия электролита через изолятор. Этот процесс ускоряется с ростом температуры и в основном определяет срок службы конденсатора.

Ниже некоторые причины, способные привести к преждевременному отказу ЭК:

• Переохлаждение (обычно ниже –30 °С). Приводит к резкому росту ESR и падению емкости.
• Перегрев (повышенная температура окружающей среды или превышение допустимого тока пульсаций). Приводит к росту ESR и тока утечки, падению емкости.
• Превышение рабочего напряжения. Приводит к росту ESR и падению емкости.
• Переходные перенапряжения. Могут привести к повышению тока утечки и внутреннему короткому замыканию ЭК.
• Воздействие высоких частот. Может привести к изменению емкости и ESR.
• Обратное напряжение. Может привести к повышению тока утечки, потере емкости, увеличению ESR, сокращению срока службы.
• Механические вибрации. Приводят к внутреннему короткому замыканию, увеличению тока утечки, потере емкости.

Выбор и расчет ЭК

Среднеквадратичное значение тока пульсаций I_RMS

Этот наиболее важный параметр, который приходится оценивать при анализе практически любой схемы, в состав которой входят ЭК. Именно значение I_RMS определяет в основном потери в ЭК. Поэтому ведущие производители конденсаторов приводят в своих технических данных предельное значение I_RMS, а не допустимую амплитуду напряжения пульсаций, как это принято в наших ТУ.

Рассмотрим для примера работу двухполупериодного выпрямителя, схема которого приведена на рис. 6. Первичное напряжение — 50 Гц, 220 В. Сопротивление нагрузки — 80 Ом, емкость конденсатора — 500 мкФ

Рис. 6. Однофазный выпрямитель

На рис. 7 показаны токи конденсатора — импульсный I_cpp и среднеквадратичный I_rmsc (вверху), напряжение на конденсаторе и выходное напряжение выпрямительного моста при отсутствии сглаживания (внизу). Предположим, что потерь в схеме нет. Заряд конденсатора начинается, когда выпрямленное напряжение превышает напряжение на ЭК. Разряд идет практически линейно. Пусть t1 — время начала заряда, t2 — время начала разряда, t3 — время начала следующего периода заряда, то есть t3 = t1 + T.

Рис. 7. Эпюры напряжений и токов однофазного выпрямителя

(310 В — амплитуда входного напряжения).

Пиковый ток конденсатора I_cpp (момент времени t1):

Ток разряда I_d определяется из соотношения:

Ток заряда ЭК имеет треугольную форму. Его среднеквадратичное значение I_rms:

Среднеквадратичное значение тока разряда I_rmsd:

Общее среднеквадратичное значение тока:

При выборе номинала конденсатора мы должны учитывать не только требования, предъявляемые к схеме, в которой он установлен, но и требования, предъявляемые к режимам работы самого ЭК. Причем последние, как правило, оказываются строже. Необходимо также учитывать разброс номиналов, временные изменения параметров и помнить о том, что ЭК должен оставаться в пределах заданных допусков в течение всего срока службы.

Обычно расчет номинала ЭК включает следующие действия:

• выбирается номинал конденсатора, обеспечивающий необходимую мощность нагрузки или заданное минимальное выпрямленное напряжение;
• найденное значение корректируется с учетом разброса номинала, временного и температурного изменения номинала;
• из каталога выбирается ближайшее минимальное значение номинала конденсатора;
• рассчитывается среднеквадратичное значение тока пульсаций для нового конденсатора, определяется температура нагрева ЭК и срок его службы.

Рассмотрим для примера методику выбора ЭК для простейшей схемы двухполупериодного выпрямителя, приведенной на рис. 6. Для упрощения расчета предположим, что диоды и сглаживающая емкость идеальные и схема не содержит паразитных сопротивлений. ЭК заряжается до амплитудного значения питающего напряжения, равного примерно 310 В. Форма напряжения на конденсаторе и токи через него приведены на эпюрах рис. 7. Для выбора номинала ЭК прежде всего необходимо знать параметры нагрузки. Иногда вместо сопротивления нагрузки задается потребляемая мощность P. Сопротивление нагрузки в этом случае можно определить из соотношения R = U²/P, где U — среднее значение выпрямленного напряжения.

Упрощенная методика расчета основана на положении, что падение напряжения на ЭК начинается на максимуме и происходит линейно, так как используется начальный участок экспоненты разряда.

Зададимся минимальным значением выпрямленного напряжения U_min = 250 В, что соответствует мощности примерно 750 Вт на сопротивлении нагрузки 80 Ом. Минимальное напряжение U_minприсутствует на ЭК в момент времени

Максимум напряжения имеет место при t2 = 5 × 10^-3 + n × T , где Т = 10 мс — период выпрямленного напряжения. Постоянная времени RC определяется по формуле:

Откуда C = 437 мкФ.

Учитывая допуск (10%), мы должны соответственно увеличить номинал в 1,1 раза (С = 480 мкФ).

Конденсатор должен быть рассчитан на постоянное напряжение 350 В и выше. RIFA приводит в своих характеристиках для таких конденсаторов так называемый фактор старения (aging factor) γ = 1 – 0,1 = 0,9. Коррекция значения емкости дает С = 530 мкФ.

Номинал ЭК необходимо также изменить с учетом уменьшения емкости при снижении температуры. Например, при –40 °С температурный коэффициент k_t = 0,94. Следовательно, С = 564 мкФ. Таким образом, окончательное табличное значение номинала ЭК — 560 мкФ. Естественно, что минимальное выпрямленное напряжение при этом конденсаторе будет больше, чем 250 В.

Наконец мы приступаем к самому главному — к нахождению среднеквадратичного тока I_RMS. Он максимален при максимальном значении номинала ЭК, который будет у нового конденсатора C_newопределяться допуском (+30%) и температурным коэффициентом (1,05 при 105 °С).

Используя формулы 18 и 19, определим новые значения t3 и U_min: t3 = 13,5 мс и U_min = 270 В. Исключив из t3 значение периода (10 мс), получим t3 = 3,5 мс.

Воспользуемся выражениями для I_cpp и I_d, приведенными выше, и найдем среднеквадратичные значения токов.

Все приведенные выше формулы и расчеты предназначены, во-первых, для лучшего понимания, а во-вторых, для людей, которые умеют и любят считать.

Более простой и быстрый способ получения значения I_rmsс(и, соответственно, более подходящий для инженеров) — моделирование схемы на PSPICE. Нарисовав с помощью схемного редактора свою схему и задав соответствующие значения сопротивления нагрузки и сглаживающей емкости, вы можете мгновенно получить график среднеквадратичного значения тока конденсатора: RMS(Ic). Необходимо только учесть, что для быстрого получения установившегося значения среднеквадратичного тока следует задать соответствующее начальное напряжение на конденсаторе.

Однако мало найти среднеквадратичный ток через конденсатор, гораздо важнее выяснить, способен ли ЭК выдержать такой ток. Мы уже приводили значения тепловых сопротивлений для ЭК, имеющих различные размеры. В нашем случае (размер А35/51):

Температура ЭК определяется рассеваемой мощностью, а она, в свою очередь, зависит от I_rmsс и ESR. Мы хотим, чтобы температура в самой нагретой точке ЭК составляла не более 105 °С. Если мы продолжим расчеты, то увидим, что перегрев ЭК оказывается совершенно недопустимым. Это наглядный пример того, как номинал конденсатора, удовлетворяющий техническим требованиям, предъявляемым к схеме, оказывается совершенно непригодным с точки зрения параметров ЭК. Поэтому для снижения тока вместо одного конденсатора 560 мкФ мы включим параллельно два по 470 мкФ и снизим тем самым Irmsc до 5 A.

Мощность, рассеиваемая в конденсаторе Pc и перегрев ΔT:

Значит, максимальная температура окружающей среды T_a должна быть не выше

Предельное состояние конденсатора наступает, когда ESR возрастает более чем в 2 раза по сравнению с начальным значением. Предположим, что это случится, когда емкость ЭК будет иметь минимальное значение. В наихудшем случае конденсатор работает при предельной температуре. Тогда емкость C_old:

где 1,05 — коэффициент коррекции емкости при высокой температуре.

В этом случае I_rmsold = 4,8 A

Значит, в конце срока службы температура окружающей среды не должна превышать 12 °С. В противном случае срок службы ЭК будет много меньше паспортного значения. Таким образом, новый конденсатор может работать при Т_a = 55 °С и температура перегрева будет 105 °С, а срок службы L_op = 30000 часов. Если при такой же температуре будет работать «старый» ЭК, его температура перегрева будет 148 °С. Воспользовавшись формулой для срока службы, мы получим, что L_op = 2500 часов.

ESR увеличивается со временем, что приводит к росту температуры ЭК и сокращению срока службы. Однако одновременное снижение емкости уменьшает I_rmsc, что несколько уравновешивает эффект от роста ESR.

Расчет L_op с учетом всех факторов чрезвычайно сложен, поэтому фирма EVOX RIFA предложила упрощенную методику с использованием графиков, отражающих основные зависимости параметров ЭК (см. рис. 8).

Пример: рассчитать для схемы однофазного выпрямителя минимальный срок службы ЭК с параметрами 470 мкФ, 400 В, 105 °C, размером 35×50, при условии, что температура окружающего воздуха — 40 °С.

1. Из справочных данных берется ESR для 20 °С и 100 Гц и пересчитывается с учетом частотного коэффициента k_f (рис. 8.4). В нашем случае k_f = 1. ESR = 190 мОм.
2. Рассчитывается среднеквадратичное значение тока пульсаций (I_rmsc = 5 A при установке двух ЭК в параллель), мощность потерь (4,7 Вт) и перегрев (50 °С). Эти цифры уже были получены в данной главе. При расчете мощности в том случае, если используется принудительное охлаждение, необходимо исправить значение теплового сопротивления с учетом (рис. 8.3)
3. Найденное значение ESR изменяется с учетом температурного коэффициента k_t (рис. 8.5, кривая 2) при температуре перегрева для нового конденсатора T_hs = T_a + ΔT = 90 °С, k_t = 0,8 – ESR = 190 × 0,8 = 152мОм. Теперь можно откорректировать значение температуры перегрева: T_hs = T_a + ΔT = 40 °С + P_c × Rth = 40 + 25 × 0,152 × 10,6 = 80 °С
4. По (рис. 8.6) определяется срок службы Lop при температуре T_hs = 80 °С – L_op

≅ 15000.

5. Уточняется значение срока службы с учетом коэффициента нагрузки по напряжению k_u = 310/400 = 0,78 по формуле (10) при n = 5 – L_op = 15000/(0,78)5 = 50000.

Заключение

Отметим, что электролитические конденсаторы долгое время не имели альтернативы для применения в силовых преобразователях благодаря высокой удельной емкости. В последнее время ситуация изменяется благодаря созданию принципиально новых технологий производства конденсаторов MPP, SMKP и MKP. Данные технологии были разработаны в компании ELECTRONICON Kondensatoren — одном из ведущих европейских предприятий, изготавливающих конденсаторы для силовых применений.

Конденсаторы MKP содержат металлизированные с двух сторон бумажные электроды с полипропиленовым диэлектриком, пропитанные маслом. Этот тип емкостей имеет низкое значение эквивалентной последовательной индуктивности (ESL), он специально разработан для использования в силовых шинах питания. Конденсаторы рассчитаны на работу при напряжении до 1300 В и имеют максимальную емкость 1500 мкФ. По сравнению с обычными ЭК с алюминиевой фольгой, СМКП способны работать при гораздо большем значении тока пульсаций. Основой почти всех конденсаторов ELECTRONICON является так называемый самовосстанавливающийся диэлектрик. На месте электрического пробоя в течение нескольких микросекунд испаряется слой металла и удаляется из центра пробоя. В результате образуется свободная от металла изолированная зона, предохраняющая от пробоя. В процессе и после пробоя конденсатор остается полностью работоспособным.

В таблице 2 приведены основные сравнительные характеристики стандартных ЭК с алюминиевой фольгой и конденсаторов MKP с полипропиленовым диэлектриком. Отметим, для того чтобы набрать аналогичный номинал (1100 мкФ) и обеспечить рабочее напряжение более 1100 В, необходимо соединить параллельно-последовательно 9 емкостей НР3! Таким образом, разница в цене (конденсаторы MKP, конечно, пока еще гораздо дороже стандартных) для высоковольтных применений может оказаться несущественной.

На рис. 1 показан модуль SEMISTACK разработанный фирмой SEMIKRON и предназначенный для применения в ветрогенераторе мощностью свыше 1 МВт. Модуль содержит конвертор и инвертор на интеллектуальных силовых модулях Trench IGBT SKiiP2403GB172 с рабочим напряжением 1700 В, размещенных на теплоотводе с жидкостным охлаждением и блок конденсаторов 2 9 [3 9 (4 9 3 последовательно)] емкостью 3300 мкФ. Номинальные емкости и количество конденсаторов в сборке рассчитаны для получения уровня тока пульсаций, обеспечивающего высокую надежность изделия. На рисунке видны полумостовые модули SKiiP, снабберные емкости и многослойные силовые шины питания с установленными на них электролитическими конденсаторами. Непосредственно на выводах конденсаторов размещены балластные резисторы, имеющие специальные полосковые выводы. Такая конструкция обеспечивает высокую стойкость к механическим воздействиям и минимальные габариты.

Tаблицa 2. Oсновные сравнительные характеристики стандартных ЭК

На рис. 9 приведены сборки SEMISTACK, разработанные для стандартных применений. Разработка и изготовление таких модулей, а также модулей на заказ является одним из приоритетных направлений работы SEMIKRON. В новейших сборках, разработанных в последние годы, стандартные ЭК практически полностью заменены на MKP. Это позволило повысить надежность изделий, уменьшить их габариты.

Рис. 9. Сборки SEMISTACK SEMIKRON для стандартных применений

Литература

1. Hitachi AIC Compact Aluminium-Electrolytic Capacitors.
2. RIFA Electrolytic Capacitors. Theory and Application.
3. А. Колпаков. Топология частотных преобразователей средней и большой мощности // Компоненты и Технологии. 2002. № 2.
4. А. Колпаков. Особенности проектирования частотных преобразователей средней и большой мощности // Электронные компоненты. 2003. № 6.

Расчет конденсатора для пуска двигателя, схема подключения

1. 
   
   Главная
   
2. 
   
   Электрические машины
   
3. 
   Конденсатор для пуска двигателя

Тема очень востребованная и вызывающая множество вопросов. Для начала разберемся какие бывают асинхронные электродвигатели переменного тока и в каких случаях применяется подключение через конденсаторы. Затем рассмотрим схемы и формулы для выбора конденсаторов. Задача, которая стоит перед нами в этой статье: подключить трехфазный двигатель к однофазному питанию используя схему с конденсаторами. Для этого будет представлена схема и формулы для выбора значения емкостей конденсаторов.

Двигатели по способу питания делятся на трехфазные и однофазные. Вначале разберемся с подключением через конденсатор трехфазного ЭД.

Коротенько про трехфазные асинхронные электродвигатели

Трехфазные асинхронные электродвигатели получили широкое применение в различных отраслях промышленности, сельского хозяйства, быту. ЭД состоит из статора, ротора, клеммной коробки, щитов с подшипниками, вентилятора и кожуха вентилятора.

Стягивающие шпильки я уже снимать не стал, чтобы добраться до статора с ротором. Но выпирающая часть, на которой сидит вентилятор и есть ротор. Ротор — вращающаяся часть, статор неподвижная (на рисунке его не видно).

Далее посмотрим на клеммник более внимательно. С одной стороны у нас С1-С2-С3, а ниже — С4-С5-С6. Это начала и концы обмоток фаз электродвигателя. У нас имеются три фазы, так как двигатель трехфазный — С1-С4, С2-С5, С3-С6. Также присутствует на фото ржавый болт заземления, он находится в клеммнике сверху слева.

Соединение, которое видно на фотографии называется “звезда”. Я уже писал про звезду и треугольник для трансформаторов — аналогично и при подключении электродвигателей. Сбоку на фотографии я добавил как выглядит схематично звезда для данного электродвигателя и треугольник. Вся разница в расположении перемычек. Их комбинации определяют схему соединения ЭД.

работа трехфазного электродвигателя без одной фазы при постоянной нагрузке

Электродвигатель может работать от однофазной сети и без дополнительных мер и схем. Например, при повреждении одной из фаз. Однако, в данном случае произойдет снижение частоты вращения. Снижение частоты вращения приведет к увеличению скольжения, что в свою очередь вызовет увеличение тока двигателя.

А возрастание тока приведет к нагреву обмоток. При такой ситуации необходимо разгрузить ЭД до 50%. Работа в таком режиме возможна, однако, если двигатель остановится, то повторно пуститься уже не получится.

почему для пуска от однофазной сети используют именно конденсаторы

Повторный пуск не произойдет, так как магнитное поле статора будет пульсирующим и, коротко говоря, из-за направленности определенных векторов в противоположные стороны ротор будет неподвижен. Чтобы двигатель пустился, нам необходимо изменить расположение этих векторов. Для этого и используют элементы, которые сдвигают фазы векторов. Рассмотрим схему, которая реализует эту возможность.

На схеме мы видим, что обмотка разделилась на две ветви — пусковую и рабочую. Пусковая используется с начала пуска до разворота двигателя, затем отключается и используется только рабочая. Для отключения пусковой можно использовать кнопку, например. Нажал и держи пока не развернулся двигатель, а потом отпускай и цепочка разорвана.

Фазосдвигающими элементами могут выступать сопротивления или конденсаторы. Разница в применении тех или иных в форме магнитного поля. И если, говорить проще, то выбирают конденсаторы, так как при одном значении пускового момента, меньший пусковой ток будет при использовании конденсаторов.

А при одинаковых пусковых токах у схем с конденсатором будет больше начальный вращающий момент, то есть движок будет быстрее разгоняться, что несомненно лучше для эксплуатации.

Важно: подключение через конденсаторы производят для двигателей до 1,5кВ. Вычислено, что для более мощных ЭД стоимость емкостных элементов превысит стоимость самого движка, следовательно, их установка является нерентабельной. Хотя, если достать их нахаляву, что в нашем пространстве не редкость, то можно и попробовать.

как подключить электродвигатель через конденсатор

Так как конденсаторы выгоднее во многих смыслах для пуска ЭД, то разберем пару схемок пуска с применением конденсаторов. Для схемы соединения “треугольник” и для схемы соединения “звезда”.

Пусковая ветвь будет использоваться до момента разворота ЭД, рабочая — напротяжении всей работы двигателя.

конденсаторы для запуска электродвигателя

Логично будет далее разобраться, как рассчитать пусковой и рабочий конденсатор для двигателя. Для правильного подбора нам необходимо знать паспортные данные ЭД, или иметь шильду с заводскими значениями.

Существуют различные схемы и в каждой конденсаторы выбираются по своему. Для схем, приведенных выше расчет емкости конденсаторов осуществляется по двум формулам:

схема “звезда”:

Рабочая емкость = 2800*Iном.эд/Uсети

схема “треугольник”:

Рабочая емкость = 4800*Iном/Uсети

Пусковая емкость в обоих случаях принимается равной 2-3 от рабочей.

В формулах выше Iном — это номинальный ток фазы электродвигателя. Если посмотреть на табличку, где через дробь указываются два тока, то это будет меньший из них. Uсети — напряжение питающей сети(~127, ~220). Значит, вычислили мы ёмкость и следующим шагом нам надо знать напряжение на конденсаторе. Для схем приведенных на рисунках выше напряжение на конденсаторе равняется 1,15 от напряжения сети. Но это напряжение переменного тока, а для выбора конденсаторов надо знать напряжение постоянного тока. Тут нам и понадобится небольшая табличка:

Например, напряжение сети ~220, умножаем на 1,15 получаем 253. В таблице смотрим переменка 250 соответствует постоянке 400В для емкости до 2мкФ, или 600В для емкостей 4-10мкФ. Нужно, чтобы номинальное напряжение конденсатора было равно или больше расчетного.

Далее, зная рабочее напряжение и требуемую емкость подбираем конденсаторы по параметрам: типы и нужное количество. Конденсаторы для пусковой цепи порой так и называются — пусковыми.

Вот так, шаг за шагом, мы разобрали как подключить трехфазный асинхронный электродвигатель в однофазную сеть и что для этого необходимо рассчитать и знать. Существуют и другие схемы для подключения двигателя через конденсатор, но эти вопросы рассмотрим в другой раз в другой статье.

Самое популярное

Как рассчитать конденсаторы, подключенные последовательно и параллельно — Kitronik Ltd

Параллельные конденсаторы

Когда конденсаторы подключаются друг к другу (бок о бок), это называется параллельным подключением. Это показано ниже. Чтобы рассчитать общую общую емкость ряда конденсаторов, подключенных таким образом, вы складываете отдельные емкости по следующей формуле: CTotal = C1 + C2 + C3 и т.д.Cобщ = C1 + C2 + C3 = 10F + 22F + 47F = 79F

Задача 1:

Рассчитайте общую емкость следующих конденсаторов, включенных параллельно.

Конденсаторы серии

Когда конденсаторы подключаются друг за другом, это называется последовательным соединением. Это показано ниже. Чтобы рассчитать общую общую емкость двух конденсаторов, подключенных таким образом, вы можете использовать следующую формулу:

Пример: чтобы рассчитать общую емкость для этих двух последовательно соединенных конденсаторов.

Задача 2:

Рассчитайте общую емкость следующих последовательно включенных конденсаторов.

Три или более конденсатора последовательно

Чтобы рассчитать общую общую емкость трех или более конденсаторов, подключенных таким образом, вы можете использовать следующую формулу: и так далее. Пример: чтобы рассчитать общую емкость для этих трех последовательно соединенных конденсаторов.

Задача 3:

Рассчитайте общую емкость следующих последовательно включенных конденсаторов.

ответы

Задача 1

1 = 232.2F 2 = 169,0F 3 = 7,0F

Задача 2

1 = 2,48F 2 = 14,99F 3 = 4,11F

Задача 3

1 = 3,33F 2 = 1,167F 3 = 0,35F Примечание Значения конденсаторов в этом листе поддерживаются высокими (близкими к единице или больше). Это сделано для упрощения процесса обучения. На самом деле типичные значения конденсаторов намного меньше единицы. Загрузите PDF-версию этой страницы здесь. Узнать больше об авторе подробнее »Если вы нашли эту статью полезной и хотели бы получать от нас обновления продуктов и бесплатные электронные ресурсы, то зарегистрируйтесь здесь.Мы тоже ненавидим спам и обещаем никогда не продавать и не сообщать свой адрес электронной почты, и вы можете отказаться от подписки в любое время.

© Kitronik Ltd — Вы можете распечатать эту страницу и добавить ссылку на нее, но не должны копировать страницу или ее часть без предварительного письменного согласия Kitronik.

конденсаторов последовательно и параллельно

Цели обучения

К концу этого раздела вы сможете:

• Выведите выражения для полной емкости последовательно и параллельно.
• Обозначение последовательной и параллельной частей в комбинации подключения конденсаторов.
• Рассчитайте эффективную емкость последовательно и параллельно с учетом индивидуальных емкостей.

Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько подключений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения.Существует два простых и распространенных типа соединений: серия и параллельная , для которых мы можем легко вычислить общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного.

Емкость серии

На рисунке 1а показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением [латекс] C = \ frac {Q} {V} \\ [/ latex].

Обратите внимание на рис. 1, что противоположные заряды величиной Q текут к обеим сторонам первоначально незаряженной комбинации конденсаторов, когда приложено напряжение В, . Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов создавались заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах. Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов.(См. Рисунок 1b.) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.

Рис. 1. (a) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине равна Q. (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d. При последовательном соединении общая емкость меньше, чем у любого из отдельных конденсаторов.

Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1.Решение [latex] C = \ frac {Q} {V} \\ [/ latex] для V дает [latex] V = \ frac {Q} {C} \\ [/ latex]. Таким образом, напряжения на отдельных конденсаторах равны [латексному] V_1 = \ frac {Q} {C_1}, V_2 = \ frac {Q} {C_2}, \ text {и} V_3 = \ frac {Q} {C_3} \\ [/латекс].

Общее напряжение складывается из отдельных напряжений:

В = В ₁ + В ₂ + В ₃ .

Теперь, называя общую емкость C _S последовательной емкостью, считайте, что

[латекс] V = \ frac {Q} {C _ {\ text {S}}} = V_1 + V_2 + V_3 \\ [/ latex].

Вводя выражения для V ₁ , V ₂ и V ₃ , получаем

[латекс] \ frac {Q} {C _ {\ text {S}}} = \ frac {Q} {C_ {1}} + \ frac {Q} {C_ {2}} + \ frac {Q} { C_ {3}} \\ [/ латекс].

Отменяя Q s, мы получаем уравнение для полной емкости в серии C _S как

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} { C_ {3}} + \ точки, \\ [/ latex]

, где «…» означает, что выражение действительно для любого количества конденсаторов, соединенных последовательно.Выражение этой формы всегда приводит к общей емкости C _S , которая меньше любой из отдельных емкостей C ₁ , C ₂ ,…, как показано в примере 1.

Общая емкость в серии,

C _с

Общая емкость в серии:

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} { C_ {3}} + \ dots \\ [/ latex]

Пример 1. Что такое серийная емкость?

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны 1.000, 5.000 и 8.000 мкФ.

Стратегия

Имея данную информацию, общую емкость можно найти, используя уравнение для емкости в серии.

Решение

Ввод заданных емкостей в выражение для [latex] \ frac {1} {C _ {\ text {S}}} \\ [/ latex] дает [latex] \ frac {1} {C _ {\ text {S} }} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} \\ [/ latex].

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {1.000 \ mu \ text {F}} + \ frac {1} {5.000 \ mu \ text {F} } + \ frac {1} {8.000 \ mu \ text {F}} = \ frac {1.325} {\ mu \ text {F}} \\ [/ latex]

Преобразование для нахождения C _S дает [латекс] C _ {\ text {S}} = \ frac {1.325} {\ mu \ text {F}} = 0,755 \ mu \ text {F} \\ [/ латекс].

Обсуждение

Общая последовательная емкость C _s меньше наименьшей индивидуальной емкости, как и было обещано. При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только целочисленные вычисления) равен 40.Таким образом,

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {40} {40 \ mu \ text {F}} + \ frac {8} {40 \ mu \ text {F} } + \ frac {5} {40 \ mu \ text {F}} = \ frac {53} {40 \ mu \ text {F}} \\ [/ latex]

так что

[латекс] C _ {\ text {S}} = \ frac {40 \ mu \ text {F}} {53} = 0,755 \ mu \ text {F} \\ [/ latex]

Параллельные конденсаторы

На рис. 2а показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти легче, чем в последовательном случае. Чтобы найти эквивалентную общую емкость C, , _p , сначала отметим, что напряжение на каждом конденсаторе составляет В, , то же самое, что и у источника, поскольку они подключены непосредственно к нему через проводник.(Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют такой же заряд, как и при индивидуальном подключении к источнику напряжения. Общая сумма начислений Q представляет собой сумму отдельных сборов: Q = Q ₁ + Q ₂ + Q ₃ .

Рис. 2. (a) Конденсаторы, включенные параллельно. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, поэтому общая параллельная емкость — это просто сумма отдельных емкостей.(b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.

Используя соотношение Q = CV , мы видим, что общий заряд составляет Q = C _p V , а индивидуальные расходы составляют Q ₁ = C ₁ V , Q ₂ = C ₂ V , и Q ₃ = C ₃ V .Ввод их в предыдущее уравнение дает

C _p V = C ₁ V + C ₂ V + C ₃ V .

Исключая В из уравнения, мы получаем уравнение для полной емкости параллельно

C _p : C _p = C ₁ + C ₂ + C ₃ +….

Общая емкость при параллельном подключении — это просто сумма отдельных емкостей. (И снова «… » означает, что выражение действительно для любого количества конденсаторов, подключенных параллельно.) Так, например, если конденсаторы в Примере 1 были подключены параллельно, их емкость была бы

C _p = 1.000 мкФ + 5.000 мкФ + 8.000 мкФ = 14000 мкФ.

Эквивалентный конденсатор для параллельного подключения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на рисунке 2b.

Общая емкость параллельно,

C _p

Общая емкость параллельно C _p = C ₁ + C ₂ + C ₃ +…

Более сложные соединения конденсаторов иногда могут быть последовательными и параллельными. (См. Рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую.

Рис. 3. (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C ₁ и C ₂ находятся последовательно; их эквивалентная емкость C _S меньше, чем у любого из них. (c) Обратите внимание, что C _S параллельно с C ₃ . Таким образом, общая емкость составляет сумму C _S и C ₃ .

Пример 2. Смесь последовательной и параллельной емкостей

Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех десятичных знаков ( C ₁ = 1.000 мкФ, C ₂ = 3.000 мкФ и C ₃ = 8.000 мкФ) и округлите ответ до трех десятичных знаков.

Стратегия

Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы включены последовательно, а какие — параллельно.Конденсаторы C ₁ и C ₂ включены последовательно. Их комбинация, обозначенная на рисунке C _S , параллельна C ₃ .

Решение

Поскольку C ₁ и C ₂ включены последовательно, их общая емкость определяется как [латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} { C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} \\ [/ latex]. Ввод их значений в уравнение дает

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} = \ frac {1} { 1.000 \ mu \ text {F}} + \ frac {1} {5.000 \ mu \ text {F}} = \ frac {1.200} {\ mu \ text {F}} \\ [/ latex].

Инвертирование дает C _S = 0,833 мкФ.

Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; Таким образом, общая сумма составляет

[латекс] \ begin {array} {lll} C _ {\ text {tot}} & = & C _ {\ text {S}} + C _ {\ text {S}} \\\ text {} & = & 0.833 \ mu \ text {F} +8.000 \ mu \ text {F} \\\ text {} & = & 8.833 \ mu \ text {F} \ end {array} \\ [/ latex]

Обсуждение

Этот метод анализа комбинаций конденсаторов по частям, пока не будет получена общая сумма, может быть применен к более крупным комбинациям конденсаторов.

Сводка раздела

• Общая емкость последовательно [латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ гидроразрыв {1} {C_ {3}} + \ dots \\ [/ latex]
• Общая емкость параллельно C _p = C ₁ + C ₂ + C ₃ +…
• Если схема содержит комбинацию конденсаторов, включенных последовательно и параллельно, определите последовательную и параллельную части, вычислите их емкости, а затем найдите общую сумму.

Концептуальные вопросы

1. Если вы хотите хранить большое количество энергии в конденсаторной батарее, подключите ли вы конденсаторы последовательно или параллельно? Объяснять.

Задачи и упражнения

1. Найдите общую емкость комбинации конденсаторов на рисунке 4.

   Рисунок 4. Комбинация последовательного и параллельного подключения конденсаторов.

2. Предположим, вам нужна конденсаторная батарея с общей емкостью 0.750 Ф, и у вас есть множество конденсаторов емкостью 1,50 мФ. Какое наименьшее число вы могли бы связать вместе, чтобы достичь своей цели, и как бы вы их связали?
3. Какую общую емкость можно получить, соединив вместе конденсатор 5,00 мкФ и конденсатор 8,00 мкФ?
4. Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.

   Рисунок 5. Комбинация последовательного и параллельного подключения конденсаторов.

5. Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.

   Рисунок 6. Комбинация последовательного и параллельного подключения конденсаторов.

6. Необоснованные результаты. (a) Конденсатор на 8,00 мкФ подключен параллельно другому конденсатору, что дает общую емкость 5,00 мкФ. Какая емкость у второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

Избранные решения проблем и упражнения

1. 0,293 мкФ

3.3,08 мкФ в последовательном соединении, 13,0 мкФ в параллельном соединении

4. 2,79 мкФ

6. (а) –3,00 мкФ; (б) У вас не может быть отрицательного значения емкости; (c) Предположение, что конденсаторы были подключены параллельно, а не последовательно, было неверным. Параллельное соединение всегда дает большую емкость, в то время как здесь предполагалась меньшая емкость. Это могло произойти, только если конденсаторы подключены последовательно.

8.3: Последовательные и параллельные конденсаторы

Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях.Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серии и параллельно , для которых мы можем легко вычислить общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.

Серия конденсаторов

На рисунке \ (\ PageIndex {1} \) показано последовательное сочетание трех конденсаторов, расположенных в ряд внутри схемы.Как и в случае любого конденсатора, емкость комбинации связана как с зарядом, так и с напряжением:

\ [C = \ dfrac {Q} {V}. \]

Когда эта последовательная комбинация подключена к аккумулятору с напряжением В, , каждый из конденсаторов получает одинаковый заряд Q . Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен \ (+ Q \), а заряд на пластине, подключенной к отрицательной клемме, равен \ (- Q \). Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю.Однако падение потенциала \ (V_1 = Q / C_1 \) на одном конденсаторе может отличаться от падения потенциала \ (V_2 = Q / C_2 \) на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть , все конденсаторы последовательной комбинации имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи удаляется с пластины первого конденсатора (который мы обозначаем как \ (- Q \)), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как \ ( + Q \)) и т. Д.

Рисунок \ (\ PageIndex {1} \): (a) Три конденсатора соединены последовательно.Величина заряда на каждой пластине равна Q. (b) Сеть конденсаторов на (a) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей на (a), а заряд на его пластинах равен Q.

Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны, соответственно, \ (V_1 = Q / C_1 \), \ (V_2 = Q / C_2 \) и \ (V_3 = Q / C_3 \). Эти потенциалы должны в сумме равняться напряжению батареи, давая следующий баланс потенциалов:

\ [V = V_1 + V_2 + V_3.\]

Потенциал \ (V \) измеряется на эквивалентном конденсаторе, который держит заряд \ (Q \) и имеет эквивалентную емкость \ (C_S \). Вводя выражения для \ (V_1 \), \ (V_2 \) и \ (V_3 \), получаем

\ [\ dfrac {Q} {C_S} = \ dfrac {Q} {C_1} + \ dfrac {Q} {C_2} + \ dfrac {Q} {C_3}. \]

Отменяя заряд Q , мы получаем выражение, содержащее эквивалентную емкость \ (C_S \) трех последовательно соединенных конденсаторов:

\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3}.\]

Это выражение можно обобщить на любое количество конденсаторов в последовательной сети.

Комбинация серии

Для конденсаторов, соединенных последовательно, эквивалентная емкость, обратная величине, является суммой обратных величин индивидуальных емкостей:

\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} + \ dots \ label {capseries} \]

Пример \ (\ PageIndex {1} \): эквивалентная емкость последовательной сети

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны \ (1.000 мкФ \), \ (5.000 мкФ \) и \ (8.000 мкФ \).

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capseries} с тремя членами.

Решение

Вводим указанные емкости в уравнение \ ref {capseries}:

\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} + \ dfrac {1} {8.000 \ mu F} \\ [4pt] & = \ dfrac {1.325} {\ mu F}. \ End {align *} \]

Теперь инвертируем этот результат и получаем

\ [\ begin {align *} C_S & = \ dfrac {\ mu F} {1.325} \\ [4pt] & = 0.755 \ mu F. \ end {align *} \ nonumber \]

Значение

Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.

Параллельная комбинация конденсаторов

Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке \ (\ PageIndex {2a} \).Поскольку конденсаторы подключены параллельно, , все они имеют одинаковое напряжение V на своих пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость \ (C_p \) параллельной сети, отметим, что общий заряд Q , хранящийся в сети, является суммой всех отдельных зарядов:

\ [Q = Q_1 + Q_2 + Q_3. \]

В левой части этого уравнения используется соотношение \ (Q = C_pV \), которое выполняется для всей сети.В правой части уравнения мы используем соотношения \ (Q_1 = C_1 V \), \ (Q_2 = C_2V \) и \ (Q_3 = C_3V \) для трех конденсаторов в сети. Таким образом получаем

\ [C_pV = C_1V + C_2V + C_3V. \]

Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:

\ [C_p = C_1 + C_2 + C_3. \]

Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.

Параллельная комбинация

Для конденсаторов, соединенных параллельно, эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,

\ [C_p = C_1 + C_2 + C_3 + … \ label {capparallel} \]

Рисунок \ (\ PageIndex {2} \): (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.

Пример \ (\ PageIndex {2} \): эквивалентная емкость параллельной сети

Найдите полезную емкость для трех конденсаторов, соединенных параллельно, учитывая, что их индивидуальные емкости равны \ (1.0 \ mu F \), \ (5.0 \ mu F \) и \ (8.0 \ mu F \).

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capparallel} с тремя членами.

Решение

Ввод заданных емкостей в уравнение \ ref {capparallel} дает

\ [\ begin {align *} C_p & = C_1 + C_2 + C_3 \\ [4pt] & = 1.0 \ mu F + 5.0 \ mu F + 8.0 \ mu F \\ [4pt] & = 14.0 \ mu F.\ end {align *} \]

Значение

Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.

Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на Рисунке \ (\ PageIndex {3} \). Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости.Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.

Рисунок \ (\ PageIndex {3} \): (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. (b) \ (C_1 \) и \ (C_2 \) идут последовательно; их эквивалентная емкость \ (C_S \) c) Эквивалентная емкость \ (C_S \) подключена параллельно с \ (C_3 \). Таким образом, эквивалентная емкость всей сети является суммой \ (C_S \) и \ (C_3 \).

Пример \ (\ PageIndex {3} \): эквивалентная емкость сети

Найдите общую емкость комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {3} \). Предположим, что емкости известны с точностью до трех десятичных знаков (\ (C_1 = 1.000 мкФ, C_2 = 5.000 мкФ, C_3 = 8.000 мкФ \)). Округлите ответ до трех десятичных знаков.

Стратегия

Сначала мы определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы \ (C_1 \) и \ (C_2 \) включены последовательно.Их комбинация, помеченная \ (C_S \), параллельна \ (C_3 \).

Решение

Поскольку \ (C_1 \) и \ (C_2 \) включены последовательно, их эквивалентная емкость \ (C_S \) получается с помощью уравнения \ ref {capseries}:

\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} \\ [4pt] & = \ dfrac {1.200} {\ mu F} \ end {align *} \]

Для этого

\ [C_S = 0,833 \ mu F. \ nonumber \]

Емкость \ (C_S \) соединена параллельно с третьей емкостью \ (C_3 \), поэтому мы используем уравнение \ ref {capparallel}, чтобы найти эквивалентную емкость C всей сети:

\ [\ begin {align *} C & = C_S + C_3 \\ [4pt] & = 0.833 \ mu F + 8.000 \ mu F \\ [4pt] & = 8.833 \ mu F. \ end {align *} \]

Сеть конденсаторов

Определите чистую емкость C комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {4} \), когда емкости равны \ (C_1 = 12,0 мкФ, C_2 = 2,0 мкФ \) и \ (C_3 = 4,0 мкФ \). Когда на комбинации поддерживается разность потенциалов 12,0 В, найдите заряд и напряжение на каждом конденсаторе.

Рисунок \ (\ PageIndex {4} \): (a) Комбинация конденсаторов.(b) Эквивалентная комбинация из двух конденсаторов. Стратегия

Сначала мы вычисляем чистую емкость \ (C_ {23} \) параллельного соединения \ (C_2 \) и \ (C_3 \). Тогда C — это чистая емкость последовательного соединения \ (C_1 \) и \ (C_ {23} \). Мы используем соотношение \ (C = Q / V \), чтобы найти заряды \ (Q_1, Q_2 \) и \ (Q_3 \), а также напряжения \ (V_1, V_2 \) и \ (V_3 \) на конденсаторы 1, 2 и 3 соответственно.

Решение Эквивалентная емкость для \ (C_2 \) и \ (C_3 \) составляет

\ [C_ {23} = C_2 + C_3 = 2.0 мк F + 4,0 мк F = 6,0 мк F. \]

Вся комбинация из трех конденсаторов эквивалентна двум последовательным конденсаторам,

\ [\ dfrac {1} {C} = \ dfrac {1} {12.0 \ mu F} + \ dfrac {1} {6.0 \ mu F} = \ dfrac {1} {4.0 \ mu F} \ Rightarrow C = 4,0 мкм F. \]

Рассмотрим эквивалентную комбинацию из двух конденсаторов на рисунке \ (\ PageIndex {2b} \). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд, \ (Q_1 = Q_ {23} \). Кроме того, конденсаторы разделяют разность потенциалов 12,0 В, поэтому

\ [12.0 V = V_1 + V_ {23} = \ dfrac {Q_1} {C_1} + \ dfrac {Q_ {23}} {C_ {23}} = \ dfrac {Q_1} {12.0 \ mu F} + \ dfrac {Q_1 } {6.0 \ mu F} \ Rightarrow Q_1 = 48.0 \ mu C. \]

Теперь разность потенциалов на конденсаторе 1 равна

.

\ [V_1 = \ dfrac {Q_1} {C_1} = \ dfrac {48,0 \ mu C} {12,0 \ mu F} = 4,0 В. \]

Поскольку конденсаторы 2 и 3 подключены параллельно, они имеют одинаковую разность потенциалов:

\ [V_2 = V_3 = 12,0 В — 4,0 В = 8,0 В. \]

Следовательно, заряды на этих двух конденсаторах равны, соответственно,

\ [Q_2 = C_2V_2 = (2.0 мкФ) (8,0 В) = 16,0 мкФ, \]

\ [Q_3 = C_3V_3 = (4,0 мкФ) (8,0 В) = 32,0 мкФ \]

Значение Как и ожидалось, чистая плата за параллельную комбинацию \ (C_2 \) и \ (C_3 \) составляет \ (Q_ {23} = Q_2 + Q_3 = 48,0 \ mu C. \)

Упражнение \ (\ PageIndex {1} \)

Определите чистую емкость C каждой сети конденсаторов, показанной ниже. Предположим, что \ (C_1 = 1,0 пФ, C_2 = 2,0 пФ, C_3 = 4,0 пФ \) и \ (C_4 = 5,0 пФ \). Найдите заряд на каждом конденсаторе, предполагая, что разность потенциалов равна 12.0 В в каждой сети.

Ответьте на

\ (C = 0,86 пФ, Q_1 = 10 пКл, Q_2 = 3,4 пКл, Q_3 = 6,8 пКл \)

Ответ б

\ (C = 2,3 пФ, Q_1 = 12 пКл, Q_2 = Q_3 = 16 пКл \)

Ответ c

\ (C = 2,3 пФ, Q_1 = 9,0 пКл, Q_2 = 18 пКл, Q_3 = 12 пКл, Q_4 = 15 пКл \)

Конденсатор

Основные расчеты — Инженерное мышление

Конденсаторы

используются во многих цепях для разных целей, поэтому мы собираемся изучить некоторые основные вычисления конденсаторов для цепей постоянного тока.

Прокрутите вниз, чтобы просмотреть обучающее видео на YouTube.

Конденсаторы в цепях постоянного тока

Конденсаторы обычно выглядят так. У нас есть конденсатор электролитического и керамического типа. Электролитик поляризован, что означает, что одна сторона должна быть подключена к плюсу, а другая — к минусу источника питания. Керамический тип обычно может быть подключен любым способом. На стороне электролитического конденсатора мы находим пунктирную линию, обозначающую отрицательную сторону, длинный вывод также указывает на положительную сторону нового конденсатора.Но обычно они обрезаются во время установки, поэтому не полагайтесь только на это. Эти два конденсатора представлены подобными символами, обратите внимание, что у поляризованного конденсатора есть маленький символ плюса, указывающий на положительную сторону.

При подключении к источнику постоянного тока напряжение аккумулятора подталкивает электроны к конденсатору, и поэтому конденсатор заряжается до того же напряжения, что и аккумулятор. Конденсаторы заряжаются почти мгновенно при подключении напрямую к батарее, но мы почти всегда используем резистор, это задерживает время зарядки, и позже в этой статье мы увидим, как это рассчитать.

Внутри конденсатора с одной стороны скопилось много электронов, им препятствует перемещение поперек из-за изоляционного материала между двумя сторонами. Поскольку электроны заряжены отрицательно, у нас есть накопление заряда на одной стороне по сравнению с другой, поэтому у нас есть разница в напряжении между двумя выводами.

Эти электроны удерживаются на месте, и конденсатор может удерживать этот заряд в течение длительных периодов времени. Получив путь, они будут разряжаться, пока не опустеют.Электроны не проходят через конденсатор; они просто накапливаются внутри, а затем высвобождаются.

Количество заряда, накопленного в конденсаторе, рассчитывается по формуле «Заряд = емкость (в фарадах), умноженная на напряжение». Итак, для этого конденсатора микрофарад на 12 В 100 мкФ мы преобразуем микрофарады в фарады (100 / 1,000,000 = 0,0001F), затем умножаем это на 12 В, чтобы увидеть, что он хранит заряд 0,0012 кулонов.

Если нам нужно сохранить заряд, скажем, 0,0002 кулонов, мы просто разделим его на напряжение, в данном случае 12 В, чтобы увидеть, что нам нужен 0.2
= 0,5 x 0,0001F x 144
= 0,0072 Дж

Мы знаем, что конденсатор будет заряжаться до напряжения батареи. Итак, если мы подключим такой конденсатор, какое будет напряжение на конденсаторе? Будет 1,5В. Если мы подключим вот так конденсатор, какое на нем будет напряжение? Тоже будет 1,5В. Это два разных способа соединения конденсаторов в цепях, последовательно или параллельно. Это заставит конденсаторы работать по-другому.

Параллельные конденсаторы

Если мы поместим конденсатор параллельно с лампой, когда батарея будет удалена, конденсатор начнет питать лампу, он медленно тускнеет по мере разряда конденсатора.Если мы используем два конденсатора, мы сможем запитать лампу дольше.

Допустим, конденсатор 1 = 10 мкФ и конденсатор 2 = 220 мкФ. Как рассчитать общую емкость? Это очень просто, ответ — 230 мкФ. Конденсаторы соединяются параллельно. Итак, 10 мкФ + 220 мкФ = 230 мкФ. Мы можем добавлять больше, например конденсатор емкостью 100 мкФ, и общая сумма будет просто суммой всех конденсаторов. Помещая их параллельно, мы, по сути, объединяем их, чтобы сформировать конденсатор большего размера. Это очень полезно, потому что, если, например, нам нужен большой конденсатор на 2000 мкФ, но у нас его не было, мы можем просто использовать более мелкие конденсаторы, такие как 2 x 1000 мкФ по 4 x 500 мкФ и т. Д.Он также часто используется для фильтрации шума и обеспечения большего тока в цепях с высокими требованиями.

Общий заряд, накопленный в параллельных конденсаторах, равен: заряд = общая емкость, умноженная на напряжение. Итак, у нас есть батарея на 9 В и два конденсатора общей емкостью 230 мкФ. Поскольку он параллелен, этот провод составляет 9 В, а это 0 В, поэтому оба конденсатора заряжены до 9 В. Следовательно, 0,00023 F, умноженное на 9V = 0,00207 кулонов. И с тремя конденсаторами у нас есть 330 мкФ (0.00033 F), умноженное на 9V = 0,00297 кулонов.

Мы также можем рассчитать заряд каждого конденсатора индивидуально. Мы просто используем одну и ту же формулу для каждого конденсатора, ответы на этот вопрос вы можете увидеть на экране.
Конденсатор 1 = 0,00001 F x 9 В = 0,00009 Кулонов
Конденсатор 2 = 0,00022 F x 9 В = 0,00198 Кулонов
Конденсатор 3 = 0,0001 F x 9 В = 0,0009 Кулонов
Всего = 0,00009 + 0,00198 + 0,0009 = 0,00297 Кулонов

Конденсаторы серии

Если мы поместим конденсатор последовательно с лампой, когда мы нажмем на переключатель, он загорится, но затем станет тусклее, когда конденсатор достигнет уровня напряжения батареи, и как только он достигнет этого уровня, лампа выключится.Помните, что электроны не могут проходить через конденсатор из-за изоляционного материала внутри. Электроны просто накапливаются внутри на одной пластине и по мере накопления отбрасывают равное количество от противоположной пластины. Таким образом, ток может течь только тогда, когда конденсатор заряжается или разряжается. В настоящее время, когда батарея снята, конденсатор не может разрядиться, поэтому он будет поддерживать напряжение на одном уровне. Неважно, подключим мы или отключим аккумулятор, лампа не загорится.Однако, если мы предоставим другой путь, при нажатии переключателя конденсатор может теперь разрядиться, поэтому электроны могут проходить через лампу и освещать ее. По мере разряда конденсатора он станет более тусклым.

Что, если бы у нас было 2 конденсатора, подключенных последовательно, опять же, конденсатор 1 — 10 мкФ, а конденсатор 2 — 220 мкФ. Как найти общую емкость? Для этого мы используем эту формулу, она может показаться сложной, но на самом деле она очень проста. Все, что нам нужно сделать, это ввести наши конденсаторы емкостью 10 и 220 мкФ.Мы можем ввести это так на наших калькуляторах или в Excel. Но при ручном вычислении мы делим 1 на 10, что равно 0,1, и 1, деленное на 220, что составляет 0,00454. Мы складываем их вместе, чтобы получить 0,10454, а затем деление 1 на это дает в сумме 9,56 мкФ. Обратите внимание, что общая емкость теперь меньше, чем конденсатор с наименьшим значением.

Если мы добавим в схему третий конденсатор емкостью 100 мкФ, мы получим общую емкость 8,73 мкФ. Так что уменьшилось еще больше. Это потому, что, комбинируя их последовательно, мы существенно увеличиваем толщину изоляционного материала, поэтому притяжение отрицательно заряженных электронов к положительно заряженным дыркам на противоположной пластине становится слабее.

Полный заряд последовательных конденсаторов определяется по формуле заряд = емкость (в фарадах), умноженная на напряжение. Итак, если мы использовали батарею 9 В, мы конвертируем микрофарады в фарады и видим, что общий заряд равен 0,00008604 кулонов
(0,00000956F x 9V = 0,00008604 кулонов)

Общий заряд конденсаторной цепи 3-й серии составляет 0,00007857 кулонов
(0,00000873 x 9 В = 0,00007857 кулонов)

Заряд, удерживаемый каждым конденсатором в отдельности, очень легко рассчитать в последовательных цепях.Это то же самое, что и общая. Каждый конденсатор содержит одинаковое количество электронов, когда они подключены последовательно. Это потому, что когда мы заряжали конденсаторы, ток был одинаковым во всех частях цепи. То же количество электронов, которые были помещены в одну пластину, вытолкнулось из противоположной пластины, поэтому каждый последовательный конденсатор может быть заряжен только до одного и того же уровня. Таким образом, наименьший конденсатор будет ограничивающим фактором.

Однако, поскольку каждый конденсатор может иметь разную емкость, напряжение каждого конденсатора будет разным.Мы находим напряжение каждого конденсатора по формуле напряжение = заряд (в кулонах), деленное на емкость (в фарадах).

Итак, для этой схемы мы видим, что конденсатор 1 — 7,8 В, конденсатор 2 — 0,35 В, а конденсатор 3 — 0,78 В. Они складываются в общее напряжение батареи, которое составляет 9 В.

Конденсатор 1: 0,00007857 C / 0,00001 F = 7,857 В
Конденсатор 2: 0,00007857 C / 0,00022 F = 0,357 В
Конденсатор 3: 0,00007857 C / 0,0001 F = 0,786 В
Общее напряжение = 7,857 В + 0,357 В + 0.786 В = 9 В

Время заряда конденсатора

Допустим, у нас есть батарея на 9 В, конденсатор на 100 мкФ, резистор на 10 кОм и переключатель, соединенные последовательно. Конденсатор полностью разряжен, и мы читаем 0 В на двух выводах.

Когда мы замыкаем выключатель, конденсатор заряжается. Напряжение будет увеличиваться до тех пор, пока не сравняется с уровнем заряда батареи. Повышение напряжения не мгновенное, оно имеет экспоненциальную кривую. Сначала напряжение быстро увеличивается, а затем замедляется, пока не достигнет того же уровня напряжения, что и аккумулятор.

Мы разделили эту кривую на 6 сегментов, но нас интересуют только первые 5, потому что на отметке 5 мы в основном находимся на полном напряжении, поэтому мы можем игнорировать все, что выходит за рамки этого. Каждый сегмент представляет собой нечто, называемое постоянной времени. Следовательно, поскольку у нас есть 5 сегментов, у нас есть 5 постоянных времени, поэтому для заряда конденсатора от 0 до чуть менее 100% потребуется 5 постоянных времени. Все, что нам нужно сделать, это вычислить длину одной постоянной времени и затем умножить ее на 5.

Чтобы вычислить одну постоянную времени, мы используем эту формулу.

Постоянная времени (в секундах) = сопротивление (в Ом), умноженное на емкость (в Фарадах). Итак, мы конвертируем наш резистор в Ом, а емкость конденсатора в фарады и видим, что 10 000 Ом, умноженные на 0,0001 Фарад, равны 1. Итак, в этом примере постоянная времени равна 1 секунде. Следовательно, 5 из них составляют 5 секунд. Это означает, что для полной зарядки этого конденсатора до 9В требуется 5 секунд.

Если бы сопротивление резистора было всего 1000 Ом, постоянная времени была бы 0,1 секунды, так что это заняло бы 0.5 секунд, чтобы достичь 9 В. Если бы емкость конденсатора была 1000 микрофарад, это заняло бы всего 50 секунд. Так что с увеличением размера конденсатора время увеличивается. При увеличении номинала резистора увеличивается и время.

Возвращаясь к нашей исходной схеме. Поэтому мы можем рассчитать уровень напряжения для каждой постоянной времени. В точке 1 напряжение всегда 63,2%, в точке 2 — 86,5%, в точке 3 — 95%, в точке 4 — 98,2% и в точке 5 — 99,3%.

Итак, в этом примере через 1 секунду напряжение конденсатора равно 5.68 В, через 2 секунды — 7,78 В, через 3 секунды — 8,55 В, через 4 секунды — 8,83 В и через 5 секунд — 8,94 В.

Если вам нужен более точный ответ, мы можем вычислить каждую точку следующим образом.

Точка 1 = 9В-0В) x0,632 = 5,6880В
Точка 2 = ((9В — 5,688В) x0,632) + 5,68В = 7,7812В
Точка 3 = ((9В-7,7812В) x0,632) + 7,7812В = 8,5515В
Точка 4 = ((9В-8,55В) x0,632) + 8,5515В = 8,8349В
Точка 5 = ((9В-8,8349В) x0,632) + 8,8349В = 8,9393В

Помните, поскольку это последовательно, ток в цепи уменьшается, а напряжение конденсатора увеличивается.После достижения полного напряжения в цепи не будет протекать ток. Если бы резистор был лампой, он бы мгновенно достигал полной яркости, когда переключатель был замкнут, но затем становился тусклее, когда конденсатор достигал полного напряжения.

Время разряда конденсатора

Когда мы обеспечиваем путь для разряда конденсатора, электроны покидают конденсатор, и напряжение на конденсаторе уменьшается. Он не разряжается мгновенно, а следует экспоненциальной кривой. Мы разбиваем эту кривую на 6 сегментов, но нас интересуют только первые 5.В точке 1 напряжение всегда 36,8%, в точке 2 будет 13,5%, в точке 3 будет 5%, в точке 4 будет 1,8% и в точке 5 будет 0,7%.

Например, если бы у нас была батарея 9 В, лампа с сопротивлением 500 Ом и конденсатор 2000 мкФ, наша постоянная времени была бы 500 Ом, умноженная на 0,002 Фарад, что составляет 1 секунду.
Итак, в тот самый момент, когда аккумулятор отключен, конденсатор будет на 9 В, и, поскольку он питает цепь, лампа также будет. Через 1 постоянную времени, в данном случае через 1 секунду, напряжение будет 36.8%, что составляет 3,312 В, через 2 секунды — 1,215 В, через 3 секунды — 0,45 В, через 4 секунды — 0,162 В и через 5 секунд — 0,063 В. Таким образом, лампа будет гореть чуть менее 3 секунд. Очевидно становится тусклее.

8.1 Конденсаторы и емкость — University Physics Volume 2

Цели обучения

К концу этого раздела вы сможете:

• Объясните понятие конденсатора и его емкости
• Опишите, как оценить емкость системы проводов

Конденсатор — это устройство, используемое для хранения электрического заряда и электрической энергии.Конденсаторы обычно состоят из двух электрических проводников, разделенных расстоянием. (Обратите внимание, что такие электрические проводники иногда называют «электродами», но, точнее, они «обкладки конденсатора».) Пространство между конденсаторами может быть просто вакуумом, и в этом случае конденсатор будет известен как «Вакуумный конденсатор». Однако пространство обычно заполнено изолирующим материалом, известным как диэлектрик. (Вы узнаете больше о диэлектриках в разделах, посвященных диэлектрикам, далее в этой главе.) Объем памяти в конденсаторе определяется свойством, называемым емкостью , , о котором вы узнаете больше чуть позже в этом разделе.

Конденсаторы

имеют различные применения: от фильтрации статического электричества от радиоприема до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как на рис. 8.2. В большинстве случаев между двумя пластинами используется диэлектрик. Когда клеммы батареи подключены к первоначально незаряженному конденсатору, потенциал батареи перемещает небольшой заряд величиной Q с положительной пластины на отрицательную.Конденсатор в целом остается нейтральным, но с зарядами + Q + Q и −Q − Q, находящимися на противоположных пластинах.

Рис. 8.2 Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них на пластинах есть заряды + Q + Q и −Q − Q (соответственно). (a) Конденсатор с параллельными пластинами состоит из двух пластин противоположного заряда с площадью A , разделенных расстоянием d . (b) Катаный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).

Система, состоящая из двух идентичных параллельно проводящих пластин, разделенных расстоянием, называется конденсатором с параллельными пластинами (рис. 8.3). Величина электрического поля в пространстве между параллельными пластинами равна E = σ / ε0E = σ / ε0, где σσ обозначает поверхностную плотность заряда на одной пластине (напомним, что σσ — это заряд Q на площадь поверхности A ). Таким образом, величина поля прямо пропорциональна Q .

Рис. 8.3 Разделение зарядов в конденсаторе показывает, что заряды остаются на поверхности пластин конденсатора.Линии электрического поля в конденсаторе с параллельными пластинами начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.

Конденсаторы с разными физическими характеристиками (такими как форма и размер пластин) накапливают разное количество заряда для одного и того же приложенного напряжения В на своих пластинах. Емкость C конденсатора определяется как отношение максимального заряда Q , который может храниться в конденсаторе, к приложенному напряжению В на его пластинах.Другими словами, емкость — это наибольшая величина заряда на вольт, которая может храниться на устройстве:

Единица измерения емкости в системе СИ — фарад (Ф), названная в честь Майкла Фарадея (1791–1867). Поскольку емкость — это заряд на единицу напряжения, один фарад равен одному кулону на один вольт, или

По определению, конденсатор емкостью 1,0 мкФ может сохранять заряд 1,0 К (очень большой заряд), когда разность потенциалов между его пластинами составляет всего 1,0 В. Следовательно, один фарад — это очень большая емкость.Типичные значения емкости варьируются от пикофарад (1пФ = 10−12Ф) (1пФ = 10−12Ф) до миллифарад (1мФ = 10−3Ф) (1мФ = 10−3Ф), что также включает микрофарады (1мкФ = 10−6F1мкФ = 10− 6F). Конденсаторы могут быть разных форм и размеров (рис. 8.4).

Рис. 8.4 Это некоторые типичные конденсаторы, используемые в электронных устройствах. Размер конденсатора не обязательно зависит от его емкости. (кредит: Windell Oskay)

Расчет емкости

Мы можем рассчитать емкость пары проводов с помощью следующего стандартного подхода.

Стратегия решения проблем

Расчет емкости

1. Предположим, что конденсатор заряжен Q .
2. Определить электрическое поле E → E → между проводниками. Если в расположении проводников присутствует симметрия, вы можете использовать закон Гаусса для этого расчета.
3. Найдите разность потенциалов между проводниками из
   VB − VA = −ABE → · dl →, VB − VA = −ABE → · dl →,

   8,2

   где путь интегрирования ведет от одного проводника к другому.Тогда величина разности потенциалов равна V = | VB-VA | V = | VB-VA |.

4. Зная В, , определите емкость непосредственно из уравнения 8.1.

Чтобы показать, как работает эта процедура, мы теперь вычисляем емкости параллельных пластин, сферических и цилиндрических конденсаторов. Во всех случаях мы предполагаем вакуумные конденсаторы (пустые конденсаторы) без диэлектрического вещества в пространстве между проводниками.

Конденсатор с параллельными пластинами

Конденсатор с параллельными пластинами (рисунок 8.5) имеет две идентичные токопроводящие пластины, каждая с площадью поверхности A , разделенными расстоянием d . Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость может зависеть от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними. Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить.Таким образом, C должно быть больше для большего значения A . Точно так же, чем ближе пластины расположены друг к другу, тем сильнее на них притяжение противоположных зарядов. Следовательно, C должно быть больше для меньшего d .

Рис. 8.5 В конденсаторе с параллельными пластинами с пластинами, разнесенными на расстояние d , каждая пластина имеет одинаковую площадь поверхности A .

Определим поверхностную плотность заряда σσ на пластинах как

Из предыдущих глав мы знаем, что, когда d мало, электрическое поле между пластинами довольно однородно (без учета краевых эффектов) и что его величина определяется как

где постоянная ε0ε0 — диэлектрическая проницаемость свободного пространства, ε0 = 8.85 × 10–12Ф / м. Ε0 = 8,85 × 10–12Ф / м. Единица СИ в Ф / м эквивалентна C2 / N · m2.C2 / N · m2. Поскольку электрическое поле E → E → между пластинами однородно, разность потенциалов между пластинами составляет

V = Ed = σdε0 = Qdε0A.V = Ed = σdε0 = Qdε0A.

Следовательно, уравнение 8.1 дает емкость конденсатора с параллельными пластинами как

C = QV = QQd / ε0A = ε0Ad.C = QV = QQd / ε0A = ε0Ad.

8,3

Обратите внимание на это уравнение, что емкость является функцией только геометрии и того, какой материал заполняет пространство между пластинами (в данном случае вакуум) этого конденсатора.Фактически, это верно не только для конденсатора с параллельными пластинами, но и для всех конденсаторов: емкость не зависит от Q или В . При изменении заряда соответственно изменяется и потенциал, так что Q / V остается постоянным.

Пример 8.1

Емкость и заряд в конденсаторе с параллельными пластинами

(a) Какова емкость пустого конденсатора с параллельными пластинами с металлическими пластинами, каждая из которых имеет площадь 1,00 м 21.00м2, разделенных расстоянием 1,00 мм? (b) Сколько заряда хранится в этом конденсаторе, если к нему приложено напряжение 3,00 × 103 В3,00 × 103 В?

Стратегия

Определение емкости C является прямым применением уравнения 8.3. Найдя C , мы сможем найти накопленный заряд, используя уравнение 8.1.

Решение

1. Ввод заданных значений в уравнение 8.3 дает
   C = ε0Ad = (8,85 × 10−12Fm) 1,00м21,00 × 10−3м = 8,85 × 10−9F = 8,85nF.C = ε0Ad = (8,85 × 10−12Fm) 1,00м21,00 × 10−3m = 8 .85 × 10−9F = 8,85 нФ.
   Это небольшое значение емкости указывает на то, насколько сложно изготовить устройство с большой емкостью.
2. Обращение уравнения 8.1 и ввод известных значений в это уравнение дает
   Q = CV = (8,85 × 10–9F) (3,00 × 103 В) = 26,6 мкКл. Q = CV = (8,85 × 10–9F) (3,00 × 103 В) = 26,6 мкКл.

Значение

Этот заряд лишь немного больше, чем в типичных приложениях для статического электричества. Поскольку воздух разрушается (становится проводящим) при напряженности электрического поля около 3.0 МВ / м, на этом конденсаторе больше нельзя накапливать заряд при увеличении напряжения.

Пример 8.2

А, 1-Ф, конденсатор с параллельными пластинами

Предположим, вы хотите сконструировать конденсатор с параллельными пластинами емкостью 1,0 F. Какую площадь вы должны использовать для каждой пластины, если пластины разделены на 1,0 мм?

Решение

Преобразуя уравнение 8.3, получаем
A = Cdε0 = (1.0F) (1.0 × 10−3m) 8.85 × 10−12F / m = 1.1 × 108m2 A = Cdε0 = (1.0F) (1.0 × 10−3m) 8,85 × 10−12F / m = 1,1 × 108 м2.

Каждая квадратная пластина должна быть 10 км в поперечнике.Раньше было обычным розыгрышем — попросить студента пойти в склад лаборатории и попросить конденсатор с параллельными пластинами 1F, пока обслуживающий персонал не устанет от шуток.

Проверьте свое понимание 8.1

Емкость конденсатора с параллельными пластинами составляет 2,0 пФ. Если площадь каждой пластины составляет 2,4 см 22,4 см2, каково расстояние между пластинами?

Проверьте свое понимание 8.2

Убедитесь, что σ / Vσ / V и ε0 / dε0 / d имеют одинаковые физические единицы.

Сферический конденсатор

Сферический конденсатор — это еще один набор проводников, емкость которых можно легко определить (Рисунок 8.dr) = Q4πε0∫R1R2drr2 = Q4πε0 (1R1−1R2).

В этом уравнении разность потенциалов между пластинами равна V = — (V2-V1) = V1-V2V = — (V2-V1) = V1-V2. Мы подставляем этот результат в уравнение 8.1, чтобы найти емкость сферического конденсатора:

C = QV = 4πε0R1R2R2 − R1.C = QV = 4πε0R1R2R2 − R1.

8,4

Рис. 8.6 Сферический конденсатор состоит из двух концентрических проводящих сфер. Обратите внимание, что заряды на проводнике находятся на его поверхности.

Пример 8.3

Емкость изолированной сферы

Вычислите емкость одиночной изолированной проводящей сферы радиуса R1R1 и сравните ее с уравнением 8.dr) = Q4πε0∫R1 + ∞drr2 = 14πε0QR1.

Следовательно, емкость изолированного шара составляет

C = QV = Q4πε0R1Q = 4πε0R1.C = QV = Q4πε0R1Q = 4πε0R1.

Значение

Тот же результат можно получить, взяв предел уравнения 8.4 при R2 → ∞R2 → ∞. Таким образом, одиночная изолированная сфера эквивалентна сферическому конденсатору, внешняя оболочка которого имеет бесконечно большой радиус.

Проверьте свое понимание 8.3

Радиус внешней сферы сферического конденсатора в пять раз превышает радиус его внутренней оболочки.Каковы размеры этого конденсатора, если его емкость 5,00 пФ?

Цилиндрический конденсатор

Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров (рисунок 8.7). Внутренний цилиндр радиуса R1R1 может быть либо оболочкой, либо полностью твердым. Внешний цилиндр представляет собой оболочку внутреннего радиуса R2R2. Мы предполагаем, что длина каждого цилиндра составляет l и что избыточные заряды + Q + Q и -Q-Q находятся на внутреннем и внешнем цилиндрах соответственно.dr) = Q2πε0l∫R1R2drr = Q2πε0llnr | R1R2 = Q2πε0llnR2R1.

Таким образом, емкость цилиндрического конденсатора составляет

C = QV = 2πε0lln (R2 / R1). C = QV = 2πε0lln (R2 / R1).

8,6

Как и в других случаях, эта емкость зависит только от геометрии расположения проводников. Важным применением уравнения 8.6 является определение емкости на единицу длины коаксиального кабеля , который обычно используется для передачи изменяющихся во времени электрических сигналов. Коаксиальный кабель состоит из двух концентрических цилиндрических проводников, разделенных изоляционным материалом.(Здесь мы предполагаем наличие вакуума между проводниками, но физика качественно почти такая же, когда пространство между проводниками заполнено диэлектриком.) Эта конфигурация защищает электрический сигнал, распространяющийся по внутреннему проводнику, от паразитных электрических полей, внешних по отношению к проводнику. кабель. Ток течет в противоположных направлениях во внутреннем и внешнем проводниках, при этом внешний проводник обычно заземлен. Теперь из уравнения 8.6 емкость коаксиального кабеля на единицу длины равна

.
Cl = 2πε0ln (R2 / R1).Cl = 2πε0ln (R2 / R1).

В практических приложениях важно выбирать конкретные значения C / l . Это может быть достигнуто за счет соответствующего выбора радиусов проводников и изоляционного материала между ними.

Проверьте свое понимание 8.4

Когда цилиндрический конденсатор получает заряд 0,500 нКл, между цилиндрами измеряется разность потенциалов 20,0 В. а) Какова емкость этой системы? (b) Если цилиндры 1.Длина 0 м, каково соотношение их радиусов?

Несколько типов конденсаторов, которые можно использовать на практике, показаны на рис. 8.4. Обычные конденсаторы часто состоят из двух небольших кусочков металлической фольги, разделенных двумя небольшими кусочками изоляции (см. Рисунок 8.2 (b)). Металлическая фольга и изоляция покрыты защитным покрытием, а два металлических вывода используются для подключения фольги к внешней цепи. Некоторые распространенные изоляционные материалы — это слюда, керамика, бумага и антипригарное покрытие Teflon ™.

Другой популярный тип конденсатора — электролитический конденсатор.Он состоит из окисленного металла в проводящей пасте. Основным преимуществом электролитического конденсатора является его высокая емкость по сравнению с другими распространенными типами конденсаторов. Например, емкость одного типа алюминиевого электролитического конденсатора может достигать 1,0 F. Однако вы должны быть осторожны при использовании электролитического конденсатора в цепи, потому что он работает правильно только тогда, когда металлическая фольга находится под более высоким потенциалом, чем проводящая паста. Когда возникает обратная поляризация, электролитическое действие разрушает оксидную пленку.Этот тип конденсатора не может быть подключен к источнику переменного тока, потому что в половине случаев переменное напряжение будет иметь неправильную полярность, поскольку переменный ток меняет свою полярность (см. Схемы переменного тока в цепях переменного тока).

Конденсатор переменного тока (рисунок 8.8) имеет два набора параллельных пластин. Один набор пластин закреплен (обозначен как «статор»), а другой набор пластин прикреплен к валу, который может вращаться (обозначается как «ротор»). Поворачивая вал, можно изменять площадь поперечного сечения в перекрытии пластин; следовательно, емкость этой системы может быть настроена на желаемое значение.Настройка конденсатора находит применение в любом типе радиопередачи и при приеме радиосигналов от электронных устройств. Каждый раз, когда вы настраиваете автомобильное радио на любимую станцию, думайте о емкости.

Рис. 8.8 В конденсаторе переменного тока емкость можно регулировать, изменяя эффективную площадь пластин. (кредит: модификация работы Робби Спроул)

Обозначения, показанные на рисунке 8.9, представляют собой схемные изображения различных типов конденсаторов. Обычно мы используем символ, показанный на рисунке 8.9 (а). Символ на Рисунке 8.9 (c) представляет конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией конденсатора с параллельными пластинами. Электролитический конденсатор представлен символом на рис. 8.9 (b), где изогнутая пластина обозначает отрицательный вывод.

Рисунок 8.9 На нем показаны три различных схемных представления конденсаторов. Символ в (а) является наиболее часто используемым. Символ в (b) представляет собой электролитический конденсатор. Символ в (c) представляет конденсатор переменной емкости.

Интересный прикладной пример модели конденсатора взят из клеточной биологии и имеет дело с электрическим потенциалом в плазматической мембране живой клетки (рис. 8.10). Клеточные мембраны отделяют клетки от их окружения, но позволяют некоторым отобранным ионам проходить внутрь или из клетки. Разность потенциалов на мембране составляет около 70 мВ. Клеточная мембрана может иметь толщину от 7 до 10 нм. Рассматривая клеточную мембрану как наноразмерный конденсатор, оценка наименьшей напряженности электрического поля на его « пластинах » дает значение E = Vd = 70 × 10−3V10 × 10−9m = 7 × 106V / m> 3MV / mE. = Vd = 70 × 10−3V10 × 10−9m = 7 × 106V / m> 3MV / m.

Этой величины электрического поля достаточно, чтобы вызвать электрическую искру в воздухе.

Рис. 8.10. Полупроницаемая мембрана биологической клетки имеет разные концентрации ионов на внутренней поверхности, чем на внешней. Диффузия перемещает ионы K + K + (калий) и Cl – Cl– (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Таким образом, внешняя поверхность мембраны приобретает положительный заряд, а ее внутренняя поверхность приобретает отрицательный заряд, создавая разность потенциалов на мембране.Мембрана обычно непроницаема для Na + (ионов натрия).

конденсаторов, подключенных последовательно и параллельно: что это такое, формула, напряжение (со схемами)

Когда вы изучаете физику электроники и хорошо разбираетесь в основах, таких как значение таких ключевых терминов, как напряжение , ток и сопротивление , наряду с важными уравнениями, такими как закон Ома — изучение того, как работают различные компоненты схемы, является следующим шагом к овладению предметом.

Конденсатор — один из наиболее важных компонентов для понимания, поскольку они широко используются практически во всех областях электроники. От конденсаторов связи и развязки до конденсаторов, которые заставляют работать вспышку камеры или играют ключевую роль в выпрямителях, необходимых для преобразования переменного тока в постоянный, трудно переоценить огромный диапазон применений конденсаторов. Вот почему так важно знать, как рассчитать емкость и общую емкость конденсаторов различной конфигурации.

Что такое конденсатор?

Конденсатор — это простой электрический компонент, состоящий из двух или более проводящих пластин, которые удерживаются параллельно друг другу и разделены воздухом или изолирующим слоем. Две пластины обладают способностью накапливать электрический заряд, когда они подключены к источнику питания, причем одна пластина вырабатывает положительный заряд, а другая — отрицательный.

По сути, конденсатор похож на небольшую батарею, производящую разность потенциалов (т.е.например, напряжение) между двумя пластинами, разделенными изолирующим разделителем, называемым диэлектриком (который может быть выполнен из многих материалов, но часто из керамики, стекла, вощеной бумаги или слюды), что предотвращает протекание тока от одной пластины. пластину к другой, тем самым сохраняя накопленный заряд.

Для данного конденсатора, если он подключен к батарее (или другому источнику напряжения) с напряжением В, , он будет хранить электрический заряд Q . Эта способность более четко определяется «емкостью» конденсатора.

Что такое емкость?

Имея это в виду, значение емкости является мерой способности конденсатора накапливать энергию в виде заряда. В физике и электронике емкость обозначается символом C и определяется как:

C = \ frac {Q} {V}

Где Q — заряд, накопленный в пластинах, а В — это разность потенциалов подключенного к ним источника напряжения. Короче говоря, емкость — это мера отношения заряда к напряжению, и поэтому единицами емкости являются кулоны заряда / вольт разности потенциалов.Конденсатор с более высокой емкостью сохраняет больше заряда при заданном значении напряжения.

Концепция емкости настолько важна, что физики дали ей уникальную единицу, названную фарад (в честь британского физика Майкла Фарадея), где 1 F = 1 C / V. Немного похоже на кулон для заряда, фарад представляет собой довольно большую емкость, при этом большинство значений емкости конденсаторов находятся в диапазоне от пикофарада (пФ = 10 ⁻¹² Ф) до микрофарада (мкФ = 10 ⁻⁶ ). F).

Эквивалентная емкость последовательных конденсаторов

В последовательной схеме все компоненты расположены на одном и том же пути вокруг контура, и таким же образом последовательные конденсаторы соединяются один за другим на едином пути вокруг схемы . Общая емкость для ряда конденсаторов, подключенных последовательно, может быть выражена как емкость одного эквивалентного конденсатора.

Формула для этого может быть получена из основного выражения для емкости из предыдущего раздела, переставленного следующим образом:

V = \ frac {Q} {C}

Поскольку закон Кирхгофа утверждает, что сумма напряжений падение напряжения вокруг полного контура цепи должно быть равно напряжению от источника питания, для ряда конденсаторов n напряжения должны складываться следующим образом:

V_ {tot} = V_1 + V_2 + V_3 + … В_н

Где В _до — полное напряжение от источника питания, а В ₁ , В ₂ , В ₃ и таковы падения напряжения на первом конденсаторе, втором конденсаторе, третьем конденсаторе и так далее.В сочетании с предыдущим уравнением это приводит к:

\ frac {Q_ {tot}} {C_ {tot}} = \ frac {Q_1} {C_1} + \ frac {Q_2} {C_2} + \ frac {Q_3 } {C_3} +… \ frac {Q_n} {C_n}

Где нижние индексы имеют то же значение, что и раньше. Однако заряд на каждой из пластин конденсатора (т. Е. Значения Q ) исходит от соседней пластины (т. Е. Положительный заряд на одной стороне пластины 1 должен соответствовать отрицательному заряду на ближайшей стороне пластины 2. и так далее), поэтому вы можете написать:

Q_ {tot} = Q_1 = Q_2 = Q_3 = Q_n

Таким образом, начисления аннулируются, в результате чего остается:

\ frac {1} {C_ {tot}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +… \ frac {1} {C_n}

Поскольку емкость комбинации равна эквивалентной емкости одиночный конденсатор, это можно записать так:

\ frac {1} {C_ {eq}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +… \ frac {1} {C_n}

для любого количества конденсаторов n .{−6} \ text {F} \\ & = 1.41 \ text {мкФ} \ end {align}

Эквивалентная емкость параллельных конденсаторов

Для параллельных конденсаторов аналогичный результат получается из Q = VC, тот факт, что падение напряжения на всех конденсаторах, подключенных параллельно (или на любых компонентах в параллельной цепи), одинаковое, и тот факт, что заряд на одном эквивалентном конденсаторе будет общим зарядом всех отдельных конденсаторов в параллельной комбинации . Результатом является более простое выражение для общей емкости или эквивалентной емкости:

C_ {eq} = C_1 + C_2 + C_3 +… C_n

, где снова n — общее количество конденсаторов.{−5} \ text {F} \\ & = 15 \ text {мкФ} \ end {align}

Комбинации конденсаторов: проблема первая

Нахождение эквивалентной емкости для комбинаций конденсаторов, расположенных последовательно и расположенных parallel просто подразумевает применение этих двух формул по очереди. Например, представьте комбинацию конденсаторов с двумя последовательно включенными конденсаторами: C ₁ = 3 × 10 ⁻³ F и C ₂ = 1 × 10 ⁻³ F. , и еще один конденсатор параллельно с C ₃ = 8 × 10 ⁻³ F.{−3} \ text {F} \ end {align}

Комбинации конденсаторов: Проблема Два

Для другой комбинации конденсаторов, три при параллельном подключении (со значениями C ₁ = 3 мкФ, C ₂ = 8 мкФ и C ₃ = 12 мкФ) и один с последовательным подключением (с C ₄ = 20 мкФ):

Подход в основном такой же, как и в последнем примере, за исключением того, что сначала вы обрабатываете параллельные конденсаторы.{−1}} \\ & = 10.7 \ text {мкФ} \ end {align}

Обратите внимание, что, поскольку все отдельные емкости были в микрофарадах, весь расчет может быть выполнен в микрофарадах без преобразования — если вы помните при цитировании ваших окончательных ответов!

Конденсаторы в схемах

• Решите расчет схемы конденсатора
• • Конденсаторы серии
• • Конденсаторы параллельно

Конденсаторы последовательно.

Подобно резисторам и индукторам, конденсаторы могут быть подключены последовательно, параллельно или последовательно-параллельно. Последовательное размещение конденсаторов эффективно увеличивает толщину диэлектрика и, таким образом, снижает общую емкость. Поскольку общая емкость обратно пропорциональна расстоянию между пластинами, формула, которую мы используем для конденсаторов в СЕРИИ:

Обратите внимание, что напряжение на каждом конденсаторе будет обратно пропорционально емкости, при этом общее напряжение распределяется между конденсаторами, наименьшая емкость имеет наибольшее напряжение на ней, а наибольшая емкость имеет наименьшее напряжение и т. Д.

Конденсаторы параллельно.

При параллельном подключении конденсаторов площадь пластин эффективно увеличивается, поэтому общая емкость определяется суммой отдельных емкостей;

Все конденсаторы заряжаются до одинакового напряжения.

Обратите внимание, что при использовании этих формул значения должны быть введены в формулу в их БАЗОВЫХ ЕДИНИЦАХ, т.е. ФАРАДЫ (не мкФ), кулоны (не мкКл) и ВОЛЬТЫ (не мВ).

Кратковременно 47 нФ; (наноФарады) вводится как; 15 EXP-09 и 25mC (милликулонов) вводятся как; 25 ЕХР-03 и т. Д.Проще всего это сделать с помощью научного калькулятора.

Попробуйте вычислить общую емкость некоторых последовательных и параллельных цепей

Примеры серий

и параллельных цепей.

Справка по математике

Нужна помощь с математикой электроники? Загрузите наш полезный буклет с советами по покупке и использованию научного калькулятора, а также по определению всех этих значений электроники. Неоценимая помощь в математике электроники в этом модуле!

.