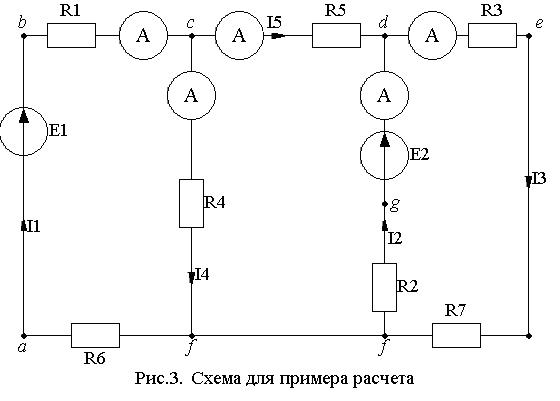
РАСЧЕТ ПОТЕНЦИАЛОВ ТОЧЕК ЦЕПИ — Мегаобучалка
Чтобы найти ток в цепи с несколькими источниками надо:
1) Сложить все Е, направленные в одну сторону;
2) Вычесть все Е, направленные в другую сторону
3) Разделить на сумму всех сопротивлений цепи
Ток течет в сторону большей суммы Е.
Пусть Е1 > Е2, тогда
Если ток и ЭДС совпадают по направлению, то источник работает в режиме генератора, если нет, то в режиме потребителя.
Е1 — генератор; Е2— потребитель
Потенциалом точки цепи называется напряжение между данной точкой и заземлённой.
φ0 = 0
При переходе через источник в режиме генератора потенциал повышается на величину ЭДС минус падение напряжения внутри источника.
φА = φ0 + Е1 — I∙Ri1
При переходе через резистор потенциал понижается на величину падения напряжений в нём:
φВ = φА — I∙R
При переходе через источник в режиме потребителя потенциал понижается на величину ЭДС и на величину падения напряжения внутри источника.
φ0 = φB — E2 — I∙Ri2
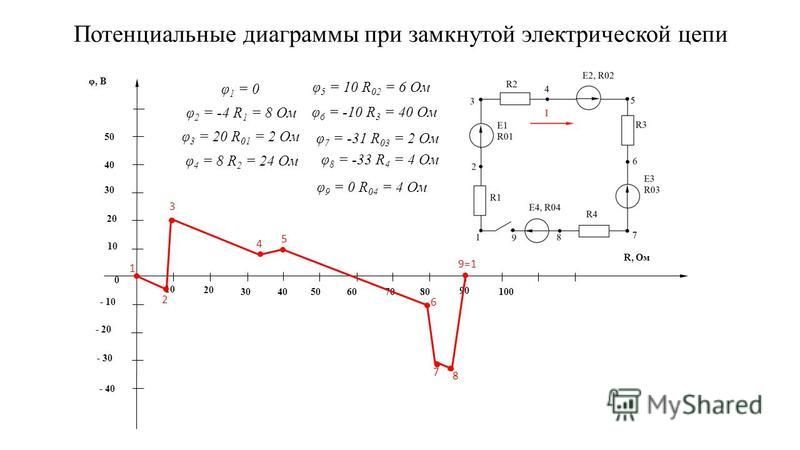
Потенциальная диаграмма — это график зависимости потенциалов точек цепи от величины сопротивления цепи.
Рассмотрим построение потенциальной диаграммы на конкретном примере. Одну точку цепи заземляем. Расставляем точки вдоль направления тока. При расчете снова должен получиться равным нулю
Пример решения задачи:
Дано:
Е1 = 25 B
Е2 = 35 В
Е3 = 18 В
Ri1 = 2 Ом
Ri2 = 1 Ом
Ri3 =2 Ом
R1 = 12 Ом
R2 = 5 Ом
R3 = 14 Ом
R4 = 6 Ом
1) Рассчитаем ток в цепи и определяем его направление:
A
2) Рассчитаем потенциалы точек:
φ0 = 0
φ1 = φ0 — I∙R1 = 0 — 12 = -12 B
φ2 = φ1 + Е1 — I∙Ri1 = -12 + 25 — 2 = 11 B
φ3 = φ2 — I∙R2 = 11 — 5 = 6 B
φ4 = φ3 + E2 — I∙Ri2 = 6 + 35 — 1 = 40 B
φ5 = φ4 — E3 — I∙Ri3 = 40 — 18 — 2 = 20 B
φ6 = φ5 — I∙R3 = 20 — 14 = 6 B
φ0 = φ6 — I∙R4 = 6 — 6 = 0
Вывод: При переходе через резистор потенциал понижается плавно, через источник в режиме генератора резко увеличивается, а в режиме потребителя резко уменьшается.
Тестовые задания:
| Задание | Варианты ответов |
| 1.Являются ли напряжение между данной точкой цепи и заземленной потенциалом точки этой цепи? | Да;
Нет. |
| 2. Источник работает в режиме генератора если… | а) ЭДС и ток направлены в разные стороны;
б) ЭДС и ток направлены в одну сторону. |
РАБОТА ИСТОЧНИКА НА НАГРУЗКУ С ПЕРЕМЕННЫМ СОПРОТИВЛЕНИЕМ.
Построение зависимостей I, U, η = F(R).
Пусть сопротивление нагрузки изменяется от Rкз=0 до Rxx= . Рассмотрим величину тока в трех режимах короткое замыкание, холостой ход и согласованный режим.
1) Iкз = =
2) Iхх =
3)
Вывод 1: с ростом величины сопротивления ток в цепи уменьшается;
Вывод 2: ток максимальный в режиме короткого замыкания;
Рассмотрим величину напряжения в трех режимах
1) Uкз=
2)
3)
Вывод 1: с ростом величины сопротивления напряжение на зажимах источника растет;
Вывод 2: напряжение максимально в режиме Х. Х.
Х.
Рассмотрим величину К.П.Д. в трех режимах
Вывод: η стремиться к 1 в режиме Х.Х., но использовать на практике этот режим невозможно, так как цепь разомкнута.
Построение зависимостей Pu, Pн = F(R)
Рассмотрим величину мощности источника в трех режимах
Pu = E∙I = E∙
Вывод: мощность источника максимальна в режиме короткого замыкания.
Рассмотрим величину мощности нагрузки в трех режимах
Исследуя функцию Pн = f(R) на экстремум доказано, что максимальная мощность выделяется в нагрузке при согласованном режиме. Поэтому линии связи и другие устройства работают в этом режиме. И хотя η = 50%, но в слаботочных цепях это не имеет значения.
Тестовые задания:
| Задание | Режим работы | Варианты ответов |
4. Укажите при каких режимах работы перечисленные в ответах величины максимальны. Укажите при каких режимах работы перечисленные в ответах величины максимальны.
| 1) режим холостого хода;
2) режим короткого замыкания; 3) согласованный режим. | а) мощность источника;
б) ток цепи; в) мощность нагрузки напряжение на зажимах источника. |
Измерение потенциалов точек электрической цепи и построение потенциальной диаграммы
любой ветви схемы можно найти по закону Ома для
участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома,
необходимо знать потенциалы узлов схемы. Метод расчета электрических цепей, в
котором за неизвестные принимают потенциалы узлов схемы, называют методом
узловых потенциалов.
Допустим, что в схеме n узлов.
Так как любая (одна) точка схемы может быть заземлена без изменения
токораспределения в схеме, то один из узлов схемы можно мысленно заземлить, т.
е. принять потенциал его равным нулю. При этом число неизвестных уменьшается с n до n-1.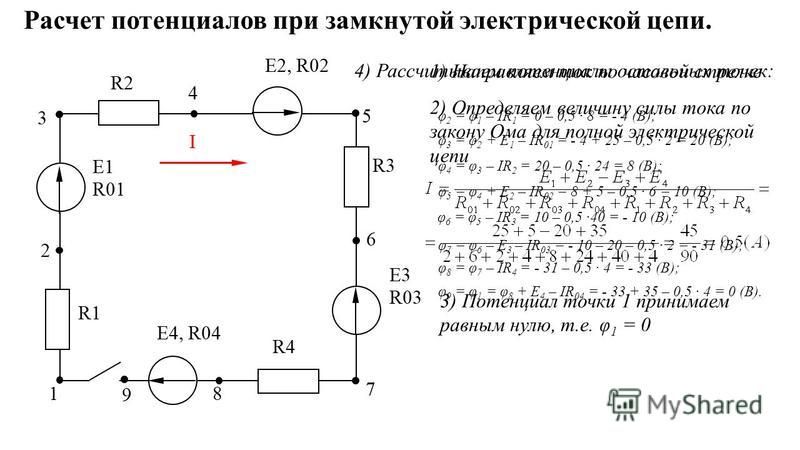
Число неизвестных в методе узловых потенциалов равно
числу уравнений, которые необходимо составить для схемы по первому закону
Кирхгофа. Метод узловых потенциалов, как и метод контурных токов, — один из
основных расчетных приемов. В том случае, когда число узлов без единицы меньше
числа независимых контуров в схеме, данный метод является более экономичным,
чем метод контурных токов.
Вывод основных расчетных уравнений проведем применительно
к схеме рис. 2, в которой три узла. Если узел 3 мысленно заземлить, т. е.
принять =0, то необходимо определить потенциалы
только двух узлов:,.
Запишем уравнения по первому закону Кирхгофа для
независимых узлов, причем токи, направленные к узлу берем со знаком минус, а от
узла – со знаком плюс.
Для первого узла ,
Для второго узла .
Рис. 2. Схема для
расчета по методу узловых потенциалов
Запишем токи по закону Ома:
, , , ,
, .
Подставим токи в уравнения по первому закону Кирхгофа:
,
.
Перепишем уравнения:
,
;
,
;
,
, где ,
, , ,
,
,
G11— сумма проводимостей
ветвей, сходящихся в первом узле,
G12— сумма проводимостей
ветвей, соединяющих первый и второй узлы, взятая со знаком минус,
G21— сумма проводимостей
ветвей, соединяющих первый и второй узлы, взятая со знаком минус,
G11— сумма проводимостей
ветвей, сходящихся во втором узле,
I11— узловой ток первого
узла,
I22 — узловой ток второго
узла.
Запишем уравнения в матричной форме:
,
, , .
Решим эти уравнения относительно искомых потенциалов и
выразим токи ветвей, используя закон Ома.
После нахождения токов ветвей любым методом всегда
делается проверка по первому закону Кирхгофа.
Потенциальная диаграмма.
Под потенциальной диаграммой понимают график
распределения потенциала вдоль какого-либо участка цепи или замкнутого контура.
По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо
произвольной точки, по оси ординат – потенциалы. Каждой точке участка цепи или
замкнутого контура соответствует своя точка на потенциальной диаграмме.
Построим потенциальную диаграмму для контура на рис.3. Пусть R1=10 Ом, R2=5 Ом, R3=15
Ом, E1=20 В, E2=10 В, I=1A.
Рис.3. Контур для
построения потенциальной диаграммы
,
,
,
,
,
.
Построим график.
Рис. 4. Потенциальная
диаграмма для контура на рис.3.
Таблица 1. Исходные
данные
Схема | R1 | R2 | R3 | R4 | R5 | R6 | E1 | E2 | |
Рис. | Ом | Ом | Ом | Ом | Ом | Ом | В | В | |
Вариант 1 | 5 | 15 | 10 | 25 | 20 | 10 | 30 | 100 | 60 |
Вариант 2 | 6 | 4 | 6 | 3 | 2 | 5 | 6 | 35 | 25 |
Вариант 3 | 7 | 5 | 1 | 6 | 4 | 2 | 6 | 10 | 30 |
Вариант 4 | 8 | 3 | 6 | 9 | 10 | 6 | 8 | 55 | 40 |
Вариант 5 | 5 | 6 | 6 | 8 | 8 | 10 | 12 | 70 | 45 |
Вариант 6 | 6 | 4 | 2 | 4 | 5 | 6 | 3 | 15 | 35 |
Вариант 7 | 7 | 1 | 2 | 5 | 1 | 3 | 3 | 10 | 15 |
Вариант 8 | 8 | 25 | 50 | 15 | 25 | 20 | 30 | 150 | 75 |
Порядок выполнения работы:
1. Нарисовать
Нарисовать
схему. Записать данные.
2. Найти токи
ветвей методом контурных токов.
3. Сделать
проверку по первому закону Кирхгофа.
4. Найти токи
ветвей методом узловых потенциалов.
5. Рассчитанные
токи занести в таблицу 2.
Таблица
2
I1,A | I2,A | I3,A | I4,A | I5,A | I6,A | |
расчет | ||||||
эксперимент |
6. Составить баланс мощностей.
Составить баланс мощностей.
7. Потенциалы точек отмеченных на схеме занести в таблицу
3.
Таблица 3
A, B | B, B | C, B | D, B | F, B | |
расчет | |||||
эксперимент |
8. Собрать
Собрать
схему в программе Electronics Workbench.
9. Измерить
токи во всех ветвях. Для чего в каждую ветвь включить амперметр. Результаты
измерений занести в таблицу 2.
10. Заземлить узел, который
заземляли при расчете по методу узловых потенциалов.
11. Измерить потенциалы точек,
отмеченных на схеме. Результаты занести в таблицу 3.
12. Построить потенциальную
диаграмму заданного контура.
13. Сравнить измеренные данные с
расчетными.
14. Сделать вывод.
Содержание отчета:
1. Тема,
цель, приборы и оборудование.
2. Схема
заданной цепи. Исходные данные.
3. Расчет по
методу контурных токов и методу узловых потенциалов.
4. Заполненная
таблица 2.
5. Проверка
по первому закону Кирхгофа.
6. Баланс
мощностей.
7. Заполненная
таблица 3.
8. Токи
ветвей и потенциалы узлов цепи, измеренные в программе Electronics Workbench .
9. Потенциальная
диаграмма.
10. Вывод.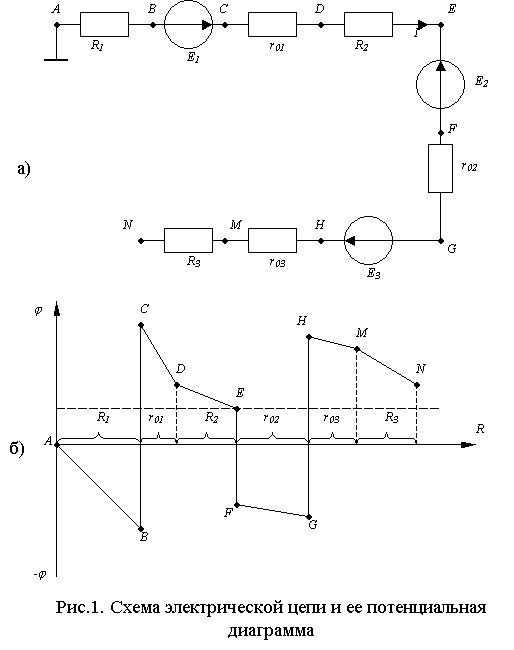
Вопросы на защиту:
1. Суть
метода контурных токов.
2. Суть
метода узловых потенциалов.
3. Какой
используется закон Кирхгофа для составления уравнений по методу контурных
токов? Сформулировать его.
4. Какой
используется закон Кирхгофа для составления уравнений по методу узловых
потенциалов? Сформулировать его.
5. Как
называется сопротивление R11? Как оно
находится?
6. Как
называется сопротивление R12? Как оно
находится?
7. Что такое
Е11 в матричной записи уравнений по методу контурных токов?
8. Как
находится собственная проводимость узла по методу узловых потенциалов?
9. Матричная
форма записи уравнений по методу узловых потенциалов.
10. Как строится потенциальная
диаграмма контура сложной цепи
Потенциальная диаграмма | Электрикам
Потенциальной диаграммой замкнутого контура называется графическая интерпретация распределения электронного потенциала вдоль замкнутого контура в зависимости от входящих в него сопротивлений.
Потребитель энергии отображается на электрической схеме как резистор с заданным сопротивлением R. Если такое элемент присутствует в участке цепи, то изменение потенциалов на концах участка будет соответствовать падению напряжения на этом резисторе.
Если на участке цепи присутствует источник напряжения, то на концах такого участка также будет наблюдаться разность потенциалов, численно равная ЭДС источника.
Построение потенциальной диаграммы
Для построения потенциальной диаграммы, замкнутый контур разбивается на участки таким образом, чтобы каждый из них содержал только одного потребителя или один источник электроэнергии.
Потенциальная диаграмма строится в декартовой системе координат, где по оси абсцисс откладывается, с соблюдением масштаба, сопротивление участков цепи, а по оси ординат – потенциалы точек. Точки замкнутого контура и сопротивления элементов откладываются (отмечаются на диаграмме) в той последовательности, в которой они встречаются при обходе контура.
В начало координат диаграммы помещается точка, потенциал которой условно выбран нулевым.
Демонстрацию алгоритма и правил построения потенциальной диаграммы выполним на примере замкнутого контура abcdef (точки a и f совпадают), представленного на рисунке 1. Положительное направление обхода контура – по часовой стрелке. Для расчетов примем:
- Е1 = 2 В, Е2 = 3 В;
- R1 = 1 Ом, R2 = 1 Ом, R3 = 2 Ом;
- I1 = 1 А, I2 = 2 А, I3 = 1 А.
Рис. 1. Схема фрагмента электрической цепи — замкнутого контура
Замкнутый контур разбит на участки, каждый из которых содержит либо источник ЭДС, либо резистор.
Примем нулевым потенциал точки а
Следующая точка согласно выбранному направлению движения – b. На участке ab находится источник ЭДС E1. Так как движение на данном участке происходит от отрицательного полюса источника к положительному (направление обхода контура совпадает со стрелкой источника ЭДС), то значение потенциалы на участке повысится на величину E1:
Следующий рассматриваемый участок – bc. На нем происходит уменьшение потенциала на величину падения напряжения на резисторе R1.
На нем происходит уменьшение потенциала на величину падения напряжения на резисторе R1.
Аналогичные процессы происходят на участках cd и de. Следовательно,
На участке ef находится еще один источник ЭДС E2. Движение по данному участку реализуется от отрицательного полюса к положительному, следовательно потенциал повысится на величину E2
Если направление обхода контура не совпадает с направлением ЭДС, тогда ЭДС записывают со знаком минус
Значения потенциалов в точках а и f совпадают , что подтверждает правильность расчетов.
На основании полученных данных можно построить потенциальную диаграмму (рисунок 2).
Рис. 2. Потенциальная диаграмма
По потенциальной диаграмме легко можно найти разность потенциалов между любыми точками электрической цепи.
Расчет потенциальной диаграммы | Учебные материалы
Потенциальной диаграммой называется график зависимости потенциала φ от сопротивления R, полученный при обходе контура.
Расчет потенциалов точек цепи выполняется после определения токов в ветвях одним из рассмотренных выше методов и нахождения истинных направлений токов.
Расчет рекомендуется производить в следующей последовательности.
- Разбивают электрическую цепь (например, внешний контур) на участки, содержащие резисторы или источники ЭДС, обозначив буквами границы участков.
- Потенциал одной из точек принимают равным нулю.
- При обходе контура (направление произвольное) разность потенциалов φA – φB между концами каждого участка вычисляются по формулам, в зависимости от элемента, включенного на рассматриваемом участке цепи:
— если на участке включен резистор с сопротивлением R, то формула имеет вид
При этом следует иметь в виду, что φA > φB, так как направление тока от большего потенциала к меньшему;
— если участок содержит источник ЭДС с внутренним сопротивлением r0, то возможны два случая:
— источник ЭДС работает в режиме источника питания (ток через источник совпадает с направлением ЭДС), тогда разность потенциалов определяется по формуле
jA — jB = E — r0 I;
— источник ЭДС работает в режиме приемника (направления тока и ЭДС противоположны),
тогда формула примет вид jA — jB = E + r0 I.
Расчетное значение потенциала точки, с которой начат обход контура, должно получиться равным нулю, что является критерием правильности расчета.
При построении потенциальной диаграммы по оси абсцисс в масштабе откладывают последовательно значения сопротивлений резисторов, включенных в контур; по оси ординат — значения потенциалов точек.
Примерный вид потенциальной диаграммы изображен на рис. 9
Рис. 9
Сакович А.Л. Точки равного потенциала
В литературе описано несколько методов преобразования электрических цепей [1; 2; 3]. В этих статьях описаны и методы упрощения схем, имеющих точки равного потенциала. Но при решении подобных задач авторы обычно пишут так: «Из симметрии ветвей цепи видно, что точки В и D имеют равные потенциалы» [2], хотя эта видимость не совсем очевидна.
Рассмотрим способы нахождения точек одинакового потенциала более подробно. Пусть нам дана электрическая цепь, состоящая из сопротивлений R1, R2, …, R8 (рис. 1 а). Проведем через точки подключения цепи прямую АВ (рис. 1 б).
1 а). Проведем через точки подключения цепи прямую АВ (рис. 1 б).
1 способ. Если схема содержит проводники с одинаковым сопротивлением, расположенные симметрично относительно определенной оси или плоскости, то концы этих проводников имеют одинаковый потенциал. При этом точки будут симметричными относительно прямой АВ, если равны сопротивления участков цепи между данными точками и любыми точками этой прямой.
Используя этой признак, можно сделать вывод, что точки С1 и С2 (рис. 1 б) будут симметричны относительно прямой АВ, если R1 = R2 (сопротивления между точкой А и С1 и между точкой А и С2 равны) и R5 = R6 (сопротивления между точкой В и С1 и между точкой В и С2 равны). Аналогично, точки С3 и С4 будут симметричны относительно прямой АВ, если R3 = R4 и R7 = R8.
а.
б.
Рис. 1.
2 способ. Точки имеют одинаковый потенциал, если равны отношения сопротивлений между данными точками и точками подключения.
Например, точки С1 и С2 (рис. 1 а) имеют одинаковый потенциал, если . Аналогично, точки С3 и С4 имеют одинаковый потенциал, если .
Покажем на примерах, как можно использовать эти способы для преобразования электрических цепей.
Метод объединения равнопотенциальных узлов:точки с одинаковыми потенциалами можно соединять в узлы.
Пример 1. Определите сопротивление электрической цепи (рис. 2), если: а) R1 = R3 = 2R, R2 = R4 = R, R5 = 3R; б) R1 = R4 = 2R, R2 = 4R, R3 = R, R5 = 5R.
Рис. 2.
а) Если провести через точки подключения прямую АВ (рис. 3 а), то равны сопротивления участков АС1 и АС2 (R1 = R3), и равны сопротивления участков ВС1 и ВС2 (R2 = R4). Следовательно, точки С1 и С2 симметричны относительно прямой АВ и имеют равные потенциалы.
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 3, б). Резисторы R1 и R3 соединены параллельно, и резисторы R2 и R4 – параллельно, участки 1/3 и 2/4 последовательно. Следовательно,
б) Если провести прямую АВ (рис. 3 а), то сопротивления участков АС1 и АС2 не равны , следовательно, точки С1 и С2 не симметричны относительно прямой АВ. НО точки С1 и С2имеют равные потенциалы, т.к. .
НО точки С1 и С2имеют равные потенциалы, т.к. .
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 3 б). Резисторы R1 и R3 соединены параллельно, и резисторы R2 и R4 – параллельно, участки 1/3 и 2/4 последовательно. Следовательно,
Пример 2. Найдите сопротивление проволочного куба между точками А1 и В3 (рис. 4). Сопротивление каждого ребра R0.
Рис. 4.
Рис. 5.
Проведем через точки подключения прямую А1В3 (рис. 5). Равны сопротивления (равны длины – ребра) участков А1В1, А1А2 и А1А4, и равны сопротивления (равны длины – диагонали) участков В3В1, В3А2 и В3А4. Следовательно точки В1, А2 и А4 симметричны относительно прямой А1В3 и имеют равные потенциалы. Равны сопротивления участков А1А3, А1В2 и А1В4, и равны сопротивления участков В3А3, В3В2 и В3В4. Следовательно точки А3, В2 и В4 симметричны относительно прямой А1В3 и имеют равные потенциалы.
Следовательно точки В1, А2 и А4 симметричны относительно прямой А1В3 и имеют равные потенциалы. Равны сопротивления участков А1А3, А1В2 и А1В4, и равны сопротивления участков В3А3, В3В2 и В3В4. Следовательно точки А3, В2 и В4 симметричны относительно прямой А1В3 и имеют равные потенциалы.
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 6). Три резистора R0 соединены параллельно между точками А1 и А2 (В1, А4), шесть резисторов R0 – параллельно между точками А2 (В1, А4) и А3 (В2, В4), три резистора R0 – параллельно между точками А3 (В2, В4) и В3, участки между этими точками соединены последовательно. Следовательно,
Следовательно,
.
Рис. 6.
Пример 3. Найдите сопротивление проволочного куба между точками А1 и В2 (рис. 4). Сопротивление каждого ребра R0.
Проведем через точки подключения прямую А1В2 (рис. 7 а). Равны сопротивления (равны длины – ребра) участков А1В1, А1А2, и равны сопротивления (равны длины – ребра) участков В2В1, В2А2. Следовательно точки В1 и А2 симметричны относительно прямой А1В2 и имеют равные потенциалы. Равны сопротивления участков А1А3 и А1В4, и равны сопротивления участков В2А3 и В2В4. Следовательно, точки А3 и В4А1 симметричны относительно прямой В2 и имеют равные потенциалы.
Следовательно, точки А3 и В4А1 симметричны относительно прямой В2 и имеют равные потенциалы.
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 7 б). Используя рекуррентный метод, схему можно упростить (рис. 7 в или г).
Точки А2 и В4имеют равные потенциалы, т.к. . Точки с одинаковыми потенциалами можно соединять в узлы (рис. 7 д). Резисторы на участке А1А2 соединены параллельно, и резисторы на участке А2В2 – параллельно, а эти участки соединены последовательно. Следовательно,
Если возможно объединение двух равнопотенциальных узлов, то возможен и обратный переход.
Метод разделения узлов: узел схемы можно разделить на два или несколько узлов, если получившиеся при этом узлы имеют одинаковые потенциалы.
Обязательным условием при этом является проверка получившихся при разделении узлов на равенство потенциалов (симметричность или пропорциональность сопротивлений).
Пример 4. Найдите сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. 8) сопротивлением R0 каждый.
Рис. 8.
Разделим узел в середине каркаса на два узла О1 и О2 так, как показано на рис. 9 а. Это можно сделать, так как точки О1 и О2 имеют равные потенциалы: равны сопротивления участков AO1, AO2, и равны сопротивления участков BO1, BO2. Перерисуем схему в стандартный вид (рис. 9 б). Используя рекуррентный метод, схему можно упростить (рис. 9 в), т.к. сопротивление участка C1F1 равно , аналогично . Тогда общее сопротивление цепи равно .
Обратите внимание. С точки зрения геометрии точки О3 и О4 симметричны относительно прямой а (рис. 9 г), но потенциалы этих точек не равны, т.к. сопротивления участков АО3 и АО4 не равны, а отношения сопротивлений участков АО3 и АО4 не равны отношению сопротивлений участков ВО3 и ВО4.
9 г), но потенциалы этих точек не равны, т.к. сопротивления участков АО3 и АО4 не равны, а отношения сопротивлений участков АО3 и АО4 не равны отношению сопротивлений участков ВО3 и ВО4.
Пример 5. Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. 10) сопротивлением R0 каждый.
Рис. 10.
Разделим узел в середине каркаса на три узла О1, О2 и О3 так, как показано на рис. 11 а. Это можно сделать, так как точки О1, О2 и О3 имеют равные потенциалы: равны сопротивления участков AO1 и BO1, участков AO2 и BO2, и участков AO3 и BO3, следовательно, отношения сопротивления этих участков равны.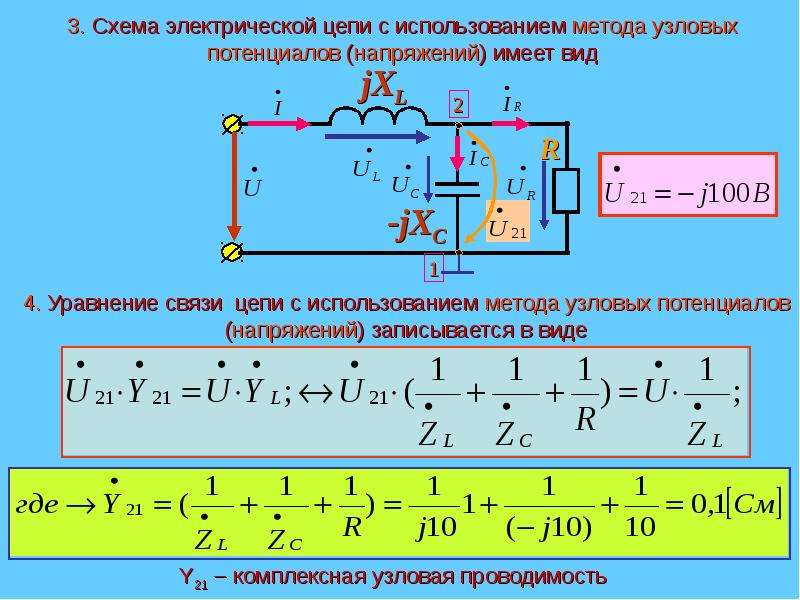
Перерисуем схему в стандартный вид (рис. 11, б). Используя рекуррентный метод, схему можно упростить (рис. 11 в), т.к. сопротивление участка C1F1 равно , аналогично , сопротивление . Тогда общее сопротивление цепи равно
Литература
- Зильберман А. Расчет электрических цепей // Квант. – 1988. – № 8. – С. 30-34.
- Петросян В.Г., Долгополова Л.В., Лихицкая И.В. Методы расчета резисторных схем постоянного тока // Физика. – 2002. – № 14, 18, 22.
- Хацет А. Методы расчета эквивалентных сопротивлений // Квант. – 1972. – № 2. – С. 54-59.
Извините такой страницы Wp-content Uploads 2014 02 Dz-1 Metod-uzlovyh-potentsialov Pdf не существует!
Выбор статьи по меткам03 (1)5 марта 2020 (1)5 мая Статград (2)9 класс (3)10 класс (1)11 класс (2)12 (1)13 (С1) (3)14 ноября (2)14 февраля (1)15 задание ЕГЭ (2)16 задача профиль (1)16 профильного ЕГЭ (1)16 января Статград (2)17 задача ЕГЭ (1)18 (С5) (2)18 задача ЕГЭ (2)18 мая 2020 физика (1)23 марта (1)25 сентября 2020 (1)31 января (1)2016 (2)140319 (1)14032019 (1)C5 (1)RC-цепь (1)RLC-контур (1)А9 (1)Александрова (2)Ампера (2)Архимед (2)Бернулли (1)Бойля-Мариотта (1)В8 (1)В12 (1)В13 (1)В15 (1)ВК (1)ВШЭ (2)ГИА физика задания 5 (1)Герона (2)Герцшпрунга-Рассела (1)Гринвич (1)ДВИ (1)ДПТ (1)Деление отрезка (1)Десятичные приставки (1)Дж (1)Диэлектрические проницаемости веществ (1)ЕГЭ 11 (2)ЕГЭ 14 (1)ЕГЭ 15 (2)ЕГЭ 18 (1)ЕГЭ С1 (1)ЕГЭ по математике (26)ЕГЭ по физике (49)ЕГЭ профиль (6)Европа (1)Задача 17 ЕГЭ (7)Задачи на движение (1)Закон Архимеда (2)Законы Ньютона (1)Земля (1)Ио (1)КПД (9)Каллисто (1)Кельвин (1)Кирхгоф (1)Кирхгофа (1)Койпера (1)Колебания (1)Коши (1)Коэффициенты поверхностного натяжения жидкостей (1)Кулона-Амонтона (1)Ломоносов (2)Лоренца (1)Луна (1)МГУ (1)МКТ (7)МФТИ олимпиада (1)Максвелл (2)Максвелла (1)Максимальное удаление тела от точки бросания (1)Менделеева-Клапейрона (3)Менелая (5)Метод наложения (2)Метод узловых потенциалов (1)Метод эквивалентных преобразований (1)НОД (1)Нансен (1)НеИСО (1)ОГЭ (11)ОГЭ (ГИА) по математике (27)ОГЭ 3 (ГИА В1) (1)ОГЭ 21 (3)ОГЭ 21 (ГИА С1) (4)ОГЭ 22 (2)ОГЭ 25 (3)ОГЭ 26 (1)ОГЭ 26 (ГИА С6) (1)ОГЭ по физике 5 (1)ОДЗ (14)Обыкновенная дробь (1)Оорта (1)Основные физические константы (1)Отношение объемов (1)Плюк (1)Погсона (1)Показатели преломления (1)Показательные неравенства (1)Противо-эдс (1)Работа выхода электронов (1)Радиус кривизны траектории (1)Расстояние между скрещивающимися (2)Релятивистское замедление времени (1)Релятивистское изменение массы (1)С1 (1)С1 ЕГЭ (1)С2 (2)С3 (1)С4 (3)С6 (5)СУНЦ МГУ (2)Савченко (1)Сиена (1)Синхронная машина (1)Снеллиуса (2)Солнечной системы (1)Солнце (2)СпБ ГУ вступительный (1)Средняя кинетическая энергия молекул (1)Статград физика (6)Таблица Менделеева (1)Текстовые задачи (8)Тьерри Даксу (1)ФИПИ (1)Фазовые переходы (1)Фаренгейт (1)Фобос (1)Френеля (1)Цельсий (1)ЭДС (6)ЭДС индукции (2)Эйлера (1)Электрохимические эквиваленты (1)Эрастофен (1)абсолютная (1)абсолютная влажность (2)абсолютная звездная величина (3)абсолютная температура (1)абсолютный ноль (1)адиабаты (1)аксиомы (1)алгоритм Евклида (2)алгоритм Робертса (1)аморфное (1)амплитуда (3)аналитическое решение (1)анекдоты (1)аннуитет (2)апериодический переходной процесс (2)апофема (1)аргумент (1)арифметическая прогрессия (5)арифметической прогрессии (1)арки (1)арккосинус (1)арккотангенс (1)арксинус (1)арктангенс (1)архимеда (3)асинхронный (1)атмосферное (2)атмосферном (1)атомная масса (2)афелий (2)афелийное (1)база (1)балка (1)банк (1)без калькулятора (1)без отрыва (1)белого карлика (1)бензин (1)бесконечная периодическая дробь (1)бесконечный предел (1)биквадратные уравнения (1)бипризма (1)биссектриса (4)биссектрисы (2)благоприятный исход (1)блеск (4)блеск компонентов (1)блок (2)блоки (3)боковой поверхности (1)большая полуось (1)большем давлении (1)бревно (2)бригада (2)бросили вертикально (1)бросили под углом (3)бросили со скоростью (2)броуновское движение (1)брошенного горизонтально (2)бруски (1)брусок (4)брусок распилили (1)бусинка (1)быстрый способ извлечения (1)ван-обеля (1)вариант (3)вариант ЕГЭ (12)вариант ЕГЭ по физике (18)вариант по физике (1)варианты ЕГЭ (6)вариент по физике (1)введение дополнительного угла (1)вектор (5)векторное произведение (2)велосипедисты (1)вероятность (3)вертикальная составляющая (1)вертикально вверх (1)вертикальные углы (1)вес (3)весов (1)вес тела (1)ветви (1)ветвь (2)ветер (1)взаимодействие зарядов (1)видеоразбор (2)видеоразбор варианта (1)видимая звездная величина (3)виртуальная работа (1)виртуальный банк (1)виртуальных перемещений (1)витка (1)витков (1)виток (1)вклад (2)влажность (3)влажность воздуха (1)влетает (2)вневписанная окружность (2)внутреннее сопротивление (1)внутреннее сопротивление источника (1)внутреннюю энергию (1)внутренняя энергия (8)вода (1)вода течет (1)воды (1)возведение в квадрат (1)возвратное уравнение (1)возвратность (1)возвратные уравнения (2)воздушный шар (1)возрастающая (1)возрастет (1)волны (1)вписанная (1)вписанная окружность (3)вписанная сфера (1)вписанной окружности (1)вписанный угол (4)в правильной пирамиде (1)вращается (1)вращение (1)времени (2)время (24)время в минутах (1)время выполнения (1)время движения (2)время минимально (1)время падения (1)все значения а (1)всесибирская олимпиада (1)в стоячей воде (1)встретились (1)встретятся (1)вступительный (1)вступительный экзамен (1)вторая половина пути (1)вторая экваториальная система координат (1)вторичная (1)вторичная обмотка (1)вторичные изображения (1)второй закон (1)второй закон Кеплера (1)второй закон Ньютона (4)выбор двигателя (1)выборка корней (4)вывод формул тригонометрии (1)выколотая точка (1)выплаты (2)выразить вектор (1)высота (5)высота Солнца (1)высота столба (1)высота столба жидкости (1)высота столбика (1)высоте (3)высоту (1)высоты (3)выталкивающая сила (2)вычисления (2)газ (3)газа (1)газов (1)газовая атмосфера (1)галочка (1)гамма-лучей (1)гармоника (2)гвоздя (1)геометрическая вероятность (1)геометрическая прогрессия (4)геометрические высказывания (1)геометрический смысл (2)геометрическую прогрессию (1)геометрия (7)гигрометр (1)гидродинамика (1)гидростатика (3)гимназия при ВШЭ (1)гипербола (2)гипотенуза (3)гистерезисный двигатель (1)главный период (1)глубина (1)глухозаземленная нейтраль (1)гомотетия (2)гонщик (1)горизонтальная сила (1)горизонтальной спицы (1)горизонтальную силу (1)горка (1)гравитационная постоянная (1)градус (1)грани (2)график (2)графики функций (5)графически (1)графический способ (1)графическое решение (3)груз (2)грузик (2)грузовик (1)грузы (1)группа (1)давление (28)давление жидкости (3)давление пара (1)дальность полета (1)две линзы (1)двигатель с активным ротором (1)движение под углом (2)движение под углом к горизонту (4)движение по кругу (1)движение по течению (1)движение с постоянной скоростью (2)движется груз (1)двойное неравенство (1)двойной фокус (1)двойным неравенством (1)двугранный угол при вершине (2)девальвация (1)действительная часть (1)действующее значение (2)деление (1)деление многочленов (2)деление уголком (1)делимость (23)делимость чисел (1)делители (1)делитель (2)делится (3)демонстрационный варант (1)деталей в час (1)диаграмма (1)диаметр (2)диаметру (1)динамика (4)диод (1)диск (2)дискриминант (5)дифракционная решетка (2)дифференцированный платеж (6)диффузия (1)диэлектрик (1)диэлектрическая проницаемость (1)длина (4)длина вектора (1)длина волны (7)длина медианы (1)длина отрезка (2)длина пружины (1)длина тени (1)длиной волны (2)длину нити (1)длины поездов (1)длительность разгона (1)длительный режим (1)добротность (1)догнал (1)догоняет (1)докажите (1)долг (1)доля (1)дополнительный угол (2)досок (1)досрочный (2)досрочный вариант (1)дптр (2)дуга (1)единицы продукции (1)единичный источник (1)единичных кубов (1)единмтвенное решение (1)единственный корень (1)ежесекундно (1)емкость (7)емкость заряженного шара (1)естественная область определения (1)желоб (2)жесткость (6)жеткость (1)живая математика (2)жидкости (1)жидкость (1)завод (1)загадка (2)задание 13 (2)задание 15 (3)задание 23 (1)задания 1-14 ЕГЭ (1)задача 4 ЕГЭ (2)задача 9 (1)задача 13 ЕГЭ (1)задача 13 профиль (1)задача 14 профиль (3)задача 15 профиль (1)задача 16 (1)задача 16 ЕГЭ (1)задача 16 профиль (4)задача 17 (1)задача 18 (1)задача 19 (2)задача 26 ОГЭ (2)задача с параметром (7)задачи (1)задачи на доказательство (4)задачи на разрезание (4)задачи на совместную работу (3)задачи про часы (1)задачи с фантазией (1)задерживающее напряжение (1)заземление (1)заказ (1)закон Бернулли (1)закон Гука (1)закон Ома (3)закон Снеллиуса (1)закон Стефана-Больцмана (1)закона сохранения (1)закон движения (1)закон кулона (7)закон палочки (6)закон сложения классических скоростей (1)закон сохранения импульса (7)закон сохранения энергии (4)законы Кирхгофа (6)законы коммутации (1)законы сохранения (1)закрытым концом (1)замена переменной (2)заметаемый сектор (1)замкнутая система (2)зануление (1)запаянная (2)заряд (9)заряда (1)заряд конденсатора (1)заряженная сфера (1)заряженный шар (1)защитная характеристика (1)звездочка (1)звезды (1)зенит (1)зенитное расстояние (1)зеркало (2)знак неравенства (1)знаменатель (1)знаменатель прогрессии (4)значение выражения (1)идеальный блок (1)идеальный газ (5)извлечение в столбик (1)излом (1)излучение (2)изменение длины (2)изменение импульса (2)изобара (1)изобаричесикй (1)изобарический (2)изобарный (1)изобарный процесс (1)изображение (3)изолированная нейтраль (1)изопроцессы (1)изотерма (2)изотермически (1)изотермический (2)изотермический процесс (1)изотоп (1)изохора (1)изохорический (1)изохорный процесс (1)импульс (11)импульса (1)импульс силы (2)импульс системы (1)импульс системы тел (4)импульс тела (4)импульс частицы (1)инвариантность (1)индуктивно-связанные цепи (1)индуктивное сопротивление (1)индуктивность (1)индукцией (1)индукция (8)интеграл Дюамеля (1)интервал (1)интересное (3)интерференционных полос (1)интерференция (1)иррациональное уравнение (2)иррациональность (2)испарение (2)исследование функции (4)источник (1)источник света (1)исход (1)камень (1)
Цепи — ток, разность потенциалов, сопротивление и элементы в последовательной и параллельной цепях, сохранение заряда
Элементы последовательно и параллельно
Ячейки в серии
Когда элементы соединены последовательно друг с другом, и все они подключены в одном направлении, общая разность потенциалов, подаваемая в цепь, представляет собой сложенные вместе индивидуальные разности потенциалов.
В всего = В 1 + В 2 + В 3
Идентичные ячейки параллельно друг другу
Когда идентичные элементы параллельны друг другу, общая разность потенциалов, подаваемая в цепь, равна разности потенциалов только одной из ячеек.
В всего = В 1 = В 2 = В 3
Итак, если три ячейки 2 В соединены параллельно друг с другом, разность потенциалов, подаваемая в цепь, составляет 2 В.
Резисторы последовательно и параллельно
Резисторы серии
Когда резисторы соединены последовательно друг с другом, общее сопротивление складывается из отдельных сопротивлений.
Резисторы параллельно
Когда резисторов соединены параллельно друг с другом, общее сопротивление определяется с помощью следующего уравнения.
Ток в последовательной и параллельной цепях
Сохранение заряда — «общий заряд, протекающий в стык проводов, должен быть равен полному заряду, вытекающему из стыка».
Первый закон Кирхгофа — «сумма токов, протекающих в месте соединения проводов, должна равняться сумме токов, исходящих от места соединения проводов».
Ток в последовательных цепях .
Когда вы включаете амперметр в последовательную цепь, ток остается неизменным, куда бы вы ни вставили амперметр.
Ток в параллельных цепях .
Полный ток, протекающий от ячейки к ветвям в цепи, всегда должен быть равен току, протекающему через каждый компонент в ветвях цепи, когда они складываются.
Если компоненты имеют разное сопротивление, тогда ток через каждый компонент может быть разным, но когда вы складываете их вместе, они должны составлять общую сумму тока, выходящего из ячейки.
Разница потенциалов в последовательной и параллельной цепях
Второй закон Кирхгофа — «сумма ЭДС в любом замкнутом контуре в цепи должна быть равна сумме разностей потенциалов в замкнутом контуре в цепи».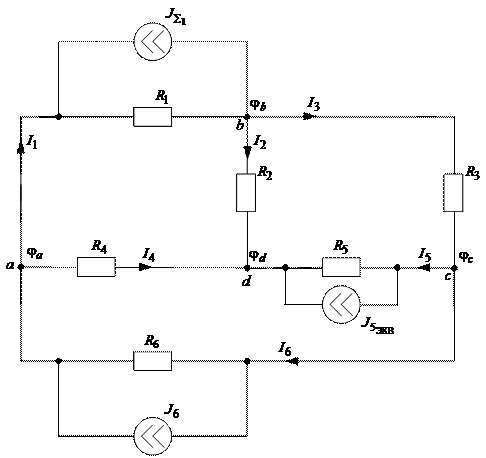
Разность потенциалов в последовательной цепи .
Полная разность потенциалов, подаваемая ячейкой, делится между компонентами. Если все компоненты имеют одинаковое сопротивление, между ними будет одинаковая разность потенциалов.
Если сопротивления не равны, они могут иметь разную величину разности потенциалов на них, но при суммировании они всегда должны равняться p.d. поставляемый ячейкой.
Разность потенциалов в параллельных цепях .
Разность потенциалов, подаваемая элементом, равна разности потенциалов каждого компонента в параллельной цепи.
14.6: Колебания в цепи LC
Цели обучения
К концу этого раздела вы сможете:
- Объясните, почему заряд или ток колеблются между конденсатором и катушкой индуктивности, соответственно, при последовательном соединении
- Опишите взаимосвязь между зарядом и током, колеблющимся между конденсатором и катушкой индуктивности, соединенными последовательно
Следует отметить, что и конденсаторы, и катушки индуктивности накапливают энергию в своих электрических и магнитных полях соответственно.Цепь, содержащая как катушку индуктивности ( L ), так и конденсатор ( C ), может колебаться без источника ЭДС, сдвигая энергию, запасенную в цепи, между электрическим и магнитным полями. Таким образом, концепции, которые мы развиваем в этом разделе, напрямую применимы к обмену энергией между электрическим и магнитным полями в электромагнитных волнах или свете. Начнем с идеализированной схемы с нулевым сопротивлением, которая содержит катушку индуктивности и конденсатор, схему LC .2} {C}. \]
Когда переключатель замкнут, конденсатор начинает разряжаться, создавая ток в цепи. Ток, в свою очередь, создает магнитное поле в индукторе. Конечным результатом этого процесса является передача энергии от конденсатора с его уменьшающимся электрическим полем к индуктору с его увеличивающимся магнитным полем.
Рисунок \ (\ PageIndex {1} \): (a – d) Колебания накопителя заряда при изменении направления тока в цепи LC . (e) Графики показывают распределение заряда и тока между конденсатором и катушкой индуктивности.2. \]
После достижения максимального значения \ (I_0 \), ток i (t) продолжает переносить заряд между пластинами конденсатора, тем самым заряжая конденсатор. Поскольку катушка индуктивности сопротивляется изменению тока, ток продолжает течь, даже если конденсатор разряжен. Этот непрерывный ток заставляет конденсатор заряжаться с противоположной полярностью. Электрическое поле конденсатора увеличивается, в то время как магнитное поле индуктора уменьшается, и общий эффект заключается в передаче энергии от индуктора обратно к конденсатору.По закону сохранения энергии максимальный заряд, который повторно приобретает конденсатор, равен \ (q_0 \). Однако, как показано на рисунке \ (\ PageIndex {1c} \), пластины конденсатора заряжены на против по сравнению с первоначальным зарядом.
После полной зарядки конденсатор снова передает свою энергию катушке индуктивности, пока она снова полностью не разрядится, как показано на рисунке \ (\ PageIndex {1d} \). Затем, в последней части этого циклического процесса, энергия возвращается к конденсатору, и исходное состояние схемы восстанавливается.2/2 \). При отсутствии трения в системе масса-пружина колебания будут продолжаться бесконечно. Точно так же колебания цепи LC без сопротивления будут продолжаться вечно, если их не нарушить; однако эта идеальная схема LC с нулевым сопротивлением неприменима, и любая схема LC будет иметь хотя бы небольшое сопротивление, которое со временем будет излучать и терять энергию.
Частоту колебаний в цепи без сопротивления LC можно найти по аналогии с системой масса-пружина.2. \]
Равнозначность двух систем очевидна. Чтобы перейти от механической системы к электромагнитной, мы просто заменяем m на L , v на i , k на 1/ C и x на q . Теперь x (t) даётся
\ [x (t) = A \, cos (\ omega t + \ phi) \], где \ (\ omega = \ sqrt {k / m} \). Следовательно, заряд конденсатора в цепи LC равен
.
\ [q (t) = q_0 \, cos (\ omega t + \ phi) \ label {14.40} \]
, где угловая частота колебаний в контуре
\ [\ omega = \ sqrt {\ frac {1} {LC}}. \ label {14.41} \]
Наконец, ток в цепи LC находится путем взятия производной по времени от q (t) :
\ [i (t) = \ frac {dq (t)} {dt} = — \ omega q_0 \, sin (\ omega t + \ phi). \]
Временные изменения q и I показаны на рисунке \ (\ PageIndex {1e} \) для \ (\ phi = 0 \).
Цепь LC
В цепи LC собственная индуктивность равна \ (2.{-5} \) C. (а) Какая угловая частота колебаний в контуре? б) Каков максимальный ток, протекающий через цепь? (c) Сколько времени нужно, чтобы конденсатор полностью разрядился? (d) Найдите уравнение, которое представляет q (t) .
Стратегия
Угловая частота цепи LC задается уравнением \ ref {14.41}. Чтобы найти максимальный ток, максимальная энергия в конденсаторе устанавливается равной максимальной энергии в катушке индуктивности.Время разряда конденсатора, если он изначально заряжен, составляет четверть периода цикла, поэтому, если мы вычислим период колебаний, мы сможем найти
Глоссарий терминов и расчетов Первоначально составлено Крисом Рандлом, бакалавром, доктором философии, ноябрь 1999 г. Щелкните подчеркнутую начальную букву, чтобы перейти к соответствующему разделу B C D E F G H I 9027 M 9027 L 9027 L 9027 L 9027 O P Q R S T UV W 000 XY Z Точность: Мера близости результата к истинному значению (ср.точность). Активность: Эффективное количество свободного иона в растворе (ср. Концентрацию). Активность иона в растворе для любой известной концентрации может быть вычислена по формуле:
Коэффициент активности: Коэффициент активности зависит от ионной силы раствора.Он становится все ниже по мере увеличения ионной силы из-за межионных взаимодействий. См. Таблицу коэффициентов активности в нашем руководстве для начинающих по ионно-селективным электродным измерениям. Коэффициент активности для любого иона в растворе можно рассчитать, используя уравнение Дебая-Хюккеля (в модификации Дэвиса): Где: Обратите внимание, что общепринято, что эта формула точна только до I = 0.1 моляр. При более высокой ионной силе начинают действовать другие факторы, которые делают расчет коэффициентов активности практически невозможным. Кроме того, это требует знания типа и концентрации всех компонентов в растворе и, таким образом, невозможно для многих природных образцов. Одним из способов преодоления разницы между активностью и концентрацией является добавление ISAB (буфер для регулировки ионной силы) как к образцам, так и к стандартам, чтобы уравнять ионную силу и, следовательно, коэффициенты активности, и позволить считывать концентрации непосредственно с калибровочных графиков.Однако следует отметить, что большинство рецептов добавления ISAB дают увеличение только на 0,1M и поэтому будут эффективны только в том случае, если IS исходного образца значительно ниже этого. Кроме того, при низких значениях ионной силы (например, ниже 0,01 М для одновалентных ионов и 0,001 М для двухвалентных ионов) разница между концентрацией и активностью относительно мала, и использование единиц концентрации вместо активности для калибровки не должно вызывать значительной ошибки в определение даже без ISAB.Например, коэффициент активности составляет около 0,9 при I = 0,01 M и 0,97 при 0,001 M для большинства одновалентных ионов и около 0,87 при I = 0,001 M и 0,96 при 0,0001 M для большинства двухвалентных ионов. Другие методы преодоления разницы между активностью и концентрацией:
Анион: Отрицательно заряженный ион. (например: Cl —, S 2-, NO 3 —, CO 3 2-) ATC = Автоматическая компенсация температуры: Автоматическая регулировка отображаемой активности или концентрации pH для корректировки отклонений наклона электрода из-за изменений температуры во время анализа. Среднее число: Количество мгновенных показаний потенциала электрода, снятых с интервалом в одну секунду, используемых для расчета среднего значения для милливольт.Переменная, выбираемая оператором в программном обеспечении компьютерного интерфейса ELIT Ion Analyzer, которая помогает снизить уровень шума и повысить точность измерений ISE. Верх
Мостовое решение: Буферный раствор: — см. ISAB (буфер для регулировки ионной силы) и TISAB. Буфер BS-1: (pH = 3,8) Специальный буфер для измерения содержания нитрит-иона в мясных экстрактах. Буфер BS-2: (pH = 3,2) Специальный буфер для измерения нитрит-иона в Верх Калибровка: Катион: Комбинированный электрод: Комбинация чувствительного электрода и электрода сравнения, содержащихся в одном устройстве. Комплексообразователь: Любое соединение, которое объединяется с ионом в растворе с образованием недиссоциированной молекулы, так что полученный комплекс остается в растворе и не выпадает в осадок. Тем не менее ион эффективно удаляется из раствора и не может быть обнаружен с помощью ISE.Комплексообразующие агенты используются в качестве титрантов и для удаления мешающих ионов. Концентрация: Общая масса иона или молекулы в данном объеме раствора (сравните активность). При измерении концентрации ионов с помощью ионоселективных электродов важно отметить, что концентрация, используемая в калибровочных графиках и рассчитанная для образцов, является концентрацией свободного иона в растворе, а не концентрацией соединения, из которого этот ион получен. Они будут такими же, только если используются единицы молярной концентрации и если обнаруженный ион имеет самую высокую валентность в соединении, или для соединений, в которых оба иона являются одновалентными.Например, 1 молярный раствор CaCl 2 содержит 1 моль / л Ca + , но 2 моль / л Cl -. Необходимо также различать концентрацию свободных несвязанных ионов и общую концентрацию, которая может включать любые ионы, связанные с комплексообразующими агентами, и любые атомы в недиссоциированных молекулах. Единицы концентрации: Единицы количества, объема или веса вещества, растворенного в данном объеме раствора. NB: не в данном объеме растворителя! грамм на литр (г / л).например, 10 граммов твердого вещества, растворенного в растворителе, а затем разбавленного до 100 мл раствора = 100 г / л (примечание: 10 г твердого вещества, добавленное к 100 мл растворителя, будет немного менее концентрированным!)
частей на миллион (ppm). При использовании в контексте единиц химической концентрации это строго вес растворенного вещества в миллионах весовых единиц раствора. например 10 микрограммов (г) растворенного вещества в 1 грамме раствора или 10 миллиграммов (мг) в 1 килограмме (кг) = 10 частей на миллион. Однако, поскольку в работе ISE всегда используются водные растворы, а масса 1 мл воды очень близка к 1 г, часто используется ppm как сокращение для микрограммов на миллилитр (г / мл) или миллиграммов на литр (мг / мл). л).
моль на литр (моль / л или моль). Число атомных масс одноатомных частиц или молекулярных масс соединений, растворенных в одном литре раствора. например, 3,55 г хлорид-иона (или 5,85 г NaCl) в 100 мл = 1 M (олар) или 1 моль / л. Также может быть выражено в микромолях (моль / л) или миллимолях (ммоль / л). Эквиваленты на литр (экв / л) . Количество эквивалентных масс вещества, растворенного в 1 литре раствора. Эквивалентный вес — это вес элемента или соединения, которые будут реагировать с 1 г водорода или 8 г кислорода.Это атомный вес, деленный на валентность. Для одновалентных ионов это то же самое, что и молекулярная масса. Также выражается в миллиэквивалентах на литр (мг-экв / л) об.% (% Об.) . Процент от общего объема, добавленный к объему нового компонента, добавленного в раствор. например при добавлении ISAB в тестовый раствор часто описывается добавление 2% об. / об. Это должно строго означать добавление 2 мл ISAB к 98 мл образца, но на практике обычно интерпретируется как добавление 2 мл ISAB к 100 мл образца. мас.% (% Мас.) . Процент общего веса раствора, приходящийся на вес растворенных веществ.
Электропроводность: Мера способности раствора проводить электричество. Это величина, обратная сопротивлению, которое связывает сопротивление проводника (в омах) с его длиной и площадью поперечного сечения. Единицы измерения проводимости — Сименс на сантиметр (См / см). Эти единицы обычно довольно большие, поэтому чаще используются миллиСименс (мСм) или микроСименс (S).Электропроводность измеряется с помощью кондуктометрической ячейки. Он содержит два платиновых электрода известной площади, жестко закрепленных на расстоянии 1 см друг от друга. Электролитическая проводимость промежуточного раствора определяется пропусканием переменного тока между электродами. Верх
Уравнение Дебая-Хюккеля: См. Коэффициент активности. Агент декомплекса: Соединение, которое добавляют к раствору для высвобождения любых ионов, которые могут быть связаны в сложные молекулы, и позволяют их обнаруживать с помощью анализа ISE. Пределы обнаружения: «Стандартный предел обнаружения» — это концентрация (или активность) измеренного иона в точке пересечения экстраполированного линейного сегмента калибровочной кривой, представляющей нормальный наклон электрода, и горизонтальной линии, представляющей напряжение, когда концентрация настолько мал, что небольшие изменения концентрации не вызывают заметного изменения отклика электрода. Участок калибровочной кривой между этой точкой и началом действительно линейного участка известен как нелинейный диапазон электрода.Образцы по-прежнему поддаются измерению в этом диапазоне при условии, что несколько стандартов используются для точного определения изменяющегося наклона кривой или когда два стандарта могут ограничивать диапазон образцов. Однако погрешность в концентрации (погрешность измерения на милливольт) будет постепенно увеличиваться по мере уменьшения крутизны. Разведение: Эффект изменения концентрации раствора путем добавления большего количества растворителя. Разбавление 1:10 означает добавление 9 объемов растворителя к 1 объему исходного раствора. Концентрация полученного раствора составляет одну десятую от исходного.> Прямая потенциометрия: Это простейший метод проведения измерений на ионоселективных электродах.Электроды погружаются в тестовый раствор, и потенциал электрода измеряется непосредственно милливольтметром. Затем концентрация напрямую связана с этим измерением, считывая ответ с калибровочного графика логарифма концентрации в зависимости от милливольт. (см. уклон для деталей расчета) Константа диссоциации (K): Число, указывающее степень диссоциации молекулы в растворе с образованием свободных ионов. Для простой двухкомпонентной системы (например,: CH 3 COONa CH 3 COO — + Na + ) это произведение молярной концентрации двух ионов на молярную концентрацию недиссоциированной молекулы. Двухвалентный ион: Двухзарядный ион.Тот, в котором исходный инертный атом или молекула потерял или получил два электрона. (например, Ca 2+ , SO 4 2-) Дрейф: Медленное изменение измеренного потенциала пары электродов. Когда электроды впервые погружают в новый раствор, сначала происходит относительно быстрое изменение потенциала, который постепенно снижается, когда ионы в растворе приходят в равновесие с ионами, проходящими через ионоселективную мембрану. Обычно через две-три минуты достигается стабильное состояние.После этого при длительном погружении может произойти второй постепенный дрейф из-за развития дополнительных потенциалов в различных жидких переходах в электродной системе. Для точных измерений важно снимать показания до того, как эти вторичные процессы станут существенными. Дополнительным явлением, которое также называется дрейфом, является постепенное изменение показаний, если один и тот же раствор повторно измеряется несколько раз, при этом электроды удаляются и промываются (и / или погружаются в другой раствор) между каждым считыванием.Это может быть связано с рядом факторов, включая эффекты гистерезиса, неспособность эталонной системы установить одинаковый потенциал жидкого перехода при каждом погружении и увеличение гидратации мембраны ISE. Верх
Головка электрода: Литой пластиковый узел, содержащий одно или несколько гнезд для вставки соответствующих электродов, снабженных штепсельными разъемами. Головка электрода имеет дорогой экранированный кабель и вилку для подключения к измерительным приборам.Доступны различные модели для использования с одним электродом (моноголовка) или комбинацией ISE / эталон (двойная головка) или комбинацией различных ISE и / или электродов pH, окислительно-восстановительного потенциала или растворенного кислорода, используемых с общим электродом сравнения для нескольких компонентный анализ (множественная головка). Электролит: Соединение, которое диссоциирует на ионы в водном растворе или растворе, содержащем ионы. Слабые электролиты диссоциируют лишь частично (например, уксусная кислота; CH 3 COOH), тогда как сильные электролиты сильно или полностью диссоциируют (например,грамм. соляная кислота; HCL или хлорид натрия; NaCl). Сильные электролиты — хорошие проводники электричества. Проводимость. является мерой прочности электролита. Электрический провод: Любая часть измерительной системы ISE, которая позволяет электронам проходить через твердую среду. В частности, хлорированная серебряная проволока погружается в раствор для внутреннего наполнения. Электролитический проводник: Любой раствор, содержащий свободные ионы, которые могут проводить электрический ток.В измерениях ISE это включает растворы для заполнения электродов и внешний тестовый раствор. Эквитрансферентный раствор: Электролитический раствор, содержащий положительные и отрицательные ионы, которые имеют равную ионную подвижность (= скорость диффузии). Поэтому они могут проходить через пористую фритту электрода сравнения с равной легкостью и, таким образом, препятствовать развитию неравномерного распределения заряда. (См. Потенциал жидкого перехода). Верх
Раствор для наполнения: Электролитический раствор внутри чувствительного электрода или электрода сравнения, который необходимо периодически пополнять.С современной твердотельной технологией и / или гелевыми растворами во многих электродах теперь это обычно применимо только к раствору внешнего заполнения электродов сравнения с двойным переходом. Это образует мост между внутренним эталонным элементом и внешним образцом и постепенно просачивается через пористую фритту во время использования. Состав заполняющего раствора выбирается таким образом, чтобы максимизировать стабильность потенциалов, возникающих на внешнем и внутреннем жидкостных переходах. В идеале он должен состоять из эквитрансферентных ионов (т.е.е. как положительные, так и отрицательные ионы пересекают границу в равных количествах), он не должен содержать измеряемый ион или любой ион, который может помешать измерению, и он должен иметь ионную силу, по крайней мере, в десять раз превышающую ионную силу измеряемого образца .
Гистерезис (память электродов): Возникновение другого значения разности потенциалов после того, как концентрация тестового раствора была изменена и затем восстановлена до исходного значения. Эта систематическая ошибка обычно связана с концентрацией предыдущего раствора. Верх
Инкрементальные методы: Методы анализа, при которых вместо соотнесения измерений пробы с заранее заданным калибровочным графиком концентрация неизвестного определяется путем снятия показаний до и после смешивания известных количеств пробы и стандарта. Преимущества этих методов заключаются в том, что они сводят к минимуму любые различия в температуре и ионной силе между стандартом и образцом и гарантируют, что калибровка и измерения образца расположены близко во времени и выполняются в очень схожих условиях без удаления электродов из раствора; таким образом сводя к минимуму любые ошибки из-за дрейфа и гистерезиса.См. Раздел «Добавление стандарта» и «Добавление образца».
Интерфейс: Электронное устройство для подключения выхода ISE / эталонной ячейки непосредственно к настольному или портативному компьютеру без необходимости в дорогостоящем ионометре. Интерфейсы снабжены сложным программным обеспечением, которое облегчает сложную обработку, отображение и хранение данных. Несколько интерфейсов могут одновременно подключать несколько электродных систем к одному ПК и обеспечивать непрерывный мониторинг периодических процессов или одновременный многокомпонентный анализ. Помехи: Влияние любых частиц, кроме измеряемого иона, присутствующих в растворе образца, влияет на измеренную разность потенциалов ячейки. Наиболее частая причина помех связана с тем, что большинство ионоселективных мембран не на 100% селективны для обнаруженного иона. Многие в некоторой степени допускают прохождение других ионов. Эти дополнительные ионы обычно увеличивают измеренный потенциал электрода и вызывают ложно высокие результаты концентрации.См. Коэффициент селективности. Другие помехи могут быть вызваны химическими реакциями с материалом мембраны, которые могут вызывать положительные или отрицательные аномалии, и реакциями в образце, которые могут вызвать осаждение, комплексообразование, окисление или восстановление измеряемого иона и, следовательно, ложно низкие результаты. Мешающий ион: Любой ион в растворе, кроме измеряемого, который реагирует с мембраной ISE, изменяя измеренный потенциал.
Внутренний электрод сравнения (ИСЭ): Та часть электрода, которая электрически соединена с экранированным кабелем, который подключается к измерительному прибору.Обычно проволока из хлорированного серебра погружается в раствор или гель хлорида серебра / хлорида калия. В случае всех твердотельных электродов материал электрода сравнения наносится непосредственно на внутреннюю поверхность ионоселективной мембраны, и внутренний заполняющий раствор не требуется. Раствор для внутреннего наполнения (ISE): Водный раствор электолита, который может превращаться в гель, содержащий фиксированную концентрацию иона, для которой внутренний электрод сравнения является обратимым; обычно хлорид-ион в случае серебряных / хлоридсеребряных электродов.Это формирует электролитический проводник, который передает заряд от обнаруженного иона в ионоселективной мембране к электрическому проводнику (серебряному проводу), который передает заряд в измерительную систему. Не присутствует в
Ионометр: Сложный измеритель pH / милливольт, содержащий микропроцессор, который позволяет обрабатывать сигналы ISE, чтобы разрешить выбор. |
Страница Не найдена | MIT
Перейти к содержанию ↓
- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Меню ↓
Поиск
Меню
Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!
Что вы ищете?
Увидеть больше результатов
Предложения или отзывы?
.