Электрическое сопротивление — металл — Большая Энциклопедия Нефти и Газа, статья, страница 1
Электрическое сопротивление — металл
Cтраница 1
Электрическое сопротивление металла зависит в некоторой степени от его состояния. Обычно холодная протяжка увеличивает, а отжиг уменьшает электрическое сопротивление. Наматывание проволоки на катушку увеличивает ее электрическое сопротивление. Для чистых металлов электрическое сопротивление приблизительно пропорционально абсолютной температуре. Для сплавов эта зависимость не выполняется.
[1]
Электрическое сопротивление металлов и их сплавов существенно изменяется в зависимости от температуры. Это свойство чистых металлов и положено в основу измерения температуры электрическими термометрами сопротивления. Изменение сопротивления проводника в зависимости от температуры фиксируется прибором, работающим по той или иной электрической схеме и имеющим температурную шкалу. Термометры сопротивления применяются в довольно широких пределах: от — 200 до 00 С. Тештовоспринимающая часть, или чувствительный элемент, термометра сопротивления представляет собой тонкую проволоку, намотанную на жесткий каркас из изоляционного материала. Длина чувствительного элемента термометра сопротивления составляет обычно несколько сантиметров ( вместо точечного спая рабочего конца термопары), поэтому при наличии перепада температур в среде термометр сопротивления измеряет некоторую среднюю температуру слоев, в которых расположен чувствительный элемент.
Термометры сопротивления применяются в довольно широких пределах: от — 200 до 00 С. Тештовоспринимающая часть, или чувствительный элемент, термометра сопротивления представляет собой тонкую проволоку, намотанную на жесткий каркас из изоляционного материала. Длина чувствительного элемента термометра сопротивления составляет обычно несколько сантиметров ( вместо точечного спая рабочего конца термопары), поэтому при наличии перепада температур в среде термометр сопротивления измеряет некоторую среднюю температуру слоев, в которых расположен чувствительный элемент.
[2]
Электрическое сопротивление металлов и сплавов измеряют при помощи двойного моста Томсона или потенциометрическим методом на проволочных образцах.
[3]
Электрическое сопротивление металлов и сплавов необходимо учитывать при плавке в индукционных пе -, чах. При достижении температуры плавления электросопротивление большинства металлов увеличивается в 2 — 10 раз по сравнению с сопротивлением при комнатной температуре.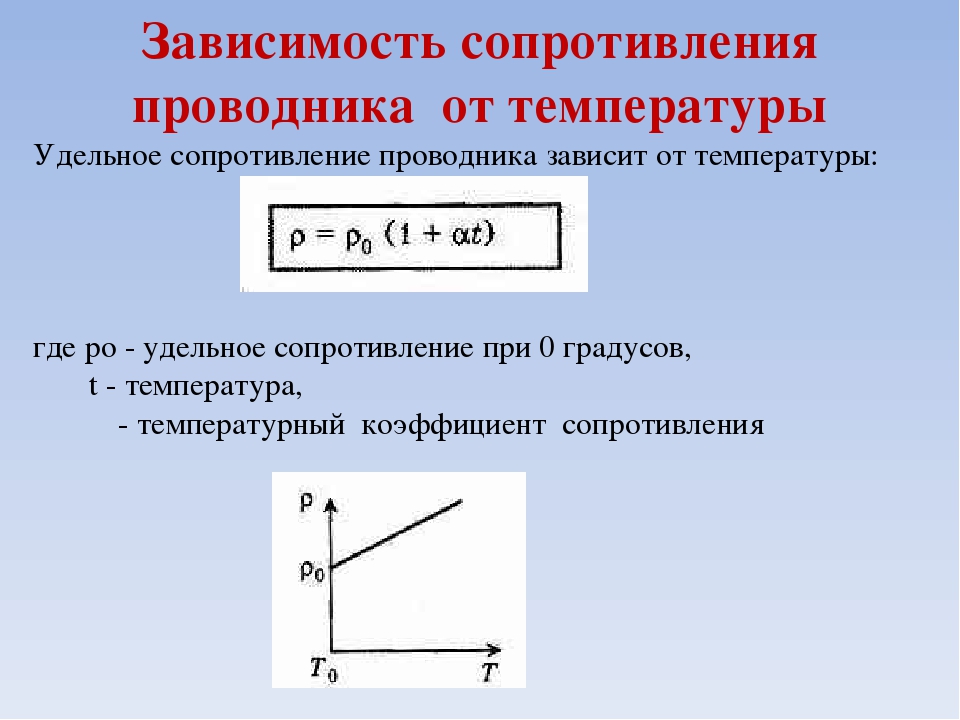
[4]
Электрическое сопротивление металлов и сплавов зависит от температуры.
[5]
Электрическое сопротивление металла можно повысить, сплавляя его с другими металлами.
[6]
Электрическое сопротивление металла зависит в некоторой степени от его состояния. Обычно холодная протяжка увеличивает, а отжиг уменьшает электрическое сопротивление. Наматывание проволоки на катушку увеличивает ее электрическое сопротивление. Для чистых металлов электрическое сопротивление приблизительно пропорционально абсолютной температуре. Для сплавов эта зависимость не выполняется.
[7]
Электрическое сопротивление металлов, а также некото-фых сплавов удовлетворяет всем требованиям, предъявляемым к термометрическому параметру. В самом деле, сопротивление R и его температурная зависимость хорошо воспроизводимы и легко могут быть сделаны независимыми от других факторов, кроме температуры.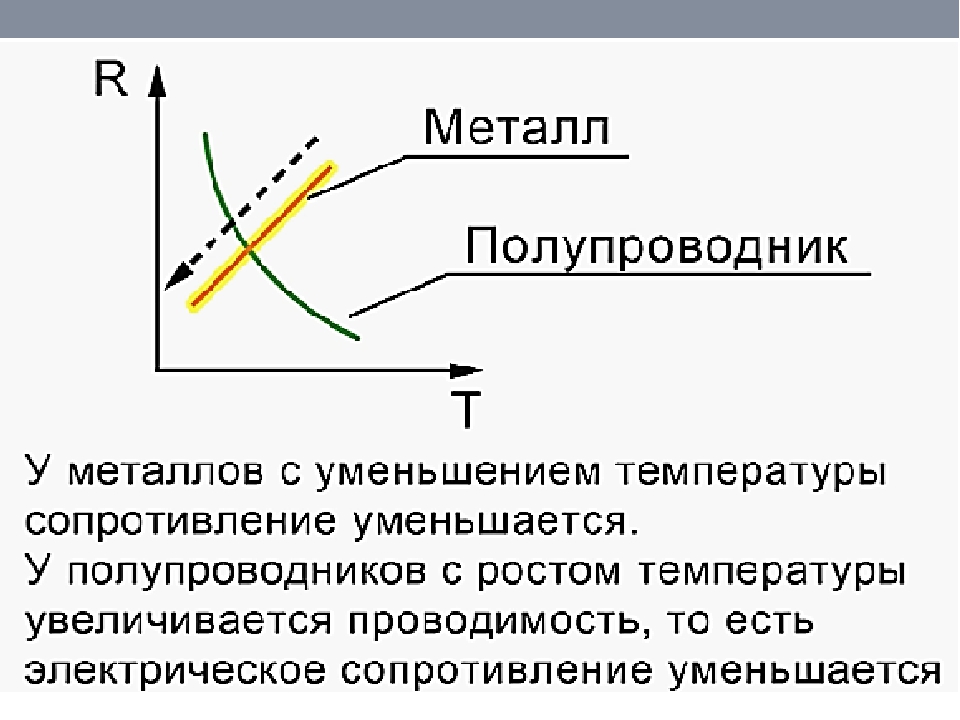
[8]
Электрическое сопротивление металлов широко используется в качестве термометрического параметра, но, как мы увидим, для топ же цели можно с успехом применять электросопротивление материалов другого класса — полупроводников. Прежде чем описывать термометры, изготовленные из полупроводников, рассмотрим природу температурной зависимости электросопротивления металлов и полупроводников.
[9]
Электрическое сопротивление металлов прямо зависит от температуры; с увеличением последней сопротивление возрастает, а с уменьшением — убывает.
[10]
Поскольку электрическое сопротивление металла обусловлено рассеянием электронов, находящихся на поверхности Ферми, рассмотрим пару электронов с энергиями ЕР.
[11]
Анализ электрического сопротивления металлов, произведенный Друде, можно непосредственно сопоставить с элементарной кинетической теорией газов.
[12]
Изменение электрического сопротивления металла при нагревании может служить косвенным методом определения его жаростойкости. Этот метод применяется часто при испытании нагревательных элементов. Испытываемая проволока нагревается до заданной температуры и выдерживается определенное время; при этом непрерывно фиксируется величина электрического сопротивления.
[13]
Анализ электрического сопротивления металлов, произведенный Друде, можно непосредственно сопоставить с элементарной кинетической теорией газов.
[14]
Увеличение электрического сопротивления металлов можно объяснить прежде всего тем, что при наклепе искажается пространственная решетка кристаллов. На значение электрического сопротивления влияет также и изменение межатомных связей, вызванных наклепом. Это изменение приводит также к увеличению межатомных расстояний.
[15]
Страницы:
1
2
3
4
Зависимость сопротивления проводника от температуры: почему увеличивается
Каждое вещество имеет свое удельное сопротивление. Причем сопротивление будет зависеть от температуры проводника. Убедимся в этом, проведя следующий опыт.
Пропустим ток через стальную спираль. В цепи со спиралью подключим последовательно амперметр. Он покажет некоторое значение. Теперь будем нагревать спираль в пламени газовой горелки. Значение силы тока, которое покажет амперметр, уменьшится. То есть, сила тока будет зависеть от температуры проводника.
Изменение сопротивления в зависимости от температуры
Пусть при температуре 0 градусов, сопротивление проводника равняется R0, а при температуре t сопротивление равно R, тогда относительное изменение сопротивления будет прямо пропорционально изменению температуры t:
В данной формуле а – коэффициент пропорциональности, который называют еще температурным коэффициентом. Он характеризует зависимость сопротивления, которым обладает вещество, от температуры.
Он характеризует зависимость сопротивления, которым обладает вещество, от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании его на 1 Кельвин.
Для всех металлов температурный коэффициент больше нуля. При изменениях температуры он будет незначительно меняться. Поэтому, если изменение температуры невелико, то температурный коэффициент можно считать постоянным, и равным среднему значению из этого интервала температур.
Растворы электролитов с ростом температуры сопротивление уменьшается. То есть для них температурный коэффициент будет меньше нуля.
Сопротивление проводника зависит от удельного сопротивления проводника и от размеров проводника. Так как размеры проводника при нагревании меняются незначительно, то основной составляющей изменения сопротивления проводника является удельное сопротивление.
Зависимость удельного сопротивления проводника от температуры
Попытаемся найти зависимость удельного сопротивления проводника от температуры.
Подставим в полученную выше формулу значения сопротивлений R=p*l/S R0=p0*l/S.
Получим следующую формулу:
Температурный коэффициент можно считать постоянным, следовательно, удельное сопротивление проводника будет прямо пропорционально температуре проводника.
Данная зависимость представлена на следующем рисунке.
Попробуем разобраться, почему увеличивается сопротивление
Когда мы повышаем температуру, то увеличивается амплитуда колебаний ионов в узлах кристаллической решетки. Следовательно, свободные электроны будут чаще с ними сталкиваться. При столкновении они будет терять направленность своего движения. Следовательно, сила тока будет уменьшаться.
Зависимость сопротивления проводника от температуры, широко используется в технике и физике. Например, в изготовлении термометров сопротивления.
Нужна помощь в учебе?
Предыдущая тема: Опыт Милликена и Иоффе: суть эксперимента и как это было
Следующая тема:   Сверхпроводимость: определение, история открытия, свойства и перспективы
Зависимость удельного сопротивления полупроводника от температуры
Зависимость удельного сопротивления полупроводника от температуры
[c. 196]
196]
Зависимость удельного сопротивления полупроводников от температуры и освещения. Опыты показывают, что при нагревании электрическое сопротивление полупроводниковых кристаллов уменьшается (рис. 157). Уменьшение электрического сопротивления полупроводников при нагревании объясняется тем, что с повышением температуры кристалла число освобождающихся [c.156]
Зависимость удельного сопротивления полупроводника от температуры может быть выражена экспоненциальной функцией
[c.207]
Рассмотрим теперь аналогичные характеристики электронных полупроводников. Эти. материалы обычно имеют удельные сопротивления в пределах от —10 дд юэ ом см при 0° С, т. е. значительно более высокие, чем у металлов, но гораздо более низкие, чем у изоляторов. На фиг. 1 приведены кривые зависимости удельного сопротивления р от температуры Т для двух типичных образцов полупроводников. Из кривых видно, что удельное
[c. 159]
159]
Таким образом, изменение удельного сопротивления полупроводника с собственной проводимостью в зависимости от температуры дается выражением [c.197]
Обычно к проводникам относят вещества с удельным сопротивлением менее 10 Ом -м, а к диэлектрикам — с р более 10 Ом -м удельное сопротивление полупроводников составляет 10″ —10 Ом -м. Однако при классификации веществ по электрическим свойствам кроме значения р необходимо учитывать и физическую природу электропроводности, в частности вид свободных носителей заряда и характер зависимости р от температуры. [c.7]
Качественное объяснение этих свойств графита было получено в результате расчетов, произведенных с помощью зонной модели [36, 37]. Установлено, что в направлении, параллельном слоям атомов углерода, вершина заполненной зоны электронных уровней касается дна проводящей зоны. Поэтому проводимость графита в этом направлении должна быть такой же, как и у полупроводника с собственной проводимостью при стремлении к нулю ширины запрещенной зоны. На основании расчетов, произведенных для чистого поликристаллического графита [36, 38], следует, что величина удельного сопротивления р изменяется при низких температурах пропорционально 1/Г. Присутствие химических загрязнений и физических неоднородностей приводит к появлению дополнительных уровней в месте соприкосновения заполненной валентной и пустой проводящей зон, в результате чего характер зависимости удельного сопротивления от температуры изменяется. Для графита с небольшим содержанием примеси величина удельного сопротивления должна возрастать при понижении температуры и принимать конечные значения при 0° К. Образцы очень загрязненного примесями графита должны обладать слабо выраженными. металлическими свойствами и иметь положительный температурный коэффициент даже при самых низких температурах.
[c.172]
На основании расчетов, произведенных для чистого поликристаллического графита [36, 38], следует, что величина удельного сопротивления р изменяется при низких температурах пропорционально 1/Г. Присутствие химических загрязнений и физических неоднородностей приводит к появлению дополнительных уровней в месте соприкосновения заполненной валентной и пустой проводящей зон, в результате чего характер зависимости удельного сопротивления от температуры изменяется. Для графита с небольшим содержанием примеси величина удельного сопротивления должна возрастать при понижении температуры и принимать конечные значения при 0° К. Образцы очень загрязненного примесями графита должны обладать слабо выраженными. металлическими свойствами и иметь положительный температурный коэффициент даже при самых низких температурах.
[c.172]
Контролируемое введение примесей в полупроводник позволяет в очень широких пределах изменять как удельное сопротивление, так и степень его зависимости от температуры. Если в полупроводник добавляется очень небольшое количество
[c.197]
Если в полупроводник добавляется очень небольшое количество
[c.197]
В разд. 5.1 показано, как влияет на свойства полупроводника введение небольшого количества примеси. Зависимость сопротивления от температуры чрезвычайно чувствительна к количеству и качеству вводимой примеси, что может использоваться для получения желаемых характеристик. Из рис. 5.7 видно, что для термометрических целей более всего интересны области III и IV. Хотя наклоном кривой и абсолютным значением удельного сопротивления можно в какой-то степени управлять, высокая чувствительность обоих этих параметров к малым изменениям концентрации примеси мешает получать
[c.235]
Цель лабораторной работы — определение зависимости величины удельного электрического сопротивления твердых проводников и полупроводников от изменения температуры с использованием стандартных методов. [c.141]
Полупроводниками называют вещества, удельное сопротивление которых при нормальной температуре находится между значениями удельных сопротивлений проводников и диэлектриков (в диапазоне от до 10 °. ..10 Омом). Основным свойством полупроводника является зависимость его электропроводности от воздействия температуры, электрического поля, излучения и других факторов. Полупроводники в отличие от проводников имеют отрицательный коэффициент температурного удельного сопротивления, электропроводность полупроводников с увеличением температуры растет экспоненциально.
[c.334]
..10 Омом). Основным свойством полупроводника является зависимость его электропроводности от воздействия температуры, электрического поля, излучения и других факторов. Полупроводники в отличие от проводников имеют отрицательный коэффициент температурного удельного сопротивления, электропроводность полупроводников с увеличением температуры растет экспоненциально.
[c.334]
На рис. 16 и 17—представлены величины удельного сопротивления карбида кремния в зависимости от давления, а на рис. 17 — в зависимости от зернистости. Электросопротивление полупроводников, как правило, снижается с повышением температуры, уменьшается под воздействием сильного электрического поля и увеличивается в магнитном поле [27]. [c.98]
Характер отклонения кривой зависимости 1п р от 1/7 от линейности для типичного термистора показывает, что удельное сопротивление термистора зависит от температуры так же, как удельное сопротивление примесного полупроводника, для которого наблюдается зависимость вида
[c. 165]
165]
Недостатками всех ферритов являются хрупкость и возможность обработки только шлифованием, а также резко выраженная зависимость магнитных свойств от температуры и механических воздействий. Ферриты являются магнитными полупроводниками и, следовательно, с ростом температуры их удельное сопротивление уменьшается, что вызывает увеличение потерь на вихревые токи. [c.86]
Прежде чем перейти к подробному обсуждению зависимости удельного сопротивления металлов и полупроводников от температуры, коснемся особенностей поведения концентрированных сплавов. Введение значительного количества примесных атомов в твердый раствор приводит к искажению кристаллической решетки. Вследствие этого появляется дополнительный вклад в рассеяние. Его величина почти не зависит от температуры и может во много раз превышать долю электрон-фонон-ного рассеяния в чистом металле. Изменение остаточного удельного сопротивления неупорядоченного сплава Си—Аи в зави-
[c. 191]
191]
Типичные температурные зависимости удельного сопротивления р полупроводниковых керамических сегнетоэлектриков приведены на рис. 21.17. Вдали от точки Кюри р снижается с ростом температуры, как и у других диэлектриков и полупроводников, однако в определенном интервале в окрестности точки Кюри наблюдается резкий аномальный рост р. Величина р увеличивается в тысячи, а иногда и миллионы раз. Это и есть позисторный эффект. Область положительного ТКр находится в области перестройки решетки при фазовом переходе. Если перестройка решетки происходит в узком интервале температур (четкий фазовый переход), то р увеличивается скачкообразно (кривые 1, 2, 5). В случае же сегнетоэлектриков с размытым фазовым переходом увеличение р с температурой плавное и происходит во всем интервале температур раз.мытия перехода (кривые 3, 4). [c.226]
Удельное сопротивление полупроводников является величиной изменчивой, зависящей от наличия примесей в материале и от технологии изготовления (многие полупроводники изготовляются посредством измельчения, смешения, прессования составных частей и последующего обжига, т. е. приемами керамической технологии (см. гл. 8). Как уже упоминалось, сопротивление полупроводников зависит от температуры в некоторых апучаях эта зависимость выражена весьма заметно, и такие полупроводники могут применяться в качестве элементов электрических устройств, для которых важна зависимость сопротивления от температуры ( т е р м о с о п р о т и в л е н и я ), В ряде случаев сопротивление полупроводников сильно зависит от освещенности, уменьшаясь при повышении последней такие полупроводники используются в качестве фотосопротивлений. Некоторые материалы типа полупроводников резко изменяют сопротивление в зависимости от величины приложенного напряжения, являясь нелинейными сопротивлениями . Полупроводники используются в качестве электронагревательных элемен-
[c.193]
е. приемами керамической технологии (см. гл. 8). Как уже упоминалось, сопротивление полупроводников зависит от температуры в некоторых апучаях эта зависимость выражена весьма заметно, и такие полупроводники могут применяться в качестве элементов электрических устройств, для которых важна зависимость сопротивления от температуры ( т е р м о с о п р о т и в л е н и я ), В ряде случаев сопротивление полупроводников сильно зависит от освещенности, уменьшаясь при повышении последней такие полупроводники используются в качестве фотосопротивлений. Некоторые материалы типа полупроводников резко изменяют сопротивление в зависимости от величины приложенного напряжения, являясь нелинейными сопротивлениями . Полупроводники используются в качестве электронагревательных элемен-
[c.193]
Простая модель электронного газа, созданная Друде в 1900 г., успещно предсказала законы Ома и Видемана — Франца. Однако она не объяснила зависимость электропроводности от температуры, а также магнитные свойства и малую величину электронной теплоемкости по сравнению с классическим значением 3/ .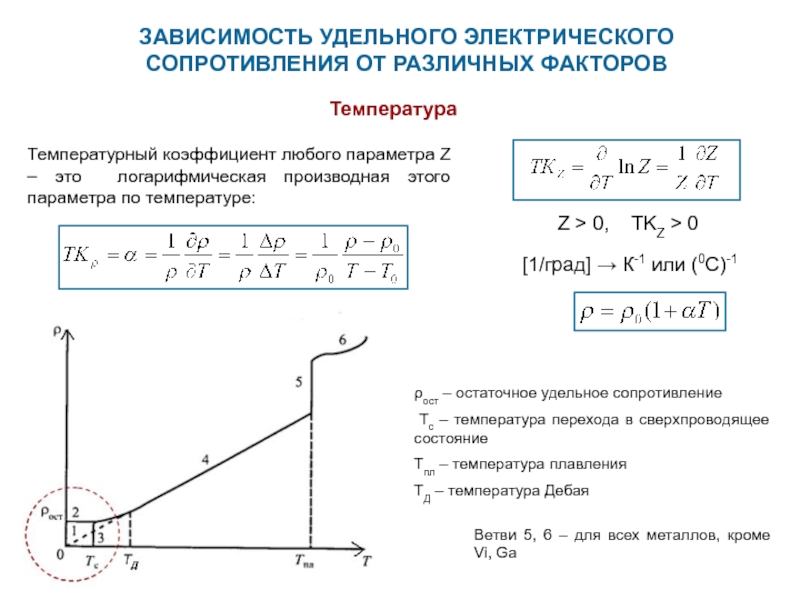 В настоящее время ясно, почему удельное сопротивление особо чистых металлов падает от типичного для комнатных температур значения 10 мкОм см до значения менее 10 з мкОм -см при температуре жидкого гелия в то время как удельное сопротивление концентрированного сплава падает всего в два раза в том же диапазоне температур. Поведение полупроводников также хорошо понято удельное сопротивление экспоненциально возрастает при уменьшении температуры, и при очень низких температурах чистые полупроводники становятся хорошими диэлектриками. Добавка в образец полупроводника небольшого количества примесей чаще всего существенно уменьшает удельное сопротивление (в противоположность чистым металлам, в которых наличие примесей ведет к увеличению удельного сопротивления).
[c.187]
В настоящее время ясно, почему удельное сопротивление особо чистых металлов падает от типичного для комнатных температур значения 10 мкОм см до значения менее 10 з мкОм -см при температуре жидкого гелия в то время как удельное сопротивление концентрированного сплава падает всего в два раза в том же диапазоне температур. Поведение полупроводников также хорошо понято удельное сопротивление экспоненциально возрастает при уменьшении температуры, и при очень низких температурах чистые полупроводники становятся хорошими диэлектриками. Добавка в образец полупроводника небольшого количества примесей чаще всего существенно уменьшает удельное сопротивление (в противоположность чистым металлам, в которых наличие примесей ведет к увеличению удельного сопротивления).
[c.187]
Существует класс полупроводниковых приборов, выполненных на основе смешанных окислов переходных металлов, которые известны под общим названием термисторов. Термин термистор происходит от слов термочувствительный резистор . Толчком к разработке термисторов послужила необходимость компенсировать изменение параметров электронных схем под влиянием колебаний температуры. Первые термисторы изготавливались на основе двуокиси урана ПОг, но затем в начале 30-х годов стали использовать шпинель MgTiOз. Оказалось, что удельное сопротивление MgTiOз и его температурный коэффициент сопротивления (ТКС) легко варьируются путем контролируемого восстановления в водороде и путем изменений концентрации MgO по сравнению со стехиометрической. Использовалась также окись меди СиО. Современные термисторы [60, 61] почти всегда представляют собой нестехиометрические смеси окислов и изготавливаются путем спекания микронных частиц компонентов в контролируемой атмосфере. В зависимости от того, в какой атмосфере происходит спекание (окислительной или восстановительной), может получиться, например, полупроводник п-типа на поверхности зерна, переходящий в полупроводник р-типа в глубине зерна, со всеми вытекающими отсюда последствиями для процессов проводимости.
Толчком к разработке термисторов послужила необходимость компенсировать изменение параметров электронных схем под влиянием колебаний температуры. Первые термисторы изготавливались на основе двуокиси урана ПОг, но затем в начале 30-х годов стали использовать шпинель MgTiOз. Оказалось, что удельное сопротивление MgTiOз и его температурный коэффициент сопротивления (ТКС) легко варьируются путем контролируемого восстановления в водороде и путем изменений концентрации MgO по сравнению со стехиометрической. Использовалась также окись меди СиО. Современные термисторы [60, 61] почти всегда представляют собой нестехиометрические смеси окислов и изготавливаются путем спекания микронных частиц компонентов в контролируемой атмосфере. В зависимости от того, в какой атмосфере происходит спекание (окислительной или восстановительной), может получиться, например, полупроводник п-типа на поверхности зерна, переходящий в полупроводник р-типа в глубине зерна, со всеми вытекающими отсюда последствиями для процессов проводимости.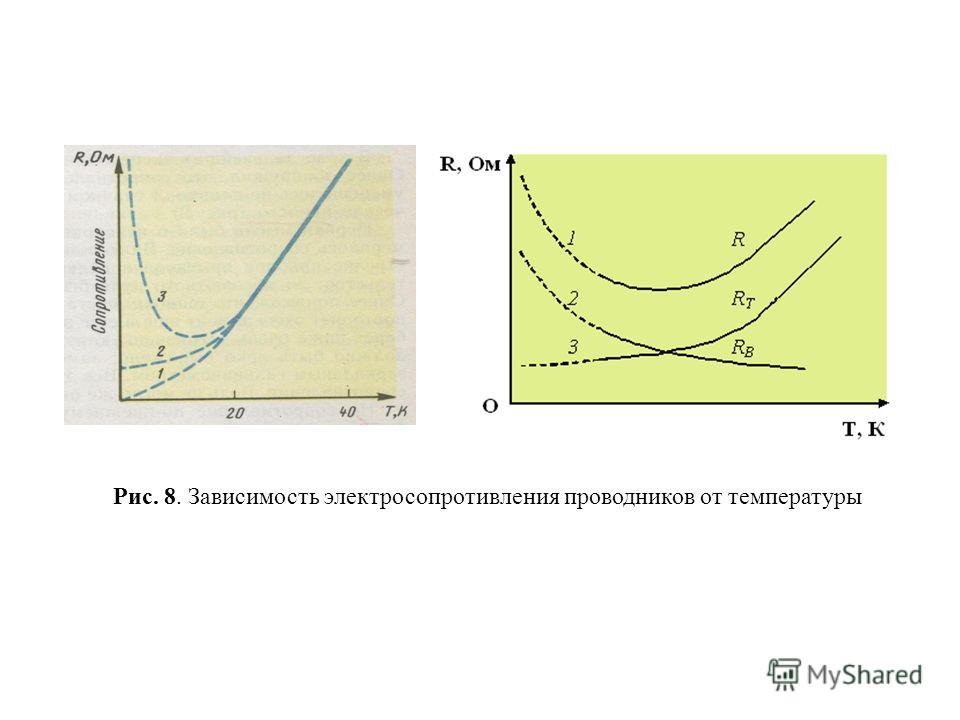 Помимо характера проводимости в отдельном зерне, на проводимость материала оказывают существенное влияние также процессы на границах между спеченными зернами. Высокочастотная дисперсия у термисторов, например, возникает вследствие того, что они представляют собой сложную структуру, образованную зонами плохой проводимости на границах зерен и зонами относительно высокой проводимости внутри зерен.
[c.243]
Помимо характера проводимости в отдельном зерне, на проводимость материала оказывают существенное влияние также процессы на границах между спеченными зернами. Высокочастотная дисперсия у термисторов, например, возникает вследствие того, что они представляют собой сложную структуру, образованную зонами плохой проводимости на границах зерен и зонами относительно высокой проводимости внутри зерен.
[c.243]
Ниже будет рассмотрено изменение электросопротивления с температурой для некоторых типов угольных термометров сопротивления. Даже качественное совпадение с тем, что дает зонная теория, наблюдается только в отдельных случаях. Для некоторых образцов величина удельного сопротивления р увеличивается почти экспоненциально при понижении температуры, указывая на то, что имеет место термическая активация носителей тока. Однако из этого не следует, что весь объем графита является элементарным полупроводником и что теоретическое предсказание оказывается несостоятельным. Характер изменения величины электросопротивления с температурой может быть объяснен тем, что частицы графита, входящие в состав образца, обычно находятся в плохом контакте друг с другом или с металлическими контактами. Поэтому носители должны быть тер.мически активированы для преодоления значительных энергетических барьеров. Этот процесс активации может привести к такой зависимости электросопротивления от температуры, которая наблюдалась выше. Очевидно, что способ изготовления угольных сопротивлений играет наиболее важную, хотя и трудно определимую роль при получении желаемых характеристик.
[c.173]
Характер изменения величины электросопротивления с температурой может быть объяснен тем, что частицы графита, входящие в состав образца, обычно находятся в плохом контакте друг с другом или с металлическими контактами. Поэтому носители должны быть тер.мически активированы для преодоления значительных энергетических барьеров. Этот процесс активации может привести к такой зависимости электросопротивления от температуры, которая наблюдалась выше. Очевидно, что способ изготовления угольных сопротивлений играет наиболее важную, хотя и трудно определимую роль при получении желаемых характеристик.
[c.173]
Пленки больщинства металлов (например, благородных металлов и неферромагнитных металлов переходной группы) толщиной в несколько сот ангстрем имеют удельное электросопротивление, величина которого изменяется с изменением температуры так же, как и у сплошных металлов. Однако пленки этих металлов толщиной в несколько ангстрем имеют большое удельное электросопротивление и большой отрицательный температурный коэффициент.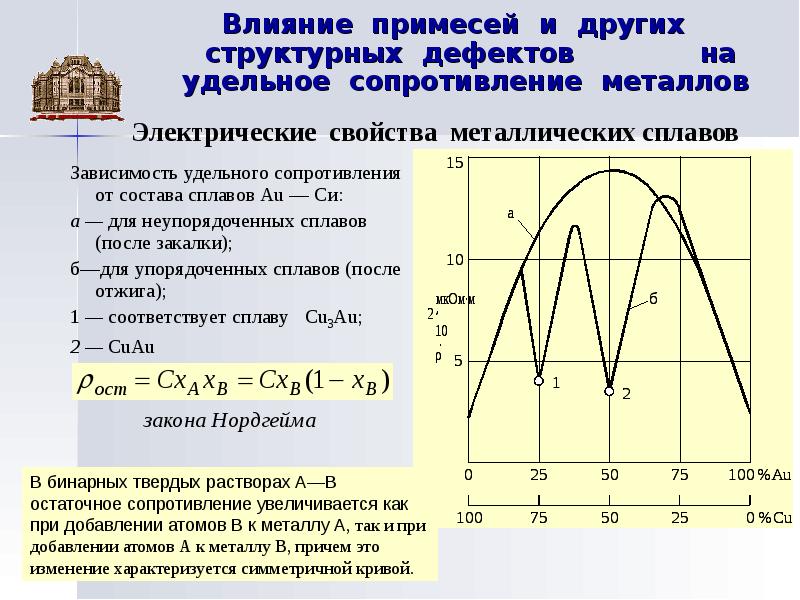 Зависи.мость сопротивления этих пленок от те.мпературы в широком интервале температур описывается уравнением, характерным для примесных полупроводников. Энергия активации в сильной степени зависит от состава пленок и их толщины. Для пленок значительной толщины, но еще не настолько толстых, чтобы появились типичные металлические свойства, зависимость сопротивления от температуры оказывается более сложной. Характеристики этих пленок и воспроизводимость их свойств сильно зависят от способа приготовления пленки, от присутствия сорбируе.мых газов, а в некоторых случаях — от старения и отжига.
[c.181]
Зависи.мость сопротивления этих пленок от те.мпературы в широком интервале температур описывается уравнением, характерным для примесных полупроводников. Энергия активации в сильной степени зависит от состава пленок и их толщины. Для пленок значительной толщины, но еще не настолько толстых, чтобы появились типичные металлические свойства, зависимость сопротивления от температуры оказывается более сложной. Характеристики этих пленок и воспроизводимость их свойств сильно зависят от способа приготовления пленки, от присутствия сорбируе.мых газов, а в некоторых случаях — от старения и отжига.
[c.181]
Выше приведено значение удельного сопротивления германия весьма высокой чистоты, близкое к значению собственного со-ттротивления германия. Примеси сильно понижают удельное сопротивление германия. С увеличением температуры удельное электросопротивление германия (как и у всех полупроводников) понижается. Характерна зависимость электросопротивления германия от давления. [c.376]
[c.376]
Удельное электрическое сопротивление любого радиоматериала в значительной степени зависит от температуры (рис. 1). Так, у проводников с повышением температуры удельное сопротивление возрастает. Это связано с более интенсивным колебанием атомов в узлах кристаллической решетки проводника, что мешает направленному перемещению свободных электронов В связи с этим общее и удельное электрические сопротивления проводников увеличиваются. У полупроводников и диэлектриков, наоборот, с возрастанием температуры общее и удельное сопротивления уменьшаются. Это объясняется увеличением энергии носителей элек-Рис. 1. Зависимость удель- тоических зяпялов ного электрического сопро- трических зарядов. [c.6]
Измерение электрофизических свойств Ag2Se показало, что при комнатной температуре селенид серебра является электронным полупроводником с удельным сопротивлением 10-10 ом-см, подвижностью электронов 2050 см (в-сек). Термоэлектродвижущая сила селенида в зависимости от способа приготовления колеблется от 140 до 160 мв град [42]. Теплопроводность АдгЗе при комнатной температуре минимальная при 40°С 5на имеет максимальную величину, составляющую 3-10 з кал (см-сек-град).
[c.109]
Теплопроводность АдгЗе при комнатной температуре минимальная при 40°С 5на имеет максимальную величину, составляющую 3-10 з кал (см-сек-град).
[c.109]
Перейдем теперь к рассмотрению менее изученного класса жидкостей с высоким удельным электрическим сопротивлением. Чистый селен изучали в течение долгого времени. По сравнению с другими жидкими полупроводниками молекулярная структура селена хорошо изучена. Жидкая сера очень похожа на жидкий селен, и было показано, что обе эти жидкости состоят из смеси цепных молекул и восьмичленных колец (а возможно и больших колец). Концентрация колец увеличивается с понижением температуры, и имеется критическая температура, ниже которой существуют только кольцевые молекулы. Критическая температура экспериментально наблюдалась только для жидкой серы для селена расчетное значение этой температуры лежит ниже точки затвердевания. Теория равновесия связей для этих жидкостей разработана очень хорошо [78, 104], и эта теория является прототипом теории для сплавов Т1—Те, описанной в гл.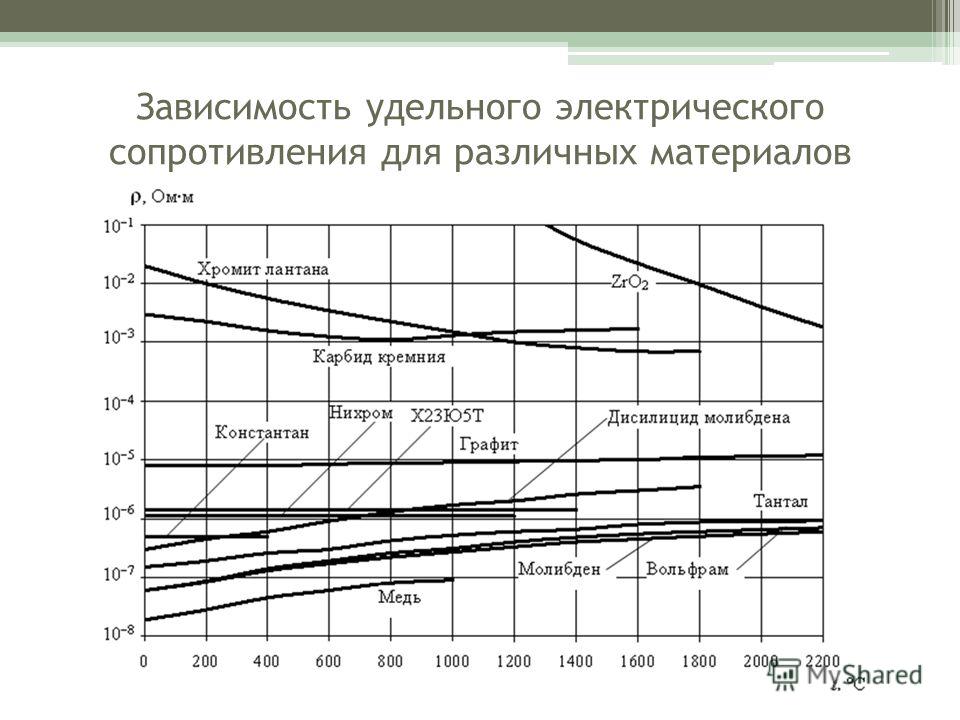 7, 3. Для настоящего обсуждения достаточно отметить, что средняя длина цепи уменьшается с температурой, а концентрация разрушенных связей описывается с помощью константы равновесия с энергией активации Еа, которая была определена различными способами. Эйзенберг и Тобольски [78] на основе данных по вязкости оценили d = 0,54 эВ. Разорванные связи являются парамагнитными центрами, и определение их концентрации в зависимости от температуры методом электронного спинового резонанса дало значение магнитной восприимчивости [175] привело к значению Еа==0,87 эВ.
[c.210]
7, 3. Для настоящего обсуждения достаточно отметить, что средняя длина цепи уменьшается с температурой, а концентрация разрушенных связей описывается с помощью константы равновесия с энергией активации Еа, которая была определена различными способами. Эйзенберг и Тобольски [78] на основе данных по вязкости оценили d = 0,54 эВ. Разорванные связи являются парамагнитными центрами, и определение их концентрации в зависимости от температуры методом электронного спинового резонанса дало значение магнитной восприимчивости [175] привело к значению Еа==0,87 эВ.
[c.210]
На первых порах накопление достоверной информации о полупроводниках существенно задерживалось тем обстоятельством, что экспериментальные данные чрезвычайно чувствительны к чистоте образца. Примером может служить фиг. 28.2, где изображенно удельное сопротивление германия в зависимости от Т для различных концентраций примесей. Отметим, что даже столь малые концентрации, как несколько примесей на 10 атомов, могут приводить к заметным эффектам и сопротивление может изменяться при данной температуре в 10 раз при изменении концентрации примесей только в 10 раз.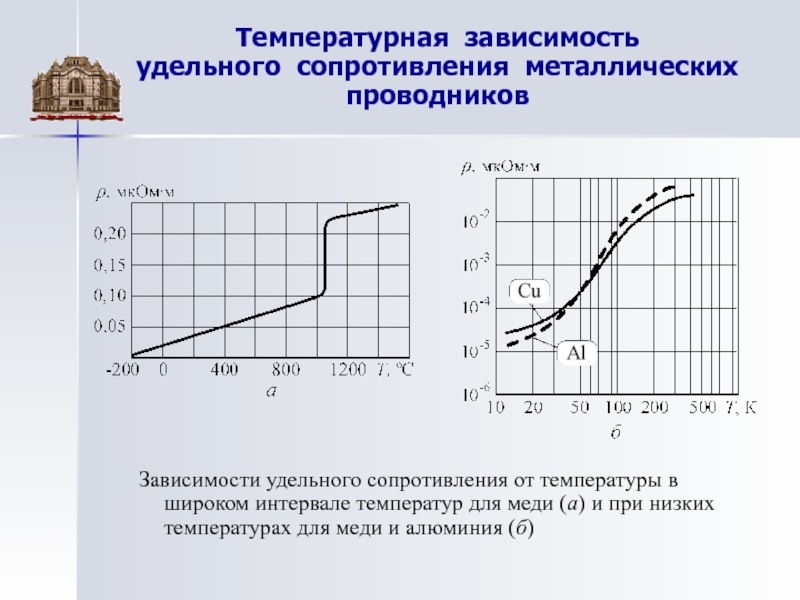 Отметим также, что при повышении температуры сопротивление образца с заданной концентрацией примесей достигает значения, лежащего на общей для всех образцов кривой. Это предельное сопротивление, которое имел бы, очевидно, идеальный, совершенно чистый образец, носит название собственного сопротивления.
[c.186]
Отметим также, что при повышении температуры сопротивление образца с заданной концентрацией примесей достигает значения, лежащего на общей для всех образцов кривой. Это предельное сопротивление, которое имел бы, очевидно, идеальный, совершенно чистый образец, носит название собственного сопротивления.
[c.186]
Как изменяется сопротивление проводника при повышении температуры
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
ho_t =
ho_0 (1 + alpha t) ,) (
R_t = R_0 (1 + alpha t) ,)
где ρ0, ρt — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R0, Rt — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1 ). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
mathcal h alpha mathcal i) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ.
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов α -1 . Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.
Формулы зависимости ρ и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором α = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
ho_t =
ho_0 (1 + alpha t) ,) (
R_t = R_0 (1 + alpha t) ,)
где ρ0, ρt — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R0, Rt — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1 ). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
mathcal h alpha mathcal i) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ.
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов α -1 . Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.
Формулы зависимости ρ и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором α = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.
В своей практической деятельности каждый электрик встречается с разными условиями прохождения носителей зарядов в металлах, полупроводниках, газах и жидкостях. На величину тока влияет электрическое сопротивление, которое различным образом изменяется под влиянием окружающей среды.
Одним из таких факторов является температурное воздействие. Поскольку оно значительно изменяет условия протекания тока, то учитывается конструкторами в производстве электрооборудования. Электротехнический персонал, участвующий в обслуживании и эксплуатации электроустановок, обязан грамотно использовать эти особенности в практической работе.
Влияние температуры на электрическое сопротивление металлов
В школьном курсе физики предлагается провести такой опыт: взять амперметр, батарейку, отрезок проволоки, соединительные провода и горелку. Вместо амперметра с батарейкой можно подключить омметр или использовать его режим в мультиметре.
Далее необходимо собрать электрическую схему, показанную на картинке и замерить величину тока в цепи. Его значение показано на шкале миллиамперметра стрелкой черного цвета.
Теперь поднесем пламя горелки к проволоке и станем ее нагревать. Если смотреть на амперметр, то будет видно, что стрелка станет перемещаться влево и достигнет положения, отмеченного красным цветом.
Результат опыта демонстрирует, что при нагревании металлов их проводимость уменьшается, а сопротивление возрастает.
Математическое обоснование этого явления приведено формулами прямо на картинке. В нижнем выражении хорошо видно, что электрическое сопротивление «R» металлического проводника прямо пропорционально его температуре «Т» и зависит еще от нескольких параметров.
Как нагрев металлов ограничивает электрический ток на практике
Ежедневно при включении освещения мы встречаемся с проявлением этого свойства у ламп накаливания. Проведем несложные измерения на лампочке с мощностью 60 ватт.
Самым простым омметром, питающемся от низковольтной батарейки 4,5 V, замерим сопротивление между контактами цоколя и увидим значение 59 Ом. Этой величиной обладает нить накала в холодном состоянии.
Вкрутим лампочку в патрон и через амперметр подключим к ней напряжение домашней сети 220 вольт. Стрелка амперметра покажет 0,273 ампера. По закону Ома для участка цепи определим сопротивление нити в нагретом состоянии. Оно составит 896 Ом и превысит предыдущее показание омметра в 15,2 раза.
Такое превышение предохраняет металл тела накала от перегорания и разрушения, обеспечивая его длительную работоспособность под напряжением.
Переходные процессы при включении
При работе нити накала на ней создается тепловой баланс между нагревом от проходящего электрического тока и отводом части тепла в окружающую среду. Но, на первоначальном этапе включения при подаче напряжения возникают переходные процессы, создающие бросок тока, который может привести к перегоранию нити.
Но, на первоначальном этапе включения при подаче напряжения возникают переходные процессы, создающие бросок тока, который может привести к перегоранию нити.
Переходные процессы протекают за короткое время и вызваны тем, что скорость возрастания электрического сопротивления от нагрева металла не успевает за увеличением тока. После их окончания устанавливается рабочий режим.
Во время длительного свечения лампы постепенно толщина ее нити доходит до критического состояния, которое приводит к перегоранию. Чаще всего этот момент возникает при очередном новом включении.
Для продления ресурса лампы различными способами уменьшают этот бросок тока, используя:
1. устройства, обеспечивающие плавную подачу и снятие напряжения;
2. схемы последовательного подключения к нити накала резисторов, полупроводников или терморезисторов (термисторов).
Пример одного из способов ограничения пускового тока для автомобильных светильников показан на картинке ниже.
Здесь ток на лампочку подается после включения тумблера SA через предохранитель FU и ограничивается резистором R, у которого номинал подбирается так, чтобы бросок тока во время переходных процессов не превышал номинальное значение.
При нагреве нити накала ее сопротивление возрастает, что ведет к увеличению разности потенциалов на ее контактах и параллельно подключенной обмотке реле KL1. Когда напряжение достигнет величины уставки реле, то нормально открытый контакт KL1 замкнется и зашунтирует резистор. Через лампочку начнет протекать рабочий ток уже установившегося режима.
Влияние температуры металла на его электрическое сопротивление используется в работе измерительных приборов. Их называют термометрами сопротивления.
Их чувствительный элемент выполняют тонкой проволочкой из металла, сопротивление которой тщательно замерено при определенных температурах. Эту нить монтируют в корпусе со стабильными термическими свойствами и закрывают защитным чехлом. Созданная конструкция помещается в среду, температуру которой необходимо постоянно контролировать.
Созданная конструкция помещается в среду, температуру которой необходимо постоянно контролировать.
На выводы чувствительного элемента монтируются провода электрической схемы, которыми подключается цепь замера сопротивления. Его величина пересчитывается в значения температуры на основе ранее произведенной калибровки прибора.
Бареттер — стабилизатор тока
Так называют прибор, состоящий из стеклянного герметичного баллона с газообразным водородом и металлической проволочной спиралью из железа, вольфрама или платины. Эта конструкция по внешнему виду напоминает лампочку накаливания, но она обладает специфической вольт-амперной нелинейной характеристикой.
На ВАХ в определенном ее диапазоне образуется рабочая зона, которая не зависит от колебаний приложенного на тело накала напряжения. На этом участке бареттер хорошо компенсирует пульсации питания и работает в качестве стабилизатора тока на подключенной последовательно к нему нагрузке.
Работа бареттера основана на свойстве тепловой инерции тела накала, которая обеспечивается маленьким сечением нити и высокой теплопроводностью окружающего ее водорода.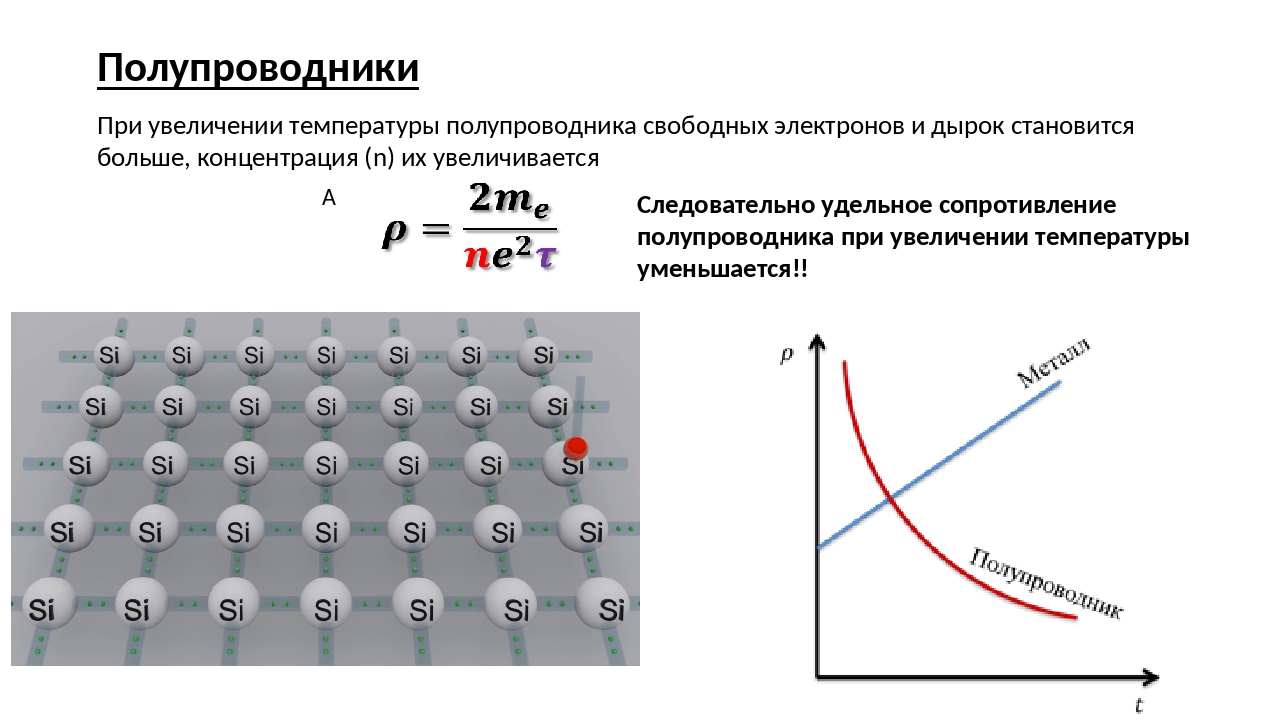 За счет этого при снижении напряжения на приборе ускоряется отвод тепла с его нити.
За счет этого при снижении напряжения на приборе ускоряется отвод тепла с его нити.
Это основное отличие бареттера от осветительных ламп накаливания, в которых для поддержания яркости свечения стремятся уменьшить конвективные потери тепла с нити.
В обычных условиях среды при охлаждении металлического проводника происходит уменьшение его электрического сопротивления.
При достижении критической температуры, близкой к нулю градусов по системе измерения Кельвина, происходит резкое падение сопротивления до нулевого значения. На правой картинке показана такая зависимость для ртути.
Это явление, названное сверхпроводимостью, считается перспективной областью для исследований с целью создания материалов, способных значительно снизить потери электроэнергии при ее передаче на огромные расстояния.
Однако, продолжающиеся изучения сверхпроводимости выявили ряд закономерностей, когда на электрическое сопротивление металла, находящегося в области критических температур, влияют другие факторы.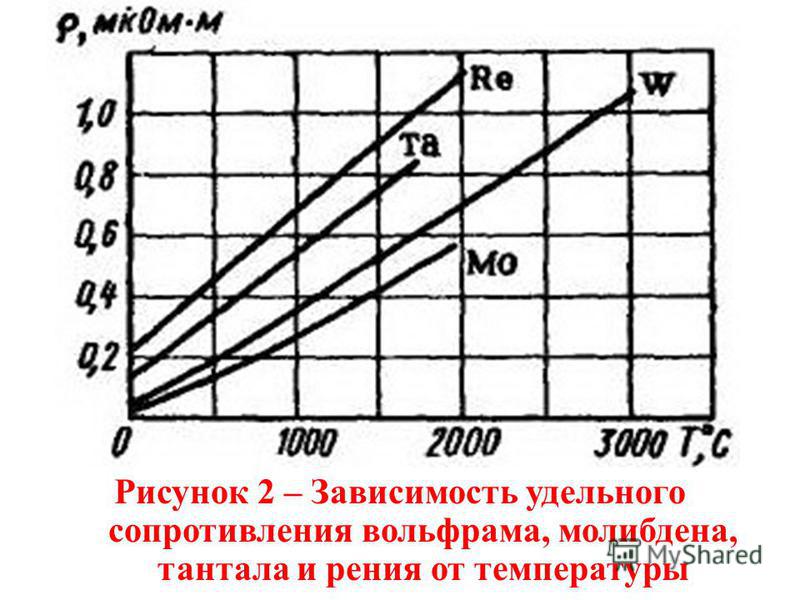 В частности, при прохождении переменного тока с повышением частоты его колебаний возникает сопротивление, величина которого доходит до диапазона обычных значений у гармоник с периодом световых волн.
В частности, при прохождении переменного тока с повышением частоты его колебаний возникает сопротивление, величина которого доходит до диапазона обычных значений у гармоник с периодом световых волн.
Влияние температуры на электрическое сопротивление/проводимость газов
Газы и обычный воздух являются диэлектриками и не проводят электрический ток. Для его образования нужны носители зарядов, которыми выступают ионы, образующиеся в результате воздействия внешних факторов.
Нагрев способен вызвать ионизацию и движение ионов от одного полюса среды к другому. Убедиться в этом можно на примере простого опыта. Возьмем то же оборудование, которым пользовались для определения влияния нагрева на сопротивление металлического проводника, только вместо проволоки к проводам подключим две металлические пластины, разделенные воздушным пространством.
Подсоединенный к схеме амперметр покажет отсутствие тока. Если между пластинами поместить пламя горелки, то стрелка прибора отклонится от нулевого значения и покажет величину проходящего через газовую среду тока.
Таким образом установили, что в газах при нагревании происходит ионизация, приводящая к движению электрически заряженных частиц и снижению сопротивления среды.
На значении тока сказывается мощность внешнего приложенного источника напряжения и разность потенциалов между его контактами. Она способна при больших значениях пробить изоляционный слой газов. Характерным проявлением подобного случая в природе является естественный разряд молнии во время грозы.
Примерный вид вольт-амперной характеристики протекания тока в газах показан на графике.
На начальном этапе под действие температуры и разности потенциалов наблюдается рост ионизации и прохождение тока примерно по линейному закону. Затем кривая приобретает горизонтальное направление, когда увеличение напряжения не вызывает рост тока.
Третий этап пробоя наступает тогда, когда высокая энергия приложенного поля так разгоняет ионы, что они начинают соударяться с нейтральными молекулами, массово образуя из них новые носители зарядов.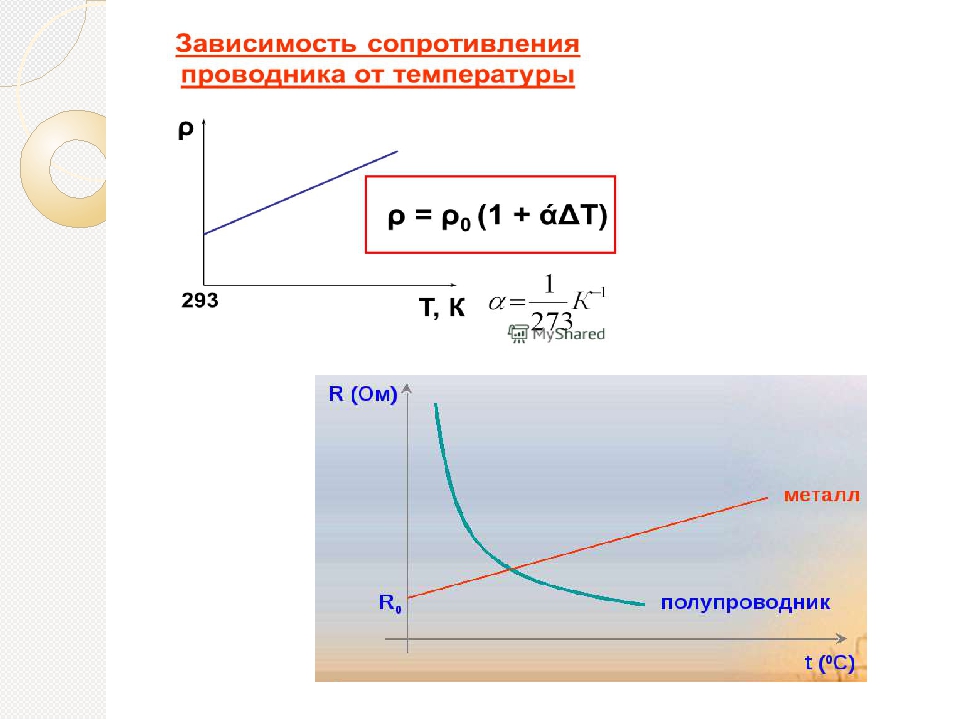 В результате ток резко возрастает, образуя пробой диэлектрического слоя.
В результате ток резко возрастает, образуя пробой диэлектрического слоя.
Практическое использование проводимости газов
Явление протекания тока через газы используется в радиоэлектронных лампах и люминесцентных светильниках.
Для этого внутри герметичного стеклянного баллона с инертным газом располагают два электрода:
У люминесцентной лампы они выполнены в виде нитей накала, которые разогреваются при включении для создания термоэлектронной эмиссии. Внутренняя поверхность колбы покрыта слоем люминофора. Он излучает видимый нами спектр света, образующийся при инфракрасном облучении, исходящем от паров ртути, бомбардируемых потоком электронов.
Ток газового разряда возникает при приложении напряжения определенной величины между электродами, расположенными по разным концам колбы.
Когда одна из нитей накала перегорит, то на этом электроде нарушится электронная эмиссия и лампа гореть не будет. Однако, если увеличить разность потенциалов между катодом и анодом, то снова возникнет газовый разряд внутри колбы и свечение люминофора возобновится.
Это позволяет использовать светодиодные колбы с нарушенными нитями накала и продлять их ресурс работы. Только следует учитывать, что при этом в несколько раз надо поднять на ней напряжение, А это значительно повышает потребляемую мощность и риски безопасного использования.
Влияние температуры на электрическое сопротивление жидкостей
Прохождение тока в жидкостях создается в основном за счет движения катионов и анионов под действием приложенного извне электрического поля. Лишь незначительную часть проводимости обеспечивают электроны.
Влияние температуры на величину электрического сопротивления жидкого электролита описывается формулой, приведенной на картинке. Поскольку в ней значение температурного коэффициента α всегда отрицательно, то с увеличением нагрева проводимость возрастает, а сопротивление падает так, как показано на графике.
Это явление необходимо учитывать при зарядке жидкостных автомобильных (и не только) аккумуляторных батарей.
Влияние температуры на электрическое сопротивление полупроводников
Изменение свойств полупроводниковых материалов под воздействием температуры позволило использовать их в качестве:
Таким названием обозначают полупроводниковые приборы, изменяющие свое электрическое сопротивление под влиянием тепла.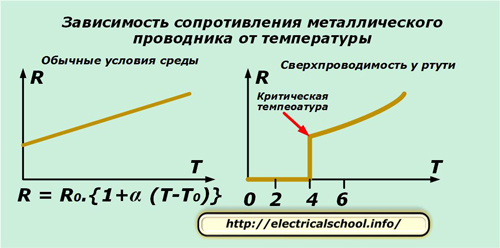 Их температурный коэффициент сопротивления (ТКС) значительно выше, чем у металлов.
Их температурный коэффициент сопротивления (ТКС) значительно выше, чем у металлов.
Величина ТКС у полупроводников может иметь положительное или отрицательное значение. По этому параметру их разделяют на позитивные «РТС» и негативные «NTC» термисторы. Они обладают различными характеристиками.
Для работы терморезистора выбирают одну из точек на его вольт-амперной характеристике:
линейный участок применяют для контроля температуры либо компенсации изменяющихся токов или напряжений;
нисходящая ветвь ВАХ у элементов с ТКС
Применение релейного терморезистора удобно при контроле или измерениях процессов электромагнитных излучений, происходящих на сверхвысоких частотах. Это обеспечило их использование в системах:
1. контроля тепла;
2. пожарной сигнализации;
3. регулирования расхода сыпучих сред и жидкостей.
Кремниевые терморезисторы с маленьким ТКС>0 используют в системах охлаждения и стабилизации температуры транзисторов.
Эти полупроводники работают на основе явления Зеебека: при нагреве спаянного места двух разрозненных металлов на стыке замкнутой цепи возникает ЭДС. Таким способом они превращают тепловую энергию в электричество.
Конструкцию из двух таких элементов называют термопарой. Ее КПД лежит в пределах 7÷10%.
Термоэлементы используют в измерителях температур цифровых вычислительных устройств, требующих миниатюрные габариты и высокую точность показаний, а также в качестве маломощных источников тока.
Полупроводниковые нагреватели и холодильники
Они работают за счет обратного использования термоэлементов, через которые пропускают электрический ток. При этом на одном месте спая происходит его нагрев, а на противоположном — охлаждение.
Полупроводниковые спаи на основе селена, висмута, сурьмы, теллура позволяют обеспечить разность температур в термоэлементе до 60 градусов. Это позволило создать конструкцию холодильного шкафа из полупроводников с температурой в камере охлаждения до -16 градусов.
Зависимость удельного сопротивления чистого металла от температуры
Зависимость удельного сопротивления чистого металла от температуры
[c.193]
На рис. 7.6, а схематически показана кривая зависимости удельного сопротивления чистых металлов от температуры, достаточно хорошо подтверждаемая экспериментально (рис. 7.6, б). [c.188]
Зависимость удельного сопротивления чистых металлов от температуры не может быть удовлетворительно объяснена в рамках классической электронной теории электропроводности. В современной квантовой теории электропроводности металлов доказывается, что при всех температурах, кроме абсолютного нуля, свободные электроны испытывают такие взаимодействия с узлами кристаллической решетки металла, что среднее время Т свободного пробега электронов в области средних температур обратно пропорционально абсолютной температуре Т металла
[c. 220]
220]
Никель и железо. Никель и железо обладают значительно более высоким температурным коэфициентом сопротивления, чем все прочие металлы 6,28 10″1 град и л= 6,4-10 . град). Кроме того, эти металлы обладают довольно высоким удельным сопротивлением, равным приблизительно 0,1—0,13 ом-мм /м. Однако возможность использования никеля и железа для изготовления термометров сопротивления ограничена в силу присущих этим металлам существенных недостатков. Получение никеля и железа в чистом виде затруднительно, а поэтому низка воспроизводимость их свойств. Далее, зависимость сопротивления этих металлов от температуры выражается к,ривыми, которые не могут быть записаны в виде простых эмпирических формул. Наконец, никель и, особенно железо чрезвычайно легко окисляются. Железные Термопары в СССР не изготовляются соверщенно. Никелевые термометры используются для технических измерений температуры в пределах до 250°. Однако щирокого распространения эти термометры до настоящего времени не нашли.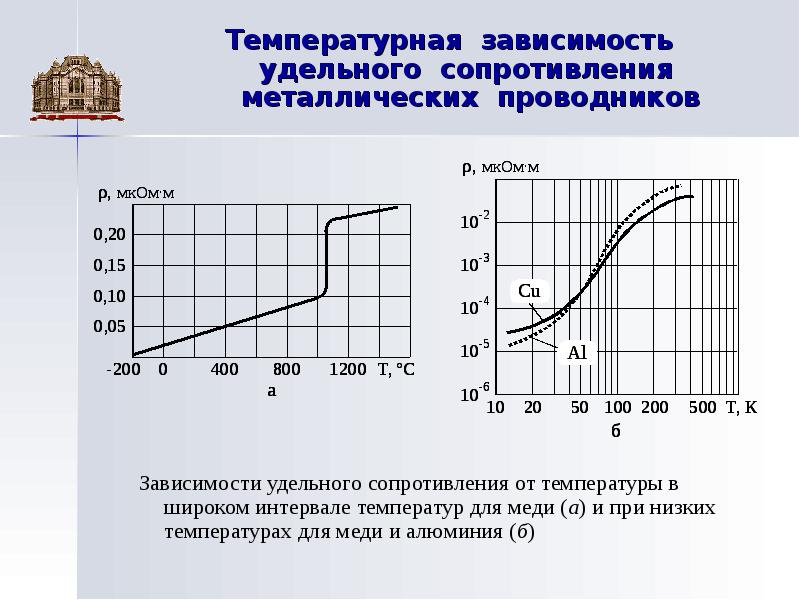 [c.77]
[c.77]
Электросопротивление алюминия высокой чистоты (99,99 %) при температуре 20 °С составляет 2,6548-10 Ом-м (0,0265 МКОМ М). В интервале температур 273—300 К температурная зависимость электрического сопротивления чистого алюминия почти линейна при постоянном коэффициенте 1,15-10 Ом-м-К . Электрическая проводимость алюминия в значительной степени зависит от чистоты металла, причем влияние различных примесей на электрическое сопротивление зависит не только от концентрации данной примеси, но и от ее нахождения в твердом растворе или вне его. Наиболее сильно повышают сопротивление алюминия примеси хрома, лития, марганца, магния, титана и ванадия [5]. Удельное электросопротивление р (мкОм м) отожженной алюминиевой проволоки в зависимости от содержания примесей (%) можно приближенно определить по следующей формуле [9] [c.12]
Для определения результирующих потоков излучения необходимо располагать данными по коэффициентам излучения. Коэффициент излучения является сложной функцией, зависящей от природы излучающего тела, его температуры, состояния поверхности, а для металлов — от степени окисления этой поверхности. Для чистых металлов с полированными поверхностями коэффициент излучения имеет низкие значения. Так, при температуре 100 °С коэффициент излучения по отношению к его величине для абсолютно черного тела не превышает 0,1. Металлы характеризуются высокой отражательной способностью, так как из-за большой электропроводности луч проникает лишь на небольшую глубину. Для чистых металлов коэффициент излучения может быть найден теоретическим путем. Относительный коэффициент (степень черноты) полного нормального излучения для них связан с удельным электрическим сопротивлением рэ зависимостью
[c.385]
Коэффициент излучения является сложной функцией, зависящей от природы излучающего тела, его температуры, состояния поверхности, а для металлов — от степени окисления этой поверхности. Для чистых металлов с полированными поверхностями коэффициент излучения имеет низкие значения. Так, при температуре 100 °С коэффициент излучения по отношению к его величине для абсолютно черного тела не превышает 0,1. Металлы характеризуются высокой отражательной способностью, так как из-за большой электропроводности луч проникает лишь на небольшую глубину. Для чистых металлов коэффициент излучения может быть найден теоретическим путем. Относительный коэффициент (степень черноты) полного нормального излучения для них связан с удельным электрическим сопротивлением рэ зависимостью
[c.385]
Наряду с малым удельным сопротивлением чистые металлы обладают хорошей пластичностью, т. е. могут вытягиваться в тонкую проволоку (до диаметра 0,01 мм), ленты (до толщины 0,01 мм) и прокатываться в фольгу толщиной менее 0,01 мм. Сплавы металлов обладают меньшей пластичностью по сравнению с чистыми металлами, они более упруги и имеют большую механическую прочность. Характерной особенностью всех металлических проводниковых, материалов является их электронная электропроводность. Удельное сопротивление всех металлических проводников увеличивается с ростом температуры и в зависимости от температурного коэффициента сопротивления, а также в результате механической обработки, вызывающей остаточную деформацию в металле. К холодной обработке (прокатка, волочение) приходится прибегать для получения проводниковых изделий с повышенным пределом прочности при разрыве, например при изготовлении проводов воздушных линий, троллейных проводов и т. д. Чтобы вернуть деформированным металлическ , проводникам прежнюю величину удельного сопротивления, их подвергают термической обработке — отжигу без доступа кислорода.
[c.225]
Сплавы металлов обладают меньшей пластичностью по сравнению с чистыми металлами, они более упруги и имеют большую механическую прочность. Характерной особенностью всех металлических проводниковых, материалов является их электронная электропроводность. Удельное сопротивление всех металлических проводников увеличивается с ростом температуры и в зависимости от температурного коэффициента сопротивления, а также в результате механической обработки, вызывающей остаточную деформацию в металле. К холодной обработке (прокатка, волочение) приходится прибегать для получения проводниковых изделий с повышенным пределом прочности при разрыве, например при изготовлении проводов воздушных линий, троллейных проводов и т. д. Чтобы вернуть деформированным металлическ , проводникам прежнюю величину удельного сопротивления, их подвергают термической обработке — отжигу без доступа кислорода.
[c.225]
Прежде чем перейти к подробному обсуждению зависимости удельного сопротивления металлов и полупроводников от температуры, коснемся особенностей поведения концентрированных сплавов. Введение значительного количества примесных атомов в твердый раствор приводит к искажению кристаллической решетки. Вследствие этого появляется дополнительный вклад в рассеяние. Его величина почти не зависит от температуры и может во много раз превышать долю электрон-фонон-ного рассеяния в чистом металле. Изменение остаточного удельного сопротивления неупорядоченного сплава Си—Аи в зави-
[c.191]
Введение значительного количества примесных атомов в твердый раствор приводит к искажению кристаллической решетки. Вследствие этого появляется дополнительный вклад в рассеяние. Его величина почти не зависит от температуры и может во много раз превышать долю электрон-фонон-ного рассеяния в чистом металле. Изменение остаточного удельного сопротивления неупорядоченного сплава Си—Аи в зави-
[c.191]
Теоретические соображения. Интересно обсудить возможный механизм частичной сверхпроводимости проволоки из фосфористой бронзы. Кеезом [25] и Бэббит и Мендельсон [45] предположили, что явление частичной сверхпроводимости обусловливается наличием большого количества сверхпроводящих включений в виде чистого металла или сверхпроводящего сплава, растворенного в фосфористой бронзе. Кроме того, они предположили, что эти включения имеют форму тонких игл, образовавшихся при протяжке и расположенных параллельно оси проволоки. Однако эти авторы дают различную интерпретацию линейной зависимости удельного сопротивления от температуры. Кеезом полагал, что благодаря очень малым и случайно распределенным размерам игл сверхпроводящие переходы в них беспорядочно распределены по всему температурному интервалу. По мере понижения температуры все большее и большее число игл становится сверхпроводящим и, таким образом, уменьшается сопротивление проволоки. Бэббит и Мендельсон, напротив, предположили, что иглы образуют цепи, и так как один и тот же ток проходит через все иглы, составляющие одну цепь, то более тонкие иглы становятся сверхпроводниками при более низких температурах, чем более толстые. Этим можно объяснить незначительный наклон кривой зависимости удельного электросопротивления от температуры.
[c.205]
Кеезом полагал, что благодаря очень малым и случайно распределенным размерам игл сверхпроводящие переходы в них беспорядочно распределены по всему температурному интервалу. По мере понижения температуры все большее и большее число игл становится сверхпроводящим и, таким образом, уменьшается сопротивление проволоки. Бэббит и Мендельсон, напротив, предположили, что иглы образуют цепи, и так как один и тот же ток проходит через все иглы, составляющие одну цепь, то более тонкие иглы становятся сверхпроводниками при более низких температурах, чем более толстые. Этим можно объяснить незначительный наклон кривой зависимости удельного электросопротивления от температуры.
[c.205]
Простая модель электронного газа, созданная Друде в 1900 г., успещно предсказала законы Ома и Видемана — Франца. Однако она не объяснила зависимость электропроводности от температуры, а также магнитные свойства и малую величину электронной теплоемкости по сравнению с классическим значением 3/ .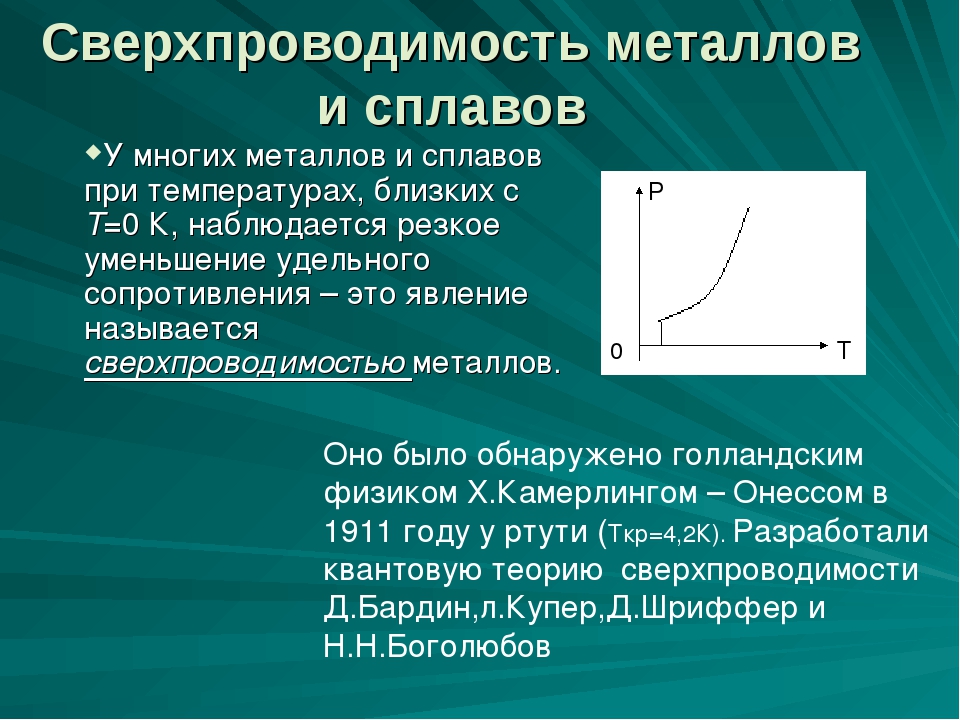 В настоящее время ясно, почему удельное сопротивление особо чистых металлов падает от типичного для комнатных температур значения 10 мкОм см до значения менее 10 з мкОм -см при температуре жидкого гелия в то время как удельное сопротивление концентрированного сплава падает всего в два раза в том же диапазоне температур. Поведение полупроводников также хорошо понято удельное сопротивление экспоненциально возрастает при уменьшении температуры, и при очень низких температурах чистые полупроводники становятся хорошими диэлектриками. Добавка в образец полупроводника небольшого количества примесей чаще всего существенно уменьшает удельное сопротивление (в противоположность чистым металлам, в которых наличие примесей ведет к увеличению удельного сопротивления).
[c.187]
В настоящее время ясно, почему удельное сопротивление особо чистых металлов падает от типичного для комнатных температур значения 10 мкОм см до значения менее 10 з мкОм -см при температуре жидкого гелия в то время как удельное сопротивление концентрированного сплава падает всего в два раза в том же диапазоне температур. Поведение полупроводников также хорошо понято удельное сопротивление экспоненциально возрастает при уменьшении температуры, и при очень низких температурах чистые полупроводники становятся хорошими диэлектриками. Добавка в образец полупроводника небольшого количества примесей чаще всего существенно уменьшает удельное сопротивление (в противоположность чистым металлам, в которых наличие примесей ведет к увеличению удельного сопротивления).
[c.187]
Зависимость удельного сопротивления металлического проводника от температуры
У металлов, не обладающих сверхпроводимостью, при низких температурах из-за наличия примесей наблюдается область 1 – область остаточного сопротивления, почти не зависящая от температуры (рис. 10.5). Остаточное сопротивление — r ост тем меньше, чем чище металл.
10.5). Остаточное сопротивление — r ост тем меньше, чем чище металл.
Рис. 10.5. Зависимость удельного сопротивления металла от температуры
Быстрый рост удельного сопротивления при низких температурах до температуры Дебая Q д может быть объяснен возбуждением новых частот тепловых колебаний решетки, при которых происходит рассеяние носителей заряда — область 2.
При Т > Q д , когда спектр колебаний возбужден полностью, увеличение амплитуды колебаний с ростом температуры приводит к линейному росту сопротивления примерно до Т пл — область 3. При нарушении периодичности структуры электрон испытывает рассеяние, приводящее к изменению направления движения, конечным длинам свободного пробега и проводимости металла. Энергия электронов проводимости в металлах составляет 3–15 эВ, что соответствует длинам волн 3–7 Å. Поэтому любые нарушения периодичности, обусловленные примесями, дефектами, поверхностью кристалла или тепловыми колебаниями атомов (фононами) вызывают рост удельного сопротивления металла.
Проведем качественный анализ температурной зависимости удельного сопротивления металлов. Электронный газ в металлах является вырожденным и основным механизмом рассеяния электронов в области высоких температур является рассеяние на фононах.
При понижения температуры до абсолютного нуля сопротивление нормальных металлов стремится к постоянному значению — остаточному сопротивлению. Исключением из этого правила являются сверхпроводящие металлы и сплавы, в которых сопротивление исчезает ниже некоторой критической температуры Тсв (температура перехода в сверхпроводящее состояние).
При увеличении температуры, отклонение удельного сопротивления от линейной зависимости у большинства металлов наступает вблизи температуры плавления Тпл . Некоторое отступление от линейной зависимости может наблюдаться у ферромагнитных металлов, в которых происходит дополнительное рассеяние электронов на нарушениях спинового порядка.
При достижении температуры плавления и переходе в жидкое состояние у большинства металлов наблюдается резкое увеличение удельного сопротивления и у некоторых его уменьшение. Если плавление металла или сплава сопровождается увеличением объема, то удельное сопротивление повышается в два–четыре раза (например, у ртути в 4 раза).
Если плавление металла или сплава сопровождается увеличением объема, то удельное сопротивление повышается в два–четыре раза (например, у ртути в 4 раза).
У металлов, объем которых при плавлении уменьшается, наоборот, происходит понижение удельного сопротивления (у галлия на 53%, у сурьмы –29% и у висмута –54%) . Подобная аномалия может быть объяснена возрастанием плотности и модуля сжимаемости при переходе этих металлов из твердого в жидкое состояние. У некоторых расплавленных (жидких) металлов удельное сопротивление с ростом температуры при постоянном объеме перестает расти, у других оно растет более медленно, чем в твердом состоянии. Такие аномалии, по-видимому, можно связать с явлениями разупорядочения решетки, которые неодинаково происходят в различных металлах при переходе их из одного агрегатного состояния в другое.
Важной характеристикой металлов является температурный коэффициент удельного электрического сопротивления, показывающий относительное изменение удельного сопротивления при изменении температуры на один Кельвин (градус)
ar— положительно, когда удельное сопротивление возрастает при повышении температуры.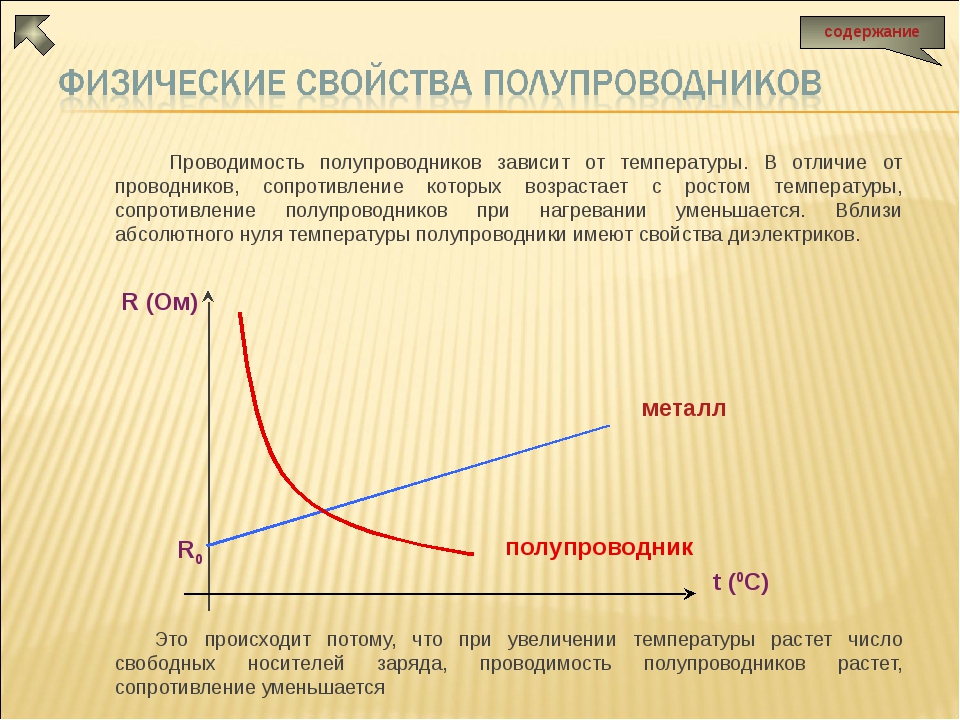 Очевидно, что величина ar также является функцией температуры. В области 3 линейной зависимости r ( T ) (см. рисунок 10.3) выполняется соотношение:
Очевидно, что величина ar также является функцией температуры. В области 3 линейной зависимости r ( T ) (см. рисунок 10.3) выполняется соотношение:
где r и ar— удельное сопротивление и температурный коэффициент удельного сопротивления при температуре T , а r — удельное сопротивление при температуре T . Экспериментальные данные показывают, что у большинства металлов ar при комнатной температуре примерно 0,004 К -1 .У ферромагнитных металлов значение ar несколько выше.
Остаточное удельное сопротивление металлов. Как говорилось выше, сопротивление нормальных металлов стремится к постоянному значению — остаточному сопротивлению, по мере снижения температуры до абсолютного нуля. У нормальных металлов (не сверхпроводников) остаточное сопротивление возникает из-за рассеяния электронов проводимости статическими дефектами
Общую чистоту и совершенство металлического проводника можно определять отношением сопротивлений r =R273/R4,2 K . Для стандартной меди чистоты 99,999 это отношение составляет 1000. Б óльших значений r можно достигнуть путем дополнительных зонных переплавок и приготовлением образцов в виде монокристаллов.
Для стандартной меди чистоты 99,999 это отношение составляет 1000. Б óльших значений r можно достигнуть путем дополнительных зонных переплавок и приготовлением образцов в виде монокристаллов.
Обширный экспериментальный материал содержит многочисленные данные по измерению сопротивления в металлах, вызванному наличием в них примесей. Можно отметить следующие наиболее характерные изменения в металлах, вызываемые легированием. Во-первых, не считая фононных возмущений, примесь является локальным нарушением идеальности решетки совершенное во всех других отношениях. Во-вторых, легирование влияет на зонную структуру, сдвигая энергию Ферми и изменяя плотность состоянии и эффективную массу, т.е. параметры, частично определяющие идеальное сопротивление металла. В-третьих, легирование может менять упругие константы и, соответственно, колебательный спектр решетки, оказывая влияние на идеальное сопротивление.
Общее удельное сопротивление проводника при температурах выше 0К складывается из остаточного сопротивления r ост и удельного сопротивления, обусловленного рассеянием на тепловых колебаниях решетки — r Т
Это соотношение известно как правило Матиссена об аддитивности удельного сопротивления. Часто, однако, наблюдаются значительные отклонения от правила Матиссена , причем некоторые их этих отклонений могут говорить не в пользу применимости основных факторов, влияющих на сопротивление металлов при введении в них примесей. Однако второй и третий факторы, отмеченные в начале этого раздела, также дают заметный вклад. Но, все же более сильное воздействие на сопротивление разбавленных твердых растворов оказывает первый фактор.
Часто, однако, наблюдаются значительные отклонения от правила Матиссена , причем некоторые их этих отклонений могут говорить не в пользу применимости основных факторов, влияющих на сопротивление металлов при введении в них примесей. Однако второй и третий факторы, отмеченные в начале этого раздела, также дают заметный вклад. Но, все же более сильное воздействие на сопротивление разбавленных твердых растворов оказывает первый фактор.
Изменение остаточного сопротивления на 1 ат . % примеси для одновалентных металлов можно найти по правилу Линде, согласно которому
где a и b — константы, зависящие от природы металла и периода, который занимает в Периодической системе элементов примесный атом; ΔΖ — разность валентностей металла-растворителя и примесного атома. Значительный практический интерес представляют расчеты сопротивления, обусловленные вакансиями и внедренными атомами. Такие дефекты легко возникает при облучении образца частицами высоких энергий, например нейтронами из реактора или ионами из ускорителя.
«Физика — 10 класс»
Какую физическую величину называют сопротивлением
От чего и как зависит сопротивление металлического проводника?
Различные вещества имеют разные удельные сопротивления. Зависит ли сопротивление от состояния проводника? от его температуры? Ответ должен дать опыт.
Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать её в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется.
Если при температуре, равной 0 °С, сопротивление проводника равно R, а при температуре t оно равно R, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t:
Коэффициент пропорциональности α называют температурным коэффициентом сопротивления.
Температурный коэффициент сопротивления — величина, равная отношению относительного изменения сопротивления проводника к изменению его температуры.
Он характеризует зависимость сопротивления вещества от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании на 1 К (на 1 °С).
Для всех металлических проводников коэффициент α > 0 и незначительно меняется с изменением температуры. Если интервал изменения температуры невелик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов
У растворов электролитов сопротивление с ростом температуры не увеличивается, а уменьшается. Для них α -1 .
При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счёт изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (16.1) подставить значения Вычисления приводят к следующему результату:
где ΔТ — изменение абсолютной температуры.
Так как а мало меняется при изменении температуры проводника, то можно считать, что удельное сопротивление проводника линейно зависит от температуры (рис. 16.2).
Увеличение сопротивления можно объяснить тем, что при повышении температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решётки, поэтому свободные электроны сталкиваются с ними чаще, теряя при этом направленность движения. Хотя коэффициент а довольно мал, учёт зависимости сопротивления от температуры при расчёте параметров нагревательных приборов совершенно необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока за счёт нагревания более чем в 10 раз.
У некоторых сплавов, например у сплава меди с никелем (Константин), температурный коэффициент сопротивления очень мал: α ≈ 10 -5 К -1 ; удельное сопротивление Константина велико: ρ ≈ 10 -6 Ом • м. Такие сплавы используют для изготовления эталонных резисторов и добавочных резисторов к измерительным приборам, т.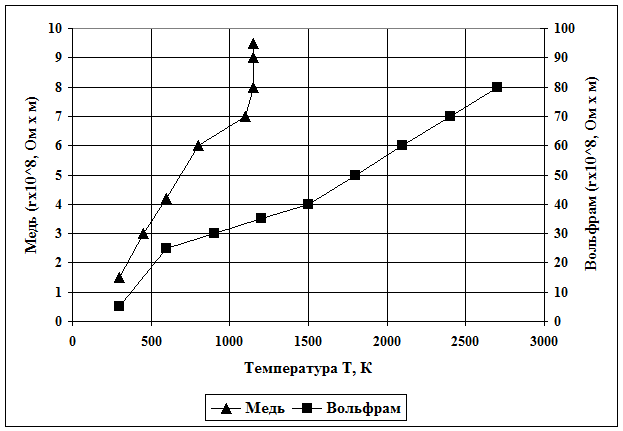 е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Существуют и такие металлы, например никель, олово, платина и др., температурный коэффициент которых существенно больше: α ≈ 10 -3 К -1 . Зависимость их сопротивления от температуры можно использовать для измерения самой температуры, что и осуществляется в термометрах сопротивления.
На зависимости сопротивления от температуры основаны и приборы, изготовленные из полупроводниковых материалов, — термисторы. Для них характерны большой температурный коэффициент сопротивления (в десятки раз превышающий этот коэффициент у металлов), стабильность характеристик во времени. Номинальное сопротивление термисторов значительно выше, чем у металлических термометров сопротивления, оно обычно составляет 1, 2, 5, 10, 15 и 30 кОм.
Обычно в качестве основного рабочего элемента термометра сопротивления берут платиновую проволоку, зависимость сопротивления которой от температуры хорошо известна.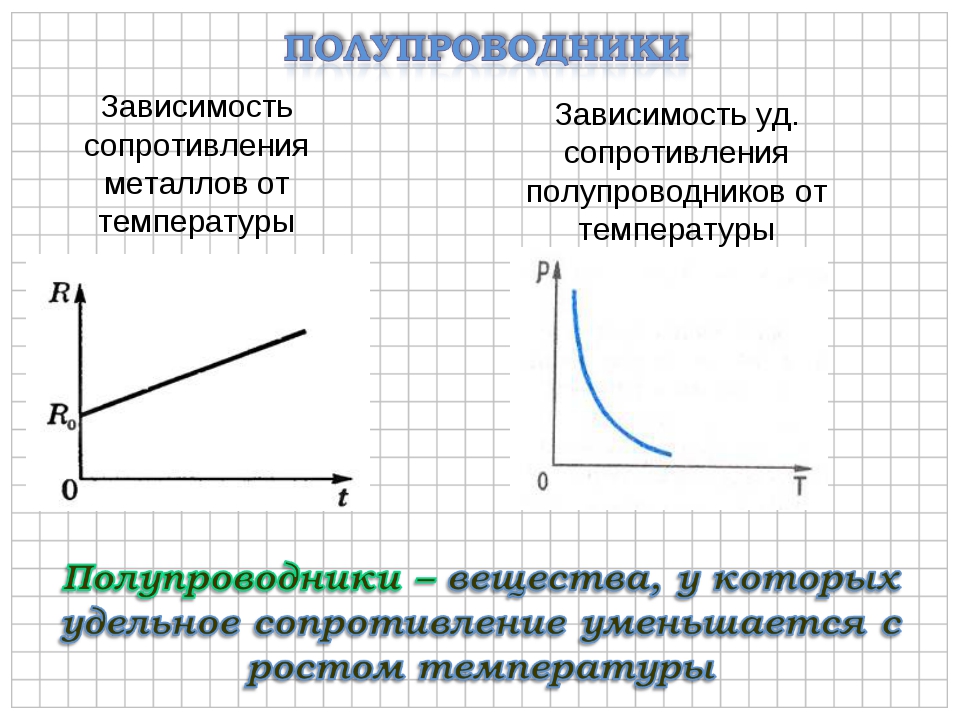 Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Сверхпроводимость.
Сопротивление металлов уменьшается с уменьшением температуры. Что произойдёт при стремлении температуры к абсолютному нулю?
В 1911 г. голландский физик X. Камерлинг-Оннес открыл замечательное явление — сверхпроводимость. Он обнаружил, что при охлаждении ртути в жидком гелии её сопротивление сначала меняется постепенно, а затем при температуре 4,1 К очень резко падает до нуля (рис. 16.3).
Явление падения до нуля сопротивления проводника при критической температуре называется сверхпроводимостью.
Открытие Камерлинг-Оннеса, за которое в 1913 г. ему была присуждена Нобелевская премия, повлекло за собой исследования свойств веществ при низких температурах. Позже было открыто много других сверхпроводников.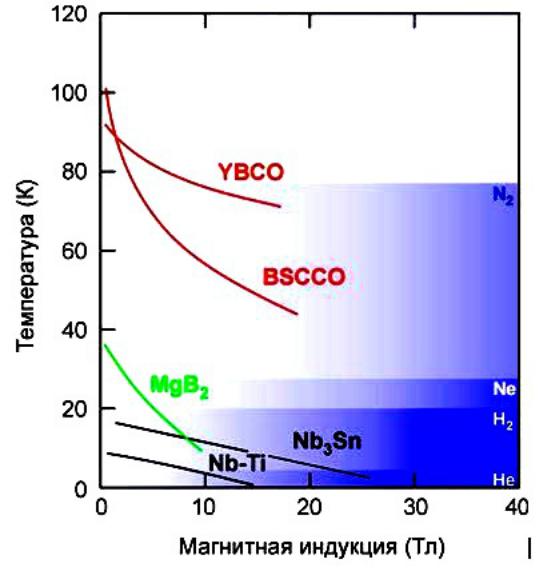
Сверхпроводимость многих металлов и сплавов наблюдается при очень низких температурах — начиная примерно с 25 К. В справочных таблицах приводятся температуры перехода в сверхпроводящее состояние некоторых веществ.
Температура, при которой вещество переходит в сверхпроводящее состояние, называется критической температурой.
Критическая температура зависит не только от химического состава вещества, но и от структуры самого кристалла. Например, серое олово имеет структуру алмаза с кубической кристаллической решёткой и является полупроводником, а белое олово обладает тетрагональной элементарной ячейкой и является серебристо-белым, мягким, пластичным металлом, способным при температуре, равной 3,72 К, переходить в сверхпроводящее состояние.
У веществ в сверхпроводящем состоянии были отмечены резкие аномалии магнитных, тепловых и ряда других свойств, так что правильнее говорить не о сверхпроводящем состоянии, а об особом, наблюдаемом при низких температурах состоянии вещества.
Если в кольцевом проводнике, находящемся в сверхпроводящем состоянии, создать ток, а затем удалить источник тока, то сила этого тока не меняется сколь угодно долго. В обычном же (несверхпроводящем) проводнике электрический ток в этом случае прекращается.
Сверхпроводники находят широкое применение. Так, сооружают мощные электромагниты со сверхпроводящей обмоткой, которые создают магнитное поле на протяжении длительных интервалов времени без затрат энергии. Ведь выделения тепла в сверхпроводящей обмотке не происходит.
Однако получить сколь угодно сильное магнитное поле с помощью сверхпроводящего магнита нельзя. Очень сильное магнитное поле разрушает сверхпроводящее состояние. Такое поле может быть создано и током в самом сверхпроводнике. Поэтому для каждого проводника в сверхпроводящем состоянии существует критическое значение силы тока, превысить которое, не нарушая сверхпроводящего состояния, нельзя.
Сверхпроводящие магниты используются в ускорителях элементарных частиц, магнитогидродинамических генераторах, преобразующих механическую энергию струи раскалённого ионизованного газа, движущегося в магнитном поле, в электрическую энергию.
Объяснение сверхпроводимости возможно только на основе квантовой теории. Оно было дано лишь в 1957 г. американскими учёными Дж. Бардиным, Л. Купером, Дж. Шриффером и советским учёным, академиком Н. Н. Боголюбовым.
В 1986 г. была открыта высокотемпературная сверхпроводимость. Получены сложные оксидные соединения лантана, бария и других элементов (керамики) с температурой перехода в сверхпроводящее состояние около 100 К. Это выше температуры кипения жидкого азота при атмосферном давлении (77 К).
Высокотемпературная сверхпроводимость в недалёком будущем приведёт наверняка к новой технической революции во всей электротехнике, радиотехнике, конструировании ЭВМ. Сейчас прогресс в этой области тормозится необходимостью охлаждения проводников до температур кипения дорогого газа — гелия.
Физический механизм сверхпроводимости довольно сложен. Очень упрощённо его можно объяснить так: электроны объединяются в правильную шеренгу и движутся, не сталкиваясь с кристаллической решёткой, состоящей из ионов.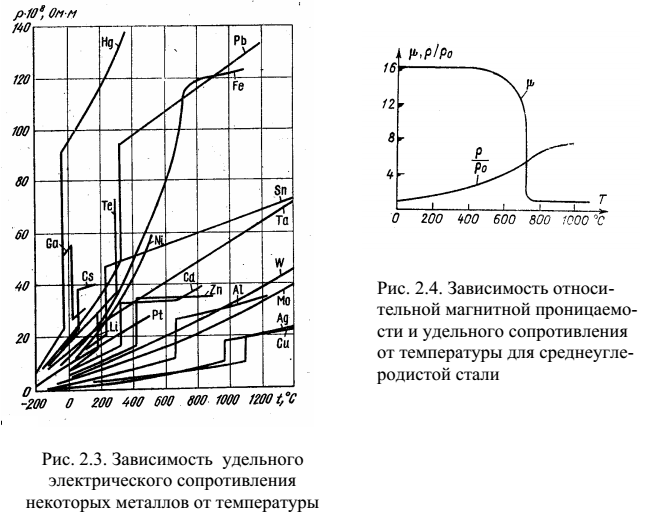 Это движение существенно отличается от обычного теплового движения, при котором свободный электрон движется хаотично.
Это движение существенно отличается от обычного теплового движения, при котором свободный электрон движется хаотично.
Надо надеяться, что удастся создать сверхпроводники и при комнатной температуре. Генераторы и электродвигатели станут исключительно компактными (уменьшатся в несколько раз) и экономичными. Электроэнергию можно будет передавать на любые расстояния без потерь и аккумулировать в простых устройствах.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электрический ток в различных средах — Физика, учебник для 10 класса — Класс!ная физика
Практически в электротехнике выло выявлено, что с увеличением температуры сопротивление проводников из металла возрастает, а с понижением уменьшается. Для всех проводников из металла это изменение сопротивления почти одинаково и в среднем равно 0,4% на 1°С.
Если быть точным, то на самом деле при изменении температуры проводника изменяется его удельное сопротивление, которое имеет следующую зависимость:
где ρ и ρ, R и R — соответственно удельные сопротивления и сопротивления проводника при температурах t и 0°С (шкала Цельсия), α — температурный коэффициент сопротивления, [α] = град -1 .
Изменение удельного сопротивления проводника приводит к изменения самого сопротивления, что видно из следующего выражения:
Зная электронную теорию строения вещества можно дать следующее объяснение увеличению сопротивления металлических проводников с повышением температуры. При увеличении температуры проводник получает тепловую энергию, которая несомненно передается всем атомам вещества, в результате чего .возрастает их тепловое движение. Увеличившееся тепловое движение атомов создает большее сопротивление направленному движению свободных электронов (увеличивается вероятность столкновения свободных электронов с атомами), от этого и возрастает сопротивление проводника.
С понижением температуры направленное движение электронов облегчается (уменьшается возможность столкновения свободных электронов с атомами), и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов. Сверхпроводимость, т. е. уменьшение сопротивления металлов до нуля, наступает при огромной отрицательной температуре —273° С, называемой абсолютным нулем. При температуре абсолютного нуля атомы металла как бы застывают на месте, совершенно не препятствуя движению электронов.
При температуре абсолютного нуля атомы металла как бы застывают на месте, совершенно не препятствуя движению электронов.
График звисимости сопротивления металлического проводника от температуры представлен на рисунке 1.
Рисунок 1. График зависимости удельного сопротивления металлического проводника от температуры
Необходимо сказать, что сопротивление электролитов и полупроводников (уголь, селен и другие) с увеличением температуры уменьшается.
Температурная зависимость сопротивления электролита объясняется также в основном изменением удельного сопротивления,однако всегда температурный коэффициент сопротивления — α
Поэтому кривая зависимости сопротивленя электролита от температуры имеет вид, представленый на рисунке 2.
Рисунок 1. График зависимости удельного сопротивления электролита от температуры
Ддя полупроводников характер изменения удельного сопротивления от температуры будет схож с таковым для элетролитов.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Как зависит сопротивление металлического проводника от температуры
Практически в электротехнике выло выявлено, что с увеличением температуры сопротивление проводников из металла возрастает, а с понижением уменьшается. Для всех проводников из металла это изменение сопротивления почти одинаково и в среднем равно 0,4% на 1°С.
Для всех проводников из металла это изменение сопротивления почти одинаково и в среднем равно 0,4% на 1°С.
Если быть точным, то на самом деле при изменении температуры проводника изменяется его удельное сопротивление, которое имеет следующую зависимость:
где ρ и ρ, R и R — соответственно удельные сопротивления и сопротивления проводника при температурах t и 0°С (шкала Цельсия), α — температурный коэффициент сопротивления, [α] = град -1 .
Изменение удельного сопротивления проводника приводит к изменения самого сопротивления, что видно из следующего выражения:
Зная электронную теорию строения вещества можно дать следующее объяснение увеличению сопротивления металлических проводников с повышением температуры. При увеличении температуры проводник получает тепловую энергию, которая несомненно передается всем атомам вещества, в результате чего .возрастает их тепловое движение. Увеличившееся тепловое движение атомов создает большее сопротивление направленному движению свободных электронов (увеличивается вероятность столкновения свободных электронов с атомами), от этого и возрастает сопротивление проводника.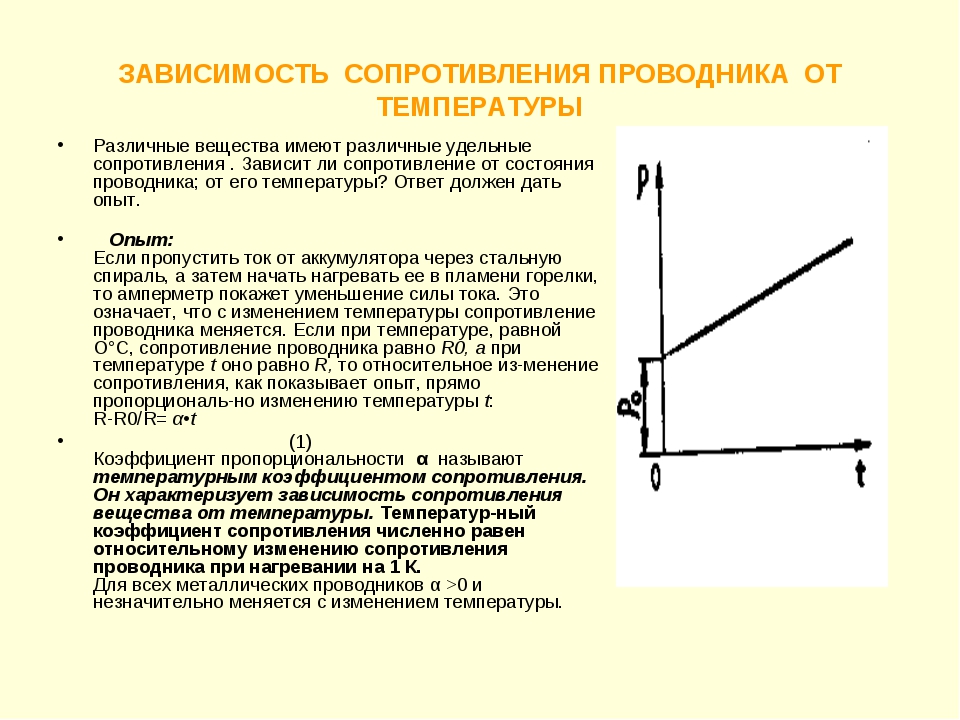
С понижением температуры направленное движение электронов облегчается (уменьшается возможность столкновения свободных электронов с атомами), и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов. Сверхпроводимость, т. е. уменьшение сопротивления металлов до нуля, наступает при огромной отрицательной температуре —273° С, называемой абсолютным нулем. При температуре абсолютного нуля атомы металла как бы застывают на месте, совершенно не препятствуя движению электронов.
График звисимости сопротивления металлического проводника от температуры представлен на рисунке 1.
Рисунок 1. График зависимости удельного сопротивления металлического проводника от температуры
Необходимо сказать, что сопротивление электролитов и полупроводников (уголь, селен и другие) с увеличением температуры уменьшается.
Температурная зависимость сопротивления электролита объясняется также в основном изменением удельного сопротивления,однако всегда температурный коэффициент сопротивления — α
Поэтому кривая зависимости сопротивленя электролита от температуры имеет вид, представленый на рисунке 2.
Рисунок 1. График зависимости удельного сопротивления электролита от температуры
Ддя полупроводников характер изменения удельного сопротивления от температуры будет схож с таковым для элетролитов.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
«Физика — 10 класс»
Какую физическую величину называют сопротивлением
От чего и как зависит сопротивление металлического проводника?
Различные вещества имеют разные удельные сопротивления. Зависит ли сопротивление от состояния проводника? от его температуры? Ответ должен дать опыт.
Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать её в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется.
Если при температуре, равной 0 °С, сопротивление проводника равно R, а при температуре t оно равно R, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t:
Коэффициент пропорциональности α называют температурным коэффициентом сопротивления.
Температурный коэффициент сопротивления — величина, равная отношению относительного изменения сопротивления проводника к изменению его температуры.
Он характеризует зависимость сопротивления вещества от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании на 1 К (на 1 °С).
Для всех металлических проводников коэффициент α > 0 и незначительно меняется с изменением температуры. Если интервал изменения температуры невелик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов
У растворов электролитов сопротивление с ростом температуры не увеличивается, а уменьшается. Для них α -1 .
При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счёт изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (16. 1) подставить значения Вычисления приводят к следующему результату:
1) подставить значения Вычисления приводят к следующему результату:
где ΔТ — изменение абсолютной температуры.
Так как а мало меняется при изменении температуры проводника, то можно считать, что удельное сопротивление проводника линейно зависит от температуры (рис. 16.2).
Увеличение сопротивления можно объяснить тем, что при повышении температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решётки, поэтому свободные электроны сталкиваются с ними чаще, теряя при этом направленность движения. Хотя коэффициент а довольно мал, учёт зависимости сопротивления от температуры при расчёте параметров нагревательных приборов совершенно необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока за счёт нагревания более чем в 10 раз.
У некоторых сплавов, например у сплава меди с никелем (Константин), температурный коэффициент сопротивления очень мал: α ≈ 10 -5 К -1 ; удельное сопротивление Константина велико: ρ ≈ 10 -6 Ом • м.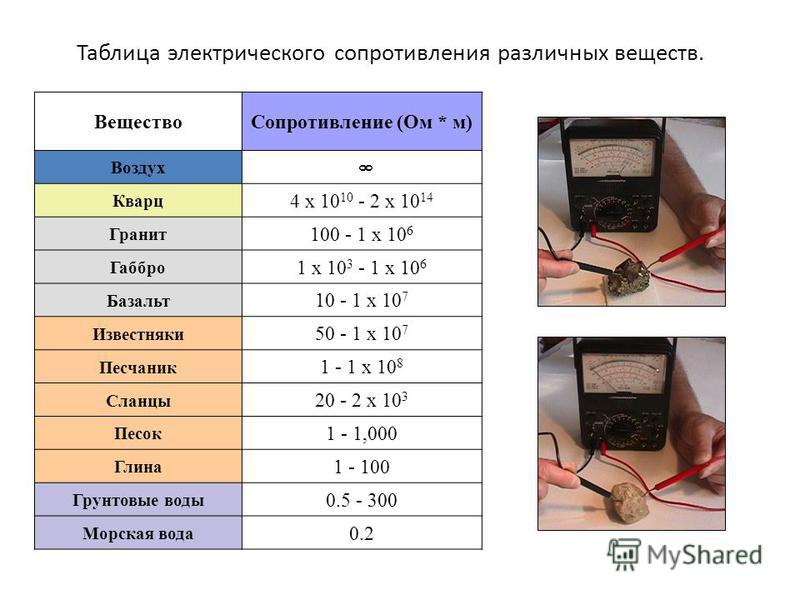 Такие сплавы используют для изготовления эталонных резисторов и добавочных резисторов к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Такие сплавы используют для изготовления эталонных резисторов и добавочных резисторов к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Существуют и такие металлы, например никель, олово, платина и др., температурный коэффициент которых существенно больше: α ≈ 10 -3 К -1 . Зависимость их сопротивления от температуры можно использовать для измерения самой температуры, что и осуществляется в термометрах сопротивления.
На зависимости сопротивления от температуры основаны и приборы, изготовленные из полупроводниковых материалов, — термисторы. Для них характерны большой температурный коэффициент сопротивления (в десятки раз превышающий этот коэффициент у металлов), стабильность характеристик во времени. Номинальное сопротивление термисторов значительно выше, чем у металлических термометров сопротивления, оно обычно составляет 1, 2, 5, 10, 15 и 30 кОм.
Обычно в качестве основного рабочего элемента термометра сопротивления берут платиновую проволоку, зависимость сопротивления которой от температуры хорошо известна.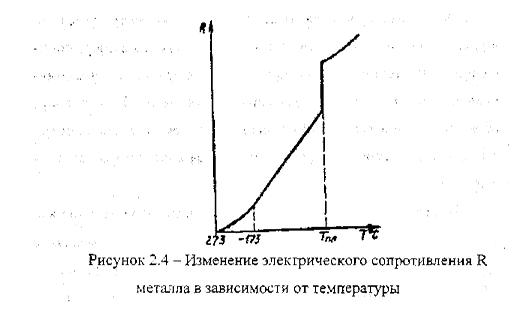 Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Сверхпроводимость.
Сопротивление металлов уменьшается с уменьшением температуры. Что произойдёт при стремлении температуры к абсолютному нулю?
В 1911 г. голландский физик X. Камерлинг-Оннес открыл замечательное явление — сверхпроводимость. Он обнаружил, что при охлаждении ртути в жидком гелии её сопротивление сначала меняется постепенно, а затем при температуре 4,1 К очень резко падает до нуля (рис. 16.3).
Явление падения до нуля сопротивления проводника при критической температуре называется сверхпроводимостью.
Открытие Камерлинг-Оннеса, за которое в 1913 г. ему была присуждена Нобелевская премия, повлекло за собой исследования свойств веществ при низких температурах. Позже было открыто много других сверхпроводников.
Сверхпроводимость многих металлов и сплавов наблюдается при очень низких температурах — начиная примерно с 25 К. В справочных таблицах приводятся температуры перехода в сверхпроводящее состояние некоторых веществ.
Температура, при которой вещество переходит в сверхпроводящее состояние, называется критической температурой.
Критическая температура зависит не только от химического состава вещества, но и от структуры самого кристалла. Например, серое олово имеет структуру алмаза с кубической кристаллической решёткой и является полупроводником, а белое олово обладает тетрагональной элементарной ячейкой и является серебристо-белым, мягким, пластичным металлом, способным при температуре, равной 3,72 К, переходить в сверхпроводящее состояние.
У веществ в сверхпроводящем состоянии были отмечены резкие аномалии магнитных, тепловых и ряда других свойств, так что правильнее говорить не о сверхпроводящем состоянии, а об особом, наблюдаемом при низких температурах состоянии вещества.
Если в кольцевом проводнике, находящемся в сверхпроводящем состоянии, создать ток, а затем удалить источник тока, то сила этого тока не меняется сколь угодно долго. В обычном же (несверхпроводящем) проводнике электрический ток в этом случае прекращается.
Сверхпроводники находят широкое применение. Так, сооружают мощные электромагниты со сверхпроводящей обмоткой, которые создают магнитное поле на протяжении длительных интервалов времени без затрат энергии. Ведь выделения тепла в сверхпроводящей обмотке не происходит.
Однако получить сколь угодно сильное магнитное поле с помощью сверхпроводящего магнита нельзя. Очень сильное магнитное поле разрушает сверхпроводящее состояние. Такое поле может быть создано и током в самом сверхпроводнике. Поэтому для каждого проводника в сверхпроводящем состоянии существует критическое значение силы тока, превысить которое, не нарушая сверхпроводящего состояния, нельзя.
Сверхпроводящие магниты используются в ускорителях элементарных частиц, магнитогидродинамических генераторах, преобразующих механическую энергию струи раскалённого ионизованного газа, движущегося в магнитном поле, в электрическую энергию.
Объяснение сверхпроводимости возможно только на основе квантовой теории. Оно было дано лишь в 1957 г. американскими учёными Дж. Бардиным, Л. Купером, Дж. Шриффером и советским учёным, академиком Н. Н. Боголюбовым.
В 1986 г. была открыта высокотемпературная сверхпроводимость. Получены сложные оксидные соединения лантана, бария и других элементов (керамики) с температурой перехода в сверхпроводящее состояние около 100 К. Это выше температуры кипения жидкого азота при атмосферном давлении (77 К).
Высокотемпературная сверхпроводимость в недалёком будущем приведёт наверняка к новой технической революции во всей электротехнике, радиотехнике, конструировании ЭВМ. Сейчас прогресс в этой области тормозится необходимостью охлаждения проводников до температур кипения дорогого газа — гелия.
Физический механизм сверхпроводимости довольно сложен. Очень упрощённо его можно объяснить так: электроны объединяются в правильную шеренгу и движутся, не сталкиваясь с кристаллической решёткой, состоящей из ионов.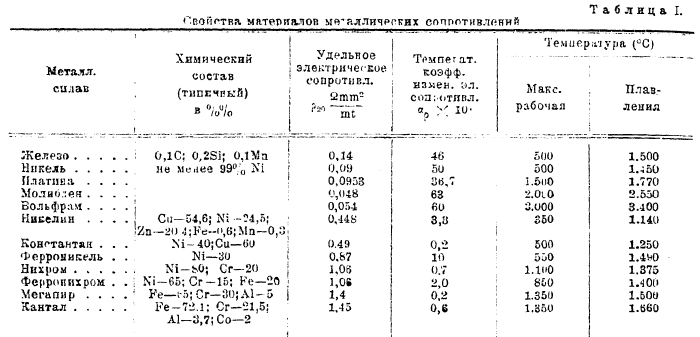 Это движение существенно отличается от обычного теплового движения, при котором свободный электрон движется хаотично.
Это движение существенно отличается от обычного теплового движения, при котором свободный электрон движется хаотично.
Надо надеяться, что удастся создать сверхпроводники и при комнатной температуре. Генераторы и электродвигатели станут исключительно компактными (уменьшатся в несколько раз) и экономичными. Электроэнергию можно будет передавать на любые расстояния без потерь и аккумулировать в простых устройствах.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электрический ток в различных средах — Физика, учебник для 10 класса — Класс!ная физика
§ 60. Зависимость сопротивления от температуры
Частицы проводника (молекулы, атомы, ионы), не участвующие в образовании тока, находятся в тепловом движении, а частицы, образующие ток, одновременно находятся в тепловом и в направленном движениях под действием электрического поля. Благодаря этому между частицами, образующими ток, и частицами, не участвующими в его образовании, происходят многочисленные столкновения, при которых первые отдают часть переносимой ими энергии источника тока вторым. Чем больше столкновений, тем меньше скорость упорядоченного движения частиц, образующих ток. Как видно из формулы I = enνS, снижение скорости приводит к уменьшению силы тока. Скалярная величина, характеризующая свойство проводника уменьшать силу тока, называется сопротивлением проводника. Из формулы закона Ома сопротивление Ом — сопротивление проводника, в котором получается ток силой в 1 а при напряжении на концах проводника в 1 в.
Чем больше столкновений, тем меньше скорость упорядоченного движения частиц, образующих ток. Как видно из формулы I = enνS, снижение скорости приводит к уменьшению силы тока. Скалярная величина, характеризующая свойство проводника уменьшать силу тока, называется сопротивлением проводника. Из формулы закона Ома сопротивление Ом — сопротивление проводника, в котором получается ток силой в 1 а при напряжении на концах проводника в 1 в.
Сопротивление проводника зависит от его длины l, поперечного сечения S и материала, который характеризуется удельным сопротивлением Чем длиннее проводник, тем больше за единицу времени столкновений частиц, образующих ток, с частицами, не участвующими в его образовании, а поэтому тем больше и сопротивление проводника. Чем меньше поперечное сечение проводника, тем более плотным потоком идут частицы, образующие ток, и тем чаще их столкновения с частицами, не участвующими в его образовании, а поэтому тем больше и сопротивление проводника.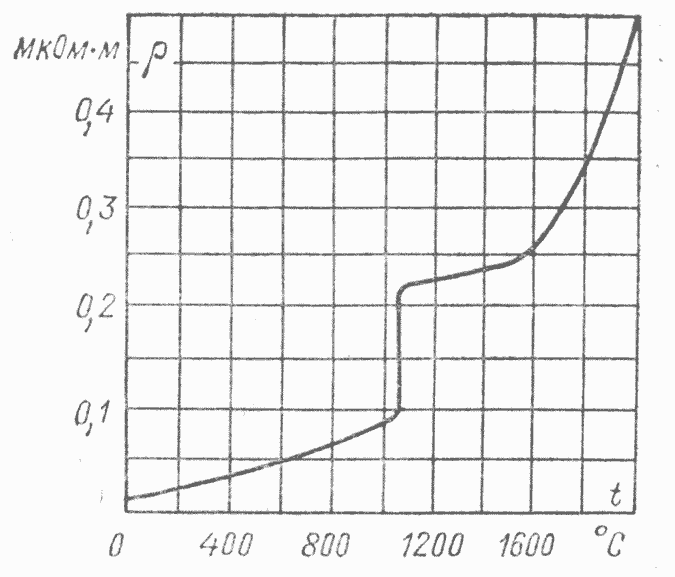
Под действием электрического поля частицы, образующие ток, между столкновениями движутся ускоренно, увеличивая свою кинетическую энергию за счет энергии поля. При столкновении с частицами, не образующими ток, они передают им часть своей кинетической энергии. Вследствие этого внутренняя энергия проводника увеличивается, что внешне проявляется в его нагревании. Рассмотрим, изменяется ли сопротивление проводника при его нагревании.
Рис. 81. Зависимость сопротивления металлов от температуры
В электрической цепи имеется моток стальной проволоки (струна, рис. 81, а). Замкнув цепь, начнем нагревать проволоку. Чем больше мы ее нагреваем, тем меньшую силу тока показывает амперметр. Ее уменьшение происходит от того, что при нагревании металлов их сопротивление увеличивается. Так, сопротивление волоска электрической лампочки, когда она не горит, приблизительно 20 ом, а при ее горении (2900° С) — 260 ом. При нагревании металла увеличивается тепловое движение электронов и скорость колебания ионов в кристаллической решетке, в результате этого возрастает число столкновений электронов, образующих ток, с ионами. Это и вызывает увеличение сопротивления проводника * . В металлах несвободные электроны очень прочно связаны с ионами, поэтому при нагревании металлов число свободных электронов практически не изменяется.
Это и вызывает увеличение сопротивления проводника * . В металлах несвободные электроны очень прочно связаны с ионами, поэтому при нагревании металлов число свободных электронов практически не изменяется.
* ( Исходя из электронной теории, нельзя вывести точный закон зависимости сопротивления от температуры. Такой закон устанавливается квантовой теорией, в которой электрон рассматривается как частица, обладающая волновыми свойствами, а движение электрона проводимости через металл — как процесс распространения электронных волн, длина которых определяется соотношением де Бройля.)
Опыты показывают, что при изменении температуры проводников из различных веществ на одно и то же число градусов сопротивление их изменяется неодинаково. Например, если медный проводник имел сопротивление 1 ом, то после нагревания на 1°С он будет иметь сопротивление 1,004 ом, а вольфрамовый — 1,005 ом. Для характеристики зависимости сопротивления проводника от его температуры введена величина, называемая температурным коэффициентом сопротивления. Скалярная величина, измеряемая изменением сопротивления проводника в 1 ом, взятого при 0° С, от изменения его температуры на 1° С, называется температурным коэффициентом сопротивления α. Так, для вольфрама этот коэффициент равен 0,005 град -1 , для меди — 0,004 град -1 . Температурный коэффициент сопротивления зависит от температуры. Для металлов он с изменением температуры меняется мало. При небольшом интервале температур его считают постоянным для данного материала.
Скалярная величина, измеряемая изменением сопротивления проводника в 1 ом, взятого при 0° С, от изменения его температуры на 1° С, называется температурным коэффициентом сопротивления α. Так, для вольфрама этот коэффициент равен 0,005 град -1 , для меди — 0,004 град -1 . Температурный коэффициент сопротивления зависит от температуры. Для металлов он с изменением температуры меняется мало. При небольшом интервале температур его считают постоянным для данного материала.
Выведем формулу, по которой рассчитывают сопротивление проводника с учетом его температуры. Допустим, что R — сопротивление проводника при 0°С, при нагревании на 1°С оно увеличится на αR, а при нагревании на t° — на αRt° и становится R = R + αRt°, или
Зависимость сопротивления металлов от температуры учитывается, например при изготовлении спиралей для электронагревательных приборов, ламп: длину проволоки спирали и допускаемую силу тока рассчитывают по их сопротивлению в нагретом состоянии.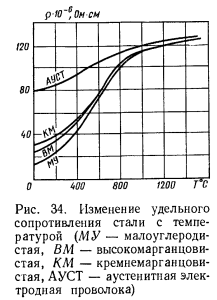 Зависимость сопротивления металлов от температуры используется в термометрах сопротивления, которые применяются для измерения температуры тепловых двигателей, газовых турбин, металла в доменных печах и т. д. Этот термометр состоит из тонкой платиновой (никелевой, железной) спирали, намотанной на каркас из фарфора и помещенной в защитный футляр. Ее концы включаются в электрическую цепь с амперметром, шкала которого проградуирована в градусах температуры. При нагревании спирали сила тока в цепи уменьшается, это вызывает перемещение стрелки амперметра, которая и показывает температуру.
Зависимость сопротивления металлов от температуры используется в термометрах сопротивления, которые применяются для измерения температуры тепловых двигателей, газовых турбин, металла в доменных печах и т. д. Этот термометр состоит из тонкой платиновой (никелевой, железной) спирали, намотанной на каркас из фарфора и помещенной в защитный футляр. Ее концы включаются в электрическую цепь с амперметром, шкала которого проградуирована в градусах температуры. При нагревании спирали сила тока в цепи уменьшается, это вызывает перемещение стрелки амперметра, которая и показывает температуру.
Величина, обратная сопротивлению данного участка, цепи, называется электрической проводимостью проводника (электропроводностью). Электропроводность проводника Чем больше проводимость проводника, тем меньше его сопротивление и тем лучше он проводит ток. Наименование единицы электропроводности Проводимость проводника сопротивлением 1 ом называется сименс.
При понижении температуры сопротивление металлов уменьшается.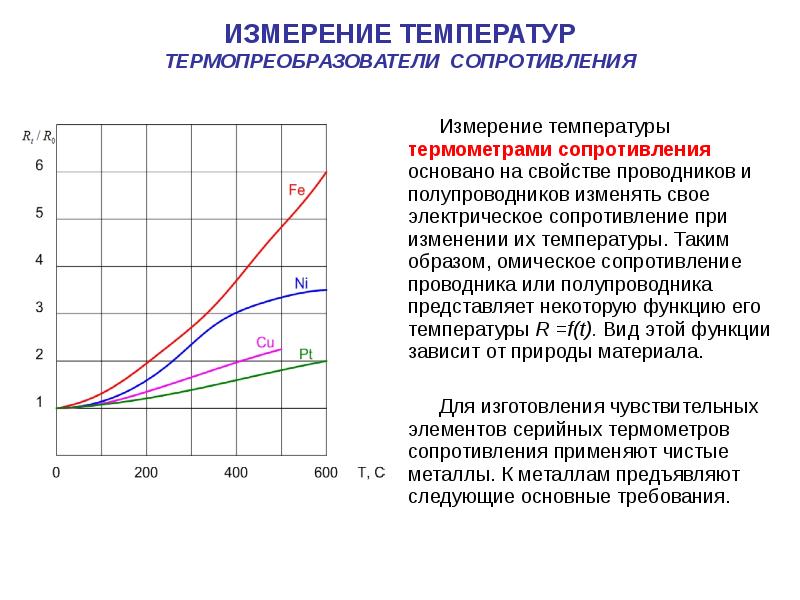 Но есть металлы и сплавы, сопротивление которых при определенной для каждого металла и сплава низкой температуре резким скачком уменьшается и становится исчезающе малым — практически равным нулю (рис. 81, б). Наступает сверхпроводимость — проводник практически не обладает сопротивлением, и раз возбужденный в нем ток существует долгое время, пока проводник находится при температуре сверхпроводимости (в одном из опытов ток наблюдался более года). При пропускании через сверхпроводник тока плотностью 1200 а /мм 2 не наблюдалось выделения количества теплоты. Одновалентные металлы, являющиеся наилучшими проводниками тока, не переходят в сверхпроводящее состояние вплоть до предельно низких температур, при которых проводились опыты. Например, в этих опытах медь охлаждали до 0,0156°К, золото — до 0,0204° К. Если бы удалось получить сплавы со сверхпроводимостью при обычных температурах, то это имело бы огромное значение для электротехники.
Но есть металлы и сплавы, сопротивление которых при определенной для каждого металла и сплава низкой температуре резким скачком уменьшается и становится исчезающе малым — практически равным нулю (рис. 81, б). Наступает сверхпроводимость — проводник практически не обладает сопротивлением, и раз возбужденный в нем ток существует долгое время, пока проводник находится при температуре сверхпроводимости (в одном из опытов ток наблюдался более года). При пропускании через сверхпроводник тока плотностью 1200 а /мм 2 не наблюдалось выделения количества теплоты. Одновалентные металлы, являющиеся наилучшими проводниками тока, не переходят в сверхпроводящее состояние вплоть до предельно низких температур, при которых проводились опыты. Например, в этих опытах медь охлаждали до 0,0156°К, золото — до 0,0204° К. Если бы удалось получить сплавы со сверхпроводимостью при обычных температурах, то это имело бы огромное значение для электротехники.
Согласно современным представлениям, основной причиной сверхпроводимости является образование связанных электронных пар. При температуре сверхпроводимости между свободными электронами начинают действовать обменные силы, отчего электроны образуют связанные электронные пары. Такой электронный газ из связанных электронных пар обладает иными свойствами, чем обычный электронный газ — он движется в сверхпроводнике без трения об узлы кристаллической решетки.
При температуре сверхпроводимости между свободными электронами начинают действовать обменные силы, отчего электроны образуют связанные электронные пары. Такой электронный газ из связанных электронных пар обладает иными свойствами, чем обычный электронный газ — он движется в сверхпроводнике без трения об узлы кристаллической решетки.
Задача 24. Для изготовления спиралей электрической плитки мастерская получила моток нихромозой проволоки, на бирке которой было написано: «Масса 8,2 кг,Λ диаметр 0,5 мм«. Определить, сколько спиралей можно изготовить из этой проволоки, если сопротивление спирали, не включенной в сеть, должно быть 22 ома. Плотность нихрома 8200 кг /м 3 .
Отсюда где S = πr 2 ; S = 3,14*0,0625 мм 2 ≈ 2*10 -7 м 2 .
Масса проволоки m = ρ1V, или m = ρ1lS, отсюда
Отв.: n = 1250 спиралей.
Задача 25. При температуре 20° С вольфрамовая спираль электрической лампочки имеет сопротивление 30 ом; при включении ее в сеть постоянного тока с напряжением 220 в по спирали идет ток 0,6 а.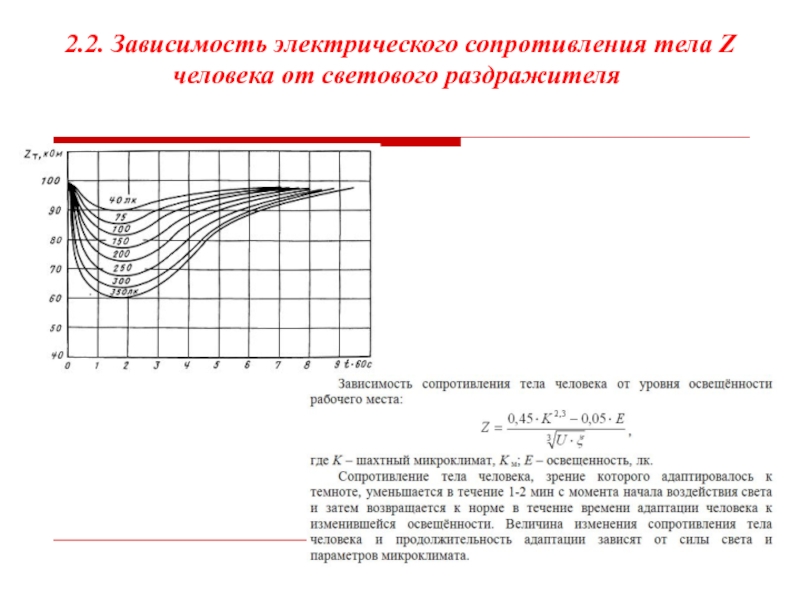 Определить температуру накала нити лампочки и напряженность стационарного электрического поля в нити лампы, если ее длина 550 мм.
Определить температуру накала нити лампочки и напряженность стационарного электрического поля в нити лампы, если ее длина 550 мм.
Сопротивление спирали при горении лампы определим из формулы закона Ома для участка цепи:
тогда
Напряженность стационарного поля в нити лампы
Влияние температуры на сопротивление
Влияние температуры на сопротивление
Электрическое сопротивление изменяется с изменением температуры. Сопротивление не только увеличивается с повышением температуры, но и уменьшается в некоторых случаях. Фактически, для разных типов материалов величина изменения сопротивления из-за изменения температуры разная, что обсуждается ниже.
Металл : Сопротивление всех чистых металлов линейно увеличивается с повышением температуры в ограниченном температурном диапазоне.При низкой температуре ионы почти неподвижны. При повышении температуры ионы внутри металла приобретают энергию и начинают колебаться вокруг своего среднего положения. Эти колеблющиеся ионы сталкиваются с электронами. Следовательно, сопротивление увеличивается с повышением температуры.
Эти колеблющиеся ионы сталкиваются с электронами. Следовательно, сопротивление увеличивается с повышением температуры.
Сопротивление всех металлов, таких как вольфрам, медь, алюминий и т. Д., Линейно увеличивается с повышением температуры в ограниченном диапазоне температур. Например, сопротивление меди составляет 100 Ом при 0 ° C, затем оно линейно увеличивается до 100 ° C.При температуре -234,5 ° C сопротивление меди почти равно нулю, как показано на рисунке.
Следовательно, чистый металл имеет положительный коэффициент сопротивления tempreature.
Сплав: Сопротивление почти всех сплавов увеличивается с повышением температуры, но скорость изменения сопротивления меньше, чем у металлов. Фактически, сопротивление некоторых сплавов, таких как манганин, эврика и константан, практически не изменяет сопротивления в значительном диапазоне температур.Благодаря этому свойству сплав используется для изготовления бокса сопротивления.
Полупроводник, изолятор и электролит: Сопротивление полупроводника, изолятора и электролита (кремний, стекло, лак и т. Д.) Уменьшается с повышением температуры. При нулевой температуре полупроводник ведет себя как идеальный изолятор. При повышении температуры некоторые электроны приобретают энергию и становятся свободными для проводимости. Следовательно, с увеличением температуры увеличивается проводимость и уменьшается сопротивление.
Полупроводник имеет отрицательный температурный коэффициент сопротивления, поэтому, поскольку с увеличением температуры сопротивление уменьшается.
Температурный коэффициент сопротивления:
Изменение сопротивления материала с повышением температуры может быть выражено через температурный коэффициент сопротивления. Рассмотрим проводник с сопротивлением R o при 0 ° C и R t при t ° c .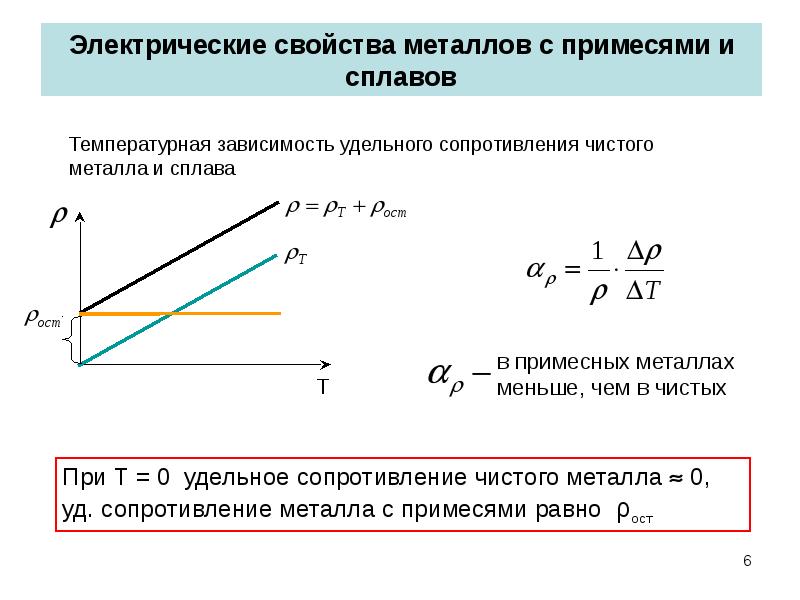 Из приведенного выше обсуждения мы можем сделать вывод, что изменение сопротивления, т.е. (R t — R o ) равно
Из приведенного выше обсуждения мы можем сделать вывод, что изменение сопротивления, т.е. (R t — R o ) равно
- , прямо пропорционально начальному сопротивлению R o
- Прямо пропорционально повышению температуры t ° c .
- Зависит от материала проводника и сплава
Отсюда
(R t — R o ) ∝ R o t
(R t — R o ) = αR o t
R t = R o (1 + α o t)
Где α o является постоянным и называется температурным коэффициентом сопротивления при 0 ° C, и его значение зависит от характера материал и температура.
Влияние температуры на температурный коэффициент сопротивления
Пусть R t1 и R t2 будет сопротивлением проводника при t 1 ° c и t 2 ° c соответственно и α 1 и α 2 — соответствующий температурный коэффициент. Пусть проводник нагревается от начальной температуры t 1 ° c до конечной температуры t 2 ° c .
Пусть проводник нагревается от начальной температуры t 1 ° c до конечной температуры t 2 ° c .
R t2 = R t1 [1 + α t1 (t 2 — t 1 )] ——————– 1
Теперь этот же провод охлаждается с t 2 ° C до t 1 ° C.
R t1 = R t2 [1 + α t2 (t 1 — t 2 )] ——————— 2
Подставляя уравнение 2 в уравнение 1
R t2 = R t2 [1 + α t2 (t 1 — t 2 )] [1 + α t1 (t 2 — t 1 )]
или
1 = [1 + α t2 (t 1 — t 2 )] [1 + α t1 (t 2 — t 1 )]
= [1 — α t2 (t 2 — t 1 )] [1 + α t1 (t 2 — t 1 )]
Примечание: Если температура изменяется от 0 ° C до t ° C, то
Влияние температуры на удельное сопротивление
Удельное сопротивление или удельное сопротивление материала зависит от температуры. Изменение температуры влияет на удельное сопротивление материала так же, как и на сопротивление. Удельное сопротивление металлов линейно увеличивается с повышением температуры. Пусть ρt 1 и ρt 2 — удельное сопротивление при температуре t 1 ° c и t 1 ° c соответственно. Пусть м — наклон линейной части кривой.
Изменение температуры влияет на удельное сопротивление материала так же, как и на сопротивление. Удельное сопротивление металлов линейно увеличивается с повышением температуры. Пусть ρt 1 и ρt 2 — удельное сопротивление при температуре t 1 ° c и t 1 ° c соответственно. Пусть м — наклон линейной части кривой.
Отношение м / ρt 1 называется температурным коэффициентом удельного сопротивления при t 1 ° c и почти равно α 1.
ρ t2 = ρ t1 [1 + α t1 (t 2 — t 1 )]
Примечание: Если температура изменяется от 0 ° C до t ° C, то
ρ t = ρ o [1 + α o t]
Вопрос1. Кусок медного провода имеет сопротивление 50 Ом при 10 ° C. Какова максимальная рабочая температура, если сопротивление провода нужно увеличить на 20%? Предположим, что α при 10 ° C = 0.0041 ° C -1 .
Sol: — R 1 = 50 Ом
R 2 = 50 + 0,2 x 50 = 60 Ом
t 2 = Неизвестная температура, при которой R 2 будет составлять 60 Ом
с
R t2 = R t1 [1 + α t1 (t 2 — t 1 )]
∴ 2 R 1 [1 + α 1 (t 2 — t 1 )]
60 = 50 [1 + 0,0041 (т 2 — 10)]
Вопрос 2. Определенная медная обмотка имеет сопротивление 100 Ом при комнатной температуре. если температурный коэффициент сопротивления меди при 0 ° C составляет 0,00428 / ° C, рассчитайте температуру сопротивления обмотки E, увеличенную до 50 ° C. Предположим, что комнатная температура составляет 25 ° C.
R 1 = 100 Ом
т 1 = 25 ° C
т 2 = 50 ° C
α o = 0,00428 / ° C
Сейчас
= 0,003866 / ° C
R 2 = R 1 [1 + α 1 (t 2 — t 1 )]
R 2 = 100 [1 + 0.003866 (50-25)]
= 109,6657 Ом
Влияние температуры на сопротивление
- Изучив этот раздел, вы должны уметь:
- • Опишите влияние температуры на сопротивление проводника.
- • Опишите влияние температуры на сопротивление изолятора.
- • Определите отрицательные и положительные температурные коэффициенты.
Как температура изменяет сопротивление
Хотя сопротивление проводника изменяется в зависимости от его размера (например, более толстые провода имеют меньшее сопротивление току, чем более тонкие), сопротивление проводника также изменяется с изменением температуры. Этого можно ожидать, потому что при изменении температуры размеры проводника будут изменяться по мере его расширения или сжатия.
Однако материалы, которые классифицируются как ПРОВОДНИКИ, имеют тенденцию ПОВЫШАТЬ свое сопротивление с повышением температуры.Однако ИЗОЛЯТОРЫ могут УМЕНЬШИТЬ свое сопротивление при повышении температуры. Материалы, используемые для изготовления изоляторов (стекло, пластик и т. Д.), Демонстрируют заметное падение сопротивления только при очень высоких температурах. Они остаются хорошими изоляторами при любых температурах, с которыми они могут столкнуться при использовании.
Следовательно, эти изменения сопротивления нельзя объяснить изменением размеров из-за теплового расширения или сжатия. Фактически, для проводника данного размера изменение сопротивления в основном связано с изменением удельного сопротивления материала и вызвано изменением активности атомов, составляющих материал.
Температура и атомная структура
Причины этих изменений удельного сопротивления можно объяснить, рассмотрев протекание тока через материал. Поток тока — это фактически движение электронов от одного атома к другому под действием электрического поля. Электроны — это очень маленькие отрицательно заряженные частицы, которые отталкиваются отрицательным электрическим зарядом и притягиваются положительным электрическим зарядом. Следовательно, если электрический потенциал приложен к проводнику (положительный на одном конце, отрицательный на другом), электроны будут «мигрировать» от атома к атому к положительному полюсу.
Однако только некоторые электроны могут свободно перемещаться. Остальные внутри каждого атома так крепко привязаны к своему конкретному атому, что даже электрическое поле не сместит их. Таким образом, ток, протекающий в материале, обусловлен движением «свободных электронов», и количество свободных электронов в любом материале по сравнению с теми, которые прочно связаны с их атомами, определяет, является ли материал хорошим проводником (много свободных электронов) или хороший изолятор (почти нет свободных электронов).
Воздействие тепла на атомную структуру материала заставляет атомы колебаться, и чем выше температура, тем сильнее колеблются атомы.
В проводнике, по которому уже проходит большое количество свободных электронов, колебания атомов вызывают множество столкновений между свободными электронами и захваченными электронами. Каждое столкновение использует некоторую энергию свободного электрона и является основной причиной сопротивления. Чем больше атомов толкается в материале, тем больше возникает столкновений и, следовательно, больше сопротивление току.
Однако в изоляторе ситуация несколько иная. Свободных электронов так мало, что ток почти не протекает. Почти все электроны прочно связаны внутри своего атома. Нагревание изолирующего материала вызывает вибрацию атомов, и при достаточном нагревании атомы вибрируют достаточно сильно, чтобы фактически освободить часть своих захваченных электронов, создавая свободные электроны, которые становятся носителями тока. Поэтому при высоких температурах сопротивление изолятора может упасть, а в некоторых изоляционных материалах — довольно резко.
В материале, сопротивление которого УВЕЛИЧИВАЕТСЯ с повышением температуры, считается, что материал имеет ПОЛОЖИТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ.
Когда сопротивление ПАДАЕТ с повышением температуры, говорят, что материал имеет ОТРИЦАТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ.
Обычно проводники имеют ПОЛОЖИТЕЛЬНЫЙ температурный коэффициент, в то время как (при высоких температурах) изоляторы имеют ОТРИЦАТЕЛЬНЫЙ температурный коэффициент.
Различные материалы в каждой группе имеют разные температурные коэффициенты.Материалы, выбранные для изготовления резисторов, используемых в электронных схемах, представляют собой тщательно отобранные проводники с очень низким положительным температурным коэффициентом. При использовании резисторы, изготовленные из таких материалов, будут иметь лишь очень небольшое увеличение удельного сопротивления и, следовательно, их сопротивления. Использование таких материалов для изготовления резисторов создает компоненты, значение которых незначительно изменяется в заданном диапазоне температур.
Материалы, выбранные в качестве изоляторов, будут иметь очень низкий ОТРИЦАТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ во всем рабочем диапазоне температур.
Electric Resistance — The Physics Hypertextbook
Обсуждение
введение
Йех! Что за беспорядок.
Проводимость: С. Грей, 1729 — Сопротивление: Георг Симон Ом, 1827.
Обычная версия…
I ∝ В
| I = | В | ⇒ | В = ИК | ⇒ | R = | В |
| R | я |
Variableogy…
- количество: сопротивление R
единица: Ом [Ом] Георг Ом (1787–1854) Германия
Причудливая версия (магнитогидродинамическая версия?)…
J ∝ E
| J = σ E | ⇐ | ⇒ | E = ρ J |
Добро пожаловать в символический ад…
| количество | символ | шт. | символ | собственности… |
|---|---|---|---|---|
| сопротивление | R | Ом | Ом | объектов |
| проводимость | г | siemens | S | |
| удельное сопротивление | ρ | омметр | Ом · м | материалов |
| проводимость | σ | siemens | См / м |
Закон Ома не серьезный закон.Это непростая физика. Разумные материалы и устройства подчиняются ему, но есть много мошенников, которые этого не делают.
резисторы
Плохая выпивка портит наши молодые кишки, но водка идет хорошо.
Лучше постройте крышу над гаражом, пока фургон не намок.
| цвет | цифра | множитель | допуск | tcr (10 −6 / К) | |
|---|---|---|---|---|---|
| нет | ± 20% | ||||
| розовый | 10 −3 | ||||
| серебристый | 10 −2 | ± 10% | |||
| золото | 10 -1 | ± 5% | |||
| черный | 0 | 10 0+ | ± 250 | ||
| коричневый | 1 | 10 1+ | ± 1% | ± 100 | |
| красный | 2 | 10 2+ | ± 2% | ± 50 | |
| оранжевый | 3 | 10 3+ | ± 0.05% | ± 15 | |
| желтый | 4 | 10 4+ | ± 0,02% | ± 25 | |
| зеленый | 5 | 10 5+ | ± 0,50% | ± 20 | |
| синий | 6 | 10 6+ | ± 0,25% | ± 10 | |
| фиолетовый | 7 | ± 0.10% | ± 5 | ||
| серый | 8 | ± 0,01% | ± 1 | ||
| белый | 9 | ||||
материалов
Сопротивление и удельное сопротивление. Факторы, влияющие на сопротивление в проводящем проводе.
Проводники и изоляторы
Лучшие электрические проводники: серебро, медь, золото, алюминий, кальций, бериллий, вольфрам
Удельное сопротивление и проводимость взаимны.
Электропроводность металлов — это статистическая / термодинамическая величина.
Удельное сопротивление определяется рассеянием электронов. Чем больше рассеяние, тем выше сопротивление.
, где…
| σ = | Электропроводность [См / м] |
| n = | плотность свободных электронов [э / м 3 ] |
| e = | заряд электрона (1.60 × 10 −19 С) |
| м e = | масса электрона (9,11 × 10 −31 кг) |
| v rms = | Среднеквадратичная скорость электронов [м / с] |
| ℓ = | средняя длина свободного пробега [м] |
Графит
Кому принадлежит эта идея? Нихром был изобретен в 1906 году, что сделало возможным электрические тостеры.
Проводящие полимеры.
| металлы | ρ (нОм м) | неметаллы | ρ (Ом м) |
|---|---|---|---|
| алюминий | 26,5 | оксид алюминия (14 ° C) | 1 × 10 14 |
| латунь | 64 | оксид алюминия (300 ° C) | 3 × 10 11 |
| хром | 126 | оксид алюминия (800 ° C) | 4 × 10 6 |
| медь | 17.1 | углерод аморфный | 0,35 |
| золото | 22,1 | карбон, алмаз | 2,7 |
| утюг | 96,1 | уголь, графит | 650 × 10 −9 |
| свинец | 208 | оксид индия и олова, тонкая пленка | 2000 × 10 −9 |
| литий | 92.8 | германий | 0,46 |
| ртуть (0 ° C) | 941 | пирекс 7740 | 40 000 |
| марганец | 1440 | кварц | 75 × 10 16 |
| нихром | 1500 | кремний | 640 |
| никель | 69,3 | диоксид кремния (20 ° C) | 1 × 10 13 |
| палладий | 105.4 | диоксид кремния (600 ° C) | 70 000 |
| платина | 105 | диоксид кремния (1300 ° C) | 0,004 |
| плутоний | 1414 | вода, жидкость (0 ° C) | 861 900 |
| серебристый | 15,9 | вода, жидкость (25 ° C) | 181 800 |
| припой | 150 | вода, жидкость (100 ° C) | 12 740 90 462 |
| сталь гладкая | 180 | ||
| сталь, нержавеющая | 720 | ||
| тантал | 131 | ||
| банка (0 ° C) | 115 | ||
| титан (0 ° C) | 390 | ||
| вольфрам | 52.8 | ||
| уран (0 ° C) | 280 | ||
| цинк | 59 |
температура
Общее правило — удельное сопротивление увеличивается с повышением температуры в проводниках и уменьшается с увеличением температуры в изоляторах. К сожалению, не существует простой математической функции для описания этих отношений.
Температурную зависимость удельного сопротивления (или обратной проводимости) можно понять только с помощью квантовой механики. Точно так же, как материя представляет собой совокупность микроскопических частиц, называемых атомами, а луч света — это поток микроскопических частиц, называемых фотонами, тепловые колебания в твердом теле представляют собой рой микроскопических частиц, называемых фононами . Электроны пытаются дрейфовать к положительному полюсу батареи, но фононы продолжают врезаться в них.Случайное направление этих столкновений нарушает попытку организованного движения электронов против электрического поля. Отклонение или рассеяние электронов на фононах — один из источников сопротивления. С повышением температуры количество фононов увеличивается, а вместе с ним и вероятность столкновения электронов и фононов. Таким образом, когда температура повышается, сопротивление повышается.
Для некоторых материалов удельное сопротивление является линейной функцией температуры.
ρ = ρ 0 (1 + α ( T — T 0 ))
Удельное сопротивление проводника увеличивается с температурой.В случае меди зависимость между удельным сопротивлением и температурой примерно линейна в широком диапазоне температур.
Для других материалов лучше работает соотношение сил.
ρ = ρ 0 ( T / T 0 ) μ
Удельное сопротивление проводника увеличивается с температурой. В случае вольфрама связь между удельным сопротивлением и температурой лучше всего описывается соотношением мощности.
см. Также: сверхпроводимость
разное
магнитосопротивление
фотопроводимость
жидкости
электролиты
газы
пробой диэлектрика
плазма
микрофоны
Угольный микрофон — ничто задом наперед
| тип | звука производят изменения в… | , что вызывает изменения… | , что приводит к изменениям… |
|---|---|---|---|
| углерод | Плотность гранул | сопротивление | напряжение |
| конденсатор | разделительная пластина | емкость | напряжение |
| динамический | расположение змеевика | флюс | напряжение |
| пьезоэлектрический | компрессия | поляризация | напряжение |
4.3: Сопротивление и температура — Physics LibreTexts
Было обнаружено, что удельное сопротивление металлов обычно увеличивается с повышением температуры, тогда как удельное сопротивление полупроводников обычно уменьшается с повышением температуры.
Возможно, стоит немного подумать о том, как электроны в металле или полупроводнике проводят электричество. В твердом металле большая часть электронов в атоме используется для образования ковалентных связей между соседними атомами и, следовательно, для удержания твердого тела вместе.Но примерно один электрон на атом не связан таким образом, и эти «электроны проводимости» более или менее свободно перемещаются внутри металла, как молекулы в газе. Мы можем приблизительно оценить скорость, с которой движутся электроны. Таким образом, мы напоминаем формулу \ (\ sqrt {3kT / m} \) для среднеквадратичной скорости молекул в газе, и, возможно, мы можем применить ее к электронам в металле только на примерный порядок величины их скорость. Постоянная Больцмана \ (k \) составляет около 1,38 \ (\ times \) 10 -23 Дж K -1 , а масса электрона m составляет около 9.11 \ (\ times \) 10 -31 кг. Если мы предположим, что температура составляет около 27 o C или 300 K, среднеквадратичная скорость электронов будет около 1,2 \ (\ times \) 10 5 м с -1 .
Теперь рассмотрим ток в 1 А, протекающий по медному проводу диаметром 1 мм, то есть площадь поперечного сечения 7,85 \ (\ times \) 10 -7 м 2 . Плотность меди составляет 8,9 г / см -3 , а ее «атомный вес» (молярная масса) составляет 63,5 г на моль, что означает, что их 6.02 \ (\ times \) 10 23 (число Авогадро) атомов в 63,5 граммах, или 8,44 \ (\ times \) 10 22 атома на см 3 или 8,44 \ (\ times \) 10 28 атом / м 3 . Если предположить, что на один атом приходится один электрон проводимости, то на 1 м приходится 8,44 \ (\ times \) 10 28 электронов проводимости, или, в нашем проводе диаметром 1 мм, 6,63 \ (\ times \ ) 10 22 электрон проводимости на метр.
Скорость, с которой электроны переносят ток в один ампер, равна току, деленному на заряд на единицу длины, при этом заряд одного электрона равен 1.60 \ (\ times \) 10 -19 C, мы находим, что скорость, с которой электроны переносят ток, составляет примерно 9,4 \ (\ times \) 10 -5 м с -1 .
Таким образом, у нас есть картина электронов, движущихся в случайных направлениях со скоростью примерно 1,2 \ (\ times \) 10 5 мс -1 (тепловое движение) и, наложенная на нее, очень медленная скорость дрейфа только 9,4 \ (\ times \) 10 -5 мс -1 для электронного тока. Если бы вы могли видеть электроны, вы бы видели, как они бегают туда-сюда с очень высокой скоростью, но вы бы даже не заметили очень медленного дрейфа в направлении тока.
Однако, когда вы подключаете длинный провод к батарее, ток (медленный дрейф электронов) начинается почти мгновенно по всей длине провода. Если бы электроны находились в полном вакууме, а не внутри металла, они бы ускорялись до тех пор, пока находились в электрическом поле. Электроны внутри металла также ускоряются, но они постоянно останавливаются на своем пути из-за столкновений с атомами металла, а затем снова запускаются. Если температура повышается, колебания атомов внутри металлической решетки увеличиваются, и это предположительно каким-то образом увеличивает сопротивление электронному потоку или уменьшает среднее время или средний путь между столкновениями.
В полупроводнике большая часть электронов требуется для валентной связи между атомами, но есть несколько (гораздо меньше одного на атом) свободных электронов проводимости. По мере повышения температуры большее количество электронов освобождается от своих валентных функций, и затем они берут на себя задачу проводить электричество. Таким образом, проводимость полупроводника увеличивается с увеличением температуры.
Температурный коэффициент сопротивления a металла (или другого вещества) — это относительное увеличение его удельного сопротивления на единицу повышения температуры:
\ [\ alpha = \ frac {1} {\ rho} \ frac {d \ rho} {dT} \ label {4.3.1} \]
В единицах СИ это было бы выражено в K -1 . Однако во многих практических приложениях температурный коэффициент определяется в зависимости от изменения сопротивления по сравнению с удельным сопротивлением при температуре 20 90 300 o 90 301 ° C и определяется уравнением
\ [\ rho = \ rho_ {20} [1+ \ alpha (t-20)], \ label {4.3.2} \]
, где t — температура в градусах Цельсия.
Примеры:
Серебро: 3.8 \ (\ times \) 10 -3 C o -1
Медь: 3.9 \ (\ раз \) 10 -3
Алюминий: 3,9 \ (\ раз \) 10 -3
Вольфрам: 4,5 \ (\ раз \) 10 -3
Железо: 5,0 \ (\ раз \) 10 -3
Углерод: -0,5 \ (\ раз \) 10 -3
Германий: -48 \ (\ times \) 10 -3
Кремний: -75 \ (\ times \) 10 -3
Некоторые металлические сплавы с коммерческими названиями, такие как нихром, манганин, константан, эврика и т. Д., Имеют довольно большое удельное сопротивление и очень низкие температурные коэффициенты.
В качестве элемента стиля обратите внимание, что кельвин — это единица измерения температуры, а метр — это единица длины. Таким образом, при обсуждении температуры нет необходимости использовать символ «градус» с кельвином. Когда вы говорите о какой-то другой температурной шкале, такой как Цельсия, нужно сказать «20 градусов по шкале Цельсия» — таким образом, 20 o C. Но когда говорят о температурном интервале , равном такому количеству градусов Цельсия , это пишется C o .Я придерживался вышеуказанного соглашения.
Удельное сопротивление платины как функция температуры используется в качестве основы для платинового термометра сопротивления , полезного в условиях и температурах, где другие типы термометров не могут быть полезны, и он также используется для определения практической шкалы температур при высокие температуры. Болометр — прибор, используемый для обнаружения и измерения инфракрасного излучения. Излучение фокусируется на почерневшем платиновом диске, который в результате нагревается.Повышение температуры измеряется путем измерения увеличения сопротивления. Термистор представляет собой полупроводниковое устройство, сопротивление которого очень чувствительно к температуре, и его можно использовать для измерения или контроля температуры.
Как температура влияет на металл?
Металлы — это элементы или соединения с отличной проводимостью как для электричества, так и для тепла, что делает их полезными для широкого круга практических целей. В настоящее время периодическая таблица Менделеева содержит 91 металл, каждый из которых имеет свои специфические свойства.Электрические, магнитные и структурные свойства металлов могут изменяться с температурой и тем самым обеспечивать полезные свойства для технологических устройств. Понимание влияния температуры на свойства металлов дает вам более глубокое понимание того, почему они так широко используются в современном мире.
TL; DR (слишком долго; не читал)
TL; DR
Температура влияет на металл по-разному. Более высокая температура увеличивает электрическое сопротивление металла, а более низкая температура снижает его.Нагретый металл подвергается тепловому расширению и увеличивается в объеме. Повышение температуры металла может вызвать аллотропное фазовое превращение, которое изменяет ориентацию составляющих его атомов и изменяет его свойства. Наконец, ферромагнитные металлы становятся менее магнитными, когда они становятся более горячими и теряют свой магнетизм выше температуры Кюри.
Рассеяние электронов и сопротивление
Когда электроны проходят через объем металла, они рассеиваются друг от друга, а также от границ материала.Ученые называют это явление «сопротивлением». Повышение температуры дает электронам больше кинетической энергии, увеличивая их скорость. Это приводит к большему рассеянию и более высокому измеренному сопротивлению. Снижение температуры приводит к уменьшению скорости электронов, уменьшению количества рассеяния и измеренного сопротивления. Современные термометры используют изменение электрического сопротивления провода для измерения изменений температуры.
Термическое расширение
Повышение температуры приводит к небольшому увеличению длины, площади и объема металла, что называется тепловым расширением.Величина расширения зависит от конкретного металла. Тепловое расширение возникает в результате увеличения колебаний атомов с температурой, и учет теплового расширения важен во множестве приложений. Например, при проектировании трубопроводов в ванных комнатах производителям необходимо учитывать сезонные изменения температуры, чтобы избежать разрыва труб.
Аллотропические фазовые превращения
Три основные фазы вещества называются твердой, жидкой и газовой.Твердое тело — это плотно упакованный массив атомов с определенной симметрией кристалла, известный как аллотроп. Нагревание или охлаждение металла может привести к изменению ориентации атомов по отношению к другим. Это известно как аллотропное фазовое превращение. Хороший пример аллотропного фазового превращения наблюдается в железе, которое переходит из альфа-фазы при комнатной температуре в гамма-фазу железа при 912 градусах Цельсия (1674 градуса Фаренгейта). Гамма-фаза железа, которая способна растворять больше углерода, чем альфа-фаза, облегчает производство нержавеющей стали.
Снижение магнетизма
Спонтанно магнитные металлы называются ферромагнитными материалами. Три ферромагнитных металла при комнатной температуре — это железо, кобальт и никель. Нагревание ферромагнитного металла снижает его намагниченность и в конечном итоге полностью теряет свой магнетизм. Температура, при которой металл теряет свою спонтанную намагниченность, известна как температура Кюри. Никель имеет самую низкую точку Кюри среди отдельных элементов и перестает становиться магнитным при 330 градусах Цельсия (626 градусов по Фаренгейту), тогда как кобальт остается магнитным до 1100 градусов Цельсия (2012 градусов по Фаренгейту).
Температурный коэффициент сопротивления | Electrical4U
Как мы обсуждали на странице под заголовком «Изменение сопротивления в зависимости от температуры», электрическое сопротивление каждого вещества изменяется с изменением его температуры.
Температурный коэффициент сопротивления — это мера изменения электрического сопротивления любого вещества на градус изменения температуры.
Возьмем проводник с сопротивлением R 0 при 0 90 300 o C и R t при t 90 300 o C соответственно.
Из уравнения изменения сопротивления в зависимости от температуры получаем
Этот α o называется температурным коэффициентом сопротивления этого вещества при 0 o C.
Из приведенного выше уравнения ясно, что изменение электрического Сопротивление любого вещества из-за температуры в основном зависит от трех факторов:
- значение сопротивления при начальной температуре,
- повышение температуры и
- температурный коэффициент сопротивления α o .
Эти α o различаются для разных материалов, поэтому влияние на сопротивление при разной температуре у разных материалов различно.
Таким образом, температурный коэффициент сопротивления при 0 o C любого вещества является обратной величиной предполагаемой температуры нулевого сопротивления этого вещества. До сих пор мы обсуждали материалы, сопротивление которых увеличивается с повышением температуры, но есть много материалов, электрическое сопротивление которых уменьшается с понижением температуры.На самом деле в металле при повышении температуры случайное движение свободных электронов и межатомные колебания внутри металла увеличиваются, что приводит к большему количеству столкновений. Больше столкновений препятствует плавному потоку электронов через металл, поэтому сопротивление металла увеличивается с повышением температуры. Итак, температурный коэффициент сопротивления считаем положительным для металла.
Но в случае полупроводника или другого неметалла количество свободных электронов увеличивается с увеличением температуры.Поскольку при более высокой температуре из-за достаточной тепловой энергии, подводимой к кристаллу, значительное количество ковалентных связей разрывается, и, следовательно, создается больше свободных электронов. Это означает, что при повышении температуры значительное количество электронов попадает в зоны проводимости из валентных зон, пересекая запрещенную энергетическую зону. По мере увеличения количества свободных электронов сопротивление этого типа неметаллического вещества уменьшается с увеличением температуры. Следовательно, температурный коэффициент сопротивления отрицателен для неметаллических веществ и полупроводников.
Если сопротивление приблизительно не изменяется с температурой, мы можем считать значение этого коэффициента равным нулю. Сплав константана и манганина имеет температурный коэффициент сопротивления, близкий к нулю.
Значение этого коэффициента не является постоянным, оно зависит от начальной температуры, на которой основано приращение сопротивления. Когда приращение основано на начальной температуре 0 o ° C, значение этого коэффициента составляет α o , что является не чем иным, как обратной величиной соответствующей предполагаемой температуры нулевого сопротивления вещества.Но при любой другой температуре температурный коэффициент электрического сопротивления не такой, как у этого α o . Фактически для любого материала значение этого коэффициента максимально при температуре 0 90 300 o 90 301 C. Скажем, значение этого коэффициента любого материала при любом t o C равно α t , тогда его значение может быть определено по следующему уравнению,
Значение этого коэффициента при температуре t 2 o C в терминах того же самого при t 1 o C определяется как,
Обзор концепции температурного коэффициента сопротивления
Электрическое сопротивление проводников, таких как серебро, медь, золото, алюминий и т. Д. ., зависит от процесса столкновения электронов внутри материала. По мере увеличения температуры этот процесс столкновения электронов ускоряется, что приводит к увеличению сопротивления с повышением температуры проводника. Сопротивление проводов обычно увеличивается с повышением температуры.
Если проводник имеет сопротивление R 1 при t 1 o C и после повышения температуры его сопротивление становится R 2 при t 2 o C.Это повышение сопротивления (R 2 — R 1 ) с повышением температуры (t 2 — t 1 ) зависит от следующих факторов:
Комбинируя указанные выше эффекты,
Где α — это температурный коэффициент сопротивления материала при t 1 o C.
Из уравнения (1)
Если при определенной температуре мы знаем сопротивление и температурный коэффициент сопротивления материала , мы можем узнать сопротивление материала при других температурах с помощью уравнения (2).
Температурный коэффициент сопротивления некоторых материалов или веществ
Температурный коэффициент сопротивления некоторых материалов / веществ при 20 o C перечислены ниже —
| Sl. № | Материал / Вещества | Химический символ / Химический состав | Температурный коэффициент сопротивления / o C (при 20 o C) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | Серебро | Ag | 0.0038 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Медь | Медь | 0,00386 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Золото | Au | 0,0034 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Алюминий | W | 0,0045 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Железо | Fe | 0,00651 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Платина | Pt | 0.003927 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Манганин | Cu = 84% + Mn = 12% + Ni = 4% | 0,000002 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Ртуть | Hg | 0,000465 | 0,000465 | Ni = 60% + Cr = 15% + Fe = 25% | 0,0004 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Константин | Cu = 55% + Ni = 45% | 0,00003 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Углерод | С | — 0.0005 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Германий | Ge | — 0,05 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Кремний | Si | — 0,07 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | 0,0015 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Никель | Ni | 0,00641 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | Олово | Sn | 0,0042 | Z0037 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Марганец | Mn | 0,00001 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Тантал | Ta | 0,0033 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CONDITION | TEMP. C | ДРОССЕЛЬНАЯ КАТУШКА | ГЕРМАНИЯ ДИОД | ТЕРМИСТОР | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | R | R | R | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Кипящая вода | 100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Горячая вода | 75 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теплая вода | 50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Комнатная температура | 25 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 45 | 45 | Для каждого устройства нарисуйте график зависимости температуры (ось x) отсопротивление (ось Y). Вопросы: 1. Какие образцы имели изменение сопротивления в зависимости от температуры? направление было это изменение? 2. Что случилось с сопротивлением при повышении температуры? проводники, полупроводники? Кажется, изменение 3. Соответствует ли какой-либо из примеров общим рекомендациям введение в лабораторию? Объяснять. 4. Опишите движение атомов или ионов в кристаллическом твердом теле. увеличивается. 5. Что заставляет электроны «дрейфовать»? 6. Опишите движение электронов при протекании тока. 7. Объясните, как повысить температуру полупроводника. сопротивление. 8. Объясните, как повышение температуры металла увеличивает его Добавочный номер: Для термистора график 1 / T (K -1 ) ln R = (E зазор / 2k) x 1 / T + ln R o где: k = 8,62 x 10 -5 эВ / К (Больцмановский E gap = энергия запрещенной зоны (разница в энергии между Определите наклон линии по графику. (E разрыв / 2k) = Заметки учителя: * Время подготовки учителя составляет около 30 минут. * Катушки сопротивления могут использоваться вместо дроссельной катушки. (Короткий * Можно попробовать другие виды проволоки, кроме меди. * Выводы разъема к устройствам можно удлинить путем пайки * Углеродное устройство должно потерять лишь небольшой процент своего помещения. * В качестве примера непроводника можно указать длину стеклянного стержня. * Используйте термопару типа K для более низких температур в сочетании * Термисторные зонды поставляются компанией Vernier. * Учитель должен продемонстрировать правильное подключение счетчиков и * Результаты диодов работают лучше всего, если температура измеряется * Для активности расширения, используя образцы данных, значение Ответы на вопросы: 1. Все устройства меняли свое сопротивление при изменении температуры. сопротивление дроссельной катушки (медной проволоки) увеличено повысился. Сопротивление диода и термистора полупроводниковый материал) уменьшалась с увеличением температуры 2. Сопротивление проводника линейно увеличивалось. В полупроводник уменьшился, но не линейно. 3.Ответы учащихся будут разными. Устройства действительно реагируют как теоретически 4. При повышении температуры атомы или ионы колеблются с вокруг их стабильного положения решетки. 5. При приложении электрического поля электроны вынуждены 6. Электроны движутся беспорядочно и движутся в противоположном направлении. приложенное электрическое поле. 7. С повышением температуры больше электронов имеют энергию зона проводимости (больше носителей заряда означает больше 8. Большая амплитуда колебаний ионов в решетке вызывает валентные электроны, что уменьшает дрейф
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
