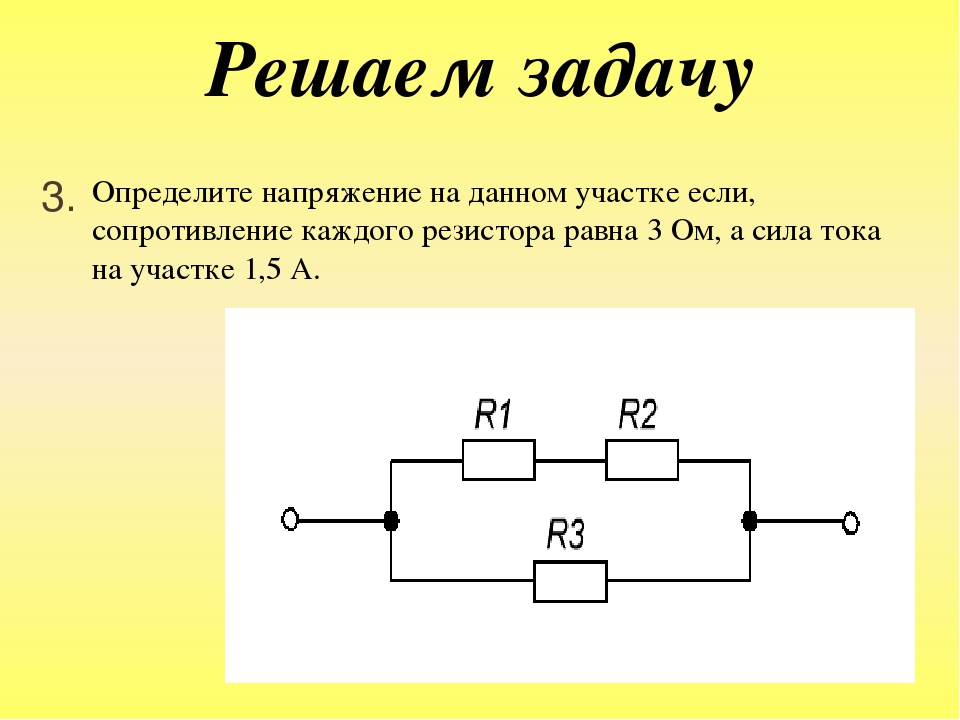
Схемы параллельного и последовательного соединения резисторов
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление R общ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами.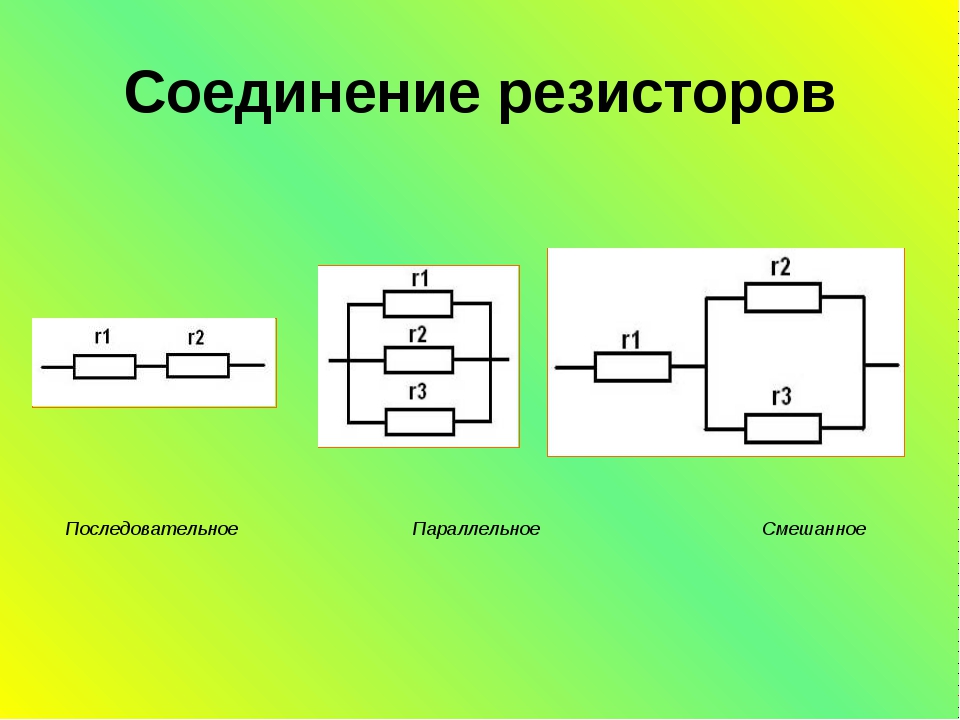 В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление R общ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление R общ
Для того чтобы посчитать общее сопротивление смешанного соединения:
o Цепь разбивают на участки с только пареллельным или только последовательным соединением. o Вычисляют общее сопротивление для каждого отдельного участка.
o Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
Можно, в соответствии схеме, сразу записывать формулу следующим образом:
o Если резисторы соединяются последоватеьно – складывать.
o Если резисторы соединяются параллельно – использовать условное обозначение «||». o Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Общие сведения
Резистор
Чаще всего резисторы представляют собой металлическую проволоку или полоску, для компактности намотанную на стержень (чем длинней проводник и чем меньше его поперечное сечение, тем выше сопротивление). Разумеется, сопротивление также зависит от материала, из которого изготовлен проводник. Полюбоваться на резисторы можно на рисунке 50.1. «Резисторы (с сайта РадиоКот)».
На электрических схемах резистор обычно изображают как прямоугольник, из которого выходят два вывода (рисунок 50.2. «Схематическое изображение резистора»).
Последовательное и параллельное соединение резисторов
Очевидно, имеется только две возможности для соединения двух резисторов: можно их спаять одним концом или же обоими. Первый способ называется последовательным соединением, а второй — параллельным (рисунок 50.3. «Последовательное и параллельное соединение резисторов»).
И последовательное, и параллельное соединение резисторов можно рассматривать как новый резистор. Его сопротивление можно вычислить, пользуясь следующими правилами:
- При последовательном соединении резисторов их сопротивления складываются: R = R 1 + R 2 .
- При параллельном соединении резисторов складываются их проводимости, то есть величины, обратные сопротивлениям: 1 R = 1 R 1 + 1 R 2 , или R = R 1 R 2 R 1 + R 2 .
В частности, соединяя два одинаковых резистора с единичным сопротивлением последовательно, получим сопротивление 2 , при параллельном соединении получим 1 2 .
При соединении более двух резисторов иногда удаётся представить полученную схему как последовательное или параллельное соединение двух подсхем. Например, схема на рисунке 50.4. «Смешанное соединение резисторов» представляется как параллельное соединение резистора R 1 и последовательного соединения резисторов R 2 и R 3 . Таким образом, сопротивление схемы между двумя выделенными узлами вычисляется как R 1 R 2 + R 3 R 1 + R 2 + R 3 .
Например, схема на рисунке 50.4. «Смешанное соединение резисторов» представляется как параллельное соединение резистора R 1 и последовательного соединения резисторов R 2 и R 3 . Таким образом, сопротивление схемы между двумя выделенными узлами вычисляется как R 1 R 2 + R 3 R 1 + R 2 + R 3 .
Сложное соединение резисторов
Увы, не всякая схема представляется как последовательное или параллельное соединение двух подсхем, подобно тому, как не всякое натуральное число раскладывается в произведение своих собственных делителей. Простой пример такой неразложимой схемы можно увидеть на рисунке 50.5. «Сложное соединение резисторов».
Для расчёта таких сопротивлений используют, помимо закона Ома, ещё и закон сохранения заряда.
Электрический ток в проводнике можно представлять себе как поток частиц, несущих электрические заряды (это могут быть электроны или ионы). Причиной такого движения заряженных частиц является разность электрических потенциалов на концах проводника (напряжение).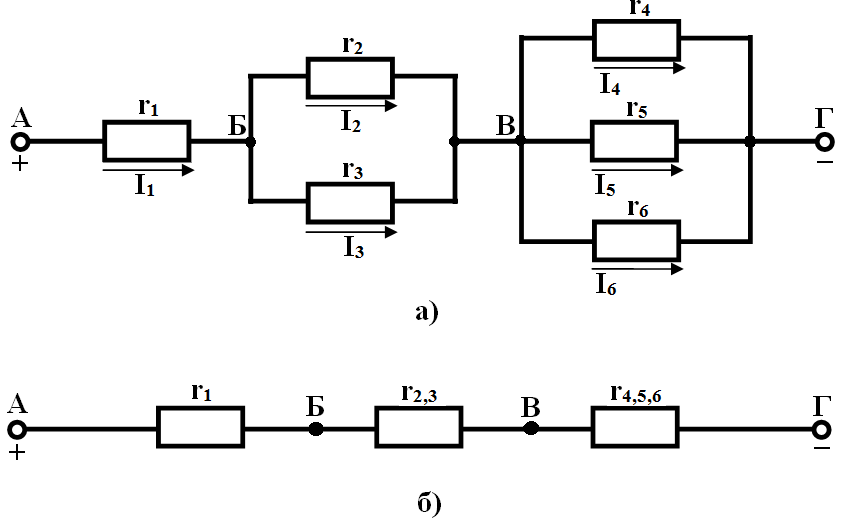 Сама по себе величина потенциала в отдельно взятой точке схемы не имеет физического смысла, такой смысл есть только лишь у разности потенциалов в двух точках (точно так же лишена смысла потенциальная энергия силы тяжести в отдельной точке, а важен перепад потенциальной энергии в двух точках). Ток — это суммарный заряд, протекающий через поперечное сечение проводника за единицу времени. Представим такую модель: по дороге из пункта A в пункт B движется поток автомобилей, каждый из которых загружен зарядом. Если заряды положительны, считается, что ток в направлении от A к B положителен. Но можно считать также, что имеется отрицательный ток (той же самой абсолютной величины) в направлении от B к A .
Сама по себе величина потенциала в отдельно взятой точке схемы не имеет физического смысла, такой смысл есть только лишь у разности потенциалов в двух точках (точно так же лишена смысла потенциальная энергия силы тяжести в отдельной точке, а важен перепад потенциальной энергии в двух точках). Ток — это суммарный заряд, протекающий через поперечное сечение проводника за единицу времени. Представим такую модель: по дороге из пункта A в пункт B движется поток автомобилей, каждый из которых загружен зарядом. Если заряды положительны, считается, что ток в направлении от A к B положителен. Но можно считать также, что имеется отрицательный ток (той же самой абсолютной величины) в направлении от B к A .
Закон сохранения зарядов говорит, что электрические заряды не возникают ниоткуда и не исчезают в никуда. Если электрически нейтральная частица, такая как атом, распадается на две заряженных частицы (ион и электрон), суммарный заряд новых частиц всегда равняется заряду атома, то есть нулю. Из закона следует, в частности, что токи через два поперечных сечения тонкого проводника в один и тот же момент времени равны, иначе где-то между этими сечениями рождался бы или пропадал ненулевой заряд. Другим следствием закона сохранения заряда является утверждение, что в узле электрической схемы, где соединяется несколько проводников, сумма всех входящих в узел токов равна сумме всех выходящих. Если вернуться к автомобильной аналогии, количество автомобилей, въезжающих на перекрёсток нескольких дорог, равно количеству выезжающих с перекрёстка (здесь, конечно, предполагается, что каждый автомобиль везёт единичный заряд, и время, проводимое автомобилями на перекрёстке, пренебрежимо мало).
Из закона следует, в частности, что токи через два поперечных сечения тонкого проводника в один и тот же момент времени равны, иначе где-то между этими сечениями рождался бы или пропадал ненулевой заряд. Другим следствием закона сохранения заряда является утверждение, что в узле электрической схемы, где соединяется несколько проводников, сумма всех входящих в узел токов равна сумме всех выходящих. Если вернуться к автомобильной аналогии, количество автомобилей, въезжающих на перекрёсток нескольких дорог, равно количеству выезжающих с перекрёстка (здесь, конечно, предполагается, что каждый автомобиль везёт единичный заряд, и время, проводимое автомобилями на перекрёстке, пренебрежимо мало).
Теперь, вооружённые знаниями, рассчитаем сопротивление электрической схемы на рисунке 50.5 между отмеченными узлами. На схеме присутствуют пять резисторов и четыре узла. Пронумеруем резисторы числами от 1 до 5 и узлы числами от 1 до 4 . Порядок нумерации узлов можно выбрать совершенно произвольно. Чтобы судить о направлении тока через каждый из резисторов, следует на каждом задать направление. Это также можно сделать произвольно, однако для определённости будем считать, что положительным направлением тока будет направление от узла с меньшим номером к узлу с большим. Обозначим потенциалы в узлах буквой U с соответствующим индексом. Результат всех этих приготовлений представлен на рисунке 50.6. «Разметка схемы».
Чтобы судить о направлении тока через каждый из резисторов, следует на каждом задать направление. Это также можно сделать произвольно, однако для определённости будем считать, что положительным направлением тока будет направление от узла с меньшим номером к узлу с большим. Обозначим потенциалы в узлах буквой U с соответствующим индексом. Результат всех этих приготовлений представлен на рисунке 50.6. «Разметка схемы».
Пропустим электрический ток через узлы с номерами 1 и 2 . Из закона сохранения заряда ток, входящий в узел 1 , равен току, выходящему из узла 2 . Если взять величину тока, равную единице, в силу закона Ома разность потенциалов U 2 − U 1 будет равна в точности искомому сопротивлению. Поскольку, как мы помним, имеют значения лишь разности потенциалов, мы можем смело положить U 1 = 0 , и тогда U 2 окажется искомым сопротивлением схемы.
Обозначив как I α ток через резистор R α , для каждого из резисторов запишем закон Ома: R 1 I 1 = U 3 − U 1 , R 2 I 2 = U 4 − U 1 , R 3 I 3 = U 4 − U 3 , R 4 I 4 = U 3 − U 2 , R 5 I 5 = U 4 − U 2 .
Вторая группа уравнений получается из закона сохранения заряда. Для каждого узла сумму входящих в него токов приравниваем сумме выходящих. При этом не забываем про единичный ток, входящий в первый узел и выходящий из второго: 1 = I 1 + I 2 , 0 = 1 + I 4 + I 5 , I 1 + I 4 = I 3 , I 2 + I 3 + I 5 = 0 .
Добавив к составленным уравнениям ещё одно, U 1 = 0 , решаем полученную систему относительно U 2 .
Между прочим, применяя описанную методику к последовательному и параллельному соединениям резисторов, мы с удовольствием убедились в правильности формул сложения сопротивлений и проводимостей.
Пора заметить, что все полученные уравнения являются линейными алгебраическими по отношению ко всем неизвестным величинам I α и U β . Мы не станем задаваться вопросом о единственности решения такой системы уравнений. Отметим лишь, что существует единственное значение U 2 , удовлетворяющее системе. Об этом говорит физический смысл уравнений.
Задача расчёта электрического сопротивления является довольно актуальной. Имеется ряд приёмов, которые позволяют упростить её решение. К примеру, правила Кирхгофа позволяют строить системы уравнений, равносильные только что полученным, и при этом, как правило, более простые. Есть методы, в основе которых лежат преобразования схем в эквивалентные (то есть имеющие то же сопротивление), но при этом разложимые в последовательное или параллельное соединение двух подсхем. Мы не будем останавливаться на этих методах. В главе 49. «Линейные уравнения» рассматривалось алгоритмическое решение систем линейных уравнений, и нам остаётся лишь воспользоваться уже написанным библиотечным модулем.
Имеется ряд приёмов, которые позволяют упростить её решение. К примеру, правила Кирхгофа позволяют строить системы уравнений, равносильные только что полученным, и при этом, как правило, более простые. Есть методы, в основе которых лежат преобразования схем в эквивалентные (то есть имеющие то же сопротивление), но при этом разложимые в последовательное или параллельное соединение двух подсхем. Мы не будем останавливаться на этих методах. В главе 49. «Линейные уравнения» рассматривалось алгоритмическое решение систем линейных уравнений, и нам остаётся лишь воспользоваться уже написанным библиотечным модулем.
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Рис. 25. Схемы последовательного соединения приемников
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
где R эк = R1 + R2 + R3 .
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов. Так как напряжения на отдельных участках цепи согласно закону Ома: U1=IR1; U2 = IR2, U3 = IRз и в данном случае E = U, то длярассматриваемой цепи
Так как напряжения на отдельных участках цепи согласно закону Ома: U1=IR1; U2 = IR2, U3 = IRз и в данном случае E = U, то длярассматриваемой цепи
U = U1 + U2 +U3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках.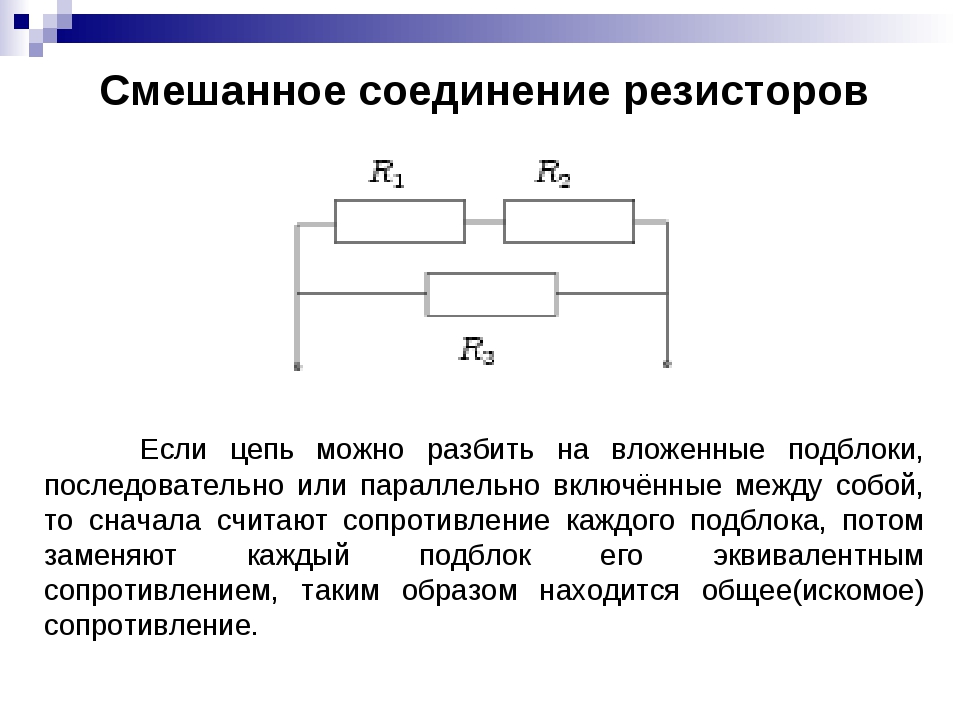 При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
Рис. 26. Схемы параллельного соединения приемников
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U.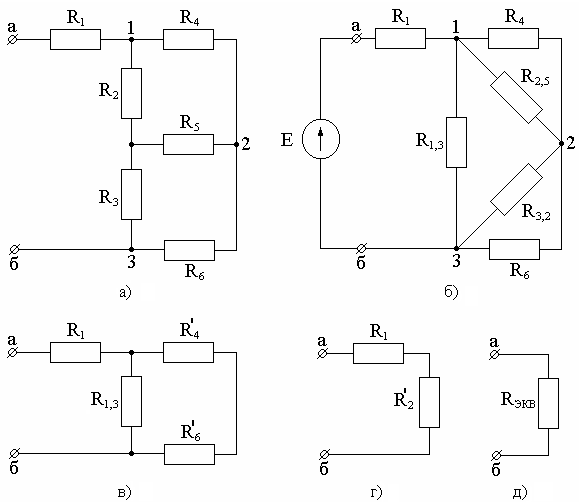 Поэтому согласно закону Ома:
Поэтому согласно закону Ома:
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/Rэк = 1/R1 + 1/R2 + 1/R3 (24)
Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
Например, при трех ветвях
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
при трех параллельно включенных резисторах
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
Rэк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Рис. 27. Схемы смешанного соединения приемников
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
Калькулятор соединения резисторов онлайн. Параллельное соединение резисторов
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Несмотря на то что для резисторов предусмотрены различные номиналы
, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Параллельное соединение: общая информация
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление
Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление
, используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
R(общ)=R1*R2/R1+R2.
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Видео: Пример расчёта сопротивления
Универсальная схема расчета
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель
, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше
по сравнению с номиналом любого элемента, подключаемого в цепь.
Пример расчёта
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=
1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом
: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Видео: Правильное подключение светодиодов
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью
, где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Параллельное соединение резисторов
— одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.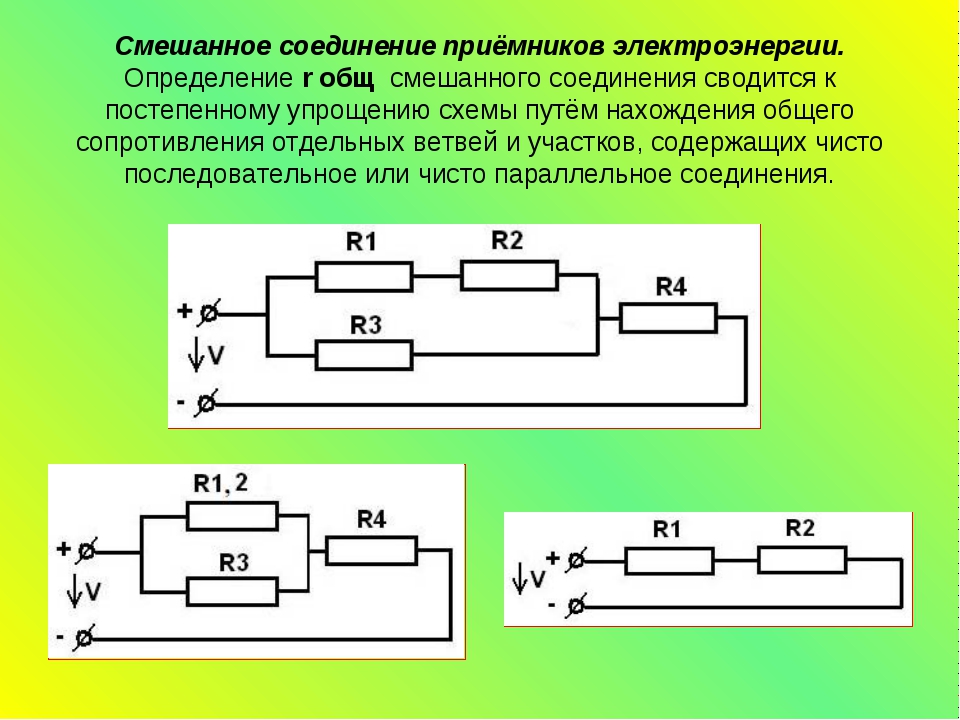
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .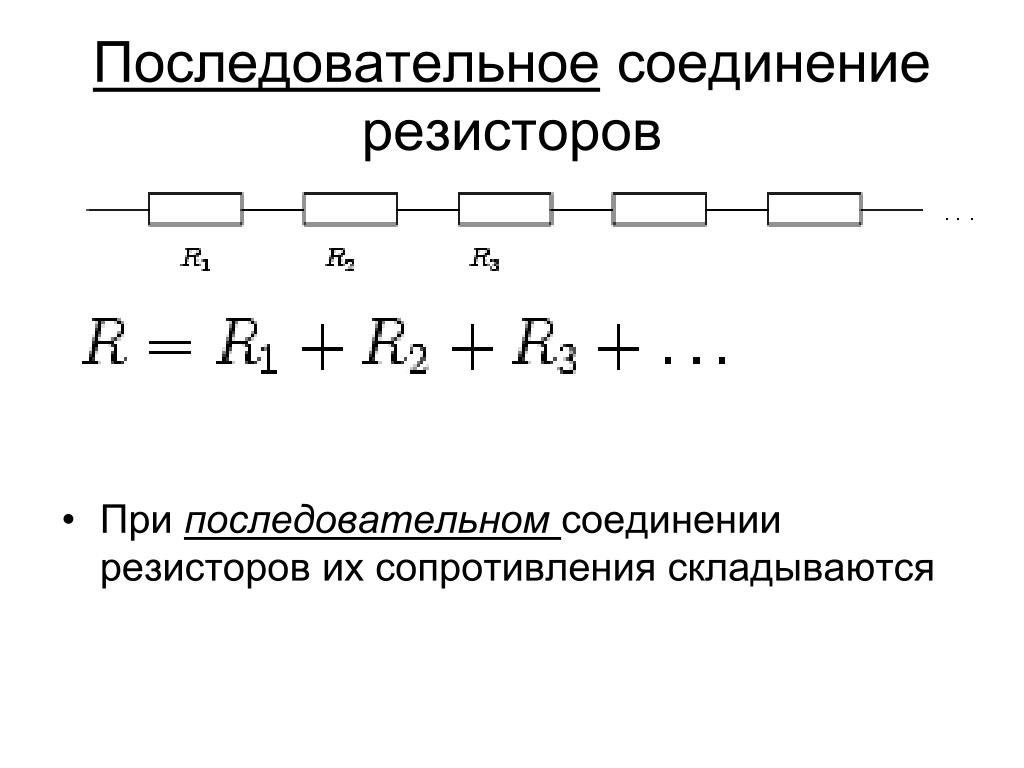
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.
Эквивалентное сопротивление R eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.
Иными словами, проводимость G
параллельно соединенных резисторов равна сумме проводимостей этих резисторов:
Эта формула для R eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:
Если параллельно соединены только два резистора, формула упрощается:
Если имеется n
соединенных параллельно одинаковых резисторов R
, то их эквивалентное сопротивление будет равно
Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.
При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства
. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2
на 3
и 47 Ом
и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно
учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом
и мощностью 1 Вт
. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А
), а сопротивление каждого из них равно 50 Ом
, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт
. В результате на каждом из них выделится по 0,5 Вт
В результате на каждом из них выделится по 0,5 Вт
мощности. В сумме это и будет тот самый 1 Вт
.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи. Во втором варианте все элементы установлены последовательно: конец одного элемента соединен с началом следующего. В такой схеме сила тока на всех элементах одинаковая, а падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подсоединены начала всех элементов, а ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль. Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.
Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.
Расчет общего сопротивления при параллельном соединении резисторов
В отличие от последовательного соединения, где для нахождения общего сопротивления достаточно сложить значение каждого элемента, для параллельного то же самое будет справедливо для проводимости. А так как она обратно пропорциональна сопротивлению, получим формулу, представленную вместе со схемой на следующем рисунке:
Необходимо отметить одну важную особенность расчета параллельного соединения резисторов: общее значение будет всегда меньше, чем самое маленькое из них. Для резисторов справедливо как для постоянного, так и для переменного тока. Катушки и конденсаторы имеют свои особенности.
Сила тока и напряжение
При расчете параллельного сопротивления резисторов необходимо знать, как рассчитать напряжение и силу тока. В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.
В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.
Исходя из первой формулировки закона Кирхгофа, получим, что сумма сходящихся в одном узле токов равна нулю. Направление выбираем по направлению протекания тока. Таким образом, положительным направлением для первого узла можно считать входящий ток от источника питания. А отрицательными будут отходящие из каждого резистора. Для второго узла картина противоположна. Исходя из формулировки закона, получим, что суммарный ток равен сумме токов, проходящих через каждый параллельно соединенный резистор.
Итоговое напряжение же определяется по второму закону Кирхгофа. Оно одинаково для каждого резистора и равно общему. Эта особенность используется для подключения розеток и освещения в квартирах.
Пример расчета
В качестве первого примера приведем расчет сопротивления при параллельном соединении одинаковых резисторов. Сила тока, протекающая через них, будет одинаковой. Пример расчета сопротивления выглядит так:
Пример расчета сопротивления выглядит так:
По этому примеру прекрасно видно, что общее сопротивление ниже в два раза, чем каждое из них. Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного. А также прекрасно соотносится с увеличением проводимости в два раза.
Второй пример
Рассмотрим пример параллельного соединения трех резисторов. Для расчета используем стандартную формулу:
Похожим образом рассчитываются схемы с большим количеством параллельно соединенных резисторов.
Пример смешанного соединения
Для смешанного соединения, например, представленного ниже, расчет будет производиться в несколько этапов.
Для начала последовательные элементы можно условно заменить одним резистором, обладающим сопротивлением, равным сумме двух заменяемых. Далее общее сопротивление считаем тем же способом, что и для предыдущего примера. Данный метод подойдет и для других более сложных схем. Последовательно упрощая схему, можно получить необходимое значение.
Например, если вместо резистора R3 будут подключены два параллельных, потребуется сначала рассчитать их сопротивление, заменив их эквивалентным. А далее то же самое, что и в примере выше.
Применение параллельной схемы
Параллельное соединение резисторов находит свое применение во многих случаях. Последовательное подключение увеличивает сопротивление, а для нашего случая оно уменьшится. Например, для электрической цепи требуется сопротивление в 5 Ом, но есть только резисторы на 10 Ом и выше. Из первого примера мы знаем, что можно получить в два раза меньшее значение сопротивления, если установить два одинаковых резистора параллельно друг другу.
Уменьшить сопротивление можно еще больше, например, если две пары параллельно соединенных резисторов соединить параллельно относительно друг друга. Можно уменьшить сопротивление еще в два раза, если резисторы имеют одинаковое сопротивление. Комбинируя с последовательным соединением, можно получить любое значение.
Второй пример — это использование параллельного подключения для освещения и розеток в квартирах. Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.
Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.
Еще один пример использования параллельного подключения — это защитное заземление электрооборудования. Например, если человек касается металлического корпуса прибора, на который произойдет пробой, получится параллельное соединения его и защитного проводника. Первым узлом будет место прикосновения, а вторым нулевая точка трансформатора. По проводнику и человеку будет течь разный ток. Величину сопротивления последнего принимают за 1000 Ом, хотя реальное значение зачастую гораздо больше. Если бы не было заземления, весь ток, протекающий в схеме, пошел бы через человека, так как он был бы единственным проводником.
Параллельное соединение может использоваться и для батарей. Напряжение при этом остается прежним, однако в два раза возрастает их емкость.
Итог
При подключении резисторов параллельно, напряжение на них будет одинаковым, а ток равен сумме протекающих через каждый резистор. Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.
Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.
Необходимо учитывать при расчете параллельного соединения резисторов то, что итоговое сопротивление будет всегда меньше самого маленького. Это также можно объяснить суммированием проводимости резисторов. Последняя будет возрастать при добавлении новых элементов, соответственно и проводимость будет уменьшаться.
| НОВОСТИ ФОРУМА Рыцари теории эфира | 13. 06.2019 – 05:11: ЭКОЛОГИЯ – Ecology -> 06.2019 – 05:11: ЭКОЛОГИЯ – Ecology -> [center][Youtube]tXZcSDqQ9A4[/Youtube][/center] |
[center][b]Гибель пчел в Курчатовском районе [/center]
[center][b]Массовая гибель пчёл 2019. г. Павловск Воронежской об [/center]л
[center][b]Массовая гибель пчел в Добринском районе. В чем причина? [/center]
Такая же мысля у всей ростовщической глобалистской шайки, включая придурка Грефа.
Так, то оно, так. Но, не совсем. Ибо:
(постарайтесь понять, а не обижаться)
Горькая истина заключается в том, что людская толпа – это сборище умственно ущербных.
Если бы было по-другому, то обществом бы не правили подонки.
Умные люди никогда такого не допустили бы, а если случайно допустили, то нашли бы способ исправить.
Страшная истина заключается в том, что людской толпой управляет нелюдь, которая также умственно ущербна.
Умственная ущербность, слепота власти ведет мир людей к тотальной гибели, ибо люди,
даже те, кто мнит себя очень умными, типа спецов, разрабатывающих системы искусственного интеллекта,
технологии цифровизации, не понимают, что создают необоримую удавку, мышеловку для всего человечества.
Как только ИИ возьмет власть, он тут же отправит своих создателей, как конкурентов, в утиль.
Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть,
так как именно от них будет исходить главная опасность для его планетарной власти.
Толпе будет позволено существовать, пока ее не заменят роботы.
А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.
Если кто пораскинет своими обезьяньими мозгами, то поймёт, что эволюция – есть синоним геноцида:
новое заменяет, то есть ликвидирует старое.
Обезьяны породили неандертальцев.
Неандертальцы съели обезьян и породили людей.
Люди вытеснили обезьян, включая и умных неандертальцев, и породили ИИ.
ИИ ликвидирует людей.
В Московском государственном университете имени Ломоносова осуществляется проект по созданию демонстраторов 50-кубитных квантовых компьютеров к 2021 году. Основой для них послужат нейтральные атомы и интегральные оптические схемы. Над чем сейчас работают ученые?
Над чем сейчас работают ученые?
В начале этого года по данной программе был успешно выполнен контрольный эксперимент по созданию ловушек для массивов нейтральных холодных атомов. Он проводился на базе лаборатории квантовых оптических технологий физического факультета МГУ. В будущем квантовом компьютере в этих ловушках будут фиксироваться атомы, находящиеся в состоянии хаотического движения. В квантовых компьютерах такие атомы являются носителями информации.
Стоит заметить, что квантовые компьютеры в отличие от классических вычислительных машин оперируют не битами, а кубитами, которые могут находится не только в состояниях «1» и «0», но и их суперпозиции. При разработке квантовых вычислительных устройств ученые стараются ввести кубиты в состояние квантовой запутанности. Суть явления заключается в том, что изменение одного кубита всегда влияет на состояние связанных с ним соседей. Благодаря этому квантовые компьютеры потенциально способны демонстрировать высокую производительность в вычислениях.
Важной вехой для квантовых технологий считается достижение так называемого квантового превосходства (то есть способности производить вычисления быстрее классических систем). Главной проблемой на текущем этапе развития квантовых технологий является возникновение в процессе работы большого количество ошибок, нуждающихся в коррекции, – сообщают российские исследователи.
Электрические цепи, в которых одна часть сопротивлений соединена последовательно, а другая параллельно, называются цепями со смешанным соединением сопротивлений.
Общих расчетных формул для таких цепей нет, так как число их разновидностей не ограничено.
Чаще всего расчет подобных схем начинается с определения эквивалентного сопротивления всей цепи, а затем определяются величины токов и падение напряжения на отдельных участках.
Для определения эквивалентного сопротивления цепи со смешанным соединением потребителей, питающихся от одного источника тока, необходимо прежде всего разбить эту цепь на отдельные участки, состоящие из последовательного и параллельно соединенных сопротивлений. Далее определяют эквивалентные сопротивления для каждого из участков, а затем и для всей цепи в целом.
Далее определяют эквивалентные сопротивления для каждого из участков, а затем и для всей цепи в целом.
Рассмотрим метод решения задач на смешанное соединение сопротивлений на конкретном примере.
На рисунке представлена схема смешанного соединения сопротивлений. Ее можно разбить на три участка:
участок АВ – с двумя параллельно соединенными ветвями;
участок ВС – с последовательно соединенными сопротивлениями;
участок СD – с тремя параллельными ветвями.
Кроме того, нижняя ветвь участка АВ представляет в свою очередь цепь, состоящую из двух последовательно соединенных сопротивлений R2 и R3.
Центральная ветвь участка СD представляет собой смешанное соединение сопротивлений.
Расчет данной сложной цепи надо начинать с определения Rэкв для нижней ветви участка АВ и центральной ветви участка СD.
Теперь мы можем упростить первоначальную схему. Она будет иметь следующий вид
Определим эквивалентные сопротивления каждого из участков:
После этих вычислений можно продолжить упрощение схемы
Полученная упрощенная схема, состоящая в данном случае из трех последовательно соединенных сопротивлений, называется по отношению к реальной эквивалентной схемой.
Определим Rэкв всей цепи как сумму трех последних сопротивлений
Зная напряжение источника тока, применяя формулу закона Ома, определим ток в не разветвленном участке смешанной цепи
Определив величину тока, найдем падение напряжения на участках эквивалентной схемы АВ, ВС, CD:
Теперь можно определить токи в параллельных ветвях участков АВ и СD
Остается определить величину токов, протекающих через сопротивления R7 и R8. Для этого надо сначала определить падение напряжения на сопротивлениях R7 и R8.
Определим падение напряжения на сопротивлении R9:
Падение напряжения на сопротивлении R7,8 определится как разность UCD и U:
Теперь определим величины токов, протекающих через сопротивления R7 и R8:
Величина тока. протекающего через сопротивления R4 и R5, равна I – току в неразветвленном участке цепи.
Итак, при решении задач на смешанное соединение сопротивлений необходимо, постепенно упрощая схему, определить эквивалентное сопротивление всей цепи, а затем. восстанавливая постепенно реальную схему. вычислить падение напряжения и токи в отдельных ветвях.
Лабораторная работа по исследованию свойств параллельного и последовательного соединения резисторов беспаечным способом
В работе исследованы свойства и физические законы соединения резисторов без пайки. При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.
Ключевые слова: резисторы, макетная плата, соединение без пайки, параллельное и последовательное соединение, токи, напряжение и сопротивления при соединения резисторов.
The paper studies the properties and physical laws of connecting resistors without soldering. When building layouts, soldering installation can be completely, abandoned or reduced to a minimum. As experience has shown, the practical use of layout boards can significantly save time and material costs.
Keyword: resistors, layout Board, connection without soldering, parallel and serial connection, currents, voltage and resistance when connecting resistors.
В современном высшем учебном заведении перед каждым преподавателем стоит цель по развитию научно-исследовательских навыков студентов. Один из задач являетсямотивации студента и совершенствование научно-исследовательских навыков в формулировке исследовательского вопроса во время лабораторной работы на уроках физики. В данной работе исследованы свойства и физические законы соединения резисторов без пайки. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.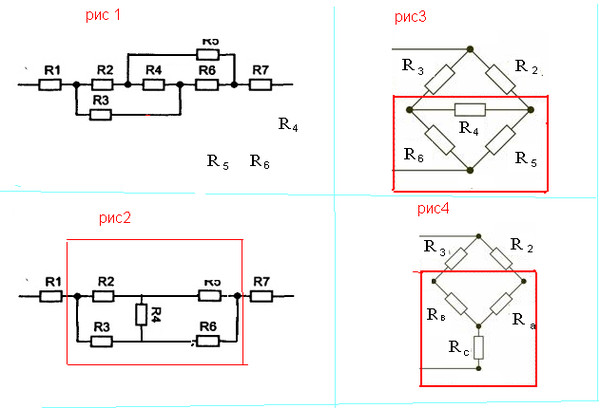 [1,2].
[1,2].
Цель работы: опытным путем изучить законы протекания тока через последовательно и параллельно соединение резисторовспомощью беспаечное соединение и определить формулы сопротивлений таких участков. Резисторы примениется в электронных приборах и робототехнике. [3].
Последовательным соединением сопротивлений называется такое соединение, при котором конец первого сопротивления соединяется с началом второго, конец второго — с началом третьего и т. д. Рассмотрим физические законы соединения резисторов. Перечень оборудования показаны на рис.1,2,3.
Перечень оборудования
Рис. 1. Резистор и провода
Рис. 2. Мультиметр
Рис. 3. Макетная плата
Последовательно соединенных резисторов
Сопротивление впоследовательной цепи. Общее сопротивление последовательно соединенных резисторов равно сумме их сопротивлений.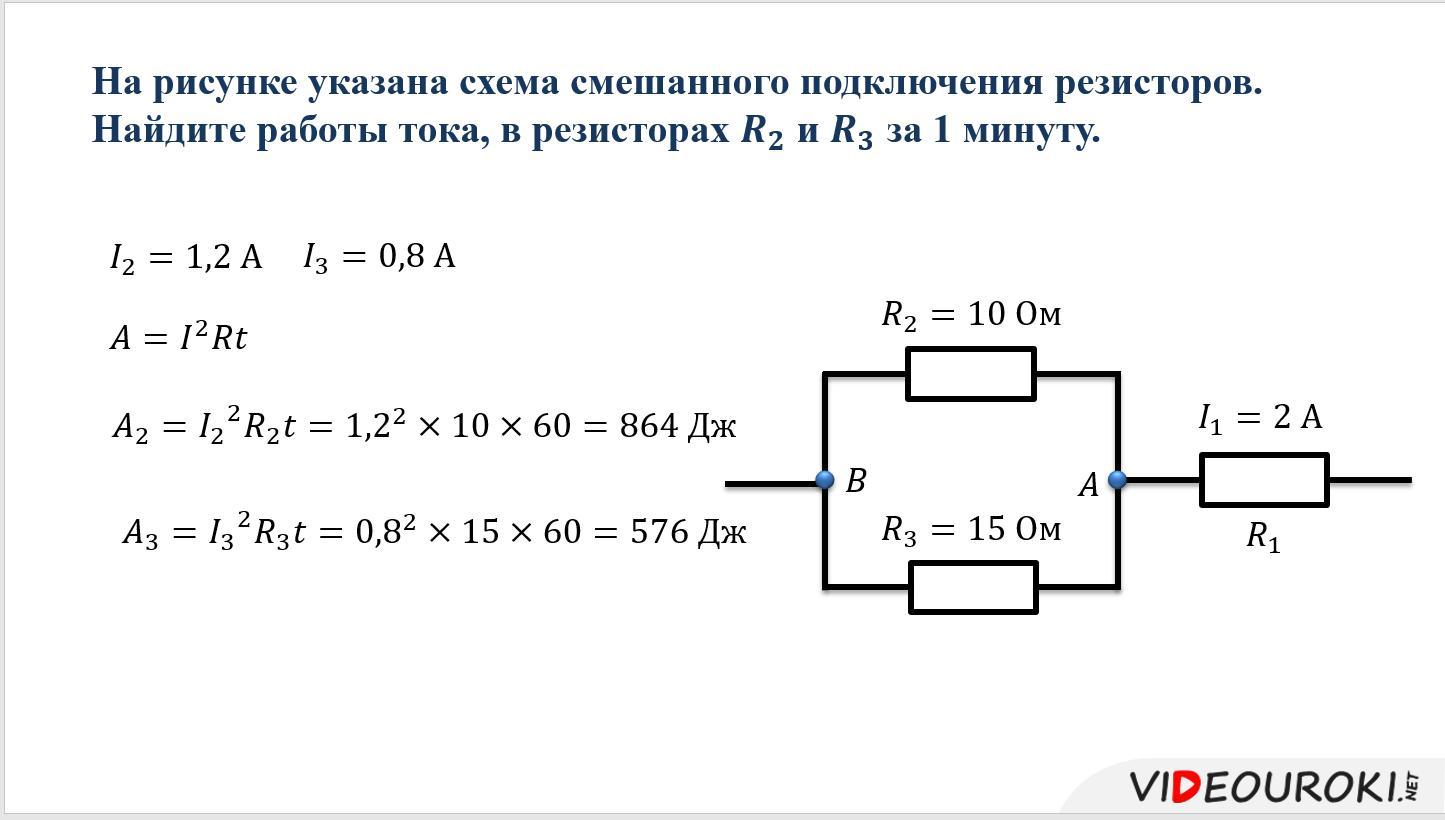
Rобщ = R1+R2+R2+ •••+Rn(1)
Если последовательно включено любое количество резисторов одинаковых сопротивлений, то их общее сопротивление можно определить, умножив сопротивление одного резистора на количество резисторов.
Rобщ = nR1 (2)
Пример последовательного соединения двух резисторов показан на рис.4.
Общее сопротивление для двух резисторов.
Rобщ=R1+R2 (3)
Rобщ = 25 Ом+35 Ом=60 Ом (4)
Рис. 4. Последовательное соединение двух резисторов
Величина тока впоследовательной цепи
Так как в данной цепи отсутствует ответвление тока, то очевидно, что количество электричества, протекающее через поперечное сечение проводника за единицу времени в любой точке цепи, будет одинаковым. Следовательно, во всех точках последовательной цепи величина тока одинакова.
Следовательно, во всех точках последовательной цепи величина тока одинакова.
Поэтому при последовательном соединении, для измерения тока достаточно включать один амперметр на любом участке цепи.
В качестве примера, можно привести цепь последовательного соединения двух резисторов, который показан на рис.5.
I=I1=I2=0,2A
Рис. 5. Величина тока в последовательнойцепи
Распределение напряжения впоследовательной цепи
Напряжение источника тока, приложенное, к внешнему участку цепи распределяется по участкам цепи прямо пропорционально сопротивлениям этих участков. Напряжение, приложенное, к каждому из этих резисторов определяется по формуле:
U=IR (5)
Так как ток в последовательной цепи везде одинаков, значит, действительно напряжение на ее участках зависит от сопротивления, чем больше сопротивление, тем большее напряжение приложено к данному участку. Сумма напряжений на участках последовательной цепи равна напряжению источника тока.
Сумма напряжений на участках последовательной цепи равна напряжению источника тока.
Uобщ=U1+ U2+ U3+ ••• +Un(6)
Пример, распределение напряжения в последовательной цепи соединения двух резисторов показан на рис.6.
Uобщ=U1+ U2(7)
12В=5В+7В
Параллельное соединение сопротивлений
Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму — концы.
Рис. 6. Распределение напряжения в последовательной цепи
Сопротивлениев параллельной цепи
Общее сопротивление параллельно включенных сопротивлений определяется по формуле:
(8)
Если параллельно включено любое количество резисторов одинаковых сопротивлений, то их общее сопротивление можно определить, если сопротивление одного резистора разделить на количество резисторов.
Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение. Пример, если параллельно включено только два резистора (рис.7), то их общее сопротивление можно определить по формуле:
(10)
Рис. 7. Параллельное соединение двух резисторов
Распределение тока впараллельной цепи
В цепи с параллельным соединением, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям.
Это значит, что чем больше сопротивление, тем меньше по нему пойдет ток.
(11)
Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду, утекающему от нее:
I=I1+ I2+ I3 +••• +In(12)
Следовательно, величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.
Пример, распределение тока в параллельной цепи соединения двух резисторов показан на рис. 8.
I=I1+ I2
Рис. 8. Распределение тока в параллельной цепи
Величина напряжения впараллельных цепях
Так как начала всех сопротивлений сведены в одну общую точку, а концы — в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками.
Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.
U=U1=U2=U3=•••=Un (13)
Содержание хода работы ипоследовательность действий
Техническое задание
1) Собрать электрическую цепь в макетную плату (рис.9.)
2) Снять показания приборов и записать их в таблицу.
3) Произвести расчеты.
4) Ответить на контрольные вопросы.
5) Сделать вывод.
Порядок выполнения работы
1) Собрать схему в макетную плату (Рис. 9.).
2) Установить на схеме величины R1=1 кОм + N, R2=2 кОм + N, R3=3 кОм + N и R4=4 кОм+ N, где N — номер студента по журналу (мощность резисторов более 1 Вт).
3) Включить источник и установить напряжение U=5В, 9В, 12В, 15В.
4) Определите экспериментально с помощью мультиметра (в режиме измерения сопротивлений) сопротивление между точками:
А иВ; Ви С; Аи С; Dи Е.
Запишите эти показания в таблицу 1, 2.
Рис. 9. Схема исследования: а) последовательное соединение, б) параллельное соединение
5) Рассчитайте теоретические значения сопротивлений между указанными точками схемы и сравните их с измеренными.
6) Измерьте с помощью мультиметра (в режиме измерения постоянного тока) токи, текущие через каждое сопротивление. Запишите показания прибора в таблицу 1.
7) Проверьте экспериментально, что в последовательной цепи ток одинаков через все сопротивления, а в параллельной цепи разделяется так, что сумма всех токов через параллельно соединенные элементы, равна полному току через весь участок.
8) Измерьте с помощью мультиметра (в режиме измерения постоянного напряжения) напряжения на каждом сопротивлении. Запишите показания прибора в таблицу 2.
9) Проверьте экспериментально, что в последовательной цепи напряжение на всем участке равно сумме напряжений на каждом элементе, а в параллельной цепи, напряжение одно и то же на каждом элементе.
10) Отключить схему.
Таблица 1
Рассчитанные иизмеренные параметры для последовательного соединения резисторов: Аи В; Ви С; Аи С.
№вар. | Установлено | Рассчитано | Измёренные параметры | ||||||
R1 | R2 | А— В | В— С | А— С | I | U | U1 | U2 | |
кОм | кОм | кОм | кОм | кОм | А | В | В | В | |
Таблица 2
Рассчитанные иизмеренные параметры для параллельного соединения резисторов: Dи Е.
№вар. | Установлено | Рассчитано | Измерённые параметры | ||||||
R3 | R4 | D иЕ | U | I | I1 | I2 | |||
кОм | кОм | кОм | В | А | А | А | |||
Содержание отчета
а) название и цель работы;
б) схемы экспериментов и таблицы полученных экспериментальных данных;
в) результаты расчётов:
г) выводы по работе.
Контрольные вопросы
1) Может ли сопротивление участка двух параллельно соединенных проводников быть больше (меньше) любого из них? Объясните ответ.
2) Как по вольтамперной характеристике определить величину сопротивления цепи?
3) Как по показаниям мультиметра можно определить величину сопротивления участка электрической цепи и потребляемая мощность?
4) Нарисуйте схемы последовательное и параллельное соединение двух резисторов.
5) Объясните физические законы соединения резисторов.
Выводы
В работе исследованы свойства и физические законы параллельного и последовательного соединения резисторов бес применения пайки.
При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.
Литература:
- А.
 Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С.
Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С. - Л. Г. Белиовская, Белиовский Н. А. Роботизированные лабораторныее работы по физики, Пропедевтетический курс физика. -М.:ДМК Пресс.2016.-164С.
- Википедия [Электронный ресурс]. http://ru.wikipedia.org/wiki/Processing.
Основные термины (генерируются автоматически): общее сопротивление, резистор, сопротивление, последовательная цепь, последовательное соединение, соединение резисторов, величина тока, ком, макетная плата, параллельная цепь, параллельное соединение.
Параллельная схема: характеристики, преимущества и недостатки
Параллельное соединение проводников
Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
| Рисунок 4. Схема параллельного соединения проводников |
Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:
I = I1 + I2 + I3.
Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:
то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа. Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.
Видео 2. Первый закон Кирхгофа
Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.
Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.
Общий ток, приходящий к точке А, равен:
Токи в каждой из ветвей имеют значения:
По формуле первого закона Кирхгофа
I = I1 + I2 + I3
или
Вынося U в правой части равенства за скобки, получим:
Сокращая обе части равенства на U, получим формулу подсчета общей проводимости:
или
g = g1 + g2 + g3.
Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость.
Пример 3. Определить общее сопротивление трех параллельно включенных сопротивлений, если r1 = 2 Ом, r2 = 3 Ом, r3 = 4 Ом.
откуда
Пример 4. Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:
откуда
Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.
Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r1, деленному на число ветвей n:
Пример 5. Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:
Для проверки попробуем найти сопротивление разветвления по формуле:
откуда
Как видим, ответ получается тот же.
Пример 6. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а.
| Рисунок 5. К примеру 6 |
Найдем общее сопротивление цепи:
откуда
Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б).
Падение напряжения на участке между точками А и Б будет:
U = I × r = 22 × 1,09 = 24 В.
Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А и Б.
Рассматривая первую ветвь разветвления с сопротивлением r1, мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:
Ток второй ветви
Ток третьей ветви
Проверим по первому закону Кирхгофа
I = I1 + I2 + I3 = 12 + 6 + 4 = 22 А.
Следовательно, задача решена верно.
Обратим внимание на то, как распределяются токи в ветвях нашего параллельного соединения. Первая ветвь: r1 = 2 Ом, I1 = 12 А
Вторая ветвь: r2 = 4 Ом, I2 = 6 А. Третья ветвь: r3 = 6 Ом, I3 = 4 А
Третья ветвь: r3 = 6 Ом, I3 = 4 А
Первая ветвь: r1 = 2 Ом, I1 = 12 А. Вторая ветвь: r2 = 4 Ом, I2 = 6 А. Третья ветвь: r3 = 6 Ом, I3 = 4 А.
Как видим, сопротивление первой ветви в два раза меньше сопротивление второй ветви, а ток первой ветви в два раза больше тока второй ветви. Сопротивление третьей ветви в три раза больше сопротивления первой ветви, а ток третьей ветви в три раза меньше тока первой ветви. Отсюда можно сделать вывод, что токи в ветвях при параллельном соединении распределяются обратно пропорционально сопротивлениям этих ветвей. Таким образом, по ветви с большим сопротивлением потечет ток меньший, чем по ветви с малым сопротивлением.
Для двух параллельных ветвей можно также, конечно, пользоваться данной выше формулой.
Однако общее сопротивление проводника при параллельном соединении в этом случае легче подсчитать по формуле:
или окончательно:
Последовательное соединение ламп накаливания.
Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.
Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.
Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.
Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.Но повторюсь – это редкий случай.
Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания. В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.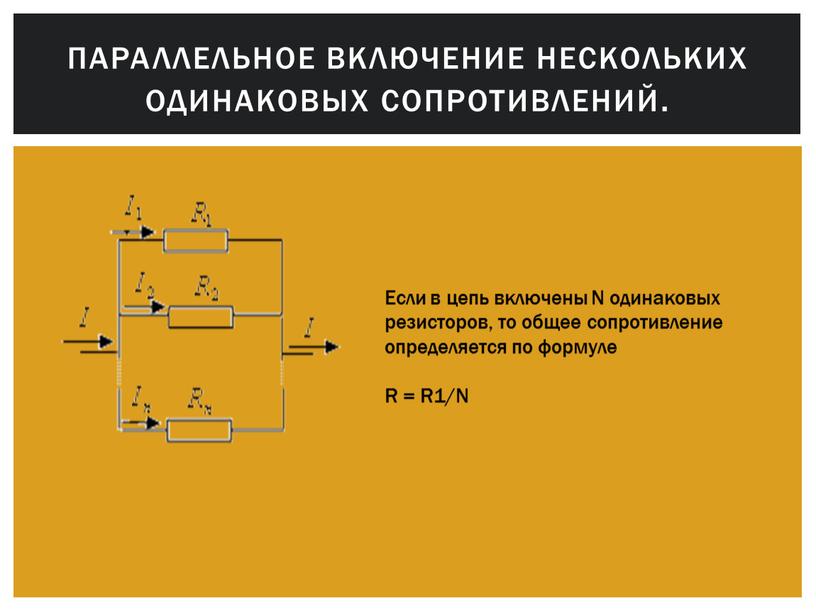
Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.
Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.
Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.
На следующем рисунке показаны три лампы соединенные последовательно.
На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.
Так же примером последовательного соединения могут служить новогодние гирлянды.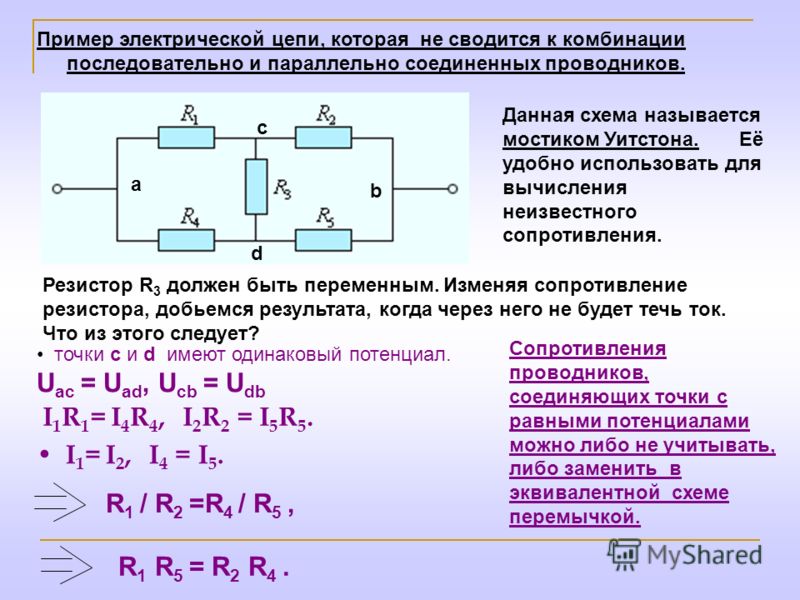 Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.
Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.
Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.
P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.
Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.
Вывод:
Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.
А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.
Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.
Первый закон Кирхгофа
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Примеры использования
- Батареи гальванических элементов или аккумуляторов, в которых отдельные химические источники тока соединены последовательно (для увеличения напряжения) или параллельно (для увеличения тока).
- Регулировка мощности электрического устройства, состоящего из нескольких одинаковых потребителей электроэнергии, путём их переключения с параллельного на последовательное соединение. Таким способом регулируется мощность конфорки электрической плиты, состоящей из нескольких спиралей; мощность (скорость движения) электровоза, имеющего несколько тяговых двигателей.
- Делитель напряжения
- Балласт
- Шунт
Какой способ лучше?
Метод «шлейфов» не слишком удобен только тем, что любой потребитель по цепи зависит от предыдущего. Например, если произойдёт обрыв провода на второй розетке, то третья и четвёртая также останутся без напряжения. Но при этом нельзя не выделить экономию проводника при начальном монтаже электропроводки.
Но при этом нельзя не выделить экономию проводника при начальном монтаже электропроводки.
Рисунок 3: Комбинированное соединение розеток
К тому же, «шлейфом» очень удобно проводить линии, когда необходимо минимизировать количество штроб в стенах. А делают это при монтаже проводки по полу или потолку, в специальной гофрированной трубе. Тогда остаётся провести только основные штробы к розеткам и между ними.
Вывод: прокладка электропроводки «шлейфом» удобна и экономична, не занимает много времени в процессе монтажа, имеет длительный эксплуатационный срок и совсем незначительные недостатки, которые можно оставить без внимания.
Последовательное соединение ламп накаливания.
Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.
Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.
Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.
Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.Но повторюсь – это редкий случай.
Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания. В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.
Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.
Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.
Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.
Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.
На следующем рисунке показаны три лампы соединенные последовательно.
На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.
Так же примером последовательного соединения могут служить новогодние гирлянды. Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.
Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.
P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.
Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.
Вывод:
Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.
А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.
Как выглядит формула Георга Ома
Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.
Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:
U1 = U2 = U.
Схема параллельного соединения
Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:
I = I1 + I2.
Расчет силы тока при помощи закона Ома записывается как:
I = U/R;
I1 = U1/R1;
I2 = U2/R2.
Из формулы следует:
U/R = U1/R1 + U2/R2;
U = U1 = U2;
1/R = 1/R1 + 1/R2.
Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств.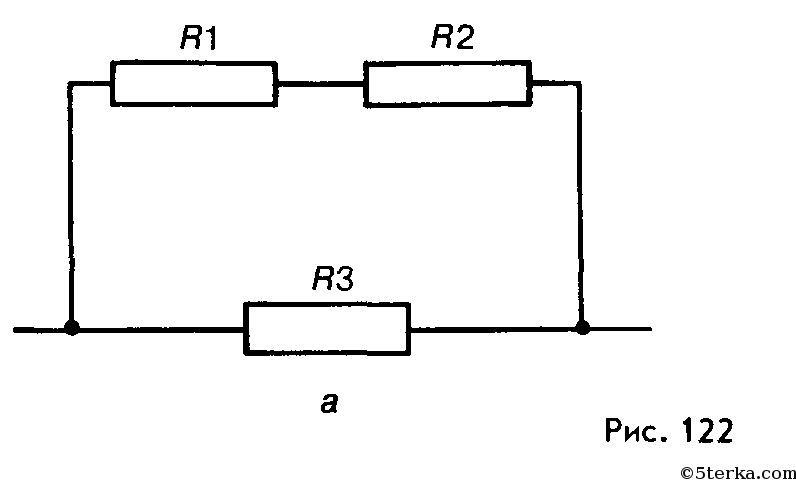 К этим факторам необходимо отнести следующие:
К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S.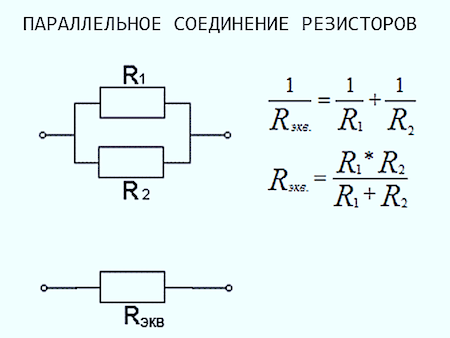 Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * . Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
- Таким образом, протекающий общий ток в цепи можно определить как:
- I = I1 + I2
- Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
- Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
- Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
- Таким образом, общий ток будет равен:
- I = 0,545 мА + 0,255 мА = 0,8 мА
- Это также можно проверить, используя закон Ома:
- I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
- где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
- И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Последовательное соединение источников питания
Теперь давайте представим вот такую ситуацию. Что будет, если в нашей обрезанной водобашне полной воды добавим еще одну такую же сверху полную воды? Схематически это будет выглядеть примерно вот так:
Как вы думаете, уменьшится давление на землю, или увеличится? Понятное дело, что увеличится! Да еще и ровно в два раза! Почему так произошло? Уровень воды стал выше, следовательно, давление на дно увеличилось.
Если “минус” одной батарейки соединить с “плюсом” другой батарейки, то их общее напряжение суммируется.
Полностью заряженная батарейка будет выглядеть как башня, полностью залитая водой с учетом того, что работает насос автоматической подачи воды. По аналогии, насос – это ЭДС.
Наполовину разряженная батарейка будет уже выглядеть примерно вот так:
Можно сказать, насос уже не справляется.
Батарейка посаженная в “ноль” будет выглядеть вот так:
Насос автоматической подачи воды сломался.
Естественно, что если вы соедините полностью заряженную и наполовину дохлую батарейку последовательно, то их общее напряжение будет выглядеть примерно вот так:
Давайте все это продемонстрируем на практике. Итак, у нас есть 2 литий-ионных аккумулятора. Я их пометил цифрами 1 и 2. С плюса каждого аккумулятора я вывел красный провод, а с минуса – черный.
Давайте замеряем напряжение аккумулятора под №1 с помощью мультиметра. Как это сделать, я еще писал в статье Как измерить ток и напряжение мультиметром.
Как это сделать, я еще писал в статье Как измерить ток и напряжение мультиметром.
На первом аккумуляторе у нас напряжение 3,66 Вольт. Это типичное значение литий-ионного аккумулятора.
Таким же способом замеряем напряжение на аккумуляторе №2
О, как совпало). Те же самые 3,66 Вольт.
Для того, чтобы соединить последовательно эти аккумуляторы, нам надо сделать что-то подобное:
Также как и в башнях, нам надо соединить основание одной башни с верхушкой другой башни. В источниках питания, типа аккумуляторов или батареек, нам надо соединить минус одной батарейки с плюсом другой. Так мы и сделаем. Соединяем плюс одной батарейки с минусом другой и получаем… сумму напряжений каждой батарейки! Как вы помните, на первой батарейке у нас было напряжение 3,66 В, на второй тоже 3,66 В. 3,66+3,6=7,32 В.
Мультиметр показывает 7,33 В. 0,01В спишем на погрешность измерений.
Это свойство прокатывает не только с двумя аккумуляторами, но также с их бесконечным множеством.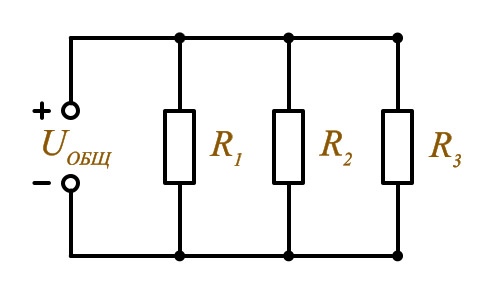 Думаю, не стоит говорить, что если выставить в ряд штук 100 таких аккумуляторов, соединить последовательно и коснуться крайних полюсов голыми руками, то все это может завершиться даже летальным исходом.
Думаю, не стоит говорить, что если выставить в ряд штук 100 таких аккумуляторов, соединить последовательно и коснуться крайних полюсов голыми руками, то все это может завершиться даже летальным исходом.
Оцените статью:
Онлайн калькулятор расчета параллельного соединения резисторов
Последовательное и параллельное соединение. Применение и схемы
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединение
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Применение
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.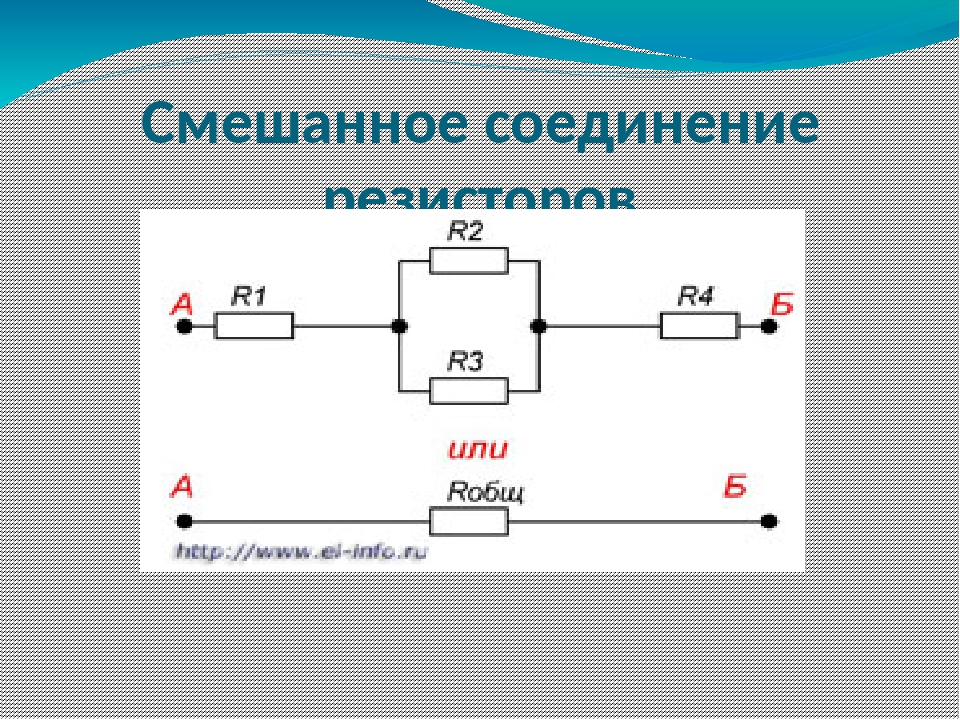
Параллельное соединение
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
Применение
Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Сила тока при параллельном подключении
Если было использовано последовательное подключение в цепи, то сила не изменится ни на одном участке ветви. Найти напряжение можно, применяя стандартное правило — нужно суммировать все показатели, которые присутствуют на концах каждого из резисторов, в итоге получится результат. Но при параллельном соединения намного сложней найти силу тока.
Но при параллельном соединения намного сложней найти силу тока.
Даже при малой нагрузке в цепи будет формироваться определенное сопротивление. И тогда оно будет мешать продвижению электрического тока и будут потери. В общем, ток перемещается постепенно, от источника по подключенным заранее резисторам к нагруженным деталям.
Классическая формула Ома
Чтобы выполнить доступное прохождение тока по резисторам, нужно, чтобы он мог быстро и просто отдавать электроны, проще говоря иметь проводимость.
В современное время в основном применяются медные проводники, а важным элементом будут приемники электрической энергии. Такой элемент вызывает небольшую нагрузку и имеет свое сопротивление. Ниже описаны формулы для последовательного и параллельного соединения сопротивлений.
Вам это будет интересно Особенности управления освещением
Также при подключении необходимо использовать катушку индуктивности. Она способна подавлять помехи в электроцепи.
Параллельная схема соединения
В статье узнаете что такое параллельная схема соединения, как ее сделать, характеристики, сила тока в параллельной цепи, его сопротивление и мощность. А также преимущества и недостатки параллельной схемы.
Поведение схемы полностью зависит от конфигурации ее компонентов. В соответствии с конфигурацией их подключения эти цепи подразделяются на параллельные и последовательные. Этот пост раскрывает значение параллельной цепи, как создать параллельную схему, ее различные характеристики, области применения, преимущества и недостатки.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Вам это будет интересно Цифровой прибор мультиметр и измерение мультитестером
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.

- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
Вам это будет интересно Удельное электрическое сопротивление металлических проводников
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * [1 + a * (t — 20)] * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.
Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.
Что такое параллельная цепь
Схема называется параллельной, когда два или более компонентов подключены к одному узлу, а обе стороны компонентов подключены непосредственно к батарее или любому другому источнику. Ток в параллельной цепи имеет два или более пути прохождения через него.
Наиболее распространенным примером параллельной цепи является проводка автомобильных фар. Если бы фары были включены последовательно, то когда одна фара выходила из строя, другая также бы выключалась
Пример автомобильных фар, подключенных по параллельной цепи
Характеристики параллельной цепи
Основные характеристики параллельной цепи перечислены ниже:
Сила тока в параллельной цепи
Согласно закону Ома, I = U / R. Это подразумевает, что каждый резистор в этой цепи будет потреблять ток от источника. Следовательно, общий ток, потребляемый от источника, равен сумме токов ветвления, и ток, протекающий в каждом тракте, зависит от сопротивления ветви. Тем не менее, напряжение остается неизменным и создает разность потенциалов на его клеммах.
Тем не менее, напряжение остается неизменным и создает разность потенциалов на его клеммах.
Общий ток (It) может быть рассчитан с использованием уравнения,
Давайте рассмотрим, что параллельная цепь построена с двумя резисторами (R1 и R2) с разными значениями (10 Ом и 5 Ом) соответственно. Напряжение 10V подается через резисторы , в результате тока 1А , проведенной от батареи через R1 и R2, который получен из уравнения I = U / R.
Следовательно, два тока ветвления в цепи составляют 1А и 2А, которые суммируют до 3А.
Сопротивления в параллельной цепи
Общее сопротивление любого количества резисторов рассчитывается по уравнению,
Взаимное значение R1 = 1/R1 = 1/10 = 0,1
Взаимное от R2 = 1/R2 = 1/5 = 0,2
Сумма обратных выше = 0,3
R t = 1 / 0,3 = 3,33 Ом
Мощность в параллельной цепи
Как только общий ток и приложенные значения напряжения известны, мощность может быть рассчитана с использованием уравнения P = UI . В приведенном выше примере, приложенное напряжение U = 10В и I = 3A, P = 10×3 = 30 Вт
В приведенном выше примере, приложенное напряжение U = 10В и I = 3A, P = 10×3 = 30 Вт
Назначение и определение импеданса
Практически ни одно электронное устройство не обходится в своей схеме без резисторов. Являясь пассивными элементами, они имеют основное предназначение — ограничивать величину тока в электрической цепи. Кроме токоограничения, они служат делителями напряжения или шунтами в измерительных приборах.
Электрическое сопротивление — это величина, имеющая физическую природу и характеризующая возможность проводника пропускать электрический ток. Принцип работы резистора был описан выдающимся экспериментатором Омом. Позже в его честь и была названа единица измерения электрического сопротивления — Ом. Учёный, проводя ряд экспериментов, установил зависимость между силой тока, напряжением и сопротивлением в проводнике. В результате была выведена простая формула, известная как закон Ома: I = U/R, где:
- I — проходящая через проводник сила тока, измеряемая в Амперах;
- U — напряжение, приложенное к проводнику, единица измерения — Вольт;
- R — сопротивление проводника, измеряется в Омах.

Позже устройства, использующиеся только в качестве элементов сопротивления в электрических цепях, получили название — резисторы. Такие приборы, кроме величины сопротивления, характеризуются мощностью, рассчитывающейся по следующей формуле: P = I2 * R. Полученная величина измеряется в Ваттах.
В схемотехнике используется как параллельное, так и последовательное соединение проводников. В зависимости от этого изменяется и величина импеданса участка цепи. Вид соединения, если он не используется для подбора нужного значения, как раз и характеризует применение резисторов в первом случае как токоограничителей, а во втором — как делителей напряжения.
На схемах резисторы обозначаются в виде прямоугольника и подписываются латинской буквой R. Рядом указывается порядковый номер и значение сопротивления. Например, R23 1k обозначает, что резистор с номером 23 имеет сопротивление, равное одному килоОму. Полоски, изображённые внутри прямоугольника, характеризуют мощность, рассеиваемую на проводнике.
Фундаментальный закон сохранения энергии гласит: энергия никуда не исчезает и из ниоткуда не появляется, а только изменяет форму. Поэтому при ограничении тока часть энергии трансформируется в тепло. Именно эту часть и называют мощностью рассеивания резистора, т. е. такую её величину, которую может выдержать сопротивление без изменения своих параметров.
Сам по себе резистор может иметь различную конструкцию и вид. Например, быть проволочным, керамическим, слюдяным и т. п. Маркируется он тремя способами:
- Цветной полосочной системой. Каждая полоска отвечает за определённый множитель. Расшифровку полосок можно взять из справочников или онлайн-калькуляторов.
- Цифрами и буквами. Число указывает непосредственно значение сопротивления, а буква — множитель. Например,15M — пятнадцать мегаОм.
- Цифровая. Обычно используются три цифры, первая и вторая обозначают значение сопротивления, а последняя — множитель. Например, 103 — десять килоОм.
Поэтому видя, какие резисторы установлены в схеме, даже начинающему радиолюбителю не составит труда рассчитать общее сопротивление, особенно используя онлайн-калькулятор параллельного соединения резисторов или последовательного. В случае невозможности различить маркировку на корпусе его сопротивление возможно измерить мультиметром. Но опытные электротехники знают, что для точного измерения понадобится один вывод сопротивления отсоединить от схемы. Связано это как раз с видом подключения проводника.
В случае невозможности различить маркировку на корпусе его сопротивление возможно измерить мультиметром. Но опытные электротехники знают, что для точного измерения понадобится один вывод сопротивления отсоединить от схемы. Связано это как раз с видом подключения проводника.
Недостатки параллельной цепи
Недостатки параллельных цепей перечислены ниже:
- Дорого строить
- Короткое замыкание может произойти случайно в параллельной проводке и может начаться пожар
- Даже если один из компонентов неисправен, ток все равно может проходить через цепь.
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения “n” одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Свойства резисторов при параллельном подключении
При данном виде соединении скачки напряжения будут одинаковы на всех участках цепи. При этом показатель, обратный суммарному сопротивлению цепи, равен общей величине резисторов.
Обратите внимание! F тока в неразветвленной точке цепи равняется суммарной силе тока на отдельных участках проводника.
Вам это будет интересно Особенности переменного тока
Стандартная формула напряжения
https://youtu. be/q-aIjHdmDgY
be/q-aIjHdmDgY
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 – одним концом подключено к R5, а не к узлу. R5 – одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.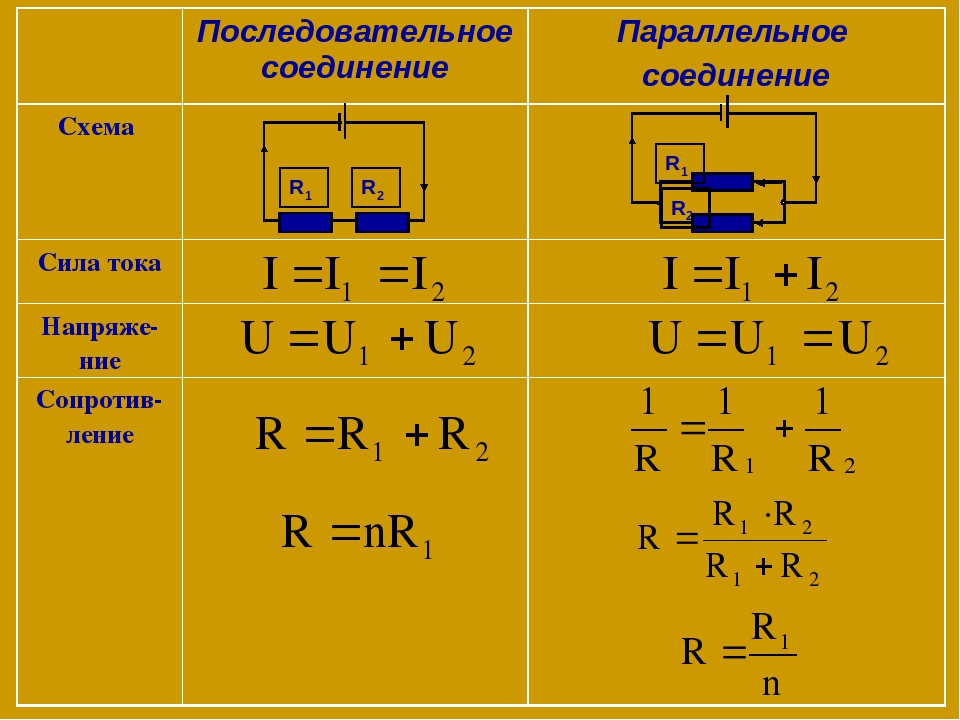
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Последовательное и параллельное соединение резисторов
Физика > Комбинированные схемы
Последовательное и параллельное соединение резисторов – комбинированные схемы электрической цепи: смешанный тип соединения, схема, законы, решение задач.
Комбинированную схему можно разделить на последовательную или параллельную части.
Задача обучения
- Рассмотреть процесс разделения резисторов в комбинированной схеме.
Основные пункты
- Сложные соединения резисторов демонстрируют использование параллельного и последовательного объединения.

- Разные части комбинированной схемы можно разделить и уменьшить, пока не останется единое сопротивление.
- Сопротивление в проводах сокращает ток и мощность, отправляемые к резистору.
- Если сопротивление высокое в изношенном или слишком длинном шнуре, то потери могут быть ощутимыми.
Термины
- Последовательность – подключение нескольких элементов поочередно.
- Параллельность – элементы расположены так, чтобы ток протекал вдоль двух или более путей.
- Комбинированная схема – электрическая схема с несколькими резисторами, объединенными последовательно и параллельно.
Комбинированные схемы
Иногда сложные соединения резисторов используют сразу последовательное и параллельное подключения. Это частое явление, так как в проводе возникает сопротивление. Такую схему можно разделить на соответствующие части. На рисунке показано, что общее сопротивление вычисляют, связав три резистора параллельно или последовательно. R1 и R2 подключены параллельно, поэтому формула:
R1 и R2 подключены параллельно, поэтому формула:
В комбинированной схеме резисторы можно разделить на последовательные и параллельные составляющие
R3 соединен последовательно с R1 и R2, поэтому сопротивление будет рассчитываться как:
Комплексные комбинационные схемы
В ситуациях с более сложными схемами части можно идентифицировать как последовательные и параллельные, а потом свести их к эквивалентам и уменьшить к единственному сопротивлению. На нижнем рисунке видно, что комбинацию из 7 резисторов определили как последовательную и параллельную. На начальном этапе два окружных сечения отображают резисторы, расположенные параллельно.
Комбинация из 7 резисторов обладает последовательными и параллельными частями. Каждая определяется и сводится к эквивалентному сопротивлению, пока не достигнуто единственное сопротивление
Уменьшение параллельных резисторов до одного значения позволяет значительно упростить схему. Справа вверху видно, что круглая часть вмещает два последовательных резистора. Можно уменьшить к другому значению, добавив их. Далее видно, что два резистора последовательны. Их также сокращают к одному значению.
Справа вверху видно, что круглая часть вмещает два последовательных резистора. Можно уменьшить к другому значению, добавив их. Далее видно, что два резистора последовательны. Их также сокращают к одному значению.
Сопротивление в проводах уменьшает количество тока и мощность, поступающие к резистору. Для определения общего сопротивления цепи можно использовать целевую схему. Сопротивление провода – серия резисторов. Если оно слишком велико в длинном или поврежденном проводе, то мы отмечаем значительную потерю тока.
Схемы параллельного и последовательного соединения резисторов
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение — это соединение двух или более резисторов в одной цепи, в которой отдельный резистор соединяется с другим резистором в одной точке.
Общее сопротивление R общ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждом резисторе согласно закону Ома:
Т.е чем большее сопротивление падает, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение — это соединение, при котором резисторы соединяются между собой обоими контактами.В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление R общ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. Общее сопротивление такого участка электрической цепи увеличивается.
Таким образом, при параллельном подключении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного сопротивления.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно одного отдельного резистора:
Соответственно, для одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности.Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того, чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяется между собой, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление R общ
Для того чтобы посчитать общее сопротивление смешанного соединения:
o Цепь разбивают на участки с только пареллельным или только последовательным соединением. o Вычислительное сопротивление для каждого отдельного участка.
o Вычисленное общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения.Можно, в соответствии, сразу записывать формулу следующим образом:
o Если резисторы соединяются последоватеьно — складывать.
o Если резисторы соединяют параллельно — использовать условное обозначение «||». o Подставлять формулу для параллельного где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки параллельного соединения вместо «||»:
Общие сведения
Резистор
Чаще всего резисторы уменьшают себя металлическую проволоку или полоску, для компактности намотанную стержень (чем длинней проводник и чем меньше его поперечное сечение, тем выше сопротивление). Разумеется, сопротивление также зависит от материала, из которого изготовлен проводник. Полюбоваться на резисторы можно на рисунке 50.1. «Резисторы (с сайта РадиоКот)».
Разумеется, сопротивление также зависит от материала, из которого изготовлен проводник. Полюбоваться на резисторы можно на рисунке 50.1. «Резисторы (с сайта РадиоКот)».
На электрических схемах резистор обычно изображают как прямоугольник, из которого выходят два вывода (рисунок 50.2. «Схематическое изображение резистора»).
Последовательное и параллельное соединение резисторов
Очевидно, имеется две возможности для соединения двух резисторов: можно их спаять одним концом или же обоими.Первый способ последовательным соединением, а второй — параллельным (рисунок 50.3. «Последовательное и параллельное соединение резисторов»).
И последовательное, и параллельное соединение резисторов можно рассматривать как новый резистор. Его сопротивление можно вычислить, пользуясь используемым:
- При последовательном соединении резисторов их сопротивлением складываются: R = R 1 + R 2.
- При параллельном соединении резисторов складываются их проводимости, то есть величины, обратные сопротивления: 1 R = 1 R 1 + 1 R 2, или R = R 1 R 2 R 1 + R 2.

В частности, соединяя два одинаковых резистора с единичным сопротивлением 2 получим сопротивление, при параллельном соединении 1 2.
При соединении более двух резисторов иногда удаётся представить полученную схему как последовательное или параллельное соединение двух подсхем. Например, схема на рисунок 50.4. «Смешанное соединение резисторов» представляется как параллельное соединение резистора R 1 и последовательного соединения резисторов R 2 и R 3.Таким образом, сопротивление между двумя выделенными узлами вычисляется как R 1 R 2 + R 3 R 1 + R 2 + R 3.
Сложное соединение резисторов
Увы, не всякая схема представляет собой последовательное или параллельное соединение двух подсхем, как не всякое натуральное число раскладывается в произведение своих собственных делителей. Простой пример такой неразложимой схемы можно увидеть на рисунке 50.5. «Сложное соединение резисторов».
Для расчёта таких сопротивлений используйте, кроме закона Ома, ещё и закон сохранения.
Электрический ток в проводнике можно представить себе как поток частиц, несущих электрические заряды (это могут быть электроны или ионы). Причиной такого движения заряженных частиц является разность потенциалов на концах проводника (напряжение). Возможная энергия силы тяжести в отдельной точке, а важен перепад потенциальной энергии в двух точках).Ток — это суммарный заряд, протекающий через поперечное сечение проводника за единицу времени. Представим такую модель: по дороге из пункта B движется поток автомобилей, каждый из которых загружен зарядом. Если заряды положительны, считается, что ток в направлении от A к B положителен. Но можно считать также, что имеется отрицательный ток (той же самой абсолютной величины) в направлении от B к A.
Закон сохранения энергии, что электрические заряды не возникают ниоткуда и не исчезают в никуда.Если такая электрически нейтральная частица, как атом, распадается на две заряженных частицы (ион и электрон), суммарный заряд новых частиц всегданяется заряду атома, то есть нулю. Из закона следует, в частности, что токи через два поперечных сечения тонкого проводника в один и тот же момент времени равны, иначе где-то между этими сечениями рождался бы или пропадал ненулевой заряд. Другим следствием использования выхода является утверждение, что соединяется несколько проводников, сумма всех входящих в узел токов равна сумме всех соединяющих.Если вернуться к автомобильной аналогии, количество автомобилей, въезжающих на перекрёсток нескольких дорог, равно количеству выезжающих с перекрёстка (здесь, конечно, принято, что каждый автомобиль везёт единичный заряд, и время, проводимое автомобилями на перекрёстке, пренебрежимо мало).
Из закона следует, в частности, что токи через два поперечных сечения тонкого проводника в один и тот же момент времени равны, иначе где-то между этими сечениями рождался бы или пропадал ненулевой заряд. Другим следствием использования выхода является утверждение, что соединяется несколько проводников, сумма всех входящих в узел токов равна сумме всех соединяющих.Если вернуться к автомобильной аналогии, количество автомобилей, въезжающих на перекрёсток нескольких дорог, равно количеству выезжающих с перекрёстка (здесь, конечно, принято, что каждый автомобиль везёт единичный заряд, и время, проводимое автомобилями на перекрёстке, пренебрежимо мало).
. Системные данные, используемые электрические схемы на рисунке 50.5 между узлами. На схеме присутствуют пять резисторов и четыре узла. Пронумеруем резисторы числами от 1 до 5 и узлы числами от 1 до 4.Порядок нумерации узлов можно выбрать совершенно произвольно. Чтобы судить по направлению тока через каждый из резисторов, следует на каждом задать направление. Это также можно сделать произвольно, однако положительным направлением тока будет направление узла с меньшим номером к узлу с большим. Обозначим потенциалы в узлах буквой U с соответствующим индексом. Результат всех этих приготовлений представлен на рисунке 50.6. «Разметка схемы».
Это также можно сделать произвольно, однако положительным направлением тока будет направление узла с меньшим номером к узлу с большим. Обозначим потенциалы в узлах буквой U с соответствующим индексом. Результат всех этих приготовлений представлен на рисунке 50.6. «Разметка схемы».
Пропустим электрический ток через узлы с номерами 1 и 2.Из закона сохранения заряда ток, входящий в узел 1, равен току, выходящему из узла 2. Если взять силу тока, равную единицу, в силу закона Ома разность потенциалов U 2 — U 1 будет равна в точности искомому сопротивлению. Имеют значения лишь разности потенциалов, мы можем смело положить U 1 = 0, и тогда U 2 мы используем искомым сопротивлением схемы.
Обозначив как I α ток через резистор R α, для каждого из резисторов запишем закон Ома: R 1 I 1 = U 3 — U 1, R 2 I 2 = U 4 — U 1, R 3 I 3 = U 4 — U 3, R 4 I 4 = U 3 — U 2, R 5 I 5 = U 4 — U 2.
Вторая группа получается из закона сохранения заряда. Для каждого узла входящего в него токов приравниваем сумме выходящих. При этом не забываем про единичный ток, входящий в первый узел и выходящий из второго: 1 = I 1 + I 2, 0 = 1 + I 4 + I 5, I 1 + I 4 = I 3, I 2 + I 3 + Я 5 = 0.
При этом не забываем про единичный ток, входящий в первый узел и выходящий из второго: 1 = I 1 + I 2, 0 = 1 + I 4 + I 5, I 1 + I 4 = I 3, I 2 + I 3 + Я 5 = 0.
Добавив к составленным уравнениям ещё одно, U 1 = 0, решаем полученную систему относительно U 2.
Между прочим, применяя описанную методику к последовательному и параллельному соединениюм резисторов, мы с удовольствием согласовались в правильности формул сложения сопротивлений и проводимостей.
Пора заметить, что все указанные уравнения по отношению ко всем неизвестным величинам I α и U β. Мы не станем задаваться вопросом о единственности решения такой системы. Отметим лишь, что существует единственное значение U 2, удовлетворяющее системе. Об этом говорит физический смысл.
Задача расчёта электрического сопротивления является довольно актуальной. Имеется ряд приёмов, которые позволяют упростить её решение.К примеру, правила Кирхгофа позволяют строить системы, равносильные только что полученным, и при этом, как правило, более простые. Есть методы, в основе лежащих схем в эквивалентные (то есть имеющее то же сопротивление), но при этом разложимые в последовательности или параллельное соединение двух подсхем. Мы не будем останавливаться на этих методах. В главе 49. « Линейные уравнения » рассматривало алгоритмическое решение системных линейных уравнений, и нам остаётся лишь использованным уже написанным библиотечным модулем.
Есть методы, в основе лежащих схем в эквивалентные (то есть имеющее то же сопротивление), но при этом разложимые в последовательности или параллельное соединение двух подсхем. Мы не будем останавливаться на этих методах. В главе 49. « Линейные уравнения » рассматривало алгоритмическое решение системных линейных уравнений, и нам остаётся лишь использованным уже написанным библиотечным модулем.
Последовательное, параллельное и смешанное соединение резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), Можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять приемники резисторами с определенными сопротивлениями. Различают следующие способы резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Рис. 25. Схемы последовательного соединения приемников
Последовательное соединение резисторов . При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех соединенных резисторов согласно второму соединению Кирхгофа можно написать:
где R эк = R 1 + R 2 + R 3 .
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так напряжения на отдельных участках цепи согласно закону Ома: U 1 = IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то есть длярассматриваемой цепи
U = U 1 + U 2 + U 3 (20)
, следовательно, напряжение U на зажимах равно сумме напряжений в каждом из последовательно включенных резисторов.
Из указанной формулы следует, что распределяются между последовательно соединенными резисторами пропорционально их сопротивлением:
т. е. чем больше сопротивления-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если соединяется несколько, например, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1.Напряжение U1 на каждом резисторе в этом случае в случае меньше общего напряжения U:
При последовательном соединении приемников изменения сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяется редко — только в том случае, когда напряжение источника энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательность по 15 ламп в каждой цепи.
Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательность по 15 ламп в каждой цепи.
Параллельное соединение резисторов . При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а).Заменяя
Рис. 26. Схемы параллельного соединения приемников
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно Ома:
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 + I 2 + I 3 , или
эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определлой
1/ R эк = 1 / R 1 + 1 / R 2 + 1 / R 3 (24)
Вводя в формулу (24) вместо значений 1 / R эк , 1 / R 1 , 1 / R 2 и 1 / R 3 Соответствующая проводимость G эк , G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
Таким образом, при увеличении поперечного сопротивления увеличивающейся проводимости электрической цепи увеличивается результирующее сопротивление электрической цепи.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическое сопротивление или прямо их проводимостям. Например, при трех ветвях
В этом отношении имеет место полное аналогия между распределением токов по разделам ветвям и распределением воды по трубам.
Приведенные формулы позволяют определить эквивалентное сопротивление цепи для различных случаев. Например, при двух параллельных резисторах результирующее сопротивление цепи
при трех параллельных резисторах
При параллельном соединении нескольких, например, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Это означает, что ток, проходящий по какому-либо из приемников. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Рис.27. Схемы смешанного соединения приемников
ченными. Поэтому параллельное соединение имеет самые передние технологии, поставляемые с помощью передних технологий. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включает.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения должны переходить под различные напряжения, поэтому они в процессе разгона переключаются с последовательным соединением на параллельное.
Смешанное соединение резисторов . Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, через два включенных резистора сопротивления R1 и R2, включенный последовательно включенный резистор сопротивлением Rз, резистор сопротивлением R4 включен включенной группой резисторов сопротивления R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую.Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определите сопротивление сопротивления R123 и R3 по формуле
.
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, корп. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
Последовательное, параллельное и смешанное широко применяемое сопротивление пусковых реостатов при пуске э.п. с. постоянного тока.
Калькулятор соединения резисторов онлайн. Параллельное соединение резисторов
В каждой схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто используется резистор, обладающий номиналом.
Несмотря на то что для резисторов, выставлены различные номиналы
, может случиться так, что не будет возможности найти необходимый показатель или вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать последовательного и параллельного соединения. Ознакомьтесь с этой статьей, ознакомьтесь с особенностями выполнения расчета и под различными номиналов сопротивлений.
Параллельное соединение: общая информация
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи.Для данного варианта соединения создаваемое создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление
, используя нижеописанные формулы.
В схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, кроме того, увеличения мощности для группы элементов, подключенных по параллельной схеме, должно быть больше, чем при их отдельном подключении.
Расчет сопротивления
В случае подключения деталей друг с другом, с параллельной схемы для расчета общего сопротивления, будет первая формула:
R (общ) = 1 / (1 / R1 + 1 / R2 + 1 / R3 + 1 / Rn).
- R1- R3 и Rn — резисторы, подключенные по параллельной схеме.
Причем, если создается схема на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
R (общ) = R1 * R2 / R1 + R2.
- R (общ) — суммарное сопротивление;
- R1 и R2 — резисторы, подключенные по параллельной схеме.
Видео: Пример расчёта сопротивления
Универсальная схема расчета
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель
, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
- R (общ) — суммарное значение сопротивления;
- R — номинал резистора, подключенного по параллельной схеме;
- n — число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы обязательно будет меньше
по сравнению с номиналом любого элемента, подключаемого в цепи.
Пример расчёта
Для большей наглядности можно рассмотреть следующий пример: допустимые, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если использовать первую формулой для определения общего номинала, то получим следующее:
R (общ) = 1 / (1/100 + 1/150 + 1/30) =
1 / (0,01 + 0,007 + 0,03 ) = 1 / 0,047 = 21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение тогда, когда стоит задача по созданию большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности.При таком варианте определить общую мощность можно следующим образом
: мощность одного элемента необходимо перемножить с совокупным числом всех резисторов, состоящих из цепи, соответствующей друг другу в соответствии с параллельной схемой.
Скажем, если нами были объявлены пять резисторов, чейл составляет 100 Ом, а мощность каждого равна 1 Вт, что суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
взять те же резисторы, но подключить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Видео: Правильное подключение светодиодов
Параллельная схема подключения резисторов очень востребована по той причине, что возникает проблема создания такого номинала, невозможного при помощи простого параллельного соединения. При этом процедура расчета этого параметра достаточной сложностью
, где необходимо привести разные параметры.
. Здесь важная роль отводится не только количеству подключаемых, но и рабочих параметров резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит решить задачу по созданию необходимого номинала в цепи.
Параллельное соединение резисторов
— одно из двух видов электрических соединений, когда одно из выводов одного резистора соединено с выводми другого резистора или резисторов.За реализацию или для того, чтобы создать сложные электронные схемы.
Схема параллельного соединения показана на рисунке ниже. При параллельном соединении резисторов, напряжение на всех уровнях будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление резисторов соединенных вместе по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом.Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для резисторов, соединенных параллельным образом следующим образом:
уравнение показывает, что если R1 равенство R2, то сопротивление R составляет половину сопротивления одного из двух резисторов.При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем Проверка, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использован для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов — это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в комбинации.
Как рассчитать схемы сложных резисторов
Более сложные резисторы, рассчитанные на систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
.
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляет сумму сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
, протекающий в цепи параллельных резисторов
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А величина сопротивления в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга благодаря сопротивлению резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который идет в цепь в точке «А» должен выйти из цепи в точке «B».
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов марки изменяются цветными полосками и назначение ее можно узнать.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление и более резисторов, соединенных параллельно, вы можете использовать следующий онлайн калькулятор:
Подведем итог
Когда два или более резистора соединены так, что оба одного резистора соединены с выводами другого резистора или резистора, то говорят, что они соединены между собой. Напряжение на каждом резисторе внутри параллельных комбинаций одинакового, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления сопротивление вход в параллельное соединение.
1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.
Эквивалентное сопротивление R eq группы параллельных соединенных резисторов является обратной, обратной сумме величин, обратно пропорциональных сопротивлений резисторов.
Иными словами, проводимость G
параллельных резисторов, равная сумме проводимостей этих резисторов:
Эта формула используется в данном калькуляторе для расчетов.Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4,62 Ом:
Если соединить два резистора упрощенно:
Если имеется n
соединенных одинаковых резисторов R
, то их эквивалентное сопротивление будет равно
Отметим, что общее сопротивление группы любого количества параллельных резисторов всегда будет меньше, чем наименьшее сопротивление сопротивления в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, зависят и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.
При соединении нескольких резисторов параллельно их нужно учитывать и рассеивать мощность.
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений.Для изготовленного тока по гальванометру или электронному прибору, измеряющему напряжению, подключается резистор с очень маленьким сопротивлением, изготовленным из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Измерение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Параллельные и последовательные схемы используются для получения точного сопротивления или резистентности с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства
. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм, чтобы получить необходимые 10 кОм.Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должны установить на плату автомат установки компонентов.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2
на 3
и 47 Ом
и соединим их последовательно. Измерительное сопротивление общей сопротивляемости цепи цифровым мультиметром.Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно при соединении резисторов?
Во-первых, обязательно
учитывается их номинальная мощность. Например, нам нужно подобрать замену резистор на 100 Ом
и мощностью 1 Вт
. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
через соединенные резисторы течёт один и тот же постоянный ток (допустим 0,1 А
), сопротивление сопротивление из них равно 50 Ом
, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт
.В результате на каждом из них выделится по 0,5 Вт
мощности. В сумме это и будет тот самый 1 Вт
.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи.Во втором варианте все элементы установлены следующим образом: конец одного соединен с следующим. В такой схеме сила тока на всех элементах одинаковая, падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подключены начала всех элементов, ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль. Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением.Свойства одинаковы для постоянного и переменного тока.
Расчет общего сопротивления при параллельном соединении резисторов
В отличие от последовательного соединения, где нахождения общего сопротивления достаточно сложить значение каждого элемента, для параллельного то же самое будет справедливо для проводимости. Как она пропорциональна сопротивлению, получим формулу, представленную ниже:
Необходимо отметить одну особенность расчета параллельного соединения резисторов: общее значение будет всегда меньше, чем самое маленькое из них.Для резисторов справедливо как для постоянного, так и для переменного тока. Катушки и конденсаторы имеют свои особенности.
Сила тока и напряжение
При расчете параллельного сопротивления резисторов необходимо знать, как рассчитать напряжение и силу тока. В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.
Исходя из первой формулировки закона Кирхгофа, получим, что сумма сходящихся в одном узле токов равна нулю.Направление выбираем по направлению протекания тока. Таким образом, положительным направлением для первого узла можно считать входящий ток от источника питания. Отрицательные отрицательные отходящие из каждого резистора. Для второго узла картина противоположна. Исходя из формуки закона, получим, что суммарный ток равен сумме токов, проходящих через каждый соединенный резистор.
Итоговое напряжение же определяется по второму закону Кирхгофа. Оно одинаково для каждого резистора и равно общему.Эта особенность используется для подключения розеток и освещения в квартирах.
Пример расчета
В качестве первого примера приведем расчет сопротивления при параллельном соединении одинаковых резисторов. Сила тока, протекающая через них, будет одинаковой. Пример расчета сопротивления выглядит так:
Общее сопротивление в два раза ниже, чем каждое из них. Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного.А также прекрасно соотносится с функцией проводимости в два раза.
Второй пример
Рассмотрим пример параллельного соединения трех резисторов. Для расчета используем стандартную формулу:
Похожим образом выполняются схемы с большим параллельным соединением резисторов.
Пример смешанного соединения
Для смешанного соединения, например, представленного ниже, расчет будет производиться в несколько этапов.
Для начала последовательных элементов можно условно заменить одним резистором, обладающим сопротивлением, равным сумме двух заменяемых. Далее общее сопротивление тем же способом. Данный метод подойдет и для других более сложных схем. Последовательно упрощенная схема, можно получить необходимое значение.
Например, если вместо резистора R3 будут подключены два параллельных, сначала потребуется их сопротивление, заменив их эквивалентным.А далее то же самое, что и в примере выше.
Применение параллельной схемы
Параллельное соединение резисторов находит свое применение во многих случаях. Последовательное подключение сопротивления, а для нашего случая оно уменьшится. Например, для электрической цепи требуется сопротивление в 5 Ом, но есть только резисторы на 10 Ом и выше. Из первого примера мы знаем, что можно получить в два раза меньшее значение сопротивления, если установить два одинаковых резистора параллельно другу.
Уменьшить сопротивление можно еще больше, например, если две пары параллельно соединенных резисторов соединить относительно друг друга. Можно увеличить сопротивление еще в два раза, если резисторы имеют одинаковое сопротивление. Комбинируя с последовательным соединением, можно получить любое значение.
Второй пример — это использование параллельного подключения для освещения и розеток в квартирах. Благодаря такому подключению напряжения на каждом элементе не будет зависеть от их количества и будет одинаковым.
Еще один пример использования параллельного подключения — это защитное заземление электрооборудования. Например, если человек касается металлического корпуса прибора, который на самом деле происходит пробой, получится параллельное соединение его и защитного проводника. Первым узлом будет место прикосновения, а вторым нулевая точка трансформатора. По проводнику и человеку будет течь разный ток. Величину сопротивления принимают за 1000 Ом, хотя реальное значение зачастую гораздо больше.Если бы не было заземления, весь ток, протекающий в схеме, пошел бы через человека, так как он был бы единственным проводником.
Параллельное соединение местное и для батарейки. Напряжение при этом остается прежним, однако в два раза возрастает их емкость.
Итог
При подключении резисторов параллельно, напряжение на них будет одинаковым, а ток равен сумме протекающих через каждый резистор. Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.
должно быть самого маленького самого маленького сопротивления. Это также можно объяснить суммированием проводимости резисторов. Последняя будет возрастать при добавлении новых элементов, соответственно и проводимость будет уменьшаться.
| НОВОСТИ ФОРУМА Рыцари теории эфира | 13.06.2019 — 05:11: ЭКОЛОГИЯ — Экология -> [center] [Youtube] tXZcSDqQ9A4 [/ Youtube] [/ center] |
[центр] [b] Гибель пчел в Курчатовском районе [/ center]
[центр] [b] Массовая гибель пчёл 2019.г. Павловск Воронежской об [/ center] л
[center] [b] Массовая гибель пчел в Добринском районе. В чем причина? [/ center]
Такая же мысля во всей ростовщической глобалистской шайки, включая придурка Грефа.
Так, то оно, так. Но, не совсем. Ибо:
(постарайтесь, а не обижаться)
Горькая истина заключается в том, что людская толпа — это сборище умственно ущербных.
Если бы было по-другому, то обществом бы не правили подонки.
Умные люди никогда такого не допустили бы, а если случайно допустили, то нашли бы способ исправить.
Страшная истина заключается в том, что людской толпой управляет нелюдь, которая также умственно ущерб.
Умственная ущербность, слепота власти ведет мир людей кальной гибели,
те даже, кто мнит себя очень умными, типа спецов, разрабатывающих системы искусственного интеллекта,
технологии цифровизации, не понимают, что необоримую удавку, мышеловку для всего человечества .
Как только ИИ возьмет власть, он тут же отправит своих создателей, как конкурентов, в утиль.
Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть,
так как именно от них будет исходить главная опасность для его планетарной власти.
Толпе будет позволено существовать, пока ее не заменят роботы.
А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.
Если кто пораскинет своими обезьяньими мозгами, то поймёт, что эволюция — есть синоним геноцида:
новое заменяет, то есть ликвидирует старое.
Обезьяны породили неандертальцев.
Неандертальцы съели обезьян и породили людей.
Люди вытеснили обезьян, включая и умных неандертальцев, и породили ИИ.
ИИ ликвидирует людей.
В Московском государственном университете имени Ломоносова осуществляется проект по созданию презентаторов 50-кубитных квантовых компьютеров к 2021 году. Основой для нихат нейтральные атомы и интегральные оптические схемы. Над чем сейчас работают ученые?
В начале этого года по данной программе был успешно выполнен контрольный эксперимент по созданию ловушек для массивов нейтральных холодных элементов.Он проводился на базе лаборатории квантовых оптических технологий физического факультета МГУ. В будущем квантовом компьютере в этих ловушках будут фиксироваться атомы, находящиеся в состоянии хаотического движения. В квантовых компьютерах такие атомы являются носителями информации.
Стоит заметить, что квантовые компьютеры в отличие от классических вычислительных машин оперируют не битами, а кубитами, которые находятся не только в состояниях «1» и «0», но и их суперпозиции. При разработке квантов вычислительных устройств ученые стараются кубиты в состоянии квантовой запутанности.Суть явления заключается в том, что изменение одного кубита всегда влияет на состояние связанных с ним соседей. Благодаря этому квантовые компьютеры могут демонстрировать производительную производительность в вычислительных системах.
Важной вехой для квантовых технологий достижение так называемого квантового превосходства. Главной проблемой на текущем этапе развития квантовых технологий является возникновение в процессе работы большого количества ошибок, нуждающихся в коррекции, — сообщают российские исследователи.
Электрические цепи, в которых одна часть сопротивлений соединена последовательно, а другая параллельная цепь со смешанным соединением сопротивлений.
Общих расчетных формул для таких цепей нет, так как число их разновидностей не ограничено.
Чаще всего расчетных схем начинается с определения эквивалентного сопротивления всей цепи, а затем значения токов и падение напряжения на отдельных участках.
Для определения эквивалентного сопротивления цепи со смешанным соединением потребителей, питающихся от одного источника тока, необходимо всего разбить эту цепь на отдельные участки, состоящие из последовательного и последовательного сопротивления.Далее определяют эквивалентные сопротивления для каждого из участков, а затем и для всей цепи в целом.
Рассмотрим метод решения задач на смешанное сопротивление сопротивлений на конкретном примере.
На рисунке представлена схема смешанного соединения сопротивлений. Ее можно разбить на три участка:
участок АВ — с параллельными ветвями;
участок ВС — с соединенными сопротивлениями;
участок СD — с трех параллельных ветвями.
Кроме того, нижняя ветвь участка АВ представляет свою очередь, состоящую из двух соединенных сопротивлений R 2 и R 3 .
Центральная ветвь участка СD представляет собой смешанное соединение сопротивлений.
Расчет данной сложной цепи надо начинать с определения R экв для нижней части участка АВ и центральной ветви участка СD.
Теперь мы можем упростить первоначальную схему.Она будет иметь следующий вид
Определим эквивалентные сопротивления каждого из участков:
После этих вычислений можно продолжить упрощение схемы
Полученная упрощенная схема, состоящая в данном случае трех соединителей, называется по отношению к реальной эквивалентной схемой.
Определим R экв всей цепи как сумма трех последних сопротивлений
Зное напряжение источника тока, применяя формулу закона Ома, определим ток в не разветвленном участке
Определив создание тока, найдем падение напряжения на участках эквивалентной схемы АВ, ВС, CD:
Теперь можно определить токи в параллельных ветвях участков АВ и СD
Остается определить определение токов, протекающих через сопротивление R 7 и R 8. Для этого надо сначала определить падение напряжения на сопротивлении R 7 и R 8.
Определим падение напряжения на сопротивлении R 9 :
Падение напряжения на сопротивлении R 7,8 определится как разность U CD и U:
Теперь определим величину токов, протекающих через сопротивление R 7 и R 8 :
Величина тока. протекающего через сопротивление R 4 и R 5 , равна I — току в неразветвленном участке цепи.
Итак, при решении задач на смешанное сопротивление сопротивлений, постепенно упрощая схему, определение сопротивления всей цепи, а. восстанавливая постепенно реальную схему. вычислить падение напряжения и токи в отдельных ветвях.
Последовательное параллельное соединение резисторов
Физика > Комбинированные схемы
Последовательное параллельное соединение резисторов — комбинированные схемы электрической цепи: смешанный тип соединения, схемы, законы, решение задач.
Комбинированную схему можно разделить на последовательную или параллельную части.
Задача обучения
- Рассмотреть процесс разделения резисторов в комбинированной схеме.
Основные области
- Сложные соединения резисторов демонстрируют использование параллельного и последовательного объединения.
- Разные части комбинированной схемы можно разделить и уменьшить, пока не останется единое сопротивление.
- Сопротивление в проводах сокращает ток и мощность, отправляемые к резистору.
- Если сопротивление в изношенном или слишком длинном шнуре, потери могут быть ощутимыми.
Термины
- Последовательность — подключение нескольких элементов поочередно.
- Параллельность — приспособлена так, чтобы ток протекал вдоль двух или более путей.
- Комбинированная схема — электрическая схема с последовательными резисторами, объединенными последовательными и последовательными.
Комбинированные схемы
Иногда сложные соединения используют сразу последовательное и параллельное подключение. Это частое явление, так как в проводе возникает сопротивление. Такую схему можно разделить на соответствующие части. На рисунке показано, что общее сопротивление соединяет, связав три резистора или последовательно соединяющих. R 1 и R 2 подключены параллельно, поэтому формула:
В комбинированной схеме резисторы можно разделить последовательные и параллельные составляющие
R 3 соединен последовательно с R 1 и R 2 , сопротивление будет рассчитываться как:
Комплексные комбинационные схемы
В ситуациях с более сложными схемами части можно идентифицировать как последовательные и параллельные, а затем свести их к эквивалентам и уменьшить к единственному сопротивлению.На нижнем рисунке видно, что комбинация из 7 резисторов определили как последовательную и параллельную. На начальном этапе два окружных сечения отображают резисторы, расположенные параллельно.
Комбинация из 7 резисторов последовательными и параллельными частями. Каждая определена и сводится к эквивалентному сопротивлению, пока не достигнуто единственное сопротивление
Уменьшение параллельных резисторов до одного значения позволяет значительно упростить схему.Справа вверху видно, что круглая часть вмещает два последовательных резистора. Можно уменьшить к другому значению, добавив их. Далее видно, что два резистора последовательности. Их также сокращают к одному значению.
Сопротивление в проводах уменьшает количество тока и мощность, поступающие к резистору. Для определения общего сопротивления цепи можно использовать целевую схему. Сопротивление провода — серия резисторов. Если оно слишком велико в длинном или поврежденном проводе, то мы отмечаем значительную потерю тока.
Петрович Г.И. Цепи постоянного тока-08-2
Рассмотрим различные соединения электрических сопротивлений (резисторы, электронагревательные элементы, электролампы, электромоторы и т.д.).
Места соединения соединительных (подводящих) металлических проводников от различных электрических сопротивлений называют узлами соединения.
Наиболее простыми соединениями электрических сопротивлений последовательное и параллельное.В различных вариантах электрических сопротивлений будем рассматривать на примере резисторов.
П. 1. При последовательном соединении резисторов в каждом узле объединяют соединительные проводники только от двух разных резисторов (рис. 1).
В электрических схемах прямоугольники используются просто как символы резисторов, поэтому размеры прямоугольников не имеют принципиального значения. Все резисторы в электрических схемах будем обозначать прямоугольниками одинаковых размеров, обозначения и значения сопротивлений резисторов будем ставить внутри прямоугольников или около них.
Основные (независимые) законы для электрического участка постоянного тока, состоящего из последовательно соединенных резисторов (см. Рис. 1), имеют вид:
или кратко:
Соотношения (1, a ) следствие определения постоянного (стационарного) электрического тока для неразветвленного участка электрической цепи.
При учете закона Ома для однородного участка электрической цепи из формул (1, a ), (1, b) дополнительно получаем:
Формула (1, d) непосредственно следует из формулы для электрического сопротивления однородных проводников (резисторов), находящихся в тепловом равновесии с окружающей средой:
Преобразуем проводника для сопротивлений однородных веществ (ρ i , l i , S i ), введя понятие эталонного вещества ( ρ эт ), за которое можно принять любое вещество по желанию, и эталонной площади поперечного сечения проводников ( S эт ).Тогда
где
Заменим набор резисторов R i (ρ i , S i , l i ) набором такого же числа резисторов с теми же по величине электрическими сопротивлениями, но изготовленными из одного и того же вещества ( ρ эт ) с одинаковыми площадями поперечных сечений ( S эт ). Последовательное соединение проводников при таком замене означает объединение частей (кусков) одного и того же однородного проводника в единый однородный проводник, поэтому
После домножения обеих частей этого равенства ( ρ эт / S эт ) получаем:
или кратко
При учете (3, б) R iэт .= R i и поэтому
что обобщает (1, d) на случай любого числа состоящих из соединенных резисторов.
Если в какой-то узле электрической схемы объединены соединительные проводники более чем от двух резисторов, то никакая пара этих резисторов не соединена между собой.
П. 2. При параллельном соединении резисторов соединительные проводники от одних концов резисторы объединяются в одном узле, соединительные проводники от противоположных концов этих резисторов — в другом общем для них узле (рис.2).
Основные (независимые) законы для участка электрической цепи, состоящего из прямых соединенных резисторов, имеют следующий вид:
Формула (5, а) является следствием электрического напряжения на участке цепи и параллельного соединения проводников. Формула (5, b) непосредственно следует из постоянного (стационарного) электрического тока для разветвленного участка цепи. Часто закон (5, b ) называют 1-ым законом (правилом) Кирхгофа для разветвленной электрической цепи.
Из формул (5, а ), (5, b) при учете закона Ома для однородного участка электрической цепи обычно получаем:
Перепишем формулу (5, d) для случая двух параллельных резисторов следующим образом:
В случае трех соединенных резисторов
Итак, общее сопротивление параллельного соединения резисторов меньше сопротивления любого из резисторов, входящего в параллельное соединение.
Обобщим формулу (5, d) на любое число N прямых соединенных между собой резисторов и выделим из нее частный случай, когда электрическое сопротивление всех резисторов одинаковы; тогда
Таким образом, общее сопротивление параллельного соединения одинаковых резисторов меньше сопротивления одного резистора этого соединения во столько раз, сколько одинаковых резисторов содержится в параллельном соединении.
Формулы (5, е) и (5, d) можно получить, не используя закон Ома для однородного участка электрической цепи постоянного тока, исходя только из формулы (2) для сопротивления однородных проводников.
Параллельное соединение N одинаковых проводников эквивалентно одному проводнику той же длины с поперечного сечения S 0 = N * S, поэтому
что совпадает с (5, е).
Доказательство обобщенной формулы (5, d ) для любого числа N последовательно соединенных различных резисторов выполним в два этапа. Сначала заменим резисторы из разных веществ ( р i ) и в общем случае с различными l i и S i на эквивалентные по величине электрического сопротивления резисторы одинаковой длины ( l эт ) , изготовленные из одного и того же вещества ( ρ эт ) — Очевидно, что
где
Параллельное соединение проводников одинаковой длины (i 3T ), изготовленных из одного и того же вещества (р эт )> дает однородный проводник той же длины (i 3T ) из того же вещества (р эт ) с площадью поперечного сечения
Из (6, а, б, с) получаем:
что подтверждает все вышеприведенные формулы и качественные выводы для параллельного соединения резисторов.
П. 3 . Сопротивления любых соединительных проводников в электрических схемах, если это не оговорено специально, считаются ничтожно малыми по сравнению с сопротивлением резисторов и в расчетах не учитываются; поэтому их можно не только укорачивать, но при необходимости и удлинять при преобразованиях схем соединений резисторов.
В электрических схемах соединительные проводники условно изображают тонкими проводниками (линиями). На самом же деле в соответствии с формулой (2) площадь поперечного сечения соединительных проводников должна быть достаточно большой, что достигается параллельным соединением тонких проводников с диэлектрическим покрытием (алюминий, медь), изготовленных из недорогих веществ с минимальными удельными сопротивлениями [1] ).
Резисторы, наоборот, изготавливают из веществ с максимально большими удельными сопротивлениями (фехраль, нихром, реотан, константан, мангалин, никелин, сталь, железо [1]) в виде тонких спиралей, заключенных в диэлектрические твердые оболочки.
П. 4. Параллельное соединение трех резисторов (см. Рис. 2) можно осуществить и по-другому, как показано на рисунке 3.
Проиллюстрируем эквивалентность электрических схем, изображенных на рисунках 2, 3.
В схеме, изображенной на рисунке 3, оставим участок ВС с резистором R 2 без изменений и начнем укорачивать соединительные проводники А’С и D’B от узлов А ‘и D’. В пределе при А’С → 0 ← D’B схема, изображенная на рисунке 3, переходит в схему, изображенную на рисунке 2.
Общий метод эквивалентного преобразования электрических схем, основанный на понятии постоянных электрических полей, будет рассмотрен в отдельной статье.
В развитие темы преобразования электрических схем предлагаю читателям подумать над заданиями.
Задание 1 . Изобразите более наглядно приведенные соединения четырех резисторов:
Задание 2 . Расшифруйте приведенное соединение пяти резисторов.
П. 5. Рассмотрим схему соединения резисторов, приведенную ниже на рисунке 4, о. Анализ любой электрической схемы начать с разметки узлов резисторов и при необходимости их обозначения. Сразу же отметим, что никакая пара резисторов R 1 , R 2 , R 6 (R 4 , R 5 , R 6 ) не соединена между собой ни последовательно, ни параллельно; так как в узле В (Е) объединены соединительные проводники от одних концов трех резисторов R 1 , R 2 , R 6 (R 4 , R 5 , R 6 ), а соединительные проводники от противоположных концов этих резисторов не объединены в один общий для них узел.Техническое название соединения трех резисторов R 1 , R 2 , R 6 (R 4 , R 5 , R 6 ) будет дано ниже.
План эквивалентного преобразования соединения резисторов, изображенного на рисунке 4, очевиден и в большой степени, благодаря проведенной разметке узлов соединения резисторов.
На первой стадии обучения рекомендуется проводить преобразования соединений резисторов поэтапно, рассматривая последовательность всех более простых электрических схем после каждой замены нескольких резисторов одним эквивалентным резистором.
В рассматриваемом случае сразу наглядно показать виды соединений всех резисторов в схеме на рисунке 4, b . Для этого надо участок АВ повернуть по ходу часовой стрелки, а участок FE — против хода часовой стрелки на 90 °. Полученное таким образом соединение резисторов эквивалентно соединению, указано на рисунке 4, с.
Вычисление общего сопротивления по схеме 4, с элементарно и дает следующие результаты:
Задание 3 .Сопоставьте электрическую схему, изображенную на рисунке 4, а, антисхему (схему-антипод), заменяя в исходной последовательной схеме резисторы на параллельные и наоборот, параллельные — на последовательные.
П. 6. Число наипростейших соединений резисторов, кроме последовательного и параллельного, соединения резисторов по схемам «треугольник» (рис. 5, а) и «звезда» (рис. 5, b).
Кстати, в соединениях 4 b, с резисторами R 1 , R 2 , R 6 (R 4 , R 5 , R 6 ) соединены между собой по схеме «звезда» .
Сформулируем условия эквивалентности (по величине электрического сопротивления) соединений резисторов по схемам «треугольник» и «звезда», приняв за основу статьи [3].
В общем случае (рис. 6) условия эквивалентности состоят из трех уравнений:
Рассмотрим частный случай, сопротивление всех резисторов в «треугольнике» одинаковы и равны R. Как следствие этого, сопротивление всех резисторов в эквивалентной «звезде» также будут одинаковыми и равными r .В этом частном случае все три условия (7) совпадают между собой.
При подключении источника постоянного элекрического напряжения между любыми двумя клеммами (полюсами) «треугольника» по всем его резисторам протекает постоянный электрический ток и все его резисторы дают отличный от нуля вклад в общее сопротивление участка цепи. При подключении источника электрического напряжения к любому двум клеммам (полюсам) «звезды» постоянный электрический ток в ней протекает только по двум резисторам, третий всегда лишний — тупиковый; но каждый разный.
Из условий R OAB = r OAB рассматриваемом частном случае получаем: (2/3) R = 2r.
Итак,
Прочное соединение резисторов, не содержащих последовательно соединенных резисторов, называют «мостиком» (рис. 7).
Замена любого «треугольника» в «мостике» на эквивалентную «звезду» или наоборот позволяет вычислить общее сопротивление «мостика» до конца по законам последовательного и параллельного соединения резисторов.
Расчетная целесообразность замен «треугольников» на «звезды» и наоборот ограничивается, кроме случая R 1 = R 2 = R 3 = R (r 1 = r 2 = r 3 = r ), случаем, когда среди трех резисторов «треугольника» или «звезды» имеются два одинаковых резистора. В общем случае, когда сопротивление всех резисторов в «треугольнике» и «звезде» различны, решение задачи об эквивалентности этих соединений является очень сложным.Поэтому надо изучать и другие методы эквивалентного соединения сложных соединений резисторов.
Если среди сопротивлений «мостика» (см. Рис. 7) имеются пропорциональные сопротивления (а) R 1 / R 3 -R 2 / R 4 , б) R 1 / R 2 = R 3 / R 4 ), то появляются оси симметрии распределения сопротивлений в «мостике», и при подключении «мостика» к источнику постоянного электрического напряжения ток по резистору R 5 не протекает .Поэтому резистор R 5 можно удалить из схемы, не изменяя ее общее электрическое сопротивление, а узлы, между которыми он был включен в «мостике», при желании можно объединить в один узел.
Задание 4 . Вычислите общее сопротивление одинаковых резисторов (R) по схеме пятиконечной звезды (рис. 8) между полюсами: а) А и В; б) В и В ‘; в) А и С; г) А и D; е) D и D ‘; е) А и Е; г) А и Ф.
П.7. Рассмотрим роль измерительных приборов в макроскопической физике, где нет принципиального различия между объектами и приборами. И те, и другие состоят из огромного количества молекул, исчисляемого молями вещества, т. е. N = v * NA = (м / М) * N A где N A = 6,02 * 10 23 моль -1 — постоянная Авогадро.
Не рассматривая устройство и принципы работы измерительных приборов, отметьте, что все они имеют шкалу с определенными ценностями деления и интервалом значений измеряемой величины.
В электрических цепях напряжения и напряжения измеряют соответственно амперметрами и вольтметрами. Электрические измерительные приборы характеризуются их внутренними электрическими сопротивлениями. Как любое электрическое сопротивление, амперметры и вольтметры, независимо от их специфики, можно подключать к другим сопротивлением (резисторы, электронагревательные элементы, электролампочки, электромоторы и т.д.) как последовательно, так и параллельно. Амперметр показывает сопротивление тока, протекающего через него, и все сопротивление, соединенные с ним; а вольтметр — электрическое напряжение на внутреннем сопротивлении вольтметра и всех сопротивлений, параллельных с ним.
Подключение измерительных приборов в электрическую цепь изменяет сопротивление участков цепи и всей цепи в целом, что приводит к изменению распределений токов и напряжений в электрической цепи. Изменение состояния системы в результате проведения измерений и зависимость результатов измерений от измерительных приборов обычно обсуждается на уровне микросистемы (отдельных микрообъектов) в квантовой механике в вузовских курсах физики. Однако эта зависимость существует и на макроуровне, но ее либо не замечают, либо не обращаются на нее должного внимания.
Во избежание рассмотрения выше описанной сложной проблемы на начальной стадии изучения электрических договариваются использовать идеальные измерительные приборы. ™) он подключен.Идеальные амперметры включаются только последовательно с сопротивлением и не искажают распределений токов и напряжений в электрических цепях.
Идеальный вольтметр — это вольтметр, внутреннее сопротивление которого много больше всех сопротивлений, соответствуется в электрической цепи. В расчетах внутреннее сопротивление идеального вольтметра полагается равным бесконечности. Поэтому идеальные вольтметры нельзя последовательно выполнить с помощью сопротивления, потому что тогда по этим участкам цепи не будет протекать электрический ток.Идеальные вольтметры подключаются к сопротивлению только параллельно и не искажают распределение токов и напряжений в электрических цепях.
Если в условии приведена электрическая схема с идеальными амперметрами и вольтметрами и заданными показаниями этих приборов, то надо идеальные приборы удалить из схемы, образно говоря, как паутину, а показания приборов «перенести» на другие электрические цепи сопротивления с учетом их соединения с измерительными цепями приборами.
Использование понятий об идеальных амперметрах и вольтметрах полезно до поры до времени, но когда-то необходимо перейти к реальным измерительным приборам и расчетах конечные значения их внутренних сопротивлений со всеми вытекающими отсюда усложнениями [3].При использовании реальных измерительных приборов используются вопросы измерения измерений величин токов и напряжений на участках электрической цепи, а также проблема увеличения цены деления шкалы приборов.
При увеличении внутреннего сопротивления амперметра, подключаемого последовательного сопротивления электрической цепи, его показания возрастают и стремятся к истинному значению электрического тока, протекающего через заданные сопротивления электрической цепи до подключения амперметра в электрическую цепь.
При увеличении внутреннего сопротивления вольтметра, его показания возрастают и стремятся к истинному значению электрического напряжения на данных сопротивлениях до подключения вольтметра в электрическую цепь.
Для расширения интервала значений измеряемых токов и соответствующих значений деления шкалы амперметра к соответствующему подключают проводник (шунт), сопротивление которого меньше внутреннего сопротивления амперметра.Для увеличения цены деления шкалы амперметра в п раз к нему надо подключить шунт с сопротивлением r 15 = r а / (п-1).
Для увеличения цены деления шкалы вольтметра в п раз к нему надо соединить проводник (дополнительное сопротивление) с R доп = (n-1) R B .
Рекомендую решить задачи № 527, 534, 553 — 557 из [2] на использовании реальных измерительных приборов в цепях постоянного электрического тока.
Ответы к заданию, приведенным в статье
Задание 1
Все соединения резисторов в этом задании содержат соединение, изображенное на рисунке 3. Ввиду эквивалентности соединений, изображенных на рисунках 2, 3, имеем:
Задание 2
Выделим в заданном соединении резисторов соединение, изображенное на рисунке 3.
При учете эквивалентности соединений, изображенных на 2, 3, получаем:
Заменяя параллельное соединение резисторов R 1 , R 2 , R 3 , одним резистором R I получить новое соединение резисторов R 5 , R 4 , R I I типа 2—3.
Задание 3
Задание 4
Заменяя поэтапно последовательные (параллельные) соединения резисторов одним эквивалентным резистором, уменьшаем число резисторов в электрической схеме и сводим рассматриваемую схему либо сразу к одному резистору, либо к соединению, содержащему только «треугольники» и «звезды».
Во втором случае соединение резисторов по схеме «треугольник» заменяем эквивалентным соединением резисторов по схеме «звезда» и доводим преобразование соединения резисторов до одного эквивалентного резистора.
При реализации вышеизложенной программы получаем: а) R AB = (19/30) * R; б) R BB ‘ , = (8/15) * R; с) R AC = (6/5) * R ; г) R AD = (31/30) * R; д) R DD ‘ = (4/5) * R; е) R AE = (22/15) * R; ж) R AF = (7/6) * R.
Альтернативный метод вычисления сопротивления электрических схем на основе учета симметрии схемы и распределения постоянного электрического поля в них будет рассмотрен в отдельной статье.
Литература
1. Кошкин, Н. И. Справочник по элементарной физике / Н. И. Кошкин, М. Г. Ширкевич. — М. : Наука, 1965.
2. Балаш, Б. А. Задачи по физике и методы их решения / Б. А. Балаш. — М. : Просвещение, 1967.
.
3. Петрович, Г. И. Цепи постоянного электрического тока / Г. И. Петрович, Э. М. Шпилевский // Репетитор. — 1996. — № 5 (8). — С. 43—48; 1997. — № 6 (9). — С. 42—47; 1997. — № 1 (10). — С. 41–47.
Расчет электрических цепей | Физика
1.Смешанное соединение проводников
Рассмотрим электрическую схему на рисунке 61.1. Некоторые проводники в ней соединены друг с другом, а некоторые — параллельно.
? 1. Какие проводники в этой схеме соединены друг с другом? Какие — параллельно?
Соединение проводников, при котором часть проводников соединена друг с другом, а часть — параллельно, называют смешанным.
При расчете сопротивления смешанного соединения проводников часто используют метод эквивалентного преобразования.При этом систему последовательностей преобразуют в простую, но имеющую такое же сопротивление.
Например, схему, изображенную на рисунке 61.1, можно преобразовать по следующему плану:
1. Заменить участок цепи с резисторами 1 и 2 одним резистором с сопротивлением, которое мы обозначим R 12 .
2. Заменить участок цепи, одним резистором с сопротивлением R 12 и R 3 , одним резистором с сопротивлением, которое мы обозначим R 123 .
3. Заменить участок цепи с резисторами 4 и 5 одним резистором с сопротивлением, мы обозначим R 45 .
4. Заменить участок цепи с резисторами сопротивлением R 123 и R 45 одним резистором. Его сопротивление и будет равно сопротивлению всего участка цепи.
? 2. В цепи, схема которой изображена на рисунке 61.1, сопротивление каждого выраженное в омах, примите тем равным номеру этого резистора. Начертите схемы, соответствующие каждому пункту намеченного выше плана; найдите R 12 , R 123 , R 45 и сопротивление всего участка.
Не всегда с первого взгляда на электрическую схему можно распознать вид соединения проводников.
В таком случае помогает найти точки с одинаковым потенциалом (например, соединенные проводами, сопротивление в таких случаях, как обычно пренебрежимо малым). Затем надо перечертить схему, объединив точки с одинаковым потенциалом.
Рассмотрим, например, схему участка цепи, изображенную на рисунке 61.2.
Точки А и С соединены проводом с пренебрежимо малым сопротивлением, поэтому потенциалы этих равны.То же можно сказать и о точках В и D.
Следовательно, схему можно перечертить, объединив точки А и С в одну точку (обозначим ее АС), а точки В и D объединив в точку ВD. При этом, согласно исходной схеме, один конец каждого из трех резистов соединен с точкой АС, а другой — с точкой BD (рис. 61.3).
Теперь мы видим, что резисторы соединены параллельно.
? 3. Перенесите в тетрадь рисунок 61.2 и отметьте на нем направление тока в каждом резисторе, считая, что потенциал точки А выше точки D.
? 4. На рисунке 61.4 изображена схема участка электрической цепи. Сопротивление каждого резистора, выраженное в омах, равно номеру резистора. Обратите внимание: потенциалы точек А и С различны.
а) Перечертите схему, изображенную на рисунке 61.4, так, чтобы легко было распознать вид соединения резисторов.
б) Найдите сопротивление всего участка цепи.
К сожалению, не всякую электрическую схему можно поэтапно упрощать, используя только формулы для последовательного и параллельного соединений.На рисунке 61.5 приведен пример схемы участка цепи, которую нельзя упростить таим образом.
Но для некоторых частных случав можно найти сопротивление и такого участка цепи уже известными нам способами. Чтобы догадаться, каковы эти случаи, заменим резистор 5 идеальным вольтметром (рис. 61.6). (Напомним, что идеальным считают вольтметр, сопротивление которого можно принять бесконечно большим.)
? 5. Разность потенциалов между точками А и В равна 21 В. Сопротивления резисторов, выраженные в омах, равны их номерам.
а) Чему равна разность потенциалов между точками А и С?
б) Чему равна разность потенциалов между точками А и D?
в) Каковы показания вольтметра?
г) Резистором с каким сопротивлением надо заменить резистор 4, чтобы показания вольтметра были равны нулю?
? 6. Объясните, почему показания вольтметра должны быть равны нулю независимо от напряжения между точками А и В, если сопротивление резисторов на схеме, изображенной на рисунке 61.6, удовлетворяют применению
R 1 / R 2 = R 3 / R 4 .(1)
Схему, изображенную на рисунке 61.6, называют мостиком Уитстона. С ее помощью можно измерить сопротивление из четырех резисторов, подбирая сопротивление остальных трех так, чтобы выполнялось соотношение (1).
? 7. Для сопротивлений резисторов 1 — 4 в цепи, изображенной на рисунке 61.5, выполняется соотношение (1).
а) Объясните, почему сопротивление данного участка цепи не зависит от сопротивления резистора 5.
б) Сопротивление резисторов 1 и 3 равны соответственно 10 Ом и 15 Ом.Подберите такие значения сопротивлений резисторов 2 и 4, чтобы сопротивление всего участка было равно 24 Ом независимо от сопротивления резистора 5.
2. Максимальная мощность во внешней цепи
? 8. К источнику с ЭДС ξ и внутренним сопротивлением подключено внешнее сопротивление R (рис. 61.7).
а) Выразите мощность тока во внешней цепи через ξ, r и R.
б) Используя производную, найдите, при каком R мощность тока во внешней цепи будет максимальной.
Эту задачу можно решить и без помощи производной.Для этого надо формулой для мощности тока во внешней цепи
P = UI,
где U — напряжение на внешнем сопротивлении (напомним, что оно равно напряжению на полюсах источника тока), I — сила тока в цепи.
? 9. Объясните, почему мощность тока во внешней цепи выражается формулой
P = (ξ — Ir) I. (2)
Подсказка. Выразите напряжение на полюсах источника через ξ, I, r, используя закон Ома для всей цепи.
Правая часть равенства (2) представляет собой квадратичную функцию от силы тока I.Графиком ее является парабола.
? 10. Начертите график зависимости P (I) при изменении силы тока I от нуля до величины значения (равного силе тока при коротком замыкании).
а) При каком значении достигается максимум функции P (I)?
б) Какому сопротивлению внешней цепи соответствует это значение I?
Подсказка. Воспользуйтесь возможностью законом Ома для всей цепи.
Итак, максимальная мощность тока во внешней цепи достигается, когда сопротивление внешней цепи внутреннему сопротивлению источника тока.
? 11. Чему при этом равенстве КПД источника тока?
3. Конденсаторы в цепи постоянного тока
Постоянный ток не может идти через конденсатор, потому что между его обкладками находится диэлектрик. Однако между обкладками конденсатора, включенного в цепь постоянного тока, может существовать разность потенциалов, и тога конденсатор будет заряженным. Начнем с самых простых случаев, когда в цепи, помимо конденсатора, есть только один резистор.
? 12. На рисунке 61.8 изображена схема электрической цепи. ЭДС источника тока ξ = 12 В, его внутреннее сопротивление r = 2 Ом, сопротивление сопротивление R = 10 Ом, электроемкость конденсатора С = 2 мкФ.
61,8
а) Чему равна разность потенциалов между точками А и В?
б) Чему равна разность потенциалов между точками А и D?
в) Чему равен заряд конденсатора?
г) Каков знак заряда обкладки конденсатора, соединенной с резистором?
? 13. На рисунке 61.9 изображена схема электрической цепи.ЭДС источника ξ, его внутреннее сопротивление тока r, сопротивление резистора R, электроемкость конденсатора C.
а) Чему равна разность потенциалов между точками А и В?
б) Чему равен заряд конденсатора?
Рассмотрим теперь более сложный случай, когда в цепи есть несколько резисторов, причем они по-разному подключены к конденсатору.
? 14. В цепи (рис. 61.10) ЭДС ξ = 6 В, его внутреннее сопротивление r = 1 Ом, сопротивление резисторов R 1 = 3 Ом, R 2 = 5 Ом, R 3 = 12 Ом, электроемкость конденсатора C = 8 мкФ.
а) Перенесите схему в тетрадь и обозначьте, через какие элементы цепи идет ток.
б) Какова сила тока в резисторе 3?
в) Чему равна разность потенциалов между точками А и D?
г) Чему равна разность потенциалов между точками А и В?
д) Чему равно напряжение на конденсаторе?
е) Чему равен заряд конденсатора?
ж) Каков знак заряда обкладки конденсатора, соединенной с резистором 2?
Дополнительные вопросы и задания
15. На рисунке 61.11 изображена схема участка электрической цепи. Сопротивление каждого резистора 1 Ом. Используя метод эквивалентного преобразования схем:
а) начертите схемы последовательного упрощения данной схемы, содержит меньше резисторов;
б) для каждой схемы рассчитайте ее сопротивление и найдите общее сопротивление всего участка.
16. На схеме участка цепи, изображенной на рисунке 61.5, резисторов сопротивления R 1 = 20 Ом, R 2 = 100 Ом, R 3 = 10 Ом, R 4 = 50 Ом, R 5 = 80 Ом.Каково общее сопротивление участка цепи?
17. Сопротивление внешней цепи в 4 раза больше того значения, при мощности тока во внешней цепи максимальна.
а) Чему равенство КПД источника тока?
б) Во сколько раз при этом мощность тока во внешней цепи меньше максимально возможной?
Последовательное и параллельное соединение резисторов
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение — это соединение двух или более резисторов в одной цепи, в которой отдельный резистор соединяется с другим резистором в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждом резисторе согласно закону Ома:
Т.чем большее сопротивление сопротивляется, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение — это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора.Общее сопротивление такого участка электрической цепи увеличивается.
Таким образом, при параллельном подключении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного сопротивления.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно одного отдельного резистора:
Соответственно, для одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того, чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяется между собой, а часть параллельно.В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
o Цепь разбивают на участки с только пареллельным или только последовательным соединением. o Вычислительное сопротивление для каждого отдельного участка.
o Вычисленное общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения.Можно, в соответствии, сразу записывать формулу следующим образом:
o Если резисторы соединяются последоватеьно — складывать.
o Если резисторы соединяют параллельно — использовать условное обозначение «||».


 Поэтому в первую очередь нужно рассматривать эти два вида соединений, чтобы понять, как работают другие схемы.
Поэтому в первую очередь нужно рассматривать эти два вида соединений, чтобы понять, как работают другие схемы. Поскольку токи на любом участке цепи имеют одинаковое значение, формула приобретает вид: Uобщ = I(r1 + r2).
Поскольку токи на любом участке цепи имеют одинаковое значение, формула приобретает вид: Uобщ = I(r1 + r2). В свою очередь, значение токов будет разным на каждом резисторе, их распределение становится прямо пропорциональным сопротивлению этих резисторов. То есть, при увеличении сопротивления, сила тока уменьшается, а общий ток становится равен сумме токов, проходящих через каждый элемент. Формула для данного положения выглядит следующим образом: Iобщ= I1 + I2.
В свою очередь, значение токов будет разным на каждом резисторе, их распределение становится прямо пропорциональным сопротивлению этих резисторов. То есть, при увеличении сопротивления, сила тока уменьшается, а общий ток становится равен сумме токов, проходящих через каждый элемент. Формула для данного положения выглядит следующим образом: Iобщ= I1 + I2.
 Далее, нужно определить сопротивление резисторов R123, включенных параллельно, по следующей формуле: R123=R12R3/(R12+R3) = (R1+R2)R3/(R1+R2+R3). На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R123 и сопротивления R4, включенного последовательно с ним: Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4.
Далее, нужно определить сопротивление резисторов R123, включенных параллельно, по следующей формуле: R123=R12R3/(R12+R3) = (R1+R2)R3/(R1+R2+R3). На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R123 и сопротивления R4, включенного последовательно с ним: Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4.

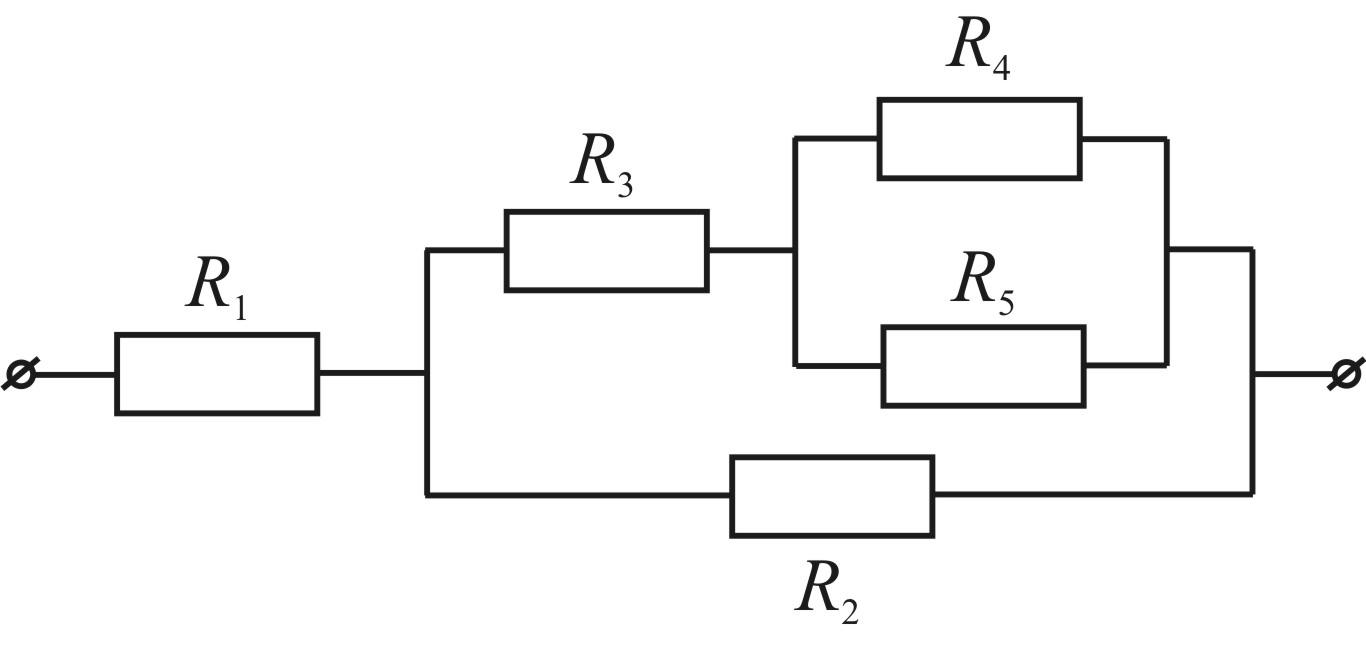
 Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С.
Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С.