Формула силы Ампера в физике
Содержание:
Определение и формула силы Ампера
Определение
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$\bar{F}, \bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
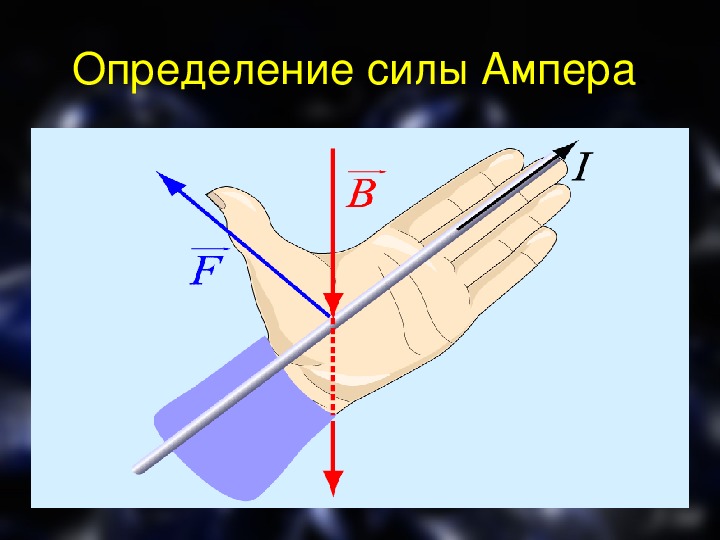
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
большой палец укажет направление силы Ампера (рис.1).
Закон Ампера
Элементарная сила Ампера
($d\bar{F}_A$) определена законом (или формулой) Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(1)$$
где I – сила тока,
$d \bar{l}$ – малый элемент длины проводника – это вектор, равный
по модулю длине проводника, направленный в таком же направлении как вектор плотности тока,
$\bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d \bar{F}_{A}=\bar{j} \times \bar{B} d V(2)$$
где $\bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I \cdot B \cdot d l \cdot \sin \alpha(3)$$
где $\alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$\bar{F}_{A}=I \int_{l} d \bar{l} \times \bar{B}(4)$$
где $\bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl.
Интегрирование в формуле (4) проводят по всей длине проводника (l). Из выражения (4) следует, что на замкнутый контур с током I,
в однородном магнитном поле действует сила Ампера равная $\bar{F}_{A}=0(H)$
Сила Ампера, которая действует на элемент (dl) прямого проводника с током I1, помещённый в магнитное поле, которое
создает другой прямой проводник, параллельный первому с током I2, равна по модулю:
$$d F=\frac{\mu_{0}}{2 \pi} \frac{I_{1} I_{2}}{d} d l(5)$$
где d – расстояние между проводниками, $\mu_{0}=4 \pi \cdot 10^{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.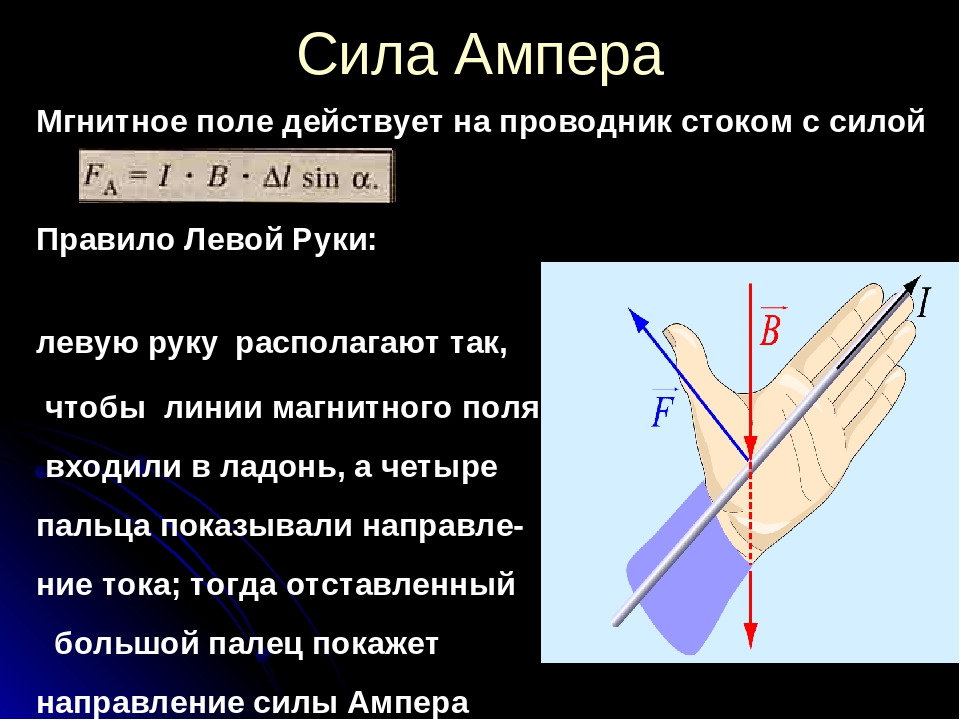
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$\frac{F}{l}=\frac{\mu_{0}}{2 \pi} \frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник
действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для
прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B \operatorname{lsin} \alpha$$
где $\alpha$ – искомый угол. Следовательно:
Следовательно:
$$\alpha=\arcsin \left(\frac{F}{I B l}\right)$$
Ответ. $\alpha=\arcsin \left(\frac{F}{I B l}\right)$
Слишком сложно?
Формула силы Ампера не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга.
Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая
на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(2.1)$$
Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости
рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
где ток, который течет в элементе проводника dx, выразим как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
где из рис.1 видно, что $a \leq x \leq a+b$, по условию задачи силу следует
найти на единицу длины, значит $0 \leq l \leq 1$ . Для нахождения суммарной силы Ампера, действующей на проводник (2) возьмем двойной интеграл от выражения (2. {a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
{a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$
Читать дальше: Формула силы выталкивания.
Формула силы Ампера в физике
Содержание:
Определение и формула силы Ампера
Определение
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$\bar{F}, \bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
большой палец укажет направление силы Ампера (рис. 1).
1).
Закон Ампера
Элементарная сила Ампера
($d\bar{F}_A$) определена законом (или формулой) Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(1)$$
где I – сила тока,
$d \bar{l}$ – малый элемент длины проводника – это вектор, равный
по модулю длине проводника, направленный в таком же направлении как вектор плотности тока,
$\bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d \bar{F}_{A}=\bar{j} \times \bar{B} d V(2)$$
где $\bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I \cdot B \cdot d l \cdot \sin \alpha(3)$$
где $\alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$\bar{F}_{A}=I \int_{l} d \bar{l} \times \bar{B}(4)$$
где $\bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl. {7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$\frac{F}{l}=\frac{\mu_{0}}{2 \pi} \frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник
действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для
прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B \operatorname{lsin} \alpha$$
где $\alpha$ – искомый угол.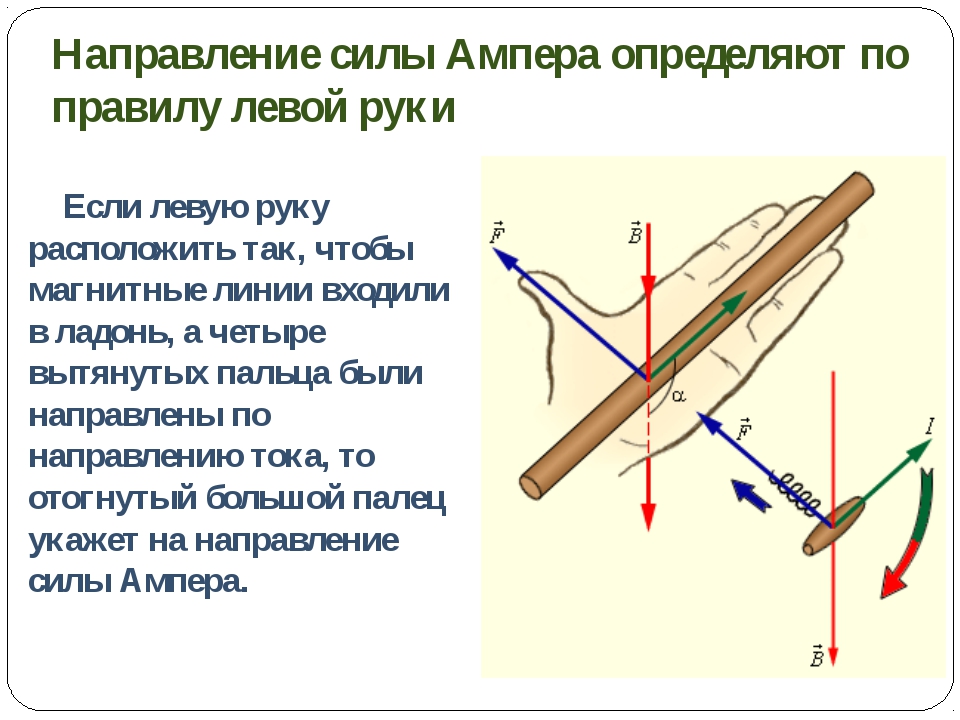 Следовательно:
Следовательно:
$$\alpha=\arcsin \left(\frac{F}{I B l}\right)$$
Ответ. $\alpha=\arcsin \left(\frac{F}{I B l}\right)$
Слишком сложно?
Формула силы Ампера не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга.
Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая
на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(2.1)$$
Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости
рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
где ток, который течет в элементе проводника dx, выразим как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
где из рис.1 видно, что $a \leq x \leq a+b$, по условию задачи силу следует
найти на единицу длины, значит $0 \leq l \leq 1$ . Для нахождения суммарной силы Ампера, действующей на проводник (2) возьмем двойной интеграл от выражения (2.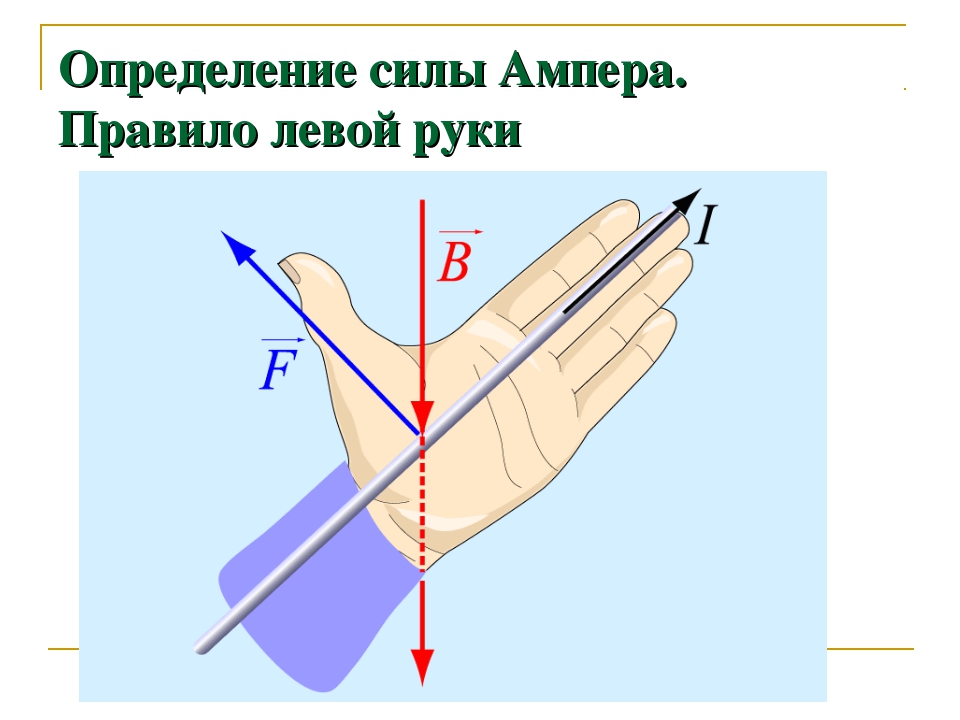 {a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
{a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$
Читать дальше: Формула силы выталкивания.
Формула силы Ампера в физике
Содержание:
Определение и формула силы Ампера
Определение
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$\bar{F}, \bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
большой палец укажет направление силы Ампера (рис. 1).
1).
Закон Ампера
Элементарная сила Ампера
($d\bar{F}_A$) определена законом (или формулой) Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(1)$$
где I – сила тока,
$d \bar{l}$ – малый элемент длины проводника – это вектор, равный
по модулю длине проводника, направленный в таком же направлении как вектор плотности тока,
$\bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d \bar{F}_{A}=\bar{j} \times \bar{B} d V(2)$$
где $\bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I \cdot B \cdot d l \cdot \sin \alpha(3)$$
где $\alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$\bar{F}_{A}=I \int_{l} d \bar{l} \times \bar{B}(4)$$
где $\bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl. {7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$\frac{F}{l}=\frac{\mu_{0}}{2 \pi} \frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник
действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для
прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B \operatorname{lsin} \alpha$$
где $\alpha$ – искомый угол. Следовательно:
Следовательно:
$$\alpha=\arcsin \left(\frac{F}{I B l}\right)$$
Ответ. $\alpha=\arcsin \left(\frac{F}{I B l}\right)$
Слишком сложно?
Формула силы Ампера не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга.
Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая
на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(2.1)$$
Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости
рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
где ток, который течет в элементе проводника dx, выразим как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
где из рис.1 видно, что $a \leq x \leq a+b$, по условию задачи силу следует
найти на единицу длины, значит $0 \leq l \leq 1$ . Для нахождения суммарной силы Ампера, действующей на проводник (2) возьмем двойной интеграл от выражения (2. {a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
{a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$
Читать дальше: Формула силы выталкивания.
Формула силы Ампера в физике
Содержание:
Определение и формула силы Ампера
Определение
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$\bar{F}, \bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
большой палец укажет направление силы Ампера (рис.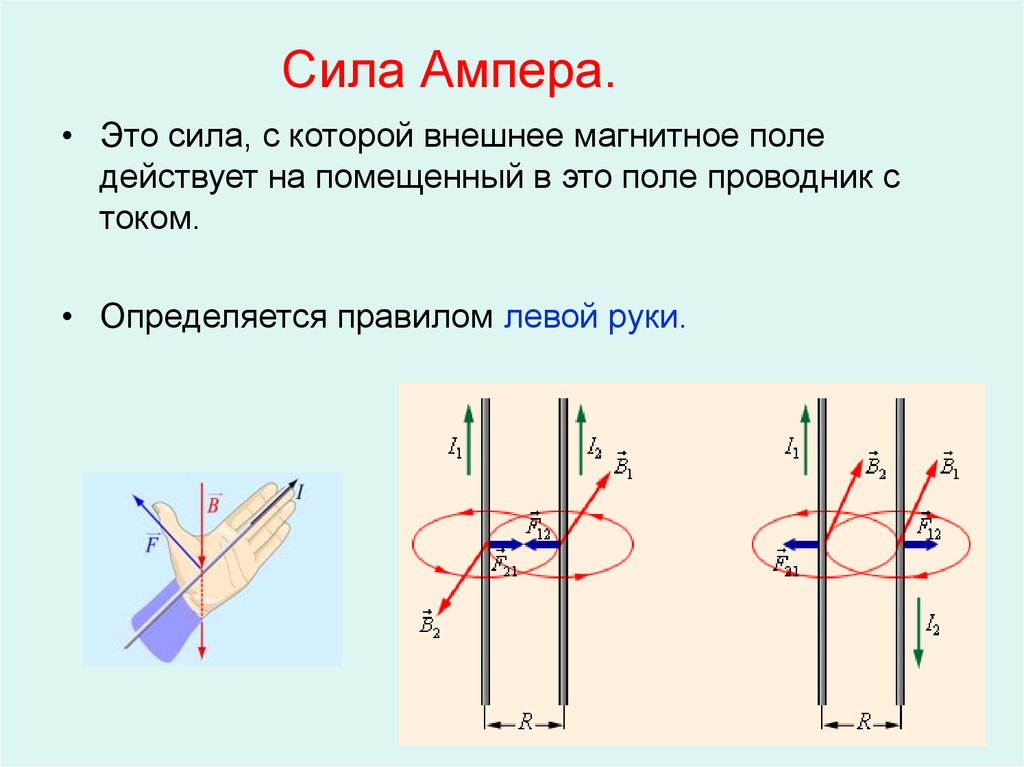 1).
1).
Закон Ампера
Элементарная сила Ампера
($d\bar{F}_A$) определена законом (или формулой) Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(1)$$
где I – сила тока,
$d \bar{l}$ – малый элемент длины проводника – это вектор, равный
по модулю длине проводника, направленный в таком же направлении как вектор плотности тока,
$\bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d \bar{F}_{A}=\bar{j} \times \bar{B} d V(2)$$
где $\bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I \cdot B \cdot d l \cdot \sin \alpha(3)$$
где $\alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$\bar{F}_{A}=I \int_{l} d \bar{l} \times \bar{B}(4)$$
где $\bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl. {7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$\frac{F}{l}=\frac{\mu_{0}}{2 \pi} \frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник
действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для
прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B \operatorname{lsin} \alpha$$
где $\alpha$ – искомый угол. Следовательно:
Следовательно:
$$\alpha=\arcsin \left(\frac{F}{I B l}\right)$$
Ответ. $\alpha=\arcsin \left(\frac{F}{I B l}\right)$
Слишком сложно?
Формула силы Ампера не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга.
Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая
на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(2.1)$$
Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника.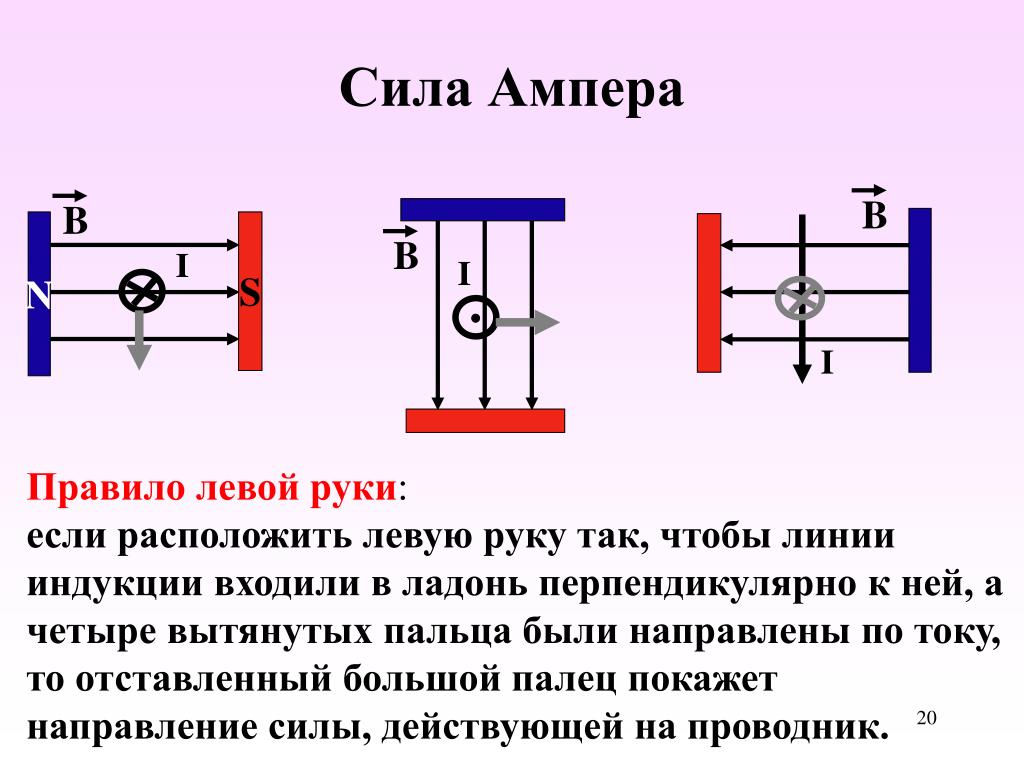 Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости
рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
где ток, который течет в элементе проводника dx, выразим как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
где из рис.1 видно, что $a \leq x \leq a+b$, по условию задачи силу следует
найти на единицу длины, значит $0 \leq l \leq 1$ . Для нахождения суммарной силы Ампера, действующей на проводник (2) возьмем двойной интеграл от выражения (2. {a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
{a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$
Читать дальше: Формула силы выталкивания.
Формула силы Ампера
ОПРЕДЕЛЕНИЕ
Сила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.
Здесь – сила Ампера, – сила тока в проводнике, – модуль вектора индукции магнитного поля, – длина участка проводника, на который воздействует магнитное поле, – угол между вектором индукции магнитного поля и направления тока.
Единица измерения силы – Н (ньютон).
Сила Ампера — векторная величина. Сила Ампера принимает своё наибольшее значение когда векторы индукции и направления тока перпендикулярны ().
Направление силы ампера определяют по правилу левой руки:
Если вектор магнитной индукции входит в ладонь левой руки и четыре пальца вытянуты в сторону направления вектора движения тока, тогда отогнутый в сторону большой палец показывает направление силы Ампера.
Исторически электрическим током принято считать движение положительного заряда, то есть направление сила тока – от плюса к минусу.
Примеры решения задач по теме «Сила Ампера»
ПРИМЕР 1
| Задание | Найти силу Ампера, действующую на прямой проводник длиной 3 м, по которому проходит ток силой 7 А. Вектор магнитной индукции составляет угол с проводником, его абсолютное значение – 2 Тл. |
| Решение | Электрический ток течёт по проводнику, значит направлен он также, как расположен проводник. Следовательно, угол между вектором магнитной индукции и проводником равен углу между ним и вектором движения тока. Остаётся только подставить значения в формулу: Следовательно, угол между вектором магнитной индукции и проводником равен углу между ним и вектором движения тока. Остаётся только подставить значения в формулу:
|
| Ответ | Сила ампера равна 21 ньютон. |
ПРИМЕР 2
| Задание | На рисунке изображены два параллельно расположенных проводника, указаны направления сил тока и вектора магнитной индукции. В ответе указать, каким образом будет действовать на них сила Ампера (сближать проводники, отталкивать или действовать как-то иначе). Как изменится ситуация, если направить вектор магнитной индукции параллельно проводникам?
|
| Решение | Определим направление силы Ампера по правилу левой руки. Очевидно, если расположить левую руку так, чтобы вектор входил в ладонь, а пальцы направить по линии движения тока в первом случае (вертикально вверх), то отогнутый большой палец будет направлен от наблюдателя.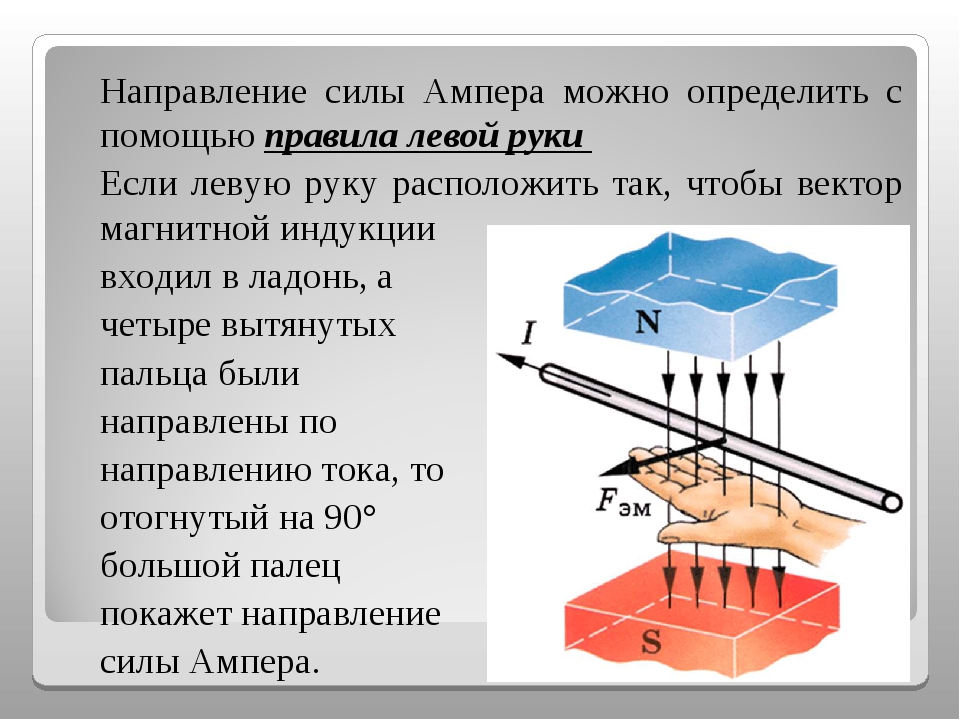 Также будет направлена и сила Ампера. Во втором проводнике ток направлен вертикально вниз, а сила Ампера – на наблюдателя. Оказалось, что под действием силы Ампера первый проводник отталкивается от наблюдателя, а второй притягивается к нему. Также будет направлена и сила Ампера. Во втором проводнике ток направлен вертикально вниз, а сила Ампера – на наблюдателя. Оказалось, что под действием силы Ампера первый проводник отталкивается от наблюдателя, а второй притягивается к нему.
Пусть вектор сонаправлен движению тока в первом проводнике, тогда
и
При вычислении силы Ампера нас интересуют не сами углы, а их синусы:
и
Сила Ампера в обоих проводниках равна нулю.
|
| Ответ | Если вектор магнитной индукции направлен так, как показано на рисунке, то сила Ампера в первом проводнике будут направлена на наблюдателя, во втором – от него. Если вектор магнитной индукции направить параллельно проводникам, то сила Ампера возникать не будет. |
|
Понравился сайт? Расскажи друзьям! |
| ||
|
Урок
|
|
|
|
|
1/1
| Что изучает физика. Физические термины. Наблюдения и опыты. Физические термины. Наблюдения и опыты. | § 1 — 3, Л № 5, 12 | |
| 2/2 | Физические величины. Измерение физических величин. Погрешность и точность измерений | § 4, 5, упр.1 | |
| 3/3 | Определение цены деления измерительного прибора | § 4, 5 | |
| 4/4 | Физика и техника | § 6, | |
| Первоначальные сведения о строении вещества | |||
| 5/1 | Строение вещества.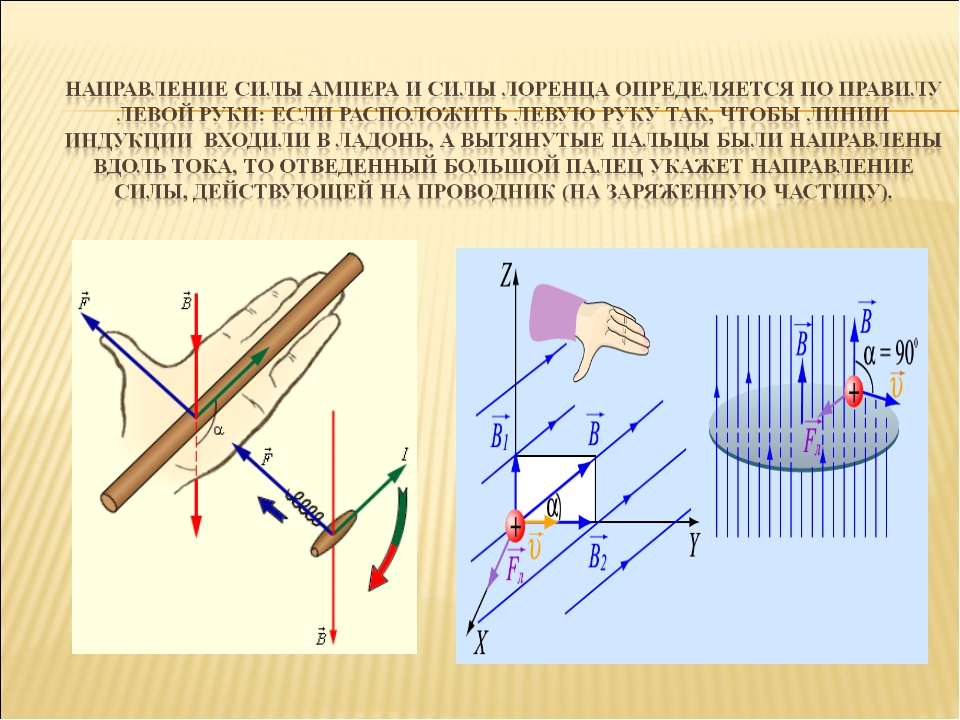 Молекулы Молекулы | § 7, 8 | |
| 6/2 | Определение размеров малых тел | § 7, 8 | |
| 7/3 | Движение молекул. Диффузия в газах, жидкостях и твердых телах | § 9, | |
| 8/4 | Взаимодействие молекул |
| |
|
9/5
| Три состояния вещества | § 11, 12 | |
| 10/6 | Повторение. Контрольная работа №1 «Первоначальные сведения о строении вещества» | § 12 | |
|
|
Электричество и магнетизм
Теперь мы готовы к обсуждению взаимодействия тока с магнитным полем.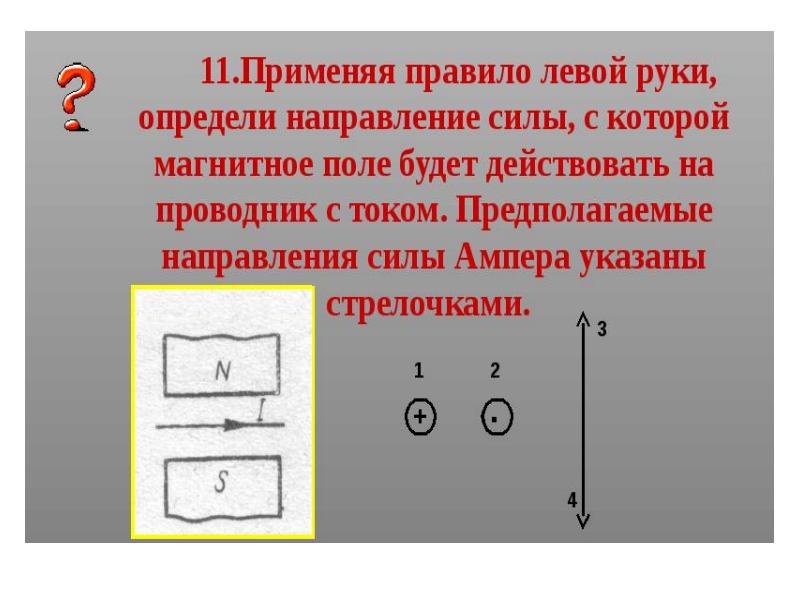
Ампер установил наличие силового взаимодействия между двумя проводниками, по которым текут электрические токи. Пусть имеются два длинных параллельных проводника (рис. 5.25-1).
Рис. 5.25. Опыт Ампера по исследованию взаимодействия параллельных токов:
1 — схема установки; 2 — отталкивание антипараллельных токов; 3 — притяжение параллельных токов
Если по ним пропускать токи, текущие в противоположных направлениях, то проводники будут отталкиваться друг от друга (см. рис. 5.25-2). Если же токи будут течь в одном направлении, то они будут притягиваться (см. рис. 5.25-3).
Видео 5.4. Взаимодействие параллельных токов.
Эксперименты, проведенные Ампером, показали, что на проводник с током, помещенный в магнитное поле, действует сила. Откуда же она берется? Обсуждая эффект Холла, мы видели, что сила электрического поля EХ уравновешивает силу Лоренца, действующую на электроны. Но холловское поле EХ действует также и на кристаллическую ионную решетку вещества. На рис. 5.23 поле EХ направлено вверх, ортогонально току и магнитной индукции. Туда же будет направлена и сила, действующая на проводник. Найдем ее величину. Если поперечное сечение проводника равно S, а его длина (в направлении тока) — dl, то в данном объеме dV = dl · S сосредоточено dN = ndV = n · dl · S электронов проводимости. Их полный заряд равен dQ = edN = en · dl · S. В силу нейтральности проводника в целом таков же по абсолютной величине и полный заряд ионов кристаллической решетки. Используя формулу (5.28), находим суммарную силу, действующую на остов кристаллической решетки рассматриваемой части проводника
Но холловское поле EХ действует также и на кристаллическую ионную решетку вещества. На рис. 5.23 поле EХ направлено вверх, ортогонально току и магнитной индукции. Туда же будет направлена и сила, действующая на проводник. Найдем ее величину. Если поперечное сечение проводника равно S, а его длина (в направлении тока) — dl, то в данном объеме dV = dl · S сосредоточено dN = ndV = n · dl · S электронов проводимости. Их полный заряд равен dQ = edN = en · dl · S. В силу нейтральности проводника в целом таков же по абсолютной величине и полный заряд ионов кристаллической решетки. Используя формулу (5.28), находим суммарную силу, действующую на остов кристаллической решетки рассматриваемой части проводника
|
|
(5. |
где мы выразили плотность тока через его силу
Обращаем внимание, что в эту формулу не вошли характеристики конкретных носителей заряда, но лишь полный ток через проводник.
У нас внешнее магнитное поле было ортогонально току. В общем случае направление тока будем характеризовать вектором dl, имеющем длину dl и направленным вдоль течения тока. В холловскую напряженность электрического поля дает вклад только компонента магнитного поля, ортогональная вектору dl. Эта компонента равна по величине
где есть угол между векторами B и dl. Тогда для величины силы имеем
|
|
(5.31) |
Учитывая направление этой силы (правило винта), можем записать ее в векторной форме
|
|
(5. |
Выражение (5.32) носит название закона Ампера, а сила называется силой Ампера (рис. 5.26).
Понимание основ закона силы Ампера
Закон силы Ампера был открыт Андре-Мари Ампера (которая легла в основу определения единицы электричества, Ампера). Не вдаваясь в утомительные математические уравнения, мы собираемся понять, что такое закон, как был определен Ампер и как этот закон изменения пути изменил физику в то время.
Закон Ампера о силе гласит, что сила притяжения или отталкивания между двумя проводами, по которым проходит ток, пропорциональна их длине и силе тока, проходящего через них.Если токи текут в одном направлении, происходит отталкивание. Если токи текут в противоположных направлениях, происходит притяжение. Закон основан на этих двух основных понятиях электростатики:
- Закон Био-Савара гласит, что каждый токоведущий провод создает вокруг себя магнитное поле, как показано на Рис.
 1 .
1 . - Сила Лоренца относится к силе, которую каждое магнитное поле оказывает на любой электрический заряд, движущийся в его поле.
Рисунок 1: Правило большого пальца для поиска магнитного поля вокруг токоведущего провода
На основании закона Био-Савара и силы Лоренца существует связь между магнитным полем и электрическим зарядом / током.Именно эту связь Ампер пытался установить с помощью экспериментов. Самый простой из этих экспериментов заключался в изучении силы между двумя токоведущими проводами, как показано на Рисунок 2 . Этот эксперимент и последующие теории, объясняющие его результаты, заложили основу электромагнетизма как области физики.
Рисунок 2: Магнитное поле между токоведущими проводами
Ампер, единица измерения электрического тока в системе СИ, определяется как сила электромагнитного поля на единицу длины между двумя проводами бесконечной длины, имеющими незначительный диаметр и расположенными на расстоянии 1 м в вакууме.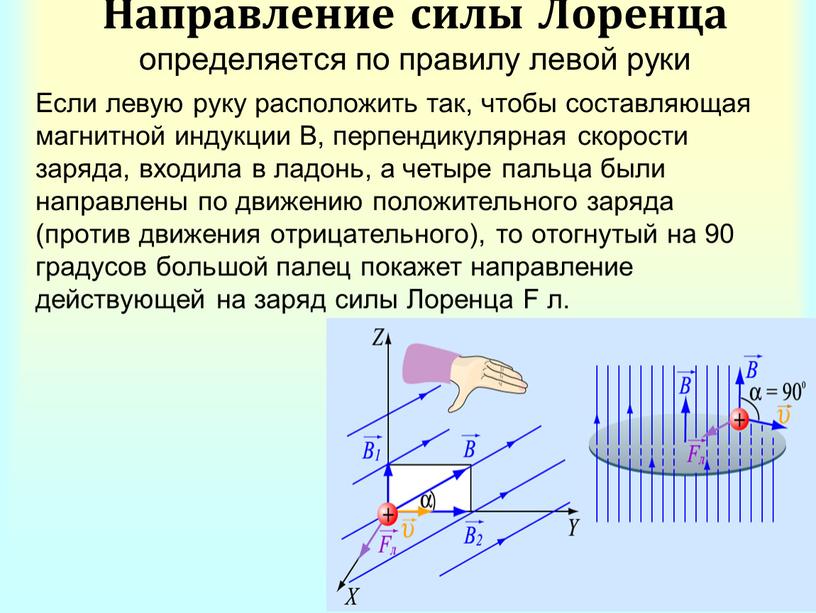 Основное предположение здесь заключается в том, что провода находятся в свободном пространстве, то есть в нем нет вещества, которое можно было бы намагнитить. Если какая-либо материя, присутствующая в окружающей среде, намагничивается, она проявляет свою собственную магнитную силу, которую необходимо принимать во внимание, поэтому следует сделать это предположение.
Основное предположение здесь заключается в том, что провода находятся в свободном пространстве, то есть в нем нет вещества, которое можно было бы намагнитить. Если какая-либо материя, присутствующая в окружающей среде, намагничивается, она проявляет свою собственную магнитную силу, которую необходимо принимать во внимание, поэтому следует сделать это предположение.
Используя закон силы Ампера, можно рассчитать магнитное поле вокруг бесконечного провода, бесконечного листа, тороида, соленоида или любой другой правильной формы, как показано на рисунках и рисунках 3 и 4 ниже.
Рисунок 3: Магнитное поле вокруг соленоида Рисунок 4: Магнитное поле вокруг тороида
Закон силы Ампера оказался настолько фундаментальным законом, что после него многие физики, такие как Джеймс Клерк Максвелл, Вильгельм Вебер, Бернард Риман и т. Д.расширил его, чтобы найти базовое определение самой силы. Возвращаясь к работе Ампера, Закон силы утверждает, что сила между токоведущими проводами пропорциональна их длине и силе протекающего тока. Это означает, что чем выше ток, тем больше притяжение или отталкивание между проводами.
Это означает, что чем выше ток, тем больше притяжение или отталкивание между проводами.
Статьи по теме:
Какой номинал батареи в ампер-часах (ампер-час или Ач)?
Напряжение в батарее: нам нужно, чтобы оно было постоянным
Как работает магнит?
ЗАКОН AMPERES
ЗАКОН AMPERES
Магнитное поле на расстоянии r от очень длинного прямого провода, несущего
установившийся ток I, имеет величину, равную
(31.)
и направление, перпендикулярное r и I. Интеграл по путям по окружности
с центром вокруг проволоки (см. рисунок 31.1) равно
(31,2)
Здесь мы использовали тот факт, что магнитное поле является касательным в любой точке
на круговой траектории интегрирования.
Рисунок 31.1. Магнитное поле, создаваемое током. Любой произвольный путь можно рассматривать как набор радиальных
сегменты (r изменяется, а [theta] остается постоянным) и круглые сегменты
([тета] изменяется, а r остается постоянным). Для радиальных сегментов магнитная
Для радиальных сегментов магнитная
поле будет перпендикулярно перемещению и продукту скейлера между
магнитное поле и смещение равны нулю. Рассмотрим теперь небольшой циркуляр
отрезок траектории вокруг проволоки (см. рисунок 31.2). Интеграл по путям
на этом круговом отрезке равно
(31.3)
Рисунок 31.2. Интеграл по небольшому круговому пути. Уравнение (31.3) показывает, что вклад этого циркуляра
отрезок к общему интегралу по путям не зависит от расстояния r и только
зависит от изменения угла [Дельта] [тета].Для замкнутого пути
общее изменение угла будет 2 [пи], и уравнение (31.3) можно переписать как
(31,4)
Это выражение — Закон Ампера :
«Интеграл от B вокруг любого замкнутого математического пути равен u 0
раз больше тока, перехваченного областью, охватывающей путь «
Пример: Задача 31,5
Шесть параллельных алюминиевых проволок небольшого, но конечного радиуса лежат в
тот же самолет. Провода разделены равным расстоянием d, и они несут равные
Провода разделены равным расстоянием d, и они несут равные
токи I в том же направлении. Найдите магнитное поле в центре
первый провод. Предположим, что токи в каждом проводе распределены равномерно.
по его поперечному сечению.
Схематическое изображение проблемы показано на рисунке 31.3. Магнитное поле
генерируется одиночным проводом равно
(31,5)
где r — расстояние от центра провода.Уравнение (31.5) имеет вид
правильно для всех точек за пределами провода, и поэтому может использоваться для определения
магнитное поле, создаваемое проводами 2, 3, 4, 5 и 6. Поле на
центр провода 1 из-за тока, протекающего в проводе 1, может быть определен с помощью
Закон Ампера и равен нулю. Суммарное магнитное поле в центре
провод 1 можно найти путем векторного сложения вкладов каждого из шести
провода. Поскольку направление каждого из этих вкладов одинаково,
полное магнитное поле в центре провода 1 равно
(31.6)
Рисунок 31.3. Задача 31. 5
5
Соленоид — это устройство, используемое для создания однородного магнитного поля. Может
быть изготовленным из тонкого проводящего провода, намотанного в спиральную спиральную катушку, состоящую из множества витков.
Магнитное поле внутри соленоида можно определить, суммируя магнитные
полей, порождаемых N отдельными кольцами (где N — количество витков
соленоид). Мы ограничимся обсуждением магнитного поля, создаваемого
соленоид к тому, который генерируется идеальным соленоидом, который бесконечно длинный, и
имеет очень плотно намотанные катушки.
Идеальный соленоид обладает поступательной и вращательной симметрией. Однако, поскольку
силовые линии магнитного поля должны образовывать замкнутые контуры, магнитное поле не может быть
направлен в радиальном направлении (в противном случае будут созданы силовые линии или
разрушен на центральной оси соленоида). Таким образом, мы заключаем, что
силовые линии в соленоиде должны быть параллельны оси соленоида. Величина
магнитного поля можно получить, применив закон Ампера.
Рисунок 31.4. Идеальный соленоид. Рассмотрим путь интеграции, показанный на рисунке 31.4. Тропинка
интеграл магнитного поля вокруг этого пути интегрирования равен
(31,7)
где L — горизонтальная длина пути интегрирования. Текущий вложенный
по пути интегрирования равен N . I 0 где N —
число витков на пути интегрирования, а I 0 — это
ток в каждом витке соленоида.Используя закон Ампера, заключаем, что
(31,8)
или
(31,9)
где n — количество витков соленоида на единицу длины. Уравнение
(31.9) показывает, что магнитное поле B не зависит от положения внутри
соленоид. Мы заключаем, что магнитное поле внутри идеального соленоида равно
униформа.
Пример: проблема 31.14
По длинному соленоиду из n витков на единицу длины проходит ток I, и через
по длинной прямой проволоке, идущей вдоль оси этого соленоида, проходит ток I ‘.Найдите суммарное магнитное поле внутри соленоида на расстоянии r от оси.
Опишите форму силовых линий магнитного поля.
Магнитное поле, создаваемое соленоидом, однородное, направленное параллельно
оси соленоида, и имеет величину, равную
(31.10)
Магнитное поле длинного прямого провода, по которому течет ток I ‘, имеет
величина равна
(31.11)
и направлена перпендикулярно направлению r и I ‘.Направление
Следовательно, провод B перпендикулярен направлению
В соль . Чистое магнитное поле внутри соленоида равно
векторная сумма проводов B и B sol . Его величина равна
на номер
(31.12)
Угол a между направлением магнитного поля и осью z равен
по
(31,13)
Пример: проблема 31.15
Коаксиальный кабель состоит из длинного цилиндрического медного провода с радиусом
r 1 в окружении цилиндрической оболочки с внутренним радиусом r 2
и внешний радиус r 3 (см. рисунок 31.5). Проволока и оболочка несут
рисунок 31.5). Проволока и оболочка несут
равные и противоположные токи I равномерно распределены по их объемам. Находить
формулы для магнитного поля в каждой из областей r
r 1
Силовые линии магнитного поля представляют собой круги с центром на оси симметрии магнитного поля.
коаксиальный кабель. Сначала рассмотрим путь интегрирования с r
Интеграл по путям B на этом пути равен
.
(31,14)
Ток, заключенный в этом пути интеграции, равен
.
(31,15)
Применяя закон Фарадея, мы можем связать вложенный ток с интегралом по путям
из Б
(31.16)
Следовательно, магнитное поле B равно
.
(31.17)
Рисунок 31.5. Проблема 31.15. В области между проводом и оболочкой закрытый
ток равен I, а интеграл по путям магнитного поля равен
уравнение (31.14). Закон Ампера гласит, что
Закон Ампера гласит, что
(31.18)
а магнитное поле равно
(31,19)
В третьей области (r 2
магнитного поля по круговой траектории радиуса r определяется выражением
экв.(31,14). Включенный ток равен
(31.20)
Следовательно, магнитное поле равно
.
(31.21)
Ток на пути интегрирования с радиусом r> r 3
равна нулю (так как ток в проводе и в оболочке течет в
противоположные направления). Следовательно, магнитное поле в этой области также
равняется нулю.
Магнитная сила, действующая на частицу с зарядом q, движущуюся со скоростью v, равна
равно
(31.22)
Эта сила всегда перпендикулярна направлению движения частицы,
и поэтому изменит только направление движения, а не величину
скорости. Если заряженная частица движется в однородной магнитной
поле с напряженностью B, перпендикулярное скорости v, то
величина магнитной силы определяется как
(31,23)
и его направление перпендикулярно v.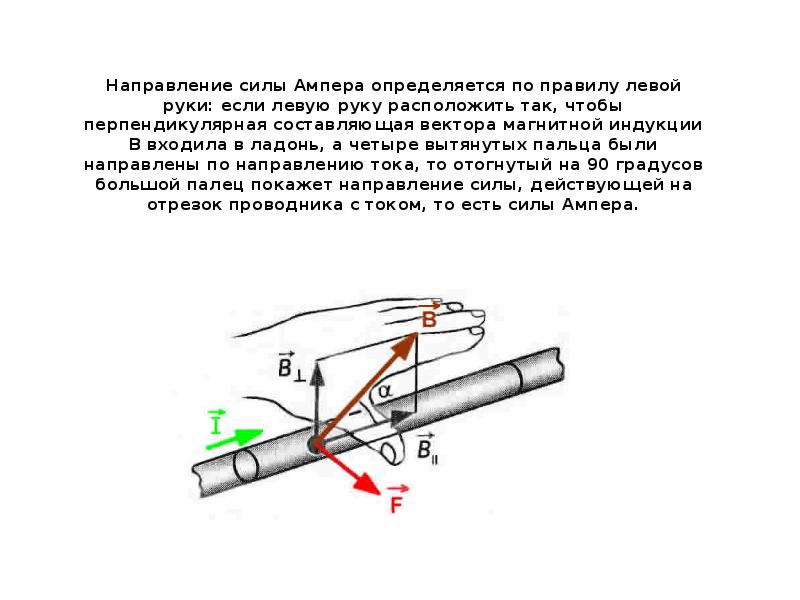 В результате этой силы
В результате этой силы
частица будет совершать равномерное круговое движение.Радиус круга равен
определяется требованием, чтобы сила магнитного поля была равна
центростремительная сила. Таким образом
(31,24)
Радиус орбиты r равен
.
(31,25)
где p — импульс заряженной частицы. Расстояние, пройденное
частица за один оборот равна
(31,26)
Время T, необходимое для совершения одного оборота, равно
.
(31.27)
Частота этого движения равна
.
(31,28)
и называется циклотронной частотой . Уравнение (31.28) показывает
что циклотронная частота не зависит от энергии частицы, и
зависит только от его массы m и заряда q.
Влияние магнитного поля на движение заряженной частицы можно использовать
для определения некоторых его свойств. Одним из примеров является измерение
заряд электрона.Электрон, движущийся в однородном магнитном поле, будет
описал круговое движение с радиусом, задаваемым уравнением (31. 25). Предположим, что
25). Предположим, что
электрон ускоряется потенциалом V 0 . Конечная кинетическая энергия
электрона равно
(31.29)
Импульс электрона p определяется его кинетической энергией
(31.30)
Таким образом, радиус кривизны траектории электрона равен
.
(31.31)
Уравнение (31.31) показывает, что измерение r можно использовать для определения
отношение массы к заряду электрона.
Еще одно приложение влияния магнитного поля на движение
заряженная частица — циклотрон. Циклотрон состоит из вакуумированного резонатора.
помещен между полюсами большого электромагнита. Полость разрезается на две части
Г-образные фигуры (называемые деэ) с промежутком между ними. Колеблющийся высокий
напряжение подается на пластины, создавая колеблющееся электрическое поле в
область между двумя деями.Заряженная частица, инжектированная в центр
циклотрон будет совершать равномерное круговое движение в течение первой половины
один оборот. Частота движения частицы зависит от ее массы, ее
Частота движения частицы зависит от ее массы, ее
заряд и напряженность магнитного поля. Частота генератора
выбирается таким образом, что каждый раз, когда частица пересекает зазор между деформациями, она
будет ускоряться электрическим полем. По мере увеличения энергии иона
его радиус кривизны будет увеличиваться, пока не достигнет края
циклотрон и извлекается.При движении в циклотроне ион будет
много раз пересеките пропасть между деями, и она будет ускорена до максимума
энергии.
До сих пор мы предполагали, что направление движения заряженного
частица перпендикулярна направлению магнитного поля. Если это
В этом случае произойдет равномерное круговое движение. Если направление движения
ион не перпендикулярен магнитному полю, это приведет к спиральному движению.
Скорость заряженной частицы можно разложить на две составляющие: одну
параллельно и один перпендикулярно магнитному полю.Магнитная сила
действующее на частицу будет определяться составляющей ее скорости
перпендикулярно магнитному полю.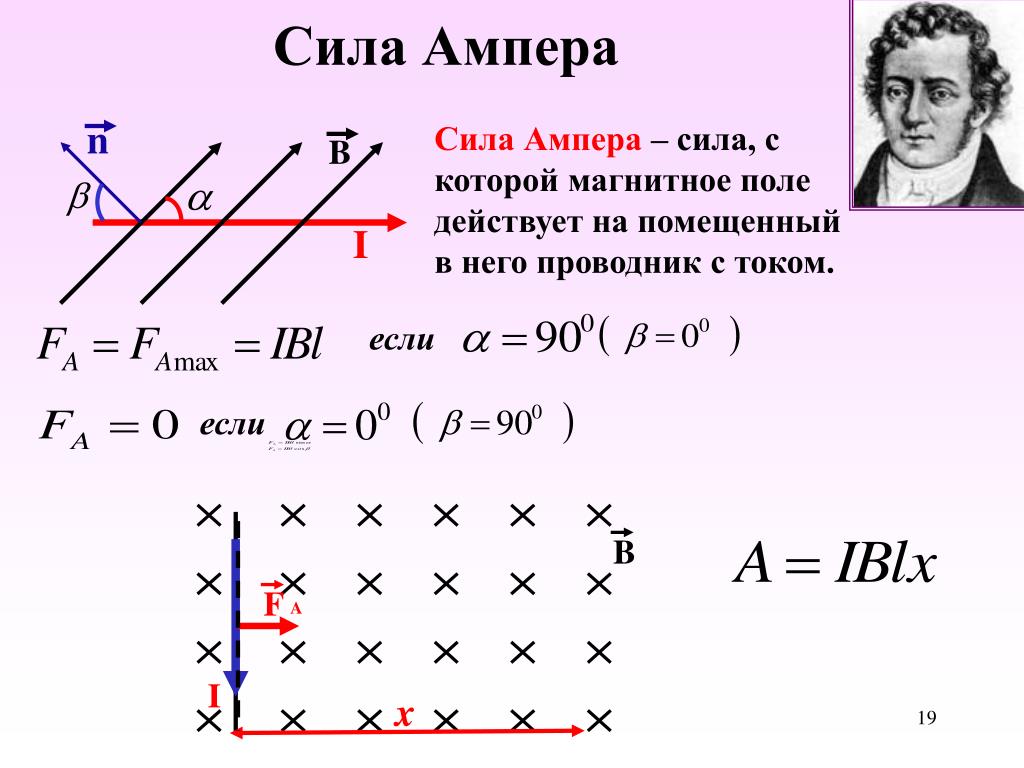 Проекция движения
Проекция движения
частица на плоскости x-y (предполагается, что она перпендикулярна магнитному полю)
будет круглым. Магнитное поле не повлияет на компонент
движение параллельно полю, и эта составляющая скорости останется
постоянный. Конечным результатом будет спиральное движение.
Заряженная частица, движущаяся в области с электрическим и магнитным полем, будет
испытать общую силу равную
(31.32)
Эта сила называется силой Лоренца .
Рисунок 31.6. Заряженная частица движется в скрещенных E и B
поля. Рассмотрим частный случай, когда электрическое поле
перпендикулярно магнитному полю. Движение заряженной частицы в таком
регион может быть достаточно сложным. Заряженная частица с положительным зарядом q
и скорость v движется в этом поле (см. рисунок 31.6). Направление
частица, показанная на рисунке 31.6 перпендикулярна как электрическому полю, так и
магнитное поле. Электрическая сила, действующая на частицу, направлена
вдоль направления электрического поля и имеет величину, равную
(31,33)
Магнитная сила, действующая на заряженную частицу, направлена перпендикулярно к
как v, так и B и имеет величину, равную
(31,34)
Суммарная сила, действующая на частицу, складывается из этих двух компонентов и имеет
величина, равная
(31. 35)
35)
Если заряженная частица имеет скорость, равную
(31,36)
тогда результирующая сила будет равна нулю, и движение частицы будет
быть равномерным линейным движением. Устройство со скрещенными электрическим и магнитным полями
называется селектором скорости. Если прорезь размещена в соответствующем
положения, он будет переносить только те частицы, скорость которых определена
величинами электрического и магнитного полей.
Рисунок 31.7. Ток в магнитном поле. Метод определения плотности и знака заряда.
носителей в металле основана на силах, действующих на скрещенные поля E и B на
носители заряда. На схеме, показанной на рисунке 31.7, показана металлическая полоса.
проводящий ток в указанном направлении и помещенный в однородный магнитный
поле с направлением магнитного поля, перпендикулярным
электрическое поле (которое генерирует ток I). Предположим, что носители заряда в
материал — электроны, то электроны будут двигаться в направлении
противоположный току (см.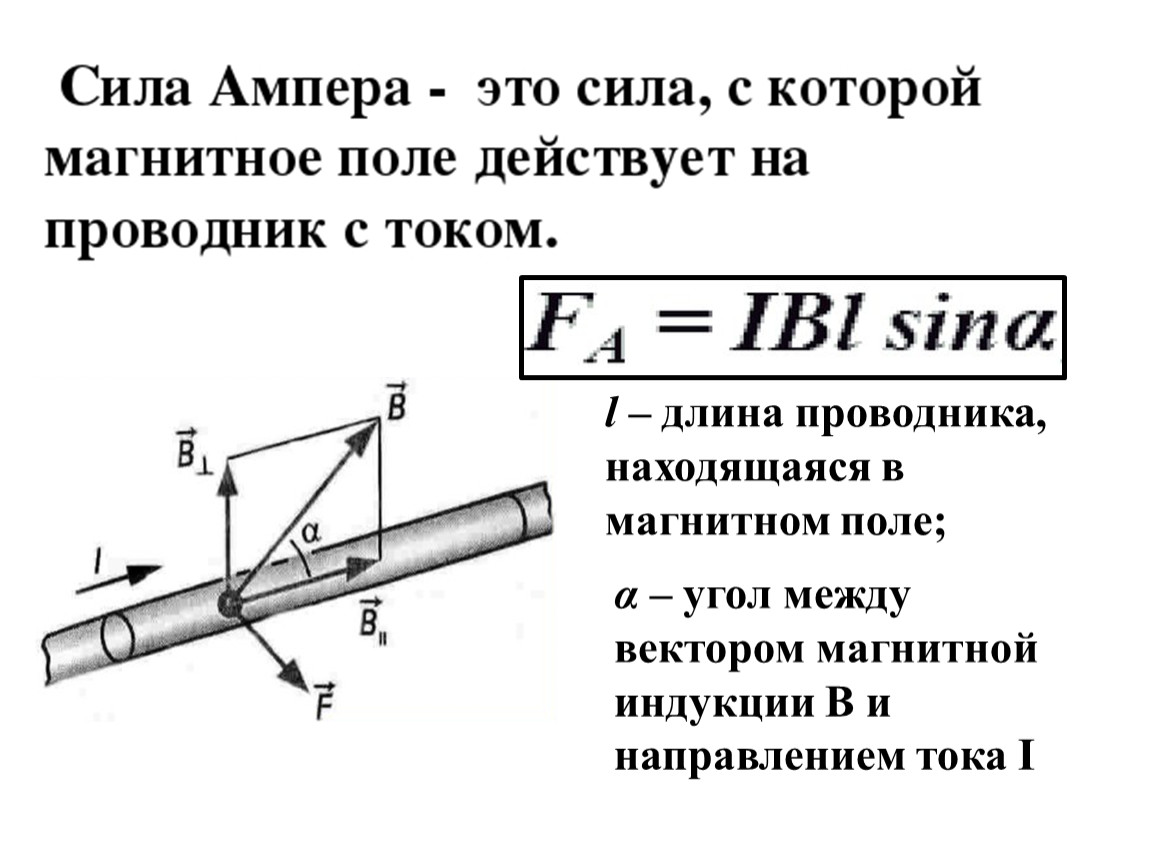 рисунок 31.7). Поскольку магнитное поле
рисунок 31.7). Поскольку магнитное поле
перпендикулярно электрическому полю, оно также перпендикулярно направлению
движения электронов. В результате действия магнитной силы электроны
отклоняются вниз, и на
низ полоски. В то же время дефицит отрицательного заряда будет
создаваться в верхней части полосы. Это распределение зарядов будет генерировать
электрическое поле, перпендикулярное внешнему электрическому полю и под действием
В условиях равновесия электрическая сила, создаваемая этим полем, уравновешивает
магнитная сила, действующая на электроны.Когда это происходит, внутренний
электрическое поле, E в , равно произведению электрона
скорость v d и напряженность магнитного поля B.
результатом внутреннего электрического поля будет создана разность потенциалов
между верхом и низом полосы. Если металлическая полоса имеет ширину w,
тогда разность потенциалов [Delta] V будет равна
(31,37)
Этот эффект называется эффектом Холла.
Скорость дрейфа электронов зависит от тока I в проводе, его
площадь поперечного сечения A и плотность электронов n (см. главу 28):
главу 28):
(31,38)
Комбинируя уравнение (31.38) и уравнение (31.37), мы получаем следующее выражение для
[Дельта] V
(31,39)
Следовательно, для определения n можно использовать измерение [Delta] V.
Ток I, протекающий по проводу, эквивалентен накоплению зарядов
движется по проволоке с определенной скоростью v d .Количество
заряд dq, присутствующий в отрезке dL провода, равен
(31,40)
Если провод помещен в магнитное поле, на него будет действовать магнитная сила.
каждый из носителей заряда, и в результате на
провод. Предположим угол между направлением тока и направлением
поля равно [theta] (см. рисунок 31.8). Магнитная сила, действующая
на отрезке dL провода равно
(31.41)
Полная сила, действующая на провод магнитным полем, может быть найдена следующим образом:
интегрируя уравнение (31.41) по всей проволоке.
Рисунок 31.8. Магнитная сила на проводе.
Пример: Задача 31.33
Весы можно использовать для измерения силы магнитного поля.
Рассмотрим петлю из провода, по которой проходит точно известный ток, как показано на рисунке.
31.9, который частично погружен в магнитное поле. Сила, которую
магнитное поле, действующее на петлю, можно измерить с помощью весов, и это
позволяет рассчитать напряженность магнитного поля.Предположим, что
длина короткой стороны петли 10,0 см, сила тока в проводе 0,225
A, а магнитная сила составляет 5,35 x 10 -2 Н. Какова сила
магнитное поле?
Рассмотрим три сегмента токовой петли, показанные на рисунке 31.9, которые
погружен в магнитное поле. Магнитная сила, действующая на сегменты 1 и 3
имеют одинаковую величину, но направлены в противоположную сторону, и поэтому
отменить. Величина магнитной силы, действующей на сегмент 2, может быть
рассчитывается с использованием ур.(31,41) и равно
(31,42)
Эта сила измеряется с помощью весов и равна 5,35 x 10 -2 .
N. Таким образом, сила магнитного поля равна
.
(31.43)
Рисунок 31.9. Токовая петля погружена в магнитное поле.
Если токовая петля погружена в магнитное поле, результирующая магнитная сила будет
быть равным нулю. Однако крутящий момент на этом контуре, как правило, не будет
равняется нулю.Предположим, прямоугольная токовая петля помещена в однородную
магнитное поле (см. рисунок 31.10). Угол между нормалью тока
петля и магнитное поле равно тета. Магнитные силы, действующие на
верхняя и нижняя части токового контура равны
(31,44)
где L — длина верхнего и нижнего края. Крутящий момент, приложенный к
токовая петля относительно ее оси равна
(31.45)
Рисунок 31.10. Токовая петля помещена в однородное магнитное поле. Используя определение магнитного дипольного момента u, обсуждалось
в главе 30 уравнение (31.45) можно переписать как
(31,46)
где
(31,47)
Используя векторные обозначения, уравнение (31. 45) можно переписать как
45) можно переписать как
(31,48)
где направление магнитного момента определяется с помощью правой
правило.
Работа, которая должна выполняться против магнитного поля, чтобы вращать ток
петля на угол d [theta] равна — [tau] d [theta]. Изменение в
потенциальная энергия токовой петли при ее вращении между
[theta] 0 и [theta] 1 равно
.
(31,49)
Обычно в качестве опорной точки выбирают [theta] 0 = 90 градусов. а также
U ([theta] 0 ) = 0 Дж. Если этот выбор сделан, мы можем переписать уравнение.(31,50)
как
(31,50)
В векторной записи:
(31.51)
Потенциальная энергия токовой петли имеет минимум, когда u и B равны
параллельно и максимум, когда u и B антипараллельны.
Отправляйте комментарии, вопросы и / или предложения по электронной почте на адрес [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса.
экспериментов Ампера
экспериментов Ампера
Далее: Закон Ампера
Up: Магнетизм
Предыдущий: Историческое введение
Эксперименты Ампера
В 1820 году датский физик Ганс Кристиан Эрстед читал лекцию.
демонстрация различных электрических и
магнитные эффекты.Вдруг, к своему изумлению, он заметил, что
стрелка компаса, которую он держал
отклонился, когда он поднес его к токопроводящей
провод. Это было очень удивительное наблюдение, поскольку до этого момента электричество и
магнетизм считался двумя совершенно не связанными друг с другом явлениями.
Слух об этом открытии быстро распространился по научной лозе.
и французский физик Андре Мари Ампер
сразу решил разобраться дальше.
Аппарат Ампера состоял (по существу) из длинного прямого провода, несущего
электрический ток
Текущий .Ампер быстро обнаружил, что стрелка небольшого компаса отображает
из ряда концентрических круговых петель в плоскости
перпендикулярно токоведущему проводу — см. рис.20.
рис.20.
Направление циркуляции вокруг этих магнитных петель принято считать равным
направление, в котором северный полюс стрелки компаса
точки.
Используя это соглашение, циркуляция петель задается
линейка правая . Если большой палец правой руки указывает в направлении
тока, то пальцы правой руки вращаются в том же смысле, что и
магнитные петли.
Следующая серия экспериментов Ампера заключалась в том, чтобы принести короткий испытательный провод,
ток,
рядом с исходным проводом и исследуя силу, приложенную к испытательному проводу.
Этот эксперимент не так ясен, как эксперимент Кулона, потому что, в отличие от
электрические заряды,
электрические токи не могут существовать как точечные сущности.Они
должны течь по замкнутым контурам. Мы должны
представьте, что цепь, которая соединяется с центральным проводом, достаточно
далеко, что это не имеет заметного влияния на исход эксперимента.
Цепь, которая соединяется с
тестовый провод более проблематичен. К счастью, если
питающие проволоки скручены друг вокруг друга, как показано на рис.21, затем
они эффективно нейтрализуют друг друга, а также не влияют на результат
эксперимент.
Ampère обнаружил, что сила, действующая на испытательный провод, прямо пропорциональна
к его длине. Он также сделал следующие наблюдения.
Если ток в тестовом проводе
(, т.е. , испытательный ток) течет параллельно току в центральном проводе.
тогда два провода притягиваются друг к другу. Если ток в тесте
провод перевернут, тогда два провода отталкиваются друг от друга.
Если испытательный ток направлен радиально к центральному проводу
(и ток в центральном проводе течет вверх), затем тестовый провод
подвергается действию направленной вниз силы.Если испытательный ток поменять местами, сила равна
вверх. Если испытательный ток вращается в одной плоскости, так что он начинается
Если испытательный ток вращается в одной плоскости, так что он начинается
параллельно центральному току и заканчивается радиально
к нему, затем сила на
испытательный провод имеет постоянную величину и всегда находится под прямым углом к
испытательный ток. Если испытательный ток параллелен магнитной петле, то есть
к испытательному проводу не прикладывалась сила. Если испытательный ток вращается в
одна плоскость, так что она начинается параллельно центральному току и заканчивается
указывая вдоль магнитной петли, то величина силы, действующей на
тестовый провод затухает как (где угол тока
перевернут, и соответствует
случай, когда испытательный ток параллелен центральному току),
и его направление снова всегда под прямым углом к
тестовый ток.Наконец, Ампер смог установить, что привлекательный
сила между двумя параллельными токоведущими проводами пропорциональна произведению
два тока, и
падает как перпендикуляр
расстояние между проводами.
Этот довольно сложный силовой закон можно кратко описать в векторных обозначениях.
при условии, что мы определяем векторное поле, называемое магнитным полем ,
который заполняет пространство, и
направление которого всюду касательно
магнитные петли, нанесенные на карту севером
полюс малого
компас.Зависимость силы на единицу длины, действующей на
испытательный провод с разными
возможные направления испытательного тока описываются
| (152) |
где — вектор, направление и величина которого такие же, как у
испытательного тока.
Изменение силы на единицу длины, действующей на
испытательный провод с прочностью
центральный ток и расстояние по перпендикуляру к центральному проводу
объясняется тем, что напряженность магнитного поля пропорциональна, и
обратно пропорционально.Таким образом, мы можем написать
| (153) |
Константа пропорциональности называется
проницаемость свободного пространства и принимает значение
| (154) |
Между прочим, единицей измерения напряженности магнитного поля в системе СИ является тесла (Тл), т. е.
е.
то же, что и ньютон на ампер на метр:
| (155) |
Понятие о магнитном поле, которое
заполняет пространство вокруг токоведущего провода
позволяет рассчитать силу при испытании
провод удобно разделить на две части.В первой части мы вычисляем
магнитное поле, создаваемое током, протекающим в центральном проводе. Это поле
циркулирует в плоскости, перпендикулярной проводу. Его величина составляет
пропорциональна центральному току и обратно пропорциональна перпендикуляру
расстояние от провода. Во второй части мы используем
Уравнение (152) для расчета силы на единицу
длина, действующая на
короткий токопроводящий провод, помещенный в магнитное поле
генерируется центральным током.
Эта сила перпендикулярна как направлению магнитного поля, так и направлению магнитного поля.
испытательный ток.Отметим, что на данном этапе у нас нет оснований предполагать, что магнитная
поле реально существует. Он введен просто для облегчения расчета.
Он введен просто для облегчения расчета.
силы, приложенной к испытательному проводу центральным проводом. Оказывается, однако,
что магнитное поле действительно существует, поскольку, как мы увидим, существует
энергия, связанная с магнитным полем, заполняющим пространство.
Далее: Закон Ампера
Up: Магнетизм
Предыдущий: Историческое введение
2007-07-14
Закон
Ампера> ИНЖИНИРИНГ.com
Закон Ампера №
, опубликовано 10 ноября 2006 г. |
Закон Ампера
Определение силы тока : Рассмотрим два длинных прямых, параллельные провода, разделенные расстоянием a и несущие токи I 1 и I 2 в одном направлении.Мы можем легко определить силу на одном проводе из-за магнитного поля, создаваемого другим проводом. Провод 2, по которому проходит ток I 2 , создает магнитное поле B 2 в месте расположения провода 1. Направление B 2 перпендикулярно проводу 1. | |
| |
| Поскольку l перпендикулярно B 2 , величина F 1 равна | |
| Мы можем переписать это в терминах силы на единицу длины как | |
Числовое значение 2×10 -7 Н / м получается из приведенного выше уравнения с I 1 = I 2 = 1 A и a = 1 м.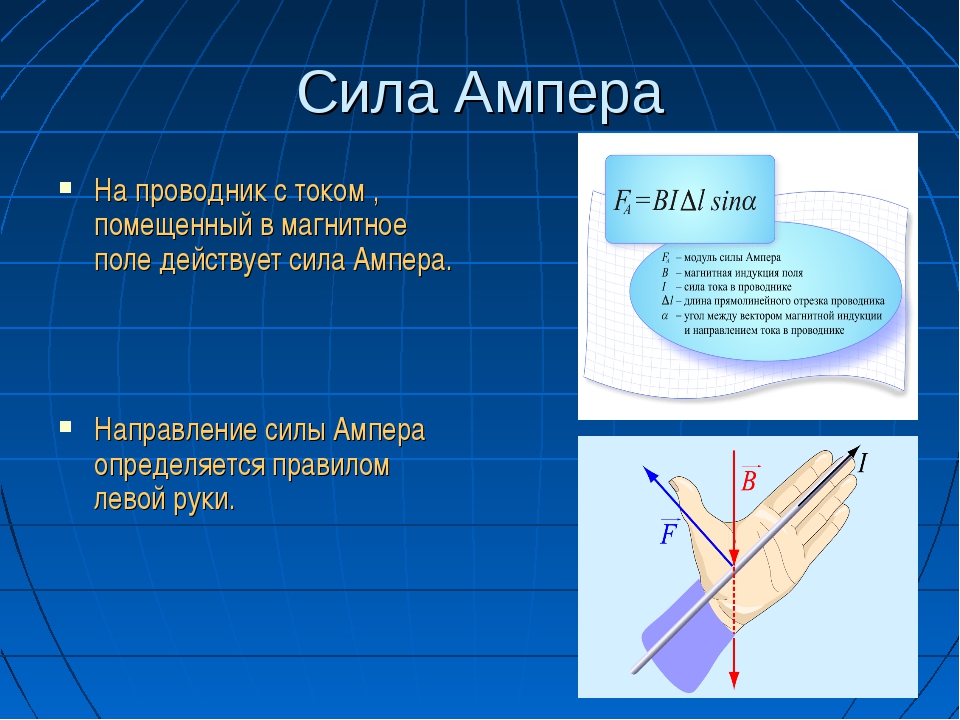 Закон Ампера гласит, что линейный интеграл B . ds вокруг любого замкнутого пути равно, где I — полный установившийся ток, проходящий через любую поверхность, ограниченную замкнутым контуром | |
| Закон Ампера действителен только для установившихся токов и полезен только для расчета магнитного поля токовых конфигураций, имеющих высокую степень симметрии. | |
Пожалуйста, включите JavaScript, чтобы просматривать комментарии от Disqus.
сил между параллельными проводниками — Учитесь — ScienceFlip
Силы между параллельными проводниками — выучить
Когда по проводу течет ток, вокруг провода возникает магнитное поле. Магнитное поле образует круговые петли вокруг провода, сила которых уменьшается по мере удаления от провода. Направление магнитного поля определяется с помощью правила для правой руки:
- обхватить пальцами токоведущий провод
- большой палец указывает направление тока
- пальцев указывают направление магнитного поля (часто описывается как по часовой стрелке или против часовой стрелки в зависимости от вида)
Два токонесущих проводника
Когда два провода, по которым проходит ток, размещаются параллельно друг другу, их магнитные поля будут взаимодействовать, в результате чего между проводами действует сила.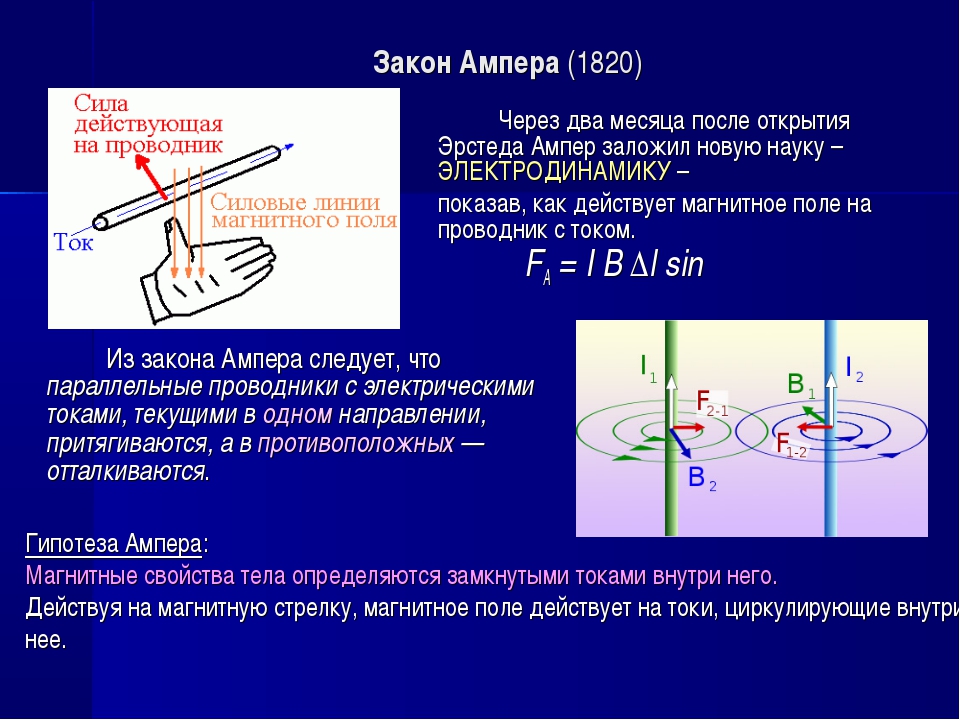 Величина силы, действующей на каждый провод, одинакова, но направления противоположны. Это верно даже в том случае, если по проводникам проходят токи разной величины.
Величина силы, действующей на каждый провод, одинакова, но направления противоположны. Это верно даже в том случае, если по проводникам проходят токи разной величины.
На приведенной ниже схеме показаны два примера, в которых направление магнитного поля вокруг каждого провода обозначено знаком • ×. Диаграмма A показывает ток в проводах, идущих в одном направлении, а диаграмма B показывает ток, идущий в противоположных направлениях:
Определение направления силы
Направление силы определяется по направлению отдельных полей в области между проводниками:
- Диаграмма A: противоположные поля создают силу притяжения
- Диаграмма B: одинаковые поля приводят к силе отталкивания
Как правило; когда ток, протекающий по проводникам в одном направлении, сила будет притягивающей, а когда токи противоположны по направлению, сила будет отталкивающей.
Определение силы между двумя параллельными проводниками
На величину силы, действующей между двумя параллельными проводниками с током, влияют несколько факторов:
- Ток в каждом проводнике
- Длина жил
- Расстояние между проводниками
Величина силы, действующей между двумя параллельными проводниками с током, рассчитывается по формуле:
Где:
— сила на единицу длины между проводниками (в Нм −1 )
— магнитная проницаемость свободного пространства (4π × 10 −7 NA −2 ) *
— ток в проводе 1 (в А)
— ток в проводе 2 (в А)
— расстояние между проводниками (в м)
* примечание: и.
Уравнение можно записать:
где
SI определение электрического тока; ампер и третий закон движения Ньютона
Международная система единиц (СИ) устанавливает, что единицей измерения электрического тока является ампер. Формальное определение ампера таково: один ампер — это постоянный ток, который, если его поддерживать в двух прямых параллельных проводниках бесконечной длины, с незначительным круглым поперечным сечением и помещать на расстоянии одного метра в вакууме, создаст между этими проводниками силу равна 2 × 10 −7 Н / м длины.
Это приложение третьего закона движения Ньютона, который гласит: в системе двух тел, если тело A оказывает силу на тело B, то тело B оказывает на тело A силу, равную по величине, но противоположную по величине. направление.
Иногда говорится о третьем законе движения Ньютона: на каждое действие существует равное и противоположное противодействие. Если один провод применяет силу ко второму проводу, второй провод прикладывает силу, равную по величине и противоположную по направлению к первому проводу.
Пример 1:
Два проводящих провода, A и B, имеют токи, протекающие в разных направлениях и разделенные расстоянием 4 см. Какова величина и направление силы на единицу длины, действующей между проводами, если у проводника A ток 2,5 А, а у проводника B — 1,5 А?
Использование:
Где:
- I 1 = 2,5 А
- Я 2 = 1.5 А
- r = 0,04 м
(сила отталкивания)
22.2: Сила между двумя токоведущими проводами
Рассмотрим два бесконечных параллельных прямых провода на расстоянии \ (h \) друг от друга, по которым проходят восходящие токи, \ (I_ {1} \) и \ (I_ {2} \), соответственно, как показано на рисунке \ (\ PageIndex {1} \).
Рисунок \ (\ PageIndex {1} \): Два параллельных токоведущих провода будут оказывать притягивающее усилие друг на друга, если их токи идут в одном направлении.
Первый провод создаст магнитное поле \ (\ vec B_ {1} \) в форме кругов, концентрических по отношению к проводу.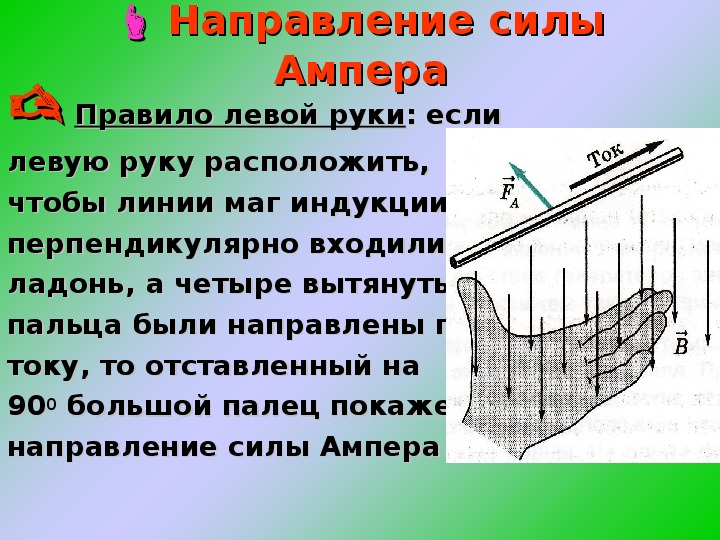 В положении второго провода магнитное поле \ (B_ {1} \) находится внутри страницы и имеет величину:
В положении второго провода магнитное поле \ (B_ {1} \) находится внутри страницы и имеет величину:
.
\ [\ begin {align} B_ {1} = \ frac {\ mu_ {0} I_ {1}} {2 \ pi h} \ end {align} \]
Поскольку второй провод проводит ток \ (I_ {2} \) вверх, он испытывает магнитную силу \ (\ vec F_ {2} \) от магнитного поля \ (B_ {1} \ ), то есть слева (как показано на рисунке \ (\ PageIndex {1} \) и определяется правилом правой руки).{◦} \). Мы ожидаем, исходя из Третьего закона Ньютона, что на первый провод должна действовать равная и противоположная сила. Действительно, второй провод создаст магнитное поле \ (\ vec B_ {2} \), которое находится за пределами страницы в месте расположения первого провода, с величиной:
.
\ [\ begin {align} B_ {2} = \ frac {\ mu_ {0} I_ {2}} {2 \ pi h} \ end {align} \]
Это приводит к магнитной силе \ (\ vec F_ {1} \), действующей на первый провод, который указывает вправо (из правила правой руки). На участке длиной \ (l \) первого провода магнитная сила от магнитного поля \ (\ vec B_ {2} \) имеет величину:
.
\ [\ begin {align} F_ {1} = I_ {1} || \ vec l \ times \ vec B_ {2} || = I_ {1} lB_ {2} \ frac {\ mu_ {0} I_ {1} I_ {2}} {2 \ pi h} \ end {align} \]
, который действительно имеет ту же величину, что и сила, действующая на второй провод.Таким образом, когда два параллельных провода проводят ток в одном направлении, они оказывают друг на друга равные и противоположные силы притяжения.
Упражнение \ (\ PageIndex {1} \)
Рисунок \ (\ PageIndex {2} \): два провода, по которым ток проходит в противоположных направлениях.
Два параллельных провода несут ток в противоположных направлениях, как показано на рисунке \ (\ PageIndex {2} \). Какую силу они оказывают друг на друга?
- Силы не будет, т. К. Токи гаснут.
- Между проводами будет сила притяжения.
- Между проводами будет сила отталкивания.
- Ответ
Сила притяжения между двумя проводами служила основой для определения Ампера, единицы S. {- 17} \ text {N} \) на метр длины ».{−19} \ text {C} \), а ампер соответствует одному кулону в секунду.
{- 17} \ text {N} \) на метр длины ».{−19} \ text {C} \), а ампер соответствует одному кулону в секунду.
Сила между двумя проводами — хорошая система, чтобы понять, как никакая физическая величина не может зависеть от нашего выбора правой руки для определения перекрестных произведений. Как упоминалось в предыдущей главе, любая физическая величина, такая как направление силы, действующей на провод, всегда будет зависеть от двух последовательных применений правой руки. В этой системе мы сначала использовали правило правой руки для аксиальных векторов, чтобы определить направление магнитного поля от одного из проводов.Затем мы использовали правило правой руки, чтобы определить направление перекрестного произведения, чтобы определить направление силы на другом проводе. Вы можете убедиться, что получите тот же ответ, если вместо этого воспользуетесь левой рукой для определения направления магнитного поля (которое будет в противоположном направлении), а затем снова для перекрестного произведения.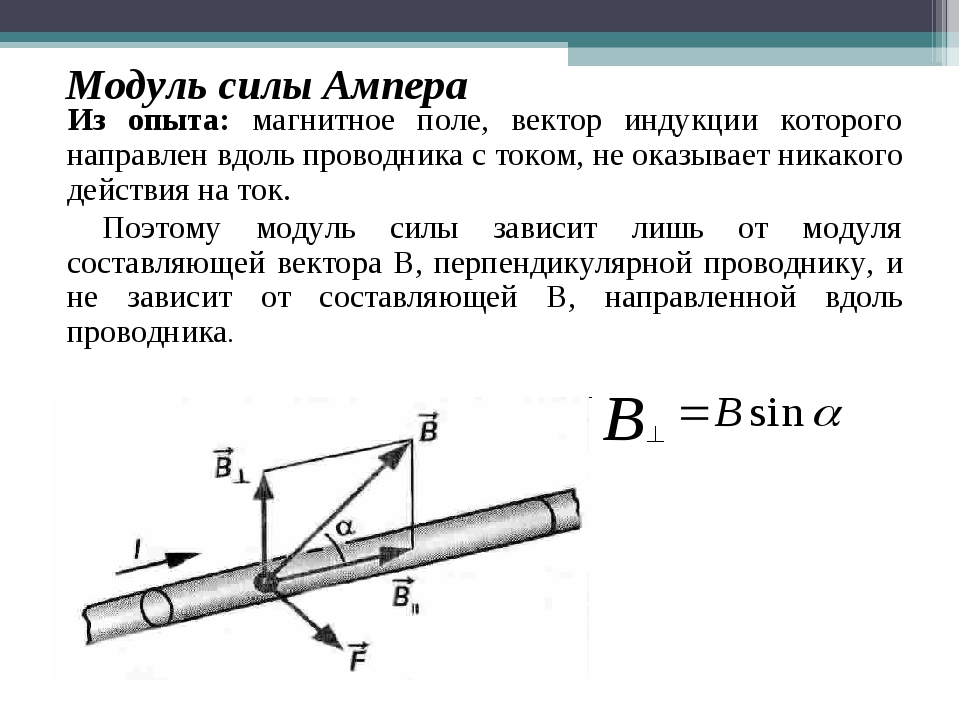 Это также подчеркивает, что магнитное поле (и электрическое поле) — это просто математический инструмент, который мы используем, в конечном итоге, для описания движения зарядов или стрелок компаса.
Это также подчеркивает, что магнитное поле (и электрическое поле) — это просто математический инструмент, который мы используем, в конечном итоге, для описания движения зарядов или стрелок компаса.
Упражнение \ (\ PageIndex {2} \)
Когда по прямому кабелю течет ток, как можно ожидать, что заряды будут распределяться радиально по поперечному сечению кабеля?
- Равномерно по радиусу (плотность тока не зависит от \ (r \)).
- На внешней стороне кабеля будет избыток положительных зарядов.
- На внешней стороне кабеля будет избыток отрицательных зарядов.
- Ответ
ампер-сила / сила Лоренца
Рисунок 1: Настройка для демонстрации Ampere Force
Алюминиевый стержень подвешен между полюсами большого магнита.Если через стержень нет тока, он свободно качается. Когда по стержню проходит ток, возникает сила, которая толкает или тянет стержень в зависимости от направления тока. Это показано на Рисунке 1 выше.
Это показано на Рисунке 1 выше.
Оснащение:
- Двойной рубильник
- Пруток алюминиевый
- Провода с открытой медной резьбой (для намотки на стержень)
- Гигантский подковообразный магнит
- Две установки штанги / стойки с другой опорной штангой / зажимами
- Источник питания постоянного тока Fisher Scientific
- Банановые шнуры (4)
- Хомуты резиновые
- Видеокамера
Рисунок 2: Принципиальная схема ампер-силы
Демо:
- Расположите алюминиевый стержень так, чтобы он висел в середине магнита (не касаясь его сторон).На магните помечены северный и южный полюсы, чтобы помочь определить направление магнитного поля.
- С ножевым выключателем прямо вверх (режим напряжения) подключите банановые кабели в соответствии со схемой на Рисунке 2 выше.
- Подключите два одинарных банановых гнезда по обе стороны от рубильника к источнику питания.

- Дважды проверьте, что текущая ручка установлена на ноль на PS, затем включите PS.
- Увеличьте напряжение примерно до 10 В.
- Поверните рубильник вправо или влево (текущий режим) и увеличьте ток.Стержень будет качаться внутрь или наружу магнита, в зависимости от направления.
- Чтобы изменить направление качания стержня, установите ток на ноль, переведите рубильник в противоположную сторону и снова увеличьте ток.
Пояснение:
Предпосылка этой демонстрации — показать, как провод с током, помещенный в магнитное поле, будет испытывать силу, известную как сила Лоренца (где электрическое поле равно 0). Это показано в уравнении ниже:
F — магнитная сила, действующая на провод, I — ток, L — длина токоведущего провода, а B — внешнее магнитное поле.
Магнитное поле, создаваемое подковообразным магнитом, представляет собой постоянное магнитное поле, силовые линии которого показаны ниже на Рисунке 3.
Рисунок 3: Магнитное поле подковообразного магнита (Подковообразный магнит. (2018, 30 декабря. Https://en.wikipedia.org/wiki/Horseshoe_magnet)
Проволока помещается между концами магнита, где мы приближаемся к однородному магнитному полю. Из-за настройки магнита на демонстрации это магнитное поле может быть как вверх, так и вниз.Провод проложен таким образом, что ток будет течь либо влево, либо вправо, если вы встречаетесь с демонстрацией. Схема этой демонстрации показана на Рисунке 1.
Как только ток начинает течь, токопроводящий провод испытывает силу, поскольку он погружен в магнитное поле. Направление этой силы определяется силой Лоренца, которая определяет, как движущийся заряд во внешнем магнитном поле будет испытывать силу. Это уравнение приведено выше.На рисунке 4 ниже показан результирующий эффект.
Рисунок 4: Эффекты реверсирования тока на алюминиевом стержне
Предположим, что магнитное поле направлено вверх на рисунке 4, чтобы соответствовать рисунку 3. На верхнем рисунке рисунка 4 мы можем определить, что сила Лоренца на проводе направлена в сторону от магнита, и мы используем наше предположение, что магнитное поле направлено вверх. Используя перекрестное произведение в уравнении Лоренца, мы можем выяснить, что ток в проводе движется слева направо относительно рисунка 4.
На верхнем рисунке рисунка 4 мы можем определить, что сила Лоренца на проводе направлена в сторону от магнита, и мы используем наше предположение, что магнитное поле направлено вверх. Используя перекрестное произведение в уравнении Лоренца, мы можем выяснить, что ток в проводе движется слева направо относительно рисунка 4.
На нижнем изображении рисунка 4 мы видим, что сила Лоренца на проводе направлена на магнит. Опять же, мы предполагаем, что магнитное поле направлено вверх. Используя векторное произведение в уравнении Лоренца, мы можем выяснить, что ток в проводе движется справа налево, как показано на рисунке 4.
Теперь, если мы предположим, что магнитное поле направлено вниз, мы могли бы использовать те же рассуждения, что и выше, чтобы обнаружить, что направление тока в проводе изменится. Чтобы убедиться в этом, давайте начнем с верхнего изображения на рисунке 4.Мы предполагаем, что магнитное поле направлено вниз, и кажется, что на провод действует сила, которая отталкивает его от магнита.

 30)
30) 32)
32) 1 .
1 .