Формула силы Ампера в физике
Содержание:
Определение и формула силы Ампера
Определение
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$\bar{F}, \bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
большой палец укажет направление силы Ампера (рис.1).
Закон Ампера
Элементарная сила Ампера
($d\bar{F}_A$) определена законом (или формулой) Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(1)$$
где I – сила тока,
$d \bar{l}$ – малый элемент длины проводника – это вектор, равный
по модулю длине проводника, направленный в таком же направлении как вектор плотности тока,
$\bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d \bar{F}_{A}=\bar{j} \times \bar{B} d V(2)$$
где $\bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I \cdot B \cdot d l \cdot \sin \alpha(3)$$
где $\alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$\bar{F}_{A}=I \int_{l} d \bar{l} \times \bar{B}(4)$$
где $\bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl.
Интегрирование в формуле (4) проводят по всей длине проводника (l). Из выражения (4) следует, что на замкнутый контур с током I,
в однородном магнитном поле действует сила Ампера равная $\bar{F}_{A}=0(H)$
Сила Ампера, которая действует на элемент (dl) прямого проводника с током I1, помещённый в магнитное поле, которое
создает другой прямой проводник, параллельный первому с током I2, равна по модулю:
$$d F=\frac{\mu_{0}}{2 \pi} \frac{I_{1} I_{2}}{d} d l(5)$$
где d – расстояние между проводниками, $\mu_{0}=4 \pi \cdot 10^{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$\frac{F}{l}=\frac{\mu_{0}}{2 \pi} \frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник
действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для
прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B \operatorname{lsin} \alpha$$
где $\alpha$ – искомый угол. Следовательно:
Следовательно:
$$\alpha=\arcsin \left(\frac{F}{I B l}\right)$$
Ответ. $\alpha=\arcsin \left(\frac{F}{I B l}\right)$
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга.
Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая
на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(2.1)$$
Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости
рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
где ток, который течет в элементе проводника dx, выразим как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$
где из рис.1 видно, что $a \leq x \leq a+b$, по условию задачи силу следует
найти на единицу длины, значит $0 \leq l \leq 1$ . {a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
{a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$
Читать дальше: Формула силы выталкивания.
Сила Ампера и закон Ампера
Закон Ампера
Трудно представить нашу современную жизнь без электричества, ведь исчезни оно, это бы мгновенно привело к глобальным катастрофическим последствиям. Так что в любом случае с электричеством мы отныне не разлучные. А вот для того, чтобы иметь с ним дело нужно знать определенные физические законы, одним из которых, безусловно, является закон Ампера. А пресловутая магнитная сила Ампера – главная составляющая этого закона.
Закон Ампера
Итак, давайте сформулируем закон Ампера: в параллельных проводниках, где электрические токи текут в одном направление, появляется сила притяжения. А в проводниках, где токи текут в противоположных направлениях, наоборот возникает сила отталкивания. Если же говорить простым житейским языком, то закон Ампера можно сформулировать предельно просто «противоположности притягиваются», и ведь в реальной жизни (а не только физике) мы наблюдаемо подобное явление, не так ли?
Но вернемся к физике, в ней также под законом Ампера понимают закон, определяющий силу действия магнитного поля на ту часть проводника, по которой протекает ток.
Что такое сила Ампера
Собственно сила ампера и является той силой действия магнитного поля на проводник, по которому идет ток. Сила Ампера вычисляется по формуле как результат умножения плотности тока, идущего по проводнику на индукцию магнитного поля, в котором находится проводник. Как результат формула силы Ампера будет выглядеть так
са=ст*дчп*ми
Где, са – сила Ампера, ст – сила тока, дчп – длина части проводника, ми – магнитная индукция.
Правило левой руки
Правило левой руки предназначено для того, чтобы помочь запомнить, куда направлена сила Ампера. Оно звучит следующим образом: если рука занимает такое положение, что линии самой магнитной индукции внешнего поля заходят в ладонь, а пальцы с мизинца по указательный указывают направление в сторону движения тока в проводнике, то отторгнутый под углом в 90 градусов большой палец ладони и будет указывать, куда направлена сила Ампера, действующая на элемент проводника.
Примерно так выглядит правило левой руки на этой схеме.
Практическое применение
Применение силы Ампера в современном мире очень широкое, можно даже без преувеличение сказать, что мы буквально окружены силой Ампера. Например, когда вы едете в трамвае, троллейбусе, электромобиле, его в движение приводит именно она, сила Ампера. Аналогичны лифты, электрические ворота, двери, любые электроприборы, все это работает именно благодаря силе Ампера.
Видео
И в завершение небольшой видео урок о силе Ампера.
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.
Урок 3. магнитная индукция. действие магнитного поля на проводник с током и движущуюся заряженную частицу — Физика — 11 класс
Физика, 11 класс
Урок 3. Магнитная индукция. Действие магнитного поля на проводник и движущуюся заряжённую частицу
Перечень вопросов, рассматриваемых на уроке:
1) магнитное поле;
2) вектор магнитной индукции, линии магнитной индукции;
3) сила Ампера, сила Лоренца;
4) правило буравчика, правило левой руки.
Глоссарий по теме
Магнитная индукция – векторная величина, характеризующая величину и направление магнитного поля.
Сила Ампера – сила, действующая со стороны магнитного поля на проводник с током.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущую частицу с зарядом.
Правило «буравчика» — правило для определения направления магнитного поля проводника с током.
Правило левой руки – правило для определения направления силы Ампера и силы Лоренца.
Соленоид – проволочная катушка.
Рамка с током – небольшой длины катушка с двумя выводами из скрученного гибкого проводника с током, способная поворачиваться вокруг оси, проходящей через диаметр катушки.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б.,. Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 3 – 20
2. А.П. Рымкевич. Сборник задач по физике. 10-11 классы. — М: Дрофа, 2009. – С.109 — 112
– С.109 — 112
Основное содержание урока
Магнитное поле – особый вид материи, которая создаётся электрическим током или постоянными магнитами. Для демонстрации действия и доказательства существования магнитного поля служат магнитная стрелка, способная вращаться на оси, или небольшая рамка (или катушка) с током, подвешенная на тонких скрученных гибких проводах.
Рамка с током и магнитная стрелка под действием магнитного поля поворачиваются так, что северный полюс (синяя часть) стрелки и положительная нормаль рамки указывают направление магнитного поля.
Магнитное поле, созданное постоянным магнитом или проводником с током, занимает всё пространство в окрестности этих тел. Магнитное поле принято (удобно) изображать в виде линий, которые называются линиями магнитного поля. Магнитные линии имеют вихревой характер, т.е. линии не имеют ни начала, ни конца, т.е. замкнуты. Направление касательной в каждой точке линии совпадает с направлением вектора магнитной индукции. Поля с замкнутыми линиями называются вихревыми.
Поля с замкнутыми линиями называются вихревыми.
Магнитное поле характеризуется векторной величиной, называемой магнитной индукцией. Магнитная индукция характеризует «силу» и направление магнитного поля – это количественная характеристика магнитного поля.
Она обозначается символом За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.
Направление магнитного поля устанавливают с помощью вектора магнитной индукции.
Направление вектора магнитной индукции прямого провода с током определяют по правилу буравчика (или правого винта).
Правило буравчика звучит следующим образом:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
Направление магнитного поля внутри соленоида определяют по правилу правой руки.
Определим модуль вектора магнитной индукции.
Наблюдения показывают, что максимальное значение силы, действующей на проводник, прямо пропорционально силе тока, длине проводника, находящегося в магнитном поле.
F_max ~ I; F ~ Δl.
Тогда, зависимость силы от этих двух величин выглядит следующим образом
Отношение зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.
Величина, численно равная отношению максимальной силы, действующей на проводник с током, на произведение силы тока и длины проводника, называется модулем вектора магнитной индукции:
Единицей измерения магнитной индукции является 1 тесла (Тл).
1Тл = 1Н/(1А∙1м).
Закон Ампера:
Сила, действующая на проводник с током в магнитном поле, равна произведению модуля магнитной индукции, силы тока, длины проводника и синуса угла между вектором магнитной индукции и направлением тока:
где α – угол между вектором B и направлением тока.
Направление силы Ампера определяется правилом левой руки:
Если ладонь левой руки развернуть так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 900 большой палец покажет направление силы Ампера.
Сила Ампера — сила, действующая на проводник с током со стороны магнитного поля.
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Её численное значение равно произведению заряда частицы на модули скорости и магнитной индукции и синус угла меду векторами скорости и магнитной индукции:
– заряд частицы;
– скорость частицы;
B – модуль магнитной индукции;
– угол между векторами скорости частицы и магнитной индукции.
Направление силы Лоренца также определяют по правилу левой руки:
Если четыре вытянутых пальца левой руки направлены вдоль вектора скорости заряженной частицы, а вектор магнитной индукции направлен в ладонь, то отведённый на 900 большой палец покажет направление силы Лоренца. Если частица имеет заряд отрицательного знака, то направление силы Лоренца противоположно тому направлению, которое имела бы положительная частица.
Если частица имеет заряд отрицательного знака, то направление силы Лоренца противоположно тому направлению, которое имела бы положительная частица.
Получим формулы для радиуса окружности и периода вращения частицы, которая влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, применяя формулы второго закона Ньютона и центростремительного ускорения.
Согласно 2-му закону Ньютона
Отсюда
Время, за которое частица делает полный оборот (период обращения), равно:
Многим юным бывает досадно, что они не родились в старые времена, когда делались открытия. Им кажется, что теперь всё известно и никаких открытий на их долю не осталось.
Одной из нераскрытых тайн является механизм земного магнитного поля. Как же и чем вызывается магнитное поле Земли? Подумайте и может быть…
Одна из возможных гипотез.
Как известно, ядро Земли имеет высокую температуру
и высокую плотность. Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.
Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.
Разбор тренировочных заданий
1. На рисунке изображён проводник с током, помещённый в магнитное поле. Стрелка указывает направление тока в проводнике. Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?
Варианты ответов:
1. вправо →;
2. влево ←;
3. вниз ↓;
4. вверх ↑.
— точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.
Используя правило левой руки, определяем направление силы Ампера:
Левую руку располагаем так, чтобы линии магнитной индукции входили в ладонь, 4 пальца направим вниз по направлению тока, тогда отогнутый на 900 большой палец покажет направление силы Ампера, т.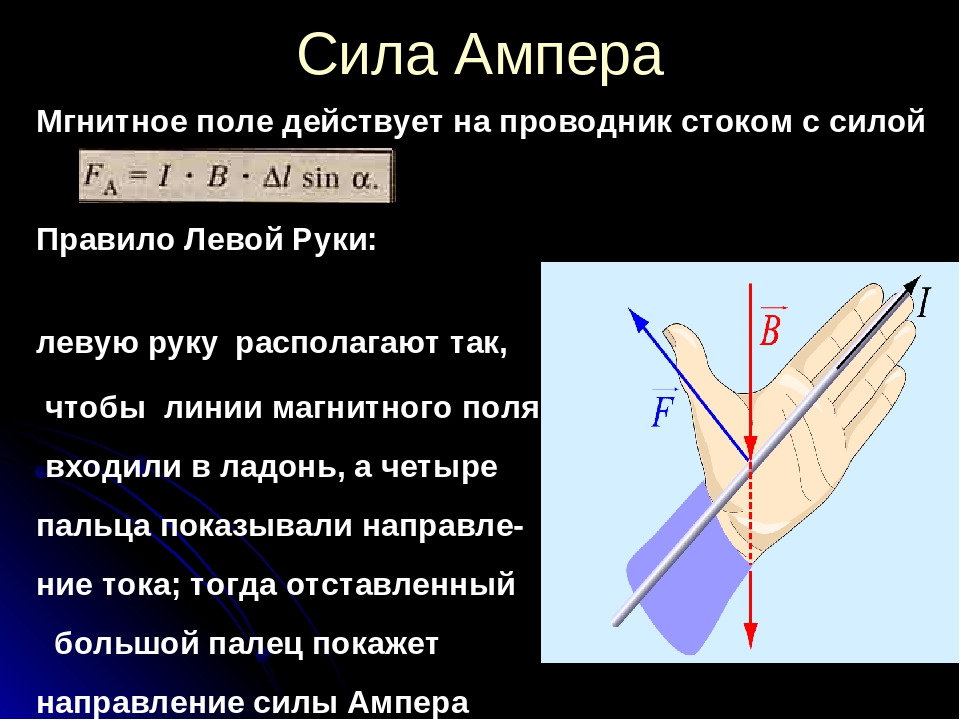 е. она направлена влево.
е. она направлена влево.
Правильный вариант:
2. влево ←.
2. По проводнику длиной 40 см протекает ток силой 10 А. Чему равна индукция магнитного поля, в которое помещён проводник, если на проводник действует сила 8 мН?
(Ответ выразите в мТл).
3. Определите модуль силы, действующей на проводник длиной 50 см при силе тока 10 А в магнитном поле с индукцией 0,15 Тл. (Ответ выразите в мН).
4. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Найдите скорость протона. (Ответ выразите в км/с, округлив до десятков)
5. С какой скоростью влетает электрон в однородное магнитное поле (индукция 1,8 Тл) перпендикулярно к линиям индукции, если магнитное поле действует на него с силой 3,6∙10—¹² Н? Ответ выразите в км/с.
6. Электрон движется в однородном магнитном поле с индукцией 3,14мТл. Чему равен период обращения электрона? (Ответ выразите в наносекундах, округлив до целых)
2. Дано:
l = 40cм = 0,4 м,
I = 10 A,
F =8 мН = 0,008 Н.
Найти: B
Решение:
Запишем формулу модуля магнитной индукции:
Делаем расчёт:
B = 0,008 Н / ( 0,4м·10 A) = 0,002 Tл = 2 мTл.
Ответ: 2 мTл.
3. Дано:
l = 50 cм = 0,5 м,
I = 10 A,
B = 0,l5 Tл.
Найти: F
Решение:
Запишем формулу силы Ампера:
Делаем расчёт:
F = 0,l5 Tл· 10 A· 0,5 м = 0,75 Н = 750 мН
Ответ: 750 мН.
4. Дано:
B = 0,0l Tл,
r = l0 cм = 0,l м.
Найти: v
Решение:
Заряд протона равен: q₀ = l,6·l0⁻ˡ⁹ Кл,
масса протона: m = l,67·l0⁻²⁷ кг.
Согласно 2-му закону Ньютона:
Отсюда следует:
Делаем расчёт:
v = ( l,6·l0⁻ˡ⁹ Кл·0,l м·0,0l Tл) / l,67·l0⁻²⁷ кг ≈ 0,00096·l0⁸ м/с ≈ l00 км/с.
Ответ: v ≈ l00 км/с.
5. Дано:
B = l,8 Tл,
F = 3,6·l0⁻¹² Н,
α = 90°.
Найти:
Решение:
Заряд электрона равен: q₀ = l,6·l0⁻ˡ⁹ Кл.
Используем формулу силы Лоренца:
.
Выразим из формулы силы скорость, учитывая, что sin90°=l,
Делаем расчёт:
v = 3,6·l0⁻¹² Н / (l,6·l0⁻ˡ⁹ Кл· l,8 Tл) = l,25·l0⁷м/с = l2500 км/с.
Ответ: v = l2500 км/с.
6. Дано:
B = 3,l4 мТл = 3,l4·l0⁻³ Tл,
q₀ = l,6·l0⁻ˡ⁹ Кл,
Найти: Т
Решение:
Масса электрона равна: m = 9,l·l0⁻³¹ кг.
Время, за которое частица делает полный оборот (период обращения), равно:
Делаем расчёт:
T = 2·3,l4·9,l·l0⁻³¹ кг/( l,6·l0⁻ˡ⁹ Кл·3,l4·l0⁻³ Tл) = ll,375·l0⁻⁹ с ≈ ll нс.
Ответ: T ≈ ll нс.
Силы Ампера и Лоренца 10 класс онлайн-подготовка на Ростелеком Лицей
Силы Ампера и Лоренца
Магнитное поле действует не только на магниты, но и на движущиеся заряды. Здесь может быть два случая:
- Действие на движение отдельных зарядов в свободном пространстве.
- Действие на движение зарядов в проводнике.
1. Действие магнитного поля на отдельный заряд
Магнитное поле не действует на неподвижные заряды – только на движущиеся. Магнитное поле действует действует на заряды не прямолинейно, а всегда вбок.
Рассмотрим заряд, движущийся с некоторой скоростью. Если магнитное поле направленно вдоль этой скорости, то никакая сила со стороны магнитного поля не действует.
Сила появляется, если магнитное поле направленно перпендикулярно скорости частицы. Эта сила перпендикулярна и вектору индукции магнитного поля B ⃗, и скорости.
Сила, действующая на отдельный заряд со стороны магнитного поля:
Когда магнитное поле перпендикулярно скорости, сила тем больше, чем сильнее магнитное поле, больше заряд и больше его скорость:
F=qυB
Если магнитное поле направленно под углом, то разложим магнитное поле на перпендикулярную и продольную составляющие. И вспомним, что продольная составляющая не действует на частицу; действует только перпендикулярная составляющая. Т.е. в выражении для силы надо вместо B написать B⊥. Если угол между магнитным полем и скоростью alpha, то можно это выражение переписать в виде:
FL=qυBsinα
Эта сила называется силой Лоренца.
Направление этой силы можно определить с помощью правила левой руки: 1. Приложить левую руку так, чтобы скорость была направленна вдоль четырех пальцев.
2. Повернуть руку так, чтобы магнитное поле входило в ладонь.
3. Оттопыренный под прямым углом большой палец укажет направление силы.
Оттопыренный под прямым углом большой палец укажет направление силы.
Это работает для положительного заряда. Если заряд отрицательный, то направление силы будет противоположным.
2. Действие магнитного поля на проводник с током
Предположим, что магнитное поле перпендикулярно проводнику. Ток – это движение заряженных частиц, поэтому их скорости в среднем направленны вдоль проводника. И на каждую из них действует магнитное поле. Поэтому на проводник будет действовать некоторая суммарная сила, называемая силой Ампера.
В общем случае выражение для силы:
FA = IBlsinα
По сути, сила Ампера – это макроскопическое проявление силы Лоренца. Поэтому полезно сравнить размерности выражений для этих сил. Если все записано правильно, они должны совпадать. Действительно, для обоих выражений мы получаем Кл⋅м/c⋅Тл.
Направление силы Ампера также определяется правилом левой руки. Четыре пальца направляются на этот раз по току, магнитное поле входит в ладонь, большой палец указывает направление силы.
Четыре пальца направляются на этот раз по току, магнитное поле входит в ладонь, большой палец указывает направление силы.
В таблице с формулами описывающими создание поля зарядами и действие поля на заряды добавились две формулы.
Задача
Рейка с сопротивлением R, массы m и длины l может без трения скользить по двум направляющим, оставаясь при этом всегда перпендикулярным им. К направляющим подключен источник, создающий напряжение U. Система помещена в однородное магнитное поле с индукцией B, перпендикулярное плоскости рисунка. Рейку отпускают без начальной скорости. До какой скорости она разгонится, пройдя расстояние L? Сопротивлением направляющих пренебречь.
Решение
Перед нами система, которая может ускорять металлические объекты
Вспомним урок «закон сохранения энергии»
Такая система называется рельсотрон. В мирных целях, она может двигать транспорт, разгонять объекты до огромных скоростей и даже имитировать падение космических микрометеоритов.
3.3.3 Сила Ампера, её направление и величина
Видеоурок 1: Правило левой руки. сила Ампера
Видеоурок 2: Задачи на закон Ампера
Лекция: Сила Ампера, её направление и величина
Существенным отличием от электрического поля, где сила взаимодействия зависит только от величины заряда и расстояния между ними, является то, что в магнитном поле существует ряд факторов, а также несколько сил, которые действуют на проводник с током и частицы в магнитном поле.
Одной из таких сил является сила Ампера. Данная сила действует на любой проводник, по которому бежит ток. Вокруг всех частиц, которые имеют направленное движение, действуют силы, в результате чего на весь проводник действует некоторая сила.
Для определения направления данной силы используют правило левой руки:
Положите проводник мысленно на левую руку так, чтобы направление тока, который по нему бежит, совпадало с направлением четырех пальцев. Линии магнитного поля должны мысленно входить вовнутрь ладони. В таком случае направление силы Ампера совпадет с большим пальцем.
Линии магнитного поля должны мысленно входить вовнутрь ладони. В таком случае направление силы Ампера совпадет с большим пальцем.
Для определения величины силы Ампера следует воспользоваться следующей формулой:
Можно сделать вывод, что сила зависит не только от величины магнитной индукции и тока, но и от размеров и расположения проводника относительно линий магнитного поля.
Пара проводников с током
Следует отметить, что проводники, по которым бежит ток, выполняют роль магнитов. Поэтому логично будет предположить, что два таких проводника будут некоторым образом взаимодействовать:
Если ток по проводникам бежит в одном направлении, то проводники притягиваются, если в разных, то отталкиваются.
Стоит отметить, что если взять проводник в форме рамки, то силы, которые будут направлены противоположно друг к другу, заставят рамку вращаться.
Закон ампера формула и определение кратко.
 Закон ампера применение закона закон ампера. Магнитное поле и его свойства
Закон ампера применение закона закон ампера. Магнитное поле и его свойства
Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются).
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения: \(\overrightarrow{F} \)
,\(\overrightarrow{F}_{A} \)
.
Сила (\(\overrightarrow{F} \)
), которая действует на прямолинейный проводник с током (I
), всегда перпендикулярна проводнику и направлению вектора магнитной индукции (\(\overrightarrow{B} \)
). В том случае, если прямолинейный проводник расположен параллельно вдоль направления линий магнитного поля, поле не действует.
Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера.
Еще Ампер установил, что два параллельных проводника с током притягиваются, если токи имеют одинаковые направления и отталкиваются, если токи текут в противоположные стороны. Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.
Закон Ампера
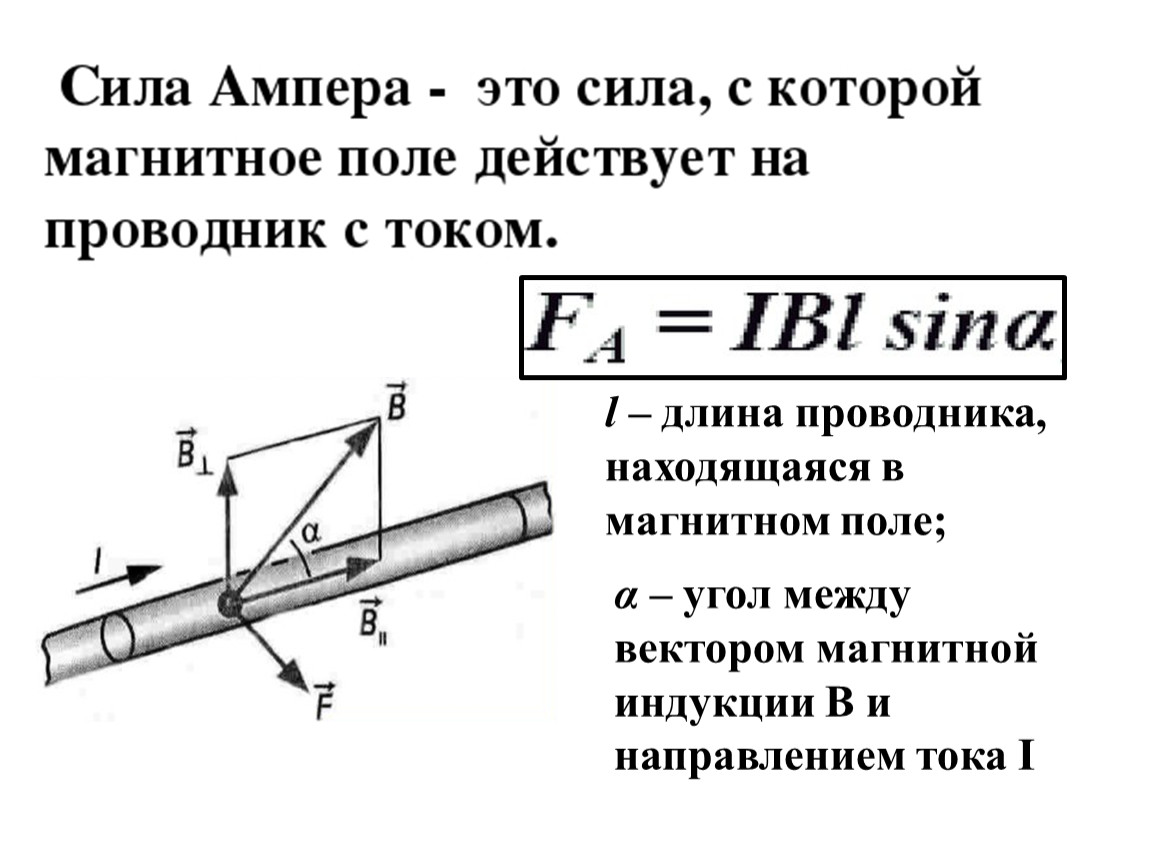
Сила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.
Для прямолинейного проводника сила Ампера
имеет вид:
\[ \large{\overrightarrow{F}_{A}} = I \cdot \overrightarrow{B} \cdot \overrightarrow{l} \cdot sin(α) \]
где: \(I \)
— сила тока, которая течет в проводнике, \(\overrightarrow{B} \)
— вектор индукции магнитного поля, в которое проводник помещен, \(\overrightarrow{l} \)
— длина проводника в поле, направление задано направлением тока, \(\alpha \)
— угол между векторами \(\overrightarrow{l\ }и\ \overrightarrow{B} \)
. {-2} \)
{-2} \)
кг, длина l=0,4м. Индукция магнитного поля равна 0,25Тл. Определите величину угла, на который отклонятся нити, на которых висит проводник с током. Проводник весь находится в поле.
Решение
Проводник расположен перпендикулярно плоскости рисунка (ток направлен от нас). Запишем условие равновесия для проводника:
\[ \overrightarrow{F_A}+\overrightarrow{mg}+2\overrightarrow{N}=0\ \left(1.1\right), \]
где \(\overrightarrow{F_A} \)
— сила Ампера, \(\overrightarrow{mg} \)
— сила тяжести, \(\overrightarrow{N} \)
— сила реакции нити.
Проектируем (1.1) на оси:
\[ X:\ -F_A-2Nsin\alpha =0\ \left(1.2\right). \]
\[ Y:\ -mg+2Ncos\alpha =0\ \left(1.3\right). \]
Разделим (1.2) на (1.3), получим:
\[ \frac{F_A}{mg}=tg\alpha \ \left(1.4\right). \]
Модуль силы Ампера для прямолинейного проводника с током, который подвешен в поле с током, причем \(\overrightarrow{B}\bot \overrightarrow{l}\ \)
равен:
\[ F_A=IBl\ \left(1.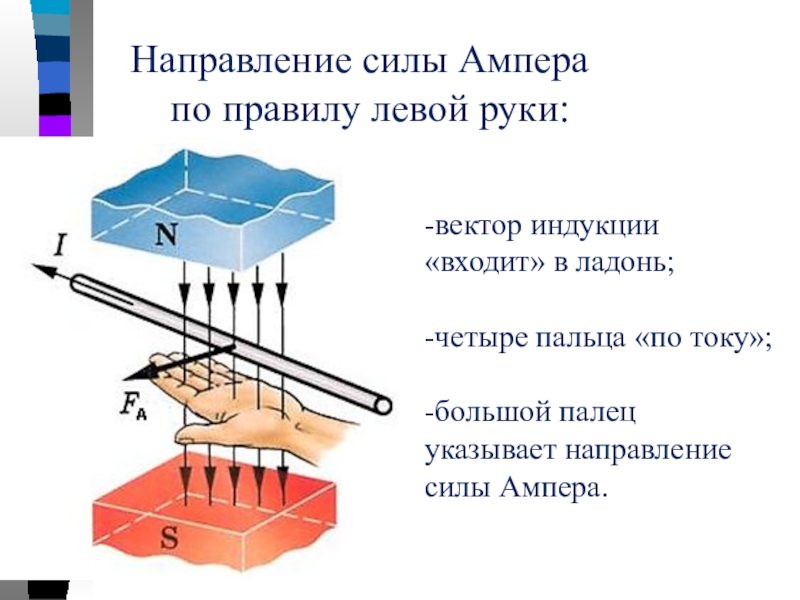 \circ \)
\circ \)
.
Пример 2
Задача
Один проводник с током имеет форму квадрата, по нему утечет ток I. В одной плоскости с рамкой лежит бесконечно длинный прямой проводник с таким же током. Расположение проводников задано на рис.3. Найдите, какова сила, действующая на рамку, если расстояние между одной из сторон рамки и проводом равно длине стороны квадрата.
Решение
Магнитное поле создается бесконечно длинным проводником с током. Модуль индукции этого поля нам известен его можно записать как:
\[ B\left(r\right)=\frac{{\mu }_0}{2\pi }\frac{I}{r}\left(2.2\right), \]
где r — расстояние от блинного проводника до точки поля.
Поле провода имеет цилиндрическую симметрию, для всех точек рамки оно будет направлено перпендикулярно. Если рассмотреть по очереди силы Ампера, которые действуют на каждый из четырех составных частей рамки, то выражение для модуля силы Ампера можно использовать в виде:
\[ F=IBlsin\alpha \ \left(2. 2}{a}. \)
2}{a}. \)
Пример 3
Задача
Однородное магнитное поле величиной двадцать Тесла удерживает от падения помещенный в него (перпендикулярно линиям магнитной индукции) прямолинейный проводник. Масса проводника четыре килограмма, длина пол метра.
Необходимо: определить силу тока в проводнике.
Данные
m=4 кг; l=0,5 м; B=20 Тл; I — ?
Решение
На прямолинейный проводник воздействуют две силы: \(F=m \cdot g \) – сила тяжести и \(F=B \cdot I \cdot l \) – сила Ампера.
Поскольку проводник не падает – эти силы равны \(m \cdot g=B \cdot I \cdot l \).
Из полученного равенства выведем формулу для определения силы тока в проводнике, помещенном в магнитное поле \(I=\dfrac{m\cdot g}{B\cdot l} \)
Подставив численные значения физических величин в формулу, определим силу тока в проводнике
\(I=\dfrac{m\cdot g}{B\cdot l}=\dfrac{4\cdot 9,8}{20\cdot 0,5}=3.92 A \)
Ответ
сила тока в проводнике равна три целых девяносто две сотых Ампера \(3.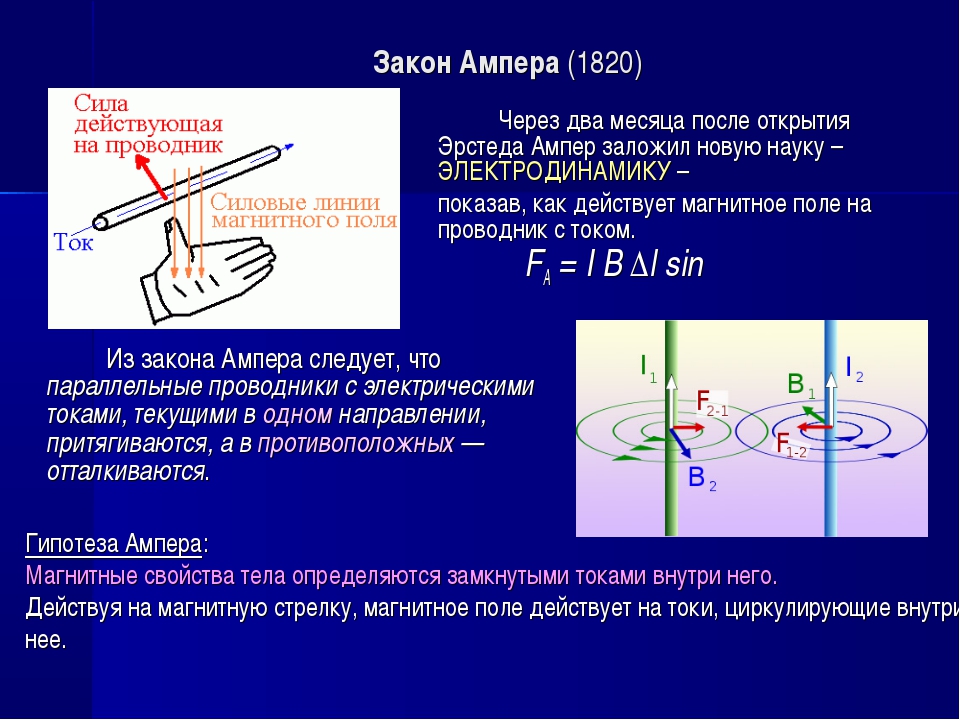 92 A \).
92 A \).
Пример 4
Задача
Прямой проводник длиной \(l = 20\) см и массой \(m = 105\) г подвешен горизонтально на двух легких нитях в однородном вертикальном магнитном поле. Модуль индукции магнитного поля \(В = 0,20\) Тл. Если по проводнику пропустить ток \(I = 5,0\) А, то нити, поддерживающие проводник, отклонятся от вертикали на угол \(\alpha \). Сколько градусов будет составлять угол \(\alpha \).
Сила,
действующая на проводник с током в
магнитном поле, называется силой
Ампера.
Сила
действия однородного магнитного поля
на проводник с током прямо пропорциональна
силе тока, длине проводника, модулю
вектора индукции магнитного поля, синусу
угла между вектором индукции магнитного
поля и проводником:
F=B . I . ℓ . sin α — закон
Ампера.
Сила,
действующая на заряженную движущуюся
частицу в магнитном поле, называется
силой
Лоренца:
Если
вектор v
частицы
перпендикуляренвектору
В
,
то
частица описывает траекторию в виде
окружности:
Роль
центростремительной силы играет сила
Лоренца:
При
этом радиус окружности: ,
Если
вектор скорости и
частицы
не перпендикулярен В,
то
частица описывает траекторию в виде
винтовой линии (спирали).
44.
Теорема о циркуляции вектора магнитной
индукции. Применение теоремы о циркуляции
вектора магнитной индукции для расчета
поля прямого тока.
Циркуляция вектора
магнитной индукции через замкнутый
контур=произведению магнитной постоянной
на алгебраическую сумму токов, охватываемых
контуром.
∫BdL=μ 0 I;
I=ΣI i
Теорема
говорит о том, что магнитное поле не
является потенциальным, а является
вихревым.
Применение
в тетради
45. Закон электромагнитной индукции. Правило Ленца
Фарадей
экспериментально установил, что при
изменении магнитного потока в проводящем
контуре возникает ЭДС индукции ε инд,
равная скорости изменения магнитного
потока через поверхность, ограниченную
контуром, взятой со знаком минус:
Эта
формула носит название закона
Фарадея
.
Опыт
показывает, что индукционный ток,
возбуждаемый в замкнутом контуре при
изменении магнитного потока, всегда
направлен так, что создаваемое им
магнитное поле препятствует изменению
магнитного потока, вызывающего
индукционный ток. Это утверждение,
Это утверждение,
сформулированное в 1833 г.,
называется правилом Ленца
.
Правило
Ленца отражает тот экспериментальный
факт, что ε инд ивсегда
имеют противоположные знаки (знак
«минус» в формуле Фарадея). Правило
Ленца имеет глубокий физический смысл
– оно выражает закон сохранения энергии.
ε i =-N,
гдеN- кол-во витков
Способ
возникновения ЭДС:
1.рамка
неподвижна, но изменяется магнитный
поток за счёт движения ккатушки или за
счет изменения силы тока в ней.
2.рамка
перемещается в поле непожвижной катушки.
46. Явление самоиндукции.
Возникновение
ЭДС индукции в проводящем контуре при
изменении в нем силы тока называется
явлением самоиндукции.
Магнитный
поток, обусловленный собственным током
контура (сцепленный с контуром),
пропорционален магнитной индукции,
которая, в свою очередь, по закону
Био-Савара-Лапласа, пропорциональна
току.
Где L –коэффициент самоиндукции или
индуктивность, «геометрическая»
характеристика проводника, так как
зависит от его формы и размеров, а также
от магнитных свойств среды.
47. Уравнения Максвелла в интегральной форме. Свойства уравнений Максвелла.
Закон
Гаусса
Поток
электрической индукции через замкнутую
поверхность s пропорционален величине
свободного заряда, находящегося в объёме
v, который окружает поверхность s.
Закон
Гаусса для магнитного поля
Поток магнитной индукции через
замкнутую поверхность равен нулю
(магнитные заряды не существуют).
Закон
индукции Фарадея
Изменение потока
магнитной индукции, проходящего через
незамкнутую поверхность,
взятое с обратным знаком, пропорционально
циркуляции электрического поля на
замкнутом контуре,
который является границей поверхности.
Теорема
о циркуляции магнитного поля
Полный
электрический ток свободных зарядов и
изменение потока электрической индукции
через незамкнутую поверхность ,
пропорциональны циркуляции магнитного
поля на замкнутом контуре,
который является границей поверхности.
Свойства
уравнений Максвелла.
А. Уравнения
Максвелла линейны
. Они содержат только
Они содержат только
первые производные полейEиBпо времени и
пространственным координатам, а так же
первые степени плотности электрических
зарядов ρ и токов γ. Свойство линейности
уравнений непосредственно связано с
принципом суперпозиции.
Б. Уравнения
Максвелла содержат уравнение непрерывности
,
выражающее закон сохранения электрического
заряда:
В. Уравнения
Максвелла выполняются во всех инерциальных
системах отсчёта
. Они являются
релятивистски-инвариантными, что
подтверждается опытными данными.
Г. О
симметрии
уравнений Максвелла
.
Уравнения
не симметричны относительно электрического
и магнитного полей. Это обусловлено
тем, что в природе существуют электрические
заряды, но нет магнитных зарядов. Вместе
с тем в нейтральной однородной среде,
где ρ = 0 и j=0 ,уравнения
Максвелла приобретают симметричный
вид, т.е.Eтак связано
с(dB/dt) ,
какBсdE/dt.
Д. Об
электромагнитных волнах
.
Из
уравнений Максвелла следует важный
вывод о существовании принципиально
нового физического явления: электромагнитное
поле способно существовать самостоятельно
без электрических зарядов и токов. При
При
этом изменение его состояния обязательно
имеет волновой характер. Всякое изменение
во времени магнитного поля возбуждает
поле электрическое, изменение
электрического поля, в свою очередь,
возбуждает магнитное поле. За счёт
непрерывного взаимопревращения они и
должны сохранятся. Поля такого рода
называются электромагнитными волнами
.
Выяснилось также, что ток
смещения(dD/dt) играет
в этом явлении первостепенную роль.
Магнитное поле и его свойства.
Магнитное поле это материя, которая возникает вокруг источников электрического тока, а также вокруг постоянных магнитов. В пространстве магнитное поле отображается как совокупление сил, которые способны оказать воздействие на намагниченные тела. Это действие объясняется наличием движущих разрядов на молекулярном уровне.
Магнитное поле формируется только вокруг электрических зарядов, которые находятся в движении. Именно поэтому магнитное и электрическое поле являются, неотъемлемыми и вместе формируют электромагнитное поле
. Компоненты магнитного поля взаимосвязаны и воздействуют друг на друга, изменяя свои свойства.
Компоненты магнитного поля взаимосвязаны и воздействуют друг на друга, изменяя свои свойства.
Свойства магнитного поля:
1. Магнитное поле возникает под воздействие движущих зарядов электрического тока.
2. В любой своей точке магнитное поле характеризуется вектором физической величины под названием магнитная индукция
, которая является силовой характеристикой магнитного поля.
3. Магнитное поле может воздействовать только на магниты, на токопроводящие проводники и движущиеся заряды.
4. Магнитное поле может быть постоянного и переменного типа
5. Магнитное поле измеряется только специальными приборами и не может быть воспринятым органами чувств человека.
6. Магнитное поля является электродинамическим, так как порождается только при движении заряженных частиц и оказывает влияние только на заряды, которые находятся в движении.
7. Заряженные частицы двигаются по перпендикулярной траектории.
Магнитные линии, определение их направления.
Направление линий магнитного поля тока зависит от направления тока в проводнике.
Эта связь может быть выражена простым правилом, которое называют правилом буравчика
(или правилом правого винта).
Правило буравчика заключается в следующем:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий, магнитного поля тока
.
С помощью правила буравчика по направлению тока можно определить направление линий магнитного поля, создаваемого этим током, а по направлению линий магнитного поля — направление тока, создающего это поле.
Сила Ампера (определение, формула, направление).
Сила Ампера это та сила, с которой магнитное поле действует на проводник, с током помещённый в это поле. Величину этой силы можно определить с помощью закона Ампера. В этом законе определяется бесконечно малая сила для бесконечно малого участка проводника.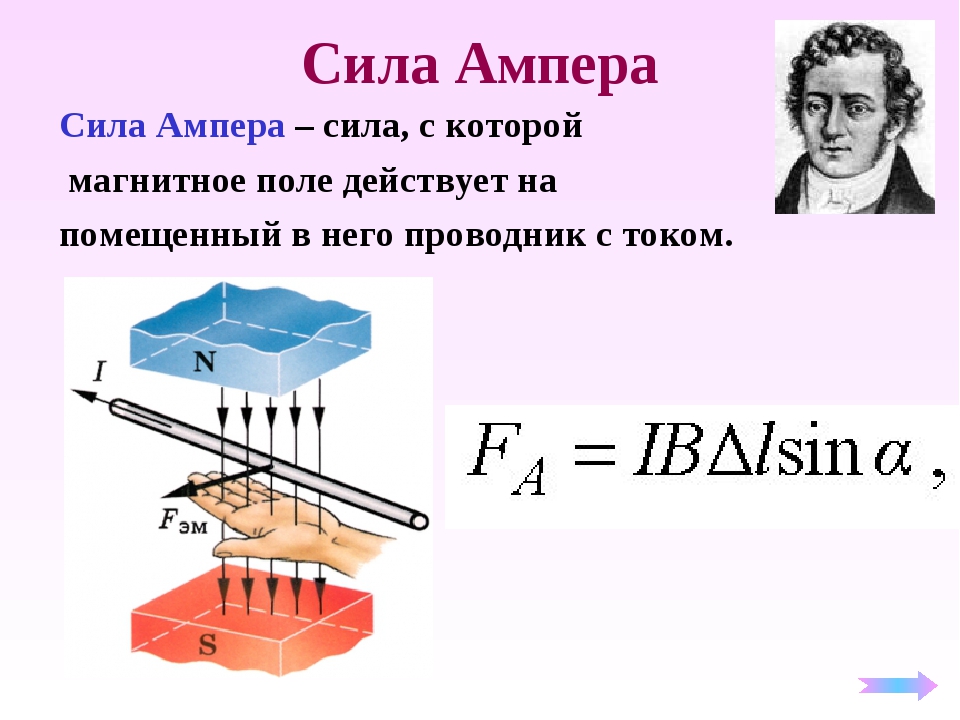 Что дает возможность применять этот закон для проводников различной формы.
Что дает возможность применять этот закон для проводников различной формы.
Направление силы Ампера находится по правилу левой руки. Когда левая рука расположена таким образом, что лини магнитной индукции внешнего поля входят в ладонь, а четыре вытянутых пальца указывают направление движения тока в проводнике, при этом отогнутый под прямым углом большой палец будет указывать направление силы, которая действует на элемент проводника.
— один из важнейших и полезнейших законов в электротехнике, без которого немыслим научно-технический прогресс. Этот закон был впервые сформулирован в 1820 году Андре Мари Ампером. Из него следует, что два расположенные параллельно проводника, по которым проходит электрический ток, притягиваются, если направления токов совпадают, а если течёт в противоположных направлениях, то проводники отталкиваются. Взаимодействие здесь происходит посредством магнитного поля, которое перманентно возникает при движении заряженных частиц. Математически закон Ампера в простой форме выглядит так:
F = BILsinα,
где F — это сила Ампера (сила, с которой проводники отталкиваются или притягиваются), где B — ; I — сила тока; L — длина проводника; α — угол между направлением тока и направлением магнитной индукции.
Интересное видео с уроком о силе Ампера:
Любые узлы в электротехнике, где под действием происходит движение каких-либо элементов, используют закон Ампера. Самый широко распространённый и используемый чуть-ли не во всех технических конструкциях агрегат, в основе своей работы использующий закон Ампера — это электродвигатель, либо, что конструктивно почти то же самое, генератор.
Именно под действием силы Ампера происходит вращение ротора, поскольку на его обмотку влияет магнитное поле статора, приводя в движение. Любые транспортные средства на электротяге для приведения во вращение валов, на которых находятся колёса, используют силу Ампера (трамваи, электрокары, электропоезда и др). Также магнитное поле приводит в движение механизмы электрозапоров (электродвери, раздвигающиеся ворота, двери лифта). Другими словами, любые устройства, которые работают на электричестве и имеющие вращающиеся узлы основаны на эксплуатации закона Ампера. Также он находит применение во многих других видах , например, в громкоговорителях.
В громкоговорителе или динамике для возбуждения мембраны, которая формирует звуковые колебания используется постоянный магнит. На него под действием электромагнитного поля, создаваемого расположенным рядом проводником с током, действует сила Ампера, которая изменяется в соответствии с нужной звуковой частотой.
Ещё одно видео о законе Ампера смотрите ниже:
 Гидравлический пресс. Золотое правило механики
Гидравлический пресс. Золотое правило механики Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы — изотерма, изобара, изохора
Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы — изотерма, изобара, изохора Электрические цепи — последовательное и параллельное соединение. Правила Кирхгофа.
Электрические цепи — последовательное и параллельное соединение. Правила Кирхгофа.Магнитное поле. Вектор магнитной индукции. Правило буравчика. Закон Ампера и сила Ампера. Сила Лоренца. Правило левой руки. Электромагнитная индукция, магнитный поток, правило Ленца, закон электромагнитной индукции, самоиндукция, энергия магнитного поля
 Зависимость массы от скорости. Основной закон релятивистский динамики…
Зависимость массы от скорости. Основной закон релятивистский динамики…Закон Ампера
Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются).
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения: \( \overrightarrow{F} \),\( \overrightarrow{F}_{A} \).
Сила (\( \overrightarrow{F} \)), которая действует на прямолинейный проводник с током (I), всегда перпендикулярна проводнику и направлению вектора магнитной индукции (\( \overrightarrow{B} \)). В том случае, если прямолинейный проводник расположен параллельно вдоль направления линий магнитного поля, поле не действует.
В том случае, если прямолинейный проводник расположен параллельно вдоль направления линий магнитного поля, поле не действует.
Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера.
Еще Ампер установил, что два параллельных проводника с током притягиваются, если токи имеют одинаковые направления и отталкиваются, если токи текут в противоположные стороны. Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.
Закон Ампера
Сила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.
Для прямолинейного проводника сила Ампера имеет вид:
\[ \large{\overrightarrow{F}_{A}} = I \cdot \overrightarrow{B} \cdot \overrightarrow{l} \cdot sin(α) \]
где: \( I \) — сила тока, которая течет в проводнике, \( \overrightarrow{B} \) — вектор индукции магнитного поля, в которое проводник помещен, \( \overrightarrow{l} \) — длина проводника в поле, направление задано направлением тока, \( \alpha \) — угол между векторами \( \overrightarrow{l\ }и\ \overrightarrow{B} \).
Этой формулой можно пользоваться:
- если длина проводника такая, что индукция во всех точках проводника может считаться одинаковой;
- если магнитное поле однородное (тогда длина проводника может быть любой, но при этом проводник целиком должен находиться в поле).
Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:
\[ \large{d\overrightarrow{F}_{A}} = I \cdot \overrightarrow{B} \cdot d\overrightarrow{l} \cdot sin(α) \]
Значение закона Ампера
На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. {-7} \) Ньютона.
{-7} \) Ньютона.
Закон взаимодействия токов – два находящихся в вакууме параллельных проводника, диаметры которых много меньше расстояний между ними, взаимодействуют с силой прямо пропорциональной произведению токов в этих проводниках и обратно пропорциональной расстоянию между ними.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsbox
Закон Ампера: определение и примеры — видео и расшифровка урока
Уравнение
Поле, создаваемое длинным прямым проводом с током, имеет форму концентрических окружностей. И по мере того, как вы удаляетесь от проволоки, эти круги становятся все дальше друг от друга — или, другими словами, поле становится слабее. Мы могли бы составить для этого уравнение, используя закон Ампера и проведя некоторые вычисления. Но на самом деле мы можем вывести это уравнение вообще без каких-либо вычислений.
Вместо интеграла будем использовать сумму.Сумма всех элементов магнитного поля, составляющих концентрическую окружность: магнитное поле B умножить на длину элемента дельта-L равно мю-ноль (проницаемость свободного пространства) умножить на ток в провод я . Это Закон Ампера.
Затем осознайте, что суммируя все эти элементы, ваша дельта-L становится окружностью концентрического круга, 2pi r .-6. I — ток, протекающий по проводу, измеряется в амперах. А r — это радиальное расстояние от вас до провода, измеряемое в метрах. Таким образом, вы можете использовать это уравнение, чтобы вычислить напряженность магнитного поля на расстоянии r от провода с током.
Благодаря уравнению можно рассчитать силу поля. Но как быть с направлением? Для этого мне нужно, чтобы вы показали мне большой палец вверх правой рукой. Нет, серьезно, сделай это прямо сейчас.
Используя эту схему токоведущего провода, укажите большим пальцем в направлении движения тока, в направлении стрелки, обозначенной I . Теперь представьте, что вы обхватываете провод пальцами, хватая его. Направление, на которое указывают ваши пальцы, представляет направление, на которое указывают линии поля — куда идут стрелки на концентрических кругах. Это называется правилом правой руки, и очень важно, чтобы вы случайно не использовали левую руку, потому что вы получите совершенно неверный ответ.
Примеры
Хорошо, давайте рассмотрим пример. Допустим, у вас есть провод с током, указывающий строго на север. Если по проводу течет ток 0,1 ампер, какова величина и направление магнитного поля на расстоянии 0,01 м над проводом?
Прежде всего, давайте запишем то, что мы знаем. Ток I равен 0,1, расстояние от провода r равно 0.-6 тесла. И в этом наша величина.
Чтобы определить направление, вы можете нарисовать ток на листе бумаги, указав вверх к верхней части страницы, которую вы можете отметить на север. Теперь поднимите большой палец вверх правой рукой, также направьте большой палец к верхней части страницы и представьте, что ваши пальцы скручиваются вокруг проволоки. Если вы сделаете это правильно, вы увидите, что ваши пальцы будут указывать налево под проволокой и направо над проволокой. Если вверху страницы север, то справа будет восток.-6 тесла на восток.
Теперь поднимите большой палец вверх правой рукой, также направьте большой палец к верхней части страницы и представьте, что ваши пальцы скручиваются вокруг проволоки. Если вы сделаете это правильно, вы увидите, что ваши пальцы будут указывать налево под проволокой и направо над проволокой. Если вверху страницы север, то справа будет восток.-6 тесла на восток.
Краткий обзор урока
Полная версия закона Ампера — одно из уравнений Максвелла, описывающих электромагнитное взаимодействие. Закон Ампера , в частности, говорит, что магнитное поле, создаваемое электрическим током, пропорционально величине этого электрического тока с константой пропорциональности, равной проницаемости свободного пространства. Стационарные заряды создают электрические поля, пропорциональные величине заряда. Но движущиеся заряды создают магнитные поля, пропорциональные току (заряд и движение).
Единственная проблема с законом Ампера заключается в том, что это дифференциальное уравнение, другими словами, чтобы его использовать, вам нужно выполнить некоторые вычисления. Но мы можем избежать этого, взглянув на результат всех этих расчетов для конкретной ситуации. Если мы изучим магнитное поле, создаваемое длинным прямым проводом с током, мы получим это окончательное уравнение для поля, создаваемого проводом с током.
Но мы можем избежать этого, взглянув на результат всех этих расчетов для конкретной ситуации. Если мы изучим магнитное поле, создаваемое длинным прямым проводом с током, мы получим это окончательное уравнение для поля, создаваемого проводом с током.
Здесь B — магнитное поле в конкретной точке пространства, измеряемое в теслах.-6. I — ток, протекающий по проводу, измеряется в амперах. А r — это радиальное расстояние от вас до провода, измеряемое в метрах. Таким образом, вы можете использовать это уравнение, чтобы вычислить напряженность магнитного поля на расстоянии r от провода с током. Чтобы определить направление этого поля, мы должны использовать правило правой руки и указать большим пальцем направление тока.
Результаты обучения
После того, как вы закончите этот урок, вы должны быть в состоянии:
- Государственный закон Ампера
- Рассчитайте магнитное поле провода с током, используя закон Ампера
- Вызов правила правой руки при вычислении текущего направления
Электромагнитная сила – Гиперучебник по физике
Обсуждение
введение
Магнетизм — это сила, с которой движущиеся заряды действуют друг на друга.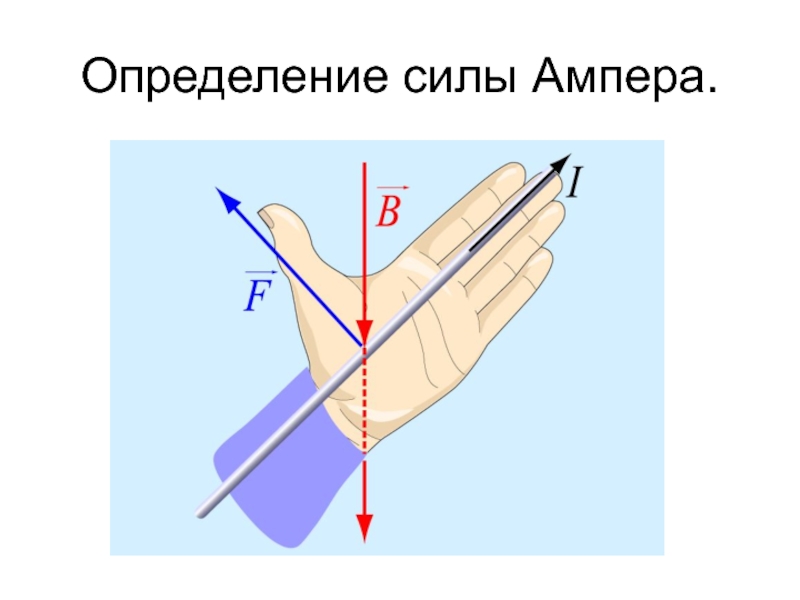 Это формальное определение основано на этом простом уравнении.
Это формальное определение основано на этом простом уравнении.
F B = q v × B
Вспомним, что электричество — это (по сути) сила, с которой заряды действуют друг на друга. Поскольку эта сила существует независимо от того, движутся заряды или нет, ее иногда называют электростатической силой. Можно сказать, что магнетизм является электродинамической силой, но так бывает редко. Сочетание электрических и магнитных сил, действующих на заряженный объект, известно как сила Лоренца .
F = q ( E + v × B )
Для больших объемов заряда…
| F B = q | v × B | ||||
| F B = q | д х | × В = | дк | ℓ × Б | |
| дт | дт | ||||
| F B = I | ℓ × B | ||||
Эта формула для магнитной силы на проводе с током является основой для эксперимента, который использовался для определения ампера с 1948 по 2019 год.
Ампер — это такой постоянный ток, который, если его поддерживать в двух прямых параллельных проводниках бесконечной длины, с ничтожно малым круглым поперечным сечением, расположенных на расстоянии одного метра друг от друга в вакууме, создавал бы между этими проводниками силу, равную 2 × 10 −7 ньютонов на метр длины
МБМВ, 1948
Используя закон Ампера, мы вывели формулу для силы магнитного поля, окружающего длинную прямолинейную проволоку с током…
Подставьте это выражение в формулу магнитной силы.(Поскольку два провода параллельны, поле одного из них падает на другой под прямым углом, и перекрестное произведение сводится к прямому умножению.) Решите силу на единицу длины, как описано в эксперименте…
| Ф Б | = | I ℓ × B | ||
| Ф Б | = | л | мк 0 I | |
| 2π р | ||||
| Ф Б | = | мк 0 I 2 | ||
| ℓ | 2π р | |||
Это устанавливает необычно точное значение проницаемости свободного пространства (необычно точное для физической константы). Подставьте значения для измерений, описанных в эксперименте BIPM, в последнее полученное уравнение…
Подставьте значения для измерений, описанных в эксперименте BIPM, в последнее полученное уравнение…
| = | ||
| (2 × 10 −7 N) | = | мк 0 (1 А) 2 |
| (1 м) | 2π(1 м) |
и решить для проницаемости свободного пространства…
| мк 0 = | 2π(1 м)(2 × 10 −7 Н) | |
| (1 м)(1 А) 2 | ||
| мк 0 = | 4π × 10 −7 Н/Д 2 | |
Возвращение к формуле для магнитной силы, действующей на провод с током, приводит к следующему определению напряженности магнитного поля и ее единицы, тесла.
| d F B = I d ℓ × × | ⇒ | В = | Ф Б | ⇒ | ⎡ ⎢ ⎣ | Т = | Н | ⎤ ⎥ ⎦ |
| л | Ам |
Третье правило правой/левой руки
Электронно-лучевая трубка: цветной телевизор (цветной монитор), осциллограф,
./lorentz/crt.svg»> Увеличить
масс-спектрометр
циклотрон
космическая погода, полярное сияние, радиационные пояса Ван Аллена
электродвигатель
электромагнитный рельсовый пистолет
ядерный магнитный резонанс?
Электромагнитные силы и поля
Стержневой магнит притягивает железные предметы к своим концам, называемым полюсами .Один конец — это северный полюс , а другой — южный полюс . Если стержень подвешен так, что он может свободно двигаться, магнит выровняется так, что его северный полюс будет указывать на географический север Земли. Подвешенный стержневой магнит действует как компас в магнитном поле Земли. Если два стержневых магнита сблизить, то одноименные полюса будут отталкиваться, а разноименные притягиваться. (Примечание: по этому определению магнитный полюс под северным географическим полюсом Земли является южным полюсом магнитного поля Земли. )
)
Это магнитное притяжение или отталкивание можно объяснить как воздействие одного магнита на другой, или можно сказать, что один магнит создает магнитное поле в области вокруг него, которое воздействует на другой магнит. Магнитное поле в любой точке является вектором. Направление магнитного поля ( B ) в указанной точке — это направление, которое северный конец стрелки компаса указывает на это положение. Линии магнитного поля , аналогичные силовым линиям электрического поля, описывают силу, действующую на магнитные частицы, помещенные в поле.Железные опилки будут выровнены, чтобы показать образцы линий магнитного поля.
Сила на движущийся заряд
Если заряд движется через магнитное поле под углом, на него действует сила. Уравнение имеет вид F = q v × B или F = qvB sin θ, где q — заряд, B — магнитное поле, v — скорость, а θ — угол между направлениями магнитного поля и скорости; таким образом, используя определение перекрестного произведения, определение магнитного поля равно
Магнитное поле выражается в единицах СИ как тесла (Тл), который также называется вебером на квадратный метр:
Направление F определяется по правилу правой руки, показанному на рисунке 1.
| ||
Чтобы найти направление силы, действующей на заряд, направьте большой палец ладони в направлении скорости положительного заряда, а остальные — в направлении магнитного поля.Направление силы выходит за пределы ладони. (Если движущийся заряд отрицателен, укажите большим пальцем направление, противоположное его движению.) Математически эта сила представляет собой перекрестное произведение вектора скорости и вектора магнитного поля.
Если скорость заряженной частицы перпендикулярна однородному магнитному полю, сила всегда будет направлена к центру окружности радиусом r , как показано на рисунке 2. x символизирует магнитное поле в плоскость бумаги — хвост стрелы.(Точка обозначает вектор вне плоскости бумаги — кончик стрелки.)
x символизирует магнитное поле в плоскость бумаги — хвост стрелы.(Точка обозначает вектор вне плоскости бумаги — кончик стрелки.)
| ||
Магнитная сила обеспечивает центростремительное ускорение:
или
Радиус пути пропорционален массе заряда.Это уравнение лежит в основе работы масс-спектрометра , который может разделять одинаково ионизированные атомы немного разных масс. Однократно ионизированным атомам даны равные скорости, и поскольку их заряды одинаковы и они проходят через одни и те же B , они будут двигаться немного разными путями и затем могут быть разделены.
Сила, действующая на проводник с током
Заряды, закрепленные в проводах, также могут испытывать силу в магнитном поле.На ток (I) в магнитном поле ( B ) действует сила ( F ), определяемая уравнением длина провода, представленная вектором, указывающим в направлении тока. Направление силы можно найти по правилу правой руки, аналогичному показанному на рис. В этом случае укажите большим пальцем направление тока — направление движения положительных зарядов.Ток не будет испытывать силы, если он параллелен магнитному полю.
Крутящий момент в токовой петле
Петля с током в магнитном поле может испытывать крутящий момент, если она может свободно вращаться. На рисунке (а) изображена квадратная петля из проволоки в магнитном поле, направленном вправо. Представьте на рисунке (b), что ось провода повернута под углом (θ) к магнитному полю, и что вид смотрит вниз на верхнюю часть петли. x в круге изображает ток, идущий на страницу от зрителя, а точка в круге изображает ток, выходящий из страницы к зрителю.
Рисунок 3
6.2: Определение силы тока
Мы видели, что электрический ток окружен магнитным полем; а также то, что если провод, по которому течет ток, находится во внешнем магнитном поле, на него действует сила, направленная под прямым углом к току. Поэтому неудивительно, что два проводника с током действуют друг на друга.
Точнее, если есть два параллельных провода, по каждому из которых течет ток в одном и том же направлении, два провода будут притягиваться друг к другу с силой, которая зависит от силы тока в каждом из них и расстояния между проводами.
Определение. Один ампер (называемый также ампером) представляет собой постоянный ток, который, протекая по каждому из двух параллельных проводов незначительного поперечного сечения на расстоянии одного метра друг от друга в вакууме , вызывает между ними силу, равную 2 × 10 — 7 ньютонов на метр их длины.
Наконец-то! Теперь мы знаем, что такое ампер, а следовательно, знаем, что такое кулон, вольт и ом. До сих пор мы оставались в состоянии неопределенности. Больше никогда!
До сих пор мы оставались в состоянии неопределенности. Больше никогда!
Но вы можете спросить: почему множитель 2 × 10 -7 ? Почему бы не определить усилитель таким образом, чтобы сила была равна 1 Н·м -1 ? Это хороший вопрос, и ответ на него связан с долгой и мучительной историей единиц в электромагнетизме.Я, вероятно, рассмотрю эту историю и различные единицы «CGS» в одной из последующих глав. Короче говоря, потребовалось много времени, чтобы понять, что электростатика, магнетизм и ток электричества были аспектами одних и тех же основных явлений, и в каждой теме развивались разные системы единиц. В частности, так называемая «практическая» единица, -ампер (определяемая по скорости осаждения серебра из раствора электролита) настолько укоренилась, что отказываться от нее казалось непрактичным.Следовательно, когда все различные системы электромагнитных единиц были объединены в двадцатом веке (начиная с предложений Георгия, основанных на метре, килограмме и секунде (МКС) еще в 1895 году) в «Международной системе» (СИ), это было определил, что основная единица тока должна быть идентична тому, что всегда было известно как ампер. (Между прочим, множитель 2 не связан с тем, что в определении они являются двумя проводами.) Усилитель — единственная единица СИ, в определение которой включено любое число, кроме «единицы», и это исключение было навязано желание сохранить усилок.
(Между прочим, множитель 2 не связан с тем, что в определении они являются двумя проводами.) Усилитель — единственная единица СИ, в определение которой включено любое число, кроме «единицы», и это исключение было навязано желание сохранить усилок.
Предложение, которое будет рассмотрено (и, возможно, принято) Генеральной конференцией по весам и размерам в 2018 году, предполагает переопределение кулона таким образом, чтобы величина заряда одного электрона была точно равна 1,60217 x 10 — 19 С.
Последний пункт перед тем, как покинуть этот раздел. В первом абзаце я написал: «Поэтому неудивительно, что два проводника с током действуют друг на друга». Тем не менее, когда я впервые узнал, будучи студентом, о взаимном притяжении двух параллельных электрических токов, я был очень удивлен.Причина, по которой это удивительно, обсуждается в главе 15 (Специальная теория относительности) раздела «Классическая механика» этих заметок.
Закон Ампера
Закон Ампера
Следующая: Сила Лоренца
Вверх: Магнетизм
Предыдущий: Эксперименты Ампера
Магнитные поля, как и электрические поля, полностью
накладной . Так что если
Так что если
поле создается током, протекающим по некоторой цепи,
а поле создается током, протекающим через другой
цепи, то когда токи и протекают по обеим цепям
одновременно генерируемое магнитное поле
.Это верно во всех точках пространства.
Рассмотрим два параллельных провода, разделенных перпендикулярным расстоянием ,
проводящие электрические токи и , соответственно. Напряженность магнитного поля во втором проводе из-за тока, протекающего в первом проводе
является
. Это поле ориентировано под прямым углом ко второму
провода, поэтому сила на единицу длины, действующая на второй провод, равна
| (156) |
Это следует из уравнения(152), справедливое как для непрерывных проводов, так и для коротких
тестовые провода. Сила, действующая на вторую проволоку, направлена радиально внутрь к
Сила, действующая на вторую проволоку, направлена радиально внутрь к
первый провод. Напряженность магнитного поля на первом проводе из-за
ток, протекающий по второму проводу, равен
. Это поле
ориентирована под прямым углом к первому проводу, поэтому сила, действующая на единицу длины
на первый провод равен и противоположен действующему на второй провод,
согласно уравнению (152). Уравнение (156) называется законом Ампера .
Кстати, уравнение. (156) является основой официального определения СИ
ампер , что составляет:
Один ампер – это величина силы тока, которая при протекании в
каждый из двух длинных параллельных проводов на расстоянии одного метра друг от друга приводит к силе
между проводами ровно
Н на метр длины.
Мы видим, что константа не случайно имеет
числовое значение ровно
.
Система единиц СИ основана на четырех стандартных единицах: метр ,
килограммов , секунд и ампер . Следовательно, система СИ
Следовательно, система СИ
иногда упоминается как система MKSA. Все остальные единицы могут быть получены
из этих четырех стандартных единиц. Например, кулон эквивалентен
ампер-секунда. Вам может быть интересно, почему ампер является стандартом
электрическая единица, а не кулон, так как последняя единица
явно более фундаментальный, чем первый. Ответ прост. Очень трудно
для точного измерения заряда, в то время как легко точно измерить электрический
Текущий. Ясно, что имеет смысл определить стандартную единицу в терминах
чего-то легко измеримого, а не того, что
трудно измерить.
Следующая: Сила Лоренца
Вверх: Магнетизм
Предыдущий: Эксперименты Ампера
2007-07-14
Устаревшая формула? · История электричества и магнетизма (сайт Ampère)
Accueil > Исторические парки… de la boussole à la Fée électricité > Des lois pour le courant: Ampère, Ohm et quelques autres… > Закон силы Ампера: устаревшая формула?
Французский
Кристин Блондель и Бертран Вольф
Перевод Эндрю Бутрики
Нередко в науке прошлого можно найти некоторые работы, которые никогда не считались недействительными, но исчезли из современной науки. Они могли быть отвергнуты последующими работами, признанными более эффективными, или от них отказались, потому что они не представляли особого интереса, или были дискредитированы по ненаучным причинам, или просто были забыты. Их статус оставался неопределенным. Однако в любой момент ученые могут взяться за такую невостребованную работу по разным причинам. Так обстоит дело с силой Ампера.
Они могли быть отвергнуты последующими работами, признанными более эффективными, или от них отказались, потому что они не представляли особого интереса, или были дискредитированы по ненаучным причинам, или просто были забыты. Их статус оставался неопределенным. Однако в любой момент ученые могут взяться за такую невостребованную работу по разным причинам. Так обстоит дело с силой Ампера.
Электродинамическая теория Ампера основана на существовании силы между двумя элементами тока, и математическое выражение этой силы подразумевает отталкивание между двумя выровненными элементами.Однако это взаимодействие между коллинеарными элементами исчезло с появлением элементарной силы Грассмана (1845 г.), силы, которая теперь составляет неотъемлемую часть современной теории электромагнетизма.
Чтобы сделать выбор между амперовским и грассмановским выражениями электродинамической силы, можно поискать опыты, основанные на существовании или отсутствии отталкивания между коллинеарными элементами электрической цепи. Тем не менее прямая проверка формулы Ампера и ее применения к частному случаю коллинеарных элементов невозможна.Действительно, нельзя изолировать токоведущие элементы внутри электрической цепи. Однако Ампер думал, что у него есть экспериментальное доказательство отталкивания коллинеарных элементов. Мы обсудим различные эксперименты, предложенные в конце двадцатого века в продолжение эксперимента Ампера и способные продемонстрировать существование этой силы. Интерпретация этих экспериментов до сих пор вызывает споры.
Тем не менее прямая проверка формулы Ампера и ее применения к частному случаю коллинеарных элементов невозможна.Действительно, нельзя изолировать токоведущие элементы внутри электрической цепи. Однако Ампер думал, что у него есть экспериментальное доказательство отталкивания коллинеарных элементов. Мы обсудим различные эксперименты, предложенные в конце двадцатого века в продолжение эксперимента Ампера и способные продемонстрировать существование этой силы. Интерпретация этих экспериментов до сих пор вызывает споры.
С теоретической точки зрения совместимость между теорией Максвелла-Лоренца и силой Ампера также является предметом споров.
Наконец, для некоторых защита силы Ампера является частью более крупного проекта, состоящего в разработке — вслед за Вебером и Нейманом — «ньютоновской» альтернативы теории Максвелла, использующей только взаимодействия на расстоянии между материальными элементами без обращения к электромагнитному полю. Этот проект может показаться безрассудным и основанным на шатком фундаменте, в то время как теория Максвелла, связанная с теорией относительности Эйнштейна, составляет главный столп современной физики.
Мы заключаем, тем не менее, вслед за самим Максвеллом, что желательно, чтобы сама жизнь науки оставляла открытым ряд путей: «Хорошо иметь два взгляда на предмет и признать, что там есть два взгляда на это.»» ( The Scientific Papers of James Clerk Maxwell , т. 1, стр. 208)
1873: «Формула, из которой можно вывести все явления…»
Согласно самому Максвеллу, «теория Ампера «суммирована в формуле, из которой могут быть выведены все явления и которая всегда должна оставаться основной формулой электродинамики». 1873, т. 2, стр. 175).
Эта фундаментальная формула Ампера выражает силу, действующую со стороны одного бесконечно малого элемента тока ids на другой элемент бесконечно малого тока i’ds’, расположенных на расстоянии r друг от друга и относительные положения которых определяются тремя углами α, β и γ [ См. стр. В поисках ньютоновского закона электродинамики ].
Рис. |
По этой формуле Ампер мог путем двойного интегрирования вычислить все взаимодействия между реальными цепями.Применяя этот метод к малым круговым токам, которые он предполагал существование внутри магнитов, он получил законы взаимодействия между двумя магнитами или между магнитом и током. Опираясь на эту формулу, можно, как писал Максвелл, «выводить все явления».
1958: формула, которая «больше не служит никакой цели»
В 1958 году Эдмон Бауэр, который сотрудничал с Полем Ланжевеном над его теорией магнетизма, перерабатывая фундаментальные идеи Ампера, переиздал великий синтез Ампера, Математическая теория электродинамических явлений, однозначно выведенная из эксперимента. В своем предисловии, которое в других местах весьма хвалебно, Бауэр писал: «»знаменитая формула Ампера больше не служит никакой цели»». Действительно, после того, как теория Ампера преобладала во Франции до 1890-х годов, постепенно от нее отказались. В начале двадцатого века физик Анри Буасс мог утверждать в своем трактате об электричестве:
Действительно, после того, как теория Ампера преобладала во Франции до 1890-х годов, постепенно от нее отказались. В начале двадцатого века физик Анри Буасс мог утверждать в своем трактате об электричестве:
«Формула Ампера не представляет больше никакого интереса, кроме исторического. Пустая трата времени обсуждать гипотезы, на которые опирался Ампер, чтобы установить его, или последствия, которые он указывает для действий между двумя элементами в определенных позициях.
Если и сегодня в некоторых текстах по физике можно встретить «формулу Ампера», то в большинстве случаев это не оригинальная формула Ампера, а формула, предложенная в 1845 году немецким математиком Германом Грассманом. Этот пионер векторного анализа определил «геометрическое произведение», из которого позже можно было получить обычное векторное произведение. Благодаря использованию этой новой математической концепции его сила оказалась более простой, чем сила Ампера. Но, в отличие от последнего, не удовлетворял принципу действия и противодействия.
Элементарная сила Грассмана (воздействующая элементом на элемент ), в современных символах: Интенсивность силы: i i’ ds ds’ sinα cosβ (β — угол между и плоскостью P). |
Эта сила, выражение которой не отводит симметричную роль двум элементам и , всегда перпендикулярна элементу .
1980-е годы: формула Ампера – новый научный вызов?
С 1980-х годов определенное число физиков, подкрепленное как теоретическими работами, так и экспериментальными результатами, считали, что необходимо вернуть из забвения первоначальную формулу Ампера, которая сейчас, спустя почти два столетия после своего «изобретения», стала предметом исследования. научный спор.
Некоторые даже утверждают, что некоторые опыты можно объяснить только формулой Ампера.
Возвращаемся ли мы в архаичное прошлое, устаревшее благодаря электромагнетизму Максвелла-Лоренца? Формула Ампера просто вышла из употребления, устарела, не оспариваемая, свергнута более плодотворной, эстетичной и простой в применении теорией, или же она несовместима с современным электромагнетизмом, объясняющим огромное количество явлений?
Двусмысленность суждения Максвелла
Хотя Максвелл считал формулу Ампера «фундаментальной», он, тем не менее, добавлял:
«Поэтому нельзя сказать, что утверждение о взаимном действии двух элементов цепи основано на чисто экспериментальных основаниях.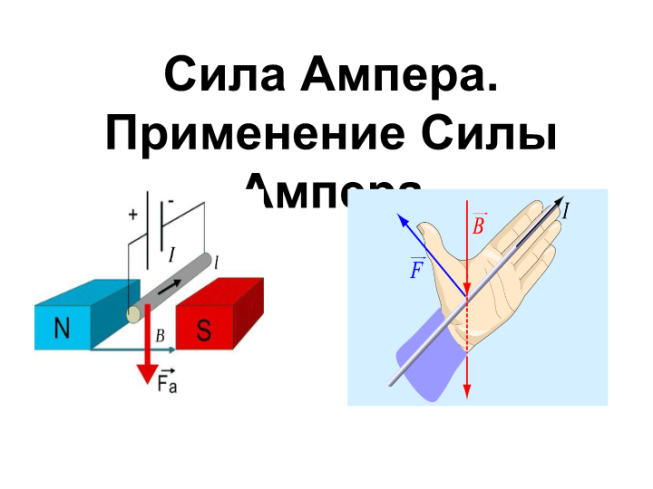 ( Трактат… , т. 2, стр. 163)
( Трактат… , т. 2, стр. 163)
Действительно, поскольку электрические токи образуют замкнутые цепи, то невозможно физически изолировать действие элемента тока (мы не рассматриваем здесь разомкнутые цепи как радиоантенну, очаг высокочастотных электрических колебаний). В то время как многие экспериментальные приемы позволяют сделать небольшой участок цепи (С’) подвижным, эта часть подвержена действию всей цепи (С), но нельзя изолировать действие одной цепи (С). элементы.
Бесконечность элементарных формул, включая формулы Ампера и Грассмана, может привести к одной и той же силе, действующей на элемент i’ds, путем интегрирования по всей цепи (C).
Почему же тот же Максвелл описывает формулу Ампера как «основную формулу электродинамики»? На самом деле это единственный, который соблюдает ньютоновский принцип действия и противодействия. В общем случае сила Грассмана не распространяется по прямой линии, соединяющей два элемента. Кроме того, сила Грассмана, действующая со стороны элемента на элемент, не имеет такой же интенсивности, как сила, действующая со стороны на , полученная путем изменения ролей двух элементов.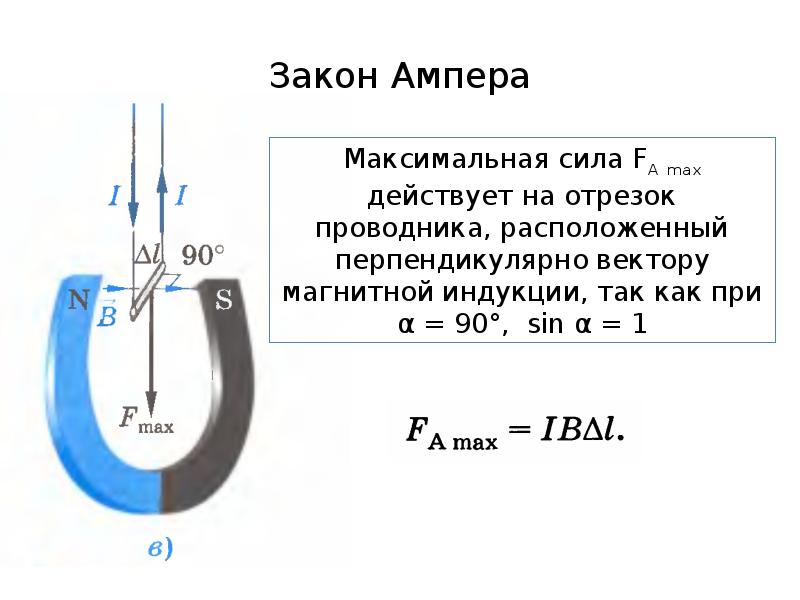
Как сказал физик Р.А.Р. Трикер подчеркнул, что сегодня мы рассматриваем принцип Ньютона как применимый только к конечным силам, имеющим физическую реальность, следовательно, к силам между контурами:
«Читатель вполне может прийти к выводу, что вопросы, которые даже в принципе не могут быть проверены опытом [такие, как правильная формула элемента], не относятся к науке, но, несмотря на это, Ампер подвергался значительная критика. Любопытно, что единственная критика, которой он был бы уязвим, заключалась именно в том, что он тоже, как и большинство его критиков, думал, что приходит к закону силы, которую текущие элементы фактически воздействовали друг на друга…» (RAR Tricker, Early Electrodynamics, 1965, стр. 99)
Формула Ампера свергнута уравнениями Максвелла и «силой Лапласа»
Интегрируя силу Грассмана по контуру (C), можно получить силу, действующую со стороны этого контура (C) на элемент контура (C’):
Результат суммирования по (C) впоследствии был идентифицирован как магнитное поле, созданное цепью (C). Таким образом, сила Грассмана принимает форму простого вектора .Эта сила перпендикулярна и , а ее интенсивность равна i’ds’B sinε, где ε угол между и . По крайней мере, во Франции этот закон известен как «сила Лапласа».
Таким образом, сила Грассмана принимает форму простого вектора .Эта сила перпендикулярна и , а ее интенсивность равна i’ds’B sinε, где ε угол между и . По крайней мере, во Франции этот закон известен как «сила Лапласа».
Сила Лапласа: |
Ампер установил аналогичный закон [см. стр. В поисках… ]. Действительно, он показал, что сила, действующая на элемент ds со стороны замкнутого контура, перпендикулярна этому элементу и прямой линии, которую он назвал направляющей .Он выразил интенсивность этой силы как:
½ D i i’ ds’ sinε.
В множителе ½ Di, связанном с направляющей , можно узнать характеристики магнитного поля В. Но Ампер видел в этом законе лишь математическое следствие действия на расстоянии между токоведущими элементами.
Триумф теории Максвелла, основанной на непрерывном распространении электромагнитных воздействий, объясняет отказ от формулы Ампера в пользу формулы Грассмана, которая идеально вписывается в рамки Максвелла, поскольку, как мы видели, ее легко связать с полем . Таким образом, дань уважения Максвеллом исторической формуле Ампера несколько парадоксальна.
Таким образом, дань уважения Максвеллом исторической формуле Ампера несколько парадоксальна.
Силы отталкивания между коллинеарными элементами?
Вопрос остается открытым. Можно ли, вопреки тому, что утверждает Максвелл, определить между элементарными формулами Ампера и Грассмана опытным путем? И если эксперимент решит в пользу силы Ампера, станет ли это вызовом зданию, возведенному Максвеллом, которое само по себе неразрывно связано с теорией относительности?
Формула Ампера предполагает, в отличие от формулы Грассмана, существование силы отталкивания между двумя коллинеарными элементами тока.В самом деле, если два элемента коллинеарны, углы α и β (рис. 1) равны нулю, а сила между ds и ds’ принимает вид:
— ½ i i’ ds ds’/ r 2 .
Поскольку сила отрицательна, это отталкивание. Напротив, формула Грассмана dF = i i’ ds ds’ sinα cosθ подразумевает, что сила между коллинеарными ds и ds’ равна нулю.
Согласно Амперу, в металлическом проводе, по которому течет ток, должна существовать сила отталкивания между двумя последовательными элементами. Итак, можем ли мы сделать выбор между двумя формулами, изучая действие, оказываемое между двумя частями одной и той же цепи?
Итак, можем ли мы сделать выбор между двумя формулами, изучая действие, оказываемое между двумя частями одной и той же цепи?
Новый взгляд на «эксперимент со шпилькой» Ампера в 1980-х годах
В 1822 году Ампер думал, что у него есть доказательство в пользу его формулы с его экспериментом с плавающим проводником, иногда называемым «экспериментом со шпилькой».[См. видео L’expérience du Conducteur Flottant на странице В поисках… ].
Рис. 2. Медная проволока нкр, в форме шпильки , изолированная, кроме оголенных концов н и р , плавает на поверхности ртути, содержащейся в двух сечениях круглой контейнер. При протекании по цепи сильного тока провод-шпилька отходит от неподвижных контактов с и м независимо от направления тока. |
В 1980-х годах несколько исследователей повторно посетили этот эксперимент.
— Питер Грано в Массачусетском технологическом институте наблюдал в 1981 году при токах в несколько сотен ампер сильную турбулентность в ртути, когда движение шпильки блокировалось. Эта турбулентность, по-видимому, свидетельствует об отталкивании части ртути, несущей ток
— Панос Т. Паппас в 1983 году заменил шпильку Ампера на проволоку, сформированную в виде прямоугольника без одной из его более коротких сторон и подвешенную в виде маятника (рис.3). Автор определил величину движения, сообщаемого маятнику, и приписал это движение силе отталкивания Ампера. Этот эксперимент был выполнен с большей точностью Питером и Нилом Грано (1986) с использованием разряда ряда конденсаторов. Рис. 3. Принцип импульсного маятника Паппаса. |
— Продолжая эксперимент Ампера, другие физики пытались «взвесить» возможную силу отталкивания. Так, Питер Грано в 1986 году, а затем Реми Сомон в 1992 году подвесили такой же мобильный проводник в форме неполного прямоугольника вертикально под чашей прецизионных весов. Затем можно было измерить вертикальную силу отталкивания, которой он подвергался от неподвижной части цепи.
Противоречивые интерпретации
На самом деле различные варианты эксперимента Ампера интерпретируются в контексте современной физики с использованием силы Лапласа и, следовательно, стихийной силы Грассмана.Действительно, на поперечную часть неполных прямоугольников действует сила Лапласа под действием магнитного поля, создаваемого контуром. Эта сила перпендикулярна поперечной части и поэтому стремится отделить подвижную часть от остальной части цепи.
Только расчет интенсивности силы, действующей на подвижную часть, мог бы решить, какой из двух основных законов выбрать. Но можно ли вычислить, интегрируя формулу Ампера, силу отталкивания между двумя частями одной и той же цепи? Если уподобить проводник линии без толщины, делящейся на «бесконечно короткие» элементы тока, то интегрирование приводит к бесконечной силе между двумя соседними коллинеарными элементами.
Но можно ли вычислить, интегрируя формулу Ампера, силу отталкивания между двумя частями одной и той же цепи? Если уподобить проводник линии без толщины, делящейся на «бесконечно короткие» элементы тока, то интегрирование приводит к бесконечной силе между двумя соседними коллинеарными элементами.
Напротив, несколько авторов предложили методы расчета, которые лучше учитывают реальную структуру проводников: токовый элемент не является бесконечно коротким, а диаметр провода не равен нулю.
| — Для Грано размер элемента тока не может быть меньше размера элементарной ячейки металлической решетки, порядка нанометра. Компьютеры выполняли численное интегрирование путем суммирования по большому количеству мелких элементов, но размер этих элементов остается намного больше нанометра.Путем экстраполяции полученных результатов надеются получить порядок величины силы [Graneau, 1986]. Рис. 4. Принцип расчета суммированием по конечным элементам [Graneau, 1986]. |
— Другие авторы, учитывая объемное распределение тока в проводнике с ненулевым диаметром, избегают выбора численных методов и проводят интегрирования.Следовательно, они должны иметь дело с шестикратными интегралами [Marcelo Bueno and A.K.T. Assis, 1996].
— Наконец, в рамках классического электромагнетизма вычисления могут быть проще выполнены с использованием выражения для индуктивности цепи, понятия, которое появилось намного позже Ампера [R.A.R. Tricker, 1965, или Bueno and Assis, 1998].
Независимо от выбранного метода расчета сила, действующая цепью на один из ее элементов, имеет значение, достаточно низкое, чтобы механические напряжения оставались незаметными в твердых проводниках, по крайней мере, до тех пор, пока ток не имеет необычно высокой силы. Но это может объяснить наблюдаемые эффекты в цепях с жидкостью или подвижной частью, как в предыдущих экспериментах.
Но это может объяснить наблюдаемые эффекты в цепях с жидкостью или подвижной частью, как в предыдущих экспериментах.
Некоторые авторы заканчивают торжеством формулы Ампера. По их мнению, интегрирование по формуле Грассмана приводит к явно более слабым силам. Однако в 1996 г. Асис и Буэно исправили ошибку в рассуждениях, лежащих в основе этих расчетов, и получили, используя формулу Грассмана, те же результаты, что и с формулой Ампера. В 1998 году они также показали, что метод индуктивности представляет собой косвенное доказательство эквивалентности формул Ампера и Грассмана.
Следовательно, не представляется возможным решить между формулами Ампера и Грассмана с помощью опытов амперовского типа.
Другие эксперименты вызывают споры
В предыдущих экспериментах рассматривалась общая сила, действующая на одну из частей цепи. Хотя формулы Грассмана и Ампера дают один и тот же результат для этой общей силы, они могут быть не эквивалентны для распределения силы по контуру. Чтобы проверить эту гипотезу, некоторые пытались выделить 90 527 местных 90 528 эффектов продольных сил, эффекты, которые могла объяснить только сила Ампера.
Чтобы проверить эту гипотезу, некоторые пытались выделить 90 527 местных 90 528 эффектов продольных сил, эффекты, которые могла объяснить только сила Ампера.
— Вдохновленный экспериментом, проведенным Нейманом для своих учеников в 1880-х годах, Грано поместил два коротких медных стержня встык в прямолинейный узкий канал, заполненный ртутью. Когда по этому каналу протекал ток силой 450 ампер, два стержня отталкивались друг от друга.
Рис. 5. В середине длинного канала ртути встык поставлены два медных стержня AB и CD. Когда течет ток, стержни отталкиваются друг от друга. (Стержни покрыты изоляцией, а проводимость меди намного больше, чем у ртути, что объясняет рисунок линий тока черным цветом).Грано, 1986. |
— В начале 1960-х годов Ян Насиловский уже заметил, что очень сильный поток тока вызывает взрыв токопроводящих проводов на серию фрагментов (рис. 6). Грано повторил эксперимент в 1980-х годах с токами более 5000 ампер, но достаточно короткой продолжительности, чтобы поддерживать температуру значительно ниже точки плавления металла. | Рис. 6. Фрагменты, образовавшиеся в результате взрыва проводов [Ян Насиловский]. |
— В другом эксперименте [Linda J. Ruscak and R.N. Bruce, 1987] медный стержень длиной один метр разрезали на отрезки по одному сантиметру и укладывали в стеклянную трубку. Пружины прочно удерживали их в контакте друг с другом. Импульсы тока от 3 до 30 килоампер заставляли их разделяться, а в промежутках прыгали электрические дуги. Рис. 7. Разделение и образование дуг между медными сегментами в опыте Русчака и Брюса. |
— Добавлю эксперимент, проведенный после наблюдения парадоксального эффекта во время экспериментов над «электромагнитным рельсотроном» для Стратегической оборонной инициативы США. В ходе этого эксперимента было замечено, что рельсы подверглись неожиданным механическим деформациям. Затем Грано модифицировал эксперимент (рис. 8, справа), заблокировав перекладину.Импульсов в 100 килоампер было достаточно, чтобы вызвать деформации в самых тонких частях рельсов, которые он приписал продольным силам Ампера. | Рис. 8: «Электромагнитный рельсотрон». В версии Грано (справа) перекладина заблокирована. |
Все эти эксперименты были представлены как доказательства существования продольных сил, но могли быть выдвинуты и альтернативные интерпретации.
Другие эксперименты, направленные на выявление продольных сил в жидких металлах и плазме. Хотя некоторые из них были очень драматичными, мы не будем упоминать их здесь, потому что они легче поддаются альтернативным интерпретациям.
Продольные силы и современный электромагнетизм
Продольные силы в проводниках отсутствуют в большинстве книг по электромагнетизму. Кроме того, их потенциальные эффекты проявляются только при необычно высокой силе тока. Тем не менее, по мнению некоторых авторов, электромагнетизм Максвелла не исключает существования продольных напряжений, которые могут играть роль в представленных выше опытах.Эти напряжения возникают в результате применения к проводникам максвелловской теории «тензоров напряжений», совершенно не связанной с силой Ампера.
Сила Лоренца и сила Ампера: противоречие?
Уравнения Максвелла имеют дело только с электромагнитным полем и не включают закон силы. Для Максвелла формулы Грассмана и Ампера были совместимы с его теорией, хотя он и отдавал предпочтение теории Ампера.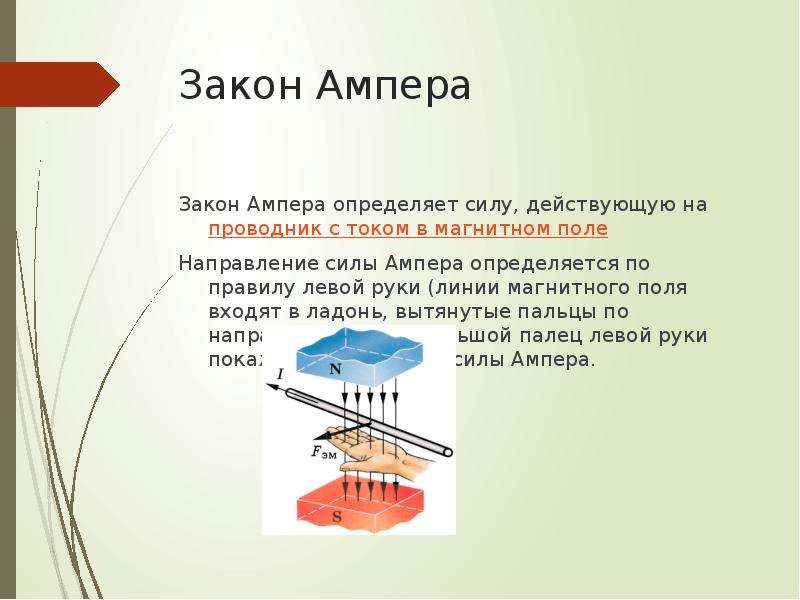
Позже Лоренц выразил силу, действующую на заряженную частицу q в вакууме в присутствии магнитного поля:
сила Лоренца |
Отныне именно сила Лоренца, замечательно проверенная экспериментально, принимается классическими объяснениями электромагнетизма в качестве элементарного закона силы.В любой момент времени эта сила перпендикулярна направлению движения частицы. Таким образом, на элемент тока, образованный движущейся заряженной частицей, действует сила, которая, как и сила Грассмана, не имеет продольной составляющей.
Выражение силы Лапласа обычно представляется как следствие силы Лоренца. В моделях, предложенных для учета проводимости в металлах, все происходит так, как если бы силы, испытываемые электронами проводимости, передавались металлической решетке.Поскольку сила перпендикулярна направлению движения электронов, металлический проводящий элемент может испытывать только поперечные силы. Таким образом, замечательная точность проверки закона Лоренца оправдывает отказ от формулы Ампера.
Таким образом, замечательная точность проверки закона Лоренца оправдывает отказ от формулы Ампера.
Тем не менее, обоснование закона Лапласа с помощью силы Лоренца было оспорено. Металлический проводник не сравним с электронным пучком в вакууме. Мы должны учитывать физическую природу элемента тока, состоящего из положительных ионов и электронов.Согласно М. Рамбо и Ж. П. Вижье, применение законов электромагнетизма Максвелла-Лоренца-Эйнштейна к коллективному поведению этого ансамбля заряженных частиц приводит в нерелятивистском приближении к формуле Ампера (1989). Токи в металлах подчинялись бы закону Ампера, а токи в вакууме подчинялись бы закону Грассмана.
Действие на расстоянии против теории поля и теории относительности Эйнштейна
Тем не менее, в то время как современный электромагнетизм предсказывает — и более простым способом — те же эффекты, что и формула Ампера, зачем же выступать — как некоторые продолжают делать — за «реабилитацию» этой формулы? Есть ли еще место для споров?
Задача на самом деле теоретическая. Сила Ампера — это сила мгновенного действия на расстоянии. В этом отношении она в корне несовместима с теорией Максвелла, основанной на непрерывном распространении электромагнитного воздействия.
Сила Ампера — это сила мгновенного действия на расстоянии. В этом отношении она в корне несовместима с теорией Максвелла, основанной на непрерывном распространении электромагнитного воздействия.
Триумф теории Максвелла основан на ее необычайной плодотворности. Его уравнения учитывают, среди прочего, распространение электромагнитных волн со скоростью c = 300 000 км/с. Электромагнитное поле, позволяющее передавать энергию, существует в вакууме, лишенном зарядов.Более того, именно теория Максвелла в некотором роде «заложила условия» для теории относительности Эйнштейна. Таким образом, здание электромагнетизма Максвелла-Лоренца и эйнштейновской теории относительности является неоспоримым столпом всей физики двадцатого века.
До Максвелла такие физики, как Вебер, а затем Нейман разработали электродинамику, основанную на формуле Ампера. Они искали закон силы или потенциала между элементами тока или между движущимися электрическими зарядами, который объяснял бы все явления, включая явление индукции, чего не делала формула Ампера. Так, Вебер предложил элементарную силу между электрическими зарядами, состоящую из трех членов, зависящих от расстояния, скорости и ускорения одного заряда относительно другого. Первый член есть не что иное, как закон Кулона, второй можно вывести из формулы Ампера, а третий объясняет явление индукции.
Так, Вебер предложил элементарную силу между электрическими зарядами, состоящую из трех членов, зависящих от расстояния, скорости и ускорения одного заряда относительно другого. Первый член есть не что иное, как закон Кулона, второй можно вывести из формулы Ампера, а третий объясняет явление индукции.
Некоторые из современных защитников силы Ампера следуют «веберианскому» электродинамическому проекту как альтернативе проекту Максвелла (А.К. Т. Ассис, Электродинамика Вебера, , 1994 или П. и Н. Грано, , Ньютоновская электродинамика, , 1996). Ссылка на Ньютона, как и на Ампера или его преемников, указывает на проект, выходящий за рамки электричества. Речь идет о построении физики, основанной на взаимодействии на расстоянии между материальными элементами. Можно было бы возразить, что сами Ньютон или Ампер далеки от того, чтобы считать мгновенное действие на расстоянии последним словом физики.За их математическими законами гравитации или электродинамики, которые включают только взаимодействующие элементы и их расстояние, оба были убеждены в существовании более глубокой реальности, основанной на непрерывной передаче в промежуточном пространстве. . Однако это не мешает попыткам объяснить явления, обычно описываемые с помощью теории Максвелла, с помощью веберовской электродинамики: эффекты излучения, распространение света… «В этом направлении потребуется много теоретической и экспериментальной работы», — писал Ассис в 1989 г.
. Однако это не мешает попыткам объяснить явления, обычно описываемые с помощью теории Максвелла, с помощью веберовской электродинамики: эффекты излучения, распространение света… «В этом направлении потребуется много теоретической и экспериментальной работы», — писал Ассис в 1989 г.
Идея применения закона, аналогичного закону Вебера для электромагнетизма (включая несколько терминов), к гравитации восходит к 1870-м годам и рассматривалась самим Вебером. К ньютоновской силе тяготения добавляют некоторые члены, зависящие от относительной скорости масс, по модели членов, добавленных Вебером к электрической силе Кулона. Согласно Ассису [ Relational Mechanics , 1999], эта веберовская механика позволяет вывести первые два закона динамики Ньютона — принцип инерции и фундаментальное соотношение динамики — и установить пропорциональность между инертной и гравитационной массой. .Прецессию перигелия планет можно рассчитать, не прибегая к уравнениям общей теории относительности.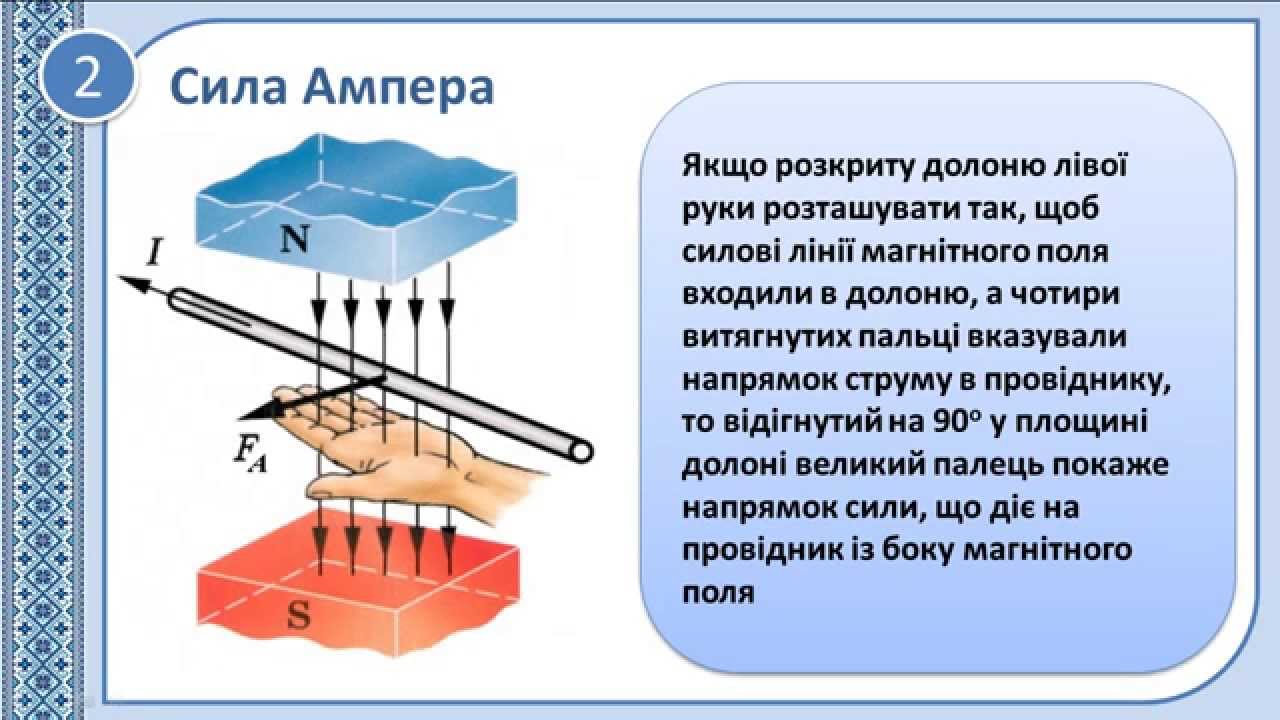 ..
..
Широко распространенное инакомыслие, которое может вызвать подозрения?
При рассмотрении публикаций некоторых сторонников реабилитации силы Ампера иногда обнаруживается оппозиция господствующему истеблишменту — «официальной науке», — которая далеко не ограничивается электромагнетизмом Максвелла. Кто-то разоблачает «аферу специальной теории относительности» или предлагает воспользоваться «бесконечной энергией вакуума».Другой противопоставляет стандартной теории Большого взрыва теорию стационарной Вселенной. Красное смещение света от далеких галактик, обычно интерпретируемое расширением Вселенной, может быть объяснено теорией «световой усталости». Также можно найти статьи о холодном синтезе и т. д.
Эти соединения могут вызывать определенные подозрения. Однако можно вспомнить, что некоторые верования Ампера, не говоря уже о его интересе к животному магнетизму, попахивали ересью для многих членов Академии.Конечно, вряд ли есть какие-либо экспериментальные основания сомневаться в электромагнетизме Максвелла, и может показаться, что работа над построением альтернативной электродинамики — это пустая трата энергии. Тем не менее, можно ли не одобрить рецензию на книгу Грано « Ньютоновская электродинамика » в журнале Scientific American : «Настоятельно рекомендуется непредубежденным и всем, кто согласен с Максвеллом в отношении благоразумной роли плюрализма в обеспечении здоровья людей». науке и, собственно, в обеспечении ее жизни.» ?»
Тем не менее, можно ли не одобрить рецензию на книгу Грано « Ньютоновская электродинамика » в журнале Scientific American : «Настоятельно рекомендуется непредубежденным и всем, кто согласен с Максвеллом в отношении благоразумной роли плюрализма в обеспечении здоровья людей». науке и, собственно, в обеспечении ее жизни.» ?»
Для получения дополнительной информации
ГИЛЬЕМО, Элен. On avait oublié la force d’Ampère, Science & Vie , 879, 1990, p. 38-46.
АССИС, Андре ; БУЭНО, М. Д. A. Расчет индуктивности и силы в электрических цепях . Нью-Йорк: Nova Science Publishers, Huntington, 2001.
ASSIS, A.K.T. & CHAIB, J.P.M.C. Электродинамический анализ Ампера значения и эволюции силы Ампера между элементами тока вместе с полным переводом его шедевра: Теория электродинамических явлений, однозначно выведенная из опыта. Монреаль: Apeiron, 2015. [см. PDF]
Библиография «вторичных источников» по истории электричества.
Французская версия: май 2009 г. (английский перевод: март 2013 г.; последняя редакция: март 2021 г.)
Магнитная сила между двумя параллельными токами – University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как параллельные провода, по которым текут токи, могут притягиваться или отталкиваться друг от друга
- Дайте определение ампера и опишите, как он связан с токоведущими проводами
- Расчет силы притяжения или отталкивания между двумя проводниками с током
Можно было бы ожидать, что два провода с током создают между собой значительные силы, поскольку обычные токи создают магнитные поля, а эти поля воздействуют на обычные токи значительными силами.Но вы можете не ожидать, что сила между проводами используется для определения ампера. Вы также можете удивиться, узнав, что эта сила как-то связана с тем, почему большие автоматические выключатели сгорают, когда они пытаются отключить большие токи.
Силу между двумя длинными, прямыми и параллельными проводниками, разделенными расстоянием r , можно найти, применяя то, что мы разработали в предыдущих разделах. (Рисунок) показывает провода, их токи, поле, создаваемое одним проводом, и последующую силу, которую другой провод испытывает от созданного поля.Рассмотрим поле, создаваемое проволокой 1, и силу, действующую на проволоку 2 (назовем силу ). Поле из-за на расстоянии r равно
(a) Магнитное поле, создаваемое длинным прямым проводником, перпендикулярно параллельному проводнику, как показано правилом правой руки (RHR)-2. (b) Вид сверху на два провода, показанные на (а), с одной линией магнитного поля, показанной для провода 1. RHR-1 показывает, что сила между параллельными проводниками притягивается, когда токи имеют одинаковое направление.Подобный анализ показывает, что сила отталкивающая между токами в противоположных направлениях.
Это поле однородно от провода 1 и перпендикулярно ему, поэтому сила, которую оно оказывает на длину l провода 2, определяется выражением
Силы на проводах равны по величине, поэтому мы просто пишем F для величины (Обратите внимание, что ) Поскольку провода очень длинные, удобно думать в терминах F/l , силы длина единицы. Подстановка выражения для в (рисунок) и перестановка членов дает
Подстановка выражения для в (рисунок) и перестановка членов дает
Отношение F/l есть сила на единицу длины между двумя параллельными токами, разделенными расстоянием r . Сила притяжения, если токи имеют одинаковое направление, и отталкивания, если они направлены в противоположные стороны.
Эта сила отвечает за пинч-эффект в электрических дугах и других плазмах. Сила существует независимо от того, есть ли токи в проводах или нет.Это очевидно только в том случае, если общая плотность заряда равна нулю; в противном случае кулоновское отталкивание преобладает над магнитным притяжением. В электрической дуге, где заряды движутся параллельно друг другу, сила притяжения сжимает токи в трубку меньшего размера. В больших автоматических выключателях, таких как те, которые используются в системах распределения электроэнергии по соседству, эффект защемления может концентрировать дугу между пластинами выключателя, пытаясь отключить большой ток, прожечь дыры и даже зажечь оборудование. Другой пример пинч-эффекта можно найти в солнечной плазме, где струи ионизированного материала, такие как солнечные вспышки, формируются под действием магнитных сил.
Другой пример пинч-эффекта можно найти в солнечной плазме, где струи ионизированного материала, такие как солнечные вспышки, формируются под действием магнитных сил.
Определение ампера основано на силе между токоведущими проводами. Обратите внимание, что для длинных параллельных проводов, разделенных 1 метром, каждый из которых несет 1 ампер, сила на метр составляет
Так как точно по определению, и потому что сила на метр точно Это и есть основа определения ампера.
Провода бесконечной длины нецелесообразны, поэтому на практике баланс токов строится из витков провода, отстоящих друг от друга на несколько сантиметров.Сила измеряется для определения силы тока. Это также дает нам метод измерения кулона. Измеряем заряд, протекающий при токе в один ампер за одну секунду. То есть, как для ампера, так и для кулона метод измерения силы между проводниками является наиболее точным на практике.
Расчет силы на проводах Два провода, по обоим проводящим ток за пределы страницы, имеют ток величиной 5,0 мА.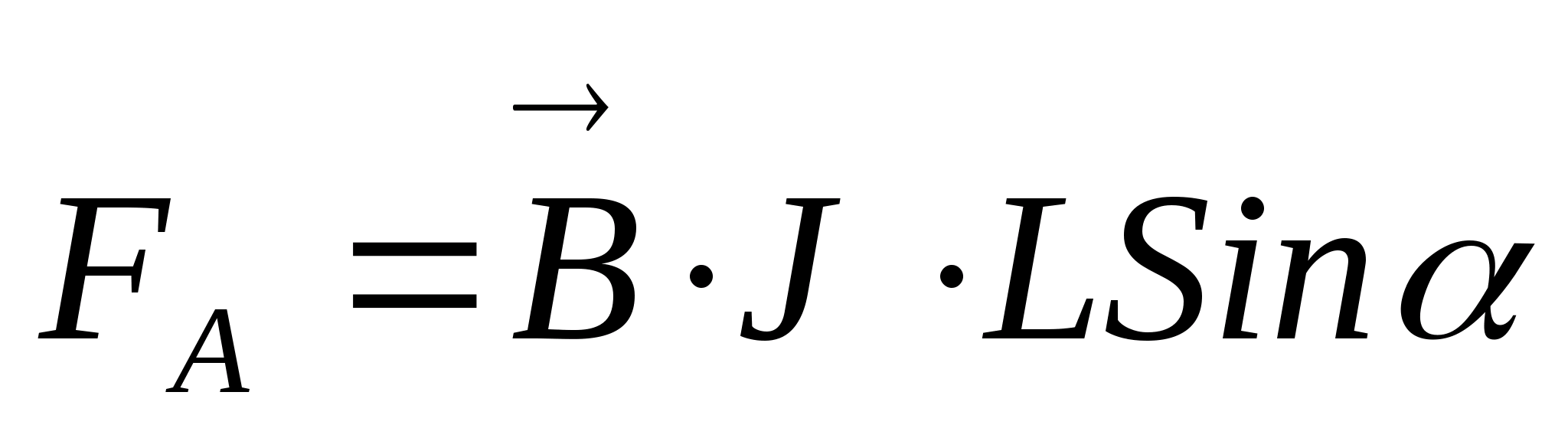 Первый провод расположен на (0,0 см, 3,0 см), а другой провод расположен на (4.0 см, 0,0 см), как показано на (рис.). Чему равна магнитная сила на единицу длины первого провода на второй и второго провода на первый?
Первый провод расположен на (0,0 см, 3,0 см), а другой провод расположен на (4.0 см, 0,0 см), как показано на (рис.). Чему равна магнитная сила на единицу длины первого провода на второй и второго провода на первый?
Два токонесущих провода в заданных местах с токами вне страницы.
Стратегия Каждый провод создает магнитное поле, ощущаемое другим проводом. Расстояние по гипотенузе треугольника между проводами — это радиальное расстояние, используемое в расчетах для определения силы на единицу длины. Поскольку по обоим проводам текут токи в одном направлении, сила направлена друг к другу.
Решение Расстояние между проводами получается из нахождения гипотенузы треугольника:
Затем можно рассчитать силу на единицу длины, используя известные токи в проводах:
Сила первого провода тянет за собой второй провод. Угол между радиусом и осью x равен
.
Единичный вектор для этого рассчитывается как
Следовательно, сила на единицу длины от провода 1 на провод 2 равна
Сила на единицу длины от провода 2 к проводу 1 равна отрицательному значению предыдущего ответа:
Значение Эти провода создавали магнитные поля одинаковой величины, но противоположного направления в местах расположения друг друга. Независимо от того, одинаковы поля или нет, силы, с которыми провода действуют друг на друга, всегда равны по величине и противоположны по направлению (третий закон Ньютона).
Независимо от того, одинаковы поля или нет, силы, с которыми провода действуют друг на друга, всегда равны по величине и противоположны по направлению (третий закон Ньютона).
Проверьте свое понимание Два провода, по обоим проводящим ток вне страницы, имеют ток величиной 2,0 мА и 3,0 мА соответственно. Первый провод расположен на (0,0 см, 5,0 см), а другой провод расположен на (12,0 см, 0,0 см). Какова величина магнитной силы на единицу длины первого провода на второй и второго провода на первый?
Оба имеют силу на единицу длины
Резюме
- Сила между двумя параллельными токами, разделенными расстоянием r , имеет величину на единицу длины, определяемую как
- Сила притяжения, если токи имеют одинаковое направление, и отталкивания, если они направлены в противоположные стороны.
Концептуальные вопросы
Сравните и сопоставьте электрическое поле бесконечной линии заряда и магнитное поле бесконечной линии тока.
Постоянна ли величина для точек, лежащих на силовой линии магнитного поля?
Линия магнитного поля указывает направление магнитного поля в любой точке пространства. Плотность силовых линий магнитного поля указывает на силу магнитного поля.
Проблемы
Два длинных прямых провода расположены параллельно и на расстоянии 25 см друг от друга.а) Если по каждому проводу течет ток силой 50 А в одном и том же направлении, какова магнитная сила на метр, действующая на каждый провод? б) Сила стягивает провода вместе или раздвигает их? в) Что произойдет, если токи текут в противоположных направлениях?
Два длинных прямых провода расположены параллельно на расстоянии 10 см друг от друга. По одному течет ток 2,0 А, по другому ток 5,0 А. (а) Если два тока текут в противоположных направлениях, какова величина и направление силы, приходящейся на единицу длины одного провода на другой? б) Какова величина и направление силы на единицу длины, если токи текут в одном направлении?
а. подальше от другого провода; б. к другому проводу
подальше от другого провода; б. к другому проводу
Два длинных параллельных провода подвешены на шнурах длиной 5,0 см, как показано на прилагаемом рисунке. Каждый провод имеет массу на единицу длины 30 г/м, и по ним течет одинаковый ток в противоположных направлениях. Какова сила тока, если шнуры висят относительно вертикали?
Цепь с током I имеет два длинных параллельных отрезка провода, по которым течет ток в противоположных направлениях. Найдите магнитное поле в точке P рядом с этими проводами, которая находится на расстоянии a от одного провода и b от другого провода, как показано на рисунке.
По бесконечному прямому проводу, показанному на прилагаемом рисунке, течет ток По прямоугольной петле, длинные стороны которой параллельны проводу, течет ток Каковы величина и направление силы, действующей на прямоугольную петлю из-за магнитного поля провод?
.


 1. Текущий элемент ds, расположенный в точке A, расположен в плоскости P; элемент ds’, расположенный в точке B, лежит в плоскости Q.
1. Текущий элемент ds, расположенный в точке A, расположен в плоскости P; элемент ds’, расположенный в точке B, лежит в плоскости Q.
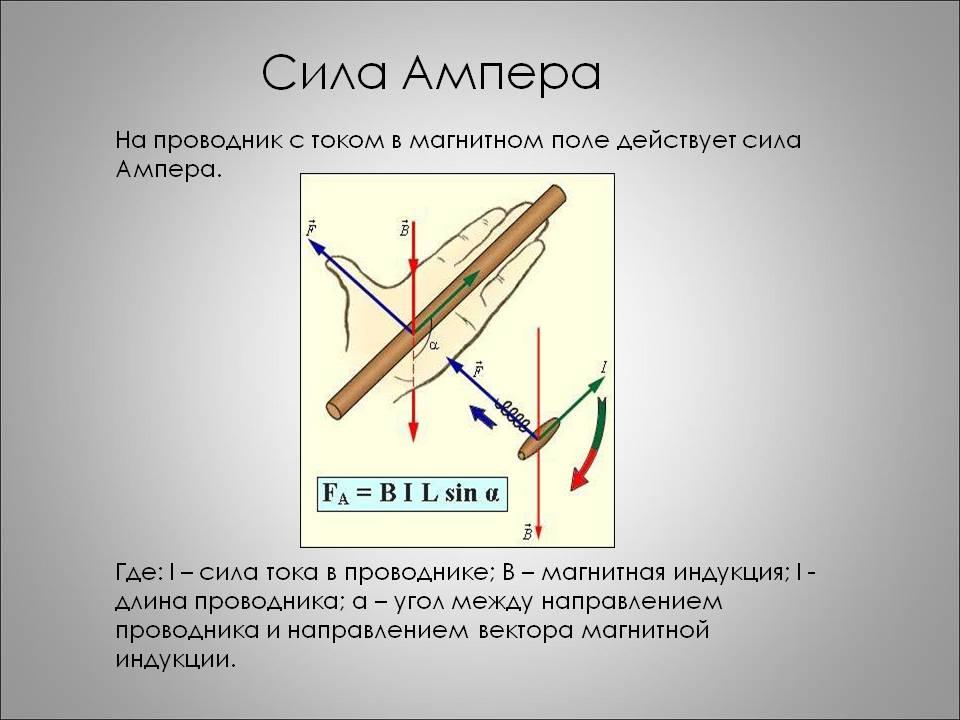
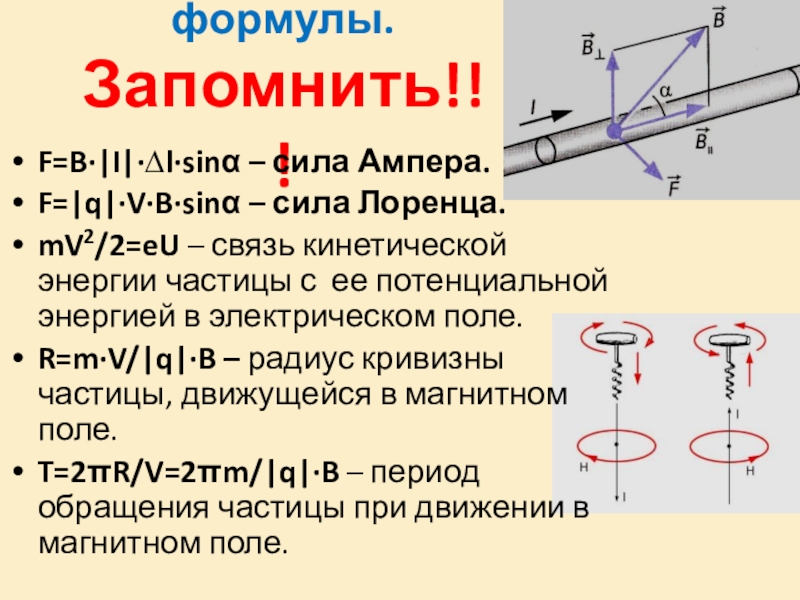 Исследование микроскопической структуры областей перелома, казалось, подтвердило механическую причину.Таким образом, переломы могли быть вызваны силой Ампера.
Исследование микроскопической структуры областей перелома, казалось, подтвердило механическую причину.Таким образом, переломы могли быть вызваны силой Ампера. В левой части рисунка 8 показан очень простой принцип работы рельсотрона или «пушки». При протекании очень сильного тока в цепи, состоящей из двух длинных горизонтальных рельсов и размещенного на этих рельсах подвижного стержня, стержень приходит в движение.Придание движения снаряду очень классически объясняется силой Лапласа, испытываемой подвижным стержнем в собственном магнитном поле цепи. В 1984 году при пиковой силе более 2 миллионов ампер можно было вести объект весом 300 г со скоростью 15 000 км/ч.
В левой части рисунка 8 показан очень простой принцип работы рельсотрона или «пушки». При протекании очень сильного тока в цепи, состоящей из двух длинных горизонтальных рельсов и размещенного на этих рельсах подвижного стержня, стержень приходит в движение.Придание движения снаряду очень классически объясняется силой Лапласа, испытываемой подвижным стержнем в собственном магнитном поле цепи. В 1984 году при пиковой силе более 2 миллионов ампер можно было вести объект весом 300 г со скоростью 15 000 км/ч.