Переменный синусоидальный ток
Переменный ток — это ток, который периодически изменяется как по модулю, так и по направлению. Появляется переменный ток благодаря электромагнитной индукции. Электромагнитная индукция это явление возникновения тока в замкнутом контуре при изменении магнитного потока проходящего через него. Чтобы понять, как именно возникает ток, представим себе рамку (кусочек проволоки прямоугольной формы), которая находится под воздействием магнитного поля B.
Пока рамка находится в покое, тока в ней нет. Но как только мы начнём её поворачивать, электроны, которые находятся в рамке, начнут перемещаться вместе с ней, то есть двигаться в магнитном поле. Вследствие этого магнитное поле начинает действовать на электроны, заставляя их двигаться по рамке. Чем больше линий магнитного поля пронизывает рамку, тем сила действующая на электроны больше, следовательно, и электрический ток тоже.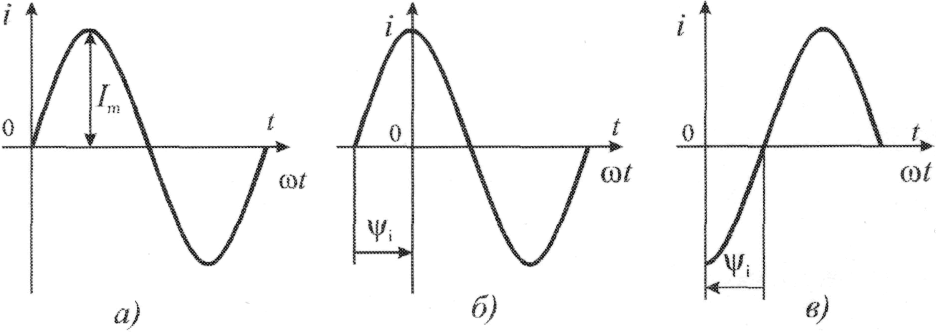 Получается, что ток достигает максимума в момент, когда рамка перпендикулярна магнитному полю (наибольшее количество линии пронизывает рамку) и равен нулю, когда параллельна (наименьшее количество линии пронизывает рамку). Соответственно и сила, которая действует на электроны, тоже изменяется. После прохождения момента, когда рамка параллельна вектору магнитной индукции B, ток в ней начинает течь в обратную сторону.
Получается, что ток достигает максимума в момент, когда рамка перпендикулярна магнитному полю (наибольшее количество линии пронизывает рамку) и равен нулю, когда параллельна (наименьшее количество линии пронизывает рамку). Соответственно и сила, которая действует на электроны, тоже изменяется. После прохождения момента, когда рамка параллельна вектору магнитной индукции B, ток в ней начинает течь в обратную сторону.
Ток, который получается при вращении рамки, изменяясь во времени, описывает синусоиду, то есть является синусоидальным. Переменный синусоидальный ток является частным случаем периодического переменного тока. Закон, описывающий изменение тока, имеет вид:
Амплитуда Im – это наибольшая абсолютная величина, которую принимает периодически изменяющийся ток.
Начальная фаза ψ — аргумент синусоидального тока (угол), отсчитываемый от точки перехода тока через нуль к положительному значению.
Время, за которое ток в проводнике дважды изменяет своё направление, называют периодом T. Период измеряется в секундах.
Циклической частотой f называется величина обратная периоду . Измеряется в Герцах, в домашней розетке циклическая частота тока равна 50 Гц, её также называют промышленной частотой. При такой частоте период тока равен , это значит, что за две сотых секунды ток в нашей розетке меняет свое направление два раза.
Угловая частота ω показывает с какой скоростью изменяется фаза тока и определяется как
Среднее значение Iср синусоидального тока за период Т определяют из геометрических представлений: площадь прямоугольника с основанием T/2 и высотой Iср приравнивают площади ограниченной кривой тока:
После упрощения получаем формулу:
Действующее значение синусоидального тока определяется из энергетических представлений: действующий ток равен по величине такому постоянному току I, который в активном сопротивлении R за период Т выделяет такое количество энергии, как и данный ток i.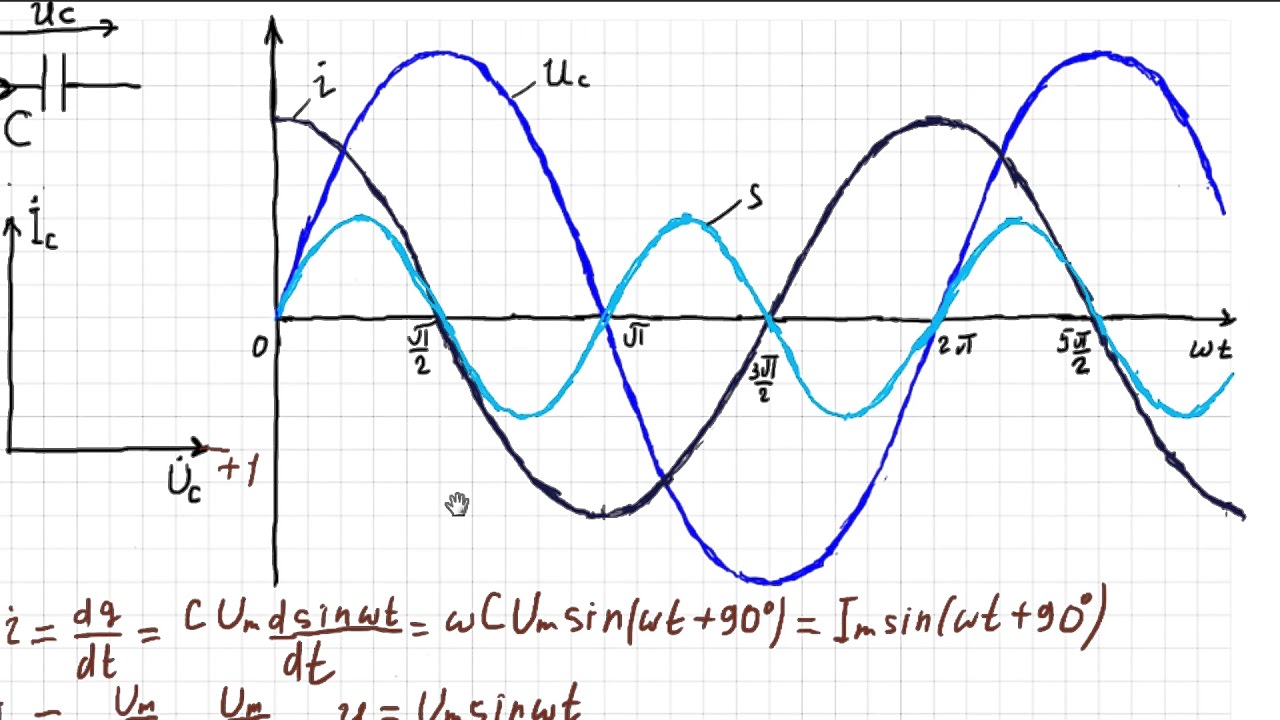 То есть действующее значение, это своеобразная аналогия между переменным и постоянным током.
То есть действующее значение, это своеобразная аналогия между переменным и постоянным током.
Для синусоидального тока действующее значение определяется по формуле:
или
Это основное что нужно знать о переменном синусоидальном токе.
Читайте также — Мгновенная мощность
Переменный (синусоидальный) ток и основные характеризующие его величины.
Переменный ток (англ. alternating current — AC) — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.
В быту для электроснабжения переменяется переменный, синусоидальный ток.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рисунок 1):
Рисунок 1
Максимальное значение функции называют амплитудой. Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:
Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:
- амплитуду тока обозначают lm;
- амплитуду напряжения Um.
Период Т— это время, за которое совершается одно полное колебание.
Частота f равна числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с-1)
f = 1/T
Угловая частота ω (омега) (единица угловой частоты — рад/с или с-1)
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)
В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j (или e(t) и j(t)).
Обратите внимание! При обозначении величин на схемах или в расчетах важен регистр букв, то есть заглавные буквы (E,I,U…) или строчные (e, i ,u…). Так как строчными буквами принято обозначать мгновенное значение, а заглавными могут обозначаться действующее значение величины (подробнее о действующем значении в следующей статье).
Синусоидальный ток и его характеристики
Лекция №3 Синусоидальный ток и его характеристики
Цепи переменного тока широко применяются в электротехнике и электронике. В отличие от цепей постоянного тока в них действуют периодически изменяющиеся ЭДС. Наиболее распространенные формы периодических ЭДС показаны на рис.3.1.
Рис. 3.1. Виды периодически изменяющихся ЭДС
Переменные ЭДС изменяются во времени как по величине, так и по направлению. Если эти изменения повторяются через равные промежутки времени, то они называются периодическими, а время повторения — периодом – Т (рис 3.1). Период измеряется в секундах.
Величина обратная периоду, называется частотой изменения ЭДС, и измеряется в герцах:
.
Диапазон применяемых частот весьма широк, от нескольких герц до нескольких гигагерц: генераторы электрических станций – 50 Гц; ЭВМ от 100 МГц до 1 ГГц.
Наиболее распространены цепи, находящиеся под воздействием синусоидальных ЭДС, поэтому в электротехнике под термином «цепи переменного тока» подразумевается, что в цепи действуют именно синусоидальные ЭДС.
Широкое распространение синусоидальных ЭДС объясняется наиболее простым способом их получения в электромашинных генераторах переменного напряжения в результате вращения токопроводящих рамок в постоянном магнитном поле.
Величина ЭДС зависит от магнитной индукции – В, скорости движения проводника в магнитном поле – V, его длины – l и угла пересечения проводником магнитных силовых линий:
где: е – мгновенное значение ЭДС;
2 – два плеча рамки, т. е. ее диаметр;
В – магнитная индукция;
V – линейная скорость движения проводников рамки;
l – длина рамки;
sin a – синус угла между направлением движения проводника рамки и направлением магнитной индукции.
Мгновенные значения ЭДС – е, тока – i, напряжения u – обозначаются строчными буквами.
При равномерном вращении рамки линейная скорость постоянна и равна:
.
где: D — диаметр рамки;
ω — угловая частота вращения рамки, которую можно выразить:
.
Тогда угол между направлением магнитной индукции и направлением движения проводника изменяется пропорционально времени:
,
тогда ЭДС будет равна:
.
Наибольшего значения ЭДС достигает при:
,
т. е. .
Следовательно:
,
где: Ет – амплитуда ЭДС, т. е. ее максимальное значение (рис 3.1).
В общем случае, если за начало отсчета принять произвольный угол – ψ, эта формула примет следующий вид:
,
где аргумент синуса — фаза – характеризует состояние колебания в данный момент времени. При t = 0 ψ – начальная фаза (рис 3.2).
Рис. 3.2
Таким же образом выражаются мгновенные значения токов, напряжений и других изменяющихся по синусоидальному закону величин.
Любая синусоидальная функция вполне определяется угловой частотой – ω; фазой – ψ; амплитудой – Ет, Uт, Iт.
Действующее значение тока и напряжения
Для оценки эффективности действия переменного тока используют его тепловое или электродинамическое действие и сравнивают с аналогичным действием постоянного тока за один и тот же интервал времени, равный одному периоду.
Значение периодического тока, равное значению такого постоянного тока, который за время одного периода производит тот же тепловой или электродинамический эффект, что и периодический ток называется действующим значением периодического тока.
Действующие значения тока, ЭДС и напряжения обозначают прописными буквами без индексов:
I; E; U.
Тепловой эффект пропорционален квадрату тока, то есть при постоянном токе количество тепла за период Т, выделяемое в резистивном элементе R, определяется по закону Джоуля-Ленца:
,
А при переменном токе
.
Тогда:
.
Решая это уравнение относительно I получим
.
Эта зависимость действующего значения от амплитудного справедлива для ЭДС и напряжения:
Электроизмерительные приборы электромагнитной, электродинамической, электростатической и тепловой систем, а также современные цифровые приборы измеряют действующие значения периодических токов и напряжений.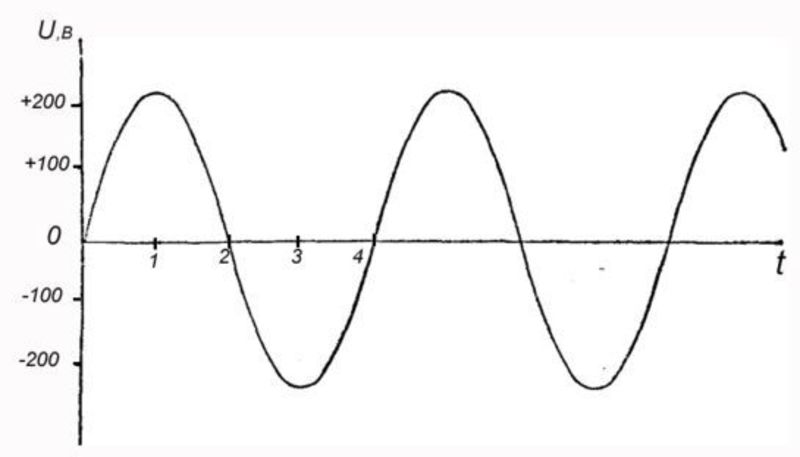
Представление синусоидальных величин векторами и комплексными числами
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями и представить в виде вращающихся векторов на комплексной плоскости.
Рассмотрим вопрос об изображении синусоидальных величин векторами на комплексной плоскости.
Комплексное число имеет действительную и мнимую части. По оси абсцисс будем откладывать действительную часть комплексного числа, а по оси ординат — мнимую часть.
Условимся на оси действительных значений ставить знак ±1, а мнимых ±ј, где .
Комплексное число изображается на комплексной плоскости вектором, численно равным единице и составляющем угол α с осью вещественных значений (осью +1) (рис 3.3). Из курса математики известна формула Эйлера для комплексных чисел:
.
Модуль функции равен единице:
Проекция функции на ось +1 равна , а проекция этой функции на ось +j равна . Возьмем теперь функцию . Очевидно, что
Возьмем теперь функцию . Очевидно, что
.
На комплексной плоскости эта функция, также как и функция изобразится под углом α к оси +1, но величина вектора будет в раз больше.
Угол α может быть любым, в том числе изменяться прямо пропорционально времени. Тогда
.
Слагаемое представляет собой действительную часть выражения , а слагаемое его мнимую часть.
Для единообразия принято изображать на комплексной плоскости векторы синусоидально изменяющихся во времени величин для момента времени ωt=0.
Тогда вектор будет равен
,
где — вектор – то есть комплексная величина, модуль ее равен , а угол, под которым вектор проведен к оси +1 на комплексной плоскости равен начальной фазе ψ. еще называют комплексной амплитудой тока i.
Изображение векторов токов и напряжений электрической цепи на комплексной плоскости позволяет произвести их геометрическое сложение и вычитание, дает наглядное представление об их величине и взаимном расположении.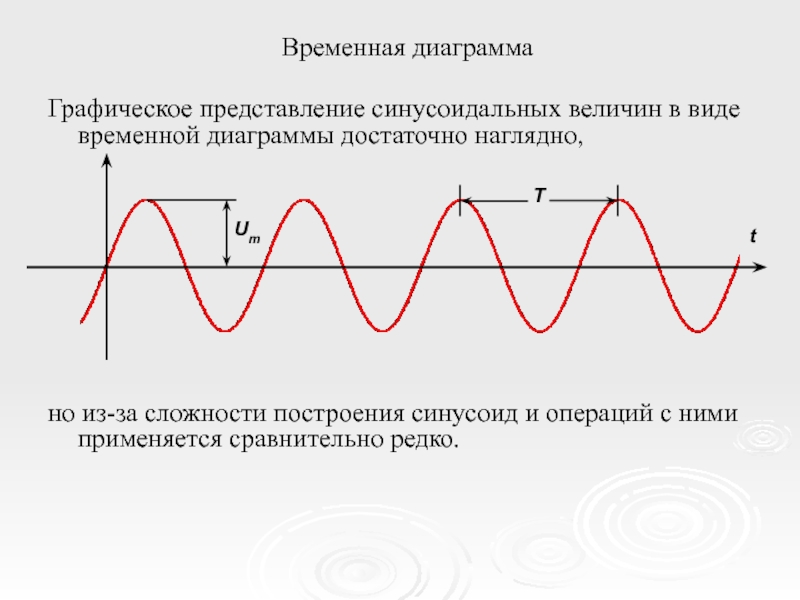
Совокупность векторов на комплексной плоскости изображающих собой синусоидально изменяющиеся функции одной и той же частоты, построенные с соблюдением правильной ориентации относительно друг друга, называется векторной диаграммой.
Применение комплексных чисел позволяет от геометрического сложения векторов на векторной диаграмме перейти к алгебраическому действию над комплексными числами этих векторов. При этом расчеты цепей переменного тока производят теми же методами, что и цепи постоянного тока.
Расчет электрических цепей переменного тока методом комплексных чисел (символическим методом).
Суть метода комплексных чисел заключается в том, что каждый вектор тока или других величин — , , а дальше мы рассмотрим и сопротивлений, раскладывается на составляющие и представляющие проекции вектора на оси комплексной плоскости (рис 3.4). Проекцию вектора на мнимую ось обозначают символом – j. Тогда можно записать:
Умножение вектора на символ j поворачивает этот вектор на угол 90º против часовой стрелки. Умножение вектора на j2 поворачивает вектор на 180º, т. е. откуда . Символ j – это мнимая единица.
Умножение вектора на j2 поворачивает вектор на 180º, т. е. откуда . Символ j – это мнимая единица.
Действующие значения токов и напряжений в комплексной форме обозначаются заглавными буквами, над которыми ставят точку или черту.
Применяют три формы записи комплексных величин:
1. Алгебраическая форма
;
2. Тригонометрическая форма
;
3. Показательная форма
Для перехода от одной формы записи к другой применяются соотношения:
— для перехода от алгебраической формы записи к показательной;
и наоборот — это вытекает из формулы Эйлера.
Алгебраическую форму записи комплексных чисел удобно применять при сложении и вычитании векторов, а показательную при делении и умножении.
Таким образом, синусоидальные величины можно рассматривать как векторы, модули которых равны соответствующим комплексным амплитудам (или действующим значениям) вращающиеся против часовой стрелки с угловой частотой ω.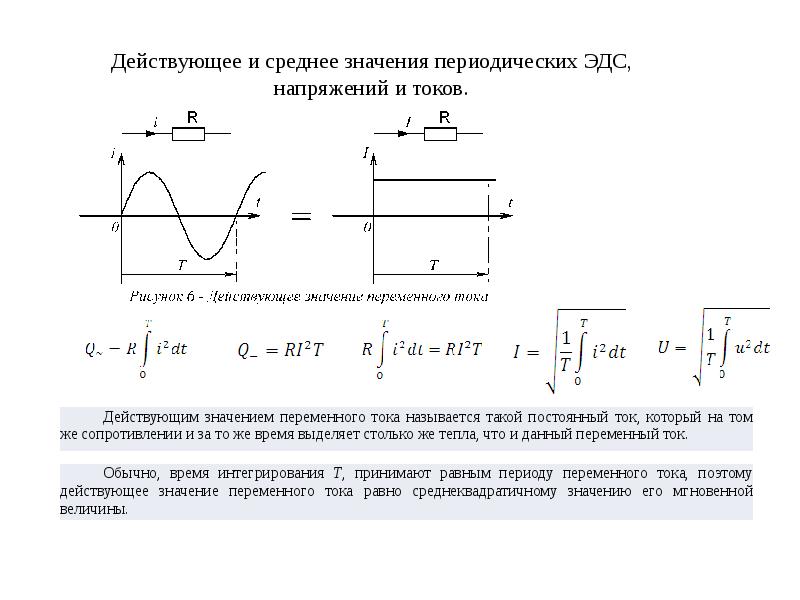 Отметим, что в практических расчетах обычно принимают t = 0 и рассматривают лишь статическое взаимное расположение комплексных ЭДС, токов и напряжений.
Отметим, что в практических расчетах обычно принимают t = 0 и рассматривают лишь статическое взаимное расположение комплексных ЭДС, токов и напряжений.
Синусоидальный ток | Цепи переменного тока
Мгновенное значение синусоидального тока определяется выражением
где — максимальное значение или амплитуда тока. Аргумент синуса называется фазой. Угол ψ равен фазе в начальный момент времени (t=0) и поэтому называется начальной фазой. Фаза с течением времени непрерывно растет. После ее увеличения на 2π весь цикл изменения тока повторяется. Поэтому, когда говорят о фазе для какого-либо момента времени, обычно отбрасывают целое число 2π так, чтобы значение фазы находилось в пределах или в пределах, от 0 до 2π. В течение периода Т фаза увеличивается на 2π. Величина 2π/Т показывает скорость изменения фазы и обозначается буквой ω. Принимая во внимание, что f=1/Т, можно написать
Это выражение, связывающее ω и f, послужило основанием называть ω угловой частотой. Измеряется w числом радианов, на которое увеличивается фаза в секунду. Так, например, при f=50 Гц имеем ω=314 рад/с. Введя в (3.1) обозначение ω для угловой частоты, получим
Измеряется w числом радианов, на которое увеличивается фаза в секунду. Так, например, при f=50 Гц имеем ω=314 рад/с. Введя в (3.1) обозначение ω для угловой частоты, получим
На рис. 3.3 построен график синусоидальных токов одинаковой частоты, но с различными амплитудами и начальными фазами:
По оси абсцисс отложены время t и пропорциональная времени величина ωt.
Начальная фаза отсчитывается всегда от момента, соответствующего началу синусоиды (нулевое значение синусоидальной величины при переходе ее от отрицательных к положительным значениям), до момента начала отсчета времени t=0 (начало координат). При начало синусоиды тока сдвинуто влево, а при для тока — вправо от начала координат.
Мгновенное значение синусоидального тока можно представить и в виде косинусоидальной функции времени
где
Если у нескольких синусоидальных функций, изменяющихся с одинаковой частотой, начала синусоид не совпадают, то говорят, что они сдвинуты относительно друг друга по фазе. Сдвиг фаз измеряется разностью фаз, которая, очевидно, равна разности начальных фаз. На рис. 3.3, например, , т.е. ток опережает по фазе ток на угол , или, что то же самое, ток отстает по фазе от тока на угол .
Сдвиг фаз измеряется разностью фаз, которая, очевидно, равна разности начальных фаз. На рис. 3.3, например, , т.е. ток опережает по фазе ток на угол , или, что то же самое, ток отстает по фазе от тока на угол .
Если у синусоидальных функций одной и той же частоты одинаковые начальные фазы, то говорят, что они совпадают по фазе, если разность их фаз равна , то говорят, что они противоположны по фазе, и, наконец, если разность их фаз равна , то говорят, что они находятся в квадратуре.
Переменный синусоидальный ток
Определение 1
В подавляющем большинстве случаев в электротехнике используются синусоидальные токи. Синусоидальными называют токи мгновенные значения которых изменяются в соответствии с законом:
\[I\left(t\right)=I_m{sin \left(\omega t- \Psi \right)\ \left(1\right).\ }\]
Подобные токи возникают как результат установившихся вынужденных колебаний в RLC контуре, если на него действует переменное напряжение вида:
Амплитуда тока ($I_m$) определяется амплитудой напряжения как:
Выражение:
называют полным электросопротивлением или импедансом.
Частные случаи значений амплитуды силы тока
В том случае, если цепь состоит только из активного сопротивления $(R)$, тогда:
ток совпадает с напряжением по фазе, амплитуда силы тока в этом случае равна:
Если сравнивать уравнение (6) с выражением (3), то можно сделать вывод о том, что если вместо конденсатора участок цепи просто закоротить, то это будет означать переход к емкости равной бесконечности.
Пусть в контуре можно сопротивлением пренебречь $(R=0)$, а емкость считать равной бесконечности, тогда:
Величину $X_L$ называют реактивным индуктивным сопротивлением (индуктивным сопротивлением), если она равна:
Из формулы следует, что индуктивность постоянному току не сопротивляется (при $\omega$=0, $X_L$=0).
Допустим, что $R=0,\ L=0.$ Тогда согласно формуле (3), получим:
Величину $X_C=\frac{1}{\omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением). 2}}=\frac{R}{Z}.$
2}}=\frac{R}{Z}.$
Мощность равную указанной в (13), развивает постоянный ток, который называют действующим (эффективным), равный:
Действующее значение напряжения, равно:
Средняя мощность может быть выражена через действующие значения силы тока и напряжения как:
$cos\varphi $- коэффициент мощности.
Пример 1
Задание: Действующее значение переменного синусоидального тока равно $14,2 А$. Чему равна амплитуда этого тока?
Решение:
В случае синусоидального тока действующее значение тока связано с его амплитудой соотношением:
\[I=\frac{I_m}{\sqrt{2}}=0,707I_m\left(1.1\right).\]
Выразим из (1.1) амплитуду, получим:
\[I_m=\sqrt{2}I(1.2).\]
Проведем вычисления:
\[I_m=\sqrt{2}\cdot 14,2=20\ \left(А\right).\]
Ответ: $I_m=20А.$
Пример 2
Задание: В проводнике с сопротивлением $R$ тек переменный ток. За время $t$ выделилось количество тепла $Q$. 2Rt\left(2.1\right)\]
2Rt\left(2.1\right)\]
выразим силу тока, получим:
\[I=\sqrt{\frac{Q}{Rt}}\left(2.2\right).\]
Для тока, который изменяется по гармоническому закону действующее значение тока связано с его амплитудой соотношением:
\[I=\frac{I_m}{\sqrt{2}}\to I_m=\sqrt{2}I\left(2.3\right).\]
Используя формулу (2.2) и (2.3), получим:
\[I_m=\sqrt{\frac{2Q}{Rt}}.\]
Ответ: $I_m=\sqrt{\frac{2Q}{Rt}}.$
§47. Основные параметры переменного тока
При подключении к источнику переменного тока с синусоидально изменяющейся э. д. с. электрических цепей с линейными сопротивлениями в них будут действовать синусоидально изменяющиеся напряжения и проходить синусоидально изменяющиеся токи. Переменные токи, э. д. с. и напряжения характеризуются четырьмя основными параметрами: периодом, частотой, амплитудой и действующим значением.
Период.
Промежуток времени Т, в течение которого э. д. с, напряжение и или ток i (рис. 169, а) совершают полный цикл изменений, называется периодом.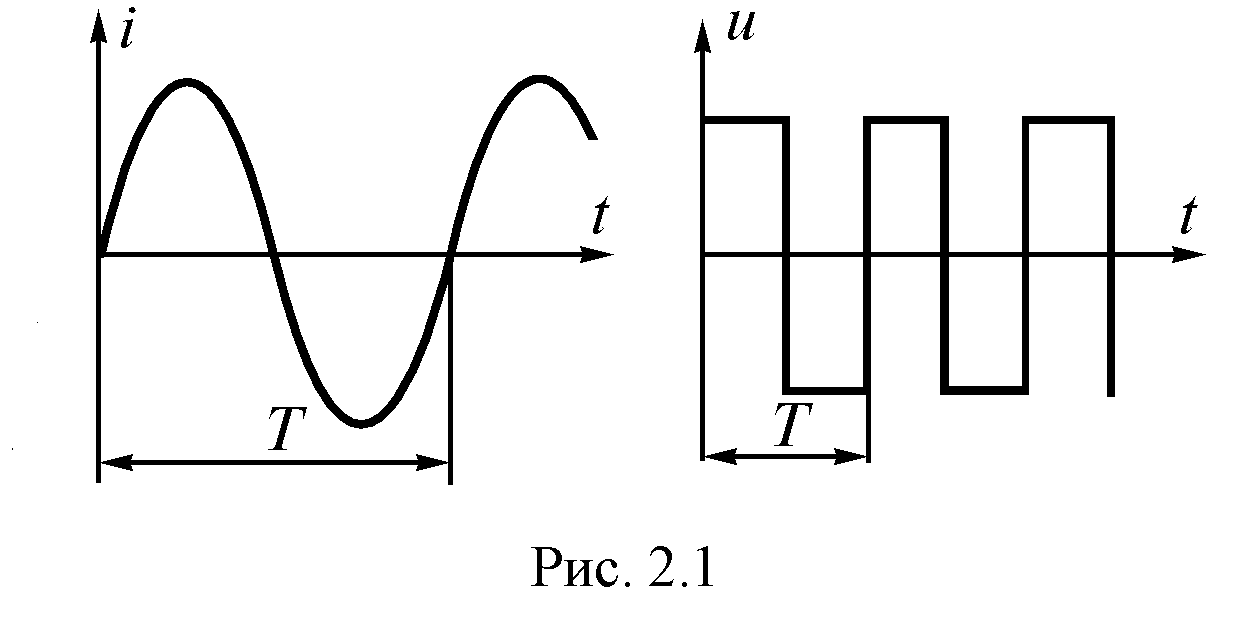 Чем быстрее вращается виток или ротор генератора переменного тока, тем меньше период изменения э. д. с. или тока.
Чем быстрее вращается виток или ротор генератора переменного тока, тем меньше период изменения э. д. с. или тока.
Частота.
Число полных периодов изменения э. д. с, напряжения или тока в 1 с называется частотой,
f = 1 / T
Она измеряется в герцах (Гц), т. е. числом периодов в секунду. Чем больше частота, тем меньше период изменения тока, напряжения или э. д. с. (рис. 169,б). В Советском Союзе все электрические станции переменного тока вырабатывают ток, изменяющийся с частотой 50 Гц, т. е. 50 периодов в секунду. В автоматике и радиотехнике применяют электрические токи и более высоких частот. Такие частоты измеряются в килогерцах (1 кГц=103 Гц) и мегагерцах (1 МГц=106 Гц).
Рис. 169. Кривые изменения синусоидального переменного тока при различной частоте
Из рис. 169,а следует, что в течение времени одного периода Т фаза ωt тока (э. д. с. или напряжения) изменяется на угол 360°, или 2π радиан. Поэтому
ω = 2π/T = 2πf
Эту величину называют угловой частотой переменного тока, она имеет размерность рад/с.
Амплитуда.
Наибольшее значение переменного тока (переменных э. д. с. и напряжения) называют амплитудным значением, или амплитудой. В рассмотренном нами простейшем генераторе переменного тока (см. рис. 168, а) э. д. с. е дважды достигает амплитудного значения: во время первого полуоборота +Ет (направлена от начала витка к его концу), а во время второго полуоборота — Ет (направлена от конца витка к его началу).
Точно так же за один период ток i 2 раза достигает амплитудного значения: Iт и — Iт. Амплитудное значение тока, напряжения и э. д. с. в формулах обозначают соответствующими буквами с индексами «т», т. е. Iт Uт, Ет и др.
Действующее значение.
Ток, напряжение и э. д. с, действующие в электрической цепи в каждый отдельный момент времени, определяются так называемыми мгновенными значениями. Эти значения принято обозначать строчными буквами i, и, е. Однако судить о переменных э. д. с, токе или напряжении по их мгновенным значениям неудобно, так как эти значения непрерывно меняются.
Поэтому оценивать способность переменного тока совершать механическую работу или создавать тепло принято по действующему его значению. Под действующим значением переменного тока понимают силу такого постоянного тока (прямая 2 на рис. 169,а), который, проходя по проводнику в течение некоторого времени (например, в течение одного периода или 1 с), выделит в нем такое же количество тепла (произведет такую же механическую работу), как и данный переменный ток (кривая 1).
Действующие значения тока, напряжения и э. д. с. обозначают соответственно I, U, Е.
При синусоидальном переменном токе:
I = Iт / √2 = 0,707 Iт
Если известно действующее значение тока I, то его амплитудное значение:
Iт = √2 I = 1,41 I
Аналогично для синусоидальных напряжений и э. д. с.:
U / Uт = Е1 / Ет = 1 / √2 = 0,707
На практике для характеристики параметров переменного тока используют, главным образом, действующие значения тока, напряжения и э. д. с. Например, когда говорят, что напряжение в осветительной сети переменного тока составляет 220 В или что по цепи проходит ток 100 А, то это значит, что в данной сети действующее значение напряжения равно 220 В или что действующее значение тока, проходящего по данной цепи, равно 100 А.
Электрическая энергия и механическая работа, создаваемые переменным током в различных электрических устройствах, пропорциональны действующим значениям тока и напряжения. Большая часть существующих приборов для измерения переменного тока измеряет действующие значения тока, напряжения и э. д. с.
Переменный синусоидальный ток
Колебания маятника также
подчиняются закону синуса.
Если
записать проекцию траектории
движения математического
маятника на
движущуюся бумажную ленту —
получится синусоида.
Синусоидальным
током называется периодический переменный
ток, который с течением времени изменяется
по закону синуса.
Синусоидальный ток —
элементарный, то есть его невозможно
разложить на другие более простые
переменные токи.
Переменный
синусоидальный ток выражается формулой:
,
где
—
амплитуда
синусоидального тока;
—
некоторый угол,
называемый фазой
синусоидального тока.
Фаза синусоидального
тока изменяется
пропорционально времени .
Множитель ,
входящий в выражение фазы —
величина постоянная, называемая угловой
частотой переменного
тока.
Угловая
частота синусоидального
тока зависит от частоты этого
тока и определяется формулой:
,
где
—
угловая частота
синусоидального тока;
—
частота синусоидального
тока;
— период синусоидального
тока;
—
центральный
угол окружности,
выраженный в радианах.
Зависимость
синусоидального тока от времени
Зависимость
синусоидального тока от угла ωt
Периоду соответствует
угол ,
половине периода угол и
так далее…
Исходя
из формулы ,
можно определить размерность угловой
частоты:
,
где
— время в секундах,
—
угол в радианах,
является безразмерной величиной.
Фаза синусоидального
тока измеряется радианами.
1
радиан = 57°17′, угол 90° = радиан,
угол 180° = радиан,
угол 270° = радиан,
угол 360° = радиан,
где радиан; — число
«Пи», ° — угловой
градус и ′ — угловая
минута.
Формула описывает
случай, когда наблюдение за изменением
переменного синусоидального тока
начинается с момента времени при .
Если не
равен нулю, тогда формула для определения
мгновенного значения переменного
синусоидального тока примет следующий
вид:
,
где
— фаза переменного
синусоидального тока;
— угол,
называемый начальной
фазой переменного синусоидального
тока.
Начальная
фаза переменного тока
Начальная
фаза переменного тока
Если
в формуле принять ,
то будем иметь
, и .
Начальная
фаза — это фаза синусоидального тока
в момент времени .
Начальная
фаза переменного синусоидального тока
может быть положительной или
отрицательной величиной.
При мгновенное
значение синусоидального тока в момент
времени положительно,
при —
отрицательно.
Если
начальная фаза ,
то ток определяется по формуле .
Мгновенное значение его в момент
времени равно
,
то есть равно положительной амплитуде
тока.
Если
начальная фаза ,
то ток определяется по формуле .
Мгновенное значение его в момент
времени равно
,
то есть равно отрицательной амплитуде
тока.
9. Идеальные элементы
электрической цепи синусоидального
тока
11.
Неразветвленная
цепь синусоидального тока. Резонанс
напряжений
Резонанс
напряжений —
резонанс, происходящий в
последовательном колебательном
контуре при
его подключении к источнику
напряжения, частота которого
совпадает с собственной
частотой контура.
Описание явления
Пусть
имеется колебательный контур с частотой
собственных колебаний f,
и пусть внутри него работает генератор
переменного тока такой же частоты f.
В
начальный момент конденсатор контура
разряжен, генератор не работает. После
включения напряжение на генераторе
начинает возрастать, заряжая конденсатор.
Катушка в первое мгновение не пропускает
ток из-за ЭДС самоиндукции. Напряжение
на генераторе достигает максимума,
заряжая до такого же напряжения
конденсатор.
Далее:
конденсатор начинает разряжаться на
катушку. Напряжение на нем падает с
такой же скоростью, с какой уменьшается
напряжение на генераторе.
Далее:
конденсатор разряжен до нуля, вся энергия
электрического поля, имевшаяся в
конденсаторе, перешла в энергию магнитного
поля катушки. На клеммах генератора в
этот момент напряжение нулевое.
Далее:
так как магнитное поле не может
существовать стационарно, оно начинает
уменьшаться, пересекая витки катушки
в обратном направлении. На выводах
катушки появляется ЭДС индукции, которое
начинает перезаряжать конденсатор. В
цепи колебательного контура течет ток,
только уже противоположно току заряда,
так как витки пересекаются полем в
обратном направлении. Обкладки
конденсатора перезаряжаются зарядами,
противоположными первоначальным.
Одновременно растет напряжение на
генераторе противоположного знака,
причем с той же скоростью, с какой катушка
заряжает конденсатор.
Далее:
катушка перезарядила конденсатор до
максимального напряжения. Напряжение
на генераторе к этому моменту тоже
достигло максимального.
Возникла
следующая ситуация. Конденсатор и
генератор соединены последовательно
и на обоих напряжение, равное напряжению
генератора. При последовательном
соединении источников питания их
напряжения складываются.
Следовательно,
в следующем полупериоде на катушку
пойдет удвоенное напряжение (и от
генератора, и от конденсатора), и колебания
в контуре будут происходить при удвоенном
напряжении на катушке.
В
контурах с низкой добротностью напряжение
на катушке будет ниже удвоенного, так
как часть энергии будет рассеиваться
(на излучение, на нагрев) и энергия
конденсатора не перейдет полностью в
энергию катушки). Соединены как бы
последовательно генератор и часть
конденсатора.
переменного тока | Безграничная физика
Фазоры
Фазоры используются для анализа электрических систем в синусоидальном устойчивом состоянии и с постоянной угловой частотой.
Цели обучения
Обсудить применение фазового вектора
Основные выводы
Ключевые моменты
- Вектор — это представление синусоидальной функции, амплитуда (A), частота (ω) и фаза (θ) не зависят от времени.Если ω используется всеми компонентами системы, его можно исключить, оставив только A и ω. Термин фазор обычно относится к двум последним факторам.
- Фазоры значительно упрощают выражение синусоидально изменяющихся сигналов.
- Фазоры могут использоваться для анализа поведения электрических систем, таких как цепи RLC, которые достигли своего рода равновесия, называемого синусоидальным устойчивым состоянием. В синусоидальном установившемся состоянии каждое напряжение и ток в системе являются синусоидальными с угловой частотой ω.
- Phasors позволяют нам применять методы, используемые для решения цепей постоянного тока, для решения цепей RC.
Ключевые термины
- синусоидальное установившееся состояние : Указывает, что все напряжение и ток в системе синусоидальны с одинаковой угловой частотой ω.
- комплексные числа : числа с мнимой частью. Обычно обозначается как i.
- phasor : представление комплексного числа в виде комплексной экспоненты.
Фазоры
Комплексные числа играют важную роль в физике. Обычно комплексные числа записываются в виде их действительной части плюс мнимая часть. Например, [latex] \ text {a} + \ text {bi} [/ latex], где a и b — действительные числа, а [latex] \ text {i} [/ latex] сигнализирует о мнимой части. Однако часто бывает удобно записывать комплексные числа в форме экспоненты, называемой фазором.
В физике фазовый вектор или фазор представляет собой представление синусоидальной функции, амплитуда ( A ), частота ( ω ) и фаза ( θ ) не зависят от времени, как показано на диаграмме.Фазоры разделяют зависимости от A , ω и θ на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид. В таких ситуациях фазоры позволяют исключить эту общую характеристику, оставляя только функции A и θ . В результате тригонометрия сводится к алгебре, а линейные дифференциальные уравнения становятся алгебраическими.Поэтому термин фазор часто относится только к этим двум факторам.
Векторная диаграмма : Пример последовательной RLC-цепи и соответствующая векторная диаграмма для определенного ω. Инженеры-электрики, инженеры-электронщики, инженеры-электронщики и авиастроители — все используют векторные диаграммы для визуализации сложных констант и переменных (векторов). Как и векторы, стрелки, нарисованные на миллиметровой бумаге или компьютерных дисплеях, представляют собой векторы.
Фазоры часто используются в электрических системах при рассмотрении напряжений и токов, которые изменяются синусоидально во времени, например, в цепях RLC.{\ text {i} \ theta} [/ латекс]. В последнем случае это сокращенное обозначение, кодирующее амплитуду и фазу лежащей в основе синусоиды.
Фазорное представление сигналов
В основе векторного представления сигнала лежат две ключевые идеи:
- реальный изменяющийся во времени сигнал может быть представлен сложным изменяющимся во времени сигналом; и
- сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа, которое не зависит от времени, и сложного сигнала, который зависит от времени.
Сигнал:
[латекс] \ text {x} (\ text {t}) = \ text {Acos} (\ omega \ text {t} + \ theta) [/ latex]
, показанный на рисунке ниже, представляет собой косинусоидальный сигнал с амплитудой A , частотой и фазой θ . Амплитуда A характеризует размах размаха 2A от пика до пика, угловая частота ω характеризует период T = 2π / ω между отрицательными и положительными пересечениями нуля (или положительными пиками или отрицательными значениями). пиков), а фаза θ характеризует время τ = — θ / ω , когда сигнал достигает своего первого пика.С таким определением сигнал x (t) также может быть записан как
[латекс] \ text {x} (\ text {t}) = \ text {Acos} (\ text {t} — \ tau) [/ latex].
Косинусоидальный сигнал : Косинусоидальный сигнал.
Если значение τ положительно, тогда τ представляет собой «временную задержку», которая описывает время (больше нуля), когда достигается первый пик. Когда τ отрицательно, тогда τ представляет собой «временной прогресс», который описывает время (меньше нуля), когда был достигнут последний пик.Подставив = 2π / T, мы получим третий способ записи x (t):
[латекс] \ text {x} (\ text {t}) = \ text {Acos} \ frac {2 \ pi} {\ text {T}} (\ text {t} — \ tau) [/ latex]
В этой форме сигнал легко построить. Просто нарисуйте косинусоидальную волну с амплитудой A и периодом T ; затем ударьте по началу координат (t = 0) так, чтобы сигнал достиг своего пика при τ . Таким образом, параметры, определяющие косинусоидальный сигнал, имеют следующие единицы:
- A , произвольно (e.g., вольт или метры / сек, в зависимости от применения)
- ω , в радианах / сек (рад / сек)
- T , в секундах (sec)
- θ , в радианах (рад)
- τ , в секундах (сек)
Синусоидальное установившееся состояние и последовательные схемы RLC CircuitPhasors могут использоваться для анализа поведения электрических и механических систем, которые достигли своего рода равновесия, называемого синусоидальным установившимся состоянием.
В синусоидальном установившемся состоянии каждое напряжение и ток (или сила и скорость) в системе синусоидальны с угловой частотой ω .Однако амплитуды и фазы этих синусоидальных напряжений и токов различны.
Например, напряжение на резисторе может опережать напряжение на конденсаторе на 90 и отставать от напряжения на катушке индуктивности на 90 ∘ . Чтобы конкретизировать наше применение векторов к электрическим системам, мы рассмотрим схему серии RLC , показанную на рисунке. Стрелка с надписью i (t) обозначает ток, который течет в ответ на приложенное напряжение.{\ text {i} \ theta} [/ латекс].
Затем мы описываем источник напряжения вектором В и помним, что мы всегда можем вычислить фактическое напряжение, умножив его на e iωt и взяв действительную часть.
Среднеквадратичные значения
Среднеквадратичное значение напряжения или тока — это усредненное по времени напряжение или ток в системе переменного тока.
Цели обучения
Связать среднеквадратичное напряжение и ток в цепи переменного тока с пиковым напряжением и током и средней мощностью.
Основные выводы
Ключевые моменты
- Напомним, что в отличие от постоянного тока и напряжения, которые постоянны, переменный ток и напряжение меняются со временем.Это называется переменным током, потому что его направление меняется.
- Среднеквадратичное значение (сокращенно RMS или RMS) — это статистическая мера величины переменной величины. Мы используем среднеквадратическое значение для выражения среднего тока или напряжения в системе переменного тока.
- Среднеквадратичные значения тока и напряжения (для синусоидальных систем) представляют собой пиковый ток и напряжение, вычисленные как квадратный корень из двух.
- Средняя мощность в цепи переменного тока является произведением среднеквадратичного значения тока и среднеквадратичного напряжения.
Ключевые термины
- среднеквадратичное значение : Квадратный корень из среднего арифметического квадратов.
- среднеквадратичный ток : среднеквадратичное значение тока, Irms = I0 / √2, где I0 — пиковый ток, в системе переменного тока
- среднеквадратичное напряжение : среднеквадратичное значение напряжения, Vrms = V0 / √2, где V0 — пиковое напряжение, в системе переменного тока
Среднеквадратичные значения и переменный ток
Напомним, что в случае переменного тока (AC) поток электрического заряда периодически меняет направление.В отличие от постоянного тока (DC), где токи и напряжения постоянны, переменные токи и напряжения меняются со временем. Напомним, что в большинстве жилых и коммерческих источников питания используется переменный ток. Часто бывает так, что нам нужно знать среднее время , равное току или напряжению. Зная ток или напряжение как функцию времени, мы можем извлечь среднеквадратичное значение с течением времени, чтобы получить средние значения.
Определение
Среднеквадратичное значение (сокращенно RMS или rms), также известное как среднее квадратичное, является статистической мерой величины переменной величины. {2} \ text {dt}} [/ latex]
RMS для функции за все время ниже.{2} \ text {dt}} [/ latex]
RMS за все время периодической функции равно RMS одного периода функции. Среднеквадратичное значение непрерывной функции или сигнала можно приблизительно оценить, взяв среднеквадратичное значение серии равномерно распределенных отсчетов.
Применение к напряжению и току
Рассмотрим случай синусоидального изменения напряжения:
Синусоидальное напряжение и ток : (a) Напряжение и ток постоянного тока постоянны во времени после установления тока.(б) График зависимости напряжения и тока от времени для сети переменного тока частотой 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления. Частоты и пиковое напряжение источников переменного тока сильно различаются.
[латекс] \ text {V} = \ text {V} _ {0} \ text {sin} (2 \ pi \ text {ft}) [/ latex]
В — это напряжение в момент времени t , В, 0, — пиковое напряжение, а f — частота в герцах. Для этой простой цепи сопротивления I = V / R, поэтому переменный ток равен:
[латекс] \ text {I} = \ text {I} _ {0} \ text {sin} (2 \ pi \ text {ft}) [/ latex]
Здесь I — ток в момент времени t, а I 0 = V 0 / R — пиковый ток.{\ text {T} _ {2}}} = \ text {V} _ {0} \ sqrt {\ frac {1} {\ text {T} _ {2} — \ text {T} _ {1} } \ frac {\ text {T} _ {2} — \ text {T} _ {1}} {2}} [/ latex]
[латекс] = \ frac {\ text {V} _ {0}} {\ sqrt {2}} [/ латекс]
Точно так же вы можете обнаружить, что среднеквадратичный ток может быть выражен довольно просто:
[латекс] \ text {I} _ {\ text {rms}} = \ text {I} _0 / \ sqrt {2} [/ latex]
Обновленные уравнения цепи для AC
Многие из полученных нами уравнений для постоянного тока в равной степени применимы и к переменному току. Если нас интересует усредненный по времени результат, и соответствующие переменные выражаются как их среднеквадратичные значения.{2} \ text {R} [/ latex]
Из приведенных выше уравнений видно, что мы можем выразить среднюю мощность как функцию пикового напряжения и тока (в случае синусоидального изменения тока и напряжения):
Средняя мощность : мощность переменного тока как функция времени. Поскольку напряжение и ток здесь синфазны, их произведение неотрицательно и колеблется между нулем и I0V0. Средняя мощность (1/2) I0V0.
[латекс] \ text {P} _ {\ text {ave}} = \ text {I} _ {\ text {rms}} \ text {V} _ {\ text {rms}} = \ frac {\ text {I} _ {0}} {\ sqrt {2}} \ frac {\ text {V} _ {0}} {\ sqrt {2}} = \ frac {1} {2} \ text {V} _ {0} \ text {I} _ {0} [/ latex]
Среднеквадратичные значения также полезны, если напряжение изменяется в зависимости от формы волны, отличной от синусоиды, например, от прямоугольной, треугольной или пилообразной волны.
Формы сигналов : синусоидальные, квадратные, треугольные и пилообразные формы сигналов
Меры предосторожности в домашнем хозяйстве
Системы и устройства электробезопасности спроектированы и широко используются для снижения рисков теплового удара и поражения электрическим током.
Цели обучения
Определить основные риски, связанные с электрическими цепями, и стратегии снижения этих рисков
Основные выводы
Ключевые моменты
- Электрические цепи могут привести к перегреву и поражению электрическим током.
- Предохранители и автоматические выключатели используются для отключения токов, превышающих установленный предел безопасности, что предотвращает перегрев.
- Трехпроводная система защищает от термического воздействия и поражения электрическим током за счет использования проводов под напряжением, нейтрали и заземления, а также заземления нейтрального провода и токопроводящих корпусов приборов.
- Прежде чем вносить изменения в какие-либо схемы, важно установить правильную цветовую схему для вашего региона (цвет проводов под напряжением, нейтрали и заземления).
- Переменный ток может вызвать ЭДС на корпусе устройства, что создает опасность поражения электрическим током, поэтому важно заземлить корпус.
Ключевые термины
- термическая опасность : опасность поражения электрическим током, вызванная перегревом (например, в резистивном элементе)
- опасность поражения электрическим током : опасность поражения электрическим током, при котором ток проходит через тело
- трехпроводная система : современная электромонтажная система с соблюдением техники безопасности; содержит провода под напряжением, нейтраль и заземление
Электробезопасность и бытовая техника
У электричества две опасности.Опасность термического воздействия возникает в случае электрического перегрева. Опасность поражения электрическим током возникает, когда через человека проходит электрический ток. Существует множество систем и устройств, предотвращающих опасность поражения электрическим током.
Цепь переменного тока, не имеющая функций безопасности : Схема простой цепи переменного тока с источником напряжения и одним устройством, обозначенным сопротивлением R. В ней отсутствуют функции безопасности.
На практике простая цепь переменного тока без функций безопасности не является способом распределения мощности.Современная бытовая и промышленная проводка требует трехпроводной системы, которая имеет несколько функций безопасности. Первая функция безопасности — это знакомый автоматический выключатель (или предохранитель), предотвращающий тепловую перегрузку. Во-вторых, вокруг прибора есть защитный чехол, как у тостера или холодильника. Корпус предотвращает прикосновение людей к оголенным проводам и электрический контакт с цепью, помогая предотвратить удары.
Трехпроводная система : Трехпроводная система соединяет нейтральный провод с землей в источнике напряжения и в месте расположения пользователя.Он существует при нулевом напряжении и обеспечивает альтернативный обратный путь для тока через землю. Корпус прибора также заземлен до нуля вольт. Автоматический выключатель или предохранитель предотвращают тепловую перегрузку и находятся последовательно на активном (токоведущем / горячем) проводе. Цвет изоляции проводов зависит от региона. Важно проверить на месте, какие цветовые коды используются, даже если они использовались в одной конкретной установке.
Есть три соединения с землей или землей (земля / земля,).Заземление — это путь с низким сопротивлением непосредственно к земле. Два соединения «земля / земля» на нейтральном проводе заставляют его существовать при нулевом вольт относительно земли, давая этому проводу свое название. Таким образом, к этому проводу безопасно прикасаться, даже если его изоляция отсутствует. Нейтральный провод — это обратный путь для тока, по которому следует замкнуть цепь.
Два соединения «земля / земля» обеспечивают альтернативный путь через землю для замыкания цепи, поскольку земля является хорошим проводником.Ближайшее к источнику питания соединение заземления может быть на электростанции, а другое — у пользователя. Третье соединение «земля / земля» связано с корпусом устройства через зеленый провод «земля / заземление», заставляя корпус быть на нуле вольт. Провод под напряжением или под напряжением (под напряжением / под напряжением) подает напряжение и ток для работы прибора. Трехпроводная система подключается к прибору через трехконтактную вилку.
Трехконтактная вилка : Стандартная трехконтактная вилка может быть вставлена только одним способом для обеспечения правильного функционирования трехпроводной системы.
Заглушка с тремя штырями
Трехпроводная система заменила старую двухпроводную систему, в которой отсутствует заземляющий провод. В обычных условиях изоляция токоведущего / горячего и нейтрального проводов предотвращает размещение корпуса непосредственно внутри цепи, так что заземляющий провод может казаться двойной защитой. Однако заземление корпуса решает несколько проблем. Самая простая проблема — это износ изоляции на токоведущем / горячем проводе, который позволяет ему контактировать с корпусом.При отсутствии заземления (некоторые люди отрезают третий контакт вилки, потому что у них только устаревшие розетки с двумя отверстиями), возможно сильное поражение электрическим током. Это особенно опасно на кухне, где хорошее заземление обеспечивается за счет воды на полу или водопроводного крана.
При неповрежденном соединении «земля / земля» сработает автоматический выключатель, что потребует ремонта устройства. Некоторые приборы по-прежнему продаются с двухконтактными вилками. Эти приборы, в том числе электроинструменты с ударопрочными пластиковыми корпусами, имеют непроводящие корпуса и называются «с двойной изоляцией».«Современные двухконтактные вилки можно вставлять в асимметричную стандартную розетку только одним способом, обеспечивая правильное подключение токоведущих / горячих и нейтральных проводов.
Цветовое кодирование
Изоляционный пластик имеет цветовую кодировку для обозначения проводов под напряжением, нейтрали и заземления, но эти коды различаются во всем мире. Провода под напряжением / под напряжением могут быть коричневыми, красными, черными, синими или серыми. Нейтральные провода могут быть синими, черными или белыми. Поскольку один и тот же цвет может использоваться для токоведущих / горячих или нейтральных проводов в разных частях мира, важно подтвердить цветовую кодировку для любого данного местного региона.Единственным исключением является провод заземления, который часто бывает зеленого цвета, но может быть желтым или оголенным. «Полосатые покрытия иногда используются в интересах дальтоников.
Индукционный ток и ток утечки
Электромагнитная индукция вызывает более тонкую проблему, решаемую путем заземления корпуса. Переменный ток в приборах может вызвать на корпусе ЭДС. В случае заземления напряжение на корпусе поддерживается близким к нулю, но если корпус не заземлен, может произойти поражение электрическим током. Ток, который создается наведенной ЭДС корпуса, называется током утечки, хотя ток не обязательно проходит от резистора к корпусу.
электричества | Определение, факты и типы
Электростатика — это изучение электромагнитных явлений, которые происходят при отсутствии движущихся зарядов, то есть после установления статического равновесия. Заряды быстро достигают своего положения равновесия, потому что электрическая сила чрезвычайно велика. Математические методы электростатики позволяют рассчитывать распределения электрического поля и электрического потенциала по известной конфигурации зарядов, проводников и изоляторов.И наоборот, имея набор проводников с известными потенциалами, можно рассчитать электрические поля в областях между проводниками и определить распределение заряда на поверхности проводников. Электрическую энергию набора зарядов в состоянии покоя можно рассматривать с точки зрения работы, необходимой для сборки зарядов; в качестве альтернативы, можно также считать, что энергия находится в электрическом поле, создаваемом этой сборкой зарядов. Наконец, энергия может храниться в конденсаторе; энергия, необходимая для зарядки такого устройства, хранится в нем как электростатическая энергия электрического поля.
Изучите, что происходит с электронами двух нейтральных объектов, тренных друг о друга в сухой среде.
Объяснение статического электричества и его проявлений в повседневной жизни.
Encyclopdia Britannica, Inc. Посмотреть все видео к этой статье
Статическое электричество — это знакомое электрическое явление, при котором заряженные частицы передаются от одного тела к другому. Например, если два предмета трутся друг о друга, особенно если они являются изоляторами, а окружающий воздух сухой, предметы приобретают одинаковые и противоположные заряды, и между ними возникает сила притяжения.Объект, теряющий электроны, становится заряженным положительно, а другой — отрицательно. Сила — это просто притяжение между зарядами противоположного знака. Свойства этой силы описаны выше; они включены в математическое соотношение, известное как закон Кулона. Электрическая сила на заряде Q 1 в этих условиях, вызванная зарядом Q 2 на расстоянии r , задается законом Кулона
Жирным шрифтом в уравнении обозначается вектор характер силы, а единичный вектор r̂ — это вектор, размер которого равен единице, и который направлен от заряда Q 2 к заряду Q 1 .Константа пропорциональности k равна 10 −7 c 2 , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10 9 ньютон-квадратный метр на квадратный кулон (Нм 2 / C 2 ). На рисунке 1 показано усилие на Q 1 , вызванное Q 2 . Числовой пример поможет проиллюстрировать эту силу. И Q 1 , и Q 2 произвольно выбраны в качестве положительных зарядов, каждый с величиной 10 −6 кулонов.Заряд Q 1 расположен в координатах x , y , z со значениями 0,03, 0, 0 соответственно, а Q 2 имеет координаты 0, 0,04, 0. Все координаты даны в метрах. Таким образом, расстояние между Q 1 и Q 2 составляет 0,05 метра.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Величина силы F на заряде Q 1 , рассчитанная с использованием уравнения (1), равна 3.6 ньютонов; его направление показано на рисунке 1. Сила, действующая на Q 2 из-за Q 1 , составляет — F , что также имеет величину 3,6 ньютона; его направление, однако, противоположно направлению F . Сила F может быть выражена через ее компоненты по осям x и y , поскольку вектор силы лежит в плоскости x y . Это делается с помощью элементарной тригонометрии из геометрии рисунка 1, а результаты показаны на рисунке 2.Таким образом, в ньютонах. Закон Кулона математически описывает свойства электрической силы между зарядами в состоянии покоя. Если заряды имеют противоположные знаки, сила будет притягивающей; притяжение было бы указано в уравнении (1) отрицательным коэффициентом единичного вектора r̂. Таким образом, электрическая сила на Q 1 будет иметь направление, противоположное единичному вектору r̂ , и будет указывать от Q 1 к Q 2 .В декартовых координатах это привело бы к изменению знаков компонентов силы x и y в уравнении (2).
компоненты кулоновской силы
Рисунок 2: Составляющие x и y силы F на рисунке 4 (см. Текст).
Предоставлено Департаментом физики и астрономии Университета штата Мичиган
Как можно понять эту электрическую силу на Q 1 ? По сути, сила возникает из-за наличия электрического поля в позиции Q 1 .Поле создается вторым зарядом Q 2 и имеет величину, пропорциональную размеру Q 2 . При взаимодействии с этим полем первый заряд на некотором расстоянии либо притягивается, либо отталкивается от второго заряда, в зависимости от знака первого заряда.
Зависимость переменного тока (AC) от постоянного (DC)
Пораженный громом!
Откуда австралийская рок-группа AC / DC получила свое название? Да ведь переменный ток и постоянный ток, конечно же! И переменный, и постоянный ток описывают типы протекания тока в цепи.В постоянного тока (DC) электрический заряд (ток) течет только в одном направлении. Электрический заряд в переменного тока (AC), с другой стороны, периодически меняет направление. Напряжение в цепях переменного тока также периодически меняется на противоположное, потому что ток меняет направление.
Большая часть созданной вами цифровой электроники будет использовать постоянный ток. Однако важно понимать некоторые концепции переменного тока. Большинство домов подключено к сети переменного тока, поэтому, если вы планируете подключить проект музыкальной шкатулки Tardis к розетке, вам нужно будет преобразовать переменный ток в постоянный.Переменный ток также имеет некоторые полезные свойства, такие как возможность преобразовывать уровни напряжения с помощью одного компонента (трансформатора), поэтому переменный ток был выбран в качестве основного средства для передачи электроэнергии на большие расстояния.
Что вы узнаете
- История создания переменного и постоянного тока
- Различные способы генерации переменного и постоянного тока
- Некоторые примеры приложений переменного и постоянного тока
Рекомендуемая литература
и nbsp
и nbsp
Переменный ток (AC)
Переменный ток описывает поток заряда, который периодически меняет направление.В результате уровень напряжения также меняется на противоположный вместе с током. Переменный ток используется для подачи электроэнергии в дома, офисные здания и т. Д.
Генерация переменного тока
переменного тока может производиться с использованием устройства, называемого генератором переменного тока. Это устройство представляет собой особый тип электрического генератора, предназначенный для выработки переменного тока.
Проволочная петля скручена внутри магнитного поля, которое индуцирует ток по проводу. Вращение провода может происходить с помощью любого количества средств: ветряной турбины, паровой турбины, проточной воды и так далее.Поскольку провод вращается и периодически меняет магнитную полярность, напряжение и ток на проводе чередуются. Вот короткая анимация, демонстрирующая этот принцип:
(Видео предоставлено: Хуррам Танвир)
Генератор переменного тока можно сравнить с нашей предыдущей аналогией с водой:
Чтобы генерировать переменный ток в наборе водопроводных труб, мы соединяем механический кривошип с поршнем, который перемещает воду по трубам вперед и назад (наш «переменный» ток).Обратите внимание, что защемленный участок трубы по-прежнему оказывает сопротивление потоку воды независимо от направления потока.
Формы сигналов
AC может быть разных форм, если напряжение и ток чередуются. Если мы подключим осциллограф к цепи переменного тока и построим график ее напряжения с течением времени, мы можем увидеть несколько различных форм сигналов. Самый распространенный тип переменного тока — это синусоида. Переменный ток в большинстве домов и офисов имеет колебательное напряжение, которое создает синусоидальную волну.
Другие распространенные формы переменного тока включают прямоугольную волну и треугольную волну:
Прямоугольные волны часто используются в цифровой и переключающей электронике для проверки их работы.
Треугольные волны используются при синтезе звука и используются для тестирования линейной электроники, такой как усилители.
Описание синусоидальной волны
Мы часто хотим описать форму волны переменного тока в математических терминах. В этом примере мы будем использовать обычную синусоидальную волну. Синусоидальная волна состоит из трех частей: амплитуда, частота и фаза .
Рассматривая только напряжение, мы можем описать синусоидальную волну как математическую функцию:
V (t) — это наше напряжение как функция времени, что означает, что наше напряжение изменяется с изменением времени. Уравнение справа от знака равенства описывает, как напряжение изменяется во времени.
V P — это амплитуда . Это описывает максимальное напряжение, которое наша синусоида может достигать в любом направлении, что означает, что наше напряжение может быть + V P вольт, -V P вольт или где-то посередине.
Функция sin () указывает, что наше напряжение будет в форме периодической синусоидальной волны, которая представляет собой плавные колебания около 0 В.
2π — это константа, которая преобразует частоту из циклов (в герцах) в угловую частоту (радианы в секунду).
f описывает частоту синусоидальной волны. Это дается в виде герц или единиц в секунду . Частота показывает, сколько раз конкретная форма волны (в данном случае один цикл нашей синусоидальной волны — подъем и спад) происходит в течение одной секунды.
t — наша независимая переменная: время (измеряется в секундах). По мере того, как меняется время, наша форма волны меняется.
φ описывает фазу синусоидальной волны. Фаза — это мера того, насколько сдвинута форма сигнала во времени. Часто это число от 0 до 360, которое измеряется в градусах. Из-за периодической природы синусоидальной волны, если форма волны сдвинута на 360 °, она снова становится такой же, как если бы она была сдвинута на 0 °.Для простоты мы предполагаем, что в остальной части этого руководства фаза равна 0 °.
Мы можем обратиться к нашей надежной розетке за хорошим примером того, как работает форма сигнала переменного тока. В Соединенных Штатах в наши дома подается питание переменного тока с размахом 170 В (амплитуда) и 60 Гц (частота). Мы можем подставить эти числа в нашу формулу, чтобы получить уравнение (помните, что мы предполагаем, что наша фаза равна 0):
Мы можем использовать наш удобный графический калькулятор, чтобы построить график этого уравнения. Если графического калькулятора нет, мы можем использовать бесплатную онлайн-программу для построения графиков, такую как Desmos (обратите внимание, что вам может потребоваться использовать «y» вместо «v» в уравнении, чтобы увидеть график).
Обратите внимание, что, как мы и предсказывали, напряжение периодически повышается до 170 В и понижается до -170 В. Кроме того, каждую секунду происходит 60 циклов синусоидальной волны. Если бы мы измеряли напряжение в розетках с помощью осциллографа, мы бы увидели именно это ( ПРЕДУПРЕЖДЕНИЕ: не пытайтесь измерять напряжение в розетке с помощью осциллографа! Это может привести к повреждению оборудования).
ПРИМЕЧАНИЕ. Возможно, вы слышали, что напряжение переменного тока в США составляет 120 В. Это тоже правильно.Как? Говоря об переменном токе (поскольку напряжение постоянно меняется), часто проще использовать среднее или среднее значение. Для этого мы используем метод под названием «Среднеквадратичный корень». (RMS). Часто бывает полезно использовать среднеквадратичное значение для переменного тока, когда вы хотите рассчитать электрическую мощность. Несмотря на то, что в нашем примере у нас было напряжение, изменяющееся от -170 В до 170 В, среднеквадратичное значение составляет 120 В RMS.
Приложения
В розетках дома и в офисе почти всегда есть кондиционер. Это связано с тем, что генерировать и транспортировать переменный ток на большие расстояния относительно просто.При высоких напряжениях (более 110 кВ) при передаче электроэнергии теряется меньше энергии. Более высокие напряжения означают более низкие токи, а более низкие токи означают меньшее тепловыделение в линии электропередачи из-за сопротивления. Переменный ток можно легко преобразовывать в высокое напряжение и обратно с помощью трансформаторов.
AC также может приводить в действие электродвигатели. Двигатели и генераторы — это одно и то же устройство, но двигатели преобразуют электрическую энергию в механическую (если вал двигателя вращается, на выводах генерируется напряжение!).Это полезно для многих крупных бытовых приборов, таких как посудомоечные машины, холодильники и т. Д., Которые работают от сети переменного тока.
Постоянный ток (DC)
Постоянный ток немного легче понять, чем переменный. Вместо того, чтобы колебаться вперед и назад, постоянный ток обеспечивает постоянное напряжение или ток.
Создание постоянного тока
постоянного тока можно создать несколькими способами:
- Генератор переменного тока, оснащенный устройством, называемым «коммутатор», может производить постоянный ток
- Использование устройства, называемого «выпрямитель», которое преобразует переменный ток в постоянный ток
- Батареи обеспечивают постоянный ток, который образуется в результате химической реакции внутри батареи
Используя нашу аналогию с водой снова, DC подобен резервуару с водой со шлангом на конце.
Бак может выталкивать воду только в одном направлении: из шланга. Как и в случае с нашей батареей постоянного тока, когда резервуар опустеет, вода больше не течет по трубам.
Описание DC
DC определяется как «однонаправленный» ток; ток течет только в одном направлении. Напряжение и ток могут изменяться с течением времени до тех пор, пока направление потока не меняется. Для упрощения предположим, что напряжение является постоянным. Например, мы предполагаем, что батарея AA обеспечивает 1.5 В, что математически можно описать как:
Если мы построим график с течением времени, мы увидим постоянное напряжение:
Что это значит? Это означает, что мы можем рассчитывать на то, что большинство источников постоянного тока обеспечат постоянное напряжение во времени. На самом деле батарея будет медленно терять заряд, а это означает, что напряжение будет падать по мере использования батареи. В большинстве случаев мы можем предположить, что напряжение постоянно.
Приложения
Практически все проекты электроники и запчасти для продажи на SparkFun работают на DC.Все, что работает от батареи, подключается к стене с помощью адаптера переменного тока или использует USB-кабель для питания, зависит от постоянного тока. Примеры электроники постоянного тока включают:
- Сотовые телефоны
- D&D Dice Gauntlet на основе LilyPad
- Телевизоры с плоским экраном (переменный ток переходит в телевизор, который конвертируется в постоянный ток)
- Фонари
- Гибридные и электромобили
Битва течений
Почти каждый дом или офис подключен к сети переменного тока.Однако это решение не было мгновенным. В конце 1880-х годов различные изобретения в Соединенных Штатах и Европе привели к полномасштабной битве между распределением переменного и постоянного тока.
В 1886 году электрическая компания Ganz Works, расположенная в Будапеште, электрифицировала весь Рим с помощью переменного тока. Томас Эдисон, с другой стороны, построил 121 электростанцию постоянного тока в Соединенных Штатах к 1887 году. Поворотный момент в битве наступил, когда Джордж Вестингауз, известный промышленник из Питтсбурга, приобрел патенты Николы Теслы на двигатели переменного тока и трансмиссию в следующем году. .
переменного тока в сравнении с постоянным током
Томас Эдисон (Изображение любезно предоставлено biography.com)
В конце 1800-х годов постоянный ток было нелегко преобразовать в высокое напряжение. В результате Эдисон предложил систему небольших местных электростанций, которые питали бы отдельные кварталы или участки города. Электроэнергия распределялась по трем проводам от электростанции: +110 вольт, 0 вольт и -110 вольт. Фонари и двигатели могут быть подключены между розеткой + 110 В или 110 В и 0 В (нейтраль). 110 В допускает некоторое падение напряжения между установкой и нагрузкой (дома, в офисе и т. Д.).).
Несмотря на то, что падение напряжения на линиях электропередач было учтено, электростанции необходимо было располагать в пределах 1 мили от конечного пользователя. Это ограничение сделало распределение электроэнергии в сельской местности чрезвычайно трудным, если не невозможным.
Используя патенты Tesla, компания Westinghouse работала над усовершенствованием системы распределения переменного тока. Трансформаторы предоставили недорогой метод повышения напряжения переменного тока до нескольких тысяч вольт и его снижения до приемлемого уровня. При более высоких напряжениях та же мощность могла передаваться при гораздо меньшем токе, что означало меньшие потери мощности из-за сопротивления проводов.В результате крупные электростанции могут быть расположены за много миль от них и обслуживать большее количество людей и зданий.
Кампания по выявлению мазков Эдисона
В течение следующих нескольких лет Эдисон провел кампанию по категорическому противодействию использованию AC в Соединенных Штатах, которая включала лоббирование законодательных собраний штатов и распространение дезинформации о AC. Эдисон также приказал нескольким техникам публично казнить животных переменным током, пытаясь показать, что переменный ток более опасен, чем постоянный ток. Пытаясь показать эти опасности, Гарольд П.Браун и Артур Кеннелли, сотрудники Edison, разработали первый электрический стул для штата Нью-Йорк с использованием переменного тока.
Возвышение AC
В 1891 году Международная электротехническая выставка проходила во Франкфурте, Германия, и показала первую передачу трехфазного переменного тока на большие расстояния, которая питала фары и двигатели на выставке. Присутствовали несколько представителей того, что впоследствии станет General Electric, и впоследствии они были впечатлены дисплеем. В следующем году была создана компания General Electric, которая начала инвестировать в технологии переменного тока.
Электростанция Эдварда Дина Адамса в Ниагарском водопаде, 1896 г. (Изображение любезно предоставлено teslasociety.com)
Westinghouse выиграл контракт в 1893 году на строительство плотины гидроэлектростанции, чтобы использовать энергию Ниагарского водопада и передавать переменный ток в Буффало, штат Нью-Йорк. Проект был завершен 16 ноября 1896 года, и электроэнергия переменного тока начала снабжать электроэнергией промышленные предприятия Буффало. Эта веха ознаменовала упадок DC в США. В то время как Европа примет стандарт переменного тока 220–240 В при 50 Гц, стандартом в Северной Америке станет 120 В при 60 Гц.
Высоковольтный постоянный ток (HVDC)
Швейцарский инженер Рене Тюри в 1880-х годах использовал серию двигателей-генераторов для создания высоковольтной системы постоянного тока, которую можно было использовать для передачи постоянного тока на большие расстояния. Однако из-за высокой стоимости и высокой стоимости обслуживания систем Thury HVDC никогда не применялся в течение почти столетия.
С изобретением полупроводниковой электроники в 1970-х годах стало возможным экономичное преобразование между переменным и постоянным током. Для генерации постоянного тока высокого напряжения (иногда до 800 кВ) может использоваться специальное оборудование.Некоторые страны Европы начали использовать линии HVDC для электрического соединения различных стран.
В линиях
HVDC потери меньше, чем в аналогичных линиях переменного тока на очень больших расстояниях. Кроме того, HVDC позволяет подключать различные системы переменного тока (например, 50 Гц и 60 Гц). Несмотря на свои преимущества, системы HVDC более дороги и менее надежны, чем обычные системы переменного тока.
В конце концов, Эдисон, Тесла и Вестингауз могут осуществить свои желания. Переменный ток и постоянный ток могут сосуществовать, и каждый из них служит определенной цели.
Ресурсы и дальнейшее развитие
Теперь вы должны хорошо понимать разницу между переменным и постоянным током. Переменный ток легче преобразовывать между уровнями напряжения, что делает передачу высокого напряжения более возможной. Напротив, постоянный ток присутствует почти во всей электронике. Вы должны знать, что они не очень хорошо сочетаются, и вам нужно будет преобразовать переменный ток в постоянный, если вы хотите подключить большую часть электроники к розетке. С этим пониманием вы должны быть готовы заняться некоторыми более сложными схемами и концепциями, даже если они содержат переменный ток.
Взгляните на следующие учебные пособия, когда будете готовы глубже погрузиться в мир электроники:
и nbsp
1.2: Синусоидальные формы сигналов — Engineering LibreTexts
AC или переменный ток назван так потому, что ток чередуется или переключается между двумя полярностями. Другими словами, ток (и, следовательно, напряжение) зависит от времени. Это принципиально отличается от постоянного тока, который имеет фиксированную полярность и, как правило, постоянный во времени.Например, лабораторный источник постоянного напряжения идеально поддерживает заданное напряжение на своих выводах и не меняется со временем. Напротив, когда форма волны переменного тока колеблется вперед и назад во времени, ее форма может иметь широкие вариации, начиная от простых регулярных путей лабораторных стандартов, таких как синусоидальные волны, треугольные волны и прямоугольные волны, до гораздо более сложных и волнообразных форм создаваемых волн. музыкальными инструментами и человеческим голосом.
Синусоидальная волна — это простейшая волна, которую можно создать.Он представляет собой движение простого вектора, вращающегося с постоянной скоростью, например, вертикальное смещение секундной стрелки часов. Пример показан на рисунке \ (\ PageIndex {1} \). По горизонтальной оси отложено время. Он увеличивается по мере того, как мы движемся слева направо (т.е. если точка A находится справа от точки B, то A возникает позже, чем B). Вертикальная ось представлена здесь, как правило, в процентах от максимума, но обычно это измерение напряжения, тока, звукового давления и т.п.
Рисунок \ (\ PageIndex {1} \): синусоида.
Обратите внимание на плавное изменение, которое начинается с нуля, поднимается до положительного пика через четверть пути, падает обратно до нуля на середине, продолжается до отрицательного пика через три четверти, а затем снова поднимается до того места, где оно началось. Затем этот процесс повторяется. Каждый повтор называется циклом. На рисунке \ (\ PageIndex {1} \) показан один полный цикл.
Синусоидальные волны демонстрируют четвертьволновую симметрию. То есть каждая четверть (по времени) волны идентична любой другой, если вы просто перевернете ее вокруг горизонтальной оси и / или повернете вертикально вокруг ее пика.Время, необходимое для завершения одного цикла, называется периодом и обозначается символом \ (T \) (для времени). Обратной величине периода является частота \ (f \).
\ [f = \ frac {1} {T} \ label {1.1} \]
Частота указывает, сколько циклов существует в одной секунде. Чтобы почтить память одного из исследователей 19 века в этой области, вместо того, чтобы называть единицу «циклов в секунду», мы используем Герц, названный в честь Генриха Герца и сокращенно Гц. На рисунке \ (\ PageIndex {2} \) показаны три синусоидальные волны с разными частотами; начальная волна (зеленый), волна с удвоенной частотой (синий) и третья с половиной частоты или с удвоенным периодом (красный).
Рисунок \ (\ PageIndex {2} \): Изменение частоты синусоидальной волны.
Амплитуда (по вертикали) волны может быть выражена как пиковая величина, которая представляет собой изменение от центральной нулевой линии до наиболее положительного значения. Амплитуда также может быть выражена от пика до пика; расстояние от самого отрицательного до самого положительного. Для синусоидальной волны это всегда будет вдвое больше пикового значения, хотя это может быть не так для других волн, которые могут быть асимметричными. Серия из трех синусоид с разными амплитудами показана на рисунке \ (\ PageIndex {3} \).Рядом с исходным (зеленый) находятся версии с двойной амплитудой (синий) и половинной амплитуды (красный).
Рисунок \ (\ PageIndex {3} \): Изменение амплитуды синусоидальной волны.
Объединив эти параметры, рассмотрим форму волны напряжения, показанную на рисунке \ (\ PageIndex {4} \). Здесь мы видим два цикла формы волны переменного напряжения.
Рисунок \ (\ PageIndex {4} \): простой пример синусоидальной волны.
Пиковое значение составляет 4 В, а значение полного размаха — 8 В (обычно сокращенно «8 В pp»).Период одного цикла составляет 0,2 секунды или \ (T = 200 \) миллисекунды. Кроме того, частота \ (f = 1/200 \) миллисекунд или 5 Гц (5 циклов за одну секунду).
сигналов переменного тока также можно комбинировать со смещением постоянного тока. Добавление положительного уровня постоянного тока сдвигает волну по вертикали, а отрицательный уровень постоянного тока смещает волну по вертикали. Это не изменяет частоту или переменную часть амплитуды (хотя абсолютные пики будут сдвинуты на величину постоянного тока). На рисунке \ (\ PageIndex {5} \) показано влияние различных смещений постоянного тока.Выше начальной волны (зеленый) находится идентичная в остальном волна с положительным смещением постоянного тока, равным 20% от исходного пикового значения (синий). Под оригиналом находится третья волна (красная), которая показывает отрицательное смещение постоянного тока, равное половине пикового значения оригинала. {\ circ} \).{\ circ} \).
Рисунок \ (\ PageIndex {6} \): Изменение фазы синусоидальной волны.
Объединение вышеупомянутых элементов позволяет нам разработать общий формат для синусоидальной волны (показано напряжение):
\ [v (t) = V_ {DC} + V_ {P} \ sin (2 \ pi f t + \ theta) \ label {1.2} \]
Где
\ (v (t) \) — напряжение в некоторый момент времени \ (t \),
\ (V_ {DC} \) — смещение постоянного тока, если оно есть,
\ (V_ {P} \) — пиковое значение,
\ (f \) — частота,
\ (\ theta \) — фазовый сдвиг (+, если опережает и рисует влево, — если отстает и рисует вправо).
В качестве быстрого и практического примера сигнал, показанный на рисунке \ (\ PageIndex {4} \), имеет пиковую амплитуду 4 вольта, частоту 5 Гц и не имеет смещения постоянного тока или фазового сдвига. Таким образом, его выражение: \ (v (t) = 4 \ sin (2 \ pi 5 t) \)
Чтобы вычислить фазовый сдвиг, сначала определите разницу во времени между формой сигнала и эталоном, которую мы назовем \ (\ Delta t \). Эталоном может быть фиксированный момент времени (например, \ (t = 0 \)) или другой сигнал. Как правило, самый простой способ сделать это — измерить разницу в точках пересечения нуля, если предположить, что смещения постоянного тока нет.{\ circ} \ frac {\ Delta t} {T} \ label {1.3} \]
Помните, что если волна смещена влево, то она является опережающей и положительной, а смещение вправо — запаздывающим или запаздывающим во времени и, следовательно, отрицательным.
Пример \ (\ PageIndex {1} \)
Запишите выражение для формы сигнала, показанной на рисунке \ (\ PageIndex {7} \).
Рисунок \ (\ PageIndex {7} \): Форма волны для примера \ (\ PageIndex {1} \).
Этот сигнал внешне может выглядеть так, как на рисунке \ (\ PageIndex {4} \), но не позволяйте этому вводить вас в заблуждение.Во-первых, другой временной масштаб. Для этого сигнала один цикл завершается за 10 миллисекунд. Следовательно, частота
\ [f = \ frac {1} {T} \ nonumber \]
\ [f = \ frac {1} {10 мс} \ nonumber \]
\ [f = 100 Гц \ nonumber \]
Вторая проблема — смещение постоянного тока. Обратите внимание, что положительный пик возникает при 4 амперах, а отрицательный пик — при -2 ампера. Это указывает на максимальное значение 6 ампер. Без смещения положительный пик будет на уровне 3 ампер, следовательно, имеется смещение по постоянному току +1 ампер.Вертикальный центр формы волны смещен вверх от 0 до +1 ампер. Эта точка находится при t = 0, следовательно, сдвига фазы нет. В результате получается выражение:
\ [i (t) = 1 + 3 \ sin (2 \ pi 100 t) \ nonumber \]
Пример \ (\ PageIndex {2} \)
Запишите выражение для формы сигнала, показанной на рисунке \ (\ PageIndex {8} \).
Рисунок \ (\ PageIndex {8} \): Форма волны для примера \ (\ PageIndex {2} \).
Во-первых, положительный пик составляет 2 вольта, а размах размаха — 4 вольта.Следовательно, смещения постоянного тока нет. Вертикальный центр волны не начинается в \ (t = 0 \), поэтому должен быть фазовый сдвиг. Значение при \ (t = 0 \) составляет 1,2 вольт. Волна достигает той же амплитуды за \ (t = 2 \) миллисекунды и начинает повторять другой цикл. Следовательно, период должен составлять 2 миллисекунды. Частота обратна этому значению, и, следовательно, \ (f = 500 \) Гц.
Форма сигнала смещена влево, что указывает на положительный или опережающий фазовый сдвиг. Если мы рассмотрим второй цикл, мы увидим, что он достигает нуля вольт при 1.{\ circ} \) представляет 72/360 или 0,2 цикла. Это соответствует временной задержке (сдвинутой вправо, потому что она отрицательна) 0,2 раза по 25 \ (\ mu \) с или 5 \ (\ mu \) s.
Изначально часто лучше построить график через серию отдельных шагов, чем пытаться нарисовать все за один присест. Сначала нарисуйте синусоидальную волну с пиковой амплитудой 5 В и периодом 25 мкс. Теперь опустите форму сигнала на 3 вольта так, чтобы положительный пик составлял всего 2 вольта, а отрицательный пик — при -8 вольт.Наконец, сдвиньте вновь сдвинутый сигнал вправо на 5 \ (\ mu \) с. Результат показан на рисунке \ (\ PageIndex {9} \).
Рисунок \ (\ PageIndex {9} \): Форма волны для примера \ (\ PageIndex {3} \).
1.2.1: Лабораторные измерения
В лаборатории генератор функций используется для генерации синусов и других форм волн. Эти устройства позволят точно контролировать как амплитуду, так и частоту волны, а также при необходимости добавить смещение постоянного тока. Пример показан на рисунке \ (\ PageIndex {10} \).Соответствующий измерительный инструмент — это осциллограф, или, для краткости, просто осциллограф.
Рисунок \ (\ PageIndex {10} \): Лабораторный генератор сигналов.
Осциллограф, пожалуй, самый полезный и универсальный измерительный прибор в лаборатории. Обычно они имеют два или четыре входных канала, хотя возможно и больше. Каждый входной канал имеет собственную настройку чувствительности, и все каналы имеют общую временную привязку. На дисплее отображаются формы сигналов так же, как на рисунках \ (\ PageIndex {1} \) — \ (\ PageIndex {9} \).Кроме того, они могут построить график зависимости одного напряжения от другого (режим X — Y). Современные осциллографы имеют дополнительные функции, такие как автоматическое измерение частоты, амплитуды, фазового сдвига и т. Д., Измерения с помощью курсора и возможность сохранять отображаемые изображения в виде графических файлов. Пример четырехканального цифрового осциллографа показан на рисунке \ (\ PageIndex {11} \).
Рисунок \ (\ PageIndex {11} \): цифровой осциллограф.
1.2.2: Условные обозначения
Что касается схем, то символы для источников переменного напряжения и тока показаны на рисунке \ (\ PageIndex {12} \).Обозначения полярности и направления не являются абсолютными; в конце концов, это источники переменного тока, полярность и направление которых меняются взад и вперед. Вместо этого маркеры используются для установления временной привязки, особенно в схемах, использующих несколько источников.
Рисунок \ (\ PageIndex {12} \): Условные обозначения для источника переменного напряжения (слева) и источника тока (справа).
Следует помнить, что отрицание источника равносильно изменению его полярности. Это было верно для источников постоянного тока и остается верным для источников переменного тока.Это показано на рисунке \ (\ PageIndex {13} \). Иногда переключение или отрицание источника делает анализ немного более очевидным или более легким для визуализации.
Рисунок \ (\ PageIndex {13} \): Эквивалентность полярности / знака.
Пример \ (\ PageIndex {4} \)
Предположим, что осциллограф отображает две волны, как показано на рисунке \ (\ PageIndex {14} \). Определите фазовый сдвиг меньшего пикового сигнала 20 В (синий) относительно сигнала большего пика 25 В (красный).
Рисунок \ (\ PageIndex {14} \): формы сигналов для примера \ (\ PageIndex {4} \).
Во-первых, обратите внимание, что ни одна из волн не имеет смещения постоянного тока. Если бы у одного или обоих было смещение, волна (волны) должна была бы быть смещена по вертикали, чтобы их нормальные точки пересечения нуля были на одном уровне. При измерении любой волны период составляет 1 миллисекунду. Сдвиг по времени проще всего найти в любом из нулевых переходов (есть четыре места на выбор). Задержка составляет одно небольшое отклонение или 0.{\ circ}) = — \ cos (2 \ pi ft) \). Взаимосвязь этих четырех волн проиллюстрирована на рисунке \ (\ PageIndex {15} \).
Рисунок \ (\ PageIndex {15} \): Временные отношения между синусами и косинусами.
Также стоит отметить, что косинусоидальная волна представляет собой первую производную или наклон синусоидальной волны. Как вы, возможно, помните из других исследований, наклон или «крутизна» линии — это отношение вертикального изменения к горизонтальному изменению, иногда называемое «подъемом над разбегом».Для напряжения это будет изменение напряжения с течением времени или \ (\ Delta V / \ Delta t \). Для гладкой, непрерывно изменяющейся кривой, такой как синусоида, наклон в данной точке правильно определяется как первая производная, или в данном случае \ (dv / dt \). Чтобы визуально убедиться в этом, обратите внимание, что самая крутая часть синусоидальной волны (зеленая) находится там, где она пересекает нулевую амплитуду. Когда он пересекает ноль при движении в положительном направлении (в точке \ (t = 0 \) или \ (t = 1 \) на рисунке \ (\ PageIndex {15} \)), косинус (синий) находится на своем положительном пике.Поскольку синус пересекает ноль при отрицательном движении (при \ (t = 0,5 \)), косинус находится на своем отрицательном пике. Кроме того, синусоидальная волна плоская с нулевым наклоном на положительных и отрицательных пиках (при t = 0,25 и t = 0,75 соответственно), и в это время амплитуда косинуса также равна нулю. . Также верно, что синусоида — это наклон отрицательной косинусоидальной волны, отрицательный косинус — это наклон отрицательной синусоиды, а отрицательный синус — наклон косинусоиды. Двигаясь в обратном направлении, мы можем сказать, что антипроизводная (неопределенный интеграл) косинусоидальной волны является синусоидальной волной, интеграл синусоидальной волны является отрицательной косинусоидальной волной и т. Д.Эти отношения окажутся наиболее полезными, когда мы обратим наше внимание на реакцию конденсаторов и катушек индуктивности в цепях переменного тока.
1.2.4: RMS — среднеквадратичное измерение
Наряду с пиком и размахом амплитуда может быть выражена как среднеквадратичное значение. Фактически, если пик или размах не указан, предполагается, что измерение является среднеквадратичным. Среднеквадратичное значение — это специальный расчет, используемый для нахождения эквивалентной мощности постоянного тока (очень часто, например, для усилителей мощности звука).Другими словами, если мы хотим найти мощность в резисторе, расчет должен выполняться с использованием значений RMS для напряжения или тока, а не пиковых или размахов. Невыполнение этого требования приведет к ошибочным полномочиям. Это верно независимо от формы волны; будь то синусоидальная волна, треугольная волна или сложные волны музыкальных сигналов. Если напряжение указано как среднеквадратичное значение, его можно рассматривать при расчетах мощности так же, как и напряжение постоянного тока эквивалентной величины. Например, среднеквадратичный синусоидальный сигнал 1 В будет производить такое же рассеивание мощности и нагрев в данном резисторе, что и 1 В постоянного тока.По этой причине среднеквадратичное значение иногда называют эффективным значением (т. Е. Эффективным значением постоянного тока).
Название среднеквадратичное описывает процесс определения действующего значения. Во-первых, вспомните, что мощность пропорциональна квадрату напряжения или тока. Таким образом, нашим первым шагом будет квадрат формы входного сигнала. Конечно, форма волны является функцией времени, и ее квадрат придаст некоторую новую форму. На этом этапе нам нужно найти среднее значение этой новой формы. Причина этого проста, но не всегда очевидна.Электрические и электронные компоненты имеют массу и поэтому не нагреваются или не охлаждаются мгновенно. У них есть тепловая постоянная времени. Следовательно, они реагируют на средний ввод с течением времени. Хотя мы могли бы вычислить каким-то образом «мгновенную пиковую мощность» в определенный момент времени, она не представляет собой эквивалентную мощность постоянного тока. Как только мы получили среднее значение этого квадрата сигнала, соответствующее значение постоянного тока будет просто квадратным корнем из среднего. Результатом является дробное значение от нуля до единицы, которое используется в качестве коэффициента масштабирования для преобразования пикового значения в среднеквадратичное значение.Значение будет уникальным для конкретной формы волны. То есть все синусы (независимо от фазы) имеют одинаковый коэффициент, все волны правильного треугольника имеют одинаковый коэффициент и так далее. Поскольку мы в основном занимаемся синусами, давайте подробнее рассмотрим определение для них RMS-фактора.
Начнем с основного выражения для синусоидальной волны без смещения постоянного тока или фазового сдвига и с амплитудой, равной единице:
\ [v (t) = \ sin (2 \ pi f t) \ nonumber \]
Первый шаг — возвести эту форму волны в квадрат.2 = \ frac {1} {2} — \ frac {1} {2} \ cos (2 \ pi 2 f t) \ nonumber \]
Это выражение описывает инвертированную косинусоидальную волну на удвоенной исходной частоте и половине исходной амплитуды, движущуюся на смещении постоянного тока, равном его пиковому значению. Другими словами, отрицательный пик косинуса равен нулю, а положительный пик равен 1. Следующий шаг — найти среднее или среднее значение этого промежуточного результата. Среднее значение равно смещению 0,5. Это можно представить как область над смещением, идеально заполняющую «провал» под смещением.Последний шаг — извлечь квадратный корень из среднего. Квадратный корень 0,5 равен единице над квадратным корнем из двух, или приблизительно 0,707. Следовательно, среднеквадратичное значение составляет 0,707 пикового значения. В качестве альтернативы вы можете разделить пик на квадратный корень из двух, или примерно 1,414. Этот процесс графически показан на рисунке \ (\ PageIndex {16} \).
Рисунок \ (\ PageIndex {16} \): процесс нахождения RMS-фактора для синусов.
В сумме для синусоидальных волн RMS всегда равно пиковому значению, умноженному на 0.707. Можно также сказать, что среднеквадратичное значение любой синусоидальной волны равно ее пику, деленному приблизительно на 1,414. Опять же, эти отношения не обязательно будут верны для несинусоидальных волн. Подробности относительно других распространенных форм можно найти в Приложении C. Наконец, отношение пикового значения к среднеквадратичному значению называется отношением пика. Это фиксированное значение для синусоидальных волн (опять же, около 1,414), но для некоторых типов аудиосигналов оно может превышать 10: 1.
1.2.5: длина волны
Еще один интересный момент — скорость распространения волны.Это сильно различается. В случае света в вакууме (или, в точном приближении, электрического тока в проводе) скорость составляет около 3E8 метров в секунду (то есть 300000 км / с) или около 186000 миль в секунду.
Учитывая скорость и период, мы можем представить, как далеко друг от друга находятся пики волны. Это расстояние называется длиной волны и обозначается греческой буквой лямбда \ (\ lambda \). Длина волны равна скорости, деленной на частоту, \ (\ lambda = v / f \). Таким образом, для громкоговорителя, производящего синусоидальную частоту 100 Гц, поскольку скорость звука в воздухе составляет 344 м / с, тогда \ (\ lambda = 344 м / с \, / \, 100 \) Гц или 3.44 метра (чуть больше 11 футов). Обратите внимание: чем выше частота, тем короче длина волны. Также обратите внимание, что чем выше скорость, тем больше длина волны. Расчеты длины волны особенно важны в области телекоммуникаций и акустики.
Цепь
переменного тока — напряжение, ток и мощность
В цепи переменного тока — переменный ток генерируется от источника синусоидального напряжения
Напряжение
Токи в цепях с чисто резистивными, емкостными или индуктивными нагрузками.
Мгновенное напряжение в синусоидальной цепи переменного тока может быть выражено в форме во временной области как
u (t) = U max cos (ω t + θ) (1)
где
u (t) = напряжение в цепи в момент времени t (В)
U max = максимальное напряжение при амплитуде синусоидальной волны (В)
t = время (с)
ω = 2 π f
= угловая частота синусоидальной волны (рад / с)
f = частота (Гц, 1 / с)
θ = фазовый сдвиг синусоидальной волны (рад)
Мгновенное напряжение альтернативно может быть выражено в частотной области (или векторе) как
U = U (jω) = U max e jθ (1а)
где
U (jω) = U = комплексное напряжение (В)
Вектор — это комплексное число, выраженное в полярной форме, состоящее из величины, равной максимальной амплитуде синусоидального сигнала, и фазы. угол, равный фазовому сдвигу синусоидального сигнала относительно косинусоидального сигнала.
Обратите внимание, что конкретная угловая частота — ω — явно не используется в выражении вектора.
Ток
Мгновенный ток может быть выражен в форме во временной области как
i (t) = I m cos (ω t + θ) (2)
где
i (t) = ток в момент времени t (A)
I max = максимальный ток при амплитуде синусоидальной волны (A)
Токи в цепях с чистая резистивная нагрузка , емкостная индуктивная нагрузка или показаны на рисунке выше.Ток в «реальной» цепи с резистивной, индуктивной и емкостной нагрузкой показан на рисунке ниже.
Мгновенный ток в цепи переменного тока альтернативно может быть выражен в частотной области (или векторном) как
I = I (jω) = I max e jθ (2a)
, где
I = I (jω) = комплексный ток (A)
Частота
Обратите внимание, что частота большинства систем переменного тока фиксированная — например, 60 Гц в Северной Америке и 50 Гц в большей части остального мира.
Угловая частота для Северной Америки составляет
ω = 2 π 60
= 377 рад / с
Угловая частота для большей части остального мира составляет
ω = 2 π 50
= 314 рад / с
Активная нагрузка
Напряжение на резистивной нагрузке в системе переменного тока можно выразить как
U = RI (4)
, где
R = сопротивление (Ом)
Для резистивной нагрузки в цепи переменного тока напряжение составляет в фазе с током.
Индуктивная нагрузка
Напряжение на индуктивной нагрузке в системе переменного тока может быть выражено как
U = j ω LI (5)
, где
L = индуктивность (генри)
Для индуктивной нагрузки ток в цепи переменного тока составляет π / 2 (90 o ) фаза после напряжения (или напряжение перед током).
Емкостная нагрузка
Напряжение на индуктивной нагрузке в системе переменного тока может быть выражено как
U = 1 / (j ω C) I (6)
где
C = емкость (фарад)
Для емкостной нагрузки ток в цепи переменного тока опережает напряжение на π / 2 (90 o ) фаза .
В реальной электрической цепи присутствует смесь резистивных, емкостных и индуктивных нагрузок с фазовым сдвигом напряжение / ток в диапазоне — π / 2 <= φ <= π / 2 , как показано на рисунок ниже.
Ток в «реальной» цепи со смесью резистивных, индуктивных и емкостных нагрузок. φ — фазовый угол между током и напряжением.
Импеданс
Закон Ома для сложного переменного тока может быть выражен как
U z = I z Z (7)
, где
U z = падение напряжения при нагрузке (вольт, В)
I z = ток через нагрузку (ампер, А)
Z = полное сопротивление нагрузки (Ом, Ом)
Полное сопротивление в цепи переменного тока можно рассматривать как комплексное сопротивление.Импеданс действует как частотно-зависимый резистор, где сопротивление является функцией частоты синусоидального возбуждения.
Импеданс в серии
Результирующий импеданс для последовательных сопротивлений может быть выражен как
Z = Z 1 + Z 2 (7b)
Сопротивление параллельно
Результирующее сопротивление для параллельных сопротивлений может быть выражено как
1 / Z = 1 / Z 1 + 1 / Z 2 (7c)
Полная проводимость
Полная проводимость — это инвертированный импеданс
Y = 1 / Z (8)
, где
Y = полная проводимость (1 / Ом)
RMS или эффективное напряжение
RMS значение — это эффективное значение синусоидального напряжения или тока.
RMS — среднеквадратичное значение — или эффективное напряжение может быть выражено как
U rms = U eff
= U max / (2) 1/2
= 0,707 U макс. (9)
где
U среднеквадратичное значение = U eff
= действующее напряжение (В)
6
6 макс = максимальное напряжение (амплитуда) источника синусоидального напряжения (В)
RMS — среднеквадратическое значение — или эффективный ток может быть выражен как
I rms = I eff
= I max / (2) 1/2
= 0.707 I макс (10)
где
I среднеквадратичное значение = I eff
= действующее значение тока (A)
I6 макс = максимальный ток (амплитуда) источника синусоидального напряжения (A)
Вольтметры и амперметры переменного тока показывают среднеквадратичное значение напряжения или тока — или 0,707 максимальных пиковых значений. Максимальные пиковые значения равны 1.В 41 раз больше значений вольтметра.
Пример
- для системы 230 В U среднеквадратичное значение = 230 В и U макс. = 324 В
- для системы 120 В U среднеквадратичное значение = 120 В и U max = 169 В
Трехфазное напряжение переменного тока — от линии к линии и от линии к нейтрали
В трехфазной системе переменного тока напряжение может подаваться между линиями и нейтралью (фазовый потенциал) или между линиями (линейный потенциал).Результирующие напряжения для двух общих систем — европейской системы 400/230 В и североамериканской системы 208/120 В указаны для одного периода на рисунках ниже.
400/230 В перем. Тока
print 400/230 В Трехфазная диаграмма
- L1, L2 и L3 — это три фазы, соединяющие потенциалы нейтрали — фазовые потенциалы
- L1 к L2, L1 к L3 и L2 — L3 — это трехфазные линейные потенциалы — линейные потенциалы
- L2, L2 и L3 — результирующий потенциал трех фаз в сбалансированной цепи — результирующий потенциал = 0
Величина линейных потенциалов равна 3 1/2 (1.73) величина фазового потенциала.
U действующее значение, линия = 1,73 U действующее значение, фаза (11)
208 В / 120 В переменного тока
распечатайте трехфазную диаграмму 208/120 В
Мощность
Активно — или реально, или истинно — мощность, которая выполняет фактическую работу в цепи — может быть рассчитана как
P = U среднеквадратичное значение I среднеквадратичное значение cos φ (12)
, где
P = активная активная мощность (Вт)
φ = фазовый угол между током и напряжением (рад, градусы)
Cos φ также называется коэффициентом мощности.
Реактивная мощность в цепи может быть рассчитана как
Q = U среднеквадратичное значение I среднеквадратичное значение sin φ (13)
Q = реактивная мощность (VAR)
Синусоидальная форма волны Базовая теория цепи переменного тока — Wira Electrical
Синусоидальная форма волны — одна из самых важных форм волны в электротехнике. После многих объяснений схемы постоянного тока, давайте перейдем к материалу следующего уровня.
В электрической схеме будет два типа источников электричества: ac (переменный ток) и dc (постоянный ток).
Обязательно сначала прочтите, что такое электрическая схема, чтобы понять следующее объяснение.
Потому что до сих пор мы ограничивали основную теорию электрических цепей только цепью постоянного тока.
Что такое синусоидальная форма волны
Прежде чем мы начнем, зачем нам изучать цепи переменного тока? Хотя этому труднее научиться, он дает много преимуществ. Для урока истории источники постоянного тока были основными источниками электроэнергии до конца 1800-х годов.
В начале следующего века был введен переменный ток.Эти двое устроили настоящую битву среди инженеров.
Поскольку переменный ток имеет более высокий КПД и лучшую экономичную передачу, он оказался победителем.
Синусоидальный источник полезен для цепи переменного тока, так же как и источник постоянного тока, который играет важную роль в цепи постоянного тока.
Обязательно прочтите:
После того, как мы изучим постоянную ценность электричества во времени, мы изучим изменяющиеся во времени напряжение и ток. Первым делом мы сосредоточимся на синусоидальной форме волны электричества или просто на синусоиде .
Синусоида — это форма сигнала, которая имеет форму косинуса или синусоиды.
В большинстве случаев переменный ток (ac) относится к синусоидальной форме волны. Синусоида означает, что значение имеет положительные и отрицательные значения в определенном интервале.
Цепь переменного тока — это цепь, которая приводится в действие источниками переменного тока или напряжения.
Зачем нам для начала изучать схему переменного тока? Что является «лучшей» стороной переменного тока, кроме того, что он более сложен, чем постоянный ток? У источников переменного тока есть несколько «лучших» причин для изучения.
Первый — это его характеристика как синусоидальная форма волны. Мы часто встречаем его в движении маятника, колебании струны или некоторой ряби на поверхности воды.
Второй , как мы упоминали ранее, синусоидальный сигнал легко генерировать и передавать. Электроэнергия, поставляемая в мир, дома, фабрики, промышленность, лаборатории и т. Д., Имеет синусоидальную форму волны.
Третий , мы можем реализовать анализ Фурье для анализа периодических сигналов, которые имеют характеристику синусоидальной формы волны.
Последний , его довольно сложно понять, но синусоиду легко анализировать, потому что ее интегральная и производная функции также являются синусоидами.
После стольких преимуществ изучения синусоидального сигнала, знаете ли вы, какую математическую теорию мы будем использовать для схемы переменного тока?
Самые базовые теории анализа цепей постоянного тока, такие как:
, будут снова применены к цепи переменного тока. Вы должны понимать некоторые параметры, обнаруженные в цепи переменного тока, такие как:
Мы будем использовать методы анализа цепей постоянного тока для цепей переменного тока, такие как:
- Анализ узлов
- Анализ сетки
Наряду с теоремами цепей постоянного тока для цепи переменного тока:
- Теорема суперпозиции
- Преобразование источника
- Thevenin и Norton
Функция синусоидальной формы сигнала
Посмотрите на синусоидальную функцию переменного напряжения:
| (1) |
где
V амплитуда синусоиды
ω = угловая частота в радианах / с
ωt = аргумент синусоиды.
Синусоидальный сигнал на рисунке (1a) показывает функцию своего аргумента, а рисунок (1b) — как функцию времени.
| Рисунок 1. Рисунок V m sin ωt : (a) в функции ωt , (b) в функции t . |
Из рисунка вы сможете получить изображение «цикла повторения» синусоиды каждые T секунд, следовательно, T называется периодом синусоиды.Из двух цифр на рисунке (1) мы заключаем, что ωT = 2π,
| (2) |
Примечание v (t) повторяется каждые T секунд отображается заменой t на t + T в уравнении (1). Получаем
| (3) |
Таким образом,
| (4) | (4) |
| (5) |
Из уравнений (2) и (5) мы можем заключить
- 00
- 6 В то время как ω выражается в радианах в секунду (рад / с), f выражается в герцах (Гц).
Рассмотрим уравнение синусоидальной волны ,
(7) , где ( ωt + ø) — аргумент, а ø — фаза .И аргумент, и фаза могут быть в радианах или градусах.
Имеются две синусоиды,
(8) , показанные на рисунке. (2). Начальная точка v 2 на рисунке (2) встречается первой по времени. Из рисунка (2) можно сказать, что v 2 опережает v 1 на ø или что v 1 отстает от v 2 на ø.
Если ø ≠ 0, мы также говорим, что v 1 и v 2 не совпадают по фазе.
Если ø = 0, то вызываются v 1 и v 2 синфазными; они достигают своих минимумов и максимумов одновременно.
Мы можем сравнить v 1 и v 2 в этом вопросе, потому что они работают с одинаковой частотой, даже если амплитуда различается. Ниже мы увидим , как построить график синусоидальных функций .
Рисунок 2.Две синусоиды с разными фазами Каждая форма синусоиды может быть выражена в косинусоидальной или синусоидальной форме. При сравнении двух синусоид целесообразно выразить в одной и той же форме волны либо косинус, либо синус с положительными амплитудами.
Это может быть достигнуто с помощью следующей тригонометрической функции:
(9) Используя эти идентификаторы, легко заметить, что
10)
С помощью этих соотношений мы можем преобразовать синусоиду из косинусной формы в синус или наоборот.
Графический рисунок может использоваться для сравнения или соотнесения в качестве альтернативного подхода к использованию тригонометрической функции в уравнениях (9) и (10).
Рис. 3. Графическое изображение (a) cos ( ωt — 90 o ) = sin ωt , (b) sin ( ωt + 180 o ) = -sin ωt Обратите внимание на набор осей на рисунке (3a).
Горизонтальная ось соответствует величине косинуса, а вертикальная ось (указывает вниз) — величине синуса.
Угол измеряется положительным значением против часовой стрелки от горизонтальной оси. Этот метод расчета можно использовать для сравнения двух синусоид.
Например, на рисунке (3a) из вычитания 90 o из cos ωt получается sin ωt , или cos ( ωt — 90 o ) = sin ωt .
Аналогичным образом, добавление 180 o к sin ωt приводит к -sin ωt или sin ( ωt + 180 o ) = -sin ωt , как видно на рисунке.(3б).
С помощью этого графического метода можно сложить две синусоиды с одинаковой частотой, если одна имеет синусоидальную форму, а другая — косинусоидальную.
Чтобы сложить A cos ωt и B sin ωt , как показано на рисунке (4a), A — величина cos ωt , а B — величина sin ωt .
Рисунок 4. (a) сложение A cos ωt и B sin ωt , (b) сложение 3 cos ωt и -4 sin ωt . Следовательно,
(11) где
- 756 9175 9175
9175 917 cos ωt и -4 sin ωt , как показано на рисунке. (4b) и результаты
(13) Из этих сообщений мы узнаем об анализе мощности переменного тока:
Мы также будем искать некоторые приложения, такие как:
После завершения однофазной цепи переменного тока мы перейдем к анализу трехфазной цепи переменного тока и прочитаем краткое объяснение того, как работает ваттметр.
Пример синусоидальной функции
Для лучшего понимания рассмотрим примеры ниже:
1. Найдите амплитуду, фазу, период и частоту из
v (t) = 12 cos (50 t + 10 o )
Решение:
Амплитуда: В м = 12 В
Фаза: ø = 10 o
Угловая частота: ω
05 = 50 рад / с
Период: T = 2π / ω = 2π / 50 = 0.1257 с
Частота: f = 1/ T = 7,958 Гц.
2. Определите фазовый угол между v 1 = -10 cos ( ωt + 50 o ) и v 2 = 12 sin ( ωt — 10 o ). Укажите, какой из них является ведущим.Решение: Есть три способа решить проблему. Мы можем использовать тригонометрические тождества для первых двух и использовать графический подход для третьего.
Метод 1 : v 1 и v 2 находятся в разных формах, поэтому нам нужно сделать их одинаковыми, например косинусоидальной.
(1,1) и
(1,2) Эта фаза может быть завершена из разница между ними составляет 30 o .Мы можем переписать v 2 как
(1.3) Сравнение (1.1) и (1.3) показывает v 2 16 v 9025 30 или .
Метод 2 : Выразим v 1 в форме синуса
Но v 2 = 12 sin ( ωt — 10 o ). Сравнение этих двух показывает v 1 отстает v 2 на ωt , то же самое с v 2 ведет v 1 на 30 o .
Метод 3 : Мы можем указать v 1 как просто -10 cos ωt с фазовым сдвигом +50 o . Мы можем нарисовать v 1 , как на рисунке 5.
Рисунок 5 Точно так же v 2 составляет 12 sin ωt с фазовым сдвигом -10 o , как показано на рисунке (5). Мы можем заключить v 2 отведений v 1 на 90 o — 50 o — 10 o = 30 o .
Что такое цепь переменного тока? — Различные термины и форма волны
Цепь, возбуждаемая переменным источником, называется цепью переменного тока . Переменный ток (AC) используется в бытовых и промышленных целях. В цепи переменного тока значение величины и направления тока и напряжений непостоянно, оно изменяется через равные промежутки времени.
Он распространяется как синусоидальная волна, завершая один цикл как половина положительного и полуотрицательного цикла и является функцией времени (t) или угла (θ = wt).
В цепи постоянного тока противодействие протеканию тока является единственным сопротивлением цепи, тогда как противодействие протеканию тока в цепи переменного тока происходит из-за сопротивления (R), индуктивного реактивного сопротивления (X L = 2πfL) и емкостное реактивное сопротивление (X C = 1/2 πfC) цепи.
В цепи переменного тока ток и напряжения представлены величиной и направлением . Переменная величина может быть или не совпадать по фазе друг с другом в зависимости от различных параметров схемы, таких как сопротивление, индуктивность и емкость.Синусоидальные переменные величины — это напряжение и ток, которые изменяются согласно синусу угла θ.
Для выработки электроэнергии во всем мире выбираются синусоидальные напряжение и ток по следующим причинам, которые приведены ниже.
- Синусоидальное напряжение и ток приводят к низким потерям в железе и меди в трансформаторах и вращающихся электрических машинах, что, в свою очередь, повышает эффективность машин переменного тока.
- Они создают меньше помех для ближайшей системы связи.
- Они вызывают меньше помех в электрической цепи.
Переменное напряжение и ток в цепи переменного тока
Напряжение, полярность и величина которого меняется через равные промежутки времени, называется переменным напряжением . Точно так же направление тока изменяется, и величина тока изменяется со временем, это называется переменным током .
Когда источник переменного напряжения подключается к сопротивлению нагрузки, как показано на рисунке ниже, ток через него течет в одном направлении, а затем в противоположном направлении при изменении полярности.
Схема цепи переменного тока
Форма волны переменного напряжения в зависимости от времени и тока, протекающего через сопротивление (R) в цепи, показана ниже.
Существуют различные типы цепей переменного тока, такие как цепь переменного тока, содержащая только сопротивление (R), цепь переменного тока, содержащая только емкость (C), цепь переменного тока, содержащую только индуктивность (L), комбинацию цепи RL, цепь переменного тока, содержащую сопротивление и емкость ( RC), цепь переменного тока, содержащая индуктивность и емкость (LC) и сопротивление, индуктивность и емкость (RLC), цепь переменного тока.
Различные термины, которые часто используются в цепи переменного тока, следующие:
Максимальное положительное или отрицательное значение, достигаемое переменной величиной за один полный цикл, называется амплитудой, или пиковым значением, или максимальным значением. Максимальные значения напряжения и тока представлены E m или V m и I m соответственно.
Половина цикла называется чередованием. Диапазон чередования составляет 180 градусов.
Когда один набор положительных и отрицательных значений дополняется переменным количеством или он проходит через электрические 360 градусов, считается, что он имеет один полный цикл.
- 756 9175 9175
