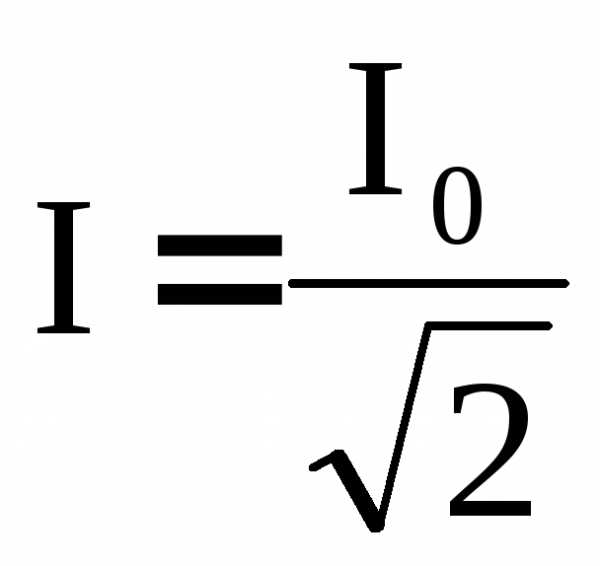Комплексное сопротивление. Сопротивление z

Комплексное сопротивление

 

Введение комплексного представления токов и напряжений требует определить и сопротивление элементов электрических цепей в комплексной форме - Z.

Хорошо известно, что сопротивление резистора определяется как отношение напряжения на резисторе к току, протекающему через него. Если напряжение и ток представлены в комплексной форме, то:

 

 

Но в предыдущей лекции было установлено, что . Поэтому:

 

(3.1)

 

Таким образом, видим, что комплексное сопротивление резистора выражается только действительным числом. Оно не вносит фазовых искажений между током и напряжением. Чтобы подчеркнуть этот факт такое сопротивление часто называют активным.

Комплексное сопротивление емкости определяется отношением:

 

. (3.2)

 

Видим, что комплексное сопротивление емкости переменному току выражается мнимым числом. Мнимая единица -j физически определяет сдвиг фаз между током и напряжением на 90о. Это хорошо согласуется с ее математическим значением:

 

Поэтому на емкости напряжение отстает от тока на 90о. Это означает, что сначала растет ток, протекающий через конденсатор, затем, с некоторым отставанием увеличивается заряд и напряжение.

Коэффициент 1/ определяет величину сопротивления в Омах. Он обратно пропорционален частоте, называется емкостным сопротивлением и обозначается ХС, т.е.:

. (3.3)

 

Комплексное сопротивление индуктивности определяется отношением:

 

. (3.4)

 

И в этом случае сопротивление выражается мнимым числом. Но так как это число положительное, то это означает, что на индуктивности напряжение опережает ток на 90о.

Коэффициент wL определяет величину сопротивления в Омах. Он пропорционален частоте, называется индуктивным сопротивлением и обозначается ХL, т.е.:

. (3.5)

 

Чтобы подчеркнуть тот факт, что сопротивления емкости и индуктивности выражаются мнимыми числами, их называют реактивными сопротивлениями, а конденсатор и индуктивность - реактивными элементами цепи.

Определим теперь комплексное сопротивление электрической цепи, содержащей активные и реактивные элементы, например последовательно включенные R, L и С элементы (рис.3.1). Такая цепь представляет замкнутый

контур, поэтому для нее справедлив второй закон Кирхгофа:

 

. (3.6)

 

В последнем выражении проведем замену символов мгновенных напряжений и ЭДС на их комплексные изображения по правилам, определенным в лекции 1.2. Такой прием получил название символического метода. Так как ток, протекающий через все элементы последовательной цепи одинаков, то (3.6) приходит к виду:

 

 

Преобразуем это выражение к виду:

 

.

 

По определению выражение в правой части последнего равенства есть ни что иное, как комплексное сопротивление цепи рис.3.1, т.е.:

 

(3.7)

 

где R - действительная часть или активное сопротивление цепи.

- мнимая часть или реактивное сопротивление цепи.

Выражение (3.7) представляет комплексное сопротивление в алгебраической форме. Соотношения между составляющими комплексного сопротивления находятся в полном соответствии с соотношениями для комплексного представления тока. Но для большей наглядности вводится

понятие треугольника сопротивления (рис.3.2).

В треугольнике - гипотенуза определяется модулем комплексного сопротивления Z, причем:

. (3.8)

 

Прилежащий к острому углу катет – активным сопротивлением цепи R, причем:

 

(3.9)

 

 

Противолежащий катет - реактивным сопротивлением Х, причем:

 

(3.10)

 

Угол определяет сдвиг фаз между током и напряжением, который вносится комплексным сопротивлением цепи, причем:

 

. (3.11)

 

Учитывая выражения (3.8) ¸ (3.11), легко перейти от алгебраической к тригонометрической форме комплексного сопротивления:

 

Z =Z (3.12)

 

a применив формулу Эйлера получить показательную форму:

 

Z =Z (3.13)

 

Теперь можно записать закон Ома для участка цепи без источника ЭДС в комплексном изображении:

(3.14)

 

Выражение (3.14) показывает, что в цепях переменного тока модуль тока определяется отношением модуля напряжения (его амплитудного значения) к модулю комплексного сопротивления, а фаза тока определяется разностью фаз напряжения и комплексного сопротивления. Отсюда вытекает еще одно полезное для практики выражение:

 

. (3.15)

 

 

Похожие статьи:

poznayka.org

1. Обзор R, X, и Z | 5. Реактивное сопротивление и импеданс -- R, L и C | Часть2

1. Обзор R, X, и Z

Обзор R, X, и Z

Прежде чем мы начнем исследовать цепи переменного тока, содержащие одновременно резисторы, катушки индуктивности и конденсаторы, давайте кратко рассмотрим некоторые основные термины и факты.

Сопротивление - это воздействие силы трения на электроны при их движении через проводник. Сопротивление в некоторой степени присутствует во всех проводниках (за исключением сверхпроводников). Особенно оно характерно для резисторов. Когда переменный ток проходит через сопротивление, произведенное им напряжение находится в фазе с этим током. Сопротивление обозначается буквой "R" и измеряется в Омах (Ом, Ω).

Реактивное сопротивление по существу - это инерция против движения электронов. Реактивное сопротивление существует там, где электрические или магнитные поля развиваются пропорционально приложенному напряжению или току. Прежде всего оно характерно для конденсаторов и катушек индуктивности. Когда переменный ток проходит через чисто реактивное сопротивление, производимое им напряжение не совпадает по фазе с током на 90o. Реактивное сопротивление обозначается буквой "X" и измеряется тоже в Омах (Ом, Ω).

Импеданс является всеобъемлющим выражением всех видов сопротивлений потоку электронов (включая активное и реактивное сопротивления). Импеданс присутствует во всех схемах и во всех компонентах. Когда переменный ток проходит через импеданс, производимое им напряжение не совпадает по фазе с током от 0o до 90o. Импеданс обозначается буквой "Z" и измеряется так же в Омах (Ом, Ω).

Идеальные резисторы обладают обычным сопротивлением, но у них нет реактивного сопротивления. Идеальные катушки индуктивности и конденсаторы обладают реактивным сопротивлением, но у них нет обычного сопротивления. Все вышеперечисленные компоненты обладают импедансом. Исходя из этого, имеет смысл перевести все значения активных и реактивных сопротивлений в соответствующие импедансы. Это будет первым шагом в анализе цепей переменного тока.

 

 

Фазовый угол импеданса любого компонента представляет собой сдвиг фазы между напряжением на этом компоненте и током через него. У идеального резистора напряжение и ток всегда находятся в фазе друг с другом, а значит, угол его импеданса составляет 0o. У идеальной катушки индуктивности напряжение всегда опережает ток на 90o, а значит, угол ее импеданса составляет +90o. У идеального конденсатора напряжение всегда отстает от тока на 90o, а значит, угол его импеданса составляет -90o.

Импедансы в цепях переменного тока ведут себя аналогично сопротивлениям в цепях постоянного тока: в последовательных цепях их значение увеличивается, а в параллельных - уменьшается. Пересмотренный на основе импеданса Закон Ома выглядит следующим образом:

 

 

Законы Кирхгофа, все методы анализа цепей и теоремы, рассмотренные нами в предыдущем разделе, верны и для цепей переменного тока (при условии, что величины представляются в комплексной, а не скалярной форме). Несмотря на то, что эта эквивалентность может быть математически сложной, она концептуально проста и изящна. Единственное различие между расчетами постоянных и переменных цепей касается мощности. Поскольку реактивное сопротивление не рассеивает мощность (как это делает обычное сопротивление), понятие мощности в цепях переменного тока в корне отличается от понятия мощности в цепях постоянного тока. Подробнее об этом мы расскажем несколько позже.

www.radiomexanik.spb.ru

Электрическое сопротивление ~ Электро мастер

Электрическое сопротивление

Любое тело, по которому протекает электрический ток, оказывает току  сопротивление – это явление называется электрическим сопротивлением.Сопротивление обозначается латинскими буквами R, X, Z. Используются также прописные буквы r, x, z.R – активное сопротивление (омическое)X – реактивное сопротивление (индуктивное, емкостное)Z – полное сопротивление (активное)Размерность сопротивления Ом, размерность записывается так – Ом.Сопротивление рассчитывается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать по формуле:

R=U/I

гдеR – сопротивлениеU – разность электрических потенциалов на концах проводника (напряжение)I – сила тока, протекающая между концами проводника под действием разности потенциалов (напряжения).Сопротивление различных проводников зависит от материала и называется удельным сопротивление, единица измерения удельного сопротивления Ом*м, а величина удельного сопротивления обозначается символом ρ (ро). Удельное сопротивление Удельное сопротивление проводника может быть рассчитано по формуле:

R= (ρ *l)/S

гдеρ – удельное сопротивление проводникаl – длинна проводника S – площадь сечения проводника

Удельное сопротивление некоторых веществ (при t 20° C)

Вещество	Удельное сопротивление,  ρОм*мм2/м
Алюминий	0,028
Вольфрам	0,055
Железо	0,098
Золото	0,023
Константан	0,44-0,52
Латунь	0,025-0,06
Манганин	0,42-0,48
Медь	0,0175
Молибден	0,057
Никелин	0,39-0,45
Никель	0,100
Олово	0,115
Ртуть	0,958
Свинец	0,221
Серебро	0,016
Тантал	0,155
Фехраль	1,1-1,3
Хром	0,027
Цинк	0,059

Чем больше сопротивление проводника, тем хуже он проводит электрический ток.Удельное сопротивление обратно пропорционально электрической проводимости.Электрическая проводимость – это способность материала пропускать через себя электрический ток. Из выше изложенного следует – чем меньше сопротивление проводника, тем больше его электрическая проводимость, тем легче электрическому току пройти через этот проводник. Виды электрического сопротивления: Существует четыре вида электрического сопротивления: 1. Омическое сопротивление (активное сопротивление постоянному току)2. Активное сопротивление (сопротивление переменному току)3. Индуктивное сопротивление (реактивное сопротивление)4. Емкостное сопротивление (реактивное сопротивление) Рассмотрим каждое подробно: Омическое сопротивление – сопротивление цепи постоянному току вызывающие безвозвратные потери энергии постоянного тока.Величина омического сопротивления не зависит от величины  тока, это сопротивление материала (удельное сопротивление) и рассчитывается по формуле:

R=U/I

гдеR – сопротивлениеU – разность электрических потенциалов на концах проводника (напряжение)I – сила тока, протекающая между концами проводника под действием разности потенциалов (напряжения). Причиной потерь постоянного тока при омическом сопротивление является преодоление противодействия материала (его удельного сопротивления), энергия затраченная на преодоления противодействия материала превращается в тепловую. Активное сопротивление – это сопротивление цепи переменному току вызывающие безвозвратные потери энергии переменного тока. Активное сопротивление обозначается латинской буквой Z и рассчитывается по формуле:

Z=R+jX

гдеZ – импедансR - величина активного сопротивленияX — величина реактивного сопротивленияj — мнимая единица Основной причиной вызывающей потери при активном сопротивление остается тоже, что и при омическом сопротивление – преодоление противодействия материала. Есть и другие причины, такие как- поверхностный эффект- вихревые токи- потери за счет излучения электромагнитной энергии и др. Абстрактно омическое и активное сопротивление можно представить как передвижение человека по узкому захламленному (препятствиями) коридору, который основную часть своей энергии будет безвозвратно тратить на преодоление этих препятствий, и чем больше удельное сопротивление проводника, тем захламленнее будет коридор. Индуктивное сопротивление - обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности  элемента и частоты  протекающего тока. Не вызывает безвозвратных потерь энергии.Индуктивное сопротивление рассчитывается по формуле:

XL=ωL=2πfL

гдеXL - индуктивное сопротивление проводника переменному токуω - циклическая частота переменного токаL - индуктивность проводника (катушки)f- частота На преодоление этого противодействия затрачивается часть энергии переменного тока генератора. Вся эта часть энергии полностью превращается в энергию магнитного поля катушки. Когда ток генератора будет убывать, магнитное поле катушки тоже будет убывать, пересекая витки катушки и индуктируя в цепи ток самоиндукции. Теперь ток самоиндукции будет идти в одном направлении с убывающим током генератора. Таким образом, вся энергия затраченная током генератора на преодоление противодействия тока самоиндукции катушки полностью вернулась в цепь в виде энергии электрического тока. Поэтому индуктивное сопротивление является реактивным, что значит не вызывающим безвозвратных потерь энергии. Абстрактно индуктивное сопротивление можно представить как воду, текущую по трубе в которой установлена крыльчатка (водомер (счетчик воды) который установлен почти в каждой квартире), крыльчатка создает индуктивное сопротивление, чем больше ток (в нашем случае напор воды), тем больше сопротивление, при убывании напора воды крыльчатка пропустить всю оставшуюся воду, так как она крутиться в том же направлении, в которой течет вода. Из этого примера видно что такое индуктивное сопротивление и почему оно не вызывает безвозвратных потерь. Индуктивную нагрузку (сопротивление) вызывают – индукционные печи и плиты, асинхронные двигатели (пылесосы, миксеры, фены) и т.д.При индуктивной нагрузке в сеть генеруется реактивная мощность (ток по фазе отстает от напряжения), которая является паразитной и приводит к перегрузке электрический сетей и требует компенсации. Подробнее об этом будет написано в следующих статьях. Емкостное сопротивление  - величина, характеризующая сопротивление, оказываемое переменному току электрической емкостью цепи (или ее участка).Емкостное сопротивление рассчитывается по формуле:

Xc=1/ωC=1/2πfC

гдеXc  - емкостное сопротивление проводника переменному токуC - емкости элемента Вся энергия затрачиваемая источником тока на преодоление емкостного сопротивления превращается в энергию электрического поля конденсатора. Когда конденсатор будет разряжаться вся энергия электрического поля вернется обратно в цепь в виде энергии электрического тока. Таким образом, емкостное сопротивление является реактивным.  Абстрактно емкостное сопротивление можно представить как кастрюлю объемом 5 литров, в нашем случае объем кастрюли это не что иное, как ее емкость. При ее наполнении водой до краев, она будет переворачиваться, и вода из неё выливаться, после чего кастрюля будет снова наполняться (так же как и конденсатор при полном заряде будет разряжаться в сеть, после чего вновь заряжаться). При емкостной нагрузке (конденсаторы) в сеть генерируется активная мощность (ток по фазе опережает напряжение). Активная мощность (конденсаторные батареи) используется для компенсации реактивной мощности.

elektro-master.blogspot.com

Полное сопротивление

Физика > Полное сопротивление

 

Это мера сопротивления, которую схема проявляет при прохождении тока в приложенном направлении.

Задача обучения

• Вывести соотношение между полным сопротивлением, сопротивлением и емкостью.

Основные пункты

• Все напряжения и токи в цепи выступают сложными экспонентами с той же частотой, что и источник.
• Отношение Z = V/I для каждого элемента не зависит от времени, но основывается на частоте источника.
• Для последовательной схемы полное сопротивление: 

Термины

• Полное сопротивление – мера противодействия потоку переменного тока в цепи (Z).
• Конденсатор – электронная составляющая, способная сберегать электрический заряд.
• Резистор – электрический компонент, передающий ток в прямой пропорциональности напряжению.

Вместо того, чтобы сталкиваться с дифференциальным уравнением, можно представить, что все источники в схеме выступают сложными экспонентами и обладают единой частотой. Этот метод идеально подходит, когда нужно учитывать соотношение фаз (фазовый сдвиг, где ток опережает напряжение).

Комплексный анализ

Для схемы RC источник переменного тока указывается как:

Последовательность RC

vin (t) = Vejωt (V – амплитуда переменного напряжения, j – мнимая единица (j2 = -1), а ω – угловая частота источника переменного тока).

Важно отметить два момента:

• Мы используем строчный алфавит для напряжения источников, чтобы разобраться в том, как они чередуются.
• Мнимая единица отображается как «j».

Комплексное сопротивление

Главное преимущество в предполагаемых источниках заключается в том, что все напряжения и токи выступают сложными экспонентами. Это помогает проследить за поведением каждого элемента в схеме.

Для резистора v = Ri. Из напряжения, приведенного выше, i = V/R ejωt. Так что, напряжение резистора сложное, как и ток с амплитудой I = V/R. Для конденсатора i = C · dv/dt. Пусть напряжение выступает сложной экспонентой (i = jωCVejωt), а амплитуда для нее: I = jωCV.

Отсюда выплывает, что отношение Z = V/I не зависит от времени, но основывается на частоте источника. Это полное сопротивление элемента. Оно отображает соотношение амплитуды напряжения к амплитуде тока. Полное сопротивление резистора приравнивается к R, а сопротивление конденсатора (C) – 1/jωC. Чтобы найти полное сопротивление схемы RС, добавим полное сопротивление двух составляющих: Z = R + 1/jωC.

Поиск реальных токов и напряжений

Так как ejωt = cos(ωt) + jsin (ωt), чтобы найти реальные токи и напряжения, нужно взять действительную часть i(t) и v(t). Полное сопротивление – реальная часть комплексного сопротивления Z. Для последовательной RC-схемы получаем Видно, что амплитуда тока 

Полное сопротивление

Оцените нашу статью

v-kosmose.com

Z в электротехнике. Какое это сопротивление?

Z=2+j6 R=2ом ХL=6ом (+это значит что это индуктивное сопротивление) <img src="//content-12.foto.my.mail.ru/mail/mayil66/_answers/i-292.jpg">Алгебраическое выражение полного сопротивления цепи имеет вид: <img src="//content-28.foto.my.mail.ru/mail/mayil66/_answers/i-294.jpg"> где Z — общее сопротивление, R — активное сопротивление, XL — индуктивное сопротивление цепи.

Z это полное сопротивление. 2 и 6 это активная и реактивная составляющие.

Импенданта, импенданс, комплексное сопротивление. Возникает в цепях переменного тока где есть индуктивность и/или ёмкость. Любая катушка и конденсатор, короче. Вообще, нормальные люди считают по формуле где учитывается индуктивность и емкость в купе с частотой тока + сопротивление резисторов, всё это в квадратах суммируется и под корнем. . А эта формула - понты теоретиков) 2 - в прикладном смысле - это таки сопротивление резисторов. А 6 - совокупное сопротивление емкости и индуктивности на определённой частоте

touch.otvet.mail.ru

Сопротивления в цепи переменного тока

Сопротивления в цепи переменного тока

Электрический ток в проводниках непрерывно связан с магнитным и электрическими полями. Элементы, характеризующие преобразование электромагнитной энергии в тепло, называются активными сопротивлениями (обозначаются R). Типичными представителями активных сопротивлений являются резисторы, лампы накаливания, электрические печи и т.д.

Индуктивное сопротивление. Формула индуктивного сопротивления.

Элементы, связанные с наличием только магнитного поля, называются индуктивностями. Индуктивностью обладают катушки реле, обмотки электродвигателей и трансформаторов. Формула индуктивного сопротивления:

где L — индуктивность.

Емкостное сопротивление. Формула емкостного сопротивления.

Элементы, связанные с наличием электрического поля, называются емкостями. Емкостью обладают конденсаторы, длинные линии электропередачи и т.д. Формула емкостного сопротивления:

где С — емкость.

Суммарное сопротивление. Формулы суммарного сопротивления.

Реальные потребители электрической энергии могут иметь и комплексное значение сопротивлений. При наличии активного R и индуктивного L сопротивлений значение суммарного сопротивления Z подсчитывается по формуле:

Аналогично ведется подсчет суммарного сопротивления Z для цепи активного R и емкостного C сопротивлений:

Потребители с активным R, индуктивным L и емкостным C сопротивлениями имеют суммарное сопротивление:

www.mtomd.info

Измерение полных сопротивлений с помощью осциллографа

Радио, 1953, №6

В статье описывается метод измерения модуля и фазового угла полного сопротивления с использованием осциллографа в качестве индикатора. При входных сопротивлениях усилителей осциллографа порядка 2 мОм, их входной ёмкости 50 пф и рабочей частоте до 1-2 кГц описываемым методом можно измерять модуль полного сопротивления до 60 кОм, с точностью +-3..4%. Измерение фазового угла обеспечивается с погрешностью, не превышающей +-3..4%.

Кроме того, косвенным путём можно измерять индуктивности и ёмкости, а также определять наличие короткозамкнутых витков в собранных дросселях и трансформаторах.

Полным сопротивлением Z цепи, как известно, называют отношение действующего на её концах напряжения к проходящему через неё току, т. е. Z = U/I.

Полное сопротивление Z можно представить в виде последовательного соединения его активной R и реактивной х составляющих. Модуль Z (абсолютная величина) и фазовый угол φ полного сопротивления определяются по формулам:

Z = (R2 + X2)0.5 = (R2 + (ωL-1/(ωC))2)0.5 ;

φ = arctg(x/R)       (1)

Измерение Z и φ можно производить с помощью схемы, показанной на рис. 1. Она состоит из двух мостовых фазовращателей АОБГ и АОБВ, на общий вход которых (на точки ЛБ) подаётся напряжение от генератора. Измеряемое сопротивление Zx является одним из плеч фазовращателя АОБВ. Напряжения с выходов фазовращателей (точки ГО к ВО) подаются на горизонтальный и вертикальный усилители осциллографа.

В зависимости от сдвига фаз между выходными напряжениями фазовращателей на экране осциллографа будут видны эллипс или окружность.

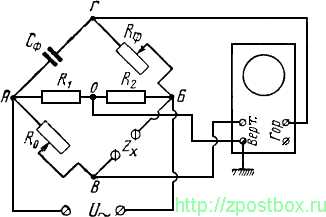
Рис. 1. Схема для измерения модуля полного сопротивления и фазового угла.

Если сопротивления R1 и R2 взять одинаковой величины, то при Rф = 1/(ωCф) между напряжением на входе фазовращателей и напряжением на входе горизонтального усилителя будет существовать сдвиг фаз в 90°. Изменяя величину введённого в схему сопротивления магазина R0, сдвиг фаз между входным напряжением фазовращателей и напряжением, поступающим на вход вертикального усилителя, также можно сделать равным 90°. Тогда на экране осциллографа получится прямая линия. При этом модуль измеряемого полного сопротивления Zx равен R0, т. е.

Zx =(R2x + (ωLx)2)0.5 - R0.       (2)

Если оба усилителя осциллографа создают одинаковые фазовые сдвиги и имеют равное усиление, то по углу а между линией на экране осциллографа и горизонталью можно определить фазовый угол φх полного сопротивления:

φx = 2α       (3)

Угол α можно измерить с помощью транспортира.

Конденсатор Сф должен обладать небольшими потерями и малой зависимостью ёмкости от частоты. Этим требованиям отвечает слюдяной конденсатор.

Если измерения будут производиться на одной фиксированной частоте, в качестве Rф можно применить сопротивление типа ВС. Для измерений в диапазоне частот на место Rф нужно включить магазин сопротивлений.

Сопротивления и R2 (также типа ВС) следует брать тем меньшими, чем выше частота, при которой производится измерение. При звуковых частотах Rl и R2 можно взять по 500-1500 Ом. При измерении полных сопротивлений обмоток дросселей, трансформаторов, реле и другой аппаратуры на промышленной частоте (50 Гц) R1 и R2 берут по 10 кОм (5 Вт). В последнем случае на вход фазовращателей приходится подавать напряжение порядка 200-400 В.

Величины R1 и R2 можно брать с допусками +-10%, но друг от друга они должны отличаться не более чем на +-1%.

При измерении полного сопротивления, имеющего ёмкостный характер, более отчётливую осциллограмму можно получить, если поменять местами магазин сопротивлений R0 и объект измерения Zx (рис. 2).

Прежде чем приступить к измерениям, нужно добиться равенства входной чувствительности и фазовых сдвигов обоих усилителей осциллографа на частоте, на которой будут производиться измерения. Это можно осуществить с помощью схемы рис. 3 (конденсатор Сф и сопротивлении Rф и могут при этом остаться подключёнными к сопротивлениям R1 и R2). Напряжение, подаваемое от генератора, при этом должно быть одного порядка с тем, которое будет применяться во время измерений. Изменением сопротивления Rд добиваются того, чтобы эллипс перешёл в прямую линию, пересекающую весь экран осциллографа.

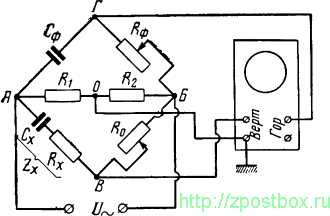
Рис. 2. Схема для измерения модуля полного сопротивления и фазового угла, если Zx имеет ёмкостный характер.

После этого точно устанавливают усиление обоих усилителей, при котором угол между указанной прямой и горизонталью составляет 45°. Если при этом осциллограмма примет вид узкого эллипса, следует вновь провести регулировку Rд и усиления, добиваясь чёткой прямой линии и угла 45°. Теперь остаётся лишь установить равенство 1/(ωCф) = Rф с погрешностью, не превышающей +-2%.

Если ёмкость Сф известна лишь приблизительно, то нужную величину Rф можно подобрать при помощи схемы рис. 4. Изменяя сопротивление Rф, добиваются того, чтобы на экране трубки при обоих положениях переключателя была видна одинаковая по амплитуде синусоида.

При изменении частоты величину сопротивления Rф следует изменять так, чтобы произведение ωRф оставалось постоянным. Помимо того, нужно производить регулировку усиления и компенсировать неравенство фазовых углов усилителей, как было указано выше.

С помощью схемы рис. 1 можно также измерять индуктивность катушек. Если катушка не имеет стального сердечника и предназначена для работы в диапазоне звуковых частот, измерения целесообразно производить на частотах 1-2 кГц, так как в этих условиях, как правило, можно пренебречь её активным сопротивлением.

Индуктивность Lx в генри вычисляется по формуле:

Lx = (R02 - Rk2)0.5       (4)

где Rk - активное сопротивление катушки в омах, измеренное омметром; ω = 2*π*f - круговая частота колебаний генератора. При ωLx > 7Rk выражение упрощается и принимает вид:

Lx ≈ R0 / ω       (5)

Если взять ω = 10000 (f = 1600 Гц), вычисления ещё упрощаются. На этой частоте можно измерять индуктивности от 100 мкГн до 16 Гн.

На частоте 50 Гц можно измерять индуктивность катушек без магнитного сердечника от 5 мГн до нескольких генри и катушек с сердечниками от 10 до 300 Гн. Если индукция в сердечнике невелика, нижний предел измерения может снизиться до 5 мГн. При увеличении индукции в сердечнике в цепи возникают гармоники. Если они велики, на экране осциллографа невозможно добиться чёткой прямой линии и точность измерений резко понижается. В этих случаях можно переходить на измерение при более высоких частотах (1 - 2 кГц).

Однако следует помнить, что индуктивность катушки со стальным сердечником зависит от приложенного напряжения и рабочей частоты, и поэтому она должна по возможности измеряться в режиме, близком к рабочему.

Рис. 3. Схема, при помощи которой производится уравнивание коэффициентов усиления и фазовых сдвигов усилителей осциллографа.

Если фигура на экране трубки сохраняет вид узкого искажённого эллипса, при изменении величины R0 не более чем на +-5% измерение индуктивности возможно в пределах от 0,005 Гн до 300 Гн.

Для определения индуктивности рассеяния первичной обмотки трансформатора низкой частоты следует измерить её полное сопротивление при замкнутой накоротко вторичной обмотке.

Рис. 4. Схема, при помощи которой подбирается сопротивление Rф, если точное значение ёмкости Сф неизвестно.

Тогда, зная рабочую частоту, полное и активное сопротивление первичной обмотки (последнее часто можно не принимать во внимание), индуктивность рассеяния можно вычислить, пользуясь формулами (4) и (5). При этом в формулу (4) вместо Rk следует подставлять активное сопротивление первичной обмотки r1. Такое измерение целесообразно производить на частоте около 1600 Гц. При слишком низкой частоте точность измерений понижается вследствие того, что при этом чрезмерно сказывается влияние активной составляющей полного сопротивления обмотки, а при слишком высокой частоте - вследствие действия междувитковой ёмкости обмотки.

Коэффициент трансформации n можно определить, измерив индуктивности рассеяния первичной и вторичной обмоток.

Если L's - индуктивность рассеяния первичной обмотки, измеренная при замкнутой накоротко вторичной обмотке, а L''s - индуктивность рассеяния вторичной обмотки, измеренная при замкнутой накоротко первичной обмотке, то коэффициент трансформации

n = (L''s/L's)0.5 = ((R022-r22)/(R012-r12))0.5,       (6)

где R01 - сопротивление магазина, обеспечивающее баланс схемы при замкнутой вторичной обмотке;r1 - активное сопротивление первичной обмотки;R02 - сопротивление магазина, обеспечивающее баланс схемы при замкнутой первичной обмотке;r2 - активное сопротивление вторичной обмотки.

При измерении на частотах 1..1,6 кГц, когда обычно R01 > 7r1 и R02 > 7r2, последнее выражение упрощается и принимает вид

n ≈ (R02/R01)0.5       (7)

Определение коэффициента трансформации таким способом более точно, чем путём измерения индуктивностей его обмоток, так как последние зависят от величины магнитной индукции в сердечнике.

С помощью описанной выше схемы можно быстро установить наличие короткозамкнутых витков в собранных трансформаторах или дросселях со стальными сердечниками даже тогда, когда их параметры неизвестны. Наличие короткозамкнутых витков уменьшает добротность катушки, в результате чего угол между линией и горизонталью уменьшается. Хорошие результаты получаются при работе на частоте 1 кГц.

При проведении этого измерения между точками А и В подключают заведомо исправный слюдяной конденсатор ёмкостью 0,02-0,05 мкф, а между точками Б и В - магазин сопротивления R0. Сопротивление последнего устанавливают таким, чтобы осциллограмма имела вид прямой линии. Уравнивая усиление вертикального и горизонтального усилителей, добиваются такого положения, при котором прямая имеет угол наклона 45° и пересекает весь экран трубки.

Затем магазин сопротивления R0 переключают на своё место (рис. 1), между точками Б и В включают обмотку испытуемого трансформатора, имеющую большее число витков, и изменением R0 вновь уравновешивают схему. При исправном трансформаторе (дросселе) угол наклона прямой на экране трубки останется равным 45°. При наличии же короткозамкнутых витков угол уменьшается, причём это уменьшение зависит от числа замкнутых накоротко витков и диаметра провода обмотки. Если, например, обмотка содержит 2500 витков провода 0,15 мм, замыкание двух витков даёт заметный на глаз эффект. При проводе диаметром 0,25 мм можно обнаружить замыкание одного витка.

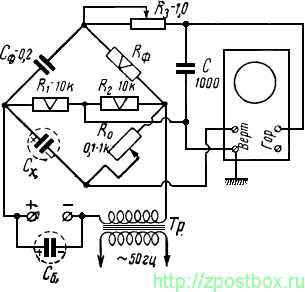
Рис. 5. Схема для измерения ёмкости электролитических конденсаторов.

Предлагаемый метод даёт также возможность измерять ёмкость.

Прямая линия на экране трубки получается при условии, что

1/(ωCx) = R0

Тогда

Cx = 1/(ωR0)       (8)

При f = 1600 Гц (ω = 10000)

Сх = 100 / R0 мкф. (9)

На этой частоте можно измерять ёмкости в пределах от 1500 пф до 100 мкф. Для измерения ёмкостей от 0,03 до 20 мкф удобно пользоваться частотой сети.

Ёмкость электролитических конденсаторов в пределах от 5 до 2000 мкф также можно измерять при f = 50 Гц, пользуясь схемой, приведённой на рис. 5. В этом случае к схеме подводятся постоянное и переменное напряжения, причём сумма постоянного напряжения и амплитуды переменного напряжения не должна превышать рабочее напряжение конденсатора. Ёмкость блокировочного конденсатора Сб должна превышать ёмкость испытуемого не менее чем в три раза, а его рабочее напряжение должно быть не ниже, чем у испытуемого.

Возможности описанных схем можно полностью реализовать лишь в случае применения в качестве R0 и Rф двух магазинов сопротивления; для верхнего фазовращателя нужен магазин сопротивления на 10 кОм, для нижнего - на 100 ком. Это затруднение радиолюбители могут преодолеть, изготовив декадные магазины сопротивления из сопротивлений типа ВС и включив последовательно с каждым из них градуированный реостат. В качестве R0 можно применить комбинацию из девяти сопротивлений по 1 кОм, девяти сопротивлений по 100 Ом, девяти сопротивлений по 10 Ом и реостата (со шкалой) на 10 Ом. Rф можно выполнить из девяти сопротивлений по 1 кОм, девяти сопротивлений по 100 Ом и градуированного реостата на 100 Ом. Сопротивления для магазинов следует подбирать с точностью +-1..1,5%.

Если возникнут затруднения с изготовлением магазинов сопротивления, в качества Rф и R0 можно взять переменные неградуированные сопротивления. При этом необходимое положение движка R0 устанавливается с помощью схемы рис. 4. Величину R0 при этом после установления баланса схемы придётся каждый раз измерять омметром.

Л. Фюрстенберг

BACK

zpostbox.ru

---

• 
  Распределительный блок
• 
  Трансформаторы тока измерительные
• 
  Виды искусственное освещение
• 
  Магнитная индукция соленоида
• 
  Счетчики электричества
• 
  Предохранитель автоматический
• 
  Бензиновый электрогенератор инверторный
• 
  Расчет теплового реле для электродвигателя
• 
  Работа переменного тока
• 
  Припои и флюсы для разных металлов и температура их плавления
• 
  1 класс электрозащиты