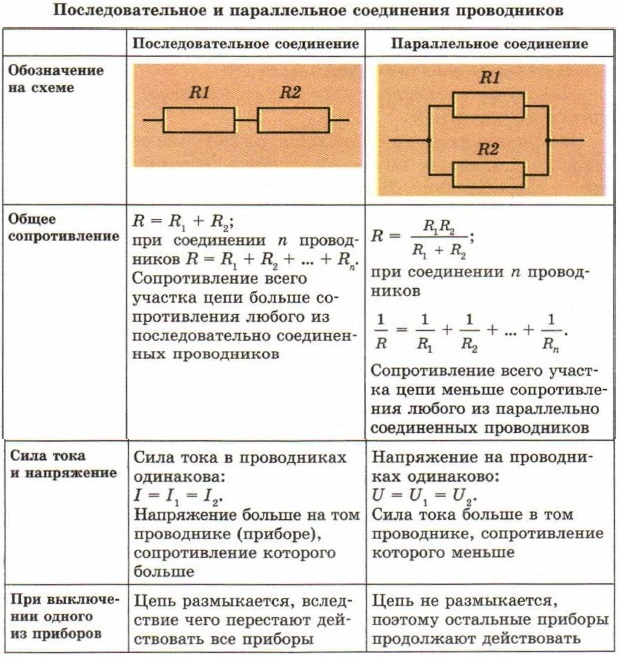
Определение параллельного соединения резисторов
Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.
В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.
В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.
Последовательное соединение резисторов.
Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.
При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.
Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.
Параллельное соединение резисторов
При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.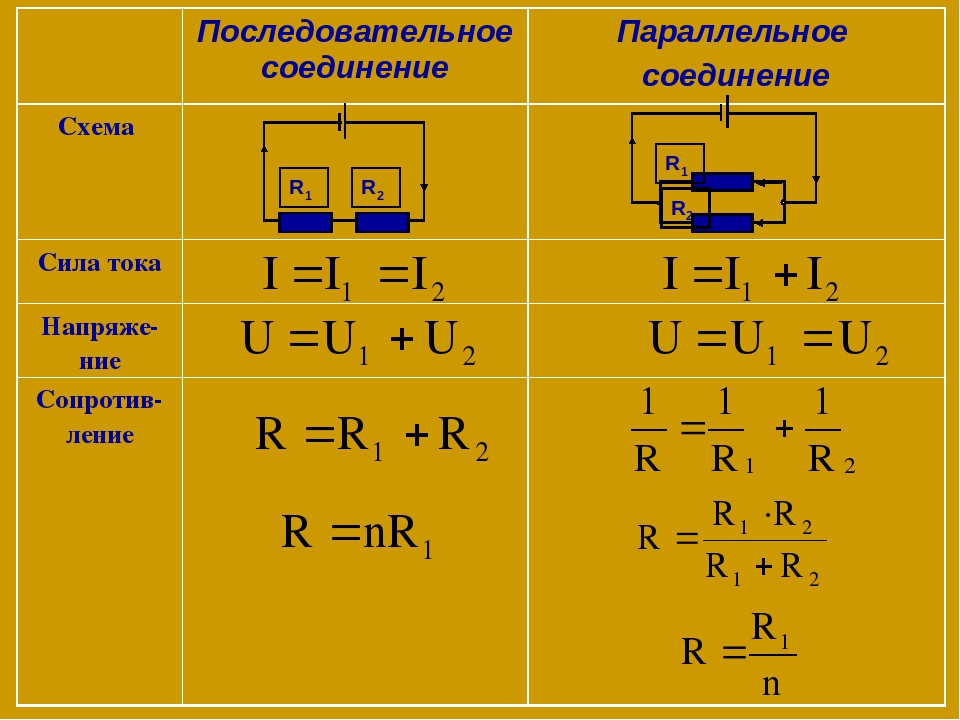
При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:
Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:
При включении трех резисторов расчет общего сопротивления будет таким:
Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.
При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.
На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.
Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.
Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!
Это такое соединение, при котором все элементы идут один за одним без разветвлений.
Свойства последовательного соединения
3.Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков – Rвх= R1+ R2+ R3;
4. Чем больше сопротивление участка, тем больше на нём падает напряжение-.
Параллельное соединение резисторов
Это такое соединение, при котором все начала элементов соединяются в одну точку, а все концы в другую и к этим точкам подводится напряжение.
Свойства параллельного соединения резистора:
1. Общее напряжение цепи равно напряжению на каждом участке-
3. Чтобы найти входное сопротивление, рассчитывают вначале величину обратную входному сопротивлению
– проводимость (G)
Общая проводимость цепи равна сумме проводимостей на каждом участке.
4.Чем больше сопротивление участка, тем меньше ток, протекающий на нем.
При параллельном соединении двух резисторов формулу входного сопротивления можно преобразовать
1.
2. Если известен общий ток, то можно найти ток ветви, умножив общий ток на сопротивление противоположной ветви и разделить на сумму сопротивлений ;.
1.Являются ли при последовательном соединении резисторов напряжения участков пропорционально сопротивлениям этих участков.
2.Являются ли при параллельном соединении резисторов токи ветвей пропорциональны сопротивлениям этих ветвей.
3.Укажите по какому из приведенных математических выражений нельзя рассчитать входное сопротивление двух параллельно соединенных резисторов.
а) ; б);
в) ; г)
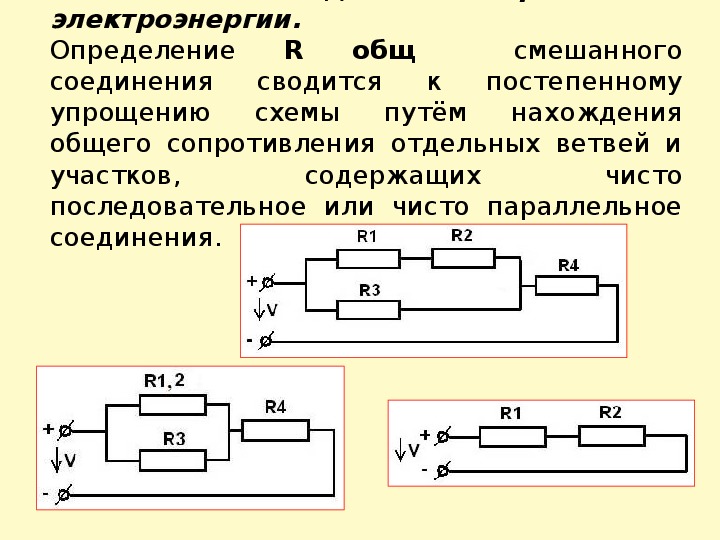
Смешанное соединение резисторов
Пример решения задач
РезисторыR2 и R3 параллельны между собой, и их общее сопротивление R2-3последовательно с R1.
А
; R4-6 = 10 Ом;
;
; R2-3 = 30 Ом
; ;
;
;
;
;
;
;
I=;
U3-6=I∙R3-6=1∙3=3В;
I3=;
I4=I5=I6=;
Cоставим подробное уравнение баланса мощностей для данной схемы. Оно является проверкой правильности решения задачи.
20Вт=20Вт- задача решена верно
Делитель напряжения- это четырёхполюсник, у которого коэффициент передачи меньше единицы.
Рассмотрим Г-образный делитель напряжения:
Чтобы рассчитать коэффициент передачи надо:
1) задать произвольное напряжение на входе;
2) любым способом рассчитать напряжение на выходе;
3) взять их отношения:
Для Г-образного делителя напряжения коэффициент передачи равен отношению выходного сопротивления ко входному.
б) Делитель напряжения с плавной регулировкой (потенциометр)
В нижнем положении движка К = 0. В верхнем положении движка К = 1
Так как в нижнем положении движка Uвых снимается с провода, а в верхнем положении
1) Если нагрузка не подключена делитель работает в режиме холостого хода и зависимость коэффициент передачи от положения движка потенциометра будет линейной.
2) Если подключить нагрузку, то характеристика будет другой: получается параллельное соединение Rн и r и при том же положении движка напряжение участка уменьшается. В крайних точках коэффициент передачи остаётся тем же, поэтому характеристика становиться нелинейной.
В крайних точках коэффициент передачи остаётся тем же, поэтому характеристика становиться нелинейной.
Вывод: чтобы при подключении нагрузки характеристика приближалась к линейной нагрузку нужно брать высокоомную.
1.Изменяется ли коэффициент передачи делителя напряжения в пределах 0 ÷ ∞?
2.Укажите среди приведенных математических выражений формулы коэффициента передачи по напряжению Г-образного делителя напряжения.
а) ; б); в); г); д).
3.Являются ли характеристики делителя напряжения с плавной регулировкой линейной, если подключить к делителю нагрузки?
Определение параллельного соединения
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) – это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 – одним концом подключено к R5, а не к узлу. R5 – одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.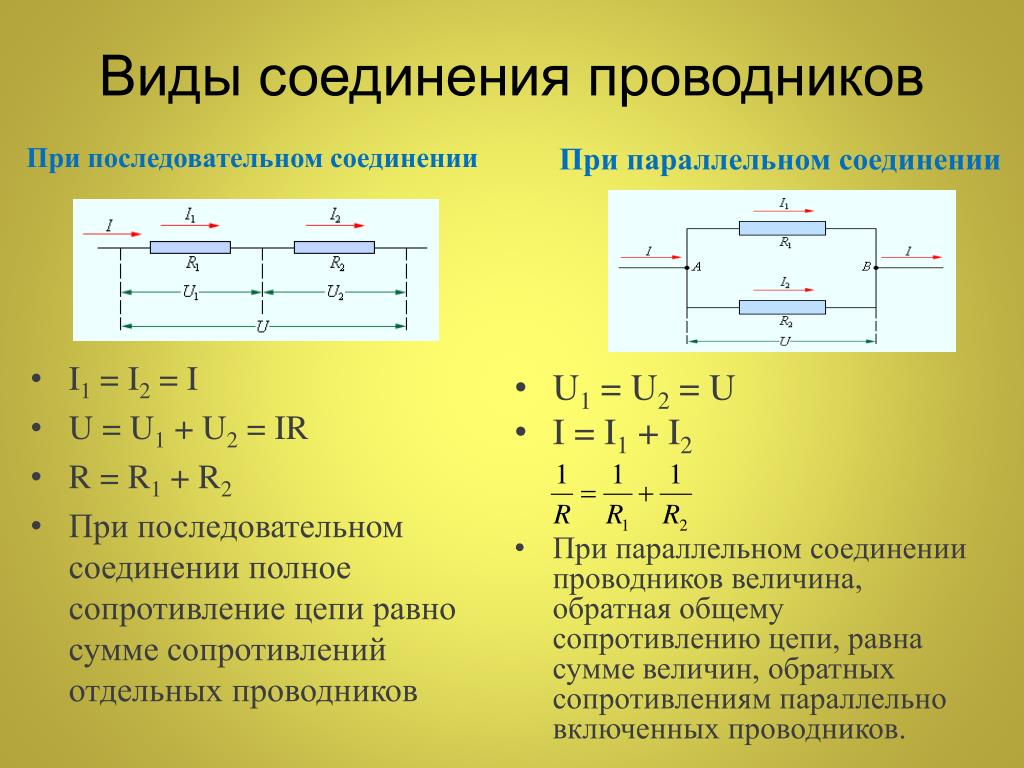
Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
Формула сопротивления при параллельном и последовательном соединении
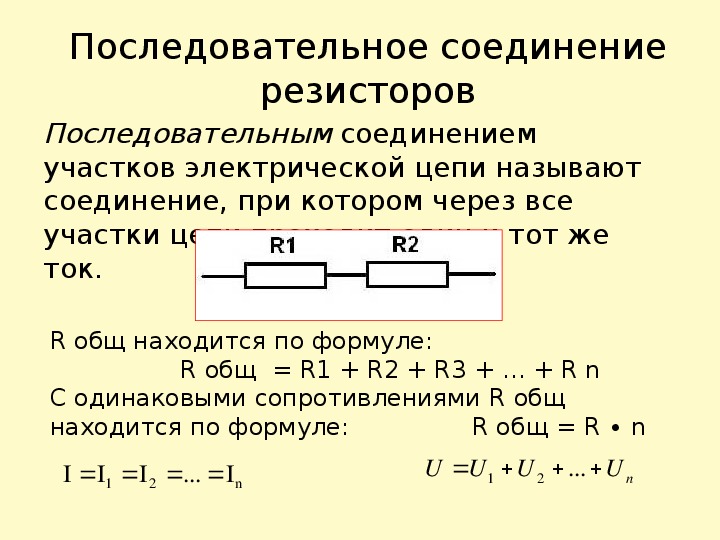
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям.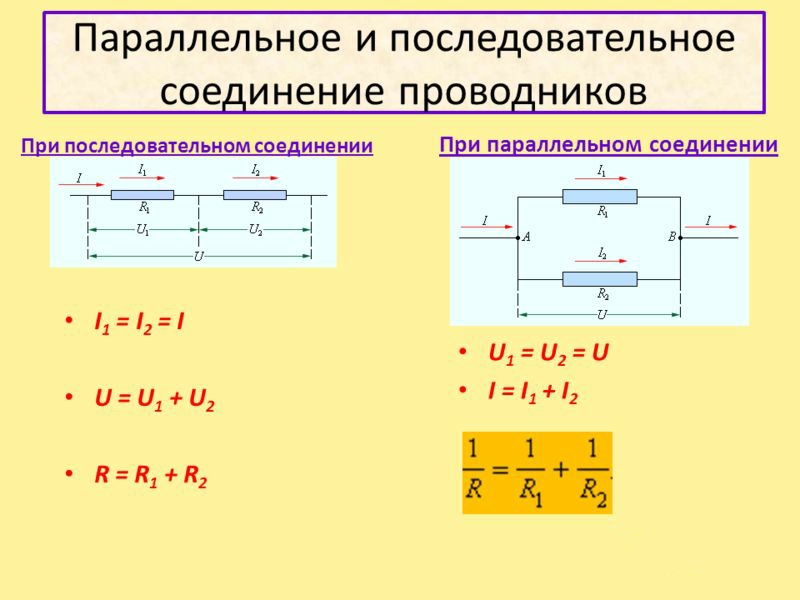 В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника.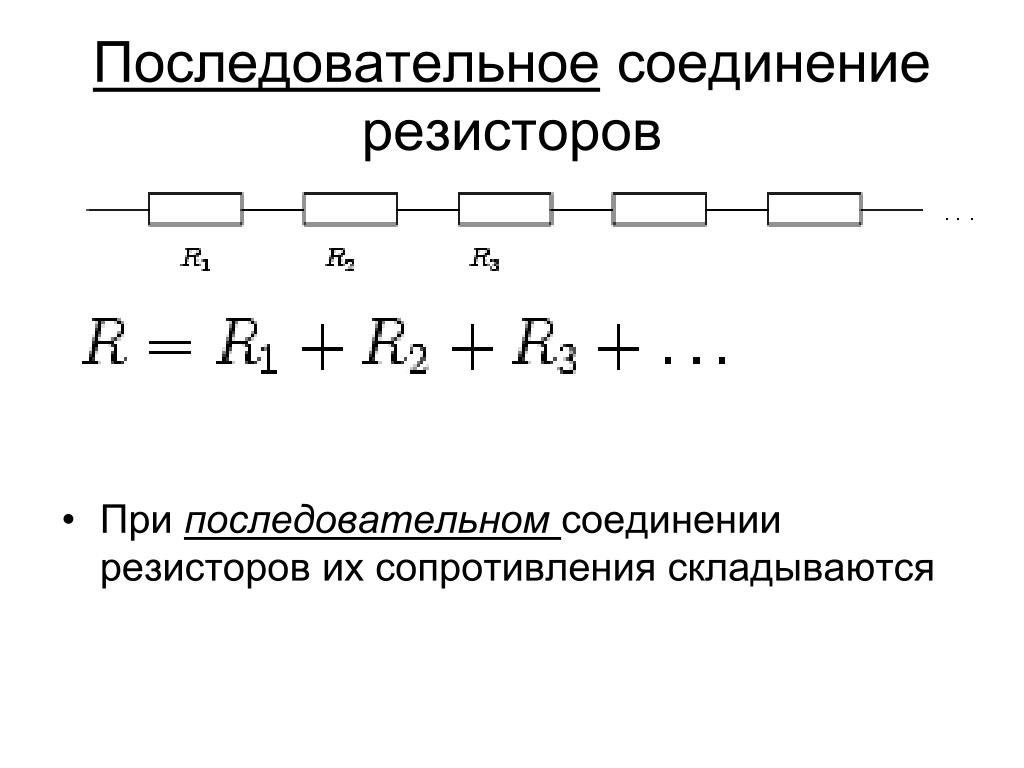 Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R – общее сопротивление, R1 – сопротивление одного элемента, а n – количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является елочная гирлянда, когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный амперметр. Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 – силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 – сопротивления обеих лампочек, U = U1 = U2 – значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях – увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- Закон ома параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения.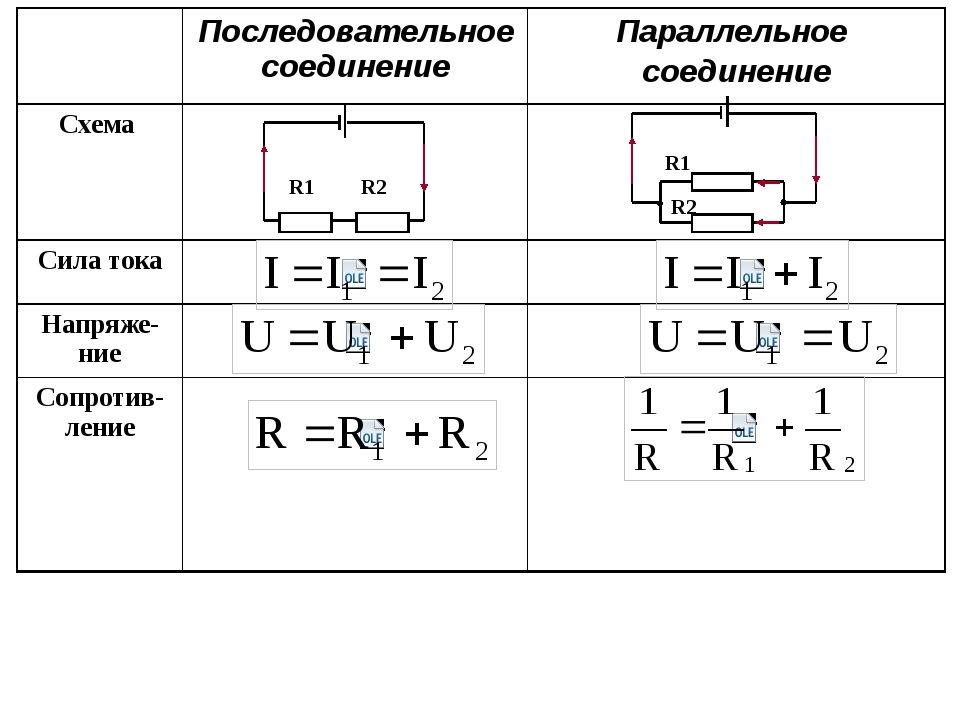 Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.
В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.
В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.
Последовательное соединение резисторов.
Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т. д.
д.
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.
При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.
Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.
Параллельное соединение резисторов
При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.
Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.
При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:
Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:
При включении трех резисторов расчет общего сопротивления будет таким:
Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.
При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.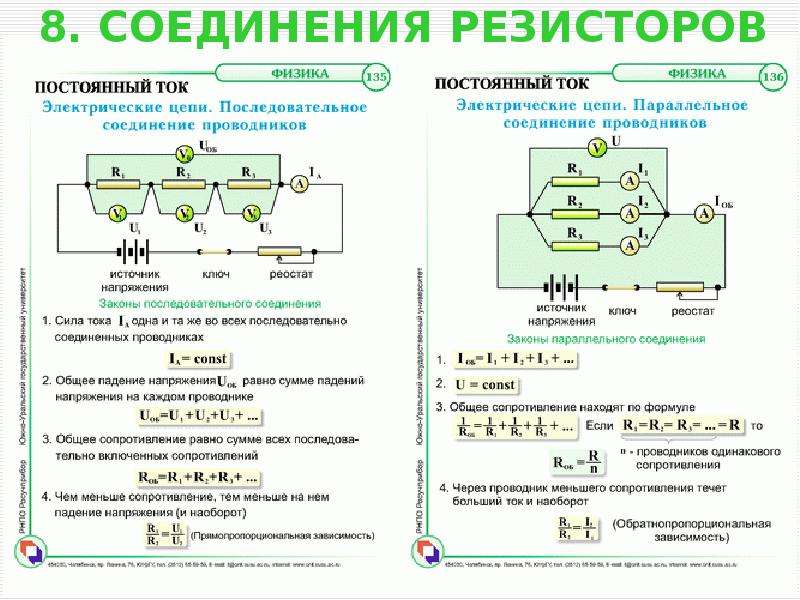
На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.
Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.
Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.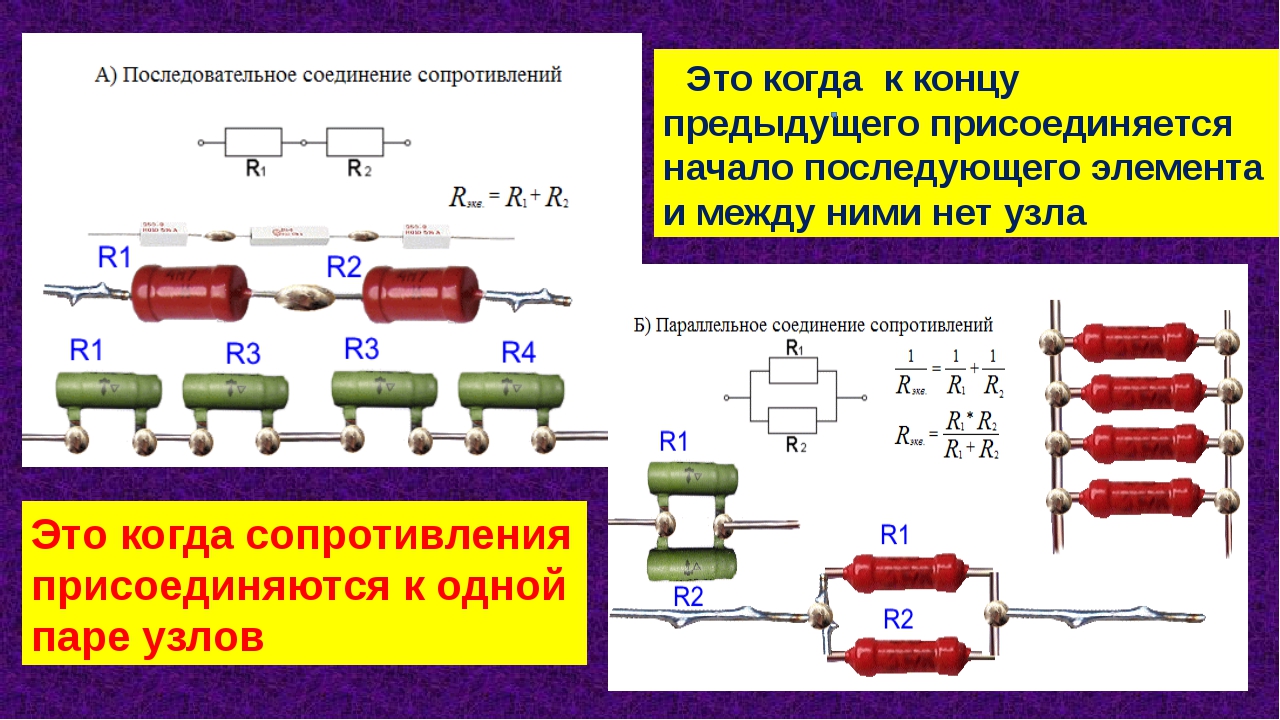
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Лабораторная работа №2 — Исследование электрических цепей при последовательном и параллельном соединении резисторов
Лабораторная работа 2
Тема: Исследование электрических цепей при последовательном и
параллельном соединении резисторов
Цель: Проверка основных закономерностей в цепях последовательного и параллельного соединения резисторов.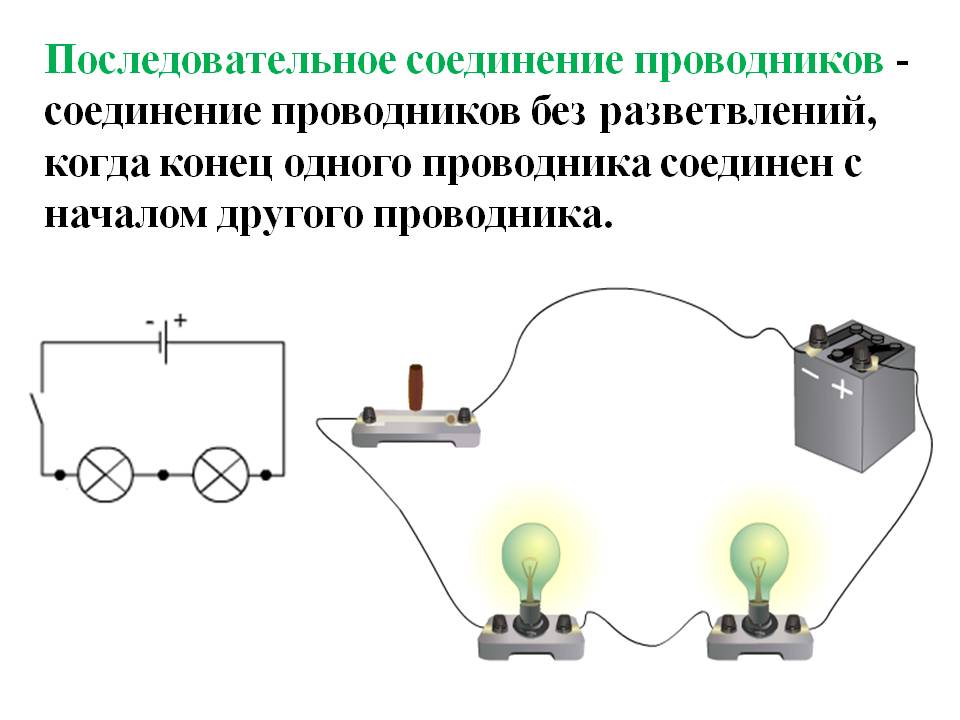
Студент должен
знать:
— основные закономерности в цепях с последовательным и параллельным соединением
резисторов;
— законы Ома;
— законы Кирхгофа;
уметь:
— рассчитывать параметры цепей при последовательном и параллельном соединении
резисторов;
— применять законы Ома, Кирхгофа.
Теоретическое обоснование
Соединение резисторов. Законы Кирхгофа позволяют анализировать и рассчитывать
электрические цепи с одним источником при различных соединениях резисторов.
Последовательным соединением участков электрической цепи называют соединение,
при котором через все участки цепи проходит один и тот же ток (см. рисунок 1.1).
Напряжение на каждом последовательно включенном участке пропорционально
величине сопротивления этого участка.
При последовательном соединении потребителей с сопротивлениями и напряжение на их зажимах равно:
Рисунок 1. 1 — Последовательное соединение резисторов
1 — Последовательное соединение резисторов
Воспользовавшись вторым законом Кирхгофа для рассматриваемой цепи (рисунок 1.1), можно записать:
или
Откуда
т. е. общее (эквивалентное) сопротивление последовательно потребителей равно сумме сопротивлений этих потребителей.
Ток в цепи последовательно включенных потребителей (рисунок 1.1) определяется
выражением:
Из этого выражения следует, что при изменении сопротивления хотя бы одного потребителя изменяется ток цепи, а, следовательно, и режим работы (напряжение)
всех последовательно включенных потребителей (резисторов).
Характерно, что при последовательном соединении потребителей на большем сопротивлении тратится большая мощность:
Параллельным соединением участков электрической цепи называют соединение, при
котором все участки цепи присоединяются к одной паре узлов, т. е. находятся под
действием одного и того же напряжения (см. рисунок 1. 2). Токи параллельно
2). Токи параллельно
включенных участков обратно пропорциональны сопротивлениям этих участков. При
параллельном соединении потребителей с сопротивлениями токи
потребителей равны:
Воспользовавшись первым законом Кирхгофа для рассматриваемой цепи, можно
определить ток в неразветвленной части цепи:
или
Рисунок 1.2 — Параллельное соединение резисторов
Т. е. обратная величина общего (эквивалентного) сопротивления (R) параллельно
включенных потребителей равна сумме обратных величин сопротивлений этих
потребителей.
Величина, обратная сопротивлению, определяет проводимость потребителя (g).
Общая (эквивалентная) проводимость цепи при параллельном соединении потребителей
определяется выражением:
Если параллельно включены п одинаковых потребителей с cпротивлением
каждое, то эквивалентное сопротивление этих потребителей .
Если параллельно включены два потребителя с сопротивлениями и , то общее
(эквивалентное) их сопротивление по (9):
Изменение сопротивления какого-либо из параллельно соединенных потребителей не
влияет на режим работы (напряжение) всех потребителей, включая изменяемый.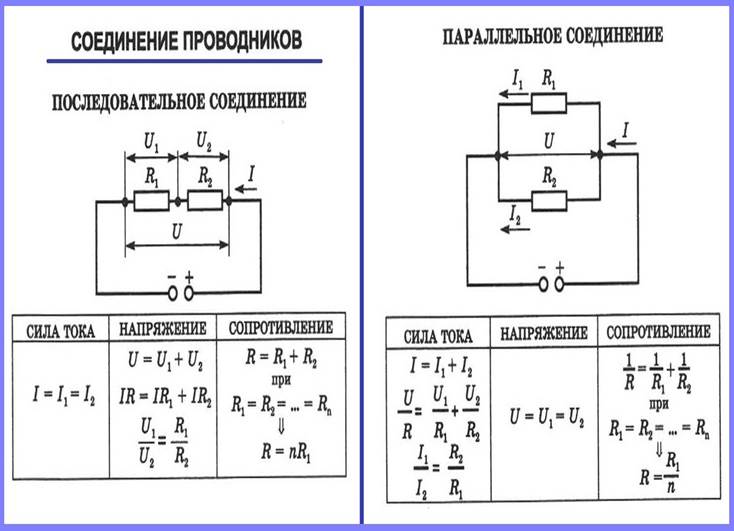
Поэтому параллельное соединение потребителей нашло широкое практическое
применение.
При параллельном соединении потребителей на большем сопротивлении тратится
меньшая мощность:
Ход работы
1 Исследование цепи при последовательном соединении резисторов
Собрать электрическую схему (рисунок 1.3) и дать проверить ее преподавателю.
Включить блок питания БП — 15. Установить напряжение цепи 20 В.
Выключатель SA включить. С помощью амперметра измерить ток в цепи, с помощью вольтметра — падения напряжений на отдельных ее участках для двух положений движков реостатов. Результаты измерений занести в таблицу 1.1.
На рисунке 1.3, 1.4 приведены электрические схемы опытов. При сборке электрических цепей по приведенным схемам используется следующее оборудование:
G1, G2 — источники постоянного напряжения БП — 15;
РА — амперметр;
PU — вольтметр;
R1 — реостат на 1 кОм;
R2 — реостат на 220 Ом;
R3 — реостат на 220 Ом;
SA — выключатель.
Рисунок 1.3 — Схема для исследования цепи с последовательным соединением
резисторов
Таблица 1.1 — Результаты исследования цепи с последовательным соединением резисторов
По результатам исследования цепи с последовательным соединением резисторов рассчитать напряжение на зажимах цепи
Результаты вычислений занести в таблицу 1.1. Сравнив результат с заданным напряжением
.
Вычислить величину эквивалентного сопротивления цепи, воспользовавшись законом Ома
Результаты вычислений нести в таблицу 1.1.
Определить сопротивления , воспользовавшись законом Ома для участка электрической цепи.
Определить эквивалентное сопротивление цепи по свойствам последовательного соединения резисторов. Сравнить с результатом, полученным в п.
 1.5.
1.5.По закону Ома для всей цепи вычислить ток . Сравнить с измеренным значением.
Вычислить отношения падений напряжений и отношения соответствующих сопротивлений и сделать вывод о распределении напряжений при последовательном соединении резисторов.
Исследование цепи при параллельном соединении резисторов
Собрать электрическую схему (рисунок 1.4) и дать проверить ее преподавателю.
Включить блок питания БП — 15. Установить напряжение цепи 20 В.
Выключатель SA включить. С помощью амперметров измерить общий ток и токи ветвей, с помощью вольтметра — падения напряжений на отдельных ее участках цепи двух положений движков реостатов. Результаты измерений занести в таблицу 1.2.
Рисунок 1.4 — Схема для исследования цепи с параллельным соединением резисторов
Таблица 1. 2 — Результаты исследования цепи с параллельным соединением резисторов
2 — Результаты исследования цепи с параллельным соединением резисторов
опыта
Вычислить эквивалентное сопротивление цепи, воспользовавшись законом Ома для всей цепи
Результаты вычислений занести в таблицу 1.2.
Определить общий ток в цепи по свойствам параллельного соединения резисторов.
Сравнить с измеренным значением тока.
Вычислить сопротивления резисторов по закону Ома для участка цепи.
Определить проводимости элементов и эквивалентную проводимость цепи по формуле
Вычислить эквивалентную проводимость цепи по свойству параллельного соединения резисторов. Сравнить с результатом в п.2.7.
Вычислить отношения для двух опытов. Сделать вывод о распределении токов при параллельном соединении резисторов.
 Проверить справедливость первого закона Кирхгофа.
Проверить справедливость первого закона Кирхгофа.
Контрольные вопросы
Как изменится ток в цепи при увеличении последовательно включенных резисторов?
Как изменится мощность цепи, если увеличить количество последовательно соединенных резисторов?
Чем объяснить равенство отношений и при любом изменении режима работы в последовательной цепи?
Перечислите свойства последовательного соединения резисторов.
Как изменится ток в цепи при увеличении числа параллельно включенных резисторов?
Как зависит величина потребляемой мощности от количества параллельно включенных резисторов?
Как изменится ток в цепи, если закоротить .
а) при последовательном соединении резисторов;
б) при параллельном соединении резисторов.
Чем объяснить равенство отношений RI/R2, и I2/I1 при любом изменении режима работы в параллельной цепи?
Перечислите свойства параллельного соединения резисторов.

Содержание отчета
Номер, тема и цель работы.
Схема опыта рисунок 1.3, 1.4.
Ход работы.
Результаты измерений и вычислений.
Сделать вывод.
Ответы на контрольные вопросы письменно.
Литература
А.К. Славинский, И.С. Туревский — Электротехника с основами электроники, 2013.-с. 40
Лоторейчук, Е.А.- Теоритические основы электротехники: 2014. –с. 24, 25
Последовательное соединение резисторов
Это такое соединение,
при котором все элементы идут один за
одним без разветвлений.
Свойства
последовательного соединения
1. Ток во всех
резисторах одинаков-
I1
= I2
= I3;
2. Общее напряжение
Общее напряжение
цепи равно сумме напряжений на всех
резисторах-
U=U1
+ U2
+ U3;
3.Сопротивление
по отношению к входным зажимам называется
входным сопротивлением и равно сумме
сопротивлений участков —
Rвх=
R1
+ R2
+ R3;
4. Чем больше
сопротивление участка, тем больше на
нём падает напряжение-.
Параллельное соединение резисторов
Это такое соединение,
при котором все начала элементов
соединяются в одну точку, а все концы в
другую и к этим точкам подводится
напряжение.
Свойства параллельного
соединения резистора:
1. Общее напряжение
цепи равно напряжению на каждом участке-
U
= U1
= U2
= U3
2. Общий ток цепи
Общий ток цепи
равен сумме токов на всех участках-
I
= I1
+ I2
+ I3
3. Чтобы найти
входное сопротивление, рассчитывают
вначале величину обратную входному
сопротивлению
— проводимость (G)
Общая проводимость
цепи равна сумме проводимостей на каждом
участке.
G
= G1
+ G2
+ G3
4.Чем больше
сопротивление участка, тем меньше ток,
протекающий на нем.
При параллельном
соединении двух резисторов формулу
входного сопротивления можно преобразовать
1.
2. Если известен
общий ток, то можно найти ток ветви,
умножив общий ток на сопротивление
противоположной ветви и разделить на
сумму сопротивлений
;.
Тестовые задания:
Задание | Варианты | |
1.Являются | Да; Нет. | |
2.Являются | Да; Нет. | |
3.Укажите | а) в) | |
Смешанное соединение резисторов
Пример
решения задач
Дано:
U
= 60 В
R1
= 7 Ом
R2
= 12 Ом
R3
= 4 Ом
Найти: I1;
I2;
I3
= ?
РезисторыR2
и R3
параллельны между собой, и их общее
сопротивление R2-3
последовательно с R1.
Rвх
= R1
+ R2
— 3
Rвх
=R1+R2∙3=
7 + 3 = 10 Ом
I1
= Iвх
= 6 А
U2
— 3 = I∙R2
— 3 — находим
напряжение разветвленного участка:
U2
— 3 = I∙R2
— 3 = 6∙3
= 18 В
U2
— 3 = U2
= U3
=18 В— т.к.
параллельное соединение
А
Дано:
U=240
В
R1
= 20 Ом
R2
= 120 Ом
R3
= 40 Ом
R4
= 60 Ом
R5
= 30 Ом
R6
= 20 Ом
Найти: I1-6
-?
;
R4-6
= 10
Ом;
;
;
R2-3
= 30
Ом
Rвх=R1+R2-3+R4-6
= 20 + 30 +10
= 60
Ом;
;
;
U2-3
=I∙R2-3=
4∙30
= 120
В;
U2
— 3
= U2
= U3;
;
;
U4-6=I∙R4-6=4∙10=40B;
U4-6=U4=U5=U6;
;
;
;
Дано:
E
= 20
В
Ri=2Ом
R1
= 9Ом
R2
= 6
Ом
R3
= 12
Ом
R4
= 1
Ом
R5
= 2
Ом
R6
= 1
Ом
R4-6
= R4
+ R5
+ R6;
;
R3-6
= 3
Ом;
Rвх
= R1
+ R3-6
+R2
= 9 + 3 + 6 = 18
Ом;
I=;
I=I1=I2=1А;
U3-6=I∙R3-6=1∙3=3В;
U3-6=U3=U4-6;
I3=;
I4=I5=I6=;
Cоставим
подробное уравнение баланса мощностей
для данной схемы.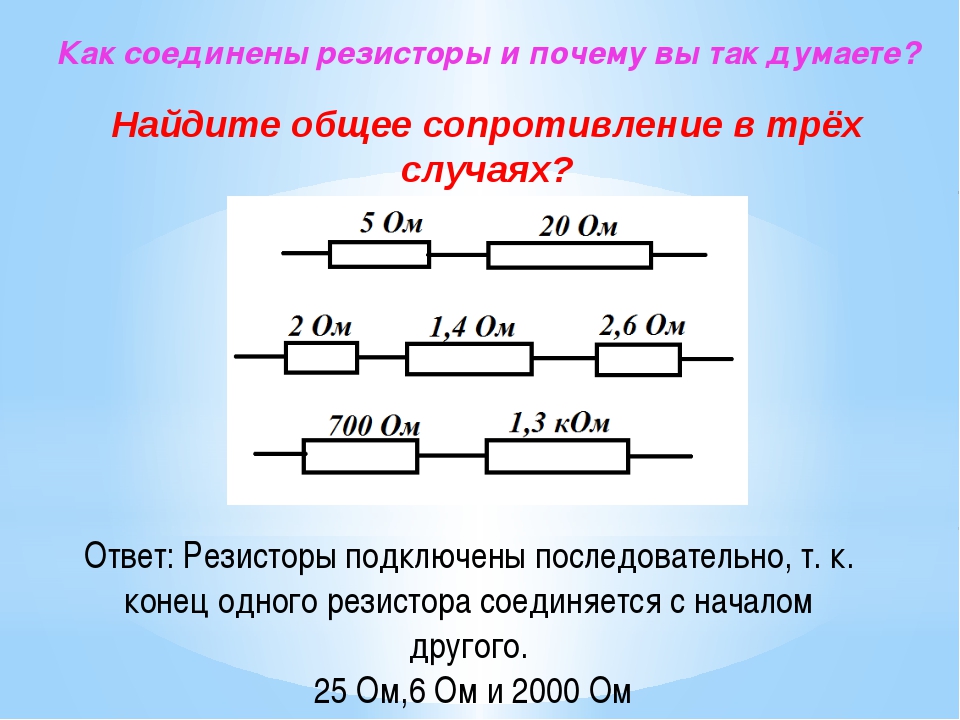 Оно является проверкой
Оно является проверкой
правильности решения задачи.
Pu=Pн+Р0;
EI=I21∙
R1+
I22∙
R2+
I23R3+I42R4+I25R5+I26+I2Ri;
20∙1=12∙9+12∙6+(0,25)2∙12+(0,75)2∙1+(0,75)22+(0,75)21+12∙2;
20Вт=20Вт- задача
решена верно
ДЕЛИТЕЛИ НАПРЯЖЕНИЯ
Делитель напряжения-
это четырёхполюсник, у которого
коэффициент передачи меньше единицы.
Рассмотрим
Г-образный делитель напряжения:
Чтобы рассчитать
коэффициент передачи надо:
1) задать произвольное
напряжение на входе;
2) любым способом
рассчитать напряжение на выходе;
3) взять их отношения:
Для Г-образного
делителя напряжения коэффициент передачи
равен отношению выходного сопротивления
ко входному.
б) Делитель
напряжения с плавной регулировкой
(потенциометр)
В нижнем положении
движка К
= 0. В верхнем положении движка К
= 1
Так как в нижнем
положении движка Uвых
снимается
с провода,
а в верхнем положении
Uвых
= Uвх
1) Если нагрузка
не подключена делитель работает в режиме
холостого хода и зависимость коэффициент
передачи от положения движка потенциометра
будет линейной.
2) Если подключить
нагрузку, то характеристика будет
другой: получается параллельное
соединение Rн
и r
и при том же положении движка напряжение
участка уменьшается. В крайних точках
коэффициент передачи остаётся тем же,
поэтому характеристика становиться
нелинейной.
Вывод: чтобы при
подключении нагрузки характеристика
приближалась к линейной нагрузку нужно
брать высокоомную.
Тестовые задания:
Задание | Варианты |
1.Изменяется | Да; Нет. |
2.Укажите | а) |
3.Являются | Да; Нет. |
Параллельное и последовательное соединение тока. Параллельное и последовательное соединение
Темы кодификатора ЕГЭ
: параллельное и последовательное соединение проводников, смешанное соединение проводников.
Есть два основных способа соединения проводников друг с другом — это последовательное
и параллельное
соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному
соединению проводников.
Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.
Проводник, обладающий сопротивлением , мы называем резистором
и изображаем следующим образом (рис. 1
1
):
Рис. 1. Резистор
Напряжение на резисторе
— это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2
):
Рис. 2.
Стационарное поле совершает при этом положительную работу .
Так как alt=»q > 0″>
и alt=»A > 0″>
, то и alt=»\varphi_a — \varphi_b > 0″>
, т. е. alt=»\varphi_a > \varphi_b»>
.
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю.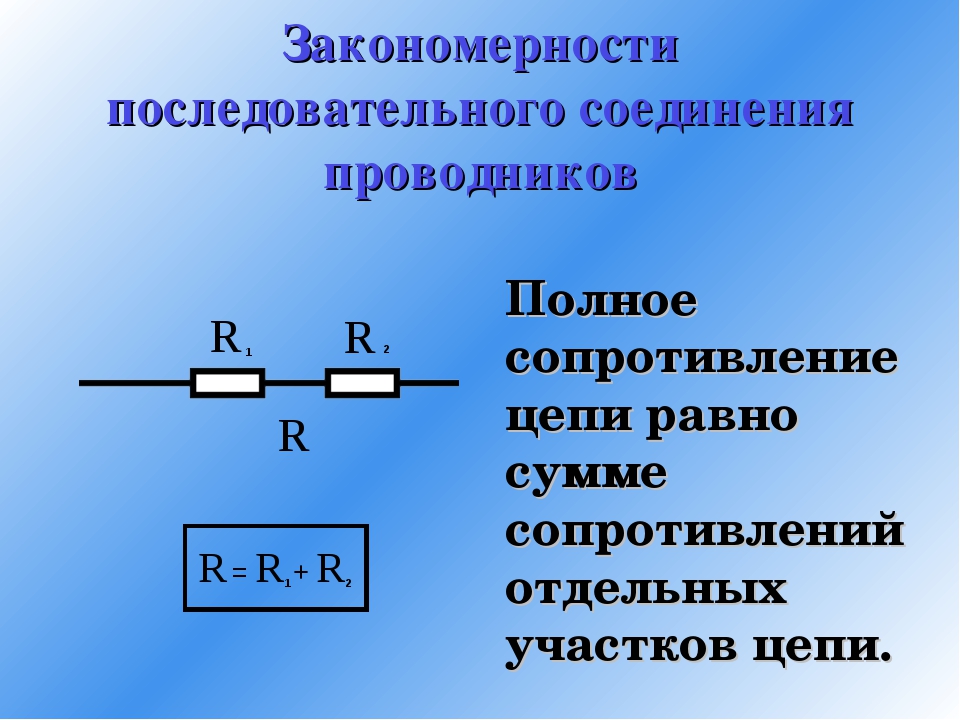 Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3
Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3
):
Рис. 3.
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным
. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении
проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4
). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.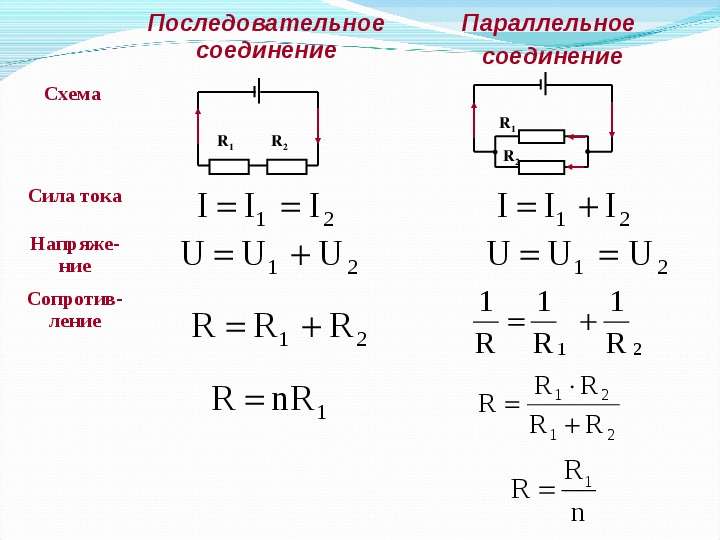
1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике
.
Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть — сопротивление участка . По закону Ома имеем:
По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении
проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис.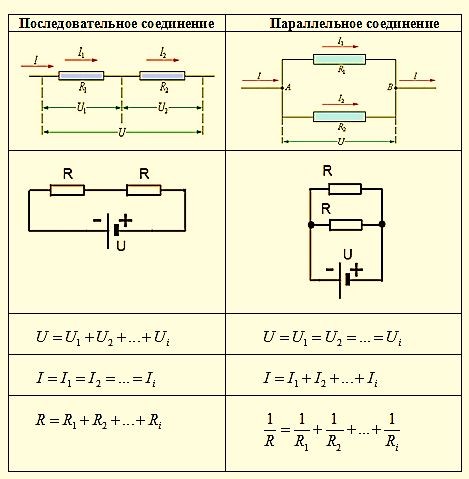 5
5
).
Рис. 5. Параллельное соединение
Резисторы подсоединены к двум точкам: и . Эти точки называются узлами
или точками разветвления
цепи. Параллельные участки называются также ветвями
; участок от к (по направлению тока) называется неразветвлённой частью
цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.
1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .
Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:
Сокращая на , получим:
(1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1)
можно найти :
(2)
К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2)
не получается, и приходится довольствоваться соотношением
(3)
Тем не менее, один полезный вывод из формулы (3)
сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:
Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное сединение
проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис. 6
).
Рис. 6. Смешанное соединение
Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :
Ом.
Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:
Ом.
Сопротивление цепи:
Ом.
Теперь находим силу тока в цепи:
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора и находятся под напряжением , поэтому:
(В сумме имеем А, как и должно быть при параллельном соединении.)
Сила тока в резисторах и одинакова, так как они соединены последовательно:
Стало быть, через резистор течёт ток A.
1. Находят эквивалентное сопротивление участков цепи с параллельным соединением резисторов. Рисунок 2. Последовательное соединение резисторов. Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов.
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Этот результат справедлив для любого числа параллельно включенных проводников.
На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений. Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения.
При последовательном соединении проводников сила тока во всех проводниках одинакова. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов.
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов. При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно.
Цепь разбивают на участки с только пареллельным или только последовательным соединением. Вычисляют общее сопротивление для каждого отдельного участка. Вычисляют общее сопротивление для всей цепи смешанного соединения.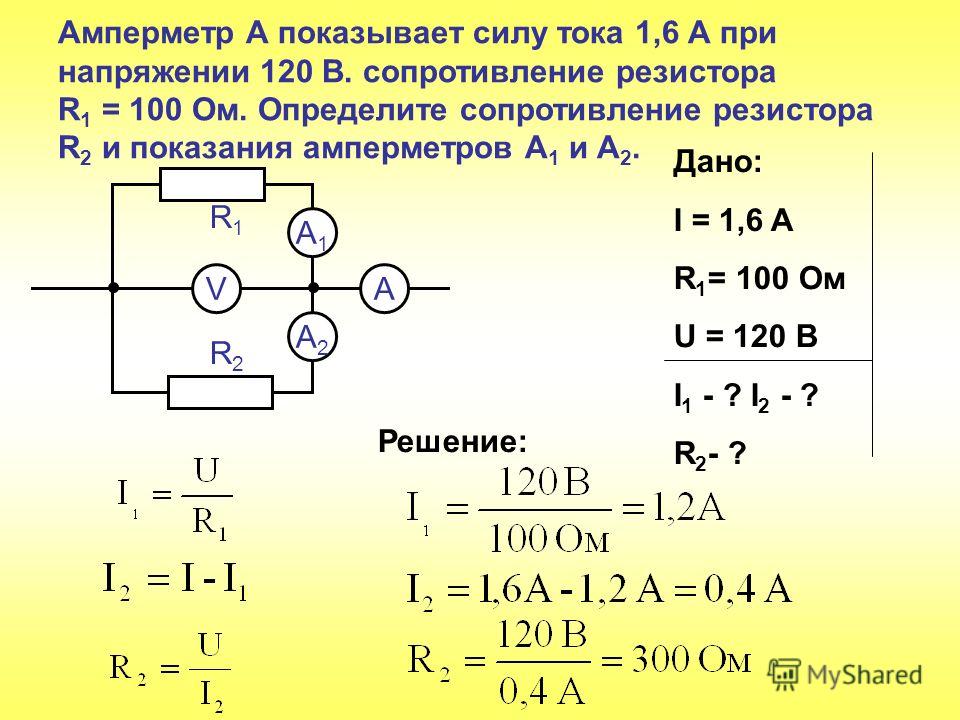 Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Если резисторы соединяются последоватеьно — складывать.
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Если резисторы соединяются последоватеьно — складывать.
То есть при последовательном соединении резисторы подключатся друг за другом. На рисунке 4 показан простейший пример смешанного соединения резисторов. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.4. Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.
В результате вы научитесь с нуля не тольно разрабатывать собственные устройства, но и сопрягать с ними различную переферию! Узел — точка разветвления цепи, в которой соединяются не менее трёх проводников. Последовательное соединение резисторов применяется для увеличения сопротивления.
Напряжение при параллельном соединении
Как видно, вычислить сопротивление двух параллельных резисторов значительно удобнее. Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением.
Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением.
Общее сопротивление Rобщ
Такое соединение сопротивлений называется последовательным. Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Точно так же для каждой ветви I1 = U1 / R1, I2 = U2 / R2, где I1 и I2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.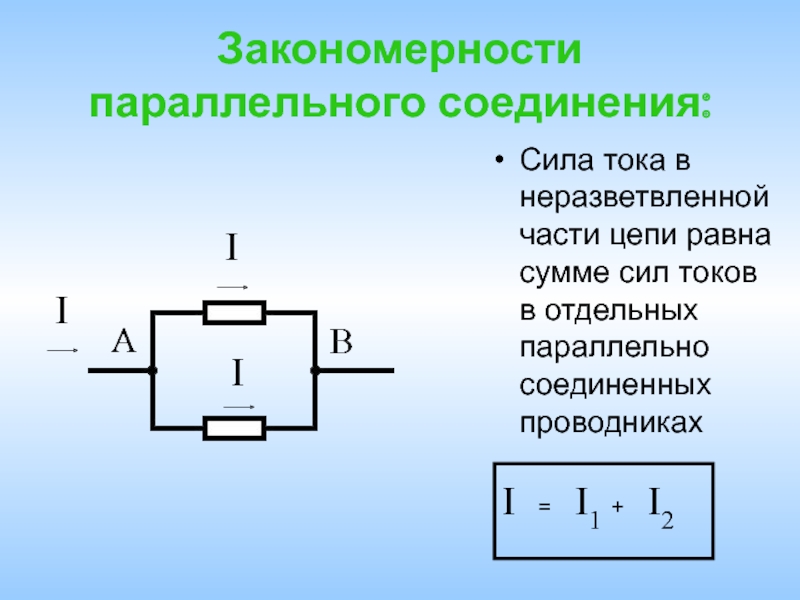
Это значит, что общее сопротивление цепи всегда будет ниже любого параллельно включенного резистора. 2. Если эти участки включают последовательно соединенные резисторы, то сначала вычисляют их сопротивление. Применяя закон Ома для участка цепи, можно доказать, что полное сопротивление при последовательном соединении равно сумме сопротивлений отдельных проводников.
Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.
Определения
Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:
- Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
- Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным.
 Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.
Использование параллельного и последовательного соединения проводников
Термины, применяемые к электрическим цепям
Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию.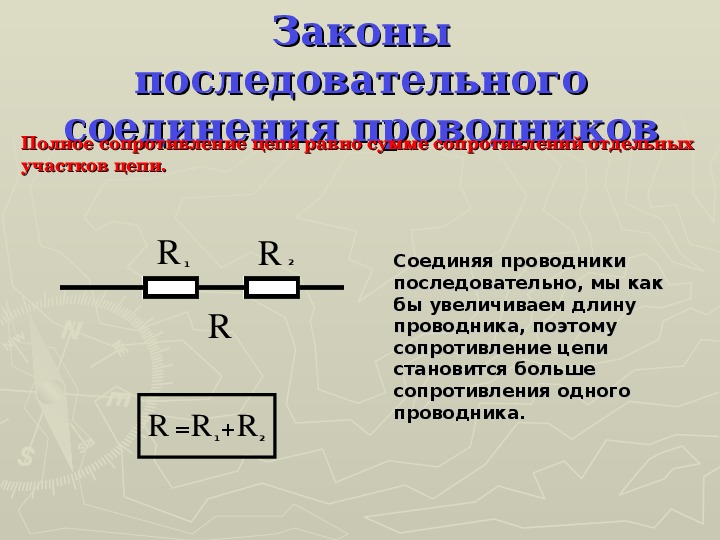 Происходит нагрев сопротивлений.
Происходит нагрев сопротивлений.
Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
- Внешняя часть цепи, где заряды движутся, увлекаемые полем.
- Внутренняя часть цепи, где заряды движутся против напряженности.

Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:
Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.
Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.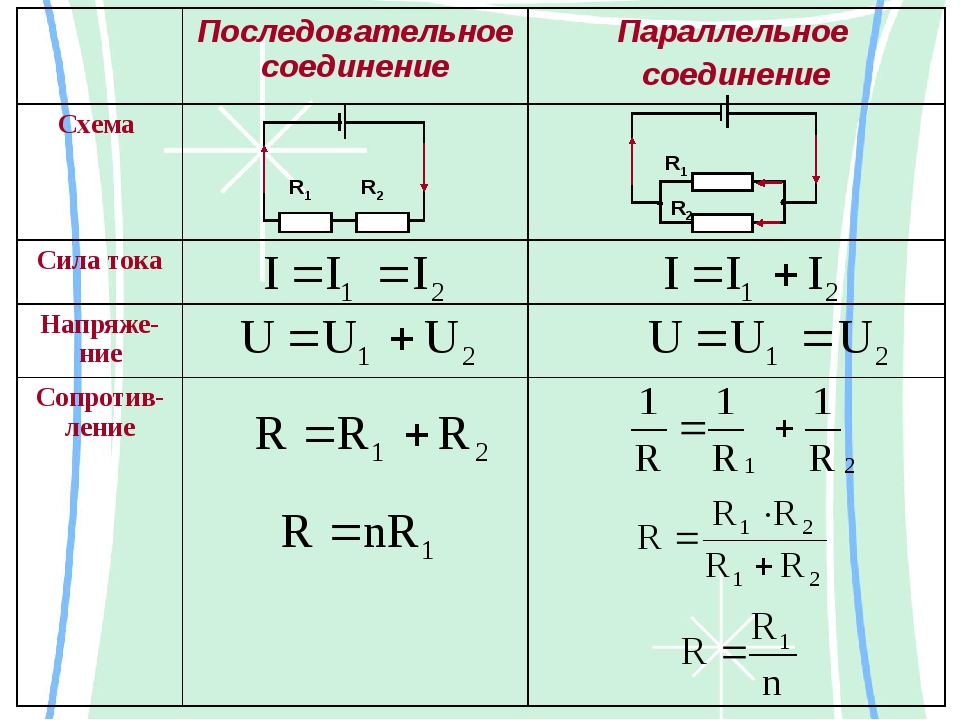
При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.
Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников
Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:
Приведем некоторые сведения, помогающие решению задачи:
Посчитать сопротивления элементов при последовательном и параллельном соединении
Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:
- При последовательном включении суммируются сопротивления, при параллельном — проводимости:
- Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
- Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
- Мнимое сопротивление емкости записывается в виде: -j/ω*С.
 Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может.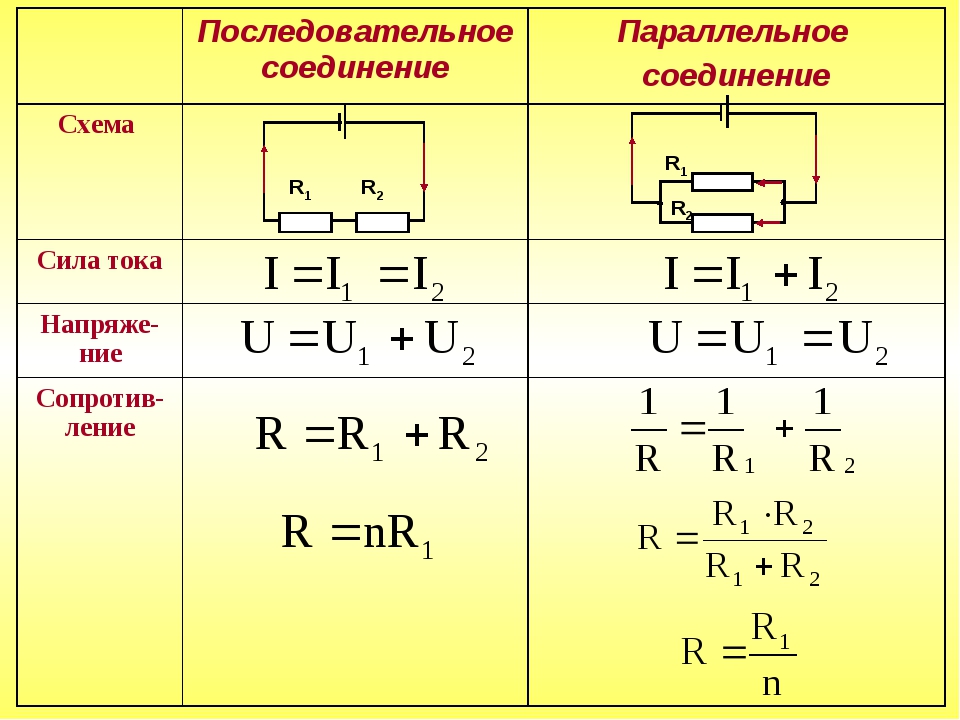 При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
Пример решения уравнений Кирхгофа
Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
- Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
- Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.
Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R
= 1/U
, где
R
= 1
Ом
А мощность будет выделяться P
=
I
*
U
,
то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым.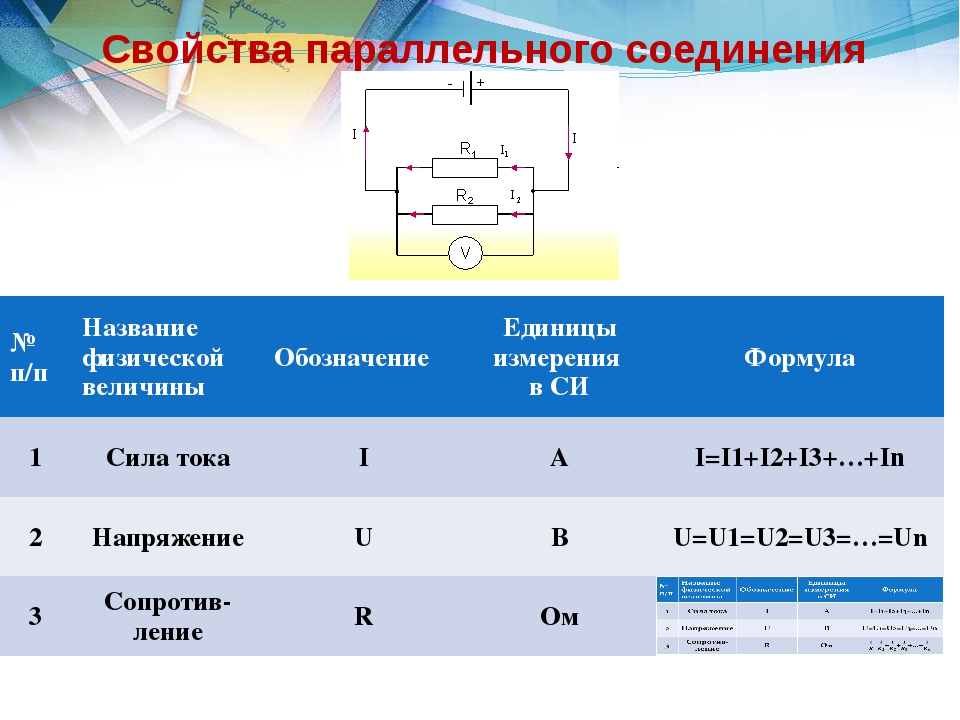 Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.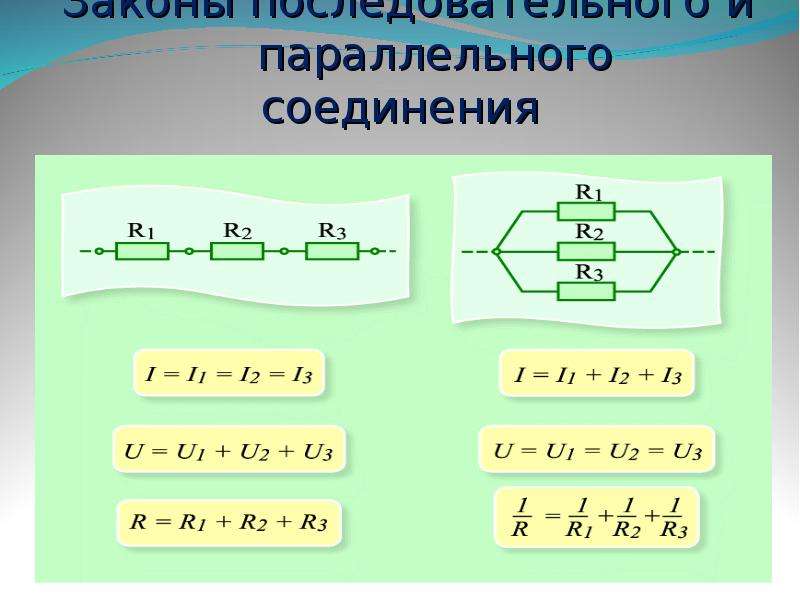
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G
, по аналогии с сопротивлением R
и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I
=
U
*
G
&
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих. Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему.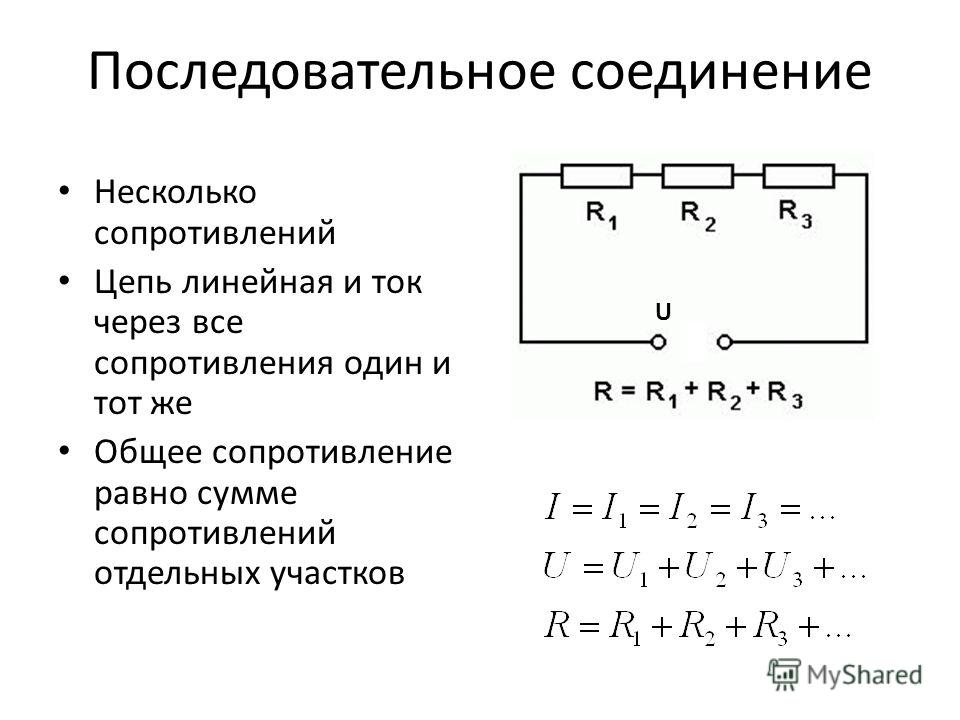 Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
В электротехнике и электронике очень широко используются резисторы. Применяются они в основном для регулирования в схемах тока и напряжения. Основные параметры: электрическое сопротивление (R) измеряется в Омах, мощность (Вт) , стабильность и точность их параметров в процессе эксплуатации. Можно вспомнить ещё множество его параметров, — ведь это обычное промышленное изделие.
Последовательное соединение
Последовательное соединение — это такое соединение, при котором каждый последующий резистор подключается к предыдущему, образуя неразрывную цепь без разветвлений. Ток I=I1=I2 в такой цепи будет одинаковым в каждой её точке. Напротив, напряжение U1, U2 в различных её точках будет разным, причём работа по переносу заряда через всю цепь, складывается из работ по переносу заряда в каждом из резисторов, U=U1+U2. Напряжение U по закону Ома равно току, умноженному на сопротивление, и предыдущее выражение можно записать так:
Напротив, напряжение U1, U2 в различных её точках будет разным, причём работа по переносу заряда через всю цепь, складывается из работ по переносу заряда в каждом из резисторов, U=U1+U2. Напряжение U по закону Ома равно току, умноженному на сопротивление, и предыдущее выражение можно записать так:
где R — общее сопротивление цепи. То есть по простому идет падение напряжения в точках соединения резисторов и чем больше подключенных элементов, тем больше происходит падение напряжения
Отсюда следует, что
, общее значение такого соединения определяется суммированием сопротивлений последовательно. Наши рассуждения справедливы для любого количества последовательно соединяемых участков цепи.
Параллельное соединение
Объединим начала нескольких резисторов (точка А). В другой точке (В) мы соединим все их концы. В результате получим участок цепи, который называется параллельным соединением и состоит из некоторого количества параллельных друг другу ветвей (в нашем случае – резисторов).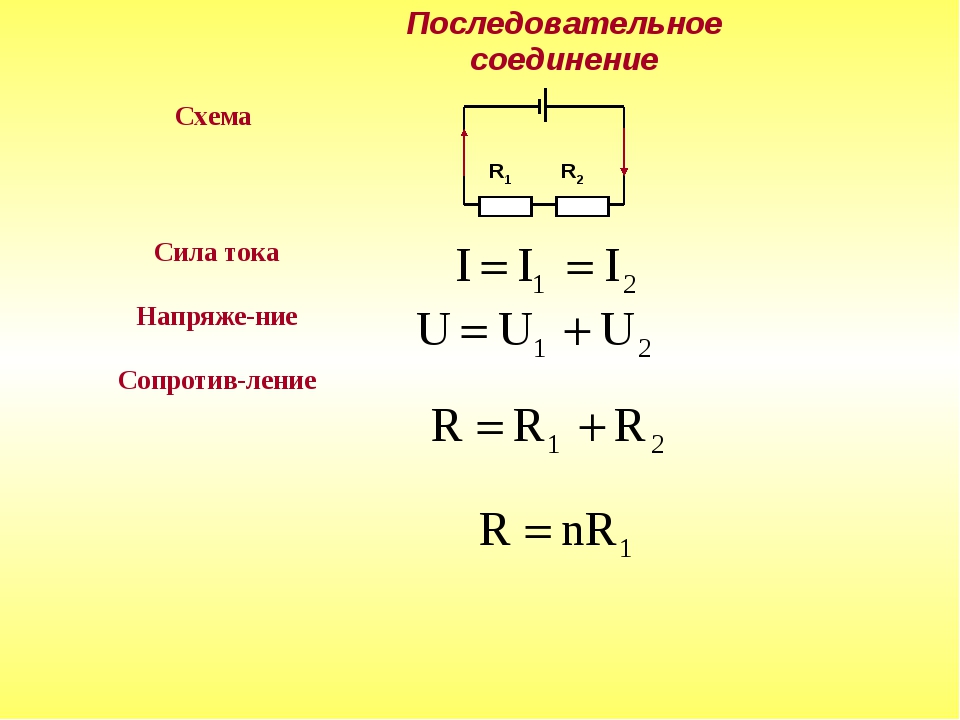 При этом электрический ток между точками А и B распределится по каждой из этих ветвей.
При этом электрический ток между точками А и B распределится по каждой из этих ветвей.
Напряжения на всех резисторах будут одинаковы: U=U1=U2=U3, их концы — это точки А и В.
Заряды, прошедшие за единицу времени через каждый резистор, в сумме образуют заряд, прошедший через весь блок. Поэтому суммарный ток через изображенную на рисунке цепь I=I1+I2+I3.
Теперь, использовав закон Ома, последнее равенство преобразуется к такому виду:
U/R=U/R1+U/R2+U/R3.
Отсюда следует, что для эквивалентного сопротивления R справедливо:
1/R=1/R1+1/R2+1/R3
или после преобразования формулы мы можем получить другую запись, такого вида:
.
Чем большее количество резисторов (или других звеньев электрической цепи, обладающих некоторым сопротивлением) соединить по параллельной схеме, тем больше путей для протекания тока образуется, и тем меньше общее сопротивление цепи.
Следует отметить, что обратная сопротивлению величина называется проводимостью.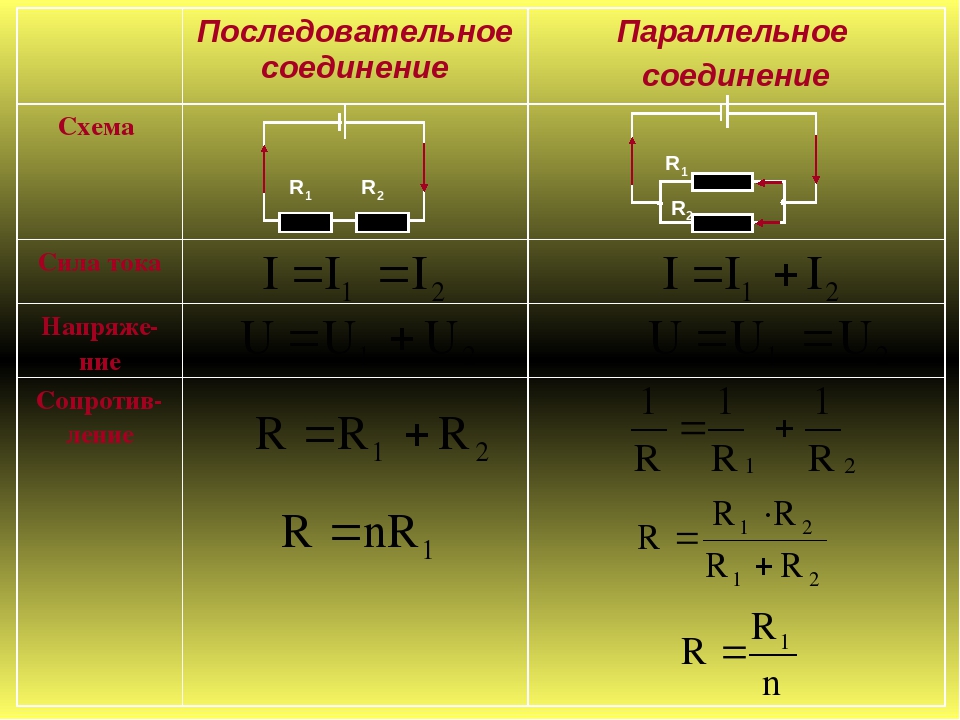 Можно сказать, что при параллельном соединении участков цепи складываются проводимости этих участков, а при последовательном соединении – их сопротивления.
Можно сказать, что при параллельном соединении участков цепи складываются проводимости этих участков, а при последовательном соединении – их сопротивления.
Примеры использования
Понятно, что при последовательном соединении, разрыв цепи в одном месте приводит к тому, что ток перестает идти по всей цепи. Например, ёлочная гирлянда перестаёт светить, если перегорит всего одна лампочка, это плохо.
Но последовательное соединение лампочек в гирлянде даёт возможность использовать большое количество маленьких лампочек, каждая из которых рассчитана на напряжение сети (220 В), делённое на количество лампочек.
Последовательное соединение резисторов на примере 3-х лампочек и ЭДС
Зато при последовательном подключении предохранительного устройства его срабатывание (разрыв плавкой вставки) позволяет обесточить всю электрическую цепь, расположенную после него и обеспечить нужный уровень безопасности, и это хорошо. Выключатель в сеть питания электроприбора включается также последовательно.
Параллельное соединение также широко используется. Например, люстра – все лампочки соединены параллельно и находятся под одним и тем же напряжением. Если одна лампа перегорит, — не страшно, остальные не погаснут, они остаются под тем же самым напряжением.
Параллельное соединение резисторов на примере 3-х лампочек и генератора
При необходимости увеличения способности схемы рассеивать тепловую мощность, выделяющуюся при протекании тока, широко используются и последовательное, и параллельное объединение резисторов. И для последовательного, и параллельного способов соединения некоторого количества резисторов одного номинала общая мощность равна произведению количества резисторов на мощность одного резистора.
Смешанное соединение резисторов
Также часто используется смешанное соединение. Если,например необходимо получить сопротивление определенного номинала, но его нет в наличии можно воспользоваться одним из выше описанных способов или воспользоваться смешанным соединением.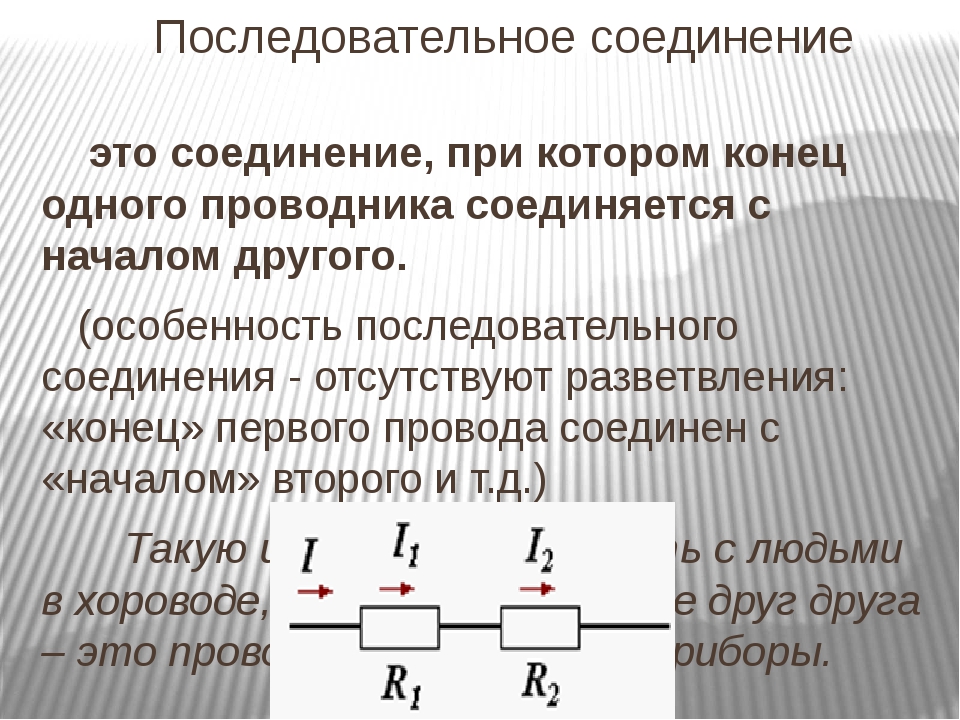
Отсюда, можно вывести формулу которая и даст нам необходимое значение:
Rобщ.=(R1*R2/R1+R2)+R3
В нашу эпоху развития электроники и различных технических устройств в основе всех сложностей лежать простые законы, которые поверхностно рассматриваются на данном сайте и думаю, что вам они помогут успешно применять в своей жизни. Если например взять ёлочную гирлянду, то соединения лампочек идет друг за другом, т.е. грубо говоря это отдельно-взятое сопротивление.
Не так давно гирлянды стали соединятся смешанным способом. Вообще, в совокупности все эти примеры с резисторами взяты условно, т.е. любым элементом сопротивления может быть ток проходящий через элемент с падением напряжения и выделением тепла.
Вконтакте
Одноклассники
Google+
Расчет мощности при параллельном соединении
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением.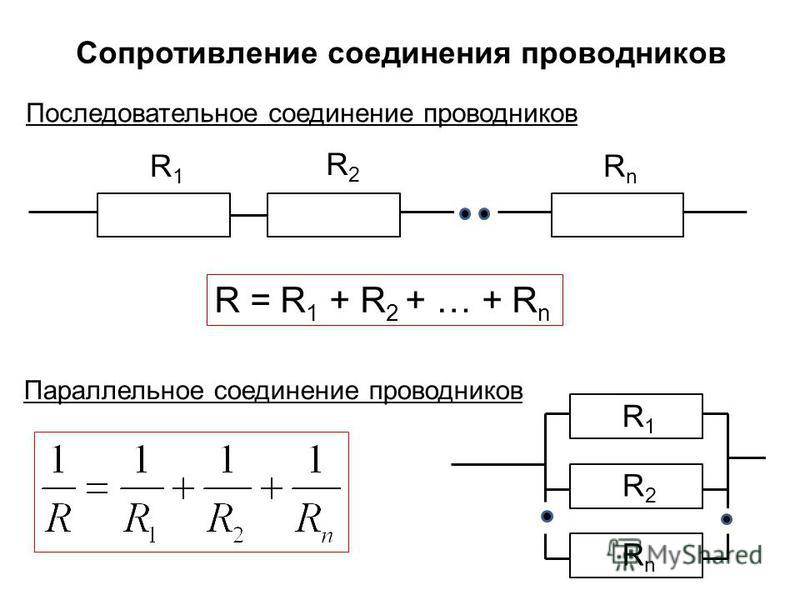 Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения – паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
- P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
- P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
- P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.

- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P1 = U 2 /R1 = 100 2 /200 = 50 Вт; P2 = U 2 /R2 = 100 2 /100 = 100 Вт; P3 = U 2 /R3 = 100 2 /51 = 195,9 Вт; P4 = U 2 /R4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.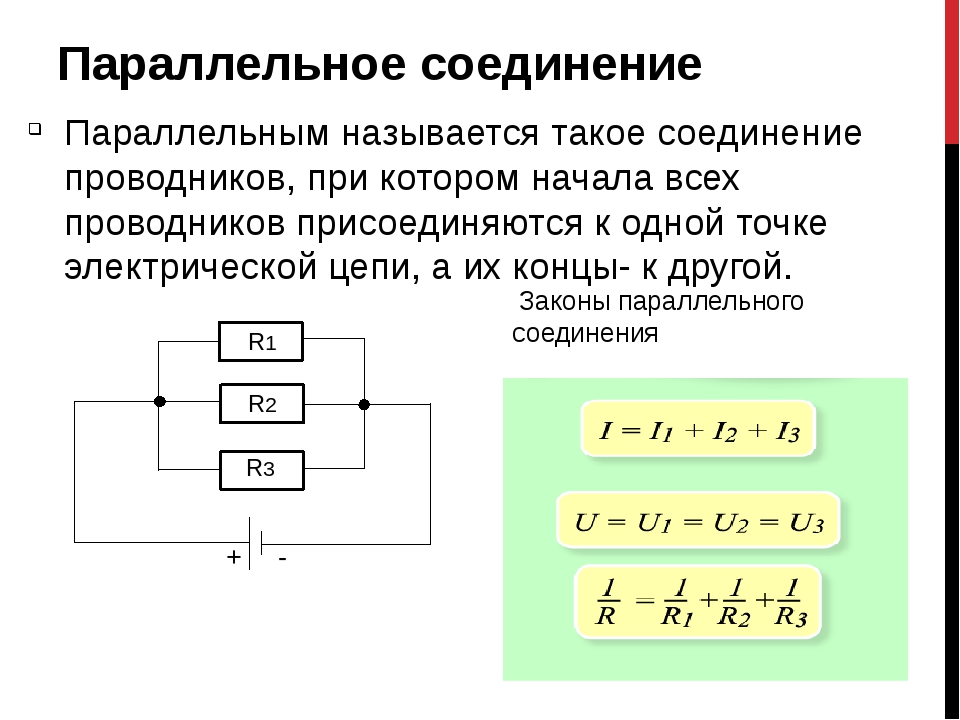
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле.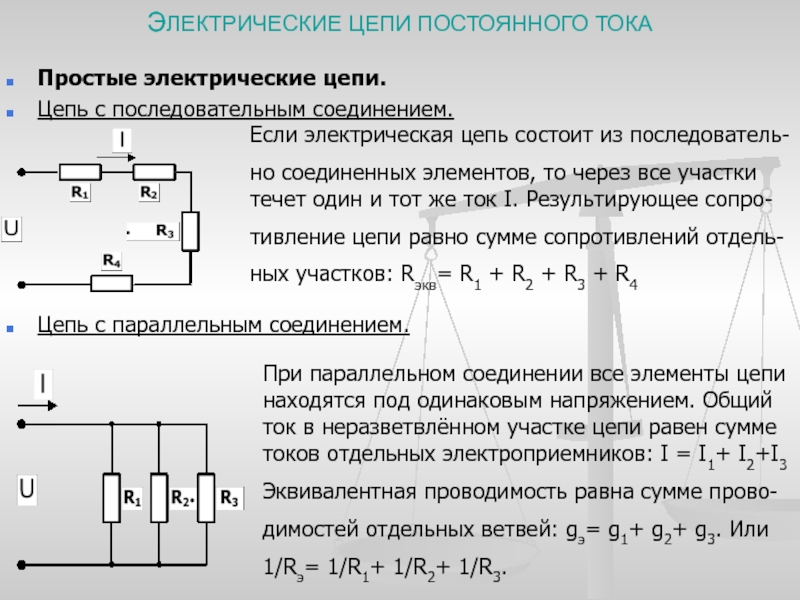 При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
youtube.com/embed/lVYhHuFjdio»/>
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте.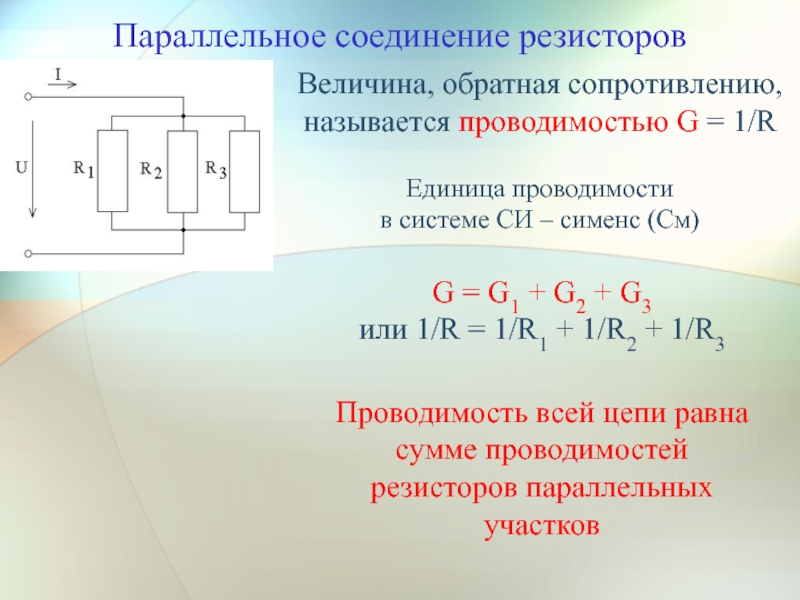 Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное.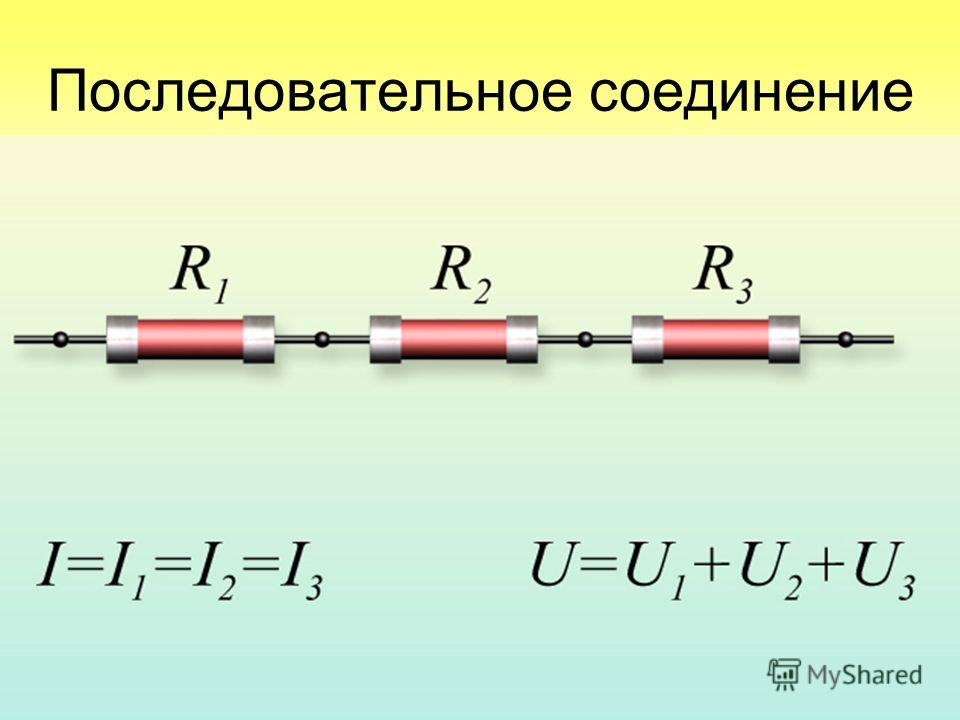 Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.
Параллельное соединение
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.
Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).

- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединение
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Следствием первых двух правил будет являться третье правило.
Применение
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединение
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.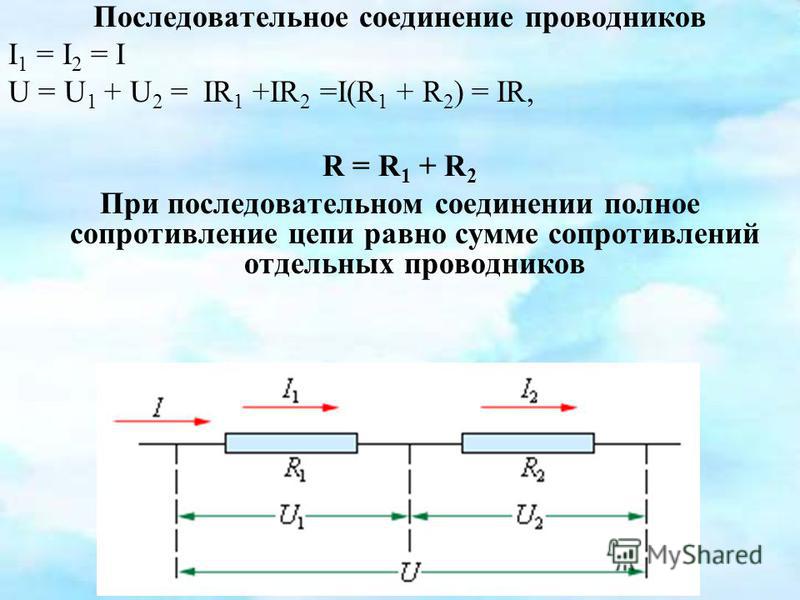
Применение
Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Работа тока
Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность тока
При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Р=U х I
После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:
Р=Р1 + Р2
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Влияние схемы соединения на новогоднюю гирлянду
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.
При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
Последовательное и параллельное соединение для конденсаторов
При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.
Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводников
В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
Формула сопротивления тока при параллельном соединении
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Параллельное соединение проводников
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.
Сопротивление проводника
Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.
Для ведения электротехнических расчётов применяется удельное сопротивление – ρ Ом·м/мм 2 . Все металлы – хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник – серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.
При расчёте сопротивления используется известная из школьного курса физики формула:
R = ρ · l/S, S – площадь сечения; l – длина.
Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.
и нагрев проводника
Для практических расчётов режимов работы проводников применяется понятие плотности тока – δ А/мм 2 , она вычисляется по формуле:
δ = I/S, I – ток, S – сечение.
Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.
Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.
Правилами регламентируется производить расчёт проводников на нагрев.
Способы соединения проводников
Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой – последовательное соединение.
На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .
Второй способ более сложный – параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.
Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.
Третий способ соединения наиболее сложный – смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.
Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.
R2,3,4 = R2,3 · R4/(R2,3 + R4).
Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.
Виды проводников
В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.
Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров – от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.
Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.
Расчёт проводов на нагрев
Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).
На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.
Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.
Расчёт проводников на потерю напряжения
При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.
Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.
Здесь S – сечение провода линии, мм 2 .
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.
С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Виды соединений
Резистор – пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:
Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:
Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.
Последовательное соединение проводников
В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.
Примером последовательного соединения проводников в быту является ёлочная гирлянда.
Параллельное соединение резисторов
При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.
Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.
В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.
Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.
Примеры параллельного соединения проводников:
- Освещение.
- Розетки в квартире.
- Производственное оборудование.
Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.
Смешанное соединение проводников
Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.
В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
Но для общего напряжение также справедлив закон Ома:
Здесь – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
Общее сопротивление будет равно:
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны (), то общее сопротивление цепи составит:
в данной формуле равно количеству элементов цепи.
С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
Подставим эти выражения в формулу общего тока:
А по закону Ома ток:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
Данную формулу можно записать и несколько иначе:
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов и – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором :
Теперь у нас образовались две группы последовательно соединенных резисторов:
Заменим эти две группы двумя резисторами, сопротивление которых равно:
Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов и одним резистором :
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
Общее сопротивление цепи получилось равным:
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов 😉
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
Что такое «последовательные» и «параллельные» схемы? | Последовательные и параллельные схемы
Цепи, состоящие только из одной батареи и одного сопротивления нагрузки, очень просто анализировать, но они не часто встречаются на практике. Обычно мы находим цепи, в которых более двух компонентов соединены вместе.
Серия
и параллельные схемы
Существует два основных способа соединения более двух компонентов схемы: серии и параллельно .
Схема конфигурации серии
Сначала пример последовательной схемы:
Здесь у нас есть три резистора (с маркировкой R 1 , R 2 и R 3 ), соединенных длинной цепочкой от одного вывода батареи к другому. (Следует отметить, что нижний индекс — эти маленькие цифры в правом нижнем углу буквы «R» — не связаны со значениями резисторов в Ом. Они служат только для идентификации одного резистора от другого.)
Определяющей характеристикой последовательной цепи является то, что существует только один путь для прохождения тока. В этой схеме ток течет по часовой стрелке от точки 1 к точке 2, точке 3 к точке 4 и обратно до 1.
Конфигурация параллельной цепи
Теперь давайте посмотрим на другой тип схемы, параллельную конфигурацию:
Опять же, у нас есть три резистора, но на этот раз они образуют более одного непрерывного пути прохождения тока.Есть один путь от 1 к 2 до 7 к 8 и снова к 1. Еще один — от 1 до 2, до 3, до 6, до 7, до 8, и снова до 1. И затем есть третий путь от 1 до 2 до 3 до 4 до 5 до 6 до 7 до 8 и снова обратно к 1. Каждый отдельный путь (через 1 рандов, 2 рандов и 3 рандов) называется ветвью .
Определяющей характеристикой параллельной цепи является то, что все компоненты подключены между одним и тем же набором электрически общих точек. Глядя на принципиальную схему, мы видим, что все точки 1, 2, 3 и 4 электрически общие.То же самое с точками 8, 7, 6 и 5. Обратите внимание, что все резисторы, а также батарея, подключены между этими двумя наборами точек.
И, конечно же, сложность не ограничивается простыми последовательностями и параллелями! У нас также могут быть цепи, которые представляют собой комбинацию последовательной и параллельной.
Последовательно-параллельная схема конфигурации
В этой схеме у нас есть две петли для протекания тока: одна от 1 до 2 до 5 до 6 и снова обратно к 1, а другая от 1 до 2 до 3 до 4 до 5 до 6 и снова обратно к 1 .Обратите внимание, как оба пути тока проходят через R 1 (от точки 1 к точке 2). В этой конфигурации мы бы сказали, что R 2 и R 3 параллельны друг другу, а R 1 — последовательно с параллельной комбинацией R 2 и R 3 .
Это всего лишь предварительный обзор того, что будет дальше. Не волнуйся! Мы рассмотрим все эти конфигурации схем подробно, по очереди! Вы можете сразу перейти к следующим страницам, посвященным последовательным и параллельным схемам, или что такое последовательно-параллельная схема? в главе 7.
Основы последовательного и параллельного подключения
Что такое последовательное соединение?
Основная идея «последовательного» соединения состоит в том, что компоненты соединяются встык в линию, образуя единый путь, по которому может течь ток:
Что такое параллельное соединение?
С другой стороны, основная идея «параллельного» подключения состоит в том, что все компоненты подключаются через выводы друг друга. В чисто параллельной схеме никогда не бывает более двух наборов электрически общих точек, независимо от того, сколько компонентов подключено.Есть много путей прохождения тока, но только одно напряжение на всех компонентах:
Последовательные и параллельные резисторы имеют очень разные электрические свойства. В следующих разделах мы рассмотрим свойства каждой конфигурации.
ОБЗОР:
- В последовательной цепи все компоненты соединены встык, образуя единый путь для прохождения тока.
- В параллельной цепи все компоненты соединены друг с другом, образуя ровно два набора электрически общих точек.
- «Ветвь» в параллельной цепи — это путь для электрического тока, образованный одним из компонентов нагрузки (например, резистором).
СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:
Характеристики параллельной цепи
Обновлено 28 декабря 2020 г.
Автор: S. Hussain Ather
Элементы схемы электрических цепей могут быть расположены последовательно или параллельно. В последовательных цепях элементы соединяются с помощью одной и той же ветви, которая пропускает электрический ток через каждую из них один за другим.В параллельных цепях элементы имеют свои отдельные ветви. В этих цепях ток может проходить по разным путям.
Поскольку ток может проходить по разным путям в параллельной цепи, ток не является постоянным во всей параллельной цепи. Вместо этого для ветвей, которые соединены параллельно друг с другом, падение напряжения или потенциала на каждой ветви является постоянным. Это связано с тем, что ток распределяется по каждой ветви в количествах, обратно пропорциональных сопротивлению каждой ветви.Это приводит к тому, что ток становится наибольшим там, где сопротивление наименьшее, и наоборот.
Эти качества позволяют параллельным цепям пропускать заряд по двум или более путям, что делает его стандартным кандидатом в домах и электрических устройствах через стабильную и эффективную систему питания. Это позволяет электричеству течь через другие части цепи, когда какая-либо часть повреждена или сломана, и они могут распределять мощность равномерно по разным зданиям. Эти характеристики можно продемонстрировать с помощью диаграммы и примера параллельной цепи.
Схема параллельной цепи
••• Syed Hussain Ather
На схеме параллельной цепи вы можете определить поток электрического тока, создавая потоки электрического тока от положительного конца батареи к отрицательному. Положительный конец обозначен плюсом на источнике напряжения, а отрицательный -.
Рисуя путь, по которому ток проходит через ветви параллельной цепи, помните, что весь ток, входящий в один узел или точку в цепи, должен равняться всему току, выходящему из этой точки или выходящему из нее.Также имейте в виду, что падение напряжения вокруг любого замкнутого контура в цепи должно быть равно нулю. Эти два утверждения представляют собой законы цепей Кирхгофа .
Характеристики параллельной цепи
В параллельных цепях используются ответвления, которые позволяют току проходить по различным маршрутам в цепи. Ток проходит от положительного конца батареи или источника напряжения к отрицательному полюсу. Напряжение остается постоянным по всей цепи, в то время как ток изменяется в зависимости от сопротивления каждой ветви.
Примеры параллельных цепей
Чтобы найти полное сопротивление резисторов, установленных параллельно друг другу, используйте формулу
\ frac {1} {R_ {total}} = \ frac {1} {R_1} + \ frac { 1} {R_2} + \ frac {1} {R_3} + … + \ frac {1} {R_n}
, в котором сопротивление каждого резистора суммируется в правой части уравнения. На приведенной выше диаграмме общее сопротивление в Ом (Ом) можно рассчитать следующим образом:
- 1 / R всего = 1/5 Ом + 1/6 Ом + 1/10 Ом
- 1 / R всего = 6/30 Ом + 5/30 Ом + 3/30 Ом
- 1 / R всего = 14/30 Ом
- R всего = 15/7 Ом или около 2.14 Ом
Обратите внимание, что вы можете «перевернуть» обе стороны уравнения с шага 3 на шаг 4 только тогда, когда есть только один член с обеих сторон уравнения (в данном случае 1 / R всего Слева и 14/30 Ом справа).
После того, как вы рассчитали сопротивление, ток и напряжение, можно рассчитать по закону Ома В = I / R , в котором В — напряжение, измеренное в вольтах, I — ток, измеренный в амперах. , а R — сопротивление в Ом.В параллельных цепях сумма токов, протекающих по каждому пути, является полным током от источника. Ток на каждом резисторе в цепи можно рассчитать, умножив напряжение на сопротивление резистора. Напряжение остается постоянным по всей цепи, поэтому напряжение является напряжением батареи или источника напряжения.
Параллельная и последовательная цепь
••• Syed Hussain Ather
В последовательных цепях ток постоянен повсюду, падение напряжения зависит от сопротивления каждого резистора, а общее сопротивление складывается из каждого отдельного резистора.В параллельных цепях напряжение постоянно, ток зависит от каждого резистора, а величина, обратная величине общего сопротивления, является суммой величин, обратных величине каждого отдельного резистора.
Конденсаторы и катушки индуктивности могут использоваться для изменения заряда в последовательной и параллельной цепях с течением времени. В последовательной цепи общая емкость цепи (заданная переменной C ), потенциал конденсатора для накопления заряда с течением времени, является обратной суммой обратных величин каждой отдельной емкости, и общая индуктивность ( I ), мощность индукторов, выделяющих заряд с течением времени, является суммой каждой индуктивности.Напротив, в параллельной цепи общая емкость является суммой каждого отдельного конденсатора, а величина, обратная величине полной индуктивности, является суммой обратных величин каждой индивидуальной индуктивности.
Последовательные и параллельные цепи также имеют разные функции. В последовательной цепи, если одна часть сломана, ток вообще не будет течь по цепи. В параллельной цепи открытие отдельной ветви останавливает только ток в этой ветви. Остальные ветви будут продолжать работать, потому что у тока есть несколько путей, которые он может пройти по цепи.
Последовательно-параллельная цепь
••• Syed Hussain Ather
Цепи, в которых есть оба разветвленных элемента, которые также соединены таким образом, что ток течет в одном направлении между этими ветвями, как последовательно, так и параллельно. В этих случаях вы можете применять правила как для последовательного, так и для параллельного подключения, в зависимости от схемы. В приведенном выше примере R1 и R2 параллельны друг другу, чтобы сформировать R5 , а также R3 и R4 , чтобы сформировать R6 . .Их можно суммировать параллельно следующим образом:
- 1 / R5 = 1/1 Ом + 1/5 Ом
- 1 / R5 = 5/5 Ом + 1/5 Ом
- 1 / R5 = 6/5 Ом
- R5 = 5/6 Ом или около 0,83 Ом
- 1 / R6 = 1/7 Ом + 1/2 Ом
- 1 / R6 = 2/14 Ом + 7/14 Ом
- 1 / R6 = 9/14 Ом
- R6 = 14/9 Ом или около 1,56 Ом
••• Syed Hussain Ather
Схема может быть упрощена для создания схемы, показанной непосредственно выше, с R5 и R6 .Эти два резистора можно просто добавить, как если бы цепь была последовательной.
R_ {total} = 5/6 \ Omega + 14/9 \ Omega = 2,38 \ Omega
При напряжении 20 В , закон Ома определяет, что общий ток равен В / R . , или 20 В / (43/18 Ом) = 360/43 А или около 8,37 А. С этим полным током вы можете определить падение напряжения на R5 и R6, используя закон Ома ( В = I / R ).
V_5 = \ frac {360} {43} \ times 5/6 = 6.98 \ text {V}
V_5 = \ frac {360} {43} \ times 14/9 = 13.02 \ text {V}
Наконец, эти падения напряжения для R5 и R6 могут быть разделено обратно на исходные параллельные схемы для расчета тока R1 и R2 для R5 и R2 и R3 для R6 с использованием закона Ома .
I1 = (1800/258 В) / 1 Ом = 1800/258 А или около т 6,98 А.
I2 = (1800/258 В) /5 Ом = 1500/43 A или около т 34.88 A.
I3 = ( 680/129 V ) / 7 Ω = 4760/129 A или около 36.90 A .
I3 = ( 680/129 В ) / 2 Ом = 1360/129 А или около 10,54 А.
Последовательные и входные резисторы Параллельные резисторы
последовательно и параллельно
следующий: Правила Кирхгофа
вверх: электрический ток
Предыдущее: ЭДС и внутреннее сопротивление
Резисторы, вероятно, встречаются чаще всего.
компоненты в электронных схемах.Практические схемы часто содержат очень сложные комбинации резисторов.
Поэтому полезно иметь набор правил для поиска эквивалентных
сопротивление некоторого общего расположения резисторов. Оказывается, мы можем
всегда находите эквивалентное сопротивление повторным применением
два простых правил. Эти правила относятся к резисторам, включенным последовательно, и
в параллели.
Рассмотрим два резистора, подключенных в серии , как показано на рис.18.
Понятно, что через оба резистора протекает одинаковый ток.
Ибо, если бы это было не так, заряд накапливался бы в одном или другом
резисторов, которые не соответствовали бы
установившаяся ситуация (таким образом нарушая
основное предположение этого раздела). Предположим, что падение потенциала
от точки к точке есть. Это падение представляет собой сумму потенциальных
падает и на двух резисторах и соответственно.
Таким образом,
| (135) |
Согласно закону Ома эквивалентное сопротивление между
и — отношение падения потенциала в этих точках
и ток, протекающий между ними.Таким образом,
| (136) |
давая
| (137) |
Здесь мы использовали тот факт, что ток является общим для
все три резистора. Следовательно, правило
Эквивалентное сопротивление двух последовательно соединенных резисторов равно
сумма отдельных сопротивлений.
Для резисторов, соединенных последовательно, уравнение.(137) обобщает
к
.
Рассмотрим два резистора, соединенных параллельно , как показано на рис. 19. Это
Из рисунка видно, что падение потенциала на двух резисторах равно
одно и тоже. В общем, однако, токи и которые текут
через резисторы и соответственно разные.
По закону Ома эквивалентное сопротивление
между и — отношение падения потенциала
через эти точки и текущий
которая течет между ними.Этот ток должен равняться сумме
токи и протекающие через два резистора, в противном случае
заряд будет накапливаться на одном или обоих переходах в цепи.
Таким образом,
| (138) |
Это следует из того
| (139) |
давая
| (140) |
Здесь мы воспользовались тем фактом, что падение потенциала
является общим для всех трех резисторов.Ясно, что правило
Обратное эквивалентное сопротивление двух сопротивлений.
соединенных параллельно — это сумма обратных величин
индивидуальные сопротивления.
Для резисторов, соединенных параллельно, уравнение. (140) обобщает на
.
следующий: Правила Кирхгофа
вверх: электрический ток
Предыдущее: ЭДС и внутреннее сопротивление
2007-07-14
Учебное пособие по физике: Параллельные схемы
Как упоминалось в предыдущем разделе Урока 4, два или более электрических устройства в цепи могут быть соединены последовательным или параллельным соединением.Когда все устройства соединены с использованием параллельных соединений, схема называется параллельной схемой . В параллельной схеме каждое устройство помещается в свою отдельную ветвь . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить через внешнюю цепь. Каждый заряд, проходящий через контур внешней цепи, будет проходить через единственный резистор, присутствующий в одной ветви. Прибыв в место разветвления или узел, плата выбирает , через какую ветвь пройти на обратном пути к терминалу с низким потенциалом.
Краткое сравнение и контраст между последовательными и параллельными цепями было сделано в предыдущем разделе Урока 4. В этом разделе было подчеркнуто, что добавление большего количества резисторов в параллельную цепь приводит к довольно неожиданному результату — уменьшению общего сопротивления. . Поскольку существует несколько путей, по которым может протекать заряд, добавление еще одного резистора в отдельную ветвь обеспечивает еще один путь, по которому заряд может проходить через основную область сопротивления в цепи.Это уменьшенное сопротивление в результате увеличения количества ветвей будет иметь эффект увеличения скорости, с которой течет заряд (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платными дорогами. Плата за проезд — это основное место сопротивления автомобильному потоку на платной дороге. Добавление дополнительных пунктов сбора платы за проезд в пределах их собственного отделения на платной дороге обеспечит больше путей для автомобилей, проезжающих через станцию сбора платы за проезд. Эти дополнительные пункты пропуска снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.
Текущий
Скорость, с которой заряд проходит через цепь, называется током. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами таким образом, что в одном месте ток меньше, чем в другом. В параллельной схеме заряд делит на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой.Тем не менее, если брать в целом, общая сумма тока во всех ветвях при сложении равна величине тока в местах за пределами ветвей. Правило, что ток везде одинаковый все еще работает, только с изюминкой. Сила тока вне ветвей равна сумме тока в отдельных ветвях. Это все еще та же величина тока, только разделенная на несколько путей.
В форме уравнения этот принцип можно записать как
I итого = I 1 + I 2 + I 3 +…
, где I всего — это общая величина тока вне ветвей (и в батарее), а I 1 , I 2 и I 3 представляют ток в отдельных ветвях цепи.
В этом блоке широко использовалась аналогия между расходом заряда и расходом воды. Еще раз вернемся к аналогии, чтобы проиллюстрировать, как сумма текущих значений в ветвях равна сумме вне ветвей.Поток заряда в проводах аналогичен потоку воды в трубах. Рассмотрим приведенные ниже схемы, на которых поток воды в трубах делится на отдельные ответвления. В каждом узле (место разветвления) вода проходит двумя или более отдельными путями. Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ветвях за пределами узла. Точно так же, когда две или более ветвей подаются в узел, скорость, с которой вода вытекает из узла, будет равна сумме расходов в отдельных ветвях, которые подаются в узел.
Тот же принцип разделения потока применяется к электрическим цепям. Скорость, с которой заряд поступает в узел, равна сумме расходов в отдельных ветвях за пределами узла. Это показано в приведенных ниже примерах. В примерах вводится новый символ схемы — буква A, заключенная в круг. Это символ амперметра — устройства, используемого для измерения силы тока в определенной точке. Амперметр может измерять ток, оказывая при этом незначительное сопротивление потоку заряда.
Диаграмма A показывает два резистора, подключенных параллельно узлам в точках A и B. Заряд течет в точку A со скоростью 6 ампер и делится на два пути — один через резистор 1, а другой через резистор 2. Ток в ветви с резистором 1 составляет 2 ампера, а ток в ветви с резистором 2 составляет 4 ампера. После того, как эти две ветви снова встретятся в точке B, чтобы сформировать единую линию, ток снова станет 6 ампер. Таким образом, мы видим, что принцип, согласно которому ток за пределами ветвей равен сумме тока в отдельных ветвях, выполняется.
I всего = I 1 + I 2
6 ампер = 2 ампера + 4 ампера
Схема B выше может быть немного более сложной, если три резистора расположены параллельно. На схеме обозначены четыре узла, обозначенные буквами A, B, C и D. Заряд течет в точку A со скоростью 12 ампер и делится на два пути: один проходит через резистор 1, а другой направляется к точке B (и резисторам 2). и 3). 12 ампер тока делятся на 2-амперную (через резистор 1) и 10-амперную (в направлении точки B).В точке B происходит дальнейшее разделение потока на два пути — один через резистор 2, а другой через резистор 3. Ток в 10 ампер, приближающийся к точке B, делится на 6-амперный канал (через резистор 2) и 4-канальный. -амперный тракт (через резистор 3). Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера, и что сумма значений тока в отдельных ветвях равна току вне ветвей.
I всего = I 1 + I 2 + I 3
12 А = 2 А + 6 А + 4 А
Анализ потока в точках C и D также может быть проведен, и будет замечено, что сумма расходов потока в этих точках равна скорости потока, находящейся непосредственно за этими точками.
Эквивалентное сопротивление
Фактическая величина тока всегда изменяется обратно пропорционально величине общего сопротивления. Существует четкая взаимосвязь между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая, когда два резистора помещены в параллельные ветви, каждый из которых имеет одинаковое значение сопротивления 4 Ом.Поскольку схема предлагает два равных путей для потока заряда, только половина заряда выберет для прохождения через данную ветвь. Хотя каждая отдельная ветвь обеспечивает сопротивление 4 Ом любому заряду, который проходит через нее, только половина всего заряда, протекающего по цепи, будет встречать сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается аккумулятора, который накачивает заряд, наличие двух параллельно подключенных резисторов 4 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи.Таким же образом, наличие двух параллельных резисторов 6 Ом было бы эквивалентно наличию одного резистора 3 Ом в цепи. А наличие двух параллельно включенных резисторов 12 Ом было бы эквивалентно наличию в цепи одного резистора 6 Ом.
Теперь давайте рассмотрим другой простой случай, когда три резистора соединены параллельно, каждый из которых имеет одинаковое сопротивление 6 Ом. При трех равных путях прохождения заряда через внешний контур только одна треть заряда будет проходить через данную ветвь.Каждая отдельная ветвь обеспечивает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через конкретную ветвь, означает, что общее сопротивление цепи составляет 2 Ом. Что касается батареи, которая накачивает заряд, наличие трех параллельно подключенных резисторов 6 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи. Таким же образом, наличие трех параллельно подключенных резисторов сопротивлением 9 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом.А наличие трех параллельно подключенных резисторов на 12 Ом было бы эквивалентно наличию в цепи одного резистора 4 Ом.
Это концепция эквивалентного сопротивления. Эквивалентное сопротивление схемы — это величина сопротивления, которая потребуется одному резистору, чтобы сравняться с общим эффектом от набора резисторов, присутствующих в схеме. Для параллельных цепей математическая формула для вычисления эквивалентного сопротивления (R eq ) составляет
.
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 +…
, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, подключенных параллельно. Приведенные выше примеры можно рассматривать как простые случаи, в которых все пути оказывают одинаковое сопротивление отдельному заряду, который проходит через них. Вышеупомянутые простые случаи были выполнены без использования уравнения. Однако это уравнение подходит как для простых случаев, когда резисторы ответвления имеют одинаковые значения сопротивления, так и для более сложных случаев, когда резисторы ответвления имеют разные значения сопротивления.Например, рассмотрим применение уравнения к одному простому и одному сложному случаю ниже.
| Случай 1 : Три резистора 12 Ом включены параллельно | 1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (12 Ом) + 1 / (12 Ом) + 1 / (12 Ом) Использование калькулятора … 1 / R экв. = 0,25 Ом -1 R экв = 1 / (0,25 Ом -1 ) R экв = 4,0 Ом |
| Случай 2 : резисторы 5,0 Ом, 7,0 Ом и 12 Ом подключены параллельно | 1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (5.0 Ом) + 1 / (7,0 Ом) + 1 / (12 Ом) Использование калькулятора … 1 / R экв = 0,42619 Ом-1 R экв = 1 / (0,42619 Ом -1 ) R экв = 2,3 Ом |
Ваша очередь попробовать
Нужно больше практики? Используйте два параллельных резистора виджет ниже, чтобы попробовать некоторые дополнительные проблемы.Введите любые два желаемых значения сопротивления. Используйте свой калькулятор, чтобы определить значения рэндов и рандов. Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте столько раз, сколько хотите, с разными значениями сопротивления.
Падения напряжения для параллельных ветвей
В разделе «Схемы» учебного пособия «Физический класс» подчеркивалось, что любое повышение напряжения, получаемое за счет заряда батареи, теряется из-за заряда, когда он проходит через резисторы внешней цепи.Общее падение напряжения во внешней цепи равно увеличению напряжения при прохождении заряда по внутренней цепи. В параллельной схеме заряд не проходит через каждый резистор; скорее, он проходит через единственный резистор. Таким образом, полное падение напряжения на этом резисторе должно соответствовать напряжению батареи. Не имеет значения, проходит ли заряд через резистор 1, резистор 2 или резистор 3, падение напряжения на резисторе, которое выбирает для прохождения , должно равняться напряжению батареи.В форме уравнения этот принцип может быть выражен как
В аккумулятор = В 1 = В 2 = В 3 = …
Если три резистора размещены в параллельных ветвях и питаются от 12-вольтовой батареи, то падение напряжения на каждом из трех резисторов составляет 12 вольт. Заряд, протекающий по цепи, встретит только один из этих трех резисторов и, таким образом, столкнется с одним падением напряжения на 12 вольт.
Диаграммы электрического потенциала были представлены в Уроке 1 этого устройства и впоследствии использовались для иллюстрации последовательных падений напряжения, происходящих в последовательных цепях.Диаграмма электрических потенциалов — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками в электрической цепи. Рассмотрим приведенную ниже принципиальную схему и соответствующую диаграмму электрических потенциалов.
Как показано на диаграмме электрического потенциала, все позиции A, B, C, E и G имеют высокий электрический потенциал. Один заряд выбирает только один из трех возможных путей; таким образом, в позиции B один заряд переместится в точку C, E или G, а затем пройдет через резистор, который находится в этой ветви.Заряд не теряет свой высокий потенциал до тех пор, пока он не пройдет через резистор, либо от C к D, от E к F или от G к H. После того, как он пройдет через резистор, заряд вернется почти до 0 вольт и вернется к отрицательному значению. клемму аккумуляторной батареи для повышения ее напряжения. В отличие от последовательных цепей, заряд в параллельной цепи встречает единственное падение напряжения на своем пути через внешнюю цепь.
Ток через данную ветвь можно предсказать, используя уравнение закона Ома и падение напряжения на резисторе и сопротивление резистора.Поскольку падение напряжения на каждом резисторе одинаковое, фактором, определяющим наибольший ток резистора, является сопротивление. Резистор с наибольшим сопротивлением испытывает наименьший ток, а резистор с наименьшим сопротивлением — наибольший ток. В этом смысле можно сказать, что заряд (как и люди) выбирает путь наименьшего сопротивления. В форме уравнения это может быть указано как
| I 1 = Δ V 1 / R 1 | I 2 = Δ V 2 / R 2 | I 3 = Δ V 3 / R 3 |
Этот принцип иллюстрируется схемой, показанной ниже.Произведение I • R одинаково для каждого резистора (и равно напряжению батареи). Тем не менее, ток у каждого резистора разный. Ток наибольший там, где сопротивление наименьшее, и ток наименьший, где сопротивление наибольшее.
Математический анализ параллельных цепей
Приведенные выше принципы и формулы могут использоваться для анализа параллельной цепи и определения значений тока и разности электрических потенциалов на каждом из резисторов в параллельной цепи.Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока через батарею (I до ), а также падений напряжения и тока для каждого из трех резисторов.
Анализ начинается с использования значений сопротивления отдельных резисторов, чтобы определить эквивалентное сопротивление цепи.
1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 = (1/17 Ом) + (1/12 Ом) + (1/11 Ом)
1 / R экв = 0.23306 Ом -1
R экв = 1 / (0,23306 Ом -1 )
R экв = 4,29 Ом
(округлено от 4,29063 Ом)
Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в батарее важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R.Расчет показан здесь:
I до = ΔV аккумулятор / R eq = (60 В) / (4,29063 Ом)
I до = 14,0 А
(округлено от 13,98396 А)
Напряжение батареи 60 В представляет собой усиление электрического потенциала за счет заряда, проходящего через батарею. Заряд теряет такое же количество электрического потенциала при любом прохождении через внешнюю цепь.То есть падение напряжения на каждом из трех резисторов такое же, как и напряжение, полученное в батарее:
ΔV аккумулятор = ΔV 1 = ΔV 2 = ΔV 3 = 60 В
Осталось определить три значения — ток каждого отдельного резистора. Закон Ома снова используется для определения значений тока для каждого резистора — это просто падение напряжения на каждом резисторе (60 В), деленное на сопротивление каждого резистора (указанное в формулировке задачи).Расчеты показаны ниже.
| I 1 = ΔV 1 / R 1 I 1 = (60 В) / (17 Ом) I 1 = 3,53 А | I 2 = ΔV 2 / R 2 I 2 = (60 В) / (12 Ом) I 2 = 5,00 А | I 3 = ΔV 3 / R 3 I 3 = (60 В) / (11 Ом) Я 3 = 5.45 ампер |
В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли вычисленные значения принципу, согласно которому сумма значений тока для каждого отдельного резистора равна общему току в цепи (или в батарее). . Другими словами, я до = Я 1 + Я 2 + Я 3 ?
Является ли I tot = I 1 + I 2 + I 3 ?
Из 14.0 ампер = 3,53 ампер + 5,00 ампер + 5,45 ампер?
14,0 А = 13,98 А?
Да !!
(Разница в 0,02 ампера — это просто результат предыдущего округления значения I до от 13,98.)
Математический анализ этой параллельной цепи включал смесь концепций и уравнений. Как это часто бывает в физике, отделение концепций от уравнений при принятии решения физической проблемы является опасным актом.Здесь необходимо учитывать концепции, согласно которым падение напряжения на каждом из трех резисторов равно напряжению батареи, а сумма тока в каждом резисторе равна общему току. Эти представления необходимы для завершения математического анализа. В следующей части Урока 4 будут исследованы комбинированные или составные схемы, в которых одни устройства включены параллельно, а другие — последовательно.
Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже.Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.
Мы хотели бы предложить …
Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие — это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключить их так, как хотите. Вольтметры и амперметры позволяют измерять ток и падение напряжения. Нажав на резистор или источник напряжения, вы можете изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванной).
Проверьте свое понимание
1. По мере того, как в цепь добавляется все больше и больше резисторов, эквивалентное сопротивление цепи ____________ (увеличивается, уменьшается), а общий ток цепи ____________ (увеличивается, уменьшается).
2.Три одинаковые лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают местоположения вдоль цепи. Какое из следующих утверждений верно?
а. Ток в точке Y больше, чем ток в точке Q.
г. Ток на Y больше, чем на P.
.
г. Ток в точке Y больше, чем ток в точке Z.
г. Ток в точке P больше, чем ток в точке Q.
.
e.Ток на Q больше, чем на P.
.
ф. Сила тока во всех местах одинакова.
3. Три одинаковые лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают местоположения вдоль цепи. В каком месте (ах), если таковые имеются, будет ток …
а. … так же, как у X?
г…. такой же, как у Q?
г. … так же, как у Y?
г. … меньше, чем у Q?
e. … меньше, чем у P?
ф. … вдвое больше, чем у Z?
г. … в три раза больше, чем в Y?
4. Какие изменения можно внести в схему ниже, чтобы уменьшить ток в ячейке? Перечислите все подходящие варианты.
а. Увеличьте сопротивление лампы X.
г. Уменьшите сопротивление лампы X.
г. Увеличьте сопротивление лампы Z.
г. Уменьшите сопротивление лампы Z.
.
e. Увеличьте напряжение ячейки (как-нибудь).
ф. Уменьшите напряжение ячейки (как-нибудь).
г. Снять лампу Y.
.
5.Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключаются, как показано. Ток в резисторе 12 Ом равен ____ току в резисторе 4 Ом.
а. 1/3
г. 1/2
г. 2/3
г. то же, что
e.1,5 раза
ф. дважды
г. трижды
ч. четыре раза
6. Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключены, как показано.Падение напряжения на резисторе 12 Ом равно ____ падению напряжения на резисторе 4 Ом.
а. 1/3
г. 1/2
г. 2/3
г. то же, что
e. 1,5 раза
ф.дважды
г. трижды
ч. четыре раза
7. Аккумулятор на 12 В и резистор на 12 Ом подключаются, как показано на схеме. К резистору 12 Ом добавлен резистор на 6 Ом, чтобы создать цепь Y, как показано.Падение напряжения на резисторе 6 Ом в цепи Y равно ____ падению напряжения на резисторе X.
а. больше, чем
г. меньше
г. то же, что
8. Используйте свое понимание эквивалентного сопротивления, чтобы заполнить следующие утверждения:
а. Два резистора сопротивлением 6 Ом, размещенные параллельно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.
г. Три резистора 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
г. Три резистора сопротивлением 8 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
г. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
e. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом размещены параллельно.Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
ф. Три резистора с сопротивлением 12 Ом, 6 Ом и 21 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
9. На основании ваших ответов на вышеуказанный вопрос заполните следующую формулировку:
Общее или эквивалентное сопротивление трех параллельно включенных резисторов будет _____.
а. больше, чем сопротивление самого большого из трех значений R.
г. меньше, чем сопротивление наименьшего значения R из трех.
г. где-то между наименьшим значением R и наибольшим значением R.
г. … ерунда! Такого обобщения сделать нельзя. Результаты меняются.
10. Три резистора включены параллельно.При размещении в цепи с источником питания 12 В. Определите эквивалентное сопротивление, общий ток цепи, падение напряжения и ток в каждом резисторе.
Последовательные и параллельные резисторы
Введение
Цепи постоянного тока (DC) характеризуются величинами тока, напряжения и сопротивления.Ток — это скорость потока заряда. Единица СИ — ампер (А). По соглашению направление тока — это направление потока заряда, даже если в металлических проводниках ток возникает из-за потока отрицательного заряда (электронов) в противоположном направлении. Из-за сохранения заряда ток одинаков во всех точках однопетлевой цепи. В точке ветвления в цепи, где проводящий путь разделяется на два или более, общий ток в точке ветвления равен полному току из этой точки.Традиционно ток течет от положительной клеммы батареи или источника питания к отрицательной клемме. Для поддержания тока в цепи должен быть полностью проводящий путь.
Напряжение — это мера разности электрических потенциалов между двумя точками в цепи. Единица СИ — вольт (В). Поскольку электрическая сила является консервативной, сумма напряжений увеличивается и уменьшается вокруг любого замкнутого контура, равная нулю.
Сопротивление — это свойство элемента схемы (проводника) препятствовать прохождению тока.Сопротивление определяется
где В, — напряжение на элементе схемы, а I — ток, протекающий через него. Если R постоянно, то же самое для всех V , то элемент схемы подчиняется закону Ома. Единицей измерения сопротивления в системе СИ является ом (Ом). Сопротивление резистивного элемента цепи изменяется в зависимости от температуры.
Два резистора R 1 и R 2 соединены последовательно, если весь ток, проходящий через R 1 , также проходит через R 2 .Следовательно, для двух последовательно соединенных резисторов ток от I 1 до R 1 совпадает с током от I 2 до R 2 , и этот ток такой же, как у ток, I , который входит в последовательную сеть:
I = I 1 = I 2 .
Общее напряжение В в последовательной сети представляет собой сумму напряжений В 1 и В 2 на каждом резисторе.То есть
V = V 1 + V 2 .
Эквивалентное сопротивление, R с , R 1 и R 2 последовательно определяется выражением
Два резистора R 1 и R 2 подключены параллельно, если напряжения В, 1 и В 2 на каждом одинаковы и равны напряжению В , через параллельную сеть.То есть
V = V 1 = V 2 .
Токи I 1 и I 2 через каждый из резисторов складываются, чтобы получить общий ток I , текущий в сеть и из нее:
I = I 1 + I 2 .
Эквивалентное сопротивление R p из R 1 и R 2 параллельно определяется выражением
Это также можно записать как
Амперметры используются для измерения тока.Амперметр подключается последовательно к цепи, так что весь измеряемый ток протекает через амперметр. Следовательно, амперметры должны иметь очень маленькое сопротивление, чтобы не изменять ток в цепи. Вольтметры используются для измерения напряжений. Вольтметр подключается параллельно в двух точках, между которыми должна быть измерена разность потенциалов. Следовательно, вольтметр должен иметь большое сопротивление, чтобы через него проходил очень небольшой ток.
Объектив
В этой лаборатории мы будем измерять и анализировать токи и напряжения для цепей, содержащих один резистор, а также для двух последовательно включенных резисторов и двух параллельно.
Аппарат
- Источник питания постоянного тока 0-40 вольт
- Лампочка на 12 В и розетка
- Резисторы 150 и 700 Ом
- Цифровой мультиметр
Процедура
Распечатайте лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.
Измерение напряжения
1
Блок питания является источником разности потенциалов (напряжения).Найдите источник питания постоянного тока за столом.
Нажмите кнопку POWER ON / OFF в положение ON. Затем нажмите кнопку RANGE в положение IN (0,85 A). Это устанавливает источник питания в диапазоне 0-35 В / 0-0,85 А.
Поверните ручку ADJUST напряжения и тока против часовой стрелки. Затем установите максимальный выходной ток для этого эксперимента, нажав кнопку CC Set и, удерживая ее, поверните ручку ADJUST по часовой стрелке, пока на дисплее AMPS не появится 0.30 A. Отпустите кнопку CC Set . Не перемещайте ручку текущей настройки ( CC Set ) ни в какой момент во время эксперимента.
2
Мультиметр — это измерительное устройство, которое используется для измерения разности напряжений, электрических токов и электрических сопротивлений. Он также может измерять другие электрические свойства. См. Рис. 1. Вверху измерителя находится ЖК-дисплей (жидкокристаллический дисплей), в середине — переключатель функций / диапазона (диск), а внизу четыре входных гнезда.
Примечание. Измеритель особенно чувствителен (и склонен к перегоранию предохранителя) при использовании входного разъема 200 мА (см. I в обозначении на Рисунке 1).
Ключ для рисунка 1:
А
3-1 / 2-разрядный ЖК-дисплей с сигнализаторами.
В
Кнопка ВКЛ / ВЫКЛ: включает и выключает питание измерителя.
С
Кнопка HI / LO: выбирает высокий или низкий уровень запуска для измерения частоты.
D
Кнопка MAX: выбирает функцию удержания максимального показания.
E
Кнопка DC / AC: выбирает напряжение постоянного или переменного тока.
Ф
Переключатель функции / диапазона: выбирает желаемую функцию и диапазон.
G
Входной разъем V Ω: входной разъем для напряжения, сопротивления, проверки диодов, целостности цепи, частоты и логики.
H
Входной разъем COM: входной разъем заземления.
Я
Входной разъем 200 мА: Входной разъем для тока до 200 мА, L x (индуктивность), C x (емкость).
Дж
Входной разъем на 10 А: входной разъем для тока до 10 А.
Чтобы измерить заданное количество, шкала должна находиться в соответствующем положении, и должны использоваться соответствующие два входных разъема.Таким образом, при повороте шкалы для перехода от одного типа измерения к другому (например, от разности напряжений к электрическому току) вам, возможно, также придется изменить входные разъемы. При перегрузке предохранитель может перегореть.
Осторожно:
Для защиты счетчик гудит при перегрузке; если гудит, немедленно отключите провода счетчика!
Чтобы защитить измеритель от перегрузки при измерении неизвестного напряжения или тока, сначала необходимо установить измеритель на высшую шкалу для этой функции.Если показание недостаточно велико, чтобы дать хотя бы три значащих цифры, шкалу следует переключить (если возможно) на такую, которая позволяет проводить точное измерение.
3
Чтобы включить мультиметр, нажимайте верхнюю левую кнопку на измерителе до тех пор, пока на циферблате не появится дисплей. Чтобы настроить мультиметр на измерение постоянного напряжения, В, , переключите верхнюю правую кнопку на постоянный ток. Убедитесь, что на дисплее счетчика отображается постоянный ток.
Установите переключатель функций / диапазонов в диапазон напряжения (В) и установите значение 20.Теперь измеритель настроен на считывание напряжений до 20 вольт постоянного тока.
Подключите банан к банановым выводам к общему разъему (COM) и к разъему напряжения (V).
4
Подключите выводы мультиметра к клеммам + и — источника питания. См. Рисунок 2. На блоке питания поверните ручку регулировки напряжения ADJUST по часовой стрелке до тех пор, пока на дисплее вольт не отобразится 5,0 вольт. Сравните показания напряжения на мультиметре и на измерителе блока питания. Эти два показания могут не совпадать.Ожидается, что мультиметр будет точнее.
Ток и напряжение для одиночного резистора
1
Уменьшите напряжение блока питания (против часовой стрелки) до нуля вольт. Подключите блок питания к резистору на печатной плате с маркировкой 700 Ом. (Не регулируйте и не изменяйте настройку тока на источнике питания.) Мы будем использовать мультиметр для измерения постоянного тока через резистор 700 Ом в зависимости от приложенного напряжения. Для этого мы должны соединить мультиметр серии с резистором, чтобы одинаковый ток проходил через оба. Так как предохранитель легко перегорит, когда мультиметр настроен на текущее значение, внимательно следуйте инструкциям.
Установите шкалу мультиметра на шкалу тока 20 мА и подключите банановые штекеры к гнездам COM и мА на измерителе.
Внимание:
Не повышайте напряжение на источнике питания, пока ТА не проверит вашу цепь.
2
После получения разрешения от вашего ТА, установите источник питания на 1 В и запишите в Таблице 1 ток через резистор, как показано на мультиметре.Повторите то же самое с источником питания, установленным на 2, 3, 4 и 5 вольт.
3
Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Инструкции по построению графиков в Excel см. В приложении к интерактивному руководству лаборатории. Если вы получите ожидаемые результаты, данные будут располагаться близко к прямой линии, проходящей через начало координат. Используйте Excel, чтобы найти наклон прямой линии, который лучше всего соответствует вашим данным, и запишите результат, включая единицы измерения.
4
Используйте закон Ома и наклон графика, чтобы рассчитать сопротивление резистора R в единицах Ом (Ом). Запишите свой результат.
Ток и напряжение для лампочки
1
УСТАНОВИТЕ НАПРЯЖЕНИЕ ПИТАНИЯ НА НУЛЬ, но не выключайте питание. Не изменяйте настройку тока на источнике питания ( CC Set ). Мы будем использовать мультиметр для измерения постоянного тока через лампочку в зависимости от приложенного напряжения.Для этого мы должны соединить мультиметр серии с лампочкой, чтобы одинаковый ток проходил через оба. Так как предохранитель легко перегорит, когда мультиметр настроен на текущее значение, внимательно следуйте инструкциям.
2
Установите шкалу мультиметра на шкалу постоянного тока 10 А. Используйте входные гнезда COM и 10 A. Подключите схему, как показано на рисунке 3.
Внимание:
Не повышайте напряжение на источнике питания, пока ТА не проверит вашу цепь.
3
После того, как ваш ТА даст добро, установите напряжение источника питания на 2 вольта. В Таблице 2 запишите текущее показание мультиметра. Повторите эти действия для напряжений источника питания 4, 6, 8, 10 и 12 вольт.
4
Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Ожидается, что ваши данные не будут приближаться к прямой. Определите и вычислите R для каждого набора значений V и I в таблице 2 и запишите в третий столбец таблицы 2. R увеличивается, уменьшается или остается таким же, как и ток, I , через лампочку увеличивается?
Два резистора последовательно
1
Подключите на печатной плате два резистора с маркировкой 150 Ом и 700 Ом, как показано на рисунке 4. Говорят, что они включены последовательно, потому что весь ток, проходящий через один, также проходит через другой. Убедитесь, что напряжение источника питания установлено на ноль. Подключите источник питания к комбинации последовательных резисторов, как показано на рисунке 4.Установите блок питания на 5 вольт. Установите шкалу мультиметра на диапазон 20 В и используйте гнезда COM и V. С помощью мультиметра измерьте и запишите разности потенциалов (напряжение) В 150 и В 700 на каждом резисторе и напряжение В на комбинации из двух резисторов.
2
Когда вы закончите эти измерения, установите напряжение источника питания на ноль и отключите мультиметр от цепи.Что из следующего лучше отражает ваши результаты?
•
В = В 150 + В 700
•
В = В 150 = В 700
3
Когда напряжение источника питания установлено на ноль, подключите мультиметр последовательно с резисторами, как показано на рисунке 5. Установите мультиметр на диапазон постоянного тока 200 мА и подключите выводы мультиметра к правильным гнездам.
Осторожно:
Перед тем, как продолжить, попросите инструктора лаборатории проверить правильность настройки: предохранитель может перегореть, если измеритель не подключен к нужным точкам в цепи.
Получив добро от ТА, включите источник питания и установите его на 5 вольт. Измерьте ток в проводе между двумя резисторами, проводе между резистором 700 Ом и источником питания и проводе между резистором 150 Ом и источником питания.Убедитесь, что эти три тока равны.
4
Продолжая схему, показанную на рисунке 5, установите напряжение источника питания на 2 вольта. В таблице 3 запишите текущее показание мультиметра. Повторите эти действия для напряжений источника питания 4, 6, 8, 10 и 12 вольт.
5
Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Используйте Excel, чтобы найти наклон прямой линии, который лучше всего соответствует вашим данным, и запишите результат, включая единицы измерения.
6
Используйте закон Ома и наклон графика, чтобы рассчитать эквивалентное сопротивление, R с , двух последовательно соединенных резисторов в единицах Ом (Ом). Запишите свой результат.
Два параллельных резистора
1
Подключите на печатной плате два резистора с маркировкой 150 Ом и 700 Ом, как показано на Рисунке 6a. Они считаются параллельными, поскольку напряжение на каждом резисторе равно напряжению источника питания, а резисторы обеспечивают параллельные пути для прохождения тока.
2
Убедитесь, что напряжение источника питания установлено на ноль. Подключите источник питания к комбинации параллельных резисторов, как показано на рисунке 6b. Установите блок питания на 5 вольт. С помощью мультиметра измерьте и запишите токи I 150 и I 700 , протекающие через каждый резистор, и общий ток I , протекающий через источник питания.
3
Когда вы закончите эти измерения, установите напряжение источника питания на ноль и отключите мультиметр от цепи.
4
Что из следующего лучше отражает ваши результаты?
•
Я = Я 150 + Я 700
•
Я = Я 150 = Я 700
5
Продолжите параллельную сеть резисторов. Когда напряжение источника питания установлено на ноль, подключите мультиметр для измерения полного тока I , протекающего через источник питания.Установите мультиметр на диапазон постоянного тока 200 мА.
Осторожно:
Перед тем, как продолжить, попросите инструктора лаборатории проверить правильность настройки: предохранитель может перегореть, если измеритель не подключен к нужным точкам в цепи.
Получив добро от ТА, включите источник питания и установите его на 2 вольта.
6
В Таблице 4 запишите текущее показание мультиметра.Повторите эти действия для напряжений источника питания 4, 6, 8, 10 и 12 вольт.
7
Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Используйте Excel, чтобы найти наклон прямой линии, который лучше всего соответствует вашим данным, и запишите результат, включая единицы измерения.
8
Используйте закон Ома и наклон графика, чтобы вычислить эквивалентное сопротивление, R p , двух резисторов, включенных параллельно, в единицах Ом (Ом). Запишите свой результат.
Авторские права © 2012-2013 Advanced Instructional Systems Inc. и | Кредиты
Анализ резисторов последовательно и параллельно
Аннотация
Несколько резисторов подключаются одновременно, образуя цепь без ответвлений посередине, которая называется резистором в последовательной цепи. А цепь, которая соединяет два или более резистора между двумя точками в цепи с одинаковым напряжением на обоих концах резистора, называется резистором в параллельной цепи.Следующие ниже в основном посвящены схемам, методам расчета, характеристикам неисправностей и устранению неисправностей резисторов, включенных последовательно и параллельно. И последняя часть вводит понятие — ESR, которое связано с последовательными резисторами и конденсаторами
.
Резисторы в электрических цепях: последовательные и параллельные
Каталог
I Резисторы в последовательной и параллельной цепях
1. Резисторы в последовательной цепи
Несколько резисторов подключаются одновременно, образуя цепь без ответвлений посередине, которая называется резистором в последовательной цепи.На рисунке ниже показан резистор в последовательной цепи, состоящей из двух резисторов.
Резистор в последовательной цепи
Характеристики последовательной цепи:
(1) Ток в последовательной цепи везде одинаковый.
Если n резисторов включены последовательно, то
(2) Общее напряжение в цепи равно сумме разделенных напряжений на последовательных резисторах.
(3) Общее сопротивление цепи равно сумме последовательного сопротивления.
R называется эквивалентным сопротивлением последовательно соединенных R1 и R2. После замены R1 и R2 на R это не влияет на ток и напряжение в цепи.
На рисунке 1 (b) представляет собой эквивалентную схему (a).
Если n резисторов включены последовательно, то
(4) Взаимосвязь между распределением напряжения и распределением мощности в последовательных цепях.
Поскольку ток в последовательной цепи везде одинаков, поэтому
Две приведенные выше формулы показывают, что напряжение на каждом резисторе в последовательной цепи пропорционально сопротивлению каждого резистора. Мощность, потребляемая каждым резистором, также пропорциональна сопротивлению каждого резистора. Следовательно, когда последовательная цепь состоит из n резисторов, может быть получена формула деления напряжения последовательной цепи.
Совет: на практике резисторы часто подключаются последовательно, чтобы расширить диапазон измерения вольтметра.
2. Резисторы в параллельных цепях
Цепь, которая соединяет два или более резистора между двумя точками в цепи с одинаковым напряжением на обоих концах резистора, называется резистором в параллельной цепи.
Резисторы в параллельных цепях
Характеристики параллельной цепи:
(1) Напряжение на каждом резисторе в цепи одинаковое.
(2) Суммарный ток резисторов в параллельной цепи равен сумме токов ветвей.
(3) Обратное полное сопротивление параллельной цепи равно сумме обратных сопротивлений каждого параллельного резистора.
(4) Взаимосвязь между распределением тока и распределением мощности резисторов в параллельных цепях.
В параллельной цепи напряжения на параллельных резисторах одинаковы, поэтому
Приведенная выше формула показывает, что ток каждой ветви параллельной цепи обратно пропорционален сопротивлению.А мощность, потребляемая резисторами каждой ветви, обратно пропорциональна сопротивлению.
Когда два резистора соединены параллельно, ток через каждый резистор можно рассчитать с помощью уравнения шунта. Формула шунта:
Приведенная выше формула показывает, что в резисторах в параллельной цепи ток ветви с малым сопротивлением велик, а ток ветви с большим сопротивлением мал.
Примечание : Резисторы в параллельных цепях широко используются в повседневной жизни.Например, электрические приборы в цепях освещения обычно подключаются параллельно. Только при параллельном использовании электроприборов другие электроприборы могут нормально работать, когда одно из электроприборов отключено, замкнуто или неисправно.
II C вычисление S и P параллельно R esistance
Один резистор можно соединить вместе с множеством других резисторов последовательно и параллельно для образования сложных резистивных цепей.
Если мы соединим различные резисторы параллельно и последовательно в одной цепи, как мы вычислим сумму сопротивления, тока и напряжения этих резисторов в цепи?
Резистивные цепи, которые объединяют последовательные и параллельные резисторы, обычно называются комбинациями резисторов или гибридными резисторными цепями. Метод расчета эквивалентного сопротивления цепи такой же, как и для любой одиночной последовательной или параллельной цепи. Теперь мы знаем, что последовательные резисторы имеют одинаковый ток, а параллельные резисторы имеют одинаковое напряжение.
1. Пример расчета 1
Рассчитайте полный ток (IT), потребляемый от источника питания 12 В в следующей схеме.
На первый взгляд это может показаться сложной задачей, но если мы внимательно рассмотрим ее, то увидим, что два резистора, R 2 и R 3, на самом деле соединены вместе последовательно. Итак, мы можем сложить сопротивление. Следовательно, суммарное сопротивление этой комбинации составляет:
R2 + R3 = 8 Ом + 4 Ом = 12 Ом
Значит, мы можем заменить резисторы R2 и R3 на резистор 12 Ом
И теперь в цепи параллельно подключены резистор RA и резистор R4.Затем мы можем уменьшить эту параллельную комбинацию до единственного эквивалентного значения сопротивления R (комбинации), используя следующую формулу сопротивления.
В результате резистивная цепь теперь выглядит так:
Мы видим, что два оставшихся сопротивления, R1 и R (гребешок) соединены последовательно, и их можно снова сложить между точками A и B.
R = R гребенчатый + R1 = 6 Ом + 6 Ом = 12 Ом
Один резистор на 12 Ом можно использовать для замены четырех исходных резисторов, включенных в исходную схему.
Теперь, используя закон Ома, текущее значение (I) цепи просто рассчитывается следующим образом:
Следовательно, используя описанные выше шаги для замены всех резисторов, соединенных последовательно или параллельно, мы можем свести любую сложную резисторную схему, состоящую из нескольких резисторов, в простую одиночную схему с одним эквивалентным резистором.
Мы также можем получить два тока ответвления, I1 и I2, используя дополнительный метод Ом:
В (R1) = I * R1 = 1 * 6 = 6 В
В (RA) = VR4 = (12-VR1) = 6 В
следовательно:
I1 = 6 В ÷ RA = 6 ÷ 12 = 0.5А или 500 мА
I2 = 6 В ÷ R4 = 6 ÷ 12 = 0,5 А или 500 мА
Поскольку сопротивления обеих ветвей составляют 12 Ом, I1 и I2 равны 0,5 А (или 500 мА). Следовательно, общий ток питания IT = 0,5 + 0,5 = 1,0А.
После этих изменений иногда легче рисовать или перерисовывать новые схемы со сложными комбинациями резисторов и цепями резисторов, что становится наглядным пособием по математике. Затем продолжайте заменять любую последовательную или параллельную комбинацию, пока не найдете эквивалентное сопротивление R EQ .Давайте попробуем еще одну более сложную схему комбинации резисторов.
2. Пример расчета 2
Чтобы найти эквивалентное сопротивление, REQ используется в следующей схеме комбинации резисторов.
Опять же, эта схема лестничных резисторов может показаться очень сложной на первый взгляд, но, как и прежде, это просто комбинация последовательно соединенных и параллельных резисторов. Начиная с правой стороны и используя упрощенную формулу двух параллельных резисторов, мы можем найти эквивалентное сопротивление / комбинацию R8 и R10 и назвать это RA.
(Формула 4-1)
Следовательно, RA + R7 = 4 + 8 = 12 Ом
Сопротивление 12 Ом теперь параллельно R6, и общее сопротивление можно рассчитать как RB.
(Формула 4-2)
RB + R5 = 4 + 4 = 8 Ом
Значение сопротивления 8 Ом теперь подключено параллельно с R4 и может быть рассчитано как RC, как показано.
(Формула 4-3)
RC подключен последовательно с R3, поэтому общее сопротивление RC + R3 = 8 Ом, что показано на рисунке.
Сопротивление 8 Ом параллельно R2, и его можно рассчитать как RD:
RD подключается последовательно с R1, поэтому общее сопротивление составляет RD + R1 = 4 + 6 = 10 Ом, как показано на рисунке.
В конечном итоге, исходная сеть комплексных резисторов, которая включает десять независимых резисторов, соединенных последовательно и параллельно, может быть заменена эквивалентным сопротивлением REQ 10 Ом.
Когда мы сталкиваемся с любыми цепями, состоящими из последовательно включенных и параллельных резисторов, сначала нам нужно определить простое последовательное и параллельное сопротивление каждой ветви, а затем заменить их эквивалентным сопротивлением.
Это позволит нам снизить сложность схемы и поможет преобразовать сложные комбинированные резистивные схемы в один эквивалентный резистор.
Однако расчет более сложных Т-образных аттенюаторов и цепей резистивных мостов нельзя упростить до простых параллельных или последовательных цепей с эквивалентным сопротивлением. Их необходимо решить, используя закон Кирхгофа и закон напряжения Кирхгофа.
III Неисправность C характеристики и T обработка R esistor s в S eries и параллельный
1.
Особенности короткого замыкания и обрыва в последовательной цепи
(1) Особенности короткого замыкания
На рисунке ниже показано короткое замыкание в последовательной цепи. В схеме резистор R1 и R2 изначально были включены последовательно, но теперь резистор R2 закорочен. В это время в последовательной цепи произойдут следующие изменения.
Короткое замыкание в последовательной цепи
1) После короткого замыкания резистора R2 в последовательной цепи остается только резистор R1.В это время уменьшается общее сопротивление цепи, которое равно сопротивлению резистора R1.
2) Поскольку рабочее напряжение постоянного тока + V в цепи не изменилось, а общее значение сопротивления последовательной цепи уменьшилось, ток последовательной цепи увеличится после короткого замыкания резистора R2.
Увеличение силы тока в цепи связано с сопротивлением сопротивления короткого замыкания R2. Если сопротивление R2 относительно велико, величина увеличения в последовательной цепи после короткого замыкания будет относительно большой, что вызовет перегрузку по току.Если блок питания не выдерживает чрезмерного тока, он может перегореть. Поэтому короткие замыкания в последовательной цепи очень вредны.
3) В то же время, поскольку повышенный ток также течет через другие резисторы (например, R1) в последовательной цепи, он также вызовет перегрузку по току в других резисторах, что также приведет к их повреждению.
4) В последовательной цепи, если ток, протекающий через определенный компонент, увеличивается, это указывает на короткое замыкание в цепи.Поскольку ток в последовательной цепи увеличивается после короткого замыкания, ток, протекающий через другие резисторы, также увеличивается, что также увеличивает падение напряжения на других резисторах.
5) Короткое замыкание в последовательной цепи относится к серьезной неисправности. Это может вызвать повреждение всех компонентов в последовательной цепи, поскольку ток, протекающий в последовательной цепи, увеличивается.
(2) Характеристики Обрыв C Схема
Когда в резисторах в последовательной цепи возникает разрыв цепи, в цепи не будет протекать ток независимо от того, какая часть последовательной цепи разомкнута.
Неисправность обрыва цепи обычно не вредит последовательным цепям. Однако иногда из-за разомкнутой цепи напряжение цепи возбуждения нагрузки повышается, что приводит к ее выходу из строя.
Обрыв в последовательной цепи
2 . F ault A анализ серии R esist ors
Следующая таблица представляет собой сводку анализа неисправностей последовательных цепей с резисторами R1 и R2.
Название компонента | Тип неисправности | Анализ неисправностей | Анализирующая мысль |
R1 | Обрыв цепи | Нет тока через R1 и R2, и невозможно измерить напряжение на R1 и R2 | Через резистор нет тока, значит, нет напряжения. |
Короткое замыкание | Ток, протекающий через R2, увеличивается, что может привести к сгоранию R2 | Общее сопротивление уменьшается, что увеличивает общий ток. Если ток, протекающий через R2, слишком велик, он сожжет R2. | |
Сопротивление увеличено | Ток, протекающий через R1 и R2, уменьшается, напряжение R1 увеличивается, а напряжение R2 уменьшается. | После увеличения сопротивления R1 общее сопротивление увеличивается, общий ток уменьшается, а падение напряжения R2 уменьшается, поэтому напряжение R1 увеличивается. | |
Сопротивление снижено | Ток, протекающий через R1 и R2, увеличивается, напряжение R1 уменьшается, а напряжение R2 увеличивается | После увеличения сопротивления R1 общее сопротивление уменьшается, а общий ток увеличивается, так что напряжение на R1 уменьшается | |
Плохой контакт | Схема будет работать нормально в одном случае и ненормально в другом. | Цепь работает нормально, когда контакт нормальный, цепь работает ненормально, когда контакт ненормальный | |
R2 | Вышеупомянутые пять ошибок | Анализ отказов такой же, как указано выше (замените R1 на R2) | Аналитическое мышление такое же, как указано выше (замените R1 на R2) |
3. Неисправность D etection of R esist ors in S eries
Есть много способов проверить отказ резисторов в последовательной цепи.Например, значение сопротивления каждого резистора в цепи можно измерить с помощью диапазона Ом мультиметра. Однако при поиске и устранении неисправностей метод проверки часто выбирается гибко.
Устройство мультиметра
(1) Метод обнаружения неисправности для Обрыв C Схема
Если устройство работает в цепи постоянного тока, используйте диапазон постоянного напряжения мультиметра для измерения напряжения на R1 (два измерительных провода соответственно подключены к двум контактам R1), тогда вы сможете определить, есть ли в цепи обрыв неисправность цепи или нет.
Если устройство работает в цепи переменного тока, переменное напряжение мультиметра и диапазон переменного напряжения цифрового измерителя можно использовать для измерения переменного напряжения на R1.
(2) F ault I nspection Средство для Short C ir circuit
Теоретически вы также можете использовать описанный выше метод для измерения напряжения на R1 при проверке короткого замыкания резисторов в последовательной цепи.Если напряжение на R1 выше, чем нормальное значение, это можно объяснить коротким замыканием в цепи. Потому что только короткое замыкание в последовательной цепи увеличит ток и напряжение на R1.
Однако есть проблема с вышеупомянутым методом проверки короткого замыкания. Необходимо знать, каково нормальное напряжение на R1, иначе невозможно определить, увеличился ли ток в цепи.
4. F a ilure Testing параллельного R esist ors
( 1) F ault D etection M ethod для разомкнутой цепи
Когда цепь отключена, используйте резистивную шестерню мультиметра для измерения общего сопротивления параллельной цепи. В нормальных условиях измеренное значение общего сопротивления должно быть Обнаружение обрыва в параллельных цепях Если измеренное значение сопротивления больше одного из R1 и R2, это означает, что R1 или R2 разомкнуты в цепи. В частности, чтобы определить, какая цепь разомкнута, мы могли измерить ток каждой ветви сопротивления. ( 2) S hort C ircuit F ault D etection M etho d Если измеренное полное сопротивление равно нулю, это означает, что в параллельной цепи произошло короткое замыкание.Если вам нужно понять детальное положение и причину отказа, вам необходимо провести дальнейшие измерения. Это имеет большое значение для поиска и устранения неисправностей, которые определяют объем неисправной цепи и направление проверки. IV E эквивалент S eries R esistance ESR — это сокращение от эквивалентного последовательного сопротивления. Это эквивалентное «последовательное» сопротивление, означающее, что при последовательном подключении двух резисторов это значение будет увеличиваться, а при параллельном подключении — уменьшиться. Появление ESR привело к отклонению поведения конденсаторов от его первоначального определения. Теоретически идеальный конденсатор сам по себе не генерирует никаких потерь энергии, но, поскольку материал, из которого изготовлен конденсатор, имеет сопротивление, а изоляционная среда имеет потери энергии, конденсатор становится несовершенным. Эти потери выглядят внешне так, как если бы резистор был подключен последовательно с конденсатором, поэтому они называются «эквивалентным последовательным сопротивлением». Считаем, что резкое изменение напряжения на конденсаторе невозможно.Когда к конденсатору внезапно подается ток, напряжение конденсатора возрастает с 0 из-за его собственной зарядки. Но с ESR сам резистор генерирует падение напряжения, которое вызывает внезапное изменение напряжения на конденсаторе. Несомненно, это снизит фильтрующий эффект конденсатора, поэтому во многих высококачественных источниках питания используются конденсаторы с низким ESR. Аналогичным образом, в случае колебательных контуров, ESR изменяет функцию контура, вызывая серьезные последствия, такие как отказ контура или даже повреждение. Таким образом, в большинстве случаев конденсаторы с низким ESR работают лучше, чем конденсаторы с высоким ESR. Но есть исключения, и иногда ESR используется для чего-то полезного. Например, в цепи стабилизации напряжения при переходной нагрузке конденсатор с определенным ESR немедленно генерирует флуктуации и запускает цепь обратной связи. Такой быстрый отклик достигается за счет определенных переходных характеристик. особенно когда скорость отклика силовой лампы мала, а объем или емкость конденсатора строго ограничены.Эта ситуация наблюдается в некоторых трехконтактных регуляторах напряжения с трубками mos в качестве регуляторов или аналогичными схемами. В это время низкое ESR снизит общую производительность. На самом деле, существует больше случаев, когда требуется более низкое ESR, а конденсаторы большой емкости с низким ESR относительно дороги. Поэтому во многих импульсных источниках питания используется параллельное соединение. Люди подключают несколько алюминиевых электролитических конденсаторов с относительно высоким ESR параллельно, чтобы сформировать конденсатор с низким ESR. Часто бывает выгодно пожертвовать определенным объемом места на печатной плате в обмен на снижение стоимости устройства. Другой концепцией, аналогичной ESR, является ESL, что означает эквивалентную последовательную индуктивность. Ранние катаные конденсаторы часто имели очень высокий ESL, и чем больше емкость, тем больше ESL. ESL часто становится частью ESR, а также вызывает сбои в некоторых цепях, например, последовательный резонанс. Однако с точки зрения емкости доля ESL слишком мала, и вероятность возникновения проблем очень мала. В дополнение к развитию процесса производства конденсаторов, ESL постепенно игнорируется, а ESR используется в качестве основного эталонного фактора помимо емкости.
Отмена ESL и ESR для конденсаторов
Кстати, у емкости есть добротность Q, аналогичная индуктивности. Этот коэффициент обратно пропорционален ESR и связан с частотой. Также редко используется.
Отказы цепи, вызванные ESR, часто трудно обнаружить, а влияние ESR легко не заметить в процессе проектирования. Самый простой способ состоит в том, что во время моделирования, если вы не можете выбрать конкретные параметры конденсатора, вы можете попытаться искусственно подключить небольшой резистор последовательно с конденсатором, чтобы имитировать эффект ESR.Как правило, ESR танталовых конденсаторов обычно ниже 100 миллиом, а алюминиевые электролитические конденсаторы выше этого значения, а ESR некоторых типов конденсаторов может достигать даже нескольких Ом.
Типичное соотношение между ESR и частотой для танталовых конденсаторов
Взаимосвязь между ESR и пульсациями напряжения может быть выражена формулой:
В = R (ESR) × I.
В этой формуле V — это пульсирующее напряжение, R — ESR конденсатора, а I — ток.Видно, что при увеличении тока пульсации напряжения удваиваются, даже если ESR остается неизменным.
Заключение
В этой статье мы в основном обсудили схемы, методы расчета, устранение неисправностей резисторов, включенных последовательно и параллельно. В последнем разделе была представлена концепция ESR — эквивалентное последовательное сопротивление. Надеюсь, вы почерпнете вдохновение из этой статьи.
Артикул Рекомендуемый:
Что такое переменный резистор?
Понимание углеродных пленочных резисторов
Руководство по прецизионным резисторам для новичков
В чем разница между подтягивающими и понижающими резисторами?
Цепь серии
— принцип работы, характеристики, применение, преимущество
Два типа цепей, которые обычно используются для подачи электроэнергии, — это последовательные и параллельные цепи.Главный принцип любой электрической схемы — подача электричества на электрическое устройство. Эта статья дает вам представление о последовательной схеме, принципе работы, характеристиках последовательной схемы, приложениях, преимуществах и недостатках.
Что такое последовательная цепь
Цепь, в которой электричество должно проходить через все компоненты в цепи и не имеет альтернативного пути, называется последовательной цепью.
В этой схеме все компоненты соединены в один контур.Наиболее распространенный пример последовательной схемы — это необычные светильники или струнные светильники.
Рис. 1 — Пример последовательной цепи
Как устроена последовательная цепь (принцип работы)
Путь для потока электронов (электричества) называется Цепью. Назначение любой электрической цепи состоит в том, чтобы подавать электричество для прибора или любого электрического устройства. Эти устройства называются нагрузками. Перед тем, как нагрузка сработает, электричество должно пройти определенный путь от источника к нагрузке и обратно к источнику.
На рисунке ниже показана типичная последовательная цепь, в которой резисторы (R1, R2, R3) последовательно подключаются, а конец одного резистора соединяется с другим концом следующего резистора, образуя петлю. Ток течет от отрицательной клеммы батарея проходит через резисторы, и, следовательно, ток одинаков для всех компонентов в последовательной цепи.
Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений. Напряжение на разных резисторах разное, а сумма падений напряжения на каждом компоненте (резисторе) равна приложенному напряжению.Обрыв в последовательной цепи остановит ток через цепь.
Рис.2 — Схематическое изображение последовательной цепи
Характеристики последовательной цепи
Ниже приведены важные характеристики цепей серии:
Сопротивление
R T = R1 + R2 + R3 +… ..R n
Где R T = Общее сопротивление
Если R1 = 10 Ом, R2 = 20 Ом, R3 = 40 Ом
р т = 10 + 20 + 40
R T = 70 Ом
Текущий
Предположим, что приложенное напряжение (В) = 10 В, тогда ток (I) можно рассчитать по формуле:
I = V / R = 10/70 = 1/7 Ампер = 0.1428 А = 142,8 мА
I = 142,8 миллиампера
Напряжение
Поскольку значения сопротивления и тока известны, напряжение можно рассчитать по формуле:
В = ИК
Обозначим напряжение на резисторе 1, 2, 3 как E R1, E R2 и E R3 соответственно.
E R1 = IxR1 = 0,142 x 10 = 1,42 v
E R2 = IxR2 = 0.142 x 20 = 2,84 В
E R3 = IxR3 = 0,142 x 40 = 5,68 В
Падение напряжения
Как мы знаем, сумма падений напряжения на каждом резисторе равна приложенному напряжению,
E T = E R1 + E R2 + E R3 = 1,42 + 2,84 + 5,68
= 9,94 В (с ошибкой округления) ≈ 10 В (приложенное напряжение)
Приложения последовательной цепи
Применения последовательных схем включают:
- Резистивные цепи серии
- используются в цепях малой мощности.
- используются в схемах делителя напряжения.
Цепи серии
Преимущества последовательной цепи
К преимуществам серии цепей относятся:
- Простота проектирования и изготовления схемы.
- Если компонент выходит из строя, текущий поток останавливается.
- Он действует как регулятор тока.
- Стоимость построения последовательной цепи меньше по сравнению с параллельной схемой.
Недостатки последовательной цепи
К недостаткам серии цепей можно отнести:
- Если перегорает одна последовательно включенная лампочка, то в цепи не будет протекать ток.
- При увеличении нагрузки, т.е. при подключении большего количества лампочек, свет становится тусклее.
Также читайте:
Что такое цифровой вольтметр - как он работает, типы, применения, преимущества
Что такое технология Li-Fi - как это работает, приложения и преимущества
Лаксми имеет степень бакалавра в области электроники и связи и имеет опыт работы в RelQ Software в качестве инженера-испытателя и HP в качестве руководителя службы технической поддержки.


 1.5.
1.5.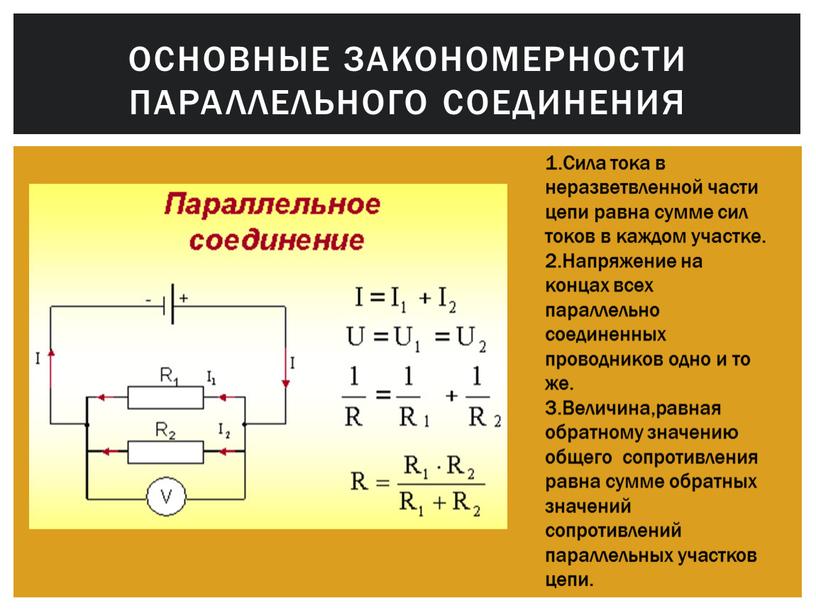 Проверить справедливость первого закона Кирхгофа.
Проверить справедливость первого закона Кирхгофа.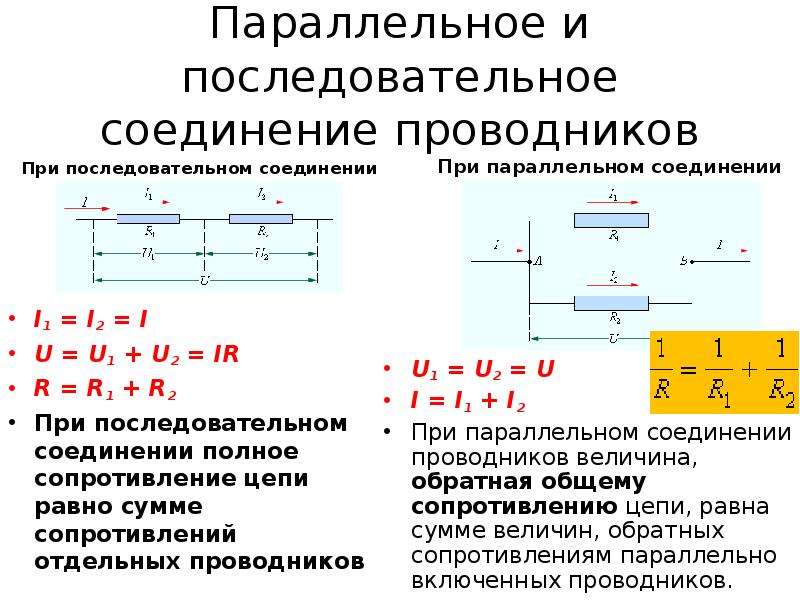
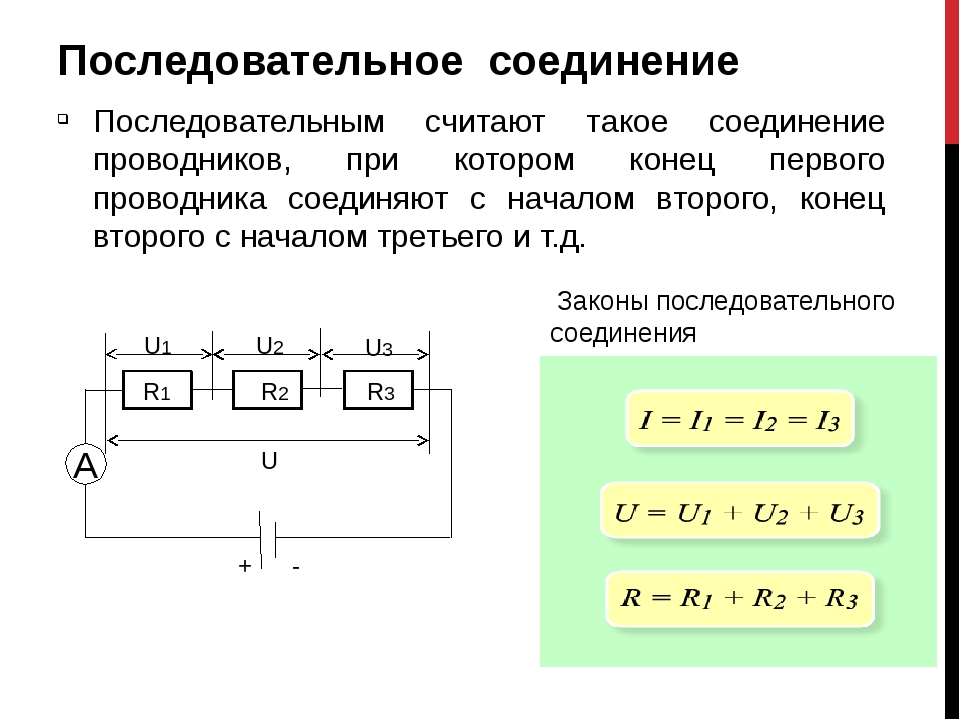
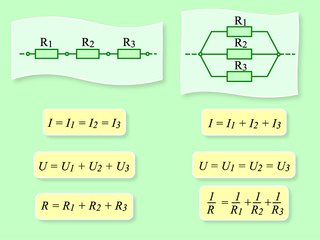 Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.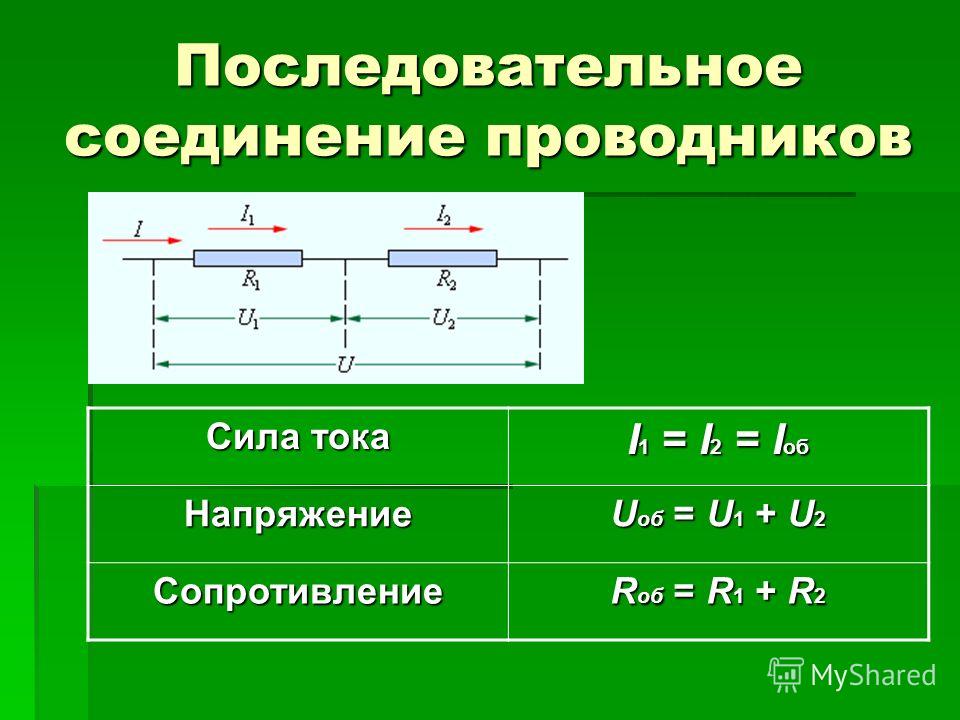
 Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.