12-02-2015_08-16-01 / ЛР 3.3. Заряд разряд конденсатора. Ток заряда конденсатора

ЛР 3.3. Заряд разряд конденсатора

Обложка

ИЗУЧЕНИЕ ПРОЦЕССОВ ЗАРЯДКИ И РАЗРЯДКИ КОНДЕНСАТОРА. ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА

Учебно-методическое пособие к лабораторной работе № 3.3

по дисциплине «Физика»

Владивосток

2013

Титул

Министерство образования и науки Российской Федерации

Дальневосточный федеральный университет

Школа естественных наук

ИЗУЧЕНИЕ ПРОЦЕССОВ ЗАРЯДКИ И РАЗРЯДКИ КОНДЕНСАТОРА. ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА

Учебно-методическое пособие к лабораторной работе № 3.3 по дисциплине «Физика»

Владивосток

Дальневосточный федеральный университет

____________________________________________________________________________________________________________

Оборот титула

УДК 53 (о76.5)

ББК 22. 343

Э41

Составитель: О.В.Плотникова

Изучение процессов зарядки и разрядки конденсатора. Определение емкости конденсатора: учебно-методич. пособие к лабораторной работе № 3.3 по дисциплине «Физика» / Дальневосточный федеральный университет, Школа естественных наук [сост. О.В.Плотникова]. – Владивосток: Дальневост. федерал. ун-т, 2013. - с.

Пособие, подготовленное на кафедре общей физики Школы естественных наук ДВФУ, содержит краткий теоретический материал по теме «Электрическая емкость. Конденсаторы» и инструктаж к выполнению лабораторной работы «Изучение процессов зарядки и разрядки конденсатора. Определение емкости конденсатора» по дисциплине «Физика».

Для студентов-бакалавров ДВФУ.

УДК 53 (о76.5)

ББК 22. 343

©ФГАОУ ВПО «ДВФУ», 2013

Цель работы: экспериментальное подтверждение законов, описывающие процессы зарядки и разрядки конденсатора, определение постоянной времени электрической цепи, определение неизвестной емкости конденсатора.

Краткая теория

1. Электроёмкость.

Проводники – это вещества, содержащие большое количество свободных заряженных частиц. В металлических проводниках такими частицами являются свободные электроны, в электролитах – положительные и отрицательные ионы, в ионизированных газах – ионы и электроны.

Если рассматривать проводник, рядом с которым нет других проводников, то он называется уединенным. Опыт показывает, что потенциал уединенного проводника прямо пропорционален находящемуся на нем заряду. Отношение заряда, сообщенного проводнику, к его потенциалу называется электроемкостью проводника (или просто емкостью):

С=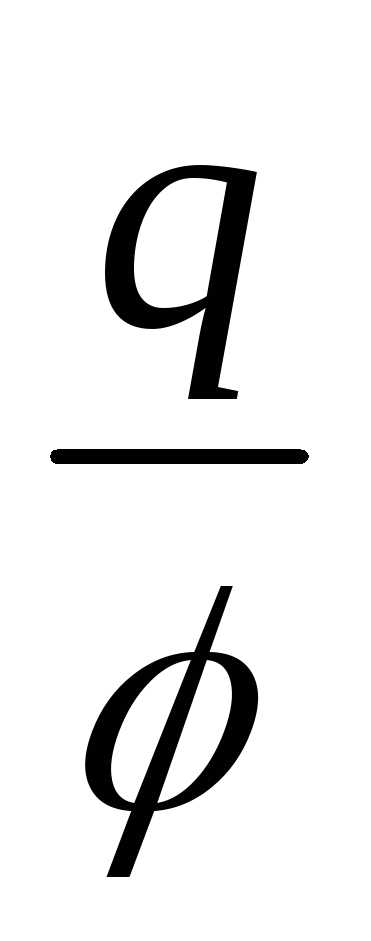

Таким образом, емкость определяется величиной заряда, который надо сообщить проводнику, чтобы увеличить его потенциал на единицу.

Емкость зависит от размеров и формы проводника, от диэлектрической проницаемости среды, от наличия рядом других проводников и не зависит ни от заряда, ни от потенциала. Так, для уединенного проводящего шара радиуса R емкость равна:

С = 4πεε0R. (т.к. потенциал φ= ).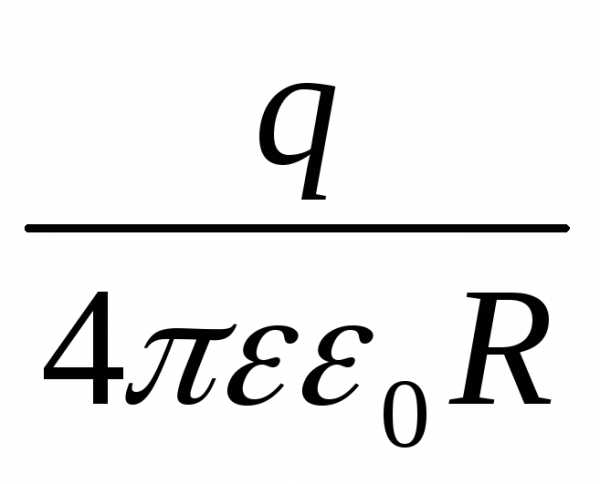

Здесь ε – диэлектрическая проницаемость среды, ε0 - электрическая постоянная.

Единица емкости в системе СИ называется Фарадой (Ф). 1Ф = 1.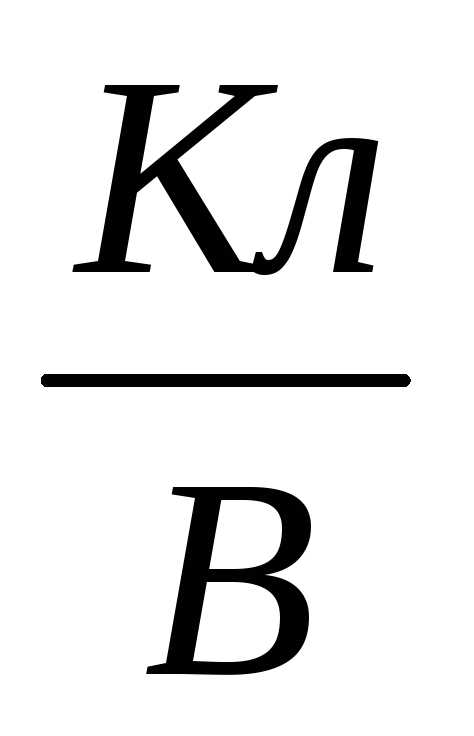

2. Конденсаторы.

Емкостью обладают не только отдельные проводники, но и системы проводников. Система, состоящая из двух проводников, разделенных слоем диэлектрика, называется конденсатором. Проводники в этом случае называются обкладками конденсатора. Заряды на обкладках имеют противоположные знаки, но по модулю – одинаковы. Практически все поле конденсатора сосредоточено между обкладками и.

Емкостью конденсатора называется величина

С= 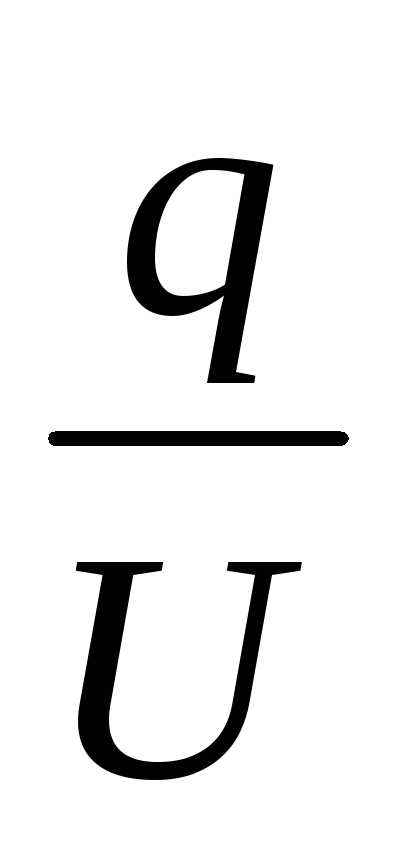, (1)

где q – абсолютная величина заряда одной из обкладок, U - разность потенциалов (напряжение) между обкладками.

В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими, цилиндрическими.

Найдем емкость плоского конденсатора, обкладки которого имеют площадь S, расположены на расстоянии d, а пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью ε.

Если поверхностная плотность заряда на обкладках равна σ (σ= 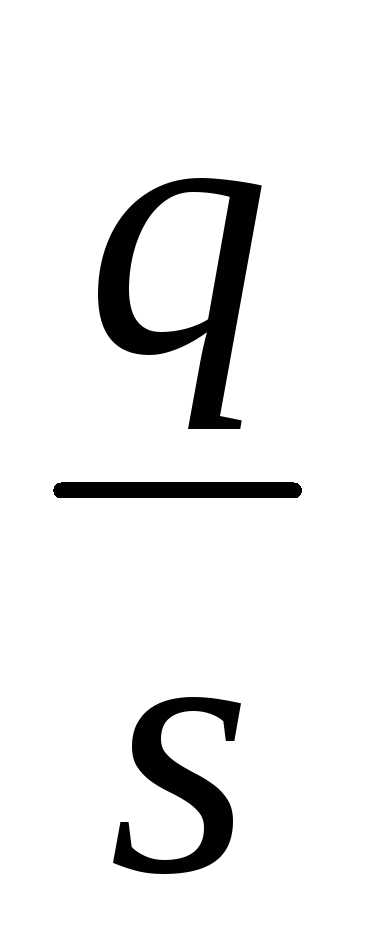), то напряженность поля конденсатора (поле считается однородным) равна:

Е= =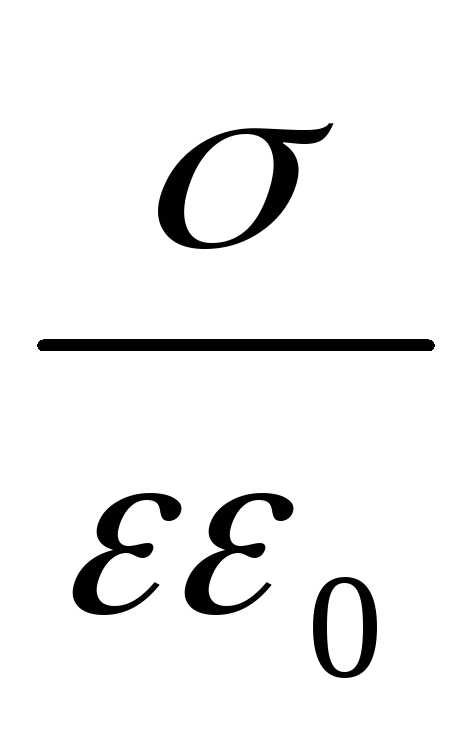

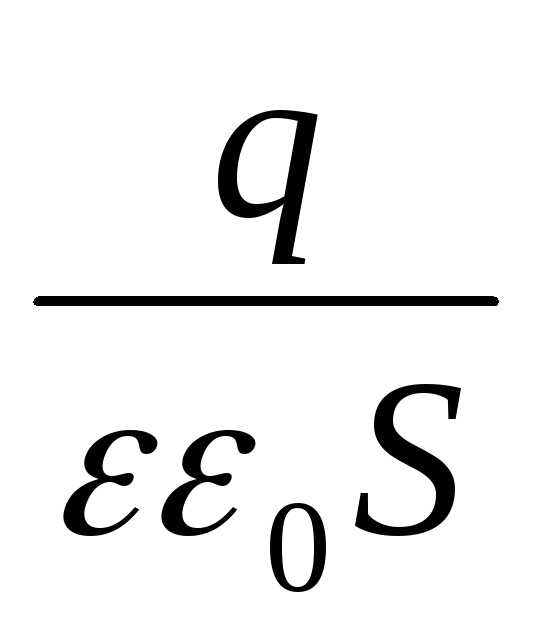
Разность потенциалов между обкладками связана с напряженностью поля: Е =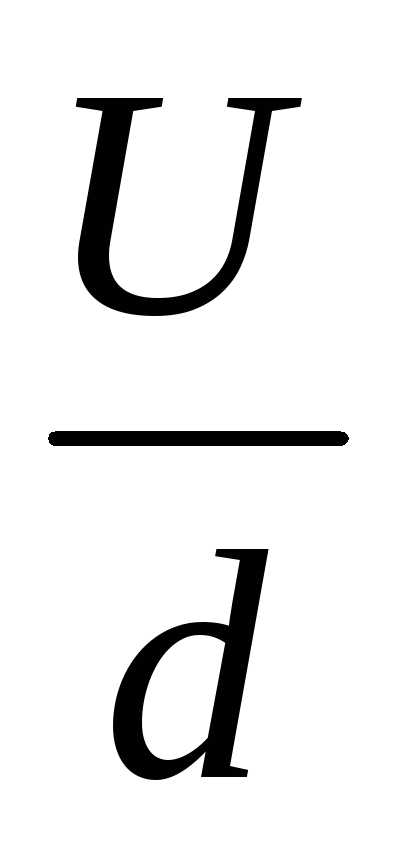 , откуда получим U=Ed = =

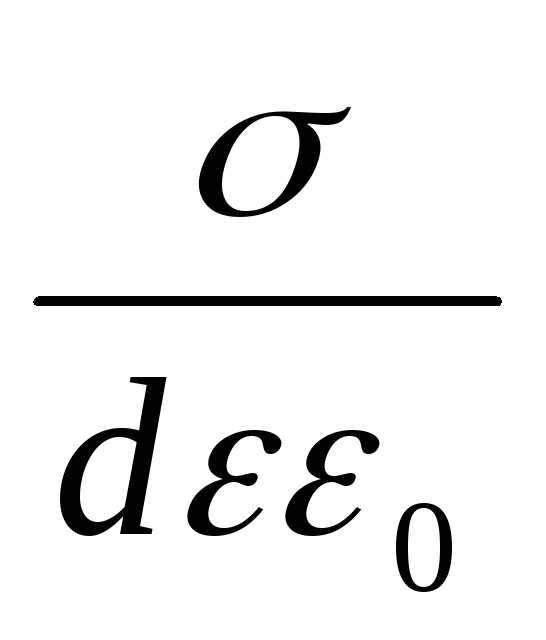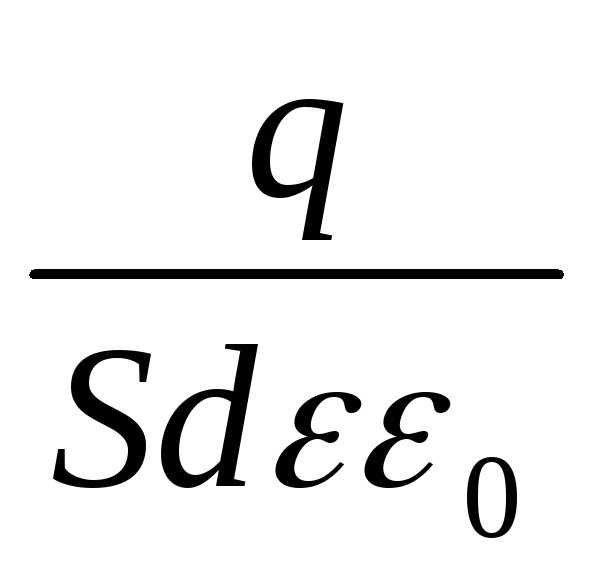
Используя формулу ( 1 ), получим для емкости плоского конденсатора выражение:

С =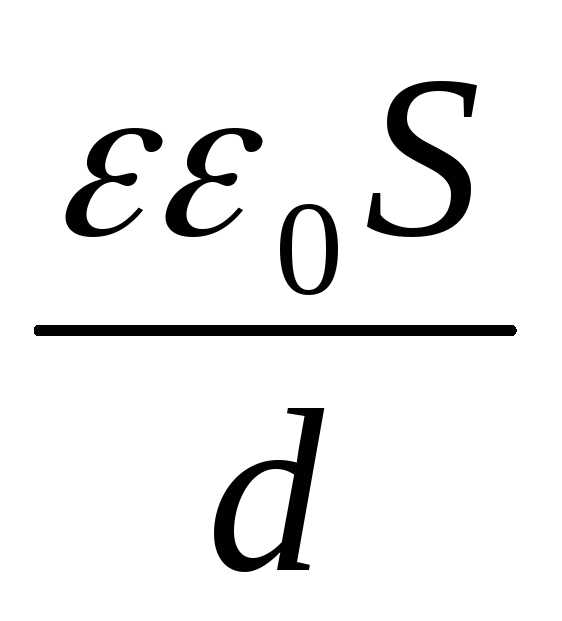(2)

3. Соединение конденсаторов.

Используются два основных вида соединения: последовательное и параллельное.

При параллельном соединении (рис 1), общая емкость батареи равна сумме емкостей всех конденсаторов:

Собщ.= С1 +С2+С3+…=ΣСi . (3)

При последовательном соединении (рис.2) величина, обратная общей емкости, равна сумме величин, обратных емкостям всех конденсаторов:

. (4)

Если последовательно соединены n конденсаторов с одинаковой емкостью С, то общая емкость: Собщ.=

Рис. 1.Параллельное соединение. Рис. 2.Последовательное соединение

4. Энергия конденсатора.

Если процесс зарядки конденсатора является медленным (квазистационарным), то можно считать, что в каждый момент времени потенциал любой из обкладок конденсатора во всех точках одинаков. При увеличении заряда на величину dq совершается работа , гдеu – мгновенное значение напряжения между обкладками конденсатора. Учитывая, что , получаем:. Если емкость не зависит от напряжения, то эта работа идет на увеличение энергии конденсатора. Интегрируя данное выражение, получим:

,

где W – энергия конденсатора, U – напряжение между обкладками заряженного конденсатора.

Используя связь между зарядом, емкостью конденсатора и напряжением, можно представить выражение для энергии заряженного конденсатора в других видах:

. (5)

5. Квазистационарные токи. Процессы зарядки и разрядки конденсатора.

При зарядке или разрядке конденсатора в цепи конденсатора течет ток. Если изменения тока происходят очень медленно, то есть за время установления электрического равновесия в цепи изменения токов и э.д.с. малы, то для определения их мгновенных значений можно использовать законы постоянного тока. Такие медленно меняющиеся токи называют квазистационарными.

Так как скорость установления электрического равновесия велика, под понятие квазистационарных токов подпадают и довольно быстрые в обычном понимании процессы: переменный ток, многие электрические колебания, используемые в радиотехнике. Квазистационарными являются и токи зарядки или разрядки конденсатора.

Рассмотрим электрическую цепь, общее сопротивление которой обозначим R. Цепь содержит конденсатор емкостью C, подключенный к источнику питания с э.д.с. ε (рис. 3).

Рис. 3. Процессы зарядки и разрядки конденсатора.

Зарядка конденсатора. Применяя к контуру εRC1ε второе правило Кирхгофа, получим: ,

где I, U – мгновенные значения силы тока и напряжения на конденсаторе (направление обхода контура указано стрелкой).

Учитывая, что 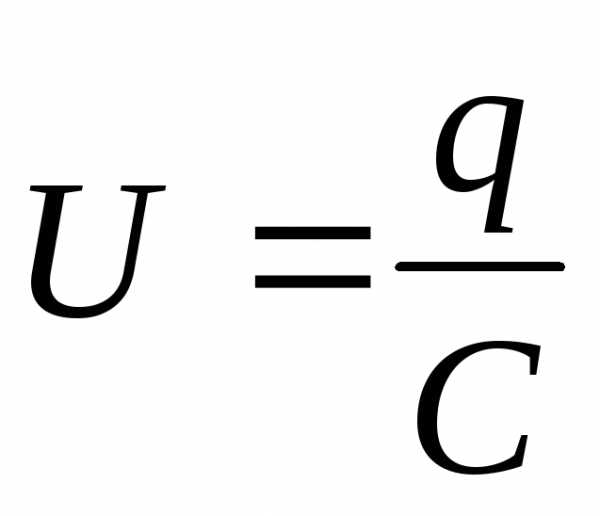,,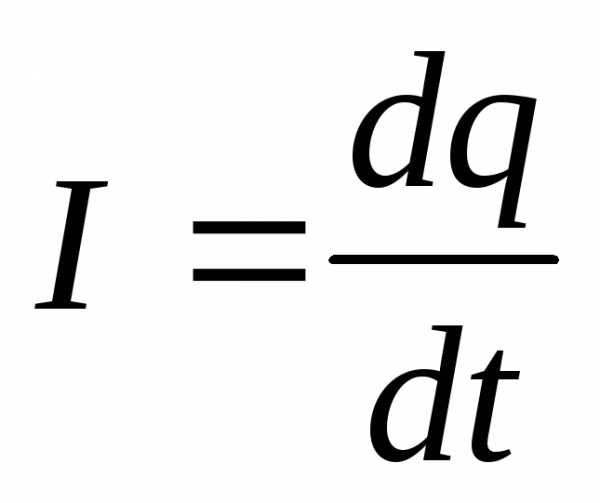 можно привести уравнение к одной переменной:

.

Введем новую переменную: . Тогда уравнение запишется:

.

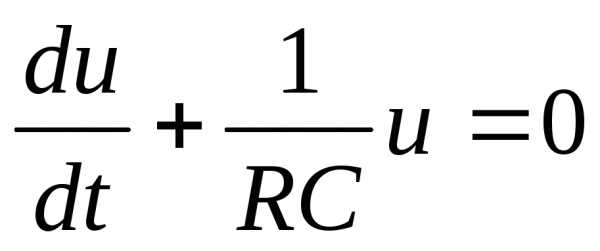Разделив переменные и проинтегрировав, получим: .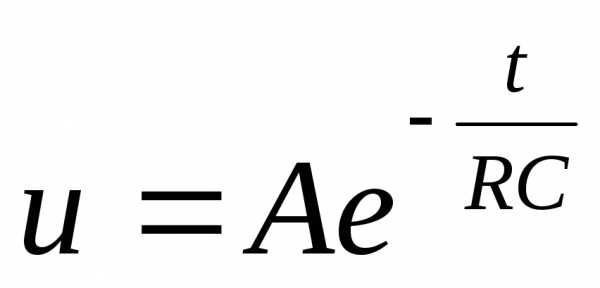

Для определения постоянной А используем начальные условия:

t=0, U=0, u= - ε. Тогда получим: А= - ε. Возвращаясь к переменной , получим окончательно для напряжения на конденсаторе выражение:

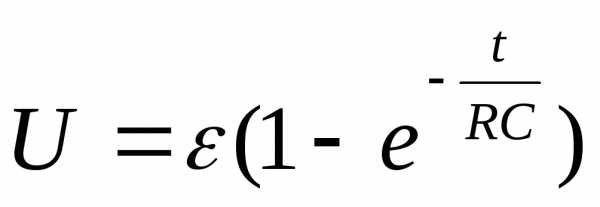. (6)

С течением времени напряжение на конденсаторе растет, асимптотически приближаясь к э.д.с. источника (рис.4, I.).

Разрядка конденсатора. Для контура CR2C по второму правилу Кирхгофа: RI=U. Используем также:

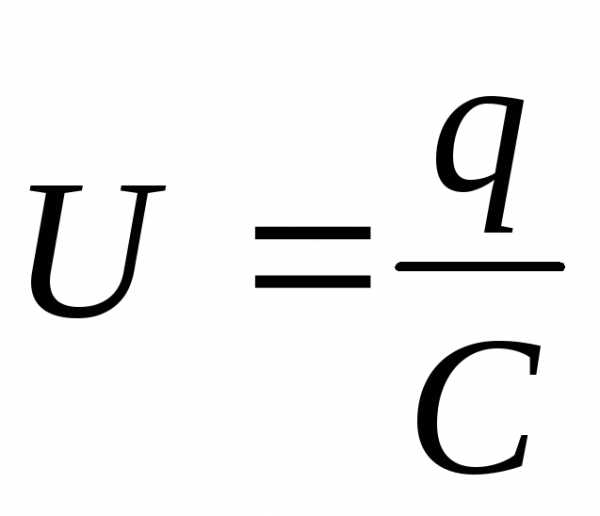, и 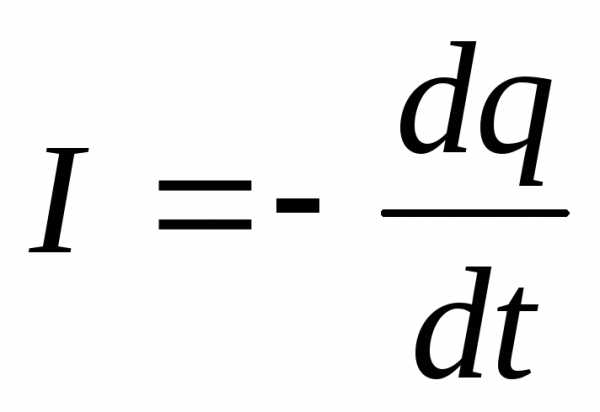(ток течет в обратном направлении).

Приведя к переменной U, получим:

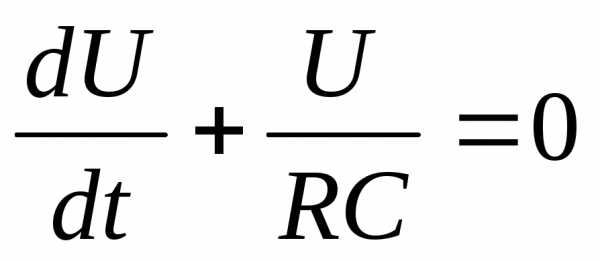. Интегрируя, получим: .

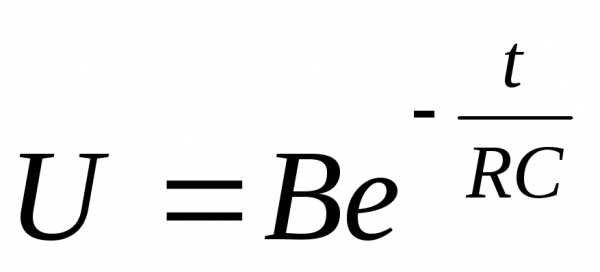Постоянную интегрирования B определим из начальных условий: t=0, U=ε. Тогда получим: В=ε.

Для напряжения на конденсаторе получим окончательно:

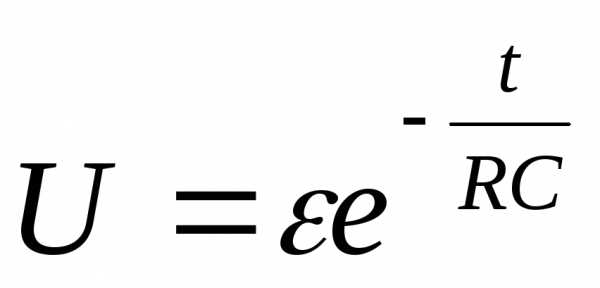. (7)

С течением времени напряжение падает, приближаясь к 0 (рис. 4, II).

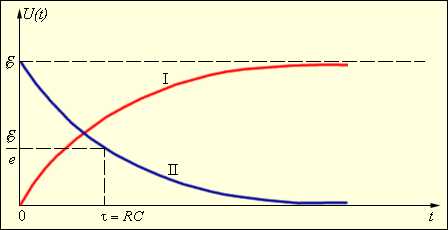
Рис. 4. Графики зарядки (I) и разрядки (II) конденсатора.

6. Постоянная времени. Характер протекания процессов зарядки и разрядки конденсатора (установление электрического равновесия) зависит от величины:

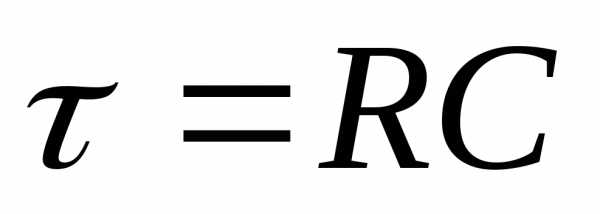, (8)

которая имеет размерность времени и называется постоянной времени электрической цепи. Постоянная времени показывает, через какое время после начала разрядки конденсатора напряжение уменьшается в e раз (е=2,71).

Теория метода

Прологарифмируем выражение (7):

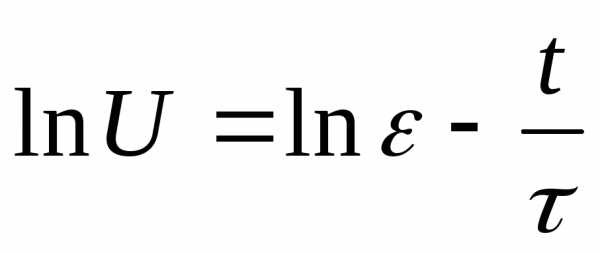(учли, что RC=τ).

График зависимости lnU от t (линейная зависимость) выражается прямой линией (рис.5), пересекающей ось y (lnU) в точке с координатами (0; lnε). Угловой коэффициент К этого графика и будет определять постоянную времени цепи: 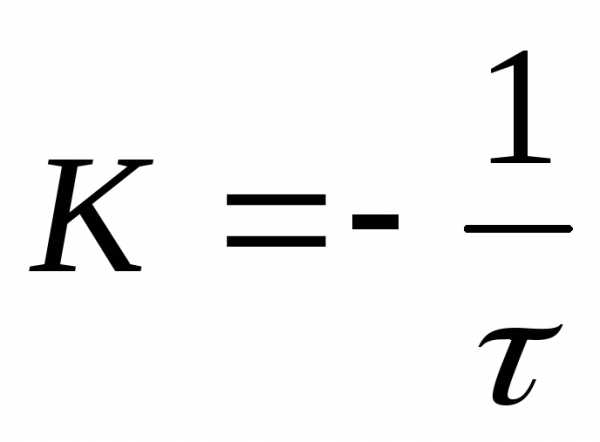,откуда:

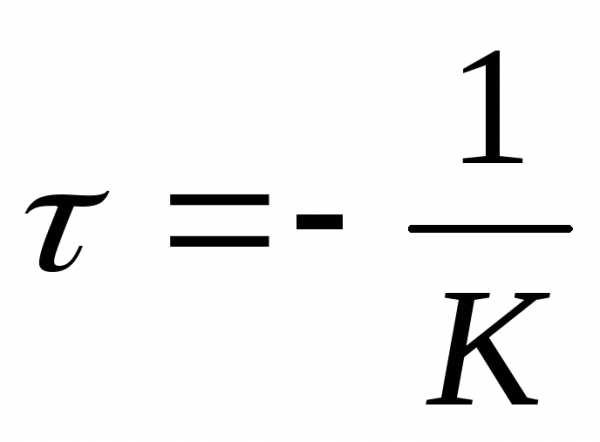. (9)

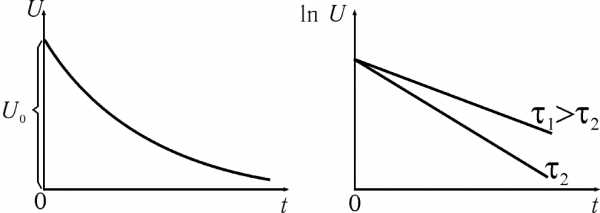
Рис. 5. Зависимость натурального логарифма напряжения от времени при разрядке конденсатора

Используя формулы: 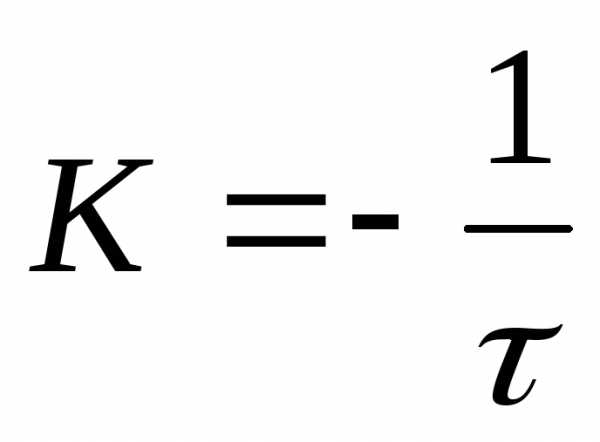и 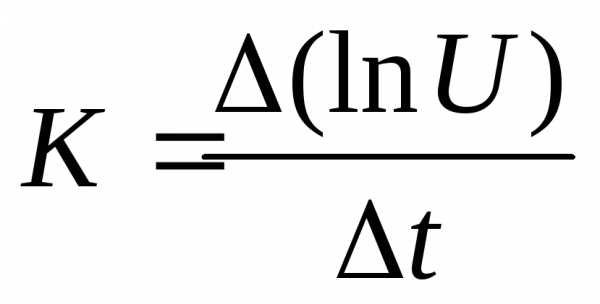,можно получить, что для одного и того же интервала времени : .

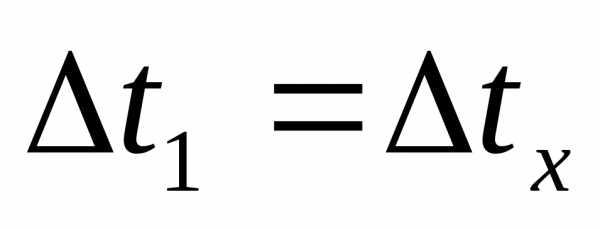Отсюда: 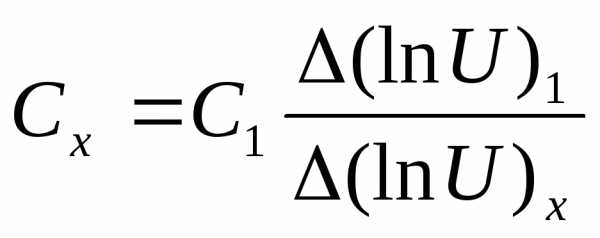.(10)

Экспериментальная установка

Установка состоит из основного блока – измерительного модуля, имеющего клеммы для подключения дополнительных элементов, источника питания, цифрового мультиметра и набора минимодулей с различными значениями сопротивления и емкости.

Для выполнения работы собирается электрическая цепь в соответствии со схемой, изображенной на верхней панели модуля. В гнезда «R1» подключается минимодуль с номиналом 1Мом, в гнезда «R2»- минимодуль с номиналом 100Ом. Параметры исследуемого конденсатора, подключаемого в гнезда «С», задаются преподавателем. В гнезда подключения амперметра устанавливается перемычка. В гнезда вольтметра подключается цифровой мультиметр в режиме вольтметра.

Следует отметить, что сопротивления резисторов заряда-разряда (минимодулей) R и цифрового вольтметра RV образуют делитель напряжения, что приводит к тому, что фактически максимальное напряжение на конденсаторе будет равно не ε, а ,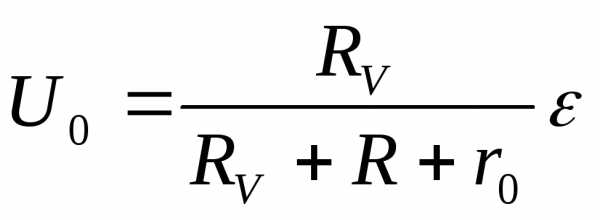

где r0- сопротивление источника питания. Соответствующие поправки необходимо будет вносить и при вычислении постоянной времени. Однако, если входное сопротивление вольтметра (107Ом) значительно превышает сопротивление резисторов, и сопротивление источника мало, то данными поправками можно пренебречь.

Порядок выполнения работы

1. Собрать электрическую цепь с заданным преподавателем значением емкости. Тумблер (переключатель заряда-разряда) установить в среднее положение (стоп). Переключатель предела измерения цифрового мультиметра установить в положение «20В» (режим измерения постоянного напряжения).

2. Подключить модуль к сети переменного тока (клавиша включения на задней панели модуля) и установить выходное напряжение , заданное преподавателем (6,5В-15В). Включить цифровой мультиметр. Нажатием кнопки «Сброс» подготовить модуль к началу измерений.

3. Тумблер перевести в положение «Заряд». При этом запускается секундомер, и начинает меняться напряжение на конденсаторе (показания вольтметра). Довести напряжение на конденсаторе до значения примерно 0,8ε.

4. Сбросить показания секундомера нажатием кнопки «Сброс». Перевести тумблер в положение «Разряд» и измерять напряжения на конденсаторе при его разрядке с интервалом времени 5с. Занести данные в таблицу 1.

5. Подключить в цепь конденсатор с неизвестным значением емкости и повторить измерения по п. 4. Данные занести в таблицу 2.

6. Подключить в цепь конденсатор и резистор с другим известным значением емкости. Повторить измерения по п. 4. Данные занести в таблицу 3.

7. Нажать кнопку «Сброс». Выключить источник питания и мультиметр. Отключить от сети измерительный модуль и отсоединить от него дополнительные элементы.

Таблица 1

ε= В, R1= Ом, , С1= Ф
Разрядка	t (с)
	U (В)
	lnU
τ1±Δτ1 (с)

Таблица 2

ε= В, R1= Ом, Сх=? Ф
Разрядка	t (с)
	U (В)
	lnU
τх±Δτх (с)
Сх±ΔСх (Ф)

Таблица 3

ε= В, R2= Ом, С2 = Ф
Разрядка	t (с)
	U (В)
	lnU
τ2±Δτ2 (с)

Обработка результатов измерения

По результатам измерений студенты выполняют одно из следующих заданий (по указанию преподавателя).

Задание 1. Построение кривых разрядки конденсаторов и экспериментальное подтверждение закона, описывающего данный процесс.

1. Используя данные, взятые из таблиц 1 и 3, постройте графики зависимости напряжения от времени при разрядке конденсаторов С1и С2. Проанализируйте их, сравните с теоретическими (рис. 4).

2. Постройте графики разрядки конденсаторов С1и С2 в осях (lnU, t). Проанализируйте их, сравните с теоретическими (рис. 5).

3. Определите по графикам угловые коэффициенты К1и К2. Среднее значение углового коэффициента находится как отношение, определяющее тангенс угла наклона прямой:

.

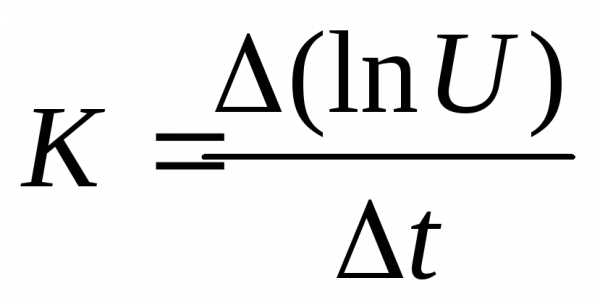4. Случайные погрешности графическим методом можно оценить по отклонению опытных точек относительно проведенной прямой. Относительная погрешность углового коэффициента может быть найдена согласно формуле:

,

где δ(lnU) – отклонение (в проекции на ось lnU) от прямой линии наиболее удаленной опытной точки, - интервал, на котором сделаны измерения.

5. По значениям угловых коэффициентов определите постоянные времени τ1 и τ2, используя формулу (9). Сравните полученные значения со значениями постоянной времени, рассчитанными по формуле (8).

6. Посчитайте относительные и абсолютные погрешности для постоянной времени: ,.

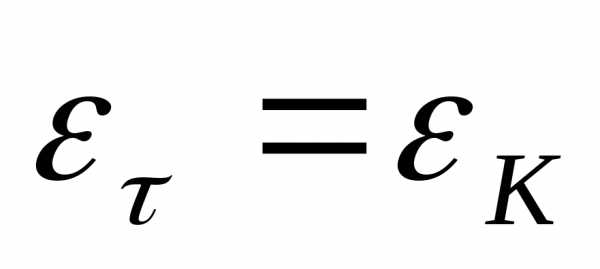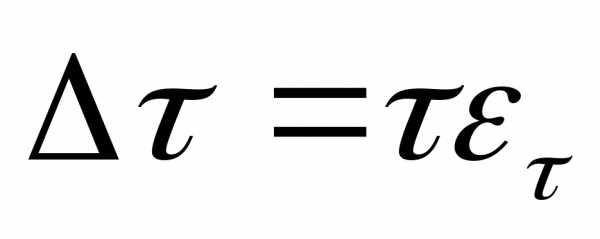7. Сделайте выводы о соответствии экспериментальных графиков экспоненциальному виду зависимости напряжения от времени, и о влиянии постоянной времени на протекание процессов зарядки и разрядки конденсатора.

Задание 2. Определение неизвестной емкости конденсатора.

1. Используя данные, взятые из таблиц 1 и 2, постройте графики зависимости напряжения от времени при разрядке конденсаторов С1 и Сх. Проанализируйте их, сравните с теоретическими (рис. 4).

2. Постройте графики разрядки конденсаторов С1 и Сх в осях (lnU, t). Сравните их и сделайте вывод о соотношении постоянных времени (см. рис.5).

3. Определите по формуле (10) неизвестную емкость, используя графики и данные таблиц 1 и 2.

4. Найдите относительные погрешности угловых коэффициентов εК1 и εкх(см. п.4 задания 1).

5. Определите относительную и абсолютную погрешности емкости:

, .

6. Сравните полученное значение Сх со значением, измеренным при помощи цифрового мультиметра в режиме измерения емкости. Сделайте вывод.

Дополнительное задание.

Рассчитайте энергию заряженного конденсатора, используя формулу (5).

Контрольные вопросы

1. Что представляет собой конденсатор? Что называется емкостью конденсатора?

2. Докажите, что электрическое поле плоского конденсатора сосредоточено между его обкладками.

2. Сколько надо взять конденсаторов емкостью 2мкФ и как их соединить,

чтобы получить общую емкость 5 мкФ?

3. Как можно найти энергию заряженного конденсатора?

4. Какие токи называются квазистационарными? Почему токи зарядки и разрядки конденсатора можно отнести к квазистационарным?

5. По какому закону изменяется напряжение на конденсаторе в процессах а) зарядки и б) разрядки?

6. Что показывает постоянная времени цепи? От чего она зависит?

7. Зачем в данной работе строится график зависимости lnU от t?

8. Как в данной работе определяется постоянная времени электрической цепи?

ЛИТЕРАТУРА

1.Трофимова Т.И. Курс физики. / Т.И. Трофимова. - М.: Высшая школа, 2006-2009 г. г. – 544с.

2 Савельев И.В. Курс физики. В 3-х томах. Том 2. Электричество. Колебания и волны. Волновая оптика. Изд. 3-е, стереотип. / И.В. Савельев - М.: Лань, 2007. - 480 с.

3. Грабовский Р. И. Курс физики / Р.И. Грабовский - СПб: издательство «Лань», 2012. – 608с.

4 Зисман Г. А., Тодес О. М. Курс общей физики. В 3-х томах. Том 2. Электричество и магнетизм / Г.А. Зисман, О.М. Тодес - СПб: «Лань», 2007. - 352c.

Концевой титул

Учебное издание

Составитель:

Плотникова Ольга Васильевна

ИЗУЧЕНИЕ ПРОЦЕССОВ ЗАРЯДКИ И РАЗРЯДКИ КОНДЕНСАТОРА. ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА

Учебно-методическое пособие к лабораторной работе № 3.3 по дисциплине «Физика»

В авторской редакции

Компьютерная верстка

Подписано в печать

Формат 60х84/16. Усл.печ.л. Уч.-изд.л.

Тираж экз. Заказ

Дальневосточный федеральный университет

690091, г. Владивосток, ул. Суханова, 8

Отпечатано на кафедре общей физики ШЕН ДВФУ

690091, г. Владивосток, ул. Суханова, 8

studfiles.net

Конденсатор и RC цепочка | Электроника для всех

Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.  

О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности: 

Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома — I=U/R, где U напряжение на выводах резистора, R — его сопротивление. 

Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.  

Чтобы визуализировать себе этот процесс, представь ган… эмм.. воздушный шарик который наполняется водой. Поток воды — это ток. Давление воды на упругие стенки — эквивалент напряжения. Теперь смотри, когда шарик пуст — вода втекает свободно, большой ток, а давления еще почти нет — напряжение мало. Потом, когда шарик наполнится и начнет сопротивляться давлению, за счет упругости стенок, то скорость потока замедлится, а потом и вовсе остановится — силы сравнялись, конденсатор зарядился. Есть напряжение натянутых стенок, но нет тока!  

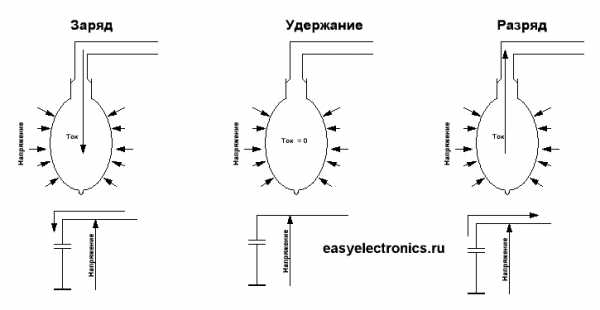Теперь, если снять или уменьшить внешнее давление, убрать источник питания, то вода под действием упругости хлынет обратно. Также и ток из конденсатора потечет обратно если цепь будет замкнута, а напряжение источника ниже чем напряжение в конденсаторе.  

Емкость конденсатора. Что это?Теоретически, в любой идеальный конденсатор можно закачать заряд бесконечного размера. Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление.А что же тогда насчет Фарад, что пишут на боку конденсатора в качестве показателя емкости? А это всего лишь зависимость напряжения от заряда (q = CU). У конденсатора малой емкости рост напряжения от заряда будет выше. 

Представь два стакана с бесконечно высокими стенками. Один узкий, как пробирка, другой широкий, как тазик. Уровень воды в них — это напряжение. Площадь дна — емкость. И в тот и в другой можно набузолить один и тот же литр воды — равный заряд. Но в пробирке уровень подскочит на несколько метров, А в тазике будет плескаться у самого дна. Также и в конденсаторах с малой и большой емкостью.Залить то можно сколько угодно, но напряжение будет разным.  

Плюс в реале у конденсаторов есть пробивное напряжение, после которого он перестает быть конденсатором, а превращается в годный проводник :)  

А как быстро заряжается конденсатор?В идеальных условиях, когда у нас бесконечно мощный источник напряжения с нулевым внутренним сопротивлением, идеальные сверхпроводящие провода и абсолютно безупречный конденсатор — этот процесс будет происходить мгновенно, с временем равным 0, равно как и разряд.  

Но в реальности всегда существуют сопротивления, явные — вроде банального резистора или неявные, такие как сопротивление проводов или внутреннее сопротивление источника напряжения.В этом случае скорость заряда конденсатора будет зависить от сопротивлений в цепи и емкости кондера, а сам заряд будет идти по экспоненциальному закону. 

 

А у этого закона есть пара характерных величин:

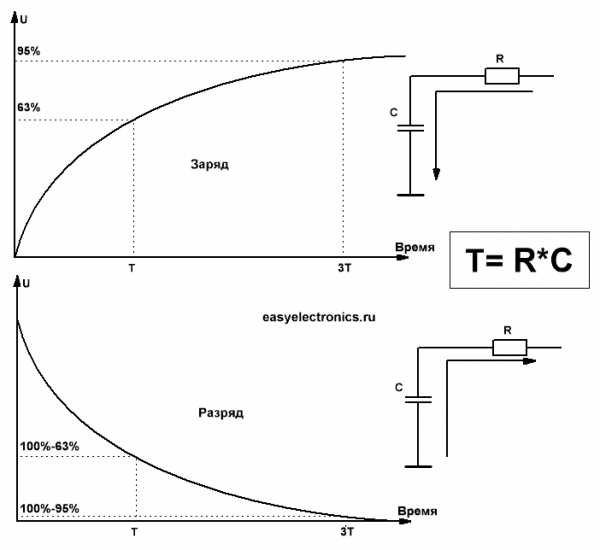
• Т — постоянная времени, это время при котором величина достигнет 63% от своего максимума. 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUET=max—1/e*max.
• 3T — а при троекратной постоянной значение достигнет 95% своего максимума.

 

Постоянная времени для RC цепи Т=R*C.  

Чем меньше сопротивление и меньше емкость, тем быстрей конденсатор заряжается. Если сопротивление равно нулю, то и время заряда равно нулю.  

Рассчитаем за сколько зарядится на 95% конденсатор емкостью 1uF через резистор в 1кОм:T= C*R = 10-6 * 103 = 0.001c3T = 0.003c через такое время напряжение на конденсаторе достигнет 95% от напряжения источника.  

Разряд пойдет по тому же закону, только вверх ногами. Т.е. через Твремени в на конденсаторе остаенется всего лишь 100% — 63% = 37% от первоначального напряжения, а через 3T и того меньше — жалкие 5%. 

Ну с подачей и снятием напряжения все ясно. А если напряжение подали, а потом еще ступенчато подняли, а разряжали также ступеньками? Ситуация тут практически не изменится — поднялось напряжение, конденсатор дозарядился до него по тому же закону, с той же постоянной времени — через время 3Т его напряжение будет на 95% от нового максимума.Чуть понизилось — подразрядился и через время 3Т напряжение на нем будет на 5% выше нового минимума.Да что я тебе говорю, лучше показать. Сварганил тут в мультисиме хитровыдрюченный генератор ступечнатого сигнала и подал на интегрирующую RC цепочку:

 

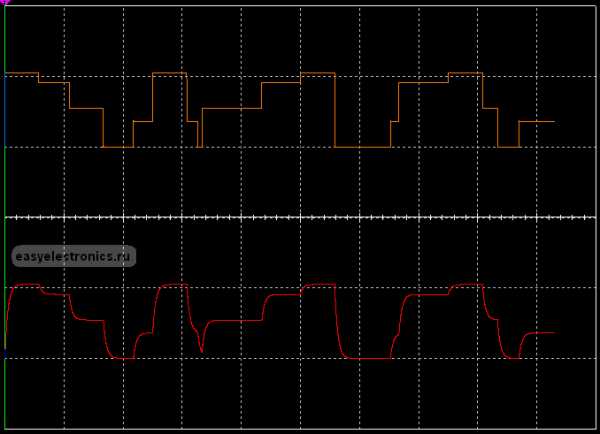Видишь как колбасится :) Обрати внимание, что и заряд и разряд, вне зависимости от высоты ступеньки, всегда одной длительности!!! 

А до какой величины конденсатор можно зарядить? В теории до бесконечности, этакий шарик с бесконечно тянущимися стенками. В реале же шарик рано или поздно лопнет, а конденсатор пробьет и закоротит. Вот поэтому у всех конденсаторов есть важный параметр — предельное напряжение. На электролитах его часто пишут сбоку, а на керамических его надо смотреть в справочниках. Но там оно обычно от 50 вольт. В общем, выбирая кондер надо следить, чтобы его предельное напряжение было не ниже того которое в цепи. Добавлю что при расчете конденсатора на переменное напряжение следует выбирать предельное напряжение в 1.4 раза выше. Т.к. на переменном напряжении указывают действующее значение, а мгновенное значение в своем максимуме превышает его в 1.4 раза.  

Что следует из вышеперечисленного? А то что если на конденсатор подать постоянное напряжение, то он просто зарядится и все. На этом веселье закончится. 

А если подать переменное? То очевидно, что он будет то заряжаться, то разряжаться, а в цепи будет туда и обратно гулять ток. Движуха! Ток есть! 

Выходит, несмотря на физический обрыв цепи между обкладками, через конденсатор легко протекает переменный ток, а вот постоянному слабо.  

Что нам это дает? А то что конденсатор может служить своего рода сепаратором, для разделения переменного тока и постоянного на соответствующие составляющие.  

Любой изменяющийся во времени сигнал можно представить как сумму двух составляющих — переменной и постоянной.

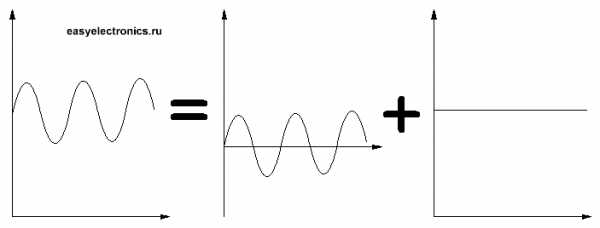Например, у классической синусоиды есть только переменная часть, а постоянная равна нулю. У постоянного же тока наоборот. А если у нас сдвинутая синусоида? Или постоянная с помехами? 

Переменная и постоянная составляющие сигнала легко разделяются!Чуть выше я тебе показал как конденсатор дозаряжается и подразряжается при изменениях напряжения. Так что переменная составляющая сквозь кондер пройдет на ура, т.к. только она заставляет конденсатор активно менять свой заряд. Постоянная же как была так и останется и застрянет на конденсаторе.  

Но чтобы конденсатор эффективно разделял переменную составляющую от постоянной частота переменной составляющей должна быть не ниже чем 1/T 

Возможны два вида включения RC цепочки:Интегрирующая и дифференцирующая. Они же фильтр низких частот и фильтр высоких частот. 

Фильтр низких частот без изменений пропускает постоянную составляющую (т.к. ее частота равна нулю, ниже некуда) и подавляет все что выше чем 1/T. Постоянная составляющая проходит напрямую, а переменная составляющая через конденсатор гасится на землю.Такой фильтр еще называют интегрирующей цепочкой потому, что сигнал на выходе как бы интегрируется. Помнишь что такое интеграл? Площадь под кривой! Вот тут она и получается на выходе.  

Как здесь вычисляется постоянная составляющая? А с виду и не скажешь, но надо помнить, что любой периодически сигнал раскладывается в ряд Фурье, превращаясь в сумму из постоянной составляющей и пачки синусоид разной частоты и амплитуды.  

Фильтр высоких частот работает наоборот. Он не пускает постоянную составляющую (т.к. ее частота слишком низка — 0) — ведь конденсатор для нее равносилен обрыву, а вот переменная пролазит через кондер без проблем.

А дифференцирующей цепью ее называют потому, что на выходе у нас получается дифференциал входной функции, который есть не что иное как скорость изменения этой функции.

• На участке 1 происходит заряд конденсатора, а значит через него идет ток и на резисторе будет падение напряжения.
• На участке 2 происходит резкое увеличение скорости заряда, а значит и ток резко возрастет, а за ним и падение напряжения на резисторе.
• На участке 3 конденсатор просто удерживает уже имеющийся потенциал. Ток через него не идет, а значит на резисторе напряжение тоже равно нулю.
• Ну и на 4м участке конденсатор начал разряжаться, т.к. входной сигнал стал ниже чем его напряжение. Ток пошел в обратную сторону и на резисторе уже отрицательное падение напряжения.

А если подать на вход прямоугольнй импульс, с очень крутыми фронтами и сделать емкость конденсатора помельче, то увидим вот такие иголки:

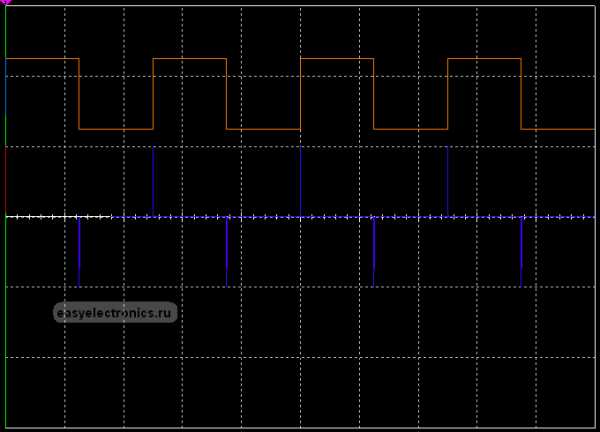Вверху идет осциллограма того что на входе, внизу то что на выходе дифференциальной цепи.Как видишь, тут мощные всплески на фронтах. Оно и понятно, в этом месте функция меняется резко, а значит производная (скорость изменения) этой функции велика, на пологих участках сигнал константа и его производная, скорость изменения, равна нулю — на графике ноль.  

А если загнать в дифференциатор пилу, то на выходе получим…

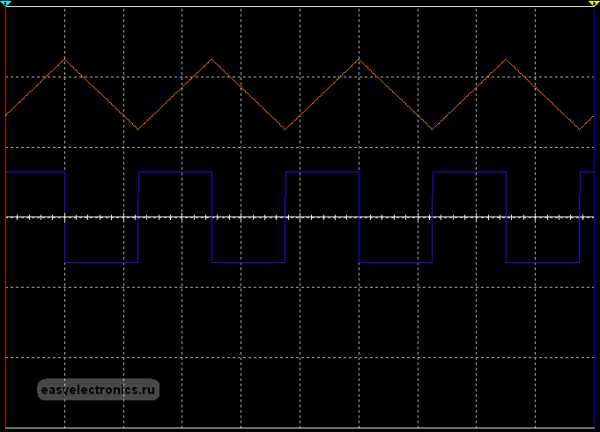прямоугольник. Ну, а чо? Правильно — производная от линейной функции есть константа, наклон этой функции определяет знак константы.  

Короче, если у тебя сейчас идет курс матана, то можешь забить на богомерзкий Mathcad, отвратный Maple, выбросить из головы матричную ересь Матлаба и, достав из загашников горсть аналоговой рассыпухи, спаять себе истинно ТРУЪ аналоговый компьютер :) Препод будет в шоке :) 

Правда на одних только резисторах кондерах интеграторы и диффернциаторы обычно не делают, тут юзают операционные усилители. Можешь пока погуглить на предмет этих штуковин, любопытная вещь :)  

А вот тут я подал обычный приямоугольный сигнал на два фильтра высоких и низких частот. А выходы с них на осциллограф:

И вот что получилось на осциллографе:

Вот, чуть покрупней один участок:

>

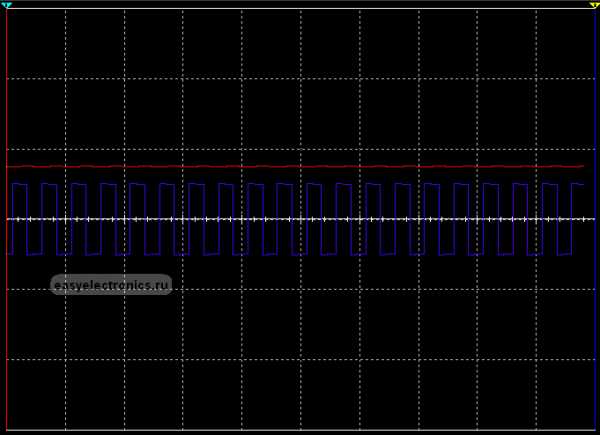Как видишь, на одном срезало постоянную составляющую, на другом переменную.  

Ладно, что то мы отвлеклись от темы.  

Как еще можно применить RC цепь?Да способов много. Часто ее используют не только в качестве фильтров, но и как формирователи импульсов. Например, на сбросе контроллера AVR, если надо чтобы МК стартанул не сразу после включения питания, а с некоторой выдержкой:

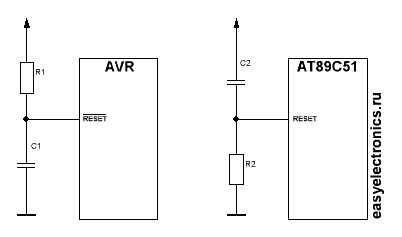При старте кондер разряжен, ток через него вваливат на полную, а напряжение на нем мизерное — на входе RESET сигнал сброса. Но вскоре конденсатор зарядится и через время Т его напряжение будет уже на уровне логической единицы и на RESET перестанет подаваться сигнал сброса — МК стартанет.А для AT89C51 надо с точностью наоборот RESET организовать — вначале подать единицу, а потом ноль. Тут ситуация обратная — пока кондер не заряжен, то ток через него течет большой, Uc — падение напряжения на нем мизерное Uc=0. А значит на RESET подается напряжение немногим меньше напряжения питания Uпит-Uc=Uпит.Но когда кондер зарядится и напряжение на нем достигнет напряжения питания (Uпит=Uс), то на выводе RESET уже будет Uпит-Uc=0  

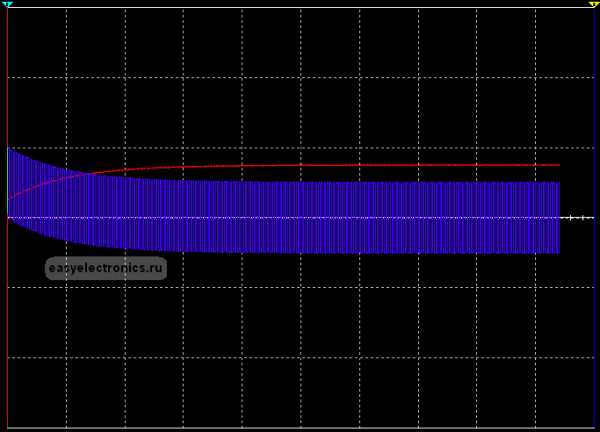
Аналоговые измеренияНо фиг сними с цепочками сброса, куда прикольней использовать возможность RC цепи для замера аналоговых величин микроконтроллерами в которых нет АЦП.Тут используется тот факт, что напряжение на конденсаторе растет строго по одному и тому же закону — экспоненте. В зависимости от кондера, резистора и питающего напряжения. А значит его можно использовать как опорное напряжение с заранее известными параметрами.  

Работает просто, мы подаем напряжение с конденсатора на аналоговый компаратор, а на второй вход компаратора заводим измеряемое напряжение. И когда хотим замерить напряжение, то просто вначале дергаем вывод вниз, чтобы разрядить конденсатор. Потом возвращем его в режим Hi-Z, cбрасываем и запускаем таймер. А дальше кондер начинает заряжаться через резистор и как только компаратор доложит, что напряжение с RC догнало измеряемое, то останавливаем таймер.

Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также зная сколько натикал таймер, мы можем довольно точно узнать чему было равно измеряемое напряжение на момент сработки компаратора. Причем, тут не обязательно считать экспоненты. На начальном этапе зарядки кондера можно предположить, что зависимость там линейная. Или, если хочется большей точности, аппроксимировать экспоненту кусочно линейными функциями, а по русски — отрисовать ее примерную форму несколькими прямыми или сварганить таблицу зависимости величины от времени, короче, способов вагон просто. 

Если надо заиметь аналоговую крутилку, а АЦП нету, то можно даже компаратор не юзать. Дрыгать ножкой на которой висит конденсатор и давать ему заряжаться через перменный резистор.  

По изменению Т, которая, напомню T=R*C и зная что у нас С = const, можно вычислить значение R. Причем, опять же необязательно подключать тут математический аппарат, в большинстве случаев достаточно сделать замер в каких-нибудь условных попугаях, вроде тиков таймера. А можно пойти другим путем, не менять резистор, а менять емкость, например, подсоединяя к ней емкость своего тела… что получится? Правильно — сенсорные кнопки!  

Если что то непонятно, то не парься скоро напишу статью про то как прикрутить к микроконтроллеру аналоговую фиговину не используя АЦП. Там подробно все разжую.  

Теперь, думаю, ты понял за что я так люблю RC цепочки и почему на моей отладочной плате PinBoard их несколько и с разными параметрами :) 

easyelectronics.ru

§6. Заряд и разряд конденсатора - Начало. Основы. - Справочник

§6. Заряд и разряд конденсатора

 

Чтобы зарядить конденсатор, надо, чтобы свободные электроны перешли из одной обкладки на другую. Переход электронов с одной обкладки конденсатора на другую происходит под действием напряжения источника по проводам, соединяющим этот источник с обкладками конденсатора.

В момент включения конденсатора зарядов на его обкладках нет и напряжение на нем равно нулю μс=0. Поэтому зарядный ток определяется внутренним сопротивлением источника rв и имеет наибольшую величину: 

IЗ max=E/ rв.

По мере накопления зарядов на обкладках конденсатора напряжение на нем увеличивается и падение напряжения на внутреннем сопротивлении источника будет равно разности ЭДС источника и напряжения на конденсаторе (Е- μс). следовательно, зарядный ток

iз=(Е- μс)/ rв.

Таким образом, с увеличением напряжения на конденсаторе ток заряда снизится и при μс=Е становится равным нулю. Процесс изменения напряжения на конденсаторе и тока заряда во времени изображен на рис. 1. В самом начале заряда напряжение на конденсаторе резко возрастает, так как зарядный ток имеет наибольшее значение и накопление зарядов на обкладках конденсатора происходит интенсивно. По мере повышения напряжения на конденсаторе зарядный ток уменьшается и накопление зарядов на обкладках замедляется. Продолжительность заряда конденсатора зависит от его емкости и сопротивления цепи, увеличение которых приводит к возрастанию продолжительности заряда. С увеличением емкости конденсатора, возрастает количество зарядов, накапливаемых на его пластинах, а если увеличить сопротивление цепи уменьшится и зарядный ток, а это замедляет процесс накопления зарядов на этих обкладках.

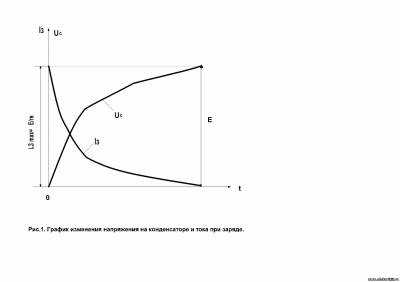
Если обкладки заряженного конденсатора подключить к какому-либо сопротивлению R, то за счет напряжения на конденсаторе будет протекать разрядный ток конденсатора. При разряде конденсатора электроны  с  одной пластины (при их избытке) будут переходить на другую (при их недостатке) и будет продолжается до тех пор, пока потенциалы обкладок не выравняются , т. е. напряжение на конденсаторе станет равным нулю. Изменение напряжения в процессе разряда конденсатора изображено на рис. 2. Ток разряда конденсатора пропорционален напряжению на конденсаторе (iр=μс/R), и его изменение во времени подобно изменению напряжения.

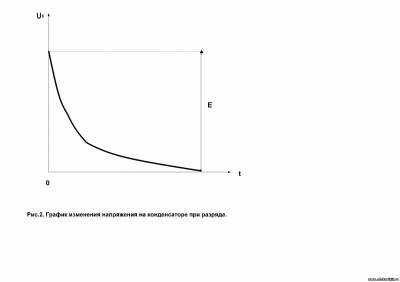
В начальный момент разряда напряжение на конденсаторе наибольшее (μс=Е) и разрядный ток максимальный (Iр max=E/R), так что разряд происходит быстро. При понижении напряжения, ток разряда снижается и процесс перехода зарядов с одной обкладки на другую затормаживается.

Время процесса разряда конденсатора зависит от сопротивления цепи и емкости конденсатора, причем возрастание как сопротивления, так и емкости увеличивает продолжительность разряда. С увеличением сопротивления разрядный ток снижается, замедляется процесс переноски зарядов с одной на другую обкладок; с увеличением емкости конденсатора повышается заряд на обкладках.

 Таким образом, в цепи, содержащей конденсатор, ток проходит только в процессе его заряда и разряда, т. е. когда напряжение на обкладках претерпевает изменение во времени. При постоянстве напряжения ток через конденсатор не проходит, т. е. конденсатор не пропускает постоянный ток, так как между его обкладками помещен диэлектрик и в результате этого цепь разомкнута.

При зарядке конденсатора, последний способен накапливать электрическую энергию, потребляя ее от энергоисточника. Накопленная энергия сохраняется определенное время. При разряде конденсатора эта энергия переходит к разрядному резистору, нагревая его, т. е. энергию электрического поля превращается в тепловую. Чем выше емкость конденсатора и напряжение на его обкладках, тем будет больше энергии, запасенной на нем. Энергия электрического поля конденсатора определяется следующим выражением

W=CU2/2.

Если конденсатор емкостью 100 мкФ заряжен до напряжения 200 В, то энергия, запасенная в электрическом поле конденсатора, W=100·10-6·2002/2=2 Дж.

www.elektrikii.ru

Поэтапный процесс зарядки и разрядки конденсатора. Схема. Ток зарядки

Итак, понятие конденсатора нами было уже введено. Включение конденсатора в цепь постоянного тока приводит к накоплению заряда на обкладках конденсатора. Однако между пластинками конденсатора находится воздух или иной диэлектрик, что говорит о том, что носитель заряда (в нашем случае, электрон) пройти от одной обкладки к другой не может. Но в итоге вся система становится заряженной. Попробуем разобраться как это происходит.

Рис. 1. Зарядка конденсатора

На рисунке 1 мы схематично видим конденсатор, подключённый в сеть постоянного тока. За счёт работы электростатического поля электрон «загоняется» на конденсатор (рис. 1.1). При этом он попадает на левую обкладку конденсатора (рис. 1.2). Обладая собственным электрическим полем, электрон выбивает другой электрон на правой обкладке конденсатора (рис. 1.3.), создавая на его месте остаточный положительный заряд (т.к. правая обкладка электронейтральна). Выбитый электрон уходит в цепь. Таким образом, через цепь проходит заряд равный заряду одного электрона, однако это не один и тот же электрон.

Тогда мы получаем суммарно нейтральную систему с разделённым зарядом на обкладках, равным по модулю и разным по знаку, т.е. систему, которую мы окрестили как конденсатор.

Поделиться ссылкой:

www.abitur.by

Заряд конденсатора постоянным током

Заряд конденсатора постоянным током

Присоединим цепь, состоящую из незаряженного конденсатора емкостью С и резистора с сопротивлением R, к источнику питания с постоянным напряжением U (рис. 16-4).

Так как в момент включения конденсатор еще не заряжен, то напряжение на нем Поэтому в цепи в начальный момент времени падение напряжения на сопротивлении R равно U и возникает ток, сила которого

Рис. 16-4. Зарядка конденсатора.

Прохождение тока i сопровождается постепенным накоплением заряда Q на конденсаторе, на нем появляется напряжение и падение напряжения на сопротивлении R уменьшается:

как и следует из второго закона Кирхгофа. Следовательно, сила тока

уменьшается, уменьшается и скорость накопления заряда Q, так как ток в цепи

С течением времени конденсатор продолжает заряжаться, но заряд Q и напряжение на нем растут все медленнее (рис. 16-5), а сила тока в цепи постепенно уменьшается пропорционально разности - напряжений

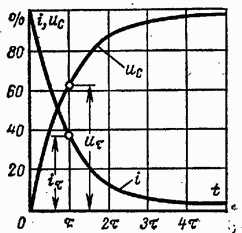
Рис. 16-5. График изменения тока и напряжения при зарядке конденсатора.

Через достаточно большой интервал времени (теоретически бесконечно большой) напряжение на конденсаторе достигает величины, равной напряжению источника питания, а ток становится равным нулю - процесс зарядки конденсатора заканчивается.

Процесс зарядки конденсатора тем продолжительней, чем больше сопротивление цепи R, ограничивающее силу тока, и чем больше емкость конденсатора С, так как при большой емкости должен накопиться больший заряд. Скорость протекания процесса характеризуют постоянной времени цепи

чем больше , тем медленнее процесс.

Постоянная времени цепи имеет размерность времени, так как

Через интервал времени с момента включения цепи, равный , напряжение на конденсаторе достигает примерно 63% напряжения источника питания, а через интервал процесс зарядки конденсатора можно считать закончившимся.

Напряжение на конденсаторе при зарядке

т. е. уменьшается по закону показательной функции (рис. 16-7).

Разрядный ток конденсатора

т. е. он, так же как и напряжение, уменьшается по тому же закону (рис. 6-7).

Вся энергия, запасенная при зарядке конденсатора в его электрическом поле, при разряде выделяется в виде тепла в сопротивлении R.

Электрическое поле заряженного конденсатора, отсоединенного от источника питания, не может долго сохраняться неизменным, так как диэлектрик конденсатора и изоляция между его зажимами обладают некоторой проводимостью.

Разряд конденсатора, обусловленный несовершенством диэлектрика и изоляции, называется саморазрядом. Постоянная времени при саморазряде конденсатора не зависит от формы обкладок и расстояния между ними.

Процессы зарядки и разряда конденсатора называются переходными процессами.

Заряд конденсатора

Для того чтобы зарядить конденсатор, необходимо включить его в цепь постоянного тока. На рис. 1 показана схема заряда конденсатора. Конденсатор С присоединен к зажимам генератора. При помощи ключа можно замкнуть или разомкнуть цепь. Рассмотрим подробно процесс заряда конденсатора.

Генератор обладает внутренним сопротивлением. При замыкании ключа конденсатор зарядится до напряжения между обкладками, равного э. д. с. генератора: Uс = Е. При этом обкладка, соединенная с положительным зажимом генератора, получает положительный заряд (+q ), а вторая обкладка получает равный по величине отрицательный заряд (-q ). Величина заряда q прямо пропорциональна емкости конденсатора С и напряжению на его обкладках: q = CUc

P ис. 1

Для того чтобы обкладки конденсатора зарядились, необходимо, чтобы одна из них приобрела, а другая потеряла некоторое количество электронов. Перенос электронов от одной обкладки к другой совершается по внешней цепи электродвижущей силой генератора, а сам процесс перемещения зарядов по цепи есть не что иное, как электрический ток, называемый зарядным емкостным током I зар.

Зарядный ток в цени протекает обычно тысячные доли секунды до тех пор, пока напряжение на конденсаторе достигнет величины, равной э. д. с. генератора. График нарастания напряжения на обкладках конденсатора в процессе его заряда представлен на рис. 2,а, из которого видно, что напряжение Uc плавно увеличивается, сначала быстро, а затем все медленнее, пока не станет равным э. д. с. генератора Е. После этого напряжение на конденсаторе остается неизменным.

Рис. 2. Графики напряжения и тока при заряде конденсатора

Пока конденсатор заряжается, по цепи проходит зарядный ток. График зарядного тока показан на рис. 2,б. В начальный момент зарядный ток имеет наибольшую величину, потому что напряжение на конденсаторе еще равно нулю, и по закону Ома io зар = E/ Ri , так как вся э. д. с. генератора приложена к сопротивлению Ri.

По мере того как конденсатор заряжается, т. е. возрастает напряженно на нем, для зарядного тока уменьшается. Когда напряженно па конденсаторе уже имеется, падение напряжения на сопротивление будет равно разности между э. д. с. генератора и напряжением на конденсаторе, т. е. равно Е - U с. Поэтому i зар = (E-Uс)/Ri

Отсюда видно, что с увеличением Uс уменьшается i зар и при Uс = E зарядный ток становится равным нулю.

Продолжительность процесса заряда конденсатора зависит от двух величии:

1) от внутреннего сопротивления генератора Ri ,

2) от емкости конденсатора С.

На рис. 2 показаны графики нарядных токов для конденсатора емкостью 10 мкф: кривая 1 соответствует процессу заряда от генератора с э. д. с. Е = 100 В и с внутренним сопротивлением Ri = 10 Ом, кривая 2 соответствует процессу заряда от генератора с такой же э. д. с, но с меньшим внутренним сопротивлением: Ri = 5 Ом.

Из сравнения этих кривых видно, что при меньшем внутреннем сопротивлении генератора сила нарядного тока в начальный момент больше, и поэтому процесс заряда происходит быстрее.

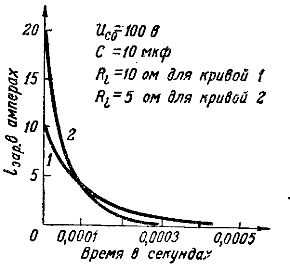
Рис. 2. Графики зарядных токов при разных сопротивлениях

На рис. 3 дается сравнение графиков зарядных токов при заряде от одного и того же генератора с э. д. с. Е = 100 В и внутренним сопротивлением Ri = 10 ом двух конденсаторов разной емкости: 10 мкф (кривая 1) и 20 мкф (кривая 2).

Величина начального зарядного тока io зар = Е/Ri = 100/10 = 10 А одинакова для обоих конденсаторов, по так как конденсатор большей емкости накапливает большее количество электричества, то зарядный его ток должен проходить дольше, и процесс заряда получается более длительным.

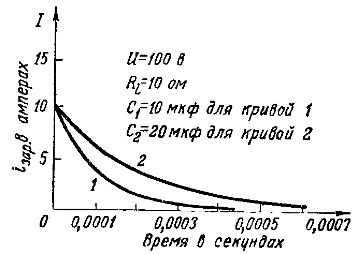
Рис. 3. Графики зарядных токов при разных емкостях

Разряд конденсатора

Отключим заряженный конденсатор от генератора и присоединим к его обкладкам сопротивление.

На обкладках конденсатора имеется напряжение U с, поэтому в замкнутой электрической цепи потечет ток, называемый разрядным емкостным током i разр.

Ток идет от положительной обкладки конденсатора через сопротивление к отрицательной обкладке. Это соответствует переходу избыточных электронов с отрицательной обкладки на положительную, где их недостает. Процесс рам ряда происходит до тех пор, пока потенциалы обеих обкладок не сравняются, т. е. разность потенциалов между ними станет равном нулю: Uc=0 .

На рис. 4, а показан график уменьшения напряжения на конденсаторе при разряде от величины Uc о =100 В до нуля, причем напряжение уменьшается сначала быстро, а затем медленнее.

На рис. 4,б показан график изменения разрядного тока. Сила разрядного тока зависит от величины сопротивления R и по закону Ома i разр = Uc /R

Рис. 4. Графики напряжения и токов при разряде конденсатора

В начальный момент, когда напряжение па обкладках конденсатора наибольшее, сила разрядного тока также наибольшая, а с уменьшением Uc в процессе разряда уменьшается и разрядный ток. При Uc=0 разрядный ток прекращается.

Продолжительность разряда зависит:

1) от емкости конденсатора С

2) от величины сопротивления R , на которое конденсатор разряжается.

Чем больше сопротивление R , тем медленнее будет происходить разряд. Это объясняется тем, что при большом сопротивлении сила разрядного тока невелика и величина заряда на обкладках конденсатора уменьшается медленно.

Это можно показать на графиках р

qptyt.ru

Электротехника :: Словарь :: Зарядный ток конденсатора

Краткий словарь по электротехнике

[ А, Б, В, Г, Д ]     [ Е, Ё, Ж, З, И ]     [ Й, К, Л, М, Н ]     [ О, П, Р, С, Т ]     [ У, Ф, Х, Ц, Ч ]     [ Ш, Щ, Ъ, Ы, Ь ]     [ Э, Ю, Я ]    

Зарядный ток конденсатора. Рассмотрим электрическую цепь, состоящую незаряженного конденсатора емкостью C, резистора с сопротивлением R, рубильника P и источника постоянного тока.

В момент включения конденсатор еще не заряжен и напряжение на нем UC=0. Падение напряжения на сопротивлении равно напряжению источника, сила тока i=U/R. Прохождение тока i сопровождается постеленным накоплением заряда Q на конденсаторе. Создается напряжение UC=Q/C, вследствие чего падение напряжения на резисторе R уменьшается iR=U-UC. Следовательно, сила тока в цепи равна i=(U-UC)/R и понижается с уменьшением скорости накопления заряда Q. Конденсатор продолжает заряжаться, но заряд и напряжение на нем растут все медленней, а сила тока уменьшается пропорционально разности U-UC.

Через промежуток времени (теоретически бесконечно большой) напряжение на конденсаторе достигнет величины источника питания, а ток станет равным нулю — процесс зарядки конденсатора заканчивается. Процесс зарядки считается законченным, когда ток уменьшился до 1% начального значения) или напряжение на конденсаторе достигло 99% напряжения источника питания U. Продолжительность процесса зарядки конденсатора зависит от сопротивления цепи R, ограничивающей силу тока, и емкости. При большей емкости накапливается больший заряд, скорость протекания процесса характеризуется постоянной времени цепи τ=RC. Через интервал времени τ с момента включения цепи напряжение на конденсаторе достигает примерно 63% напряжения источника U питания, а через интервал 5τ процесс зарядки конденсатора закончится. Напряжение на конденсаторе при зарядке равно UC=U-Ue-t/τ=U(1-e-t/τ), т. е. оно равно разности постоянного напряжения источника питания и напряжения Ue-t/τ, убывающего с течением времени по закону показательной функции от значения U до 0. Зарядный ток конденсатора равен величине iC=Ue-t/τ/R=Ie-t/τ и постепенно уменьшается от начального значения I=U/R по закону показательной функции.

www.goldcrocus.ru

Что скажите по схеме ограничения тока зарядка электролитического конденсатора?

После нескольких уточнений наконец выяснилось, чего же вы хотите добиться: общий источник питания для нескольких цепей последовательно включённых светодиодов. Главной проблемой вы сочли узел плавного заряда фильтрового конденсатора. На мой взгляд, в такой схеме есть несколько куда более критичных мест. Но сначала по теме вопроса.

1000 мкф - это значение подходяще для тока нагрузки 0,5...3 ампера, а не десятки миллиампер (там достаточно 22...50 мкф). Транзистор можно ставить, если надо сделать плавное, на 4...20 секунд, нарастание яркости - но ведь у вас несколько гирлянд! Неужели они должны во всей квартире стартовать одновременно? Да и насчёт выключателей - вы хотите вместо штатных, коммутирующих цепь ~220 вольт, коммутировать цепь =310 вольт, ставя выключатель между конденсатором и гирляндой? Такое решение выглядит хоть как-то оправданным для "умного дома" (да и то не всё в нём понятно), но в обычной квартире так делать смысла нет. В ней правильнее установить для каждой гирлянды свой отдельный БП - и тогда куда выгоднее применять обычные супердешёвые (и куда более надёжные!) ленты с параллельными светодиодами на 12 вольт, а не с самодельными последовательными, в которых выгорание одного диода полностью лишает вас света.Другое назначение узла плавного заряда - защита выпрямительных диодов от многократной перегрузки в момент включения, когда конденсатор полностью разряжен. Но эта задача полностью решается куда более простым методом - вместо T1 и R1, R3 надо вставить терморезистор сопротивлением в несколько десятков ом, снижающимся при прогреве до 0,5...3 ом, так сделано в сотнях миллионов компьютерных БП, надёжно работающих годами при примерно таком же токе нагрузки, как и у вас. Добыть такой термистор можно из любого дохлого компьютерного БП.

И наконец о том, чего в вашем вопросе нет, а оно бросается в глаза - о стабилизаторе тока на LM317, поглощающем излишек сетевого напряжения. Дело в том, что такой стаб работоспособен только в диапазоне от 3 до 40 вольт. Допуск на сетевое напряжение в городской исправной сети 10%, т.е. от 198 до 242 вольт. Значит, если вы рассчитали стаб на нижний предел (а так обычно и делается), то на верхнем пределе напряжение на стабе выйдет за допустимые 40 вольт. Если же вы настроите его на верх диапазона (т.е. на 242), то на нижнем пределе напряжение на стабе понизится ниже 3 вольт, и он перестанет стабилизировать ток. И я уж умолчу, что будет с этой схемой в сельской местности, где колебания сетевого напряжения куда шире. Так что такая схема будет нормально работать только при стабильном напряжении сети - но при стабильной сети стабилизатор не нужен, его прекрасно заменит простой резистор.

toster.ru

---

• 
  Какой бесперебойник для котла лучше
• 
  Антипаническое освещение
• 
  Справочник монтажника электрика
• 
  До какого числа передавать показания счетчиков воды в москве
• 
  Травма вызванная воздействием электрического тока называется
• 
  Ippon back comfo pro new 600 инструкция
• 
  Технология монтажа кабельных линий в земле
• 
  Схема логического элемента и
• 
  Основные средства защиты свыше 1000 вольт
• 
  Электротехнические работы это
• 
  Определение схема электроснабжения