Вектор магнитной индукции от чего зависит: Вектор магнитной индукции — основная характеристика магнитного поля — МАГНИТНОЕ ПОЛЕ

Модуль вектора магнитной индукции. Сила Ампера

Модуль вектора магнитной индукции. Сила Ампера

Подробности

Просмотров: 785

«Физика — 11 класс»

Магнитное поле действует с некоторой силой на проводник с током, а точнее на все элементы этого проводника.

В 1820 г. А. А м п е р сумел установить выражение для силы, действующей на отдельный элемент тока.

Позднее в память о заслугах А. Ампера выражение для магнитной силы, действующей на проводник с током со стороны магнитного поля, назвали законом Ампера.

Модуль вектора магнитной индукции

От чего зависит сила, действующая на проводник с током в магнитном поле?

Пусть свободно подвешенный горизонтально проводник находится в поле постоянного подковообразного магнита.

Поле магнита сосредоточено в основном между его полюсами, поэтому магнитная сила действует практически только на часть проводника длиной , расположенную между полюсами.

Сила направлена горизонтально, перпендикулярно проводнику и линиям магнитной индукции.

Сила достигает максимального значения _m, когда вектор магнитной индукции перпендикулярен проводнику.

Модуль вектора магнитной индукции определяется отношением максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока на длину этого отрезка:

Итак, в каждой точке магнитного поля можно определить направление вектора магнитной индукции и его модуль, если измерить силу, действующую на отрезок проводника с током.

Модуль силы Ампера.

В общем случае вектор магнитной индукции ожет составлять угол α с направлением отрезка проводника с током (с направлением тока).

Вектор магнитной индукции можно разложить на две составляющие.

Модуль силы зависит лишь от модуля составляющей вектора , перпендикулярной проводнику, т. е. от В_⊥ = В sin α, и не зависит от составляющей В, направленной вдоль проводника.

Закон Ампера для силы, действующей на участок проводника с током в магнитном поле:

F = I | | Δl sin α

Модуль силы Ампера равен произведению силы тока, модуля вектора магнитной индукции, длины отрезка проводника и синуса угла между направлениями вектора магнитной индукции и элемента тока.

Направление силы Ампера.

Направление силы Ампера определяется правилом левой руки:

Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец укажет направление силы, действующей на отрезок проводника.

Единица магнитной индукции.

За единицу модуля вектора магнитной индукции можно принять магнитную индукцию однородного поля, в котором на отрезок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила F_m = 1 Н.

Единица магнитной индукции равна

Единица магнитной индукции получила название тесла (Тл) в честь сербского ученого-электротехника Н. Тесла (1856—1943).

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Магнитное поле. Физика, учебник для 11 класса — Класс!ная физика

Магнитное поле и взаимодействие токов —
Магнитная индукция. Линии магнитной индукции —
Модуль вектора магнитной индукции. Сила Ампера —
Электроизмерительные приборы. Громкоговоритель —
Действие магнитного поля на движущийся заряд. Сила Лоренца —
Магнитные свойства вещества —
Примеры решения задач —
Краткие итоги главы

Направление вектора магнитной индукции

Магнитное поле характеризуют при помощи вектора магнитной индукции ().

Если свободно вращающуюся магнитную стрелку, которая является небольшим магнитом, обладающим полюсами (северным (N) и южным(S)), поместить в магнитное поле, то она будет поворачиваться до тех пор, пока не установится определённым образом.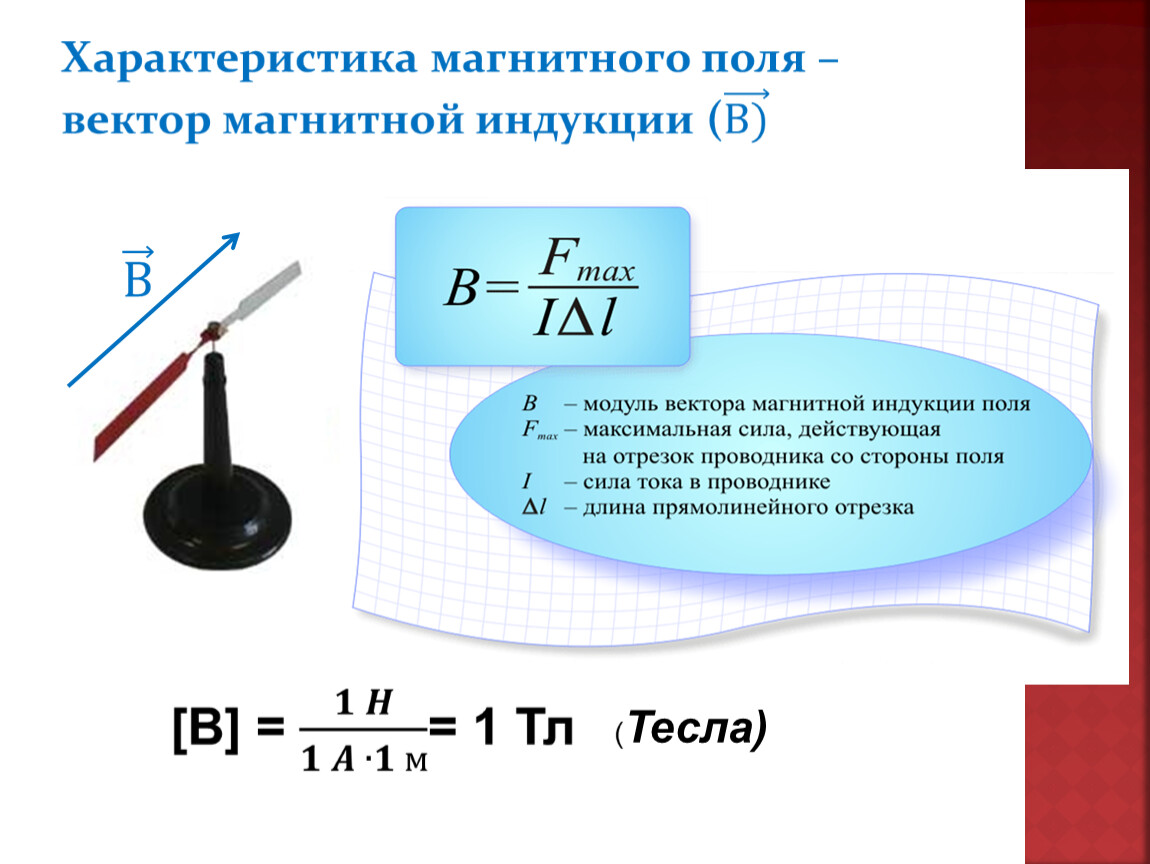 Аналогично ведет себя рамка с током, повешенная на гибком подвесе, имеющая возможность поворачиваться. Способность магнитного поля ориентировать магнитную стрелку используют для того, чтобы определить направление вектора магнитной индукции.

Направление вектора магнитной индукции

Так, направлением вектора магнитной индукции считают направление, которое указывает северный полюс магнитной стрелки, которая может свободно поворачиваться в магнитном поле.

Такое же направление имеет положительная нормаль к замкнутому контуру с током. Направление положительной нормали определяют при помощи правила правого винта (буравчика): положительная нормаль направлена туда, куда поступательно перемещался бы буравчик, если бы его головку вращали по направлению течения тока в контуре.

Применяя контур с током или магнитную стрелку, можно выяснить, как направлен вектор магнитной индукции магнитного поля в любой точке.

Для определения направления вектора иногда удобно использовать так называемое правило правой руки. Его применяют следующим образом. Пытаются в воображении охватить правой рукой проводник таки образом, чтобы при этом большой палец указывал направление силы тока, тогда кончики остальных пальцев направлены так же как вектор магнитной индукции.

Частные случаи направления вектора магнитной индукции прямого тока

Если магнитное поле в пространстве создается прямолинейным проводником с током, то магнитная стрелка будет в любой точке поля устанавливаться по касательной к окружностям, центры которых лежат на оси проводника, а плоскости перпендикулярны проводу. При этом направление вектора магнитной индукции определим, используя правило правого винта. Если винт вращать так, что он будет поступательно двигаться по направлению силы тока в проводе, то вращение головки винта совпадает с направлением вектора . На рис. 1 направлен от нас, перпендикулярно плоскости рисунка.

Ориентируясь на местности при помощи компаса, мы каждый раз проводим опыт по определению направления вектора Земного поля.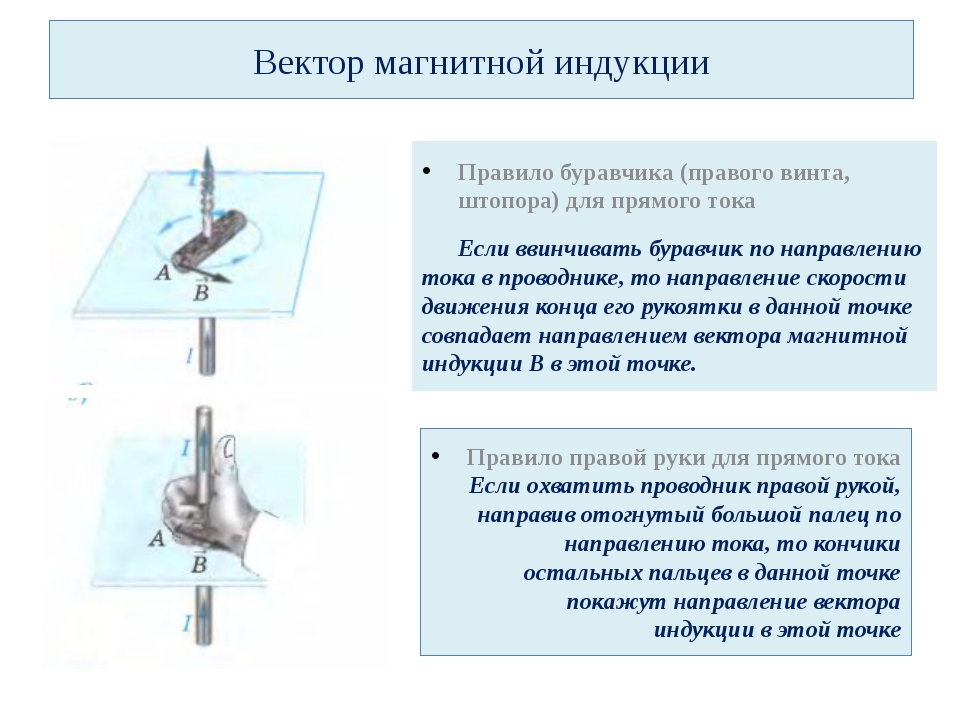

Пусть в магнитном поле движется заряженная частица, тогда на нее действует сила Лоренца (), которая определена как:

где q – заряд частицы; – вектор скорости частицы. Сила Лоренца и вектор магнитной индукции всегда взаимно перпендикулярны. Для заряда большего нуля (), тройка векторов и связана правилом правого винта (рис.2).

Линии магнитного поля и направление вектора B

Визуализировать картину магнитного поля можно при помощи линий магнитной индукции. Линиями магнитной индукции поля называют линий, для которых касательными в любой точке являются векторы магнитной индукции рассматриваемого поля. Для прямого проводника с током линиями магнитной индукции являются концентрические окружности, плоскости их перпендикулярны проводнику, центры на оси провода. Специфика линий магнитного поля заключена в том, что они бесконечны и являются всегда замкнутыми (или уходящими в бесконечность). Это означает, что магнитное поле является вихревым.

Принцип суперпозиции вектора B

Если магнитное поле создано не одним, а совокупностью токов или движущихся зарядов, то оно находится как векторная сумма отдельных полей, создаваемых каждым током или движущимся зарядом отдельно.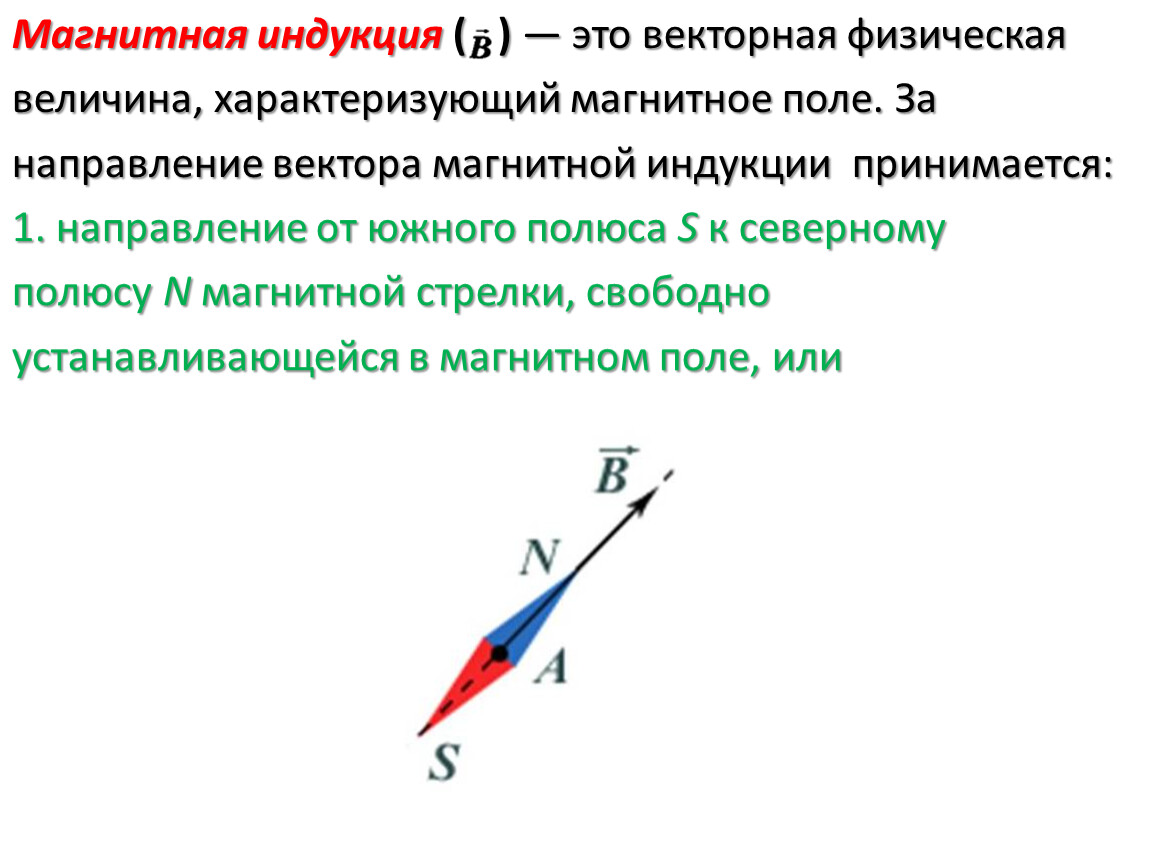 В виде формулы принцип суперпозиции записывают как:

Или:

Примеры решения задач

Вектор магнитной индукции

Качественно величину магнитного поля в данной области пространства можно характеризовать по густоте магнитных линий.

Для количественной характеристики поля вводится физическая величина вектор магнитной индукции.

Согласно экспериментальным данным сила, с которой магнитное поле действует на проводник с током, зависит от силы тока в проводнике (F ~ I), от длины проводника (F ~ Δl), от положения проводника относительно магнитных линий, а также от величины магнитного поля.

Отношение максимальной силы, действующей на проводник со стороны магнитного поля, к силе тока и длине проводника не будет зависеть от свойств проводника, а будет характеризовать только величину магнитного поля. Это отношение определяет модуль вектора магнитной индукции B:

В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера, равная 1 Н. Эта единица называется тесла (Тл).

Направление вектора магнитной индукции определяется как направление от южного полюса (S) к северному (N) магнитной стрелки, свободно устанавливающейся в магнитном поле. Другими словами, вектор магнитной индукции в каждой точке лежит на касательной к магнитной линии и совпадает по направлению с магнитной линией.

За направление вектора магнитной индукции принимают направление от южного полюса N к северному полюсу S магнитной стрелки, свободно устанавливающейся в магнитном поле.

Рамка с током в отсутствие силы упругости, препятствующей ориентации рамки, поворачивается до тех пор, пока не установится определённым образом. Таким образом, рамка ведёт себя как магнитная стрелка. Поэтому для определения направления вектора магнитной индукции можно использовать рамку с током: направление магнитной индукции совпадает с направлением положительной нормали к замкнутому контуру с током. Положительная нормаль направлена в ту сторону, куда перемещается буравчик с правой нарезкой, если вращать его по направлению тока в рамке.

Конспект урока «Модуль вектора магнитной индукции.

Сила Ампера.» (11 класс)

Урок 2/68

Тема урока: Модуль вектора магнитной индукции. Сила Ампера.

Класс: «11»

Тип урока: урок изучения нового материала

Методы изучения: объяснительно-иллюстративный с элементами эвристической беседы

Вид урока: урок-беседа.

Цель: Сформировать у учащихся понятие о модуле вектора магнитной индукции, понятие о силе Ампера, оценить уровень знаний учащихся по данной теме.

Задачи:

Образовательные:

1. Научить учащихся правильно определять модуль вектора магнитной индукции и силы Ампера.

2. Научить применять правило левой руки для определения направления силы Ампера.

3. Научить решать задачи по данной теме, учить применять знания на практике.

Воспитательные: формирование умения культуры общения (внимательно слушать друг друга, анализировать услышанное), умения работать коллективно и в парах.

Развивающие: Развитие физического мышления учащихся, расширение понятийного аппарата учащихся, формирование умений анализировать информацию, делать выводы из наблюдений и опытов.

Ход урока:

Организационный этап.

1 мин

-Здравствуйте, ребята, садитесь.

Ученики настраиваются на урок, проверяют домашнее задание.

Актуализация знаний.

8 мин

Проверяем домашнее задание с разбором у доски.

Упражнение 1

Задание №1

Задание №2

Какое явление рассматривается в задаче?

Как определить направление вектора магнитной индукции? По какому правилу?

Как определить направление вектора магнитной индукции внутри рамки с током?

Мотивационный этап.

3 мин

Мы с вами на прошлом уроке говорили, если частицы в проводнике двигаются, то вокруг проводника с током возникает магнитное поле – особый вид материи. Обнаружить магнитное поле можно либо с помощью проводника с током, магнитной стрелки или рамки с током. Магнитную стрелку разворачивает и за направление магнитного поля принимают направление указывающее северным концом стрелки свободно расположившейся в магнитном поле (никто не заставляет занят определенное положение, точнее ничто кроме магнитного поля). Магнитное поле описывается численно и направлением. Это векторная величина вектор магнитной индукции и направление поля это тоже самое что и направления вектора магнитной индукции В. Кроме того мы познакомились с графическим описанием магнитного поля – это линии магнитного поля. Прошлый урок мы говорили о направлении магнитного поля, то есть как определить направление вектора магнитной индукции. Сегодня мы поговорим о том, как описать, как найти модуль этого вектора(подробно).

Запишем тему урока.

Запись темы на доске: «Модуль вектора магнитной индукции. Сила Ампера»

Дом раб. №830-834 Сборник задач Рымкевич.

Изучение нового материала.

18 мин

Обратите внимание на рисунок:

Рисовать его не надо. Давайте то, что здесь нарисовано в трехмерной проекции, изобразим в пользуясь обозначениями (вниз, вверх, от нас, к нам, вправо, влево).

Магнитное поле на рисунке направлено сверху вниз. Ток течет по проводнику от нас. Направление силы Ампера определяется правилом левой руки.

Параллельно рассмотрим другой случай:

Направим проводник с током следующим образом. Магнитное поле сверху вниз. Ток течет вверх. В такой ситуации сила ампера будет равна нулю, т.е. не действует. А если перпендикулярно, то сила Ампера максимальна. Т.е. в данном случае 2 разных расположения проводника в магнитном поле.

А сейчас мы с вами будем говорить и выводить от чего зависит максимальное значение силы Ампера.

В данном случаи умозрительно можно получить результаты, которые мы запишем. 1. сила А ͂ силе тока в проводнике (представьте, что у вас здесь течет ток 2А и в направлении действует сила. А давайте проводник разрежем вдоль и у нас получится 2 проводника, по каждому из которых течет ток 1А. На каждый из этих проводников действует сила А., но если эти проводники складываем, то получится удвоение силы, т.е. сложим 2 проводника и получим ток в 2А и сумму 2х сил, действующих на каждый проводник, следовательно, данное утверждение работает.

Кроме того, максимальное значение, силы А˜длине, предполагается, что магнитное поле везде одинаковое, такое поле называется однородное. На каждый см. действует некоторая сила, если мы возьмем не 1 см, а 10 см проводника, то сила будет складываться, т.е. дает удесятеренное значение.

И наконец сила А ˜ Il, тогда от чего зависит коэффициент пропорциональности. Он зависит от того в каком магнитном поле находится проводник, в более сильном, там сила больше, или в более слабом, и сила меньше. Коэффициент пропорциональности зависит от величины поля, в котором находится проводник. Коэффициент пропорциональности обозначается буквой В.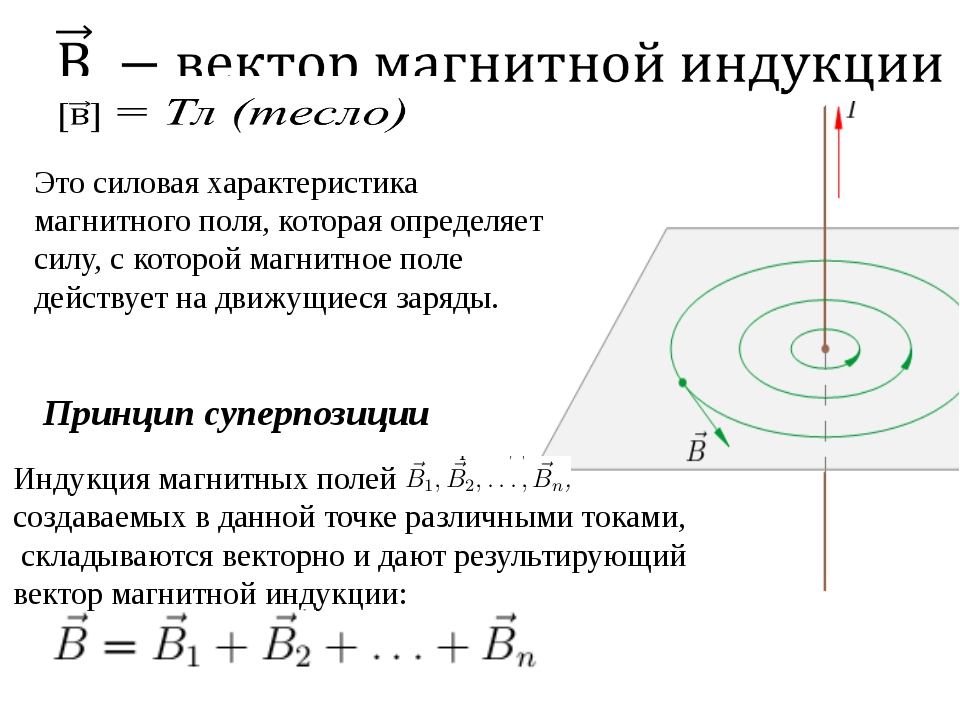

F_A=BIL

Следовательно модуль вектора магнитной индукции равен

В=F/IL

Модуль вектора магнитной индукции физическая величина равная отношению максимальной силы действующей на участке проводника со стороны магнитного поля к длине участка и силе тока в нем.

Модуль силы Ампера.

Пусть вектор магнитной индукции составляет угол α с направлением отрезка проводника с током (элементом тока). (За направление элемента тока принимают направление, в котором по проводнику идет ток.) Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает никакого действия на ток. (Показ опыта). Модуль силы зависит лишь от модуля составляющей вектора , перпендикулярной проводнику, т. е. от B_┴ = В sinα, и не зависит от составляющей B_II, направленной вдоль проводника.

Максимальная сила Ампера равна: ей соответствует угол α = . При произвольном значении угла α сила пропорциональна не В, а составляющей B_┴ = В sin α. Поэтому выражение для силы F, действующей на малый отрезок проводника Δ l, при силе тока в нем I, со стороны магнитного поля с индукцией В, составляющей с элементом тока угол, имеет вид

F = I │B│Δl sin α.

Это выражение называют законом Ампера. Сила Ампера равна произведению модуля силы тока, вектора магнитной индукции, длины отрезка проводника и синуса угла между направлениями векторов магнитной индукции и тока.

Запишем это.

Направление силы Ампера определяется правилом левой руки:

если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90⁰ большой палец укажет направление силы, действующей на отрезок проводника. Это правило справедливо во всех случаях.

Единица магнитной индукции. Мы ввели новую величину — вектор магнитной индукции. За единицу модуля вектора магнитной индукции можно принять магнитную индукцию однородного поля, в котором на отрезок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила F т = 1 Н. Согласно формуле единица магнитной индукции равна 1

Единица магнитной индукции получила название тесла (Тл) в честь югославского ученого-электротехника Н. Тесла (1856-1943).

Отвечают на вопросы, вступают в дискуссию, делают выводы, делают записи в тетрадях.

Действующая на проводник сила также увеличивается в 2 раза.

Сила при этом также увеличится в 2 раза.

Когда вектор магнитной индукции перпендикулярен проводнику.

Закрепление изученного материала

13 мин

Решим несколько задач:
см. Приложение 1

Решают на месте и у доски.

Задача 1

а)

б)

в)

г)

д)

е)

ж)

з)

Задача 2

В задаче рассматривается действия магнитного поля на проводник с током.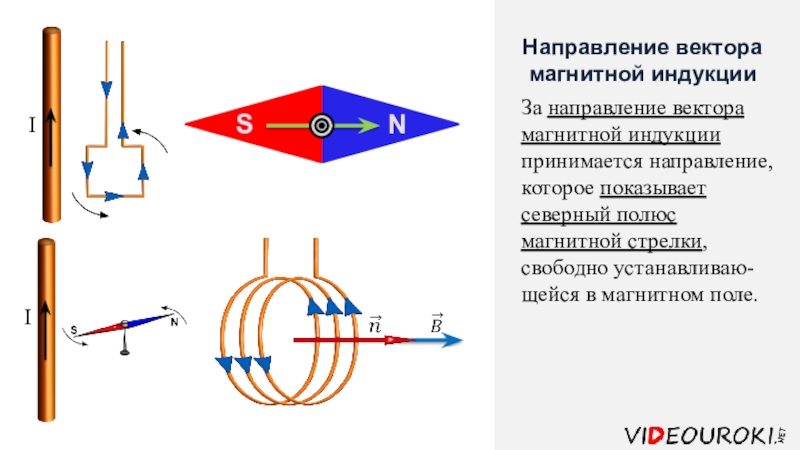 Вектор индукции магнитного поля находится из закона Ампера.

Задача 3

В задаче рассматривается действия магнитного поля и силы тяжести на проводник с током.

Задача 4

В задаче рассматривается работа источника тока при перемещении проводника на определенное расстояние.

Подведение итогов.

2 мин

Организуется беседа по выставлению и обоснованию отметок.

Выражают свое мнение по выставленным отметкам .

Вывод по уроку:

5. Резюме — Physics LibreTexts

5. Резюме — Physics LibreTexts
Перейти к основному содержанию

1. Последнее обновление

2. Сохранить как PDF

Без заголовков

1. Постоянные магниты имеют два конца, условно обозначенные северным и южным в зависимости от того, как они выравниваются с магнитным полем Земли. Магнитных монополей не существует; каждый магнит имеет северный и южный полюс.
2. Магнитное поле, или поле \(\mathbf{B}\), является векторным полем и указывает направление, в котором компас указывал бы на «север», если бы он был помещен в поле.
3. Электрический заряд чувствует силу в магнитном поле, только если заряд находится в движении. Величина силы задается \[| \mathbf{F} | = | д | |\mathbf{v}| |\mathbf{B}| |\sin\тета| = | д | |\mathbf{v}_{\perp}| |\mathbf{B}| \]Величина силы зависит от величины скорости , перпендикулярной к полю .\(|\mathbf{v}_{\perp} |=|\mathbf{v}| |\sin \theta|\) где \(\theta\) — угол между вектором поля и вектором скорости.
4. Движущиеся заряды также создают магнитные поля. Постоянные магниты испускают \(\mathbf{B}\) поля из-за коллективного движения электронов внутри них.
5. Мы изучили правило правой руки для нахождения направления силы, действующей на движущийся заряд в магнитном поле. Мы изучили правило правой руки для нахождения направления магнитного поля вокруг провода с током.
6. Можно индуцировать ток в цепи, изменяя поток поля \(\mathbf{B}\) через область, ограниченную цепью. Закон Фарадея гласит, что индуцированная ЭДС \(\mathcal{E}\) (напряжение) пропорциональна изменению потока во времени: \[\mathcal{E} = -N \dfrac{\Delta \Phi}{\Delta t}\]Закон Ленца гласит, что индуцированные токи текут в направлении, которое препятствует изменению потока.

Зависящий от времени вектор адиабатического магнитного поля B ( t ) восходит к …

Контекст 1

… движущаяся классическая заряженная частица подвергается действию силы Лоренца в магнитном поле и следует так называемому гиродвижению по винтовой орбите. В сильно замагниченной плазме быстрое гироскопическое движение частиц делает исследование замагниченной плазмы громоздким из-за смешения различных временных и пространственных масштабов. Магнитогидродинамика и традиционные теории гирокинетики решили исключить быстрое гиромиации путем усреднения гирофазной переменной, чтобы упростить задачу как для аналитических, так и для численных целей. Давая много важных результатов, эти гениальные методы игнорируют некоторую физику, переносимую гирофазой, которая иногда имеет решающее значение. Гирофаза выживает в современной гирокинетике, которая строго отделяет, а не устраняет гирофазу от других медленных компонентов динамики частиц. 1–3 Гирофаза вносит свой вклад во многие интересные явления, такие как плотность поляризации, сдвиговые альфвеновские волны и нагрев радиочастотными волнами. В гирокинетической теории мы начинаем обращать внимание на физику гирофазы, особенно на ее реакцию на высокочастотное электромагнитное поле.4–6 С другой стороны, гирофаза в медленно меняющихся магнитных полях имеет немалый физический смысл. В этой статье мы раскроем интересную физику гирофазы в адиабатически изменяющемся магнитном поле. Исследуется динамика гирофазы заряженной частицы в магнитном поле, однородном в пространстве, но медленно меняющемся во времени. Если магнитное поле не меняется со временем, то частица будет вращаться с постоянной угловой скоростью X 1/4 qB = m в плоскости, перпендикулярной магнитному полю, где q — электрический заряд, переносимый частицей, m — масса частицы, а B — величина магнитного поля. Гирофазу частицы в момент времени t можно легко записать как h ( t ) 1/4 qBt = m , учитывая, что h 1/4 0 при t 1/4 0. Поскольку магнитное поле медленно меняется со временем, изменение гирофаза оказывается состоящей из двух частей. Первая часть представляет собой динамическую фазу hd ð t Þ 1⁄4 Ð 0 t X d ð t 0 Þ dt 0 , которая представляет собой просто временной интеграл мгновенной угловой скорости X d ( t ) 1/4 qB ( t ) = m в результате действия силы Лоренца. Конечно, в этой динамичной фазе нет ничего удивительного. Интересно, что помимо фазы динамики гирофаза содержит еще одну часть h g , называемую геометрической фазой.Название происходит от его изящного геометрического смысла и его геометрического происхождения, некоммутативности операций вращения. 7 Если эволюция магнитного поля B(t) образует замкнутую петлю C в пространстве параметров, состоящем из (Bx,By,Bz), величина геометрической фазы равна телесному углу a, натянутому петлей С (см. рис. 1). Его значение зависит только от замкнутого пути C, а не от других физических составляющих, таких как масса частицы, скорость, скорость изменения поля и т. д.Эта геометрическая фаза, связанная с гирофазой, является примером общей геометрической фазы в физике. Еще в 1958 году Лайман Спитцер предвидел существование геометрической фазы, изучая преобразования вращения, и изобрел стелларатор Фигура-8. 8 В 1984 году Берри изучал квантовую адиабатическую систему. 9 Согласно адиабатической теореме, впервые введенной Борном и Фоком, 10 если начальное состояние системы является собственным состоянием ее начального гамильтониана, оно должно оставаться в соответствующем собственном состоянии мгновенного гамильтониана во время адиабатического процесса.Берри обнаружил, что помимо динамической фазы требуется дополнительный фазовый фактор, чтобы мгновенная собственная функция удовлетворяла уравнению Шедингера. Этот дополнительный фазовый фактор называется фазой Берри, которая является квантовой версией геометрической фазы. 9,11,12 Вскоре Ханней опубликовал свою классическую версию фазы Берри, известную как угол Ханнея. 13 Саймон изучал геометрическую фазу с точки зрения более абстрактной математики. 14 В 1988 г. Литтлджон исследовал геометрическую фазу, связанную с гиродвижением заряженной частицы в пространственно-неоднородном магнитном поле.15 В 1992 г. Бхаттачарджи и др. . указал на глубокую связь между геометрической фазой и изменением продольного инварианта среди различных типов орбит ведущего центра. 16 Все эти геометрические фазы имеют четкий геометрический смысл в пространстве, состоящем из адиабатических параметров окружающей среды. С тех пор геометрическая фаза стала интенсивно изучаться и стала играть важную роль почти во всех разделах физики. 17–19 Поэтому неудивительно, что геометрическая фаза находит свое применение в физике плазмы или, точнее, в гирофазе.Для сравнения с геометрической фазой, связанной с гиродвижением, мы также изучаем геометрическую фазу (фазу Берри) спиновой волновой функции электрона, помещенного в то же адиабатически изменяющееся магнитное поле. Мы используем уравнение Шедингера и представление Паули для получения спиновой волновой функции электрона. Фазовый фактор волновой функции, как и следовало ожидать, помимо динамической части имеет геометрическую часть, фазу Берри. Интересно обнаружить, что фаза Берри в волновой функции спина электрона имеет много общих свойств с геометрической фазой, связанной с гирофазой.Его величина равна половине телесного угла a, натянутого замкнутой петлей C в пространстве параметров. Эта фаза Берри зависит только от пути эволюции магнитного поля B(t) в пространстве параметров, как и в случае гиродвижения. Эти сходства, а также некоторые различия отражают связь между классической теорией и квантовой теорией и глубину геометрической фазы. Эта статья организована следующим образом. В разд. II мы изучаем геометрическую фазу, связанную с классическим гиродвижением.Начиная с уравнения Ньютона, гирофаза строго определяется с помощью преобразования гироцентра. После получения выражения геометрической фазы, связанной с гирофазой, изучаются ее интересные свойства. Обсуждаются его геометрические свойства в пространстве параметров, физическая наблюдаемость и выбор калибровки. В разд. III мы получаем фазу Берри электрона со спином 1 = 2 в том же зависящем от времени адиабатическом магнитном поле. Хотя геометрические фазы, связанные с гиродвижением и спином электрона, подчиняются совершенно разным динамическим правилам, они имеют много общего, что обсуждается в гл.IV. Сначала рассмотрим классическое движение заряженной частицы в зависящем от времени адиабатическом магнитном поле. Предполагается, что поле однородно в пространстве, но медленно меняется со временем. Эта простая модель сохраняет здесь всю важнейшую физику интереса, делая проблему разрешимой. Начнем с управляющего уравнения частицы …

Контекст 2

… C — замкнутая кривая, а S — поверхность, заключенная C в пространстве (B x , B y , B z ) (см. Рисунок 1). В конфигурационном пространстве определен телесный угол…

Магнитное поле и зависящая от угла фотолюминесценция алмаза, богатого вакансиями азота, связанного волокном: Журнал прикладной физики: Том 130, № 12 РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ ЗАКЛЮЧЕНИЕ И ПЕРСПЕКТИВЫДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛЛИТЕРАТУРААлмаз является материалом-основой одного из выдающихся объектов исследований в прикладной квантовой физике твердого тела в последнее десятилетие — отрицательно заряженного азотного вакансионного дефектного центра (НВ-центра).

Этот центр окраски проявляет поляризацию электронного спина в основное состояние |m=0⟩ при оптическом возбуждении ¹ 1. G.M.H. Thiering and A. Gali, Phys. B 98 , 085207 (2018). https://doi.org/10.1103/PhysRevB.98.085207 (схему уровней см. в дополнительном материале). Это позволяет когерентно управлять отдельными электронными спинами при комнатной температуре с временем когерентности в несколько миллисекунд. ² 2. N. Bar-Gill, L. Pham, A. Jarmola, D. Budker, and R. Walsworth, Nat.коммун. 4 , 45 (2013). https://doi.org/10.1038/ncomms2771 Таким образом, было достигнуто исследование фундаментальных проблем квантовой механики, таких как запутанность, и разработка высокочувствительных датчиков, основанных на квантовых свойствах или ядерной гиперполяризации. ^3–6 3. Д. Р. Гленн, Д. Б. Бучер, Дж. Ли, М. Д. Лукин, Х. Парк и Р. Л. Уолсворт, Nature 555 , 351 (2018). https://doi.org/10.1038/nature257814. Г. Баласубраманян, И. Ю. Чан, Р. Колесов, М. Аль-Хмуд, Дж.Тислер, К. Шин, К. Ким, А. Войцик, П. Р. Хеммер, А. Крюгер, Т. Ханке, А. Лейтенсторфер, Р. Брачич, Ф. Железко и Дж. Врахтруп, Nature 455 , 648 (2008 г.). ). https://doi.org/10.1038/nature072785. T. Wolf, P. Neumann, K. Nakamura, H. Sumiya, T. Ohshima, J. Isoya и J. Wrachtrup, Phys. Ред. X 5 , 041001 (2015 г.). https://doi.org/10.1103/PhysRevX.5.0410016. R. Wunderlich, J. Kohlrautz, B. Abel, J. Haase и J. Meijer, Phys. Ред. B 96 , 220407 (2017). https://дои.org/10.1103/PhysRevB.96.220407 Например, такие датчики широко использовались для получения магнитных изображений (анти)ферромагнитных материалов или для изучения скирмионов. ^7–11 7. Маккаллиан Б.А., Табт А.М., Грей Б.А., Мелендес А.Л., Вольф М.С., Сафонов В.Л., Пелехов Д.В., Бхалламуди В.П., Пейдж М.Р., Хаммель П.С., Nat. коммун. 11 , 453 (2020). https://doi.org/10.1038/s41467-020-19121-08. С. Фу, К. Кан, К. Шаян, А. Йошимура, С. Дадрас, С. Ван, Л. Чжан, С.Chen, N. Liu, A. Jindal, X. Li, A.N. Pasupathy, A.N. Vamivakas, V. Meunier, S. Strauf и E.-H. Ян, Нат. коммун. 11 , 777 (2020). https://doi.org/10.1038/s41467-019-13943-39. А. Финко, А. Хайкал, Р. Танос, Ф. Фабр, С. Шуайеб, В. Ахтар, И. Робер-Филип, В. Легран, Ф. Ажехас, К. Бузехуан, Н. Рейрен, Т. Деволдер, Ж.-П. Адам, Дж.-В. Kim, V. Cros и V. Jacques, Nat. коммун. 12 , 231 (2021). https://doi.org/10.1038/s41467-021-20995-x10. Ф. Фабр, А. Финко, А.Purbawati, A. Hadj-Azzem, N. Rougemaille, J. Coraux, I. Philip и V. Jacques, Phys. Преподобный Матер. 5 , 034008 (2021). https://doi.org/10.1103/PhysRevMaterials.5.03400811. I. Gross, W. Akhtar, A. Hrabec, J. Sampaio, L. J. Martinez, S. Chouaieb, B. J. Shields, P. Maletinsky, A. Thiaville, S. Rohart, and V. Jacques, Phys. Преподобный Матер. 2 , 024406 (2018). https://doi.org/10.1103/PhysRevMaterials.2.024406 Традиционный принцип измерения для этого известен как оптически детектируемый магнитный резонанс (ODMR) и основан на спин-зависимой оптической флуоресценции NV-центра. ^12,13 12. E. van Oort, N.B. Manson, and M. Glasbeek, J. Phys. C: Физика твердого тела. 21 , 4385 (1988). https://doi.org/10.1088/0022-3719/21/23/02013. П. Делани, Дж. К. Грир и Дж. А. Ларссон, Nano Lett. 10 , 610 (2010). https://doi.org/10.1021/nl

6p Измерения можно проводить как на ансамблях, так и на отдельных центрах окраски. Для измерения внешних полей, например магнитных, их целесообразно выполнять на ансамблях из-за более высокого отношения сигнал/шум (SNR~n, n — число зондирующих спинов).Однако обязательное использование микроволн вместе с соответствующим оборудованием и экспериментальными усилиями делает этот метод сложным и дорогостоящим. Во многих случаях более простой метод без микроволнового излучения гораздо более эффективен с точки зрения затрат и результатов. Из-за внешнего магнитного поля происходит зеемановское расщепление NV-подуровней. В общем случае это также приводит к смешению этих квантово-механических спиновых состояний. Это напрямую влияет на интенсивность фотолюминесценции (ФЛ) центров NV при оптическом возбуждении.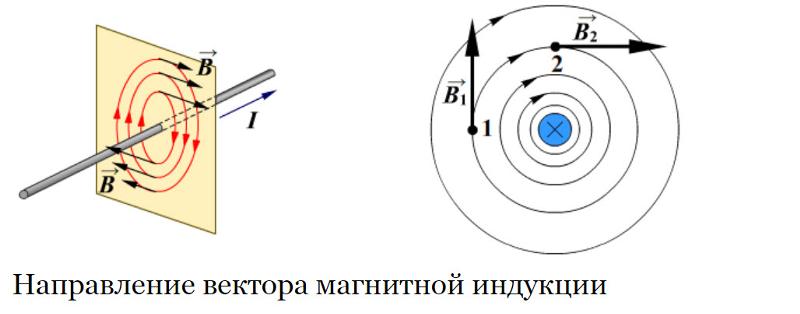 ¹⁴ 14. Ж.-П. Тетьен, Л. Ронден, П. Спиничелли, М. Шипо, Т. Дебюшерт, Ж.-Ф. Roch и V. Jacques, New J. Phys. 14 , 103033 (2012). https://doi.org/10.1088/1367-2630/14/10/103033 Соответственно, магнитное поле можно определить, измерив интенсивность ФЛ. ^15–17 15. A. Wickenbrock, H. Zheng, L. Bougas, N. Leefer, S. Afach, A. Jarmola, V.M. Acosta, and D. Budker, Appl. физ. лат. 109 , 053505 (2016). https://doi.org/10.1063/1.496017116.R. Staacke, R. John, R. Wunderlich, L. Horsthemke, W. Knolle, C. Laube, P. Glösekötter, B. Burchard, B. Abel и J. Meijer, Adv. Квантовая технология. 3 , 2000037 (2020). https://doi.org/10.1002/qute.20200003717. H. Zheng, Z. Sun, G. Chatzidrosos, C. Zhang, K. Nakamura, H. Sumiya, T. Ohshima, J. Isoya, J. Wrachtrup, A. Wickenbrock и D. Budker, Phys. Преподобный заявл. 13 , 044023 (2020). https://doi.org/10.1103/PhysRevApplied.13.044023 В отличие от схемы датчика на основе микроволн, чувствительность этого подхода без микроволнового излучения в основном ограничена шумом интенсивности лазера, электронным шумом и качеством оптических элементов и, в основном, наклон сигнала ФЛ при внешнем приложенном поле. Чтобы воспользоваться преимуществами ансамблевых измерений, здесь была изучена ФЛ на красном бриллианте, который чрезвычайно богат NV. Здесь образец считается NV-богатым, если его фотолюминесценция показывает типичный провал около 59,5 мТл, что указывает на взаимодействие NV-NV и, следовательно, на небольшое среднее расстояние между NV-центрами (см. дополнительный материал). Все выявленные особенности в зависимая от магнитного поля фотолюминесценция алмазов с высоким содержанием NV, вызванная смешением спиновых состояний, проливает свет на квантово-механические взаимодействия NV-центров с окружающей их средой.Таким образом, ансамблевые измерения при высокой плотности NV позволяют проводить систематические исследования на малых расстояниях дефект-NV из-за высокого SNR. Это возможно только в ограниченной степени для одиночных измерений, например, с ODMR, поскольку по статистическим причинам пара дефектов, такая как пара NV-NV, встречается редко. Таким образом, представленные здесь измерения не только полезны в контексте потенциальных применений датчиков магнитного поля на основе NV, но и могут способствовать исследованию связи дефект-NV для обработки квантовой информации с использованием связанных NV-центров. ^18,19 18. F. Dolde, I. Jakobi, B. Naydenov, N. Zhao, S. Pezzagna, C. Trautmann, J. Meijer, P. Neumann, F. Jelezko, J. Wrachtrup, Nat. физ. 9 , 139 (2013). https://doi.org/10.1038/nphys254519. M.W.Doherty, C.A.Meriles, A.Alkauskas, H.Fedder, M.J.Sellars, and N.B.Manson, Phys. X 6 , 041035 (2016). https://doi.org/10.1103/PhysRevX.6.041035 (При написании статьи нам стало известно, что группа Будкера работает над аналогичной темой. Работы ведутся самостоятельно.)

МАТЕРИАЛ И МЕТОДЫ ЭКСПЕРИМЕНТА

Раздел:

ВыбратьВерх страницыРЕФЕРАТВВЕДЕНИЕМАТЕРИАЛ И ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ… <<РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ ЗАКЛЮЧЕНИЕ И ПЕРСПЕКТИВЫ ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛЛИТЕРАТУРА Образец с высоким содержанием NV изготовлен из HPHT-алмаза с высокой начальной концентрацией одиночных замещающих атомов азота. В образце алмаза с помощью электронного пучка с энергией 10 мэВ было создано большое количество вакансий. При этом электронный пучок проникает в образец миллиметровой толщины. Один электрон порождает всего несколько вакансий (∼3 см–1), которые, таким образом, имеют большое среднее расстояние. Это снижает вероятность нежелательного скопления вакансий. Таким образом, за счет одновременного отжига может быть достигнута высокая плотность NV. Здесь температура (900°C) контролируется током пучка, а чистая плотность вакансий — накопленным флюенсом облучения (2×1018 см-2). ²⁰ 20. Ю. Миндарава, Р. Блиндер, К. Лаубе, В. Кнолле, Б. Абель, К. Джентгенс, Дж. Исоя, Дж. Шойер, Дж. Ланг, И.Шварц, Б. Найденов и Ф. Железко, Carbon 170 , 182 (2020). https://doi.org/10.1016/j.carbon.2020.07.077 В результате этого процесса в образце образуется смесь замещающих азотных (P1) центров и NV-центров. Концентрации дефектов в исследуемом образце алмаза, оцененные по ЭПР-измерениям, составляют [N]=30 ppm и [NV]=3 ppm соответственно. Измерения ФЛ проводились на самодельной установке (рис. 1). В качестве источника освещения используется печатная плата (PCB) с лазерным диодом (Osram Pl520B, 520 nm) с электронным драйвером (icHaus iC-HKB). Магнитное поле создается цилиндрической системой магнитного поля, в которой расположен двухосный вращатель. Система магнитного поля состоит из трех концентрических цилиндрических катушек для создания крупномасштабного однородного поля и подключена к источнику питания (EA PS 5000 A для полей до 111 мТл и R&S HMP2020 для разверток ниже 50 мТл). Образец алмаза размером около 2 мм прикрепляют к концу оптического волокна, не поддерживающего поляризацию (NA0,5, сердечник 400 мкм), и располагают гониометрически в центре системы магнитного поля.Лазерный свет вводится в оптическое волокно для возбуждения фотолюминесценции (Pexc≈25 мВт). ^21–25 21. Блейкли С.М., Федотов И.В., Килин С.Ю., Желтиков А.М. // Опт. лат. 40 , 3727 (2015). https://doi.org/10.1364/OL.40.00372722. Федотов И.В., Блейкли С.М., Серебрянников Э.Е., Хеммер П., Скалли М.О., Желтиков А.М. // Опт. лат. 41 , 472 (2016). https://doi.org/10.1364/OL.41.00047223. Д. Дуан, Г. Х. Ду, В. К. Каватамане, С. Арумугам, Ю.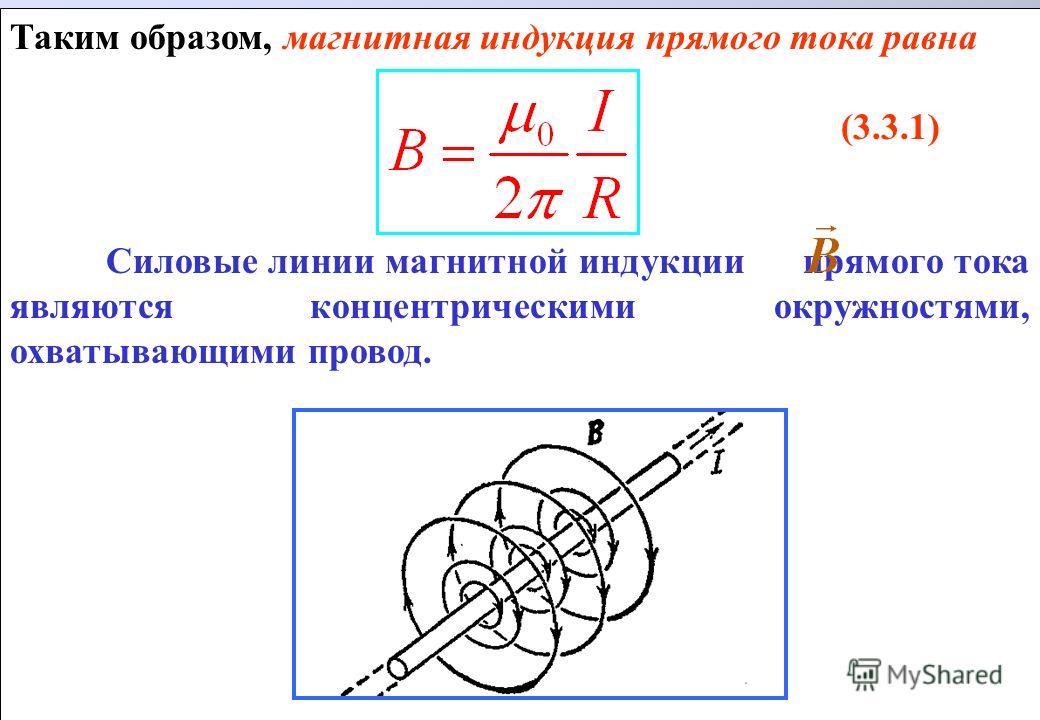 -К. Ценг, Х.-С. Chang, and G. Balasubramanian, Opt. Экспресс 27 , 6734 (2019). https://doi.org/10.1364/OE.27.00673424. D. Bai, M. H. Huynh, D. A. Simpson, P. Reineck, S. A. Vahid, A. D. Greentree, S. Foster, H. Ebendorff-Heidepriem и B. C. Gibson, APL Mater. 8 , 081102 (2020). https://doi.org/10.1063/5.001347325. Д. Дуан, В. К. Каватамане, С. Р. Арумугам, Ю.-К. Ценг, Х.-К. Chang и G. Balasubramanian, Appl. физ. лат. 116 , 113701 (2020). https://doi.org/10.1063/1.5140785 Одновременно используется для сбора ФЛ и направления ее на фотодиод (Hamamatsu S5971) через дихроичное зеркало (отсечка на 600 нм). Фотодиод смонтирован на другой печатной плате вместе с электроникой усилителя (простой трансимпедансный усилитель). Для измерения напряжения трансимпедансного усилителя использовался синхронный усилитель (Zurich Instruments MFLI). Лазер и фотодиод питались от экранированной батареи 12 В для минимизации шума. Импульсный режим лазера осуществлялся с помощью генератора сигналов (Keysight 33500B) на частотах 375 и 250 кГц для сканирования полного диапазона магнитного поля соответственно. Время задержки для измерения ФЛ на значение магнитного поля варьировалось от 1 до 3  мс без учета предыдущего времени установления магнитного поля. Если не указано иное, PL нормируется на значение без магнитного поля. В дальнейшем термин «рассогласование» используется как угол относительно направления ⟨111⟩ решетки алмаза, а для «соосных» NV-центров всегда следует предполагать, что их ось симметрии параллельна приложенному извне магнитному поле.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Раздел:

ВыбратьНаверх РЕФЕРАТВВЕДЕНИЕМАТЕРИАЛ И ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ…РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ <<ЗАКЛЮЧЕНИЕ И ПЕРСПЕКТИВЫДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛЛИТЕРАТУРА На рис. 2(а) показана ФЛ во всем исследованном диапазоне магнитных полей от 0 до 111  мТл, когда магнитное поле ориентировано на одно из четырех эквивалентных направлений NV (<1°). Для сравнения показан результат простой модели, вычисляющей ФЛ ансамбля NV-центров, равномерно распределенных по всем направлениям в решетке алмаза при соответствующем векторе магнитного поля на основе [1]. 1414.Ж.-П. Тетьен, Л. Ронден, П. Спиничелли, М. Шипо, Т. Дебюшерт, Ж.-Ф. Roch и V. Jacques, New J. Phys. 14 , 103033 (2012). https://doi.org/10.1088/1367-2630/14/10/103033. Форма модельной кривой обусловлена ​​тем, что, когда образец выровнен с одним направлением НВ вдоль внешнего магнитного поля, три оставшихся направления НВ наклонены на угол около 109° относительно вектора магнитного поля в соответствии с тетрагональной симметрией. . Для этого подансамбля это приводит к увеличению смешивания спиновых состояний с увеличением магнитного поля.Поскольку это смешивание определяет ФЛ NV-центра, то с увеличением магнитного поля ФЛ уменьшается до тех пор, пока, в зависимости от мощности оптического возбуждения, не будет достигнуто насыщение. Вкратце, модель показывает ФЛ ансамбля невозмущенных отдельных NV-центров. ²⁶ 26. R.J. Epstein, F.M. Mendoza, Y.K. Kato, and D.D. Awschalom, Nat. физ. 1 , 94 (2005). https://doi.org/10.1038/nphys141 Очевидно, что измеренная кривая имеет некоторые особенности, которые не могут быть воспроизведены этой простой моделью. Разница между моделью и измерением показана на рис. 2(б). Выраженный спад (по сравнению с модельной кривой) в ФЛ наблюдается при 0–10, 34, 51, 59,5 и 102 мТл с некоторыми малозаметными субструктурами. (GSLAC) выровненных центров NV. ^27,28 27. Х.-Ф. He, N.B. Manson и P.T.H. Fisk, Phys. Rev. B 47 , 8809 (1993). https://doi.org/10.1103/PhysRevB.47.880928. Л. Дж. Роджерс, Р. Л. Макмертри, М.J. Sellars и N. B. Manson, New J. Phys. 11 , 063007 (2009 г.). https://doi.org/10.1088/1367-2630/11/6/063007 Согласно литературным данным, субструктура обусловлена ​​связью с соседними спинами 13C. ^15,29 15. A. Wickenbrock, H. Zheng, L. Bougas, N. Leefer, S. Afach, A. Jarmola, V.M. Acosta, and D. Budker, Appl. физ. лат. 109 , 053505 (2016). https://doi.org/10.1063/1.496017129. В. Ивади, Х. Чжэн, А. Викенброк, Л. Бугас, Г. Чацидросос, К. Накамура, Х.Sumiya, T. Ohshima, J. Isoya, D. Budker, I.A. Abrikosov, and A. Gali, Phys. B 103 , 035307 (2021 г.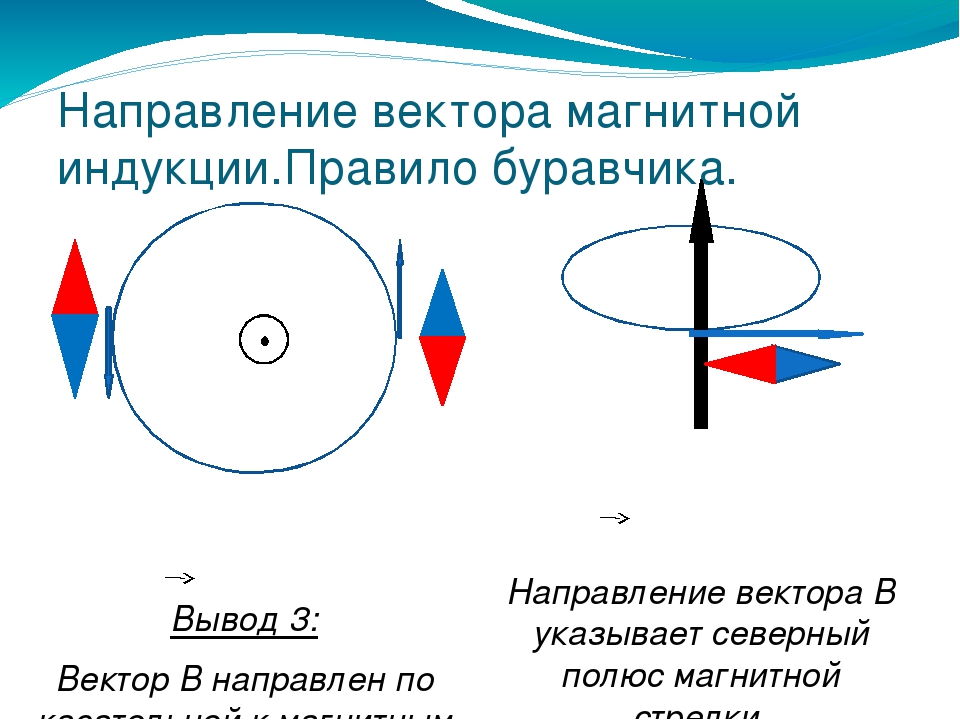 ). https://doi.org/10.1103/PhysRevB.103.035307 Поскольку выход преобразования центров P1 в центры NV находится в низком процентном диапазоне, существует также много пар NV-P1 с расстоянием спаривания ниже порога, при котором перекрестная релаксация (CR) происходит. Это имеет место для выровненных центров NV примерно при 51 мТл. Вследствие анизотропного сверхтонкого взаимодействия электронного спина дефекта P1 с его собственным ядерным спином азота происходит наблюдаемое расщепление провалов ФЛ. ^30–32 30. W.V. Smith, P.P. Sorokin, I.L. Gelles, G.J. Lasher, Phys. 115 , 1546 (1959). https://doi.org/10.1103/PhysRev.115.154631. K. Holliday, N.B. Manson, M. Glasbeek, and E. van Oort, J. Phys.: Condens. Материя 1 , 7093 (1989). https://doi.org/10.1088/0953-8984/1/39/02132. R. Lazda, L. Busaite, A. Berzins, J. Smits, F. Gahbauer, M. Auzinsh, D. Budker, R. Ferber, Phys. B 103 , 134104 (2021 г.). https://doi.org/10.1103/PhysRevB.103.134104 С увеличением плотности НВ среднее расстояние между ними уменьшается, и, таким образом, субансамбль, которым уже нельзя пренебречь, падает ниже критического расстояния (несколько нм) до соседнего центра НВ. Если только один из двух NV-центров выровнен, CR между ними происходит примерно при 59,5  мТл, и, следовательно, ФЛ выровненного NV-центра снижается. ³³ 33. S. Armstrong, L.J. Rogers, R.L. McMurtrie, and N.B. Manson, Phys. Procedia 3 , 1569 (2010). https://doi.org/10.1016/j.phpro.2010.01.223 Если магнитное поле не идеально выровнено по оси NV, в результате образуются три подгруппы пар с разными углами относительно выровненного магнитного поля. Соответственно, эта функция PL разделяется на три провала [например, см. рис. 4 (a) для смещения 3°]. Другая конфигурация пары NV-NV существует, когда обе составляющие выровнены в одном направлении; т. е. они магнитно эквивалентны. Затем, при выравнивании вдоль магнитного поля примерно при 34  мТл, энергетические уровни трехспинового состояния основного состояния 3A2 становятся равноотстоящими друг от друга. ^34,35 34. E. van Oort, M. Glasbeek, Phys. Rev. B 40 , 6509 (1989). https://doi.org/10.1103/PhysRevB. 40.650935. E. van Oort и M. Glasbeek, Appl. Магн. Резон. 2 , 291 (1991). https://doi.org/10.1007/BF03166042 Однако CR этих двух переходов (|m⟩:|0⟩↔|1⟩ и |−1⟩↔|+1⟩) запрещен, так как спин не сохраняется в этот процесс скольжения. Переход становится разрешенным, когда задействованные функции уровней энергии изменяются от чистых состояний (|0⟩, |±1⟩) к линейным комбинациям триплетных состояний.Это происходит, с одной стороны, когда ориентация NV-центров уже не соответствует ориентации внешнего магнитного поля или, с другой стороны, когда возмущение состояний, например взаимодействие хотя бы с одним другим спином, происходит. В представленном измерении совмещение лучше 1°; следовательно, наблюдение этой особенности ФЛ можно отнести только к NV-NV CR, предполагая достаточную дипольную связь между двумя NV-центрами или взаимодействие по крайней мере с одним другим спином.Рисунок 2(c) показывает подробное сканирование этой функции. Для анализа расщепления мы вычли линейный фон из измеренного сигнала и аппроксимировали его симметричной мультигауссовой функцией (рис. 2(г)]. Сходство резонансной структуры с особенностью GSLAC при 102 mT позволяет предположить, что она обусловлена ​​взаимодействием с соседними спинами 13C. ¹⁵ 15. A. Wickenbrock, H. Zheng, L. Bougas, N. Leefer, S. Afach, A. Jarmola, V.M. Acosta, and D. Budker, Appl. физ. лат. 109 , 053505 (2016).https://doi.org/10.1063/1.4960171 Далее мы предлагаем простую модель зависимости этой функции от мощности лазера. На рис. 3(а) показано моделирование населенности уровней, зависящих от мощности лазера, отдельного центра NV. Здесь термин «популяция» используется как синоним вероятности занятости. Авто-КП между двумя НВ-центрами предполагает переход с 1-го уровня на 2-й для одного НВ-центра и с 3-го на 2-й уровень для другого. Если мы теперь предположим, что два NV-центра представляют собой единую систему, соответствующий переход можно записать как |levelNValevelNVb=13⟩→|22⟩.Это показано на вставке к рис. 3(б). Обратите внимание, что состояния помечены уровнями, а не магнитными квантовыми числами. Уменьшение PL при 34 mT может быть описано уменьшением популяции состояния |13⟩ (|светлое состояние, более темное состояние) с помощью авто-CR до состояния |22⟩ (|более темное состояние, более темное состояние⟩). Для фиксированной скорости авто-CR (w5) можно найти коэффициент p, который пропорционален вероятности авто-CR и зависит только от населенности задействованных уровней. Для низких и умеренных мощностей лазера, используемых в этом исследовании, этот пропорциональный коэффициент увеличивается с увеличением мощности лазера в соответствии с увеличением заселенности уровня 1 для одного центра NV.В области очень больших мощностей лазера вероятность авто-КП снова снижается из-за уменьшения заселенности вовлеченных уровней, например, накачки заселенности в возбужденном и синглетном состоянии (рис. 3(б)]; другими словами, особенность ФЛ ожидается только при умеренных мощностях лазера, так что только один из двух NV-центров поляризован в основном состоянии |0⟩. Поскольку мы работаем с низкими мощностями лазера, можно измерить только увеличение провала ФЛ [рис.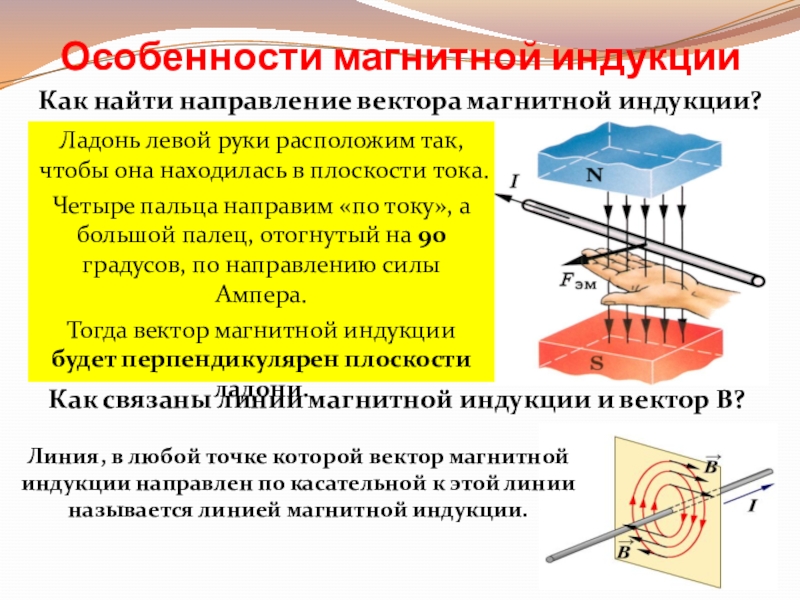 3(с)]. Подробности в дополнительных материалах.Падение ФЛ ниже 10 мТл было предложено в качестве объяснения дипольной связи между соседними NV-центрами (d≲15нм), приводящей к смешиванию спиновых состояний. ^36,37 36. Анищик С.В., Винс В.Г., Елисеев А.П., Лукзен Н.Н., Лаврик Н.Л., Багрянский В.А. // New J. Phys. 17 , 023040 (2015). https://doi.org/10.1088/1367-2630/17/2/02304037. Ахмеджанов Р., Гущин Л., Низов Н., Низов В., Собгайда Д., Зеленский И., Хеммер П. // Phys. Ред. A 96 , 013806 (2017 г.).https://doi.org/10.1103/PhysRevA.96.013806 Однако при ближайшем рассмотрении обнаруживаются дополнительные подструктуры, которые нельзя объяснить таким образом [рис. 2(е)]. Мы попытались воспроизвести эти провалы ФЛ с помощью различных модельных расчетов, таких как CR NV-P1, NV-NV и NV-(NV+P1) или даже между отрицательным и нейтральным состоянием заряда центра NV (NV—NV0). . Ни одна из моделей не могла удовлетворительно объяснить наблюдаемые резонансы при малых магнитных полях (B<14 мТл). Также ЛАК, вызванные взаимодействием электронного спина НВ-центра и его собственного ядерного спина азота в сочетании с малым поперечным магнитным полем (В нашем случае это справедливо для подансамбля НВ-центров не с их симметрией ось параллельна B→.) не может объяснить наблюдаемые особенности. ³⁸ 38. H. Clevenson, E.H. Chen, F. Dolde, C. Teale, D. Englund, and D. Braje, Phys. Ред. A 94 , 021401 (2016 г.). https://doi.org/10.1103/PhysRevA.94.021401 Как недавно было предложено для PL образцов алмазов, выращенных методом CVD, мы исследуем потенциальную CR с отрицательно заряженными центрами VH- и WAR1. ³⁹ 39. C. Pellet-Mary, P. Huillery, M. Perdriat, A. Tallaire, and G. Hétet, Phys. B 103 , L100411 (2021 г.).https://doi.org/10.1103/PhysRevB.103.L100411 Соответствующие магнитные поля показаны на рис. 2(f) красными пунктирными (синими пунктирно-штриховыми) вертикальными линиями для центра VH− (центр WAR1). Хотя некоторые из провалов ФЛ, возможно, можно отнести к этим дефектам, есть и такие, которые не могут быть объяснены таким образом (например, провал 6,1 мТл среди прочих). Подробности в дополнительных материалах. Для алмазов HPHT дефект, связанный с железом, никелем или кобальтом, более вероятен, поскольку эти элементы используются в качестве катализаторов в процессе выращивания. ⁴⁰ 40. Якубовский К. // Физ. Ред. B 70 , 205211 (2004 г.). https://doi.org/10.1103/PhysRevB.70.205211 Эти дефектные центры в основном имеют спин S=1/2, что не может объяснить наблюдаемые провалы ФЛ в этой области магнитного поля. ^41–44 41. Надолинный В.А., Елисеев А.П., Юрьева О.П., Фейгельсон Б.Н. Магн. Резон. 12 , 543 (1997). https://doi.org/10.1007/BF0316413442. К. Джонстон, А. Мейнвуд, А. Т. Коллинз, Г. Дэвис, Д. Твитчен, Дж. Бейкер и М.Newton, Physica B 273–274 , 647 (1999). https://doi.org/10.1016/S0921-4526(99)00595-543. Надолинный В.А., Елисеев А.П., Бейкер Дж.М., Ньютон М.Е., Твитчен Д.Дж., Лоусон С.С., Юрьева О.П., Фейгельсон Б.Н. // J. Phys.: Condens. Материя 11 , 7357 (1999). https://doi.org/10.1088/0953-8984/11/38/31444. Надолинный В.А., Бейкер Дж.М., Юрьева О.П., Ньютон М.Е., Твитчен Д.Дж., Пальянов Ю.Н. // Прикл. Магн. Резон. 28 , 365 (2005). https://doi.org/10.1007/BF03166768 Однако если предположить, что наблюдаемые провалы ФЛ вызваны КЛ, то следует предположить, что он вызван дефектным центром с расщеплением в нулевом поле (ZFS). Ni-родственный центр AB5 имеет спин S=1, но при ZFS около 32 ГГц по оси ⟨111⟩ имеет значение более чем на порядок выше, чем у NV-центра и, следовательно, не может также объяснить наблюдаемые провалы. ⁴⁵ 45. A. Neves, R. Pereira, N. Sobolev, M. Nazaré, W. Gehlhoff, A. Naser, and H. Kanda, Diam.Относ. Матер. 9 , 1057 (2000). https://doi.org/10.1016/S0925-9635(99)00329-5 Таким образом, происхождение этих особенностей PL в настоящее время остается неизвестным. На рисунках 4(a) и 4(c) показан набор измерений PL для различных магнитное поле колеблется под разными углами смещения. На рис. 4(а) показан участок (0°–10°) из серии измерений углов смещения до 109° с шагом 1° (полное измерение в дополнительном материале).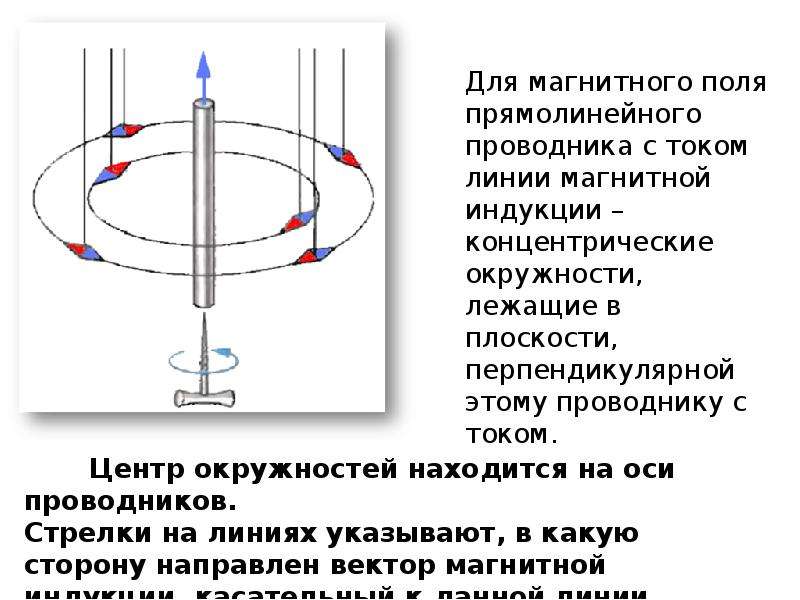 С увеличением угла описанные выше особенности становятся менее выраженными.Зависящий от угла контраст ФЛ различных особенностей ФЛ относительно ФЛ (B=0) также был извлечен из полной серии измерений и показан на рис. 4(b). Контраст фотолюминесценции быстро уменьшается с увеличением рассогласования, что может быть связано со смешиванием спиновых состояний изначально выровненных NV-центров. от ° до +8° угла наклона [рис. 4(с)]. Затем было извлечено точное положение магнитного поля этой особенности.Для этого к кривой для каждого сканирования магнитного поля подгоняли симметричную мультигауссову функцию [сравните рис. 2(d)], а результирующее положение строили как функцию угла [рис. 4(г)]. Сравнение с численно рассчитанными значениями положения наклона показывает основное соответствие формы кривой. Однако расчетное значение положения магнитного поля отклоняется от измеренного на 0,3 мТл, а также кривизна кривых не совпадает в точности. Причиной этого могло быть то, что в расчет не была включена связь с дополнительными спинами, такими как спины 13C. Кроме того, известно, что в алмазах могут возникать сильные внутренние напряжения, приводящие к сдвигу энергетических уровней, а значит, и к энергетическим резонансам, приводящим к КЛ. Из-за геометрии и оптического поглощения образца невозможно выполнить измерения оптической кросс-поляризации, которые могли бы указывать на внутреннее напряжение; следовательно, мы не можем исключить это в измеренном образце.

ЗАКЛЮЧЕНИЕ И ПРОГНОЗ

Раздел:

ChooseВерх страницыРЕФЕРАТВВЕДЕНИЕМАТЕРИАЛ И ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ…РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ ЗАКЛЮЧЕНИЕ И ПЕРСПЕКТИВЫ <<ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫССЫЛКИ

Алмаз с высоким содержанием NV был создан с помощью электронного облучения и прикреплен к концу оптического волокна. С помощью метода синхронизации ФЛ может быть записана в зависимости от угла в магнитных полях от 0 до 111  мТл. Это выявило связи с разными соседними спинами по сравнению с моделью ФЛ для ансамбля отдельных NV-центров. В дополнение к GSLAC и связи с соседними центрами P1 также может быть обнаружена связь между центрами NV.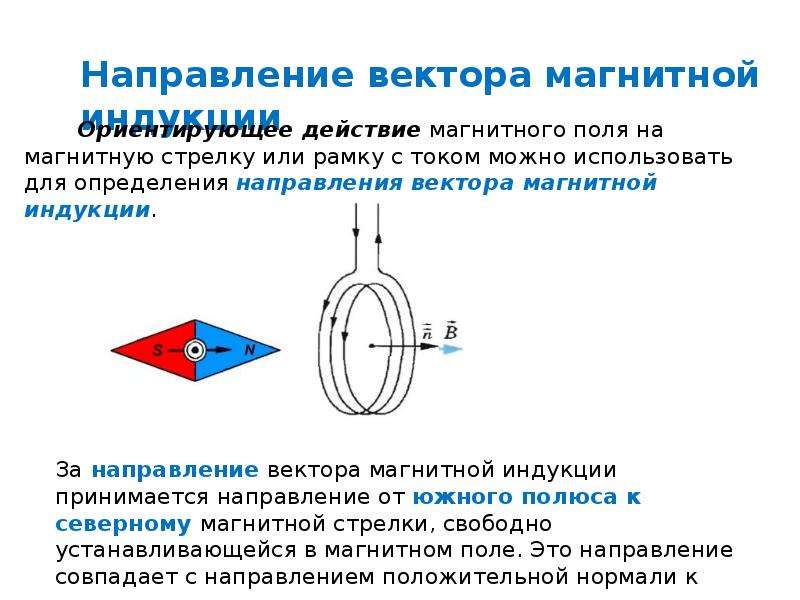 Выбирая умеренные мощности облучения, можно было показать связь магнитно-эквивалентных NV-центров в дополнение к магнитно-неэквивалентным.

Кроме того, измерения показывают возможность изучения парамагнитных дефектов в алмазе в целом. Для области магнитного поля ниже примерно 10  мТл в измерениях ФЛ появляются дополнительные провалы. Эти провалы PL сравнивали с литературными значениями. Однако не удалось найти простую модель, включающую спиновые дефекты, обсуждаемые в тексте, для воспроизведения каждого провала ФЛ.В будущих исследованиях особенности ФЛ следует систематически связывать с концентрацией примесей. Их можно определить, например, с помощью ЭПР или PIXE. Более того, не следует исключать многоспиновые взаимодействия как источник необъяснимых особенностей ФЛ. В частности, возможность изучения трехспинового взаимодействия между NV–NV–P1 или NV–P1–P1 потенциально возникает при очень высоких плотностях NV.

Что такое единица СИ магнитного потока? Является ли он вектором класса 12 физики CBSE

Подсказка: Магнитный поток определяется количеством магнитных линий, проходящих через определенную замкнутую область. Это скалярное произведение магнитного поля через петлю и площадь замкнутой петли. Мы можем использовать основное определение магнитного потока, чтобы определить единицу измерения.

Полный пошаговый ответ:
Магнитный поток представляет собой поверхностный интеграл нормальных составляющих силовых линий магнитного поля, проходящих через замкнутый контур. Мы можем определить магнитное поле следующим образом:
${{\phi}_{B}}=BA=BA\cos\Theta $

магнитный поток
$B$ — магнитное поле
$A$ — площадь замкнутой области
$\Theta $ — угол между вектором магнитного поля и вектором площади.
Следовательно, основной единицей измерения магнитного потока является вольт-секунда.
Однако единицей измерения магнитного потока в системе СИ является Вебер (Вб).
Это очень важная единица в электромагнетизме, и мы часто используем эту единицу для выражения других величин.

Магнитный поток зависит от двух величин — Магнитное поле и Площадь.
Обе эти компоненты являются векторными величинами. Однако магнитный поток зависит только от линий магнитного поля, которые перпендикулярны поверхности замкнутого контура (или вдоль вектора площади).Это замкнутая поверхностная интеграция всех этих силовых линий магнитного поля.

Уравнение, о котором мы говорили выше, работает для фиксированного магнитного поля. В противном случае мы должны использовать эту формулу.
${{\phi}_{B}}={{B}_{1}}.d{{A}_{1}}+{{B}_{2}}.d{{A}_ {2}}+{{B}_{3}}.d{{A}_{3}}+…=\sum\nolimits_{all}{{{B}_{i}}.d{ {A}_{i}}}$
Или мы можем записать это следующим образом:
${{\phi }_{B}}=\oint\limits_{A}{B.dA}$
Здесь , мы используем интегрирование по замкнутому кругу.
Поскольку мы используем скалярное произведение, магнитный поток является скалярной величиной.

Примечание:
Когда магнитное поле проходит вдоль площади замкнутой поверхности, магнитный поток равен 0. Это происходит потому, что угол между вектором площади и вектором магнитного поля равен 90°.
Принимая во внимание, что магнитный поток максимален, когда угол между этими векторами равен 0°.

Магниты — дополнительная документация SIMION 2020

Что касается магнитных полей, обычно необходимо рассчитать поле и/или
рассчитать, как магнитное поле влияет на движение заряженных частиц
(и часто наложенное электрическое поле).

Последнее, движение заряженных частиц, обычно управляется
Закон силы Лоренца.

Возможно, ваше магнитное поле уже известно из аналитического
уравнение, экспериментальные данные или расчет из другого магнитного поля
программа решения, и в этом случае вам просто нужно импортировать из уравнения
или из файла данных.

Расчет магнитного поля зависит
от того, что генерирует это магнитное поле
(например, магнитные и/или проволочные токи) и может включать
ряд методов, таких как закон Био-Савара и
Уравнение Пуассона.Расчет магнитного поля вызывает больше вопросов,
в зависимости от того, какие типы магнитных материалов задействованы и
2D по сравнению с 3D.
Расчеты магнитного поля могут быть немного более сложными, чем
электростатические, так как потенциал является вектором и существуют
усложнения проницаемости, плотности тока и гистерезиса.
SIMION не является полной программой решения магнитных задач (например, проблемы с гистерезисом)
но может импортировать из таких программ.
Бета-версия SIMION имеет некоторые дополнительные магнитные решения.
(решатель Пуассона), которые расширяют область применения.

Генерация магнитных полей из переменных электрических полей и
наоборот, не учитываются (квазистатическое приближение
к уравнениям Максвелла).

В SIMION существует три основных способа определения магнитного поля:

• в терминах магнитных скалярных потенциалов
• в терминах магнитного векторного потенциала (экспериментальный в 8.1.0.45).
• по векторам магнитного поля

Эти случаи описаны ниже:

• в терминах магнитных скалярных потенциалов – Скалярный магнитный
  потенциал аналогичен скалярному потенциалу в электрических полях (т.е.
  Напряжение). Вектор магнитного поля представляет собой отрицательный градиент
  скалярный магнитный потенциал, как и вектор электрического поля
  отрицательный градиент электростатического потенциала. SIMION может решить
  скалярный магнитный потенциал с использованием уравнения Лапласа в том же
  как решается электрический потенциал, и после этого
  вектор магнитного поля можно сразу получить и использовать для
  решение траектории частицы. Однако не все магнитные поля
  могут быть выражены как скаляры, а скорее как векторы, и значение
  потенциала может быть менее интуитивным с магнитными полями.Магнитный
  потенциал будет скаляром при определенных условиях, например, когда
  в моделируемой области отсутствует плотность тока (а в
  иначе, если система имеет двумерную симметрию).
  Подробности см. в разделе «Магнитный потенциал».
  SIMION Early Access Mode добавляет поддержку Permeability.
• по магнитному векторному потенциалу –
  Магнитный векторный потенциал может учитывать ненулевую плотность тока
  в космосе.
  Режим раннего доступа SIMION имеет экспериментальную поддержку магнитного вектора
  потенциал.См. Магнитный потенциал.
• по векторам магнитного поля –
  Магнитные поля здесь определяются непосредственно через векторы поля.
  При интегрировании траектории вектор магнитного поля, видимый
  частица может быть определена программно. У вас может быть аналитический
  математическое выражение для него, или у вас могут быть полевые данные
  (рассчитывается из какой-то внешней программы и хранится в текстовом файле)
  которые можно интерполировать (SIMION 8.0.3 включает сетку полей
  подпрограммы интерполяции и SIMION 8.1.0 позволяет обычным файлам PA
  представлять это), или магнитное поле может быть определено через
  конфигурация проводных токов (SIMION 8.0.3 поддерживает
  Расчеты по закону Био-Савара). Во всех этих случаях магнитное поле
  может быть наложен на систему через пользовательскую программу mfield\_adjust
  сегмент, прикрепленный к пустой массиву магнитных потенциалов. Эта программа
  сегмент определяет вектор магнитного поля напрямую, как вам угодно.
  SIMION 8.1.0.22 добавляет некоторые возможности и примеры, которые делают это
  проще использовать с точки зрения хранения векторных данных в обычных файлах PA
  и визуализация векторов поля (и/или проволок Био-Савара)
  на экране просмотра. См. Пример SIMION: field_array,
  SIMION Пример: контур (contourlib81), SIMION Пример: helmholtz_coil,
  и пример SIMION: соленоид).

Связанные ресурсы:

• SIMION 8.0.3 включает функции для расчетов Био-Савара
  магнитные поля от проволочных токов и соленоидов.
  См. Закон Био-Савара.
• SIMION 8.0.3 включает функции импорта магнитного поля
  массивы из текстового файла (см. пример field_array)
• Примеры _Magnet в SIMION 7/8 (массивы скалярных потенциалов,
  включая простой магнитный сектор).Также см
  examples\geometry\sector.gem (простая геометрия секторов
  пример добавлен в 8.1.0)
• Следующие ресурсы больше относятся к версиям SIMION до
  8.0.3:

Применение постоянного магнитного поля

Очень часто требуется просто постоянное магнитное поле, поэтому мы
опишите это здесь. Существует два основных метода определения константы.
магнитное поле в SIMION: с пользовательской программой или без пользователя
программа. Каждый объясняется ниже. Оба метода почти одинаково
подходит, но рекомендуется использовать программу пользователя, поскольку она
избегает магнитных потенциалов и, следовательно, может быть более интуитивным.

Через программу пользователя в SIMION 8/8.1

В этом примере мы предположим, что вам нужна постоянная 100 гаусс.
магнитное поле в направлении +X.

1. Создать пустой базовый УМ типа «магнитный».
   Предположим, что этот PA называется «mag.pa».
   Этот PA не будет определять само магнитное поле, а скорее
   просто определяет объем, в котором должно находиться магнитное поле.
   прикладной (пользовательской программой).
   Значит, он должен быть соответствующего размера.
   Он не содержит полюсных точек и не нуждается в уточнении.Для экономии памяти рекомендуется сделать это
   PA быть двумерным плоским или двумерным цилиндрическим (нет необходимости в
   массив 3D), и неважно, если ваш магнитный
   поле на самом деле не имеет такой симметрии, поскольку оно
   просто определение объема.
   Примечание: этого шага можно избежать при использовании sim_segment_global .
   (в версии 8.2EA).

2. Добавьте экземпляр PA в рабочую среду (View > PAs > Add).
   Предположим, что этот IOB называется «system.iob».
   Соответствующий размер и положение экземпляра PA
   в верстаке (Вид | ПА | Позиционирование).Если вы используете 2D планар, убедитесь, что
   чтобы правильно установить значение «nz use» в «View | ПА».
   Вы также можете масштабировать размер массива на верстаке.
   («Вид | PAs | Позиционирование | Масштаб»).
   Магнитный усилитель мощности может перекрывать ваши электрические усилители мощности.
   если вы хотите, чтобы электрические и магнитные поля перекрывались.
   Заметим, что если частица находится в точке
   внутри нескольких экземпляров PA он видит только электрическое поле
   от электрического PA с наивысшим номером приоритета и видит только
   магнитное поле от магнитного УМ с наивысшим приоритетным номером.(Номера приоритета видны в списке экземпляров PA.
   на вкладке PAs и переключаются с помощью кнопок L-/L+).

3. Добавьте пользовательскую программу на свое рабочее место.
   Самый простой способ — нажать «Пользовательская программа…».
   на вкладке Частицы.
   (При этом создается файл «system.lua», т.е. с тем же
   базовое имя файла «system», как у файла IOB и в той же папке.)
   Вставьте в него следующий текст и сохраните:

   .

    simion.workbench_program()
   регулируемый bx = 100 -- Гаусс
   регулируется на = 0 -- гаусс
   регулируемый bz = 0 -- Гаусс
   функциональный сегмент.mfield_adjust()
     ion_bfieldx_gu = bx
     ion_bfieldy_gu = автор
     ion_bfieldz_gu = бз
   конец
    

   Это работает следующим образом. SIMION видит, что в system.iob есть
   соответствующий system.lua, и всякий раз, когда частица летит
   внутри mag.pa эта пользовательская программа
   прикладывает к частице постоянное магнитное поле.

4. Проверка правильности магнитного поля с SIMION Data
   Запись.
   Внимание: магнитное поле, заданное через пользовательскую программу
   (а не без него) обычно не будет виден с
   Варианты просмотра PE/контуров (хотя их можно визуализировать с помощью
   контурlib81 в SIMION Пример: контур).

Описанный выше подход используется в примере SIMION: icrcell.
Пример SIMION: mfield_adjust (добавлено в SIMION 8.1.0.19) демонстрирует простой
mfield_adjust сегмент, как описано выше.

Через программу пользователя в SIMION 6 или 7 (также работает в 8)

SIMION 7 может сделать это с помощью программы PRG. Создайте файл пользовательской программы
«mag.prg» (т. е. с тем же базовым именем файла «mag», что и у файла PA, а не у файла IOB,
и в той же папке):

 дефа бх 100 ; Гаусс
дефа на 0 ; Гаусс
дефа бз 0 ; Гаусс
сегмент mfield_adjust
  rcl bx sto ion_bfieldx_gu
  rcl от sto ion_bfieldy_gu
  rcl bz sto ion_bfieldz_gu
 

Через магнитные потенциалы в усилителе мощности

Альтернативный метод создания магнитного поля заключается в создании
магнитный полюс в магнитном УМ.Отрицательный градиент скаляра
тогда магнитный потенциал определяет магнитное поле. Это
предложено на стр. 2-10 руководств SIMION 8.0 и 7. 0.
Это описано в Магнитном Потенциале.

Сочетание электрического и магнитного полей

Электрические и магнитные поля не могут сочетаться в одном УМ.
Скорее, вам нужны два PA, один электрический и один магнитный. Ты тогда
перекрывают ПА на верстаке. Если частица находится внутри нескольких PA,
он увидит электрическое поле от электрического УМ с наивысшим приоритетом
номер (в списке PA Instances на вкладке PAs) и магнитное поле
магнитного УМ с наивысшим приоритетным номером.См. также
Пример SIMION: пример магнита (magnet1.iob), который делает это, или
СИМИОН Пример: icrcell.

Зависимая от магнитного поля квантовая эмиссия в гексагональном нитриде бора при комнатной температуре

Подготовка и монтаж образцов

В более ранних работах подчеркивалось сильное влияние взаимодействия с подложкой во время облучения и отжига на видимую флуоресценцию h-BN ²¹ . Чтобы устранить эти эффекты, мы изучаем эмиттеры, присутствующие в свободно подвешенных мембранах h-BN, которые были отслоены от коммерчески доступных объемных монокристаллов и обработаны, как описано. Все измерения выполняются в условиях окружающей среды. Образцы

H-BN готовятся путем расслаивания монокристаллического h-BN, приобретенного у графена HQ, на структурированный тепловой SiO ₂ толщиной 90 нм на кремниевых подложках. Узорчатые отверстия диаметром в несколько микрон создаются в опорной пластине с помощью оптической литографии с последующим сухим травлением, создавая в подложке протравленные отверстия в несколько микрон шириной и ~ 5   мкм глубиной. Представляют интерес расслоенные монокристаллические чешуйки h-BN, которые подвешиваются над узорчатым отверстием ²¹ .Толщина пленки определяется с помощью атомно-силовой микроскопии; толщина исследуемого чешуйка около 400 нм в окрестности подвешенной области; см. Дополнительный рисунок 2.

После расслаивания образцы подвергаются плазменной очистке O ₂ в озолительном аппарате с кислородным баллоном (Anatech SCE 108) и отжигаются в Ar при 850°C в течение 30 мин. Их визуализируют с помощью сканирующего электронного микроскопа (СЭМ), работающего при напряжении 3 кВ (FEI Strata DB235 FIB SEM), обычно в течение <5 мин, хотя образцы могут находиться в камере до 30 мин. После РЭМ образцы снова отжигают в Ar при 850 °C в течение 30 мин. Этот процесс надежно создает квантовые излучатели с индивидуальной адресацией в подвешенных областях хлопьев h-BN, из которых несколько процентов демонстрируют реакцию, зависящую от магнитного поля.

Отслоенный и подготовленный образец устанавливается на поворотный столик, обеспечивающий вращение образца и, следовательно, оптических диполей отдельных дефектов в плоскости по отношению к остальной части установки в самодельном конфокальном флуоресцентном микроскопе с длиной волны 592 нм. непрерывное волновое возбуждение; см. дополнительный рисунок 1.Мощность возбуждения, используемая как для обесцвечивания, так и для визуализации, находится в диапазоне от 175 до 550  мкВт, измеренная непосредственно перед объективом, и изменение ФЛ в этом диапазоне примерно постоянно; см. Дополнительный рисунок 3. Дополнительный контроль над направлением линейной поляризации возбуждения облегчается с помощью полуволновой пластины. Внешнее магнитное поле прикладывается с помощью неодимовых магнитов, установленных на самодельном гониометре, который позволяет варьировать направление приложенного поля по отношению к плоскости образца, как показано на рис. 1г. Изменение расстояния между магнитом и образцом позволяет использовать диапазон прикладываемых магнитных полей от 0 до 890 G.

PL-изображения

Составные поляризованные PL-изображения, как на рис. 1b, построены из серии конфокальных PL-сканов, записанных для 4 различные настройки линейной поляризации возбуждающего лазера с длиной волны 592 нм (0°, 45°, 90° и 135°) при сборе фотолюминесценции между 650 и 900 нм. Отдельные изображения раскрашиваются в соответствии с настройкой поляризации, совмещаются друг с другом и суммируются для создания составного изображения таким образом, чтобы результирующий цвет, значение и насыщенность соответствовали ориентации диполя возбуждения, видимости и яркости фотолюминесценции соответственно ^21,47 .

Дифференциальные изображения PL, как на рис. 1c, построены с использованием координаты значения (т.е. яркости) из составных изображений, полученных с магнитным полем и без него. Небольшое постоянное изменение PL [≈8% на рис.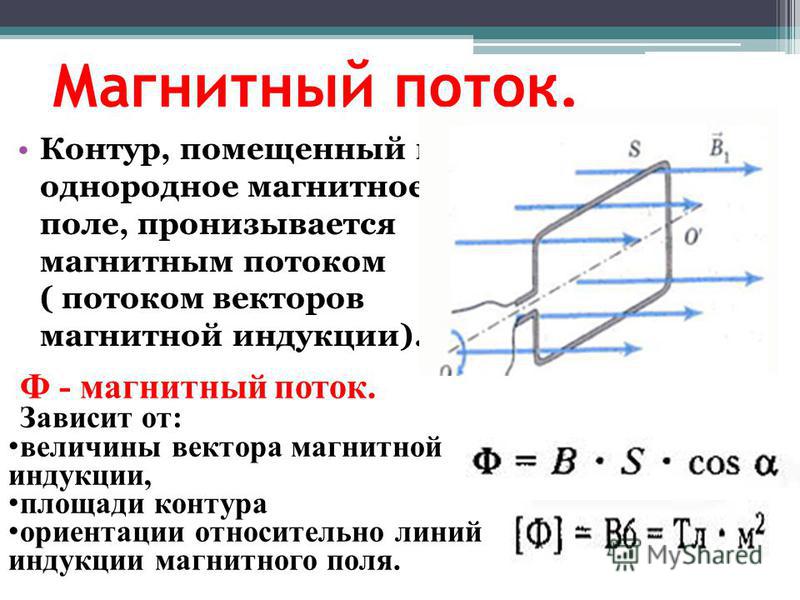 1c], рассчитанное путем усреднения по всем пикселям, вычитается для учета вызванных полем изменений юстировки микроскопа.

Спектры ФЛ

Спектры ФЛ сняты с использованием спектрометра Princeton Instruments IsoPlane 160 и ПЗС-матрицы PIXIS 100 со спектральным разрешением 0.7 нм. Собираются множественные экспозиции (> 2), вычитается темновой счет и отбрасываются космические лучи, а затем усредняются вместе. Спектры ФЛ не корректируются с учетом эффективности сбора фотонов в зависимости от длины волны. Краевой фильтр с длиной волны 633 нм (Semrock, BLP01-633R-25) в линии сбора блокирует лазер с длиной волны 592 нм. На рис. 1f линия комбинационного рассеяния света h-BN видна на краю полосы сбора при ~644 нм. Независимая от поля особенность около 650 нм связана с фоном.

Изменение PL в зависимости от магнитного поля

Устранение экспериментальных артефактов, которые могут указывать на ложный отклик на магнитные поля, является ключом к определению зависимости QE от поля в h-BN.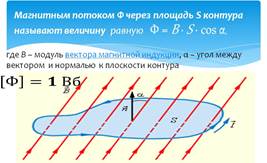 Мы предприняли шаги для учета экспериментальных артефактов, включая построение графика процентного изменения PL, а не необработанного PL с магнитным полем и без него. Для расчета вариации ФЛ при различных ( α , ε ) ориентациях и при различных напряженностях магнитного поля, ФЛ за вычетом фона определяется из комбинации гауссовских подгонок к изображениям ФЛ и, если доступно, измерений временн усредненная скорость излучения, обнаруженная путем фокусировки непосредственно на излучателе в течение 30–120   с при каждой настройке.Все данные об интенсивности выбросов вычитаются из фона перед формированием коэффициента вариации PL. Фон, определенный с помощью гауссовой аппроксимации конфокальных фотолюминесценций, используется для вычитания фона из усредненных по времени данных об интенсивности выбросов, полученных в идентичных условиях. При B  = 0 G измеряется зависящее от ориентации пропускание ФЛ от обведенного кружком излучателя через линию сбора конфокального микроскопа, чтобы нормализовать небольшие вариации (<6%) ФЛ, которые возникают, когда образец вращается. При каждой ориентации образца поляризация возбуждения совпадает с поглощающим диполем.

Автокорреляционный анализ

Автокорреляционные данные получены с использованием установки Hanbury Brown-Twiss с модулем счета одиночных фотонов с временной корреляцией (PicoQuant PicoHarp 300) в режиме сбора данных с временными метками и временным разрешением. Автокорреляционная функция второго порядка, g ⁽²⁾ ( t ), рассчитывается по временам прихода фотонов с использованием метода, описанного в ref. ⁴⁸ , а кривые подобраны с использованием эмпирических функций, как описано в тексте. Выбор модели основан на качестве взвешенного метода наименьших квадратов с учетом пуассоновской неопределенности каждого бина.

Амплитуды с поправкой на фон, \(\тильда C_i\), рассчитываются с использованием отдельных калибровочных измерений отношения сигнал/фон при каждой местной настройке. Используя усредненное измерение фона пуассоновской фотолюминесценции, взятое из нескольких соседних мест на подвесной мембране, мы оцениваем параметр коррекции фона, ρ  =  I /( I  +  I _bkgd ), где I — QE PL, а I _bkgd — фоновый PL. {(2)}(0) < 0,5\), на \(0,8\сигма\). Точность этого измерения ограничена дробовым шумом и дрожанием синхронизации детектора из-за короткой временной шкалы антигруппировки, \(\tau _1 = 0,8 \pm 0,2\) нс.

Молекулярно-орбитальная теория и моделирование оптической динамики

Целью нашего теоретического исследования является перечисление набора упрощенных моделей электронной структуры дефектов на основе соображений симметрии ⁵⁰ , а затем выполнение полуклассических расчетов для моделирования их оптических и спиновых динамика при стационарном освещении, для сравнения с экспериментальными результатами.С этой целью мы не начинаем с конкретной модели дефекта и не изучаем ее подробно; скорее мы исследуем качественные сходства и различия между различными электронными конфигурациями, чтобы сузить пространство возможностей. Мы надеемся, что это будет мотивировать будущие усилия по сравнению этих качественных предсказаний с количественными, ab initio, расчетами предполагаемых конфигураций дефектов в h-BN.

Отправной точкой любого расчета в теории молекулярных орбит является идентификация соответствующей группы точек, описывающей симметрию молекулы или системы дефектов.Сосредоточимся на точечной группе C _{2 v} по причинам, описанным в тексте, и выберем систему координат с \(\hat x\) в качестве главной оси симметрии, лежащей в плоскости h-BN , причем ось \(\hat z\) ориентирована нормально к плоскости h-BN. Более подробная информация, включая таблицу символов и таблицу умножения групп для C _{2 v} , доступна в дополнительных методах (раздел IG).

Здесь мы рассматриваем только электронные степени свободы, т.е.2),$$

(3)

, где μ _B — магнетон Бора, а \({\hat{\mathbf S}}\) — оператор проектирования спина. Поскольку спин-орбитальная связь в h-BN относительно слаба, мы предполагаем, что компоненты g -тензора изотропны и почти равны затравочному значению g  ~  2.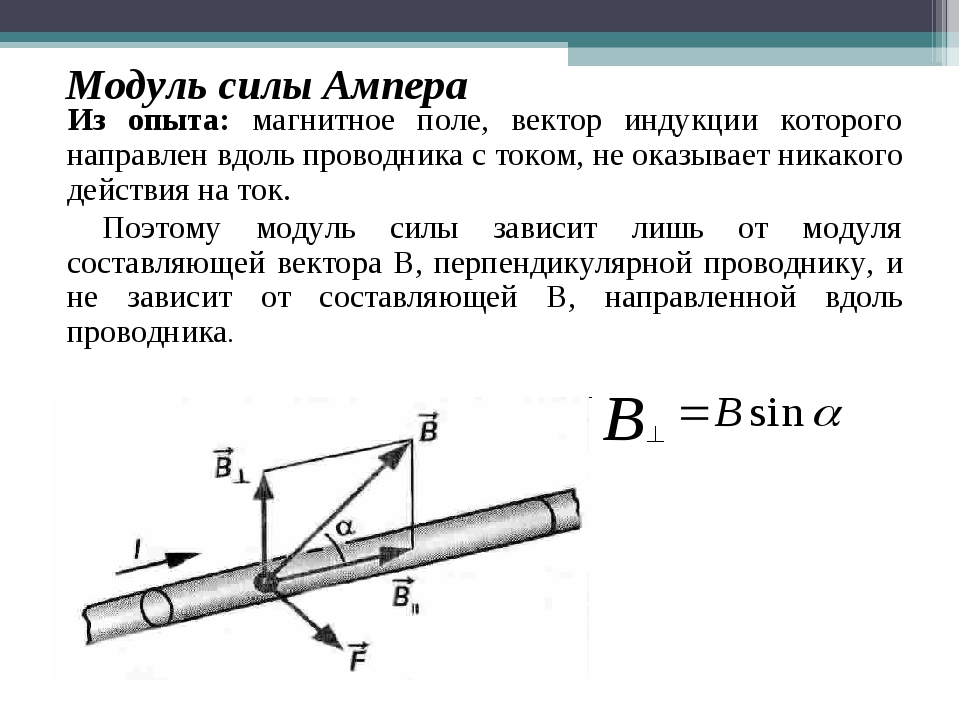 Параметры D и E – параметры расщепления в нулевом поле; Оба термина ненулевые в C _{2 V} , в отличие от случаев высшего симметрии, такие как C _{3 V} или 9 D _{3 H} , где E исчезают к симметрии.Их источником могут быть спин-спиновые взаимодействия первого порядка или спин-орбитальные взаимодействия второго порядка, хотя спин-спиновые взаимодействия, вероятно, преобладают из-за слабой спин-орбитальной связи в h-BN. Для конкретных орбитальных конфигураций их значения можно вычислить явно через двухэлектронные интегралы ^32,51,52 , но в нашей общей трактовке D и E являются эмпирическими параметрами. Явные матричные представления уравнения. (3) представлены в Разделе IG Дополнительных методов.

В остальном мы сосредоточимся на случае синглетно-триплетных конфигураций, поскольку они больше согласуются с нашими экспериментальными наблюдениями, чем дублетно-квартетные конфигурации, основанные на аргументах симметрии (см. Раздел IG 2 Дополнительных методов). Начиная с минимальной конфигурации произвольных одночастичных орбиталей (две для случая синглетно-основного состояния, три для триплетно-основного состояния), мы строим диаграммы Яблонского, включающие оптические основные и возбужденные состояния вместе с возможными метастабильными состояниями с различными С .Учет разрешенных правил отбора оптических диполей уменьшает количество конфигураций, поскольку в экспериментах мы наблюдаем линейно поляризованное излучение в плоскости. Предполагается, что безызлучательные ISC-переходы возникают в результате спин-орбитальных взаимодействий. Правила отбора определяются путем определения симметричных спин-триплетных базисных состояний \(\{ |s_x\rangle,|s_y\rangle,|s_z\rangle\} \sim \{A_2,B_2,B_1\}\) и использования таблица группового умножения для определения спинового состояния (если есть), чья спин-орбитальная симметрия соответствует симметрии доступной спин-синглетной конфигурации.2,$$

(4)

, где μ  ∈ { x , y , z } и i  ∈ {1, 2, 3}. .. \rangle = R\langle {\mathbf{x}}\rangle = 0\), т. е. из нулевого пространства R . Предполагая, что радиационные переходы сохраняют спин, стационарная PL определяется выражением \(\langle {\mathrm{PL}}\rangle = \Gamma _s\mathop {\sum}\nolimits_{i \in {\mathrm{ES }}} \langle x_i\rangle\), где GS (ES) относится к основному состоянию (возбужденному состоянию). Автокорреляционная функция рассчитывается путем численного интегрирования основного уравнения, начиная с начального условия, соответствующего конфигурации, следующей за испусканием фотона.{(2)} (t) = \ frac {{{\ mathrm {PL}} (t)}} {\ langle {\ mathrm {PL}} \ rangle}} = \ frac {{\ mathop {\ sum } \ limit_ {i \ in {\ mathrm {GS}}, j \ in {\ mathrm {ES}}} R_ {ij} x_j (t)}} {\ langle {\ mathrm {PL}} \ rangle} }.$$

(6)

Дополнительные сведения о моделировании различных спиновых конфигураций, структур энергетических уровней, PL, автокорреляции и моделирования ODMR представлены в дополнительной информации.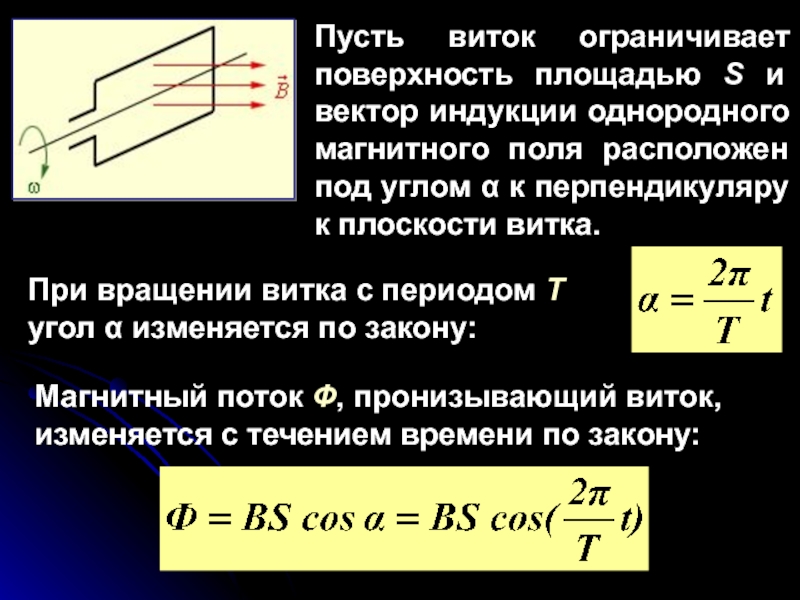

Наличие кода

Коды, используемые для анализа данных автокорреляции и моделирования оптической динамики с помощью основного уравнения, можно получить у соответствующего автора по запросу.

Уравнения Максвелла

Уравнения электромагнетизма Максвелла

Уравнения Максвелла представляют собой набор из четырех уравнений, описывающих поведение электрических и магнитных полей и их взаимосвязь. В конечном итоге они демонстрируют, что электрические и магнитные поля — это два проявления одного и того же явления.

В вакууме без заряда и тока уравнения Максвелла в дифференциальной форме имеют вид: b / ∂ / ∂ t)

∇ x b = μ b = μ 0 = μ 0 = ∂ ε 8 0 9 ( ∂ E / ∂ t)

где E и B — электрическое поле и плотность магнитного потока, а ∇· и ∇× — операторы дивергенции и ротора соответственно.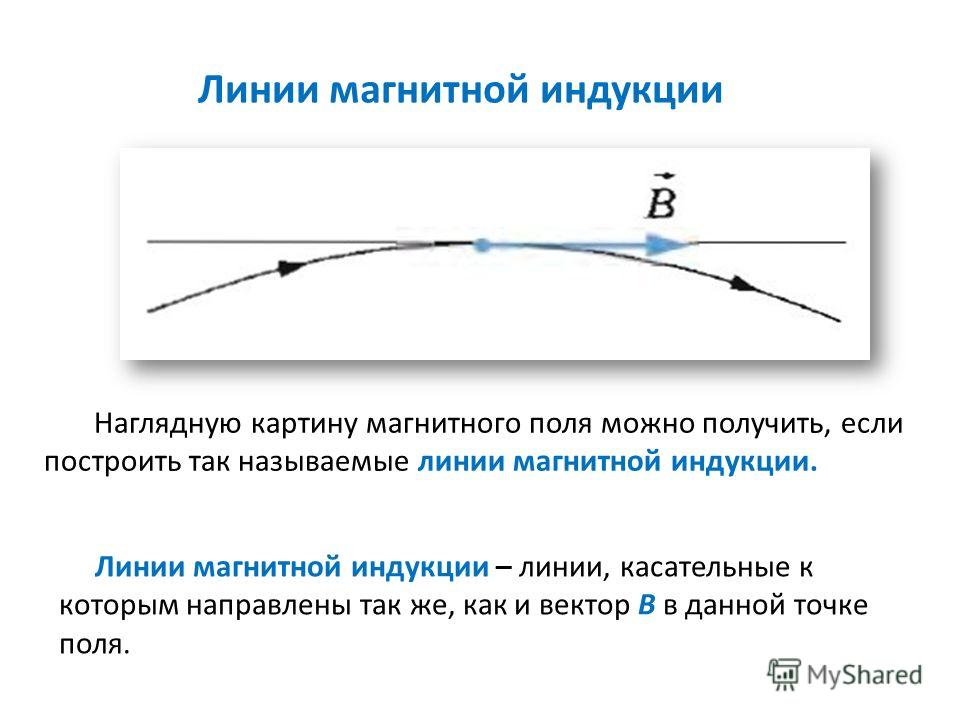 Переменные µ ₀ и ε ₀ являются фундаментальными универсальными константами, называемыми проницаемостью свободного пространства и диэлектрической проницаемостью свободного пространства соответственно. В вакууме без электрических зарядов математические решения этих дифференциальных уравнений представляют собой синусоидальные плоские волны с электрическим и магнитным полями, перпендикулярными друг другу и направлению движения, со скоростью

, где c распознается как скорость света.

Уравнения Максвелла являются макроскопическими выражениями; они относятся к средним полям и не включают квантовые эффекты.

Уравнения Максвелла: общая форма

В самом общем виде уравнения Максвелла можно записать в виде магнетизма)

∇ x E = -(∂ B /∂t) (закон индукции Фарадея)

∇ x H = J + ∂A’ттр D

В первом уравнении ρ — плотность свободного электрического заряда. В последнем уравнении Дж — это плотность свободного тока.

для линейных материалов, отношения между E , D , B , и H , и H D = ε E

B = μ H

здесь, ε — электрическая проницаемость, µ — магнитная проницаемость. Для нелинейных материалов e и µ зависят от напряженности поля. В изотропных средах e и µ не зависят от положения.В неизотропных средах e и µ можно описать как матрицы 3 × 3, которые представляют различные значения диэлектрической и магнитной проницаемости вдоль разных пространственных осей среды. Во всех средах e и µ также меняются в зависимости от частоты излучения.

Чтобы соответствовать уравнениям Максвелла, величины векторов электрического и магнитного полей должны удовлетворять следующему соотношению:

Таким образом, в электромагнитном излучении вектор электрического поля имеет гораздо большую амплитуду, чем вектор магнитного поля.