Векторная диаграмма онлайн. Построение векторных диаграмм токов и напряжений
Рисунок 25- Векторная диаграмма токов в точке КЗ
Рисунок 26-Векторная диаграмма токов в сечении А-А
Рисунок 27- Векторная диаграмма напряжений в сечении А-А
Рисунок 28- Векторная диаграмма токов в сечении В-В
Рисунок 29- Векторная диаграмма напряжений сечении В-В
Расчет периодической слагающей тока КЗ методом типовых кривых.
Задача III. Расчет периодической слагающей тока трехфазного КЗ
Методом типовых кривых.
При определении периодического тока трехфазного КЗ составляется схема прямой последовательности для начального момента времени, в которой генераторы представляются сверхпереходными параметрами; нагрузки не учитываются (рисунок 2). Общая методика расчета описана в . После эквивалентирования получена промежуточная схема, (рисунок 30) , которая преобразуется к лучевому виду относительно точки КЗ (рисунок 31). При этом используются коэффициенты токораспределения .
Общая методика расчета описана в . После эквивалентирования получена промежуточная схема, (рисунок 30) , которая преобразуется к лучевому виду относительно точки КЗ (рисунок 31). При этом используются коэффициенты токораспределения .
В процессе упрощений схемы замещения получены следующие сопротивления: Х 15 =Х 1 +Х 2 /2=0+0,975425/2=0,4877125 о.е.
Х 16 =Х 4 +Х 5 =0,84+1,53=2,37 о.е.
Рисунок 30- Промежуточная схема Рисунок 31- Расчетная схема
Х 17 =Х 6 +Х 7 =0,88+0=0,88 о.е.
Х 18 =Х 11 +Х 9 /2=0+1,240076/2=0,620038 о.е.
Х 19 =Х 12 +Х 13 =2,117202+0,192308=2,30951 о.е.
Х ЭК =Х 18 *Х 19 /(Х 18 +Х 19)=0,620038*2,30951/(0,620038+2,30951)=0,488807 о.е.
С 1 =Х ЭК /Х 18 =0,488807/0,620038=0,78835.
С 2 =Х ЭК /Х 19 =0,488807/2,30951=0,21165.
Х 20 =(Х эк +Х 17) /С 1 =1,736294 о.е.
Х 21 =(Х эк +Х 17) /С 2 =6,467324 о.е.
Получена схема, изображенная на рисунке 31. Далее находятся начальные периодические токи в месте КЗ.
I » Г =Е 2 /Х 16 *I Б =1,13/2,27*2,5102=1,196846 кА.
I » С1 =Е 1 /Х 15 *I Б =1/0,4877125*2,5102=5,146885 кА.
I » С2 =Е 3 /Х 20 *I Б =1/1,736294*2,5102=1,445723 кА.
I » С3 =Е 4 /Х 21 *I Б =1/6,467324*2,5102=0,388136 кА.
Токи от систем постоянны. Периодический ток, по типовым кривым, определяется для синхронного генератора с тиристорной или высокочастотной системой возбуждения. В соответствии с методикой рассчитывается номинальный ток синхронного генератора и далее определяется номер типовой кривой.
I ГН = S ГН / *U Б = 100/( *0,85*230) = 0,295320 кА;
I * ПО =I Г2 » /I ГН =1,196846/0,295320 = 4,05»4.
Так как отношение I Г2 » /I ГН » 4,то по выбирается 4 типовая кривая:
I КЗПОСТ =I » С2 +I » С3 +I » С1 =5,1468885+1,445723+0,388136=6,980748 кА
| t, сек | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| I Г t /I ” Г, о.е | 0,85 | 0,78 | 0,755 | 0,75 | 0,745 | |
| I Г t , кА | 1,1968 | 1,017 | 0,933 | 0,903 | 0,897 | 0,891 |
| Суммарный I К t , кА | 8,1775 | 7,9977 | 7,9137 | 7,8837 | 7,8777 | 7,872 |
В качестве примера рассмотрим нахождение периодического тока для момента времени 0,1 сек.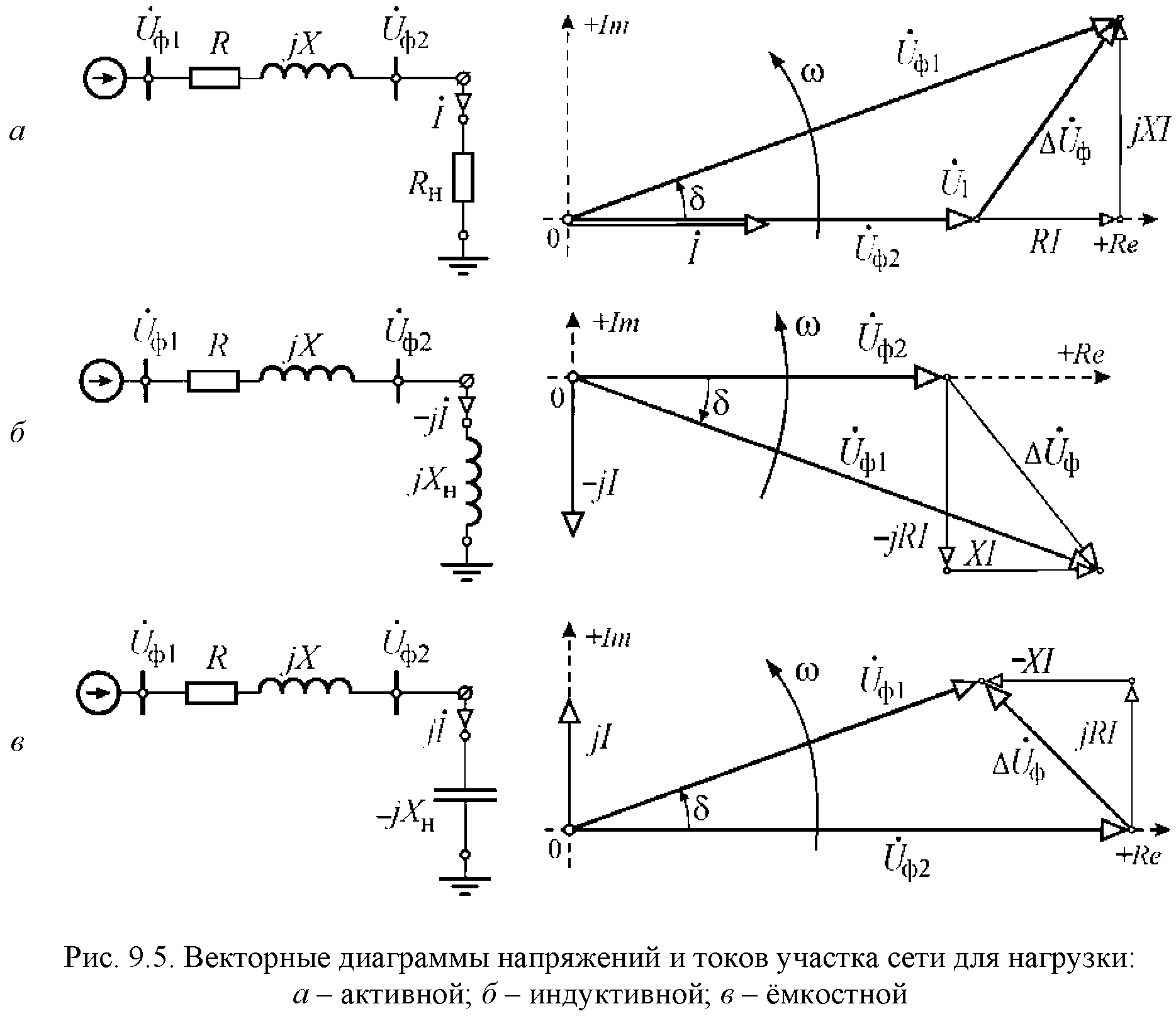 По кривой 4 для этого момента времени определяется отношение In,t,г/Inoг=0,85.
По кривой 4 для этого момента времени определяется отношение In,t,г/Inoг=0,85.
Определяется действующее значение периодической составляющей тока КЗ от генератора: In,t,г=0,85 * Inо*I НОМ =0,85 * 4,05*0,2953 = 1,017 кА.
Суммарный периодический ток при К (3) в узле К с учетом типовых кривых изображен на рисунке 32.
Рисунок 32- График зависимости суммарного периодического тока от времени КЗ Iкt=f(t)
Задача IV. Расчет периодической слагающей тока несимметричного КЗ методом типовых кривых.
Для определения периодических токов КЗ при К (1.1) методом типовых кривых составляется схема замещения обратной последовательности без учета нагрузок (рисунок 33). Далее производится упрощение схемы замещения и получение эквивалентного сопротивления обратной последовательности. Последовательность упрощений приведена ниже и на рисунках 34-37.
Х 15 =Х 1 +Х 2 /2=0+0,975425/2=0,487713 о.е. Х 16 =Х 4 +Х 5 =0,84+1,87=2,71 о.е.
Х 17 =Х 6 +Х 7 =0+0,88=0,88 о. е. Х 18 =Х 11 +Х 9 /2=0+1,240076/2=0,620038 о.е.
е. Х 18 =Х 11 +Х 9 /2=0+1,240076/2=0,620038 о.е.
Х 19 =Х 12 +Х 13 =2,117202+0,230769=2,347971 о.е.
Х 20 =Х 15 *Х 16 /(Х 15 +Х 16)=0,487713*2,71/(0,487713+2.71)=0,413327 о.е.
Х 22 =Х 17 +Х 21 =0,88+0,490508=1,370508 о.е. Х ЭК2 =Х 20 *Х 22 /(Х 20 +Х 22)=0,413327*1,370508/ /(0,413327+1,370508)=0,317556 о.е.
Рисунок 33- Схема замещения обратной последовательности
Рисунок 34- Упрощение схемы №1
Рисунок 35- Упрощение схемы №2
Рисунок 36- Упрощение схемы №3
Рисунок 37- Эквивалентная схема замещения обратной
Последовательности
Аналогично составим схему замещения нулевой последовательности (рисунок 38). Порядок упрощения схемы замещения приведен ниже на рисунках 39-42.
Рисунок 38 –Расчетная схема замещения нулевой последовательности
Х 13 =Х 1 +Х 2 /2=0+4,585/2=2,292 о.е. Х 14 =Х 10 +Х 9 /2=0+6,82/2=3,41 о. е.
е.
Х 15 =Х 11 +Х 12 =7,41+0,769= 8,18 о.е. Х 16 =Х 13 *Х 4 /(Х 13 +Х 4)=2,29225*0,84/(2,29+0,84)=0,615 о.е.
Х 18 =Х 6 +Х 17 =0,88+1,338581=2,219 о.е.
Х 17 =1 / (1/Х 7 +1/Х 15 +1/Х 14)=1 /(1/3,016+1/8,18+1/3,41)=1,34 о.е.
Рисунок 39- Упрощение схемы №1
Рисунок 40- Упрощение схемы №2
Рисунок 41 — Упрощение схемы № 3
Рисунок 42- Эквивалентная схема замещения нулевой
Последовательности
Для решения поставленной задачи используются эквивалентные данные по прямой последовательности из предыдущей задачи. С учетом особенностей К (1.1) получаем схему, приведенную на рисунке 43. Эта схема приводится к виду, изображенному на рисунке 44.
Рассмотрен для случая с исправным нулевым проводом. Векторные диаграммы напряжений и токов даны на рисунках 15 и 16; на рисунке 17 дана совмещенная диаграмма токов и напряжений
1. Строятся оси комплексной плоскости: действительных величин (+1) — горизонтально, мнимых величин (j) — вертикально.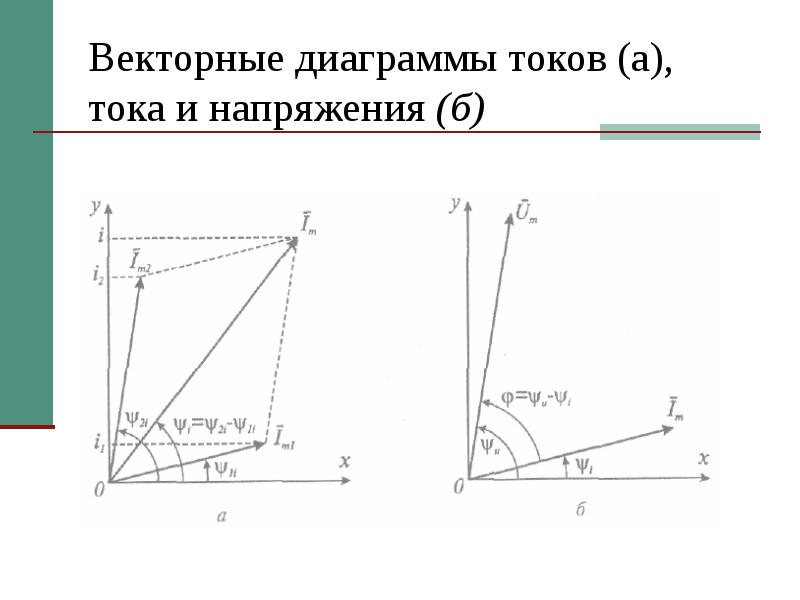
2. Исходя из значений модулей токов и напряжений и размеров полей листов, отведеных для построения диаграмм, выбираются масштабы тока mI и напряжения mU. При использовании формата А4 (размеры 210х297 мм) при наибольших модулях (см. табл. 8) тока 54 А и напряжения 433 В приняты масштабы: mI = 5 А/см, mU = 50 В/см.
3. С учетом принятых масштабов mI и mU определяется длина каждого вектора, если диаграмма строится с использованием показательной формы его записи; при использовании алгебраической формы находятся длины проекций векторов на оси действительных и мнимых величин, т.е. длины действительной и мнимой частей комплекса.
Например, для фазы А:
Длина вектора тока / ф.А / = 34,8 А/ 5 А/см = 6,96 см; длина его действительной части
I ф.А = 30 А/ 5 А/см = 6 см,
длина его мнимой части
I ф.А = -17,8 А/5 А/см = — 3,56 см;
Длина вектора напряжения / А нагр./ = 348 В/ 50 В/см = 6,96 см; длина его действительной части
U А нагр. = 340,5 В/ 50 В/см = 6,8 см;
= 340,5 В/ 50 В/см = 6,8 см;
длина его мнимой части
U Анагр. = 37,75 В/ 50 В/см = 0,76 см.
Результаты определения длин векторов, их действительных и мнимых частей отражены в таблице 9.
Таблица 9 — Длины векторов тока и напряжения, их действительных и мнимых частей для случая неповрежденного нулевого провода.
| Величина | Масштаб, 1/см | Длина вектора, см | Длина действительной части, см | Длина мнимой части, см | |
| Напряжения фаз сети | U А | 50 В/см | 7,6 | 7,6 | |
| UВ | 7,6 | — 3,8 | — 6,56 | ||
| UС | 7,6 | — 3,8 | 6,56 | ||
| Напряжения фаз нагрузки | U Анагр. | 50 В/см | 6,96 | 6,8 | 0,76 |
| UВ нагр. | 7,4 | — 4,59 | — 5,8 | ||
| UС нагр. | 8,66 | -4,59 | 7,32 | ||
| U0 | 1,08 | 0,79 | — 0,76 |
Продолжение таблицы 9
| Токи фаз нагрузки | I ф. А А | 5 А/см | 6,96 | 6.0 | — 3,56 |
| I ф.В | 7,4 | 1,87 | — 7,14 | ||
| I ф.С | 3,13 | 0,1 | 3,12 | ||
| I 0 | 10,8 | 7,9 | — 7,6 |
4. Построение векторной диаграммы напряжений.
4.1 На комплексной плоскости строятся векторы фазных напряжений питающей сети А, В, С; соединив их концы, получают векторы линейных напряжений АВ, ВС, СА. Затем строятся векторы фазных напряжений нагрузки А нагр., В нагр., С нагр. Для их построения можно использовать обе формы записи комплексов токов и напряжений.
Например, вектор А нагр. строится по показательной форме следующим образом: от оси +1 под углом 6 10 , т.е. против часовой стрелки, откладывается отрезок длиной 6,96 см; по алгебраической форме его можно построить, отложив по оси +1 отрезок длиной 6,81 см, а по оси + j отрезок длиной 0,76 см, концы этих отрезков являются координатами конца вектора А нагр.
4.2 Т.к. линейные напряжения нагрузки заданы питающей сетью, для определения положения нейтрали нагрузки необходимо выполнить параллельный перенос векторов фазных напряжений нагрузки А нагр., В нагр., С нагр. так, чтобы их концы совпали с концами фазных напряжений питающей сети.
Точка 0, в которой окажутся их начала, есть нейтраль нагрузки. В этой точке находится конец вектора напряжения смещения нейтрали 0, его начало расположено в точке 0. Этот вектор можно также построить, используя данные таблицы 9.
5. Построение векторной диаграммы токов.
5.1 Построение векторов фазных токов нагрузки ф.А, ф.В, ф.С подобно построению векторов фазных напряжений.
5.2 Сложением векторов фазных токов находится вектор тока в нулевом проводе 0; его длина и длины его проекций на оси должны совпасть с указанными в таблице 8.
Векторные диаграммы токов и напряжений для случая обрыва нулевого провода строятся аналогично.
Следует выполнить анализ результатов расчета и построения векторных диаграмм и сделать выводы о влиянии несимметрии нагрузки на величину ее фазных напряжений и на напряжение нейтрали; особое внимание необходимо обратить на последствия обрыва нулевого провода сети при несимметричной нагрузке.
Примечание
. Допускается совмещение диаграмм токов и напряжений при условии их выполнения разными цветами.
Рисунок 15. Векторная диаграмма напряжений
Рисунок 16. Векторная диаграмма токов.
Рисунок 17. Совмещенная векторная диаграмма напряжений и токов.
а) Понятие о векторах
На рис. 1-4 приведена кривая изменения переменного тока во времени. Ток сначала растет от нуля (при = 0°) до максимального положительного значения + I M (при = 90°), затем убывает, переходит через нуль (при = 180°), достигает максимального отрицательного значения — I M (при = 270°) и, наконец, возвращается к нулю (при = 360°). После этого весь цикл изменения тока повторяется.
Кривая изменения переменного тока во времени, построенная на рис. 1-4, называется синусоидой. Время Т, в течение которого происходит полный цикл изменения тока, соответствующий изменению угла до 360°, называется периодом переменного тока. Число периодов за 1 с называется частотой переменного тока. В промышленных установках и в быту в СССР и в других странах Европы используется главным образом переменный ток частотой 50 Гц. Этот ток 50 раз в секунду принимает положительное и отри цательное направление.
Число периодов за 1 с называется частотой переменного тока. В промышленных установках и в быту в СССР и в других странах Европы используется главным образом переменный ток частотой 50 Гц. Этот ток 50 раз в секунду принимает положительное и отри цательное направление.
Изменение переменного тока во времени можно записать в следующем виде:
где i — мгновенное значение тока, т. е. значение тока в каждый момент времени; I м — максимальное значение тока; — угловая частота переменного тока, f= 50 Гц, = 314; — начальный угол, соответствующий моменту времени, с которого начинается отсчет времени (при t = 0).
Для частного случая, показанного на рис. 1-4,
Анализируя действие устройств релейной защиты и автоматики, необходимо сопоставлять токи и напряжения, складывать или вычитать их, определять углы между ними и производить другие операции. Пользоваться при этом кривыми, подобными приведенной на рис. 1-4, неудобно, поскольку построение синусоид тока и напряжения занимает много времени и не дает простого и наглядного результата. Поэтому для упрощения принято изображать токи и напряжения в виде отрезков прямых линий, имеющих определенную длину и направление, — так называемых векторов (ОА на рис. 1-4). Один конец вектора закреплен в точке О — начало координат, а второй вращается против часовой стрелки.
Поэтому для упрощения принято изображать токи и напряжения в виде отрезков прямых линий, имеющих определенную длину и направление, — так называемых векторов (ОА на рис. 1-4). Один конец вектора закреплен в точке О — начало координат, а второй вращается против часовой стрелки.
Мгновенное значение тока или напряжения в каждый момент времени определяется проекцией на вертикальную ось вектора, длина которого равна максимальному значению электрической величины тока или напряжения. Эта проекция будет становиться то положительной, то отрицательной, принимая максимальные значения при вертикальном расположении вектора.
За время Т, равное периоду переменного тока, вектор совершит полный оборот по окружности (360°), занимая последовательно положения и т. д. При
частоте переменного тока 50 Гц вектор будет совершать 50 об/с.
Таким образом, вектор тока или напряжения — это отрезок прямой, равный по величине максимальному значению тока или напряжения, вращающийся относительно точки О против движения часовой стрелки со скоростью, определяемой частотой переменного тока. Зная положение вектора в каждый момент времени, можно определить мгновенное значение тока или напряжения в данный момент. Так, для положения вектора тока ОА, показанного на
Зная положение вектора в каждый момент времени, можно определить мгновенное значение тока или напряжения в данный момент. Так, для положения вектора тока ОА, показанного на
рис. 1-5, его мгновенное значение определяется проекцией на вертикальную ось, т. е.
На основании рис. 1-5 можно также сказать, что ток в данный момент времени имеет положительную величину. Однако это еще не дает полного представления о протекании процесса в цепи переменного тока, так как неизвестно, что значит положительный или отрицательный ток, положительное или отрицательное напряжение.
Для того чтобы векторные диаграммы токов и напряжений давали полную картину, их нужно увязать с фактическим протеканием процесса в цепи переменного тока,
т. е. необходимо предварительно принять условные положительные направления токов и напряжений в рассматриваемой схеме.
Без выполнения этого условия, если не заданы положительные направления токов и напряжений, любая векторная диаграмма не имеет никакого смысла.
Рассмотрим простую однофазную цепь переменного тока, приведенную на рис. 1-6, а. От однофазного генератора энергия передается в активное сопротивление нагрузки R. Зададимся положительными направлениями токов и напряжений в рассматриваемой цепи.
За условное положительное направление напряжения и э д. с. примем направление, когда потенциал вывода генератора или нагрузки, связанного с линией, выше потенциала вывода, соединенного с землей. В соответствии с правилами, принятыми в электротехнике, положительное направление для э. д. с. обозначено стрелкой, направленной в сторону более высокого потенциала (от земли к линейному выводу), а для напряжения — стрелкой, направленной в сторону более низкого потенциала (от линейного вывода к земле).
Построим векторы э. д. с. и тока, характеризующие работу рассматриваемой цепи (рис. 1-6, б). Вектор э. д. с. произвольно обозначим вертикальной линией со стрелкой, направленной вверх. Для построения вектора тока запишем для цепи уравнение согласно второму закону Кирхгофа:
Поскольку знаки векторов тока и э.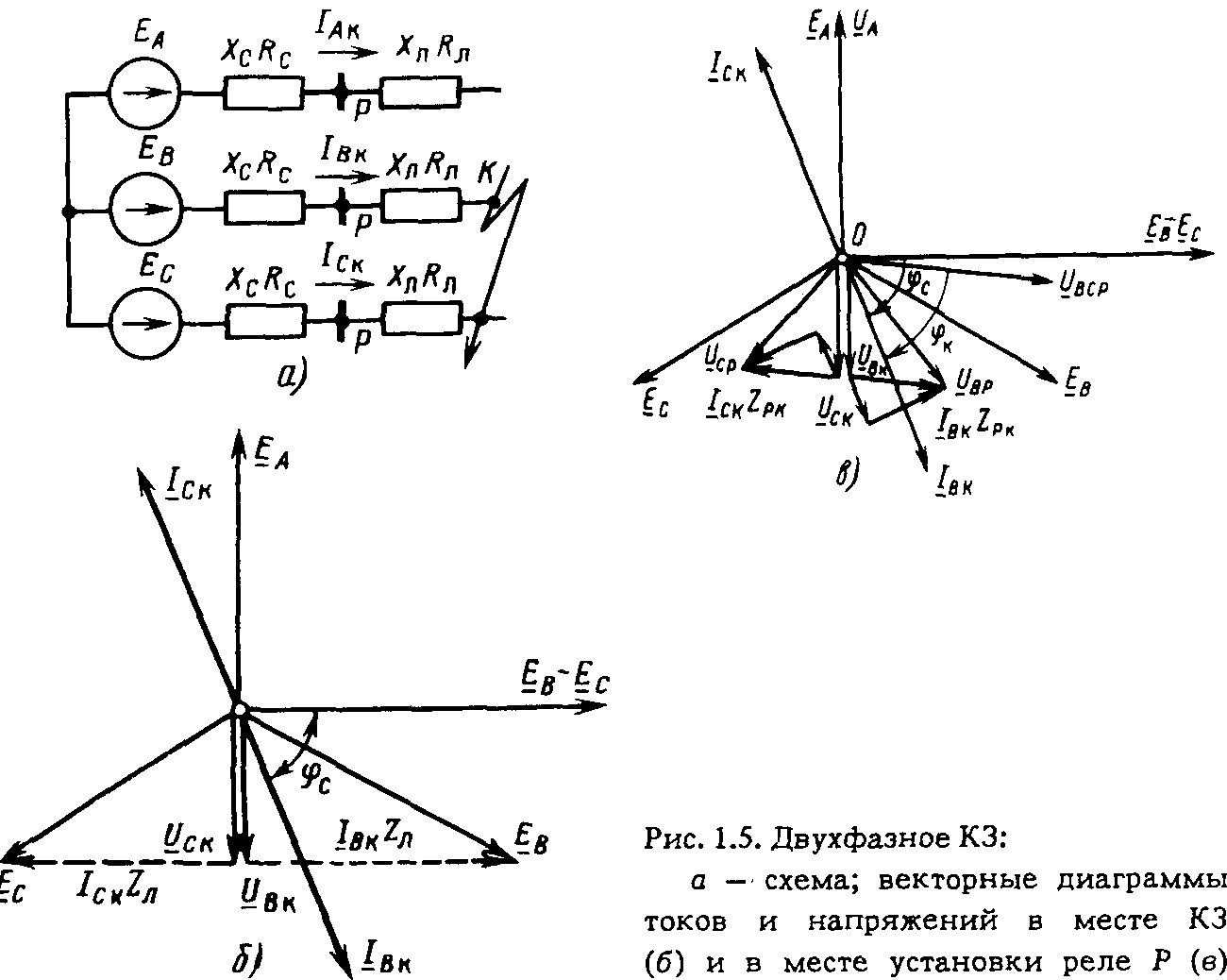 д. с. в выражении (1-7) совпадают, вектор тока будет совпадать с вектором э. д. с. и на рис. 1-6, б.
д. с. в выражении (1-7) совпадают, вектор тока будет совпадать с вектором э. д. с. и на рис. 1-6, б.
Здесь и в дальнейшем при построении векторов будем откладывать их по величине равными эффективному значению тока и напряжения, что удобно для выполнения различных математических операций с векторами. Как известно, эффективные значения тока и напряжения в раз меньше соответствующих максимальных (амплитудных) значений.
При заданных положительных направлениях тока и напряжения однозначно определяется и знак мощности. Положительной в рассматриваемом случае будет считаться мощность, направленная от шин генератора в линию:
так как векторы тока и э. д. с. на рис. 1-6, б совпадают.
Аналогичные соображения могут быть высказаны и для
трехфазной цепи переменного тока, показанной па рис. 1-7,а.
В этом случае во всех фазах приняты одинаковые положительные направления, чему соответствует симметричная диаграмма токов и напряжений, приведенная на рис. 1-7, б. Отметим, что симметричной называется такая трехфазная система векторов, когда все три вектора равны но величине и сдвинуты относительно друг друга на угол 120°.
Вообще говоря, совсем не обязательно принимать одинаковые положительные направления во всех фазах. Однако принимать разные положительные направления в разных фазах неудобно, так как пришлось бы изображать несимметричную систему векторов при работе электрической цепи в нормальном симметричном режиме, когда все три фазы находятся в одинаковых условиях.
б) Операции с векторами
Когда мы рассматриваем только одну кривую тока или напряжения, начальное значение угла, с которого начинается отсчет или, иначе говоря, положение вектора на диаграмме, соответствующее начальному моменту времени, может быть принято произвольным. Если же одновременно рассматриваются два или несколько токов и напряжений, то, задавшись начальным положением на диаграмме одного из векторов, мы тем самым уже определяем положение всех других векторов.
Все три вектора фазных напряжений показанные на рис. 1-7, б, вращаются против часовой стрелки с одинаковой скоростью, определяемой частотой переменного тока. При этом они пересекают вертикальную ось, совпадающую с направлением вектора на рис. 1-7,б, поочередно с определенной последовательностью, а именно которая называется чередованием фаз напряжения (или тока).
При этом они пересекают вертикальную ось, совпадающую с направлением вектора на рис. 1-7,б, поочередно с определенной последовательностью, а именно которая называется чередованием фаз напряжения (или тока).
Для того чтобы определить взаимное расположение двух векторов, обычно говорят, что один из них опережает или отстает от другого. При этом опережающим считается вектор, который при вращении против часовой стрелки раньше пересечет вертикальную ось. Так, например, можно сказать, что вектор напряжения на рис. 1-7, б опережает на угол 120°, или, с другой стороны, вектор отстает от вектора на угол 120°. Как видно из рис. 1-7, выражение «вектор отстает на угол 120°» равноценно выражению «вектор опережает на угол 240°».
При анализе разных электрических схем возникает необходимость складывать или вычитать векторы тока и напряжения. Сложение векторов производится геометрическим суммированием по правилу параллелограмма, как показано на рис. 1-8, а, на котором построена сумма токов
Так как вычитание — действие обратное сложению, очевидно, что для определения разности токов (например, достаточно к току прибавить вектор, обратный
Вместе с тем на рис. 1-8, а показано, что вектор разности токов можно построить проще, соединив
1-8, а показано, что вектор разности токов можно построить проще, соединив
линией концы векторов При этом стрелка вектора разности токов направлена в сторону первого вектора, т. е.
Совершенно аналогично строится векторная диаграмма междуфазных напряжений, например (рис. 1-8, б).
Очевидно, что положение вектора на плоскости определяется его проекциями на две любые оси. Так, например, для
того чтобы определить положение вектора ОА (рис. 1-9), достаточно знать его проекции на взаимно перпендикулярные оси
Отложим на осях координат проекции вектора и и восстановим из точек перпендикуляры
к осям. Точка пересечения этих перпендикуляров и есть точка А — один конец вектора, вторым концом которого является точка О — начало координат.
в) Назначение векторных диаграмм
Работникам, занимающимся проектированием и эксплуатацией релейной защиты, весьма часто приходится использовать в своей работе так называемые векторные диаграммы — векторы токов и напряжений, построенные на плоскости в определенном сочетании, соответствующем электрическим процессам, происходящим в рассматриваемой схеме.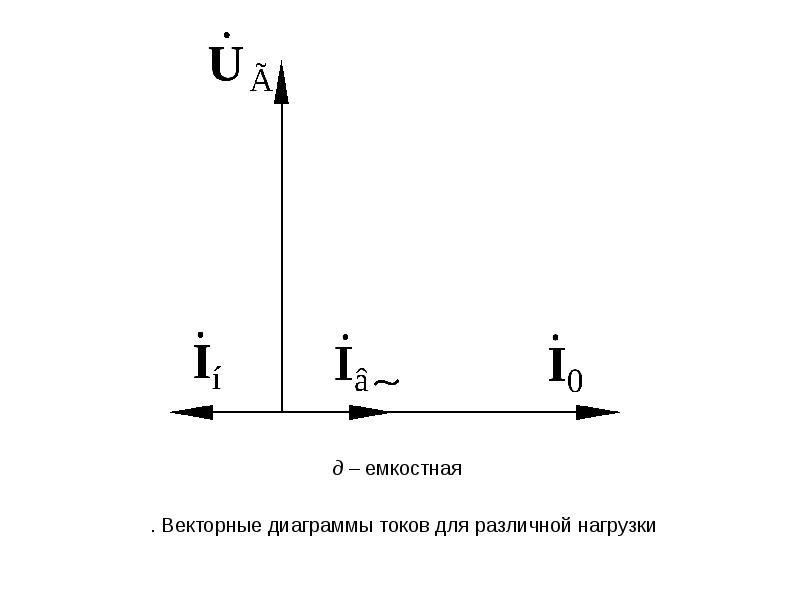
Векторные диаграммы токов и напряжений строятся при расчете коротких замыканий, при анализе токораспре-деления в нормальном режиме.
Анализ векторных диаграмм токов и напряжений является одним из основных, а в ряде случаев единственным способом проверки правильности соединения цепей тока и напряжения и включения реле в схемах дифференциальных и направленных защит.
По сути дела, построение векторной диаграммы целесообразно во всех случаях, когда к рассматриваемому реле подаются две или больше электрических величин: разность токов в максимальной токовой или дифференциальной защите, ток и напряжение в реле направления мощности или в направленном реле сопротивления. Векторная диаграмма позволяет сделать заключение о том, как рассматриваемая защита будет работать при коротком замыкании, т. е. оценить правильность ее включения. Взаимное расположение векторов токов и напряжений на диаграмме определяется характеристикой рассматриваемой цепи, а также условно принятыми положительными направлениями токов и напряжений.
Для примера рассмотрим две векторные диаграммы.
На рис. 1-10, а показана однофазная цепь переменного тока, состоящая из генератора и последовательно соединенных емкостного активного и индуктивного сопротивлений (примем, что индуктивное сопротивление больше емкостного x L > x C). Положительные направления токов и напряжений, так же как и в случаях, рассмотренных выше, обозначены на рис. 1-10, а стрелками. Построение векторной диаграммы начнем с вектора э. д. с, который расположим на рис. 1-10, б вертикально. Величина тока, проходящего в рассматриваемой цепи, определится из следующего выражения:
Поскольку в рассматриваемой цепи имеются активные и реактивные сопротивления, причем x L > x C , вектор тока отстает от вектора напряжения на угол :
На рис. 1-10, б построен вектор отстающий от
вектора на угол 90°. Напряжение в точке n
определяется разностью векторов .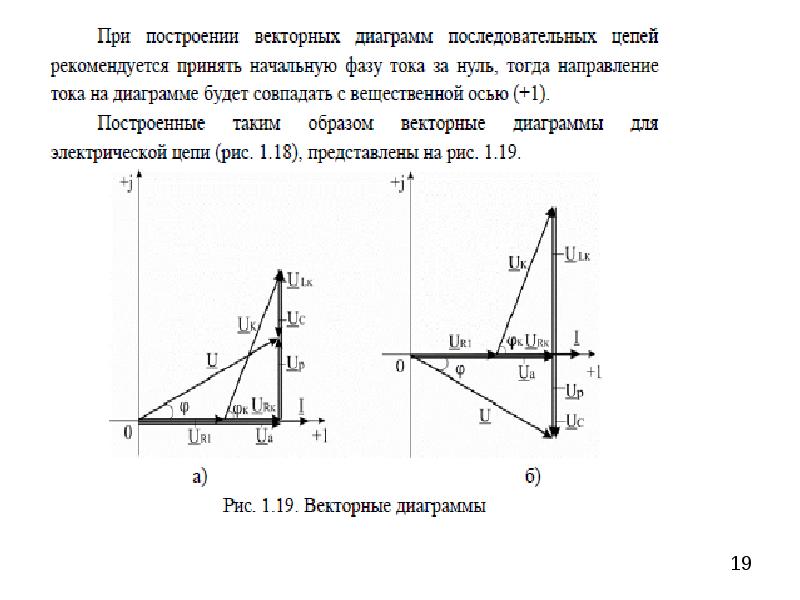 Напряжение в точке m определится аналогично:
Напряжение в точке m определится аналогично:
г) Векторные диаграммы при наличии трансформации
При наличии в электрической цепи трансформаторов необходимо ввести дополнительные условия, для того чтобы сопоставлять векторные диаграммы токов и напряжений на разных сторонах трансформатора. Положительные направления токов при этом следует задавать с учетом полярности обмоток трансформатора.
В зависимости от направления намотки обмоток трансформатора взаимное направление токов в них меняется. Для того чтобы определять направление токов в обмотках силового трансформатора и сопоставлять их между собой, обмоткам трансформатора дают условные обозначения «начало» и «конец».
Нарисуем схему, приведенную на рис. 1-6, только между источником э. д. с. и нагрузкой включим трансформатор (рис. 1-12, а). Обозначим начала обмоток силового трансформатора буквами А и а, концы — X и х. При этом следует иметь в виду, что «начало» одной из обмоток принимается произвольно, а второй — определяется на основании условных положительных направлений токов, заданных для обеих обмоток трансформатора.На рис. 1-12, а указаны положительные направления токов в обмотках силовых трансформаторов. В первичной обмотке положительным считается направление тока от «начала» к «концу», а во вторичной — от «конца» к «началу».
При этом следует иметь в виду, что «начало» одной из обмоток принимается произвольно, а второй — определяется на основании условных положительных направлений токов, заданных для обеих обмоток трансформатора.На рис. 1-12, а указаны положительные направления токов в обмотках силовых трансформаторов. В первичной обмотке положительным считается направление тока от «начала» к «концу», а во вторичной — от «конца» к «началу».
В результате при таких положительных направлениях направление тока в сопротивлении нагрузки остается таким же, что и до включения трансформатора (см. рис. 1-6 и 1-12).
где — магнитные потоки в магнитопроводс трансформатора, а
— создающие эти потоки намагничивающие силы (н. с).
Из последнего уравнения
Согласно равенству (1-11) векторы имеют одинаковые знаки и, следовательно, будут совпадать по направлению (рис. 1-12, б).
Принятые положительные направления токов в обмотках трансформатора удобны тем, что векторы первичного и
Вторичного токов на векторной диаграмме совпадают по направлению (рис. 1-12, б). Для напряжений также удобно принять такие положительные направления, чтобы векторы вторичного и первичного напряжений совпадали, как показано на рис. 1-12.
1-12, б). Для напряжений также удобно принять такие положительные направления, чтобы векторы вторичного и первичного напряжений совпадали, как показано на рис. 1-12.
В рассматриваемом случае имеет место соединение трансформатора по схеме 1/1-12. Соответственно для трехфазного трансформатора схема соединений и векторная
диаграмма токов и напряжений показаны на рис. 1-14.
На рис. 1-15, б построены векторные диаграммы напряжений, соответствующие схеме соединения трансформатора
На стороне высшего напряжения, где обмотки соединены в звезду, междуфазные напряжения в раз превышают фазные напряжения. На стороне же низшего напряжения, где обмотки соединены в треугольник, междуфазные и фазные напряжения равны. Междуфазные напряжения стороны низшего напряжения отстают на 30° от аналогичных междуфазных напряжений стороны высшего напряжения, что и соответствует схеме соединений
Для рассматриваемой схемы соединений обмоток трансформатора можно построить и векторные диаграммы токов, проходящих с обеих его сторон. При этом следует иметь в виду, что на основании принятых нами условий определяются только положительные направления токов в обмотках трансформатора. Положительные же направления токов в линейных проводах, соединяющих выводы обмоток низшего напряжения трансформатора с шинами, могут быть приняты произвольно независимо от положительных направлений токов, проходящих в треугольнике.
При этом следует иметь в виду, что на основании принятых нами условий определяются только положительные направления токов в обмотках трансформатора. Положительные же направления токов в линейных проводах, соединяющих выводы обмоток низшего напряжения трансформатора с шинами, могут быть приняты произвольно независимо от положительных направлений токов, проходящих в треугольнике.
Так, например, если принять положительные направления токов в фазах на стороне низшего напряжения от выводов, соединенных в треугольник, к шинам (рис. 1-15, а), можно записать следующие равенства:
Соответствующая векторная диаграмма токов показана на рис. 1-15, в.
Аналогично можно построить векторную диаграмму токов и для случая, когда положительные направления токов приняты от шин к выводам треугольника (рис. 1-16, а). Этому случаю соответствуют следующие равенства:
и векторные диаграммы, приведенные на рис.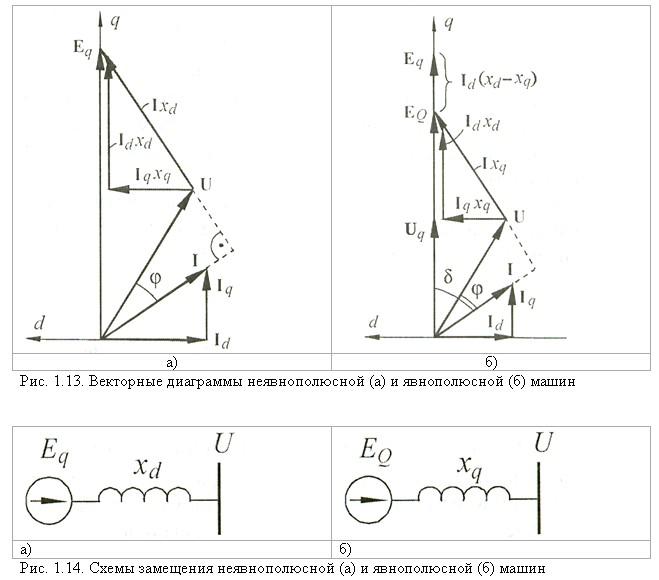 1-16, б. Сравнивая диаграммы токов, приведенные на рис. 1-15, в и 1-16, б, можно сделать вывод, что векторы фазных токов, проходящих в проводах, соединяющих выводы обмоток низ-
1-16, б. Сравнивая диаграммы токов, приведенные на рис. 1-15, в и 1-16, б, можно сделать вывод, что векторы фазных токов, проходящих в проводах, соединяющих выводы обмоток низ-
Шего напряжения трансформатора и шины, находятся в про-тивофазе. Конечно, как те, так и другие диаграммы верны.
Таким образом, при наличии в схеме обмоток, соединенных в треугольник, необходимо задаваться положительными направлениями токов как в самих обмотках, так и в линейных проводах, соединяющих треугольник с шинами.
В рассматриваемом случае при определении группы соединений силового трансформатора удобно за положительные принимать направления от выводов низшего напряжения к шинам, так как при этом векторные диаграммы токов совпадают с принятым обозначением групп соединения силовых трансформаторов (сравните рис. 1-15, б и в). Аналогично могут быть построены векторные диаграммы токов и для других групп соединения силовых трансформаторов. Сформулированные выше правила построения векторных диаграмм токов и напряжений в схемах с трансформаторами действительны и для измерительных трансформаторов тока и напряжения.
Опыт коротких замыканий | Проект РЗА
Приветствую, коллеги!
Сегодня будем строить векторные диаграммы токов однофазного, двухфазного и двухфазного на землю коротких замыканий. Это означает, что мы приступаем ко второму опыту в нашей Виртуальной лаборатории.
Есть много хороших книг, где вы можете посмотреть, как это делается, но на Проекте “РЗА” вы сможете построить векторную диаграмму самостоятельно!
Вот, что мы сделаем – возьмем наш рабочий файл и сымитируем все виды коротких замыканий при помощи связанных векторных диаграмм (первый опыт мы делали здесь). Посмотрим, как изменяются составляющие симметричных последовательностей (прямой, обратной и нулевой) по величине и направлению. И самое главное – сравним это все с классическим учебником по переходным электромеханическим процессам. Уверен, эта книга многим знакома по учебе в институте. — С.А. Ульянов “Электромагнитные переходные процессы” (стр. 315-323):
Например, вот так выглядит классическое однофазное короткое замыкание в учебнике (1) и в нашем сегодняшнем опыте (2):
Как видите, диаграммы очень похожи.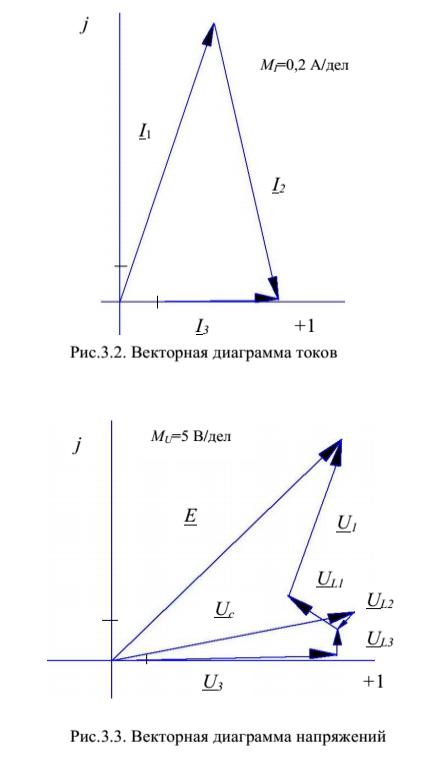
По ходу опытов с векторными диаграммами токов КЗ мы будем останавливаться на физическом смысле полученных результатов и даже немного посчитаем для того, чтобы убедиться в полном соответствии с учебником.
Вы в реальном времени увидите, как меняются симметричные последовательности при изменении фазных векторов, и как они связаны друг с другом
Изменяйте фазные вектора, чтобы увидеть, как меняются последовательности. Поэкспериментируйте, придумайте свои опыты и пишите в комментариях, что получилось. Самое интересное потом выложим на проекте.
А вот и само видео опытов моделирования несимметричных КЗ:
Отдаем программу в хорошие руки!
Наша рубрика называется Виртуальная лаборатория релейной защиты поэтому, после просмотра видео предлагаю вам самим провести опыты в нашей программе.
Вы сможете скачать Программу для построения векторных диаграмм и изучить все, что связано с методом симметричных составляющих самостоятельно!
Для этого оформите подписку на наши новости в этой форме
После подтверждения подписки в течении 10-15 минут вам придет письмо с ссылкой на скачку программы.
Внимание! Для работы с программой требуется MS Visio 2003-2010
Политика конфиденциальности сайта Проект «РЗА»
P.S. Коллеги, мы надеемся, что наши материалы приносят пользу и хотим, чтобы Проект “РЗА” развивался и становился более популярным. Поэтому просим отставлять ссылки на сайт внутри скачанной программы. Спасибо!
Пример построения качественных векторных диаграмм Электротех…
Привет, мой друг, тебе интересно узнать все про построения качественных векторных диаграмм, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
построения качественных векторных диаграмм , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства
Задача 3
Построить качественную векторную диаграмму.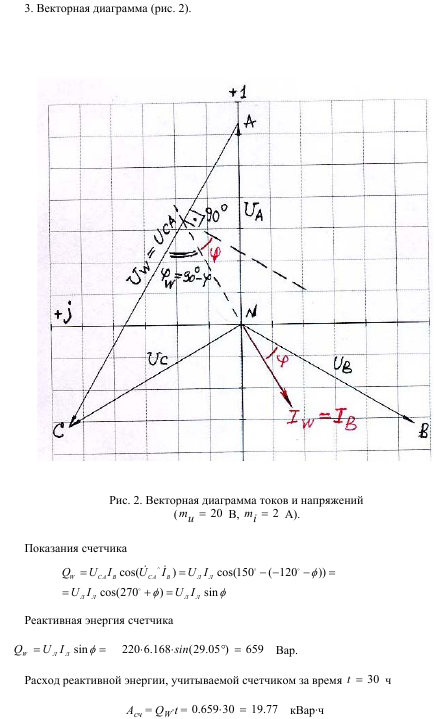
Построение проводим, используя свойства элементов. Первым строится вектор тока, затем вектора напряжений.
Задача 4
Построить качественную векторную диаграмму.
Построение проводим, используя свойства элементов.
Задача 5
Построить качественную векторную диаграмму для цепи, при условии, если XL>XC.
Построение проводим, используя свойства элементов.
Задача
В последовательной цепи определить показания приборов, составить и рассчитать баланс мощностей , определить коэффициент мощности, построить топографическую векторную диаграмму.
R1 = 10 Ом
R2 = 20 Ом
C = 31,8 мкФ
L = 0,127 Гн
f = 50 Гц
Решение:
1) . Об этом говорит сайт https://intellect.icu . Определим полные комплексные сопротивления реактивных элементов
2). Переведем в алгебраическую форму напряжение источника
3). Определим эквивалентное сопротивление цепи
Схема имеет активно-емкостной характер
4). Определим ток в цепи
Определим ток в цепи
5). Амперметр покажет действующее значение тока
6). Определим показание вольтметра, действующее значение напряжения на конденсаторе
7). Определим мощности источника и приемников
Мощность приемников
Из расчетов видно, что баланс сходится с погрешностью меньше процента
8). Определим коэффициент мощности
9) построение топографической векторной диаграммы
Определим напряжения на элементах цепи
Выбор масштаба по току 2 см – 1 А; по напряжению 2см – 50 В
Правило построения векторной диаграммы, при последовательном включении элементов:
строим вектор тока
строим вектора напряжений
складываем вектора напряжений по правилу параллелограмма.
пример параллельное соединение
Определить токи в ветвях.
Дано:
R1 = 10 Ом
R2 = 10 Ом
f = 50 Гц
Решение:
3 ветви, 2 узла.
Токи определяем по закону Ома. Запишем полные сопротивления ветвей:
Запишем полные сопротивления ветвей:
Общий ток определяем по первому закону Кирхгофа
Векторная диаграмма
Задача
E = Uo + Um•sin(ωt + 45), Uo = 45 B, U = 39 B,
R1= R2 =50 Ом, L= 0,127 Гн, C= 3,18 мкФ
Определить Uc, I2
Решение
по постоянной составляющей
Е1 = Uo = 45 B I2 = Uo/R1 = 0,9 A I3 = 0
По переменной составляющей XL= 40, Ом Xc = 1000 Ом
Как ты считаеешь, будет ли теория про построения качественных векторных диаграмм улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое построения качественных векторных диаграмм
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятелно рекомендую изучить комплексно всю информацию в категории
Электротехника, Схемотехника, Аналоговые устройства
Векторная диаграмма токов и напряжений для трехфазной
Векторная диаграмма — способ изображения переменных напряжений и токов с помощью векторов.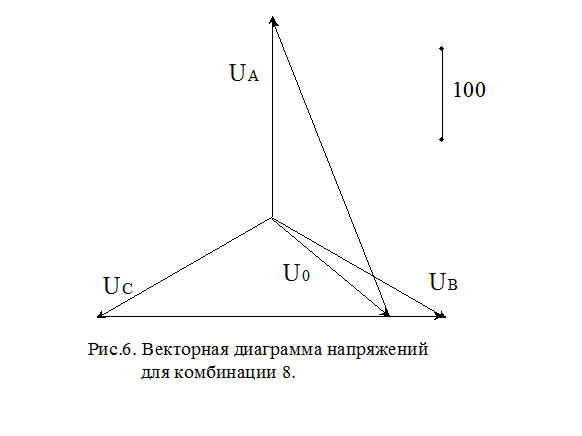
Векторная диаграмма трехфазной системы ЭДС и график ЭДС фаз А, B и С:
Векторная диаграмма трехфазной симметричной системы ЭДС:
Векторная диаграмма напряжений симметричной нагрузки, соединенной звездой:
Построение диаграммы напряжений симметричной нагрузки, соединенной звездой:
Векторная диаграмма токов активной несимметричной нагрузки, соединенной звездой:
Построение векторной диаграммы для несимметричной нагрузки при обрыве нейтрального провода:
Несимметричная нагрузка при обрыве нейтрального провода:
Построение диаграммы для несимметричной нагрузки. Звезда без нейтрального провода:
Векторная диаграмма симметричной нагрузки, соединенной звездой:
Векторные диаграммы напряжений и токов при соединении приемников треугольником:
Векторная диаграмма напряжений и токов при соединении приемников треугольником:
Векторная диаграмма напряжений и токов при соединении приемников треугольником (несимметричная нагрузка):
Векторная диаграмма напряжений и токов несимметричной нагрузки, соединенной треугольником:
Векторная диаграмма — способ изображения переменных напряжений и токов с помощью векторов.
Векторная диаграмма трехфазной системы ЭДС и график ЭДС фаз А, B и С:
Векторная диаграмма трехфазной симметричной системы ЭДС:
Векторная диаграмма напряжений симметричной нагрузки, соединенной звездой:
Построение диаграммы напряжений симметричной нагрузки, соединенной звездой:
Векторная диаграмма токов активной несимметричной нагрузки, соединенной звездой:
Построение векторной диаграммы для несимметричной нагрузки при обрыве нейтрального провода:
Несимметричная нагрузка при обрыве нейтрального провода:
Построение диаграммы для несимметричной нагрузки. Звезда без нейтрального провода:
Векторная диаграмма симметричной нагрузки, соединенной звездой:
Векторные диаграммы напряжений и токов при соединении приемников треугольником:
Векторная диаграмма напряжений и токов при соединении приемников треугольником:
Векторная диаграмма напряжений и токов при соединении приемников треугольником (несимметричная нагрузка):
Векторная диаграмма напряжений и токов несимметричной нагрузки, соединенной треугольником:
Несимметричные режимы в простейших характерных случаях (короткое замыкание и холостой ход) могут быть проанализированы на основе построения векторных диаграмм.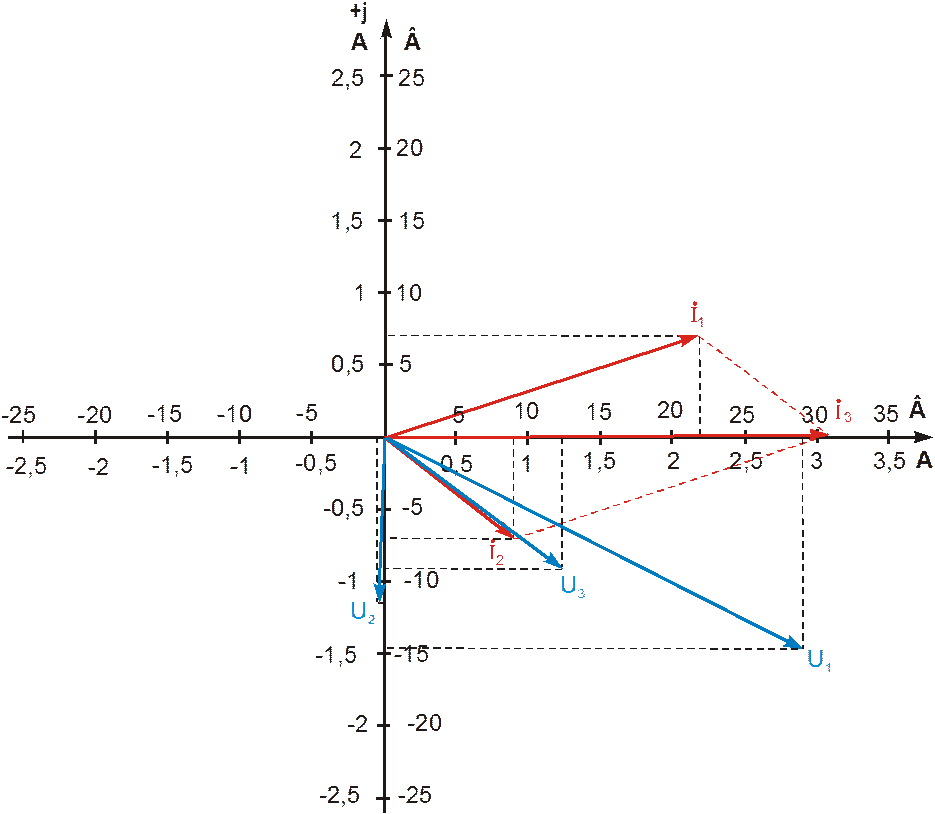
Рассмотрим режимы обрыва и короткого замыкания фазы при соединении в звезду для трех- и четырехпроводной систем. При этом будем проводить сопоставление с симметричным режимом работы цепи, фазные напряжения и токи в которой будут базовыми. Для этой цепи (см. рис.1,а) векторная диаграмма токов и напряжений приведена на рис. 1,б (принято, что нагрузка носит активно-индуктивный характер). Здесь
При обрыве фазы А нагрузки приходим к векторной диаграмме на рис. 2.
.
При коротком замыкании фазы А (трехпроводная система) имеет место векторная диаграмма на рис. 3. Из нее вытекает: ; ; ; ; .
При обрыве фазы А в четырехпроводной системе (нейтральный провод на рис. 1,а показан пунктиром, а вектор тока – пунктиром на рис. 1,б) ; ; .
Симметричный трехфазный приемник при соединении в треугольник и соответствующая этому случаю векторная диаграмма напряжений и токов приведены на рис. 4.
Здесь при том же способе соединения фаз генератора ; ; ; ; ; .
При обрыве провода в фазе А-В нагрузки, как это видно из схемы на рис. 5, ; , при этом сами токи и в силу автономности режима работы фаз при соединении нагрузки в треугольник такие же, как и в цепи на рис. 4,а. Таким образом,
; ; .
Цепь при обрыве линейного провода А-А’ и соответствующая этому случаю векторная диаграмма приведены на рис.6.
; ; .
Мощность в трехфазных цепях
Мгновенная мощность трехфазного источника энергии равна сумме мгновенных мощностей его фаз:
.
Активная мощность генератора, определяемая как среднее за период значение мгновенной мощности, равна
.
Соответственно активная мощность трехфазного приемника с учетом потерь в сопротивлении нейтрального провода
,
.
Суммарная активная мощность симметричной трехфазной системы
| . | (1) |
Учитывая, что в симметричном режиме для звезды имеют место соотношения
и для треугольника –
на основании (1) для обоих способов соединения фаз получаем
,
где j – угол сдвига между фазными напряжением и током.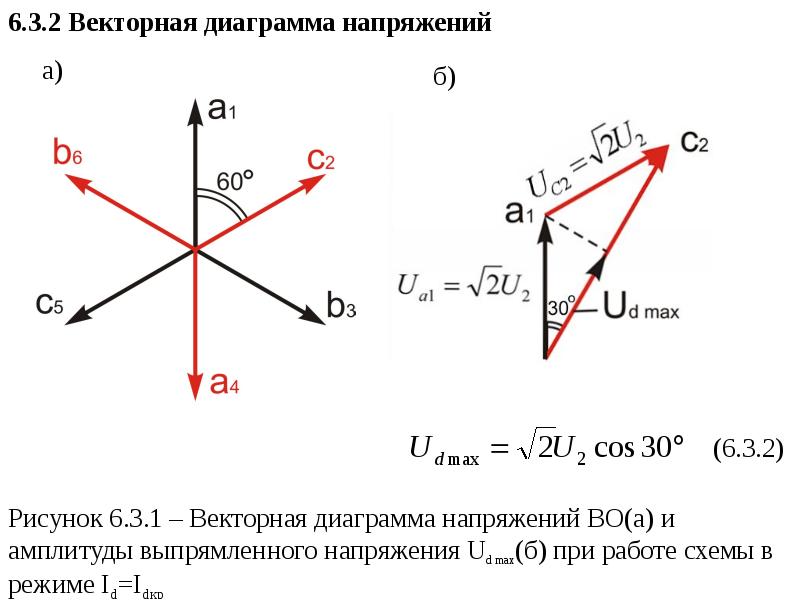
Докажем теперь указанное ранее свойство уравновешенности двухфазной системы Тесла и симметричной трехфазной системы.
1. Двухфазная система Тесла
В соответствии с рис. 7
| (2) |
| . | (3) |
.
Таким образом, суммарная мгновенная мощность фаз есть величина постоянная, равная суммарной активной мощности источника.
2. Симметричная трехфазная цепь
,
т.е. и для симметричной трехфазной цепи свойство уравновешенности доказано.
Измерение мощности в трехфазных цепях
Ниже рассмотрены практические схемы включения ваттметров для измерения мощности в трехфазных цепях.
1. Четырехпроводная система, несимметричный режим.
Представленная на рис. 8 схема называется схемой трех ваттметров.
Суммарная активная мощность цепи определяется как сумма показаний трех ваттметров
.
2. Четырехпроводная система, симметричный режим.
Если режим работы цепи симметричный, то для определения суммарной активной мощности достаточно ограничиться одним ваттметром (любым), включаемым по схеме на рис. 8. Тогда, например, при включении прибора в фазу А,
| . | (4) |
3. Трехпроводная система, симметричный режим.
При отсутствии доступа к нейтральной точке последняя создается искусственно с помощью включения трех дополнительных резисторов по схеме «звезда», как показано на рис. 9 – схема ваттметра с искусственной нейтральной точкой. При этом необходимо выполнение условия , где – собственное сопротивление обмотки ваттметра. Тогда суммарная активная мощность трехфазной системы определяется согласно (4).
4. Трехпроводная система, симметричный режим; измерение реактивной мощности.
С помощью одного ваттметра при симметричном режиме работы цепи можно измерить ее реактивную мощность. В этом случае схема включения ваттметра будет иметь вид по рис. 10,а. Согласно векторной диаграмме на рис. 10,б измеряемая прибором мощность
В этом случае схема включения ваттметра будет иметь вид по рис. 10,а. Согласно векторной диаграмме на рис. 10,б измеряемая прибором мощность
Таким образом, суммарная реактивная мощность
5. Трехпроводная система, несимметричный режим.
Представленная на рис. 11 схема называется схемой двух ваттметров. В ней сумма показаний приборов равна суммарной активной мощности цепи.
Действительно, показания приборов в данной схеме:
.
В заключение отметим, что если в схеме на рис. 11 имеет место симметричный режим работы, то на основании показаний приборов можно определить суммарную реактивную мощность цепи
| . | (5) |
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов.
 –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
–7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В симметричной трехпроводной цепи произошел обрыв фазы. Что покажет вольтметр, включенный между найтральными точками источника и приемника?
Ответ: .
Во сколько раз мощность в цепи на рис. 6,а меньше мощности в цепи на рис. 4,а?
Ответ: в два раза.
В цепи на рис. 10,а симметричная нагрузка составлена из резистивных элементов. Что покажет ваттметр?
Ответ: .
В цепи на рис. 10,а симметричная нагрузка с фазным сопротивлением соединена в звезду. Линейное напряжение .
Определить показание ваттметра.
Ответ: .
В цепи на рис. 11 нагрузкой служат два одинаковых конденсатора с ХС=100 Ом, включенные между линейными проводами А и В, В и С соответственно. Линейное напряжение .
Определить показания ваттметров.
Ответ: .
 11 доказать соотношение (5).
11 доказать соотношение (5).Пример решения задачи однофазного синусоидального тока
Для цепи, изображенной на рис. 1 требуется:
- Определить комплексным методом действующие значения напряжений и токов на всех участках цепи.
- Определить активные, реактивные и полные мощности каждого участка цепи и всей цепи.
- Составить баланс активных и реактивных мощностей и оценить погрешность расчета.
- Построить векторную диаграмму токов и напряжений.
Частота питающего напряжения 50 Гц.
Рис. 1
Исходные данные:
U = 127 В , r1 = 15 Ом , C1 = 60 мкФ, r2 = 10 Ом , L2 = 80 мГн, r3 = 15 Ом , C3 = 90 мкФ.
Решение. Заказать у нас работу!
Решить онлайн! (New!!!)
- Определим комплексные сопротивления каждой ветви.
(Ом)
(Ом)
(Ом)
2. Определим полное сопротивление цепи.
(Ом)
3. Приняв найдем токи и напряжения в ветвях.
(А)
(В)
(В)
(А)
(А)
4. Определим активные, реактивные и полные мощности участков цепи и всей цепи целиком.
Определим активные, реактивные и полные мощности участков цепи и всей цепи целиком.
Мощность первого участка:
(ВА)
Мощность второго участка:
(ВА)
Мощность третьего участка:
(ВА)
Полная мощность всей цепи:
(ВА)
Проверим баланс активных мощностей:
P = P1 + P2 + P3
P = 205,2 (BA)
P1 + P2 + P3 = 61,25 + 82,44 + 61,22 = 204,91 (Вт)
Абс. погр-ть Δ = P – (P1 + P2 + P3) = 205,2 – 204,91 = 0,29 (Bт)
Отн. погр-ть
Проверим баланс реактивных мощноcтей:
S = S1 + S2 + S3
S =- 153,96 (BA)
S1 + S2 + S3 = — 216,7 + 207,19 – 144,5 = — 154,01 (ВА)
Абс. погр-ть Δ = |S – (S1 + S2 + S3)| = |153,96 – 154,01| = 0,05 (BA)
Отн. погр-ть
5. Построим векторную диаграмму на комплексной плоскости.
Для этого определим напряжения на каждом элементе схемы.
(В)
(В)
(В)
(В)
(В)
(В)
Рис. 2. Векторная диаграмма.
Заказать у нас работу!
Решить онлайн! (New!!!)
Векторная диаграмма | Электротехника
Векторная диаграмма трансформатора. Она позволяет наглядно представить соотношения и углы сдвига фаз между различными величинами, характеризующими работу трансформатора.
Она позволяет наглядно представить соотношения и углы сдвига фаз между различными величинами, характеризующими работу трансформатора.
Кроме того, ее построение полезно для вывода некоторых соотношений, которые упрощают анализ рабочих характеристик трансформатора.
Векторную диаграмму строим на основании уравнений электрического состояния и уравнения токов с учетом сдвигов фаз между магнитным потоком, ЭДС и токами для приведенного трансформатора – в этом случае масштаб всех величин вторичной обмотки одинаков с масштабом величин первичной обмотки. Диаграмма на рис. 2.8 для активно-индуктивной нагрузки () построена следующим образом. Из точки О в произвольном направлении в выбранном масштабе для токов строится вектор и при активно-индуктивной нагрузке в направлении опережения под углом сдвига фаз в масштабе, выбранном для напряжения, вектор . Для получения вектора к вектору прибавляется вектор активного падения напряжения во вторичной обмотке (направлен параллельно вектору ) и вектор индуктивного падения напряжения (опережает вектор на угол ). Замыкающий вектор .
Замыкающий вектор .
Вектор магнитного потока отстает по фазе от вектора на угол . Вектор тока холостого хода опережает вектор на угол потерь .
С вектором складывается вектор и получается вектор тока в первичной обмотке . Вектор напряжения первичной обмотки находится (см. (2.8)) как сумма векторов , вектора падения напряжения на активном сопротивлении первичной обмотки (откладывается из конца вектора параллельно вектору ) и вектора падения напряжения на индуктивном сопротивлении рассеяния (откладывается из конца вектора и опережает вектор тока на угол ).
Читайте также:
§63. Назначение и принцип действия трансформатора
§65. Режимы работы трансформатора и его характеристики
§69. Регулирование напряжения трансформаторов
Режим холостого хода трансформатора
Векторные диаграммы трансформатора
Уравнения трансформатора (16) могут быть решены аналитическим или графическим методом.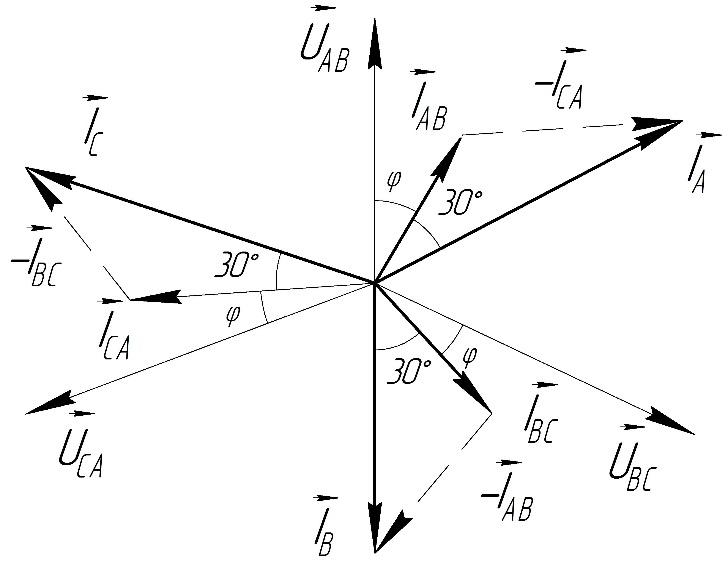 Графический метод решения основан на построении векторных диаграмм. Он является более наглядным и часто используется для качественного анализа различных режимов работы трансформатора.
Графический метод решения основан на построении векторных диаграмм. Он является более наглядным и часто используется для качественного анализа различных режимов работы трансформатора.
Режим холостого хода
В режиме холостого хода первичная обмотка трансформатора включена в сеть на напряжение , а вторичная разомкнута . Для этого режима справедливы уравнения
(17)
Ток первичной обмотки представляет собой намагничивающий ток трансформатора. Построение векторной диаграммы (рис.10) начинают с вектора потока . ЭДС и отстают от потока на угол 90°. Реактивная составляющая тока намагничивания совпадает по фазе с потоком, а его активная составляющая опережает поток на 90°. Намагничивающий ток несколько опережает поток . Для получения вектора первичного напряжения необходимо построить вектор и прибавить к нему падения напряжений на активном и индуктивном сопротивлениях. Из векторной диаграммы видно, что очень мал. Обычно . Трансформатор потребляет из сети реактивную мощность на создание магнитного поля в трансформаторе.
Из векторной диаграммы видно, что очень мал. Обычно . Трансформатор потребляет из сети реактивную мощность на создание магнитного поля в трансформаторе.
Режим короткого замыкания
Режимом короткого замыкания называют режим при замкнутой накоротко вторичной обмотке . Схема замещения трансформатора в этом режиме имеет вид, представленный на рис. 11. Для режима короткого замыкания справедливы следующие уравнения:
Векторная диаграмма (рис. 12) в этом режиме строится аналогично векторной диаграмме для режима холостого хода. Угол определяется параметрами вторичной обмотки:
.
Особенность этого режима состоит в том, что ЭДС значительно отличается от напряжения из-за больших токов короткого замыкания. Учитывая, что , током можно пренебречь. Тогда схема замещения может быть упрощена (рис. 13).
Тогда схема замещения может быть упрощена (рис. 13).
Из схемы замещения получаем
.
Если принять, что , то действующее значение ЭДС будет равно половине действующего значения напряжения :
.
Поэтому в режиме короткого замыкания магнитопровод трансформатора оказывается ненасыщенным.
Действующее значение тока короткого замыкания в соответствии с рис. 13
,
где — модуль комплексного сопротивления короткого замыкания трансформатора.
При ток короткого замыкания может превосходить номинальное значение в 10-50 раз. Поэтому в условиях эксплуатации режим короткого замыкания является аварийным. Однако этот режим часто проводится при пониженном напряжении для определения параметров трансформатора.
Напряжение , при котором ток короткого замыкания равен номинальному, называется напряжением короткого замыкания и обозначается
.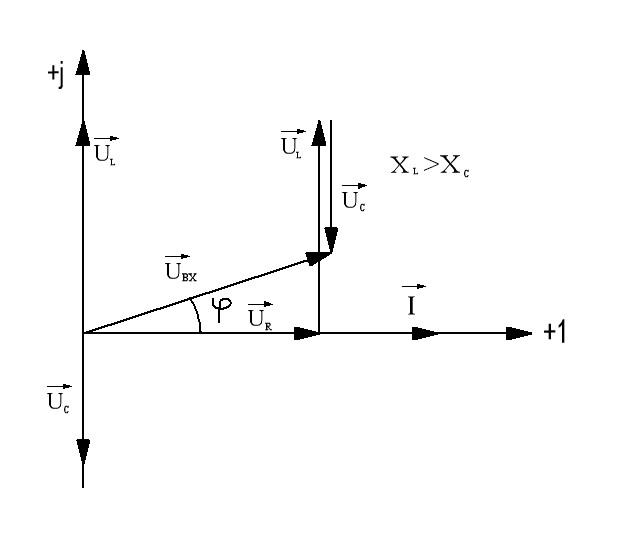
Отсюда следует, что напряжение короткого замыкания представляет собой падение напряжения на внутреннем сопротивлении трансформатора при номинальном токе и поэтому является важной характеристикой трансформатора.
Если совместить вещественную ось с вектором тока , то комплексное значение можно представить как , где , — активная и реактивная составляющие напряжения короткого замыкания. Обычно модуль выражают в относительных единицах,
,
либо в процентах,
.
Величина оказывает существенное влияние на свойства трансформатора в рабочих и аварийных режимах. Поэтому является паспортной величиной наряду с номинальными данными.
Режим нагрузки трансформатора
Векторные диаграммы при нагрузке строят по уравнениям (16). Вид векторной диаграммы зависит от характера нагрузки (рис. 14).
Векторная диаграмма а рис. 14 соответствует активно-индуктивной нагрузке, а векторная диаграмма б — активно-емкостной нагрузке.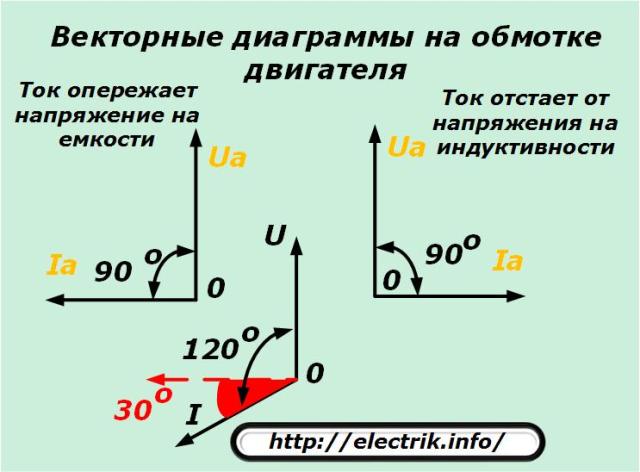
Сопоставляя обе диаграммы, можно заключить, что при и увеличение активно-индуктивной нагрузки вызывает снижение напряжения , а при увеличении активно-емкостной нагрузки напряжение возрастает. Это объясняется тем, что при активно-индуктивной нагрузке происходит некоторое размагничивание трансформатора (поток Ф уменьшается, так как ток имеет составляющую, направленную навстречу току ), а при активно-емкостной нагрузке трансформатор дополнительно намагничивается (поток Ф возрастает, так как ток имеет составляющую, совпадающую с ).
Для оценки диапазона изменения напряжения вводится величина , представляющая собой арифметическую разность между вторичным напряжением трансформатора при холостом ходе () и при номинальной нагрузке (). Напряжение первичной обмотки принимается постоянным и равным номинальному .
. (18)
Для расчета примем допущение , тогда, используя
упрощенную схему замещения (рис. 15), получим
15), получим
. (19)
Уравнению (19) соответствует векторная диаграмма, представленная на рис. 16. Из векторной диаграммы следует, что
.
Подставляя приближенное выражение для в уравнение (18), получим
.
Отрезок можно выразить через составляющие напряжения короткого замыкания:
,
где . Учитывая, что , , получим для простое выражение
.
На рис. 17 представлена зависимость при .
Максимальное снижение напряжения имеет место при , а при напряжение не зависит от нагрузки.
Онлайн график вектор. Построение векторных диаграмм токов и напряжений
Рисунок 25- Векторная диаграмма токов в точке короткого замыкания
Рисунок 26-Векторная диаграмма токов в сечении AA
Рисунок 27- Векторная диаграмма напряжений в сечении AA
Рисунок 28 — Векторная диаграмма токов в сечении BB
Рисунок 29- Векторная диаграмма напряжений поперечного сечения BB
Расчет периодической составляющей тока короткого замыкания методом стандартных кривых.
Задача III. Расчет периодической составляющей тока трехфазного КЗ
Метод типовых кривых.
При определении периодического тока трехфазного короткого замыкания составляется диаграмма прямой последовательности для начального момента времени, в которой генераторы представлены параметрами суперперехода; нагрузки не учитываются (рисунок 2). Общая процедура расчета описана в.После эквивалентности была получена промежуточная цепь (рисунок 30), которая преобразуется в радиальный вид относительно точки короткого замыкания (рисунок 31). В этом случае используются коэффициенты распределения тока.
В процессе упрощения схемы замещения были получены следующие сопротивления: X 15 = X 1 + X 2/2 = 0 + 0,975425 / 2 = 0,4877125 о.е.
Х 16 = Х 4 + Х 5 = 0,84 + 1,53 = 2,37 о.е.
Рисунок 30- Промежуточная схема Рисунок 31- Расчетная схема
Х 17 = Х 6 + Х 7 = 0.88 + 0 = 0,88 о.е.
Х 18 = Х 11 + Х 9/2 = 0 + 1,240076 / 2 = 0,620038 о.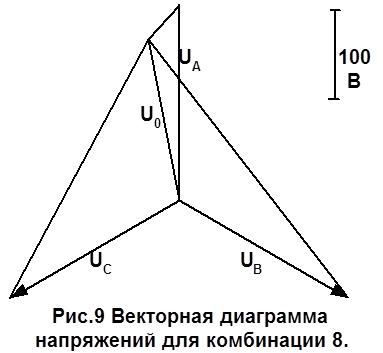 е.
е.
Х 19 = Х 12 + Х 13 = 2,117202 + 0,192308 = 2,30951 о.е.
Х ЭК = Х 18 * Х 19 / (Х 18 + Х 19) = 0,620038 * 2,30951 / (0,620038 + 2,30951) = 0,488807 о.е.
C 1 = X EC / X 18 = 0,488807 / 0,620038 = 0,78835.
C 2 = X EC / X 19 = 0,488807 / 2,30951 = 0,21165.
Х 20 = (Х экв + Х 17) / С 1 = 1.736294 о.е.
Х 21 = (Х экв + Х 17) / С 2 = 6,467324 о.е.
Получается схема, показанная на рисунке 31. Далее идут начальные периодические токи в месте повреждения.
I «G = E 2 / X 16 * I B = 1,13 / 2,27 * 2,5 · 102 = 1,196846 кА.
I «C1 = E 1 / X 15 * I B = 1 / 0,4877125 * 2,5102 = 5,146885 кА.
I «C2 = E 3 / X 20 * I B = 1 / 1,736294 * 2,5102 = 1,445723 кА.
I «C3 = E 4 / X 21 * I B = 1/6.467324 * 2,5102 = 0,388136 кА.
Токи в системах постоянны. Периодический ток по типовым кривым определяется для синхронного генератора с тиристорной или высокочастотной системой возбуждения. В соответствии с методикой рассчитывается номинальный ток синхронного генератора и затем определяется номер типовой кривой.
I GN = S GN / * U B = 100 / (* 0,85 * 230) = 0,295320 кА;
I * PO = I Г2 «/ I ГН = 1.196846 / 0,295320 = 4,05 «4.
Так как соотношение I Г2 «/ I ГН» 4, то выбираются 4 типовые кривые:
I KZPOST = I «C2 + I» C3 + I «C1 = 5,1468885 + 1,445723 + 0,388136 = 6,980748 кА
| т, сек | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| I Г т / I ”Г, о.е | 0,85 | 0,78 | 0,755 | 0,75 | 0,745 | |
| I G t, кА | 1,1968 | 1 017 | 0,933 | 0,903 | 0,897 | 0,891 |
| Итого I K t, кА | 8,1775 | 7,9977 | 7,9137 | 7,8837 | 7 8777 | 7 872 |
В качестве примера рассмотрим поиск периодического тока в момент времени 0.1 сек. По кривой 4 для этого момента времени определяется отношение In, t, g / Inog = 0,85.
Определяется действующее значение периодической составляющей тока короткого замыкания от генератора: In, t, r = 0,85 * Ino * I NOM = 0,85 * 4,05 * 0,2953 = 1,017 кА.
Полный периодический ток в точке K (3) в узле K с учетом типичных кривых показан на рисунке 32.
Рисунок 32- График зависимости полного периодического тока от времени короткого замыкания Ikt = f (t)
Задача IV.Расчет периодической составляющей несимметричного тока короткого замыкания методом стандартных кривых.
Для определения периодических токов короткого замыкания при K (1.1) методом типовых кривых составляется эквивалентная схема замены последовательности без учета нагрузок (рисунок 33). Далее получают упрощение эквивалентной схемы и эквивалентное сопротивление обратной последовательности. Последовательность упрощений приведена ниже и на рисунках 34-37.
Х 15 = Х 1 + Х 2/2 = 0 + 0,975425 / 2 = 0,487713 о.е. Х 16 = Х 4 + Х 5 = 0,84 + 1,87 = 2,71 о.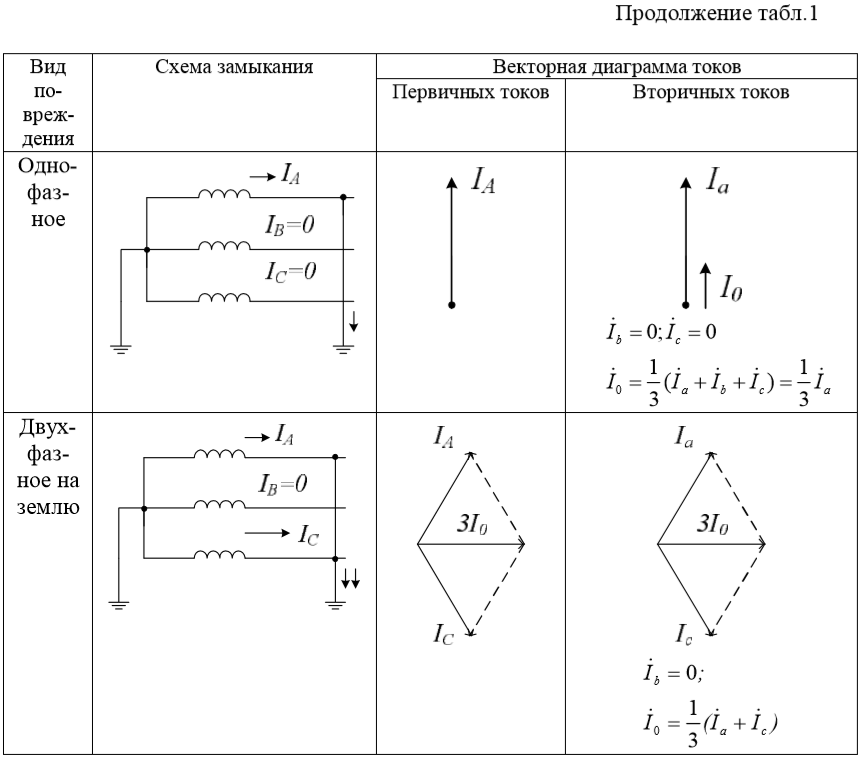 е.
е.
Х 17 = Х 6 + Х 7 = 0 + 0,88 = 0,88 о.е. Х 18 = Х 11 + Х 9/2 = 0 + 1,240076 / 2 = 0,620038 о.е.
Х 19 = Х 12 + Х 13 = 2,117202 + 0,230769 = 2,347971 о.е.
Х 20 = Х 15 * Х 16 / (Х 15 + Х 16) = 0,487713 * 2,71 / (0,487713 + 2,71) = 0,413327 о.е.
Х 22 = Х 17 + Х 21 = 0.88 + 0,4 = 1,370508 о.е. X EC2 = X 20 * X 22 / (X 20 + X 22) = 0,413327 * 1,370508 / / (0,413327 + 1,370508) = 0,317556 о.е.
Рисунок 33 — Порядок замены обратной последовательности
Рисунок 34- Упрощение схемы № 1
Рисунок 35- Упрощение схемы № 2
Рисунок 36- Упрощение схемы №3
Рисунок 37 — Эквивалентная обратная эквивалентная схема
Последовательности
Аналогично составляем эквивалентную схему нулевой последовательности (рисунок 38). Процедура упрощения эквивалентной схемы показана ниже на рисунках 39-42.
Рисунок 38 — Расчетная эквивалентная схема нулевой последовательности
Х 13 = Х 1 + Х 2/2 = 0 + 4,585 / 2 = 2292 п.u. Х 14 = Х 10 + Х 9/2 = 0 + 6,82 / 2 = 3,41 о.е.
Х 15 = Х 11 + Х 12 = 7,41 + 0,769 = 8,18 о.е. Х 16 = Х 13 * Х 4 / (Х 13 + Х 4) = 2,29225 * 0,84 / (2,29 + 0,84) = 0,615 о.е.
Х 18 = Х 6 + Х 17 = 0,88 + 1,338581 = 2,219 о.е.
X 17 = 1 / (1 / X 7 + 1 / X 15 + 1 / X 14) = 1 / (1 / 3,016 + 1 / 8,18 + 1 / 3,41) = 1,34 о.е.
Рисунок 39- Упрощение схемы №1
Рисунок 40- Упрощение схемы № 2
Рисунок 41 — Упрощение схемы № 3
Рисунок 42 — Схема эквивалентного нулевого эквивалента
Последовательности
Для решения проблемы используются эквивалентные данные в прямой последовательности из предыдущей задачи. Учитывая особенности K (1.1), получаем схему, показанную на рисунке 43. Эта схема приведена к виду, показанному на рисунке 44.
Эта схема приведена к виду, показанному на рисунке 44.
Рассмотрен для случая с исправным нулевым проводом. Векторные диаграммы напряжений и токов приведены на рисунках 15 и 16; На рисунке 17 показана комбинированная диаграмма токов и напряжений
.
1. Построены оси комплексной плоскости: реальные значения (+1) — по горизонтали, мнимые значения (j) — по вертикали.
2. На основании значений модулей токов и напряжений и размеров выделенных для построения диаграмм полей листа выбираются шкалы токов mI и напряжения mU.При использовании формата А4 (размеры 210х297 мм) с самыми крупными модулями (см. Табл. 8), током 54 А и напряжением 433 В принимаются следующие масштабы: mI = 5 А / см, mU = 50 В / см.
3. С учетом принятых масштабов mI и mU определяется длина каждого вектора, если диаграмма построена с использованием экспоненциальной формы его записи; при использовании алгебраической формы находятся длины проекций векторов на оси действительных и мнимых величин, т. е.е. длины действительной и мнимой частей комплекса.
е.е. длины действительной и мнимой частей комплекса.
Например, для фазы A:
Длина вектора тока / f.A / = 34,8 А / 5 А / см = 6,96 см; длина его реальной части
I ф.А = 30 А / 5 А / см = 6 см,
длина его мнимой части
И ф.А = -17,8 А / 5 А / см = — 3,56 см;
Длина вектора напряжения / А нагрузка / = 348 В / 50 В / см = 6,96 см; длина его реальной части
У А нагрузка = 340.5 В / 50 В / см = 6,8 см;
длина его мнимой части
У Анагр. = 37,75 В / 50 В / см = 0,76 см.
Результаты определения длин векторов, их действительной и мнимой частей приведены в таблице 9.
Таблица 9 — Длины векторов тока и напряжения, их действительная и мнимая части для случая неповрежденного нулевого провода.
| Значение | Шкала, 1 / см | Длина вектора, см | Длина реальной части, см | Длина воображаемой части, см | |
| Напряжение фаз сети | U A | 50 В / см | 7,6 | 7,6 | |
| УВ | 7,6 | — 3,8 | — 6,56 | ||
| UС | 7,6 | — 3,8 | 6,56 | ||
| Нагрузка фазы напряжения | У Анагр. | 50 В / см | 6,96 | 6,8 | 0,76 |
| УВБ | 7,4 | — 4,59 | — 5,8 | ||
| Нагрузка UC | 8,66 | -4,59 | 7,32 | ||
| U0 | 1,08 | 0,79 | — 0,76 |
Продолжение таблицы 9
| Токи фаз нагрузки | I ф.A | 5 А / см | 6,96 | 6,0 | — 3,56 |
| I ф. B | 7,4 | 1,87 | — 7,14 | ||
| I ф. C | 3,13 | 0,1 | 3,12 | ||
| I 0 | 10,8 | 7,9 | — 7,6 |
4. Построение векторной диаграммы напряжений.
4.1 На комплексной плоскости строятся векторы фазных напряжений питающей сети A, B, C; соединяя их концы, получаем линейные векторы напряжений AB, BC, CA. Затем строятся векторы фазных напряжений нагрузки A. В., В., С. Для их построения можно использовать обе формы регистрации комплексов токов и напряжений.
Затем строятся векторы фазных напряжений нагрузки A. В., В., С. Для их построения можно использовать обе формы регистрации комплексов токов и напряжений.
Например, вектор нагрузки А. строится в экспоненциальной форме следующим образом: от оси +1 под углом 6 10, т.е. против часовой стрелки, задерживается длина 6,96 см; в алгебраической форме его можно построить, отложив отрезок длиной 6,81 см вдоль оси +1 и отрезок длиной 0,76 см вдоль оси + j, концы этих отрезков являются координатами конца вектора A Загрузка.
4.2 Поскольку линейные напряжения нагрузки задаются питающей сетью, для определения положения нейтральной нагрузки необходимо выполнить параллельную передачу фазовых векторов фазного напряжения нагрузки A., In load., С нагрузкой. так, чтобы их концы совпадали с концами фазных напряжений питающей сети.
Точка 0, в которой появляются их начала, является нейтральной нагрузкой. В этой точке находится конец вектора напряжения смещения нейтрали 0, его начало находится в точке 0.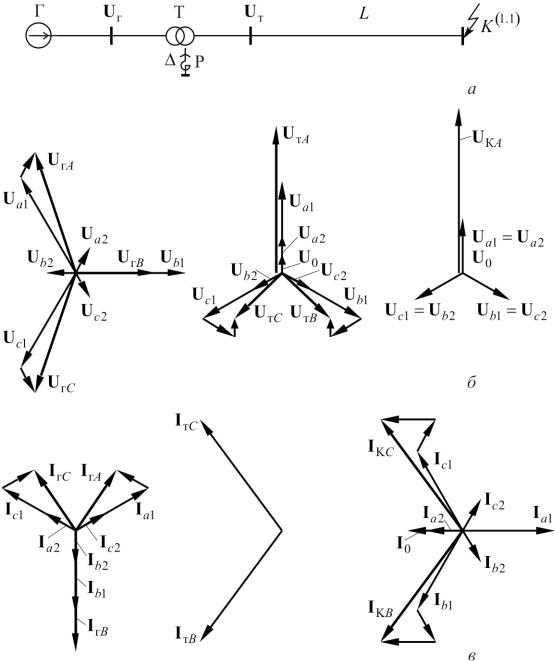 Этот вектор также можно построить, используя данные таблицы 9.
Этот вектор также можно построить, используя данные таблицы 9.
5. Построение векторной диаграммы токов.
5.1. Построение векторов фазных токов нагрузки f.A, f.V, f.C аналогично построению векторов фазных напряжений.
5.2 Суммирование векторов фазных токов — это вектор тока в нейтральном проводе 0; его длина и длины выступов на оси должны совпадать с указанными в таблице 8.
Векторные диаграммы токов и напряжений для случая обрыва нулевого провода строятся аналогично.
Необходимо проанализировать результаты расчета и построения векторных диаграмм и сделать выводы о влиянии несимметрии нагрузки на величину ее фазных напряжений и на напряжение нейтрали; Особое внимание необходимо обратить на последствия обрыва сети нулевого провода при несимметричной нагрузке.
Примечание . Допускается совмещение диаграмм токов и напряжений при условии, что они выполнены разного цвета.
Рис. 15. Векторная диаграмма напряжений
Рисунок 16. Векторная диаграмма токов.
Векторная диаграмма токов.
Рисунок 17. Совмещенная векторная диаграмма напряжений и токов.
а) Концепция векторов
На рис. На рис. 1-4 показана зависимость переменного тока от времени. Ток изначально увеличивается от нуля (при = 0 °) до максимального положительного значения + IM (при = 90 °), затем уменьшается, проходит через ноль (при = 180 °), достигает максимального отрицательного значения — IM ( при = 270 °) и окончательно возвращается к нулю (при = 360 °).После этого повторяется весь цикл изменения тока.
Кривая изменения переменного тока во времени, представленная на рис. 1-4, называется синусоидой. Время T, в течение которого происходит полный цикл изменения тока, соответствующий изменению угла до 360 °, называется периодом переменного тока. Количество периодов в 1 с называется частотой переменного тока. В промышленных установках и в быту в СССР и других странах Европы используется в основном переменный ток частотой 50 Гц.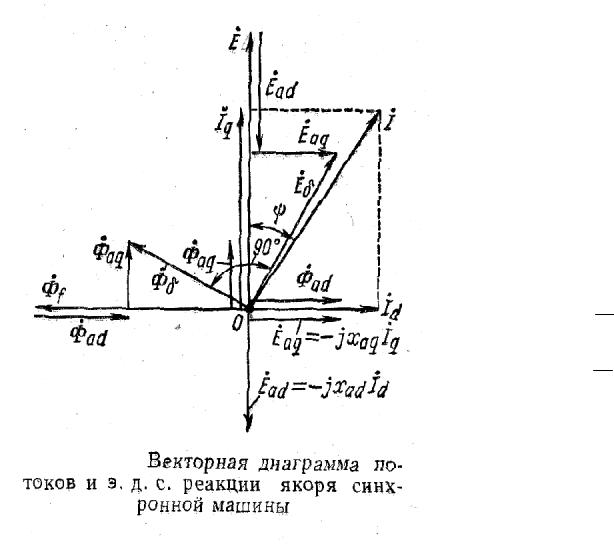 Этот ток 50 раз в секунду принимает положительное и отрицательное направление.
Этот ток 50 раз в секунду принимает положительное и отрицательное направление.
Изменение переменного тока во времени можно записать следующим образом:
, где i — мгновенное значение тока, т.е. значение тока в каждый момент времени; I м — максимальное значение тока; — угловая частота переменного тока, f = 50 Гц, = 314; — начальный угол, соответствующий моменту времени, с которого начинается отсчет времени (при t = 0).
Для особого случая, показанного на рис.1-4,
Анализируя действие устройств релейной защиты и автоматики, необходимо сравнить токи и напряжения, сложить или вычесть их, определить углы между ними и выполнить другие операции. В этом случае использовать кривые, аналогичные приведенным на рис. 1-4, неудобно, так как построение синусоидального тока и напряжения занимает много времени и не дает простого и интуитивно понятного результата. Поэтому для упрощения принято изображать токи и напряжения в виде отрезков прямых, имеющих определенную длину и направление, так называемые векторы (ОА на рис.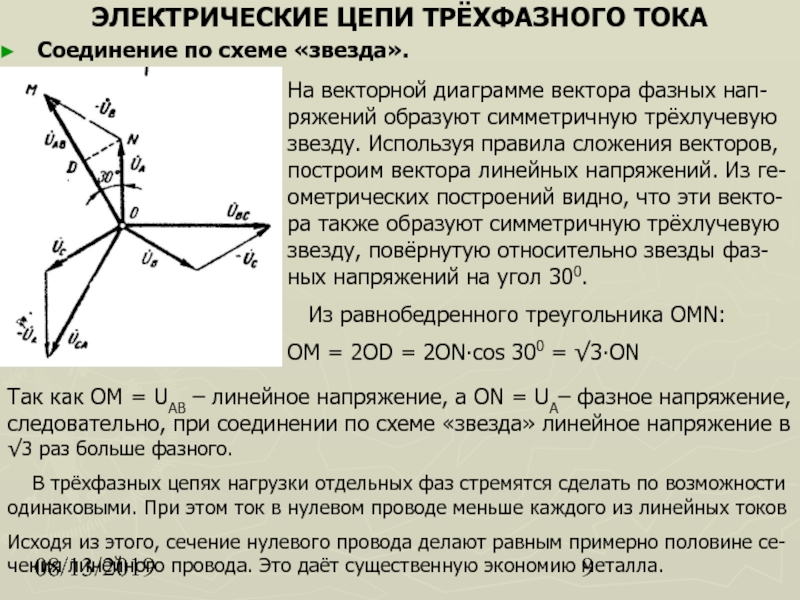 1-4). Один конец вектора фиксируется в точке O — начале координат, а второй вращается против часовой стрелки.
1-4). Один конец вектора фиксируется в точке O — начале координат, а второй вращается против часовой стрелки.
Мгновенное значение тока или напряжения в каждый момент времени определяется проекцией на вертикальную ось вектора, длина которого равна максимальному значению электрического значения тока или напряжения. Эта проекция станет либо положительной, либо отрицательной, принимая максимальные значения при вертикальном расположении вектора.
За время T, равное периоду переменного тока, вектор совершит полный оборот по окружности (360 °), последовательно занимая позиции и т. Д.При частоте переменного тока 50 Гц вектор составит 50 об / мин.
Таким образом, вектор тока или напряжения представляет собой отрезок прямой, равный по величине максимальному значению тока или напряжения, вращающийся относительно точки O против часовой стрелки со скоростью, определяемой частотой переменного тока. Зная положение вектора в каждый момент времени, можно определить мгновенное значение тока или напряжения в данный момент. Итак, для положения вектора тока ОУ, показанного на рис.1-5, его мгновенное значение определяется проекцией на вертикальную ось, т.е.
Итак, для положения вектора тока ОУ, показанного на рис.1-5, его мгновенное значение определяется проекцией на вертикальную ось, т.е.
На основе рис. 1-5, мы также можем сказать, что ток в данный момент времени имеет положительное значение. Однако это все еще не дает полной картины процесса в цепи переменного тока, поскольку неизвестно, что означает положительный или отрицательный ток, положительное или отрицательное напряжение.
Чтобы векторные диаграммы токов и напряжений давали полную картину, их необходимо связать с реальным процессом в цепи переменного тока, т.е.е., необходимо предварительно принять условные положительные направления токов и напряжений в рассматриваемой цепи.
Без выполнения этого условия, если не указаны положительные направления токов и напряжений, любая векторная диаграмма не имеет смысла.
Рассмотрим простую однофазную цепь переменного тока, показанную на рис. 1-6, а. От однофазного генератора энергия передается на активное сопротивление нагрузки R. Зададим положительные направления токов и напряжений в рассматриваемой цепи.
Зададим положительные направления токов и напряжений в рассматриваемой цепи.
Для условного положительного направления напряжения и э.с. мы выбираем направление, когда выходной потенциал генератора или нагрузки, связанной с линией, выше, чем выходной потенциал, подключенный к земле. В соответствии с правилами, принятыми в электротехнике, положительное направление для эл. d.s он указывается стрелкой, направленной в сторону более высокого потенциала (от земли к линейному выходу), а для напряжения — стрелкой, направленной в сторону более низкого потенциала (от линейного выхода к земле).
Построим векторы e. d.s и ток, характеризующий работу рассматриваемой цепи (рис. 1-6, б). Вектор е. d.s произвольно обозначают вертикальную линию со стрелкой, направленной вверх. Для построения вектора тока запишем для схемы уравнение по второму закону Кирхгофа:
Так как знаки векторов тока и эл. d.s в выражении (1-7) совпадут, текущий вектор будет совпадать с вектором e. d.s и на рис. 1-6, стр.
1-6, стр.
Здесь и в дальнейшем при построении векторов мы будем откладывать их по величине, равной действующим значениям тока и напряжения, что удобно для выполнения различных математических операций с векторами.Как известно, действующие значения тока и напряжения в разы меньше соответствующих максимальных (амплитудных) значений.
Для заданных положительных направлений тока и напряжения знак мощности также определяется однозначно. В этом случае мощность, направляемая от шин генератора в линию, будет считаться положительной:
, так как текущие векторы и e. d.s на рис. 1-6, б матч.
Аналогичные соображения можно сделать для трехфазной цепи переменного тока, показанной на рис.1-7, а.
В этом случае во всех фазах берутся одинаковые положительные направления, что соответствует симметричной диаграмме токов и напряжений, показанной на рис. 1-7, б. Обратите внимание, что трехфазная система векторов называется симметричной, если все три вектора равны по величине и сдвинуты относительно друг друга на угол 120 °.
Вообще говоря, вовсе не обязательно следовать одним и тем же положительным направлениям на всех фазах. Однако брать разные положительные направления в разных фазах неудобно, так как было бы необходимо изобразить асимметричную систему векторов, когда электрическая цепь работает в нормальном симметричном режиме, когда все три фазы находятся в одинаковых условиях.
б) Операции с векторами
Когда мы рассматриваем только одну кривую тока или напряжения, начальное значение угла, с которого начинается отсчет, или, другими словами, положение вектора на диаграмме, соответствующее начальному моменту времени, может быть принято произвольным. Если одновременно рассматриваются два или несколько токов и напряжений, то, задав начальное положение на схеме одного из векторов, мы тем самым уже определяем положение всех остальных векторов.
Все три вектора фазного напряжения, показанные на рис. 1-7, б, вращаются против часовой стрелки с одинаковой скоростью, определяемой частотой переменного тока.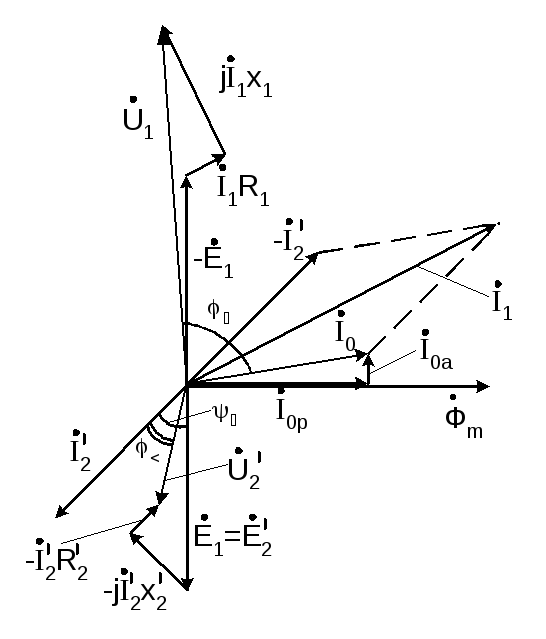 При этом они пересекают вертикальную ось, которая совпадает с направлением вектора на рис. 1-7, б, попеременно с определенной последовательностью, а именно, которая называется чередованием фаз напряжения (или тока ).
При этом они пересекают вертикальную ось, которая совпадает с направлением вектора на рис. 1-7, б, попеременно с определенной последовательностью, а именно, которая называется чередованием фаз напряжения (или тока ).
Для определения относительного положения двух векторов обычно говорят, что один из них впереди или позади другого.В этом случае ведущим вектором считается тот, который при повороте против часовой стрелки раньше пересекает вертикальную ось. Так, например, мы можем сказать, что вектор напряжения на рис. 1-7, b опережает вектор на угол 120 °, или, с другой стороны, вектор отстает от вектора на 120 °. Как видно из рис. 1-7 выражение «вектор на 120 ° позади» эквивалентно выражению «вектор на 240 ° впереди».
При анализе различных электрических цепей возникает необходимость складывать или вычитать векторы тока и напряжения.Сложение векторов производится геометрическим суммированием по правилу параллелограмма, как показано на рис. 1-8, а, по которому строится сумма токов
Поскольку вычитание противоположно сложению, очевидно, что для определения разности токов (например, достаточно прибавить обратный вектор к току
Однако на рис.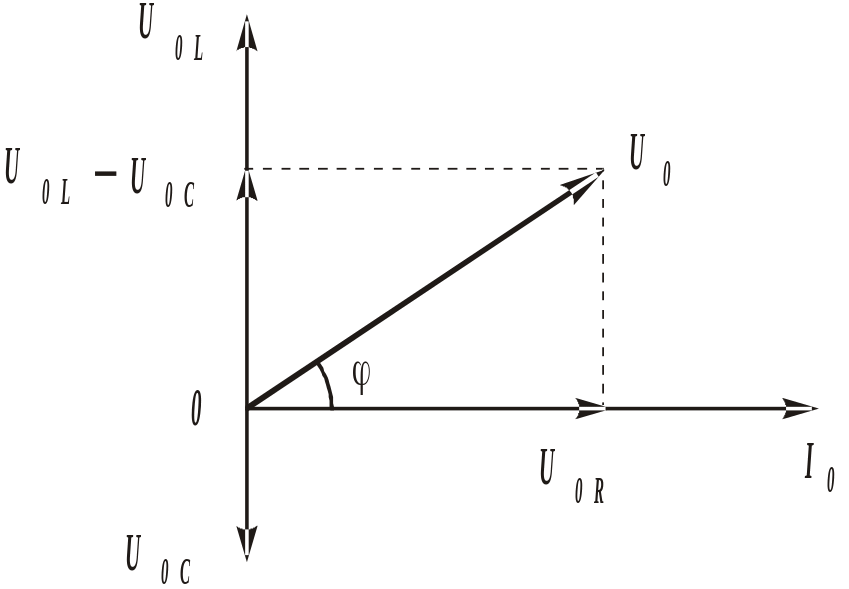 1-8, а это Показано, что вектор текущей разности может быть проще построить, соединив концы векторов линией.В этом случае стрелка вектора разности токов направлена в сторону первого вектора, т.е.
1-8, а это Показано, что вектор текущей разности может быть проще построить, соединив концы векторов линией.В этом случае стрелка вектора разности токов направлена в сторону первого вектора, т.е.
Векторная диаграмма межфазных напряжений строится точно так же, например (рис. 1-8, б).
Очевидно, что положение вектора на плоскости определяется его проекциями на любые две оси. Так, например, чтобы определить положение вектора OA (рис. 1-9), достаточно знать его проекции на взаимно перпендикулярные оси
Откладываем проекции вектора на оси координат и восстанавливаем перпендикуляры к осям из точек.Точкой пересечения этих перпендикуляров является точка A — один конец вектора, второй конец которого — точка O — начало координат.
в) Назначение векторных диаграмм
Работникам, занимающимся проектированием и эксплуатацией релейной защиты, очень часто приходится пользоваться так называемыми векторными диаграммами — векторами тока и напряжения, построенными на плоскости в определенной комбинации, соответствующей электрическим процессам, происходящим в рассматриваемой цепи.
Векторные диаграммы токов и напряжений строятся при расчете коротких замыканий, при анализе распределения тока в нормальном режиме.
Анализ векторных диаграмм токов и напряжений является одним из основных, а в некоторых случаях единственным способом проверки правильности подключения цепей тока и напряжения и включения реле в цепях дифференциальной и направленной защиты.
Фактически построение векторной диаграммы целесообразно во всех случаях, когда на рассматриваемое реле подаются две или более электрических величин: разница токов в максимальной токовой или дифференциальной защите, ток и напряжение в переключателе направления мощности или в реле направленного сопротивления.Векторная диаграмма позволяет сделать вывод о том, как сработает рассматриваемая защита при КЗ, т.е. оценить правильность ее включения. Взаимное расположение векторов тока и напряжения на схеме определяется характеристикой рассматриваемой цепи, а также условно принятыми положительными направлениями токов и напряжений.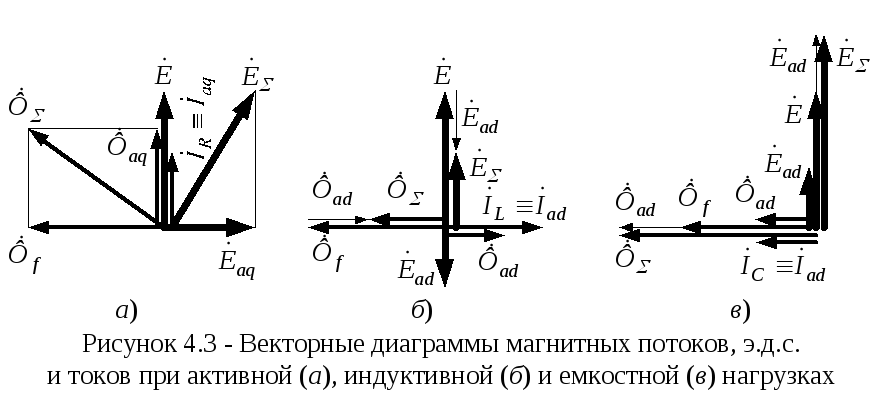
Например, рассмотрим две векторные диаграммы.
На рис.1-10, а изображена однофазная цепь переменного тока, состоящая из генератора и последовательно соединенных емкостного активного и индуктивного сопротивлений (мы предполагаем, что индуктивное сопротивление больше емкостного x L> x C). Положительные направления токов и напряжений, как и в случаях, рассмотренных выше, показаны на рис. 1-10 и стрелками. Начнем построение векторной диаграммы с вектора e. d. s, который расположен на рис. 1-10, б вертикально. Величина протекающего в рассматриваемой цепи тока определяется из следующего выражения:
Так как рассматриваемая схема имеет активное и реактивное сопротивления, причем x L> x C, вектор тока отстает от вектора напряжения на угол:
На рис.1-10, б построен вектор, отстоящий от вектора на 90 °. Напряжение в точке n
определяется разностью векторов. Напряжение в точке m определяется аналогично:
Напряжение в точке m определяется аналогично:
г) Векторные диаграммы при наличии трансформации
Если в электрической цепи есть трансформаторы, необходимо ввести дополнительные условия для сравнения векторных диаграмм токов и напряжений на разных сторонах трансформатора.Положительное направление токов в этом случае следует устанавливать с учетом полярности обмоток трансформатора.
В зависимости от направления намотки обмоток трансформатора меняется взаимное направление токов в них. Для определения направления токов в обмотках силового трансформатора и сравнения их между собой, обмоткам трансформатора присвоены символы «начало» и «конец».
Нарисуем схему, показанную на рис.1-6, только между источником e. d.s и включите трансформатор с нагрузкой (рис. 1-12, а). Обозначим начало обмоток силового трансформатора буквами А и а, концы — X и x. При этом следует учитывать, что «начало» одной из обмоток берется произвольно, а вторая определяется исходя из условных положительных направлений токов, заданных для обеих обмоток трансформатора. 1-12, а также указаны положительные направления токов в обмотках силовых трансформаторов.В первичной обмотке направление тока от «начала» к «концу» считается положительным, а во вторичной — от «конца» к «началу».
При этом следует учитывать, что «начало» одной из обмоток берется произвольно, а вторая определяется исходя из условных положительных направлений токов, заданных для обеих обмоток трансформатора. 1-12, а также указаны положительные направления токов в обмотках силовых трансформаторов.В первичной обмотке направление тока от «начала» к «концу» считается положительным, а во вторичной — от «конца» к «началу».
В результате при таких положительных направлениях направление тока в сопротивлении нагрузки остается таким же, как и до включения трансформатора (см. Рис. 1-6 и 1-12).
где — магнитные потоки в магнитной цепи трансформатора, а — силы намагничивания, создающие эти потоки (n.с.).
Из последнего уравнения
Согласно равенству (1-11), векторы имеют одинаковые знаки и, следовательно, будут совпадать по направлению (рис. 1-12, б).
Принятые положительные направления токов в обмотках трансформатора удобны тем, что первичный и
вторичный токи на векторной диаграмме совпадают по направлению (рис.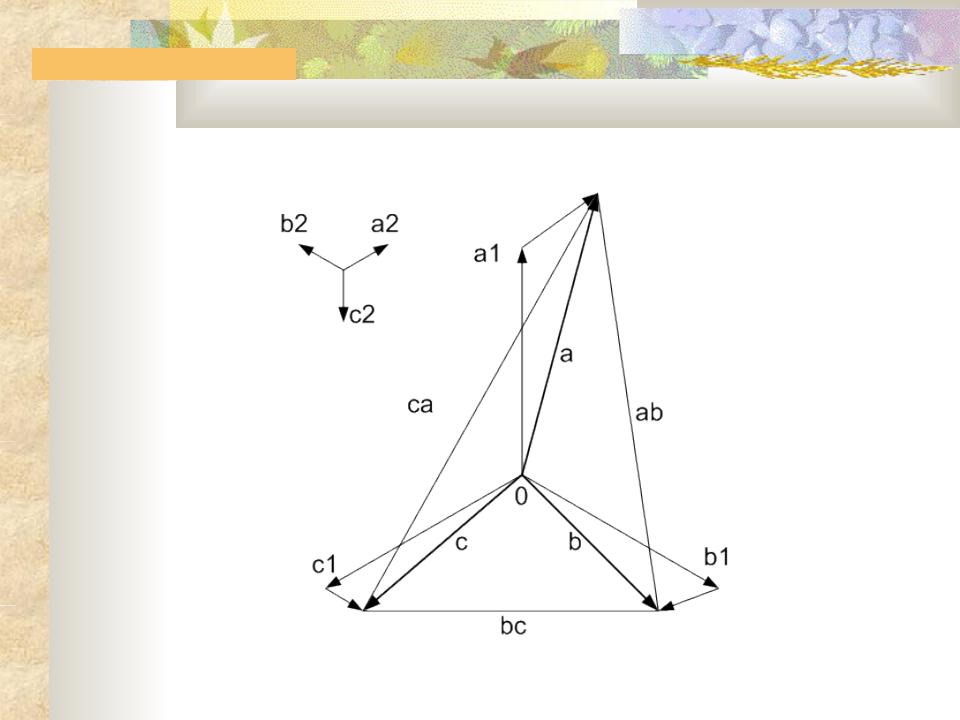 1-12, б). Также удобно, чтобы напряжения принимали такие положительные направления, чтобы векторы вторичных и первичных напряжений совпадали, как показано на рис.1-12.
1-12, б). Также удобно, чтобы напряжения принимали такие положительные направления, чтобы векторы вторичных и первичных напряжений совпадали, как показано на рис.1-12.
В данном случае происходит трансформаторное подключение по схеме 1 / 1-12. Соответственно, для трехфазного трансформатора электрическая схема и векторная диаграмма токов и напряжений показаны на рис. 1-14.
На рис. 1-15, б построены векторные диаграммы напряжения, соответствующие схеме подключения трансформатора
.
На стороне высокого напряжения, где обмотки соединены звездой, межфазные напряжения превышают фазные напряжения в один раз.На стороне более низкого напряжения, где обмотки соединены треугольником, межфазное и фазное напряжения равны. Межфазные напряжения стороны низкого напряжения на 30 ° отстают от аналогичных межфазных напряжений стороны высокого напряжения, что соответствует схеме подключения
Для рассматриваемой схемы подключения обмоток трансформатора можно построить векторные диаграммы протекающих токов. с обеих сторон. При этом следует учитывать, что исходя из принятых нами условий определяются только положительные направления токов в обмотках трансформатора.Положительные направления токов в линейных проводах, соединяющих выводы низковольтных обмоток трансформатора с шинами, могут быть приняты произвольно независимо от положительных направлений токов, проходящих в треугольнике.
с обеих сторон. При этом следует учитывать, что исходя из принятых нами условий определяются только положительные направления токов в обмотках трансформатора.Положительные направления токов в линейных проводах, соединяющих выводы низковольтных обмоток трансформатора с шинами, могут быть приняты произвольно независимо от положительных направлений токов, проходящих в треугольнике.
Так, например, если взять положительные направления токов в фазах на стороне более низкого напряжения от клемм, соединенных треугольником с шинами (рис. 1-15, а), то можно записать следующее равенство:
Соответствующая векторная диаграмма токов представлена на рис.1-15, в.
Аналогичным образом можно построить векторную диаграмму токов для случая, когда положительные направления токов снимаются от шин к выводам треугольника (рис. 1-16, а). Этому случаю соответствуют следующие равенства:
Этому случаю соответствуют следующие равенства:
и векторные диаграммы, показанные на рис. 1-16, стр. Сравнивая токовые диаграммы, представленные на рис. 1-15, в и 1-16, б, можно сделать вывод, что векторы фазных токов, проходящих в проводах, соединяющих выводы обмоток, малы
Напряжения трансформатора и шины находятся в пределах противофазный.Конечно, и те, и другие диаграммы верны.
Таким образом, при наличии в цепи обмоток, соединенных треугольником, необходимо задать положительные направления токов как в самих обмотках, так и в линейных проводах, соединяющих треугольник с шинами.
В этом случае при определении группы соединений силового трансформатора направления от выводов низкого напряжения к сборным шинам удобно принять как положительные, так как векторные диаграммы токов совпадают с принятым обозначением групп соединений. силовых трансформаторов (ср. рис.1-15, б и в). Аналогично векторные диаграммы тока могут быть построены для других групп подключения силовых трансформаторов. Приведенные выше правила построения векторных диаграмм токов и напряжений в цепях с трансформаторами справедливы и для измерения трансформаторов тока и напряжения.
Приведенные выше правила построения векторных диаграмм токов и напряжений в цепях с трансформаторами справедливы и для измерения трансформаторов тока и напряжения.
% PDF-1.6
%
1 0 obj
>
endobj
2 0 obj
>
endobj
3 0 obj
>
>>
/ Вкладки / S
/ Содержание [22 0 R 23 0 R 24 0 R 25 0 R 26 0 R 27 0 R 28 0 R 29 0 R]
/ Тип / Страница
>>
endobj
4 0 obj
>
>>
/ Содержание 31 0 руб.
/ Родитель 1 0 R
/ StructParents 1
/ Тип / Страница
/ Аннотации 32 0 R
/ Вкладки / S
>>
endobj
5 0 obj
>
/ XObject
>
/Шрифт
>
>>
/ Вкладки / S
/ Содержание 36 0 руб.
/ Тип / Страница
>>
endobj
6 0 obj
>
/ XObject
>
/Шрифт
>
>>
/ Содержание 39 0 руб.
/ Родитель 1 0 R
/ StructParents 4
/ Группа 40 0 р
/ Тип / Страница
/ Вкладки / S
>>
endobj
7 0 объект
>
/ XObject
>
/Шрифт
>
>>
/ Содержание 44 0 руб.
/ Родитель 1 0 R
/ StructParents 5
/ Группа 40 0 р
/ Тип / Страница
/ Вкладки / S
>>
endobj
8 0 объект
>
/ XObject
>
/Шрифт
>
>>
/ Содержание 47 0 руб.
/ Родитель 1 0 R
/ StructParents 6
/ Группа 40 0 р
/ Тип / Страница
/ Вкладки / S
>>
endobj
9 0 объект
>
/ XObject
>
/Шрифт
>
>>
/ Содержание 52 0 руб.
/ Родитель 1 0 R
/ StructParents 7
/ Группа 40 0 р
/ Тип / Страница
/ Вкладки / S
>>
endobj
10 0 obj
>
/Цветовое пространство
>
/ XObject
>
/Шрифт
>
>>
/ Содержание 56 0 руб.
/ Родитель 1 0 R
/ StructParents 8
/ Группа 40 0 р
/ Тип / Страница
/ Вкладки / S
>>
endobj
11 0 объект
>
/Цветовое пространство
>
/ XObject
>
/Шрифт
>
>>
/ Содержание 61 0 руб.
/ Родитель 1 0 R
/ StructParents 9
/ Группа 40 0 р
/ Тип / Страница
/ Вкладки / S
>>
endobj
12 0 объект
>
/ XObject
>
/Шрифт
>
>>
/ Вкладки / S
/ Содержание 66 0 руб.
/ Тип / Страница
>>
endobj
13 0 объект
>
/ XObject
>
/Шрифт
>
>>
/ Вкладки / S
/ Содержание 68 0 руб.
/ Тип / Страница
>>
endobj
14 0 объект
>
/ XObject
>
/Шрифт
>
>>
/ Вкладки / S
/ Содержание 70 0 руб.
/ Тип / Страница
>>
endobj
15 0 объект
>
>>
/ Вкладки / S
/ Содержание 71 0 руб.
/ Тип / Страница
>>
endobj
16 0 объект
>
>>
/ Содержание 73 0 руб.
/ Родитель 1 0 R
/ StructParents 14
/ Тип / Страница
/ Аннотации 74 0 руб.
/ Вкладки / S
>>
endobj
18 0 объект
>
/Шрифт
>
/ ProcSet [/ PDF / Text / ImageC]
>>
endobj
19 0 объект
>
транслировать
x ڭَ6} B @ bEl & $ o 䁖 hGG6PZifù; q’NŮU7oy $ R: PđABF #] ŝ] sq + tR37 / 䉓 i $ «Qi0ϝ! Wn» ݎ8 = 87 w BzNwi
4% — # Gv \? BX ~ dmzS ި :. WReb !!
WReb !!
Как использовать фазорную диаграмму?
Когда вы выполняете обследование энергии или качества электроэнергии, вам нужно измерить данные за дни или недели, представьте себе разочарование, если, вернувшись к регистратору по истечении этого времени, вы обнаружите, что вам не удалось выполнить правильные измерения. В службу поддержки Fluke слишком часто звонят пользователи, которые не понимают измеренных значений, которые они зарегистрировали, обычно они думают, что неисправен прибор. Обычно, хотя проблема возникает из-за того, что пользователь совершает ошибку подключения, это может быть связано с неправильным подключением напряжения или постоянным током подключения.Проблему можно легко предотвратить, проверив и дважды проверив эти соединения перед запуском сеанса регистрации.
Отображение векторной диаграммы
Самым мощным инструментом трехфазных анализаторов Fluke для выполнения этой проверки является отображение векторной диаграммы. На одном экране вы можете быстро увидеть, правильно ли вы подключили напряжение и ток, и что датчики тока правильно измеряют направление тока, входящего в нагрузку, или в случае генератора, измеряющего ток, обеспечиваемый генератор.
Как только вы поймете основы векторной диаграммы, вы сможете использовать ее, чтобы каждый раз при входе в журнал регистрировать нужные вам данные.
Основы
- Векторы напряжения, представленные толстыми линиями со стрелками, обычно с разделением 120 °, это немного варьируется в зависимости от степени дисбаланса в системе.
- Current использует более тонкую линию, оканчивающуюся треугольником, таким же образом с разделением около 120 ˚. Угол между векторами напряжения и тока указывает на коэффициент мощности схемы, если угол небольшой, коэффициент мощности будет хорошим и близким к 1.Если коэффициент мощности плохой, скажем, менее 0,9, угол будет больше.
- Длина вектора указывает величину напряжения и тока (для удобства показания напряжения и тока отображаются в вольтах и амперах). Проверка этих показаний важна для обеспечения выбора правильных диапазонов перед регистрацией.
- Угол между напряжением и током меняется, но если он больше 90 °, то это связано с неправильным подключением.

- Важно отметить, что и при вращении векторов напряжения фаза L1 должна быть направлена горизонтально вправо, затем фаза L2 должна быть следующей в направлении против часовой стрелки и, наконец, фаза L3 должна быть последней.В этом примере правильное направление обозначено L1L2L3 в верхней части дисплея.
В этом примере мы видим ошибку:
- Здесь вектор тока направлен почти на 180 ° от напряжения. Это связано с тем, что датчик тока (гибкий зонд или зажим) указывает неправильное направление. На датчике тока вы найдете стрелку, все они должны указывать на нагрузку. Если один или несколько из них указывают в неправильном направлении, вы увидите угол больше 90˚
Проверка того, что все ваши фазы правильно чередуются, а датчики тока правильно ориентированы каждый раз, когда вы подключаетесь для выполнения съемки, избавит от разочарования при возвращении к вашему прибору только для того, чтобы обнаружить, что вы потратили впустую дни или недели времени регистрации.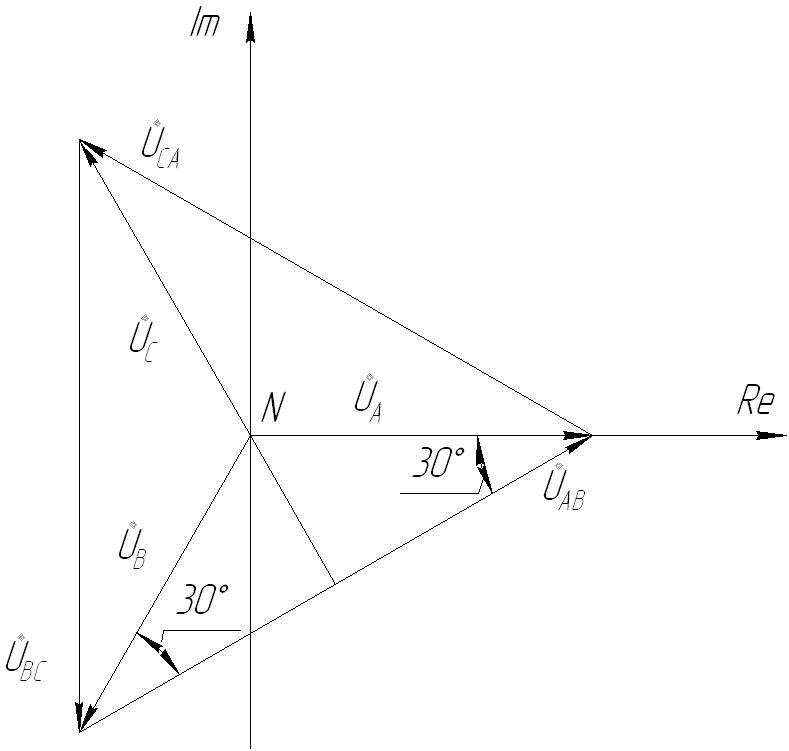
Некоторые из новых продуктов Fluke указывают на наличие ошибки подключения и позволяют автоматическое исправление без необходимости перемещать какое-либо соединение.
Цепь последовательного RLC серии
(схема и фазовая диаграмма)
Что такое последовательная цепь RLC?
Последовательная цепь RLC — это резистор, катушка индуктивности и конденсатор, соединенные последовательно через источник напряжения. Результирующая цепь называется цепью RLC серии . Схема и векторная диаграмма для последовательной цепи RLS показаны ниже.
Векторная диаграмма последовательной цепи RLC
Векторная диаграмма последовательной RLC-цепи построена путем объединения векторной диаграммы резистора, катушки индуктивности и конденсатора. Перед тем как это сделать, необходимо понять взаимосвязь между напряжением и током в случае резистора, конденсатора и катушки индуктивности.
- Резистор
В случае резистора напряжение и ток находятся в одной фазе, или мы можем сказать, что разность фаз между напряжением и током равна нулю.
- Катушка индуктивности
В катушке индуктивности напряжение и ток не совпадают по фазе. Напряжение опережает ток на 90 ° или, другими словами, напряжение достигает своего максимального значения и нулевого значения на 90 ° до того, как его достигает ток. - Конденсатор
В случае конденсатора ток опережает напряжение на 90 ° или, другими словами, напряжение достигает своего максимального значения и нулевого значения 0 ° после того, как ток достигает его, то есть векторная диаграмма конденсатора прямо противоположна индуктивности.
- Резистор
ПРИМЕЧАНИЕ: Чтобы запомнить соотношение фаз между напряжением и током, выучите это простое слово под названием «ГРАЖДАНСКИЙ», т.е.e в конденсаторах, ток в проводах, напряжение и напряжение, ток в индуктивности.
Цепь RLC
Для построения векторной диаграммы последовательной цепи RLC выполните следующие действия:
Шаг — I. В случае последовательной цепи RLC; резистор, конденсатор и индуктор соединены последовательно; Таким образом, ток, протекающий во всех элементах, одинаков, т. е. I r = I l = I c = I. Для построения векторной диаграммы возьмите вектор тока в качестве эталона и проведите его по горизонтальной оси, как показано на диаграмме .
е. I r = I l = I c = I. Для построения векторной диаграммы возьмите вектор тока в качестве эталона и проведите его по горизонтальной оси, как показано на диаграмме .
Шаг — II. В случае резистора напряжение и ток находятся в одной фазе. Итак, нарисуйте вектор напряжения V R вдоль той же оси или направления, что и вектор тока, то есть V R находится в фазе с I.
Шаг — III. Мы знаем, что в катушке индуктивности напряжение ведет ток на 90 °, поэтому проводите V l (падение напряжения на катушке индуктивности) перпендикулярно вектору тока в опережающем направлении.
Шаг — IV. В случае конденсатора, напряжение отстает от тока на 90 °, поэтому потяните V c (падение напряжения на конденсаторе) перпендикулярно вектору тока в направлении вниз.
Шаг — V. Чтобы нарисовать получившуюся диаграмму, начертите V c в направлении вверх. Теперь нарисуйте результат, V s , который представляет собой векторную сумму напряжений V r и V L — V C .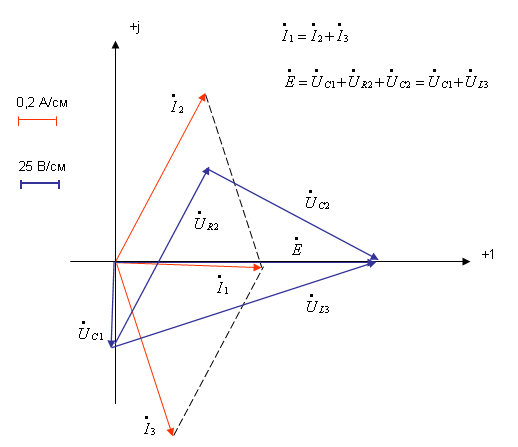
Полное сопротивление для последовательной цепи RLC
Импеданс Z последовательной RLC-цепи определяется как сопротивление протеканию тока из-за сопротивления цепи R, индуктивного реактивного сопротивления X L и емкостного реактивного сопротивления X С .Если индуктивное реактивное сопротивление больше, чем емкостное, то есть X L > X C , тогда цепь RLC имеет запаздывающий фазовый угол, и если емкостное реактивное сопротивление больше, чем индуктивное, то есть X C > X L , тогда цепь RLC имеет опережающий фазовый угол, и если и индуктивная, и емкостная одинаковы, то есть X L = X C , тогда схема будет вести себя как чисто резистивная цепь.
Мы знаем, что,
Подставив значения V S 2 = (IR) 2 + (IX L — IX C ) 2
Из этого треугольника импеданса: с помощью Пифагора теорему получаем;
Изменение сопротивления, реактивного сопротивления и импеданса с частотой
В последовательной цепи RLC задействованы три типа импеданса —
- Электрическое сопротивление — Сопротивление не зависит от частоты, поэтому оно остается постоянным при изменении частоты.

- Индуктивное реактивное сопротивление, X L — Мы знаем, что X L = 2πfL. Таким образом, индуктивное реактивное сопротивление напрямую зависит от частоты. Таким образом, график между частотой и индуктивным сопротивлением представляет собой прямую линию, проходящую через центр, как показано кривой
a
. - Емкостное реактивное сопротивление, X C — Из формулы емкостного реактивного сопротивления, X C = 1 / 2πfC, поэтому емкостное реактивное сопротивление изменяется обратно пропорционально частоте. Поскольку чистое реактивное сопротивление равно (X L — X C ).Итак, для построения кривой (X L — X C ) сначала нарисуйте график (-X C ), который показан кривой
b
, а затем нарисуйте кривую чистого реактивного сопротивления, которое показано как криваяс
. - Полный импеданс цепи показан кривой
d
, которая получается добавлением постоянного сопротивления резистора к общему реактивному сопротивлению.
Страница не найдена | MIT
Перейти к содержанию ↓
- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Меню ↓
Поиск
Меню
Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!
Что вы ищете?
Увидеть больше результатов
Предложения или отзывы?
Калькулятор импеданса цепи RLC серии
• Калькуляторы электрических, радиочастот и электроники • Онлайн-преобразователи единиц
Этот калькулятор импеданса последовательной цепи RLC определяет импеданс и угол разности фаз резистора, катушки индуктивности и конденсатора, соединенных последовательно для заданной частоты синусоидальный сигнал. Также определяется угловая частота.
Также определяется угловая частота.
Пример: Рассчитайте полное сопротивление катушки индуктивности 1 Ом, конденсатора 100 мкФ и резистора 100 Ом на частоте 16 Гц. В этом примере показано почти резонансное сопротивление около 100,006 Ом. Если вы хотите проверить импеданс почти при точном резонансе, введите 15,9154 Гц вместо 16 Гц. На этой частоте импеданс является немного емкостным, потому что угол разности фаз φ <0. Если вы введете немного более высокую частоту 15.9155 Гц, импеданс изменится на слегка индуктивный, и вы заметите, что угол разности фаз стал положительным.
Вход
Сопротивление, R
миллиом (мОм) Ом (Ом) килоом (кОм) мегом (МОм)
Индуктивность, л
генри (H) миллигенри (мГн) микрогенри (мкГн) ) пикогенри (pH)
Емкость, C
фарад (F) микрофарад (мкФ, мкФ) нанофарад (нФ) пикофарад (пФ)
Частота, f
герц (Гц) миллигерц (мГц) килогерц (мГц) кГц (МГц) гигагерцы (ГГц)
Выход
Угловая частота ω = рад / с
Емкостное реактивное сопротивление X C = Ω
Индуктивное реактивное сопротивление X
5
всего
Ом Импеданс RLC | Z RLC | = Ом
Разность фаз φ = ° = рад
Коэффициент качества Q =
Резонансная частота
f 0 = Гц ω 0 = рад / с
Введите сопротивление, значения емкости, индуктивности и частоты, выберите единицы и нажмите или коснитесь кнопки Calculate . Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.
Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.
Для расчета используются следующие формулы:
φ 90 °, если 1/2 πfC <2 πfL 9029
φ = –90 °, если 1/2 πfC > 2 πfL и R = 0
φ = 0 °, если 1/2 πfC = 2 πfL и R = 0
где
Z LC — полное сопротивление цепи LC в омах (Ω),
ω = 2πf — угловая частота в рад / с,
f — частота в герцах (Гц),
R — сопротивление в омах (Ом),
L — индуктивность в генри (Гн),
C — емкость в фарадах ( F),
Q — добротность Схема RLC (безразмерная),
ω 0 — резонансная угловая частота в радианах в секунду (рад / с),
f 0 — резонансная частота в герцах (Г),
φ — это фазовый сдвиг между полным напряжением V T и полным током I T в градусах (°) и радианах, а
j — мнимая единица.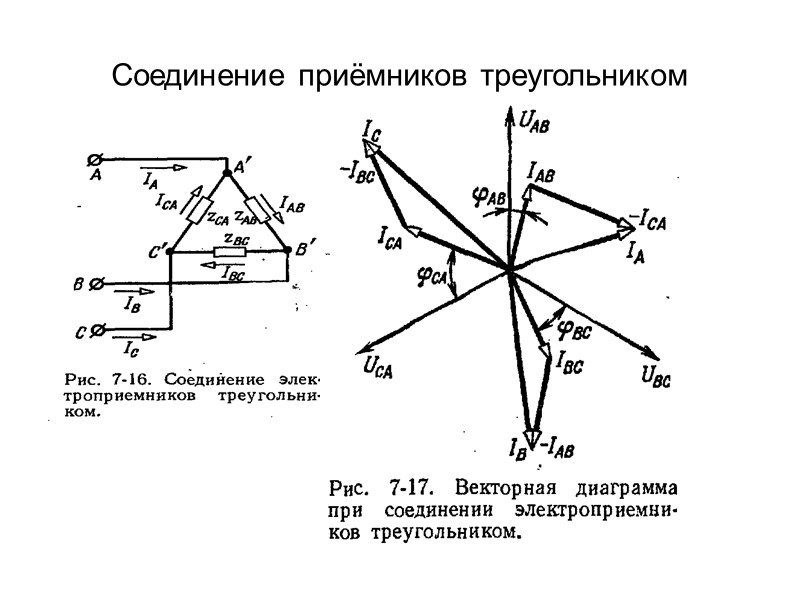
Для расчета введите сопротивление, индуктивность, емкость и частоту, выберите единицы измерения, и результат для полного сопротивления RLC будет отображаться в омах, а для разности фаз — в градусах. Также будут рассчитаны добротность, реактивное сопротивление C и L и резонансная частота. Щелкните или коснитесь Рассчитать на резонансной частоте , чтобы увидеть, что произойдет при резонансе.
Последовательная цепь RLC состоит из последовательно соединенных резистора R, индуктора L и конденсатора C.Последовательность букв в названии цепи может быть разной: RLC, RCL, LCR и т. Д. Как и в чисто последовательном LC-контуре, RLC-контур может резонировать на резонансной частоте, а резистор увеличивает затухание колебаний на этой частоте.
Резонанс возникает на частоте, на которой полное сопротивление цепи минимально, то есть, если в цепи нет реактивного сопротивления. Другими словами, если импеданс чисто резистивный (или реальный). Это явление происходит, когда реактивные сопротивления катушки индуктивности и конденсатора равны, и из-за их противоположных знаков они компенсируют друг друга (подавление можно увидеть на правой векторной диаграмме ниже).
Калькулятор определяет резонансную частоту контура RLC, и вы можете ввести эту частоту или значение немного выше или ниже, чтобы увидеть, что произойдет с другими расчетными значениями при резонансе.
Калькулятор также может определить коэффициент добротности последовательного RLC-контура — параметр, который используется для характеристики резонансных контуров и не только электрических, но и механических резонаторов. Цепи RLC с затуханием и потерями с высоким сопротивлением имеют низкий коэффициент добротности и широкополосный диапазон, тогда как схемы с низким сопротивлением имеют высокий коэффициент добротности.Для последовательной цепи RLC коэффициент добротности можно рассчитать по формуле выше.
Слева представлен график полного сопротивления Z RLC последовательного RLC-контура в зависимости от частоты f для заданного сопротивления, индуктивности и емкости, показывает только резистивное сопротивление на резонансных частотах.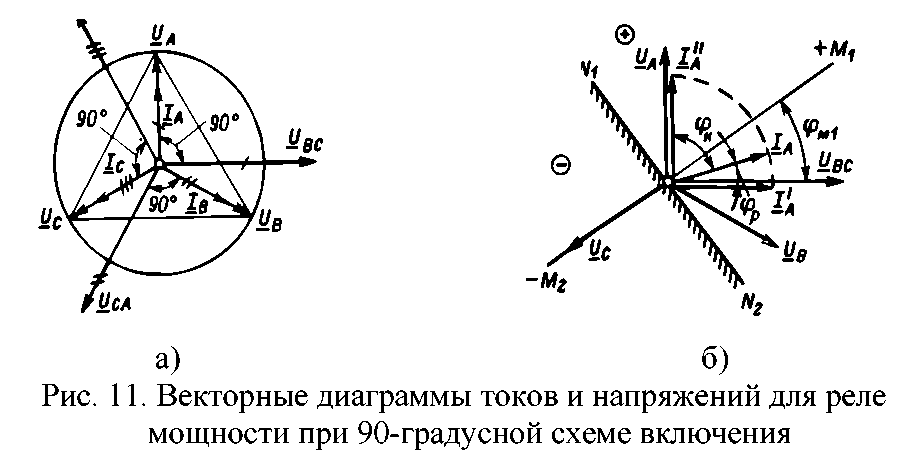 Когда частота увеличивается, реактивное сопротивление катушки индуктивности увеличивается, а реактивное сопротивление конденсатора уменьшается. Однако, если частота приближается к нулю (или постоянному току), реактивное сопротивление катушки индуктивности уменьшается до нуля, а реактивное сопротивление конденсатора увеличивается до бесконечности.На нулевой частоте последовательная цепь RLC действует как разомкнутая цепь. Правый график показывает зависимость импеданса и фазового угла последовательной RLC-цепи от частоты. Справа от резонансной частоты импеданс является индуктивным, а слева от резонансной частоты — емкостным.
Когда частота увеличивается, реактивное сопротивление катушки индуктивности увеличивается, а реактивное сопротивление конденсатора уменьшается. Однако, если частота приближается к нулю (или постоянному току), реактивное сопротивление катушки индуктивности уменьшается до нуля, а реактивное сопротивление конденсатора увеличивается до бесконечности.На нулевой частоте последовательная цепь RLC действует как разомкнутая цепь. Правый график показывает зависимость импеданса и фазового угла последовательной RLC-цепи от частоты. Справа от резонансной частоты импеданс является индуктивным, а слева от резонансной частоты — емкостным.
Векторная диаграмма для последовательного RLC-контура для емкостного (слева), индуктивного (в центре) и чисто резистивного (справа) импеданса. Векторы напряжения на диаграмме образуют прямоугольный треугольник напряжения с гипотенузой V T , вертикальным участком V L — V C и горизонтальным участком V R .
В последовательной цепи один и тот же ток протекает через резистор, катушку индуктивности и конденсатор, но отдельные напряжения на компонентах различаются.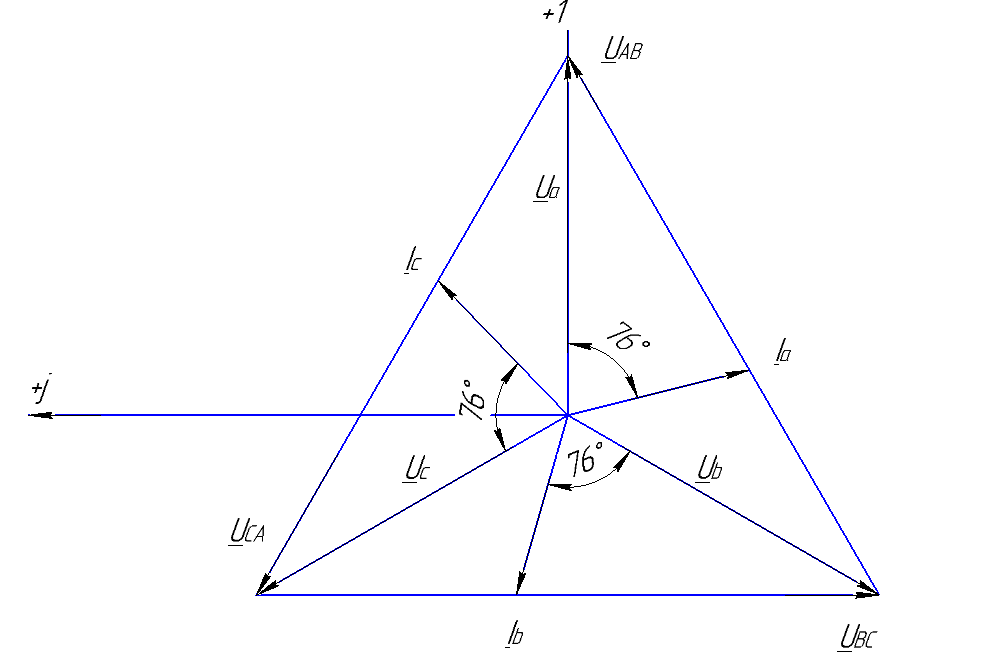 На векторной диаграмме показано напряжение V T идеального источника синусоидального напряжения. Падение напряжения на резисторе V T показано на горизонтальной оси в фазе с током, протекающим по цепи. Вектор напряжения индуктивности V L отстает от тока в векторе индуктивности на 90 °, поэтому он нарисован под + 90 °.Вектор напряжения емкости V C опережает ток в векторе конденсатора на 90 ° и проходит под углом –90 °. Векторная сумма двух противоположных векторов может быть направлена вниз или вверх в зависимости от падения напряжения на катушке индуктивности и конденсаторе. Вектор полного напряжения V T получается с использованием теоремы Пифагора.
На векторной диаграмме показано напряжение V T идеального источника синусоидального напряжения. Падение напряжения на резисторе V T показано на горизонтальной оси в фазе с током, протекающим по цепи. Вектор напряжения индуктивности V L отстает от тока в векторе индуктивности на 90 °, поэтому он нарисован под + 90 °.Вектор напряжения емкости V C опережает ток в векторе конденсатора на 90 ° и проходит под углом –90 °. Векторная сумма двух противоположных векторов может быть направлена вниз или вверх в зависимости от падения напряжения на катушке индуктивности и конденсаторе. Вектор полного напряжения V T получается с использованием теоремы Пифагора.
На резонансной частоте емкостное и индуктивное реактивные сопротивления равны, и если мы посмотрим на уравнение для | Z | выше, мы увидим, что эффективное сопротивление равно сопротивлению R , потому что два противоположных напряжения просто компенсируют друг друга. Ток, протекающий через катушку индуктивности и конденсатор, одинаков, а напряжения на них равны и противоположны. Таким образом, на резонансной частоте ток, потребляемый от источника, ограничивается только сопротивлением, потому что идеальный последовательный LC-контур на резонансной частоте действует как короткое замыкание.
Ток, протекающий через катушку индуктивности и конденсатор, одинаков, а напряжения на них равны и противоположны. Таким образом, на резонансной частоте ток, потребляемый от источника, ограничивается только сопротивлением, потому что идеальный последовательный LC-контур на резонансной частоте действует как короткое замыкание.
Резонансная частота последовательного RLC-контура определяется с учетом того, что
Умножая обе части уравнения на частоту f , мы получим
Разделив обе стороны на 2 πL , взяв квадратный корень из обеих частей уравнения и упрощая, мы получим
Режимы отказа
Что, если что-то пойдет не так в этой цепи? Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных режимах отказа:
Специальные режимы
Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах:
Различные режимы постоянного тока
Короткое замыкание
Обрыв цепи
Чисто емкостная цепь
Резонансная цепь
Чисто индуктивная цепь
Индуктивная цепь
Примечания
- В наших объяснениях поведения этой цепи нулевая частота означает постоянный ток.
 Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения.
Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения. - При нулевой частоте мы считаем реактивное сопротивление конденсатора равным нулю, если его емкость бесконечно велика. Если конденсатор имеет конечную емкость, его реактивное сопротивление при нулевой частоте бесконечно велико, и для источника постоянного напряжения оно представляет собой разомкнутую цепь или, другими словами, удаленный конденсатор.
- При нулевой частоте мы считаем реактивное сопротивление идеальной катушки индуктивности бесконечно большим, если ее индуктивность бесконечно велика.Если катушка индуктивности имеет конечную индуктивность, ее реактивное сопротивление при нулевой частоте равно нулю, а для источника постоянного напряжения оно представляет собой короткое замыкание.
Индукторы в радиочастотном модуле телевизионного приемника
Фазорное представление синусоидальных переменных
Фазорное представление синусоидальных переменных
В следующем обсуждении анализа цепей переменного тока все синусоидальные
переменные (токи и напряжения) считаются одинаковыми
частота. В общем, арифметические операции над синусоидальными функциями
В общем, арифметические операции над синусоидальными функциями
неудобны, поскольку потребуют использования тригонометрических тождеств.Например, учитывая две синусоиды одинаковой частоты:
| (16) |
мы можем найти их сумму как:
С другой стороны, мы предполагаем, что эта сумма имеет вид
| (18) |
Сравнивая два приведенных выше уравнения, мы видим, что
| (19) |
которые мы обозначили через и.
Из этих уравнений мы можем получить
| (20) |
Решая эти уравнения, получаем
| (21) |
Добавление двух реальных синусоидальных функций выше может быть
выполняется с использованием альтернативного подхода, если обе функции
рассматривается как действительная (или мнимая) часть вращающихся векторов в
комплексная плоскость. Затем их арифметические операции (сложение,
Затем их арифметические операции (сложение,
умножение и т. д.) может быть более удобно проводить на основе
на векторе представления синусоидальных переменных.
В частности, сумма
двух синусоидальных
функции, когда-то представленные в векторной форме на комплексной плоскости, могут
можно найти как действительную часть векторной суммы в следующих
три шага:
(обзор сложной арифметики)
Пример
Рассмотрим три источника синусоидального напряжения
,
и
последовательно.По данным КВЛ,
общее напряжение будет алгебраической суммой трех:
| (29) |
Хотя сложение этих синусоидальных функций непросто.
(еще помните все тригонометрические тождества?), вполне прям
вперед, чтобы найти векторную сумму, если напряжения представлены в виде векторов:
Результирующее напряжение равно
Фазор и преобразование Фурье
Синусоидальная функция
можно выразить в
либо преобразование Фурье (ряд Фурье), либо представление вектора:
куда
| (32) |
Мы видим, что вектор и коэффициенты Фурье
и по сути одинаковы в том смысле, что они оба
коэффициенты, представляющие амплитуду и фазу комплекса
экспоненциальная функция
.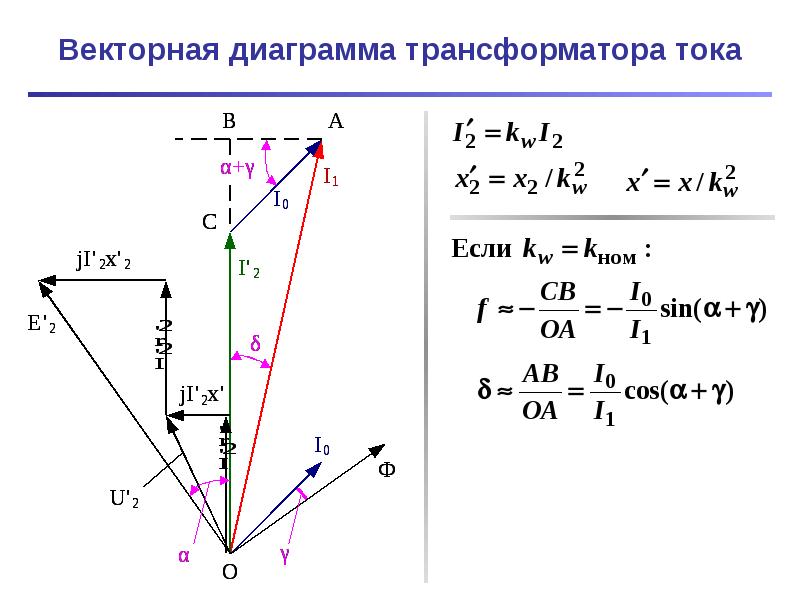

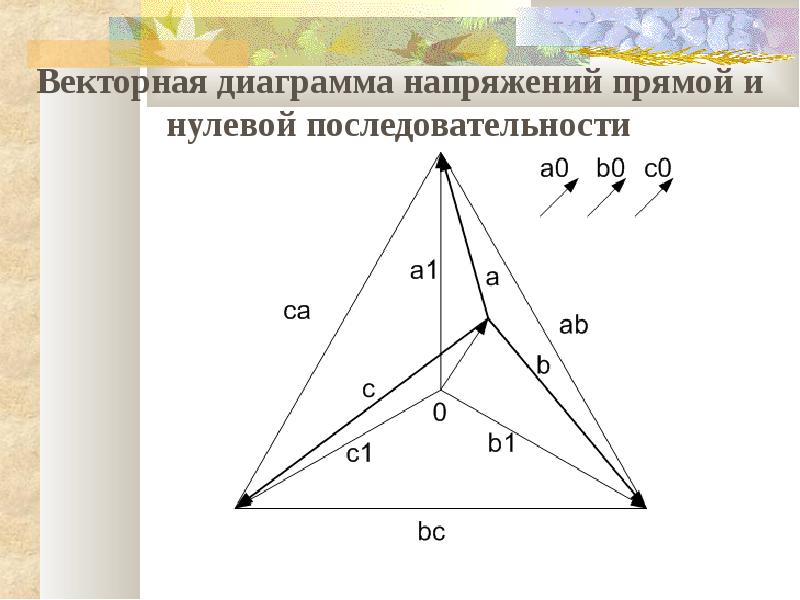 –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
–7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
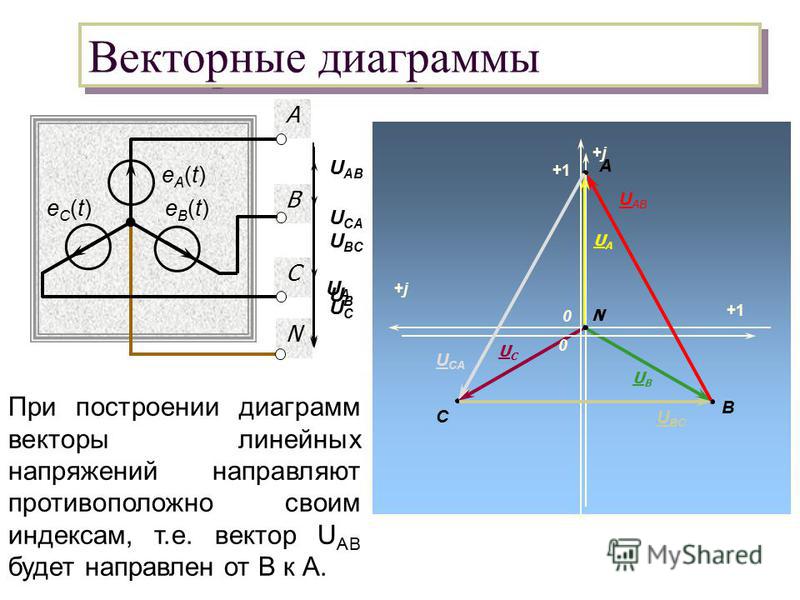
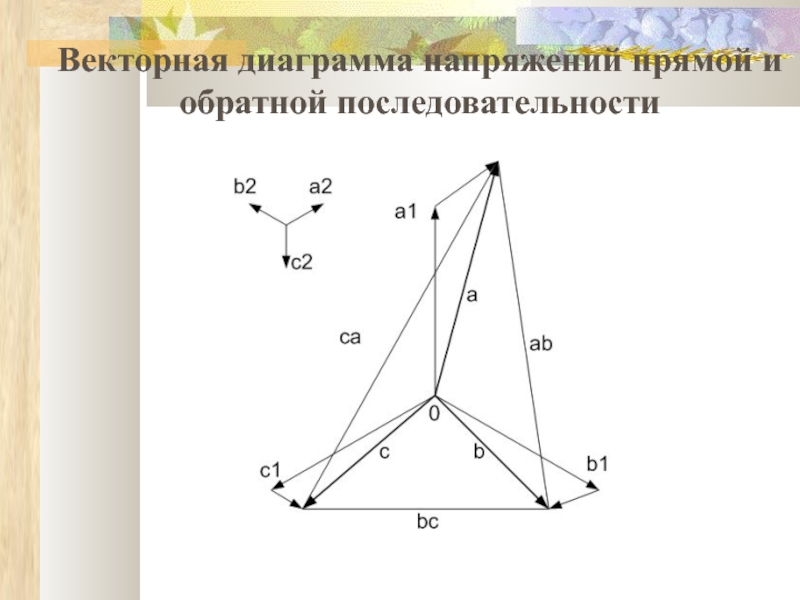

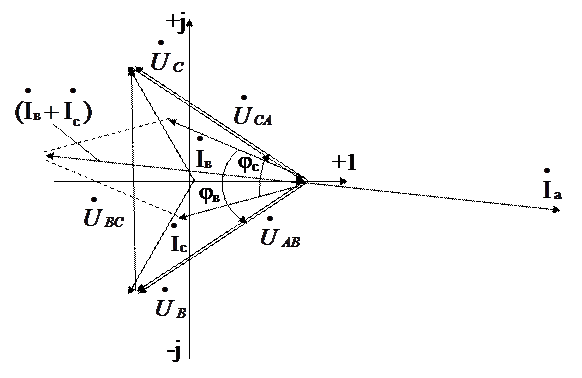 Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения.
Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения.