Закон Ома для участка цепи. Последовательное и параллельное соединение проводников
Как мы уже говорили,
чтобы создать электрический ток в проводнике, необходимо существование
электрического поля. Иными словами, на концах этого проводника должны быть
разные потенциалы, то есть проводник должен находиться под напряжением. Как вы
понимаете, чем больше будет разность потенциалов, тем больше будет
напряженность электрического поля. Следовательно, поле будет действовать на
заряды сильнее, и они будут двигаться по проводнику быстрее. Это приведет к
увеличению силы тока. Таким образом, мы можем заключить, что для каждого
проводника существует определенная взаимосвязь между напряжением и силой тока.
Зависимость силы тока от напряжения в данном проводнике называют вольт-амперной
характеристикой проводника.
Подавая различное
напряжение на концы проводника можно измерять силу тока и, таким образом,
вывести зависимость между силой тока и напряжением.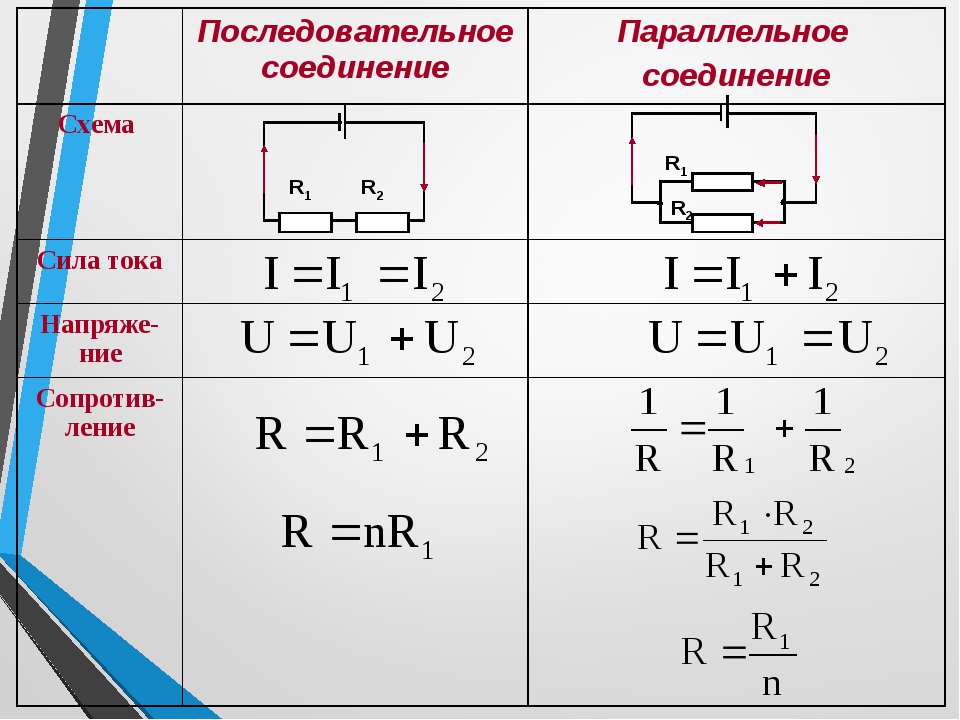 Наиболее простую форму
Наиболее простую форму
имеет вольт-амперная характеристика металлов и растворов электролитов. Итак,
эту вольт-амперную характеристику установил Георг Ом, проведя многочисленные
опыты. Он доказал, что сила тока в проводнике прямо пропорциональна
напряжению на концах этого проводника.
Как вы знаете из курса
физики восьмого класса, закон Ома для участка цепи звучит так: сила тока на
участке цепи прямо пропорциональна приложенному к нему напряжению и обратно
пропорциональна сопротивлению данного участка:
Единица измерения
сопротивления названа в честь Георга Ома:
Как видно из формулы,
проводник обладает сопротивлением 1 Ом, если при напряжении 1 В, в этом проводнике
возникает сила тока в 1 А.
Если мы изобразим эту
зависимость графически, то графики будут представлять собой прямые линии. Это
говорит нам о линейной зависимости силы тока от напряжения.
Угол наклона прямой,
соответствующей каждому проводнику будет обусловлен сопротивлением проводника.
Используя наш график, мы можем с уверенностью сказать, что проводник номер 3
обладает самым маленьким сопротивлением, а проводник номер 1 обладает самым
большим сопротивлением:
То есть, при одинаковом
напряжении во всех трех проводниках будет различная сила тока, в зависимости от
сопротивления данного проводника.
Очевидно, что
сопротивление — это основная электрическая характеристика проводника, которая и
обуславливает индивидуальную вольт-амперную характеристику. Разумеется,
пользуясь законом Ома, можно определить сопротивление того или иного проводника
экспериментально. Рассмотрим участок цепи между точками 1 и 2, обладающими
различными потенциалами.
Подключим вольтметр для
измерения разности потенциалов и подключим амперметр для измерения силы тока в
проводнике. Тогда сопротивление проводника будет равно отношению напряжения
между точками 1 и 2 к силе тока:
В восьмом классе мы уже
говорили, чем обусловлено сопротивление проводников.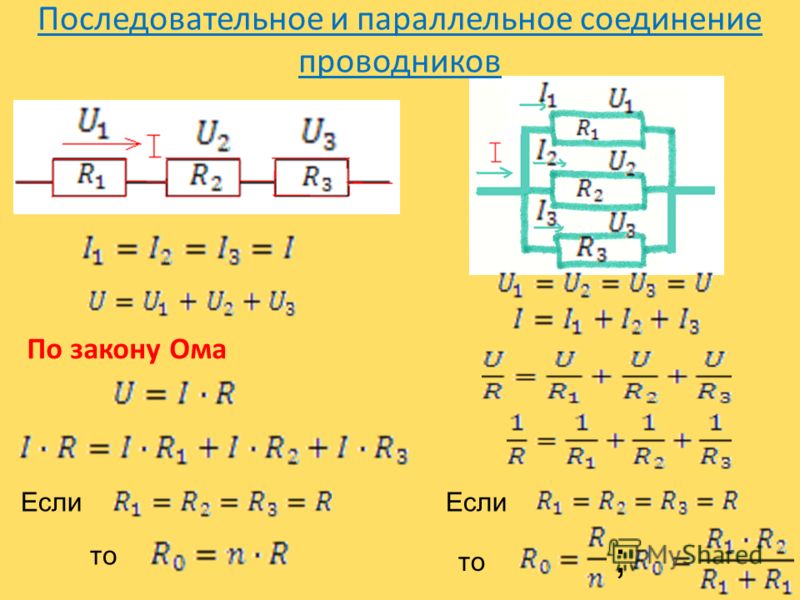 Дело в том, что свободные
Дело в том, что свободные
электроны, перемещаясь по проводнику, неизбежно взаимодействуют с
кристаллической решеткой, соударяясь с ее узлами, с ионами или различными
примесями. Все это приводит к замедлению движения электронов, то есть, к
уменьшению силы тока. Исходя из этого, можно сделать вывод, что чем длиннее
проводник, тем больше его сопротивление.
Чем толще проводник, тем
меньше его сопротивление.
И, конечно же, сопротивление
проводника зависит от самого вещества, из которого сделан проводник.
Также, сопротивление
зависит от внешних условий (в первую очередь от температуры), но к этому
вопросу мы вернемся чуть позже — при изучении полупроводников. Таким образом,
сопротивление проводника рассчитывается по формуле:
Напомним, какие величины
входят в эту формулу. l
—
это длина проводника, S —
это площадь поперечного сечения проводника, а ρ0 — это удельное
сопротивление проводника.
Удельным сопротивлением
проводника называется сопротивление проводника из данного вещества длиной 1 м и
площадью поперечного сечения 1 м2.
Если мы выразим удельное
сопротивление из формулы, по которой рассчитывается сопротивление проводника,
то убедимся, что удельное сопротивление измеряется в омах умноженных на метр:
Конечно, удельные
сопротивления многих материалов уже давно измерены экспериментально и сведены в
таблицы.
Как вы видите, в таблице
все вещества разделены на три группы: проводники, полупроводники и диэлектрики.
Нетрудно догадаться, что проводники обладают очень маленьким удельным
сопротивлением (поэтому они и хорошо проводят ток). Диэлектрики, напротив,
обладают огромным удельным сопротивлением (поэтому их используют для изоляции).
Полупроводники занимают промежуточную стадию, но их удельные сопротивления
интереснее рассматривать в таблицах, показывающих зависимость удельного
сопротивления полупроводников от температуры. Если вы обратили внимание, то в
Если вы обратили внимание, то в
таблице указано, что данные значения удельных сопротивлений тех или иных
веществ наблюдаются при определенной температуре. Поэтому, следует понимать,
что при других температурах, эти значения могут быть иными.
Закон Ома для участка
цепи имеет огромное значение для расчета электрических цепей, поэтому, было бы
хорошо, если бы вы запомнили формулу, описывающую закон Ома.
Пример решения задачи.
Задача. В
лампе накаливания используется вольфрамовая нить, радиус которой равен 0,01 мм.
Длина этой нити составляет 20 см. Если лампочка рассчитана на 80 мА, то, каково
напряжение на ней?
Последовательное и параллельное сопротивление проводников. Закон Ома. Соединение проводников
Одним из китов, на котором держатся многие понятия в электронике, является понятие последовательного и параллельного подключения проводников. Знать основные отличия указанных типов подключения просто необходимо. Без этого нельзя понять и прочитать ни одной схемы.
Без этого нельзя понять и прочитать ни одной схемы.
Основные принципы
Электрический ток движется по проводнику от источника к потребителю (нагрузке). Чаще всего в качестве проводника выбирается медный кабель. Связано это с требованием, которое предъявляется к проводнику: он должен легко высвобождать электроны.
Независимо от способа подключения, электрический ток двигается от плюса к минусу. Именно в этом направлении убывает потенциал. При этом стоит помнить, что провод, по котору идет ток, также обладает сопротивлением. Но его значение очень мало. Именно поэтому им пренебрегают. Сопротивление проводника принимают равным нулю. В том случае, если проводник обладает сопротивлением, его принято называть резистором.
Параллельное подключение
В данном случае элементы, входящие в цепь, объединены между собой двумя узлами. С другими узлами у них связей нет. Участки цепи с таким подключением принято называть ветвями. Схема параллельного подключения представлена на рисунке ниже.
Если говорить более понятным языком, то в данном случае все проводники одним концом соединены в одном узле, а вторым — во втором. Это приводит к тому, что электрический ток разделяется на все элементы. Благодаря этому увеличивается проводимость всей цепи.
При подключении проводников в цепь данным способом напряжение каждого из них будет одинаково. А вот сила тока всей цепи будет определяться как сумма токов, протекающих по всем элементам. С учетом закона Ома путем нехитрых математических расчетов получается интересная закономерность: величина, обратная общему сопротивлению всей цепи, определяется как сумма величин, обратных сопротивлениям каждого отдельного элемента. При этом учитываются только элементы, подключенные параллельно.
Последовательное подключение
В данном случае все элементы цепи соединены таким образом, что они не образуют ни одного узла. При данном способе подключения имеется один существенный недостаток. Он заключается в том, что при выходе из строя одного из проводников все последующие элементы работать не смогут. Ярким примером такой ситуации является обычная гирлянда. Если в ней перегорает одна из лампочек, то вся гирлянда перестает работать.
Ярким примером такой ситуации является обычная гирлянда. Если в ней перегорает одна из лампочек, то вся гирлянда перестает работать.
Последовательное подключение элементов отличается тем, что сила тока во всех проводниках равна. Что касается напряжения цепи, то оно равно сумме напряжения отдельных элементов.
В данной схеме проводники включаются в цепь поочередно. А это значит, что сопротивление всей цепи будет складываться из отдельных сопротивлений, характерных для каждого элемента. То есть общее сопротивление цепи равно сумме сопротивлений всех проводников. Эту же зависимость можно вывести и математическим способом, используя закон Ома.
Смешанные схемы
Бывают ситуации, когда на одной схеме можно увидеть одновременно последовательное и параллельное подключение элементов. В таком случае говорят о смешанном соединении. Расчет подобных схем проводится отдельно для каждой из группы проводников.
Так, чтобы определить общее сопротивление, необходимо сложить сопротивление элементов, подключенных параллельно, и сопротивление элементов с последовательным подключением. При этом последовательное подключение является доминантным. То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.
При этом последовательное подключение является доминантным. То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.
Подключение светодиодов
Зная основы двух типов подключения элементов в цепи, можно понять принцип создания схем различных электроприборов. Рассмотрим пример. во многом зависит от напряжения источника тока.
При небольшом напряжении сети (до 5 В) светодиоды подключают последовательно. Снизить уровень электромагнитных помех в данном случае поможет конденсатор проходного типа и линейные резисторы. Проводимость светодиодов увеличивают за счет использования системных модуляторов.
При напряжении сети 12 В может использоваться и последовательное, и параллельное подключение сети. В случае последовательного подключения используют импульсные блоки питания. Если собирается цепь из трех светодиодов, то можно обойтись без усилителя. Но если цепь будет включать большее количество элементов, то усилитель необходим.
Во втором случае, то есть при параллельном подключении, необходимо использование двух открытых резисторов и усилителя (с пропускной способностью выше 3 А). Причем первый резистор устанавливается перед усилителем, а второй — после.
При высоком напряжении сети (220 В) прибегают к последовательному подключению. При этом дополнительно используют операционные усилители и понижающие блоки питания.
Последовательное, параллельное и смешанное соединения резисторов.
Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление.
Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов
(приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов
.
При последовательном соединении
нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк
(19)
где R
эк
=
R 1 + R 2 + R 3
.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3
(20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3
(21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов
. При параллельном соединении
нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
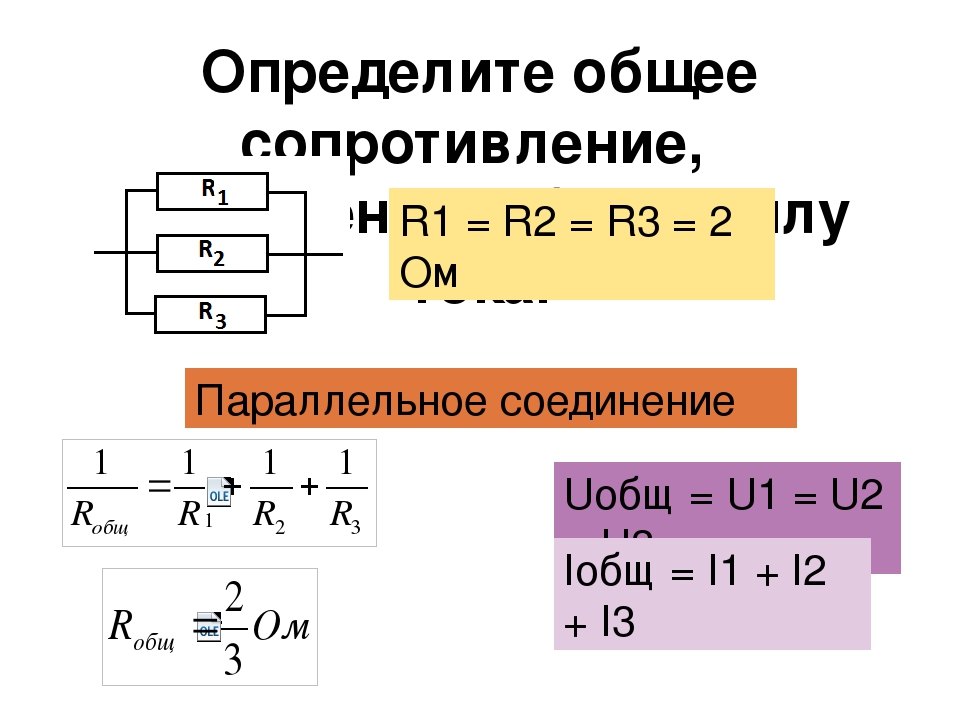
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк
(23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк
=
1/R 1 + 1/R 2 + 1/R 3
(24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов
:
G эк = G 1 + G 2 +G 3
(25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3
(26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n
(27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n
(28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных.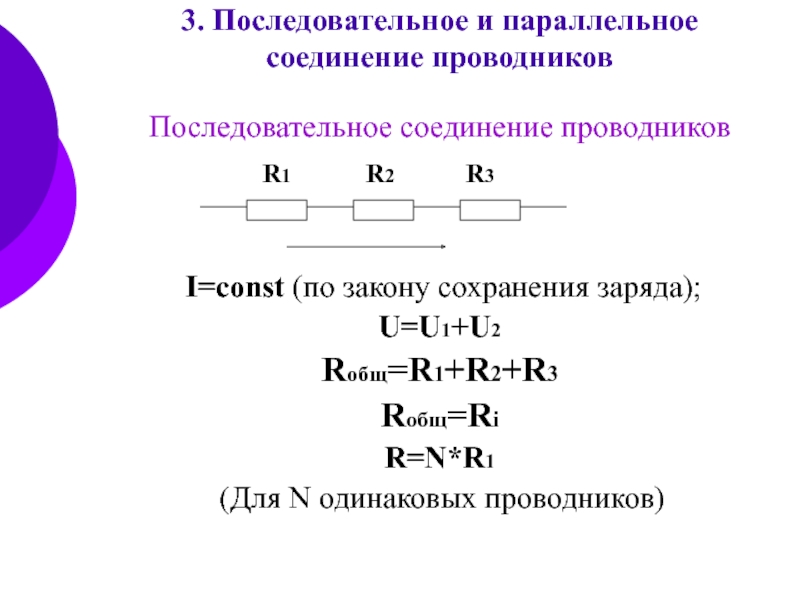 Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов
. Смешанным соединением
называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.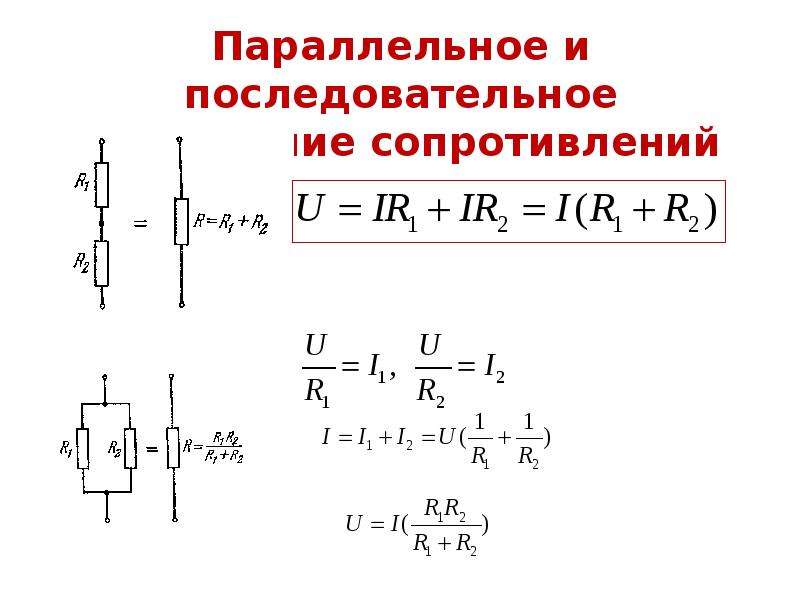
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
п. с. постоянного тока.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2
на 3
и 47 Ом
и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно
учитывается их номинальная мощность.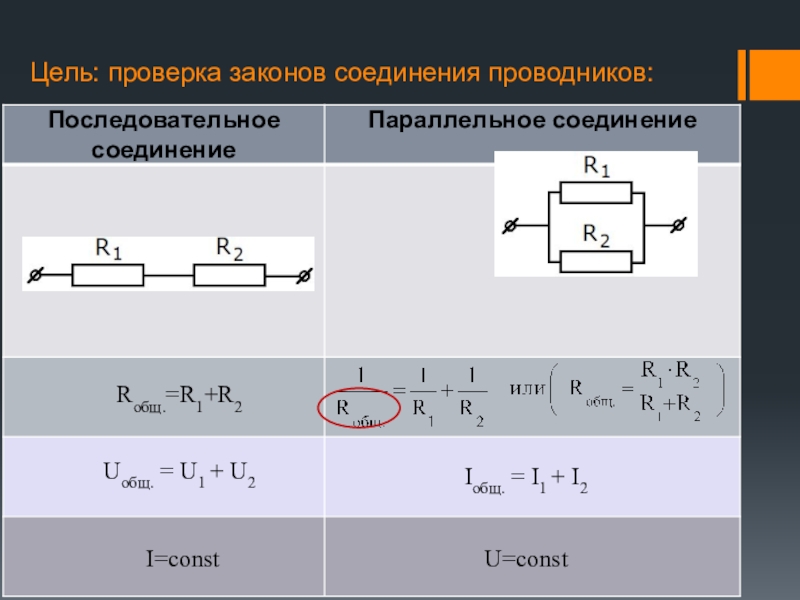 Например, нам нужно подобрать замену резистору на 100 Ом
Например, нам нужно подобрать замену резистору на 100 Ом
и мощностью 1 Вт
. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А
), а сопротивление каждого из них равно 50 Ом
, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт
. В результате на каждом из них выделится по 0,5 Вт
мощности. В сумме это и будет тот самый 1 Вт
.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Причем это могут быть не только проводники, но и конденсаторы.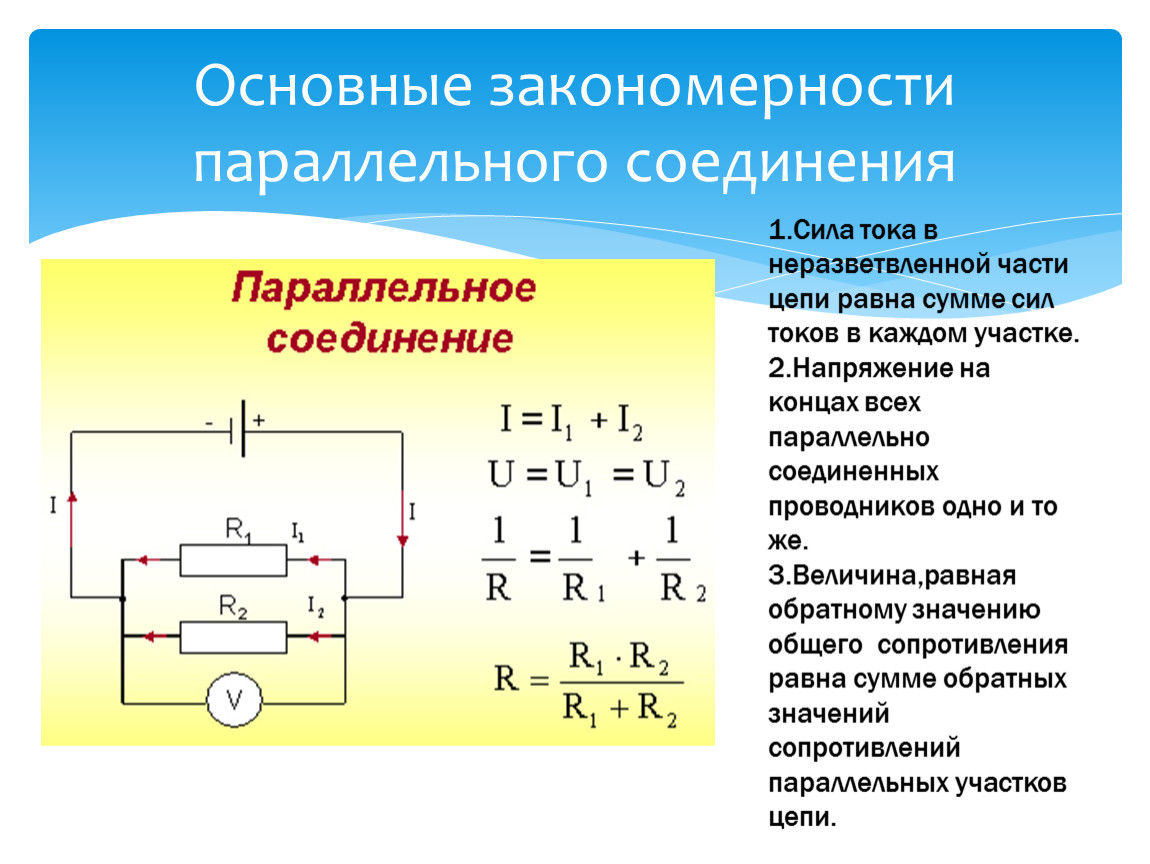 Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.
Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.
Как различить эти два соединения?
Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.
Формулы для силы тока
О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.
Параллельное и последовательное соединение по-разному влияют на величину в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.
Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:
I общ = I 1 = I 2
Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.
Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при :
Формула общей силы тока при :
I общ = I 1 + I 2
Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.
Формулы для напряжения
Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.
Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:
U общ = U 1 + U 2
, где U — обозначение, принятое для
Другая ситуация складывается, если рассматривается Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек.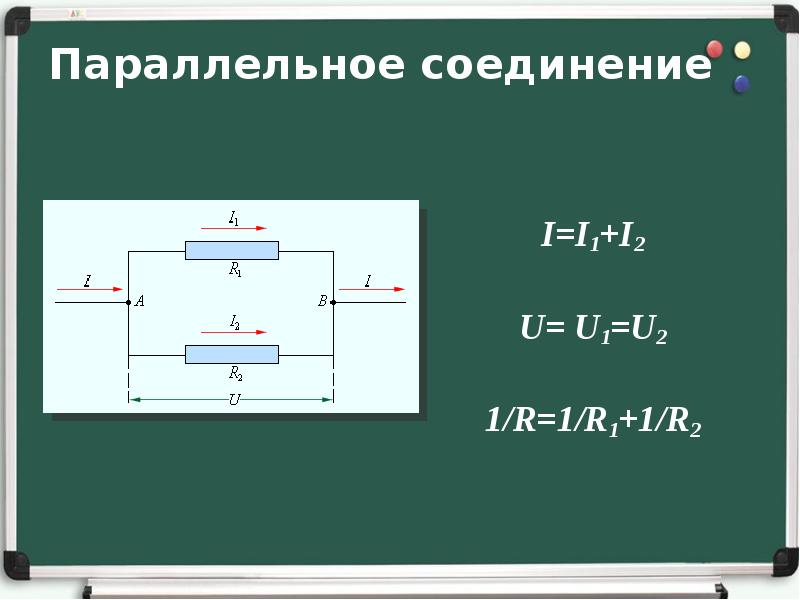 Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:
Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:
U общ = U 1 = U 2
Формулы для электрического сопротивления
Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.
Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:
- последовательно, значит, нужно равенство для напряжения — I общ * R общ = I 1 * R 1 + I 2 * R 2;
- параллельно необходимо пользоваться формулой для силы тока — U общ / R общ = U 1 / R 1 + U 2 / R 2 .
Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны.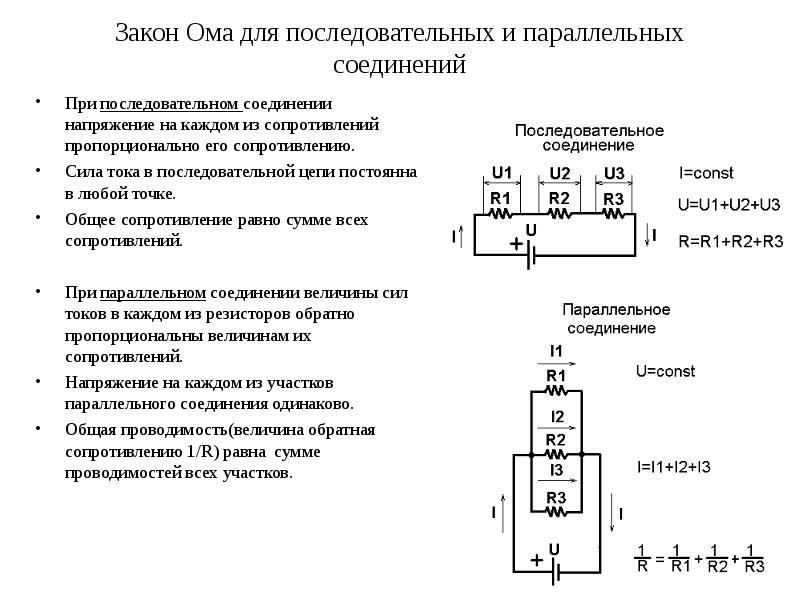 Значит, их можно сократить. То есть получаются такие выражения:
Значит, их можно сократить. То есть получаются такие выражения:
- R общ = R 1 + R 2 (для последовательного соединения проводников).
- 1 / R общ = 1 / R 1 + 1 / R 2 (при параллельном соединении).
При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.
Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.
Работа тока
Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t
, где А — работа тока, t — время его прохождения по проводнику.
Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U 1 + U 2) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.
Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А 1 + А 2 .
Мощность тока
При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I.
После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р 1 + Р 2 .
То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.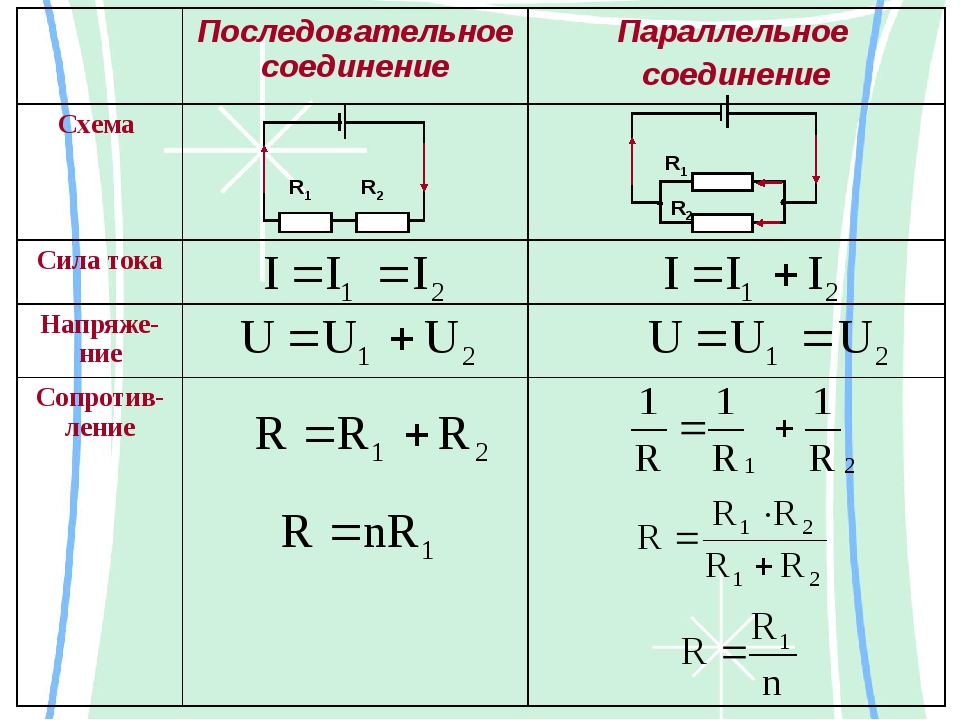
Как влияет соединение проводников на ремонт новогодней гирлянды?
Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее — и гирлянда станет работать.
Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.
Что происходит с цепью, если в нее включены не резисторы, а конденсаторы?
При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:
Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:
q общ = q 1 = q 2 .
Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С.
В ней С — емкость конденсатора.
Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:
С = q / (U 1 + U 2).
Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С 1 + 1 / С 2 .
Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное. Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:
Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:
С = (q 1 + q 2) / U.
То есть эта величина считается, как сумма каждого из использованных в соединении приборов:
С = С 1 + С 2.
Как определить общее сопротивление произвольного соединения проводников?
То есть такого, в котором последовательные участки сменяют параллельные, и наоборот. Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.
Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).
Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.
Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.
Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:
- сначала ту, которая приведена для последовательного соединения;
- потом для параллельного;
- и снова для последовательного.
Подобным образом можно развернуть любую, даже очень сложную схему.
Задача на последовательное соединение проводников
Условие.
В цепи друг за другом подсоединены две лампы и резистор. Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?
Решение.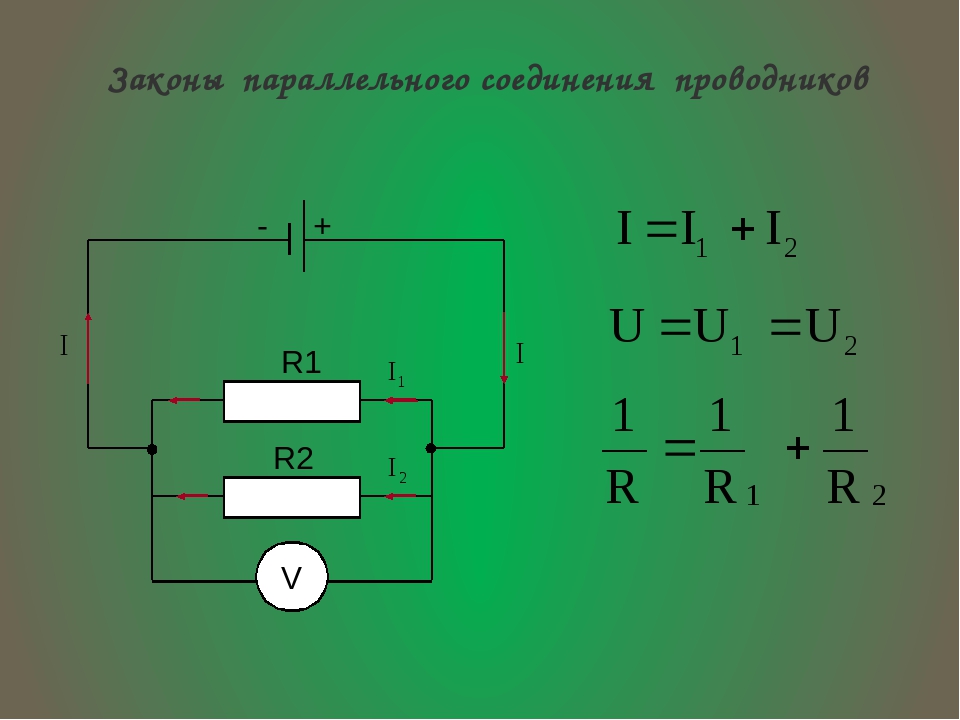
Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.
Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.
Ответ.
Сопротивление резистора равно 2,5 Ом.
Задача на параллельное и последовательное
Условие.
Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.
Решение.
Проще начать с В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.
Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.
Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.
Ответ.
Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.
Если нам надо, чтобы электроприбор работал, мы должны подключить его к . При этом ток должен проходить через прибор и возвращаться вновь к источнику, то есть цепь должна быть замкнутой.
Но подключение каждого прибора к отдельному источнику осуществимо, в основном, в лабораторных условиях. В жизни же приходится иметь дело с ограниченным количеством источников и довольно большим количеством потребителей тока. Поэтому создают системы соединений, позволяющие нагрузить один источник большим количеством потребителей. Системы при этом могут быть сколь угодно сложными и разветвленными, но в их основе лежит всего два вида соединения: последовательное и параллельное соединение проводников.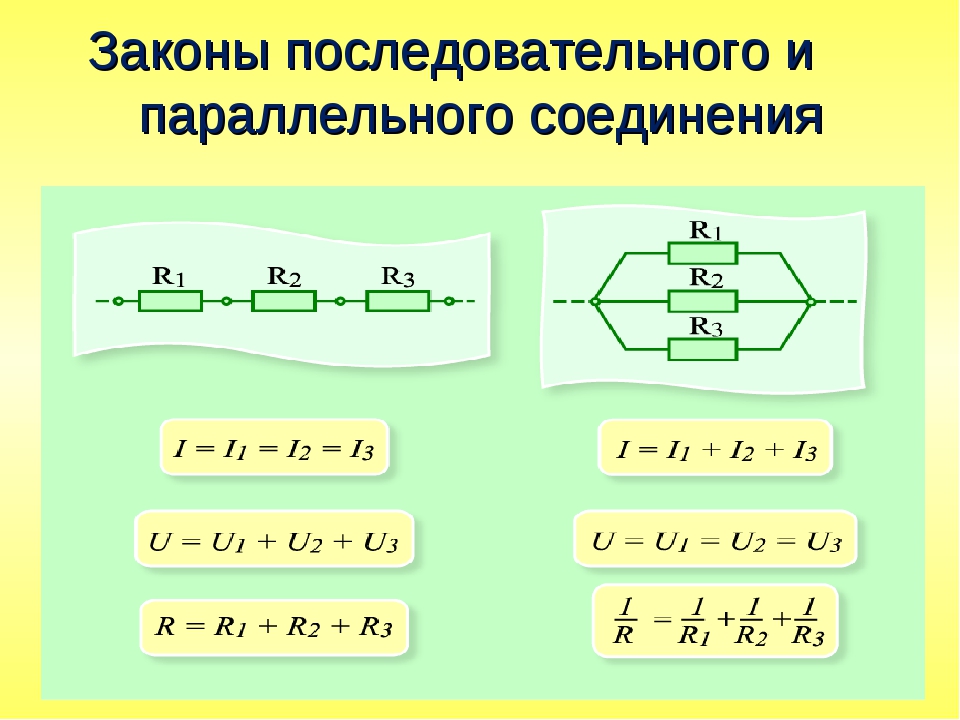 Каждый вид имеет свои особенности, плюсы и минусы. Рассмотрим их оба.
Каждый вид имеет свои особенности, плюсы и минусы. Рассмотрим их оба.
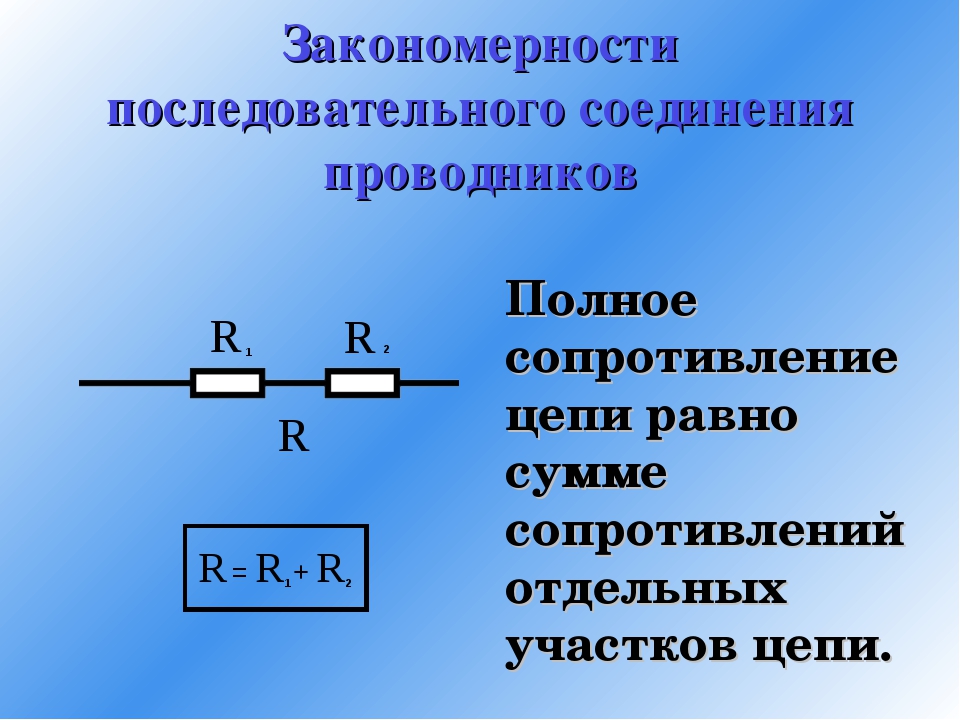
Последовательное соединение проводников
Последовательное соединение проводников – это включение в электрическую цепь нескольких приборов последовательно, друг за другом. Электроприборы в данном случае можно сравнить с людьми в хороводе, а их руки, держащие друг друга – это провода, соединяющие приборы. Источник тока в данном случае будет одним из участников хоровода.
Напряжение всей цепи при последовательном соединении будет равно сумме напряжений на каждом включенном в цепь элементе. Сила тока в цепи будет одинакова в любой точке. А сумма сопротивлений всех элементов составит общее сопротивление всей цепи. Поэтому последовательное сопротивление можно выразить на бумаге следующим образом:
I=I_1=I_2=⋯=I_n ; U=U_1+U_2+⋯+U_n ; R=R_1+R_2+⋯+R_n ,
Плюсом последовательного соединения является простота сборки, а минусом – то, что если один элемент выйдет из строя, то ток пропадет во всей цепи. В такой ситуации неработающий элемент будет подобен ключу в выключенном положении. Пример из жизни неудобства такого соединения наверняка припомнят все люди постарше, которые украшали елки гирляндами из лампочек.
В такой ситуации неработающий элемент будет подобен ключу в выключенном положении. Пример из жизни неудобства такого соединения наверняка припомнят все люди постарше, которые украшали елки гирляндами из лампочек.
Если в такой гирлянде выходила из строя хотя бы одна лампочка, приходилось перебирать их все, пока не найдешь ту самую, перегоревшую. В современных гирляндах эта проблема решена. В них используют специальные диодные лампочки, в которых при перегорании сплавляются вместе контакты, и ток продолжает беспрепятственно проходить дальше.
Параллельное соединение проводников
При параллельном соединении проводников все элементы цепи подключаются к одной и той же паре точек, можно назвать их А и В. К этой же паре точек подключают источник тока. То есть получается, что все элементы подключены к одинаковому напряжению между А и В. В то же время ток как бы разделяется на все нагрузки в зависимости от сопротивления каждой из них.
Параллельное соединение можно сравнить с течением реки, на пути которой возникла небольшая возвышенность. Вода в таком случае огибает возвышенность с двух сторон, а потом вновь сливается в один поток. Получается островок посреди реки. Так вот параллельное соединение – это два отдельных русла вокруг острова. А точки А и В – это места, где разъединяется и вновь соединяется общее русло реки.
Вода в таком случае огибает возвышенность с двух сторон, а потом вновь сливается в один поток. Получается островок посреди реки. Так вот параллельное соединение – это два отдельных русла вокруг острова. А точки А и В – это места, где разъединяется и вновь соединяется общее русло реки.
Напряжение тока в каждой отдельной ветви будет равно общему напряжению в цепи. Общий ток цепи будет складываться из токов всех отдельных ветвей. А вот общее сопротивление цепи при параллельном соединении будет меньше сопротивления тока на каждой из ветвей. Это происходит потому, что общее сечение проводника между точками А и В как бы увеличивается за счет увеличения числа параллельно подключенных нагрузок. Поэтому общее сопротивление уменьшается. Параллельное соединение описывается следующими соотношениями:
U=U_1=U_2=⋯=U_n ; I=I_1+I_2+⋯+I_n ; 1/R=1/R_1 +1/R_2 +⋯+1/R_n ,
где I — сила тока, U- напряжение, R – сопротивление, 1,2,…,n – номера элементов, включенных в цепь.
Огромным плюсом параллельного соединения является то, что при выключении одного из элементов, цепь продолжает функционировать дальше. Все остальные элементы продолжают работать. Минусом является то, что все приборы должны быть рассчитаны на одно и то же напряжение. Именно параллельным образом устанавливают розетки сети 220 В в квартирах. Такое подключение позволяет включать различные приборы в сеть совершенно независимо друг от друга, и при выходе их строя одного из них, это не влияет на работу остальных.
Все остальные элементы продолжают работать. Минусом является то, что все приборы должны быть рассчитаны на одно и то же напряжение. Именно параллельным образом устанавливают розетки сети 220 В в квартирах. Такое подключение позволяет включать различные приборы в сеть совершенно независимо друг от друга, и при выходе их строя одного из них, это не влияет на работу остальных.
Нужна помощь в учебе?
Предыдущая тема: Расчёт сопротивления проводников и реостаты: формулы
Следующая тема:   Работа и мощность тока
Закон Ома для полной цепи при последовательном соединении источников тока | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Тема:
Законы электромагнетизма
| Рис. 5.20. Последовательное соединение источников тока |
Знание закона Ома для полной цепи позволяет решать задачи соединения источников тока в батареи, что имеет немаловажное значение для практики. Даже в карманном фонарике применяются батареи из трех-четырех гальванических элементов или аккумуляторов. Такое соединение может быть, как и у проводников,— последовательным, параллельным или смешанным.
Даже в карманном фонарике применяются батареи из трех-четырех гальванических элементов или аккумуляторов. Такое соединение может быть, как и у проводников,— последовательным, параллельным или смешанным.
Последовательным является такое соединение, когда соединяют друг с другом разноименные полюса источников: положительный полюс предшествующего с отрицательным полюсом следующего и т. д. (рис. 5.20). Чаще всего в батареи соединяют одинаковые источники. Поэтому при последовательном соединении источников электродвижущая сила батареи будет в n раз больше, чем электродвижущая сила одного источника, где n — количество соединенных в батарею источников
Ɛбат = nƐ.
Внутреннее сопротивление такой батареи также больше в n раз, чем внутреннее сопротивление одного источника
rбат = nr.
Закон Ома для полной цепи в случае последовательного соединения источников Материал с сайта http://worldofschool.ru
I = Ɛбат / (R + rбат) = nƐ / (R + nr).
Последовательное соединение источников удобно тогда, когда сопротивление внешней части цепи (нагрузка) больше по сравнению с внутренним сопротивлением источника. При этом необходимо позаботиться, чтобы сила тока в цепи не превышала допустимой силы тока для одного источника.
Вопросы по этому материалу:
Для чего источники тока соединяют последовательно?
Электрический ток. Закон Ома для участка цепи. Виды соединения проводников.
Электрический ток — упорядоченное движение заряженных частиц под действием сил электрического поля или сторонних сил.
За направление тока выбрано направление движения положительно заряженных частиц.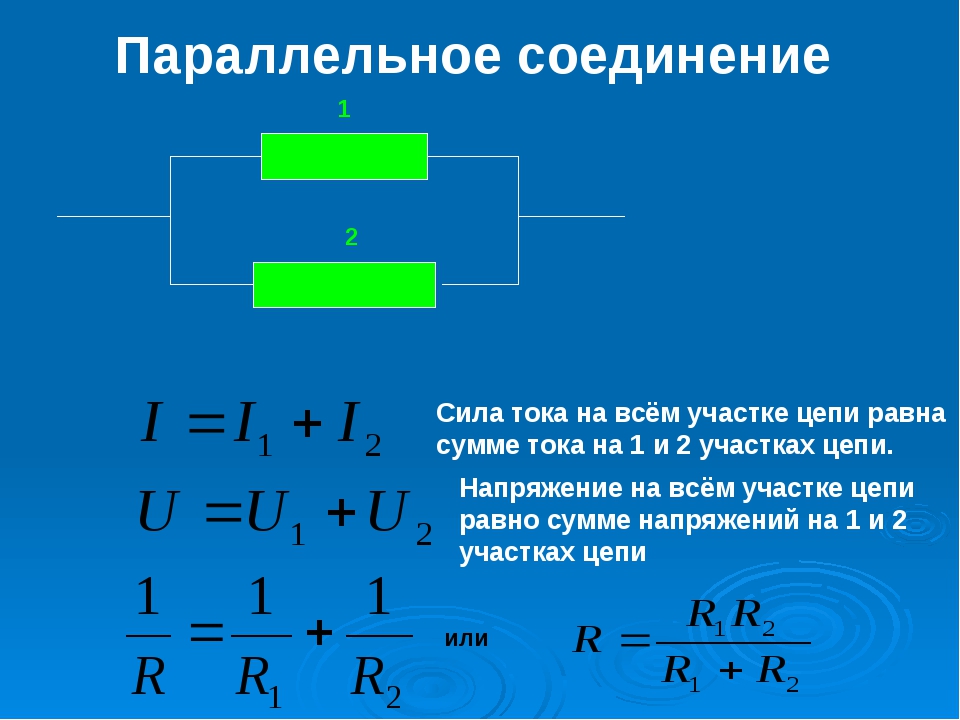
Электрический ток называют постоянным, если сила тока и его направление не меняются с течением времени.
Пусть цилиндрический проводник имеет поперечное сечение
площадью S. За положительное направление в проводнике примем направление
слева направо. Заряд каждой частицы будем считать равным q0.
В объеме проводника, ограниченном поперечными сечениями 1
и 2 с расстоянием Δl между
ними, содержится общий заряд q = q0nSΔl. Если частицы движутся слева
направо со средней скоростью v, то за время Δt = Δl / v все
частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение
2. Поэтому сила тока равна:
В СИ единицей силы тока является ампер (А). Эту
единицу устанавливают на основе магнитного взаимодействия токов.
Измеряют силу тока амперметрами. Принцип устройства
этих приборов основан на магнитном действии тока.
Скорость упорядоченного движения электронов в проводнике. Найдем скорость упорядоченного перемещения электронов в
Найдем скорость упорядоченного перемещения электронов в
металлическом проводнике. Согласно формуле v = I /enS, где
е — модуль заряда электрона. Пусть, например, сила тока I = 1 A,
а площадь поперечного сечения проводника S = 10-6 м2.
Модуль заряда электрона е = 1,6•10-19 Кл. Число электронов в
1 м3 меди равно числу атомов в этом объеме, так как один из
валентных электронов каждого атома меди коллективизирован и является свободным.
Это число есть n = 8,5•1028 м3. Следовательно,
Очевидно, что скорость
упорядоченного перемещения электронов очень мала.
Основная количественная
характеристика электрического тока — сила тока. Она определяется электрическим
зарядом, переносимым через поперечное сечение проводника за единицу времени.
Скорость заряженных частиц (электронов) в проводнике очень мала — около 0,1
мм/с.
Условия
существования постоянного электрического тока.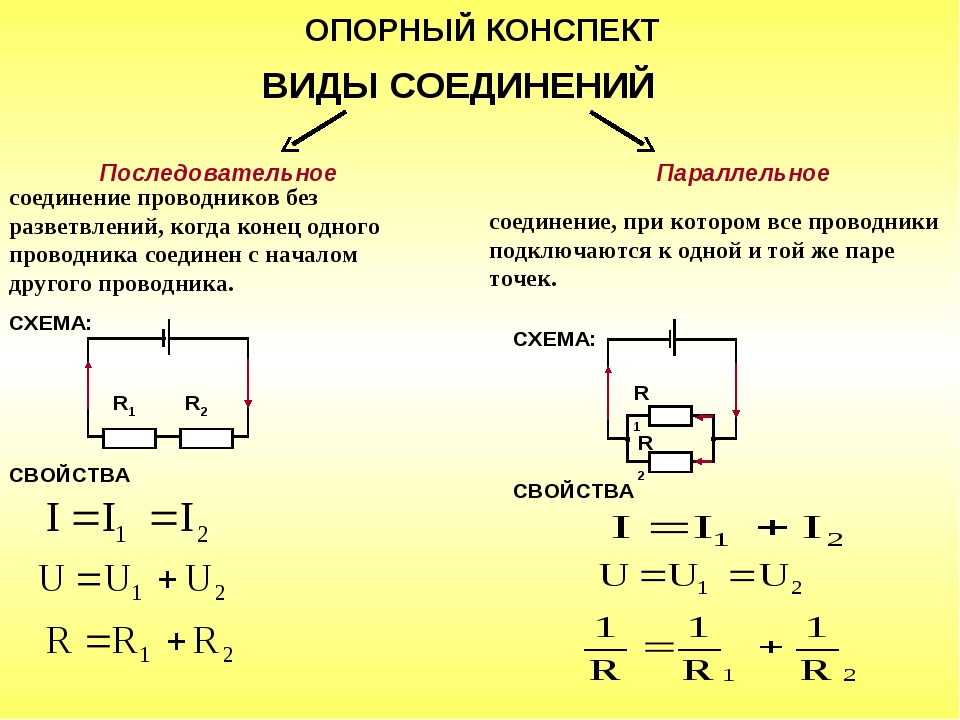
Для существования постоянного электрического тока необходимо наличие
свободных заряженных частиц и наличие источника тока, в котором осуществляется
преобразование какого-либо вида энергии в энергию электрического поля.
Источник тока — устройство, в котором
осуществляется преобразование какого-либо вида энергии в энергию электрического
поля. В источнике тока на заряженные частицы в замкнутой цепи действуют
сторонние силы. Причины возникновения сторонних сил в различных источниках тока
различны. Например, в аккумуляторах и гальванических элементах сторонние силы
возникают благодаря протеканию химических реакций, в генераторах электростанций
они возникают при движении проводника в магнитном поле, в фотоэлементах —
при действия света на электроны в металлах и полупроводниках.
Закон Ома для участка цепи.
Немецкий ученый
Георг Ом в 1827 г. связал воедино три физические величины и вывел закон,
который назвали его именем. Закон Ома для участка цепи гласит:
Сила тока в
участке цепи прямо пропорциональна напряжению на концах этого участка и обратно
пропорциональна его сопротивлению.
I=U/R,
где I – сила
тока, U – напряжение, R – сопротивление.
Последовательное и параллельное соединение
проводников.
Электрическая цепь включает в себя источника
тока и проводники (потребители, резисторы и др), которые могут соединятся
последовательно или параллельно.
Смешанное соединение
— комбинация параллельного и последовательного соединений.
Урок решения задач по теме «Закон Ома для участка цепи, последовательное и параллельное соединения»
Цель урока: Закрепить изученный
материал путем решения задач.
Задачи:
Образовательные:
- Научить учащихся решать задачи на
последовательное и параллельное соединение
проводников; - Углубить и расширить знания о данных видах
соединения проводников; - Научить определять силу тока, напряжение,
сопротивление при последовательном и
параллельном соедини проводников; - Научить решать задачи на смешанное соединение
проводников; - Научить учащихся разбираться в схемах
электрических цепей.
Воспитательные:
- Развить личные качества учащихся: аккуратность,
внимание, усидчивость; - Воспитывать культуру общения при работе в
группах.
Развивающие:
- Продолжить развитие навыков решения задач на
данную тему; - Продолжить развитие умений анализировать
условия задач и ответов, умений делать выводы,
обобщения; - Продолжить развитие памяти, творческих
способностей.
План урока
| № | Этап | Время | Метод |
| Организационный момент | 2 мин | Словесный | |
| I | Актуализация знаний | 5 мин | Письменная работа в парах |
| II | Вводная часть | 2 мин | Слово учителя, опрос учащихся |
| III | Решение задач | 45-50 мин | Работа учителя, учащихся у доски |
| IV | Работа учащихся в группах | 20 мин | Групповой работы, устный, письменный |
| V | Итог урока | 1-2 мин | Словесный метод |
Оформление класса: Проектор с экраном, доска с
мелом.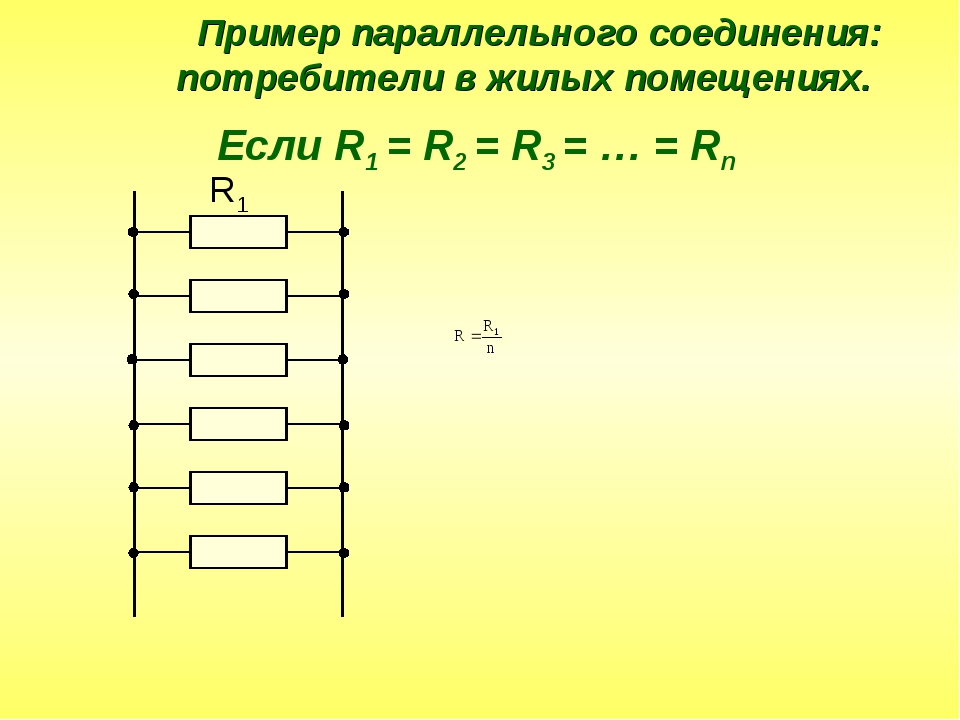 Раздаточный материал.
Раздаточный материал.
Слайд 1 включен в начале урока.
Урок начинается с физического диктанта.
I. Актуализация знаний.
На слайде физический диктант. (Слайд
2). Учащимся выдается таблица для заполнения.
1. Заполнить двенадцать ячеек таблицы на
карточке:
| Ученый | Физическая величина | Формула | Единица измерения |
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| Выполнил ______________ Проверил
__________ Оценка__________ | |||
2. После заполнения таблиц учащиеся меняют
После заполнения таблиц учащиеся меняют
карточками с соседом по парте, проверяют вместе с
учителем и выставляют оценку:
| Кол-во ошибок | 1 | 2-3 | 4-6 | 7 и более |
| Оценка | 5 | 4 | 3 | 2 |
II. Вводное слово.
Сегодня на уроке мы с вами будем решать задачи
на закон Ома, на последовательное и параллельное
соединение проводников. (Слайд 3).
Запишите тему урока. (Слайд 4).
Для этого вспомним формулы и законы, которые
нам пригодятся при решении задач.
III. Решение задач.
(3 ученика выходят к доске и записывают:
первый закон Ома и выражает и него напряжение и
сопротивление; второй – формулы справедливые
для последовательного соединения; третий –
формулы справедливые для последовательного
соединения).
Задача 1. Для начала решим устную
задачу на запоминание закона Ома. (Слайд
5)
a) U = 20B,R=10Om,I-?
б) I=10A,R = 5Om, R-?
в) I = 5A,U=15B,R-?
Ответ: а) I = 2А; б) U= 50 Ом; в) R = 3 Ом.
Задача 2. (Решает учитель с
использованием презентации) Слайд
6.
Рассчитать силу тока, проходящую по медному
проводу длиной 100м, площадью поперечного сечения
0,5мм2, если к концам провода приложено
напряжение 6,8B.
Дано:
I=100м
S=0,5мм2
U=6,8В
I-?
Решение:
Ответ: Сила тока равна 2А.
Вопросы: Что известно из условия
задачи? Какую величину необходимо определить? По
какому закону будем определять силу тока? Какие
величины нам неизвестны для нахождения силы тока
и как их найти? ( – берется из таблицы). Теперь найдем
Теперь найдем
R и полученное значение подставим в формулу
для нахождения силы тока. (Перевод S в м2
не нужно делать, т.к. в единицах измерения
плотности тоже присутствуют тоже мм2)
Задача 3. (Решает у доски
сильный ученик) Условия задачи Слайд
7.
В электрическую цепь включены
последовательно резистор сопротивлением 5 Ом и
две электрические лампы сопротивлением 500 Ом.
Определите общее сопротивление проводника.
Дано:
RAB=5 Ом
RBC=500 Ом
RCD=500 Ом
RAD-?
Решение:
Ответ: Общее сопротивление
проводника равно 1005 Ом.
Вопросы: Какие элементы цепи нам даны?
Как найти общее сопротивление?
Задача 4. (Класс делится на 2
группы, каждая из которой решает задачу своим
способом (одни находя силу тока используя закон
Ома, вторые используя формулу параллельного
соединения). Затем по одному представителю пишут
Затем по одному представителю пишут
решения на доске) Условия задачи Слайд
8.
Два резистора сопротивлением r 1 = 5 Ом и r2=
30 Ом включены, как показано на рисунке, к зажимам
источника тока напряжением 6В. Найдите силу тока
на всех участках цепи.
Дано:
r1=5 Ом
r2=30 Ом
U=6B
I0-?
Решение:
Ответ: Сила тока на всех участках
цепи равна 1,4 А.
Вопросы: Какой тип соединения
рассматривается в задаче? Что известно из
условия? Какие величины необходимо найти? Как
найти I0? Что для этого неизвестно? Как найти
I 1 и I2?
Второй способ решения данной задачи:
Дано:
r1=5 Ом
r2=30 Ом
U=6B
I0-?
Решение:
Ответ: Сила тока на всех
участках цепи равна 1,4А.
Вопросы: Какой тип соединения
рассматривается в задаче? Что известно из
условия? Какие величины необходимо найти? По
какой формуле будем находить общий ток в цепи?
Какая величина нам неизвестна при нахождении
силы тока и как ее найти?
Задача 5. (Решает ученик, можно
вызвать два ученика по очереди). Определите
полное сопротивление цепи и токи в каждом
проводнике, если проводники соединены так, как
показано на рисунке, а r1=1 Ом, r2=2 Ом, r3=
3 Ом, UAC = 11В. Условие задачи Слайд
9.
Дано:
r1=1 Ом
r2=2 Ом
r3=3 Ом
UAB=11B
RAC-?
I1-?
I2-?
I3-?
Решение:
Ответ: RАС =2,2 Ом, I1=2A, I2=3
А, I3=2A.
Вопросы: Какие типы соединения
изображены на рисунке? Что нужно определить? Как
найти полное сопротивление и величины в него
входящие? Как найти силу тока в цепи? Как
определить I1 и 12? Как определить UBC?
Задача 6. Условия задачи Слайд
10. (Вопросы 1,2,5 решаются устно. 3,4 – два
ученика).
- Какому значению силы тока и напряжения
соответствует точка А? - Какому значению силы тока и напряжения
соответствует точка В? - Найдите сопротивление в точке А и в точке В.
- Найдите по графику силу тока в проводнике при
напряжении 8 В и вычислите сопротивление в этом
случае. - Какой вывод можно проделать по результатам
задачи?
Ответ:
- Сила тока = 0,4 А, напряжение – 4В.

- Сила тока = 0,6 А, напряжение – 6В.
- Сопротивление в т.А – 10 Ом, в т.В – 10 Ом.
- Сила тока = 0,8А, сопротивление – 10 Ом.
- При изменении силы тока и напряжения на
одинаковую величину, сопротивление остается
постоянным.
IV. Самостоятельная работа в группах.
Учащиеся делятся на 4 группы и каждой группе
дается карточка с заданием.
Учитель объясняет критерии выставления оценок:
Во время работы в группах ведется наблюдение за
более и менее активными участниками группы.
Соответственно это будет влиять на более или
менее высокую оценку при проверке записей в
тетради, также будет учитываться уровень
сложности решенных задач. Тетради с записями
сдаются в конце урока. Время для решения задач
ограниченное.
Задание 1. Слайд 11. (8
мин.)
Вопросы к карточкам:
- Перечислите все элементы цепи.

- Какие виды соединения используются?
- Рассчитайте напряжение на лампе.
- Рассчитайте напряжение на реостате.
- Рассчитайте силу тока на всем участке цепи.
Задание 2. Слайд 12. (4 мин.)
Определить общее сопротивление в цепи.
R1 = 2 Ом, R2 = 102 Ом, R 3 = 15 Ом, R4
= 4 Ом.
Задание 3. Слайд 13. (3 мин.)
Определите силу тока I при заданных U и R.
| Группа | R, Ом | U, В | I, А |
| I | 2 | 55 | ? |
| II | 14,2 | 87,4 | ? |
| III | 21 | 100 | ? |
| IV | 0,16 | 0,28 | ? |
Задание 4. Слайд 14. (5 мин)
Слайд 14. (5 мин)
Моток проволоки имеет сопротивление R и
длину l .
Вычислить площадь поперечного сечения S.
| Группа | Материал | Параметры | ||
| Сопротивление | Длина проводника | Удельное сопротивление | ||
| R, Ом | l, мм2 | p, Ом·мм2/м | ||
| I | Медь | 0,83 | 33,9 | 1,7·10-2 |
| II | Алюминий | 16,1 | 83,1 | 2,8·10-2 |
| III | Серебро | 0,39 | 0,234 | 1,6·10-2 |
| IV | Сталь | 23,2 | 3,06 | 12·10-2 |
После выполнения заданий группами, тетради
сдаются учителю.
V. Итог урока.
На сегодня все. Мы с вами научились решать
задачи на последовательное и параллельное
соединение проводников, закрепили знания о
законе Ома для участка цепи.
Домашнее задание. Повторить все
формулы и физические величины.
21.1 Резисторы, включенные последовательно и параллельно – College Physics
Резюме
- Нарисуйте цепь с параллельными и последовательными резисторами.
- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Сравните способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
- Объясните, почему общее сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Рассчитайте общее сопротивление цепи, содержащей смесь резисторов, соединенных последовательно и параллельно.
Большинство цепей имеют более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением . Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они соединены.
Мера этого предела потока заряда называется сопротивлением . Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они соединены.
Рис. 1. (а) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.
Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то $latex \boldsymbol{R_1} $ на рис. 1(a) может быть сопротивлением стержня отвертки, $latex \boldsymbol{R_2} $ сопротивление ее ручки, $latex \boldsymbol{R_3} $ сопротивление тела человека и $latex \boldsymbol{R_4} $ сопротивление ее обуви.
На рис. 2 показаны резисторы, последовательно подключенные к источнику напряжения .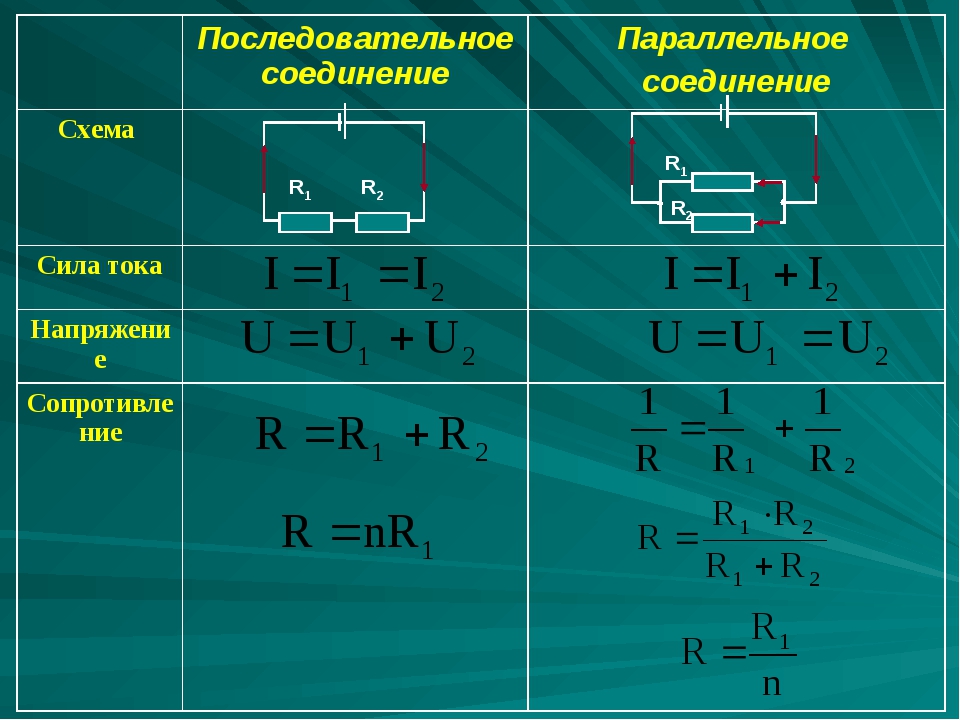 Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев высокоомную обувь на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для устройство, уменьшающее рабочий ток.)
Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев высокоомную обувь на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для устройство, уменьшающее рабочий ток.)
Рисунок 2. Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа).
Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потери электроэнергии, называемые падением напряжения , в каждом резисторе на рисунке 2.
Согласно закону Ома , падение напряжения $latex \boldsymbol{V} $ на резисторе при протекании через него тока рассчитывается по уравнению $latex \boldsymbol{V = IR} $, где $latex \ boldsymbol{I} $ соответствует току в амперах (А), а $latex \boldsymbol{R} $ — сопротивлению в омах. $latex \boldsymbol{(\Omega )} $.Другой способ представить это так: $latex \boldsymbol{V} $ — это напряжение, необходимое для протекания тока $latex \boldsymbol{I} $ через сопротивление $latex \boldsymbol{R} $.
$latex \boldsymbol{(\Omega )} $.Другой способ представить это так: $latex \boldsymbol{V} $ — это напряжение, необходимое для протекания тока $latex \boldsymbol{I} $ через сопротивление $latex \boldsymbol{R} $.
Таким образом, падение напряжения на $latex \boldsymbol{R_1} $ равно $latex \boldsymbol{V_1 = IR_1} $, на $latex \boldsymbol{R_2} $ равно $latex \boldsymbol{V_2 = IR_2} $, и что через $latex \boldsymbol{R_3} $ есть $latex \boldsymbol{V_3 = IR_3} $. Сумма этих напряжений равна выходному напряжению источника; то есть
$латекс \boldsymbol{V = V_1 + V_2 + V_3}.$
Это уравнение основано на законах сохранения энергии и сохранения заряда. Электрическая потенциальная энергия может быть описана уравнением $latex \boldsymbol{PE = qV} $, где $latex \boldsymbol{q} $ — электрический заряд, а $latex \boldsymbol{V} $ — напряжение. Таким образом, энергия, подаваемая источником, равна $latex \boldsymbol{qV} $, а энергия, рассеиваемая резисторами, равна
$латекс \boldsymbol{qV_1 + qV_2 + qV_3}.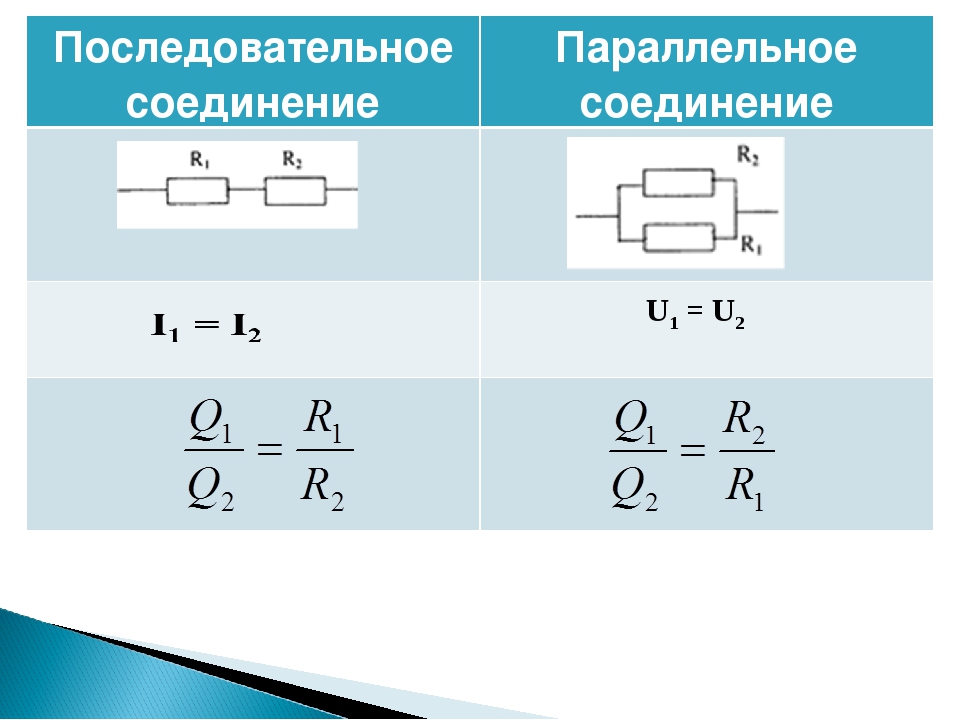 $
$
Связи: законы сохранения
Выводы выражений для последовательного и параллельного сопротивления основаны на законах сохранения энергии и сохранения заряда, которые утверждают, что полный заряд и полная энергия постоянны в любом процессе.Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого места назначения энергии. Таким образом, $latex \boldsymbol{qV = qV_1 + qV_2 + qV_3} $. Заряд $latex \boldsymbol{q} $ отменяется, что дает $latex \boldsymbol{V = V_1 + V_2 + V_3} $, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
$латекс \boldsymbol{V = IR_1 + IR_2 + IR_3 = I(R_1+R_2+R_3)}. $
$
Обратите внимание, что для эквивалентного однорядного сопротивления $latex \boldsymbol{R_s} $ мы имеем
$латекс \boldsymbol{V = IR_s}. $
Это означает, что общее или эквивалентное последовательное сопротивление $latex \boldsymbol{R_s} $ трех резисторов равно
.
$латекс \boldsymbol{R_s = R_1 + R_2 + R_3} $.
Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, полное сопротивление $latex \boldsymbol{R_s}$ последовательного соединения равно
$ $латекс \boldsymbol{R_s = R_1 + R_2 + R_3 + \dots} $
как предложено.Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.
Пример 1. Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рис. 2 равно $latex \boldsymbol{12,0 \;\textbf{V}} $, а сопротивления равны $latex \boldsymbol{R_1 = 1,00 \;\Omega} $, $latex \ boldsymbol{R_2 = 6,00 \;\Omega} $, а $latex \boldsymbol{R_3 = 13. 0 \;\Омега } $. а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
0 \;\Омега } $. а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление представляет собой просто сумму отдельных сопротивлений, определяемую следующим уравнением:
$latex \begin{array}{r @{{}={}} l} \boldsymbol{R_s} & \boldsymbol{R_1 + R_2 + R_3} \\[1em] & \boldsymbol{1.00 \;\Omega + 6.00 \;\Omega + 13.0 \;\Omega} \\[1em] & \boldsymbol{20.0 \;\Omega}. \end{массив} $
Стратегия и решение для (b)
Ток находится по закону Ома, $latex \boldsymbol{V = IR} $. Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
$латекс \boldsymbol{I =} $ $латекс \boldsymbol{=} $ $латекс \boldsymbol{= 0,600 \;\textbf{A}}.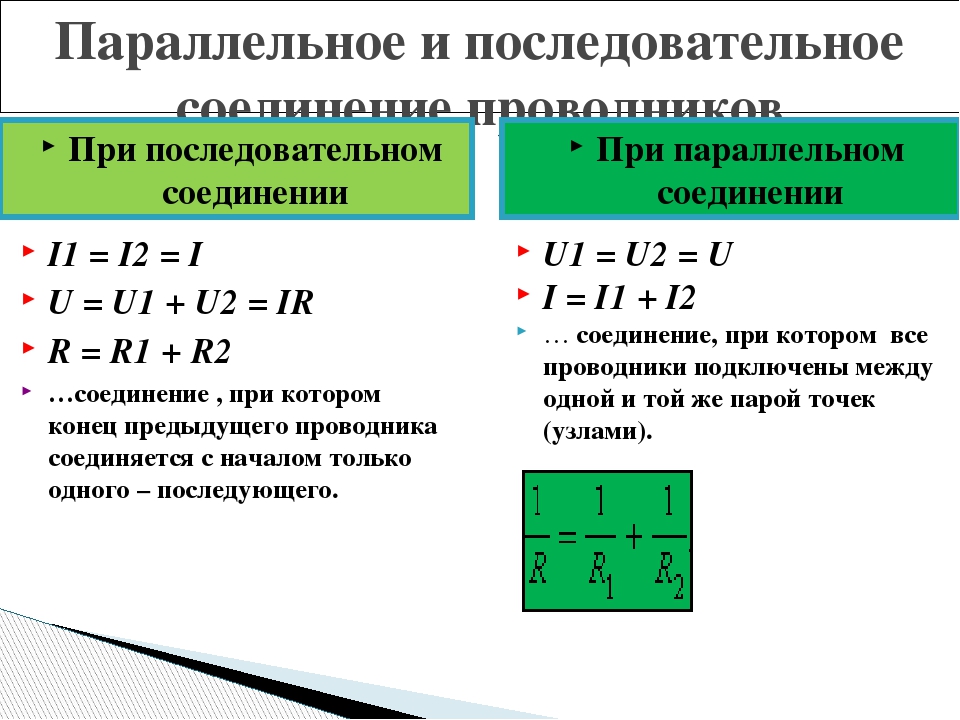 $
$
Стратегия и решение для (c)
Напряжение — или $latex \boldsymbol{IR} $ падение — на резисторе определяется законом Ома.Ввод тока и значения первого сопротивления дает
$латекс \boldsymbol{V_1 = IR_1 = (0,600 \;\textbf{A})(1,0 \;\Omega) = 0,600 \;\textbf{V}}. $
Аналогично,
$латекс \boldsymbol{V_2 = IR_2 = (0,600 \;\textbf{A})(6,0 \;\Omega) = 3,60 \;\textbf{V}} $
и
$латекс \boldsymbol{V_3 = IR_3 = (0,600 \;\textbf{A})(13,0 \;\Omega) = 7,80 \;\textbf{V}}. $
Обсуждение для (с)
Три капли $latex \boldsymbol{IR} $ добавляются к $latex \boldsymbol{12.0 \;\textbf{V}} $, как и было предсказано:
$латекс \boldsymbol{V_1 + V_2 + V_3 = (0,600 + 3,60 + 7,80) \;\textbf{V} = 12,0 \;\textbf{V}}. $
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля , $latex \boldsymbol{P = IV} $, где $latex \boldsymbol{P} $ — электрический сила. 2 R_1 = (0.2}{R}} $, где $latex \boldsymbol{V} $ — падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.
2 R_1 = (0.2}{R}} $, где $latex \boldsymbol{V} $ — падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать $latex \boldsymbol{P = IV} $, где $latex \boldsymbol{V} $ — напряжение источника. Это дает
$латекс \boldsymbol{P = (0,600 \;\textbf{A})(12,0 \;\textbf{V}) = 7,20 \;\textbf{W}}. $
Обсуждение для (е)
Обратите внимание, по совпадению, что общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность выдает источник. То есть
$латекс \boldsymbol{P_1 + P_2 + P_3 = (0,360 + 2,16 + 4,68) \;\textbf{W} = 7,20 \;\textbf{W}}. $
Мощность — это энергия в единицу времени (ватты), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Сопротивления серии добавить: $latex \boldsymbol{R_s = R_1 + R_2 + R_3 + \dots} $ .

- Один и тот же ток протекает через каждый резистор последовательно.
- Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.
На рис. 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое верно и в вашем доме, или в любом здании. (См. рис. 3(b).)
Рисунок 3. (a) Три резистора, подключенные параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление.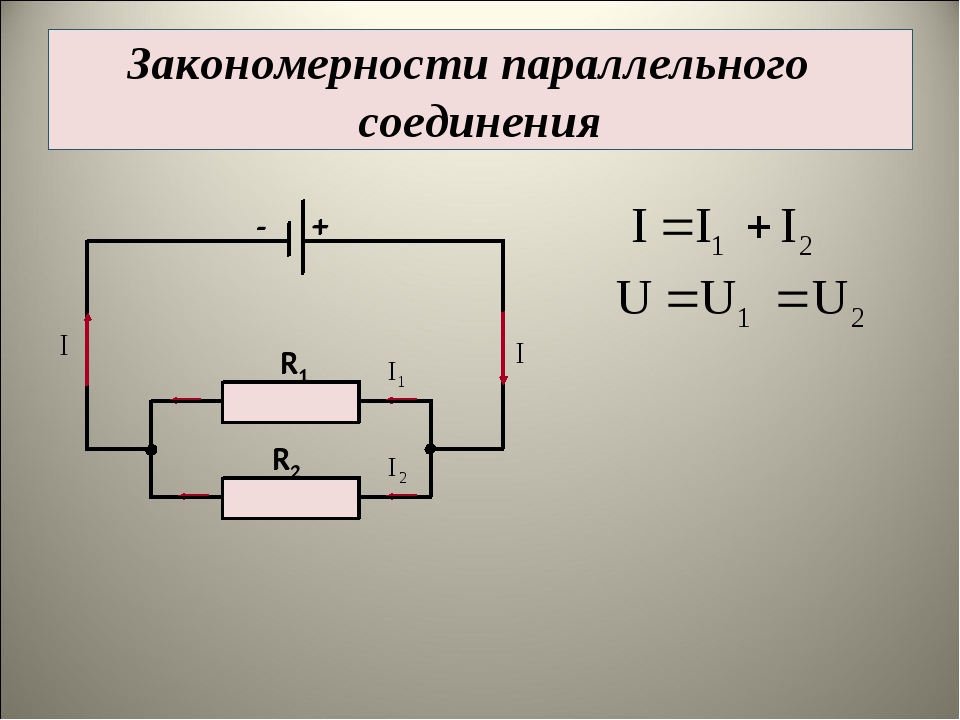 (b) Установка электроснабжения в доме. (Фото: Dmitry G, Wikimedia Commons)
(b) Установка электроснабжения в доме. (Фото: Dmitry G, Wikimedia Commons)
Чтобы найти выражение для эквивалентного параллельного сопротивления $latex \boldsymbol{R_{\textbf{p}}} $, давайте рассмотрим протекающие токи и то, как они связаны с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны $latex \boldsymbol{I_1 = \frac{V}{R_1}} $, $latex \boldsymbol{I_2 = \frac{V}{ R_2}} $ и $latex \boldsymbol{I_3 = \frac{V}{R_3}} $. Сохранение заряда подразумевает, что полный ток $latex \boldsymbol{I} $, производимый источником, представляет собой сумму этих токов:
$латекс \boldsymbol{I = I_1 + I_2 + I_3}. $
Подстановка выражений для отдельных токов дает
Обратите внимание, что закон Ома для эквивалентного единичного сопротивления дает
$латекс \boldsymbol{=} $ $латекс \boldsymbol{= V} $
Члены в скобках в последних двух уравнениях должны быть равны.Обобщая на любое количество резисторов, общее сопротивление $latex \boldsymbol{R_p} $ параллельного соединения связано с отдельными сопротивлениями как
.
$латекс \boldsymbol{=} $ $латекс \boldsymbol{+} $ $латекс \boldsymbol{+} $ $латекс \boldsymbol{+ \cdots} $
Это соотношение приводит к тому, что общее сопротивление $latex \boldsymbol{R_p} $ меньше, чем наименьшее из отдельных сопротивлений. (Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.
Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рис. 3 такие же, как при рассмотренном ранее последовательном соединении: $latex \boldsymbol{V = 12,0 \;\textbf{V}} $, $latex \boldsymbol{ R_1 = 1,00 \;\Omega} $, $latex \boldsymbol{R_2 = 6,00 \;\Omega} $ и $latex \boldsymbol{R_3 = 13,0 \;\Omega} $. а) Чему равно полное сопротивление? б) Найдите полный ток.(c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов определяется по приведенной ниже формуле. Ввод известных значений дает
Таким образом,
(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны инвертировать это, чтобы найти полное сопротивление $latex \boldsymbol{R_p} $. Это дает
$латекс \boldsymbol{R_p =} $ $латекс \boldsymbol{\Omega = 0,8041 \;\Omega}. $
Общее сопротивление с правильным количеством значащих цифр равно $latex \boldsymbol{R_p = 0,804 \;\Omega} $
Обсуждение для (а)
$latex \boldsymbol{R_p} $, как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, подставив $latex \boldsymbol{R_p} $ вместо полного сопротивления. Это дает
Это дает
$latex \boldsymbol{I =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 14,92 \;\textbf{A}} $
Обсуждение для (б)
Ток $latex \boldsymbol{I} $ для каждого устройства намного больше, чем для таких же устройств, соединенных последовательно (см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.
Стратегия и решение для (c)
Индивидуальные токи легко рассчитать по закону Ома, так как на каждый резистор подается полное напряжение.Таким образом,
$latex \boldsymbol{I_1 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 12.0 \;\textbf{A}}. $
Аналогично,
$latex \boldsymbol{I_2 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 2.00 \;\textbf{A}} $
и
$latex \boldsymbol{I_3 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 0,92 \;\textbf{A}}. $
Обсуждение для (с)
Общий ток представляет собой сумму отдельных токов:
$латекс \boldsymbol{I_1 + I_2 + I_3 = 14. 2}{R}} $, так как на каждый резистор подается полное напряжение. Таким образом,
2}{R}} $, так как на каждый резистор подается полное напряжение. Таким образом,
$latex \boldsymbol{P_1 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 144 \;\textbf{W}}. $
Аналогично,
$latex \boldsymbol{P_2 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 24,0 \;\textbf{W}} $
и
$latex \boldsymbol{P_3 =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 11.1 \;\textbf{W}} .$
Обсуждение для (д)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к одному и тому же источнику напряжения.
Стратегия и решение для (e)
Общая мощность также может быть рассчитана несколькими способами. Выбор $latex \boldsymbol{P = IV} $ и ввод общего тока дает
$латекс \boldsymbol{P = IV = (14,92 \;\textbf{A})(12,0 \;\textbf{V}) = 179 \;\textbf{W}}. $
Обсуждение для (е)
Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт:
$латекс \boldsymbol{P_1 + P_2 + P_3 = 144 \;\textbf{W} + 24. 0 \;\textbf{W} + 11,1 \;\textbf{W} = 179 \;\textbf{W}}. $
0 \;\textbf{W} + 11,1 \;\textbf{W} = 179 \;\textbf{W}}. $
Это согласуется с законом сохранения энергии.
Общее обсуждение
Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.
Основные характеристики резисторов, включенных параллельно
- Параллельное сопротивление находится из $latex \boldsymbol{\frac{1}{R_p} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \cdots } $, и оно меньше, чем любое отдельное сопротивление в комбинации.
- К каждому параллельно подключенному резистору приложено одинаковое полное напряжение источника. (Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо.)
- Параллельные резисторы не получают суммарный ток каждый; они его делят.
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения.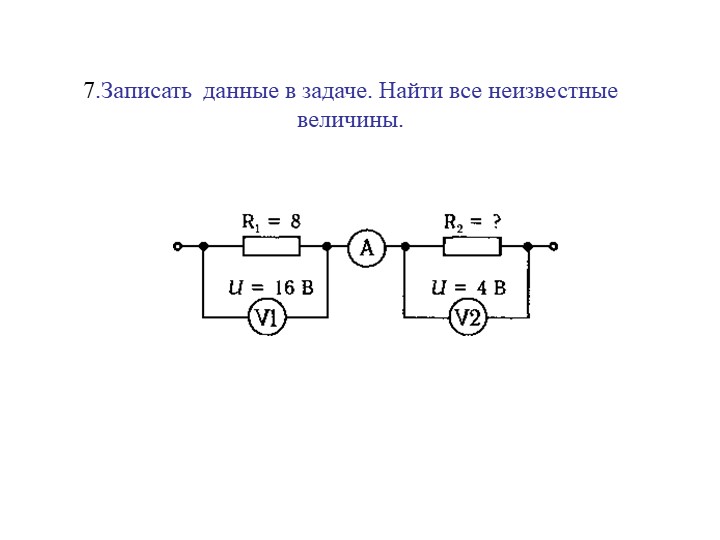 Они часто встречаются, особенно когда учитывается сопротивление проводов.В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Они часто встречаются, особенно когда учитывается сопротивление проводов.В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения могут быть сведены к одному эквивалентному сопротивлению с помощью метода, показанного на рис. 4. Различные части идентифицируются как последовательные или параллельные, сводятся к их эквивалентам и далее уменьшаются до тех пор, пока не останется одно сопротивление. Процесс скорее трудоемкий, чем сложный.
Рисунок 4. Эта комбинация семи резисторов имеет как последовательные, так и параллельные части.Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единственное эквивалентное сопротивление.
Простейшая комбинация последовательного и параллельного сопротивлений, показанная на рис. 5, также является наиболее поучительной, поскольку она встречается во многих приложениях. Например, $latex \boldsymbol{R_1} $ может быть сопротивлением проводов от автомобильного аккумулятора до его электрических устройств, находящихся параллельно. $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $ могут быть стартером и освещением салона.Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Например, $latex \boldsymbol{R_1} $ может быть сопротивлением проводов от автомобильного аккумулятора до его электрических устройств, находящихся параллельно. $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $ могут быть стартером и освещением салона.Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 3. Расчет сопротивления, $latex \boldsymbol{IR} $ падения, тока и рассеиваемой мощности: объединение последовательных и параллельных цепей
На рис. 5 показаны резисторы из двух предыдущих примеров, соединенные другим способом — последовательно и параллельно. Мы можем считать $latex \boldsymbol{R_1} $ сопротивлением проводов, ведущих к $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $.а) Найдите полное сопротивление. (b) Что такое падение $latex \boldsymbol{IR} $ в $latex \boldsymbol{R_1} $? (c) Найдите текущий $latex \boldsymbol{I_2} $ до $latex \boldsymbol{R_2} $.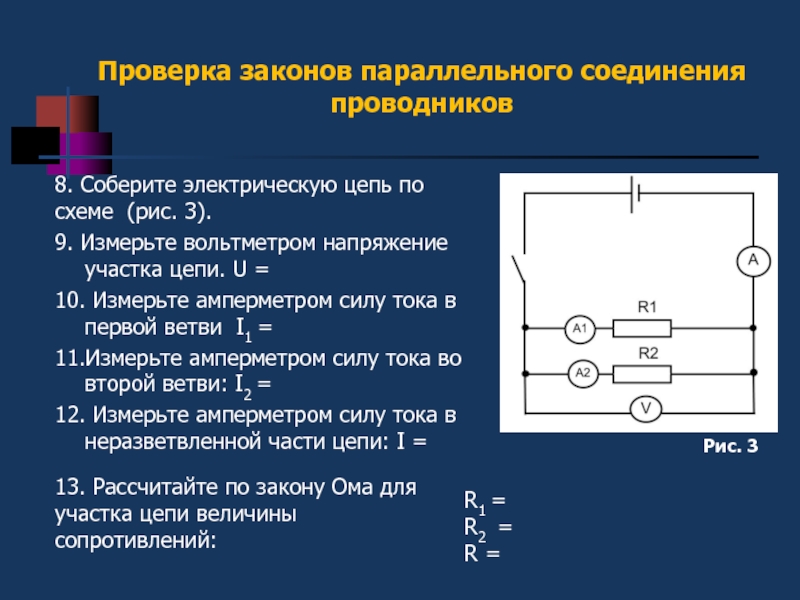 (d) Какую мощность рассеивает $latex \boldsymbol{R_2} $?
(d) Какую мощность рассеивает $latex \boldsymbol{R_2} $?
Рисунок 5. Эти три резистора подключены к источнику напряжения таким образом, что R 2 и R 3 соединены параллельно друг другу, а эта комбинация последовательно с 3 R 7 1 .
Стратегия и решение для (а)
Чтобы найти полное сопротивление, заметим, что $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $ параллельны, а их комбинация $latex \boldsymbol{R_p} $ последовательно с $latex \boldsymbol{ Р_1} $. Таким образом, общее (эквивалентное) сопротивление этой комбинации равно
.
$латекс \boldsymbol{R_{\textbf{tot}} = R_1 + R_p}. $
Сначала находим $latex \boldsymbol{R_p} $, используя уравнение для параллельных резисторов и вводя известные значения:
Инвертирование дает
$латекс \boldsymbol{R_p =} $ $латекс \boldsymbol{\Omega = 4.11 \;\Омега}. $
$
Таким образом, общее сопротивление равно
.
$латекс \boldsymbol{R_{\textbf{tot}} = R_1 + R_p = 1,00 \;\Omega + 4,11 \;\Omega = 5,11 \;\Omega}. $
Обсуждение для (а)
Суммарное сопротивление этой комбинации занимает промежуточное положение между чистыми последовательными и чисто параллельными значениями ($latex \boldsymbol{20,0 \;\Omega} $ и $latex \boldsymbol{0,804 \;\Omega} $ соответственно), найденными для одного и того же резисторы в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти падение $latex \boldsymbol{IR} $ в $latex \boldsymbol{R_1} $, заметим, что полный ток $latex \boldsymbol{I} $ протекает через $latex \boldsymbol{R_1} $.Таким образом, его $latex \boldsymbol{IR} $ drop равен
$латекс \boldsymbol{V_1 = IR_1}. $
Мы должны найти $latex \boldsymbol{I} $, прежде чем мы сможем вычислить $latex \boldsymbol{V_1} $. Полный ток $latex \boldsymbol{I} $ находится по закону Ома для цепи. То есть
То есть
$latex \boldsymbol{I =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{= 2,35 \;\textbf{A}}. $
Подставив это в выражение выше, мы получим
$латекс \boldsymbol{V_1 = IR_1 = (2,35 \;\textbf{A})(1.00 \;\Омега) = 2,35 \;\textbf{V}}. $
Обсуждение для (б)
Напряжение, подаваемое на $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $, меньше суммарного напряжения на величину $latex \boldsymbol{V_1} $. Когда сопротивление проводов велико, это может существенно повлиять на работу устройств, представленных $latex \boldsymbol{R_2} $ и $latex \boldsymbol{R_3} $.
Стратегия и решение для (c)
Чтобы найти ток через $latex \boldsymbol{R_2} $, мы должны сначала найти приложенное к нему напряжение.Мы называем это напряжение $latex \boldsymbol{V_{\textbf{p}}}$, потому что оно приложено к параллельной комбинации резисторов. Напряжение, подаваемое как на $latex \boldsymbol{R_2} $, так и на $latex \boldsymbol{R_3} $, уменьшается на величину $latex \boldsymbol{V_1} $, поэтому оно равно
.
$латекс \boldsymbol{V_p = V – V_1 = 12,0 \;\textbf{V} – 2,35 \;\textbf{V} = 9,65 \;\textbf{V}}. $
Теперь текущий $latex \boldsymbol{I_2} $ через сопротивление $latex \boldsymbol{R_2} $ находится по закону Ома:
$латекс \boldsymbol{I_2 =} $ $латекс \boldsymbol{=} $ $латекс \boldsymbol{ = 1.2(6,00 \;\Омега) = 15,5 \;\textbf{W}}. $
Обсуждение для (д)
Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение $latex \boldsymbol{IR} $ в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет.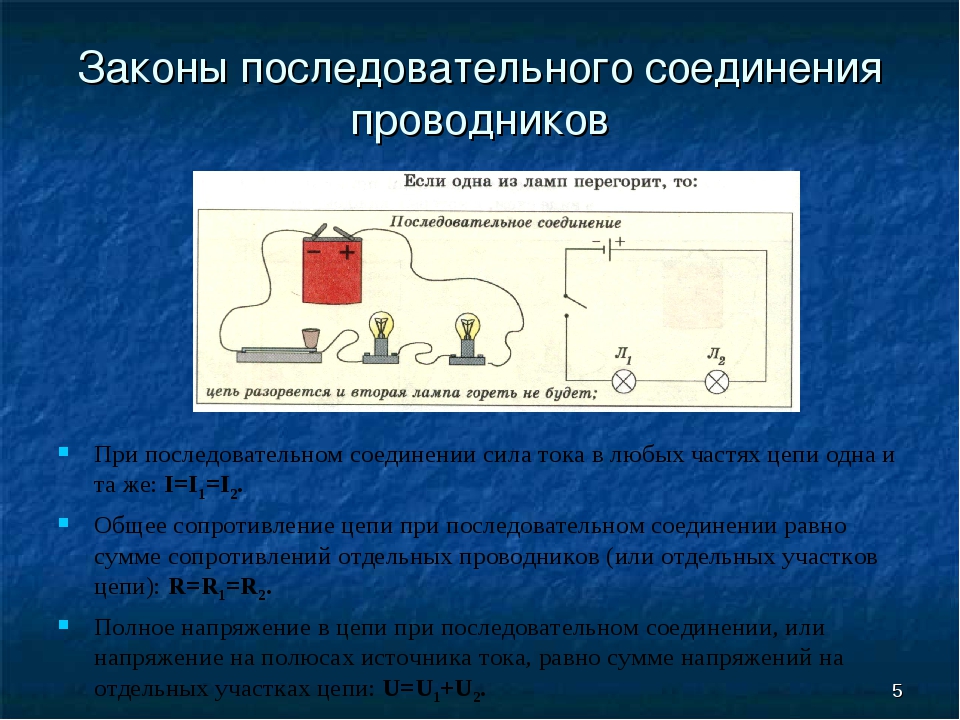 Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, представленное $latex \boldsymbol{R_3} $, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток.Этот увеличенный ток вызывает большее падение $latex \boldsymbol{IR} $ в проводах, представленных $latex \boldsymbol{R_1} $, уменьшая напряжение на лампочке (которое равно $latex \boldsymbol{R_2} $), что потом заметно тускнеет.
Рисунок 6. Почему гаснет свет при включении большого электроприбора? Ответ заключается в том, что большой ток, потребляемый двигателем электроприбора, вызывает значительное падение напряжения в проводах и снижает напряжение на лампе.
Проверьте свое понимание
1: Можно ли любую произвольную комбинацию резисторов разбить на последовательные и параллельные комбинации? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательных и параллельных соединений.
Стратегии решения проблем для последовательных и параллельных резисторов
- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме.
- Точно определите, что нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или как последовательно, так и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных. Если в вашей задаче сочетаются последовательные и параллельные соединения, уменьшите ее пошагово, рассмотрев отдельные группы последовательных или параллельных соединений, как это делается в этом модуле и в примерах.
 Особое примечание: при нахождении $latex\boldsymbol{R_p} $ необходимо соблюдать осторожность.
Особое примечание: при нахождении $latex\boldsymbol{R_p} $ необходимо соблюдать осторожность. - Проверьте, разумны ли и последовательны ли ответы. Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.
- Общее сопротивление электрической цепи с последовательно соединенными резисторами равно сумме сопротивлений отдельных элементов: $latex \boldsymbol{R_s = R_1 + R_2 + R_3 + \cdots} $
- Каждый резистор в последовательной цепи имеет одинаковую величину тока, протекающего через него.
- Падение напряжения или рассеиваемая мощность на каждом отдельном резисторе в серии различны, и их общая сумма составляет входную мощность источника питания.
- Общее сопротивление электрической цепи с параллельно соединенными резисторами меньше наименьшего сопротивления любого из компонентов и может быть определено по формуле:
$latex \boldsymbol{=} $ $latex \boldsymbol{+} $ $latex \boldsymbol{+} $ $latex \boldsymbol{+ \;\cdots} $ - К каждому резистору в параллельной цепи приложено одинаковое полное напряжение источника.

- Ток, протекающий через каждый резистор в параллельной цепи, различен в зависимости от сопротивления.
- Если более сложное соединение резисторов представляет собой комбинацию последовательного и параллельного сопротивления, его можно свести к единому эквивалентному сопротивлению, обозначив различные его части как последовательные или параллельные, сведя каждую к эквиваленту и продолжая до тех пор, пока в конечном итоге не будет достигнуто единое сопротивление .
Концептуальные вопросы
1: Выключатель имеет переменное сопротивление, близкое к нулю в замкнутом состоянии и очень большое в разомкнутом, и включается последовательно с управляемым им устройством.Объясните влияние переключателя на рисунке 7 на ток в разомкнутом и замкнутом состоянии.
Рисунок 7. Переключатель обычно подключается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в закрытом состоянии, но чрезвычайно большое сопротивление в разомкнутом состоянии.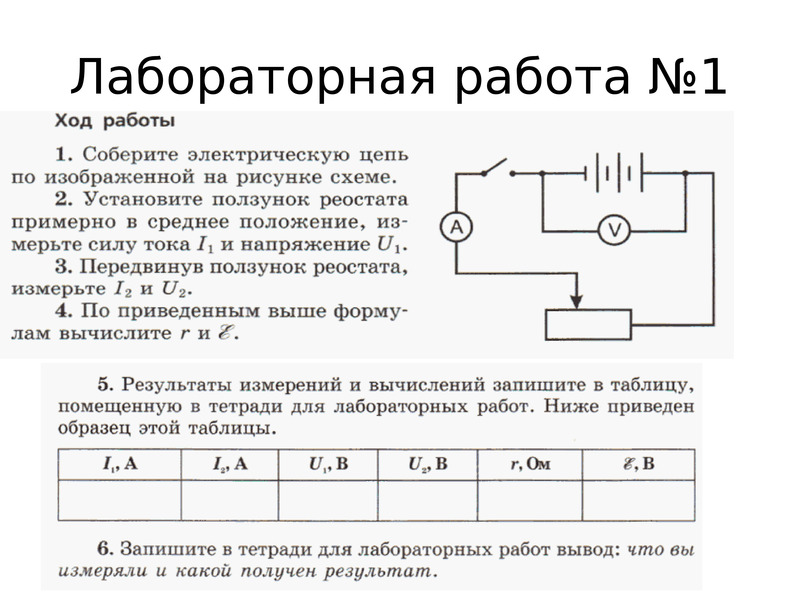 (Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи.)
(Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи.)
2: Какое напряжение на разомкнутом переключателе на рисунке 7?
3: На разомкнутом переключателе присутствует напряжение, как показано на рисунке 7.Почему же тогда мощность, рассеиваемая открытым ключом, мала?
4: Почему мощность, рассеиваемая замкнутым выключателем, таким как на рисунке 7, мала?
5: Студент в лаборатории физики по ошибке подключил лампочку, батарею и выключатель, как показано на рис. 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и выключается, когда выключатель замкнут. (Не пытайтесь это сделать — это плохо для батареи!)
Рисунок 8. Ошибка проводки поместила этот переключатель параллельно с устройством, представленным R .(Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи.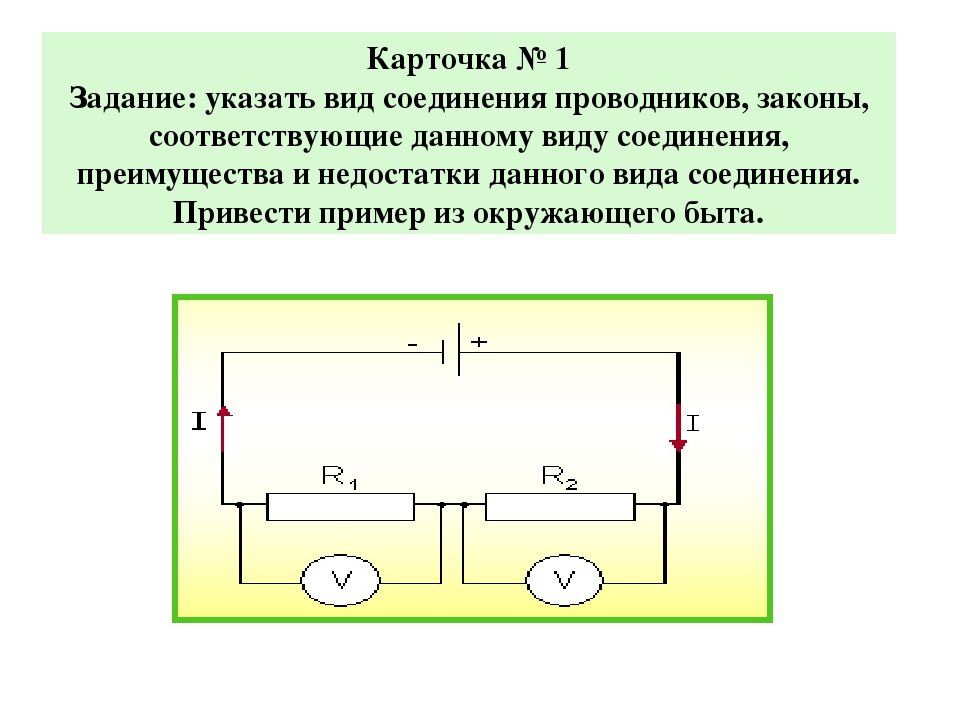 )
)
6: Зная, что сила удара зависит от силы тока, протекающего через ваше тело, вы бы предпочли быть включенным последовательно или параллельно с сопротивлением, например, с нагревательным элементом тостера, если оно поражено им? Объяснять.
7: Погасли бы фары при запуске двигателя автомобиля, если бы провода в автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.
8: Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые разрывали электрическое соединение, как разомкнутый выключатель, когда они перегорали. Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампочки, у которых короткое замыкание, как у замкнутого выключателя, когда они перегорают.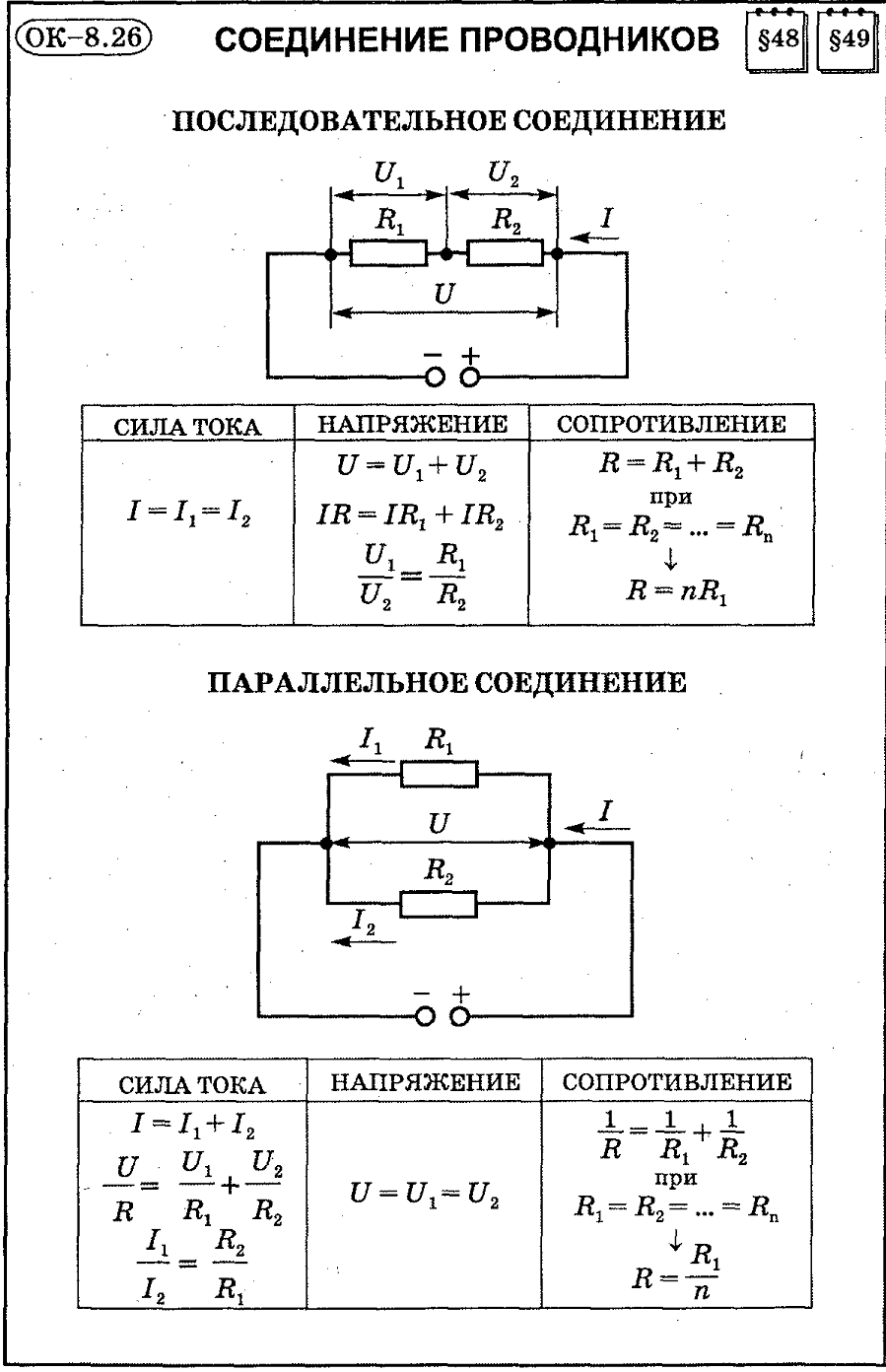 Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 одинаковых лампочек, каково тогда рабочее напряжение каждой?
Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 одинаковых лампочек, каково тогда рабочее напряжение каждой?
9: Если две бытовые лампочки мощностью 60 Вт и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.
10: Предположим, вы выполняете лабораторную работу по физике, в которой вас просят включить резистор в цепь, но все поставляемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее требуемое значение?
11: До Второй мировой войны некоторые радиоприемники получали питание через «резистивный шнур», который имел значительное сопротивление. Такой шнур сопротивления снижает напряжение до желаемого уровня для радиоламп и т.п., а также экономит расходы на трансформатор.Объясните, почему шнуры сопротивления нагреваются и расходуют энергию, когда радио включено.
12: Некоторые лампочки имеют три уровня мощности (не считая нуля), получаемые из нескольких нитей накала, которые включаются по отдельности и соединяются параллельно. Какое минимальное количество нитей необходимо для трех режимов мощности?
Проблемные упражнения
Примечание. Можно предположить, что данные, взятые из рисунков, имеют точность до трех значащих цифр.
1: (a) Чему равно сопротивление десяти $латексных \boldsymbol{275 – \;\Omega} $ резисторов, соединенных последовательно? б) Параллельно?
2: (a) Чему равно сопротивление $latex \boldsymbol{1.2 – \;\Omega} $ a $latex \boldsymbol{2.50 – \;\textbf{k} \Omega} $ и резистор $latex \boldsymbol{4.00 – \;\textbf{k} \Omega} $ подключены последовательно? б) Параллельно?
3: Какое наибольшее и наименьшее сопротивление можно получить, соединив $латекс \boldsymbol{36,0 – \;\Omega} $, $латекс \boldsymbol{50,0 – \;\Omega} $ и $ латекс \boldsymbol{700 – \;\Omega} $ резистор вместе?
4: Тостер мощностью 1800 Вт, электрическая сковорода мощностью 1400 Вт и лампа мощностью 75 Вт подключены к одной розетке в сети 15 А, 120 В. (Три устройства подключены параллельно, когда они подключены к одной и той же розетке.). а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
(Три устройства подключены параллельно, когда они подключены к одной и той же розетке.). а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
5: Фара вашего автомобиля мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в системе 12,0 В. Какую мощность будет потреблять одна фара и стартер при последовательном подключении к аккумулятору 12,0 В? (Любым другим сопротивлением в цепи и любым изменением сопротивления в двух устройствах пренебречь.)
6: (а) Учитывая 48.Батарея 0 В и резисторы $latex \boldsymbol{24.0 – \;\Omega} $ и $latex \boldsymbol{96.0 – \;\Omega} $, найти ток и мощность каждого из них при последовательном соединении. (b) Повторите, когда сопротивления параллельны.
7: Ссылаясь на пример объединения последовательных и параллельных цепей и рисунок 5, рассчитайте $latex \boldsymbol{I_3} $ двумя следующими способами: (a) по известным значениям $latex \boldsymbol{I} $ и $латекс \boldsymbol{I_2} $; (б) используя закон Ома для $latex \boldsymbol{R_3} $.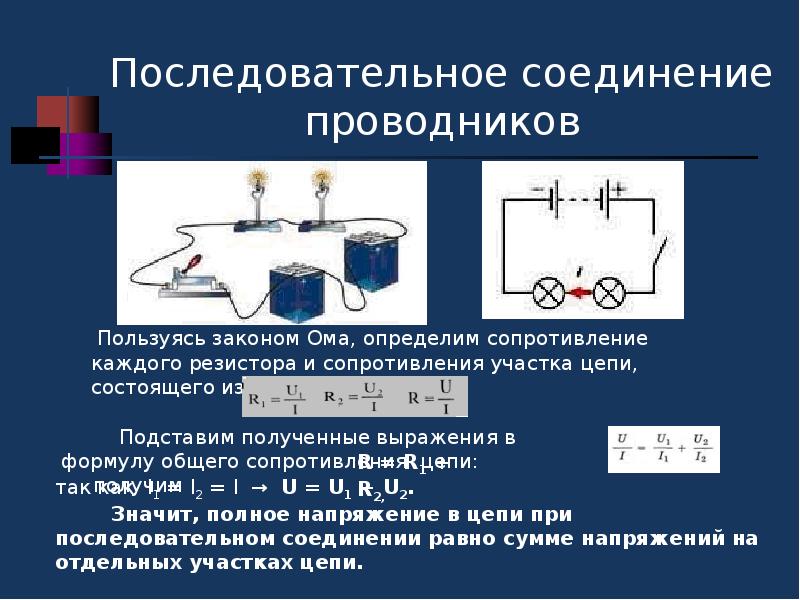 В обеих частях подробно показано, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».
В обеих частях подробно показано, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».
8: Ссылаясь на рисунок 5: (a) Вычислите $latex \boldsymbol{P_3} $ и обратите внимание на то, как это сравнивается с $latex \boldsymbol{P_3} $, найденным в первых двух примерах задач в этом модуле. б) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.
9: См. рис. 6 и обсуждение затемнения света при включении тяжелого электроприбора.9 — \;\Omega} $ сопротивление. Рис. 9. (а) Каково сопротивление заземления 100 таких изоляторов? б) Рассчитайте мощность, рассеиваемую 100 из них. в) Какую долю мощности несет линия? Подробно покажите, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».
Рисунок 9. Высоковольтная линия электропередачи (240 кВ), по которой проходит 5,00 × 10 2 Линия подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивают 1.00 × 10 9 Ом сопротивления каждый.
Ряд керамических изоляторов обеспечивают 1.00 × 10 9 Ом сопротивления каждый.
11: Покажите, что если объединить два резистора $latex \boldsymbol{R_1} $ и $latex \boldsymbol{R_2} $ и один из них намного больше другого ($latex \boldsymbol{R_1 >> R_2} $) : (a) Их последовательное сопротивление почти равно большему сопротивлению $latex \boldsymbol{R_1} $. (b) Их параллельное сопротивление почти равно меньшему сопротивлению $latex \boldsymbol{R_2} $.
12: необоснованные результаты
Два резистора, один из которых имеет сопротивление $latex \boldsymbol{145 \;\Omega} $, соединены параллельно, чтобы получить общее сопротивление $latex \boldsymbol{150 \;\Omega} $.а) Какова величина второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
13: необоснованные результаты
Два резистора, один из которых имеет сопротивление $latex \boldsymbol{900 \;\textbf{k} \Omega} $, соединены последовательно, чтобы получить общее сопротивление $latex \boldsymbol{0,500 \;\textbf{M} \Омега} $. а) Какова величина второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
а) Какова величина второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
Глоссарий
- серия
- последовательность резисторов или других компонентов, включенных в цепь один за другим
- резистор
- компонент, обеспечивающий сопротивление току, протекающему по электрической цепи
- сопротивление
- вызывает потерю электроэнергии в цепи
- Закон Ома
- связь между током, напряжением и сопротивлением в электрической цепи: $latex \boldsymbol{V=IR} $
- напряжение
- электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например батареей
- падение напряжения
- потеря электроэнергии при протекании тока через резистор, провод или другой компонент
- текущий
- поток заряда через электрическую цепь мимо заданной точки измерения
- Закон Джоуля
- соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое как: $latex \boldsymbol{P_e = IV} $
- параллельный
- соединение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
Решения
Проверьте свое понимание
1: Нет, существует множество способов соединения резисторов, не являющихся комбинациями последовательного и параллельного, включая петли и переходы. В таких случаях правила Кирхгофа, которые будут представлены в главе 21.3 «Правила Кирхгофа», позволят вам проанализировать схему.
В таких случаях правила Кирхгофа, которые будут представлены в главе 21.3 «Правила Кирхгофа», позволят вам проанализировать схему.
Проблемы Упражнения
1: (a) $latex \boldsymbol{2.75 \;\textbf{k} \Omega} $
(б) $латекс \boldsymbol{27.5 \;\Omega} $
3: (a) $латекс \boldsymbol{786 \;\Omega} $
(б) $латекс \boldsymbol{20.3 \;\Omega} $
5: 29,6 Вт
7: (а) 0.74 А
(б) 0,742 А
9: (а) 60,8 Вт
(б) 3,18 кВт
11: (a) $латекс \begin{array}{c} \boldsymbol{R_s = R_1 + R_2} \\[1em] \boldsymbol{\Rightarrow R_s \ приблизительно R_1(R_1 >> R_2)} \end {массив} $
(b) $латекс \boldsymbol{=} $ $латекс \boldsymbol{+} $ $латекс \boldsymbol{=} $
так что
$latex \boldsymbol{R_p =} $ $latex \boldsymbol{\приблизительно} $ $latex \boldsymbol{= R_2 \; (R_1 >> R_2)}.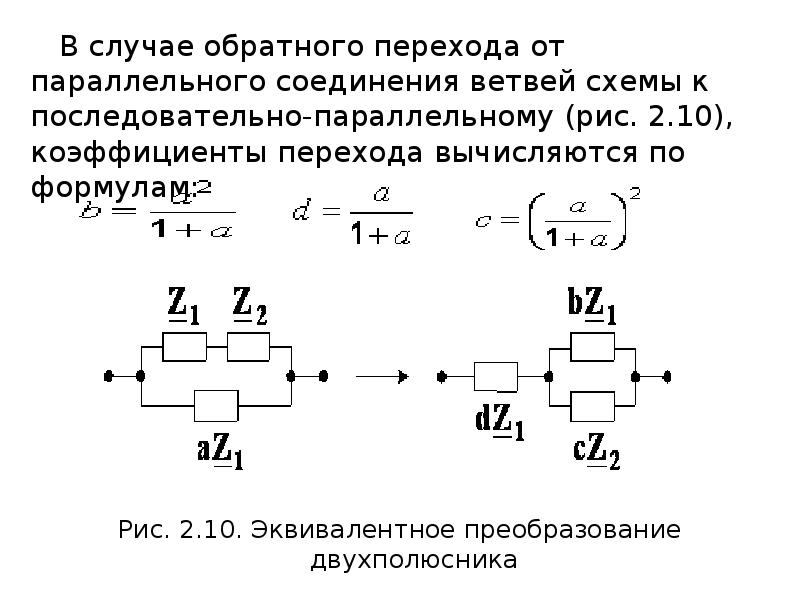 $
$
13: (a) $latex \boldsymbol{-400 \;\textbf{k} \Omega} $
(b) Сопротивление не может быть отрицательным.
(c) Говорят, что последовательное сопротивление меньше одного из резисторов, но оно должно быть больше любого из резисторов.
Серия
и параллельная схема | bartleby
Параллельная цепь
Параллельная цепь — это разветвленная цепь с несколькими путями протекания тока. Элементы при параллельном соединении имеют общие узлы, и падение напряжения на каждом компоненте будет одинаковым.
Равное напряжение означает, что каждый электрический компонент подключен между двумя наборами электрически подобных точек. Ток, протекающий через каждую ветвь цепи, зависит от компонента, подключенного к этой ветви. Если подключенный компонент представляет собой резистор, то ветвь с низким сопротивлением будет иметь больший ток по сравнению с ветвью с более высоким сопротивлением.
Параллельные цепи состоят из множества ответвлений, поэтому удаление одного компонента не приведет к размыканию цепи.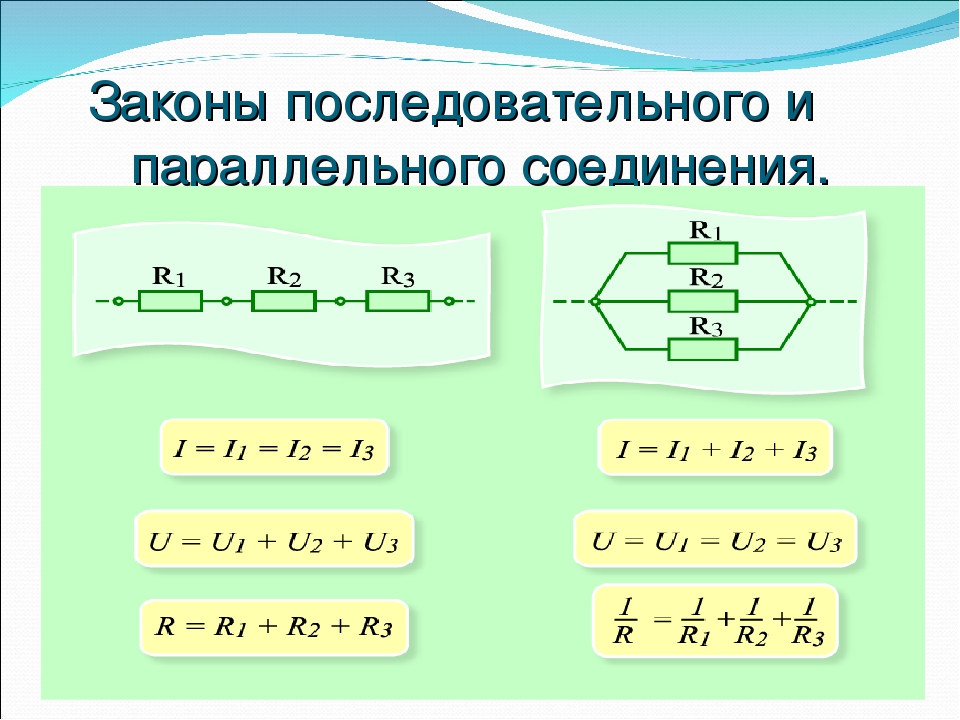 Большинство измерительных приборов подключаются по параллельным цепям. Например, вольтметр подключается параллельно компоненту для измерения напряжения.
Большинство измерительных приборов подключаются по параллельным цепям. Например, вольтметр подключается параллельно компоненту для измерения напряжения.
Параллельные цепи в основном используются для проводки электрических точек в зданиях и автомобилях. В сложных соединениях сильноточных электрических цепей используются параллельные схемы. Параллельные схемы также используются при разработке компьютерного оборудования.
Резистор, включенный параллельно
Поскольку параллельные соединения имеют одинаковое напряжение по всей цепи, два или более резистора, подключенных между двумя общими узлами, будут иметь одинаковое напряжение.Напряжение на источнике будет равно напряжению на каждом резисторе.
Ток, протекающий через каждый резистор, будет разным и может быть рассчитан по закону Ома. Общий ток, протекающий по цепи, будет суммой токов, протекающих по каждой ветви. Следовательно,
I=VRItotal = I1 + I2 + I3 +….VtotalRtotal=V1R1+V2R2+V3R3+.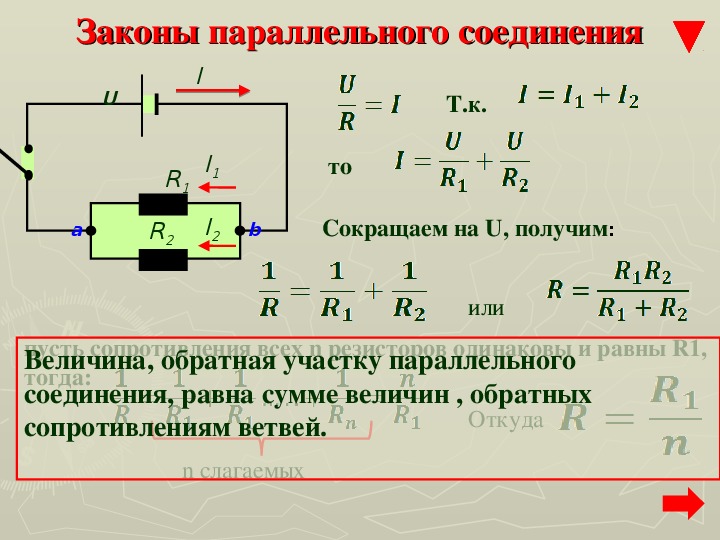 …..
…..
Поскольку напряжение в цепи равно индивидуальному падению напряжения.
Vобщ= V1=V2=V3=…
Условия напряжения в левой и правой частях будут компенсированы. Таким образом,
1Rtotal=1R1+1R2+1R3+…..
R total равно результирующему сопротивлению параллельной цепи.
Конденсаторы в параллельной цепи
Когда отдельные конденсаторы подключены к одним и тем же клеммам, эта цепь будет иметь параллельное соединение. Каждый конденсатор будет иметь одинаковое падение напряжения, значение будет равно значению источника напряжения.
Несколько конденсаторов при параллельном соединении действуют как один конденсатор.Конечная емкость представляет собой сумму емкостей отдельных компонентов.
Ctotal= C1 + C2 + C3 +…
Катушки индуктивности в параллельной цепи
Две или более катушки индуктивности, соединенные между одним и тем же набором клемм, образуют параллельную цепь.
Напряжение при параллельном соединении остается прежним, но изменяется ток.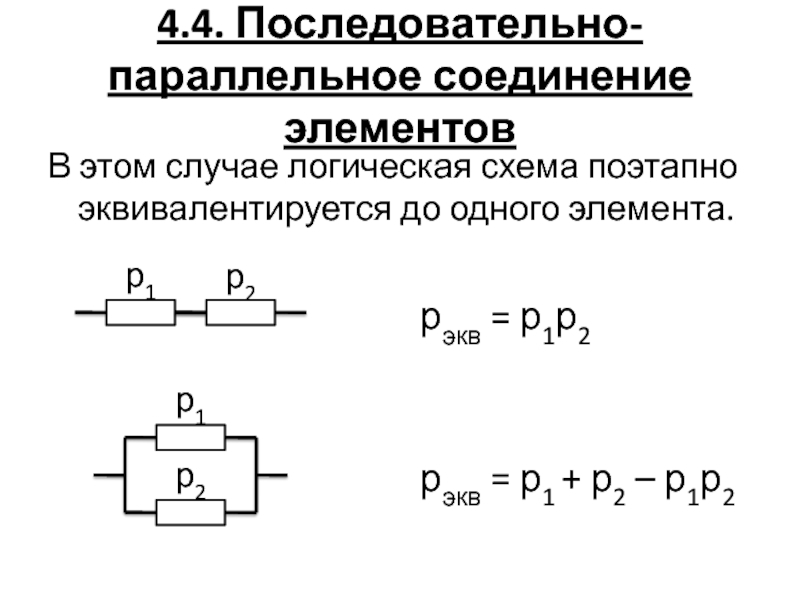 Индуктивность катушки зависит от скорости изменения тока. Поскольку каждый компонент имеет различную величину тока, результирующее напряжение не будет прямой суммой отдельных индуктивностей.
Индуктивность катушки зависит от скорости изменения тока. Поскольку каждый компонент имеет различную величину тока, результирующее напряжение не будет прямой суммой отдельных индуктивностей.
1Ltotal = 1L1+1L2+1L3+…….
Ток течет по пути с наименьшим сопротивлением, поэтому в параллельной цепи партия с наименьшим сопротивлением будет иметь больший ток. Результирующее значение также зависит от явления взаимной индуктивности.
Серия
и параллельные сети
Серийные и параллельные сети
Конфигурация последовательных и параллельных цепей может существовать в одной и той же сети.
Для решения последовательных и параллельных сетей выполните следующие действия:- Набросайте общий подход, который вы планируете использовать
- Рассматривать каждую ветвь отдельно
- После решения проверьте соответствие результатов сезонным
Пример 1: Найдите I 1 , I 2 , I 3 и V R3
Решение: R 2 и R 3 параллельно Общее сопротивление , Найти R T , I 1 , I 2 , I 3 в заданной цепи Затем Общее сопротивление Текущий I 1 можно найти как , Также |
Пример 2: Найти R T , v a , v b в следующей схеме
Решение: Найдите R T , v a , v b в следующей схеме Этап 1 Для v б |
Пример 3: Найдите силу тока в следующей цепи
Решение Два разных решения Этап 1 1 к Ом и 3 к Ом серии Этап 2 Этап 3 6 кОм и 2. Этап 4 Этап 5 Использование схемы шага 2 Ступень 6 Использование данной схемы |
Пример 4: ????
- Найти V 1
- Найти V 2
- Проверка закона напряжения Кирхгофа для замкнутого контура
Примеры:
Пример 1: Для следующей цепи:
Ток можно рассчитать как |
Пример 2: Каков ток через резистор мощностью 100 Вт в следующей цепи с падением потенциала 20 В?
Ток можно рассчитать как |
Пример 3: Рассчитайте напряжение на резисторе 120 Вт следующей цепи, имеющей 1. 2 А ток через.
2 А ток через.
Напряжение можно рассчитать как |
Пример 4 Рассчитайте сопротивление лампы накаливания в следующей цепи, через которую проходит ток 0,5 А и напряжение 120 В.
Ток можно рассчитать как |
Пример 5 .Какая мощность будет рассеиваться на резисторе мощностью 10 Вт, если ток через него равен 2А?
Мощность можно рассчитать как |
Практические задачи :
(Щелкните изображение, чтобы посмотреть решение)
Практическое занятие 1 Каков ток i через резистор R в следующей цепи?
Просмотреть решение
Решение: Ток можно рассчитать как |
Практическое занятие 2: Найдите напряжения В 1 , В 2 , В 3 , В g и ток I 1 в следующей цепи.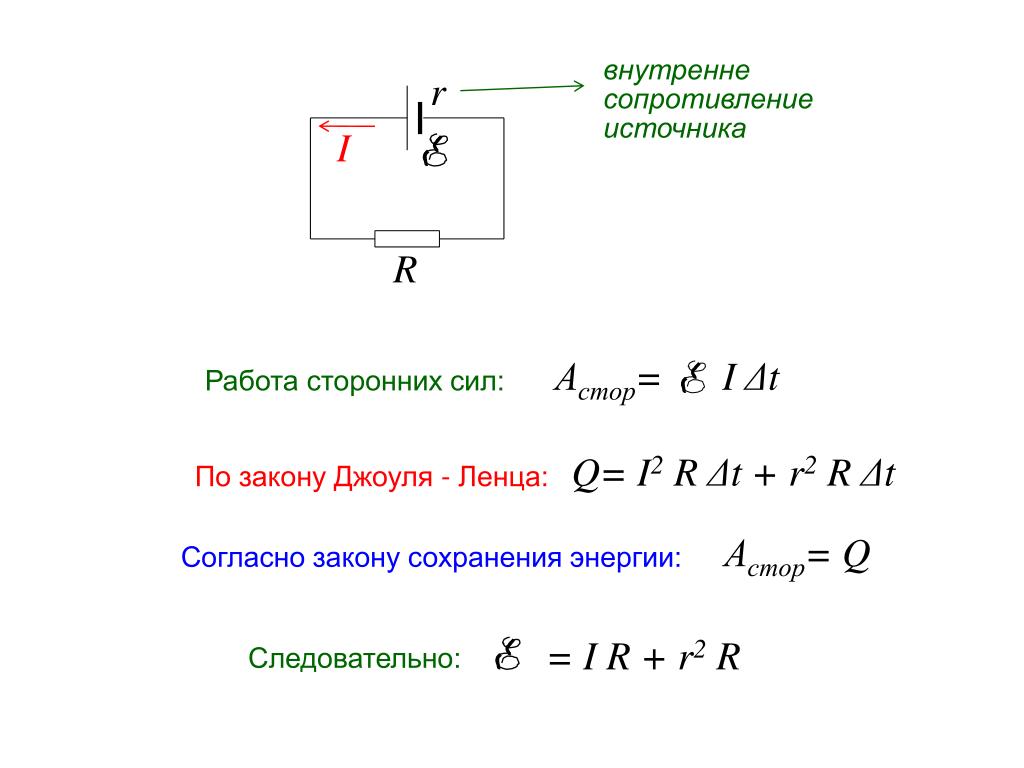
Просмотреть решение
Практика 3 Найти ток i через резистор R
Просмотреть решение
Решение: Ток можно рассчитать как |
Практическое занятие 4 Найдите напряжение источника v в следующей цепи.
Просмотреть решение
Решение: Напряжение можно рассчитать как |
Практика 5 . в следующей схеме:
в следующей схеме:
а. Найдите ток и через лампочку.
б. Найдите номинал резистора лампочки в следующей цепи
Просмотреть решение
Решение: Уравнение степени Тогда ток можно рассчитать как Номинал резистора лампочки |
Упражнения:
.

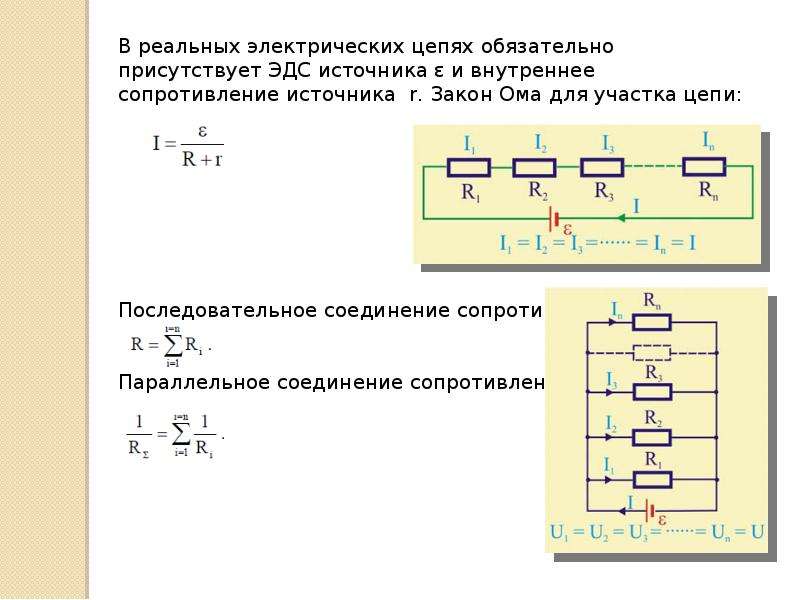

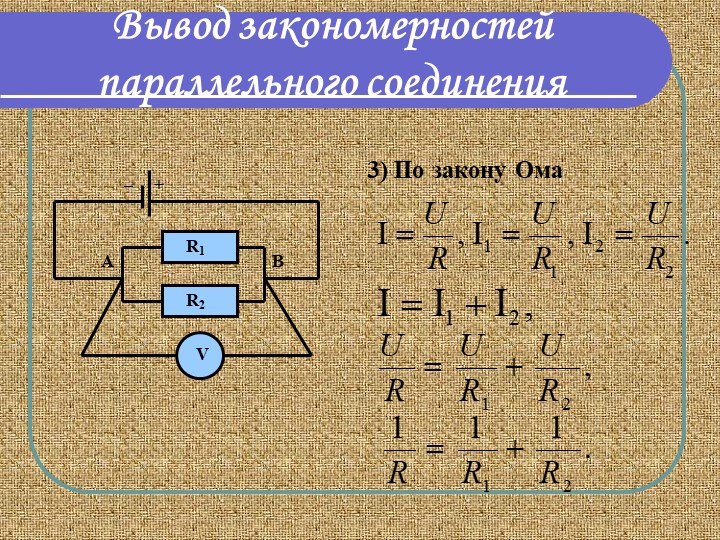
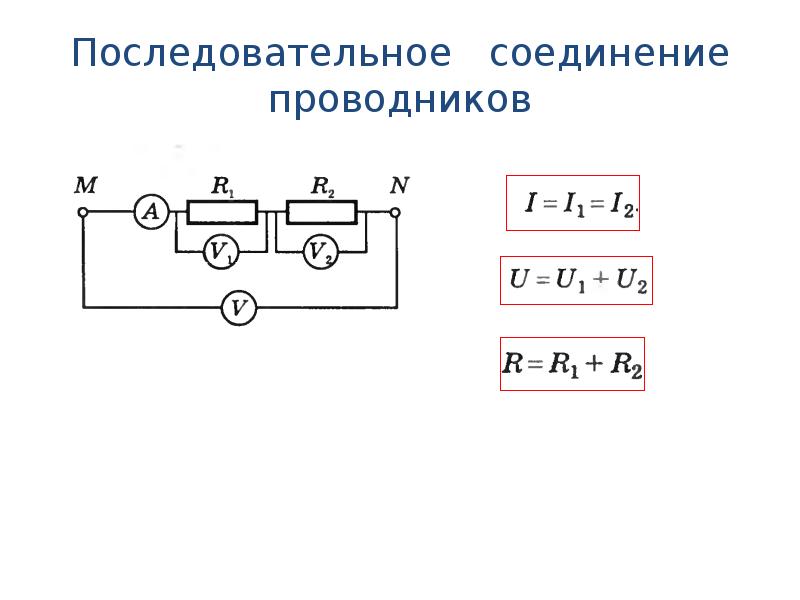
 Особое примечание: при нахождении $latex\boldsymbol{R_p} $ необходимо соблюдать осторожность.
Особое примечание: при нахождении $latex\boldsymbol{R_p} $ необходимо соблюдать осторожность.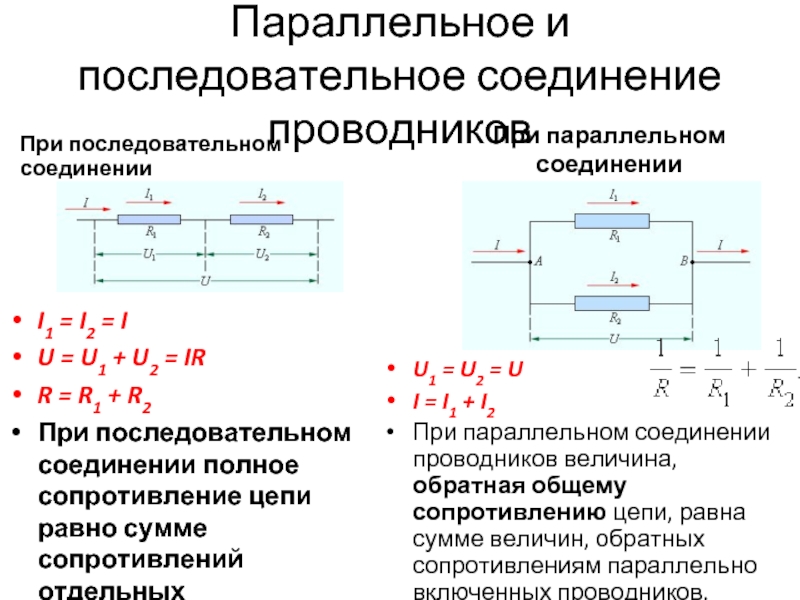
 66 кОм
66 кОм