Законы Кирхгофа — подробное и понятное объяснение на примерах | Pro Физику
Для расчета электрической цепи применяют два закона Кирхгофа. (Скорее их можно отнести не к законам, а к правилам. Но в большинстве учебников пишут именно о “законах” Кирхгофа. Поэтому и здесь будем обращаться к законам).
Первый закон Кирхгофа
Первый закон Кирхгофа применяют к узлам электрической цепи и выражают баланс токов в них. Первый закон Кирхгофа гласит:
Алгебраическая сумма токов сходящихся в узле электрической цепи равна 0.
Под словом “алгебраическая” имеется в виду, что учитывается знак перед током: “плюс” или “минус”.
В общем виде первый закон Кирхгофа можно записать как:
Рисунок 1 — Первый закон Кирхгофа
Для примера возьмем узел, в котором протекают токи, указанные стрелками (далее рассмотрим это все на конкретных схемах).
Рисунок 2 — Узел электрической цепи, в котором сходятся 4 ветви
Токи, втекающие и вытекающие из узла, берутся с противоположными знаками.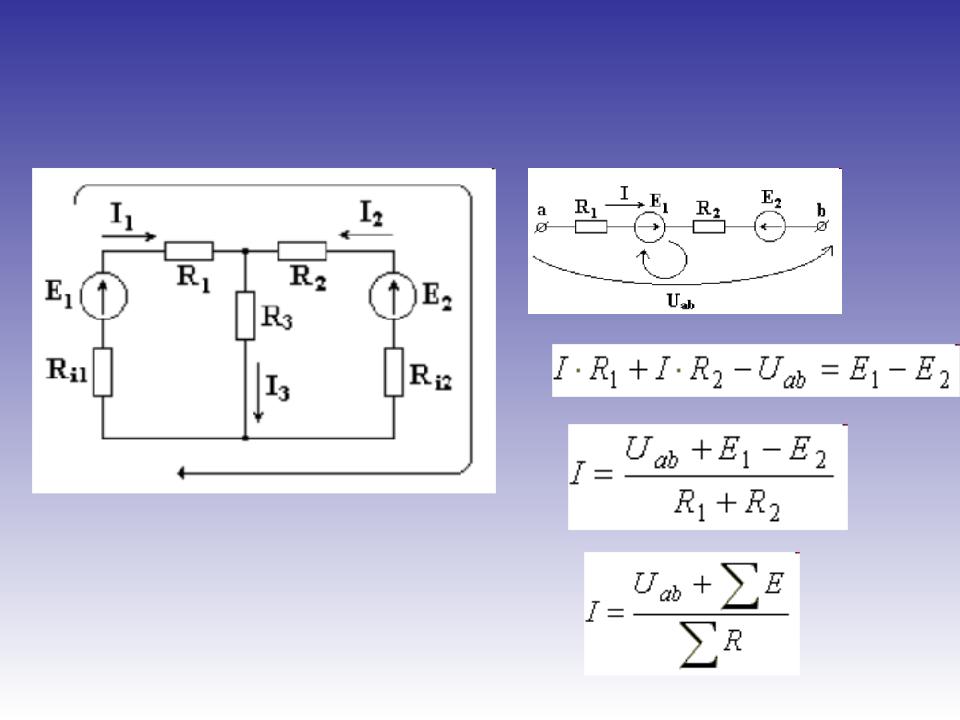 Втекающие в узел токи берутся со знаком, например, “+”, а вытекающие с “-“ (можно вытекающие брать с “+”, а втекающие с “-“). Главное, чтобы втекающие и вытекающие токи отличались по знаку.
Втекающие в узел токи берутся со знаком, например, “+”, а вытекающие с “-“ (можно вытекающие брать с “+”, а втекающие с “-“). Главное, чтобы втекающие и вытекающие токи отличались по знаку.
Будем считать токи положительными, если они втекают в узел, а вытекающие из узла – отрицательными. Тогда первый закон Кирхгофа для узла, представленного на рисунке 2, запишется:
I1-I2+I3+I4=0
Это выражение можно записать и в следующем виде:
I2=I1+I3+I4;
Ток I2 мы перенесли за знак равенства, его знак поменялся на противоположный (был с “минусом”, стал с “плюсом”).
Остальные токи мы не переносим, поэтому их знаки не меняются.
Согласно последнему выражению, первый закон Кирхгофа можно сформулировать по-другому:
Сумма токов, втекающих (подходящих) в узел, равна сумме токов, вытекающих (отходящих) из узла.
Все это говорит о том, что в узле эти токи не остаются и заряд в узле не накапливается.
Для более полного понимания, представим электрическую цепь (схему электрической цепи), для которой запишем первый закон Кирхгофа.
Рисунок 3 — Электрическая схема цепи для записи первого закона Кирхгофа
Запишем для этой цепи первый закон Кирхгофа для узла “a” (о том, как определить количество уравнений по первому и второму законам Кирхгофа, рассмотрим в конце ).
I1+I2-I3=0 или I3=I1+I2.
Второй закон Кирхгофа
Этот закон применяется к контурам электрической цепи и выражает баланс напряжений в них. Второй закон Кирхгофа звучит так:
Алгебраическая сумма ЭДС в замкнутом контуре (с учетом направления обхода контура) равна алгебраической (учитывается знак “+” или “-“) сумме падений напряжений на всех сопротивлениях (элементах) этого контура.
Для того, чтобы правильно составить уравнения по второму закону Кирхгофа, нужно пользоваться следующим правилом:
ЭДС берется со знаком “+”, если ее действие совпадает с направлением обхода контура. Напряжение на элементе контура берется со знаком “+”, если направление тока через данный элемент совпадает с направлением обхода контура. Если не совпадает направление обхода контура с направлением тока через элемент, то напряжение этого элемента берется со знаком “-“.
Если не совпадает направление обхода контура с направлением тока через элемент, то напряжение этого элемента берется со знаком “-“.
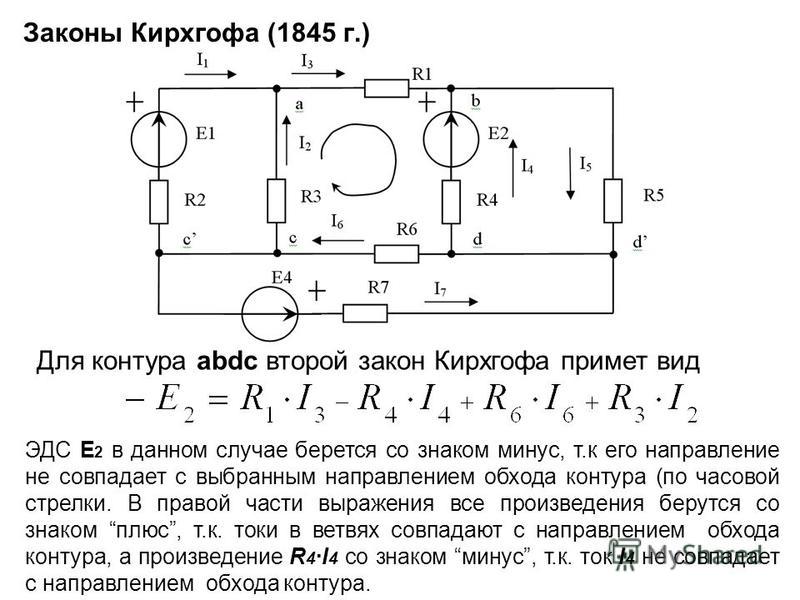
Запишем второй закон Кирхгофа для цепи, представленной ниже:
Рисунок 4 — Электрическая схема цепи для записи второго закона Кирхгофа(1 пример)
Выбираем направление обхода контура по часовой стрелке. В данном случае направление тока и направление обхода контура совпадают, поэтому I·R1 и I·R2 взяли со знаком “+”. А также совпадает направление обхода контура и действие ЭДС, поэтому ЭДС также записали со знаком “+”.
Возьмем еще один пример.
Рисунок 5 — Электрическая схема цепи для записи второго закона Кирхгофа(2 пример)
Запишем для этой цепи второй закон Кирхгофа. Обход выбираем по часовой стрелке (указали обход контура на схеме круговой стрелкой внутри контура). Как видим, направление обхода контура и направление тока I1 совпадают, а ток I2 направлен напротив обхода контура.
Следовательно, падение напряжения на резисторе R1 запишется со знаком “+”, т. е. +I1·R1. А падение напряжения на R2 запишется со знаком “-“, т. е. –I2·R2.
е. +I1·R1. А падение напряжения на R2 запишется со знаком “-“, т. е. –I2·R2.
Направление действия ЭДС совпадает с обходом контура, поэтому ЭДС E берем со знаком “+”.
Запишем второй закон Кирхгофа для этой цепи:
I1·R1-I2·R2=E
Ну и напоследок рассмотрим сложную электрическую цепь, состоящую из нескольких источников и резисторов.
Рисунок 6 — Схема сложной электрической цепи
Введем произвольно направление токов в ветвях, а также укажем на схеме в виде круговых стрелок направление обхода контуров.
Рисунок 7 — Схема сложной электрической цепи с введенными токами, наименованиями узлов и направлением обхода контура
Токи в ветвях направили произвольно, обход контура выбрали по часовой стрелке, а также узлы в этой схеме обозначили буквами a и b. Для того, чтобы понять, как и сколько уравнений по первому и второму законам Кирхгофа нужно составить для данной цепи, необходимо посчитать количество ветвей, узлов и независимых контуров.
Подробно вышесказанные понятия электрической цепи мы рассмотрим в следующих статьях.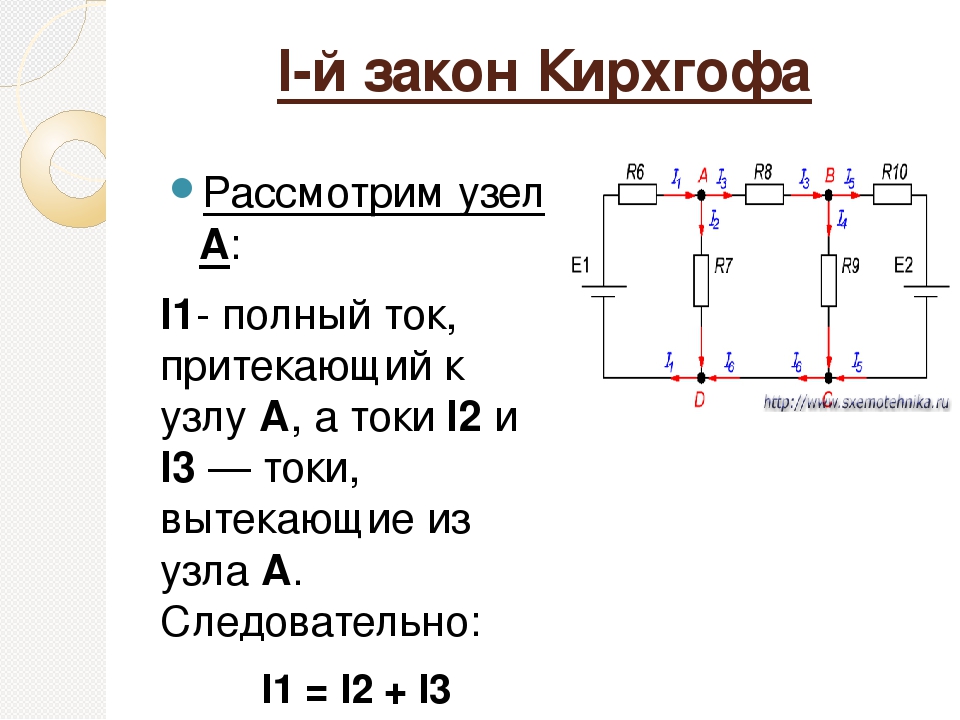 А пока вкратце.
А пока вкратце.
Узел – это место соединения трех и более ветвей в электрической цепи (в данном случае таких узлов два. Это узлы «a» и «b».
Ветвь – это участок электрической цепи, который образуется одним или несколькими последовательно соединенными элементами и через все эти элементы протекает один и тот же ток.
Рисунок 8 — Ветви электрических цепей
Контур – это любой замкнутый путь электрической цепи, проходящий по двум или нескольким ветвям.
Рисунок 9 — Схема электрической цепи с введенными обходами контуров
Так же есть такое понятие как независимый контур.
Независимый контур должен включать в себя хотя бы одну ветвь, не входящую в другие контуры.
На рисунке 9 будет три контура, два из которых независимые. Если контур 1 независимый, контур 2 независимый(таким образом все три ветви этой схемы цепи вошли в эти независимые контуры). Тогда контур 3 уже независимым не будет, поскольку все ветви “заняты” остальными двумя контурами.
Или если контур 1 независимый (он включает в себя ветви с элементами E и R1). Контур 3 независимый (он включает в себя ветви с элементом E и ветвь с элементом R3. Элемент R3 ранее не входил в первый независимый контур), поэтому контур 3 считается независимым.
Получается, что все ветви “заняты”. Тогда контур 2 независимым уже не будет, поскольку в него не входят ветви или ветвь ранее не входящую в другие контура. Все ветви вошли в ранее независимые контуры 1 и 3.
В цепи на рисунке 9, в общем случае, три ветви, два узла и два независимых контура. Общее количество уравнений по законам(правилам) Кирхгофа составляется столько, сколько ветвей в схеме цепи за вычетом количества ветвей, где есть источник тока (именно источник тока, а не ЭДС). В нашей схеме нет источников тока, следовательно, составляются три уравнения по законам Кирхгофа. Теперь осталось определить, сколько уравнений нужно составить по первому и второму законам Кирхгофа. Общее количество уравнений будет три. Формула для определения количества уравнений по первому закону Кирхгофа следующая:
Формула для определения количества уравнений по первому закону Кирхгофа следующая:
N1з.к.=Ny-1, где Ny – количество узлов.
Ny=2, тогда
N1.з.к.=Ny-1=2-1=1
Т. е. по первому закону Кирхгофа составляется одно уравнение для данной цепи, а общее количество уравнений – три. Таким образом, мы получаем, что по второму закону Кирхгофа нужно составить два уравнения. Или для определения количества уравнений по второму закону Кирхгофа есть формула:
N2.з.к.=Nв-(Ny-1), где Nв – количество ветвей
Nв=3, тогда:
N2.з.к.=3-(2-1)=2
По второму закону Кирхгофа составляется два уравнения. Составим систему, состоящую из трех уравнений. Одно уравнение по первому закону Кирхгофа (это уравнение составляется для любого узла a или b) и двух уравнений по второму закону Кирхгофа для двух любых независимых контуров, например, составим для контуров 1 и 2.
Рисунок 10 — Система уравнений для схемы цепи, изображенной на рисунке 9
Неизвестными в данной системе являются токи I1, I2 и I3.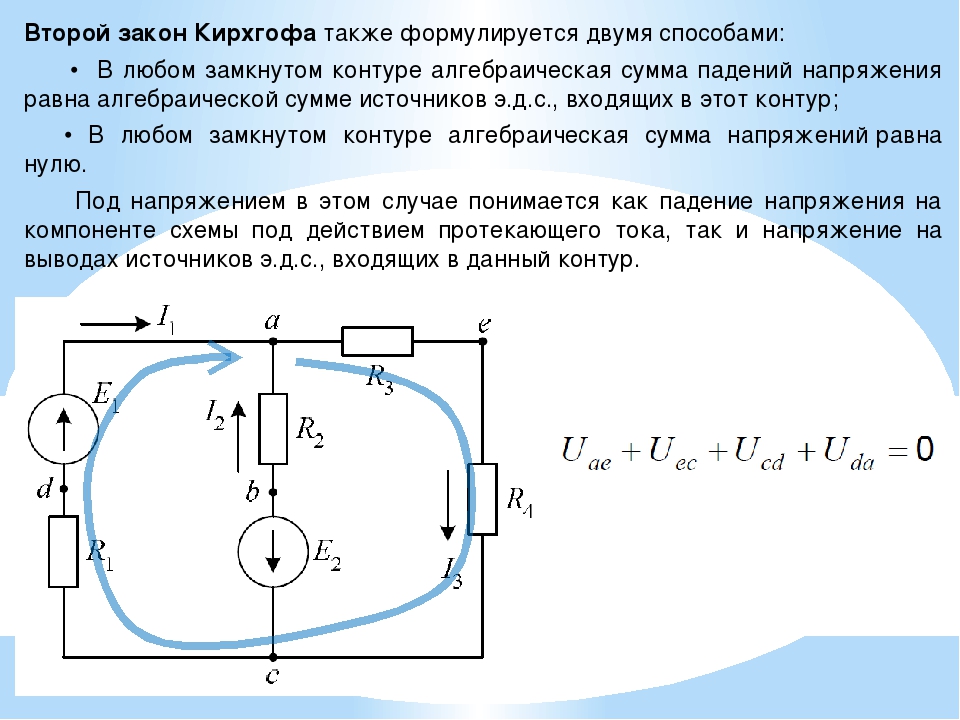 Решая данную систему, находят эти неизвестные.
Решая данную систему, находят эти неизвестные.
О том, как решаются задачи с более сложными цепями, мы поговорим в следующих статьях.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток — простыми словами;
Законы Кирхгофа простыми словами: определения и формулы
По всем проводникам, которые являются частью электрической цепи, протекает электрический ток. При проведении расчётов не редкостью являются случаи, когда необходимо вычислить параметры тока и напряжения в цепях сложной формы, то есть в тех, где имеются разветвления. Для получения точных расчётов применяют правила Кирхгофа, которые иногда называют законами. Используя их вместе с законами Ома, можно с легкостью определять параметры независимых контуров в самых разветвленных и сложных цепях.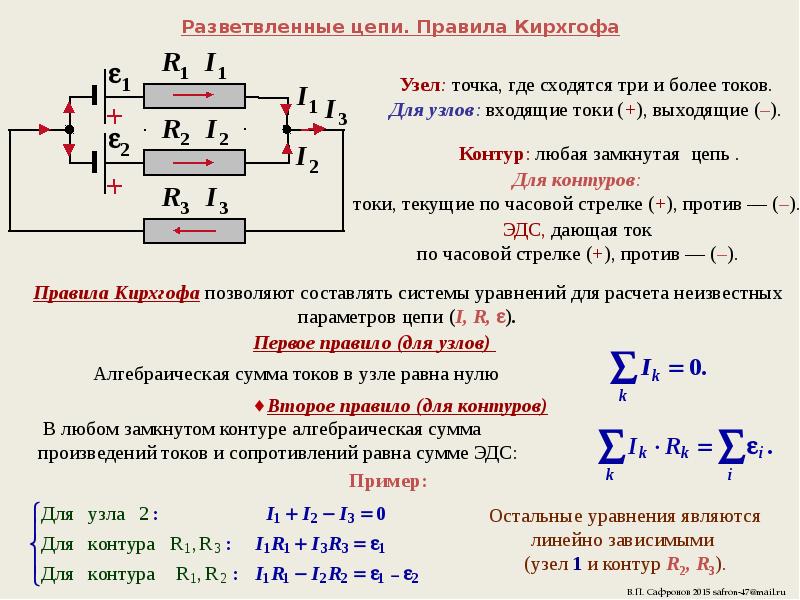 Важным преимуществом данных законов является то, что не нужно использовать глубокие расчёты, благодаря приведенным алгоритмам посчитать сможет даже неопытный физик, сложные и многоуровневые расчёты превращаются в простые односложные сложения.
Важным преимуществом данных законов является то, что не нужно использовать глубокие расчёты, благодаря приведенным алгоритмам посчитать сможет даже неопытный физик, сложные и многоуровневые расчёты превращаются в простые односложные сложения.
Закон Кирхгофа своими словами, кратко и понятно для чайников
История возникновения закона начинается с первого упоминания немецкого учёного Кирхгофа в XIX веке. В этот период в стране проходили репрессии, остро ощущалась нехватка новых технологий. Учёные искали решения, способные ускорить развитие промышленности. Вышеупомянутый учёный занимался исследованиями в области электричества. Он точно осознавал, что будущее за технологиями. Однако была проблема: как провести точные математические вычисления в цепях сложной формы. Тогда и возник закон.
К узлу подходят два провода, в то время как отходит всего один. Значение тока, который протекает по направлению от узла, равняется сумме протекающего по оставшимся двум проводникам, иными словами, идущим к нему.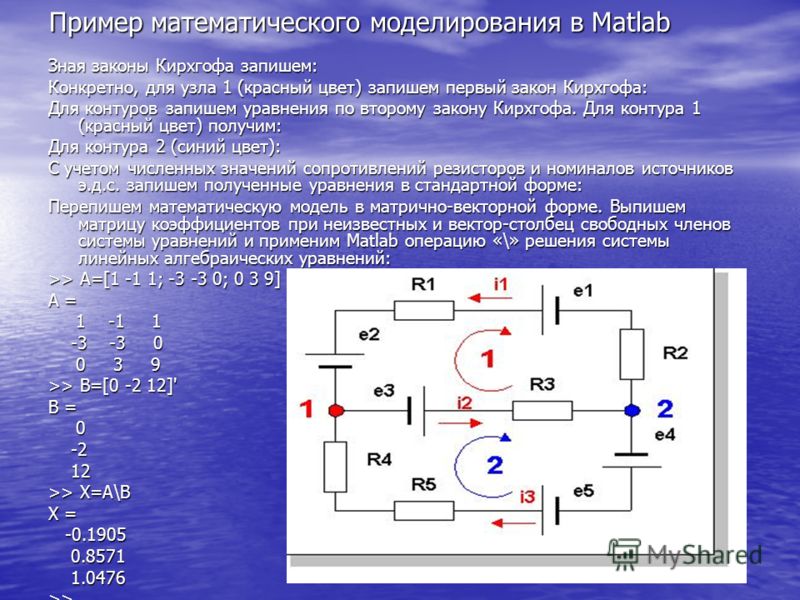 Правило, о котором идёт речь в статье, даёт понятное объяснение тому, что в противном случае происходило бы накопление заряда, однако такого никогда не бывает. Каждый физик на практике знает, что любую сложную цепь можно разделить на небольшие участки.
Правило, о котором идёт речь в статье, даёт понятное объяснение тому, что в противном случае происходило бы накопление заряда, однако такого никогда не бывает. Каждый физик на практике знает, что любую сложную цепь можно разделить на небольшие участки.
Возникает другая сложность: трудно определить путь, по которому он проходит. Более того, важно понимать, что на различных участках сопротивления разные, а из этого следует, что энергия будет распределяться неравномерно.
Первый закон Кирхгофа: определение
Первый закон, или, как он известен некоторым, правило, Густава Кирхгофа был выведен на основании другого закона – сохранения заряда. Как уже было упомянуто раннее, физик осознавал, что в узле надолго заряд задержаться не сможет, так как распределится по ветвям контура, которые образуют эти соединения.
Важно! У Кирхгофа было предположение, которое он впоследствии сумел доказать, благодаря проведенным экспериментам, что количество зарядов, оказавшихся в узле, равняется количеству тока, вытекающего из него.
Схема первого закона Кирхгофа
На рисунке показана схема, состоящая из нескольких контуров. Все части рисунка подписаны. Итак, закон № 1 утверждает, что сумма токов в любом узле абсолютно любой электрической цепи равняется нулю. Согласно правилу, входящий ток равен сумме выходящих, поэтому I1 = I2 + I3. Узлами сети называются такие участки, в которых соединяются несколько проводников. Ток, который оказывается в узле, обозначается стрелкой, направленной к узлу, в то время вытекающий ток – стрелкой от узла. Таким образом, обозначение воспринимается проще в любой задаче.
Наглядно это показано на картинке.
Первый закон Кирхгофа
На основании вышесказанного запишем уравнение первого закона ученого:
I1 + I2 − I3 − I4 − I5 = 0
Эта же формула может быть записана в более сокращенном виде:
I1 + I2 = I3 + I4 + I5
Важно! Положительные или же противоположные – отрицательные – знаки токам присвоены в условном порядке.
Их можно поменять, значение не поменяется.
Для примера разберём схему, изображённую на картинке выше.
Источник питания может быть абсолютно любой природы, им могут быть пальчиковые батарейки или же полноценный блок питания с возможностью регулировки. Итак, следуя первому закону, верным будет уравнение:
I1 − I2 − I3 = 0 или же I1 = I2 + I3
Чтобы продолжить измерения, необходимо в место на схеме, где указан амперметр, подключить мультиметр, который покажет, что закон полностью работает.
Формула для электрической и магнитной цепи
При проведении расчётов используют вышеупомянутые законы.
Первый закон для магнитных цепей вытекает из принципа непрерывности магнитного потока, который известен ещё из курса физики.
Второй же закон, если разобрать по частям, понятно, является иной формой записи закона полного тока. Прежде чем записать уравнения, необходимо в любом порядке остановить свой выбор на положительном направлении потоков в ветвях, аналогичное действие необходимо провести с напряжением обхода контуров. Если направление магнитного потока на определённом участке совпадает с направлением обхода, то магнитное напряжение на этом участке будет положительным, если же оно определяется как противоположное, то значение будет отрицательным.
Если направление магнитного потока на определённом участке совпадает с направлением обхода, то магнитное напряжение на этом участке будет положительным, если же оно определяется как противоположное, то значение будет отрицательным.
Схожий случай, если МДС совпадает с направлением обхода, тогда знак положительный, в противном случае – отрицательный.
Закон для магнитных цепей
Для примера рассмотрим схему. Левая ветвь пусть будет первой, все относящиеся к ней величины будут записаны с индексом 1. Средняя весть будет второй, и величины получат индекс 2. Соответственно, величины правой ветви – индекс 3.
В произвольном порядке выберем направление потоков в ветвях. Предположим, что направление всех потоков будет вверх. Следуя первому закону, необходимо составить для каждого узла цепи уравнение. В цепи всего два узла, соответственно, составим всего одно уравнение:
Ф1 + Ф2 + Ф3 = 0
Далее используем второй закон Кирхгофа, по которому нужно составить столько уравнений, сколько ветвей, не учитывая числа уравнений, составленных по первому закону.
Итак, запишем уравнения. Первое будет предназначено для контура, образованного первой и второй ветвями, второе – для контура, который будет образован первой и третьей ветвями.
Перед тем как составлять уравнения по второму закону, нужно выбрать положительное направление обхода контуров. Контуры будем обходить по часовой стрелке.
Итак, итоговое уравнение имеет вид:
H1l1 + Hδ1δ1 − H2l2 − Hδ2δ2 = I1w1 − I2w2
В левую часть уравнения были включены слагаемые со знаком плюс, потому что на первом участке поток направлен соответственно обходам контура, а слагаемые – с отрицательным знаком, потому что поток направлен в противоположную обходу контура сторону.
Второй закон Кирхгофа: определение
Второй закон вызывает у многих вопросы, так как он несколько труднее первого, но этот миф легко можно развеять, объяснив принцип работы. Для начала необходимо разобрать определение закона, который звучит таким образом: в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех пассивных элементах цепи.
Для начала необходимо разобрать определение закона, который звучит таким образом: в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех пассивных элементах цепи.
Формулировка определения несколько затрудняет его понимание, поэтому можно упростить: сумма ЭДС в замкнутом контуре равняется сумме падений напряжений. Так намного проще и понятнее.
Закон напряжения и формула для магнитной цепи
Формула, которая выражает этот закон, примет такой вид:
Формула второго закон Кирхгофа
В качестве примера возьмём самый элементарный и понятный для всех случай. Нам понадобится взять батарейку и резистор – всё в одном экземпляре. Так как резистор в единичном количестве, так же как и батарейка, то ЭДС батарейки будет равняться 1,5 ватт, и это равно падению напряжения на резисторе.
Если для примера взять уже два резистора и подключить их к батарейке, то 1,5 ватт будут распределяться равномерно на обоих резисторах, то есть на каждом окажется по 0,75 ватт. Если взять уже три резистора по 1 кОм, то падение напряжения будет на них уже по 0,5 ватт. Логика расчётов сохраняется в любом случае. Формула примет вид:
Если взять уже три резистора по 1 кОм, то падение напряжения будет на них уже по 0,5 ватт. Логика расчётов сохраняется в любом случае. Формула примет вид:
| Формула | Е1 = IR1 + IR2 + IR3 |
| Преобразование | 1,5 Вт = 0,5 Вт + 0,5 Вт + 0,5 Вт |
| Итог | 1,5 Вт = 1,5 Вт |
Важно! Второй закон будет работать независимо от того, сколько использовано источников питания и нагрузок. Не влияет на расчёты и место их расположения в контуре схемы. Так что даже у разных схем решение может быть одинаковым, но должно быть соблюдено условие – количество элементов должно быть идентичным.
Закон Кирхгофа для теплового излучения
Данный закон имеет другое название «третий закон». Сперва для лучшего понимания введем понятие теплового излучения. Принято называть тепловым излучение электромагнитное излучение, возникающее благодаря чужеродной энергии вращательного и колебательного движения атомов, молекул. Данное явление можно обнаружить абсолютно у всех тел, имеющих температуру не равняющуюся нулю или меньше. Основной количественной характеристикой теплового излучения выступает энергетическая светимость. Она должна быть вычислена одной из первых или же указана в условиях. Рассчитать её самостоятельно весьма проблематично. Её значение не постоянное, оно может меняться в зависимости от определенных характеристик: оказывает влияние температура окружающей среды, а также уровень нагретости тела. Имеет значение и длина, чем длиннее — тем значение меньше.
Данное явление можно обнаружить абсолютно у всех тел, имеющих температуру не равняющуюся нулю или меньше. Основной количественной характеристикой теплового излучения выступает энергетическая светимость. Она должна быть вычислена одной из первых или же указана в условиях. Рассчитать её самостоятельно весьма проблематично. Её значение не постоянное, оно может меняться в зависимости от определенных характеристик: оказывает влияние температура окружающей среды, а также уровень нагретости тела. Имеет значение и длина, чем длиннее — тем значение меньше.
Формула выглядит таким образом:
R = E/(S·t), [Дж/(м2с)] = [Вт/м2]
Ещё одной характеристикой остаётся спектральная плотность энергетической светимости.
Важно ввести ещё одно понятие: коэффициент поглощения – это отношение поглощенной телом энергии к падающей энергии. Только теперь перейдем непосредственно к выделенному закону. Первое, что нужно сказать, что тепловое излучение является равновесной величиной. Это указывает на то, что сколько энергии будет излучаться телом, столько и им же и поглотится. При расчётах данное заявление имеет существенное значение. Можно сразу приравнивать оба значение. Таким образом, для трёх тел, которые находятся в замкнутой полости, формула примет вид:
Это указывает на то, что сколько энергии будет излучаться телом, столько и им же и поглотится. При расчётах данное заявление имеет существенное значение. Можно сразу приравнивать оба значение. Таким образом, для трёх тел, которые находятся в замкнутой полости, формула примет вид:
Закон для теплового излучения
Раннее указанная формула будет верной даже тогда, когда какое-либо тело из указанных будет АЧ:
Закон звучит данным образом: отношение спектральной плотности энергетической светимости тела к его монохроматическому коэффициенту поглощения (при определенной температуре и для определенной длины волны) не зависит от природы тела и равно для всех тел спектральной плотности энергетической светимости при тех же самых температуре и длине волны.
Законы Кирхгофа в комплексной форме
Итак, для того, чтобы вывести математическую формулировку первого закона в комплексной формуле, необходимо представить все синусоидальные токи в комплексных значениях. Формула примет данный вид:
Комплексная форма первого закона Кирхгофа
Расшифровывая формулу получим, что алгебраическая сумма комплексных значений токов всех ветвей, которые сходятся в узле цепи, будет равняться нулю.
Закон №2 сформулирован не менее просто. Для контура замещения, который содержит лишь неактивные элементы и источники ЭДС, в каждую секунду алгебраическая сумма напряжений на данных элементах контура равняется числовой сумме ЭДС. Некоторым может показаться данная формулировка трудной, но при реальном разборе станет ясно, что все весьма просто и элементарно:
Комплексная форма второго закона Кирхгофа
Например, рассмотрим рисунок. Для выбранного на схеме замещения контура 1
u1-u2-u3+u4=0
Для второго контура:
ur-uL=e1-e2
В комплексной записи закон выглядит таким образом:
Контур 1
Контур 2
Задачи и примеры на законы Кирхгофа с решением
На картинках ниже подробно разобраны 2 задачи с применением законов Кирхгофа. Полное решение с наглядным примером на схемах и ответ.
Пример решения задачи по законам Кирхгофа
7.2. Порядок решения задач на законы Кирхгофа
1. Нарисовать схему
Нарисовать схему
цепи. На рисунке выбрать и показать
направления токов на всех участках
цепи, при этом надо учесть, что в узел
токи не могут только входить или только
выходить из узла. Это следует из первого
закона Кирхгофа.
2. Выбрать замкнутые
контуры обхода для применения второго
закона Кирхгофа. Показать на рисунке
направление обхода по контуру. Контуров
может быть несколько. Число независимых
уравнений, которые можно составить по
второму закону Кирхгофа, меньше чем
число контуров. Чтобы составить
необходимое число независимых уравнений
надо придерживаться следующего правила:
Выбирать контуры так, чтобы в каждый
новый контур входил хотя бы один участок
цепи, которого бы не было нив одном ранее
рассмотренных контуров.
3.
Используя первый закон Кирхгофа можно
написать ( n
– 1) уравнений, где n—
число
узлов в
рассматриваемой цепи.
4.
Воспользоваться вторым законом Кирхгофа
и записать такое число уравнений, чтобы
число уравнений, составленных по первому
и второму законам Кирхгофа, равнялось
числу неизвестных величин в задаче.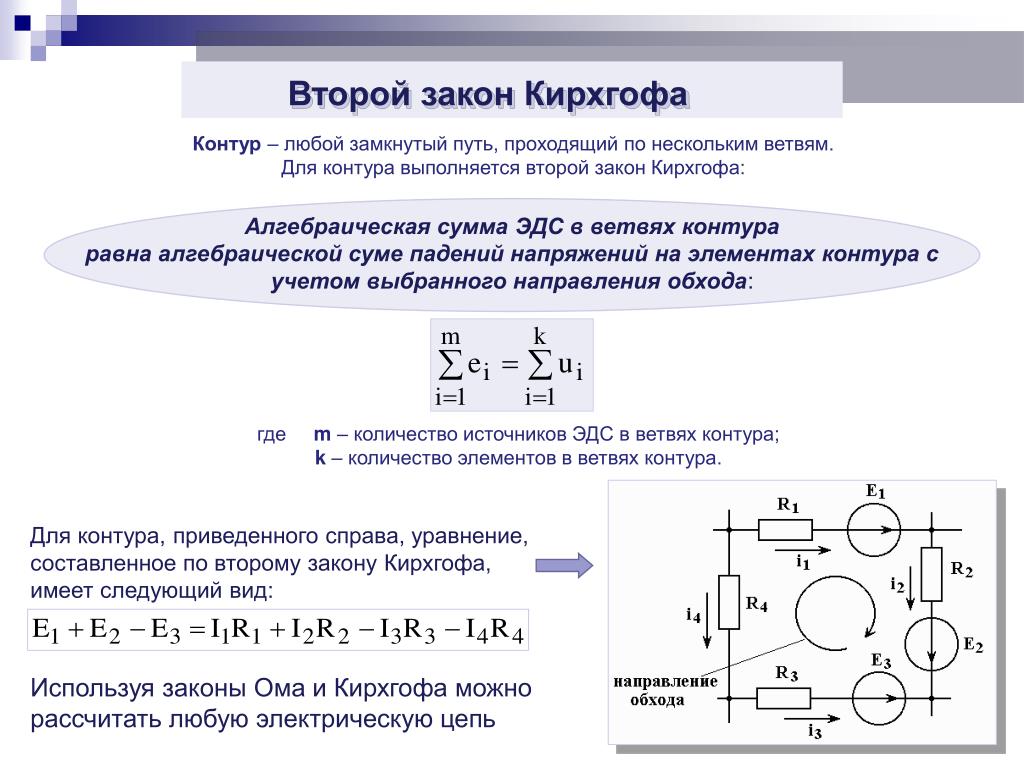 При
При
этом надо учитывать следующее правило
знаков: падение напряжения на каждом
участке записывается со знаком «+», если
направление обхода по этому участку
совпадает с направлением тока на нем.
И наоборот, если обход совершался по
этому сопротивлению обратно направлению
тока, то ставится знак « – ».
ЭДС записывается
со знаком «+» в том случае, когда
направление обхода совпадает с
направлением поля сторонних сил в
источнике тока и наоборот.
Поле сторонних
сил внутри источника всегда направлено
от отрицательного полюса к положительному.
5. Решить полученную
систему уравнений и найти искомые
величины.
В результате
решения полученной системы уравнений
определяемые величины могут получаться
отрицательными. Отрицательное значение
тока указывает на то, что фактическое
направление тока на данном участке цепи
обратно тому, которое мы выбрали.
7.3. Примеры решения задач на законы Кирхгофа
П
р и м е р 1.
Два
элемента с одинаковыми ЭДС e1
= e2
= 2В и внутренними сопротивлениями r1
= 1 Ом, r2
= 2 Ом замкнуты на внешнее сопротивление
R.
Через первый элемент течет ток I1
= 1 А. Найдите сопротивление R,
ток I2,
текущий через второй элемент, и ток
I,
текущий через сопротивление R.
Схема соединения показана на рисунке.
Дано:
e1
= e2
= 2 D;
r1
= 1 Ом;
r2
= 2 Ом;
I1
=
1 A
________
Найти:
I2
=? R=?
I=?
Решение:
1.Выберем
направления токов на всех участках цепи
так, как показано на рисунке. Видим, что
в узлах 1 и 2 есть входящие и есть выходящие
токи, значит, направления токов выбраны
разумно.
2. Выберем контуры
обхода и покажем направления обхода по
ним. Контуров выбрали два и нарисовали
направления обхода по ним.
3. Составим
уравнение, используя первый закон
Кирхгофа. Узлов два, поэтому можно
составить только одно уравнение, например
для первого узла:
I1
+ I2
— I
= 0.
Токи, входящие в
узел, пишем со знаком «+», а выходящие
с знаком»–». Уравнение для второго
узла будет тождественно первому.
4.
Применим второй закон Кирхгофа для
первого контура обхода. Падение напряжения
на всех участках этого контура пишем
со знаком «+», т.к. направление обхода
на всех участках совпадает с направлением
тока на этих участках
Uå
= IR
+I1
r.
В
этот контур входит только один источник
тока e1,
и направление обхода по контуру совпадает
с направлением поля сторонних сил, т.к.
силы этого поля направлены от отрицательного
полюса к положительному, т.е. вниз.
Запишем уравнение
IR
+ I1r1
= e1.
Для
второго контура, рассуждая аналогично,
получим
U2
= +I2r2
+ IR.
ЭДС будет входить в уравнение также со
знаком «+».
Второе
уравнение имеет вид:
I2R2
+ IR
= e2.
5. Получили систему
из трех уравнений с тремя неизвестными.
Решая
систему, находим величину тока
I2
.
Полный
ток через сопротивление R
равен сумме токов
I
= I1
+ I2
= 1,5 A.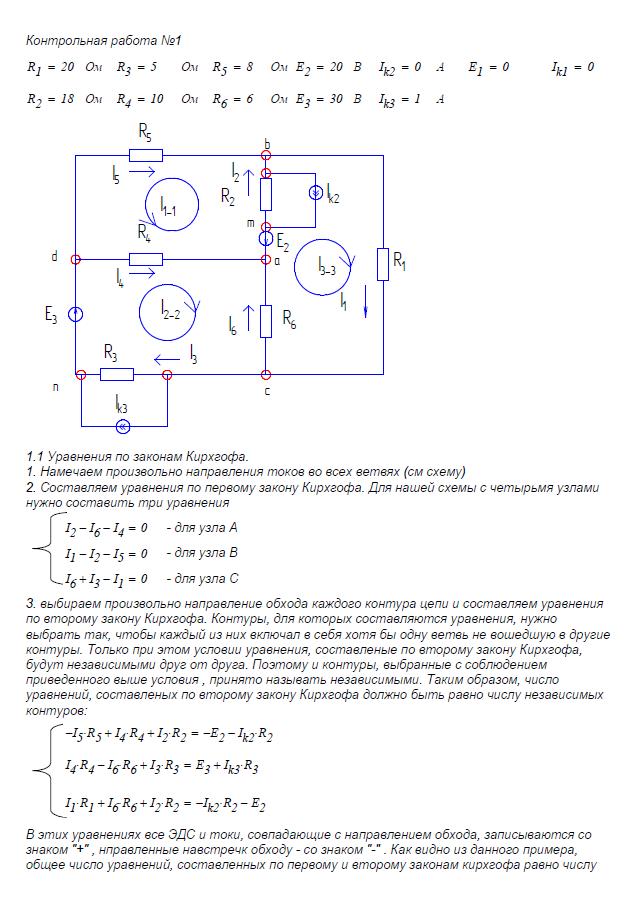
Сопротивление
R
находим из одного из уравнений системы:
.
Ответ:
ток через второй источник равен I2
= 0,5 А, суммарный ток
I
= I1
+ I2
= 1,5 А. Внешнее сопротивление R
= 0,66 Ом.
П р и м е р 2.
Два
одинаковых элемента имеют ЭДС e1
= e2
= 2 В и внутренние сопротивления r1
= r
2 = 0,5 Ом.
Найдите токи I1
и I2,
текущие через сопротивления R1
= 0,5 Ом и R2
= 1,5 Ом, а также ток I
через первый элемент. Схема заданной
цепи изображена на рисунке.
Дано:
e1
= e2
= 2 В;
r1=r2=0,5
Ом;
R1
=
0,5 Ом;
R2
= 1,5 Ом
I1
– ?
I2
– ?
I
– ?
Решение:
1. Выберем направления
Выберем направления
токов на всех участках так, как показано
на рисунке. Видим, что в узлах 1 и 2 есть
входящие и есть выходящие токи, значит,
направления токов выбраны верно.
2. Выберем два
контура обхода: большой и малый. Укажем
направления обходов по контурам. Контуров
обхода в заданной цепи можно выбрать
три, но для нахождения трех неизвестных
величин достаточно трех уравнений.
Узлов всего два, поэтому можно составить
только одно уравнение, применяя первый
закон Кирхгофа. Недостающих два уравнения
составим используя второй закон Кирхгофа.
3. Для первого узла
запишем:
I2
+ I1
– I
= 0.
4. Учитывая правила
определения знаков всех слагаемых при
применении второй закон Кирхгофа для
большого контура, получаем уравнение:
I
r1
+ I2r2
+ I2R2
= e1
+ e2.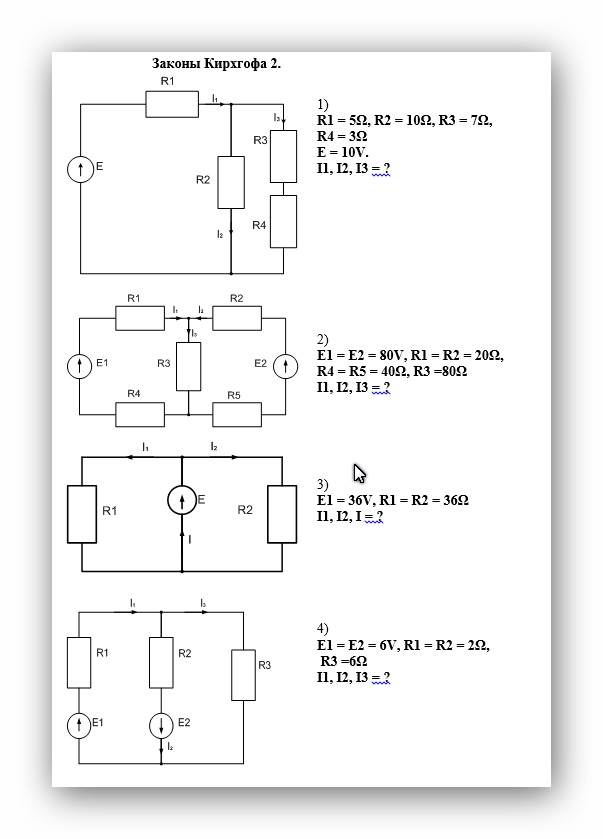
Для малого контура:
I
r1
+ I1R1
= e1.
5.Получили
систему из трех уравнений с тремя
неизвестными величинами I1;
I2
и I.
Решать
систему линейных уравнений можно разными
способами. В случае, когда система
состоит из большого числа уравнений
удобно пользоваться методом Крамера
(методом определителей). Проиллюстрируем
применение этого метода решения на
нашей системе уравнений. Для этого
перепишем систему ещё раз:
или
в численном виде;
если поделить правую и левую части
второго и третьего уравнении на « 0,5»
получим
Искомые
величины токов по методу определителей
находятся следующим образом:
и
,
где
определители
—
определитель системы уравнений,
и
-определители,
которые получаются заменой соответствующих
столбцов определителя
столбцами,
полученными из свободных членов уравнений
образующих систему (с учетом заданных
числовых значений). Запишем эти
Запишем эти
определители:
По приведенным
выше формулам, получаем
и
.
Значение третьего
тока можно найти аналогичным способом,
но проще его значение получить из первого
уравнения нашей системы:
I2
+ I1
– I
= 0
или
I
= I2
+ I1
= 1,33 + 1,33 = 2,66 А
Знаки
у всех полученных значений силы тока
положительные, это свидетельствует о
том, что при произвольном выборе
направлений токов, указанных на рисунке,
все направления токов были выбраны
правильно.
Ответ:
I1
= 1,33 А
; I2
=
1.33 А;I
= I1
+ I2
= 2.66 А.
П
р и м е р 3.
Два
элемента с одинаковыми ЭДС 1
= 2
= 2В и внутренними сопротивлениями r1
= 1 Ом, r2
= 2 Ом замкнуты на внешнее сопротивление
R.
Через элемент с ЭДС 1
— течет ток I1
= 1 А. Найти сопротивление R
и ток I2,
текущий через элемент с ЭДС 2.
Какой ток течет через сопротивление R.
Схема соединения показана на рисунке.
Д
ано:
1
= 2
= 2 D;
r1
= 1 Ом;
r2
= 2 Ом;
I1
= 1 A
__________
+I2
— ?
R
— ? I
— ?
Выберем
направления токов на всех участках
цепи. Видим, что в узлах 1 и 2 есть входящие
и есть выходящие токи, значит, направления
токов выбраны разумно.
Выберем контуры
обхода и покажем направления обхода по
ним.
Составим уравнение,
используя первый закон Кирхгофа для
первого узла:
I1
+ I2
— I
= 0.
Токи,
входящие в узел, пишем со знаком «+»,
а входящие с «–». Всего можно
написать одно уравнение, т.к. второе
будет тождественно первому.
Воспользуемся
вторым законом Кирхгофа. Запишем
уравнение для первого контура обхода.
Падение напряжения на всех участках
1-го контура напишем со знаком «+», т.к.
направление обхода на этих участках
совпадает с направлением тока
U
= IR
+I1
r.
В
этот контур входит только ЭДС 1,
и направление обхода по контуру совпадает
с направлением поля сторонних сил, т.к.
силы этого поля направлены от отрицательного
полюса к положительному.
Запишем уравнение
IR
+ I1r1
= 1.
Для
второго контура U2
= +I2r2
+ IR.
И ЭДС будет входить в уравнение также
со знаком «+».
Запишем
уравнение
I2R2
+ IR
= 2.
Получим систему
из трех уравнений с тремя неизвестными.
Решая систему,
получаем
.
Полный
ток через сопротивление R
равен сумме токов
I
= I1
+ I2
= 1,5 A.
Сопротивление
R
находим из одного из уравнений
.
Ответ.
Ток через второй источник равен I2
= 0,5 А, суммарный ток
I
= I1
+ I2
= 1,5 А. Внешнее сопротивление R
= 2/3 Ом.
П р и м е р 4.
Два
одинаковых элемента имеют ЭДС 1
= 2
= 2 В и внутренние сопротивления r1
= l2
=0,5 Ом. Найти токи I1
и I2,
текущие через сопротивления R1
= 0,5 Ом и R2
= 1,5 Ом, а также ток I
через элемент с ЭДС. Схема изображена
Схема изображена
на рисунке.
Д
ано:
1
= 2
= 2 В;
r1
= r2
= 0,5 Ом;
R1
= 0,5 Ом;
R2
= 1,5 Ом
_____________
I1
— ?
I2
— ?
I
— ?
Решение:
Выберем
направления токов на всех участках.
Запишем первый закон Кирхгофа для 1-го
узла
I2
+ I1
= I
.
Выберем
большой и малый контуры обхода. Для
большого контура уравнение будет иметь
вид:
Ir1
+ I2r2
+ I2R2
= 1
+ 2.
Для малого контура
Ir1
+ I1R1
= 1.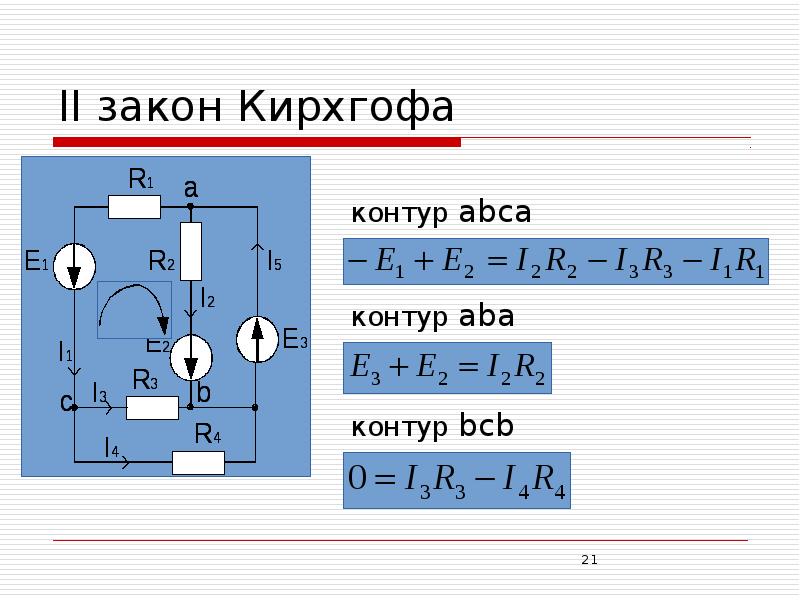
Получили три
уравнения
В
эти уравнения входят три неизвестных
величины I1;
I2
и I.
Решаем систему уравнений и находим
I1
= 2,28 А ; I2
= 0,56 А;I
= I1
+ I2
= 1,72 А.
как они проявляются в работе электромагнитной цепи, примеры расчета
Считается, что каждый образованный человек должен обладать минимальными знаниями физики, например, знать закон Ома.
Но знать закон Ома мало, ведь вокруг нас действует гораздо больше. Ученый из Германии Г. Кирхгоф, занимавшийся рядом естественных наук, вывел закон, по которой сегодня работают все электрические цепи.
Закон Кирхгофа объясняют, как распределяется ток на контуре цепи. Поговорим о правилах, которые вывел немецкий учёный.
Первое правило
В первом определении закона Кирхгофа описано, что общее суммирование токов, проходящим по веткам, равняется 0. Постоянство токов объясняется тем, что неважно, сколько токов втекает в узлы пересечения — такое же количество будет вытекать.
Постоянство токов объясняется тем, что неважно, сколько токов втекает в узлы пересечения — такое же количество будет вытекать.
Точку в соединении ветвей обозначают как узел в электрической цепи. В каждой ветке на своё сопротивление есть свой ток.
Эта формула соответствует тем электрическим цепям, где ток считается постоянным.
Когда закон Кирхгофа применяется для цепи, где ток считается переменным, используется I, обозначающее мгновенное напряжение.
Формула производится в форме комплекса, но расчёт при этом не изменится:
Благодаря такому подходу к расчётам учитывается реактивные и активные значения, присутствующие в цепи.
Второе правило Кирхгофа
Первое правило закона Кирхгофа существует для описания распределения тока среди веток цепи.
Второе правило Кирхгофа описывает, что суммарное падение напряжения будет равно суммарному количеству электродвижущих сил.
Это значит, что электродвижущие силы, воздействующие на определённые места в цепи, распределятся пропорционально сопротивлению. Об этом говорится в законах Ома.
Об этом говорится в законах Ома.
Для переменного тока суммарное количество электродвижущих сил будет равна сумме падений напряжений в ветках электрической цепи.
В формуле Z означает абсолютное сопротивление, включающее реактивную и резистивную элементы, зависящие от частоты переменного тока. Формула суммы сопротивления и индуктивности:
Более наглядно данная формула может выглядеть следующим образом:
При этом:
Какими могут быть варианты расчёта правила Кирхгофа
Теперь рассмотрим, как можно применять описанные правила в жизни. Выбрав направления обходов контура Вы сможете верно разместить знаки в формуле. Рассмотрим следующий вариант:
Выберем путь, идущий параллельно стрелке часов, отметим на примере:
Пунктиром мы обозначили, как будет проходить ток в схеме.
Далее составим само уравнение закона Кирхгофа согласно правилам, сначала по второму.
Перед ЭДС ставим минус, если сила будет двигаться против часовой стрелки.
Для всех контуров используются свои знаки.
При первом контуре сила будет совпадать с направлением контура. Первый будет выглядеть так:
Второе будет выглядеть так:
Третий будет выглядеть так:
Напряжение зависит от направления. По часовой стрелке значения будут положительными. Против часовой стрелки значения будут отрицательными.
Обход контура является своего рода условным значением, который нужен для того, чтобы правильно поставить знаки в формулах. На правильность вычисления это значение не влияет. Иногда это может затруднить расчёт в целом, но скорее всего значение останется то же.
Теперь посмотрим на эту цепь:
В этой схеме у электродвижущей силы четыре источника. Не забудьте сначала выбрать направление контура.
Составляем формулу по первому рассмотренному закону. Начальный узел рассчитывается следующим образом:
Второй будет таким:
Третий таким:
Узла 4, но уравнения при этом 3, и эти цифры не являются ошибкой. Число формул согласно первому правилу выглядит так:
Число формул согласно первому правилу выглядит так:
Так, уравнений будет на одно меньше, чем узлов, и при этом все токи будут описаны.
Строим формулы по второму закону Кирхгофа. Первый контур будет выглядеть так:
Второй контур будет таким:
Третий контур вычисляется следующим образом:
Подставляя значения из реальной жизни Вы сможете убедиться, что все эти законы действующие и правильные. Примеры к закону Кирхгофа, о которых мы рассказали, достаточно лёгкие, задачи из жизни бывают гораздо сложнее.
При вычислении путём применения данных правил главным образом нужно следить за тем, куда направлен ток и как обходит контур, чтобы подставить в уравнение правильные значения.
Действие правил и закона Кирхгофа в электромагнитной цепи
Расчёты магнитных цепей необходимы для вычислений верных значений. Расчёт будет тем же, но числа изменятся.
МДС, или магнитная движущая силы, определена витками в катушке и проходящее через них электричество:
МДС является множителем поля и тока.
Можно провести вычисление через сопротивление:
В этих формулах средняя длина участок цепи и проницаемость магнита разделены. Для магнитной цепи формула будет выглядеть следующим образом:
Через узел общее число магнитного потока будет равно нулю.
Сумма магнитной движущей силы в контуре равно сумме напряжения магнита.
Магнитный поток можно высчитать следующим образом:
А переменное поле магнита рассчитывается так:
Применяя эти знания на практике, посмотрим на следующий вариант контура.
Математическая формула будет следующей:
При наличии зазора рисунок будет выглядеть так:
Сопротивление магнитного потока будет вычисляться согласно описанным законам:
Сопротивление в зазоре будет таким:
Лучше понять всё написанное помогут наглядный урок по закону Кирхгофа от ведущего эксперта и профессора в области физики. Для того, чтобы разобраться в написанном и понять происходящее, советуем посмотреть данный урок:
Правила Кирхгофа» data-lazy-type=»iframe» data-src=»https://www.youtube.com/embed/-dGngUpT2xA?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Учёные веками вносили неоценимый вклад в развитие науки и объяснения жизни вокруг нас, это касается и Г. Кирхгофа.
Благодаря его правилам и выведенному закону можно рассчитать многие значения в электрической цепи. Пользуйтесь ими, чтобы легко проводить расчёты!
Законы Кирхгофа — формулы и примеры использования
Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач.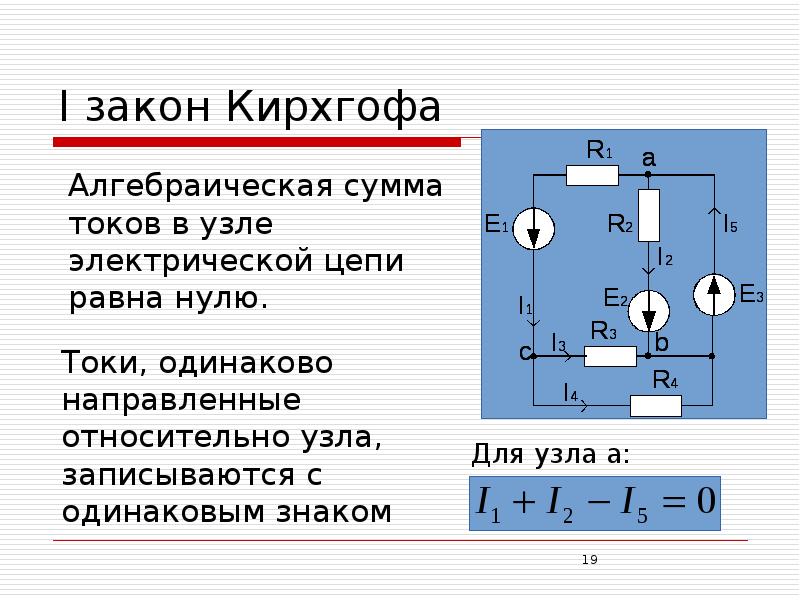 Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.
Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.
Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.
где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0
Рис. 1
В этом уравнении токи, направленные к узлу, приняты положительными.
Физически первый закон Кирхгофа – это закон непрерывности электрического тока.
Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.
Рис. 2
Так, для замкнутого контура схемы (рис. 2) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4
2) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4
Замечание о знаках полученного уравнения:
1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;
2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.
Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.
Расчет разветвленной электрической цепи с помощью законов Кирхгофа
Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.
Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b, следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.
Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только (y – 1) уравнений являются независимыми друг от друга.
Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b — (y — 1) = b — y +1.
Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.
Составим систему уравнений Кирхгофа для электрической цепи (рис. 3). Схема содержит четыре узла и шесть ветвей.
Поэтому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3, также три уравнения.
Произвольно выберем положительные направления токов во всех ветвях (рис. 4). Направление обхода контуров выбираем по часовой стрелке.
Рис. 3
Составляем необходимое число уравнений по первому и второму законам Кирхгофа
Полученная система уравнений решается относительно токов.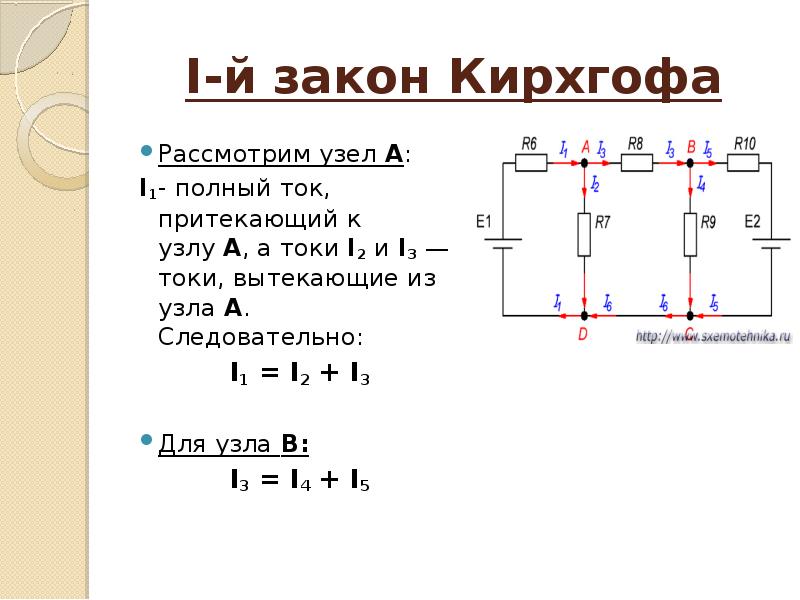 Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.
Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.
Потенциальная диаграмма – это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях. Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми.
Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.
Рис. 4. Контур для построения потенциальной диаграммы
Потенциал любого узла принимаем равным нулю (например, ?а=0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а — I1R1, ?b = ?к + Е1, ?с = ?b — I2R2, ?d = ?c — Е2, ?a = ?d + I3R3 = 0
При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5).
Рис. 5. Потенциальная диаграмма
Законы Кирхгофа в комплексной форме
Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.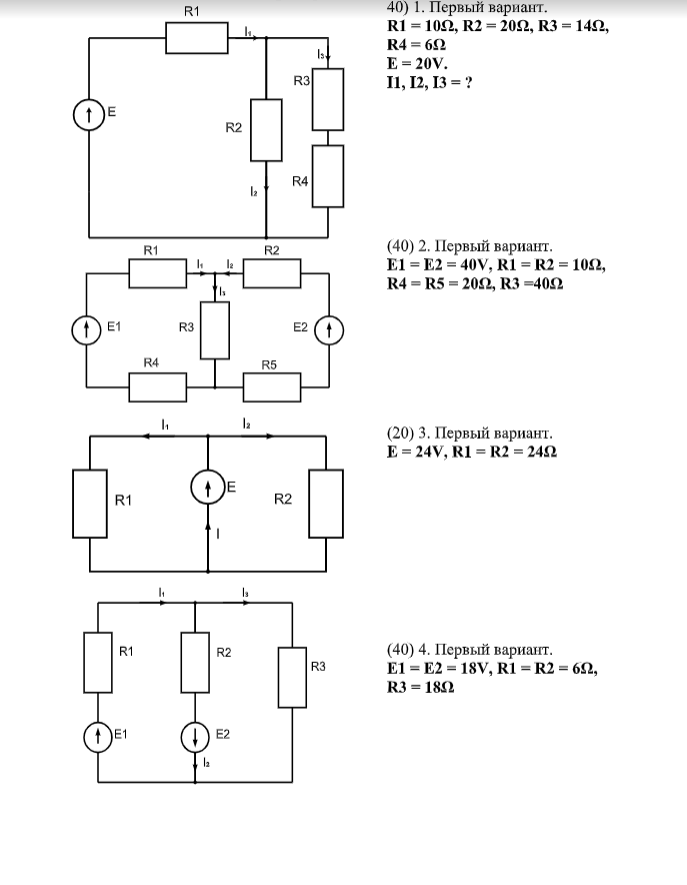
Первый закон Кирхгофа: «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»
Второй закон Кирхгофа: «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».
Расчет электрических цепей с применением законов Кирхгофа и Ома
Законы Кирхгофа наиболее общие. Они являются отдельным случаем универсальных уравнений электрического поля относительно произвольных электрических цепей с сосредоточенными параметрами. Закон Ома используется для расчета только линейных цепей.
Алгоритм расчета:
1. Начертить по принципиальной схеме схему замещения; упростить схему, преобразовав последовательно и параллельно соединенные резисторы в эквивалентные, пронумеровать ЭДС соответствующих ветвей, узлы; произвольно выбрать и обозначить положительные направления токов в ветвях.
2. Записать n – 1 уравнений по первому и m – (n – 1) уравнений по второму закону Кирхгофа, где n – количество узлов, m – количество ветвей в цепи. Если бы мы записывали n уравнений по первому закону Кирхгофа, то одно из них – это линейная комбинация оставшихся, что привело бы к линейной зависимости уравнений.
Если бы мы записывали n уравнений по первому закону Кирхгофа, то одно из них – это линейная комбинация оставшихся, что привело бы к линейной зависимости уравнений.
Источник тока J входит только в уравнение первого закона Кирхгофа (баланс тока в узлах) и переносится как известное в правую часть уравнения.
Для схемы (рис. 1) n = 3, m = 4.
Смотрите еще:
Пример решения задачи по правилам Кирхгофа № 1
Пример решения задачи по правилам Кирхгофа № 2
Пример решения задачи по правилам Кирхгофа № 3
Рис. 1.
Ветвь с идеальным источником тока не учитывается, поскольку ее сопротивление бесконечно велико.
Уравнение по первому закону Кирхгофа при n – 1 = 2 для узла 1: – I1 – I3 + I4 + J = 0; для узла 2: I1 + I2 – I4 = 0.
Уравнение по второму закону Кирхгофа при m – (n – 1) = 4 – 2 = 2 для контура 1 (направление обхода указано пунктиром):
I1R1 + I2R2 = E1; для контура 2 (направление обхода то же самое, но можно было взять и противоположное): I2R2 – I3R3 – I4R4 = – E2.
3. Решить систему уравнений относительно тока I:
Если среди компонент вектора I есть отрицательные, то это означает, что их направление противоположно положительному направлению, приведенному в схеме (рис. 1).
4. По закону Ома определить напряжения на элементах.
Сложность использования этого метода связана с чрезмерно большой размерностью систем уравнений.
Законы Кирхгофа • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Карьера Густава Кирхгофа во многом типична для немецкого физика XIX столетия. Германия позже своих западных соседей подошла к индустриальной революции и потому сильнее нуждалась в передовых технологиях, которые способствовали бы ускоренному развитию промышленности. В результате ученые, прежде всего естественники, ценились в Германии очень высоко. В год окончания университета Кирхгоф женился на дочери профессора, «соблюдя, тем самым, — как пишет один из его биографов, — два обязательных условия успешной академической карьеры». Но еще до этого, в возрасте двадцати одного года, он сформулировал основные законы для расчета токов и напряжений в электрических цепях, которые теперь носят его имя.
Но еще до этого, в возрасте двадцати одного года, он сформулировал основные законы для расчета токов и напряжений в электрических цепях, которые теперь носят его имя.
Середина XIX века как раз стала временем активных исследований свойств электрических цепей, и результаты этих исследований быстро находили практические применения. Базовые правила расчета простых цепей, такие как закон Ома, были уже достаточно хорошо проработаны. Проблема состояла в том, что из проводов и различных элементов электрических цепей технически уже можно было изготовлять весьма сложные и разветвленные сети — но никто не знал, как смоделировать их математически, чтобы рассчитать их свойства. Кирхгофу удалось сформулировать правила, позволяющие достаточно просто анализировать самые сложные цепи, и законы Кирхгофа до сих пор остаются важным рабочим инструментом специалистов в области электронной инженерии и электротехники.
Оба закона Кирхгофа формулируются достаточно просто и имеют понятную физическую интерпретацию. Первый закон гласит, что если рассмотреть любой узел цепи (то есть точку разветвления, где сходятся три или более проводов), то сумма поступающих в цепь электрических токов будет равна сумме исходящих, что, вообще говоря, является следствием закона сохранения электрического заряда. Например, если вы имеете Т-образный узел электрической цепи и по двум проводам к нему поступают электрические токи, то по третьему проводу ток потечет в направлении от этого узла, и равен он будет сумме двух поступающих токов. Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит.
Первый закон гласит, что если рассмотреть любой узел цепи (то есть точку разветвления, где сходятся три или более проводов), то сумма поступающих в цепь электрических токов будет равна сумме исходящих, что, вообще говоря, является следствием закона сохранения электрического заряда. Например, если вы имеете Т-образный узел электрической цепи и по двум проводам к нему поступают электрические токи, то по третьему проводу ток потечет в направлении от этого узла, и равен он будет сумме двух поступающих токов. Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит.
Второй закон не менее прост. Если мы имеем сложную, разветвленную цепь, ее можно мысленно разбить на ряд простых замкнутых контуров. Ток в цепи может различным образом распределяться по этим контурам, и сложнее всего определить, по какому именно маршруту потекут токи в сложной цепи. В каждом из контуров электроны могут либо приобретать дополнительную энергию (например, от батареи), либо терять ее (например, на сопротивлении или ином элементе).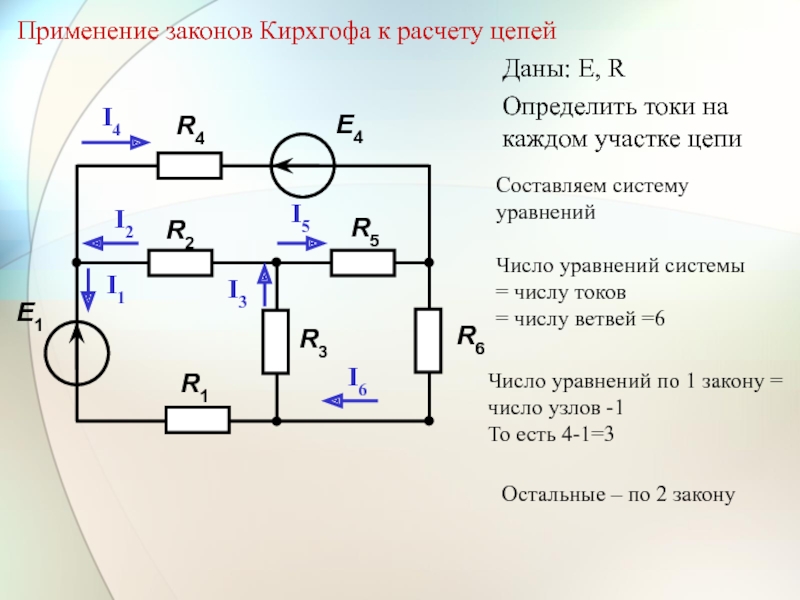 Второй закон Кирхгофа гласит, что чистое приращение энергии электронов в любом замкнутом контуре цепи равно нулю. Этот закон также имеет простую физическую интерпретацию. Если бы это было не так, всякий раз, проходя через замкнутый контур, электроны приобретали или теряли бы энергию, и ток бы непрерывно возрастал или убывал. В первом случае можно было бы получить вечный двигатель, а это запрещено первым началом термодинамики; во втором — любые токи в электрических цепях неизбежно затухали бы, а этого мы не наблюдаем.
Второй закон Кирхгофа гласит, что чистое приращение энергии электронов в любом замкнутом контуре цепи равно нулю. Этот закон также имеет простую физическую интерпретацию. Если бы это было не так, всякий раз, проходя через замкнутый контур, электроны приобретали или теряли бы энергию, и ток бы непрерывно возрастал или убывал. В первом случае можно было бы получить вечный двигатель, а это запрещено первым началом термодинамики; во втором — любые токи в электрических цепях неизбежно затухали бы, а этого мы не наблюдаем.
Самое распространенное применение законов Кирхгофа мы наблюдаем в так называемых последовательных и параллельных цепях. В последовательной цепи (яркий пример такой цепи — елочная гирлянда, состоящая из последовательно соединенных между собой лампочек) электроны от источника питания по серии проводов последовательно проходят через все лампочки, и на сопротивлении каждой из них напряжение падает согласно закону Ома.
В параллельной цепи провода, напротив, соединены таким образом, что на каждый элемент цепи подается равное напряжение от источника питания, а это означает, что в каждом элементе цепи сила тока своя, в зависимости от его сопротивления.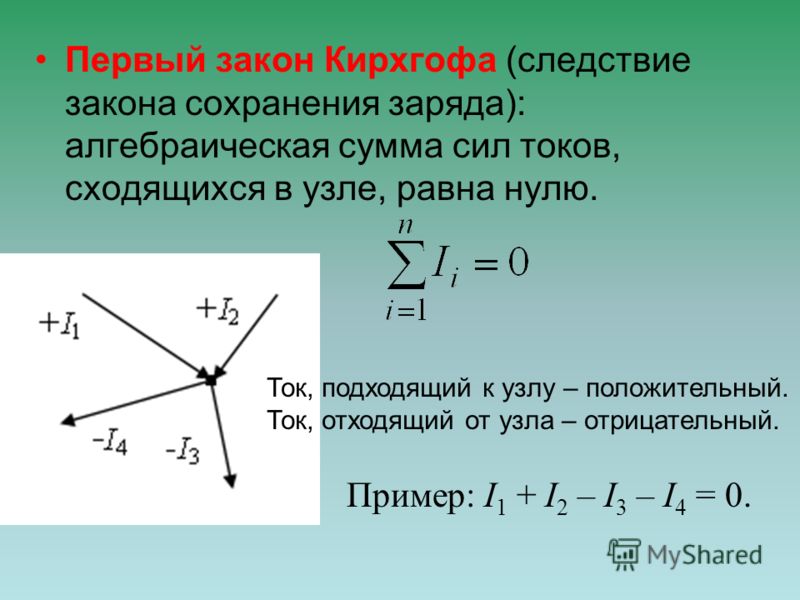 Примером параллельной цепи является соединение ламп «лесенкой»: напряжение подается на шины, а лампы смонтированы на поперечинах. Токи, проходящие через каждый узел такой цепи, определяются по первому закону Кирхгофа.
Примером параллельной цепи является соединение ламп «лесенкой»: напряжение подается на шины, а лампы смонтированы на поперечинах. Токи, проходящие через каждый узел такой цепи, определяются по первому закону Кирхгофа.
10.4: Правила Кирхгофа — Physics LibreTexts
Мы только что увидели, что некоторые схемы можно анализировать, сводя схему к одному источнику напряжения и эквивалентному сопротивлению. Многие сложные схемы невозможно проанализировать с помощью последовательно-параллельных методов, разработанных в предыдущих разделах. В этом разделе мы подробно рассмотрим использование правил Кирхгофа для анализа более сложных схем. Например, схема на рисунке \ (\ PageIndex {1} \) известна как многоконтурная схема , которая состоит из переходов.Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы имеют четкую последовательную или параллельную конфигурацию, которую можно уменьшить. Попробуйте. Резисторы \ (R_1 \) и \ (R_2 \) включены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое и с резисторами \ (R_4 \) и \ (R_5 \). Но что же тогда делать?
Попробуйте. Резисторы \ (R_1 \) и \ (R_2 \) включены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое и с резисторами \ (R_4 \) и \ (R_5 \). Но что же тогда делать?
Несмотря на то, что эта схема не может быть проанализирована с помощью уже изученных методов, два правила анализа схемы могут использоваться для анализа любой схемы, простой или сложной.Правила известны как Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).
Теперь мы даем объяснения этих двух правил, за которыми следуют советы по решению проблем по их применению и рабочий пример, в котором они используются.
Первое правило Кирхгофа
Первое правило Кирхгофа (правило соединения ) применяется к заряду, входящему в соединение и выходящему из него (рисунок \ (\ PageIndex {2} \)). Как говорилось ранее, соединение или узел — это соединение трех или более проводов.Ток — это поток заряда, и заряд сохраняется; таким образом, любой заряд, попадающий в переход, должен вытекать.
Рисунок \ (\ PageIndex {2} \): Заряд должен быть сохранен, поэтому сумма токов в переходе должна быть равна сумме токов на выходе.
Хотя это чрезмерное упрощение, можно провести аналогию с водопроводными трубами, соединенными в водопроводной разветвлении. Если провода на рисунке \ (\ PageIndex {2} \) были заменены водопроводными трубами и вода считалась несжимаемой, объем воды, текущей в соединение, должен быть равен объему воды, вытекающей из соединения.
Второе правило Кирхгофа
Второе правило Кирхгофа (правило петли ) применяется к разности потенциалов. Правило цикла сформулировано в терминах потенциала В , а не потенциальной энергии, но они связаны, поскольку \ (U = qV \). В замкнутом контуре, какая бы энергия ни поступала от источника напряжения, энергия должна передаваться в другие формы устройствами в контуре, поскольку нет других способов, которыми энергия может быть передана в цепь или из нее.Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжение, подаваемое источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простой цикл без соединений, как на рисунке \ (\ PageIndex {3} \).
Например, рассмотрим простой цикл без соединений, как на рисунке \ (\ PageIndex {3} \).
Рисунок \ (\ PageIndex {3} \): простой цикл без переходов. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.
Схема состоит из источника напряжения и трех внешних нагрузочных резисторов.Ярлыки a , b , c и d служат в качестве ссылок и не имеют другого значения. Скоро станет очевидна полезность этих этикеток. Петля обозначена как Loop abcda , и метки помогают отслеживать разницу напряжений при перемещении по цепи. Начните с точки a и двигайтесь к точке b . Напряжение источника напряжения добавляется к уравнению, а падение потенциала резистора \ (R_1 \) вычитается.От точки b до c вычитается падение потенциала на \ (R_2 \). Из c до d вычитается падение потенциала на \ (R_3 \). От точек d до a ничего не делается, потому что нет компонентов.
От точек d до a ничего не делается, потому что нет компонентов.
На рисунке \ (\ PageIndex {4} \) показан график напряжения при движении по контуру. Напряжение увеличивается при прохождении через батарею, тогда как напряжение уменьшается при прохождении через резистор. Падение потенциала , или изменение электрического потенциала, равно величине тока через резистор, умноженной на сопротивление резистора.Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
Рисунок \ (\ PageIndex {4} \): график напряжения при перемещении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор. Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
Тогда правило петли Кирхгофа утверждает
\ [V — IR_1 — IR_2 — IR_3 = 0. \]
\]
Уравнение контура можно использовать для определения тока в контуре:
\ [I = \ frac {V} {R_1 + R_2 + R_3} = \ frac {12.00 \, V} {1.00 \, \ Omega + 2.00 \, \ Omega + 3.00 \, \ Omega} = 2.00 \, A . \]
Этот цикл можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем мощь метода Кирхгофа в следующем разделе.
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы генерируем набор линейных уравнений, которые позволяют нам находить неизвестные значения в схемах.Это могут быть токи, напряжения или сопротивления. Каждый раз, когда применяется правило, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то проблема может быть решена.
Использование метода анализа Кирхгофа требует нескольких шагов, перечисленных в следующей процедуре.
Стратегия решения проблем: правила Кирхгофа
- Обозначьте точки на принципиальной схеме строчными буквами a , b , c ,….
 Эти ярлыки просто помогают ориентироваться.
Эти ярлыки просто помогают ориентироваться. - Найдите соединения в цепи. Соединения — это точки соединения трех или более проводов. Пометьте каждое соединение токами и направлениями в него и из него. Убедитесь, что хотя бы один ток направлен на соединение, и хотя бы один ток выходит из соединения.
- Выбрать петли в схеме. Каждый компонент должен содержаться хотя бы в одном цикле, но компонент может содержаться более чем в одном цикле.
- Примените правило соединения. Опять же, некоторые стыки не следует включать в анализ. Вам нужно использовать достаточно узлов только для включения каждого тока.
- Примените правило цикла. Используйте карту на рисунке \ (\ PageIndex {5} \).
Рисунок \ (\ PageIndex {5} \): Каждый из этих резисторов и источников напряжения проходит от до до до . (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном току, добавьте падение потенциала. (c) При перемещении через источник напряжения от отрицательного вывода к положительному, добавьте падение потенциала. (d) При перемещении через источник напряжения от положительной клеммы к отрицательной вычтите падение потенциала.
(c) При перемещении через источник напряжения от отрицательного вывода к положительному, добавьте падение потенциала. (d) При перемещении через источник напряжения от положительной клеммы к отрицательной вычтите падение потенциала.
Давайте рассмотрим некоторые этапы этой процедуры более подробно. При размещении переходов в цепи не беспокойтесь о направлении токов. Если направление потока тока неочевидно, выбора любого направления достаточно при условии, что хотя бы один ток направлен в соединение и хотя бы один ток выходит из соединения.Если стрелка находится в направлении, противоположном направлению обычного тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.
Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.
Рассмотрим рисунок \ (\ PageIndex {6} \).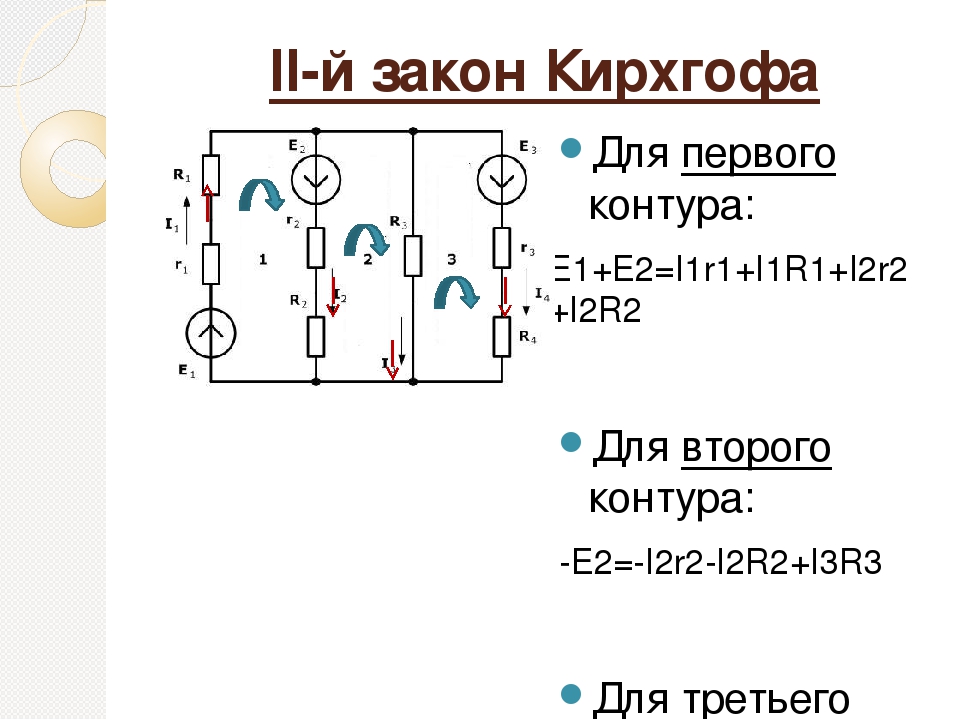 В этой цепи два соединения: соединение b и соединение e .Точки a , c , d и f не являются перекрестками, поскольку стык должен иметь три или более соединений. Уравнение для соединения b : \ (I_1 = I_2 + I_3 \), а уравнение для соединения e — \ (I_2 + I_3 = I_1 \). Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.
В этой цепи два соединения: соединение b и соединение e .Точки a , c , d и f не являются перекрестками, поскольку стык должен иметь три или более соединений. Уравнение для соединения b : \ (I_1 = I_2 + I_3 \), а уравнение для соединения e — \ (I_2 + I_3 = I_1 \). Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.
Рисунок \ (\ PageIndex {6} \): На первый взгляд, эта схема содержит два соединения, соединение b и соединение e , но следует рассматривать только один, поскольку их уравнения соединения эквивалентны.
При выборе петель в схеме вам необходимо достаточное количество петель, чтобы каждый компонент был покрыт один раз, без повторения петель. На рисунке \ (\ PageIndex {7} \) показаны четыре варианта петель для решения примерной схемы; варианты (a), (b) и (c) содержат достаточное количество циклов для полного решения схемы. Вариант (d) отражает больше петель, чем необходимо для решения схемы.
Вариант (d) отражает больше петель, чем необходимо для решения схемы.
Рисунок \ (\ PageIndex {7} \): Панели (a) — (c) достаточно для анализа схемы. В каждом случае два показанных контура содержат все элементы схемы, необходимые для полного решения схемы.Панель (d) показывает три использованных контура, что больше, чем необходимо. Любые две петли в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла дает избыточную информацию.
Рассмотрим схему на рисунке \ (\ PageIndex {8a} \). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала промаркируйте схему, как показано в части (b).
Рисунок \ (\ PageIndex {8} \): (a) Многоконтурная схема. (b) Пометьте цепь, чтобы облегчить ориентацию.
Далее определяем перекрестки.В этой схеме точки b и e имеют по три соединенных провода, что делает их соединениями. Начните применять правило соединения Кирхгофа \ (\ left (\ sum I_ {in} = \ sum I_ {out} \ right) \), рисуя стрелки, представляющие токи, и маркируя каждую стрелку, как показано на рисунке \ (\ PageIndex {9 } \). Соединение b показывает, что \ (I_1 = I_2 + I_3 \), а соединение e показывает, что \ (I_2 + I_3 = I_1 \). Поскольку соединение и дает ту же информацию, что и соединение b , ее можно не принимать во внимание.Эта схема имеет три неизвестных, поэтому для ее анализа нам понадобятся три линейно независимых уравнения.
Соединение b показывает, что \ (I_1 = I_2 + I_3 \), а соединение e показывает, что \ (I_2 + I_3 = I_1 \). Поскольку соединение и дает ту же информацию, что и соединение b , ее можно не принимать во внимание.Эта схема имеет три неизвестных, поэтому для ее анализа нам понадобятся три линейно независимых уравнения.
Рисунок \ (\ PageIndex {9} \): (a) Эта схема имеет два соединения, помеченных b и e, но в анализе используется только узел b. (b) Обозначенные стрелки представляют токи в переходах и на выходе из них.
Далее нам нужно выбрать петли. На рисунке \ (\ PageIndex {10} \) контур abefa включает в себя источник напряжения \ (V_1 \) и резисторы \ (R_1 \) и \ (R_2 \). Цикл начинается в точке a , затем проходит через точки b , e и f , а затем возвращается к точке a .Второй контур, Loop ebcde , начинается в точке e и включает резисторы \ (R_2 \) и \ (R_3 \), а также источник напряжения \ (V_2 \).
Рисунок \ (\ PageIndex {10} \): Выберите петли в схеме.
Теперь мы можем применить правило цикла Кирхгофа, используя карту на рисунке \ (\ PageIndex {5} \). Начиная с точки a и двигаясь к точке b , резистор \ (R_1 \) пересекается в том же направлении, что и ток \ (I_1 \), поэтому падение потенциала \ (I_1R_1 \) вычитается.При перемещении от точки b к точке e резистор \ (R_2 \) пересекается в том же направлении, что и ток \ (I_2 \), поэтому падение потенциала \ (I_2R_2 \) вычитается. При перемещении от точки e к точке f , источник напряжения \ (V_1 \) пересекается от отрицательной клеммы к положительной клемме, поэтому добавляется \ (V_1 \). Между точками f и a нет компонентов. Сумма разностей напряжений должна равняться нулю:
\ [Петля \, abefa: \, -I_1R_1 — I_2R_2 + V_1 = 0 \ или \, V_1 = I_1R_1 + I_2R_2.\]
Наконец, проверяем цикл ebcde .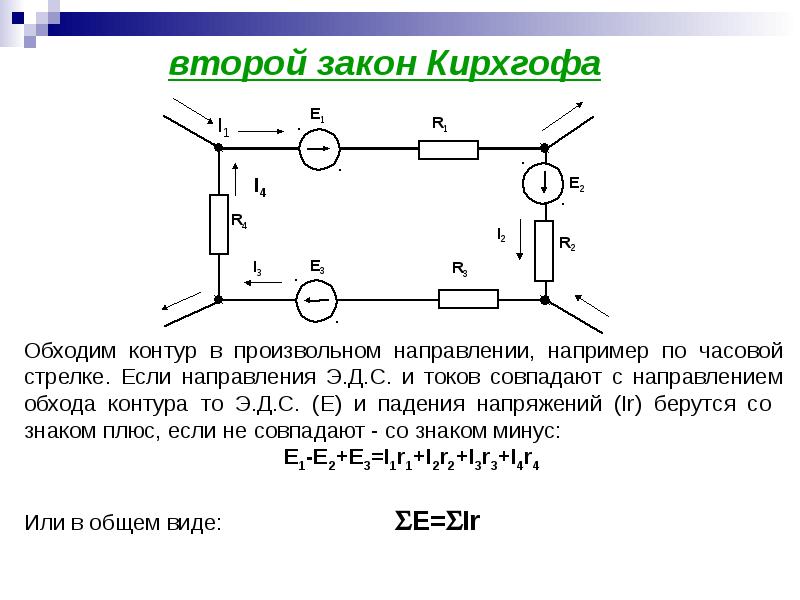 Мы начинаем с точки e и переходим к точке b , пересекая \ (R_2 \) в направлении, противоположном текущему потоку \ (I_2 \). Потенциальное падение \ (I_2R_2 \) добавлено. Затем мы пересекаем \ (R_3 \) и \ (R_4 \) в том же направлении, что и текущий поток \ (I_3 \), и вычитаем потенциальные падения \ (I_3R_3 \) и \ (I_3R_4 \). Обратите внимание, что ток через резисторы \ (R_3 \) и \ (R_4 \) одинаков, потому что они соединены последовательно. Наконец, источник напряжения переключается с положительной клеммы на отрицательную, а источник напряжения \ (V_2 \) вычитается.Сумма этих разностей напряжений равна нулю и дает уравнение контура
Мы начинаем с точки e и переходим к точке b , пересекая \ (R_2 \) в направлении, противоположном текущему потоку \ (I_2 \). Потенциальное падение \ (I_2R_2 \) добавлено. Затем мы пересекаем \ (R_3 \) и \ (R_4 \) в том же направлении, что и текущий поток \ (I_3 \), и вычитаем потенциальные падения \ (I_3R_3 \) и \ (I_3R_4 \). Обратите внимание, что ток через резисторы \ (R_3 \) и \ (R_4 \) одинаков, потому что они соединены последовательно. Наконец, источник напряжения переключается с положительной клеммы на отрицательную, а источник напряжения \ (V_2 \) вычитается.Сумма этих разностей напряжений равна нулю и дает уравнение контура
\ [Петля \, ebcde: \, I_2R_2 — I_3 (R_3 + R_4) — V_2 = 0. \]
Теперь у нас есть три уравнения, которые мы можем решить относительно трех неизвестных.
\ [\ text {Перекресток b:} \, I_1 — I_2 — I_3 = 0. \ label {eq1} \]
\ [\ text {Петля abefa:} \, I_1R_1 + I_2R_2 = V_1. \ label {eq2} \]
\ [\ text {Loop ebcde:} \, I_2R_2 — I_3 (R_3 + R_4) = V_2. \ label {eq3} \]
\ label {eq3} \]
Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока \ (I_2 \).Сначала добавьте уравнение \ ref {eq1} times \ (R_2 \) к уравнению \ ref {eq2}. Результатом будет уравнение \ ref {eq4}:
.
\ [(R_1 + R_2) I_1 — R_2I_3 = V_1. \]
\ [6 \, \ Omega I_1 — 3 \ Omega I_3 = 24 \, V. \ label {eq4} \]
Затем вычтите уравнение \ ref {eq3} из уравнения \ ref {eq2}. Результатом будет уравнение \ ref {eq5}:
.
\ [I_1R_1 + I_3 (R_3 + R_4) = V_1 — V_2. \]
\ [3 \ Omega I_1 + 7 \ Omega I_3 = -5 \, V. \ label {eq5} \]
Мы можем решить уравнения \ ref {eq4} и \ ref {eq5} для тока \ (I_1 \).Если сложить семикратное уравнение \ ref {eq4} и трехкратное уравнение \ ref {eq5}, получится \ (51 \, \ Omega I_1 = 153 \, V \) или \ (I_1 = 3.00 \, A \). Использование уравнения \ ref {eq4} приводит к \ (I_3 = -2,00 \, A \). Наконец, уравнение \ ref {eq1} дает \ (I_2 = I_1 — I_3 = 5,00 \, A \). Один из способов проверить соответствие решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:
\ [P_ {in} = I_1V_1 + I_3V_2 = 130 \, W, \ nonumber \]
\ [P_ {out} = I_1 ^ 2R_1 + I_2 ^ 2R_2 + I_3 ^ 2R_3 + I_3 ^ 2R_4 = 130 \, W. \ nonumber \]
\ nonumber \]
Обратите внимание, что решение для текущего \ (I_3 \) отрицательно. Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединений, имеет направление, противоположное направлению обычного тока. Мощность от второго источника напряжения составляет 58 Вт, а не −58 Вт.
Пример \ (\ PageIndex {1} \): расчет тока с использованием правил Кирхгофа
Найдите токи, протекающие в цепи, показанной на рисунке \ (\ PageIndex {11} \).
Рисунок \ (\ PageIndex {11} \): Эта схема представляет собой комбинацию последовательной и параллельной конфигураций резисторов и источников напряжения.Эта схема не может быть проанализирована с использованием методов, обсуждаемых в «Электродвижущей силе», но может быть проанализирована с использованием правил Кирхгофа.
Стратегия
Эта схема достаточно сложна, поэтому токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа.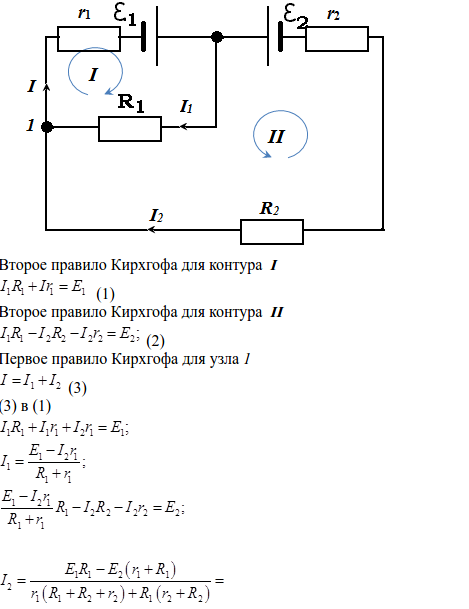 На рисунке токи обозначены \ (I_1, \, I_2 \) и \ (I_3 \), и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от до до h .В решении мы применяем правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.
На рисунке токи обозначены \ (I_1, \, I_2 \) и \ (I_3 \), и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от до до h .В решении мы применяем правила соединения и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.
Решение
Применение правил соединения и петли дает следующие три уравнения. У нас есть три неизвестных, поэтому требуется три уравнения.
\ [Перекресток \, c: \, I_1 + I_2 = I_3. \]
\ [Петля \, abcdefa: \, I_1 (R_1 + R_4) — I_2 (R_2 + R_5 + R_6) = V_1 — V_3. \]
\ [Петля \, cdefc: \, I_2 (R_2 + R_5 + R_6) + I_3R_3 = V_2 + V_3.\]
Упростите уравнения, поместив неизвестные в одну сторону уравнений.
\ [Соединение \, c: \, I_1 + I_2 — I_3 = 0. \]
\ [Петля \, abcdefa: \, I_1 (3 \ Omega) — I_2 (8 \ Omega) = 0,5 \, V — 2,30 \, V. \]
\ [Цикл \, cdefc: \, I_2 (8 \ Omega) + I_3 (1 \ Omega) = 0,6 \, V + 2. 2R_1 = 0.2R_1 = 0,18 \, W. \]
2R_1 = 0.2R_1 = 0,18 \, W. \]
\ [P_ {disipated} = 1.09 \, W. \]
\ [P_ {источник} = I_1V_1 + I_2V_3 + I_3V_2 = 0,10 \, + 0,69 \, W + 0,30 \, W = 1,09 \, W. \]
Подаваемая мощность равна мощности, рассеиваемой резисторами.
Упражнение \ (\ PageIndex {1} \)
При рассмотрении следующей схемы и мощности, подаваемой и потребляемой схемой, будет ли источник напряжения всегда обеспечивать питание схемы или может ли источник напряжения потреблять мощность?
- Ответ
Схема может быть проанализирована с использованием правила петли Кирхгофа.2R_2 = 7,2 \, мВт. \)
Пример \ (\ PageIndex {2} \): расчет тока с использованием правил Кирхгофа
Найдите ток, протекающий в цепи, показанной на рисунке \ (\ PageIndex {12} \).
Рисунок \ (\ PageIndex {12} \): Эта схема состоит из трех резисторов и двух последовательно соединенных батарей. Обратите внимание, что батареи подключены с противоположной полярностью.
Стратегия
Эта схема может быть проанализирована с использованием правил Кирхгофа. Есть только один цикл и нет узлов.Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки a к точке b . Рассмотрим цикл abcda и воспользуемся рисунком \ (\ PageIndex {5} \), чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку \ (\ PageIndex {5} \), батарея \ (V_1 \) будет добавлена, а батарея \ (V_2 \) вычтена.
Решение
Применение правила соединения дает следующие три уравнения. У нас есть одно неизвестное, поэтому требуется одно уравнение:
\ [Цикл \, abcda: \, -IR_1 -V_1 -IR_2 + V_2 -IR_3 = 0.\]
Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.
\ [I (R_1 + R_2 + R_3) = V_2 — V_1. \]
\ [I = \ frac {V_2 — V_1} {R_1 + R_2 + R_3} = \ frac {24 \, V — 12 \, V} {10.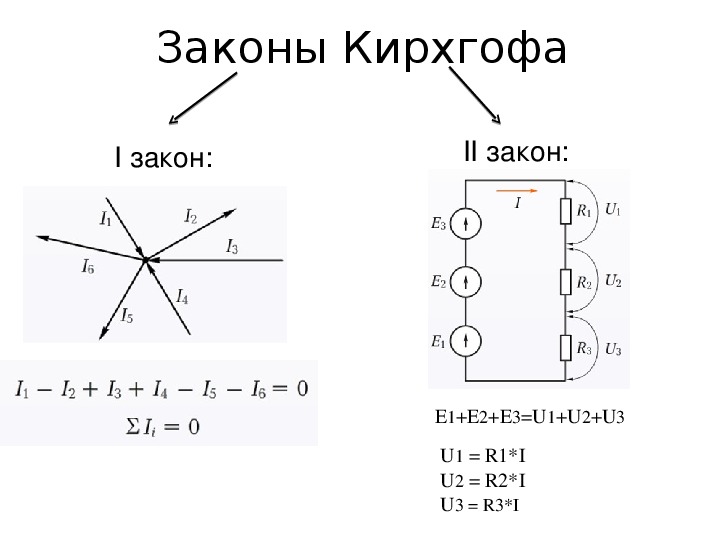 0 \, \ Omega + 30.0 \, \ Omega + 10.0 \, \ Омега} = 0,20 \, А. \]
0 \, \ Omega + 30.0 \, \ Omega + 10.0 \, \ Омега} = 0,20 \, А. \]
Значение
Мощность, рассеиваемая или потребляемая схемой, равна мощности, подаваемой в схему, но обратите внимание, что ток в батарее \ (V_1 \) протекает через батарею от положительной клеммы к отрицательной клемме и потребляет энергию.2R_3 = 0,80 \, Вт \]
\ [P_ {V_1} = IV_1 = 2,40 \, W \]
\ [P_ {рассеивается} = 4.80 \, Вт \]
\ [P_ {источник} = IV_2 = 4.80 \, W \]
Подаваемая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей \ (V_1 \).
Упражнение \ (\ PageIndex {2} \)
При использовании законов Кирхгофа вам необходимо решить, какие петли использовать, и направление тока, протекающего через каждую петлю. При анализе схемы в примере \ (\ PageIndex {2} \) было выбрано направление тока по часовой стрелке от точки a до точки b .Как бы изменились результаты, если бы направление тока было выбрано против часовой стрелки, от точки b до точки a ?
- Ответ
Расчетный ток будет равен \ (I = -0.
 20 \, A \) вместо \ (I = 0.20 \, A \). Сумма рассеиваемой мощности и потребляемой мощности все равно будет равна подаваемой мощности.
20 \, A \) вместо \ (I = 0.20 \, A \). Сумма рассеиваемой мощности и потребляемой мощности все равно будет равна подаваемой мощности.
Несколько источников напряжения
Для многих устройств требуется более одной батареи.Несколько источников напряжения, например батареи, могут быть подключены в последовательной конфигурации, параллельной конфигурации или их комбинации.
Последовательно положительная клемма одной батареи соединена с отрицательной клеммой другой батареи. Любое количество источников напряжения, в том числе аккумуляторы, можно подключать последовательно. Две последовательно соединенные батареи показаны на рисунке \ (\ PageIndex {13} \). Использование правила петли Кирхгофа для схемы в части (b) дает результат
\ [\ epsilon_1 — Ir_1 + \ epsilon_2 — Ir_2 — IR = 0, \]
\ [[(\ epsilon_1 + \ epsilon_2) — I (r_1 + r_2)] — IR = 0.\]
Рисунок \ (\ PageIndex {13} \): (a) Две батареи, соединенные последовательно с нагрузочным резистором. (b) Принципиальная схема двух батарей и нагрузочного резистора, где каждая батарея смоделирована как идеализированный источник ЭДС и внутреннего сопротивления.
(b) Принципиальная схема двух батарей и нагрузочного резистора, где каждая батарея смоделирована как идеализированный источник ЭДС и внутреннего сопротивления.
Когда источники напряжения включены последовательно, их внутренние сопротивления можно складывать, а их ЭДС можно складывать вместе, чтобы получить общие значения. Последовательное соединение источников напряжения является обычным явлением, например, в фонариках, игрушках и других приборах.Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС. На рисунке \ (\ PageIndex {13} \) напряжение на клеммах равно
.
\ [V_ {терминал} = (\ epsilon_1 — Ir_1) + (\ epsilon_2 — Ir_2) = [(\ epsilon_1 + \ epsilon_2) — I (r_1 + r_2) — I (r_1 + r_2)] = (\ epsilon_1 + \ epsilon_2) + Ir_ {eq}. \]
Обратите внимание, что одинаковый ток I присутствует в каждой батарее, потому что они соединены последовательно. Недостаток последовательного соединения ячеек в том, что их внутренние сопротивления складываются.
Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь. Например, светодиодный фонарик может иметь две батареи типа AAA, каждая с напряжением на клеммах 1,5 В, чтобы обеспечить 3,0 В для фонарика.
Любое количество батарей можно подключать последовательно. Для последовательно включенных аккумуляторов N напряжение на зажимах равно
Примечание
\ [V_ {терминал} = (\ epsilon_1 + \ epsilon_2 +… + \ Epsilon_ {N-1} + \ epsilon_N) — I (r_1 + r_2 +.№ р_и \]
Когда нагрузка подключается к источникам напряжения последовательно, как показано на рисунке \ (\ PageIndex {14} \), мы можем найти ток:
\ [(\ epsilon_1 — Ir_1) + (\ epsilon_2 — Ir_2) = IR, \]
\ [Ir_1 + Ir_2 + IR = \ epsilon_1 + \ epsilon_2, \]
\ [I = \ frac {\ epsilon_1 + \ epsilon_2} {r_1 + r_2 + R}. \]
Как и ожидалось, внутренние сопротивления увеличивают эквивалентное сопротивление.
Рисунок \ (\ PageIndex {14} \): две батареи последовательно подключаются к светодиодной лампе, как в фонарике.
Источники напряжения, такие как батареи, также можно подключать параллельно. На рисунке \ (\ PageIndex {15} \) показаны две батареи с одинаковыми ЭДС, включенные параллельно и подключенные к сопротивлению нагрузки. Когда батареи подключаются параллельно, положительные клеммы соединяются вместе, а отрицательные клеммы соединяются вместе, а сопротивление нагрузки подключается к положительной и отрицательной клеммам. Обычно источники напряжения, включенные параллельно, имеют идентичные ЭДС. В этом простом случае, поскольку источники напряжения подключены параллельно, общая ЭДС равна индивидуальной ЭДС каждой батареи.
Рисунок \ (\ PageIndex {15} \): (a) Две батареи подключаются параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея как источник ЭДС и внутренний резистор. Два источника ЭДС имеют идентичные ЭДС (каждый из которых обозначен как \ (\ epsilon \)), соединенные параллельно, которые создают одинаковую ЭДС.
Рассмотрим анализ Кирхгофа схемы на рисунке \ (\ PageIndex {15b} \). {- 1} \]
{- 1} \]
Например, в некоторых грузовиках с дизельным двигателем используются две батареи на 12 В параллельно; они производят полную ЭДС 12 В, но могут обеспечить больший ток, необходимый для запуска дизельного двигателя.
Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме индивидуальных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют равные ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше, чем отдельные внутренние сопротивления. Аккумуляторы подключаются последовательно, чтобы увеличить напряжение на клеммах нагрузки.Аккумуляторы подключаются параллельно для увеличения тока нагрузки.
Законы Кирхгофа
Действующий закон Кирхгофа (KCL)
Закон Кирхгофа о напряжении (KVL)
Действующий закон Кирхгофа (KCL) :
Алгебраическая сумма всех токов, входящих в узел, всегда должна быть равна нулю , где i n — ток n th . Обычное задание:
Для следующего рисунка Уравнение узла можно записать как Чтобы использовать KCL для анализа схемы,
|
Пример: Найдите ток через сопротивление 20 Ом и ток через сопротивление 40 Ом
Закон Кирхгофа о напряжении (KVL):
Алгебраическая сумма всех напряжений в замкнутом контуре всегда должна быть равна нулю.
, где v n — напряжение n th . N — количество элементов в контуре Обычное задание:
Для следующего рисунка Чтобы использовать KVL для анализа схемы,
|
Примеры:
Пример 2 : Найдите ток i и напряжение v на каждом резисторе.
Пример 3: Найдите v1 и v2 в следующей схеме
(примечание: стрелки указывают положительное положение поля, а отрицательное — в конце поля)
Пример 4 : Найдите V1, V2 и V3.
(примечание: стрелки указывают положительное положение поля, а отрицательное — в конце поля)
Пример 5: Найдите V1, V2, V3 и V4
(примечание: стрелки указывают положительное положение прямоугольника, а отрицательное — в конце поля)
Практические задачи :
(Щелкните изображение, чтобы просмотреть решение)
Задача 1: Найдите V1 в следующей цепи.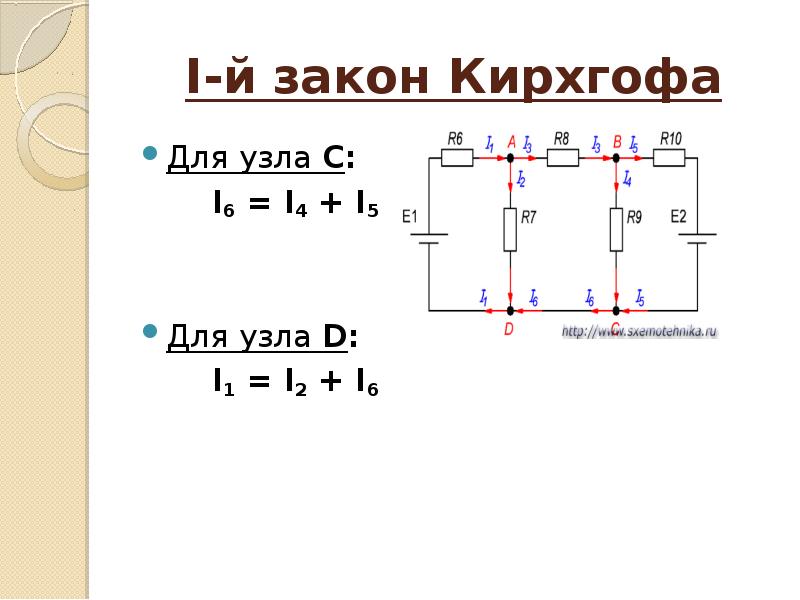
Просмотреть решение
Задача 2: Найдите V0 в следующей схеме.
Просмотреть решение
Задача 3: Найдите V1, V2 и V3 в следующей схеме.
Просмотреть решение
Задача 4 : Найдите I 1 , I 2 , I 3 в следующей цепи
Просмотреть решение
Проблема 5 : Найдите значение резистора R в следующей цепи.
Просмотреть решение
Операции:
- В 1 = 8 В, В 2 = -4 В, В 4 = 14 В.
 Найдите V 3 и V 5 в следующей схеме
Найдите V 3 и V 5 в следующей схеме - Найдите V x и V y в следующей схеме
- Найдите V x , V y и V z в следующей схеме
- Найдите уравнения узлов KCL в узлах A, B, C и D
- Если I 1 = 4A, I 2 = 5A и I 3 = 3A, то с помощью KCL найдите I 4 и, I 5 в следующей схеме
- Ответы:
- В 3 = 12 В и В 5 = -2 В
- В x = 12 В и В y = 9 В
- V x = 35V, V y = 5V и V z = 15V
- На узле A:
На узле B:
На узле C:
На узле D:
- I 4 = 2A и I 5 = 1A
Закон Кирхгофа по току и напряжению (KCL и KVL)
Первый и второй законы Кирхгофа с решенным примером
Немецкий физик Роберт Кирхгоф ввел в 1847 году два важных электрических закона, с помощью которых мы можем легко найти эквивалентное сопротивление сложная сеть и протекающие токи в разных проводниках. Как цепи переменного, так и постоянного тока можно решить и упростить, используя эти простые законы, известные как закон Кирхгофа по току (KCL) и закон Кирхгофа по напряжению (KVL).
Как цепи переменного, так и постоянного тока можно решить и упростить, используя эти простые законы, известные как закон Кирхгофа по току (KCL) и закон Кирхгофа по напряжению (KVL).
Также обратите внимание, что KCL выводится из уравнения непрерывности заряда в электромагнетизме, а KVL выводится из уравнения Максвелла-Фарадея для статического магнитного поля (производная B по времени равна 0)
Закон Кирхгофа (KCL):
Согласно KCL, в любой момент алгебраическая сумма текущих токов через точку (или соединение) в сети равна нулю (0) или в любой электрической сети алгебраическая сумма токов, встречающихся в точке (или соединение) равно нулю (0).Этот закон также известен как точечный закон или текущий закон.
В любой электрической сети алгебраическая сумма входных токов в точку и выходных токов из этой точки равна нулю. Или входящие токи в точку равны выходным токам этой точки.
Другими словами, сумма токов, текущих к точке, равна сумме токов, текущих от нее.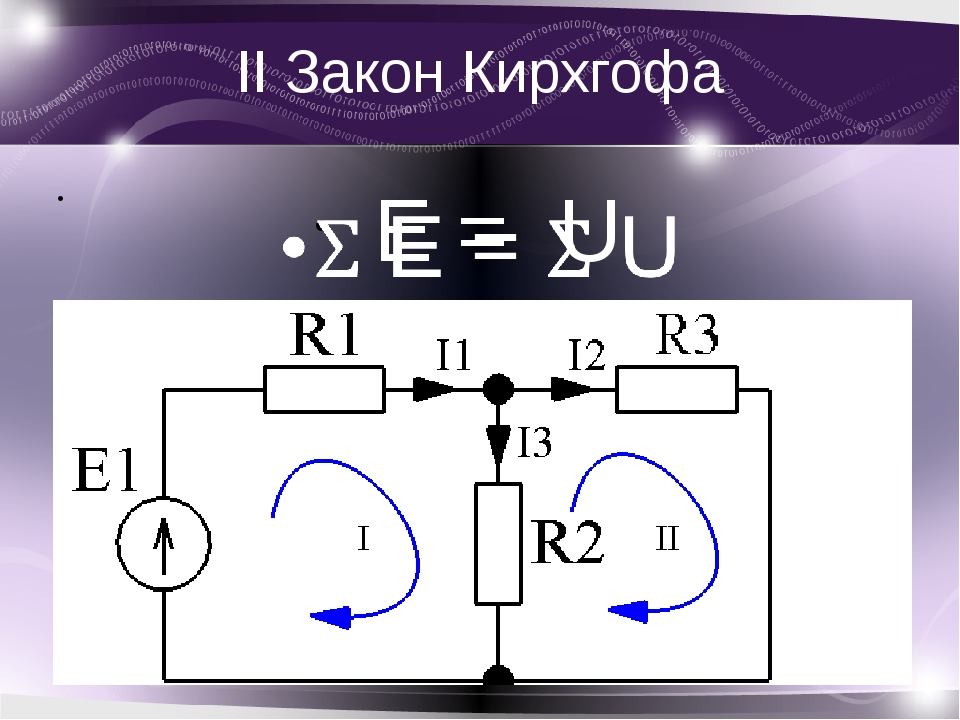 Или алгебраическая сумма токов, входящих в узел, равна алгебраической сумме выходящих из него токов.
Или алгебраическая сумма токов, входящих в узел, равна алгебраической сумме выходящих из него токов.
Пояснение к KCL:
Предположим, что некоторые проводники встречаются в точке «A», как показано на рис. 1.a. в некоторых проводниках токи поступают в точку «А», тогда как в других проводниках токи уходят или исходят из точки «А».
Считайте входящие или входящие токи «положительными (+) в направлении точки« A », в то время как уходящие или исходящие токи из точки« A »являются« отрицательными (-) ».
, затем:
I 1 + (-I 2 ) + (-I 3 ) + (-I 4 ) + I 5 = 0
OR
I 1 + I 5 -I 2 -I 3 -I 4 = 0
OR
I 1 + I 5 = I 2 + I 3 + I 4 = 0
и.е.
Входящие или входящие токи = выходящие или исходящие токи
или
ΣI Вход = ΣI Выход
Например, 8A приближается к точке, а 5A плюс 3A выходят из этой точки на рис.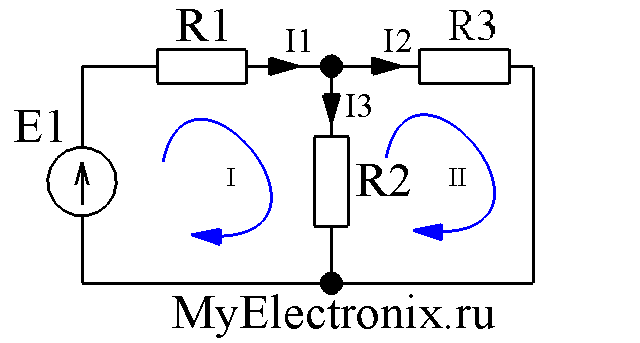 1.b, следовательно,
1.b, следовательно,
8A = 5A + 3А
8А = 8А.
Демонстрация действующего закона Кирхгофа (KCL)
Закон Кирхгофа о напряжении (KVL):
Второй закон Кирхгофа гласил:
В любом замкнутом пути (или цепи) в сети алгебраическая сумма IR-продукта равна ЭДС в этом пути.
Другими словами, в любом замкнутом контуре (который также известен как Mesh) алгебраическая сумма приложенной ЭДС равна алгебраической сумме падений напряжения в элементах. Второй закон Кирхгофа также известен как закон напряжения или закон сетки.
ΣIR = ΣE
Пояснение к KVL:
Замкнутый контур показан на рис., Который содержит два соединения батарей E 1 и E 2 . Общая сумма E.M.F батарей обозначена E 1 -E 2 .Воображаемое направление тока также показано на рис.
E 1 управляют током в таком направлении, которое должно быть положительным, в то время как E 2 мешает в направлении тока (то есть в направлении, противоположном предполагаемому направлению тока), следовательно, это принято как отрицательный. Падение напряжения в этой замкнутой цепи зависит от произведения напряжения и тока.
Падение напряжения в этой замкнутой цепи зависит от произведения напряжения и тока.
Падение напряжения в предполагаемом направлении тока известно как положительное падение напряжения, а другое — отрицательное падение напряжения.
На приведенном выше рисунке I 1 R 1 и I 2 R 2 — положительное падение напряжения, а I 3 R 3 и I 4 R 4 — отрицательное напряжение V.D.
Если мы обойдем замкнутую цепь (или каждую сетку) и умножим сопротивление проводника на протекающий в нем ток, то сумма IR будет равна сумме приложенных источников ЭДС, подключенных к цепи.
Общее уравнение для вышеуказанной схемы:
E 1 -E 2 = i 1 R 1 + i 2R 2 — i 4 3 R 9047 3 — i 4 R 4
Если мы пойдем в предполагаемом направлении тока, как показано на рисунке, то произведение IR будет положительным, в противном случае отрицательным.
Полезно знать:
Направление тока:
Очень важно определять направление тока при решении схем по законам Кирхгофа.
Направление тока можно предполагать по часовой стрелке или против часовой стрелки. После того как вы выберете собственное направление тока, вам нужно будет применить и поддерживать одно и то же направление для всей цепи до окончательного решения схемы.
Если мы получили окончательное значение как положительное, это означает, что предполагаемое направление тока было правильным.В случае отрицательных значений, тогда ток направления будет обратным по сравнению с предполагаемым.
Анализ цепей по законам Кирхгофа
Решенный пример для KCL и KVL (законы Кирхгофа)
Пример:
Резисторы R 1 = 10 Ом, R 4 Ом и 2 90 = 8 Ом подключаются до двух батарей (с незначительным сопротивлением), как показано. Найдите ток через каждый резистор.
Найдите ток через каждый резистор.
Решение:
Предположим, что токи текут в направлениях, указанных стрелками.
Примените KCL к соединениям C и A.
Следовательно, ток в ячейке ABC = i 1
Ток в ячейке CA = i 2
Затем ток в ячейке CDA = i 1 — i 2
Теперь примените KVL к сетке ABC, 20 В действуют по часовой стрелке. Приравнивая сумму IR произведений, получаем:
10 i 1 + 4 i 2 = 20 ……………. (1)
В сетевом ACD 12 вольт действуют по часовой стрелке, затем:
8 ( i 1 — i 2 ) — 4 i 2 = 12
8 i 1 — 8 i 2 — 4 i 2 = 12
8 i 1 — 12 i 2 = 12 …………….(2)
Умножение уравнения (1) на 3;
30 i 1 + 12 i 2 = 60
Решение для i 1
30 i 1 + 12 i 2 905 905 905 1 — 12 i 2 = 12
______________
38 i 1 = 72
Вышеупомянутое уравнение также можно упростить с помощью правила исключения или правила Крамера.
i 1 = 72/38 = 1,895 Ампер = Ток в резисторе 10 Ом
Подставляя это значение в (1), получаем:
10 (1,895) + 4 i 2 = 20
4 i 2 = 20-18,95
i 2 = 0,263 Ампер = Ток в резисторах 4 Ом.
Сейчас,
i 1 — i 2 = 1.895 — 0,263 = 1,632 Ампер
Применение законов Кирхгофа
- Законы Кирхгофа можно использовать для определения значений неизвестных значений, таких как ток, напряжение, ток, а также направление потока. значения в цепи.
- Эти законы могут применяться к любой цепи * (см. Ограничение Законов Кирхгофа в конце статьи), но полезны для поиска неизвестных значений в сложных схемах и сетях.
- Также используется в узловом и сеточном анализе для определения значений тока и напряжения.

- Ток через каждую независимую петлю передается за счет применения KVL (каждая петля) и тока в любом элементе схемы путем подсчета всего тока (применимо в методе тока петли).
- Ток через каждую ветвь передается за счет применения KCL (каждого перехода) KVL в каждом контуре цепи (применимо в методе тока контура).
- Законы Кирхгофа полезны для понимания передачи энергии через электрическую цепь.
Полезно знать:
Эти полезные правила необходимо учитывать при упрощении и анализе электрических цепей по законам Кирхгофа:
- Падение напряжения в контуре из-за тока по часовой стрелке считается положительным (+) Падение напряжения.
- Падение напряжения в контуре из-за тока, направленного против часовой стрелки, считается отрицательным (-) падением напряжения.
- Ток, потребляемый батареей по часовой стрелке, считается положительным (+).
- Ток, потребляемый батареей против часовой стрелки, считается положительным (-).

Ограничения по закону Кирхгофа:
- KCL применяется при условии, что ток течет только по проводам и проводам. В то время как в высокочастотных цепях, паразитная емкость больше не может игнорироваться. В таких случаях ток может течь в разомкнутой цепи, потому что в этих случаях проводники или провода действуют как линии передачи.
- KVL применимо при условии отсутствия флуктуирующего магнитного поля, связывающего замкнутый контур.В то время как при наличии изменяющегося магнитного поля в высокочастотных, но коротковолновых цепях переменного тока электрическое поле не является консервативным векторным полем. Таким образом, электрическое поле не может быть градиентом любого потенциала, а линейный интеграл электрического поля вокруг петли не равен нулю, что прямо противоречит KVL. Поэтому КВЛ в таком состоянии неприменим.
- Во время передачи энергии от магнитного поля к электрическому, когда в KVL необходимо ввести помаду, чтобы заставить P.
 d (разность потенциалов) вокруг цепи равна 0.
d (разность потенциалов) вокруг цепи равна 0.
Вы также можете проверить другие схемы, анализируя теоремы:
Закон Кирхгофа | Основы резистора
Густав Роберт Кирхгоф
Законы Кирхгофа необходимы для теории резисторных цепей. Они были сформулированы немецким ученым Густавом Кирхгофом в 1845 году. Законы описывают сохранение энергии и заряда в электрических сетях. Их также называют схемными законами Кирхгофа. Кирхгоф внес свой вклад и в другие области науки, поэтому общий термин закон Кирхгофа может иметь разные значения.Оба закона схемы, закон тока Кирхгофа (KCL) и закон напряжения Кирхгофа (KVL), будут подробно объяснены.
Текущий закон Кирхгофа (KCL)
Закон Кирхгофа по току (KCL) гласит, что сумма всех токов, выходящих из узла в любой электрической сети, всегда равна нулю. В его основе лежит принцип сохранения электрического заряда. Этот закон также называют первым законом Кирхгофа. В форме формулы это дается как:
KCL легче понять на примере. Посмотрите на произвольный «узел А» из резисторной сети. К этому узлу подключены три ветви. Известны два тока: I 1 — 2 ампера и I 2 — 4 ампера. Действующий закон гласит, что сумма I 1 , I 2 и I 3 должна быть равна нулю:
Посмотрите на произвольный «узел А» из резисторной сети. К этому узлу подключены три ветви. Известны два тока: I 1 — 2 ампера и I 2 — 4 ампера. Действующий закон гласит, что сумма I 1 , I 2 и I 3 должна быть равна нулю:
Закон Кирхгофа о напряжении (KVL)
Второй закон также называется законом напряжения Кирхгофа (KVL). В нем говорится, что сумма возрастаний и падений напряжения на всех элементах замкнутого контура равна нулю.В форме формулы:
Давайте рассмотрим пример, чтобы объяснить второй закон. Рассмотрим часть резисторной сети с внутренним замкнутым контуром, как показано на рисунке ниже. Нам нужно знать падение напряжения между узлами B и C (V BC ). Сумма падений напряжения в контуре ABCD должна быть равна нулю, поэтому мы можем написать:
Два закона схемы поясняются на видео ниже.
Пример закона Кирхгофа
Законы Кирхгофа составляют основу теории сетей.В сочетании с законом Ома и уравнениями для последовательных и параллельных резисторов можно решить более сложные схемы. Дано несколько примеров резисторных схем, чтобы проиллюстрировать, как можно использовать Кирхгофа.
Пример 1: мостовая схема
Мостовые схемы — очень распространенный инструмент в электронике. Они используются в схемах измерения, преобразователя и переключения. Рассмотрим мостовую схему ниже. В этом примере будет показано, как использовать законы Кирхгофа для определения перекрестного тока I 5 .Схема имеет четыре перемычки с резисторами R1 — R4. Имеется одно поперечное соединение с резистором R5. На мост действует постоянное напряжение V и I.
Первый закон Кирхгофа гласит, что сумма всех токов в одном узле равна нулю. Результат:
Результат:
Второй закон Кирхгофа гласит, что сумма всех напряжений на всех элементах контура равна нулю. Это приводит к:
Шесть приведенных выше наборов уравнений можно переписать с использованием нормальной алгебры, чтобы найти выражение для I 5 (ток в поперечной ветви):
Уравнение показывает, что ток моста равен нулю, мост сбалансирован:
Пример 2: соединение звезда-треугольник
Законы Кирхгофа можно использовать для преобразования соединения звезды в соединение треугольником.Это часто делается для решения сложных сетей. Широко распространенное применение соединения звезда-треугольник — ограничение пускового тока электродвигателей. Высокий пусковой ток вызывает высокие падения напряжения в энергосистеме. В качестве решения обмотки двигателя подключаются по схеме звезды во время пуска, а затем меняются на подключение по схеме треугольник.
Соединение звездой, как показано на рисунке выше, имеет те же падения напряжения и токи, что и соединение треугольником, показанное справа, только если справедливы следующие уравнения:
законов Кирхгофа
законов Кирхгофа
Вот несколько терминов для электрических цепей:
- Узел: точка, в которой три или более токоведущих элемента
(ветви) связаны; - Ветвь: путь, соединяющий два узла, по которому проходит
один или несколько элементов последовательно; - Цикл: последовательность нескольких путей, образующих замкнутый цикл.
На принципиальной схеме как направление тока, так и
полярность напряжения на элементе может быть обозначена произвольно.
Фактическое направление и полярность будут определяться знаком
конкретные значения, полученные после решения схемы. Например,
ток, обозначенный слева направо с отрицательным значением
фактически течет справа налево.
Законы Кирхгофа
- Действующий закон Кирхгофа (KCL)
Алгебраическая сумма токов в узле равна нулю:
(70) за счет принципа сохранения электрического заряда (электрический
заряд не может быть создан или разрушен в цепи).Здесь можно принять направления всех токов через элементы
находятся либо в узле, либо вне его. - Закон Кирхгофа о напряжении (KVL)
Алгебраическая сумма всех падений напряжения в контуре равна нулю:
(71) за счет принципа сохранения энергии (энергия не может быть
созданы или уничтожены в цепи).Здесь мы можем предположить полярности всех напряжений на элементах
от высокого (+) до низкого (-), при обходе цикла в любом
по часовой стрелке или против часовой стрелки.
Пример 1:
Предположим, что токи, текущие в узел, положительны, а токи, выходящие из
узел отрицательный, KCL заявляет:
.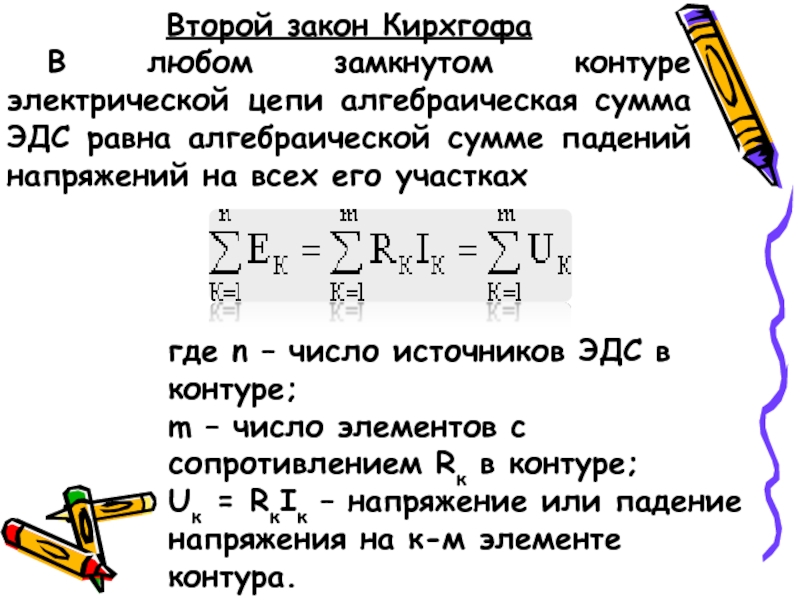
Предположим, что ток течет по петле по часовой стрелке, KVL
состояния:
.
Пример 2: Для приведенной ниже схемы найти,,,
и .
По закону Ома имеем
.
Нанесите КВЛ на петлю справа, чтобы получить:
| (72) |
По закону Ома имеем
.
Примените KCL к среднему узлу сверху, чтобы получить:
| (73) |
Опять же по закону Ома получаем
.
Нанесите КВЛ на петлю слева, чтобы получить:
| (74) |
Последовательные и параллельные комбинации компонентов схемы
- Последовательные резисторы:
Согласно КВЛ, сумма напряжений на
резисторы равны входному напряжению:куда
(76) и
(77) - Делитель напряжения:
По закону Ома напряжение на k-м резисторе может быть равным
установлено, что:(78) В частности, если мы имеем
(79) - Сопротивления параллельно:
Согласно KCL, сумма токов через резисторы равна
входной ток:куда
(81) и
(82) В частности, когда,
(83) - Делитель тока:
По закону Ома ток через k-й резистор может быть
установлено, что:(84) В частности, если мы имеем
(85) (86) - Последовательные индукторы: Согласно KVL, сумма напряжений на
индукторы равны входному напряжению:(87) я.
 е.,
е.,(88) - Параллельные индукторы: Согласно KCL, сумма токов через
индуктивности равняется входному току:(89) мы получили
(90) - Параллельно подключенные конденсаторы: Согласно KCL, сумма токов через
резисторы равны входному току:(91) я.е.,
(92) - Последовательные конденсаторы: По КВЛ сумма напряжений на
конденсаторы равны входному напряжению:(93) т.е.
(94)
Пример 3 Рассмотрим следующие шесть цепей как ток
или делители напряжения.
- Для каждой из трех параллельных цепей найдите и в
условия данного тока и сопротивлений, емкостей или
индуктивности.
- Цепь резистора:
(95) - Цепь конденсатора:
(96) - Цепь индуктивности:
(97)
- Цепь резистора:
- Для каждой из трех последовательных цепей найдите и в
с точки зрения данного напряжения и сопротивлений, емкостей или
индуктивности.- Цепь резистора:
(98) - Цепь конденсатора:
(99) - Цепь индуктивности:
(100)
- Цепь резистора:
Действующий закон Кирхгофа (KCL) | Делительные схемы и законы Кирхгофа
Что такое действующий закон Кирхгофа?
Закон Кирхгофа о течениях, часто сокращаемый до KCL, гласит, что «алгебраическая сумма всех токов, входящих и выходящих из узла, должна быть равна нулю. ”
”
Этот закон используется для описания того, как заряд входит и покидает точку соединения или узел провода.
Вооружившись этой информацией, давайте теперь рассмотрим пример применения закона на практике, почему он важен и как он был разработан.
Обзор параллельной цепи
Давайте внимательнее рассмотрим эту последнюю параллельную схему примера:
Решение для всех значений напряжения и тока в этой цепи:
На данный момент мы знаем значение тока каждой ветви и общего тока в цепи.Мы знаем, что полный ток в параллельной цепи должен равняться сумме токов ответвления, но в этой цепи происходит нечто большее, чем просто это. Взглянув на токи в каждой точке соединения проводов (узле) в цепи, мы должны увидеть кое-что еще:
Токи, входящие в узел и выходящие из него
В каждом узле положительной «шины» (провод 1-2-3-4) у нас есть разделение тока от основного потока к каждому последующему резистору ответвления. В каждом узле отрицательной «шины» (провод 8-7-6-5) у нас есть ток, сливающийся вместе, чтобы сформировать основной поток от каждого последующего резистора ответвления. Этот факт должен быть довольно очевиден, если вы подумаете об аналогии контура водопровода с каждым ответвленным узлом, действующим как тройник, разделением или слиянием водяного потока с основным трубопроводом, когда он движется от выхода водяного насоса к обратному каналу. резервуар или отстойник.
В каждом узле отрицательной «шины» (провод 8-7-6-5) у нас есть ток, сливающийся вместе, чтобы сформировать основной поток от каждого последующего резистора ответвления. Этот факт должен быть довольно очевиден, если вы подумаете об аналогии контура водопровода с каждым ответвленным узлом, действующим как тройник, разделением или слиянием водяного потока с основным трубопроводом, когда он движется от выхода водяного насоса к обратному каналу. резервуар или отстойник.
Если мы более внимательно рассмотрим один конкретный узел «тройник», такой как узел 6, мы увидим, что ток, входящий в узел, равен по величине току, выходящему из узла:
Сверху и справа у нас есть два тока, входящие в проводное соединение, обозначенное как узел 6.Слева у нас есть единственный ток, выходящий из узла, равный по величине сумме двух входящих токов. Чтобы обратиться к аналогии с водопроводом: пока в трубопроводе нет утечек, поток, поступающий в фитинг, должен также выходить из фитинга. Это верно для любого узла («подгонки»), независимо от того, сколько потоков входит или выходит. Математически мы можем выразить это общее соотношение как таковое:
Математически мы можем выразить это общее соотношение как таковое:
Действующий закон Кирхгофа
Г-н Кирхгоф решил выразить это в несколько иной форме (хотя и математически эквивалентной), назвав ее Текущий закон Кирхгофа (KCL):
Текущий закон Кирхгофа, изложенный в одной фразе, гласит:
«Алгебраическая сумма всех токов, входящих и выходящих из узла, должна быть равна нулю»
То есть, если мы присвоим каждому току математический знак (полярность), обозначающий, входят ли они (+) или выходят (-) из узла, мы можем сложить их вместе, чтобы получить гарантированно нулевое значение.
Взяв наш пример узла (номер 6), мы можем определить величину тока, выходящего слева, задав уравнение KCL с этим током в качестве неизвестного значения:
Отрицательный знак (-) на значении 5 миллиампер говорит нам, что ток равен на выходе из узла, в отличие от токов 2 миллиампер и 3 миллиампер, которые оба должны быть положительными (и, следовательно, входит в узел) .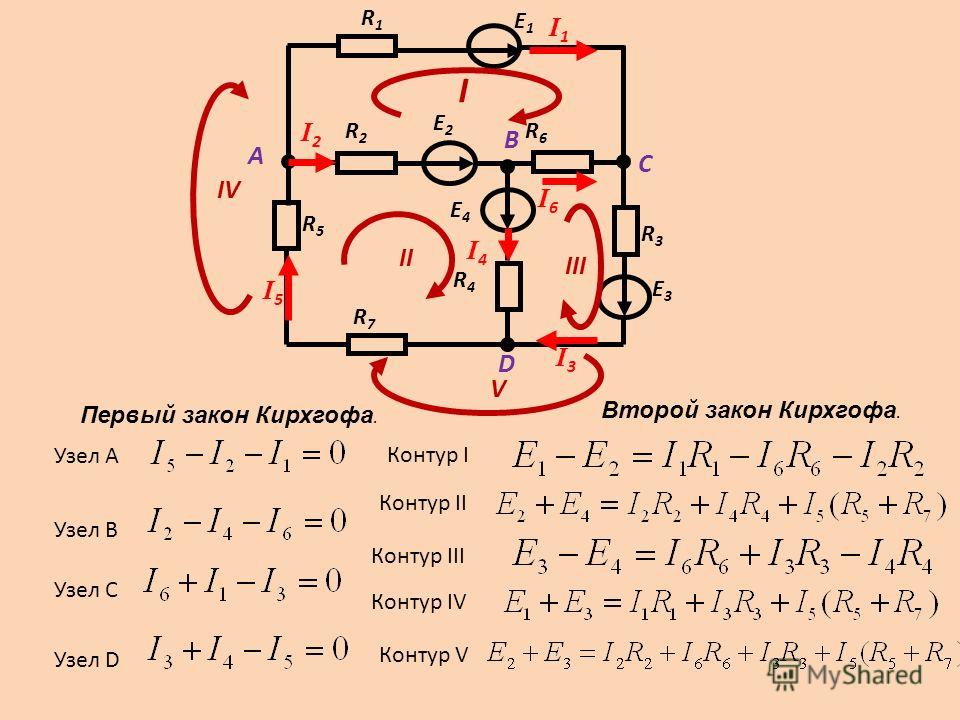 Независимо от того, обозначает ли отрицательное или положительное значение текущий вход или выход, совершенно произвольно, если они являются противоположными знаками для противоположных направлений и мы остаемся последовательными в наших обозначениях, KCL будет работать.
Независимо от того, обозначает ли отрицательное или положительное значение текущий вход или выход, совершенно произвольно, если они являются противоположными знаками для противоположных направлений и мы остаемся последовательными в наших обозначениях, KCL будет работать.
Вместе законы напряжения и тока Кирхгофа представляют собой замечательную пару инструментов, полезных при анализе электрических цепей. Их полезность станет еще более очевидной в следующей главе («Сетевой анализ»), но достаточно сказать, что эти законы заслуживают того, чтобы их запомнил изучающий электронику не меньше, чем закон Ома.
ОБЗОР:
- Текущий закон Кирхгофа (KCL): «Алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю»
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Руководство для начинающих по законам Кирхгофа
В этом руководстве мы узнаем о законах Кирхгофа.Закон Кирхгофа или KCL и Закон напряжения Кирхгофа или KVL — два очень важных математических равенства в анализе электрических цепей.
Введение
Многие электрические цепи являются сложными по своей природе, и вычисления, необходимые для нахождения неизвестных величин в таких цепях, с использованием простого закона Ома и методов упрощения последовательной / параллельной комбинации невозможны. Поэтому для упрощения этих схем используются законы Кирхгофа.
Эти законы являются фундаментальными аналитическими инструментами, которые используются для нахождения решений для напряжений и токов в электрической цепи, будь то переменный или постоянный ток.Элементы в электрической цепи соединяются множеством возможных способов, поэтому для определения параметров в электрической цепи эти законы очень полезны.
Прежде чем узнать больше о законе Кирхгофа, мы должны рассмотреть некоторые термины, относящиеся к электрическим цепям.
Узел : Узел или соединение — это точка в цепи, в которой соединены два или более электрических элемента. Это определяет уровень напряжения с опорным узлом в цепи.
Ветвь : Непрерывный проводящий путь между двумя соединениями, который содержит электрический элемент в цепи, называется ветвью.
Петля : В электрической цепи петля — это независимый замкнутый путь в цепи, который следует за последовательностью ветвей таким образом, что он должен начинаться и заканчиваться одним и тем же узлом и не должен касаться какого-либо другого соединения или узла. чем однажды.
Сетка: Сетка в электрической цепи — это петля, не содержащая никаких других петель внутри.
Вернуться к началу
Законы Кирхгофа
В 1847 году немецкий физик Густав Роберт Кирхгоф разработал эти законы для описания соотношения напряжения и тока в электрической цепи.Это следующие законы: закон Кирхгофа по напряжению (KVL) и закон Кирхгофа по току (KCL).
Вернуться к началу
Действующий закон Кирхгофа (KCL)
Это также называется законом сохранения заряда, потому что заряд или ток не могут быть созданы или разрушены на стыке или узле. Он утверждает, что алгебраическая сумма токов в любом узле равна нулю. Таким образом, ток, поступающий в узел, должен быть равен сумме тока, выходящего из узла.
Он утверждает, что алгебраическая сумма токов в любом узле равна нулю. Таким образом, ток, поступающий в узел, должен быть равен сумме тока, выходящего из узла.
На приведенном выше рисунке токи I1 и I2 поступают в узел, а токи I3 и I4 уходят из узла.Применяя KCL в узле, предположим, что входящие токи положительны, а выходящие токи отрицательны, мы можем записать как
I1 + I2 + (-I3) + (-I4) = 0
I1 + I2 = I3 + I4
Вернуться к началу
Пример проблемы KCL
Рассмотрим рисунок ниже, на котором мы должны определить токи IAB и Ix с помощью KCL.
Применяя Закон Кирхгофа в точке А, получаем
IAB = 0,5 — 0,3
IAB = 0.2 ампер
Аналогично, применяя KCL в точке B, получаем
IAB = 0,1 + Ix
0,2 = 0,1 + Ix
Ix = 0,2 — 0,1 = 0,1 А
Вернуться к началу
Закон Кирхгофа о напряжении (KVL)
Закон Кирхгофа о напряжении гласит, что алгебраическая сумма напряжений в замкнутом контуре равна нулю, то есть сумма напряжений источника равна сумме падений напряжения в цепи.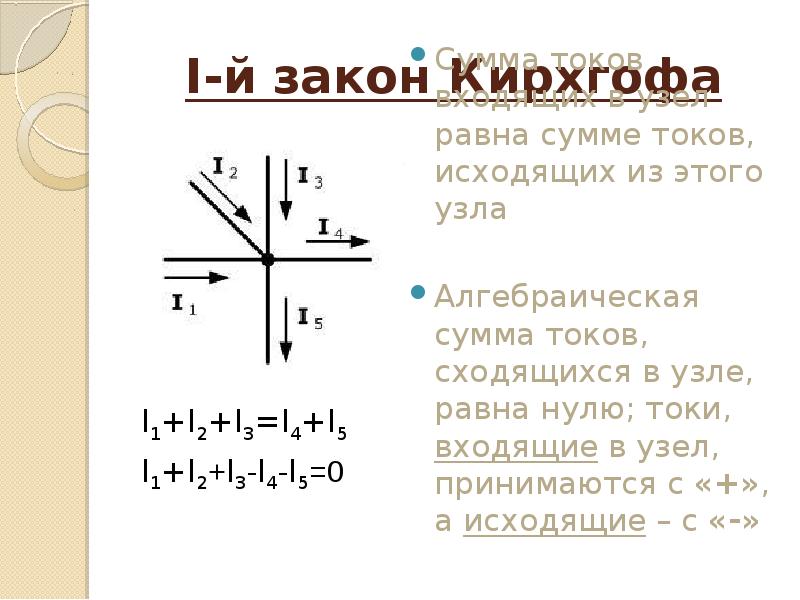 Если ток течет от более высокого потенциала к более низкому в элементе, мы рассматриваем это как падение напряжения.
Если ток течет от более высокого потенциала к более низкому в элементе, мы рассматриваем это как падение напряжения.
Если ток течет от более низкого потенциала к более высокому, мы рассматриваем это как повышение напряжения. Таким образом, энергия, рассеиваемая током, должна быть равна энергии, отдаваемой источником питания в электрической цепи.
Рассмотрим схему выше, в которой направление тока взято по часовой стрелке. Различные падения напряжения в приведенной выше схеме: V1 — положительное, IR1 — отрицательное (падение напряжения), IR2 — отрицательное (падение напряжения), V2 — отрицательное, IR3 — отрицательное (падение напряжения), IR4 — отрицательное (падение напряжения). , V3 положительный, IR5 отрицательный и V4 отрицательный.Применяя КВЛ, получаем
V1 + (-IR1) + (-IR2) + (-V2) + (-IR3) + (-IR4) + V3 + (-IR5) + (-V4) = 0
V1 — IR1 — IR2 — V2 — IR3 — IR4 + V3 — IR5 — V4 = 0
V1 — V2 + V3 — V4 = IR1 + IR2 + IR3 + IR4 + IR5
Следовательно, KVL также известен как закон сохранения электрической энергии, потому что сумма падений напряжения (произведение сопротивления и тока) равна сумме источников напряжения в замкнутом контуре.
Вернуться к началу
Пример закона Кирхгофа о напряжении
1.Давайте рассмотрим одноконтурную схему, показанную ниже, и примем направление потока тока как замкнутый путь DEABCD. В этой схеме, используя KVL, мы должны найти напряжение V1.
Применяя KVL к этому замкнутому контуру, мы можем записать как
VED + VAE + VBA + VCB + VDC = 0
Где
Напряжение точки E относительно точки D, VED = -50 В
Напряжение точки D относительно точки C, В = -50 В
Напряжение точки А относительно точки Е.VAE = I * R
VAE = 500 м * 200
VAE = 100 В
Аналогично Напряжение в точке C относительно контакта B, VCB = 350 м * 100
VCB = 35 В
Рассмотрим напряжение в точке A относительно точки B, VAB = V1
VBA = -V1
Затем с помощью KVL
-50 + 100 — V1 + 35-50 = 0
V1 = 35 Вольт
2. Рассмотрим нижеприведенную типичную двухконтурную схему, в которой мы должны найти токи I1 и I2, применяя законы Кирхгофа.
Внутри схемы есть два контура, и рассмотрите пути контура, как показано на рисунке.
Применяя КВЛ к этим петлям, получаем
Для первого контура,
2 (I1 + I2) + 4I1 — 28 = 0
6I1 + 2I2 = 28 ——— (1)
Для второго контура,
-2 (I1 + I2) — 1I2 + 7 = 0
-2I1 — 3I2 = -7 ——– (2)
Решая приведенные выше уравнения 1 и 2, мы получаем
I1 = 5A и I2 = -1 A
Вернуться к началу
Пример задачи о законах Кирхгофа
Теперь давайте воспользуемся законами Кирхгофа по току и напряжению, чтобы найти падение тока и напряжения в цепи ниже.Подобно описанной выше задаче, эта схема также содержит два контура и два соединения. Учитывайте текущее направление, указанное на рисунке.
Применяем действующий закон Кирхгофа на обоих перекрестках, получаем
На стыке 1, I = I1 + I2
На стыке 2 I1 + I2 = I
Применим закон напряжения Кирхгофа к обоим контурам, тогда получим
В первом контуре,
1,5 В — 100 I1 = 0
I1 = 1,5 / 100
= 0,015 А
Во втором контуре
100 (I1- I2) — 9В — 200I2 = 0
100I1- 300I2 = 9
Подставив значение I1 в приведенное выше уравнение, тогда
1. 5 — 300I2 = 9
5 — 300I2 = 9
— 300I2 = 7,5
I2 = -0,025
Тогда ток в переходе I = I1 + I2
I = 0,015 — 0,025
I = — 0,01
Вернуться к началу
Применение законов Кирхгофа
- Используя эти законы, мы можем найти неизвестные сопротивления, напряжения и токи (как направление, так и значение).
- В методе ответвлений определение токов, проходящих через каждую ветвь, путем применения KCL на каждом переходе и KVL в каждом контуре цепи.
- В методе тока контура определение тока через каждый независимый контур осуществляется путем применения KVL для каждого контура и подсчета всех токов в любом элементе контура.
- Используется в узловом методе определения напряжений и токов.
- Эти законы можно применить для анализа любой схемы, независимо от ее состава и структуры.
К началу
.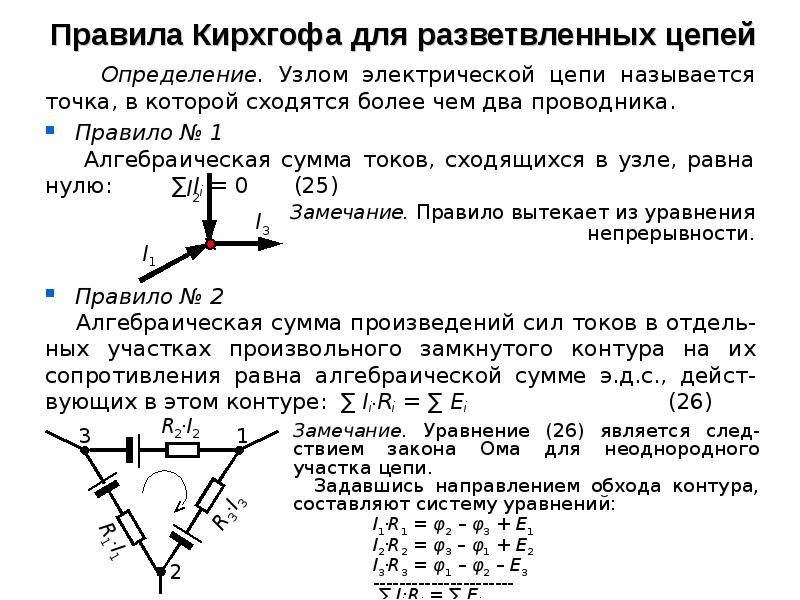

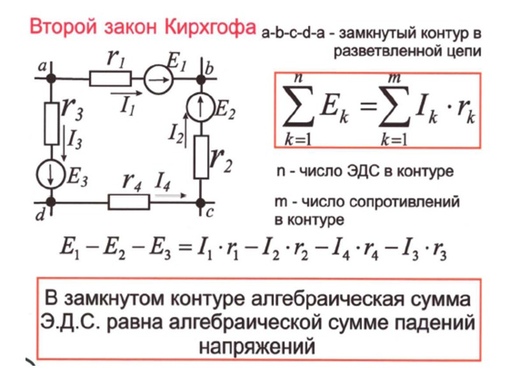
 Их можно поменять, значение не поменяется.
Их можно поменять, значение не поменяется. Для всех контуров используются свои знаки.
Для всех контуров используются свои знаки.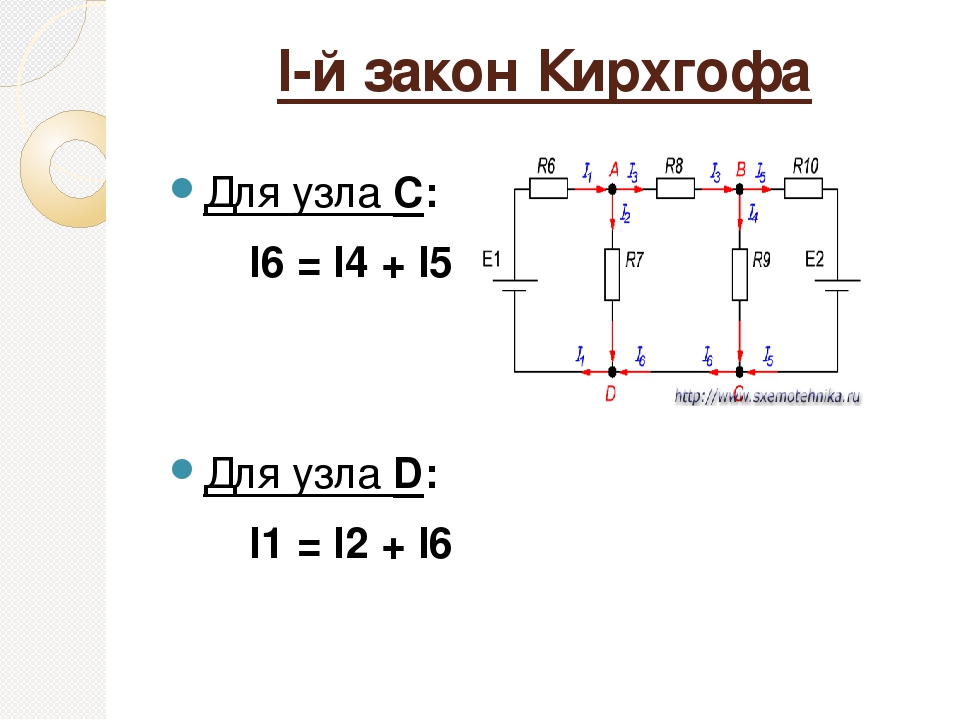 Эти ярлыки просто помогают ориентироваться.
Эти ярлыки просто помогают ориентироваться. 20 \, A \) вместо \ (I = 0.20 \, A \). Сумма рассеиваемой мощности и потребляемой мощности все равно будет равна подаваемой мощности.
20 \, A \) вместо \ (I = 0.20 \, A \). Сумма рассеиваемой мощности и потребляемой мощности все равно будет равна подаваемой мощности. N — количество ветвей.
N — количество ветвей.
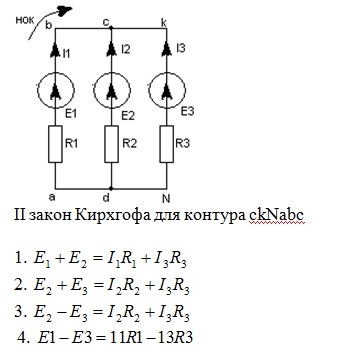 Найдите V 3 и V 5 в следующей схеме
Найдите V 3 и V 5 в следующей схеме

 d (разность потенциалов) вокруг цепи равна 0.
d (разность потенциалов) вокруг цепи равна 0. е.,
е.,