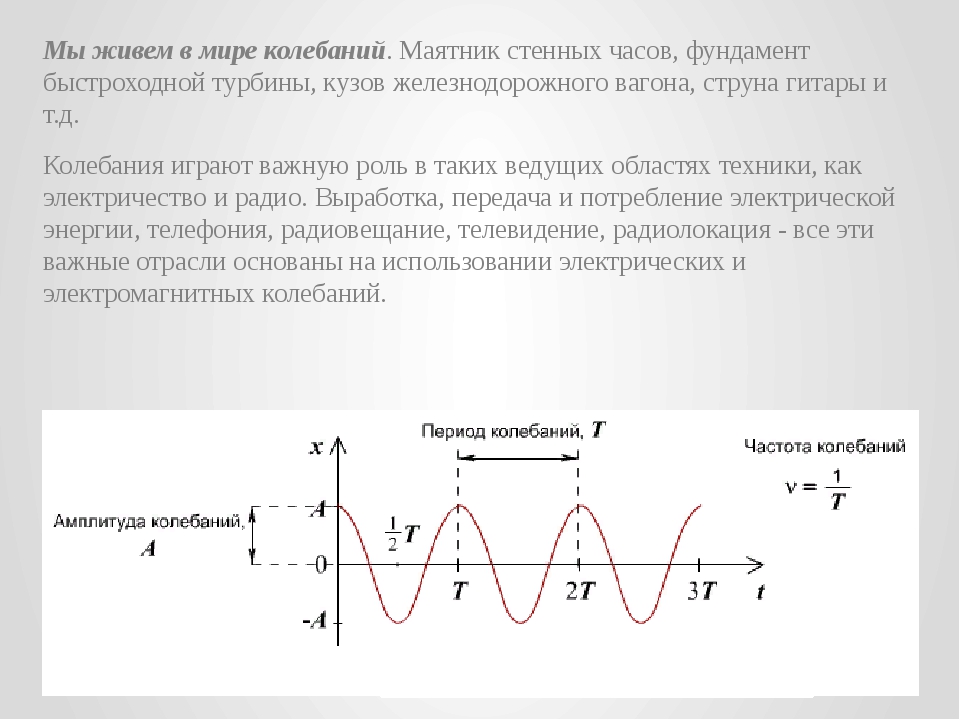
Амплитуда, частота, период колебаний — урок. Физика, 9 класс.
Рассмотрим величины, с помощью которых можно охарактеризовать колебания.
Рис. \(1\). Движение пустых качелей и качелей с мальчиком
Сравним колебания двух качелей на рисунке \(1\) — пустых качелей и качелей с мальчиком. Качели с мальчиком колеблются с большим размахом, то есть их крайние положения находятся дальше от положения равновесия, чем у пустых качелей.
Амплитудой колебаний \(A\) называется максимальное отклонение колеблющегося тела от положения равновесия.
\([A]=1~м\)
Полным колебанием называют движение, за которое тело возвращается в исходную точку (из которой началось колебание).
За одно полное колебание тело дважды максимально отклоняется от положения равновесия, поэтому один полный путь одного полного колебания равен четырём амплитудам: \(s=4A\).
Период колебаний — это промежуток времени, за который тело совершает одно полное колебание.
\([T]=1~с\)
Пример:
ударим по столу двумя линейками — металлической и деревянной (рис. \(2\)) Линейки после этого начнут колебаться, но за один и тот же промежуток времени металлическая линейка (B) сделает больше колебаний, чем деревянная (A).
Рис. \(2\). Колебания металлической (B) и деревянной (A) линеек
Число колебаний в единицу времени называется частотой колебаний.
Обрати внимание!
Обозначается частота греческой буквой ν («ню»). За единицу частоты принято одно колебание в секунду. Эта единица в честь немецкого учёного Генриха Герца названа герцем (Гц).
Период колебания \(T\) и частота колебаний ν связаны следующей зависимостью:
T=1ν.
Свободные колебания в отсутствие трения и сопротивления воздуха называются собственными колебаниями, а их частота — собственной частотой колебательной системы.
Для описания закономерностей колебательной системы необходимо учитывать зависимость параметров колебания от параметров системы. Например, период колебаний и их частота зависят от массы груза и жёсткости пружины для физического маятника.
Например, период колебаний и их частота зависят от массы груза и жёсткости пружины для физического маятника.
Рис. \(3\). Движение пустых качелей и качелей с мальчиком
Рассмотрим колебания двух одинаковых пустых качелей на рисунке \(3\). В один и тот же момент времени красные качели из положения равновесия начинают движение вперед, а зелёные качели из положения равновесия движутся назад. Движение качелей таково, что их амплитуды и периоды колебаний одинаковы. А если одинаковы периоды, то и частота колебаний совпадает. Однако, направлений движения качелей противоположно. О таких движениях говорят, что они движутся в противофазах.
Красные пустые качели и качели с мальчиком тоже колеблются с одинаковыми частотами. Направление скоростей этих качелей тоже совпадает. Это означает, что колебания происходят в одинаковых фазах, т.е. совпадают по фазе.
Фаза — физическая величина. Её используют для описания колебания тела.
Исходя из выше сказанного следует, что характеристиками колебательного движения являются:
- амплитуда,
- частота (можно использовать период),
- фаза.

Источники:
Рис. 1, 3. Движение пустых качелей и качелей с мальчиком.
Рис. 2. Колебания металлической и деревянной линеек.
Лабораторная работа №3 Исследование зависимости периода и частоты свободных колебаний
В
прошлых темах говорилось о простейших колебательных системах, которые совершают
свободные гармонические колебания — это математический и пружинный маятники.
Математический
маятник — это материальная точка, подвешенная на невесомой нерастяжимой
нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
Пружинный
маятник — это система, состоящая из материальной точки массой mи
пружины, которая совершает колебания в вертикальной плоскости.
В
данной лабораторной работе подробно остановимся на математическом маятнике и
рассмотрим, от чего зависит период его колебаний.
Цель
лабораторной работы: выяснить, как
зависит период и частота свободных колебаний математического маятника от его
длины. А также выяснить, существует ли математическая зависимость между длиной
А также выяснить, существует ли математическая зависимость между длиной
маятника и периодом его колебаний.
Оборудование:
штатив с муфтой и лапкой, шарик с нитью, секундомер, ластик и линейка.
Результаты
опытов необходимо свести в таблицу.
Порядок выполнения
работы.
Соберите установку в
соответствии с рисунком. В лапке штатива укрепите кусочек ластика так, чтобы
через него была передернута нить. Это делается для того, чтобы можно было
регулировать ее длину.
Длину нити необходимо
измерять с помощью линейки от точки подвеса маятника, до середины шарика. Время
измеряется секундомером.
При проведении опытов,
шарик следует отклонять от положения равновесия на небольшую амплитуду, порядка
1 — 3 см. Все результаты измерений заносятся в таблицу.
Длину маятника в каждом
опыте меняется в соответствии со значениями, указанными в таблице.
После проведения серии
экспериментов, вычисляется период и частота колебаний маятника каждого из
опытов: для периода по формуле — время полных колебаний деленное на их
количество; а для частоты, как величину, обратную периоду.
После снятия всех
прямых и косвенных измерений сделайте вывод о том, как зависят период и частота
свободных колебаний маятника от его длины.
В качестве
дополнительного задания, выясните, какая математическая зависимость существует
между длиной маятника и периодом его колебаний, сравнив отношения периодов
колебаний и длин маятника, по формуле
где k
— это номер опыта, начиная со второго.
В
конце работы подведите итоги и сделайте общий вывод.
Презентация: Лабораторная работа «Изучение зависимости периода и частоты колебаний нитяного маятника от длины нити»
библиотека
материалов
Содержание слайдов
Номер слайда 1
Государственное автономное учреждение Калининградской области профессиональная образовательная организация «Колледж сервиса и туризма» преподаватель физики Литвиненко Ирина Витальевна г. Калининград – 2019 год *
Калининград – 2019 год *
Номер слайда 2
Математическим маятником пользовались такие выдающиеся ученые, как Сократ, Аристотель, Платон, Плутарх, Архимед. Многие из них верили в то, что эта механическая система может влиять на судьбу и жизнь человека. Архимед использовал математический маятник при своих вычислениях.
Номер слайда 3
Мои предсказания, в рамках урока: — вам не будет скучно; — большинство из вас получат отличные оценки за урок!
Номер слайда 4
На прошлом уроке мы изучили…
Номер слайда 5
…величины, характеризующие колебательное движение. Теоретически или практически?
Теоретически или практически?
Номер слайда 6
Что мы будем делать сегодня на уроке?
Номер слайда 7
Выполнять лабораторную работу
Номер слайда 8
Проверка домашнего задания:
Номер слайда 9
Решение Тело совершает гармонические колебания с частотой 5 Гц. Определите время, за которое тело пройдёт расстояние от положения равновесия до точки, соответствующей максимальному смещению от положения равновесия. Задача №1 Математический маятник за 13 с совершил 6,5 полных колебаний. Найти период колебаний. Решение: т.к. T= t/N = 13/6,5 = 2с Ответ: 2с Задача №2 Тело совершает гармонические колебания с частотой 5 Гц. Определите время, за которое тело пройдёт расстояние от положения равновесия до точки соответствующей максимальному смещению от положения равновесия. Решение: Т.к. тело пройдет от точки равновесия до максимального значения, то оно потратит 1/4 периода Т.к. T=1/ν, то t= T/4=1/4ν =1/20= 0,05c Ответ: 0,05с
Определите время, за которое тело пройдёт расстояние от положения равновесия до точки, соответствующей максимальному смещению от положения равновесия. Задача №1 Математический маятник за 13 с совершил 6,5 полных колебаний. Найти период колебаний. Решение: т.к. T= t/N = 13/6,5 = 2с Ответ: 2с Задача №2 Тело совершает гармонические колебания с частотой 5 Гц. Определите время, за которое тело пройдёт расстояние от положения равновесия до точки соответствующей максимальному смещению от положения равновесия. Решение: Т.к. тело пройдет от точки равновесия до максимального значения, то оно потратит 1/4 периода Т.к. T=1/ν, то t= T/4=1/4ν =1/20= 0,05c Ответ: 0,05с
Номер слайда 10
Ответьте на вопросы: Колебание — это …? Что называется периодом колебаний? Определительная формула? Что называется частотой колебаний? Определительная формула? Нитяной маятник? Математический маятник? От чего зависят период и частота свободных колебаний нитяного маятника?
Номер слайда 11
Лабораторная работа №1 «Изучение зависимости периода и частоты колебаний нитяного маятника от длины нити»
Номер слайда 12
Цель лабораторной работы?
Номер слайда 13
Цель работы: Выяснить, как зависят период и частота свободных колебаний нитяного маятника от его длины.
Номер слайда 14
Оборудование: укладочный пенал, груз 100г, нить, ластик, измерительная лента, секундомер, стержень штатива с муфтой и лапкой.
Номер слайда 15
Ваша гипотеза?
Номер слайда 16
Правила ТБ: До начала работы приборы не трогать и не приступать к выполнению лабораторной работы до указания преподавателя. Будьте внимательны, дисциплинированы, осторожны, точно выполняйте указания преподавателя. Не оставляйте рабочее место без разрешения преподавателя. Не держите на рабочем месте предметы, не требующиеся при выполнении задания. Не отклоняйте маятник от положения равновесия на большие расстояния. Берегите оборудование и используйте его по назначению. При получении травмы обратитесь к преподавателю.
Будьте внимательны, дисциплинированы, осторожны, точно выполняйте указания преподавателя. Не оставляйте рабочее место без разрешения преподавателя. Не держите на рабочем месте предметы, не требующиеся при выполнении задания. Не отклоняйте маятник от положения равновесия на большие расстояния. Берегите оборудование и используйте его по назначению. При получении травмы обратитесь к преподавателю.
Номер слайда 17
Таблица для записи результатов измерений и вычислений Физическая величина 1 2 3 4 5 l, см 5 20 40 80 125 N 30 t, с T, с ν, Гц
Номер слайда 18
ФИЗКУЛЬТ-МИНУТКА ГИМНАСТИКА ДЛЯ ГЛАЗ
Номер слайда 19
Выполните задания: Рассчитайте период колебаний Рассчитайте частоту колебаний Запишите вывод о том, как зависят период и частота свободных колебаний нитяного маятника от его длины Ответьте на вопросы Дополнительное задание
Номер слайда 20
1. Увеличили или уменьшили длину маятника, если: А) период его колебаний сначала был 0, 3 с, а после изменения длины стал 0,1 с; Б)частота его колебаний вначале была равна 5 Гц, а потом уменьшилась до 3 Гц? Ответьте на вопросы:
Увеличили или уменьшили длину маятника, если: А) период его колебаний сначала был 0, 3 с, а после изменения длины стал 0,1 с; Б)частота его колебаний вначале была равна 5 Гц, а потом уменьшилась до 3 Гц? Ответьте на вопросы:
Номер слайда 21
Закономерность! Т ~
Номер слайда 22
Христиан Гюйгенс (14 апреля 1629- 8 июля 1695) — нидерландский механик, физик, математик, астроном и изобретатель.
Номер слайда 23
Мы исследовали зависимость периода и частоты свободных колебаний нитяного маятника от его длины. ВЫВОД ?
Номер слайда 24
Домашнее задание: Повторить все формулы и определения § 18-22, упр. 3 (2) Сделать презентацию на тему: «Механические волны» и «Ультразвук и его применение»
3 (2) Сделать презентацию на тему: «Механические волны» и «Ультразвук и его применение»
Номер слайда 25
Рефлексия: Ваше настроение на уроке (обвести) 2. Исполнилось ли предсказание?
Номер слайда 26
Спасибо за внимание!
(Ф9) ЛР Исследование зависимости периода частоты свободных колебаний маятника от его длины
Цель работы: выяснить, как зависят период и частота свободных колебаний нитяного маятника от его длины.
Дополнительное задание
Цель задания: выяснить, какая математическая зависимость существует между длиной маятника и периодом его колебаний.
При изменении длины нитяного маятника меняется его частота и период. В данной работе мы должны определить эту зависимость. Период и частоту определяем следующим образом. Отклоним шарик маятника от положения равновесия на небольшую амплитуду и засечем время t, в течение которого маятник совершит N . колебаний. Тогда период и амплитуду можно посчитать по формулам:
Измеряя период и частоту при разных значениях длины маятника, мы тем самым получаем зависимость периода и частоты от длины.
Пример выполнения работы.
№ опыта Физ. вел. | 1 | 2 | 3 | 4 | 5 |
5 | 20 | 45 | 80 | 125 | |
30 | 30 | 30 | 30 | 30 | |
13 | 27 | 40 | 53 | 67 | |
0,43 | 0,9 | 1,33 | 1,77 | 2,23 | |
2,31 | 1,11 | 0,75 | 0,57 | 0,45 |
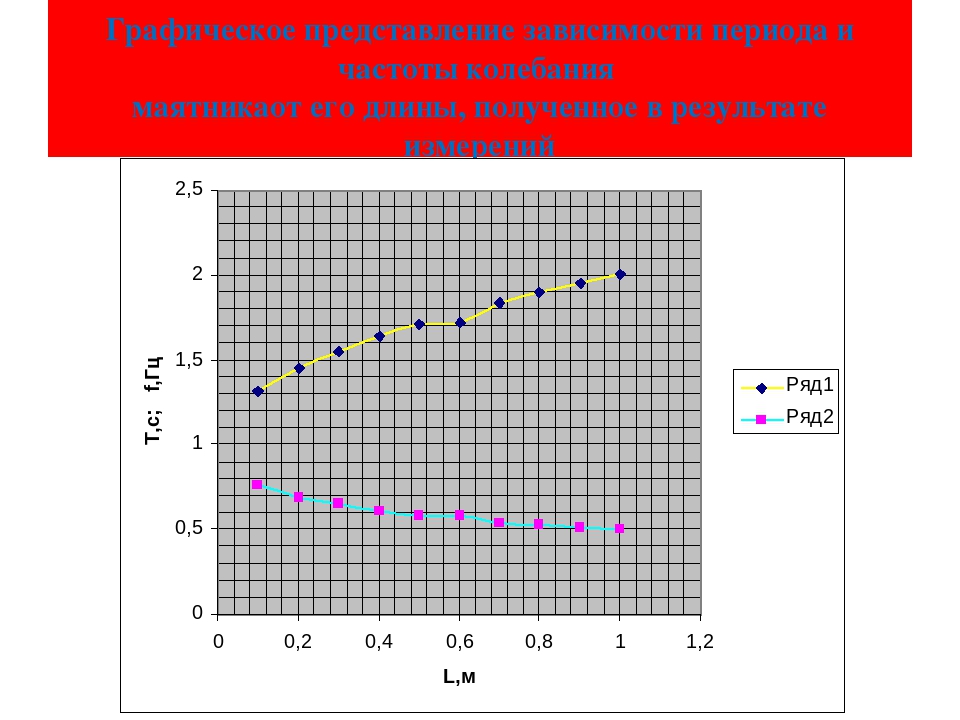
Из данных в таблице можно заметить такую закономерность: чем больше длина маятника, тем больше период и меньше частота, и наоборот.
Дополнительное задание.
Цель задания: выяснить, какая математическая зависимость существует между длиной маятника и периодом его колебаний.
Из данных в таблице хорошо просматривается связь между периодом колебаний маятника и его длиной:
Физика — 10
4.3
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ МАТЕМАТИЧЕСКОГО
МАЯТНИКА
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г.Гапилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
- Предложите свою гипотезу: К каким результатам привели исследования Галилея — от чего зависят период и частота колебаний нитевого маятника?
Исследование-1. Исследование колебаний нитевого маятника
Оборудование: маленький шарик, закрепленный на длинной нити, линейка, секундомер,
штатив с муфтой и зажимом.
Ход исследования:
I. Исследование зависимости периода и частоты колебания нитевого маятника от амплитуды.
- Поместите штатив на край стола. Свободный конец нити с шариком закрепите в зажиме штатива так, чтобы шарик находился от пола на высоте 1-2 см(a).
- Измерьте расстояние от точки закрепления свободного конца нити в зажиме штатива до центра шарика (длина маятника), оно должно быть порядка 160 см.

- Приведите в колебательное движение маятник с малой амплитудой колебания xm1, и измерьте секундомером время t1 затраченное на совершение N = 5
полных колебаний. - Определите период и частоту нитевого маятника при помощи формул T1 = t1/N
и v1 = N/t1, соответственно. - Незначительно увеличьте амплитуду маятника (xm2) и, повторив опыт, вычислите период(T2 ) и частоту
(v2) колебаний. - Сравните периоды T1 и T2, а также частоты v1 и v2 колебаний нитевого маятника.

II. Исследование зависимости периода и частоты колебания нитевого маятника от массы подвешенного груза.
- Замените шарик на нити другим, с несколько большей массой. Приведите в колебательное движение маятник с той же малой амплитудой колебания xm1 и измерьте секундомером время t2, затраченное на совершение N = 5 полных колебаний.
- Определите период T2‘ и частоту v2‘ колебаний.
- Сравните периоды T1 и T2‘, а также частоты v1
и v2‘ колебаний нитевого маятника.
III. Исследование зависимости периода и частоты колебания нитевого маятника от
длины маятника.
- Намотав нить на держатель штатива, укоротите длину маятника в 4 раза и приведите в колебательное движение маятник с той же малой амплитудой колебания
xm1. Измерьте секундомером время, затраченное на совершение N=5 полных колебаний. - Определите период T2» и частоту v2» колебаний.
- Запишите проведенные измерения и вычисления в таблицу 4.2 и сравните нижеприведенные соотношения:
T»2
T1
и l2
l1 ;
v»2
v1
и l2
l1 ;
Разница между периодом и частотой
Основное различие между периодом и частотой заключается в их определении. Оба они являются вибрационными характеристиками. Колебания и вибрации механических систем являются важными областями изучения в физике. Почти все системы свободно колеблются или вибрируют по-разному.
Оба они являются вибрационными характеристиками. Колебания и вибрации механических систем являются важными областями изучения в физике. Почти все системы свободно колеблются или вибрируют по-разному.
Колебание – это повторяющееся движение инструмента, обычно во времени, вокруг центрального состояния или между двумя или более отдельными точками. Именно термин «вибрация» описывает механические колебания.Чтобы узнать больше о разнице между колебаниями и вибрацией, вы можете посетить эту ссылку. Типичными примерами колебаний являются качающийся маятник, гитарные струны, биение сердца и переменный ток. Даже атомы нашего тела вибрируют.
Каждая колебательная система имеет нечто общее, включая силу и энергию. Раскачивая ребенка на качелях, начинается движение. Также при использовании тепла увеличивается энергия атомов, и они вибрируют. Таким образом, колебания порождают волны.
Характерной чертой всех волн является периодичность.Ясно, что несколько фундаментальных принципов описывают все явления, которые доказывают, что они более распространены, чем вы думали. В каждом явлении вы видите определенную модель движения, которая повторяется снова и снова. Периодические движения, такие как движение струны гитары или движение ребенка вперед и назад на качелях, повторяются через равные промежутки времени. Время, необходимое для завершения цикла вибрации или колебаний, называется периодом волны. Частота – это параметр, равный количеству циклов колебаний в секунду.
В каждом явлении вы видите определенную модель движения, которая повторяется снова и снова. Периодические движения, такие как движение струны гитары или движение ребенка вперед и назад на качелях, повторяются через равные промежутки времени. Время, необходимое для завершения цикла вибрации или колебаний, называется периодом волны. Частота – это параметр, равный количеству циклов колебаний в секунду.
Основы периода и частоты
Основное различие между периодом и частотой восходит к их определению.
Период
Период определяется как время, необходимое для одного полного цикла вибрации или колебаний. Это относится ко времени периодического возникновения, измеряемому в секундах за цикл. Период обычно обозначается буквой «Т».
Частота
Частота волны означает количество полных циклов вибрации или колебаний, происходящих за одну секунду.Единицей измерения частоты являются циклы в секунду или герц (Гц). Частота обычно обозначается буквой «f».
Оба значения периода времени и частоты обратно пропорциональны друг другу. На математическом языке период и частота связаны следующим уравнением:
T=\frac{1}{f}
или
f=\frac{1}{T}
0
2 Природа периода и частоты
Определения периода и частоты показывают, что природа этих двух параметров различна.
Период
Исходя из определения периода как продолжительности завершения волнового цикла в его единице, т. е. времени, природа периода — время.
Частота
Частота как количество полных циклов, происходящих в единицу времени, является величиной скорости.
Схемы периода и частоты
В этом разделе мы хотим проиллюстрировать концепции периода и частоты волны на диаграммах.
Период
Если мы посмотрим на диаграмму распространения повторяющихся волн во времени, мы можем представить период как расстояние между двумя последовательными гребнями волны (или идентичными последовательными точками) на оси времени.
Волна как функция времени для отображения периода (Ссылка: afsharphysics.wordpress.com )
Частота
Рассмотрим волну, которая совершает два полных цикла в секунду (как показано ниже). Следовательно, частота этой волны равна 2 Гц.
Волна как функция времени для отображения периода (Ссылка: Circuitglobe.com )
Отношение периода и частоты к длине волны
Рассмотрим распространение волны со скоростью v в м/с. Расстояние между двумя последовательными идентичными точками (например, двумя гребнями или впадинами) на волновой диаграмме как функция расстояния называется длиной волны. Обозначается греческой буквой «λ» и измеряется в метрах.
Волна как функция расстояния для отображения длины волны (Ссылка: afsharphysics.wordpress.com )
Период
Период и длина волны связаны следующим уравнением: а длина волны определяется уравнением ниже:
f=\frac{v}{\lambda}
Это может быть очевидно, поскольку период и частота обратно пропорциональны друг другу.
Пример периода и частоты
Чтобы лучше понять частоту и период, посмотрите на этот пример. Рассмотрим человеческое сердце, бьющееся 75 раз в минуту. Если каждый раз рассматривать полный цикл, то нам придется вычислять период и частоту:
Период
Использование математического определения периода приводит к:
T=\frac{Overall\ time}{Number \ of\ cycles}=\frac{60}{75}=0.8\ (s)
Частота
Для расчета частоты имеем:
f=\frac{Количество\ циклов} {Общее\ время}=\frac{1}{T}=\frac{75}{60}=1.25\ (Гц)
Период и частота в физике
Понятия периода и частоты широко используются в физике, особенно в области энергетики.
Период
Хорошо известным примером применения периода является движение маятника. Период этого движения – это время, затрачиваемое на перемещение из одной стороны в другую и обратно.
Другим физическим примером является электрон, движущийся по винтовой орбите. Его период определяется выражением:
Его период определяется выражением:
T=\frac{2\pi m}{qB}
, где m , q и B — масса электрона, заряд электрона, и магнитное поле в регионе.
Частота
Частота является важным параметром в инженерных и научных приложениях. Он определяет скорость колебательных и вибрационных событий, таких как механические вибрации, звуковые сигналы, радиоволны и свет.
Частота волны совпадает с частотой вибрации, создающей волну. Чтобы создать волну с более высокой частотой в веревке, вы должны перемещать веревку вверх и вниз с большей скоростью. При этом потребляется больше энергии, и эта энергия передается волне.Следовательно, высокочастотные волны обладают большей энергией, чем низкочастотные волны той же амплитуды.
Частота обычно представлена в двух формах:
Угловая частота
Угловая частота определяет количество оборотов за фиксированный интервал времени. Единицей угловой частоты является Герц.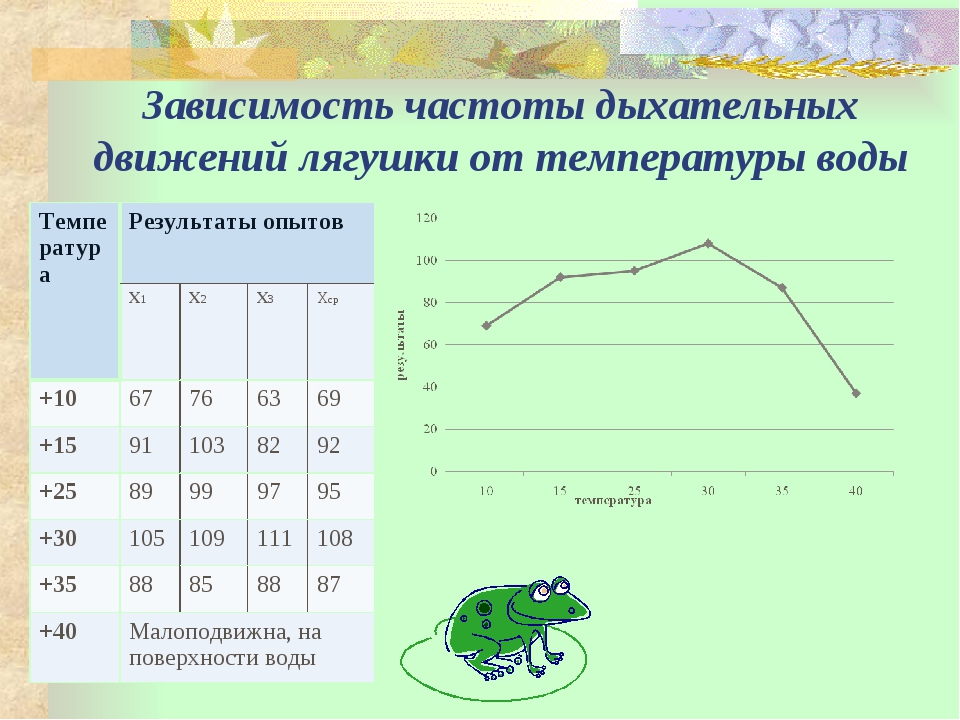 Следующее уравнение выражает связь между частотой и угловой частотой:
Следующее уравнение выражает связь между частотой и угловой частотой:
\omega =2\pi f
Где ω — угловая частота.
Пространственная частота
Пространственная частота зависит от пространственной координаты и обратно пропорциональна длине волны. Пространственная частота содержит характеристику системы, периодически работающей в пространстве.
Низкие и высокие пространственные частоты (Ссылка: cns.nyu.edu )
Параметры волны: длина волны, амплитуда, период, частота и скорость — видео и стенограмма урока
Период и частота
Период — это время, которое требуется волне для завершения одного цикла.Мы измеряем период в секундах и обозначаем его заглавной буквой T . Вы можете думать о периоде как о времени, которое требуется одной частице в среде, чтобы двигаться вперед и назад. Если бы это была водная волна, все частицы в воде двигались бы вверх и вниз по мере прохождения волны. Время, за которое одна молекула воды движется вверх, опускается вниз и затем возвращается в исходное положение, называется периодом.
Время, за которое одна молекула воды движется вверх, опускается вниз и затем возвращается в исходное положение, называется периодом.
Хорошо знать период волны, но нам часто приходится говорить о волнах с точки зрения того, как часто приходят волновые циклы.Другими словами, мы хотим знать частоту волны. Частота волны — это количество циклов, которые совершаются за определенный промежуток времени. Частота обозначается строчными буквами f , и мы измеряем ее в циклах в секунду, что соответствует единице измерения в герцах. Волна с частотой 20 Гц каждую секунду совершает 20 волновых циклов.
Будьте осторожны, не перепутайте частоту с периодом. Это распространенная ошибка. Частота и период имеют обратную зависимость.В то время как период измеряется в секундах за цикл, частота измеряется в циклах в секунду. Рассмотрим нашу волну с периодом 2 секунды. Так как волна совершает один цикл каждые две секунды, то ее частота равна половине или 0,5 Гц. Итак, вы видите — период и частота обратны друг другу. Мы можем представить их отношения с помощью простого уравнения:
Мы можем представить их отношения с помощью простого уравнения:
Чем больше период волны, тем меньше волновых циклов может уместиться в секунду, и тем ниже становится частота.Точно так же волна с большей частотой должна была бы умещать больше волновых циклов в каждую секунду, а это означает, что период каждого цикла должен быть меньше. Независимо от того, на какую волну вы смотрите, период и частота всегда будут обратно пропорциональны друг другу.
Амплитуда и энергия
Итак, теперь мы знаем, как измерить волну на основе циклов и времени, но как насчет высоты волны? Можем ли мы измерить, как высоко достигает гребень волны или как низко опускается впадина? Мы уже упоминали амплитуду в нашем предыдущем уроке.Это расстояние между средней линией волны и ее гребнем или впадиной. Амплитуда измеряет, сколько энергии переносится волной. Чем больше амплитуда, тем больше энергии имеет волна.
Чем больше амплитуда, тем больше энергии имеет волна.
Амплитуда обозначается заглавной буквой A . Будьте осторожны, чтобы не ошибиться, думая, что амплитуда — это расстояние от гребня до впадины. Это только расстояние от точки покоя. Возьмем в качестве примера гигантскую водную волну.
Мы видим, что гребни достигают полуметра выше точки покоя, а впадины достигают полуметра ниже точки покоя. Неважно, смотрим ли мы на гребень или корыто. Амплитуда этой волны составляет 0,5 метра.
Скорость и длина волны
Если волны несут энергию, а энергия волны иллюстрируется ее амплитудой, значит ли это, что волны с большой амплитудой движутся быстрее, чем волны с малой амплитудой? У вас может возникнуть соблазн так подумать.Но скорость волны не имеет ничего общего с амплитудой ее гребней и впадин. Скорость измеряется расстоянием, которое волна проходит за определенное время. В частности, она измеряется в метрах в секунду. У нас уже есть часть «в секунду». Помните, частота говорит нам, сколько циклов совершается в секунду. Но откуда мы знаем, каково расстояние для каждого полного цикла?
В частности, она измеряется в метрах в секунду. У нас уже есть часть «в секунду». Помните, частота говорит нам, сколько циклов совершается в секунду. Но откуда мы знаем, каково расстояние для каждого полного цикла?
Расстояние за цикл волны называется длиной волны .Легче всего найти длину волны, измерив пространственное расстояние между двумя гребнями волн. Ранее мы измеряли время, необходимое для завершения одного цикла. Но сейчас мы измеряем длину одного полного цикла волны. Длина волны длинных волн может быть измерена в метрах, но мы используем нанометры для измерения длины более коротких волн. Символом, обозначающим длину волны, является греческая буква лямбда.
Итак, теперь мы можем узнать скорость волны? Конечно! У нас есть мера расстояния по длине волны, и у нас есть мера времени по частоте.Длина волны в метрах на цикл. Частота циклов в секунду. Итак, умножение двух дает нам метры в секунду. В науке мы используем строчные буквы и для обозначения скорости, потому что это также называется скоростью. Итак, теперь мы можем суммировать наши выводы с помощью уравнения: скорость равна длине волны, умноженной на частоту.
Частота циклов в секунду. Итак, умножение двух дает нам метры в секунду. В науке мы используем строчные буквы и для обозначения скорости, потому что это также называется скоростью. Итак, теперь мы можем суммировать наши выводы с помощью уравнения: скорость равна длине волны, умноженной на частоту.
Ну, это было не так уж и плохо, не так ли? Вы узнали пять способов описания волны, используя ваши параметры волны .Период, частота, амплитуда, скорость и длина волны используются для различения и разделения волн на группы. Позже мы узнаем о множестве различных типов волн и о том, как использовать эти параметры, чтобы понять их все.
Краткий обзор урока
Волна — это возмущение, которое периодически проходит через среду, перенося энергию без переноса материи. Волны описываются и измеряются пятью волновыми параметрами: периодом, частотой, амплитудой, длиной волны и скоростью. Период волны – это время, необходимое для завершения одного цикла. Частота прямо противоположна; это количество волновых циклов, которые совершаются за одну секунду. Амплитуда и длина волны являются мерами расстояния. Амплитуда измеряет высоту гребня волны от средней линии. Длина волны измеряет горизонтальное расстояние между циклами. Скорость волны находится путем умножения длины волны на частоту. Изучив пять основных параметров волн, мы можем легче узнать о волнах и классифицировать их на основе их характеристик.
Период волны – это время, необходимое для завершения одного цикла. Частота прямо противоположна; это количество волновых циклов, которые совершаются за одну секунду. Амплитуда и длина волны являются мерами расстояния. Амплитуда измеряет высоту гребня волны от средней линии. Длина волны измеряет горизонтальное расстояние между циклами. Скорость волны находится путем умножения длины волны на частоту. Изучив пять основных параметров волн, мы можем легче узнать о волнах и классифицировать их на основе их характеристик.
Результаты обучения
После этого урока вы сможете:
- Описывать каждый из пяти параметров волны: период, частоту, амплитуду, длину волны и скорость
- Объясните, как найти каждый из пяти параметров и определить их символы
- Приведите уравнение для определения скорости волны
Период волны
: определение и формула — видео и стенограмма урока
Частота волны
Прежде чем мы найдем период волны, полезно знать частоту волны, то есть количество раз, которое цикл волны повторяется в заданный период времени. Этот график показывает нам пять разных волн с разными частотами. Вы можете видеть, что разное количество циклов за один и тот же период времени. Мы могли бы найти точное число, посчитав пики или впадины. Красная волна имеет самую низкую частоту среди пяти, потому что она имеет наименьшее количество повторяющихся циклов, а розовая волна имеет самую высокую частоту потому что она имеет наибольшее количество повторяющихся циклов.
Этот график показывает нам пять разных волн с разными частотами. Вы можете видеть, что разное количество циклов за один и тот же период времени. Мы могли бы найти точное число, посчитав пики или впадины. Красная волна имеет самую низкую частоту среди пяти, потому что она имеет наименьшее количество повторяющихся циклов, а розовая волна имеет самую высокую частоту потому что она имеет наибольшее количество повторяющихся циклов.
Частота ( f ) может быть получена путем деления скорости волны, обычно обозначаемой буквой v , на ее длину волны.Помните, мы представляем его греческим символом: лямбда. Обычно мы измеряем длину волны в метрах и скорость в метрах в секунду. Частота, найденная с использованием этих единиц измерения, будет измеряться в 90 209 Гц (герц) 90 210 , иначе говоря, циклов в секунду.
Допустим, мы определили, что волна движется с частотой 60 Гц; эта волна будет иметь 60 циклов в секунду. При написании формул Герц обычно сокращается до Гц.
При написании формул Герц обычно сокращается до Гц.
Нахождение периода волны
Так как же знание частоты может помочь нам найти период волны? Чем выше частота волны, тем меньше период волны.В конце концов, если вы собираетесь уместить больше циклов в определенный период времени, циклы должны быть короче.
Можно сказать, что частота и период волны обратно пропорциональны друг другу, поэтому если частота увеличивается, период уменьшается, и наоборот. Другими словами, если частота большая, , то период короткий , а если частота малая, , то период длинный.
Помните, что длина волны и скорость влияют на частоту, поэтому мы также можем сказать, чем больше длина волны, тем больше период волны и чем меньше скорость, тем больше период волны.’
Период волны на самом деле является величиной, обратной частоте, что означает, что любая волна будет иметь период волны, на 1 превышающий частоту волны. Стандартной единицей измерения периода является секунда, сокращенно буква S.
Стандартной единицей измерения периода является секунда, сокращенно буква S.
Практические вопросы
Давайте немного потренируемся.Вот задача со словами:
Пример 1:
Вы в отпуске на пляже, и сегодня ветреный день. Глядя на океанские волны, вы заметили, что приблизительная скорость волны составляет 3 м/с, а расстояние между пиками двух волн составляет примерно 20 м. Каковы частота и период этих волн?
Решение:
Итак, мы знаем скорость, которая равна 3 м/с. Мы также знаем длину волны , помните, что это расстояние между двумя пиками, поэтому мы можем назвать длину волны 20 метров.-15 секунд. Это сложные цифры, но мы все же можем ответить на второй вопрос: у какого цвета период волны больше? В этом случае ответ красный, чей волновой цикл немного медленнее. Мы также можем понять это, зная частоты двух волн. Помните, что частота обратно пропорциональна периоду волны . Это означает, что чем выше частота волны, тем меньше будет период ее волны.
Это означает, что чем выше частота волны, тем меньше будет период ее волны.
Фиолетовые волны имеют более высокую частоту, чем красные волны. Это означает, что мы знаем, что у красных волн более высокие периоды волн, чем у фиолетовых волн, и нам не нужно подключать это к каким-либо уравнениям.
Итоги урока
Каждый день мы сталкиваемся с волнами. Иногда мы видим их, когда идем на пляж и смотрим на океан. В других случаях они невидимы, например, волны в микроволнах и радиоволны. Разные волны имеют разные частоты и периоды.
Период волны — это время, необходимое для завершения одного цикла. Стандартная единица измерения периода волны в секундах, и обратно пропорциональна частоте волны , которая является числом циклов волн, возникающих в одну секунду.Другими словами, чем выше частота волны, тем меньше период волны.
Период волны также зависит от длины волны и скорости. Чем выше скорость, тем меньше период волны, и чем больше длина волны, тем больше период волны.
Период волны – термины и определения
- Период волны : время, необходимое для завершения одного цикла волны
- Гребни/пики : самые высокие точки волны
- Впадины : самые низкие точки волны
- Длина волны : измерение в метрах от одного пика до следующего пика волны
- Волновые циклы : одно завершение повторяющегося восходящего и нисходящего паттерна волны
- Частота : количество повторений цикла волны в заданный период времени
- Скорость : скорость длин волн измеряется в метрах в секунду
- Гц (герц) : циклов в секунду
- Частота и период волны обратно пропорциональны : если частота волны увеличивается, период волны уменьшается, и наоборот
Результаты обучения
Когда вы закончите изучение периода волны с помощью этого урока, убедитесь, что вы можете успешно:
- Написать определение периода волны
- Вербализация значения частоты волны
- Используйте частоту, чтобы найти период волны
Частота, амплитуда, длина волны, цикл, период
Определения частоты, амплитуды, длины волны, цикла и периода должны быть известны всем специалистам-электрикам. Ниже я дам вам определения и сравнения этих важных терминов. Это сделает вашу жизнь проще.
Ниже я дам вам определения и сравнения этих важных терминов. Это сделает вашу жизнь проще.
Что такое частота?
Частота переменного тока — это количество циклов в секунду синусоидальной волны переменного тока. Другими словами, частота — это количество раз, когда синусоида повторяет положительный и отрицательный циклы.
Частота обычно используется для описания работы электрического оборудования. Некоторые распространенные диапазоны частот:
Частота линии электропередачи (например, в большинстве стран Европы частота составляет 50 Гц, а в Америке — 60 Гц)
Низкая частота: от 300 кГц до 3 мегагерц (МГц).
Средняя частота: 3–30 МГц.
Высокая частота: 30-300 МГц.
Диапазон радиочастот: от 118 до 137 МГц
Диапазон звуковых частот: от 15 Гц до 20 кГц (диапазон человеческого слуха).
Радиочастота: 30-300 кГц.
Стандартной единицей измерения частоты является герц (Гц), определяемый как количество событий или циклов в секунду . Частота электрических сигналов часто измеряется в герцах, включая килогерцы (кГц), мегагерцы (МГц) или гигагерцы (ГГц), где 1 кГц равен одной тысяче (10³) событий в секунду, 1 МГц равен одному миллиону (10⁶ ) событий в секунду, а 1 ГГц соответствует одному миллиарду (10⁹) событий в секунду.
Частота электрических сигналов часто измеряется в герцах, включая килогерцы (кГц), мегагерцы (МГц) или гигагерцы (ГГц), где 1 кГц равен одной тысяче (10³) событий в секунду, 1 МГц равен одному миллиону (10⁶ ) событий в секунду, а 1 ГГц соответствует одному миллиарду (10⁹) событий в секунду.
В 1930 году Международная электротехническая комиссия (МЭК) удостоила имени Генриха Рудольфа Герца , назвав единицу измерения частоты.
Для измерения частоты подсчитывается количество раз, когда событие происходит в заданном временном интервале, затем это число делится на временной интервал.
ф = 1/Т
f: Частота
Т: Период
Другая формула частоты:
f = с/λ
f: Частота
c: Скорость волны (скорость электромагнитной волны = скорость света = 3 x 10 м/сек)
λ: Длина волны
Что такое период?
Период — это время в секундах, в течение которого сигнал повторяется от начала до конца. Обозначается буквой «Т». Он обратно пропорционален частоте. Его единица — секунда.
Обозначается буквой «Т». Он обратно пропорционален частоте. Его единица — секунда.
Что такое амплитуда?
Амплитуда может быть просто определена несколькими способами:
- Амплитуда равна половине расстояния по вертикали от гребня волны до ее впадины.
- Его также можно определить как максимальный уровень в периодическом движении.
- Амплитуда – максимальное абсолютное значение периодически изменяющейся величины.
Что такое длина волны?
Длина волны — это расстояние между повторяющимися единицами группы волн. Обозначается символом с буквой лямбда (λ).
Длина волны обратно пропорциональна частоте. Чем длиннее длина волны, тем ниже частота.
Расчет длины волны:
λ = v/f
λ: Длина волны
v: Скорость волны
f: Частота
В большинстве случаев скорость волны (v) выбирается как скорость света (c) в предположении, что волна распространяется в пространстве.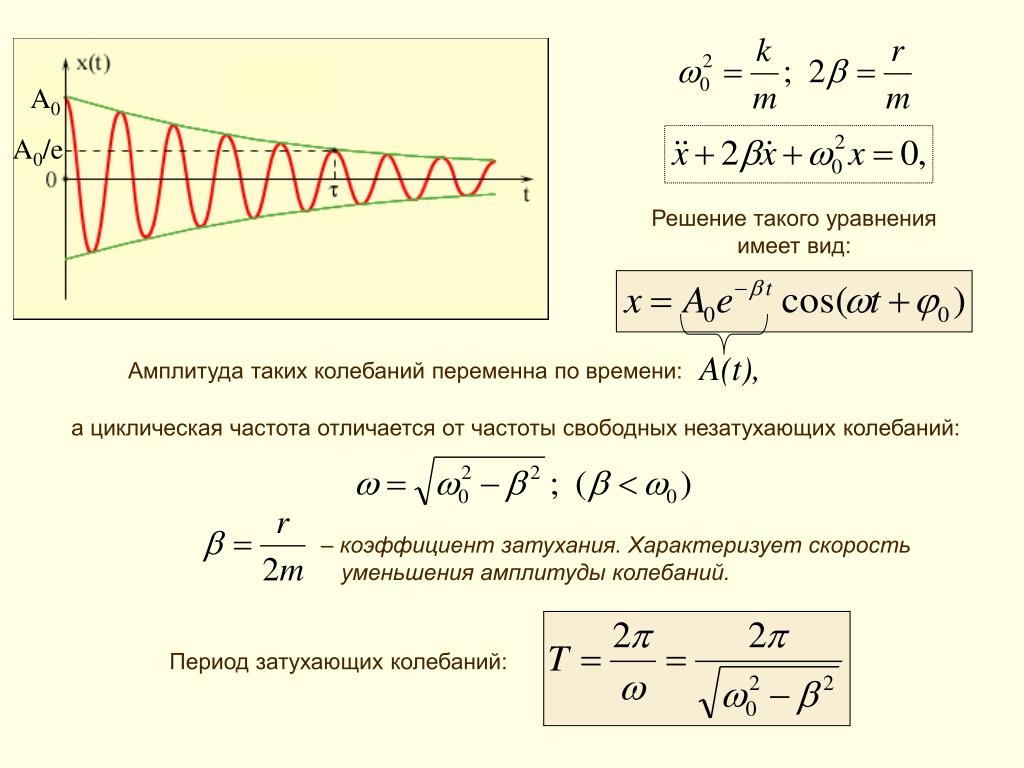 В этом случае формула будет следующей:
В этом случае формула будет следующей:
λ = с/ф
λ: Длина волны
c: Скорость света
f: Частота
Соотношение длины волны и периода следующее:
λ = T x v
λ: Длина волны
Т: Период
v: Скорость волны
Что такое цикл?
Цикл – это полная волна переменного тока или напряжения.Другими словами, подъем кривой, начинающийся с нуля до положительного максимального значения, снова уменьшающийся до нуля и отрицательного максимального значения, а затем снова достигающий нуля, называется «циклом».
Разница между циклом и периодом:
Время, необходимое для завершения цикла, называется периодом. Таким образом, цикл представляет собой полную волну. Период — это время в секундах, в течение которого сигнал повторяется от начала до конца.
Продолжить чтение
Формула частоты период времени частота цикл в секунду герц Гц амплитуда продолжительность периодический период времени к угловой частоте формула длины волны акустическое уравнение отношение длина волны Гц миллисекунда расчет мс расчет калькулятор t=1/f Гц герц в мс T в f рабочий лист
Формула частоты период время частота цикл в секунду герц Гц амплитуда продолжительность периодический период времени к угловой частоте формуляр длины волны акустическое уравнение соотношение длина волны Гц миллисекунды расчет мс вычислить калькулятор t=1/f Гц герц в мс рабочий лист T в f — sengpielaudio Sengpiel Berlin
Заполните серое поле выше и щелкните на панели расчета соответствующего столбца.
Частота означает количество колебаний (циклов) в секунду в Гц = герц = 1/с.
1 секунда = 1 с = 1000 мс | 1 мс = 0,001 с | 1 мкс = 0,000001 с
cps = число циклов в секунду
| Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обе стороны знака ↔ . |
Осциллоскоп: Ввод ящиков (разд.) и временная развертка (Y) дают частоту.
Формула для периода (длительности цикла) T
| Физическое значение | символ | шт. | аббревиатура | формула |
| Продолжительность цикла | Т = 1 / ж | второй | с | Т = λ/с |
| Частота | f = 1 / Т | герц | Гц = 1/с | f = с / λ |
| Длина волны | λ | метр | м | λ = х/ф |
| Скорость волны | с | метр в секунду | м/с | с = λ × f |
Преобразование времени — по ходу времени
Формулы и уравнения для частоты и длины волны
Формула для частоты: f (частота) = 1 / T (период).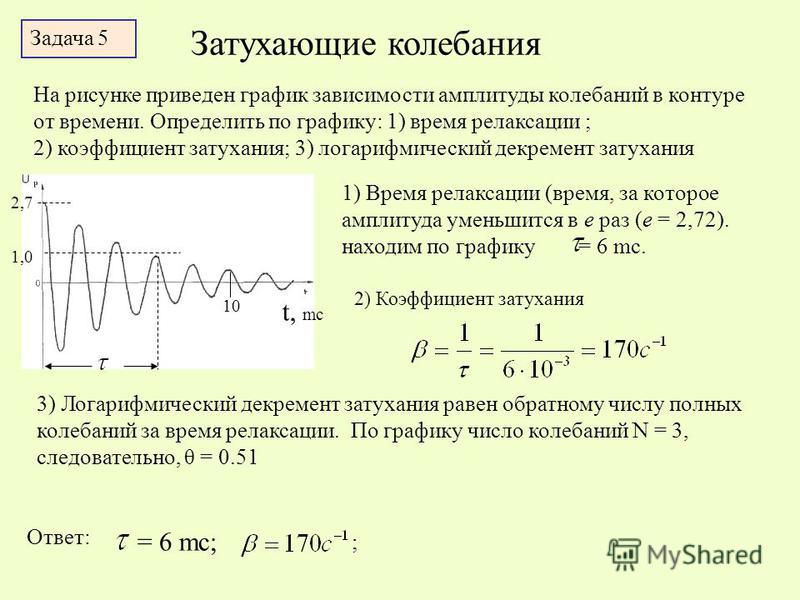 f = c / λ = скорость волны c (м/с) / длина волны λ (м). Формула для времени: T (период) = 1 / f (частота). Формула для длины волны λ (M) = C / F λ = C / F = скорость волны C (м / с) / частота f (Гц). Единица измерения герц (Гц) когда-то называлась cps = циклы в секунду. |
c = λ × f λ = c / f = c × T f = c / λ
Различие скорости среды:
Скорость звука или скорость света
| Выберите: Скорость звука в воздухе при температуре 20°C: c = 343 м/с или скорость радиоволн и света в вакууме: c = 299 792 458 м/с. Скорость распространения электрических сигналов по оптическому волокну составляет около 9/10 . 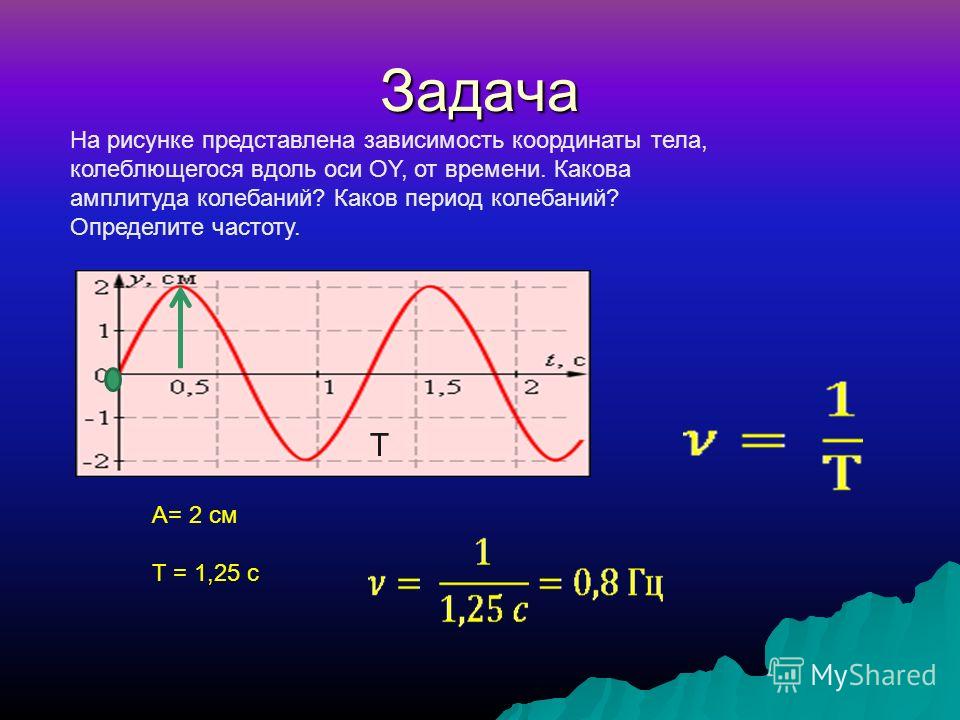 скорость света, то есть ≈ 270 000 км/с. Скорость распространения электрических сигналов по медным кабелям составляет около 2/3 . скорость света, то есть ≈ 200 000 км/с. Скорость звука c = 343 м/с также равна 1235 км / ч, 767 миль в час, 1125 фут/с. |
Волна состоит из четырех частей:
длина волны, период, частота и амплитуда 90 210
Изменение частоты (герц, Гц) никогда не меняет амплитуду и наоборот
Угловая частота равна ω = 2 π × f
| Дано уравнение: y = 50 sin (5000 t) Определить частоту и амплитуду. Ответ: амплитуда 50 и Ω = 5000. , поэтому частота F = 1/ T = Ω /2 π = 795,77 Гц. 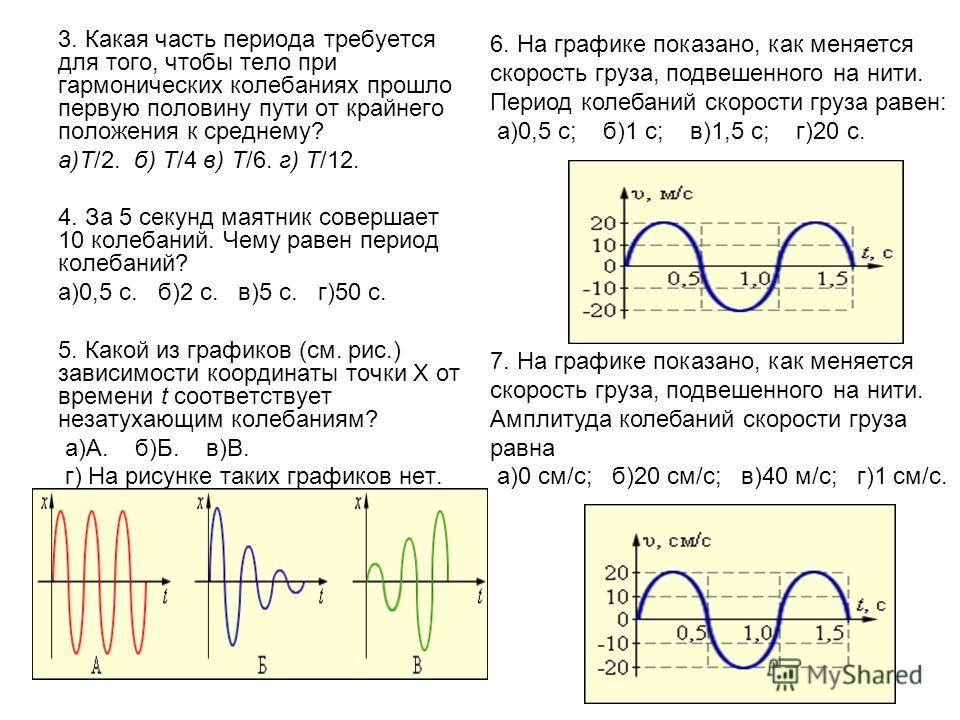 |
| Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обе стороны знака ↔ . |
Преобразование: частота в длину волны и наоборот
Синусоида или синусоида и период T
| В физике и электротехнике для синусоидального процесса часто используется угловая частота ω вместо частоты f .Скорость или частота вращения представляет собой размер при — предпочтительно механических — вращательных движениях с указанием частоты революций. Например, это важная функция для двигателей. Будет дано в 1/мин, как число оборотов в минуту или как число оборотов в минуту.  |
| Ось y показывает звуковое давление p (амплитуда звукового давления). Если на графике по оси X отобразить время t , мы увидим период T = 1 / f . Если на графике по оси x отобразить расстояние d , мы увидим длину волны λ . Наибольшее отклонение или удлинение называется амплитудой a . |
| Амплитуда не имеет абсолютно никакого отношения к частоте… тоже ничего с длиной волны. |
● Графики волн ●
Волны можно отображать в виде графика как функцию времени или расстояния. Одна частота Одна частота волна будет выглядеть как синусоида (синусоида) в любом случае. С расстояния график длина волны может быть определена. На временном графике период и частоту можно получить. От обоих вместе скорость волны может быть определенный. Источник: http://hyperphysics.phy-astr.gsu.edu/hbase/sound/wavplt.html |
| В акустике выражение для синусоиды записывается в виде y = A sin (2 π f T + φ ).Где ω = 2 π f и A — амплитуда и где f — частота волны, измеряемая в герцах. Сравнивая математическую форму y = A sin ( B T + φ ): С этой акустической формой мы видим, что | Б | = 2 π ж .  Следовательно, у нас есть Следовательно, у нас есть частота f = | Б | / 2 π и период T = 2 π / | Б | = 1 / f . |
| Коэффициенты SI для герц (Гц) | ||||||
| Значение | Символ | Имя | Значение | Символ | Имя | |
| 10 −1 Гц | дБ | децигерц | 10 1 Гц | даГц | декагерц | |
| 10 −2 Гц | Гц | сантигерц | 10 2 Гц | Гц | гектогерц | |
| 10 −3 Гц | МГц | миллигерц | 10 3 Гц | кГц | килогерц | |
| 10 −6 Гц | мкГц | микрогерц | 10 6 Гц | МГц | мегагерц | |
| 10 −9 Гц | нГц | наногерц | 10 9 Гц | ГГц | гигагерц | |
| 10 −12 Гц | пГц | пикогерц | 10 12 Гц | ТГц | терагерц | |
| 10 −15 Гц | фГц | фемтогерц | 10 15 Гц | Гц | петагерц | |
| 10 −18 Гц | Гц | аттогерц | 10 18 Гц | Гц | экзагерца | |
| 10 −21 Гц | Гц | зептогерц | 10 21 Гц | Гц | зеттагерц | |
| 10 −24 Гц | Гц | йоктогерц | 10 24 Гц | Гц | йоттагерц | |
Общие единицы с префиксом выделены жирным шрифтом. | ||||||
Типичный вопрос: как связаны длина волны, температура и частота?
| Объясните взаимосвязь между расстоянием, временем и частотой при определении Длина волны или: Что такое уравнение с частотой, расстоянием и временем? Скорость = расстояние/время |
Калькулятор Masterclock (тактовая частота)
| Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обе стороны знака ↔ . |
Калькулятор опорной частоты
Для настройки вниз можно изменить опорную частоту и настройку фортепиано.
100 центов эквивалентны полутону (полутону).
Названия примечаний: сравнение английской и немецкой систем
Расчет гармоник по основной частоте
Волны
Частота
Частота — это мера того, как часто повторяющееся событие, такое как волна, происходит в течение измеряемого промежутка времени.Одно завершение повторяющегося шаблона называется циклом. Частотой обладают только движущиеся волны, меняющие свое положение во времени. Частота — это один из способов определить скорость движения волны.
Волны могут двигаться двумя способами. Частоты прогрессивных волн или тех, которые движутся вперед, показывают, насколько быстро волна движется вперед в единицах циклов в единицу времени. Частоты стоячих волн или тех, которые колеблются на месте, представляют собой скорость колебаний в единицах циклов в единицу времени.
| Определение Словарное определение частоты: Физика.  а) количество периодов или регулярно происходящих событий любого вида в единицу времени, обычно одну секунду. а) количество периодов или регулярно происходящих событий любого вида в единицу времени, обычно одну секунду.б) число циклов или завершенных чередований в единицу времени волны или колебания. Символ: f ; Сокр.: част. |
Единицы
Частота выражается в единицах циклов в единицу времени.
Хотя частота является мерой скорости движения, она не идентична скорости. Например, если мы думаем об автомобиле, который движется со скоростью 60 миль в час, мы имеем в виду именно это. Однако если мы говорим, что волна имеет частоту 60 циклов в час, точки на волне могут двигаться быстрее или медленнее в зависимости от длины волны. Сравнивая две волны с одинаковой длиной волны, более высокая частота связана с более быстрым движением. Сравнивая две волны с разной длиной волны, более высокая частота не всегда указывает на более быстрое движение, хотя и может.Волны разной длины могут иметь одинаковую частоту. Для некоторых целей частота измерения более полезна, чем абсолютная скорость.
Для некоторых целей частота измерения более полезна, чем абсолютная скорость.
Единица, Герц
Единица Герц (Гц) используется для описания частоты в циклах в секунду. В предложении правильный формат для записи этого отношения:
Один цикл соответствует перемещению на одну длину волны.
Номера радиотелефонов
Часто вы можете слышать радиочастоты, указанные в мегагерцах (МГц)… (в разработке).
Период волны
Частота волны также связана с другим измерением, называемым периодом волны (T). Период волны — это то, сколько времени требуется для прохождения одного цикла, и единицы измерения всегда выражены во времени. Чем быстрее движется волна, тем меньше период ее волны.
Вместо измерения в фиксированной единице времени, секунды, период волны использует фиксированное количество циклов, один цикл …
Как измерить период волны?
Период волны можно определить, измерив, сколько времени требуется двум пикам для прохождения определенной точки. Вы можете сделать это для океанских волн, стоя на пирсе и используя секундомер.
Вы можете сделать это для океанских волн, стоя на пирсе и используя секундомер.
Строится…
Объясните связь между частотой и периодом времени
Мы знаем, что число полных колебаний колеблющейся частицы за одну секунду называется ее частотой. Частота обозначается f. Опять же, период времени — это время одной полной вибрации. Частота и период являются обратно пропорциональными величинами.Частота (f) волны — это количество полных сигналов, генерируемых в секунду. Это то же самое, что количество повторений в секунду или количество колебаний в секунду.
Период времени (T) — количество секунд на сигнал или количество секунд на колебание. Ясно, что частота и период времени обратны.
Если период времени T, то за T секунд количество вибраций равно 1
Следовательно, количество вибраций в одну секунду = 1/T
Количество вибраций в 1 секунду – это частота.Итак, частота f = 1/T
Частота означает, как часто что-то происходит; тогда как период относится ко времени, которое требуется для того, чтобы что-то произошло. Частота означает, сколько раз периодическое событие происходит в секунду.
Частота означает, сколько раз периодическое событие происходит в секунду.
Период — это время между любыми двумя событиями. Как правило, период должен быть обратен частоте, отсюда и уравнение: Период = 1/Частота.
Частота, f, представляет собой количество циклов колебаний в секунду и измеряется в циклах в секунду или герцах (Гц).Период волны Т — это время, за которое волна совершает один полный цикл колебаний. Эти два члена обратно пропорциональны друг другу: f = 1/T и T = 1/f.
Например, если волне требуется 1 секунда, чтобы колебаться вверх и вниз, период волны равен 1 секунде. Частота обратно пропорциональна 1 циклу в секунду, потому что в секунду происходит только один цикл.
Математический пример: Длина волны звука, издаваемого объектом в воздухе, составляет 20 см.Если скорость звука в воздухе 340 мс -1 , найдите частоту и период объекта.
Здесь, Длина волны, γ = 20 см = 0,2 м
Скорость звука = 340 мс -1
Частота, f =?
Период (время), T = ?
Мы знаем, Скорость = fγ
Итак, f = v/γ = 340 мс -1 / 0,20 м = 1700 Гц
А T = 1/f = 1/1700 с -1 = 0,000 = 5,88 x 10 -4 с Частота 1700 Гц; Период (время) 5.