«исследование зависимости периода и частоты механических колебаний от параметров колебательной системы». Зависимость периода от частоты

Движение по окружности, угловая скорость, частота, период, центростремительное ускорение. Формулы, определения, пояснения

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T - это время, за которое тело совершает один оборот.

Частота вращение - это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено - это есть период T. Путь, который преодолевает точка - это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение - изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

fizmat.by

Частота, период, циклическая частота, амплитуда, фаза колебаний.

ЧАСТОТА КОЛЕБАНИЙ, числоколебаний в 1 с. Обозначается. Если T -периодот колебаний, то= 1/T; измеряется в герцах (Гц).Угловая частотаколебаний= 2= 2/T рад/с.

ПЕРИОД колебаний, наименьший промежуток времени, через который совершающая колебания системавозвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период -величина, обратная частоте колебаний.Понятие"период" применимо, например, в случае гармонических колебаний, однако часто применяется и для слабо затухающих колебаний.

Круговая или циклическая частотаω

При изменении аргумента косинуса, либо синуса на 2π эти функции возвращаются к прежнему значению. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2π .

ω(t + T) + α = ωt + α + 2π, или ωT = 2π.

.

Время T одного полного колебания называется периодом колебания. Частотой ν называют величину, обратную периоду

.

Единица измерения частоты - герц (Гц), 1 Гц = 1 с-1.

Так как

, то .

Круговая, или циклическая частоты ω в 2π раз больше частоты колебаний ν. Круговая частота - это скорость изменения фазы со временем. Действительно:

.

АМПЛИТУДА (от латинского amplitudo - величина), наибольшее отклонение от равновесного значения величины, колеблющейся по определенному, в том числе гармоническому, закону; смотри такжеГармонические колебания.

ФАЗА КОЛЕБАНИЙ аргумент функцииcos (ωt + φ), описывающей гармонический колебательный процесс (ω — круговая частота, t — время, φ — начальная фаза колебаний, т. е. фаза колебаний вначальный момент времениt = 0)

Смещение, скорость, ускорение колеблющейся системы частиц.

Энергия гармонических колебаний.

Гармонические колебания

Важным частным случаем периодических колебаний являются гармонические колебания, т.е. такие изменения физической величины, которые идут по закону

где . Из курса математики известно, что функция вида (1) меняется в пределах от А до -А , и что наименьший положительный период у нее. Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом.

Не следует путать циклическую частоту и частоту колебаний. Между ними простая связь. Так как, а, то.

Величина называется фазой колебания. При t=0 фаза равна, потомуназывают начальной фазой.

Отметим, что при одном и том же t:

где - начальная фаза .Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точнотью до. Поэтому из множества возможных значений начальной фазы выбирается обычно значение начальной фазы наименьшее по модулю или наименьшее положительное. Но делать это необязательно. Например, дано колебание, то его удобно записать в видеи работать в дальнейшем с последним видом записи этого колебания.

Можно показать, что колебания вида:

где имогут быть любого знака, с помощью простых тригонометрических преобразований всегда приводится к виду (1), причем,, ане равна, вообще говоря. Таким образом, колебания вида (2) являются гармоническими с амплитудойи циклической частотой. Не приводя общего доказательства, проиллюстрируем это на конкретном примере.

Пусть требуется показать, что колебание

будет гармоническим и найти амплитуду , циклическую частоту, периоди начальную фазу. Действительно,

-

Видим, что колебание величины S удалось записать в виде (1). При этом ,.

Попробуйте самостоятельно убедится, что

.

Естественно, что запись гармонических колебаний в форме (2) ничем не хуже записи в форме (1), и переходить в конкретной задаче от записи в данной форме к записи в другой форме обычно нет необходимости. Нужно только уметь сразу находить амплитуду, циклическую частоту и период, имея перед собой любую форму записи гармонического колебания.

Иногда полезно знать характер изменения первой и второй производных по времени от величины S, которая совершает гармонические колебания (колеблется по гармоническому закону). Если , то дифференцирование S по времени t дает,. Видно, что S' и S'' колеблются тоже по гармоническому закону с той же циклической частотой, что и величина S, и амплитудамии, соответственно. Приведем пример.

Пусть координата x тела, совершающего гармонические колебания вдоль оси x, изменяется по закону , где х в сантиметрах, время t в секундах. Требуется записать закон изменения скорости и ускорения тела и найти их максимальные значения. Для ответа на поставленный вопрос заметим, что первая производная по времени от величины х есть проекция скорости тела на ось х, а вторая производная х есть проекция ускорения на ось х:,. Продифференцировав выражение для х по времени, получим,. Максимальные значения скорости и ускорения :.

studfiles.net

Гармонические колебания - Класс!ная физика

Гармонические колебания

«Физика - 11 класс»

Ускорение — вторая производная координаты по времени.

Мгновенная скорость точки - это производная координаты точки по времени. Ускорение точки — это производная ее скорости по времени, или вторая производная координаты по времени. Поэтому уравнение движения маятника можно записать так:

где х" — вторая производная координаты по времени.

При свободных колебаниях координата х изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.

Гармонические колебания

Из математики: вторые производные синуса и косинуса по их аргументу пропорциональны самим функциям, взятым с противоположным знаком, и никакие другие функции таким свойством не обладают. Поэтому: Координата тела, совершающего свободные колебания, меняется с течением времени по закону синуса или косинуса.

Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются гармоническими колебаниями.

Амплитуда колебаний

Амплитудой гармонических колебаний называется модуль наибольшего смещения тела от положения равновесия.

Амплитуда определяется начальными условиями, а точнее энергией, сообщаемой телу.

График зависимости координаты тела от времени представляет собой косинусоиду.

х = xm cos ω0t

где

Тогда уравнение движения, описывающее свободные колебания маятника:

Период и частота гармонических колебаний.

При колебаниях движения тела периодически повторяются. Промежуток времени Т, за который система совершает один полный цикл колебаний, называется периодом колебаний.

Частота колебаний - это число колебаний в единицу времени. Если одно колебание совершается за время Т, то число колебаний за секунду

В Международной системе единиц (СИ) единица частоты называется герцем (Гц) в честь немецкого физика Г. Герца.

Число колебаний за 2π с равно:

Величина ω0 — это циклическая (или круговая) частота колебаний. Через промежуток времени, равный одному периоду, колебания повторяются.

Частоту свободных колебаний называют собственной частотой колебательной системы. Часто для краткости циклическую частоту называют просто частотой.

Зависимость частоты и периода свободных колебаний от свойств системы.

1. для пружинного маятника

Собственная частота колебаний пружинного маятника равна:

Она тем больше, чем больше жесткость пружины k, и тем меньше, чем больше масса тела m. Жесткая пружина сообщает телу большее ускорение, быстрее меняет скорость тела, а чем тело массивнее, тем медленнее оно изменяет скорость под влиянием силы.

Период колебаний равен:

Период колебаний пружинного маятника не зависит от амплитуды колебаний.

2. для нитяного маятника

Собственная частота колебаний математического маятника при малых углах отклонения нити от вертикали зависит от длины маятника и ускорения свободного падения:

Период же этих колебаний равен:

Период колебаний нитяного маятника при малых углах отклонения не зависит от амплитуды колебаний.

Период колебаний возрастает с увеличением длины маятника. От массы маятника он не зависит.

Чем меньше g, тем больше период колебаний маятника и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут за сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета (высота 200 м). И это только за счет уменьшения ускорения свободного падения с высотой.

Источник: «Физика - 11 класс», учебник Мякишев, Буховцев, Чаругин

Механические колебания. Физика, учебник для 11 класса - Класс!ная физика

Свободные, затухающие и вынужденные колебания --- Условия возникновения свободных колебаний. Математический маятник --- Динамика колебательного движения. Уравнение движения маятника --- Гармонические колебания --- Фаза колебаний --- Превращение энергии при гармонических колебаниях --- Вынужденные колебания. Резонанс --- Примеры решения задач --- Краткие итоги главы

class-fizika.ru

Гармонические колебания: амплитуда и период колебаний

 

Гармонические колебания – колебания, совершаемые по законам синуса и косинуса. На следующем рисунке представлен график изменения координаты точки с течением времени по закону косинуса.

картинка

Амплитуда колебаний

Амплитудой гармонического колебания называется наибольшее значение смещения тела от положения равновесия. Амплитуда может принимать различные значения. Она будет зависеть от того, насколько мы сместим тело в начальный момент времени от положения равновесия.

Амплитуда определяется начальными условиями, то есть энергией сообщаемой телу в начальный момент времени. Так как синус и косинус могут принимать значения в диапазоне от -1 до 1, то в уравнении должен присутствовать множитель Xm, выражающий амплитуду колебаний. Уравнение движения при гармонических колебаниях:

x = Xm*cos(ω0*t).

Период колебаний

Период колебаний – это время совершения одного полного колебания. Период колебания обозначается буквой Т.  Единицы измерения периода соответствуют единицам времени. То есть в СИ - это секунды.

Частота колебаний – количество колебаний совершенных в единицу времени. Частота колебаний обозначается буквой ν. Частоту колебаний можно выразить через период колебания.

ν = 1/Т.

Единицы измерения частоты в СИ 1/сек. Эта единица измерения получила название Герца.  Число колебаний за время 2*pi секунд будет равняться:

ω0 = 2*pi* ν = 2*pi/T.

Частота колебаний

 

Данная величина называется циклической частотой колебаний. В некоторой литературе встречается название круговая частота. Собственная частота колебательной системы – частота свободных колебаний. 

Частота собственных колебаний рассчитывается по формуле:

ω0 = √(k/m)

Частота собственных колебаний зависит от свойств материала и массы груза.  Чем больше жесткость пружины, тем больше частота собственных колебаний.  Чем больше масса груза, тем меньше частота собственных колебаний.

Эти два вывода очевидны. Чем более жесткая пружина, тем большее ускорение она сообщит телу, при выведении системы из равновесия. Чем больше масса тела, тем медленнее будет изменяться это скорость этого тела.

Период свободных колебаний:

T = 2*pi/ ω0 = 2*pi*√(m/k)

Примечателен тот факт, что при малых углах отклонения период колебания тела на пружине и период колебания маятника не будут зависеть от амплитуды колебаний.

Запишем формулы периода и частоты свободных колебаний для математического маятника.

ω0 = √(g/l),

тогда период будет равен

T = 2*pi*√(l/g).

Данная формула будет справедлива лишь для малых углов отклонения. Из формулы видим, что период колебаний возрастает с увеличением длины нити маятника. Чем больше будет длина, тем медленнее тело будет колебаться.

От массы груза период колебаний совершенно не зависит. Зато зависит от ускорения свободного падения. При уменьшении g, период колебаний будет увеличиваться. Данное свойство широко используют на практике. Например, для измерения точного значения свободного ускорения.

Нужна помощь в учебе?

Предыдущая тема: Математический маятник: динамика колебательного движения Следующая тема:&nbsp&nbsp&nbspФаза колебаний, сдвиг фаз

Все неприличные комментарии будут удаляться.

www.nado5.ru

Ответы@Mail.Ru: помогите пожалуйста!!!

В данной работе исследовали зависимость периода и частоты свободных колебаний нитяного маятника от его длины. в следствии чего было выявлена зависимость такая: чем больше длина тем меньше период свободных колебаний.

проделав данную работу, я выяснила, как зависят период и частота свободных колебаний нитяного маятника от его длины и убедилась, что чем больше длина маятника, тем больше период свободных колебаний.

Вывод: Законы физики выполняются.

Издателем первой русской печатной книги является

touch.otvet.mail.ru

Зависимость частоты и периода свободных колебаний от свойств системы. Фаза колебаний Помощь школьнику

Цель урока: сформировать представление о частоте, периоде и фазе свободных колебаний; обратить внимание на практическое применение маятников; рассмотреть алгоритм решения задач.

Ход урока

Проверка домашнего задания методом фронтального опроса

1. Какие колебания называются гармоническими? Начертить график гармонического колебания.

2. Что такое смещение и амплитуда гармонических колебаний?

3. Как решается уравнение движения для свободных колебаний?

4. Характеристики колебательных процессов: период, частота, циклическая частота.

5. Задача. Определите период колебания иглы швейной машинки, если за один оборот игла совершает одно колебание, а частота вращения вала 1200 об/мин.

Решение. Т= 1/γ; T = 60/1200=0,05c

6.Задача. Определить число взмахов крыльев вороны, которая пролетела путь 650 м со скоростью 13 м/с. Частота взмахов ее крыльев в среднем равна 3 Гц.

Решение. t =S/V; T= 1/γ; n= t/T; n= 150.

Изучение нового материала

1. Формула Гюйгенса. ω0= QUOTE – собственная частота колебаний тела прикрепленного к пружине.

Она изменяется в зависимости от жесткости пружины, от массы тела.

T= QUOTE = 2π QUOTE

ω₀= QUOTE — собственная частота колебаний математического маятника; она изменяется в зависимости от длины маятника и ускорения свободного падения.

Т = 2π QUOTE — формула Гюйгенса (голл.)

На практике используется зависимость периода колебания маятника от значения ускорения свободного падения. С изменением географической широты значение g ≈9,8 м/с2 –меняется.

Меняется эта величина в зависимости от плотности земной коры, которая не везде одинаковая.

2. Фаза колебаний.

Для...

характеристики гармонических колебаний введем еще одну величину – фазу колебаний.

Фазой колебаний называют величину 𝝋, стоящую под знаком синуса или косинуса.

Измеряется фаза в угловых единицах – радианах. Значение фазы влияет на величины: координаты, скорости, ускорения, которые изменяются по гармоническому закону.

То есть фаза при определенной амплитуде задает состояние колебательной системы.

Колебания с одинаковыми амплитудами и частотами могут иметь разные фазы.

ω0= 2π/Т; 𝝋 = ω0t = 2π QUOTE ; QUOTE – указывает, какая часть периода прошла от начала колебаний.

Любому значению фазы, выраженному в радианах, соответствует значение времени, выраженное в долях периода.

Рассмотрим законы, по которым изменяется координата тела со временем, обращая внимание на фазу. Косинус отличается от синуса сдвигом аргумента на π/2;

QUOTE ; X= Xm QUOTE

Значение фазы в момент времени t=0, равна π/2.

3. Сдвиг фаз.

На графиках мы видим колебания отличающиеся друг от друга разностью фаз или как чаще говорят сдвигом фаз.

Чтобы определить разность фаз, колеблющуюся величину выражают через одну функцию синус или косинус.

Закрепление изученного материала

1. Почему частота колебаний математического маятника не зависит от массы, а частота колебаний тела на пружине от массы зависит.

2. Через 5 секунд от начала колебания, на какую величину изменилась фаза колебаний?

3. На рисунке видим графики трех разных гармонических колебаний. Определить амплитуды и периоды этих колебаний.

Подведем итоги урока

Домашнее задание: § 22 (часть), 23, упр. 3, № 3. 4.

Прислал: Щербакова Анастасия . 2017-10-15 17:52:18

pomosh-shkolniky.iusite.ru

«исследование зависимости периода и частоты механических колебаний от параметров колебательной системы» - Исследование

Муниципальное образовательное учреждение

«МОРОЗОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»

РЕФЕРАТ ПО ФИЗИКЕ

на тему

«ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА И ЧАСТОТЫ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ ОТ ПАРАМЕТРОВ КОЛЕБАТЕЛЬНОЙ СИСТЕМЫ»

(ГОСУДАРСТВЕННАЯ (ИТОГОВАЯ) АТТЕСТАЦИЯ)

Ученицы 9 класса

КОШЕЛЬ АНАСТАСИИ ЮРЬЕВНЫ

Руководитель Н.А. Баландина

С. Морозово, 2010 год

ОГЛАВЛЕНИЕ

1. Введение. 3 стр.

2. Основная часть. 4 стр.

1. Теоретическое обоснование работы. 4 стр.

2. Исследование зависимости периода и частоты

колебаний математического маятника от его параметров. 8 стр.

3. Исследование зависимости периода и частоты

колебаний пружинного маятника от его параметров. 9 стр.

4. Исследование зависимости периода и частоты

колебаний физического маятника от его параметров. 10 стр.

5. Исследование зависимости периода и частоты

колебаний оборотного маятника от его параметров. 11 стр.

6. Некоторые применения колебательных систем. 13 стр.

III. Заключение. 16 стр.

IV. Литература. 17 стр.

V. Приложения. 18 стр.

I. ВВЕДЕНИЕ

Я выбрала данную тему для исследования, так как в школьном курсе физики она рассматривается довольно кратко, а встречаются колебания в жизни широко. Мне было интересно познакомиться не только с теми колебательными системами, которые рассмотрены в школьном учебнике, но и с другими. Кроме того, эксперимент по данной теме не предполагает каких-то сложных приборов, колебательные системы можно изготовить самостоятельно.

Предмет исследования – зависимость периода и частоты колебаний от параметров колебательной системы.

Объект исследования – различные колебательные системы: математический маятник, пружинный маятник, физический маятник, оборотный маятник.

Цели исследования:

1) Подготовка к государственной итоговой аттестации за курс основной школы.

2) Углубление и расширение знаний по теме «Механические колебания».

Задачи исследования:

1) Определить период и частоту колебаний пружинного, математического, физического, оборотного маятников.

2) Выяснить зависимость периода и частоты колебаний указанных колебательных систем от их характеристик.

3) Совершенствовать навыки физического эксперимента.

4) Расширить знания о применении колебательных систем.

II. ОСНОВНАЯ ЧАСТЬ

1. Теоретическое обоснование работы.

Механические колебания – это периодически повторяющиеся движения тела в двух противоположных направлениях около положения равновесия.

Виды колебаний

Свободные колебания

Вынужденные колебания

Авто-колебания

Свободные колебания – колебания, происходящие под действием внутренних сил. Для того чтобы в системе могли возникнуть свободные колебания, трение в системе должно быть мало.

Вынужденные колебания – колебания, происходящие под действием внешних сил.

Система, в которой генерируются незатухающие колебания за счет поступления энергии от источника внутри системы, называется автоколебательной. Незатухающие колебания, существующие в системе без воздействия на нее внешних периодических сил, называются автоколебаниями.

Колебательная система – система тел, которая способна совершать свободные колебания.

Примеры колебательных систем: математический маятник, пружинный маятник, физический маятник, оборотный маятник.

Математический маятник – это материальная точка, подвешенная на длинной, невесомой, нерастяжимой нити. В реальных условиях математическим маятником можно считать шар, подвешенный на нити при условии, что размеры шара много меньше длины нити, масса нити много меньше массы шара, растяжение нити шаром настолько мало, что им можно пренебречь (рис. 1).

Параметрами математического маятника можно считать длину нити маятника (L, м) и массу шарика (m, кг).

Рис. 1

С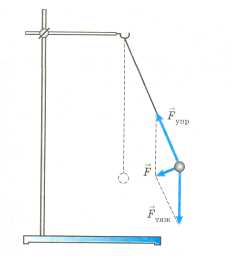илой, возвращающей математический маятник к положению равновесия, является равнодействующая сил тяжести и упругости нити (рис. 2).

Под действием этих сил шарик движется к положению равновесия, при этом равнодействующая уменьшается, а скорость шарика увеличивается. В положении равновесия равнодействующая сил тяжести и упругости нити равна нулю, скорость шарика достигает максимального значения, поэтому он по инерции движется дальше. Снова появляется возвращающая сила, которая будет направлена к Рис. 2

положению равновесия, скорость шарика уменьшается до нуля. Затем все повторяется.

Пружинный маятник – груз, подвешенный на пружине (рис. 3). Параметрами пружинного маятника будем считать жесткость пружины (k, Н/м) и массу груза (m, кг).

Рис. 3

Возвращающей силой в пружинном маятнике является равнодействующая силы тяжести и силы упругости пружины.

Физическим маятником называется тело произвольной формы, которое может вращаться вокруг горизонтальной оси, не проходящей через центр тяжести тела. Маятник находится в устойчивом равновесии, если его центр тяжести находится ниже оси вращения. Выведенный из положения равновесия маятник совершает колебания под действием момента силы тяжести. В данной работе в качестве физического маятника использовался деревянный параллелепипед, в котором проделано отверстие для горизонтальной оси (рис. 4).

Рис. 4

Параметры физического маятника – его масса (m, кг) и расстояние от оси вращения до центра тяжести (l, м). Центром тяжести называется точка, к которой приложена сила тяжести, действующая на тело (рис. 5)

N О – ось вращения физического маятника.

S – центр тяжести

O

O - сила реакции подвеса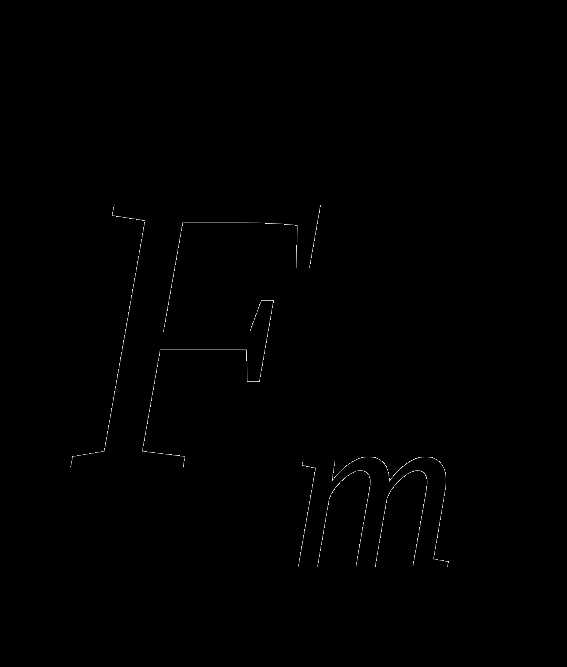

- сила тяжести

S

Рис. 5

Fт

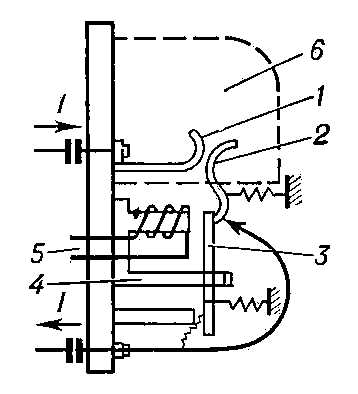
Оборотный маятник является частным случаем физического маятника и состоит из стального стержня, на котором укреплены два шарика. Стержень подвешен на вертикальной проволоке (рис. 6).

Параметры оборотного маятника – длина подвеса (L, м), длина горизонтального стержня (l, м), масса шаров на горизонтальном стержне (m, кг).

Рис. 6

Колебания, происходящие по закону синуса или косинуса, называются гармоническими. Гармонические колебания описываются следующими характеристиками: период колебаний, частота колебаний, амплитуда колебаний, фаза колебаний.

Амплитуда колебаний – максимальное отклонение колеблющегося тела от положения равновесия. Амплитуда обозначается буквой А, измеряется в метрах (м).

Период колебаний – время, в течение которого тело совершает одно полное колебание. Период обозначается буквой Т, измеряется в секундах (с).

Частота колебаний – число колебаний, совершенных телом за 1 секунду. Частота обозначается буквой ν, измеряется в герцах (Гц). 1 герц – частота колебаний, при которой за 1 с тело совершает одно полное колебание. Период и частота колебаний – величины, обратные друг другу, то есть Т= или ν=.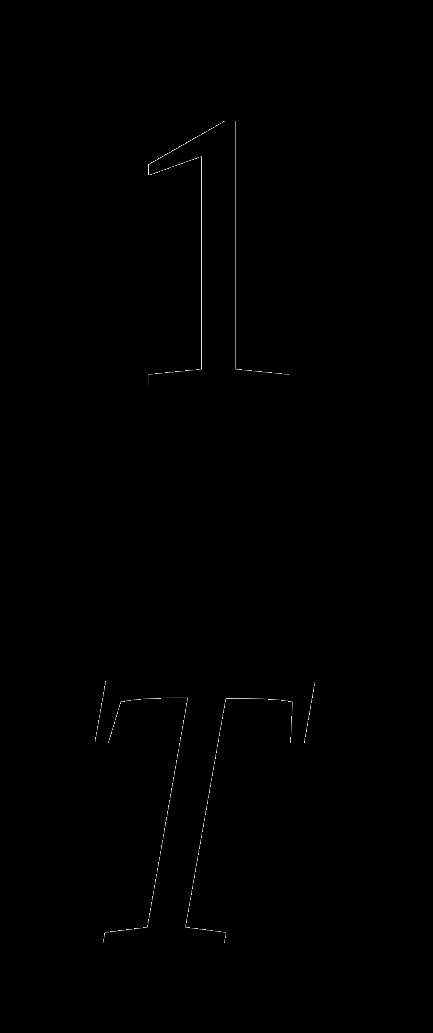

Теперь рассмотрим колебания двух одинаковых маятников (рис. 7). В один и тот же момент времени левый маятник из крайнего левого положения начинает движение вправо, а правый маятник из крайнего правого положения движется влево. Оба маятника колеблются с одной и той же частотой и с одинаковыми амплитудами. Однако эти колебания отличаются друг от друга: в любой момент времени скорости маятников направлены в противоположные стороны, это значит, что они колеблются в разных (противоположных) фазах.

Рис. 7

Гармонические колебания описываются следующими уравнениям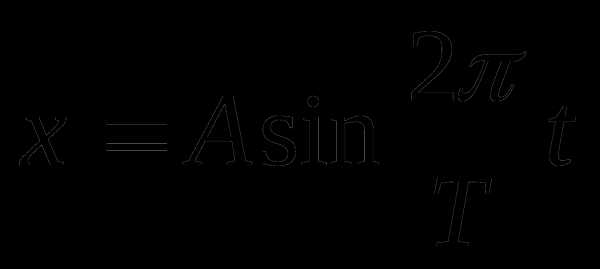и: или .

При малых амплитудах колебания всех перечисленных выше колебательных систем можно считать гармоническими.

2. Исследование зависимости периода и частоты колебаний

математического маятника от его параметров.

Оборудование: штатив с муфтой и лапкой, шарик на нити длиной около 1,3 м, лента измерительная, секундомер, груз массой 100 г, весы с разновесами.

Гипотеза № 1 - период и частота колебаний математического маятника зависят от длины нити: чем больше длина нити маятника, тем больше период колебаний и меньше частота колебаний.

N – количество колебаний, сделанных маятником за время t.

Т=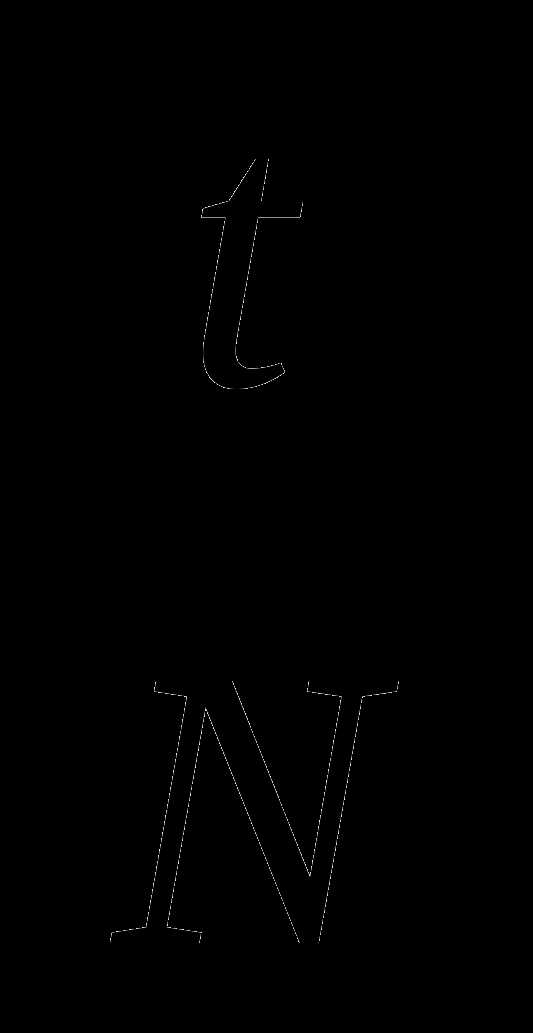, ν =

Таблица 1

№ опыта	1	2	3	4
L, м	0,2	0,45	0,8	1,25
N	30	30	30	30
t, с	27,43	40,38	54,13	67,26
T, с	0,91	1,35	1,8	2,24
ν, Гц	1,1	0,74	0,56	0,45

Вывод: при увеличении длины нити математического маятника период его колебаний увеличивается, а частота колебаний уменьшается (гипотеза № 1 подтвердилась).

Сравним следующие отношения:

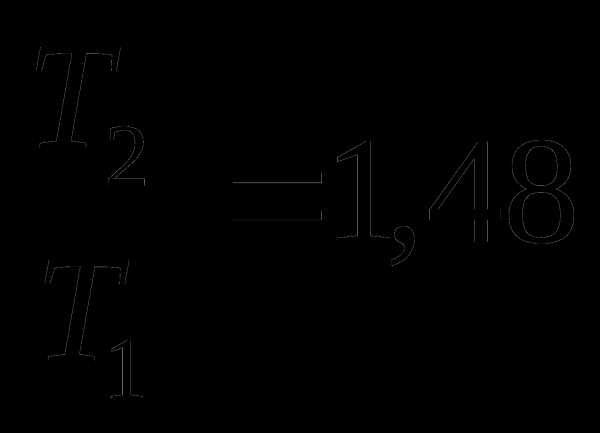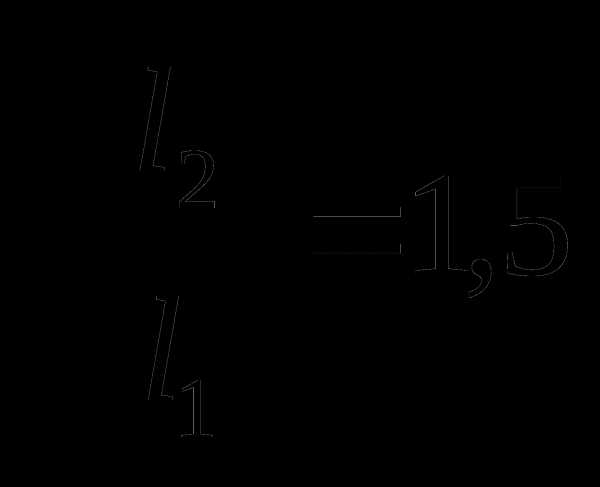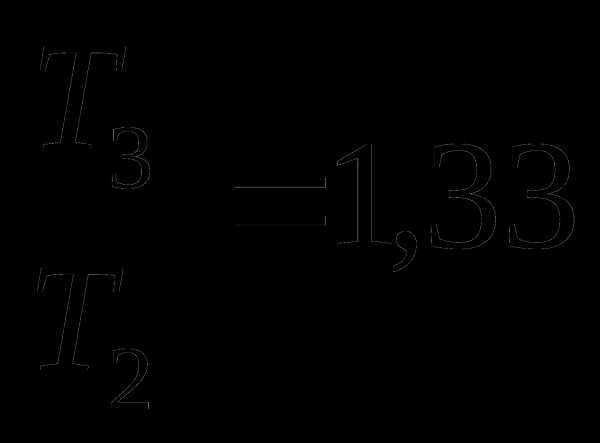и 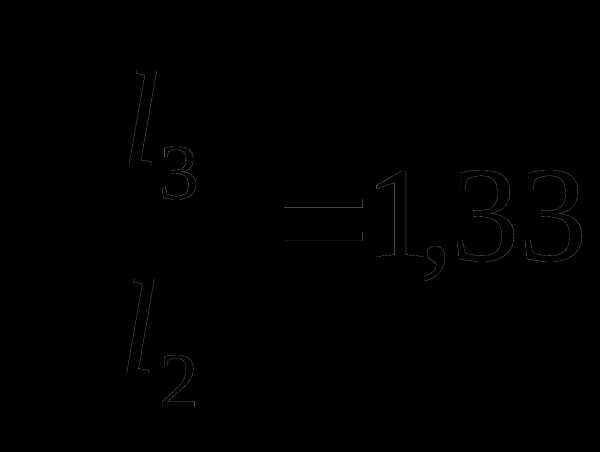; 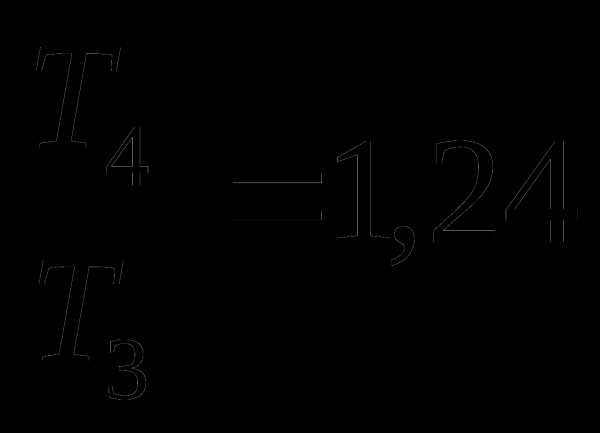и ; и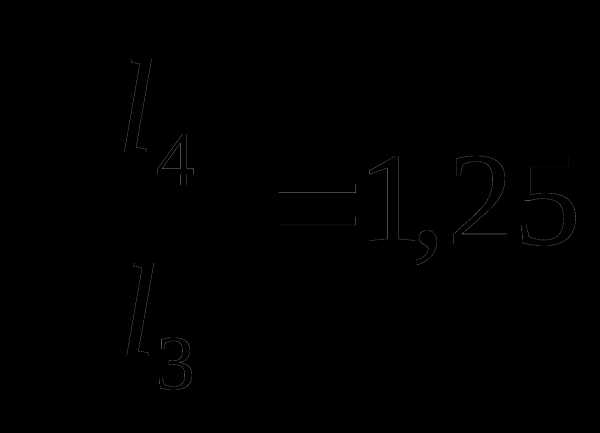

Можно видеть, что период колебаний математического маятника пропорционален корню квадратному из длины нити маятника, а частота колебаний, соответственно, обратно пропорциональна корню квадратному из длины нити маятника: Т~; ν~.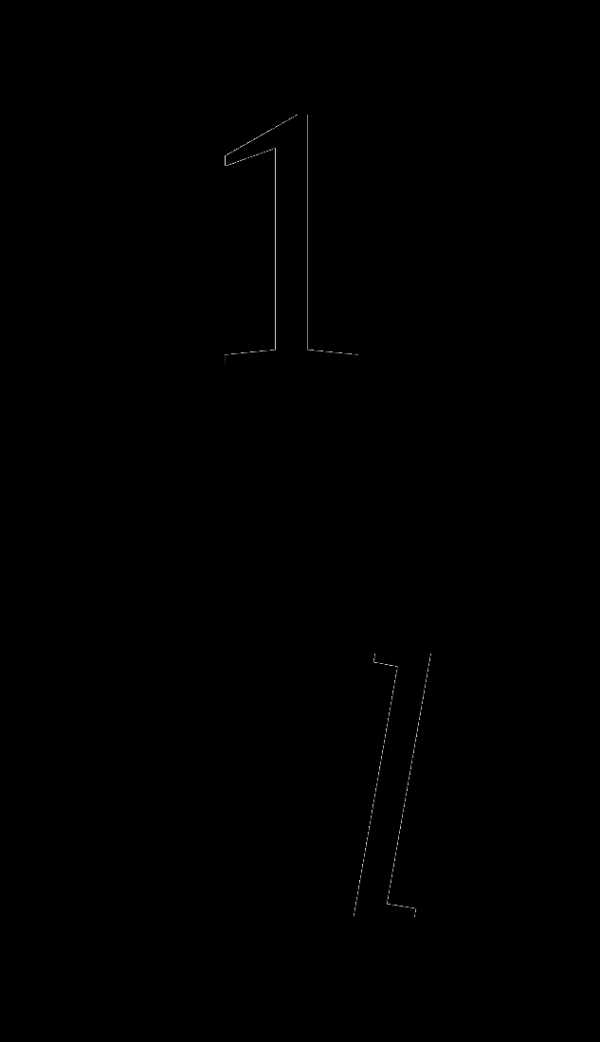

Гипотеза № 2 – период и частота колебаний математического маятника зависят от амплитуды колебаний: чем больше амплитуда, тем больше частота колебаний и меньше период колебаний.

Таблица 2

№ опыта	N	L, м	A, м	t, c	Т, с	ν, Гц
1	30	0,52	0,05	41,2	1,4	0,7
2	30	0,52	0,1	41,6	1,4	0,7
3	30	0,52	0,15	42	1,4	0,7

Вывод: период и частота колебаний математического маятника не зависят от амплитуды колебаний (гипотеза № 2 не подтвердилась).

Гипотеза № 3 – период и частота колебаний математического маятника зависят от массы груза: чем больше масса груза, тем больше частота колебаний и меньше период колебаний.

В первом опыте на нити подвешен один шарик, а во втором опыте к шарику добавлен груз массой 100 г.

Таблица 3

№ опыта	m, кг	N	L, м	t, c	Т, с	ν, Гц
1	0,63	30	0,52	42	1,4	0,7
2	1,63	30	0,52	43	1,4	0,7

Вывод: Период и частота колебаний математического маятника не зависят от массы груза (гипотеза № 3 не подтвердилась).

2. Исследование зависимости периода и частоты колебаний

refdb.ru

---

• 
  Как заменить выключатель в квартире
• 
  Расстояние от газопровода до зданий и сооружений
• 
  Формула расчета тока короткого замыкания
• 
  Дизель генератор 200 квт
• 
  Регулируемый линейный стабилизатор напряжения
• 
  Измерение сопротивления методом вольтметра и амперметра
• 
  Допустимая температура воздуха на рабочем месте в холодное время года
• 
  Как не платить за не воду
• 
  Ремонт коллектора электродвигателя
• 
  Что такое электрический контактор
• 
  Гост размеры резистор