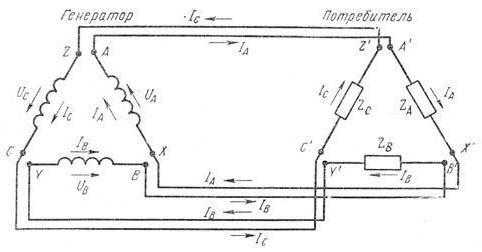
4. Потери и падения напряжения в электрических сетях. Что такое падение напряжения потеря напряжения

3.4. Падение и потеря напряжения в линии

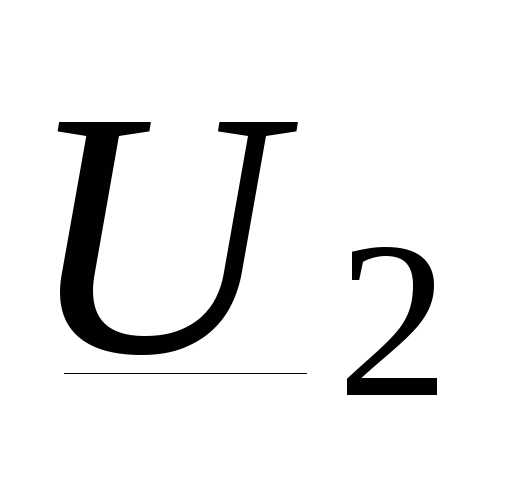На рис. 3.2, е приведена векторная диаграмма для ли­- нейных напряжений в начале и в конце линии и . Эта диаграмма аналогична диаграмме на рис. 3.2, в.

Падение напряжения—геометрическая (векторная) разность между комплексами напряжений начала и конца линии. На рис. 3.2, е падение напряжения — это вектор , т. е.

. (3.26)

Продольной составляющей падения напряжения называют проекцию падения напряжения на действитель­- ную ось или на напряжение 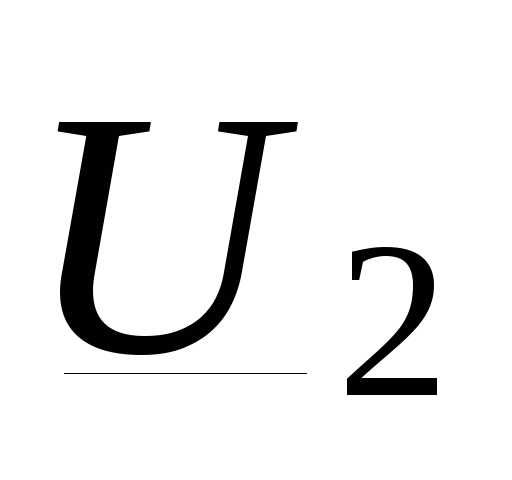, =АС на рис. 3.2, е. Индекс «к» означает, что — проекция на напряжение конца линии 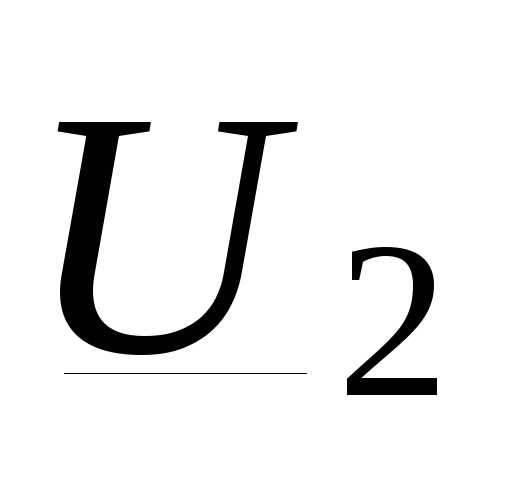. Обычно 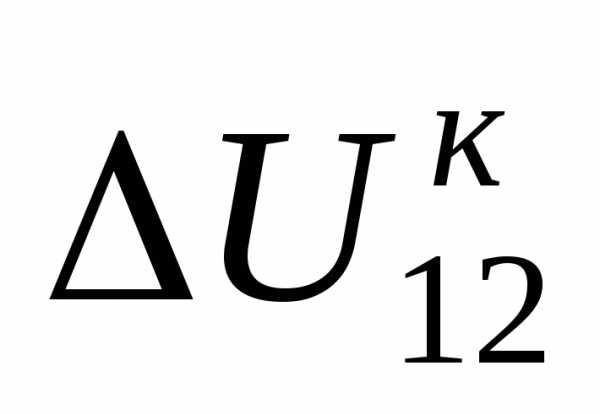выражается через данные в конце линии: , , .

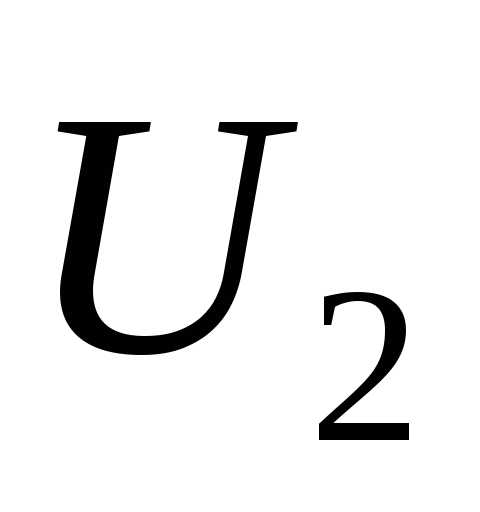Поперечная составляющая падения напряжения 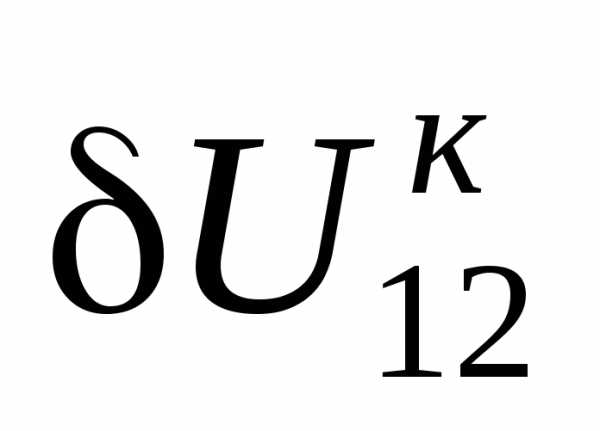- это проекция падения напряжения на мнимую ось, 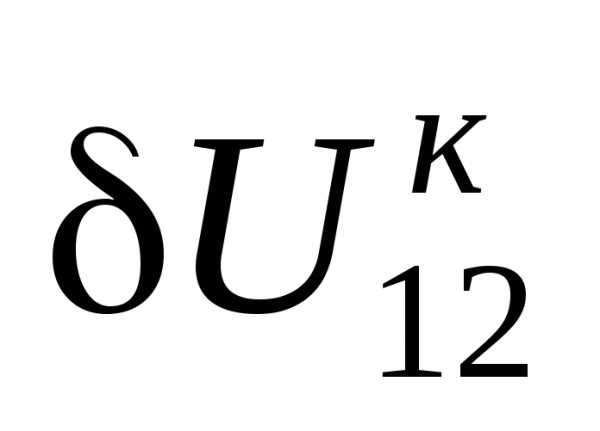==СВ на рис. 3.2, е. Таким образом,

. (3.27)

Часто используют понятие потеря напряжения — это ал- гебраическая разность между модулями напряжений на­- чала и конца линии. На рис. 3.2,е . Если попе­- речная составляющая 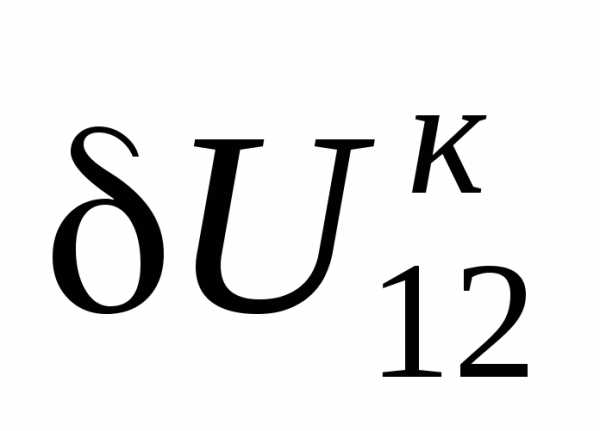мала (например, в сетях кВ), то можно приближенно считать, что потеря напряжения равна продольной составляющей падения на­- пряжения.

Расчет режимов электрических сетей ведется в мощно­- стях, поэтому выразим падение напряжения и его состав­- ляющие через потоки мощности в линии.

Известны мощность и напряжение в конце линии (рас- чет напряжения в начале линии по данным конца). Выра­- зим ток в линии 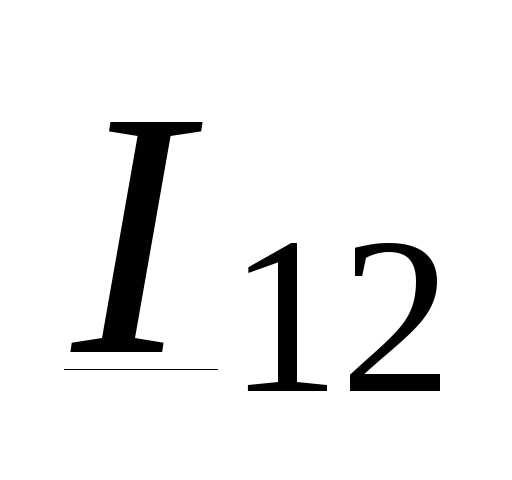в (3.27) через мощность в конце про­- дольной части линии и напряжение :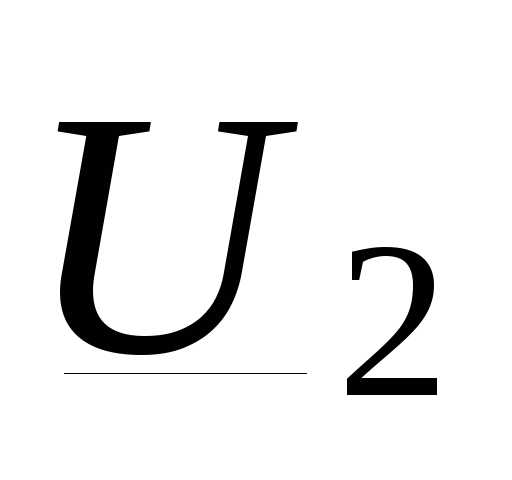

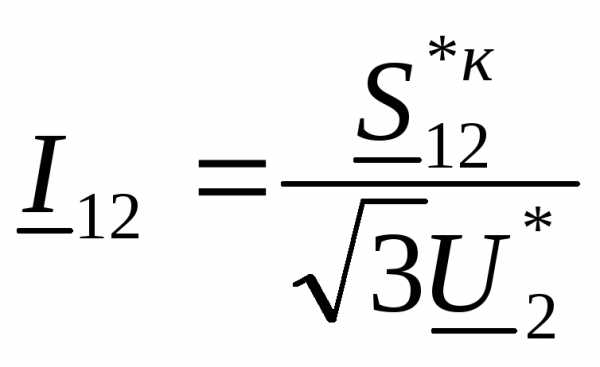. (3 28)

В результате получим

. (3.29)

Приравняв в (3.29) действительные и мнимые части, по­- лучим выражения продольной и поперечной составляющих падения напряжения по данным конца:

; (3.30)

. (3.31)

Напряжение в начале линии

, (3.32)

где 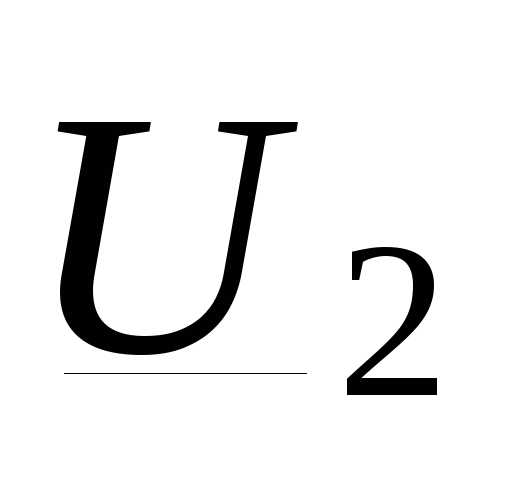известно; , 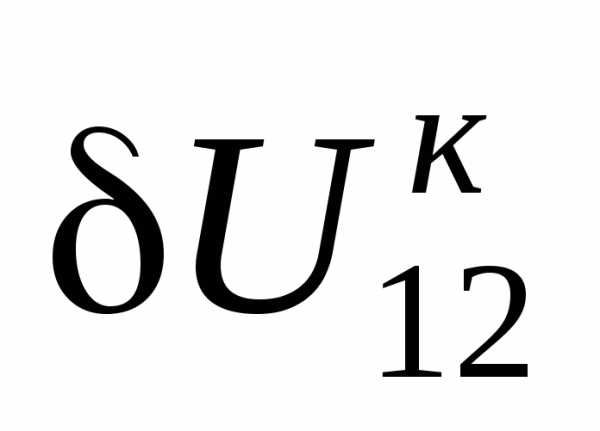определяем из (3.30) и (3.31).

Соответственно модуль и фаза напряжения в начале ли­- нии (см. рис. 3.2, е)

; (3.33)

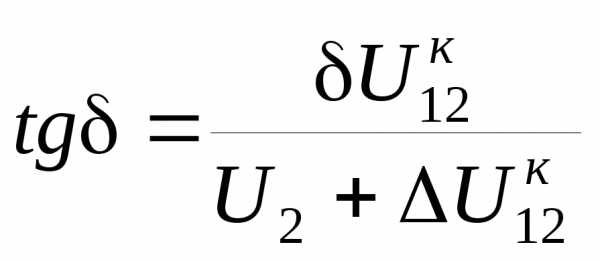. (3.34)

Определение напряжения в начале линии по данным конца по выражениям (3.32), а также (3.30), (3.31) экви­- валентно использованию закона Ома.

Пример 3.2. Определим падение и потерю напряжения в линии, рас­- смотренной в примере 3.1, по известным мощности нагрузки =15+ +j10 МВА и напряжению в конце линии j2,65 кВ.

Используя параметры линии, а также мощность в конце линии 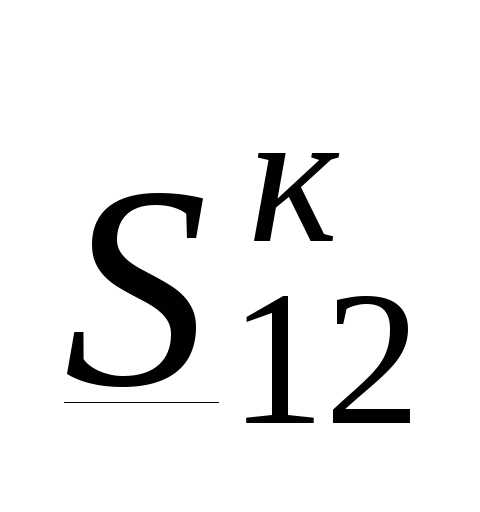, приведенные в примере 3.1, по (3.30), (3.31) найдем продольную и поперечную составляющие падения напряжения по данным конца:

кВ ;

кВ .

Напряжения и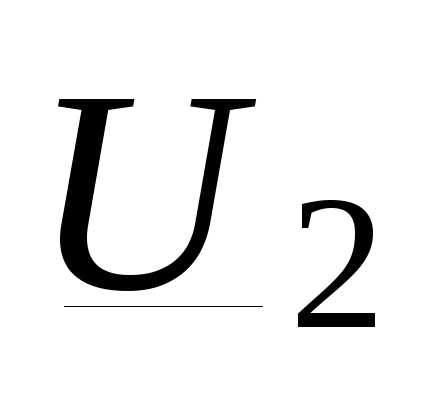приведены на рис. 3.2, з. В большем мас­- штабе продольная и поперечная составляющие падения напряжения изображены на рис 3.2, и.

Напряжение в начале линии по (3.32) равно

кВ.

Модуль напряжения в начале линии

кВ.

Потеря напряжения

кВ.

Известны мощность и напряжение в начале линии (рас- чет напряжения в конце линии по данным начала). Напра­- вим по действительной оси, т.е. примем, что 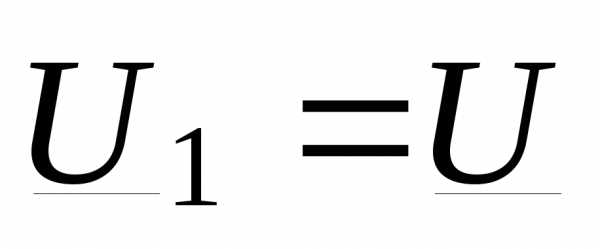(рис. 3.2, ж). На рис. 3.2, ж изменилось положение осей в сравнении с рис. 3.2, е. Продольная составляющая паде­- ния напряжения =ВС'—это проекция падения на­- пряжения на действительную ось или на 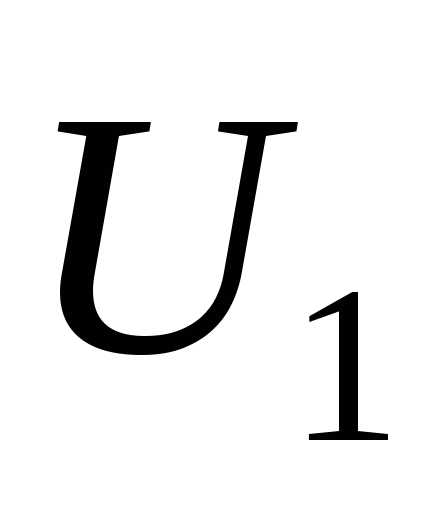. Поперечная составляющая падения напряжения 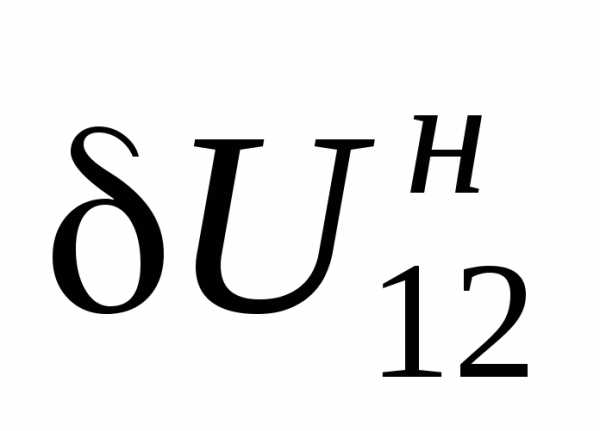=АС'—это про­- екция падения напряжения на мнимую ось. Один и тот же вектор падения напряжения проектируется на различ­- ные оси. Поэтому

,.

Если выразить ток в линии 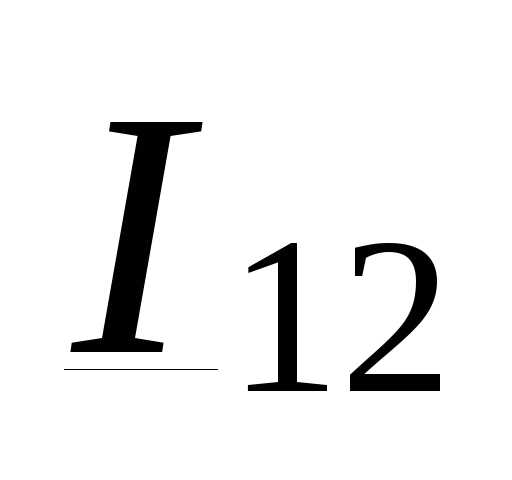аналогично (3.28) через известные в данном случае мощность в начале продольной ветви лини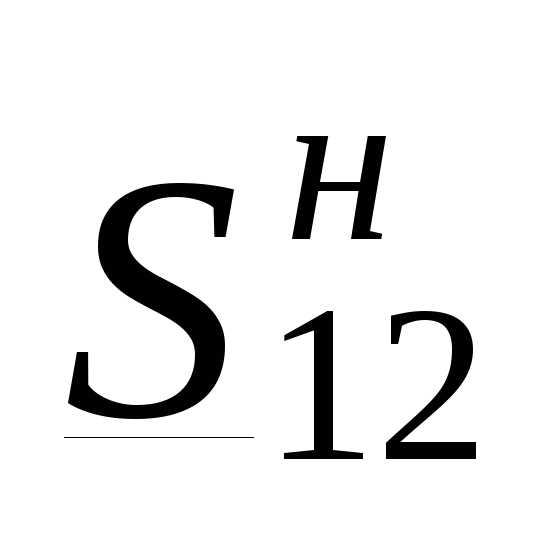и и 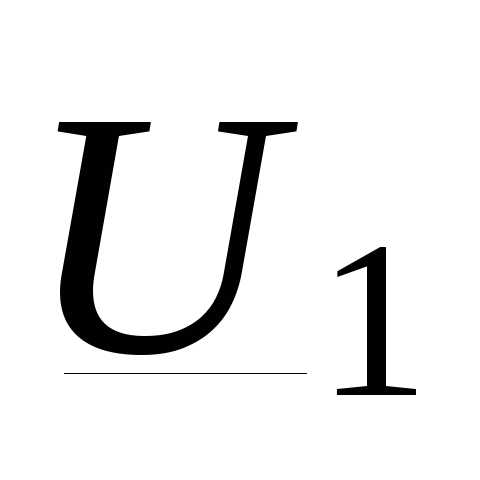, то получим выражения, аналогичные (3.30), (3.31):

; (3.35)

. (3.36)

Напряжение в конце линии

, (3.37)

где 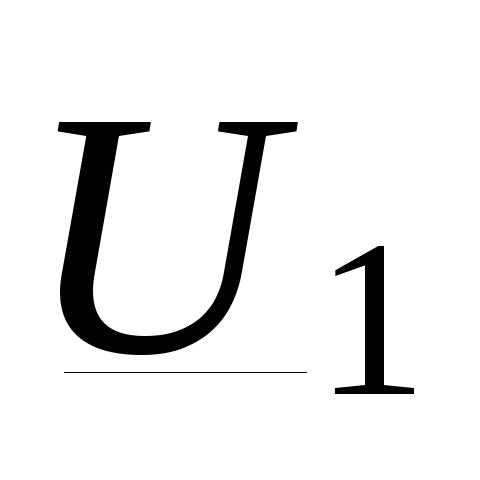известно; , 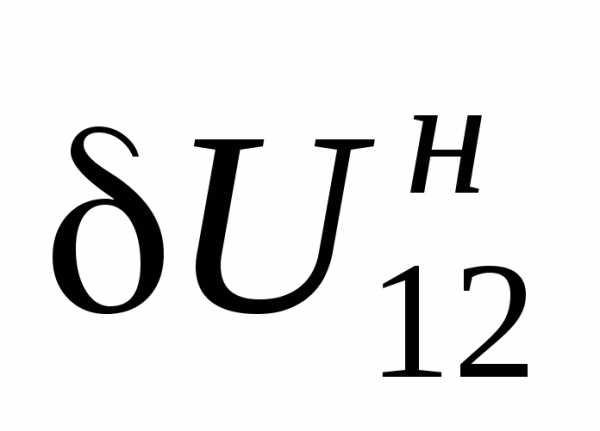определяются из(3.35), (3.36). Модуль и фаза 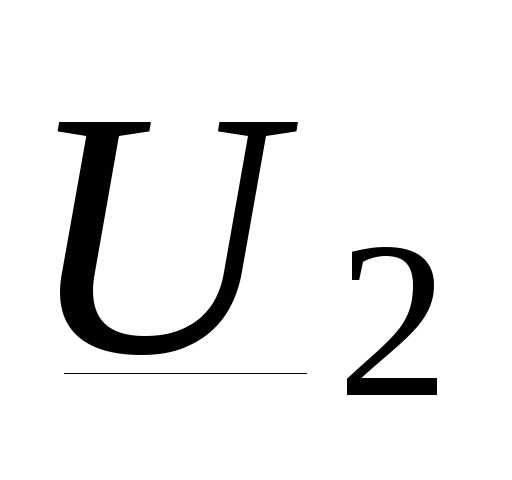равны

; (3.38)

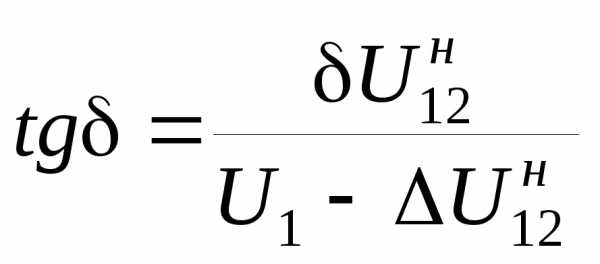. (3.39)

Определение напряжения в конце линии по данным на­- чала по выражениям (3.37), а также (3.35), (3.36) эквива­- лентно применению закона Ома в виде (3.25).

Пример 3.3. Определим падение и потерю напряжения в линии, рассмотренной в примере 3.1, по известным мощности в начале линии 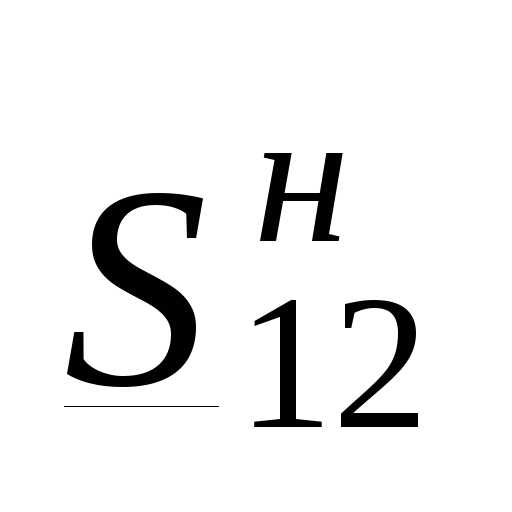=15,61+j9,6 МВА и напряжению в начале линии 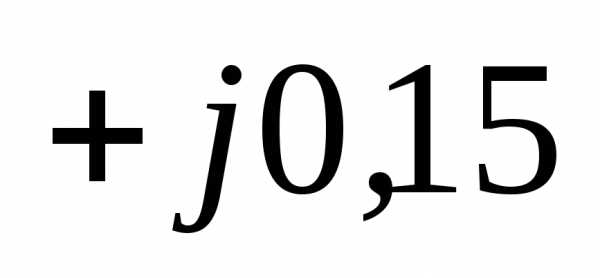кВ; 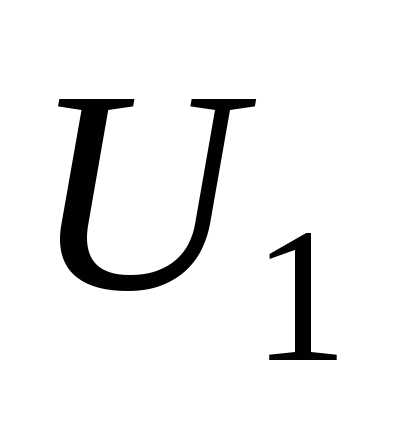= 115,9 кВ.

Используя параметры линии, приведенные в примере 3.1, по выра­- жениям (3.35), (3.36) найдем продольную и поперечную составляющие падения напряжения по данным начала:

кВ:

кВ.

Напряжение в конце линии по (3.37)

кВ.

Модуль напряжения в конце линии

кВ.

Потеря напряжения кВ.

Результаты определения напряжений в примерах 3.1, 3.2 и 3.3 раз­- личаются на погрешность округления, в примере 3.1 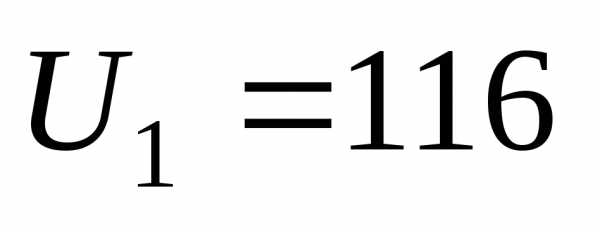кВ, а в примере 3.2 кВ. Соответственно в примерах 3.2, 3.3 потери напряжения равны 6,1 и 6,2 кВ. При проведении расчетов напряжений с четырьмя значащими цифрами погрешность округления при опреде­- лении, например, 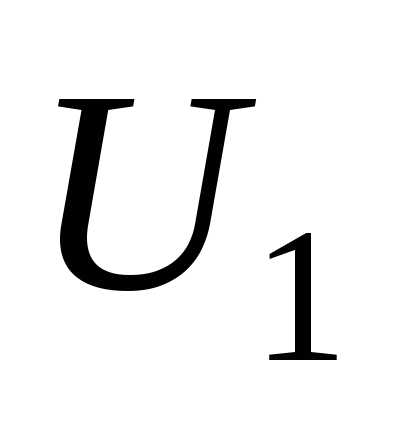в данных примерах равна 116—115,9=0,1 кВ. Ес­- ли проводить расчеты с восемью значащими цифрами, то результаты определения 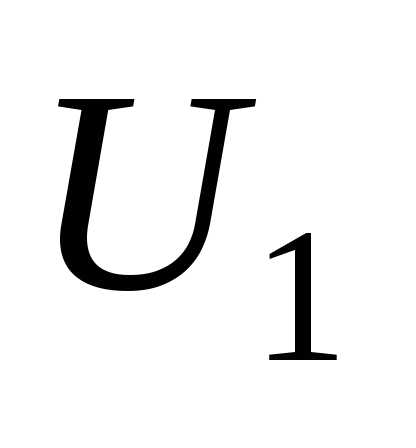и 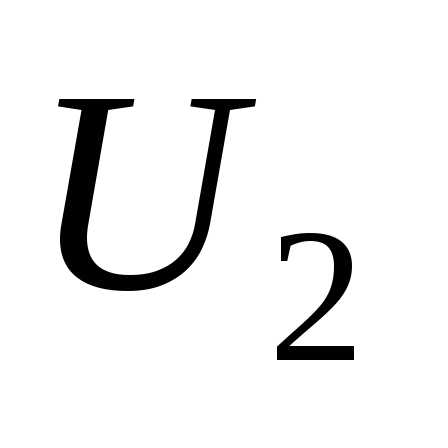различаются на 0,00094 кВ, т. е. погрешность ок­- ругления равна 0,001 кВ.

studfiles.net

4. Потери и падения напряжения в электрических сетях

Рассмотрим линию электропередачи, по которой протекает ток I и передается мощность S, а напряжения в начале (со стороны источника питания) и в конце (со стороны нагрузки) соответственно равны U1 и U2 (рис. 4.1).

Падением напряжения называется разность комплексов напряжений в начале и в конце элемента сети (в данном случае линии) .

Потерей напряжения называется разность модулей напряжений в начале и в конце элемента сети .

Падение напряжения – величина векторная, а потеря напряжения – скалярная.

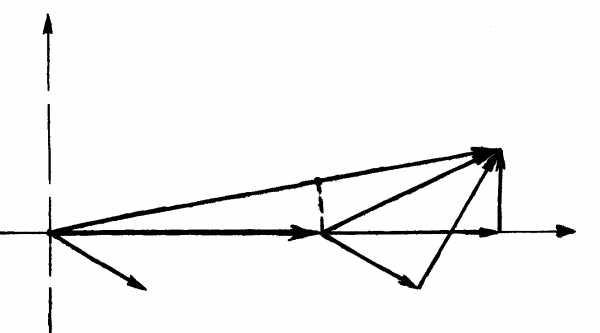
На рис. 4.2 изображена векторная диаграмма линии (емкостные токи не показаны). Напряжения на этой диаграмме по модулю равны линейным, а по фазе – фазным. Фактически это линейные напряжения, фазы которых изменены на 30°. Такие напряжения используются во всех дальнейших выкладках и расчетах.

Zл

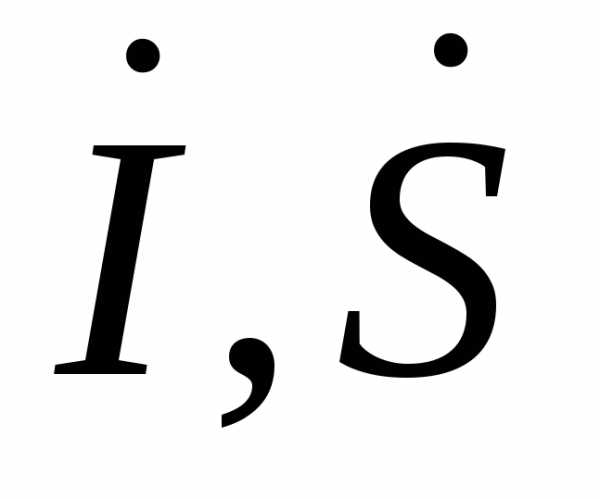
Р

Bл

Bл

ис. 4.1. Схема замещения линии для

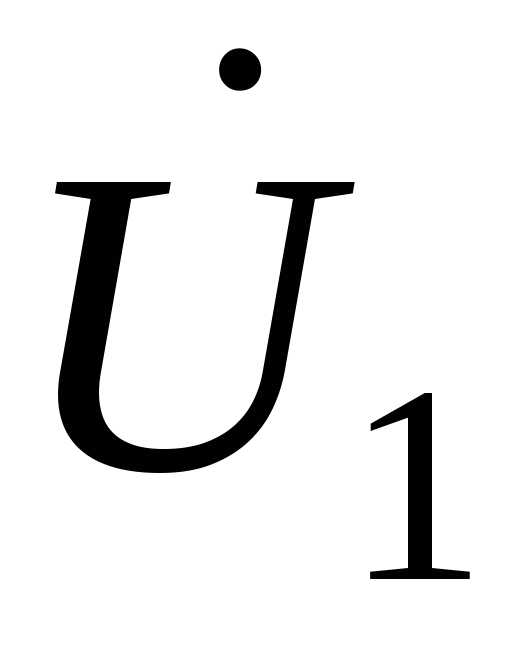
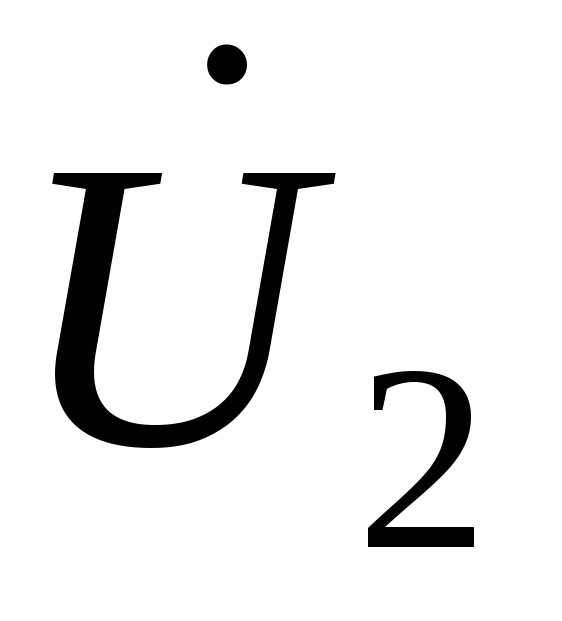
расчета падения и потери напряжения

+j

D

C

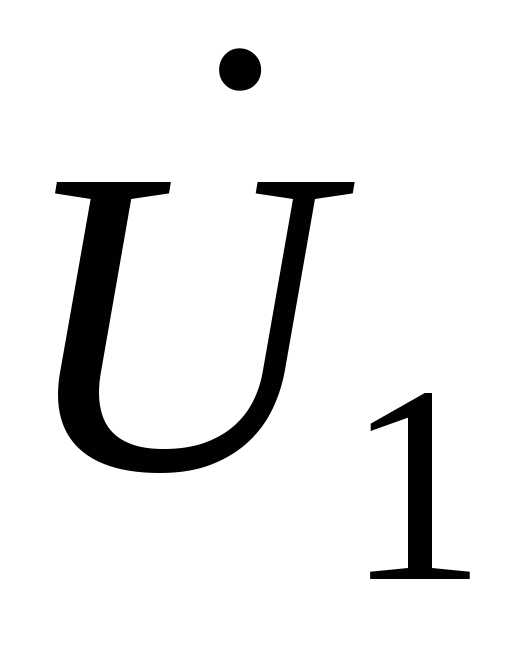
+1

A

B

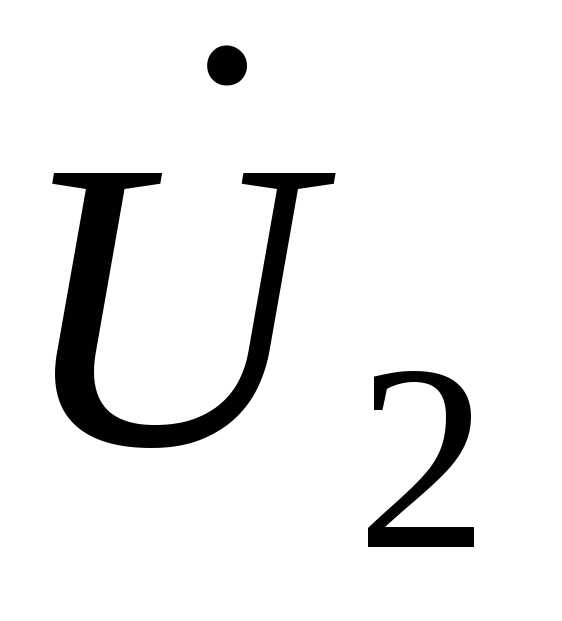
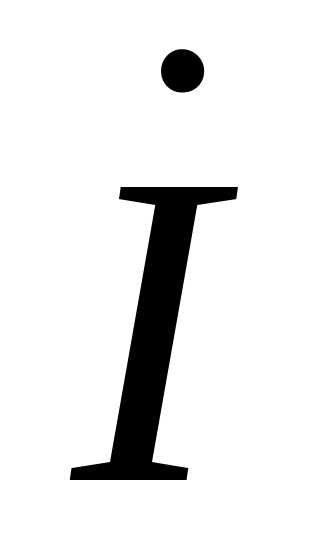
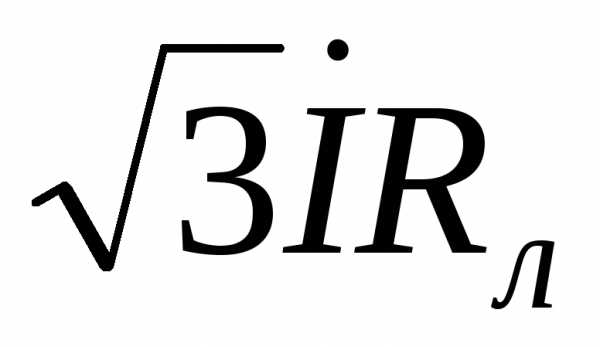
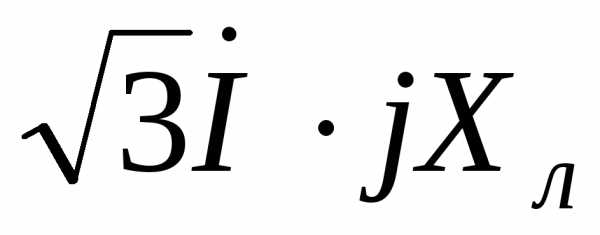
Рис. 4.2. Векторная диаграмма линии электропередачи

Построение векторной диаграммы начинается с векторов 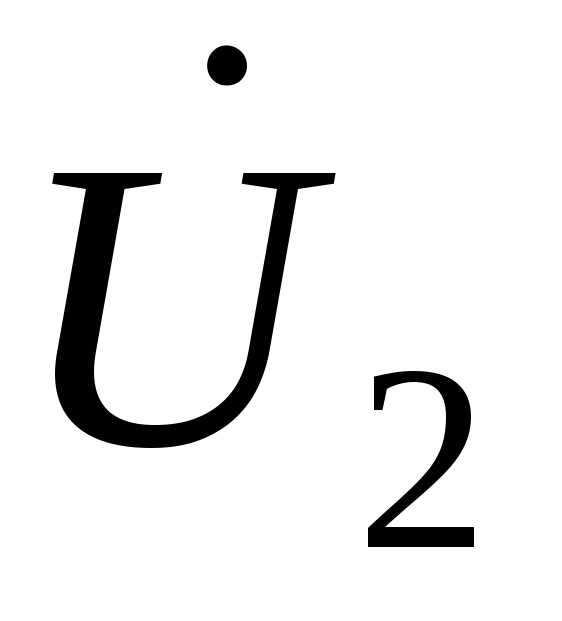и 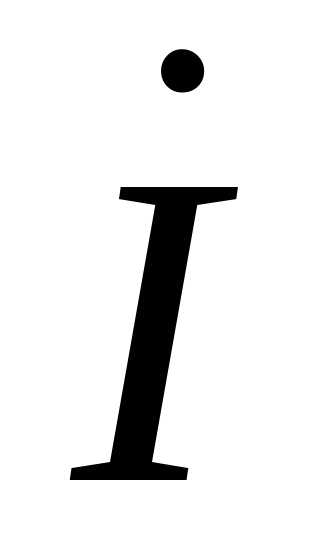при условии, что ток имеет активно-индуктивный характер. Затем строятся падения напряжения на активном, реактивном и полном сопротивлении лини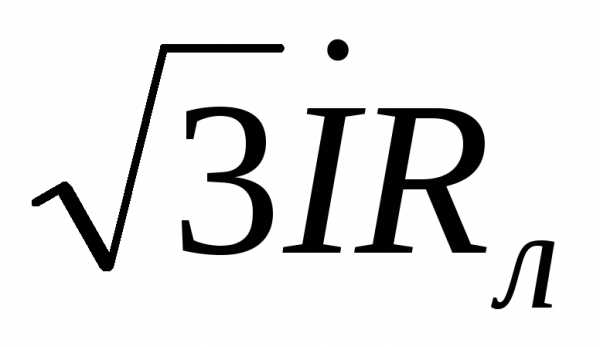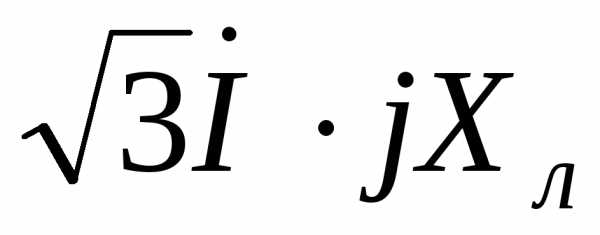и ,и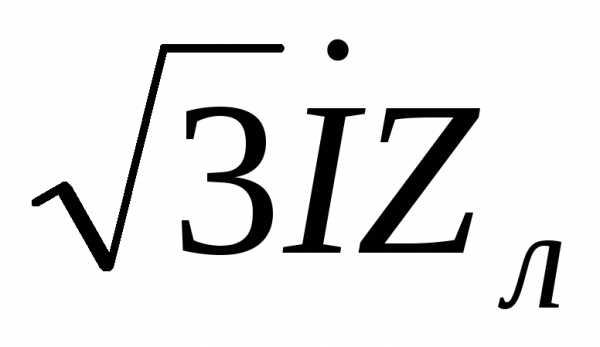. Прибавив последний вектор к 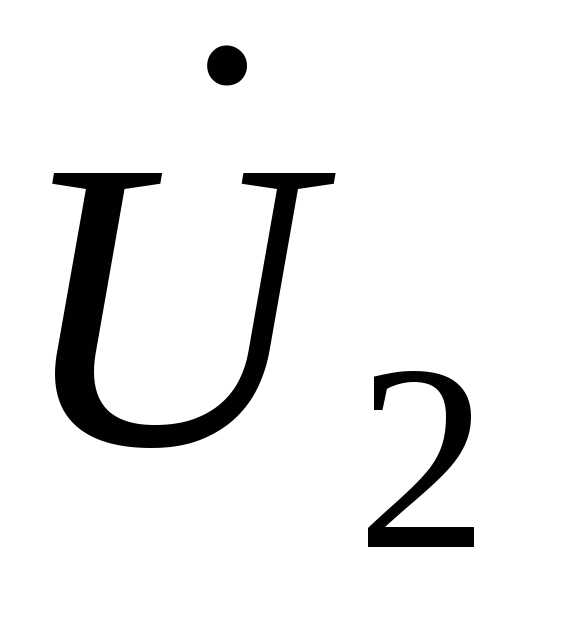, получим напряжение в начале линии.

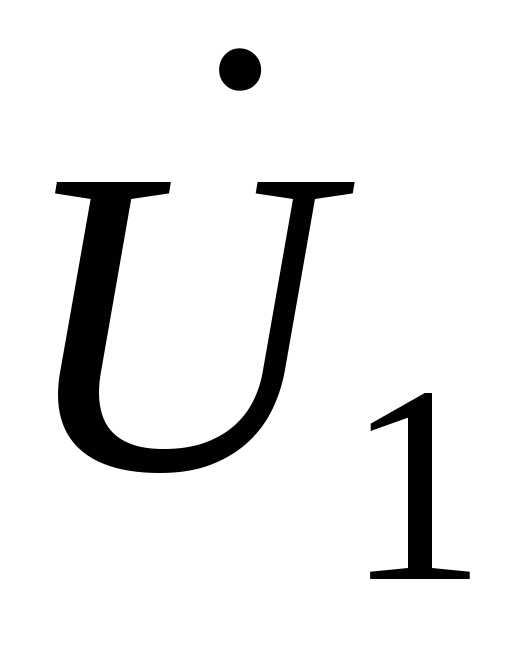Вектор 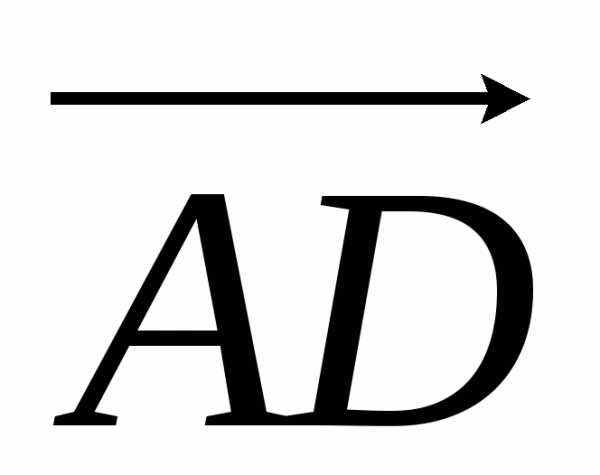представляет собой падение напряжения в линии , а отрезокCD – потерю напряжения . Точка С получена путем поворота вектора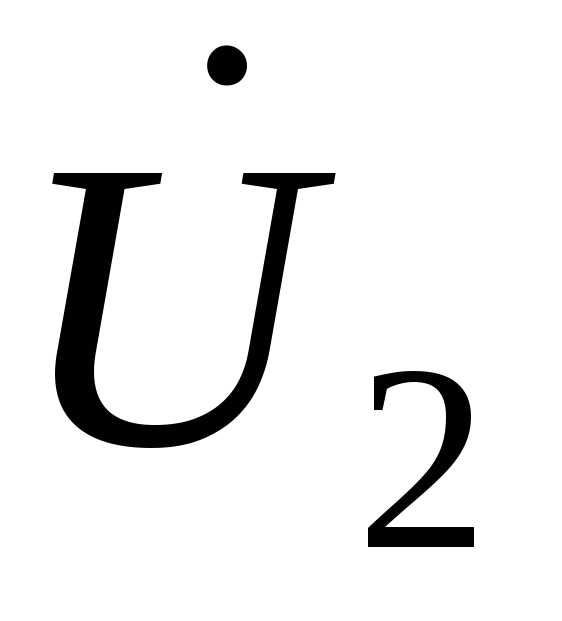 до совмещения с вектором .

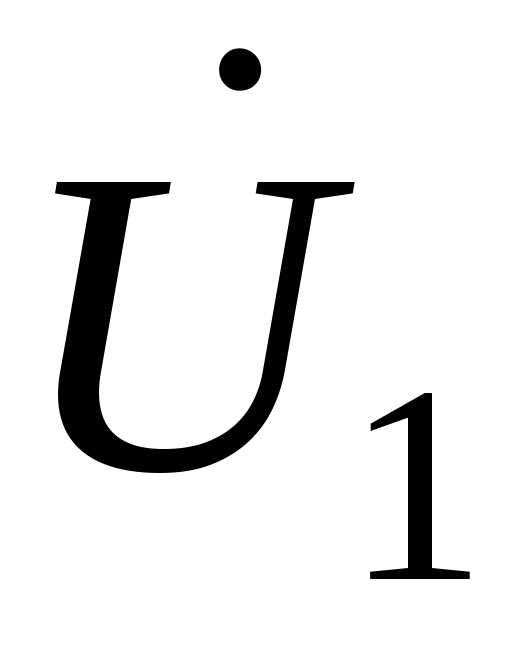Выразим падение напряжения через передаваемую мощность, которая связана с током соотношением

. (4.1)

Верхний индекс «*» здесь и далее обозначает сопряженные комплексы.

Из (4.1) при нулевой фазе напряжения следует

. (4.2)

Тогда

, (4.3)

где U – напряжение, в качестве которого может быть принято напряжение либо в начале, либо в конце данного элемента сети (при приближенных расчетах может использоваться также номинальное напряжение).

Величина ΔUnp называется продольной составляющей падения напряжения и представляет собой действительную часть падения напряжения (вектор 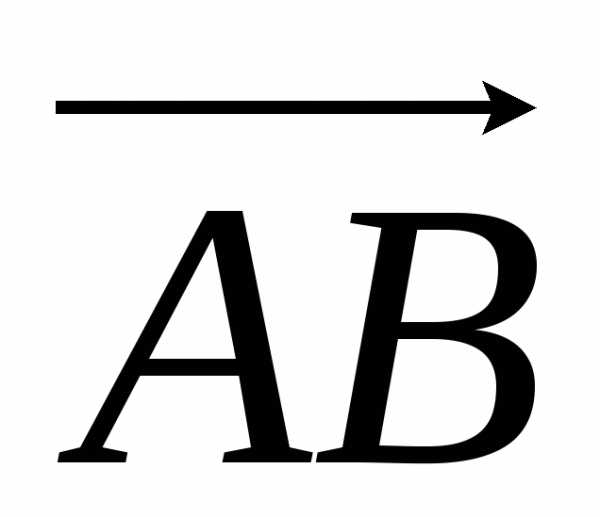на рис. 4.2).

Величина ΔUnon называется поперечной составляющей падения напряжения и представляет собой мнимую часть падения напряжения (вектор ).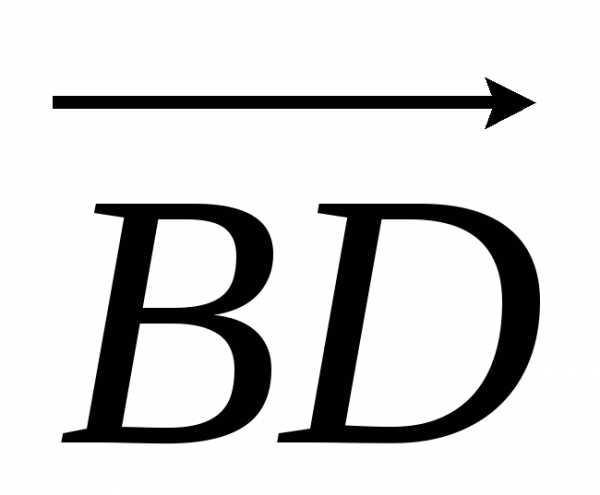

Значения продольной и поперечной составляющей падения напряжения зависят от того, через какое напряжение они рассчитаны. В случае, рассмотренном на рис. 4.2, этим напряжением является U2. Модуль и фаза напряжения U1 равны

, (4.4)

. (4.5)

С практической точки зрения модуль напряжения более важен, чем его фаза. Поэтому в некоторых случаях поперечная составляющая падения напряжения может не учитываться, так как она изменяет главным образом только фазу. При таком допущении потеря и падение напряжения равны друг другу.

studfiles.net

ПАДЕНИЕ И ПОТЕРЯ НАПРЯЖЕНИЯ В ЛИНИИ

Рассмотрим векторную диаграмму для линейных напряжений в начале и в конце линии и . Очевидно, что эта векторная диаграмма подобна диаграмме для фазных напряжений в начале и в конце линии и , рассмотренной ранее

 

Рис. 2.8. К оценке падения и потери напряжения в линии

Падение напряжения –геометрическая (векторная) разность между комплексами напряжений начала и конца линии. На рис. 2.8 падение напряжения – это вектор , т.е.

.

Продольной составляющей падения напряжения DU1,2 называют проекцию падения напряжения на действительную ось или на напряжение , т.е. величину DU1,2 = АС на рис. 2.8. Обычно DU1,2выражается через известные в конце линии значения , , .

Поперечная составляющая падения напряжения dU1,2 – это проекция падения напряжения на мнимую ось, dU1,2 = СВ на рис. 2.8. Таким образом,

.

Часто используют понятие потеря напряжения – это алгебраическая разность между модулями напряжений начала и конца линии.

На рис. 2.8 определено . Если поперечная составляющая падения напряжения dU1,2 мала (например, в сетях Uном £ 110 кВ), то можно приближенно считать, что потеря напряжения равна продольной составляющей падения напряжения.

Расчет режимов электрических сетей ведется в мощностях. Поэтому падения напряжения в целом и его составляющие принято выражать через потоки мощности в линии.

 

Похожие статьи:

poznayka.org

Что такое потери напряжения и причины образования потерь напряжения

Утраты напряжения в полосы

Для осознания, что такое утрата напряжения, разглядим векторную диаграмму напряжения трехфазной полосы переменного тока (рис. 1) с одной нагрузкой в конце полосы (I).

Представим, что вектор тока разложен на составляющие Iа и Iр. На рис. 2 в масштабе построены векторы фазного напряжения в конце полосы U3ф и тока I, отстающего от него по фазе на угол φ2.

Для получения вектора напряжения сначала полосы U1ф следует у конца вектора U2ф выстроить в масштабе напряжения треугольник падений напряжения в полосы (abc). Для этого вектор аb, равный произведению тока на активное сопротивление полосы (IR), отложен параллельно току, а вектор bc, равный произведению тока на индуктивное сопротивление полосы (IХ), — перпендикулярно вектору тока. При этих критериях ровная, соединяющая точки О и с, соответствует величине и положению в пространстве вектора напряжения сначала полосы (U1ф) относительно вектора напряжения в конце полосы (U2ф). Соединив концы векторов U1ф и U2ф, получим вектор падения напряжения на полном сопротивлении полосы ac=IZ.

Рис. 1. Схема с одной нагрузкой на конце полосы

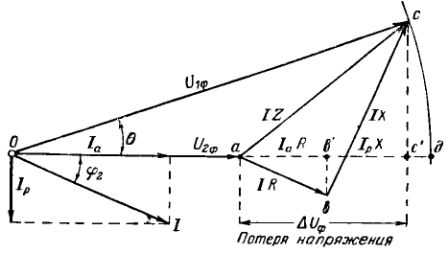
Рис. 2. Векторная диаграмма напряжений для полосы с одной нагрузкой. Утраты напряжения в полосы.

Договорились именовать потерей напряжения алгебраическую разность фазных напряжений сначала и конце полосы, т. е. отрезок ad либо практически равный ему отрезок ас’.

Векторная диаграмма и выведенные из нее соотношения демонстрируют, что утрата напряжения находится в зависимости от характеристик сети, также от активной и реактивной составляющих тока либо мощности нагрузки.

При расчете величины утраты напряжений в сети активное сопротивление нужно учесть всегда, а индуктивным сопротивлением можно пренебречь в осветительных сетях и в сетях, выполненных сечениями проводов до 6 мм2 и кабелей до 35 мм2.

Определение утраты напряжения в полосы

Утрату напряжения для трехфазной системы принято обозначать для линейных величин определять по формуле

где l — протяженность соответственного участка сети, км.

Если поменять ток мощностью, то формула воспримет вид:

где Р — активная мощность, Q— реактивная мощность, кВар; l — протяженность участка, км; Uн — номинальное напряжение сети, кВ.

Допустимые утраты напряжения

Для каждого приемника электроэнергии допускаются определенные утраты напряжения. К примеру, асинхронные движки в обычных критериях допускают отклонение напряжения ±5%. Это означает, что если номинальное напряжение данного электродвигателя составляет 380 В, то напряжения U‘доп = 1,05 Uн = 380 х1,05 = 399 В и U«доп = 0,95 Uн = 380 х 0,95 = 361 В следует считать его максимально допустимыми значениями напряжения. Естественно, что все промежные напряжения, заключенные меж значениями 361 и 399 В, также будут удовлетворять потребителя и составят некую зону, которую можно именовать зоной хотимых напряжений.

Потому что при работе предприятия имеет место неизменное изменение нагрузки (мощность либо ток, протекающий по проводам в данное время суток), то в сети будут иметь место и разные утраты напряжения, изменяющиеся от больших значений, соответственных режиму наибольшей нагрузки dUmaх, до меньших dUmin, соответственных малой нагрузке потребителя.

Для подсчета величины этих утрат напряжения следует пользоваться формулой:

Из векторной диаграммы напряжений (рис. 2) следует, что действительное напряжение у приемника U2ф можно получить, если из напряжения сначала полосы U1ф отнять величину dUф, либо, переходя к линейным, т. е. междуфазным напряжениям, получим U2 = U1 — dU

Расчет утрат напряжения

Пример. Потребитель, состоящий из асинхронных движков, подключен к шинам трансформаторной подстанции предприятия, на которых поддерживается неизменное в течение суток напряжение U1 = 400 В.

Большая нагрузка потребителя отмечена в 11 ч утра, при всем этом утрата напряжения dUмакс = 57 В, либо dUмакс% = 15%. Меньшая нагрузка потребителя соответствует обеденному перерыву, при всем этом dUмин — 15,2 В, либо dUмин% = 4%.

Нужно найти действительное напряжение у потребителя в режимах большей и меньшей нагрузок и проверить лежи г ли оно в зоне хотимых напряжений.

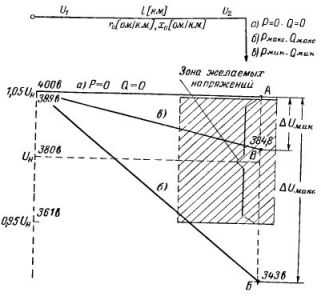
Рис. 3. Возможная диаграмма для полосы с одной нагрузкой для определения утрат напряжения

Решение. Определяем действительные значения напряжений:

U2макс = U1 — dUмакс = 400 — 57 = 343 В

U2мин = U1 — dUмин = 400 — 15,2 = 384,8 В

Желаемые напряжения для асинхронных движков с Uн = 380 В должны удовлетворять условию:

399 ≥ U2жел ≥ 361

Подставив в неравенство вычисленные значения напряжений, убеждаемся, что для режима больших нагрузок соотношение 399 > 343 > 361 не удовлетворяется, а для меньших нагрузок 399 > 384,8 > 361 удовлетворяется.

Вывод. В режиме больших нагрузок утрата напряжения так велика, что напряжение у потребителя выходит за границы зоны хотимых напряжений (понижается) и не удовлетворяет потребителя.

Этот пример можно проиллюстрировать графически возможной диаграммой рис. 3. При отсутствии тока напряжение у потребителя будет численно равно напряжению на питающих шинах. Потому что утрата напряжения пропорциональна длине питающей полосы, то напряжение при наличии нагрузки меняется повдоль полосы по наклонной прямой от величины U1 = 400 В до величины U2макс = 343 В и величины U2мин = 384,8 В.

Как видно из диаграммы, напряжение в режиме большей нагрузки вышло из зоны хотимых напряжений (точка Б графика).

Таким макаром, даже при неизменной величине напряжения на шинах питающего трансформатора, резкие конфигурации нагрузки могут сделать у приемника недопустимую величину напряжения.

Не считая того, возможно окажется, что при конфигурациях нагрузки в сети от большей нагрузки в дневное время до меньшей нагрузки в ночное время сама энергетическая система не сумеет обеспечить подабающей величины напряжения на выводах трансформатора. В обоих этих случаях следует прибегнуть к средствам местного, приемущественно, ступенчатого конфигурации напряжения.

Утрата напряжения в трансформаторе (в картинах)

elektrica.info

Что такое падение напряжения? | Voltstab.ru

Падение напряжения

Падение напряжения — это термин, используемый для описания любого снижения напряжения питания в полной электрической цепи. Этот термин может использоваться для описания потерь напряжения на конкретном компоненте в цепи, потерь напряжения, измеренных по всей цепи, или в качестве широкого описания явления потери напряжения в цепи в целом. Все электрические схемы, независимо от того, насколько просты, представляют определенную степень сопротивления потоку электрического тока через них. Это сопротивление эффективно усиливает работу электрического тока и, таким образом, поглощает энергию. Это расходование энергии приводит к уменьшению напряжения, описываемого термином падения напряжения.

Например, простая схема может состоять из 9-вольтовой батареи, прикрепленной к простой лампе накаливания с помощью маленького переключателя. Если бы измерить напряжение на клеммах батарей с открытым переключателем, показание мультиметра будет приблизительно 9 вольт. Если нужно закрыть выключатель и осветить лампочку, это показание снизится примерно на 1,5 вольта. Это снижение напряжения — это то, что известно как падение напряжения, и это происходит в результате работы, которую батарея должна делать, чтобы осветить лампу. Каждый компонент в цепи, включая проводку, обеспечивает определенную степень сопротивления потоку электрического тока и вызывает связанное падение напряжения.

В приложениях, которые являются чрезвычайно чувствительными к напряжению питания, например электронным устройствам, эти потери напряжения должны быть тщательно рассчитаны и напряжение питания отрегулировано таким образом, чтобы обеспечить их. Например, источник питания с постоянным током 12 В (DC), как правило, производит выход 13,8 вольт для удовлетворения этого явления падения напряжения. В приложениях, требующих очень длинных кабельных трасс, общепринятой практикой является использование довольно тяжелых кабелей, которые оказывают меньшее сопротивление потоку электрического тока в попытке минимизировать влияние потерь напряжения. Таким образом, полная потенциальная потеря напряжения в любой цепи должна быть тщательно рассчитана на этапе проектирования и спецификации проекта, чтобы гарантировать, что конечный результат соответствует всем требованиям.

К счастью, любые потери напряжения в цепи можно вычислить с большой точностью, используя формулу падения напряжения. Это позволяет достичь согласованных и прогнозируемых результатов в конце установки. Эти расчеты будут различаться в зависимости от типа схемы, напряжения питания и задействованных компонентов и могут быть чрезвычайно сложными, часто требуя использования калькулятора падения напряжения. Тем не менее, они выполняют предположения о точном регулировании характеристик источника питания для обеспечения сопротивления цепи.

voltstab.ru

2.Чем отличаются потери от падения напряжения и как их определяют?

Падение напряжения - геометрическая (векторная) разность между комплексами напряжений начала и конца линии. Падение напряжения — это вектор АВ, т. е.

AB → = U1 – U2 = √3I12Z12

Продольной составляющей падения напряжения ∆U12К называют проекцию падения напряжения на действитель­ную ось или на напряжение ∆U12К = АС.

Индекс «к» означает, что ∆U12К - проекция на напряжение конца линии U2. Обычно ∆U12К выражается через данные в конце линии: U2, P12К, Q12К.

Поперечная составляющая падения напряжения δU12К - это проекция падения напряжения на мнимую ось, δU12К= СВ. Таким образом,

U1 – U2 = √3I12Z12 = ∆U12К + jδU12К

Часто используют понятие потеря напряжения — это ал­гебраическая разность между модулями напряжений на­чала и конца линии.U1 – U2 =AD. Если попе­речная составляющая -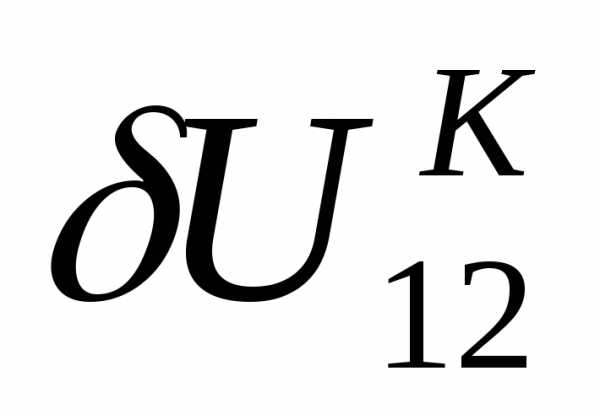 мала (например, в сетях Uном ≥ 110 кВ), то можно приближенно считать, что потеря напряжения равна продольной составляющей падения на­пряжения.

3.Компенсация реактивной мощности на промпредприятиях.

Мероприятия по уменьшению потребления реактивной мощности можно разделить на следующие группы:

а)снижение потребления реактивной мощности приемниками электроэнер­гии без применения компенсирующих устройств;

б)применение компенсирующих устройств.

Мероприятия по снижению потребления реактивной мощности должны рас­сматриваться в первую очередь, поскольку для их осуществления, как правило, не требуется значительных капитальных затрат. К ним относятся следующие:

1)упорядочение технологического процесса, ведущее к улучшению энерге­тического режима оборудования;

2)замена малозагруженных асинхронных двигателей двигателями меньшей мощности;

3)понижение напряжения у двигателей, систематически работающих с малой загрузкой;

4)ограничение холостой работы двигателей;

5)применение синхронных двигателей вместо асинхронных тон же мощности в случаях, когда это возможно по условиям технологического процесса;

6)повышение качества ремонта двигателей;

7)замена и перестановка малозагруженных трансформаторов.

Понижение напряжения у малозагруженных дви­гателей. При невозможности замены малозагруженного асинхронного дви­гателя следует проверить целесообразность снижения напряжения на его зажимах. Снижение напряжения на выводах асинхронного двигателя до определенного ми­нимально допустимого значения (Умин приводит к уменьшению потребления им реактивной мощности (за счет уменьшения тока намагничивания) и тем самым к увеличению коэффициента мощности. При этом одновременно уменьшаются потери активной мощности и, следовательно, увеличивается к. п. д. двигателя. На практике применяются следующие способы снижения напряжения у мало-загруженных асинхронных двигателей:

1)переключение статорной обмотки с треугольника на звезду;

2)секционирование статорных обмоток;

3)понижение напряжения в фабрично-заводских силовых сетях путем пере­ключения ответвлений понижающих трансформаторов.

Ограничение холостого хода работающих асин­хронных двигателей. Работа большинства асинхронных двигателей характерна тем, что в перерывах между нагрузками они вращаются на холостом ходу. Для ряда потребителей время работы двигателей на холостом ходу дости­гает 50-65% всего времени работы. Если промежутки работы на холостом ходу достаточно велики, то целесообразно на это время отключать двигатель от сети. Потребление активной и особенно реактивной энергии при этом значительно умень­шится. В случае применения ограничителей холостого хода подсчет экономии производится по графикам активной и реактивной мощности, потребляемой асин­хронными двигателями.

Повышение качества ремонта асинхронных дви­гателей. При выполнении ремонта двигателей необходимо учитывать и точно соблюдать номинальные данные двигателей. В противном случае из ремонта могут быть выпущены двигатели с повышенным потреблением реактивной мощности, большой неравномерностью нагрузки отдельных фаз, увеличенным током холос­того хода, значительным отклонением от заводских обмоточных данных и другими серьезными недостатками. Все это создает повышенные потери энергии и ухудшает естественный коэффициент мощности предприятия.

Замена и перестановка трансформаторов. Больших успехов в повышении естественного коэффициента мощности промышленного предприятия можно достигнуть за счет рационализации работы трансформаторов, которая проводится путем их замены и перегруппировки, а также путем отклю­чения некоторых трансформаторов в часы малых нагрузок. Если при этих меро­приятиях снижается потребление реактивной мощности и уменьшаются потери активной мощности, то осуществление их, несомненно, целесообразно.

Билет №18

studfiles.net

Что такое падение напряжения

Для человека, который знаком с электрооборудованием на уровне простого пользователя (знает, где и как включить/выключить), многие используемые электриками термины кажутся какой-то бессмыслицей. Например, чего только стоит «падение напряжения» или «сборка схемы». Куда и что падает? Кто разобрал схему на детали? На самом же деле, физический смысл происходящих процессов, скрывающийся за большинством этих слов, вполне доступен для понимания даже со школьными знаниями физики.

Чтобы объяснить, что такое падение напряжения, необходимо вспомнить, какие вообще напряжения бывают в электрической цепи (имеется в виду глобальная классификация). Их всего два вида. Первый – это напряжение источника питания, который подключен к рассматриваемому контуру. Оно может также называться приложенным ко всей цепи. А второй вид – это именно падение напряжения. Может быть рассмотрено как в отношении всего контура, так и любого отдельно взятого элемента.

На практике это выглядит следующим образом. Например, если взять обычную лампу накаливания, вкрутить ее в патрон, а провода от него подключить в домашнюю сетевую розетку, то приложенное к цепи (источник питания – проводники – нагрузка) напряжение составит 220 Вольт. Но стоит нам с помощью вольтметра замерять его значение на лампе, как станет очевидно, что оно немного меньше, чем 220. Так произошло потому, что возникло падение напряжения на электрическом сопротивлении, которым обладает лампа.

Пожалуй, нет человека, который не слышал бы о законе Ома. В общем случае формулировка его выглядит так:

I = U / R,

где R – активное сопротивление цепи или ее элемента, измеряется в Омах; U – электрическое напряжение, в Вольтах; и, наконец, I – ток в Амперах. Как видно, все три величины непосредственно связаны между собой. Поэтому, зная любые две, можно довольно просто вычислить третью. Конечно, в каждом конкретном случае придется учесть род тока (переменный или постоянный) и некоторые другие уточняющие характеристики, но основа – вышеуказанная формула.

Электрическая энергия – это, фактически, движение по проводнику отрицательно заряженных частиц (электронов). В нашем примере спираль лампы обладает высоким сопротивлением, то есть замедляет перемещающиеся электроны. Благодаря этому возникает видимое свечение, но общая энергия потока частиц снижается. Как видно из формулы, с уменьшением тока уменьшается и напряжение. Именно поэтому результаты замеров у розетки и на лампе различаются. Эта разница и является падением напряжения. Данная величина всегда учитывается, чтобы предотвратить слишком большое снижение на элементах в конце схемы.

Падение напряжения на резисторе зависит от его внутреннего сопротивления и силы протекающего по нему тока. Также косвенное влияние оказывают температура и характеристики тока. Если в рассматриваемую цепь включить амперметр, то падение можно определить умножением значения тока на сопротивление лампы.

Но далеко не всегда удается вот так просто с помощью простейшей формулы и измерительного прибора выполнить расчет падения напряжения. В случае параллельно подключенных сопротивлений нахождение величины усложняется. На переменном токе приходится дополнительно учитывать реактивную составляющую.

Рассмотрим пример с двумя параллельно включенными резисторами R1 и R2. Известно сопротивление провода R3 и источника питания R0. Также дано значение ЭДС – E.

Приводим параллельные ветки к одному числу. Для этой ситуации применяется формула:

R = (R1*R2) / (R1+R2)

Определяем сопротивление всей цепи через сумму R4 = R+R3.

Рассчитываем ток:

I = E / (R4+r)

Остается узнать значение падение напряжения на выбраном элементе:

U = I * R5

Здесь множитель "R5" может быть любым R - от 1 до 4, в зависимости от того, какой именно элемент схемы нужно рассчитать.

fb.ru

---

• 
  Треугольник в электрической схеме
• 
  Льготы мосэнерго
• 
  Почему нельзя допустить перегрузку и недогрузку машин
• 
  Отличие синхронного двигателя от асинхронного двигателя
• 
  Если нет тепла куда звонить
• 
  Асинхронные двигатели серии 4а справочник
• 
  Антенна для укв приемника своими руками
• 
  Кто отвечает за тепло в квартире
• 
  Центр сбк передать показания счетчика нижегородская область
• 
  Люстра из светодиодной ленты
• 
  Что такое субсидия и кому она положена