Электрические цепи с одним источником тока или эдс
Рассмотрим электрическую цепь, схема которой изображена на рис. 1, Пусть известны значения сопротивления резисторов R1, R2, R3, R4, R5, R6, эдс E и ее внутреннее сопротивление R0. Требуется определить токи во всех участках цепи и напряжение, которое покажет вольтметр (сопротивление его бесконечно велико), включенный между точками схемы а и d.
Рисунок 1
Такие задачи решаются методом свертывания схемы, по которому отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению относительно зажимов источников питания. Схема упрощается с помощью замены группы последовательно или параллельно соединенных резисторов одним эквивалентным по сопротивлению. Так, резисторы R4 и R5 соединены последовательно, а резистор R6 — с ними параллельно, поэтому их эквивалентное сопротивление
После произведенных преобразований схема принимает вид, показанный на рис. 2, а эквивалентное сопротивление всей цепи найдем из уравнения
2, а эквивалентное сопротивление всей цепи найдем из уравнения
Рисунок 2
Ток I1 в неразветвленной части схемы определим по закону Ома:
Воспользовавшись схемой (рис. 2), найдем токи I2 и I3:
Переходя к рис. 1, определим токи I4, I5, I6 по аналогичным уравнениям:
Зная ток I1, можно найти ток I2 по-другому. Согласно второму закону Кирхгофа,
Показания вольтметра можно определить, составив уравнение по второму закону Кирхгофа, например, для контура acda:
Для проверки решения можно воспользоваться первым законом Кирхгофа и уравнением баланса мощностей, которые для схемы, изображенной на рис. 1, примут вид
Электрические цепи с одним источником можно рассчитывать методом подобия (метод пропорциональных величин), который применим только для расчета линейных цепей, т. е. цепей с неизменными значениями сопротивлений. Воспользуемся свойствами линейных цепей для определения токов схемы, изображенной на рис. 1, в такой последовательности: задаемся произвольным значением тока I6/ в резисторе R6, наиболее удаленном от источника питания. По заданному току I6/ и сопротивлению резистора R6 определяем напряжение .
1, в такой последовательности: задаемся произвольным значением тока I6/ в резисторе R6, наиболее удаленном от источника питания. По заданному току I6/ и сопротивлению резистора R6 определяем напряжение .
Далее определяем
Рис. 3
Наконец, находим значение э.д.с. Е’:
Однако найденное значение E/ в общем случае отличается от заданной величины э.д. с. E. Поэтому для определения действительных и
значений токов и напряжений
вычисляем так называемый коэффициент подобия К=Е/Е’. Умножив на него полученные при расчете значения токов и напряжений, находим действительные значения токов цепи. Метод пропорциональных величин особенно эффективен при расчете разветвленных электрических цепей с одним источником.
Рассмотрим электрическую цепь, схема которой изображена на рис. 3. К источнику тока J=0,1 А подключены резисторы с сопротивлениями R1 = 12 Ом; R2=10 Ом; R3 = 16 Ом; R4 Ом; R5=60 Ом. Определить напряжение Uab источника тока и все токи. Составить баланс мощностей. Задача решается методом свертывания схемы.
Определить напряжение Uab источника тока и все токи. Составить баланс мощностей. Задача решается методом свертывания схемы.
Находим входное сопротивление Rab схемы относительно зажимов источника тока:
Находим напряжение на зажимах источника тока Uab
По закону Ома находим ток I2
Ток I3 определяем из уравнения закона Кирхгофа:
Этот ток распределяется обратно пропорционально сопротивлениям R4 и R5:
Уравнение баланса мощностей отражает равенство мощностей, отдаваемой источником н расходуемой приемниками, т, е.
определение, элементы, схемы. Топология и методы расчета
Эта статья для тех, кто только начинает изучать теорию электрических цепей. Как всегда не будем лезть в дебри формул, но попытаемся объяснить основные понятия и суть вещей, важные для понимания. Итак, добро пожаловать в мир электрических цепей!
Итак, добро пожаловать в мир электрических цепей!
Хотите больше полезной информации и свежих новостей каждый день? Присоединяйтесь к нам в телеграм.
Электрические цепи
Электрическая цепь – это совокупность устройств, по которым течет электрический ток.
Рассмотрим самую простую электрическую цепь. Из чего она состоит? В ней есть генератор – источник тока, приемник (например, лампочка или электродвигатель), а также система передачи (провода). Чтобы цепь стала именно цепью, а не набором проводов и батареек, ее элементы должны быть соединены между собой проводниками. Ток может течь только по замкнутой цепи. Дадим еще одно определение:
Электрическая цепь – это соединенные между собой источник тока, линии передачи и приемник.
Конечно, источник, приемник и провода – самый простой вариант для элементарной электрической цепи. В реальности в разные цепи входит еще множество элементов и вспомогательного оборудования: резисторы, конденсаторы, рубильники, амперметры, вольтметры, выключатели, контактные соединения, трансформаторы и прочее.
Электрическая цепь
Кстати, о том, что такое трансформатор, читайте в отдельном материале нашего блога.
По какому фундаментальному признаку можно разделить все цепи электрического тока? По тому же, что и ток! Есть цепи постоянного тока, а есть – переменного. В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.
Сейчас переменный ток используется повсеместно. О том, что для этого сделал Никола Тесла, читайте в нашей статье.
Элементы электрических цепей
Все элементы электрических цепей можно разделить на активные и пассивные. Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники.
Приемники и источники тока, с точки зрения топологии цепей, являются двухполюсными элементами (двухполюсниками). Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи.
Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи.
Резисторы – элементы электрической цепи, которые обладают сопротивлением. Вообще, все элементы реальных цепей, вплоть до самого маленького соединительного провода, имеют сопротивление. Однако в большинстве случаев этим можно пренебречь и при расчете считать элементы электрической цепи идеальными.
Существуют условные обозначения для изображения элементов цепи на схемах.
Кстати, подробнее про силу тока, напряжение, сопротивление и закон Ома для элементов электрической цепи читайте в отдельной статье.
Вольт-амперная характеристика – фундаментальная характеристика элементов цепи. Это зависимость напряжения на зажимах элемента от тока, который проходит через него.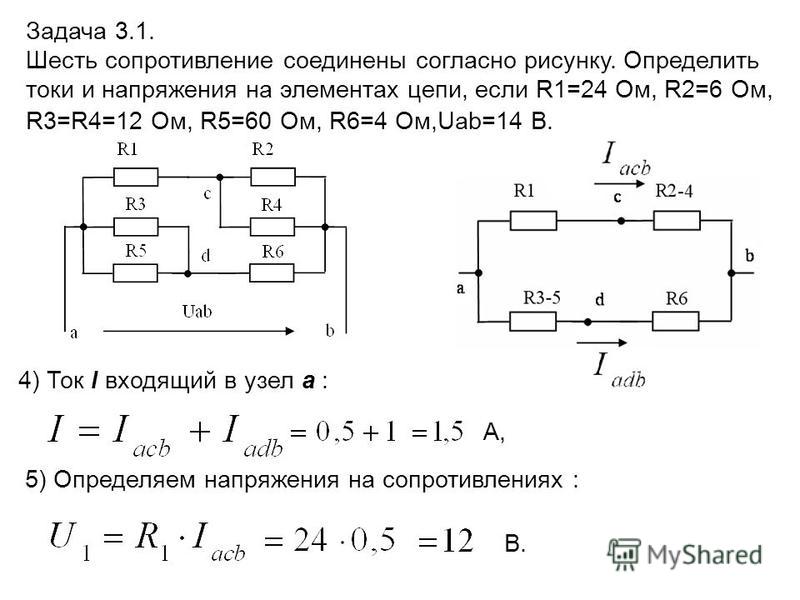 Если вольт-амперная характеристика представляет собой прямую линию, то говорят, что элемент линейный. Цепь, состоящая из линейных элементов – линейная электрическая цепь. Нелинейная электрическая цепь – такая цепь, сопротивление участков которой зависит от значений и направления токов.
Если вольт-амперная характеристика представляет собой прямую линию, то говорят, что элемент линейный. Цепь, состоящая из линейных элементов – линейная электрическая цепь. Нелинейная электрическая цепь – такая цепь, сопротивление участков которой зависит от значений и направления токов.
Какие есть способы соединения элементов электрической цепи? Какой бы сложной ни была схема, элементы в ней соединены либо последовательно, либо параллельно.
При решении задач и анализе схем используют следующие понятия:
- Ветвь – такой участок цепи, вдоль которого течет один и тот же ток;
- Узел – соединение ветвей цепи;
- Контур – последовательность ветвей, которая образует замкнутый путь. При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.
Чтобы понять, что есть что, взглянем на рисунок:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Классификация электрических цепей
По назначению электрические цепи бывают:
- Силовые электрические цепи;
- Электрические цепи управления;
- Электрические цепи измерения;
Силовые цепи предназначены для передачи и распределения электрической энергии. Именно силовые цепи ведут ток к потребителю.
Именно силовые цепи ведут ток к потребителю.
Также цепи разделяют по силе тока в них. Например, если ток в цепи превышает 5 ампер, то цепь силовая. Когда вы щелкаете чайник, включенный в розетку, Вы замыкаете силовую электрическую цепь.
Электрические цепи управления не являются силовыми и предназначены для приведения в действие или изменения параметров работы электрических устройств и оборудования. Пример цепи управления – аппаратура контроля, управления и сигнализации.
Электрические цепи измерения предназначены для фиксации изменений параметров работы электрического оборудования.
Расчет электрических цепей
Рассчитать цепь – значит найти все токи в ней. Существуют разные методы расчета электрических цепей: законы Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Рассмотрим применение метода контурных токов на примере конкретной цепи.
Сначала выделим контуры и обозначим ток в них. Направление тока можно выбирать произвольно. В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:
В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:
Полученная система решается с подставкой исходных данных задачи. Токи в ветвях исходной цепи находим как алгебраическую сумму контурных токов
Какую бы цепь Вам ни понадобилось рассчитать, наши специалисты всегда помогут справится с заданиями. Мы найдем все токи по правилу Кирхгофа и решим любой пример на переходные процессы в электрических цепях. Получайте удовольствие от учебы вместе с нами!
Направление тока в цепи, куда течет?
Свободные электроны.. Электрический ток.. Измерение тока.. Амперметр.. Единица силы тока — Ампер.. Направление электрического тока.. Направление движения электронов..
Когда электрическое поле прикладывается к проводнику, свободные электроны (носители отрицательного заряда) начинают дрейфовать в соответствии с направлением электрического поля – возникает электрический ток.
Движение электронов означает движение отрицательных зарядов, следовательно, – электрический ток является мерой количества электрического заряда, переносимого через поперечное сечение проводника за единицу времени.
В международной системе СИ единица измерения заряда – Кулон, а единица времени – секунда. Поэтому единица силы тока – Кулон в секунду (Кл/сек).
Измерение тока
Единица силы тока Кулон в секунду в системе СИ имеет конкретное название Ампер (А) – в честь знаменитого французского ученого Андре-Мари Ампера (на фото в заголовке статьи).
Как мы знаем, величина отрицательного электрического заряда электрона -1,602 • 10-19 Кулона. Поэтому один Кулон электрического заряда состоит из 1 / 1,602 • 10-19 = 6,24 • 1018 электронов.
Следовательно, если 6,24 • 1018 электронов пересекает поперечное сечение проводника за одну секунду, то величина такого тока равна одному амперу.
Для измерения силы тока существует измерительный прибор — амперметр.
Рис. 1
Амперметр включается в электрическую цепь (рис. 1) последовательно с тем элементом цепи, силу тока в котором необходимо измерить. При подключении амперметра нужно соблюдать полярность: «плюс» амперметра подключается к «плюсу» источника тока, а «минус» амперметра — к «минусу» источника тока.
1) последовательно с тем элементом цепи, силу тока в котором необходимо измерить. При подключении амперметра нужно соблюдать полярность: «плюс» амперметра подключается к «плюсу» источника тока, а «минус» амперметра — к «минусу» источника тока.
Направление электрического тока
Если в электрической цепи, показанной на рис. 1 замкнуть контакты выключателя, то по этой цепи потечет электрический ток. Возникает вопрос: «А в каком направлении?»
Мы знаем, что электрическим током в металлических проводниках называется упорядоченное движение отрицательно заряженных частиц – электронов (в других средах это могут быть ионы или ионы и электроны). Отрицательно заряженные электроны во внешней цепи двигаются от минуса источника к плюсу (одноименные заряды отталкиваются, противоположные — притягиваются), что хорошо иллюстрирует рис. 2.
Рис. 2
Учебник физики за 8 класс дает нам другой ответ: «За направление электрического тока в цепи принято направление движения положительных зарядов», — то есть от плюса источника энергии к минусу источника.
Выбор направления тока, противоположного истинному, иначе как парадоксальным назвать нельзя, но объяснить причины такого несоответствия можно, если проследить историю развития электротехники.
Дело в том, что электрические заряды стали изучать задолго до того, как были открыты электроны, поэтому природа носителей заряда в металлах была еще неизвестна.
Понятие о положительном и отрицательном заряде ввёл американский ученый и политический деятель Бенджамин Франклин.
В своей работе «Опыты и наблюдения над электричеством» (1747 г.) Франклин предпринял попытку теоретически объяснить электрические явления. Именно он первым высказал важнейшее предположение об атомарной, «зернистой» природе электричества: «Электрическая материя состоит из частичек, которые должны быть чрезвычайно мелкими».
Франклин полагал, что тело, которое накапливает электричество, заряжается положительно, а тело, теряющее электричество, заряжается отрицательно. При их соединении избыточный положительный заряд перетекает туда, где его недостает, то есть к отрицательно заряженному телу (по аналогии с сообщающими сосудами).
Эти представления о движении положительных зарядов широко распространились в научных кругах и вошли в учебники физики. Так и получилось, что действительное направление движения электронов в проводнике противоположно принятому направлению электрического тока.
После открытия электрона ученые решили оставить все как есть, поскольку пришлось бы очень многое изменять (и не только в учебниках), если указывать истинное направление тока. Также это связано и с тем, что знак заряда практически ни на что не влияет, пока все используют одно и то же соглашение.
Истинное направление движения электронов используется только, когда это необходимо, чтобы объяснить некоторые физические эффекты в полупроводниковых устройствах (диоды, транзисторы, тиристоры и др.).
Статьи по теме: 1. Что такое электрический ток?
2. Взаимодействие электрических зарядов. Закон Кулона
3. Постоянный и переменный ток
4. Проводники и изоляторы. Полупроводники
5. О скорости распространения электрического тока
6. Электрический ток в жидкостях
Электрический ток в жидкостях
7. Проводимость в газах
8. Электрический ток в вакууме
9. О проводимости полупроводников
Внимание! Всех интересующихся практической электротехникой приглашаю на страницы своего нового сайта «Электрика для дома». Он посвящен основам электротехники и электричества с акцентом на домашние электрические установки и происходящие в них процессы.
Некоторые реки текут вспять, они могут вытекать из моря
Вода всегда течет вниз согласно закону всемирного тяготения. Это известно многим. Точно так же происходит и с природными водотоками Земли – реками, ручьями, потоками. Но бывают и исключения. Иногда некоторые реки текут вспять, они могут вытекать из моря или другого крупного водоема. Об этих примерах — в этой статье.
Река и ее русло
У любого водотока имеется исток (точка его начала) и устье (место, где он впадает в водоем или какой-либо другой водоток). Все реки текут по своему руслу – природному углублению в земле, ими же и созданному. При этом они плавно огибают те препятствия, которые встречаются им на пути: скальные выступы, кристаллические массивы, пласты твердых горных пород. Как результат, русло реки почти всегда имеет множество изгибов (по-научному они называются меандрами).
При этом они плавно огибают те препятствия, которые встречаются им на пути: скальные выступы, кристаллические массивы, пласты твердых горных пород. Как результат, русло реки почти всегда имеет множество изгибов (по-научному они называются меандрами).
На своем длинном или коротком пути река принимает в себя ряд других притоков. Они могут быть большими или крошечными, полноводными или пересыхающими. Река со всеми своими притоками образует речную (гидрографическую) систему, а территория, с которой она собирает свои воды, называется речным (водосборным) бассейном.
Как правило, реки текут в пониженных формах рельефа – так называемых долинах. В русле глубоководные участки (плеса) чередуются с мелководными (перекатами). Последние нередко усложнены каскадами и водопадами, особенно в горной местности. Реки могут изменять свои русла вследствие сезонных изменений климата, миграций песчаных массивов, активной человеческой деятельности и прочих факторов.
Но речь пойдет о том, как и в каком направлении текут реки. И о самых любопытных гидрографических объектах, существующих на нашей планете. На много проще понять на конкретном примере, в этой https://gkd.ru/408205a-reka-don-kuda-vpadaet-otkuda-beret-nachalo-istoki-protyajennost-glubina-pritoki-i-sudohodstvo статье хорошо описана река Дон, советуем прочесть.
И о самых любопытных гидрографических объектах, существующих на нашей планете. На много проще понять на конкретном примере, в этой https://gkd.ru/408205a-reka-don-kuda-vpadaet-otkuda-beret-nachalo-istoki-protyajennost-glubina-pritoki-i-sudohodstvo статье хорошо описана река Дон, советуем прочесть.
Какие реки текут вспять?
Есть водотоки, которые, подобно женщинам, отличаются непостоянностью. Сегодня они текут в одну сторону, а завтра – уже в обратную.
Так, однажды жители Новгорода решили выгнать из города своего епископа Иоанна. Они посадили его на деревянный плот и пустили вниз по реке Волхов. Но каким же было их удивление, когда плавсредство с епископом вернулось обратно в город. Новгородцы восприняли это как «божий знак». Но они не знали, что Господь не имел никакого отношения к этому удивительному событию.
Река Волхов вытекает из озера Ильмень и впадает в Ладожское озеро. Земная поверхность по направлению русла наклонена незначительно. И время от времени случается так, что уровень воды в нижнем течении реки становится выше, чем в ее верховьях (например, весной в результате скопления в низовьях обломков льда). В эти периоды Волхов меняет свое направление на противоположное.
В эти периоды Волхов меняет свое направление на противоположное.
Это далеко не единственный пример «непостоянства» у рек. Та же Амазонка иногда течет вспять в своем нижнем течении. Это происходит тогда, когда мощная приливная волна из океана входит в речное русло. И тогда амазонские воды поворачивают назад, затапливая прибрежные участки суши.
3. Положительные направления тока и напряжения.
Электрический ток в общем случае представляет собой движения электрических зарядов отрицательного и положительного знаков в разные стороны.
Численно ток определяется как придел отношения количества электричества, переносимого заряженными частицами сквозь рассматриваемое поперечное сечение проводника за некоторый промежуток времени, к этому времени, при условии, что данный промежуток времени стремится к нулю:
где q — количество электричества, прошедшее через рассматриваемое сечение проводника за время t.
Количество электричества (заряд) измеряется в Кулонах , промежуток времени в секундах , а единицей измерения тока служит Ампер .
Электрическому току приписывают направление.
За положительное направление тока принимают направление перемещения положительных зарядов от точки высшего потенциала к точке меньшего потенциала.
Направление тока характеризуется знаком тока. Понятия положительный или отрицательный ток имеют смысл, если сравнивать направление тока в проводнике с некоторым заранее выбранным направлением – так называемым положительным направлением тока.
Положительное направление тока выбирается произвольно и указывается стрелкой.
Рассмотрим пассивный участок электрической цепи с выбранным положительным направлением тока:
При протекании тока от точки 1 к точке 2 подразумевается, что потенциал точки 1 выше потенциала точки 2.
Под напряжением на данном участке подразумевается разность электрических потенциалов точек 1 и 2.
Единица измерения напряжения Вольт .
При условии, что 1 больше 2 U12 = 1 — 2 будет положительным.
Порядок индексов при напряжении означают его выбранное положительное направление.
Чаще всего положительное направление напряжения выбирают совпадающим с положительным направлением тока и указывают стрелкой.
4. Источник напряжения и источник тока.
В теории электрических цепей используют понятия идеальные источники электрической энергии: источник напряжения и источник тока.
Им приписывают следующие свойства:
Источник напряжения представляет собой активный элемент с двумя зажимами, напряжение на котором не зависит от тока, проходящего через источник
Рис.2. Идеальный источник напряжения и
его вольтамперная характеристика(BAX).
Предполагается, что внутри идеального источника напряжения пассивные сопротивление, индуктивность и емкость отсутствуют и, следовательно, прохождение тока не вызывает падения напряжения.
Упорядоченное перемещение положительных зарядов в источнике напряжения от меньшего потенциала к большему возможно за счет работы сторонних сил, которые присущи источнику.
Величина работы, производимой данными сторонними силами по перемещению единицы положительного заряда от отрицательного полюса источника напряжения к положительному по полюсу, называется электродвижущей силой (э. д.с.) источника и обозначается e(t).
д.с.) источника и обозначается e(t).
На рис.2(а) указано направление напряжения на зажимах идеального источника, которое всегда равно э.д.с. источника по величине и противоположно ей по направлению.
Идеальный источник напряжения называют еще источником бесконечной мощности. Это — теоретическое понятие. Величина тока в пассивной цепи зависит от параметров этой цепи и e(t). Если зажимы идеального источника напряжения замкнуть накоротко, то ток цепи должен быть теоретически равен бесконечности. В действительности при замыкании зажимов источника ток имеет конечное значение, так как реальный источник обладает внутренним сопротивлением.
Обычно внутренние параметры источника конечной мощности незначительны по сравнению с параметрами внешней цепи и в некоторых случаях (по условию задачи) могут вообще не учитываться. Внутреннее сопротивление источника напряжения на схемах замещения изображается последовательно соединенным с самим источником.
Рис.3. Источник напряжения конечной мощности.
Источник тока представляет собой активный элемент, ток которого не зависит от напряжения на его зажимах.
Рис.4. Идеальный источник тока и его вольтамперная характеристика.
Предполагается, что внутренне сопротивление идеального источника тока равно бесконечности, и поэтому параметры внешней цепи, от которых зависит напряжение на зажимах источника тока, не влияют на ток источника.
При увеличении напряжения внешней цепи, присоединенной к источнику тока, напряжение на его зажимах, и следовательно, мощность возрастают. Поэтому идеальный источник тока теоретически так же рассматривается как источник бесконечной мощности.
Источник тока конечной мощности изображен на рис.5. g0 – внутренняя проводимость источника. Она характеризует внутренние параметры источника и ограничивает мощность, отдаваемую в цепь.
Рис.5. Источник тока конечной мощности.
Часто при решении задач методом эквивалентных преобразований возникает необходимость заменить реальный источник напряжения эквивалентным источником тока или наоборот. Преобразование осуществляется по схеме и формулам рис.6.
Преобразование осуществляется по схеме и формулам рис.6.
Расчёт сложной цепи постоянного тока » СтудИзба
Выполнение домашнего задания № 1 (первая часть)
Тема «Расчёт сложной цепи постоянного тока»
Методические указания
Цель работы: освоение методов анализа линейных электрических цепей постоянного тока.
- Задание:
1) Начертить схему согласно варианту.
2) Определить количество ветвей, узлов и контуров.
3) Составить уравнения по первому и второму законам Кирхгофа.
4) Определить токи всех ветвей методом узловых потенциалов и методом контурных токов.
5) Составить и рассчитать баланс мощностей.
6) Определить ток в ветви (номер ветви в таблице соответствует номеру резистора в схеме) методом эквивалентного генератора.
7) Определить показания приборов.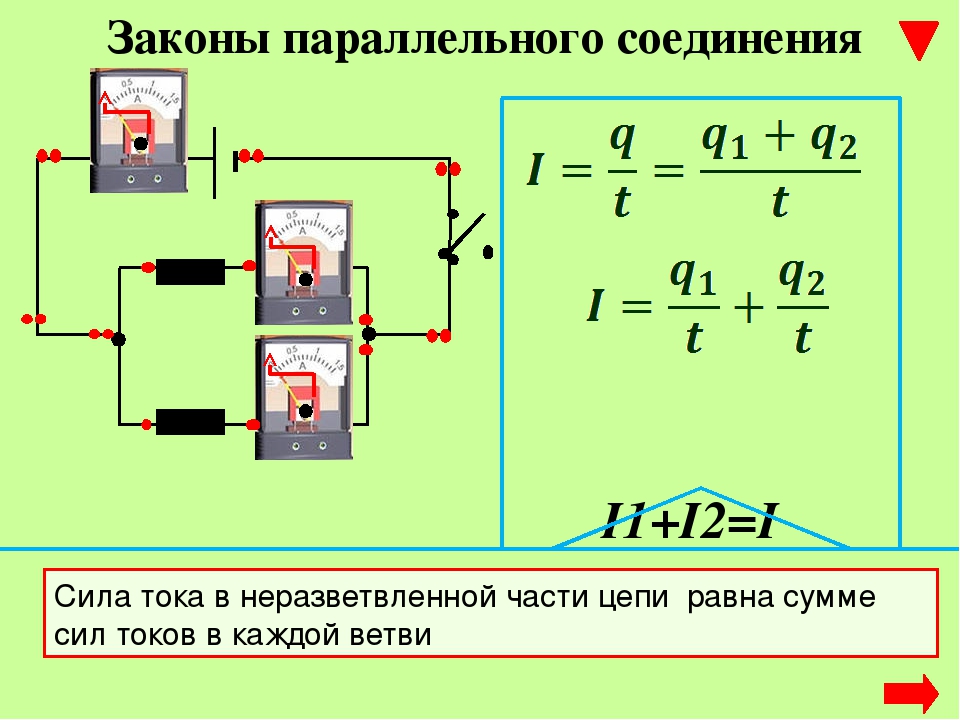
8) Построить потенциальную диаграмму.
9) Сделать выводы.
2. Указания по оформлению расчетно-графической работы
1) Начертить схему в соответствии с номером варианта (схема Приложение 1, таблица Приложение 2). Номер варианта соответствует номеру в учебном журнале.
2) Домашнее задание выполняется на листах формата А4 с одной стороны листа, желательно использовать компьютерные программы.
3) Выполнить чертеж схемы и её элементов в соответствии с ГОСТом.
4) Образец оформления титульного листа представлен в Приложении 3.
5) Каждый пункт задания должен иметь заголовок. Формулы, расчёты, диаграммы должны сопровождаться необходимыми пояснениями и выводами. Полученные значения сопротивлений, токов, напряжений и мощностей должны заканчиваться единицами измерения в соответствии с системой СИ.
6) Графики (диаграммы) должны выполняться на мм бумаге с обязательной градуировкой по осям и указанием масштабов по току и напряжению.
7) Если студент сделал ошибки при выполнении домашнего задания, то исправление проводится на отдельных листах с заголовком «Работа над ошибками».
8) Срок выполнения домашнего задания 5 неделя семестра.
3. Теоретическое введение
3.1 Топологические компоненты электрических схем
а) ветвь — участок электрической цепи с одним и тем же током | ветвь активная | |
ветвь пассивная |
Количество ветвей — р
б) узел – q место соединения трех и более ветвей, узлы бывают потенциальные или геометрические рис. 1
Рис. 1
Четыре узла геометрических (abcd) и три потенциальных (abc) так как потенциалы узлов с и d равны: φс = φd
в) Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвленной электрической цепи – abcd , рис. 1. Независимый контур имеющий хотя бы одну новую ветвь.
1. Независимый контур имеющий хотя бы одну новую ветвь.
3.2. Баланс мощностей
Составляем уравнения для определения мощности приемника:
ΣРпр = Σ I²·R
Составляем уравнения для определения мощности источника:
ΣPист =Σ E·I
Баланс сходится при условии равенства уравнений мощностей источника и приемника, т.е.: ΣРпр = ΣPист
Баланс считается сошедшимся, если погрешность не сходимости составляет не более 2%.
3.3. Эквивалентные преобразования пассивных участков электрической цепи
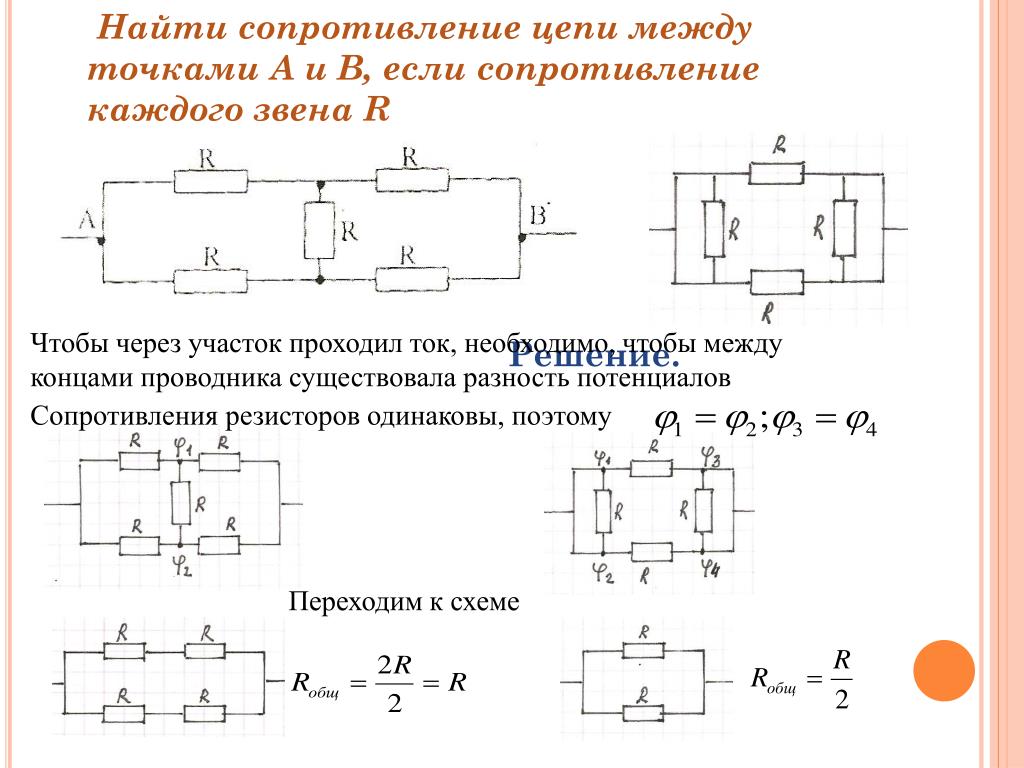
Соединения бывают: последовательное, параллельное и смешанное, звезда, треугольник, мостовое.
1. Последовательное соединение, когда ток в каждом элементе один и тот же.
U1 U2 U3 R1 R2 R3 I U | Rэкв = R1+R2+R3 I = E/Rэкв U = U1+U2+U3 = =R1·I + R2·I + R3·I = Rэкв ·I |
Свойства последовательного соединения:
а) Ток цепи и напряжения зависит от сопротивления любого из элементов;
б) Напряжение на каждом из последовательно соединенных элементов меньше входного;
Ui< U
в) Последовательное соединение является делителем напряжения.
2. Параллельное соединение
Соединение, при котором все участки цепи присоединяются к одной паре узлов, находящихся под воздействием одного и того же напряжения.
Iвх= I1+I2+I3 I1 = U/R1 = UG1 I2 = U/R2 = UG2 I3 =U/R3 = UG3 Iвх = U·ΣGi |
Свойства параллельного соединения:
1) Эквивалентное сопротивление всегда меньше наименьшего из сопротивлений ветвей;
2) Ток в каждой ветви всегда меньше тока источника. Параллельная цепь является делителем тока;
Параллельная цепь является делителем тока;
3) Каждая ветвь находится под одним и тем же напряжением источника.
3. Смешанное соединение
Это сочетание последовательных и параллельных соединений.
Метод эквивалентных преобразований
Решение любой задачи с одним источником питания с помощью законов Ома, Кирхгофа и умением сворачивания схемы.
3.4 Методы расчета электрических цепей с несколькими источниками питания
3.4.1 Метод с помощью законов Кирхгофа.
Самый точный метод, но с его помощью можно определять параметры схемы с небольшим количеством контуров (1-3).
Алгоритм:
1. Определить количество узлов q, ветвей p и независимых контуров;
2. Задаться направлениями токов и обходов контуров произвольно;
3. Установить число независимых уравнений по 1-ому закону Кирхгофа (q — 1) и составить их, где q-количество узлов;
4. Определить число уравнений по 2-ому закону Кирхгофа (p – q + 1) и составить их;
Определить число уравнений по 2-ому закону Кирхгофа (p – q + 1) и составить их;
5. Решая совместно уравнения, определяем недостающие параметры цепи;
6. По полученным данным производится проверка расчетов, подставляя значения в уравнения по 1-ому и 2-ому законам Кирхгофа или составив и рассчитав баланс мощностей.
Пример:
Рис 1. | Согласно предложенному алгоритму, определим количество узлов и ветвей схемы рис. 1 q = 3, p = 5, следовательно, уравнений по 1-ому закону Кирхгофа равно 2, а уравнений по 2-ому закону Кирхгофа равно 3. |
Запишем эти уравнения согласно правилам:
для узла «а» I1 — I2 — I4 = 0
для узла «b» I4 — I5 — I3 = 0
для контура 1 R1·I1+R2·I2 = E1 — E2
для контура 2 R4·I4+R5·I5 — R2·I2 = E2
для контура 3 R3·I3 — R5·I5 =E3
Правило: если ЭДС и ток имеют одинаковое направление с направлением обхода контура, то они берутся с «+», если нет, то с «-».
Составим уравнения баланса мощностей:
Pпр= R1·I1² + R2·I2² + R3·I3² + R4·I4² + R5·I5²
Pист= E1·I1 + E3·I3 — E2·I2
3.4.2 Метод контурных токов
Используя этот метод, сокращается число уравнений, а именно исключаются уравнения по 1-ому закону Кирхгофа. Вводится понятие контурный ток (таких токов в природе не бывает – это виртуальное понятие), составляются уравнения по второму закону Кирхгофа.
Рассмотрим наш пример рис. 2
Рис.2
Контурные токи обозначены Iм, Iн, Iл, заданы их направления, как показано на рис. 2
2
Алгоритм решения:
1. Запишем действительные токи через контурные: по внешним ветвям I1 = Iм,
I3 = Iл, I4 = Iн и по смежным ветвям I2 = Iм — Iн, I5 = Iн — Iл
2. Составим уравнения по второму закону Кирхгофа, так, как контура три, следовательно будет и три уравнения:
для первого контура Iм·(R1 + R2) — Iн·R2 = E1 — E2, знак «–» перед Iн ставится потому, что этот ток направлен против Iм
для второго контура — Iм·R2 + (R2 + R4 + R5) ·Iн — Iл·R5 = E2
для третьего контура — Iн·R5 + (R3 + R5) ·Iл = E3
3. Решая полученную систему уравнений, находим контурные токи
Решая полученную систему уравнений, находим контурные токи
4. Зная контурные токи, определяем действительные токи схемы (см. пункт 1.)
3.4.3 Метод узловых потенциалов
Предлагаемый метод самый эффективный из предложенных методов.
Ток в любой ветви схемы можно найти по обобщённому закону Ома. Для этого необходимо определить потенциалы узлов схемы.
Если схема содержит n-узлов, то уравнений будет (n-1):
- Заземлим любой узел схемы φ = 0;
- Необходимо определить (n-1) потенциалов;
- Составляются уравнения согласно первому закону Кирхгофа по типу:
φ1·G11 + φ2·G12 +…+ φ(n-1)·G1,(n-1) = I11
φ1·G21+ φ2·G22 +…+ φ(n-1)·G2,(n-1) = I22
…………………………………………………
…………………………………………………
φ1·G(n-1),1 + φ2·G(n-1),2 +…+ φ(n-1)·G(n-1),(n-1) = I (n-1), (n-1)
где I11… I (n-1), (n-1) узловые токи в ветвях с ЭДС подключенных к данному узлу, Gkk– собственная проводимость (сумма проводимостей ветвей в узле k), Gkm– взаимная проводимость (сумма проводимостей ветвей соединяющие узлы k и m), взятая со знаком «–».
- Токи в схеме определяются по обобщенному закону Ома.
Пример:
Заземлим узел с, т.е. φс = 0 |
φа ( + + ) — φb = E1 + E2
φb(++) — φa = — E3
определив потенциалы φа и φb, найдем токи схемы. Составление формул для расчета токов осуществляется в соответствии с правилами знаков ЭДС и напряжений, при расчете по обобщенному закону Ома (см. лекция 1).
Правильность расчета токов проверяется с помощью законов Кирхгофа и баланса мощностей.
3.4.4 Метод двух узлов
Метод двух узлов это частный случай метода узловых потенциалов. Применяется в случае, когда схема содержит только два узла (параллельное соединение).
Применяется в случае, когда схема содержит только два узла (параллельное соединение).
Алгоритм:
- Задаются положительные направления токов и напряжение между двумя узлами произвольно;
- Уравнение для определения межузлового напряжения
,
где G – проводимость ветви, J – источники тока;
- Правило: G·E и J берутся со знаком «+», если Е и J направлены к узлу с большим потенциалом;
- Токи схемы определяются по обобщенному закону Ома
Пример:
Составление формул для расчета токов осуществляется в соответствии с правилами знаков ЭДС и напряжений, при расчете по обобщенному закону Ома (см. лекция 1).
3.4.5 Метод активного двухполюсника
Данный метод применяется, когда необходимо рассчитать параметры одной ветви в сложной схеме.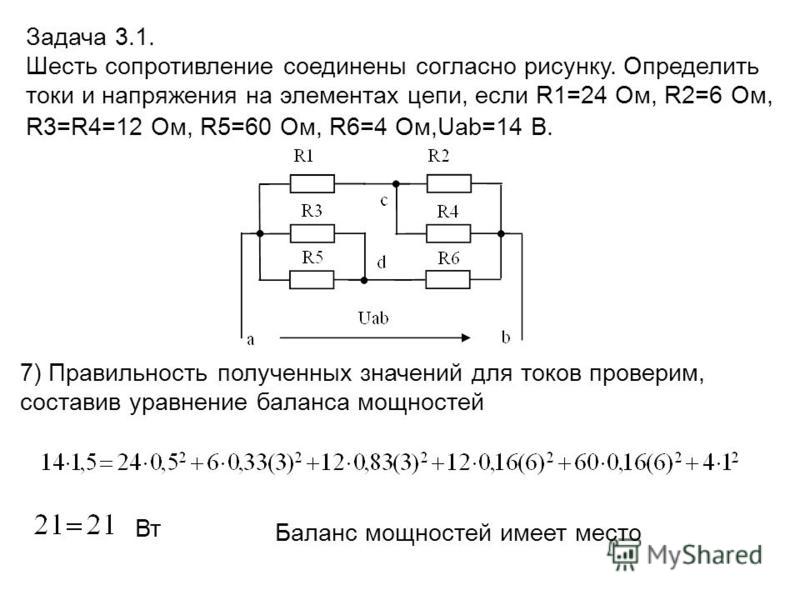 Метод основан на теореме об активном двухполюснике: «Любой активный двухполюсник может быть заменен эквивалентным двухполюсником с параметрами Еэкв и Rэкв или Jэкв и Gэкв , режим работы схемы при этом не изменится».
Метод основан на теореме об активном двухполюснике: «Любой активный двухполюсник может быть заменен эквивалентным двухполюсником с параметрами Еэкв и Rэкв или Jэкв и Gэкв , режим работы схемы при этом не изменится».
Алгоритм:
1. Разомкнуть ветвь, в которой необходимо определить параметры.
2. Определить напряжение на разомкнутых зажимах ветви, т.е. при режиме холостого хода Еэкв = Uхх любимым методом.
3. Заменить активный двухполюсник, т.е. схему без исследуемой ветви, пассивным (исключить все источники питания, оставив их внутренние сопротивления, не забывая, что у идеальной ЭДС Rвн = 0, а у идеального источника тока Rвн = ∞). Определить эквивалентное сопротивление полученной схемы Rэкв.
4. Найти ток в ветви по формуле I = Eэкв/(R+Rэкв) для пассивной ветви и
I = E ± Eэкв/(R+Rэкв) для активной ветви.
3.5 Построение потенциальной диаграммы
Распределение потенциалов в электрической цепи можно представить с помощью потенциальной диаграммы.
Потенциальная диаграмма представляет собой зависимость φ(R) в виде графика, на котором по вертикальной оси отложены значения потенциалов последовательного ряда точек выбранного контура, а по горизонтальной – сумма значений сопротивлений последовательно проходимых участков цепи этого контура. Построение потенциальной диаграммы начинается из произвольно выбранной точки контура, потенциал которой принят за нулевой φ1 = 0. Последовательно обходим выбранный контур. Если построение диаграммы начали в точке 1, то и закончиться она должна в этой же точке 1. Скачки потенциала на графике соответствуют включенным в цепь источникам напряжения.
1.1. Определение показаний приборов
Вольтметр измеряет напряжение (разность потенциалов) между двумя точками в электрической цепи. Для определения показания вольтметра необходимо составить уравнение по второму закону Кирхгофа по контуру, в который входит измеряемое напряжение.
Для определения показания вольтметра необходимо составить уравнение по второму закону Кирхгофа по контуру, в который входит измеряемое напряжение.
Ваттметр показывает мощность участка электрической цепи, которая определяется по закону Джоуля – Ленца.
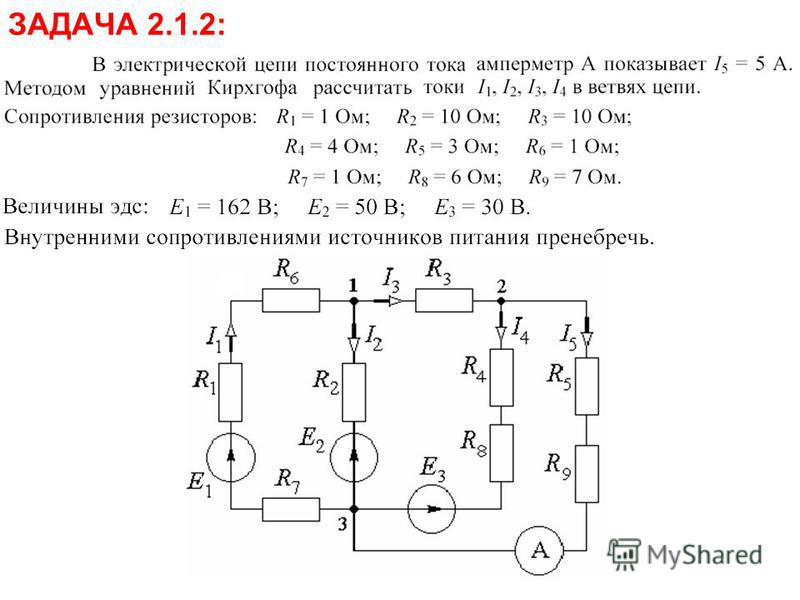
4. Пример:
Дано: R1 = R5 =10 Ом, R4 = R6 = 5 Ом, R3 = 25 Ом, R2 = 20 Ом, Е1 =100 В, Е2 =80 В, Е3 =50 В
Определить токи в ветвях разными методами, составить и рассчитать баланс мощностей.
Решение:
Определяем количество узлов, ветвей и независимых контуров: q = 3, p = 5, контуров 3. Составляем уравнения по законам Кирхгофа: уравнений по 1-ому закону Кирхгофа равно 2, а уравнений по 2-ому закону Кирхгофа равно 3 для узлов а и b. |
1) Метод контурных токов
Так как три контура, то будет три контурных тока I11, I22, I33. Направления этих токов выбираем по часовой стрелке рис 3. Запишем настоящие токи через контурные:
I1 = I11 — I33, I2 = — I22, I3 = — I33, I4 = I11, I5 = I11— I22
Запишем уравнения по второму закону Кирхгофа для контурных уравнений в соответствии с правилами.
Правило: если ЭДС и ток имеют одинаковое направление с направлением обхода контура, то они берутся с «+», если нет, то с «–».
Решим систему уравнений математическим методом Гаусса или Крамера.
Решив систему, получаем значения контурных токов:
I11 = 2,48 А, I22 = — 1,84 А, I33 = — 0,72 А
Определим настоящие токи: I1 = 3,2 А, I2 = 1,84 А, I3 = 0,72 А, I4 = 2,48 А, I5 = 4,32 А
Проверим правильность расчёта токов, подставив их в уравнения по законам Кирхгофа.
Составим уравнения для расчёта баланса мощностей:
Из расчёта видно, что баланс мощностей сошёлся. Погрешность меньше 1%.
2) Метод узловых потенциалов
Решаем туже задачу методом узловых потенциалов
Составим уравнения:
Ток в любой ветви схемы можно найти по обобщённому закону Ома. Для этого необходимо определить потенциалы узлов схемы. Заземлим любой узел схемы φс = 0.
Решая систему уравнений, определяем потенциалы узлов φaиφb
φa= 68 B φb= 43,2 B
По обобщенному закону Ома определяем токи в ветвях. Правило: ЭДС и напряжение берутся со знаком «+», если их направления совпадают с направлением тока, и со знаком «–», если нет.
3)Построение потенциальной диаграммы внешнего контура
Определим значение потенциалов узлов и точек схемы.
Правило: обходим контур против часовой стрелки, если ЭДС совпадает с обходом тока, то ЭДС бреется с «+» (φе). Если ток по обходу, то падение напряжения на резисторе, т.е «-» (φb).
Потенциальная диаграмма:
- Список рекомендуемой литературы
- Бессонов Л.А. Теоретические основы электротехники. В 2-х томах. М.: Высшая школа, 1978.
- Электротехника и электроника. Учебник для вузов. / Под редакцией В.Г.Герасимова. — М.: Энергоатомиздат, 1997.
- Сборник задач по электротехнике и основам электроники. / Под редакцией В.Г. Герасимова. Учебное пособие для вузов.- М.: Высшая школа, 1987.
- Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника. Учебник для вузов – М.: Энергоатомиздат, 1985.
- Липатов Д.Н. Вопросы и задачи по электротехнике для программированного обучения. Учебное пособие для студентов вузов.
 – М.: Энергоатомиздат, 1984.
– М.: Энергоатомиздат, 1984. - Волынский Б.А., Зейн Е.Н., Шатерников В.Е. Электротехника, -М.: Энергоатомиздат, 1987.
- Контрольные вопросы
- Свойства последовательной цепи
- Свойства параллельной цепи
- Правила составления баланса мощностей
- Правила составления уравнений по первому закону Кирхгофа
- Как определяется мощность источника питания?
- Независимый контур. Напишите уравнение по 2-ому закону Кирхгофа любого контура Вашей схемы.
- Правила составления уравнений по 2-ому закону Кирхгофа
- Как определяется мощность приемника?
- Как определить количество уравнений по 1-ому закону Кирхгофа?
- Алгоритм метода эквивалентного генератора
- Как включается вольтметр в цепь?
- Как включается амперметр в цепь?
- Как определить количество уравнений по 2-ому закону Кирхгофа?
- С помощью какого закона определяем ток в ветви, в методе эквивалентного генератора?
- В чём смысл метода эквивалентных преобразований?
Приложение 1
Схема 1 и данные для группы СМ3 – 41
E1=50 В, E2 = 100 В, E3 = 80 В, R1= 40 Ом, R2 = 30 Ом, R3 = 20 Ом, R4 = 30 Ом, R5 = 20 Ом, R6 = 30 Ом, Е = 60 В |
Схема 1 и данные для группы СМ3 – 42
E1=100 В, E2 = Е4= 50 В, E3 = 80 В, R1= 80 Ом, R2 = 50 Ом, R3 = 40 Ом, R4 = 30 Ом, R5= R7= 20 Ом, R6 =30 Ом, Е =40 В |
Приложение 2.
Для группы СМ3 – 41
Вариант | ветвь | Заменить |
1 | 1 | R3→E |
2 | 2 | R1→0 |
3 | 4 | R1→E |
4 | 3 | R1→(-E) |
5 | 2 | R2→0 |
6 | 6 | R2→E |
7 | 5 | R2→(-E) |
8 | 1 | R3→0 |
9 | 3 | R4→E |
10 | 2 | R4→(-E) |
11 | 6 | R6→E |
12 | 1 | R5→E |
13 | 5 | R6 и R5→(-E) |
14 | 4 | R6 и R5→0 |
15 | 3 | R5→0 |
16 | 1 | R5→(-E) |
17 | 2 | R6 и R5→(E) |
18 | 3 | R6→0 |
19 | 4 | R1→R2 |
20 | 3 | E2→R4 |
21 | 2 | R2→E |
22 | 1 | R4→E |
23 | 5 | R1→0 |
24 | 1 | E1→R4 |
25 | 3 | E2→R5 |
26 | 2 | E3→R1 |
27 | 5 | E2→R2 |
28 | 4 | R3→E |
29 | 3 | R1→R4 |
30 | 6 | E2→R6 |
Для группы СМ3 – 42
Вариант | ветвь | Заменить |
1 | 1 | R3→E |
2 | 5 | E1→0 |
3 | 4 | R1→E |
4 | 3 | R1→(-E) |
5 | 2 | E2→0 |
6 | 6 | R4→E |
7 | 5 | R2→(-E) |
8 | 4 | E3→0 |
9 | 3 | R4→E |
10 | 2 | R7→(-E) |
11 | 1 | E4→0 |
12 | 3 | R5→E |
13 | 5 | R6 и R5→(-E) |
14 | 4 | R6 и R7→0 |
15 | 6 | R7→0 |
16 | 1 | R3 и E3→0 |
17 | 2 | R6 и R4→0 |
18 | 3 | R6 и R2→0 |
19 | 4 | R3 и R4→0 |
20 | 5 | E2→R4 |
21 | 6 | R2→E |
22 | 1 | R4 и R7→E |
23 | 2 | R1→0 |
24 | 5 | E1→R4 |
25 | 3 | E2→R5 |
26 | 2 | E3→R1 |
27 | 5 | E2→R2 |
28 | 4 | R3→E |
29 | 3 | R1→R4 |
30 | 2 | E2→R6 |
Выполнение домашнего задания № 1 вторая часть
по курсу «Электротехника и электроника»
тема «Расчёт линейных цепей синусоидального тока»
Методические указания
Цель работы: освоение анализа электрических цепей однофазного синусоидального тока с использованием символического метода.
- Задание
1) Изучить теоретическое введение и методические указания по выполнению домашнего задания.
2) Начертить схему с элементами согласно варианту.
3) Определить количество узлов, ветвей и независимых контуров.
4) Определить количество уравнений по первому и второму законов Кирхгофа.
5) Составить уравнения по первому и второму законов Кирхгофа.
6) Рассчитать эквивалентное сопротивление схемы и определить характер цепи.
7) Определить токи в ветвях методом эквивалентных преобразований.
Записать токи в алгебраической, показательной и во временной форме.
8) Составить и рассчитать баланс мощностей. Определить коэффициент мощности цепи.
9) Рассчитать напряжения на элементах и построить векторную диаграмму токов и напряжений всей цепи.
10) Определить показания приборов.
11) Начертить схему замещения исходя из характера цепи. Ввести в схему замещения дополнительный элемент, обеспечивающий в цепи резонанс напряжений. Рассчитать напряжения и ток, построить векторную диаграмму.
Ввести в схему замещения дополнительный элемент, обеспечивающий в цепи резонанс напряжений. Рассчитать напряжения и ток, построить векторную диаграмму.
12) Ввести в схему замещения дополнительный элемент, обеспечивающий в цепи резонанс токов. Рассчитать напряжение и токи, построить векторную диаграмму.
13) Собрать исходную схему в среде MULTISIM. Поставить приборы и измерить токи, напряжение и мощность.
- Указания по оформлению расчетно-графической работы
9) Выписать параметры сопротивлений ветвей схемы в соответствии с номером варианта (таблица приложение1). Номер варианта соответствует номеру в учебном журнале.
10) Домашнее задание выполняется на листах формата А4 с одной стороны листа, желательно использовать компьютерные программы.
11) Выполнить чертеж схемы и её элементов в соответствии с ГОСТом. Схема представлена в приложении 2.
12) Образец оформления титульного листа представлен в приложении 2.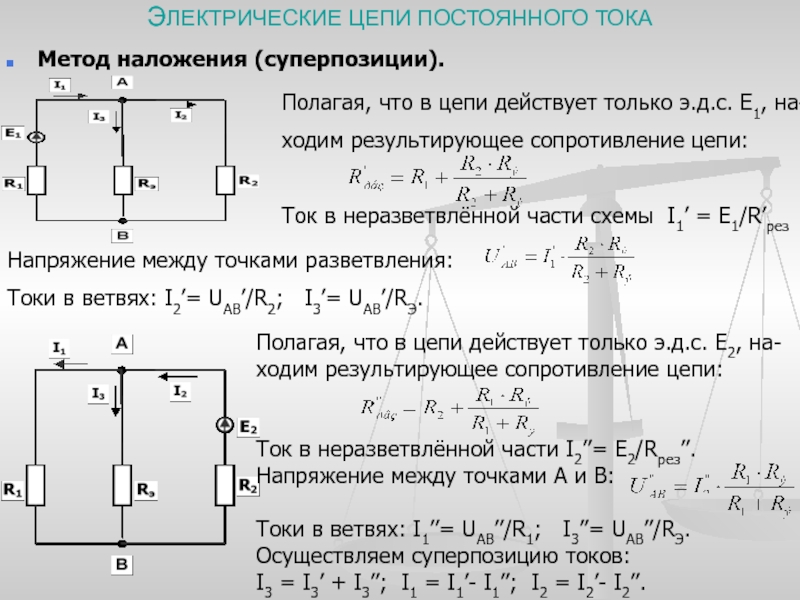
13) Каждый пункт задания должен иметь заголовок. Формулы, расчёты, диаграммы должны сопровождаться необходимыми пояснениями и выводами. Полученные значения сопротивлений, токов, напряжений и мощностей должны заканчиваться единицами измерения в соответствии с системой СИ.
14) Графики (векторные диаграммы) должны выполняться на миллиметровой бумаге с обязательной градуировкой по осям и указанием масштабов по току и напряжению.
15) При работе с программой MULTISIM необходимо в рабочем поле собрать схему, подключить в ветви амперметры. Перевести картинку с результатами в Word. Амперметры убрать из ветвей. Подключить вольтметр и ваттметр и измерить напряжение и мощность. Перевести картинку с результатами в Word. Результаты включить в отчет.
16) Если студент сделал ошибки при выполнении домашнего задания, то исправление проводится на отдельных листах с заголовком «Работа над ошибками».
17) Срок выполнения домашнего задания 10 неделя семестра.
- Теоретическое введение
3.1 Временная форма представления электрических величин, при синусоидальных воздействиях
Аналитическое выражение мгновенных значений тока, ЭДС и напряжения определяется тригонометрической функцией:
i(t) = Im sin(ωt + ψi)
u(t) = Um sin(ωt + ψu)
e(t) = Em sin(ωt + ψe),
где Im, Um, Em— амплитудные значения тока, напряжения и ЭДС.
(ωt + ψ) — аргумент синуса, который определяют фазовый угол синусоидальной функции в данный момент времени t.
ψ — начальная фаза синусоиды, при t = 0.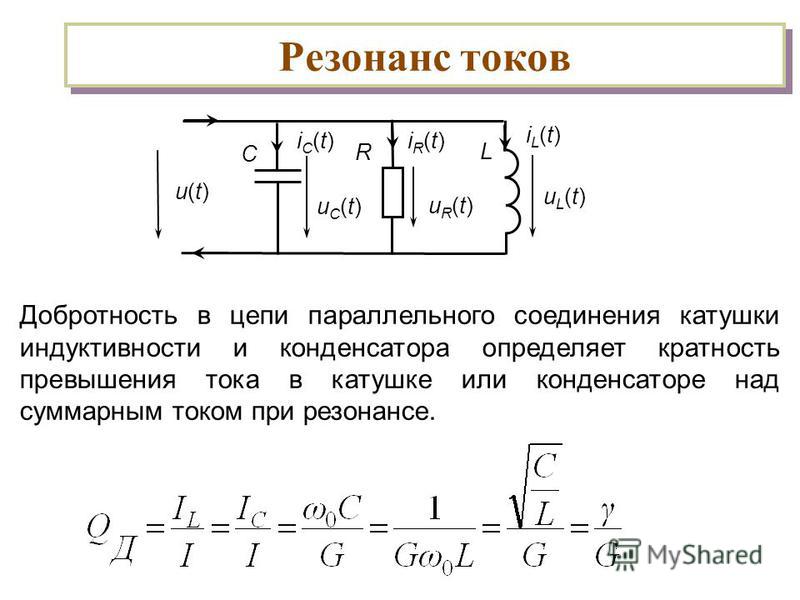
i(t), u(t) временные формы тока и напряжения.
По ГОСТу ƒ = 50 Гц, следовательно, ω = 2πƒ = 314 рад/сек.
Временную функцию можно представить в виде временной диаграммы, которая полностью описывает гармоническую функцию, т.е. дает представление о начальной фазе, амплитуде и периоде (частоте).
3.2 Основные параметры электрических величин
При рассмотрении нескольких функций электрических величин одной частоты интересуются фазовыми соотношениями, называемой углом сдвига фаз.
Угол сдвига фаз φ двух функций определяют как разность их начальных фаз. Если начальные фазы одинаковые, то φ = 0 , тогда функции совпадают по фазе, если φ = ± π, то функции противоположны по фазе.
Особый интерес представляет угол сдвига фаз между напряжением и током: φ = ψu — ψi
На практике используют не мгновенные значения электрических величин, а действующие значения. Действующим значением называют среднеквадратичное значение переменной электрической величины за период.
Действующим значением называют среднеквадратичное значение переменной электрической величины за период.
Для синусоидальных величин действующие значения меньше амплитудных в √2 раз, т.е.
Электроизмерительные приборы градуируются в действующих значениях.
3.3 Применение комплексных чисел
Расчет электрических цепей с использованием тригонометрических функций весьма сложен и громоздок, поэтому при расчете электрических цепей синусоидального тока используют математический аппарат комплексных чисел. Комплексные действующие значения записываются в виде:
Синусоидальные электрические величины, представленные в комплексной форме, можно изображать графически. На комплексной плоскости в системе координат с осями +1 и +j, которыми обозначены положительные действительная и мнимая полуоси, строятся комплексные векторы. Длина каждого вектора пропорциональна модулю действующих значений. Угловое положение вектора определяется аргументом комплексного числа. При этом отсчет положительного угла ведется против часовой стрелки от положительной действительной полуоси.
Угловое положение вектора определяется аргументом комплексного числа. При этом отсчет положительного угла ведется против часовой стрелки от положительной действительной полуоси.
Пример: построение вектора напряжения на комплексной плоскости рисунок 1.
Напряжение в алгебраической форме записывается:
Длина вектора напряжения:
Комплексное сопротивление выражается через комплексные действующие значения напряжения и тока в соответствии с законом Ома:
3.4 Законы Ома и Кирхгофа в комплексной форме
Закон Ома в комплексной форме:
Комплексное сопротивление выражается через комплексные действующие значения напряжения и тока в соответствии с законом Ома:
• Анализ цепей синусоидального тока происходит при условии, что все элементы цепи R, L, C идеальны (таблица 1).
• Электрическое состояние цепей синусоидального тока описывается теми же законами и рассчитываются теми же методами, что и в цепях постоянного тока.
Первый закон Кирхгофа в комплексном виде:
Второй закон Кирхгофа в комплексном виде:
Сводная таблица идеальных элементов и их свойств.
Таблица 1
Элемент | Сопротивление | Угол сдвига фаз | Закон Ома | Мощность | Векторная диаграмма |
R | Z = R | 0 | S = P | ||
C | Z = — jXC | -90o | S = — jQ |
| |
L | Z = jXL | 90o | S = jQ |
3. 5 Баланс мощностей в цепях синусоидального тока
5 Баланс мощностей в цепях синусоидального тока
Для приемников вычисляем раздельно активную мощность
и реактивную мощность
.
При выполнении реальных расчетов мощности источников и приемников могут несколько отличаться. Эти погрешности обусловлены погрешностями метода, округления результатов расчётов.
Точность выполненного расчета схемы оценивают с помощью относительной погрешности при вычислении баланса активных мощностей
δР% =
и реактивных мощностей
δQ% =
При выполнении расчетов погрешности не должны превышать 2%.
3.6 Определение коэффициента мощности
Электрооборудование энергетически выгодно эксплуатировать, если он совершает максимальную работу. Работа в электрической цепи определяется активной мощностью Р.
Коэффициент мощности показывает, насколько эффективно используется генератор или электрооборудование.
λ = P/S = cosφ ≤ 1
Мощность максимальна в случае, когда Р = S, т.е. в случае резистивной цепи.
3.7 Резонансы в цепях синусоидального тока
3.7.1 Резонанс напряжений
Режим работы RLC цепи рисунок 2 или LC—цепи, при условии равенства реактивных сопротивлений XC = XL, когда общее напряжение цепи совпадает по фазе с её током , называется резонансом напряжения.
XC= XL – условие резонанса
Признаки резонанса напряжения:
1. Напряжение на входе совпадает по фазе с током, т.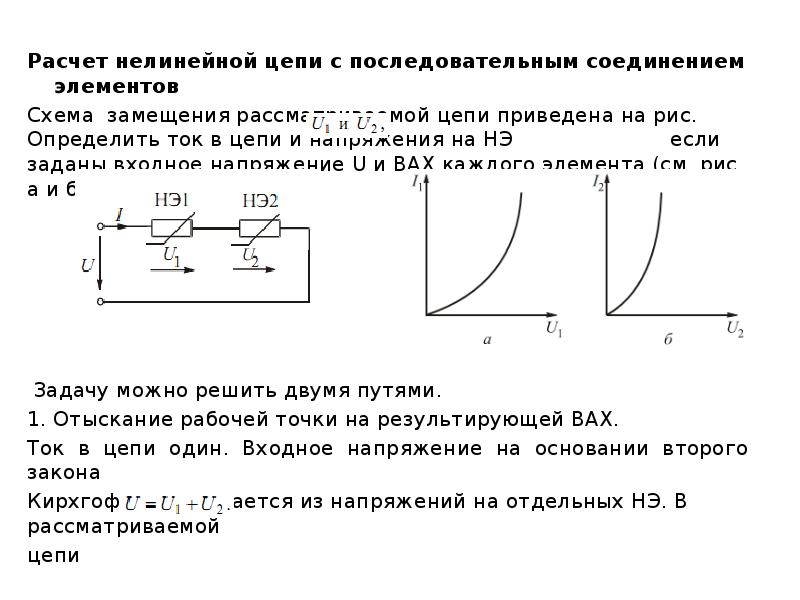 е. сдвиг фаз между I и U φ = 0, cos φ = 1
е. сдвиг фаз между I и U φ = 0, cos φ = 1
2. Ток в цепи будет наибольшим и как следствие Pmax= I2maxR мощность тоже максимальна, а реактивная мощность равна нулю.
3. Резонансная частота
4.
Резонанс можно достигнуть, изменяя L, C или ω.
Векторные диаграммы при резонансе напряжений
LC цепь RLC цепь
3.7.2. Резонанс токов
Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.
Условие резонанса токов: разность реактивных проводимостей параллельных ветвей равна 0
В1 – реактивная проводимость первой ветви,
В2 – реактивная проводимость второй ветви
Признаки резонанса токов:
- Реактивные составляющие токов ветвей равны IPC = IPL и находятся в противофазе в случае, когда напряжение на входе чисто активное;
- Токи ветвей превышают общий ток цепи, который имеет минимальное значение;
- и совпадают по фазе
RLC – цепь Векторная диаграмма
LC – цепь Векторная диаграмма
- Методические указания
4. 1 Начертить схему с элементами согласно варианту.
1 Начертить схему с элементами согласно варианту.
Схема рисунок 1 преобразуем согласно варианту ( Z1 – RC, Z2 – R, Z3 – RL).
Рисунок 1 Исходная схема
4.2 Рассмотрим схему рисунок 2, и запишем уравнения по законам Кирхгофа.
Схема содержит два узла, два независимых контура и три ветви.
Рисунок 2 Схема с элементами
Запишем первый закон Кирхгофа для узла а:
Запишем второй закон Кирхгофа для первого контура:
Запишем второй закон Кирхгофа для второго контура:
4.3 Определим эквивалентное сопротивление цепи.
Свернём схему рис 2.
По эквивалентному сопротивлению определяется характер цепи и чертится схема замещения.
Рисунок 3 свернутая схема
4.4 Определяем токи в ветвях схемы рисунок 2, методом эквивалентных преобразований: зная эквивалентное сопротивление, определяем ток первой ветви .
Рассчитываем ток в комплексной форме по закону Ома в соответствии со схемой рисунок 3:
Чтобы определить токи в остальных ветвях, нужно найти напряжение между узлами «ab» рисунок 2:
Определяем токи:
4.5 Запишем уравнения баланса мощностей:
где I1, I2, I3 – действующие значения токов.
Определение коэффициента мощности
Расчёт коэффициента мощности проводят, определив активную и полную мощности: P/S = cosφ . Используем рассчитанные мощности, которые найдены при расчёте баланса.
модуль полной мощности .
4.6 Рассчитаем напряжения на элементах, используя схему рисунок 2:
4.7 Построение векторной диаграммы
Построение векторной диаграммы ведется после полного расчета всей цепи, определения всех токов и напряжений. Построение начинаем с задания осей комплексной плоскости [+1; +j]. Выбираются удобные для построения масштабы для токов и напряжений. Сначала строим на комплексной плоскости вектора токов (рисунок 4), в соответствии с первым законом Кирхгофа для схемы 2. Сложения векторов осуществляется по правилу параллелограмма.
Выбираются удобные для построения масштабы для токов и напряжений. Сначала строим на комплексной плоскости вектора токов (рисунок 4), в соответствии с первым законом Кирхгофа для схемы 2. Сложения векторов осуществляется по правилу параллелограмма.
Рисунок 4 векторная диаграмма токов
Затем строим на комплексной плоскости вектора рассчитанных напряжений проверка по таблице 1 рисунок 5.
Рисунок 5 Векторная диаграмма напряжений и токов
4.8 Определение показаний приборов
Амперметр измеряет ток, проходящий через его обмотку. Он показывает действующее значение тока в ветви, в которую он включен. В схеме (рис.1) амперметр показывает действующее значение (модуль) тока . Вольтметр показывает действующее значение напряжения между двумя точками электрической цепи, к которым он подключен. В рассматриваемом примере (рис.1) вольтметр подключен к точкам а и b.
Вычисляем напряжение в комплексной форме:
Ваттметр измеряет активную мощность, которая расходуется на участке цепи, заключенном между точками, к которым подключена обмотка напряжения ваттметра, в нашем примере (рис. 1) между точками а и b.
1) между точками а и b.
Активную мощность, измеряемую ваттметром, можно вычислить по формуле
,
где — угол между векторами и .
В этом выражении действующее значение напряжения, на которое подключена обмотка напряжения ваттметра, и действующее значение тока, проходящего через токовую обмотку ваттметра.
Или рассчитываем полную комплексную мощность
ваттметр покажет активную мощность Р.
4.9 Расчёт резонансных цепей
4.9.1 Добавить в схему замещения элемент для получения резонанса напряжений. Например, схема замещения представляет RL цепь. Тогда необходимо добавить последовательно включённый конденсатор С – элемент. Получается последовательная RLC цепь.
Рассчитать ток и все напряжения цепи в комплексной форме, при выполнении условия резонанса, построить векторную диаграмму, см.теоретическое введение пункт 3.7.1
4. 9.2 Добавить в схему замещения элемент для получения резонанса токов. Например, схема замещения представляет RL цепь. Тогда необходимо добавить параллельно включённый конденсатор С – элемент.
9.2 Добавить в схему замещения элемент для получения резонанса токов. Например, схема замещения представляет RL цепь. Тогда необходимо добавить параллельно включённый конденсатор С – элемент.
Рассчитать проводимости ветвей, токи и напряжения, при выполнении условия резонанса. Построить векторную диаграмму, см.теоретическое введение пункт 3.7.2
5. Собрать схему в среде MULTISIM. Поставить приборы и измерить токи, напряжение и мощность.
Сборка схемы в среде Multisim 10.1. На рисунке 6 рабочее окно в среде Multisim. Панель приборов располагается справа.
Рисунок 6 рабочее окно в среде Multisim
Разместить на рабочем поле необходимые для схемы элементы. Для этого на верхней панели инструментов слева нажмём кнопку «Place Basic» (см. Рисунок 7 ). Выбор резистор: появится окно «Select a Component», где из списка «Family» выбрать «Resistor». Под строкой «Component» появятся номинальные значения сопротивлений, выбираем нужное нажатием левой кнопки мыши или же непосредственным введением в графу «Component» необходимого значения. В Multisim используются стандартные приставки системы СИ (см. Таблицу 1)
Под строкой «Component» появятся номинальные значения сопротивлений, выбираем нужное нажатием левой кнопки мыши или же непосредственным введением в графу «Component» необходимого значения. В Multisim используются стандартные приставки системы СИ (см. Таблицу 1)
Таблица 1
Обозначение Multisim (международное) | Русское обозначение | Русская приставка | Порядок |
m | м | мили | 10−3 |
µ (u) | мк | микро | 10−6 |
n | н | нано | 10−9 |
p | п | пико | 10−12 |
f | ф | фемто | 10−15 |
Рисунок 7
В поле «Symbol» выбираем элемент. После выбора, нажимаем кнопку «OK» и размещаем элемент на поле схемы нажатием левой кнопки мыши. Далее можно продолжать размещение необходимых элементов или нажать кнопку «Close», чтобы закрыть окно «Select a Component». Все элементы можно поворачивать для более удобного и наглядного расположения на рабочем поле. Для этого необходимо навести курсор на элемент и нажать левую кнопку мыши. Появится меню, в котором надо выбрать опцию «90 Clockwise» для поворота на 90° по часовой стрелке или «90 CounterCW» для поворота на 90° против часовой стрелки. Размещённые на поле элементы необходимо соединить проводами. Для этого наводим курсор на клемму одного из элементов, нажимаем левую кнопку мыши. Появляется провод, обозначенный пунктиром, подводим его к клемме второго элемента и снова нажимаем левую кнопку мыши. Проводу так же можно придавать промежуточные изгибы, обозначая их кликом мыши (см. Рисунок 8). Схему необходимо заземлить.
После выбора, нажимаем кнопку «OK» и размещаем элемент на поле схемы нажатием левой кнопки мыши. Далее можно продолжать размещение необходимых элементов или нажать кнопку «Close», чтобы закрыть окно «Select a Component». Все элементы можно поворачивать для более удобного и наглядного расположения на рабочем поле. Для этого необходимо навести курсор на элемент и нажать левую кнопку мыши. Появится меню, в котором надо выбрать опцию «90 Clockwise» для поворота на 90° по часовой стрелке или «90 CounterCW» для поворота на 90° против часовой стрелки. Размещённые на поле элементы необходимо соединить проводами. Для этого наводим курсор на клемму одного из элементов, нажимаем левую кнопку мыши. Появляется провод, обозначенный пунктиром, подводим его к клемме второго элемента и снова нажимаем левую кнопку мыши. Проводу так же можно придавать промежуточные изгибы, обозначая их кликом мыши (см. Рисунок 8). Схему необходимо заземлить.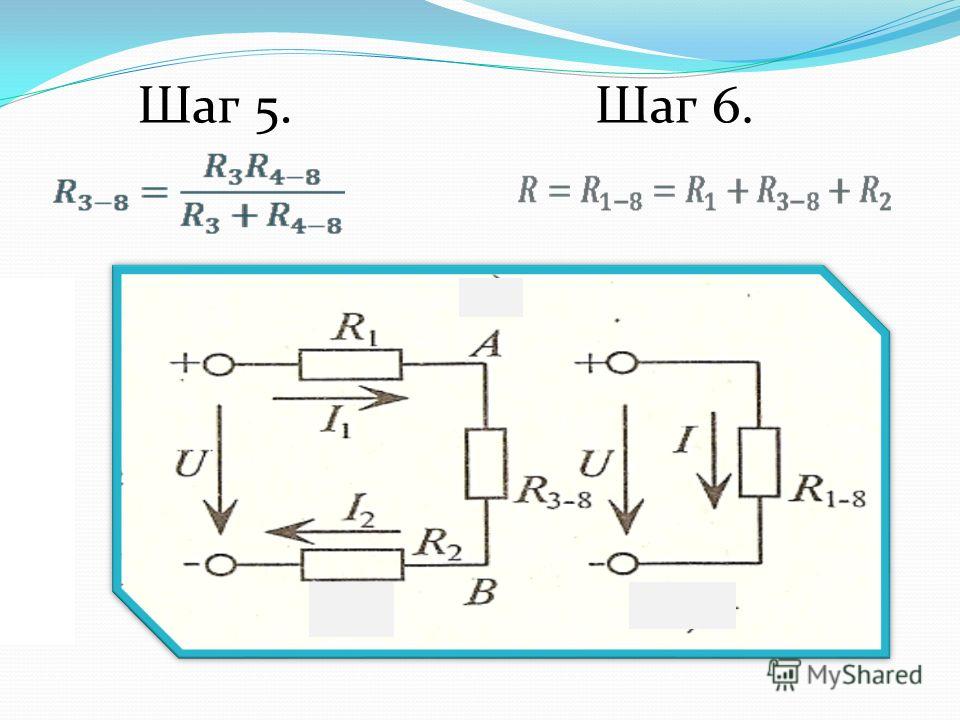
Подключаем к цепи приборы. Для того, чтобы подсоединить вольтметр, на панели инструментов выбираем «Place Indicator», в списке Family» открывшегося окна выбираем тип элемента «Voltmetr_V», приборы перевести в режим измерения переменного тока (АС).
Измерение токов
Соединив все размещённые элементы, получаем разработанную схему рисунок .
На панели инструментов выбираем «Place Source». В списке «Family» открывшегося окна выбираем тип элемента «Power Souces», в списке «Component» — элемент «DGND».
Измерение напряжения
Измерение мощности
6. Контрольные вопросы
1. Сформулируйте законы Кирхгофа и объясните правила составления системы уравнений по законам Кирхгофа.
2. Метод эквивалентных преобразований. Объясните последовательность расчета.
3. Уравнение баланса мощностей для цепи синусоидального тока. Объясните правила составления уравнения баланса мощностей.
Объясните правила составления уравнения баланса мощностей.
4. Объясните порядок расчета и построения векторной диаграммы для Вашей схемы.
5. Резонанс напряжений: определение, условие, признаки, векторная диаграмма.
6. Резонанс токов: определение, условие, признаки, векторная диаграмма.
7. Объясните, как рассчитать показания приборов (амперметра, вольтметра, ваттметра).
8. Сформулируйте понятия мгновенного, амплитудного, среднего и действующего значений синусоидального тока.
9. Напишите выражение для мгновенного значения тока в цепи, состоящей из соединенных последовательно элементов R и L, если к зажимам цепи приложено напряжение .
10. От каких величин зависит значение угла сдвига фаз между напряжением и током на входе цепи с последовательным соединением R , L , C ?
11. Как определить по экспериментальным данным при последовательном соединении сопротивлений R , XL и XC значения величин Z , R , X , ZК , RК , L , XC , C ,cosφ , cosφК?
12. В последовательной RLC цепи установлен режим резонанса напряжений. Сохранится ли резонанс, если:
В последовательной RLC цепи установлен режим резонанса напряжений. Сохранится ли резонанс, если:
а) параллельно конденсатору подключить активное сопротивление;
б) параллельно катушке индуктивности подключить активное сопротивление;
в) последовательно включить активное сопротивление?
13. Как должен изменяться ток I в неразветвленной части цепи при параллельном соединении потребителя и батареи конденсаторов в случае увеличения емкости от С = 0 до С = ∞ , если потребитель представляет собой:
а) активную,
б) емкостную,
в) активно-индуктивную,
г) активно-емкостную нагрузку?
6. Литература
1. Бессонов Л.А. Теоретические основы электротехники- М.: Высшая школа, 2012г.
2. Беневоленский С.Б., Марченко А.Л. Основы электротехники. Учебник для ВУЗов – М.,Физматлит, 2007г.
3. Касаткин А.С., Немцов М.В. Электротехника. Учебник для вузов- М.: В. ш, 2000г.
4. Электротехника и электроника. Учебник для вузов, книга 1. / Под редакцией
В.Г.Герасимова. — М.: Энергоатомиздат, 1996г.
4. Волынский Б.А., Зейн Е.Н., Шатерников В.Е. Электротехника, -М.:
Энергоатомиздат, 1987г.
Приложение 1
Схема группа 1
Схема группа 2
Приложение 2
Вариант | Z1 | Z2 | Z3 | Z4 | U |
1 | 2+j2 | 5 | 5+j3 | 8-j2 | 40 |
2 | 2-j2 | -j5 | 8-j2 | 4-j4 | 50 |
3 | 3 | j5 | 4-j4 | 6+j3 | 80 |
4 | -j5 | 2+j2 | 6+j3 | 2-j5 | 60 |
5 | j4 | 2-j2 | 6 | 3 | 20 |
6 | 5-j2 | 4 | 5+j3 | j4 | 80 |
7 | 2-j5 | -j6 | 8-j2 | 5+j3 | 40 |
8 | 5+j3 | 3-j4 | 4-j4 | 8-j2 | 100 |
9 | 4+j6 | 4-j3 | 3 | 2-j5 | 20 |
10 | 6-j3 | 5+j5 | 7 | j4 | 70 |
11 | 3-j6 | 8-j2 | 2-j5 | -j5 | 50 |
12 | 5 | 2+j4 | 8-j2 | 6+j3 | 90 |
13 | 8+j4 | 5 | 6+j3 | 8 | 40 |
14 | 6 | 5+j3 | j4 | 2 | 60 |
15 | -j3 | j4 | 6 | -j5 | 40 |
16 | j8 | -j5 | 5+j3 | 2-j5 | 20 |
17 | 5 | 5+j3 | -j5 | 4 | 60 |
18 | 6+j3 | 8-j2 | 2-j5 | 5+j3 | 80 |
19 | 4-j4 | j4 | 8 | 8-j2 | 60 |
20 | 4+j4 | 5+j3 | 4-j4 | 6+j3 | 50 |
21 | 2 | j6 | 2 | 5 | 120 |
22 | -j5 | 5 | 5-j5 | 8 | 110 |
23 | 2+j4 | -j4 | 7 | j5 | 70 |
24 | 3-j4 | 3-j4 | 2 | 9 | 150 |
25 | j4 | 2+j6 | 7 | -j2 | 130 |
Электрическая цепь | Физика
Электрическая цепь и выключатели
Электрический ток может возникнуть только в замкнутой электрической цепи.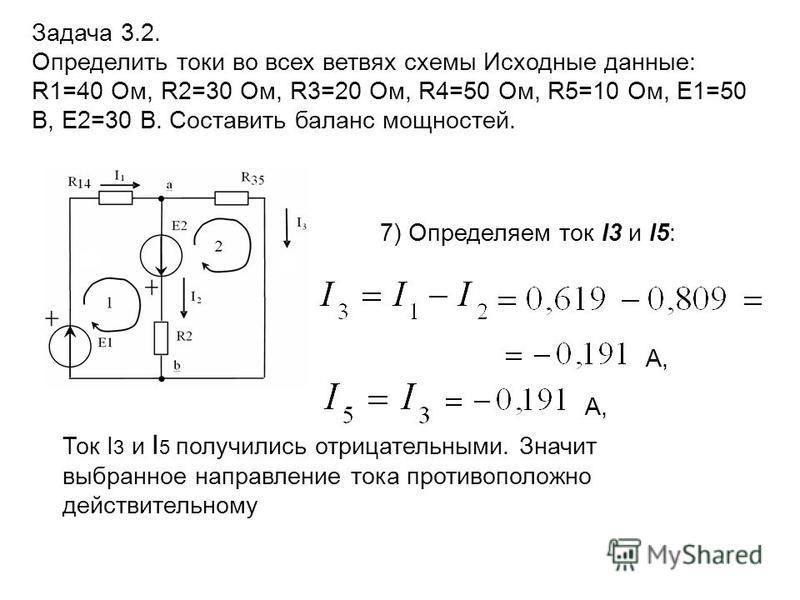 Электрическая цепь состоит как минимум из следующих составляющих: источника электрического тока, проводников и какого-нибудь электрического устройства. Источник тока всегда имеет два полюса — плюс и минус.
Электрическая цепь состоит как минимум из следующих составляющих: источника электрического тока, проводников и какого-нибудь электрического устройства. Источник тока всегда имеет два полюса — плюс и минус.
Одним выключателем мы можем замыкать и размыкать электрическую цепь.
Существуют различные виды механических выключателей. Например, кнопочный, как кнопка дверного звонка или планочный, как выключатель света в комнате.
Переключатель одновременно размыкает одну электрическую цепь и замыкает другую. Кроме механических переключателей существуют электрические, которые называются реле.
Условные обозначения
Для изображения сложных электрических цепей используют условные обозначения тех или иных электрических устройств и правила их соединения. Проводники электрического тока обозначаются прямыми линиями, которые всегда пересекаются под прямым углом. Если мы хотим показать, что в точке пересечения существует контакт проводников, то это место обозначается жирной точкой.
Проводники и изоляторы
Разные материалы имеют различную электропроводность. Особенно хорошо проводят электрический ток серебро, медь, алюминий и железо. Не так хорошо проводят электрический ток уголь и кислоты. Плохими проводниками являются стекло, фарфор и искусственные материалы. Эти материалы используются при работе с электрическим током в качестве изоляторов.
Атомная структура и заряд
Любое тело состоит из атомов.
Каждый атом имеет ядро из положительно заряженных протонов и нейтрально заряженных нейтронов. Это ядро окружено отрицательно заряженными электронами. В целом атом электрически нейтрален, так как количество положительных и отрицательных частиц одинаково.
Рассмотрим эбонитовую палочку. Если мы потрем палочку о шелковый платок, то с нее часть электронов перейдет на платок. Таким образом, на палочке уменьшается количество отрицательно заряженных частиц. Равновесие нарушится, и палочка приобретет положительный заряд.
Из окружающего пространства положительно заряженная палочка начинает притягивать отрицательно заряженные частички пыли. Когда пылинки касаются палочки, электроны возвращаются на нее, и через некоторое время палочка снова становится электрически нейтральной.
Гроза
Грозовые облака образуются при определенных погодных условиях, когда теплый и влажный воздух быстро поднимается вверх, а холодные слои опускаются вниз.
Потоки теплого воздуха переносят частички воды вверх. При этом происходит разделение зарядов — точно такое же, как при трении эбонитовой палочки о шелковый платок. Воздушные течения поднимают положительно заряженные частички в верхнюю часть облака, в то время как отрицательный заряд концентрируется в его нижней части.
Таким образом, в большом грозовом облаке возникает огромная разница зарядов. Молния возникает в тот момент, когда заряды начинают перемещаться. При этом за очень короткое время протекает мощнейший электрический ток. Под его действием воздух нагревается и начинает интенсивно светиться. Большинство молний находится внутри облака.
Под его действием воздух нагревается и начинает интенсивно светиться. Большинство молний находится внутри облака.
Молния может возникнуть также между грозовым облаком и возвышенностью на поверхности Земли.
Благодаря выделению огромного количества энергии воздух вокруг молнии резко нагревается, расширяется и начинает быстро распространяться в виде волны. Эту ударную волну мы слышим как раскаты грома.
Направление тока
Металлы имеют определенное атомное строение, которое является причиной их хорошей электропроводности. Рассмотрим строение медной проволоки. Атомы меди расположены на одинаковом расстоянии один от другого, образуя атомную решетку. Вокруг каждого атома двигаются отрицательно заряженные свободные электроны, которые играют огромную роль для электропроводности металла.
Возьмем медную проволоку в качестве проводника в замкнутой электрической цепи. Тогда свободные электроны будут притягиваться положительным полюсом источника и одновременно отталкиваться от отрицательного полюса. В результате свободные электроны в медной проволоке движутся от отрицательного полюса источника к его положительному полюсу.
В результате свободные электроны в медной проволоке движутся от отрицательного полюса источника к его положительному полюсу.
В источнике электрического тока электроны перемещаются от плюса к минусу под действием определенной химической реакции.
Когда в 18 веке открыли электрический ток, то об электронах не знали практически ничего. Действие электрического тока наблюдали только по внешним проявлениям, поэтому направление тока определили произвольно, от плюса к минусу. Такое направление тока называется техническим, и оно используется по сей день.
Сила тока, напряжение, сопротивление
Чтобы измерить электрический ток, необходимо узнать количество электронов, проходящих через поперечное сечение проводника за одну секунду. Эта величина называется силой тока и измеряется в амперах (A).
Если мы возьмем более сильный источник тока, то через поперечное сечение проводника пройдет большее количество заряженных частиц за одну секунду. Сила тока увеличилась, так как более мощный источник тока действует на электроны с большей силой притяжения. Эта сила притяжения источника тока называется электрическим напряжением и измеряется в вольтах (В).
Эта сила притяжения источника тока называется электрическим напряжением и измеряется в вольтах (В).
(во втором случае электроны двигаются быстрее)
Если заменить батарею постоянным источником тока, то можно определить воздействие электрического напряжения на силу тока.
Сила тока и напряжение зависят один от другого. Большее напряжение означает также и большую силу тока.
Любой материал обладает электрическим сопротивлением, которое характеризует способность материала препятствовать движению электрического тока. Это означает, что сила тока будет тем больше, чем меньше электрическое сопротивление материала при условии постоянного напряжения.
Это пропорциональное соотношение называется законом Ома: напряжение (U), деленное на силу тока (I), есть величина постоянная (R). Эта величина называется электрическим сопротивлением и измеряется в омах. 1 ом равняется 1 вольту, деленному на 1 ампер.
Последовательное соединение
В гирлянде лампочки располагаются последовательно. Такое соединение называется последовательным соединением проводников.
Такое соединение называется последовательным соединением проводников.
Если замерить силу тока в такой цепи в любом ее месте, то амперметр будет показывать одну и ту же величину. В нашем случае это 0,2 ампера.
Вольтметр, в свою очередь, в разных точках показывает различные значения напряжения. Напряжение на отдельных лампочках суммируются в общее напряжение, равное 14 В. Это означает, что все потребители электрического тока должны делить эти 14 В между собой. Если мы, например, уберем из цепи 2 лампы с сопротивлением 20 Ом, то общее напряжение будет делиться на оставшиеся 3 лампы. Теперь на каждой лампе будет напряжение в 4,6 В.
Uобщ = U1 + U2 + U3 + U4 + U5
Таким образом, общее сопротивление цепи рассчитывается следующим образом:
Параллельное соединение
Большинство домашних электрических приборов функционируют при напряжении 220 В. Они не могут быть подключены в цепь последовательно, так как тогда на каждый прибор будет приходиться напряжение намного меньшее, чем 220 В. Подобным образом можно подключить только один прибор, который будет работать в полную силу.
Подобным образом можно подключить только один прибор, который будет работать в полную силу.
В связи с этим домашние приборы подключаются к источнику тока параллельно, что позволяет каждому прибору получить нужное напряжение — 220 В.
При параллельном подключении приборов на каждом приборе будет одинаковое напряжение в 220 В.
При помощи амперметра измерим силу тока на трех участках электрической цепи. Общая сила тока составляет 12,6 А. Сила тока на измеренных участках: I1 = 3,5 A, I2 = 8,7 A, I3 = 0,4 A, что в сумме дает 12,6 А. Из этого следует, что при параллельном подключении общая сила тока равна сумме всех токов в цепи.
V = V1 = V2 = V3
I = I1 + I2 + I3
При параллельном подключении мы можем высчитать общее сопротивление и сопротивление на каждом отдельном участке цепи: Rобщ = Uобщ / Iобщ и в нашем случае: Rобщ = 220 / 12. 6 = 17.5 Ом. Это сопротивление меньше, чем наименьшее отдельное сопротивление. Если мы хотим вычислить общее сопротивление цепи, зная сопротивление отдельных частей, то нам необходимо произвести следующее суммирование: 1/Rобщ = 1/R1 + 1/R2 + 1/R3. Так выглядит закон вычисления общего сопротивления для параллельного подключения.
6 = 17.5 Ом. Это сопротивление меньше, чем наименьшее отдельное сопротивление. Если мы хотим вычислить общее сопротивление цепи, зная сопротивление отдельных частей, то нам необходимо произвести следующее суммирование: 1/Rобщ = 1/R1 + 1/R2 + 1/R3. Так выглядит закон вычисления общего сопротивления для параллельного подключения.
Постоянный и переменный ток
Если мы используем батарею или аккумулятор в качестве источника напряжения, то мы получим постоянный ток в электрической цепи. В цепи постоянного тока электроны текут медленно и всегда в одном направлении: вне батареи от минусового полюса к плюсовому полюсу, а внутри батареи наоборот.
Для большинства электрических приборов не имеет значения, используется постоянный или переменный ток. В любом случае, электростанции поставляют переменный ток. При переменном токе источник напряжения регулярно меняет полярность. Напряжение, которое мы можем измерить в розетке, составляет 220 В и имеет частоту 50 Гц. Это значит, что ток меняет направление 100 раз за секунду. Электроны в переменном токе текут, постоянно меняя направление, то в одну, то в другую сторону.
Это значит, что ток меняет направление 100 раз за секунду. Электроны в переменном токе текут, постоянно меняя направление, то в одну, то в другую сторону.
(на первой картинке электроны медленно перемещаются слева направо, на второй — дергаются туда-сюда)
Передавать электрическую энергию можно при помощи как постоянного, так и переменного тока. Использование переменного тока более выгодно, так как в этом случае потери энергии значительно снижаются.
Действие электрического тока
Если в цепь подключить кусок проволоки, то она скоро нагреется. Это нагревание происходит за счет движения электронов, которые, как говорят, «трутся» об атомы. Скорость и величина нагревания зависят от материала, из которого изготовлена проволока. Чем больше сопротивление материала, тем быстрее нагревается проволока.
Если мы хотим с помощью электрического тока нагреть электрическую плиту или утюг, то надо использовать материалы с высоким сопротивлением и хорошей теплопроводностью. Длинная проволока выделит больше тепла, чем короткая, но для удобства использования, ее надо свернуть в спираль.
Длинная проволока выделит больше тепла, чем короткая, но для удобства использования, ее надо свернуть в спираль.
Если на спираль накаливания подать большее напряжение, то вместе с теплом она будет давать и свет. Это явление используется с 1879 года, когда Эдисоном была изобретена лампочка накаливания.
Если напряжение слишком высокое, то проволока может расплавиться. Это связано с тем, что выделяется большое количество энергии, которого достаточно, чтобы расплавить проволоку.
Электрический ток способствует протеканию химических реакций в жидких проводниках. Примером жидких проводников являются кислоты, щелочи, растворы солей. Химическое действие электрического тока можно показать на следующем примере. Возьмем угольную палочку и железный гвоздь и опустим их в раствор хлорида меди. Эти, так называемые электроды, подключим к источнику напряжения. Гвоздь подсоединим к минусу, после чего будем называть его катодом, а угольную палочку — к плюсу, и назовем ее анодом.
Спустя некоторое время на поверхности угольной палочки начнут образовываться пузырьки газа, а поверхность железного гвоздя покроется коричневым налетом. Эту химическую реакцию вызвал электрический ток. Такой процесс называется электролизом.
В растворе хлорида меди перемещаются положительно заряженные ионы меди и отрицательно заряженные хлорид-ионы. Ионами называются заряженные частички, которые притягиваются противоположным электродом. Там они отдают свой заряд и становятся нейтральными. Это означает, что хлорид-ионы перемещаются к угольной палочке, а ионы меди к гвоздю.
Когда ион меди подходит к металлическому гвоздю и получает два электрона, то он превращается в металлическую медь, которая осаждается на поверхности гвоздя. В свою очередь, хлорид-ион отдает электрон положительному угольному электроду и превращается в чистый хлор, который имеет газообразную форму и выделяется из раствора. Такой вид электролиза можно использовать для покрытия металлических изделий тонким слоем различных металлов. Подобный процесс называется гальванизацией.
Подобный процесс называется гальванизацией.
В свободном состоянии стрелка компаса всегда показывает на север. Н если компас поместить под кабель, по которому течет электрический ток, то стрелка обязательно отклониться. Электричество и магнетизм тесно связаны. Это явление в 1820 году впервые открыл Кристиан Эрстед.
Закон
Ома: сопротивление и простые схемы
Цели обучения
К концу этого раздела вы сможете:
- Объясните происхождение закона Ома.
- Рассчитывайте напряжения, токи или сопротивления по закону Ома.
- Объясните, что такое омический материал.
- Опишите простую схему.
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока.Все такие устройства создают разность потенциалов и условно называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов В, , которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В. . Немецкий физик Георг Симон Ом (1787–1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
[латекс] I \ propto {V} \\ [/ латекс].
Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная взаимосвязь возникает не всегда.
Сопротивление и простые схемы
Если напряжение увеличивает ток, что ему мешает? Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением R . Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току, или
Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току, или
[латекс] I \ propto \ frac {1} {R} \\ [/ latex].
Так, например, при удвоении сопротивления ток уменьшается вдвое. Комбинируя отношения тока к напряжению и тока к сопротивлению, получаем
[латекс] I = \ frac {V} {R} \\ [/ латекс].
Это соотношение также называется законом Ома.Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых справедлив закон Ома, называются омическими . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R , которое не зависит от напряжения В и тока I . Объект с простым сопротивлением называется резистором , даже если его сопротивление невелико. Единица измерения сопротивления — Ом, и обозначается символом Ω (заглавная греческая омега). Перестановка I = V / R дает R = V / I , и поэтому единицы сопротивления равны 1 Ом = 1 вольт на ампер:
Единица измерения сопротивления — Ом, и обозначается символом Ω (заглавная греческая омега). Перестановка I = V / R дает R = V / I , и поэтому единицы сопротивления равны 1 Ом = 1 вольт на ампер:
[латекс] 1 \ Omega = 1 \ frac {V} {A} \\ [/ latex].
На рисунке 1 показана схема простой схемы. Простая схема имеет один источник напряжения и один резистор. Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в R .
Рис. 1. Простая электрическая цепь, в которой замкнутый путь для прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленной красными параллельными линиями. Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.
Пример 1. Расчет сопротивления: автомобильная фара
Какое сопротивление проходит у автомобильной фары? 2.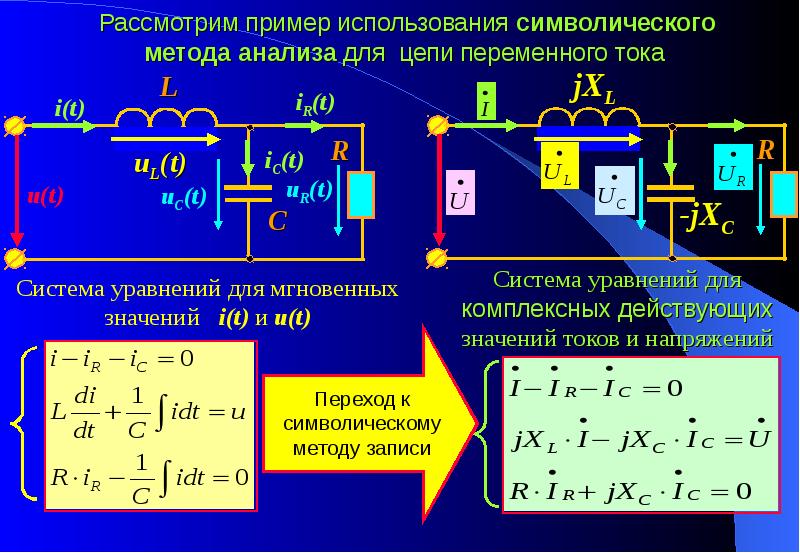 50 А при подаче на него 12,0 В?
50 А при подаче на него 12,0 В?
Стратегия
Мы можем изменить закон Ома в соответствии с I = V / R и использовать его для определения сопротивления.
Решение
Перестановка I = V / R и замена известных значений дает
[латекс] R = \ frac {V} {I} = \ frac {\ text {12} \ text {.} \ Text {0 V}} {2 \ text {.} \ Text {50 A}} = \ text {4} \ text {.} \ text {80 \ Omega} \\ [/ latex].
Обсуждение
Это относительно небольшое сопротивление, но оно больше, чем хладостойкость фары.Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампа имеет меньшее сопротивление при первом включении и потребляет значительно больший ток в течение короткого периода прогрева.
Сопротивления варьируются от многих порядков. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 12 Ом или более. Сопротивление сухого человека может составлять 10 5 Ом, в то время как сопротивление человеческого сердца составляет примерно 10 3 Ом.Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10 −5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделах «Сопротивление и удельное сопротивление». Дополнительную информацию можно получить, решив I = V / R для V , что дает
Сопротивление сухого человека может составлять 10 5 Ом, в то время как сопротивление человеческого сердца составляет примерно 10 3 Ом.Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10 −5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделах «Сопротивление и удельное сопротивление». Дополнительную информацию можно получить, решив I = V / R для V , что дает
В = ИК
Это выражение для В, можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I .Для этого напряжения часто используется фраза IR drop . Например, у фары в Пример 1 выше падение IR составляет 12,0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе.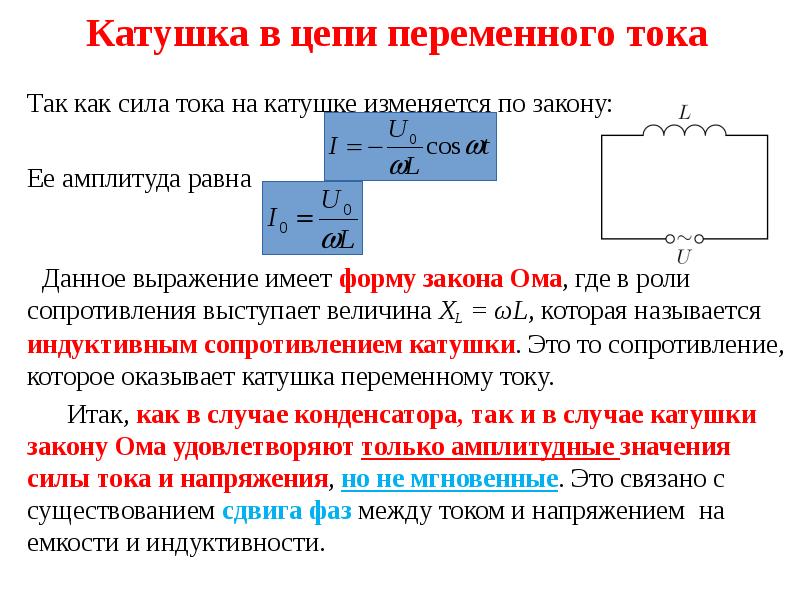 Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывая ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления.Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как PE = q Δ V , и то же самое q протекает через каждую. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.(См. Рисунок 2.)
Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывая ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления.Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как PE = q Δ V , и то же самое q протекает через каждую. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.(См. Рисунок 2.)
Рис. 2. Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Подключение: сохранение энергии
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним резистором. Мы обнаружим, что сохранение энергии имеет и другие важные применения в схемах и является мощным инструментом анализа схем.
Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним резистором. Мы обнаружим, что сохранение энергии имеет и другие важные применения в схемах и является мощным инструментом анализа схем.
Исследования PhET: закон Ома
Посмотрите, как уравнение закона Ома соотносится с простой схемой. Отрегулируйте напряжение и сопротивление и посмотрите, как изменяется ток по закону Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Щелкните, чтобы запустить моделирование.
Сводка раздела
- Простая схема — это схема , в которой есть один источник напряжения и одно сопротивление.
- Одно из утверждений закона Ома дает соотношение между током I , напряжением В и сопротивлением R в простой схеме как [латекс] I = \ frac {V} {R} \\ [/ latex] .
- Сопротивление выражается в единицах Ом (Ом), относящихся к вольтам и амперам на 1 Ом = 1 В / А.

- Существует падение напряжения IR на резисторе, вызванное протекающим через него током, равным В = IR .
Концептуальные вопросы
- Падение напряжения IR на резисторе означает изменение потенциала или напряжения на резисторе.Изменится ли ток при прохождении через резистор? Объяснять.
- Как падение давления IR в резисторе похоже на падение давления в жидкости, протекающей по трубе?
Задачи и упражнения
1. Какой ток протекает через лампочку фонаря на 3,00 В, когда ее горячее сопротивление составляет 3,60 Ом?
2. Рассчитайте эффективное сопротивление карманного калькулятора с батареей на 1,35 В, через которую протекает ток 0,200 мА.
3.Каково эффективное сопротивление стартера автомобиля, когда через него проходит 150 А, когда автомобильный аккумулятор подает на двигатель 11,0 В?
4. Сколько вольт подается для работы светового индикатора DVD-плеера с сопротивлением 140 Ом при прохождении через него 25,0 мА?
5.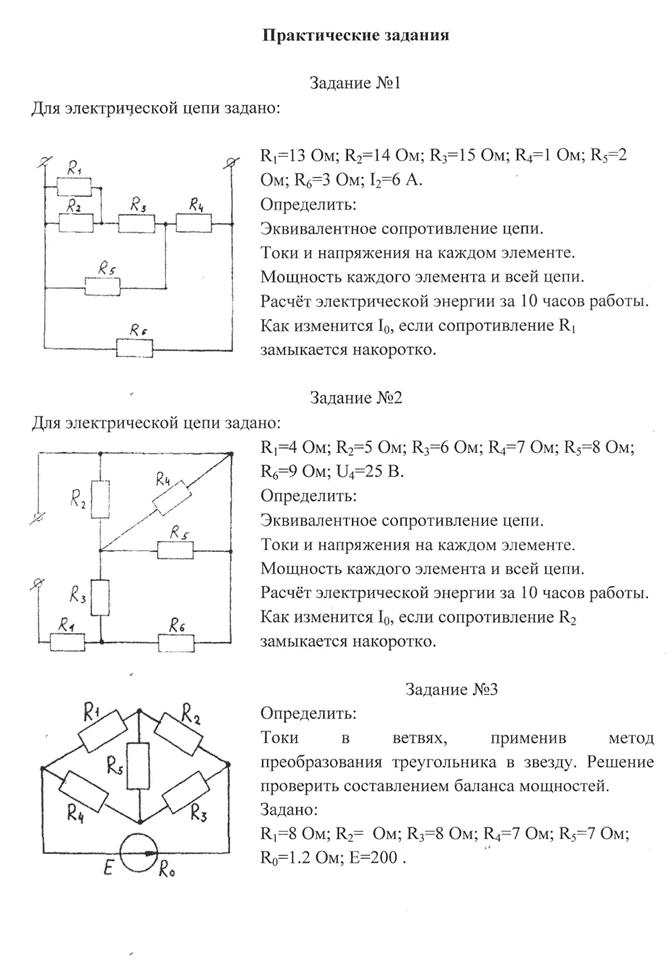 (a) Найдите падение напряжения на удлинителе с сопротивлением 0,0600 Ом, через который проходит ток 5,00 А. (b) Более дешевый шнур использует более тонкую проволоку и имеет сопротивление 0.300 Ом. Какое в нем падение напряжения при протекании 5.00 А? (c) Почему напряжение на любом используемом приборе снижается на эту величину? Как это повлияет на прибор?
(a) Найдите падение напряжения на удлинителе с сопротивлением 0,0600 Ом, через который проходит ток 5,00 А. (b) Более дешевый шнур использует более тонкую проволоку и имеет сопротивление 0.300 Ом. Какое в нем падение напряжения при протекании 5.00 А? (c) Почему напряжение на любом используемом приборе снижается на эту величину? Как это повлияет на прибор?
6. ЛЭП подвешена к металлическим опорам со стеклянными изоляторами, имеющими сопротивление 1,00 × 10 9 Ом. Какой ток протекает через изолятор при напряжении 200 кВ? (Некоторые линии высокого напряжения — постоянного тока.)
Глоссарий
- Закон Ома:
- — эмпирическое соотношение, указывающее, что ток I, пропорционален разности потенциалов В, , ∝ В, ; его часто записывают как I = V / R , где R — сопротивление
- сопротивление:
- электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V / I
- Ом:
- единица сопротивления, равная 1Ω = 1 В / A
- омическое:
- тип материала, для которого действует закон Ома
- простая схема:
- схема с одним источником напряжения и одним резистором
Избранные решения проблем и упражнения
1. 0,833 А
0,833 А
3. 7,33 × 10 −2 Ом
5. (а) 0,300 В
(б) 1,50 В
(c) Напряжение, подаваемое на любой используемый прибор, снижается, поскольку общее падение напряжения от стены до конечного выхода прибора является фиксированным. Таким образом, если падение напряжения на удлинителе велико, падение напряжения на приборе значительно уменьшается, поэтому выходная мощность прибора может быть значительно уменьшена, что снижает способность прибора работать должным образом.
Электрический ток — Веб-формулы
Электрический ток определяется по формуле:
I = В / R
Соответствующие единицы:
ампер (А) = вольт (В) / Ом (Ом)
Эта формула получена из закона Ома . Где у нас:
В: напряжение
I: ток
R: сопротивление
Если электрическая мощность и полное сопротивление известны, то ток можно определить по следующей формуле:
I = √ ( P / R )
Соответствующие единицы:
Ампер (А) = √ (Ватт (Вт) / Ом (Ом))
Где P — электрическая мощность.
Электрический ток
Скорость потока заряда через поперечное сечение некоторой области металлической проволоки (или электролита) называется током, протекающим через эту область.
Если скорость потока заряда непостоянна, то ток в любой момент задается дифференциальным пределом: I = dQ / dt.
Если заряд Q течет по цепи в течение времени t, то
I = Q / t.
Единица измерения тока S.I называется ампер (А) (кулон в секунду).
1 ампер = 6,25 × 10 8 электронов / сек
В металлических проводниках ток возникает из-за движения электронов, тогда как в электролитах и ионизированных газах и электроны, и положительные ионы движутся в противоположном направлении. Направление тока принимается за направление движения положительных зарядов.
В проводимости, хотя ток возникает только за счет электронов, ранее предполагалось, что ток возникает из-за положительных зарядов, протекающих от положительного полюса батареи к отрицательному.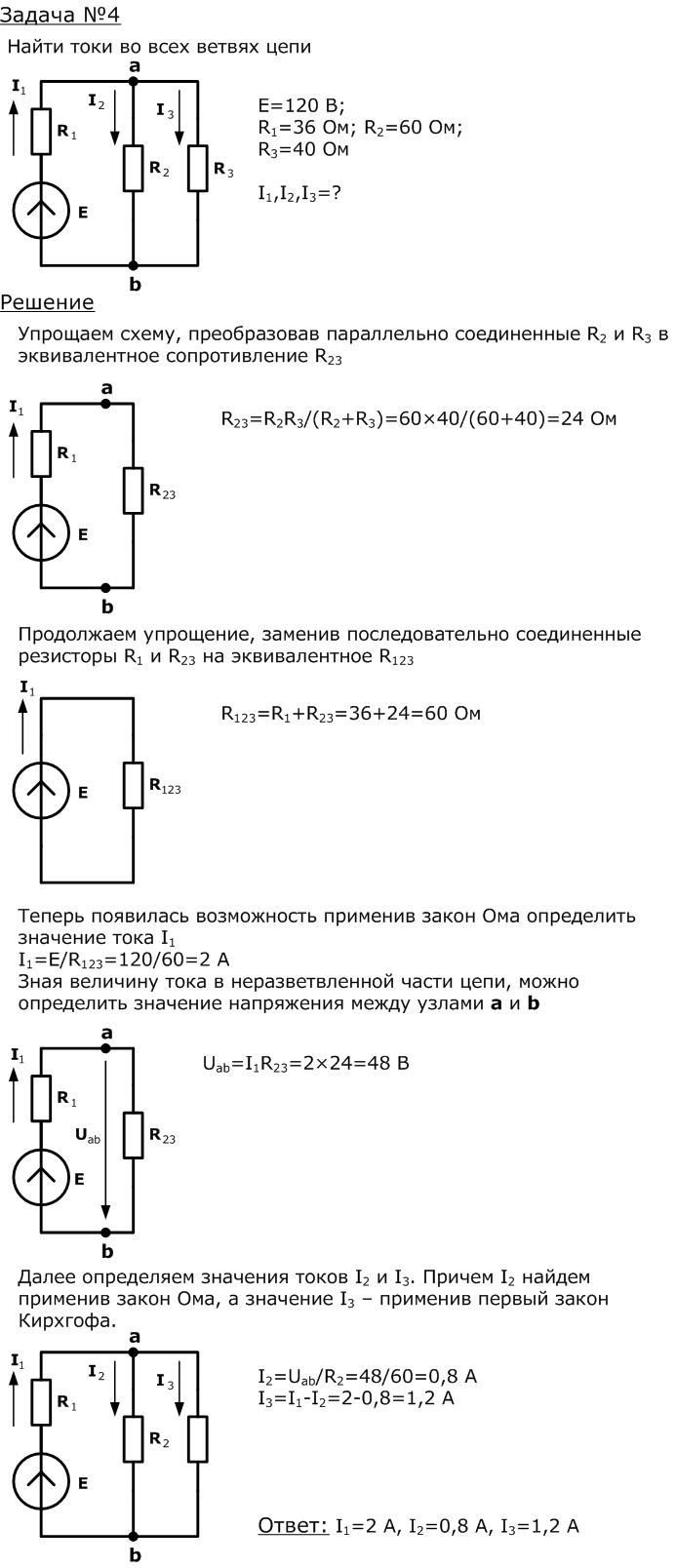 Поэтому направление тока считается противоположным потоку электронов.
Поэтому направление тока считается противоположным потоку электронов.
Если ток постоянный: Δq = I.Δt
функция времени:
Заряд = Площадь под графиком = ½ × t 0 × I 0
To Найти ток в электрической цепи
Для простой цепи или одиночного провода мы имеем:
Для сложной цепи с более чем одним проводом мы можем определить ток с помощью двух законов Кирхгофа
Первый закон: Этот закон основан на на принципе сохранения заряда и утверждает, что в электрической цепи (или сети проводов) алгебраическая сумма токов, встречающихся в точке, равна нулю.
Стрелка, отмеченная на схеме, представляет направление обычного тока, то есть направление потока положительного заряда, тогда как направление потока электронов дает направление электронного тока, которое противоположно направлению обычного тока.
I 1 + I 4 + I 5 = I 3 + I 2 + I 6
Второй закон: Алгебраическая сумма произведения тока и сопротивление в любом замкнутом контуре цепи равно алгебраической сумме электродвижущих сил, действующих в этом контуре.
Математически.
Электродвижущие силы — ЭДС (𝜖) источника определяется как работа, совершаемая на единицу заряда при прохождении положительного заряда через гнездо ЭДС от конца с низким потенциалом к концу с высоким потенциалом. Таким образом,
𝜖 = w / Q
Когда ток не течет, ЭДС источника точно равна разности потенциалов между его концами. Единица ЭДС такая же, как и у потенциала, то есть вольт.
Средний поток электронов в проводнике, не подключенном к батарее, равен нулю, т.е. количество свободных электронов, пересекающих любой участок проводника слева направо, равно количеству электронов, пересекающих участок проводника справа налево. ток по проводнику не течет, пока он не будет подключен к батарее.
Скорость дрейфа свободных электронов в металлическом проводнике
В отсутствие электрического поля свободные электроны в металле беспорядочно вращаются во всех направлениях, поэтому их средняя скорость равна нулю. При приложении электрического поля они ускоряются в направлении, противоположном направлению поля, и поэтому имеют общий дрейф в этом направлении. Однако из-за частых столкновений с атомами их средняя скорость очень мала. Эта средняя скорость, с которой электроны движутся в проводнике под действием разности потенциалов, называется дрейфовой скоростью .
При приложении электрического поля они ускоряются в направлении, противоположном направлению поля, и поэтому имеют общий дрейф в этом направлении. Однако из-за частых столкновений с атомами их средняя скорость очень мала. Эта средняя скорость, с которой электроны движутся в проводнике под действием разности потенциалов, называется дрейфовой скоростью .
Если E — приложенное поле, e — заряд электрона, m — масса электрона и τ — временной интервал между последовательными столкновениями (время релаксации), то ускорение электрона составляет
Так как средняя скорость сразу после столкновения равна нулю, а непосредственно перед следующим столкновением это τ, скорость дрейфа должна быть:
Если I — ток через проводник и n — это количество свободных электронов на единицу объема, тогда можно показать, что:
Подвижность µ носителя заряда определяется как скорость дрейфа на единицу электрического поля:
Плотность тока (J)
(i)
(ii) S.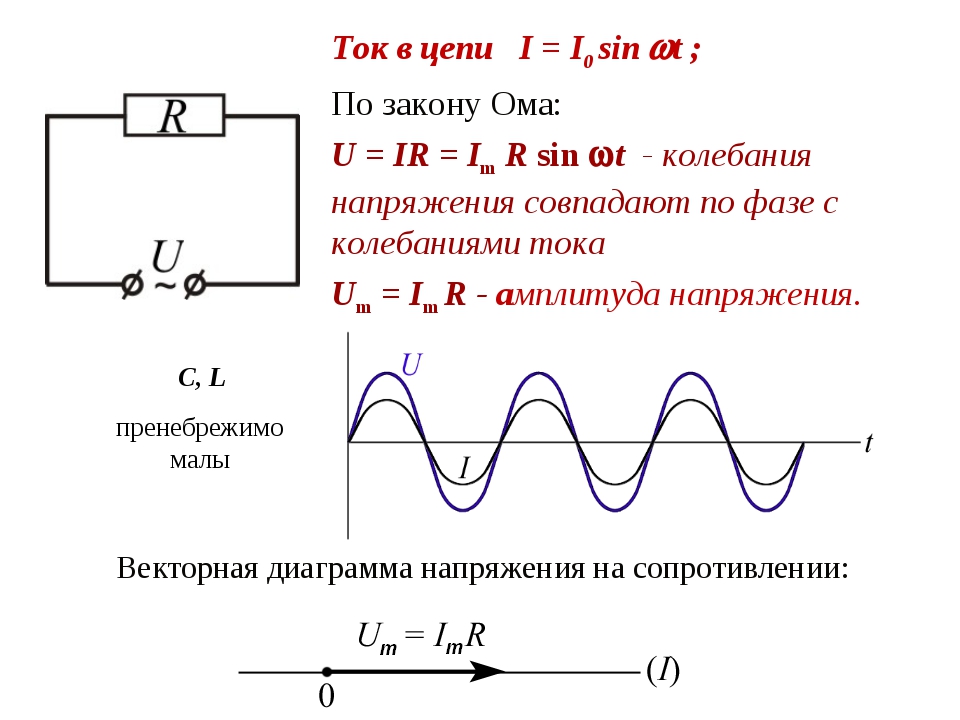 I Единица J = Am -2 .
I Единица J = Am -2 .
(iii) Плотность тока — это векторная величина, ее направление — это направление потока положительного заряда в данной точке внутри проводника.
(iv) Размеры плотности тока = [M 0 L -2 T o A 1 ]
Носители тока: заряженные частицы, поток которых в определенном направлении составляет электрический ток, являются носителями тока. . Носители тока могут иметь положительный или отрицательный заряд.Ток переносится электронами в проводниках, ионами в электролитах, электронами и дырками в полупроводниках.
Пример 1: Частица с зарядом q кулонов описывает круговую орбиту. Если радиус орбиты равен R, а частота орбитального движения частиц равна f, то найти ток на орбите.
Решение: Через любой участок орбиты заряд проходит f раз за одну секунду. Следовательно, через этот участок общий заряд, проходящий за одну секунду, равен fq.По определению i = fq.
Пример 2: Ток в проводе изменяется со временем в соответствии с уравнением I = 4 + 2t, где I — в амперах, а t — в секундах. Вычислите количество заряда, прошедшего через поперечное сечение провода за время от t = 2 с до t = 6 с.
Решение: Пусть dq будет изменением, которое произошло за небольшой интервал времени dt.
Тогда dq = I dt = (4 + 2t) dt
Следовательно, общий заряд, прошедший за интервал t = 2 секунды и t = 6, равен
q = ∫ 6 2 (4 + 2t) dt = 48 кулонов
Пример 3: Дан токоведущий провод неоднородного сечения.Что из следующего является постоянным по всей сети?
(a) Только ток
(b) Ток и скорость дрейфа
(c) Только скорость дрейфа
(d) Ток, скорость дрейфа
Решение : (a)
Пример4 : Когда разность потенциалов на данном медном проводе увеличивается, скорость дрейфа составляет
носители заряда:
(a) Уменьшается
(b) Увеличивается
(c) Остается прежним
(d) Уменьшается до нуля
Решение : (b)
Как использовать теорему Тевенина | EAGLE
Существует множество методов, доступных для анализа сложных электрических цепей, например, анализ сетки, узловой анализ или законы Кирхгофа для цепей.Проблема в том, что при проектировании сети постоянного тока у вас будет нагрузка, значение которой будет меняться по мере развития процесса проектирования. Вместо того, чтобы пересчитывать ток и напряжение всей вашей цепи каждый раз при изменении нагрузки, вы можете упростить этот процесс с помощью теоремы Тевенина. В этом блоге мы рассмотрим, как упростить любую сложную линейную схему до единого источника напряжения и последовательного сопротивления. Оттуда мы можем использовать нашу эквивалентную схему Тевенина, чтобы быстро рассчитать ток и напряжение.Давай начнем.
Что такое теорема Тевенина?
Как и все другие математические и научные теории / законы, теорема Тевенина была изобретена самим человеком, Леоном Шарлем Тевенином, французским телеграфным инженером, родившимся в Мо, Франция.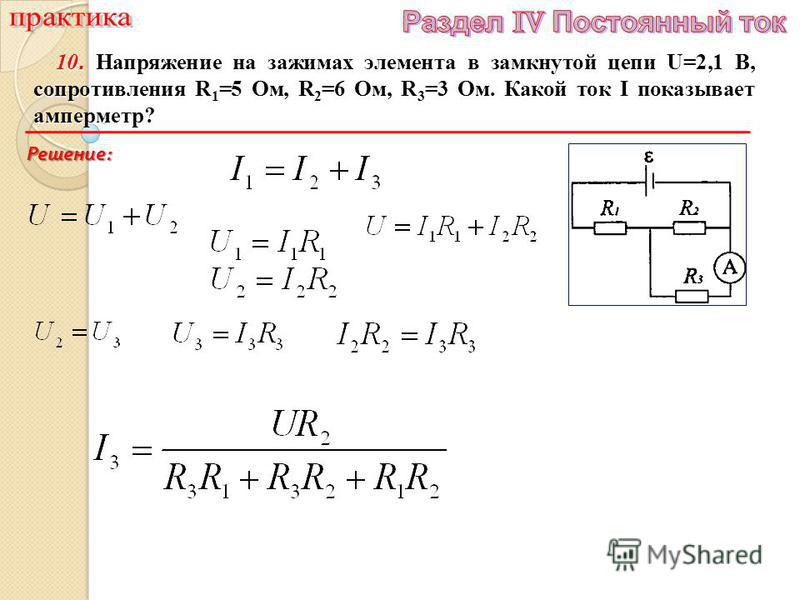 После прохождения службы в корпусе инженеров-телеграфистов, Тевенен был назначен инспектором по обучению в Высшей школе телеграфии в 1882 году. Именно здесь он заинтересовался измерением электрических цепей с использованием двух доступных в то время методов — схемы Кирхгофа. Законы и закон Ома.
После прохождения службы в корпусе инженеров-телеграфистов, Тевенен был назначен инспектором по обучению в Высшей школе телеграфии в 1882 году. Именно здесь он заинтересовался измерением электрических цепей с использованием двух доступных в то время методов — схемы Кирхгофа. Законы и закон Ома.
Леон Шарль Тевенин (Источник изображения)
В попытке упростить анализ сложных схем для каждого инженера, Тевенин разработал свою теперь известную теорему Тевенина, которая сводит сложные схемы к упрощенным эквивалентным схемам Тевенина.
Эта теорема утверждает, что вы можете взять любую линейную цепь, которая может содержать несколько ЭДС и резистивных компонентов, и упростить схему до одного источника напряжения и последовательного сопротивления, подключенного к нагрузке.
Упрощенная эквивалентная схема Тевенина с одним источником напряжения и сопротивлением. (Источник изображения)
В данном случае линейная цепь — это цепь, которая включает в себя пассивные компоненты, такие как резисторы, катушки индуктивности и конденсаторы. Однако, если вы работаете со схемой, которая включает газоразрядные или полупроводниковые компоненты, то у вас нелинейная схема. Теорема Тевенина не для этого годилась. Так зачем использовать эту теорему для анализа линейных цепей?
Однако, если вы работаете со схемой, которая включает газоразрядные или полупроводниковые компоненты, то у вас нелинейная схема. Теорема Тевенина не для этого годилась. Так зачем использовать эту теорему для анализа линейных цепей?
- КПД .Теорема Тевенина обеспечивает простой метод анализа силовых цепей, которые обычно имеют нагрузку, которая меняет значение в процессе анализа. Эта теорема обеспечивает эффективный способ вычисления напряжения и тока, протекающих через нагрузку, без необходимости заново рассчитывать всю схему.
- Фокус . Теорема Тевенина также предоставляет эффективный способ сосредоточить анализ на определенной части схемы. Это позволяет вам рассчитать напряжение и ток на конкретном терминале, упростив остальную часть схемы с помощью эквивалента Тевенина.
Посмотрите на пример схемы ниже. Здесь в качестве нагрузки используется резистор R2. Мы хотим рассчитать напряжение и ток, протекающие через этот резистор, без необходимости использовать трудоемкие методы анализа, такие как Branch Current, Mesh Current и т. Д., Каждый раз, когда значение резистора нагрузки изменяется.
Д., Каждый раз, когда значение резистора нагрузки изменяется.
(Источник изображения)
Чтобы упростить эту задачу, мы можем использовать теорему Тевенина, чтобы удалить сопротивление нагрузки и напряжения. Затем мы упрощаем остальную часть схемы как единый источник напряжения и последовательное сопротивление.В этой упрощенной схеме Тевенина два резистора R1 и R3 вместе с вторичным напряжением B2 упрощены до единого источника напряжения и последовательного сопротивления. Что касается нагрузочного резистора, то упрощенные напряжение и сопротивление будут работать так же, как и наша оригинальная схема. Теперь у нас есть только две простые переменные, с которыми мы будем работать в наших расчетах.
(Источник изображения)
Теорема Тевенина в действии
Давайте посмотрим на пример схемы и вычислим ток, протекающий через нагрузочный резистор между двумя выводами.Процесс анализа цепи постоянного тока с использованием теоремы Тевенина требует следующих шагов:
- Найдите сопротивление Тевенину, удалив все источники напряжения и нагрузочный резистор.

- Найдите напряжение Thevenin, подключив напряжение.
- Используйте сопротивление и напряжение Thevenin, чтобы найти ток, протекающий через нагрузку.
Вот пример схемы, с которой мы будем работать:
(Источник изображения)
Шаг 1 — Thevenin Resistance
Сначала нам нужно снять нагрузочный резистор 40 Ом, соединяющий клеммы A и B, вместе со всеми источниками напряжения.Это даст нам разомкнутую цепь при нулевом напряжении, в результате чего останется только два резистора, подключенных последовательно.
(Источник изображения)
Чтобы рассчитать общее сопротивление тевенину, мы можем использовать следующий процесс:
Шаг 2 — Напряжение Thevenin
Затем мы можем использовать закон Ома для вычисления полного тока, протекающего по цепи, следующим образом:
Поскольку эти резисторы соединены последовательно, они будут иметь одинаковый 0.33 ампера.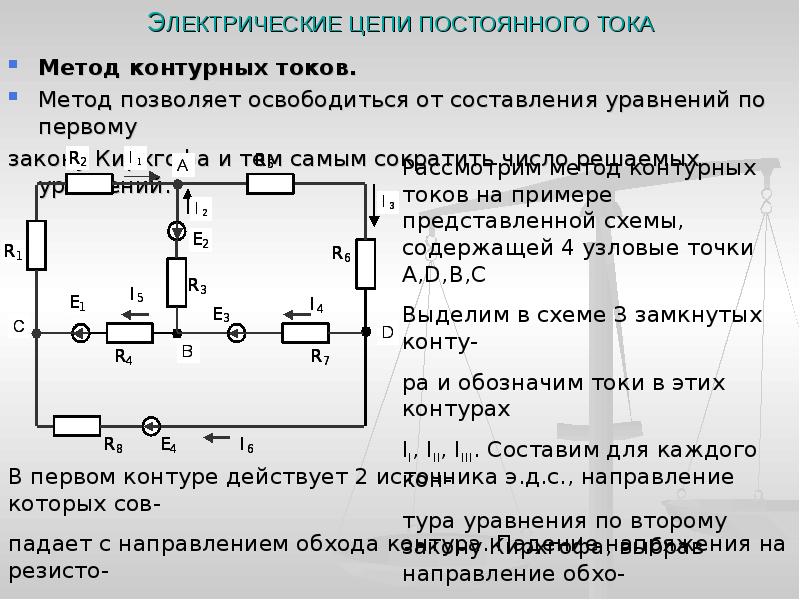 Мы можем использовать эти значения резисторов и наш ток для расчета падения напряжения, которое составляет:
Мы можем использовать эти значения резисторов и наш ток для расчета падения напряжения, которое составляет:
Шаг 3 — Ток нагрузки
Теперь, когда у нас есть сопротивление и напряжение Тевенина, мы можем соединить нашу эквивалентную схему Тевенина с нашим исходным нагрузочным резистором, как показано ниже.
Отсюда мы можем использовать закон Ома для расчета полного тока, протекающего через нагрузочный резистор, следующим образом:
Готовы проверить свои навыки? Используйте теорему Тевенина, чтобы найти iload и vload для схемы ниже!
Запомните трехэтапный процесс:
- Найдите сопротивление Тевенину, отключив все источники напряжения и нагрузку.
- Найдите напряжение Thevenin, повторно подключив источники напряжения.
- Используйте сопротивление и напряжение Тевенина, чтобы найти общий ток, протекающий через нагрузку.
Сохраняйте простоту
Планируете разработать схему питания постоянного тока? Скорее всего, вы включите нагрузку, значение которой изменится во время анализа схемы. Вместо того, чтобы пересчитывать всю схему каждый раз, когда вы меняете значение этой нагрузки, теперь у вас есть теорема Тевенина, которая упрощает вашу работу.
Вместо того, чтобы пересчитывать всю схему каждый раз, когда вы меняете значение этой нагрузки, теперь у вас есть теорема Тевенина, которая упрощает вашу работу.
Эта теорема позволяет вам взять любую сложную линейную схему с множеством резистивных компонентов и ЭДС и упростить ее до эквивалентной схемы Тевенина. С помощью этой упрощенной схемы вы можете легко рассчитать полный ток и напряжение, протекающие через нагрузку. Это огромная экономия времени для любого инженера, которому необходимо эффективно анализировать схемы для силовых конструкций и других сложных приложений.
Тем из вас, кто изучает визуальное / кинестетическое мышление, обязательно посмотрите видео ниже, в котором показано, как использовать теорему Тевенина шаг за шагом.
Готовы спроектировать свою первую силовую цепь? Попробуйте Autodesk EAGLE бесплатно сегодня!
Что такое закон Ома? | Fluke
Закон Ома — это формула, используемая для расчета взаимосвязи между напряжением, током и сопротивлением в электрической цепи.
Для изучающих электронику закон Ома (E = IR) столь же фундаментально важен, как уравнение относительности Эйнштейна (E = mc²) для физиков.
E = I x R
Если прописано, это означает напряжение = ток x сопротивление , или вольт = ампер x ом , или В = A x Ω .
Названный в честь немецкого физика Георга Ома (1789-1854), закон Ома определяет ключевые величины, действующие в цепях:
| Количество | Закон Ома символ | Единица измерения (аббревиатура) | Роль в схемы | Если вам интересно: |
|---|---|---|---|---|
| Напряжение | E | Вольт (В) | Давление, которое запускает поток электронов | E = электродвижущая сила (старая школа) |
| Ток | I | Ампер, ампер (A) | Скорость потока электронов | I = интенсивность |
| Сопротивление | R | Ом (Ом) | Буква ингибитора потока | Ом = omega |
Если известны два из этих значений, технические специалисты могут перенастроить закон Ома для вычисления третьего.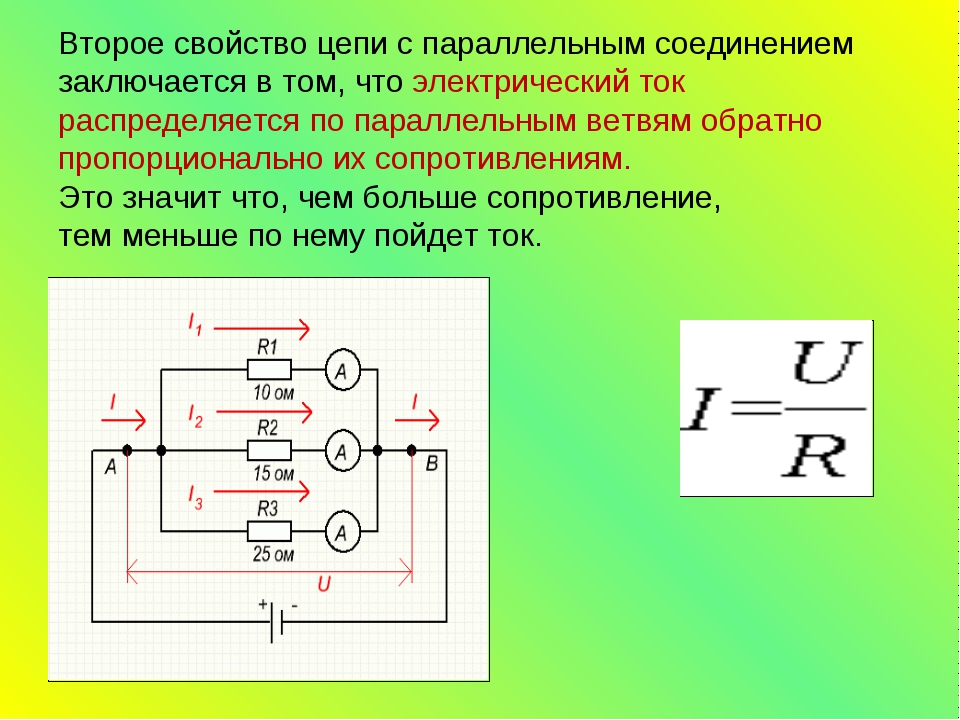 Просто измените пирамиду следующим образом:
Просто измените пирамиду следующим образом:
Если вы знаете напряжение (E) и ток (I) и хотите узнать сопротивление (R), вытяните X-образную букву R в пирамиде и вычислите оставшееся уравнение (см. Первое или дальнее слева, пирамида вверху).
Примечание: Сопротивление нельзя измерить в рабочей цепи, поэтому закон Ома особенно полезен, когда его нужно вычислить. Вместо того, чтобы отключать цепь для измерения сопротивления, техник может определить R, используя вышеуказанный вариант закона Ома.
Теперь, если вы знаете напряжение (E) и сопротивление (R) и хотите узнать ток (I), вытяните X-I и вычислите оставшиеся два символа (см. Среднюю пирамиду выше).
И если вы знаете ток (I) и сопротивление (R) и хотите знать напряжение (E), умножьте нижние половины пирамиды (см. Третью или крайнюю правую пирамиду выше).
Попробуйте несколько примеров расчетов на основе простой последовательной схемы, которая включает только один источник напряжения (аккумулятор) и сопротивление (свет). В каждом примере известны два значения. Используйте закон Ома для вычисления третьего.
В каждом примере известны два значения. Используйте закон Ома для вычисления третьего.
Пример 1: Напряжение (E) и сопротивление (R) известны.
Какой ток в цепи?
I = E / R = 12 В / 6 Ом = 2 А
Пример 2: Напряжение (E) и ток (I) известны.
Какое сопротивление создает лампа?
R = E / I = 24 В / 6 A = 4 Ом
Пример 3: Ток (I) и сопротивление (R) известны. Какое напряжение?
Какое напряжение в цепи?
E = I x R = (5A) (8 Ом) = 40 В
Когда Ом опубликовал свою формулу в 1827 году, его ключевым выводом было то, что величина электрического тока, протекающего через проводник, прямо пропорциональна приложенному напряжению. в теме.Другими словами, требуется один вольт давления, чтобы протолкнуть один ампер тока через один ом сопротивления.
Что проверять с помощью закона Ома
Закон Ома можно использовать для проверки статических значений компонентов схемы, уровней тока, источников напряжения и падений напряжения.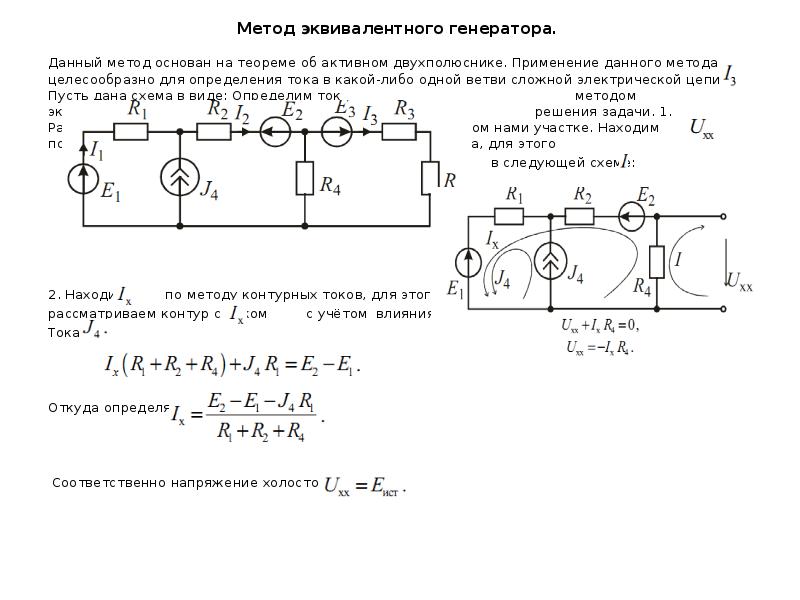 Если, например, измерительный прибор обнаруживает более высокое значение измерения тока, чем обычно, это может означать, что сопротивление уменьшилось или что напряжение увеличилось, вызывая ситуацию высокого напряжения. Это может указывать на проблему с питанием или цепью.
Если, например, измерительный прибор обнаруживает более высокое значение измерения тока, чем обычно, это может означать, что сопротивление уменьшилось или что напряжение увеличилось, вызывая ситуацию высокого напряжения. Это может указывать на проблему с питанием или цепью.
В цепях постоянного тока (dc) измерение тока ниже нормального может означать, что напряжение уменьшилось или сопротивление цепи увеличилось. Возможные причины повышенного сопротивления — плохие или неплотные соединения, коррозия и / или поврежденные компоненты.
Нагрузки в цепи потребляют электрический ток. Нагрузками могут быть любые компоненты: небольшие электрические устройства, компьютеры, бытовая техника или большой двигатель. На большинстве этих компонентов (нагрузок) есть паспортная табличка или информационная наклейка.На этих паспортных табличках указаны сертификаты безопасности и несколько ссылочных номеров.
Технические специалисты обращаются к заводским табличкам на компонентах, чтобы узнать стандартные значения напряжения и тока. Во время тестирования, если технические специалисты обнаруживают, что обычные значения не регистрируются на их цифровых мультиметрах или токоизмерительных клещах, они могут использовать закон Ома, чтобы определить, какая часть цепи дает сбой, и на основании этого определить, где может заключаться проблема.
Во время тестирования, если технические специалисты обнаруживают, что обычные значения не регистрируются на их цифровых мультиметрах или токоизмерительных клещах, они могут использовать закон Ома, чтобы определить, какая часть цепи дает сбой, и на основании этого определить, где может заключаться проблема.
Основы науки о схемах
Схемы, как и вся материя, состоят из атомов.Атомы состоят из субатомных частиц:
- Протонов (с положительным электрическим зарядом)
- Нейтронов (без заряда)
- Электронов (с отрицательным зарядом)
Атомы остаются связанными силами притяжения между ядром атома и электронами в его внешняя оболочка. Под воздействием напряжения атомы в цепи начинают преобразовываться, и их компоненты проявляют потенциал притяжения, известный как разность потенциалов. Взаимно притягиваемые свободные электроны движутся к протонам, создавая поток электронов (ток).Любой материал в цепи, ограничивающий этот поток, считается сопротивлением.
Ссылка: Принципы цифрового мультиметра, автор — Глен А. Мазур, American Technical Publishers.
Сопутствующие статьи
Измерение электрического тока | IOPSpark
Электрическая цепь
Электричество и магнетизм
Измеритель электрического тока
Повествование о физике
для 11-14
Ток — это расход заряда
Электрический ток состоит из движущихся заряженных частиц.Итак, заряженные частицы движутся по контуру.
Чтобы разобраться в электрических цепях, вам нужно смоделировать поведение токов в цепях. Теперь мы рассмотрим, как можно измерить электрические токи и как мы можем разобраться в этих измерениях.
Электрический ток в одной части цепи измеряется амперметром, который дает показание в амперах.
Для проведения измерения в цепи делается зазор, и в этот зазор включается амперметр, так что заряженные частицы, движущиеся по цепи, должны проходить через измеритель.
Поскольку амперметр подключается непосредственно к цепи, он должен иметь низкое сопротивление, чтобы не уменьшать поток заряда, который он используется для измерения.
Повышение тока
Что на самом деле измеряет амперметр, когда он включен в цепь? Вы можете представить себе работу амперметра как подсчет зарядов по мере их прохождения через прибор, чтобы узнать, сколько зарядов проходит каждую секунду. Количество проходящего заряда в секунду является мерой электрического тока:
Количество заряженных частиц, проходящих в секунду: большой ток
Мало заряженных частиц проходит в секунду: небольшой ток
Мы можем уточнить это до электрический ток = количество заряда, проходящего в секунду
.
Это эквивалентно электрическому току = скорости потока заряда
.
Более формально, возможно:
ток = зарядка
Вы можете записать это символами:
I = Q т
Где I — ток; Q — заряд; t — время, за которое течет заряд (продолжительность).
Вы также можете записать все отношения с помощью единиц:
ток в амперах = заряд в кулонах время в секундах
Для увеличения величины электрического тока,
- Либо нужно привести в движение больше заряженных частиц (изменить материал или толщину проволоки),
- Или нужно заставить заряженные частицы быстрее перемещаться по цепи.
Оба этих действия приводят к тому, что через любую точку цепи каждую секунду проходит больше заряда, и это больший электрический ток. В эпизоде 02 вы увидите, как можно увеличить электрический ток.
Ампер: мера электрического тока, которая представляет собой скорость протекания заряда
Когда амперметр используется для измерения силы электрического тока, показания счетчика выражаются в единицах ампер. Включите амперметр в цепь последовательно, чтобы не было разветвлений: ток в проводах будет таким же, как и в амперметре.
Включите амперметр в цепь последовательно, чтобы не было разветвлений: ток в проводах будет таким же, как и в амперметре.
Постоянный электрический ток в 1,0 ампер означает, что в секунду проходит один кулон заряда.
Что это значит? Сколько электронов составляют заряд на один кулон? Поскольку заряд одного электрона составляет 1,6 × 10 -19 кулонов, то в одном кулонах заряда должно быть около 6 × 10 18 электронов (6 миллионов, миллионов, миллионов!).
Думая об электрических токах в проводах, хорошая мысленная картина — это огромное количество электронов, перемещающихся по цепи с довольно умеренной скоростью!
Единица измерения электрического тока — ампер.
Обозначение ампера: A
Каким бы ни был проводник, независимо от заряда, связь между током и накопленным количеством прошедшего заряда универсальна.
Изучение закона Ома | BCHydro Power Smart для школ
Вы построите схему и проведете демонстрацию, чтобы ваши ученики могли наблюдать взаимосвязь между напряжением, током и сопротивлением.
Инструкции
Введение в тему
Настройте схему, как показано здесь:
Просмотрите рабочий лист «Изучение закона Ома» со студентами.
Проведите демонстрацию
- Используя амперметр и вольтметр, покажите учащимся, как считывать значения тока и напряжения в цепи. Пока вы проводите измерения, запишите данные на доске и попросите учащихся записать данные на своих листах.Напомните им преобразовать мА в А; 1 ампер = 1000 миллиампер.
- Последовательно добавьте сухую ячейку и повторите измерения.
- Если у вас больше сухих ячеек, добавляйте их последовательно по одной и повторяйте измерения каждый раз.
Постройте график сопротивления
Используя данные из таблицы, попросите учащихся построить график зависимости напряжения от тока (V от I). Убедитесь, что они помечают все части своего графика. Объясните, какая линия лучше всего подходит, и попросите учащихся нарисовать ее на своем графике.
Объясните, какая линия лучше всего подходит, и попросите учащихся нарисовать ее на своем графике.
Попросите учащихся вычислить наклон линии по наиболее подходящей линии:
- Выберите две точки на прямой (точка A и точка B).
- Рассчитайте разницу между напряжениями в двух точках (НАРАЩИВАНИЕ наклона).
- Вычислите разницу между током в двух точках (РАСХОД наклона).
- Разделите ПОДЪЕМ на БЕГ. Это наклон линии.
Сопротивление цепи математически отображается в виде алгебраического уравнения:
- Сопротивление = напряжение / ток.
Интерпретация данных
Сравните наклон графиков, созданных вашими учениками, с заявленным сопротивлением резистора, который вы использовали. Цифры должны быть похожими (разные числа являются результатом индивидуальных различий в выборе наиболее подходящей линии).
Связь между напряжением и током — это закон Ома, а наклон линии на графике этих двух величин является значением сопротивления в цепи. Уравнение закона Ома можно представить тремя способами:
Уравнение закона Ома можно представить тремя способами:
- R = V / I (сопротивление = напряжение, деленное на ток)
- V = I x R (напряжение = ток x сопротивление)
- I = V / R (ток = напряжение, деленное на сопротивление)
Мощность в цепи переменного тока — University Physics Volume 2
Цели обучения
К концу раздела вы сможете:
- Опишите, как можно записать среднюю мощность от цепи переменного тока через пиковый ток и напряжение, а также среднеквадратичное значение тока и напряжения
- Определите соотношение между фазовым углом тока и напряжения и средней мощностью, известное как коэффициент мощности
Элемент схемы рассеивает или производит мощность в зависимости от того, где I — ток через элемент, а В — напряжение на нем.Поскольку в цепи переменного тока и ток, и напряжение зависят от времени, мгновенная мощность также зависит от времени.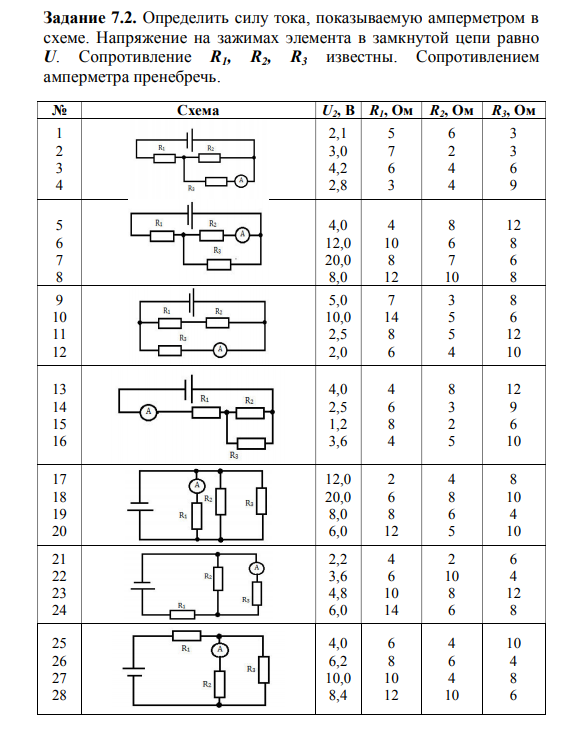 График p ( t ) для различных элементов схемы показан на (Рисунок). Для резистора i ( t ) и v ( t ) синфазны и поэтому всегда имеют один и тот же знак (см. (Рисунок)). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разницы фаз (см. (Рисунок) и (Рисунок)).Следовательно, p ( t ) в некоторые моменты является положительным, а в другое — отрицательным, что указывает на то, что емкостные и индуктивные элементы вырабатывают мощность в одни моменты и поглощают ее в другие.
График p ( t ) для различных элементов схемы показан на (Рисунок). Для резистора i ( t ) и v ( t ) синфазны и поэтому всегда имеют один и тот же знак (см. (Рисунок)). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разницы фаз (см. (Рисунок) и (Рисунок)).Следовательно, p ( t ) в некоторые моменты является положительным, а в другое — отрицательным, что указывает на то, что емкостные и индуктивные элементы вырабатывают мощность в одни моменты и поглощают ее в другие.
Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. Что нас почти всегда интересует, так это усредненная по времени мощность, которую мы называем средней мощностью. Он определяется средним по времени мгновенной мощностью за один цикл:
Что нас почти всегда интересует, так это усредненная по времени мощность, которую мы называем средней мощностью. Он определяется средним по времени мгновенной мощностью за один цикл:
где — период колебаний.С заменами и этот интеграл становится
Используя тригонометрическое соотношение, получаем
Вычисление этих двух интегралов дает
и
Следовательно, средняя мощность, связанная с элементом схемы, равна
В инженерных приложениях известен как коэффициент мощности, который представляет собой величину, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе.Для резистора средняя рассеиваемая мощность
Сравнение p ( t ) и показано на (Рисунок) (d). Чтобы он выглядел как его аналог постоянного тока, мы используем среднеквадратичные значения тока и напряжения. По определению это
где
С получаем
Затем мы можем написать для средней мощности, рассеиваемой резистором,
Это уравнение дополнительно подчеркивает, почему при обсуждении выбирается среднеквадратичное значение, а не пиковые значения.Оба уравнения для средней мощности верны для (рисунок), но среднеквадратичные значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не требуется.
Переменные напряжения и токи обычно описываются их действующими значениями. Например, напряжение 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника равна. Поскольку большинство измерителей переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, установленный в бытовой розетке, будет показывать 110 В.
Для конденсатора и катушки индуктивности соответственно. Поскольку мы находим из (Рисунок), что средняя мощность, рассеиваемая любым из этих элементов, равна Конденсаторам, а катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем разряжают ее обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках (Рисунок), (b) и (c), которые показывают, что p ( t) колеблются синусоидально около нуля.
Фазовый угол генератора переменного тока может иметь любое значение.Если генератор производит мощность; если он поглощает энергию. В терминах среднеквадратичных значений средняя мощность генератора переменного тока записывается как
Для генератора в цепи RLC ,
и
Отсюда средняя мощность генератора
Это также можно записать как
, который означает, что мощность, производимая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного напряжения на импеданс.
Проверьте свое понимание Вольтметр переменного тока, подключенный к клеммам генератора переменного тока 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.
Проверьте свое понимание Покажите, что действующие значения напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичный ток выражается соответственно. Определите эти значения для компонентов цепи RLC (рисунок).
Сводка
- Средняя мощность переменного тока определяется путем умножения действующего значения тока и напряжения.
- Ома для среднеквадратичного значения переменного тока находится делением действующего напряжения на полное сопротивление.
- В цепи переменного тока существует фазовый угол между напряжением источника и током, который можно найти, разделив сопротивление на импеданс.
- Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла.
- Коэффициент мощности находится в диапазоне от –1 до 1.
Закон
Концептуальные вопросы
При каком значении фазового угла между выходным напряжением источника переменного тока и током средняя выходная мощность источника является максимальной?
Обсудите разницу между средней мощностью и мгновенной мощностью.
Мгновенная мощность — это мощность в данный момент. Средняя мощность — это мощность, усредненная за цикл или количество циклов.
Средний переменный ток, подаваемый в цепь, равен нулю.Несмотря на это, мощность в цепи рассеивается. Объяснять.
Может ли мгновенная выходная мощность источника переменного тока быть отрицательной? Может ли средняя выходная мощность быть отрицательной?
Мгновенная мощность может быть отрицательной, но выходная мощность не может быть отрицательной.
Номинальная мощность резистора, используемого в цепях переменного тока, относится к максимальной средней мощности, рассеиваемой в резисторе. Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?
Глоссарий
- средняя мощность
- среднее по времени мгновенной мощности за один цикл
- Коэффициент мощности
- величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе
.

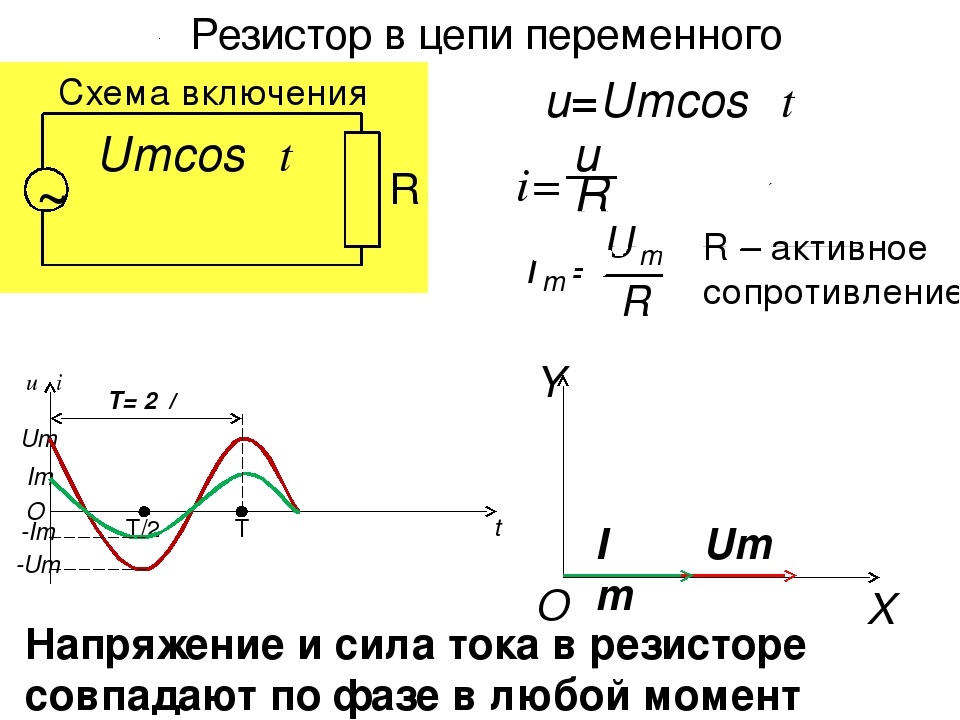 Для контуров выбираем обходы по часовой стрелке:
Для контуров выбираем обходы по часовой стрелке: – М.: Энергоатомиздат, 1984.
– М.: Энергоатомиздат, 1984.
