Электрическое сопротивление и проводимость. Как зависит проводимость ветви от сопротивления
Закон Ома. Сопротивление и проводимость
⇐ ПредыдущаяСтр 2 из 8Следующая ⇒
Вспомните хорошо известные из школьного курса физики понятия.
Электрический ток (или сила тока) - количество заряда, проходящего через поперечное сечение проводника в единицу времени или производная заряда по времени i(t) = dq/dt.
Единица измерения тока – Ампер – А = Кл/с
Для цепей постоянного тока i(t) = const = I
Напряжение – разность электрических потенциалов между двумя точками цепи u(t) = φ1 - φ2.
В цепях постоянного тока u(t) = const = U.
Единица измерения напряжения – Вольт (В).
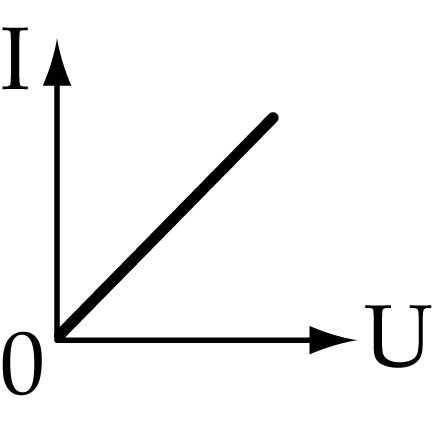
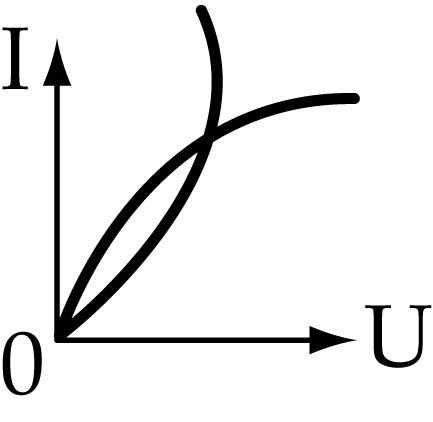
Одной из основных характеристик элемента цепи является зависимость тока от напряжения I = f (U), называемая вольт-амперная характеристика (ВАХ). Пример графиков двух ВАХ показан на рисунке 1.2.
ВАХ бывают линейные (если график – прямая линия) и нелинейные. На рисунке 1.2 характеристики 1 и 3 – линейные, а 2 – нелинейная. Соответственно, элементы цепи с линейной ВАХ называются линейными, а с нелинейной – нелинейными.
Линейная цепь - это цепь, состоящая только из линейных элементов. Если хотя бы один элемент цепи имеет нелинейную ВАХ, то цепь уже является нелинейной.
Важным параметром элемента цепи является его сопротивление R – коэффициент пропорциональности между током и напряжением.
В линейной цепи сопротивление элемента при любом напряжении постоянно и не зависит ни от напряжения, ни от тока. Зависимость тока от напряжения определяется законом Ома:
U = IR, где R = const.
Сопротивление R легко определить по графику ВАХ по любым двум точкам. R = ΔU/ΔI.
Определите: на какой из линейных ВАХ на рисунке 2 сопротивление больше: 1 или 3?
В нелинейной цепи сопротивление в каждой точке ВАХ различно. В данном разделе будем рассматривать только более простые, линейные цепи. Нелинейные цепи будут рассматриваться в последующих главах.
Сопротивление R является характеристикой провод-ника и определяется следующим образом:
R = , где l – длина проводника, ρ – удельное со-противление, характеризующее материал проводника, S – площадь поперечного сечения.
Теоретически любой элемент цепи обладает сопро-тивлением, но на практике в расчётах цепь идеализирует-ся, и сопротивлением проводов пренебрегают и считают, что всё сопротивление заключается в нагрузках.
Элемент цепи, обладающий сопротивлением, назы-вают резистором, на схеме обозначается так:
Размеры резистора – 4х10.
Часто удобно использовать величину, обратную сопротивлению, и называемую проводимость G.
G = 1/R
Единицей проводимости называется Сименс (См).
1 См = 1/1 Ом.
Закон Ома в этом случае выглядит: I = GU
G = , где γ = 1/ ρ – удельная проводимость.
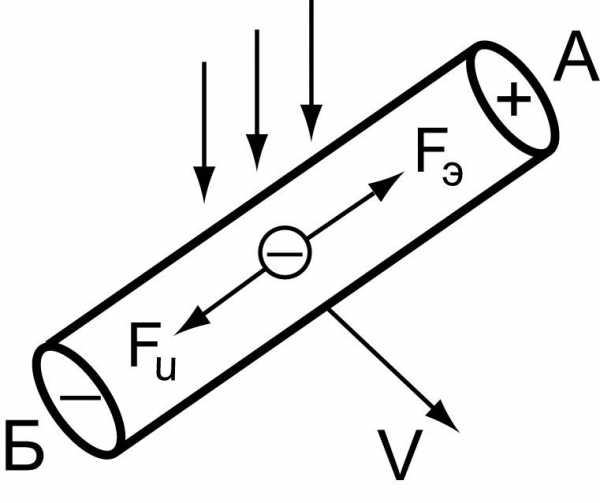
Рассмотрим участок ветви с резистором R (смотреть рисунок 1.3) и полярности величин.
Очевидно, всегда R > 0
Uab = φa - φb
Если φa > φb то Uab > 0 – напряжение положительно.
Ток считается положительным, если направление тока совпадает с направлением положительного напряжения и отрицательным, если его направление противоположно направлению положительного напряжения.
Рассмотрим теперь источник ЭДС (рисунок 1.4)
Стрелка источника ЭДС показывает направление положительного тока, который вызывает источник. Интересно, что направление напряжения на самом источнике ЭДС противоположно току.
Рассмотрим участок ветви, содержащий источник ЭДС и резистор (рисунок 1.5).
Некоторые студенты испытывают затруднения при анализе данной цепи. При данном направлении ЭДС, правильная формула:
Uab = UR – E = IR – E
Проанализируйте схему и запишите самостоятельно формулы при различных вариантах направлений напряжений, токов и источника.
Соединение сопротивлений
Во многих случаях расчёт электрической цепи можно упростить, путём преобразования её из сложного вида в более простой. При этом уменьшается число узлов, ветвей либо и то и другое.
Необходимое условие преобразования: токи и напряжения в остальных частях схемы, не подвергающих-ся преобразованию, не изменяются. Такое преобразование называется эквивалентным.
а) Последовательное соединение сопротивлений
Последовательное соединение – это такое, при ко-тором во всех элементах цепи течёт одинаковый ток. Элементы ветви соединены последовательно (рис. 1.6).
Такую ветвь можно заменить одним резистором с сопротивлением Rэкв, равным сумме сопротивлений всех резисторов.
Rэкв = = R1+R2+R3+…+Rn
Эквивалентное сопротивление при таком соедине-нии всегда больше сопротивления любого из элементов. Если все сопротивления равны
R1= R2= R3=…= R, то Rэкв = nR
Для проводимостей G формула будет выглядеть так:
Напряжение на зажимах ab равно сумме напряжений на каждом элементе ветви.
б) Параллельное соединение сопротивлений
Параллельное соединение сопротивлений – это такое соединение, при котором ко всем элементам цепи приложено одинаковое напряжение.
Параллельно соединены элементы между двумя узлами (рисунок 1.7).
Ток I в неразветвлённой части равен сумме токов в каждом элементе.
I = I1= I2+ I3+…+ In
Эквивалентная проводимость в этом случае равна сумме проводимостей всех элементов:
Gэкв = = G1+ G2+ G3+…+ Gn
Для сопротивлений R формула будет выглядеть так:
Как видите, формулы симметричны: при последова-тельном соединении складываются сопротивления, а при параллельном – проводимости.
Эквивалентное сопротивление при таком соедине-нии всегда меньше сопротивления любого из элементов.
Если все сопротивления равны R1= R2= R3=…= R, то
Rэкв = R/n
Ток в любой ветви пропорционален проводимости этой ветви.
в) Смешанное соединение сопротивлений
Смешанное соединение сопротивлений – это такое соединение, которое можно представить в виде параллельного и последовательного.
На первый взгляд кажется, что любую схему соединения элементов можно представить в виде смешанного соединения и найти эквивалентное сопротивление путём преобразования параллельных и последовательных участков. Однако бывают случаи, когда соединение элементов не является смешанным. Примером такого случая может служить распространённая в электронике мостовая схема, показанная на рисунке 1.8.
Как найти сопротивление между точками a и d? После нескольких попыток упростить схему, легко убе-диться, что здесь нет участков ни с последовательным, ни с параллельным соединением. Для этого нужно приме-нить преобразование, описанное в следующем параграфе.
г) Преобразование «Звезда-треугольник»
Существует возможность эквивалентного преобра-зования треугольника сопротивлений, показанного на ри-сунке 1.9, в трёхлучевую звезду (рисунок 1.10).
При преобразовании одной схемы в другую, напря-жения и токи, как при любом эквивалентном преобразова-нии, не изменяются.
Формулы для преобразования из треугольника в звезду:
Формулы для преобразования из звезды в треугольник:
Rab = Ra+ Rb+ RaRb/Rс
Rac = Ra+ Rc+ RaRc/Rb
Rbc = Rc+ Rb+ RcRb/Ra
Если все сопротивления равны, то легко убедиться, что сопротивления в треугольнике в три раза больше, чем в звезде.
Теперь вернёмся к мостовой схеме на рисунке 8. Можно преобразовать в ней треугольник abc в звезду. Получим схему на рисунке 1.11.
В этой схеме сопротивления треугольника R1, R2, R3 преобразованы в звезду Ra, Rb, Rc.
Теперь не вызывает затруднения найти сопротивле-ние Rad. Для этого нужно найти последовательные соеди-нения Rb-R4 и Rc-R5, затем параллельное соединение двух получившихся и затем - последовательное соедине-ние с Ra.
Также и в других подобных случаях преобразование «звезда-треугольник» может быть незаменимым.
Читайте также:
lektsia.com
4. Проводимость | 4. Последовательные и параллельные цепи | Часть1
4. Проводимость
Проводимость
Когда начинающие радиолюбители видят уравнение для расчета общего сопротивления параллельной цепи, у них возникает естественный вопрос, "Откуда оно взялось?". В этой статье мы попытаемся дать ответ на данный вопрос.
Ввиду того что электроны, сталкиваясь с частицами проводника, преодолевают некоторое сопротивление движению, принято говорить, что проводники обладают электрическим сопротивлением. Сопротивление обозначается буквой "R" и измеряется в Омах. Однако, всякий проводник можно характеризовать не только его сопротивлением, но и так называемой проводимостью — способностью проводить электрический ток. Проводимость есть величина, обратная сопротивлению:
Чем больше сопротивление, тем меньше проводимость и наоборот. Сопротивление и проводимость являются противоположными способами обозначения одного и того же электрического свойства материалов. Если при сравнении сопротивлений двух компонентов выясняется, что сопротивление компонента "А" составляет половину от сопротивления компонента "Б", то мы можем альтернативно выразить эту связь, сказав, что проводимость компонента "А" в два раза выше проводимости компонента "Б". Если сопротивление компонента "А" составляет одну треть от сопротивления компонента "Б", то можно сказать, что компонент "А" в три раза проводимее компонента "Б", и так далее.
Обозначается проводимость буквой "G", а ее единицей измерения первоначально было "Мо", то есть "Ом" записанный задом наперед. Но, несмотря на уместность этой единицы, позже она была заменена на "Сименс" (сокращенно - См или S).
Теперь давайте вернемся к нашему примеру параллельной цепи. Если рассматривать ее с точки зрения сопротивления, то наличие нескольких путей (ветвей) для потока электронов снижает общее сопротивление этой цепи, так как электронам легче течь по нескольким путям, чем по одному, обладающему некоторым сопротивлением. Если рассматривать цепь с точки зрения проводимости, то несколько путей для потока электронов наоборот, увеличивают проводимость схемы.
Общее сопротивление параллельной цепи меньше любого из ее отдельных сопротивлений, поскольку несколько параллельных ветвей создают меньше препятствий потоку электронов, чем каждый резистор по отдельности:
Общая проводимость параллельной цепи больше проводимости любой ее отдельной ветви, поскольку параллельно соединенные резисторы лучше проводят электрический ток, чем каждый резистор по отдельности:
Точнее будет сказать, что общая проводимость параллельной цепи равна сумме ее отдельных проводимостей:
Зная, что проводимость равна 1/R, мы можем преобразовать эту формулу в следующий вид:
Из данной формулы видно, что общее сопротивление параллельной цепи будет равно:
Ну вот мы и нашли ответ на поставленный в начале статьи вопрос! Вам следует знать, что проводимость очень редко используется на практике, в связи с чем данная статья носит чисто образовательный характер.
Краткий обзор:
- Проводимость - это величина противоположная сопротивлению.
- Проводимость обозначается буквой "G" и измеряется в Мо или Сименсах.
- Математически проводимость обратна сопротивлению: G=1/R
www.radiomexanik.spb.ru
Комплексные сопротивления и проводимости
Отношение комплексного напряжения к комплексному току называют комплексным сопротивлением цепи и обозначают .
,
где R, X и z – активное, реактивное и полное сопротивления цепи.
С другой стороны:
.
Тогда полное сопротивление z получим из соотношений:
В случае последовательного соединения элементов R,L,C комплексное сопротивление запишется в виде:
.
Отношение комплексного тока к комплексному напряжению называют комплексной проводимостью цепи и обозначают :
,
где –активная, реактивная и полная проводимости цепи.
Поскольку комплексная проводимость есть величина обратная комплексному сопротивлению, то:
.
Пусть: ;.
Тогда: .
С другой стороны: .
Тогда полную проводимость у получим из соотношений:
В случае параллельного соединения элементов G,L,C комплексная проводимость запишется в виде:
.
Очевидно, что .
Перевод комплексных величин в показательную форму:
3 + j2
1. Находим модуль: .
2. Находим аргумент: .
Окончательно: .
3 − j2
1. Находим модуль: .
2. Находим аргумент: .
Окончательно: .
Перевод показательных величин в комплексную форму:
;
.
Основные законы электрических цепей в комплексной форме
Законы электрических цепей переменного тока в комплексной форме имеют такой же вид, как и для цепей постоянного тока, с заменой соответствующих постоянных величин комплексными: ,,,,,.
Закон Ома в комплексной форме имеют вид: .
Достоинство этих выражений заключается в том, что в них учитывается как связь между действующими значениями тока и напряжения, так и сдвиг фаз между ними.
Первый закон Кирхгофа в применении к узлу: .
Второй закон Кирхгофа применительно к контуру: .
Возможность использовать соотношения для цепей постоянного тока справедлива и для эквивалентных преобразований.
При последовательном соединении комплексное сопротивление всей цепи равно алгебраической сумме комплексных сопротивлений отдельных ее участков: .
При параллельном соединении комплексная проводимость всей цепи равна алгебраической сумме комплексных проводимостей отдельных ее участков:
.
При смешанном соединении:
Расчет сложных цепей переменного тока комплексным методом осуществляется с помощью тех же методов, что и цепей постоянного тока при замене соответствующих величин их комплексными аналогами.
Мощность в комплексной форме. Баланс мощностей
В качестве комплексной мощности понимают произведение комплексного напряжения на сопряженную комплексную величину тока. В результате чего, получаем комплексную мощность:
.
Вещественная часть комплексной мощности равна активной мощности Р, а мнимая часть Q (без j) реактивной мощности. Модуль комплексной мощности равен полной мощности .
Баланс мощности:
1. Сумма комплексных мощностей для всех ветвей электрической цепи равна 0.
, откуда .
Такое равенство возможно только в том случае, если и.
2. Поскольку в каждой цепи есть источники и приемники, то
Источники ЭДС и токов можно разделить:
.
Действительно, мощность, потребляемую приемником, мы можем представить как:
.
С другой стороны,
и для мощности источников
.
Следовательно, и.
Резонансные явления в электрических цепях. Частотные характеристики.
Ранее было доказано, что действующее значение силы тока в R, L,C цепочке определяет соотношение:
.
Так как индуктивное и емкостное сопротивления зависят от частоты (), то сила тока вR, L,C также будет зависеть от частоты источника питания. Из приведенного выражения следует, что ток будет максимален при:
,
где −резонансная частота контура.
В том случае, когда в цепи наблюдаетсяявление резонанса.
На этой резонансной частоте , а, следовательно, в цепи действует чисто активное сопротивлениеR, поэтому напряжение и ток при резонансе совпадают по фазе.
Частоты, при которых наблюдается явление резонанса, называются резонансными частотами.
Покажем зависимость I (ω) для фиксированных значениях напряжения U, индуктивности L и емкости С при двух различных значения R:
Резонансными называют электрические цепи, в которых могут возникать явления резонанса напряжения или тока.
studfiles.net
3. Электродвижущая сила
|
| Если цепь замкнута, то разделение зарядов протекает непрерывно. |
Сопротивление и проводимость
Электрическое сопротивление
Проводник оказывает противодействие электрическому току, которое характеризует электрическое сопротивление проводника.
За единицу эл. сопротивления принят Ом. Более крупными единицами электрического сопротивления являютсякОм иМом.
Устройства, имеющие сопротивления и включаемые в электрическую цель для ограничения или регулирования тока, называются резисторами иреостатами.
Сопротивление, которым обладает изготовленный из данного материала провод длиной 1мс поперечным сечением1мм2 при температуре 200С, называют удельным электрическим сопротивлением.Удельное сопротивление обозначаюти выражают в.
Выясним влияние длины металлического проводника lи его сеченияSна электрическое сопротивление.
Известно, что сопротивление проводника вызвано столкновением движущихся электронов с атомами и молекулами проводника. Количество таких столкновений, а значит, и электрическое сопротивление возрастает при удлинении проводника и уменьшается с увеличением его поперечного сечения. Поэтому сопротивление проводника при температуре 200Сопределяют по формуле:
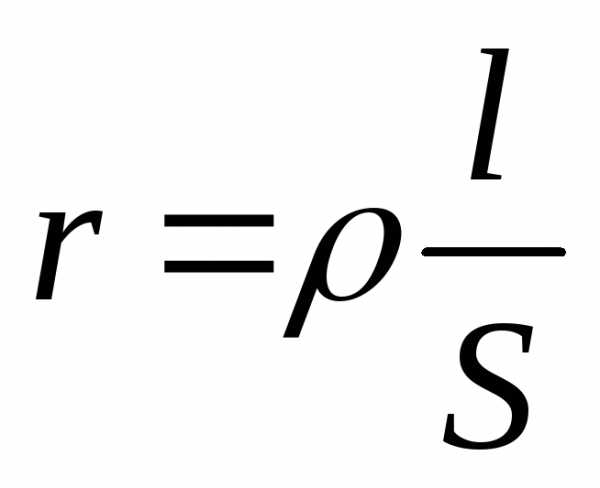
l – длина проводника,м;
S – площадь поперечного сечения,мм2.
Зависимость эл. сопротивления от температуры
Для определения сопротивления проводника при температуре, отличной от 200С, необходимо знать его температурный коэффициент сопротивления.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления при изменении температуры проводника на 10С.
Реостаты и резисторы
Резистор – прибор, имеющий сопротивление и предназначенный для ограничения или регулирования тока в электрической цепи. Резисторы бывают регулируемые, нерегулируемые, проволочные и непроволочные. Зависимость тока резистора Iот подводимого напряженияUназывают еговольт-амперной характеристикой.
Различают линейные инелинейные сопротивления резисторов. Если сопротивление резистора не зависит от тока, его вольт-амперная характеристика представляет собой прямую, проходящую через начало координат.
|
| Такое сопротивление называется линейным. |
Нелинейные сопротивления являются функцией тока или напряжения. Вольт-амперная характеристика нелинейных резисторов отклоняется от прямой линии.
|
| К нелинейным сопротивлениям относятся осветительные лампы с вольфрамовой и угольной нитью накаливания, вентильные элементы (селеновые, германиевые, кремниевые). |
Электрические цепи, содержащие только линейные элементы, называют линейными. Если в цепи имеется хотя бы один нелинейный элемент, то вся цепь называетсянелинейной.
Проводимость
Величина, обратная сопротивлению называется проводимостьюи обозначаетсяg: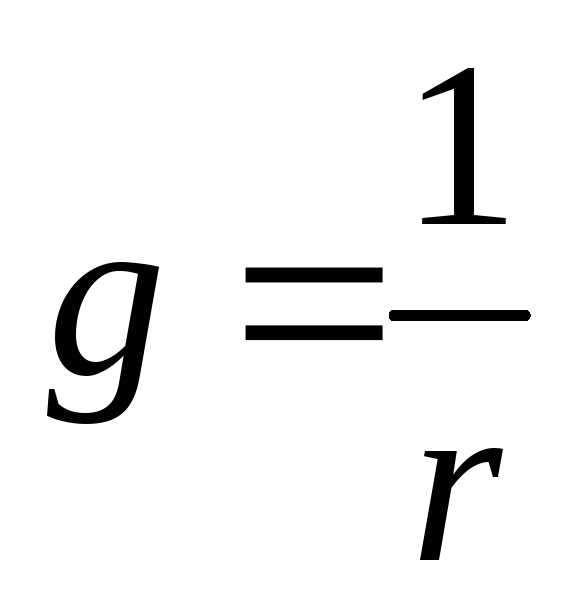 .
.
Единица проводимости называется сименсом:, а величина, обратная удельному сопротивлению –удельной проводимостью: 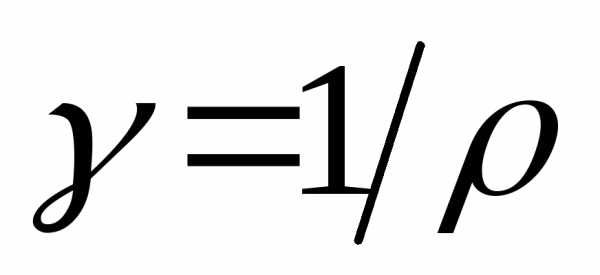 .
.
Если удельное сопротивление выражается в , то удельная проводимость – в.
Чем меньше сопротивление проводника, тем больше его проводимость, и, следовательно, он лучше проводит ток.
studfiles.net
Реактивная проводимость - Большая Энциклопедия Нефти и Газа, статья, страница 1
Реактивная проводимость
Cтраница 1
Реактивная проводимость равна нулю, так как емкостная и индуктивная проводимости одинаковы по величине. [1]
Реактивная проводимость при отсутствии г в цепи также имеет три характерные частоты - два нуля ( со 0, со оо), при которых b 0, и один полюс ( со со0), при котором b оо. [2]
Реактивная проводимость Ъ ( как и следует по общему правилу) равна их разности. [3]
Реактивная проводимость bL не является величиной, обратной реактивному сопротивлению, так как при ее определении учитывается и активное сопротивление ветви. [4]
Реактивная проводимость для ветви с индуктивностью bL записывается со знаком плюс, а для ветви с емкостью Ьс - со знаком минус. [5]
Реактивная проводимость при отсутствии г в цепи также имеет три характерные частоты - два нуля ( со 0, со оо), при которых b о, и один полюс ( со сос), при котором b оо. [6]
Реактивная проводимость при отсутствии г в цепи также имеет три характерные частоты - два нуля ( со 0, со оо), при которых b О, и один полюс ( со со), при котором b оо. [7]
Реактивная проводимость обусловливается наличием емкости у каждой из фаз по отношению к другой фазе, а также по отношению к земле. [8]
Реактивная проводимость Ь0 зависит от напряжения ( / и является нелинейной величиной. В т - Если же потери на гистерезис изменяются непропорционально квадрату амплитуды индукции, то величина gu в некоторой мере зависит от ( / и также является нелинейной. [9]
Реактивная проводимость Ь0 зависит от напряжения U0 и явЛяется нелинейной величиной. Если же потери на гистерезис изменяются непропорционально квадрату амплитуды индукции, то величина g9 в некоторой мере зависит от t / 0 и также является нелинейной. [10]
Реактивная проводимость при отсутствии г в цепи также ь имеет три характерные частоты - два нуля ( со 0, со оо), при которых b О, и один полюс ( со со0), при котором b - оо. [11]
Реактивная проводимость определяется магнитным потоком взаимоиндукции в обмотках трансформатора. [12]
Реактивная проводимость шлейфов изменяется путем перемещения короткозамыкаю-щих мостиков или поршней. [13]
Суммарная реактивная проводимость на выходе каскада В2 О, что соответствует индуктивному характеру расстройки контура, образованного в выходной цепи каскада. [14]
Реактивная проводимость шлейфа должна быть равной по величине и противоположной по знаку реактивной проводимости линии в точке соединения. Единственным дополнительным требованием является необходимость найти такую точку присоединения, чтобы действительная часть полного сопротивления или проводимости по направлению к нагрузке была равна волновому сопротивлению или проводимости линии. [15]
Страницы: 1 2 3 4 5
www.ngpedia.ru
Электрический ток, электрическое сопротивление и проводимость
Электрический ток. В веществе, помещенном в электрическое поле, под действием сил поля возникает процесс движения элементарных носителей электричества — электронов или ионов. Движение этих электрически заряженных частиц материи называют электрическим током.
За единицу силы тока принят ампер (А). Это такой ток, при котором через поперечное сечение проводника каждую секунду проходит количество электричества, равное 1 Кл.
, [А];
Постоянным называют ток, значение и направление которого в любой момент времени остаются неизменными.Т оки, значение и направление которых не остаются постоянными, называют переменными.
Количество электричества, прошедшего через поперечное сечение проводника в течение одной секунды, называется величиной токаи обозначается буквой I:
; ; ;
Ток в цепи измеряется электрическим прибором – амперметром. Амперметр включают последовательно, т. е. разрывают цепь в каком-либо месте и образовавшиеся концы подключают к зажимам прибора.
Для того чтобы постоянно протекал ток по проводнику необходимо разность потенциалов на его концах.
Электропроводность. Свойство вещества проводить электрический ток под действием электрического поля называют электропроводностью. Электропроводность различных веществ зависит от концентрации свободных электрически заряженных частиц. Чем больше концентрация этих частиц, тем больше электропроводность данного вещества. Все вещества в зависимости от электропроводности делят на три группы: проводники, диэлектрики (изолирующие материалы) и полупроводники.
Электрическое сопротивление.При движении свободных электронов в проводнике они сталкиваются на своем пути с положительными ионами, атомами и молекулами вещества, из которого выполнен проводник, и передают им часть своей энергии. При этом энергия движущихся электронов в результате столкновения их с атомами и молекулами частично выделяется и рассеивается в виде тепла, нагревающего проводник.
Проводники обладают электрическим сопротивлением – способностью проводника препятствовать прохождению тока.
,
где с – удельное сопротивление проводников в;
l – длинна проводника в м;
S – площадь поперечного сечения проводника в мм .
За единицу сопротивления принят Ом.
Сопротивлением в 1 Ом обладает проводник , по которому проходит ток в 1 А при разности потенциала на его концах, равной 1 В.
Проводимость. Всякий проводник можно характеризовать не только его сопротивлением, но и так называемой проводимостью — способностью проводить электрический ток. Проводимость есть величина, обратная сопротивлению. Единица проводимости называется сименсом (См).
О способности проводить электрический ток различных материалов можно судить по их удельному электрическому сопротивлению (ро) – сопротивление проводника длиной 1м, сечением 1 мм .
| Удельное сопротивление ( ) некоторых материалов | ||
| Материал | ||
| Серебро | 0,0063 | |
| Медь | 0,0175 | |
| Алюминий | 0,03 | |
| Цинк | 0,063 | |
| Сталь | 0,12 | |
| Нихром | 0,43 | |
| Константан | 0,5 | |
Электропроводность всех материалов зависит от их температуры. В металлических проводниках при нагревании размах и скорость колебаний атомов в кристаллической решетке металла увеличиваются, вследствие чего возрастает и сопротивление, которое они оказывают потоку электронов. При охлаждении происходит обратное явление.
Для металлов зависимость сопротивления от температуры выражается формулой:
где - при начальной температуре;
- изменение температур;
- температурный коэффициент, какая доля соответствует изменению сопротивления проводника от начальной величины при изменении температуры на 1°С.
При увеличении температуры сопротивление проводников увеличивается.
Похожие статьи:
poznayka.org
|
ТОП 10: |
Физическая природа электрического сопротивления.При движении свободных электронов в проводнике они сталкиваются на своем пути с положительными ионами 2 (см. рис. 10, а), атомами и молекулами вещества, из которого выполнен проводник, и передают им часть своей энергии. При этом энергия движущихся электронов в результате столкновения их с атомами и молекулами частично выделяется и рассеивается в виде тепла, нагревающего проводник. Ввиду того что электроны, сталкиваясь с частицами проводника, преодолевают некоторое сопротивление движению, принято говорить, что проводники обладают электрическим сопротивлением. Если сопротивление проводника мало, он сравнительно слабо нагревается током; если сопротивление велико, проводник может раскалиться. Провода, подводящие электрический ток к электрической плитке, почти не нагреваются, так как их сопротивление мало, а спираль плитки, обладающая большим сопротивлением, раскаляется докрасна. Еще сильнее нагревается нить электрической лампы. За единицу сопротивления принят ом. Сопротивлением 1 Ом обладает проводник, по которому проходит ток 1 А при разности потенциалов на его концах (напряжении), равной 1 В. Эталоном сопротивления 1 Ом служит столбик ртути длиной 106,3 см и площадью поперечного сечения 1 мм2 при температуре 0 °С. На практике часто сопротивления измеряют тысячами ом — килоомами (кОм) или миллионами ом — мегаомами (МОм). Сопротивление обозначают буквой Я (г). Проводимость.Всякий проводник можно характеризовать не только его сопротивлением, но и так называемой проводимостью — способностью проводить электрический ток. Проводимость есть величина, обратная сопротивлению. Единица проводимости называется сименсом (См). 1 См равен 1/1 Ом. Проводимость обозначают буквой О (§). Следовательно, Удельное электрическое сопротивление и проводимость.Атомы разных веществ оказывают прохождению электрического тока неодинаковое сопротивление. О способности отдельных веществ проводить электрический ток можно судить по их удельному электрическому сопротивлению р. За величину, характеризующую удельное сопротивление, обычно принимают сопротивление куба с ребром 1 м. Удельное электрическое сопротивление измеряют в Ом-м. Для суждения об электропроводности материалов пользуются также понятием удельная электрическая проводимость а=1/р. Удельная электрическая проводимость измеряется в сименсах на метр (См/м) (проводимость куба с ребром 1 м). Часто удельное электрическое сопротивление выражают в ом-сантиметрах (Ом • см), а удельную электрическую проводимость — в сименсах на сантиметр (См/см). При этом 1 Ом-см = 10~~2 Ом-м, а 1 См/см = = 102 См/м. Проводниковые материалы применяют, главным образом, в виде проволок, шин или лент, площадь поперечного сечения которых принято выражать в квадратных миллиметрах, а длину — в метрах. Поэтому для удельного электрического сопротивления подобных материалов и удельной электрической проводимости введены и другие единицы измерения: р измеряют в Ом-мм2/м (сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2), а а — в См-м/мм2 (проводимость проводника длиной 1 м и площадью поперечного сечения 1 мм2). Из металлов наиболее высокой электропроводностью обладают серебро и медь, так как структура их атомов позволяет легко передвигаться свободным электронам, затем следует золото, хром, алюминий, марганец, вольфрам и т. д. Хуже проводят ток железо и сталь. Чистые металлы всегда проводят электрический ток лучше, чем их сплавы. Поэтому в электротехнике используют преимущественно очень чистую медь, содержащую только 0,05 % примесей. И наоборот, в тех случаях, когда необходим материал с высоким сопротивлением (для различных нагревательных приборов, реостатов и пр.). применяют специальные сплавы: константан, манганин, нихром, фехраль. В табл. 1 приведены значения удельного сопротивления некоторых проводниковых материалов, применяемых в электрическом оборудовании локомотивов. 16 Таблица 1
Следует отметить, что в технике, кроме металлических проводников, используют и неметаллические. К таким проводникам относится, например, уголь, из которого изготовляют щетки электрических машин, электроды для прожекторов и пр. Проводниками электрического тока являются толща земли, живые ткани растений, животных и человека. Проводят электрический ток сырое дерево и многие другие изоляционные материалы во влажном состоянии. Электрическое сопротивление проводника зависит не только от материала проводника, но и его длины / и площади поперечного сечения 5. (Электрическое сопротивление подобно сопротивлению, оказываемому движению воды в трубе, которое зависит от площади сечения трубы и ее длины.) Сопротивление прямолинейного проводника Если удельное сопротивление р выражено в Ом-мм2/м, то для того, чтобы получить сопротивление проводника в омах, длину его надо подставлять в формулу (5) в метрах, а площадь поперечного сечения — в квадратных миллиметрах. Зависимость сопротивления от температуры.Электропроводность всех материалов зависит от их температуры. В металлических проводниках при нагревании размах и скорость колебаний атомов в кристаллической решетке металла увеличиваются, вследствие чего возрастает и сопротивление, которое они оказывают потоку электронов. При охлаждении происходит обратное явление: беспорядочное колебательное движение атомов в узлах кристаллической решетки уменьшается, сопротивление их потоку электронов понижается и электропроводность проводника возрастает. В природе, однако, имеются некоторые сплавы: фехраль, константан, манганин и др., у которых в определенном интервале температур электрическое сопротивление меняется сравнительно мало. Подобные сплавы применяют в технике для изготовления различных резисторов, используемых в электроизмерительных приборах и некоторых аппаратах для компенсации влияния температуры на их работу. О степени изменения сопротивления проводников при изменении температуры судят по так называемому температурному коэффициенту сопротивления а. Этот коэффициент представляет собой относительное приращение сопротивления проводника при увеличении его температуры на 1 °С. В табл. 1 приведены значения температурного коэффициента сопротивления для наиболее применяемых проводниковых материалов. Сопротивление металлического проводника /?/ при любой температуре / Свойство металлических проводников увеличивать свое сопротивление при нагревании часто используют в современной технике для измерения температуры. Например, при испытаниях тяговых двигателей после ремонта температуру нагрева их обмоток определяют измерением их сопротивления в холодном состоянии и после работы под нагрузкой в течение установленного периода (обычно в течение 1 ч). Исследуя свойства металлов при глубоком (очень сильном) охлаждении, ученые обнаружили замечательное явление: вблизи абсолютного нуля ( — 273,16 °С) некоторые металлы почти полностью утрачивают электрическое сопротивление. Они становятся идеальными проводниками, способными длительное время пропускать ток по замкнутой цепи без всякого воздействия источника электрической энергии. Это явление названо сверхпроводимостью. В настоящее время созданы опытные образцы линий электропередачи и электрических машин, в которых используется явление 18 сверхпроводимости. Такие машины имеют значительно меньшие массу и габаритные размеры по сравнению с машинами общего назначения и работают с очень высоким коэффициентом полезного действия. Линии электропередачи в этом случае можно выполнить из проводов с очень малой площадью поперечного сечения. В перспективе в электротехнике будет все больше и больше использоваться это явление. |
infopedia.su
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.