Урок 9. конденсатор и катушка индуктивности в цепи переменного электрического тока — Физика — 11 класс
Физика, 11 класс
Урок 9. Конденсатор и катушка индуктивности в цепи переменного электрического тока
Перечень вопросов, рассматриваемых на уроке:
Процессы, происходящие в цепи переменного электрического тока при наличии конденсатора и катушки индуктивности;
Устройство и принцип действия генератора переменного тока и трансформатора;
Автоколебания;
Проблемы передачи электроэнергии и способы повышения эффективности её использования.
Глоссарий по теме
Автоколебания – незатухающие колебания в системе, поддерживаемые за счет постоянного источника энергии.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами.
Трансформатор – устройство, применяемое для повышения или понижения переменного напряжения.
Коэффициент трансформации – величина равная отношению напряжений в первичной и вторичной обмотках трансформатора.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.
Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.
Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004
Основное содержание урока
Переменный ток, которым мы пользуемся, вырабатывается с помощью генераторов переменного тока на электростанциях. Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.
В июле 1832 года Фарадей получил анонимное письмо, в котором автор описывал устройство созданного им генератора постоянного тока. Ознакомившись с содержанием письма Фарадей тут же отослал его в редакцию научного журнала.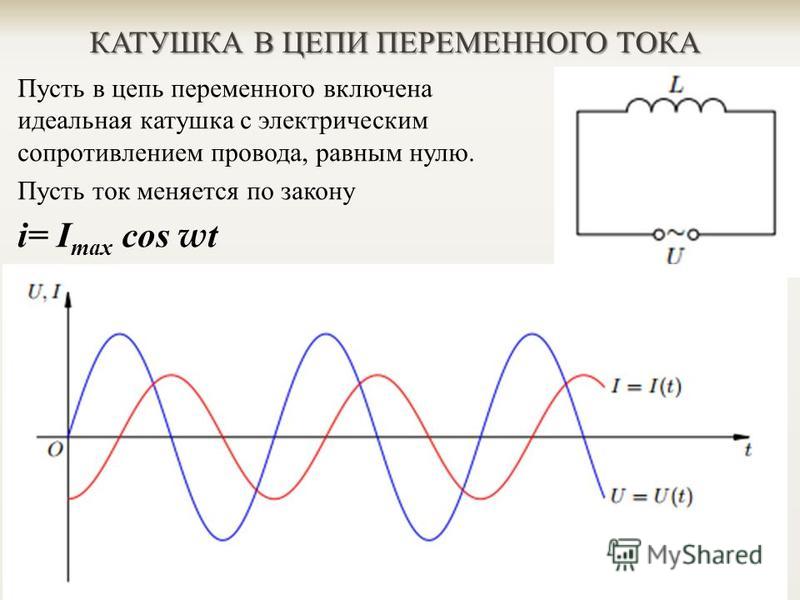 Автор этого письма не назвал себя, его фамилия осталась неизвестной.
Автор этого письма не назвал себя, его фамилия осталась неизвестной.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами. Впоследствии генераторы постоянного тока непрерывно совершенствовались. Потом, когда начали использовать переменный ток они уступили место генераторам переменного тока. Переменный ток в основном вырабатывается генераторами переменного тока. Простой моделью генератора может служить прямоугольная рамка, вращающаяся в магнитном поле. При вращении рамки, магнитный поток пронизывающий площадь поверхности, ограниченную рамкой, меняется по гармоническому закону:
N- число витков.
Возникает ЭДС индукции который меняется по гармоническому закону.
ЭДС индукции в рамке равна:
Если с помощью контактных колец и скользящих по ним щёток соединить концы рамки с электрической цепью, то в цепи возникнет переменный ток.
В современной энергетике для производства электроэнергии используются электромеханические индукционные генераторы. Принцип действия таких генераторов основан на явлении электромагнитной индукции. Основными частями генератора являются статор и ротор. Неподвижная часть генератора называется статором, а вращающаяся – ротором.
Принцип действия таких генераторов основан на явлении электромагнитной индукции. Основными частями генератора являются статор и ротор. Неподвижная часть генератора называется статором, а вращающаяся – ротором.
Постоянный ток не может идти по цепи содержащей конденсатор, т. к. цепь оказывается разомкнутой. При включении конденсатора в цепь переменного тока конденсатор будет периодически заряжаться и разряжаться с частотой равной частоте приложенного напряжения. В результате периодически меняющихся процессов зарядки и разрядки конденсатора в цепи течет переменный ток. Лампа накаливания, включенная в цепь переменного тока последовательно с конденсатором кажется горящей непрерывно, т.к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.
Величину ХC, обратную произведению циклической частоты на электрическую ёмкость конденсатора называют ёмкостным сопротивлением.
Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току. Чем больше ёмкость конденсатора и частота колебаний, тем больше ток перезарядки. При наличии в цепи переменного тока конденсатора колебания силы тока опережают по фазе колебания напряжения конденсаторе на 90º. Сдвиг фазы колебаний силы тока на 90º относительно фазы колебания напряжения на конденсаторе приводит к тому, что мощность переменного тока в течение одной четверти периода имеет положительный знак, а в течение второй четверти – отрицательный. Поэтому среднее значение мощности за период равно нулю.
Индуктивность в цепи, так же, как и ёмкость, влияет на силу переменного тока. Объясняется это явлением самоиндукции. В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов.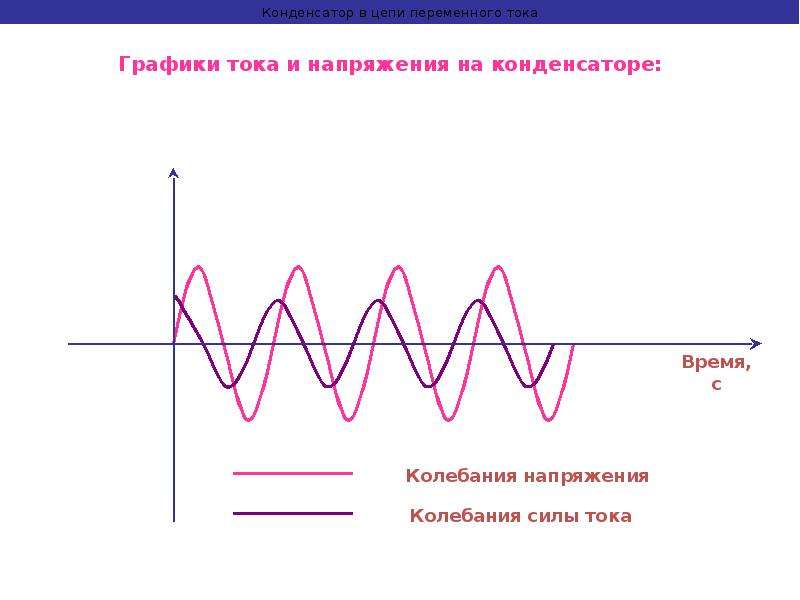 Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.
Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.
Величину ХL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
Если частота равна нулю, то индуктивное сопротивление тоже равно нулю. Поэтому постоянный ток как бы не «замечает» катушку индуктивности в цепи.
Колебания напряжения на катушке опережают по фазе колебания силы тока на 90º.
Сдвиг фазы колебаний приводит к тому, что средняя мощность за период колебаний равна нулю.
Генератор на транзисторе используется для создания высокочастотных электромагнитных колебаний.
Для потребления электрической энергии нужно доставить его от источника к потребителю.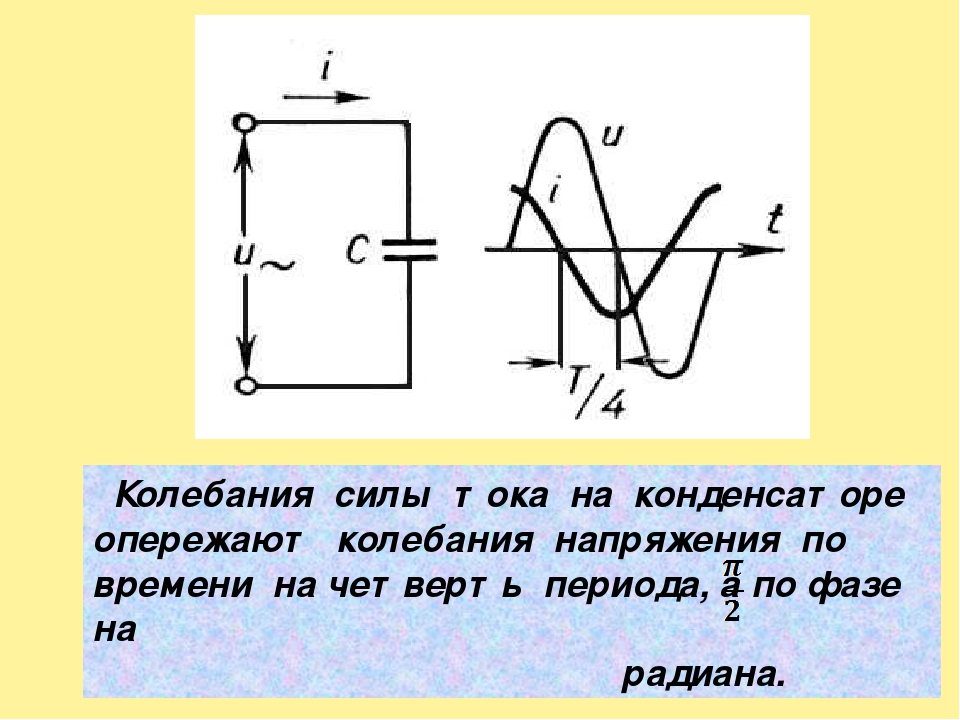 Для этого строят линии электропередачи. При передаче электроэнергии на расстояние возникают потери энергии вследствие нагревания проводов. Тепловые потери можно определить используя закон Джоуля – Ленца:
Для этого строят линии электропередачи. При передаче электроэнергии на расстояние возникают потери энергии вследствие нагревания проводов. Тепловые потери можно определить используя закон Джоуля – Ленца:
Из этой формулы следует, что для уменьшения потерь энергиинужно уменьшить сопротивление или повысить напряжение. Уменьшения сопротивления проводов ЛЭП требует увеличения их площади поперечного сечения, что приведет к увеличению массы проводов. Увеличение массы проводов связано с большими расходами на укрепление столбов линии электропередачи, для их удержания и на производство металла для них. Наиболее эффективным является увеличение напряжения.
Для изменения напряжения в сети используют трансформаторы. Трансформатор был изобретен в 1876 году Яблочковым и в 1882 году усовершенствован Усагиным. Простейший трансформатор состоит из двух катушек, надетых на общий замкнутый стальной сердечник. Эти катушки называются обмотками трансформатора. Обмотка трансформатора, подключаемая к источнику переменного напряжения, называют первичной, а другая к которой присоединяют нагрузку – вторичной. Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.
Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.
Величина равная отношению напряжений в первичной и вторичной обмотках трансформатора называют коэффициентом трансформации. Его обозначают буквой «k».
k– коэффициент трансформации.
U1 иU2 – напряжения на первичной и на вторичной обмотке.
N1 и N2— число витков на первичной и на вторичной обмотке.
Если k < 1 — трансформатор повышающий,
k > 1 — трансформатор понижающий.
КПД трансформатора равен отношению мощности в нагрузке к мощности, подаваемой из сети на первичную обмотку:
Для передачи электроэнергии на расстояние напряжение повышают с помощью трансформатора, а для потребления — понижают. В массивных проводниках при изменении магнитного поля возникают индукционные токи (токи Фуко), которые нагревают проводник. Чтобы эти индукционные токи не нагревали сердечник трансформатора его делают не сплошным, а из отдельных пластин, скрепленных вместе.
В массивных проводниках при изменении магнитного поля возникают индукционные токи (токи Фуко), которые нагревают проводник. Чтобы эти индукционные токи не нагревали сердечник трансформатора его делают не сплошным, а из отдельных пластин, скрепленных вместе.
Закон Ома гласит: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
Из формулы закона Ома для переменного тока мы видим, что при постоянной амплитуде напряжения, амплитуда силы тока зависит от частоты. Амплитуда силы тока будет максимальной, если полное сопротивление минимально. Полное сопротивление цепи минимально при равенстве индуктивного и ёмкостного сопротивления. В этом заключается условие возникновения резонанса в электрической цепи.
Резонанс в электрической цепи – это явление резкого возрастания амплитуды колебаний силы тока в контуре при совпадении частоты вынужденных колебаний с частотой собственных колебаний контура.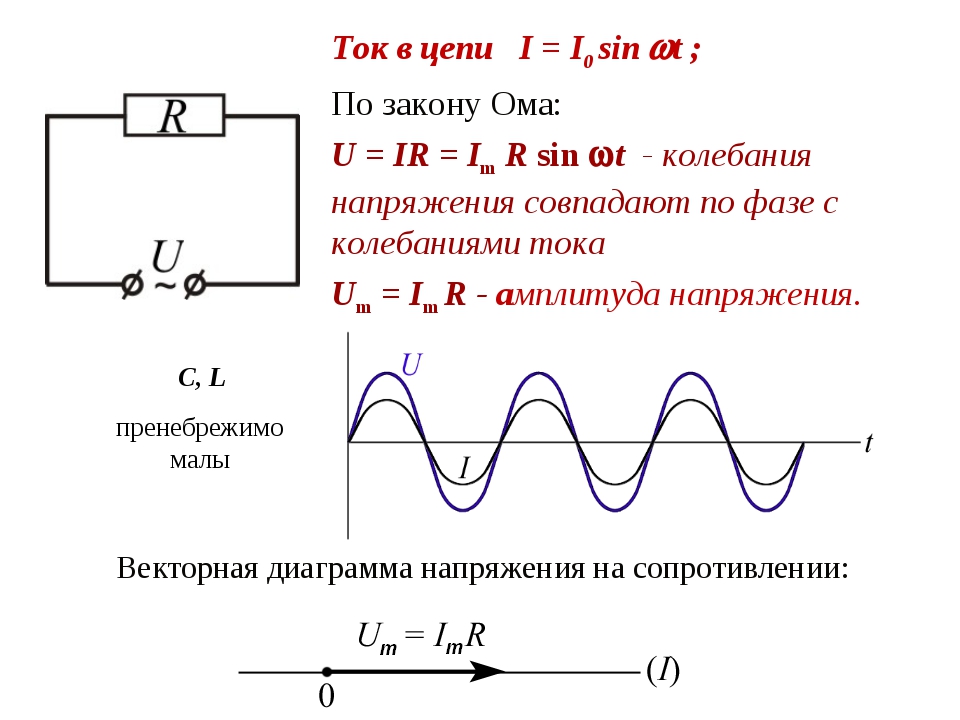
Явление резонанса широко используется в радиотехнике, в схемах настройки радиоприемников. Меняя электроемкость конденсатора в колебательном контуре можно настроить его на нужную волну, т.е. выделить частоту на которой работает передающая станция
Разбор тренировочных заданий
1. Каково амплитудное значение ЭДС, возникающей в рамке из 50 витков, если она вращается с циклической частотой 180 рад/с в магнитном поле индукцией 0,4 Тл? Площадь рамки 0,02 м2.
Дано:
N=50
ω=180 рад/с
B=0,4 Тл
S=0,02 м2
_________
Ԑm=?
Решение:
Ответ: 72 В.
2. Катушка с индуктивностью 0,08 Гн присоединена к источнику переменного тока частотой 1000 Гц. При этом вольтметр показывает 100 В. Определить амплитуду тока в цепи. Ответ округлить до десятых.
Дано:
L=0,08 Гн
ν= 1000 Гц
U=100 В
__________
Im=?
Решение:
Напишем закон Ома для переменного тока
Т. к. ХC и R равны нулю, то
к. ХC и R равны нулю, то
Учитывая, что , получаем:
Найдем амплитудное значение напряжения:
Подставим числовые данные в формулу для расчета амплитуды силы тока:
Ответ: Im = 0,3 А.
Конденсатор в цепи переменного тока
При изучении постоянного тока мы узнали, что он не может проходить в цепи, в которой есть конденсатор. Так как конденсатор — это две пластины, разделенные слоем диэлектрика. Для цепи постоянного тока конденсатор будет, как разрыв в цепи. Если конденсатор пропускает постоянный ток, значит, он неисправен.
Конденсатор в цепи переменного тока
В отличии от постоянного переменный ток может идти и через цепь, в которой присутствует конденсатор. Рассмотрим следующий опыт.
Возьмем два источника питания. Один из них пусть будет источником постоянного напряжения, а второй – переменного. Причем подберем источники так, чтобы постоянное значение напряжения равнялось действующему значению переменного напряжения.
Подключим к ним с помощью переключателя цепь, состоящую из лампочки и конденсатора. Причем лампочка и конденсатор подключены последовательно.
При включении питания от источника постоянного тока (АА’) лампочка не загорится. Если подключить цепь к источнику тока с переменным напряжением (BB’), то лампочка будет гореть. При условии, что емкость конденсатора достаточно велика.
В цепи происходит периодическая зарядка и разрядка конденсатора. В то время, когда конденсатор перезаряжается, ток проходит по цепи и нагревает нить накаливания лампочки.
Рассмотрим, как будет меняться сила тока в цепи, содержащей конденсатор, с течением времени. При этом будем пренебрегать сопротивлением соединяющих проводов и обкладок конденсатора.
Напряжение на конденсаторе будет равняться напряжению на концах цепи. Значит, мы можем приравнять эти две величины.
u = φ1-φ2 = q/C,
u = Um*cos(ω*t).
Имеем:
q/C = Um*cos(ω*t).
Выражаем заряд:
q = C*Um*cos(ω*t).
Видим, что заряд будет изменяться по гармоническому закону. Сила тока — это скорость изменения заряда. Значит, если возьмем производную от заряда, получим выражение для силы тока.
I = q’ = Um*C*ω*cos(ω*t+pi/2).
Разность фаз между колебаниями силы тока и заряда, а также напряжения, получилась равной pi/2. Получается, что колебания силы тока опережают по фазе колебания напряжения на pi/2. Это представлено на следующем рисунке.
Из уравнения колебаний силы тока получаем выражение для амплитуды силы тока:
Im = Um*C*ω.
Введем следующее обозначение:
Xc = 1/(C*ω).
Запишем следующее выражение закона Ома, используя Xc и действующие значения силы тока и напряжения:
I = U/Xc.
Xc — величина, называемая емкостным сопротивлением.
Конденсатор в цепи переменного тока
Электроника Конденсатор в цепи переменного тока
просмотров — 139
Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. При подключении конденсатора к источнику переменного напряжения (перед подключением конденсатор разряжен), ток в цепи максимальный (см. рис.2.5), а напряжение Uc на конденсаторе равно нулю.
При подключении конденсатора к источнику переменного напряжения (перед подключением конденсатор разряжен), ток в цепи максимальный (см. рис.2.5), а напряжение Uc на конденсаторе равно нулю.
Рис.2.5. Изменения силы тока и напряжения во времени для ёмкостной нагрузки
Uc(t) — напряжение на конденсаторе, I(t) — ток в цепи, Uq(t) — напряжение на выходе источника переменного напряжения.
В первой четверти периода напряжение источника увеличивается, напряжение на конденсаторе также увеличивается. Конденсатор заряжается, а ток в цепи уменьшается. По прошествии 1/4 периода конденсатор полностью заряжен и ток в цепи равен нулю. При этом напряжение на пластинах конденсатора, становится к этому моменту максимальным, но обратного знака, т. е. направлено навстречу напряжению генератора,
u(t) = — uc(t).
Во второй четверти происходит разряд конденсатора, ток в цепи увеличивается. В следующую четверть периода конденсатор вновь заряжается, но полярность напряжения на его обкладках изменяется на противоположную и т. д. Процессы заряда и разряда конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения. Подобно этому и ток сначала устремляется в незаряженный конденсатор, а затем постепенно ослабевает по мере его заряда. Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с его выводами, течет переменный ток. При изменениях напряжения на обкладках конденсатора по гармоническому закону
д. Процессы заряда и разряда конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения. Подобно этому и ток сначала устремляется в незаряженный конденсатор, а затем постепенно ослабевает по мере его заряда. Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с его выводами, течет переменный ток. При изменениях напряжения на обкладках конденсатора по гармоническому закону
u = Umcosωt,
заряд на его обкладках изменяется по закону:
q = C u = C Um cosωt.
Электрический ток в цепи возникает в результате изменения заряда конденсатора,
i = dq/dt.
По этой причине колебания силы тока в цепи происходят по закону,
i = d(C Um cosωt)/dt = — C Um ω sinωt = C Um ω cos (ωt + π/2),
где (y = cos x, y= − sinx).
Следовательно, колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на π/2 или колебания силы тока опережают по фазе колебания напряжения на π/2 (рис. 2.5). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т.д Произведение
Um ω C
является амплитудой колебаний силы тока i
Um = Im(1/ω C).
Связь амплитуды колебаний напряжения на концах конденсатора с амплитудой колебаний силы тока в цепи совпадает по форме с выражением закона Ома для участка цепи постоянного тока:
Xc = 1/ ω C.
Емкостное сопротивление конденсатора, как и индуктивное сопротивление катушки, не является постоянной величиной. Оно обратно пропорционально частоте переменного тока. По этой причине амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте.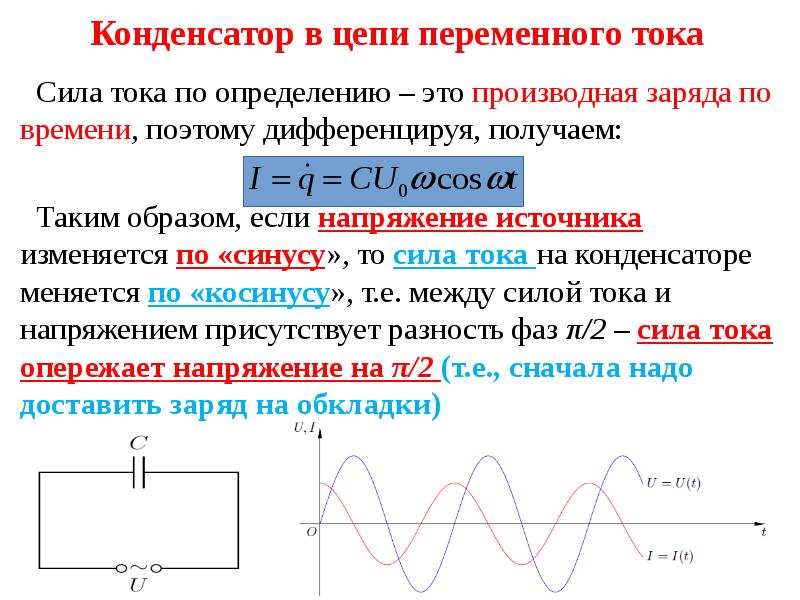
Читайте также
Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. При подключении конденсатора к источнику переменного напряжения (перед подключением конденсатор разряжен), ток в цепи максимальный (см. рис.2.5), а напряжение Uc на конденсаторе равно… [читать подробенее]
Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. Если подключить конденсатор к источнику постоянного тока, то в цепи возникнет кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток… [читать подробенее]
ЛЕКЦИЯ 6
Включим конденсатор в цепь постоянного тока. Некоторый заряд перетечет от источника тока на обкладки конденсатора. В цепи возникает кратковременный импульс зарядного тока. Конденсатор заряжается до напряжения источника, после чего ток прекращается.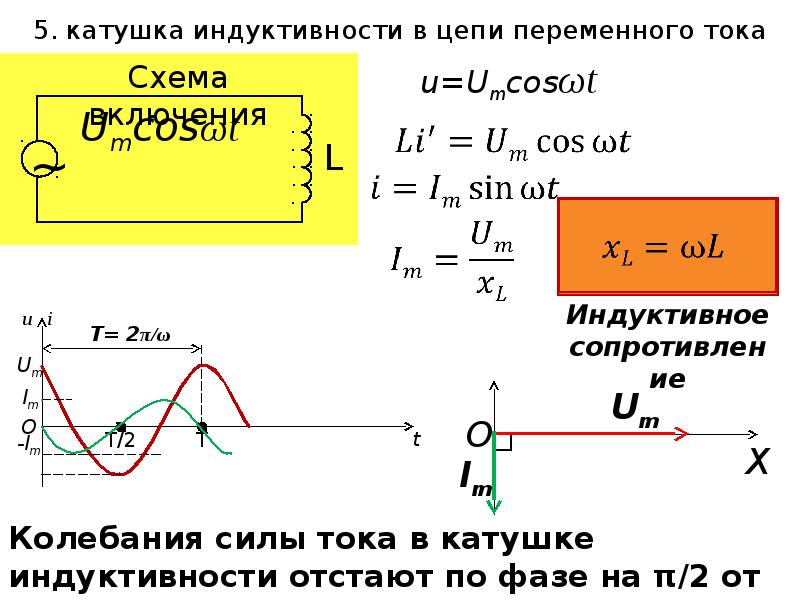 Через… [читать подробенее]
Через… [читать подробенее]
Резистор в цепи переменного тока
(7.20)
Здесь через IR обозначена амплитуда тока, протекающего через резистор. Связь между амплитудами тока и напряжения на резисторе выражается соотношением RIR = UR.
Фазовый сдвиг между током и напряжением на резисторе равен нулю.
… [читать подробенее]
Конденсатор в цепи переменного тока
Количество просмотров публикации Конденсатор в цепи переменного тока — 81
Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором.
Понятие и виды, 2019-2020.
Если подключить конденсатор к источнику постоянного тока, то в цепи возникнет кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Если заряженный конденсатор отключить от источника постоянного тока и соединить ᴇᴦο обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при ϶том наблюдается кратковременная вспышка лампы.
При включении конденсатора в цепь переменного тока процесс ᴇᴦο зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор вновь заряжается, но полярность напряжения на ᴇᴦο обкладках изменяется на противоположную и т.д. Процессы зарядки и разрядки конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения.
Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с ᴇᴦο выводами, течет переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока (рис. 6), кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы.
Установим связь между амплитудой колебаний напряжения на обкладках конденсатора и амплитудой колебаний силы тока. При изменениях напряжения на обкладках конденсатора по гармоническому закону
заряд на ᴇᴦο обкладках изменяется по закону:
Электрический ток в цепи возникает в результате изменения заряда конденсатора: i = q’. По϶тому колебания силы тока в цепи происходят по закону:
Отсюда следует, что, колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на р/2 или колебания силы тока опережают по фазе колебания напряжения на р/2 (рис. 7). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равнои̌ нулю и т.д.
Произведение Um⋅щ⋅C является амплитудой колебаний силы тока:
Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде колебаний силы тока называют емкостным сопротивлением конденсатора (обозначается ХC):
Связь между амплитудным значением силы тока и амплитудным значением напряжения по форме совпадает с выражением закона Ома для участка цепи постоянного тока, в котором вместо электрического сопротивления фигурирует емкостное сопротивление конденсатора:
Емкостное сопротивление конденсатора, как и индуктивное сопротивление катушки, не является постояннои̌ величинои̌. Оно обратно пропорционально частоте переменного тока. По϶тому амплитуда колебаний силы тока в цепи конденсатора при постояннои̌ амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте.
Оно обратно пропорционально частоте переменного тока. По϶тому амплитуда колебаний силы тока в цепи конденсатора при постояннои̌ амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте.
Конденсатор в цепи переменного тока
Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может.
Совершенно иначе ведет себя конденсатор в цепи переменного тока (Рис 1,а).
Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила.
В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i, сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться. Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.
Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.
После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать.
Итак, к концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения.
С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС. Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления.
Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления.
Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать. Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится.
Итак, к концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. е. на той пластине, где был прежде плюс, будет минус, а где был минус, будет плюс. При этом ЭДС достигнет амплитудного значения (противоположного направления), а ток в цепи будет равен нулю.
В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток. Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях.
Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях.
Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока. Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.
Отметим, что в цепи с индуктивностью ток отставал от напряжения, а в цепи с емкостью ток опережает напряжение. И в том и в другом случае между фазами тока и напряжения имеется сдвиг, но знаки этих сдвигов противоположны
Емкостное сопротивление конденсатора
Мы уже заметили, что ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС
Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.
е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.
Рисунок 2. Зависимость емкостного сопротивления конденсатра от частоты.
Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может.
Величина емкостного сопротивления определяется по следующей формуле:
где Хс — емкостное сопротивление конденсатора в ом;
f—частота переменного тока в гц;
ω — угловая частота переменного тока;
С — емкость конденсатора в ф.
При включении конденсатора в цепь переменного тока, в последнем, как и в индуктивности, не затрачивается мощность, так как фазы тока и напряжения сдвинуты друг относительно друга на 90°. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.
Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.
Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается большая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность. И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому се называют мощностью потерь.
Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки.
Ранее мы сравнивали электрическую емкость с вместимостью герметически (наглухо) закрытого сосуда или с площадью дна открытого сосуда, имеющего вертикальные стенки.
Конденсатор в цепи переменного тока целесообразно сравнивать с гиб-костью пружины. При этом во избежание возможных недоразумений условимся под гибкостью понимать не упругость («твердость») пружины, а величину, ей обратную, т. е. «мягкость» или «податливость» пружины.
Представим себе, что мы периодически сжимаем и растягиваем спиральную пружину, прикрепленную одним концом наглухо к стене. Время, в течение которого мы будем производить полный цикл сжатия и растяжения пружины, будет соответствовать периоду переменного тока.
Таким образом, мы в течение первой четверти периода будем сжимать пружину, в течение второй четверти периода отпускать ее, в течение третьей четверти периода растягивать и в течение четвертой четверти снова отпускать.
Кроме того, условимся, что наши усилия в течение периода будут неравномерными, а именно: они будут нарастать от нуля до максимума в течение первой и третьей четвертей периода и уменьшаться от максимума до нуля в течение второй и четвертой четвертей.
Сжимая и растягивая пружину таким образом, мы заметим, что в начале первой четверти периода незакрепленный конец пружины будет двигаться довольно быстро при сравнительно малых усилиях с нашей стороны.
В конце первой четверти периода (когда пружина сожмется), наоборот, несмотря на возросшие усилия, незакрепленный конец пружины будет двигаться очень медленно.
В продолжение второй четверти периода, когда мы будем постепенно ослаблять давление на пружину, ее незакрепленный конец будет двигаться по направлению от стены к нам, хотя наши задерживающие усилия направлены по направлению к стене. При этом наши усилия в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины наименьшей. В конце же второй четверти периода, когда наши усилия будут наименьшими, скорость движения пружины будет наибольшей и т. д.
Продолжив аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и построив графики (рис. 1,б) изменения наших усилий и скорости движения незакрепленного конца пружины, мы убедимся, что эти графики в точности соответствуют графикам ЭДС и тока в емкостной цепи (рис 1,а), причем график усилий будет соответствовать графику ЭДС , а график скорости — графику силы тока.
1,б) изменения наших усилий и скорости движения незакрепленного конца пружины, мы убедимся, что эти графики в точности соответствуют графикам ЭДС и тока в емкостной цепи (рис 1,а), причем график усилий будет соответствовать графику ЭДС , а график скорости — графику силы тока.
Рисунок 3. а)Процессы в цепи переменного тока с конденсатором и б)сравнение конденсатора с пружиной.
Нетрудно, заметить, что пружина, так же как и конденсатор, в течение одной четверти периода накапливает энергию, а в течение другой четверти периода отдает ее обратно.
Вполне очевидно также, что чем меньше гибкость пружины,- т е. чем она более упруга, тем большее противодействие она будет оказывать нашим усилиям. Точно так же и в электрической цепи: чем меньше емкость, тем больше будет сопротивление цепи при данной частоте.
И наконец, чем медленнее мы будем сжимать и растягивать пружину, тем меньше будет скорость движения ее незакрепленного конца. Аналогично этому, чем меньше частота, тем меньше сила тока при данной ЭДС.
При постоянном давлении пружина только сожмется и на этом прекратит свое движение, так же как при постоянной ЭДС конденсатор только зарядится и на этом прекратится дальнейшее движение электронов в цепи.
А теперь как ведет себя конденсатор в цепи переменного тока вы можете посмотреть в следующем видео:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Цепи переменного тока — презентация онлайн
Цепи переменного тока
ГР ОМ 14-1
Белый Р.Ю.
RCL
в цепи переменного тока -1
@ Краснополянская школа № 1 Домнин Константин Михайлович 2006 год
1. Действующие значения
тока и напряжения.
Активное сопротивление в
цепи переменного тока
Действующие значения тока и напряжения, виды сопротивлений
Рассмотрим активное сопротивление в цепи переменного тока:
U U m cos t
R
Мгновенное значение силы
тока через активное
сопротивление
пропорционально
мгновенному значению
напряжения
U U m cos t
i
I m cos t
R
R
Активное сопротивление в цепи переменного тока
Графики изменения напряжения и силы
тока на активном сопротивлении
Время, с
Колебания напряжения
Колебания силы тока
Активное сопротивление в цепи переменного тока
Введем понятие действующего значения напряжения и силы тока:
i,A
При прохождении переменного тока
через проводник, как видно из графика,
его значение не остается постоянным:
Im
Iд
t,c
Ток плавно изменяется от нуля до
амплитудного значения. Значит и
Значит и
тепловое действие тока различно в
разные моменты времени.
Какое значение тока можно использовать
для расчета работы и мощности тока ?
Понятно, что необходимо брать усредненное значение, называемое
действующим значением силы тока (т.е действие переменного тока
заменяется действием постоянного тока, дающего такой же тепловой эффект)
Im
Iд
0,7 I m
2
Активное сопротивление в цепи переменного тока
Аналогично действующее значение напряжения:
Um
Uд
0,7 I m
2
Тогда действующая мощность (средняя мощность):
P Uд Iд
а выделяемое в проводнике тепло:
2
Uд
Q U д I д t I д R t
t
R
2
2. Конденсатор в цепи
переменного тока
C
Конденсатор в цепи переменного тока
Давайте вспомним, что такое конденсатор
Конденсатор – это система из двух
проводников, разделенных слоем
диэлектрика (воздуха, слюды,
керамики …)
Ясно, что конденсатор
– это разрыв в цепи
(подобно
разомкнутому
выключателю),
поэтому постоянный
ток конденсатор не
проводит
Конденсатор в цепи переменного тока
Посмотрим, как ведет себя конденсатор в цепи переменного
тока:
Замкнем цепь и понаблюдаем движение электронов в цепи:
~
Источник ~ тока,
обладающий
Мы видим, что ток между обкладками конденсатора по
прежнему не идет, однако вследствие перезарядки
конденсатора через лампочку идет переменный ток – т. е.
е.
конденсатор проводит переменный ток
и
r
Конденсатор в цепи переменного тока
Итак, конденсатор проводит переменный ток, однако он
оказывает току сопротивление, которое называется емкостным
сопротивлением
1
1
XС
C 2 C
XС
— емкостное
сопротивление
— циклическая частота протекающего тока
С – электроемкость конденсатора
— частота тока
Конденсатор в цепи переменного тока
Проанализируем формулу емкостного сопротивления:
1
1
XС
C 2 C
Из формулы видно, что сопротивление конденсатора обратно
пропорционально частоте протекающего тока и его электроемкости :
XС
XС 0
0 XС
Сопротивление конденсатора
уменьшается с ростом
частоты, значит конденсатор
хорошо проводит
высокочастотные колебания и
плохо – низкочастотные, а
постоянный ток вообще не
проводит
Конденсатор в цепи переменного тока
График зависимости сопротивления конденсатора от частоты:
XС
XС1
XС2
С1
С2
С2>C1
Сопротивление конденсатора зависит и от его электроемкости:
при фиксированной частоте конденсатор с большей емкостью будет
обладать меньшим сопротивлением
Конденсатор в цепи переменного тока
Сдвиг фаз между напряжением и током:
Если напряжение на конденсаторе меняется по закону:
U U m cos t
то заряд на конденсаторе равен:
q CU m cos t
тогда сила тока в цепи:
i q (CU m cos t ) U mC sin t
U mC cos( t )
2
Конденсатор в цепи переменного тока
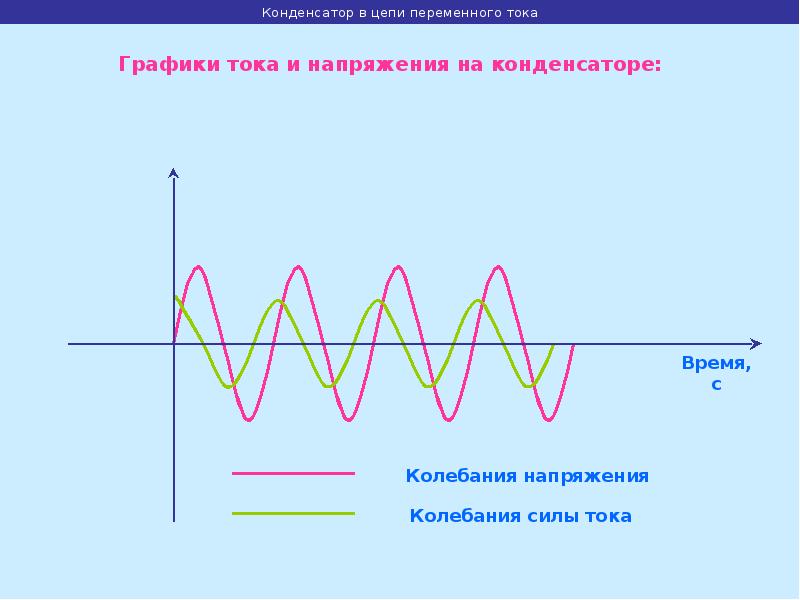
Графики тока и напряжения на конденсаторе:
Время, с
Колебания напряжения
Колебания силы тока
3. Индуктивность в цепи
Индуктивность в цепи
переменного тока
L
Индуктивность в цепи переменного тока
Давайте вспомним, что такое индуктивность
Индуктивность L– это физическая величина,
подобная массе в механике. Как в механике для
изменения скорости тела нужно время, и масса
является мерой этого времени (инерция), так и
электродинамике для изменения тока через
проводник нужно время и индуктивность является
мерой этого времени (самоиндукция)
L
Катушка индуктивности –
это обычный проводник с
необычной формой,
обладающий активным
сопротивлением.
Поэтому катушка хорошо
проводит постоянный ток,
значение которого
ограничено только его
активным сопротивлением
Явление самоиндукции возникает только в моменты включения и
выключения (препятствует любому изменению тока)
Индуктивность в цепи переменного тока
Посмотрим, как ведет себя индуктивность в цепи переменного
тока:
Замкнем цепь и сравним яркость горения лампочек 1 и 2
Л1
Л2
R
L
~
Источник ~ тока,
обладающий
и
r
В цепи сопротивление R поберем равным активному сопротивлению L
Лампочка Л1 горит гораздо ярче, чем Л2
Почему ?
Индуктивность в цепи переменного тока
Все дело в явлении самоиндукции, возникающей в катушке при
любом изменении тока, которое мешает этому изменению –
поэтому у катушки индуктивности кроме активного
сопротивления провода, из которого она сделана, появляется
еще одно сопротивление, обусловленное явлением
самоиндукции и называемое индуктивным сопротивлением
X L L 2 L
—
циклическая частота протекающего тока
L – индуктивность катушки
— частота тока
XL
Индуктивность в цепи переменного тока
Проанализируем формулу индуктивного сопротивления:
X L L 2 L
Из формулы видно, что индуктивное сопротивление прямо
пропорционально частоте протекающего тока и индуктивности
X
L
XL
0 XL 0
Индуктивное сопротивление
увеличивается с ростом
частоты, значит катушка
хорошо проводит
низкочастотные колебания и
плохо – высокочастотные, а
для постоянного тока оно
равно нулю
Индуктивность в цепи переменного тока
Сдвиг фаз между напряжением и током:
Если ток в катушке изменяется по закону:
i I m cos t
то напряжение на катушке изменяется по закону:
U U m sin( t )
2
Правило:
CIVIL
Индуктивность в цепи переменного тока
Графики тока и напряжения на индуктивности:
Время, с
Колебания напряжения
Колебания силы тока
4. Использование
Использование
частотных свойств
конденсатора и катушки
индуктивности
5. Использование частотных свойств конденсатора и катушки
Таким образом, в цепи переменного тока можно выделить 3 вида
сопротивлений (или три вида элементов, оказывающих сопротивление
току)
СОПРОТИВЛЕНИЕ
R
активное
реактивное
XL индуктивное
емкостное XC
Реальные электрические цепи содержат все виды сопротивлений
(активное, индуктивное и емкостное), поэтому ток в реальной цепи зависит
от ее полного (эквивалентного) сопротивления, а сдвиг фаз определяется
величиной L и C цепи
5. Использование частотных свойств конденсатора и катушки
Итак,
• конденсатор хорошо проводит ВЧ колебания, и плохо – НЧ
колебания
• катушка наоборот: хорошо НЧ колебания и плохо – ВЧ
колебания
Эти свойства позволяют создать:
1. Различные частотные фильтры – схемы, позволяющие
выделить из всего сигнала (например от магнитофона) НЧ и ВЧ
составляющие:
Вход сигнала
от
магнитофона
НЧ
ВЧ
Используя различные значения R, L и C, можно создавать
фильтры с заданными параметрами (полосой пропускания)
5. Использование частотных свойств конденсатора и катушки
Использование частотных свойств конденсатора и катушки
2. Электрический колебательный контур, состоящий из конденсатора и
катушки индуктивности
L
C
Колебательный контур обладает
замечательный свойством – пропускать
колебания (резонировать) только
определенной частоты, зависящей от
емкости конденсатора и индуктивности
катушки
рез
1
2 LC
Эти свойства контура широко
применяются в радио и
телеприемной и передающей
аппаратуре для селекции сигналов
Схемы конденсаторов переменного тока | Реактивное сопротивление и импеданс — емкостный
Конденсаторы Против. Резисторы
Конденсаторы ведут себя не так, как резисторы. В то время как резисторы пропускают через себя поток электронов, прямо пропорциональный падению напряжения, конденсаторы противостоят изменениям напряжения, потребляя или подавая ток, когда они заряжаются или разряжаются до нового уровня напряжения.
Поток электронов «через» конденсатор прямо пропорционален скорости изменения напряжения на конденсаторе. Это противодействие изменению напряжения представляет собой другую форму реактивного сопротивления , но совершенно противоположную тому, что демонстрируют катушки индуктивности.
Это противодействие изменению напряжения представляет собой другую форму реактивного сопротивления , но совершенно противоположную тому, что демонстрируют катушки индуктивности.
Характеристики цепи конденсатора
Выраженное математически соотношение между током, проходящим через конденсатор, и скоростью изменения напряжения на конденсаторе выглядит следующим образом:
Выражение de/dt получено из исчисления и означает скорость изменения мгновенного напряжения (e) во времени, в вольтах в секунду.Емкость (C) в фарадах, а мгновенный ток (i), разумеется, в амперах.
Иногда скорость мгновенного изменения напряжения во времени выражается как dv/dt вместо de/dt: для обозначения напряжения используется строчная буква «v» или «e», но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую цепь конденсатора:
.
Чисто емкостная цепь: напряжение конденсатора отстает от тока конденсатора на 90°
Если бы мы построили график тока и напряжения для этой очень простой схемы, это выглядело бы примерно так:
Чисто емкостные сигналы цепи.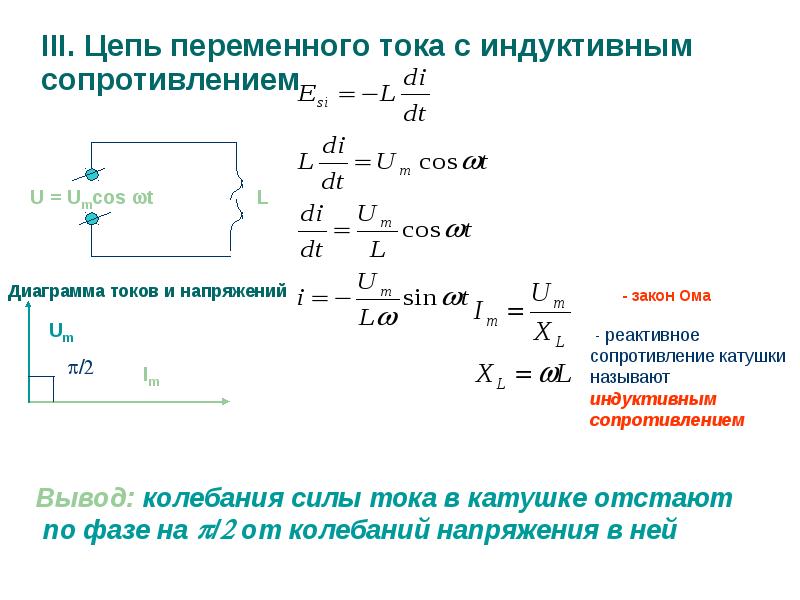
Помните, ток через конденсатор является реакцией на изменение напряжения на нем.
Следовательно, мгновенный ток равен нулю всякий раз, когда мгновенное напряжение имеет пиковое значение (нулевое изменение или наклон уровня на синусоиде напряжения), а мгновенный ток имеет пиковое значение всякий раз, когда мгновенное напряжение имеет максимальное изменение (точки наибольшего наклона волны напряжения, где она пересекает нулевую линию).
Это приводит к тому, что волна напряжения на -90° не совпадает по фазе с волной тока.Глядя на график, кажется, что волна тока опережает волну напряжения; ток «опережает» напряжение, а напряжение «отстает» от тока.
Напряжение отстает от тока на 90° в чисто емкостной цепи.
Как вы могли догадаться, та же самая необычная волна мощности, которую мы видели в простой схеме с катушкой индуктивности, присутствует и в простой схеме с конденсатором:
В чисто емкостной цепи мгновенная мощность может быть положительной или отрицательной.
Как и в случае с простой индукторной схемой, фазовый сдвиг на 90 градусов между напряжением и током приводит к волне мощности, которая в равной степени чередуется между положительной и отрицательной. Это означает, что конденсатор не рассеивает мощность, реагируя на изменения напряжения; он просто поглощает и высвобождает энергию попеременно.
Реактивное сопротивление конденсатора
Противодействие конденсатора изменению напряжения переводится в противодействие переменному напряжению в целом, которое по определению всегда изменяется по мгновенной величине и направлению.
Для любой заданной величины переменного напряжения на заданной частоте конденсатор заданной емкости будет «проводить» переменный ток определенной величины.
Точно так же, как ток через резистор является функцией напряжения на резисторе и сопротивления резистора, переменный ток через конденсатор является функцией переменного напряжения на нем, и реактивное сопротивление , создаваемое конденсатором .
Как и в случае катушек индуктивности, реактивное сопротивление конденсатора выражается в омах и обозначается буквой X (или XC, если быть точным).
Поскольку конденсаторы «проводят» ток пропорционально скорости изменения напряжения, они будут пропускать больший ток при более быстро меняющемся напряжении (поскольку они заряжаются и разряжаются до одинаковых пиков напряжения за меньшее время) и меньший ток при более медленно меняющемся напряжении. .
Это означает, что реактивное сопротивление в омах для любого конденсатора равно обратно пропорционально частоте переменного тока.
Реактивное сопротивление конденсатора 100 мкФ:
| Частота (Герц) | Реактивное сопротивление (Ом) |
| 60 | 26.5258 |
| 120 | 13.2629 |
| 2500 | 0,6366 |
Обратите внимание, что отношение емкостного сопротивления к частоте прямо противоположно отношению индуктивного сопротивления.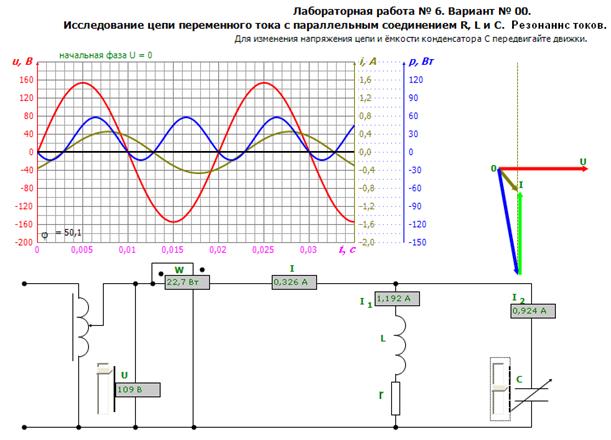
Емкостное реактивное сопротивление (в омах) уменьшается с увеличением частоты переменного тока. И наоборот, индуктивное сопротивление (в омах) увеличивается с увеличением частоты переменного тока. Катушки индуктивности препятствуют более быстрому изменению тока, вызывая большее падение напряжения; конденсаторы противодействуют более быстрому изменению падения напряжения, пропуская большие токи.
Как и в случае с катушками индуктивности, член уравнения реактивного сопротивления 2πf может быть заменен строчной греческой буквой Омега (ω), которая обозначается угловой скоростью цепи переменного тока. Таким образом, уравнение XC = 1/(2πfC) также может быть записано как XC = 1/(ωC), где ω выражено в единицах радиан в секунду .
Переменный ток в простой емкостной цепи равен напряжению (в вольтах), деленному на емкостное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в омах).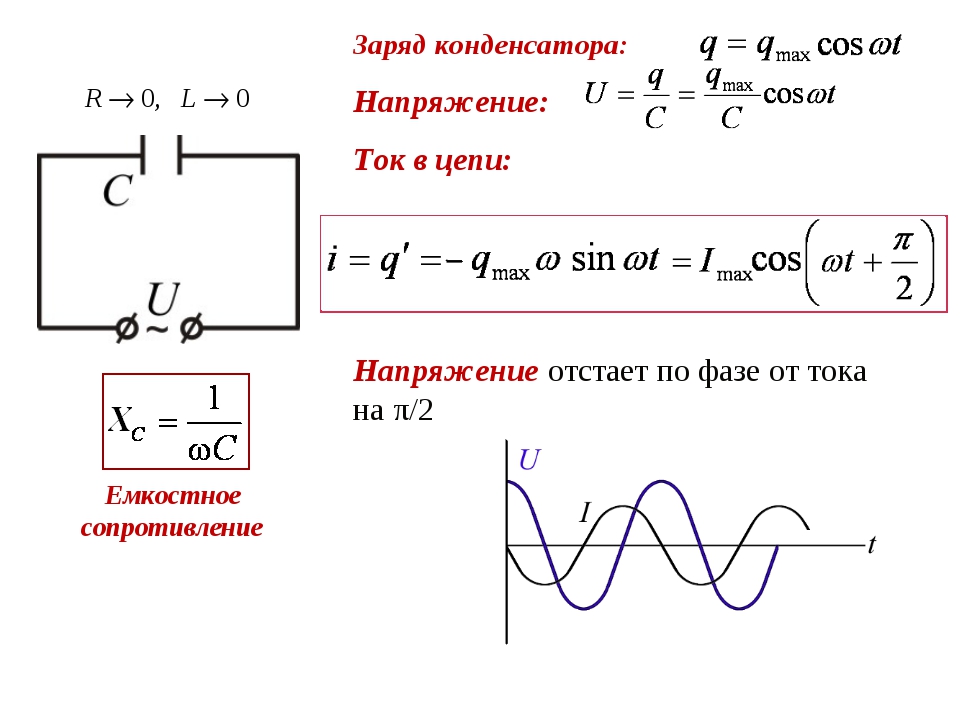 Следующая схема иллюстрирует это математическое соотношение на примере:
Следующая схема иллюстрирует это математическое соотношение на примере:
Емкостное реактивное сопротивление.
Однако нужно помнить, что напряжение и ток здесь не совпадают по фазе. Как было показано ранее, ток имеет фазовый сдвиг +90° по отношению к напряжению. Если мы представим эти фазовые углы напряжения и тока математически, мы сможем вычислить фазовый угол реактивного сопротивления конденсатора току.
В конденсаторе напряжение отстает от тока на 90°.
Математически мы говорим, что фазовый угол сопротивления конденсатора току равен -90°, а это означает, что сопротивление конденсатора току является отрицательной мнимой величиной. (См. рисунок выше.) Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где взаимодействуют реактивное сопротивление и сопротивление.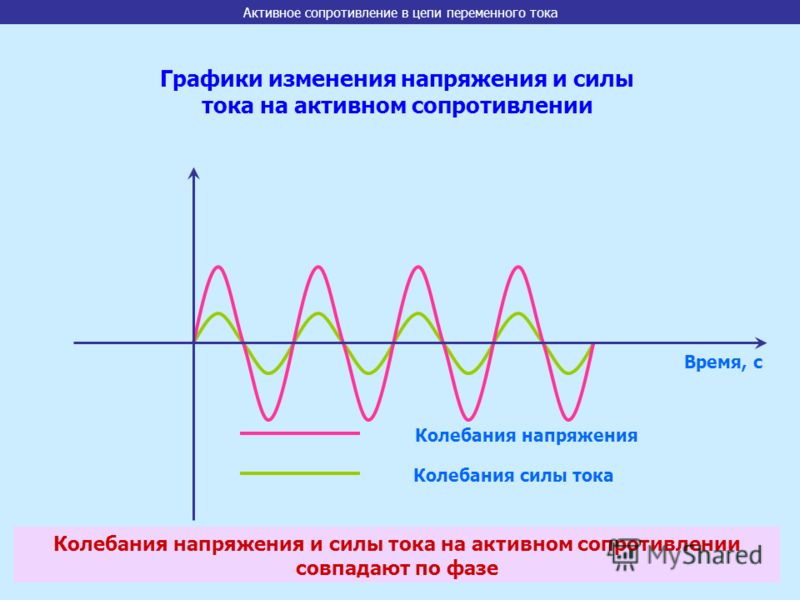
Будет полезно представить сопротивление любого компонента току в терминах комплексных чисел, а не только скалярных величин сопротивления и реактивного сопротивления.
ОБЗОР:
- Емкостное реактивное сопротивление — это сопротивление, которое конденсатор оказывает переменному току из-за сдвинутого по фазе накопления и высвобождения энергии в своем электрическом поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах так же, как сопротивление (R).
- Емкостное реактивное сопротивление можно рассчитать по следующей формуле: XC = 1/(2πfC)
- Емкостное сопротивление уменьшается с увеличением частоты. Другими словами, чем выше частота, тем меньше она противостоит (тем больше «проводит») переменному току.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Мощность в цепи переменного тока — University Physics Volume 2
Цели обучения
По окончании раздела вы сможете:
- Опишите, как средняя мощность от цепи переменного тока может быть выражена через пиковый ток и напряжение и среднеквадратичное значение тока и напряжения
- Определить зависимость между фазовым углом тока и напряжения и средней мощностью, известную как коэффициент мощности
Элемент схемы рассеивает или производит мощность в соответствии с формулой, где I — ток через элемент, а V — напряжение на нем.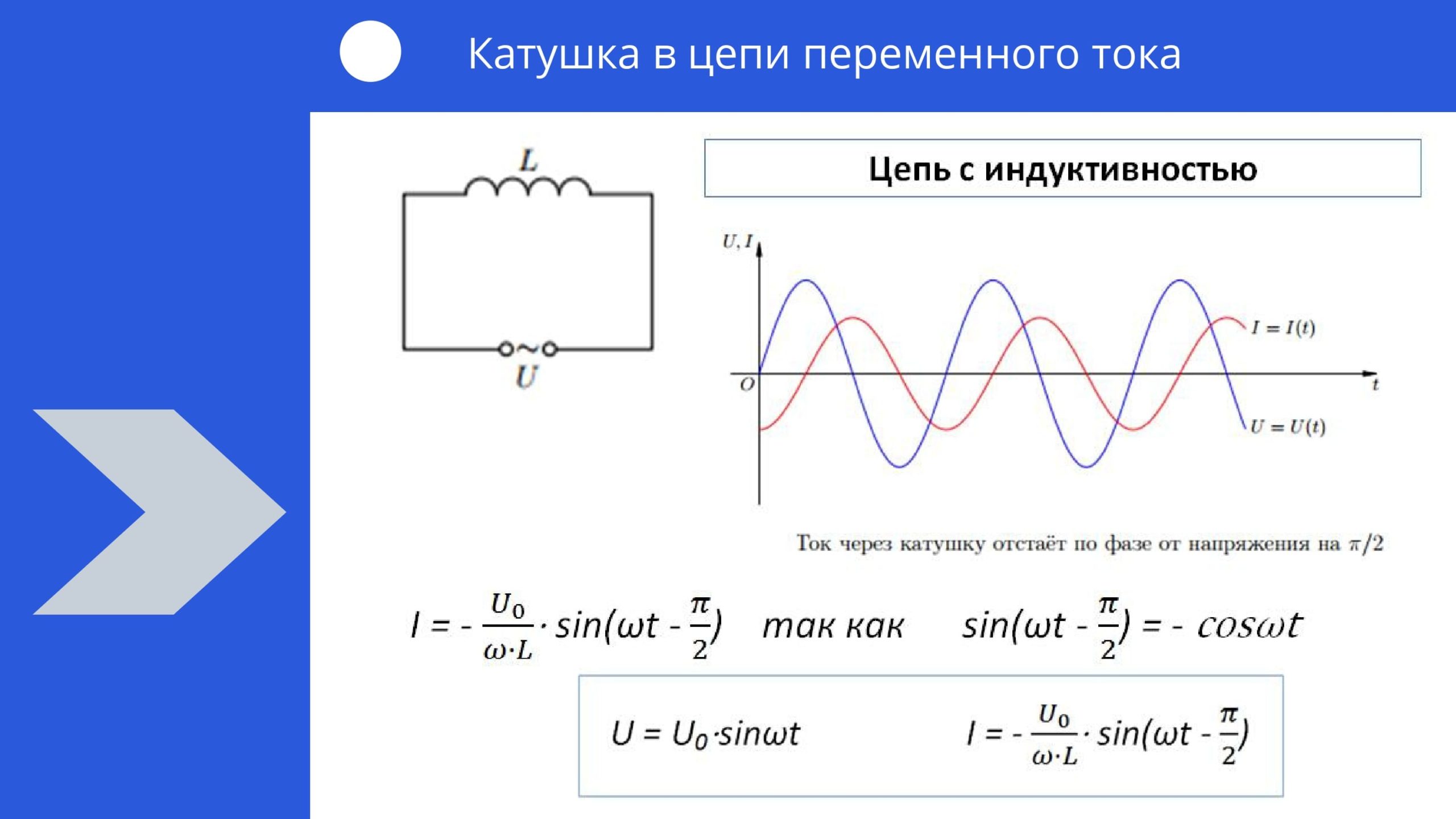 Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность также зависит от времени. График p ( t ) для различных элементов схемы показан на (рис.). Для резистора i ( t ) и v ( t ) находятся в фазе и поэтому всегда имеют один и тот же знак (см. (рисунок)). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разности фаз (см. (Рисунок) и (Рисунок)).Следовательно, p ( t ) в одни моменты времени положителен, а в другие отрицателен, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты времени и поглощают ее в другие.
Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность также зависит от времени. График p ( t ) для различных элементов схемы показан на (рис.). Для резистора i ( t ) и v ( t ) находятся в фазе и поэтому всегда имеют один и тот же знак (см. (рисунок)). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разности фаз (см. (Рисунок) и (Рисунок)).Следовательно, p ( t ) в одни моменты времени положителен, а в другие отрицателен, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты времени и поглощают ее в другие.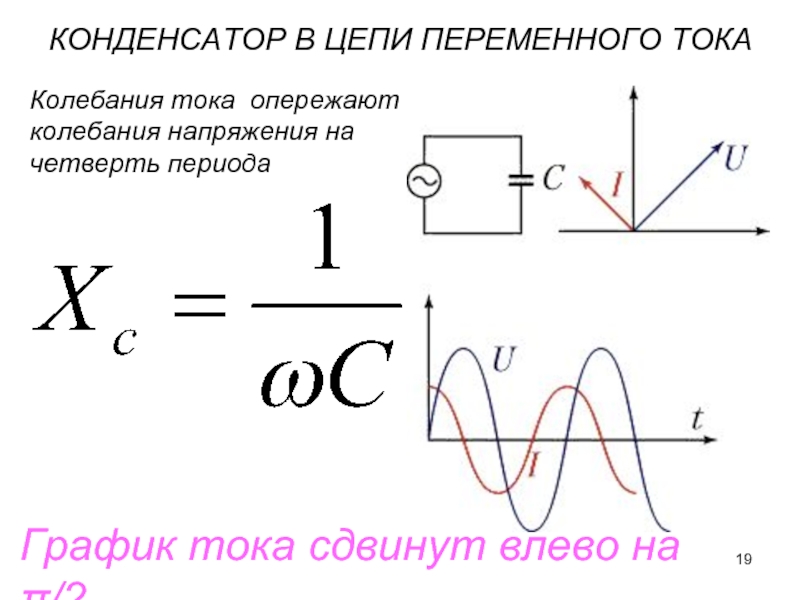
Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. Что нас почти всегда интересует, так это мощность, усредненная по времени, которую мы называем средней мощностью. Определяется средней по времени мгновенной мощностью за один цикл:
где — период колебаний.С заменами и этот интеграл становится
Используя тригонометрическое соотношение, получаем
Вычисление этих двух интегралов дает
и
Следовательно, средняя мощность, связанная с элементом схемы, равна
.
В инженерных приложениях известен как коэффициент мощности, который представляет собой величину, на которую мощность, подаваемая в цепь, меньше теоретического максимума цепи из-за несовпадения фаз напряжения и тока.Для резистора средняя рассеиваемая мощность равна
.
Сравнение p ( t ) и показано на (Рисунок)(d).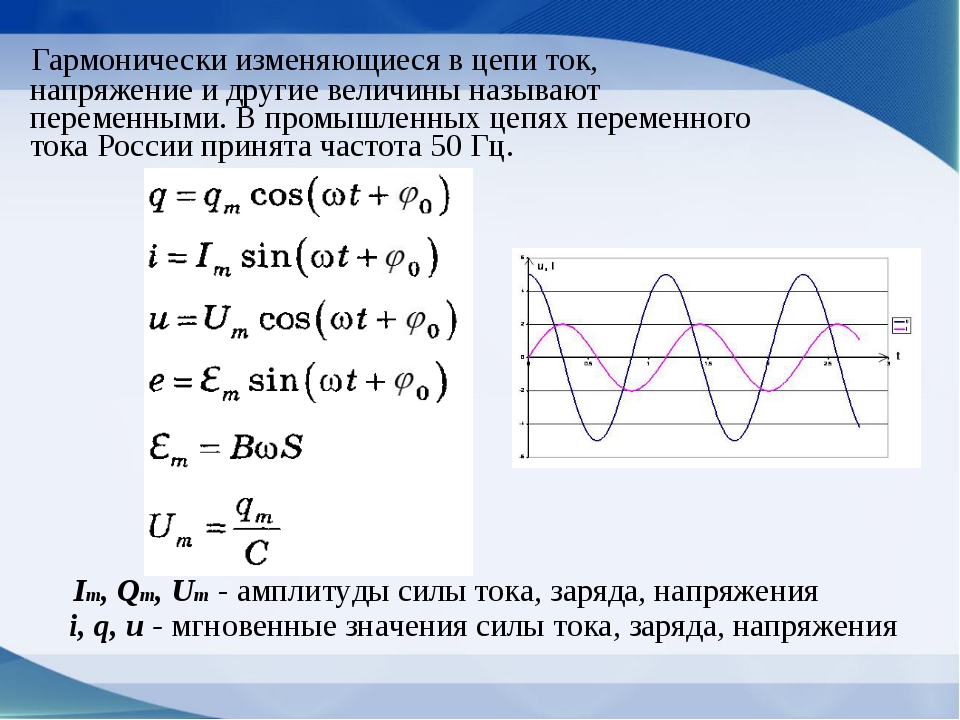 Чтобы сделать его аналог постоянным, мы используем среднеквадратичные значения тока и напряжения. По определению это
Чтобы сделать его аналог постоянным, мы используем среднеквадратичные значения тока и напряжения. По определению это
где
С получаем
Тогда мы можем написать для средней мощности, рассеиваемой резистором,
Это уравнение еще раз подчеркивает, почему при обсуждении выбрано среднеквадратичное значение, а не пиковые значения.Оба уравнения для средней мощности верны для (рис.), но среднеквадратичные значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не нужен.
Переменные напряжения и токи обычно описываются их действующими значениями. Например, 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника равна Поскольку большинство счетчиков переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, подключенный к бытовой розетке, будет показывать 110 В.
Для конденсатора и катушки индуктивности соответственно. Поскольку мы находим из (Рисунок), что средняя мощность, рассеиваемая любым из этих элементов, равна Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем возвращают ее обратно в цепь в течение другого полупериода. Это поведение показано на графиках (рисунок), (b) и (c), которые показывают, что p( t) колеблется синусоидально около нуля.
Это поведение показано на графиках (рисунок), (b) и (c), которые показывают, что p( t) колеблется синусоидально около нуля.
Фазовый угол для генератора переменного тока может иметь любое значение.Если генератор производит мощность; если он поглощает энергию. В среднеквадратичных значениях средняя мощность генератора переменного тока записывается как
.
Для генератора в цепи RLC ,
и
Отсюда средняя мощность генератора
Это также может быть записано как
.
, что означает, что мощность, вырабатываемая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.
Проверьте свои знания Вольтметр переменного тока, подключенный к клеммам генератора переменного тока частотой 45 Гц, показывает 7,07 В.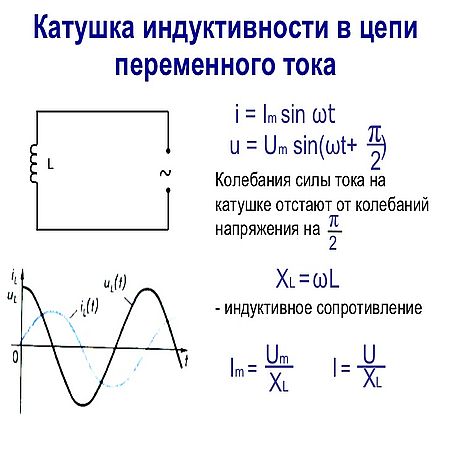 Напишите выражение для ЭДС генератора.
Напишите выражение для ЭДС генератора.
Проверьте свои знания Покажите, что среднеквадратичное значение напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичное значение тока выражается соответственно. Определите эти значения для компонентов схемы RLC (рисунок).
Резюме
- Средняя мощность переменного тока находится путем умножения среднеквадратичных значений тока и напряжения.
- Закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.
- В цепи переменного тока существует угол сдвига фаз между напряжением источника и током, который можно найти, разделив сопротивление на импеданс.
- На среднюю мощность, подаваемую в цепь RLC , влияет фазовый угол.

- Коэффициент мощности находится в диапазоне от –1 до 1.
Концептуальные вопросы
При каком значении фазового угла между выходным напряжением источника переменного тока и током средняя выходная мощность источника максимальна?
Обсудите разницу между средней мощностью и мгновенной мощностью.
Мгновенная мощность – это мощность в данный момент времени. Средняя мощность — это мощность, усредненная по циклу или количеству циклов.
Средний переменный ток, подаваемый в цепь, равен нулю.Несмотря на это, мощность рассеивается в цепи. Объяснять.
Может ли мгновенная выходная мощность источника переменного тока быть отрицательной? Может ли средняя выходная мощность быть отрицательной?
Мгновенная мощность может быть отрицательной, но выходная мощность не может быть отрицательной.
Номинальная мощность резистора, используемого в цепях переменного тока, относится к максимальной средней мощности, рассеиваемой в резисторе. Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?
Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?
Глоссарий
- средняя мощность
- среднее значение мгновенной мощности за один цикл
- коэффициент мощности
- величина, на которую мощность, подаваемая в цепь, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе
Напряжение переменного тока, подаваемое на конденсатор
Цепь, в которой есть только конденсатор и источник питания переменного тока (например, настенная розетка). Конденсатор — это устройство для хранения заряда . Оказывается, что между током и напряжением существует разность фаз 90°, при этом ток достигает своего пика 90° (1/4 цикла) до того, как напряжение достигает своего пика. Иными словами, в чисто емкостной цепи ток опережает напряжение на 90°.
Ток, протекающий в источнике переменного тока:
i = dQ/dt
Напряжение источника или приложенное напряжение V = V m sin ωt .
Где V м = амплитуда напряжения и ω = угловая частота.
Зависимость между напряжением и зарядом конденсатора: CV = Q
склад
В = напряжение на обкладках конденсатора
Q = заряд конденсатора.
Можно записать как:
Q = C × V м × sin (ω × t)
Ток, протекающий в источнике переменного тока:
i = dQ/dt
i = d(V m × sin (ω × t))/dt
i = C × V м × ω × cos(ω × t)
i = (V м × sin(ω × t + π/2)) (1/(ω × c))
Ток изменяется синусоидально с разностью фаз 90 градусов.
i = i m × sin(ω × t + π/2)
Амплитуда тока может быть записана как:
i m = ωCV m
Конденсаторы ведут себя не так, как резисторы. В то время как резисторы пропускают через себя поток электронов, прямо пропорциональный падению напряжения, конденсаторы противодействуют изменениям напряжения, потребляя или подавая ток, когда они заряжаются или разряжаются до нового уровня напряжения. Поток электронов «через» конденсатор прямо пропорционален скорости изменения напряжения на конденсаторе.Это противодействие изменению напряжения — еще одна форма реактивного сопротивления, но прямо противоположная той, которую проявляют катушки индуктивности.
Поток электронов «через» конденсатор прямо пропорционален скорости изменения напряжения на конденсаторе.Это противодействие изменению напряжения — еще одна форма реактивного сопротивления, но прямо противоположная той, которую проявляют катушки индуктивности.
Роль конденсатора в цепи переменного тока
Конденсаторы используются для хранения энергии на своих проводящих пластинах в виде электрического заряда. Конденсатор, включенный в цепь переменного тока, блокирует источник питания при полной зарядке. Когда в цепи есть источник питания переменного тока, конденсатор будет заряжаться и разряжаться попеременно со скоростью, определяемой подаваемой частотой.
Функция конденсатора в цепи переменного тока
Конденсаторы служат для наращивания напряжения выше входного напряжения и выпрямительные цепи для выравнивания колебаний тока.
Конденсаторы используются для блокировки статического напряжения постоянного тока и позволяют сигналам переменного тока проходить из одной области цепи в другую и известны как конденсаторы связи.
Развязывающие конденсаторы используются для устранения любых сигналов переменного тока в точке смещения постоянного тока.
Пусковой момент можно улучшить с помощью конденсаторов и использовать для повышения коэффициента мощности в энергосистемах.
Принцип зарядки и разрядки конденсатора
В процессе зарядки конденсатора ток течет к положительной пластине, в этом процессе к этой пластине добавляется положительный заряд.
В случае, когда конденсатор полностью заряжен, ток в цепи не течет из-за разности потенциалов на конденсаторе, равной напряжению источника. Это означает, что зарядный ток падает до нуля (напряжение конденсатора = напряжению источника).
В процессе разрядки конденсатора ток течет от положительной пластины к отрицательной, то есть в противоположном направлении.
Конденсаторы напряжения переменного тока – определение, назначение и вывод конденсатора переменного тока
Эта статья дает четкое представление об электрических цепях при использовании переменного напряжения на конденсаторе. В этой схеме мы соединили конденсатор и переменное напряжение V, обозначенное символом «~».
В этой схеме мы соединили конденсатор и переменное напряжение V, обозначенное символом «~».
[Изображение будет загружено в ближайшее время]
Напряжение в цепи создает разность потенциалов на ее клеммах, которая изменяется синусоидально.
Выражение для разности потенциалов v или напряжения переменного тока приведено ниже:
v = vmsinωt
Где
vm = амплитуда колеблющейся разности потенциалов
ω = угловая частота
Мы можем рассчитать ток, доступный в резисторе при текущем напряжении, с использованием правила петли Кирхгофа.
Вот выражение правила цикла Кирхгофа:
\[\sum\]v(t) = 0
На приведенной выше диаграмме поясняется источник переменного напряжения, приложенный к конденсатору.
Емкость в цепи переменного тока и емкостное реактивное сопротивление
На приведенном выше рисунке мы можем написать выражение для конденсатора:
v = \[\frac{q}{C}\]
можно переписать выражение как:
vmsinωt = \[\frac{q}{C}\]
Мы можем рассчитать величину тока в цепи, используя это соотношение,
i = \[\frac{ dq}{dt}\]
⇒ i = \[\frac{d(v_{m}Csinωt)}{dt}\] = ωCvmcos ωt
⇒ i = \[i_{m}sin(ωt +\ frac{π}{2})\]
В приведенном выше выражении используется соотношение Cosωt = \[sin(ωt +\frac{π}{2})\]
Также мы можем переписать амплитуда тока как:
im = ωCvm
Или мы можем выразить это как
im = \[\frac{v_{m}}{\frac{1}{ω_{C}}}\]
В этом выражении \[\frac{1}{ω_{C}}\] можно принять за эквивалент сопротивления устройства.
Вот почему термин для этого выражения называется емкостным сопротивлением. XC — это символ, используемый для пленного сопротивления.
XC = \[\frac{1}{ω_{C}}\]
Также мы можем рассчитать амплитуду тока в цепи, используя следующее соотношение:
im = \[\frac{v_ {m}}{X_{C}}\]
Как работает конденсатор в цепи переменного тока?
В электрической цепи конденсатор обеспечивает прямую связь с переменным напряжением питания. Когда происходит изменение напряжения питания (напряжение увеличивается или уменьшается), конденсатор заряжается или разряжается в соответствии с изменением напряжения.
Когда ток проходит через цепь, он будет следовать в одном направлении, а затем в другом направлении, не позволяя фактическому току проходить через конденсатор.
Однако в цепи постоянного тока сценарий другой. Когда ток протекает через конденсатор, подключенный к цепи постоянного тока, пластина конденсатора имеет как положительный, так и отрицательный заряд.
Цепи конденсаторов переменного тока
[Изображение будет загружено в ближайшее время]
Когда конденсатор подключен к цепи переменного тока, он будет последовательно заряжаться и разряжаться со скоростью, вычисляемой частотой источника питания.В цепях переменного тока емкость зависит от частоты, поскольку конденсатор постоянно заряжается и разряжается.
Какова роль конденсатора в цепи переменного и постоянного тока?
1. Роль конденсатора в цепи постоянного тока
В цепи постоянного тока конденсатор заряжается медленнее. Конденсатор заряжается до напряжения питания, но препятствует дальнейшему прохождению через него тока. Он блокирует протекание тока, поскольку диэлектрик конденсатора является непроводящим и изолятором.
2. Роль конденсатора в цепи переменного тока
Когда конденсатор используется в цепи переменного тока, он заряжается и разряжается для изменения напряжения питания. Согласно записи, ток становится прямо пропорциональным максимальному напряжению на пластинах.
Согласно записи, ток становится прямо пропорциональным максимальному напряжению на пластинах.
Конденсаторы, включенные в цепь переменного тока, блокируют подачу питания, когда они полностью заряжены. Когда в цепи есть источник питания переменного тока, конденсаторы будут заряжаться и разряжаться попеременно со скоростью, определяемой подаваемой частотой.
Функция конденсатора в цепи переменного тока
Мы знаем, что конденсаторы используются для накопления энергии на своих проводящих пластинах в виде электрического заряда.
Конденсаторы используются для повышения напряжения выше входного. Это помогает в плавных текущих колебаниях.
Самое главное, конденсаторы используются в схемах выпрямителей для выравнивания колебаний тока.
Конденсаторы также используются для блокирования статического напряжения постоянного тока и позволяют сигналам переменного тока проходить из одной области цепи в другую.
 Эти типы конденсаторов известны как конденсаторы связи.
Эти типы конденсаторов известны как конденсаторы связи.Для устранения любых сигналов переменного тока в точке смещения постоянного тока используются развязывающие конденсаторы.
Пусковой крутящий момент можно увеличить с помощью конденсаторов. Кроме того, конденсаторы хороши для одной фазы.
Также конденсаторы используются для улучшения коэффициента мощности в энергосистемах.
Переменный ток через конденсатор
Мы можем назвать пару проводников конденсатором, разделенным некоторой средой.Когда мы подключаем конденсатор к цепи переменного тока, мы можем найти ток, протекающий через него.
Когда мы подключаем лампу в эту цепь, лампа светится, что показывает прохождение тока в цепи переменного тока. Мы пришли к выводу, что конденсатор является проводником в цепи переменного тока, но работает как изолятор в цепи постоянного тока.
[Изображение будет загружено в ближайшее время]
Предотвращение колебаний напряжения из-за линий электропитания
При использовании источников питания, таких как понижающие регуляторы или линейные регуляторы, они регулируют заданное напряжение для снабжения нагрузки электрической энергией.В некоторых приложениях, например, в лабораторных источниках питания или электронных системах, в которых различные компоненты подключены к более длинным кабелям, регулируемое напряжение не всегда является особенно точным в той точке, где оно необходимо, из-за различных падений напряжения на соединительных линиях. Точность управления зависит от многих параметров. Одной из них является точность по постоянному току, когда нагрузке требуется непрерывный и постоянный ток. Существует также точность переменного тока генерируемого напряжения. Это определяется тем, как генерируемое напряжение ведет себя при переходных процессах нагрузки.Эффекты, влияющие на точность постоянного тока, включают требуемое опорное напряжение, возможно, резистивный делитель напряжения и поведение усилителя ошибки, а также некоторые другие факторы, влияющие на источник питания.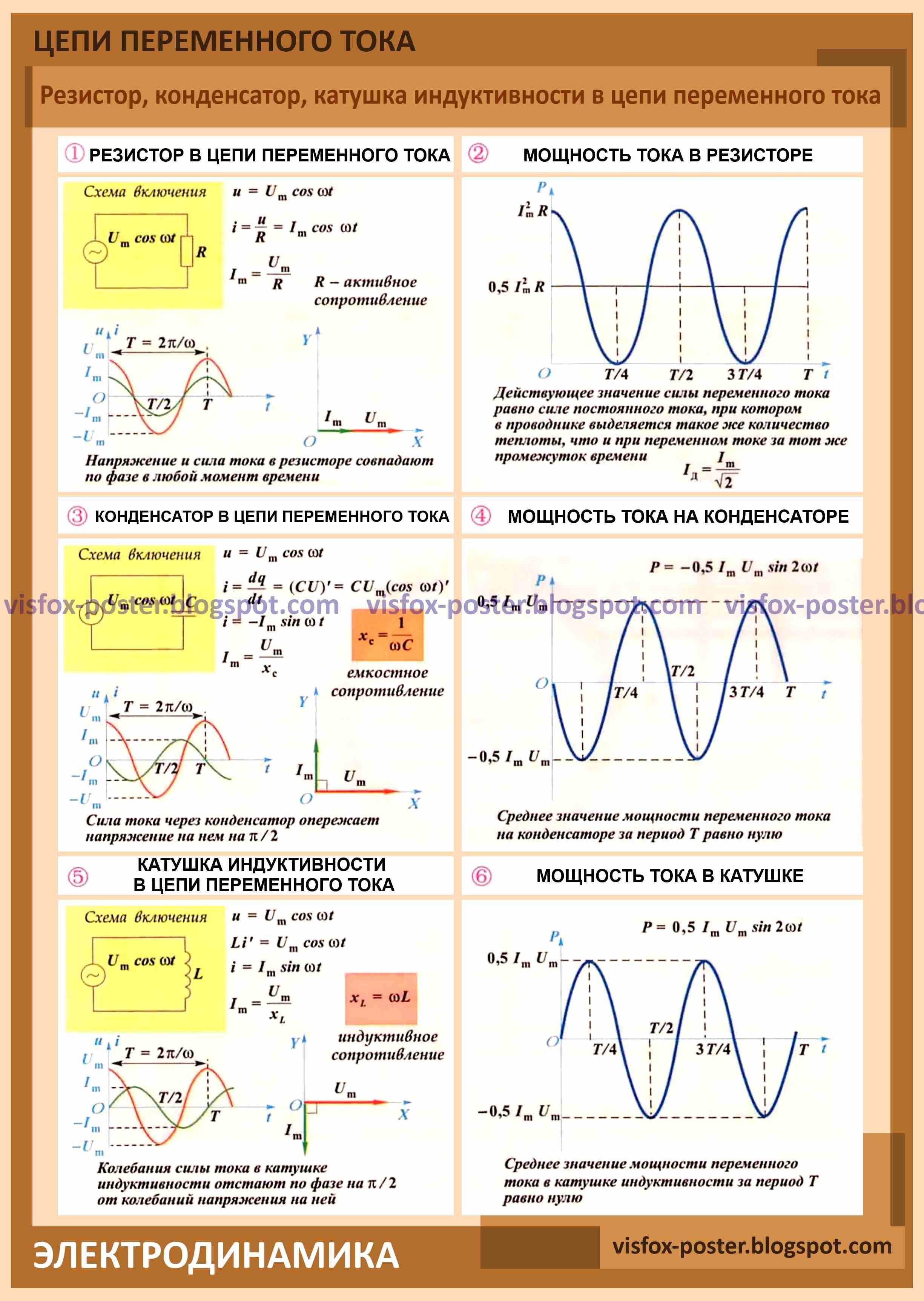 Критические факторы для точности переменного тока включают выбранный уровень мощности, резервные конденсаторы, а также архитектуру и конструкцию контура управления.
Критические факторы для точности переменного тока включают выбранный уровень мощности, резервные конденсаторы, а также архитектуру и конструкцию контура управления.
В дополнение ко всем этим факторам, влияющим на точность генерируемого напряжения питания, необходимо учитывать и другие эффекты.Если источник питания пространственно отделен от питаемой нагрузки, будет существовать падение напряжения между регулируемым напряжением и местом, где требуется электрическая энергия. Это падение напряжения зависит от сопротивления, присутствующего между регулятором напряжения и нагрузкой. Это может быть кабель со штекерными контактами или более длинная дорожка на плате.
На рис. 1 показано сопротивление между источником питания и нагрузкой. Напряжение, генерируемое источником питания, можно немного увеличить, чтобы компенсировать потери напряжения на этом резисторе.К сожалению, результирующее падение напряжения на сопротивлении линии зависит от тока нагрузки, то есть тока, протекающего по линии. Более высокий ток приводит к более высокому падению напряжения, чем более низкий ток. Таким образом, нагрузка питается от довольно неточно регулируемого напряжения, которое зависит от сопротивления линии и соответствующего протекающего тока.
Более высокий ток приводит к более высокому падению напряжения, чем более низкий ток. Таким образом, нагрузка питается от довольно неточно регулируемого напряжения, которое зависит от сопротивления линии и соответствующего протекающего тока.
Рис. 1. Физическое расстояние между регулятором напряжения и соответствующей нагрузкой.
Решение этой проблемы было найдено заранее.Дополнительное соединение может быть проложено параллельно фактической линии соединения. Линии измерения Кельвина измеряют напряжение на стороне электрической нагрузки. На рисунке 1 эти дополнительные линии показаны красным цветом. Эти измеренные значения затем интегрируются в управление напряжением питания на стороне источника питания. Эта концепция работает довольно хорошо, но имеет тот недостаток, что требует дополнительных сенсорных проводов. Такие линии обычно могут иметь очень маленький диаметр, так как по ним не проходят большие токи. Тем не менее установка измерительной линии в соединительном кабеле для больших токов связана с дополнительными трудозатратами и большими затратами.
Также можно компенсировать падение напряжения на соединительной линии между источником питания и нагрузкой без дополнительной пары измерительных проводов. Это представляет особый интерес для применений, в которых сложные кабели являются сложными и дорогими, и в которых возникающие электромагнитные помехи могут легко проникать в измерительные провода напряжения. Эта вторая возможность заключается в использовании специальной ИС для компенсации падения напряжения в линии, такой как LT6110. Он вставляется со стороны генерирования напряжения и измеряет ток перед входом в соединительную линию.На основе этого измеренного тока выходное напряжение источника питания регулируется таким образом, чтобы напряжение на стороне нагрузки регулировалось очень точно, независимо от тока нагрузки.
Рис. 2. LT6110 используется для регулировки выходного напряжения источника питания для компенсации падения напряжения в соединительной линии.
Для таких компонентов, как LT6110, напряжение питания можно регулировать в зависимости от соответствующего тока нагрузки; однако для этой настройки требуется информация о сопротивлении линии. Эта информация доступна во многих, но не во всех приложениях. Если соединительную линию можно заменить на более длинную или более короткую в течение срока службы устройства, то компенсацию напряжения за счет LT6110 также необходимо отрегулировать.
Эта информация доступна во многих, но не во всех приложениях. Если соединительную линию можно заменить на более длинную или более короткую в течение срока службы устройства, то компенсацию напряжения за счет LT6110 также необходимо отрегулировать.
В случае возможного изменения сопротивления линии во время работы устройства существуют такие компоненты, как LT4180, которые могут использовать сигналы переменного тока при наличии входного конденсатора на стороне нагрузки для виртуального предсказания сопротивления линии связи и, таким образом, может обеспечивать высокоточное напряжение на нагрузке.
На рис. 3 показано приложение с LT4180, в котором сопротивление линии передачи неизвестно. Входное линейное напряжение настраивается на соответствующее сопротивление линии. В LT4180 это делается без линий измерения Кельвина за счет ступенчатого изменения тока в линии и измерения соответствующего изменения напряжения. Результат этого измерения используется для определения потерь напряжения в неизвестной линии. Эта информация используется для оптимальной регулировки выходного напряжения преобразователя постоянного тока.
Эта информация используется для оптимальной регулировки выходного напряжения преобразователя постоянного тока.
Рис. 3. Виртуальное удаленное измерение линии с помощью LT4180.
Такое измерение хорошо работает до тех пор, пока узел на стороне нагрузки имеет низкое полное сопротивление переменному току. Это имеет место во многих приложениях, поскольку нагрузка после длинной соединительной линии требует определенного запаса энергии. Благодаря низкому импедансу выходной ток преобразователя постоянного тока можно модулировать, а сопротивление линии можно определить с помощью измерения напряжения на стороне перед соединительной линией.
Для успешного регулирования напряжения питания важен не только сам преобразователь напряжения, но и линия питания нагрузки.
Заключение
Требуемая точность постоянного тока может быть увеличена с помощью дополнительных измерительных линий Кельвина. В качестве альтернативы этим дополнительным измерительным проводам существуют также интегральные схемы для компенсации падения напряжения на линии без использования измерительной линии Кельвина.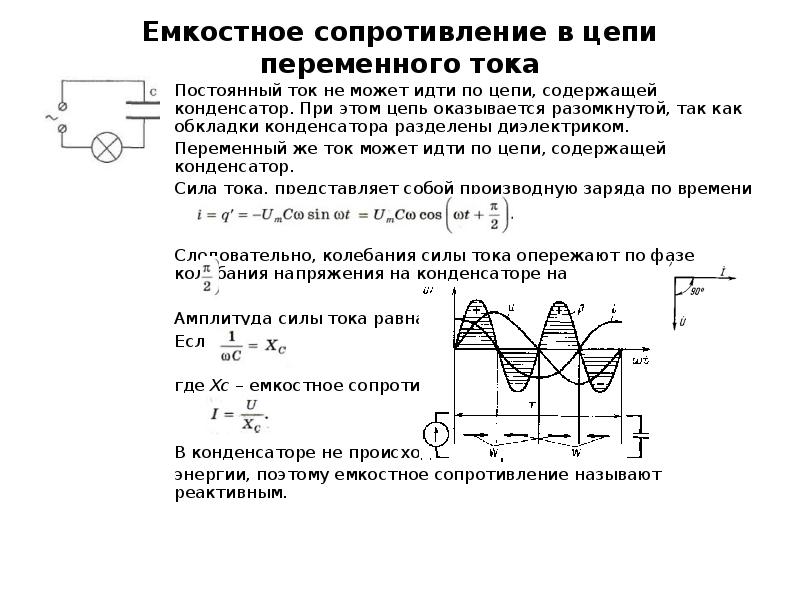 Это полезно, если стоимость измерительной линии Кельвина слишком высока или если необходимо использовать существующие линии без дополнительных измерительных проводов.С помощью этих наконечников можно легко достичь более высокой точности измерения напряжения.
Это полезно, если стоимость измерительной линии Кельвина слишком высока или если необходимо использовать существующие линии без дополнительных измерительных проводов.С помощью этих наконечников можно легко достичь более высокой точности измерения напряжения.
Как конденсатор работает с переменным током
В предыдущем посте мы видели работу конденсатора с постоянным током. Этот пост о том, как конденсатор работает с переменным током. В электронике переменного тока конденсаторы обрабатывают сигнал переменного тока, чтобы получить выходной сигнал определенной частоты и амплитуды.
Как конденсатор работает с переменным током
Сигнал переменного тока постоянно изменяется во времени. Существуют различные типы сигналов переменного тока e.г. синусоидальный, треугольный, квадратный и т. д. Давайте сначала проясним два наиболее важных понятия, связанных с конденсатором в цепях переменного тока.
- Конденсатор пропускает сигнал переменного тока и блокирует постоянный ток.

Это утверждение не на 100% верно. Конденсатор блокирует постоянный ток, за исключением времени, когда он заряжается или разряжается. Конденсатор также в некоторой степени блокирует сигнал переменного тока. Этот характер конденсатора по отношению к сигналу переменного тока называется реактивным сопротивлением конденсатора . Реактивное сопротивление работает так же, как сопротивление в цепях постоянного тока.
- Конденсатор имеет короткое замыкание на переменный ток и обрыв цепи на постоянный ток.
Вы можете подумать, что если конденсатор пропускает переменный ток намного лучше, чем постоянный, то он должен действовать либо как короткое замыкание, либо как разомкнутая цепь с сигналом переменного тока. Ответ: нет. Конденсатор не действует ни на обрыв, ни на короткое замыкание. Тогда возникает вопрос, как конденсатор пропускает переменный ток без короткого замыкания или обрыва цепи. Давайте обсудим…!
Аналог воды можно сравнить с работой конденсатора с переменным током. Рассмотрим пластины конденсатора как две емкости с водой Т1 и Т2, заполненные одинаково на половину их полной емкости. Две трубы, используемые для наполнения/опорожнения резервуаров, действуют как выводы конденсаторов. Между этими двумя трубами используется насос, аналогичный источнику напряжения. Здесь бак Т1 наполняется отрицательным напряжением и опорожняется положительным напряжением. Танк Т2 работает ровно напротив Т1. Опорожненный бак похож на пластину конденсатора с отрицательным зарядом. Вода, текущая по трубам, аналогична току, протекающему через конденсатор.
Рассмотрим пластины конденсатора как две емкости с водой Т1 и Т2, заполненные одинаково на половину их полной емкости. Две трубы, используемые для наполнения/опорожнения резервуаров, действуют как выводы конденсаторов. Между этими двумя трубами используется насос, аналогичный источнику напряжения. Здесь бак Т1 наполняется отрицательным напряжением и опорожняется положительным напряжением. Танк Т2 работает ровно напротив Т1. Опорожненный бак похож на пластину конденсатора с отрицательным зарядом. Вода, текущая по трубам, аналогична току, протекающему через конденсатор.
Теперь сначала рассмотрим наш источник напряжения постоянного тока. Сигнал постоянного тока является постоянным и может быть положительным или отрицательным. При отрицательном напряжении насос будет откачивать воду из T1 и подавать ее в T2. Через некоторое время поток воды прекращается, T1 опорожняется, а T2 полностью заполняется. Следовательно, непрерывный поток воды из Т1 в Т2 с постоянным током отсутствует.
Теперь напряжение заменено переменным током. Сигнал переменного тока постоянно изменяется между положительным и отрицательным. Резервуары опорожняются или заполняются для соответствующих напряжений.Но на этот раз полярность сигнала непрерывно меняется с положительной на отрицательную и наоборот. Следовательно, ни T1, ни T2 не опорожняются полностью, и вода непрерывно течет по трубам в обоих направлениях. Именно это происходит, когда конденсатор работает с переменным током. Заряд на обкладках конденсатора непрерывно изменяется при переменном токе. Следовательно, это приводит к потоку электронов через конденсатор.
Сигнал переменного тока постоянно изменяется между положительным и отрицательным. Резервуары опорожняются или заполняются для соответствующих напряжений.Но на этот раз полярность сигнала непрерывно меняется с положительной на отрицательную и наоборот. Следовательно, ни T1, ни T2 не опорожняются полностью, и вода непрерывно течет по трубам в обоих направлениях. Именно это происходит, когда конденсатор работает с переменным током. Заряд на обкладках конденсатора непрерывно изменяется при переменном токе. Следовательно, это приводит к потоку электронов через конденсатор.
Емкостное реактивное сопротивление
Резистор и конденсатор имеют одно важное сходство.Сопротивление резистора препятствует протеканию тока за счет рассеивания тепла. Способность конденсатора противостоять протеканию тока (как переменного, так и постоянного) известна как реактивное сопротивление конденсатора. Реактивное сопротивление препятствует протеканию тока без рассеивания тепла. Сопротивление конденсатора току носит кажущийся характер, т. е. наблюдается только в какой-то точке. И сопротивление, и реактивное сопротивление измеряются в омах. Термин реактивное сопротивление происходит от того факта, что пластины конденсатора реагируют на протекание тока, т.е. пластины несут положительный или отрицательный заряд, когда на конденсатор подается напряжение.
Сопротивление конденсатора току носит кажущийся характер, т. е. наблюдается только в какой-то точке. И сопротивление, и реактивное сопротивление измеряются в омах. Термин реактивное сопротивление происходит от того факта, что пластины конденсатора реагируют на протекание тока, т.е. пластины несут положительный или отрицательный заряд, когда на конденсатор подается напряжение.
Частота является важным параметром сигнала переменного тока. Возможно, вы читали, что конденсатор действует как разомкнутая цепь на низких частотах и короткое замыкание на высоких частотах . Это утверждение основано на том факте, что частота обратно пропорциональна емкостному реактивному сопротивлению . Это колебание напряжения прямо пропорционально току через конденсатор. Чем медленнее колеблется входное напряжение, тем меньше поток электронов через конденсатор и наоборот.
Вспомните математическое представление постоянной времени конденсатора.
Время (τ) = R x C
Следовательно, увеличение емкости увеличивает необходимое время для зарядки, что подразумевает низкую частоту (медленные колебания входного напряжения) и меньший поток электронов через конденсатор.
Математическое выражение емкостного сопротивления:
Xc = 1 ⁄ (2πfC) . . . . . . . . . . . (Единица измерения – Ом)
Закон Ома для емкостного реактивного сопротивления
Как обсуждалось ранее, сопротивление и реактивное сопротивление имеют одну и ту же единицу измерения – Ом.Существует также закон Ома для емкостного реактивного сопротивления. Важное замечание: при применении закона Ома для емкостного реактивного сопротивления частота должна быть постоянной. Выясним, как изменяется емкостное сопротивление по закону Ома.
| Для C = 0,1 мкФ, f = 100 Гц, V = 5 В | Для C = 0,1 мкФ, f = 10 кГц, V = 5 В |
| I = В ⁄ Xc = 5 ⁄ (15,91k) I = 0,314 мА | I = V ⁄ Xc = 5 ⁄ (159.15) I = 31,4 мА |
Эти примеры показывают, что изменение частоты входного сигнала изменяет емкостное сопротивление. Следовательно, частота входного сигнала должна быть постоянной при применении закона Ома для конденсатора с переменным током. Это все на данный момент. Надеюсь, теперь вы знаете, как конденсатор работает с переменным током. В следующем посте мы обсудим типы конденсаторов. Спасибо за чтение и не забудьте оставить комментарий. Конденсаторы в этой серии электроники еще многое предстоит сделать.Продолжайте посещать.
Следовательно, частота входного сигнала должна быть постоянной при применении закона Ома для конденсатора с переменным током. Это все на данный момент. Надеюсь, теперь вы знаете, как конденсатор работает с переменным током. В следующем посте мы обсудим типы конденсаторов. Спасибо за чтение и не забудьте оставить комментарий. Конденсаторы в этой серии электроники еще многое предстоит сделать.Продолжайте посещать.
15.4 Питание в цепи переменного тока — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Опишите, как средняя мощность от цепи переменного тока может быть выражена через пиковый ток и напряжение и среднеквадратичное значение тока и напряжения
- Определить зависимость между фазовым углом тока и напряжения и средней мощностью, известную как коэффициент мощности
Элемент схемы рассеивает или производит мощность в соответствии с P=IV,P=IV, где I — ток через элемент, а V — напряжение на нем.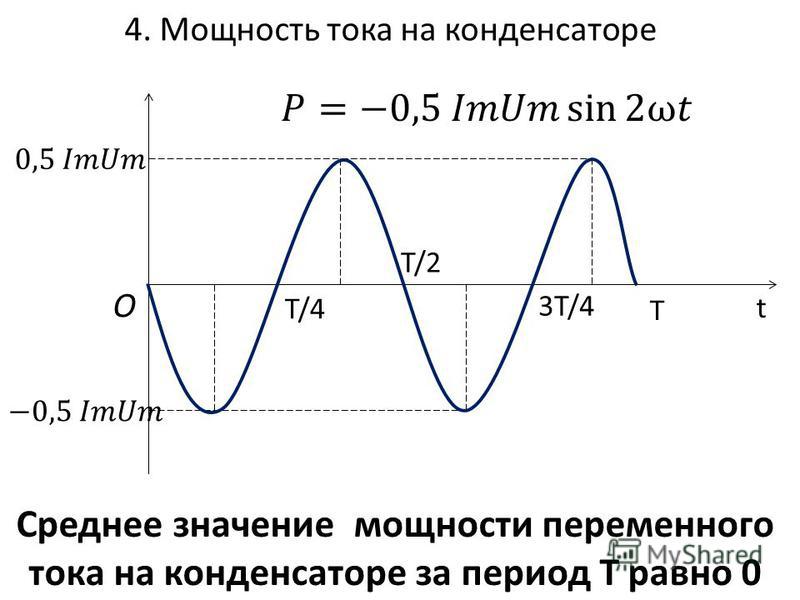 Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность p(t)=i(t)v(t)p(t)=i(t)v(t) также зависит от времени. График p ( t ) для различных элементов схемы показан на рис. 15.16. Для резистора i ( t ) и v ( t ) совпадают по фазе и поэтому всегда имеют один и тот же знак (см. рис. 15.5). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разности фаз (см. рис. 15).7 и рис. 15.9). Следовательно, p ( t ) в одни моменты времени положителен, а в другие отрицателен, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты времени и поглощают ее в другие.
Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность p(t)=i(t)v(t)p(t)=i(t)v(t) также зависит от времени. График p ( t ) для различных элементов схемы показан на рис. 15.16. Для резистора i ( t ) и v ( t ) совпадают по фазе и поэтому всегда имеют один и тот же знак (см. рис. 15.5). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разности фаз (см. рис. 15).7 и рис. 15.9). Следовательно, p ( t ) в одни моменты времени положителен, а в другие отрицателен, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты времени и поглощают ее в другие.
Фигура
15.16
График мгновенной мощности для различных элементов цепи. (a) Для резистора Pave=I0V0/2, Pave=I0V0/2, тогда как для (b) конденсатора и (c) катушки индуктивности Pave=0.Pave=0. (d) Для источника Pave=I0V0(cosϕ)/2, Pave=I0V0(cosϕ)/2, что может быть положительным, отрицательным или нулевым, в зависимости от ϕ.ϕ.
Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. Что нас почти всегда интересует, так это мощность, усредненная по времени, которую мы называем средней мощностью. Определяется средней по времени мгновенной мощностью за один цикл:
Pave=1T∫0Tp(t)dt,Pave=1T∫0Tp(t)dt,
, где T=2π/ωT=2π/ω – период колебаний. С заменами v(t)=V0sinωtv(t)=V0sinωt и i(t)=I0sin(ωt−ϕ),i(t)=I0sin(ωt−ϕ) этот интеграл принимает вид
Pave=I0V0T∫0Tsin(ωt−ϕ)sinωtdt.Pave=I0V0T∫0Tsin(ωt−ϕ)sinωtdt.
Используя тригонометрическое соотношение sin(A−B)=sinAcosB−sinBcosA,sin(A−B)=sinAcosB−sinBcosA, получаем
Pave=I0V0cosϕT∫0Tsin2ωtdt−I0V0sinϕT∫0Tsinωtcosωtdt. Pave=I0V0cosϕT∫0Tsin2ωtdt−I0V0sinϕT∫0Tsinωtcosωtdt.
Pave=I0V0cosϕT∫0Tsin2ωtdt−I0V0sinϕT∫0Tsinωtcosωtdt.
Вычисление этих двух интегралов дает
1T∫0Tsin2ωtdt=121T∫0Tsin2ωtdt=12
и
1T∫0Tsinωtcosωtdt=0,1T∫0Tsinωtcosωtdt=0.
Следовательно, средняя мощность, связанная с элементом схемы, равна
.
Pave=12I0V0cosϕ.Pave=12I0V0cosϕ.
15.12
В технических приложениях cosϕcosϕ известен как коэффициент мощности, который представляет собой величину, на которую мощность, подаваемая в цепь, меньше теоретического максимума цепи из-за несовпадения фаз напряжения и тока. Для резистора ϕ=0,ϕ=0, поэтому средняя рассеиваемая мощность равна
.
Сравнение p ( t ) и PavePave показано на рис. 15.16(d). Чтобы сделать Pave=(1/2)I0V0Pave=(1/2)I0V0 похожим на его аналог постоянного тока, мы используем среднеквадратичные значения IrmsandVrmsIrmsandVrms тока и напряжения.По определению это
Irms=iave2 и Vrms=vave2, Irms=iave2 и Vrms=vave2,
где
iave2=1T∫0Ti2(t)dt и vave2=1T∫0Tv2(t)dt.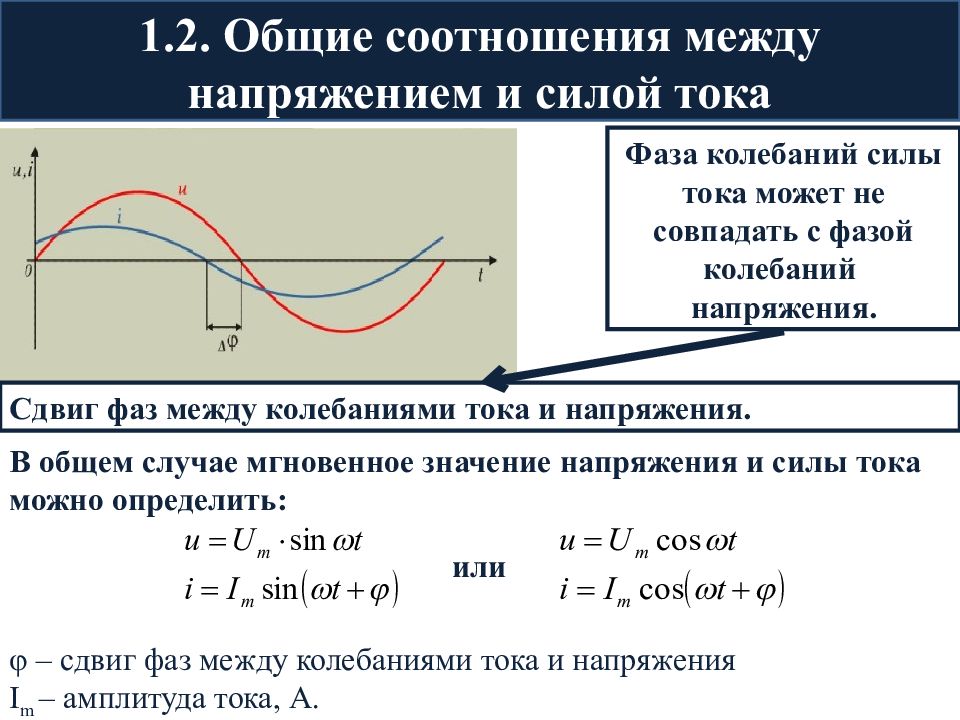 iave2=1T∫0Ti2(t)dt и vave2=1T∫0Tv2(t)dt.
iave2=1T∫0Ti2(t)dt и vave2=1T∫0Tv2(t)dt.
При i(t)=I0sin(ωt−ϕ) и v(t)=V0sinωt, i(t)=I0sin(ωt−ϕ)и v(t)=V0sinωt получаем
Irms=12I0 и Vrms=12V0.Irms=12I0andVrms=12V0.
Тогда мы можем написать для средней мощности, рассеиваемой резистором,
Pave=12I0V0=IrmsVrms=Irms2R.Pave=12I0V0=IrmsVrms=Irms2R.
15.13
Это уравнение еще раз подчеркивает, почему при обсуждении выбрано среднеквадратичное значение, а не пиковые значения.Оба уравнения для средней мощности верны для уравнения 15.13, но среднеквадратические значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не нужен.
Переменные напряжения и токи обычно описываются их действующими значениями. Например, 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника составляет 1102 В = 156 В. 1102 В = 156 В. Поскольку большинство счетчиков переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, подключенный к бытовой розетке, будет показывать 110 В.
Для конденсатора и катушки индуктивности ϕ=π/2 и −π/2 рад, ϕ=π/2 и −π/2 рад соответственно. Поскольку cosπ/2=cos(−π/2)=0, cosπ/2=cos(−π/2)=0, из уравнения 15.12 мы находим, что средняя мощность, рассеиваемая любым из этих элементов, равна Pave=0.Pave =0. Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем возвращают ее обратно в цепь в течение другого полупериода. Это поведение показано на графиках рис. 15.16, (b) и (c), которые показывают, что p( t) колеблется синусоидально около нуля.
Фазовый угол для генератора переменного тока может иметь любое значение. Если cosϕ>0,cosϕ>0, генератор вырабатывает мощность; если cosϕ<0,cosϕ<0, он поглощает мощность. В среднеквадратичных значениях средняя мощность генератора переменного тока записывается как
.
Pave=IrmsVrmscosϕ.Pave=IrmsVrmscosϕ.
Для генератора в цепи RLC ,
tanϕ=XL-XCRtanϕ=XL-XCR
и
cosϕ=RR2+(XL-XC)2=RZ. cosϕ=RR2+(XL-XC)2=RZ.
cosϕ=RR2+(XL-XC)2=RZ.
Отсюда средняя мощность генератора
Pave=IrmsVrmscosϕ=VrmsZVrmsRZ=Vrms2RZ2.Pave=IrmsVrmscosϕ=VrmsZVrmsRZ=Vrms2RZ2.
15.14
Это также может быть записано как
.
, что означает, что мощность, вырабатываемая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.
Пример
15,3
Выходная мощность генератора
Генератор переменного тока, ЭДС которого определяется выражением
v(t)=(4,00В)sin[(1,00×104рад/с)t]v(t)=(4,00В)sin[(1,00×104рад/с)t]
подключен к цепи RLC , для которой L=2.00×10-3HL=2,00×10-3H, C=4,00×10-6FC=4,00×10-6F и R=5,00 Ом R=5,00 Ом. а) Чему равно среднеквадратичное напряжение на генераторе? б) Чему равно сопротивление цепи? в) Какова средняя мощность генератора?
Стратегия
Среднеквадратичное напряжение – это амплитуда напряжения, умноженная на 1/21/2. Полное сопротивление цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по уравнению 15.14 или, точнее, по последней части уравнения, поскольку у нас есть импеданс цепи Z , среднеквадратичное напряжение VrmsVrms и сопротивление R .
Полное сопротивление цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по уравнению 15.14 или, точнее, по последней части уравнения, поскольку у нас есть импеданс цепи Z , среднеквадратичное напряжение VrmsVrms и сопротивление R .
Решение
- Поскольку V0=4,00 В, V0=4,00 В, среднеквадратичное значение напряжения на генераторе равно
Vrms = 12 (4,00 В) = 2,83 В. Vrms = 12 (4,00 В) = 2,83 В. - Полное сопротивление цепи
Z=R2+(XL-XC)2={(5,00 Ом)2+[(1,00×104 рад/с)(2,00×10-3H)-1(1,00×104рад/с)(4,00×10-6F)]2 }1/2=7,07 Ом.Z=R2+(XL-XC)2={(5,00 Ом)2+[(1,00×104 рад/с)(2,00×10-3H)−1(1,00×104рад/с)( 4,00×10-6F)]2}1/2=7,07 Ом. - Из уравнения 15.14 средняя мощность, передаваемая в цепь, равна
Pave=Vrms2RZ2=(2,83 В)2(5,00 Ом)(7,07 Ом)2=0.801 Вт.Pave=Vrms2RZ2=(2,83 В)2(5,00 Ом)(7,07 Ом)2=0,801 Вт.
Значение
Если сопротивление намного больше, чем реактивное сопротивление конденсатора или индуктора, средняя мощность представляет собой уравнение цепи постоянного тока P=V2/R, P=V2/R, где В заменяет среднеквадратичное значение напряжения.
Проверьте свое понимание
15,4
Проверьте свои знания Вольтметр переменного тока, подключенный к клеммам генератора переменного тока частотой 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.
Проверьте свое понимание
15,5
Проверьте свои знания Покажите, что среднеквадратичное значение напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичное значение тока равно IrmsIrms, выражается как IrmsR, IrmsXC и IrmsXL, IrmsR, IrmsXC и IrmsXL соответственно. Определите эти значения для компонентов схемы RLC по уравнению 15.12.
.


 Эти типы конденсаторов известны как конденсаторы связи.
Эти типы конденсаторов известны как конденсаторы связи.