Магнитная индукция. Магнитная индукция кратко

Магнитная индукция - это... Что такое Магнитная индукция?

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 104 Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в системе единиц СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе[4] наиболее важными являются:

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :

• Формула силы Лоренца
  • Следствия из нее, такие как
    • Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
    • выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
    • выражение для потенциальной энергии магнитного диполя в магнитном поле:
    • а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т.д..
    • Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
      • (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля
  • Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Примечания

1. ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид: При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведенную в основном тексте.
2. ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
3. ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
4. ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
5. ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).

См. также

dik.academic.ru

Магнитная индукция.

 

Интенсивность магнитного поля в каждой его точке характеризуется магнитной индукцией (обозначается буквой В).

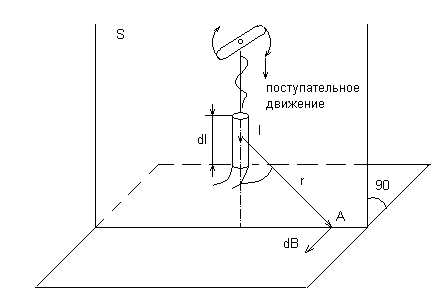
Закон Био и Савара – Лапласа.

 

Т.е. индукция dB прямо пропорциональна длине элемента dl, величине тока I, синусу угла между направлением тока и радиусом – вектором, соединяющим данный элемент с точкой поля, и обратно пропорциональна квадрату длины радиуса – вектора.

 

Магнитная индукция по системе СИ измеряется в теслах

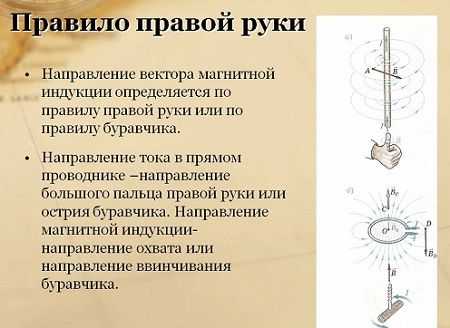
Магнитная индукция – векторная величина. Вектор dB направлен перпендикулярно плоскости S, в которой расположены радиус – вектор r и элемент dl. Направление вектора dB определяется по правилу Буравчика.

Магнитное поле, в различных точках которого индукция имеет различные значения, называется неоднородным, и наоборот, магнитное поле называется однородным, если во всех точках поля векторы магнитной индукции имеют одинаковую величину и направлены друг к другу.

 

Магнитная проницаемость.

Для того, чтобы получить представление о магнитных свойствах среды, нужно сравнить магнитное поле вокруг повода с током в данной среде с магнитным полем вокруг того же провода, но находящегося в вакууме. Материалы или среды, в которых поле получается сильнее, чем в вакууме, называется – парамагнитными, а в которых слабее – диамагнитными.

Магнитные свойства среды характеризует абсолютная магнитная проницаемость , имеющая различную величину для разных веществ.

Абсолютная магнитная проницаемость вакуума называется магнитной постоянной .

Отношение абсолютной магнитной проницаемости какого – либо вещества к магнитной постоянной называется магнитной проницаемостью вещества.

Для диамагнитных веществ 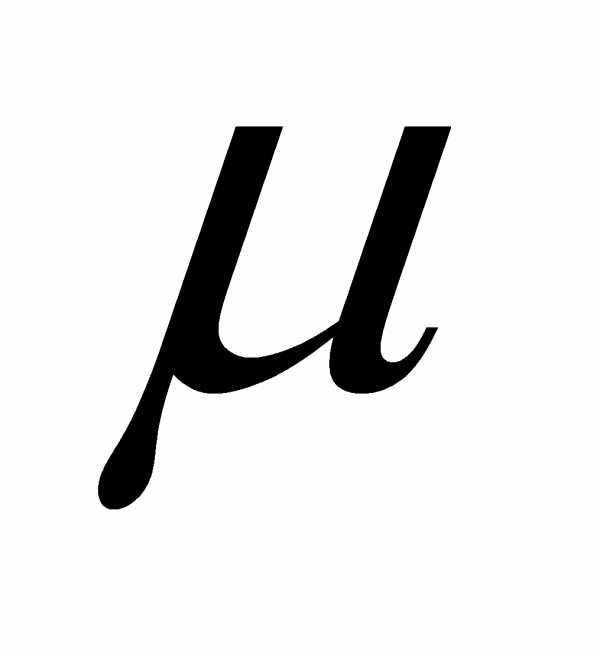<1 (медь 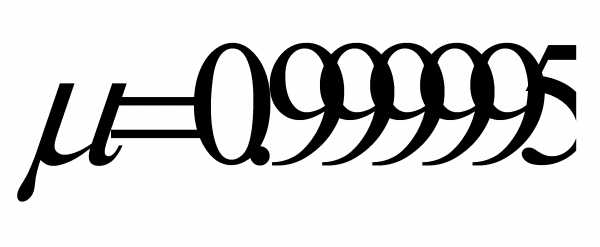), для парамагнитных 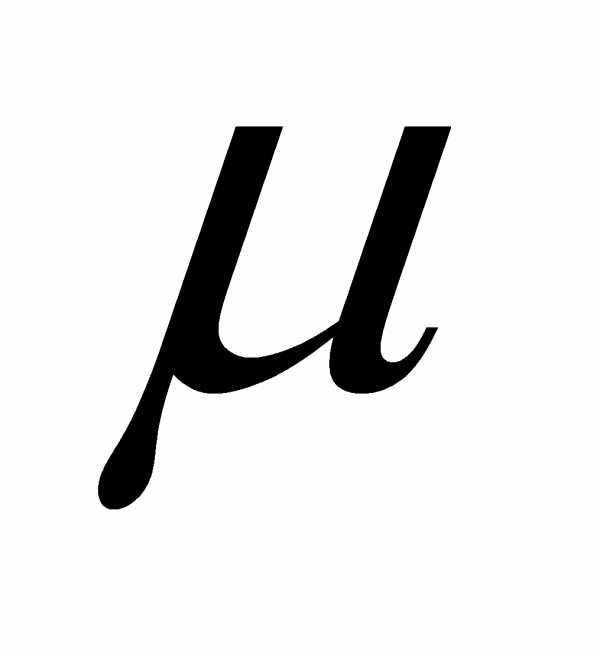>1 (воздух ).

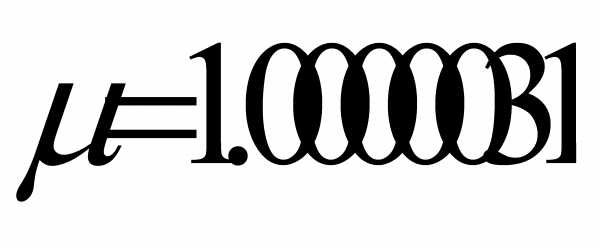Особую группу составляют так называемые ферромагнитные материалы. Магнитная проницаемость этих материалов может достигать десятки тысяч (железо, кобальт).

 

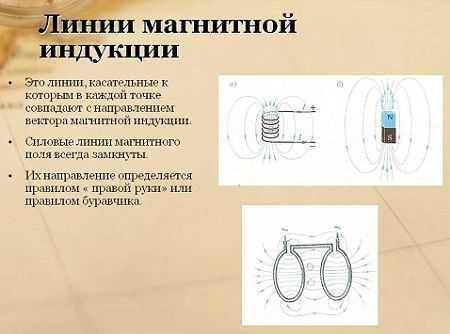
Линии магнитной индукции.

Применяются для изображения магнитного поля. Линии магнитной индукции проводят так, чтобы вектор магнитной индукции в каждой точке был направлен по касательной к линии в этой точке.

 

Магнитное поле витка с током

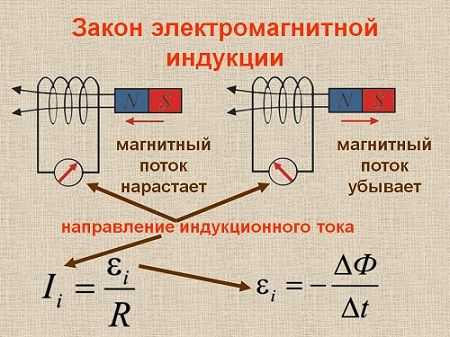
Магнитный поток

 

 

Магнитный поток (Ф) через площадку, перпендикулярную вектору магнитной индукции, в однородном поле равен произведению магнитной индукции на величину площади.

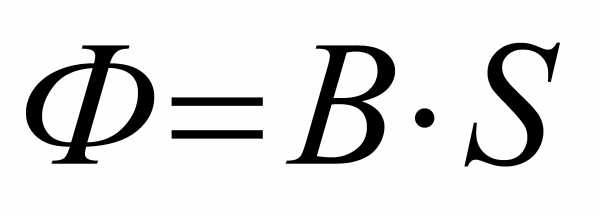
Более мелкой единицей измерения магнитного потока является максвелл (мкс)

 

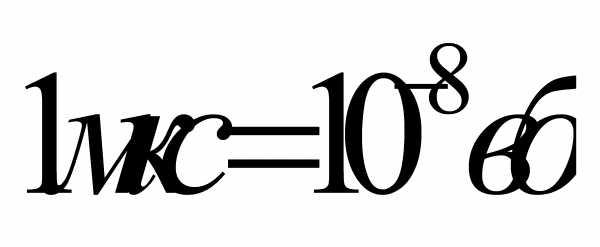
Похожие статьи:

poznayka.org

Магнитная индукция - это... Что такое Магнитная индукция?

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 104 Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в системе единиц СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе[4] наиболее важными являются:

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :

• Формула силы Лоренца
  • Следствия из нее, такие как
    • Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
    • выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
    • выражение для потенциальной энергии магнитного диполя в магнитном поле:
    • а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т.д..
    • Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
      • (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля
  • Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Примечания

1. ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид: При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведенную в основном тексте.
2. ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
3. ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
4. ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
5. ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).

См. также

dikc.academic.ru

Индукция магнитного поля

Все магниты разделяются между собой по силе своего воздействия. Таким образом, существует определенная величина, которая характеризует степень проявления силы того или иного магнита. Если быть более точными, то данная сила создается не самими магнитами, а их магнитными полями. Само магнитное поле зависит от векторной величины, которая известна, как индукция магнитного поля или просто магнитная индукция. Формула Для определения величины электромагнитной индукции используется формула B=F/(I*l), где магнитная индукция В, представляющая собой модуль вектора, определяется, как отношение модуля силы F, воздействующей на проводник с током, расположенным перпендикулярно с магнитными линиями, к значению силы тока I, имеющейся в проводнике и длине l самого проводника. Зависимость магнитной индукции На электромагнитную индукцию абсолютно не влияют, ни сила тока, ни длина проводника. Она находится в прямой зависимости и связи, только с магнитным полем. Таким образом, при уменьшении силы тока в проводнике, без изменения каких-либо других показателей, происходит уменьшение не индукции, прямо пропорционально связанной с силой тока, а той силы, с которой магнитное поле воздействует на проводник. При этом, значение самой магнитной индукции остается постоянным. Благодаря этим качествам, электромагнитная индукция выступает в роли количественной характеристики магнитного поля. Измерение магнитной индукции производится в теслах, по формуле: 1 Тл=1 Н/(А*м). Физическую зависимость этой величины от различных факторов, можно определить в ходе проведения несложного эксперимента. Необходимо взять весы, где на одной стороне прикрепляется проводник, а на другой стороне расположены гири. Проводник находится в постоянном электромагнитном поле, при этом, его масса и вес гирь имеют одинаковое значение. После уравновешивания весов, по проводнику пропускается электрический ток. Вокруг него происходит образование магнитного поля, определяемое в соответствии с правилом правой руки. В результате, наблюдается взаимодействие полей постоянного магнита и самого проводника. При этом, равновесие весов будет нарушено. Из-за протекания тока, сторона весов с проводником начинает опускаться. Для того, чтобы вычислить силу воздействия поля на этот проводник, нужно уравновесить его с помощью гирь. Сила их тяжести рассчитывается по специальной формуле, и будет равняться силе магнитного поля, воздействующей на проводник с током. Соотношение этой силы с длиной проводника и силой тока является постоянной величиной. Данная количественная характеристика находится в зависимости только от поля и представляет собой ни что иное, как модуль вектора магнитной индукции. Линии магнитной индукции Сама индукция магнитного поля характеризуется определенным направлением, представляющим собой линии, отображаемые графически. Эти линии, также получили название магнитных линий, или линий магнитных полей. Так же, как и магнитная индукция, ее линии имеют собственное определение. Они представляют собой линии, к которым проведены касательные во всех точках поля. Эти касательные и вектор магнитной индукции совпадают между собой. Однородное магнитное поле отличается параллельными линиями магнитной индукции, совпадающими с направлением вектора во всех точках. Если же магнитное поле является неоднородным, произойдет изменение вектора электромагнитной индукции в каждой пространственной точке, расположенной вокруг проводника. Касательные, проведенные к этому вектору, приведут к созданию концентрических окружностей вокруг проводника. Таким образом, в данном случае, линии индукции будут выглядеть в виде расширяющихся окружностей.

electric-220.ru

Магнитная индукция - это... Что такое Магнитная индукция?

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 104 Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в системе единиц СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе[4] наиболее важными являются:

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :

• Формула силы Лоренца
  • Следствия из нее, такие как
    • Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
    • выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
    • выражение для потенциальной энергии магнитного диполя в магнитном поле:
    • а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т.д..
    • Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
      • (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля
  • Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Примечания

1. ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид: При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведенную в основном тексте.
2. ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
3. ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
4. ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
5. ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).

См. также

dic.academic.ru

Магнитная индукция - это... Что такое Магнитная индукция?

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 104 Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в системе единиц СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе[4] наиболее важными являются:

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :

• Формула силы Лоренца
  • Следствия из нее, такие как
    • Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
    • выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
    • выражение для потенциальной энергии магнитного диполя в магнитном поле:
    • а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т.д..
    • Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
      • (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля
  • Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Примечания

1. ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид: При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведенную в основном тексте.
2. ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
3. ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
4. ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
5. ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).

См. также

med.academic.ru

Магнитная индукция - это... Что такое Магнитная индукция?

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 104 Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в системе единиц СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе[4] наиболее важными являются:

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :

• Формула силы Лоренца
  • Следствия из нее, такие как
    • Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
    • выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
    • выражение для потенциальной энергии магнитного диполя в магнитном поле:
    • а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т.д..
    • Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
      • (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля
  • Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Примечания

1. ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид: При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведенную в основном тексте.
2. ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
3. ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
4. ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
5. ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).

См. также

dal.academic.ru

---

• 
  Определение распределительный газопровод
• 
  Электроэнергетика атомная
• 
  Температурный коэффициент химия формула
• 
  Ночная зона электроэнергии с какого часа
• 
  Плата за содержание и ремонт
• 
  Как напрямую заключить договор с мосэнергосбытом
• 
  Единицы измерения си
• 
  Как перекрыть стояк отопления в многоквартирном доме
• 
  Как подключить асинхронный двигатель
• 
  Что делает молния
• 
  Масса нейтрона протона и электрона