Последовательное и параллельное соединение проводников — урок. Физика, 8 класс.
В быту и в промышленности в электрическую цепь соединяются сразу несколько потребителей электрической энергии. Различают три вида соединения сопротивлений (резисторов):
- последовательное соединение проводников
- параллельное соединение проводников
- смешанное соединение проводников
Последовательное соединение проводников
Схема соединения выглядит следующим образом:
Обрати внимание!
При последовательном соединении все входящие в него проводники соединяются друг за другом, т.е. конец первого проводника соединяется с началом второго.
Опыт показывает:
Сила тока в любых частях цепи одна и та же (об этом свидетельствуют показания амперметров): I=I1=I2.
Если выкрутить одну лампу, то цепь разомкнётся, а другая лампа тоже погаснет.
Опыт показывает следующее:
При последовательном соединении сопротивлений результирующее напряжение равно сумме напряжений на участках: U=U1+U2.
Результирующее сопротивление последовательно соединённых потребителей равно сумме сопротивлений потребителей: R=R1+R2.
Для проверки данного утверждения можно использовать омметр. При подключении омметра ключ должен быть разомкнут!
Омметр подключают по очереди к каждому потребителю, а потом к обоим одновременно.
Сопротивление цепи \(R\), состоящей из \(n\) одинаковых ламп, сопротивлением R1 каждая, в \(n\) раз больше сопротивления одной лампы: \(R\) = R1* \(n\).
Параллельное соединение проводников
Схема соединения выглядит следующим образом:
Обрати внимание!
При параллельном соединении все входящие в него проводники одним своим концом присоединяются к одной точке цепи А, а вторым концом — к другой точке В.
Опыт доказывает:
Сила тока в неразветвлённой части цепи равна сумме сил тока в отдельных параллельно соединённых проводниках.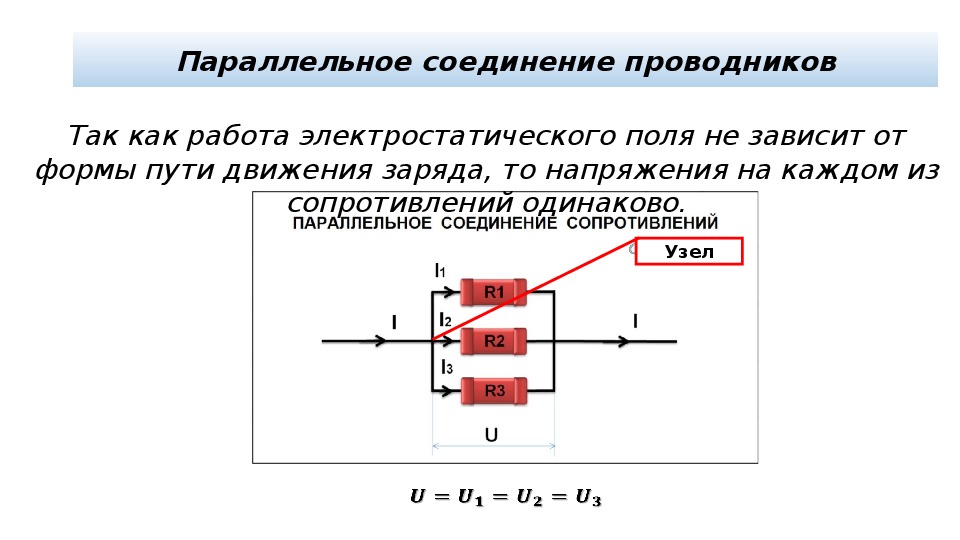
Об этом свидетельствуют показания амперметров: I=I1+I2.
Если выкрутить одну лампу, то другая лампа продолжает гореть. Это свойство используют для подключения бытовых приборов в помещении.
Опыт свидетельствует, что:
Напряжение на участке цепи АВ и на концах всех параллельно соединённых проводников одно и то же.
Об этом свидетельствуют показания вольтметров:
U=U1=U2.
Общее сопротивление цепи при параллельном соединении проводников определяется по формуле:
1R=1R1+1R2.
Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников.
Для проверки формулы можно использовать омметр. При подключении омметра ключ должен быть разомкнут!
Сопротивление цепи \(R\), состоящей из \(n\) одинаковых ламп, сопротивлением R1 каждая, в \(n\) раз меньше сопротивления одной лампы: \(R\) = R1/ \(n\).
Источники:
http://files. school-collection.edu.ru/dlrstore/669ba073-e921-11dc-95ff-0800200c9a66/3_17.swf
school-collection.edu.ru/dlrstore/669ba073-e921-11dc-95ff-0800200c9a66/3_17.swf
http://files.school-collection.edu.ru/dlrstore/669ba074-e921-11dc-95ff-0800200c9a66/3_18.swf
http://class-fizika.narod.ru/8_33.htm
Параллельное соединение — урок. Физика, 8 класс.
При параллельном соединении все потребители подключены к источнику тока независимо друг от друга и образуют разветвлённую цепь.
При параллельном соединении все потребители подключены к одному источнику тока, между клеммами которого имеется определённое напряжение.
Каждый потребитель получает полное напряжение цепи.
U=U1=U2=U3=…
При параллельном соединении общий ток является суммой токов, протекающих через отдельные потребители.
I=I1+I2+I3+…
Общее сопротивление потребителей, находящихся в параллельном соединении, будет наименьшим (меньше, чем наименьшее из сопротивлений параллельно подключённых потребителей).
Если параллельно соединены \(n\) потребителей, а сопротивление каждого из них одинаково и равно \(R\), тогда общее сопротивление цепи будет равно \(R : n\).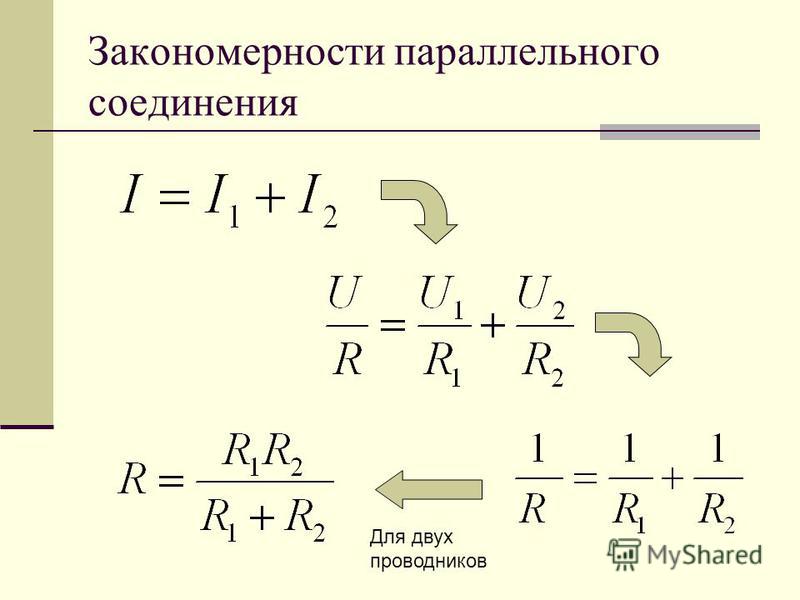
Можно сделать вывод о том, что при увеличении числа потребителей общая сила тока неограниченно возрастает, что может привести к пожару.
Обрати внимание!
В одну розетку нельзя включать несколько мощных потребителей, так как перенагруженные провода нагреваются и могут загореться.
В квартире потребители включены в параллельное соединение. Подводка электричества, входящего в квартиру, состоит из нескольких проводов, которые проходят через счётчик, измеряющий потребление электроэнергии. Электрический ток течёт через предохранители, которые подключены последовательно и предусмотрены для определённой силы тока в цепи. Они размыкают цепь в случае опасной перегрузки.
Электрический кабель, который используется в электрической цепи квартиры, имеет три провода. Третий провод является заземлением.
Преимуществом параллельного соединения является то, что при отключении одного из потребителей, остальные продолжают работать.
Источники:
http://www.ndg.lv/latvian/Macibas/FizInter/b2.2.4.htm
http://www.goerudio.com/demo/paralelais_slegums
http://www.ndg.lv/latvian/Macibas/FizInter/b2.2.4.htm
Параллельное соединение проводников | Физика
При параллельном соединении все проводники (резисторы, лампы и т.д.) подключаются к одной и той же паре точек A и B (рис. 43). Связь между общими значениями силы тока, напряжения и сопротивления с их значениями на отдельных участках цепи при этом отличается от той, что была при последовательном соединении. Теперь соответствующие формулы имеют вид
I = I1 + I2, (17.1) U = U1 = U2, (17.2) R = (R1R2) / (R1 + R2). (17.3)
Чтобы убедиться в справедливости этих соотношений, следует собрать цепь и с помощью амперметра и вольтметра произвести необходимые измерения.
Итак, при параллельном соединении проводников напряжение на всех участках цепи одно и то же, общая сила тока равна сумме сил токов на отдельных проводниках, а общее сопротивление двух проводников находится как отношение произведения их сопротивлений к их сумме.
Первые две из этих закономерностей справедливы для любого числа параллельно соединенных проводников, последняя — только для двух.
Если R1 = R2, то
R = (R1R2) / (R1 + R2) = R12/2R1 = R1/2 (17.4)
Мы видим, что общее сопротивление двух одинаковых проводников в 2 раза меньше сопротивления одного проводника. Эта закономерность допускает обобщение: если параллельно соединено n одинаковых потребителей электроэнергии (резисторов, ламп и т.д.), то их общее сопротивление в n раз меньше сопротивления каждого из них:
R = R1/n (17.5)
Отсюда следует, что с увеличением числа проводников общее сопротивление будет становиться все меньше и меньше. Это может показаться странным. На самом деле ничего удивительного в этом нет: ведь при параллельном соединении проводников происходит как бы увеличение общей площади их поперечного сечения, а с увеличением площади сечения проводника, как известно, его сопротивление уменьшается.
Отличительной особенностью параллельного соединения нескольких потребителей является то, что при выключении одного из них остальные продолжают работать. Так, например, вывернув одну лампу в цепи, изображенной на рисунке 44, мы увидим, что другая будет по-прежнему гореть.
Большинство потребителей электроэнергии — электронагревательные приборы, холодильники, швейные машины, магнитофоны, телевизоры и т. д. — рассчитаны на напряжение сети 220 В. Поэтому все они должны включаться в сеть параллельно, ибо только в этом случае они окажутся под одним и тем же напряжением (220 В) и будут продолжать работать при выключении одного из них.
На рисунке 45 приведена упрощенная схема квартирной электропроводки. Провода сети, между которыми существует напряжение 220 В, обозначены буквами Ф и О. Первый из них называют фазным, второй — нулевым. Нулевой провод соединен с землей. Именно с ним соединяют все потребители. И наоборот, все выключатели соединяют с фазным проводом. Такой порядок подключения потребителей и выключателей обеспечивает наибольшую безопасность человека.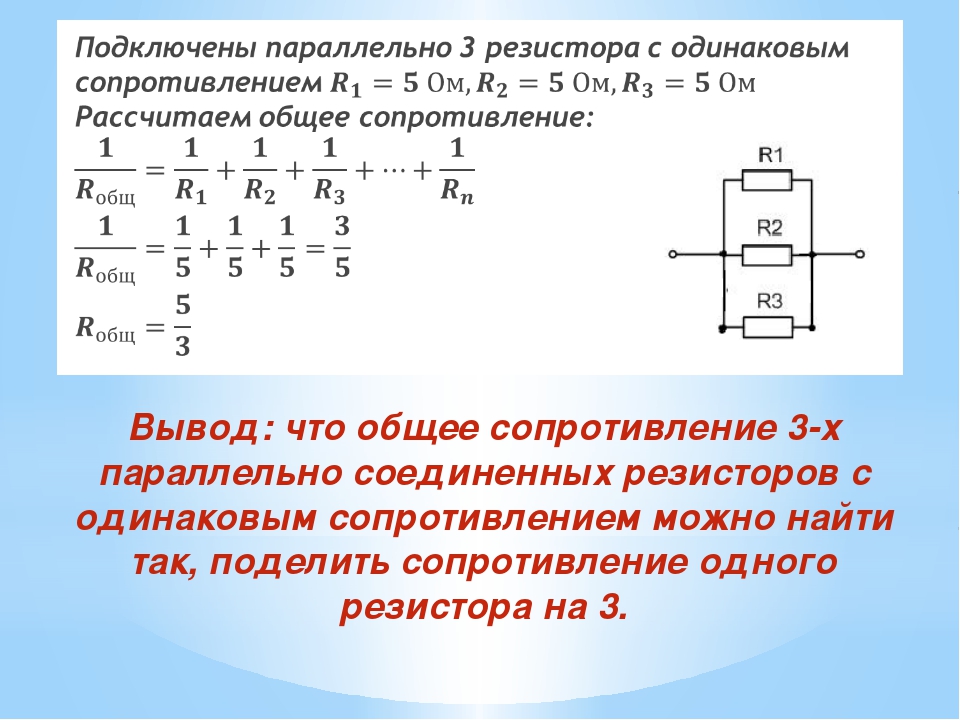
??? 1. Какое соединение называют параллельным? 2. Начертите схему цепи, изображенной на рисунке 44. 3. Какие три закономерности справедливы для параллельного соединения проводников? 4. Как находится общее сопротивление параллельно соединенных проводников, когда они одинаковые? 5. Перечислите все элементы электрической цепи, изображенной на рисунке 45. 6. Предположим, что при замене лампы человек случайно коснулся металлического контакта в патроне лампы и одновременно с этим какой-либо заземленной части здания (например, батареи отопления). Под каким напряжением он окажется? Рассмотрите ситуацию, когда лампа и выключатель подсоединены к проводам сети так, как это показано на рисунке 45. Что произойдет, если лампу и выключатель поменять местами? 7. Почему у вольтметров делают большое внутреннее сопротивление, а у амперметров — малое?
Чему равна сила тока в параллельном соединении. Мощность при параллельном и последовательном соединении резисторов
Последовательным
называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т. д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому
д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому
\(~I = I_1 = I_2 .\)
Амперметр А
измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R
A → 0).
Включенные вольтметры V
1 и V
2 измеряют напряжение U
1 и U
2 на сопротивлениях R
1 и R
2 . Вольтметр V
измеряет подведенное к клеммам Μ
и N
напряжение U
. Вольтметры показывают, что при последовательном соединении напряжение U
равно сумме напряжений на отдельных участках цепи:
\(~U = U_1 + U_2 . \qquad (1)\)
Применяя закон Ома для каждого участка цепи, получим:
\(~U = IR ; \ U_1 = IR_1 ; \ U_2 = IR_2 ,\)
где R
— общее сопротивление последовательно соединенной цепи.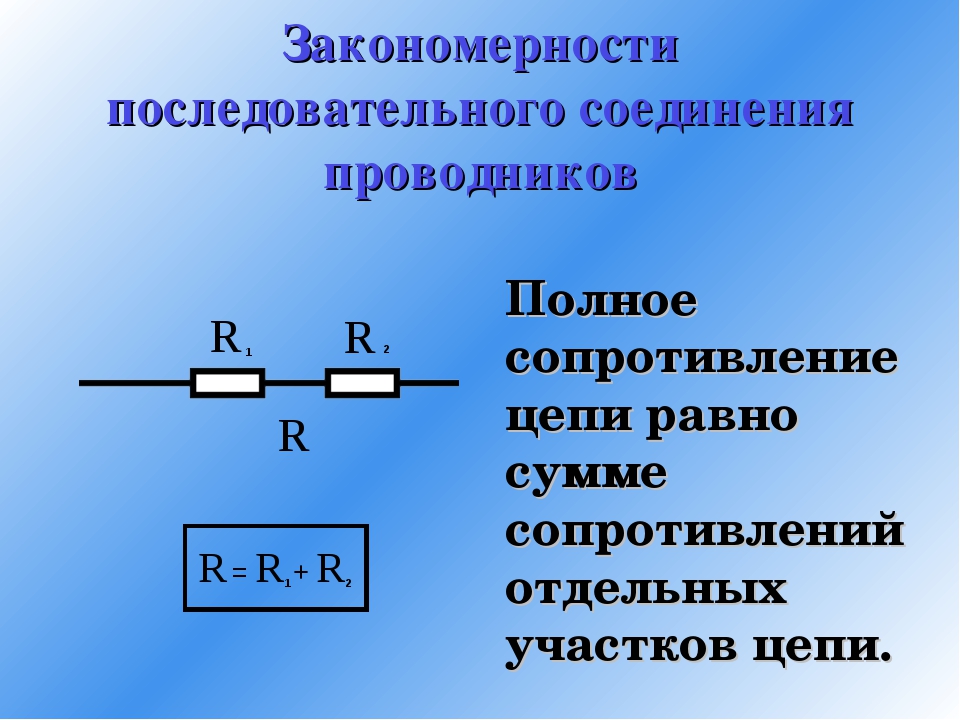 n R_i .\)
n R_i .\)
Если сопротивления отдельных резисторов равны между собой, т.е. R
1 = R
2 = … = R
n , то общее сопротивление этих резисторов при последовательном соединении в n
раз больше сопротивления одного резистора: R
= nR
1 .
При последовательном соединении резисторов справедливо соотношение \(~\frac{U_1}{U_2} = \frac{R_1}{R_2}\), т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.
Параллельным
называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам Μ
и N
подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R
1 и R
2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:
\(~U = U_1 = U_2 . n \frac{1}{R_i} .\)
n \frac{1}{R_i} .\)
Если сопротивления всех n
параллельно соединенных резисторов одинаковы и равны R
1 то \(~\frac 1R = \frac{n}{R_1}\) . Откуда \(~R = \frac{R_1}{n}\) .
Сопротивление цепи, состоящей из n
одинаковых параллельно соединенных резисторов, в n
раз меньше сопротивления каждого из них.
При параллельном соединении резисторов справедливо соотношение \(~\frac{I_1}{I_2} = \frac{R_2}{R_1}\), т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 257-259.
В предыдущем конспекте был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R
Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R
. Этот закон, установленный экспериментально, называется закон Ома
(для участка цепи).
Закон Ома
для участка цепи
: сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника.
Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).
Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи. Д
ва основных типа соединения проводников
: последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.
Последовательное соединение проводников
При последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец — с началом третьего и т.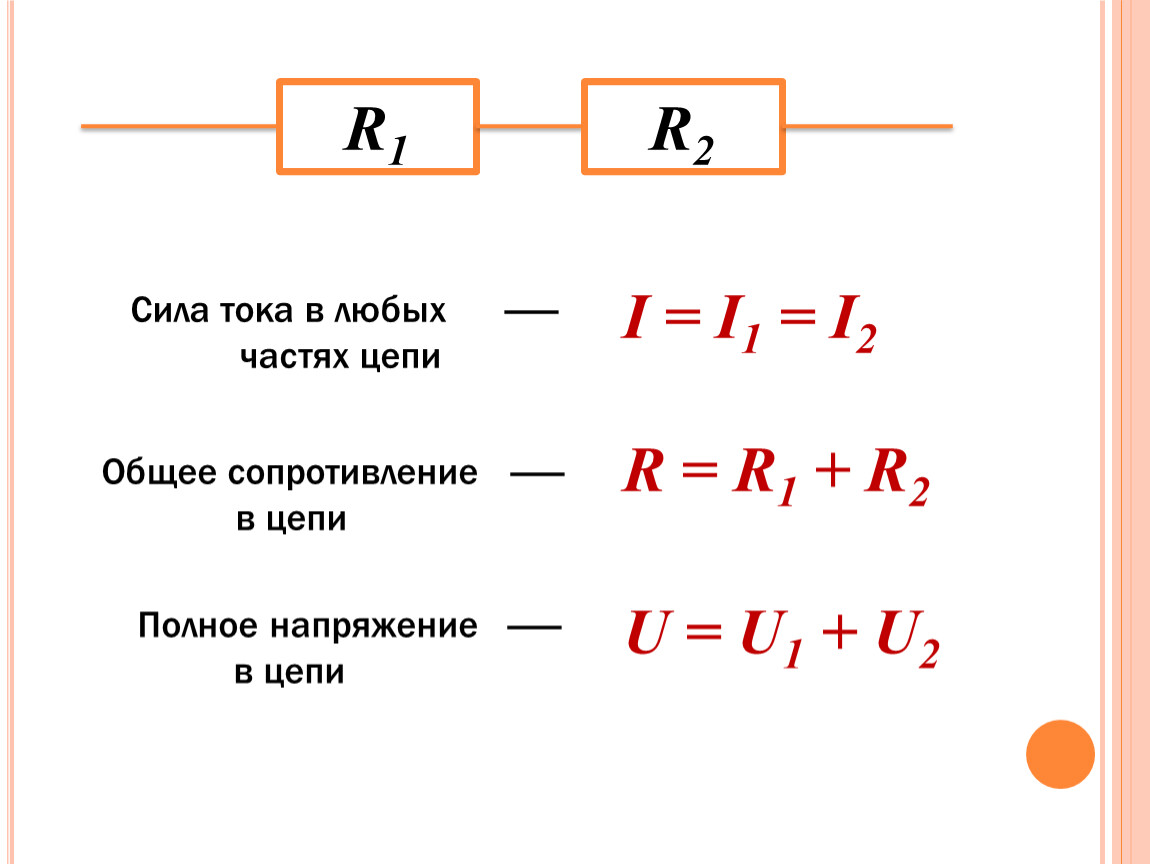 д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.
д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.
Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова:
I 1 =
I 2 =
I
.
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений
: R 1 + R 2 = R
. Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: U 1 =
I*
R 1
, U 2 = I*R 2
. В таком случае общее напряжение равно U = I (
R 1 +
R 2)
. Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике
: U = U 1 + U 2
.
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
Для последовательного соединения проводников справедливы законы
:
1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Параллельное соединение проводников
Примером параллельного соединения
проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U
.
При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I =
I 1 +
I 2
.
В соответствии с законом Ома I = U/R, I 1 = U 1 /R 1 , I 2 = U 2 /R 2
. Отсюда следует: U/R = U 1 /R 1 + U 2 /R 2
, U = U 1 = U 2
,
1/R = 1/R 1 + 1/R
2
Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г
, то их общее сопротивление равно: R = г/2
. Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.
Для параллельного соединения проводников справедливы законы:
1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.
Содержание:
Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой. Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.
Способы подключения и их особенности
Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.
Последовательное соединение
Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего. Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.
Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.
Параллельное соединение
Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.
Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом. В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.
Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.
Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.
Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.
Последовательно-параллельное соединение
Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.
Подведем итог
Подводя итог всему вышеизложенному можно сделать следующие выводы:
- При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
- При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
- Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
- Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
- Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.
В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки. По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.
Содержание:
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R
= 1/U
, где
R
= 1
Ом
А мощность будет выделяться P
=
I
*
U
,
то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G
, по аналогии с сопротивлением R
и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I
=
U
*
G
&
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих. Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Последовательное и параллельное соединение
В данной статье речь пойдет о последовательном и параллельном соединении проводников. На примерах будут рассмотрены данные соединения и как при таких соединениях будут изменяться такие величины как:
- ток;
- напряжение;
- сопротивление.
В таблице 1.8 [Л2, с.24] приведены схемы и формулы по определению сопротивлений, токов и напряжений при параллельном и последовательном соединении.
Последовательное соединение
Последовательным соединением называются те участки цепи, по которым всегда проходят одинаковые токи.
При последовательном соединении:
- сила тока во всех проводниках одинакова;
- напряжение на всём соединении равно сумме напряжений на отдельных проводниках;
- сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Пример 1
Последовательно подключены две лампы накаливания одинаковой мощности Рл1=Рл2=100 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляет Rл1=Rл2=122 Ом. Номинальное напряжение для ламп равно 220 B. На рис.1 показано последовательное включение ламп.
Решение
Составляем схему замещения, выражая каждую из входящих элементов цепи (в данном случае лампы накаливания) в виде сопротивлений.
1. Определяем ток протекающей по участкам цепи:
Iн = Uн/Rл1+ Rл2 = 220/122+122 = 0,9 A
2. Определяем напряжение на каждой из ламп накаливания, так как мощность ламп у нас одинаковая, то и напряжение для каждой из ламп будет одинаково:
Uл1=Uл2 = Iн*R = 0,9*122 = 110 B
Как мы видим напряжение источника (в данном примере 220 В) разделиться поровну, между обоими последовательно включенными лампами. При этом лампы будут ели светит, их накал будет неполным.
Для того чтобы лампы горели с полным накалом, нужно увеличить напряжение источника с 220В до 440В, при этом на каждой из ламп установиться номинальное (рабочее) напряжение равное 220В.
Пример 2
Последовательно подключены две лампы накаливания мощность Рл1 = 100 Вт и Рл2 = 75 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляют Rл1= 122 Ом для стоваттной лампы и Rл2= 153 Ом для семидесяти пяти ватной лампы.
Решение
1. Определяем ток протекающей по участкам цепи:
Iн = Uн/Rл1+ Rл2 = 220/100+75 = 0,8 A
2. Определяем напряжение на каждой из ламп накаливания:
Uл1= Iн*Rл1 = 0,8*122 = 98 B
Uл2= Iн*Rл2 = 0,8*153 = 122 B
Исходя из результатов расчетов, более мощная лампа 100 Вт получает при этом меньшее напряжение. Но ток в двух последовательно включенных даже разных лампах остается одинаковым. Например, если одна из ламп перегорит (порвется ее нить накаливания), погаснут обе лампы.
Данное соединение лампочек, например, используется в трамвайном вагоне для освещения салона.
Параллельное соединение
Параллельное соединение – это соединение, при котором начала всех проводников присоединяются к одной точке цепи, а их концы к другой.
Точки цепи, к которым сходится несколько проводов, называют узлами. Участки цепи, соединяющие между собой узлы, называют ветвями.
При параллельном соединении:
- напряжение на всех проводниках одинаково;
- сила тока в месте соединения проводников равна сумме токов в отдельных проводниках;
- величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.
Пример 3
Определить токи и напряжения всех участков цепи (рис.5), если известно:
- Номинальное напряжение сети Uн = 220В;
- Сопротивление нити в лампах HL1 и HL2 составляют Rл1 = Rл2 = 122 Ом.
- Сопротивление нити в лампе HL3 составляют Rл3 = 153 Ом.
Решение
Составляем схему замещения для схемы, представленной на рис.5.
1. Определяем проводимость всей цепи [Л1, с.47] и согласно таблицы 1.8:
2. Определяем сопротивление всей цепи [Л1, с.47]:
3. Определяем силу тока цепи по закону Ома:
4. Определяем токи для каждой цепи [Л1, с.47]:
5. Выполним проверку, согласно которой, сила тока в месте соединения проводников равна сумме токов в отдельных проводниках:
Iл1+ Iл2+ Iл3=Iобщ.=1,8+1,8+1,44=5,04=5,04 (условие выполняется)
Смешанное соединение
Смешанным соединением – называется последовательно-параллельное соединение сопротивлений или участков цепи.
Пример 4
Определить токи и напряжения всех участков цепи (рис.7), если известно:
- Номинальное напряжение сети Uн = 220В;
- Сопротивление нити в лампах HL1, HL2, HL3 составляют Rл1 = Rл2 = Rл3 = 122 Ом.
- Сопротивление нити в лампе HL4 составляют Rл4 = 153 Ом.
- Результаты расчетов для участка цепи ВС (параллельное соединение проводников) применим из примера 3:
Сопротивление цепи ВС составляет Rвс = 43,668 Ом.
Решение
Составляем схему замещения для схемы, представленной на рис.7.
1. Определяем сопротивление всей цепи:
Rобщ = Rав+Rвс = Rл1+Rвс = 122+43,688 = 165,688 Ом
2. Определяем силу тока цепи, согласно закона Ома:
3. Определяем напряжение на первом сопротивлении:
Uав=Uл1= Iобщ*Rл1 = 1,33*122 = 162 B
4. Определяем напряжение на участке ВС:
Uвс= Iобщ*Rвс = 1,33*43,688 = 58,1 B
5. Определяем токи для каждой цепи участка ВС:
6. Выполним проверку для участка цепи ВС:
Iл2+ Iл3+ Iл4= Iобщ.=0,48+0,48+0,38=1,33=1,33 (условие выполняется)
Литература:
- Общая электротехника с основами электроники, В.С. Попов, 1972 г.
- Справочная книга электрика. В.И. Григорьева. 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи,
в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление R
общ
При таком соединении, через все резисторы проходит один и тот же электрический ток.
Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него.
Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается,
и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами.
В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление R
общ
При таком соединении, через каждый резистор потечет отдельный ток.
Сила данного тока будет обратно пропорциональна сопротивлению резистора.
В результате общая проводимость такого участка электрической цепи увеличивается,
а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением,
общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности.
Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора.
Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов
соединяются между собой последовательно, а часть параллельно.
В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление R
общ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения.
Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Последовательное и параллельное соединения проводников – FIZI4KA
1. Потребители электрической энергии: электрические лампочки, резисторы и пр. — могут по-разному соединяться друг с другом в электрической цепи. Существует два основных типа соединения проводников: последовательное и параллельное. При последовательном соединении проводников конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т.д. (рис. 85).
Примером последовательного соединения проводников может служить соединение электрических лампочек в ёлочной гирлянде.
При последовательном соединении проводников ток проходит через все лампочки, при этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд, т.е. заряд не скапливается ни в какой части проводника. Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: \( I_1=I_2=I \).
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений: \( R_1=R_2=R \). Это следует из того, что при последовательном соединении проводников их общая длина увеличивается, она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: \( U_1=IR_1 \), \( U_2=IR_2 \), а общее напряжение равно \( U=I(R_1+R_2) \). Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике: \( U=U_1+U_2 \).
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
2. Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи (А), а вторым концом к другой точке цепи (В) (рис. 86).
Поэтому вольтметр, подключенный к этим точкам, покажет напряжение как на проводнике 1, так и на проводнике 2. Таким образом, напряжение на концах всех параллельно соединённых проводников одно и то же: \( U_1=U_2=U \).
При параллельном соединении проводников электрическая цепь разветвляется, в данном случае в точке В. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: \( I=I_1+I_2 \).
В соответствии с законом Ома \( I=\frac{U}{R} \), \( I_1=\frac{U_1}{R_1} \), \( I_2=\frac{U_2}{R_2} \). Отсюда следует: \( \frac{U}{R}=\frac{U_1}{R_1}+\frac{U_2}{R_2} \). Так как \( U_1=U_2=U \), \( \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2} \). Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление \( r \), то их общее сопротивление равно: \( R=r/2 \). Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения, соответственно уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно: они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них и соответствие суммарной силы тока предельно допустимой силе тока.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением \( R_1 \) и \( R_2 \). Напряжения на резисторах соответственно \( U_1 \) и \( U_2 \).
По какой из формул можно определить напряжение U на участке АВ?
1) \( U=U_1+U_2 \)
2) \( U=U_1-U_2 \)
3) \( U=U_1=U_2 \)
4) \( U=\frac{U_1U_2}{U_1+U_2} \)
2. На рисунке изображёна схема электрической цепи, содержащая два параллельно включённых резистора сопротивлением \( R_1 \) и \( R_2 \). Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
1) \( I=I_1=I_2 \)
2) \( I=I_1+I_2 \)
3) \( U=U_1+U_2 \)
4) \( R=R_1+R_2 \)
3. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением R} и R2. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
1) \( U=U_1+U_2 \)
2) \( I=I_1+I_2 \)
3) \( U=U_1=U_2 \)
4) \( R=\frac{R_1R_2}{R_1+R_2} \)
4. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением \( R_1 \) и \( R_2 \). Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?
1) \( U=U_1=U_2 \)
2) \( I=I_1+I_2 \)
3) \( I=I_1=I_2 \)
4) \( R=\frac{R_1R_2}{R_1+R_2} \)
5.2 \)
2) \( R=2R_1 \)
3) \( R=\frac{R_1}{2} \)
4) \( R=\sqrt{R_1} \)
6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов \( R_1 \) и \( R_2 \) равны. Чему равно сопротивление каждого резистора?
1) 81 Ом
2) 18 Ом
3) 9 Ом
4) 4,5 Ом
7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?
1) 1/3 Ом
2) 3 Ом
3) 9 Ом
4) 27 Ом
8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 10 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 5 Ом?
1) 9 Ом
2) 11 Ом
3) 16 Ом
4) 26 Ом
9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 3 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 10 Ом?
1) 9 Ом
2) 10 Ом
3) 14 Ом
4) 24 Ом
10. Если ползунок реостата (см. схему) переместить влево, то сила тока
1) в резисторе \( R_1 \) уменьшится, а в резисторе \( R_2 \) увеличится
2) увеличится в обоих резисторах
3) в резисторе \( R_1 \) увеличится, а в резисторе \( R_2 \) уменьшится
4) уменьшится в обоих резисторах
11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как изменяются при передвижении ползунка реостата вправо его сопротивление, сила тока в цепи и напряжение на резисторе 1?
Для каждой физической величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) сопротивление реостата 2
Б) сила тока в цепи
B) напряжение на резисторе 1
ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется
12. Установите соответствие между физическими величинами и правильной электрической схемой для измерения этих величин при последовательном соединении двух резисторов \( R_1 \) и \( R_2 \). Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) сила тока в резисторе \( R_1 \) и \( R_2 \)
Б) напряжение на резисторе \( R_2 \)
B) общее напряжение на резисторах \( R_1 \) и \( R_2 \)
Часть 2
13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов \( R_1 \) = 10 Ом, \( R_2 \) = 5 Ом, \( R_3 \) = 5 Ом. Каково напряжение на резисторе 1, если амперметр показывает силу тока 2 А?
Ответы
Последовательное и параллельное соединения проводников
3.1 (62.86%) 7 votes
Учебное пособие по физике: Параллельные схемы
Как упоминалось в предыдущем разделе Урока 4, два или более электрических устройства в цепи могут быть соединены последовательным или параллельным соединением. Когда все устройства соединены с использованием параллельных соединений, схема называется параллельной схемой . В параллельной схеме каждое устройство помещается в свою отдельную ветвь . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить через внешнюю цепь.Каждый заряд, проходящий через контур внешней цепи, будет проходить через единственный резистор, присутствующий в одной ветви. Прибыв в место разветвления или узел, плата выбирает , через какую ветвь пройти на обратном пути к терминалу с низким потенциалом.
Краткое сравнение и контраст между последовательными и параллельными цепями было сделано в предыдущем разделе Урока 4. В этом разделе было подчеркнуто, что добавление большего количества резисторов в параллельную цепь приводит к довольно неожиданному результату — уменьшению общего сопротивления. .Поскольку существует несколько путей, по которым может протекать заряд, добавление еще одного резистора в отдельную ветвь обеспечивает еще один путь, по которому заряд может проходить через основную область сопротивления в цепи. Это уменьшенное сопротивление в результате увеличения количества ветвей будет иметь эффект увеличения скорости, с которой течет заряд (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платными дорогами. Плата за проезд — это основное место сопротивления автомобильному потоку на платной дороге.Добавление дополнительных пунктов сбора платы за проезд в пределах их собственного отделения на платной дороге обеспечит больше путей для автомобилей, проезжающих через станцию сбора платы за проезд. Эти дополнительные пункты пропуска снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.
Текущая
Скорость, с которой заряд проходит через цепь, называется током. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах.Заряд НЕ расходуется резисторами таким образом, что в одном месте ток меньше, чем в другом. В параллельной схеме заряд делит на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой. Тем не менее, если брать в целом, общая сумма тока во всех ветвях при сложении равна величине тока в местах за пределами ветвей. Правило, что ток везде один и тот же , все еще работает, только с изюминкой.Сила тока вне ветвей равна сумме токов в отдельных ветвях. Это все еще та же величина тока, только разделенная на несколько путей.
В форме уравнения этот принцип можно записать как
I всего = I 1 + I 2 + I 3 + …
, где I всего — это общая сумма тока вне ветвей (и в батарее), а I 1 , I 2 и I 3 представляют ток в отдельных ветвях цепи.
В этом блоке широко использовалась аналогия между расходом заряда и расходом воды. Еще раз вернемся к аналогии, чтобы проиллюстрировать, как сумма текущих значений в ветвях равна сумме вне ветвей. Поток заряда в проводах аналогичен потоку воды в трубах. Рассмотрим приведенные ниже схемы, на которых поток воды в трубах делится на отдельные ответвления. В каждом узле (место разветвления) вода проходит двумя или более отдельными путями.Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ветвях за пределами узла. Точно так же, когда две или более ветви подаются в узел, скорость, с которой вода вытекает из узла, будет равна сумме расходов в отдельных ветвях, которые подаются в узел.
Тот же принцип разделения потока применяется к электрическим цепям. Скорость, с которой заряд поступает в узел, равна сумме расходов в отдельных ветвях за пределами узла.Это проиллюстрировано в приведенных ниже примерах. В примерах вводится новый символ схемы — буква A, заключенная в круг. Это символ амперметра — устройства, используемого для измерения силы тока в определенной точке. Амперметр способен измерять ток, оказывая при этом незначительное сопротивление потоку заряда.
Диаграмма A показывает два резистора, подключенных параллельно с узлами в точках A и B. Заряд течет в точку A со скоростью 6 ампер и делится на два пути — один через резистор 1, а другой — через резистор 2.Ток в ветви с резистором 1 составляет 2 ампера, а ток в ветви с резистором 2 — 4 ампера. После того, как эти две ветви снова встретятся в точке B, чтобы сформировать единую линию, ток снова станет равным 6 ампер. Таким образом, мы видим, что принцип, согласно которому ток вне ветвей равен сумме тока в отдельных ветвях, справедлив.
I итого = I 1 + I 2
6 ампер = 2 ампера + 4 ампера
Схема B выше может быть немного сложнее, если три резистора расположены параллельно.На схеме обозначены четыре узла, обозначенные буквами A, B, C и D. Заряд течет в точку A со скоростью 12 ампер и делится на два пути: один проходит через резистор 1, а другой направляется к точке B (и резисторам 2). и 3). 12 ампер тока делятся на 2-амперную (через резистор 1) и 10-амперную (в направлении точки B). В точке B происходит дальнейшее разделение потока на два пути — один через резистор 2, а другой через резистор 3. Ток в 10 ампер, приближающийся к точке B, делится на 6-амперный канал (через резистор 2) и 4-канальный. -амперный тракт (через резистор 3).Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера, и что сумма значений тока в отдельных ветвях равна току вне ветвей.
I всего = I 1 + I 2 + I 3
12 ампер = 2 ампер + 6 ампер + 4 ампер
Анализ потока в точках C и D также может быть проведен, и будет замечено, что сумма расходов потока в этих точках равна скорости потока, находящейся непосредственно за этими точками.
Эквивалентное сопротивление
Фактическая величина тока всегда изменяется обратно пропорционально величине общего сопротивления. Существует четкая взаимосвязь между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая, когда два резистора помещены в параллельные ветви, каждый из которых имеет одинаковое значение сопротивления 4 Ом.Поскольку схема предлагает два равных путей для потока заряда, только половина заряда выберет для прохождения через данную ветвь. В то время как каждая отдельная ветвь предлагает сопротивление 4 Ом любому заряду, который проходит через нее, только половина всего заряда, протекающего по цепи, будет встречать сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается батареи, которая накачивает заряд, наличие двух параллельно подключенных резисторов 4 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи.Таким же образом, наличие двух параллельно подключенных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом. А наличие двух параллельных резисторов 12 Ом было бы эквивалентно наличию в цепи одного резистора 6 Ом.
Теперь давайте рассмотрим другой простой случай, когда три резистора включены параллельно, каждый из которых имеет одинаковое сопротивление 6 Ом. При трех равных путях прохождения заряда через внешнюю цепь только одна треть заряда будет проходить через данную ветвь.Каждая отдельная ветвь обеспечивает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через определенную ветвь, означает, что общее сопротивление цепи составляет 2 Ом. Что касается батареи, которая нагнетает заряд, наличие трех параллельных резисторов 6 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи. Таким же образом, наличие трех параллельно подключенных резисторов сопротивлением 9 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом.А наличие трех параллельных резисторов 12 Ом было бы эквивалентно наличию одного резистора 4 Ом в цепи.
Это концепция эквивалентного сопротивления. Эквивалентное сопротивление схемы — это величина сопротивления, которая потребуется одному резистору, чтобы сравняться с общим эффектом от набора резисторов, присутствующих в схеме. Для параллельных цепей математическая формула для вычисления эквивалентного сопротивления ( R eq ) составляет
.
1/ экв. = 1/ 1 + 1/ 2 + 1/ 3 +…
, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, подключенных параллельно. Приведенные выше примеры можно рассматривать как простые случаи, в которых все пути обладают одинаковым сопротивлением отдельному заряду, который проходит через них. Приведенные выше простые случаи были выполнены без использования уравнения. Тем не менее, уравнение подходит как для простых случаев, когда резисторы ответвления имеют одинаковые значения сопротивления, так и для более сложных случаев, когда резисторы ответвления имеют разные значения сопротивления.Например, рассмотрим применение уравнения к одному простому и одному сложному случаю ниже.
| Случай 1 : три резистора 12 Ом включены параллельно | 1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (12 Ом) + 1 / (12 Ом) + 1 / (12 Ом) Использование калькулятора … 1 / R экв. = 0,25 Ом -1 R экв = 1 / (0,25 Ом -1 ) R экв = 4,0 Ом |
| Случай 2 : резисторы 5,0 Ом, 7,0 Ом и 12 Ом включены параллельно | 1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (5.0 Ом) + 1 / (7,0 Ом) + 1 / (12 Ом) Использование калькулятора … 1 / R экв = 0,42619 Ом-1 R экв = 1 / (0,42619 Ом -1 ) R экв. = 2,3 Ом |
Ваша очередь попробовать
Нужно больше практики? Используйте два параллельных резистора виджет ниже, чтобы попробовать некоторые дополнительные проблемы.Введите любые два желаемых значения сопротивления. Используйте свой калькулятор, чтобы определить значения рэндов и рэндов. Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте столько раз, сколько хотите, с разными значениями сопротивления.
Падения напряжения для параллельных ветвей
В разделе «Схемы» учебного курса «Физический класс» подчеркивалось, что любое повышение напряжения, полученное за счет заряда в батарее, теряется из-за заряда, когда он проходит через резисторы внешней цепи.Общее падение напряжения во внешней цепи равно увеличению напряжения при прохождении заряда через внутреннюю цепь. В параллельной схеме заряд не проходит через каждый резистор; скорее, он проходит через единственный резистор. Таким образом, полное падение напряжения на этом резисторе должно соответствовать напряжению батареи. Не имеет значения, проходит ли заряд через резистор 1, резистор 2 или резистор 3, падение напряжения на резисторе, которое выбирает для прохождения , должно равняться напряжению батареи.В форме уравнения этот принцип можно было бы выразить как
В аккумулятор = В 1 = В 2 = В 3 = …
Если три резистора размещены в параллельных ветвях и питаются от 12-вольтовой батареи, то падение напряжения на каждом из трех резисторов составляет 12 вольт. Заряд, протекающий по цепи, встретит только один из этих трех резисторов и, таким образом, столкнется с одним падением напряжения на 12 вольт.
Диаграммы электрических потенциалов были представлены в Уроке 1 этого устройства и впоследствии использовались для иллюстрации последовательных падений напряжения, происходящих в последовательных цепях.Диаграмма электрического потенциала — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим приведенную ниже принципиальную схему и соответствующую диаграмму электрических потенциалов.
Как показано на диаграмме электрических потенциалов, все позиции A, B, C, E и G имеют высокий электрический потенциал. Один заряд выбирает только один из трех возможных путей; таким образом, в позиции B один заряд будет двигаться к точкам C, E или G, а затем пройдет через резистор, находящийся в этой ветви.Заряд не теряет свой высокий потенциал до тех пор, пока не пройдет через резистор, либо от C к D, от E к F или от G к H. После того, как он пройдет через резистор, заряд вернется почти до 0 вольт и вернется к отрицательному клемму аккумуляторной батареи для повышения ее напряжения. В отличие от последовательных цепей, заряд в параллельной цепи встречает единственное падение напряжения на своем пути через внешнюю цепь.
Ток через заданную ветвь можно предсказать, используя уравнение закона Ома, падение напряжения на резисторе и сопротивление резистора.Поскольку падение напряжения на каждом резисторе одинаково, фактором, определяющим, что резистор имеет наибольший ток, является сопротивление. Резистор с наибольшим сопротивлением испытывает наименьший ток, а резистор с наименьшим сопротивлением — наибольший ток. В этом смысле можно сказать, что заряд (как и люди) выбирает путь наименьшего сопротивления. В форме уравнения это может быть указано как
| I 1 = Δ V 1 / R 1 | I 2 = Δ V 2 / R 2 | I 3 = Δ V 3 / R 3 |
Этот принцип иллюстрируется схемой, показанной ниже.Произведение I • R одинаково для каждого резистора (и равно напряжению батареи). Тем не менее, ток у каждого резистора разный. Ток наибольший там, где сопротивление наименьшее, и ток наименьший, где сопротивление наибольшее.
Математический анализ параллельных цепей
Приведенные выше принципы и формулы могут использоваться для анализа параллельной цепи и определения значений тока и разности электрических потенциалов на каждом из резисторов в параллельной цепи.Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока через батарею (I до ), а также падений напряжения и тока для каждого из трех резисторов.
Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.
1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 = (1/17 Ом) + (1/12 Ом) + (1/11 Ом)
1 / R экв = 0.23306 Ом -1
R экв = 1 / (0,23306 Ом -1 )
R экв = 4,29 Ом
(округлено от 4,29063 Ом)
Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в батарее важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R.Расчет показан здесь:
I до = ΔV аккумулятор / R eq = (60 В) / (4,29063 Ом)
I до = 14,0 А
(округлено от 13,98396 А)
Напряжение батареи 60 В представляет собой усиление электрического потенциала за счет заряда, проходящего через батарею. Заряд теряет такое же количество электрического потенциала при любом прохождении через внешнюю цепь.То есть падение напряжения на каждом из трех резисторов такое же, как и напряжение, полученное в батарее:
ΔV аккумулятор = ΔV 1 = ΔV 2 = ΔV 3 = 60 В
Осталось определить три значения — ток каждого отдельного резистора. Закон Ома снова используется для определения значений тока для каждого резистора — это просто падение напряжения на каждом резисторе (60 В), деленное на сопротивление каждого резистора (указанное в формулировке задачи).Расчеты показаны ниже.
| I 1 = ΔV 1 / R 1 I 1 = (60 В) / (17 Ом) I 1 = 3,53 А | I 2 = ΔV 2 / R 2 I 2 = (60 В) / (12 Ом) I 2 = 5,00 А | I 3 = ΔV 3 / R 3 I 3 = (60 В) / (11 Ом) Я 3 = 5.45 ампер |
Для проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли вычисленные значения принципу, согласно которому сумма значений тока для каждого отдельного резистора равна общему току в цепи (или в батарее). . Другими словами, I to = I 1 + I 2 + I 3 ?
Является ли I tot = I 1 + I 2 + I 3 ?
Из 14.0 ампер = 3,53 ампер + 5,00 ампер + 5,45 ампер?
14,0 А = 13,98 А?
Да !!
(Разница в 0,02 ампера — это просто результат предыдущего округления значения I до от 13,98.)
Математический анализ этой параллельной цепи включал смесь концепций и уравнений. Как это часто бывает в физике, отделение понятий от уравнений при принятии решения физической проблемы является опасным актом.Здесь необходимо учитывать концепции, согласно которым падение напряжения на каждом из трех резисторов равно напряжению батареи и что сумма тока в каждом резисторе равна общему току. Эти представления необходимы для завершения математического анализа. В следующей части Урока 4 будут исследованы комбинированные или составные схемы, в которых одни устройства включены параллельно, а другие — последовательно.
Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже.Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.
Мы хотели бы предложить …
Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключить их так, как захотите. Вольтметры и амперметры позволяют измерять ток и падение напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).
Проверьте свое понимание
1. По мере того, как в цепь добавляется все больше и больше резисторов, эквивалентное сопротивление цепи ____________ (увеличивается, уменьшается) и общий ток цепи ____________ (увеличивается, уменьшается).
2.Три одинаковых лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают местоположения вдоль цепи. Какое из следующих утверждений верно?
а. Ток в точке Y больше, чем ток в точке Q.
г. Ток на Y больше, чем на P.
.
г. Ток в точке Y больше, чем ток в точке Z.
г. Ток в точке P больше, чем ток в точке Q.
.
e.Ток на Q больше, чем на P.
.
ф. Сила тока одинакова во всех местах.
3. Три одинаковые лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают местоположения вдоль цепи. В каком (а) месте (ах), если таковые имеются, будет ток …
а. … так же, как у X?
г…. такой же, как у Q?
г. … так же, как у Y?
г. … меньше, чем у Q?
e. … меньше, чем у P?
ф. … вдвое больше, чем у Z?
г. … в три раза больше, чем в Y?
4. Какие настройки можно внести в схему ниже, чтобы уменьшить ток в ячейке? Перечислите все подходящие варианты.
а. Увеличьте сопротивление лампы X.
г. Уменьшите сопротивление лампы X.
г. Увеличьте сопротивление лампы Z.
г. Уменьшите сопротивление лампы Z.
.
e. Увеличьте напряжение ячейки (как-нибудь).
ф. Уменьшите напряжение ячейки (как-нибудь).
г. Снять лампу Y.
.
5.Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключаются, как показано на рисунке. Ток в резисторе 12 Ом равен ____ току в резисторе 4 Ом.
а. 1/3
г. 1/2
г. 2/3
г. то же, что
e.1,5 раза
ф. дважды
г. трижды
ч. четыре раза
6. Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключены, как показано.Падение напряжения на резисторе 12 Ом равно ____ падению напряжения на резисторе 4 Ом.
а. 1/3
г. 1/2
г. 2/3
г. то же, что
e. 1,5 раза
ф.дважды
г. трижды
ч. четыре раза
7. Аккумулятор на 12 В и резистор на 12 Ом подключаются, как показано на схеме. Резистор на 6 Ом добавлен к резистору на 12 Ом, чтобы создать цепь Y, как показано.Падение напряжения на резисторе 6 Ом в цепи Y равно ____ падению напряжения на резисторе в цепи X.
а. больше, чем
г. меньше
г. то же, что
8. Используйте свое понимание эквивалентного сопротивления, чтобы заполнить следующие утверждения:
а. Два резистора сопротивлением 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.
г. Три резистора 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.
г. Три резистора сопротивлением 8 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.
г. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
e. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом размещены параллельно.Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
ф. Три резистора с сопротивлением 12 Ом, 6 Ом и 21 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
9. На основании ваших ответов на вышеуказанный вопрос заполните следующую формулировку:
Общее или эквивалентное сопротивление трех параллельно включенных резисторов будет _____.
а. больше, чем сопротивление самого большого значения R.
г. меньше, чем сопротивление наименьшего значения R из трех.
г. где-то между наименьшим значением R и наибольшим значением R.
г. … бред какой то! Такого обобщения сделать нельзя. Результаты меняются.
10. Три резистора включены параллельно.Если поместить в цепь с источником питания 12 В. Определите эквивалентное сопротивление, полный ток цепи, падение напряжения и ток в каждом резисторе.
Ток в параллельной цепи
Ток в параллельной цепи
Закон
Ома гласит, что ток в цепи обратно пропорционален сопротивлению цепи.Это верно как для последовательных, так и для параллельных цепей.
Существует единственный путь для тока в последовательной цепи. Величина тока определяется общим сопротивлением цепи и приложенным напряжением. В параллельной цепи ток источника делится между доступными путями.
Поведение тока в параллельных цепях будет показано серией иллюстраций с использованием примеров цепей с разными значениями сопротивления для заданного значения приложенного напряжения.
Часть (A) рисунка 3-40 показывает базовую последовательную схему.Здесь полный ток должен проходить через единственный резистор. Величину тока можно определить.
Рисунок 3-40. — Анализ тока в параллельной цепи.
Дано:
Решение:
На части (B) рисунка 3-40 показан тот же резистор (R 1 ) со вторым резистором (R 2 ) равного номинала, подключенным параллельно через напряжение источник. Когда применяется закон Ома, ток, протекающий через каждый резистор, оказывается таким же, как ток через единственный резистор в части (A).
Дано:
Решение:
Очевидно, что если через каждый из двух резисторов проходит ток 5 ампер, то должен быть ОБЩИЙ ТОК 10 ампер от источника.
Общий ток в 10 ампер, как показано на рисунке 3-40 (B покидает отрицательную клемму батареи и течет в точку а. Поскольку точка а является точкой соединения двух резисторов, она называется СОЕДИНЕНИЕМ. В переходе а общий ток делится на два тока по 5 ампер каждый.Эти два тока протекают через соответствующие резисторы и снова соединяются в переходе b. Затем полный ток течет от перехода b обратно к положительной клемме источника. Источник обеспечивает общий ток 10 ампер, и каждый из двух одинаковых резисторов несет половину общего тока.
Каждый отдельный путь тока в цепи на рисунке 3-40 (B) называется ОТВЕТЛЕНИЕМ. Каждая ветвь несет ток, который составляет часть общего тока. Два или более филиала образуют СЕТЬ.
Из предыдущего объяснения характеристики тока в параллельной цепи могут быть выражены в терминах следующего общего уравнения:
I T = I 1 + I 2 +. . . I n
Сравните часть (A) рисунка 3-41 с частью (B) схемы на рисунке 3-40. Обратите внимание, что удвоение значения резистора второй ветви (R 2 ) не влияет на ток в первой ветви (I R1 ), но снижает ток второй ветви (I R2 ) вдвое. его первоначальная стоимость.Полный ток в цепи падает до значения, равного сумме токов ответвления. Эти факты подтверждаются следующими уравнениями.
Дано:
Решение:
Рисунок 3-41. — Текущее поведение в параллельных цепях.
Сила тока, протекающего в ответвленных цепях, и общий ток в цепи, показанной на рисунке 3-41 (B), определяются с помощью следующих вычислений.
Дано:
Решение:
Обратите внимание, что сумма омических значений в каждой цепи, показанной на рисунке 3-41, равна (30 Ом), и что приложенное напряжение одинаково (50 вольт) .Однако общий ток в 3-41 (B) (15 ампер) в два раза больше, чем в 3-41 (A) (7,5 ампер). Таким образом, очевидно, что способ подключения резисторов в цепи, а также их фактические омические значения влияют на общий ток.
Разделение тока в параллельной сети происходит по определенной схеме. Этот образец описывается ЗАКОНОМ ТОКА КИРХГОФА, который гласит:
«Алгебраическая сумма токов, входящих и выходящих из любого соединения проводников, равна нулю.»
Математически этот закон можно сформулировать следующим образом:
I a + I b + … I n + 0
где: I a , I b и т. Д. токи, входящие и выходящие из соединения. Токи, входящие в соединение, считаются ПОЛОЖИТЕЛЬНЫМИ, а токи, выходящие из соединения, считаются ОТРИЦАТЕЛЬНЫМИ. При решении проблемы с использованием закона Кирхгофа, токи должны быть помещены в уравнение СО ЗНАКАМИ НАДЛЕЖАЩЕЙ ПОЛЯРНОСТИ ПРИКРЕПИЛ.
Пример. Найдите значение I 3 на рисунке 3-42.
Дано:
Решение:
I a + I b +. . . I
a + 0
Рисунок 3-42. — Цепь например проблема.
Токи указаны в уравнении с соответствующими знаками.
I 3 имеет значение 2 ампера, и отрицательный знак показывает, что это ток, ПОХОДЯЩИЙ из соединения.
Пример.Используя рисунок 3-43, найдите величину и направление I 3 .
Рисунок 3-43. — Цепь например проблема.
Дано:
Решение:
I 3 составляет 2 ампера, и его положительный знак показывает, что это ток, поступающий в соединение.
Существует взаимосвязь между общим током и током через отдельные компоненты в цепи. Что это за отношения в последовательной и параллельной цепях?
На что указывает полярность тока при применении закона Кирхгофа?
параллельных цепей
Ваш браузер не поддерживает Java-апплеты
Схема с более чем одним
Путь прохождения тока представляет собой параллельную цепь.
НАПРЯЖЕНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ
Общее напряжение равно
напряжение любого параллельного сопротивления.
ТОК В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ
Полный ток равен
сумма тока каждого параллельного компонента.
ПАРАЛЛЕЛЬНОЕ СОПРОТИВЛЕНИЕ
ЦЕПИ
Общее сопротивление может быть
рассчитывается по закону Ома, если известны напряжение и полный ток.
Общее сопротивление всегда
меньше наименьшего значения сопротивления.
Метод равных значений
Для параллельных сопротивлений в
какие все резисторы имеют одинаковое значение, сопротивление можно рассчитать по формуле
разделив номинал одного из резисторов на количество резисторов.
Взаимный метод
Для параллельных сопротивлений в
какие все резисторы имеют одинаковое значение, сопротивление можно рассчитать по формуле
разделив номинал одного из резисторов на количество резисторов.
1 / R T = 1 / R 1 + 1 / R 2 + 1 / R N
R EQ = 1 / (1 / R 1 + 1 / R 2 +
… + 1 / R N
)
Метод произведения на сумму
Для расчета сопротивления
двух резисторов параллельно можно использовать эту формулу:
рэндов EQ = ( 1 рэндов * рэндов 2 ) / ( 1 рэндов + 2 рэндов)
Правило приближения 10 к 1
Если подключены два резистора
параллельно, и один резистор в 10 или более раз больше, чем другой
резистор, резистор большего номинала можно не учитывать.
ПРОВОДИМОСТЬ
Общая проводимость равна
сумме проводимости каждого компонента.
ПИТАНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ
Суммарная мощность равна
сумма мощности каждого компонента. (Это то же самое, что и с серией
схемы).
Правила для параллельных цепей постоянного тока
- Такое же напряжение существует
на каждой ветви параллельной цепи и равно напряжению источника. - Ток через
параллельная ветвь обратно пропорциональна величине сопротивления
ветка. - Полный ток
параллельная цепь равна сумме отдельных токов ответвления
цепь - Эквивалентное сопротивление
параллельная цепь находится по общему уравнению Req = 1 / (1 / R1 + 1 / R2 +
1 / р-н) - Общая мощность, потребляемая в
параллельная схема равна сумме мощности, потребляемой индивидуумом
резисторы.
ПАРАЛЛЕЛЬНЫЙ АНАЛИЗ ЦЕПЕЙ
- Соблюдайте принципиальную схему
внимательно или при необходимости нарисуйте. - Обратите внимание на указанные значения и
значения, которые необходимо найти. - Выберите подходящий
уравнения, которые будут использоваться при решении для неизвестных величин на основе известных
количества. - Подставьте известные значения
в выбранном вами уравнении и найдите неизвестное значение.
ПАРАЛЛЕЛЬНОЕ УСТРАНЕНИЕ НЕПОЛАДОК
ЦЕПИ
Когда в
ветви параллельной сети сопротивление ветви увеличивается и
общее сопротивление цепи увеличивается. Это вызывает уменьшение общего
Текущий.
Короткое замыкание всегда приводит
в отсутствие тока, протекающего через другие ветви цепи.
Комбинированная серия
/ Параллельные схемы — Устранение неисправностей двигателей и органов управления
Кен Диксон-Селф
В простых последовательных цепях все компоненты соединены встык, образуя только один путь для прохождения электронов по цепи:
В простых параллельных цепях все компоненты подключаются между одними и теми же двумя наборами электрически общих точек, создавая несколько путей для прохождения электронов от одного конца батареи к другому:
Для каждой из этих двух базовых конфигураций схемы у нас есть определенные наборы правил, описывающих отношения напряжения, тока и сопротивления.
- Цепи серии :
- Падения напряжения прибавляются к общему напряжению.
- Все компоненты имеют одинаковый (равный) ток.
- единиц сопротивления добавляют к равному общему сопротивлению.
- Параллельные цепи:
- Все компоненты имеют одинаковое (равное) напряжение.
- Токи ответвления добавляют к равному общему току.
- Сопротивления уменьшаются до полного сопротивления.
Однако, если компоненты схемы соединены последовательно в одних частях и параллельно в других, мы не сможем применить единый набор правил к каждой части этой цепи.Вместо этого нам придется определить, какие части этой цепи являются последовательными, а какие — параллельными, а затем выборочно применять правила последовательного и параллельного подключения, если это необходимо, чтобы определить, что происходит. Возьмем, к примеру, следующую схему:
Эта схема не является ни простой последовательной, ни простой параллельной. Скорее, он содержит элементы обоих. Ток выходит из нижней части батареи, разделяется, чтобы пройти через R 3 и R 4 , снова присоединяется, затем снова разделяется, чтобы пройти через R 1 и R 2 , затем снова присоединяется, чтобы вернуться к верх аккумуляторной батареи.Существует более одного пути для прохождения тока (не последовательно), но в цепи более двух наборов электрически общих точек (не параллельных).
Поскольку схема представляет собой комбинацию как последовательной, так и параллельной, мы не можем применить правила для напряжения, тока и сопротивления «поперек стола», чтобы начать анализ, как мы могли бы, когда цепи были тем или иным образом. Например, если бы вышеприведенная схема была простой последовательной, мы могли бы просто сложить R 1 — R 4 , чтобы получить общее сопротивление, вычислить общий ток, а затем вычислить все падения напряжения.Точно так же, если бы вышеуказанная схема была простой параллельной, мы могли бы просто решить для токов ответвления, сложить токи ответвления, чтобы вычислить общий ток, а затем вычислить общее сопротивление из общего напряжения и общего тока. Однако решение этой схемы будет более сложным.
Таблица по-прежнему поможет нам управлять различными значениями для последовательно-параллельных комбинированных цепей, но мы должны быть осторожны, как и где применять разные правила для последовательного и параллельного подключения. Закон Ома, конечно, по-прежнему работает точно так же для определения значений в вертикальном столбце таблицы.
Если мы можем определить, какие части схемы являются последовательными, а какие — параллельными, мы можем анализировать их поэтапно, подходя к каждой части по очереди, используя соответствующие правила для определения отношений напряжения, тока и сопротивления. . Остальная часть этой главы будет посвящена тому, чтобы показать вам, как это сделать.
Процесс анализа последовательно-параллельной цепи резисторов
Целью анализа последовательно-параллельной цепи резисторов является определение всех падений напряжения, токов и рассеиваемой мощности в цепи.Общая стратегия достижения этой цели следующая:
- Шаг 1. Определите, какие резисторы в цепи соединены вместе простой последовательностью или простой параллелью.
- Шаг 2: Изобразите схему заново, заменив каждую из комбинаций последовательных или параллельных резисторов, определенных на шаге 1, одним резистором эквивалентного номинала. При использовании таблицы для управления переменными создайте новый столбец таблицы для каждого эквивалента сопротивления.
- Шаг 3: Повторяйте шаги 1 и 2, пока вся цепь не будет уменьшена до одного эквивалентного резистора.
- Шаг 4: Рассчитайте общий ток из общего напряжения и общего сопротивления (I = E / R).
- Шаг 5: Взяв значения общего напряжения и полного тока, вернитесь к последнему шагу в процессе сокращения цепи и вставьте эти значения, где это возможно.
- Шаг 6: Из известных значений сопротивления и значений полного напряжения / полного тока из шага 5 используйте закон Ома для вычисления неизвестных значений (напряжения или тока) (E = IR или I = E / R).
- Шаг 7: Повторяйте шаги 5 и 6, пока все значения напряжения и тока не будут известны в исходной конфигурации схемы.По сути, вы будете шаг за шагом переходить от упрощенной версии схемы к ее исходной сложной форме, вставляя значения напряжения и тока, где это необходимо, до тех пор, пока не будут известны все значения напряжения и тока.
- Шаг 8: Рассчитайте рассеиваемую мощность на основе известных значений напряжения, тока и / или сопротивления.
Это может показаться пугающим процессом, но его гораздо легче понять на примере, чем через описание.
В приведенном выше примере схемы R 1 и R 2 соединены в простую параллельную схему, как и R 3 и R 4 .После идентификации эти секции необходимо преобразовать в эквивалентные одиночные резисторы и заново нарисовать схему:
Символы двойной косой черты (//) обозначают «параллельность», чтобы показать, что эквивалентные значения резисторов были рассчитаны по формуле 1 / (1 / R). Резистор 71,429 Ом в верхней части схемы эквивалентен R 1 и R 2 , включенным параллельно друг другу. Резистор 127,27 Ом внизу эквивалентен R 3 и R 4 , включенным параллельно друг другу.
Наша таблица может быть расширена, чтобы включить эти эквиваленты резисторов в отдельные столбцы:
Теперь должно быть очевидно, что схема была уменьшена до простой последовательной конфигурации только с двумя (эквивалентными) сопротивлениями. Последний шаг в уменьшении — сложить эти два сопротивления, чтобы получить общее сопротивление цепи. Когда мы складываем эти два эквивалентных сопротивления, мы получаем сопротивление 198,70 Ом. Теперь мы можем перерисовать схему как единое эквивалентное сопротивление и добавить значение общего сопротивления в крайний правый столбец нашей таблицы.Обратите внимание, что столбец «Итого» был переименован (R 1 // R 2 —R 3 // R 4 ), чтобы указать, как он электрически связан с другими столбцами цифр. Символ «-» здесь используется для обозначения «серии», так же как символ «//» используется для обозначения «параллельности».
Теперь общий ток цепи можно определить, применив закон Ома (I = E / R) к столбцу «Всего» в таблице:
Вернемся к нашему рисунку эквивалентной схемы, наше общее текущее значение 120.Здесь показан только ток 78 миллиампер:
Теперь мы начинаем работать в обратном направлении в нашей прогрессии переделки схем до исходной конфигурации. Следующим шагом является переход к схеме, в которой последовательно находятся R 1 // R 2 и R 3 // R 4 :
Поскольку R 1 // R 2 и R 3 // R 4 включены последовательно друг с другом, ток через эти два набора эквивалентных сопротивлений должен быть одинаковым.Кроме того, ток через них должен быть таким же, как и полный ток, поэтому мы можем заполнить нашу таблицу соответствующими текущими значениями, просто скопировав текущую цифру из столбца Total в R 1 // R 2 и R 3 // R 4 столбцов:
Теперь, зная ток через эквивалентные резисторы R 1 // R 2 и R 3 // R 4 , мы можем применить закон Ома (E = IR) к двум правым вертикальным столбцам, чтобы найти падение напряжения на них:
Поскольку мы знаем, что R 1 // R 2 и R 3 // R 4 являются эквивалентами параллельных резисторов, и мы знаем, что падения напряжения в параллельных цепях одинаковы, мы можем передавать соответствующие падения напряжения в соответствующие столбцы таблицы для этих отдельных резисторов.Другими словами, мы делаем еще один шаг назад в нашей последовательности рисования к исходной конфигурации и заполняем таблицу соответствующим образом:
Наконец, исходный раздел таблицы (столбцы R 1 — R 4 ) заполнен достаточным количеством значений для завершения. Применяя закон Ома к остальным вертикальным столбцам (I = E / R), мы можем определить токи через R 1 , R 2 , R 3 и R 4 по отдельности:
Размещение значений напряжения и тока на диаграммах
Найдя все значения напряжения и тока для этой цепи, мы можем показать эти значения на принципиальной схеме как таковые:
В качестве последней проверки нашей работы мы можем увидеть, складываются ли рассчитанные текущие значения должным образом в общую сумму.Поскольку R 1 и R 2 подключены параллельно, их комбинированные токи в сумме должны составить 120,78 мА. Аналогичным образом, поскольку R 3 и R 4 подключены параллельно, их комбинированные токи в сумме также должны составлять 120,78 мА. Вы можете проверить сами, чтобы убедиться, что эти цифры складываются так, как ожидалось.
Эта глава является адаптацией книги « уроков по электрическим схемам» Тони Р. Купхальда (на allaboutcircuits.com) и используется в соответствии с лицензией на научный дизайн.
Расчет тока в последовательно-параллельных цепях
Расчет тока в последовательно-параллельных цепях
| Рисунок 1. Последовательно-параллельные резисторы. |
В цепи с резисторами, включенными как последовательно, так и
параллельно, рассматривать схему как комбинацию параллельных частей и последовательных
части.
Используйте формулы сопротивления для определения общего сопротивления
серийных и параллельных частей.Затем используйте закон Ома, чтобы вычислить напряжение
падает поперек и токи через каждую часть.
В схеме на Рисунке 1 сначала используйте параллельное сопротивление
формула для нахождения эквивалентного сопротивления R 123 .
Тогда формула последовательного сопротивления говорит нам R TOT = R 123 + R 4 . Итак, закон Ома дает полный ток цепи:
I TOT равняется как текущим I 4 через R 4 и текущему I 123 входу / выходу из параллельной части.Используя закон Ома:
Итак, зная значение В 123 , снова применим закон Ома, чтобы найти ток I 1 через параллельный резистор R 1 :
и аналогично для I 2 и I 3 .
Пример
Для схемы на рисунке 1 предположим, что E = 9 В, R 1 = 500 Ом, R 2 = 1.0 кОм, R 3 = 1,5 кОм и R 4 = 220 Ом. Тогда R 123 = 273 Ом и R TOT = 493 Ом, поэтому
и, следовательно,
Аналогично для I 2 и I 3 .
Примечание: Важно осторожно обращаться с единицами измерения с метрическими префиксами. Выше мы отрегулировали десятичную точку и единицы измерения так, чтобы наша формула для тока давала вольт / Ом = ампер.
резисторов последовательно и параллельно
Резисторы
серии
Общее сопротивление в цепи с последовательно включенными резисторами равно сумме отдельных сопротивлений.
Цели обучения
Рассчитайте общее сопротивление в цепи с последовательно включенными резисторами
Основные выводы
Ключевые моменты
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
- Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений: [латекс] \ text {RN} (\ text {series}) = \ text {R} _1 + \ text {R} _2 + \ text {R} _3 +… + \ text {R} _ \ text {N} [/ latex].
Ключевые термины
- серия : ряд элементов, которые следуют одно за другим или связаны друг за другом.
- сопротивление : Противодействие прохождению электрического тока через этот элемент.
Обзор
В большинстве схем имеется более одного компонента, называемого резистором, который ограничивает поток заряда в цепи. Мера этого предела для потока заряда называется сопротивлением. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Цепи серии : Краткое введение в анализ последовательных и последовательных цепей, включая закон Кирхгофа по току (KCL) и закон Кирхгофа по напряжению (KVL).
Резисторы серии
Резисторы включены последовательно всякий раз, когда заряд или ток должны проходить через компоненты последовательно.
Резисторы в серии : Эти четыре резистора подключены последовательно, потому что, если бы ток подавался на один конец, он бы протекал через каждый резистор последовательно до конца.
показывает резисторы, последовательно подключенные к источнику напряжения. Общее сопротивление в цепи равно сумме отдельных сопротивлений, поскольку ток должен последовательно проходить через каждый резистор.
Резисторы, подключенные последовательно. : Три резистора, подключенные последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Использование закона Ома для расчета изменений напряжения в резисторах серии
Согласно закону Ома падение напряжения V на резисторе при протекании через него тока рассчитывается по формуле V = IR, где I — ток в амперах (A), а R — сопротивление в омах (Ω). .
Таким образом, падение напряжения на R 1 равно V 1 = IR 1 , на R 2 равно V 2 = IR 2 , а на R 3 равно V 3 = IR 3 .Сумма напряжений будет равна: V = V 1 + V 2 + V 3 , исходя из сохранения энергии и заряда. Если подставить значения отдельных напряжений, получим:
[латекс] \ text {V} = \ text {IR} _1 + \ text {IR} _2 + \ text {IR} _3 [/ latex]
или
[латекс] \ text {V} = \ text {I} (\ text {R} _1 + \ text {R} _2 + \ text {R} _3) [/ латекс]
Это означает, что полное сопротивление в серии равно сумме отдельных сопротивлений. Следовательно, для каждой цепи с Н количество резисторов, подключенных последовательно:
[латекс] \ text {RN} (\ text {series}) = \ text {R} _1 + \ text {R} _2 + \ text {R} _3 +… + \ text {R} _ \ text {N }.[/ латекс]
Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Поскольку напряжение и сопротивление имеют обратную зависимость, отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Об этом свидетельствует пример, когда две лампочки соединены в последовательную цепь с аккумулятором. В простой схеме, состоящей из одной батареи 1,5 В и одной лампочки, падение напряжения на лампе будет равно 1.5V через него. Однако, если бы две лампочки были соединены последовательно с одной и той же батареей, на каждой из них было бы падение напряжения 1,5 В / 2 или 0,75 В. Это будет очевидно по яркости света: каждая из двух последовательно соединенных лампочек будет в два раза слабее, чем одиночная лампочка. Следовательно, резисторы, соединенные последовательно, потребляют такое же количество энергии, как и один резистор, но эта энергия распределяется между резисторами в зависимости от их сопротивлений.
Параллельные резисторы
Общее сопротивление в параллельной цепи равно сумме обратных сопротивлений каждого отдельного сопротивления.
Цели обучения
Рассчитайте общее сопротивление в цепи с параллельно включенными резисторами
Основные выводы
Ключевые моменты
- Общее сопротивление в параллельной цепи меньше наименьшего из отдельных сопротивлений.
- Каждый резистор, включенный параллельно, имеет то же напряжение, что и приложенный к нему источник (напряжение в параллельной цепи постоянно).
- Параллельные резисторы не получают суммарный ток каждый; они делят его (ток зависит от номинала каждого резистора и общего количества резисторов в цепи).
Ключевые термины
- сопротивление : Противодействие прохождению электрического тока через этот элемент.
- параллельно : Расположение электрических компонентов, при котором ток течет по двум или более путям.
Обзор
Резисторы в цепи могут быть включены последовательно или параллельно. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Parallel Circuits : Краткий обзор анализа параллельных цепей с использованием таблиц VIRP для студентов-физиков средней школы.
Параллельные резисторы
Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения путем соединения проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Параллельные резисторы : Параллельное соединение резисторов.
Каждый резистор потребляет такой же ток, как если бы он был единственным резистором, подключенным к источнику напряжения. Это верно для схем в доме или квартире. Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.
Закон и параллельные резисторы Ом
Каждый резистор в цепи имеет полное напряжение. Согласно закону Ома токи, протекающие через отдельные резисторы, равны [латекс] \ text {I} _1 = \ frac {\ text {V}} {\ text {R} _1} [/ latex], [latex] \ text {I} _2 = \ frac {\ text {V}} {\ text {R} _2} [/ latex] и [latex] \ text {I} _3 = \ frac {\ text {V}} {\ text {R} _3} [/ латекс].Сохранение заряда подразумевает, что полный ток является суммой этих токов:
Параллельные резисторы : Три резистора, подключенные параллельно батарее, и эквивалентное одиночное или параллельное сопротивление.
[латекс] \ text {I} = \ text {I} _1 + \ text {I} _2 + \ text {I} _3. [/ Latex]
Подстановка выражений для отдельных токов дает:
[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R} _1} + \ frac {\ text {V}} {\ text {R} _2} + \ frac {\ текст {V}} {\ text {R} _3} [/ latex]
или
[латекс] \ text {I} = \ text {V} (\ frac {1} {\ text {R} _1} + \ frac {1} {\ text {R} _2} + \ frac {1} { \ text {R} _3}) [/ latex]
Это означает, что полное сопротивление в параллельной цепи равно сумме обратных сопротивлений каждого отдельного сопротивления.Следовательно, для каждой схемы с числом [latex] \ text {n} [/ latex] или резисторов, подключенных параллельно,
[латекс] \ text {R} _ {\ text {n} \; (\ text {parallel})} = \ frac {1} {\ text {R} _1} + \ frac {1} {\ text { R} _2} + \ frac {1} {\ text {R} _3}… + \ frac {1} {\ text {R} _ \ text {n}}. [/ Latex]
Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Каждый резистор, включенный параллельно, имеет такое же полное напряжение источника, как на него, но делит общий ток между ними. Примером может служить соединение двух лампочек в параллельную цепь с аккумулятором на 1,5 В. В последовательной цепи две лампочки будут вдвое менее тусклыми при подключении к одному источнику батареи. Однако, если бы две лампочки были подключены параллельно, они были бы столь же яркими, как если бы они были подключены к батарее по отдельности. Поскольку к обеим лампочкам подается одинаковое полное напряжение, батарея также разряжается быстрее, поскольку она по существу обеспечивает полную энергию для обеих лампочек.В последовательной цепи батарея будет работать столько же, сколько и с одной лампочкой, только тогда яркость будет разделена между лампочками.
Комбинированные схемы
Комбинированная цепь может быть разбита на аналогичные части, работающие последовательно или параллельно.
Цели обучения
Описать расположение резисторов в комбинированной цепи и его практическое значение
Основные выводы
Ключевые моменты
- Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного.
- Различные части комбинированной схемы могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление.
- Сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление в проводах относительно велико, как в изношенном (или очень длинном) удлинительном шнуре, то эти потери могут быть значительными и влиять на выходную мощность в устройствах.
Ключевые термины
- серия : ряд элементов, которые следуют одно за другим или связаны друг за другом.
- параллельно : Расположение электрических компонентов, при котором ток течет по двум или более путям.
- Комбинированная схема : электрическая цепь, содержащая несколько резисторов, которые соединены как последовательным, так и параллельным соединением.
Комбинированные схемы
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Это часто встречается, особенно если учитывать сопротивление проводов.В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинированная цепь может быть разбита на аналогичные части, которые являются последовательными или параллельными, как показано на схеме. На рисунке общее сопротивление может быть вычислено путем соединения трех резисторов друг с другом последовательно или параллельно. R 1 и R 2 соединены параллельно друг другу, поэтому мы знаем, что для этого подмножества сопротивление, обратное сопротивлению, будет равно:
Сеть резисторов : В этой комбинированной схеме цепь может быть разбита на последовательный компонент и параллельный компонент.
Комбинированные схемы : Два параллельно включенных резистора с одним резистором.
[латекс] \ frac {1} {\ text {R} _1} + \ frac {1} {\ text {R} _2} [/ latex] или [латекс] \ frac {\ text {R} _1 \ text {R} _2} {\ text {R} _1 + \ text {R} _2} [/ latex]
R 3 соединены последовательно с как R 1 , так и R 2 , поэтому сопротивление будет рассчитано как:
[латекс] \ text {R} = \ frac {\ text {R} _1 \ text {R} _2} {\ text {R} _1 + \ text {R} _2} + \ text {R} _3 [/ latex ]
Сложные комбинированные схемы
Для более сложных комбинированных схем различные части могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление, как показано на.На этом рисунке комбинация из семи резисторов была идентифицирована как включенные последовательно или параллельно. На исходном изображении две обведенные кружком секции показывают резисторы, включенные параллельно.
Уменьшение комбинированной схемы : Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто одно эквивалентное сопротивление.
Уменьшение этих параллельных резисторов до одного значения R позволяет нам визуализировать схему в более упрощенном виде.На верхнем правом изображении мы видим, что обведенная кружком часть содержит два последовательно соединенных резистора. Мы можем дополнительно уменьшить это до другого значения R, добавив их. Следующий шаг показывает, что два обведенных резистора включены параллельно. Уменьшение тех бликов, что последние два соединены последовательно и, таким образом, могут быть уменьшены до одного значения сопротивления для всей цепи.
Одним из практических следствий комбинированной схемы является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Комбинированная цепь может быть преобразована в последовательную цепь на основе понимания эквивалентного сопротивления параллельных ветвей комбинированной цепи. Последовательная цепь может использоваться для определения общего сопротивления цепи. По сути, сопротивление провода является последовательным с резистором. Таким образом, увеличивается общее сопротивление и уменьшается ток. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение ИК-излучения в проводах также может быть значительным.
Зарядка аккумулятора: последовательные и параллельные ЭДС
При последовательном включении источников напряжения их ЭДС и внутренние сопротивления складываются; параллельно они остаются прежними.
Цели обучения
Сравнить сопротивления и электродвижущие силы для источников напряжения, подключенных с одинаковой и противоположной полярностью, последовательно и параллельно
Основные выводы
Ключевые моменты
- ЭДС, соединенные последовательно с одинаковой полярностью, являются аддитивными и приводят к более высокой общей ЭДС.
- Две ЭДС, соединенные последовательно с противоположной полярностью, имеют общую ЭДС, равную разнице между ними, и могут использоваться для зарядки источника более низкого напряжения.
- Два источника напряжения с идентичными ЭДС, соединенные параллельно, имеют чистую ЭДС, эквивалентную одному источнику ЭДС, однако чистое внутреннее сопротивление меньше и, следовательно, дает более высокий ток.
Ключевые термины
- параллельно : расположение электрических компонентов, при котором ток течет по двум или более путям.
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
- серия : ряд элементов, которые следуют одно за другим или связаны друг за другом.
Когда используется более одного источника напряжения, они могут быть подключены последовательно или параллельно, аналогично резисторам в цепи.Когда источники напряжения включены последовательно в одном направлении, их внутренние сопротивления складываются, а их электродвижущая сила или ЭДС складываются алгебраически. Эти типы источников напряжения распространены в фонариках, игрушках и других приборах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС.
Фонарик и лампочка : Последовательное соединение двух источников напряжения в одном направлении. Эта схема представляет собой фонарик с двумя последовательно включенными ячейками (источниками напряжения) и одной лампочкой (сопротивление нагрузки).
Батарея представляет собой соединение нескольких гальванических элементов. Однако недостатком такого последовательного соединения ячеек является то, что их внутреннее сопротивление увеличивается. Иногда это может быть проблематично. Например, если вы поместите в машину две батареи на 6 В вместо обычной батареи на 12 В, вы должны добавить как ЭДС, так и внутреннее сопротивление каждой батареи. Таким образом, у вас будет такая же ЭДС 12 В, хотя внутреннее сопротивление тогда будет удвоено, что вызовет у вас проблемы, когда вы захотите запустить двигатель.
Но, если ячейки противостоят друг другу — например, когда одна вставляется в прибор задом наперед, — общая ЭДС меньше, так как это алгебраическая сумма отдельных ЭДС. Когда он перевернут, он создает ЭДС, которая противодействует другой, и приводит к разнице между двумя источниками напряжения.
Зарядное устройство : представляет два источника напряжения, соединенных последовательно с противоположными ЭДС. Ток течет в направлении большей ЭДС и ограничивается суммой внутренних сопротивлений.(Обратите внимание, что каждая ЭДС представлена на рисунке буквой E.) Зарядное устройство, подключенное к аккумулятору, является примером такого подключения. Зарядное устройство должно иметь большую ЭДС, чем батарея, чтобы через него протекал обратный ток.
Когда два источника напряжения с одинаковыми ЭДС соединены параллельно и также подключены к сопротивлению нагрузки, общая ЭДС равна индивидуальным ЭДС. Но общее внутреннее сопротивление уменьшается, поскольку внутренние сопротивления параллельны. Таким образом, параллельное соединение может производить больший ток.
Две идентичные ЭДС : Два источника напряжения с одинаковыми ЭДС (каждый помечен буквой E), подключенные параллельно, создают одинаковую ЭДС, но имеют меньшее общее внутреннее сопротивление, чем отдельные источники. Параллельные комбинации часто используются для подачи большего тока.
ЭДС и напряжение на клеммах
Выходное напряжение или напряжение на клеммах источника напряжения, такого как аккумулятор, зависит от его электродвижущей силы и внутреннего сопротивления.
Цели обучения
Выразите взаимосвязь между электродвижущей силой и напряжением на клеммах в форме уравнения
Основные выводы
Ключевые моменты
- Электродвижущая сила (ЭДС) — это разность потенциалов источника при отсутствии тока.
- Напряжение на клеммах — это выходное напряжение устройства, измеренное на его клеммах.
- Напряжение на клеммах рассчитывается по формуле V = ЭДС — Ir.
Ключевые термины
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
- напряжение на клеммах : Выходное напряжение устройства, измеренное на его клеммах.
- разность потенциалов : разница в потенциальной энергии между двумя точками в электрическом поле; разница в заряде между двумя точками в электрической цепи; Напряжение.
Когда вы забываете выключить автомобильные фары, они постепенно тускнеют по мере разрядки аккумулятора. Почему они просто не мигают, когда батарея разряжена? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разряда батареи. Причина снижения выходного напряжения для разряженных или перегруженных батарей заключается в том, что все источники напряжения состоят из двух основных частей — источника электрической энергии и внутреннего сопротивления.
Электродвижущая сила
Все источники напряжения создают разность потенциалов и могут подавать ток, если подключены к сопротивлению. В небольшом масштабе разность потенциалов создает электрическое поле, которое воздействует на заряды, вызывая ток. Мы называем эту разность потенциалов электродвижущей силой (сокращенно ЭДС). ЭДС — это вообще не сила; это особый тип разности потенциалов источника при отсутствии тока. Единицы измерения ЭДС — вольты.
Электродвижущая сила напрямую связана с источником разности потенциалов, например, с конкретной комбинацией химических веществ в батарее.Однако при протекании тока ЭДС отличается от выходного напряжения устройства. Напряжение на выводах батареи, например, меньше, чем ЭДС, когда батарея подает ток, и оно падает дальше, когда батарея разряжается или разряжается. Однако, если выходное напряжение устройства можно измерить без потребления тока, то выходное напряжение будет равно ЭДС (даже для сильно разряженной батареи).
Напряжение на клеммах
представляет схематическое изображение источника напряжения.Выходное напряжение устройства измеряется на его выводах и называется напряжением на выводах В . Напряжение на клеммах определяется уравнением:
Схематическое изображение источника напряжения : Любой источник напряжения (в данном случае углеродно-цинковый сухой элемент) имеет ЭДС, связанную с источником разности потенциалов, и внутреннее сопротивление r, связанное с его конструкцией. (Обратите внимание, что сценарий E означает ЭДС.) Также показаны выходные клеммы, на которых измеряется напряжение на клеммах V.Поскольку V = ЭДС-Ir, напряжение на клеммах равно ЭДС, только если ток не течет.
[латекс] \ text {V} = \ text {emf} — \ text {Ir} [/ latex],
где r — внутреннее сопротивление, а I — ток, протекающий во время измерения.
I является положительным, если ток течет от положительного вывода. Чем больше ток, тем меньше напряжение на клеммах. Точно так же верно, что чем больше внутреннее сопротивление, тем меньше напряжение на клеммах.
Серия
и параллельные схемы в источниках питания
Фотоэлектрические модули и батареи являются строительными блоками системы.Хотя каждый модуль или батарея имеют номинальное напряжение или силу тока, их также можно соединить вместе, чтобы получить желаемое напряжение в системе.
1. Цепи серии
Соединения проводов серии
выполняются на положительном (+) конце одного модуля с отрицательным (-) концом другого модуля. Когда нагрузки или источники питания подключаются последовательно, напряжение увеличивается. Последовательная проводка не увеличивает производимую силу тока. На изображении справа показаны два модуля, подключенных последовательно, что дает 24 В и 3 А.Цепи серии
можно также проиллюстрировать с помощью батареек для фонарей. Батареи фонарей часто подключаются последовательно для увеличения напряжения и питания лампы с более высоким напряжением, чем одна батарея могла бы питать в одиночку.
Вопрос: Каково результирующее напряжение при последовательном подключении четырех батарей 1,5 В постоянного тока?
Ответ: 6 вольт
2. Параллельные цепи
Параллельные подключения проводов выполняются от положительных (+) к положительным (+) клеммам и от отрицательных (-) к отрицательным (-) клеммам между модулями.Когда нагрузки или источники подключаются параллельно, токи складываются, а напряжение одинаково во всех частях цепи. Чтобы увеличить силу тока в системе, источники напряжения должны быть подключены параллельно. На изображении справа показаны фотоэлектрические модули, подключенные параллельно, чтобы получить систему на 12 В, 6 А. Обратите внимание, что параллельная проводка увеличивает производимый ток и не увеличивает напряжение.
Батареи также часто подключаются параллельно для увеличения общего количества ампер-часов, что увеличивает емкость накопителя и продлевает время работы.s
3. Последовательные и параллельные схемы
Системы могут использовать сочетание последовательной и параллельной проводки для получения требуемых значений напряжения и силы тока. На изображении справа показаны четыре модуля на 3 А, 12 В постоянного тока, подключенных последовательно и параллельно. Гирлянды из двух модулей соединены последовательно, увеличивая напряжение до 24 В. Каждая из этих струн подключается параллельно цепи, увеличивая силу тока до 6 ампер. В результате получилась система на 6 ампер и 24 В постоянного тока.
4. Последовательные и параллельные батареи
Преимущества параллельной схемы можно проиллюстрировать, наблюдая, как долго проработает фонарик, прежде чем батареи полностью разрядятся.Чтобы фонарик прослужил вдвое дольше, необходимо вдвое увеличить емкость аккумулятора.
На картинке слева последовательно добавлена цепочка из четырех батарей параллельно другой цепочке из четырех батарей для увеличения емкости (ампер-часов). Новая цепочка батарей подключается параллельно, что увеличивает доступные ампер-часы, тем самым добавляя дополнительную емкость и увеличивая время использования. Вторую цепочку нельзя было добавить последовательно, потому что общее напряжение будет 12 вольт, что несовместимо с 6-вольтовой лампой.
5. Высоковольтные фотоэлектрические массивы
До сих пор в этой главе мы обсуждали только входное напряжение до номинального 24 В. Сегодня для большинства инверторов с подключением к сети без батарей требуется вход постоянного тока высокого напряжения. Это входное окно обычно находится в диапазоне от 350 до 550 В постоянного тока. Из-за требований инвертора к входу высокого напряжения фотоэлектрические модули должны быть подключены последовательно, чтобы в достаточной степени увеличить напряжение.
6. Примеры и инструкции последовательного и параллельного подключения
1. Подключите фотоэлектрические модули (массив) последовательно или параллельно, чтобы получить желаемое напряжение в системе.
2. Рассчитайте общую выходную мощность модуля для вольт и ампер.
3. Подключите массив к контроллеру заряда.
4. Подключите батареи последовательно или параллельно, чтобы получить желаемое напряжение в системе.
5. Рассчитайте общее напряжение аккумуляторной батареи и емкость ампер-часов.
6. Подключите аккумуляторную батарею к контроллеру заряда.
Источник : «ФОТОЭЛЕКТРОЭНЕРГИЯ — Руководство по проектированию и установке» компании Solar Energy International.
Тренинг по сертификации солнечной энергии от профессиональных установщиков солнечных батарей
С 18 сертифицированными IREC-ISPQ инструкторами по солнечной фотоэлектрической установке и 24 сертифицированными специалистами по установке солнечных фотоэлектрических систем, сертифицированными NABCEP — больше, чем в любой другой учебной организации по солнечной энергии, — опытная команда Solar Energy International находится в авангарде образования в области возобновляемых источников энергии. Если вы ищете онлайн-обучение по солнечной энергии или личное лабораторное обучение для сдачи экзамена начального уровня NABCEP или сертификации установщика NABCEP, почему бы не получить свое образование от команды самых опытных специалистов по установке солнечных батарей в отрасли? Многие инструкторы SEI участвовали в самых известных солнечных установках в своих общинах в США и в развивающихся странах.
