Магнитное поле: частицы в поле-2
В этой статье мы рассмотрим задачи, в которых частицы перемещаются в магнитном поле. Частицы будут двигаться по спиралям и окружностям, тормозиться и разгоняться электрическими полями. Эта статья – вторая из серии статей о магнитном поле. В этой серии мы не только рассмотрим движение частиц по сложным траекториям, но и будем двигать рамки в магнитном поле, словом, самое интересное – впереди!
Задача 1. Прямолинейный проводник подвешен горизонтально на двух нитях в однородном магнитном поле с индукцией мТл. Вектор магнитной индукции горизонтален и перпендикулярен проводнику.
Рисунок 1
Какой ток следует пропустить по проводнику, чтобы сила натяжения нитей увеличилась вдвое? Ответ выразить в А, округлив до целых.
В каком направлении для этого необходимо пропустить ток?
Масса единицы длины проводника г/м. Ускорение свободного падения принять равным м/с.
Запишем второй закон Ньютона для состояния до включения тока:
При пропускании тока возникнет сила Ампера, направленная, как мы можем догадаться, вниз – поскольку натяжение нитей возросло (для этого ток должен быть направлен от нас).
По условию, натяжение стало вдвое больше. Записываем второй закон Ньютона для состояния, когда ток в проводнике протекает:
Или
Ответ: А.
Задача 2. Однородные электрическое и магнитное поля расположены взаимно перпендикулярно. Напряженность электрического поля равна кВ/м, а индукция магнитного поля мТл. В каком направлении и с какой скоростью должен двигаться электрон, чтобы его движение в пространстве, занимаемом полями, было равномерным и прямолинейным? Ответ выразить в км/с, округлив до целых.
Рисунок 2
Сила Лоренца должна быть равна силе, с которой электрическое поле действует на электрон:
Откуда
Ответ: м/с, или км/с.
Задача 3. Электрон влетает в плоский слой однородного магнитного поля шириной см со скоростью м/с. Индукция магнитного поля мТл. Скорость электрона перпендикулярна как направлению поля, так и границам слоя. Под каким углом к первоначальному направлению электрон вылетит из магнитного поля? В ответе записать синус угла, округлив до десятых. Элементарный заряд равен Кл, масса электрона кг.
Скорость электрона перпендикулярна как направлению поля, так и границам слоя. Под каким углом к первоначальному направлению электрон вылетит из магнитного поля? В ответе записать синус угла, округлив до десятых. Элементарный заряд равен Кл, масса электрона кг.
Рисунок 3
В магнитном поле электрон начнет двигаться по окружности. Определим ее радиус. По второму закону Ньютона:
Откуда
Получилось, что радиус 11,375 см. Но область магнитного поля (слой) имеет ширину 9,1 – следовательно, электрон не пройдет и четверти окружности и вылетит из области поля. Отметим, какой угол нам надо найти:
Рисунок 4
Даже не сам угол, а его синус:
Ответ: .
Задача 4. Пучок протонов, ускоренных напряжением , попадает в однородное магнитное поле с индукцией Тл, перпендикулярное скорости протонов. После того, как пучок прошёл путь см, скорость пучка изменилась по направлению на угол . Отношение заряда протона к его массе равно Кл/кг. Найдите ускоряющее напряжение . Ответ выразить в кВ, округлив до целых.
Отношение заряда протона к его массе равно Кл/кг. Найдите ускоряющее напряжение . Ответ выразить в кВ, округлив до целых.
Рисунок 5
В магнитном поле протоны начнут двигаться по окружности. Определим ее радиус. По второму закону Ньютона:
Откуда
По условию, пучок прошел путь 10 см – а это длина дуги окружности. Найдем всю длину – из нее можно определить радиус: так как 10 см соответствуют , то будет соответствовать длина дуги см. Тогда
Работа электрического поля равна кинетической энергии протонов пучка:
Ответ: 73 кВ.
Задача 5. Частица массой мг с положительным зарядом нКл находится в однородном электрическом и магнитном полях. Линии индукции магнитного поля параллельны силовым линиям электрического поля (см. рис.). В начальный момент частице сообщают скорость м/с, направленную под углом к линиям индукции. Через время с частица возвращается в исходную точку. Чему равна напряженность электрического поля ? Ответ выразить в В/м, округлив до целых. При каком минимальном значении индукции магнитного поля это возможно?
Чему равна напряженность электрического поля ? Ответ выразить в В/м, округлив до целых. При каком минимальном значении индукции магнитного поля это возможно?
Рисунок 6
На частицу будут действовать две силы: сила со стороны электрического поля , и сила Лоренца со стороны магнитного поля. Эта сила будет перпендикулярна линиям магнитной индукции и скорости частицы, найдем ее:
Под действием электрической силы частица движется сначала равнозамедленно, а потом (после остановки) равноускоренно с тем же по величине ускорением. Запишем второй закон Ньютона и формулы кинематики для частицы. Второй закон Ньютона в проекции на ось, направленную горизонтально вправо, имеет вид
Из кинематики горизонтальная скорость частицы
После возвращения в первоначальную точку горизонтальная составляющая скорости частицы по величине будет совпадать с первоначальной, но будет направлена в противоположную сторону. Таким образом, получаем, что
Где
откуда
В плоскости, перпендикулярной силовым линиям E и B, под действием силы Лоренца частица совершает круговые движения. Найдем период обращения частицы по окружности радиуса . Из второго закона Ньютона получаем, что
Найдем период обращения частицы по окружности радиуса . Из второго закона Ньютона получаем, что
Отсюда радиус окружности
Период обращения
Подставим радиус:
Для того, чтобы частица вернулась в начальную точку, необходимо, чтобы она совершила целое число оборотов по окружности в плоскости, перпендикулярной силовым линиям E и B, за время τ, то есть
где N − любое натуральное число. Отсюда получается, что частица возвращается в начальную точку при значениях B, равных
Поскольку в условии просят найти минимальную индукцию поля, подставляем в эту формулу минимальное и окончательно получаем, что
Ответ: В/м, мТл.
Идз №3 1 курс, 2 семестр Электродинамика
Вариант 3
На проводник
длиной 0,5 м, расположенный перпендикулярно
магнитному полю с индукцией 2·10–2
Тл, действует сила 0,15 Н. Найдите силу
Найдите силу
тока, протекающую в проводнике.П
рямой
проводник АВ длиной 20 см и массой 5 г
подвешен горизонтально на двух тонких
лёгких нитях ОА и ОВ в однородном
магнитном поле, вектор индукции которого
имеет горизонтальное направление и
перпендикулярен проводнику. Какой ток
надо пропустить по проводнику, чтобы
одна из нитей разорвалась? Индукция
магнитного поля 0,5 Тл. Каждая нить
разрывается при нагрузке 0,04 Н.
В направлении,
перпендикулярном линиям магнитной
индукции, влетает в магнитное поле
электрон со скоростью 10 Мм/с. Найдите
индукцию поля, если электрон описал
окружность радиусом 1 см.Перпендикулярно
линиям магнитной индукции перемещается
проводник длиной 1,8 м со скоростью 6,0
м/с. ЭДС индукции 1,44 В. Найдите магнитную
индукцию поля.Однородные
электрическое и магнитное поля
расположены взаимно перпендикулярно.
Напряжённость электрического поля 1
кВ/м, а индукция магнитного поля 1 мТл.
Какими должны быть направление и модуль
скорости электрона, чтобы траектории
движения его оказалась прямолинейной?Магнитная индукция
в данном бруске металла B=0,75
Тл, а индукция внешнего намагничивающего
поля В0=0,0375
Тл. Какова относительная магнитная
проницаемость металла?
ИДЗ №3
1 курс, 2 семестр
Электродинамика
Вариант 4
На провод обмотки
якоря электродвигателя при силе тока
20 A
действует сила 1,0 H.
Определите магнитную индукцию в месте
расположения провода, если длина провода
0,2 м.Медная пластинка
высотой в и толщиной a
расположена перпендикулярно магнитному
полю с индукцией B.
По пластинке течёт ток I.
Вследствие отклонения электрона к
одной из граней внутри пластинки
возникает однородное электрическое
поле, направленное поперёк проводника
(эффект Холла). Какова напряжённость
Какова напряжённость
этого поля? Чему равно отношение
напряжённости электрического поля,
возникшего в пластинке, к напряжённости
электрического поля, создающего ток в
проводнике? Концентрация электронов
проводимости в меди известна и равна
n.
Протон в магнитном
поле с индукцией 0,01 Тл описал окружность
радиусом 10см. Найдите скорость протона.Электрон, обладающий
кинетической энергией W0,
влетает в однородное магнитное поле с
индукцией B.
Скорость электрона направлена
перпендикулярно полю. Определите: а)
силу, действующую на частицу; б) радиус
кривизны траектории; в) период обращения
электрона.Проводник MN
с длиной активной части 1 м и сопротивлением
2 Ом находится в однородном магнитном
поле с индукцией 0,1 Тл. Проводник
подключен к источнику, ЭДС которого
равна 1 B
(внутренним сопротивлением источника
и сопротивлением проводящих проводников
пренебречь). Какова сила тока в проводнике,
Какова сила тока в проводнике,
если: а) проводник покоится; б) проводник
движется вправо со скоростью 4 м/с; в)
проводник движется влево с той же
скоростью. В каком направлении и с какой
скоростью надо перемещать проводник,
чтобы через него не шёл ток?
По графику
определите магнитную проницаемость
стали при индукции В0
намагничивающего поля 0,4 Тл и 1,2 мТл.
ИДЗ №3
1 курс, 2 семестр
Задачи по физике и математике с решениями и ответами
Задача по физике — 7688
Пучок нерелятивистских протонов проходит, не отклоняясь, через область, в которой созданы однородные поперечные взаимно перпендикулярные электрическое и магнитное поля с $E = 120 кВ/м$ и $B = 50 мТ$. { \circ}$ с осью х. Найти шаг винтовой линии, по которой будут двигаться протоны после выключения электрического поля.
{ \circ}$ с осью х. Найти шаг винтовой линии, по которой будут двигаться протоны после выключения электрического поля.
Подробнее
Задача по физике — 7690
Пучок нерелятивистских заряженных частиц проходит, не отклоняясь, через область А (рис.), в которой созданы поперечные взаимно перпендикулярные электрическое и магнитное поля с напряженностью $E$ и индукцией $B$. Если магнитное поле выключить, след пучка на экране Э смещается на $\Delta x$. Зная расстояния $a$ и $b$, найти удельный заряд $q/m$ частиц.
Подробнее
Задача по физике — 7691
Частица с удельным зарядом $q/m$ движется в области, где созданы однородные взаимно перпендикулярные электрическое и магнитное поля с напряженностью $\vec{E}$ и индукцией $\vec{B}$ (рис. ). В момент $t = 0$ частица находилась в точке О и имела нулевую скорость. Найти для нерелятивистского случая:
). В момент $t = 0$ частица находилась в точке О и имела нулевую скорость. Найти для нерелятивистского случая:
а) закон движения частицы $x(t)$ и $y(t)$; какой вид имеет траектория;
б) длину участка траектории между двумя ближайшими точками, в которых скорость частицы обращается в нуль;
в) среднее значение проекции вектора скорости частицы на ось $x$ (дрейфовая скорость).
Подробнее
Задача по физике — 7693
Магнетрон — это прибор, состоящий из нити накала радиуса а и коаксиального цилиндрического анода радиуса $b$, которые находятся в однородном магнитном поле, параллельном нити. Между нитью и анодом приложена ускоряющая разность потенциалов $U$. Найти значение индукции магнитного поля, при котором электроны, вылетающие с нулевой начальной скоростью из нити, будут достигать анода.
Подробнее
Задача по физике — 7694
Заряженная частица с удельным зарядом $q/m$ начинает двигаться в области, где созданы однородные взаимно перпендикулярные электрическое и магнитное поля. Магнитное поле постоянно и имеет индукцию $B$, электрическое же меняется во времени как $E = E_{m} \cos \omega t$, где $\omega = qB/m$. Найти для нерелятивистского случая закон движения частицы $x(t)$ и $y(t)$, если в момент $t = 0$ она находилась в точке О (см. рис.). Какой примерно вид имеет траектория частицы?
Магнитное поле постоянно и имеет индукцию $B$, электрическое же меняется во времени как $E = E_{m} \cos \omega t$, где $\omega = qB/m$. Найти для нерелятивистского случая закон движения частицы $x(t)$ и $y(t)$, если в момент $t = 0$ она находилась в точке О (см. рис.). Какой примерно вид имеет траектория частицы?
Подробнее
Задача по физике — 7695
Частота генератора циклотрона $\nu = 10 МГц$. Найти эффективное ускоряющее напряжение на дуантах этого циклотрона, при котором расстояние между соседними траекториями протонов с радиусом $r = 0,5 м$ не меньше, чем $\Delta r = 1,0 см$.
Подробнее
Задача по физике — 7696
Протоны ускоряют в циклотроне так, что максимальный радиус кривизны их траектории $r = 50 см$. { +}$ ускоряют в циклотроне так, что максимальный радиус орбиты $r = 60 см$. Частота генератора циклотрона $\nu = 10,0 МГц$, эффективное ускоряющее напряжение между дуантами $U = 50 кВ$. Пренебрегая зазором между дуантами, найти:
{ +}$ ускоряют в циклотроне так, что максимальный радиус орбиты $r = 60 см$. Частота генератора циклотрона $\nu = 10,0 МГц$, эффективное ускоряющее напряжение между дуантами $U = 50 кВ$. Пренебрегая зазором между дуантами, найти:
а) полное время процесса ускорения иона;
б) приближенное значение пути, пройденного ионом за весь цикл ускорения.
Подробнее
Задача по физике — 7698
Так как период обращения электронов в однородном магнитном поле с ростом энергии быстро увеличивается, циклотрон оказывается непригодным для их ускорения. Этот недостаток устраняется в микротроне (рис.), где изменение периода обращения электрона $\Delta T$ делают кратным периоду ускоряющего поля $T_{0}$. Сколько раз электрону необходимо пройти через ускоряющий промежуток микротрона, чтобы приобрести энергию $W = 4,6 МэВ$, если $\Delta T = T_{0}$, индукция магнитного поля $B = 107 мТ$ и частота ускоряющего поля $\nu = 3000 МГц$?
Подробнее
Задача по физике — 7699
Чтобы в циклотроне не возникала расстройка, связанная с изменением периода обращения частицы при возрастании ее энергии, медленно изменяют (модулируют) частоту ускоряющего поля. По какому закону надо изменять эту частоту $\omega(t)$, если индукция магнитного поля равна $B$ и частица приобретает за один оборот энергию $\Delta W$? Заряд частицы $q$, масса $m$.
По какому закону надо изменять эту частоту $\omega(t)$, если индукция магнитного поля равна $B$ и частица приобретает за один оборот энергию $\Delta W$? Заряд частицы $q$, масса $m$.
Подробнее
Задача по физике — 7700
Частица с удельным зарядом $q/m$ находится внутри соленоида круглого сечения на расстоянии $r$ от его оси. В обмотке включили ток, и индукция магнитного поля стала равной $B$. Найти скорость частицы и радиус кривизны ее траектории, считая, что за время нарастания тока в соленоиде ее смещение пренебрежимо мало.
Подробнее
Задача по физике — 7701
В бетатроне магнитный поток внутри равновесной орбиты радиуса $r = 25 см$ возрастает за время ускорения практически с постоянной скоростью $\Phi = 5,0 Вб/с$. При этом электроны приобретают энергию $W = 25 МэВ$. Найти число оборотов, совершенных электроном за время ускорения, и соответствующее значение пройденного им пути.
При этом электроны приобретают энергию $W = 25 МэВ$. Найти число оборотов, совершенных электроном за время ускорения, и соответствующее значение пройденного им пути.
Подробнее
Задача по физике — 7702
Показать, что электроны в бетатроне будут двигаться по круговой орбите постоянного радиуса при условии, что индукция магнитного поля на орбите равна половине среднего значения индукции поля внутри орбиты (бетатронное условие).
Подробнее
ДЗ 11.1. Конкурсные и олимпиадные задачи по теме «Магнетизм». — Студопедия
1.Пучок однозарядных ионов гелия и неона попадают в область пространства, где имеется однородное электрическое поле с напряженностью E = 100 В/м и однородное магнитное поле с индукцией B = 0,01 Тл. Векторы E и B направлены под прямым углом друг к другу, и оба перпендикулярны пучку. Ионы проходят эти скрещенные электрическое и магнитное поля без отклонения и проникают в область однородного магнитного поля с индукцией B1 = 0,1 Тл, направленной перпендикулярно направлению движения ионов. На каком расстоянии друг от друга ионы гелия и неона окажутся, пройдя половину окружности? Силами кулоновского взаимодействия между ионами в пучке пренебречь. (2004).
Ионы проходят эти скрещенные электрическое и магнитное поля без отклонения и проникают в область однородного магнитного поля с индукцией B1 = 0,1 Тл, направленной перпендикулярно направлению движения ионов. На каком расстоянии друг от друга ионы гелия и неона окажутся, пройдя половину окружности? Силами кулоновского взаимодействия между ионами в пучке пренебречь. (2004).
2.Заряженная частица попадает в среду, где на нее действует сила сопротивления, пропорциональная скорости. До полной остановки частица проходит путь s = 10 см. Если в среде имеется магнитное поле, перпендикулярное скорости частицы, то она при той же начальной скорости остановится на расстоянии L1 = 6 см от точки входа в среду. На каком расстоянии L2 от точки входа в среду остановилась бы частица, если бы индукция магнитного поля была в два раза меньше? (2001).
3.+ В объеме плоского конденсатора созданы взаимно перпендикулярные электрическое и магнитное поля с напряженностью E и индукцией B такими, что пучок заряженных частиц движется вдоль оси x до центра O экрана Э прямолинейно.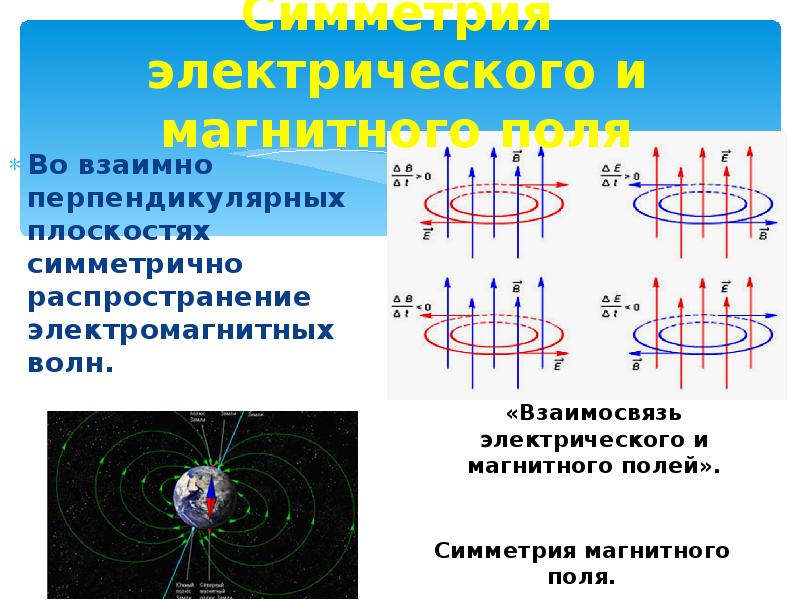 При выключении магнитного поля след пучка на экране сместился на величину Dy (см. рис.). Считая известными расстояния L1 и L2, определите отношение заряда частицы к его массе (удельный заряд частицы). Силу тяжести не учитывать. (2004).
При выключении магнитного поля след пучка на экране сместился на величину Dy (см. рис.). Считая известными расстояния L1 и L2, определите отношение заряда частицы к его массе (удельный заряд частицы). Силу тяжести не учитывать. (2004).
Рис. к зад. 3.
4.Пучок протонов движется прямолинейно в области, где созданы однородные взаимно перпендикулярные электрическое поле с напряженностью E и магнитное поле с индукцией B. Траектория протонов лежит в плоскости xz (см. рис.) и составляет угол j с осью x. Определите шаг винтовой линии, по которой будут двигаться протоны после выключения электрического поля. (2004)
Рис. к зад. 4. Рис. к зад. 5.
5.Из начала координат со скоростью v0, направленной вдоль оси x, влетает протон в область, где созданы однородные параллельные оси y электрическое и магнитное поля с напряженностью E и индукцией B (см. рис.). Определите координату yn частицы в момент времени, когда она в n-й раз пересечет ось y. (2004)
(2004)
6.Незаряженный металлический цилиндр радиуса R вращается в магнитном поле с угловой скоростью w вокруг своей оси. Индукция магнитного поля направлена вдоль оси цилиндра. Какова должно быть значение индукции магнитного поля, чтобы в цилиндре не возникало электрическое поле? (2006).
7.+По металлической ленте, толщина которой равна h, течет ток I. Лента помещена в однородное магнитное поле, индукция которого равна В и направлена перпендикулярно поверхности ленты (см. рис.). Определите разность потенциалов (jА — jС) между точками А и С ленты, если концентрация свободных электронов в металле равна n. (2008, 2009).
Рис. к зад. 7. Рис. к зад. 8.
8.+ Незаряженный металлический брусок представляет собой прямоугольный параллелепипед со сторонами d, b, c (c << b, c << d). Брусок движется в магнитном поле вдоль стороны d. Индукция магнитного поля В перпендикулярна основанию бруска со сторонами d и с (см. рис.). Определите скорость движения бруска v, если плотность электрических зарядов на боковых поверхностях параллелепипеда, образованных сторонами d и b, равняется s. (2008, 2009).
Индукция магнитного поля В перпендикулярна основанию бруска со сторонами d и с (см. рис.). Определите скорость движения бруска v, если плотность электрических зарядов на боковых поверхностях параллелепипеда, образованных сторонами d и b, равняется s. (2008, 2009).
9.+-Из проволоки, единица длины которой имеет сопротивление r, сделан плоский замкнутый контур, состоящий из двух квадратов площадью S1 и S2 (см. рис.). Контур находится в однородном магнитном поле с индукцией B0, направленной перпендикулярно плоскости контура. Какой заряд протечет через поперечное сечение провода при равномерном уменьшении индукции поля до нуля? Между пересекающимися на рисунке проводами контакта нет (2002).
Рис. к зад. 9. Рис. к зад. 10.
10.Контур состоит из участка OA полукольца AC и стержня OD сопротивлением R длины L, который может скользить по полукольцу, вращаясь вокруг его центра – точки O. Сопротивления остальных участков контура и скользящего контакта пренебрежимо малы. Контур помещен в однородном магнитном поле с индукцией B, линии которой перпендикулярны плоскости контура (см. рис.). Найдите модуль минимальной силы F, которую надо приложить к стержню на расстоянии ⅓ L от точки O, чтобы вращать его с постоянной угловой скоростью w. (2006)
Сопротивления остальных участков контура и скользящего контакта пренебрежимо малы. Контур помещен в однородном магнитном поле с индукцией B, линии которой перпендикулярны плоскости контура (см. рис.). Найдите модуль минимальной силы F, которую надо приложить к стержню на расстоянии ⅓ L от точки O, чтобы вращать его с постоянной угловой скоростью w. (2006)
11.+-Прямоугольную рамку, сделанную из проволоки сопротивлением R = 1 Ом, перемещают с постоянной скоростью v = 10 м/с через область однородного магнитного поля с индукцией B = 0,5 Тл (см. рис.). Какое количество теплоты Q выделится в рамке, если L1 = 0,10 м, L2 = 0,05 м и L3 > L2? (2006).
Рис. к зад. 11. Рис. к зад. 12.
12.+-По двум гладким медным шинам, установленным под углом a к горизонту, скользит под действием силы тяжести медная перемычка массы m. Шины замкнуты на сопротивление R. Расстояние между шинами L. Система находится в однородном магнитном поле с индукцией B, перпендикулярном плоскости, в которой перемещается перемычка (см.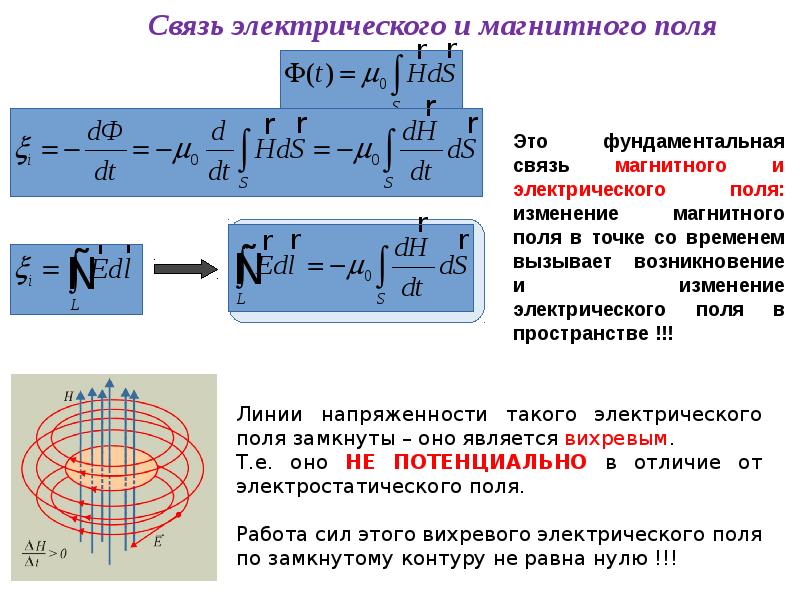 рис.). Сопротивления шин, перемычки и скользящих контактов, а также самоиндукция контура пренебрежимо малы. Найдите установившуюся скорость перемычки. (2006)
рис.). Сопротивления шин, перемычки и скользящих контактов, а также самоиндукция контура пренебрежимо малы. Найдите установившуюся скорость перемычки. (2006)
13.По двум параллельным металлическим направляющим, наклоненным под углом a к горизонту и расположенным на расстоянии b друг от друга, может скользить без трения металлическая перемычка массой m. Направляющие замкнуты снизу на незаряженный конденсатор емкостью C, и вся конструкция находится в магнитном поле, индукция которого B направлена вертикально. В начальный момент перемычку удерживают на расстоянии L от основания «горки» (см. рис.). Определите время t, за которое перемычка достигнет основания «горки» после того, как ее отпустят. Какую скорость vк она будет иметь у основания? Сопротивлением направляющих и перемычки пренебречь. (2004).
Рис. к зад. 13. Рис. к зад. 14.
14.Проводник, состоящий из двух участков, описываемых уравнениями и , находится в однородном магнитном поле В, перпендикулярном плоскости ху (см.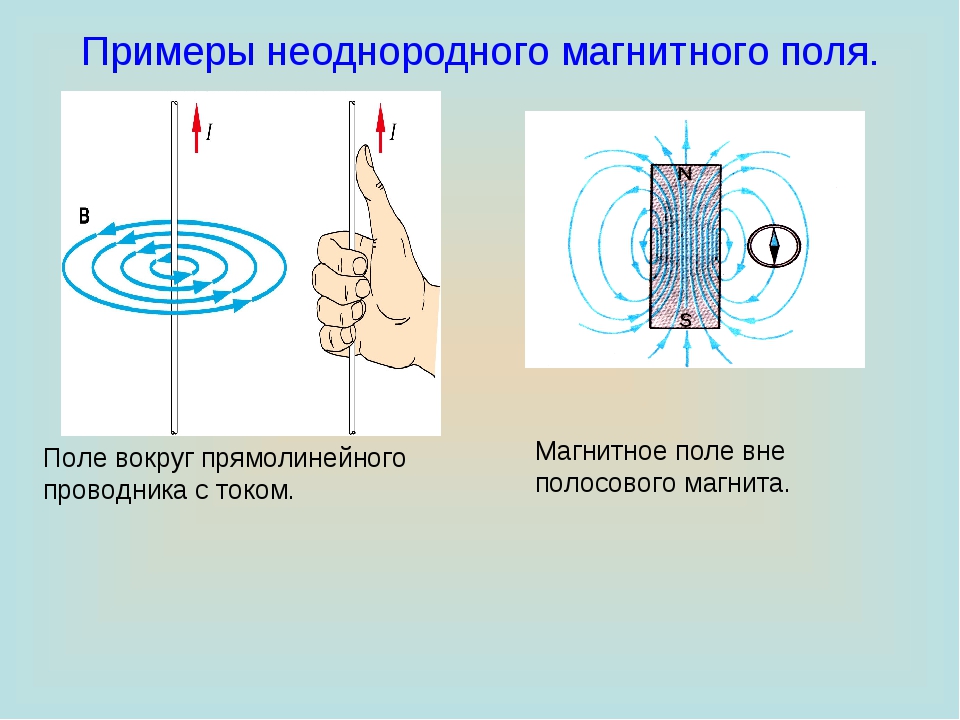 рис.). Из вершины параболы перемещают поступательно и без начальной скорости перемычку, параллельную оси Ох с постоянным ускорением а, направленным вдоль оси Оу. Найдите ЭДС индукции в образовавшемся контуре при значении координаты у = с. (2005).
рис.). Из вершины параболы перемещают поступательно и без начальной скорости перемычку, параллельную оси Ох с постоянным ускорением а, направленным вдоль оси Оу. Найдите ЭДС индукции в образовавшемся контуре при значении координаты у = с. (2005).
15.+Проводник АОК, согнутый под углом 120°, расположен в плоскости xy, как показано на рис., в однородном постоянном магнитном поле индукции B, перпендикулярной плоскости xy (см. рис.). По проводнику из начала координат O перемещают поступательно вдоль оси y с постоянной скоростью v перемычку MN, параллельную оси x. Сопротивление единицы длины перемычки равно r. Пренебрегая сопротивлением проводника и скользящих контактов, а также индуктивностью контура, найдите полное количество теплоты Q, выделившейся в перемычке, за время её движения до точки C. Длина отрезка OC равна L. (2007 — 2009)
Рис. к зад. 15.
16.Два параллельных идеально проводящих рельса расположены на расстоянии L = 0,1 м друг от друга в плоскости, перпендикулярной однородному магнитному полю индукции B = 1 Тл.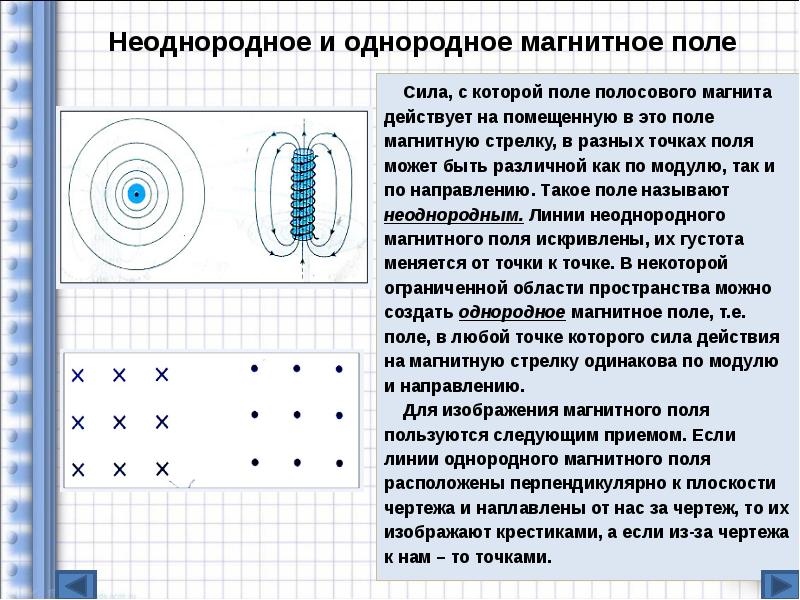 Между рельсами включены, как показано на рисунке, сопротивление R0 = 3 Ом и два конденсатора: C1 = 3×10-3 Ф и C2 = 6×10-3 Ф (см. рис.). По рельсам в разные стороны от сопротивления R0 скользят две перемычки, скорости которых V1 = 0,3 м/с и V2 = 0,2 м/с. Сопротивления перемычек R1 = 1 Ом и R2 = 2 Ом. Найдите электрическую энергию батареи конденсаторов C1, C2. (2007).
Между рельсами включены, как показано на рисунке, сопротивление R0 = 3 Ом и два конденсатора: C1 = 3×10-3 Ф и C2 = 6×10-3 Ф (см. рис.). По рельсам в разные стороны от сопротивления R0 скользят две перемычки, скорости которых V1 = 0,3 м/с и V2 = 0,2 м/с. Сопротивления перемычек R1 = 1 Ом и R2 = 2 Ом. Найдите электрическую энергию батареи конденсаторов C1, C2. (2007).
Рис. к зад. 16.
17.В однородном магнитном поле, вектор индукции которого B направлен вертикально, на горизонтальной поверхности расположена катушка, состоящая из легкого изолирующего цилиндра радиуса r, скрепленного с помощью спиц с двумя обручами радиуса R = 2r и массы 0,5m каждый (см. рис.). Вдоль оси цилиндра закреплен тонкий металлический стержень длины L и массы m. На цилиндр намотана нить, перекинутая через блок, к концу которой прикреплен груз массы m, как показано на рисунке. В процессе движения ось катушки, вектор ее скорости и вектор магнитной индукции остаются взаимно перпендикулярными. Определите скорость изменения разности потенциалов на концах металлического стержня, считая, что обручи при качении не проскальзывают. Массами цилиндра, спиц, нити и блока, а также трением в блоке пренебречь. (2003)
В процессе движения ось катушки, вектор ее скорости и вектор магнитной индукции остаются взаимно перпендикулярными. Определите скорость изменения разности потенциалов на концах металлического стержня, считая, что обручи при качении не проскальзывают. Массами цилиндра, спиц, нити и блока, а также трением в блоке пренебречь. (2003)
Рис. к зад. 17.
18.+Сверхпроводящее круглое кольцо радиуса а, имеющее индуктивность L, находится в однородном магнитном поле с индукциейВ. Первоначально плоскость кольца была параллельна вектору В, а ток в кольце равен нулю. Какую работу нужно совершить, чтобы повернуть кольцо так, чтобы его плоскость стала перпендикулярна линиям индукции? (2006).
Дифференцированное обучение 10 класс контрольные и самостоятельные работы трех уровней сложности | Учебно-методический материал по физике (10 класс) по теме:
Самостоятельная работа на тему:
«Движение заряженных частиц в электрическом и магнитном поле».
Вариант №1 (п).
Задача №1. Между пластинами плоского незаряженного конденсатора параллельно им пропускают поток электронов. Модуль скорости электронов 106. В пространстве, где находится конденсатор, создано однородное магнитное поле индукцией 1,2мТл, линии индукции которого параллельны пластинам и перпендикулярны скорости электронов. Расстояние между пластинами конденсатора 1см. Вычислить напряжение, которое установится между пластинами конденсатора.
Задача №2. Электрон движется в однородном магнитном поле с индукцией 1,4мТл по винтовой линии, шаг которой 4,6мм, а диаметр 5,2мм. Определить модуль скорости электрона.
Задача №3. Электрон влетает в область пространства, где силовые линии электрического и магнитного полей совпадают по направлению и перпендикулярны начальной скорости электрона. Модуль напряженности электрического поля 6к, модуль индукции магнитного поля 1,4мТл. Модуль скорости электрона 2. Вычислить модуль результирующего ускорения электрона в момент вхождения в эту область.
Самостоятельная работа на тему:
«Движение заряженных частиц в электрическом и магнитном поле».
Вариант №2 (в).
Задача №1. Электрон влетает в однородное магнитное поле с индукцией 1,2Тл со скоростью 1,6. Магнитное поле создано в области пространства шириной 38см. Скорость электрона перпендикулярна границе области магнитного поля и его линиям индукции. Вычислить угол, под которым он вылетит из области поля (к начальному направлению движения).
Задача №2. Электрон описывает в магнитном поле окружность радиусом 4,8мм. Вычислить модуль скорости электрона, если модуль индукции магнитного поля 3,8мТл.
Задача №3. Электрон влетает в плоский конденсатор параллельно его пластинам со скоростью 6,4. Модуль напряженности электрического поля в конденсаторе 16к, длина пластин 10см. После конденсатора электрон попадает в магнитное поле, линии индукции которого перпендикулярны линиям напряженности электрического поля, а модуль индукции 12мТл. Определить радиус винтовой линии, по которой движется электрон в магнитном поле.
Самостоятельная работа на тему:
«Движение заряженных частиц в электрическом и магнитном поле».
Вариант №1 (п).
Задача №1. Между пластинами плоского незаряженного конденсатора параллельно им пропускают поток электронов. Модуль скорости электронов 106. В пространстве, где находится конденсатор, создано однородное магнитное поле индукцией 1,2мТл, линии индукции которого параллельны пластинам и перпендикулярны скорости электронов. Расстояние между пластинами конденсатора 1см. Вычислить напряжение, которое установится между пластинами конденсатора.
Задача №2. Электрон движется в однородном магнитном поле с индукцией 1,4мТл по винтовой линии, шаг которой 4,6мм, а диаметр 5,2мм. Определить модуль скорости электрона.
Задача №3. Электрон влетает в область пространства, где силовые линии электрического и магнитного полей совпадают по направлению и перпендикулярны начальной скорости электрона. Модуль напряженности электрического поля 6к, модуль индукции магнитного поля 1,4мТл. Модуль скорости электрона 2. Вычислить модуль результирующего ускорения электрона в момент вхождения в эту область.
Модуль скорости электрона 2. Вычислить модуль результирующего ускорения электрона в момент вхождения в эту область.
Самостоятельная работа на тему:
«Движение заряженных частиц в электрическом и магнитном поле».
Вариант №2 (в).
Задача №1. Электрон влетает в однородное магнитное поле с индукцией 1,2Тл со скоростью 1,6. Магнитное поле создано в области пространства шириной 38см. скорость электрона перпендикулярна границе области магнитного поля и его линиям индукции. Вычислить угол, под которым он вылетит из области поля (к начальному направлению движения).
Задача №2. Электрон описывает в магнитном поле окружность радиусом 4,8мм. Вычислить модуль скорости электрона, если модуль индукции магнитного поля 3,8мТл.
Задача №3. Электрон влетает в плоский конденсатор параллельно его пластинам со скоростью 6,4. Модуль напряженности электрического поля в конденсаторе 16к, длина пластин 10см. После конденсатора электрон попадает в магнитное поле, линии индукции которого перпендикулярны линиям напряженности электрического поля, а модуль индукции 12мТл. Определить радиус винтовой линии, по которой движется электрон в магнитном поле.
Определить радиус винтовой линии, по которой движется электрон в магнитном поле.
Самостоятельная работа на тему:
«Движение заряженных частиц в электрическом и магнитном поле».
Вариант №3 (б).
Задача №1. Электрон движется по окружности радиусом 10см в однородном магнитном поле с индукцией 0,02Тл. Определить частоту вращения частицы, если её масса 10-30кг.
Задача №2. Протон и электрон влетают в однородное магнитное поле с одинаковой скоростью, направленной перпендикулярно полю. Во сколько раз радиус орбиты протона больше радиуса орбиты электрона?
Задача №3. Однородные электрическое и магнитное поле расположены взаимно перпендикулярно. Протон движется в этих полях равномерно и прямолинейно перпендикулярно силовым линиям обоих полей со скоростью 0,6м/с. Напряженность электрического поля 0,6кВ/м. Чему равна индукция магнитного поля?
Самостоятельная работа на тему:
«Движение заряженных частиц в электрическом и магнитном поле».
Вариант №3 (б).
Задача №1. Электрон движется по окружности радиусом 10см в однородном магнитном поле с индукцией 0,02Тл. Определить частоту вращения частицы, если её масса 10-30кг.
Задача №2. Протон и электрон влетают в однородное магнитное поле с одинаковой скоростью, направленной перпендикулярно полю. Во сколько раз радиус орбиты протона больше радиуса орбиты электрона?
Задача №3. Однородные электрическое и магнитное поле расположены взаимно перпендикулярно. Протон движется в этих полях равномерно и прямолинейно перпендикулярно силовым линиям обоих полей со скоростью 0,6м/с. Напряженность электрического поля 0,6кВ/м. Чему равна индукция магнитного поля?
Самостоятельная работа на тему:
«Движение заряженных частиц в электрическом и магнитном поле».
Вариант №3 (б).
Задача №1. Электрон движется по окружности радиусом 10см в однородном магнитном поле с индукцией 0,02Тл. Определить частоту вращения частицы, если её масса 10-30кг.
Задача №2. Протон и электрон влетают в однородное магнитное поле с одинаковой скоростью, направленной перпендикулярно полю. Во сколько раз радиус орбиты протона больше радиуса орбиты электрона?
Во сколько раз радиус орбиты протона больше радиуса орбиты электрона?
Задача №3. Однородные электрическое и магнитное поле расположены взаимно перпендикулярно. Протон движется в этих полях равномерно и прямолинейно перпендикулярно силовым линиям обоих полей со скоростью 0,6м/с. Напряженность электрического поля 0,6кВ/м. Чему равна индукция магнитного поля?
Самостоятельная работа на тему:
«Движение заряженных частиц в электрическом и магнитном поле».
Вариант №3 (б).
Задача №1. Электрон движется по окружности радиусом 10см в однородном магнитном поле с индукцией 0,02Тл. Определить частоту вращения частицы, если её масса 10-30кг.
Задача №2. Протон и электрон влетают в однородное магнитное поле с одинаковой скоростью, направленной перпендикулярно полю. Во сколько раз радиус орбиты протона больше радиуса орбиты электрона?
Задача №3. Однородные электрическое и магнитное поле расположены взаимно перпендикулярно. Протон движется в этих полях равномерно и прямолинейно перпендикулярно силовым линиям обоих полей со скоростью 0,6м/с. Напряженность электрического поля 0,6кВ/м. Чему равна индукция магнитного поля?
Напряженность электрического поля 0,6кВ/м. Чему равна индукция магнитного поля?
Движение заряженной частицы в магнитном поле
Электрические силы против магнитных
И электрические, и магнитные силы влияют на траекторию заряженных частиц, но качественно по-разному.
Цели обучения
Сравните влияние электрического и магнитного полей на заряженную частицу
Основные выводы
Ключевые моменты
- Сила, действующая на заряженную частицу из-за электрического поля, направлена параллельно вектору электрического поля в случае положительного заряда и антипараллельно в случае отрицательного заряда.Это не зависит от скорости частицы.
- Напротив, магнитная сила, действующая на заряженную частицу, ортогональна вектору магнитного поля и зависит от скорости частицы. Правило правой руки можно использовать для определения направления силы.
- Электрическое поле может действовать на заряженную частицу, в то время как магнитное поле не действует.

- Сила Лоренца — это комбинация электрической и магнитной сил, которые часто рассматриваются вместе в практических приложениях.
- Линии электрического поля генерируются на положительных зарядах и оканчиваются на отрицательных. Силовые линии изолированного заряда направлены прямо радиально наружу. Электрическое поле касается этих линий.
- Линии магнитного поля в случае магнита генерируются на северном полюсе и заканчиваются на южном полюсе. Магнитные полюса не существуют изолированно. Как и в случае силовых линий электрического поля, магнитное поле касается силовых линий. Заряженные частицы будут вращаться вокруг этих силовых линий.
Ключевые термины
- ортогонально : из двух объектов под прямым углом; перпендикулярны друг другу.
Электрические силы против магнитных
Сила, создаваемая как электрическими, так и магнитными силами, влияет на движение заряженных частиц. Однако результирующее изменение траектории частиц будет качественно отличаться между двумя силами. Ниже мы кратко рассмотрим два типа сил, а также сравним и сопоставим их влияние на заряженную частицу.
Ниже мы кратко рассмотрим два типа сил, а также сравним и сопоставим их влияние на заряженную частицу.
Электростатическая сила и магнитная сила на заряженной частице
Напомним, что в статическом неизменном электрическом поле E сила, действующая на частицу с зарядом q, будет:
[латекс] \ text {F} = \ text {qE} [/ латекс]
Где F — вектор силы, q — заряд, а E — вектор электрического поля. Обратите внимание, что направление F идентично направлению E в случае позитивистского заряда q и в противоположном направлении в случае отрицательно заряженной частицы.{2}} [/ латекс]
Следует подчеркнуть, что электрическая сила F действует параллельно электрическому полю E . Ротор электрической силы равен нулю, т.е .:
[латекс] \ bigtriangledown \ times \ text {E} = 0 [/ латекс]
Следствием этого является то, что электрическое поле может работать, и заряд в чистом электрическом поле будет следовать по касательной к линии электрического поля.
Напротив, напомним, что магнитная сила, действующая на заряженную частицу, ортогональна магнитному полю, так что:
[латекс] \ text {F} = \ text {qv} \ times \ text {B} = \ text {qvBsin} \ theta [/ latex]
, где B — вектор магнитного поля, v — скорость частицы, а θ — угол между магнитным полем и скоростью частицы.Направление F можно легко определить с помощью правила правой руки.
Правило правой руки : Магнитные поля действуют на движущиеся заряды. Эта сила — одна из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует правилу правой руки –1 (RHR-1), как показано. Величина силы пропорциональна q, v, B и синусу угла между v и B.
Если скорость частицы выровнена параллельно магнитному полю или равна нулю, магнитная сила будет равна нулю.Это отличается от случая электрического поля, где скорость частицы не имеет отношения в любой данный момент к величине или направлению электрической силы.
Угловая зависимость магнитного поля также заставляет заряженные частицы двигаться перпендикулярно линиям магнитного поля по кругу или спирали, в то время как частица в электрическом поле будет двигаться по прямой линии вдоль линии электрического поля.
Еще одно различие между магнитными и электрическими силами состоит в том, что магнитные поля не работают, , поскольку движение частицы является круговым и, следовательно, заканчивается в одном и том же месте.Мы выражаем это математически как:
[латекс] \ text {W} = \ oint \ text {B} \ cdot \ text {dr} = 0 [/ latex]
Лоренц Форс
Сила Лоренца — это объединенная сила, действующая на заряженную частицу за счет как электрического, так и магнитного полей, которые часто рассматриваются вместе для практических приложений. Если частица заряда q движется со скоростью v в присутствии электрического поля E и магнитного поля B , то на нее будет действовать сила:
[латекс] \ text {F} = \ text {q} [\ text {E} + \ text {vBsin} \ theta] [/ latex]
Линии электрического и магнитного поля
Выше мы кратко упомянули, что движение заряженных частиц относительно силовых линий различается в зависимости от того, имеем ли мы дело с электрическими или магнитными полями. Есть некоторые заметные различия между концептуальными представлениями линий электрического и магнитного поля. Линии электрического поля от положительного изолированного заряда представляют собой просто последовательность равномерно расположенных радиально направленных линий, направленных наружу от заряда. В случае отрицательного заряда направление поля меняется на противоположное. Электрическое поле направлено по касательной к силовым линиям. Конечно, мы предполагаем, что силовые линии тем плотнее упакованы, чем больше заряды. Хорошо видно, что ротор электрической силы равен нулю.
Есть некоторые заметные различия между концептуальными представлениями линий электрического и магнитного поля. Линии электрического поля от положительного изолированного заряда представляют собой просто последовательность равномерно расположенных радиально направленных линий, направленных наружу от заряда. В случае отрицательного заряда направление поля меняется на противоположное. Электрическое поле направлено по касательной к силовым линиям. Конечно, мы предполагаем, что силовые линии тем плотнее упакованы, чем больше заряды. Хорошо видно, что ротор электрической силы равен нулю.
Электрическое поле, создаваемое точечными зарядами : электрическое поле, окружающее три различных точечных заряда: (а) положительный заряд; (б) отрицательный заряд равной величины; (c) больший отрицательный заряд.
Если задействовано несколько зарядов, силовые линии создаются на положительных зарядах и заканчиваются на отрицательных.
В случае магнитов силовые линии формируются на северном полюсе (+) и заканчиваются на южном полюсе (-) — см. Рисунок ниже.Однако магнитные «заряды» всегда идут парами — магнитных монополей (изолированных северных или южных полюсов) нет. Таким образом, ротор магнитного поля, создаваемого обычным магнитом, всегда отличен от нуля. Заряженные частицы будут вращаться по спирали вокруг этих силовых линий до тех пор, пока частицы имеют ненулевую составляющую скорости, направленную перпендикулярно силовым линиям.
Рисунок ниже.Однако магнитные «заряды» всегда идут парами — магнитных монополей (изолированных северных или южных полюсов) нет. Таким образом, ротор магнитного поля, создаваемого обычным магнитом, всегда отличен от нуля. Заряженные частицы будут вращаться по спирали вокруг этих силовых линий до тех пор, пока частицы имеют ненулевую составляющую скорости, направленную перпендикулярно силовым линиям.
Модель магнитного полюса : Модель магнитного полюса: два противоположных полюса, Северный (+) и Южный (-), разделенные расстоянием d, создают H-поле (линии).
Магнитное поле может также создаваться током, силовые линии которого представляют собой концентрические круги вокруг токоведущего провода. Магнитная сила в любой точке в этом случае может быть определена с помощью правила правой руки и будет перпендикулярна обоим ток и магнитное поле.
При постоянной скорости получается прямолинейный
Если скорость заряженной частицы параллельна магнитному полю, результирующая сила отсутствует и частица движется по прямой линии.
Цели обучения
Определить условия, при которых частица движется по прямой в магнитном поле
Основные выводы
Ключевые моменты
- Первый закон движения Ньютона гласит, что если объект не испытывает чистой силы, то его скорость постоянна.
- Частица с постоянной скоростью будет двигаться по прямой в пространстве.
- Если скорость заряженной частицы полностью параллельна магнитному полю, магнитное поле не будет оказывать силы на частицу и, таким образом, скорость останется постоянной.
- В случае, если вектор скорости не параллелен и не перпендикулярен магнитному полю, составляющая скорости, параллельная полю, останется постоянной.
Ключевые термины
- прямолинейное движение : движение, которое происходит в одном направлении
Постоянная скорость обеспечивает прямолинейное движение
Вспомните первый закон движения Ньютона. Если объект не испытывает чистой силы, то его скорость постоянна: объект либо находится в состоянии покоя (если его скорость равна нулю), либо он движется по прямой с постоянной скоростью (если его скорость отлична от нуля).
Во многих случаях частица может не испытывать чистой силы. Частица могла существовать в вакууме вдали от любых массивных тел (которые проявляют гравитационные силы) и электромагнитных полей. Или на частицу могут действовать две или более силы, уравновешенные таким образом, что результирующая сила равна нулю. Так обстоит дело, скажем, с частицей, подвешенной в электрическом поле, электрическая сила которого точно уравновешивает гравитацию.
Если результирующая сила, действующая на частицу, равна нулю, то ускорение обязательно равно нулю согласно второму закону Ньютона: F = ma.Если ускорение равно нулю, любая скорость частицы будет поддерживаться бесконечно (или до тех пор, пока результирующая сила не станет равной нулю). Поскольку скорость является вектором, направление остается неизменным вместе со скоростью, поэтому частица продолжает движение в одном направлении, например, по прямой.
Заряженные частицы, движущиеся параллельно магнитным полям
Сила, которую заряженная частица «ощущает» из-за магнитного поля, зависит от угла между вектором скорости и вектором магнитного поля B . Напомним, что магнитная сила составляет:
Напомним, что магнитная сила составляет:
Нулевая сила, когда скорость параллельна магнитному полю : В приведенном выше случае магнитная сила равна нулю, потому что скорость параллельна силовым линиям магнитного поля.
[латекс] \ text {F} = \ text {qvBsin} \ theta [/ latex]
Если магнитное поле и скорость параллельны (или антипараллельны), тогда sinθ равен нулю и сила отсутствует. В этом случае заряженная частица может продолжать прямолинейное движение даже в сильном магнитном поле.Если находится между 0 и 90 градусами, то составляющая v параллельно B остается неизменной.
Круговое движение
Так как магнитная сила всегда перпендикулярна скорости заряженной частицы, частица будет совершать круговое движение.
Цели обучения
Опишите условия, которые приводят к круговому движению заряженной частицы в магнитном поле.
Основные выводы
Ключевые моменты
- Магнитное поле не работает, поэтому кинетическая энергия и скорость заряженной частицы в магнитном поле остаются постоянными.
 {2}} {\ text {r}} [/ latex].
{2}} {\ text {r}} [/ latex]. - Решение для r выше дает гриорадиус, или радиус кривизны траектории частицы с зарядом q и массой m, движущейся в магнитном поле с напряженностью B. Тогда гриорадиус определяется как [латекс] \ text {r} = \ frac {\ text {mv}} {\ text {qB}} [/ latex].
- Циклотронная частота (или, эквивалентно, гирочастота) — это количество циклов, которые частица совершает вокруг своего кругового цикла каждую секунду, и задается как [latex] \ text {f} = \ frac {\ text {qB}} {2 \ пи \ текст {м}} [/ латекс].
Ключевые термины
- гирорадиус : Радиус кругового движения заряженной частицы в присутствии однородного магнитного поля.
- циклотронная частота : частота заряженной частицы, движущейся перпендикулярно направлению однородного магнитного поля B (постоянная величина и направление). Дается равенством центростремительной силы и магнитной силы Лоренца.
Круговое движение заряженной частицы в магнитном поле
Магнитные силы могут заставлять заряженные частицы двигаться по круговой или спиральной траектории. Ускорители элементарных частиц удерживают протоны на круговых траекториях с помощью магнитной силы. Космические лучи будут следовать по спирали при встрече с магнитным полем астрофизических объектов или планет (одним из примеров является магнитное поле Земли). На фотографии пузырьковой камеры на рисунке ниже показаны заряженные частицы, движущиеся по таким искривленным траекториям. Изогнутые траектории заряженных частиц в магнитных полях являются основой ряда явлений и могут даже использоваться аналитически, например, в масс-спектрометре.показывает путь, пройденный частицами в пузырьковой камере.
Ускорители элементарных частиц удерживают протоны на круговых траекториях с помощью магнитной силы. Космические лучи будут следовать по спирали при встрече с магнитным полем астрофизических объектов или планет (одним из примеров является магнитное поле Земли). На фотографии пузырьковой камеры на рисунке ниже показаны заряженные частицы, движущиеся по таким искривленным траекториям. Изогнутые траектории заряженных частиц в магнитных полях являются основой ряда явлений и могут даже использоваться аналитически, например, в масс-спектрометре.показывает путь, пройденный частицами в пузырьковой камере.
Пузырьковая камера : Следы пузырьков создаются заряженными частицами высокой энергии, движущимися через перегретый жидкий водород в изображении пузырьковой камеры этим художником. Существует сильное магнитное поле, перпендикулярное странице, которое вызывает искривленные траектории частиц. Радиус пути можно использовать для определения массы, заряда и энергии частицы.
Итак, вызывает ли магнитная сила круговое движение? Магнитная сила всегда перпендикулярна скорости, поэтому она не действует на заряженную частицу.Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Это влияет на направление движения, но не на скорость. Это типично для равномерного кругового движения. Самый простой случай возникает, когда заряженная частица движется перпендикулярно однородному B-полю, как показано на рисунке. (Если это происходит в вакууме, магнитное поле является доминирующим фактором, определяющим движение.) Здесь магнитная сила (Лоренц сила) обеспечивает центростремительную силу
Круговое движение заряженной частицы в магнитном поле : отрицательно заряженная частица движется в плоскости страницы в области, где магнитное поле перпендикулярно к странице (представлено маленькими кружками с крестиками — как хвосты стрелок) .{2}} {\ text {r}} [/ latex]
решение для r дает
[латекс] \ text {r} = \ frac {\ text {mv}} {\ text {qB}} [/ latex]
Здесь r , называемый гирорадиусом или циклотронным радиусом, представляет собой радиус кривизны пути заряженной частицы с массой m и зарядом q , движущейся со скоростью v перпендикулярно магнитному полю прочность B . Другими словами, это радиус кругового движения заряженной частицы в присутствии однородного магнитного поля.Если скорость не перпендикулярна магнитному полю, то v — составляющая скорости, перпендикулярная полю. Компонент скорости, параллельный полю, не изменяется, поскольку магнитная сила равна нулю для движения, параллельного полю. Последствия этого случая мы рассмотрим в следующем разделе, посвященном спиральному движению.
Другими словами, это радиус кругового движения заряженной частицы в присутствии однородного магнитного поля.Если скорость не перпендикулярна магнитному полю, то v — составляющая скорости, перпендикулярная полю. Компонент скорости, параллельный полю, не изменяется, поскольку магнитная сила равна нулю для движения, параллельного полю. Последствия этого случая мы рассмотрим в следующем разделе, посвященном спиральному движению.
Частица, совершающая круговое движение из-за однородного магнитного поля, называется циклотроном , резонанс .Этот термин происходит от названия циклотронного ускорителя частиц, который показан на рисунке. Циклотронная частота (или, что то же самое, гирочастота) — это количество циклов, которые частица совершает вокруг своего кругового контура каждую секунду, и может быть найдена путем решения для v выше и подставив частоту обращения так, чтобы
Циклотрон : Французский циклотрон, произведенный в Цюрихе, Швейцария, в 1937 г.
[латекс] \ text {f} = \ frac {\ text {v}} {2 \ pi \ text {r}} [/ latex]
становится
[латекс] \ text {f} = \ frac {\ text {qB}} {2 \ pi \ text {m}} [/ latex]
Циклотронная частота тривиально выражается в радианах в секунду как
.
[латекс] \ omega = \ frac {\ text {qB}} {\ text {m}} [/ latex].
Спиральное движение
Движение по спирали возникает, когда вектор скорости не перпендикулярен вектору магнитного поля.
Цели обучения
Опишите условия, которые приводят к спиральному движению заряженной частицы в магнитном поле.
Основные выводы
Ключевые моменты
- Ранее мы видели, что круговое движение возникает, когда скорость заряженной частицы перпендикулярна магнитному полю. Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой.
- Если скорость не перпендикулярна магнитному полю, мы учитываем только компонент v, который перпендикулярен полю при проведении наших расчетов.

- Составляющая скорости, параллельная полю, не изменяется, поскольку магнитная сила равна нулю для движения, параллельного полю. Это вызывает спиральное движение.
- Заряды могут двигаться по спирали вдоль силовых линий. Если сила магнитного поля увеличивается в направлении движения, поле будет оказывать силу, замедляющую заряды и даже меняющую их направление.Это называется магнитным зеркалом.
Ключевые термины
- спиральное движение : движение, которое создается, когда один компонент скорости постоянен по величине и направлению (т. Е. Прямолинейное движение), в то время как другой компонент постоянен по скорости, но равномерно изменяется по направлению (т. Е. Круговое движение ). Это суперпозиция прямолинейного и кругового движения.
- магнитное зеркало : Конфигурация магнитного поля, при которой напряженность поля изменяется при движении вдоль силовой линии.Эффект зеркала приводит к тенденции заряженных частиц отскакивать от области сильного поля.

Спиральное движение
В разделе о круговом движении мы описали движение заряженной частицы с вектором магнитного поля, направленным перпендикулярно скорости частицы. В этом случае магнитная сила также перпендикулярна скорости (и, конечно, вектору магнитного поля) в любой момент, что приводит к круговому движению. Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой.быстро рассматривает эту ситуацию в случае отрицательно заряженной частицы в магнитном поле, направленном внутрь страницы.
Круговое движение заряженной частицы в магнитном поле : отрицательно заряженная частица движется в плоскости страницы в области, где магнитное поле перпендикулярно к странице (представлено маленькими кружками с крестиками — как хвосты стрелок) . Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине.2} {\ text {r}} [/ latex]
[латекс] \ text {F} = \ text {qvBsin} \ theta = \ text {qv} _ {\ perp} \ text {B} [/ latex]
Составляющая скорости, параллельная полю, не изменяется, поскольку магнитная сила равна нулю для движения, параллельного полю. Это производит спиральное движение (т.е. спиральное движение), а не круговое движение.
Это производит спиральное движение (т.е. спиральное движение), а не круговое движение.
показывает, как электроны, движущиеся не перпендикулярно силовым линиям магнитного поля, следуют за силовыми линиями. Компонент скорости, параллельный линиям, не изменяется, поэтому заряды вращаются по спирали вдоль силовых линий.Если напряженность поля увеличивается в направлении движения, поле будет оказывать силу, замедляющую заряды (и даже меняющую их направление), образуя своего рода магнитное зеркало.
Спиральное движение и магнитные зеркала : Когда заряженная частица движется вдоль силовой линии магнитного поля в область, где поле становится сильнее, частица испытывает силу, которая уменьшает составляющую скорости, параллельную полю. Эта сила замедляет движение вдоль силовой линии и переворачивает его, образуя «магнитное зеркало».«
Движение заряженных частиц в магнитных полях связано с такими разными вещами, как Северное сияние или Северное сияние (северное и южное сияние) и ускорители частиц. Заряженные частицы, приближающиеся к линиям магнитного поля, могут быть захвачены спиральными орбитами вокруг линий, а не пересекать их. , как видно выше. Некоторые космические лучи, например, следуют за линиями магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере.Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются составной частью радиационного фона; следовательно, они дают более высокую дозу излучения на полюсах, чем на экваторе.
Заряженные частицы, приближающиеся к линиям магнитного поля, могут быть захвачены спиральными орбитами вокруг линий, а не пересекать их. , как видно выше. Некоторые космические лучи, например, следуют за линиями магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере.Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются составной частью радиационного фона; следовательно, они дают более высокую дозу излучения на полюсах, чем на экваторе.
Заряженные частицы вращаются по спирали вдоль линий магнитного поля Земли : Энергичные электроны и протоны, составляющие космических лучей, исходящие от Солнца и дальнего космоса, часто следуют за линиями магнитного поля Земли, а не пересекают их.(Напомним, что северный магнитный полюс Земли на самом деле является южным полюсом в смысле стержневого магнита. )
)
Примеры и приложения
Циклотроны, магнетроны и масс-спектрометры представляют собой практические технологические приложения электромагнитных полей.
Цели обучения
Обсудить применение масс-спектрометров, движение заряженных частиц в циклотроне и то, как микроволны генерируются в магнетроне с резонатором.
Основные выводы
Ключевые моменты
- Циклотрон — это тип ускорителя частиц, в котором заряженные частицы ускоряются наружу от центра по спиральной траектории.Частицы удерживаются на спиральной траектории с помощью статического магнитного поля и ускоряются быстро меняющимся электрическим полем.
- Магнетрон с резонатором представляет собой мощную вакуумную лампу, которая генерирует микроволны, используя взаимодействие потока электронов с магнитным полем. Магнетрон находит применение в радарах, обогреве и освещении.
- Масс-спектрометры измеряют отношение массы к заряду заряженных частиц с помощью электромагнитных полей для разделения частиц с разными массами и / или зарядами.
 Его можно использовать для определения элементного состава молекулы или образца.
Его можно использовать для определения элементного состава молекулы или образца.
Ключевые термины
- циклотрон : ускоритель ранних частиц, в котором заряженные частицы генерировались в центральном источнике и ускорялись по спирали наружу посредством фиксированного магнитного и переменного электрического поля.
- масс-спектрометр : устройство, используемое в масс-спектрометрии для определения массового состава данного вещества.
- магнетрон : устройство, в котором электроны заставляют резонировать в камере особой формы и, таким образом, производить микроволновое излучение; используется в радарах и микроволновых печах.
Примеры и приложения — движение заряженной частицы в магнитном поле
Обзор
Напомним, что заряженные частицы в магнитном поле будут двигаться по круговой или спиральной траектории в зависимости от совмещения их вектора скорости с вектором магнитного поля.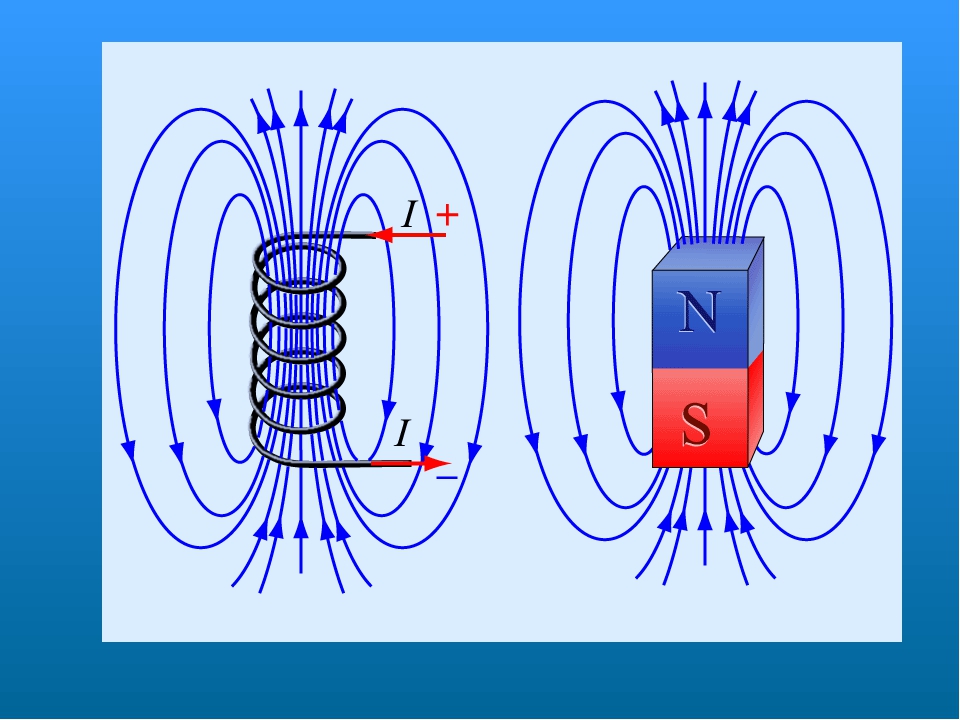 Последствия такого движения могут иметь глубокое практическое применение. Многие технологии основаны на движении заряженных частиц в электромагнитных полях. Мы рассмотрим некоторые из них, включая циклотрон и синхротрон, магнетрон с резонатором и масс-спектрометр.
Последствия такого движения могут иметь глубокое практическое применение. Многие технологии основаны на движении заряженных частиц в электромагнитных полях. Мы рассмотрим некоторые из них, включая циклотрон и синхротрон, магнетрон с резонатором и масс-спектрометр.
Циклотроны и синхротроны
Циклотрон — это тип ускорителя частиц, в котором заряженные частицы ускоряются наружу от центра по спиральной траектории. Частицы удерживаются на спиральной траектории с помощью статического магнитного поля и ускоряются быстро меняющимся (радиочастотным) электрическим полем.
Cyclotron Sketch : Эскиз частицы, которая ускоряется в циклотроне и выбрасывается через канал.
Циклотроны ускоряют пучки заряженных частиц, используя высокочастотное переменное напряжение, которое прикладывают между двумя электродами в форме буквы «D» (также называемыми «деээ»).Дополнительное статическое магнитное поле прикладывается перпендикулярно плоскости электрода, позволяя частицам повторно сталкиваться с ускоряющим напряжением много раз в одной и той же фазе. Для этого частота напряжения должна соответствовать частоте циклотронного резонанса частицы,
Для этого частота напряжения должна соответствовать частоте циклотронного резонанса частицы,
.
[латекс] \ text {f} = \ frac {\ text {qB}} {2 \ pi \ text {m}} [/ latex]
с релятивистской массой м и его зарядом q . Эта частота задается равенством центростремительной силы и магнитной силы Лоренца.Частицы, инжектируемые около центра магнитного поля, увеличивают свою кинетическую энергию только при рециркуляции через зазор между электродами; таким образом, они движутся наружу по спирали. Их радиус будет увеличиваться до тех пор, пока частицы не попадут в цель по периметру вакуумной камеры или не покинут циклотрон с помощью лучевой трубки, что позволит их использовать. Частицы, ускоренные циклотроном, могут использоваться в терапии частицами для лечения некоторых видов рака. Кроме того, циклотроны являются хорошим источником пучков высоких энергий для ядерно-физических экспериментов.
Синхротрон является усовершенствованием циклотрона, в котором ведущее магнитное поле (изгибание частиц по замкнутому пути) зависит от времени, синхронизировано с пучком частиц с увеличивающейся кинетической энергией. Синхротрон — одна из первых концепций ускорителей, которые позволяют создавать крупномасштабные объекты, поскольку изгиб, фокусировка пучка и ускорение могут быть разделены на разные компоненты.
Синхротрон — одна из первых концепций ускорителей, которые позволяют создавать крупномасштабные объекты, поскольку изгиб, фокусировка пучка и ускорение могут быть разделены на разные компоненты.
Полостной магнетрон
Магнетрон с резонатором представляет собой мощную вакуумную лампу, которая генерирует микроволны, используя взаимодействие потока электронов с магнитным полем.Все магнетроны с резонатором состоят из горячего катода с высоким (непрерывным или импульсным) отрицательным потенциалом, создаваемым высоковольтным источником постоянного тока. Катод встроен в центр откачанной круглой камеры с лепестками. Магнитное поле, параллельное нити накала, создается постоянным магнитом. Магнитное поле заставляет электроны, притянутые к (относительно) положительной внешней части камеры, двигаться по спирали наружу по круговой траектории, что является следствием силы Лоренца. По краю камеры расположены цилиндрические полости.Полости открыты по своей длине и соединяют общее пространство полости.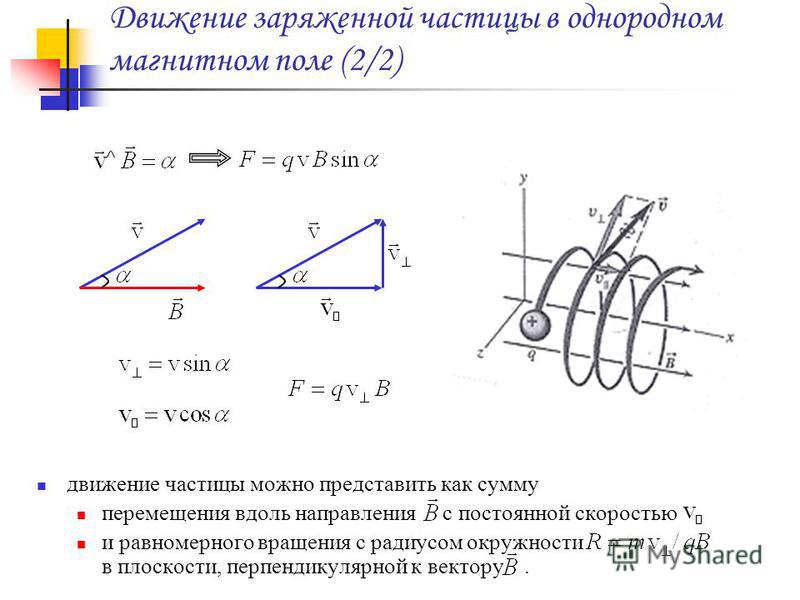 Когда электроны проходят мимо этих отверстий, они создают резонансное высокочастотное радиополе в полости, которое, в свою очередь, заставляет электроны группироваться в группы.
Когда электроны проходят мимо этих отверстий, они создают резонансное высокочастотное радиополе в полости, которое, в свою очередь, заставляет электроны группироваться в группы.
Схема магнетрона с резонатором : Поперечное сечение магнетрона с резонатором. Магнитные силовые линии параллельны геометрической оси этой конструкции.
Размеры полостей определяют резонансную частоту и, следовательно, частоту излучаемых микроволн.Магнетрон — это автоколебательное устройство, не требующее никаких внешних элементов, кроме источника питания. Магнетрон находит практическое применение в радарах, обогреве (как основной компонент микроволновой печи) и освещении.
Масс-спектрометрия
Масс-спектрометрия — это аналитический метод, позволяющий измерять отношение массы к заряду заряженных частиц. Он используется для определения массы частиц и определения элементного состава образца или молекулы.
Масс-анализаторы разделяют ионы в соответствии с их отношением массы к заряду. Следующие два закона управляют динамикой заряженных частиц в электрическом и магнитном полях в вакууме:
Следующие два закона управляют динамикой заряженных частиц в электрическом и магнитном полях в вакууме:
[латекс] \ text {F} = \ text {Q} (\ text {E} + \ text {v} \ times \ text {B}) [/ latex] (сила Лоренца)
[латекс] \ text {F} = \ text {ma} [/ latex]
Приравнивая приведенные выше выражения для силы, приложенной к иону, получаем:
[латекс] (\ text {m} / \ text {Q}) \ text {a} = \ text {E} + \ text {v} \ times \ text {B} [/ latex]
Это дифференциальное уравнение вместе с начальными условиями полностью определяет движение заряженной частицы в терминах m / Q.Есть много типов масс-анализаторов, использующих статические или динамические поля, а также магнитные или электрические поля, но все они работают в соответствии с приведенным выше дифференциальным уравнением.
На следующем рисунке показан один тип масс-спектрометра. Отклонения частиц зависят от отношения массы к заряду. В случае изотопного диоксида углерода каждая молекула имеет одинаковый заряд, но разные массы. Масс-спектрометр будет разделять частицы в пространстве, позволяя детектору измерять отношение массы к заряду каждой частицы.Поскольку заряд известен, абсолютную массу можно определить тривиально. Относительные содержания могут быть выведены путем подсчета количества частиц каждой данной массы.
Масс-спектрометр будет разделять частицы в пространстве, позволяя детектору измерять отношение массы к заряду каждой частицы.Поскольку заряд известен, абсолютную массу можно определить тривиально. Относительные содержания могут быть выведены путем подсчета количества частиц каждой данной массы.
Масс-спектрометрия : Схема простого масс-спектрометра с масс-анализатором секторного типа. Он предназначен для измерения соотношения изотопов диоксида углерода (IRMS), как в дыхательном тесте с мочевиной углерода-13.
Электромагнетизм
Электромагнетизм
5 Электромагнетизм
5.1 Магнетизм
До сих пор мы обсуждали силы между зарядами, которые находятся в состоянии покоя с
уважение друг к другу. Когда заряды движутся относительно друг друга, они
приложить дополнительную силу , магнитную силу. Эта сила, как мы и будем
см. ниже, играет незначительную роль в межатомных и межмолекулярных связях.
Однако влияние магнитных полей на атомы и молекулы широко используется в
всевозможные спектроскопии, и нам нужно будет оценить магнитное поведение
чтобы понять взаимодействие света и других электромагнитных
излучение с атомами и молекулами.
5.1.1 Сила Лоренца
Магнитные материалы были открыты задолго до электростатических эффектов
натирание янтаря. Магнитный оксид железа — магнетит — добывали в Малой Азии.
до Рождества Христова, действительно, примерно к 100 г. до н.э. китайцы уже
обнаружил, что такие минералы будут соответствовать северному и южному полюсам. К
В начале XIX века было известно, что такие стержневые магниты будут
отталкивать, если одинаковые полюса обращены друг к другу, и притягивать, если полюса
противоположный смысл, и сходство с поведением электрических зарядов имело
некоторое время интересовало ученых того времени.
В 1820 году датский ученый Ганс Кристиан Эрстед выполнил серию
эксперименты, которые продемонстрировали, что движущийся заряд оказывает силу на
постоянный магнит. В том же году Ампер показал, что третий Ньютон
закон предсказывал, что верно и обратное, что магнит оказывает силу на
движущийся заряд.
Они сделали следующие наблюдения
* сила пропорциональна величине и знаку заряда на
частица
* сила пропорциональна скорости заряженной частицы
* сила пропорциональна величине магнитного поля
* величина силы зависит от взаимной ориентации
линия полета и направление магнитного поля
* и сила всегда действует перпендикулярно линии движения частицы.
полет.
Последнее утверждение является наименее ожидаемым, поскольку пока мы встретили только силы
которые действуют в том же направлении, что и поле. Математически единственный способ
которая умножает две векторные величины, в данном случае скорость и
поле, приводит к вектору, который является взаимно перпендикулярным, сила равна
применить векторное векторное произведение.
F = q v x B (5.1.1)
где B — магнитное поле (единица магнитного поля —
Тесла (Т)).Обратите внимание, что направление поля было задано
требование, чтобы F был перпендикулярен v . Тем не мение,
это гарантирует, что если мы воспользуемся стрелкой компаса для нанесения на карту поля, то северный полюс
будет указывать в направлении магнитного поля.
Эта сила называется силой Лоренца. (Лоренц был голландским физиком,
релятивистские преобразования координат были использованы Эйнштейном в его теории
специальная теория относительности.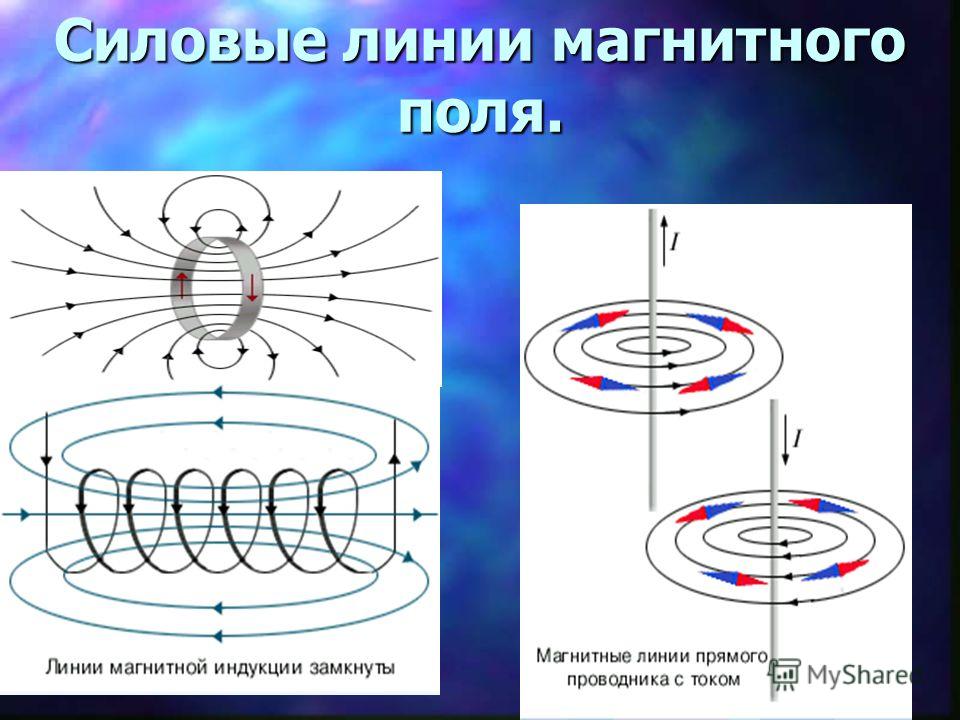 Правила специальной теории относительности демонстрируют, что
Правила специальной теории относительности демонстрируют, что
магнитная сила на самом деле просто электростатическая сила при релятивистском
трансформация.Этот интересный факт нас здесь не касается.)
Величина силы определяется как
.
F = Bqv sinθ (5.1.2).
Величина θ — это угол между магнитным полем и частицей.
направление движения. Итак, если заряд, движущийся в области магнитного
поле не испытывает силы, мы бы сказали, что по определению оно движется
параллельно силовой линии. Максимальная сила проявляется при полете.
перпендикулярно полю.
Направление этой силы легче всего увидеть на чертеже.
Рисунок 5.1.1. Сила Лоренца на положительно заряженном ионе.
Один из способов запомнить относительное направление силы — представить
направление, в котором двигался бы правосторонний винт, если бы его повернули на угол
θ от v до B .
5.1.2 Масс-спектрометр
Классическое использование силы Лоренца в химической лаборатории — это
масс-спектрометр, рисунок 5. 1.2.
1.2.
Здесь неизвестная молекула в паровой фазе ионизируется (и диссоциирует) посредством
бомбардируют электронами высокой энергии. Некоторые ионные фрагменты всплывают
через небольшое отверстие в область однородного электрического поля между двумя
параллельные плоские проводники с большой разностью потенциалов между ними.
Здесь они ускоряются, образуя пучок ионов, который выходит через
второе отверстие, после которого они проходят через область однородного магнитного
поле под прямым углом к их линии полета, прежде чем они будут обнаружены.
Сначала займемся ускорением ионизированных фрагментов. Если
напряжение, V, приложено к проводящим пластинам, потенциальная энергия
однократно ионизированный фрагмент с зарядом е при входе в область, заполненную полем, равен эВ.
Кинетическая энергия в этой точке практически равна нулю. На выходе из
во второй апертуре больше нет значительного электрического поля и, следовательно,
конечная кинетическая энергия должна быть эВ. Отсюда скорость выходящего иона
(5. 1.3),
1.3),
где m — масса осколка.
Рисунок 5.1.1. Масс-спектрометр. Поле B представлено кружком
с крестиком в центре, чтобы показать, что поле находится на странице, т.е.
стрелка, если смотреть со спины.
Теперь частица попадает в область однородного магнитного поля. С
B и v взаимно перпендикулярны величине
сила на ион
(5.1.4).
Поле B показано входящим на страницу, поэтому сила действует в
направление показано на рисунке 5.1.2. Поскольку сила всегда направлена под прямым углом к
v и B частица должна следовать по круговой траектории.
Это означает, что сила Лоренца равна массе частицы, умноженной на
центростремительное ускорение и заменяя скорость, получаем
(5.1.5).
Следовательно, радиус пути, пройденного ионизированным фрагментом, равен
.
(5.1.6).
Таким образом, записывая количество ионизированных фрагментов как функцию расстояния r в
На плоскости детектора мы можем измерить массу напрямую.
5.1.3 Магнитное поле и силовые линии
Чтобы определить магнитную силу, действующую на ионизированный атом или молекулу, магнитный
поле должно быть известно. Определение магнитного поля — нетривиальное упражнение
которые мы опустим (кроме смелых, см. [[раздел]] 5.1.4). Вместо этого мы
увидит, какие силовые линии магнитного поля для заряда, движущегося в линии и в
круг будет выглядеть.
Наиболее яркая характеристика силовых линий магнитного поля для прямой
Линия тока состоит в том, что силовые линии сплошные, рисунок 5.1.2. То есть,
в отличие от силовых линий электростатического поля, они не происходят из одного места и
конец в другом. Эта непрерывность линий поля всегда верна для
магнитное поле. Чтобы соответствовать нашему определению поля в
силу Лоренца определяем направление силовых линий правой рукой
винт правило.
Рисунок 5.1.2. Магнитное поле вокруг прямого носителя тока.
Вы можете запомнить правило правой руки, указав большим пальцем правой руки
по направлению тока и сжав остальные пальцы в кулак. Направление, в котором указывают ваши пальцы, указывает направление поля. В
Направление, в котором указывают ваши пальцы, указывает направление поля. В
Единственное, что вам нужно помнить, это то, что ток определяется как движущийся
в направлении движения положительного заряда!
Образец поля для токовой петли можно набросать, вспомнив, что
линии непрерывны и проходят вокруг проводника, рисунок 5.1.3. В
картина поля имеет очевидное сходство с электростатическим диполем и является
называется по аналогии магнитным диполем. Ясно, что электрон вращается вокруг
ядро будет представлять собой токовую петлю, и поэтому мы ожидаем, что оно будет
создают магнитное дипольное поле.На самом деле не только атом обладает
магнитное дипольное поле, а также электроны и протоны. Магнитный диполь
из них не могут быть описаны классически, они являются внутренним квантовым
механическое свойство. Однако способы взаимодействия этих магнитных диполей
друг с другом и с внешними полями важны для интерпретации
спектроскопическое поведение атомов и молекул.
Рисунок 5. 1.3. Магнитный диполь. Текущий цикл выходит из
1.3. Магнитный диполь. Текущий цикл выходит из
страницу и был разрезан пополам.
5.1.4 Определение магнитного поля
Теперь перейдем к определению магнитного поля с помощью прибора Био-Савара.
закон. Это магнитный эквивалент принципа суперпозиции, но его
внешний вид намного сложнее!
Закон Био-Савара выражает магнитное поле как сумму крошечных участков
токоведущая цепь.
Рисунок 5.1.4. Конструкция Био-Савара.
Вклад в магнитное поле в точке, определяемой вектором положения
r от элемента цепи d l ‘(который указывает на
направление тока) задается
(5.1,7),
где I — ток, r — r ‘- вектор
указывая от элемента схемы к месту, где поле
рассчитывается, а μ0 — универсальная константа, проницаемость свободного пространства,
что составляет 4πx10 -7 кг. м.C -2 точно. Текущий
определяется как поток заряда в единицу времени в цепи и имеет единицы измерения
Ампер (1А = 1 кулон в секунду).
Чтобы увидеть, как можно использовать это уравнение, мы рассмотрим расчет
магнитное дипольное поле вдоль оси токовой петли.
Рисунок 5.1.5. Конструкция для расчета поля аксиального диполя.
Помещаем начало координат в центр петли и пусть r —
r ‘= R для простоты, рисунок 5.1.5. Поле
вклад от d l ‘перпендикулярен к R и
обращен радиально наружу от оси для показанной циркуляции тока. Этот
означает, что если просуммировать все элементы d l ‘, то составляющая поля
перпендикулярно оси должно быть по симметрии равным нулю.Поле будет только добавлять
вверх по оси. Осевой вклад, dBaxis, от нашего элемента составляет
(5.1.8),
где мы пока опускаем векторные обозначения. Суммируя все элементы, видим
что все величины не зависят от dl ‘, поэтому получаем
(5.1.9).
Полная длина токовой петли, конечно, составляет 2πa и выражает R и
sinα через a и r мы получаем магнитное поле вдоль диполя
ось.
(5.1.10),
где единичный вектор показан на рисунке и может быть определен правым
правило ручного винта.
Когда r 2 >> a 2 , мы можем аппроксимировать знаменатель, как
мы сделали ранее, чтобы получить
(5.1.11),
где м — магнитный дипольный момент, по аналогии с
электростатический случай, и равен Iπa 2 n , т.е.
величина дипольного момента определяется площадью, ограниченной петлей.
раз больше текущего.
Аналогичными методами можно показать, что величина осевого
симметричное тангенциальное поле вокруг прямого проводника равно
(5.1.12),
где r — перпендикулярное расстояние, измеренное от проводника.
5.1.5 Крутящий момент на магнитном диполе — прецессионное движение
Мы рассчитали крутящий момент на электростатическом диполе из-за
электрического поля, поэтому давайте теперь вычислим крутящий момент на магнитном диполе из-за
внешнее магнитное поле.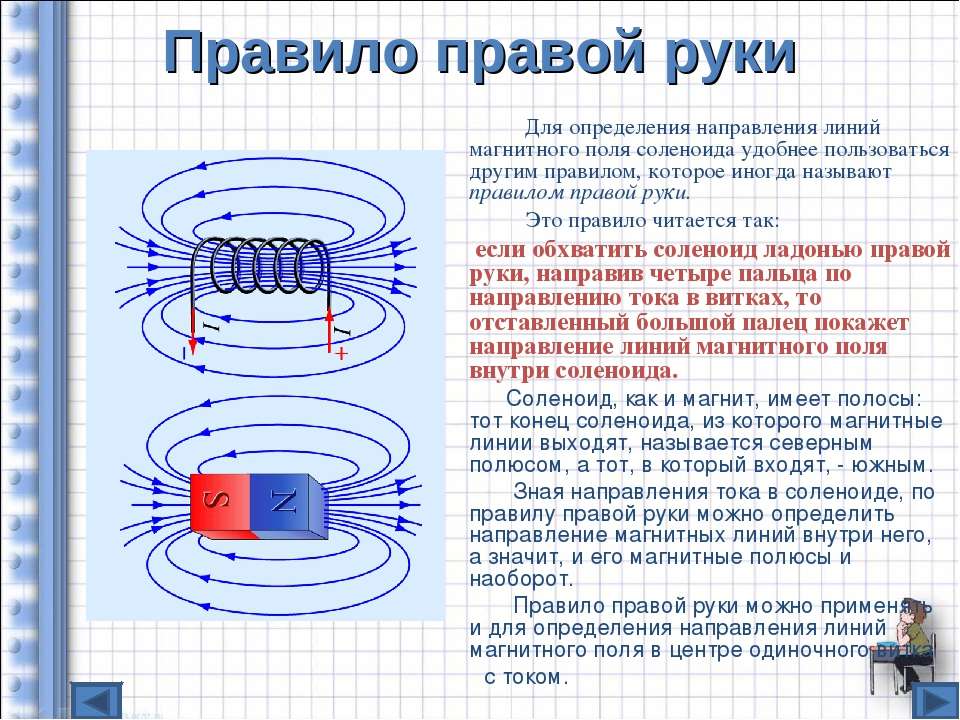
Чтобы упростить задачу (но не теряя общности), будем моделировать
диполь как ток, циркулирующий по квадратному пути, а не по круговой
один, рисунок 5.1.6.
Рисунок 5.1.6. Крутящий момент на магнитном диполе. Индексы силы
вектор относятся к количеству каждого ребра.
Диполь помещается в однородное поле так, чтобы края 2 и 4 были перпендикулярны
к силовым линиям, а 1 и 3 ориентированы под углом φ (на рис.
фигура). Положительный заряд q, циркулирующий по квадрату со скоростью v, будет
испытывают силу Лоренца величиной Bqv на ребрах 2 и 4 и Bqvsinφ на
1 и 3. Направление силы на кромках 1 и 3 одинаково и противоположно и
не производит крутящего момента.Направление сил на кромках 2 и 4 также равно
и наоборот, но здесь крутящий момент
(5.1.13),
где l — длина каждой кромки, а Τ — длина
общий крутящий момент на диполе. Теперь ток I, циркулирующий вокруг диполя
(единиц заряда за единицу времени) равна qv / l . Следовательно, мы можем перебросить
Следовательно, мы можем перебросить
выражение для полного крутящего момента
(5.1.14).
Теперь I l 2 — текущее значение площади, ограниченной
циркулирующий ток и по аналогии с электростатическим дипольным моментом это
магнитный дипольный момент м .Вектор дипольного момента равен
перпендикулярно плоскости, определяемой циркулирующим током, и его направлением
дается правилом правого винта. Векторная версия (5.1.14) имеет вид
следовательно
(5.1.15).
Теперь мы переходим к рассмотрению того, что происходит с молекулой, имеющей как угловые
импульс, т.е. молекула вращается, и магнитный момент, т.е.
циркулирующие электроны. L и м указывать не обязательно
в том же направлении, поэтому мы рассмотрим два случая; L и
м взаимно перпендикулярно друг другу и B ,
рисунок 5.1,7, и L и м параллельно, но
перпендикулярно к B , рисунок 5. 1.8.
1.8.
Рисунок 5.1.7. В этом примере приложенный крутящий момент
( м x B ) находится в том же
направление как L и, следовательно, изменение углового
импульс во времени dt равен ( m x
B ) dt.
На рисунке 5.1.7 мы видим, что крутящий момент, возникающий в результате взаимодействия
между диполем и магнитным полем увеличивает величину углового
импульс, но не меняет своего направления. (Если бы магнитное поле было
точки в противоположном направлении, это, конечно, уменьшило бы угловой
импульс.)
Рисунок 5.1.8. В этом случае крутящий момент перпендикулярен
L , и молекула прецессирует.
Когда L , м параллельны, но перпендикулярны
B происходит нечто довольно неожиданное. Теперь крутящий момент правильный
углов до L и с T = d L / dt
ясно, что изменение в L после короткого интервала dt равно
T dt. Это вектор, указывающий перпендикулярно к L
Это вектор, указывающий перпендикулярно к L
в этом случае и поэтому не меняет величину L , но
действительно меняет свое направление.Другими словами, поскольку L и
м зафиксированы относительно молекулы, молекула поворачивается
по кругу (гораздо медленнее, чем по L )
перпендикулярно к B . Это движение называется прецессией.
Прецессия вращающихся молекул, обладающих магнитным моментом, когда они
помещать в магнитное поле — обычное явление. Скорость прецессии
зависит от окружающей химической среды и может быть исследован
электромагнитно.Вы будете использовать этот эффект каждый раз, когда исследуете соединение.
с помощью ядерного магнитного резонанса.
5.2 Происхождение электромагнитных волн
Сейчас мы находимся в положении, которое позволит нам, по крайней мере качественно,
описать происхождение электромагнитного излучения и его взаимодействие с
атомы и молекулы. Описание, данное здесь, во многом следует описанию, данному
Описание, данное здесь, во многом следует описанию, данному
Блатт.
Мы уже знаем, как выглядит дипольное поле. Если бы мы измерили
поля в точке P, на большом расстоянии от диполя, мы бы нашли
поле, указывающее в отрицательном направлении оси z.
Рисунок 5.2.1. Электрическое поле при t = 0.
Пусть это первое измерение будет выполнено в момент времени t = 0. Если начисления выполняются простыми
гармоническое движение и инвертируются в момент времени t = T / 2, и мы измеряем поле
в точке P снова поле имеет ту же величину, но теперь указывает на положительное значение y
направление. Следовательно, можно предположить, что E будет отличаться
синусоидально на P.
Вопрос в том, происходит ли это синусоидальное изменение в E на
в тот же момент, что и синусоидальное изменение атомных позиций? Максвелл нашел
что на самом деле вариация в E требует времени, чтобы
Космос.Скорость, с которой он это делает, определяется как
.
(5.2.1),
которая является скоростью света, обычно обозначаемой c. Итак, изменения в области
распространяются со скоростью света! Мы будем использовать этот факт для наброска электрического
и вариации магнитного поля для нашего дипольного осциллятора.
Представим, что мы остановили колебание через половину цикла, т.е. в момент t
= T / 2, и измерить картину электрического поля при t = T. На расстоянии r <
cT / 2 и расстояние r> cT силовые линии строго диполярны, но с
направления поля инвертированы.В части пространства между cT / 2 и cT
силовые линии можно определить, вспомнив, что в области, которая свободна
зарядов линии должны быть либо непрерывными, либо продолжаться до бесконечности. Единственный
способ сделать это показано ниже.
Рисунок 5.2.2. Электрическое поле после полупериода диполя
колебание.
Следовательно, если мы позволим диполю совершать простое гармоническое движение, электрическое
изменение поля в P будет соответствовать
E = E 0sin (kx — ωt) (5.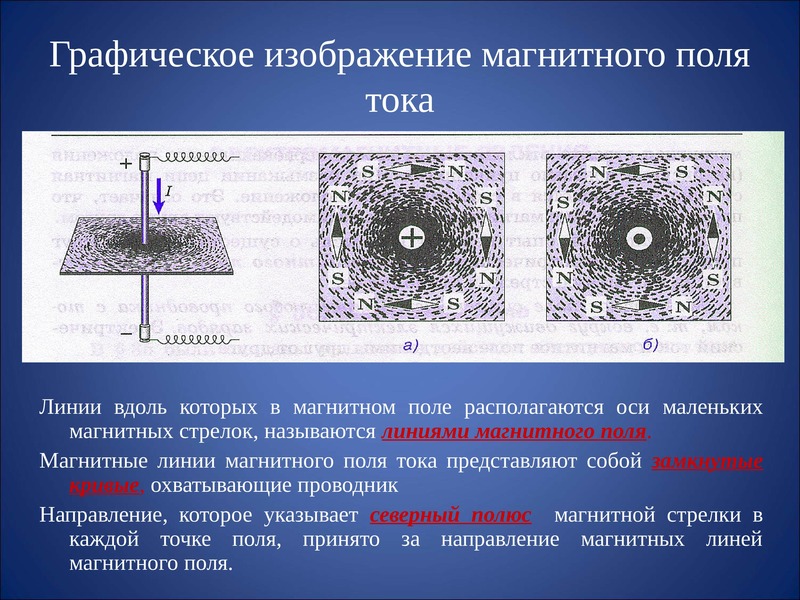 2.2),
2.2),
где E 0 — амплитуда при t = 0 в позиции P, и в этом случае
точек в направлении z, ω — частота колебаний диполя.
k называется волновым числом и определяется как
(5.2.3),
где λ — длина волны волнистости электрического поля.
Движущиеся дипольные заряды, конечно, также являются источником магнитного поля.
Здесь направление движения положительного заряда и отрицательного заряда находится в
противоположного направления, но поскольку знак зарядов противоположен текущему
произведенный будет указывать в том же направлении.
Рисунок 5.2.3. Магнитное поле колеблющегося диполя эквивалентно
в поле от прямого проводника.
По правилу правой руки ясно, что силовые линии магнитного поля в точке
P всегда перпендикулярны электрическому полю, т.е.
плоскость x-y и точка в направлении y. Мы не можем сделать нашу упрощенную картину
электромагнитной волны слишком далеко в этой точке. Это предсказывает, что
магнитное и электрическое поля были в противофазе, тогда как на самом деле они
фаза. Эта ошибка связана с тем, что мы только научились определять
Эта ошибка связана с тем, что мы только научились определять
магнитное поле, которое является статическим, когда оно изменяется, добавляет сложности
происходит. Полная теория предсказывает, что результирующая электромагнитная волна на
P движется в направлении x и совершает поперечные колебания в направлении z.
электрического поля и в направлении y магнитного поля и что
они находятся в фазе.
(5.2.4).
Рисунок 5.2.4. Электромагнитная волна. E
колеблется в направлении z B в направлении y.
(Код см. В разделе «Физическая химия: молекулярные взаимодействия: электромагнитные.
Волна.)
Из того, что мы уже видели о крутящем моменте, создаваемом электрическим и
магнитных полей на диполях, можно было бы ожидать, что электромагнитная волна будет
заставляют молекулы вращаться и прецессировать. Дополнительно электростатический диполь
выровненные вдоль направления z в нашем примере будут вынуждены колебаться. Эти эффекты замечательны, потому что закон сохранения энергии говорит нам, что
Эти эффекты замечательны, потому что закон сохранения энергии говорит нам, что
мы можем передавать колебательную энергию через пустое пространство в виде
электромагнитные волны, и тем самым заставляют другие диполи колебаться или
повернуть.
Вернуться к оглавлению
8.3 Движение заряженной частицы в магнитном поле — Введение в электричество, магнетизм и электрические схемы
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Объясните, как заряженная частица во внешнем магнитном поле совершает круговое движение
- Опишите, как определить радиус кругового движения заряженной частицы в магнитном поле
Заряженная частица испытывает силу при движении в магнитном поле.Что произойдет, если это поле будет однородным при движении заряженной частицы? По какому пути следует частица? В этом разделе мы обсуждаем круговое движение заряженной частицы, а также другое движение, возникающее в результате попадания заряженной частицы в магнитное поле.
Самый простой случай возникает, когда заряженная частица движется перпендикулярно однородному полю (рис. 8.3.1). Если поле находится в вакууме, магнитное поле является доминирующим фактором, определяющим движение. Поскольку магнитная сила перпендикулярна направлению движения, заряженная частица следует по кривой траектории в магнитном поле.Частица продолжает двигаться по этому изогнутому пути, пока не образует полный круг. Другой способ взглянуть на это состоит в том, что магнитная сила всегда перпендикулярна скорости, так что она не действует на заряженную частицу. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Это влияет на направление движения, но не на скорость.
(рисунок 8.3.1)
Рис. 8.3.1. Отрицательно заряженная частица движется в плоскости бумаги в области, где магнитное поле перпендикулярно бумаге (обозначено маленькой буквой s — как хвосты стрелок).Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине.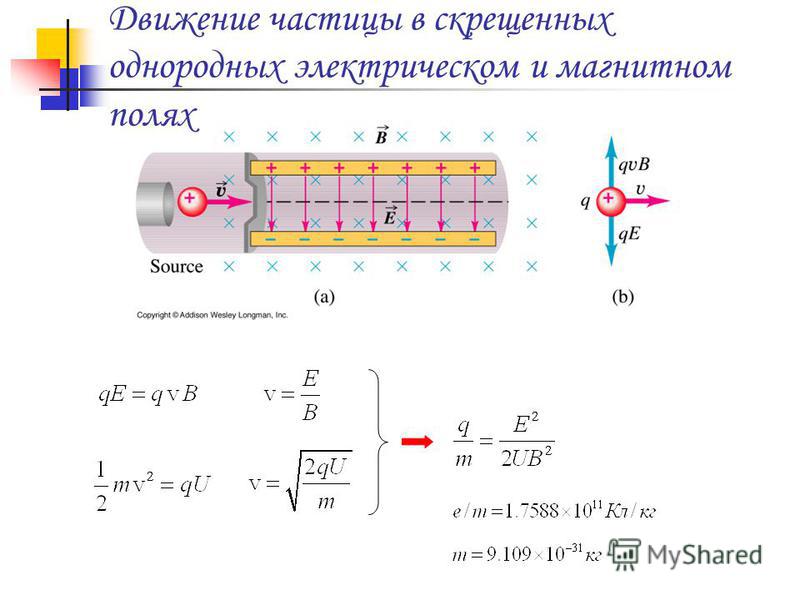 Результат — равномерное круговое движение. (Обратите внимание, что поскольку заряд отрицательный, сила противоположна предсказанию правила правой руки.)
Результат — равномерное круговое движение. (Обратите внимание, что поскольку заряд отрицательный, сила противоположна предсказанию правила правой руки.)
В этой ситуации магнитная сила обеспечивает центростремительную силу. Учитывая, что скорость перпендикулярна магнитному полю, величина магнитной силы уменьшается до. Поскольку магнитная сила обеспечивает центростремительную силу, мы имеем
(8.3.1)
Решение для урожайности
(8.3.2)
Здесь — радиус кривизны пути заряженной частицы с массой и зарядом, движущейся со скоростью, перпендикулярной напряженности магнитного поля. Время прохождения заряженной частицы по круговой траектории определяется как период, который равен пройденному расстоянию (окружности), деленному на скорость. На основании этого и 8.3.1, мы можем получить период движения как
.
(8.3.3)
Если скорость не перпендикулярна магнитному полю, то мы можем сравнить каждую составляющую скорости отдельно с магнитным полем.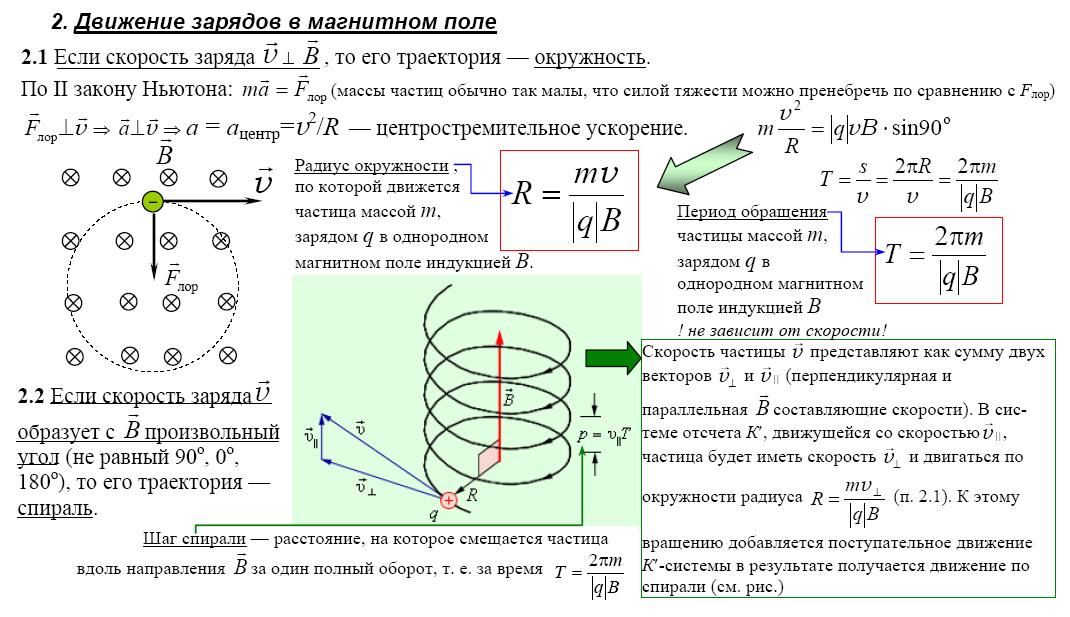 Компонент скорости, перпендикулярный магнитному полю, создает магнитную силу, перпендикулярную как этой скорости, так и полю:
Компонент скорости, перпендикулярный магнитному полю, создает магнитную силу, перпендикулярную как этой скорости, так и полю:
(8.3.4)
где — угол между и. Компонент, параллельный магнитному полю, создает постоянное движение в том же направлении, что и магнитное поле, также показанное на 8.3.4. Параллельное движение определяет шаг спирали, то есть расстояние между соседними витками. Это расстояние равно параллельной составляющей скорости, умноженной на период:
(8.3.5)
В результате получается спиральное движение , как показано на следующем рисунке.
(рисунок 8.3.2)
Рис. 8.3.2. Заряженная частица движется со скоростью, не совпадающей с направлением магнитного поля. Компонента скорости, перпендикулярная магнитному полю, создает круговое движение, тогда как составляющая скорости, параллельная полю, перемещает частицу по прямой.Шаг — это горизонтальное расстояние между двумя последовательными кругами.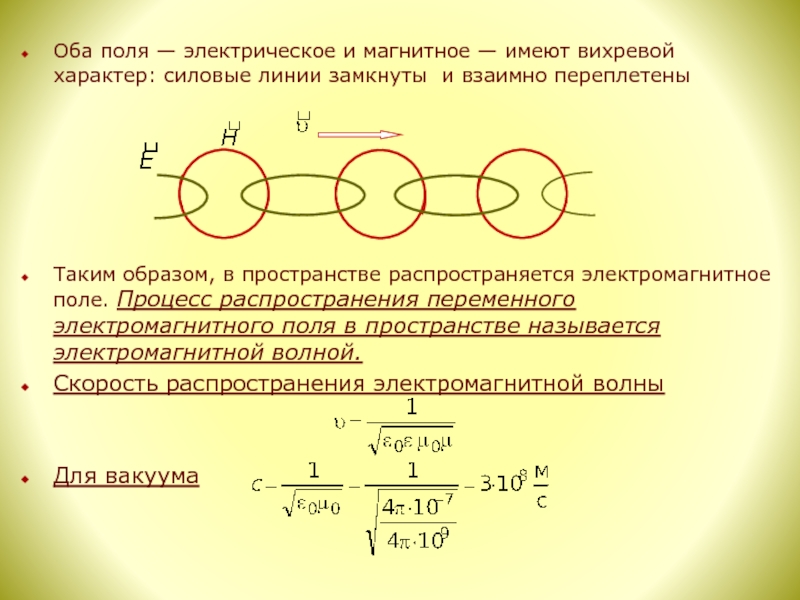 Результирующее движение — спиральное.
Результирующее движение — спиральное.
Пока заряженная частица движется по спирали, она может попасть в область, где магнитное поле неоднородно. В частности, предположим, что частица перемещается из области сильного магнитного поля в область более слабого поля, а затем обратно в область более сильного поля. Частица может отразиться до того, как войдет в область более сильного магнитного поля. Это похоже на волну на струне, которая проходит от очень легкой тонкой струны к твердой стене и отражается назад.Если отражение происходит с обоих концов, частица оказывается захваченной в так называемую магнитную бутылку.
Захваченные частицы в магнитных полях обнаружены в радиационных поясах Ван Аллена вокруг Земли, которые являются частью магнитного поля Земли. Эти пояса были обнаружены Джеймсом Ван Алленом при попытке измерить поток космических лучей на Земле (частицы высокой энергии, приходящие извне Солнечной системы), чтобы увидеть, похоже ли это на поток, измеренный на Земле. Ван Аллен обнаружил, что из-за вклада частиц, захваченных магнитным полем Земли, поток на Земле был намного выше, чем в космическом пространстве. Aurorae , как и знаменитое полярное сияние (северное сияние) в Северном полушарии (рис. 8.3.3), представляют собой прекрасные проявления света, излучаемого при рекомбинации ионов с электронами, входящими в атмосферу, по мере их движения вдоль силовых линий магнитного поля. (Ионы — это в основном атомы кислорода и азота, которые первоначально ионизируются при столкновении с энергичными частицами в атмосфере Земли.) Полярные сияния также наблюдались на других планетах, таких как Юпитер и Сатурн.
Ван Аллен обнаружил, что из-за вклада частиц, захваченных магнитным полем Земли, поток на Земле был намного выше, чем в космическом пространстве. Aurorae , как и знаменитое полярное сияние (северное сияние) в Северном полушарии (рис. 8.3.3), представляют собой прекрасные проявления света, излучаемого при рекомбинации ионов с электронами, входящими в атмосферу, по мере их движения вдоль силовых линий магнитного поля. (Ионы — это в основном атомы кислорода и азота, которые первоначально ионизируются при столкновении с энергичными частицами в атмосфере Земли.) Полярные сияния также наблюдались на других планетах, таких как Юпитер и Сатурн.
(рисунок 8.3.3)
Рис. 8.3.3. (a) Радиационные пояса Ван Аллена вокруг Земли улавливают ионы, образованные космическими лучами, падающими на атмосферу Земли. (b) Великолепное зрелище северного сияния, или северного сияния, сияет в северном небе над Беар-Лейк недалеко от базы ВВС Эйлсон, Аляска. Этот свет, сформированный магнитным полем Земли, создается светящимися молекулами и ионами кислорода и азота.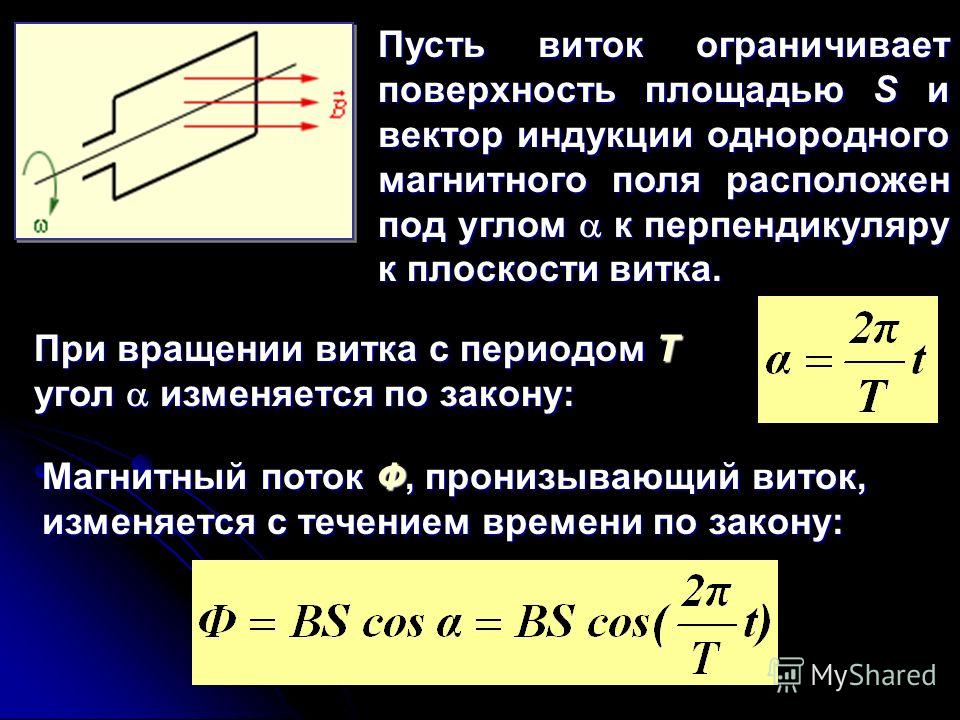 (кредит b: модификация работы старшего летчика ВВС США Джошуа Стрэнга)
(кредит b: модификация работы старшего летчика ВВС США Джошуа Стрэнга)
ПРИМЕР 8.3.1
Дефлектор луча
Группа исследователей занимается изучением короткоживущих радиоактивных изотопов. Им необходимо разработать способ транспортировки альфа-частиц (ядер гелия) от места их создания к месту, где они столкнутся с другим материалом с образованием изотопа. Пучок альфа-частиц изгибается через область градусов с однородным магнитным полем (рис. 8.3.4). а) В каком направлении следует приложить магнитное поле? (б) Сколько времени требуется альфа-частицам, чтобы пересечь область однородного магнитного поля?
(рисунок 8.3.4)
Рисунок 8.3.4. Вид сверху на установку дефлектора балки.
Стратегия
а. Направление магнитного поля показано RHR-1. Ваши пальцы указывают в направлении, а большой палец должен указывать в направлении силы, влево. Следовательно, поскольку альфа-частицы заряжены положительно, магнитное поле должно указывать вниз.
г. Период движения альфа-частицы по окружности
.
(8.3.6)
Поскольку частица движется только по четверти круга, мы можем умножить этот период, чтобы найти время, необходимое для обхода этого пути.
Решение
а. Начнем с того, что сфокусируемся на альфа-частице, входящей в поле в нижней части изображения. Сначала покажите пальцем вверх по странице. Чтобы ваша ладонь открывалась влево, куда указывает центростремительная сила (и, следовательно, магнитная сила), ваши пальцы должны менять ориентацию, пока они не будут указывать на страницу. Это направление приложенного магнитного поля.
г. Период движения заряженной частицы по кругу рассчитывается с использованием заданных в задаче массы, заряда и магнитного поля.Получается
Однако для данной задачи альфа-частица обходит четверть круга, поэтому время, необходимое для этого, составит
Значение
Это время может быть достаточно быстрым, чтобы добраться до материала, который мы хотели бы бомбардировать, в зависимости от того, насколько короткоживущий радиоактивный изотоп и продолжает испускать альфа-частицы.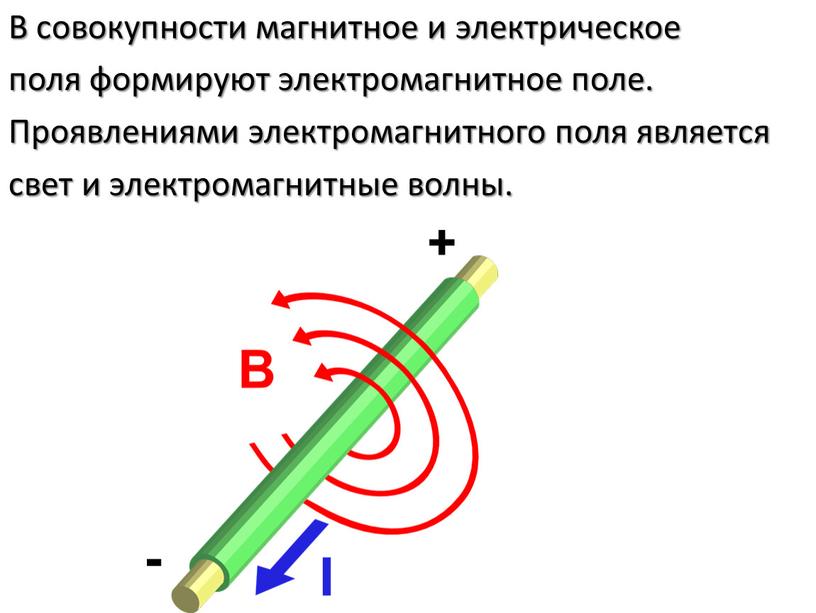 Если бы мы могли усилить магнитное поле, приложенное к области, это сократило бы время еще больше.Путь, по которому частицы должны пройти, можно было бы сократить, но это может оказаться неэкономичным с учетом экспериментальной установки.
Если бы мы могли усилить магнитное поле, приложенное к области, это сократило бы время еще больше.Путь, по которому частицы должны пройти, можно было бы сократить, но это может оказаться неэкономичным с учетом экспериментальной установки.
ПРОВЕРЬТЕ ПОНИМАНИЕ 8.2
Однородное магнитное поле магнитуды направлено горизонтально с запада на восток. а) Какова магнитная сила, действующая на протон в момент, когда он движется вертикально вниз в поле со скоростью? (б) Сравните эту силу с весом протона.
ПРИМЕР 8.3.2
Движение по спирали в магнитном поле
Протон входит в однородное магнитное поле со скоростью.Под каким углом должно быть магнитное поле от скорости, чтобы шаг результирующего спирального движения был равен радиусу спирали?
Стратегия
Шаг движения относится к параллельной скорости, умноженной на период кругового движения, тогда как радиус относится к перпендикулярной составляющей скорости. После установки равных друг другу радиуса и шага найдите угол между магнитным полем и скоростью или.
После установки равных друг другу радиуса и шага найдите угол между магнитным полем и скоростью или.
Решение
Шаг задается уравнением 8.3.5 период определяется уравнением 8.3.3, а радиус кругового движения задается уравнением 8.3.2. Обратите внимание, что скорость в уравнении радиуса связана только с перпендикулярной скоростью, в которой происходит круговое движение. Поэтому мы подставляем синусоидальную составляющую общей скорости в уравнение радиуса, чтобы приравнять шаг и радиус:
Значение
Если бы этот угол был, имел бы место только параллельная скорость, а спираль не образовывалась бы, потому что не было бы кругового движения в перпендикулярной плоскости.Если бы этот угол был, то было бы только круговое движение, и не было бы движения кругов, перпендикулярных движению. Это то, что создает спиральное движение.
Кандела Цитаты
Лицензионный контент
CC, особая атрибуция
- Загрузите бесплатно по адресу http://cnx.
 org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Электромагнетизм
Электромагнетизм описывает взаимосвязь между магнетизмом и электричеством.Понятие электрического поля было впервые введено Майклом Фарадеем; электрическое поле описывает не только область, окружающую электрически заряженное тело, но, кроме того, силу, испытываемую любыми дополнительными зарядами, помещенными в эту область. Когда электрические заряды находятся в движении, они вызывают магнитное поле.
поля. Такие явления наблюдаются, когда железная стружка выравнивается в присутствии магнитного поля, вызванного прохождением тока через соседний провод. Изменяющееся магнитное поле вызовет электрическое поле; аналогично изменяющееся электрическое поле будет индуцировать магнитное поле.Это концепция электромагнитной индукции, это принцип, используемый для привода генераторов, двигателей, трансформаторов,
усилители и многие другие электрические устройства.
Теория электрического поля
Закон Кулона
Электрическая сила между двумя заряженными телами — это неконтактная сила. Эти силы действуют вдоль линии, соединяющей геометрические центры двух зарядов. Сила пропорциональна произведению зарядов и обратно пропорциональна квадрату их разделения.{-1} $ (электрическая постоянная)
$ F $ — Сила
$ \ bf r $ — разделение между центрами заряда
$ Q $ — Заряд
$ \ bf {r_ {12}} $ — это единичный вектор, который указывает от центра заряда один к центру заряда два. Сила отталкивающая, если два заряда одного знака, и притягивающая, если заряды противоположного знака. Следует отметить, что обычная материя приобретает лишь небольшое количество заряда (измеряется в кулонах). Пример ниже лучше всего иллюстрирует это.
Пример:
Найдите силу между двумя точечными зарядами, каждый из которых заряжен +1 кулон и находится на расстоянии 1 метра.9 $ N
Очевидно, это чрезвычайно большая сила; обычно заряженное тело несет заряд порядка нано / микрокулонов.
Электрический потенциал
Разность потенциалов между двумя точками — это работа, выполняемая (или им) единицей положительного заряда при перемещении из одной точки в другую. Когда заряд проходит через импеданс (когда цепь приводится в движение постоянным током, нет разницы между импедансом и сопротивлением), он должен работать, но при прохождении через батарею с ним выполняется работа.b \ bf {E} d \ bf {r} $
Чтобы определить электрический потенциал в какой-то точке, мы должны найти разность потенциалов между этой точкой и другой точкой, в которой потенциал равен нулю (это условие выполняется в бесконечное расстояние от точечного заряда, поле которого мы описываем). Следовательно, электрический потенциал — это работа, совершаемая против электрического поля при перемещении единичного положительного заряда от бесконечности к некоторому
расстояние r от центра заряда, в поле которого он входит. Математически это описывается следующим образом:
$ \ bf V = \ int_ {r} ^ {\ infty} \ bf {E} \ bf {dl} $
Электрический потенциал обычно измеряется в джоулях на кулон или в вольтах. 2} $.Фактически, это правда, что любой точечный источник, который распространяет свое влияние одинаково во всех направлениях, будет подчиняться такому закону, это можно вывести только из геометрических соображений, примеры включают гравитационные поля, электромагнитное излучение и звук.
2} $.Фактически, это правда, что любой точечный источник, который распространяет свое влияние одинаково во всех направлениях, будет подчиняться такому закону, это можно вывести только из геометрических соображений, примеры включают гравитационные поля, электромагнитное излучение и звук.
Общие условные обозначения, принятые для рисования электрических полей, описаны ниже.
Плотность силовых линий:
Плотность силовых линий описывает величину поля. Более плотная упаковка силовых линий указывает на более сильное поле.Силовые линии обычно расходятся по мере увеличения расстояния от заряженного тела — это указывает на уменьшение напряженности поля.
Ориентация силовых линий для проводников:
Силовые линии всегда проводят перпендикулярно поверхности тела, поле которой они описывают; никогда не бывает компонента электрического поля, параллельного поверхности тела.
Пересечение силовых линий:
Силовые линии электрического поля никогда не должны пересекаться. Линии электрического поля указывают направление электромагнитной силы в данной области пространства.Если бы силовые линии могли пересекаться в некоторой точке пространства, тогда направление силы было бы неопределенным в этой точке пересечения (мы бы фактически определяли два отдельных поля)
Линии электрического поля указывают направление электромагнитной силы в данной области пространства.Если бы силовые линии могли пересекаться в некоторой точке пространства, тогда направление силы было бы неопределенным в этой точке пересечения (мы бы фактически определяли два отдельных поля)
Electric Flux
Электрический поток равен общее количество электрического поля, проходящего через область виртуальной поверхности, перпендикулярную полю.
Flux = $ \ phi = \ int \ bf {E} \ cdot \ bf {dA} $
Здесь $ \ bf E $ — электрическое поле, а $ dA $ — дифференциальный элемент единичной площади на замкнутой поверхность с обращенной наружу нормалью, определяющей ее направление.
Суперпозиция
Принцип суперпозиции гласит, что отклик любой линейной системы на несколько входов равен сумме ответов, произведенных, если каждый из входов был применен отдельно. Применяя эту идею к электростатике, мы видим, что при наличии нескольких зарядов результирующее электрическое поле может быть найдено путем векторного суммирования электрического поля, создаваемого каждым отдельным зарядом. Это
Это
Следует отметить, что принцип суперпозиции — очень важная концепция, встречающаяся во многих инженерных приложениях.
Закон Гаусса
Закон Гаусса гласит, что общее количество электрического потока, исходящего от поверхности и перпендикулярного ей, равно общему приложенному электрическому заряду. Как следствие, электрический заряд, заключенный внутри поверхности, равен нулю, когда поток, входящий в поверхность, равен выходящему потоку. В интегральной форме закон Гаусса выглядит следующим образом:
$ \ int \ bf {D} \ cdot \ bf {da} = Q $,
, где
$ \ bf {D} $ — напряженность диэлектрического поля, Напряженность диэлектрического поля принимает одинаковое значение при переходе от одного диэлектрика к другому.2 $
Для линии заряда мы должны выбрать цилиндр в качестве нашей гауссовой поверхности. $ A = 2 \ pi r l $
Для плоскости заряда (например, конденсатора) мы должны просто выбрать плоскость в качестве нашей гауссовой поверхности. Следует позаботиться о том, чтобы учитывались обе стороны плоскости.
Емкость
Мы определяем емкость как заряд, накопленный на единицу вольт:
$ C = \ frac {dQ} {dV} $
Конденсатор — это просто пара проводников, разделенных диэлектрическим материалом, устройство, которое обеспечивает кратковременное хранение энергии в виде смещенного заряда.Когда к проводникам прикладывается разность потенциалов, в диэлектрике создается электрическое поле, и именно это электрическое поле обеспечивает средство хранения энергии. При достаточно высоком напряжении молекулярная структура
изолятора разрушается, электроны вырываются из атомов, и материал начинает проводить. Максимальное напряжение, которое мы можем приложить к материалу, прежде чем он схлопнется и начнет проводить, известно как напряжение пробоя. Мы всегда должны использовать конденсатор ниже этого напряжения пробоя.Выбор диэлектрического материала будет определять применение конденсатора, типичные области применения
перечислены ниже.
Air: Используется в устройствах настройки радио.
Стекло. Известно, что НАСА, используемое в высоковольтных устройствах, использует стеклянные диэлектрические конденсаторы для инициализации схем космических челноков и помощи в развертывании космических зондов.
Керамика: Используется в высокочастотных устройствах, таких как антенны и рентгеновские аппараты.
Мы знаем, что напряжение — это работа, совершаемая на единицу заряда, теперь мы можем использовать эту идею, чтобы найти энергию, запасенную в электрическом поле.2} {2}
$
Простейшей формой конденсатора является конденсатор с параллельными пластинами, показанный ниже:
Каждая пластина заряжается равным и противоположным зарядом, если пластины бесконечного размера, однородное электрическое поле будет существуют между ними. Равномерное распределение заряда, вызванное взаимным отталкиванием одноименных зарядов (на пластине), приводит к генерации однородного поля. На практике площадь пластины, намного превышающая расстояние между пластинами, дает минимальное расхождение поля на концах пластины.
(эффекты окантовки), поэтому мы можем рассматривать поле как однородное.
Вопрос:
Используя концепции закона Гаусса, суперпозиции, электрического потенциала и емкости, докажите, что поле E между пластинами конденсатора с параллельными пластинами однородно, и найдите емкость. Расстояние между пластинами равно d, а относительная диэлектрическая проницаемость диэлектрика $ \ epsilon_r $, кроме того, можно предположить, что A намного больше d.
Решение:
Шаг 1: Закон Гаусса определяет электрическое поле, создаваемое одной пластиной.
$ \ int \ bf {D} \ cdot \ bf {da} $ = $ \ epsilon_0 \ epsilon_r \ bf {E} A = Q $
$ \ bf {E} = \ frac {Q} {A \ epsilon_0 \ epsilon_r} $
Шаг 2: Принцип суперпозиции
У нас есть две пластины; каждая пластина накапливает заряд и, следовательно, создает электрическое поле.На расстоянии x от верхней пластины каждая из верхней и нижней пластины создает поле размером
$ \ bf {E} = \ frac {Q} {A \ epsilon_0 \ epsilon_r} $
Входит только половина этого поля. диэлектрик между проводниками, другая половина выступает с противоположной стороны пластины и не вносит вклад. Таким образом, полное электрическое поле находится суперпозицией.
диэлектрик между проводниками, другая половина выступает с противоположной стороны пластины и не вносит вклад. Таким образом, полное электрическое поле находится суперпозицией.
$ \ bf E = \ frac {1} {2} \ frac {Q} {A \ epsilon_0 \ epsilon_r} + \ frac {1} {2} \ frac {Q} {A \ epsilon_0 \ epsilon_r} = \ frac {Q} {A \ epsilon_0 \ epsilon_r} $
Эта функция $ \ bf E $ не зависит от положения между пластинами (x), поэтому поле однородно.d \ frac {Q} {A \ epsilon_0 \ epsilon_r} dr $ = $ \ frac {Qd} {A \ epsilon_0 \ epsilon_r} $
Шаг 4: Емкость
$ C = \ frac {dq} {dv} $
Если заряд не меняется со временем.
$ C = \ frac {Q} {V} $
$ C = \ frac {Q} {V} $ = $ \ frac {A \ epsilon_0 \ epsilon_r} {d} $
Это показывает нам, что Емкость пропорциональна площади пластин и обратно пропорциональна их расстоянию.
Зарядка и разрядка конденсатора
Это разность потенциалов между источником питания и конденсатором, которая заставляет заряд течь от одной пластины к другой. Система желает находиться в состоянии равновесия. Таким образом, заряд будет течь до тех пор, пока разность потенциалов на конденсаторе не совпадет с разностью потенциалов источника питания (пока не исчезнет разность потенциалов между источником питания и конденсатором). Электроны берутся с одной пластины и переносятся
Система желает находиться в состоянии равновесия. Таким образом, заряд будет течь до тех пор, пока разность потенциалов на конденсаторе не совпадет с разностью потенциалов источника питания (пока не исчезнет разность потенциалов между источником питания и конденсатором). Электроны берутся с одной пластины и переносятся
к другому; один становится положительным, а другой — все более отрицательным. По мере накопления заряда на конденсаторе напряжение на нем увеличивается, разность потенциалов между батареей и конденсатором уменьшается, и, следовательно, скорость зарядки уменьшается.Это может быть проанализировано с помощью закона напряжения Кирхгофа; мы знаем, что сумма ЭДС равна сумме падений напряжения.
$ V_ {supply} = V_c + V_R = V_c + IR $
$ I = \ frac {V_ {supply} — V_c} {R}
$
Мы видим, что ток (скорость потока заряда) и, следовательно, скорость зарядки / разрядки пропорциональна разности потенциалов между источником питания и конденсатором. Напряжение источника питания постоянно, но напряжение конденсатора меняется в зависимости от заряда согласно $ C = \ frac {Q} {V} $
Заряд: $ V = V_0 e ^ {\ frac {-t} {RC} } $
Разряд: $ V = V_0 (1 — e ^ {\ frac {-t} {RC}}) $
Вопрос:
Используйте закон Ома, закон Кирхгофа и определение емкости для получения уравнение зарядного конденсатора для простой схемы, состоящей из ячейки, резистора и конденсатора. {\ frac {-t} {RC}}) $
{\ frac {-t} {RC}}) $
Конденсаторы в серии:
Что касается конденсаторов, соединенных последовательно, мы знаем, что каждый из них будет хранить одинаковое количество заряда, но может иметь разное напряжение на нем.
$ V_ {total} = V_1 + V_2 + … + V_n $
$ C = \ frac {Q} {V} $
$ \ frac {Q} {C_ {total}} = \ frac { Q} {C_1} + \ frac {Q} {C_2} + … + \ frac {Q} {C_n} $
$ \ frac {1} {C_ {total}} = \ frac {1} {C_1 } + \ frac {1} {C_2} + … + \ frac {1} {C_n} $
Параллельно подключенные конденсаторы:
Для конденсаторов, подключенных параллельно, мы знаем, что каждый из них имеет одинаковое напряжение, но может иметь хранится другой заряд.{-6} = 3,67 мкФ $
Теория магнитного поля
Магнитные поля являются результатом движения электрических зарядов; это могут быть токи, протекающие по проводам, или просто электроны на своих атомных орбитах.
Напряженность магнитного поля
Плотность магнитного потока (или напряженность поля) $ \ bf {B} $ определяется силой Лоренца. Сила Лоренца описывает силу, действующую на заряд $ Q $, движущийся со скоростью $ \ bf {v} $ в наложенных электрическом и магнитном полях.
Сила Лоренца описывает силу, действующую на заряд $ Q $, движущийся со скоростью $ \ bf {v} $ в наложенных электрическом и магнитном полях.
$ \ bf {F} = q (\ bf {E} + \ bf {V} \ times \ bf {B}) $
В отсутствие электрического поля указанное выше становится
$ \ bf {F } = q \ bf V \ times \ bf {B} $,
где:
$ q $ — величина заряда
$ V $ — вектор скорости заряда
$ B $ — плотность магнитного потока
Приведенное выше уравнение описывает Учитывая векторную природу поля B, следует обратить внимание на перекрестное произведение в приведенном выше уравнении, оно указывает на то, что поле B всегда перпендикулярно как потоку заряда, так и магнитной силе.Направление плотности магнитного потока можно найти из правила большого пальца правой руки. Когда большой палец правой руки указывает в направлении тока (в
направление вектора скорости), ваши пальцы будут сгибаться в направлении $ \ bf {B} $.
Отметив, что I = $ \ frac {dq} {dt} $, мы можем получить силу, испытываемую проводом с током, помещенным в магнитное поле. Если мы подставим $ q = It $ в закон сил Лоренца, то получим:
Если мы подставим $ q = It $ в закон сил Лоренца, то получим:
$ \ bf {F} = q \ bf {V} \ times \ bf {B} = It \ bf {V} \ times \ bf {B}
$
Но скорость заряда, умноженная на величину заряда, — это просто длина провода, пройденного за единицу времени ($ L $).
$ \ bf F = L \ bf I \ times \ bf B = BIL \ sin \ theta $
Если мы знаем направление любого из силы, поля или тока, то два других могут быть выведены с помощью левой формулы Флеминга. ручное правило. Вытяните большой, указательный и средний пальцы левой руки так, чтобы все три пальца были взаимно перпендикулярны друг другу, если большой палец указывает в направлении силы, то указательный палец указывает в направлении поля B и среднего пальца. в
направление течения.Это проиллюстрировано ниже.
Магнитный поток
Концепция магнитного потока очень удобна для описания закона Фарадея (который будет обсуждаться ниже). Магнитный поток — это общая величина магнитного поля, проходящего через виртуальную площадь поверхности, перпендикулярную полю.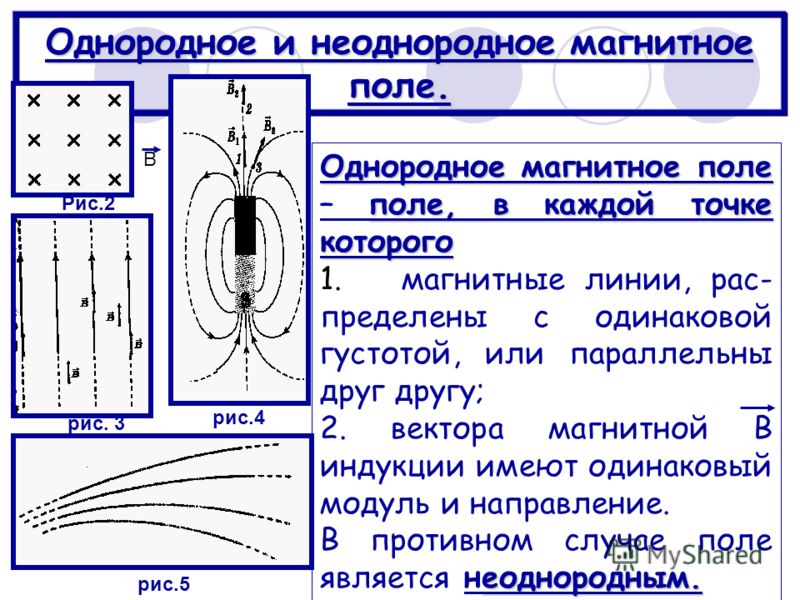
Поток $ \ phi = \ int \ bf {B} \ cdot \ bf {dA} $
Где $ B $ — плотность магнитного потока, а $ dA $ — дифференциальная область на замкнутой поверхности с обращенной наружу поверхностью. нормаль, определяющая его направление.
Потоковая связь равна произведению магнитного потока на количество витков связываемого объекта.
$ \ phi ‘= \ phi N $
Закон Ампера
Закон Ампера описывает взаимосвязь между магнитными полями и токами аналогично тому, как закон Гаусса описывает взаимосвязь между электрическими полями и зарядом. Закон Ампера гласит, что для любого замкнутого контура линейный интеграл напряженности поля ($ H = \ frac {B} {\ mu_0 \ mu_r} $) равен связанному току.
$ \ int \ bf {H} dl = N I $
Закон Ампера позволяет нам найти выражение для поля B как функции тока. Ниже приведен пример, иллюстрирующий это.
Вопрос:
Используя закон Ампера, найдите выражение для напряженности магнитного поля вокруг токоведущего провода.
Решение:
Сначала мы должны определить путь, по которому будет идти B-поле. Используя правило правой руки, мы знаем, что B-поле будет окружать ток, следовательно, дифференциальный путь, по которому будет проходить ток, равен dl = $ 2 \ pi dr $ (где r — расстояние от провода).
$ \ int \ bf {H} dl = \ int \ bf {H} 2 \ pi dr = I $ (N = 1, поскольку мы рассматриваем только один провод)
$ \ frac {B 2 \ pi r} {\ mu_0 \ mu_r} = I $
$ B = \ frac {\ mu_0 \ mu_r I} {2 \ pi r} $
Закон индукции Фарадея
Закон электромагнитной индукции Фарадея является чрезвычайно важным принципом, он имеет фундаментальное значение для производства большей части электроэнергии в современном мире. Закон Фарадея описывает, как изменение магнитного потока, пронизывающего цепь, индуцирует напряжение, стремящееся противодействовать этому изменению потока.Индуцированное напряжение пропорционально скорости изменения магнитной связи.
$ V = — N \ frac {d \ phi} {dt} $
Знак минус просто указывает на то, что направление индуцированного тока таково, что его магнитное поле противодействует изменению потока (закон Ленца). Обычно существует два метода создания напряжения: резка флюса и флюсовая связь.
Обычно существует два метода создания напряжения: резка флюса и флюсовая связь.
Резка флюса: когда линии флюса перерезаются проводниками. Например. Пропускание магнита через моток проволоки.
Flux Linking: изменение направления или величины B-поля.{-4} \ times 42 \ times 130 = 2,73 В $
Катушки индуктивности
Катушки индуктивности — это пассивные электрические компоненты. Они хранят энергию в виде движущегося заряда (или магнитного поля). Обычно индукторы имеют форму проволочной катушки (похожей на соленоид). Причина создания петли в катушке — увеличить потокосцепление и, следовательно, увеличить потенциал накопления энергии. Электрический ток, проходящий через индуктор, индуцирует вокруг него магнитное поле, время
переменный ток создаст изменяющееся во времени магнитное поле и, в соответствии с Фарадеем, напряжение.Следовательно, индуктивность — это напряжение, индуцированное на единицу заряда, ее единицы — Генри (Гн).
$ V = L \ frac {dI} {dt} = Lq $
Показан символ идеального индуктора:
Последовательные индукторы:
Для катушек, соединенных последовательно, мы знаем, что ток через каждую быть таким же, но может иметь другое напряжение на нем.
$ V_ {total} = V_1 + V_2 + … + V_n $
$ L = \ frac {V} {Q} $
$ \ frac {L_ {total}} {Q} = \ frac {L_1 } {Q} + \ frac {L_2} {Q} +… + \ frac {L_3} {Q} $
$ L_ {total} = L_1 + L_2 + … + L_n $
Параллельные индукторы:
Мы знаем, что для катушек, подключенных параллельно, мы знаем, что каждый имеет одинаковый напряжение на нем, но через него может проходить другой ток.
$ Q_ {total} = Q_1 + Q_2 + … + Q_n $
$ \ frac {V} {L_ {total}} = \ frac {V} {L_1} + \ frac {V} {L_2} + … + \ frac {V} {L_n} $
$ \ frac {1} {L_ {total}} = \ frac {1} {L_1} + \ frac {1} {L_2} + … + \ frac {1} {L_n} $
Применение электромагнитной индукции
Многие электрические устройства работают по принципу электромагнитной индукции.К ним относятся двигатели, генераторы, трансформаторы, микрофоны и динамики (некоторые из которых описаны ниже).
Генератор переменного тока
Генераторы переменного тока работают по принципу электромагнитной индукции; это устройства, преобразующие механическую энергию в электрическую. Вращение катушки в магнитном поле вызывает разность потенциалов на катушке и, следовательно, ток через нее. Индуцированная ЭДС заставляет заряд (уже присутствующий в проводе) проходить через внешнюю цепь и, следовательно, производить электричество.Первоначальная механическая энергия может быть произведена рядом устройств, таких как вода, проходящая через турбину, ветряные турбины или паровые турбины.
Вращение катушки в магнитном поле вызывает разность потенциалов на катушке и, следовательно, ток через нее. Индуцированная ЭДС заставляет заряд (уже присутствующий в проводе) проходить через внешнюю цепь и, следовательно, производить электричество.Первоначальная механическая энергия может быть произведена рядом устройств, таких как вода, проходящая через турбину, ветряные турбины или паровые турбины.
Двигатель переменного тока
Токоведущий провод в магнитном поле испытывает силу; это основной принцип двигателя. Ток проходит через катушку, это создает B-поле вокруг катушки, это B-поле затем взаимодействует с постоянным B-полем, в котором находится катушка, векторное суперпозиция полей приводит к отмене в некоторых областях и сложению в других , чистый эффект является результирующим
сила и, следовательно, вращающий момент относительно катушки.Этот крутящий момент заставляет проволоку вращаться; Таким образом, механическая энергия была преобразована в электрическую.
Трансформатор
Трансформатор — это устройство, которое используется для преобразования электроэнергии с одного уровня напряжения и тока на другой.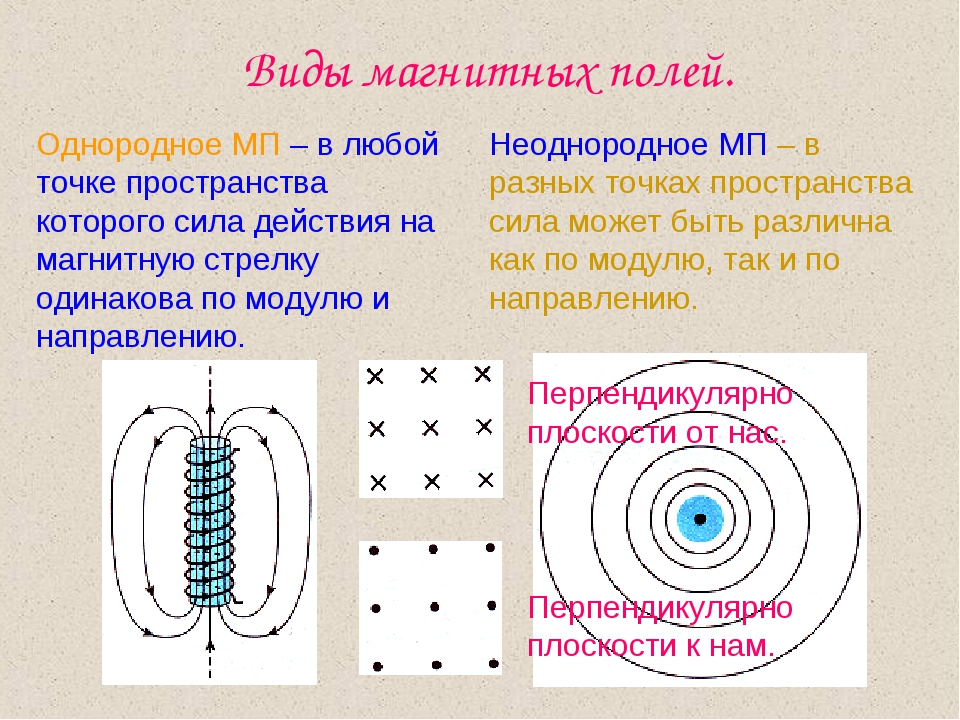 В своей самой простой форме трансформатор состоит из первичной обмотки, вторичной обмотки и железного сердечника. железный сердечник передает поток от одной обмотки к другой, это показано ниже.
В своей самой простой форме трансформатор состоит из первичной обмотки, вторичной обмотки и железного сердечника. железный сердечник передает поток от одной обмотки к другой, это показано ниже.
Трансформаторы работают в соответствии с законом Фарадея об электромагнитной индукции.Пропуская переменный ток через первичную обмотку, мы индуцируем изменяющееся во времени B-поле, которое затем передается через железный сердечник во вторичную обмотку. Изменение этого B-поля на вторичной обмотке вызовет на ней переменное напряжение и, следовательно, переменный ток через нее. Если
трансформатор идеален, индуцированное напряжение описывается формулой ниже.
$ \ frac {V_1} {V_2} = \ frac {N_1} {N_2} $
Таким образом, мы видим, что возможны два типа трансформаторов: один, который повышает напряжение, а другой — понижает.Если количество витков вторичной обмотки больше, чем количество витков первичной, напряжение будет увеличиваться. Если количество витков первичной обмотки больше, чем количество витков вторичной обмотки, напряжение будет понижаться. 2 R $ и очень сильно зависят от величины тока.На высоких частотах возникают дополнительные потери из-за явления, известного как скин-эффект, электрический ток пропускается только через внешнюю оболочку проводника. Мы знаем от Фарадея и Ленца, что индуцированное
2 R $ и очень сильно зависят от величины тока.На высоких частотах возникают дополнительные потери из-за явления, известного как скин-эффект, электрический ток пропускается только через внешнюю оболочку проводника. Мы знаем от Фарадея и Ленца, что индуцированное
напряжение пропорционально скорости изменения магнитного потока, кроме того, оно действует в направлении, противоположном изменению, вызвавшему его. Следовательно, ток высокой частоты будет вызывать большой ток, который будет противодействовать самому себе. Мы знаем, что B-поле, индуцированное токоведущим проводом, затухает с расстоянием от центра провода, B-поле и, следовательно, противоположный ток, следовательно, является самым большим в центре
в обмотке этот сильный противоположный ток приводит к гашению тока по центру провода, следовательно, ток течет только по коже.
Потери в стали чаще всего связаны с гистерезисом и вихревыми токами. Каждый раз, когда магнитное поле меняет направление на противоположное, оно должно выполнять некоторую работу с атомными диполями, которые оно ранее выровняло, это известно как потеря гистерезиса. 2 R $, связанных с джоулями. обогрев.Когда питание поступает к потребителю, напряжение необходимо снова понизить перед использованием в домашних условиях.
2 R $, связанных с джоулями. обогрев.Когда питание поступает к потребителю, напряжение необходимо снова понизить перед использованием в домашних условиях.
Измерение высоких напряжений и токов:
Трансформаторы часто используются для понижения высокого напряжения или тока до безопасного уровня перед измерением.
Непрерывное изменение уровней напряжения и тока:
Машинному оборудованию часто требуется питание при постоянно меняющемся уровне напряжения и тока.
Метод комплексного изображения для расчета магнитных и электрических полей, создаваемых на поверхности Земли авроральным электроджетом | Международный геофизический журнал
Сводка
Для изучения аврорального электроджета и изучения эффектов, которые он может вызывать в энергосистемах на земле, полезно иметь возможность вычислять магнитные и электрические поля, которые электроджет создает на поверхности Земли.Учет эффектов индуцированных в Земле токов приводит к набору интегральных выражений, численное вычисление которых сложно и требует компьютерных ресурсов. Приблизительное решение может быть достигнуто путем представления индуцированных токов током изображения на сложной глубине. Мы представляем простой вывод выражений для сложных изображений и используем их для расчета полей, создаваемых авроральным электроджетом на поверхности земли, представленных моделями слоистой проводимости.Сравнение этих результатов с результатами, полученными с использованием точного интегрального решения, показывает, что внесенные ошибки незначительны по сравнению с неопределенностями используемых параметров. Таким образом, метод комплексного изображения обеспечивает простые, быстрые и точные средства расчета магнитных и электрических полей.
Приблизительное решение может быть достигнуто путем представления индуцированных токов током изображения на сложной глубине. Мы представляем простой вывод выражений для сложных изображений и используем их для расчета полей, создаваемых авроральным электроджетом на поверхности земли, представленных моделями слоистой проводимости.Сравнение этих результатов с результатами, полученными с использованием точного интегрального решения, показывает, что внесенные ошибки незначительны по сравнению с неопределенностями используемых параметров. Таким образом, метод комплексного изображения обеспечивает простые, быстрые и точные средства расчета магнитных и электрических полей.
Введение
Знание электромагнитных полей, создаваемых авроральным электроджетом, необходимо для работы в ряде областей. Наземные измерения магнитного поля используются для изучения морфологии токовой системы электроджета (например,грамм. Cramoysan, Bunting & Orr 1995) и структурированные поля источника электроджета усложняют интерпретацию магнитотеллурических измерений структуры проводимости Земли в авроральных областях (например, Mareschal 1986). Система аврорального электроджета также является основной причиной магнитных возмущений, которые вызывают проблемы в энергосистемах в результате геомагнитно индуцированных токов (например, Boteler, Pirjola & Nevanlinna 1997). Последнее приложение, в частности, требует быстрого метода расчета, который можно использовать со схемами прогнозирования в реальном времени, которые планируются для следующего солнечного максимума.
Cramoysan, Bunting & Orr 1995) и структурированные поля источника электроджета усложняют интерпретацию магнитотеллурических измерений структуры проводимости Земли в авроральных областях (например, Mareschal 1986). Система аврорального электроджета также является основной причиной магнитных возмущений, которые вызывают проблемы в энергосистемах в результате геомагнитно индуцированных токов (например, Boteler, Pirjola & Nevanlinna 1997). Последнее приложение, в частности, требует быстрого метода расчета, который можно использовать со схемами прогнозирования в реальном времени, которые планируются для следующего солнечного максимума.
Расчеты электромагнитных полей, связанных с авроральным электроджетом, усложняются действием наведенных в Земле электрических токов. Эти индуцированные токи сами по себе создают электромагнитное поле, которое добавляется к полю, создаваемому электроджетом. Процесс индукции зависит от частоты колебаний источника и структуры проводимости Земли. Пространственная протяженность полей источника также имеет значение, и полное решение на каждой частоте включает интегрирование по всем пространственным волновым числам. Решения этого интеграла были получены, но связаны со сложными вычислениями, которые требуют компьютерных ресурсов и не подходят для вычислений в реальном времени.
Решения этого интеграла были получены, но связаны со сложными вычислениями, которые требуют компьютерных ресурсов и не подходят для вычислений в реальном времени.
Быстрые и простые решения для полей, создаваемых линейным током над Землей, получены в электроэнергетике с использованием техники, которая включает представление токов, наведенных в Земле током изображения на сложной глубине ниже внешнего линейного тока. . Этот метод «сложного изображения» был первоначально предложен Уэйт и Спайс (1969) и широко использовался для исследования полей, создаваемых проводниками вблизи поверхности Земли (например,грамм. Баннистер 1970, 1986). Этот метод также был принят в электроэнергетике (Deri et al. 1981), где он широко используется для расчета взаимного импеданса между соседними проводниками. При частотах и высотах проводов, используемых в энергетике, метод комплексного изображения дает результаты, неотличимые от более сложных точных расчетов. Расчеты сложных изображений использовались Томсоном и Уивером (1975) для изучения влияния линейного источника тока на магнитотеллурические отклики, полученные на земле. Однако в целом методика сложных изображений не применялась к задаче расчета магнитных и электрических полей, создаваемых авроральным электроджетом.
Однако в целом методика сложных изображений не применялась к задаче расчета магнитных и электрических полей, создаваемых авроральным электроджетом.
В этой статье мы представляем простой вывод сложных изображений для магнитных и электрических полей, создаваемых на поверхности Земли бесконечным линейным током над Землей. Бесконечный линейный ток — это первое приближение к реальной системе аврорального электроджета, которая включает продольные токи, а также ионосферные токи.Чтобы проверить точность сложных выражений изображения, мы используем их для расчета полей, создаваемых на поверхности земли, представленных двумя различными слоистыми моделями земли. Одна модель земли представляет структуру Квебека и является примером региона с высоким сопротивлением. Другая модель Земли представляет север Британской Колумбии и является примером более проводящего региона. Во всех случаях для расчета полей также используется точное интегральное решение, основанное на общей модели электроджеты Хаккинена и Пирйолы (1986).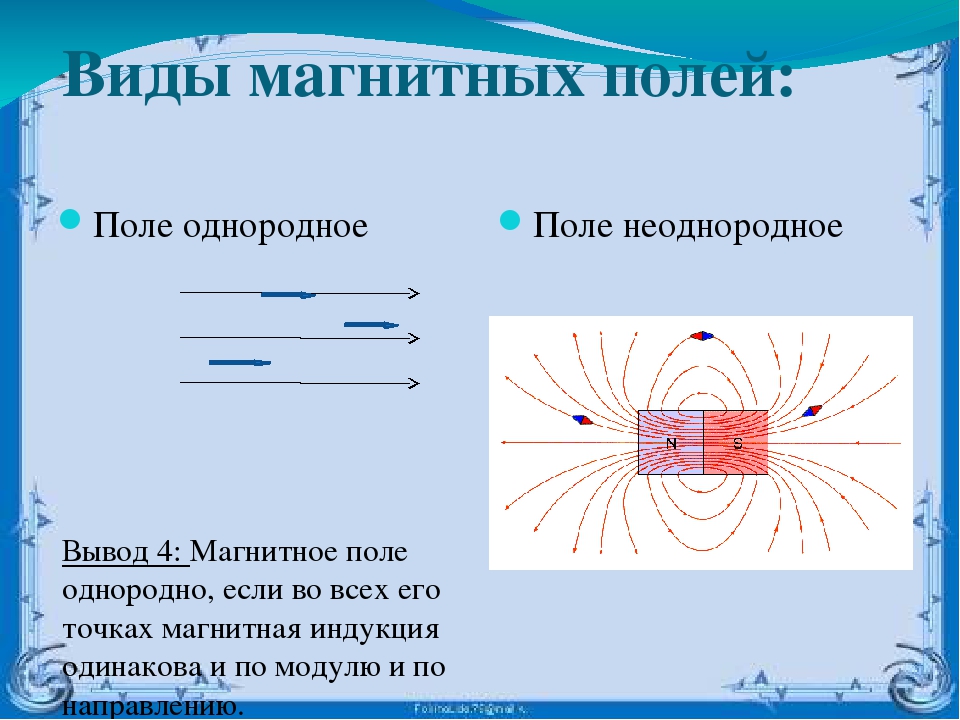 Сравнение результатов показывает, что метод сложного изображения почти так же точен, как и точный метод, и имеет дополнительные преимущества, заключающиеся в том, что он намного проще и быстрее.
Сравнение результатов показывает, что метод сложного изображения почти так же точен, как и точный метод, и имеет дополнительные преимущества, заключающиеся в том, что он намного проще и быстрее.
Точное решение
Модель электроджетной системы, применимая для определения геоэлектромагнитного поля на авроральных широтах, была представлена Хаккиненом и Пирйолой (1986). В модели электроджет описывается горизонтальным слоем на заданной высоте над поверхностью Земли, и его ток может быть любой функцией координат пространства и времени.Слойный ток сопровождается токами, направленными по геомагнитному полю, величины которых подобраны таким образом, чтобы общий ток не расходился. Хаккинен и Пирйола (1986) представили точные и строгие формулы для расчета геоэлектромагнитного поля, обусловленного рассматриваемой общей системой электродвигателей, в любой точке на поверхности Земли, с учетом индукции в слоистой Земле. Их решение основано на работе в трехмерной области Фурье ( ω , ν , ψ ) относительно времени t и горизонтальных пространственных координат x и y .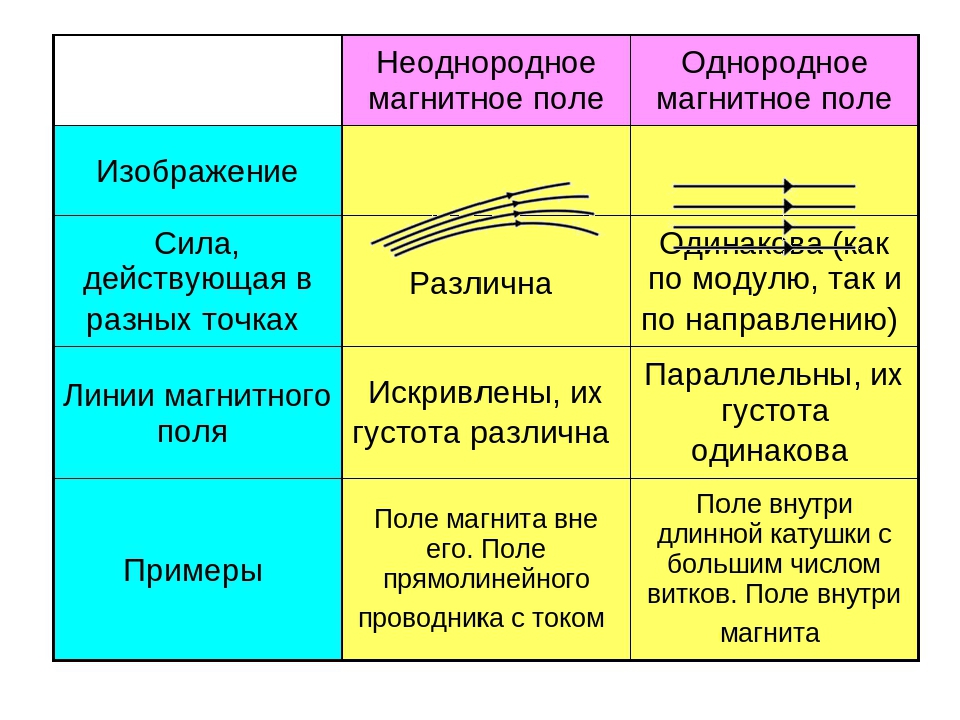
Случай простой бесконечно длинной линии тока, обсуждаемый в настоящей статье, является частным случаем, когда волновое число в направлении y , ψ , стремится к нулю. Поля на поверхности Земли определяются выражением (1) (2) (3), где h — высота линии тока, I и x — горизонтальное расстояние от линии тока. R — коэффициент отражения и зависит от структуры проводимости земли, а также от частоты ω и волнового числа ν .Эти формулы также были представлены Hermance & Peltier (1970) и Wait (1992).
Был разработан компьютерный код для изучения полей в соответствии с общей моделью электроджетной системы, упомянутой выше (Pirjola & Häkkinen 1991). Численный расчет электромагнитного поля, создаваемого на поверхности земли на одной частоте ω , требует вычисления обратных двойных интегралов Фурье из пространства ( νψ ) до x и y .Чаще всего это достигается с помощью формулы интеграции Гаусса (Abramowitz & Stegun 1970). Как при интегрировании ν , так и при интегрировании ψ интервал разделен на подинтервалы, на каждом из которых используется формула интегрирования Гаусса восьмого порядка (Pirjola & Häkkinen 1991). Другой подход заключается в использовании быстрого преобразования Ханкеля (Johansen & Sørensen, 1979) и расширенного правила Симпсона (Abramowitz & Stegun, 1970), как это было сделано Пирджолой (1992). Независимо от выбранного численного алгоритма вычисления отнимают много времени, и требуется эффективный компьютер.
Как при интегрировании ν , так и при интегрировании ψ интервал разделен на подинтервалы, на каждом из которых используется формула интегрирования Гаусса восьмого порядка (Pirjola & Häkkinen 1991). Другой подход заключается в использовании быстрого преобразования Ханкеля (Johansen & Sørensen, 1979) и расширенного правила Симпсона (Abramowitz & Stegun, 1970), как это было сделано Пирджолой (1992). Независимо от выбранного численного алгоритма вычисления отнимают много времени, и требуется эффективный компьютер.
Комплексное изображение: выражения магнитного поля
Падающие части в выражениях (1) и (2) могут быть записаны (см. Приложение) в формах (4) и (5), которые являются просто выражениями Био – Савара для внешнего сетевого тока.
Сложное изображение: выражения электрического поля
Используя приближение R (ν) = e −2pν в ур. (3) и выразив cos νx через экспоненциальные функции, получим (19) Используя интегральное соотношение, после малой алгебры это становится (20) где два квадратных корня в члене ln — это расстояния до прямой ток и ток изображения, как показано на рис.1.
(3) и выразив cos νx через экспоненциальные функции, получим (19) Используя интегральное соотношение, после малой алгебры это становится (20) где два квадратных корня в члене ln — это расстояния до прямой ток и ток изображения, как показано на рис.1.
Рисунок 1.
Линейное представление аврорального электроджета и положение тока изображения на комплексной глубине, используемое для представления эффекта индуцированных токов в Земле.
Рисунок 1.
Линейное представление аврорального электроджета и положение тока изображения на комплексной глубине, используемое для представления эффекта индуцированных токов в Земле.
Сравнение результатов точных и сложных изображений
В рамках оценки геомагнитной опасности для энергосистем Канады мы выполнили расчеты магнитных и электрических полей, создаваемых на поверхности Земли электроджетом в 1 миллион ампер.Эти расчеты были выполнены для слоистых моделей земли, представляющих структуру проводимости в различных частях страны (Ferguson, частное сообщение, 1996). Здесь мы представляем результаты исследования области вулканических пород Квебека, которая является частью Канадского щита, и области более молодых пород в северной части Британской Колумбии. Модели земли для этих двух регионов показаны на рис. 2. Эти две модели представляют область с высоким сопротивлением, а также область с более высокой проводимостью, и они представляют ряд структур земли, для которых, как ожидается, будут выполнены эти расчеты.
Здесь мы представляем результаты исследования области вулканических пород Квебека, которая является частью Канадского щита, и области более молодых пород в северной части Британской Колумбии. Модели земли для этих двух регионов показаны на рис. 2. Эти две модели представляют область с высоким сопротивлением, а также область с более высокой проводимостью, и они представляют ряд структур земли, для которых, как ожидается, будут выполнены эти расчеты.
Рисунок 2.
Модели Земли Квебека и северной части Британской Колумбии.
Рис. 2.
Модели Земли Квебека и северной части Британской Колумбии.
Сложные формулы изображения (уравнения 17, 18, 20) используются для расчета горизонтального и вертикального магнитных полей и горизонтального электрического поля на расстоянии до 1000 км по обе стороны от линии тока на высоте 100 км. Эти результаты сравниваются с точными расчетами, выполненными с использованием интегрального решения Häkkinen & Pirjola (1986), как указано ранее.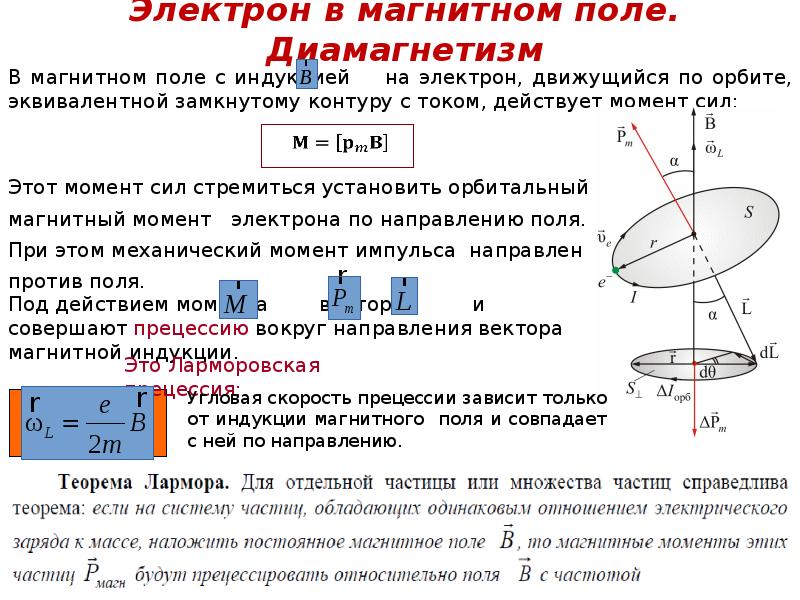 Для этого длина электроджеты устанавливается на большое значение, которое подходящим образом представляет бесконечный линейный ток, и интегрирование выполняется с использованием метода, основанного на формуле интегрирования Гаусса. Расчеты производились для ряда периодов от 2 мин до 2 часов. На рисунках 3 и 4 показаны результаты (* для метода комплексных изображений и сплошные линии для точных расчетов) для слоистой модели земли Квебека за периоды 5 и 30 минут. На рисунках 5 и 6 показаны результаты в те же периоды, но для слоистой модели земли Британской Колумбии.
Для этого длина электроджеты устанавливается на большое значение, которое подходящим образом представляет бесконечный линейный ток, и интегрирование выполняется с использованием метода, основанного на формуле интегрирования Гаусса. Расчеты производились для ряда периодов от 2 мин до 2 часов. На рисунках 3 и 4 показаны результаты (* для метода комплексных изображений и сплошные линии для точных расчетов) для слоистой модели земли Квебека за периоды 5 и 30 минут. На рисунках 5 и 6 показаны результаты в те же периоды, но для слоистой модели земли Британской Колумбии.
Рисунок 3.
Горизонтальное ( B x ) и вертикальное ( B z ) магнитные поля и горизонтальное ( E y ) электрическое поле, создаваемое линией ток в 1 миллион ампер на 100 км над поверхностью Земли. Расчеты производятся для периода 5 минут и модели земли, представляющей Квебек. Звездочками показаны результаты расчетов, выполненных методом комплексного изображения; сплошными линиями показаны результаты точных расчетов, выполненных с использованием метода Häkkinen & Pirjola.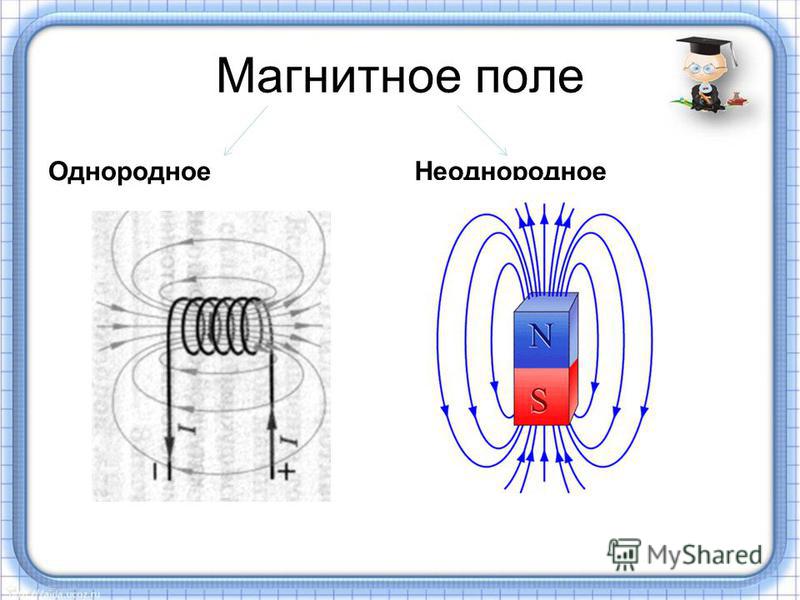
Рисунок 3.
Горизонтальное ( B x ) и вертикальное ( B z ) магнитные поля и горизонтальное ( E y ) электрическое поле, создаваемое линейный ток в 1 миллион ампер на 100 км над поверхностью Земли. Расчеты производятся для периода 5 минут и модели земли, представляющей Квебек. Звездочками показаны результаты расчетов, выполненных методом комплексного изображения; сплошными линиями показаны результаты точных расчетов, выполненных с использованием метода Häkkinen & Pirjola.
Рис. 4.
Расчеты магнитного и электрического поля с использованием модели земли для Квебека, как на рис. 3, но для периода 30 мин.
Рисунок 4.
Расчеты магнитного поля и электрического поля с использованием модели земли для Квебека, как на рис. 3, но для периода 30 мин.
Рис. 5.
Расчеты магнитного и электрического поля, как на рис. 3, для периода 5 минут и модели земли, представляющей север Британской Колумбии.
Рис. 5.
Расчеты магнитного и электрического полей, как на рис. 3, для периода 5 минут и модели земли, представляющей север Британской Колумбии.
Рис. 6.
Расчеты магнитного и электрического поля, как на рис. 3, для периода 30 минут и модели земли, представляющей север Британской Колумбии.
Рис. 6.
Расчеты магнитного и электрического поля, как на рис. 3, для периода 30 минут и модели земли, представляющей север Британской Колумбии.
Для горизонтальной и вертикальной составляющих магнитного поля вклад в поле самого электроджета и вклад индуцированных токов показаны отдельно. Также отображается общее поле, представляющее собой сумму этих «внешних» и «внутренних» частей. На отдельных графиках изображены действительная и мнимая части полей (принимая поля в фазе с электроджетом как реальные). Таким образом, внешняя часть магнитных полей не имеет мнимой части. Расчет сложного изображения внешней части не требует аппроксимации и поэтому всегда согласуется с точным решением. Внешняя часть показана на рисунках, чтобы можно было сравнить относительные вклады внутренней и внешней частей магнитного поля. Аппроксимация, сделанная при выводе метода сложного изображения, включает коэффициент отражения и поэтому влияет только на внутреннюю часть.
Внешняя часть показана на рисунках, чтобы можно было сравнить относительные вклады внутренней и внешней частей магнитного поля. Аппроксимация, сделанная при выводе метода сложного изображения, включает коэффициент отражения и поэтому влияет только на внутреннюю часть.
Горизонтальное магнитное поле имеет максимальную амплитуду непосредственно под электроджетом. Здесь внешняя часть поля вносит основной вклад. Однако вклад электроджета падает быстрее, чем вклад индуцированных токов, и на горизонтальном расстоянии 200 км от электроджета наведенные токи составляют 50% от общего поля, а на больших расстояниях они вносят преобладающий вклад.
Вертикальное магнитное поле направлено вверх с одной стороны электроджета и вниз с другой стороны, поэтому оно проходит через ноль непосредственно под электроджетом. Максимальная амплитуда наблюдается на горизонтальном расстоянии примерно 100 км по обе стороны от электроджета. Здесь вклад индуцированных токов снова мал по сравнению с вкладом самого электроджета. Вертикальные поля, создаваемые наведенными токами, направлены противоположно полям электроджета. При увеличении горизонтального расстояния от электроджета вклад индуцированных токов приближается к той же амплитуде, что и вклад электроджета, и, таким образом, полное поле стремится к нулю.Насколько быстро это происходит, зависит от плотности индуцированных токов, на которую влияют проводимость земли и период колебаний.
Вертикальные поля, создаваемые наведенными токами, направлены противоположно полям электроджета. При увеличении горизонтального расстояния от электроджета вклад индуцированных токов приближается к той же амплитуде, что и вклад электроджета, и, таким образом, полное поле стремится к нулю.Насколько быстро это происходит, зависит от плотности индуцированных токов, на которую влияют проводимость земли и период колебаний.
Электрические поля, возникающие на поверхности Земли, также показаны на рисунках с 3 по 6 (где * показывает результаты метода комплексного изображения, а сплошные линии — результаты точных расчетов). Электрическое поле имеет максимальное значение непосредственно под электроджетом и падение амплитуды с обеих сторон.
Изучая отдельные графики, можно видеть, что обычно существует очень хорошее согласие между расчетами сложных изображений и точным решением.(Помните, что вычисление внешней части магнитного поля по сложному изображению само по себе является точным. ) Для горизонтального магнитного поля наибольшая разница в сложном изображении и точных расчетах внутренней части составляет около 10 процентов и происходит непосредственно под ним. Электроджет. Однако в этот момент внешняя часть вносит основной вклад в магнитное поле, поэтому разница между комплексным изображением и точным расчетом полных полей незначительна. Для вертикального магнитного поля наибольшая разница (около 10%) наблюдается по сторонам электроджета, вблизи того места, где амплитуда максимальна.Однако, опять же, поскольку приближение сложного изображения влияет только на внутреннюю часть, результаты полного поля, полученные методом сложного изображения, почти такие же, как и точные вычисления. Для электрических полей сложное изображение и точные вычисления практически неразличимы.
) Для горизонтального магнитного поля наибольшая разница в сложном изображении и точных расчетах внутренней части составляет около 10 процентов и происходит непосредственно под ним. Электроджет. Однако в этот момент внешняя часть вносит основной вклад в магнитное поле, поэтому разница между комплексным изображением и точным расчетом полных полей незначительна. Для вертикального магнитного поля наибольшая разница (около 10%) наблюдается по сторонам электроджета, вблизи того места, где амплитуда максимальна.Однако, опять же, поскольку приближение сложного изображения влияет только на внутреннюю часть, результаты полного поля, полученные методом сложного изображения, почти такие же, как и точные вычисления. Для электрических полей сложное изображение и точные вычисления практически неразличимы.
Выражения сложного изображения такие же, как и точное решение, когда комплексная глубина скин-слоя намного меньше горизонтальной длины волны поля источника. Однако, даже когда это условие не достигается, уравнения (10) и (11) показывают, что результаты сложного изображения будут мало отличаться от точных результатов. Для источника с одной длиной волны и однородной землей легко оценить, насколько точно достигается это условие. Однако поля, создаваемые линейным током, представляют собой сумму нескольких вкладов с разными длинами волн. Кроме того, для слоистой земли комплексная глубина скин-слоя имеет действительные и мнимые компоненты, относительные размеры которых меняются с частотой. Таким образом, было сочтено необходимым провести численные расчеты, чтобы сравнить метод сложного изображения с точными результатами.
Для источника с одной длиной волны и однородной землей легко оценить, насколько точно достигается это условие. Однако поля, создаваемые линейным током, представляют собой сумму нескольких вкладов с разными длинами волн. Кроме того, для слоистой земли комплексная глубина скин-слоя имеет действительные и мнимые компоненты, относительные размеры которых меняются с частотой. Таким образом, было сочтено необходимым провести численные расчеты, чтобы сравнить метод сложного изображения с точными результатами.
Изучение результатов для всех периодов от 2 минут до 2 часов показывает, что существует общая тенденция к тому, что ошибка в результатах комплексного изображения будет немного больше при более длительных периодах, как и следовало ожидать.Однако различие между комплексным изображением и точным решением также зависит от структуры проводимости. Для модели Квебека значения комплексного изображения для B x непосредственно под линейным током всегда меньше, чем точное решение. Однако результаты Британской Колумбии показывают, что значения комплексного изображения выше точных значений на периодах 2, 5 и 10 минут (см. Рис. 5) и уменьшаются до значений ниже точных результатов на более длительных периодах (см. Рис. 6). .Ошибки в действительной и мнимой частях результатов комплексного изображения также ведут себя по-разному и усложняют любое сравнение результатов для различных структур проводимости. Например, за период в 5 минут реальная и мнимая части комплексной глубины скин-слоя в Квебеке (132 — j 80,95 км) значительно больше, чем в Британской Колумбии (36,83 — j 48,54 км), из-за более высокое сопротивление земной коры в Квебеке. Однако за период в 30 минут поля проникают глубже в Землю, и сейчас сложные поверхностные глубины в Квебеке и Британской Колумбии составляют (253.55 — j 113,41 км) и (116,13 — j 122,61 км) соответственно. Реальная часть сложной толщины скин-слоя в Британской Колумбии все еще меньше половины от таковой в Квебеке, но мнимая часть для Британской Колумбии теперь больше, чем для Квебека.
Однако результаты Британской Колумбии показывают, что значения комплексного изображения выше точных значений на периодах 2, 5 и 10 минут (см. Рис. 5) и уменьшаются до значений ниже точных результатов на более длительных периодах (см. Рис. 6). .Ошибки в действительной и мнимой частях результатов комплексного изображения также ведут себя по-разному и усложняют любое сравнение результатов для различных структур проводимости. Например, за период в 5 минут реальная и мнимая части комплексной глубины скин-слоя в Квебеке (132 — j 80,95 км) значительно больше, чем в Британской Колумбии (36,83 — j 48,54 км), из-за более высокое сопротивление земной коры в Квебеке. Однако за период в 30 минут поля проникают глубже в Землю, и сейчас сложные поверхностные глубины в Квебеке и Британской Колумбии составляют (253.55 — j 113,41 км) и (116,13 — j 122,61 км) соответственно. Реальная часть сложной толщины скин-слоя в Британской Колумбии все еще меньше половины от таковой в Квебеке, но мнимая часть для Британской Колумбии теперь больше, чем для Квебека.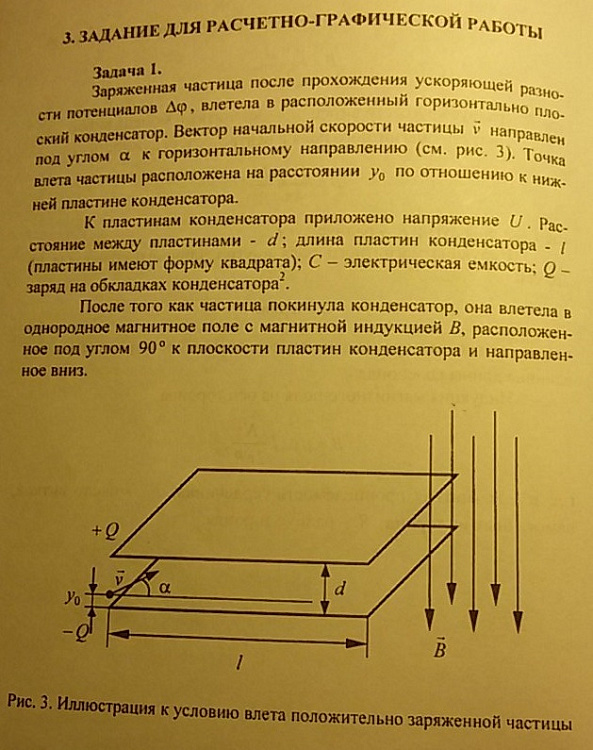
Обсуждение
Сравнения, представленные выше, показывают, что метод комплексного изображения обеспечивает значения магнитных и электрических полей, создаваемых линейным током на высоте 100 км, которые очень хорошо согласуются с точными результатами.Линейный ток представляет собой сильно структурированный источник и является серьезным испытанием для техники сложного изображения. В действительности авроральный электроджет имеет значительную ширину и может быть смоделирован множественными линейными токами. Горизонтальные длины волн полей в этом случае будут больше, чем длины волн, создаваемых линейным током, и результаты комплексного изображения даже лучше согласуются с точными результатами. Система аврорального электроджета также включает продольные токи, которые вносят вклад в магнитные поля, наблюдаемые на поверхности Земли.В настоящее время для включения продольных токов в расчеты поля необходимо использовать точное решение, такое как решение Häkkinen & Pirjola (1986). Необходима дальнейшая работа, чтобы изучить, можно ли применить подход комплексного изображения к моделированию продольных токов.
Необходима дальнейшая работа, чтобы изучить, можно ли применить подход комплексного изображения к моделированию продольных токов.
Метод комплексных изображений позволяет моделировать Землю несколькими слоями с различной проводимостью. Это усовершенствование расчетов, которые аппроксимируют Землю однородным полупространством, но все же не представляют реальную неоднородную структуру проводимости Земли.Таким образом, модель линейного тока над слоистой структурой проводимости является лишь грубым приближением к системе аврорального электроджета над Землей. Ошибки, вносимые при использовании метода комплексного изображения, несущественны по сравнению с различиями между моделью и реальной ситуацией. Таким образом, для практических расчетов полей, создаваемых авроральным электроджетом, выбор метода расчета не влияет на точность результатов, поэтому простота и большая скорость метода сложных изображений делают его очевидным.
В этой статье мы упоминали «метод сложного изображения», который известен в других дисциплинах. Однако важно отметить, что метод фактически включает реальное изображение на сложной глубине. Токи изображения ранее использовались в расчетах электроджетов (например, Kisabeth & Rostoker 1977; Pirjola & Viljanen 1989; Cramoysan et al . 1995), но они всегда использовали изображение на реальной глубине. В таких исследованиях Земля представляет собой идеальный проводник на заданной глубине, и индуцированные токи текут по поверхности этого проводника.Глубина идеального проводника соответствует глубине скин-слоя только с реальной частью, а токи на поверхности проводника отражают электромагнитное поле электроджета и поэтому могут быть представлены током изображения на реальной глубине ниже дирижер. Эта техника идеального проводника проста, но не может должным образом представить влияние проводимости Земли на электрические и магнитные поля. Метод сложных изображений теперь обеспечивает сопоставимую по простоте технику, которая должным образом учитывает индуцированные токи на Земле.
Однако важно отметить, что метод фактически включает реальное изображение на сложной глубине. Токи изображения ранее использовались в расчетах электроджетов (например, Kisabeth & Rostoker 1977; Pirjola & Viljanen 1989; Cramoysan et al . 1995), но они всегда использовали изображение на реальной глубине. В таких исследованиях Земля представляет собой идеальный проводник на заданной глубине, и индуцированные токи текут по поверхности этого проводника.Глубина идеального проводника соответствует глубине скин-слоя только с реальной частью, а токи на поверхности проводника отражают электромагнитное поле электроджета и поэтому могут быть представлены током изображения на реальной глубине ниже дирижер. Эта техника идеального проводника проста, но не может должным образом представить влияние проводимости Земли на электрические и магнитные поля. Метод сложных изображений теперь обеспечивает сопоставимую по простоте технику, которая должным образом учитывает индуцированные токи на Земле.
Простота метода комплексного изображения делает его пригодным для критических по времени приложений, таких как расчет геомагнитно-индуцированных токов (GIC), создаваемых в энергосистемах авроральным электроджетом. Цепи магнитометров используются для отслеживания амплитуды и положения аврорального электроджета. Затем метод комплексного изображения обеспечивает удобный способ расчета магнитных и электрических полей, испытываемых энергосистемами на земле, и эту информацию можно использовать для расчета потока GIC в энергосистеме.Ряд сотрудников также пытается разработать алгоритмы для использования данных о солнечном ветре в реальном времени со спутника WIND (и в будущем со спутника ACE), расположенного в точке L1 между Солнцем и Землей, для прогнозирования положения и амплитуды солнечного ветра. авроральный электродвигатель Petschek & Feero, 1997). С такой информацией можно использовать метод комплексного изображения для обеспечения прогноза величин GIC, ожидаемых в энергосистеме.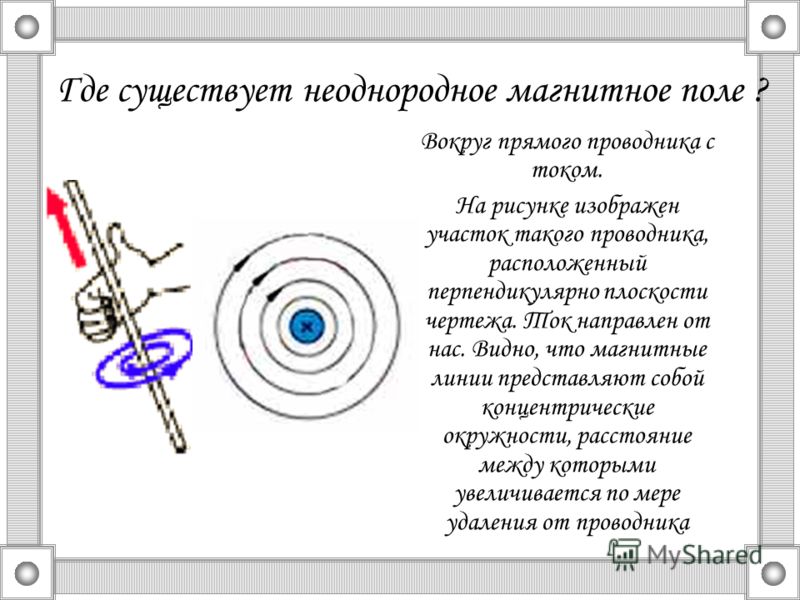
Выводы
Магнитные поля и электрические поля, создаваемые на поверхности Земли авроральным электроджетом, в близком приближении задаются выражениями (21) (22) (23) Это соответствует полям, создаваемым линейным током на высоте h и ток изображения на комплексной глубине h +2 p , где p — комплексная глубина скин-слоя, связанная с поверхностным импедансом по формуле (24) Сравнение результатов этих выражений с полученными результатами Использование точного решения показывает различия, которые незначительны по сравнению с неопределенностями в некоторых параметрах, используемых в расчетах, таких как поверхностный импеданс Земли и положение электроджеты.Таким образом, метод комплексного изображения обеспечивает быстрый и простой метод, пригодный для расчетов в реальном времени магнитных полей и электрических полей, создаваемых на поверхности Земли авроральным электроджетом.
Благодарности
Мы благодарны Питеру Дику из Ontario Hydro Technologies за предложение использовать метод комплексного изображения.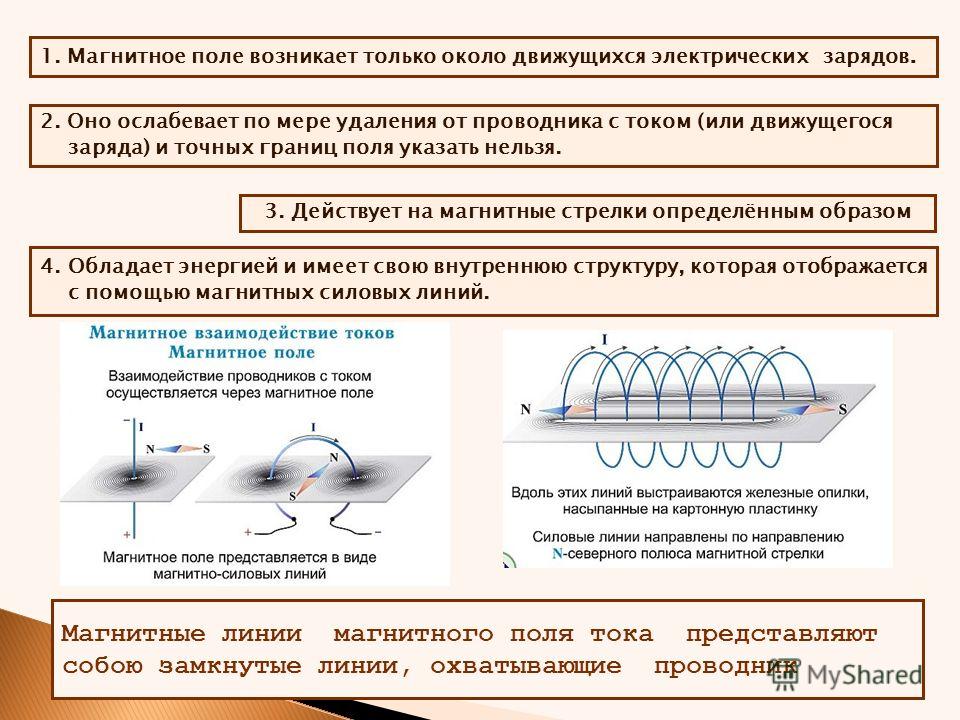 Вклад Геологической службы Канады № 1996422.
Вклад Геологической службы Канады № 1996422.
Ссылки
,
1970
.
Справочник по математическим функциям с формулами, графиками и математическими таблицами.
9-я печать,
886
—
888
,
Dover Publications
,
New York, NY
.
,
1970
.
Использование методов теории изображений для определения взаимной связи между возвышенными источниками с длинными горизонтальными линиями,
Radio Sci.,
5,
1375
—
1381
.
,
1986
.
Приложения теории сложных изображений,
Radio Sci.,
21,
605
—
616
.
,
1997
.
Влияние геомагнитных возмущений на электрические системы на поверхности земли,
Adv. пространство Res.
.
,
1995
.
Использование модельного токового клина для определения положения токовых систем суббури,
Ann. Геофиз.,
Геофиз.,
13,
583
—
594
.
,
1981
.
Комплексная плоскость заземления: упрощенная модель для однородного и многослойного заземления,
IEEE Trans. Power App. & Sys.,
ПАС-100,
3866
—
3693
.
,
1986
.
Расчет электрических и магнитных полей из-за системы электрического тока над слоистой землей,
Geophysica,
22,
31
—
44
.
,
1970
.
Магнитотеллурические поля линейного тока,
J. Gephys. Res.,
75,
3351
—
3356
.
,
1970
.
Фурье-анализ,
пересмотренный edn,
Simon and Schuster
,
New York, NY
.
,
1979
.
Быстрые преобразования Хенкеля,
Geophys. Проспект,
27,
876
—
901
.
,
1977
.
Моделирование трехмерных токовых систем, связанных с магнитосферными суббурями,
Geophys. J. R. astr. Soc.,
J. R. astr. Soc.,
49,
655
—
683
.
,
1986
.
Моделирование естественных источников магнитосферного происхождения в интерпретации региональных индукционных исследований: обзор,
Surv. Геофиз.,
8,
261
—
300
.
,
1997
.
Мастерская посвящена влиянию космической погоды на электроэнергию,
EOS, Trans. Являюсь. геофизики. Ед.,
78,
217
—
218
.
,
1992
.
Об эффектах магнитотеллурических источников, вызванных авроральной электроджетной системой,
Radio Sci.,
27,
463
—
468
.
,
1991
.
Электромагнитное поле, вызванное системой аврорального электроджета, модель,
Экологическая и космическая электромагнетизм,
288
—
298
,
Springer-Verlag
,
Токио
.
,
1989
.
О геомагнитно-индуцированных токах в финской энергосистеме 400 кВ за счет аврорального тока электроджеты,
IEEE Trans. Электроснабжение,
Электроснабжение,
4,
1239
—
1245
.
,
1975
.
Комплексное приближение изображения для индукции в многослойной земле,
J. geophys. Res.,
80,
123
—
129
.
,
1992
.
Теория электромагнитных волн,
J.R. Wait
,
Tucson, AZ
.
,
1969
.
О представлении квазистатических полей линейного источника тока над землей,
Кан.J. Phys.,
47,
2731
—
2733
.
Приложение
Приложение А. Косинус и синусоидальные преобразования Фурье
Заметки автора
© 1998 РАН
Распространение
— Почему электрическое поле ортогонально магнитному полю от антенны?
Короткий ответ: нет, не бывает случаев, когда радиоволны не имели бы ортогональных магнитных и электрических полей.
В физике радиоволна, как и все электромагнитное излучение, называется поперечной волной, что по определению означает, что колебания волн перпендикулярны направлению передачи и распространения энергии.
Электрическая и магнитная части поля находятся в фиксированном соотношении сил, чтобы удовлетворять двум уравнениям Максвелла, которые определяют, как одно создается из другого. Эти поля $ \ mathbf {E} $ и $ \ mathbf {B} $ (в физике по какой-то причине магнитная часть использует B, я буду придерживаться этого соглашения, чтобы физикам было легче исправлять любые ошибки) также являются в фазе, причем оба достигают максимума и минимума в одних и тех же точках пространства.
Хорошо, мы уже это знаем, но почему ?
Спросите Джеймса Клерка Максвелла; его уравнение электромагнитной волны — это уравнение в частных производных второго порядка, которое описывает распространение электромагнитных волн через среду или в вакууме. Это трехмерная форма волнового уравнения. 2 {\ partial B \ over \ частичное z} \, = \, {\ partial E \ over \ partial t} $.Поскольку расходимость электрического и магнитного полей равна нулю, в направлении распространения нет полей.
2 {\ partial B \ over \ частичное z} \, = \, {\ partial E \ over \ partial t} $.Поскольку расходимость электрического и магнитного полей равна нулю, в направлении распространения нет полей.
Список литературы
Введение в теорию электромагнитных волн
Электромагнетизм
Электромагнитные волны
Электромагнитные волны в средах без бесплатных зарядов
Уравнения Максвелла в среде с диэлектрической проницаемостью,; магнитная проницаемость,; и электропроводность в среде без свободных зарядов принимают следующие формы:
| Название уравнения | Дифференциальная форма | Комментарий |
|---|---|---|
| Закон Максвелла – Ампера | Электрическое поле вместе со скоростью его изменения создает магнитное поле. | |
| Закон Фарадея | Скорость изменения магнитного поля создает электрическое поле. | |
| Закон Гаусса | Предполагается, что свободных электрических зарядов нет. | |
| Магнитный закон Гаусса | Нет свободных магнитных зарядов. |
Закон Максвелла – Ампера и закон Фарадея можно объединить в волновое уравнение второго порядка, взяв ротор одного уравнения и подставив его в другое.Другими словами, система, образованная этими двумя уравнениями первого порядка, представляет собой электромагнитные волны.
Делители луча могут разделять луч света, например, с длиной волны 700 нм, на два. Один из методов создания светоделителя заключается в нанесении слоя металла между двумя призмами из стекла. Внутри слоя луч слегка ослабляется и затем разделяется на два разных пути. Изображение показывает величину электромагнитной волны, где красный и синий — высокие и низкие значения соответственно.
Делители луча могут разделять луч света, например, с длиной волны 700 нм, на два. Один из методов создания светоделителя заключается в нанесении слоя металла между двумя призмами из стекла. Внутри слоя луч слегка ослабляется и затем разделяется на два разных пути. Изображение показывает величину электромагнитной волны, где красный и синий — высокие и низкие значения соответственно.
Один из методов создания светоделителя заключается в нанесении слоя металла между двумя призмами из стекла. Внутри слоя луч слегка ослабляется и затем разделяется на два разных пути. Изображение показывает величину электромагнитной волны, где красный и синий — высокие и низкие значения соответственно.
Формулировки поля для электромагнитных волн
Чтобы вывести одно волновое уравнение второго порядка для электрического поля, сначала предположим, что материал не зависит от времени.Затем проницаемость может быть взята за пределы производной по времени в законе Фарадея и инвертирована:
Теперь возьмем локон этого уравнения:
Сбор терминов на одну сторону дает:
Аналогичный вывод дает следующее уравнение относительно магнитного поля:
В этой формулировке мы предположили, что свойства материала не зависят от пространства. Выведя вместо этого волновое уравнение из магнитного векторного потенциала, это ограничение можно ослабить, как показано ниже.
Электромагнитные волны в свободном пространстве
В свободном месте ,,, и. Уравнение для электрического поля можно записать в виде:
Эквивалентная формула:
где скорость света:
Закон Гаусса в свободном пространстве равен, что вместе с векторным тождеством:
дает следующую и, возможно, более знакомую форму волнового уравнения:
и аналогично дает следующий вид для магнитного поля:
Уравнения электромагнитных волн
Наиболее важные уравнения для электромагнитных волн приведены в следующей таблице:
Здесь — магнитный поток через замкнутый контур C , а — поверхностная плотность тока.
Предельный процесс для вывода граничных условий, соответствующих поверхностным интегралам в законе Максвелла – Ампера и законе Фарадея, включает потоки, которые проходят перпендикулярно предельной поверхности. Вклад процесса равен нулю для исчезающей площади поверхности, и по этой причине граничные условия, соответствующие закону Максвелла – Ампера и закону Фарадея, идентичны таковым для статических случаев.
Участок воздуха, окружающий прямоугольную идеально проводящую металлическую пластину, на которую падает плоская электромагнитная волна с частотой 10 ГГц.Пластина 1,5 на 1,5 на 1 мм. Электрическое и магнитное векторные поля представлены красными и синими стрелками соответственно. Электрическое поле поляризовано в направлении y . -Компонент поля визуализируется в определенный момент времени цветом на двух пересекающихся плоскостях, где синий и красный представляют низкие и высокие значения поля соответственно. Картина поля около пластины является результатом того, что касательное электрическое поле к металлической пластине равно нулю.
Участок воздуха, окружающий прямоугольную идеально проводящую металлическую пластину, на которую падает плоская электромагнитная волна с частотой 10 ГГц.Пластина 1,5 на 1,5 на 1 мм. Электрическое и магнитное векторные поля представлены красными и синими стрелками соответственно. Электрическое поле поляризовано в направлении y . -Компонент поля визуализируется в определенный момент времени цветом на двух пересекающихся плоскостях, где синий и красный представляют низкие и высокие значения поля соответственно. Картина поля около пластины является результатом того, что касательное электрическое поле к металлической пластине равно нулю.
Электрическое поле поляризовано в направлении y . -Компонент поля визуализируется в определенный момент времени цветом на двух пересекающихся плоскостях, где синий и красный представляют низкие и высокие значения поля соответственно. Картина поля около пластины является результатом того, что касательное электрическое поле к металлической пластине равно нулю.
Формулировка векторного потенциала для электромагнитных волн
С помощью векторного магнитного потенциала можно вывести волновое уравнение второго порядка.Для этого начните с предположения о временной калибровке вместе с определением векторного потенциала и подставьте их в закон Максвелла – Ампера:
Сбор терминов на одну сторону дает:
Обратите внимание, что эта формулировка предназначена для материала, не зависящего от времени. Для материала, зависящего от времени, диэлектрическая проницаемость не может быть взята за пределы производной по времени.
Составы с гармониками во времени
Поле временной гармоники, может быть расширено до:
as can and, где члены высшего порядка включают обертоны, пропорциональные, и т. Д.Для синусоидального поля обертоны исчезают, и остаются только нулевой (постоянный) член Фурье и члены Фурье первого порядка.
При работе с выражениями и уравнениями, включающими гармонические по времени поля, не зависящая от времени часть рассматривается как комплексное векторное поле. Преобразование обратно от формулировок векторных полей к действительным, зависящим от времени количествам:
Формулировки гармонических по времени электромагнитных волн следующие:
Обратите внимание, что уравнение для идентично уравнению из-за связи.
Комплексные значения диэлектрической проницаемости и показателей преломления
В оптике предпочтительным свойством материала является показатель преломления. Показатель преломления определяется как:
где — скорость света в вакууме, а — фазовая скорость света в среде.
Показатель преломления также может быть записан как функция относительной диэлектрической проницаемости ,, и проницаемости, в соответствии с.
Во многих важных оптических материалах он близок к 1, а показатель преломления приблизительно равен:
Чтобы смоделировать затухание в формулировке гармонической во времени электромагнитной волны, мы можем учесть комплексную диэлектрическую проницаемость (см. Также: Электроквазистатика, Теория и, следовательно, комплексный показатель преломления:
Плоская волновая форма уравнений Максвелла
Плоская волна, выраженная в гармоническом во времени электрическом поле, может быть записана как комплекснозначное векторное поле:
где — постоянный вектор; — волновой вектор; — пространственная координата; и является независимым от времени комплексным векторным полем.
Условие плоской формы волны соответствует векторному полю в предположении, что материал изотропный.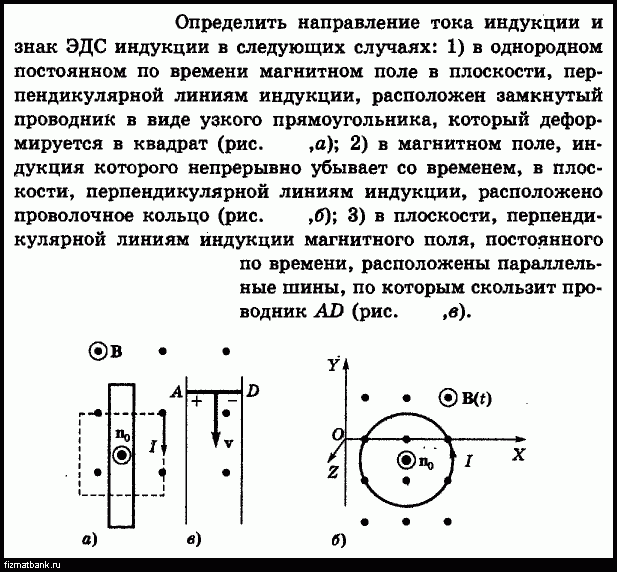
Закон Фарадея
Для линейной среды гармоническая по времени версия закона Фарадея принимает форму.
Для плоской волны мы имеем следующее векторное тождество:
, так что закон Фарадея для плоской волны принимает вид, или, что то же самое,.
Закон Максвелла – Ампера
Гармоническая по времени версия закона Максвелла – Ампера для линейной среды:
Для плоской волны в среде с изотропной однородной проницаемостью это уравнение принимает вид:
или:
Уравнение плоской волны
Теперь напишите:
и объединить в:
Некоторая манипуляция дает:
или:
Условия сбора в левой части дают:
Для материала с уравнение принимает следующий вид:
Это уравнение плоской волны, которое ограничено средами с однородной изотропной проницаемостью, как объясняется ниже.
В качестве альтернативы можно ввести комплексную диэлектрическую проницаемость:
В этом случае уравнение плоской волны принимает следующий вид:
Материальные отношения и поперечные поля
Если среда имеет анизотропную проницаемость, то из-за этого мы можем иметь это и не выровнены.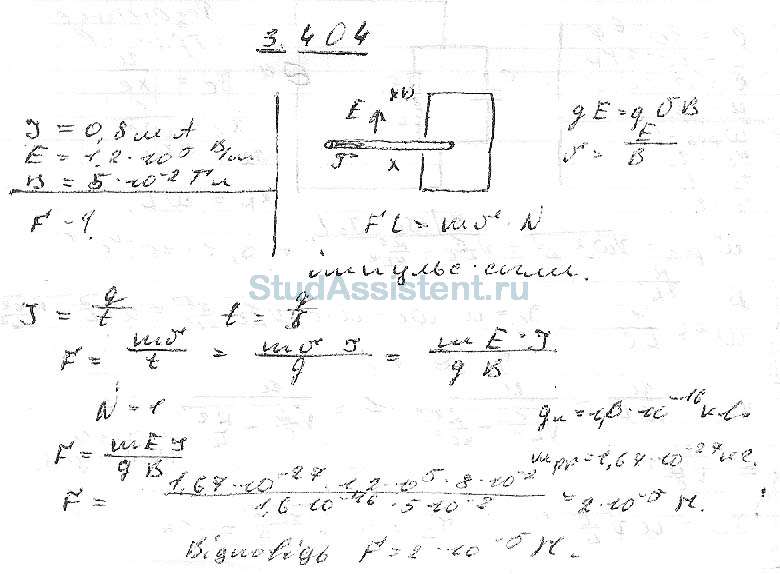 Таким образом,, и не обязательно взаимно перпендикулярны.
Таким образом,, и не обязательно взаимно перпендикулярны.
С другой стороны, и всегда выравниваются для среды с изотропной однородной проницаемостью.Согласно магнитному закону Гаусса, он утверждает, что:
так, чтобы гарантированно быть перпендикулярно обоим и.
Кроме того, поскольку и, мы имеем, что перпендикулярно обоим и.
Однако, если допустить анизотропную диэлектрическую проницаемость, то и выровняться нельзя, т.к. Это означает, что он не может быть перпендикулярным или поперечным по отношению к.
Смещено и / или смещено и соответствует волновому вектору, не выровненному с вектором Пойнтинга,.Эквивалентно, поток импульса не совмещен с вектором Пойнтинга.
Опубликовано: 13 февраля 2019 г.
Последнее изменение: 13 февраля 2019 г.
.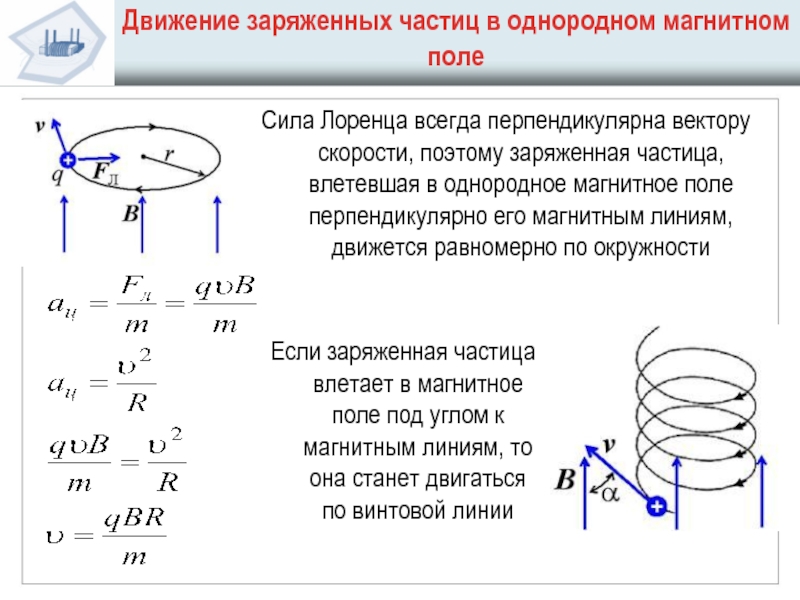

 Найдите силу
Найдите силу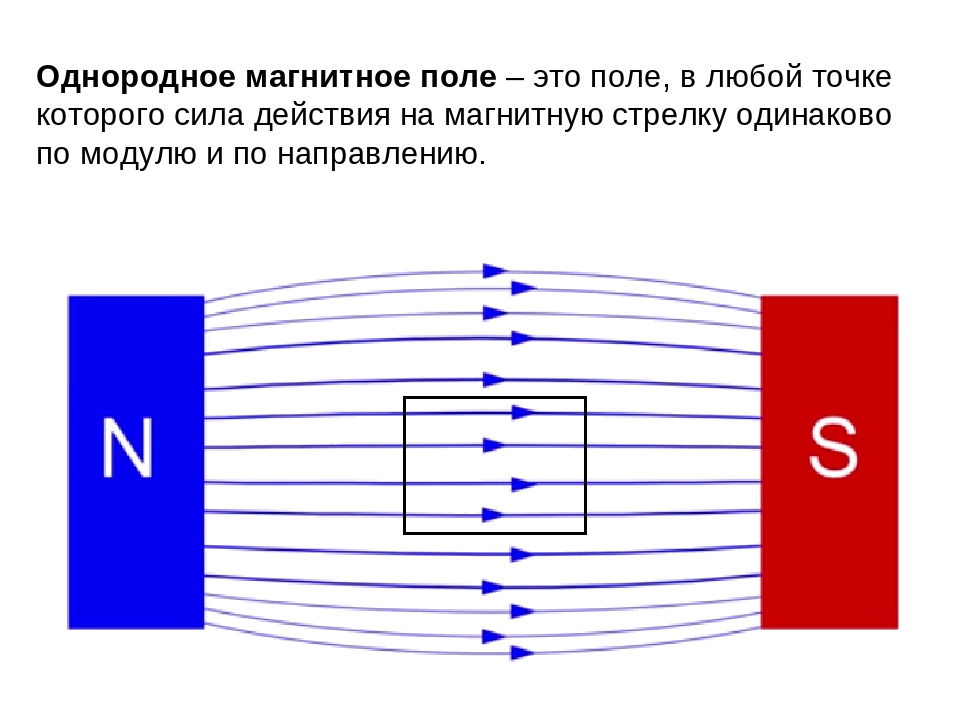
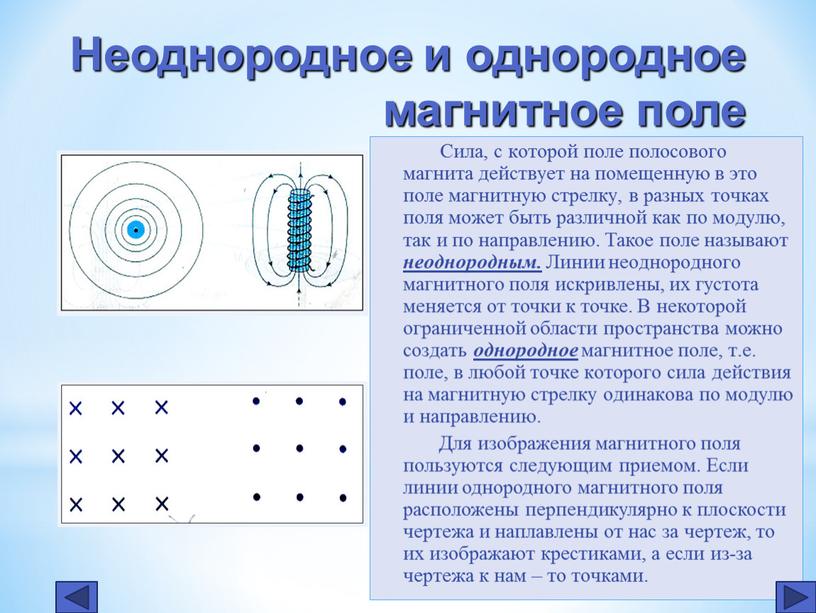 Какова напряжённость
Какова напряжённость Какова сила тока в проводнике,
Какова сила тока в проводнике,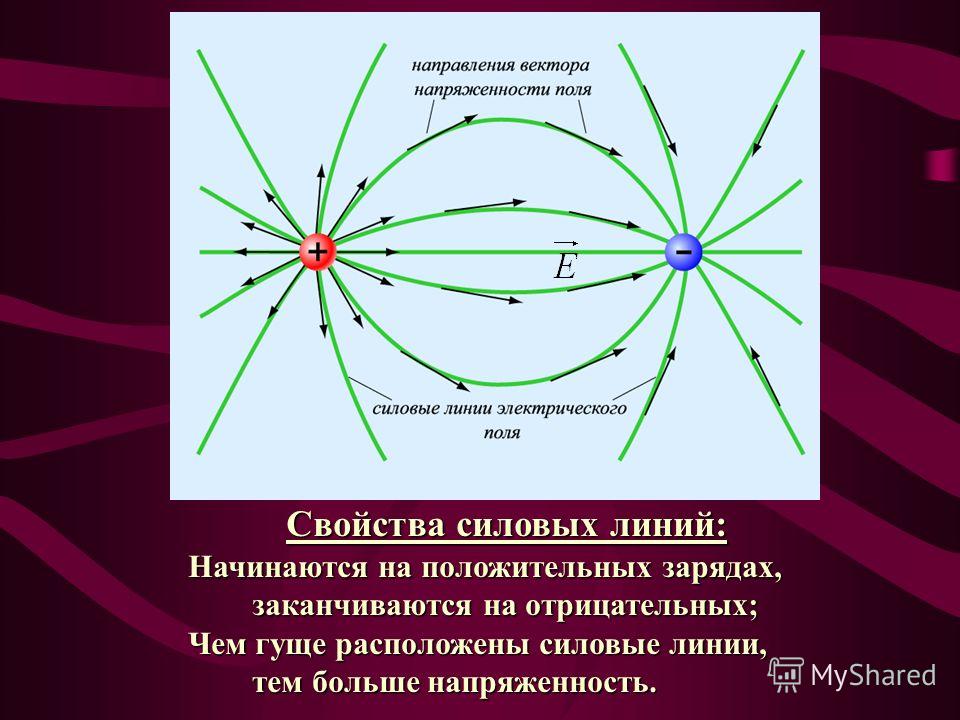
 {2}} {\ text {r}} [/ latex].
{2}} {\ text {r}} [/ latex].

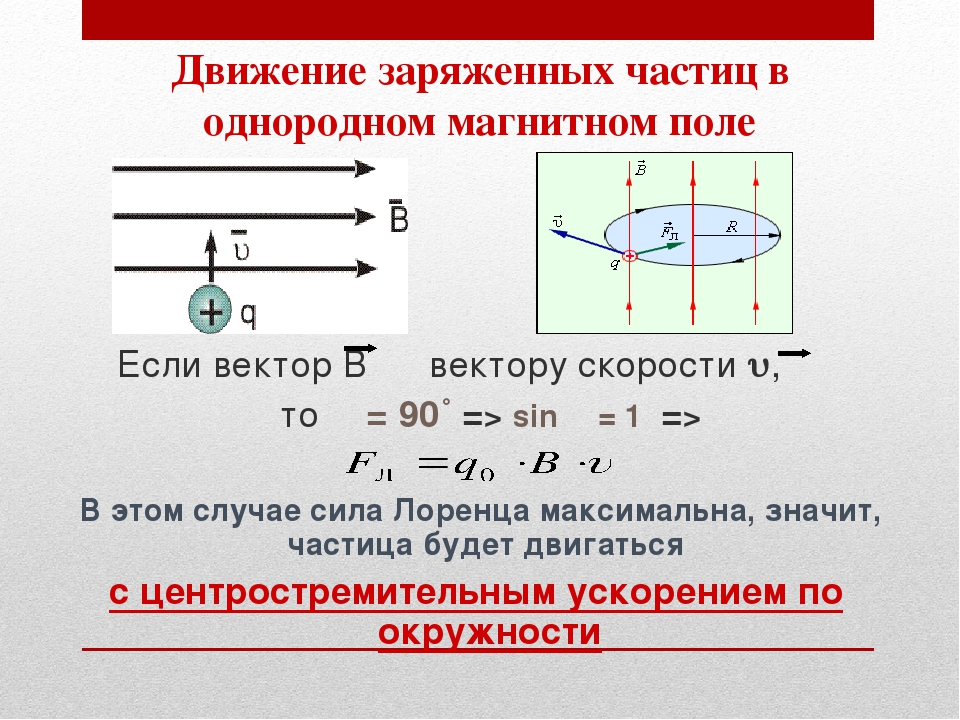 Его можно использовать для определения элементного состава молекулы или образца.
Его можно использовать для определения элементного состава молекулы или образца. org/contents/
org/contents/