1.8. Расчет цепей методом контурных токов. Определить токи в ветвях методом контурных токов
Метод контурных токов
Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах. На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I11 и I22 - контурные токи.
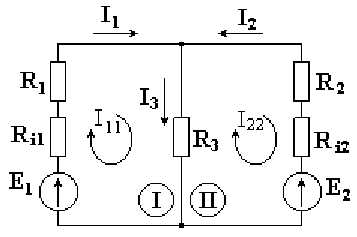Рис. 4.2 Токи в сопротивлениях R1 и R2 равны соответствующим контурным токам. Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви с R3 встречно.
Порядок расчета
Выбираются независимые контуры, и задаются произвольные направления контурных токов. В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:
Перегруппируем слагаемые в уравнениях
(4.4)
(4.5)
Суммарное сопротивление данного контура называется собственным сопротивлением контура. Собственные сопротивления контуров схемы
, .
Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.
,
где R12 - общее сопротивление между первым и вторым контурами; R21 - общее сопротивление между вторым и первым контурами. E11 = E1 и E22 = E2 - контурные ЭДС. В общем виде уравнения (4.4) и (4.5) записываются следующим образом:
, .
Собственные сопротивления всегда имеют знак "плюс". Общее сопротивление имеет знак "минус", если в данном сопротивлении контурные токи направлены встречно друг другу, и знак "плюс", если контурные токи в общем сопротивлении совпадают по направлению. Решая уравнения (4.4) и (4.5) совместно, определим контурные токи I11 и I22, затем от контурных токов переходим к токам в ветвях. Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви. В схеме на Рис. 4.2
.
Рекомендации
Контуры выбирают произвольно, но целесообразно выбрать контуры таким образом, чтобы их внутренняя область не пересекалась ни с одной ветвью, принадлежащей другим контурам. Контурные токи желательно направлять одинаково (по часовой стрелке или против). Если нужно определить ток в одной ветви сложной схемы, необходимо сделать его контурным. Если в схеме имеется ветвь с известным контурным током, этот ток следует сделать контурным, благодаря чему количество уравнений становится на единицу меньше.
4.3. Метод узловых потенциалов
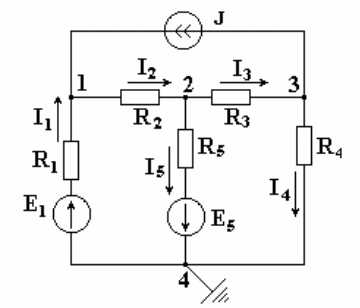Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла. Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем в схеме произвольно направления токов. Примем для схемы ?4 = 0. Рис. 4.3
Запишем уравнение по первому закону Кирхгофа для узла 1.
(4.6)
В соответствии с законами Ома для активной и пассивной ветви
,
где - проводимость первой ветви.
,
где - проводимость второй ветви.
Подставим выражения токов в уравнение (4.6).
(4.7)
где g11 = g1 + g2 - собственная проводимость узла 1.
Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле. g12 = g2 - общая проводимость между узлами 1 и 2. Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.
-сумма токов источников, находящихся в ветвях, сходящихся в узле 1. Если ток источника направлен к узлу, величина его записывается в правую часть уравнения со знаком "плюс", если от узла - со знаком "минус". По аналогии запишем для узла 2:
studfiles.net
1.8. Расчет цепей методом контурных токов.
Этот метод рационально использовать при расчете цепей с большим количеством узлов, т.к. он позволяет почти вдвое сократить количество уравнений по сравнению с методом непосредственного применения законов Кирхгофа. В методе контурных токов независимыми переменными являются контурные токи, условно замыкающиеся по элементам независимых контуров.
Чтобы найти контурные токи каждого независимого контура, необходимо составить уравнения второго закона Кирхгофа и решить полученную систему уравнений.
При расчете рекомендуется придерживаться следующей последовательности:
– выделить все независимые контуры
– указать направления обхода контуров (желательно одно и то же для всех контуров)
– указать направления контурных токов в каждом контуре (рекомендуется направления контурных токов выбирать совпадающими с направлением обхода)
– для всех независимых контуров составить уравнения второго закона Кирхгофа
– решить полученную систему уравнений любым известным методом
– по вычисленным значениям контурных токов определить величины токов в ветвях и их направления.
Рассмотрим цепь, представленную на рис. 1.10. Она имеет два независимых контура: E1R3R1E1и R3E2R2R3. Направления контурных токов и направления обхода указаны на рисунке. Нетрудно видеть, что в смежной ветви R3, которая принадлежит двум контурам сразу, протекают два контурных тока IK1и IK2, но в противоположных направлениях.
E1 = IK1 (R1 + R3) – IK2R3
– E2= –IK1R3+IK2(R2+R3)
Решение полученной системы уравнений проводится так же, как изложено выше для метода непосредственного применения законов Кирхгофа. Токи в ветвях, принадлежащих одному контуру, равны соответствующему контурному току. Если же контурный ток отрицателен, то ток в ветви, принадлежащей только этому контуру, будет равен контурному току по величине, но будет иметь противоположное направление.
Например, пусть контурные токи в ветвях цепи, представленной на рис. 1.10 равны: IK1=7 A, IK2= – 5 A. Тогда I1= IK1= 7 = 7 A и протекает в резисторе R1так же, как контурный ток IK1по схеме сверху вниз. Ток I2= – IK2= – 5 А и протекает в резисторе R2по схеме снизу вверх. Токи в смежных ветвях, принадлежащие одновременно двум контурам и по которым протекают два контурных тока, находятся как алгебраическая сумма протекающих в этих ветвях контурных токов. Направление тока в смежной ветви определяется направлением большего контурного тока в этой ветви. Например, в ветви R3 , цепи представленной на рис. 1.10, протекают контурный ток IK1= 7 А по схеме сверху вниз и контурный ток I2= – 5 А по схеме снизу вверх. IK1> IK2и I3= IK1– IK2= 7 – (–5) = 12 А. Ток I3имеет такое же направление, что и ток IK1 , т.е. по схеме сверху вниз.
1.9. Расчет цепей методом эквивалентного преобразования.
Расчет цепей методом эквивалентного преобразования применяют для цепей с одним источником электроэнергии со смешанным соединением приемников. Смешанным соединением приемников называется сочетание их последовательных и параллельных соединений.
По методу эквивалентных преобразований отдельные участки цепи с последовательным или параллельным включением приемников заменяют одним эквивалентным приемником. Постепенным преобразованием участков цепь приводят к простейшей, состоящей из одного эквивалентного элемента.
Рис. 1.11. Цепь со смешанным соединением приемников (а) и эквивалентные ей схемы (б) и (в)
Например, в цепи представленной на рис. 1.11а приемники R3и R4соединены последовательно и их можно заменить одним эквивалентным с сопротивлением
R34= R3+ R4.
После замены цепь принимает вид, представленный на рис. 1.11б, в которой приемник R2 и эквивалентный приемник R34включены параллельно. Параллельный участок R2– R34также можно заменить одним эквивалентным с сопротивлением
после чего цепь принимает вид, представленный на рис. 1.11.в, элементы которой соединены последовательно.
Входное сопротивление этой цепи R1234= R1+ R234
позволяет найти ток I1исходной цепи рис. 1.11а, пользуясь законом Ома
.
Напряжение на участке R234легко найти по закону Ома для пассивного участка цепи
U234= I1R234.
Токи в ветвях R2и R34также находятся по закону Ома
.
Токи I3= I4, т.к. приемники R3и R4включены последовательно, они равны току I34.
studfiles.net
Метод контурных токов
Метод контурных токов является одним из основных методов расчета сложных электрических цепей, которым широко пользуются на практике.
При расчете методом контурных токов полагают, что в каждом независимом контуре течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего определяют токи ветвей через контурные токи.
Таким образом, метод контурных токов можно определить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по II закону Кирхгофа, т.е. . Следовательно, этот метод более экономичен при вычислениях, чем метод уравнений Кирхгофа.
Разработаем алгоритм расчета цепей методом контурных токов на примере приведенной на рис. 2.3. схемы, в которой три независимых контура. Предположим, что в каждом контуре протекает свой контурный ток в указанном направлении. Для каждого из контуров составим уравнения по II закону Кирхгофа. При этом учтем, что по смежной ветви для контурных токов и(ветвьbd, содержащая сопротивление ) протекает ток, по смежной ветви для контурных токови(ветвьdс, содержащая сопротивление ) протекает ток, по смежной ветви для контурных токови(ветвьаd, содержащая сопротивление ) протекает ток.
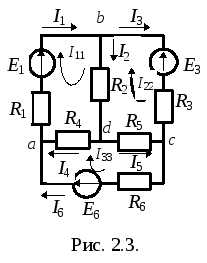
Сгруппируем слагаемые при одноименных токах:
(2.5)
Введем обозначения:
В окончательном виде система уравнений для контурных токов приобретает следующий вид:
(2.6)
в матричной форме
(2.7)
Собственное сопротивление контура (Rii) представляет собой арифметическую сумму сопротивлений всех потребителей, находящихся в i-ом контуре.
Общее сопротивление контура (Rij = Rji) представляет собой алгебраическую сумму сопротивлений потребителей ветви (нескольких ветвей), одновременно принадлежащих i-ому и j-ому контурам. В эту сумму сопротивление входит со знаком «+», если контурные токи протекают через данное сопротивление в одном направлении (согласно), и знак «–», если они протекают встречно.
Контурные ЭДС представляют собой алгебраическую сумму ЭДС источников, входящих в контур. Со знаком «+» в эту сумму входят ЭДС источников, действующих согласно с обходом контура, со знаком «–» входят ЭДС источников, действующих встречно.
Решение полученной системы удобно выполнить методом Крамера
, (2.8)
где , 1, 2, 3, – соответственно определители матриц:
(2.9)
По найденным контурным токам при помощи I закона Кирхгофа определяются токи ветвей.
Таким образом, методика расчета цепи постоянного тока методом контурных токов следующая:
Обозначить все токи ветвей и их положительное направление.
Произвольно выбрать совокупность p независимых контуров, нанести на схему положительное направление контурных токов, протекающих в выбранных контурах.
Определить собственные, общие сопротивления и контурные ЭДС и подставить их в систему уравнений вида (2.3).
Разрешить полученную систему уравнений относительно контурных токов, используя метод Крамера.
Определить токи ветвей через контурные токи по I закону Кирхгофа.
В случае необходимости, с помощью обобщенного закона Ома определить потенциалы узлов.
Проверить правильность расчетов при помощи баланса мощности.
Если в цепи содержится q источников тока, количество совместно рассматриваемых уравнений сокращается на q и становится равным р – q, поскольку токи в таких ветвях известны (для контуров с Iii = J уравнение можно не записывать). В этом случае следует выбирать такую совокупность независимых контурных токов, чтобы часть из них стала известными. Для этого необходимо, чтобы каждый источник тока входил только в один контур. Напряжения UJ источников войдут в качестве неизвестных в правые части уравнений, т.е. в состав контурных ЭДС.
Пример.
Тогда система уравнений по методу контурных токов примет следующий вид:
Причем, , решив первое уравнение, можно получить. Далее
UJ можно определить из второго уравнения системы или, составив уравнение по II закону Кирхгофа для любого контура, в который входит источник тока.
Баланс мощности:
studfiles.net
1.8. Расчет цепей методом контурных токов.
Этот метод рационально использовать при расчете цепей с большим количеством узлов, т.к. он позволяет почти вдвое сократить количество уравнений по сравнению с методом непосредственного применения законов Кирхгофа. В методе контурных токов независимыми переменными являются контурные токи, условно замыкающиеся по элементам независимых контуров.
Чтобы найти контурные токи каждого независимого контура, необходимо составить уравнения второго закона Кирхгофа и решить полученную систему уравнений.
При расчете рекомендуется придерживаться следующей последовательности:
– выделить все независимые контуры
– указать направления обхода контуров (желательно одно и то же для всех контуров)
– указать направления контурных токов в каждом контуре (рекомендуется направления контурных токов выбирать совпадающими с направлением обхода)
– для всех независимых контуров составить уравнения второго закона Кирхгофа
– решить полученную систему уравнений любым известным методом
– по вычисленным значениям контурных токов определить величины токов в ветвях и их направления.
Рассмотрим цепь, представленную на рис. 1.10. Она имеет два независимых контура: E1R3R1E1и R3E2R2R3. Направления контурных токов и направления обхода указаны на рисунке. Нетрудно видеть, что в смежной ветви R3, которая принадлежит двум контурам сразу, протекают два контурных тока IK1и IK2, но в противоположных направлениях.
E1 = IK1 (R1 + R3) – IK2R3
– E2= –IK1R3+IK2(R2+R3)
Решение полученной системы уравнений проводится так же, как изложено выше для метода непосредственного применения законов Кирхгофа. Токи в ветвях, принадлежащих одному контуру, равны соответствующему контурному току. Если же контурный ток отрицателен, то ток в ветви, принадлежащей только этому контуру, будет равен контурному току по величине, но будет иметь противоположное направление.
Например, пусть контурные токи в ветвях цепи, представленной на рис. 1.10 равны: IK1=7 A, IK2= – 5 A. Тогда I1= IK1= 7 = 7 A и протекает в резисторе R1так же, как контурный ток IK1по схеме сверху вниз. Ток I2= – IK2= – 5 А и протекает в резисторе R2по схеме снизу вверх. Токи в смежных ветвях, принадлежащие одновременно двум контурам и по которым протекают два контурных тока, находятся как алгебраическая сумма протекающих в этих ветвях контурных токов. Направление тока в смежной ветви определяется направлением большего контурного тока в этой ветви. Например, в ветви R3 , цепи представленной на рис. 1.10, протекают контурный ток IK1= 7 А по схеме сверху вниз и контурный ток I2= – 5 А по схеме снизу вверх. IK1> IK2и I3= IK1– IK2= 7 – (–5) = 12 А. Ток I3имеет такое же направление, что и ток IK1 , т.е. по схеме сверху вниз.
1.9. Расчет цепей методом эквивалентного преобразования.
Расчет цепей методом эквивалентного преобразования применяют для цепей с одним источником электроэнергии со смешанным соединением приемников. Смешанным соединением приемников называется сочетание их последовательных и параллельных соединений.
По методу эквивалентных преобразований отдельные участки цепи с последовательным или параллельным включением приемников заменяют одним эквивалентным приемником. Постепенным преобразованием участков цепь приводят к простейшей, состоящей из одного эквивалентного элемента.
Рис. 1.11. Цепь со смешанным соединением приемников (а) и эквивалентные ей схемы (б) и (в)
Например, в цепи представленной на рис. 1.11а приемники R3и R4соединены последовательно и их можно заменить одним эквивалентным с сопротивлением
R34= R3+ R4.
После замены цепь принимает вид, представленный на рис. 1.11б, в которой приемник R2 и эквивалентный приемник R34включены параллельно. Параллельный участок R2– R34также можно заменить одним эквивалентным с сопротивлением
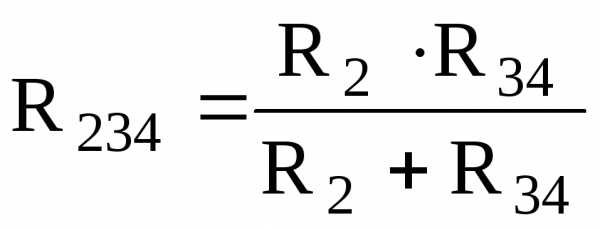
после чего цепь принимает вид, представленный на рис. 1.11.в, элементы которой соединены последовательно.
Входное сопротивление этой цепи R1234= R1+ R234
позволяет найти ток I1исходной цепи рис. 1.11а, пользуясь законом Ома
.
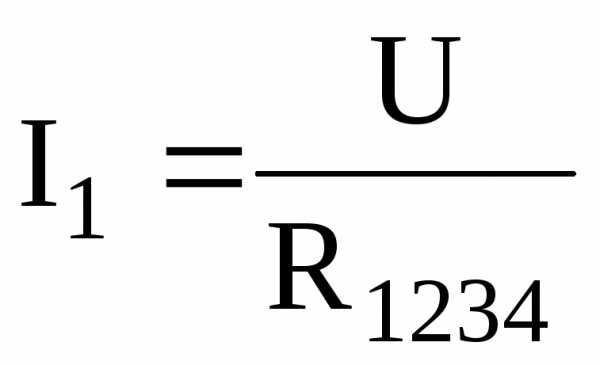Напряжение на участке R234легко найти по закону Ома для пассивного участка цепи
U234= I1R234.
Токи в ветвях R2и R34также находятся по закону Ома
.
Токи I3= I4, т.к. приемники R3и R4включены последовательно, они равны току I34.
studfiles.net
4. Анализ сложных электрических цепей с несколькими источниками энергии
4.1. Метод непосредственного применения законов Кирхгофа
На рис. 4.1 изображена схема разветвленной электрической цепи. Известны величины сопротивлений и ЭДС, необходимо определить токи. В схеме имеются четыре узла, можно составить четыре уравнения по первому закону Кирхгофа.
Укажем произвольно направления токов. Запишем уравнения::
(4.1)
Рис. 4.1
Сложим эти уравнения. Получим тождество 0 = 0. Система уравнений (4.1) является зависимой. Если в схеме имеется n узлов, количество независимых уравнений, которые можно составить по первому закону Кирхгофа, равно n - 1. Для схемы на рис. 4.1 число независимых уравнений равно трем.
(4.2)
Недостающее количество уравнений составляют по второму закону Кирхгофа. Уравнения по второму закону составляют для независимых контуров. Независимым является контур, в который входит хотя бы одна новая ветвь, не вошедшая в другие контуры. Выберем три независимых контура и укажем направления обхода контуров. Запишем три уравнения по второму закону Кирхгофа.
(4.3)
Решив совместно системы уравнений (4.2) и (4.3), определим токи в схеме. Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному нами.
Метод контурных токов
Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах. На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I11 и I22 - контурные токи.
Рис. 4.2 Токи в сопротивлениях R1 и R2 равны соответствующим контурным токам. Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви с R3 встречно.
Порядок расчета
Выбираются независимые контуры, и задаются произвольные направления контурных токов. В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:
Перегруппируем слагаемые в уравнениях
(4.4)
(4.5)
Суммарное сопротивление данного контура называется собственным сопротивлением контура. Собственные сопротивления контуров схемы
, .
Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.
,
где R12 - общее сопротивление между первым и вторым контурами; R21 - общее сопротивление между вторым и первым контурами. E11 = E1 и E22 = E2 - контурные ЭДС. В общем виде уравнения (4.4) и (4.5) записываются следующим образом:
,
.
Собственные сопротивления всегда имеют знак "плюс". Общее сопротивление имеет знак "минус", если в данном сопротивлении контурные токи направлены встречно друг другу, и знак "плюс", если контурные токи в общем сопротивлении совпадают по направлению. Решая уравнения (4.4) и (4.5) совместно, определим контурные токи I11 и I22, затем от контурных токов переходим к токам в ветвях. Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви. В схеме на Рис. 4.2
.
Рекомендации
Контуры выбирают произвольно, но целесообразно выбрать контуры таким образом, чтобы их внутренняя область не пересекалась ни с одной ветвью, принадлежащей другим контурам. Контурные токи желательно направлять одинаково (по часовой стрелке или против). Если нужно определить ток в одной ветви сложной схемы, необходимо сделать его контурным. Если в схеме имеется ветвь с известным контурным током, этот ток следует сделать контурным, благодаря чему количество уравнений становится на единицу меньше.
4.3. Метод узловых потенциалов
Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла. Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем в схеме произвольно направления токов. Примем для схемы ?4 = 0.
Рис. 4.3
Запишем уравнение по первому закону Кирхгофа для узла 1.
(4.6)
В соответствии с законами Ома для активной и пассивной ветви
,
где - проводимость первой ветви.
,
где - проводимость второй ветви.
Подставим выражения токов в уравнение (4.6).
(4.7)
где g11 = g1 + g2 - собственная проводимость узла 1.
Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле. g12 = g2 - общая проводимость между узлами 1 и 2. Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.
- сумма токов источников, находящихся в ветвях, сходящихся в узле 1. Если ток источника направлен к узлу, величина его записывается в правую часть уравнения со знаком "плюс", если от узла - со знаком "минус". По аналогии запишем для узла 2:
(4.8) для узла 3:
(4.9) Решив совместно уравнения (4.7), (4.8), (4.9), определим неизвестные потенциалы ?1, ?2, ?3, а затем по закону Ома для активной или пассивной ветви найдем токи. Если число узлов схемы - n, количество уравнений по методу узловых потенциалов - (n - 1).
Замечание.
Если в какой-либо ветви содержится идеальный источник ЭДС, необходимо один из двух узлов, между которыми включена эта ветвь, выбрать в качестве базисного, тогда потенциал другого узла окажется известным и равным величине ЭДС. Количество составляемых узловых уравнений становится на одно меньше.
4.4. Метод двух узлов
Схема на рис. 4.4 имеет два узла. Потенциал точки 2 примем равным нулю ?2 = 0. Составим узловое уравнение для узла 1.
,
,
Рис. 4.4
где , , - проводимости ветвей.
В общем виде:
.
В знаменателе формулы - сумма проводимостей параллельно включенных ветвей. В числителе - алгебраическая сумма произведений ЭДС источников на проводимости ветвей, в которые эти ЭДС включены. ЭДС в формуле записывается со знаком "плюс", если она направлена к узлу 1, и со знаком "минус", если направлена от узла 1. После вычисления величины потенциала ?1 находим токи в ветвях, используя закон Ома для активной и пассивной ветви.
4.5. Метод эквивалентного генератора
Этот метод используется тогда, когда надо определить ток только в одной ветви сложной схемы. Чтобы разобраться с методом эквивалентного генератора, ознакомимся сначала с понятием "двухполюсник". Часть электрической цепи с двумя выделенными зажимами называется двухполюсником. Двухполюсники, содержащие источники энергии, называются активными. На рис. 4.5 показано условное обозначение активного двухполюсника. Двухполюсники, не содержащие источников, называются пассивными. На эквивалентной схеме пассивный двухполюсник может быть заменен одним элементом - внутренним или входным сопротивлением пассивного двухполюсника Rвх. На рис. 4.6 условно изображен пассивный двухполюсник и его эквивалентная схема.
Рис. 4.5 Рис. 4.6
Входное сопротивление пассивного двухполюсника можно измерить. Если известна схема пассивного двухполюсника, входное сопротивление его можно определить, свернув схему относительно заданных зажимов. Дана электрическая цепь. Необходимо определить ток I1 в ветви с сопротивлением R1 в этой цепи. Выделим эту ветвь, а оставшуюся часть схемы заменим активным двухполюсником (рис. 4.7). Согласно теореме об активном двухполюснике, любой активный двухполюсник можно заменить эквивалентным генератором (источником напряжения) с ЭДС, равным напряжению холостого хода на зажимах этого двухполюсника и внутренним сопротивлением, равным входному сопротивлению того же двухполюсника, из схемы которого исключены все источники (рис. 4.8). Искомый ток I1 определится по формуле:
(4.10)
Рис. 4.7 Рис. 4.8
Параметры эквивалентного генератора (напряжение холостого хода и входное сопротивление) можно определить экспериментально или расчетным путем. Ниже показан способ вычисления этих параметров расчетным путем в схеме на рис. 4.2. Изобразим на рис. 4.9 схему, предназначенную для определения напряжения холостого хода. В этой схеме ветвь с сопротивлением R1 разорвана, это сопротивление удалено из схемы. На разомкнутых зажимах появляется напряжение холостого хода. Для определения этого напряжения составим уравнение для первого контура по второму закону Кирхгофа
,
откуда находим
, (4.11)
где определяется из уравнения, составленного по второму закону Кирхгофа для второго контура
. (4.12)
Так как первая ветвь разорвана, ЭДС Е1 не создает ток. Падение напряжения на сопротивлении Rвн1 отсутствует. На рис. 4.10 изображена схема, предназначенная для определения входного сопротивления.
.
Рис. 4.9 Рис. 4.10
Из схемы на рис. 4.9 удалены все источники (Е1 и Е2), т.е. эти ЭДС мысленно закорочены. Входное сопротивление Rвх определяют, свертывая схему относительно зажимов 1-1'
. (4.13)
Для определения параметров эквивалентного генератора экспериментальным путем необходимо выполнить опыты холостого хода и короткого замыкания. При проведении опыта холостого хода от активного двухполюсника отключают сопротивление R1, ток I1 в котором необходимо определить. К зажимам двухполюсника 1-1' подключают вольтметр и измеряют напряжение холостого хода Uxx (рис. 4.11). При выполнении опыта короткого замыкания соединяют проводником зажимы 1-1' активного двухполюсника и измеряют амперметром ток короткого замыкания I1кз (рис. 4.12).
Рис. 4.11 Рис. 4.12
откуда
(4.14)
nwpi-fsap.narod.ru
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
