Урок 28. электрическая ёмкость. конденсатор — Физика — 10 класс
Физика, 10 класс
Урок 28. Электрическая ёмкость. Конденсатор
Перечень вопросов, рассматриваемых на уроке:
- Электрическая ёмкость
- Плоский конденсатор
- Энергия конденсатора
Глоссарий по теме:
Конденсатор – устройство для накопления электрического заряда.
Электроёмкостью конденсатора называют физическую величину, численно равную отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Под зарядом конденсатора понимают модуль заряда одной из его обкладок.
Последовательное соединение – электрическая цепь не имеет разветвлений. Все элементы цепи включают поочередно друг за другом. При параллельном соединении концы каждого элемента присоединены к одной и той же паре точек.
Смешанное соединение — это такое соединение, когда в цепи присутствует и последовательное, и параллельное соединение.
Энергия конденсатора прямо пропорциональна квадрату напряжённости электрического поля внутри его:
Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения.
Основная и дополнительная литература по теме:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 321-330.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. С. 97-100.
Теоретический материал для самостоятельного изучения
Конденсатор при переводе с латиницы означает, то что уплотняет, сгущает – устройство, предназначенное для накопления зарядов энергии электрического поля. Конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга. Главной характеристикой этого прибора, является его электроёмкость, которая зависит от площади его пластин, расстояния между ними и свойств диэлектрика.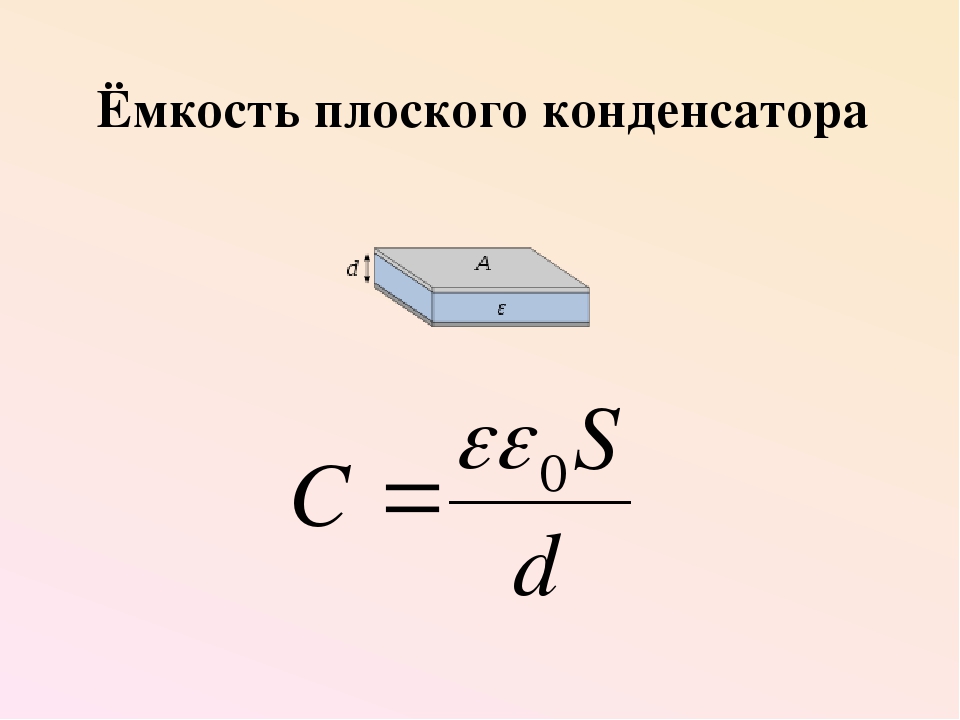
Заряд конденсатора определяется – модулем заряда на любой одной из её обкладок. Заряд конденсатора прямо пропорционален напряжению между обкладками конденсатора. Коэффициент пропорциональности С называется электрической ёмкостью, электроёмкостью или просто ёмкостью конденсатора.
Электрической ёмкостью конденсатора называется физическая величина, которая численно равна отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Чем больше площадь проводников и чем меньше пространство заполняющего диэлектриком, тем больше увеличивается ёмкость обкладок конденсатора.
Измеряется электрическая ёмкость в Международной системе СИ в Фарадах. Эта единица имеет своё название в честь английского физика экспериментатора Майкла Фарадея который внёс большой вклад в развитие теории электромагнетизма. Один Фарад равен ёмкости такого конденсатора, между пластинами которого возникает напряжение, равное одному Вольту, при сообщении заряда в один Кулон.
Электрическая ёмкость конденсаторов определяется их конструкцией, самыми простыми из них являются плоские конденсаторы.
Чем больше площадь взаимного перекрытия обкладок и чем меньше расстояние между ними, тем значительнее будет увеличение ёмкости обкладок конденсатора. При заполнении в пространство между обкладками стеклянной пластины, электрическая ёмкость конденсатора значительно увеличивается, получается, что она зависит от свойств используемого диэлектрика.
Электрическая ёмкость плоского конденсатора зависит от площади его обкладок, расстояния между ними, диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками и определяется по формуле:
где – электрическая постоянная.
Для того чтобы получить необходимую определённую ёмкость, берут несколько конденсаторов и собирают их в батарею применяя при этом параллельное, последовательное или смешанное соединения.
Параллельное соединение:
q = q1 + q2 + q3
u = u1 = u2 = u3
с = с1+с2+с3
с = n∙с
Последовательное соединение:
q = q1 = q2 = q3
u = u1 + u2 + u3
Энергия конденсатора равна половине произведения заряда конденсатора напряжённости поля и расстояния между пластинами конденсатора: u = Еd
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин, это поле совершает положительную работу. При этом энергия электрического поля уменьшается:
При этом энергия электрического поля уменьшается:
Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения:
Примеры и разбор решения заданий:
1. Плоский конденсатор, расстояние между пластинами которого равно 3 мм, заряжен до напряжения 150 В и отключен от источника питания. Разность потенциалов между пластинами возросла до 300 В.
- Во сколько раз увеличилась разность потенциалов между пластинами?
- Какое расстояние между пластинами конденсатора стало после того, как пластины были раздвинуты?
- Во сколько раз изменилось расстояние между пластинами.
Решение:
Электрическая ёмкость конденсатора определяется по формуле:
1.По условию разность потенциалов увеличилось в два раза. U1 = 150В→ U2 = 300В.
2.По условию d = 3 мм, если разность потенциалов увеличилось в два раза, по формуле соответственно и расстояние между пластинами увеличилось в два раза, и d =2·3 мм = 6 мм.
3.Расстояние между пластинами увеличилось в два раза.
Ответ:
1. 2
2. 6мм
3. 2
2. Конденсатор электроёмкостью 20 мкФ имеет заряд 4 мкКл. Чему равна энергия заряженного конденсатора?
Дано: С = 20 мкФ = 20 · 10-6 Ф, q = 4 мкКл = 4·10-6 Кл.
Найти: W.
Решение:
Энергия заряженного конденсатора W через заряд q и электрическую ёмкость С определяется по формуле:
Ответ: W = 0,4 мкДж.
как рассчитать по току и напряжению, формула
Что такое плоские конденсаторы
Определение
Конденсатор — это устройство для накопления заряда и энергии электрического поля.
Определение
Плоский конденсатор — конденсатор, который представляет собой две параллельные проводящие плоскости (обкладки), которые разделяет небольшой промежуток, заполненный диэлектриком. На обкладках сосредоточены равные по модулю и противоположные по знаку заряды.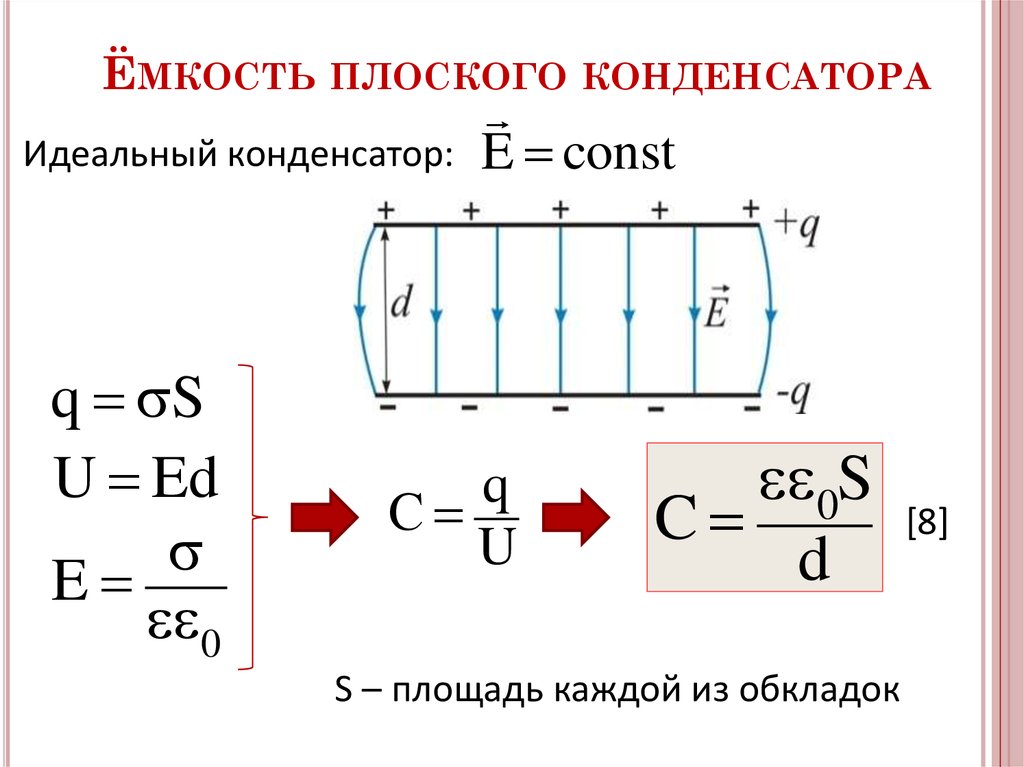
Емкость конденсатора не слишком велика, но энергия при разрядке отдается почти мгновенно. Свойство конденсаторов быстро выдавать импульс большой мощности находит применение в лампах-вспышках для фотографирования, электромагнитных ускорителях, импульсных лазерах.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Примером может служить генератор Ван де Граафа, позволяющий создавать в лабораторных условиях напряжение в миллионы вольт, чтобы моделировать разряды молний. Также конденсаторы используют в радиотехнике.
Описание и технические характеристики
Конденсатор состоит из двух проводников, разделенных слоем диэлектрика.
Простейший конденсатор — две металлические пластины-обкладки, расположенные параллельно, с тонкой прослойкой воздуха между ними. Когда заряды пластин противоположны по знаку, электрическое поле оказывается сосредоточено внутри конденсатора и почти не взаимодействует с внешним миром, что позволяет накапливать на пластинах заряд.
Конденсатор обладает следующими техническими параметрами:
- номинальной и реальной емкостью — заявленной и фактической способностью накапливать заряд;
- удельной емкостью — отношением емкости к массе или объему диэлектрика;
- плотностью энергии;
- номинальным напряжением;
- полярностью — электролитические конденсаторы требуют корректной полярности напряжения для безопасной работы;
- электрическим сопротивлением изоляции диэлектрика;
- временем самостоятельной потери заряда;
- эквивалентным последовательным сопротивлением — внутренним электрическим сопротивлением диэлектрика, материала обкладок, выводов, контактов;
- эквивалентной последовательной индуктивностью и собственной частотой резонанса;
- температурным коэффициентом емкости — относительным изменением емкости при изменении температуры окружающей среды;
- диэлектрической абсорбцией — поглощением и сохранением части заряда при быстрой разрядке;
- пьезоэффектом — генерацией напряжения на обкладках при механических деформациях.
 {-12}\;\frac Фм\).
{-12}\;\frac Фм\).Таким образом, емкость плоского конденсатора легко изменить, погрузив его в жидкость или иную среду с нужной диэлектрической проницаемостью.
Способы расчета по току и напряжению
Конденсатор — это два проводящих тела, которые разделены диэлектриком. Они несут равные по величине и противоположные по знаку заряды \(q_1\) и \(q_2 \) имеют потенциалы \(\varphi_1\) и \(\varphi_2\).
Электроемкость изолированного проводника С равна отношению изменения заряда q к изменению потенциала проводника \(\varphi.\) Их зависимость выражается формулой:\(С\;=\;\frac qU\)
Где U — разность потенциалов тел, т. е. обкладок конденсатора, или напряжение на конденсаторе.
Если порции заряда малы, для простоты расчетов можно предположить, что напряжение между пластинами не меняется. Оно вычисляется по формуле:
\( U\;=\;\varphi2\;-\;\varphi_1\)
Заряд измеряется в кулонах. Заряд и сила тока связаны следующим соотношением: один кулон равен величине заряда, прошедшего через проводник за одну секунду при силе тока в один ампер.
 Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:
Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:\(q\;=\;I\;\times\;t\)
Когда конденсатор включен в колебательный контур, то, зная период электромагнитных колебаний T и индуктивность катушки контура L, можно вычислить емкость, воспользовавшись формулой Томсона:
\(T\;=\;2\mathrm\pi\sqrt{\mathrm{LC}}\)
При решении задач часто требуется вычислить емкости каждого конденсатора в цепи параллельно или последовательно соединенных, а также напряжение на каждом из них. Чтобы составить необходимые уравнения, нужно воспользоваться формулами для вычисления общей емкости цепи.
При параллельном соединении:\({\mathrm С}_{\mathrm{общ}\;}\;=\;{\mathrm С}_1\;+\;{\mathrm С}_2\;+\;{\mathrm С}_{3\;}+\;…\;+\;{\mathrm С}_{\mathrm n}\)
При последовательном:
\(\frac{1\;}{{\mathrm С}_{\mathrm{общ}\;}}=\;\frac1{{\mathrm С}_1}\;+\;\frac1{{\mathrm С}_2}\;+\;\frac1{{\mathrm С}_{3\;}}+\;.
 ..\;+\;\frac1{{\mathrm С}_{\mathrm n}}\)
..\;+\;\frac1{{\mathrm С}_{\mathrm n}}\)Примечание
Эти формулы справедливы для любого конденсатора, не только для плоского.
Блок разноуровневых задач по физике по теме: «Электроемкость плоского конденсатора»
Блок разноуровневых задач по физике
по теме: «Электроемкость плоского конденсатора»
Семенова Галина Андреевна учитель физики ГБОУ СОШ с. Ольгино Безенчукского района Самарской области
Вступительная часть.
Предлагаемый блок разноуровневых задач предназначен для проведения тематического контроля знаний учащихся 10 класса в ходе изучения раздела «Электростатика» «Электроемкость плоского конденсатора» УМК Г.Я. Мякишева.
Блок содержит 4 задачи разных уровней сложности. Это задачи на геометрию конденсаторов и на соединение конденсаторов.
Первая задача соответствует базовому уровню подготовки выпускников, вторая задача соответствует достаточному уровню.
 Третья и четвертая задачи соответствуют высокому и превосходному уровню сложности, они рассчитаны на углубленное изучение физики. Решение данных задач предусматривают применение и актуализацию теоретических знаний учащихся, контроль качества усвоения материала. Блок содержит подробное решение каждой задачи.
Третья и четвертая задачи соответствуют высокому и превосходному уровню сложности, они рассчитаны на углубленное изучение физики. Решение данных задач предусматривают применение и актуализацию теоретических знаний учащихся, контроль качества усвоения материала. Блок содержит подробное решение каждой задачи.Цель формирования учебной ситуации: тематический контроль усвоения основных понятий в ходе изучения раздела «Электростатика» темы: «Электроемкость плоского конденсатора» учащимися 10 классов УМК Г. Я. Мякишева.
Объект учебной ситуации: электрическая емкость плоского конденсатора, подключенного или отключенного от источника тока; электрическая емкость батареи конденсаторов, соединенных последовательно или параллельно.
Внешняя среда, действующая на объект: диэлектрик; источник тока;
Взаимодействия объекта учебной ситуации с внешней средой: электрические; механические.

Блок разноуровневых задач по физике по теме «Электрическая емкость плоского конденсатора».
1 уровень: базовый.
Задача 1. Определите толщину диэлектрика плоского конденсатора, емкость которого 1400пФ, а площадь перекрывающих друг друга пластин равна 1,4 см, если диэлектрическая проницаемость диэлектрика равна 6.
Решение:
СИ
Решение:
С=1400пФ
d=1,4 см
e=6
1,4*10-9 Ф
1,4*10-2 м
Электроемкость конденсатора вычисляется по формуле: С=e eS\d , следовательно d=eeₒS\C, где eₒ -электрическая постоянная, eₒ=8,85*10-12 Кл2\(Н*м2), подставляя значения в формулу, получим: d=(6*8,85*10-12 Кл2\(Н*м2)*1,4*10-2 м)\1,4*10-9Ф=53,1*10-2м = 0,53мм
d=?
м
Ответ: d=0,53 мм
2 уровень: достаточный.

Задача 2. Два последовательно соединенных конденсатора, емкости, которых равны соответственно С1=2 мкФ и С2=4 мкФ присоединены к источнику постоянного напряжения U=120 В. Определите напряжение на каждом конденсаторе.
Решение:
СИ
Решение:
С1= 2 мкФ
С2 = 4 мкФ
Uобщ = 120 В
2* 10-6 Ф
4* 10-6 Ф
Так как конденсаторы присоединены к источнику и соединены последовательно, то их заряды одинаковы и равны, т.е. q=q1=q2.
Также при последовательном соединении общая емкость двух конденсаторов вычисляется по формуле: 1\Собщ= 1\С1+1\С2), отсюда следует, что Собщ = С1С2\(С1+С2), общее напряжение: Uобщ = U1 +U2.
Так как заряд q = CU, то, зная, что q= q1 =q2, имеем: C общU общ=C 1U1=C 2U2, отсюда: U1 = C2Uобщ\(C1+C2) =4*10-6Ф*120 В\(2*106Ф+4*10-6Ф)= 80В и U2= C1Uобщ\(C1+C2) = 2*10-6 Ф *120 В\(2*10-6 Ф+ 4*10-6) = 40 В.

U1= ? U2= ?
В
Ответ: U1 =80B и U2= 40B.
3 уровень: высокий
Задача 3. Три конденсатора одинаковой емкости зарядили до напряжений U1 =30 B, U2 = 70 B и U3=80 B, отключили от источника и соединили параллельно собой одноименными полюсами. Какое установится напряжение на батарее конденсаторов? Какое установилось бы напряжение, если бы перепутали полюса первого конденсатора?
Решение:
Решение
U1= 30 B
U2= 70 B
U3= 80 B
отключены от источника
соединены параллельно
При соединении проводников перераспределение зарядов будет продолжаться до тех пор, пока не выровняются их потенциалы, т.е. UI1=UI2 = UI3 = Uобщ. По закону сохранения заряда имеем: q1 + q2 + q3 = qI1 + qI2 + qI3 или CU1 + CU2 + CU3 = 3CUобщ, отсюда следует, что: Uобщ = (U1 + U2 + U3)\3 = (30B + 70 B+ 80 B)\3 = 60 B.

Если при соединении перепутать полюса первого конденсатора, то он будет иметь отрицательный заряд и по закону сохранения заряда получим: -q1 + q2 + q3 = qI1 + qI2 + qI3, аналогично решая, получим значения для общего напряжения: UIобщ = (-U1 + U2 + U3)\3= ( -30В +70В + 80 В)\3 = 40 B
Uобщ = ? U1общ = ?
Ответ: Uобщ = 60В; UIобщ = 40 В.
4уровень: превосходный.
Задача 4 Определите эквивалентную электрическую ёмкость в цепи, изображённой на рисунке ( а), если ёмкости конденсаторов известны.
Решение: Часто при решении задач, в которых требуется определить эквивалентную электрическую ёмкость, соединение конденсаторов не очевидно. В этом случае если удаётся определить точки цепи, в которых потенциалы равны, то можно соединить эти точки или исключить конденсаторы, присоединённые к этим точкам, так как они не могут накапливать заряд (Δφ = 0) и, следовательно, не играют роли при распределении зарядов.
 Рассмотрим два случая:
Рассмотрим два случая:1 случай. В приведённой на рисунке (а) схеме нет очевидного параллельного или последовательного соединения конденсаторов, так как в общем случае φA ≠ φB в и к конденсаторам С1 и С2 приложены разные напряжения. Однако заметим, что в силу симметрии и равенства ёмкостей соответствующих конденсаторов потенциалы точек А и В равны. Следовательно, можно, например, соединить точки А и В. Схема преобразуется к виду, изображённому на рисунке (б). Тогда конденсаторы С1, так же как и конденсаторы С2, будут соединены параллельно и Сэкв определим по формуле 1/Сэкв = 1/2С1 + 1/2С2, откуда
2 случай. Можно также просто не учитывать присутствие в схеме конденсатора СЗ, так как заряд на нём равен нулю. Тогда схема преобразуется к виду, изображённому на рисунке (в). Конденсаторы С1 и С2 соединены последовательно, следовательно,
Эквивалентные конденсаторы с С’экв соединены параллельно, так что окончательно получим такое же выражение для эквивалентной ёмкости:
Примечание: Всякое смешанное соединение конденсаторов путем упрощений может быть сведено либо к параллельному соединению, либо к последовательному.

Алгоритм расчета имеет вид:
1.Определяют эквивалентную емкость участков с последовательным соединением конденсаторов. 2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость. 3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов. 4. Рассчитывают емкость полученной схемы.
Алгоритм сворачивания схемы при смешанном соединении конденсаторов Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке :
В задачах на расчет электроемкости конденсаторов, последовательного соединения плоских конденсаторов, следует учитывать, что:
а) если плоский конденсатор подключить к источнику питания, зарядить его и затем отключить, то при изменении емкости конденсатора вследствие раздвижения (сближения) пластин, внесения диэлектрика заряд на конденсаторе не меняется;
б) если конденсатор подключен к источнику постоянного напряжения, то могут меняться величины заряда, электроемкости и др.
 , но при всех изменениях емкости остается неизменным напряжение.
, но при всех изменениях емкости остается неизменным напряжение.В задачах на систему заряженных тел (обычно плоских конденсаторов) прежде всего, необходимо установить тип соединения, и учитывать, что соединение конденсаторов может не относиться ни к последовательному, ни к параллельному.
Знание общей емкости соединения значительно упростит все дальнейшие расчеты, в последнем случае общую емкость сложного соединения можно найти просто в тех случаях, когда в схеме есть точки с одинаковыми потенциалами. Такие точки можно соединить и разъединить, распределение зарядов и потенциалов на конденсаторах от этого не изменится.
Следует также помнить, что потенциал земли и всех тел, соединенных с проводником с землей, принимается равным нулю.
2.4.2. Более сложные задачи на параллельное соединение конденсаторов рекомендуется решать, придерживаясь следующей последовательности действий:
1. Определить емкость каждого конденсатора до соединения в батарею.
2.
 Определить общую электроемкость соединения.
Определить общую электроемкость соединения.3. Найти общее напряжение после соединения.
4. Определить общий заряд после соединения.
5. Найти искомое неизвестное.
Мкость плоского конденсатора.
Электроника Мкость плоского конденсатора.
просмотров — 90
Плоским конденсатором принято называть конденсатор, обкладки которого – плоские проводящие пластины. В случае идеального плоского конденсатора (см. рис. 1.9.5), у которого обкладки – бесконечные равномерно заряженные плоскости, электрическое поле внутри конденсатора – однородное, и его напряженность вычисляется по формуле:
, (1.9.5)
где q – заряд конденсатора, S – площадь его пластин.
Разность потенциалов U между обкладками равна
, (1.9.6)
где d – расстояние между обкладками.
Пользуясь определением (1.9.4) и формулами (1.9.5) и (1.9.6), получим следующее выражение для емкости плоского конденсатора:
.
 (1.9.7)
(1.9.7)Читайте также
- — Электроемкость плоского конденсатора
Электроемкость
а) уединенного проводника:
,
где Q – заряд проводника, &… [читать подробенее] - — Тема 4. Емкость плоского конденсатора
Тема 3. Электроемкость проводника
1. На шаре сосредоточен заряд 6·10-8 Кл, а потенциал его 18 кВ. Найдите радиус шара, если он находится в вакууме.
2. До какого потенциала зарядится проводник емкостью 10 см, если ему сообщить заряд 2·10-10Кл?
3. Каким должен быть радиус шара, чтобы… [читать подробенее] - — Мкость плоского конденсатора
Сообщим обкладкам плоского конденсатора заряды +Q и –Q. Плотность заряда на обкладках станет равной , а напряжённость однородного электрического поля, возникшего в конденсаторе (см. 2.17):
.
Воспользовавшись связью напряжённости и потенциала в электрическом поле, вычислим… [читать подробенее] - — Конденсаторы.
 Электроемкость конденсатора. Электроемкость плоского конденсатора.
Электроемкость конденсатора. Электроемкость плоского конденсатора.Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов или напряжение U. Проще всего сообщить проводникам заряды, равные по модулю и противоположные по знаку. Если подключить проводники к разным… [читать подробенее]
- — Мкость плоского конденсатора.
Плоским конденсатором называется конденсатор, обкладки которого – плоские проводящие пластины. В случае идеального плоского конденсатора (см. рис. 1.9.5), у которого обкладки – бесконечные равномерно заряженные плоскости, электрическое поле внутри конденсатора –… [читать подробенее]
- — Емкость плоского конденсатора
Плоский конденсатор представляет собой две пластины, расположенные на некотором расстоянии друг от друга, пространство между которыми заполнено слоем диэлектрика.
Если площадь одной из обкладок S , а заряд на ней q ,то напряженность электрического поля между. .. [читать подробенее]
.. [читать подробенее] - — Электроемкость плоского конденсатора.
Получим формулу для емкости бесконечного плоского конденсатора. Если площадь обкладки заряд на ней , а диэлектрическая проницаемость вещества между обкладками , то напряженность поля между обкладками равна , где — поверхностная плотность заряда. Разность потенциалов… [читать подробенее]
- — Электроемкость. Конденсаторы. Емкость плоского конденсатора
Потенциал уединенного проводника пропорционален сообщенному ему заряду, поэтому отношение заряда проводника к его потенциалу не зависит от заряда и является характеристикой данного проводника.
Электроемкостью уединенного проводника называют величину, равную… [читать подробенее] - — Электроемкость плоского конденсатора
Конденсаторы
Емкость проводника изменяется, если вблизи него находятся проводящие тела. Пусть одна пластина заряжена положительно, тогда, вследствие электростатической индукции, другая пластина, находящаяся на расстоянии d, будет заряжена отрицательно.
Если… [читать подробенее] - Воздушные. Их емкость невелика, редко превышает 1000 пФ.
- Слюдяные. В нем диэлектриком служит слюда. Слюда – это минерал, кристаллическое вещество, у которого очень интересная кристаллическая структура. Атомы расположены слоями, расстояние между которыми гораздо больше, чем расстояние между атомами в одном слое. Поэтому, слюда при попытке расколоть кристалл слюды колется на очень тонкие пластинки. У них большая диэлектрическая проницаемость. Толщина пластинок получается очень маленькой. Эти пластинки хорошо работают в быстропеременных электрических полях, обладают хорошей электрической плотностью.
 Поэтому слюдяные конденсаторы получили широкое распространение.
Поэтому слюдяные конденсаторы получили широкое распространение. - Бумажные. Диэлектриком служит бумага, пропитанная парафином. Это хороший диэлектрик, но в быстро меняющихся полях ведет себя не очень хорошо, поляризуется медленно. Используются ограниченно.
- Керамические. Люди научились делать различные сорта керамики. Есть диэлектрики с проницаемостью более 1000, они сделаны из керамики. Можно получить большую емкость. Керамика хорошо работает на высоких частотах в быстропеременных электрических полях.
- Электролитические. Они имеют самую большую емкость при заданных размерах.
- Хранение аналоговых сигналов.
- Сохранение цифровых данных.
- Сфера телекоммуникационной связи.
 В этом случае главная функция — регулировка частоты, настройка профессионального оборудования.
В этом случае главная функция — регулировка частоты, настройка профессионального оборудования. - Использование при создании различных источников питания.
- Сглаживание выпрямленного напряжения на выходе устройств. Другой вопрос — в чём измеряется ёмкость конденсаторов.
- Показатель номинальной ёмкости.
- Отклонения от номинального значения.
- Номинальное напряжение. Благодаря ему проще понять, как определить ёмкость конденсатора, формула которой остаётся одинаковой.
- Рабочие температуры, постоянный и переменный ток — характеристики дополнительные, информация о них не всегда выносится на этикетку.
- Конденсаторы бывают однофазными и трёхфазными, для внутренней или наружной установки.
- Зависимость между ёмкостью и температурой.
- Потери диэлектрического характера.
- Сопротивление материала, из которого изготовлены обкладки.
- Ток утечки.
- Уровень полярности.
- Номинальное напряжение.
- Фоторопласт.
- Полистирол.
- Полипропилен.
- Полисульфон.
- Поликарбонат.

- Полиамид.
- Полиэтилентерифталат.
- Нижняя представляет собой тонкий кусок резины. Толщина его выбирается из соображений эффективности устройства. Если выбрать кусок более солидный, то значительная часть энергии будет накапливаться внутри диэлектрика на ориентацию его молекул. Что и наблюдается в современном плоском конденсаторе, куда диэлектрик помещается для увеличения электроёмкости.
- Верхняя пластина из тонкой стали кладётся сверху, когда заряд уже накоплен трением. За счёт влияния на верхней поверхности образуется избыток отрицательного заряда, и он должен быть снят на заземлитель, чтобы при расстыковке двух обкладок не произошло взаимной компенсации.

- Слюдяные.
- Воздушные.
- Электролитические (оксидные).
- Керамические.
- Вспомнить, что такое конденсатор, назначение конденсаторов и примеры конденсаторов
- Определить емкость
- Укажите уравнение, которое дает определение емкости, и уравнение для определения емкости плоского конденсатора
- Переменный конденсатор
- Электрометр
- Регулируемый блок питания
- Перемычки
- Провода электрометра
- Измерьте диаметр пластин конденсатора в сантиметрах. Ваше измерение должно быть около 17,8 см
- Разделите диаметр на 100, чтобы получить значение в метрах.Результат 0,178м. Разделите это на два, чтобы получить радиус: 0,089 м
- Площадь пластины определяется по общей формуле A=πr 2.
 Подставьте числа, чтобы получить A = π(0,089) 2 = 0,0249 м 2
Подставьте числа, чтобы получить A = π(0,089) 2 = 0,0249 м 2 - Преобразуйте расстояние между пластинами (1 мм) в метры, разделив на 1000. 1/1000 = 0,001 м.
- Используйте эти числа в формуле C = ε 0A/d, чтобы определить расчетную емкость следующим образом: C = 8,85×10 -12(0,0249)/0,001 = 2,20×10 -10. Это равно 220×10 -12F или 220pF
- Добавьте встроенную емкость электрометра (50 пФ) к теоретической емкости, чтобы получить 270 пФ.
- Запишите этот результат (270 пФ) в столбце «Расчетная емкость» и в строке 1 мм.
- Повторите этот процесс для других промежутков между пластинами. Обратите внимание, что площадь пластины одинакова для всех, поэтому все, что вам нужно сделать, это повторить шаги 5, 6 и 7, вставляя правильные значения интервала в каждом случае.
- Теперь вы рассчитаете теоретическое напряжение для каждого интервала. Мы примем напряжение 10 В для расстояния 1,0 мм, поэтому вы можете просто ввести это значение непосредственно в таблицу.
 Во-первых, вы определяете количество заряда в конденсаторе при этом расстоянии и напряжении. Используйте формулу Q=CV, чтобы определить заряд таким образом: Q=270×10-12F(10V)=2700×10-12C. Этот заряд остается одинаковым при любом расстоянии между пластинами, поэтому вы можете ввести одно и то же значение во весь столбец «Расчетный заряд»! Теперь используйте это значение заряда, чтобы определить расчетное напряжение на всех других расстояниях. Например, при расстоянии 5 мм используйте формулу V=Q/C, таким образом: V=2700×10-12C/94,0×10-12F=28,7В. Введите это значение в столбец Расчетное напряжение в строке 5 мм.
Во-первых, вы определяете количество заряда в конденсаторе при этом расстоянии и напряжении. Используйте формулу Q=CV, чтобы определить заряд таким образом: Q=270×10-12F(10V)=2700×10-12C. Этот заряд остается одинаковым при любом расстоянии между пластинами, поэтому вы можете ввести одно и то же значение во весь столбец «Расчетный заряд»! Теперь используйте это значение заряда, чтобы определить расчетное напряжение на всех других расстояниях. Например, при расстоянии 5 мм используйте формулу V=Q/C, таким образом: V=2700×10-12C/94,0×10-12F=28,7В. Введите это значение в столбец Расчетное напряжение в строке 5 мм. - Повторите тот же расчет напряжения для остальных промежутков между пластинами. Используйте расчетную емкость и постоянный заряд для каждого интервала и введите значение напряжения в столбец Расчетное напряжение таблицы.
- Поздравляем! Вы закончили предварительные расчеты! Все, что вам нужно сделать сейчас, это сделать фактические измерения!
- Поместите переменный конденсатор в центр лабораторного стола так, чтобы отметка 0 см находилась слева от вас. Не ставьте конденсатор слишком близко к краю стола!
- Поместите блок питания за переменным конденсатором. Подключите блок питания, но не включайте его.
- Подсоедините красный и черный провода перемычки к красной и черной клеммам источника питания. Просто прикрепите зажим типа «крокодил» к отверстию и оставьте другой конец провода свободным.
- Поместите электрометр слева от конденсатора.
- Прикрепите лепестковые выводы проводов электрометра к клеммам на задней стороне каждой пластины конденсатора. Красный провод идет к правой пластине, черный провод идет к левой пластине.
- Вставьте разъем BNC в электрометр.

- Установите пластины на расстоянии не менее 1 мм.Белые бамперы препятствуют тому, чтобы пластины располагались ближе друг к другу. Если пластины не параллельны друг другу, используйте регулировочные ручки в середине правой опоры, чтобы выровнять пластины. Левый край пластикового язычка, обращенный к шкале, должен быть совмещен с отметкой 1 мм.
- Убедитесь, что установка оборудования завершена и выполнена правильно.
- Полностью поверните все четыре регулятора на блоке питания против часовой стрелки.
- Поверните крайнюю левую ручку (Fine Current) в положение «12 часов» (прямо вверх!)
- Включите питание. Дисплеи должны загореться.
- Используйте ручки Fine и Coarse Voltage (две самые правые ручки), чтобы установить напряжение на 10,0 В.
- Установите пластины на минимум
- Установите электрометр на шкалу 30 В.

- Нажмите кнопку питания на электрометре. Должен загореться светодиод 30 В.
- Нажмите кнопку нуля на электрометре. Это обнуляет счетчик и гарантирует, что пластины находятся при нулевом напряжении относительно друг друга.
- На мгновение прикоснитесь проводами от источника питания к пластинам, черным к левой пластине и красным к правой пластине.
- В этот момент на электрометре должно быть 12 В (12 В — это первая небольшая отметка над «1» на нижней шкале. Если это не проверит настройку, попробуйте еще раз.Иногда приходится несколько раз прикасаться к контактам пластин, чтобы получить правильное значение 12 В.
- С этого момента вы должны быть осторожны, чтобы не касаться пластин. Если вы дотронетесь до них, вы измените заряд пластин и испортите данные!
- Следите за электрометром, чтобы убедиться, что заряд удерживается. Если вы видите падение более чем на вольт за 30 секунд, остановитесь и выясните, что не так, прежде чем продолжить.

- Переключите электрометр на настройку 100 В. Счетчик по-прежнему должен показывать 12 В, но по шкале 100 В.
- Осторожно раздвиньте пластины на расстояние 5 мм.
- Снимите показания электрометра и запишите их в таблицу в столбце «Измеренное напряжение».
- Повторите предыдущие два шага для других расстояний между пластинами и запишите соответствующие данные.
- На миллиметровой бумаге отобразите расчетную емкость по оси x (горизонтальной) в зависимости от напряжения по оси y (вертикальной).
 Нанесите расчетное значение и измеренное значение напряжения, используя разные цвета или стили линий, чтобы различить две кривые. Убедитесь, что вы выбрали подходящие масштабы и четко обозначьте оси и масштабы. Лучше всего ориентировать бумагу длинной осью в горизонтальном направлении («альбомный режим»).
Нанесите расчетное значение и измеренное значение напряжения, используя разные цвета или стили линий, чтобы различить две кривые. Убедитесь, что вы выбрали подходящие масштабы и четко обозначьте оси и масштабы. Лучше всего ориентировать бумагу длинной осью в горизонтальном направлении («альбомный режим»). - Изучите свой график и ответьте на следующие вопросы:
- Подтверждают ли ваши измеренные данные измеренные значения?
- Две кривые имеют одинаковую форму? Если да, то о чем это свидетельствует?
- Что бы вы сделали, чтобы повысить точность собираемых данных?
- Формула для энергии, запасенной в конденсаторе: U e=½CV 2.Остается ли запасенная в конденсаторе энергия постоянной при изменении расстояния между пластинами? Он идет вверх или вниз? Обсудите, откуда пришла или куда ушла энергия.
- Время активности
150 минут - Уровень
Передовой - Демонстрация: зарядка конденсатора (10 минут)
- Обсуждение: Определение емкости и фарад (20 минут)
- Студенческий эксперимент: Зарядка пропорциональна напряжению – два варианта (30 минут)
- Обсуждение: Факторы, влияющие на C (10 минут)
- Студенческий эксперимент: Факторы, влияющие на C (30 минут)
- Обсуждение: Диэлектрическая проницаемость (20 минут)
- Обсуждение: Работа с реальными конденсаторами (10 минут)
- Вопросы учащихся и обсуждение: Расчеты с реальными конденсаторами (20 минут)
- (10 -9 ) или пико- (10 -12 ) фарад.Емкость планеты Земля, рассматриваемой как изолированная сфера радиусом R , рассчитанная с использованием
- GW Parker
- электрическое поле в середине вакуумного промежутка \(E\)= 0,1127 В/Å;
- расстояние между двумя плоскостями изображения \(d\)=8,88 Å.
Плоский воздушный конденсатор. Емкость и пластины конденсатора
Две плоские пластины, находящиеся параллельно между собой, с диэлектриком внутри, образуют плоский конденсатор. Это наиболее простая модель конденсатора, накапливающая энергию разноименного заряда. Если на пластины подать заряд, одинаковый по размеру, но различающийся по модулю, то поле, а точнее его напряженность между проводниками повысится в два раза. Отношение размера заряда одного проводника к разности потенциалов между пластинами – это электроемкость.
Применение
Во всех электронных и радиотехнических устройствах, кроме микросхем и транзисторов используются конденсаторы. В разных схемах конденсаторов присутствует разное количество. Нет таких схем, где бы они не использовались. Они выполняют различные задачи: являются емкостями в фильтрах, служат передающим элементом для сигнала каскадов усиления, входят в состав частотных фильтров, для выдержки временного диапазона, для подбора частоты колебаний в генерирующих устройствах.
Конструкция и принцип действия
Устройство конденсатора заключается в двух обкладках с диэлектриком между ними. На всех схемах они так и отображаются.
S – площадь поверхности обкладок в м2, d – расстояние от обкладок, м, С – емкость, Ф, е – проницаемость диэлектрика. Все показатели выражены в системе СИ. Формула подходит плоскому конденсатору, помещают две пластины из металла с выводами, диэлектрик не нужен, так как им будет являться воздух.
Это показывает: емкость плоского конденсатора прямо зависит от площади пластин, и имеет обратную зависимость расстояния от пластин. Если геометрическая форма конденсатора иная, то формула емкости будет отличаться. Для вычисления кабеля. Но смысл зависимости остается таким же.
Пластины конденсаторов бывают и другой формы. Существуют металлобумажные конденсаторы с обкладками из алюминиевой фольги, которая свернута вместе с бумагой в клубок по форме корпуса.
Для повышения электрической прочности бумага конденсатора пропитывается специальным составом для изоляции, в основном это масло для трансформатора. Такое устройство дает возможность повысить емкость в разы. По такому же принципу сделаны конденсаторы других конструкций.
Такое устройство дает возможность повысить емкость в разы. По такому же принципу сделаны конденсаторы других конструкций.
В формуле нет ограничений на размер пластин S и расстояние d. Если пластины отодвинуть далеко, и уменьшить их площадь, то малая емкость останется. Два соседних провода имеют электрическую емкость.
В технике высокой частоты такое свойство широко применяется. Конструкцию конденсаторов выполняют дорожками на печатном монтаже или скручивают два провода в полиэтилене. Простой провод, который называют «лапшой», имеет свою емкость. Чем длиннее провод, тем больше емкость.
Все кабели еще имеют сопротивление R, кроме емкости С. Свойства распределяются по длине кабеля, во время сигналов в виде импульсов являются цепочкой интеграции RС.
Импульс искажается специально. Для этого собрана схема. Емкость кабеля влияет на сигнал. На выходе появится измененный сигнал – «колокол», при коротком импульсе сигнал совсем пропадает.
Свойства материалов-диэлектриков
В формуле значение проницаемости диэлектрика находится в знаменателе, увеличение ведет к повышению емкости. Для воздуха, лавсана, фторопласта величина не отличается от вакуумного состояния. Существуют вещества-диэлектрики, у которых проницаемость больше. Конденсатор, залитый спиртом, повышает свою емкость в 20 раз.
Для воздуха, лавсана, фторопласта величина не отличается от вакуумного состояния. Существуют вещества-диэлектрики, у которых проницаемость больше. Конденсатор, залитый спиртом, повышает свою емкость в 20 раз.
Такие вещества кроме проницаемости имеют хорошую проводимость. Конденсатор с таким веществом держит заряд хуже, разряжается быстрее. Это свойство назвали током утечки. В качестве диэлектриков применяют материалы, позволяющие создавать нормальные токи утечки при большой удельной емкости. Поэтому существует много видов конденсаторов для различных условий применения.
Накопление энергии в конденсаторе
На схеме показан конденсатор с большой емкостью для медленного течения разряда. Можно взять лампочку от фонарика и проверить работу схемы. Такую лампочку можно найти в любом магазине электротоваров. Когда переключатель SA находится во включенном состоянии, то конденсатор получает заряд от батареи через резистор. Процесс изображен на рисунке.
Напряжение повышается по кривой-экспоненте.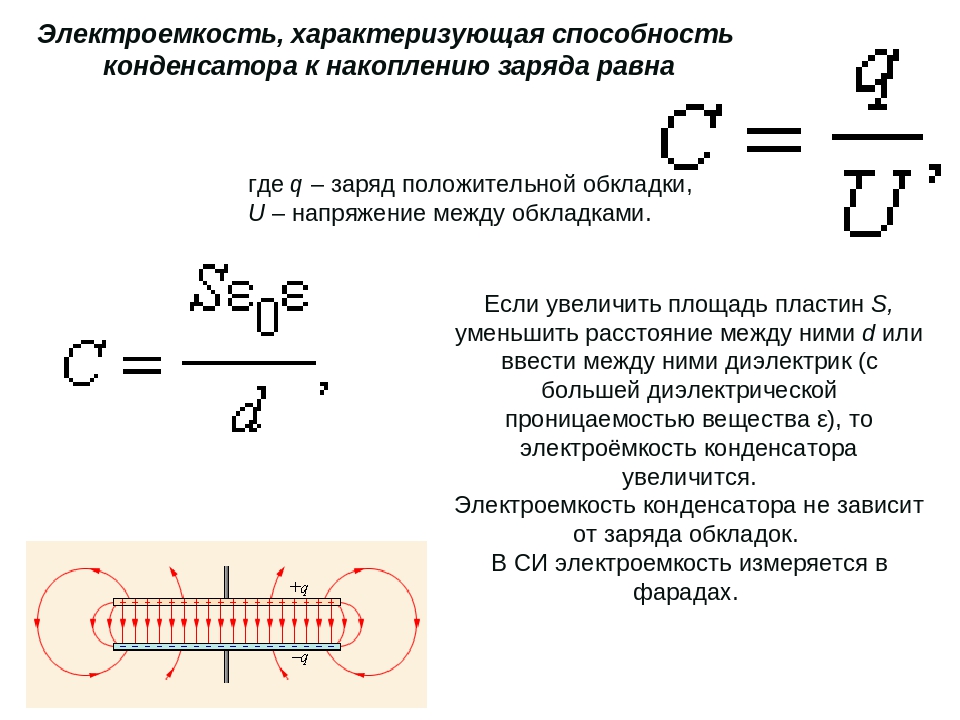 Ток отражается на графике в зеркальном виде, и имеет обратную зависимость от напряжения. Только в самом начале он подходит для приведенной формулы.
Ток отражается на графике в зеркальном виде, и имеет обратную зависимость от напряжения. Только в самом начале он подходит для приведенной формулы.
Через определенное время конденсатор получит заряд от источника до значения 4,5 вольт. Как можно вычислить время заряда конденсатора?
В формуле τ = R*C величины умножаются, итог получается в секундах. Это количество времени нужно для заряда уровня 36,8% от источника. Чтобы зарядить конденсатор полностью, нужно время = 5*т.
Если в формулу ставить емкость в мкФ, сопротивление в Ом, то время будет в микросекундах. Для нас удобнее секунды. На схеме емкость 2000 мкФ, сопротивление 500 Ом, время получается т = R * C = 500 * 2000 = 1000000 микросекунд. Это равнозначно одной секунде. В итоге, чтобы конденсатор получил полный заряд, необходимо время 5 секунд.
После этого времени переключатель переводим вправо, конденсатор разряжается по лампочке. Будет видна вспышка разряда конденсатора. Время, необходимое для разряда вычисляется величиной «т».
По схеме можно убедиться в вышеописанном утверждении.
При замыкании переключателя лампа вспыхивает — конденсатор получил заряд по лампочке. На графике видно, что в момент включения значение тока наибольшее, с течением заряда ток снижается до полного прекращения. При качественном конденсаторе и небольшой степенью саморазряда включение не выдаст вспышку лампы. Чтобы лампа снова вспыхнула, нужно разрядить конденсатор.
Любой проводник создает вокруг себя электрическое поле. Электрическое поле можно описать с помощью такой величины, как электрический потенциал. В каждой точке пространства потенциал имеет какое-то значение. Потенциал на бесконечном расстоянии равен нулю. Приближаемся мысленно от бесконечности к проводнику. Чтобы пробиться к проводнику, необходимо совершить работу. Эта работа идет на увеличение потенциальной энергии пробного заряда.
Максимальное значение потенциальная энергия достигнет тогда, когда мы вплотную подойдем к проводнику. После проникновения внутрь проводника, потенциальная энергия перестает меняться. Если мы разделим потенциальную энергию на величину пробного заряда, то получим электрический потенциал.
После проникновения внутрь проводника, потенциальная энергия перестает меняться. Если мы разделим потенциальную энергию на величину пробного заряда, то получим электрический потенциал.
Потенциал проводника зависит от заряда. Если мы удвоим заряд проводника, то потенциал так же удвоится. Потенциал проводника прямо пропорционален заряду, который несет на себе этот проводник. Отношение заряда проводника к потенциалу является характеристикой проводника, называется электрической емкостью.
Чтобы понять это определение электроемкости, представим себе высоту жидкости в сосуде, имеющим широкое дно. Высота жидкости будет мала, то есть, потенциал мал. Если сосуд узкий и высокий, то такое же количество жидкости приведет к тому, что уровень жидкости будет высоким.
Применение емкостей в фильтрах
В фильтрах емкость устанавливается в конце выпрямителя, который сделан двухполупериодным.
Такие выпрямители применяются с малой мощностью. Достоинством выпрямителей с одним полупериодом является его простота. Он состоит из трансформатора и диода. Емкость конденсатора рассчитывается по формуле:
Он состоит из трансформатора и диода. Емкость конденсатора рассчитывается по формуле:
C=1000000*Po/2 * U * f * dU, где С – емкость в мкФ, Po – мощность, ватт, U — напряжение, вольт, f – частота, герц, dU амплитуда, В.
В числителе находится большое значение, это определяет емкость в мкФ. В знаменателе число 2 – это количество полупериодов, для однополупериодного – это 1.
Классификация
По материалу диэлектрика:
Слюдяные конденсаторы
Пластинка слюды, две пластинки-электрода с прикрепленными выводами. Если вы хотите, чтобы емкость конденсатора была больше, то можно поступить следующим образом. Взять несколько пластинок слюды в качестве диэлектрика, между пластинами поместить много обкладок. Получается конденсатор, который состоит из нескольких конденсаторов, соединенных вместе, параллельно.
Воздушные конденсаторы могут быть с переменной емкостью. Они состоят из двух систем пластин.
Подвижные пластины вращающиеся, это ротор. Неподвижные – это статор. Промежутки между подвижными и неподвижными пластинами – это слой диэлектрика из воздуха. Если подвижные пластины выдвинуты из неподвижных, то эта емкость будет минимальная. Площадь перекрытия маленькая. Если пластины задвинуты, то площадь максимальная. Это воздушный конденсатор.
Существуют и керамические переменные конденсаторы. Они используются для перемены емкости в небольших пределах.
Диэлектриком служит керамика. Обкладка представляет собой покрытие из слоя серебра. Сбоку указана емкость в пФ. Отверткой вращают винт, меняется площадь перекрытия пластин. Это подстроечный керамический конденсатор.
Пишите комментарии, дополнения к статье, может я что-то пропустил. Загляните на карту сайта, буду рад если вы найдете на моем сайте еще что-нибудь полезное.
Похожее
Максимальный заряд пластины конденсатора формула
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.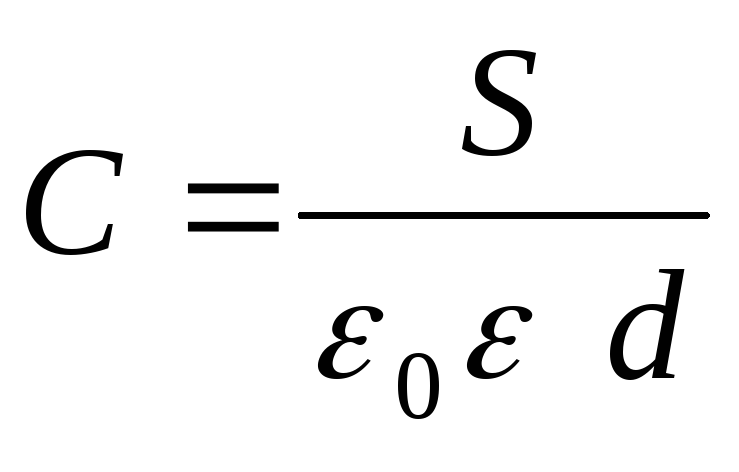
Заряд на обкладках сферического конденсатора найдем как:
где – радиусы обкладок конденсатора.
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
| Задание | Каковы заряды на обкладках конденсаторов, если они имеют емкости Ф и Ф, соединены последовательно и присоединены к батарее с ЭДС равной В (рис. 3)? Чему равен суммарный заряд соединения? 3)? Чему равен суммарный заряд соединения? |
Заряд на первом конденсаторе при этом равен:
Заряд на обкладках второго конденсатора:
Суммарный заряд системы можно найти как:
Тогда суммарный заряд равен:
| Задание | Емкость пускового устройства электрического двигателя равна C. Энергии имеющейся в конденсаторе достаточно для того чтобы поднять груз массы m на высоту h. Чему равен заряд конденсатора? |
| Решение | При поднятии груза на высоту h происходит переход энергии поля конденсатора () в потенциальную энергию тела (), поднятого над Землей, поэтому запишем: |
Энергию найдем как:
Энергию электрического поля конденсатора будет удобнее выразить:
Подставим в выражение (2. 1) правые части (2.2) и (2.3), имеем:
1) правые части (2.2) и (2.3), имеем:
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
где – радиусы обкладок конденсатора.
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
| Задание | Каковы заряды на обкладках конденсаторов, если они имеют емкости Ф и Ф, соединены последовательно и присоединены к батарее с ЭДС равной В (рис. 3)? Чему равен суммарный заряд соединения? 3)? Чему равен суммарный заряд соединения? |
Заряд на первом конденсаторе при этом равен:
Заряд на обкладках второго конденсатора:
Суммарный заряд системы можно найти как:
Тогда суммарный заряд равен:
| Задание | Емкость пускового устройства электрического двигателя равна C. Энергии имеющейся в конденсаторе достаточно для того чтобы поднять груз массы m на высоту h. Чему равен заряд конденсатора? |
| Решение | При поднятии груза на высоту h происходит переход энергии поля конденсатора () в потенциальную энергию тела (), поднятого над Землей, поэтому запишем: |
Энергию найдем как:
Энергию электрического поля конденсатора будет удобнее выразить:
Подставим в выражение (2. 1) правые части (2.2) и (2.3), имеем:
1) правые части (2.2) и (2.3), имеем:
В схемах электронных устройств конденсаторы выполняют большое количество полезных функций. Хотя конструкция этих приспособлений остаётся максимально простой. Но надо внимательно изучить ёмкость конденсатора и сами устройства, чтобы узнать, какого эффекта можно от них добиться.
Что это такое
Конденсатор — устройство, внутри которого сгущается или собирается электрический заряд в определённых количествах. Можно назвать это приспособление своеобразным аккумулятором. Отличие от существующих аналогов — в готовности сразу отдать всё накопленное, буквально в несколько секунд. Ещё одна отличительная черта — отсутствие внутри источника ЭДС. Как найти ёмкость, будет рассказано далее.
Для чего нужен
Эти устройства отличаются также широкой сферой применения. Вот лишь некоторые допустимые варианты:
Ещё одна возможная функция — генерация высокого напряжения, которое во много раз больше по сравнению с входными параметрами. Конденсаторы могут быть отличным хранилищем для электронов. Даже при отключении цепи от заряда энергия продолжает сохраняться внутри, на протяжении длительного времени.
Принцип действия
Основные элементы любого конденсатора — это две проводящие обкладки. У каждой из них — свой электрический заряд, знаки у них противоположные. Этот заряд сохраняется благодаря диэлектриком, который разделяет обкладки.
В конденсаторах используется несколько разновидностей материалов в качестве изоляции. Это касается таких решений:
Воздух вместе с бумагой и пластиком тоже популярные материалы, с помощью которых создают конденсаторы.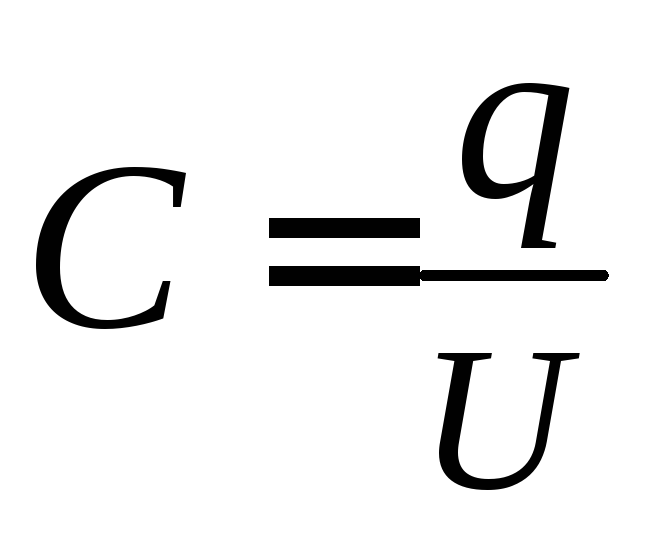 Благодаря их применению обкладки внутри не соприкасаются друг с другом.
Благодаря их применению обкладки внутри не соприкасаются друг с другом.
Характеристики
На корпусе устройства обычно пишут о том, какие параметры для него характерны. Из других важных сведений из маркировки — дата выпуска, наименование фирмы производителя, тип конденсатора.
Интересно. Один из самых важных. ГОСТ 2.702 — основной документ, регулирующий это направление. На схемах без указания единиц измерения пишут ёмкость, если она находится в пределах от 0 до 9 999 пФ. Если диапазон больше — то о микрофарадах обязательно упоминают. На самом конденсаторе соответствующая маркировка тоже стоит.
Для работы рекомендуется брать конденсаторы, у которых есть некоторый запас относительно данного параметра. С меньшим значением применять приборы не рекомендуют. Иначе диэлектрик пострадает от пробоя, устройство выйдет из строя раньше указанного времени.
Иначе диэлектрик пострадает от пробоя, устройство выйдет из строя раньше указанного времени.
Величина заряда конденсатора
Как уже говорилось, конденсаторы — это электронные устройства, главное предназначение которых — накопление заряда в определённых количествах. Эта способность зависит от другой главной характеристики, получившей название ёмкости.
Её можно определить по формуле:
Это как соотношение между количеством электрического заряда и напряжением. Самое простое объяснение, какой может быть ёмкость конденсатора, формула через площадь у которой несколько иная.
В чём измеряется
Для этого используются величины, названные фарадами и микрофарадами. В честь учёного, который открыл соответствующее явление.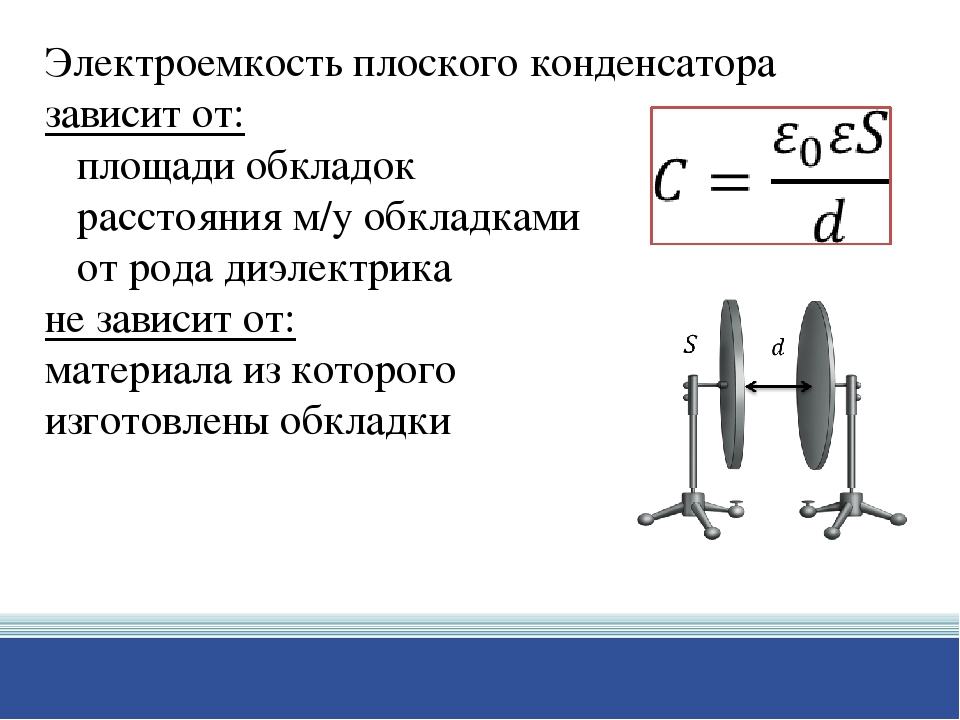
Формула ёмкости
Основная формула уже была описана выше. Ёмкость относят к величинам постоянного характера. Её определяют другие параметры, например — размер конденсатора, конструктивные особенности.
За единицу ёмкости принимают ёмкость конденсатора, которому хватает единичного заряда для получения разности потенциалов в 1 Вольт. Определять конечные цифры благодаря этому очень просто.
Плоского
Обычно между обкладками внутри плоского конденсатора создаётся так называемое однородное поле. Только около краёв подобное свойство может быть нарушено. Этими эффектами у краёв часто пренебрегают, когда организуют расчёты. Но такой подход допустим, только если расстояние между пластинами достаточно маленькое по сравнению с линейными размерами.
Плоский конденсатор отличается ёмкостью, которую считают по формуле:
E0 — постоянная электрическая величина.
S — площадь каждой пластины. Часто учитывают детали конструкции с минимальной площадью.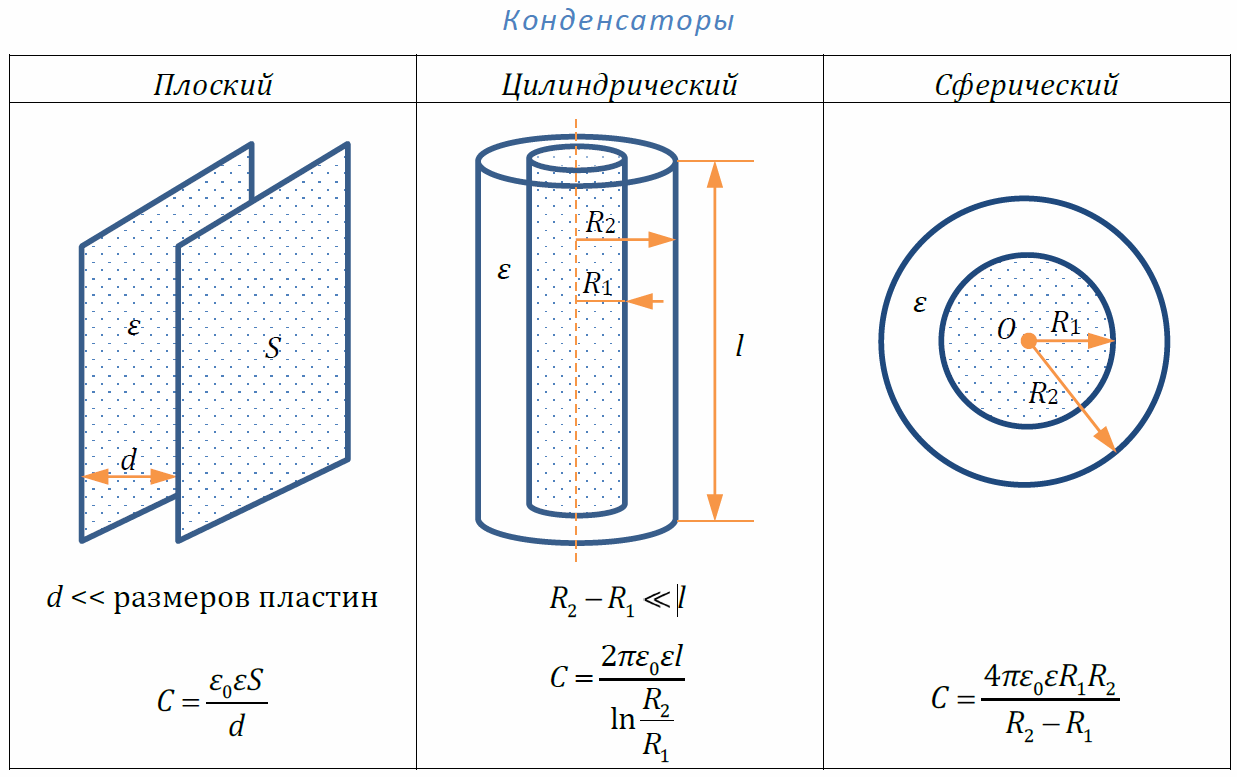
D — обозначение расстояния между пластинами.
Другое дело — когда конструкцию строят на нескольких слоях диэлектрика. Тогда их тоже включают в формулу, обычно добавляют к знаменателю. Без объёма в такой ситуации тоже не обойтись.
Сферического
Сферический — это конденсатор, обкладки которого выполнены в виде двух сферических проводящих поверхностей. Диэлектрик заполняет пространство между указанными выше деталями. В таком случае формула в знаменателе содержит дополнительные обозначения R — радиус каждой из пластин.
Цилиндрического
В данном случае пластины выглядят как две соосные или коаксиальные цилиндрические поверхности с проводящим эффектом. При этом радиус у каждого элемента разный. И здесь пространство между разными частями заполнено диэлектриком. L — обозначение высоты цилиндра. И к формуле добавляют символ для диаметра. Его измеряют отдельно для обкладки внутри и снаружи.
Как с помощью закона Гаусса рассчитать ёмкость конденсатора?
Главное — чтобы изначально присутствовала ёмкость с заданной геометрией у конденсатора. Остаётся вставить в стандартную формулу разность между потенциалами. Благодаря этому уменьшается общий уровень нагрузки, который обозначают как Q.
Остаётся вставить в стандартную формулу разность между потенциалами. Благодаря этому уменьшается общий уровень нагрузки, который обозначают как Q.
Соотношения между полями E и V применяют для поиска характеристик, которые остались неизвестными для формулы. Закон Гауса — универсальный инструмент, упрощающий любые вычисления в этой сфере. Измеряться так могут многие показатели.
Эксплуатационные характеристики
Не идеальные, но реальные конденсаторы обладают рядом дополнительных характеристик помимо тех, о которых сказано выше. Среди них:
Важно разобраться, какой источник может быть у потерь. Но для этого необходимо разобраться с таким понятием, как графики синусоидного тока, различные направления этого вида энергии. В обкладках ток равен нулю, когда конденсатор набрал максимальный заряд. Напряжение в этом случае у изделия отсутствует. То есть, по фазе напряжение вместе с током сдвигаются на угол в 90 градусов. Идеальная ситуация — когда у конденсатора появляется только реактивная мощность.
В обкладках ток равен нулю, когда конденсатор набрал максимальный заряд. Напряжение в этом случае у изделия отсутствует. То есть, по фазе напряжение вместе с током сдвигаются на угол в 90 градусов. Идеальная ситуация — когда у конденсатора появляется только реактивная мощность.
Важно. Но реальность такова, что у обкладок появляется собственное сопротивление. Часть энергии нужна, чтобы температура диэлектрика повысилась до определённого уровня. Из-за этого и появляются потери внутри конструкции. Эта характеристика в большинстве случаев остаётся незначительной, но в некоторых ситуациях пренебрегать ей не получится.
Тангенс угла диэлектрических потерь — главная единица измерения, применяемая в этом случае. Это соотношение между активной и реактивной разновидностями мощности. Измерение величины возможно, но только в теоретическом плане. Иначе рассчитать результаты невозможно.
Каким ещё бывает техническое исполнение конденсаторов?
Постоянные и переменные, подстроечные — группы конденсаторов, которые выделяются в зависимости от возможности регулировать основные рабочие параметры. Форма позволяет выделить плоские и цилиндрические, сферические разновидности. Но тип диэлектрика — главное свойство, по которому чаще всего проводят классификацию.
Форма позволяет выделить плоские и цилиндрические, сферические разновидности. Но тип диэлектрика — главное свойство, по которому чаще всего проводят классификацию.
Бумажные
Бумага, чаще всего — промасленная — вот главный диэлектрик для таких ситуаций. Конденсаторы данного вида известны крупными габаритами. Без промасливания можно изменить характеристику в меньшую сторону. Обычно служат устройствами со стабилизирующей и накопительной функциями. Но из современной электроники их всё чаще вытесаняют плёночные аналоги, которые считают более современными.
Если промасливание отсутствует, появляется серьёзный недостаток — реакция на влажность воздуха, даже если упаковка остаётся абсолютно герметичной. Энергопотери увеличиваются при наличии промокшей бумаги.
Диэлектрики-органические плёнки
Выполняются из органических полимеров, например:
Размеры таких конденсаторов более компактные, если сравнить с предыдущим вариантом. При этом диэлектрические потери не становятся больше, даже если влажность увеличивается. Но при перегреве многие устройства часто выходят из строя. А если недостаток отсутствует — приобретение прибора связано с дополнительными расходами.
Твёрдые неорганические материалы
Примеры — стекло и керамика, слюда.
Стабильность, линейность указанных характеристик — главное преимущество. Некоторые устройства реагируют даже на уровень радиации окружающей среды. Но иногда такая зависимость может стать и проблемой. Чем менее выражены недостатки — тем дороже стоит устройство.
Оксидные диэлектрики
Подходят для производства танталовых и твердотельных конденсаторов, моделей из алюминия. Отличаются такой характеристикой, как полярность. При неправильном подключении могут быстро выйти из строя. То же касается ситуации с высоким номиналом напряжения. Но зато это компактные устройства со стабильной работой, достаточными показателями по ёмкости. Могут проработать около 60 тысяч часов, если эксплуатировать устройство правильно.
Но зато это компактные устройства со стабильной работой, достаточными показателями по ёмкости. Могут проработать около 60 тысяч часов, если эксплуатировать устройство правильно.
Маркировка конденсаторов
Ёмкость вместе с номинальным напряжением — характеристики, которые должны быть отражены в маркировке. Ещё применяют циферно-буквенную разновидность обозначений для основных параметров.
Интересно. В российской практике существует четыре буквы для обозначения устройств.
Первая буква К позволяет понять, что перед покупателем — именно конденсатор. Далее идёт цифра для обозначения разновидности применяемого диэлектрика. Следующим указывают назначение, тоже в виде буквы. Последние значки могут иметь разное назначение.
Выбор и эксплуатация
Главное — использовать приборы в режимах, не превышающих номинальные значения. Тогда никаких дефектов и проблем появиться не должно.
Обратите внимание. Электрохимические процессы диэлектрика — главная причина старения основных элементов при воздействии постоянного напряжения. Причина — постоянный ноль, увеличение влажности и температуры в окружающей среде. Вид диэлектрика, конструктивное исполнение определяют, как поведёт себя то или иное устройство в этих условиях.
Причина — постоянный ноль, увеличение влажности и температуры в окружающей среде. Вид диэлектрика, конструктивное исполнение определяют, как поведёт себя то или иное устройство в этих условиях.
Ионизационные процессы станут причиной старения в случае с переменным напряжением, импульсными режимами.
Защищённые керамические конденсаторы считаются наиболее прочными и надёжными моделями из всех. Либо стоит отдавать предпочтение оксидно-полупроводниковым вариантам. Каждый из них гарантирует максимальный срок службы.
Со временем любой конденсатор теряет ёмкость. Это нормальный процесс, проходящий в оборудовании. Поэтому не рекомендуется размещать устройства с другими предметами, которые подвержены сильному нагреву. Электролиты могут стать слабым местом для любой электроники. Качество детали во многом зависит от того, какого выбрать производителя. Но такая проблема заслуживает отдельного разговора.
Площадь обкладки конденсатора.
 Наука техника технологии
Наука техника технологии
Плоский конденсатор состоит из двух
параллельных пластин, разделённых
небольшим зазором шириной
,
заполненным однородным диэлектриком.
Нам известно, что поле между двумя
разноимённо заряженными пластинами с
одинаковой по величине поверхностной
плотностью
равно,
где,S– площадь каждой пластины.
Напряжение между обкладками:
Используя
определение емкости конденсатора,
получаем:
Отметим, что полученная формула является
приближенной, так как выведена без учета
искажения поля у краев пластин. Расчет
по этой формуле дает завышенное значение
ёмкости и тем точнее, чем меньше зазор
по сравнению с линейными размерами
пластин.
Ёмкость сферического конденсатора.
Сферический конденсатор представляет
собой систему двух концентрических
сфер с радиусами
и.
Электрическое поле между обкладками
сферического конденсатора согласно
теореме Гаусса определяется зарядом
внутренней сферы. Напряжение между
обкладками равно:
.
Для
ёмкости сферического конденсатора
получаем:
Это
формула точная.
Если
,
полученная формула переходит в выражение
для ёмкости плоского конденсатора.
Ёмкость
цилиндрического конденсатора.
Цилиндрический конденсатор составляет
систему двух коаксиальных цилиндров с
радиусами
и,
длиной.
Рассуждая
аналогично выводу ёмкости сферического
конденсатора, получаем:
..
Полученная формула является приближенной
и при малом зазоре
переходит в формулу емкости плоского
конденсатора.
Соединение
конденсаторов.
В практике для получения необходимых
значений емкости используют соединения
конденсаторов: а) последовательное, б)
параллельное, в) смешанное (см. рисунок).
Ёмкость
последовательного соединения
конденсаторов.
Заряды последовательно соединенных
конденсаторов равны
,
а напряжение на батарее.
Из определения емкости следует:
Если
,
то(ёмкость последовательного соединения
меньше наименьшей ёмкости в последовательном
соединении).
Для
последовательно соединенных конденсаторов
емкость вычисляется по формуле:
Ёмкость
параллельного соединения конденсаторов.
Заряд
батареи равен сумме зарядов:
а
напряжение
.
По определению емкости получаем:
Для
параллельно соединенных конденсаторов:.
В
случае одинаковых конденсаторов:
.
Оценить
емкость батареи (см. рисунок)
.
Используя
свойство бесконечности можно представить
цепь в виде соединения (см. рисунок).
Для
расчета ёмкости батареи получаем:
Откуда:
,
так как,
то.
Лекция 7.
Диэлектрики
в электрическом поле.
Диэлектриками (изоляторами) называют
вещества, не проводящие постоянного
электрического тока. Это означает, что
в диэлектриках отсутствуют «свободные»
заряды, способные перемещаться на
значительные расстояния.
Диэлектрики состоят либо из нейтральных
молекул, либо из ионов, находящихся в
узлах кристаллической решетки. Сами же
молекулы могут быть полярными
инеполярными.
Полярные молекулы
обладают дипольным моментом, у неполярных
молекул дипольный момент равен нулю.
Поляризация.
В электрическом поле диэлектрики
поляризуются. Это явление связано с
появлением в объеме и на поверхности
диэлектрика «связанных
» зарядов.
При этом конечный объем диэлектрика
приобретает дипольный момент. Механизм
поляризации связан с конкретным строением
диэлектрика. Если диэлектрик состоит
из неполярных молекул, то в пределах
каждой молекулы происходит смещение
зарядов – положительных по полю,
отрицательных против поля, т.е. молекулы,
приобретают дипольный момент. У
диэлектрика с полярными молекулами в
отсутствии внешнего электрического
поля их дипольные моменты ориентированы
хаотично.
Под действием электрического поля
диполи ориентируются преимущественно
в направлении поля. Рассмотрим подробнее
этот механизм (см. рисунок). Пара сил
исоздает
вращательный момент равный,
где-
дипольный момент молекулы. Этот момент
стремится ориентировать диполь вдоль
поля. В ионных кристаллах под действием
В ионных кристаллах под действием
электрического поля все положительные
ионы смещаются по полю, отрицательные
– против поля. Отметим, что смещение
зарядов очень малы даже по сравнению с
размерами молекул. Это связано с тем,
что напряженность внешнего электрического
поля обычно много меньше напряженности
внутренних электрических полей в
молекулах.
Отметим, что существуют диэлектрики,
поляризованные даже при отсутствии
внешнего поля (электреты, сегнетоэлектрики).
Мы остановимся на рассмотрении только
однородных диэлектриков, в которых
отсутствует остаточная поляризация, а
объемный и «связанный» заряд всегда
равен нулю
.
Плоский конденсатор – это физическое упрощение, взявшее начало из ранних исследований электричества, представляющее собой конструкцию, где обкладки имеют форму плоскостей и в каждой точке параллельны.
Формулы
Многие ищут формулы, описывающие ёмкость плоского конденсатора. Если это так, то не читайте ниже любопытные и малоизвестные факты, потому что сухие математические знаки, конечно же, важнее.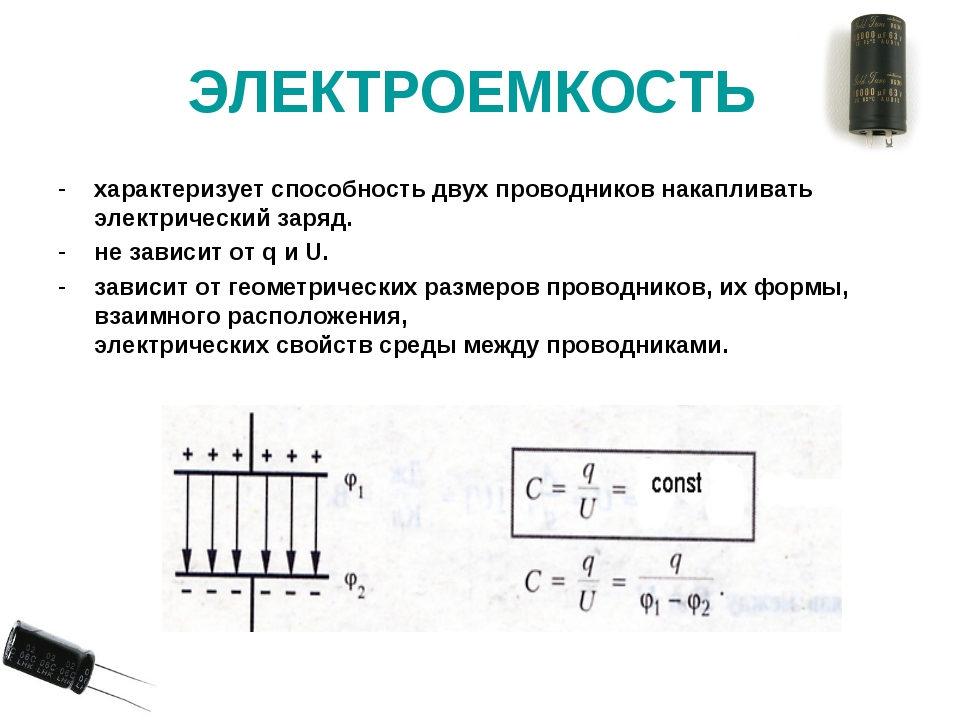
Первым определил ёмкость плоского конденсатора Вольта. В его распоряжении ещё не было такой величины, как разница потенциалов, именуемая напряжением, но интуитивно он совершенно правильно объяснил суть явления. Что касается количества зарядов, то он трактовал её, как объем электрического флюида атмосферы – не совсем правильно, но в конечном итоге похоже на правду. Согласно этому мировоззрению ёмкость плоского конденсатора может быть найдена, как отношение объёма накопленного электрического флюида к разнице атмосферных потенциалов, то есть:
Эта формула применима к любому конденсатору, вне зависимости от его конструкции. То есть, является универсальной. Специально для плоских конденсаторов имеется формула ёмкости, выраженная через свойства материала диэлектрика и геометрические размеры:
В этой формуле через S обозначена площадь обкладок, вычисляемая через произведение сторон, а d – показывает расстояние между обкладками. Прочие символы – электрическая постоянная (8,854 пФ/м) и диэлектрическая проницаемость материала диэлектрика, да простит Тот столь откровенные тавтологии. Электролитические конденсаторы обладают столь большой ёмкостью по той причине, что проводящий раствор отделен от металла очень тонким слоем оксида. Следовательно, d в этом случает будет минимальным. Единственный минус в том, что электролитические конденсаторы полярные, их нельзя подключать в цепи переменного тока. С этой целью на каждом анод или катод обозначены значками плюса или минуса.
Электролитические конденсаторы обладают столь большой ёмкостью по той причине, что проводящий раствор отделен от металла очень тонким слоем оксида. Следовательно, d в этом случает будет минимальным. Единственный минус в том, что электролитические конденсаторы полярные, их нельзя подключать в цепи переменного тока. С этой целью на каждом анод или катод обозначены значками плюса или минуса.
Плоские конденсаторы сегодня редко встречаются, и это преимущественно плёночные микроскопические технологии, где такой род поверхностей является доминирующим. Все пассивные и активные элементы образуются через трафарет. И, следовательно, имеют вид плёнок. Плоские индуктивности, резисторы и конденсаторы наносятся в виде токопроводящих паст.
От материала диэлектрика ёмкость зависит по той причине, что у каждого из них структура своя. Считается, что аморфное вещество состоит из неориентированных диполей, упруго укреплённых на своих местах. При приложении внешнего электрического поля они обратимо ориентируются вдоль силовых линий, ослабляя напряжённость. В результате заряд продолжает накапливаться, пока этот процесс не прекратится. По мере выхода энергии из обкладок диполи возвращаются на свои места, делая возможным следующий рабочий цикл. Так функционирует плоский электрический конденсатор.
В результате заряд продолжает накапливаться, пока этот процесс не прекратится. По мере выхода энергии из обкладок диполи возвращаются на свои места, делая возможным следующий рабочий цикл. Так функционирует плоский электрический конденсатор.
Из истории
Исторически первым начал исследовать накопление заряда великий Алессандро Вольта. В докладе Королевскому научному обществу за 1782 год он впервые озвучил слово конденсатор. В понимании Вольты электрофорус, представляющий собой две параллельные обкладки, выкачивал из эфира электрический флюид.
В то время все познания сводились к тому, что учёные думали, будто атмосфера Земли содержит в себе нечто, что не может быть определено приборами. Существовали только простейшие электроскопы, способные определить знак заряда и его наличие, но не дававшие представления о количестве. Учёные просто натирали мехом поверхность тела и подносили его для исследования в область влияния прибора. Ещё Гильберт показал, что электрические и магнитные взаимодействия ослабевают с расстоянием. Поэтому учёные примерно знали, что нужно делать, но исследования не продвигались ни на йоту.
Поэтому учёные примерно знали, что нужно делать, но исследования не продвигались ни на йоту.
Гипотеза об атмосферном электричестве высказана Бенджамином Франклином. Он активно исследовал молнии и пришёл к выводу, что это проявления все той же единой силы. Запуская воздушного змея в небо, он соединял его шёлковой нитью с землёй и наблюдал дуговой разряд. Это были достаточно опасные опыты, и Бенджамин много раз рисковал своей жизнью ради развития науки. О том, что шёлковая нить проводит статический заряд, было известно от Стивена Грея, первым собравшего в 1732 году электрическую цепь.
Уже через 20 лет (1752 год) Бенджамин Франклин предложил конструкцию первого громоотвода, осуществлявшего молниезащиты близлежащих построек. Только вдуматься! – до этого всякий мог ожидать того, что его дом сгорит от случайного удара. Именно Бенджамин Франклин предложил один из видов заряда называть положительным (стеклянный), а другой отрицательным (смоляной). Так физики были введены в заблуждение относительно истинного направления движения электронов.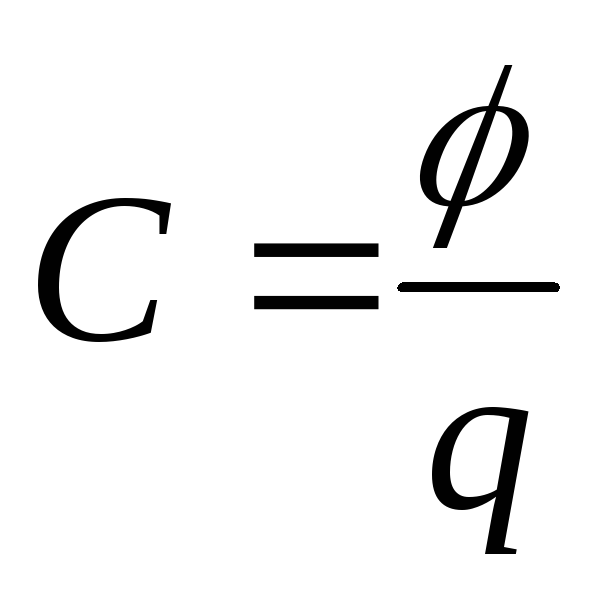 Но как они могли думать иначе, когда в 1802 году на примере опытов нашего соотечественника Петрова увидели, что на аноде образуется ямка? Следовательно, положительные частицы переносили заряд на катод, вот только это были ионы воздушной плазмы.
Но как они могли думать иначе, когда в 1802 году на примере опытов нашего соотечественника Петрова увидели, что на аноде образуется ямка? Следовательно, положительные частицы переносили заряд на катод, вот только это были ионы воздушной плазмы.
К началу исследования Вольтой электрических явлений, таким образом, были уже известны статические заряды и факт наличия у них двух знаков, кроме того люди упорно считали, что весь «флюид» берётся из воздуха. На эту мысль их натолкнули опыты с натиранием янтаря шерстью, которые не могли быть проведены под водой. Следовательно, логичным было предположить, что электричество может происходить только из атмосферы Земли, что, конечно же, совершенно неверно. В частности, многие растворы, исследованные Хампфри Дэви, могут проводить электрический ток.
Причина, следовательно, была в другом – при натирании янтаря под водой силы трения снижались в десятки и сотни раз, а заряд рассеивался по всему объёму жидкости. Следовательно, этот процесс был всего лишь неэффективным. Но сегодня каждый добытчик знает, что нефть прекрасно электризуется трением о трубы и без воздуха. Следовательно, атмосфера для «флюида» не является обязательным компонентом.
Но сегодня каждый добытчик знает, что нефть прекрасно электризуется трением о трубы и без воздуха. Следовательно, атмосфера для «флюида» не является обязательным компонентом.
Самый большой в мире плоский конденсатор
Столь систематизированные, но в корне неверные толкования все-таки не смогли остановить Вольту на его исследовательском пути. Он упорно изучал электрофорус, как один из самых совершенных генераторов, существовавших в то время. Вторым был серный шар Отто фон Герике, изобретённый более чем за век до этого (1663 год). С тех самых пор его конструкция мало менялась, но после открытий Стивена Грея заряд начали снимать при помощи проводников. В частности, в для этого служат металлические гребёнки-нейтрализаторы.
Долгое время учёные ходили вокруг да около. Электрофорная машина 1880 года может считаться первым мощным генератором разряда, позволявшим получить дугу, но своей настоящей силы электроны достигли в генераторе Ван де Граафа (1929 год), где разница потенциалов составила единицы мегавольта. Для сравнения грозовое облако, согласно данным Википедии, может иметь потенциал относительно Земли в единицы гигавольт (на три порядка больше, чем в человеческой машине).
Для сравнения грозовое облако, согласно данным Википедии, может иметь потенциал относительно Земли в единицы гигавольт (на три порядка больше, чем в человеческой машине).
Суммируя сказанное, можно с определённой долей уверенности сказать, что природные процессы используют в качестве принципа своего действия электризацию трением, влиянием и некоторые другие её виды, а мощный циклон является самым большим из известных нам плоских конденсаторов. Молния показывает, что бывает, когда диэлектрик (атмосфера) не выдерживает приложенной разницы потенциалов и пробивается. В точности то же самое происходит в любом плоском конденсаторе, созданном человеком, если вольтаж оказывается для него непомерным. Пробой твёрдого диэлектрика необратим, а возникающая электрическая дуга часто служит причиной расплавления обкладок и выхода изделия из строя.
Электрофорус
Итак, Вольта взялся за исследование модели природных процессов. Первый электрофорус появился в 1762 году сконструированный Йоханом Карлом Вильке. По-настоящему популярным прибор становится после докладов Вольты Королевскому научному обществу (середина 70-х годов XVIII века). Вольта же и дал прибору его нынешнее название.
По-настоящему популярным прибор становится после докладов Вольты Королевскому научному обществу (середина 70-х годов XVIII века). Вольта же и дал прибору его нынешнее название.
Электрофорус способен накапливать электростатический заряд, образованный трением резины куском шерсти. Он состоит из двух плоских, параллельных друг другу обкладок:
Принцип действия этого плоского конденсатора должен быть уже понятен. Оператор трёт резину шерстью, оставляя на ней отрицательный заряд. Затем сверху кладётся кусок металла. Из-за значительной шероховатости поверхностей они не соприкасаются, но находятся на некотором расстоянии друг от друга. В результате металл электризуется влиянием. Электроны отталкиваются поверхностным зарядом резины и уходят на внешнюю плоскость, где оператор их снимает через заземлитель лёгким кратковременным прикосновением.
Низ металлической обкладки остаётся заряженным положительно. При расстыковке двух поверхностей этот эффект сохраняется, потому что в материале наблюдается дефицит электронов. И можно наблюдать искру, если дотронуться до металлической обкладки. Этот опыт можно на одном и том же заряде резины проделывать сотни раз, поскольку её поверхностное статическое сопротивление весьма велико. Это не даёт заряду растекаться. Демонстрируя этот опыт, Вольта привлёк внимание всего научного мира, но исследования никак не двигались вперёд, если не считать открытий Шарля Кулона.
В 1800 году сам Алессандро даёт толчок развитию изысканий в области электричества, изобретя свой знаменитый гальванический источник питания.
Конструкция плоского конденсатора
Электрофорус по сути представляет собой первый из когда-либо сконструированных плоских конденсаторов. Его обкладки способны хранить только статический заряд, потому что иначе наэлектризовать резину невозможно. Поверхность очень долго хранит электроны. Вольта даже предлагал снимать их пламенем свечи через ионизированный воздух или ультрафиолетовым излучением Солнца. Сегодня каждый школьник знает, что то же самое можно проделать и водой. Правда, электрофорус нужно будет после этого высушить.
В современном мире нижней обкладкой может служить тефлоновое покрытие или пластик. Они тоже хорошо набирают статический заряд. Диэлектриком здесь служит воздух. Чтобы перейти к конструкции современного конденсатора, нужно обе обкладки сделать металлическими. Тогда при возникновении на одной из них заряда влиянием электризация распространится на вторую, и если другой контакт заземлён, накопленная энергия может храниться какое-то время.
Запас электронов напрямую зависит от материала диэлектриков. Так например, среди современных конденсаторов встречаются:
В эти названия как раз и заложен материал диэлектрика. От его состава зависит напрямую ёмкость, которая может быть увеличена во много раз. Роль диэлектриков объяснялась выше, в частности их параметры определяются непосредственно строением вещества. Однако многие материалы, обладающие высокими характеристиками, использовать не удаётся по причине их непригодности. Так например, вода обладает высокой диэлектрической проницаемостью.
Характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников. Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин.
Под зарядом конденсатора понимают заряд одной пластины.
Так же есть:
Энергия конденсатора:
Ёмкость цилиндрического конденсатора:
Емкость сферического конденсатора:
В формуле мы использовали:
Электрическая ёмкость (ёмкость конденсатора)
Относительная диэлектрическая проницаемость
Электрическая постоянная
Емкость: Единицы измерения и формула — Видео и стенограмма урока
Уравнения емкости
Определение емкости дается следующим уравнением: емкость C , измеренная в фарадах, равна заряду Q , измеренному в кулонах, деленному на напряжение В , измеренное в вольтах.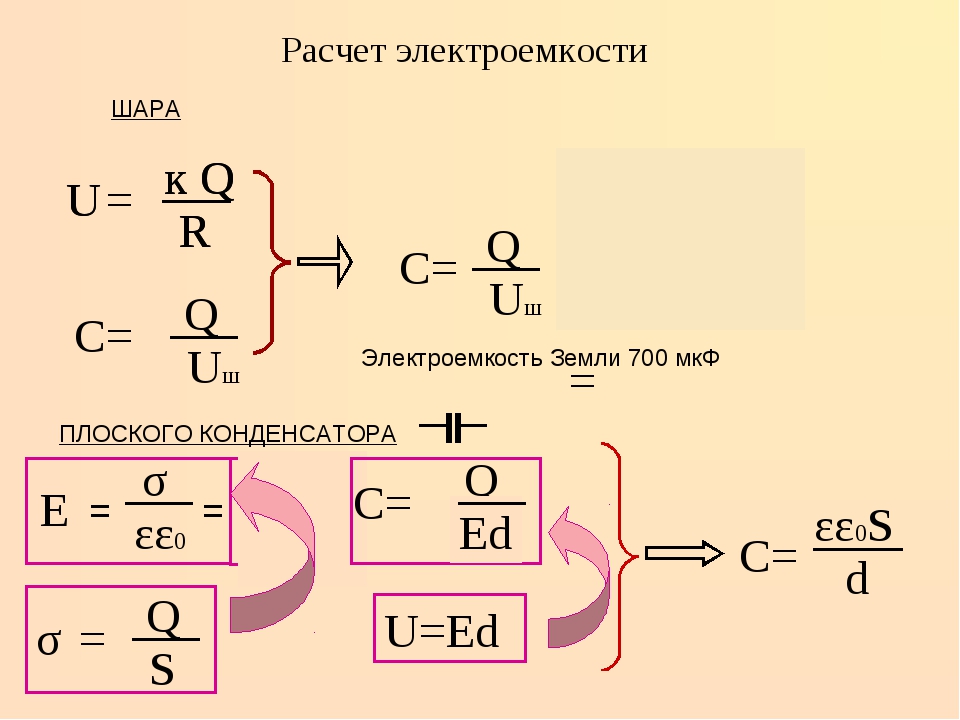 Так, например, если вы подключаете 12-вольтовую батарею к конденсатору, и эта батарея заряжает конденсатор зарядом 4 кулона, его емкость должна быть 4/12, что равно 0.33 фарад.
Так, например, если вы подключаете 12-вольтовую батарею к конденсатору, и эта батарея заряжает конденсатор зарядом 4 кулона, его емкость должна быть 4/12, что равно 0.33 фарад.
Если бы емкость конденсатора была выше, то при подключении к той же батарее он сохранял бы больше заряда. Из этого уравнения мы можем видеть, что емкость измеряется в кулонах на вольт. Таким образом, он показывает, сколько кулонов заряда будет храниться в конденсаторе на вольт, который вы на него подали.
Хорошо, но что физически заставляет конкретный конденсатор иметь другую емкость? Что определяет, сколько заряда он хранит? Ну, это основано на фактических физических характеристиках конденсатора.Итак, у нас есть еще одно уравнение для емкости, которое выглядит так:
Емкость плоского конденсатора, простого конденсатора, состоящего из двух параллельных пластин, разделенных расстоянием d , равна относительной диэлектрической проницаемости материала между местами, K , умноженной на диэлектрическая проницаемость свободного пространства, эпсилон-ноль, которая всегда равна 8.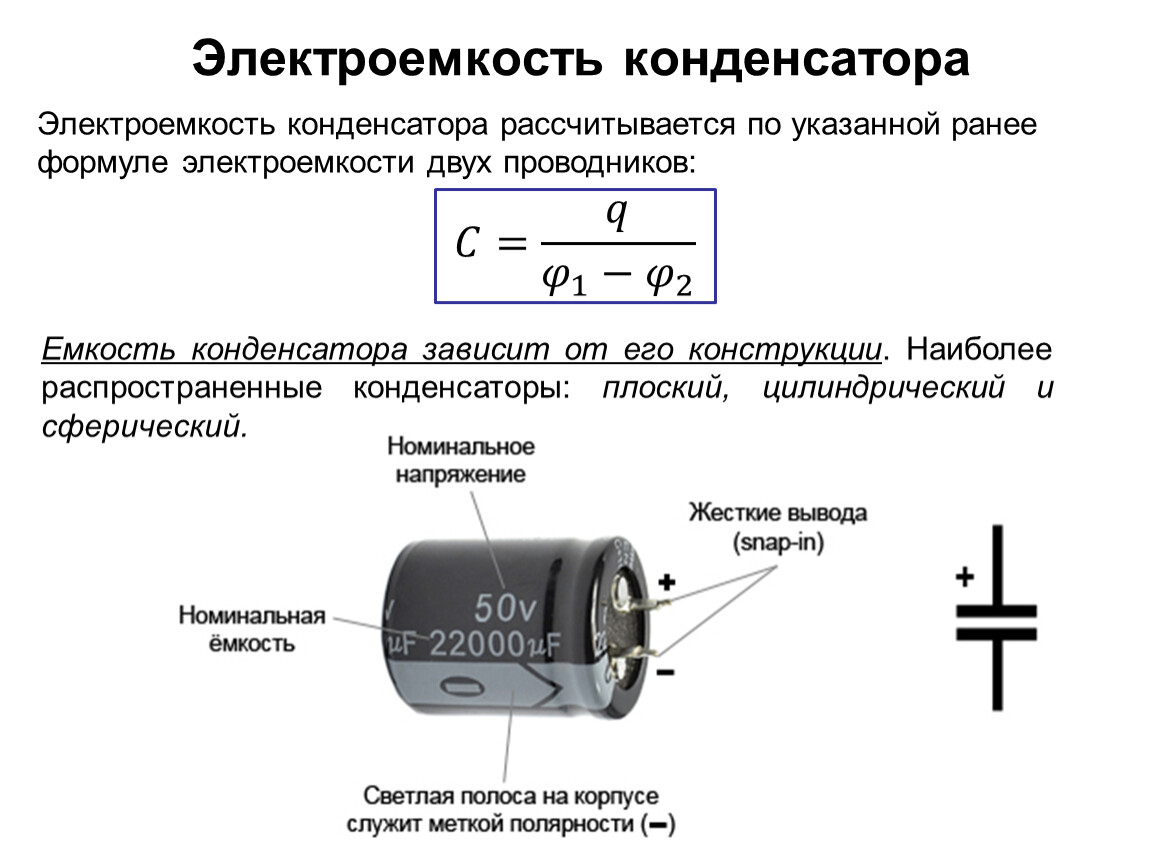 -12, умноженное на площадь плит, А , измеренное в метрах в квадрате, деленное на расстояние между местами, d , измеренное в метрах.
-12, умноженное на площадь плит, А , измеренное в метрах в квадрате, деленное на расстояние между местами, d , измеренное в метрах.
Большая часть этого не требует пояснений, но K относительная диэлектрическая проницаемость так называемого «диэлектрического» материала между пластинами обычно равна 1 или больше. Если между пластинами ничего нет, К = 1; если между пластинами воздух, то К почти все равно равно 1; а если это другой материал, то число будет больше единицы, в зависимости от конкретного материала.
Итак, это наши два основных уравнения для емкости, и, как обычно, пришло время попробовать использовать их в примере задачи.
Пример расчета
Допустим, у вас есть конденсатор площадью 0,1 м2 с пластинами, отстоящими друг от друга на 0,01 м, и между пластинами находится воздух. Если вы подключите его к батарее 9В, сколько заряда останется на пластинах?
Ну, во-первых, давайте запишем то, что мы знаем. Площадь равна 0,1 метра в квадрате, поэтому · = 0.1; пластины находятся на расстоянии 0,01 метра друг от друга, поэтому d = 0,01; и это воздух между пластинами, поэтому К примерно 1. У вас также есть напряжение, поэтому В = 9 вольт, и нас просят найти заряд, Q , поэтому Q равно знаку вопроса . Мы пока не можем найти Q , потому что у нас есть V , но у нас нет C . Итак, нам нужно использовать наше другое уравнение, чтобы сначала найти емкость C .
Площадь равна 0,1 метра в квадрате, поэтому · = 0.1; пластины находятся на расстоянии 0,01 метра друг от друга, поэтому d = 0,01; и это воздух между пластинами, поэтому К примерно 1. У вас также есть напряжение, поэтому В = 9 вольт, и нас просят найти заряд, Q , поэтому Q равно знаку вопроса . Мы пока не можем найти Q , потому что у нас есть V , но у нас нет C . Итак, нам нужно использовать наше другое уравнение, чтобы сначала найти емкость C .
Подставляя числа в это уравнение, мы получаем, что емкость равна 1, умноженному на 8.-10 кулонов. И все — это наш ответ.
Краткий обзор урока
Конденсатор — это компонент, который накапливает заряд (аккумулирует электрическую энергию) до тех пор, пока он не заполнится, а затем высвобождает его в виде импульса. Есть много причин, по которым вы можете захотеть это сделать. Вы можете хранить заряд в конденсаторе на случай отключения внешнего питания, чтобы устройство не отключилось мгновенно, позволяя завершить процессы восстановления. Вы можете захотеть, чтобы схема получала регулярный «импульс» энергии каждые x периодов времени.Вы найдете конденсаторы почти в любом электронном устройстве: компьютерах, телевизорах, автомобильных стартёрах — что угодно.
Вы можете захотеть, чтобы схема получала регулярный «импульс» энергии каждые x периодов времени.Вы найдете конденсаторы почти в любом электронном устройстве: компьютерах, телевизорах, автомобильных стартёрах — что угодно.
Емкость — это мера способности конденсатора накапливать заряд, измеряемая в фарадах; конденсатор с большей емкостью будет хранить больше заряда. Определение емкости дается следующим уравнением: емкость Кл , измеренная в фарадах, равна заряду Кл , измеренному в кулонах, деленному на напряжение В , измеренное в вольтах. Емкость зависит от физических характеристик конденсатора.-12, умноженное на площадь плит, А , измеренное в метрах в квадрате, деленное на расстояние между местами, d , измеренное в метрах. Значение K равно 1 для пустого пространства и очень близко к 1 для воздуха. Эти два уравнения вместе позволяют решить множество простых задач, связанных с конденсаторами.
Результаты обучения
По окончании этого урока вы сможете:
Конденсаторы и расчеты емкости Формулы Уравнения
Конденсаторы — это пассивные устройства, используемые
в электронных схемах для хранения энергии в виде электрического поля. Они являются комплиментом
Они являются комплиментом
катушки индуктивности, которые хранят энергию в виде магнитного поля. Идеальный конденсатор
является эквивалентом разомкнутой цепи (бесконечное сопротивление) для постоянного тока и представляет импеданс (реактивное сопротивление) для
переменный ток (AC), который зависит от частоты тока (или напряжения). Реактивное сопротивление (противодействие току
расход) конденсатора обратно пропорциональна частоте воздействующего на него сигнала. Изначально были конденсаторы.
называемые «конденсаторами» по причине, которая восходит ко временам Лейденской банки, где считалось, что электрические заряды
накапливаться на тарелках в результате процесса конденсации.
Свойство емкости противодействовать изменению напряжения используется для проведения сигналов с
компонент более высокой частоты, предотвращая прохождение сигналов компонентов более низкой частоты. Общее применение
конденсатор в ВЧ (радиочастотной) цепи — это место, где есть напряжение смещения постоянного тока, которое необходимо заблокировать.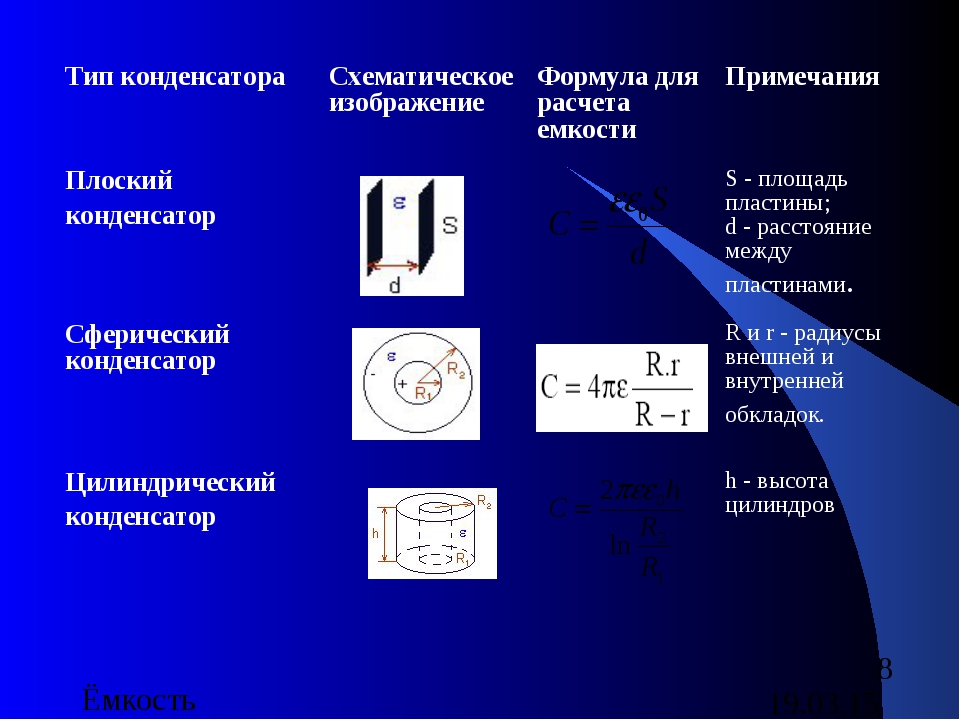
в цепи, позволяя радиочастотному сигналу проходить. Источники питания постоянного тока используют большие значения емкости параллельно с выходом
клеммы для сглаживания низкочастотных пульсаций из-за выпрямления и/или коммутации сигналов.
При использовании последовательно (левый рисунок) или параллельно (правый рисунок) с
комплемент цепи, катушка индуктивности, комбинация катушка индуктивности и конденсатора образует цепь, которая резонирует на определенной частоте
это зависит от значений каждого компонента. В последовательной цепи полное сопротивление току на резонансной частоте
равен нулю с идеальными компонентами. В параллельной цепи (справа) полное сопротивление протеканию тока бесконечно с идеальными компонентами.
Реальные конденсаторы, изготовленные из физических компонентов, обладают не только чистой емкостью, когда
присутствует в цепи переменного тока.Слева показана модель симулятора общей схемы. Он включает реальный идеальный конденсатор с параллельным резистивным
компонент («Утечка»), реагирующий на переменный ток. Эквивалентная резистивная составляющая постоянного тока
Эквивалентная резистивная составляющая постоянного тока
(«ESR») включен последовательно с идеальным конденсатором и эквивалентным последовательным индуктивным компонентом.
(«ESL») присутствует из-за металлических выводов (если они есть) и характеристик поверхностей пластин.
Эта индуктивность в сочетании с емкостью создает резонансную частоту, при которой конденсатор выглядит как
чистое сопротивление.
По мере увеличения рабочей частоты после резонанса (также называемой собственной резонансной частотой или SRF),
схема ведет себя как индуктивность, а не как емкость. Следовательно, необходимо тщательное рассмотрение SRF, когда
подбор конденсаторов. Симуляторы типа SPICE используют эту или еще более сложную модель для облегчения более точных расчетов.
в широком диапазоне частот.
Уравнения для соединения конденсаторов последовательно и параллельно приведены ниже.Дополнительные уравнения даны для конденсаторов
различных конфигураций. Как показывают эти цифры и формулы, емкость является мерой способности двух поверхностей
для хранения электрического заряда. Разделенные и изолированные диэлектриком (изолятором), суммарный положительный заряд накапливается на
Разделенные и изолированные диэлектриком (изолятором), суммарный положительный заряд накапливается на
одной поверхности, а чистый отрицательный заряд накапливается на другой поверхности. В идеальном конденсаторе заряд будет храниться бесконечно;
однако конденсаторы реального мира постепенно теряют заряд из-за токов утечки через неидеальный диэлектрик.
|
|
Связанные страницы в RF Cafe
— Конденсаторы и
Расчет емкости
—
Конденсатор
Цветовые коды
— преобразование емкости
—
Конденсатор Диэлектрики
—
Стандартные значения конденсаторов
—
Поставщики конденсаторов
—
Благородное искусство разъединения
Отслеживание динамики Конденсатор Цепи Волновой резервуар Оптическая скамья | Конденсатор с параллельными пластинами Заряд конденсатора, разделение пластин и напряжение Конденсатор используется для накопления электрического заряда. Чем большее напряжение (электрическое давление) вы прикладываете к конденсатору, тем больше заряда попадает в конденсатор. Кроме того, чем большей емкостью обладает конденсатор, тем больше заряда будет вызвано данным напряжением.Это соотношение описывается формулой q=CV, где q — накопленный заряд, C — емкость, а V — приложенное напряжение. Глядя на эту формулу, можно задаться вопросом, что произошло бы, если бы заряд оставался постоянным, а емкость изменялась. Ответ, конечно же, что напряжение изменится! Это то, что вы будете делать в этой лаборатории. Лабораторный конденсатор Конденсатор с плоскими пластинами — это прибор, используемый для изучения конденсаторов. Этот конденсатор работает путем создания противоположных зарядов на параллельных пластинах, когда напряжение подается с одной пластины на другую. Количество заряда, перемещающегося на пластины, зависит от емкости и приложенного напряжения по формуле Q=CV, где Q — заряд в кулонах, C — емкость в фарадах, а V — разность потенциалов между пластинами в вольт. Конденсаторы для хранения энергии Если на конденсатор подается напряжение, а затем он отключается, заряд, хранящийся в конденсаторе, сохраняется до тех пор, пока конденсатор не разрядится каким-либо образом. Тогда между пластинами возникает электрическое поле, которое позволяет конденсатору накапливать энергию. Это один из полезных аспектов конденсаторов, способность накапливать энергию в электрическом поле, чтобы ее можно было использовать позже. От чего зависит емкость? Количество заряда, которое может храниться на один приложенный вольт, определяется площадью поверхности пластин и расстоянием между ними.Чем больше пластины и чем ближе они расположены друг к другу, тем больше заряда может храниться на каждый вольт разности потенциалов между пластинами. Заряд, сохраняемый на приложенный вольт, представляет собой емкость, измеряемую в фарадах. Может ли изменение емкости заряженного конденсатора изменить его напряжение? Лабораторный конденсатор можно регулировать, поэтому мы можем провести интересный эксперимент с емкостью и напряжением. Если конденсатор имеет постоянный заряд, изменение емкости должно привести к изменению напряжения.Раздвигание пластин уменьшит емкость, поэтому напряжение должно увеличиться. Как математически определить емкость нашего конденсатора? С = ε 0A/d Где C — емкость в фарадах, ε 0 — константа диэлектрической проницаемости свободного пространства (8,85×10 -12), A — площадь пластин в квадратных метрах, а d — расстояние между пластинами в метрах. Фарад — это очень большое значение емкости, поэтому мы будем использовать метрические префиксы для получения более удобных чисел. Емкость обычно измеряется в микрофарадах (мкФ), что составляет 1,0×10 -6 Ф, или в пикофарадах (пФ), что составляет 1,0×10 -12 Ф. 1,0Ф = 1 000 000 мкФ = 1 000 000 000 000 пФ! Будьте очень осторожны с расчетами! Этот расчет даст вам приблизительное значение емкости лабораторного конденсатора. Однако есть и другие факторы, которые вносят ошибки в реальное измерение емкости и напряжения.Вы должны быть осторожны, чтобы принять во внимание эти факторы. Лабораторное оборудование: Чтобы получить хорошие результаты, эта лабораторная работа требует специального оборудования. Вам нужен хороший регулируемый источник питания, чтобы напряжение, подаваемое на конденсатор, было одинаковым в каждом испытании. Вам также нужен очень точный способ измерения напряжения между пластинами без приложения резистивной нагрузки к конденсатору. Одна проблема с электрометром заключается в том, что он имеет некоторую собственную емкость. Поскольку эта емкость параллельна емкости конденсатора, встроенная емкость выводов должна быть добавлена к емкости конденсатора. Назначение: Целью этой лабораторной работы является исследование взаимосвязи между расстоянием между пластинами и напряжением в конденсаторе с параллельными пластинами, поддерживаемом при постоянном заряде. Оборудование: Меры предосторожности: Это хрупкое оборудование. Ваша первая задача — предсказать, что произойдет с напряжением конденсатора, когда вы зарядите его источником 10 В, а затем раздвинете пластины (что уменьшит емкость). Вы сделаете это в следующем разделе. Теоретические расчеты: Сначала необходимо рассчитать теоретическую емкость для каждого расстояния между пластинами. Мы сделаем первое, а потом вы сможете сделать все остальное! Самое сложное в этом — правильно подобрать единицы измерения. Самый простой способ продолжить — перевести все в метры для расчетов: В следующих разделах вы проведете реальный эксперимент, чтобы проверить (или, возможно, не проверить!) свои теоретические расчеты. Процедура настройки переменного конденсатора (если лаборатория уже настроена, переходите к следующему разделу!) Сбор экспериментальных данных
Анализ данных:
|
Эпизод 126: Емкость и уравнение C=Q/V
К=К/В
Электричество и магнетизм
Эпизод 126: Емкость и уравнение C=Q/V
Урок
за
16-19
Установив наличие заряда на каждой пластине конденсатора, следующим этапом является установление зависимости между зарядом и разностью потенциалов на конденсаторе.
Итоги урока
Демонстрация: зарядка конденсатора
Экспериментальная демонстрация зарядки конденсатора с постоянной скоростью
показывает, что разность потенциалов на конденсаторе пропорциональна заряду.
Эпизод 126-1: Зарядка конденсатора постоянным током (Word, 34 КБ)
Обсуждение: Определение емкости и фарад
Эксперимент показывает, что
Q ∝ V , или
Q = константа × В . Эта постоянная называется емкостью конденсатора Кл и измеряется в фарадах (Ф). Таким образом, емкость — это заряд, хранящийся на вольт, и
Эта постоянная называется емкостью конденсатора Кл и измеряется в фарадах (Ф). Таким образом, емкость — это заряд, хранящийся на вольт, и
фарад = кулонвольт.
Следует отметить, что 1 фарад — это очень большая емкость и что большинство конденсаторов будут микро, мк, – (10 -6 ), нано
C = 4 π ε 0 ε r R
составляет 710 мФ.
Студенческий эксперимент: заряд, пропорциональный напряжению — первый вариант
Зависимость между зарядом и разностью потенциалов может быть дополнительно исследована самими учащимися. Возможны два эксперимента; в этом используется кулоновый метр.
Заряжая подходящий конденсатор до различных напряжений и каждый раз измеряя накопленный заряд, вы быстро подтверждаете соотношение Q ∝ В .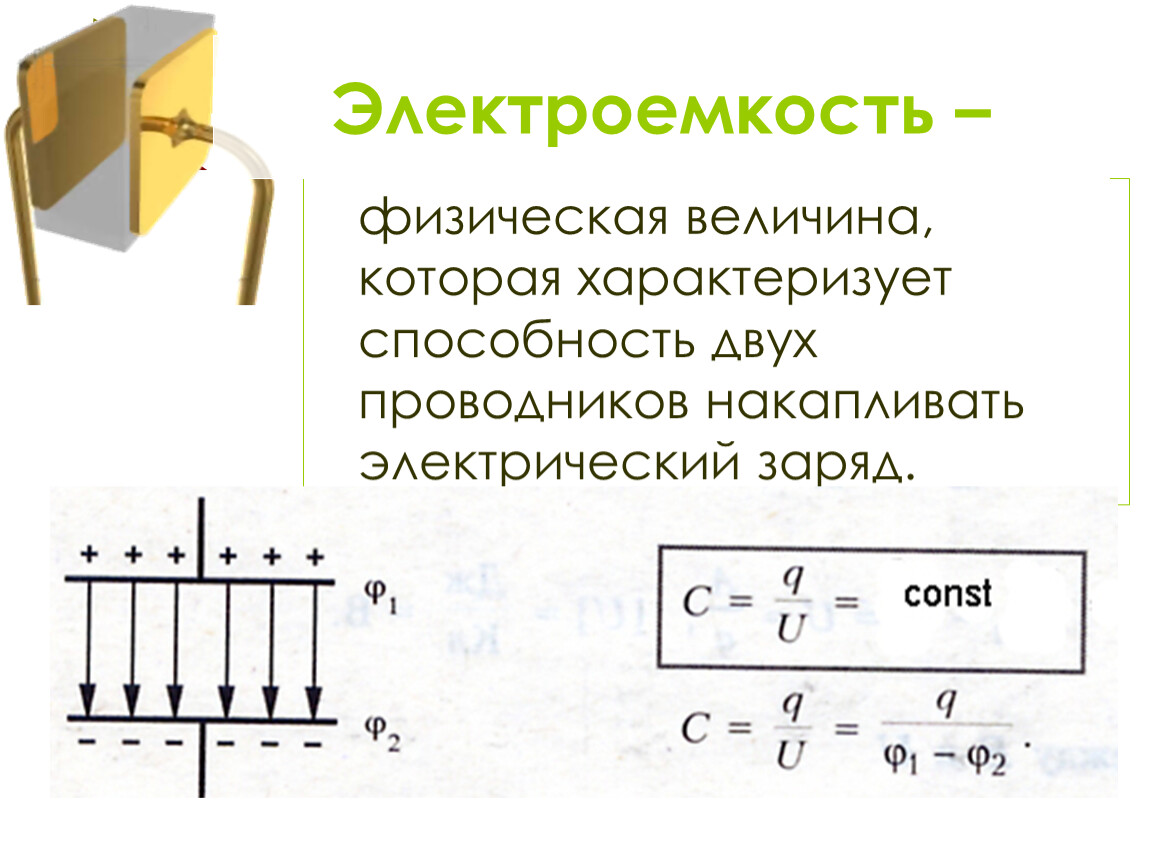 Эксперимент можно повторить с другими конденсаторами. Постройте график Q против V .
Эксперимент можно повторить с другими конденсаторами. Постройте график Q против V .
Эпизод 126-2: Измерение заряда конденсатора (Word, 47 КБ)
Зарядка пропорциональна напряжению – второй вариант
Во втором исследовании зависимости между зарядом и pd используется герконовый переключатель. Учащиеся могли встречать простые герконы включения/выключения в технике или даже в начальной школе.
Хотя это более сложный эксперимент, он имеет ценность, поскольку его можно расширить для исследования факторов, определяющих емкость конденсатора с плоскими пластинами, если это необходимо для вашей спецификации.
Из любого эксперимента можно построить график зависимости Q от V . Это пригодится позже при обсуждении энергии, хранящейся в конденсаторе. (Примечание. График эксперимента с герконом не проходит через начало координат, поэтому необходимо объяснить влияние паразитной емкости в эксперименте)
Эпизод 126-3. Использование геркона для измерения емкости (Word, 46 КБ)
Использование геркона для измерения емкости (Word, 46 КБ)
Обсуждение: Факторы, влияющие на
C
Если ваша спецификация требует изучения уравнения C = ε 0 ε r × A d
, то это удобный момент для покрытия этой работы.
Самое время представить идею о том, что многие трубчатые конденсаторы в форме
на самом деле представляют собой конденсаторы с параллельными пластинами, свернутые и заполненные диэлектриком. Почему? (Большая площадь с малым зазором дает приемлемые значения емкости; диэлектрик увеличивает емкость; прокатка уменьшает общий размер.)
Студенческий эксперимент: факторы, влияющие на C
С помощью геркона или цифрового измерителя емкости исследуйте факторы, определяющие емкость плоского конденсатора.
Если у вас нет геркона, многие дешевые цифровые мультиметры теперь оснащены измерителем емкости, покрывающим диапазоны пФ и нФ, который здесь будет эффективно работать.
При использовании параллельных пластин в качестве конденсатора в этом эксперименте соотношение между емкостью и площадью может быть найдено путем изменения площади перекрытия, в то время как использование прокладок приводит к соотношению между емкостью и разделением. Размещение пластиковых листов между пластинами показывает эффект диэлектрика и показывает, почему относительная диэлектрическая проницаемость появляется в формуле.Если времени мало, эти три эксперимента можно провести как групповые занятия, когда группы сообщат о своих выводах.
Обсуждение: Диэлектрическая проницаемость
Обсудите результаты экспериментов и значение ε 0 } , диэлектрической проницаемости свободного пространства. Выведите его единицы F m -1 или C 2 N -1 m -2 .
Обсуждение: Работа с реальными конденсаторами
Возьмите несколько конденсаторов и посмотрите на информацию, написанную на каждом из них. Это будет включать емкость и максимальное рабочее напряжение. На электролитическом конденсаторе также будет указание полярности для каждого вывода (и может быть максимальный ток пульсаций).
Это будет включать емкость и максимальное рабочее напряжение. На электролитическом конденсаторе также будет указание полярности для каждого вывода (и может быть максимальный ток пульсаций).
Обсудите, что означают маркировки, и сравните заряд, сохраняемый каждым конденсатором при максимальном напряжении (попрактикуйтесь в использовании
).
Q = C × V .
Как это связано с физическим размером конденсатора? (Вряд ли это просто потому, что чем больше емкость, тем больше конденсатор.Рабочее напряжение важно, как и материал между пластинами.)
Вопросы учащихся: Расчеты с реальными конденсаторами
Последующие вопросы завершат этот эпизод.
Эпизод 126-4: Вопросы о зарядных конденсаторах (Word, 62 КБ)
Эпизод 126-5: Проблемы с конденсаторами (Word, 37 КБ)
Основные расчеты конденсатора
— инженерное мышление
Конденсаторы
используются во многих цепях для разных целей, поэтому мы собираемся изучить некоторые основные расчеты конденсаторов для цепей постоянного тока.
Прокрутите вниз, чтобы посмотреть обучающее видео на YouTube
Конденсаторы в цепях постоянного тока
Конденсаторы
обычно выглядят так. У нас есть конденсатор электролитического и керамического типа. Электролитик поляризован, что означает, что одна сторона должна быть подключена к плюсу, а другая к минусу источника питания. Керамический тип, как правило, может быть подключен любым способом. На стороне электролитического конденсатора мы находим пунктирную линию, указывающую на отрицательную сторону, длинный вывод также указывает на положительную сторону нового конденсатора.Но они обычно обрезаются во время установки, поэтому не полагайтесь только на это. Эти два конденсатора представлены такими символами, обратите внимание, что поляризованный конденсатор имеет небольшой символ плюса, указывающий на положительную сторону.
При подключении к источнику постоянного тока напряжение батареи будет выталкивать электроны в конденсатор, поэтому конденсатор заряжается до того же напряжения, что и батарея.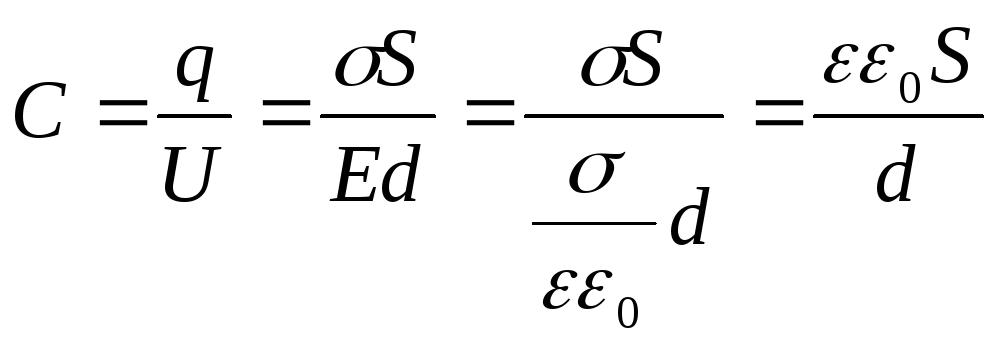 Конденсаторы заряжаются почти мгновенно при прямом подключении к батарее, но мы почти всегда используем резистор, это задержит время зарядки, и позже в этой статье мы увидим, как это рассчитать.
Конденсаторы заряжаются почти мгновенно при прямом подключении к батарее, но мы почти всегда используем резистор, это задержит время зарядки, и позже в этой статье мы увидим, как это рассчитать.
Внутри конденсатора с одной стороны скопилось много электронов, они не могут двигаться из-за изолирующего материала между двумя сторонами. Поскольку электроны заряжены отрицательно, у нас есть накопление заряда на одной стороне по сравнению с другой, поэтому у нас есть разница в напряжении между двумя выводами.
Эти электроны удерживаются на месте, и конденсатор может удерживать этот заряд в течение длительного периода времени. Когда указан путь, они будут разряжаться, пока не опустеют.Электроны не проходят через конденсатор; они просто накапливаются внутри, а затем высвобождаются.
Количество заряда, накопленного в конденсаторе, рассчитывается по формуле Заряд = емкость (в фарадах), умноженная на напряжение. Итак, для этого конденсатора 12 В 100 мкФ микрофарад мы конвертируем микрофарады в фарады (100/1 000 000 = 0,0001 Ф). Затем умножаем это на 12 В, чтобы увидеть, что он хранит заряд 0,0012 кулона.
Затем умножаем это на 12 В, чтобы увидеть, что он хранит заряд 0,0012 кулона.
Если нам нужно сохранить заряд, скажем, 0,0002 кулона, то мы просто делим его на напряжение, в данном случае 12 В, чтобы увидеть, что нам нужен 0.2
= 0,5 x 0,0001F x 144
= 0,0072 Дж
Мы знаем, что конденсатор будет заряжаться до напряжения аккумулятора. Итак, если мы подключим конденсатор таким образом, каково будет напряжение на конденсаторе? Будет 1,5В. Если мы вот так подключим конденсатор, каково будет его напряжение? Тоже будет 1,5В. Это два разных способа соединения конденсаторов в цепях, последовательное или параллельное. Это приведет к тому, что конденсаторы будут работать по-разному.
Параллельные конденсаторы
Если мы поставили конденсатор параллельно с лампой, то при извлечении батарейки конденсатор начнет питать лампу, она медленно тускнеет по мере разрядки конденсатора.Если бы мы использовали два конденсатора, мы могли бы питать лампу дольше.
Допустим, конденсатор 1 = 10 мкФ, а конденсатор 2 = 220 мкФ. Как рассчитать общую емкость? Это очень просто, ответ 230 мкФ. Конденсаторы соединены параллельно. Итак, 10 мкФ + 220 мкФ = 230 мкФ. Мы можем продолжать добавлять больше, например, конденсатор на 100 мкФ, и общее количество будет просто суммой всех конденсаторов. Размещая их параллельно, мы, по сути, объединяем их, чтобы сформировать больший конденсатор. Это очень полезно, потому что, если, например, нам нужен большой конденсатор на 2000 мкФ, но у нас его нет, мы можем просто использовать более мелкие конденсаторы, такие как 2x 1000 мкФ или 4x 500 мкФ и т. д.Он также часто используется для фильтрации шума и обеспечения большего тока в цепях с высоким спросом.
Как рассчитать общую емкость? Это очень просто, ответ 230 мкФ. Конденсаторы соединены параллельно. Итак, 10 мкФ + 220 мкФ = 230 мкФ. Мы можем продолжать добавлять больше, например, конденсатор на 100 мкФ, и общее количество будет просто суммой всех конденсаторов. Размещая их параллельно, мы, по сути, объединяем их, чтобы сформировать больший конденсатор. Это очень полезно, потому что, если, например, нам нужен большой конденсатор на 2000 мкФ, но у нас его нет, мы можем просто использовать более мелкие конденсаторы, такие как 2x 1000 мкФ или 4x 500 мкФ и т. д.Он также часто используется для фильтрации шума и обеспечения большего тока в цепях с высоким спросом.
Общий заряд, хранящийся в параллельных конденсаторах, равен: заряд = общая емкость, умноженная на напряжение. Итак, у нас есть батарея на 9 В и два конденсатора общей емкостью 230 мкФ. Поскольку это параллельно, этот провод 9 В, а этот 0 В, поэтому оба конденсатора заряжены до 9 В. Следовательно, 0,00023 Ф, умноженное на 9 В = 0,00207 кулона. И с тремя конденсаторами у нас есть 330 мкФ (0.00033 F), умноженное на 9V = 0,00297 кулонов.
И с тремя конденсаторами у нас есть 330 мкФ (0.00033 F), умноженное на 9V = 0,00297 кулонов.
Мы также можем рассчитать заряд каждого конденсатора в отдельности. Мы просто используем одну и ту же формулу для каждого конденсатора, вы можете увидеть ответы на экране.
Конденсатор 1 = 0,00001 F x 9v = 0,00009 Coulombs
Конденсатор 2 = 0,00022 F x 9V = 0,00198 Кулонс
Конденсатор 3 = 0,0001 F x 9v = 0,0009 Coulombs
Всего = 0,00009 + 0,00198 + 0,0009 = 0,00297 Coulombs
Конденсаторы серии
Если мы поместим конденсатор последовательно с лампой, когда мы нажмем переключатель, она загорится, но затем станет тусклее, когда конденсатор достигнет уровня напряжения батареи, и как только он достигнет этого, лампа погаснет.Помните, что электроны не могут проходить через конденсатор из-за изолирующего материала внутри. Электроны просто накапливаются внутри одной пластины и по мере их накопления отбрасывают такое же количество с противоположной пластины. Таким образом, ток может течь только тогда, когда конденсатор заряжается или разряжается. В настоящее время, когда батарея удалена, конденсатор не может разрядиться, поэтому он будет удерживать напряжение на том же уровне. Неважно, подключаем мы аккумулятор или отключаем, лампа не включится.Однако, если мы обеспечим другой путь, то при нажатии переключателя конденсатор теперь может разряжаться, так что электроны могут течь через лампу и освещать ее. Он станет тусклее по мере разрядки конденсатора.
Таким образом, ток может течь только тогда, когда конденсатор заряжается или разряжается. В настоящее время, когда батарея удалена, конденсатор не может разрядиться, поэтому он будет удерживать напряжение на том же уровне. Неважно, подключаем мы аккумулятор или отключаем, лампа не включится.Однако, если мы обеспечим другой путь, то при нажатии переключателя конденсатор теперь может разряжаться, так что электроны могут течь через лампу и освещать ее. Он станет тусклее по мере разрядки конденсатора.
Что, если бы у нас было 2 конденсатора, соединенных последовательно, опять же, конденсатор 1 — 10 мкФ, а конденсатор 2 — 220 мкФ. Как найти полную емкость? Для этого мы используем эту формулу, она может показаться сложной, но на самом деле она очень проста. Все, что нам нужно сделать, это ввести значения наших конденсаторов 10 и 220 мкФ.Мы можем ввести это как это на наших калькуляторах или в Excel. Но при ручном вычислении мы делаем 1, деленное на 10, что равно 0,1, и 1, деленное на 220, что равно 0,00454. Мы сложим их вместе, чтобы получить 0,10454, а затем 1, деленная на это, даст в общей сложности 9,56 мкФ. Обратите внимание, что общая емкость теперь меньше конденсатора с наименьшим значением.
Если мы добавили в схему третий конденсатор на 100 мкФ, то получим общую емкость 8,73 мкФ. Значит, уменьшилось еще больше. Это потому, что, объединяя их последовательно, мы существенно увеличиваем толщину изоляционного материала, поэтому притяжение отрицательно заряженных электронов к положительно заряженным отверстиям на противоположной пластине становится слабее.
Общий заряд последовательных конденсаторов находится по формуле: заряд = емкость (в фарадах), умноженная на напряжение. Итак, если мы использовали батарею на 9 В, мы конвертируем микрофарады в фарады и видим, что общий заряд равен 0,00008604 кулона
(0,00000956F x 9В = 0,00008604 кулона)
.
Общий заряд цепи конденсатора из 3 рядов составляет 0,00007857 кулонов
(0,00000873 x 9 В = 0,00007857 кулонов)
Заряд, удерживаемый каждым конденсатором в отдельности, очень легко рассчитать в последовательных цепях.Это то же самое, что общее количество. Каждый конденсатор содержит одинаковое количество электронов при последовательном соединении. Это потому, что когда мы заряжали конденсаторы, ток был одинаковым во всех частях цепи. То же самое количество электронов, которые были вытолкнуты в одну пластину, были вытеснены из противоположной пластины, поэтому каждый последовательный конденсатор может быть заряжен только до одного и того же уровня. Таким образом, наименьший конденсатор будет ограничивающим фактором.
Однако, поскольку каждый конденсатор может иметь разную емкость, напряжение каждого конденсатора будет разным.Напряжение каждого конденсатора находим по формуле напряжение = заряд (в кулонах) деленное на емкость (в фарадах).
Итак, для этой схемы мы видим, что конденсатор 1 на 7,8 В, конденсатор 2 на 0,35 В и конденсатор 3 на 0,78 В. Они объединяются в общее напряжение батареи, которое составляет 9 В.
Конденсатор 1: 0.00007857 C / 0.000077857 C / 0.00001 F = 7.857V
Конденсатор 2: 0.00007857 C / 0.00022 F = 0,357 В
Конденсатор 3: 0.00007857 C / 0,0001 F = 0,786 В
Общее напряжение = 7,857 В + 0,357 В + 0.786В = 9В
Время заряда конденсатора
Допустим, у нас есть батарея 9 В, конденсатор 100 мкФ, резистор 10 кОм и переключатель, все последовательно. Конденсатор полностью разряжен, и мы считываем 0 В на двух выводах.
Когда мы замыкаем переключатель, конденсатор заряжается. Напряжение будет увеличиваться до тех пор, пока не сравняется с напряжением батареи. Рост напряжения не мгновенный, он имеет экспоненциальную кривую. Сначала напряжение быстро увеличивается, а затем замедляется, пока не достигнет того же уровня напряжения, что и батарея.
Мы разделили эту кривую на 6 сегментов, но нас интересуют только первые 5, потому что на 5 маркере мы в основном находимся на полном напряжении, поэтому мы можем игнорировать все, что дальше этого. Каждый сегмент представляет нечто, называемое постоянной времени. Следовательно, поскольку у нас есть 5 сегментов, у нас есть 5 постоянных времени, поэтому потребуется 5 постоянных времени, чтобы зарядить конденсатор от 0 до чуть менее 100%. Все, что нам нужно сделать, это вычислить длину одной постоянной времени, а затем умножить ее на 5.
Чтобы вычислить одну постоянную времени, мы используем эту формулу.
Постоянная времени (в секундах) = сопротивление (в Омах), умноженное на емкость (в Фарадах). Итак, мы конвертируем резистор в омы, а емкость конденсатора в фарады и видим, что 10 000 Ом, умноженные на 0,0001 фарад, равняются 1. Итак, в этом примере постоянная времени равна 1 секунде. Следовательно, 5 из них — это 5 секунд. Это означает, что для полной зарядки этого конденсатора до 9 В требуется 5 секунд.
Если бы резистор был всего 1000 Ом, постоянная времени была бы 0,1 секунды, поэтому это заняло бы 0.5 секунд, чтобы достичь 9В. Если бы конденсатор был 1000 микрофарад, это заняло бы всего 50 секунд. Таким образом, с увеличением размера конденсатора время, затрачиваемое на это, увеличивается. Если значение резистора увеличивается, время, необходимое для этого, также увеличивается.
Возвращаясь к нашей первоначальной схеме. Таким образом, мы можем рассчитать уровень напряжения для каждой постоянной времени. В точке 1 напряжение всегда равно 63,2 %, в точке 2 — 86,5 %, в точке 3 — 95 %, в точке 4 — 98,2 % и в точке 5 — 99,3 %.
Итак, в этом примере через 1 секунду напряжение на конденсаторе равно 5.68 В, через 2 секунды 7,78 В, через 3 секунды 8,55 В, через 4 секунды 8,83 В и через 5 секунд 8,94 В
Если вам нужен более точный ответ, мы можем рассчитать каждую точку следующим образом.
Точка 1 = 9В-0В)x0,632 = 5,6880В
Точка 2 = ((9В – 5,688В)x0,632)+5,68В = 7,7812В
Точка 3 = ((9В-7,7812В)x0,632) +7,7812В = 8,5515В
Точка 4 = ((9В-8,55В)x0,632)+8,5515В = 8,8349В
Точка 5 = ((9В-8,8349В)x0,632)+8,8349В = 8,9393В
Помните, что при последовательном соединении ток в цепи уменьшается, а напряжение на конденсаторе увеличивается.При полном напряжении ток в цепи не течет. Если бы резистор был лампой, он мгновенно достиг бы полной яркости, когда переключатель был замкнут, но затем стал бы тусклее, когда конденсатор достиг полного напряжения.
Время разрядки конденсатора
Когда мы обеспечиваем путь для разрядки конденсатора, электроны покидают конденсатор, и напряжение на конденсаторе уменьшается. Он не разряжается мгновенно, а следует экспоненциальной кривой. Мы разделяем эту кривую на 6 сегментов, но нас интересуют только первые 5.В точке 1 напряжение всегда будет 36,8%, в точке 2 будет 13,5%, в точке 3 будет 5%, в точке 4 будет 1,8% и в точке 5 будет 0,7%.
Например, если бы у нас была батарея на 9 В, лампа с сопротивлением 500 Ом и конденсатор на 2000 мкФ, наша постоянная времени была бы 500 Ом, умноженная на 0,002 фарад, что составляет 1 секунду.
Итак, в тот момент, когда батарея отключена, конденсатор будет на 9 В, и, поскольку он питает цепь, лампа также будет. Через 1 постоянную времени, в данном случае 1 секунду, напряжение будет равно 36.8%, что составляет 3,312 В, через 2 секунды — 1,215 В, через 3 секунды — 0,45 В, через 4 секунды — 0,162 В и через 5 секунд — 0,063 В. Таким образом, лампа будет гореть чуть менее 3 секунд. Явно становится тусклее.
%PDF-1.4
%
1 0 объект
>поток
2022-01-06T16:01:55-08:002013-07-17T13:36:22+05:302022-01-06T16:01:55-08:00application/pdf
uuid:2847878b-2330-4669 -8b08-ed86c4980f3fuuid:c358df81-e9d9-4eaf-93d4-0e7970412763iText 4.2.0 от 1T3XT
конечный поток
эндобдж
2 0 объект
>
эндобдж
3 0 объект
>поток
xV]oH}WGa?4U&VU8[cSۨ;6n1FaswPHWUL9-*_9hj( $aJ9g8C,S~7+/^`Bn[h
ћhVO1J59`OQ
isW::'(˒nN_’a~n[.3F2″-|\Kg8MAgigQi, !s] EI@K3[dd=fM]yuu
0Jפ5Z4NS5UY2n7YZ=’xXJF3u*)8&*lܴ[ycwOq+H/B@ZC2?3G{LZ»춶T7W pnf5r63
Atom емкость | QuantumATK S-2021.06 Документация
Подход на основе индуцированного заряда
Конечное смещение создаст суммарный положительный/отрицательный заряд на двух
золотые поверхности, как показано на графиках ниже.
Теперь емкость в принципе может быть вычислена как \(C=dq/dV\),
где \(q\) — полный накопленный заряд на одной поверхности в виде
функция смещения.От наклона прямой можно
поэтому получаем емкость наноконденсатора:
Графики выше, а также весь анализ данных на основе Малликена
популяции, можно выполнить, запустив этот скрипт:
mulliken-analysis.py .
Это длинный сценарий, но отличная возможность узнать о пользовательских данных.
анализ в Python и QuantumATK.
Результаты
Скрипт сообщает емкость 7,27*10 -22 Фарад,
как вычислено путем подгонки прямой линии к точкам данных.Поместить это
число в перспективе, рассмотрим емкость идеального параллельного
пластинчатый конденсатор, записываемый как \(C = \varepsilon A/d\), где
\(\varepsilon=1\) для диэлектрической проницаемости вакуума и площади \(A\)
каждой пластины можно рассчитать исходя из конструкции устройства. Затем вы можете
рассчитать расстояние до параллельной пластины \(d=A/C\). Это также делается
в сценарии и сообщает \(d\)=8,77 Å.
Сравнивая это значение с расстоянием между поверхностными атомами золота
(11,89 Å) положение так называемой плоскости изображения оценивается как
1.56 Å над поверхностью золота.
Анализ электростатической энергии
Чтобы вычислить емкость, используя более общий и точный метод,
вам нужно будет сначала рассчитать электростатическую энергию \(E\) как
функция приложенного смещения \(V\):
\[E(V)=\frac{1}{2}\int \delta v(\mathbf{r},V) \delta n(\mathbf{r}, V)d\mathbf{r}\]
, где \(\дельта v\) — индуцированный электростатический потенциал, а
\(\delta n\) — индуцированная плотность.
Скрипт потенциальный_участок.ру
извлекает потенциал и плотность при смещении 1 В из существующего HDF5
файл и производит графики наведенной плотности и электростатического потенциала.
Скрипт также сообщает два параметра:
Наконечник
Положение плоскостей изображения определяется как точка, в которой
электрическое поле равно нулю, то есть там, где электростатический потенциал
становится плоским.2/2\). Сценарий
v-e-plot.py
вычисляет электростатическую энергию и соответствует емкости, как показано ниже.
Результаты
Скрипт сообщает емкость \(C\)=6,81*10 -22 Фарад,
в качественном согласии со значением, полученным из простого подхода
используя анализ заряда Малликена.
Этот скрипт также сообщает \(d\)=9,36 Å, что соответствует изображению
плоскости на 1,27 Å над поверхностью золота, в очень точном соответствии с
положение пика наведенной плотности.
Внимание
В чем разница между двумя методами?
В анализе заряда Малликена предполагается, что все электроны на
левая поверхность имеет такой же потенциал, как и правая поверхность.
Когда мы свернем электронную плотность и электростатический потенциал
мы учитываем тот факт, что некоторая часть электронной плотности находится
в области с конечным электрическим полем. Электростатическая энергия
поэтому анализ является более точным для расчета емкости.
Анализ электростатической энергии также имеет то преимущество, что он
не требуют от исследователя разделения атомов как однозначно «левых» и
«правильно» — это тривиально для двух золотых поверхностей, но может и не
всегда быть так.
.

 {-12}\;\frac Фм\).
{-12}\;\frac Фм\). Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:
Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле: ..\;+\;\frac1{{\mathrm С}_{\mathrm n}}\)
..\;+\;\frac1{{\mathrm С}_{\mathrm n}}\) Третья и четвертая задачи соответствуют высокому и превосходному уровню сложности, они рассчитаны на углубленное изучение физики. Решение данных задач предусматривают применение и актуализацию теоретических знаний учащихся, контроль качества усвоения материала. Блок содержит подробное решение каждой задачи.
Третья и четвертая задачи соответствуют высокому и превосходному уровню сложности, они рассчитаны на углубленное изучение физики. Решение данных задач предусматривают применение и актуализацию теоретических знаний учащихся, контроль качества усвоения материала. Блок содержит подробное решение каждой задачи.

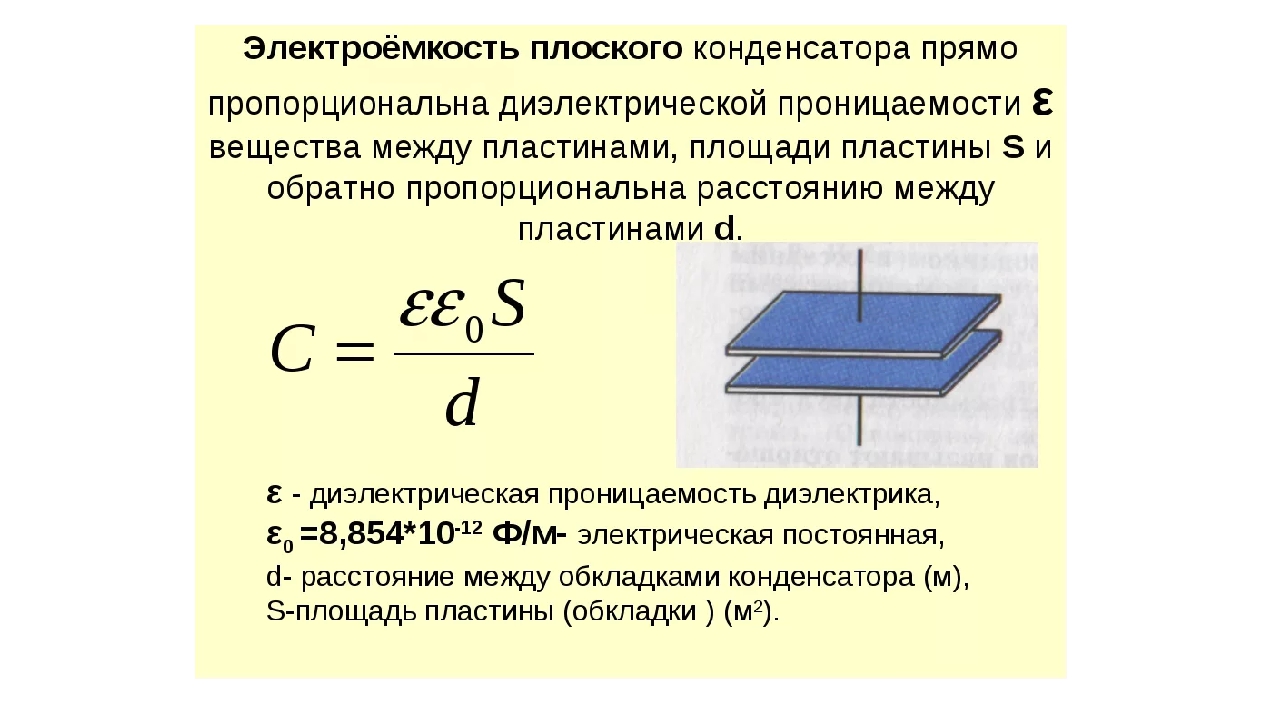
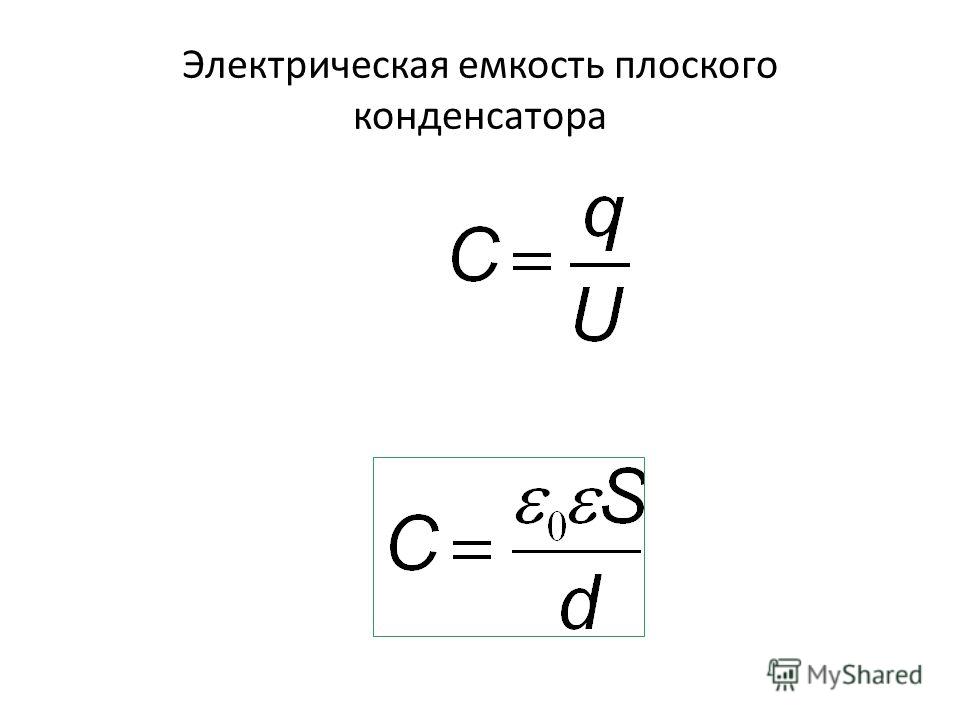
 Рассмотрим два случая:
Рассмотрим два случая:
 , но при всех изменениях емкости остается неизменным напряжение.
, но при всех изменениях емкости остается неизменным напряжение. Определить общую электроемкость соединения.
Определить общую электроемкость соединения. (1.9.7)
(1.9.7) Электроемкость конденсатора. Электроемкость плоского конденсатора.
Электроемкость конденсатора. Электроемкость плоского конденсатора. .. [читать подробенее]
.. [читать подробенее]
 Поэтому слюдяные конденсаторы получили широкое распространение.
Поэтому слюдяные конденсаторы получили широкое распространение. В этом случае главная функция — регулировка частоты, настройка профессионального оборудования.
В этом случае главная функция — регулировка частоты, настройка профессионального оборудования.

 Обратите внимание, что единицы длины и площади могут быть метрическими.
Обратите внимание, что единицы длины и площади могут быть метрическими. Сохраняйте единицы измерения постоянными.
Сохраняйте единицы измерения постоянными.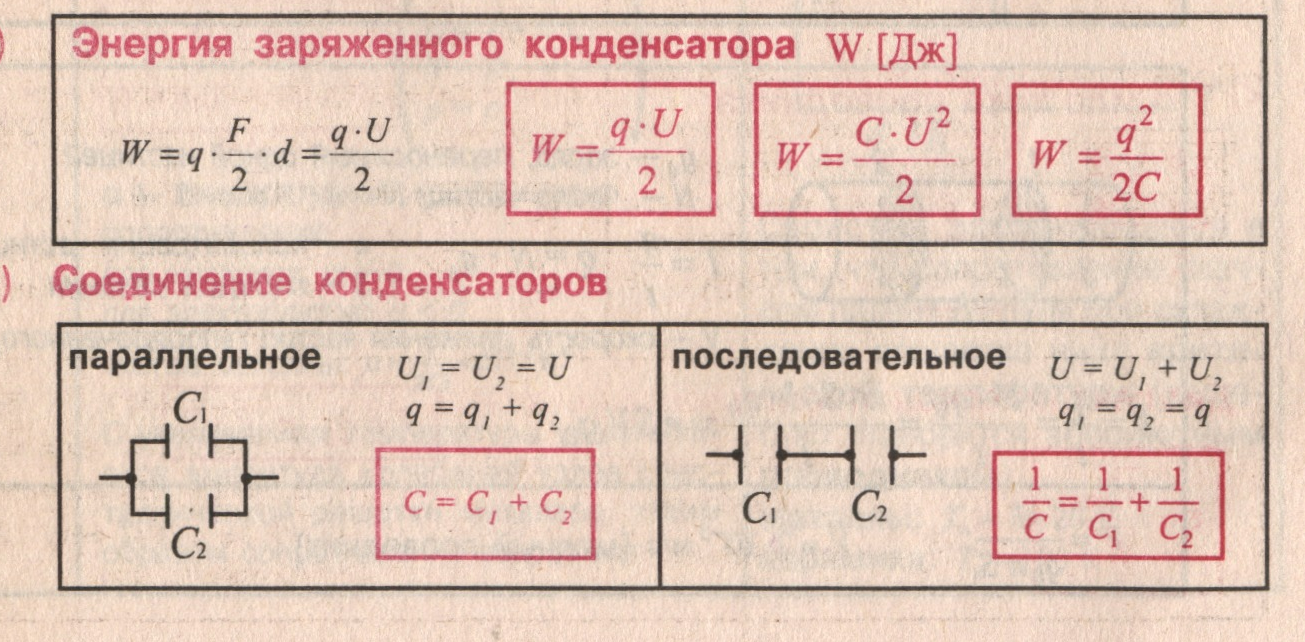

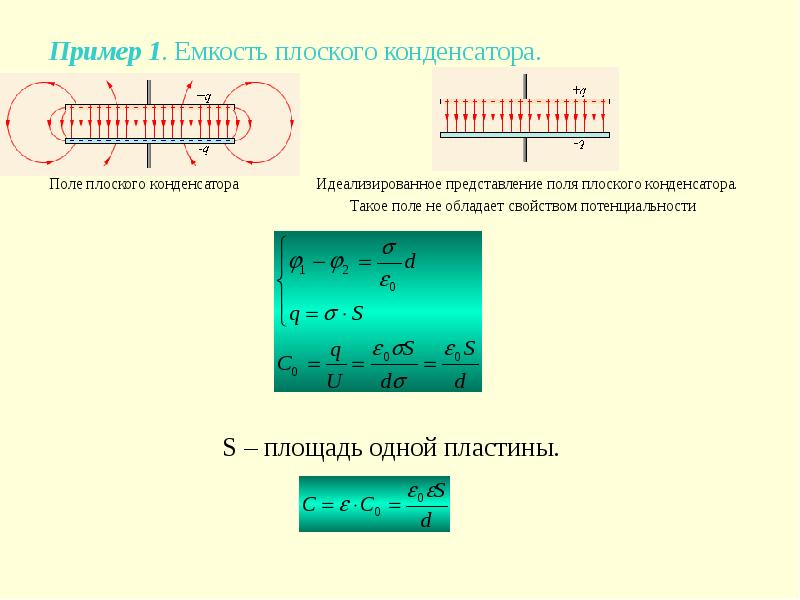
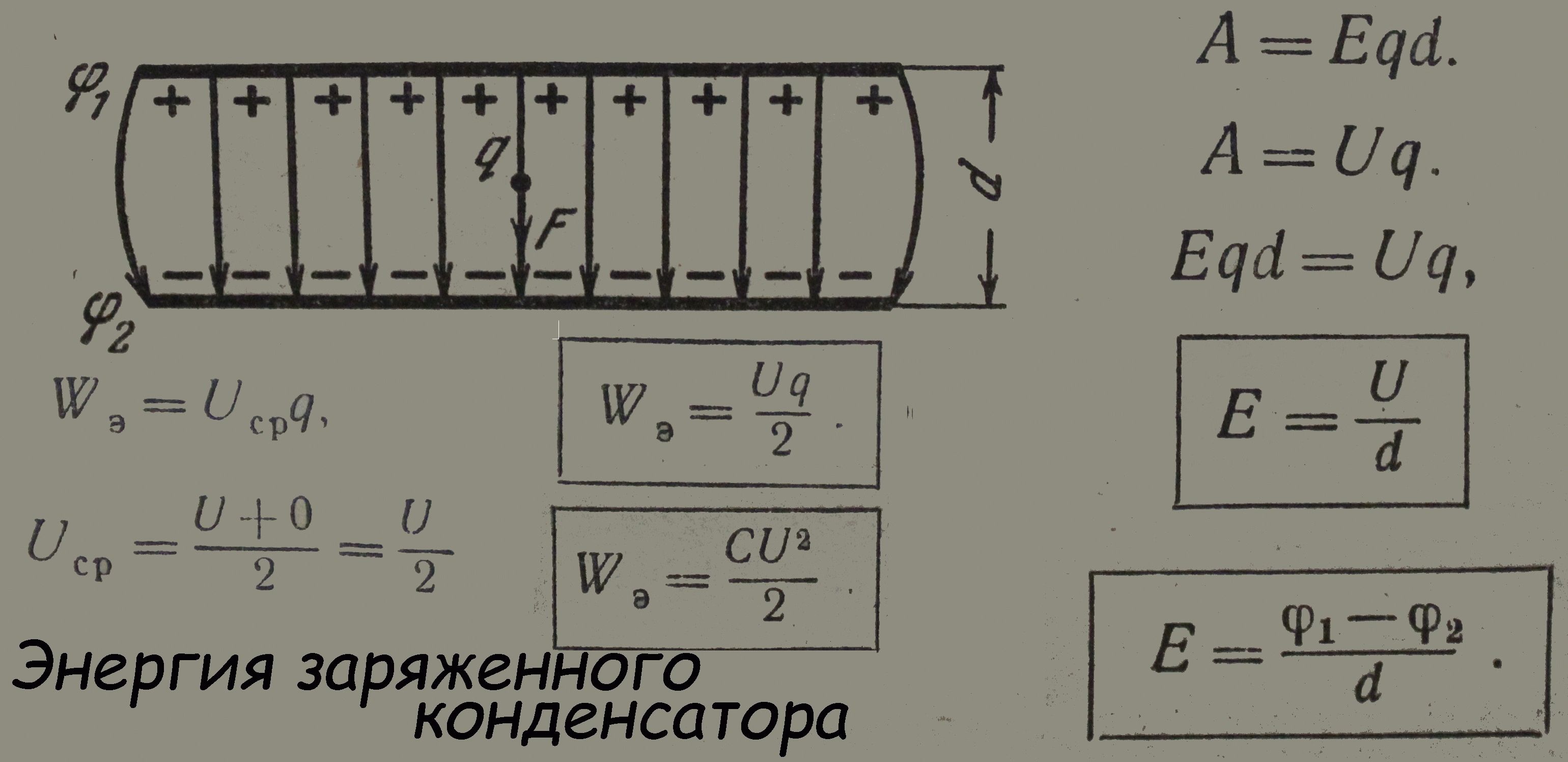 Это сводит к минимуму функцию конденсатора. Конденсаторы в реальном мире обычно свернуты в спирали в небольших упаковках, поэтому конденсатор с плоскими пластинами значительно упрощает привязку функции к устройству.
Это сводит к минимуму функцию конденсатора. Конденсаторы в реальном мире обычно свернуты в спирали в небольших упаковках, поэтому конденсатор с плоскими пластинами значительно упрощает привязку функции к устройству.

 Количество сохраняемого заряда очень мало, поэтому обычный вольтметр не подойдет.Небольшой заряд, накопившийся в конденсаторе, просто разрядился бы через измеритель, сделав любое измерение бесполезным. Вы будете использовать специальное устройство для измерения напряжения, называемое электрометром, которое измеряет напряжение без разрядки конденсатора.
Количество сохраняемого заряда очень мало, поэтому обычный вольтметр не подойдет.Небольшой заряд, накопившийся в конденсаторе, просто разрядился бы через измеритель, сделав любое измерение бесполезным. Вы будете использовать специальное устройство для измерения напряжения, называемое электрометром, которое измеряет напряжение без разрядки конденсатора.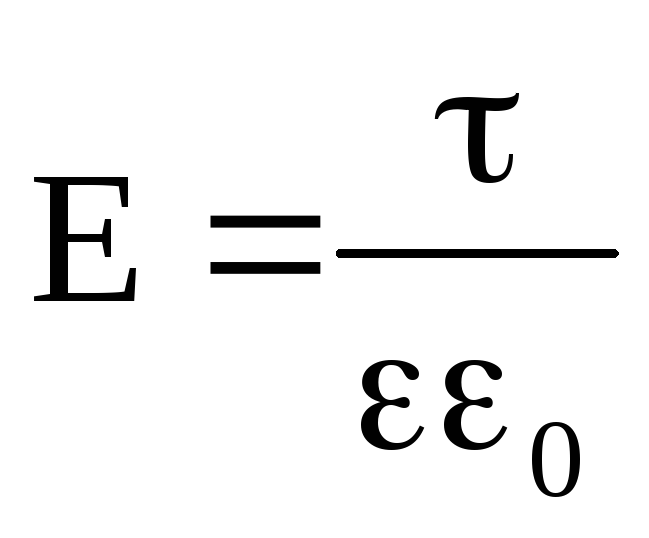 Все должно сочетаться с самыми легкими прикосновениями. Ничего не форсировать!
Все должно сочетаться с самыми легкими прикосновениями. Ничего не форсировать! Подставьте числа, чтобы получить A = π(0,089) 2 = 0,0249 м 2
Подставьте числа, чтобы получить A = π(0,089) 2 = 0,0249 м 2 Во-первых, вы определяете количество заряда в конденсаторе при этом расстоянии и напряжении. Используйте формулу Q=CV, чтобы определить заряд таким образом: Q=270×10-12F(10V)=2700×10-12C. Этот заряд остается одинаковым при любом расстоянии между пластинами, поэтому вы можете ввести одно и то же значение во весь столбец «Расчетный заряд»! Теперь используйте это значение заряда, чтобы определить расчетное напряжение на всех других расстояниях. Например, при расстоянии 5 мм используйте формулу V=Q/C, таким образом: V=2700×10-12C/94,0×10-12F=28,7В. Введите это значение в столбец Расчетное напряжение в строке 5 мм.
Во-первых, вы определяете количество заряда в конденсаторе при этом расстоянии и напряжении. Используйте формулу Q=CV, чтобы определить заряд таким образом: Q=270×10-12F(10V)=2700×10-12C. Этот заряд остается одинаковым при любом расстоянии между пластинами, поэтому вы можете ввести одно и то же значение во весь столбец «Расчетный заряд»! Теперь используйте это значение заряда, чтобы определить расчетное напряжение на всех других расстояниях. Например, при расстоянии 5 мм используйте формулу V=Q/C, таким образом: V=2700×10-12C/94,0×10-12F=28,7В. Введите это значение в столбец Расчетное напряжение в строке 5 мм.


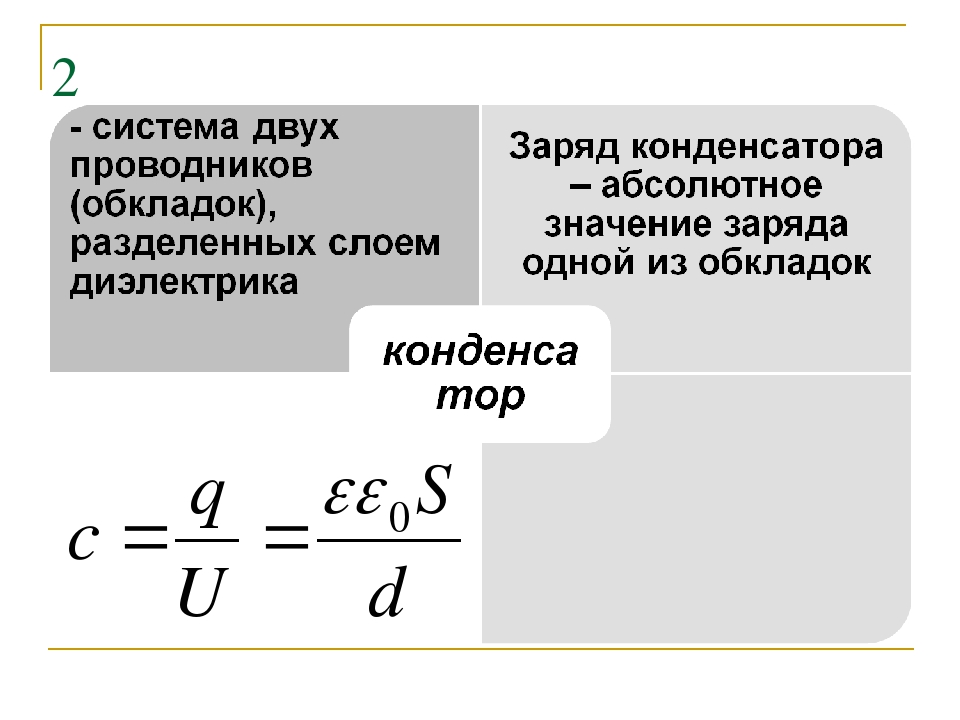
 Нанесите расчетное значение и измеренное значение напряжения, используя разные цвета или стили линий, чтобы различить две кривые. Убедитесь, что вы выбрали подходящие масштабы и четко обозначьте оси и масштабы. Лучше всего ориентировать бумагу длинной осью в горизонтальном направлении («альбомный режим»).
Нанесите расчетное значение и измеренное значение напряжения, используя разные цвета или стили линий, чтобы различить две кривые. Убедитесь, что вы выбрали подходящие масштабы и четко обозначьте оси и масштабы. Лучше всего ориентировать бумагу длинной осью в горизонтальном направлении («альбомный режим»).