Расчет потерь мощности в трансформаторах — Студопедия
Потери активной и реактивной мощности в трансформаторах и автотрансформаторах разделяются на потери в стали и потери в меди (нагрузочные потери). Потери в стали – это потери в проводимостях трансформаторов. Они зависят от приложенного напряжения. Нагрузочные потери – это потери в сопротивлениях трансформаторов. Они зависят от тока нагрузки.
Потери активной мощности в стали трансформаторов – это потери на перемагничивание и вихревые токи. Определяются потерями холостого хода трансформатора , которые приводятся в его паспортных данных.
Потери реактивной мощности в стали определяются по току холостого хода трансформатора, значение которого в процентах приводится в его паспортных данных:
Потери мощности в обмотках трансформатора можно определить двумя путями:
— по параметрам схемы замещения;
— по паспортным данным трансформатора.
Потери мощности по параметрам схемы замещения определяются по тем же формулам, что и для ЛЕП:
,
где S – мощность нагрузки;
U – линейное напряжение на вторичной стороне трансформатора.
Для трехобмоточного трансформатора или автотрансформатора потери в меди определяются как сумма потерь мощности каждой из обмоток.
Получим выражения для определения потерь мощности по паспортным данным двухобмоточного трансформатора.
Потери короткого замыкания, приведенные в паспортных данных, определены при номинальном токе трансформатора:
(7.1)
При любой другой нагрузке потери в меди трансформатора равны:
(7.2)
Разделив выражение (7.1) на (7.2), получим:
Откуда найдем :
Если в выражение для расчета , подставить выражение для определения реактивного сопротивления трансформатора, то получим:
Таким образом, полные потери мощности в двухобмоточном трансформаторе равны:
Если на подстанции с суммарной нагрузкой S работает параллельно n одинаковых трансформаторов, то их эквивалентные сопротивления в n раз меньше, а проводимости в n раз больше. Тогда,
Для n параллельно работающих одинаковых трехобмоточных трансформаторов (автотрансформаторов) потери мощности рассчитываются по формулам:
где Sв, Sс, Sн – соответственно мощности, проходящие через обмотки высшего, среднего и низшего напряжений трансформатора.
Потери мощности в трансформаторе
 КПД трансформатора никогда не достигает 100 %, поскольку в нём всегда присутствуют потери электроэнергии. Потери в трансформаторах принято разделять на два вида: потери в меди (медные витки обмоток) и потери в стали (материал сердечника).
КПД трансформатора никогда не достигает 100 %, поскольку в нём всегда присутствуют потери электроэнергии. Потери в трансформаторах принято разделять на два вида: потери в меди (медные витки обмоток) и потери в стали (материал сердечника).
Потери в меди возникают из-за собственного сопротивления медного проводника. Ток, протекая по обмотке, обуславливает некоторое падение напряжения, которое и является потерей мощности. При этом электрическая энергия преобразуется в тепловую, которая разогревает обмотку.
Потери в стали в свою очередь состоят из потерь, вызванных вихревыми токами, и обусловленых циклическим перемагничиванием (гистерезис).
 Вихревые токи возникают в проводнике, который находится в переменном магнитном поле. Этим условиям удовлетворяет стальной сердечник, на который намотаны медные витки. В нем постоянно возникают вихревые токи, величина которых может достигать достаточно больших значений, из-за которых в свою очередь происходит нагрев сердечника.
Вихревые токи возникают в проводнике, который находится в переменном магнитном поле. Этим условиям удовлетворяет стальной сердечник, на который намотаны медные витки. В нем постоянно возникают вихревые токи, величина которых может достигать достаточно больших значений, из-за которых в свою очередь происходит нагрев сердечника.
Величина потерь, вызванных необходимостью циклического перемагничивания определяется в первую очередь качеством стали, из которой сделан сердечник. В сердечнике как бы находится большое количество диполей, которые под действием переменного магнитного поля периодически изменяют своё направление (поворачиваются с периодичностью изменения магнитного поля). В ходе пространственного изменения положения диполей возникают механические силы трения между ними, что вызывает дополнительный нагрев сердечника. Таким образом происходит преобразование магнитной энергии в тепловую (потери мощности на гистерезис).
Чтобы снизить эти потери, применяется ряд мер. Потери, вызванные циклическим перемагничиванием, могут быть уменьшены, если использовать специальный структурированный особым образом магнитомягкий материал для изготовления сердечника (электротехническая сталь). Такой материал обладает большой магнитной проницаемостью, но при этом малой коэрцитивной силой.
Для снижения потерь в меди применяется увеличение сечения проводников обоих обмоток, при этом электросопротивление их уменьшается. С другой стороны, это вызывает увеличение стоимости и веса трансформатора, поэтому достаточным считается такое сечение, при котором не возникает заметного нагрева обмоток.
Чтобы уменьшить вихревые токи, сердечник выполняется не в виде единого монолитного блока, а собирается из множества электроизолированных пластин. Толщина каждой из них может равняться всего нескольким десятым долям миллиметра. Также электрическую проводимость сильно снижает специально вводимый в сталь легирующий элемент — кремний.
Комплексное использование мер по снижению потерь мощности позволяет довести КПД трансформаторов до 85-90%.
Пример расчета реактивной мощности трансформатора
В данном примере нужно будет определить реактивную мощность трансформатора при холостом ходе и при коэффициенте загрузки β=0,5.
Пример
Определить реактивную мощность трансформатора типа ТМЗ-1000-10/0,4 при холостом ходе и при коэффициенте загрузки β=0,5.
Исходные данные:
Технические характеристики трансформатора принимаем, согласно таблицы 2.110 [Л1., с.221] (ГОСТ 16555-75 (действующий)), также данные технические характеристики можете принимать из каталога завода-изготовителя:
- I% = 1,2% — ток холостого хода, %;
- Uк% = 5,5% — напряжение КЗ, %.
- Sн = 1000 кВА – номинальная полная мощность трансформатора, кВА.
Решение
1. Определяем реактивную мощность трансформатора при холостом ходе по выражению 17 [Л2, с.26]:
2. Определим реактивную мощность, зависящую от нагрузки по выражению 18 [Л2, с.27] для номинальной нагрузки:
3. Определяем полную реактивную мощность по выражению 19 [Л2, с.28] для номинальной нагрузки:
4. Определим полную реактивную мощность при загрузке трансформатора на 50% (β=0,5) по выражению 19 [Л2, с.28]:
Как видно из результатов расчетов, реактивная мощность трансформатора состоит из двух частей — реактивной мощности холостого хода Q0, не зависящей от нагрузки, и реактивной мощности рассеяния Qp, зависящей от тока нагрузки. В результате при уменьшении нагрузки трансформатора от номинальной до холостого хода реактивная мощность уменьшается от 100 примерно до 10%.
Читать еще: «Выбор устройства компенсации реактивной мощности».
Литература:
- Справочник по проектированию электроснабжению. Ю.Г. Барыбина. 1990 г.
- Реактивная мощность (2-е издание) Минин Г.П. 1978 г.
Поделиться в социальных сетях
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.
20. Определение потерь мощности и энергии в силовых трансформаторах
Потери мощности в трансформаторах
складываются из потерь активной и
реактивной мощности. Активные
потери состоят из потерь, идущих на
нагрев обмоток трансформатора и потерь
зависящих от тока нагрузки, потерь на
нагрев стали не зависящих от нагрузки.
Потери на нагрев обмоток

где RT– активное сопротивление трансформатора

РМ– активные потери в меди
обмотки, кВт
SН– номинальная
мощность трансформатора, кВА.
Полные активные потери определяются
суммой выше названных потерь

где РСТ–
потери в стали, кВт.
При известной нагрузке по паспортным
данным можно рассчитать потери

или

где
 — коэффициент загрузки трансформатора,
— коэффициент загрузки трансформатора,
РМ.Н– номинальные активные
потери в меди.
Реактивные потери — потери, вызванные
рассеянием магнитного потока в
трансформаторе, зависящие от тока
нагрузки и потерь на намагничивание.
Потери вызванные рассеянием магнитного
потока

xТ– реактивное
сопротивление обмоток трансформатора,
равное

UК– напряжение
короткого замыкания трансформатора, %
Полные реактивные потери трансформатора,
также определяются суммой потерь

где


 —
—
ток холостого тока, %
Полные реактивные потери с учетом
каталожных данных трансформатора

или

При передаче реактивной мощности
появляются потери активной мощности,
определяемые экономическим эквивалентом
реактивной мощности kЭК.
Приведенные потери активной мощности
на холостом ходу с учетом передачи
реактивной мощности определяются

Приведенные потери активной мощности
при коротком замыкании с учетом передачи
реактивной мощности определяются

При наличии на ПС nодинаковыхпараллельно
работающих трансформаторов,
приведенные активные потери мощности
составят

Для практических расчетов потери
мощности в трансформаторах рассчитываются
по выражениям:
активные потери
 ,
,
где n–
число трансформаторов подстанции,
 — паспортные данные трансформатора,
— паспортные данные трансформатора,
 — коэффициент загрузки трансформатора,
— коэффициент загрузки трансформатора,
реактивные потери
 ,
,
где
 — потери в режиме ХХ и режиме КЗ.
— потери в режиме ХХ и режиме КЗ.
Значения потерь учитываются при
определении мощности нагрузки на высоком
напряжении трансформатора в форме
Ф202-90 таблицы электрических нагрузок.
Потери электроэнергии
в в трансформаторах
Потери активной электроэнергии
в меди можно определить по потерям
мощности в меди РМ,
максимальной нагрузке SPи времени потерь .
Время потерь определяется по кривым рисунок 7.1, где
по кривым рисунок 7.1, где приниматся неизменным за определенное
приниматся неизменным за определенное
время (сутки, год).

Потери активной электроэнерги в стали
определяются потерями мощности на
холостом ходу и продолжительностью
включения трансформатора

где РСТ=РХХ
Суммарные активные потери электроэнергии
 (7.18)
(7.18)
Суммарные реактивные потери электроэнергии
определяются по реактивным потерям
мощности с учетом времени потерь и
времени включения трансформатора

или

21. Мероприятия по снижению потерь мощности и напряжения.
Составляющие потерь мощности и
напряжения, зависимость от показателей
качества напряжения. Пути снижения
потерь.
Пути снижения потерь электроэнергии
1) Рациональный выбор числа и мощности
трансформаторов
2) Исключение режима ХХ при малых загрузках
3) Количество одновременно работающих
трансформаторов выбирается из условия
минимума потерь
4) Снижение потерь в линиях снижением
сопротивления (параллельное включение)
5) Повышение уровня напряжения
6) При выборе схемы электроснабжения
принимать вариант без реактора или с
минимальными потерями в реакторе
7) Формирование более равномерного
графика нагрузки. Это позволит снизить
суммарный максимум нагрузки при
неизменяемой установленной мощности
и обеспечить питание большего числа
потребителей
8) Снижение активного сопротивления
шинопроводов, что достигается
соответствующим расположением шин и
конфигурацией шинного пакета (2-4 полосы
на фазу)
9) Экономное и рациональное использование
расходование электроэнергии, чему
способствует чистота световых проемов,
чистка светильников, побелка помещений,
правильное размещение осветительных
приборов, своевременное включение и
отключение светильников, применение
энергосберегающих ламп.
Компенсация реактивной мощности, поглощаемой трансформатором
Индуктивные реактивные сопротивления трансформатора
При измерении на стороне высокого напряжения трансформатора потери реактивной мощности в трансформаторе могут |
До сих пор в роли потребителей реактивной мощности рассматривались устройства с параллельным подключением к сети. Они потребляют наибольшее количество реактивной мощности. Однако, реактивные сопротивления с последовательным соединением, такие как индуктивные реактивные сопротивления силовых линий и реактивные сопротивления рассеяния обмоток трансформатора, также поглощают реактивную мощность.
При учете на стороне высокого напряжения трансформатора потери реактивной энергии в трансформаторе могут (в зависимости от тарифа) требовать компенсации. Поскольку рассматриваются только потери реактивной мощности, трансформатор может быть представлен с помощью элементарной схемы (рис. L19). Все значения реактивных сопротивлений приведены к вторичной обмотке трансформатора, на которой параллельное ответвление представляет путь намагничивающего тока. Намагничивающий ток остается практически постоянным (около 1,8% номинального тока) при изменении нагрузки от нуля до номинальной в нормальном режиме, т.е. при постоянном напряжении на первичной обмотке. Поэтому на стороне высокого или низкого напряжения может устанавливаться постоянный (нерегулируемый) шунтирующий конденсатор для компенсации потерь реактивной мощности намагничивания.
Рис. L19 : Реактивные сопротивления трансформатора на фазу
Потери реактивной мощности в последовательно включенном реактивном сопротивлении XL, обусловленном магнитным потоком рассеяния
Простая иллюстрация этого явления приводится на векторной диаграмме (рис. L20).
Реактивная составляющая тока через нагрузку = I sin φ, так что, QL = VI sin φ.
Реактивная составляющая тока от источника = I sin φ’ так что, QE = EI sin φ’
где V и E выражены в кВ.
Можно видеть, что E > V и sin φ’ > sin φ.
Разница между EI sin φ’ и VI sin φ XL дает значение квар на фазу (поглощение XL).
Можно показать, что такое значение квар равно I2XL (аналог потерь активной мощности (кВт) I2R — потери в последовательно соединенных элементах).
Из формулы I2XL легко вывести поглощаемое значение квар при любом значении нагрузки для заданного трансформатора.
Если используются значения в относительных единицах (вместо значений в процентах), можно выполнить прямое умножение I на XL.
Рис. L20 : Поглощение реактивной энергии последовательным индуктивным сопротивлением
Реактивная мощность, поглощаемая трансформатором, не может не приниматься во внимание и может составлять около 5% от номинальной мощности трансформатора при его номинальной нагрузке. |
Пример:
Трансформатор 630 кВА с реактивной составляющей напряжения короткого замыкания 4% работает при полной нагрузке.
Каковы его нагрузочные потери реактивной мощности (квар)?
4% = 0,04 о.е., Iо.е. = 1
Потери = I2XL = 12 x 0,04 о.е.,
единица мощности = 630 кВА
Трехфазные нагрузочные потери реактивной мощности (квар) = 630 х 0,04 = 25,2 квар (или 4% от 630 кВА).
При половине нагрузки, т.е. I = 0,5 о.е. потери составят: 0,52 x 0,04 = 0,01 о.е. или в квар: 630 x 0,01 = 6,3 квар.
Данный пример и векторная диаграмма (рис. L22) показывают, что:
- Коэффициент мощности на стороне первичной обмотки нагруженного трансформатора отличается (нормально ниже) от коэффициента на вторичной обмотке (из-за потерь реактивной мощности (квар).
- Нагрузочные потери реактивной мощности (квар) при полной нагрузке равны реактивному сопротивлению трансформатора в о.е. умноженному на Sном. (нагрузочные потери реактивной мощности (квар), равные 4% номинальной мощности кВА трансформатора).
- Нагрузочные потери реактивной мощности (квар) изменяются согласно квадрату тока (или мощности кВА).
Для определения общих потерь реактивной мощности (квар) трансформатора необходимо добавить постоянные потери в цепи намагничивающего тока (приблизительно 1,8% номинального значения кВА трансформатора) к указанным нагрузочным потерям. Рис. L21 показывает потери реактивной мощности (квар) при холостом ходе и при полной нагрузке для типового распределительного трансформатора. В принципе, последовательно включенные индуктивные сопротивления могут компенсироваться последовательно включенными нерегулируемыми конденсаторами (как в общем случае протяженных высоковольтных линий передачи). Однако, такая схема сложна для выполнения, тем более, что при уровнях напряжения, рассматриваемых в данном руководстве, всегда применима параллельная компенсация.
В случае учета на стороне высокого напряжения достаточно повысить коэффициент мощности до значения, при котором потери реактивной мощности в трансформаторе плюс потребление реактивной мощности нагрузки ниже уровня, при котором взимается дополнительная плата за электроэнергию. Этот уровень зависит от тарифа, но часто соответствует значению tg φ = 0,31 (cos φ = 0,955).
| Номинальная мощность (кВА) | Реактивная мощность (квар), подлежащая компенсации | |
|---|---|---|
| Без нагрузки | Полная нагрузка | |
| 100 | 2,5 | 6,1 |
| 160 | 3,7 | 9,6 |
| 250 | 5,3 | 14,7 |
| 315 | 6,3 | 18,4 |
| 400 | 7,6 | 22,9 |
| 500 | 9,5 | 28,7 |
| 630 | 11,3 | 35,7 |
| 800 | 20 | 54,5 |
| 1000 | 23,9 | 72,4 |
| 1250 | 27,4 | 94,5 |
| 1600 | 31,9 | 126 |
| 2000 | 37,8 | 176 |
Рис. L21 : Потери реактивной мощности для распределительных трансформаторов с первичными обмотками 20 кВ
Теоретически, потери реактивной мощности (квар) в трансформаторе могут быть полностью компенсированы путем регулирования блока конденсаторов таким образом, чтобы создать небольшой избыток реактивной мощности конденсаторов (QC) по сравнению с реактивной мощностью нагрузки (QL) (QC — QL > 0). При этом коэффициент мощности на стороне НН (cos φ) увеличится и будет опережающим. В таком случае вся реактивная мощность потерь трансформатора поступает от КБ, а на стороне высокого напряжения трансформатора коэффициент мощности 1, как показано на рис. L22.
Рис. L22 : Перекомпенсация нагрузки до полной компенсации потерь реактивной мощности в трансформаторе
С практической точки зрения, компенсация реактивной энергии в трансформаторе осуществляется конденсаторами, главным образом предназначенными для повышения коэффициента мощности нагрузки (централизовано, по группам или индивидуально). В отличие от большинства других элементов, потребляющих реактивную мощность, потребление трансформатором (из-за реактивного сопротивления рассеяния) значительно изменяется при изменении уровня нагрузки, так что, если для трансформатора применяется индивидуальная компенсация, то средний уровень нагрузки должен приниматься в качестве гарантированного.
Однако, такое потребление реактивной мощности составляет, как правило, относительно небольшую часть общей реактивной мощности установки, и поэтому рассогласование компенсации с временным изменением нагрузки не представляет проблемы.
Рис. L21 показывает типовые значения потерь реактивной энергии для намагничивающей цепи (строка «Без нагрузки»), а также общие потери при полной нагрузке для стандартных распределительных трансформаторов с первичным напряжением 20 кВ (с учетом нагрузочных потерь).zh:对变压器吸收的无功电能进行补偿
Потери мощности и энергии в трансформаторах — Студопедия
Потери мощности через трансформатор всегда связаны с потерями мощности в активном и реактивном сопротивлениях его обмоток и потерями, связанными с намагничиванием стали. Потери, возникающие в обмотках, зависят от протекающего по ним тока. Потери, идущие на намагничивание, определяются приложенным напряжением и могут быть приняты неизменными и равными потерям холостого хода.
В двухобмоточных трансформаторах потери мощности определяются как
, (3.32)
. (3.33)
В тех случаях, когда напряжение U неизвестно, принимают его равным номинальному напряжению трансформатора, к которому приведены его сопротивления R и X.
При параллельной работе n одинаковых трансформаторов их эквивалентное сопротивление уменьшается в n раз, а потери на намагничивание увеличиваются в n раз.
, (3.34)
. (3.35)
Потери мощности могут быть найдены непосредственно по каталожным параметрам трансформаторов без предварительного вычисления сопротивлений r и х. Поскольку потери короткого замыкания определяются при номинальном токе трансформатора
=3,
а при любом другом токе, потери активной мощности в обмотках
,
то справедлива зависимость
.
Значит при одном трансформаторе
, (3.36)
а при параллельной работе n одинаковых трансформаторов
. (3.37)
Подставив значение реактивного сопротивления (3.12) в (3.35), получим
. (3.38)
Из (3.38) следует, что при S=S напряжение короткого замыкания U численно равно потере реактивной мощности в обмотках трансформатора, выраженной в долях от его номинальной мощности.
В трехобмоточных трансформаторах и автотрансформаторах потери активной мощности определяются суммированием потерь мощности в каждой из обмоток
(3.39)
где S, S, S — соответственно мощности, протекающие по обмоткам высшего, среднего и низшего напряжений.
Потери реактивной мощности определяются
. (3.40)
Потери энергии в трансформаторах определяют следующим образом:
. (3.41)
для трехобмоточных и автотрансформаторов
. (3.42)
Потери мощности и энергии в трансформаторах. — КиберПедия
Передача электрической энергии от источников питания к потребителям связана с потерей части мощности и энергии в системе электроснабжения (трансформаторах, линиях, реакторах). Эти потери определяются током, протекающим по линии, и величиной передаваемого напряжения. Применение повышенного напряжения в электрических сетях, например 10 кВ (вместо 6 кВ), а также глубокого ввода напряжения 35 кВ и выше значительно снижает потери мощности и электроэнергии. Этому также способствует повышение коэффициента мощности.
Следует подчеркнуть, что потери в трансформаторахопределяются также числом часов их работы, поэтому одним из условий, обеспечивающих экономию электроэнергии в трансформаторах, является отключениеихпри малых загрузках. Это возможно осуществить, если в ночное (не рабочее) время питать электроустановки, предназначенные для ремонтных работ, дежурного освещения и пр., от одного трансформатора. Питание указанных потребителей при этом обеспечивается наличием перемычек на низшем напряжении между цеховыми подстанциями.
Другим условием экономии электроэнергии в трансформаторах является установление рационального режима работывключенных трансформаторов, что обеспечивается установлением оптимального коэффициента загрузки, зависящего от соотношения между активными и реактивными составляющими потерь.
Потери мощности и электроэнергии в трансформаторах.
Потери мощности в трансформаторах состоят из потерь активной D Рх и потерь реактивной мощности D Qх.
Потери активной мощности.
Они состоят из двух составляющих:
1) потерь, идущих на нагревание обмоток трансформатора D Р, зависящих от тока нагрузки,
2) потерь, идущих на нагревание стали D Рст, не зависящих от тока нагрузки.
Потери мощности, идущие на нагревание обмоток трансформатора
При этом полные активные потери
где Rт — активное сопротивление (0м) обмоток трансформатора, определяемое по величине потерь в меди D Рх (кВт), мощности трансформатора Sном (кВА), номинальному напряжению Uном (кВ) обмотки трансформатора, присоединенной к рассчитываемой линии:
Потери реактивной мощности.
Они состоят из двух составляющих:
1)потерь, вызванных рассеянием магнитного потока в трансформаторе D Q, зависящих от квадрата тока нагрузки,
2) потерь, идущих на намагничивание трансформатора D Qm , не зависящих от тока нагрузки, которые определяются током х.х.
Потери мощности, вызванные рассеянием магнитного потока
При этом полные реактивные потери
где Хт — реактивное сопротивление обмоток трансформатора, определяемое напряжением короткого замыкания uкз,% и сопротивлением Rт.
С помощью каталожных данных потери мощности в трансформаторах можно определить иначе. Если даны потери короткого замыкания D Рм,ном соответствующие потерям в меди при номинальной нагрузке трансформатора Sном, и известна его фактическая загрузка S, то активные потери
где кз — коэффициент загрузки трансформатора.
Сопротивление и реактивные потери трансформатора могут быть определены также по каталожным данным:
где uкз — напряжение короткого замыкания, %; Iхх — ток холостого хода трансформатора, %; Sном — номинальная мощность, кВA.
Компенсация реактивной энергии, потребляемой трансформатором
Если учет осуществляется на стороне СН трансформатора, может потребоваться компенсация потерь реактивной энергии в трансформаторе (в зависимости от тарифа).
Природа индуктивных сопротивлений трансформатора
Все предыдущие ссылки были связаны с шунтирующими подключенными устройствами, такими как те, которые используются в обычных нагрузках, конденсаторных батареях с коррекцией коэффициента мощности и т.д. ; однако последовательно соединенные реактивные сопротивления, такие как индуктивные реактивные сопротивления линий электропередач и реактивное сопротивление рассеяния обмоток трансформатора и т. д., также поглощают реактивную энергию.
Если измерение выполняется на стороне среднего напряжения трансформатора, потери реактивной энергии в трансформаторе могут (в зависимости от тарифа) должны быть компенсированы. Что касается только потерь реактивной энергии, трансформатор может быть представлен в виде элементарной схемы , рисунок L20. Все значения реактивного сопротивления относятся к вторичной обмотке трансформатора, где шунтирующая ветвь представляет путь тока намагничивания. Ток намагничивания остается практически постоянным (около 1.8% от тока полной нагрузки) от холостого хода до полной нагрузки в нормальных условиях, т. Е. С постоянным первичным напряжением, так что шунтирующий конденсатор фиксированного значения может быть установлен на стороне среднего или низкого напряжения для компенсации реактивной энергии впитывается.
Рис. L20 — Реактивные сопротивления трансформатора на фазу
Потребление реактивной мощности при последовательном включении (поток рассеяния) реактивное сопротивление XL
Реактивной мощностью, потребляемой трансформатором, нельзя пренебрегать, и она может составлять (около) 5% от номинальной мощности трансформатора при питании его полной нагрузки.Компенсация может быть обеспечена батареей конденсаторов. В трансформаторах реактивная мощность поглощается как шунтирующим (намагничивающее), так и последовательным (поток утечки) реактивными сопротивлениями. Полная компенсация может быть обеспечена за счет установки параллельно подключенных низковольтных конденсаторов.
Простую иллюстрацию этого явления дает векторная диаграмма , рис. L21.
Составляющая реактивного тока через нагрузку = I sin φ, так что QL = VI sin φ.
Составляющая реактивного тока от источника = I sin φ, так что QE = EI sin φ ‘.
Видно, что E> V и sin φ ‘> sin φ.
Разница между EI sin φ ‘и VI sin φ дает квар на фазу, поглощаемую XL.
Можно показать, что это значение квар равно I 2 XL (что аналогично потерям активной мощности (кВт) I 2 R из-за последовательного сопротивления линий электропередач и т. Д.).
Из формулы I 2 X L очень просто вывести потребляемую квар, потребляемую при любом значении нагрузки для данного трансформатора, следующим образом:
Если используются удельные значения (вместо процентных значений), можно выполнить прямое умножение I и X L .
Пример
Трансформатор 630 кВА с реактивным напряжением короткого замыкания 4% полностью загружен.
Каковы его потери реактивной мощности (квар)?
X L = 0,04 о.е. и I = 1 о.е.
потери = I 2 X L = 1 2 x 0,04 = 0,04 о.е. квар
, где 1 о.е. = 630 кВА
Потери в трехфазной кВАр составляют 630 x 0,04 = 25,2 кВАр (или, проще говоря, 4% от 630 кВА).
При половинной нагрузке, т.е. I = 0,5 о.е., потери будут
0.5 2 x 0,04 = 0,01 pu = 630 x 0,01 = 6,3 квар и так далее …
Этот пример и векторная диаграмма Рис. L21 показывают, что:
- Коэффициент мощности на первичной стороне нагруженного трансформатора отличается (обычно ниже), чем на вторичной стороне (из-за поглощения вар.)
- Потери квар при полной нагрузке из-за реактивного сопротивления утечки равны процентному реактивному сопротивлению трансформатора (реактивное сопротивление 4% означает потерю квар, равную 4% от номинальной мощности трансформатора в кВА).
Потери - квар из-за реактивного сопротивления утечки зависят от тока (или нагрузки в кВА) в квадрате
Рис.L21 — Потребление реактивной мощности последовательной индуктивностью
Для определения общих потерь в кВАр трансформатора необходимо добавить потери в цепи постоянного тока намагничивания (примерно 1,8% от номинальной мощности трансформатора, кВА) к вышеуказанным «последовательным» потерям. На рисунке L21 показаны кварцевые потери холостого хода и полной нагрузки для типичных распределительных трансформаторов. В принципе, последовательные индуктивности можно компенсировать последовательными конденсаторами постоянной емкости (как это обычно бывает в длинных линиях передачи среднего напряжения).Однако такая компоновка трудна в эксплуатации, поэтому на уровнях напряжения, описываемых в данном руководстве, всегда применяется шунтирующая компенсация.
В случае измерения среднего напряжения достаточно поднять коэффициент мощности до точки, при которой трансформатор плюс потребление реактивной мощности нагрузки ниже уровня, при котором производится выставление счетов. Этот уровень зависит от тарифа, но часто соответствует значению tan ϕ, равному 0,31 (cos φ, равному 0,955).
Рис. L22 — Потребляемая реактивная мощность распределительных трансформаторов с первичной обмоткой 20 кВ
| Номинальная мощность (кВА) | Реактивная мощность (квар) для компенсации | |
|---|---|---|
| Без нагрузки | Полная нагрузка | |
| 100 | 2.5 | 6,1 |
| 160 | 3,7 | 9,6 |
| 250 | 5,3 | 14,7 |
| 315 | 6,3 | 18,4 |
| 400 | 7,6 | 22,9 |
| 500 | 9,5 | 28,7 |
| 630 | 11,3 | 35,7 |
| 800 | 20 | 54.5 |
| 1000 | 23,9 | 72,4 |
| 1250 | 27,4 | 94,5 |
| 1600 | 31,9 | 126 |
| 2000 | 37,8 | 176 |
Интересно, что потери квар в трансформаторе могут быть полностью компенсированы путем регулировки конденсаторной батареи, чтобы дать нагрузке (немного) опережающий коэффициент мощности. В таком случае вся квар трансформатора питается от конденсаторной батареи, в то время как вход на стороне среднего напряжения трансформатора имеет единичный коэффициент мощности, как показано на Рис. L23.
Рис. L23 — Чрезмерная компенсация нагрузки для полной компенсации потерь реактивной мощности трансформатора
Таким образом, на практике компенсация потребляемой трансформатором квар включается в конденсаторы, в первую очередь предназначенные для коррекции коэффициента мощности нагрузки, глобально, частично или в индивидуальном режиме. В отличие от большинства других устройств, поглощающих квар, поглощение трансформатора (то есть часть, обусловленная реактивным сопротивлением утечки) значительно изменяется при изменении уровня нагрузки, поэтому, если к трансформатору применяется индивидуальная компенсация, то средний уровень нагрузки должен быть предполагаться.
К счастью, это потребление квар обычно составляет лишь относительно небольшую часть общей реактивной мощности установки, и поэтому несоответствие компенсации при изменении нагрузки вряд ли будет проблемой.
На рисунке L22 показаны типичные значения потерь в квар для цепи намагничивания (столбцы «квар без нагрузки»), а также для общих потерь при полной нагрузке для стандартного ряда распределительных трансформаторов, питаемых напряжением 20 кВ (включая потери из-за реактивного сопротивления утечки).
.
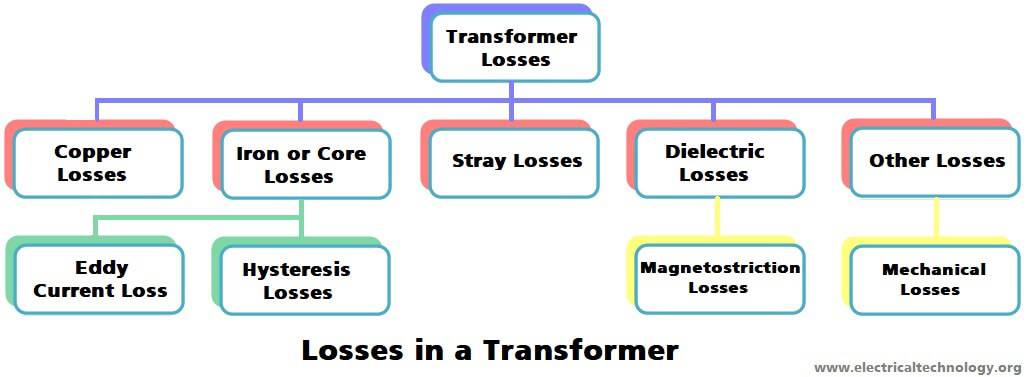
Типы потерь в трансформаторе
В трансформаторе есть различные типы потерь, такие как потери в стали, потери в меди, гистерезисные потери, потери на вихревые токи, паразитные потери и диэлектрические потери. Гистерезисные потери возникают из-за изменения намагниченности в сердечнике трансформатора, а потери в меди возникают из-за сопротивления обмотки трансформатора.
Различные типы потерь подробно описаны ниже.
В комплекте:
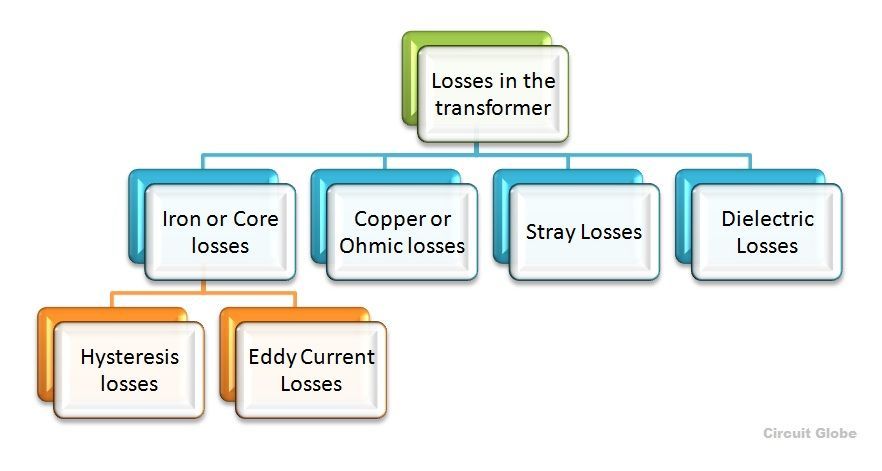
Виды потерь в трансформаторе
Потери железа
Потери в стали вызваны переменным магнитным потоком в сердечнике трансформатора, так как эти потери происходят в сердечнике, они также известны как Потери в сердечнике .Потери в железе подразделяются на гистерезис и потери на вихревые токи.
Гистерезис потери
На сердечник трансформатора действует переменная сила намагничивания, и для каждого цикла ЭДС прослеживается петля гистерезиса. Мощность рассеивается в виде тепла, известного как гистерезисные потери, и определяется уравнением, показанным ниже:
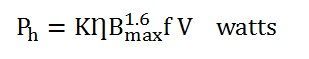
Где
- KȠ — постоянная пропорциональности, которая зависит от объема и качества материала сердечника, используемого в трансформаторе,
- f — частота питания,
- Bmax — максимальное или пиковое значение плотности потока.
Потери в железе или сердечнике могут быть минимизированы за счет использования кремнистой стали для изготовления сердечника трансформатора.
Потери на вихревые токи
Когда магнитный поток соединяется с замкнутой цепью, в цепи индуцируется ЭДС и течет ток, значение тока зависит от величины ЭДС вокруг цепи и сопротивления цепи.
Так как сердечник изготовлен из проводящего материала, эти ЭДС циркулируют токи внутри тела материала.Эти циркулирующие токи называются Вихревые токи . Они возникают, когда проводник испытывает изменяющееся магнитное поле. Поскольку эти токи не отвечают за выполнение какой-либо полезной работы, и они вызывают потери (I 2 R потери) в магнитном материале, известные как потери на вихревые токи .
Потери на вихревые токи минимизированы за счет изготовления сердечника из тонких пластин.
Уравнение потерь на вихревые токи имеет вид:
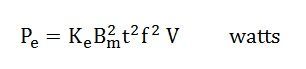
Где,
- K e — коэффициент вихревого тока.Его значение зависит от природы магнитного материала, такого как объем и удельное сопротивление материала сердечника, толщина слоев
- B м — максимальное значение плотности потока в Вт / м 2
- T — толщина ламинации в метрах
- F — частота разворота магнитного поля в Гц
- В — объем магнитного материала, м 3
Потери в меди или омические потери
Эти потери возникают из-за омического сопротивления обмоток трансформатора.Если I 1 и I 2 — это первичный и вторичный ток. R 1 и R 2 — это сопротивление первичной и вторичной обмоток, тогда потери в меди, возникающие в первичной и вторичной обмотках, будут равны I 1 2 R 1 и I 2 2 R 2 соответственно.
Таким образом, общие потери в меди будут
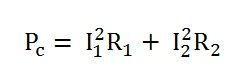 Эти потери варьируются в зависимости от нагрузки и известны, следовательно, также известны как переменные потери.Потери в меди изменяются как квадрат тока нагрузки.
Эти потери варьируются в зависимости от нагрузки и известны, следовательно, также известны как переменные потери.Потери в меди изменяются как квадрат тока нагрузки.
Рассеянная потеря
Возникновение этих паразитных потерь связано с наличием поля утечки. Процент этих потерь очень мал по сравнению с потерями в чугуне и меди, поэтому ими можно пренебречь.
Диэлектрические потери
Диэлектрические потери возникают в изоляционном материале трансформатора, который находится в масле трансформатора, или в твердой изоляции. Когда качество масла ухудшается, или твердая изоляция, либо ее качество ухудшается, и из-за этого снижается КПД трансформатора.
.
Потери в трансформаторе — Типы потерь энергии в трансформаторе
Типы потерь энергии в трансформаторе
Идеальный трансформатор не имеет потерь энергии, т.е. нулевые потери, и 100% КПД. но в реальных (на практике) трансформаторах энергия рассеивается в обмотках, сердечнике и окружающих конструкциях. Трансформаторы большего размера обычно более эффективны, а трансформаторы распределительного трансформатора обычно работают лучше 98%.
Экспериментальные трансформаторы, использующие сверхпроводящие обмотки (сверхпроводник — это тот, в котором потери отсутствуют) достигают КПД 99.85%, т.е. нулевые потери в трансформаторе, но это будет доступно в ближайшие годы.
Потери в трансформаторе
Различные потери в трансформаторе следующие
Щелкните изображение, чтобы увеличить

Потери в меди (сопротивление обмотки)
Ток, протекающий через обмотки, вызывает резистивный нагрев проводники. На более высоких частотах скин-эффект и эффект близости создают дополнительное сопротивление обмотки и потери.
Общие потери меди. = I 1 2 . R 1 + I 2 2 R 2 = I 1 2 . R 01 + I 2 2 R 02
Потери в сердечнике или в железе
В трансформаторе есть два типа потерь в сердечнике или в железе.
a) Гистерезисные потери
Каждый раз, когда магнитное поле меняет направление, небольшое количество энергии теряется из-за гистерезиса внутри сердечника.Для данного материала сердечника потери трансформатора пропорциональны частоте и являются функцией максимальной плотности магнитного потока, которой он подвергается.
Мы можем найти гистерезисные потери по этой формуле.
Вт ч = η B 1,6 макс фв ватт
b) Потери на вихревые токи
Ферромагнитные материалы также являются хорошими проводниками, и сердечник, сделанный из такого материала, также составляет один короткозамкнутый виток по всей длине.Поэтому вихревые токи циркулируют внутри сердечника в плоскости, перпендикулярной потоку, и ответственны за резистивный нагрев материала сердечника.
Потери на вихревые токи являются сложной функцией квадрата частоты питания и обратного квадрата толщины материала. Потери на вихревые токи можно уменьшить, сделав сердечник пакета пластин электрически изолированным друг от друга, а не сплошным блоком; все трансформаторы, работающие на низких частотах, используют ламинированные или аналогичные сердечники.
По этой формуле можно найти потери на вихревые токи.
Вт e = PB 2 max .f 2 t 2 Вт
Параллельные потери (поток утечки)
Индуктивность утечки сама по себе в значительной степени без потерь, поскольку энергия подается на его магнитные поля возвращаются в источник питания в следующем полупериоде. Однако любой поток утечки, который захватывает соседние проводящие материалы, такие как опорная конструкция трансформатора, вызывает вихревые токи и преобразуется в тепло.Существуют также радиационные потери из-за колеблющегося магнитного поля, но они обычно невелики и пренебрежимо малы.
Диэлектрические потери
В твердой изоляции или трансформаторном масле, т. Е. Изоляционном материале трансформатора, диэлектрические потери возникают, когда твердая изоляция повреждается, или масло ухудшается, или его качество со временем ухудшается. Следовательно, эта потеря может повлиять на общий КПД трансформатора.
Прочие потери
Магнитострикционные потери
Магнитный поток в ферромагнитном материале, таком как сердечник, заставляет его физически расширяться и слегка сжиматься с каждым циклом магнитного поля, эффект, известный как магнитострикция.Это создает жужжащий звук, обычно связанный с трансформаторами, и может вызвать потери из-за нагрева от трения.
Вы также можете прочитать: Фазирование трансформатора: точечная нотация и условные обозначения
Механические потери
Помимо магнитострикции, переменное магнитное поле вызывает колебания сил между первичной и вторичной обмотками. Они вызывают вибрацию в ближайших металлических конструкциях, усиливают жужжание и потребляют небольшое количество энергии.

 Потери трансформатора: Siemens 1500 кВА Трансформатор
Потери трансформатора: Siemens 1500 кВА Трансформатор
Вы также можете прочитать:
.
Основные операции трансформатора
- Изучив этот раздел, вы сможете описать:
- • Принцип работы трансформатора.
- • Передаточное число.
- • Коэффициент мощности.
- • Коэффициент трансформации.
- • Потери в трансформаторе: медь, гистерезис и вихревые токи.
- • КПД трансформатора и ток холостого хода.
Трансформаторы.
Трансформатор использует принципы электромагнетизма для переключения одного уровня переменного напряжения на другой. Работа Фарадея в 19 веке показала, что изменяющийся ток в проводнике (например, первичной обмотке трансформатора) создает изменяющееся магнитное поле вокруг проводника. Если другой проводник (вторичная обмотка) поместить в это изменяющееся магнитное поле, в этой обмотке будет индуцироваться напряжение.
Передаточное число.
Фарадей также рассчитал, что напряжение, индуцированное во вторичной обмотке, будет иметь величину, которая зависит от ОТНОШЕНИЯ ОБОРОТОВ трансформатора. т.е. если вторичная обмотка имеет половину числа витков первичной обмотки, то вторичное напряжение будет вдвое меньше напряжения на первичной обмотке. Аналогично, если вторичная обмотка имеет вдвое больше витков первичной обмотки, вторичное напряжение будет вдвое больше первичного напряжения.
Коэффициент мощности.
Поскольку трансформатор является пассивным компонентом (у него нет внешнего источника питания), он не может выдавать больше мощности из вторичной обмотки, чем подается на первичную обмотку. Следовательно, если вторичное напряжение больше, чем первичное напряжение на определенную величину, вторичный ток будет меньше, чем первичный ток на аналогичную величину, то есть если напряжение удвоится, ток будет уменьшен вдвое.

Рис. 11.1.1 Основные операции трансформатора.
Коэффициент трансформации.
Работа трансформатора
Basic может быть описана двумя формулами, связывающими коэффициент трансформации с числом витков обмоток трансформатора.
- В P = первичное напряжение.
- I P = первичный ток.
- В S = вторичное напряжение.
- I S = вторичный ток.
- N P = количество витков в первичной обмотке.
- N S = количество витков вторичной обмотки.
Потери трансформатора.
Формулы на рис. 11.1.1 относятся к идеальному трансформатору, то есть трансформатору без потерь мощности, в котором первичный вольт-ампер = вторичный вольт-ампер.
Хотя практические трансформаторы могут быть чрезвычайно эффективными, некоторые потери будут возникать, потому что не весь магнитный поток, создаваемый первичной обмоткой, будет связываться со вторичной обмоткой. Потери мощности, возникающие в трансформаторе, бывают трех типов;
1.Медные потери.
Эти потери также можно назвать потерями в обмотке или потерями I2R, поскольку они могут возникать в обмотках, сделанных не из меди, а из других металлов. Потери проявляются в виде тепла, выделяемого в обмотках (медных) проводов, поскольку они рассеивают мощность из-за сопротивления провода.
Потери мощности в обмотке трансформатора можно рассчитать, используя ток в обмотке и ее сопротивление в формуле для мощности P = I 2 R. Эта формула является причиной того, что потери в меди иногда называют I 2 R убытки.Чтобы свести к минимуму потери, сопротивление обмотки должно быть низким с использованием провода подходящей площади сечения и низкого удельного сопротивления.
2. Гистерезисные потери.
Каждый раз, когда переменный ток меняет направление на противоположное (один раз в каждом цикле), крошечные «магнитные домены» в материале сердечника меняются местами. Это физические изменения в основном материале, требующие некоторой энергии. Количество используемой энергии зависит от «сопротивления» материала сердечника; в больших сердечниках силовых трансформаторов, где потери на гистерезис могут быть проблемой, они в значительной степени решаются использованием специальной стали с низким сопротивлением «ориентированной зернистостью» в качестве материала сердечника.
3. Вихретоковые потери.
Поскольку железный или стальной сердечник является электрическим проводником, а также магнитной цепью, изменяющийся ток в первичной обмотке будет иметь тенденцию создавать ЭДС внутри сердечника, а также во вторичной обмотке. Токи, индуцируемые в сердечнике, будут противодействовать изменениям магнитного поля, происходящим в сердечнике. По этой причине эти вихревые токи должны быть как можно меньше. Это достигается разделением металлического сердечника на тонкие листы или «ламинаты», каждый из которых изолирован от других изолирующим слоем лака или оксида.Ламинированные сердечники значительно уменьшают образование вихревых токов, не влияя на магнитные свойства сердечника.
Ферритовые сердечники.
В высокочастотных трансформаторах потери на вихревые токи уменьшаются за счет использования сердечника из керамического материала, содержащего большую долю мельчайших металлических частиц, железной пыли или марганцево-цинка. Керамика изолирует металлические частицы друг от друга, давая аналогичный эффект ламинированным слоям и лучше работая на высоких частотах.
Благодаря способам снижения потерь, описанным выше, практические трансформаторы по своим характеристикам близки к идеальным.В мощных силовых трансформаторах может быть достигнут КПД около 98%. Поэтому для большинства практических расчетов можно считать трансформатор «идеальным», если не указаны его потери. Фактические вторичные напряжения в практическом трансформаторе будут лишь немного меньше, чем рассчитанные с использованием теоретического коэффициента трансформации.
Ток выключения.
Поскольку трансформатор работает почти идеально, мощность как в первичной, так и во вторичной обмотках одинакова, поэтому, когда на вторичную обмотку не подается нагрузка, вторичный ток не течет, а мощность во вторичной обмотке равна нулю (V x I = 0).Следовательно, хотя к первичной обмотке приложено напряжение, ток не будет течь, поскольку мощность в первичной обмотке также должна быть равна нулю. В практических трансформаторах «ток холостого хода» в первичной обмотке на самом деле очень мал.
Вольт на оборот.
Трансформатор с первичной обмоткой на 1000 витков и вторичной обмоткой на 100 витков имеет соотношение витков 1000: 100 или 10: 1. Следовательно, 100 вольт, приложенное к первичной обмотке, создаст вторичное напряжение 10 вольт.
Другой способ измерения напряжения трансформатора — вольт / виток; если 100 вольт, приложенное к 1000 витков первичной обмотки, дает 100/1000 = 0.1 вольт на виток, тогда каждый отдельный виток 100-витковой вторичной обмотки будет производить 0,1 В, поэтому общее вторичное напряжение будет 100 × 0,1 В = 10 В.
Тот же метод можно использовать для определения значений напряжения, возникающего на отдельных ответвлениях автотрансформатора, если известно количество витков на ответвление.
Просто разделите общее напряжение по всей обмотке на общее количество витков и умножьте этот результат на количество витков в конкретном ответвлении.
.
