Сдвиг фаз
Могут ли чем-либо отличаться друг от друга два гармонических колебания, имеющих одинаковые амплитуды и частоты? Возьмем два одинаковых маятника и отклоним их в одну и ту же сторону на один и тот же угол от вертикали. Если теперь их отпустить, то мы получим два гармонических колебания с одинаковыми амплитудами и частотами. Казалось бы, никакого различия между ними быть не может.
Рис. 11. Колебания маятников сдвинуты на четверть периода
Рис. 12. Колебания маятников сдвинуты на полпериода
Однако стоит нам отпустить маятники не одновременно, и мы сразу же увидим разницу: колебания будут сдвинуты по времени.
Отпустим сначала один маятник, а второй отпустим только тогда, когда первый будет проходить через положение равновесия, т. е. спустя четверть периода. С этим сдвигом по времени на четверть периода маятники и будут колебаться дальше (рис. 11).
Мы могли бы выждать полпериода от момента пуска первого маятника и тогда отпустить второй.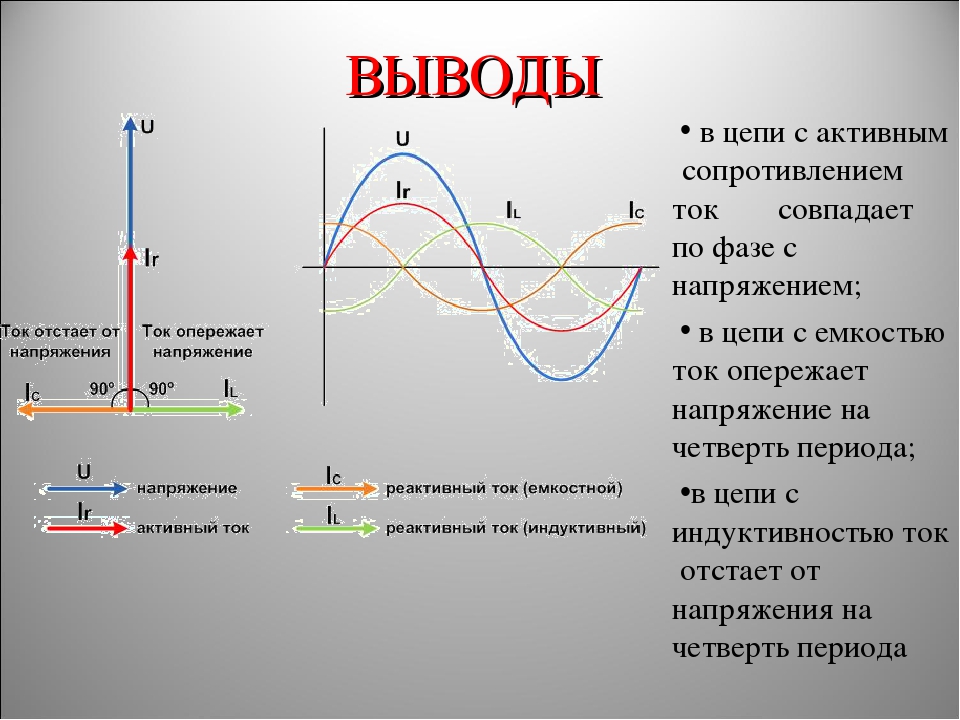 Колебания были бы сдвинуты на полпериода: маятники одновременно проходят при этом через положения равновесия, но движутся все время в противоположные стороны; при наибольшем отклонении одного из них вправо другой сильнее всего отклонен влево, и наоборот (рис. 12).
Колебания были бы сдвинуты на полпериода: маятники одновременно проходят при этом через положения равновесия, но движутся все время в противоположные стороны; при наибольшем отклонении одного из них вправо другой сильнее всего отклонен влево, и наоборот (рис. 12).
Нетрудно получить такие сдвинутые по времени колебания в опыте с теневой проекцией. Если на равномерно вращающемся диске укреплены два шарика в двух диаметрально противоположных точках (рис. 13), то их тени будут колебаться со сдвигом в полпериода, т. е. будут все время двигаться в противоположные стороны, одновременно проходя через среднее положение. Для того чтобы получить сдвиг в четверть периода, надо расположить шарики под центральным углом
друг к другу (рис. 14). В этом случае одна тень проходит через среднее положение тогда, когда другая наиболее отклонена. Вообще колебания на тени будут сдвинуты на такую часть периода, какую часть от полной окружности (360°) составляет угол между радиусами, на которых укреплены шарики.
Рис. 13. Колебания теней сдвинуты на
Рис. 14. Колебания теней сдвинуты по фазе на
Про колебания одинаковой частоты, но смещенные по времени, говорят, что они сдвинуты по фазе, Смещение по времени выражается в долях периода, а сдвиг, или разность, фаз — в угловых единицах (градусах или радианах).
Если второе колебание запаздывает по сравнению с первым на
периода, то это значит, что оно отстает по фазе на
, или сдвинуто по фазе на
. Если же второе колебание опережает первое на
периода, то говорят, что оно опережает его по фазе на
, или сдвинуто по фазе на
.
Если колебания происходят без запаздывания, то их называют синфазными, или говорят, что они совершаются в фазе (т. е. в одинаковой фазе), При запаздывании одного из колебаний на полпериода говорят, что колебания происходят в противофазе.
Понятие сдвига, или разности, фаз характеризует, как мы видим, соотношение по времени между двумя гармоническими колебаниями. Можно, однако, говорить о фазе одного единственного гармонического колебания. Фазой гармонического колебания называется угол, соответствующий времени, протекшему от какого-нибудь произвольно выбранного момента. Разумеется, один период колебания соответствует при этом по-прежнему
Можно, однако, говорить о фазе одного единственного гармонического колебания. Фазой гармонического колебания называется угол, соответствующий времени, протекшему от какого-нибудь произвольно выбранного момента. Разумеется, один период колебания соответствует при этом по-прежнему
.
Итак, фаза колебания зависит от того, какой момент принят за начало отсчета времени. Разность же фаз двух колебаний не зависит от этого произвольного выбора.
Сдвиг фаз между током и напряжением. Понятие двухполюсника — Студопедия
Рассмотрим электрическую цепь состоящую из последовательно включенных сопротивления r, индуктивности L и емкости C (рис. 1 а)).
Протекающий ток i создает на всех элементах цепи падения напряжения, сумма которых равна напряжению на входе u. Для синусоидальных функций времени это можно записать в виде выражения
| . | (1) |
Пусть ток в цепи равен i = Imsin(wt+yi). Подставим это выражение в (1) и получим:
Подставим это выражение в (1) и получим:
| . | (2) |
Очевидно, что определить из выражения (2) амплитуду и начальную фазу напряжения u сложно. Поэтому перейдем в выражении (1) от оригиналов величин к их символическим изображениям комплексными числами или векторами.
| . | (3) |
Формально выражение (3) совпадает с записью закона Ома для цепи постоянного тока. Отличие заключается в том, что все величины входящие в него являются комплексными числами изображающими реальные функции времени. Поэтому его можно назвать законом Ома в области изображений.
Графически выражение (3) можно представить векторной диаграммой рис. 1 б). Здесь вектор входного напряжения U складывается из трех составляющих. Вектор падения напряжения на резистивном сопротивлении rI совпадает по направлению с током I , т.к. отличается от него только вещественным коэффициентом r . Вторая составляющая jxLI перпендикулярна вектору тока I и опережает его по фазе на 90°. Это связано с умножением на оператор поворота j вектора xLI , совпадающего по направлению с током. Третий вектор —jxСI отстает по фазе от тока на 90° , т.к. образуется из него умножением на оператор поворота —j .
Вторая составляющая jxLI перпендикулярна вектору тока I и опережает его по фазе на 90°. Это связано с умножением на оператор поворота j вектора xLI , совпадающего по направлению с током. Третий вектор —jxСI отстает по фазе от тока на 90° , т.к. образуется из него умножением на оператор поворота —j .
Величина Z = r+j(xL— xC) = r+jx = Ze jj в выражении (3), имеющая размерность сопротивления, называется комплексным сопротивлением. Его вещественная часть r называется резистивным сопротивлением, а мнимая x = xL— xC — реактивным сопротивлением. Из выражения (3) следует, что комплексное сопротивление является отношением комплексного падения напряжения к комплексному току
| , | (4) |
поэтому его модуль Z можно определить через отношение модулей напряжения и тока Z=U/I или через резистивную и реактивную составляющую . Модуль комплексного сопротивления называется полным сопротивлением.
Модуль комплексного сопротивления называется полным сопротивлением.
Аргумент комплексного сопротивления j есть разность начальных фаз напряжения и тока, но его можно также определить по вещественной и мнимой составляющим комплексного сопротивления как j = arctg(X/R). Следовательно, сдвиг фаз между напряжением и током определяется только параметрами нагрузки и не зависит от параметров тока и напряжения в цепи. Из выражения (4) необходимо следует, что положительные значения j соответствуют отставанию тока по фазе, а отрицательные — опережению.
Таким образом, изображение напряжения на входе цепи можно представить через комплексное сопротивление в виде
| . | (5) |
Теперь можно вернуться к определению оригинала напряжения u на входе цепи рис. 1 а) преобразованием изображения (5) —
| . | (6) |
Из выражения (3) можно представить комплексное сопротивление суммой трех величин в виде
| Z=r+jxL— jxC=Zr+ZL+ZC | (7) |
и изобразить эти соотношения на векторной диаграмме (рис.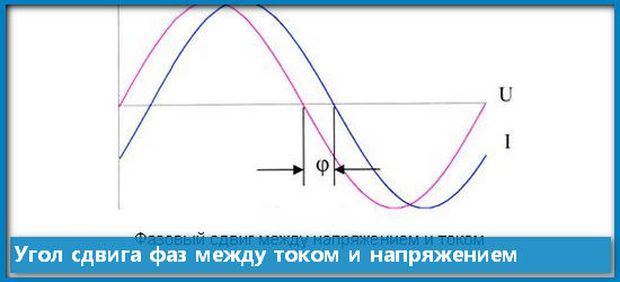 1 в)). Векторная диаграмма сопротивлений подобна векторной диаграмме напряжений, т.к. комплексное сопротивление Z аналитически можно получить делением комплексного напряжения U на комплексный ток I . Графически это соответствует повороту векторной диаграммы напряжений на угол -y i и изменению ее масштаба на 1/I.
1 в)). Векторная диаграмма сопротивлений подобна векторной диаграмме напряжений, т.к. комплексное сопротивление Z аналитически можно получить делением комплексного напряжения U на комплексный ток I . Графически это соответствует повороту векторной диаграммы напряжений на угол -y i и изменению ее масштаба на 1/I.
Соотношение между напряжением и током в электрической цепи можно выразить также величиной обратной сопротивлению
| . | (8) |
Величина Y называется комплексной проводимостью. Ее модуль является величиной обратной модулю комплексного сопротивления, а аргумент всегда равен его аргументу, но имеет противоположный знак.
Вещественная составляющая комплексной проводимости называется резистивной проводимостью, а мнимая — реактивной проводимостью.
Между резистивными (R и G) и реактивными (X и B)составляющими комплексной проводимости и сопротивления существует очевидное соответствие, вытекающее из понятия комплексного числа.
| . | (9) |
Отсюда следует:
- резистивные и реактивные составляющие комплексного сопротивления и проводимости в общем случаене являются взаимно обратными величинами;
- резистивные и реактивные составляющие комплексного сопротивления и проводимости являются взаимно обратными величинами только в случае отсутствия второй составляющей;
- реактивные составляющие комплексного сопротивления и проводимости всегда противоположного знака.
Начальная фаза. Сдвиг фаз — Студопедия
Предположим, что в магнитном поле генератора находится два одинаковых витка, сдвинутых в пространстве друг относительно друга на угол . При вращении в них буду находится ЭДС одинаковой частоты и амплитуды. При вращении в них буду находится ЭДС одинаковой частоты и амплитуды. |
Но т.к. витки сдвинуты в пространстве, то наводимая в них ЭДС будет достигать амплитудных и нулевых значений не одновременно.
В начальный момент времени ЭДС витка будет:
В этих выражениях углы и называются фазными, или фазой. Углы и называются начальной фазой. Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
Разность начальных фаз двух синусоидальных величин одинаковой частоты и амплитуды называется углом сдвига фаз
Разделив угол сдвига фаз на угловую частоту, получим время, прошедшее с начала периода:
| Если угол сдвига фаз составляет 1800, то такие ЭДС находятся в противофазе |
Графическое изображение синусоидальных величин
Синусоидальные величины можно изображать графически при помощи синусоид или вращающихся векторов.
Любая синусоидальная величина характеризуется:
1. Амплитудой;
2. Угловой частотой;
3. Начальной фазой.
При изображении величины с помощью синусоиды ординаты синусоиды в масштабе представляют собой мгновенное значение, абсциссы – промежутки времени.
При этом длина вектора равна амплитудному значению величины, угол между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью . Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.
Совокупность нескольких синусоид называется синусоидальной (волновой) диаграммой.
Совокупность нескольких векторов называется векторной диаграммой.
Сложение и вычитание синусоидальных величин
.
Для сложения двух синусоидальных величин с помощью синусоид необходимо сложить их ординаты в каждый момент времени.
Для того, чтобы сложить две величины с помощью векторов, необходимо к концу первого вектора добавить второй, не изменяя его величины и направления. Соединив начало первого вектора с концом второго, получим суммарный вектор.
Цепи переменного тока с активным сопротивлением
На величину тока и его характер в цепях переменного тока оказывает влияние не только сопротивление, определяемое материалом и геометрическими размерами, но и наличием в цепи емкости и индуктивности. Любая электрическая цепь обладает сопротивлением, индуктивностью и емкостью. Однако, часто тот или иной элемент преобладает над другим, поэтому их влиянием можно пренебречь.
Один и тот же проводник имеет различное сопротивление в цепях постоянного и переменного тока, причем, в цепях переменного тока это сопротивление больше.
| — постоянный ток | |
| — переменный ток |
Это объясняется тем, что переменный ток в отличие от постоянного, который протекает по сечению проводника с равномерной плотностью, частично вытесняется из внутренних слоев проводника к наружным. В результате чего плотность тока в различных слоях неодинакова. Это явление называется поверхностным эффектом. Это объясняется тем, что внутренние слои проводника сцеплены с большим числом магнитных силовых линий, чем наружные, и поэтому в них наводится большая ЭДС самоиндукции, которая препятствует протеканию тока и вытесняет его к наружным слоям, где ЭДС самоиндукции меньше.
Разделив обе части равенства на , получим действующие значения .
Ток и напряжение в цепи с активным сопротивлением совпадают по фазе.
Таким образом, мощность состоит из постоянной составляющей и переменной составляющей , среднее значение которых за период равно нулю. Таким образом, постоянная составляющая мощности выражает среднее за период значение мощности и называется активной мощностью:
Мощность в оба полупериода положительна. Это означает, что цепь с сопротивлением r только потребляет энергию из сети и назад ее не возвращает, т.к. она преобразуется в другие виды энергии.
Цепи переменного тока с индуктивностью
| Допустим, что под действием напряжения в этой цепи протекает ток. Под действием переменного тока в катушке возникает переменный магнитный поток, который наводи в ней ЭДС самоиндукции. |
ЭДС самоиндукции в любой момент времени уравновешивается напряжением:
Т. о. в цепи с индуктивностью напряжение опережает ток на угол 900.
о. в цепи с индуктивностью напряжение опережает ток на угол 900.
— индуктивное (реактивное) сопротивление.
— закон Ома для цепи с индуктивностью.
Физически индуктивное сопротивление характеризует препятствие, оказываемое переменному току в результате наличия ЭДС самоиндукции.
Мощность цепи:
Т.о. мощность изменяется с двойной частотой и может быть положительной и отрицательной. Когда она «+» индуктивность потребляет электрическую энергию от источника и запасает ее от магнитного поля. Когда мощность «-» индуктивность возвращает запасенную энергию обратно к источнику.
Т.о. между источником и индуктивностью происходит непрерывный обмен энергией, при котором:
— цепь работает потребителем
— цепь работает генератором.
Максимальное значение мощности цепи индуктивности называется реактивной мощностью:
Энергия, запасенная в магнитном поле катушки, равна
Цепь переменного тока с емкостью
Под действием этого напряжения конденсатор будет разряжаться и заряжаться. Мгновенное значение заряда на обкладках конденсатора: Мгновенное значение заряда на обкладках конденсатора: |
— закон Ома для цепи с емкостью.
— реактивное емкостное сопротивление
Т.о. ток в цепи с емкостью опережает напряжение на угол 900.
Физически емкостное сопротивление характеризует препятствие, оказываемое переменному току цепью с емкостью. В результате поляризации диэлектрика конденсатора в нем образуется свое внутренне электрическое поле, которое направлено противоположно внешнему полю, приложенному к диэлектрику.
Мощность цепи:
Мощность изменяется с двойной частотой относительно тока и напряжения. В течении первой четверти периода, когда напряжение, приложенное к конденсатору, возрастает, мгновенная мощность положительна. Это означает, что конденсатор получает и запасает энергию источника в виде электрического поля.
В течении второй четверти, когда напряжение, приложенное к конденсатору, уменьшается, запасенная энергия возвращается к источнику, т. е.
е.
— цепь работает потребителем;
— цепь работает источником.
Максимальное значение мощности цепи с емкостью называют реактивной емкостной мощностью:
Она характеризует скорость обмена энергией между источником и цепью с емкостью.
Максимальное значение энергии, запасенной в цепи:
Неразветвленная цепь переменного тока с активным сопротивлением и индуктивностью
Таким сопротивлением (активным и индуктивным) обладают катушки индуктивности, обмотки трансформаторов и электрических машин.
Т.о. напряжение опережает ток в этой цепи на угол , причем .
Мощность цепи:
Т.о. мгновенная мощность состоит из двух составляющих: постоянной и переменной , среднее значение за период которой равно нулю.
Мощность принимает как положительные так и отрицательный значения. Когда мощность положительна, то цепь потребляет энергию, а когда мощность отрицательна, то цепь возвращает запасенную энергию в цепь. Но т.к. потребляет энергию и активное сопротивление и индуктивное, а возвращает в цепь только индуктивность, то положительная будет значительно больше.
Треугольники напряжений, сопротивлений, мощностей
| Если стороны треугольника напряжений уменьшить или разделить на величину тока, то получим треугольник сопро-тивлений |
| — полное сопротивление цепи |
| — закон Ома для цепи с активным и индуктивным сопротивлением. |
Если стороны треугольника напряжений уменьшить на ток, то получим треугольник мощностей.
| — коэффициент мощности |
— реактивная мощность
— активная мощность
Коэффициент мощности показывает, какая часть полной мощности потребляется безвозвратно.
Цепь переменного тока с активным сопротивлением, емкостью и индуктивностью
Допустим:
1.
2.
Общий случай неразветвленной цепи
Резонанс напряжений
Результирующий ток резко увеличивается, т.к. индуктивное и емкостное сопротивления компенсируют друг друга.
Если параметры цепи подобрать так, что , то напряжения на емкости и индуктивности будут превышать напряжение на зажимах цепи в раз. Отношение называется добротностью цепи (контура).
Т.о. напряжение на емкости и индуктивности будут превышать напряжение сети в раз, что может привести к пробою диэлектрика в конденсаторе или сопротивлений изоляции индуктивности, поэтому явление резонанса напряжений в электрических цепях нежелательно, но в то же время в радиотехнике его используют (колебательные контуры приемника и передатчика).
Возникновение напряжений на L и С, превышающих напряжение на зажимах цепи объясняется способностью емкости и индуктивности накапливать электрическую энергию.
Между емкостью и индуктивностью происходит непрерывный обмен энергией, который называется собственными колебаниями.
Частоту собственных колебаний можно определить при условии, что .
| Т.о. резонанс можно получить, изменяя частоту тока питающей сети, или изменяя емкость или индуктивность. |
Резонансные кривые
Зависимость параметров цепи от частоты характеризуется резонансными кривыми.
Разветвленные цепи переменного тока
Рассмотрим цепь с двумя параллельно соединенными катушками.
Для определения тока неразветвленной части цепи необходимо разложить токи и на активные и реактивные составляющие.
Характеристики синусоидальных величин: мгновенное, амплитудное, действующее, среднее значение, период, частота (угловая и циклическая), фаза − мгновенные значения синусоидальных функций обозначают маленькими буквами: i, e, u. Они являются функциями времени.
Зависимость их от времени выражается соотношениями:
;
− фаза — аргумент синусоидальной функции (wt + j) — показывает, какое значение имеет синусоидальная функция в данный момент времени;
− начальная фаза j — показывает, какое значение имеет синусоидальная функция в момент на чала отсчета, т.е. при t = 0;
− угловая (циклическая) частота изменения тока:
, рад/c.
Для нашей сети w = 314 рад/c.
− Действующее значение переменного тока.
Действующим значением I переменного тока называют такое значение постоянного I, который, протекая по сопротивлению R, за время, равное одному периоду Т изменения тока, выделяет в нем такое же количество теплоты Q, что и переменный ток i. Поясним определение на примере:
.
После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:
.
Аналогичные соотношения могут быть получены также для напряжения и ЭДС:
.
Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.
Учитывая, например, что действующее значение напряжения в нашей сети составляет 220 В, можно определить амплитудное значение фазного напряжения Um = UÖ2 = 307 В. Связь между действующим и амплитудным значениями напряжений важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.
Цепи переменного тока с резистором: напряжение, ток, мощность, векторная диаграмма
Мгновенное значение мощности. В цепи, содержащей активное, индуктивное и емкостное сопротивления, в которой ток I и напряжение u в общем случае сдвинуты по фазе на некоторый угол ?, мгновенное значение мощности р равно произведению мгновенных значений силы тока i и напряжения u. Кривую мгновенной мощности р можно получить перемножением мгновенных значений тока i и напряжения u при различных углах t (рис. 199, а. Из этого рисунка видно, что в некоторые моменты времени, когда ток и напряжение направлены навстречу друг другу, мощность имеет отрицательное значение.
Возникновение в электрической цепи отрицательных значений мощности является вредным. Это означает, что в такие периоды времени приемник возвращает часть полученной электроэнергии обратно источнику; в результате уменьшается мощность, передаваемая от источника к приемнику. Очевидно, что чем больше угол сдвига фаз, тем больше время, в течение которого часть электроэнергии возвращается обратно к источнику, и тем больше возвращаемая обратно энергия и мощность.
Активная и реактивная мощности. Мгновенная мощность может быть представлена в виде суммы двух составляющих 1 и 2 (рис. 199,б). Составляющая 1 соответствует изменению мощности в цепи с активным сопротивлением (см. рис. 175,б).
Среднее ее значение, которое называют активной мощностью,
P = UI cos
Она представляет собой среднюю мощность, которая поступает от источника к электрическим установкам при переменном токе.
Составляющая 2 изменяется подобно изменению мощности в цепи с реактивным сопротивлением (индуктивным или емкостным, см. рис. 179, а и б). Среднее ее значение равно нулю, поэтому для оценки этой составляющей пользуются ее амплитудным значением, которое называют реактивной мощностью:
Q = UI sin
Рассматривая кривые мощности (см. рис. 199,б), можно установить, что только активная мощность может обеспечить преобразование в приемнике электрической энергии в другие виды энергии. Эта мощность в течение всего периода имеет положительный знак, т. е. соответствующая ей электрическая энергия 2, называемая активной, непрерывно переходит от источника 1 к приемнику 4 (рис. 200, а). Реактивная мощность никакой полезной работы создать не может, так как среднее значение ее в течение одного периода равно нулю. Как видно из рис. 199,б, эта мощность становится то положительной, то отрицательной, т. е. соответствующая ей электрическая энергия ,3, называемая реактивной,
Рис. 199. Зависимость мгновенной мощности р (а) и ее составляющих (б) от угла t
Рис. 200. Диаграмма, иллюстрирующая передачу электрической энергии между источником и приемником, содержащим активное и реактивное сопротивления, при отсутствии компенсатора (а) и при наличии его (б): 1 — источник; 2,3 — условные изображения активной и реактивной энергии; 4 — приемник; 5 — компенсатор непрерывно циркулирует по электрической цепи от источника электрической энергии 1 к приемнику 4 и обратно (см. рис. 200, а).
Возникновение реактивной мощности в цепи переменного тока возможно только при включении в эту цепь накопителей энергии, таких как катушка индуктивности или конденсатор. В первом случае электрическая энергия, поступающая от источника, накапливается в электромагнитном поле катушки индуктивности, а затем отдается обратно; во втором случае она накапливается в электрическом поле конденсатора, а затем возвращается обратно к источнику. Постоянная циркуляция реактивной мощности от источника к приемникам загружает генераторы переменного тока и электрические сети реактивными токами, не создающими полезной работы, и тем самым не дает возможности использовать их по прямому назначению для выработки и передачи потребителям активной мощности. Поэтому в производственных условиях стараются по возможности уменьшить реактивную мощность, потребляемую электрическими установками.
Полная мощность. Источники электрической энергии переменного тока (генераторы и трансформаторы) рассчитаны на определенный номинальный ток Iном и определенное номинальное напряжение Uном, которые зависят от конструкции машины, размеров ее основных частей и пр. Увеличить значительно номинальный ток или номинальное напряжение нельзя, так как это может привести к недопустимому нагреву обмоток машины или пробою их изоляции. Поэтому каждый генератор или трансформатор может длительно отдавать без опасности аварии только вполне определенную мощность, равную произведению его номинального тока на номинальное напряжение. Произведение действующих значений тока и напряжения называется полной мощностью,
S = UI
Следовательно, полная мощность представляет собой наибольшее значение активной мощности при заданных значениях тока и напряжения. Она характеризует ту наибольшую мощность, которую можно получить от источника переменного тока при условии, что между проходящим по нему током и напряжением отсутствует сдвиг фаз. Полную мощность измеряют в вольт-амперах (В*А) или киловольт-амперах (кВ*А).
Связь между мощностями Р, Q и S можно определить из векторной диаграммы напряжений (рис. 201, а). Если умножить на ток I все стороны треугольника ABC, то получим треугольник мощностей А’В’С’ (рис. 201,б), стороны которого равны Р, Q и S. Из треугольника мощностей имеем:
S = (P2 + Q2)
Из этого выражения следует, что при заданной полной мощности S (т. е. напряжении U и токе I) чем больше реактивная мощность Q, которая проходит через генератор переменного тока или трансформатор, тем меньше активная мощность Р, которую он может отдать приемнику. Иными словами, реактивная мощность не позволяет полностью использовать всю расчетную мощность источников переменного тока для выработки полезно используемой электрической энергии.
То же самое относится и к электрическим сетям. Ток I = (Ia2 + Ip2), который можно безопасно пропускать по данной электрической сети, определяется, главным образом, поперечным сечением ее проводов. Поэтому если часть Iр проходящего по сети тока (см. рис. 194,б) идет на создание реактивной мощности, то должен быть уменьшен активный ток Iа, обеспечивающий создание активной мощности, которую можно пропустить по данной сети.
Рис. 201. Векторная диаграмма напряжений (а) и треугольник мощностей (б) для цепи переменного тока
Если задана активная мощность Р, то при увеличении реактивной мощности Q возрастут реактивный ток Iр и общий ток I, проходящий по проводам генераторов переменного тока, трансформаторов, электрических сетей и приемников электрической энергии. При этом увеличиваются и потери мощности Р = I2Rпp в активном сопротивлении Rпp этих проводов.
Таким образом, бесполезная циркуляция электрической энергии между источником переменного тока и приемником, обусловленная наличием в нем реактивных сопротивлений, требует также затраты определенного количества энергии, которая теряется в проводах всей электрической цепи.
Коэффициент мощности. Из формулы (75) следует, что активная мощность Р зависит не только от тока I и напряжения U, но и от величины cos, называемой коэффициентом мощности:
cos = P/(UI) = P/S = P/(P2 + Q2)
По значению cos можно судить, как использует мощность источника данный приемник или электрическая цепь. Чем больше cos ?, тем меньше sin, следовательно, согласно формулам (75) и (76) при заданных U и I, т. е. S, тем больше активная и меньше реактивная мощности, отдаваемые источником. При повышении cos и постоянной активной мощности Р, поступающей в приемник, уменьшается ток в цепи I = P/(U cos). При этом уменьшаются потери мощности P = I2Rпp в проводах и обеспечивается возможность дополнительной загрузки источника и электрической сети, т. е. лучшего их использования.
Если приемник питается от источника при неизменном токе нагрузки, то повышение cos ведет к возрастанию активной мощности Р, используемой приемником. При cos = 1 реактивная мощность равна нулю, и вся мощность, отдаваемая источником, является активной. Поэтому на всех предприятиях и во всех отраслях народного хозяйства стремятся всемерно повышать коэффициент мощности и доводить его по возможности до единицы.
Значения коэффициента мощности электрических установок переменного тока различны. Электрические лампы обладают, главным образом, активным сопротивлением, поэтому при их включении сдвиг фаз между током и напряжением практически отсутствует. Следовательно, для осветительной нагрузки коэффициент мощности можно считать равным единице. Коэффициент мощности для двигателей переменного тока зависит от нагрузки. При номинальной расчетной нагрузке двигателя cos = 0,8-0,9, а у крупных двигателей даже выше. При недогрузке двигателей коэффициент мощности их резко снижается (при холостом ходе cos = 0,25-0,3).
Повышение коэффициента мощности. Cos повышают различными способами. Основной из них — включение параллельно приемникам электрической энергии специальных устройств, называемых компенсаторами. В качестве последних чаще всего используют батареи конденсаторов (статические компенсаторы), но могут быть применены также и синхронные электрические машины (вращающиеся компенсаторы).
Способ повышения cos с помощью статического компенсатора (рис. 202, а) называют компенсацией сдвига фаз, или компенсацией реактивной мощности. При отсутствии компенсатора от источника к приемнику, содержащему активное и индуктивное сопротивления, поступает ток i1 который отстает от напряжения и на некоторый угол сдвига фаз. При включении компенсатора Хс по нему проходит ток ic, опережающий напряжение и на 90°. Как видно из векторной диаграммы (рис. 202,б), при этом в цепи источника будет проходить ток i < i1 и угол сдвига фаз его относительно напряжения также будет меньше.
Для полной компенсации угла сдвига фаз, т. е. для получения cos = 1 и минимального значения тока Imin, необходимо, чтобы ток компенсатора Iс был равен реактивной составляющей I1p = I1 sin1 тока I1.
При включении компенсатора 5 (см. рис. 200,б) источник 1 и электрическая сеть разгружаются от реактивной энергии 3, так как она циркулирует уже по цепи «приемник — компенсатор». Благодаря этому достигаются существенное повышение использования генераторов переменного тока и электрических сетей и уменьшение потерь энергии, возникающих при бесполезной циркуляции реактивной энергии между источником 1 и приемником 4.
Рис. 202. Схема, иллюстрирующая способ повышения cos с помощью компенсатора (а), и векторная диаграмма (б)
Компенсатор в этом случае выполняет роль генератора реактивной энергии, так как токи Iсв конденсаторе и I1р в катушке индуктивности (см, рис. 202,б) направлены навстречу один другому (первый опережает по фазе напряжение на 90°, второй отстает от него на 90°), вследствие чего включение компенсатора уменьшает общий реактивный ток Iр и сдвиг фаз между током I и напряжением U. При надлежащем подборе реактивной мощности компенсатора можно добиться, что вся реактивная энергия 3 (см. рис. 200,б), поступающая в приемник 4, будет циркулировать внутри контура «приемник — компенсатор», а генератор и сеть не будут участвовать в ее передаче. При этих условиях от источника 1 к приемнику 4 будет передаваться только активная мощность 2, т. е. cos будет равен единице.
В большинстве случаев по экономическим соображениям в электрических установках осуществляют неполную компенсацию угла сдвига фаз и ограничиваются значением cos = 0,95.
Последовательное соединение активного и реактивного элементов
В общем случае в цепях переменного тока обычно имеются все виды сопротивлений: активное, индуктивное и емкостное. Например, электрические двигатели переменного тока могут быть представлены эквивалентной схемой, состоящей из индуктивного сопротивления имеющихся в нем катушек и активного сопротивления образующих эти катушки проводов.
Рис. 192. Схема цепи переменного тока, содержащей последовательно включенные активное, индуктивное и емкостное сопротивления (а), векторные диаграммы (б и а), кривые тока и напряжения и (г)
Воздушные линии электропередачи или кабельные линии обычно представляют в виде совокупности активного, индуктивного и емкостного сопротивлений. Активное сопротивление обусловлено сопротивлением электрических проводов, индуктивное — индуктивностью линии, а емкостное — емкостью, возникающей между отдельными проводами, между проводами и землей или же между отдельными жилами кабеля и между жилами кабеля и его оболочкой.
Расчет электрических цепей переменного тока существенно отличается от расчета цепей постоянного тока, так как при переменном токе в активном, индуктивном и емкостном сопротивлениях имеют место различные сдвиги фаз между токами и напряжениями.
Ток, напряжение и полное сопротивление. При последовательном включении в цепь переменного тока активного R, индуктивного XL и емкостного Хс сопротивлений (рис. 192, а) к ним приложены напряжения: активное ua = iR, индуктивное uL = iXL и емкостное uc = iXc. Мгновенное значение напряжения и, приложенного к данной цепи, согласно второму закону Кирхгофа равно алгебраической сумме напряжений:
u = ua + uL + uc
Но для действующих значений эта формула неприменима, так как между всеми указанными напряжениями имеется сдвиг по фазе (амплитудные значения этих напряжений не совпадают по времени).
Рис. 193. Треугольник со противлении
Для этого строят векторную диаграмму, на которой откладывают в определенном масштабе векторы тока и напряжений. Из этих напряжений первое совпадает по фазе с током, второе опережает его на 90°. Векторная диаграмма (рис. 192,б) построена для цепи, в которой индуктивное сопротивление XL больше емкостного Xc, а рис. 192, в — для цепи, в которой XL меньше Хс. Напряжение U (действующее значение) может быть определено из треугольника ЛВС по теореме Пифагора:
U = (U2a + (UL – Uc)2)
Таким образом, из-за наличия угла сдвига фаз напряжение U всегда меньше алгебраической суммы Ua + UL + UC. Разность UL – UC = Up называется реактивной составляющей напряжения.
Рассмотрим, как изменяются ток и напряжение в последовательной цепи переменного тока.
В цепи, содержащей все три вида сопротивления, ток i и напряжение и оказываются сдвинутыми по фазе на некоторый угол ср (рис. 192, г).
Полное сопротивление и угол сдвига фаз. Если подставить в формулу (71) значения Ua = IR; UL = lL и UC=I/(C), то будем иметь: U = ((IR)2+ [IL-I/ (С) ]2), откуда получаем формулу закона Ома для последовательной цепи переменного тока:
I = U / ( (R2+ [L-1 / (С) ]2) ) = U / Z (72)
где Z = (R2+ [L-1 / (С) ]2) = (R2+ (XL – Xc)2)
Величину Z называют полным сопротивлением цепи, оно измеряется в омах. Разность L — l/(C) называют реактивным сопротивлением цепи и обозначают буквой X. Следовательно, полное сопротивление цепи
Z = (R2+ X2)
Соотношение между активным, реактивным и полным сопротивлениями цепи переменного тока можно также получить по теореме Пифагора из треугольника сопротивлений (рис. 193). Треугольник сопротивлений А’В’С’ можно получить из треугольника напряжений ABC (см. рис. 192,б), если разделить все его стороны на ток I.
Угол сдвига фаз определяется соотношением между отдельными сопротивлениями, включенными в данную цепь. Из треугольника А’В’С (см. рис. 193) имеем:
sin ? = X / Z; cos? = R / Z; tg? = X / R
Например, если активное сопротивление R значительно больше реактивного сопротивления X, угол сравнительно небольшой. Если в цепи имеется большое индуктивное или большое емкостное сопротивление, то угол сдвига фаз возрастает и приближается к 90°. При этом, если индуктивное сопротивление больше емкостного, напряжение и опережает ток i на угол; если же емкостное сопротивление больше индуктивного, то напряжение и отстает от тока i на угол.
Идеальная катушка индуктивности, реальная катушка и конденсатор в цепи переменного тока.
Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.
Угол сдвига фаз между током и напряжением. Измерение и вычисление | ENARGYS.RU
Начальные фазы электромагнитных синусоидальных колебаний первичного и вторичного напряжения, с частотой одинаковой величины, могут существенно различаться на некоторый угол сдвига фаз (угол φ). Переменные величины могут неоднократно в течение определенного периода некоторого времени изменяются с определенной частотой. Если электрические процессы имеют неизменный характер, а сдвиг фаз равен нулю, это свидетельствует о синхронизме источников величин переменного напряжения, например, трансформаторов. Сдвиг фазы служит определяющим фактором коэффициента мощности в электрических сетях переменного тока.
Угол сдвига фаз находится при необходимости, тогда, если один из сигналов является опорным, а второй сигнал с фазой в самом начале совпадает с углом сдвига фаз.
Измерение угла сдвига фаз производится прибором, в котором присутствует нормированная погрешность.
Фазометр может производить измерение угла сдвига в границах от 0о до 360о в некоторых случаях от -180оС до +180оС, а диапазон измеряемых частот сигналов может колебаться от 20Гц до 20 ГГц. Измерение гарантируется в том случае если напряжение входного сигнала равно от 1 мВ до 100 В, если же напряжение входного сигнала превышает эти границы точность измерения не гарантируется.
Методы измерения угла сдвига фаз
Существует несколько способов измерения угла сдвига фаз, это:
- Использование двухлучевого или двухканального осциллографа.
- Компенсационный метод основан на сравнении измеряемого фазового сдвига, с фазовым сдвигом, который предоставляется образцовым фазовращателем.
- Суммарно-разностный метод, он заключается в использовании гармонических или сформированных прямоугольных сигналов.
- Преобразование сдвига фаз во временном интервале.
Как измеряется угол сдвига фаз осциллографом
Осциллографический способ можно отнести к самому простейшему с погрешностью в районе 5о. Определение сдвига осуществляется при помощи осциллограмм. Существует четыре осциллографических метода:
- Применение линейной развертки.
- Метод эллипса.
- Метод круговой развертки.
- Использование яркостных меток.
Определение угла сдвига фаз зависит от характера нагрузки. При определении фазного сдвига в первичной и вторичной цепях трансформатора, углы могут считаться равными и практически не отличаются друг от друга.
Угол сдвига фаз напряжений, измеряемый по эталонному источнику частоты и при использовании измерительного органа лает возможность обеспечить точность всех последующих измерений. Фазные напряжения и угол сдвига фаз зависят от нагрузки, так симметричная нагрузка обуславливает равенство фазного напряжения , токов нагрузки и угол фазного сдвига, также будет равна нагрузка по потребляемой мощности на всех фазах электроустановки.
Угол сдвига фаз между током и напряжением в несимметричных трехфазных цепях не равны друг другу. Для того чтобы вычислить угол сдвига фаз (угол φ) в цепь включают последовательно присоединенные сопротивления (резисторы), индуктивности и конденсаторы (емкости).
Рис. №1. Последовательное соединение сопротивления, индуктивности и емкости для вычисления угла сдвига фаз. В этом контуре протекает переменный ток, который способствует возникновению ЭДС.
Рис. №2. Схема проведения опыта по определению сдвига фаз между током и напряжением. Слева показаны схемы подключения конденсаторов, катушек индуктивности и резисторов, справа показаны результаты опыта.
Из результатов опыта можно определить, что сдвиг фаз между напряжением и током служит при определении нагрузки и не может зависеть от переменных величины тока и напряжения в электрической сети.
Как вывод, можно сказать, что:
- Составляющие элементы комплексного сопротивления, такие как резистор и емкость, а также проводимость не будут взаимообратными величинами.
- Отсутствие одного из элементов делает резистивные и реактивные значения, которые входят в состав комплексного сопротивления и проводимости и делают их величинами взаимообратными.
- Реактивные величины в комплексном сопротивлении и проводимости используются с противоположным знаком.
Угол сдвига фаз между напряжением и током всегда выражается, как главный аргументированный фактор комплексного сопротивления φ.
Урок 43-2 (продолжение) Переменный ток
Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R, конденсатору емкости C и катушки индуктивности L. Во всех трех случаях напряжения на резисторе, конденсаторе и катушке равны напряжению источника переменного тока.
1. Резистор в цепи переменного тока
Сопротивление R называют активным, потому что цепь с таким сопротивлением поглощает энергию.
Активное сопротивление — устройство, в котором энергия электрического тока необратимо преобразуется в другие виды энергии (внутреннюю, механическую)
Пусть напряжение в цепи меняется по закону: u = Umcos ωt ,
тогда сила тока меняется по закону: i = u/R = IRcosωt
u – мгновенное значение напряжения;
i – мгновенное значение силы тока;
IR — амплитуда тока, протекающего через резистор.
Связь между амплитудами тока и напряжения на резисторе выражается соотношением RIR = UR
Колебания силы тока совпадают по фазе с колебаниями напряжения. (т.е. фазовый сдвиг между током и напряжением на резисторе равен нулю).
2. Конденсатор в цепи переменного тока
При включении конденсатора в цепь постоянного напряжения сила тока равна нулю, а при включении конденсатора в цепь переменного напряжения сила тока не равна нулю. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока.
Соотношение между амплитудами тока IC и напряжения
UC:
Ток опережает по фазе напряжение на угол π/2.
3. Катушка в цепи переменного тока
В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для той же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения.
Соотношение между амплитудами тока IL и напряжения UL:
ωLIL = UL
Ток отстает по фазе от напряжения на угол π/2.
Теперь можно построить векторную диаграмму для последовательного RLC-контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I0. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги.
Векторная диаграмма на рисунке построена для случая, когда или В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.
Векторная диаграмма для последовательной RLC-цепи
Из рисунка видно, что
откуда следует
Из выражения для I0 видно, что амплитуда тока принимает максимальное значение при условии
или
Явление возрастания амплитуды колебаний тока при совпадении частоты ω внешнего источника с собственной частотой ω0 электрической цепи называется электрическим резонансом. При резонансе
Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).
При последовательном резонансе (ω = ω0) амплитуды UC и UL напряжений на конденсаторе и катушке резко возрастают:
Рисунок иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды UC напряжения на конденсаторе к амплитуде 0 напряжения источника от его частоты ω. Кривые на рисунке называются резонансными кривыми.
Блог » Смещение фаз и реактивная мощность
Реактивная мощность необходима для создания электромагнитных полей машин, например, трехфазных электродвигателей, трансформаторов, сварочных установок и т.п. Поскольку эти поля непрерывно исчезают и возникают заново, реактивная мощность перемещается между генератором и потребителем. В отличие от активной мощности ее нельзя использовать, то есть преобразовать в другую форму энергии, поэтому она создает нагрузку на сеть электроснабжения и генераторные установки (генераторы и трансформаторы). Кроме того, из-за реактивного тока распределительные установки должны иметь большую мощность.
Поэтому целесообразно снижать возникающую индуктивную реактивную мощность в непосредственной близости от потребителя с помощью противодействующей емкостной реактивной мощности равной величины. Эту процедуру называют компенсацией. В ходе компенсации доля индуктивной реактивной мощности в сети снижается на величину реактивной мощности силового конденсатора или установки для компенсации реактивной мощности (КРМ). Генераторные установки и системы электропередачи освобождаются при этом от реактивного тока. Сдвиг фаз между током и напряжением уменьшается или, в идеальном случае, при коэффициенте мощности 1, полностью устраняется.
Коэффициент мощности (Power Factor) – это параметр, зависящий от таких сбоев в сети, как искажение или асимметрия. Он снижается при увеличении сдвига фаз между током и напряжением и при росте искажения кривой тока. Вычисляется как отношение поглощаемой нагрузкой активной мощности к полной и является, таким образом, показателем эффективности использования нагрузкой электрической энергии. Чем больше коэффициент мощности, тем эффективнее используется электроэнергия, так выше КПД.
Коэффициент мощности – Power Factor (арифметический)
Коэффициент мощности может принимать только положительные значения
Cos (phi) – Fundamental Power Factor
- Для расчета cos (phi) используется только основная гармоническая составляющая.
- Знак cos (phi) (φ): «-» при выработке активной мощности; «+» при потреблении активной мощности.
Поскольку при нагрузке высшими гармониками невозможно указать единый угол сдвига фаз, нельзя путать коэффициент мощности λ и часто используемый коэффициент смещения cos(φ1). Из формулы
где I1 = эффективное значение первой гармоники тока, I = общий эффективный ток, g1 = доля первой гармоники тока и cos(φ1) = коэффициент сдвига. Видно, что только при синусоидальном напряжении и токе (g = 1) коэффициент мощности λ равен коэффициенту сдвига cos(φ1). Таким образом, только при синусоидальном напряжении и токе коэффициент мощности λ равен косинусу угла сдвига фаз φ и
равен коэффициенту мощности.
Регистрацию значений реактивной мощности производит любой анализатор качества электроэнергии.
Расчет фазового угла, время задержки, частота, расчет фазового сдвига, временной сдвиг между разностью напряжений, время прихода, осциллограф ITD, измерение двух сигналов, формула, угол, текущее напряжение, phi, фазовый сдвиг, временная разница
, расчет фазового угла, временная задержка, частота, вычисление фазового запаздывания, временной сдвиг между разностью напряжений, время прихода Осциллограф ITD для измерения двух сигналов, формула, угол, текущее, напряжение, фазовый сдвиг, фазовый сдвиг, разница во времени — sengpielaudio Sengpiel Berlin
| Вопрос: Какова формула фазы синусоидальной волны? Нет фазы синусоидальной волны.Синусоидальная волна не имеет фазы. Фаза может развиваться только между двумя синусоидальными волнами. Две синусоидальные волны взаимно сдвинуты по фазе, если моменты времени его нулевые отрывки не совпадают. |
| Слово фаза имеет четкое определение для двух чистых бегущих синусоидальных волн переменного тока, но не для музыкальных сигналов. Все эквалайзеры сдвигают фазу вместе с частотой. Без каких-либо с фиксированной точкой «смещение» (смещение) невозможно. Особые приемы: Фильтр 90 ° с двумя универсальными фильтрами. Фазы всегда разности фаз . Реверс полярности (pol-rev) никогда не сдвиг фазы на оси времени t . Синусоидальные сигналы одинаковой частоты могут иметь разность фаз. Если есть фазовый сдвиг (разность фаз) или фазовая задержка фазовый угол φ |
Что такое на самом деле амплитуда?
| Один полный цикл волны связан с «угловым» смещением 2 π радиан. Фаза φ — угол участка сигнала, он указывается в угловых градусах и |
Какое отношение задержка имеет к фазовому углу?
Разница во времени (длительность) звука на метр
Влияние температуры на разницу во времени Δ t
Зависимость скорости звука только от температуры воздуха
| Температура воздуха в ° C | Скорость звука c м / с | Время на 1 м Δ t в мс / м |
| +40 | 354.9 | 2,818 |
| +35 | 352,0 | 2,840 |
| +30 | 349,1 | 2,864 |
| +25 | 346,2 | 2,888 |
| +20 | 343,2 | 2,912 |
| +15 | 340,3 | 2,937 |
| +10 | 337.3 | 2,963 |
| +5 | 334,3 | 2,990 |
| ± 0 | 331,3 | 3,017 |
| −5 | 328,2 | 3,044 |
| −10 | 325,2 | 3,073 |
| −15 | 322,0 | 3,103 |
| −20 | 318.8 | 3,134 |
| −25 | 315,7 | 3,165 |
| Звукорежиссеры обычно руководствуются практическим правилом: Для расстояния r = 1 м звук требует около t = 3 мс в воздухе. Δ t = r / c и r = Δ t × c Скорость звука c = 343 м / с при 20 ° C. |
Для фиксированной выдержки времени Δ t = 0,5 мс получаем
следующий фазовый сдвиг φ ° (град) сигнала:
| Разность фаз φ ° (град) | Разность фаз φ Bogen (рад) | Частота f | Длина волны λ = c / f |
| 360 ° | 2 π = 6.283185307 | 2000 Гц | 0,171 м |
| 180 ° | π = 3,141592654 | 1000 Гц | 0,343 м |
| 90 ° | π /2 = 1,5 70796327 | 500 Гц | 0,686 м |
| 45 ° | π /4 = 0,785398163 | 250 Гц | 1.372 м |
| 22,5 ° | π /8 = 0,392699081 | 125 Гц | 2.744 м |
| 11,25 ° | π /16 = 0,196 349540 | 62,5 Гц | 5,488 м |
Преобразование: радианы в градусы и наоборот
Фазовый угол: φ ° = 360 × f × Δ t
Для стереофонии на основе времени Δ t = a × sin α / c
Частота f = φ ° / 360 × Δ t
Фазовый угол (град.) φ = временная задержка Δ t × частота f × 360
Если взять разницу во времени Δ t = длина пути a / скорость звука c , тогда получаем
Разность фаз φ ° = длина пути a × частота f × 360 / скорость звука c
Введите два значения , будет вычислено третье значение
Дополнительная помощь: Время, частота, фаза и задержка
| Автор Lord Rayleigh (Джон Уильям Струтт, 3-й лорд Рэлей, 1907 г.) была показана теория дуплекса .Эта теория способствует пониманию процедуры «естественного ». слух »с людьми. Это очень простое понимание, что межуральное время прибытия различия ITD важны на частотах ниже 800 Гц как разности фаз с направлением локализации как ушные сигналы , а на частотах выше 1600 Гц эффективны только межуровневые различия ILD. Между ушами максимальная задержка равна 0.63 мс. Разница фаз для отдельные частоты могут быть рассчитаны. |
Схема фазовращателя для фазовых углов от φ = 0 до 180
Векторы напряжения фазовращателя
Для R = 0 Ом составляет В OUT = V IN . Выход не должен быть нагружен низким импедансом.
Вы можете сдвигать отдельные чистые частоты (синусоидальные волны),
но с такой схемой музыкальных программ это невозможно.
Два синусоидальных напряжения со сдвигом по фазе: φ = 45 °
Условия для передачи без искажений
От Шопса — Йорг Вуттке: «Микрофонбух» — Глава 7
| В то время как потребность в постоянной частотной характеристике очевидна, для «линейной» фазы требуется скорее объяснение. Есть инженеры, которые ожидают, что идеальная фаза будет такой же постоянной, как и амплитудная характеристика. Это неправда. Первоначально фаза начинается с 0 °, потому что самая низкая частота заканчивается на 0 Гц, на . ОКРУГ КОЛУМБИЯ. (Между напряжениями постоянного тока отсутствует фазовый угол). При заданной частоте фазовый угол не имеет значения, если фазовый угол равен . только в два раза больше в случае двойной частоты и в три раза больше в случае трех экземпляров и т. д. |
Предоставлено David Moulton Laboratories
(о гребенчатой фильтрации, фазовом сдвиге и обращении полярности)
| Электронный эквивалент потока сигнала и его отложенной итерации, рекомбинированный в единый сигнал.В случае, который мы будем рассматривать, линия задержки имеет задержку в 1 миллисекунду, уровни исходного и задержанного сигналов, поступающих в микшер, равны, а сигнал представляет собой синусоидальную волну с частотой 1 кГц. |
| Синусоидальная волна 1500 Гц. частота (период T = 0,667 мс) и ее задержка итерация с задержкой 1 мс. Результирующий смешанный сигнал будет сигналом без . амплитуда, либо полная гашение сигнала. |
| Фазовый сдвиг для любой частоты с задержкой в 1 миллисекунду. Диагональная линия представляет возрастающий фазовый сдвиг как функцию частоты. Обратите внимание, что мы можем Считайте, что 540 фактически то же самое, что 180. |
Время, фаза, частота, задержка — Учебное пособие по теории звуковых сигналов
Реверс полярности нет Фазовый сдвиг из 180 (временная задержка)
| (phi) = сдвиг фазы, сдвиг фазы, разность фаз, сдвиг фазы, фазовая задержка, фазовый угол часто неверно используются как: pol-rev = изменение полярности. |
Полярность и фаза часто используются так, как будто они означают одно и то же. Они не.
«Кнопка реверса фазы» не меняет фазу. Это меняет полярность.
| Реверс полярности без сдвига фаз. Изменение полярности (или Pol-Rev) — это термин, который часто путают с фазой Ø (phi) но не включает фазового сдвига или временной задержки. Изменение полярности происходит всякий раз, когда мы «изменить знак» значений амплитуды сигнала.В аналоговой области это можно сделать с инвертирующим усилителем, трансформатором или в симметричной линии на простое переключение соединений между контактами 2 и 3 (разъем XLR) на одном конце кабель. В цифровой сфере это делается простой заменой всех плюсов на . минусы и наоборот в потоке данных аудиосигнала. |
Два пилообразных колебаний
| вверху: исходный сигнал a / b (пилообразный зуб) посередине: сигнал со сдвигом фазы 180 внизу: сигнал b / a- с обратной (инвертированной) полярностью , |
| Хорошо видно, что обратная полярность не может быть такой же, как не совпадает по фазе. |
| Речь идет о широко обсуждаемой теме: «Фазовый сдвиг в зависимости от инвертирования сигнала» и «фаза . сдвиг в зависимости от временного сдвига сигнала ». Термин фазовый сдвиг предположительно определен только для одночастотные синусоидальные сигналы и угол сдвига фаз явно задан только для синусоидальные величины. |
Типичная кнопка Ø (phi) — только переключатель полярности
Абсолютно отсутствует фазовый сдвиг
| Примечание. Время, частота и фаза тесно связаны. Высота амплитуды не влияет на эти параметры. |
Угловая частота составляет ω = 2 π × f
| Дано уравнение: y = 50 sin (5000 t) Определите частоту и амплитуду. Ответ: Амплитуда 50 и ω = 5000. Итак, частота f = 1/ T = ω /2 π = 795.77 Гц. |
| Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обоих направлениях знака ↔ . |
Общие сведения о коаксиальных линиях передачи РЧ посредством измерений и расчетов Стр. 8
Общие сведения о коаксиальных линиях передачи РЧ путем измерений и расчетов Стр. 8
5.5) Относительная фаза ОТРАЖЕННЫХ напряжений от ОТКРЫТОГО и КОРОТКОГО состояния
Теперь мы можем сравнить фазы, полученные при измерении напряжений на ОТКРЫТОМ и КОРОТКОМ выводах.
Фаза при ОТКРЫТОМ состоянии
В параграфе 5.2 с ОТКРЫТОМ на конце кабеля детектор V / C показал нулевое напряжение на четверти волны от ОТКРЫТОГО. Поскольку и очень малые ИНЦИДЕНТНЫЕ и ОТРАЖЕННЫЕ токи, которые проходили через вольтметр в одном направлении, токи были суммированы. Таким образом, нулевой результат указывает на то, что ИНЦИДЕНТНЫЙ и ОТРАЖЕННЫЙ токи, проходящие через вольтметр, были сдвинуты по фазе на 180 °. Поскольку фазовый сдвиг в кабеле в одном направлении составлял 90 °, что давало общий фазовый сдвиг в кабеле в обоих направлениях на 180 °, то в ОТКРЫТОМ состоянии сдвига фазы не было.OPEN ведет себя так, как будто сигнал идет полностью.
путь до конца ОТКРЫТОГО, а затем просто отражается без изменения фазы.
Короткая фаза
В параграфе 5.4, с КОРОТКОМ на конце кабеля, детектор V / C показал сумму напряжений на четверти волны от КОРОТКОГО. И малый ИНЦИДЕНТНЫЙ, и ОТРАЖЕННЫЙ токи проходили через вольтметр в одном направлении, и токи суммировались. Следовательно, результат удвоения напряжения источника указывает на то, что напряжения ИНЦИДЕНТА и ОТРАЖЕНИЯ были в фазе.Поскольку фазовый сдвиг в кабеле в одном направлении составлял 90 °, что давало общий фазовый сдвиг в кабеле в обоих направлениях на 180 °, то общий фазовый сдвиг «туда и обратно» при SHORT составлял 180 °.
Относительные фазы
Теперь можно просто вывести, что фазовый сдвиг напряжения с SHORT составляет 180 °, а фазовый сдвиг напряжения с OPEN равен 0 °, что дает разность 180 °. Эти относительные фазы можно наблюдать с помощью векторного анализатора цепей, и большинство опытных пользователей ВАЦ знакомы с этим.На диаграмме Смита точка в правой части дисплея означает ОТКРЫТОЕ, а точка в левой части дисплея — КОРОТКОЕ.
5.6) Относительная фаза АВАРИЙНОГО и ОТРАЖЕННОГО токов от КОРОТКОГО
Когда испытательное оборудование настроено, как показано на рисунке 5.1, цифровой мультиметр переключается на токовый выход детектора напряжения и тока.
Генератор сигналов снова настроен на выход +0 дБмВт на частоте 37,5 МГц, рассчитанной для кабеля длиной 2 м в параграфе 5.2. Это дает выход усилителя приблизительно +15 дБмВт (1,26 Вольт, действующее значение при 0,025 А на нагрузке 50 Ом). SHORT Termination теперь подключен к выходу двухметрового кабеля.
Наблюдая за цифровым мультиметром, частота генератора сигналов медленно снижается, пока ток не будет равен нулю. Частота генератора сигналов вернется практически к той же частоте, что и ранее записанная для нуля напряжения в ОТКРЫТОМ состоянии в параграфе 5.2.
На рисунке 5.4 показано, как токи (I f и I r ), протекающие через трансформатор тока детектора напряжения и тока, протекают в противоположных направлениях, что вызывает принципиальное вычитание токов.Из рисунка 5.4 видно, что имеется сдвиг фазы на 90 ° вдоль кабеля в направлении ИНЦИДЕНТА плюс 90 ° на КОРОТКОМ, затем 90 ° на КОРОТКОМ в ОТРАЖЕННОМ направлении плюс еще 90 ° вдоль кабеля, всего 360 ° фазового сдвига Таким образом, сигналы INCIDENT и REFLECTED имеют одинаковую фазу на трансформаторе тока. Поскольку два тока в трансформаторе находятся в фазе, и трансформатор вычитается, конечным результатом является аннулирование, и цифровой мультиметр считывает нулевой ток.
Рисунок 5.4
5.7) Относительная фаза АВАРИЙНОГО и ОТРАЖЕННОГО токов от ОТКРЫТОГО
Когда испытательная установка остается такой же, как указано выше, а частота генератора сигналов все еще установлена, как в параграфе 5.6, на оконечной коробке выбирается ОТКРЫТО. Цифровой мультиметр теперь показывает ток примерно 0,05 А, потому что ИНЦИДЕНТНЫЙ и ОТРАЖЕННЫЙ токи теперь суммируются. Два сигнала сдвинуты по фазе на 180 ° на трансформаторе тока, потому что в ОТКРЫТОМ состоянии нет изменения фазы, но они текут в противоположных направлениях, и два отрицательных сигнала дают положительный результат, что дает сумму.Фактически, указывается разность векторов пикового тока.
Рисунок 5.2
5.8) Относительная фаза ОТРАЖЕННЫХ токов от ОТКРЫТОГО и КОРОТКОГО
Теперь мы можем сравнить фазы, полученные при измерении токов от ОТКРЫТОГО и КОРОТКОГО выводов.
Короткая фаза
В параграфе 5.6 с КОРОТКОМ на конце кабеля детектор V / C показал нулевой ток на четверть волны от КОРОТКОГО.Поскольку ИНЦИДЕНТНЫЙ и ОТРАЖЕННЫЙ токи, проходящие через трансформатор, были в противоположных направлениях, токи в основном вычитались. Следовательно, нулевой результат указывает на то, что токи ИНЦИДЕНТА и ОТРАЖЕНИЯ, проходящие через вольтметр, были в фазе. Поскольку фазовый сдвиг в кабеле в одном направлении составлял 90 °, что давало общий фазовый сдвиг в кабеле в обоих направлениях на 180 °, то при коротком замыкании был фазовый сдвиг на 180 °.
Фаза при ОТКРЫТОМ состоянии
В п. 5.7, с ОТКРЫТОМ на конце кабеля, детектор V / C показал сумму тока в четверти волны от ОТКРЫТОГО. Поскольку ИНЦИДЕНТНЫЙ и ОТРАЖЕННЫЙ токи, проходящие через трансформатор, были в противоположных направлениях, токи в основном вычитались. Следовательно, результат удвоения тока источника указывает, что ИНЦИДЕНТНЫЙ и ОТРАЖЕННЫЙ токи не совпадают по фазе на 180 °. Поскольку фазовый сдвиг в кабеле в одном направлении составлял 90 °, что давало общий фазовый сдвиг в кабеле в обоих направлениях на 180 °, то в ОТКРЫТОМ состоянии сдвига фазы не было.
Относительные фазы
Теперь можно просто вывести, что текущий фазовый сдвиг с SHORT составляет 180 °, а текущий фазовый сдвиг с OPEN равен 0 °. Точно такой же сдвиг, что и для напряжений в пункте 5.5.
5.9) Несоответствие относительных фаз напряжения и тока
Используя данные, собранные в ходе продолжающихся измерений, можно проводить дальнейшие наблюдения. Если учесть измерения напряжения и тока в ОТКРЫТОМ состоянии под углом 90 °, можно увидеть, что цифровой мультиметр показывает минимум напряжения и максимум тока.И наоборот, если рассматривать измерения напряжения и тока в КОРОТКОМ состоянии под углом 90 °, можно увидеть, что цифровой мультиметр показывает максимум напряжения и минимум тока. Мы заметили, что эта разница в показаниях между напряжением и током связана с тем, что измерение напряжения является сложением, а измерение тока — вычитанием. Из этого видно, что напряжение и ток в любом одном направлении определенно совпадают по фазе. В классическом исследовании ЛЭП указание счетчиков,
напряжение было на максимуме, когда ток был на минимуме (и наоборот), означало, что ток и напряжение были не в фазе на 180 °, что
явно не соответствует действительности.
Теперь работа линии передачи имеет смысл. Сигнал, проходящий по линии, состоит из заряженных частиц. Напряжение любой заряженной частицы связано с количеством заряда на этой отдельной частице, а ток в любой момент связан с количеством заряженных частиц. Этот заряд дает частице электрическое поле и магнитное поле, и все они движутся вместе как единое целое. Нелогичное представление о том, что напряжение или ток могут двигаться независимо от частицы, больше не требуется.
< 1 2 3 4 5 6 7 8 9 > Страницы
Индекс линии передачи
Указатель технических статей
Напряжение, ток, мощность и энергия: определения :: электронные измерения
Последняя модификация: 17 февраля 2013 г.
Правильное подключение измерительного прибора — это только одно. Но, чтобы определить правильный параметр, необходимо больше соображений.
Очень важный вопрос: с какой целью я делаю это измерение?
Выполнение измерения тока для изучения тепловыделения в проводе требует другого параметра, чем измерение тока, для определения состояния заряда конденсатора или батареи.
Параметры могут быть выражены как среднее, среднеквадратичное, мгновенное или пиковое значение. Важен не только тип нагрузки, но и то, является ли она источником переменного или постоянного тока, а также то, как выглядят напряжение и форма тока.
На этой странице, с другой стороны, будет обсуждаться тесно связанное взаимодействие между напряжением и током, а также мощностью и энергией.
Мгновенные значения
Мгновенное напряжение v , ток i и мощность p имеет значение, которое соответствует определенному времени t . Каждая форма волны имеет бесконечное количество мгновенных значений. Такая форма волны описывается как параметр как функция времени. В случае напряжения это будет записано как v (t) .
В приведенном ниже примере ситуация последовательной цепи резистора и катушки, подключенных к синусоидальному напряжению с пиковым напряжением 3 В и частотой f 50 Гц.
Рис. 1: Напряжение, ток и мощность как функции времени.
Синусоидальное напряжение как функция времени записывается как:
[экв. 1]
Максимальное значение тока составляет 2 А и смещено на 60 ° относительно напряжения.
[экв. 2]
Мощность как функция времени является произведением соответствующих мгновенных значений напряжения и тока:
[экв.3]
На рис. 1 показано графическое представление напряжения, тока и мощности. Например; мгновенные значения показаны для времени t = 4,2 мс, отмечены серой линией:
v (4,2 мс) = 2,906 В
i (4,2 мс) = 0,538 A
p (4,2 мс) = 1,563 Вт
В определенный момент мгновенное напряжение и ток всегда можно умножить для расчета мгновенной мощности.
Средние значения
Среднее значение, также называемое средним значением, является наиболее часто используемым параметром.Если мультиметр настроен для измерения значений постоянного тока, измеряется среднее напряжение или ток. Также измеряется среднее значение переменного напряжения или тока, когда счетчик установлен на постоянный ток. В случае симметричного переменного напряжения мультиметр покажет 0 В, что является правильным значением.
Напряжение и ток
Среднее значение — это сумма всех произведений мгновенных значений x , умноженных на бесконечно малое время dt , деленное на период T , в котором измеряется.Такое суммирование с бесконечно малыми шагами по времени называется интегрированием. Обычно записывается как:
[экв. 4]
X, например, может представлять напряжение или ток. Заполнено для напряжения:
[экв. 5]
Мультиметр
Рис. 2: RC-фильтр усредняет напряжение.
Как упоминалось ранее, мультиметр, выбранный в диапазоне постоянного тока, измеряет среднее значение напряжения или тока. В цифровых измерителях это среднее значение устанавливается с помощью RC-фильтра. Это входной сигнал, непрерывно усредняемый за время RC.В форме формулы:
[экв. 6]
Энергия и мощность
Уравнение 3 показывает, что произведение мгновенного напряжения и тока дает мгновенную мощность p (t) . Если эти мгновенные мощности, умноженные на бесконечно малое время dt , непрерывно суммировать, это вернет энергию в системе, поскольку t = 0 с:
[экв. 7]
В самом деле, энергия — это мощность, умноженная на время: E = P · t, и пакеты энергии всегда можно складывать вместе, чтобы вычислить полную энергию.
Ниже снова показаны сигналы из примера последовательной цепи с сопротивлением катушки, как описано в разделе «Мгновенные значения». На этом рисунке черной линией показано изменение энергии во времени, рассчитанное по уравнению 7.
Рис. 3: Энергия как функция времени.
В результате переменной полярности напряжения и тока кривая мощности также имеет периодическое изменение амплитуды с удвоенной частотой. Поскольку энергия рассеивается в сопротивлении, положительная область серого цвета на кривой мощности больше, чем отрицательная область.
Значение черной энергетической линии в любой момент времени равно предыдущей области под кривой мощности. Ясно видно, что линия энергии периодически поднимается больше, чем опускается, в результате амплитудной асимметрии кривой мощности вокруг оси x.
На рисунке 3 показан период времени T . Энергия внутри этого времени (0 … T s), которая вводится в систему, обозначена E на и будет рассчитана следующим образом:
[экв. 8]
Средняя мощность за определенный период времени равна общему количеству энергии за это время, деленному на время, в котором измеряется:
[экв.9]
Если это деление по времени вставлено в экв. 8, средняя мощность может быть рассчитана для любой формы сигнала:
[экв. 10]
Это уравнение согласуется с общим уравнением для расчета среднего значения (уравнение 4). Активная мощность — это всегда средняя мощность.
Это уравнение для расчета средней рассеиваемой мощности всегда актуально, поскольку расчет основан на мгновенных значениях. Не имеет значения, является ли это постоянным или переменным током, как выглядит напряжение и форма тока, и существует ли фазовый сдвиг между напряжением и током.
Приведенное выше уравнение для расчета средней мощности — это метод, на котором основана работа измерителя мощности. Счетчик энергии, такой как счетчик киловатт-часов в домах и на производстве, работает в соответствии со сравнением 8. Или иначе записывается как:
Полномостовой контроллер с фазовым сдвигом обеспечивает эффективное изолированное преобразование мощности для приложений с высокой мощностью
В распределенных системах электропитания большого оборудования для обработки данных и связи используются изолированные преобразователи большой мощности для генерации промежуточных напряжений распределения шины и более низких напряжений для ЦП, запоминающих устройств и схем ввода-вывода.Изоляция источника питания необходима для соблюдения требований регулирующих органов, экранирования чувствительных цепей и устранения контура заземления. К сожалению, добавление изоляции увеличивает сложность и снижает эффективность из-за множества факторов, включая потери в магнитном сердечнике и медных потерях силового трансформатора. Эти проблемы усиливаются по мере увеличения уровня мощности и входного напряжения. Кроме того, паразитная индуктивность рассеяния может вызывать переходные процессы высокого напряжения на силовых полевых МОП-транзисторах, еще больше снижая эффективность и создавая нежелательные электромагнитные помехи.Любое повышение эффективности этих источников питания приводит к снижению требований к охлаждению, уменьшению объема, веса и стоимости. Мостовые преобразователи мощности со сдвигом фазы привлекли внимание из-за их способности использовать обычно нежелательные элементы силового трансформатора и полевых МОП-транзисторов для значительного снижения коммутационных потерь и шума.
LTC1922-1 в корпусе G или N с 20 выводами (рис. 1) представляет собой полнофункциональный контроллер для фазосдвинутого полномостового преобразователя. Предлагая широкий диапазон (0% –99.5%) фазовый модулятор, LTC1922-1 также сочетает в себе программируемую (от 10 кГц до 1 МГц) фиксированную частоту, управление режимом тока с новой схемой для включения переключения при нулевом напряжении (ZVS) во всех рабочих условиях, оптимизируя эффективность. Встроенное управление синхронным выпрямлением с удвоением тока дополнительно повышает эффективность и снижает пульсации выходного напряжения. Низкие пусковые токи и рабочие токи покоя снижают нагрузку на внешние цепи смещения, в то время как точный стабилизатор с малым падением напряжения 5 В обеспечивает до 15 мА для питания вспомогательных цепей.Кроме того, LTC1922-1 обеспечивает простую программируемость для ограничения тока, гашения переднего фронта, плавного пуска и защиты от короткого замыкания, уменьшая сложность схемы и время разработки.
Рис. 1. Блок-схема LTC1922.
Вместо того, чтобы жестко переключать силовые полевые МОП-транзисторы, как обычный полномостовой или прямой преобразователь, полномостовой преобразователь со сдвигом фазы фиксирует и рециркулирует энергию, накопленную в индуктивности рассеяния силового трансформатора, чтобы плавно включить каждый из четырех силовых полевых МОП-транзисторов в полной мере. мост.ZVS (переключение при нулевом напряжении) происходит, когда внешние силовые полевые МОП-транзисторы включаются и выключаются, когда их соответствующие напряжения сток-исток равны или близки к нулю, что эффективно устраняет мгновенные потери мощности при включении полевых МОП-транзисторов, вызванные C OSS ( емкость сток-исток) и разряд паразитной емкости (см. рисунок 2). Это повышает эффективность, снижает электромагнитные помехи, связанные с переключением, и устраняет необходимость в демпферах на первичной стороне.
Рис. 2. Мгновенные потери переключения из-за емкостного разряда.
Как показано на рисунке 3, альтернативные диагональные переключатели в полном мосту (A-D или B-C) работают одновременно, чтобы подавать энергию на нагрузку (вторичную). Каждый сигнал переключателя-привода имеет рабочий цикл 50% за вычетом небольшой задержки включения ZVS. Выходы A и B сдвинуты по фазе на 180 градусов и изменяют состояние каждый раз, когда генератор синхронизирует внутренний триггер PWM. Точно так же выходы C и D сдвинуты по фазе на 180 градусов и меняют состояние каждый раз, когда RAMP превышает уровень управления PWM, определенный COMP.По мере увеличения уровня управления ШИМ происходит соответствующее увеличение перекрытия проводимости переключателя (A – D или B – C) или фазового сдвига. Максимальное перекрытие на пару переключателей составляет 50%. Поскольку обе пары переключателей проводят ток во время цикла трансформатора, максимально достижимый рабочий цикл составляет 100%. Когда переключатель выключается, собственный импульс намагничивания трансформатора и индуктивности рассеяния при управлении фазовым сдвигом помогает коммутировать напряжения соответствующих плеч моста в сторону нулевого напряжения.
Рисунок 3.Временная диаграмма LTC1922.
LTC1922-1 реализует ZVS с технологией замкнутого контура DirectSense. Оптимальное время задержки ZVS является сложной нелинейной функцией тока нагрузки, MOSFET C OSS , межобмоточной емкости трансформатора, индуктивности рассеяния и намагничивания, а также выходной индуктивности. Кроме того, каждая опора моста демонстрирует уникальное поведение, что требует различных задержек. Оптимальное время задержки предотвращает резкое переключение и / или повышенную проводимость основного диода, увеличивает диапазон рабочего цикла и минимизирует электромагнитные помехи.Как показано на рисунке 4, LTC1922 определяет каждую ветвь полного моста с делителем напряжения на PDLY и ADLY и определяет входное питание с делителем напряжения на SBUS. Внутренние высокоскоростные компараторы с фиксацией состояния, логика состояния и ШИМ, а также отказоустойчивые схемы дают команду соответствующим полевым МОП-транзисторам верхнего плеча (MA, MC) включаться, когда возрастающие напряжения на PDLY и ADLY пересекают пороговый уровень, определяемый напряжением на SBUS. Кроме того, каждый нарастающий фронт ADLY и PDLY инициирует точный ток из ADLY и PDLY соответственно.Этот ток вместе с внешним резистивным делителем создает более низкий пороговый уровень для использования, когда ветви моста коммутируются к земле, обеспечивая ZVS для нижних полевых МОП-транзисторов (MB, MD). После перехода по заднему фронту ток сбрасывается. Определяя мост и входное питание напрямую, LTC1922-1 может интеллектуально адаптироваться к любым изменениям тока нагрузки, температуры, допусков компонентов, смещения задержки схемы драйвера или входного напряжения. Преимущества включают простую конструкцию, высокую эффективность, увеличенный рабочий цикл, более низкий уровень электромагнитных помех и стабильную производительность без дополнительных настроек.
Рис. 4. Прямое определение полного моста.
Синхронное выпрямление может обеспечить значительное повышение эффективности, особенно при более низких выходных напряжениях и когда синхронное переключение оптимально. LTC1922-1 включает внутреннюю синхронизацию и логику, необходимые для генерации управляющих сигналов для синхронных выпрямителей вторичной стороны, как показано на рисунке 3. Эти интервалы переключения были внутренне запрограммированы для предотвращения преждевременного включения и отложенного выключения внешних синхронных выпрямителей. максимальное преимущество над кремниевыми выпрямителями или выпрямителями Шоттки и устранение внешней логической схемы и дискретных схем синхронизации.
MOSFET синхронного выпрямителя и вторичный силовой каскад трансформатора сконфигурированы как удвоитель тока с чередованием. В удвоителе тока используются две катушки индуктивности, которые поровну распределяют выходной ток и, что более важно, сдвинуты по фазе на 180 градусов. Эти свойства значительно снижают ток пульсаций выходного конденсатора в зависимости от продолжительности включения (см. Рисунок 5), уменьшая пульсации напряжения и повышая надежность выходного конденсатора, обеспечивая при этом удвоение выходного тока на объем катушки индуктивности по сравнению с сопоставимыми силовыми каскадами с одной катушкой индуктивности.
Рис. 5. Пульсации выходного индуктора в зависимости от рабочего цикла.
В схеме на рисунке 6 используется LTC1922-1, регулирующий 3,3 В при токе до 40 А от изолированного входного напряжения 36 В до 72 В. В этой конструкции используются только компоненты для поверхностного монтажа. Пиковая эффективность составляет чуть более 90%, снижаясь до 85% при нагрузке 40 А (рис. 7). Высокая эффективность устраняет необходимость в принудительном воздушном охлаждении, лицевых панелях или громоздких радиаторах. Один LTC1693-1 и миниатюрные сигнальные трансформаторы используются для управления затвором двух полевых МОП-транзисторов верхнего плеча.Второй LTC1693-1 обеспечивает питание вторичных синхронных выпрямителей. LT1431 и стандартный оптический ответвитель предоставляют информацию о регулировании напряжения на границе изоляции.
Рис. 6. Преобразователь LTC1922 для поверхностного монтажа 3,3 В / 40 А.
Рис. 7. Эффективность преобразования 48V в 3.3V.
Осциллограммы первичного осциллографа (рис. 8) демонстрируют очень четкие переходы, типичные для полного моста со сдвигом фазы. Поскольку LTC1922-1 является контроллером режима тока, он легко адаптируется к стандартным методам распределения нагрузки, используемым в приложениях системы резервного питания.Дополнительные функции этого преобразователя включают блокировку пониженного напряжения, плавный пуск, гашение переднего фронта, ограничение тока и защиту от короткого замыкания.
Рис. 8. Формы сигналов на входе от 48 В до 3,3 В / 20 А.
Полномостовой преобразователь со сдвигом фазы является идеальным кандидатом для изолированного преобразования мощности высокой мощности, что подтверждается его высокой эффективностью и низким уровнем шума. LTC1922-1 — это решение нового поколения для управления преобразователем этого типа, предлагающее оптимальное переключение при нулевом напряжении и интегрированное управление синхронным выпрямлением, а также ряд других функций, предназначенных для приложений с большой мощностью.
Работа при отказе в обрыве в многофазных асинхронных двигателях
Аннотация
В последние несколько лет многофазные машины были признаны привлекательной альтернативой традиционным трехфазным. Это связано с их полезностью в той нише, где требуется снижение общей мощности на фазу и, в основном, высокая общая надежность системы и возможность использования многофазной машины в неисправных условиях. Электромобиль и железнодорожная тяга, полностью электрические корабли, электрические самолеты или системы ветроэнергетики являются примерами современных реальных приложений, использующих многофазные машины, большинство из которых используют возможность продолжения работы в неисправных условиях.Среди доступных многофазных машин симметричные пятифазные индукционные машины, вероятно, являются одними из наиболее часто рассматриваемых многофазных машин в недавних исследованиях. Однако другие многофазные машины также использовались в последние несколько лет в связи с разработкой более мощных микропроцессоров. В этой главе анализируется поведение обычных n-фазных машин (n любое нечетное число больше 3) при неисправной работе (с учетом наиболее распространенной неправильной работы, то есть обрыва фазы).Затем полученные результаты будут конкретизированы для 5-фазного случая, где будут представлены некоторые результаты моделирования и экспериментов, чтобы показать поведение всей системы в исправных и неисправных условиях. Глава будет организована следующим образом. Во-первых, анализируются различные неисправности многофазной машины. Подробно описаны и объяснены условия неисправности, а также указана заинтересованность многофазной машины в управлении неисправностями. Затем изучается влияние короткого замыкания на обрыв в модели машины.Рассматривается общая n-фазная машина, где n любое нечетное число больше трех. Затем анализ конкретизируется для 5-фазной машины, в которой состояние короткого замыкания обрыва фазы управляется с использованием различных методов управления, и полученные результаты сравниваются. Наконец, выводы представлены в последнем разделе главы.
1. Введение
Многофазные машины были признаны в последние несколько лет привлекательной альтернативой обычным трехфазным.Это связано с их полезностью в той нише, где требуется снижение общей мощности на фазу, а также высокая общая надежность системы и возможность использования многофазной машины в неисправных условиях. Электромобиль и железнодорожная тяга, полностью электрические корабли, электрические самолеты или системы ветроэнергетики являются примерами современных реальных приложений, использующих многофазные машины, большинство из которых используют возможность продолжения работы в неисправных условиях.Среди доступных многофазных машин симметричные пятифазные индукционные машины, вероятно, являются одними из наиболее часто рассматриваемых многофазных машин в недавних исследованиях. Однако другие многофазные машины также использовались в последние несколько лет в связи с разработкой более мощных микропроцессоров. В этой главе анализируется поведение типовых машин с фазой n ( n — любое нечетное число больше 3) при неисправной работе (учитывая наиболее частую неисправную работу, т.е.е. обрыв фазы). Затем полученные результаты будут конкретизированы для 5-фазного случая, где будут представлены некоторые результаты моделирования и экспериментов, чтобы показать поведение всей системы в исправных и неисправных условиях.
Глава будет организована следующим образом:
Во-первых, анализируются различные неисправности в многофазной машине. Подробно описаны и объяснены условия неисправности, а также указана заинтересованность многофазной машины в управлении неисправностями. Затем изучается влияние короткого замыкания на обрыв в модели машины.Рассматривается типовая машина с фазой n , где n — любое нечетное число больше трех. Затем анализ конкретизируется для 5-фазной машины, в которой состояние короткого замыкания обрыва фазы управляется с использованием различных методов управления, и полученные результаты сравниваются. Наконец, выводы представлены в последнем разделе главы.
2. Неисправности в электромеханических многофазных приводах
Электропривод — это электромагнитное оборудование, подверженное различным электрическим и механическим неисправностям, которые, в зависимости от его характера и особых характеристик системы, могут привести к ненормальной работе или отключению.Чтобы расширить использование электроприводов в критически важных для безопасности и востребованных приложениях, настоятельно необходима разработка экономичных, прочных и надежных систем. Этот вопрос в последнее время стал одной из последних задач в области проектирования электроприводов [1]. Следовательно, отказоустойчивость, которую можно определить как способность обеспечивать надлежащее отслеживание заданной скорости или крутящего момента в электроприводе в ненормальных условиях, была рассмотрена в трехфазных электроприводах с учетом различных подходов к проектированию и исследованиям, включая резервное оборудование. и крупногабаритные конструкции, ведущие к эффективным и жизнеспособным, но дорогостоящим решениям, устраняющим неисправности.Отказоустойчивость трехфазных приводов при различных типах неисправностей — это жизнеспособная и зрелая область исследований, в которой производительность привода и возможность управления гарантируются за счет дополнительного оборудования [1]. Однако это не относится к области многофазных приводов, несмотря на большее количество фаз, которыми обладает многофазная машина, что способствует более высокой отказоустойчивости по сравнению с обычными трехфазными приводами. Многофазные приводы не нуждаются в дополнительном электрическом оборудовании для управления работой после отказа, требуя только надлежащих методов управления после отказа для продолжения работы [2].Поэтому они идеальны для тяговых и аэрокосмических применений по соображениям безопасности или на морских ветряных электростанциях, где корректирующее обслуживание может быть затруднено в плохих погодных условиях [3-6].
Рисунок 1.
Типы неисправностей пятифазного привода.
Неисправности в электромеханическом приводе также можно классифицировать в зависимости от характера (электрический или механический), местоположения или влияния, которое они оказывают на систему в целом (обратите внимание, что разные типы неисправностей могут привести к одинаковому ненормальному поведению машины).Наиболее распространенная классификация неисправностей электроприводов определяет три основные группы неисправностей, которые могут возникнуть в электроприводе. Преобразователь энергии, электронные датчики (тока, температуры, скорости и напряжения) и электрическая машина определяют основные неисправности в электроприводе, как показано на Рисунке 1. Эти неисправности подробно описаны ниже.
Неисправности электрических машин, которые могут быть вызваны электрическими или механическими проблемами / нагрузками и подразделяются следующим образом [7-11]:
Неисправности статора: обрыв или короткое замыкание одного или нескольких статоров фазные обмотки.Эти виды неисправностей возникают из-за механического повреждения соединений, вызванного нарушением изоляции, экстремальных электрических условий эксплуатации (высокие температуры в сердечнике статора или обмоток, пусковые напряжения, работа при повышенном или пониженном напряжении, электрические разряды, несбалансированное напряжение статора) или несоответствующие условия окружающей среды (грязь, загрязнение масла и влаги) [10-12], что приводит к межвитковым замыканиям [12], обмоткам статора [13] и различным фазным замыканиям обмоток [10-11], что может привести к дальнейшему обрыву -фазные замыкания одной или нескольких фазных обмоток [14-15].
Неисправности ротора: короткое замыкание обмотки возбуждения ротора, сломанные стержни ротора и трещины на концевых кольцах ротора. Они вызваны электрическими (короткое замыкание обмоток ротора) или механическими (сломанные стержни и трещины в кольцах ротора). Эти типы неисправностей возникают из-за термического напряжения (работа привода в условиях перегрузки и несбалансированной нагрузки), электромагнитного напряжения, производственных проблем, динамического напряжения от крутящего момента вала, условий окружающей среды и усталости механических частей [10-11].
Неравномерность воздушного зазора из-за статического или динамического эксцентриситета.Эксцентриситет вызван производственными и конструктивными ошибками, которые приводят к неравномерному воздушному зазору между статором и ротором, что приводит к неуравновешенным радиальным силам и возможному контакту ротор-статор [10]. Статический эксцентриситет появляется, когда положение неравенства воздушного зазора фиксировано, тогда как динамический эксцентриситет возникает, когда центр ротора не выровнен должным образом в центре вращения, а положение воздушного зазора не вращается одинаково.
Неисправности подшипников, которые в основном вызваны ошибками сборки (несоосность подшипников), которые приводят к тому, что вибрация подшипника проникает в вал [16].
Неисправности изогнутого вала, аналогичные неисправностям динамического эксцентриситета [10]. Эти неисправности возникают, когда происходит силовой дисбаланс или несоосность нагрузки машины, что приводит к вибрации машины и дальнейшему отказу машины [11].
Статистически наиболее распространенными неисправностями в электрических машинах являются отказы подшипников, неисправности обмотки статора, поломка стержня ротора, неисправности вала и муфты, трещины на концевых кольцах ротора и эксцентриситет воздушного зазора [7-9], приводящие к несимметричные токи и напряжения статора, появление определенных гармоник в фазных токах, общие колебания и уменьшение крутящего момента, вибрация машин, шум, перегрев и снижение КПД [10-11].
Неисправности датчика. Электрические приводы обычно включают в себя датчики скорости, напряжения и тока для целей управления и защиты (Рисунок 1). В случае многофазного привода стандартные методы FOC и прогнозирующего управления требуют измерения скорости и по крайней мере n-1 (для n -фазного привода) измерений тока, чтобы гарантировать надлежащее поведение управления. В случае ненормальной работы датчика, несуществующие или неточные сигналы могут снизить производительность системы или привести к полному отказу привода [17-20].Неисправности датчиков в основном анализировались для трехфазных приводов, и недавние работы также рассматривали этот тип неисправностей для многофазного случая [21-23]. Обратите внимание, что в зависимости от неисправного датчика (например, напряжения, тока или скорости в промежуточном контуре) эффект в обычном трехфазном или многофазном приводе в основном одинаков. В любом случае, анализ таких неисправностей в основном сосредоточен на работе только с одним неисправным датчиком из-за малой вероятности неисправности более чем одного датчика [24], что может включать неисправности датчиков тока и скорости, которые являются наиболее важными в электрические приводы.Основная причина этого заключается в том, что высокопроизводительные приводы основаны на контроллерах скорости и тока с обратной связью и, следовательно, на датчиках скорости и тока. Любое изменение или систематическая ошибка в измеряемых величинах может привести к мгновенным потребляемым управляющим воздействиям мощности, подвергая всю систему возможному электрическому напряжению [17].
