Закон Ома для переменного тока
 Приветствую всех на нашем сайте! В этот раз речь пойдёт про закон Ома для переменного тока.
Приветствую всех на нашем сайте! В этот раз речь пойдёт про закон Ома для переменного тока.
Когда-то люди жили без электричества. Потом научились делать батарейки, и так появился постоянный электрический ток. Есть у электриков шутка: «Что такое переменный ток? Это нет-нет, да шарахнет…» А вот тут возникает логичный вопрос: «Почему не остановились на постоянном токе, раз он безопаснее»? Исключительно с экономической точки зрения. Переменный ток гораздо удобнее и дешевле преобразовывать, то есть повышать или понижать. Точнее не сам ток, а напряжение. Когда протекает ток, он совершает работу, работа сопровождается выделением тепла. Мощность, это произведение тока и напряжения, а значит, повышая напряжение и понижая ток мы передадим ту же мощность, но с меньшим тепловыделением, а значит и с меньшими потерями. А ещё, чем выше напряжение, тем меньше сопротивление проводов, по которым протекает ток, это оказывает влияние на потери напряжения. Как-нибудь поговорим более подробно об этом. А пока обратимся к школьному курсу физики – ток протекает только по замкнутому контуру и возможен только при условии, что к этому контуру будет приложено напряжение и контур будет иметь какое-то сопротивление. Подробно об этом вы можете прочитать в статье Закон Ома для замкнутой цепи. А мы двинемся дальше.
Сейчас вы поймете, почему так важен и что даёт закон Ома для цепи переменного тока. В современной жизни без этого закона никак не обойтись. Поскольку ток, это работа, а работа есть выделение тепла, то существенная задача электротехники в том, чтобы соблюдался термический режим, проще говоря, чтобы не произошло перегрева электроцепей. Итак, закон Ома гласит, что:

Измерить напряжение довольно просто, для этого понадобится вольтметр, в нашем случае для переменного напряжения. В цепях постоянного тока измерить сопротивление тоже не составляет сложности, для этого потребуется омметр. Почему же возникают сложности с переменным током? А проблема, именно, в его переменности, а точнее понятиях емкости и индукции, которые ведут себя при переменном токе несколько иначе, нежели при постоянном.
Формула Закона Ома для переменного тока:

Кому-то эта формула может показаться неожиданной, потому что все привыкли видеть другую формулу:

Теперь давайте разберёмся, что такое полное сопротивление цепи и всё сразу встанет на свои места. В цепях постоянного тока конденсаторы могут только накапливать заряд, а катушки индуктивности становятся обычным проводом, но в цепях переменного тока они становятся сопротивлениями. Поэтому в переменном токе существует две составляющие: активный ток и реактивный. Как это происходит, сейчас увидите.
Ёмкостное сопротивление. При подаче напряжения на конденсатор сначала возникает сильный ток и потом поднимается напряжение, то есть в идеальных условиях ток опережает напряжение на угол 90. Другими словами, ток совершает работу из-за наличия сопротивления в цепи, которое можно посчитать по формуле:
Таким образом, чем выше частота переменного тока и чем выше емкость конденсатора, тем меньше ёмкостное сопротивление.
Индуктивное сопротивление. Здесь все происходит наоборот, сначала возникает напряжение, затем запускается индукционный процесс который препятствует возрастанию тока. Подробнее об этом читайте в статьях про индукцию.

Поэтому здесь мы видим уже обратную картину – чем выше частота и чем больше индуктивность катушки, тем больше индуктивное сопротивление переменному току.
Почему эти понятия не встречаются в цепях постоянного тока? Ответ можно узнать, посмотрев на формулы. Если ток постоянный, то f=0. То есть, емкостное сопротивление станет бесконечно большим, а это значит, что конденсатор в цепи постоянного тока становится похож на выключатель, который размыкает цепь и ток по ней не идёт, но при этом, конденсатор будет пропускать переменный ток. А индуктивное сопротивление станет равно нулю, значит, у нас останется просто провод, который имеет свое собственное сопротивление, которое еще называется активным, и его можно измерить обычным омметром. В отличие от конденсатора, у которого нет активного сопротивления, сопротивление катушки, если оно довольно большое, должно приниматься в расчёт. Как правило, активное сопротивление катушки очень маленькое по сравнению с индуктивным, поэтому его в расчёт не берут, но всё же правильно формула сопротивления катушки выглядит так:

По такому принципу в электронике изготавливают фильтры, которые должны отсечь переменный ток от постоянного, то есть пропускать только переменный ток или наоборот заглушить переменный ток, оставив только постоянный, или даже заглушить токи какой-то одной или нескольких частот.
А сейчас совсем вас запутаю… И катушка может иметь ёмкостные свойства и конденсатор – индуктивные, но как правило они слишком малы и носят паразитический характер.
Ну а сейчас мы рассмотрим закон Ома для электрической цепи переменного тока наглядно.

Допустим, у нас есть цепь из последовательно включенных резистора (активное сопротивление), конденсатора (реактивное ёмкостное сопротивление) и катушка (активно-реактивное индуктивное сопротивление). Теперь, чтобы узнать силу тока в цепи нам нужно правильно посчитать полное сопротивление цепи.

Осталось применить всё изложенное выше.
Реактивное сопротивление Х это разница между индуктивным сопротивлением XL и ёмкостным сопротивлением XC. Ну а дальше векторным сложением можем узнать полное реактивное сопротивление

следовательно:

дальнейший расчет:

или:

Что можно сказать в заключении. Как вы можете видеть, закон Ома для переменного тока точно такой же, как и для постоянного. Разница лишь в том, как считать сопротивление. Если в постоянном токе мы имеем только активное сопротивление, то в переменном токе добавляется еще и реактивное, а именно индуктивное и емкостное. И, кстати говоря, реактивный ток – явление, с которым в электротехнике стараются бороться различными методами, поскольку эти токи паразитные и не несут полезной нагрузки. Об этом мы поговорим в других статьях. Пока сообщу лишь, что идеальный вариант, к которому пока никто не смог приблизиться, чтобы нагрузка была исключительно активной.
Поделиться ссылкой:
Похожее
«Закон Ома для участка цепи»
Аннотация к разработке урока.
Урок открытия новых знаний и первичного закрепления по теме «Закон Ома для участка цепи и сопротивление» составлен в соответствие с требованиями ФГОС второго поколения.
В разработанном уроке реализованы следующие приёмы развития критического мышления с учётом личностно ориентированного подхода:
1.ФИШБОУН (рыбный скелет)
Голова-вопрос темы, верхние косточки — основные понятия темы ,середина- основная часть темы, нижние косточки – суть понятий, хвост – ответ на вопрос. Записи краткие и представляют собой ключевые слова или фразы отражающие суть темы.
2.КЛАСТЕР (гроздь) – предполагает выделение смысловых единиц текста и его графическое оформление в виде грозди.
3.СИНКВЕЙН (пятистишье) нерифмованное стихотворение, состоящее из пяти строк, используемое как дидактический приём на этапе актуализации или рефлексии.
4.ИНСЕРТ — маркировка текста значками по мере чтения.
«_»- думал иначе
«+»-новые знания
«?»- не понял, есть вопросы
«у»- знал раньше
5.Вопросы по Б. Блуму:
-Простые вопросы. Для ответа на них нужны конкретные знания о понятиях.
-Уточняющие вопросы, например: «Если я правильно понял, то…..» То есть, ты говоришь, что…»
-Интерпретационные, например: «Почему вольтметр соединяют в цепь параллельно , а амперметр последовательно…..»
— Творческие вопросы, например «Как вы думаете, что будет если…..»
— Оценочные вопросы: «Почему вы считаете, что это хорошо, а что-то плохо…?
-Практические вопросы: « Где в обычной жизни это встречается, наблюдается……. «
6.Работа в группах или в парах. Обучение сообща.
7.Приём «Совместный поиск»
8.Стратегия решения проблем ИДЕАЛ
И — Идентифицируйте проблему
Д — Доберитесь до сути
Е – Есть варианты решения
А — А теперь — за работу
Л – Логические выводы.
Применение перечисленных технологий позволяет развить у учащихся ряд личностных качеств:
1. Готовность к планированию. Мысли часто возникают хаотично. Важно упорядочить их, выстроить последовательность изложения. Упорядоченность мысли — признак уверенности.
2.Гибкость ума. Если учащийся не готов воспринимать идеи других ,он никогда не сможет стать генератором собственных идей и мыслей.
3. Настойчивость. Вырабатывая настойчивость в напряжении ума ,ученик обязательно добьётся лучших результатов в обучении.
4.Готовность исправлять свои ошибки.
5.Осознание. Отслеживать ход своих рассуждений.
6.Поиск компромиссных решений.
Тема урока: « Закон Ома для участка цепи. Сопротивление»
Цель урока: установить зависимость силы тока от разности потенциалов на концах участка цепи и сопротивления этого участка.
Задачи урока:
Обучающие:
познакомить учащихся с законом Ома; исследовать зависимость силы тока от разности потенциалов и сопротивления виртуально, экспериментально, графически, теоретически.
Развивающие: развить приёмы исследовательской работы, умение планировать время и достигать цель, развить умение строить логические цепочки.
Воспитательные: продолжить воспитание личностных качеств, формирование мировоззрения, эстетических и нравственных представлений.
Формирование УУД:
1.Личностные: умение создавать дружелюбную атмосферу вокруг себя, принимать активное участие на уроке, быть вежливыми и корректными работая в группе.
2.Регулятивные: уметь планировать свою деятельность, ставить перед собой цель, уметь делать выводы, контролировать свои действия, быть внимательными.
3.Познавательные: научить на опытах, исследовать зависимость силы тока от разности потенциалов и сопротивления познать способы исследования этой зависимости.
4. Коммуникативные: сформировать умение работать в группе, паре, умение принимать равное участие в исследовательской работе, уметь выслушать товарища и помочь, делать выводы, выдвигать гипотезы.
Тип урока: Урок – исследования с проведением демонстрационного эксперимента.
Вид урока: урок практических самостоятельных работ (исследовательского типа).
Возраст учащихся: 10 класс.
Программное обеспечение: Microsoft Word, Power Point, Publisher, Internet Explorer, виртуальный практикум по теме «Закон Ома» тест к уроку «Закон Ома для участка цепи».
Дидактический материал: бланк лабораторной работы (по числу учащихся в классе), тест по теме «Закон Ома» (4 варианта, число экземпляров – по числу учащихся в классе), «Реостаты и их применение» — текст по числу учащихся.
Техническое оснащение: лабораторное оборудование (электронный вольтметр, амперметр, источники питания, 3 резистора различного сопротивления, ключ, соединительные провода), персональные компьютеры; мультимедийный проектор; документ — камера.
Наглядные пособия: компьютерная модель «Закон Ома» и тест к уроку «Закон Ома для участка цепи», презентация (текст, графики, таблицы).
Формы работы учащихся:
Фронтальная
Индивидуальная
Групповая деятельность
Проектная деятельность
Исследовательская деятельность
План урока:
1.Организационный момент (1 минута).
2.Актуализация и мотивация (подготовка к основному этапу занятий обозначение темы и цели урока; повторение основных вопросов темы) (7 минут).
3.Изучен
Электротехника. Основы. Закон Ома — Всё об энергетике
Электротехника. Основы. Закон Ома
В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.
Закон Ома
Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.
Закон Ома для участка цепи без ЭДС
Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:
\begin{equation}
I = {U_{ab}\over R};
\end{equation}
Где:
- I — ток через участок ab электрической цепи;
- Uab — напряжение на участке ab электрической цепи;
- R — сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation}
I = U_{ab} × G;
\end{equation}
Где:
- G — проводимость участка ab электрической цепи.
Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.

Рисунок 1 — Участок цепи без ЭДС
Закон Ома для участка цепи содержащего ЭДС
Или обобщённый закон Ома. Формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation}
I = {U_{ab} + E\over R};
\end{equation}
Где:
- I — ток через участок ac электрической цепи;
- Uab — напряжение на участке ab электрической цепи;
- E — ЭДС на участке bс электрической цепи;
- R — сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation}
I = {(U_{ab} + E) × G};
\end{equation}
Где:
- G — проводимость участка ab электрической цепи.
Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.

Рисунок 2 — Участок цепи содержащий ЭДС
Закон Ома для полной цепи
Закон формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation}
I = {E\over {R + r}};
\end{equation}
Где:
- I — ток в электрической цепи;
- E — ЭДС электрической цепи;
- R — сопротивление электрической цепи;
- r — внутреннее сопротивление источника ЭДС.
Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).

Рисунок 3 — Полная цепь
На схеме видно, что R и r соединены последовательно, а в формуле это отражено как сумма R (сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на Rп
\begin{equation}
I = {E\over R_п};
\end{equation}
Где:
- Rп — полное сопротивление электрической цепи (включая сопротивление источника ЭДС).
Закон Ома в дифференциальной форме
Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].
\begin{equation}
\vec E = {ρ × \vec\jmath};
\end{equation}
Где:
- \(\vec\jmath\) — плотность тока;
- ρ — удельное сопротивление;
- \(\vec E\) — напряжённость электрического поля.
Примеры применения
Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.
Пример 1
Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.

Рисунок 4 — Схема к 1 и 2-му примеру
Для решения задания воспользуемся выражением (1):
\begin{equation}
I = {U\over R} = {26\over 5,2} = {5 \ А;}
\end{equation}
Пример 2
Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.
Для решения задания преобразуем выражение (2) относительно G:
\begin{equation}
I = {U × G} \ \Rightarrow \ G = {I\over U} = {1,5\over 24} = {0,0625 \ См;}
\end{equation}
Пример 3
Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.

Рисунок 5 — Схема к 3-му примеру
Для решения задания преобразуем выражение (3) относительно E:
\begin{equation}
I = {U — E\over R} \ \Rightarrow \ {I × R} = {U — E} \ \Rightarrow \ E = {U — I × R};
\end{equation}
Подставим в выражение (10) известные величины:
\begin{equation}
E = {U — I × R} = {220 — 0,5 × 140} = {150 \ В;}
\end{equation}
Пример 4
Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь — 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.
Преобразуем выражение (5) относительно r:
\begin{equation}
I = {E\over {R + r}} \ \Rightarrow \ {I × (R + r)} = E \ \Rightarrow \ {I × r} = {E — I × R} \ \Rightarrow \ r = {E — I × R\over I};
\end{equation}
Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:
\begin{equation}
r = {E — I × R\over I} = {9 — 0,72 × 12\over 0,72} = {0,36\over 0,72} = {0,5 \ Ом;}
\end{equation}
Использованные термины
Электрический потенциал точки:
Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.
Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.
Электрическое напряжение:
Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: Uab = φa — φb.
Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение — скалярная величина, но на электрических схемах указывают его положительное направление.
Электродвижущая сила (ЭДС):
Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.
ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС — скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.
Электрическое ток:
Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление — направленное движение заряженных частиц.
Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11].
Плотность тока:
Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.
Плотность тока обозначается буквой \(\vec\jmath\) латинского алфавита и измеряется в амперах на метр квадратный (А/м2). Плотность тока — векторная величина [4].
Электрическое сопротивление:
Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.
Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление — скалярная величина.
Электрическая проводимость:
Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.
Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость — скалярная величина.
Удельное сопротивление:
Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м2.
Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].
В дальнейшем при использовании вышеперечисленных терминов слово «электрический» будет упускаться.
Список использованных источников
- Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов — Москва: Высшая школа, 1996. — 623 с.
- Иванова, С.Г. Теоретические основы электротехники: Версия 1.0 [Электронный ресурс] : учеб. пособие / С. Г. Иванова, В. В. Новиков – Красноярск: ИПК СФУ, 2008. — 318 с.
- Википедия — Удельное электрическое сопротивление [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление
- Википедия — Плотность тока [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Плотность_тока
Электротехника. Основы. Закон Ома — Всё об энергетике
Электротехника. Основы. Закон Ома
В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.
Закон Ома
Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.
Закон Ома для участка цепи без ЭДС
Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:
\begin{equation}
I = {U_{ab}\over R};
\end{equation}
Где:
- I — ток через участок ab электрической цепи;
- Uab — напряжение на участке ab электрической цепи;
- R — сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation}
I = U_{ab} × G;
\end{equation}
Где:
- G — проводимость участка ab электрической цепи.
Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.

Рисунок 1 — Участок цепи без ЭДС
Закон Ома для участка цепи содержащего ЭДС
Или обобщённый закон Ома. Формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation}
I = {U_{ab} + E\over R};
\end{equation}
Где:
- I — ток через участок ac электрической цепи;
- Uab — напряжение на участке ab электрической цепи;
- E — ЭДС на участке bс электрической цепи;
- R — сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation}
I = {(U_{ab} + E) × G};
\end{equation}
Где:
- G — проводимость участка ab электрической цепи.
Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.

Рисунок 2 — Участок цепи содержащий ЭДС
Закон Ома для полной цепи
Закон формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation}
I = {E\over {R + r}};
\end{equation}
Где:
- I — ток в электрической цепи;
- E — ЭДС электрической цепи;
- R — сопротивление электрической цепи;
- r — внутреннее сопротивление источника ЭДС.
Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).

Рисунок 3 — Полная цепь
На схеме видно, что R и r соединены последовательно, а в формуле это отражено как сумма R (сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на Rп
\begin{equation}
I = {E\over R_п};
\end{equation}
Где:
- Rп — полное сопротивление электрической цепи (включая сопротивление источника ЭДС).
Закон Ома в дифференциальной форме
Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].
\begin{equation}
\vec E = {ρ × \vec\jmath};
\end{equation}
Где:
- \(\vec\jmath\) — плотность тока;
- ρ — удельное сопротивление;
- \(\vec E\) — напряжённость электрического поля.
Примеры применения
Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.
Пример 1
Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.

Рисунок 4 — Схема к 1 и 2-му примеру
Для решения задания воспользуемся выражением (1):
\begin{equation}
I = {U\over R} = {26\over 5,2} = {5 \ А;}
\end{equation}
Пример 2
Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.
Для решения задания преобразуем выражение (2) относительно G:
\begin{equation}
I = {U × G} \ \Rightarrow \ G = {I\over U} = {1,5\over 24} = {0,0625 \ См;}
\end{equation}
Пример 3
Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.

Рисунок 5 — Схема к 3-му примеру
Для решения задания преобразуем выражение (3) относительно E:
\begin{equation}
I = {U — E\over R} \ \Rightarrow \ {I × R} = {U — E} \ \Rightarrow \ E = {U — I × R};
\end{equation}
Подставим в выражение (10) известные величины:
\begin{equation}
E = {U — I × R} = {220 — 0,5 × 140} = {150 \ В;}
\end{equation}
Пример 4
Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь — 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.
Преобразуем выражение (5) относительно r:
\begin{equation}
I = {E\over {R + r}} \ \Rightarrow \ {I × (R + r)} = E \ \Rightarrow \ {I × r} = {E — I × R} \ \Rightarrow \ r = {E — I × R\over I};
\end{equation}
Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:
\begin{equation}
r = {E — I × R\over I} = {9 — 0,72 × 12\over 0,72} = {0,36\over 0,72} = {0,5 \ Ом;}
\end{equation}
Использованные термины
Электрический потенциал точки:
Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.
Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.
Электрическое напряжение:
Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: Uab = φa — φb.
Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение — скалярная величина, но на электрических схемах указывают его положительное направление.
Электродвижущая сила (ЭДС):
Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.
ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС — скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.
Электрическое ток:
Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление — направленное движение заряженных частиц.
Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11].
Плотность тока:
Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.
Плотность тока обозначается буквой \(\vec\jmath\) латинского алфавита и измеряется в амперах на метр квадратный (А/м2). Плотность тока — векторная величина [4].
Электрическое сопротивление:
Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.
Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление — скалярная величина.
Электрическая проводимость:
Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.
Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость — скалярная величина.
Удельное сопротивление:
Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м2.
Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].
В дальнейшем при использовании вышеперечисленных терминов слово «электрический» будет упускаться.
Список использованных источников
- Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов — Москва: Высшая школа, 1996. — 623 с.
- Иванова, С.Г. Теоретические основы электротехники: Версия 1.0 [Электронный ресурс] : учеб. пособие / С. Г. Иванова, В. В. Новиков – Красноярск: ИПК СФУ, 2008. — 318 с.
- Википедия — Удельное электрическое сопротивление [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление
- Википедия — Плотность тока [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Плотность_тока
Закон Ома | РАЗМЫШЛЯЕМ
Лекция № 17 Электрическое сопротивление. Закон Ома для участка цепи, для полной цепи.
1 Закон Ома
Рассмотрим некоторый элемент электрической цепи постоянного тока. Это может быть что угодно — например, металлический проводник, раствор электролита, лампочка накаливания или газоразрядная трубка.
Будем менять напряжение U, поданное на наш элемент, и измерять силу тока I, протекающего через него. Получим функциональную зависимость I = I(U). Эта зависимость называется вольт-амперной характеристикой элемента и является важнейшим показателем его электрических свойств.
Вольт-амперные характеристики различных элементов цепи могут выглядеть по-разному. Очень простой вид имеет вольт-амперная характеристика металлического проводника. Эту зависимость экспериментально установил Георг Ом.
1.1 Закон Ома для участка цепи
Оказалось, что сила тока в металлическом проводнике прямо пропорциональна напряжению на его концах: I ∼ U. Коэффициент пропорциональности принято записывать в виде 1/R:
I = U/R . (1)
Величина R называется сопротивлением проводника. Измеряется сопротивление в омах (Ом). Как видим, Ом=В/А.
Дадим словесную формулировку закона Ома.
Закон Ома для участка цепи. Сила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению участка.
Закон Ома оказался справедливым не только для металлов, но и для растворов электролитов.
Сформулированный закон имеет место для так называемого однородного участка цепи — участка, не содержащего источников тока. Закон Ома для неоднородного участка (на котором имеется источник тока) мы обсудим позже.
Вольт-амперная характеристика (1) является линейной функцией. Её графиком служит прямая линия (рис. 1).
Рис. 1 Вольт-амперная характеристика металлического проводника
По этой причине металлические проводники (и электролиты) называются линейными элементами. А вот газоразрядная трубка, например, является нелинейным элементом — её вольт- амперная характеристика уже не будет линейной функцией. Но об этом мы поговорим позднее.
2 ЭДС. Закон Ома для полной цепи
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд q:
- уходит во внешнюю цепь с положительной клеммы источника;
- перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
- приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду q нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила Fэл, направленная против движения заряда (т. е. против направления тока).
2.1 Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 2).
Рис. 2 Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила Fст не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через Aст работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы Aст называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда q вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, Aст — это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа Aст прямо пропорциональна перемещаемому заряду q. Поэтому отношение Aст/q уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается ε:
ε = Аст/q (2)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
2.2 Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением r, которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной E, и внутренним сопротивлением r подключён к резистору R (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 3).
Рис. 3 Полная цепь
Наша задача — найти силу тока I в цепи и напряжение U на резисторе R.
За время t по цепи проходит заряд q = It. Согласно формуле (60) источник тока совершает при этом работу:
Aст = εq = εIt. (3)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, кото- рая выделяется на сопротивлениях R и r.
Данное количество теплоты определяется законом Джоуля–Ленца:
Q = I2Rt + I2 rt = I2 (R + r)t. (4)
Итак, Aст = Q, и мы приравниваем правые части формул (3) и (4):
εIt = I2 (R + r)t.
После сокращения на It получаем:
ε = I(R + r).
Вот мы и нашли ток в цепи:
I = ε /(R + r ). (5)
Формула (5) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0), то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Iкз = ε /r .
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (5)), мы можем найти напряжение на резисторе R с помощью закона Ома для участка цепи:
U = IR = εR/(R + r) . (6)
Это напряжение является разностью потенциалов между точками a и b (рис. 3). Потенциал точки a равен потенциалу положительной клеммы источника; потенциал точки b равен потенциалу отрицательной клеммы. Поэтому напряжение (6) называется также напряжением на клеммах источника.
Мы видим из формулы (6), что в реальной цепи будет U < ε — ведь ε умножается на дробь, меньшую единицы. Но есть два случая, когда U = ε.
1.Идеальный источник тока. Это источник с нулевым внутренним сопротивлением. При r = 0 формула (6) даёт U = ε.
2.Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: R = ∞. Тогда величина R + r неотличима от R, и формула (6) снова даёт нам U =ε.
Смысл этого результата прост: если источник не подключён к цепи, то идеальный вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
3 Электрическое сопротивление
А сейчас давайте подумаем вот о чём. Пусть к концам проводника приложено постоянное напряжение U. Тогда на свободные заряды проводника действует сила со стороны стационарного электрического поля. Раз есть сила — значит, эти заряды должны двигаться с ускорением; скорость их направленного движения будет увеличиваться, а вместе с ней будет возрастать и сила тока. Но закон Ома гласит, что сила тока будет постоянной. Как же так?
Дело в том, что сила со стороны стационарного поля — не единственная сила, действующая на свободные заряды проводника.
Например, свободные электроны металла, совершая направленное движение, сталкиваются с ионами кристаллической решётки. Возникает своего рода сила сопротивления, действующая со стороны проводника на свободные заряды. Эта сила уравновешивает электрическую силу, с которой на свободные заряды действует стационарное поле. В результате скорость направленного движения заряженных частиц не меняется по модулю; вместе с ней остаётся постоянной и сила тока.
Так что величина R названа сопротивлением не случайно. Она и в самом деле показывает, в какой степени проводник «сопротивляется» прохождению тока.
3.1 Удельное сопротивление
Возьмём два проводника из одинакового материала с равными поперечными сечениями; пусть отличаются только их длины. Ясно, что сопротивление будет больше у того проводника, у которого больше длина. В самом деле, при большей длине проводника свободным зарядам труднее пройти сквозь него: каждый свободный электрон встретит на своём пути больше ионов кристаллической решётки. Аналогия такая: чем длиннее заполненная машинами улица, тем труднее будет через неё проехать.
Пусть теперь проводники отличаются только площадью поперечного сечения. Ясно, что чем больше площадь, тем меньше сопротивление проводника. Снова аналогия: чем шире шоссе, тем больше его пропускная способность, т. е. тем меньше его «сопротивление» движению машин.
Опыт подтверждает эти соображения и показывает, что сопротивление проводника прямо пропорционально его длине l и обратно пропорционально площади поперечного сечения S:
R = ρ l /S . (7)
Коэффициент пропорциональности ρ уже не зависит от геометрии проводника; он является характеристикой вещества проводника и называется удельным сопротивлением данного вещества. Величины удельных сопротивлений различных веществ можно найти в соответствующей таблице.
В каких единицах измеряется удельное сопротивление? Давайте выразим его из формулы (7):
ρ = RS/l .
Получим:
[ρ] = Ом · м 2 /м = Ом · м.
Однако такая «теоретическая» единица измерения не всегда удобна. Она вынуждает при расчётах переводить площадь поперечного сечения в квадратные метры, тогда как на практике чаще всего речь идёт о квадратных миллиметрах (для проводов, например). На такой случай предусмотрена «практическая» единица:
Ом · мм2/ м .
В таблице задачника Рымкевича удельное сопротивление даётся как в «теоретических» единицах, так и в «практических».
Лекция по основам электротехники «Соединение резисторов. Закон Ома»
ТЕМА: Соединения резисторов. Законы Ома.
План
Последовательное соединение резисторов.
Параллельное соединение резисторов.
Смешанное соединение резисторов.
Законы Ома.
Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.
Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов.
Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.
Рисунок 1. Соединение резисторов
Последовательное соединение резисторов
Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).

Рисунок 2. Последовательное соединение резисторов
То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток.
Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.
Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает.
Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле:
Rобщ = R1 + R2 + R3+…+ Rn.
Где можно наблюдать последовательное соединение сопротивлений? — Да допустим в той же самой новогодней гирлянде. Каждая лампочка в новогодней гирлянде, как правило, обладает одинаковым сопротивлением. При последовательном соединении, если перегорает одна лампочка, то в электрической цепи будет наблюдаться разрыв и соответственно, в этом случае, новогодняя гирлянда не будет гореть полностью.
Параллельное соединение резисторов
Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).

Рисунок 3. Параллельное соединение резисторов
При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением:
1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn
Следует отметить, что здесь действует правило «меньше — меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.
Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле:
Что такое закон Ома? Объяснение и ограничения закона Ома
Когда к проводнику приложена разность электрических потенциалов (В) , как показано на рисунке ниже, через него протекает ток (I) . Протеканию тока противодействует сопротивление проводника и цепи. Связь между напряжением, током и сопротивлением объясняется законом Ома.
Законы
Ома гласят, что ток через любые две точки проводника прямо пропорционален разности потенциалов, приложенной к проводнику, при условии физических условий i.е. температура и т. д. не меняются. Измеряется в ( Ом, ) Ом.
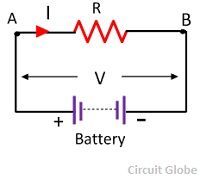
Математически это выражается как
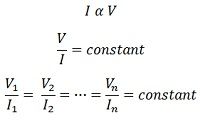
Другими словами, закон Ома также можно сформулировать как;
Отношение разности потенциалов в конечной точке проводника к току, протекающему между ними, всегда постоянное, но физические условия проводника, то есть температура и т. Д., Остаются неизменными.
Эту постоянную также называют сопротивлением (R) проводника (или цепи)
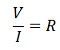
Его можно записать как
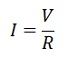
В цепи, когда ток течет через резистор, разность потенциалов на резисторе известна как падение напряжения на нем, т.е.е., В = ИК.
Ограничения закона Ома
- Закон Ома не применяется в односторонних сетях. Односторонние сети позволяют току течь в одном направлении. Такие типы сетей состоят из таких элементов, как диод, транзистор и т. Д.
- Не применяется для нелинейной сети. В нелинейной сети параметр сети изменяется в зависимости от напряжения и тока. Их параметр включает сопротивление, индуктивность, емкость, частоту и т. Д., не оставаться неизменным со временем. Итак, закон Ома не применим к нелинейной сети.
Закон Ома используется для определения сопротивления цепи, а также для определения напряжения и тока цепи.
Законов постоянного тока. Электрический ток. Мощность и плотность тока. ЭДС и напряжение. Закон Ома. Закон Ома для однородного участка цепи. Закон Ома для неоднородной области цепи в интегрированной форме. Закон Ома для всей цепочки.Закон Ома в дифференциальной форме.
ЗАКОН ПРЯМОТОК
§ 1 Электрический ток .
Мощность и плотность тока .
ЭДС и напряжение
И.Любое упорядоченное (направленное) движение электрических зарядов называется электрическим текущим . При внешнем электрическом поле E в проводнике начинает движение зарядов, т.е. генерируется электрический ток. С положительными зарядами движутся по полю, а с отрицательными — по полю. Примите направление текущего направления движения положительных зарядов. Для возникновения и существования электрического тока требуется два условия:
1) наличие свободных носителей заряда (т.е. вещество должно быть проводником или полупроводником при высоких температурах),
2) Наличие внешнего электрического поля.
Для количественного описания электрического тока вводится — сила тока — скалярная физическая величина, равная количеству электрического заряда, передаваемого в единицу времени через поперечное сечение S .
— для постоянного тока и
— для переменного тока.
Ток, сила и направление которого не меняются со временем, называют постоянным.
Плотность тока — векторная физическая величина, численно равная силе тока, протекающего через единицу площади перпендикулярно току.
— для постоянного тока и
— для переменного тока.
II. К рассматриваемой части проводника идет ток I , необходимый для поддержания постоянной разности потенциалов между этими точками проводника. Для того, чтобы поддерживать постоянную разность потенциалов на концах проводника, он должен быть подключен к источнику питания. Источник тока действительно перемещает электрические заряды по цепи.Эта работа совершается за счет внешних сил — сил не электростатического происхождения, действующих на заряды стороны источника питания. Характер внешних сил может быть
разных (кроме фиксированных):
1) химическая реакция — в гальванических элементах (батареях), аккумуляторных батареях,
2) Электромагнитный — в генераторах. Генератор может использовать а) механическую энергию — гидро, б) ядерный — ядерный реактор) тепло — ТЭС, з) приливы — ПЭС, Г) ветер — ветряная электростанция и т. Д.
3) использование фотоэффекта — фотоэдс в калькуляторах и солнечной энергии; 4) пьезоэлектрик — пьезоЭДС, например, пьезоэлемент,
5) контактный потенциал — термоЭДС в термопарах и т. Д.
В поле внешних сил электрические заряды движутся внутри источника питания против сил электростатического поля, в результате чего на клеммах источника тока и поддерживается разность потенциалов, в цепи протекает ток.
Источник тока характеризуется электродвижущей силой — ЭДС.
ЭДС определяется работой, совершаемой внешними силами по перемещению единицы положительного заряда по замкнутой цепи.
Сторона силы равна:
, где — поле внешних сил. Работа внешних сил по перемещению заряда q на замкнутом участке цепи составляет:
т.е. ЭДС циркуляции равна вектору интенсивности внешних сил. На участке 1 — 2 (см. Рисунок) кроме внешних сил, действующих на электростатическое поле
т.е. равнодействующая сила на участке 1-2 равна
, затем
Для замкнутого контура
Напряжение U на участке 1-2 называется физической величиной, определяемой работой, совершаемой суммарным электростатическим (кулоновским) полем и внешними силами при перемещении единичного положительного заряда по этой части цепи
в
§ 2 Закон Ома
1.Закон Ома для однородного участка цепи.
Называется однородной зоной, свободной от ЭМП.
Ток в однородном участке цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению цепи
1 Ом — сопротивление проводника, по которому при напряжении 1 В 1 А протекает ток.
г –
Электропроводность.(Сименс).
Сопротивление R проводника зависит от его размера и формы, а также от материала проводника.
,
где ρ — удельное сопротивление проводника — сопротивление на единицу длины проводника.
ℓ — длина провода; S — площадь поперечного сечения проводника.
2. Закон Ома для неоднородной области цепочки
Неоднородный называется участком цепи, содержащим ЭДС.
— Закон Ома для неоднородной области цепи в интегрированной форме
3. Закон Ома для замкнутой цепи (полная цепь).
где
где R — сопротивление внешней цепи,
r — импеданс ЭДС источника, то
-Закон Ома для полной цепи
4.Закон Ома в дифференциальной форме
σ — электропроводность;
–
Закон Ома в дифференциальной форме.
Плотность тока прямо пропорциональна электрическому полю E . Коэффициент пропорциональности σ — удельная электропроводность.
% PDF-1.5
%
5322 0 объект>
endobj
xref
5322 1386
0000000016 00000 н.
0000058340 00000 п.
0000058531 00000 п.
0000058584 00000 п.
0000058819 00000 п.
0000058924 00000 п.
0000059091 00000 п.
0000265893 00000 н.
0000265968 00000 н.
0000266065 00000 н.
0000266156 00000 н.
0000266206 00000 н.
0000266231 00000 п.
0000266393 00000 н.
0000266533 00000 н.
0000266583 00000 н.
0000266608 00000 н.
0000266733 00000 н.
0000266918 00000 н.
0000267080 00000 п.
0000267130 00000 н.
0000267155 00000 н.
0000267265 00000 н.
0000267448 00000 н.
0000267603 00000 п.
0000267652 00000 н.
0000267677 00000 н.
0000267787 00000 н.
0000267973 00000 п.
0000268157 00000 н.
0000268205 00000 н.
0000268230 00000 н.
0000268340 00000 н.
0000268447 00000 н.
0000268495 00000 н.
0000268520 00000 н.
0000268628 00000 н.
0000268676 00000 н.
0000268701 00000 н.
0000268815 00000 н.
0000268863 00000 н.
0000268888 00000 н.
0000269028 00000 н.
0000269075 00000 н.
0000269100 00000 н.
0000269149 00000 н.
0000269174 00000 н.
0000269286 00000 н.
0000269335 00000 н.
0000269360 00000 н.
0000269521 00000 н.
0000269643 00000 н.
0000269692 00000 н.
0000269717 00000 н.
0000269840 00000 н.
0000270009 00000 н.
0000270118 00000 п.
0000270167 00000 н.
0000270192 00000 п.
0000270323 00000 н.
0000270522 00000 н.
0000270625 00000 н.
0000270674 00000 н.
0000270699 00000 н.
0000270860 00000 н.
0000271033 00000 н.
0000271164 00000 н.
0000271213 00000 н.
0000271238 00000 н.
0000271373 00000 н.
0000271537 00000 н.
0000271668 00000 н.
0000271717 00000 н.
0000271742 00000 н.
0000271868 00000 н.
0000271980 00000 н.
0000272029 00000 н.
0000272054 00000 н.
0000272219 00000 н.
0000272324 00000 н.
0000272373 00000 н.
0000272398 00000 н.
0000272510 00000 н.
0000272685 00000 н.
0000272794 00000 н.
0000272843 00000 н.
0000272868 00000 н.
0000273005 00000 н.
0000273181 00000 н.
0000273286 00000 н.
0000273335 00000 н.
0000273360 00000 н.
0000273498 00000 н.
0000273610 00000 н.
0000273659 00000 н.
0000273684 00000 н.
0000273864 00000 н.
0000273966 00000 н.
0000274015 00000 н.
0000274040 00000 н.
0000274186 00000 н.
0000274354 00000 н.
0000274470 00000 н.
0000274519 00000 н.
0000274544 00000 н.
0000274674 00000 н.
0000274859 00000 н.
0000274991 00000 н.
0000275039 00000 н.
0000275064 00000 н.
0000275212 00000 н.
0000275261 00000 н.
0000275286 00000 н.
0000275396 00000 н.
0000275445 00000 н.
0000275470 00000 н.
0000275607 00000 н.
0000275656 00000 н.
0000275681 00000 п.
0000275812 00000 н.
0000275861 00000 п.
0000275886 00000 н.
0000276015 00000 н.
0000276064 00000 н.
0000276089 00000 н.
0000276220 00000 н.
0000276269 00000 н.
0000276294 00000 н.
0000276407 00000 н.
0000276456 00000 н.
0000276481 00000 н.
0000276614 00000 н.
0000276663 00000 н.
0000276688 00000 н.
0000276830 00000 н.
0000276879 00000 н.
0000276904 00000 н.
0000277043 00000 н.
0000277092 00000 н.
0000277117 00000 н.
0000277265 00000 н.
0000277313 00000 н.
0000277338 00000 н.
0000277386 00000 н.
0000277411 00000 н.
0000277460 00000 н.
0000277485 00000 н.
0000277626 00000 н.
0000277675 00000 н.
0000277700 00000 н.
0000277749 00000 н.
0000277774 00000 н.
0000277823 00000 н.
0000277848 00000 н.
0000277965 00000 н.
0000278014 00000 н.
0000278039 00000 н.
0000278158 00000 н.
0000278207 00000 н.
0000278232 00000 н.
0000278349 00000 н.
0000278398 00000 н.
0000278423 00000 н.
0000278567 00000 н.
0000278616 00000 н.
0000278641 00000 н.
0000278754 00000 н.
0000278803 00000 н.
0000278828 00000 н.
0000278947 00000 н.
0000278996 00000 н.
0000279021 00000 н.
0000279139 00000 н.
0000279188 00000 н.
0000279213 00000 н.
0000279329 00000 н.
0000279378 00000 н.
0000279403 00000 н.
0000279452 00000 н.
0000279477 00000 н.
0000279526 00000 н.
0000279551 00000 н.
0000279693 00000 н.
0000279742 00000 н.
0000279767 00000 н.
0000279887 00000 н.
0000279936 00000 н.
0000279961 00000 н.
0000280082 00000 н.
0000280131 00000 п.
0000280156 00000 н.
0000280277 00000 н.
0000280326 00000 н.
0000280351 00000 н.
0000280400 00000 н.
0000280425 00000 н.
0000280474 00000 н.
0000280499 00000 н.
0000280626 00000 н.
0000280675 00000 н.
0000280700 00000 н.
0000280833 00000 н.
0000280882 00000 н.
0000280907 00000 н.
0000281025 00000 н.
0000281074 00000 н.
0000281099 00000 н.
0000281222 00000 н.
0000281271 00000 н.
0000281296 00000 н.
0000281443 00000 п.
0000281492 00000 н.
0000281517 00000 н.
0000281649 00000 н.
0000281698 00000 н.
0000281723 00000 н.
0000281839 00000 н.
0000281888 00000 н.
0000281913 00000 н.
0000282038 00000 н.
0000282087 00000 н.
0000282112 00000 н.
0000282226 00000 н.
0000282275 00000 н.
0000282300 00000 н.
0000282415 00000 н.
0000282464 00000 н.
0000282489 00000 н.
0000282616 00000 н.
0000282665 00000 н.
0000282690 00000 н.
0000282739 00000 н.
0000282764 00000 н.
0000282813 00000 н.
0000282947 00000 н.
0000282996 00000 н.
0000283021 00000 н.
0000283178 00000 п.
0000283227 00000 н.
0000283252 00000 н.
0000283390 00000 н.
0000283439 00000 п.
0000283464 00000 н.
0000283578 00000 н.
0000283627 00000 н.
0000283652 00000 п.
0000283783 00000 н.
0000283832 00000 н.
0000283857 00000 н.
0000284008 00000 н.
0000284057 00000 н.
0000284082 00000 н.
0000284216 00000 н.
0000284265 00000 н.
0000284290 00000 н.
0000284339 00000 н.
0000284364 00000 н.
0000284413 00000 н.
0000284438 00000 н.
0000284559 00000 н.
0000284608 00000 н.
0000284633 00000 н.
0000284787 00000 н.
0000284836 00000 н.
0000284861 00000 н.
0000285010 00000 н.
0000285059 00000 н.
0000285084 00000 н.
0000285225 00000 н.
0000285274 00000 н.
0000285299 00000 н.
0000285417 00000 н.
0000285466 00000 п.
0000285491 00000 н.
0000285540 00000 н.
0000285565 00000 н.
0000285614 00000 н.
0000285639 00000 н.
0000285760 00000 н.
0000285809 00000 н.
0000285834 00000 н.
0000285958 00000 п.
0000286007 00000 н.
0000286032 00000 н.
0000286149 00000 н.
0000286198 00000 п.
0000286223 00000 н.
0000286336 00000 н.
0000286385 00000 п.
0000286410 00000 н.
0000286524 00000 н.
0000286573 00000 н.
0000286598 00000 н.
0000286735 00000 н.
0000286784 00000 н.
0000286809 00000 н.
0000286858 00000 н.
0000286883 00000 н.
0000286932 00000 н.
0000286957 00000 н.
0000287081 00000 п.
0000287130 00000 н.
0000287155 00000 н.
0000287273 00000 н.
0000287322 00000 н.
0000287347 00000 н.
0000287471 00000 н.
0000287520 00000 н.
0000287545 00000 н.
0000287668 00000 н.
0000287717 00000 н.
0000287742 00000 н.
0000287874 00000 н.
0000287923 00000 п.
0000287948 00000 н.
0000288072 00000 н.
0000288121 00000 н.
0000288146 00000 н.
0000288270 00000 н.
0000288319 00000 н.
0000288344 00000 п.
0000288478 00000 н.
0000288527 00000 н.
0000288552 00000 н.
0000288685 00000 н.
0000288734 00000 н.
0000288759 00000 н.
0000288875 00000 н.
0000288924 00000 н.
0000288949 00000 н.
0000289065 00000 н.
0000289114 00000 н.
0000289139 00000 н.
0000289256 00000 н.
0000289305 00000 н.
0000289330 00000 н.
0000289457 00000 н.
0000289506 00000 н.
0000289531 00000 н.
0000289658 00000 н.
0000289707 00000 н.
0000289732 00000 н.
0000289913 00000 н.
0000289962 00000 н.
0000289987 00000 н.
00002
00000 н.
00002 00000 н.
00002
00000 н.
0000290329 00000 н.
0000290378 00000 п.
0000290403 00000 н.
0000290528 00000 н.
0000290577 00000 н.
0000290602 00000 н.
0000290651 00000 н.
0000290676 00000 н.
0000290725 00000 н.
0000290750 00000 н.
0000290868 00000 н.
0000290917 00000 н.
0000290942 00000 н.
0000291067 00000 н.
0000291116 00000 н.
0000291141 00000 н.
0000291270 00000 н.
0000291319 00000 н.
0000291344 00000 н.
0000291465 00000 н.
0000291514 00000 н.
0000291539 00000 н.
0000291671 00000 н.
0000291720 00000 н.
0000291745 00000 н.
0000291871 00000 н.
0000291920 00000 н.
0000291945 00000 н.
0000291994 00000 н.
0000292019 00000 н.
0000292068 00000 н.
0000292093 00000 н.
0000292213 00000 н.
0000292262 00000 н.
0000292287 00000 н.
0000292417 00000 н.
0000292466 00000 н.
0000292491 00000 н.
0000292609 00000 н.
0000292658 00000 н.
0000292683 00000 п.
0000292818 00000 н.
0000292867 00000 н.
0000292892 00000 н.
0000293023 00000 н.
0000293072 00000 н.
0000293097 00000 н.
0000293224 00000 н.
0000293273 00000 н.
0000293298 00000 н.
0000293421 00000 н.
0000293470 00000 н.
0000293495 00000 н.
0000293617 00000 н.
0000293666 00000 н.
0000293691 00000 н.
0000293740 00000 н.
0000293765 00000 н.
0000293863 00000 н.
0000293911 00000 н.
0000293936 00000 н.
0000294096 00000 н.
0000294144 00000 п.
0000294169 00000 н.
0000294314 00000 н.
0000294362 00000 п.
0000294387 00000 н.
0000294518 00000 н.
0000294566 00000 н.
0000294591 00000 н.
0000294721 00000 н.
0000294769 00000 н.
0000294794 00000 н.
0000294929 00000 н.
0000294977 00000 н.
0000295002 00000 н.
0000295111 00000 п.
0000295159 00000 н.
0000295184 00000 н.
0000295292 00000 н.
0000295340 00000 н.
0000295365 00000 н.
0000295474 00000 н.
0000295522 00000 н.
0000295547 00000 н.
0000295657 00000 н.
0000295705 00000 н.
0000295730 00000 н.
0000295778 00000 н.
0000295803 00000 н.
0000295853 00000 п.
0000295878 00000 н.
0000295990 00000 н.
0000296040 00000 н.
0000296065 00000 н.
0000296243 00000 н.
0000296346 00000 н.
0000296396 00000 н.
0000296421 00000 н.
0000296561 00000 н.
0000296724 00000 н.
0000296827 00000 н.
0000296877 00000 н.
0000296902 00000 н.
0000297027 00000 н.
0000297139 00000 н.
0000297189 00000 н.
0000297214 00000 н.
0000297376 00000 н.
0000297479 00000 н.
0000297529 00000 н.
0000297554 00000 н.
0000297678 00000 н.
0000297846 00000 н.
0000297949 00000 н.
0000297999 00000 н.
0000298024 00000 н.
0000298154 00000 н.
0000298266 00000 н.
0000298316 00000 н.
0000298341 00000 п.
0000298513 00000 н.
0000298642 00000 н.
0000298692 00000 н.
0000298717 00000 н.
0000298851 00000 н.
0000299016 00000 н.
0000299119 00000 н.
0000299169 00000 н.
0000299194 00000 н.
0000299321 00000 н.
0000299505 00000 н.
0000299608 00000 н.
0000299658 00000 н.
0000299683 00000 н.
0000299829 00000 н.
0000300012 00000 н.
0000300132 00000 н.
0000300182 00000 н.
0000300207 00000 н.
0000300352 00000 п.
0000300464 00000 н.
0000300514 00000 н.
0000300539 00000 п.
0000300721 00000 н.
0000300824 00000 н.
0000300873 00000 п.
0000300898 00000 н.
0000301042 00000 н.
0000301092 00000 н.
0000301117 00000 н.
0000301235 00000 н.
0000301285 00000 н.
0000301310 00000 н.
0000301439 00000 н.
0000301488 00000 н.
0000301513 00000 н.
0000301655 00000 н.
0000301704 00000 н.
0000301729 00000 н.
0000301845 00000 н.
0000301894 00000 н.
0000301919 00000 н.
0000302033 00000 н.
0000302082 00000 н.
0000302107 00000 н.
0000302230 00000 н.
0000302279 00000 п.
0000302304 00000 н.
0000302353 00000 п.
0000302378 00000 н.
0000302428 00000 н.
0000302453 00000 н.
0000302590 00000 н.
0000302640 00000 н.
0000302665 00000 н.
0000302793 00000 н.
0000302843 00000 н.
0000302868 00000 н.
0000302998 00000 н.
0000303048 00000 н.
0000303073 00000 н.
0000303186 00000 п.
0000303236 00000 н.
0000303261 00000 н.
0000303382 00000 н.
0000303432 00000 н.
0000303457 00000 н.
0000303587 00000 н.
0000303637 00000 н.
0000303662 00000 н.
0000303790 00000 н.
0000303840 00000 н.
0000303865 00000 н.
0000303993 00000 н.
0000304043 00000 н.
0000304068 00000 н.
0000304203 00000 н.
0000304253 00000 н.
0000304278 00000 н.
0000304412 00000 н.
0000304462 00000 н.
0000304487 00000 н.
0000304537 00000 н.
0000304562 00000 н.
0000304612 00000 н.
0000304637 00000 н.
0000304766 00000 н.
0000304816 00000 н.
0000304841 00000 н.
0000304977 00000 н.
0000305027 00000 н.
0000305052 00000 н.
0000305183 00000 п.
0000305233 00000 п.
0000305258 00000 н.
0000305388 00000 п.
0000305438 00000 н.
0000305463 00000 н.
0000305593 00000 н.
0000305643 00000 п.
0000305668 00000 н.
0000305798 00000 н.
0000305848 00000 н.
0000305873 00000 н.
0000305923 00000 н.
0000305948 00000 н.
0000305998 00000 н.
0000306023 00000 н.
0000306183 00000 п.
0000306233 00000 н.
0000306258 00000 н.
0000306392 00000 н.
0000306442 00000 н.
0000306467 00000 н.
0000306603 00000 п.
0000306653 00000 н.
0000306678 00000 н.
0000306818 00000 н.
0000306868 00000 н.
0000306893 00000 н.
0000307030 00000 н.
0000307080 00000 н.
0000307105 00000 н.
0000307242 00000 н.
0000307292 00000 н.
0000307317 00000 н.
0000307445 00000 н.
0000307495 00000 н.
0000307520 00000 н.
0000307659 00000 н.
0000307709 00000 н.
0000307734 00000 н.
0000307870 00000 п.
0000307920 00000 н.
0000307945 00000 н.
0000308070 00000 н.
0000308120 00000 н.
0000308145 00000 н.
0000308195 00000 н.
0000308220 00000 н.
0000308270 00000 н.
0000308295 00000 н.
0000308439 00000 н.
0000308489 00000 н.
0000308514 00000 н.
0000308658 00000 н.
0000308708 00000 н.
0000308733 00000 н.
0000308867 00000 н.
0000308917 00000 н.
0000308942 00000 н.
0000309064 00000 н.
0000309114 00000 п.
0000309139 00000 н.
0000309269 00000 н.
0000309319 00000 п.
0000309344 00000 п.
0000309473 00000 п.
0000309523 00000 н.
0000309548 00000 н.
0000309676 00000 н.
0000309726 00000 н.
0000309751 00000 п.
0000309886 00000 н.
0000309936 00000 н.
0000309961 00000 н.
0000310092 00000 н.
0000310142 00000 п.
0000310167 00000 н.
0000310294 00000 н.
0000310344 00000 п.
0000310369 00000 п.
0000310419 00000 п.
0000310444 00000 н.
0000310494 00000 п.
0000310519 00000 п.
0000310657 00000 н.
0000310707 00000 п.
0000310732 00000 н.
0000310877 00000 н.
0000310927 00000 н.
0000310952 00000 п.
0000311100 00000 н.
0000311150 00000 н.
0000311175 00000 н.
0000311293 00000 н.
0000311343 00000 п.
0000311464 00000 н.
0000311514 00000 н.
0000311539 00000 н.
0000311659 00000 н.
0000311709 00000 н.
0000311734 00000 н.
0000311857 00000 н.
0000311907 00000 н.
0000311932 00000 н.
0000311982 00000 н.
0000312007 00000 н.
0000312057 00000 н.
0000312082 00000 н.
0000312208 00000 н.
0000312258 00000 н.
0000312283 00000 н.
0000312409 00000 н.
0000312459 00000 н.
0000312484 00000 н.
0000312614 00000 н.
0000312664 00000 н.
0000312689 00000 н.
0000312817 00000 н.
0000312867 00000 н.
0000312892 00000 н.
0000313015 00000 н.
0000313065 00000 н.
0000313090 00000 н.
0000313215 00000 н.
0000313265 00000 н.
0000313290 00000 н.
0000313428 00000 н.
0000313478 00000 н.
0000313503 00000 н.
0000313635 00000 н.
0000313685 00000 н.
0000313710 00000 н.
0000313850 00000 н.
0000313900 00000 н.
0000313925 00000 н.
0000314054 00000 н.
0000314104 00000 п.
0000314129 00000 н.
0000314268 00000 н.
0000314318 00000 н.
0000314343 00000 п.
0000314480 00000 н.
0000314530 00000 н.
0000314555 00000 н.
0000314694 00000 п.
0000314744 00000 н.
0000314769 00000 н.
0000314908 00000 н.
0000314958 00000 н.
0000314983 00000 п.
0000315033 00000 н.
0000315058 00000 н.
0000315108 00000 н.
0000315133 00000 н.
0000315252 00000 н.
0000315302 00000 н.
0000315327 00000 н.
0000315461 00000 н.
0000315511 00000 н.
0000315536 00000 н.
0000315660 00000 н.
0000315710 00000 н.
0000315735 00000 н.
0000315871 00000 н.
0000315921 00000 н.
0000315946 00000 н.
0000316097 00000 н.
0000316147 00000 н.
0000316172 00000 н.
0000316302 00000 н.
0000316352 00000 н.
0000316377 00000 н.
0000316494 00000 н.
0000316544 00000 н.
0000316569 00000 н.
0000316704 00000 н.
0000316754 00000 н.
0000316779 00000 н.
0000316903 00000 н.
0000316953 00000 н.
0000316978 00000 н.
0000317132 00000 н.
0000317182 00000 н.
0000317207 00000 н.
0000317327 00000 н.
0000317377 00000 н.
0000317402 00000 н.
0000317546 00000 н.
0000317596 00000 н.
0000317621 00000 н.
0000317761 00000 н.
0000317811 00000 н.
0000317836 00000 н.
0000317966 00000 н.
0000318016 00000 н.
0000318041 00000 н.
0000318172 00000 н.
0000318222 00000 н.
0000318247 00000 н.
0000318297 00000 н.
0000318322 00000 п.
0000318372 00000 п.
0000318397 00000 н.
0000318539 00000 н.
0000318589 00000 н.
0000318614 00000 н.
0000318747 00000 н.
0000318797 00000 н.
0000318822 00000 н.
0000318969 00000 н.
0000319019 00000 н.
0000319044 00000 н.
0000319194 00000 н.
0000319244 00000 н.
0000319269 00000 н.
0000319412 00000 н.
0000319462 00000 п.
0000319487 00000 н.
0000319637 00000 н.
0000319687 00000 н.
0000319712 00000 н.
0000319856 00000 н.
0000319906 00000 н.
0000319931 00000 н.
0000320074 00000 н.
0000320124 00000 н.
0000320149 00000 н.
0000320271 00000 н.
0000320321 00000 н.
0000320346 00000 н.
0000320478 00000 н.
0000320528 00000 н.
0000320553 00000 н.
0000320684 00000 н.
0000320734 00000 н.
0000320759 00000 н.
0000320868 00000 н.
0000320918 00000 н.
0000320943 00000 н.
0000321103 00000 н.
0000321153 00000 н.
0000321178 00000 н.
0000321328 00000 н.
0000321378 00000 н.
0000321403 00000 н.
0000321525 00000 н.
0000321575 00000 н.
0000321600 00000 н.
0000321744 00000 н.
0000321794 00000 н.
0000321819 00000 н.
0000321869 00000 н.
0000321894 00000 н.
0000321997 00000 н.
0000322046 00000 н.
0000322071 00000 н.
0000322187 00000 н.
0000322236 00000 н.
0000322371 00000 н.
0000322420 00000 н.
0000322445 00000 н.
0000322589 00000 н.
0000322638 00000 н.
0000322663 00000 н.
0000322784 00000 н.
0000322833 00000 н.
0000322858 00000 н.
0000322986 00000 н.
0000323035 00000 н.
0000323060 00000 н.
0000323183 00000 н.
0000323232 00000 н.
0000323257 00000 н.
0000323389 00000 н.
0000323438 00000 н.
0000323463 00000 н.
0000323593 00000 н.
0000323642 00000 н.
0000323667 00000 н.
0000323788 00000 н.
0000323837 00000 н.
0000323862 00000 н.
0000323911 00000 н.
0000323936 00000 н.
0000323986 00000 н.
0000324011 00000 н.
0000324124 00000 н.
0000324174 00000 н.
0000324199 00000 н.
0000324382 00000 н.
0000324485 00000 н.
0000324535 00000 н.
0000324560 00000 н.
0000324705 00000 н.
0000324872 00000 н.
0000324975 00000 н.
0000325025 00000 н.
0000325050 00000 н.
0000325179 00000 н.
0000325357 00000 н.
0000325460 00000 н.
0000325510 00000 н.
0000325535 00000 н.
0000325675 00000 н.
0000325840 00000 н.
0000325943 00000 н.
0000325993 00000 н.
0000326018 00000 н.
0000326145 00000 н.
0000326258 00000 н.
0000326308 00000 н.
0000326333 00000 н.
0000326493 00000 н.
0000326596 00000 н.
0000326646 00000 н.
0000326671 00000 н.
0000326793 00000 н.
0000326954 00000 н.
0000327082 00000 н.
0000327132 00000 н.
0000327157 00000 н.
0000327280 00000 н.
0000327460 00000 н.
0000327596 00000 н.
0000327646 00000 н.
0000327671 00000 н.
0000327812 00000 н.
0000327925 00000 н.
0000327975 00000 н.
0000328000 00000 н.
0000328167 00000 н.
0000328313 00000 н.
0000328363 00000 н.
0000328388 00000 н.
0000328517 00000 н.
0000328705 00000 н.
0000328808 00000 н.
0000328858 00000 н.
0000328883 00000 н.
0000329033 00000 н.
0000329199 00000 н.
0000329302 00000 н.
0000329352 00000 н.
0000329377 00000 н.
0000329505 00000 н.
0000329618 00000 н.
0000329668 00000 н.
0000329693 00000 н.
0000329896 00000 н.
0000330018 00000 н.
0000330068 00000 н.
0000330093 00000 н.
0000330258 00000 н.
0000330448 00000 н.
0000330551 00000 п.
0000330601 00000 н.
0000330626 00000 н.
0000330778 00000 н.
0000330891 00000 н.
0000330941 00000 п.
0000330966 00000 н.
0000331147 00000 н.
0000331250 00000 н.
0000331300 00000 н.
0000331325 00000 н.
0000331467 00000 н.
0000331641 00000 н.
0000331744 00000 н.
0000331794 00000 н.
0000331819 00000 п.
0000331955 00000 н.
0000332135 00000 н.
0000332247 00000 н.
0000332297 00000 н.
0000332322 00000 н.
0000332464 00000 н.
0000332645 00000 н.
0000332748 00000 н.
0000332798 00000 н.
0000332823 00000 н.
0000332950 00000 н.
0000333062 00000 н.
0000333112 00000 н.
0000333137 00000 н.
0000333317 00000 н.
0000333420 00000 н.
0000333470 00000 н.
0000333495 00000 н.
0000333637 00000 н.
0000333815 00000 н.
0000333918 00000 н.
0000333968 00000 н.
0000333993 00000 н.
0000334133 00000 п.
0000334294 00000 н.
0000334397 00000 н.
0000334447 00000 н.
0000334472 00000 н.
0000334595 00000 н.
0000334707 00000 н.
0000334757 00000 н.
0000334782 00000 н.
0000334953 00000 п.
0000335056 00000 н.
0000335106 00000 п.
0000335131 00000 п.
0000335264 00000 н.
0000335469 00000 н.
0000335572 00000 н.
0000335622 00000 н.
0000335647 00000 н.
0000335780 00000 н.
0000335983 00000 п.
0000336086 00000 н.
0000336136 00000 п.
0000336161 00000 п.
0000336292 00000 н.
0000336342 00000 п.
0000336367 00000 н.
0000336492 00000 н.
0000336542 00000 н.
0000336567 00000 н.
0000336617 00000 н.
0000336642 00000 н.
0000336692 00000 н.
0000336717 00000 н.
0000336844 00000 н.
0000336894 00000 н.
0000336919 00000 п.
0000337063 00000 н.
0000337113 00000 п.
0000337138 00000 н.
0000337188 00000 п.
0000337213 00000 н.
0000337263 00000 н.
0000337288 00000 н.
0000337417 00000 н.
0000337467 00000 н.
0000337492 00000 н.
0000337646 00000 н.
0000337696 00000 н.
0000337721 00000 н.
0000337857 00000 н.
0000337907 00000 н.
0000337932 00000 н.
0000338076 00000 н.
0000338126 00000 н.
0000338151 00000 п.
0000338201 00000 н.
0000338226 00000 н.
0000338276 00000 н.
0000338301 00000 п.
0000338434 00000 н.
0000338484 00000 н.
0000338509 00000 н.
0000338651 00000 п.
0000338701 00000 п.
0000338726 00000 н.
0000338776 00000 н.
0000338801 00000 п.
0000338851 00000 н.
0000338876 00000 н.
0000339025 00000 н.
0000339075 00000 н.
0000339100 00000 н.
0000339214 00000 н.
0000339264 00000 н.
0000339289 00000 н.
0000339413 00000 н.
0000339463 00000 п.
0000339488 00000 н.
0000339614 00000 н.
0000339664 00000 н.
0000339689 00000 н.
0000339802 00000 н.
0000339852 00000 н.
0000339877 00000 н.
0000339998 00000 н.
0000340048 00000 н.
0000340073 00000 н.
0000340123 00000 н.
0000340148 00000 н.
0000340198 00000 н.
0000340223 00000 п.
0000340358 00000 н.
0000340408 00000 н.
0000340433 00000 н.
0000340564 00000 н.
0000340614 00000 н.
0000340639 00000 н.
0000340762 00000 н.
0000340812 00000 н.
0000340837 00000 н.
0000340967 00000 н.
0000341017 00000 н.
0000341042 00000 п.
0000341092 00000 н.
0000341117 00000 н.
0000341167 00000 н.
0000341192 00000 н.
0000341336 00000 н.
0000341386 00000 н.
0000341411 00000 н.
0000341569 00000 н.
0000341619 00000 п.
0000341644 00000 н.
0000341694 00000 н.
0000341719 00000 н.
0000341769 00000 н.
0000341794 00000 н.
0000341913 00000 н.
0000341963 00000 н.
0000341988 00000 н.
0000342038 00000 н.
0000342063 00000 н.
0000342113 00000 п.
0000342138 00000 п.
0000342274 00000 н.
0000342324 00000 н.
0000342349 00000 п.
0000342399 00000 н.
0000342424 00000 н.
0000342474 00000 н.
0000342499 00000 н.
0000342643 00000 п.
0000342693 00000 н.
0000342718 00000 н.
0000342839 00000 н.
0000342889 00000 н.
0000342914 00000 н.
0000343037 00000 н.
0000343087 00000 н.
0000343112 00000 н.
0000343162 00000 п.
0000343187 00000 п.
0000343237 00000 н.
0000343262 00000 н.
0000343392 00000 н.
0000343442 00000 н.
0000343467 00000 н.
0000343597 00000 н.
0000343647 00000 н.
0000343672 00000 н.
0000343803 00000 п.
0000343853 00000 н.
0000343878 00000 н.
0000343928 00000 н.
0000343953 00000 н.
0000344003 00000 п.
0000344028 00000 н.
0000344151 00000 п.
0000344201 00000 н.
0000344226 00000 п.
0000344276 00000 н.
0000344301 00000 п.
0000344351 00000 п.
0000344376 00000 п.
0000344501 00000 н.
0000344551 00000 н.
0000344576 00000 н.
0000344707 00000 п.
0000344757 00000 н.
0000344782 00000 н.
0000344921 00000 н.
0000344971 00000 н.
0000344996 00000 н.
0000345136 00000 п.
0000345186 00000 п.
0000345211 00000 н.
0000345375 00000 п.
0000345425 00000 н.
0000345450 00000 н.
0000345573 00000 п.
0000345623 00000 п.
0000345648 00000 н.
0000345796 00000 н.
0000345846 00000 н.
0000345871 00000 н.
0000345921 00000 н.
0000345946 00000 н.
0000345996 00000 н.
0000346021 00000 н.
0000346157 00000 н.
0000346207 00000 н.
0000346232 00000 н.
0000346397 00000 н.
0000346447 00000 н.
0000346472 00000 н.
0000346522 00000 н.
0000346547 00000 н.
0000346597 00000 н.
0000346622 00000 н.
0000346755 00000 н.
0000346805 00000 н.
0000346830 00000 н.
0000346966 00000 н.
0000347016 00000 н.
0000347041 00000 п.
0000347194 00000 н.
0000347244 00000 н.
0000347269 00000 н.
0000347391 00000 н.
0000347441 00000 п.
0000347466 00000 н.
0000347601 00000 п.
0000347651 00000 п.
0000347676 00000 н.
0000347813 00000 н.
0000347863 00000 н.
0000347888 00000 н.
0000347938 00000 п.
0000347963 00000 н.
0000348013 00000 н.
0000348038 00000 п.
0000348173 00000 п.
0000348223 00000 п.
0000348248 00000 п.
0000348390 00000 н.
0000348440 00000 н.
0000348465 00000 н.
0000348598 00000 н.
0000348648 00000 н.
0000348673 00000 п.
0000348799 00000 н.
0000348849 00000 н.
0000348874 00000 н.
0000348994 00000 н.
0000349044 00000 н.
0000349069 00000 н.
0000349193 00000 п.
0000349243 00000 п.
0000349268 00000 н.
0000349385 00000 п.
0000349435 00000 п.
0000349460 00000 н.
0000349510 00000 п.
0000349535 00000 п.
0000349585 00000 п.
0000349610 00000 п.
0000349756 00000 н.
0000349806 00000 н.
0000349831 00000 н.
0000349971 00000 н.
0000350021 00000 н.
0000350046 00000 н.
0000350207 00000 н.
0000350257 00000 н.
0000350282 00000 н.
0000350416 00000 н.
0000350466 00000 н.
0000350491 00000 п.
0000350630 00000 н.
0000350680 00000 н.
0000350705 00000 н.
0000350846 00000 н.
0000350896 00000 н.
0000350921 00000 н.
0000351066 00000 н.
0000351116 00000 н.
0000351141 00000 н.
0000351191 00000 н.
0000351216 00000 н.
0000351266 00000 н.
0000351291 00000 н.
0000351424 00000 н.
0000351474 00000 н.
0000351499 00000 н.
0000351628 00000 н.
0000351678 00000 н.
0000351703 00000 н.
0000351873 00000 н.
0000351923 00000 н.
0000351948 00000 н.
0000352067 00000 н.
0000352117 00000 н.
0000352142 00000 н.
0000352316 00000 н.
0000352366 00000 н.
0000352391 00000 н.
0000352514 00000 н.
0000352564 00000 н.
0000352589 00000 н.
0000352718 00000 н.
0000352768 00000 н.
0000352793 00000 н.
0000352843 00000 н.
0000352868 00000 н.
0000352918 00000 н.
0000352943 00000 н.
0000353075 00000 н.
0000353125 00000 н.
0000353150 00000 н.
0000353282 00000 н.
0000353332 00000 н.
0000353357 00000 н.
0000353519 00000 н.
0000353569 00000 н.
0000353594 00000 н.
0000353724 00000 н.
0000353774 00000 н.
0000353799 00000 н.
0000353928 00000 н.
0000353978 00000 н.
0000354003 00000 п.
0000354123 00000 н.
0000354173 00000 п.
0000354198 00000 н.
0000354370 00000 н.
0000354420 00000 н.
0000354445 00000 н.
0000354580 00000 н.
0000354630 00000 н.
0000354655 00000 н.
0000354705 00000 н.
0000354730 00000 н.
0000354780 00000 н.
0000354805 00000 н.
0000354939 00000 н.
0000354989 00000 н.
0000355014 00000 н.
0000355135 00000 н.
0000355185 00000 н.
0000355210 00000 п.
0000355340 00000 н.
0000355390 00000 н.
0000355415 00000 н.
0000355540 00000 н.
0000355590 00000 н.
0000355615 00000 н.
0000355737 00000 н.
0000355787 00000 н.
0000355812 00000 н.
0000355932 00000 н.
0000355982 00000 н.
0000356007 00000 н.
0000356057 00000 н.
0000356082 00000 н.
0000356132 00000 н.
0000356157 00000 н.
0000356304 00000 н.
0000356354 00000 п.
0000356379 00000 н.
0000356530 00000 н.
0000356580 00000 н.
0000356605 00000 н.
0000356742 00000 н.
0000356792 00000 н.
0000356817 00000 н.
0000357008 00000 н.
0000357058 00000 н.
0000357083 00000 н.
0000357221 00000 н.
0000357271 00000 н.
0000357296 00000 н.
0000357452 00000 н.
0000357502 00000 н.
0000357527 00000 н.
0000357667 00000 н.
0000357717 00000 н.
0000357742 00000 н.
0000357792 00000 н.
0000357817 00000 н.
0000357867 00000 н.
0000357892 00000 н.
0000358015 00000 н.
0000358065 00000 н.
0000358090 00000 н.
0000358240 00000 н.
0000358290 00000 н.
0000358315 00000 н.
0000358480 00000 н.
0000358530 00000 н.
0000358555 00000 н.
0000358729 00000 н.
0000358779 00000 н.
0000358804 00000 н.
0000358943 00000 н.
0000358993 00000 н.
0000359018 00000 н.
0000359152 00000 н.
0000359202 00000 н.
0000359227 00000 н.
0000359378 00000 н.
0000359428 00000 н.
0000359453 00000 п.
0000359604 00000 н.
0000359654 00000 н.
0000359679 00000 н.
0000359729 00000 н.
0000359754 00000 н.
0000359857 00000 н.
0000359907 00000 н.
0000359932 00000 н.
0000360058 00000 н.
0000360108 00000 п.
0000360133 00000 п.
0000360293 00000 п.
0000360343 00000 п.
0000360368 00000 н.
0000360536 00000 н.
0000360586 00000 н.
0000360611 00000 н.
0000360750 00000 н.
0000360800 00000 н.
0000360825 00000 н.
0000360947 00000 н.
0000360997 00000 н.
0000361022 00000 н.
0000361173 00000 н.
0000361223 00000 н.
0000361248 00000 н.
0000361298 00000 н.
0000361323 00000 н.
0000361373 00000 н.
0000361398 00000 н.
0000361513 00000 н.
0000361563 00000 н.
0000361588 00000 н.
0000361702 00000 н.
0000361752 00000 н.
0000361777 00000 н.
0000361827 00000 н.
0000361852 00000 н.
0000361902 00000 н.
0000028016 00000 п.
трейлер
] >>
startxref
0
%% EOF
6707 0 obj> поток
x ڤ} \ Te, 2 «0d # 8» «%.знак равно
* 2 * (**% = «If! Zje =}} gΙ9c] avrH (]` $ O G * 0Ec $ 0swP «Jl%
.
